The circular restricted eight-body problem

Abstract

We study the motion of infinitesimal mass in the vicinity of the dominant primaries under the Newtonian law of gravitation in the restricted eight-body problem. The proposed problem is a particular case of n + 1-body problem studied by Kalvouridis (Astrophys. Space Sci 260: 309 325, 1999). We consider six peripheral primaries P₁, P₂, …, P₆, each of mass m, revolve in a circular orbit of radius a with an angular velocity ω about their common center of mass. The primaries P_i (i = 1, 2, …, 6) are revolve in a way such that P₁, P₃, P₅ and P₂, P₄, P₆ always form equilateral triangles of side l and have a common circumcenter where the seventh more massive primary P₀ of mass m₀ rests. The primaries form a symmetric configuration with respect to the origin at any instant of time. This is observed that there exist 18 equilibrium points out of which four equilibrium points are on x-axis, two on y-axis and rest are in orbital plane of the primaries. All the equilibrium points lie on the concentric circles C₁, C₂ and C₃ centered at origin and there exists exactly six equilibrium points on each circle. The equilibrium points on circle C₂ are stable for the critical mass parameter β₀ while the equilibrium points on circles C₁ and C₃ are unstable for all values of mass parameter β. The regions of motion for infinitesimal mass are also analyzed in this paper.

1 Introduction

In the last decades many authors have put their efforts in solving the restricted problem of more than three-bodies in different aspects. Their work is appreciable and encouraged us to develop a configuration in restricted problem of eight bodies’ to describe the motion of spacecraft in the vicinity of the dominant primaries.

The restricted three-body problem plays an important role to understand the behavior of satellite in the vicinity of two dominant primaries. This model is suitable to understand the dynamics of satellite in Earth-Moon and Sun-Earth planet system. A lot of research papers have been written in last five decades to show the significance of the equilibrium points obtained in these systems by including many parameters as oblateness of the primaries, radiation pressure, PR-drag effect, albedo effect etc. The stability of the triangular points in the elliptic restricted problem of three bodies is studied by Danby [12]. A concise solution to the restricted three-body problem in the circular as well as in the elliptical case has been found by Szebehely [41]. The restricted three-body problem under the consideration of radiation pressure has been studied by Chernikov [8]. The equilibrium points in the generalized elliptic restricted three-body problem are investigated by Choudhary [9]. Bhatnagar and Hallan [4] have studied the effect of perturbed potentials on the stability of equilibrium points in the restricted problem of three bodies. Asymptotic solutions to the restricted problem near equilateral equilibrium points have been investigated by Cid et al. [10]. Markellos et al. [31] have discussed the nonlinear stability zones around triangular equilibria in the plane circular restricted three-body problem with oblateness. Roberts [37] has examined the linear stability of the triangular equilibrium points in the elliptic restricted three-body problem. Douskos [14] has analyzed the collinear equilibrium points of Hill’s problem with radiation and oblateness and their fractal basins of attraction. Idrisi and Taqvi [18, 19] have solved the circular restricted three-body problem in terms of elliptic integrals. The restricted three-body problem under the consideration of albedo effects in circular and elliptic cases is studied by Idrisi [20], Idrisi and Ullah [21,22,23, 25, 43]. Ershkov and Leshchenko [15] have presented an approach for solving the Euler-Poisson equations of momentum near the liberation points for planets in our Solar System whose orbital plane is inclined relative to Earth's orbit. In a recent study conducted by Ershkov et al. [16], a semi-analytical approach was employed to analyze the bi-elliptic problem of four bodies and explore possible stable positioning for elements of a Dyson sphere.

The following researchers have extended the restricted three-body problem to 4-body, 5-body, 6-body and in general n-body problem: Michalodimitrakis [32] has investigated the equilibrium points, zero velocity curves and periodic orbits around the equilibrium points in the restricted four-body problem. Pacella [33] has used the equivariant Morse theory in three-dimensional n-body problem to estimate the minimal number of central configurations. In this study it is shown that the non-planar central configurations exist for n ≥ 4. Casasayas et al. [5] have considered a restricted charged four-body problem and proved the existence of infinite symmetric periodic orbits with arbitrarily large extremal period. The global solution of the n-body problem using a new ‘blowing up’ transformation is given by Qiu-Dong [36]. Roy et al. [38] have investigated some special cases of restricted four-body problems. Kalvouridis [27] has studied n + 1-body problem by arranging the peripheral primaries in equal arcs on an ideal ring with a central body of different mass is considered at the center of mass of the system. Bang et al. [3] have proved results on the existence and on linear stability of equilibrium points in the restricted N + 1 body problem. Celli [6] has studied the central configurations of four masses in detail. Baltagiannis et al. [2] have studied the existence of equilibrium points and their linear stability in the equilateral configuration of restricted four-body problem. A study of finding central configurations of the four-body problem with a dominant mass was carried out by Corbera et al. [11]. Kumari et al. [28] have plotted the equilibrium points and zero velocity surfaces in the restricted four-body problem with solar wind drag. Papadouris et al. [34] have examined the existence of equilibrium points and their linear stability in the equilateral configuration of restricted four-body problem with radiation pressure. A new perturbative method for solving the gravitational n-body problem in the general theory of relativity is given by Turyshev and Toth [42]. Marchesin [30] has considered a rhomboidal configuration of restricted five-body problem and discussed the stability of rhomboidal equilibria. Gao et al. [17] have analyzed the equilibrium points and zero velocity surfaces in the axisymmetric central configuration of restricted five-body problem. A special case of the restricted four-body problem has been investigated by Ansari [1] by treating the three primaries as a triaxial rigid body and the infinitesimal body as variable mass. An inverse problem of central configurations in the collinear five-body problem has been investigated by Davis et al. [13]. Ullah et al. [43] have studied the elliptic Sitnikov five-body problem under the consideration of radiation pressure. Idrisi and Ullah [23] have studied the existence and stability of equilibrium points in restricted six-body problem under a square configuration model. Chen and Yang [7] have examined the central configurations of five-body problem with four infinitesimal particles out of which two particles have unequal mass. Pappalarado et al. [35] have used an analytical approach based on the direct linearization of the index-three form to analyze the stability of multibody mechanical systems in the framework of Lagrangian mechanics. Ullah et al. [44] have probed the Sitnikov five-body problem with combined effects of radiation pressure and oblateness. Idrisi et al. [24] have shown the effect of perturbations in Coriolis and centrifugal forces on equilibrium points in the restricted six-body problem. The stability analysis of rhomboidal restricted six-body problem is studied by Siddique et al. [39]. The motion of infinitesimal mass around out-of-plane equilibrium points in the frame of restricted six-body problem under radiation pressure is examined by Idrisi and Ullah [26]. Siddique and Kashif [40] have explored the stable equilibrium points in the rhomboidal restricted six-body problem. The periodic solutions of circular Sitnikov restricted four-body problem using multiple scales method are analyzed by Kumari et al. [29].

In this paper, we have considered a symmetric configuration of restricted eight-body problem in which the dominant primary is located at the center of mass of the system. The paper is organized as follows: In Sect. 1, some notable researches related to the theme of the research are given. The mathematical model of the system and equations of motion of infinitesimal mass are obtained in Sect. 2. The graphical and numerical solution to equilibrium points are given in Sect. 3. In Sect. 4, the stability of equilibrium points is discussed. The regions of motion or zero velocity regions are discussed in brief in Sect. 5. In the last section, conclusions are drawn.

2 Mathematical model and equations of motion

Let six peripheral primaries P₁, P₂, …, P₆, each of mass m, revolve in a circular orbit of radius a with an angular velocity ω about their common center of mass O. The primaries P_i (i = 1, 2, …, 6) are revolve in a way such that P₁, P₃, P₅ and P₂, P₄, P₆ always form equilateral triangles of side l and have a common circumcenter where the seventh more massive primary P₀ of mass m₀ rests (Fig. 1). It is also assumed that the mass of central primary is greater than the sum of all masses of peripheral primaries, i.e., m₀ > Ʃm_i, i = 1, 2, …, 6. The orbit lies in the Oxy plane of the inertial frame of reference, and has its center at the origin. According to Newton's law of gravitation, primaries attract each other and at any instant of time form a symmetric configuration with respect to the origin. Suppose that a test particle P with infinitesimal mass m′ <  < 1 moves under the gravitational field of P_i (i = 0, 1,…, 6) in the same plane. The distances of P from O and P_i (i = 1, 2, …, 6) are r₀ and r_i (i = 1, 2, …, 6), respectively. From Fig. 1, it can be seen that the proposed configuration is possible if l = √3a where l and a are the dimensionless lengths of side of equilateral triangles and radius of circular orbit, respectively.

Fig. 1

Configuration of restricted eight-body problem

In order to maintain the configuration of the primaries, the sum of the gravitational forces applied by P₀, P₂, P₃, P₄, P₅ and P₆ on P₁ must be equal to the centrifugal force, i.e.,

$$m_{1} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{{OP_{1} }} \omega^{2} = \frac{{Gm_{0} m_{1} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{{OP_{1} }} }}{{|OP_{1} |^{3} }} + \sum\limits_{j = 2}^{6} {\frac{{Gm_{j} m_{1} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{{P_{j} P_{1} }} }}{{|P_{j} P_{1} |^{3} }}} ,$$

which gives

$$\omega^{2} = \frac{{Gm_{0} }}{{a^{3} }}\left( {1 + \kappa \frac{m}{{m_{0} }}} \right),\,\kappa = 1.82735.$$

Now, we choose the units of distance, mass and time in such a way that G = 1, m₀ = 1 and ω = 1, therefore we have a = (1 + k β)^1/3, β = m/m₀ is the mass parameter having the range 0 < β < 1/6. Obviously, a is an increasing function in terms of β and thus as mass parameter β increases the radius of the orbit of primaries also increases (Fig. 2).

Fig. 2

a with respect to β

2.1 Equations of motion

The equations of motion of the particle P(x, y, z) in the synodic coordinate system and dimensionless variables are given by

$$\ddot{x} - 2\dot{y} = \frac{\partial U}{{\partial x}},\,\,\,\,\ddot{y} + 2\dot{x} = \frac{\partial U}{{\partial y}}\,\,{\text{and}}\,\,\,\ddot{z} = \frac{\partial U}{{\partial z}}$$

(1)

where the effective potential U may be written as

$$\begin{aligned} &U = \frac{1}{2}(x^{2} + y^{2} ) + \frac{1}{{r_{0} }} + \sum\limits_{\upsilon = 1}^{6} {\frac{\beta }{{r_{\upsilon } }}} ,\\ & r_{0}^{2} = x^{2} + y^{2} + z^{2} , \\ & r_{\upsilon }^{2} = (x - x_{\upsilon } )^{2} + (y - y_{\upsilon } )^{2} + z^{2} , \\ & x_{\upsilon } = a\cos \left[ {(\upsilon - 1)\frac{\pi }{3}} \right],\,y_{\upsilon } = a\sin \left[ {(\upsilon - 1)\frac{\pi }{3}} \right],\upsilon = 1,\,2,\,...,\,6. \end{aligned}$$

The integral analogous to Jacobi integral is

$$v^{{2}} = {2}U - c,$$

(2)

where v is the velocity of the particle P having infinitesimal mass m′ and c is Jacobian constant.

3 Equilibrium points in orbital plane

The equilibrium points in orbital plane are the solution of the Eqns. U_x = 0, U_y = 0 and z = 0, i.e.,

$$\left. \begin{gathered} U_{x} = \left( {1 - \frac{1}{{r_{0}^{3} }}} \right)x - \beta \,\sum\limits_{\upsilon = 1}^{6} {\frac{{(x - x_{\upsilon } )}}{{r_{\upsilon }^{3} }}} = 0, \hfill \\ U_{y} = \left( {1 - \frac{1}{{r_{0}^{3} }}} \right)y - \beta \,\sum\limits_{\upsilon = 1}^{6} {\frac{{(y - y_{\upsilon } )}}{{r_{\upsilon }^{3} }}} = 0.\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \hfill \\ \end{gathered} \right\}$$

(3)

3.1 Graphical solution to equilibrium points

Clearly, the equilibrium points are the intersection of the curves U_x(x, y) and U_y(x, y). On plotting the corresponding curves it turns out that there are 18 equilibrium points, four of which are collinear and fourteen are non-collinear (Fig. 3). All points of equilibrium lie on the concentric circles C₁, C₂ and C₃ centered at the origin. The equilibrium points E_i (i = 1, 2, …, 6) lie on circle C₁, E_j (j = 7, 8, …, 12) on C₂ and E_k (k = 13, 14, …, 18) on C₃. Further, it is observed that the six equilibrium points are on the axes and twelve are in orbital plane of the primaries, i.e., E₁, E₄, E₁₃ and E₁₆ are on x-axis, E₈ and E₁₁ on y-axis and rest are in the orbital plane.

Fig. 3

Equilibrium Points E_i (i = 1, 2, …, 18) in orbital plane for β = 0.1

3.2 Numerical solution

In this section, we locate the equilibrium points numerically on the circles C₁, C₂ and C₃ using Newton–Raphson iteration method. Instead of finding all the equilibrium points, we focus on just one equilibrium point on each circle C₁, C₂ and C₃, i.e., E₁, E₈ and E₁₃ and the locations of other equilibrium points can be found by symmetricity. Let us assume that the coordinates of E₁, E₈ and E₁₃ be (a + ρ, 0), (0, a + λ) and (a–δ, 0), respectively (Fig. 4), where ρ, λ, δ ∈ R⁺.

Fig. 4

Locations of E₁, E₈ and E₁₃

3.2.1 Equilibrium points on C ₁

First we find the location of equilibrium point E₁ and then by symmetricity we can locate other equilibrium points on C₁. Let the coordinates of E₁ be (a + ρ, 0). Thus, on substituting x = a + ρ and y = 0 in Eq. (3), we have f(ρ) = 0, where

$$\begin{aligned} & f({\rho} ) = f_{1} ({\rho} ) - \beta f_{2} ({\rho} ) = 0, \\ &f_{1} ({\rho} ) = (a + {\rho} )\left( {1 - \frac{1}{{(a + {\rho} )^{3} }}} \right), \hfill \\ & f_{2} ({\rho} ) = \frac{1}{{{\rho}^{2} }} + \frac{1}{{(2a + {\rho} )^{2} }} + \frac{a + 2{\rho} }{{(a^{2} + a{\rho} + {\rho}^{2} )^{3/2} }} + \frac{3a + 2{\rho} }{{(3a^{2} + 3a{\rho} + {\rho}^{2} )^{3/2} }}. \hfill \\ \end{aligned}$$

(4)

The solution of Eq. (4) provides the location of E₁. Since the general solution of Eq. (4) is not possible therefore we apply Newton–Raphson iteration method to solve it. On solving Eq. (4) for various values of mass parameter β, we have only one positive real root as shown in Fig. 5. It is observed that as the mass parameter β increases, ρ increases and the equilibrium point E₁ moves away from the primary P₁ along x-axis. The numerical positions of E₁ and other equilibrium points on C₁ for various values of mass parameter β are given in Table 1. The coordinates of the equilibrium points E_i(x_i, y_i) lying on C₁ are given by:

$$x_{i} = \Lambda \cos \left( {(i - 1)\frac{\pi }{3}} \right),\,y_{i} = \Lambda \sin \left( {(i - 1)\frac{\pi }{3}} \right),\,\,i = 1,\,2,\,...,\,6$$

where Λ = a + ρ is the radius of circle C₁.

Fig. 5

Zeroes of f(ρ) for different values of mass parameter β

Table 1 Equilibrium points on C₁

3.2.2 Equilibrium points on C ₂

Let the coordinates of E₈ be (0, a + λ). Thus on substituting x = 0 and y = a + λ in Eq. (3), we have g(λ) = 0, where

$$g(\lambda ) = g_{1} (\lambda ) - \beta g_{2} (\lambda ) = 0,$$

(5)

$$g_{1} (\lambda ) = (a + \lambda )\left( {1 - \frac{1}{{(a + \lambda )^{3} }}} \right),$$

$$\begin{aligned} g_{2} (\lambda ) = & \frac{2(a + \lambda )}{{(2a^{2} + 2a\lambda + \lambda^{2} )^{3/2} }} + \frac{(2 - \sqrt 3 )a + 2\lambda }{{((2 - \sqrt 3 )a^{2} + (2 - \sqrt 3 )a\lambda + \lambda^{2} )^{3/2} }} \\ & + \frac{(2 + \sqrt 3 )a + 2\lambda }{{((2 + \sqrt 3 )a^{2} + (2 + \sqrt 3 )a\lambda + \lambda^{2} )^{3/2} }}. \\ \end{aligned}$$

On solving Eq. (5) for different values of mass parameter β by Newton–Raphson iteration method, we have location of E₈. Eq. (5) possesses only one real root for 0 < β < 1/6 as shown in Fig. 6. It is found that λ increases as the mass parameter β increases and the equilibrium point E₈ moves in upward direction along y-axis. The numerical positions of E₈ and other equilibrium points on C₂ for various values of mass parameter β are given in Table 2. The coordinates of the equilibrium points E_j(x_j, y_j) lying on C₂ are given by:

$$x_{j} = \tau \cos \left( {(2j - 13)\frac{\pi }{6}} \right),\,y_{j} = \tau \sin \left( {(2j - 13)\frac{\pi }{6}} \right),\,\,j = 7,\,8,\,...,\,12$$

where τ = a + λ is the radius of circle C₂.

Fig. 6

Zeroes of g(λ) for different values of mass parameter β

Table 2 Equilibrium points on C₂

3.2.3 Equilibrium points on C ₃

Let the coordinates of E₁₃ be (a − δ, 0). Thus on substituting x = a − δ and y = 0 in Eq. (3), we have h(δ) = 0, where

$$h(\delta ) = h_{1} (\delta ) - \beta \,h_{2} (\delta ) = 0,$$

(6)

$$\begin{gathered} h_{1} (\delta ) = (a - \delta )\left( {1 - \frac{1}{{(a - \delta )^{3} }}} \right), \hfill \\ h_{2} (\delta ) = \frac{1}{{\delta^{2} }} + \frac{1}{{(2a - \delta )^{2} }} + \frac{a - 2\delta }{{(a^{2} - a\delta + \delta^{2} )^{3/2} }} + \frac{3a - 2\delta }{{(3a^{2} - 3a\delta + \delta^{2} )^{3/2} }}. \hfill \\ \end{gathered}$$

On solving Eq. (6) for various values of mass parameter β by Newton–Raphson iteration method, we have location of E₁₃. Eq. (6) possesses only one real root for 0 < β < 1/6 as shown in Fig. 7. It is observed that as the mass parameter β increases, δ decreases and the equilibrium point E₁₃ moves toward the primary P₁ along x-axis. The numerical positions of E₁₃ and other equilibrium points on C₃ for various values of mass parameter β are given in Table 3. The coordinates of the equilibrium points E_k(x_k, y_k) on C₃ are given by:

$$x_{k} = \varepsilon \cos \left( {(k - 13)\frac{\pi }{3}} \right),\,y_{k} = \varepsilon \sin \left( {(k - 13)\frac{\pi }{3}} \right),\,\,k = 13,\,14,\,...,\,18$$

where ε = a − δ is the radius of circle C₃.

Fig. 7

Zeroes of h(δ) for different values of mass parameter β

Table 3 Equilibrium points on C₃

Finally, it is concluded that there exist 18 equilibrium points (E₁, E₂, …, E₁₈) in total and in particular 6 equilibrium points on each circle C₁, C₂ and C₃, respectively. The equilibrium points E₁, E₂, …, E₆ are lying on circle C₁; E₇, E₈, …, E₁₂ on circle C₂ and E₁₃, E₁₄, …, E₁₈ on circle C₃. The numerical locations of all equilibrium points on circles C₁, C₂ and C₃ for various values of mass parameter β are given in Tables 1, 2 and 3, respectively. This is also observed that as the mass parameter β increases, the radius of circle C₁ and C₂ increases while the radius of circle C₃ decreases. Hence the equilibrium points on C₁ and C₂ move away from the peripheral primaries and the equilibrium points on C₃ come closer to central primary (Fig. 8).

Fig. 8

Radius of C₁, C₂, C and C₃ with respect to β

4 Stability of equilibrium points in orbital plane

In this section, we study the possible motion of infinitesimal mass around all the equilibrium points E₁, E₂, …, E₁₈. Instead of discussing the stability of all equilibrium points we focus only on one equilibrium point on each circle C₁, C₂ and C₃, respectively. The stability of one equilibrium point on any circle C₁, C₂ and C₃ implies the stability of other equilibrium points on the same circle. Therefore, let us assume that the coordinates of these equilibrium points are (x₀, y₀). On giving small displacement (ζ, η) to (x₀, y₀) and considering only linear terms in ζ and η, the variation ζ and η can be written as: ζ = x–x₀ and η = y–y₀ and the equation of the motion (1) become

$$\left. \begin{gathered} \ddot{\zeta } - 2\,\dot{\eta } = U_{x} (x_{0} + \zeta ,y_{0} + \eta ) = \zeta \mathop {U_{xx} }\limits^{o} + \,\eta \,\mathop {U_{xy} }\limits^{o} , \hfill \\ \ddot{\eta } + 2\,\dot{\zeta } = U_{y} (x_{0} + \zeta ,y_{0} + \eta ) = \zeta \mathop {U_{yx} }\limits^{o} + \,\eta \,\mathop {U_{yy} }\limits^{o} .\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \hfill \\ \end{gathered} \right\}$$

(7)

The characteristic equation of Eq. (7) is given by

$$\Pi^{4} + (4 - \mathop U\limits^{o}_{xx} \, - \mathop U\limits^{o}_{yy} \,)\,\Pi^{2} + \,\,\mathop U\limits^{o}_{xx} \,\mathop U\limits^{o}_{yy} - \mathop {(U}\limits^{o}_{xy} )^{2} = 0$$

(8)

is a fourth degree equation in Π, where

$$\mathop U\limits^{o}_{xx} = \left. {\frac{{\partial^{2} U}}{{\partial x^{2} }}} \right|_{{(x_{0} ,y_{0} )}} = 1 - \frac{1}{{r_{00}^{3} }}\left( {1 - \frac{{3x_{o}^{2} }}{{r_{00}^{2} }}} \right) - \beta \sum\limits_{\upsilon = 1}^{6} {\frac{1}{{r_{0\upsilon }^{3} }}\left( {1 - \frac{{3(x_{0} - x_{\upsilon } )^{2} }}{{r_{0\upsilon }^{2} }}} \right)} ,$$

$$\mathop U\limits^{o}_{xy} = \frac{\partial }{\partial x}\left. {\left( {\frac{\partial U}{{\partial y}}} \right)} \right|_{{(x_{0} ,y_{0} )}} = \frac{\partial }{\partial y}\left. {\left( {\frac{\partial U}{{\partial x}}} \right)} \right|_{{(x_{0} ,y_{0} )}} = \mathop U\limits^{o}_{yx} = \frac{{3x_{o} y_{o} }}{{r_{00}^{5} }} + 3\beta \sum\limits_{\upsilon = 1}^{6} {\frac{{(x_{o} - x_{v} )(y_{o} - y_{\upsilon } )}}{{r_{0\upsilon }^{5} }}} ,$$

$$\mathop U\limits^{o}_{yy} = \left. {\frac{{\partial^{2} U}}{{\partial y^{2} }}} \right|_{{(x_{0} ,y_{0} )}} = 1 - \frac{1}{{r_{00}^{3} }}\left( {1 - \frac{{3y_{o}^{2} }}{{r_{00}^{2} }}} \right) - \beta \sum\limits_{\upsilon = 1}^{6} {\frac{1}{{r_{0\upsilon }^{3} }}\left( {1 - \frac{{3(y_{0} - y_{\upsilon } )^{2} }}{{r_{0\upsilon }^{2} }}} \right)} ,$$

$$r_{00}^{2} = x_{o}^{2} + y_{o}^{2} ,r_{0\upsilon }^{2} = (x_{o} - x_{\upsilon } )^{2} + (y_{o} - y_{\upsilon } )^{2} ,\,\upsilon = 1,\,2,\,...,\,6.$$

Let Π² = χ, therefore the characteristic Eq. (8) becomes

$$\chi^{2} + (4 - \mathop U\limits^{o}_{xx} \, - \mathop U\limits^{o}_{yy} \,)\,\chi + \,\,\mathop U\limits^{o}_{xx} \,\mathop U\limits^{o}_{yy} - \mathop {(U}\limits^{o}_{xy} )^{2} = 0$$

(9)

which is a quadratic equation in χ. If χ₁ and χ₂ are the roots of Eq. (9) then

$$\chi_{1,2} = \frac{1}{2}\left( { - p \pm \sqrt D } \right),$$

(10)

where D is the discriminant of Eq. (9) and defined as D = p² – 4q, $p = 4 - \mathop U\limits^{o}_{xx} \, - \mathop U\limits^{o}_{yy} ,$ $q = \mathop U\limits^{o}_{xx} \,\mathop U\limits^{o}_{yy} - \mathop {(U}\limits^{o}_{xy} )^{2} .$

Therefore, the roots corresponding to characteristic Eq. (8) are given by

$$\Pi_{\,1,2} = \pm \sqrt {\chi_{1} } \,\,{\text{and}}\,\,\Pi_{\,3,4} = \pm \sqrt {\chi_{2} } .$$

(11)

The equilibrium point (x₀, y₀) is said to be stable if χ_1,2 < 0.

4.1 Stability of equilibrium points on C ₁

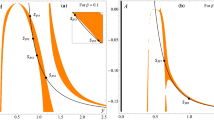
For E₁: The discriminant of Eq. (9) is positive, i.e., D > 0 for all values of mass parameter β (Fig. 9) and thus the roots of Eq. (9) are real and unequal. The roots of Eq. (9), i.e., χ_1,2 for different values of mass parameter μ are plotted in Fig. 10 and it is observed that χ₁ > 0 and χ₂ < 0 and hence the roots of characteristic Eq. (8) are of the form Π_1,2 =  ± u and Π_3,4 =  ± iv, u, v ϵ R which leads to instability of equilibrium point E₁ (Table 4). Hence the other equilibrium points on C₁ are also unstable for all values of mass parameter μ.

Fig. 9

D with respect to β for E₁

Fig. 10

χ_1,2 with respect to β for E₁

Table 4 Stability of E₁

4.2 Stability of equilibrium points on C ₂

For E₈: D ≥ 0 if and only if 0 < β ≤ 0.0027284 (Fig. 11) and thus Eq. (9) possesses real roots in the interval 0 < β ≤ 0.0027284. The roots of Eq. (9), i.e., χ_1,2 for 0 < β ≤ 0.0027284 are plotted in Fig. 12 and it is observed that χ₁ < 0 and χ₂ < 0 and hence the roots of characteristic Eq. (8) are of the form Π_1,2 =  ± iu₁ and Π_3,4 =  ± iv₁, u₁, v₁ ϵ R which leads to stability of equilibrium point E₈ (Table 5). Hence the other equilibrium points on C₂ are also stable for the critical mass parameter 0 < β ≤ β₀, β₀ = 0.0027284.

Fig. 11

D with respect to β for E₈

Fig. 12

χ_1,2 with respect to β for E₈

Table 5 Stability of E₈

4.3 Stability of equilibrium points on C ₃

For E₁₃: D > 0 for all values of mass parameter β (Fig. 13) and thus the roots of Eq. (9) are real and unequal. The roots of Eq. (9), i.e., χ_1,2 for different values of mass parameter β are plotted in Fig. 14 and it is observed that χ₁ > 0 and χ₂ < 0 and hence the roots of characteristic Eq. (8) are of the form Π_1,2 =  ± u₂ and Π_3,4 =  ± iv₂, u₂, v₂ ϵ R which leads to instability of equilibrium point E₁₃ (Table 6). Hence the other equilibrium points on C₂ are also unstable for all values of mass parameter β.

Fig. 13

D with respect to β for E₁₃

Fig. 14

χ_1,2 with respect to β for E₁₃

Table 6 Stability of E₁₃

5 Regions of motion

In this section, the regions of motion for a fixed value of mass parameter β and different values of Jacobi constant c have been plotted. The values of Jacobi constant c are computed numerically at all the equilibrium points (E₁, E₂, …, E₁₈) using Eq. 2U–c = 0 in Table 7. Figure 15a, the zero velocity regions have been plotted for c = 3.5 and a circular white region around the central primary has been observed. The white and shaded regions correspond to permitted and restricted regions of motion, respectively for the motion of infinitesimal mass. For c = 3.25, some small white regions appear around the primaries P₁, P₂, P₃, P₅ and P₆ which allow to move infinitesimal mass in the vicinity of P₁, P₂, P₃, P₅ and P₆ only (Fig. 15b). For c = c₃, a transition exists at the equilibrium points E₁₃, E₁₄, E₁₅, E₁₆, E₁₇ and E₁₈ which allow the infinitesimal mass to move from central primary to other peripheral primaries but it cannot move to the outer region, Fig. 15c. For c = c₁, again some transitions exist at the equilibrium points E₁, E₂, E₃ E₄, E₅ and E₆ which allow the infinitesimal mass to move from E₁₃, E₁₄, E₁₅, E₁₆, E₁₇ and E₁₈ to outer region and the forbidden region constitutes six branches containing equilibrium points E₇, E₈, E₉, E₁₀, E₁₁and E₁₂, respectively, Fig. 15d. For c = 3.015, the forbidden region get reduced and the infinitesimal mass is allowed to move in the entire xy-plane except the forbidden region containing equilibrium points E₇, E₈, E₉, E₁₀, E₁₁ and E₁₂, Fig. 15e. For c = c₂, all the forbidden regions has been disappeared and the infinitesimal mass can move in the entire xy-plane, Fig. 15f. Thus, it is observed that the forbidden region decreases as the value of Jacobi constant c decreases.

Table 7 Jacobi constant c at E_i (i = 1, 2, …, 18) for β = 0.01

Fig. 15

Regions of motion for β = 0.01 and different values of Jacobi constant c; a: c = 3.5; b: c = 3.4; c: c = 3.28; d: c = 3.265; e: c = c₁; f: c = c₂

6 Conclusion

We have studied the dynamics of infinitesimal mass around the equilibrium points in the restricted eight-body problem. This problem is a particular case of n + 1-body problem studied by Kalvouridis [27]. In this paper, we considered six peripheral primaries P₁, P₂, …, P₆, each of mass m, revolve in a circular orbit of radius a with an angular velocity ω about their common center of mass O. The primaries P_i (i = 1, 2, …, 6) are revolve in a way such that P₁, P₃, P₅ and P₂, P₄, P₆ always form equilateral triangles of side l and have a common circumcenter where the seventh more massive primary P₀ of mass m₀ rests. The equations of motion for the infinitesimal mass in synodic coordinate system and dimensionless variables are given by Eq. (1). On solving the Eqns. U_x(x, y) = 0, U_y(x, y) = 0 and z = 0 we found 18 equilibrium points such that four equilibrium points are on x-axis, two on y-axis and rest are in orbital plane of the primaries. All the equilibrium points lie on the concentric circles C₁, C₂ and C₃ centered at origin. It is observed that as the mass parameter β increases, the radius of circles C₁ and C₂ also increases and the equilibrium points on C₁ and C₂ move away from the peripheral primaries. On the other hand, the radius of circle C₃ decreases as β increases and the equilibrium points on C₃ come closer to the central primary. The stability of equilibrium points depends upon the nature of roots of characteristic Eq. (8). On solving the characteristic Eq. (8) for various values of mass parameter β in the interval 0 < β < 1/6 we found that the equilibrium points on circle C₂ are stable for the critical mass parameter β₀ while the equilibrium points on circles C₁ and C₃ are unstable for all values of mass parameter β. In the last section of this paper, the regions of motion for infinitesimal mass are investigated and it is found that the forbidden region decreases as the value of Jacobi constant c decreases.