Thermal effect on the transient waves in piezoelectric half-space subjected to dynamic loading

Abstract

Propagation of transient waves in the piezoelectric half-space under anti-plane dynamic force and in-plane electrical displacement loading is studied theoretically when thermal effect considered. One-sided and two-sided Laplace transforms are firstly employed in obtaining the solutions of mechanical displacement, electrical potential, shear stress and electrical displacement in Laplace space. Cagniard-de Hoop method is then adopted for inverse Laplace transform in determining the analytical transient solutions in time domain. Transient response of the mechanical displacement, shear stress, electric potential and displacement are finally evaluated numerically, and the effect of thermal stress on the transient waves propagating in the piezoelectric half-space is discussed in details. Furthermore, two different electro-mechanic boundary conditions are considered for the propagation of transient waves in the piezoelectric half-space.

1 Introduction

Piezoelectric materials find a wide range of applications in many technological industries because of the coupling characteristics between mechanical and electric fields. A number of devices, such as piezoelectric sensors and transducers [1,2,3,4,5], acoustic amplification devices [6, 7] and semiconductor devices [8,9,10], involve the use of piezoelectric materials. For these piezoelectric devices, the ability to manipulate the propagation of elastic waves has a significant effect on the sensitivity of signal output and energy loss [11,12,13,14,15]. In recent years, the propagation and regulation of steady waves in piezoelectric materials have been studied extensively when different materials properties and interface conditions are considered. For instance, Wang et al. [16] investigated the shear surface waves propagating along the surface of a functionally graded piezoelectric semiconductor half-space, and it was found that the piezoelectric gradient index could hinder the wave propagation in the medium. Chaudhary et al. [17] investigated the SH wave developed in an irregular piezoelectric layer, and they found that phase velocity of the SH wave increased with higher piezoelectric constant and dielectric constant. Singh [18] studied the shear wave propagating in the piezoelectric solids when steel/PZT4 and PZT4/PZT-5H interfaces were taken into consideration, and it showed that the piezoelectric field had a significant effect on the ratio of amplitude and energy. Furthermore, Nirwal et al. [19] conducted the analysis of wave velocity in a piezo-structure with flexoelectric effect under different boundary conditions, and the influences of layer thickness, flexoelectric parameter and imperfect interface on the phase velocity were presented in their research. Nie et al. [20] and Pang et al. [21] found that the thickness ratio of piezoelectric and piezomagnetic layer had an important effect on the dispersion relation and wave velocity of SH waves and Lamb waves, and the imperfect bonding of the interface generally reduced the wave velocity. Rakshit et al. [22, 23] extended the research about the effect of interface imperfection on the propagation of SH wave in a porous piezoelectric composite and love wave in a layered piezoelectric/elastic composite having interfacial imperfection.

However in practical applications, the time-dependent stimulus and response is more important than those static ones in engineering. For example, structural health monitoring system under impact loading [24], forced vibration response of smart composite structure [25] and spatiotemporal carrier dynamics induced by piezoelectric surface acoustic wave [26]. Thus, investigation on the transient waves propagating in the piezoelectric solids is very essential and significant. Ma et al. [27] analyzed the propagation of transient waves in the piezoelectric materials subjected to anti-plane loading or electrical charge, and the result showed that existence of the surface waves was limited when velocities of the shear waves in the bi-materials were very close. Lin et al. [28] employed the Durbin method in studying the transient waves propagating in the functionally graded piezoelectric slabs, and they found that the ground boundary could produce instantaneous shear waves at the beginning under the action of electric displacement loading. As an extension, Ing et al. [29] conducted theoretical and numerical investigation on the transient response of a layered piezoelectric solids, and it showed that the transient waves vibrated near the static value and then quickly approached the static solution. When studying the electromagnetic waves in the piezoelectric solids, Li [30] considered the contribution from the rotational part of the electrical field and derived the closed-form solution for the Bleustein-Gulyaev wave. Different from the traditional quasi-static approximation, quasi-hyperbolic approximation was employed in this research, where the hyperbolicity of piezoelectric governing equations can be preserved. This brings great convenience in analyzing the transient response of the piezoelectric material [31].

It is found that the thermal effect has a significant influence on the propagating of elastic waves in the solids. For example, Bajpai et al. [32] studied the effects of different thermal conductivity and diffusivity on the infinite thermo-elastic diffusion circular plate using two-temperature generalized thermo-elastic diffusion theory. Zhou and Shui [33] investigated the influence of thermal effect on transient waves propagating in the multilayered composite structure, and the results showed that magnitude of the transient wave became smaller when change of the environmental temperature is higher. Shariyat [34] also studied the thermo-elastic waves propagating and reflecting in the functionally graded thick cylinder when under different thermo-mechanical shock loadings, and influence from the thermal and elastic waves was further investigated. Furthermore, Ashida et al. [35] studied the dynamic response of the functionally graded medium when under thermal loading, and the result revealed that oscillation of the thermal stress changed with different mechanical impedance, which depends on the space variables. Recently, Wang et al. [36] proposed a theoretical analysis in exploring the influence of thermo-mechanical interactions, which involves the micro-scale effect of the FGM hollow cylindrical structures, on the propagating of thermal waves.

Considering the importance of understanding the transient waves in the piezoelectric material, and the fact that the thermal effect is seldom concerned when analyzing transient response of the piezoelectric structure, propagation of transient waves in the piezoelectric half-space under anti-plane dynamic force and in-plane electrical loading will be studied theoretically with thermal effect considered in this study. Closed-form solution in Laplace and time space will be obtained by employing Laplace transform and Cagniard-de Hoop method. Transient response of the mechanical displacement, shear stress, electric potential and electrical displacement is evaluated numerically, and effects of the temperature variation and boundary condition on the transient waves are then discussed.

2 Theoretical model

When analyzing the dynamic response of a piezoelectric device, the wavelength of the transient wave propagating in the elastic medium is generally small compared with the geometry dimension of the device. The piezoelectric structure is thus modeled as a half-space. For a transversely isotropic piezoelectric half-space, the constitutive equations for mechanical and electric fields are [37]:

$$ \sigma_{{{\text{ij}}}} {\,=\,}c_{{{\text{ijkl}}}} S_{{{\text{kl}}}} - e_{{{\text{kij}}}} E_{{\text{k}}} $$

(1a)

$$ D_{{\text{i}}} {\,=\,}e_{{{\text{ikl}}}} S_{{{\text{kl}}}} + \in_{{{\text{ik}}}} E_{{\text{k}}} $$

(1b)

where $\sigma_{{{\text{ij}}}}$, $S_{{{\text{kl}}}}$, $E_{{\text{k}}}$ and $D_{{\text{i}}}$ are components of stress, strain, electrical field and displacement; $c_{{{\text{ijkl}}}}$, $e_{{{\text{kij}}}}$ and $\in_{{{\text{ik}}}}$ are elastic constants, piezoelectric and permittivity tensors of the solids.

When the body force and free charge density are not considered, the equations of motion and electric displacement for linear piezoelectric medium can be expressed as follows [37]:

$$ \sigma_{{\text{ij,i}}} = \rho \ddot{u}_{{\text{i}}} $$

(2)

$$ D_{{{\text{i}},i}} = 0 $$

(3)

where $u_{{\text{i}}}$ and $\rho$ are displacement and mass density. The strain tensor $S_{kl}$ and electric field $E_{i}$ are defined as [31]:

$$ S_{{{\text{kl}}}} = \frac{1}{2}\left( {u_{{i,{\text{j}}}} + u_{{{\text{j}},i}} } \right) $$

(4)

$$ E_{{\text{i}}} = - \left( {\phi_{{\text{,i}}} + \frac{1}{{c_{{\text{l}}} }}\frac{{\partial {\varvec{A}}_{{\text{i}}} }}{\partial t}} \right) $$

(5)

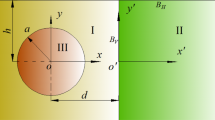
where $\phi$ and ${\varvec{A}}_{{\text{i}}}$ are scalar potential and vector potential, and the constant $c_{{\text{l}}} = 1/\sqrt {\mu_{0} \in_{11} }$ is light speed of the piezoelectric solids, $\mu_{0}$ is magnetic permeability constant in the vacuum. As shown in Fig. 1, when considering the coupling between anti-plane wave field and in-plane electromagnetic field, we have:

$$ u_{{\text{x}}} = u_{{\text{y}}} = 0,u_{{\text{z}}} = w\left( {x,y,t} \right) $$

(6a)

$$ E_{{\text{x}}} = E_{{\text{x}}} \left( {x,y,t} \right),E_{{\text{y}}} = E_{{\text{y}}} \left( {x,y,t} \right),E_{{\text{z}}} = 0 $$

(6b)

Fig. 1

Schematic diagram of the piezoelectric half-space

Therefore, the constitutive equations can be simplified as:

$$ \tau_{{{\text{yz}}}} {\,=\,}c_{44} \frac{\partial w}{{\partial y}} - e_{15} E_{{\text{y}}} $$

(7)

$$ \tau_{{{\text{xz}}}} {\,= \,}c_{44} \frac{\partial w}{{\partial x}} - e_{15} E_{{\text{x}}} $$

(8)

$$ D_{{\text{y}}} {\,=\,}e_{15} \frac{\partial w}{{\partial y}}{ + } \in_{11} E_{{\text{y}}} $$

(9)

$$ D_{{\text{x}}} {\,=\,}e_{15} \frac{\partial w}{{\partial x}}{ + } \in_{11} E_{{\text{x}}} $$

(10)

According to Lorentz gauge, the scalar and vector potentials of the electric field can be uniquely determined by:

$$ \nabla \cdot \user2{\rm A} + \frac{1}{{c_{{\text{l}}} }}\frac{\partial \phi }{{\partial t}} = 0 $$

(11)

Substituting Eqs. (5), (6) and (8)–(11) into Eqs. (3) and (4), the equations of motion can be obtained as following forms:

$$ c_{44} \nabla^{2} w - \rho \frac{{\partial^{2} w}}{{\partial t^{2} }} = - e_{15} \left( {\nabla^{2} \phi - \frac{1}{{c_{{\text{l}}}^{2} }}\frac{{\partial^{2} \phi }}{{\partial t^{2} }}} \right) $$

(12)

$$ \frac{{e_{15} }}{{ \in_{11} }}\nabla^{2} w = \nabla^{2} \phi - \frac{1}{{c_{{\text{l}}}^{2} }}\frac{{\partial^{2} \phi }}{{\partial t^{2} }} $$

(13)

where $\nabla^{2} = \frac{{\partial^{2} }}{{\partial x^{2} }} + \frac{{\partial^{2} }}{{\partial y^{2} }}$ is the Laplace operator with respect to variables x and y. Introducing a function:

$$ \psi \equiv \phi - \frac{{e_{15} }}{{ \in_{{{11}}} }}C_{{\text{f}}} w $$

(14)

and with following definitions:

$$ \overline{c}_{44} = c_{44} + \frac{{e_{15}^{2} }}{{ \in_{{{11}}} }} $$

(15)

$$ c_{{\text{s}}} = \sqrt {\frac{{\overline{c}_{44} }}{\rho }} $$

(16)

$$ C_{{\text{f}}} = \frac{{c_{{\text{l}}}^{2} }}{{c_{{\text{l}}}^{2} - c_{{\text{s}}}^{2} }} $$

(17)

where $c_{{\text{s}}}$ is the speed of acoustic shear wave; Eqs. (13) and (14) can then be decoupled into two equations, which are:

$$ \nabla^{2} w - \frac{1}{{c_{{\text{s}}}^{2} }}\frac{{\partial^{2} w}}{{\partial t^{2} }} = 0 $$

(18)

$$ \nabla^{2} \psi - \frac{1}{{c_{{\text{l}}}^{2} }}\frac{{\partial^{2} \psi }}{{\partial t^{2} }} = 0 $$

(19)

Letting $\tilde{c}_{44} = \overline{c}_{44} - \left( {1 - C_{{\text{f}}} } \right)e_{15}^{2} {/} \in_{{{11}}}$, and substituting Eq. (6) into constitutive Eqs. (8)–(11), we have

$$ \tau_{{{\text{yz}}}} {\,=\,}\tilde{c}_{44} \frac{\partial w}{{\partial y}} + e_{15} \frac{\partial \psi }{{\partial y}} + \frac{{e_{15} }}{{c_{{\text{l}}} }}\frac{{\partial A_{{\text{y}}} }}{\partial t} $$

(20)

$$ \tau_{{{\text{xz}}}} {\,=\,}\tilde{c}_{44} \frac{\partial w}{{\partial x}} + e_{15} \frac{\partial \psi }{{\partial x}} + \frac{{e_{15} }}{{c_{{\text{l}}} }}\frac{{\partial A_{{\text{x}}} }}{\partial t} $$

(21)

$$ D_{{\text{y}}} {\,=\,}e_{15} \left( {1 - C_{{\text{f}}} } \right)\frac{\partial w}{{\partial y}} - \in_{11} \frac{\partial \psi }{{\partial y}} - \frac{{ \in_{11} }}{{c_{{\text{l}}} }}\frac{{\partial A_{{\text{y}}} }}{\partial t} $$

(22)

$$ D_{{\text{x}}} {\,=\,}e_{15} \left( {1 - C_{{\text{f}}} } \right)\frac{\partial w}{{\partial x}} - \in_{11} \frac{\partial \psi }{{\partial x}} - \frac{{ \in_{11} }}{{c_{l} }}\frac{{\partial A_{{\text{x}}} }}{\partial t} $$

(23)

Please note that $C_{{\text{f}}}$ is quite close to 1 according to Eq. (17), because the speed of acoustic shear wave is much smaller than that of light. However, to have a comprehensive understanding of the contributions of acoustic shear wave, electroacoustic head wave and electric wave to the electrical displacement D analytically, $C_{{\text{f}}}$ is thus preserved in the subsequent process of theoretical derivation.

When there is a change of the environment temperature, additional stress will be produced due to thermal deformation of the solids. Considering that the results are similar when analyzing the thermal stress in x- and y- directions, the case only with thermal stress in y-direction will be studied and discussed. Thermal stress in y-direction is expressed as:

$$ \sigma_{{{\text{Ty}}}} = - \frac{E\beta T}{{1 - 2\nu }} $$

(24)

where E is the Yong’s modulus, $\beta$ is the coefficient of thermal expansion in y-direction, T is the change of temperature, $\nu$ is the Poisson ratio. Governing equations can then be expressed as [38]:

$$ \left\{ \begin{gathered} \frac{{\partial^{2} w}}{{\partial x^{2} }} + \left( {1 + \frac{{\sigma_{{{\text{Ty}}}} }}{{\overline{c}_{44} }}} \right)\frac{{\partial^{2} w}}{{\partial y^{2} }} = \frac{1}{{c_{{\text{s}}}^{2} }}\frac{{\partial^{2} w}}{{\partial t^{2} }} \hfill \\ \nabla^{2} \psi - \frac{1}{{c_{{\text{l}}}^{2} }}\frac{{\partial^{2} \psi }}{{\partial t^{2} }} = 0 \hfill \\ \end{gathered} \right. $$

(25)

Because intensity of the induced electric field generated in the piezoelectric material under magnetic field is very small, rotational part of the electric field satisfies [31]:

$$ \left| {\frac{{1}}{{c_{{\text{l}}} }}\frac{{\partial A_{{\text{y}}} }}{\partial t}} \right| \ll \left| {\frac{\partial \phi }{{\partial y}}} \right| $$

(26)

$$ \left| {\frac{1}{{c_{{\text{l}}} }}\frac{{\partial A_{{\text{x}}} }}{\partial t}} \right| \ll \left| {\frac{\partial \phi }{{\partial x}}} \right| $$

(27)

With the aid of Eqs. (27)–(28), the constitutive equations are finally expressed as:

$$ \tau_{{{\text{yz}}}} { = }\tilde{c}_{44} \frac{\partial w}{{\partial y}} + e_{15} \frac{\partial \psi }{{\partial y}} $$

(28)

$$ \tau_{{{\text{xz}}}} { = }\tilde{c}_{44} \frac{\partial w}{{\partial x}} + e_{15} \frac{\partial \psi }{{\partial x}} $$

(29)

$$ D_{{\text{y}}} { = }e_{15} \left( {1 - C_{{\text{f}}} } \right)\frac{\partial w}{{\partial y}} - \in_{11} \frac{\partial \psi }{{\partial y}} $$

(30)

$$ D_{{\text{x}}} { = }e_{15} \left( {1 - C_{{\text{f}}} } \right)\frac{\partial w}{{\partial x}} - \in_{11} \frac{\partial \psi }{{\partial x}} $$

(31)

As shown in Fig. 1, an anti-plane force $- \tau_{0} \delta \left( x \right)H\left( t \right)$ is applied on the surface of the piezoelectric half-space, where $\tau_{0}$ is magnitude of the dynamic force, $\delta \left( x \right)$ is the Dirac delta function, and $H\left( t \right)$ is the Heaviside function. Mechanical and short-circuit boundary conditions on the surface can be expressed as:

$$ \tau_{{{\text{yz}}}} \left( {x,0,t} \right) = - \tau_{0} \delta \left( x \right)H\left( t \right)\; $$

(32)

$$ \phi \left( {x,0,t} \right) = 0\; $$

(33)

3 Transient solution in Laplace space

The double Laplace transformation and corresponding inverse transformation of the function $f\left( {x,y,t} \right)$ are defined as:

$$ \overline{f}^{*} \left( {\vartheta ,y,\kappa } \right) = \int_{ - \infty }^{\infty } {\int_{0}^{\infty } {f\left( {x,y,t} \right){\text{e}}^{ - \kappa \vartheta x - \kappa t} } dtdx} $$

(34)

$$ f\left( {x,y,t} \right){ = } - \frac{\kappa }{{4\pi^{{2}} }}\int_{{\vartheta_{1} - {\text{i}}\infty }}^{{\vartheta_{1} {\text{ + i}}\infty }} {\int_{{\kappa_{1} - {\text{i}}\infty }}^{{\kappa_{1} {\text{ + i}}\infty }} {\overline{f}^{*} \left( {\vartheta ,y,\kappa } \right){\text{e}}^{\kappa t + \kappa \vartheta x} d\kappa d\vartheta } } $$

(35)

Applying the double Laplace transformation on the boundary conditions, we have:

$$ \overline{\tau }^{*}_{yz} \left( {\vartheta ,0,\kappa } \right) = - \frac{{\tau_{0} }}{\kappa } $$

(36)

$$ \overline{\phi }^{*} \left( {\vartheta ,0,\kappa } \right) = 0 $$

(37)

The transformed expressions of stress and potential in Eqs. (29)–(32) are thus written as:

$$ \overline{\tau }^{*}_{{{\text{yz}}}} { = }\tilde{c}_{44} \frac{{\partial \overline{w}^{*} }}{\partial y} + e_{15} \frac{{\partial \overline{\psi }^{*} }}{\partial y} $$

(38)

$$ \overline{\tau }^{*}_{{{\text{xz}}}} { = }\kappa \vartheta \tilde{c}_{44} \overline{w}^{*} + \kappa \vartheta e_{15} \overline{\psi }^{*} $$

(39)

$$ \overline{D}^{*}_{{\text{y}}} { = }e_{15} \left( {1 - C_{{\text{f}}} } \right)\frac{{\partial \overline{w}^{*} }}{\partial y} - \in_{11} \frac{{\partial \overline{\psi }^{*} }}{\partial y} $$

(40)

$$ \overline{D}_{{\text{x}}}^{*} { = }\kappa \vartheta e_{15} \left( {1 - C_{{\text{f}}} } \right)\overline{w}^{*} - \kappa \vartheta \in_{11} \overline{\psi }^{*} $$

(41)

Letting

$$ a\left( \vartheta \right) = q\sqrt {s_{{\text{s}}}^{2} - \vartheta^{2} } $$

(42)

$$ q = \sqrt {\frac{{\overline{c}_{44} }}{{\overline{c}_{44} + \sigma_{{{\text{Ty}}}} }}} $$

(43)

$$ e\left( \vartheta \right) = \sqrt {s_{{\text{l}}}^{2} - \vartheta^{2} } $$

(44)

The governing equations can then be expressed as ordinary differential equations:

$$ \frac{{d^{2} \overline{w}^{*} \left( {\vartheta ,y,\kappa } \right)}}{{dy^{2} }} - \kappa^{2} a^{2} \left( \vartheta \right)\overline{w}^{*} \left( {\vartheta ,y,\kappa } \right) = 0 $$

(45)

$$ \frac{{d^{2} \overline{\psi }^{*} \left( {\vartheta ,y,\kappa } \right)}}{{dy^{2} }} - \kappa^{2} e^{2} \left( \vartheta \right)\overline{\psi }^{*} \left( {\vartheta ,y,\kappa } \right) = 0 $$

(46)

where $s_{{\text{s}}}$ and $s_{{\text{l}}}$ are slowness of acoustic shear wave and electromagnetic wave.

After solving transformed governing equations Eqs. (46) and (47), displacement and electrical potential can then be written as:

$$ \overline{w}^{*} \left( {\vartheta ,y,\kappa } \right) = A\left( {\vartheta ,\kappa } \right)\exp \left[ { - \kappa a\left( \vartheta \right)y} \right] $$

(47)

$$ \overline{\psi }^{*} \left( {\vartheta ,y,\kappa } \right) = B\left( {\vartheta ,\kappa } \right)\exp \left[ { - \kappa e\left( \vartheta \right)y} \right] $$

(48)

Substituting Eqs. (48) and (49) into transformed boundary conditions in Eqs. (37) and (38), we have:

$$ \kappa \left[ {\tilde{c}_{44} a\left( \vartheta \right)A\left( {\vartheta ,\kappa } \right) + e_{15} e\left( \vartheta \right)B\left( {\vartheta ,\kappa } \right)} \right] = \tau_{0} F^{*} \left( \kappa \right) $$

(49)

$$ \frac{{e_{15} }}{{ \in_{{{11}}} }}C_{f} A\left( {\vartheta ,\kappa } \right) + B\left( {\vartheta ,\kappa } \right) = 0 $$

(50)

So, $A\left( {\vartheta ,\kappa } \right)$ and $B\left( {\vartheta ,\kappa } \right)$ can be obtained as follows:

$$ A\left( {\vartheta ,\kappa } \right) = \frac{1}{{\kappa^{2} }}\frac{{\tau_{0} }}{{\tilde{c}_{44} \left( {{1} - k_{{\text{e}}}^{4} } \right)}}\frac{{a\left( \vartheta \right) + k_{{\text{e}}}^{2} e\left( \vartheta \right)}}{{s_{{{\text{bge}}}}^{2} - \vartheta^{2} }} $$

(51)

$$ B\left( {\vartheta ,\kappa } \right) = - \frac{{e_{15} }}{{ \in_{{{11}}} }}C_{{\text{f}}} A\left( {\vartheta ,\kappa } \right) $$

(52)

where $s_{{{\text{bge}}}}$ and $c_{{{\text{bge}}}}$ are wave slowness and speed of Bleustein-Gulyaev wave, with $s_{{{\text{bge}}}} = \sqrt {\frac{{s_{{\text{s}}}^{2} - k_{{\text{e}}}^{4} s_{{\text{l}}}^{2} }}{{{1} - k_{{\text{e}}}^{4} }}}$ and $c_{{{\text{bge}}}} = 1/s_{{{\text{bge}}}}$. And $k_{{\text{e}}}^{2} = \frac{{e_{15}^{2} }}{{\tilde{c}_{44} \in_{{{11}}} }}C_{{\text{f}}}$ is the electro-mechanical coupling coefficient.

Substituting Eqs. (48) and (49) into equations Eqs. (39)–(42), and subsequently performing inverse Laplace transform about variable x, we can get the expressions of mechanical displacement, electrical potential, shear stress and electrical displacement in Laplace space as:

$$ w^{*} \left( {x,y,\kappa } \right){ = }\frac{\kappa }{{{2}\pi {\text{i}}}}\int_{{\vartheta_{a} - {\text{i}}\infty }}^{{\vartheta_{a} {\text{ + i}}\infty }} {A\left( {\vartheta ,\kappa } \right)\exp \left[ { - \kappa \left( {a\left( \vartheta \right)y - \vartheta x} \right)} \right]d\vartheta } $$

(53)

$$ \begin{gathered} \phi^{*} \left( {x,y,\kappa } \right) = \frac{\kappa }{{{2}\pi {\text{i}}}}\frac{{e_{15} }}{{ \in_{{{11}}} }}C_{f} \left\{ {\int_{{\vartheta_{a} - {\text{i}}\infty }}^{{\vartheta_{a} {\text{ + i}}\infty }} {A\left( {\vartheta ,\kappa } \right)\exp \left[ { - \kappa \left( {a\left( \vartheta \right)y - \vartheta x} \right)} \right]d\vartheta } } \right. \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. { - \int_{{\vartheta_{e} - {\text{i}}\infty }}^{{\vartheta_{e} {\text{ + i}}\infty }} {A\left( {\vartheta ,\kappa } \right)\exp \left[ { - \kappa \left( {e\left( \vartheta \right)y - \vartheta x} \right)} \right]d\vartheta } } \right\} \hfill \\ \end{gathered} $$

(54)

$$ \begin{gathered} \tau_{{{\text{yz}}}}^{*} \left( {x,y,\kappa } \right){ = } - \frac{{\tilde{c}_{44} \kappa^{2} }}{{2\pi {\text{i}}}}\left\{ {\int_{{\vartheta_{a} - {\text{i}}\infty }}^{{\vartheta_{a} + {\text{i}}\infty }} {a\left( \vartheta \right)A\left( {\vartheta ,\kappa } \right)\exp \left[ { - \kappa \left( {a(\vartheta )y - \vartheta x} \right)} \right]d\vartheta } } \right. \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. { - k_{e}^{2} \int_{{\vartheta_{e} - {\text{i}}\infty }}^{{\vartheta_{e} + {\text{i}}\infty }} {e(\vartheta )A\left( {\vartheta ,\kappa } \right)\exp \left[ { - \kappa \left( {e(\vartheta )y - \vartheta x} \right)} \right]d\vartheta } } \right\} \hfill \\ \end{gathered} $$

(55)

$$ \begin{gathered} \tau^{*}_{xz} \left( {x,y,\kappa } \right){ = }\frac{{\tilde{c}_{44} \kappa^{2} }}{{{2}\pi {\text{i}}}}\left\{ {\int_{{\vartheta_{a} - {\text{i}}\infty }}^{{\vartheta_{a} {\text{ + i}}\infty }} {\vartheta A\left( {\vartheta ,\kappa } \right)\exp \left[ { - \kappa \left( {a\left( \vartheta \right)y - \vartheta x} \right)} \right]d\vartheta } } \right. \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. { - \int_{{\vartheta_{e} - {\text{i}}\infty }}^{{\vartheta_{e} {\text{ + i}}\infty }} {\vartheta k_{e}^{2} A\left( {\vartheta ,\kappa } \right)\exp \left[ { - \kappa \left( {e\left( \vartheta \right)y - \vartheta x} \right)} \right]d\vartheta } } \right\} \hfill \\ \end{gathered} $$

(56)

$$ \begin{gathered} D_{{\text{y}}}^{*} \left( {x,y,\kappa } \right){ = } - \frac{{e_{15} \kappa^{2} }}{{{2}\pi {\text{i}}}}\left\{ {\left( {1 - C_{{\text{f}}} } \right)\int_{{\vartheta_{a} - {\text{i}}\infty }}^{{\vartheta_{a} {\text{ + i}}\infty }} {a\left( \vartheta \right)A\left( {\vartheta ,\kappa } \right)\exp \left[ { - \kappa \left( {a\left( \vartheta \right)y - \vartheta x} \right)} \right]d\vartheta } } \right. \hfill \\ \left. {\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \quad+ C_{f} \int_{{\vartheta_{e} - {\text{i}}\infty }}^{{\vartheta_{e} {\text{ + i}}\infty }} {e\left( \vartheta \right)A\left( {\vartheta ,\kappa } \right)\exp \left[ { - \kappa \left( {e\left( \vartheta \right)y - \vartheta x} \right)} \right]d\vartheta } } \right\} \hfill \\ \end{gathered} $$

(57)

$$ \begin{gathered} D_{{\text{x}}}^{*} \left( {x,y,\kappa } \right){ = }\frac{{e_{15} \kappa^{2} }}{{{2}\pi {\text{i}}}}\left\{ {\left( {1 - C_{{\text{f}}} } \right)\int_{{\vartheta_{1} - {\text{i}}\infty }}^{{\vartheta_{1} {\text{ + i}}\infty }} {\vartheta A\left( {\vartheta ,\kappa } \right)\exp \left[ { - \kappa \left( {a\left( \vartheta \right)y - \vartheta x} \right)} \right]d\vartheta } } \right. \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \quad+ C_{{\text{f}}} \int_{{\vartheta_{1} - {\text{i}}\infty }}^{{\vartheta_{1} {\text{ + i}}\infty }} {\vartheta A\left( {\vartheta ,\kappa } \right)\exp \left[ { - \kappa \left( {e\left( \vartheta \right)y - \vartheta x} \right)} \right]d\vartheta } \; \hfill \\ \end{gathered} $$

(58)

4 Analytical solution in time space

In theoretical analysis of transient waves in elastic media, integral transform is essential in solving the equation of motion. Cagniard [39] introduced a clever transformation which can easily get the original function through a process of contour integration based on Cauchy theorem. This method, which is then improved by De Hoop [40], has been widely employed to get the exact analytical solution in time space for transient waves. Using this method, Sánchez-Sesma et al. [41] conducted effective investigation on the exact solution for the problem with line loading, Shan et al. [42] got the solutions for the transient waves in an elastic half-space subjected to a buried cylindrical line source, and Dehestani et al. [43] studied the transient stresses in the isotropic semi-infinite solids loaded by a force moving at subsonic speed. Furthermore, Lee [44] and Ma et al. [45, 46] discussed the transient response of a layered composite structure subjected to anti-plane force using Cagniard-de Hoop method.

When applying Cagniard-de Hoop method, the integral with respect to variable $\vartheta$ is converted to the definition of an integral with respect to variable t. In the derivation, the integrating path and positions of the singular points are changed in a suitable way. To do this, a new integration with respect to variable t is obtained as:

$$ \mathcal{L}^{ - 1} \left\{ {\int_{{t_{1} }}^{\infty } {{\text{e}}^{ - pt} f(t)dt} } \right\} = f(t)H(t - t_{1} ) $$

(59)

Next, inverse transformation of Eqs. (54)–(59) will be conducted using Cagniard-de Hoop method. Taken electrical potential in Eq. (54) as an example. The integral in Eq. (54) has two branch points $\vartheta_{{\text{s}}} = - s_{{\text{s}}}$ and $\vartheta_{l} = - s_{l}$, and a pole point $\vartheta_{{{\text{bge}}}} = - s_{{{\text{bge}}}}$. According to Cagniard-de Hoop method, an integral variable t is introduced as:

$$ t = a\left( \vartheta \right)y - \vartheta x $$

(60)

where t is positive and real. Equation (61) means a conformal transform from t-plane to $\vartheta$-plane. $\vartheta$ is thus expressed as:

$$ \vartheta_{{\text{a}}}^{( \pm )} = - \frac{xt}{{x^{2} + q^{2} y^{2} }} \pm {\text{i}}\frac{{qy\sqrt {t^{2} - t_{{\text{a}}}^{2} } }}{{x^{2} + q^{2} y^{2} }},\;\;\;\;\;t_{{\text{a}}} \le t < \infty $$

(61)

where $t_{{\text{a}}}$ is the arriving time of acoustic shear waves, and it can be expressed as:

$$ t_{{\text{a}}} = s_{{\text{s}}} \sqrt {x^{2} + q^{2} y^{2} } $$

(62)

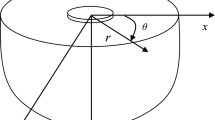
Equation (62) is a hyperbola in $\vartheta$-plane, as shown in Fig. 2. This integral path corresponds to the propagating ray of the shear waves. When $t = t_{{\text{a}}}$, the imaginary part of $\vartheta$ is zero. Because the branch points, pole and saddle points satisfy the condition of $\vartheta_{{{\text{bge}}}} < \vartheta_{{\text{s}}} < \vartheta_{{{\text{saddle}}}} < \vartheta_{{\text{l}}}$; the integral path is composed of two segments and a circle, which is centered at $\vartheta_{l}$ with radius $\varepsilon$. The expressions of additional two segments $\vartheta_{{{\text{ae}}}}^{( \pm )}$ are:

$$ \vartheta_{{{\text{ae}}}}^{( \pm )} = - \frac{xt}{{x^{2} + q^{2} y^{2} }} + \frac{{qy\sqrt {t_{{\text{a}}}^{2} - t^{2} } }}{{x^{2} + q^{2} y^{2} }} \pm {\text{i}}\varepsilon ,\;\;\;\;\;t_{{{\text{ae}}}} \le t < t_{{\text{a}}} $$

(63)

where $t_{{{\text{ae}}}}$ is the arriving time of electroacoustic head wave, and it is:

$$ t_{{{\text{ae}}}} = \sqrt {s_{{\text{s}}}^{2} - s_{{\text{l}}}^{2} } qy + s_{{\text{l}}} x, \, \varepsilon \to 0 $$

(64)

Fig. 2

The integration path of employing Cagniard-de Hoop method in the $\vartheta$-plane for Eq. (54)

According to Cauchy’s theorem and Jordan’s lemma, Eq. (54) is then rewritten as:

$$ \begin{gathered} w^{*} \left( {x,y,\kappa } \right) = \frac{1}{\pi \kappa }\frac{P}{{\tilde{c}_{44} \left( {{1} - k_{e}^{4} } \right)}}\left\{ {\int_{{t_{{\text{a}}} }}^{\infty } {\left. {{\text{Re}} \left[ {\frac{{a\left( \vartheta \right) + k_{e}^{2} e\left( \vartheta \right)}}{{s_{{{\text{bge}}}}^{2} - \vartheta^{2} }}\frac{a\left( \vartheta \right)}{{\sqrt {t^{2} - t_{a}^{2} } }}} \right]} \right|_{{\vartheta_{{\text{a}}}^{ + } }} \exp \left( { - \kappa t} \right)dt} } \right. \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. { - \int_{{t_{{{\text{ae}}}} }}^{{t_{a} }} {\left. {{\text{Im}} \left[ {\frac{{a\left( \vartheta \right) + k_{{\text{e}}}^{2} e\left( \vartheta \right)}}{{s_{{{\text{bge}}}}^{2} - \vartheta^{2} }}\frac{a\left( \vartheta \right)}{{\sqrt {t_{a}^{2} - t^{2} } }}} \right]} \right|_{{\vartheta_{{{\text{ae}}}}^{ + } }} \exp \left( { - \kappa t} \right)dt} } \right\} \hfill \\ \end{gathered} $$

(65)

With Eq. (60) and considering the convolution theorem:

$$ \mathcal{L}^{ - 1} \left[ {F_{1} \left( \kappa \right) \cdot F_{2} \left( \kappa \right)} \right] = f_{1} \left( t \right) * f_{2} \left( t \right) = \int_{0}^{t} {f_{1} \left( \tau \right)} f_{2} \left( {t - \tau } \right)d\tau $$

(66)

where $F_{1} \left( \kappa \right)$ and $F_{2} \left( \kappa \right)$ are Laplace transforms of $f_{1} \left( t \right)$ and $f_{2} \left( t \right)$. We can obtain the inverse transform of the displacement as:

$$ w\left( {x,y,t} \right) = \int_{{0}}^{t} {w^{\prime}\left( {x,y,\tau } \right)H(t - \tau )d\tau } $$

(67)

where

$$ w^{\prime}\left( {x,y,t} \right) = \frac{{\tau_{0} }}{{\pi \tilde{c}_{44} \left( {{1} - k_{e}^{4} } \right)}}\left\{ {{\text{Re}} \left( {{\Omega }_{a} } \right)H\left( {t - t_{a} } \right) - {\text{Im}} \left( {{\Omega }_{ae} } \right)\left[ {H\left( {t - t_{ae} } \right) - H\left( {t - t_{a} } \right)} \right]} \right\} $$

(68)

$$ {\Omega }_{{\text{a}}} { = }\frac{{a\left( {\vartheta_{a}^{ + } } \right) + k_{{\text{e}}}^{2} e\left( {\vartheta_{{\text{a}}}^{ + } } \right)}}{{s_{{{\text{bge}}}}^{2} - \vartheta_{{\text{a}}}^{ + 2} }}\frac{{a\left( {\vartheta_{{\text{a}}}^{ + } } \right)}}{{\sqrt {t^{2} - t_{{\text{a}}}^{2} } }} $$

(69)

$$ {\Omega }_{{{\text{ae}}}} = \frac{{a\left( {\vartheta_{{{\text{ae}}}}^{ + } } \right) + k_{{\text{e}}}^{2} e\left( {\vartheta_{{{\text{ae}}}}^{ + } } \right)}}{{s_{{{\text{bge}}}}^{2} - \vartheta_{{{\text{ae}}}}^{ + 2} }}\frac{{a\left( {\vartheta_{{{\text{ae}}}}^{ + } } \right)}}{{\sqrt {t_{{\text{a}}}^{2} - t^{2} } }} $$

(70)

Subsequently, a similar procedure is employed in the same way to obtain $\phi \left( {x,y,t} \right)$. Letting

$$ t = e\left( \vartheta \right)y - \vartheta x $$

(71)

solution of Eq. (72) can thus be obtained as:

$$ \vartheta_{{\text{e}}}^{( \pm )} = - \frac{xt}{{x^{2} + y^{2} }} \pm i\frac{{y\sqrt {t^{2} - \left( {x^{2} + y^{2} } \right)s_{{\text{l}}}^{2} } }}{{x^{2} + y^{2} }},\;\;\;\;\;t_{{\text{e}}} \le t < \infty $$

(72)

where $t_{e}$ is the arriving time of electric waves, and it can be expressed as:

$$ t_{{\text{e}}} = s_{{\text{l}}} \sqrt {x^{2} + y^{2} } $$

(73)

Shown in Fig. 3 is the integration contour of employing Cagniard-de Hoop method in $\vartheta$-plane for $\phi^{*} \left( {x,y,\kappa } \right)$, where the saddle point is $\vartheta_{{{\text{saddle}}}} = - xs_{{\text{l}}} \left( {x^{2} + y^{2} } \right)^{{ - \frac{1}{2}}}$. The branch points, point pole and saddle point satisfy the relationship $\vartheta_{{{\text{bge}}}} < \vartheta_{{\text{s}}} < \vartheta_{{\text{l}}} < \vartheta_{{{\text{saddle}}}}$. For this case, the hyperbola does not intersect with the branch cut.

Fig. 3

The integration contour of employing Cagniard-de Hoop method in $\vartheta$-plane for Eq. (55)

With similar procedure of derivation, the transient solutions for electrical potential, shear stress and electrical displacement can be expressed explicitly as follows:

$$ \phi \left( {x,y,t} \right) = \int_{{0}}^{t} {\phi^{\prime}\left( {x,y,\tau } \right)H(t - \tau )d\tau } $$

(74)

$$ \begin{gathered} \tau_{{{\text{yz}}}} \left( {x,y,t} \right) = \frac{{\tau_{0} }}{{\pi \left( {{1} - k_{{\text{e}}}^{4} } \right)}}\left\{ {{\text{Re}} \left[ {a\left( {\vartheta_{{\text{a}}}^{ + } } \right){\Omega }_{{\text{a}}} } \right]H\left( {t - t_{{\text{a}}} } \right)} \right. \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. \quad{ - {\text{Im}} \left[ {a\left( {\vartheta_{{{\text{ae}}}}^{ + } } \right){\Omega }_{{{\text{ae}}}} } \right]\left[ {H\left( {t - t_{{{\text{ae}}}} } \right) - H\left( {t - t_{{\text{a}}} } \right)} \right] + k_{{\text{e}}}^{2} {\text{Re}} \left[ {e\left( {\vartheta_{{\text{e}}}^{ + } } \right){\Omega }_{{\text{e}}} } \right]H\left( {t - t_{{\text{e}}} } \right)} \right\} \hfill \\ \end{gathered} $$

(75)

$$ \begin{gathered} \tau_{{{\text{xz}}}} \left( {x,y,t} \right){ = } - \frac{{\tau_{0} }}{{\pi \left( {{1} - k_{{\text{e}}}^{4} } \right)}}\left\{ {{\text{Re}} \left( {\vartheta_{{\text{a}}}^{ + } {\Omega }_{{\text{a}}} } \right)H\left( {t - t_{{\text{a}}} } \right)} \right. \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. \quad{ - {\text{Im}} \left( {\vartheta_{{{\text{ae}}}}^{ + } {\Omega }_{{{\text{ae}}}} } \right)\left[ {H\left( {t - t_{{{\text{ae}}}} } \right) - H\left( {t - t_{{\text{a}}} } \right)} \right] + k_{{\text{e}}}^{2} {\text{Re}} \left( {\vartheta_{{\text{e}}}^{ + } {\Omega }_{{\text{e}}} } \right)H\left( {t - t_{{\text{e}}} } \right)} \right\} \hfill \\ \end{gathered} $$

(76)

$$ \begin{gathered} D_{{\text{y}}} \left( {x,y,t} \right){ = }\frac{{\tau_{0} e_{15} }}{{\pi \tilde{c}_{44} \left( {{1} - k_{{\text{e}}}^{4} } \right)}}\left\{ {\left( {1 - C_{{\text{f}}} } \right){\text{Re}} \left[ {a\left( {\vartheta_{{\text{a}}}^{ + } } \right){\Omega }_{{\text{a}}} } \right]H\left( {t - t_{{\text{a}}} } \right)} \right. \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \quad - \left( {1 - C_{{\text{f}}} } \right){\text{Im}} \left[ {a\left( {\vartheta_{{{\text{ae}}}}^{ + } } \right){\Omega }_{{{\text{ae}}}} } \right]\left[ {H\left( {t - t_{{{\text{ae}}}} } \right) - H\left( {t - t_{{\text{a}}} } \right)} \right] \hfill \\ \left. {\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \quad+ C_{{\text{f}}} {\text{Re}} \left[ {e\left( {\vartheta_{{\text{e}}}^{ + } } \right){\Omega }_{{\text{e}}} } \right]H\left( {t - t_{{\text{e}}} } \right)} \right\} \hfill \\ \end{gathered} $$

(77)

$$ \begin{gathered} D_{{\text{x}}} \left( {x,y,t} \right) = - \frac{{\tau_{0} e_{15} }}{{\pi \tilde{c}_{44} \left( {{1} - k_{e}^{4} } \right)}}\left\{ {\left( {1 - C_{{\text{f}}} } \right){\text{Re}} \left( {\vartheta_{{\text{a}}}^{ + } {\Omega }_{{\text{a}}} } \right)H\left( {t - t_{{\text{a}}} } \right)} \right. \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; - \left( {1 - C_{{\text{f}}} } \right){\text{Im}} \left( {\vartheta_{{{\text{ae}}}}^{ + } {\Omega }_{{{\text{ae}}}} } \right)\left[ {H\left( {t - t_{{{\text{ae}}}} } \right) - H\left( {t - t_{{\text{a}}} } \right)} \right]\left. { + C_{{\text{f}}} {\text{Re}} \left( {\vartheta_{{\text{e}}}^{ + } {\Omega }_{{\text{e}}} } \right)H\left( {t - t_{{\text{e}}} } \right)} \right\} \hfill \\ \end{gathered} $$

(78)

where

$$ \begin{gathered} \phi^{\prime}\left( {x,y,t} \right) = \frac{{\tau_{0} e_{15} C_{f} }}{{\pi \tilde{c}_{44} \in_{{{11}}} \left( {{1} - k_{e}^{4} } \right)}}\left\{ {{\text{Re}} \left( {{\Omega }_{a} } \right)H\left( {t - t_{{\text{a}}} } \right)} \right. \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. \quad{ - {\text{Im}} \left( {{\Omega }_{{{\text{ae}}}} } \right)\left[ {H\left( {t - t_{{{\text{ae}}}} } \right) - H\left( {t - t_{{\text{a}}} } \right)} \right] - {\text{Re}} \left( {\Omega_{{\text{e}}} } \right)H\left( {t - t_{{\text{e}}} } \right)} \right\} \hfill \\ \end{gathered} $$

(79)

$$ {\Omega }_{{\text{e}}} = \frac{{a\left( {\vartheta_{{\text{e}}}^{ + } } \right) + k_{{\text{e}}}^{2} e\left( {\vartheta_{{\text{e}}}^{ + } } \right)}}{{s_{{{\text{bge}}}}^{2} - \vartheta_{{\text{e}}}^{ + 2} }}\frac{{e\left( {\vartheta_{{\text{e}}}^{ + } } \right)}}{{\sqrt {t^{2} - t_{{\text{e}}}^{2} } }} $$

(80)

Expressed in Eqs. (77) and (78) are electrical displacements in x- and y-direction. The first and second terms on the right of the equations are contributions of acoustic shear wave and electroacoustic head wave to the electrical displacement, and the third term is the contribution of electric wave to the electrical displacement. Because C_f is very close to 1, the electrical displacement is obviously dominated by the electric wave.

5 Numerical calculation and discussion

5.1 Verification of the numerical calculation

Based on the analytical expression of the transient response for mechanical displacement, electrical potential, shear stress and electric displacement in time domain, numerical examples will be presented and discussed in this section. For convenience, dimensionless variables are introduced as:

$$ \begin{gathered} x^{\prime} = \frac{x}{L},y^{\prime} = \frac{y}{L},\tau = \frac{t}{{s_{{\text{s}}} L}},\tau_{l} = \frac{{s_{l} }}{{s_{{\text{s}}} }},\tau_{{{\text{bge}}}} = \frac{{s_{{{\text{bge}}}} }}{{s_{{\text{s}}} }} \hfill \\ \tau_{{\text{a}}} = \frac{{t_{a} }}{{s_{{\text{s}}} L}},\tau_{{{\text{ae}}}} = \frac{{t_{{{\text{ae}}}} }}{{s_{{\text{s}}} L}},\tau_{{\text{e}}} = \frac{{t_{{\text{e}}} }}{{s_{{\text{s}}} L}} \hfill \\ \end{gathered} $$

(81)

where L is the horizontal distance from the exciting point. Please refer to Appendix 1 for the expressions of mechanical displacement, electrical potential, shear stress and electrical displacement when above dimensionless variables are employed. Please note that the waves presented in Figs. 4–11 are composed of electric wave, electroacoustic head wave and acoustic wave, which are denoted by subscript e, ae and a, respectively.

Fig. 4

The integrand function of displacement on the surface without thermal effect

Before discussing the thermal effect on the transient response, the numerical result based on the solution of this research is first validated. As shown in Fig. 4 are the curves of the integrand function $\frac{{\pi \tilde{c}_{44} L}}{{c_{s} \tau_{0} }}w^{\prime}\left( {x,y,t} \right)$ of transient displacement for receiver at location (L, 0) when change of the temperature is not considered. Due to the singularity of electroacoustic head wave and acoustic shear wave, we can see that integrand function of the displacement varies rapidly near the wave front. After the last acoustic shear wave passes the receiver, the transient displacement integrand function finally comes to the static value in the end. With increasing electro-mechanical coupling coefficient k_e, it shows that the moment exhibiting singular behavior increases, and magnitude of the static value increases correspondingly. To this point, the result consists well with that given by Li [31], who studied the transient waves in a transversely isotropic piezoelectric half-space under the action of a line loading when without temperature effect.

Considering that only the curves of the integrand function are presented in Ref. 31, transient displacement is further provided in this research. As shown in Fig. 5 are transient displacements for receivers with different depths. Dimensionless arriving time of the electric wave, electroacoustic head wave and acoustic shear wave are $\tau_{e} = 0.001$, $\tau_{{{\text{ae}}}} = 1.007$ and $\tau_{{\text{a}}} = 1.414$ when y = L; $\tau_{{\text{e}}} = 0.0016$, $\tau_{{{\text{ae}}}} = 2.007$ and $\tau_{{\text{a}}} = 2.236$ when y = 2L; $\tau_{{\text{e}}} = 0.0023$, $\tau_{{{\text{ae}}}} = 3.001$ and $\tau_{{\text{a}}} = 3.162$ when y = 3L, respectively. Although the first arrived wave should be electric wave, it has no contribution to the transient displacement according to the derived expression given by Eq. (68). The electroacoustic head wave is the second wave arriving at the receiver, as shown in the small illustration window in Fig. 5, where the contribution is clearly observed from the electroacoustic head waves. It is also found that magnitude of the displacement induced by electroacoustic head waves is bigger when the receiver is further away in vertical direction. The last arrived wave is acoustic shear wave, and it can be seen that the displacement is larger for the receiver closer to the source point. After the last shear acoustic shear wave arrives at the receiver, the displacement grows steadily with increasing time.

Fig. 5

Transient displacements for receivers located vertically without thermal effect

The transient stress $\tau_{{{\text{xz}}}}$ of receivers located in different vertical points is shown in Fig. 6. Dimensionless arrival time of the electric wave, electroacoustic head wave and acoustic shear wave are $\tau_{{\text{e}}} = 7.288 \times 10^{ - 4}$, $\tau_{{{\text{ae}}}} = 7.288 \times 10^{ - 4}$ and $\tau_{{\text{a}}} = 1$ when y = 0; $\tau_{{\text{e}}} = 0.001$, $\tau_{{{\text{ae}}}} = 1.007$ and $\tau_{{\text{a}}} = 1.414$ when y = L; $\tau_{{\text{e}}} = 0.0016$, $\tau_{{{\text{ae}}}} = 2.007$ and $\tau_{{\text{a}}} = 2.236$ when y = 2L, respectively. From Fig. 6, we can find that electric wave has little contribution to the shear stress. For each stress wave, there are two opposite peaks because of the electroacoustic head wave and acoustic shear wave. It also can be seen that magnitude of the transient response contributed by electroacoustic head wave and acoustic shear wave is higher for receiver closer to the surface. After the acoustic wave passes the receiver, the transient stress eventually approaches to the static value.

Fig. 6

Transient shear stress $\tau_{{{\text{xz}}}}$ for receivers located vertically without thermal effect

5.2 Thermal effects on the transient waves

In engineering application of piezoelectric devices, it is of great importance to learn about the propagation of waves in the solids. For example, influence of external mechanical dynamic loading and environmental temperature on the mechanical displacement, electric potential, arrival time of acoustic shear wave, electroacoustic head wave and electric wave. This is helpful in manipulating the propagation of waves in such structures as acoustic amplification devices, piezoelectric sensors and transducers and semiconductor devices. Effects of the thermal stress on the transient response of the piezoelectric half-space subjected to anti-plane dynamic loading will be first discussed in this section. Presented in Fig. 7 is the displacement of receiver located at (x, y) = (L, L) for different change of temperature. Corresponding dimensionless arriving time is $\tau_{{\text{e}}} = 0.001$, $\tau_{{{\text{ae}}}} = 1.001$ and $\tau_{{\text{a}}} = 1.414$ when q = 1; $\tau_{{\text{e}}} = 0.001$, $\tau_{{{\text{ae}}}} = 1.501$ and $\tau_{{\text{a}}} = 1.803$ when q = 1.5; $\tau_{{\text{e}}} = 0.001$, $\tau_{{{\text{ae}}}} = 2.001$ and $\tau_{{\text{a}}} = 2.236$ when q = 2, respectively. According to the definition in Eq. (43), q = 1 when the thermal stress is zero, and q is greater for higher thermal stress. It is found that the arrival time of electroacoustic head wave and acoustic wave increases when the environmental temperature increases. In addition, magnitude of the transient displacement is greater with higher environmental temperature. Figure 8 presents the transient responses of electrical potential $\phi$ under different variation of environmental temperature. Similarly, arriving time of acoustic wave and magnitude of electrical potential increase with higher variation of the temperature. Contribution of the electric wave to electrical potential is almost instantaneous, and then, the electrical potential increases gradually.

Fig. 7

Transient responses of displacement with different temperature changes

Fig. 8

Transient responses of electrical potential with different temperature changes

Presented in Fig. 9 are the transient dimensionless shearing stresses $\tau_{xz}$ at points (L, L) under different temperature variations. The corresponding dimensionless arriving time are $\tau_{{\text{e}}} = 0.001$, $\tau_{{{\text{ae}}}} = 1.001$ and $\tau_{{\text{a}}} = 1.414$ when q = 1; $\tau_{e} = 0.001$, $\tau_{{{\text{ae}}}} = 1.501$ and $\tau_{{\text{a}}} = 1.803$ when q = 1.5; $\tau_{{\text{e}}} = 0.001$, $\tau_{{{\text{ae}}}} = 2.001$ and $\tau_{{\text{a}}} = 2.236$ when q = 2, respectively. It shows that there are more contributions from the electroacoustic head wave and acoustic shear wave with increment of temperature variation, which results in higher magnitude of the transient stress. Furthermore, the arriving time of the transient stress corresponding to electroacoustic head wave and acoustic waves also increases with higher variation of environmental temperature, which implies that change of the environment temperature has influence on the speed of electroacoustic head wave and acoustic wave.

Fig. 9

Transient responses of transient shear stress $\tau_{{{\text{yz}}}}$ at (L, L) with different temperature changes

Figure 10 is the transient electrical displacement $D_{x}$ at point (L, L) with different temperature changes. The corresponding dimensionless arriving time is $\tau_{{\text{e}}} = 0.001$, $\tau_{{{\text{ae}}}} = 1.001$ and $\tau_{{\text{a}}} = 1.414$ when q = 1; $\tau_{{\text{e}}} = 0.001$, $\tau_{{{\text{ae}}}} = 1.501$ and $\tau_{{\text{a}}} = 1.803$ when q = 1.5; and $\tau_{{\text{e}}} = 0.001$, $\tau_{{{\text{ae}}}} = 2.001$ and $\tau_{{\text{a}}} = 2.236$ when q = 2, respectively. From the small illustration window, it is found that the electric waves generate excitation around the time $t/s_{{\text{s}}} L = \tau_{{\text{e}}} = 0.001$. Considering that speed of the electric wave is five orders of magnitude faster than that of acoustic shear wave in a typical medium, the parameter $C_{{\text{f}}}$ is thus close to 1. According to the expression given by Eq. (79), the electric wave contributes most to the response of electric displacement, while the electroacoustic head wave and acoustic wave only have a little contribution to the electric displacement. In addition, with the increment of thermal stress, magnitude of the electric displacement increases correspondingly. When the last acoustic shear wave passes the receiver, the electric displacement approaches to static value.

Fig. 10

Transient responses of electric displacements $D_{{\text{x}}}$ at (L, L) with different temperature changes

5.3 Transient response subjected to mechanical and electrical loading

Transient behavior of the piezoelectric half-space simultaneously subjected to anti-plane line force and in-plane electrical line loading will be further investigated, as shown in Fig. 11. The boundary conditions are:

$$ \tau_{{{\text{yz}}}} \left( {x,0,t} \right) = - \tau_{0} \delta \left( x \right)H\left( t \right)\;;\;t > 0 $$

(82)

$$ E_{{\text{x}}} \left( {x,0,t} \right) = E_{{\text{x}}}^{v} \left( {x,0,t} \right) $$

(83)

$$ D_{{\text{y}}} \left( {x,0,t} \right) - D_{{\text{y}}}^{v} \left( {x,0,t} \right) = - D_{0} \delta \left( x \right)H\left( t \right)\;;\;t > 0 $$

(84)

where the superscript “$v$” represents the corresponding physical quantity when in the vacuum. As presented in Sect. 3, general solutions of the equations for the waves are:

$$ \overline{w}^{*} \left( {\vartheta ,y,\kappa } \right) = A\left( {\vartheta ,\kappa } \right)\exp \left[ { - \kappa a\left( \vartheta \right)y} \right] $$

(85)

$$ \overline{\psi }^{*} \left( {\vartheta ,y,\kappa } \right) = B\left( {\vartheta ,\kappa } \right)\exp \left[ { - \kappa e\left( \vartheta \right)y} \right] $$

(86)

$$ \overline{\phi }^{v*} \left( {\vartheta ,y,\kappa } \right) = C\left( {\vartheta ,\kappa } \right)\exp \left[ {\kappa g\left( \vartheta \right)y} \right] $$

(87)

where $g\left( \vartheta \right) = \sqrt {s_{0}^{2} - \vartheta^{2} }$, with $s_{0}$ the slowness of electromagnetic wave in the vacuum. By using Cagniard-de Hoop method for inverse transform, which is similar to the process of derivation in Sect. 5.1, analytical expressions of the displacement, electric potential, shear stress and electric displacement in time domain are given directly as:

$$ w\left( {x,y,t} \right) = \int_{{0}}^{t} {w^{\prime}\left( {x,y,\tau } \right)H(t - \tau )d\tau } $$

(88)

$$ \phi \left( {x,y,t} \right) = \int_{0}^{t} {\phi^{\prime}\left( {x,y,t} \right)H(t - \tau )d\tau } $$

(89)

$$ \begin{aligned} \tau_{{{\text{yz}}}} \left( {x,y,t} \right){\,=\,} & \frac{1}{\pi }\frac{{\tilde{c}_{44} \tau^{v} }}{{c_{44}^{v} \left( {1 - k_{{\text{e}}}^{v4} } \right)}}\left\{ {{\text{Re}} \left[ {a\left( {\vartheta_{{\text{a}}}^{ + } } \right)\Omega_{{\text{a}}}^{v} } \right]H\left( {t - t_{{\text{a}}} } \right) - {\text{Im}} \left[ {a\left( {\vartheta_{{{\text{ae}}}}^{ + } } \right)\Omega_{{{\text{ae}}}}^{v} } \right]\left[ {H\left( {t - t_{{{\text{ae}}}} } \right) - H\left( {t - t_{{\text{a}}} } \right)} \right]} \right\} \\ & \, + \frac{1}{\pi }\frac{{e_{15} \tau^{v} }}{{c_{44}^{v} \left( {1 - k_{e}^{v4} } \right)}}\left\{ {{\text{Re}} \left[ {e\left( {\vartheta_{e}^{ + } } \right)\Omega_{e1}^{v} } \right]H\left( {t - t_{{\text{e}}} } \right) - {\text{Im}} \left[ {e\left( {\vartheta_{{{\text{ef}}}}^{ + } } \right)\Omega_{ef1}^{v} } \right]\left[ {H\left( {t - t_{{{\text{ef}}}} } \right) - H\left( {t - t_{{\text{e}}} } \right)} \right]} \right\} \\ & \, - e_{15} \frac{{D_{0} }}{\pi }\left\{ {{\text{Re}} \left[ {e\left( {\vartheta_{{\text{e}}}^{ + } } \right)\Omega_{e2}^{v} } \right]H\left( {t - t_{{\text{e}}} } \right) - {\text{Im}} \left[ {e\left( {\vartheta_{{\text{e}}}^{ + } } \right)\Omega_{ef2}^{v} } \right]\left[ {H\left( {t - t_{{{\text{ef}}}} } \right) - H\left( {t - t_{e} } \right)} \right]} \right\} \\ \end{aligned} $$

(90)

$$ \begin{aligned} \tau_{{{\text{xz}}}} \left( {x,y,t} \right){\,=\,} & - \frac{1}{\pi }\frac{{\tilde{c}_{44} \tau^{v} }}{{c_{44}^{v} \left( {1 - k_{e}^{v4} } \right)}}\left\{ {{\text{Re}} \left( {\vartheta_{{\text{a}}}^{ + } \Omega_{{\text{a}}}^{v} } \right)H\left( {t - t_{{\text{a}}} } \right)} \right.\left. { - {\text{Im}} \left( {\vartheta_{{{\text{ae}}}}^{ + } \Omega_{{{\text{ae}}}}^{v} } \right)\left[ {H\left( {t - t_{{{\text{ae}}}} } \right) - H\left( {t - t_{{\text{a}}} } \right)} \right]} \right\} \\ & \, - \frac{1}{\pi }\frac{{e_{15} \tau^{v} }}{{c_{44}^{v} \left( {1 - k_{{\text{e}}}^{v4} } \right)}}\left\{ {{\text{Re}} \left( {\vartheta_{{\text{e}}}^{ + } \Omega_{e1}^{v} } \right)H\left( {t - t_{{\text{e}}} } \right)} \right.\left. { - {\text{Im}} \left( {\vartheta_{{{\text{ef}}}}^{ + } \Omega_{ef1}^{v} } \right)\left[ {H\left( {t - t_{{{\text{ef}}}} } \right) - H\left( {t - t_{{\text{e}}} } \right)} \right]} \right\} \\ & \, + e_{15} \frac{{D_{0} }}{\pi }\left\{ {{\text{Re}} \left( {\vartheta_{{\text{e}}}^{ + } \Omega_{e2}^{v} } \right)H\left( {t - t_{{\text{e}}} } \right)} \right.\left. { - {\text{Im}} \left( {\vartheta_{{{\text{ef}}}}^{ + } \Omega_{ef2}^{v} } \right)\left[ {H\left( {t - t_{{{\text{ef}}}} } \right) - H\left( {t - t_{{\text{e}}} } \right)} \right]} \right\} \\ \end{aligned} $$

(91)

$$ \begin{gathered} D_{{\text{y}}} \left( {x,y,t} \right){\,=\,}\left( {1 - C_{f} } \right)\frac{1}{\pi }\frac{{e_{15} \tau^{v} }}{{c_{44}^{v} \left( {1 - k_{e}^{v4} } \right)}}\left\{ {{\text{Re}} \left[ {a\left( {\vartheta_{a}^{ + } } \right)\Omega_{a}^{v} } \right]H\left( {t - t_{a} } \right)} \right. \hfill \\ \left. {\quad \quad \quad \quad \quad \quad \,\, - {\text{Im}} \left[ {a\left( {\vartheta_{{{\text{ae}}}}^{ + } } \right)\Omega_{{{\text{ae}}}}^{v} } \right]\left[ {H\left( {t - t_{{{\text{ae}}}} } \right) - H\left( {t - t_{{\text{a}}} } \right)} \right]} \right\} \hfill \\ \quad \quad \quad \quad \quad \quad \quad \quad \quad \,\, + \frac{1}{\pi }\frac{{ \in_{11} \tau^{v} }}{{c_{44}^{v} \left( {1 - k_{e}^{v4} } \right)}}\left\{ {{\text{Re}} \left[ {e\left( {\vartheta_{e}^{ + } } \right)\Omega_{e1}^{v} } \right]H\left( {t - t_{{\text{e}}} } \right)} \right.\left. { - {\text{Im}} \left[ {e\left( {\vartheta_{{{\text{ef}}}}^{ + } } \right)\Omega_{ef1}^{v} } \right]\left[ {H\left( {t - t_{{{\text{ef}}}} } \right) - H\left( {t - t_{{\text{e}}} } \right)} \right]} \right\} \hfill \\ \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \,\, - \in_{11} \frac{{D_{0} }}{\pi }\left\{ {{\text{Re}} \left[ {e\left( {\vartheta_{{\text{e}}}^{ + } } \right)\Omega_{e2}^{v} } \right]H\left( {t - t_{{\text{e}}} } \right)} \right.\left. { - {\text{Im}} \left[ {e\left( {\vartheta_{{\text{e}}}^{ + } } \right)\Omega_{ef2}^{v} } \right]\left[ {H\left( {t - t_{{{\text{ef}}}} } \right) - H\left( {t - t_{{\text{e}}} } \right)} \right]} \right\} \hfill \\ \end{gathered} $$

(92)

$$ \begin{gathered} D_{{\text{x}}} \left( {x,y,t} \right){\,=\,} - \left( {1 - C_{f} } \right)\frac{1}{\pi }\frac{{e_{15} \tau^{v} }}{{c_{44}^{v} \left( {1 - k_{e}^{v4} } \right)}}\left\{ {{\text{Re}} \left( {\vartheta_{a}^{ + } {\Omega }_{a}^{v} } \right)H\left( {t - t_{a} } \right)} \right. \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. { - {\text{Im}} \left( {\vartheta_{ae}^{ + } {\Omega }_{{{\text{ae}}}}^{v} } \right)\left[ {H\left( {t - t_{{{\text{ae}}}} } \right) - H\left( {t - t_{a} } \right)} \right]} \right\} \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\; - \frac{1}{\pi }\frac{{ \in_{11} \tau^{v} }}{{c_{44}^{v} \left( {1 - k_{e}^{v4} } \right)}}\left\{ {{\text{Re}} \left( {\vartheta_{e}^{ + } {\Omega }_{e1}^{v} } \right)H\left( {t - t_{e} } \right)} \right.\left. { - {\text{Im}} \left( {\vartheta_{{{\text{ef}}}}^{ + } {\Omega }_{{{\text{ef}}1}}^{v} } \right)\left[ {H\left( {t - t_{{{\text{ef}}}} } \right) - H\left( {t - t_{{\text{e}}} } \right)} \right]} \right\} \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\; + \in_{11} \frac{{D_{0} }}{\pi }\left\{ {{\text{Re}} \left( {\vartheta_{{\text{e}}}^{ + } {\Omega }_{e2}^{v} } \right)H\left( {\;t - t_{{\text{e}}} } \right)} \right.\left. { - {\text{Im}} \left( {\vartheta_{{{\text{ef}}}}^{ + } {\Omega }_{{{\text{ef}}2}}^{v} } \right)\left[ {H\left( {t - t_{{{\text{ef}}}} } \right) - H\left( {\;t - t_{{\text{e}}} } \right)} \right]} \right\} \hfill \\ \end{gathered} $$

(93)

where

$$ t_{{{\text{ef}}}} = \sqrt {s_{l}^{2} - s_{0}^{2} } y + s_{0} x $$

(94)

$$ \tau^{v} = \tau_{0} + \frac{{e_{15} }}{{ \in_{11} + \in_{0} }}D_{0} $$

(95)

$$ k_{e}^{v} = k_{e} \sqrt {\frac{{\tilde{c}_{44} \in_{0} }}{{\overline{c}_{44} \in_{11} + \tilde{c}_{44} \in_{0} }}} $$

(96)

$$ s_{{{\text{bge}}}}^{v} = \sqrt {\frac{{s_{{\text{s}}}^{2} - k_{{\text{v}}}^{4} s_{{\text{l}}}^{2} }}{{1 - k_{{\text{v}}}^{4} }}} $$

(97)

$$ c_{{{44}}}^{v} = \left( {\frac{{ \in_{11} + \in_{0} }}{{\overline{c}_{44} \in_{11} + \tilde{c}_{44} \in_{0} }}} \right)^{{ - 1}} $$

(98)

$$ w^{\prime}\left( {x,y,t} \right){ = }\frac{1}{\pi }\frac{{\tau^{v} }}{{c_{44}^{v} \left( {1 - k_{e}^{v4} } \right)}}\left\{ {{\text{Re}} \left( {\Omega_{a}^{v} } \right)H\left( {\;t - t_{a} } \right) - {\text{Im}} \left( {\Omega_{ae}^{v} } \right)\left[ {H\left( {t - t_{ae} } \right) - H\left( {\;t - t_{a} } \right)} \right]} \right\} $$

(99)

$$ \begin{gathered} \phi^{\prime}\left( {x,y,t} \right) = \frac{{e_{15} \tau^{v} C_{f} }}{{\pi \in_{{{11}}} c_{44}^{v} \left( {1 - k_{{\text{e}}}^{v4} } \right)}}\left\{ {{\text{Re}} \left( {\Omega_{{{\text{e}}1}}^{v} } \right)H\left( {t - t_{{\text{e}}} } \right)} \right.\left. { - {\text{Im}} \left( {\Omega_{{{\text{ef}}1}}^{v} } \right)\left[ {H\left( {t - t_{{{\text{ef}}}} } \right) - H\left( {t - t_{{\text{e}}} } \right)} \right]} \right\} \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;{ + }\frac{1}{\pi }\frac{{\tau^{v} }}{{c_{44}^{v} \left( {1 - k_{{\text{e}}}^{v4} } \right)}}\left\{ {{\text{Re}} \left( {\Omega_{{{\text{e}}1}}^{v} } \right)H\left( {t - t_{{\text{e}}} } \right)} \right.\left. { - {\text{Im}} \left( {\Omega_{{{\text{ef}}1}}^{v} } \right)\left[ {H\left( {t - t_{{{\text{ef}}}} } \right) - H\left( {t - t_{{\text{e}}} } \right)} \right]} \right\} \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\; - \frac{{D_{0} }}{\pi }\left\{ {{\text{Re}} \left( {\Omega_{{{\text{e}}2}}^{v} } \right)H\left( {t - t_{{\text{e}}} } \right)} \right.\left. { - {\text{Im}} \left( {\Omega_{{{\text{ef}}2}}^{v} } \right)\left[ {H\left( {t - t_{{{\text{ef}}}} } \right) - H\left( {t - t_{{\text{e}}} } \right)} \right]} \right\} \hfill \\ \end{gathered} $$

(100)

$$ \vartheta_{{{\text{ef}}}}^{ + } = - \frac{xt}{{x^{2} + y^{2} }} + \frac{{y\sqrt {t_{{\text{e}}}^{2} - t^{2} } }}{{x^{2} + y^{2} }} $$

(101)

Fig. 11

Transversely isotropic piezoelectric half-space subjected to anti-plane force and in-plane electrical loading

The following dimensionless variables are introduced as:

$$ \tau_{{{\text{bgv}}}} = \frac{{s_{{{\text{bgv}}}} }}{{s_{{\text{s}}} }}, \in = \frac{{ \in_{11} }}{{ \in_{0} }},\tau_{{\text{e}}} = \frac{{t_{{\text{e}}} }}{{s_{{\text{s}}} L}} $$

(102)

To investigate the influence of the mechanical loading and electrical loading on the transient responses, the electromechanical ratio factor is introduced as:

$$ E_{{{\text{cf}}}} = \frac{{e_{15} D_{0} }}{{ \in_{11} \tau_{0} }} $$

(103)

where $\tau_{0}$ and $D_{0}$ are magnitudes of the stress and electric loading. Please refer to Appendix for the dimensionless expressions of response of the displacement, electric potential, shear stress and electric displacement (Fig. 11).

The waves shown in Figs. 12–14 are composed of purely electric head waves, electric waves, electroacoustic head waves and acoustic shear waves, which are denoted by subscript ef, e, ae and a, respectively.

Fig. 12

Transient responses of electrical potential when E_cf = 0.5, 1, 2 and at (L, L)

Figure 12 is the transient electrical potential for receiver at (L, L) when E_cf = 0.5, 1 and 2, respectively. The corresponding dimensionless arriving time is $\tau_{{{\text{ef}}}} = 7.48 \times 10^{ - 4}$, $\tau_{{\text{e}}} = 0.001$, $\tau_{{{\text{ae}}}} = 0.99$ and $\tau_{{\text{a}}} = 1.4$. We can see that the electrical potential gradually increases after purely electric head wave arrives. In addition, it is found that the responses have a little change at the moment $t/s_{{\text{s}}} L = \tau_{{\text{a}}} = 1.4$. This can be attributed to the coupling between mechanical and electric fields. As the shear wave arrives at the receiving point, electrical wave will be generated at the same time, which will then have effect on the magnitude of electrical potential. Moreover, it can be observed that magnitude of the electrical potential is higher as the electromechanical ratio factor increases.

Presented in Fig. 13 is the transient shear stress for receiver at (L, L) when E_cf = 0.5, 1 and 2, respectively. This response is the result of purely electric head waves, electric waves, electroacoustic head waves and acoustic shear waves, and the corresponding dimensionless arriving time is $\tau_{{{\text{ef}}}} = 7.48 \times 10^{ - 4}$, $\tau_{{\text{e}}} = 0.001$, $\tau_{{{\text{ae}}}} = 0.99$ and $\tau_{{\text{a}}} = 1.4$. As illustrated in the small window, we can see that the influence of purely electric head wave and electrical wave on the transient response of shear stress $\tau_{{{\text{xz}}}}$ is instantaneous, and the stress rapidly comes to the static value after the acoustic shear wave passes the receiver. When subjected to anti-plane Heaviside function H(t), the stress has a square root singularity at the arrival of the acoustic wave. In addition, it can be observed that before arriving of acoustic waves at $t/s_{{\text{s}}} L = \tau_{{\text{a}}} = 1.4$, magnitude of the transient stress is higher when the electromechanical ratio factor increases. However, it is exact opposite after propagation of the acoustic wave. This is because of the interaction of the electric wave and acoustic wave.

Fig. 13

Transient responses of stress $\tau_{{{\text{xz}}}}$ when E_cf = 0.5, 1, 2 and at (L, L)

Presented in Fig. 14 is the response of electrical displacement $D_{{\text{x}}}$ for different electromechanical ratio factor. The corresponding dimensionless arriving time is $\tau_{{{\text{ef}}}} = 7.48 \times 10^{ - 4}$, $\tau_{{\text{e}}} = 0.001$, $\tau_{{{\text{ae}}}} = 0.99$ and $\tau_{{\text{a}}} = 1.4$, respectively. Similar to $\tau_{{{\text{xz}}}}$ in Fig. 13, the influence of both purely electric head wave and electrical wave on the transient electrical displacement $D_{{\text{x}}}$ is instantaneous. The electrical displacement response drops to the static value rapidly after electrical wave passes the receiver, while the acoustic shear waves have no contribution to the electric displacement. Magnitude of the transient electric displacement is higher when the electromechanical ratio factor E_cf increases.

Fig. 14

Transient responses of electric displacements D_x when E_cf = 0.5, 1, 2 at (L, L)

6 Conclusion

This study investigates the propagation of transient waves in the piezoelectric half-space under anti-plane dynamic force and in-plane electrical displacement loading when thermal effect considered. It shows that variation of environmental temperature and external loading has obvious influence on the propagation of transient waves in the piezoelectric half-space. We can come to the following conclusions:

• (1) The arrival time of electroacoustic head wave and acoustic wave becomes longer when the environmental temperature increases, and magnitude of the transient displacement is greater with higher environmental temperature. Arriving time of acoustic wave and magnitude of electrical potential increase with higher variation of the temperature.

• (2) For the shearing stresses, there are more contributions from the electroacoustic head wave and acoustic shear wave with increment of temperature variation, which results in higher magnitude of the transient stress. The arriving time of the transient stress corresponding to electroacoustic head wave and acoustic waves also increases with higher variation of environmental temperature.

• (3) With the increment of thermal stress, magnitude of the electric displacement increases correspondingly. The electric wave contributes most to the response of electric displacement, while the electroacoustic head wave and acoustic wave only have a little contribution to the electric displacement.

• (4) When the piezoelectric half-space is simultaneously under the action of anti-plane line force and in-plane electrical line loading, the transient response is influenced by the electromechanical ratio factor. Magnitudes of the displacement, electrical potential, stress, and electric displacement increase with higher electromechanical ratio factor. Acoustic shear wave has little contribution to electrical potential and electrical displacement.

Appendices

Appendix 1

The transient response of the displacement field can be expressed as:

$$ \frac{{\pi \tilde{c}_{44} L}}{{c_{s} P}}w^{\prime}\left( {x,y,t} \right) = \frac{1}{{{1} - k_{e}^{4} }}\left\{ {{\text{Re}} \left( {{\Omega }_{{\text{a}}}^{\prime } } \right)H\left( {\tau - \tau_{a} } \right) - {\text{Im}} \left( {{\Omega }_{{{\text{ae}}}}^{\prime } } \right)\left[ {H\left( {\tau - \tau_{{{\text{ae}}}} } \right) - H\left( {\tau - \tau_{{\text{a}}} } \right)} \right]} \right\} $$

(104)

The transient response of electrical potential, stress and electric displacement can be expressed as:

$$ \begin{gathered} \frac{{\pi \tilde{c}_{44} \in_{{{11}}} L}}{{\tau_{0} c_{s} e_{15} }}\phi^{\prime}\left( {x,y,t} \right) = \frac{{C_{f} }}{{{1} - k_{e}^{4} }}\left\{ {{\text{Re}} \left( {{\Omega }_{{\text{a}}}^{\prime } } \right)H\left( {\tau - \tau_{{\text{a}}} } \right)} \right. \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. { - {\text{Im}} \left( {{\Omega }_{{{\text{ae}}}}^{\prime } } \right)\left[ {H\left( {\tau - \tau_{{{\text{ae}}}} } \right) - H\left( {\tau - \tau_{{\text{a}}} } \right)} \right] - {\text{Re}} \left( {{\Omega }_{{\text{e}}}^{\prime } } \right)H\left( {\tau - \tau_{{\text{e}}} } \right)} \right\} \hfill \\ \end{gathered} $$

(105)

$$ \begin{gathered} \frac{\pi L}{{\tau_{0} }}\tau_{{{\text{yz}}}} \left( {x,y,t} \right) = \frac{1}{{{1} - k_{e}^{4} }}\left\{ {{\text{Re}} \left( {q\sqrt {1 - \vartheta_{{\text{a}}}^{\prime + 2} } {\Omega }_{a}^{\prime } } \right)H\left( {\tau - \tau_{a} } \right)} \right. \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \quad- {\text{Im}} \left( {q\sqrt {1 - \vartheta_{{{\text{ae}}}}^{\prime + 2} } {\Omega }_{ae}^{\prime } } \right)\left[ {H\left( {\tau - \tau_{{{\text{ae}}}} } \right) - H\left( {\tau - \tau_{{\text{a}}} } \right)} \right] \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {\;\;\;\;\quad + k_{e}^{2} {\text{Re}} \left( {\sqrt {\tau_{l}^{2} - \vartheta_{{\text{e}}}^{\prime + 2} } {\Omega }_{{\text{e}}}^{\prime } } \right)H\left( {\tau - \tau_{{\text{e}}} } \right)} \right\} \hfill \\ \end{gathered} $$

(106)

$$ \begin{gathered} \frac{\pi L}{{\tau_{0} }}\tau_{{{\text{xz}}}} \left( {x,y,t} \right){ = } - \frac{1}{{{1} - k_{{\text{e}}}^{4} }}\left\{ {{\text{Re}} \left( {\vartheta_{{\text{a}}}^{\prime + } {\Omega }_{{\text{a}}}^{\prime } } \right)H\left( {\tau - \tau_{a} } \right)} \right. \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \quad- {\text{Im}} \left( {\vartheta_{ae}^{\prime + } {\Omega }_{{{\text{ae}}}}^{\prime } } \right)\left[ {H\left( {\tau - \tau_{{{\text{ae}}}} } \right) - H\left( {\tau - \tau_{{\text{a}}} } \right)} \right] \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. { \quad+ k_{{\text{e}}}^{2} {\text{Re}} \left( {\vartheta_{{\text{e}}}^{\prime + } {\Omega }_{e}^{\prime } } \right)H\left( {\tau - \tau_{{\text{e}}} } \right)} \right\} \hfill \\ \end{gathered} $$

(107)

$$ \begin{gathered} \frac{{\pi \tilde{c}_{44} L}}{{\tau_{0} e_{15} }}D_{y} \left( {x,y,t} \right) = \frac{1}{{{1} - k_{{\text{e}}}^{4} }}\left\{ {\left( {1 - C_{f} } \right){\text{Re}} \left( {q\sqrt {1 - \vartheta_{{\text{a}}}^{\prime + 2} } {\Omega }_{{\text{a}}}^{\prime } } \right)H\left( {\tau - \tau_{{\text{a}}} } \right)} \right. \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\quad - \left( {1 - C_{{\text{f}}} } \right){\text{Im}} \left( {q\sqrt {1 - \vartheta_{{{\text{ae}}}}^{\prime + 2} } {\Omega }_{{{\text{ae}}}}^{\prime } } \right)\left[ {H\left( {\tau - \tau_{{{\text{ae}}}} } \right) - H\left( {\tau - \tau_{{\text{a}}} } \right)} \right] \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {\quad + C_{{\text{f}}} {\text{Re}} \left( {\sqrt {\tau_{{\text{l}}}^{2} - \vartheta_{{\text{e}}}^{\prime + 2} } {\Omega }_{{\text{e}}}^{\prime } } \right)H\left( {\tau - \tau_{{\text{e}}} } \right)} \right\} \hfill \\ \end{gathered} $$

(108)

$$ \begin{gathered} \frac{{\pi \tilde{c}_{44} L}}{{\tau_{0} e_{15} }}D_{{\text{x}}} \left( {x,y,t} \right) = - \frac{1}{{{1} - k_{e}^{4} }}\left\{ {{\text{Re}} \left( {\vartheta_{{\text{a}}}^{\prime + } {\Omega }_{{\text{a}}}^{\prime } } \right)H\left( {\tau - \tau_{{\text{a}}} } \right)} \right. \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \quad- \left( {1 - C_{{\text{f}}} } \right){\text{Im}} \left( {\vartheta_{{{\text{ae}}}}^{\prime + } {\Omega }_{{{\text{ae}}}}^{\prime } } \right)\left[ {H\left( {\tau - \tau_{{{\text{ae}}}} } \right) - H\left( {\tau - \tau_{{\text{a}}} } \right)} \right] \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \quad+ C_{{\text{f}}} \left. {{\text{Re}} \left( {\vartheta_{{\text{e}}}^{\prime + } {\Omega }_{{\text{e}}}^{\prime } } \right)H\left( {\tau - \tau_{{\text{e}}} } \right)} \right\} \hfill \\ \end{gathered} $$

(109)

where

$$ \begin{gathered} {\Omega }_{{\text{a}}}^{\prime } = \frac{{q\sqrt {1 - \vartheta_{{\text{a}}}^{\prime + 2} } + k_{{\text{e}}}^{2} \sqrt {\tau_{l}^{2} - \vartheta_{a}^{\prime + 2} } }}{{\tau_{{{\text{bge}}}}^{2} - \vartheta_{{\text{a}}}^{\prime + 2} }}\frac{{q\sqrt {1 - \vartheta_{a}^{\prime + 2} } }}{{\sqrt {\tau^{2} - \tau_{a}^{2} } }} \hfill \\ {\Omega }_{{{\text{ae}}}}^{\prime } = \frac{{q\sqrt {1 - \vartheta_{{{\text{ae}}}}^{\prime + 2} } + k_{e}^{2} \sqrt {\tau_{l}^{2} - \vartheta_{ae}^{\prime + 2} } }}{{\tau_{{{\text{bge}}}}^{2} - \vartheta_{{{\text{ae}}}}^{\prime + 2} }}\frac{{q\sqrt {1 - \vartheta_{{{\text{ae}}}}^{\prime + 2} } }}{{\sqrt {\tau_{a}^{2} - \tau^{2} } }} \hfill \\ {\Omega }_{{\text{e}}}^{\prime } = \frac{{q\sqrt {1 - \vartheta_{a}^{\prime + 2} } + k_{e}^{2} \sqrt {\tau_{l}^{2} - \vartheta_{a}^{\prime + 2} } }}{{\tau_{{{\text{bge}}}}^{2} - \vartheta_{e}^{\prime + 2} }}\frac{{\sqrt {\tau_{l}^{2} - \vartheta_{e}^{\prime + 2} } }}{{\sqrt {\tau^{2} - \left( {x^{\prime 2} + q^{2} y^{\prime 2} } \right)\tau_{l}^{2} } }} \hfill \\ \end{gathered} $$

(110)

$$ \begin{gathered} \vartheta_{a}^{\prime \left( \pm \right)} = - \frac{{x^{\prime}\tau }}{{x^{\prime 2} + q^{2} y^{\prime 2} }} \pm {\text{i}}\frac{{qy^{\prime}\sqrt {\tau^{2} - \left( {x^{\prime 2} + q^{2} y^{\prime 2} } \right)} }}{{x^{\prime 2} + q^{2} y^{\prime 2} }} \hfill \\ \vartheta_{ae}^{\prime \left( \pm \right)} = - \frac{{x^{\prime}\tau }}{{x^{\prime 2} + q^{2} y^{\prime 2} }} \pm \frac{{qy^{\prime}\sqrt {\left( {x^{\prime 2} + q^{2} y^{{\prime}{2}} } \right) - \tau^{2} } }}{{x^{\prime 2} + q^{2} y^{\prime 2} }} \hfill \\ \vartheta_{e}^{\prime \left( \pm \right)} = - \frac{{x^{\prime}\tau }}{{x^{\prime 2} + y^{\prime 2} }} \pm {\text{i}}\frac{{y^{\prime}\sqrt {\tau^{2} - \left( {x^{\prime 2} + y^{\prime 2} } \right)\tau_{l}^{2} } }}{{x^{\prime 2} + y^{\prime 2} }} \hfill \\ \end{gathered} $$

(111)

Appendix 2

After dimensionless processing, each physical quantity can be expressed as:

$$ \frac{{\pi c_{44}^{v} L}}{{c_{s} \tau^{v} }}w^{\prime}\left( {x,y,t} \right){ = }\frac{1}{{1 - k_{e}^{v4} }}\left\{ {{\text{Re}} \left( {{\Omega }_{a}^{v\prime } } \right)H\left( {\tau - \tau_{{\text{a}}} } \right) - {\text{Im}} \left( {{\Omega }_{{{\text{ae}}}}^{v\prime } } \right)\left[ {H\left( {\tau - \tau_{{{\text{ae}}}} } \right) - H\left( {\tau - \tau_{{\text{a}}} } \right)} \right]} \right\} $$

(112)

$$ \begin{gathered} \frac{{\pi c_{44}^{v} \in_{{{11}}} L}}{{\tau^{v} c_{{\text{s}}} e_{15} }}\phi^{\prime}\left( {x,y,t} \right) = \frac{{C_{f} }}{{1 - k_{e}^{v4} }}\left\{ {{\text{Re}} \left( {\Omega_{a}^{v\prime } } \right)H\left( {\tau - \tau_{{\text{a}}} } \right)} \right. \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. { - {\text{Im}} \left( {\Omega_{ae}^{v\prime } } \right)\left[ {H\left( {\tau - \tau_{{{\text{ae}}}} } \right) - H\left( {\tau - \tau_{{\text{a}}} } \right)} \right]} \right\} \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; + \frac{{ \in_{{{11}}} }}{{ \in_{0} }}\frac{1}{{1 - k_{e}^{v4} }}\left\{ {{\text{Re}} \left( {\Omega_{e1}^{v\prime } } \right)H\left( {\tau - \tau_{e} } \right)} \right. \hfill \\ \left. {\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; - {\text{Im}} \left( {\Omega_{{{\text{ef}}1}}^{v\prime } } \right)\left[ {H\left( {\tau - \tau_{{{\text{ef}}}} } \right) - H\left( {\tau - \tau_{{\text{e}}} } \right)} \right]} \right\} \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; - \frac{{ \in_{{{11}}} }}{{ \in_{0} }}\frac{{c_{44}^{v} }}{{\frac{{e_{15}^{2} }}{{E_{cf} \in_{11} }} + \frac{{e_{15}^{{2}} }}{{ \in_{11} + \in_{0} }}}}\left\{ {{\text{Re}} \left( {\Omega_{e2}^{v\prime } } \right)H\left( {\tau - \tau_{{\text{e}}} } \right)} \right. \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. { - {\text{Im}} \left( {\Omega_{{{\text{ef}}2}}^{v\prime } } \right)\left[ {H\left( {\tau - \tau_{{{\text{ef}}}} } \right) - H\left( {\tau - \tau_{{\text{e}}} } \right)} \right]} \right\} \hfill \\ \end{gathered} $$

(113)

$$ \begin{gathered} \frac{{\pi c_{44}^{v} L}}{{\tau^{v} \tilde{c}_{44} }}\tau_{yz} \left( {x,y,t} \right){ = }\frac{1}{{1 - k_{e}^{v4} }}\left\{ {{\text{Re}} \left( {q\sqrt {1 - \vartheta_{a}^{\prime + 2} } {\Omega }_{a}^{v\prime } } \right)\left( {\tau - \tau_{{\text{a}}} } \right)} \right. \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. { - {\text{Im}} \left( {q\sqrt {1 - \vartheta_{{{\text{ae}}}}^{\prime + 2} } {\Omega }_{{{\text{ae}}}}^{v\prime } } \right)\left[ {H\left( {\tau - \tau_{{{\text{ae}}}} } \right) - H\left( {\tau - \tau_{a} } \right)} \right]} \right\} \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; + \frac{{e_{15}^{2} }}{{\tilde{c}_{44} \in_{0} }}\frac{1}{{1 - k_{e}^{v4} }}\left\{ {{\text{Re}} \left( {\sqrt {\tau_{l}^{2} - \vartheta_{e}^{\prime + 2} } {\Omega }_{e1}^{v\prime } } \right)H\left( {\tau - \tau_{e} } \right)} \right. \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. { - {\text{Im}} \left( {\sqrt {\tau_{l}^{2} - \vartheta_{ef}^{\prime + 2} } {\Omega }_{ef1}^{v\prime } } \right)\left[ {H\left( {\tau - \tau_{ef} } \right) - H\left( {\tau - \tau_{e} } \right)} \right]} \right\} \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; - \frac{{e_{15} }}{{\frac{{e_{15} }}{{E_{cf} \in_{11} }} + \frac{{e_{15} }}{{ \in_{11} + \in_{0} }}}}\frac{{c_{44}^{v} }}{{\tilde{c}_{44} \in_{0} }}\left\{ {{\text{Re}} \left( {\sqrt {\tau_{l}^{2} - \vartheta_{e}^{\prime + 2} } {\Omega }_{e2}^{v\prime } } \right)H\left( {\tau - \tau_{{\text{e}}} } \right)} \right. \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. { - {\text{Im}} \left( {\sqrt {\tau_{l}^{2} - \vartheta_{{{\text{ef}}}}^{\prime + 2} } {\Omega }_{ef2}^{v\prime } } \right)\left[ {H\left( {\tau - \tau_{{{\text{ef}}}} } \right) - H\left( {\tau - \tau_{{\text{e}}} } \right)} \right]} \right\} \hfill \\ \end{gathered} $$

(114)

$$ \begin{gathered} \frac{{\pi c_{44}^{v} L}}{{\tau^{v} \tilde{c}_{44} }}\tau_{{{\text{xz}}}} \left( {x,y,t} \right) = - \frac{1}{{1 - k_{{\text{e}}}^{v4} }}\left\{ {{\text{Re}} \left( {\vartheta_{{\text{a}}}^{\prime + } \Omega_{{\text{a}}}^{v\prime } } \right)H\left( {\tau - \tau_{{\text{a}}} } \right)} \right. \hfill \\ \left. {\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad - {\text{Im}} \left( {\vartheta_{{{\text{ae}}}}^{\prime + } \Omega_{{{\text{ae}}}}^{v\prime } } \right)\left[ {H\left( {\tau - \tau_{{{\text{ae}}}} } \right) - H\left( {\tau - \tau_{{\text{a}}} } \right)} \right]} \right\} \hfill \\ \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad - \frac{{e_{15}^{2} }}{{\tilde{c}_{44} \in_{0} }}\frac{1}{{1 - k_{{\text{e}}}^{v4} }}\left\{ {{\text{Re}} \left( {\vartheta_{{\text{e}}}^{\prime + } \Omega_{{{\text{e}}1}}^{v\prime } } \right)H\left( {\tau - \tau_{{\text{e}}} } \right)} \right. \hfill \\ \left. {\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad - {\text{Im}} \left( {\vartheta_{{{\text{ef}}}}^{\prime + } \Omega_{{{\text{ef}}1}}^{v\prime } } \right)\left[ {H\left( {\tau - \tau_{{{\text{ef}}}} } \right) - H\left( {\tau - \tau_{{\text{e}}} } \right)} \right]} \right\} \hfill \\ \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad + \frac{{e_{15} }}{{\frac{{e_{15} }}{{E_{{{\text{cf}}}} \in_{11} }} + \frac{{e_{15} }}{{ \in_{11} + \in_{0} }}}}\frac{{c_{44}^{v} }}{{\tilde{c}_{44} \in_{0} }}\left\{ {{\text{Re}} \left( {\vartheta_{{\text{e}}}^{\prime + } \Omega_{{{\text{e}}2}}^{v\prime } } \right)H\left( {\tau - \tau_{{\text{e}}} } \right)} \right. \hfill \\ \left. {\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad - {\text{Im}} \left( {\vartheta_{{{\text{ef}}}}^{\prime + } \Omega_{ef2}^{v\prime } } \right)\left[ {H\left( {\tau - \tau_{{{\text{ef}}}} } \right) - H\left( {\tau - \tau_{{\text{e}}} } \right)} \right]} \right\} \hfill \\ \end{gathered} $$

(115)

$$ \begin{gathered} \frac{{\pi c_{44}^{v} L}}{{\tau^{v} e_{15} }}D_{{\text{y}}} \left( {x,y,t} \right) = \frac{{1 - C_{{\text{f}}} }}{{1 - k_{{\text{e}}}^{v4} }}\left\{ {{\text{Re}} \left( {q\sqrt {1 - \vartheta_{{\text{a}}}^{\prime + 2} } \Omega_{{\text{a}}}^{v\prime } } \right)H\left( {\tau - \tau_{{\text{a}}} } \right)} \right. \hfill \\ \left. {\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad - {\text{Im}} \left( {q\sqrt {1 - \vartheta_{{{\text{ae}}}}^{\prime + 2} } \Omega_{{{\text{ae}}}}^{v\prime } } \right)\left[ {H\left( {\tau - \tau_{{{\text{ae}}}} } \right) - H\left( {\tau - \tau_{{\text{a}}} } \right)} \right]} \right\} \hfill \\ \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad + \frac{{ \in_{11} }}{{ \in_{0} \left( {1 - k_{v}^{4} } \right)}}\left\{ {{\text{Re}} \left( {\sqrt {\tau_{l}^{2} - \vartheta_{{\text{e}}}^{\prime + 2} } \Omega_{{{\text{e}}1}}^{v\prime } } \right)H\left( {\tau - \tau_{{\text{e}}} } \right)} \right. \hfill \\ \left. {\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad - {\text{Im}} \left( {\sqrt {\tau_{l}^{2} - \vartheta_{{{\text{ef}}}}^{\prime + 2} } \Omega_{{{\text{ef}}1}}^{v\prime } } \right)\left[ {H\left( {\tau - \tau_{{{\text{ef}}}} } \right) - H\left( {\tau - \tau_{{\text{e}}} } \right)} \right]} \right\} \hfill \\ \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \;\;\; - \frac{{c_{44}^{v} }}{{\frac{{e_{15}^{2} }}{{E_{{{\text{cf}}}} \in_{11} }} + \frac{{e_{15}^{2} }}{{ \in_{11} + \in_{0} }}}}\frac{{ \in_{11} }}{{ \in_{0} }}\left\{ {{\text{Re}} \left( {\sqrt {\tau_{l}^{2} - \vartheta_{{\text{e}}}^{\prime + 2} } \Omega_{{{\text{e}}2}}^{v\prime } } \right)H\left( {\tau - \tau_{{\text{e}}} } \right)} \right. \hfill \\ \left. {\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \;\; - {\text{Im}} \left( {\sqrt {\tau_{l}^{2} - \vartheta_{{{\text{ef}}}}^{\prime + 2} } \Omega_{{{\text{ef}}2}}^{v\prime } } \right)\left[ {H\left( {\tau - \tau_{{{\text{ef}}}} } \right) - H\left( {\tau - \tau_{{\text{e}}} } \right)} \right]} \right\} \hfill \\ \end{gathered} $$

(116)

$$ \begin{gathered} \frac{{\pi c_{44}^{{\text{v}}} L}}{{\tau^{{\text{v}}} e_{15} }}D_{{\text{x}}} \left( {x,y,t} \right){ = } - \frac{{1 - C_{{\text{f}}} }}{{1 - k_{{\text{e}}}^{v4} }}\left\{ {{\text{Re}} \left( {\vartheta_{{\text{a}}}^{\prime + } {\Omega }_{{\text{a}}}^{v\prime } } \right)H\left( {\tau - \tau_{{\text{a}}} } \right)} \right. \hfill \\ \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \left. { - {\text{Im}} \left( {\vartheta_{{{\text{ae}}}}^{\prime + } {\Omega }_{{{\text{ae}}}}^{v\prime } } \right)\left[ {H\left( {\tau - \tau_{{{\text{ae}}}} } \right) - H\left( {\tau - \tau_{{\text{a}}} } \right)} \right]} \right\} \hfill \\ \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad - \frac{{ \in_{11} }}{{ \in_{0} \left( {1 - k_{v}^{4} } \right)}}\left\{ {{\text{Re}} \left( {\vartheta_{e}^{\prime + } {\Omega }_{e1}^{v\prime } } \right)H\left( {\tau - \tau_{{\text{e}}} } \right)} \right. \hfill \\ \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \left. { - {\text{Im}} \left( {\vartheta_{{{\text{ef}}}}^{\prime + } {\Omega }_{{{\text{ef}}1}}^{v\prime } } \right)\left[ {H\left( {\tau - \tau_{{{\text{ef}}}} } \right) - H\left( {\tau - \tau_{{\text{e}}} } \right)} \right]} \right\} \hfill \\ \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad + \frac{{c_{44}^{v} }}{{\frac{{e_{15}^{2} }}{{E_{{{\text{cf}}}} \in_{11} }} + \frac{{e_{15}^{2} }}{{ \in_{11} + \in_{0} }}}}\frac{{ \in_{11} }}{{ \in_{0} }}\left\{ {{\text{Re}} \left( {\vartheta_{{\text{e}}}^{\prime + } {\Omega }_{e2}^{v\prime } } \right)H\left( {\tau - \tau_{{\text{e}}} } \right)} \right. \hfill \\ \quad \quad \quad \quad \quad \quad \quad \quad \quad \left. {\quad \quad \quad - {\text{Im}} \left( {\vartheta_{{{\text{ef}}}}^{\prime + } {\Omega }_{{{\text{ef}}2}}^{v\prime } } \right)\left[ {H\left( {\tau - \tau_{{{\text{ef}}}} } \right) - H\left( {\tau - \tau_{{\text{e}}} } \right)} \right]} \right\} \hfill \\ \end{gathered} $$

(117)

$$ \begin{gathered} \Omega_{{\text{a}}}^{v\prime } = \frac{{q\sqrt {1 - \vartheta_{{\text{a}}}^{\prime + 2} } + k_{{\text{e}}}^{v2} \sqrt {\tau_{{\text{l}}}^{2} - \vartheta_{{\text{a}}}^{\prime + 2} } }}{{\tau_{{{\text{bge}}}}^{v2} - \vartheta_{{\text{a}}}^{\prime + 2} }}\frac{{q\sqrt {1 - \vartheta_{{\text{a}}}^{\prime + 2} } }}{{\sqrt {\tau^{2} - \tau_{{\text{a}}}^{2} } }} \hfill \\ \Omega_{{{\text{ae}}}}^{v\prime } = \frac{{q\sqrt {1 - \vartheta_{{{\text{ae}}}}^{\prime + 2} } + k_{e}^{v2} \sqrt {\tau_{l}^{2} - \vartheta_{{{\text{ae}}}}^{\prime + 2} } }}{{\tau_{{{\text{bge}}}}^{v2} - \vartheta_{{{\text{ae}}}}^{\prime + 2} }}\frac{{q\sqrt {1 - \vartheta_{{{\text{ae}}}}^{\prime + 2} } }}{{\sqrt {\tau_{{\text{a}}}^{2} - \tau^{2} } }} \hfill \\ \end{gathered} $$

(118)

$$ \begin{gathered} \Omega_{e1}^{v\prime } = \frac{{q\sqrt {1 - \vartheta_{{\text{e}}}^{\prime + 2} } + k_{{\text{e}}}^{v2} \sqrt {\tau_{{\text{l}}}^{2} - \vartheta_{{\text{e}}}^{\prime + 2} } }}{{\tau_{{{\text{bge}}}}^{v2} - \vartheta_{{\text{e}}}^{\prime + 2} }} \cdot \hfill \\ \frac{{\sqrt {\tau_{l}^{2} - \vartheta_{{\text{e}}}^{\prime + 2} } \left[ {\left( {1 - C_{{\text{f}}} } \right)q\sqrt {1 - \vartheta_{{\text{e}}}^{\prime + 2} } - \frac{{ \in_{0} }}{{ \in_{11} }}C_{{\text{f}}} \sqrt {\tau_{0}^{2} - \vartheta_{{\text{e}}}^{\prime + 2} } } \right]}}{{\left( { \in \sqrt {\tau_{{\text{l}}}^{2} - \vartheta_{{\text{e}}}^{\prime + 2} } + \sqrt {\tau_{0}^{2} - \vartheta_{{\text{e}}}^{\prime + 2} } } \right)\sqrt {\tau^{2} - \tau_{{\text{e}}}^{2} } }} \hfill \\ \Omega_{ef1}^{v\prime } = \frac{{q\sqrt {1 - \vartheta_{{{\text{ef}}}}^{\prime + 2} } + k_{e}^{v2} \sqrt {\tau_{l}^{2} - \vartheta_{ef}^{\prime + 2} } }}{{\tau_{{{\text{bge}}}}^{{v{2}}} - \vartheta_{{{\text{ef}}}}^{\prime + 2} }} \cdot \hfill \\ \frac{{\sqrt {\tau_{{\text{l}}}^{2} - \vartheta_{{{\text{ef}}}}^{\prime + 2} } \left[ {\left( {1 - C_{{\text{f}}} } \right)q\sqrt {1 - \vartheta_{{{\text{ef}}}}^{\prime + 2} } - \frac{{ \in_{0} }}{{ \in_{11} }}C_{{\text{f}}} \sqrt {\tau_{0}^{2} - \vartheta_{{{\text{ef}}}}^{\prime + 2} } } \right]}}{{\left[ { \in \sqrt {\tau_{{\text{l}}}^{2} - \vartheta_{{{\text{ef}}}}^{\prime + 2} } + \sqrt {\tau_{0}^{2} - \vartheta_{{{\text{ef}}}}^{\prime + 2} } } \right]\sqrt {\tau_{{\text{e}}}^{2} - \tau^{2} } }} \hfill \\ \end{gathered} $$

(119)

$$ \begin{gathered} \Omega_{e2}^{v\prime } = \frac{{\sqrt {\tau_{{\text{l}}}^{2} - \vartheta_{{\text{e}}}^{\prime + 2} } }}{{\left[ { \in \sqrt {\tau_{{\text{l}}}^{2} - \vartheta_{{\text{e}}}^{\prime + 2} } + \sqrt {\tau_{0}^{2} - \vartheta_{{\text{e}}}^{\prime + 2} } } \right]\sqrt {\tau^{2} - \tau_{{\text{e}}}^{2} } }} \hfill \\ \Omega_{ef2}^{v\prime } = \frac{{\sqrt {\tau_{l}^{2} - \vartheta_{ef}^{\prime + 2} } }}{{\left[ { \in \sqrt {\tau_{{\text{l}}}^{2} - \vartheta_{{{\text{ef}}}}^{\prime + 2} } + \sqrt {\tau_{0}^{2} - \vartheta_{{{\text{ef}}}}^{\prime + 2} } } \right]\sqrt {\tau_{{\text{e}}}^{2} - \tau^{2} } }} \hfill \\ \end{gathered} $$

(120)