1 Introduction

In light of their utility and importance in aerospace, marine, automotive, and many other fields, nano-reinforcements are currently being thoroughly studied. This class of materials has admirable properties, including high fracture toughness, low weight, and relatively high strength [1], that make them highly desirable for such applications. Recent research work in this field has not only focused on the interface and structural morphology, and the determination of effective mechanical properties of nano-reinforcements but also on their architecture to help design functional composite materials using Artificial intelligence (AI) technology [2]. Due to their exceptional mechanical, thermal, and electrical properties, CNTs are considered to be an excellent candidate for the reinforcement of polymer composites [3,4,5,6], used in many applications ranging from marine and aerospace structures to the high technology of nuclear plants [7]. The combination of CNTs and polymer matrix (i.e., carbon nanotube-reinforced composite (CNTRC)) leads to composite structural components in the form of beams, plates, and shells to gain higher stiffness and strength coupled with a lower weight, which can be four times less for an equivalent cross section made of metallic materials [8, 9]. It has been reported in [10, 11] that the dispersion of low concentrated CNTs into polymeric matrices can remarkably enhance their mechanical properties. For instance, Qian et al. [12] found that mixing polystyrene with a 1% weight fraction of multi-walled carbon nanotubes (MWCNTs) can enhance the neat polystyrene in the elastic modulus of 36–42%. Moreover, many reported research works have noted that dispersing nano-reinforcements such as CNTs in a non-uniform fashion following kind patterns leads to improve mechanical properties of nanocomposite structures. In this context, an excellent review was reported by Liew et al. [13] on recent advances in functionally graded carbon nanotube-reinforced composite (FG-CNTRC) structures.

Recently, many of studies on the mechanical analysis of plates, shells, and beams made from functionally graded materials (FGMs) have been published in the literature [14,15,16,17,18]. In such research works, FGMs are generally characterized by a gradual variation of compositions (typically ceramic and metal) and mechanical properties to achieve the required performance criteria.

Using the FGM concept, Shen [19] first addressed an analysis of the CNT-based FGM to study the nonlinear bending behavior of FG-CNT-reinforced composite plates in thermal environments. Since then, a large number of works have been reported to investigate the effect of CNT volume fraction and their distribution patterns together with other influencing factors, including: (i) dynamic analysis [20], (ii) static analysis [21, 22], (iii) buckling analysis [23, 24] and (iv) post-buckling analysis [25]. Additionally, the vibrational response has been analyzed for FG-CNTs reinforced composite elliptical plates [26], circular plate [27], triangular plates [28], skew plates [29, 30], quadrilateral plates [31], shell plates [32, 33], arbitrary-shaped plates [34], sandwich plates [35, 36] and laminated plates [37].

The most-reported works in terms of investigating the mechanical behavior of FG-CNT composites deal only with the linear form of the distributed nanofillers across the thickness direction of the plate structures. On the one hand, this may lead to an incorrect numerical prediction, because during manufacturing processes, carbon nanotubes, may not disperse in a perfectly linear form, which causes uncertainty in the distribution of CNTs [38, 39]. And, on the other hand, this nonconformity may also lead to limitations in maximizing the overall strength and the high potential for using carbon-based nanocomposite structures. In this area of research, only a limited number of researchers have studied the influence of the uncertainty in the distribution patterns of the nano-reinforcements (i.e., the nonlinear dispersion of the nanofillers). In this context, Mirjavad et al. [40] studied the nonlinear free/forced vibration of FG graphene platelets (FG-GPL) reinforced microbeam employing the couple stress theory; in this study, the nanofillers are assumed to be either uniformly distributed or linearly and nonlinearly functionally graded along the thickness direction of the structure. From the results obtained, it was concluded that the lowest and highest vibration frequencies were obtained in the case of linear and nonlinear dispersion of GPL, respectively. However, Vo-Duy et al. [41] examined the static, free vibration, and buckling analyses of FG-CNT-reinforced composite beams using third-order shear deformation theory (TSDT). In this study, a type of novel nonlinear distribution of the FG-CNT was used to improve the stiffness of the structural beams. The Authors concluded that the dispersion of the CNT closer to the bottom and top surfaces of the beam structures makes it stiffer. Successfully, Tornabene et al. [42] investigated the effect of agglomeration on the natural frequencies of FG-CNT laminated composite doubly curved shells using the generalized differential quadrature method (GDQM); they considered various laminations schemes and several CNT exponential distributions across the thickness of the structures; the presented applications have proven that the presence of CNTs, in terms of both concentration and mass fraction, affects the stiffness of the structure. The same observations were made by Fantuzzi et al. [43] by studying the free vibration behavior of arbitrarily shaped FG-CNT-reinforced composite plates using the GDQ method. While, Jiao et al. [44] studied the effects of the uncertainty in the distributions of CNTs as well as their volume fractions on the buckling behavior of thin rectangular FG-CNT-reinforced composite plate subjected to an arbitrarily distributed partial edge compression loads. Their research results show that the critical buckling load of the CNTRC plates is affected by the uncertainty in the grading of CNT from one type of distribution to another. Using the FSDT, Garcia et al. [45] compared the bending and free vibration analysis of FG graphene versus carbon nanotube-reinforced composite plates. It has been found that the best way to improve the structure's stiffness is to disperse more nanofillers near the bottom and top surfaces of the structure. The same remarks were made by Chiker et al. [46] when investigating the free vibration behavior of functionally graded carbon-based nanofillers, including CNT and GPL, using the FSDT. In their study, the CNT's volume fraction was assumed to be piece-wise functionally graded across the plate thickness employing a layer-wise formulation model. Based on the same methodology, Chiker et al. [47] studied the effect of the uncertainty in the grading profile for the vibrational behavior of hybrid laminated plates containing CNTRC plies. The reported results have proven that the configuration of the laminated plate structures with a special layout arrangement using the CNT distribution patterns can remarkably enhance its performance indices in terms of specific strength and/or specific stiffness.

Recently, the mechanical behavior of various laminated FG-CNTRC structures has been investigated under several influencing parameters, including CNT volume fractions, distribution patterns, plate geometry, number of layers, boundary conditions, and lamination sequences. In this subject area, Tran et al. [48] examined the static analysis of smart laminated CNTRC plates integrated with a piezoelectric layer employing a new four-variable refined plate theory. Using the FSDT and the meshless kp-Ritz method, Lei et al. [49] investigated the buckling behavior of FG-CNT-reinforced composite laminated plate. Employing the higher-order shear deformation theory (HSDT) together with Hamilton's principle, Chakraborty et al. [50] studied the stability and vibration analyses of FG-CNT-reinforced composite laminated cylindrical shell panels. Moreover, Arani et al. [51] presented the free and forced vibration analyses of multi-layered FG composite cylindrical panels reinforced with single-wall CNTs using the Reddy’s TSDT and Hamilton’s principle. Furthermore, Nguyen-Quang et al. [52] investigated the dynamic response of FG-CNT-reinforced composite laminated plates integrated with piezoelectric layers using the HSDT. While Fu et al. [53] carried out the static and free vibration analyses of laminated FG-CNT-reinforced composite rectangular plates on an elastic foundation employing nth-order shear deformation theory and Hamilton’s principle. Using both Maxwell’s equation and Hamilton’s principle, Tran et al. [54] investigated the free vibration analysis of smart laminated FG-CNT-reinforced composite plates integrated with a piezoelectric layer. Employing the FSDT and differential quadrature method, Malekzadeh et al. [55] studied the free vibration behavior of quadrilateral laminated thin-to-moderately thick plates with CNT-reinforced composite layers. The static and free vibration analyses of FG-CNT-reinforced composite laminated plates using a semi-analytical approach based on a layer-wise-differential quadrature method were examined by Malekzadeh and Heydarpour [56]. Whereas, Zhang and Selim [57] studied the vibration analysis of FG-CNT-reinforced composite thick laminated plates employing the Reddy’s HSDT and element-free IMLS-Ritz method, where the Mori–Tanaka approach was employed to obtain the effective material properties. Using the FSDT and kp-Ritz method, Lei et al. [58] conducted the free vibration behavior of laminated FG-CNT-reinforced composite thin-to-moderately thick plates. Likewise, the free vibration and bending analyses of antisymmetrically laminated CNT-reinforced FG plates using the four-variable theory and Hamilton’s principle were investigated by Huang et al. [59].

A literature survey on the background of the present work has been carefully introduced. The review revealed that several recent valuable studies on the analysis of FG-CNTRC had been performed. Nevertheless, it is relevant to examine some novel aspects that can affect the mechanical behavior of carbon-based nanocomposite structures. The literature review reveals the lack of existing studies on the matter of the effect of the uncertainty in the distribution of the nano-reinforcements on the specific stiffness and strength of FG-CNT-reinforced composite. Aiming to fill this gap, the present paper investigates the effect of linear and nonlinear distribution forms of CNT reinforcements on the free vibration behavior of nanocomposite laminated plates using the frameworks of a FEM.

In this article, two types of laminated plate configurations are considered and compared in terms of the layout arrangement of CNT distribution patterns. The effective mechanical properties of the nanocomposite are derived using the extended rule of mixture. Both the FSDT and Lagrange's equations are employed to obtain the governing equations. In addition, various illustrative results are provided to highlight the effects of (i) CNT distribution patterns, (ii) uncertainty in the distribution of CNTs, (iii) plate configurations, (iv) number of plies constituting the plate thickness, (v) CNT volume fraction, (vi) plate width/thickness and length/width ratios, (vii) CNTs orientation angle and (viii) plate boundary conditions on the natural frequencies of the CNTRC laminated plates.

2 Theoretical formulations and field equations

2.1 Geometrical and mechanical characterization

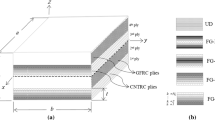
The structure under consideration is a perfectly bonded laminated multi-layer FG-CNT-reinforced composite plate with a total thickness h, width b, and length a (see Fig. 1a). The laminated plates contain n plies of multi-layer CNTRC. Assuming that each ply of the CNTRC laminated plate is divided into NL layers, the ply thickness is given by (\(t = \Delta h \times N_{L}\)), in which \(\Delta h\) is the thickness of each individual layer. The CNTRC plies are made of a polymeric material reinforced with CNTs. Taking into account the functionally graded and uniform distributions form of the CNTs, five different patterns are considered in the present study, with the following abbreviations identifying them: FG-V, FG-Λ, FG-O, FG-X, and UD, as illustrated in Fig. 1b. The CNT volume fraction (\(f_{{{\text{CNT}}}}\)) is assumed to change from layer-to-layer along the ply thickness (in layer-wise form) to provide the functionally graded dispersion. Accordingly, the CNT volume fraction in the k-th ply layer (\(f_{{{\text{CNT}}}}^{(k)}\)) for the considered distribution patterns are given as follows [46]:

$$ UD:f_{{{\text{CNT}}}}^{(k)} = f_{{{\text{CNT}}}}^{*} $$
(1a)
$$ {\text{FG}} - \Lambda :f_{{{\text{CNT}}}}^{(k)} = (1 + {\text{p}}_{{{\text{in}}}} )\left( {\frac{{\left( {0.5 - k + N_{L} } \right)}}{{N_{L} }}} \right)^{{{\text{P}}_{{{\text{in}}}} }} f_{{{\text{CNT}}}}^{*} $$
(1b)
$$ {\text{FG}} - {\text{V }}:f_{{{\text{CNT}}}}^{(k)} = (1 + {\text{p}}_{{{\text{in}}}} )\left( {\frac{k - 0.5}{{N_{L} }}} \right)^{{{\text{P}}_{{{\text{in}}}} }} f_{{{\text{CNT}}}}^{*} $$
(1c)
$$ {\text{FG}} - {\text{X}}:f_{{{\text{CNT}}}}^{(k)} = (1 + {\text{p}}_{{{\text{in}}}} )\left( {\frac{{\left| {2k - N_{L} - 1} \right|}}{{N_{L} }}} \right)^{{{\text{P}}_{{{\text{in}}}} }} f_{{{\text{CNT}}}}^{*} $$
(1d)
$$ {\text{FG}} - {\text{O}}: f_{{{\text{CNT}}}}^{(k)} = (1 + {\text{p}}_{{{\text{in}}}} )\left( {1 - \frac{{\left| {2k - N_{L} - 1} \right|}}{{N_{L} }}} \right)^{{{\text{P}}_{{{\text{in}}}} }} f_{{{\text{CNT}}}}^{*} $$
(1e)
Fig. 1
figure 1

Schematic of: a a laminated composite plate made from multi-layer CNTRC plies; b different distribution patterns of CNT fillers

Full size image

in which \(k =\) 1, 2, 3 …\(N_{L}\). The Pin is the power-law index that sets out the uncertainty in the distribution of the nano-reinforcements, and \(f_{CNT}^{*}\) is the total volume fractions of CNTs. This latter is expressed as follows:

$$ f_{{{\text{CNT}}}}^{*} = \frac{{w_{{{\text{CNT}}}} }}{{w_{{{\text{CNT}}}} + (1 - w_{{{\text{CNT}}}} )({{\rho_{{{\text{CNT}}}} } \mathord{\left/ {\vphantom {{\rho_{{{\text{CNT}}}} } {\rho_{m} }}} \right. \kern-\nulldelimiterspace} {\rho_{m} }})}}, $$
(2)

where \(w_{CNT}\) is the weight fraction of the CNTs; \(\rho_{{{\text{CNT}}}}\) and \(\rho_{m}\) are the CNT and matrix mass density, respectively. The subscripts “CNT” and “m” are referred to as the carbon nanotube and polymer matrix, respectively. In order to make a meaningful comparison, the total volume fraction of CNT (\(f_{CNT}^{*}\)) is kept constant for the five considered FG-CNT patterns.

According to the rule of mixture, the volume fraction of the polymer matrix is given as follows:

$$ f_{m}^{(k)} = 1 - f_{{{\text{CNT}}}}^{(k)}. $$
(3)

Based on the extended rule of mixture micromechanics model [60], the effective elastic properties of the k-th CNTRC ply layer can be expressed as follows [61]:

$$ E_{11}^{(k)} = f_{{{\text{CNT}}}}^{(k)} \eta_{1} E_{11}^{{{\text{CNT}}}} + E_{m} \left( {1 - f_{{{\text{CNT}}}}^{(k)} } \right) $$
(4)
$$ E_{22}^{(k)} = \frac{{\eta_{2} }}{{\frac{{f_{{{\text{CNT}}}}^{(k)} }}{{E_{22}^{{{\text{CNT}}}} }} + \frac{{(1 - f_{{{\text{CNT}}}}^{(k)} )}}{{E_{m} }}}} $$
(5)
$$ G_{12}^{(k)} = \frac{{\eta_{3} }}{{\frac{{f_{{{\text{CNT}}}}^{(k)} }}{{G_{12}^{{{\text{CNT}}}} }} + \frac{{(1 - f_{{{\text{CNT}}}}^{(k)} )}}{{G_{m} }}}} $$
(6)

In Eqs. (4–6), elastic and shear moduli of the polymeric CNT-reinforced-composite are characterized by \(E_{11}^{{{\text{CNT}}}}\), \(E_{22}^{{{\text{CNT}}}}\), \(G_{12}^{{{\text{CNT}}}}\) and \(E_{m}\), \(G_{m}\), respectively, while \(\eta_{i}\) (i = 1,2,3) are the CNT/matrix efficiency parameters, which are introduced to deal with the small scale effect [4, 62].

Using the rule of mixture, the effective Poisson’s ratio and mass density are expressed as follows [63]:

$$ \rho^{(k)} = f_{{{\text{CNT}}}}^{(k)} \rho^{{{\text{CNT}}}} + \left( {1 - f_{{{\text{CNT}}}}^{(k)} } \right)\rho_{m} $$
(7)
$$ \nu_{12}^{(k)} = f_{CNT}^{*} \nu_{12}^{{{\text{CNT}}}} + \left( {1 - f_{{{\text{CNT}}}}^{(k)} } \right)\nu_{m} $$
(8)

where \(\nu_{m}^{{}}\) and \(\nu_{12}^{{{\text{CNT}}}}\) are the Poisson's ratios of matrix and CNT, respectively.

Figure 2 shows the variation of the CNT volume fraction ratios (\({{f_{{{\text{CNT}}}}^{(k)} } \mathord{\left/ {\vphantom {{f_{{{\text{CNT}}}}^{(k)} } {f_{{{\text{CNT}}}}^{*} }}} \right. \kern-\nulldelimiterspace} {f_{{{\text{CNT}}}}^{*} }}\)) across the thickness direction of a single ply of CNTRC plate with different FG-CNT patterns, including UD, FG-V, FG-Λ, FG-X, and FG-O patterns. As can be seen from Fig. 2, the CNT reinforcements follow three forms of distribution across the thickness of the plate, notably: (i) the uniform distribution form (Pin = 0), (ii) the linear distribution form (Pin = 1), and (iii) the nonlinear distribution form (\({\text{P}}_{{{\text{in}}}} \ne\) 0 and 1). Since the CNT volume fraction (1) decreases from the bottom and top layers to the mid-layers for the FG-X pattern, (2) increases from the top and bottom layers to the mid-layers for the FG-O pattern, (3) decreases from the top to the bottom layers for FG-V pattern, and (4) increases from the top to the bottom layers for FG- Λ pattern, the volume fraction ratio as a function of the thickness direction ratio (z/h) varies in a symmetric way for both FG-X and FG-O patterns and in an unsymmetrical way for FG-V and FG-Λ patterns, as shown in Fig. 2a–d.

Fig. 2
figure 2

Variation of CNT volume fraction ratio along the thickness direction ratio for plates with: a FG-V, b FG-Λ, c FG-X and d FG-O patterns

Full size image

A comparison of frequency parameters of two laminated plate configurations is performed, and the plates arrangement depends on the distribution patterns that contain, namely Configuration-I and Configuration-II, (see Fig. 3). For both configurations, laminated plates have four plies of CNTRC. In Configuration-I, the laminated plates contain FG-X distribution patterns, and in Configuration-II the laminated plates contain a combination of FG-Λ and FG-V patterns which are located in the lower and the upper half of the laminated plate, respectively.

Fig. 3
figure 3

Configuration types of the CNTRC laminated plates: a Configuration-I; b Configuration-II

Full size image

2.2 Governing equations of the CNTRC laminated plate

The displacement fields of any point M (x, y, z) in the laminated plate are obtained by using the first-order shear deformation theory (FSDT) [64]:

$$ \left\{ \begin{gathered} u(x,y,z) \hfill \\ v(x,y,z) \hfill \\ w(x,y,z) \hfill \\ \end{gathered} \right\} = \left\{ \begin{gathered} u_{0} (x,y) \hfill \\ v_{0} (x,y) \hfill \\ w_{0} (x,y) \hfill \\ \end{gathered} \right\} + z\left\{ {\begin{array}{*{20}c} {\theta_{x} (x,y)} \\ {\theta_{y} (x,y)} \\ 0 \\ \end{array} } \right\}, $$
(9)

in which \(u_{0} (x,y)\), \(v_{0} (x,y)\) and \(w_{0} (x,y)\) are the translational displacements of a point (x, y) at the mid-plane of the laminated plate; \(\theta_{y} (x,y)\) and \(\theta_{x} (x,y)\) denote the rotations of the transverse normal about the x and y axes, respectively.

According to the FSDT, strain and displacement relationships are expressed as:

$$ \left\{ {\begin{array}{*{20}c} {\varepsilon_{xx} } \\ {\varepsilon_{yy} } \\ {\gamma_{xy} } \\ \end{array} } \right\} = \varepsilon_{0} + z\kappa {,}\quad \quad \quad \left\{ {\begin{array}{*{20}c} {\gamma_{yz} } \\ {\gamma_{xz} } \\ \end{array} } \right\} = \gamma_{0} ,$$
(10)

where

$$ \varepsilon_{0} = \left\{ {\begin{array}{*{20}c} {\frac{{\partial u_{0} }}{\partial x}} \\ {\frac{{\partial v_{0} }}{\partial y}} \\ {\frac{{\partial u_{0} }}{\partial y} + \frac{{\partial v_{0} }}{\partial x}} \\ \end{array} } \right\},\quad \kappa = \left\{ {\begin{array}{*{20}c} {\frac{{\partial \theta_{x} }}{\partial x}} \\ {\frac{{\partial \theta_{y} }}{\partial y}} \\ {\frac{{\partial \theta_{x} }}{\partial y} + \frac{{\partial \theta_{y} }}{\partial x}} \\ \end{array} } \right\},\quad \gamma_{0} = \left\{ {\begin{array}{*{20}c} {\theta_{y} + \frac{{\partial w_{0} }}{\partial y}} \\ {\theta_{x} + \frac{{\partial w_{0} }}{\partial x}} \\ \end{array} } \right\} .$$
(11)

The stress–strain relationship for the k-th layer of the CNTRC ply is given as:

$$\left\{ {\begin{array}{*{20}c} {\sigma_{x} } \\ {\sigma_{y} } \\ {\tau_{xy} } \\ {\tau_{yz} } \\ {\tau_{xz} } \\ \end{array} } \right\}^{(k)} = \left[ {\begin{array}{*{20}c} {Q_{11} } & {\quad Q_{12} } & 0 & 0 & 0 \\ {Q_{12} } & {\quad Q_{22} } & 0 & 0 & 0 \\ 0 & 0 & {\quad Q_{66} } & 0 & 0 \\ 0 & 0 & 0 & {\quad Q_{44} } & 0 \\ 0 & 0 & 0 & 0 & {\quad Q_{55} } \\ \end{array} } \right]^{(k)} \left\{ {\begin{array}{*{20}c} {\varepsilon_{x} } \\ {\varepsilon_{y} } \\ {\varepsilon_{xy} } \\ {\varepsilon_{yz} } \\ {\varepsilon_{xz} } \\ \end{array} } \right\}^{(k)},$$
(12)

where

$$ Q_{11}^{(k)} = \frac{{E_{11}^{(k)} }}{{1 - \nu_{12}^{(k)} \nu_{21}^{(k)} }},\;Q_{12}^{(k)} = \frac{{v_{21}^{(k)} E_{11}^{(k)} }}{{1 - \nu_{12}^{(k)} \nu_{21}^{(k)} }},\;Q_{22}^{(k)} = \frac{{E_{22}^{(k)} }}{{1 - \nu_{12}^{(k)} \nu_{21}^{(k)} }},\,Q_{44}^{(k)} = G_{23}^{(k)} ,\;Q_{55}^{(k)} = G_{13}^{(k)} ,\;Q_{66}^{(k)} = G_{12}^{(k)} .$$
(13)

The axial forces \((N_{x} ,N_{y} ,N_{xy} )\), moment resultants \((M_{x} ,M_{y} ,M_{xy} )\) and shear forces \((Q_{x} ,Q_{y} )\) are related to the strain components by:

$$ \left\{ \begin{gathered} N_{x} \hfill \\ N_{y} \hfill \\ N_{xy} \hfill \\ \end{gathered} \right\} = \left[ {\begin{array}{*{20}c} {A_{11} } & {\quad A_{12} } & {\quad A_{16} } \\ {A_{12} } & {\quad A_{22} } & {\quad A_{26} } \\ {A_{16} } & {\quad A_{26} } & {\quad A_{66} } \\ \end{array} } \right]\varepsilon_{0} + \left[ {\begin{array}{*{20}c} {B_{11} } & {\quad B_{12} } & {\quad B_{16} } \\ {B_{12} } & {\quad B_{22} } & {\quad B_{26} } \\ {B_{16} } & {\quad B_{26} } & {\quad B_{66} } \\ \end{array} } \right]\kappa, $$
(14a)
$$ \left\{ \begin{gathered} M_{x} \hfill \\ M_{y} \hfill \\ M_{xy} \hfill \\ \end{gathered} \right\} = \left[ {\begin{array}{*{20}c} {B_{11} } & {\quad B_{12} } & {\quad B_{16} } \\ {B_{12} } &\quad {B_{22} } & {\quad B_{26} } \\ {B_{16} } & {\quad B_{26} } & {\quad B_{66} } \\ \end{array} } \right]\varepsilon_{0} + \left[ {\begin{array}{*{20}c} {D_{11} } & {\quad D_{12} } & {\quad D_{16} } \\ {D_{12} } & {\quad D_{22} } & {\quad D_{26} } \\ {D_{16} } & {\quad D_{26} } &\quad {D_{66} } \\ \end{array} } \right]\kappa, $$
(14b)
$$ \left\{ \begin{gathered} Q_{y} \hfill \\ Q_{x} \hfill \\ \end{gathered} \right\} = k_{s} \left[ {\begin{array}{*{20}c} {F_{44} } & {\quad F_{45} } \\ {F_{45} } & {\quad F_{55} } \\ \end{array} } \right]\gamma_{0} ,$$
(14c)

in which \(k_{s}\) is the shear correction factor, and the value \(k_{s}\) is taken as 5/6 in this analysis.

The stiffness elements \(A_{ij} ,B_{ij} ,D_{ij}\) and \(F_{ij}\) of the ply are defined as follows:

$$ (A_{ij} ,B_{ij} ,D_{ij} ) = \sum\limits_{k = 1}^{n} {\int\limits_{{Z_{k} }}^{{Z_{k + 1} }} {Q_{ij}^{(k)} (1,z,z^{2} )} } dz,\;\left( {i, j = { 1},{2},{6}} \right) $$
(15)

and

$$ F_{ij} = \sum\limits_{k = 1}^{n} {\int\limits_{{Z_{k} }}^{{Z_{k + 1} }} {Q_{ij}^{(k)} } } dz,\,\left( {i \, ,j = { 4},{5}} \right) .$$
(16)

Equations (14) can be written in compact matrix form as follows:

$$ \left\{ {\begin{array}{*{20}c} N \\ M \\ Q \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} A & B & 0 \\ B & D & 0 \\ 0 & 0 & F \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\varepsilon_{0} } \\ \kappa \\ \gamma \\ \end{array} } \right\}. $$
(17)

2.3 Finite element formulation

The numerical analysis in this work is performed based on a nine-node isoparametric quadrilateral element. Each node possesses five independent degrees of freedom (three displacements (i.e., u, v, w) and two rotations (i.e., θx, θy). Thus, the elementary displacement field can be written as:

$$ \left\{ {\begin{array}{*{20}c} {u_{0} } \\ {v_{0} } \\ {w_{0} } \\ {\theta_{x} } \\ {\theta_{y} } \\ \end{array} } \right\} = \sum\limits_{i = 1}^{9} {\left[ {\begin{array}{*{20}c} {N_{i} } & 0 & 0 & 0 & 0 \\ 0 & {\quad N_{i} } & 0 & 0 & 0 \\ 0 & 0 & {\quad N_{i} } & 0 & 0 \\ 0 & 0 & 0 & {\quad N_{i} } & 0 \\ 0 & 0 & 0 & 0 & {\quad N_{i} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {u_{0i} } \\ {v_{0i} } \\ {w_{0i} } \\ {\theta_{xi} } \\ {\theta_{yi} } \\ \end{array} } \right\}}, $$
(18a)

in which Ni are the shape functions. Equation (18a) can also be expressed in a compact matrix form as follows:

$$ \{ \delta \} = [N]\{ \delta_{e} \} .$$
(18b)

The relationship between the elementary strain and displacement is derived from Eq. (18) as

$$ \left\{ {\begin{array}{*{20}c} {\varepsilon_{0x} } \\ {\varepsilon_{0y} } \\ {\gamma_{0xy} } \\ {\kappa_{x} } \\ {\kappa_{y} } \\ {\kappa_{xy} } \\ {\gamma_{xz} } \\ {\gamma_{yz} } \\ \end{array} } \right\} = \sum\limits_{i = 1}^{9} {\left[ {\begin{array}{*{20}c} {{{\partial N_{i} } \mathord{\left/ {\vphantom {{\partial N_{i} } {\partial x}}} \right. \kern-\nulldelimiterspace} {\partial x}}} & 0 & 0 & 0 & 0 \\ 0 & {\quad {{\partial N_{i} } \mathord{\left/ {\vphantom {{\partial N_{i} } {\partial y}}} \right. \kern-\nulldelimiterspace} {\partial y}}} & 0 & 0 & 0 \\ {{{\partial N_{i} } \mathord{\left/ {\vphantom {{\partial N_{i} } {\partial y}}} \right. \kern-\nulldelimiterspace} {\partial y}}} & {\quad {{\partial N_{i} } \mathord{\left/ {\vphantom {{\partial N_{i} } {\partial x}}} \right. \kern-\nulldelimiterspace} {\partial x}}} & 0 & 0 & 0 \\ 0 & 0 & 0 & {\quad {{\partial N_{i} } \mathord{\left/ {\vphantom {{\partial N_{i} } {\partial x}}} \right. \kern-\nulldelimiterspace} {\partial x}}} & 0 \\ 0 & 0 & 0 & 0 & {\quad {{\partial N_{i} } \mathord{\left/ {\vphantom {{\partial N_{i} } {\partial y}}} \right. \kern-\nulldelimiterspace} {\partial y}}} \\ 0 & 0 & 0 & {\quad {{\partial N_{i} } \mathord{\left/ {\vphantom {{\partial N_{i} } {\partial y}}} \right. \kern-\nulldelimiterspace} {\partial y}}} & {\quad {{\partial N_{i} } \mathord{\left/ {\vphantom {{\partial N_{i} } {\partial x}}} \right. \kern-\nulldelimiterspace} {\partial x}}} \\ 0 & 0 & {\quad {{\partial N_{i} } \mathord{\left/ {\vphantom {{\partial N_{i} } {\partial x}}} \right. \kern-\nulldelimiterspace} {\partial x}}} & {\quad N_{i} } & 0 \\ 0 & 0 & {\quad {{\partial N_{i} } \mathord{\left/ {\vphantom {{\partial N_{i} } {\partial y}}} \right. \kern-\nulldelimiterspace} {\partial y}}} & 0 & {\quad N_{i} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {u_{0i} } \\ {v_{0i} } \\ {w_{0i} } \\ {\theta_{xi} } \\ {\theta_{yi} } \\ \end{array} } \right\}}, $$
(19a)

or in compact matrix form as

$$ \{ \varepsilon \} = [B]\{ \varepsilon_{e} \} .$$
(19b)

According to the Lagrange equations and finite element discretization process, the equilibrium equation for free vibration behavior can be written as

$$ [M]\{ \ddot{\delta }\} + [K]\{ \delta \} = \{ 0\}, $$
(20)

where [K] and [M] are, respectively, the global stiffness and global mass matrix, and \(\{ \ddot{\delta }\}\) and \(\{ \delta \}\) are the acceleration and nodal displacement vector, respectively.

[M] and [K] are obtained by assembling the elementary mass matrix \([M_{e} ]\) and stiffness matrix \([K_{e} ]\); these latter are expressed as follows:

$$ [M_{e} ] \, = \int\limits_{{\Lambda_{e} }} {[N]^{T} [\overline{m}][N]} \, d\Lambda_{e} ,$$
(21)
$$ [K_{e} ] = \int\limits_{{\Lambda_{e} }} {[B]^{T} [C][B]}^{{}} d\Lambda_{e} ,$$
(22)

where Λe is the elementary surface, \([\overline{m}]\) is the inertia matrix and \([C]\) is the elasticity matrix; they are expressed as:

$$ \overline{m} = \left[ {\begin{array}{*{20}c} {I_{0} } & 0 & 0 & {\quad I_{1} } & 0 \\ 0 & {\quad I_{0} } & 0 & 0 & {\quad I_{1} } \\ 0 & 0 & {\quad I_{0} } & 0 & 0 \\ {I_{1} } & 0 & 0 & {\quad I_{2} } & 0 \\ 0 & {\quad I_{1} } & 0 & 0 & {\quad I_{2} } \\ \end{array} } \right],\;C = \left[ {\begin{array}{*{20}c} A & B & 0 \\ B & D & 0 \\ 0 & 0 & F \\ \end{array} } \right], $$
(23)

in which \(I_{i} = \sum\nolimits_{k = 1}^{n} {\int\limits_{{z_{k - 1} }}^{{z_{k} }} {z^{i} \rho^{k} dz} }\), i = 0,1,2 and \(\rho^{k}\) is the material density of the kth ply layer.

3 Numerical applications

The numerical applications reported in this section are performed using an in-house finite element computer code, developed and maintained by our research team. Initially, the validity of the present approach is examined by comparing the achieved results with those reported in the literature; then, many applications and parametric studies, as shown in Sect. 1, are carried out.

The armchair (10,10) single-walled carbon nanotubes (SWCNTs) are selected as reinforcements, and the poly(m-phenylenevinylene)-co-[(2,5-dioctoxy-p-phenylene) vinylene] (PmPV) is selected as matrix. The mechanical properties of both constituent materials at a temperature of 300 K are listed in Table 1. The CNT/matrix efficiency parameters for three levels of CNT volume fractions are given in Table 2. It is assumed that \(G_{12} = G_{13} = G_{23}\).

Table 1 Material properties of the polymer matrix and (10,10) SWCNTs [19, 62]
Full size table
Table 2 CNT/matrix efficiency parameters [19]
Full size table

For the proposed applications, the plates are discretized into 8 × 8 elements and the following boundary conditions (BCs) are considered:

1. Simply supported edge (S):

Angle-ply laminate (45°/−45°/45°/−45°):

  • at x = 0, a: \(u_{0} = w_{0} = \theta_{y} = 0,\)

    at y = 0, b: \(v_{0} = w_{0} = \theta_{x} = 0.\)

cross-ply laminate (0°/90°/0°/90°):

  • at x = 0, a: \(v_{0} = w_{0} = \theta_{y} = 0,\)

    at y = 0, b: \(u_{0} = w_{0} = \theta_{x} = 0.\)

2. Clamped edge (C):

  • at x = 0, a: and y = 0, b: \(u_{0} = v_{0} = w_{0} = \theta_{x} = \theta_{x} = 0,\) for both angle-ply and cross-ply laminates.

Natural frequencies are expressed in non-dimensional form by using the following expression:

$$ \overline{\omega } = \omega ({{b^{2} } \mathord{\left/ {\vphantom {{b^{2} } h}} \right. \kern-\nulldelimiterspace} h})\sqrt {{{\rho^{m} } \mathord{\left/ {\vphantom {{\rho^{m} } {E^{m} }}} \right. \kern-\nulldelimiterspace} {E^{m} }}}. $$
(24)

3.1 Comparative studies

Three comparative studies are performed; the first one concerns the case of a functionally graded alumina/aluminum (Al2O3/Al) square simply supported plate. The mechanical properties of the Al2O3 and Al materials are given as follows [65]:

$$ E_{{{\text{Al}}_{{2}} {\text{O}}_{{3}} }} = 380.0\;{\text{GPa}},\quad \rho_{{{\text{Al}}_{{2}} {\text{O}}_{{3}} }} = 3800\;{\text{kg}}/{\text{m}}^{{3}}, \quad \nu_{{{\text{Al}}_{{2}} {\text{O}}_{{3}} }} = 0.3, $$
$$ E_{{{\text{Al}}}} = 70.0\;{\text{GPa}},\quad \rho_{{{\text{Al}}}} = 2702\;{\text{kg}}/{\text{m}}^{{3}} ,\quad \nu_{{{\text{Al}}}} = 0.3. $$

The effective material properties of the functionally graded Al2O3/Al plates are estimated using the following layer-wise formulation [46]:

$$ E^{(k)} = (E_{{{\text{Al}}_{2} {\text{O}}_{3} }} - E_{Al} )\left( {\frac{k - 0.5}{{N_{L} }}} \right)^{{{\text{P}}_{{{\text{in}}}} }} + E_{{{\text{Al}}}}, $$
(25a)
$$ \rho^{(k)} = \left( {\rho^{{{\text{Al}}_{2} {\text{O}}_{3} }} - \rho_{{{\text{Al}}}} } \right)\left( {\frac{k - 0.5}{{N_{L} }}} \right)^{{{\text{P}}_{{{\text{in}}}} }} + \rho_{{{\text{Al}}}}, $$
(25b)
$$ \nu^{(k)} = 0.3. $$
(25c)

Herein, NL is the number of plate layers and k = 1, 2, 3… NL.

Results in terms of non-dimensional frequencies, \({\overline{\omega }}_{{}} { = }_{{}} {\upomega }_{{}} h_{{}} \sqrt {{{\rho_{{Al_{2} O_{3} }} } \mathord{\left/ {\vphantom {{\rho_{{Al_{2} O_{3} }} } {E_{{Al_{2} O_{3} }} }}} \right. \kern-\nulldelimiterspace} {E_{{Al_{2} O_{3} }} }}}\), are presented in Table 3 and are compared with those reported by Matsunaga [65]. As can be observed from Table 3, the obtained results and those reported in Ref. [65] are in good agreement. In this analysis, the width/thickness ratio (b/h) and the number of ply layers (NL) are set to 5 and 10, respectively.

Table 3 Comparison of the first six non-dimensional natural frequency (\(\overline{\omega } = \omega h\sqrt {{{\rho_{{{\text{AL}}_{2} {\text{O}}_{3} }} } \mathord{\left/ {\vphantom {{\rho_{{{\text{AL}}_{2} {\text{O}}_{3} }} } {E_{{{\text{AL}}_{2} {\text{O}}_{3} }} }}} \right. \kern-\nulldelimiterspace} {E_{{{\text{AL}}_{2} {\text{O}}_{3} }} }}}\)) of square FG (Al/Al2O3) plates (b/h = 05; NL = 10; SSSS)
Full size table

For the second comparison study, a cross-ply (0°/90°/0°/90°/0°) CNTRC square laminated plate is considered. The first six dimensionless frequencies, obtained for the different CNT distribution patterns (i.e., UD, FG-O, FG-V, and FG-X), are tabulated in Table 4 and are compared with the results published by Lie et al. [58]. The number of ply layers (NL), width/thickness ratio (b/h), and CNT volume fraction (\(f_{CNT}^{*}\)) are selected to be 20, 10 and 0.14, respectively, whereas the SSSS and CCCC boundary conditions are used. The material properties are listed in Tables 1 and 2. By way of comparison, it can be seen that the obtained results are in good agreement with those given by Lie et al. [58], where the maximum percentage difference is about 2.32%.

Table 4 Comparison of the first six non-dimensional natural frequencies \(\overline{\omega } = \omega ({{b^{2} } \mathord{\left/ {\vphantom {{b^{2} } h}} \right. \kern-\nulldelimiterspace} h})\sqrt {{{\rho_{m} } \mathord{\left/ {\vphantom {{\rho_{m} } {E_{m} }}} \right. \kern-\nulldelimiterspace} {E_{m} }}}\) of CNT-reinforced composite square laminated plates with (0°/90°/0°/90°/0°) stacking sequence (\(f_{CNT}^{*} = 0.14\); b/h = 10; a/b = 1; NL = 20)
Full size table

The third comparison study concerns the case of a simply supported CNTRC square laminated plate with two cases of stacking sequences, namely (0°/90°)n and (45°/− 45°)n where (n = 1, 2 and 3). The number of ply layers (NL), width/thickness ratio (b/h) and CNT volume fraction (\(f_{CNT}^{*}\)) are chosen as 20, 50 and 0.14, respectively. As can be seen after comparison in Table 5, the obtained results agree well with those obtained by Hang et al. [59].

Table 5 Comparison of the first natural frequency (\(\overline{\omega } = \omega ({{b^{2} } \mathord{\left/ {\vphantom {{b^{2} } h}} \right. \kern-\nulldelimiterspace} h})\sqrt {{{\rho_{m} } \mathord{\left/ {\vphantom {{\rho_{m} } {E_{m} }}} \right. \kern-\nulldelimiterspace} {E_{m} }}}\)) of simply supported CNT-reinforced composite square laminated plates (\(f_{CNT}^{*} = 0.14\); b/h = 50; a/b = 1; NL = 20)
Full size table

It can be concluded from the above comparative studies that the numerical model used in the present paper can provide accurate predictions for the free vibration of FG nanocomposite laminated plate structures.

3.2 Free vibration analysis of CNTRC laminated plates

3.2.1 Effect of the number of layers constituting the plies

To determine the minimum number of layers (NL) constituting the plies, which can properly assess the desired distribution patterns of the nano-reinforcements through the ply thickness, a study on the convergence of the first non-dimensional frequency parameter \({\overline{\omega }}\) versus the number of layers (NL) constituting the plies is performed. Let us start with the case of a single ply CNTRC square plate with width/thickness ratio b/h = 10 and CNT volume fraction \(f_{CNT}^{*}\) = 0.11. The boundary conditions used for the plates investigated are either fully simply supported (SSSS) or fully clamped (CCCC). Three distribution patterns are considered, namely FG-Λ, FG-V, and FG-X. The analysis is performed for different power-law indexes (Pin = 0, 0.4, 0.8, 1, 1.4, and 1.8). It can be seen from Fig. 4 that when Pin = 0, the fundamental non-dimensional frequency (\({\overline{\omega }}\)) remains constant with the increase in NL which occurs for all considered cases of distribution patterns. The physical reason for this matter is believed to be related to the fact that the CNTs are uniformly distributed across the ply thickness. Results also reveal that when \({\text{P}}_{{{\text{in}}}} \ne 0\), the frequency parameter \(\overline{\omega }\) increases with the increase of NL for the FG-X distribution type; whereas for the two other non-uniform distribution patterns (i.e., FG-Λ and FG-V), the frequency parameter \(\overline{\omega }\) decreases. According to Figs. 4a and b, the convergence of the frequency parameter \({\overline{\omega }}\) shows a similar trend for both SSSS and CCCC boundary conditions. Moreover, Fig. 4 indicates that the fundamental non-dimensional frequency remains constant when \(N_{L} \ge 20\). Therefore, for the upcoming applications, NL will be set to 20.

Fig. 4
figure 4

Convergence of the first non-dimensional frequency \({\overline{\omega }}\) parameter versus the layer number of a single ply of CNTRC plates with different CNT distribution patterns, power-law indexes, and boundary conditions (b/h = 10; a/b = 1; \(f_{{{\text{CNT}}}}^{*} = 0.11\))

Full size image

3.2.2 Effects of plate width/thickness ratio and CNT volume fraction

The combined influences of the plate configuration, CNT volume fraction, power-law index, and plate width/thickness ratio on the fundamental non-dimensional, frequency (\({\overline{\omega }}\)) parameter of the SSSS cross-ply (0°/90°/0°/90°) laminated plate are reported in Table 6. Two configurations for the stratification of plies with respect to the CNT distribution patterns are proposed, namely (a) Configuration-I: [X-X-X-X] and (b) Configuration-II: [Λ-Λ-V-V] as shown in Fig. 3. Table 6 shows that for a fixed value of Pin, the \({\overline{\omega }}\) parameter increases whenever the CNT volume fraction is added. Also, one can see that by increasing the width/thickness ratio, the value of \({\overline{\omega }}\) increases for both types of plate configurations. Results also indicate that the frequencies obtained with Configuration-II are higher than those obtained with Configuration-I with a value of \({\text{P}}_{{{\text{in}}}} \ne 0\). Table 7 presents the results of the first non-dimensional frequency of simply supported CNTRC laminated plate for an angle-ply staking sequence (45°/− 45°/45°/− 45°). The results indicate that the fundamental frequencies of the angle-ply CNTRC laminated plates are affected by the width/thickness ratio, plate configuration, and CNT volume fraction in the same way as the cross-ply CNTRC laminated plates were affected.

Table 6 First non-dimensional frequency (\({\overline{\omega }}_{{}} { = }_{{}} {\upomega }_{{}} {(}{{b^{2} } \mathord{\left/ {\vphantom {{b^{2} } h}} \right. \kern-\nulldelimiterspace} h}{)}\sqrt {{{\rho_{m} } \mathord{\left/ {\vphantom {{\rho_{m} } {E_{m} }}} \right. \kern-\nulldelimiterspace} {E_{m} }}}\)) of cross-ply (0°/90°/0°/90°) simply supported CNTRC laminated plates with different power-law indexes, plate configurations, CNT volume fractions, and width/thickness ratios (a/b = 1)
Full size table
Table 7 First non-dimensional frequency (\({\overline{\omega }}_{{}} { = }_{{}} {\upomega }_{{}} {(}{{b^{2} } \mathord{\left/ {\vphantom {{b^{2} } h}} \right. \kern-\nulldelimiterspace} h}{)}\sqrt {{{\rho_{m} } \mathord{\left/ {\vphantom {{\rho_{m} } {E_{m} }}} \right. \kern-\nulldelimiterspace} {E_{m} }}}\)) of angle-ply (45°/− 45°/45°/− 45°) simply supported CNTRC laminated plates with different power-law indexes, plate configurations, CNT volume fractions, and width/thickness ratios (a/b = 1)
Full size table

3.2.3 Effects of plate length/width ratio and CNT volume fraction

The effect of CNT volume fraction associated with the effects of plate length/width ratio, power-law index, and plate configuration on the non-dimensional fundamental frequency (\({\overline{\omega }}\)) of a simply supported cross-ply (0°/90°/0°/90°) CNTRC laminated plate are reported in Table 8, where b/h is taken equal to 10. It is observed that for a fixed value of Pin, the parameter \({\overline{\omega }}\) increases once the CNT volume fraction increases for the three values of length/width ratio considered, i.e., 2.0, 1.5, 1.0. For both types of plate configurations (I and II), the parameter \({\overline{\omega }}\) decreases when a/b increases. Also, it is evident that the values of \({\overline{\omega }}\) obtained with configuration-I are smaller than the ones obtained with configuration-II having \({\text{P}}_{{{\text{in}}}} \ne 0\). However, this advance is only provided when a/b is equal to 1 and 1.5. In other words, when a/b is equal to 2, the parameter \({\overline{\omega }}\) for both types of plate configurations (I and II) is nearly identical. Likewise, Table 9 presents the non-dimensional fundamental frequency (\({\overline{\omega }}\)) of simply supported angle-ply (45°/− 45°/45°/− 45°) CNTRC laminated plates. One can conclude that for different values of CNT volume fractions, width/thickness ratios, and plate configurations, the parameter \({\overline{\omega }}\) of the angle-ply and cross-ply CNTRC laminated plates is affected in the same manner.

Table 8 First non-dimensional frequency (\({\overline{\omega }}_{{}} { = }_{{}} {\upomega }_{{}} {(}{{b^{2} } \mathord{\left/ {\vphantom {{b^{2} } h}} \right. \kern-\nulldelimiterspace} h}{)}\sqrt {{{\rho_{m} } \mathord{\left/ {\vphantom {{\rho_{m} } {E_{m} }}} \right. \kern-\nulldelimiterspace} {E_{m} }}}\)) of cross-ply (0°/90°/0°/90°) simply supported CNTRC laminated plate with different power-law indexes, plate configurations, CNT volume fractions, and length/width ratios (b/h = 10)
Full size table
Table 9 First non-dimensional frequency (\({\overline{\omega }}_{{}} { = }_{{}} {\upomega }_{{}} {(}{{b^{2} } \mathord{\left/ {\vphantom {{b^{2} } h}} \right. \kern-\nulldelimiterspace} h}{)}\sqrt {{{\rho_{m} } \mathord{\left/ {\vphantom {{\rho_{m} } {E_{m} }}} \right. \kern-\nulldelimiterspace} {E_{m} }}}\)) of angle-ply (45°/− 45°/45°/− 45°) simply supported CNTRC laminated plates with different power-law indexes, plate configurations, CNT volume fractions, and length/width ratios (b/h = 10)
Full size table

3.2.4 Effect of power-law index

Regarding the influence of the power-law index (Pin) that describes the nano-reinforcements dispersion through the ply thickness, or in other words, the parameter that describes uncertainty in the grading nano-reinforcements on the vibrational behavior of CNTRC laminated plates, it is evident from Tables 6, 7, 8 and 9 that the dimensionless fundamental frequency (\({\overline{\omega }}\)) of the plates with configurations I and II increases when Pin increases from 0 to 1.8. The reason for achieving these results for Configuration-I is explained by the fact that as the power-law index increases the CNT-reinforcements accumulation at both the top and bottom ply surfaces. In fact, according to the widespread thought of many researchers, this is the best way to develop high-performance polymeric FG composite structures. On the other hand, due to the special arrangement of Configuration-II, which contains two types of CNT distribution patterns (i.e., FG-Λ and FG-V), it appears that accumulating the CNTs on one surface of each ply also provides excellent results in strengthening the plates that contain several plies and exceeding even the performance of laminated plates that contain FG-X patterns. These results also confirm the main feature of FG materials, which can enhance the overall stiffness of nanocomposite structures by adjusting the distribution of the nano-reinforcements across the plate thickness. From these observations, it can be concluded that the nonlinear distributions of nano-reinforcements along the thickness of the plies, as may emerge in the manufacturing process as a source of uncertainty, also have a considerable effect on the stiffness of CNTRC plate structures.

3.2.5 Effect of number of plies

The influence of the number of plies together with the plate configuration and power-law index on the \({\overline{\omega }}\) parameter of simply supported CNTRC laminated plates for cross-ply (0°/90°/0°/90°) and angle-ply (45°/− 45°/45°/− 45°) stacking sequences are examined in Table 10. In the analysis, the following parameter values are chosen \(f_{CNT}^{*} = 0.11\), b/h = 10 and a/b = 1. By increasing the number of plies (n), the parameter \({\overline{\omega }}\) largely increases for both plate configurations. For \({\text{P}}_{{{\text{in}}}} \ne 0\), it can be seen that when n = 1, the plates with [X-X]n arrangement yield the largest \({\overline{\omega }}\) while the plates with [Λ-V]n arrangement produce the smallest \({\overline{\omega }}\). However, when n = 2, 4 and 6, the highest first non-dimensional frequency parameter \({\overline{\omega }}\) characterizes the plate with [Λ-V]n arrangement and the smallest one parameter goes to characterizes the plate with [X-X]n arrangement. It can be concluded from this analysis that the best way to enhance the laminated plate structural performance containing 4, 8, or 12 plies of CNTRC is to put the FG-Λ distribution patterns in the lower half of the laminated plate and to put the FG-V distribution patterns in its upper half and accumulate the CNTs to the exterior surfaces of plies.

Table 10 First non-dimensional frequency (\({\overline{\omega }}_{{}} { = }_{{}} {\upomega }_{{}} {(}{{b^{2} } \mathord{\left/ {\vphantom {{b^{2} } h}} \right. \kern-\nulldelimiterspace} h}{)}\sqrt {{{\rho_{m} } \mathord{\left/ {\vphantom {{\rho_{m} } {E_{m} }}} \right. \kern-\nulldelimiterspace} {E_{m} }}}\)) of simply supported cross-ply (0°/90°)n and angle-ply (45°/− 45°)n CNTRC laminated plates with different number of plies, power-law indexes, and plate configurations (b/h = 50; a/b = 1; \(f_{CNT}^{*} = 0.11\))
Full size table

3.2.6 Effect of Pin on the first eight non-dimensional frequencies

The first eight non-dimensional frequencies versus the power-law index of CNTRC cross-ply (0°/90°/0°/90°) and angle-ply (45°/− 45°/45°/− 45°) laminated plates are plotted in Figs. 5 and 6, respectively. The SSSS and CCCC boundary conditions are considered in this study, where b/h, a/b, and \(f_{CNT}^{*}\) are set to be 50, 1, and 0.11, respectively. The obtained results reveal that increasing the power-law index leads to an increase in the first eight non-dimensional frequencies for the two types of boundary conditions, the staking sequences and the plate configurations. Indeed, one can see that the influence of the power-law index on the first eight \({\overline{\omega }}\) parameters can be better observed for the laminated plates with Configuration-II. In other words, the observations reveal that when Pin increases, the gap between the first eight non-dimensional frequencies corresponding to the plate with Configuration-I is too small compared to those of the plate with Configuration-II. Moreover, it can be observed that the fully clamped and fully simply supported plates provide the highest and lowest values of the first eight non-dimensional frequencies, respectively.

Fig. 5
figure 5

Effect of power-law index and plate configuration on the first eight non-dimensional \({\overline{\omega }}\) parameters of cross-ply (0°/90°/0°/90°) CNTRC laminated plates for different boundary conditions: a & b SSSS; c & d CCCC (\(f_{{{\text{CNT}}}}^{*} = 0.11\), a/b = 1; b/h = 50)

Full size image
Fig. 6
figure 6

Effect of power-law index and plate configuration on the first eight non-dimensional \({\overline{\omega }}\) parameters of angle-ply (45°/ − 45°/45°/ − 45°) CNTRC laminated plates for different boundary conditions: a & b SSSS; c & d CCCC (\(f_{{{\text{CNT}}}}^{*} = 0.11\), a/b = 1; b/h = 50)

Full size image

3.2.7 Effect of CNTs orientation angle

Figure 7 shows the effects of CNTs orientation angle (θ), plate configuration, power-law index, and CNT volume fraction on the non-dimensional fundamental frequency (\({\overline{\omega }}\)) of SSSS and CCCC angle-ply (θ/-θ/ θ/ −θ) CNTRC laminated plates. In the analysis, b/h and a/b are taken equal to 10 and 1, respectively. For the considered values of θ, one can observe that the fundamental frequency curves present symmetric increase and decrease with respect to the line of θ = 45°; in other words, Fig. 7 shows that the \({\overline{\omega }}\) parameter of the CNTRC laminated plates increases from 15° to 45°, and decreases from 45° to 75° for different values of CNT volume fractions, plate configurations, and boundary conditions.

Fig. 7
figure 7

Effects of CNTs orientation angle θ, power-law index, CNT volume fraction, and plate configuration on the \({\overline{\omega }}\) parameter of SSSS and CCCC angle-ply (θ / − θ /θ / − θ) CNTRC laminated plates (a/b = 1; b/h = 10)

Full size image

The effects of CNTs orientation angle, power-law index, plate configuration, and width/thickness ratio on the non-dimensional fundamental frequency (\({\overline{\omega }}\)) parameter of SSSS and CCCC CNTRC laminated plates are depicted in Fig. 8. In this modeling, a/b and \(f_{CNT}^{*}\) are taken to be equal to 1 and 0.11, respectively. It is obvious that the results of Fig. 7 can be discerned again, i.e., the fundamental frequency varies symmetrically on either side of the line of θ = 45°. In contrast, this trend is reversed for thinner (b/h = 50) CCCC CNTRC laminated plates, where the \({\overline{\omega }}\) parameter decreases and increases when θ varies from 15° to 45° and from 45° to 75°, respectively, as depicted in Fig. 8f.

Fig. 8
figure 8

Effect of CNTs orientation angle θ, power-law index, CNT volume fraction, and plate configuration on the first \({\overline{\omega }}\) parameter of SSSS and CCCC angle-ply (θ / − θ /θ / − θ) CNTRC laminated plates (\(f_{{{\text{CNT}}}}^{*} = 0.11\); a/b = 1)

Full size image

The effects of CNTs orientation angle, power-law index, plate configuration, and different values of length/width ratio on the \({\overline{\omega }}\) parameter of SSSS and CCCC CNTRC laminated plates are plotted in Fig. 9, for b/h = 10 and \(f_{{{\text{CNT}}}}^{*} = 0.11\). It can be seen that the curves of the plate fundamental frequencies with a/b = 1 vary symmetrically with respect to the line of θ = 45°, while the curves of the fundamental frequencies corresponding to the plates with a/b = 1.5 and a/b = 2.0, increase with the increase of angle θ to become almost unchanged when θ increases from 60° to 75°. In addition to the above observations, the results illustrated in Figs. 7, 8 and 9 indicate that the stiffening effect of the plates with Configuration-II overtakes that of Configuration-I for all values of CNTs orientation angle.

Fig. 9
figure 9

Effect of CNTs orientation angle θ, power-law index, CNT volume fraction, and plate configuration on the first \({\overline{\omega }}\) parameter of SSSS and CCCC angle-ply (θ / − θ /θ /-θ) CNTRC laminated plates (\(f_{{{\text{CNT}}}}^{*} = 0.11\); b/h = 10)

Full size image

3.2.8 Effect of the plate boundary conditions

The combined effects of plate configuration, power-law index, and various combinations of boundary conditions on the fundamental non-dimensional frequency \({\overline{\omega }}\) parameter are examined in Table 11. The combinations of boundary conditions considered are shown in Fig. 10, for which S denotes simply supported, C clamped and F free. In this analysis, b/h, a/b and \(f_{{{\text{CNT}}}}^{*}\) are taken equal to 10, 1, and 0.11, respectively. As can be seen from Table 11, within every single boundary condition combination, the \({\overline{\omega }}\) parameter increases as Pin increases for both plates configurations I and II. However, for \({\text{P}}_{{{\text{in}}}} \ne 0\), it is evident that plates with configuration-II are more affected by Pin than those with Configuration-I for all the considered boundary conditions. The obtained frequencies are arranged in Table 11 from highest to lowest for the different combinations of boundary conditions. One can conclude that the more the plate edges are restrained (from free to simply supported, then to clamped), the higher the fundamental frequencies.

Table 11 First non-dimensional frequency (\({\overline{\omega }}_{{}} { = }_{{}} {\upomega }_{{}} {(}{{b^{2} } \mathord{\left/ {\vphantom {{b^{2} } h}} \right. \kern-\nulldelimiterspace} h}{)}\sqrt {{{\rho_{m} } \mathord{\left/ {\vphantom {{\rho_{m} } {E_{m} }}} \right. \kern-\nulldelimiterspace} {E_{m} }}}\)) of cross-ply (0°/90°/0°/90°) CNTRC laminated plates with various boundary conditions, and power-law indexes (b/h = 10; a/b = 1; \(f_{CNT}^{*} = 0.11\))
Full size table
Fig. 10
figure 10

Boundary conditions combinations

Full size image

3.2.9 Discussion on the mode shapes

Let us now consider a square CNTRC laminated plate with b/h = 20, \(f_{{{\text{CNT}}}}^{*} = 0.11\), and SSSS boundary conditions. The angle-ply (θ/−θ/ θ/ −θ) stacking sequence and the Configuration-II layout arrangement are chosen in this analysis, which aims to study the dependency of the plate mode shapes in terms of contour curves on the in-plane CNTs orientation angle θ and the power-law index Pin. The contour curves of the first six mode shapes related to the associated natural mode shapes are depicted in Fig. 11 for three values of CNTs orientation angle (θ = 15°, θ = 30°, and θ = 45°) and three levels of power-law indexes (Pin = 0.0, Pin = 1.0, and Pin = 1.8). From Fig. 11, it is discernible that the increase in Pin does not make any change in the mode shapes, except when θ is equal to 15° (cases (a), (b), and (c)), where mode interchange is observed: Mode 4 in case (a) tends to be Mode 5 in cases (b) and (c), while Mode 5 in case (a) tends to be Mode 4 in cases (b) and (c). On the other hand, it is clear that the mode shapes of the CNTRC laminated plate are highly affected by the reinforcement orientation angle, this aspect can be observed by comparing cases characterized by different values of θ, but have the same values of Pin (case (a), case (d), and case (g), for instance).

Fig. 11
figure 11

Contour curves of the first six mode shapes of square simply supported angle-play [θ/-θ/ θ/ -θ] CNTRC laminated plate. (Configuration-II, b/h = 20, \(f_{{{\text{CNT}}}}^{*} = 0.11\))

Full size image

4 Conclusion

The free vibration response of multi-layer functionally graded carbon nanotube-reinforced composite laminated plates using the finite element method was analyzed in this paper. The homogenization of each ply was done via the extended rule of mixture. Kinematic relations were obtained employing Lagrange's equations and the first-order shear deformation theory. Focusing on the effect of the linear and nonlinear distribution forms of the nano-reinforcements based CNTs and the plate configuration, the numerical results obtained show the influence of several parameters, including the effects of (i) number of ply layers, (ii) CNT volume fractions and distribution patterns, (iii) geometry of the plate, (iv) ply orientation angle, (v) number of plies and (vi) boundary conditions on the free vibration behavior of CNTRC laminated plates. The following points summarize the most crucial findings of the present study:

  • The minimum number of ply layers needed to produce accurate predictions for free vibration response of CNTRC plates is 20 layers per ply.

  • The natural frequencies of the CNTRC laminated plates can be amplified by using a greater volume fraction of CNTs.

  • The use of high width/thickness ratios can increase the natural frequency of the CNTRC laminated plate structure, while high aspect ratios can weaken it.

  • The appropriate strengthening way for FG-CNTRC laminated plates that contain more than four plies, is to put the FG-Λ patterns in the lower half of the laminated plates and the FG-V patterns in their upper half.

  • Natural frequencies of the CNTRC laminated plates that contain FG-X or both FG-Λ and FG-V patterns can be increased when CNTs fillers are accumulated to the lateral surfaces of the plies.

  • The orientation angle of CNTs and the number of plies have a remarkable influence on the natural frequencies of the CNTRC laminated plates, as discussed in Sect. 3.2.7.

  • Plate structures with fully clamped boundary conditions yield larger natural frequencies than plates with fully simply supported boundary conditions.