Nonlinear effects of induced unbalance in the rod fastening rotor-bearing system considering nonlinear contact

Abstract

Rod fastening rotor (RFR) is characterized by discontinuity of contact interface and unbalance of multiple disks. There are few researches that focus on unbalance effect including magnitude and phase difference on the nonlinear dynamic characteristics of RFR considering contact feature. A typical RFR model is proposed to investigate the nonlinear dynamic characteristics. The nonlinear motion governing equation considering unbalance excitation, nonlinear oil-film force and nonlinear contact characteristics between disks is derived by D’Alembert principle. The contact effects are simulated by bending spring with nonlinear stiffness. The research focuses on the effects of unbalance on the onset of low-frequency instability and nonlinear response of RFR. The obtained results evidently show the distinct phenomena brought about by the variations of unbalance, which confirms that unbalance magnitude and phase difference are critical parameters for the RFR system response. To restrain large amplitude of nonsynchronous vibration and retard the occurrence of instability, the unbalance magnitude of rotor is suggested to be kept at range from U5 to U6. Meaningfully, RFR can operate relatively well with small vibration and higher instability threshold when the residual unbalance between disks is controlled at an enough-reasonable unbalance phase difference. Phase difference adjustment can accomplish active balance. The total vibration and nonsynchronous components could be reduced, and onset speed of instability could be delayed effectively by using the proposed method, which is helpful for the dynamic design, assembly, balance and vibration control of such RFR.

1 Introduction

Rod fastening rotor (RFR) consists of disks compressed together by tie rods, and its operating speed often exceeds first critical speed or even higher critical speed to achieve higher efficiency and good dynamic characteristics. They already have been widely used in gas turbines or small- and medium-sized turboshaft aero engines [1]. It is well known that RFR is a core part of heavy-duty gas turbine or other applications and has become more and more common used in industrial power generation set and naval ship due to its green, high-efficiency and fast-startup-speed characteristics. In the meantime, the hydrodynamic bearings are the common type used for high-speed RFR under high-speed and heavy-load working condition. The vibration response of RFR is complicated and highly nonlinear due to the high operation speed, nonlinear oil-film force and discontinuous structure feature between disks.

The rotor dynamic characteristics directly affect the performance, efficiency and service life of rotating machine. An RFR with small inappropriate unbalance may induce excessive vibration when it runs at high speed, which may perturb its normal operation, even lead to loss of stability and generate some unexpected vibration accidents. Obviously, the RFR design must ensure safe and stable operation throughout the speed range. The demands for higher rotation speed, efficient performance, longer life and better NVH performance, along with low manufacturing cost, continue to motivate the rotordynamics investigation of RFR. Many efforts were made to investigate the rotordynamics of RFR-bearing system. Wang et al. [2] built a nonlinear dynamic model of RFR system with a transverse open crack based on FE model to investigate the stability and bifurcation. The stability of RFR system was decreased due to the presence of crack. Using the Floquet theory, shooting method and path-following technique, Liu et al. [3] investigated the stability and bifurcation phenomena of a flexible RFR-bearing system considering contact stiffness. Liu et al. [4] also studied the nonlinear dynamic response of a flexible RFR-bearing system, which indicated that mass eccentricity and unbalanced pretightening force of rod have great influence on stability and bifurcation of system. Based on D’Alembert principle, Hu et al. [5, 6] mainly investigated the nonlinear coupled dynamics of an RFR under the condition of rub-impact and initial permanent. The contact effects between two disks were equivalent to a flexural spring with a nonlinear stiffness. The corresponding result showed the larger radial stiffness of stator, and big unbalance force can simplify the motion of rotor system to some extent. Zhou et al. [7] calculated the contact stiffness by using two methods of FE method and Greenwood model with Hertz contact theory and investigated their influences on dynamics of combined rotor. Hei et al. [8] modeled an RFR supported in fixed-tilting pad bearings to investigate the nonlinear dynamic behavior and bifurcation. It was shown that RFR is more stable than the integral rotor system. On the base of experimental transition processes, Lyantsev et al. [9] put forward an identification method of nonlinear dynamic model of gas turbine on acceleration mode. He et al. [10] established a tighten force test rig to investigate the effect of pretightening force on the critical speed. Rotor imbalance is a typical structure parameter which can induce vibration in the high-speed rotor-bearing system. Ma et al. [11] investigated the influence of eccentric phase difference between two disks on instability in an integral rotor-bearing system. It was shown that the instability threshold increases when the phase difference becomes larger and it increases almost linearly when the eccentric phase difference is greater than $20^\circ$. Liu et al. [12] investigated the effect of unbalanced pretightening force on nonlinear dynamic characteristics of 3D RFR-bearing system considering linear contact stiffness and a constant mass eccentricity. Due to the nonlinear flexural stiffness of contact interface between disks, especially when the contact regions are partially separated, the dynamics of the RFR may be different from that of the integral rotors. Yuan et al. [13] calculated the flexural stiffness by using the FE method and then adopted the harmonic balance method to analyze the dynamics of rod-fastened Jeffcott rotor, which confirmed dynamics of the rotor were nonlinear when it was subjected to a large unbalance force. Li et al. [14] studied the effect of contact stiffness on natural frequencies and unbalance responses. Using an improved transfer matrix method, Meng et al. [15] built a dynamic model of RFR including linear bearing dynamic coefficients and equivalent contact stiffness to obtain the critical speed, mode shapes and unbalance response of four balance plane. According to the improved 2D FEM, Yuan et al. [16] developed a program to calculate the critical speed and unbalance response of gas turbine rotors, in which the contact stiffness has been taken as control parameter. Yang et al. [17] investigated the linear unbalance response based on the transfer matrix models. It is well known that the elimination of sub-synchronous vibration is a major task for rotating machinery engineers. Yi et al. [18] proposed a simplified model for flexible RFR to investigate the global nonlinear dynamic characteristics and indicated the mass eccentricity would be the most nonlinear source for the nonlinear instability. Some published reports also indicated increasing unbalance is an effective way to suppress the sub-synchronous vibration [19,20,21,22]. In a word, many researchers devoted to investigate the contact stiffness, pretightening force effect, natural characteristics, nonlinear dynamic phenomena under certain fault conditions and vibration response considering different levels of mass unbalance eccentricity. Moreover, the researches on the effect of unbalance on nonlinear dynamic characteristics and instability mainly focus on integral rotor rather than RFR with discontinuous characteristics. Besides, the contact characteristics must be considered in the model. Suitable unbalance can suppress the sub-synchronous vibration of low frequency and improve the dynamic behavior of rotor-bearing system as many researchers mentioned before, which is determined by the special structure, operational speed and nonlinear force. Due to the unbalance force, nonlinear oil-film and contact characteristics between disks, the dynamic characteristics of RFR become more complicated. However, the nonlinear analysis is also rare at high speed for the RFR considering nonlinear contact characteristics. The available publications, involving a systematic research and discussion on the influence of unbalance magnitude and phase difference on the dynamic behaviors of the RFR-bearing system considering nonlinear contact, have not been found.

Interestingly, for an initially relative-perfect balanced rotor in assumption, the disks may gradually exist some uncertain carbon deposition and wear under the extreme operation condition with high temperature and varying operation speed. Hence, the induced unbalance on disks may be formed after running a certain period for the high-speed RFR. Furthermore, the unbalance magnitude can be grown with the operating time, which directly influences the high-efficiency operation for the high-speed RFR and even causes seriously nonlinear vibration accident. In addition, RFR, even after dynamic balancing through adding weights or subtracting weights in the automatic balancer, would still exist residual unbalance at two discontinuous disks. For an assembled RFR, the unbalance phase difference between two disks may not be identical under allowably residual unbalance amplitude for each other, which may lead to the occurrence of different dynamic behaviors for a same type rotor. Driven by the continuous desire for higher efficiency and safe operating performance, it is necessary to investigate the effects of unbalance magnitude and phase difference on the dynamic characteristics, retard the instability threshold in low frequency and reduce the vibration to an acceptable level by controlling the unbalance magnitude or phase difference for the high-speed RFR-bearing system. This study will provide theoretical foundation and technical supports to RFR’s assemblage, dynamic design, vibration control, etc.

Fig. 1

Schematic diagram of an RFR-bearing system

Using the bifurcation diagrams, Lyapunov index, waterfall plots, vibration root-mean-square value, frequency spectrum, vibration time waveforms, rotor orbits, Poincaré maps, etc., this paper numerically investigates the influence of unbalance magnitude and phase difference on the nonlinear dynamic behaviors of a RFR-bearing system, considering nonlinear oil-film force based on short bearing theory, and nonlinear contact characteristics. Some interesting, distinct phenomena, which are rarely reported in previous reports, are systematically shown and analyzed in this paper. The onset speed of instability caused by oil-film instability will be mainly addressed. This paper includes four sections. After this introduction, in Sect. 2, the mathematical models of an RFR-bearing system considering unbalance excitation, nonlinear oil-film force based on short bearing theory and nonlinear contact characteristics between disks are developed to characterize the dynamic characteristics of rotor. Section 3 systematically discusses the effects of the unbalance magnitude and phase difference between disks on low-frequency instability and nonlinear dynamic response under different rotational speeds. Finally, some conclusions and vibration suppression strategy are presented in Sect. 4.

2 RFR-bearing system model description

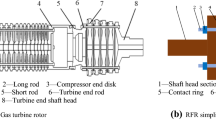
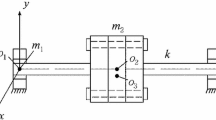
RFRs are widely applied to gas turbines or small- and medium-sized turboshaft engines. The rod rotor can be divided into circumferential rod and central rod fastening rotor, of which the disks are connected by the curving couplings or surface contact. It is difficult to build a dynamic model because of the multi-interface contact and multi-tie rods. It is urgent to know the unbalance nonlinear response characteristics and how to control the fractional frequency vibration of large amplitude with the consideration of nonlinear oil-film forces and interface contact characteristics. Note that the circumferential rod fastening rotors with annular flat contact are investigated in this paper. The details of the RFR-bearing system under investigation are shown in Fig. 1. In order to efficiently study the nonlinear dynamic response and oil-film instability, a mathematical model considering nonlinear contact of a typical RFR-bearing system simulated by four lumped mass points is simplified according to the following assumptions.

• (a) The small rotor displacements in torsional and axial directions are negligible, the journal and disks are simulated by four lumped mass points, and the corresponding points are connected by massless elastic shaft sections of lateral stiffness [23].

• (b) The left and right bearings mounted outboard shown in Fig. 1 are identical hydrodynamic sliding bearings. For the purpose of simplicity, the bearing feeding holes and feeding conditions will not be considered. In addition, the isothermal fluid flow condition, constant oil-film viscosity and incompressible fluid are assumed for the proposed model based on infinite short bearing theory.

• (c) The contact characteristics for rods and interface are equivalent to the added flexible bending spring with nonlinear stiffness.

2.1 Nonlinear bearing model

In some cases, such as large external disturbance, investigation of shaft orbit after instability and nonlinear vibration response, the nonlinear relation between oil-film force, displacement and velocity should be considered. Hence, the nonlinear oil-film forces should be obtained under investigation. Figure 2 shows the oil-film bearing model. $\theta$ is taken as the angular coordinate starting from the maximum oil-film thickness corresponding to the fixed coordinate system. $F_{e}$ and $F_{\psi }$ are the radial component and circumferential component of oil-film force, respectively. Nonlinear oil-film force of Capone model [24, 25] is used in this paper under the assumptions mentioned above.

Fig. 2

Bearing model

Based upon the short bearing theory, the dimensionless Reynolds equation [26] can be derived $\hbox {as}_{\mathrm {:}}$

$$\begin{aligned} \left( {\frac{R}{L}} \right) ^{\text{2 }}\frac{\partial }{\partial Z}\left( {h^{3}\frac{\partial p}{\partial Z}} \right) =X\sin \theta -Y\cos \theta -2\left( {\dot{{X}}\text{ cos }\theta +\dot{{Y}}\text{ sin }\theta } \right) , \end{aligned}$$

(1)

where X and Y are the dimensionless displacement of journal center in horizontal and vertical direction, $X=x/c$, and $Y=y/c$, respectively. Z is the bearing dimensionless displacement in axial direction, c is the bearing clearances, p is the dimensionless oil-film pressure, h is the oil-film thickness, R is the bearing radius, and L is the bearing width.

Dimensionless pressure distribution p in oil films, as illustrated in Eq. (2), can be solved by integrating Eq. (1).

$$\begin{aligned} p=\frac{1}{8}\left( {\frac{L}{R}} \right) ^{2}\frac{\left( {X-2\dot{{Y}}} \right) \sin \theta -\left( {Y+2\dot{{X}}} \right) \cos \theta }{\left( {1-X\cos \theta -Y\sin \theta } \right) ^{3}}(4Z^{2}-1). \end{aligned}$$

(2)

Then, the $F_{e}$ and $F_{\psi }$ can be obtained as follows:

$$\begin{aligned} F_{e}= & {} -\int _{-L/2}^{L/2} {\text {d}z} \int _0^{2\pi } {p(\theta ,z)\cos \theta R\text {d}\theta } , \end{aligned}$$

(3)

$$\begin{aligned} F_{\psi }= & {} \int _{-L/2}^{L/2} {\text {d}z} \int _0^{2\pi } {p(\theta ,z)\sin \theta R\text {d}\theta } . \end{aligned}$$

(4)

Obviously, the horizontal component $F_{x}$, vertical component $F_{y}$ of oil-film force, $F_{e}$ and $F_{\psi }$ have the following relationship:

$$\begin{aligned} F_{x}= & {} -F_{e} \sin \psi +F_{\psi } \cos \psi , \end{aligned}$$

(5)

$$\begin{aligned} F_{y}= & {} F_{e} \cos \psi +F_{\psi } \sin \psi . \end{aligned}$$

(6)

Integrating the oil-film pressure, the dimensionless nonlinear oil-film force in x and y directions can be solved as follows:

$$\begin{aligned}&\left( {\begin{array}{l} f_{x} \\ f_{y} \\ \end{array}} \right) =\frac{1}{sP}\left( {\begin{array}{l} F_{x} \\ F_{y} \\ \end{array}} \right) \nonumber \\= & {} -\frac{\sqrt{(X-2\dot{{Y}})^{2}+(Y+2\dot{{X}})^{2}} }{1-X^{2}-Y^{2}}\times \left( {\begin{array}{l} 3X\times V(X,Y,\varphi )-\sin \varphi \times G(X,Y,\varphi )-2\cos \varphi \times S(X,Y,\varphi ) \\ 3Y\times V(X,Y,\varphi )+\cos \varphi \times G(X,Y,\varphi )-2\sin \varphi \times S(X,Y,\varphi ) \\ \end{array}} \right) ,\nonumber \\ \end{aligned}$$

(7)

where the functions of $V({X,Y,}\varphi ), S({X,Y,}\varphi ), G({X,Y,}\varphi )$ and $\varphi$ are, respectively, given in Eqs. (8)–(11):

$$\begin{aligned} V(X,Y,\varphi )= & {} \frac{2+(Y\cos \varphi -X\sin \varphi )\times G(X,Y,\varphi )}{1-X^{2}-Y^{2}}, \end{aligned}$$

(8)

$$\begin{aligned} S(X,Y,\varphi )= & {} \frac{X\cos \varphi +Y\sin \varphi }{1-(X\cos \varphi +Y\sin \varphi )^{\text{2 }}}, \end{aligned}$$

(9)

$$\begin{aligned} G(X,Y,\varphi )= & {} \frac{2}{\sqrt{1-X^{2}-Y^{2}} }\times \left( {\frac{\pi }{2}+~\hbox {arctan}\frac{Y\cos \varphi -X\sin \varphi }{\sqrt{1-X^{2}-Y^{2}} }} \right) , \end{aligned}$$

(10)

$$\begin{aligned} \varphi= & {} \arctan \frac{Y+2\dot{{X}}}{X-2\dot{{Y}}}-\frac{\pi }{2}~\hbox {sign}\frac{Y+2\dot{{X}}}{X-2\dot{{Y}}}-\frac{\pi }{2}~\hbox {sign}~(Y+2\dot{{X}}), \end{aligned}$$

(11)

where $s=\frac{\eta \omega RL}{P}\left( {\frac{R}{c}} \right) ^{2}\left( {\frac{L}{2R}} \right) ^{2}$ denotes the Sommerfeld correction factor, $\eta$ represents the constant oil-film viscosity, $\omega$ is the rotating velocity, and P denotes the disk’s half mass. The nonlinear fluid film forces are dependent on the motions of the journal, and the interaction of journal and nonlinear oil-film forces will exhibit highly nonlinear dynamic behavior.

2.2 Nonlinear restoring force for interface contact

Because of the existence of multiple contact surfaces, the RFR has the discontinuous characteristics of physical structure. Figure 3 depicts a cross section of contact surface at rod fastening rotor, d represents the diameter of rod, and D represents the diameter of matching holes. There are gaps between rod holes and rods for easy assembly of gas turbine rotor, that is, $d <D$. The nonlinear elastic force [6] between disks is analyzed below.

Fig. 3

A cross section at RFR contact surface

Fig. 4

Nonlinear restoring force for additional tangential stiffness

Define the relative displacement of x direction between disks as a, and b for y direction; then, $a=x_{i}-x_{j}, b=y_{i}-y_{j}$, where $i=2, j=3$, as described in Fig. 1, respectively. Taking $\varepsilon =({D-d})/2$, when $a \le -\varepsilon$ or $a \ge \varepsilon$, the rod and matching hole is in contact in x direction. Interestingly, the rotor system will generate an additional tangential contact stiffness with a segmental linear function described in Eq. (12), the same rules for y direction.

$$\begin{aligned} F_{cx} =\left\{ {\begin{array}{ll} k_{2} (a-\varepsilon ),&{}a\ge \varepsilon \\ 0,&{}-\varepsilon<a<\varepsilon \\ k_{2} (a+\varepsilon ).&{}a<\varepsilon \\ \end{array}} \right. , \end{aligned}$$

(12)

While the gap of $\varepsilon$ between the rod and matching hole is small, the restoring force in x direction can be expressed by a nonlinear function of three-order power about the relative displacement [27]. So, as shown in Fig. 4, the nonlinear restoring force of contact layer between disks can be derived as follows:

$$\begin{aligned} \left( {\begin{array}{l} F_{cx1} \\ F_{cy1} \\ \end{array}} \right) =\left( {\begin{array}{l} -F_{cx2} \\ -F_{cy2} \\ \end{array}} \right) =\left( {\begin{array}{l} k_{1} (x_{i} -x_{j} )+k_{1}^{\prime } (x_{i} -x_{j} )^{3} \\ k_{1} (y_{i} -y_{j} )+k_{1}^{\prime } (y_{i} -y_{j} )^{3} \\ \end{array}} \right) . \end{aligned}$$

(13)

2.3 Unbalance force model

As shown in Eqs. (14) and (15), F$_{\mathbf{ub}}$ is the unbalance force vector, which only exists at two disks. $m_{\mathrm {2}}, m_{\mathrm {3}}$ denote the mass of the 1# disk and 2# disk, respectively. $e_{i}\, (i=1, 2)$ is the mass unbalance eccentricity. $\alpha$ is the rotational angle of rotor around the Z direction. $\phi _{\mathrm {1}}$ and $\phi _{\mathrm {2}}$ represent the initial phase of the imposed unbalance at Node 2 and Node 3 with a red arrow line for two disks (see Fig. 1), respectively. The positive initial phase angle is measured in the direction of rotation from positive x-axis [28].

$$\begin{aligned} {{\varvec{F}}}_{\mathbf {ub1}} =\left( {\begin{array}{l} F_{\mathrm{ub}_{x1} } \\ F_{\mathrm{ub}_{y1} } \\ \end{array}} \right) =\left( {\begin{array}{l} m_{2} e_{1} \dot{{\alpha }}^{2}\cos (\alpha +\phi _{1} )+m_{2} e_{1} \ddot{{\alpha }}\sin (\alpha +\phi _{1} ) \\ m_{2} e_{1} \dot{{\alpha }}^{2}\sin (\alpha +\phi _{1} )-m_{2} e_{1} \ddot{{\alpha }}\cos (\alpha +\phi _{1} ) \\ \end{array}} \right) , \end{aligned}$$

(14)

$$\begin{aligned} {{\varvec{F}}}_{\mathbf {ub}_{{\mathbf {2}}} } =\left( {\begin{array}{l} F_{\mathrm{ub}_{x2} } \\ F_{\mathrm{ub}_{y2} } \\ \end{array}} \right) =\left( {\begin{array}{l} m_{3} e_{2} \dot{{\alpha }}^{2}\cos (\alpha +\phi _{2} )+m_{3} e_{2} \ddot{{\alpha }}\sin (\alpha +\phi _{2} ) \\ m_{3} e_{2} \dot{{\alpha }}^{2}\sin (\alpha +\phi _{2} )-m_{3} e_{2} \ddot{{\alpha }}\cos (\alpha +\phi _{2} ) \\ \end{array}} \right) . \end{aligned}$$

(15)

The eccentric (unbalance) phase difference of 1# disk and 2# disk is

$$\begin{aligned} \phi =\left. {\left| {\phi _{1} -\phi _{2} } \right. } \right| . \end{aligned}$$

(16)

The steady-state conditions are investigated in this paper, so, angular acceleration $\ddot{{\alpha }}= 0$ and angular velocity $\dot{{\alpha }}=\omega$, Eqs. (14)–(15) can be rewritten as follows:

$$\begin{aligned}&{{\varvec{F}}}_{\mathbf {ub1}} =\left( {\begin{array}{l} F_{\mathrm{ub}_{x1} } \\ F_{\mathrm{ub}_{y1} } \\ \end{array}} \right) =\left( {\begin{array}{l} m_{2} e_{1} \omega ^{2}\cos (\omega t+\phi _{1} ) \\ m_{2} e_{1} \omega ^{2}\sin (\omega t+\phi _{1} ) \\ \end{array}} \right) , \end{aligned}$$

(17)

$$\begin{aligned}&{{\varvec{F}}}_{\mathbf {ub}_{{\mathbf {2}}} } =\left( {\begin{array}{l} F_{\mathrm{ub}_{x2} } \\ F_{\mathrm{ub}_{y2} } \\ \end{array}} \right) =\left( {\begin{array}{l} m_{3} e_{2} \omega ^{2}\cos (\omega t+\phi _{2} ) \\ m_{3} e_{2} \omega ^{2}\sin (\omega t+\phi _{2} ) \\ \end{array}} \right) . \end{aligned}$$

(18)

2.4 RFR-bearing system motion equations

The motion equation of the RFR-bearing system can be deduced from D’Alembert principle. Consider a system composed of n mass points, assuming that the mass of ith mass point, with active force of F$_{i}$ and constraining force of F$_{Ni}$, is $m_{i}$, radius vector is r$_{i}$, and acceleration is $\ddot{\varvec{r}}_{i}$ . The inertia force of ith mass point can be written in the form:

$$\begin{aligned} {{\varvec{F}}}_{Ii} = -m_i\ddot{{{\varvec{r}}}}_{i}. \end{aligned}$$

(19)

If the system is only subject to ideal constraints, the general equation of dynamics can be written in the form:

$$\begin{aligned} \sum \limits _{i=1}^n {({{\varvec{F}}}_{i} -m_{i} {\varvec{{\ddot{{r}}}}}_{i} )\times \delta {{\varvec{r}}}_{i} =0} , \end{aligned}$$

(20)

Substituting the constraining force into Eq. (20), it can be expressed as follows:

$$\begin{aligned} \sum \limits _{i=1}^n {({{\varvec{F}}}_{i} +{{\varvec{F}}}_{Ni} +{{\varvec{F}}}_{\text{ I }i} )\times \delta {{\varvec{r}}}_{i} \text{=0 }} . \end{aligned}$$

(21)

Write it as an analytic expression:

$$\begin{aligned} \sum \limits _{i=1}^n {\text{(( }F_{xi} +F_{Nxi} -m_{i} \ddot{{x}}_{ci} \text{) }\delta x_{ci} \text{+( }F_{yi} +F_{Nyi} -m_{i} \ddot{{y}}_{ci} \text{) }\delta y_{ci} \text{+( }F_{zi} +F_{Nzi} -m_{i} \ddot{{z}}_{ci} \text{) }\delta z_{ci} \text{=0 }} . \end{aligned}$$

(22)

From D’Alembert principle, the system of active force, constraining force and inertial force acting on each mass point should constitute the equilibrium force system. Consider every constraining force in each mass point, then

$$\begin{aligned} \left\{ {\begin{array}{l} F_{xi} +F_{Nxi} -m_{i} \ddot{{x}}_{ci} =0 \\ F_{yi} +F_{Nyi} -m_{i} \ddot{{y}}_{ci} =0 \\ F_{zi} +F_{Nzi} -m_{i} \ddot{{z}}_{ci} =0 \\ \end{array}} \right. , i=1,ldots , n. \end{aligned}$$

(23)

Due to the neglect of axial vibration, $z_{i}$ is set to zero in the above equations. According to the structural parameters and lubricating conditions, the active force, constraining force and inertia force of the RFR system investigated can be expressed as:

$$\begin{aligned}&\left\{ {\begin{array}{l} F_{xi} =-c_{\text{1 }} \dot{{x}}_{i} +F_{x} \left( {x_{i} ,y_{i} ,\dot{{x}}_{i} ,\dot{{y}}_{i} } \right) \\ F_{yi} =-c_{\text{1 }} \dot{{y}}_{i} -m_{i} g+F_{y} \left( {x_{i} ,y_{i} ,\dot{{x}}_{i} ,\dot{{y}}_{i} } \right) \\ \end{array}} \right. (i = 1, 4), \end{aligned}$$

(24)

$$\begin{aligned}&\left\{ {\begin{array}{l} F_{xi} =-c_{2} \dot{{x}}_{i} \\ F_{yi} =-c_{2} \dot{{y}}_{i} -m_{i} g \\ \end{array}} \right. (i = 2, 3), \end{aligned}$$

(25)

$$\begin{aligned}&\left\{ {\begin{array}{l} F_{Nx\text{1 }} =-k_{s} \left( {x_{1} -x_{2} } \right) \\ F_{Ny\text{1 }} =-k_{s} \left( {y_{1} -y_{2} } \right) \\ \end{array}} \right. ~\hbox {and} ~\left\{ {\begin{array}{l} F_{Nx\text{2 }} =-c_{3} \left( {\dot{{x}}_{2} -\dot{{x}}_{3} } \right) -k_{s} \left( {x_{2} -x_{1} } \right) -F_{cx1} \\ F_{Ny\text{2 }} =-c_{3} \left( {\dot{{y}}_{2} -\dot{{y}}_{3} } \right) -k_{s} \left( {y_{2} -y_{1} } \right) -F_{cy1} \\ \end{array}} \right. , \end{aligned}$$

(26)

$$\begin{aligned}&\left\{ {\begin{array}{l} F_{Nx\text{3 }} =-c_{3} \left( {\dot{{x}}_{\text{3 }} -\dot{{x}}_{\text{2 }} } \right) -k_{s} \left( {x_{\text{3 }} -x_{\text{4 }} } \right) -F_{cx2} \\ F_{Ny\text{3 }} =-c_{3} \left( {\dot{{y}}_{2} -\dot{{y}}_{3} } \right) -k_{s} \left( {y_{3} -y_{4} } \right) -F_{cy2} \\ \end{array}} \right. , ~\hbox {and }~\left\{ {\begin{array}{l} F_{Nx\text{4 }} =-k_{s} \left( {x_{\text{4 }} -x_{\text{3 }} } \right) \\ F_{Ny\text{4 }} =-k_{s} \left( {y_{\text{4 }} -y_{\text{3 }} } \right) \\ \end{array}} \right. , \end{aligned}$$

(27)

$$\begin{aligned}&\left\{ {\begin{array}{l} F_{\text{ I }xi} =-m_{i} \ddot{{x}}_{i} \\ F_{\text{ I }yi} =-m_{i} \ddot{{y}}_{i} \\ \end{array}} \right. (i=1, 4),~\hbox { and }~\left\{ {\begin{array}{l} F_{\text{ I }xi} =-m_{i} \ddot{{x}}_{i} +F_{ubx_{i-1} } \\ F_{\text{ I }yi} =-m_{i} \ddot{{y}}_{i} +F_{uby_{i-1} } \\ \end{array}} \right. (i=2, 3) . \end{aligned}$$

(28)

Substituting Eqs. (24–28) into Eq. (23), the motion governing equations for the investigated RFR-bearing system shown in Fig. 1 are as follows, in which considering the nonlinear oil-film forces, nonlinear contact restoring forces and the unbalance force.

$$\begin{aligned} \left\{ {\begin{array}{l} m_{1} \ddot{{x}}_{1} +c_{1} \dot{{x}}_{1} +k_{s} (x_{1} -x_{2} )-F_{x} (x_{1} ,y_{1} ,\dot{{x}}_{1} ,\dot{{y}}_{1} )=0 \\ m_{1} \ddot{{y}}_{1} +c_{1} \dot{{y}}_{1} +k_{s} (y_{1} -y_{2} )-F_{y} (x_{1} ,y_{1} ,\dot{{x}}_{1} ,\dot{{y}}_{1} )+P_{1} =0 \\ m_{2} \ddot{{x}}_{2} +c_{2} \dot{{x}}_{2} +c_{3} (\dot{{x}}_{2} -\dot{{x}}_{3} )+k_{s} (x_{2} -x_{1} )+F_{cx1} -F_{ub_{x1} } =0 \\ m_{2} \ddot{{y}}_{2} +c_{2} \dot{{y}}_{2} +c_{3} (\dot{{y}}_{2} -\dot{{y}}_{3} )+k_{s} (y_{2} -y_{1} )+F_{cy1} -F_{ub_{y1} } +P_{2} =0 \\ m_{3} \ddot{{x}}_{3} +c_{2} \dot{{x}}_{3} +c_{3} (\dot{{x}}_{3} -\dot{{x}}_{2} )+k_{s} (x_{3} -x_{4} )+F_{cx2} -F_{ub_{x2} } =0 \\ m_{3} \ddot{{y}}_{3} +c_{2} \dot{{y}}_{3} +c_{3} (\dot{{y}}_{3} -\dot{{y}}_{2} )+k_{s} (y_{3} -y_{4} )+F_{cy2} -F_{ub_{y2} } +P_{3} =0 \\ m_{4} \ddot{{x}}_{4} +c_{1} \dot{{x}}_{4} +k_{s} (x_{4} -x_{3} )-F_{x} (x_{4} ,y_{4} ,\dot{{x}}_{4} ,\dot{{y}}_{4} )=0 \\ m_{4} \ddot{{y}}_{4} +c_{1} \dot{{y}}_{4} +k_{s} (y_{4} -y_{3} )-F_{y} (x_{4} ,y_{4} ,\dot{{x}}_{4} ,\dot{{y}}_{4} )+P_{4} =0 \\ \end{array}} \right. , \end{aligned}$$

(29)

where $m_{\mathrm {1}}, m_{\mathrm {2}}, m_{\mathrm {3}}$ and $m_{\mathrm {4}}$ are the lumped mass at 1# bearing, 1# disk, 2# disk and 2# bearing, respectively; $k_{s}$ represents the shaft stiffness; and $c_{\mathrm {1}}, c_{\mathrm {2}}$ and $c_{\mathrm {3}}$ denote the bearing damping coefficient, damping coefficient of disks and the damping coefficient at contact interface, respectively. $F_{x}$ and $F_{y}$ are the nonlinear oil-film forces in x direction and y direction. $F_{\mathrm {ub}}$ is mass unbalance force expressed in Eqs. (17–18); $P_{i}\, (i=1, 2, 3, 4)$ is the gravity for four different lumped masses.

$$\begin{aligned} \tau= & {} \omega t, \end{aligned}$$

(30)

$$\begin{aligned} X_{i}= & {} x_{i} /c,Y_{i} =y_{i} /c,~\text{ where }~i=\left( {\text{1, } \text{2, } \text{3, } \text{4 }} \right) . \end{aligned}$$

(31)

Equation (29) can be rewritten in terms of the dimensionless time and dimensionless displacement expressed in Eqs. (30–31) so that the following nondimensional motion equation systems are obtained:

$$\begin{aligned} \left\{ {\begin{array}{l} \ddot{{X}}_{1} +\frac{c_{1} }{m_{1} \omega }\dot{{X}}_{1} +\frac{k_{s} }{m_{1} \omega ^{2}}(X_{1} -X_{2} )-\frac{sP}{m_{1} c\omega ^{2}}f_{x} (X_{1} ,Y_{1} ,\dot{{X}}_{1} ,\dot{{Y}}_{1} )=0 \\ \ddot{{Y}}_{1} +\frac{c_{1} }{m_{1} \omega }\dot{{Y}}_{1} +\frac{k_{s} }{m_{1} \omega ^{2}}(Y_{1} -Y_{2} )-\frac{sP}{m_{1} c\omega ^{2}}f_{y} (X_{1} ,Y_{1} ,\dot{{X}}_{1} ,\dot{{Y}}_{1} )+\frac{g}{c\omega ^{2}}=0 \\ \ddot{{X}}_{2} +\frac{c_{2} }{m_{2} \omega }\dot{{X}}_{2} +\frac{c_{3} }{m_{2} \omega }(\dot{{X}}_{2} -\dot{{X}}_{3} )+\frac{k_{s} }{m_{2} \omega ^{2}}(X_{2} -X_{1} )+\frac{F_{cx1} }{m_{2} c\omega ^{2}}-\frac{e_{1} }{c}\cos (\tau +\phi _{1} )=0 \\ \ddot{{Y}}_{2} +\frac{c_{2} }{m_{2} \omega }\dot{{Y}}_{2} +\frac{c_{3} }{m_{2} \omega }(\dot{{Y}}_{2} -\dot{{Y}}_{3} )+\frac{k_{s} }{m_{2} \omega ^{2}}(Y_{2} -Y_{1} )+\frac{F_{cy1} }{m_{2} c\omega ^{2}}-\frac{e_{1} }{c}\sin (\tau +\phi _{1} )+\frac{g}{c\omega ^{2}}=0 \\ \ddot{{X}}_{3} +\frac{c_{2} }{m_{3} \omega }\dot{{X}}_{3} +\frac{c_{3} }{m_{3} \omega }(\dot{{X}}_{3} -\dot{{X}}_{2} )+\frac{k_{s} }{m_{3} \omega ^{2}}(X_{3} -X_{4} )+\frac{F_{cx2} }{m_{3} c\omega ^{2}}-\frac{e_{2} }{c}\cos (\tau +\phi _{2} )=0 \\ \ddot{{Y}}_{3} +\frac{c_{2} }{m_{3} \omega }\dot{{Y}}_{3} +\frac{c_{3} }{m_{3} \omega }(\dot{{Y}}_{3} -\dot{{Y}}_{2} )+\frac{k_{s} }{m_{3} \omega ^{2}}(Y_{3} -Y_{4} )+\frac{F_{cy2} }{m_{3} c\omega ^{2}}-\frac{e_{2} }{c}\sin (\tau +\phi _{2} )+\frac{g}{c\omega ^{2}}=0 \\ \ddot{{X}}_{4} +\frac{c{ }_{1}}{m_{4} \omega }\dot{{X}}_{4} +\frac{k_{s} }{m_{4} \omega ^{2}}(X_{4} -X_{3} )-\frac{sP}{m_{4} c\omega ^{2}}f_{x} (X_{4} ,Y_{4} ,\dot{{X}}_{4} ,\dot{{Y}}_{4} )=0 \\ \ddot{{Y}}_{4} +\frac{c_{1} }{m_{4} \omega }\dot{{Y}}_{4} +\frac{k_{s} }{m_{4} \omega ^{2}}(Y_{4} -Y_{3} )-\frac{sP}{m_{4} c\omega ^{2}}f_{y} (X_{4} ,Y_{4} ,\dot{{X}}_{4} ,\dot{{Y}}_{4} )+\frac{g}{c\omega ^{2}}=0 \\ \end{array}} \right. . \end{aligned}$$

(32)

The details of the RFR-bearing system under investigation are listed in Table 1. 1# and 2# bearings are consistent with the same hydrodynamic lubrication bearing parameters and lubricating conditions. It is assumed that 1# and 2# bearings are simulated by rigid supports, and the approximate natural frequency of a given rotor-bearing system calculated by formula $\omega _0={\sqrt{k/m}}$ is about 441 rad/s. In practice, the first critical speed should be less than 441 rad/s because of the effects of hydrodynamic bearing dynamic coefficients and rotating speed, etc., as demonstrated in Sect. 3.

Table 1 Details of rotor-bearing system

3 Numerical simulations and discussions

In this section, four-order Runge–Kutta method is adopted to get the solution because it is a high precision algorithm to solve the nonlinear motion equation system and successfully fulfills the simulation purpose in the time domain. The rotating speed, mass unbalance and the unbalance phase difference are taken as control parameters in the performed simulations, respectively. The magnitude of the imposed unbalance changes through varying the unbalance eccentric displacement $e_{\mathrm {1}}$ [see Eqs. (17) and (18)]. The bifurcation diagram is used to depict continuous changes of motion patterns of the RFR-bearing system. The 3D waterfall spectrums are used to show the change of the frequency components and its instability onset speed with the change of control parameters. The Poincaré map is adopted to exhibit the motion nature. The rotor orbit is used to indicate the motion behavior. The vibration time waveform and the frequency spectrum are adopted to show the moving orbits and frequency-domain features at some certain parameters. Note that 1X frequency corresponds to the precession speed equal to rotor spinning speed, 0.5X frequency corresponds to the whirl speed approximately equal to half of rotor spinning speed, and the rest will be the same.

As can be seen from the following, the obtained results systematically reveal the effects of imposed unbalance on the investigated dynamic behaviors of a given RFR system considering nonlinear contact. In the performed simulations, with varying unbalance magnitude, phase difference and rotational speed, interesting and distinct phenomena, which have not been reported previously, will be displayed.

3.1 Bifurcation and nonlinear response analysis

Under the almost perfect-balanced condition, in which the mass unbalance parameter is set to $e_{\mathrm {1}}=0.002$ mm, $e_{\mathrm {2}}=0$ mm and $\phi = 0^\circ$, a comparison of bifurcation diagram and Lyapunov stability map of 1# bearing horizontal dimensionless displacement($X_{\mathrm {1}})$ at speed up and speed down simulation, $\omega \in [100, 5000]$ rad/s, is depicted in Fig. 5. For the bifurcation diagram from speed down simulation, it can be seen from Fig. 5b that the motion is synchronous vibration with period-one at speed below 1018 rad/s and only one isolated point is correspondingly shown in the bifurcation diagram for each rotational speed (see Fig. 5b). Meanwhile, the corresponding Lyapunov index $\lambda$ is less than zero, which confirms that the motion is Lyapunov stable. Figure 6 shows the vibration waveform, rotor orbit, frequency spectrum and Poincaré map at a typical speed of 518 rad/s. Only one point exists in Poincaré map, one peak value of 1X frequency, which equals to rotational speed, exists in the frequency spectrum of Fig. 6, and rotor orbit is elliptic. All those also show the rotor performs period-one motion at $\omega <1018$ rad/s. When the spinning speed is greater than 1018 rad/s, the rotor system motion turns into quasi-periodic pattern until to top speed and the Lyapunov index $\lambda$ closes to 0. For the results from speed up simulation, the corresponding bifurcation diagram and Lyapunov stability map are shown in Fig. 5a, c, and in comparison with speed down case, it is apparent that there are great differences for two cases. In the case at speed up, the rotor motion is period-one pattern at speed interval of 1018 rad/s $<\omega <4508$ rad/s, while the rotor motion keeps quasi-periodic motion pattern in the case at speed down. In other words, a bi-stable state region exists in the bifurcation diagram from 1018 to 4508 rad/s. In the meantime, when the rotation speed gets into or out of this region when speed up or speed down, the jump phenomenon will occur. The reason for this is that different initial values may lead to different steady solutions in numerical simulation.

Fig. 5

Bifurcation diagram and Lyapunov index of $X_{\mathrm {1}}$ at $\omega \in$[100, 5000] rad/s for a relative-perfect balanced RFR

Figure 7 shows the vibration responses of the RFR at 1528 rad/s through speed up or speed down simulation. It can be seen that the nonlinear vibration characteristics at the same speed point through speed up and speed down are clearly different. The rotor with elliptical orbit behaves as quasi-periodic motion pattern which can be verified by a closed loop in Poincaré map at 1528 rad/s when speed down, while performs period-one motion pattern verified by the corresponding Poincaré map with one isolated point when speed up. Obviously, the vibration amplitude at speed down is much greater than that at speed up. What’s more, the vibration frequency spectrum is also different, the major difference is that the whip frequency $\hbox {f}_{\mathrm {n1}}$ of 0.42X with large amplitude is clearly visible on the spectrum, and the $2\hbox {f}_{\mathrm {n1}}$ of 0.84X frequency can also be observed when speed down, but only rotational speed frequency exists in the spectrum when speed up.

At 4729 rad/s when speed down or speed up, the system motion with elliptical orbit is always quasi-periodic pattern, and only one whip frequency $\hbox {f}_{\mathrm {n1}}$ of 0.14X with large peak appears in the frequency spectrum. The system quasi-periodic motion can also be verified by a closed loop in Poincaré map. The time-domain waveform will have little phase difference due to the different initial value in the numerical simulation, as shown in Fig. 8. Therefore, based on the above analysis, by analyzing and comparing bifurcation diagram and Lyapunov index $\lambda$ between speed up and speed down in Fig. 5, and vibration response characteristics at 518 rad/s in Fig. 6, at 1528 rad/s in Fig 7, and at 4729 rad/s in Fig. 8, the investigated FRR response may show fold bifurcation [29] at speed of 1018 rad/s and subcritical Hopf bifurcation [29,30,31] at speed of 4508 rad/s. To further understand and confirm the fold bifurcation and subcritical Hopf bifurcation phenomena, the analyses and numerical simulations under no imbalance are conducted; subsequently, the discussions are as follows.

Fig. 6

Vibration waveform, rotor orbit, frequency spectrum, Poincaré map at $\omega =518$ rad/s

Fig. 7

Vibration waveform, rotor orbit, frequency spectrum, Poincaré map at $\omega =1528$ rad/s through speed up/down simulation

Fig. 8

Vibration waveform, rotor orbit, frequency spectrum, Poincaré map at $\omega =4729$ rad/s

At first, two types of Hopf bifurcation, i.e., supercritical Hopf bifurcation and subcritical Hopf bifurcation, and fold bifurcation [29] are introduced by using the simple 2D system cases through the phase plane diagram, as shown in Figs. 9, 10 and 11. For a 2D system, ${\dot{r}}=\mu {r}-r^{3}$, ${\dot{\theta }}=\omega +\hbox {b}r^2$ there is one stable focus in Fig. 9a when $\mu <0$, and there are one unstable fixed point and one stable limit cycle when $\mu \>0$, so the system occurs supercritical Hopf bifurcation. (According to the flow in the phase space, a supercritical Hopf bifurcation occurs when a stable focus becomes an unstable focus surrounded by an approximate small elliptical limit cycle.) For another 2D system, when $\mu _{c}<\mu <0$, there are two attractors: One is the stable limit cycle and the other is the stable fixed point; interestingly, there is an unstable cycle between them, when $\mu = 0$, subcritical Hopf bifurcation occurs, where the unstable cycle shrinks to zero amplitude and engulfs the origin and makes the origin unstable. When $\mu \>0$, the limit cycle with large amplitude becomes attractor. The third bifurcation type is so-called fold bifurcation. As shown in Fig. 11, it can be found that the system experiences a fold bifurcation when $\mu =\mu _{c}=-1/4$. (At the bifurcation point, two limit cycles are combined and disappeared. Such bifurcation of fixed point is called folding bifurcation in Ref. [29].) It should be noted that the origin does not change at the bifurcation, and it is stable from beginning to end. Figures 12 and 13 show the time-domain waveform and shaft center orbit at some speed points, respectively. When the rotor rotation speed $\omega <1018$ rad/s, such as 508 rad/s, the solution is asymptotic stability and an equilibrium point exists in the shaft orbit from Fig. 13a, i.e., all trajectories at different initial values spiral into an equilibrium point. However, as shown in Fig. 12b, when 1018 rad/s$\le \omega <4508$ rad/s, such as 1528 rad/s, there are two stable states: One is stable limit cycle, and the other is stable equilibrium point, i.e., bi-stable state. As depicted in Fig. 13c, different initial conditions at the start of simulation may lead to different steady solutions at that speed region, when the initial value is such as A1, A2, A3, A4 or A5, the system orbit will finally enter into a stable limit cycle; however, when the initial value is such as B1, B2 or B3, the system orbit will finally enter into a stable equilibrium point. There might be a semi-stable ring around 1018 rad/s, but it is very difficult to be found due to the high-dimension system, and with the increasing rotation speed, it splits into a stable limit cycle and an unstable cycle. Note that the equilibrium point state always exists. Based on the determining criteria mentioned above, the rotor system occurs fold bifurcation at 1018 rad/s, as depicted in Figs. 5,  6,  7,  12a, b and  13a, c. With the increasing rotation speed, the other type of bifurcation will occur. When the rotational speed $\omega \ge$ 4508 rad/s, there is one stable limit cycle existed in the shaft center orbit for different initial conditions at the start simulation, and the equilibrium point is unstable, so the subcritical Hopf bifurcation occurs at speed of 4508 rad/s, as indicated in Figs. 5,  7,  8,  12b, c, d and  13b, c. Two typical bifurcations are confirmed through the numerical method.

In order to further investigate the characteristics of nonlinear dynamic for a given RFR-bearing system, under the almost perfect-balanced condition, a comparison of 3D waterfall spectrum plot when speed up and speed down is presented in Fig. 14. Figure 15 depicts the root-mean-square (RMS) level of rotor amplitude, single peak value(SPV) of rotor amplitude and maximum value (max) of dimensionless displacement $X_{\mathrm {1}}$ when speed up and speed down, respectively. Figure 16 depicts the rotor orbits for speed down simulation at different speeds, and Fig. 17 represents the shaft orbits mode at a constant speed of 2000 rad/s for speed down simulation. The numerical results exhibit the following dynamic phenomena.

Fig. 9

Supercritical Hopf bifurcation (${\dot{r}}={\mu }r+r^{3}, {\dot{\theta }}=\omega +\hbox {b}r^{2}$)

Fig. 10

Subcritical Hopf bifurcation (${\dot{r}}={\mu }r+r^{3} \hbox {-}r^{5}, {\dot{\theta }}=\omega +\hbox {b}r^{2}$)

Fig. 11

Fold bifurcation of 2D system (${\dot{r}}={\mu }r+r^{3} \hbox {-}r^{5}, {\dot{\theta }}=\omega +\hbox {b}r^{2}$)

Fig. 12

Time-domain waveform under no imbalance condition

• (a) When the rotational speed is small for speed down or speed up simulation, only synchronous lateral vibrations with tiny amplitude are observed, which is confirmed in Fig. 14. These forced vibrations are caused by the smallest mass unbalance force of an almost perfectly balanced rotor. At rotational speed $\omega <1018$ rad/s, these vibrations are stable, that is, shortly after an impulse disturbance of the rotor causes a transient process; the same stable vibration mode is rebuilt.

Fig. 13

Shaft orbit under no imbalance condition at different initial values at the start of simulation

Fig. 14

Waterfall plot at $X_{\mathrm {1}}$ for a relative-perfect balanced RFR

• (b) Interestingly, at the speed region from 1018 to 4508 rad/s, there are great differences between speed up and speed down simulation. For speed up simulation, only 1X frequency exists in the 3D spectrum. However, for the speed down simulation, there are three frequency components, such as at $\omega = 1018$ rad/s, they are rotational speed frequency 1X($\hbox {f}_{\mathrm {r}})$, subharmonic frequency $\hbox {f}_{\mathrm {n1}}$ with 0.42X and subharmonic frequency $2\hbox {f}_{\mathrm {n1}}$ with 0.84X. $\hbox {f}_{\mathrm {n1}}$ belongs to oil whirl, in which the frequency is close to, and usually smaller than, half of the rotation speed. Note that nonsynchronous frequency $\hbox {f}_{\mathrm {n1}}$ mainly results from oil-film instability and the whirl speed of $2\hbox {f}_{\mathrm {n1}}$ approximately equals to double frequency of $\hbox {f}_{\mathrm {n1}}$. Most notably, the dominant frequency component jumps from 1X frequency to $\hbox {f}_{\mathrm {n1}}$ with largest amplitude and the 1X frequency bifurcates to 1X and $2\hbox {f}_{\mathrm {n1}}$, which causes sudden instability of rotor motion. The $\hbox {f}_{\mathrm {n1}}$ frequency dominates the vibration of RFR-bearing system. In summary, speed from 1018 to 4508 rad/s is the bi-stable state region.

• (c) For speed down simulation, at the higher speed which is greater than 1018 rad/s, the oil whirl mode is quickly replaced by oil whip with a constant frequency about 110 Hz, which is a lateral forward processional subharmonic vibration of the rotor with a locking frequency equaling to double of first critical speed. Independent of the increasing rotation speed, the oil whip frequency remains close to double first natural frequency of rotor. However, for speed up simulation, the system loses its stability when the speed is greater than 4508 rad/s, which is much greater than that of 1018 rad/s, compared to speed down situation.

• (d) The different nonlinear jumping phenomena with large vibration offset jumping directly from the lower value to the higher value can also be obtained for speed up and speed down simulation in Fig. 15. The jump speed is 1018 rad/s for speed down and 4508 rad/s for speed up. Figure 16 shows that the rotor performs limit cycle oscillation [21] due to the large amplitude of predominated 0.42X frequency at $\omega \ge$ 1018 rad/s when speed down. At 2000 rad/s when speed down, Fig. 17 demonstrates that predominated $\hbox {f}_{\mathrm {n1}}$ is a bending forward mode with in-phase of Nodes 1–4.

Fig. 15

Dimensionless displacement ($X_{\mathrm {1}})$ in horizontal direction at $\omega \in$[100, 5000] rad/s

Both oil whirl and oil whip are phenomena of dynamic instability induced by the interaction between the rotor and the bearing, and they both produce severe rotor vibrations. It may be dangerous that the investigated rotor runs at $\omega \ge 1018$ rad/s due to the existence of bi-stable state at $\omega \in$[1018, 4508] rad/s, the occurrence of fold bifurcation phenomena at 1018 rad/s and subcritical Hopf bifurcation phenomena at 4508 rad/s and oil whip. The potential danger should be avoided in the dynamic design for a real rotor. High amplitude shaft vibrations that can sustain themselves over a wide range of rotational speed may not only perturb the normal running, but also cause serious unexpected damage to the whole machine.

Fig. 16

Orbits of 1# bearing for speed down simulation

Fig. 17

Vibration mode at 2000 rad/s for speed down simulation

3.2 Effects of induced unbalance magnitude

The magnitude of the imposed unbalance(me) changes through varying the unbalance eccentric displacement $e_{\mathrm {1}}$ in 1# disk, while the unbalance eccentric displacement $e_{\mathrm {2}}$ in 2# disk was set to zero.

3.2.1 Effects of the unbalance magnitude at a constant speed

Figure 18 shows the bifurcation diagram and the vibration response of the RFR-bearing system with $e_{\mathrm {1}}$ as a control parameter in the range of $e_{\mathrm {1}}\in$[0.01,0.7] mm at $e_{\mathrm {2}}=0$ mm, $\phi =0^\circ$ and $\omega =2000$ rad/s. It shows that system keeps period-one motion state when mass unbalance eccentricity $e_{\mathrm {1 }}$ is below 0.036 mm, and the response value versus unbalance can be regarded as approximately linear increase at $e_{\mathrm {1}}\in$[0.01,0.036] mm. The system response remains quasi-periodic motion in the range of $e_{\mathrm {1}}\in$[0.036,0.1036] mm. Figure 19 shows the vibration waveform, rotor orbit, frequency spectrum, Poincaré map at $e_{\mathrm {1}}=0.1036$ mm, it is clearly shown that the system occurs quasi-periodic motion verified by a closed cycle in Poincaré map and some disperse frequency components without a common divisor in frequency spectrum. With the increase in unbalance, the system behaves as period-three motion at eccentricity range from 0.1051 mm to 0.114 mm. Figure 20 also shows the period-three motion pattern with three isolated points shown in Poincaré map. Again, the rod fastening rotor performs quasi-periodic motion at $e_{\mathrm {1}}\in$[0.1155,0.1868] mm. It is interesting that the bifurcation diagram once again exists period-three window at $e_{\mathrm {1}}\in$[0.1881,0.1933] mm. And then, the rotor response becomes quasi-periodic motion at $e_{\mathrm {1}}\in$[0.195,0.2354] mm. After a short periodic-three motion, the system enters synchronous periodic-one motion. Note that the dimensionless displacement $X_{\mathrm {1}}$ remains almost constant value over a wide range of unbalance eccentricity with $e_{\mathrm {1}}$, as shown in Fig. 18b. The above-mentioned bifurcation sequences, which are period-one, quasi-period, period-three, quasi-period, period-three, quasi-period and period-one motion, can also be demonstrated in Poincaré map for different unbalance eccentricities, as shown in Fig. 21.

Fig. 18

Bifurcation diagram and rotor response with unbalance eccentricity $e_{\mathrm {1}}$ from 0.01 mm to 0.7 mm at 2000 rad/s

Fig. 19

Vibration waveform, rotor orbit, frequency spectrum, Poincaré map at $e_{\mathrm {1}}=0.1036\hbox {mm}$ and $\omega =2000$ rad/s

Fig. 20

Vibration waveform, rotor orbit, frequency spectrum, Poincaré map at $e_{\mathrm {1}}=0.1071$ and $\omega =2000$ rad/s

Fig. 21

Poincaré map at different unbalance eccentricities of 1# disk

Fig. 22

Waterfall plots of the rotor-bearing system in x direction at 2000 rad/s

In order to further understand the rotor vibration state, the waterfall plots corresponding to the bifurcation diagram of dimensionless amplitude $X_{\mathrm {1}}$ are depicted in Fig. 22. The RFR system occurs oil whip instability with constant whip frequency about 110 Hz at unbalance level of eccentricity range from 0.036 to 0.2354 mm. The frequency components of oil whip region include frequency $\hbox {f}_{\mathrm {n1}}, \hbox {f}_{\mathrm {r}}$, and combined frequencies of both, such as $2\hbox {f}_{\mathrm {n1}} and \hbox {f}_{\mathrm {r}}+\hbox {f}_{\mathrm {n1}}$. The elaborate spectrum waterfall plot in the range of $e_{\mathrm {1}}\in$[0.01, 0.24] rad/s is displayed in Fig. 22b, which shows the process from synchronous vibration, through oil whip, to the pure unbalance forced vibration. In short, the motion pattern of the RFR-bearing system is diverse for different levels of induced unbalance and may become instability with large amplitude for some specific unbalance region at a certain speed. Therefore, the unbalance level should be strictly controlled and detected under the working condition of a constant rotation speed.

3.2.2 Effects of the induced unbalance magnitude at different speeds

Based upon the above analyses, it is clearly shown that mass unbalance magnitude replaced by eccentricity $e_{\mathrm {1}}$ is an important parameter affecting the nonlinear behavior of the RFR-bearing system when the rotor remains at a constant speed of 2000 rad/s. However, the majority of rod fastening rotor applications usually operate at high-speed and wide speed range conditions, such as naval ship gas turbine rotor. In this section, the magnitude of the imposed unbalance me (see Table 2) changes from $0.02m_{\mathrm {2}}$ to $0.7m_{\mathrm {2}}~ \hbox {kg}\,\hbox {mm}$ with an increasing ratio of 2 for 1# disk, and the value of unbalance magnitude was decided by the empirical formula of many statistical data from the results of high-speed dynamic balancing. The nonlinear vibration responses of the rotor-bearing system will be analyzed for six different unbalance amplitudes at different rotating speeds from 100 to 3000 rad/s. Note that U1 to U6 represent the induced unbalance magnitudes on the N2 of the rod fastening rotor system shown in Fig. 1.

Table 2 Six different magnitudes of induced unbalance

Figure 23 depicts the bifurcation diagrams at speeds range from 100 to 3000 rad/s when the variable value of U2 and U3 is imposed, respectively. By comparing the bifurcation diagrams of U2 and U3, it shows that the bifurcating trend is basically similar except the onset speed of two kinds of instability. For the unbalance magnitude of U2, the system motion is periodic-one when rotor speed is below 543.4 rad/s. With the increase in rotational speed, the rotor system occurs double period bifurcation phenomenon at 543.4 rad/s, which is caused by the half-speed whirl instability of oil film. The speed region of period-two motion pattern corresponding to the first instability is from 543.4 to 659.6 rad/s, only two isolated points are shown in Poincaré map, and the half-frequency amplitude dominates the motion of rotor system at 552 rad/s as shown in Fig. 24. And then, the system motion is from period-one at 659.6 rad/s $<\omega <1517$ rad/s to quasi-period at $\omega \ge 1517$ rad/s. What’s more, the system response occurs the second instability at speed of 1517 rad/s, which is caused by the oil whirl/whip instability with large magnitude.

Two instability speed regions of [543.4,659.6] rad/s and [1517,3000] rad/s can be determined by the above analysis. Nonlinear factors in the rod fastening rotor mainly come from contact and bearing, especially for the high-nonlinear oil-film bearing, which makes rich high-nonlinear dynamic characteristics. Due to the interaction of nonlinear contact characteristics and nonlinear oil-film force and unbalance, the rotor may reach the second instability of oil whip at higher speed. (The second instability phenomena are also reported in Refs. [11,12,13,14,15,16,17,18,19,20,21].) The first instability speed range and vibration amplitude are significantly less than the second one, so this paper focuses on the second onset speed of instability.

Fig. 23

Bifurcation diagrams of dimensionless displacement $X_{\mathrm {1}}$ at two unbalance magnitudes

Fig. 24

Vibration waveform, rotor orbit, frequency spectrum, Poincaré map for induced unbalance of U2 at $\omega =552$ rad/s

Fig. 25

Waterfall plots of dimensionless displacement $X_{\mathrm {1}}$ under different unbalance magnitudes

Figure 25 shows the waterfall plots of the dimensionless displacement($X_{\mathrm {1}}$) for six kinds of unbalance magnitude at speeds range from 100 to 3000 rad/s. Root-mean-square level and Max value of rotor response corresponding to the waterfall spectrum are presented in Fig. 26. The main results of simulation are summarized as follows.

• (a) By analyzing the results from Figs. 25 and 26, the first two critical speeds are about 318 rad/s and 1256 rad/s, respectively. When rotor speed is below first critical speed, the vibration amplitude increases faster as the increase in unbalance, and rod fastening rotor system performs pure unbalance forced vibration around the equilibrium position, which is defined as a rigid rotor.

• (b) The first instability with small speed range only exists in the induced unbalance of U2, U3 and U4, in which the first unstable region is [543.4,659.6] rad/s, [521.6,528.8] rad/s, [572.4,1030] rad/s and [986.7,1147] rad/s, respectively. Complicated frequency components of second whirl/whip region are nearly consistent for six different unbalance magnitudes, which include whirl frequencies of $\hbox {f}_{\mathrm {n1}}$ and $\hbox {f}_{\mathrm {n2}}$, rotating frequency of $\hbox {f}_{\mathrm {r}}$ and combined frequencies of both, such as $\hbox {f}_{\mathrm {r}}$-$2\hbox {f}_{\mathrm {n1}}$ and $2\hbox {f}_{\mathrm {n1}}, 2\hbox {f}_{\mathrm {r}}$. Moreover, the first mode oil whip frequency (about 110 Hz) remains close to the double of first critical speed, as mentioned in Sect. 3.2.1.

• (c) When rotor speed exceeds second instability threshold, the amplitude of $\hbox {f}_{\mathrm {n1}}$ frequency vibration increases rapidly and dominates the system motion with the increasing rotation speed, which gives rise to the critical limit cycle oscillation. It is very unstable and dangerous for RFR-bearing system under operating speed of second instability region due to the complex motion with large amplitude of low-frequency $\hbox {f}_{\mathrm {n1}}$, which may lead to rapid fatigue failure or shaft fracture accident. For the six different magnitudes of induced unbalance, the major difference is that the onset speed of second instability is not identical, which is 1408 rad/s, 1517 rad/s, 1692 rad/s, 1881 rad/s, 2106 rad/s and 2382 rad/s, respectively. With the increase in the unbalance magnitude, the instability threshold is delayed from 1408 rad/s at U1 to 2382 rad/s at U6. This is because the increasing amplitude of synchronous vibration restrains oil-film instability. Hence, the increase in the unbalance magnitude can improve the stability of the rotor-bearing system to some extent.

• (d) When higher unbalance values are introduced, e.g., U5 and U6 (see Fig. 25e, f), it is surprising to see that the dominant vibration component changes from nonsynchronous vibration component of frequency $\hbox {f}_{\mathrm {n1 }}$ to synchronous vibration component of rotating frequency $\hbox {f}_{\mathrm {r}}$ by comparing with U1, U2, U3 and U4, that is, the nonsynchronous vibration amplitudes are inhibited by bigger unbalance force. As shown in Fig. 26, the rod fastening rotor operates stable without big wave for the state of U5 and U6 at speed above the first critical speed, while the vibration RMS of U5 is relatively lower than those of U6 throughout the entirely considered rotor speed range. Therefore, in order to restrain the amplitude of nonsynchronous vibration components of $\hbox {f}_{\mathrm {n1}}$ and retard the occurrence of second instability, the unbalance magnitude of rotor system is suggested to be kept at unbalance range from U5 to U6.

Fig. 26

RMS level and MAX value of rotor response for different magnitudes of induced unbalance

Fig. 27

Bifurcation diagrams of dimensionless displacement $X_{\mathrm {1}}$ from 100 to 3000 rad/s

Fig. 28

Waterfall plots of dimensionless displacement $X_{\mathrm {1}}$ at $\phi =0^\circ$

Fig. 29

Vibration waveform, rotor orbit, frequency spectrum, Poincaré map at $\phi =0^\circ$ and $\omega =785$ rad/s

Fig. 30

Poincaré maps of different speeds ($\phi =0^\circ$ )

Fig. 31

Waterfall plots at different unbalance phase differences from rotor speed of 100 rad/s to 3000 rad/s

3.3 Effects of induced unbalance phase difference

Variation of the unbalance phase difference, $\phi$, is considered in the performed simulations, while both mass unbalance eccentricities of 1# disk and 2# disk were set to 0.02 mm

Figure 27 shows the bifurcation diagrams with $\omega$ as control parameter from 100 to 3000 rad/s at $\phi =0^\circ$ and $\phi =180^\circ$, respectively. The detailed waterfall spectrum plots of dimensionless displacement $X_{\mathrm {1}}$ at $\phi =0^\circ$ are presented in Fig. 28. Under the condition of $0^\circ$ phase difference, obviously, the motion is period-one pattern at speeds range from 100 to 543.4 rad/s, period-two pattern caused by half-frequency whirl instability (first instability) at speed above 543.6 rad/s but below 666.9 rad/s, period-one pattern at $\omega \in$[666.9,761.4] rad/s, quasi-periodic pattern caused by the $\hbox {f}_{\mathrm {s1}}$ whirl frequency with 0.4X and $\hbox {f}_{\mathrm {s2}}$ whirl frequency with 0.6X at speed above 761.4 but below 863.2 rad/s, period-one pattern at speeds range from 863.2 to 1030 rad/s, period-two pattern caused by 0.5X sub-synchronous vibration component at 1030 rad/s$<\omega <1067$ rad/s, period-three pattern mainly caused by the frequencies of $\hbox {f}_{\mathrm {n1}}$ at $\omega \in$[1067,1125] rad/s and quasi-period pattern caused by the frequencies of $\hbox {f}_{\mathrm {n1}}$ and $\hbox {f}_{\mathrm {r}}$-$2\hbox {f}_{\mathrm {n1}}$ at speed above 1125 rad/s up to top speed. Most notably, as mentioned in Sect. 3.2.2, the system motion occurs the second instability when rotor speed is above 1067 rad/s at $0^\circ$ phase difference. For the unbalance phase difference of $180^\circ$ , interestingly, there is no first instability in bifurcation diagram and the onset speed of second instability is shifted to higher speed location of 1525 rad/s than those in $0^\circ$ phase difference.

Fig. 32

Max value and RMS level of rotor response for different unbalance phase differences

Fig. 33

Instability speed at different differences of $\phi$

As shown in Fig. 29, it is clearly demonstrated that the system is quasi-periodic motion with a complex shaft orbit due to the appearance of a closed cycle in Poincaré map and some discrete frequency component without a common divisor in frequency spectrum for $0^\circ$ phase difference at speed of 785 rad/s. The above-mentioned bifurcation sequences, which are period-one, period-two, period-one, quasi-period, period-one, period-two, period-three and quasi-period motions, can also be verified in Poincaré map of different speeds, as shown in Fig. 30.

In order to deeply know the dynamic characteristics effects about other unbalance phase difference, the waterfall spectrum and vibration RMS level are presented in Figs. 31 and 32, respectively. The instability speeds are summarized and depicted in Fig. 33. The conclusions of the obtained results are generally drawn as follows.

• (a) Interestingly, the first instability with small speed range only exists at $\phi =0^\circ , 30^\circ , 60^\circ , 90^\circ$, which is caused by the nonsynchronous whirl frequencies, such as 0.4X, 0.5X and 0.6X. Half-frequency components can lead to period-two motion, while 0.4X and 0.6X frequencies can lead to period-three motion, which causes first instability of rotor. Complicated frequency components of second instability region are nearly consistent for different unbalance phase differences, which include low frequency of $\hbox {f}_{\mathrm {n1}}$, rotating frequency of $\hbox {f}_{\mathrm {r}}$ and combined frequencies of both, such as $\hbox {f}_{\mathrm {r}}$-$2\hbox {f}_{\mathrm {n1}} and 2\hbox {f}_{\mathrm {n1}}, \hbox {f}_{\mathrm {r}}+\hbox {f}_{\mathrm {n1}}$. The first mode oil whip frequency (about 110 Hz) remains close to the double of first critical speed, which dominates the motion of rotor system, as mentioned before. At second instability region, namely oil whip, the dimensionless displacement $X_{\mathrm {1}}$ in horizontal direction consistently ascending to an extremely high value (see Fig. 31 or 32) with the rotor speed leads to an exceedingly dangerous state for the safe operation of the RFR applications.

• (b) The second instability speed is low and does not change significantly with the increase in phase difference at $\phi \le 40^\circ$. However, the second instability speed rises dramatically when phase difference is from $40^\circ$ to $50^\circ$ , which increases by about 247 rad/s. Then, the instability speed can be regarded as approximately linear increase at $50^\circ \le \phi <120^\circ$ and remains constant value at $120^\circ \le \phi \le 180^\circ$. Most notably, the speed difference between maximum instability of 1525 rad/s and minimum instability of 1067 rad/s is about 458 rad/s, which increases by 43%. So, a certain-enough range of unbalance phase difference can improve the instability of the RFR-bearing system to some extent, which is from $120^\circ$ to $180^\circ$ .

• (c) By comparing the RMS level for different phase differences, it is concluded that reasonable unbalance phase difference can also reduce the vibration amplitude, such as first-order amplitude reduced by 95%, restrain the appearance of first instability and decay the occurrence of second instability. Under the condition of allowably residual unbalance in two disks, the vibration RMS level for $180^\circ$ phase difference is relatively small compared to other phase differences in the considered speed range. The unbalance phase difference of $180^\circ$ is relative-optimum phase difference for the allowable magnitude of residual unbalance.

Under the condition of allowably residual unbalance, the results show that reasonable-enough unbalance phase difference not only can increase the instability, but also reduce the amplitude; moreover, the RFR can operate relatively well with small vibration amplitude and higher instability threshold when the unbalance between two disks is controlled at $180^\circ$ phase difference through reassembly or balancing process. What’s more, the operating speed of the investigated RFR should be designed below the threshold of second instability, even second critical speed.

4 Conclusions

The model or nonlinear motion governing equation considering unbalance excitation, nonlinear oil-film force and nonlinear contact property between disks is built to systematically investigate the nonlinear effects produced by the unavoidably residual unbalance on the dynamic characteristics for an RFR-bearing system. The rotating speed, mass unbalance magnitude and unbalance phase difference are taken as control parameters in the performed simulations. All of them need to be carefully considered and controlled during the design, manufacture, assembly, operation and maintenance process of RFR. Unbalance phase difference is the most important controlled parameter for such RFR-bearing system through high-speed balancing. Special considerations should be required for the RFR-bearing system due to the low-frequency vibration component caused by nonlinear oil-film force and nonlinear contact at high speed. Large amplitude of low-frequency vibration of $\hbox {f}_{\mathrm {n1}}$ may lead to excessive vibration in RFR, even rapid failure or shaft fracture.

• (1) Under the almost perfect-balanced condition, a bi-stable state region exists at speed range from 1018 to 4508 rad/s. In the meantime, when the rotation speed gets into or out of this region when speed up or speed down, the jump phenomenon will occur. The investigated FRR response may show fold bifurcation at speed of 1018 rad/s and subcritical Hopf bifurcation at speed of 4508 rad/s. Two typical bifurcations are confirmed through the numerical method. The different nonlinear jumping phenomena with large vibration offset jumping directly from the lower value to the higher value can also be obtained for speed up and speed down simulation. The jump speed is 1018 rad/s for speed down and 4508 rad/s for speed up. The dominant frequency component transforms from 1X frequency to $\hbox {f}_{\mathrm {n1}}$ with largest amplitude, and the 1X frequency bifurcates to 1X and $2\hbox {f}_{\mathrm {n1}}$, which causes sudden instability of rotor motion. Accordingly, it may be dangerous that the investigated RFR runs at $\omega \ge$ 1018 rad/s due to the occurrence of nonlinear bifurcation phenomena and oil whip.

• (2) The unbalance magnitude is a key parameter for the investigated RFR-bearing system. The system will exhibit distinct motion types for different regions of unbalance magnitude, such as synchronous period-one motion, period-two motion, period-three motion and quasi-periodic motion. The increase in the unbalance magnitude can improve the stability and increase the operating speed of rotor-bearing system to some extent. In order to restrain the large amplitude of nonsynchronous vibration components of $\hbox {f}_{\mathrm {n1}}$ and retard the occurrence of instability, the unbalance magnitude of rotor system is suggested to be kept at unbalance range from U5 to U6.

• (3) Under the condition of allowably residual unbalance, an enough-reasonable unbalance phase difference, $\phi \in [120^\circ ,180^\circ ]$, may not only increase the instability, but also reduce the vibration amplitude. Interestingly, by further comparing the dynamic characteristics in $\phi \in [120^\circ ,180^\circ ]$, the RFR can operate relatively well with small vibration amplitude and higher instability threshold when the unbalance between two disks is controlled at $180^\circ$ phase difference through reassembly of disks or balancing process. The onset speed of instability is increased by 43%, and first-order amplitude of total vibration is reduced by 95%. The proposed unbalance phase difference is an effective way to achieve more small vibration and stable operation for the high-speed RFR, which is helpful for vibration control and rotor high-speed balancing without adding weights or subtracting weights. The proposed method may be further applied to other combined rotor types.