1 Introduction

A rotor bearing system is one of the key components in rotating machines. Its dynamic characteristics affect the performance, efficiency and service life of the machine directly. Recently, the studies on the nonlinear dynamic behaviors and stability of the integral rotor bearing have been reported in many literature [1–7]. Wang et al. [1] built a general model of a rub-impact rotor system supported by oil-film journal bearings. Nonlinear dynamic characteristics and stability of the system are investigated. Mohammad et al. [2] established the model of a high-speed rotor bearing system using 3D finite element model and one-dimensional finite element model. The nature frequencies and mode shapes were investigated, and the results were compared with those obtained from the modal test. Yang et al. [3] proposed a new nonlinear dynamic analysis method for a rotor system supported by oil-film journal bearings used mainly to investigate effects of mass eccentricity on dynamic behaviors of the rotor system. Results showed that the proposed method has universal applicability and can easily obtain the nonlinear dynamic characteristic of rotor systems. Transverse crack in a rotor shaft acts just as “breathing” by opens and closed when the rotor rotates at a constant speed. This effect displays the time-periodic stiffness of the shaft and hence generates a parametrically excited. The instability and severe vibration under certain operating conditions caused by parametric excitation from time-varying stiffness were studied by Han et al. [4]. Li et al. [5] proposed a novel nonlinear model of rotor–bearing–seal system based on the Hamilton principle. Musznyska model and unsteady bearing oil-film force were applied to describe the nonlinear steam excitation force and oil-film force, the dynamic behavior of the rotor-bearing-seal system was analyzed by using Runge–Kutta method.

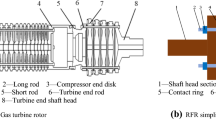
The studies above mainly focus on the integral rotor bearing system. Rod fastening rotor bearing system has many advantages, such as light weight, good strength and ease of cooling. The rod fastening rotors are widely used in high-power gas turbines. The rotor consists of rods and disks, and the disks are connected by rods. The dynamic behavior of the rod rotor has been studied in various ways. Hei et al. [8, 9] established the model of a rod fastening rotor with the journal bearings support. The nonlinear dynamic characteristics and bifurcation of the rotor bearing system has been investigated. He et al. [10] studied the variations of the critical speeds of the rod fastening rotor with rod pre-tightening force through experimental method. Comparison with theoretical analysis shows that the critical speeds of the simulation are close to experimental results. Li et al. [11, 12] revealed the evolution laws of stress distribution and interface contact states with different pre-tightening force and operation conditions. Yuan et al. [13] calculated the flexural stiffness of a rod-fastened rotor by using finite element method (FEM) and then analyzed the dynamic behavior of the rotor system under large unbalance force by using harmonic balance method.

Rod pre-tightening force has a great influence on the dynamic behavior of the rotor bearing system. Unsuitable or unbalance pre-tightening force may cause the severe vibration and catastrophe failure. Liu et al. [14, 15] built the dynamic model of rod fastening rotor bearing system by using Hamilton principle and obtained the general expressions of the additional stiffness matrix and additional generalized moment caused by unbalanced rods pre-tightening force. The result shows that unbalanced pre-tightening force has great influence on nonlinear dynamic and stability of the system. Gao et al. [16] studied the effects of bending moments and pre-tightening forces on the flexural stiffness of contact interfaces in rod-fastened rotors.

It should be noted that the current researches about the dynamic characteristics of the rod fastening rotors focus on the contact stiffness, natural characteristics of the rod fastening rotor. In fact, the unbalanced rod pre-tightening force has a great influence on the nonlinear dynamic characteristics of the rod fastening. In this paper, a dynamic model of rod fastening rotor bearing system is established, considering the nonlinear oil-film force, unbalance mass, unbalanced rod pre-tightening force, etc. The fourth-order Runge–Kutta method is used to get the solution of the nonlinear model. Bifurcation diagram, vibration waveform, frequency spectrum, phase trajectory and Poincare map are applied to analyze the nonlinear dynamic phenomena of the rod fastening rotor.

2 Dynamic modeling of rod fastening rotor

Rod fastening rotor bearing system is complex, in order to analyze the dynamic behavior caused by unbalanced pre-tightening force, and the system is simplified according to the following assumptions:

  1. (a)

    Torsional and axial vibration of the rotor is neglected;

  2. (b)

    Rod pre-tightening force is large enough, ignoring stiffness changes caused by unbalanced single rod pre-tightening force.

2.1 Equation of motion

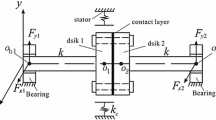
As shown in Fig. 1, the rotor is supported by the same journal bearings, the lumped mass in journal bearing is \(m_{1}\), and the lumped mass in disks is \(m_{2}\). Assuming that rod pre-tightening force is large enough, relative movement between the disks will not occur, bearing and disks are connected by a massless elastic shaft, the shaft stiffness is k, \(c_{1}\) and \(c_{2}\) are the damping coefficient in the journal bearing and disks. The displacements of journal bearing and disks in lateral and vertical direction are expressed by \(x_{1}\), \(x_{2}\) and \(y_{1}\), \(y_{2}\), respectively.

Fig. 1
figure 1

Dynamic model of a rod fastening rotor

Full size image

The equation of motion of the rod fastening can be deduced from Lagrange’s equations. The Lagrange’s equations are described by

$$\begin{aligned} \frac{\hbox {d}}{\hbox {d}t}\left( {\frac{\partial L}{\partial \dot{q}_i }} \right) -\frac{\partial L}{\partial q_i }+\frac{\partial D}{\partial \dot{q}_i }=Q_{q_i}\quad (i=1,2,\ldots ,n) \end{aligned}$$
(1)

where \(q_{i}\) and \(\dot{q}_i \) are the generalized coordinates and generalized velocity, L is Lagrange’s function and \(L=V-U\), V and U are kinetic and potential energies. D is dissipation function, and \(D=\frac{1}{2}\sum \nolimits _{i=1}^n {\sum \nolimits _{j=1}^n {c_{ij} } } \dot{q}_i \dot{q}_j \), \(c_{ij} \) is damping force in generalized coordinate \(q_{i}\) direction when the system has generalized unit velocity in \(q_{i}\) direction. \(Q_{q_i } \) are the external forces corresponding to \(q_{i}\). The symbol “\(\cdot \)” refers to the differentiation with respect to time t.

The kinetic and potential energies and dissipation function of the rod fastening rotor bearing system can be expressed as

$$\begin{aligned} V= & {} m_1 \dot{x}_1^2 +m_1 \dot{y}_1^2 +\frac{1}{2}m_2 \dot{x}_O^2 +\frac{1}{2}m_2 \dot{y}_O^2 \end{aligned}$$
(2)
$$\begin{aligned} U= & {} \frac{1}{2}k(x_1 -x_2 )^{2}+\frac{1}{2}k(y_1 -y_2 )^{2}+m_1 gy_1 +\frac{1}{2}k(x_2 -x_1 )^{2}\nonumber \\&+\,\frac{1}{2}k(y_2 -y_1 )^{2}+m_2 gy_O +\frac{1}{2}\frac{M^{2}L_0 }{EI} \end{aligned}$$
(3)
$$\begin{aligned} D= & {} \frac{1}{2}c_1 \dot{x}_1^2 +\frac{1}{2}c_1 \dot{y}_1^2 +\frac{1}{2}c_2 \dot{x}_2^2 +\frac{1}{2}c_2 \dot{y}_2^2 \end{aligned}$$
(4)

where \((x_O ,y_O )\) is the center of mass coordinate of the disk, and \(x_O =x_2 +e\cos \omega t\), \(y_O =y_2 +e\sin \omega t\), e is eccentric distance. M is the additional bending moment caused by the unbalanced rod pre-tightening force, \(L_{0}\) is the length of the disk, E is elasticity modulus, and I is the inertia moments.

The generalized coordinates of the system are \(q_i =(x_1 ,y_1 ,x_2 ,y_2 )^{T}\), and according to Eq. (1), the Lagrange’s equations are as follows

$$\begin{aligned} \left\{ {\begin{array}{l} \frac{\hbox {d}}{\hbox {d}t}\left( {\frac{\partial L}{\partial \dot{x}_1 }} \right) -\frac{\partial L}{\partial x_1 }+\frac{\partial D}{\partial \dot{x}_1 }=Q_{x_1 } \\ \frac{\hbox {d}}{\hbox {d}t}\left( {\frac{\partial L}{\partial \dot{y}_1 }} \right) -\frac{\partial L}{\partial y_1 }+\frac{\partial D}{\partial \dot{y}_1 }=Q_{y_1 } \\ \frac{\hbox {d}}{\hbox {d}t}\left( {\frac{\partial L}{\partial \dot{x}_2 }} \right) -\frac{\partial L}{\partial x_2 }+\frac{\partial D}{\partial \dot{x}_2 }=Q_{x_2 } \\ \frac{\hbox {d}}{\hbox {d}t}\left( {\frac{\partial L}{\partial \dot{y}_2 }} \right) -\frac{\partial L}{\partial y_2 }+\frac{\partial D}{\partial \dot{y}_2 }=Q_{y_2 } \\ \end{array}} \right. \end{aligned}$$
(5)

Submitting Eqs. (2), (3), (4) into Eq. (5), the equation of motion of the rotor bearing system is as follows

$$\begin{aligned} \left\{ {\begin{array}{l} m_1 \ddot{x}_1 +c_1 \dot{x}_1 +k(x_1 -x_2 )=F_x \\ m_1 \ddot{y}_1 +c_1 \dot{y}_1 +k(y_1 -y_2 )=F_y -m_1 g \\ m_2 \ddot{x}_2 +c_2 \dot{x}_1 +2k(x_2 -x_1 )=k\delta _0 \cos (\omega t+\varphi )+m_2 e\omega ^{2}\cos \omega t \\ m_2 \ddot{y}_2 +c_2 \dot{y}_1 +2k(y_2 -y_1 )=k\delta _0 \sin (\omega t+\varphi )+m_2 e\omega ^{2}\sin \omega t-m_2 g \\ \end{array}} \right. \end{aligned}$$
(6)

where \(F_{x}, F_{y}\) are the nonlinear film force in x direction and y direction, \(\delta _{0}\) is the initial deflection caused by the unbalanced rod pre-tightening force, \(\varphi \) is the angle between initial deflection and unbalance mass.

2.2 Dimensionless equation of motion

In order to simplify the calculation, the dimensionless transformations are given as follows

$$\begin{aligned} x_i =x_i /c, \quad y_i =y_i /c \quad (i=1,2) \end{aligned}$$
(7)

Defining the dimensionless time \(\tau \), \(\tau =\omega t\). Through Eq. (7), dimensionless equation of Eq. (6) can be rewritten as follows

$$\begin{aligned} \left\{ {\begin{array}{l} \ddot{x}_1 =-\frac{c_1 }{m_1 \omega }\dot{x}_1 -\frac{k}{m_1 \omega ^{2}}(x_1 -x_2 )+\frac{\delta P}{m_1 c\omega ^{2}}f_x (x_1 ,y_1 ,\dot{x}_1 ,\dot{y}_1 ) \\ \ddot{y}_1 =-\frac{c_1 }{m_1 \omega }\dot{y}_1 -\frac{k}{m_1 \omega ^{2}}(y_1 -y_2 )+\frac{\delta P}{m_1 c\omega ^{2}}f_y (x_1 ,y_1 ,\dot{x}_1 ,\dot{y}_1 )-\frac{g}{c\omega ^{2}} \\ \ddot{x}_2 =-\frac{c_2 }{m_2 \omega }\dot{x}_2 -\frac{2k}{m_2 \omega ^{2}}(x_2 -x_1 )+\frac{k\delta _0 }{m_2 c\omega ^{2}}\cos (\tau +\varphi )+\frac{e}{c}\cos (\tau ) \\ \ddot{y}_2 =-\frac{c_2 }{m_2 \omega }\dot{y}_2 -\frac{2k}{m_2 \omega ^{2}}(y_2 -y_1 )+\frac{k\delta _0 }{m_2 c\omega ^{2}}\sin (\tau +\varphi )+\frac{e}{c}\sin (\tau )-\frac{g}{c\omega ^{2}} \\ \end{array}} \right. \end{aligned}$$
(8)

where \(f_{x}\) and \(f_{y}\) are dimensionless nonlinear film force in x direction and y direction, and \(f_x =\frac{F_x }{\delta P}\), \(f_y =\frac{F_y }{\delta P}\). \(\delta \) is Sommerfeld correction coefficient, and \(\delta =\frac{\mu \omega RL_1 }{P}(\frac{R}{c})^{2}(\frac{L_1 }{2R})^{2}\), \(\mu \), \(L_{1}\) and R are oil viscosity, bearing length and bearing radius, respectively, \(\omega \) is the excitation frequency, and P is the half mass of the disk.

Equation (8) can be converted to a first-order differential equation form as follows

$$\begin{aligned} \left\{ {\begin{array}{l} \dot{x}_1 =x_{1v} \\ \dot{x}_{1v} =-\frac{c_1 }{m_1 \omega }x_{1v} -\frac{k}{m_1 \omega ^{2}}(x_1 -x_2 )+\frac{\delta P}{m_1 c\omega ^{2}}f_x (x_1 ,y_1 ,x_{1v} ,y_{1v} ) \\ \dot{y}_1 =y_{1v} \\ \dot{y}_{1v} =-\frac{c_1 }{m_1 \omega }y_{1v} -\frac{k}{m_1 \omega ^{2}}(y_1 -y_2 )+\frac{\delta P}{m_1 c\omega ^{2}}f_y (x_1 ,y_1 ,x_{1v} ,y_{1v} )-\frac{g}{c\omega ^{2}} \\ \dot{x}_2 =x_{2v} \\ \dot{x}_{2v} =-\frac{c_2 }{m_2 \omega }x_{2v} -\frac{2k}{m_2 \omega ^{2}}(x_2 -x_1 )+\frac{k\delta _0 }{m_2 c\omega ^{2}}\cos (\tau +\varphi )+\frac{e}{c}\cos \tau \\ \dot{y}_2 =y_{2v} \\ \dot{y}_{2v} =-\frac{c_2 }{m_2 \omega }y_{2v} -\frac{2k}{m_2 \omega ^{2}}(y_2 -y_1 )+\frac{k\delta _0 }{m_2 c\omega ^{2}}\cos (\tau +\varphi )+\frac{e}{c}\sin \tau -\frac{g}{c\omega ^{2}} \\ \end{array}} \right. \end{aligned}$$
(9)

2.3 Nonlinear oil-film force

The nonlinear oil-film force can be obtained by solving the Reynolds equation. Based on the theory of the short bearing [17], Capone nonlinear oil-film force model [18] gives the following assumption: Lubricating oil is isothermal, laminar flow, lubricant dynamic viscosity is constant, and lubricating oil is incompressible fluid.

Under short bearing theory assumption, the dimensionless Reynolds equation is expressed as follows [18, 19]

$$\begin{aligned} \left( {\frac{R}{L}} \right) ^{2}\frac{\partial }{\partial z}\left( {h^{3}\frac{\partial p}{\partial z}} \right) =x\sin \theta -y\cos \theta -2({x}'\cos \theta +{y}'\sin \theta ) \end{aligned}$$
(10)

According to Eq. (10), the dimensionless oil-film pressure is the following

$$\begin{aligned} p=\frac{1}{2}\left( {\frac{L}{D}} \right) ^{2}\frac{\left( {x-2{y}'} \right) \sin \theta -\left( {y+2{x}'} \right) \cos \theta }{\left( {1-x\cos \theta -y\sin \theta } \right) ^{3}} \end{aligned}$$
(11)

The dimensionless oil-film force can be obtained with Eq. (11) through integration along the lubricated arc of bearing

$$\begin{aligned} \left\{ {\begin{array}{l} f_x \\ f_y \\ \end{array}} \right\}= & {} -\frac{[(x-2\dot{y})^{2}+(y+2\dot{x})^{2}]^{1/2}}{1-x^{2}-y^{2}} \nonumber \\&\times \,\left\{ {\begin{array}{l} 3xV(x,y,\alpha )-\sin \alpha G(x,y,\alpha )-2\cos \alpha S(x,y,\alpha ) \\ 3yV(x,y,\alpha )+\cos \alpha G(x,y,\alpha )-2\sin \alpha S(x,y,\alpha ) \\ \end{array}} \right\} \end{aligned}$$
(12)

where \(V(x,y,\alpha )\), \(S(x,y,\alpha )\), \(G(x,y,\alpha )\), \(\alpha \) are expressed as follows

$$\begin{aligned}&V(x,y,\alpha )=\frac{2+(y\cos \alpha -x\sin \alpha )G(x,y,\alpha )}{1-x^{2}-y^{2}} \end{aligned}$$
(13)
$$\begin{aligned}&S(x,y,\alpha )=\frac{x\cos \alpha +y\sin \alpha }{1-(x\cos \alpha +y\sin \alpha )^{2}} \end{aligned}$$
(14)
$$\begin{aligned}&G(x,y,\alpha )=\frac{2}{(1-x^{2}-y^{2})^{1/2}}\left[ {\frac{\pi }{2}+\arctan \frac{y\cos \alpha -x\sin \alpha }{(1-x^{2}-y^{2})^{1/2}}} \right] \end{aligned}$$
(15)
$$\begin{aligned}&\alpha =\arctan \frac{y+2\dot{x}}{x-2\dot{y}}-\frac{\pi }{2}\hbox {sign}\left[ {\frac{y+2\dot{x}}{x-2\dot{y}}} \right] -\frac{\pi }{2}\hbox {sign}(y+2\dot{x}) \end{aligned}$$
(16)

2.4 Initial deflection

The totally number of the rod is 8, as shown in Fig. 2. Rods are uniformly distributed on the circle in which radius is r. The pre-tightening force of the ith rod is \(\mathbf{F}_{\mathbf{i}}\), and the bending moment, in which rod pre-tightening force acts on the disk center, is \(\mathbf{M}_{\mathbf{i}}\).

$$\begin{aligned} \mathbf{M}=\sum _{i=1}^8 {\mathbf{M}_\mathbf{i} } =\sum _{i=1}^8 {\mathbf{F}_\mathbf{i} \cdot \mathbf{r}} \end{aligned}$$
(17)

The bending moments, in which rods pre-tightening force acts on the disk center, are sum to zero when rods pre-tightening forces are equal; otherwise, the disk will be subjected to the effect of additional bending moment. Assume that the rods pre-tightening force is F, if one rod has unbalanced pre-tightening force \(\mathbf{F^{\prime }}\), defined the unbalanced level of the rod pre-tightening force \(\Delta \) and \(\Delta =\frac{\mathbf{F}-{\mathbf{F}'}}{\mathbf{F}}\). The bending moment acting on the disk is as follows

$$\begin{aligned} \mathbf{M}=\sum _{i=1}^8 {\mathbf{M}_\mathbf{i} } =\sum _{i=1}^8 {\mathbf{F}_\mathbf{i} \cdot \mathbf{r}} =\Delta \mathbf{F}\cdot \mathbf{r} \end{aligned}$$
(18)
Fig. 2
figure 2

Uniform distribution of the rods

Full size image
Fig. 3
figure 3

Schematic of rotor deformation

Full size image

Figure 3 is the schematic of rotor deformation. The length of the rotor is L, and additional bending moment M is caused by the unbalanced pre-tightening force. As shown in Fig. 3, according to the definition of bending stiffness, the \(\theta \) is expressed by

$$\begin{aligned} \theta =\frac{ML}{EI} \end{aligned}$$
(19)

where E is elasticity modulus, \(E=2.08\times 10^{11}\) Pa, and I is the inertia moments.

The initial deflection of the disk under the bending moment M is the following

$$\begin{aligned} \delta _0 =\frac{L}{\theta }\left( {1-\cos \left( {\frac{\theta }{2}} \right) } \right) =\frac{EI}{M}\left( {1-\cos \left( {\frac{\theta }{2}} \right) } \right) . \end{aligned}$$
(20)

3 Solving method

Considering the nonlinear oil-film force, unbalance mass and the initial deflection caused by the unbalanced pre-tightening force, the established model of the rotor bearing system has strong nonlinearity, and it is difficult to solve the model using analytical method. Numerical integration methods play an important role in studying the dynamic characteristics of strong nonlinear system, and it can calculate the response of the system and calculate the effect of parameters on the system behavior.

Runge–Kutta method is one of the numerical methods to solve differential equations, and fourth-order Runge–Kutta method is mostly used and also has high precision relatively.

The normal form of the Runge–Kutta method is as follows

$$\begin{aligned} \left\{ {\begin{array}{ll} Y_{n+1} =Y_n +h\sum \limits _{i=1}^r {c_i } K_i &{} \quad i=2,3,\ldots ,r \\ K_1 =F(t_n ,Y_n ) \\ K_i =F\left( t_n +\lambda _i h,Y_n +h\sum \limits _{j=1}^{i-1} {\mu _{ij} } K_j \right) &{}\quad \lambda _i =\sum \limits _{j=1}^{i-1} {\mu _{ij} } \\ \end{array}} \right. \end{aligned}$$
(21)

After determining the order number, through Taylor expansion and comparing coefficient of both sides, the coefficient \(c_{i}\), \(\lambda _{i}\), \(\mu _{ij}\) can be determined.

The fourth-order Runge–Kutta method is expressed as follows

$$\begin{aligned} \left\{ {\begin{array}{l} Y_{n+1} =Y_n +\frac{h}{6}\left[ {K_1 +2K_2 +2K_3 +K_4 } \right] \\ K_1 =F(t_n ,Y_n ) \\ K_2 =F\left( t_n +\frac{1}{2}h,Y_n +\frac{h}{2}K_1 \right) \\ K_3 =F\left( t_n +\frac{1}{2}h,Y_n +\frac{h}{2}K_2\right) \\ K_4 =F\left( t_n +h,Y_n +hK_3\right) \\ \end{array}} \right. . \end{aligned}$$
(22)

4 Results and discussion

The parameters of the rod fastening rotor and journal bearing are shown in Table 1. The stiffness of the right journal bearing is the same as that of the left bearing. The critical speed of the system without considering initial deflection is 710 rad/s approximately as shown in Fig. 4a. The nonlinear dynamic behaviors of the rod fastening rotor bearing system are performed by using the fourth-order Runge–Kutta method and implemented in MATLAB. Bifurcation diagram, vibration waveform, frequency spectrum, phase trajectory and Poincare map are presented to illustrate the nonlinear dynamic phenomena of system.

Table 1 Parameters of the rotor and bearing
Full size table

Unbalanced pre-tightening force of rod will generate additional bending moments acting on disk and initial deflection. Initial deflection is an important nonlinear factor in the dynamic analysis of the rotor bearing system. Figure 4 is the curve of the maximum vibration displacement of disk in radial direction changing with speed under different initial deflections. It can be seen from Fig. 4a that the curve appears one peak near 710 rad/s, and a small pear near 1130 rad/s. The first critical speed of the system is about 710 rad/s without initial deflection. Compared with Fig. 4a, the response amplitude of the first critical speed decreases when the initial deflection is a small value. As shown in Fig. 4c, d, the response amplitude of the first critical speed increased with the increase in initial deflection.

Fig. 4
figure 4

The maximum vibration displacement of disk in radial direction a \(\delta _{0}=0\), b \(\delta _{0}=10\,\upmu \hbox {m}\), c \(\delta _{0}=30\,\upmu \hbox {m}\) and d \(\delta _{0}=50\,\upmu \hbox {m}\)

Full size image
Fig. 5
figure 5

Bifurcation diagram of rotor with a \(\delta _{0}=0\), b \(\delta _{0}=10\,\upmu \hbox {m}\), c \(\delta _{0}=30\,\upmu \hbox {m}\) and d \(\delta _{0}=50\,\upmu \hbox {m}\)

Full size image

Figure 5 is the bifurcation diagrams of horizontal displacement at the bearing location for four different initial deflections \(\delta _{0}=0\), \(\delta _{0}=10\,\upmu \hbox {m}\), \(\delta _{0}=30\,\upmu \hbox {m}\), \(\delta _{0}=50\,\upmu \hbox {m}\). In Fig. 5a, it can be seen that at a lower speed, \(\omega \leqslant 864\) rad/s, the system keeps periodic-1 motion, which is shown as one isolated point in Fig. 6d and one obvious frequency component in Fig. 6b, at a speed of \(\omega =731\) rad/s the system occurs subcritical bifurcation and generates a jump, and the system may occur multiple attractors near the 731 rad/s. When the speed reaches near the 864 rad/s, the system turns into a periodic-2 motion. It can be seen from Fig. 7a that the time domain waveform of the response has two frequency components, which performs as two obvious peaks in Fig. 7b and two isolated points in Fig. 7d. When the speed is in the range of \(946\,\hbox {rad/s}\leqslant \omega \leqslant 1039\,\hbox {rad/s}\), the system becomes a periodic-4 motion, which is shown as four isolated points in Fig. 8d. When \(1039\,\hbox {rad/s}\leqslant \omega \leqslant 1369\,\hbox {rad/s}\), the system returns into periodic-2 motion again. With the increasing speed, the system response finally presents a periodic-1 motion.

Fig. 6
figure 6

Numerical analysis results at \(\omega =821\) rad/s, \(\delta _{0}=0\). a Time domain waveform, b frequency spectrum, c phase trajectory and d Poincare map

Full size image
Fig. 7
figure 7

Numerical analysis results at \(\omega =906\) rad/s, \(\delta _{0}=0\). a Time domain waveform, b frequency spectrum, c phase trajectory and d Poincare map

Full size image
Fig. 8
figure 8

Numerical analysis results at \(\omega =962\) rad/s, \(\delta _{0}=0\). a Time domain waveform, b frequency spectrum, c phase trajectory and d Poincare map

Full size image

Figure 5b is the bifurcation diagram of the rod fastening rotor bearing with \(\delta _{0}=10\,\upmu \hbox {m}\). It can be seen from Fig. 5a, b that the bifurcation diagrams of the system have a little difference. The system still keeps periodic-1 motion at a low speed, \(\omega \leqslant 825\) rad/s, and the jump phenomenon disappears. Before the system comes into periodic-2 motion, the system has experienced a transient quasiperiodic process with \(825\,\hbox {rad/s}<\omega <872\,\hbox {rad/s}\). As shown in Fig. 9d, the Poincare map of the quasiperiodic motion presents a closed loop, and the frequency spectrum in Fig. 9b contains presumably incommensurate frequencies. At the speed of \(\omega =919\) rad/s, the system occurs bifurcation, the periodic-2 motion turns into periodic-4 motion, and at \(\omega =1042\) rad/s, the system returns to the periodic-2 motion again. Figure 10 is the numerical analysis results at \(\omega =1020\) rad/s, \(\delta _{0}=10\,\upmu \hbox {m}\), the main components in frequency spectrum are the n/4 times excitation frequency, and the system is in frequency locking. With the increase in speed, the system finally presents periodic-1 motion when the speed over 1367 rad/s.

Fig. 9
figure 9

Numerical analysis results at \(\omega =864\) rad/s, \(\delta _{0}=10\,\upmu \hbox {m}\). a Time domain waveform, b frequency spectrum, c phase trajectory and d Poincare map

Full size image
Fig. 10
figure 10

Numerical analysis results at \(\omega =1020\) rad/s, \(\delta _{0}=10\,\upmu \hbox {m}\). a Time domain waveform, b frequency spectrum, c phase trajectory and d Poincare map

Full size image

It can be seen from Fig. 5c that the system response becomes more complicated under \(\delta _{0}=30\,\upmu \hbox {m}\). Compared with Fig. 5b, the quasiperiodic motion happens earlier and the quasiperiodic region expands with \(721\,\hbox {rad/s}<\omega <835\,\hbox {rad/s}\). With the increase in the speed, the periodic-4 motion is destroyed and the system occurs periodic-6 motion under certain conditions. Figure 11 is the response of the system at \(\omega =946\) rad/s, and the system presents periodic-6 motion, which is shown as six isolated points in Fig. 11d and six obvious frequency components in Fig. 11b.

Fig. 11
figure 11

Numerical analysis results at \(\omega =946\) rad/s, \(\delta _{0}=30\,\upmu \hbox {m}\). a Time domain waveform, b frequency spectrum, c phase trajectory and d Poincare map

Full size image

Figure 5d is the bifurcation diagram of the rod fastening rotor bearing with \(\delta _{0}=50\,\upmu \hbox {m}\). With the increase in initial deflection, the quasiperiodic motion disappears. The system keeps a periodic-1 motion at a lower speed, and near the critical speed, the system occurs jump phenomenon and turns into periodic-2 motion. The system keeps periodic-4 motion with \(901\,\hbox {rad/s}<\omega <1120\,\hbox {rad/s}\), and the trajectory of the bifurcation diagram intersects at certain points. Continuing to increasing the speed, the system keeps periodic-2 motion, and when the speed is over 1403 rad/s, the system finally presents a periodic-1 motion.

5 Conclusions

In this paper, a model of a rod fastening rotor bearing system is established based on the Lagrange’s equations. The nonlinear dynamic and bifurcation characteristics of the rod fastening rotor bearing system under unbalanced pre-tightening force have been investigated by the fourth-order Runge–Kutta method. Bifurcation diagram, vibration waveform, frequency spectrum, phase trajectory and Poincare map are presented to illustrate the nonlinear dynamic phenomena of system. The following conclusions can be obtained from the above research.

  1. (1)

    With the changing of rotational speed and initial deflection, the system status alternates among period-1, multiperiodic, quasiperiodic motion. Under certain conditions, the system occurs amplitude jump and frequency locking.

  2. (2)

    When the initial deflection equals to zero, at a lower speed, the nonlinear oil-film force is small, and the system keeps period-1 motion. With the increase in speed, the influence of nonlinear oil-film force on the system response becomes bigger, and the system occurs half frequency oil whirl near the critical speed.

  3. (3)

    With the increase in initial deflection, the system occurs quasiperiodic motion. When the initial deflection reaches 50 \(\upmu \hbox {m}\) the quasiperiodic motion disappears. The system bifurcation for period-2 motion happens earlier with the increasing of initial deflection.

  4. (4)

    The critical speed of the system is about 710 rad/s, and the response amplitude of the disk is near the critical speed changing with initial deflection.

The corresponding results can provide the guidance for the fault diagnose of a rod fastening rotor with unbalanced pre-tightening force; meanwhile, the study may contribute to the further understanding of the nonlinear dynamic characteristics of a rod fastening rotor with unbalanced pre-tightening force.

The further research work will be concentrated on the modeling of the stability analysis of the rod fastening rotor with initial deflection caused by the unbalanced pre-tightening force in detail.