Modelling of a Cellular Rubber with Nonlinear Viscosity Functions

Abstract

In this paper a porous carbon black-filled rubber is investigated under uniaxial tension. On the experimental site the main focus of attention lies on the Mullins effect, the thixotropic and the viscoelastic behaviour. Because of the two phase character of cellular rubber, the Theory of Porous Media is taken into account. Performing a proper preconditioning, the Mullins effect can be eliminated. Hence, it is not included in the material model. The constitutive model for the basic elasticity is based on a polynomial approach for an incompressible material which is expanded by a volumetric term to include the structural compressibility. Finally, the concept of finite viscoelasticity is applied introducing an intermediate configuration. Nonlinear relaxation functions are used to model the process dependent relaxation times, to simulate the thixotropy and the highly nonlinear behaviour concerning the deformation and feedrate. The material parameters of the model are estimated using a stochastic identification algorithm.

Introduction

Cellular rubber is a mixed open- and closed-cell foamed rubber enclosed by a moulding skin. Because of its diverse range of application [1] and also of other polymer foams [2], e. g. in the automotive engineering, researchers are interested in describing the mechanical behaviour of this material. While a variety of research concerns the manufacturing process of the investigated material [3–6], this paper introduces an experimentally motivated material model based on the Theory of Porous Media. Therefore, uniaxial cyclic tests and relaxation tests are performed. These experiments are evaluated to quantify the Mullins effect [7–11] and the thixotropic behaviour [12]. Furthermore the basic elasticity and the viscoelastic behaviour are observed. On the theoretical side a phenomenological material model for cellular rubber is formulated. As the Mullins effect can be eliminated using a proper preconditioning, it can be neglected in the model at this moment. The particular difficulty related to the structural compressibility is solved by the use of a so-called hybride two-phase model consisting of a materially incompressible porous matrix saturated by a compressible pore gas [13, 14]. Therein the pore pressure is simulated by the ideal gas law introduced by Clapeyron [15], and in the case of the basic elasticity a modified Yeoh model [16] with an extended compression term [17] is taken into account. Furthermore, the observed thixotropic behaviour and the viscoelasticity are included in the model. For the thixotropy no additional structural parameter is used, as proposed by Haupt [18] or Sedlan [19]. It can be represented by the conventional theory for viscoelastic materials, see [9, 20–25]. Moreover a dependency of the relaxation behaviour on the deformation is found during the experiments. In the case of the cyclic tests the following anomaly is also found: Both the size of the hysteresis loop and the maximum of the overstress are nearly independent of the different feedrates, i.e. variations of the feedrate in a certain range only have small influence on the hysteresis. To simulate these high nonlinearities with respect to the deformation and feedrates, nonlinear relaxation times in four Maxwell elements are introduced.

Experiments

Samples and Measurements

The investigations are accomplished to foamed EPDM. The porosity of the used material amounts to approximately 50%. While the investigated material is commercially available from the industry no statement can be made according to the chemical composition. The pore size is around 2–3 · 10^− 4 m. For the experiments two different sample geometries are used. On the one hand dogbone specimens are investigated according to ISO 527, see Fig. 1, and on the other hand cylindrical specimens, cf. Fig. 2. The dogbone samples are diecut from car door gaskets. The cylindrical specimens have a diameter of 9 mm and a length of 130 mm. They are cut from bulk stock used in this form by industry. These different sample forms have been used to study the influence of geometry on the material behaviour. The cardinal difference of the two geometries lies in the moulding skin. The cylindrical samples are surrounded by a closed moulding skin, while in the case of the dogbone specimen the pores are visible at all edges. Therein the moulding skin is only on the upper and lower surface of the sample.

Fig. 1

Dogbone specimen according to ISO 527

Fig. 2

Cylindrical specimen

With both sample geometries the experiments are accomplished in a custom-made tensile tester, see Figs. 3 and 4. The testing device is based on a uniaxial force-way measuring system where the specimen is fixed by clamps at both ends and streched by a linear table. The deformation is measured by an optical method. Therefore, the specimen is marked with silkscreen colour. At the beginning of the investigation the painted measuring field is mapped by a camera. With the help of the image editing software NI VISION ASSISTANT the initial length l ₀ and width b ₀ of the measuring field are calculated by counting the pixels over a clamp function in length direction and in transverse direction, see Fig. 5. Afterwards different machine ways are approached and at each stage a picture is taken. Again, using the clamps function, the length l and the width b are calculated corresponding to the current machine way.

Fig. 3

Custom-made tensile tester

Fig. 4

Custom-made tensile tester

Fig. 5

Clamp function on the mark

In Fig. 6 a series of the recorded measuring fields during a measurement is shown. To avoid errors in this method, the contrast between the sample and the mark is elected as large as possible. Besides attention must be paid to the fact that no cracks result in the mark, i.e. the silkscreen colour must not be totally dried. Based on the correlations

$$ \lambda_1\,=\,\frac{l}{l_0},\lambda_2\,=\,\frac{b}{b_0} $$

(1)

the stretch in tension direction λ ₁ and in transverse direction λ ₂ can be calculated depending on the machine way U. A linear relation between the stretches and the machine way is established

$$\begin{array}{lll} \lambda_1(U)&=&1+0.032\,\displaystyle\frac{1}{\rm{mm}}\,U, \\ \lambda_2(U)&=&1-0.005\,\displaystyle\frac{1}{\rm{mm}}\,U.\end{array}$$

(2)

A similar method is used in [26] and [27].

Fig. 6

Series of the sample mark for different deformations

Another way to determine the deformation is the digital image correlation (DIC). In this method, a speckle pattern is applied on the sample. With the help of an image editing software the speckle patterns of the undeformed sample are compared to those of the deformed sample, see [28]. With these results, the deformation of the sample is determined everywhere inside a measurement window, while the method described before only determines the average deformation in the center of the sample. DIC is used especially in inhomogeneous deformation states, but for the used specimen geometries it can be assumed that the deformation field in the middle of the sample is homogeneous. To verify this statement, results of both measurement methods are compared. As expected, it is found that there do not exist any differences in the investigated case. In general the application of both methods is possible, but in view of the homogeneity of the measuring field the easier one is used.

Thereon in the case of the dogbone specimen, the thickness direction is mapped by the camera to approve the isotropy assumption. In this way the same machine ways as before are applied and λ ₃ is determined in analogy to λ ₁ and λ ₂. Therewith, the isotropy assumption is approved, that means λ ₃  =  λ ₂. This study is not necessary in the case of the cylindrical specimen due to the symmetry. Using these values, the Jacobian J can be calculated. The Jacobian is the determinant of the deformation gradient F and yields in the homogeneous uniaxial tension test under the isotropy assumption

$$ J\,=\,\det\,{\bf F}\,=\,\lambda_1\,\lambda_2\,\lambda_3\,=\,\lambda_1\,\lambda_2^2. $$

(3)

The Jacobian is a measure for the volume change. In the case of incompressible materials it is 1 during the whole experiment. Due to the porous structure of cellular rubber the Jacobian changes during the experiment and thus it is a key size for the used material representing the structural compressibility.

The stretches are also required to calculate the Cauchy stress. Thereby the force F in loading direction is measured via a force sensor in form of a S-bracket. With the relation

$$ T_{11}\,=\,\frac{F}{A_0\,\lambda_2^2} $$

(4)

the Cauchy stress T ₁₁ in tension direction is determined, wherein A ₀ stands for the initial cross section surface.

The relationship between machine way and deformation is also used for the implementation of the cyclic experiments. In these experiments the sample is loaded repetitively up to a maximum value and afterwards it is unloaded, see Fig. 7. These tests are performed with different deformation rates. Therefore, a constant feed rate is pretended and over the relation (2) this can be converted in the material deformation rates $\dot{\lambda}_1,\,\dot{\lambda}_2$. Because of the linear relation between machine way and deformation the deformation rate is constant.

Fig. 7

Saw tooth function of the deformation over the time as measured during cyclic tests

Experiments and Analysis

At first the effect of the different sample forms is examined concerning the material behaviour. Therefore the basic elasticity of both forms is investigated. The specimens are submitted first to a pretreatment. Besides, the samples are deformed ten times up to a maximum. This serves to eliminate the Mullins effect appearing in rubber like materials. On this effect it is even more exactly entered later. After the pretreatment, the basic elasticity is examined. Therefore three different methods exist:

• In the first method a quasi-static process with the slowest possible feedrate is performed. In our case this results in $\dot{\lambda}_1\,=\,0.000265$ s^− 1. In this experiment the rubber still shows a hysteresis in the stress-strain diagram. Thus, the basic elasticity cannot be obtained with this process.

• As a second possiblity the basic elasticity is obtained from relaxation tests. These stepwise tests are performed at the loading and unloading paths. After 30 min of holding time the stress values of the two relaxation tests still differ around 30% for the used material. For that reason, the basic elasticity cannot be determined by this method.

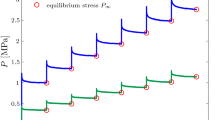
• The third method to obtain the basic elasticity is based on cyclic tests around a medial strain. In these tests a certain deformation is chosen and cyclic tests around this deformation are performed. In Fig. 8 a medial strain of 60% is chosen corresponding to λ ₁ = 1.6. Increasing the number of cycles leads to a decrease of the stress-strain curves until a stationary hysteresis loop is obtained. In Fig. 8 the first 50 cycles are shown. If the last cycle is assumed to represent the stationary hysteresis the value of the equilibrium stress at λ ₁ = 1.6 is found as average value of the stress values in the rising and falling branches of the hysteresis at this point. The stress-strain response is constructed by repeating this procedure for different values of λ ₁.

For the used material the basic elasticity can be obtained more easily and faster with the third method. In that respect the basic elasticity is recorded by this method and the results of the two geometries are shown in Fig. 9. It can be seen that there exists no difference between the two geometries in the case of the basic elasticity. During these tests the viscoelastic behaviour is observed, too. And also there are no great differences. For that reason, no additional parameter for the sample form is needed in the model and in the following the investigations are only examined with the dogbone specimens.

Fig. 8

Cyclic tests to get the basic elasticity

Fig. 9

Basic elasticity of cellular rubber for two different geometries

As described before, an effect of carbon black-filled rubber is the Mullins effect which should be clearly explained in this section. There exist two different explanations of the Mullins effect in the literature. On the one hand the Mullins effect is described as stress softening, see [29]. It contents of an irreversible and a reversible stress softening. The irreversible part can be explained with the breakage of some network junction points and it appears only in the first cycle of a virgin specimen. The reversible part is the decay of the hysteresis in the follwing cycles. This part can be observed each time after a certain period of recovery.

On the other hand researchers see and model the Mullins effect as an irreversible effect. Nevertheless if the specimen is loaded once the stress-strain curve of the first cycle will never be obtained, see [30] and [31]. In the following the name Mullins effect is used for the irreversible stress softening observed in the first loading cycle. At the beginning the magnitude of the Mullins effect is investigated. Therefore, a previously unloaded (virgin) specimen is loaded ten times and recovered for 1 week. Then the same test is performed again, see Fig. 10. The red curve shows the first run while the black curve shows the results of the second run. A significant stress drop can be observed after the first cycle of the first run. Then the hysteresis loop falls slower. The first cycle of the second run, obtained after a recovery of 1 week, is above the last cycle of the first run, but below the first cycle of the virgin specimen. Thus, it was found that there exists an irreversible breakage of bondings, which cannot be recovered without an external input of energy. Hence, this irreversible effect will be neglected in the model, because it has no importance for the application. The gasket can be loaded one time before use. Thus, as a pretreatment every specimen is loaded ten times until the maximum of the investigated deformation range and recovered 1 week for each experiment. Hence, reversible material behaviour will be included into the model.

Fig. 10

Mullins effect of cellular rubber

During these experiments another effect can be observed. After the recovery time the stress of the first cycle is above the last one of the experiment performed on the virgin specimen. This healing effect can have two causes: On the one hand this healing results from the viscoelasticity itself and on the other hand a thixotropic effect can occur. The item thixotropy originates from rheology and it is used to describe viscous effects of fluids [32]. One assumes that damage and healing effects lead to a softening by cyclic loadings and hardening during the recovery, respectively, as can be seen in the experiment. Moreover, thixotropic material behaviour has an influence on the relaxation time, cf. Sedlan [19]. To specify this effect the same test is repeated after a recovery of 1 day, see Fig. 11. It can be seen that the stress level during the first cycle of the experiment after a recovery of 1 day is below that one of 1 week. Thus the healing process is not finished after 1 day. For more information concerning this effect relaxation tests with different pretreatments are performed. The blue curve in Fig. 12 shows the relaxation without any pretreatment, the red curve with a cyclic pretreatment and the black one shows the corresponding basic elasticity. In this figure it can be clearly seen that the relaxation time is strongly depending on the pretreatment. Using these experiments the investigated material could be identified as thixotropic, but the behaviour could be explained by pure viscoelasticity, if very long relaxation times are taken into account. Because of the specimens’ geometry the material buckles at the end of a cycle, so the required stress to get the same deformation in the second cycle is below to that one of the first cycle. During the recovery, a relaxation takes place and therefore the required stress is above the last one of the cycles before. The phenomenon during the relaxation tests can be explained by the same argumentation. Consequently it cannot be said doubtlessly whether this material is thixotropic or only viscoelastic. However vulcanised materials do not contain healing effects at constant room temperature. For that reason it is assumed that the observed effect originates from the viscoelasticity only. For this physical reason the observed phenomenon should not be modelled with an additional structural parameter as introduced e. g. in [18, 19, 33, 34], but only with the theory of viscoelasticity including sufficiently long relaxation times. To quantify the viscoelastic behaviour additional relaxation tests are needed. Therefore, investigations at seven different deformation levels are performed, see Fig. 13. It can be seen that the greater the deformation, the greater the overstress. To see the difference between relaxation times at different deformation levels, three of the performed experiments are plotted in Fig. 14 with the corresponding stress answer of the basic elasticity. In each experiment the basic elasticity is not reached after a holding time of 30 min. It can also be seen that the relaxation time is depending on the deformation. After 30 min the obtained stress value for a deformation of 31% is 36% above the basic elasticity value. In the case of 60% deformation the value is around 18% and in the last case of 86% deformation only 13% above. For that reason it can be said that for larger deformation levels less time is needed to reach the basic elasticity. This has to be included in the constitutive model.

Fig. 11

Cyclic tests after different time of recovery

Fig. 12

Relaxation tests with different pretreatments

Fig. 13

Relaxation tests for different deformation levels

Fig. 14

Three different relaxation tests with the corresponding basic elasticity

After these examinations one relaxation test is performed over 20,000 s. It is observed that even after 20,000 s the stress is steadily decline and the basic elasticity can not be reached, see Fig. 15 in a logarithmic presentation. For that reason relaxation times greater than 20,000 s are needed in the model to represent the measured data.

Fig. 15

Relaxation tests with the corresponding basic elasticity over 20,000 s

Moreover cyclic tests at three different feedrates from 0.265 to 0.00265 s^− 1 are performed using five cycles. Figure 16 shows the results of the fastest feedrate, Fig. 17 the medial one and Fig. 18 the slowest one. In every experiment a rapid decay of the stress with respect to the first cycle is observed. It is also important to mention that concerning the feedrate both the size of the hysteresis loop and the maximum stress value do not change significantly. This nonlinearity has to be recognised in the model.

Fig. 16

Cyclic test with a constant feedrate of 0.265 s^− 1

Fig. 17

Cyclic test with a constant feedrate of 0.0265 s^− 1

Fig. 18

Cyclic test with a constant feedrate of 0.00265 s^− 1

With these experimental data at hand conclusions can be made to introduce an experimentally based material model in the following chapter.

Modelling Aspects and Parameter Identification

Theoretical Modelling

The cellular rubber is macroscopically characterised as a two phase material. It consists of a solid and a gas phase. Such problems show a special challenge in mechanics. They can be solved in different ways. On the one hand each individual component of the material can be looked at independently with the help of the one phase material theory. This possibility is very costly and, besides, additional contact and intersection conditions must be formulated. This is very difficult on account of the often unknown internal pore structure and the geometry of the single bodies. Another modelling approach consists on a homogenisation procedure of the mixture. On this occasion, not the single bodies are investigated, but the physical properties of the material are returned on average. This association is the basis of the mixture theory which was introduced in Truesdell [35] and Truesdell and Toupin [36]. However, in this theory no volumetric measure of the immiscible constituents of the mixture is included, so that with porous media is recoursed, in addition, to the concept of volume fraction, see [37]. The Theory of Porous Media [37, 38] consists of these two concepts and is used in the following for the description of the material. In Fig. 19 one can see on the left the porous structure of the material under scanning electron micrograph under 300-fold enlargement. In the middle the microstructure is shown schematically and on the right the macro model of the structure within the scope of the Theory of Porous Media with the volume fraction of the gas phase dv ^G and of the solid phase dv ^S. According to the saturation constrain it holds for the total volume dv  =  dv ^S + dv ^G. Because the material consists of an incompressible solid phase and a compressible gas phase, it is fallen back on the so-called hybride model, see [13, 14]. Thereby the structural compressibility of the material can be illustrated. From the physical point of view macroscopic volumetric deformations result from changes of the pore space. For simplicity closed pores are assumed, i.e. the porous solid and the pore gas undergo the same motion and the flow of the gas relative to the deforming matrix is neglected. While the basic elasticity of the cellular rubber is influenced by the solid and the gas phase, one supposes that the viscoelastic behaviour originates only from the solid phase. Viscous effects resulting from the gas flow are neglected. To illustrate the finite viscoelastic behaviour of the material a rheological model is used consisting of a parallel connection of a single spring which illustrates the basic elasticity, and a series of spring-dashpot-elements (Maxwell elements), see Fig. 20. Starting with this basic elasticity the internal energy balance and the entropy balance are coupled to the Clausius–Duhem inequality or, because isothermal processes are assumed, to the Clausius–Planck inequality

$$\label{clausius} -\,\rho^S\,\dot{\Psi}^S_{eq}\,-\,\rho^G\,\dot{\Psi}^G_{eq}+\,\big({\bf T}^S_{eq}\,+\,{\bf T}^G_{eq}\big)\,:\,{\bf D}\,\geq\,0 $$

(5)

with the density of the solid phase ρ ^S and that one of the gas phase ρ ^G, the equilibrium parts of the Cauchy stress tensor of the solid ${\bf T}_{eq}^S$ and of the gas phase ${\bf T}_{eq}^G$ and the deformation rate D. The partial densities ρ ^α are related to the effective densities ρ ^αR by the volume fraction ρ ^α  =  n ^α ρ ^αR. $\Psi_{eq}^S$ is the equilibrium part of the specific free Helmholtz energy of the solid phase and $\Psi_{eq}^G$ that one of the gas phase. Each value is defined with respect to the current configuration. The concept of constitutive seperation of variables is applied. The process variables are ${\cal S}\,=\,\{\,\rho^{GR},\,{\bf B}\}$, wherein ρ ^GR stands for the effective gas density and B  =  F · F ^T is the left Cauchy–Green deformation tensor. The evaluation of the entropy principle according to Coleman and Noll [39] yields in the following form for the Cauchy stress for the two phases

$$\begin{array}{lll}\label{Teq1} {\bf T}^S_{eq}&=&-n^S\,p^{GR}\,{\bf I}+2\,{\bf B}\,\rho^S\,\displaystyle\frac{\partial \Psi_{eq}^S}{\partial {\bf B}}, \\{\bf T}^G_{eq}&=&-n^G\,p^{GR}\,{\bf I},\end{array}$$

(6)

with the partial density of the solid ρ ^S  =  n ^S ρ ^SR, the pore pressure p ^GR and the volume fractions of solid n ^S and gas phase n ^G in the current configuration. This expression results from the assumption of an in-phase motion of the gas and solid phase, i.e. from the assumption that all pores are closed. Therewith the Cauchy stress of the mixture can be calculated as

$$\label{Teq} {\bf T}_{eq}\,=\,{\bf T}_{eq}^S\,+\,{\bf T}_{eq}^G\,=\,-\,p^{GR}\,{\bf I}+2\,{\bf B}\,\rho^S\,\displaystyle\frac{\partial \Psi_{eq}^S}{\partial {\bf B}}. $$

(7)

At this point the pressure term is needed. Therefore the relation between the reference and the current configuration has to be determined, see Fig. 21. On account of the effective incompressibility of the solid phase one receives after some arithmetic steps the following connection between the reference volume V ₀ and the current volume V of the mixture

$$\label{volume} V\,=\,J\,V_0. $$

(8)

Because of the assumption of the closed pores, the mass of the gas phase enclosed in the pores is identical in both configurations. This statement in combination with (8) yield in

$$ \frac{\rho_0^{GR}}{\rho^{GR}}\,=\,\frac{n^G\,J}{n_0^G}, $$

(9)

with the effective density $\rho_0^{GR}$ of the gas phase in the reference configuration, ρ ^GR in the current configuration and the volume fraction $n_0^G$ of the gas phase in the reference configuration. With the saturation condition

$$ n^G\,=\,1\,-\,n^S $$

(10)

and the ideal gas law [15] the pressure term results in

$$ p^{GR}\,=\,p_0\,\left(\frac{1-J}{J-n_0^S}\right), $$

(11)

with the initial solidity $n_0^S$ and the ambient pressure p ₀. For the free Helmholtz energy a modified Yeoh model [16] with a point of compaction [17] is introduced:

$$\begin{array}{lll}\label{psi_eq} \rho_0^S\,\Psi_{eq}^S&=&c_{10}\,\left({\rm I}_{\bf B}\,-\,3\right)\,+\,c_{20}\,\left(\frac{1}{2}{\rm I}_{\bf B}^2\,-\,3\,{\rm I}_{\bf B}\right) \\ &&+\,c_{30}\,\left(\frac{1}{3}{\rm I}_{\bf B}^3\,-\,9\,{\rm I}_{\bf B}\right)\,-\,2\,c_{10}\,\ln\,J \\ &&+\,\displaystyle\lambda\,(1-n_0^S)^2\,\left[\frac{J-1}{1-n_0^S}-\ln\,\frac{J-n_0^S}{1-n_0^S}\right],\end{array}$$

(12)

with the first invariant of the left Cauchy–Green deformation tensor I _B  = B:I. The model parameters for the basic elasticity are the stiffness parameters c ₁₀, c ₂₀ and c ₃₀ and the structural bulk modulus of the mixture λ. At this point only uniaxial tension tests are performed. For this kind of experiments the second invariant does not give any benefit. The extended volumetrical term leads to an infinite energy if the pores are closed, i.e. J  =  n ^S. Further improvements may also be needed if the data pool contains results of compression tests. Using the free Helmholtz energy (12) and equation (7) with $\rho^S\,=\,J^{-1}\,\rho_0^S$ the Cauchy stress for the equilibrium part reads

$$\begin{array}{lll} \label{teq} {\bf T}_{eq}&=&-\,p^{GR}\,{\bf I}\\ &&+\,2\,J^{-1}\,\left(\,\left[c_{10}\,+\,c_{20}\big({\rm I}_{\bf B}-3\big)\,+\,c_{30}\big({\rm I}_{\bf B}^2-9\big)\right]\,{\bf B}\vphantom{\frac12}\right.\\ &&{\kern40pt}-\,c_{10}\,{\bf I}+\,\frac{1}{2}\,\lambda\,\big(1-n_0^S\big)^2 \\ &&{\kern40pt} \left.\times\left[\frac{J}{1-n_0^S}-\frac{J}{J-n_0^S}\right]\,{\bf I}\right). \end{array}$$

(13)

Therewith the stress in the single spring of Fig. 20 can be modelled completely. The total stress is the summation of the equilibrium part in the single spring T _eq and n non-equilibrium parts of the Maxwell elements ∑  _n T _neq representing the viscoelastic parts of the system.

Fig. 19

Porous structure under a scanning electron micrograph (left), schematic microstructure (middle), smeared macro model (right)

Fig. 20

Rheological model of the viscoelastic behaviour with n Maxwell elements

Fig. 21

Reference configuration of the macro model (left); volumetrical tension of the macro model (right)

In the theory of finite viscoelasticity a multiplicative split of the deformation gradient tensor F into an elastic part F _e and an inelastic part F _i is introduced for each Maxwell element F  =  F _e · F _i . The implementation is realised applying the concept of deformation-valued internal variables. At this point only some of the existing works should be mentioned [9, 19–21, 23–25, 39–49]. In this context a fictitious intermediate configuration is introduced for each Maxwell element. Because of the multiplicative split of the deformation gradient, the Jacobian can also be split in an elastic part J _e and an inelastic part J _i . The used material is compressible on the macroscale, therefore the Jacobian is unequal to 1. The elastic part and the inelastic part of the Jacobian have to be unequal to 1 if a deformation is applied. The inelastic deformation of the dashpots in the reference configuration is described by the inelastic right Cauchy–Green deformation tensors ${\bf C}_i^j:=\,{\bf F}_i^{jT}\,\cdot\,{\bf F}_i^j$. The deformation of the spring within the Maxwell elements are meanwhile described in the current configuration by the elastic left Cauchy–Green deformation tensors ${\bf B}_e^j:=\,{\bf F}_e^j\,\cdot\,{\bf F}_e^{jT}$. Besides in the case of the non-equilibrium stresses the Clausius–Planck inequality can be derived to

$$ -\,\hat{\rho}\,\dot{\Psi}_{neq}^j\,+\,{\bf M}_{neq}^j\,:\,(\stackrel{\triangle}{\bf \Gamma})^j\,\geq\,0, $$

(14)

with the corresponding values of equation (5) defined on the intermediate configuration, the non- equilibrium stress of the Mandel type M _neq and the objective rate $(\stackrel{\triangle}{\bf \Gamma})^j$ of the deformation tensor Γ = $\frac{1}{2}\,\left[{\bf F}_e^T\,\cdot\,{\bf F}_e\,-\,{\bf F}_i^{-T}\,\cdot\,{\bf F}_i^{-1}\right]$. After some calculations the Clausius–Planck inequality may be re-written with the process variable ${\bf C}_e^j$

$$\begin{array}{lll} &&{\kern-6pt} \displaystyle{\bf M}_{neq}^j\,:\,(\stackrel{\triangle}{\bf \Gamma})^j-\displaystyle2\,\hat{\rho}\,\frac{\partial\,\Psi_{neq}^j}{\partial {\bf C}_e^j}\,:\,(\stackrel{\triangle}{\bf \Gamma})^j\notag\\ &&-\displaystyle\hat{\rho}\,\frac{\partial\,\Psi_{neq}^j}{\partial {\bf C}_e^j}\,:\,\big({\bf F}_e\,\cdot\,(\stackrel{\triangle}{\bf \Gamma})_i\,\cdot\,{\bf F}_e^T\big)\geq 0.\end{array}$$

(15)

The evaluation of the entropy principle concerning the argumentation of Coleman and Noll [39] yields in the following set of constitutive equations for the n non-equilibrium stresses of the Mandel type on the intermediate configuration

$${\bf M}_{neq}^j\,=\,2\,\hat{\rho}\,\frac{\partial\,\Psi_{neq}^j}{\partial {\bf C}_e^j}. $$

(16)

With the push forward operation and $\hat{\rho}\,=\,J^{-1}_i\,\rho_0$ the n non-equilibrium Cauchy stresses can be calculated to

$${\bf T}_{neq}^j\,=\,2\,J^{-1}\,\frac{\rho_0\,\partial\,\Psi_{neq}^j}{\partial {\bf C}_e^j}\,\cdot\,{\bf B}_e^j. $$

(17)

After this evaluation the dissipation inequalities remain

$$ \hat{\rho}\,\frac{\partial\,\Psi_{neq}^j}{\partial {\bf C}_e^j}\,:\,\big({\bf F}_e^j\,\cdot\,(\stackrel{\triangle}{\bf \Gamma})_i^j\,\cdot\,{\bf F}_e^{jT}\big)\,\geq\,0, $$

(18)

from which n evolution equations can be motivated, cf. Sedlan [19] and Lion [23]. This dissipation inequality is fulfilled if the two appeared tensors are coaxial. Therefore a proportionality function

$$ \eta^j\,=\,\hat{\eta}^j\,({\bf C}\,,\,{\bf D})\,\geq 0 $$

(19)

is introduced depending on the right Cauchy–Green deformation tensor C and the deformation rate D. This approach is chosen related to the experimental data. With a pull back operation the evolution equations for each Maxwell element are obtained as

$$ \dot{\bf C}_i^j\,=\,\frac{4}{J_i\,\eta^j}\frac{\partial\,\rho_0\,\Psi_{neq}^j}{\partial {\bf C}_e^j}. $$

(20)

To represent the measured data a modified Neo–Hooke model [50, 51] is used for each Maxwell element. The free Helmholtz energy functions are

$$ \rho_0\,\Psi_{neq}^j\,=\,c_{10}^j\,\big(\rm{I}_{{\bf C}_e^j}\,-\ln\,{\bf C}_e^j\big). $$

(21)

Therein $c_{10}^j$ represent the shear moduli and ${\bf C}_e^j$ the elastic right Cauchy–Green deformation tensors in the different Maxwell elements. The logarithm function allows a stress-relieved undeformed state. Hence, the Cauchy stress of the Maxwell elements can be calculated by

$$\label{tneq} \sum\limits_j\,{\bf T}_{neq}\,=\,\frac{2}{J}\,\sum\limits_{j=1}^n\,c_{10}^j\,\big({\bf B}_e^j\,-\,{\bf I}\big) $$

(22)

and the evolution equations follow to

$$ \dot{\bf C}_i^j\,=\,\frac{4\,c_{10}^j}{J_i^j\,\eta^j}\,\big({{\bf C}}-{\bf C}_i^j\big). $$

(23)

The process dependent relaxation time is defined as

$$ r^j\,=\,\frac{\hat{\eta}^j({\bf C}\,,\,{\bf D})}{c_{10}^j}. $$

(24)

The viscosity functions $\hat{\eta}^j$ have to be determined from the experimental data. On the one hand it is shown by the experiments that the viscosity decreases with the deformation rate. For that reason an exponential equation is required. On the other hand it can be seen that the viscosity decreases with increasing deformation. In this case a rational function is needed. Using this information the relaxation time functions are adopted in the individual Maxwell elements either to

$$\label{relax1} r_j\,=\,r_{j1}\,+\,r_{j2}\,\exp\big(-\,k_j\,|{\bf D}|\big),j=1\dots J $$

(25)

and to

$$\label{relax2} r_j=\frac{1}{|{\bf C}|^4}\big(\,r_{j1}+r_{j2}\exp\big(\!-\!k_j\,|{\bf D}|\big)\big),\,j=J\dots n, $$

(26)

respectively. Therein the r _j1 and r _j2 represent the relaxation times and k _j are fit parameters. It was observed that four Maxwell elements are sufficient to represent the measured data. In two Maxwell elements the relaxation times regarding to equation (25) are used and in the other two elements equation (26) is taken into account. Hence, the stress can be calculated by equations (13) and (22) to

$${\bf T}\,=\,{\bf T}_{eq}\,+\,\sum\limits_n\,{\bf T}_{neq}. $$

(27)

Parameter Identification and Simulation

Identifying the model parameters is an inverse problem. The material parameters must be determined under the condition that the simulation results match the data obtained in the real experiments. For solving this inverse problem, a target or objective function is set in the form of a quality criterion that reflects the match between simulation and experiment. This target function is formulated as the sum of residual errors between simulation and experiment

$$ f\,=\,\sum\limits_i\,\big|T_{11_i}^{exp}\,-\,T_{11_i}^{num}\big|\,\rightarrow\,{\rm min} $$

(28)

and it is minimised by incrementally changing the material parameters. The index i counts the discrete points where data is sampled in the experiments. For an optimum set of parameters, this sum must be zero. A gradient-free optimisation method [52, 53] for the computer-aided optimisation (CAO) is used. The algorithm generates the set of parameters applying evolution strategies. Other possibilities are described in [54]. The first important mechanism of the evolution strategies is the mutation-selection principle. In the design variable space $X\subseteq{\mathbb R}^n$ every set of variables is represented by a point. Outgoing from this view the mutation-selection principle runs off for a two-dimensional parameter space n = 2 in the following steps, see Fig. 22 [55]:

• 1. A circle with the radius N is generated around a set of parental variables E ^(g) of the generation g.

• 2. The radius N is modified λ-times. Thus λ new circles originate which scatter normal-distributed around the first circle.

• 3. On each of the new circles a point is selected by chance, with the same probability. λ descendants of the generation g have originated from it.

• 4. The quality of the descendants is checked. The best descendant and the accompanying radius are noticed.

• 5. The noticed set of variables becomes the parents E ^(g + 1) of the generation g + 1. With the accompanying radius it is repeated from 1..

Beside the mutation the second important mechanism of the evolution strategies is the recombination. For two sets of variables in the two-dimensional design variable space $X\subseteq{\mathbb R}^2$ the mechanism is as follows, see Fig. 23 [55]:

• 1. Two really different sets of parental variables $E_1^{(g)}\,\neq\,E_2^{(g)}$ of the generation g are given.

• 2. The distance of both sets of variables is halved defining the centre of a circle on both sets of variables.

• 3. On the circle points are selected by chance, with the same probability ρ (recombinations). ρ new sets of variables have originated. Here the whole circle is used to the production of the recombinations.

• 4. The quality of the descendants is checked. Both best descendants are added to the parents of the new generation g + 1. It is repeated from 1..

The identification of all model parameters is performed stepwise. The strategy for the parameter identification is as follows:

Fig. 22

Mutation-selection principle

Fig. 23

Recombination mechanism [55]

At first the material parameters governing the basic elasticity are determined. With the following parameters c ₁₀ = 0.085 MPa, c ₂₀ = 0.0015 MPa, c ₃₀ = 0.002 MPa and λ = 0.0054 MPa a good match is found, see Fig. 24. For the parameter p ₀ the ambient pressure of 0.1 MPa and the known average porosity of $n_0^S\,=\,0.5$ are used. In a second step the parameters for the Maxwell elements are identified using the data of the relaxation and cyclic tests, see Table 1. Therefore the cyclic experiments are investigated first. The preserve set of parameters is used as a starting value to adapt the relaxation experiment over 20,000 s, in addition. Thereon all values are held steady except the relaxation times which depend on the deformation. Then the indentification is carried out in addition for the relaxation experiments with deformations λ ₁  =  1.16, λ ₁  =  1.98 and additionally for the experiment with pretreatment. The relaxation experiments with other deformations served for the verification. All in all four Maxwell elements are used, the first two elements with relaxation times of type (25) and the other ones with type (26). The Maxwell elements with the large relaxation times need the deformation dependence. With these parameters the experiments are simulated.

Fig. 24

(color online) Comparison of simulation and experimental data of the basic elastcity

Table 1 Identified viscoelastic material parameters, respectively

At the beginning the simulation of the relaxation tests is performed. In Fig. 25 seven relaxation tests for different deformation levels are simulated. The experimental data are plotted in black and the simulation data in red. The simulations represent the experimental data very accurately. Only in the cases of 16% and 31% deformation discrepances arise, but the error is around 10% and for that reason this discrepances are acceptable. Therefore the relaxation tests can be simulated with the introduced model and the chosen relaxation time functions represent the real material behaviour.

Fig. 25

(color online) Comparison of simulation (red) and experimental data (black) for different relaxation tests

In Fig. 26 the results of three relaxation tests are plotted and compared to the corresponding basic elasticity. In each experiment the stress value after 30 min is acceptable for experiment and simulation, although the basic elasticity is more than 15% lower, i.e. the stationary value of deformation is not yet reached. For that reason, it can be stated, that the chosen relaxation times in the last two elements are satisfactory.

Fig. 26

(color online) Comparison of simulation (red) and experimental data (black) for different relaxation tests with the corresponding basic elasticity (dashed line)

Finally also the relaxation test over 20,000 s is simulated, see Fig. 27. The results are nearly perfect for this case. Only at the end of the experiment differences of less than 1% exist, although the basic elasticity (grey line) is not reached. In general, the introduced model represents the experimental data of the relaxation tests very well. With the established dependency on the deformation the relaxation behaviour can be described over a great range of deformations.

Fig. 27

(color online) Comparison of simulation (red) and experimental data (black) for a relaxation test over 20,000 s with the corresponding basic elasticity (dashed line)

After the relaxation tests, cyclic tests are also simulated to see whether the dependency of the relaxation time on the deformation rate can represent the experimental data. Figure 28 shows the experiment (black) and the simulation (red) of the first five cycles of the slowest feedrate. Therein the Cauchy stress is presented related to the deformation and in Fig. 29 with respect to the time. Therein it can be seen, that the maximum values differ around 8% between experiment and simulation, but the other values are acceptable. The same plots are presented for the medium feedrate in Fig. 30 and Fig. 31 and for the fast one, see Fig. 32 and Fig. 33. The same problems as seen in Fig. 28 can be observed here, but the maximums differ less than before. Concluding, the obtained results are satisfying for all feedrates, so the used dependency of the relaxation time on the deformation rate represents the measured data. The only arising but acceptable discrepancy is observed in range of large deformations.

Fig. 28

Cauchy stress of a cyclic test with a constant feedrate of 0.00265 s^− 1 over the deformation

Fig. 29

Cauchy stress of a cyclic test with a constant feedrate of 0.00265 s^− 1 over the time

Fig. 30

Cauchy stress of a cyclic test with a constant feedrate of 0.0265 s^− 1 over the deformation

Fig. 31

Cauchy stress of a cyclic test with a constant feedrate of 0.0265 s^− 1 over the time

Fig. 32

Cauchy stress of a cyclic test with a constant feedrate of 0.265 s^− 1 over the deformation

Fig. 33

Cauchy stress of a cyclic test with a constant feedrate of 0.265 s^− 1 over the time

Special emphasis is now placed on the “thixotropic” behaviour. That means the fast decay of the overstress in the first cycle and the slow decline of the hysteresis after this cycle. This behaviour is well represented for each feedrate. At last more about the thixotropic behaviour is shown. The dependency of the relaxation time on the pretreatment can be simulated with the presented viscoelastic model without taking into account additional structural variables. Figure 34 shows the simulations and the experimental data for relaxation tests at a deformation of 60% during 1,800 s. The experiment shows a dependency of the relaxation behaviour on the pretreatment. Both, the maximum value at the beginning and the value after 1,800 s differ from relaxation tests with and without pretreatment, respectively. It is pointed out that the model using the identified material parameters represents this phenomenon very precisely, although the basic elasticity is not reached after 1,800 s in the experiment and in the simulation. Moreover the model does not need any additional structural parameter to represent this effect. Therefore, the statement can be made that in the case of the investigated cellular rubber the so-called thixotropic effect is only of viscoelastic nature. This interpretation is in accordance with the microscopic interpretation, that a crosslinked polymer does not allow for healing effects without additional energy supply.

Fig. 34

Comparison of simulation and experimental data for different pretreatment

After these experiments simulations are done to verify the model. Therefore relaxation tests at deformation levels of 45% and 73% are carried out, see Fig. 35. Also in this case a good correspondence can be ascertained between experiment and simulation. Additionally a relaxation experiment with another pretreatment is carried out. In the investigation shown before the material is pretreated with ten cycles. In Fig. 36 the material is pretreated only with one cycle. Again the simulation matches the experiment well even if the equilibrium stress is not reached after 2,000 s.

Fig. 35

Relaxation test at two different deformations

Fig. 36

Relaxation test with a pretreatment of 1 cycle

At last a cyclic experiment with a rate of 0.13 s^− 1 is carried out, see Figs. 37 and 38. Here a good correspondence can be ascertained by experiment and simulation. All in all, the model is able to generate reasonable simulations for the material behaviour of the investigated cellular rubber for a wide range of deformation, feedrate and pretreatment.

Fig. 37

Cauchy stress of a cyclic test with a constant feedrate of 0.13 s^− 1 over the deformation

Fig. 38

Cauchy stress of a cyclic test with a constant feedrate of 0.13 s^− 1 over the time

Conclusion and Outlook

In this study a porous cellular rubber is characterised with respect to its mechanical properties. Therefore, uniaxial tension tests were performed on dogbone specimens. Many important effects for rubber materials, like the Mullins effect, thixotropy and viscoelasticity are experimentally investigated for the chosen material. Based on these results a continuum mechanical material model is developed. The basic elasticity is described by a modified Yeoh model with an extended pressure term and the viscoelastic behaviour is represented with four highly nonlinear Maxwell elements. To capture the special behaviour which looks like thixotropy, and the nonlinear character with respect to the deformation and feedrate strongly nonlinear relaxation time functions are introduced. The model contains a number of parameters. In order to determine them a successful sequential strategy is presented which allows for an efficient quantification of the required parameters. It is shown that the model predicts the experiments for a wide range of parameters, i.e. maximum deformation, feedrate and pretreatment. In future works the data pool is extended by hydrostatic compression tests in order to include multiaxial stress states. Theoretically, the material model should reflect the measured data. Furthermore experiments at different isothermal temperatures will be performed to enlarge the data pool concerning the thermo-viscoelasticity.