Mechanical Characterisation of Polymeric Materials Using Nanoindentation

Abstract

This chapter describes the mechanical behaviour of polymeric and soft materials through combined computational and experimental studies. Many soft materials exhibit time-dependent or a very large non-linear strain behaviour known as viscoelasticity/viscoplasticity and hyper elasticity or viscous-hyper elasticity respectively. A comparative study using nano-indentation of polymeric materials has been performed through combined experimental and Finite Element methods. Several constitutive models are available in the literature to analyse the experimental response of polymeric materials, however, the correct constitutive models are required to accurately model the mechanical behaviour of a given material system. Three widely used hyper elastic models, including the Mooney-Rivlin, Ogden and Arruda-Boyce models are studied for the analysis using the Finite Element software ANSYS. Also, due to the time dependent behaviour of soft materials the viscoelasticity and viscoplasicity behaviour based on the Prony series and Perzyna/modified time hardening models are discussed. Conventional macroscopic mechanical tests have been performed on PMMA, epoxy resin and polyurethane rubber materials using uniaxial tensile testing in conjunction with digital image correlation (DIC) technique to provide input data for Finite Element modelling of the indentation process. FE analysis of the indentation tests was then carried out and the results are compared with experimental data. This study helps to identify the deformation behaviour and mechanical characteristics of soft materials.

1 Introduction

Soft biomaterials are produced from a wide range of polymers (Shtil′man 2003). One of the main advantages of using polymers as a biomaterial is that their chemical structure and functionality can be easily modified which allows the tailoring of properties such as mechanical response, bioadherence, etc. (Zadpoor 2015). Many polymers are therefore extensively used in biomedical applications as implants, scaffolds, or wound-dressing foams (Shtil′man 2003; Ifkovits and Burdick 2007; Ulery et al. 2011). However, any chemical and physical changes in the structure of soft polymeric materials significantly influences their mechanical properties (Piskin 1995; Dutcher and Marangoni 2004). For instance, where soft materials mainly reside in aqueous environments, chemical degradation can result in material failure (Piskin 1995; Oyen 2008). Therefore, understanding the mechanical behaviour is essential and this often needs to take place at very high spatial resolution. Unlike metals and ceramics, which show predominantly elastic-plastic behaviour, characterising the mechanical properties of soft polymeric materials is very complex and challenging (Oyen 2008; Sinha and Briscoe 2009). Most of the soft polymeric materials exhibit both elastic/hyper elastic and viscoelastic/viscoplastic properties at different strain rates and temperatures (Alfrey and Doty 1945; Li et al. 2018). Viscoelastic/viscoplastic behaviour such as strain rate dependency and time dependent relaxation requires diverse range of analyses to evaluate mechanical response.

A mathematical framework to determine the stress-strain behaviour of a loaded material is called a constitutive model (Dorfmann and Muhr 1999; Dean et al. 2011). A number of existing constitutive models, such as linear, bilinear, hyper elastic, or viscoelastic/viscoplastic models, can be used to characterise the mechanical behaviour of soft materials (Gurtin 1973; Dean et al. 2011; Fill et al. 2012). However, the structure of soft materials such as polymers and elastomers is complex and the constitutive response can be entirely different compared to the typical engineering materials (Ogden 1973; Blatz et al. 1974; MacManus et al. 2016). Therefore, obtaining an accurate constitutive model is a key issue in the better understanding of the mechanical behaviour of polymers, elastomers or soft biomaterials used in implants, scaffolds, etc. Depending on the structure and composition, soft materials often exhibit elastic, plastic, viscous (time-dependent) and hyper elastic behaviours (Ogden 1973; Dorfmann and Muhr 1999; Dean et al. 2011). For soft materials under small deformation the stress can be considered proportional to strain and can be fitted to linear elastic models, i.e., (σ = Eε (Gurtin 1973)); typically linear elasticity can be described with two material constants (i.e Young’s modulus and Poisson’s ratio) (Gurtin 1973). In the case of hyper elastic soft materials, these show a large deformation when a load is applied which returns to the original shape after the load is released, and a stress that varies nonlinearly with respect to strain (Mooney 1940). This hyper elasticity is described by a few constitutive models to precisely characterise the nonlinear stress-strain data of such soft materials (which are described in the Sect. 1.4).

The mechanical properties of soft materials can be determined using conventional methods such as, tensile, compression, or bending tests (Moerman et al. 2009; Nie et al. 2009). But soft materials display large deformation behaviour at a given applied load, and their surfaces or sub surfaces are often very different from bulk materials (Mooney 1940). Therefore, in order to locally investigate the mechanical properties and deformation characteristics of soft materials at small (micro/nano) scale such as thin films, composites, or nanobiological applications, the nanoindentation test method is probably the most suitable test method (Li and Bhushan 2002). However, nanoindentation measurements on soft materials can vary considerably with applied loading conditions (Li and Bhushan 2002; Zhang et al. 2010). In particular, the time dependent nature of soft materials must be considered when measuring their properties. Numerous studies have shown the mechanical characterisation and measurement sensitivity using nanoindentation with varying load conditions (Li and Bhushan 2002; Fischer-Cripps and Nicholson 2004; Zhang et al. 2010). Understanding the effect of the test time, and the degree to which mechanical response is dependent on intrinsic materials properties, is necessary to fully explain the mechanical behaviour of soft materials using nanoindentation testing under different loading conditions.

In this chapter an overview of the mechanical properties of soft materials is presented. The mechanical behaviour of most soft materials displays both nonlinearity and viscoelasticity as well as viscoplasticity. Therefore, a detailed understanding of the mechanical properties of soft and elastomeric (rubber-like) materials is an important part of our investigation. Firstly, as a consequence of effect of test time, nanoindentation relaxation of polymeric materials such as PMMA and epoxy resin materials has been studied. In PMMA, Prony series parameters obtained from nanoindentation experiments were determined using an analytical expression from the literature and subsequently the parameters were input into the Finite Element model of nanoindentation in order to validate the experimental results. In case of epoxy resin, the results of creep testing (variation of the strain versus time) and also the results of tensile testing at various strain rates were used to determine the Viscoplastic model parameters (modified time hardening and Perzyna models), subsequently the parameters were used as input data into the Finite Element model to verify the experimental parameters.

Secondly, polyurethane rubber is used as a model hyper elastic material. The Mooney Rivlin, Ogden and Arruda-Boyce models were used for the Finite Element analysis. Numerical solutions were compared with experimental data which were utilised to understand the stress strain behaviour of hyper elastic materials. It is found that different constitutive models are required for the different materials studied.

1.1 Structure and Mechanical Response

The mechanical response of biomaterials based on polymeric systems is much more variable than that of metals or ceramics. A major part of this comes from the different structures that these largely amorphous materials can adopt and the fact that these are not as dense and predictable as those of crystalline materials. This results in different stress-strain behaviour depending on the initial structure and how it changes during loading; therefore an understanding of the engineering and true stress-strain response of different materials and how it relates to the structure is paramount. Figure 8.1a shows the tensile engineering stress-strain curve for a typical ductile metal. The initial linear behaviour is reversible and is due to elastic behaviour (the slope gives the Youngs Modulus of the material) and the deviation from linear behaviour is due to plasticity which is related to the propagation of mobile defects (dislocations) in the material. The engineering stress continues to rise after the onset of plastic deformation up to the point when a plastic instability develops and the test sample cross-section is locally reduced (necking). From this point the engineering stress which is based on the original cross-sectional area of the test sample is reduced with increasing strain up to the point of fracture, but the true stress continues to increase as the load carrying area reduces. In ceramic materials fracture may occur prior to plastic deformation and only the elastic behaviour is seen.

Fig. 8.1

Stress-strain response of (a), ductile metal, (b), semi crystalline polymer and (c), elastomer

In a semi crystalline polymer a similar curve is often observed (Fig. 8.1b). An initial linear elastic section is followed by a non-linear (plastic) behaviour but the curve shows a maximum stress and then a plateau of stress at a lower level with a considerable change in extension and a final increase before failure. In this case the neck that forms does not continue shrinking until the specimen fails. Rather, the material in the neck stretches only to a certain “draw ratio” beyond which the material in the neck stops stretching and new material at the neck shoulders necks down. The neck then propagates until it spans the full gauge length of the specimen, a process called drawing. The increase in strain hardening rate needed to sustain the drawing process in semi crystalline polymers arises from a dramatic transformation in the material’s microstructure. These materials are initially “spherulitic,” containing flat lamellar crystalline plates, perhaps 10 nm thick, arranged radially outward in a spherical domain. As the induced strain increases, these spherulites are first deformed in the straining direction. As the strain increases further, the spherulites are broken apart and the lamellar fragments rearranged with a predominantly axial molecular orientation to become what is known as the fibrillar microstructure. With the strong covalent bonds now dominantly lined up in the load-bearing direction, the material exhibits markedly greater strength and stiffness than in the original material.

In elastomeric materials (Fig. 8.1c) a non-linear stress-strain curves is also observed but this is often completely reversible. The behaviour is elastic but the stiffness depends on the applied strain. The effect of tensile load is to stretch and align the polymer chains in the loading direction within the movements that are allowed by their original arrangement, available free space in the structure and degree of entanglement. This hyper elastic behaviour generally results in a reduction of stiffness with increasing strain at low loads followed by an increase at high strain once chain alignment is maximised.

The structure of materials based on polymer chains (and molecular films) is also more likely to be changed by thermal effects even at temperatures around room temperature. Most amorphous polymeric materials show a glass transition temperature where behaviour changes from elastomeric to glassy on cooling. The value of Tg depends on the mobility of polymer chains and for many polymers this lies between 170 and 500 K. Some polymers (like PMMA) are used in their glassy state and are relatively hard and brittle. Other polymers (e.g. polyurethane elastomers, polyisoprene) are used above Tg and are soft and flexible in nature; their Tg vales are below room temperature.

In addition, changes in the polymer chain structure by rotation and untangling can occur even a modest temperature giving a viscous component to the deformation process. Viscoelastic response is thus key in understanding the behaviour of polymeric materials. Elastic materials deform instantaneously when a load is applied, and “remember” their original configuration, returning there instantaneously when the load is removed. In solids, the relaxation of the structure at the molecular level is extremely small and, therefore, their response is essentially elastic. On the other hand, viscous materials do not show such characteristics, but instead exhibit a time-dependent behaviour. While under a constant stress, a viscous body strains at a constant rate, and when this load is removed, the material has “lost” its original configuration, remaining in the deformed state. In liquids, molecular reorganization generally occurs very rapidly and structural memory at the molecular level is very short. The response is essentially viscous unless the testing experiment is very fast. Viscoelastic materials exhibit certain characteristics of these two behaviours and show time-dependent behaviour, a “fading memory”, partial recovery, energy dissipation, etc. This may be linear (stress and strain are proportional) or nonlinear.

Polymers are the most important viscoelastic systems. Above the glass transition temperature, the response of these materials to a mechanical perturbation involves several types of molecular motions. For instance, the rearrangement of flexible chains may be very fast on the length scale of a repeated unit. These movements imply some type of cooperativity in the conformational transitions that produce them. Cooperativity occurs even as the relaxation propagates along the chains, involving a growing number of segments of the backbone as time passes. At very long times, disentanglements of the chains takes place, and the longest relaxation time associated with this process shows a strong dependence on both the molecular weight and the molecular architecture of the system. The disentanglement process governs the flow in the system. As a consequence of the complexity of the molecular response, polymer chains exhibit a wide distribution of relaxation times that extend over several orders of magnitude in the time or frequency domain. At short time or at high frequency the response is mainly elastic, whereas at long time or low frequency it is mainly viscous. Obviously, the elastic component of the deformation is recoverable but the viscous component is not.

These differences in mechanical behaviour lead to differences in response in any mechanical test including nanoindentation tests which are used when material is only available in small amounts. A range of different load-displacement responses are measured (Fig. 8.2) and it is not possible to use a single analysis method to derive useful comparative data or a mechanistic understanding of the deformation processes occurring. Careful modelling of the measured data is therefore necessary.

Fig. 8.2

Typical load-displacement fingerprints for (a) a glassy material (elastic-plastic (b) an elastic/viscoelastic material (c) an elastic/hyper elastic material (d) an elastic-viscoplastic material

Appropriate constitutive models for deformation are needed for all of the above cases. Whereas a single value for elastic modulus may be sufficient for crystalline materials this is not generally the case for polymers. In Sects. 1.3.2, 1.3.3 and 1.4 some of the constitutive models for hyper elastic, viscoelastic and viscoplastic materials which may be required are described.

1.2 Conventional Mechanical Testing vs Nanoindentation

For mechanical characterization, traditional mechanical methods such as tensile, compression, shear or bending tests can provide macro-scale information which can differ at the nano-scale level since most soft materials are non-homogeneous materials. Also, these testing methods have some challenges such as complex gripping geometry and the requirement for specific shapes and sizes of test samples (Nie et al. 2009). Therefore, in order to locally investigate the mechanical properties and deformation characteristics of soft materials at micro/nanoscale, the nanoindentation test method is probably the most common test method.

Nanoindentation is a depth sensing technique in which continuously measures load, displacement and time providing the mechanical response to the contact deformation; from this mechanical testing method, parameters such as hardness and modulus can be calculated (Fischer-Cripps and Nicholson 2004). Nanoindentation is easy to use, it does not generally require specialised laboratory infrastructure or a vacuum chamber. Properties such as viscoelasticity, creep, fracture toughness, and strain hardening effects localised to the contact region can be also extracted from the analysis of loading-unloading cycles (Ebenstein and Pruitt 2006). In contrast, the traditional mechanical methods such as tensile, compression, shear and flexural tests can only provide global deformation information which can differ to that from the nanoscale level since most soft materials are non-homogeneous (Bradley et al. 2001). Also, these conventional testing methods have some challenges which were described earlier (Dvir et al. 2011).

In the nanoindentation process, the load is applied through the transducer and the probe displacement is continuously measured to provide a load-displacement curve. The displacement is usually measured by capacitance while the force actuation is provided by force generation due to expansion of a piezoelectric element, magnetic coils, or electrostatically (Fischer-Cripps and Nicholson 2004). A schematic representation of nanoindentation is shown in Fig. 8.3, where the tip mounted directly onto the middle plate of a three-plate capacitor and a normal load is applied to move the tip downwards. The resulting load-displacement curve serves as the mechanical fingerprints of the material, from where the mechanical properties can be determined.

Fig. 8.3

Schematic representation of a nanoindenter machine

When testing compliant such as biomaterials three typical types of load-displacement fingerprint are often observed depending on the material tested:

• 1. Totally elastic or hyper-elastic response in which the loading and unloading curves are identical (Fig. 8.2c). This is typical of elastomeric materials with very low elastic moduli where the stresses generated during the indentation cycle are too small to drive plasticity.

• 2. Elastic-viscoelastic response in which the loading and unloading curves are offset from each other by the viscoelastic behaviour during a hold period (Fig. 8.2b). This is typically observed in non-crosslinked polymers such as PMMA at low test loads. The deformation is reversible and no visible impression is observed but the rate of recovery is slow enough that a visible offset between the loading and unloading curves is observed that disappears when the test is completed.

• 3. Elastic-viscoplastic response in which a permanent impression is created which does not recover fully after the test. A load-displacement curve that is similar to that seen when testing elastic-plastic materials is produced (Fig. 8.2d). This involves breaking of bonds and is more commonly observed for cross-linked polymers like epoxy resin systems.

This chapter discusses the analysis of all these types of curves and compares the results to the widely used conventional nanoindentation analysis method developed by Oliver and Pharr (Oliver and Pharr 1992) which is introduced in the next section.

1.3 Nanoindentation Theory

Nanoindentation has emerged as a convenient technique to determine the mechanical properties of polymeric materials. Thanks to the recent technological advances to the transducer sensitivity of nanoindentation equipment, continuous checking and monitoring of the load and contact depth is permitted throughout the load-unload cycles. Depth sensing micro-indentation was first conducted by Fröhlich (Fröhlich et al. 1977) and then used as a method to characterize the surface properties of materials. Although for conventional macro and micro-scale hardness testing, an indenter geometry of a four faceted pyramidal Vickers tip (Fig. 8.4b) is mainly used, when it comes to the nanoscale measurement, the three faceted pyramidal Berkovich indenter (Fig. 8.4a) is preferred. The Berkovich tip shape was invented by a Russian scientist (Berkovich 1950) where the area to depth ratio of this indenter geometry is similar to that of the Vickers indenter.

Fig. 8.4

Geometry of indenter tips (a) Berkovich, (b) Vickers

In the Nano-indentation process, either under displacement or load control mode, a diamond indenter tip is pushed into the bulk material. During the indentation cycle, the displacement is monitored with respect to the load. A typical load displacement curve from nanoindentation experiment is shown in Fig. 8.5b. The Oliver and Pharr (2010) method is the main used method to analyse the unloading part of load displacement curves and therefore to determine hardness and elastic modulus. The hardness H is defined as

Fig. 8.5

(a) A schematic representation of surface showing the section before and after indenting, (b) A schematic representation of typical nanoindentation load-displacement curve, also showing the graphical interpretation of the contact depth (Oliver and Pharr 1992)

$$ H=\frac{P_{max}}{A} $$

(8.1)

Where P _max is the maximum applied load, and A is the projected area. The contact area, A which can be evaluated from the contact depth, h _c, at the maximum load of P _max, can be expressed as

$$ A={c_0{h}_c}^2 $$

(8.2)

where c ₀, is the coefficient and it depends on the indenter tip geometry. For a Berkovich tip, the value of c ₀ is about 24.5. As can be seen in Fig. 8.5 the contact depth, h _c, which is the actual contact depth between the indenter and material, is different from the maximum contact depth, h _max at the maximum applied load, due to the elastic deformation surrounding the indenter area. The contact depth, h _c is given by

$$ {h}_c={h}_{max}-\epsilon \frac{P_{max}}{S} $$

(8.3)

where S, is the contact stiffness, and can be extracted from the slope of unloading curve. ϵ is a constant, that depends on geometry of indenter. The projected contact area can be calculated either from the cross-sectional image of the indenter shape or directly measured from the imprint geometry under the scanning electron microscope (Briscoe et al. 1998; Pharr et al. 2010). However, determining actual contact area is highly dependent on contact depth and the cross-sectional shape along the contact depth (Pharr et al. 2010). In order to consider the bluntness of the tip Oliver & Pharr proposed an area function which is mainly applicable for a Berkovich tip and is given as

$$ A=24.5\ {h_c}^2+{c_1{h}_c}^1+{c_2{h}_c}^{0.5}+{c_3{h}_c}^{0.25}\dots $$

(8.4)

Once the contact area, A and stiffness, S are determined, the reduced modulus, E _r can be calculated following the pioneering work of Bulychev, Alekhin, Shorshorov (BASh) and their co-workers from the analysis of the frictionless contact problem. This gives

$$ {E}_r=\frac{S\sqrt{\pi }}{2\beta \sqrt{A}} $$

(8.5)

where β is correction factor (β = 1.034) for a Berkovich indenter tip. The reduced modulus, E _r represents the elastic modulus occurring both in the indenter and the materials, and the Young’s modulus can be extracted from the given equation

$$ {E}_r=\frac{1-{\nu_s}^2}{E_s}+\frac{1-{\nu_i}^2}{E_i} $$

(8.6)

where ν _s and ν _i are the Poission’s ratios of the sample and indenter respectively, and E _s and E _i are the elastic modulus of the sample and indenter respectively.

In summary, it must be noted that the determination of elastic modulus of polymeric materials using nanoindentation data has been shown to be erroneous. The Oliver and Pharr method explained earlier is inaccurate and cannot be applied to the nanoindentation unloading curves obtained for polymeric materials (Tranchida et al. 2007); due to the effects of pile up, viscoelasticity/viscoplasticity and hydrostatic stress, a clear difference exists between the elastic modulus calculated using macroscopic tensile testing of polymers and those calculated using nanoindentation, with indentation modulus normally overestimating the elastic modulus.

1.3.1 Material Pile Up

According to the elastic contact theory (Sneddon 1965), during the indentation, the “sink-in” behaviour occurs in the region around the indentation. Based on this behaviour, the projected contact area is calculated from the indentation load displacement data and therefore Hardness and Modulus of the indented material are calculated. However, depending on the material under indentation (i.e. occurrence of plastic deformation), the material at the maximum indentation depth, may sink in or pile up around the indenter as shown in Fig. 8.6. When pile-up occurs, the contact depth (h _c) is bigger than the maximum indentation depth (h _max). As a result, the contact area can be underestimated by the theory of nanoindentation and the mechanical properties extracted by the Oliver and Pharr method are overestimated. It has been shown that the nanoindentation theory has failed to acceptably calculate the exact projected contact area for the elastic-plastic indentation, therefore the contact area can be underestimated significantly depending on the work hardening and the ratio of modulus to the yield stress (Bolshakov and Pharr 1998).

Fig. 8.6

Pile up and sink in behavior of material at max indentation depth. (Hardiman et al. 2016)

1.3.2 Viscoelasticity

The difference between indentation modulus and macroscopic tensile modulus has been related to the viscoelastic (time dependent) behaviour of materials (VanLandingham et al. 2001; Oyen 2007; Tranchida et al. 2007; King et al. 2013). In fact, the initial part of unloading curve of load displacement data is affected by the viscoelastic creep. This results in a ‘nose’ in the load displacement curves and therefore a negative value for the unloading slope (contact stiffness). For example, during the nanoindentation unloading curve, the occurrence of a ‘nose’ is seen when the indentation is conducted on PMMA (Briscoe et al. 1998). In an attempt to reduce the influence of viscoelastic effects on the unloading part of a nanoindentation test, adding a constant load hold segment between the loading and unloading segment has been proposed (Hochstetter et al. 1999). Therefore, determination of the optimum holding time for each material to adequately reduce the influence of creep on the initial part of the unloading data is necessary when characterizing the nano-mechanical behaviour of materials.

Polymers and soft materials exhibit time dependent behaviour such as creep, stress relaxation, or frequency dependent of dynamic properties (Brinson and Brinson 2008). These viscoelastic materials show both elastic and time dependent response, that are primarily responsible for energy loss since they store as well as dissipate mechanical energy under the deformation, with the response of stress-relaxation or creep.

Recently, nanoindentation has been considered as a possible way to measure the viscoelastic properties as well. For example, Cheng et al. (2000) demonstrated an analytical solution for linearly viscoelastic deformation using flat-punch indentation. Lu et al. (2003) and Huang et al. (2004) developed methods for viscoelastic functions of polymers in the time domain and frequency domain respectively. Odegard et al. (2005) studied the dynamic viscoelastic behaviour of various polymers. Vanlandingham et al. (2005) determined the relaxation modulus and creep compliance. Thereafter numerous studies have been performed using nanoindentation with conical, spherical and Berkovich indentation on polymers and soft materials (Briscoe et al. 1998; Dean et al. 2011).

As mentioned above, almost all soft biomaterials exhibit time-dependent behaviour. Apart from typical indentation methods to characterize time-dependent behaviour, dynamic testing is also widely used, where instead of a trapezoidal load function, a sinusoidal load is applied for measuring the storage and loss modulus directly as a function of loading frequency. Dynamic indentation tests have been shown to be pivotal for both in identification of mechanical properties of soft materials and assessing their viability. This allows for the continuous evaluation of the hardness and Young’s modulus of the given material over the depth of the indentation. Apart from hardness and Young’s modulus measurements, this method is useful for the experimental determination of the local creep and strain-rate dependent mechanical properties of materials, as well as the local damping of viscoelastic materials. Mishuris et al. (Argatov et al. 2013) has provided useful insights on mechanical properties of biological tissues (articular cartilage) using dynamic spherical indentation tests at various geometrical parameters of the indenter.

Considering the complexity of the loading conditions and time-dependent behaviour, including complicated constitutive response and some explicit analysis connected with physiological conditions is more likely to be necessary in future studies of soft biomaterials. The dependency of the stress-strain behaviour of soft biomaterials with respect to time is largely responsible for the absorption of energy, where the approach to quantifying the material response is not straightforward since most of the data analysis is complex due to the viscoelastic models used. For instance, in the case of a nonlinear viscoelastic model, there is no direct analytical expression for the indentation behaviour and not always a complete range of the required material property data at the sample scale. This necessitates the use of finite element analysis (FEA) modelling approaches with an appropriate materials response included, such as from a fitted database, or an inverse FEA analysis method for data optimisation. Therefore, in order to evaluate a more realistic analysis and materials behaviour both experimental approaches and modelling need to be used (Fig. 8.7).

Fig. 8.7

Schematic representation of time-dependent behaviour of stress- relaxation (left) and creep (right)

Experimental results of indentation tests can be fitted to determine viscoelastic parameters. A generalized Maxwell model is extensively used to consider the correlation between nanoindentation load-displacement data and the relaxation modulus as a function of time (Huang and Lu 2006). Typically, the model is formulated by Prony series expressions, to characterize the continuous viscoelastic contribution of the materials in terms of a number of different relaxation processes with different shear modulus and relaxation time.

$$ G(t)={G}_{\infty }+\sum_{j=1}^N{G}_J.{e}^{-t/{\tau}_j} $$

(8.7)

where G _∞ is the equilibrium shear modulus, G _j is the magnitude of the shear modulus, and τ _j is its relaxation time. Due to its simplicity, this model is widely used to describe viscoelastic materials such as polymers and many soft biomaterials.

1.3.3 Viscoplasticity

As mentioned in the above section, many soft materials exhibit the time dependent behaviours that include creep, stress relaxation, or frequency dependence of dynamic properties (Lu et al. 2003; Huang et al. 2004). If these are reversible they can be regarded as viscoelastic but this is not always the case. Viscoplasticity also occurs depending on the rate of the applied loading, but the time-dependent material response is irreversible and accompanied by unrecoverable plastic deformation (Perzyna 1966; Batra and Kim 1990). A viscoplastic model is required for large strain deformation. For qualitative analysis, several tests such as hardening, creep, or stress relaxation at constant elongation are performed to describe the viscoplasticity (Batra and Kim 1990). To predict the stress-strain curve the viscoplasticity is generally modelled using Perzyna approach (Simo and Hughes 2006).

1.3.3.1 Perzyna and Modified Time Hardening Models

In viscoplasticity, the material deformation is rate dependent and undergoes unrecoverable deformation. The rate-dependent behaviour of polymers and soft materials in general is widely modelled using a viscoelastic constitutive law (Odegard et al. 2005). However for viscoplasticity, the Perzyna and Modified time hardening models can be used for rate dependent behaviour of soft materials (Simo and Hughes 2006). The Perzyna model as a function of plastic strain can be expressed as

$$ {\dot{\varepsilon}}_{pl}=\gamma {\left(\frac{\sigma }{\sigma_0}-1\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$m$}\right.} $$

(8.8)

where ε _pl is the plastic strain, m is the hardening parameter, γ is the viscosity parameter, and σ ₀ is the static stress. In the Perzyna model, the results of stress-strain response of polymeric samples under tensile testing at various strain rates are used to determine the Perzyna parameters (Perzyna 1963a, b, 1966). The model assumes that the plastic strain rate (έ _pl) is a function of a hardening/softening parameter (m), the material viscosity parameter (γ), and the static yield stress (σ ₀). The stress strain rate graph is created and fitted with Perzyna material model of viscoplasticity to identify the required parameters.

To identify the modified time hardening parameters, the variation of strain versus time (creep test) is used in curve fitting and, as a result, Modified Time hardening parameters (i.e. constants C ₁ to C ₄ in Eq. 8.9 are determined.

$$ {\varepsilon}_r=\frac{C_1\times {\sigma}^{C_2}\times {t}^{c_3+1}\left(\exp \left(-\frac{C_4}{T}\right)\right)}{C_3+1} $$

(8.9)

where ε _r is the strain rate, σ is the stress level where creep test is performed, t is the time and T is the temperature.

1.3.4 Hydrostatic Stress

When applying nanoindentation testing on materials (in particular polymers), the stressed material beneath the indenter tip is constrained by the neighbouring relaxed material (unstressed), this leads to the accumulation of great compressive hydrostatic stress in the indentation region (Atkins and Tabor 1965), which is why many researchers believe that the effect of hydrostatic stress state is the main reason for the difference between modulus of polymers calculated by macroscopic tensile testing and nanoindentation (Doerner and Nix 1986; Briscoe and Sebastian 1996; VanLandingham et al. 1999). In the literature an expression (Eq. 8.10) has been developed in order to calculate the indentation modulus, free from the influence of hydrostatic stress (Hardiman et al. 2016).

$$ {E}_{(0)}=E-2\left(H-\frac{H}{C}\right)\left(5-4\nu \right)\left(1-\nu \right) $$

(8.10)

Where E ₍₀₎ is the elastic modulus, E is the affected indentation modulus by hydrostatic stress state, ν is the Poisson’s ratio, H is the indentation Hardness and C is the factor of constraint suggested by (Atkins and Tabor 1965). It has been shown that taking into consideration the effect of hydrostatic stress by the above expression can result in a 15% increase in the match between indentation modulus and macroscopic modulus of polymeric materials.

1.4 General Hyper Elastic Models

Most soft materials such as elastomers exhibit non-linear stress-strain behaviour known as hyper elasticity, in which the stress-strain behaviour is usually derived from a strain energy density function. The strain energy density function depends on properties such as isotropy, incompressibility, initial level of porosity, etc. (Boyce and Arruda 2000; Horgan and Saccomandi 2002). Numerous constitutive models such as Neo-Hookean, Ogden, Mooney-Rivlin, or Arruda Boyce models based on energy density functions are available in the literature for large strain deformation (Gent 1996). The Ogden model is older and widely used in finite element simulations, whereas Neo-Hookean, Mooney-Rivlin or Arruda-Boyce are mainly used for low, moderate and high strain analyses, respectively (Gent 1996; Dorfmann and Muhr 1999).

1.4.1 Mooney-Rivlin Model

The Mooney-Rivlin model is one of the most widely used models to predict the stress-strain behaviour of hyper elastic materials (Mooney 1940). It is based on two invariants of the left Cauchy-Green deformation tensor, and it works well with the large strain in uniaxial elongation and shear (Mooney 1940; Rivlin and Saunders 1951). Mooney-Rivlin can be derived from the following relationship between the strain density function and the stretch ratio

$$ W={C}_1\left({\overline{I}}_1-3\right)+{C}_2\left({\overline{I}}_2-3\right) $$

(8.11)

Where C ₁ and C ₂ are empirical parameters, and $\overline{I}$ ₁ and $\overline{I}$ ₂ are the first and second deviatoric invariants of the left Cauchy-Green deformation tensor. The invariants ($\overline{I}$ ₁ = λ ₁ ² + λ ₂ ² + λ ₃ ² and $\overline{I}$ ₂ = λ ₁ ² λ ₂ ² + λ ₂ ² λ ₃ ² + λ ₃ ² λ ₁ ²) are described in terms of principal stretch ratios λ ₁, λ ₂ and λ ₃.

1.4.2 Neo-Hookean Model

The Neo-Hookean model is a hyper elastic material model, which can be used to predict the stress-strain behaviour of hyper elastic materials at low strains; this model is very similar to Hooke’s law (Ogden 1997). At the beginning the Neo-Hookean model’s stress-strain behaviour is linear, but after certain point the stress-strain behaviour changes to non-linear (Ogden 1997; Gent 2012). A neo-Hookean model is one of the simplest models that can make good approximation at relatively small strain analysis (Ogden 1997). It is based on one invariant of the right Cauchy-Green deformation tensor. The strain density function of an incompressible Neo-Hookean model material can be expressed as

$$ W={C}_1\left({\overline{I}}_1-3\right) $$

(8.12)

Where C ₁ is empirical parameter, and $\overline{I}$ ₁ is the first deviatoric component of the right Cauchy-Green deformation tensor.

1.4.3 Ogden Model

The Ogden model is a hyper elastic material model, which can be used to predict the stress-strain behaviour of complex hyper elastic materials at larger strain levels (Ogden 1973). This model is the most widely used model up to now since it is capable of modelling stress-strain curves for strains up to 700%, whereas Mooney-Rivlin is typically best for strains below 100% (Ogden 1973). The strain density function for the Ogden model can be expressed as

$$ W=\sum_{I=1}^N\frac{\mu_i}{\alpha_i}\left({\lambda}_1^{\alpha_i}+{\lambda}_2^{\alpha_i}+{\lambda}_3^{\alpha_i}-3\right) $$

(8.13)

Where λ ₁, λ ₂ and λ ₃ are the principal stretch ratios, whilst μ _i and α _i are the empirically determined materials parameters.

1.4.4 Arruda-Boyce Model

The Arruda-Boyce model is a hyper elastic material model, which is based on an eight-chain model in which hyper elastic material is represented by eight identical polymer chains. This model requires two material parameters (the rubbery chain modulus and the limiting chain extensibility) and it works well to capture the collective nature of network deformation (Arruda and Boyce 1993). The strain density function for an Arruda-Boyce model, using the first five terms of the inverse Langevin function can be expressed as

$$ W=\mu \sum_{I=1}^5\frac{C_i}{\lambda_m^{2i-2}}\left({\overline{I}}_1^i-3\right) $$

(8.14)

here, μ is the initial rubbery shear modulus, and λ _m is the initial chain extensibility. $\overline{I}$ ₁ is the first deviatoric strain invariant.

2 Experimental and Numerical Methodology

2.1 Nanoindentation Test

In this work, depth sensing nanoindentation testing was conducted on viscoelastic and viscoplastic materials (i.e. PMMA and epoxy resin) using a Hysitron Triboindenter fitted with the Berkovich diamond indenter (500 nm tip end radius). An array of nine indents (3 × 3) was created. The distance between the indent was maintained 15 μm to avoid the interaction between the indents. To make sure that the nanoindentation results are not influenced by errors due to the shape of indenter, standard fused silica specimen was initially used to calibrate the tip area function. The tests were performed under displacement control mode using a single cycle indentation (load-hold-unload) protocol and during each cycle, a 5 s hold was imposed at the peak displacement. This was done to account for the effect of creep and viscosity. In addition, before the indentation testing, specimens were held for 24 h inside the nanoindentation enclosure in order to minimize the effect of thermal drift and to minimise the offset the specimen temperature with that of the environment. In this study, Atomic force microscopy (AFM) scans contributed to identify the occurrence of epoxy resin pile up and therefore the effect of pile up was corrected using the FEM method. The blunt Berkovich used can be regarded as a conical indenter with a spherical cap. For displacements less than about 60 nm the contact can be regarded as dominated by the spherical cap whereas at greater displacements the contact is dominated by the conical indenter geometry.

Nanomechanical response of hyper elastic material (polyurethane rubber) was conducted numerically, however the input parameters for the FE model were calculated experimentally. The numerical tests were performed under displacement control mode using a single cycle indentation (load-hold-unload) protocol and during each cycle, a 1 s hold was imposed at the peak displacement. More details about the methodology of computational nanoindentation on the hyper elastic material are given in Sect. 3.3.

2.2 Finite Element Modelling of the Nanoindentation

In this study, because of the complexity of the contact problem in soft polymers (large deformation and the stress-strain relationship with strong nonlinear features), the ANSYS Finite Element program was used to simulate the nanoindentation process for the nonlinear elastic materials. For this purpose, a 2D axisymmetric FE model with a conical indenter (half angle of 70.3 ^°) and a tip radius of 50 or 500 nm was used in order to accurately reproduce the nanoindentation experiment through the simulation. To build the nanoindentation model in this study, a 4-node planar element (PLANE182) was used to model the entire areas of the indenter and the bulk material. The element has axisymmetric modelling functionality and can be used for the large deformation problems in nanoindentation. In addition, it can be integrated with CONTA171 and TARGE169 elements to define the surface-to-surface contact model (bottom surface of the indenter and the top surface of the bulk material). Since a large localized strain/deformation occurs in the contact region beneath the indenter, a very fine mesh (2.5 nm × 2.5 nm) was used close to the contact zone, while a coarser mesh was used outside this region. The appropriate number of elements and element size were obtained by improving mesh density using mesh sensitivity study of the load versus displacement curve; therefore the FE model is mesh independent. Symmetric boundary conditions were applied along the axis of symmetry (the horizontal direction displacement was set to zero). The bottom side of the bulk material is also constrained by a fixed boundary condition. The height and the width of the model were set to a value of 300 times bigger than maximum indentation depth to minimize the samples edge and free boundary effects. The friction coefficient between the tip indenter and the upper surface of bulk material was set to 0.1(Johnson and Johnson 1987; Mata and Alcala 2004).

The indenter was modelled as deformable body in the ANSYS program, with its elastic properties the same as diamond (Young’s modulus of 1140 GPa and Poisson’s ratio of 0.08). The mechanical properties (hyper elastic model parameters), determined from macroscopic tension testing were supplied to the Finite Element code to simulate the nanoindentation testing. The indented sample was modelled as a hyper elastic material following Mooney Rivlin, Ogden and Arruda Boyce constitutive laws (Table 8.6), while when it comes to the viscoelastic and viscoplastic polymeric materials such as PMMA and epoxy resin, the Prony shear relaxation model and Perzyna/modified time hardening parameters are used in the FE model of the indented sample respectively. More details about how these parameters are identified are explained in later Sections (3.1 and 3.2).

To optimize the efficiency and avoid the convergence issues, a displacement control mode was used for the movement of the indenter. A downward displacement was applied to the indenter to simulate the indentation process. The corresponding load was obtained by the reaction force for a given indentation depth. In order to consider the effect of hyper elasticity and viscous hyper elasticity, the loading procedures of loading-holding- unloading indentation were applied with the maximum displacement varied from 50 nm to 1000 nm. The indenter reaches the maximum displacement within 1 s and then is held for 1 s and finally gets back to the initial place within a second. The analysis of the FE calculated load-displacement curve provides the contact modulus and hardness of the bulk material following the procedure based on the Oliver and Pharr method (Oliver and Pharr 1992). In this method, the contact stiffness (S) is calculated from the initial slope of unloading curve (Fig. 8.8a). This is related to the contact modulus (E _r) using equation:

Fig. 8.8

(a) A typical load-displacement curve obtained from the numerical Nano-indentation test on sample with purely hyper elastic properties and a sample with combined viscos hyper elasticity properties showing their contact stiffness which were used to calculate the elastic modulus, (b) Deformed and un deformed shape of bulk material under indentation showing the contact area used in Oliver and Pharr method to calculate the elastic modulus

$$ S=\frac{dP}{dh}=\frac{2{E}_r\sqrt{A_c}}{\sqrt{\pi }} $$

(8.15)

Where, A _c is the contact area at the indentation depth. According to the Oliver and Pharr method, the contact area is calculated via the area function for the indenter tip geometry used.

However, since the load-displacement curve in this study is based on Finite Element simulation, the contact area (A _c) is determined in the FE model from the last point of contact at maximum load (Fig. 8.8b).

3 Results

3.1 Viscoelasticity

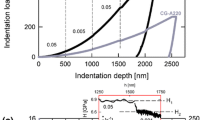
Viscoelasticity which has elastic and viscous components is usually characterized by relaxation testing. Generally in a relaxation experiment, either a constant tensile, compressive or shear strain is applied on the material, thereafter stress relaxation occurs over time. The variation of stress versus time is fitted with a number of models (e.g. Prony series model). The nanoindentation process in polymeric materials such as PMMA involves nonlinear contact mechanics and time dependent properties (viscoelasticity). A methodology based on combined FEM and nanoindentation experiments was used for developing an analysis procedure to characterize the micromechanical behaviour of PMMA. Initially, an FEM based inverse method is implemented to account for the effect of viscoelasticity (Prony series) parameters of the bulk polymer. These parameters can be calculated using the analytical expression derived based on the conical indentation of a homogeneous linear viscoelastic half space (Baral et al. 2017). The analytical expression used to calculate the Prony series parameters (Eq. 8.16) is used for fitting the load-time curve which was obtained during the holding time in (Fig. 8.9), with results in (Table 8.1). These parameters are then reused in the FE model of nanoindentation of bulk PMMA to predict the experimental load displacement data in Fig. 8.10 (Baral et al. 2017).

Fig. 8.9

Variation of load during the holding time and curve fitting using exponential function

Table 8.1 Prony series parameters of PMMA used in FE model

Fig. 8.10

Comparing numerically and experimentally calculated load displacement curves

$$ F(t){=}\frac{\pi \tan \left(\beta \right)}{1{-}\nu }{\left(\frac{a}{h}\right)}^2\times \left[{G}_0.{h}_1^2{+}2\sum_{i=1}^n{G}_i.{r}_1^2{\tau}_i\exp \left({-}\frac{t{-}{t}_1}{\tau_i}\right)\times \left[\frac{h_1}{r_1}{+}{\tau}_i\exp \left({-}\frac{h_1}{r_1{\tau}_i}\right){-}1\right]\right] $$

(8.16)

Using the above Prony series parameters and the mechanical properties of PMMA (obtained from macroscopic tensile testing, elastic modulus: 3.00 GPa and Poisson’s ratio: 0.35) in the FE model indicates that there is a good correlation between the experimental data and the FE simulation. The agreement between numerical and experimental result can be used to validate the viscoelasticity parameters introduced into the FE model. The von Mises strain fields developed in the 2D FE model of PMMA is shown in Fig. 8.11 providing an insight into the strain distribution when characterizing the bulk PMMA using the nanoindentation method.

Fig. 8.11

Von Mises strain fields (a) at maximum displacement, (b) after complete unloading

3.2 Viscoplasticity

The nanoindentation process on polymeric materials such as epoxy resin involves nonlinear contact mechanics and strain rate dependent properties (viscoplasticity) as well as the effect of material pile up. To account for these effects, an FE based inverse method (combined FEM and nanoindentation experiment) was used for developing an analysis procedure to characterize the micromechanical behaviour of bulk epoxy resin. Initially, the FEM based inverse method is implemented to account for the effect of viscoplasticity of the bulk polymer. To do this, viscoplasticity parameters are determined using tensile and creep testing (at various strain rates) on epoxy resin and then these parameters are used in FE models of nanoindentation on bulk epoxy resin for verification of load displacement data. To correct for the effect of pile up, rather than estimating the projected contact area using the Oliver and Pharr method, the FE calculated contact area was used by detecting the last contact point at maximum load in the FE mesh, resulting in a more accurate measurement of the indentation modulus of the epoxy resin.

3.2.1 Viscoplasticity Models

In order to analyse the time dependent response of the epoxy resin under nanoindentation, viscoplasticity models were applied in the numerical simulation for verification using the static properties in Table 8.2. To account for the effect of viscoplasticity, two methods based on Perzyna and Modified time hardening were implemented. On the Perzyna model, the results of stress-strain response of the epoxy resin under the tensile tests at various strain rates were used to determine the Perzyna parameters. This was done based on the ideas presented by Perzyna (1963a, b, 1966). The model assumes that the plastic strain rate (έ _pl) is a function of a hardening/softening parameter (m), the material viscosity parameter (γ), and the static yield stress (σ ₀). The stress strain rate graph is created and fitted with Perzyna material model of viscoplasticity (Table 8.3) to identify the required parameters. To identify the modified time hardening parameters (Table 8.3), the variation of strain versus time at the stress level of 10 MPa (obtained from a creep test) was determined and fitted with the Modified Time hardening model.

Table 8.2 Isotropic elastic-perfectly plastic properties of bulk epoxy resin (obtained from macroscopic tension test) used for the FE model of nanoindentation

Table 8.3 Viscoplasticity models and calculated parameters of epoxy resin used in FE model

3.2.2 Comparison with Experiment

An AFM images of the residual impression from an indentation on bulk epoxy resin and the amounts of pile up around it are shown in Fig. 8.12. The data from the AFM scans was post-processed using the AFM data analysis software Gwyddion. The tests were performed under displacement control mode using a single cycle indentation (load-hold-unload) protocol and during each cycle, a 5 s hold was imposed at the peak displacement.

Fig. 8.12

AFM image of a residual impression from an indentation carried out on the bulk epoxy resin, highlighting locations of line scans, (b) Line scans A, B and C

When performing indentations on a polymer such an epoxy resin, due to the effect of pile up (Fig. 8.12), the Oliver and Pharr method underestimates the contact area. In this study, because of the viscoelastic recovery which the epoxy resin experiences on reduction of the maximum indentation load; methods of calculating the projected contact area based on the residual impression (Saha and Nix 2001; Beegan et al. 2003; Kese and Li 2006; Zhou et al. 2008; Hardiman et al. 2016) as well as depth-corrected contact area based on the measured pile up profile (Cao et al. 2006; Zhou et al. 2008; Hardiman et al. 2016) fail to correct the effect of material pile up on indentation modulus of epoxy resin as the height of the measured pile-up is a not representative of the state of pile-up under the indenter at maximum indentation load. In addition, the Oliver and Pharr method does not take into account the effect of viscoplasticity, therefore, in order to correct the effect of above phenomena (material pile up and viscoplasticity effects) for the measurement of elastic modulus, FE calculated load displacement curves are generated and compared with experimentally generated load displacement curves (Fig. 8.13). Agreement is good but the small difference between experimental load displacement curves and the computed results from the FE model is probably due to the effect of surface roughness, adhesion force and indentation process-associated factors (e.g. sample mounting and fame compliance) which are not considered in the numerical model. The maximum load reached by all the nanoindentations experiments on bulk epoxy resin only varies between 280–300 μN indicating that the resulting data curves for all indentations are relatively consistent and reproducible due to the careful and uniform process of polishing the sample. The agreement between numerical and experimental results validates the viscoplasticity parameters introduced into the FE model. The von Mises stress fields developed in the 2D FE model of bulk epoxy resin at the maximum indentation depth are shown in Fig. 8.14 providing an insight into the stress distribution when characterizing the bulk epoxy resin using the nanoindentation method.

Fig. 8.13

Force-displacement curve on bulk epoxy resin

Fig. 8.14

Von Mises stress field on 2D axisymmetric FE model of nanoindentation of bulk epoxy resin

In order to correct the effect of pile up, the ratio of contact area calculated from the FE model to the contact area calculated from the Oliver and Pharr method (Eq. 8.4) is used and therefore an area correction factor was applied to the experimental indentation test data (Table 8.4). The elastic modulus of bulk epoxy resin calculated from the experimentally generated load displacement curves is corrected by the area correction and reported in Table 8.5. It must be noted that, the elastic modulus of the bulk epoxy resin has been calculated by averaging data from 4 × 4 (8.16) indentations using the Oliver and Pharr method and the mean value of modulus was calculated as 5.22 GPa with a standard deviation of 0.3 GPa. After accounting for the effect of material pile up (using the area correction in Table 8.4) and the effect of hydrostatic stress using the relation (Eq. 8.10) which is detailed in (Rodríguez et al. 2012; Hardiman et al. 2016), the remaining difference of about 11.5% between the indentation modulus of bulk epoxy resin (i.e. 4.21 GPa) and the macroscopic tensile modulus (i.e. 3.78 GPa) is mainly due to the effect of creep/viscoplasticity. Although the effect of creep has been considered by addition of a constant displacement hold segment between the loading and unloading segments (i.e. 5 s hold segment), the FE analysis of indentation on the bulk epoxy resin at various holding time and/or displacement rate shows that increasing holding time or reducing strain rate result in an indentation modulus of the epoxy resin which compares very well with the bulk tensile modulus. As can be seen in Fig. 8.15, the results can be produced free from the effect of time dependent deformation behaviour of the epoxy resin by either increasing holding time (to 500 s) or reducing the displacement rate to 0.002 μm/s. It was found that nullifying the effects of the viscoplastic deformation can lead to reductions of the modulus of the order of 10–12%.

Table 8.4 Ratio of contact area calculated from FEM to the contact area calculated from Oliver and Pharr method

Table 8.5 Experimentally calculated indentation modulus of epoxy resin and the effect of pile up (using FEM) and hydrostatic stress

Fig. 8.15

Effect of loading rate (at the constant hold time of zero) and holding time (at the constant loading rate of 0.2 μm/s) on elastic modulus calculated using the FE model of nanoindentation on bulk epoxy resin, Normalized modulus is the ratio of indentation modulus calculated from the FE load displacement curve over the macroscopic tensile modulus

3.3 Viscous-Hyper Elastic Materials

Soft materials such as biological tissues can have both the large strain and time dependent behaviour at once, therefore viscous behaviour needs to be considered for obtaining the mechanical properties of such soft materials. In order to study the viscous response of the soft materials using nanoindentation, a viscoelasticity model and hyper elasticity models were applied simultaneously in the FE model. As described in earlier sections, the three hyper elastic models, namely Mooney-Rivlin, Ogden and Arruda-Boyce models were used to determine the nonlinear behaviour. The viscoelasticity demonstrates the time dependent behaviour that includes creep, stress relaxation, or frequency-dependent dynamic properties. The viscoelasticity can be described using a power law variation of stress with respect to time. One widely used model for this is known as the Prony series model described previously. The constitutive model for viscous-hyper elasticity is a combination of the hyper elastic Mooney-Rivlin, Ogden and Arruda Boyce models, and the time dependent Prony series model.

3.3.1 Methodology of Tension Testing and Determination of Viscoelastic/Hyper Elastic Model Parameters

In this study, the parameters of various hyper elastic material models that characterize the soft polymer (bulk specimen in nanoindentation) were obtained from the uniaxial tension test. The various hyperelastic strain energy functions and their corresponding uniaxial stress-strain relationships were used in this study for the curve fitting to find their parameters following the Nelder-Mead optimization method are listed in Table 8.6.

Table 8.6 Hyper elastic strain energy function with their uniaxial stress strain equations

The tensile test was conducted in conjunction with a video gauge system (DIC measurement set up) to measure the components of strain and Poisson’s ratio. Subsequently this information was used to build the stress-strain curve. In order to use the DIC technique during the tensile testing, a camera was placed perpendicular to the specimen surface to register digital images of it during the deformation. The image acquisition was started as soon as the tension test began. The registered images were processed using an algorithm in the DIC software (VIC 2D) (Solutions 2009) which outputs full field strain measurement with high spatial resolution. The DIC technique is based on the recognition of geometrical changes in the grey intensity distribution of the surface speckle patterns before and after deformation. Therefore in order to make the process work, the specimen surface is marked with a random speckle pattern (Fig. 8.16). In this work, this was done by alternately spraying white and coloured paint. The artificial stochastic spot pattern (random speckle pattern) of the specimen surface is used as the carrier of the surface displacement/strain information.

Fig. 8.16

Geometry of tensile test specimen marked with random speckle pattern

In order to evaluate the viscous hyper elasticity response of the polymeric specimen under nanoindentation, a viscoelasticity model and hyper elasticity model were combined and applied in the FE model. The hyper elasticity component was described by Mooney Rivlin, Ogden or Arruda Boyce constitutive laws. The viscoelasticity which has elastic and viscous parts is usually characterized by relaxation or creep testing. Generally in relaxation experiments, either a constant tensile, compressive or shear strain is applied on the material, and the stress variation is recorded. Therefore, because of the viscous effects in the material stress relaxation occurs over the time. The variation of stress with respect to time is fitted with a number of models (in this study Prony series model was used). In shear relaxation experiment, the Prony series is:

$$ G(t)={G}_0-\sum_{i=1}^N{G}_i\left(1-\exp \left(\frac{-t}{\tau_i}\right)\right) $$

(8.17)

Where G ₀, G _i and τ _i are the elastic shear modulus, relative modulus and relaxation time. In this study it is assumed that N =1, G ₁ =0.33 and τ _i =1.

3.3.2 Tensile Testing Results

Obtaining complete stress-strain curves during contact loading is complex in soft materials due to the inhomogeneity of the stress state, whereas the stress-strain curves under uniaxial loading can be easily assessed. Therefore, determining the constitutive parameters from the hyper elastic stress-strain behaviour of rubber required uniaxial tensile experiments. Figure 8.17 shows a typical stress-strain response of polyurethane rubber determined at a strain rate of 10 min⁻¹. To build the stress-strain curve, stress was calculated based on the variation of load obtained from the load cell of the testing machine divided by the original cross sectional area of the sample and the strain data was extracted from the DIC. For a representative tension stress-strain curve up to 120% strain (Fig. 8.17), the DIC calculated strain field (i.e. longitudinal component of strain) is shown illustrating the localized strains and the areas on the surface of the sample where damage develops. The polynomial fit to the tensile stress strain data was used to determine the corresponding variation of tangent modulus versus strain (Fig. 8.18). Although it is not possible to define the equivalent Elastic modulus and Poisson’s ratio that characterize the mechanical performance of this material, an initial value for elastic modulus can be calculated when the material begins to deform in tension. During the tension test, it was found that initially strain softening occurs (decrease in the elastic modulus) and later strain hardening (increase in the elastic modulus) occurs. As it can be seen from Figs. 8.17 and 8.18, the initial response of the specimen under tensile loading is linear with the average Elastic modulus and Poisson’s ratio of 62 ± 5 MPa and 0.5 respectively. This is followed by a drop-in modulus from 62 MPa to less than 10 MPa until the nominal value of strain is about 0.8, and thereafter hardening behaviour was observed.

Fig. 8.17

Tensile stress-strain response and DIC calculated strain maps during the deformation

Fig. 8.18

Variation of tangent modulus versus strain using the Polynomial fit

In order to describe the nonlinear mechanical behaviour of the studied material, three widely used hyper elastic material models including Mooney Rivlin, Ogden and Arruda-Boyce were used. Figure 8.19 shows the uniaxial stress-strain curve which was used to fit with the above material models. In this study, the FE software ANSYS was used to determine the unknown hyper elastic parameters depending on the chosen model. This fitting approach avoids any material stability issues that occur when trying to generate optimum fitting parameter for an elastomeric material using the Ogden model as may be encountered in some dedicated fitting packages (e.g. hyperfit). The hyper elastic material parameters obtained from the results after fitting the constitutive models are provided in Table 8.7. As can be seen in Fig. 8.19, the Mooney-Rivlin model appears to be a better fit with a relatively good match to experimental data when compared to the Ogden and Arruda-Boyce models. This indicates that the Mooney-Rivlin method matched to the experimental results of the specific rubber material we have chosen; this mainly depends on the rubber-material used since the Ogden model is the best fit choice for the rubber material used in ‘O’ ring seals. However, in this study the numerical simulation of displacement-controlled nanoindentation using all these above-mentioned hyperelastic models was analysed. Given the varying fit quality it is interesting to note what effect the selection of model will have on modelled indentation behaviour.

Fig. 8.19

Fitting the uniaxial test data using different hyperplastic models. (Mooney-Rivlin, Ogden and Arruda Boyce)

Table 8.7 Hyperplastic material parameters of obtained results after fitting the constitutive models

3.3.3 Finite Element Modelling

For indenting soft materials, the load-displacement behaviour is different from that of stiff materials, a relatively large displacement is achieved for a given (small) applied load. Thus, the contact area plays an important role in mechanical characterisation of soft materials. In the literature, commonly dull tips such as spherical or flat ended tips are widely used. In order to analyse the mechanical behaviour of hyper elastic and viscous hyper elastic material under nanoindentation testing, 2D axisymmetric FE simulations were carried out. This resulted in the generation of reaction forces (P) versus displacement (h) during the indentation process. To understanding the effect of the tip, the FE simulation was done using two different tip radii, namely 50 nm and 500 nm. Also, the contact depth varied from 50 nm to 1000 nm in each case. The mechanical properties (hyper elastic model parameters), known from macroscopic tension testing was supplied to the Finite Element code (ANSYS) to simulate the nanoindentation testing. The FE modelling of nanoindentation was performed under the displacement control mode using a single cycle indentation (load-hold-unload) protocol and during each cycle, a 1 s hold was imposed at the peak displacement. The indented sample was modelled as a hyper elastic material following Mooney Rivlin, Ogden and Arruda Boyce constitutive laws. The FE projected contact area under nanoindentation was determined from the last contact point at maximum load in the FE mesh.

Fig. 8.20

FE calculated load-depth curves of nanoindentation on hyper-elastic and viscos hyper elastic material model (a) tip radius of 500 nm, (b) tip radius of 50 nm. Mooney Rivlin hyper elastic = MR-H, Mooney Rivlin viscos hyper elastic = MR-VH, Ogden hyper elastic = O-H, Ogden viscos hyper elastic = O-VH, Arruda Boyce hyper elastic = AB-H, Arruda Boyce viscos hyper elastic = AB-VH

3.3.4 Model Predictions and Experiment

Figure 8.20, shows the FE calculated load-contact depth (P-h) curves obtained from the nanoindentation on the specimen with purely hyper elastic and viscous hyper elastic properties. As can be seen, compared to different purely hyper elastic material models, the maximum load required to achieve the displacement of 500 nm is higher when the Mooney Rivlin model is used in the FE model of the indented sample. Combining viscosity (Prony shear relaxation model) with the hyper elasticity in the FE model of the indented sample results in lower load throughout the indentation cycle. In addition, compared with the Ogden and the Arruda Boyce model, conducting indentation on the sample with Mooney Rivlin behaviour, results in a steeper slope in the initial part of the unloading curve indicating an increase in the contact stiffness. The indentation force generated during nanoindentation with two different tip radii (50 nm and 500 nm) was also investigated and it is shown that, at the same indentation depth, the larger tip radius (blunt tip) induces a higher indentation load irrespective of material model used. This is due this fact that, at a given indentation depth, the larger tip radius deforms a greater amount of material compared to the smaller radius tip (sharp tip) during the indentation processes; as a result, higher indentation load is needed to apply enough pressure on the indenter to penetrate into the specimen to the target contact depth. Comparing Fig. 8.25 to Fig. 8.26 or Fig. 8.27 to Fig. 8.28, it can be seen that bigger deforming volumes are also created when using the larger tip radius. Although, due to limited space, only the FE calculated load contact depth curves for the maximum applied displacement of 500 nm are shown here (Fig. 8.20), for different displacements similar load displacement behaviour can be seen. Of course the magnitude of maximum load at different displacement is also different (Fig. 8.21).

Following the procedure based on the Oliver and Pharr method (described in Sect. 1.3 and 2.1), the analysis of the FE calculated load-displacement curve provides an elastic modulus of the material using either the purely hyperelastic material model or the viscous hyper elastic material model. The effect of indenter tip geometry and contact depth, on the elastic modulus for the different material models is shown in Figs. 8.22, 8.23 and Fig. 8.24. Using the Arruda Boyce model (Fig. 8.22), hyper-elasticity effects are insensitive to the both varied tip radius and indentation depth. Although viscous effects are sensitive to the variation in indentation depth, they are insensitive to the varied tip radius for indentation depths less than 250 nm and become more sensitive when indentation depth increases.

Fig. 8.21

Variation of maximum force versus displacement (a) tip radius of 50 nm, (b) tip radius of 500 nm for hyper-elastic and viscos hyper elastic material model, Mooney Rivlin hyper elastic = MR-H, Mooney Rivlin viscos hyper elastic = MR-VH, Ogden hyper elastic = O-H, Ogden viscos hyper elastic = O-VH, Arruda Boyce hyper elastic = AB-H, Arruda Boyce viscos hyper elastic = AB-VH

Fig. 8.22

Variation of elastic modulus versus displacement during the nanoindentation testing on specimen with (a) purely hyper elastic model (Arruda Boyce), (b) Viscous hyper elasticity model (Combined Prony shear relaxation and Arruda Boyce model)

Fig. 8.23

Variation of elastic modulus versus displacement during the nanoindentation testing on specimen with (a) purely hyper elastic model (Mooney Rivlin), (b) Viscous hyper elasticity model (Combined Prony shear relaxation and Mooney Rivlin model)

Fig. 8.24

Variation of elastic modulus versus applied displacement during the nanoindentation testing on specimen with (a) purely hyper elastic model (Ogden), (b) Viscous hyper elasticity model (Combined Prony shear relaxation and Ogden model)

Using the Mooney Rivlin material model (Fig. 8.23) shows that both hyper-elasticity and viscosity effects are insensitive to the varied tip radius, however, their effects are sensitive to the varied indentation depth. Comparing the variation of elastic modulus obtained from the hyper elastic and viscous hyper elastic models for different indentation depths the elastic modulus obtained from the viscous hyper elastic model can be replaced by a purely hyper elastic model and vice versa to calculate the elastic modulus. In addition comparing Fig. 8.23 with Fig. 8.18, shows that for a small indentation depth (0–250 nm) the elastic modulus obtained from either a hyper elastic model or a viscous hyper elastic model matches well with tangent modulus obtained from the initial linear part of tensile stress strain curve, however, as the indentation depth increases, the FE model of nanoindentation overestimate the elastic modulus.

Using the Ogden material model (Fig. 8.24) shows that for indentation depth less than 250 nm, hyper-elasticity effects are insensitive to the variation in tip radius but it becomes a bit more sensitive when indentation depth increases. In addition, the viscosity effects are insensitive to the variation in tip radius, while they are also insensitive to the contact depth (for indentation depth less than 500 nm)

In order to understand the effect of indenter tip radius on the mechanics of nanoindentation of soft polymeric materials with either purely hyper elastic or viscous hyper elastic properties, FE calculated Von Mises stress distribution are shown in Figs. 8.25, 8.26, 8.27 and 8.28. As it can be seen in these figures, the stress fields in nanoindentation testing of specimen is affected by the size of the indenter. Regardless of the indentation depths and material models, a sharper tip induces higher stress values. For example for testing a sample with purely hyper elastic behaviour (Mooney Rivlin model) at the maximum displacement of 500 nm, a conical indenter tip with 500 nm radius induces maximum stress of 30 MPa as opposed to 52 MPa when the tip radius is 50 nm. In addition, sharper conical tip produces a smaller deforming volume compared to a larger tip. Similar comparison can be made for testing a sample with viscous hyper elastic behaviour (Prony shear relaxation model combined with Mooney Rivlin). Obviously, because of the relaxation model used in the FE model in the material of a nanoindented sample, the maximum stress values are lower compared to the purely hyper elastic model. In addition, compared to the purely hyper elastic model of an indented sample, the residual stress after complete unloading, shows the effect of viscoelasticity (Prony shear relaxation) in the FE model. Regardless of the material models used for the FE analysis of nanoindentation, the highest stress value is located under the contact area between the indenter tip and specimen (not at the surface of tested specimen but deeper under the indenter as might be expected from Hertzian contact theory). The stress fields of other hyper elastic and viscous hyper elastic material models (Ogden and Arruda Boyce) are similar to the stress fields of the Mooney Rivlin model, while the maximum stress values obtained by Ogden and Arruda Boyce are lower.

Fig. 8.25

Evolution of von Mises stress distribution during the nanoindentation of viscos hyper elastic material using combined Prony shear relaxation and Mooney-Rivlin model) with the indenter tip radius of 50 nm after (a), 1 s, (b) 2 s (c) 3 s

Fig. 8.26

Evolution of von Mises stress distribution during the nanoindentation of viscous hyper elastic material using combined Prony shear relaxation and Mooney-Rivlin model and indenter tip radius of 500 nm after (a), 1 s, (b) 2 s (c) 3 s

Fig. 8.27

Evolution of von Mises stress distribution during the nanoindentation of pure hyper elastic material using Mooney-Rivlin model and indenter tip radius of 50 nm after (a), 1 s, (b) 2 s (c) 3 s

Fig. 8.28

Evolution of von Mises stress distribution during the nanoindentation of pure hyper elastic material using Mooney-Rivlin model and indenter tip radius of 500 nm after (a), 1 s, (b) 2 s (c) 3 s

Figure 8.29 compares the elastic modulus measured experimentally using the uniaxial tensile test and that reconstructed numerically from nanoindention by giving the tensile data as input to the FE model of nanoindentation to extract constitutive parameters using various hyperelastic models. From the Fig. 8.29 it can be observed that the finite element simulations output of averaged modulus of different hyperelastic materials using the Mooney Rivlin, Ogden and Arruda-Boyce model closely matches with the experimental data. The numerical validation of the experimental results of elastic modulus was appropriately fit over the entire range of the strain. The Mooney-Rivlin model was found to be suitable to represent accurately nonlinear mechanical behaviour and shown the excellent agreement with numerical validation of the experimental results over a wide range of strains. The average elastic modulus E was about 62 MPa for Mooney-Rivlin. Both the Arruda-Boyce and Ogden models predicted the lower elastic modulus compared with the Mooney Rivlin model. The average elastic modulus E was about 17.3 MPa for Arruda-Boyce model, and the average elastic modulus E was about 28.5 MPa for Ogden model. Thus the results confirm that the Mooney-Rivlin approach is most suitable for small strain hyperelasticity whilst the other models are more suitable at larger strains.

Fig. 8.29

Comparison between the elastic modulus obtained from FE calculated nanoindentation load displacement data and experimentally tensile stress-strain data

4 Conclusions

The extraction of mechanical behaviour of soft materials using nanoindentation is performed through combined experimental and numerical simulations. Hyper elastic constitutive models such as the Mooney Rivlin model, the Ogden model and the Arruda-Boyce model as well as viscoelastic/viscoplastic models such as Prony shear relaxation, Perzyna and Modified time hardening models are required for the FEM. The input parameters can be extracted from the uniaxial tensile test and digital image correlation (DIC) technique on PMMA, epoxy resin and polyurethane rubber materials.

In a rubber-like polymer with hyper elastic properties, the Mooney-Rivlin model was found to be suitable to represent accurately nonlinear mechanical behaviour and shows excellent agreement with numerical validation of the experimental results over a wide range of strains. When it comes to the combined viscoelasticity and hyperelasticity properties of rubber like materials, it was found that viscosity effects are sensitive to the varied indentation depth and insensitive to tip radius respectively when this material model is used.

In polymers like epoxy resin, although atomic force microscopy images of residual impressions showed regions of material pile-up, the viscoplastic recovery which occurs following indenter unloading makes the determination of the contact areas problematic. The use of FEM to predict the projected indentation contact area, given the viscoplasticity parameters (e.g. Modified time hardening and/or Perzyna) of epoxy resin, is shown to be useful when extracting the mechanical properties from the nanoindentation technique. It was also shown that the overestimation of the elastic modulus calculated by the nanoindentation test method in relation to the macroscopic conventional test methods (e.g. tensile and/or compressive tests) is mainly related to the effects of material pile up, viscoplasticity and hydrostatic stress. It was found that, the FE calculated indentation modulus will be in a good agreement with macroscopic tensile modulus values provided that the viscoplastic deformation is allowed to finish prior to unloading. FEA suggested that, this can be obtained by altering indentation settings (i.e. holding segment and/or strain rate), therefore the elastic modulus of bulk epoxy resin can be determined, independent of the viscous effects.

In polymeric materials which only show viscoelasticity properties (e.g. PMMA), it was found that analytical expression developed in the literature can be successfully used to determine the Prony series parameters. Using these parameters in an FE model, resulted similar load displacement data obtained from the experimental nanoindentation.

Thus, the combined FE and experimental nanoindentation approach used in this study shows that appropriate constitutive models are needed to characterize mechanical and deformation behaviour of polymers and therefore, careful modelling of experimental data is necessary for understanding deformation mechanisms.