The peculiar elongational viscosity of concentrated solutions of monodisperse PMMA in oligomeric MMA

Abstract

Concentrated solutions of nearly monodisperse poly(methyl methacrylate), PMMA-270k and PMMA-86k, in oligo(methyl methacrylate), MMA o-4k and MMA o-2k, investigated by Wingstrand et al. (Phys Rev Lett 115:078302, 2015) and Wingstrand (2015) do not follow the linear-viscoelastic scaling relations of monodisperse polystyrenes (PS) dissolved in oligomeric styrene (Wagner in Rheol Acta 53:765–777, 2014a, in Non-Newtonian Fluid Mech 222:121–131, 2014b; Wagner et al. in J Rheol 59:1113–1130, 2015). Rather, PMMA-270k shows an attractive interaction with MMA, in contrast to the interaction of PMMA-86k and MMA. This different behavior can be traced back to different tacticities of the two polymers. The attractive interaction of PMMA-270k with o-4k creates pseudo entanglements, which increase the interchain tube pressure, and therefore, the solution PMMA-270k/o-4k shows, as reported by Wingstrand et al. (Phys Rev Lett 115:078302, 2015), qualitatively a similar scaling of the elongational viscosity with ${\left(\dot{\varepsilon}{\tau}_R\right)}^{-1/2}$ as observed for polystyrene melts. For the solution PMMA-270/o-2k, this effect is only seen at the highest elongation rates investigated. The elongational viscosity of PMMA-86k dissolved in oligomeric MMA is determined by the Rouse time of the melt, as in the case of polystyrene solutions.

Introduction

Experimental data of elongational properties of polymer solutions and melts of monodisperse and polydisperse polymers obtained by the filament stretching technique (see, e.g., Bhattacharjee et al. 2002, 2003; McKinley and Sridhar 2002; Bach et al. 2003; Nielsen et al. 2008) have challenged the predictive capabilities of the classical Doi-Edwards (DE) tube model. In elongational flow, the tube model with the so-called independent alignment assumption predicts an upper limit of the tensile stress equal to five times the plateau modulus G_N (Doi and Edwards 1986). The tube diameter and tension in the polymer chain are assumed to be constant, and the macroscopic stress is a consequence of chain orientation only, resulting in a scaling of the steady-state elongational viscosity at strain rates $\dot{\varepsilon}$ larger than the inverse reptation time according to ${\dot{\varepsilon}}^{-1}$. Various reptation-based models have invoked chain stretch when the deformation rate is larger than the inverse Rouse time τ_R of the chain (see e.g. Pearson et al. 1989; Mead et al. 1995, 1998; Fang et al. 2000), and these models seem to capture the essential features seen in the elongational viscosity of polymer solutions (Bhattacharjee et al. 2002), i.e., a decrease of the elongational viscosity proportional to ${\dot{\varepsilon}}^{-1}$ for elongation rates less than the inverse Rouse time, and a sudden increase at larger elongation rates.

In strong contrast to polymer solutions, elongational viscosity measurements of Bach et al. (2003) on narrow molar mass distribution polystyrene melts revealed that the elongational viscosity scales approximately with ${\left(\dot{\varepsilon}{\tau}_R\right)}^{-1/2}$ in the nonlinear viscoelastic regime. To account for this behavior and relaxing the assumption of a constant tube diameter, Marrucci and Ianniruberto (2004, 2005) introduced an interchain pressure term arising from lateral forces between polymer chain and tube wall into the DE model, which limits chain stretching. Their analysis was restricted to scalar arguments and to the steady-state viscosity. A full constitutive equation, which describes time-dependent as well as steady-state rheology of nearly monodisperse polymer melts, was presented by Wagner et al. (2005), and predictions are in excellent agreement with the elongational viscosity data of Bach et al. (2003), Hassager (2004), Nielsen et al. (2008), and Rolón-Garrido et al. (2006). Later, Wagner and Rolón-Garrido (2009a, b) proposed a combination of Rouse relaxation and tube diameter relaxation in agreement with experimental evidence of elongational flow data of monodisperse linear polymer melts and showed that the tube diameter relaxation time is equal to three times the Rouse time. This concept was extended to bidisperse polymer systems consisting of a short and a long-chain component, and demonstrated that the effective tube diameter relaxation time of the long-chain component is increased in accordance with the expansion of the tube diameter due to dynamic tube dilation (Wagner 2011).

Huang et al. (2013a, b) investigated elongational viscosities of two polystyrene melts as well as of several concentrated solutions of the same polystyrenes with polymer volume fractions φ≥44% in oligomeric styrene, and they reported that polymer solutions show much stronger strain hardening than the corresponding melts. They also speculated on a nematic interaction between the polymer and the oligomeric styrene (Huang et al. 2013b). In agreement with the experimental data of Huang et al., Wagner (2014a, b) presented a unifying concept of modeling the elongational viscosity of polymer melts and concentrated solutions. Later, Narimissa et al. (2015, 2016), Narimissa and Wagner (2016a, b, c) extended this idea to a Hierarchical Multi-mode Molecular Stress Function (HMMSF) model for polydisperse linear and long-chain branched polymer melts.

Recently, Wingstrand et al. (2015) reported elongational viscosity data of two PMMA polymers dissolved in oligomeric MMAs. Their aim was to demonstrate linear and nonlinear universality in the rheology of polymer melts and solutions by comparing the two PMMA solutions to two polystyrene melts, PS-285k and PS-100k, with supposedly the same number of entanglements and the same number of Kuhn steps per entanglement. Also, by using MMA as solvent, the flow-induced monomeric friction reduction as proposed by Ianniruberto et al. (2012) should be similar as in the melt. Wingstrand et al. (2015) came to the conclusion that the two PMMA solutions show indeed a similar elongational viscosity as the polystyrene melts. However, their analysis was based on an empirical relation for the number of entanglements per polymer chain of the PMMA solutions. Here, we examine the interaction of the two PMMA polymers with the oligomeric MMA and present quantitative modeling of the steady-state and start-up elongational viscosities of the PMMA solution data of Wingstrand et al. (2015) and Wingstrand (2015), based on the extended interchain pressure model.

Experimental data and linear-viscoelastic characterization

The experimental data discussed are those presented by Wingstrand et al. (2015) and Wingstrand (2015) on nearly monodisperse poly(methyl methacrylate) PMMA-270k and PMMA-86k. Forty-four percent of PMMA-270k was diluted in 4k oligo(methyl methacrylate) (o-4k), and 43% was diluted in 2k oligo(methyl methacrylate) (o-2k). The solutions were denoted as PMMA-270k/o-4k and PMMA-270/o-2k, respectively. Also, 51% of PMMA-86k was diluted in o-4k, and 43% was diluted in o-2k, and the solutions were denoted as PMMA-86k/o-4k and PMMA-86k/o-2k, respectively. Details of molecular characterization and sample preparation are given by Wingstrand et al. (2015). Elongational viscosities were measured using a filament stretching rheometer capable of measuring at high temperatures. Measurements were performed at 150 °C, or shifted to 150 °C by standard time-temperature shifting. The elongational viscosity data of PMMA-270k and PMMA-86k diluted in o-2k (Wingstrand 2015) have not been published previously and are reported here for the first time.

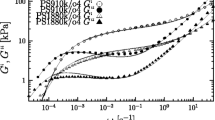
From linear-viscoelastic mastercurves of G’ and G”, Wingstrand et al. (2015) determined continuous Baumgärtel-Schausberger-Winter (BSW) relaxation spectra (Baumgaertel et al. 1990). The relaxation modulus G(t) is found from the spectrum H(τ) by

$$ G(t)=\underset{0}{\overset{\infty }{\int }}\frac{H\left(\tau \right)}{\tau}\exp \left(-t/\tau \right) d\tau $$

(1)

H(τ) is composed of two part, the entanglement contribution H_e(τ) and the glassy contribution H_g(τ),

$$ H\left(\tau \right)={H}_e\left(\tau \right)+{H}_g\left(\tau \right) $$

(2)

with

$$ {H}_e\left(\tau \right)={n}_e{G}_N{\left(\frac{\tau }{\tau_m}\right)}^{n_e}h\left(1-\tau /{\tau}_t\right) $$

(3)

and

$$ {H}_g\left(\tau \right)={n}_e{G}_N{\left(\frac{\tau }{\tau_c}\right)}^{-{n}_g}h\left(1-\tau /{\tau}_t\right) $$

(4)

G_N is the plateau modulus, τ_t the longest or “terminal” relaxation time, τ_c the characteristic time constant of the glassy contribution, and h(x) the Heaviside step function. The values of n_e and n_g are fixed to 0.23 and 0.70, respectively, as in the case of polystyrene melts and polystyrene diluted in oligomeric styrene (Huang et al. 2013a, b). The other characteristic material constants of the BSW spectra for the melts and solutions investigated are summarized in Tables 1 and 2.

Table 1 Molecular characterization and material parameters of PMMA-270k and its solutions in o-4k and o-2k at 150 °C. Quantities in parenthesis as reported by Wingstrand et al. (2015)

Table 2 Molecular characterization and material parameters of PMMA-86k and its solutions in o-4k and o-2k at 150 °C. Quantities in parenthesis as reported by Wingstrand et al. (2015)

The zero-shear viscosity calculated from the BSW spectrum is given by

$$ {\eta}_0=\underset{0}{\overset{\infty }{\int }}G(s) ds={n}_e{G}_N{\tau}_t\left(\frac{1}{1+{n}_e}+\frac{1}{1-{n}_g}{\left(\frac{\tau_c}{\tau_t}\right)}^{n_g}\right)\cong {n}_e{G}_N{\tau}_t\left(\frac{1}{1+{n}_e}\right) $$

(5)

However, due to the slight polydispersity of PMMA-276k and PMMA-86k, we prefer to determine η₀ from a parsimonious spectrum fitted to the mastercurves of G’ and G”, and this value of η₀ is reported in Tables 1 and 2 and is used in the following.

The entanglement molar mass M_e is obtained from the plateau modulus G_N by the relation of classical rubber elasticity as

$$ {M}_e=\frac{\rho RT}{G_N}\varphi $$

(6)

with density ρ at 150 °C taken as ρ = 1.130g/cm³ and gas constant R. φ is the volume fraction of polymer in the solution with φ = 1 specifying the melt. With M being the molar mass of the polymer, the number of entanglements per chain, Z, follows then from

$$ Z=\frac{M}{M_e} $$

(7)

The Rouse stretch relaxation time τ_R is calculated according to Osaki et al. (1982), Menezes and Graessley (1982), Takahashi et al. (1993), and Isaki et al. (2003),

$$ {\tau}_R=\frac{12\;M{\eta}_0}{\pi^2\rho \kern0.62em RT\varphi}{\left(\frac{M_{cm}}{M\varphi}\right)}^{2.4} $$

(8)

M_cm indicates the critical molar mass in the melt state and was taken as M_cm = 2M_em (see, e.g., Fuchs et al. 1996), with M_em being the entanglement molar mass of the melt. The characteristic quantities of all PMMA melts and solutions investigated are summarized in Tables 1 and 2.

We note that the analysis of Wingstrand et al. (2015) was based on the empirical relations

$$ Z\propto {\left(\frac{\tau_t}{\tau_c}\right)}^{\frac{1}{3.4}} $$

(9)

and

$$ {\tau}_R={\tau}_c{Z}^2 $$

(10)

which in some cases led to substantially different values for Z, M_e, and τ_R (see values in parenthesis in Tables 1 and 2). These relations depend sensitively on the experimental determination of τ_c, and deviation from values derived by relations (6) to (8) are not surprising.

The horizontal shift factors a_T used to obtain mastercurves of G’ and G” at the reference temperature T₀ = 150 °C (see Wingstrand et al. 2015) are shown in Figs. 1a and 2a. The shift factors of the melts are fitted by the WLF equation

$$ {\log}_{10}{a}_T=\frac{-{c}_1^0\left(T-{T}_0\right)}{c_2^0+\left(T-{T}_0\right)} $$

(11)

with ${c}_1^0=10.08$ and ${c}_2^0=102.38$ for PMMA-270k, and ${c}_1^0=13.84$ and ${c}_2^0=180.43$ for PMMA-86k. The WLF parameters ${c}_1^0$ and ${c}_2^0$ are in the range of WLF parameters reported by Fuchs et al. (1996), and the difference in the temperature dependence of PMMA-270k and PMMA-86k is due to a difference in the tacticity of the two melts. The glass transition temperatures T_g of the solvents (oligomeric MMA) are much lower than the glass transition temperature of the melts, and are reported as 98.9 °C for o-4k and 72.5 °C for o-2k. Therefore, the glass transition temperature of the solutions as indicated in Tables 1 and 2 is shifted by a temperature difference

$$ \Delta {T}_g={T}_{gm}-{T}_g $$

(12)

relative to the glass transition temperature T_gm of the melt to lower values. The change in the glass transition temperature leads to a reduction of the friction factor of the polymer solutions relative to the friction factor of the melt. Following Wagner (2014a, b), this is characterized by a shift factor a_Tg, which is obtained by inserting ΔT_g from Eq. (12) into Eq. (11),

$$ {\log}_{10}{a}_{Tg}=\frac{-{c}_1^0\Delta {T}_g}{c_2^0+\Delta {T}_g} $$

(13)

Fig. 1

a Temperature shift factors a_T as a function of temperature for PMMA-270k melt and solutions at reference temperature of T₀ = 150 °C as reported by Wingstrand et al. (2015). Solid line for PMMA-270k is given by Eq. (11). b Same temperature shift factors a_T as a function of T-T_g and vertically shifted by multiplication with shift factor a_Tg. Solid line is given by Eq. (11)

Fig. 2

a Temperature shift factors a_T as a function of temperature for PMMA-86k melt and solutions at reference temperature of T₀ = 150 °C as reported by Wingstrand et al. (2015) and Wingstrand (2015). Solid line for PMMA-270k is given by Eq. (11). b Same temperature shift factors a_T as a function of T-T_g and vertically shifted by multiplication with shift factor a_Tg. Solid line is given by Eq. (11)

The temperature dependence of melts and solutions is then given by

$$ {\log}_{10}{a}_T{a}_{Tg}=\frac{-{c}_1^0\left(T+\Delta {T}_g-{T}_0\right)}{c_2^0+\left(T+\Delta {T}_g-{T}_0\right)}=\frac{-{c}_1^0\left[\left(T-{T}_g\right)-\left({T}_0-{T}_{gm}\right)\right]}{c_2^0\left[\left(T-{T}_g\right)-\left({T}_0-{T}_{gm}\right)\right]} $$

(14)

The experimentally determined shift factors a_T are plotted in Figs. 1b and 2b according to Eq.(14), and agreement of the temperature dependence of melts and solutions is excellent for PMMA-86k, while for PMMA-270k dissolved in MMA deviations appear at temperatures 60 K (for o-2k) and 100 K (for o-4k) above the glass transition temperature. A possible explanation for this is given below.

For a range of polystyrenes dissolved in oligomeric styrene with polymer volume fractions between 0.10 and 0.72, Huang et al. (2013a, b) found a dilution exponent of α = 1, and the scaling relations with the exponents shown in Tables 3 and 4 for polystyrene were confirmed by comparison with the experimental data (Wagner 2014a, b; Wagner et al. 2015). Recently, Shahid et al. (2017) showed the apparent dilution exponent as determined from the maximum of the loss modulus or the minimum of the loss angle scales with α = 1.3, and attribute this to constraint release effects. It is obvious from Tables 3 and 4 that these scaling relations are not followed by the PMMA solutions. The entanglement molar mass M_e of both PMMA-270k/o-4k and PMMA-270k/o-2k increases with dilution much less than expected from the relation M_e = M_emφ⁻¹ with dilution exponents of α = 0.5 and α = 0.4, respectively (Table 3). This may be due to attractive interactions between polymer and the oligomeric solvents leading to the effective formation of pseudo entanglements between PMMA and oligomeric MMA which enhance the elastic plateau modulus of the solutions, in spite of the fact that the molar masses of the solvents o-4k and o-2k with 3.5 and 2.1 kg/mol, respectively, are much smaller than the entanglement molar mass M_e = 9.7 kg/mol of PMMA-270k.

Table 3 Exponents “x” of scaling relations for polystyrene (PS) solutions and PMMA solutions in o-4k and o-2k at 150 °C

Table 4 Exponents “x” of scaling relations for polystyrene (PS) solutions and PMMA solutions in o-4k and o-2k at 150 °C

In contrast to PMMA-270k, the entanglement molar mass M_e of both PMMA-86k/o-4k and PMMA-86k/o-2k increases with dilution more than expected from the relation M_e = M_emφ⁻¹ (Table 4), which may be due to a repulsive interaction between polymer and solvent, but we also note that the exponents observed are not far from the apparent dilution exponent of α = 1.3 reported by Shahid et al. (2017). The entanglement molar mass of melt PMMA-86k resulting from Eq. (6) is M_em = 3.1 kg/mol (Table 2), and therefore similar to the molar mass of the solvents o-4k and o-2k. By using the relation (9), Wingstrand et al. (2015) report instead an entanglement molar mass of M_em = 6.1 kg/mol. This value would result in a dilution exponent of α ≈ 1 for both PMMA-86k/o-4k and PMMA-86k/o-2k instead of α = 1.6 and α = 1.5, respectively, bringing it in line with the dilution coefficient found for polystyrene dissolved in oligomeric styrene.

Unfortunately, no information on the tacticity of the PMMA polymers and solvents investigated by Wingstrand et al. (2015) is available. However, we note that Fetters et al. (1999) report values of the plateau modulus of 310 and 760 kPa for an atactic and a predominantly syndiotactic PMMA, respectively. By comparison with the data given in Tables 1 and 2, this indicates that PMMA-270k with G_N = 408 kPa is predominantly atactic, while PMMA-86k with G_N = 1070 kPa has a very high tacticity. Considering the difference in the temperature dependence of the shift factors of PMMA-270k and its solutions at higher temperatures as shown in Fig. 1b, the attractive interaction of PMMA-270k and the oligomeric solvents seems to be temperature dependent, while the shift factors of PMMA-86k and its solutions coincide perfectly (Fig. 2b). In summary, from the scalings presented in Tables 3 and 4, it is obvious that the characteristic properties of the PMMA solutions of PMMA-270k and PMMA-86k such as plateau modulus and entanglement molar mass are largely influenced by the different tacticities of the two PMMA polymers, which lead to different interactions with MMA.

The extended interchain tube pressure model

The tube model of Doi and Edwards (1986) assumes that the diameter a₀ of the tube is constant, or equivalently the tension in the macromolecular chain remains constant and equal to its equilibrium value even for nonlinear deformations. The extra stress tensor σ(t) is then a consequence of the orientation of tube segments due to the flow. The resulting constitutive equation is of the single integral form,

$$ \boldsymbol{\sigma} (t)=\underset{-\infty }{\overset{t}{\int }}\frac{\partial G\left(t-{t}^{\hbox{'}}\right)}{\partial {t}^{\hbox{'}}}{\mathbf{S}}_{\mathrm{DE}}^{\mathrm{IA}}\left(t,{t}^{\hbox{'}}\right){dt}^{\hbox{'}} $$

(15)

if the tube segments are assumed to align independently of each other in the flow field (the “Independent Alignment (IA)” approximation). G(t) is the linear-viscoelastic shear relaxation modulus, and the relative strain measure ${\mathbf{S}}_{\mathrm{DE}}^{\mathrm{IA}}$is given by

$$ {\mathbf{S}}_{\mathrm{DE}}^{\mathrm{IA}}\left(t,{t}^{\hbox{'}}\right)\equiv 5{\left\langle \frac{{\mathbf{u}}^{\hbox{'}}{\mathbf{u}}^{\hbox{'}}}{u{\hbox{'}}^2}\right\rangle}_{\mathrm{o}}=5\mathbf{S}\left(t,{t}^{\hbox{'}}\right) $$

(16)

S is the relative second order orientation tensor. The bracket denotes an average over an isotropic distribution of unit vectors u(t^') at time t’ and can be expressed as a surface integral over the unit sphere,

$$ {\left\langle \kern0.5em \right\rangle}_{\mathrm{o}}\equiv \frac{1}{4\pi}\oiint \left[\right]\sin {\theta}_od{\theta}_od{\varphi}_o $$

(17)

At the observation time t, the unit vectors are deformed to vectors u', which are calculated from the affine deformation hypothesis (with F⁻¹(t, t^') as the relative deformation gradient tensor) as

$$ {\mathbf{u}}^{\hbox{'}}\left(t,{t}^{\hbox{'}}\right)={\mathbf{F}}^{-1}\left(t,{t}^{\hbox{'}}\right).\mathbf{u}\left({t}^{\hbox{'}}\right) $$

(18)

u' indicates the length of the vector u'.

The DE model does not account for any strain hardening. Doi and Edwards (1986) added a stretch process with a stretch λ of the tube segments to their model in order to explain the discrepancies of the DE theory at start-up of extensional flows. Pre-averaging the stretch, i.e., assuming that the stretch is uniform along the chain contour length and an explicit function λ(t) of the observation time, the extra stress tensor is given by

$$ \boldsymbol{\sigma} (t)={\lambda}^2(t)\underset{-\infty }{\overset{t}{\int }}\frac{\partial G\left(t-{t}^{\hbox{'}}\right)}{\partial {t}^{\hbox{'}}}{\mathbf{S}}_{\mathrm{DE}}^{\mathrm{IA}}\left(t,{t}^{\hbox{'}}\right){dt}^{\hbox{'}} $$

(19)

Equation (19) required finding a stretch evolution equation, and a vast variety of concepts based on different kinetic ideas has been proposed in recent years (see e.g. Doi and Edwards 1986; Pearson et al. 1989; McLeish and Larson 1998; Mead et al. 1998). However, it should be noted that Eq. (19) with any function λ²(t) is not in agreement with experimental results of reversed elongational flow of a monodisperse polystyrene melt (Nielsen and Rasmussen 2008).

While in models with pre-averaged stretch, the tube diameter is always assumed to stay constant and equal to its equilibrium value a_o; stretch can also be introduced by the assumption of a strain-dependent tube diameter, as first suggested by Marrucci and de Cindio (1980). In this way, also the pre-averaging of the stretch can be avoided, which is inherently present in models based on Eq. (19) or its differential approximations. A generalized tube model with strain-dependent tube diameter was presented by Wagner and Schaeffer (1992, 1993, 1994), and Wagner et al. (2001). In the Molecular Stress Function (MSF) theory, tube segment stretch f = f(t,t’) is the inverse of the relative tube diameter a,

$$ f\left(t,{t}^{\hbox{'}}\right)={a}_0/a\left(t,{t}^{\hbox{'}}\right) $$

(20)

which decreases from its equilibrium value a_o with increasing stretch. Taking into account that the tube diameter a represents the mean field of the surrounding chains, it is assumed that the tube diameter is independent of tube segment orientation. The extra stress is then given as

$$ \boldsymbol{\sigma} (t)=\underset{-\infty }{\overset{t}{\int }}\frac{\partial G\left(t-{t}^{\hbox{'}}\right)}{\partial {t}^{\hbox{'}}}{f}^2{\mathbf{S}}_{DE}^{IA}\left(t,{t}^{\hbox{'}}\right){dt}^{\hbox{'}} $$

(21)

In contrast to Eq. (19), stretch in Eq. (21) does not only depend on the observation time t, but depends on the strain history: for time-dependent strain histories, chain segments with long relaxation times (i.e., at the center of the chain) experience higher stretches than chain segments with short relaxation times (i.e., at the chain ends).

Based on the so-called “interchain tube pressure” concept of Marrucci and Ianniruberto (2004), Wagner and Rolón-Garrído (2009a, b) developed an Extended Interchain Pressure (EIP) model consisting of Eq. (21) and an evolution equation for the molecular stretch f,

$$ \frac{\partial f}{\partial t}=f\left(\kappa :\mathbf{S}\right)-\frac{1}{3}\frac{f-1}{\tau_{Rm}}-\frac{2}{3}\frac{f^2\left({f}^3-1\right)}{3{\tau}_{Rm}} $$

(22)

with the initial conditions f_i(t, t) = 1. The first term on the right hand side represents an on average affine stretch rate with κ the velocity gradient tensor, the second term takes into account Rouse relaxation in the longitudinal direction of the tube, and the third term limits molecular stretch due to the interchain tube pressure in the lateral direction of a tube segment. τ_Rm is the Rouse time of the melt according to Eq. (8) with φ = 1. Excellent agreement of the EIP model with elongational viscosity data of the monodisperse melts PS390k and PS200k (Wagner et al. 2008; Wagner and Rolón-Garrido 2009a, b) was shown, as well as excellent agreement for melt PS-285k (Wagner 2014a, b), which is used as a comparison here and is shown in Figs.4 and 5.

In the case of the monodisperse melts PS100k and PS50k with lower molar masses, it was necessary to account for the self-dilution due to fluctuating chain ends (Wagner 2011). Introducing an effective polymer volume fraction w_i with

$$ {w}_i=\frac{M-{M}_{cm}}{M} $$

(23)

into the evolution Eq. (22),

$$ \frac{\partial f}{\partial t}=f\left(\kappa :\mathbf{S}\right)-\frac{1}{3}\frac{f-1}{\tau_{Rm}}-\frac{2}{3}{w}_i^2\frac{f^2\left({f}^3-1\right)}{3{\tau}_{Rm}} $$

(24)

resulted in improved agreement with experimental data, as shown in Fig. 7 for PS100k.

For polystyrene dissolved in oligomeric styrene, due to the shift in the glass transition temperature, the Rouse time of the solutions is much smaller than the Rouse time of the melts (Wagner 2014a, b). The additional free volume created by the solvent speeds up Rouse relaxation along the tube axis, but does not affect the interchain tube pressure created by binary contacts of polymer chains. The tube diameter relaxation of the solutions is then the same as in the melt state, resulting in an evolution equation of the form

$$ \frac{\partial f}{\partial t}=f\left(\kappa :\mathbf{S}\right)-\left(1-\frac{2}{3}\frac{\tau_R}{\tau_{Rm}}\right)\frac{f-1}{\tau_R}-\frac{2}{3}\frac{f^2\left({f}^3-1\right)}{3{\tau}_{Rm}} $$

(25)

Thus, even in the case of solutions, the interchain tube pressure is characterized by the Rouse time of the corresponding melt. The Rouse time τ_R of the PS solution can be expressed in terms of the Rouse time τ_Rm of the PS melt as τ_R = a_Tgτ_Rm, leading to an alternative formulation of the evolution equation in terms of the Rouse time τ_Rm of the melt,

$$ \frac{\partial f}{\partial t}=f\left(\kappa :\mathbf{S}\right)-\left(1-\frac{2}{3}{a}_{Tg}\right)\frac{f-1}{a_{Tg}{\tau}_{Rm}}-\frac{2}{3}\frac{f^2\left({f}^3-1\right)}{3{\tau}_{Rm}} $$

(26)

Evolution Eq. (26) was successfully used in modeling the elongational viscosity of PS dissolved in oligomeric styrene as well as in small molecule solvents (Wagner et al. 2015).

Comparison to experimental data

Predictions of the EIP model are now confronted with experimental evidence as presented by Wingstrand et al. (2015) and Wingstrand (2015). The parameters of the relaxation spectra for melts and solutions, Eqs. (3) and (4), are given in Tables 1 and 2, as well as the Rouse times calculated by Eq. (8).

Solutions of PMMA-270k

Predictions assuming that the PMMA solutions in oligomeric MMA behave in the same way as PS solutions in oligomeric styrene, i.e., using the evolution Eq. (26) with the Rouse time of the solution defined by ${\tau}_R^{\ast }={a}_{Tg}{\tau}_{Rm}$, are shown in Fig. 3. Predictions are in agreement with experimental evidence up to elongation rates when the Rouse relaxation term in the evolution equation diverges, i.e., for Weissenberg numbers

$$ {Wi}_{Rm}=\dot{\varepsilon}\kern0.5em {a}_{Tg}{\tau}_{Rm}\to 1 $$

(27)

Fig. 3

Steady-state elongational viscosity data (symbols) and predictions (lines) by Eqs. (21) and (26)

For PMMA-270k/o-4k and PMMA-270k/o-2k, the critical elongation rates are ${\dot{\varepsilon}}_c=\frac{1}{a_{Tg}{\tau}_{Rm}}=0.016{s}^{-1}$ and ${\dot{\varepsilon}}_c=0.090{s}^{-1}$, respectively. At larger elongation rates, the divergence of the Rouse relaxation term is suppressed by the interchain pressure term, which, after the maximum, leads to a decreasing viscosity with a slope corresponding to ${\left(\dot{\varepsilon}{\tau}_{Rm}\right)}^{-1/2}$. The predicted behavior up to the maximum of the elongational viscosity is qualitatively similar to what is reported for PMMA dissolved in small molecule solvents (Bhattacharjee et al. 2002; Wagner et al. 2015).

On the other hand, when the PMMA solutions in oligomeric MMA are considered as melts, i.e., when the evolution Eq. (22) for melts is used with the Rouse times of the solutions according to Eq. (8) and Tables 1 and 2,

$$ \frac{\partial f}{\partial t}=f\left(\kappa :\mathbf{S}\right)-\frac{1}{3}\frac{f-1}{\tau_R}-\frac{2}{3}\frac{f^2\left({f}^3-1\right)}{3{\tau}_R} $$

(28)

qualitative agreement between experimental evidence and predictions is obtained for PMMA-270k/o-4k, while the agreement with the data of PMMA-270k/o-2k is marginal (Fig. 4). Predictions of ${\eta}_E\left(\dot{\varepsilon}\right)$scale with ${\left(\dot{\varepsilon}{\tau}_R\right)}^{-1/2}$ at higher strain rates, which is a signature of the interchain pressure effect. Qualitatively, as observed by Wingstrand et al. (2015), PMMA-270k/o-4k can be considered to behave as a pseudo polymer melt with the Rouse time of the solution being taken as the characteristic Rouse time of the pseudo melt, while the data of PMMA-270/o-2k show clearly a different behavior.

Fig. 4

Steady-state elongational viscosity data (symbols) and predictions (lines) by Eqs. (21) and (28)

Nearly quantitative agreement between data and model can be obtained as shown in Fig. 5, when the evolution Eq. (26) for the solutions is used, but with the Rouse time of the melt in the interchain pressure term replaced by the Rouse time of the solution,

$$ \frac{\partial f}{\partial t}=f\left(\kappa :\mathbf{S}\right)-\left(1-\frac{2}{3}\frac{a_{Tg}{\tau}_{Rm}}{\tau_R}\right)\frac{f-1}{a_{Tg}{\tau}_{Rm}}-\frac{2}{3}\frac{f^2\left({f}^3-1\right)}{3{\tau}_R} $$

(29)

Fig. 5

Steady-state elongational viscosity data (symbols) and predictions (solid blue and red lines for PMMA solutions) by Eqs. (21) and (29). Dotted blue and red lines for PMMA solutions and solid black line for PS are predictions by Eqs. (21) and (28)

We note that in the limit of small elongation rates, Eq. (29) reduces to the small stretch limit of evolution Eq. (26) (Wagner and Rolón-Garrido 2009a, b; Wagner 2014a, b),

$$ \frac{\partial f}{\partial t}=f\left(\kappa :\mathbf{S}\right)-\frac{1}{3}\frac{f-1}{a_{Tg}{\tau}_{Rm}} $$

(30)

while at high elongation rates, Eq. (29) approaches the high stretch limit of evolution Eq. (28),

$$ \frac{\partial f}{\partial t}=f\left(\kappa :\mathbf{S}\right)-\frac{2}{3}\frac{f^2\left({f}^3-1\right)}{3{\tau}_R} $$

(31)

This means that Rouse relaxation in the longitudinal direction of the tube, which is effective at small elongation rates, is determined by the true Rouse relaxation time of the diluted PMMA polymer chains ${\tau}_R^{\ast }={a}_{Tg}{\tau}_{Rm}$, unaffected by the attractive interaction with oligomeric MMA, while the interchain pressure in the perpendicular direction of the tube, which limits chain stretch at higher elongation rates, is increased by the interaction with the oligomers and is determined by the Rouse time τ_R of the solution as calculated from Eq. (8). Note that ${\tau}_R^{\ast }$ is smaller than τ_R, with ${\tau}_R^{\ast }={a}_{Tg}{\tau}_{Rm}$ being 62.1 s for PMMA-270k/o-4k and 11.1 s for PMMA-270k/o-2k, respectively. Especially for PMMA-270k/o-2k, the effect of Rouse relaxation is important due to the low value of a_Tg, and the increase of the interchain pressure due to the presence of the MMA oligomer is only significant at the highest elongation rates investigated.

Evolution Eq. (29) also gives a quantitative description of the start-up elongational viscosities of both PMMA-270k/o-4k and PMMA-270k/o-2k within experimental accuracy as demonstrated in Fig. 6.

Fig. 6

a, b Start-up elongational viscosity data (symbols) and predictions (lines) by Eqs. (21) and (29)

Solutions of PMMA-86k

Figure 7 shows predictions of the EIP model by use of evolution Eqs. (22) and (24), respectively, for PS100k. Taking into account the dilution effect of the chain ends results in a qualitative improvement of the agreement between data and model (Wagner 2011). The solutions of PMMA-86k can be considered as solutions with no attractive interaction of polymer and oligomeric solvent, and the appropriate Rouse relaxation time is, as in the case of the solutions of PS in oligomeric styrene, governed by the Rouse relaxation of the melt. Using the evolution Eqs. (22) and (24) results in the predictions presented in Fig. 7. The enhanced maximum seen in the prediction of the steady-state elongational viscosity of PMMA-86k/o-2k is caused by the terminal relaxation time τ_t being smaller than the Rouse time τ_Rm of the melt, τ_t < τ_Rm. Due to the lower value of the entanglement molar mass of PMMA-86k (Table 2), the effect of dilution by chain end fluctuations is less pronounced than in the case of PS100k. Nevertheless, qualitative agreement between data of the steady-state (Fig. 7) as well as the start-up elongational viscosity (Fig. 8) and model is achieved. For a more quantitative evaluation an improved modeling of the effect of chain end fluctuations would be needed, which is outside the scope of the present paper.

Fig. 7

Steady-state elongational viscosity data (symbols) and predictions (full lines) by Eqs. (21) and (24); dotted lines predictions by Eqs. (21) and (22)

Fig. 8

a, b Start-up elongational viscosity data (symbols) and predictions (lines) by Eqs. (21) and (24)

Conclusions

The experimental data in elongational flow of two monodisperse PMMA polymers with different tacticity dissolved in two oligomeric MMAs are consistent with the assumption that the tube, i.e., the confinement of a test chain, is characterized by the orientation in the direction along the tube and the diameter of the tube in the lateral dimension. Chain stretch is associated with a reduction of the tube diameter and is balanced by a linear spring force in the longitudinal direction and a nonlinear interchain tube pressure in the lateral direction.

By dilution of the polymer with a solvent, the glass transition temperature T_g of the polymer in solution is reduced relative to T_g of the melt, resulting in a temperature shift factor a_Tg, which enters the scaling relations between melt and solutions. The PMMA solutions in oligomeric MMA investigated by Wingstrand et al. (2015) and Wingstrand (2015) do not follow the scaling of polystyrene dissolved in oligomeric styrene. Rather, PMMA-270k shows an attractive interaction with MMA, in contrast to the interaction of PMMA-86k and MMA. This different behavior can be traced back to different tacticities of the two polymers. The attractive interaction of PMMA-270k with o-4k creates pseudo entanglements increasing the interchain tube pressure, and the solution PMMA-270k/o-4k shows, as observed by Wingstrand et al. (2015), qualitatively a similar scaling of the elongational viscosity with ${\left(\dot{\varepsilon}{\tau}_R\right)}^{-1/2}$ as melt PS-285k. For PMMA-270/o-2k, this effect is only observed at the highest elongation rates investigated. The elongational viscosity of PMMA-86k dissolved in oligomeric MMA is determined by the Rouse time of the melt, as in the case of polystyrene solutions. While the steady-state elongational viscosity data of PMMA-86k/o-4k show qualitatively a similar trend as PS100k with a well-defined maximum followed by a decrease of the viscosity with increasing elongation rate, PMMA-86k/o-2k features a nearly constant elongational viscosity within the experimental window.