Introduction

The significance of the extensional rheological analysis of polymer melts is due to the subjection of nearly all polymer processing systems to extensional deformation at narrowing profile sections, where extensional flow dominates the rheological characteristics of the deformation (Gupta 2002; Padmanabhan and Macosko 1997; Revenu et al. 1993; Sampers and Leblans 1988). This dominance is accentuated in processes such as blow moulding, melt spinning, biaxial stretching of extruded sheets, etc., and the extensional deformation may be the last step before solidification which triggers molecular orientation (Meissner and Hostettler 1994; Soon et al. 2009). The occurrence of strain hardening behaviour prevents the formation of local weak spots as the starting point of cracks in plastic melts in free surface flows. Moreover, extensional deformations are very sensitive to macromolecular structure of the polymeric systems including degree of branching, molecular weight distribution and cross-linking (Meissner and Hostettler 1994; Narimissa et al. 2014). Extensional characteristics of polymeric systems can be strongly impacted by processing properties such as thermomechanical history (due to extrusion speed and temperature), residence time, homogeneity of deformation (e.g. in spinning), degree of delamination of fillers within the polymeric matrix and the effect of stretching and relaxation (e.g. in capillary flow). Therefore, the simple-term modelling of the extensional viscosity of polymers in general, and their strain hardening behaviour in particular, is of great importance for polymer processing.

In this research, we propose a novel hierarchical multi-mode molecular stress function (HMMSF) model for long-chain branched (LCB) polymers, which implements the basic ideas of the pom-pom model, of hierarchal relaxation, of dynamic dilution and of the interchain pressure. This model can accurately predict the elongational viscosity of several LCB polymer melts based exclusively on their linear viscoelastic characterization and features a single non-linear parameter. The paper is organized as follows: in “Pom-pom model” section and “Molecular stress function model” section, we sketch the basic assumptions of the pom-pom and the MSF model. “The interchain pressure term” section introduces the interchain pressure concept, and “Dynamic dilution” section discusses dynamic dilution. The HMMSF model for LCB polymers is developed in “HMMSF model of LCB polymer melts” section and confronted with experimental evidence of elongational viscosity data of several LCB polymers in “Experimental” section.

Pom-pom model

The pom-pom model for polymeric systems was developed by McLeish and Larson (1998) for an idealized long-chain branched (LCB) polymer starting from a H-polymer but allowing an arbitrary number q of side branches attached to the two branch points at both ends of the backbone. Thus, the pom-pom polymer can be simplistically defined as a combination of one linear polymer with two star polymers attached to its ends. The main observable difference between the pom-pom polymer and linear polymers occurs during the start-up of the elongational deformation when the pom-pom polymers exhibit substantial strain hardening behaviour. Additionally, the strain softening behaviour at high shear rates is less pronounced (only quantitatively) for the pom-pom polymers when compared to linear polymers. According to the pom-pom model, the backbone chain with molar mass M b is kept inside the tube by means of the net Brownian force excreted on the free chain ends (McLeish and Larson 1998). Therefore, the maximum possible stretch magnitude of the backbones of the pom-pom polymer is equal to the number of free chain ends, λ max = q. Branch point withdrawal, i.e. withdrawal of the branches into the tube of the backbone, occurs once the maximum stretch is reached. Accordingly, the path length of the arms drawn into the backbone tube, S c(t), is measured in the unit of the constant tube diameter a 0 as 0 < S c (t) < M a /M e , where M a is the molar mass of the arm and M e the entanglement molar mass.

The non-linear response of the pom-pom model begins when the strain rate is larger than the inverse of the reptation time of the backbone and smaller than the inverse of arm relaxation time, \( {\tau}_b^{-1}<\overset{\bullet }{\varepsilon }<{\tau}_{\mathrm{arm}}^{-1} \), and the main contributor to the stress in this region is the backbone segments. On the other hand, when S c  > 0, the arms also contribute to the stress. Thus, the mentioned contributions to the stress from the backbones, as well as the portion of arms pulled into the backbone tube, are both reflected in the stress tensor equation of the original pom-pom model as

$$ \sigma ={G}_N^0{\phi}_b\left({\phi}_b{\lambda}^2(t)+\frac{2q{S}_c(t)}{2q{S}_c(t)+{Z}_b}\right)\overline{\mathbf{S}} $$
(1)

Here, G 0 N is the plateau modulus, and the first and second terms in the bracket exhibit the contribution of the backbone and the arms to the stress tensor, respectively, and S c (t) denotes the branch point withdrawal path.

The configuration integral \( \overline{\mathbf{S}} \) of the pom-pom model was based on the Doi and Edwards strain tensor S DE (Doi and Edwards 1986) by taking into account the rate of creation and destruction of the backbone segments, τ − 1 b (t), due to the flow-induced reduction of the effective friction constant of the branch points,

$$ \overline{\mathbf{S}}(t)={\displaystyle \underset{-\infty }{\overset{t}{\int }}\frac{dt^{\prime }}{\tau_b\left(t^{\prime}\right)} \exp \left(-{\displaystyle \underset{t^{\prime }}{\overset{t}{\int }}\frac{dt^{\prime\prime }}{\tau_b\left(t^{\prime\prime}\right)}}\right)\ }{\mathbf{S}}_{\mathbf{DE}}\left(t,t^{\prime}\right) $$
(2)

with

$$ {\mathbf{S}}_{\mathbf{DE}}\left(t,t^{\prime}\right)=\frac{1}{<\mathrm{u}^{\prime }>}\left\langle \frac{\mathbf{u}\mathbf{^{\prime }}\mathbf{u}\mathbf{^{\prime }}}{\mathrm{u}^{\prime }}\right\rangle $$
(3)

Here, τ − 1 b (t ’) and τ − 1 b (t ”) indicate the segmental creation and destruction rates, respectively; u′ presents the length of the deformed unit vector u′, and the bracket denotes an average over an isotropic distribution of unit vectors at time t′, u(t′), which can be expressed as a surface integral over the unit sphere,

$$ \left\langle \right\rangle \equiv \frac{1}{4\pi }{\displaystyle \oiint \left[\right]} \sin {\theta}_0d{\theta}_0d{\varphi}_0 $$
(4)

The relative deformation gradient tensor, F − 1(t, t ’), signifies the deformation of the unit vector u at observation time t to u′ according to affine deformation assumption,

$$ \mathbf{u}\mathbf{^{\prime }}\left(t,t^{\prime}\right)={\mathbf{F}}^{-1}\left(t,t^{\prime}\right).\mathbf{u}\left(t^{\prime}\right) $$
(5)

The quantity ϕ b in the original pom-pom model presents the volume fraction of the backbone material,

$$ {\phi}_b={Z}_b/\left({Z}_b+2q{Z}_a\right) $$
(6)

where Z b  = M b /M e represents the number of entanglements of the backbone, and the volume fraction of the 2q arm material is ϕ a  = 1 − ϕ b . Note that in Eq. 1, the dilution exponent is set equal to one.

The force balance between the dissipative drag and elastic recovery is the governing factor in the evolution of the molecular dynamics of the backbone stretch λ(t) (McLeish and Larson 1998); hence, the evolution equation of the dimensionless stretch parameter of the pom-pom model is given as

$$ \frac{\partial }{\partial t}\lambda (t)=\overset{\bullet }{\lambda }=\lambda \left(\mathbf{K}:\overline{\mathbf{S}}\right)-\frac{1}{\tau_s}\left(\lambda -1\right)\kern0.84em \mathrm{f}\mathrm{o}\mathrm{r}\kern0.24em \lambda \le q $$
(7)

K is the deformation rate tensor, \( \mathbf{K}:\overline{\mathbf{S}} \) is the average increase of length per unit length of the tube, and τ s is the stretch relaxation time. Additionally, the abrupt cessation of the backbone stretch at λ max = q of the original pom-pom model was rectified by Blackwell et al. (2000) via the inclusion of a smoothing exponential term in Eq. 7 in order to accelerate the relaxation of stretch when λ becomes large,

$$ \overset{\bullet }{\lambda }=\lambda \left(\mathbf{K}:\overline{\mathbf{S}}\right)-\frac{1}{\tau_s}\left(\lambda -1\right){e}^{v^{*}\left(\lambda -1\right)} $$
(8)

Here, v ∗ = 2/q delivered the best fit to the data considered by Blackwell et al. (2000), and this approach was termed “drag-strain coupling.” Furthermore, the branch point withdrawal path of Eq. 1 was set to zero, S c  = 0, and consequently, the arms contribution, \( \frac{2q{S}_c(t)}{2q{S}_c(t)+{Z}_b} \), was neglected, and also, a constant backbone relaxation time was assumed, τ b  = τ b (0) (Dealy and Larson 2006).

Due to the complexity in the branching structure of LCB polymers compared to the pom-pom system, a multi-mode version of the pom-pom model was introduced by Inkson et al. (1999). This multi-mode version presents the stress tensor as sum of the partial stresses σ i of each mode of relaxation with partial relaxation modulus g i and backbone relaxation time τ bi ,

$$ \sigma ={\displaystyle \sum_i{\sigma}_{\boldsymbol{i}}}={\displaystyle \sum_i{g}_i{\lambda}_i^2(t){\overline{\mathbf{S}}}_i} $$
(9)

The configuration integral of the multi-mode pom-pom model was evaluated by means of the differential version of the configuration integral (Eq. 2) introduced by McLeish and Larson (1998) with mode index i as

$$ {\overset{\bullet }{\mathbf{A}}}_i-\mathbf{K}\cdot {\mathbf{A}}_{\boldsymbol{i}}-{\mathbf{A}}_{\boldsymbol{i}}\cdot {\mathbf{K}}^T=-\frac{1}{\tau_{bi}}\left({\mathbf{A}}_{\boldsymbol{i}}-\boldsymbol{\delta} \right) $$
(10)

and

$$ {\overline{\mathbf{S}}}_i=\frac{{\mathbf{A}}_{\boldsymbol{i}}}{tr\left({\mathbf{A}}_{\boldsymbol{i}}\right)} $$
(11)

where A i is the auxiliary tensor of mode i used to compute the configuration tensor of this mode. Moreover, the stretch λ i of mode i of the multi-mode pom-pom model is given as

$$ \overset{\bullet }{\lambda_i}={\lambda}_i\left(\mathbf{K}:{\mathbf{S}}_{\boldsymbol{i}}\right)-\frac{1}{\tau_{si}}\left({\lambda}_i-1\right){e}^{v^{*}\left({\lambda}_i-1\right)} $$
(12)

with v ∗ = 2/q i . Additionally, the backbone relaxation times of the multi-mode version, τ bi , are considered to be constant due to the application of the drag-strain coupling.

Ultimately, the extra stress tensor of the multi-mode pom-pom model may be reintroduced as an integral equation,

$$ \sigma (t)={\displaystyle \sum_i{\lambda}_i^2(t){\displaystyle \underset{-\infty }{\overset{+\infty }{\int }}\frac{g_i}{\tau_{bi}}{e}^{\left(t-t\prime \right)/{\tau}_i}{\mathbf{S}}_{\mathbf{DE}}\left(t,t^{\prime}\right)dt=}}{\displaystyle \sum_i{\lambda}_i^2(t){\displaystyle \underset{-\infty }{\overset{+\infty }{\int }}\frac{\partial {G}_i\left(t-t^{\prime}\right)}{\partial t^{\prime }}{\mathbf{S}}_{\mathbf{DE}}\left(t,t^{\prime}\right)dt}} $$
(13)

Here, G i (t) is the partial relaxation modulus of mode i. Thus, the pom-pom model is based on the assumption that stretch and orientation of the backbone chain can be decoupled and that stretch is an explicit function of the observation time t with its own dynamics as defined by the stretch relaxation times τ si and the maximum stretches λ i max ≅ q i (Eq. 12). Orientation depends on the backbone relaxation times τ bi , which are identified with the time constants of the linear viscoelastic relaxation spectrum, i.e. τ bi  = τ i . Therefore, for each mode i, in addition to the two parameters g i and τ i defined by linear viscoelasticity, two non-linear viscoelastic parameters τ si and q i are needed. We also note that the multi-mode version of the pom-pom model does no longer consider the dilution of the backbone chain segments by the side chains, as implemented in the original model (Eq. 1).

We finish this section by reporting that Read et al. (2011) considered the “hierarchical” occurrence of the chain reconfiguration in LCB polymers commencing from the extremities of the arms. This hierarchical relaxation of the entangled branched polymers is indicative of the existence of variable relaxation mechanism along the chains which it is fastest at the extremities of the entangled arms and slower at the segments adjacent to the branch points of the backbone. In comparison with linear polymers with only one reptation time, the hierarchical reconfiguration of LCB melts results in (i) a suppression of the reptation process when the relaxation of the backbone occurs via exponentially slower arm retraction mode and (ii) the observation of a broad range of relaxation times for an entangled arm (Read et al. 2011).

Molecular stress function model

Marrucci and de Cindio (1980) suggested a strain-dependent tube diameter which dismisses the decoupling assumption of stretch and orientation in Eq. 13. Based on this idea, Wagner and Schaeffer (1992, 1993, 1994) proposed a generalized tube segment model with strain-dependent tube diameter, i.e. the molecular stress function (MSF) model. According to this model, the segmental chain stretch, f, is directly related to the diameter a of a tube segment. The tube diameter can be viewed as the mean field of the surrounding chains which is independent of the orientation of tube segments, and it decreases from its equilibrium value a 0 with increasing stretch. The extra stress tensor σ of the MSF model is expressed as

$$ \sigma (t)={\displaystyle {\int}_{\kern-.8em -\infty}^t\frac{\partial G\left(t-t^{\prime}\right)}{\partial t^{\prime }}{f}^2\left(t,t^{\prime}\right){\mathbf{S}}_{DE}^{IA}\left(t,t^{\prime}\right)dt^{\prime }} $$
(14)

Here, G(t) is the linear viscoelastic relaxation modulus, and S IA DE is the Doi and Edwards orientation tensor assuming an independent alignment (IA) of tube segments (Doi and Edwards 1986), which is five times the second-order orientation tensor S,

$$ {\mathbf{S}}_{DE}^{IA}\left(t,t^{\prime}\right)\equiv 5\left\langle \frac{\mathbf{u}\mathbf{^{\prime }}\mathbf{u}^{\prime }}{\mathrm{u}{\prime}^2}\right\rangle =5\mathbf{S}\left(t,t^{\prime}\right) $$
(15)

The MSF f = f(t, t ’) is the inverse of the relative tube diameter,

$$ f\left(t,t^{\prime}\right)={a}_0/a\left(t,t^{\prime}\right) $$
(16)

f = f(t, t ’) is a function of both the observation time t and the time t ’ of creation of tube segments by reptation. Thus, chain segments with long relaxation times, i.e. those preferably in the middle of the tube, are exposed to higher stretches than chain segments with short relaxation times, i.e. those at the chain ends. This is in contrast to the pom-pom model where stretch and orientation are decoupled and stretch is assumed to be the same for all tube segments of the backbone chain. In the MSF model, stretch is considered to be a relative quantity (i.e. a quantity depending on times t and t ’) in the same way as the strain tensor.

Considering the change of free energy of backbone chain segments due to stretch and irreversible energy dissipation by a constraint release (CR) process, the evolution equation for f was found to be (Wagner et al. 2003)

$$ \frac{\partial f}{\partial t}=\frac{1}{2}\frac{\beta f}{1+\frac{\beta -1}{f^4}}\left[\left(\mathbf{K}:\mathbf{S}\right)-\frac{CR}{f^2-1}\right] $$
(17)

with the starting condition f(t = t ’, t ’) = 1. The parameter β takes the value of 1 for linear polydisperse polymers and has typically a value of 2 for LCB polymers. In constant strain rate elongation, the evolution Eq. 17 can then be expressed as

$$ \frac{\partial f}{\partial t}=\frac{1}{2}\overset{\bullet }{\varepsilon}\frac{\beta f}{1+\frac{\beta -1}{f^4}}\left({S}_{11}-{S}_{33}-\frac{f^2-1}{f_{\max}^2-1}\sqrt{S_{11}+\frac{1}{2}{S}_{33}}\right) $$
(18)

\( \overset{\bullet }{\varepsilon } \) is the elongation rate in the direction of the 1-coordinate, and S11 and S33 are the corresponding components of the orientation tensor S in the directions parallel and perpendicular to the elongation, respectively. In the case of irrotational flows, the MSF model (Eqs. 14 and 17) features only two non-linear parameters, β and f max, which were sufficient to model the extensional viscosity of a wide variety of polydisperse linear and LCB polymers (for more details, see the review by Rolón-Garrido 2014).

The interchain pressure term

When modelling the rheology of linear monodisperse polymers, usually the assumption is made that the stretch created by affine deformation of the chain is balanced by a linear spring force (Pearson et al. 1989). The corresponding evolution equation of the MSF model is then

$$ \frac{\partial f}{\partial t}=f\left(\mathbf{K}:\mathbf{S}\right)-\frac{1}{\tau_R}\left(f-1\right) $$
(19)

where τ R is the Rouse time of the chain. In elongational flow, this leads to unbounded stretch at Weissenberg numbers \( Wi=\overset{\bullet }{\varepsilon }{\tau}_R\to 1 \), which is easily seen by considering the maximum stretch resulting from Eq. 19,

$$ {f}_{\max }=\frac{1}{1-\overset{\bullet }{\varepsilon }{\tau}_R} $$
(20)

However, evolution Eq. 19 is not in agreement with the steady-state elongational viscosity data of monodisperse polystyrene melts (Wagner 2011), which show a continuously decreasing elongational viscosity with a scaling of approximately \( {\left(\overset{\bullet }{\varepsilon}\right)}^{-1/2} \).

To account for this experimental observation, Marrucci and Ianniruberto (2004) proposed an interchain pressure (IP) term based on the free energy of a polymer chain confined by fixed walls of a tube with diameter a. As shown by Doi and Edwards (1986), when a chain made up of Kuhn segments is confined to an anisotropic box, the pressure exerted by the chain on the walls of this box is also anisotropic and increases as the size of the confinement decreases. Marrucci and Ianniruberto (2004) assumed that the reduction of the tube diameter due to deformation is balanced by the increase of the radial pressure of the confined chain, and for elongational flow with strain rate \( \overset{\bullet }{\varepsilon } \), they proposed the following scalar evolution equation of the tube diameter a,

$$ \frac{\partial a}{\partial t}=-\overset{\bullet }{\varepsilon }a+\frac{a_0}{\tau_a}\left(\frac{a_0^3}{a^3}-1\right) $$
(21)

τ a denotes the tube diameter relaxation time. Replacing the strain rate with the general tensorial description of the deformation rate and expressing the rate of change in tube diameter (\( \frac{\partial a}{\partial t} \) in Eq. 21) in terms of the MSF, i.e. \( \frac{\partial a}{\partial t}=-{a}_0\frac{1}{f^2}\frac{\partial f}{\partial t} \) in Eq. 14, the evolution equation for the tension in a chain segment is derived as (Wagner et al. 2005)

$$ \frac{\partial f}{\partial t}=f\left(\mathbf{K}:\mathbf{S}\right)-\frac{f^2\left({f}^3-1\right)}{\tau_a} $$
(22)

Here, \( \frac{f^2\left({f}^3-1\right)}{\tau_a} \) represents the nonlinear restoring IP term. Subsequently, it was shown that the tube diameter relaxation time can be identified with three times the Rouse time of the chain (Wagner and Rolón-Garrido 2009a, 2009b), τ a  = 3τ R . Considering the original findings of Doi and Edwards (1986), i.e. that the pressures of a chain exerted on the walls of a confining box are anisotropic if the dimensions of the box are anisotropic, an extended interchain pressure (EIP) model was later developed with 1/3 Rouse relaxation in the longitudinal direction (no walls) and 2/3 IP in the lateral direction of a tube segment (Wagner et al. 2005),

$$ \frac{\partial f}{\partial t}=f\left(\mathbf{K}:\mathbf{S}\right)-\frac{1}{3}\frac{f-1}{\tau_R}-\frac{2}{3}\frac{f^2\left({f}^3-1\right)}{3{\tau}_R} $$
(23)

Note that Eq. 23 becomes equivalent to Eq. 19 in the first order of stretch, i.e. for f − 1 < < 1. It emits the singularity in the classical relation when Wi → 1 and does not contain any non-linear parameter since the Rouse time of the chain can be evaluated from linear viscoelasticity. Furthermore, Eq. 23 together with Eq. 14 represents a non-linear integro-differential constitutive relation with no free parameters, which was shown to be in excellent agreement with start-up and steady-state elongational viscosity data of several linear monodisperse polystyrene melts (Wagner 2011) and of concentrated solutions of polystyrene in oligomeric styrene (Wagner 2014). These findings demonstrate the importance of the IP term in polymer rheology.

Dynamic dilution

When a polymer is diluted by a low-molar-mass solvent, the entanglement molar mass of the polymer increases, the tube diameter increases, and the plateau modulus G N decreases according to

$$ {G}_N={G}_N^0{w}^2 $$
(24)

Here, G 0 N is the plateau modulus of the melt and w the mass fraction of the polymer (a dilution exponent of 1 is assumed here and in the following). In a bidisperse melt system with a high molar mass fraction w and a low-molar-mass fraction 1- w, two relaxation steps can simplistically be assumed to arise sequentially as a function of the reptation or disengagement times of the long and short chains, i.e. τ wL and τ wS , respectively: (i) a drop of the relaxation modulus from G 0 N to G 0 N w 2 at the reptation time τ wS of the short chains and (ii) a terminal relaxation from G 0 N w 2 to zero at the reptation time τ wL of the long chains. On the timescale of the long chains, the short chains act as a solvent, thereby increasing the tube diameter of the long chains and reducing the relaxation modulus in proportion to w 2. In general, this concept is denoted as “dynamic dilution” referring to the dynamic dilation of the tube diameter of the non-relaxed chains through the solvent effect of the already relaxed ones.

Dynamic dilution does not only affect the linear viscoelastic properties, but it has also an effect on chain stretch, due to the dilation of tube diameter. This leads to an effective tube diameter relaxation time of the high molar mass fraction of bidisperse polystyrene blends which was shown to have an inverse proportionality to the square of the mass fraction, τ a  ∝ w − 2, resulting in an evolution equation for the MSF f L of the long chains of the form (Wagner 2011),

$$ \frac{\partial {f}_L}{\partial t}={f}_L\left(\mathbf{K}:\mathbf{S}\right)-\frac{f_L-1}{\tau_{RL}}\left(1-\frac{2}{3}{w}^2\right)-\frac{2}{3}\frac{f_L^2\left({f}_L^3-1\right)}{3{\tau}_{RL}}{w}^2 $$
(25)

τ RL is the Rouse time of the long chains. Note that evolution Eq. 25 is formulated here such that Eq. 19 is retained in the first order of stretch, i.e. for f − 1 < < 1. In fast elongational flow, the steady-state tensile stress contribution of the long chains, σ L , reaches the limit,

$$ {\upsigma}_L\cong 5{G}_N^0{w}^2{f}^2=\frac{15}{2}{G}_N^0w\sqrt{2{\tau}_{RL}\dot{\varepsilon}} $$
(26)

This shows that although the plateau modulus of the long chains is reduced in proportion to w 2 by dynamic dilution, the effective contribution of the long chains to the non-linear tensile stress is eventually, i.e. at sufficiently high strain rates, proportional to their mass fraction w. This means that in fast flows, the effect of dynamic dilution vanishes and that for flows with Weissenberg numbers \( W{i}_{wS}=\dot{\varepsilon}{\tau}_{wS}>1 \), long and short chains remain entangled.

HMMSF model of LCB polymer melts

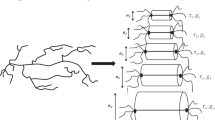
We follow the pom-pom model idea to the extent that we assume an LCB polymer to be equivalent to a combination of individual pom-pom macromolecules with two branch points, characterized by the parameters {g i , τ i } of a discrete relaxation spectrum. However, we take the hierarchical relaxation starting from the extremities of the multi-branched arms of the LCB molecules into account: We assume that this is directly reflected in the relaxation spectrum and that the pom-pom macromolecule with the shortest relaxation time represents chain segments at the extremities of the arms, while the ones with longer and longer relaxation times correspond to chain segments closer and closer to the “centre” of the LCB molecule. Figure 1 displays a schematic illustration of the proposed conversion of an LCB macromolecule into a hierarchical series of pom-pom polymers, where the pom-poms with short relaxation times dynamically dilute those with longer relaxation times. As shown schematically, the tube diameter and the contour length increase with increasing relaxation time, when the already relaxed pom-poms with shorter relaxation times dilute the ones with longer relaxation times. Note that we do not take the branch point withdrawal mechanism into consideration here, which may become important in the modelling of the occurrence of maxima at the end of the strain-hardening region and prior to the steady-state zone as observed by Bach et al. (2003) and Rasmussen et al. (2005). We rather assume that the stretch of the backbone segments is balanced by the IP, which leads to a prediction of a steady-state extensional viscosity without a maximum.

Fig. 1
figure 1

Schematic representation of a long-chain branched polymer by a hierarchical series of pom-pom polymers with τ i + 1 > τ i

Full size image

In correspondence with the multi-mode pom-pom model (Eq. 13) and a multimode version of the MSF model used earlier to model the elongational viscosity of mixtures of LCB and linear polypropylene (Wagner et al. 2006), the stress tensor of the hierarchical multi-mode molecular stress function (HMMSF) model is given as

$$ \sigma (t)={\displaystyle \sum_i{\displaystyle \underset{-\infty }{\overset{+\infty }{\int }}\frac{\partial {G}_i\left(t-t^{\prime}\right)}{\partial t^{\prime }}{f}_i^2\left(t,t^{\prime}\right){\mathbf{S}}_{DE}^{IA}\left(t,t^{\prime}\right)dt^{\prime }}} $$
(27)

where f i (t = t ’, t ’) represents the MSFs of each mode i.

To account for the dilution effect, we split dilution into (i) permanent dilution and (ii) dynamic dilution. Permanent dilution occurs due to the fast Rouse-like relaxation of non-entangled oligomeric chains, which are often present in commercial LCB polymers, and of copious short chains with molar mass less than the entanglement molar mass attached to the LCB molecules. Dynamic dilution, on the other hand, describes the hierarchical dilution of pom-poms with longer relaxation times by those with shorter relaxation times. The relaxation modulus G(t) of a polymer can be divided into three distinct relaxation regimes: (i) a very fast “glassy” relaxation region during early times, (ii) a plateau over a range of relaxation times characterized by a plateau modulus G N and (iii) a terminal relaxation region (Fig. 2). The relaxation modulus of the multi-mode pom-pom model can be represented by discrete Maxwell modes {g i , τ i },

$$ G(t)={\displaystyle \sum_{j=1}^n{g}_j \exp \left(-t/{\tau}_j\right)} $$
(28)
Fig. 2
figure 2

Relaxation modulus of a long-branch chained polymer melt in view of permanent and dynamic dilution mechanisms (for details, see the text)

Full size image

We assume that the onset of dynamic dilution starts when the relaxation process has reached a “dilution modulus” G D  ≤ G N . This modulus is a free parameter, which needs to be fitted to non-linear viscoelastic experimental evidence, since the mass fraction of oligomeric chains and un-entangled side chains is not known a priori. The time when G(t) has relaxed to the value of G D , i.e. t = τ D , denotes the commencement of the dynamic dilution zone, while at relaxation times t ≤ τ D , the pom-poms are permanently diluted by the un-entangled chain fraction. Figure 2 illustrates the permanent and dynamic dilution zones, which are separated by the dilution modulus G D and the relaxation time t = τ D . Following the discussion in “Dynamic dilution” section, we estimate the mass fraction w i of a dynamically diluted pom-pom polymer with relaxation time τ i  > τ D by considering the ratio of the relaxation modulus at time t = τ i to the dilution modulus G D ,

$$ {w}_i^2=\frac{G\left(t={\tau}_i\right)}{G_D}=\frac{1}{G_D}{\displaystyle \sum_{j=1}^n{g}_j \exp \left(-{\tau}_i/{\tau}_j\right)} $$
(29)

We make the assumption that the value of w i obtained at t = τ i can be attributed to the pom-pom with relaxation time τ i . Although this may seem to be a very rough estimate, it is (as will be shown in “Experimental” section) a sufficiently robust assumption to model the rheology of broadly distributed LCB polymers, largely independent of the number of discrete Maxwell modes used to represent the relaxation modulus G(t).

We are now in the position to formulate the evolution equation of the MSFs f i (t, t ’) for each mode i. We maintain the following three assumptions from the evolution Eq. 23 for bidisperse blends: we assume that (i) affine deformation is balanced by (ii) a linear stretch relaxation term and (iii) a non-linear IP term, which is a consequence of tube diameter reduction by deformation. The third assumption also includes the effect of dynamic dilution. However, while the stretch relaxation dynamics of linear polymers is governed by the Rouse time, the relaxation dynamics of a pom-pom polymer (restricted by two branch points in their relaxation) is governed by its relaxation time. Therefore, we replace the Rouse time in Eq. 25 by the relaxation time τ i ; i.e. we make the constitutive assumption that the stretch relaxation time and the orientational relaxation time of a pom-pom polymer are identical. Hence, in consideration of the IP (“The interchain pressure term” section), as well as the dynamic dilution mechanism (“Dynamic dilution” section), the MSF of each mode can be reformulated with respect to Eq. 25 as

$$ \frac{\partial {f}_i}{\partial t}={f}_i\left(\mathbf{K}:\mathbf{S}\right)-\frac{f_i-1}{\tau_i}\left(1-\frac{2}{3}{w}_i^2\right)-\frac{2}{3}\frac{f_i^2\left({f}_i^3-1\right)}{3{\tau}_i}{w}_i^2 $$
(30)

with the starting conditions f i (t = t ’, t) = 1. Thus, the HMMSF model consists of the multi-mode stress equation (Eq. 27), a set of evolution equations for the molecular stresses f i (Eq. 30), and a hierarchical procedure to evaluate the effect of dynamic dilution (Eq. 29) with only one free non-linear parameter, the dilution modulus G D .

Once the linear viscoelastic relaxation spectrum of an LCB polymer is known, the mass fractions w i of the diluted pom-poms can be iteratively obtained by fitting the value of G D to the experimental evidence. It should be noted that Maxell modes with relaxation times τ i  ≤ τ D are considered to be permanently diluted. Permanent dilution is already reflected in the values of the partial relaxation moduli g i ; thus, as far as the non-linear effect of dilution in the evolution Eq. 30 is concerned, their corresponding mass fractions w i in Eq. 30 are set equal to 1.

In fast elongational flow, the steady-state tensile stress reaches the limit

$$ \sigma \left(\overset{\bullet }{\varepsilon}\right)=5{\displaystyle \sum_i{g}_i{f}_{i \max}^2} $$
(31)

The maximum stretches f i max of the pom-poms are limited by the IP term,

$$ {f}_{i \max}^2=\frac{3}{2{w}_i}\sqrt{2\overset{\bullet }{\varepsilon }{\tau}_i} $$
(32)

resulting in a tensile stress of

$$ \sigma \left(\overset{\bullet }{\varepsilon}\right)=\frac{15}{2}{\displaystyle \sum_i\frac{g_i}{w_i}\sqrt{2\overset{\bullet }{\varepsilon }{\tau}_i}} $$
(33)

Equation 33 clearly features the signature of dynamic dilution through the term w i in the denominator, which augments the stress contribution of the long relaxation modes with high dilution, and also the signature of the IP, which predicts a scaling of the stress contribution according to \( {\left(\overset{\bullet }{\varepsilon}\right)}^{1/2} \).

Experimental

Materials

The elongational rheological modellings of this study were conducted on different grades of low-density polyethylene (LDPE) melts previously characterized and tested by Bastian (2001), Rolón-Garrido et al. (2013) and Pivokonsky et al. (2006), as well as long-chain branched polypropylene (LCB-PP) melt characterized by Wagner et al. (2006). Tables 1, 2 and 3 display the weight average molecular weight (M w), number average molecular weight (M n), polydispersity index (M w/M n), melting temperature (T m), room temperature density (ρ RT), testing temperature density (ρ T), activation energy (E a), dilution modulus G D obtained by modelling of the elongational data and the linear viscoelastic relaxation spectrum of LDPE I to LDPE VI at their testing temperature. Likewise, Table 4 shows the characterization of Lupolen 1840D, Escorene, Bralen and LCB-PP samples.

Table 1 Characterization of LDPE I and LDPE II melts
Full size table
Table 2 Characterization of LDPE III and LDPE IV melts
Full size table
Table 3 Characterization of LDPE V and LDPE VI melts
Full size table
Table 4 Characterization of Lupolen 1840D, Escorene, Bralen and LCP-PP melts
Full size table

Rheological measurements

The extensional rheological measurements of LDPE I-VI were performed by Bastian (2001) through a commercial form of Meissner rheometer manufactured by Rheometric Scientific and named Rheometrics Melt Extensional Rheometer (RME). The comprehensive aspects of this commercial rheometer, as well as the rheological theories behind it, have been explained elsewhere (Meissner and Hostettler 1994; Narimissa et al. 2015). Rolón-Garrido et al. (2009, 2013) and Pivokonsky et al. (2006) conducted their uniaxial elongational measurements of Lupolen 1840D, Escorene and Bralen through Sentmanat Extensional Rheometer (Sentmanat 2004) universal testing platform from Xpansion Instruments, i.e. models SER2-P and SER-HV-A01, respectively. Extensional viscosity of LCB-PP and also LDPE II melts were investigated by Münstedt-type extensional rheometer (MTR) (Münstedt 1979) which is capable of measuring the time-dependent elongational viscosity at constant elongation rates up to the Hencky strain of 3.8.

Comparison between the predictions of the HMMSF model and the elongational viscosity data

The aim of the following discussion is to present a comparative analysis between the experimental results and the HMMSF model, as defined by the equation of stress (Eq. 27), the set of evolution equations for the MSFs (Eq. 30) and the hierarchical procedure to evaluate the effect of dynamic dilution with only one free non-linear parameter, the dilution modulus G D (Eq. 29).

Figures 3, 4 and 5 present the experimental elongational viscosity results of LDPE I-VI conducted by Bastian (2001) using the RME rheometer, as well as LDPE 1840D (Rolón-Garrido et al. 2013), Escorene and Bralen (Pivokonsky et al. 2006) measured by the SER rheometer. The elongational viscosity data of LCB-PP (Wagner et al. 2006) measured by the MTR are shown in Fig. 6. Figure 4 verifies the accuracy of the RME data of Bastian by comparison with independently measured data of the same polymer through the application of a different elongational rheometer, MTR (Münstedt 1979), at nearly the same strain rates.

Fig. 3
figure 3

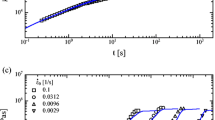
a Comparison of elongational viscosity data (open symbols) of LDPE I with predictions of the HMMSF model. Continuous lines and crosses represent predictions for spectrum A and spectrum B (Table 1), respectively. G D  = 1.0 × 104 Pa. b Spectral decomposition for relaxation spectrum A of LDPE I at strain rate of 0.093/s. Modes are indicated by relaxation times. c Stretches f i of the long relaxation modes as a function of Hencky strain ε. Modes are indicated by relaxation times

Full size image
Fig. 4
figure 4

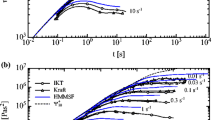
Comparison of elongational viscosity data (symbols) of LDPE II (characterized in Table 1) with predictions of the HMMSF model (lines). Data measured by MTR and RME

Full size image
Fig. 5
figure 5figure 5

Comparison of elongational viscosity data (symbols) of LDPE III to LDPE VI measured by RME rheometer (Bastian 2001), as well as LDPE 1840D (Rolón-Garrido et al. 2013), Escorene and Bralen (Pivokonsky et al. 2006) measured by SER rheometer and characterized in Tables 2, 3 and 4 with predictions of HMMSF model (continuous lines)

Full size image
Fig. 6
figure 6

Comparison of elongational viscosity data (symbols) of LCB-PP characterized in Table 4 and measured by MTR (symbols) with predictions of HMMSF model (continuous lines)

Full size image

Table 1 displays two sets of relaxation spectra for LDPE I, i.e. Spectra A and B, with 7 and 17 modes, respectively. Both sets of relaxation spectra were applied to demonstrate that the best fit of the dilution modulus, G D, is independent of the number of modes. For the same G D , the predictions of spectrum A (7 modes, shown in Fig. 3a by continuous lines) are the same as the predictions of spectrum B (17 modes, identified in Fig. 3a by cross symbols) within line width. This demonstrates the robustness of the hierarchical procedure to evaluate the effect of dynamic dilution from the relaxation spectrum, irrespective of the number of relaxation modes used to represent linear viscoelasticity.

For spectrum A (7 modes), Fig. 3b shows the contribution of the individual relaxation modes to the prediction of elongational viscosity of LDPE I at \( \overset{\bullet }{\varepsilon }=0.093\;/\mathrm{s} \). The dotted lines in this figure show the spectral decomposition of the prediction (continues line) by individual modes of relaxation (indicated by the relaxation times); i.e. the prediction is the sum of the contributions of individual modes. The spectral decomposition demonstrates the importance of the modes with long relaxation times τ i , which feature a high dynamic dilution and, therefore, a lower mass fraction w i after dilution, and hence, a large effect on the prediction of the elongational viscosity. Figure 3c presents the stretches f i as a function of Hencky strain ε and confirms the outcome of the spectral decomposition in the prediction of the elongational viscosity by the HMMSF model: Only the four longest relaxation modes show stretches f i  > 1, while the stretch of the shorter relaxation modes remains negligibly small. Furthermore, the findings of Fig. 3a, b are in accordance with the general expectation that in elongational flow, the strain hardening behaviour is created predominantly by the long relaxation modes.

The predictions of the elongational viscosity of LDPE I-IV (continuous lines in Figs. 3, 4 and 5) are, in general, in excellent agreement with the experimental data for the time-dependent strain-hardening regime and, also, as far as accessible by the experiments, in the transition to what seems to be a steady-state elongational viscosity. It is obvious that the experimental data do not allow inferring a definite steady-state elongational viscosity at all strain rates, and thus, the prediction represents rather a lower limit of the steady-state value. The only quantitative discrepancies between the experimental data and the prediction are observed for LDPE IV and LDPE VI at the lowest strain rates, \( \overset{\bullet }{\varepsilon }=0.1\kern0.24em \mathrm{and}\kern0.24em 0.0274\;/\mathrm{s} \), respectively (Fig. 5). The underpredictions observed may be due to the limited extension of the relaxation spectrum of the two LDPEs and, consequently, the underestimation of the weight of the longest relaxation time, which leads to poor prediction of the elongational viscosity of these polymers at low strain rates.

Predictions of the elongational viscosity of Lupolen 1840D, Escorene and Bralen are also demonstrated in Fig. 5. The elongational viscosity data of Lupolen 1840D are well consistent with the prediction. The model underpredicts the strain hardening region of Escorene and Bralen at extremely high strain rates, while it showed good agreement with the data otherwise. Here, the main cause of the observed underpredictions at high strain rates, \( \overset{\bullet }{\varepsilon }=10\kern0.5em \mathrm{and}\kern0.5em 20\;/\mathrm{s} \), may be due to the instrumental errors as a result of extremely short measurement times (0.1 and 0.2 s, respectively) leading to possibly inaccurate determination of the elongational viscosity at such high rates. Despite of the claimed maximum operational strain rate of 20/s of the SER, the rheological data produced by this rheometer at \( \overset{\bullet }{\varepsilon}\ge 10\;/\mathrm{s} \) must be taken into consideration rather cautiously.

Figure 6 exhibits the comparison between the elongational viscosity data of long-chain branched polypropylene (LCB-PP) (Wagner et al. 2006) and prediction of the HMMSF model. The MTR rheometer was utilized to investigate the extensional behaviour of LCB-PP at \( \overset{\bullet }{\varepsilon}\le 1\;/\mathrm{s} \). The prediction of the HMMSF model accords well with the experimental data of LCB-PP at all strain rates investigated. As in this case, no indication of a transition to a steady-state elongational viscosity is observed within the experimentally accessible strain, and the value of the dilution modulus G D and the steady-state viscosity predicted represent only a lower limit of the true values.

Overall, the comparison between the experimental elongational viscosity data and the prediction of the HMMSF model shows very good agreement for data measured with three different extensional rheometers at different experimental temperatures and for a wide range of strain rates investigated. The accuracy of the predictions of the HMMSF model is in all cases at least comparable to the predictions of the MSF model (Eqs. 14 and 17), which features two non-linear parameters (β and f max) in elongational flow. The dependence on only the linear viscoelastic data plus merely one non-linear parameter, the dilution modulus G D , signifies the ease of application in modelling elongational viscosity of LCB polymer melts by the HMMSF model.

Conclusions

The proposed hierarchical multi-mode molecular stress function (HMMSF) model for long-chain branched (LCB) polymer melts implements the basic ideas of (i) the pom-pom model, of (ii) hierarchal relaxation, of (iii) dynamic dilution and of (iv) interchain pressure (IP). The advantage of the HMMSF model over the pom-pom model lies in the fact that the HMMSF model is not based on the assumption of stretch-orientation decoupling of the backbone chain. Stretch-orientation decoupling necessitates a separate dynamics of the stretch as defined by the stretch relaxation times τ si , while the assumption of a constant tube diameter leads to the absence of the IP mechanism in the pom-pom model, which initiates the necessity of defining the maximum stretches in terms of the number of hypothetical free chain ends, λ i max ≅ q i . Thus, the multi-mode pom-pom model features two non-linear parameters for each mode (e.g. 16 parameters for eight modes). In contrast, the HMMSF model maintains that stretch and orientation dynamics are coupled by assuming that stretch is implemented through a tube diameter which decreases with increasing deformation. Therefore, stretch and orientation of tube segments have the same dynamics. In addition, a decrease of the tube diameter increases the IP which, in combination with the effect of hierarchical dilution, sets a limit on the minimum tube segment diameter and, thereby, the maximum stretch of the backbone chain segment for a given deformation rate. In this way, the HMMSF model reduces the number of free non-linear parameters to only one parameter for modelling of elongational flow, namely the dilution modulus G D . The effect of hierarchical dilution is independent of the number of linear viscoelastic relaxation modes used; i.e. the value of the dilution modulus G D does not depend on the number of modes. Due to the dilution effect, the strain-hardening effect of LCB polymers in elongational flows is largely influenced by the long relaxation modes as seen from the spectral decomposition.

Excellent agreement was found between the predictions of the HMMSF model and the elongational viscosity data of a broad range of LCB melts measured by five different research groups with three different extensional rheometers at different experimental temperatures as well as a wide range of strain rates.