A generalized equation for rheology of emulsions and suspensions of deformable particles subjected to simple shear at low Reynolds number

Abstract

We present analyses to provide a generalized rheological equation for suspensions and emulsions of non-Brownian particles. These multiparticle systems are subjected to a steady straining flow at low Reynolds number. We first consider the effect of a single deformable fluid particle on the ambient velocity and stress fields to constrain the rheological behavior of dilute mixtures. In the homogenization process, we introduce a first volume correction by considering a finite domain for the incompressible matrix. We then extend the solution for the rheology of concentrated system using an incremental differential method operating in a fixed and finite volume, where we account for the effective volume of particles through a crowding factor. This approach provides a self-consistent method to approximate hydrodynamic interactions between bubbles, droplets, or solid particles in concentrated systems. The resultant non-linear model predicts the relative viscosity over particle volume fractions ranging from dilute to the the random close packing in the limit of small deformation (capillary or Weissenberg numbers) for any viscosity ratio between the dispersed and continuous phases. The predictions from our model are tested against published datasets and other constitutive equations over different ranges of viscosity ratio, volume fraction, and shear rate. These comparisons show that our model, is in excellent agreement with published datasets. Moreover, comparisons with experimental data show that the model performs very well when extrapolated to high capillary numbers (C a≫1). We also predict the existence of two dimensionless numbers; a critical viscosity ratio and critical capillary numbers that characterize transitions in the macroscopic rheological behavior of emulsions. Finally, we present a regime diagram in terms of the viscosity ratio and capillary number that constrains conditions where emulsions behave like Newtonian or Non-Newtonian fluids.

Introduction

Suspensions and emulsions of a Newtonian fluid including dispersed non-Brownian particles are ubiquitous in nature (Faroughi et al. 2013), and have many applications in industry (Schramm 2006). When the Brownian motion due thermal energy is neglected, the dynamics of suspensions/emulsions is mainly governed by external body forces, interparticle forces, and long-range hydrodynamic interactions due to the presence of other particles (Brady and Bossis 1988). It is known that the existence of a cloud of particles in a Newtonian fluid at low Reynolds number dramatically changes the mechanism by which momentum is exchanged between particles and the ambient fluid. Moreover, the macroscopic rheological behavior of suspensions and emulsions, which are heterogeneous microscopically, depends mainly on the particle size distribution, particle concentration, shear dynamic viscosity of the matrix (continuous phase) and dispersed phase, the order of the particle deformation, and the rate of deformation.

In the last century, since the calculation conducted independently by Sutherland (1905) and Einstein (1911) to obtain the viscosity of a very dilute suspension of non-deformable solid spheres, the macroscopic rheological behavior of multiparticle systems has received a remarkable attention. Solutions are mainly based on conceptual models that account for the change in hydrodynamic interactions based on the particle concentration and deformation. Einstein-Sutherland theory was first extended to very dilute emulsions by Taylor (1932) where he assumed that fluid particles remain spherical, i.e., the dimensionless capillary number, C a, (the ratio of viscous force to the force associated with the surface tension) is assumed C a≪1. These models predict an increase in the macroscopic shear viscosity of the system that is linearly proportional to the particle concentration, with a greater effect for solid spheres. The Einstein-Sutherland law for a dilute suspension of identical rigid spheres was then extended to second-order in volume fraction by Batchelor and Green (1972). Other investigations by Mackenzie (1950), Ducamp and Raj (1989), and Bagdassarov and Dingwell (1992) have constrained expressions for the rheology of dilute emulsions including highly deformable fluid particles (C a≫1). More generalized constitutive equations for the rheology of dilute systems were derived by Oldroyd (1959) for emulsions of two immiscible Newtonian fluids, by Goddard and Miller (1967) for suspensions including deformable Hookian solid sphere, and by Frankel and Acrivos (1970) for emulsions consisting of deformable fluid particles up to the first order of the particle deformation. These constitutive equations predict the macroscopic viscosity of relatively dilute systems over a wide range of deformation rates (capillary number) and viscosity ratios.

For concentrated systems, Pal (2003b) and Pal (2004) employed the differential effective medium (DEM) theory (Norris et al. 1985) to determine phenomenologically the relative viscosity for elastic solid particle suspension ($\lambda \to \infty$) and bubbly emulsion (λ→0). Pal (2003c) developed a more general model for concentrated emulsions with different viscosity ratio and deformable particle using the analogy between shear modulus and shear viscosity. In these studies, different interpretations and definitions are used for the change in the volume available for adding particles (termed “free volume” by Robinson (1949)), which leads to different sub-models. More recently, new rheological equations for concentrated suspensions of rigid solid particles have been proposed by Mendoza (2011) using DEM theory, and by Brouwers (2010) who matched the viscosity of bimodal suspensions with identically sized particles to yield a closed form solution for the relative viscosity of monomodal suspensions. Faroughi and Huber (2014) also proposed a crowding-based rheological model to quantify the shear dynamic viscosity of suspensions of rigid and spherical bimodal-sized particles with interfering size ratios.

These theoretical models have been tested and complemented with several numerical and experimental studies. For instance, Brady and Bossis (1988) used numerical modeling based on Stokesian dynamics and took into account lubrication forces at high particle density to study the rheology of monosize suspensions. They showed that microstructures can form in sheared suspension, and outlined the role of particle clusters on the rheological behavior of concentrated suspensions. Schaink et al. (2000) extended the Stokesian dynamics method to study the rheology of suspensions of rigid spheres suspended in viscous and viscoelastic matrices. The rheological behavior of suspensions of rigid particles has also been investigated using other numerical techniques (for example Aidun (1995) and Ladd and Verberg (2001) who used Lattice Boltzmann method and studies of Koelman and Hoogerbrugge (1993) and Strating (1999) for Brownian dynamics method, see also the recent numerical studies by Rexha and Minale (2011) and D’Avino et al. (2013) and Villone et al. (2014)).

Experimental studies also have provided a great insight into the role of particles on the suspension rheology (e.g., Rutgers (1962), Thomas (1965), Chan and Powell (1984), Rodriguez et al. (1992), Segre et al. (1995), Cheng et al. (2002), Pasquino et al. (2008), Mueller et al. (2009), Boyer et al. (2011), and Dai et al. (2013)) and bubbly emulsion rheology (e.g., Stein and Spera (2002), Manga and Loewenberg (2001), and Rust and Manga (2002) and Llewellin and Manga (2005)). Additionally, the role of the viscosity ratio and capillary number on the viscoelastic properties and rheology of dilute and concentrated emulsions has been studied extensively by Pal and Rhodes (1021), Pal (1245), Pal (1996), Pal (2001), and Pal (2003c). These studies provided many experimental data on the viscosity of emulsions which will be used here to validate the accuracy of our new theoretical model for predicting the shear viscosity in multiparticle systems.

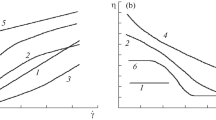
We summarize the contribution and applicability of several studies (non-exhaustive) for the rheology of suspensions and emulsions as function of the particle volume fraction, ψ, viscosity ratio, λ, and capillary number, C a in Fig. 1. For example, the model proposed by Lim et al. (2004) is suitable for ψ<0.2, λ→0 and C a≪1, while models of Pal (2003a) and Pal (2004) cover the entire range of ψ and capillary number within the limit of λ→0. This diagram serves to clearly identify regions of the volume fraction, viscosity ratio, and capillary number parameter space that need to be further explored. It also points to the lack of unified model valid over the entire space. A more complete list of published equations developed for solid particle suspensions and emulsions along with the range over which they are deemed applicable is reported in Tables 1 and 2, respectively.

Fig. 1

Summary of some of published rheological models and their range of applicability with respect to particle volume fraction, ψ, viscosity ratio, λ, and capillary number, C a. See Tables 1 and 2 for more details about published models

Table 1 Selected published models to predict the relative viscosity of suspensions of rigid solid particles and the range of volume fraction over which they intend to be applied

The present study is undertaken for three reasons. The first goal is to present a complete derivation of the macroscopic rheology for both dilute and concentrated monosized suspensions/emulsions under simple steady shearing flow conditions. The effective viscosity is determined from the knowledge of the influence of individual particles on the fluid flow and the pressure field by taking two steps of volume correction into consideration. The first volume correction serves to build a general rheological model for dilute systems. With this correction, each particle inside the finite volume can interact with all particles added simultaneously to the system through a decrease in the volume of the ambient fluid. We then introduce the second volume correction to extend the model phenomenologically to highly concentrated systems (up to the random close packing). This correction accounts for the interaction of particles added during the differential effective medium procedure with particles already present in the system. Therefore, the second volume correction includes a term that carries the effect of the particle shape and size distribution as a geometrical constraint on the amount of volume that can be eventually filled by particles (i.e., the second volume correction accounts for the volume of matrix trapped in interstices formed by particles through a crowding factor). The second objective of the present work is to provide a robust and general equation for the macroscopic rheology of emulsions applicable for a wide range of viscosity ratio, capillary number, and particle concentration which is missing in the literature (see Fig. 1). This general equation shall reduce to the well-known relative viscosity law developed by Sutherland-Einstein (1911) and Taylor (1932) in the limiting cases when ψ≪1 along with either $\lambda \to \infty$ or λ→0, respectively. The third objective is to provide a regime diagram which illustrates how the relative viscosity for emulsions depends on the viscosity ratio and capillary number. We find different regimes that are delimited by two critical dimensionless numbers; a critical viscosity ratio and a critical capillary number. These regimes constrain the influence of different parameters on the deformation of particles, and provide insight on transitions in the rheology of non-Brownian emulsions from Newtonian to shear thinning due to the particle deformation (the effect of microstructure changes such as shear-induced migration, wall-slip, and heterogeneity is not considered in this study).

In the following sections, we present a brief physical description of the perturbation in the flow fields due to the presence of a single fluid particle. Next, we discuss the homogenization process and the application of the first volume correction to obtain the macroscopic property of dilute systems. Then, we explain the procedure of the fixed volume differential effective method including the second volume correction to extend the relative viscosity model to concentrated systems. The model is then tested against a number of experimental data and published constitutive equations. Finally, the ability of the model to approximate the relative viscosity for polydisperse systems including non-deformable particles is discussed.

Physical description

We shall consider two incompressible and immiscible Newtonian fluids forming a matrix (the continuous phase) and the dispersed phase (a single fluid particle at this stage). The fluid flow at large distances from the fluid particle satisfies the conditions of a simple steady straining flow:

$$\begin{array}{@{}rcl@{}} \mathbf{u}_{\odot }(\mathbf{x}) = \boldsymbol{\Upsilon \cdot x}. \end{array} $$

(1)

Here, x denotes the position vector with respect to the origin located at the center of the fluid particle, and Υ is a given velocity gradient tensor for which the incompressibility of the matrix imposes t r Υ=0. We shall assume that inertial forces can be neglected (small Reynolds number, R e≪1), and the density of dispersed particles is the same as that of the matrix. The force balance which governs the equation of motion is characterized by Stokes creeping equations

$$\begin{array}{@{}rcl@{}} \boldsymbol{\nabla \cdot \sigma}^{m} = 0, \boldsymbol{\sigma}^{m} = -p^{m}\mathbf{I} + {\upmu}_{m} \left[ \boldsymbol{\nabla u}^{m} + (\boldsymbol{\nabla u}^{m})^{T}\right], \end{array} $$

(2)

where sub/superscript m refers to properties associated with the matrix, σ ^m is the total stress tensor, p ^m is the dynamic pressure, I is the unit tensor, and μ _m denotes the shear dynamic viscosity of the matrix. u ^m is the velocity vector that satisfies the continuity equation, ∇⋅u ^m=0. Similar expressions can be formulated for the fluid flow inside the particle just by changing the superscript m to d which refers to the dispersed phase. We assume that the particle deforms due to the shearing. To the first order, the stress that acts to elongate the particle is proportional to μ _m Υ where Υ=|Υ| is the magnitude of the velocity gradient (or the shear rate magnitude) with unit [t ⁻¹]. The resisting stress on the surface of the particle opposing the induced shear stress is of order γ/R _d where γ is the surface tension, and R _d is the radius of the particle. For the case of a deformable elastic solid particle, the resisting stress will be proportional to the shear modulus G. The equilibrium state between these two counteracting surface stresses on the surface of particle controls the final shape of the particle, and leads to the definition of the dimensionless deformation number; the capillary number,

$$\begin{array}{@{}rcl@{}} Ca= \frac{\Upsilon {\upmu}_{m} R_{d}}{\gamma}, \end{array} $$

(3)

for the case of fluid particles and the Weissenberg number,

$$\begin{array}{@{}rcl@{}} Wi= \frac{\Upsilon {\upmu}_{m}}{G}, \end{array} $$

(4)

for the case of solid particles. The required sets of boundary conditions directly depends on the order of particle deformation considered. Here, we shall consider a homogeneous straining flow at a large distance from the center of the fluid particle, (1), along with the continuity of tangential velocity and tangential components of the stress tensor at the surface of the particle in order to find the zeroth order of deformation solution (assuming the particle remains spherical). We can also obtain the first order of deformation solution by using the discontinuity in normal components of the stress tensor across the particle surface based on Laplace’s equation. Overall, the velocity, pressure, and stress fields outside the particle are decomposed up to the second order of the particle deformation O(D ²) as follows

$$\begin{array}{@{}rcl@{}} \mathbf{u}^{t} &=& \mathbf{u}_{\odot} + \mathbf{u}^{0,d} + D\mathbf{u}^{1,d} +O(D^{2}), \\ p^{t} &=& p_{\odot} + p^{0,d} + Dp^{1,d} +O(D^{2}), \\ \boldsymbol{\sigma}^{t}&=& \boldsymbol{\sigma}_{\odot} + \boldsymbol{\sigma}^{0,d} + D\boldsymbol{\sigma}^{1,d} +O(D^{2}). \end{array} $$

(5)

Here, D is a dimensionless parameter which specifies the amount of deformation (departure from the spherical shape), and it is proportional to either C a or W i number, respectively, for fluid particle and solid particle. p _⊙ is an arbitrary constant pressure at a large distance from the particle which is normally assumed to be zero. At large distances from the particle, the zeroth and first-order correction terms (parameterized by superscript 0,d and 1,d) vanish.

Zeroth order deformation

Using the general solution for Stokes equations formulated by Lamb, and considering appropriate solid spherical harmonics of degree j (p _j a n d ϕ _j ) for the exterior fluid, one can express both velocity and pressure fields. The zeroth order deformation solution was first provided by Taylor (1932) who used the following solid spherical harmonic functions of degree −3:

$$\begin{array}{@{}rcl@{}} p^{0,d}_{-3} &=& {\upmu}_{m}A^{0,d}_{-3}\left( \frac{R_{d}}{r^{2}}\right)^{3}{r}(\boldsymbol{{\Upsilon}^{\mathcal{S}} : xx}), \\ \phi^{0,d}_{-3} &=& B^{0,d}_{-3}\left( \frac{R_{d}}{r}\right)^{5}(\boldsymbol{{\Upsilon}^{\mathcal{S}} : xx}), \end{array} $$

(6)

where r is the the magnitude of the position vector at the interface between phases, and $\boldsymbol {{\Upsilon }^{\mathcal {S}}}$ is the normalized pure shear rate tensor (the rate of deformation tensor as the symmetric part of the velocity gradient normalized by the magnitude of the shear flow). By applying the aforementioned boundary conditions for the zeroth order, Taylor (1932) arrived at the following expression for the constants in Eq. 6:

$$\begin{array}{@{}rcl@{}} A^{0,d}_{-3} =-5{\Upsilon} \left( \frac{\lambda + \frac{2}{5}}{\lambda +1}\right) , ~~~~ B^{0,d}_{-3}= -\frac{\Upsilon}{2}\left( \frac{\lambda}{\lambda+1}\right), \end{array} $$

(7)

in which λ is the viscosity ratio defined as,

$$\begin{array}{@{}rcl@{}} \lambda =\frac{{\upmu}_{d}}{{\upmu}_{m}}. \end{array} $$

(8)

First-order deformation

The solution for a first-order deformation can be obtained with the same method, and by using Laplace’s equation as a proper boundary condition to define the stress jump at the boundary of the particle (see Frankel and Acrivos (1967) and Frankel and Acrivos (1970) for more details). The solid spherical harmonics p ₋₃ are the only functions needed for the integration of the stress components over a large volume, owing to the fact that other solid spherical harmonics vanish. The final result for the solid spherical harmonic reduces to the following expression (Schowalter et al. 1968):

$$\begin{array}{@{}rcl@{}} p^{1,d}_{-3} &=& \frac{20}{7}{\upmu}_{m}{\Upsilon} \frac{25\lambda^{2} + 41\lambda +4}{25(\lambda+1)^{2}}\left( \frac{R_{d}}{r}\right)^{3} \\ &\cdot & \left[ \boldsymbol{({\Upsilon}^{\mathcal{S} }: {\Upsilon}^{\mathcal{S} } )} \,-\, \frac{3}{r^{2}}(\boldsymbol{{\Upsilon}^{\mathcal{S}} \cdot x})^{2}\right] \,+\, 12{\upmu}_{m}{\Upsilon} \frac{19\lambda + 16}{15(\lambda +1)} \\ & \cdot {r}&\left ( \frac{R_{d}}{r^{2}}\right)^{3} \left[ (\frac{\mathbf{u}_{\odot}}{\Upsilon} \,-\, \boldsymbol{{\Upsilon}^{\mathcal{S}} \cdot x} ) \boldsymbol{\cdot} (\boldsymbol{{\Upsilon}^{\mathcal{S}} \cdot x})\right]. \end{array} $$

(9)

Furthermore, the shape of the particle up to the second order of the deformation (O(D ²)) is calculated as:

$$\begin{array}{@{}rcl@{}} r - R_{d} \left[ 1+ \frac{2}{r^{2}}\underbrace{\frac{Ca}{16 }\frac{19\lambda + 16}{\lambda +1}}_{D} (\boldsymbol{{\Upsilon}^{\mathcal{S}} : xx}) \right] = 0. \end{array} $$

(10)

Second-order deformation

To proceed to higher orders deformation, for instance to C a ², one needs to derive the complete second-order solutions of the spherical harmonics for the pressure and velocity fields and an expression for the particle shape. Deriving these solutions following the same methodology is complex and tedious (Chaffey and Brenner 1967; Greco 2002). Alternatively, Greco (2002) presented an analysis that calls for rotational invariance to find all unknown fields (velocity and pressure) and the particle shape. According to Greco (2002), one arrives to the following function for the fluid particle shape up to the third order of the deformation (O(D ³)),

$$\begin{array}{@{}rcl@{}} r - R_{d} \left[ 1+ \frac{2}{r^{2}}\frac{Ca}{16}\frac{19\lambda + 16}{\lambda +1} (\boldsymbol{{\Upsilon}^{\mathcal{S}} : xx}) + Ca^{2}\right. \\ \cdot \left( \frac{S_{1} (\lambda)}{r^{3}} (\boldsymbol{{\Upsilon}^{\mathcal{S}} {\Upsilon}^{\mathcal{S}} :: xxx}) + \frac{S_{2} (\lambda)}{r^{2}} (\boldsymbol{{\Upsilon}^{\mathcal{S}} {\Upsilon}^{\mathcal{S}} : xx}) \right. \\ \left. \left. + S_{3} (\lambda) (\boldsymbol{{\Upsilon}^{\mathcal{S}}: {\Upsilon}^{\mathcal{S}}}) + \frac{S_{4} (\lambda)}{r^{2}} (\boldsymbol{\Pi : xx}) \right) \right] = 0, \end{array} $$

(11)

where coefficients S ₁ through S ₄ depend only on the viscosity ratio and are listed in the Appendix F of Greco (2002). In Eq. 11, π is the second Rivlin-Ericksen tensor (Astarita and Marrucci 1974) that, under simple shear flow conditions, reduces to

$$\begin{array}{@{}rcl@{}} \boldsymbol{\Pi} = 2(\boldsymbol{{\Upsilon}^{\mathcal{S}} \cdot {\Upsilon}^{\mathcal{A}} } - \boldsymbol{{\Upsilon}^{\mathcal{A}} \cdot {\Upsilon}^{\mathcal{S}} }) + 4 \boldsymbol{{\Upsilon}^{\mathcal{S}} \cdot {\Upsilon}^{\mathcal{S}} }, \end{array} $$

(12)

where $\boldsymbol {{\Upsilon }^{\mathcal {A}}}$ is the normalized spin tensor (skew-symmetric part of the velocity gradient normalized by the magnitude of the shear flow).

While Greco (2002) provides a starting point to further develop our model to higher orders of particle deformation, we restrict our derivation to the first order of the deformation (up to O(D ²), therefore the model is theoretically applicable only for small particle deformations). Interestingly, we show below that our model predictions for emulsions sheared at high C a are in good agreement with experiments which suggest that the second-order truncation with respect to particle deformation does not introduce significant errors when extrapolated to high C a.

The harmonic functions for the case of a matrix including a Hookean elastic solid particle are obtained with the same methodology to the zeroth order of deformation. For first-order deformations, we replace Laplace’s equation with another stress boundary condition at the fluid-elastic solid interface (Goddard and Miller 1967). This is the case even for a fluid particle which has a infinite viscosity where the spherical shape of the particle is not maintained by surface tension forces, but rather by its shear modulus G.

Relative viscosity of a dilute system

According to Batchelor (1967), the rate of energy dissipation per unit volume inside a suspension (or emulsion) increases when more solid particles (or fluid particles possessing high surface tension or shear viscosity) are fed to the system. Therefore, a multiparticle systems can be treated as a homogeneous Newtonian fluid of the same average density in a fixed volume of $V_{\psi } = {V^{r}_{m}}+{V^{t}_{p}}$ (in which ${V^{t}_{p}}$ is the total volume occupied by particles, and ${V^{r}_{m}}$ is the remaining volume of the matrix) and with viscosity μ _ψ . The stress tensor at any point of the system (outside particles), σ ^t, is given by

$$\begin{array}{@{}rcl@{}} \boldsymbol{\sigma}^{t} = -p^{m}\mathbf{I} + 2{\upmu}_{m}\boldsymbol{\Upsilon} \underbrace{-p^{\prime}\mathbf{I} + {\upmu}_{m}\left[ \boldsymbol{\nabla u}^{\prime} + (\boldsymbol{\nabla u}^{\prime})^{T}\right] }_{\boldsymbol{\sigma}^{\prime}}, \end{array} $$

(13)

where the primed terms are associated with the disturbance in stress tensor, velocity and pressure fields due to the presence of particles, and consequently they include both perturbation arising from zeroth and first order of deformation. Namely,

$$\begin{array}{@{}rcl@{}} \boldsymbol{\sigma}^{\prime} = \boldsymbol{\sigma}^{0,d} + D\boldsymbol{\sigma}^{1,d}. \end{array} $$

(14)

Besides, the stress tensor for the homogeneous equivalent fluid at any point can be calculated as

$$\begin{array}{@{}rcl@{}} \boldsymbol{\sigma}^{\psi} = -p^{\psi}\mathbf{I} + 2{\upmu}_{\psi}\boldsymbol{\Upsilon}. \end{array} $$

(15)

The equivalence assumption implies the equality of the total rate of work done on the boundary of the emulsion/suspension, A _ψ , in both structures characterized with the stress tensors defined in Eqs. 13 and 15.

In previous models (Einstein 1911; Taylor 1932; Batchelor 1967; Goddard and Miller 1967; Frankel and Acrivos 1970; Schowalter et al. 1968; Landau and Lifshitz 1987), the matrix is considered unbounded (infinite volume). Therefore, the excluded volume taken by particles has been overlooked which results in particles being represented as mass points. These models provide valuable results only in cases where the particle concentration is low (less than 5 %). In this study, a finite volume for the matrix is considered; however, it is assumed large enough to satisfy the fact that the perturbation of single particles on the flow fields are independent of each other (no hydrodynamic interactions in the dilute limit). The model, thus, takes into account the excluded volume of the matrix replaced by particles using a first-volume correction. Using this correction, particles added simultaneously interact by decreasing the volume available in the ambient fluid. We note that the consideration of a finite volume is physically more consistent when the model is tested against experiments.

Owing to the fact that the rate of work associated with the isotropic component of the stress tensors stated in Eqs. 13 and 15 are the same on the boundary of the physical domain (far from particles), the equality of the rate of work exerted by the deviatoric components, represented by τ, yields

$$\begin{array}{@{}rcl@{}} {\int}_{A_{\psi}} \mathbf{u}_{\odot}^{\psi} \boldsymbol{\tau}^{\psi} \boldsymbol{\cdot n } dA = {\int}_{A_{\psi}} \mathbf{u}_{\odot} (\boldsymbol{\tau}_{\odot}+\boldsymbol{\sigma^{\prime}}) \boldsymbol{\cdot n } dA, \end{array} $$

(16)

$$\begin{array}{@{}rcl@{}} {\int}_{A_{\psi}} {\Upsilon}_{ik}(2{\upmu}_{\psi}{\Upsilon}_{ij} )x_{k}n_{j}dA &=& {\int}_{A_{\psi}} {\Upsilon}_{ik}(2{\upmu}_{m}{\Upsilon}_{ij})x_{k}n_{j}dA \\ &+ &{\int}_{A_{\psi}} {\Upsilon}_{ik} \sigma^{\prime}_{ij} x_{k}n_{j} dA, \end{array} $$

(17)

where n is a outward unit vector normal to the surface. We proceed by transforming the first two surface integrals into integrals over the boundary of the remaining ambient fluid, A _m , (a surface enclosing the matrix). Thus, by applying the divergence theorem, Eq. 17 can be recast as

$$\begin{array}{@{}rcl@{}} {\int}_{V_{\psi}-{V^{r}_{m}}} 2{\upmu}_{\psi}{\Upsilon}_{ij}\frac{\partial u_{i}}{\partial x_{j}}dV+{\int}_{A_{m}}2{\upmu}_{\psi}{\Upsilon}_{ij}{\Upsilon}_{ik} x_{k}n_{j}dA &=& \\ {\int}_{V_{\psi}-{V^{r}_{m}}} 2{\upmu}_{m}{\Upsilon}_{ij}\frac{\partial u_{i}}{\partial x_{j}}dV+ {\int}_{A_{m}}2{\upmu}_{m}{\Upsilon}_{ij}{\Upsilon}_{ik} x_{k}n_{j}dA &+& \\ {\int}_{A_{\psi}} {\Upsilon}_{ik} \sigma^{\prime}_{ij}x_{k}n_{j}dA. \end{array} $$

(18)

Assuming that equations governing the perturbation in the fluid flow caused by particles are in Stokes regime, we obtain

$$\begin{array}{@{}rcl@{}} \frac{\partial (\sigma^{\prime}_{ij}x_{k})}{\partial x_{j}} = \sigma^{\prime}_{ik}. \end{array} $$

(19)

Using Eq. 19, the third integral in the right-hand side of Eq. 18 can be expressed as

$$\begin{array}{@{}rcl@{}} {\int}_{A_{\psi}} {\Upsilon}_{ik} \sigma^{\prime}_{ij}x_{k}n_{j}dA &=& \\ \underbrace{{\int}_{V_{\psi}-NV_{p}} {\Upsilon}_{ik} \sigma^{\prime}_{ik} dV}_{-N{\int}_{A_{p}} 2{\Upsilon}_{ik} {\upmu}_{m}u^{\prime}_{i}n_{k}dA} &+& N{\int}_{A_{p}} {\Upsilon}_{ik} \sigma^{\prime}_{ij}x_{k}n_{j}dA. \end{array} $$

(20)

N is the number of particles fed to the system, and A _p is the surface of a particle. Integrals in Eq. 20 are treated in such a way that it is assumed particles are far apart, and the disturbance they generate does not affect the flow field around other particles. Therefore, the averaged rate of energy dissipation per unit of volume is calculated only for one particle and then generalized (linearly summed) to account for the effect of other particles on the rate of dissipation. This assumption is true only for very dilute suspensions/emulsions where $V_{\psi } \rightarrow {V^{r}_{m}}$. As a result, the following equation can be retrieved from Eq. 18 by a simple integration,

$$\begin{array}{@{}rcl@{}} 2{\Upsilon}_{ij}{\Upsilon}_{ij} ({\upmu}_{\psi} - {\upmu}_{m}) {V^{r}_{m}} &=& \\ N{\int}_{A_{p}} ({\Upsilon}_{ik} \sigma^{\prime}_{ij}x_{k}n_{j} &-&2{\Upsilon}_{ik} {\upmu}_{m}u^{\prime}_{i}n_{k}) dA. \end{array} $$

(21)

The integral in the right-hand side of Eq. 21 indicates the average additional rate of energy dissipation caused by a single particle (Batchelor 1967; Happel and Brenner 1983). To calculate this integral, we can use the reciprocal theorem developed by Happel and Brenner (1983) or simply replace A _p by an arbitrary large surface, A _a , enclosing a single particle at its center. For the latter method, the ambient stress and velocity fields of the fluid disturbed by the presence of this particle should be considered as well, namely

$$\begin{array}{@{}rcl@{}} \mathbf{u}^{\prime\prime} &=& \mathbf{u}_{\odot} + \mathbf{u}^{\prime} \\ \boldsymbol{ \sigma}^{\prime\prime} &=& \boldsymbol{ \sigma}_{\odot} + \boldsymbol{ \sigma}^{\prime}. \end{array} $$

(22)

Therefore, we shall restate Eq. 21 as follows

$$\begin{array}{@{}rcl@{}} \tau_{ik} &=& 2{\upmu}_{m}{\Upsilon} {\Upsilon}^{S}_{ik} + \frac{{V^{t}_{p}}}{V_{\psi}-{V^{t}_{p}}} \\ &\cdot & \left( \frac{1}{V_{p}} {\int}_{A_{a}} \sigma^{\prime\prime}_{ij}x_{k}n_{j} dA - \frac{2}{V_{p}}{\int}_{A_{a}} {\upmu}_{m}u^{\prime\prime}_{i}n_{k} ~dA \right), \end{array} $$

(23)

where ${V^{t}_{p}} = N V_{p}$, Using Lamb’s general solution, we have

$$\begin{array}{@{}rcl@{}} \mathbf{u}^{\prime\prime} =\mathbf{u}_{\odot} +\frac{1}{2{\upmu}_{m}} \mathbf{x}p_{-3}, \end{array} $$

(24)

and

$$\begin{array}{@{}rcl@{}} \boldsymbol{\sigma}^{\prime\prime} &=& {\upmu}_{m}\left[ \boldsymbol{\nabla u}_{\odot} + (\boldsymbol{\nabla u}_{\odot})^{T}\right] \\ &+& \frac{1}{2}\left[ \boldsymbol{\nabla} (\mathbf{x}p_{-3}) + (\boldsymbol{\nabla} (\mathbf{x}p_{-3})^{T}\right] - \mathbf{I}p_{-3}, \end{array} $$

(25)

with

$$\begin{array}{@{}rcl@{}} p_{-3} = p^{0,d}_{-3} + \left( \frac{\Upsilon\mu_{m}R_{d}}{16\gamma }\right) \left( \frac{19\lambda + 16}{\lambda +1}\right) p^{1,d}_{-3}. \end{array} $$

(26)

In Eq. 23, the first correction that accounts for the volume taken by particles appears in the homogenization process. Models which overlook this correction underpredict the shear dynamic viscosity of the equivalent fluid in a finite system. Therefore, if a set of particles are added to the matrix (forming a dilute system), the position of each particles is restricted by the presence of other particles.

The detailed solution to integrals in Eq. 23 can be found in Landau and Lifshitz (1987) and Batchelor (1967) for system of non-deformable particles and in Goddard and Miller (1967), Frankel and Acrivos (1970), and Schowalter et al. (1968) for systems composed of deformable particles. Finally,

$$\begin{array}{@{}rcl@{}} \boldsymbol{\tau} &=& 2{\upmu}_{m}{\Upsilon} \left[ 1 + \frac{\psi }{1- \psi} \left( \frac {1+2.5\lambda}{1+\lambda}\right) \right] \boldsymbol{{\Upsilon}^{\mathcal{S}}} \\ &+& \frac{{{\upmu}^{2}_{m}}{\Upsilon}^{2}R_{d}}{\gamma}\left( \frac{\psi }{1-\psi}\right) (\boldsymbol{\mathfrak{A }} - \boldsymbol{\mathfrak{B }} ), \end{array} $$

(27)

where $\psi \equiv \frac {NV_{p}}{V_{\psi }}$ is the particle volume fraction and

$$\begin{array}{@{}rcl@{}} \boldsymbol{\mathfrak{A}} &=& \frac{3(19\lambda +16)(25\lambda^{2} +41\lambda+4)}{140(\lambda+1)^{3}} \\ &\cdot & \left[ \boldsymbol{{\Upsilon}^{\mathcal{S}} \cdot {\Upsilon}^{\mathcal{S}}} -\frac{1}{3}\boldsymbol{I \left( {\Upsilon}^{\mathcal{S}} : {\Upsilon}^{\mathcal{S}}\right) }\right], \end{array} $$

(28)

and

$$\begin{array}{@{}rcl@{}} \boldsymbol{\mathfrak{B}} = \frac{1}{40}\left( \frac{19\lambda+16}{\lambda+1}\right)^{2}\left( \boldsymbol{{\Upsilon}^{\mathcal{A}} \cdot} \boldsymbol{{\Upsilon}^{\mathcal{S}}} - \boldsymbol{{\Upsilon}^{\mathcal{S}}} \boldsymbol{ \cdot {\Upsilon}^{\mathcal{A}}}\right). \end{array} $$

(29)

Equation 27 is a special case of simple fluids family of constitutive equations (Schowalter et al. 1968). We note that the deformation introduces a non-linear relationship between the stress and the rate of strain. Thus, emulsions/suspensions behave as non-Newtonian fluids. Following Frankel and Acrivos (1970), we can apply the operator

$$\begin{array}{@{}rcl@{}} 1+ {\Lambda} \frac{\mathfrak{D}}{\mathfrak{D}t}, \end{array} $$

(30)

on both sides of Eq. 27. In Eq. 30, $\frac {\mathfrak {D}}{\mathfrak {D}t}$ denotes the Jaumann derivative (Goddard and Miller 1967), which is defined as follows for an arbitrary tensor α,

$$\begin{array}{@{}rcl@{}} \frac{\mathfrak{D}}{\mathfrak{D}t} \boldsymbol{\alpha} = \frac{d}{dt} \boldsymbol{\alpha}+ \boldsymbol{u \cdot \nabla \alpha } + {\Upsilon} \left( \boldsymbol{{\Upsilon}^{\mathcal{A}} \cdot \alpha } - \boldsymbol{ \alpha \cdot {\Upsilon}^{\mathcal{A}} }\right). \end{array} $$

(31)

In Eq. 30, Λ is determined as

$$\begin{array}{@{}rcl@{}} {\Lambda} = \frac{(2\lambda+3)(19\lambda+16)}{40(\lambda+1)}\left( \frac{{\upmu}_{m}R_{d}}{\gamma}\right), \end{array} $$

(32)

has unit of time and is defined as the relaxation time (Oldroyd 1959) that characterizes the time-dependency of the flow response to deformation (the time required for a slightly deformed particle to relaxes exponentially to its spherical equilibrium shape). The value of the relaxation time diverges as the viscosity ratio approaches to infinity or as surface tension approaches zero.

In a steady and laminar simple straining flow, when $\boldsymbol { \alpha } = \boldsymbol {{\Upsilon }^{\mathcal {S}} }$, the material derivative part of the Jaumann derivative, first two terms of the RHS of Eq. 31, vanishes. This simplification is valid even when the Jaumann derivative is applied to the stress tensor associated with dilute systems subjected to a steady simple shear. For these systems, fluctuations caused by variation in particle arrangement and deformation far away from the considered particle remain relatively small, therefore, we expect this simplification does not affect our model under steady conditions.

By applying the operator defined in Eq. 30 to 27, we obtain Eq. 33,

$$\begin{array}{@{}rcl@{}} \boldsymbol{\tau} + {\Lambda} {\Upsilon}\left( \boldsymbol{{\Upsilon}^{\mathcal{A}} \cdot \tau } - \boldsymbol{ \tau \cdot {\Upsilon}^{\mathcal{A}} }\right) = 2{\upmu}_{m}{\Upsilon} \left[ 1 + \frac{\psi }{1- \psi} \left( \frac {1+2.5\lambda}{1+\lambda}\right) \right] \times \left[ \boldsymbol{{\Upsilon}^{\mathcal{S}}} + {\Lambda} {\Upsilon} \boldsymbol{\left( \boldsymbol{{\Upsilon}^{\mathcal{A}} \cdot {\Upsilon}^{\mathcal{S}} } - \boldsymbol{ {\Upsilon}^{\mathcal{S}} \cdot {\Upsilon}^{\mathcal{A}} }\right) } \right] + \\ \\ \frac{{{\upmu}^{2}_{m}}{\Upsilon}^{2}R_{d}}{\gamma}\left( \frac{\psi }{1- \psi}\right) (\boldsymbol{\mathfrak{A }} - \boldsymbol{\mathfrak{B }} ) + \frac{{{\upmu}^{2}_{m}}{\Upsilon}^{3}R_{d}}{\gamma}\left( \frac{\psi }{1- \psi}\right) {\Lambda} \left( \boldsymbol{{\Upsilon}^{\mathcal{A}} \cdot }(\boldsymbol{\mathfrak{A }} - \boldsymbol{\mathfrak{B }} ) - (\boldsymbol{\mathfrak{A }} - \boldsymbol{\mathfrak{B }} ) \boldsymbol{ \cdot {\Upsilon}^{\mathcal{A}} }\right), \end{array} $$

(33)

in which $\boldsymbol {\mathfrak {A}}$ and $\boldsymbol {\mathfrak {B}}$ are defined in Eqs. 28 and 29, respectively. We drop the last term in Eq. 33 to maintain the order of deformation in Eq. 33 similar to that of Eq. 27 (second order with respect to Υ).

For a simple steady straining flow with the following dimensionless symmetric and skew-symmetric part of the velocity gradient

$$\begin{array}{@{}rcl@{}} \boldsymbol{{\Upsilon}^{\mathcal{S}}} = \frac{1}{2} \left[ {\begin{array}{ccc} 0 & 1 &0\\ 1 & 0 &0\\ 0 & 0 &0\\ \end{array} } \right], ~~~~~~~~ \boldsymbol{{\Upsilon}^{\mathcal{A}}} = \frac{1}{2} \left[ {\begin{array}{ccc} 0 & -1 &0\\ 1 & 0 &0\\ 0 & 0 &0\\ \end{array} } \right], \end{array} $$

we can restate Eq. 33 in a matrix form, see Eq. 34.

$$\begin{array}{@{}rcl@{}} ~ \left[ {\begin{array}{ccc} \tau_{11} - {\Lambda}{\Upsilon}\tau_{12} & \tau_{12} + \frac{\Lambda{\Upsilon}}{2}(\tau_{11} - \tau_{22}) &0\\ \tau_{12} + \frac{\Lambda{\Upsilon}}{2}(\tau_{11} - \tau_{22}) & \tau_{22} + {\Lambda}{\Upsilon}\tau_{12} &0\\ 0 & 0 &\tau_{33}\\ \end{array} } \right] = {\upmu}_{m}{\Upsilon} \left[ 1 + \frac{\psi }{1- \psi} (\frac {1+2.5\lambda}{1+\lambda}) \right] \left[ {\begin{array}{ccc} -{\Lambda}{\Upsilon} & 1 &0\\ 1& {\Lambda} {\Upsilon} &0\\ 0 & 0 &0\\ \end{array} } \right] + \\ \left( \frac{ {\upmu}_{m}{\Upsilon}^{2} {\Lambda}}{14(2\lambda+3)(\lambda+1)^{2}} (\frac{\psi }{1-\psi}) \right) \times \left[ {\begin{array}{ccc} (158\lambda^{2} +286\lambda+116) & 0 &0\\ 0& -(108\lambda^{2} +204\lambda+108) &0\\ 0 & 0 & -(50\lambda^{2} +82\lambda+8)\\ \end{array} } \right], \end{array} $$

(34)

The deviatoric stress components in the direction of the first and second principal axes are obtained in Eq. 35.

$$\begin{array}{@{}rcl@{}} \tau_{11} = {\Lambda}{\Upsilon}\tau_{12} - {\upmu}_{m} {\Lambda}{\Upsilon}^{2} \left( 1 + \frac{70\lambda^{3} +45\lambda^{2}- 111 \lambda - 74}{14(2\lambda+3)(\lambda+1)^{2}}(\frac{\psi }{1- \psi})\right), \\ \tau_{22} = -{\Lambda}{\Upsilon}\tau_{12} + {\upmu}_{m} {\Lambda}{\Upsilon}^{2} \left( 1 + \frac{70\lambda^{3} +95\lambda^{2}-29\lambda - 66}{14(2\lambda+3)(\lambda+1)^{2}}(\frac{\psi }{1- \psi}) \right), \\ \tau_{12} = -\frac{1}{2}{\Lambda}{\Upsilon} (\tau_{11}-\tau_{22}) + {\upmu}_{m}{\Upsilon} \left( 1 + \frac {1+2.5\lambda}{1+\lambda} (\frac{\psi }{1- \psi})\right). \end{array} $$

(35)

A simple manipulation of Eq. 35 yields an expression for τ ₁₂ which can be used to find the macroscopic viscosity of the emulsion, μ _ψ =τ ₁₂/Υ. Finally, we obtain

$$\begin{array}{@{}rcl@{}} \frac{{\upmu}_{\psi}}{{\upmu}_{m}} &=& 1 + \frac{1}{1+{\Lambda}^{2}{\Upsilon}^{2}}(\frac{\psi }{1- \psi}) \\ &\cdot & \left[ \frac {1+2.5\lambda}{1+\lambda} + \frac{140(\lambda^{3}+\lambda^{2}- \lambda -1)}{28(2\lambda+3)(\lambda+1)^{2}}{\Lambda}^{2}{\Upsilon}^{2}\right]. \end{array} $$

(36)

Now, by substituting Λ from Eq. 32 into Eq. 36, and using the definition of the capillary number in Eq. 3, we can recast Eq. 36 into the following general equation for any capillary number and finite viscosity ratio

$$\begin{array}{@{}rcl@{}} \frac{{\upmu}_{\psi}}{{\upmu}_{m}} &=& 1 + \frac{1}{1+\kappa Ca^{2}}(\frac{\psi }{1- \psi}) \\ &\cdot & \left[ \frac {1+2.5\lambda}{1+\lambda} + \frac{140(\lambda^{3}+\lambda^{2}-\lambda-1)}{28(2\lambda+3)(\lambda+1)^{2}}\kappa Ca^{2}\right] , \end{array} $$

(37)

where

$$\begin{array}{@{}rcl@{}} \kappa = \left( \frac{(2\lambda+3)(19\lambda+16)}{40(\lambda+1)}\right)^{2}. \end{array} $$

(38)

It should be noted again that the model stated in Eq. 37 is only valid for a dilute system up to the second order of particle deformation for any finite viscosity ratios and capillary number. Note for the case of infinite viscosity ratio, the fluid particle acts like a Hookian solid particle and remains spherical because of the large shear dynamic viscosity, not surface tension. Therefore, another proper set of boundary conditions for the normal components of the stresses on the surface of the deformed particle should be used (Goddard and Miller 1967). Applying the boundary condition of Goddard and Miller (1967) and introducing the first volume correction in the homogenization process, we find

$$\begin{array}{@{}rcl@{}} \frac{{\upmu}_{\psi}}{{\upmu}_{m}} = 1 + \frac{2.5}{1+\frac{9}{4}Wi^{2}}\left( \frac{\psi }{1- \psi}\right) \left[ 1 - \frac{3}{2} Wi^{2}\right], \end{array} $$

(39)

for suspensions of elastically deformable solid particles.

We note that at low particle volume fraction, where $\frac {\psi }{1- \psi } = \psi + O(\psi ^{2})$, Eq. 37 recovers the equation of Taylor (1932) using λ→0 and C a≪1, the equation of Mackenzie (1950) using λ→0 and C a≫1 and that of Oldroyd (1959) using λ→0 (see Table 1. Similarly, at low solid particle volume fraction, Eq. 39 reduces to the well-known Einstein-Sutherland law when W i≪1 (see Table 2).

Table 2 Selected published models to predict the relative viscosity of emulsions of deformable fluid particles and the range of volume fraction, viscosity ratio, λ, and capillary number, C a, over which they intend to be applied

An extension of rheological model to concentrated systems requires a self consistent approach to account for particle hydrodynamic interactions. Additionally, for a multiparticle system of rigid solid or non-deformable fluid particles, the relative viscosity should satisfy

$$\begin{array}{@{}rcl@{}} \lim_{\psi \to \psi_{M} } \frac{{\upmu}_{\psi}}{{\upmu}_{m}} \simeq \infty, \end{array} $$

(40)

where ψ _M is the threshold packing (commonly known as the maximum random close packing, RCP) fraction for spherical particles. We note that in the case of emulsions including deformable fluid particles, the relative viscosity at ψ=ψ _M exhibits considerable increase but does not diverge (Pal 2000), however, to the first-order deformation for emulsions of slightly deformable fluid particles, we will assume that (40) still holds. We note that ψ _M depends strongly on the particle size distribution, particle shape and deformation, and the protocol employed to produce the random packing (Faroughi and Huber 2014). This quantity is also defined as the maximally random jammed state by Torquato et al. (2000), who argued that the concept of the RCP as the highest possible density that a random sphere packing can attain is ill-defined. For these reasons, in the literature, the value of ψ _M for mono-disperse spheres is found in the range of 0.56<ψ<0.74 which is related to the mechanically stability of packing starting from the random loose packing to face-centered cubic structure, respectively (Rust and Manga 2002; Song et al. 2008; Boyer et al. 2011). Under static conditions, the value of 0.637 is reported for ψ _M in classical studies (e.g., Scott and Kilgour (1969)), and it is assumed to be an acceptable value for the remaining of this study. We keep this parameter constant; however, our model allows to modify it freely, if necessary, to account for different packing protocols in experiments, especially when high shear stresses (or shear rates) are imposed.

Extension to concentrated suspension

We use a phenomenological approach based on the differential effective medium (DEM) method (Norris et al. 1985) operating in a fixed volume to extend our model to high concentration systems. The DEM approach is an incremental method in which, at each conceptual step, a few particles are introduced into the suspension/emulsion and interact with particles present in the medium. The homogenized macroscopic property (effective viscosity) is then computed for the whole system. It should be noted that the differential effective medium theory is physically appropriate only in the case where the incremental addition is sufficiently sparse that it does not form a preferential connected network throughout the system. Due to the first volume correction, particles added simultaneously can interact with each other. Therefore, we only need to account for interactions between a new generation of particles and previous generations. We should account for the fact that this procedure cannot be followed until the entire volume of the matrix is replaced by particles ($\psi \nrightarrow 1$). This restriction arises because of the geometrical constraint dictated by the shape and size distribution of particles. Firstly, we will extend the model for the relative viscosity of a dense system in the case of zeroth order of particle deformation. Then, we can find an expression for the geometrical constraint by utilizing the packing limit condition of Eq. 40.

Relative viscosity for a dense system of non-deformable particles

To start the procedure, we can rewrite Eq. 37 in the following form (assuming C a≪1)

$$\begin{array}{@{}rcl@{}} \frac{{\upmu}_{\psi}}{{\upmu}_{m}}= 1+ \psi_{c}\left( \frac{1+2.5\lambda}{1+\lambda}\right) , \,\, \psi_{c} = \frac{\psi}{1- \psi}. \end{array} $$

(41)

Here, ψ _c is called the corrected volume fraction of particles for the dilute system (first volume correction). In other words, this volume correction considers the finite space taken by other particles of the same generation. Based on the fixed volume DEM theory, the homogenization process is characterized by taking a portion of the ambient fluid out and replacing it with particles at each step. We define the particle fraction added to the system during each step as d ψ ⁱ, and the corresponding corrected particle fraction (effective concentration) added to be ${\Delta }{\psi ^{i}_{c}}$. Therefore, the viscosity change of the homogenized equivalent fluid during step i+1 is

$$\begin{array}{@{}rcl@{}} {\upmu}_{i+1} - {\upmu}_{i} = {\upmu}_{i} {\Delta}\psi^{i+1}_{c}\left( \frac{1+2.5\lambda}{1+\lambda}\right), \end{array} $$

(42)

where the current value μ _i represents the matrix viscosity μ _m and the next value μ _i+1 denotes the effective suspension viscosity μ _ψ . The effective concentration in Eq. 42 is defined as,

$$\begin{array}{@{}rcl@{}} {\Delta} \psi^{i+1}_{c} = \frac{d \psi^{i+1}}{1-{\Omega} \psi^{i}}, \end{array} $$

(43)

where ψ ⁱ is the total volume fraction of particles inside the medium at step i. In Eq. 43, the effective concentration at step i+1, ${\Delta } \psi ^{i+1}_{c}$, introduces the second volume correction combining the first volume correction ψ _c and a self-crowding factor parameter denoted by Ω. This parameter, Ω, is a positive constant that accounts for the fact that particles cannot fill all the volume of the suspension/emulsion (a geometrical constraint). Theoretically, this parameter takes the effective volume of particles into consideration knowing that some fluid located in interstices formed by particles is no longer available to suspend particles. Ω is called the self-crowding factor because we assume that all particles have the same size (volume). In general, we argue that Ω is related to the size distribution (assuming small deformation) through the maximum random close packing concentration, ψ _M . Substituting Eq. 43 into Eq. 42 yields

$$\begin{array}{@{}rcl@{}} \frac{{\upmu}_{i+1} - {\upmu}_{i}}{{\upmu}_{i}} = \frac{d \psi^{i+1}}{1-{\Omega} \psi^{i}} \left( \frac {1+2.5\lambda}{1+\lambda}\right). \end{array} $$

(44)

Upon integrating Eq. 44 from a system with zero particle and shear dynamic viscosity μ _m to a desired particle volume fraction ψ _c and shear dynamic viscosity μ _ψ ,

$$\begin{array}{@{}rcl@{}} {\int}_{{\upmu}_{m}}^{{\upmu}_{\psi}} \frac{1}{\upmu}d\upmu = {\int}_{0}^{\psi_{c}} \frac{1}{1-{\Omega} \psi} \left( \frac {1+2.5\lambda}{1+\lambda}\right) d\psi , \end{array} $$

(45)

Eq. 41 becomes

$$\begin{array}{@{}rcl@{}} \frac{{\upmu}_{\psi}}{\mu_{m}}= \left( 1- {\Omega} \frac{\psi}{1- \psi}\right)^{-\frac {1+2.5\lambda}{\Omega(1+\lambda)}}. \end{array} $$

(46)

The model described by Eq. 46 predicts the relative viscosity for a dense system at any finite viscosity ratio to the zeroth order of particle deformation. The self-crowding factor Ω is determined by applying the constraint stated in Eq. 40

$$\begin{array}{@{}rcl@{}} \lim_{\psi \to \psi_{M}}\frac{\Omega \psi}{1-\psi} = 1 \longrightarrow {\Omega} = \frac{1-\psi_{M}}{\psi_{M}}. \end{array} $$

(47)

Based on Eq. 47, we find that Ω<1 if ψ _M >0.5. This implies that the added particle volume fraction, say ψ=a, practically occupies an effective volume of a/Ω. This is also equivalent to argue that the volume a(1/Ω−1) of the matrix is trapped in interstitial spaces between particles.

Substituting Eq. 47 into Eq. 46 yields the following equation for the relative viscosity of emulsions of non-deformable fluid particles

$$\begin{array}{@{}rcl@{}} \frac{{\upmu}_{\psi}}{{\upmu}_{m}}=\left( \frac{\psi_{M}-\psi}{\psi_{M}(1-\psi)}\right)^{-\frac {\psi_{M}(1+2.5\lambda)}{(1-\psi_{M})(1+\lambda)}}. \end{array} $$

(48)

For the particular case of a suspension of rigid solid particles ($\lambda \to \infty$ and $G \to \infty$), Eq. 48 reduces to

$$\begin{array}{@{}rcl@{}} \frac{{\upmu}_{\psi}}{{\upmu}_{m}}= \left( \frac{\psi_{M}-\psi}{\psi_{M}(1-\psi)}\right)^{-\frac {2.5\psi_{M}}{1-\psi_{M}}}. \end{array} $$

(49)

Equation 49 is plotted for intermediate- and high-volume fractions of particles, respectively, in Figs. 2 and 3 where it is compared to published experimental data and well-known equations listed in Table 1. Figure 2 shows a monotonically increasing relative viscosity with particle concentration. The shaded area in Fig. 2 highlights the region that regroups most of the experimental data. Our model agrees very well with published experiments for suspensions. One can observe that commonly used models for concentrated suspensions, like Krieger and Dougherty (1959), Barnea and Mizrahi (1973), and Eilers (1943), deviate from the experimental data as the particle concentration increases. As mentioned earlier, ignoring the first volume correction (e.g., Einstein (1911)) results in underpredicting the shear viscosity of even dilute suspensions. It is also interesting to stress that our model closely follows the empirical model proposed by Mooney (1951) when the free parameter in his model is set to 1.35 (see Table 1). In Fig. 3, the relative viscosity predicted with our model Eq. 49 is plotted for dense systems up to the packing limit ψ→ψ _M , and shows an excellent agreement with experimental data. Here, again the shaded area indicates the range observed in experiments. Over this range of particle concentration (0.35<ψ<0.6), we observe that models that do not include the volume corrections discussed above underpredict the relative viscosity by up to two orders of magnitude. As a note, we emphasize here that the model does not include free parameters to fit the data and that we used ψ _M =0.637 which corresponds to the volume fraction for the random close packing of spherical particles under static conditions.

Fig. 2

Rheology of suspension of rigid solid particles ($\lambda \to \infty$ and $G \to \infty$). Comparison of the model in Eq. 49 with previous published models (see Table 1) and experimental data from dilute up to the intermediate particle concentration. The shaded area highlights the region that regroups most of the experimental data

Fig. 3

Rheology of suspension of rigid solid particles ($\lambda \to \infty$ and $G \to \infty$). Comparison of the model in Eq. 49 with previous published models (see Table 1) and experimental data at intermediate to high particle volume fraction

We compare the model in Eq. 48 with published data for dense emulsions in the limit of C a→0. The predicted value of the relative viscosity as function of particle volume fraction is depicted in Fig. 4 for an emulsion of non-deformable fluid particles where λ→0 (bubbly emulsion). Similarly to the results for solid suspensions in Fig. 2, we observe that the relative viscosity increases monotonically with volume fraction, but with a smaller rate than for solid particles. Based on Fig. 4, one can see that our model performs very well to reproduce experimental data in the limit of λ→0. Predicted results from other well-known models reported in Table 2 that are applicable to this range of ψ, C a≪1, and λ→0 are also depicted in Fig. 4 for comparison. Figures 2 to 4 clearly show the importance of considering a finite volume (the influences of the first volume correction in the range of dilute emulsions ψ<0.15) and defining an appropriate self-crowding factor (second volume correction) to improve the model’s ability to describe interparticle hydrodynamic interactions at high-volume fraction.

Fig. 4

Rheology of emulsion of non deformable inviscid fluid particles (bubbly emulsion where λ→0 and C a≪1). Comparison of the model in Eq. 48 with existing models (see Table 2) and published experimental data

Relative viscosity for a dense system of deformable particles

To extend our model to concentrated systems with deformable particles, we shall first rewrite Eq. 37 as

$$\begin{array}{@{}rcl@{}} \frac{{\upmu}_{\psi}}{{\upmu}_{m}} = 1 + \frac{1}{1+\kappa \mathcal{L}^{2} {{\upmu}_{m}^{2}}}(\frac{\psi }{1- \psi}) \left[ \mathcal{N} + \mathcal{M}\kappa \mathcal{L}^{2}{{\upmu}_{m}^{2}}\right] , \end{array} $$

(50)

in which $\mathcal {L} = {\Upsilon } R_{d} / \sigma$ and

$$\begin{array}{@{}rcl@{}} \mathcal{N} = \frac {1+2.5\lambda}{1+\lambda}, ~~~ \mathcal{M} = \frac{140(\lambda^{3}+\lambda^{2}-\lambda-1)}{28(2\lambda+3)(\lambda+1)^{2}}. \end{array} $$

(51)

Applying the same procedure (fixed volume DEM theory) to Eq. 50 leads to the following ordinary differential equation

$$\begin{array}{@{}rcl@{}} \left( \frac{1}{\upmu}- \frac{\mathcal{M}\kappa\mathcal{L}^{2}\upmu}{\mathcal{N}+\mathcal{M}\kappa\mathcal{L}^{2}{\upmu}^{2}} + \kappa\mathcal{L}^{2}\upmu - \frac{\mathcal{M}\kappa^{2}\mathcal{L}^{4}{\upmu}^{3}}{\mathcal{N}+\mathcal{M}\kappa\mathcal{L}^{2}{\upmu}^{2}}\right) d\upmu \\ = \mathcal{N}\frac{d\psi}{1-{\Omega} \psi}. \end{array} $$

(52)

Upon integrating this equation with respect to the volume fraction from zero to ψ _c , with corresponding viscosity of μ _m and μ _ψ , we can find the following non-linear relation for the relative viscosity

$$\begin{array}{@{}rcl@{}} \frac{{\upmu}_{\psi}}{{\upmu}_{m}} \left( \frac{\mathcal{N}+\mathcal{M}\kappa\mathcal{L}^{2}{\upmu}_{\psi}^{2}}{\mathcal{N}+\mathcal{M}\kappa\mathcal{L}^{2}{{\upmu}_{m}^{2}}} \right)^{{\frac{1}{2}}(\frac{\mathcal{N}}{\mathcal{M}} -1)} = \left( \frac{\psi_{M}-\psi}{\psi_{M}(1-\psi)}\right)^{-\frac {\mathcal{N}\psi_{M}}{1-\psi_{M}}}. \end{array} $$

(53)

Alternatively, defining $f^{\upmu }(\psi ,\lambda ,Ca) = {\upmu }_{\psi }/ {\upmu }_{m}$ and $Ca = \mathcal {L} {\upmu }_{m}$, Eq. 53 can be restated in the following general form

$$\begin{array}{@{}rcl@{}} f^{\upmu} \left( \frac{\mathcal{N}+\mathcal{M}\kappa Ca^{2} (f^{\upmu})^{2}} {\mathcal{N}+\mathcal{M}\kappa Ca^{2}} \right)^{{\frac{1}{2}}(\frac{\mathcal{N}}{\mathcal{M}} -1)} = \\ \left(\frac{\psi_{M}-\psi}{\psi_{M}(1-\psi)}\right)^{-\frac {\mathcal{N}\psi_{M}}{1-\psi_{M}}}. \end{array} $$

(54)

We note that for bubbly emulsions (where $\lambda \to 0,~ \mathcal {N} =1, ~\mathcal {M} = -5/3$ and κ=(6/5)²), the left-hand side of Eq. 54 reduces to the phenomenological equation of Pal (2003a). Furthermore, for non-deformable particles, Eq. 54 reduces to Eq. 48 or Eq. 49 that have been successfully compared with experiments in Figs. 2 to 4.

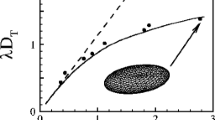
To validate the effective viscosity model for emulsions of deformable particles defined in Eq. 54, we compare it with experiments conducted by Rust and Manga (2002) for bubbly emulsion (λ→0) over intermediate capillary number ranges (small deformation) and relatively dilute systems with ψ=0.115 and ψ=0.163, respectively (see Fig. 5a, b). Based on these comparisons, one can see that using ψ _M =0.637, our model provides a satisfying fit to experimental data. In addition, in panels (c) and (d) of Fig. 5, we show that Eq. 54 is in excellent agreement with experiments conducted by Stein and Spera (2002) at high shear rate (high capillary number) for relatively concentrated bubbly emulsions of ψ=0.29 and ψ=0.45. These results suggest that the errors associated with neglecting higher orders of particle deformation have a limited impact on the rheology of emulsions at (C a≫1).

Fig. 5

Rheology of emulsion of deformable inviscid fluid particles (λ→0) versus capillary number. Comparison between our model (solid line), containing no fitting parameter, and experimental data for four different measured particle concentrations

For systems containing deformable particles, the physics of interactions between particles becomes more complicated when the particle volume fraction approaches or exceeds the maximum random close packing. Dense systems have displayed elastic and plastic behavior at small and large strains, respectively (Marmottant et al. 2008). Even at very low shear rates, high particle concentration leads to deformation, possibly coarsening and drainage phenomena (Benito et al. 2008). It should be emphasized that our rheological model defined in Eq. 54 does not account for these processes such as plastic flow resulting from particle rearrangements and compaction, aging, and yield stress. Our model is therefore limited to volume fractions below the random close packing, ψ _M . Nevertheless, Eq. 54 provides a valid rheological model for 0≤ψ<ψ _M ) over any of finite viscosity ratio and capillary number.

The relative viscosity as function of the capillary number predicted by Eq. 54 for two viscosity ratios λ=0 and λ=1.1 and different particle volume fractions is plotted in panels a–b of Fig. 6. We distinguish three regions: (i) the relative viscosity is constant at low values of capillary numbers (C a≤10⁻³), (ii) the relative viscosity decreases over intermediate values of capillary numbers (10⁻³<C a<10), and, finally, (iii) the relative viscosity is constant again at high values of capillary numbers (C a≥10). Furthermore, the viscosity ratio exerts a significant control on the viscosity of emulsions. For instance, based on the relation between the relative viscosity and capillary number in the limit of λ→0, (Fig. 6a), we observe that at capillary number values smaller than a critical capillary number (where curves intersect each other), the relative viscosity is greater than unity (f ^μ>1), and its value increases with particle concentration. At higher capillary numbers, an opposite trend is captured where the relative viscosity is smaller than one (f ^μ<1 ), and higher particle concentration leads to lower relative viscosity. All curves intersect at a critical capillary number where the viscosity of the system is independent of particle concentration, and is equal to the viscosity of the matrix (f ^μ=1). This behavior does not exist for the system shown in Fig. 6b, where the viscosity of the matrix is slightly smaller than that of the dispersed phase (λ=1.1). In this case, the relative velocity is greater than one (f ^μ>1) over the entire range of capillary number. At small capillary number, the force associated with capillary stresses controls the resistance against deformation, and a higher particle concentration (greater surface area) results in a greater macroscopic shear viscosity for the emulsion. At high capillary number, the resisting force against deformation is mostly controlled by shear stresses (Fig. 6b). As a consequence, introducing more particle does not significantly affect the overall viscosity of the emulsion.

Fig. 6

Relative viscosity, $f^{\upmu } = {\upmu }_{\psi } / {\upmu }_{m}$, as a function of capillary number for different particle concentrations calculated with Eq. 54 for a system where a the viscosity ratio is zero (bubbly emulsion) and b the viscosity ratio is λ=1.1. Our model predicts that a critical capillary number exists only when the viscosity ratio λ<1, while for emulsions with λ>1, the effective viscosity is greater than that of the ambient fluid for all C a

Interestingly, the relative viscosity is more sensitive to the capillary number in the intermediate regime (Fig. 6b), and this sensitivity is enhanced at higher particle concentration. It suggests that shear thinning occurs dominantly when 0.1<C a<1, and that the reduction in viscosity is greater at higher particle concentration. Zinchenko and Davis (2003) observed a similar behavior for λ=1 using a hybrid approach between a boundary integral method and a multi-pole approach.

The relative viscosity of emulsions behaves differently for different combinations of the viscosity ratio and capillary number at a given particle concentration. This interesting behavior captured by Eq. 54 is demonstrated in Fig. 7a, b. These results suggest that the capillary number does not have a comparable effect on the dynamics of the problem over the entire range of viscosity ratio. At low viscosity ratio (λ<10⁻¹), the effect of the capillary number remains constant and then increases gradually until it reaches unity viscosity ratio (λ=1) at which the capillary number exerts the greatest influence on the viscosity of the emulsion (maximum possible shear thinning). For viscosity ratios λ>1, the effect of the capillary number decreases. At high viscosity ratio (λ>10³), the capillary number plays a negligible role on the rheology of emulsions (Fig. 7a, b). In addition, at λ>10³, the relative viscosity of emulsions for a given particle volume fraction does no longer depend on the viscosity ratio. This effect is clearly depicted in Fig. 7b. It suggests that when the shear viscosity of the dispersed phase is much greater than that of the matrix, the deformation of the particle is no longer controlled by surface tension (and consequently the capillary number). Under these conditions, the physical property that acts to keep the particle’s shape spherical is the shear viscosity of the dispersed phase.

Fig. 7

The effect of the capillary number and viscosity ratio on the relative viscosity at a constant particle volume fraction ψ=0.4; a shows that increasing the viscosity ratio results in an increase in relative viscosity up to a point (λ>10³) beyond which increasing viscosity ratio does not affect the relative viscosity. Also the sensitivity of the shear thinning behavior to viscosity ratio first increases from zero to unity, and then as viscosity ratio increases the shear thinning behavior decreases. The shear thinning behavior vanishes for systems where λ>10³. b Shows the effect of the capillary number in different viscosity ratios. We observe that the effect of the capillary number on the relative viscosity is maximum around the critical viscosity ratio, and decreases as the viscosity ratio increases

For solid suspensions, $\lambda \to \infty$, of elastic particles (Hookian particles), the deformation is controlled by the Weissenberg number. The rheological behavior of these concentrated suspensions is also obtained by applying the fixed volume DEM theory along with the second volume correction to account for the geometrical constraint described by Eq. 39. This leads to

$$\begin{array}{@{}rcl@{}} f^{\upmu} \left( \frac{1-\frac{3}{2} Wi^{2} (f^{\upmu})^{2}} {1-\frac{3}{2} Wi^{2}} \right)^{-\frac{5}{4}}= \left( \frac{\psi_{M}-\psi}{\psi_{M}(1-\psi)}\right)^{-\frac {2.5\psi_{M}}{1-\psi_{M}}}, \end{array} $$

(55)

which is a non-linear equation in terms of the relative viscosity, f ^μ. As expected, the relative viscosity of a suspension including Hookian solid particles increases as more particles are fed to the system. At a fixed particle volume fraction, when the Weissenberg number increases (i.e., particles deform), shear thinning behavior occurs. The shear thinning behavior decreases as the particle shear modulus increases, and at $G \to \infty$, the suspension behaves like a Newtonian fluid. It is also worth mentioning that W i = 0.816 calculated based on Eq. 55 is a critical Weissenberg number at which the shear viscosity of the deformable solid suspensions is independent of the particle volume fraction, and it is equivalent to the shear viscosity of the matrix.

Regime diagram

The macroscopic responses of emulsions to shear, and more specifically the role of λ and C a observed in Figs. 6 and 7, suggest that there should be a set of critical numbers that controls transitions in the behavior of the relative viscosity. Based on Eq. 54, we can deduce that a critical capillary number, C a _{c r} , at which the viscosity of the emulsion is identical to that of the matrix and hence is independent of the particle volume fraction satisfies

$$\begin{array}{@{}rcl@{}} \mathcal{N}+\mathcal{M}\kappa Ca_{cr}^{2} = 0. \end{array} $$

(56)

Equation 56 has a real and physical root only in cases where $\mathcal {M} < 0$, owing to the fact that $\mathcal {N}$ and κ are always positive. For a bubbly emulsion, λ→0, the critical capillary number is found to be 0.645 (Fig. 6a), while for a system where λ≥1, the relative viscosity is always a function of the particle concentration. In other words, there is no critical capillary number for such system (because $\mathcal {M} > 0$) as depicted in Fig. 6b. Thus, the presence of the critical capillary number strongly depends on the viscosity ratio between the two phases which controls the sign of the parameter $\mathcal {M}$. Following this assertion, we define the critical viscosity ratio λ _{c r} such that $\mathcal {M}(\lambda _{cr}) = 0$. Therefore, the critical viscosity ratio satisfies

$$\begin{array}{@{}rcl@{}} \lambda_{cr}^{3} +\lambda_{cr}^{2} - \lambda_{cr} - 1 = 0, \end{array} $$

(57)

which has only one real physical root, λ _{c r} =1. For λ<λ _{c r} , a critical capillary number exists and consequently a behavior similar to that shown in Fig. 6a will be expected. For a viscosity ratio greater than λ _{c r} , the behavior of the system (the relation between the relative viscosity, capillary number, and the particle concentration) will be similar to that displayed in Fig. 6b. Note that the critical viscosity ratio and capillary numbers are independent of the particle volume fraction.

We summarize the prediction of our rheological model for the relative viscosity of emulsions as function of the viscosity ratio λ and capillary number C a in a regime diagram in Fig. 8. This regime diagram includes three regions A, B, and C, which are delimited by the critical numbers discussed above. In the region where the viscosity of the dispersed phase is greater than the viscosity of the matrix (region A in Fig. 8 where λ>λ _{c r} ), the viscosity of the emulsion is always greater than the viscosity of the matrix for any given particle concentration. In this region of the diagram, the high viscosity of the dispersed phase generates a resisting stress that balances the shear applied on the surface of the particles. We note that increasing the volume fraction of particles results in an increase in the effective viscosity of the emulsion.

Fig. 8

A regime diagram constrained by the critical viscosity ratio (λ _{c r} ) and critical capillary number (C a _{c r} ) shown by solid lines. In region A, where the viscosity ratio is bigger than λ _{c r} , the relative viscosity is always greater than unity. While at smaller viscosity ratio (λ<λ _{c r} ), regions B and C, there is a critical capillary number determined by Eq. 56 at which a transition in the macroscopic rheological behavior occurs. Right at C a _{c r} , the relative viscosity is always unity and is independent of the particle volume fraction. In region C, where C a<C a _{c r} , the relative viscosity is greater than unity, whereas at C a>C a _{c r} , the shear viscosity of the emulsion becomes lower than that of matrix (region B). The dashed line separates regions where different parameters control the stress partitioning between the matrix and particles, and the shape of the fluid particles (deformation), surface tension in region ⓐ , and shear viscosity of the dispersed phase in region ⓑ

As the viscosity ratio of the emulsion decreases below the critical viscosity ratio λ _{c r} =1, two opposite scenarios emerge for the relative viscosity depending on the capillary number. When the capillary number is smaller than its critical value C a _{c r} (region C in Fig. 8 where λ<λ _{c r} and C a<C a _{c r} ), the viscosity of the emulsion is greater than the viscosity of the matrix. The large capillary stresses between the two phases strongly oppose particle deformation. On the other hand, when the capillary number increases beyond its critical value (region B in Fig. 8 where λ<λ _{c r} and C a>C a _{c r} ), the viscosity of the emulsion is lower than the viscosity of the matrix. This reduction is more pronounced as more particles are fed to the system (see Figs. 6a and 8). This shear thinning behavior results from the accommodation of most of the induced shear stress by low viscosity and deformable particles. Finally, considering a viscosity ratio smaller than λ _{c r} and a capillary number equals to that of determined by Eq. 56 for that specific viscosity ratio (C a=C a _{c r} ∣ _λ ), the viscosity of the emulsion is identical to the viscosity of the matrix regardless of particle concentration. From Fig. 8, we can also observe the limiting behavior of the relative viscosity at λ=λ _{c r} and γ→0 where the two phase fluid flow actually reduces to a single phase flow. In this scenario, the shear viscosity of the emulsion is independent of the particle concentration and morphology, and hence the critical capillary number approaches infinity.

This regime diagram can be interpreted differently by highlighting four regions as shown in Fig. 9. The solid lines that delimit these regions represent transitions in the general rheological behavior (Newtonian or non-Newtonian) of emulsions. In region ①, the resistance to deformation of fluid particles is controlled by surface tension, γ. According to Fig. 6, at C a≪1 where the capillary stresses are important, an increase in the viscosity of the emulsion is expected. Therefore, at low capillary numbers (region ①), emulsions behave like a Newtonian fluid, i.e., the shear dynamic viscosity of the emulsion is independent of the strain rate for a given particle volume fraction. When the capillary number increases beyond C a _{c r} , the emulsion displays a non-Newtonian behavior indicated by region ② in Fig. 9. This implies that an increase in the strain rate leads to a decrease in the viscosity of the emulsion). We observe that the range of capillary number over which shear thinning occurs is the broadest at λ=0, and decreases as the viscosity ratio increases. However, it is worth mentioning that for a given particle volume fraction, the amount of viscosity reduction due the shear thinning is the greatest at λ=λ _{c r} . This range shrinks gradually when the viscosity ratio decreases, and it also decreases significantly as the viscosity ratio increases beyond λ _{c r} as illustrated in Fig. 7.

Fig. 9

Same regime diagram highlighting four regions that distinguish different rheological responses for emulsions. In region ①, where the capillary stresses between two phases are important, an increase in the viscosity of the emulsion is expected, and emulsions behave like Newtonian fluid. Region ② illustrates the shear thinning behavior that occurs when the capillary number at a given viscosity ratio is increased. The largest shear thinning occurs at λ=1. Region ③, where the resistance force against deformation is dominated by the shear dynamic viscosity of the dispersed phase, is characterized by a Newtonian behavior for emulsions. However, it has lower shear viscosity than that obtained for the region ①. The hatched area (region ④) represents a region where the value of the relative viscosity is independent of both capillary number and viscosity ratio and behaves like a Newtonian fluid

In regions ③ and ④ of Fig. 9, the resisting force against deformation is dominated by the shear viscosity of the dispersed phase which tends to keep the particle spherical regardless of surface tension. Therefore, the viscosity of emulsions in these region strongly depends on the viscosity ratio and particle concentration. Region ③ is characterized by a Newtonian behavior for emulsions; however, it has lower shear viscosity than that obtained in region ①. In the portion of region ③ where the viscosity ratio is smaller than λ _{c r} (which belongs to the region B in Fig. 8), the resisting forces imposed by both surface tension and the viscosity of the dispersed phase are small compared to the external shear force exerted by the ambient fluid. As a results, particles deform and align with the flow direction. Owing to the smaller viscosity of the dispersed phase, as the particle volume fraction increases, the shear viscosity of emulsions decreases (see Fig. 6a). Thus, in this portion of the regime diagram, the relative (Newtonian) viscosity is smaller than unity. However, for parts of the region ③ that belong to region A in Fig. 8 (λ>λ _{c r} ), the relative (Newtonian) viscosity is greater than unity.

The hatched area (region ④ in Fig. 9) represents a region where the value of the relative viscosity is independent of both capillary number and viscosity ratio (Fig. 7b), and emulsions behave macroscopically like Newtonian fluids. Beyond a viscosity ratio of O(10³), the viscosity of emulsions is only controlled by the volume fraction of particles (e.g., it will be roughly 8.2 and 3.4 times greater than the viscosity of the matrix for fluid particle concentrations of ψ=0.4 and ψ=0.3, respectively). Mathematically, for the hatched region, we have

$$\begin{array}{@{}rcl@{}} \lim_{\lambda \to \lambda \geq O(10^{3}) } \mathcal{M} \simeq \lim_{\lambda \to \lambda \geq O(10^{3}) } \mathcal{N} \to 2.5, \end{array} $$

(58)

consequently, the non-linear part of Eq. 54 vanishes, and the expression to estimate the relative viscosity of emulsions becomes

$$\begin{array}{@{}rcl@{}} f^{\upmu} \approx \left( \frac{\psi_{M}-\psi}{\psi_{M}(1-\psi)}\right)^{-\frac {2.5\psi_{M}}{1-\psi_{M}}} \end{array} $$

(59)

which is similar to the relative viscosity of a suspension of rigid spherical particles in Eq. 49.

It is important to stress that for an emulsion possessing a viscosity ratio exactly equal to λ _{c r} , the model presented here diverges because $\mathcal {M}(\lambda _{cr}) = 0$. Thus, we consider two emulsions of viscosity ratios λ=λ _{c r} +ε and λ=λ _{c r} −ε, where ε is an arbitrary small number. We then determine the relative viscosity of the emulsion by matching solutions in the limit where ε→0.

Our model for the rheology of emulsions ($\lambda < \infty$) or suspension ($\lambda = \infty$) relies on our choice for the maximum random close packing ψ _M . For slightly deformable particles (up to the first order of deformation), we expect ψ _M to deviate slightly from its value for the random close packing of spherical particles. In the majority of published models for monosized systems, ψ _M has been used as a fitting parameter. ψ _M must be a function of particle shape, size distribution, and dynamical conditions (order of deformation). However, for monosized spherical particles undergoing no or small deformation, which is assumed to be the case here, it should remain mostly constant. We test this hypothesis by comparing the predictions from our model, Eq. 54 with the experimental and numerical data published in Lejeune et al. (1999), Stein and Spera (2002), and Pal (2004) and Manga and Loewenberg (2001) in Fig. 10. These datasets for bubbly emulsions (λ→0) provide useful test for our model in the limit of non-deformable (C a=10⁻⁴) and highly deformable bubbles (C a=10⁴). As shown in Fig. 10, both limits are successfully modeled by our model Eq. 54 using a fixed maximum packing ψ _M =0.637, corresponding to the random close packing of uniform spherical particles. The model developed by Pal (2003a) (model 4) fits these datasets with a varying maximum random packing limit that increases significantly with C a (ψ _M is changed from 0.54 to 0.7). In Fig. 10, we also show the relative viscosity of bubbly emulsion predicted by our model at C a _{c r} to highlight the transition in the rheological behavior across C a=C a _{c r} , and the fact that at C a=C a _{c r} , the relative viscosity is independent of particle concentration.

Fig. 10

Comparison between our model and published experimental and numerical data for the rheology of bubbly emulsion (λ→0) over a range of volume fraction. The comparison is performed for two bounding values of the capillary number representing emulsions including non-deformable fluid particles (small capillary number) and deformable fluid particles (large capillary number) using Eq. 54. The dashed line represents the relative viscosity versus particle volume fraction for a bubbly emulsion at C a=C a _{c r}

Polydisperse systems

Providing a theoretical value for ψ _M in polydisperse emulsions/suspensions is more challenging because the void space between large particles can be filled by smaller particles (Faroughi and Huber 2014). This causes ψ _M to reach a higher limit in polydisperse systems. Therefore, we expect to observe lower effective viscosities in polydisperse suspensions/ emulsions compared to monodisperse systems for a given volume fraction (below ψ _M ). For a multimodal system (with a wide range of particle sizes), the particle size distribution and the particle size ratio have significant impact on the rheological behavior of the system. The greatest effect of polydispersity occurs when the modality is changed from monomodal to bimodal, subsequent modality changes have lesser influences on rheology (Farris 1968; Faroughi and Huber 2014). Experiments on bimodal suspensions reported by Chong et al. (1971) at constant fraction of smaller size particles revealed that the effective viscosity decreases as the size ratio of spheres (small to large) decreases. They also showed a negligible reduction in the shear viscosity when the particle size ratio decreases below 0.1 (Chong et al. 1971; Stickel and Powell 2005). For bimodal suspensions of any size ratio, the largest fraction for the random close packing (and hence the minimum relative shear viscosity) in a fixed volume of total particles occurs when suspensions consist of 65 to 80% large particles, or in other words, 20 to 35% of the total particle volume fraction is made of small particles (Santiso and Muller 2002; Stickel and Powell 2005; Faroughi and Huber 2014). Quemada (1977) discussed that for a highly polydisperse systems, ψ _M approaches unity because the broad distribution of particle sizes decreases the void ratio to a negligible value. It is important to stress that, using multimodal size distribution, we can produce an emulsion/suspension possessing a fixed shear viscosity but with various amount of particles. For example, in a bimodal suspension, the particle concentration can be increased while maintaining the shear viscosity fixed by varying the size ratio. This is illustrated in Fig. 11 where we compare the relative viscosity for two bimodal suspensions possessing particle size ratio of P S R=0.35 and P S R=0.1 and containing 25 % of small particles with a monodispersed suspension (P S R=1). The maximum packing for these bimodal systems are estimated with the experimental correlation (Chong et al. 1971; Costa et al. 2009)

$$\begin{array}{@{}rcl@{}} {\psi^{b}_{M}} = \psi_{M}\left( \frac{{R^{s}_{p}}}{{R^{l}_{p}}}\right)^{-0.104}, \end{array} $$

(60)

where ${\psi ^{b}_{M}}$ denotes the estimated critical fraction for a bimodal system, and ${R^{s}_{p}}$ and ${R^{l}_{p}}$ are the radius of the smaller and larger particles, respectively. Other models for the maximum close packing of bimodal systems with different size ratios and fraction of sizes have been published recently and can be used alternatively (Boumonville et al. 2005; Qi and Tanner 2011; Brouwers 2013; Faroughi and Huber 2014). The maximum attainable packing for bimodal systems is around 0.869 (Faroughi and Huber 2014), which occurs when the size ratio (small to large) approaches zero. Therefore, we expect that the maximum random close packing can be even higher than 0.869 for multimodal systems involving a broad range of particle sizes where the smaller particles fill void spaces between larger particles. In Fig. 12, we use our rheological model for monosized particles Eq. 54 and test it against experimental data provided for polydispersed emulsions at C a≪1. For this comparison, we use ψ _M =0.9 in Eq. 54 and plot the results from the model against experimental data over a wide range of viscosity ratio and particle volume fraction. For example, the experiments associated with λ=5.52 (inset of Fig. 12), was conducted with particle sizes ranging from 1 to 24 μm (Pal 2001). While our model, in the limit of C a≪1, provides satisfying approximation of the rheology of multimodal emulsions by considering a corrected maximum packing limit, a more rigorous account of polydisperse dynamics is required to find more accurate results, and extend the model to predict the relative viscosity of multimodal emulsions at (C a≫1).

Fig. 11

Relative viscosity versus solid phase concentrations and particle size ratio (PSR) for bimodal systems obtained from Eq. 49. The maximum packing is computed from Eq. 60 where it is assumed that the fraction of the small size particles is 25 %

Fig. 12

Comparison between experimental data and our model in Eq. 54 at ψ=0.5, C a→0 and assuming ψ _M =0.9 for the maximum packing of multimodal emulsions. The two insets also show how the relative viscosity of multimodal emulsions varies as function of volume fraction for two different viscosity ratios at C a→0

Conclusion

The primary goal of this paper is to provide a generalized equation to determine the relative viscosity of both dilute and concentrated emulsions made of two Newtonian incompressible and immiscible fluids under a simple straining flow. First, we obtain a constitutive equation in the dilute limit using the perturbation of the flow field caused by a single fluid particle. The model is then extended to concentrated systems using the differential effective medium theory operating in a fixed volume. In our derivation, two volume corrections are introduced. The first correction accounts for a finite spatial domain where the addition of a particle requires the removal of the same volume of the matrix. The second volume correction accounts for the amount of the matrix inaccessible to other particles and trapped in the interstices formed by particles through a self-crowding factor. The resulting general equation is a function of the viscosity ratio, capillary number, particle volume fraction, and the maximum fraction for random close packing of particles. The maximum packing is expected to depend on dynamical conditions (deformation) that affect particles. However, to the first order, assuming small deformations, we use the static packing limit for spheres (ψ _M =0.637). The model is then tested against published experimental data, and we find an excellent agreement with these data sets. The proposed model provides a generalized framework to accurately predict the viscosity of emulsions over a wide range of capillary number, volume fraction, and viscosity ratios.

Our theoretical model allows us to construct a regime diagram to highlight the transition in rheological behavior in emulsions as a function of two critical dimensionless numbers. The critical viscosity ratio, λ _{c r} =1, determines whether the system has a critical capillary number or not. The existence of a critical capillary number requires a viscosity ratio smaller than λ _{c r} . The critical capillary number defines a regime where the relative viscosity is unity (i.e., the relative viscosity is independent of the particle volume fraction). At C a<C a _{c r} , the relative viscosity is greater than unity, while the viscosity of emulsions is smaller than that of the matrix when C a>C a _{c r} .

In addition, the regime diagram provides information regarding parameters that control the stress partitioning between the matrix and particles, and regions where the emulsion behaves like a Newtonian or non-Newtonian fluid. We find that beyond a viscosity ratio of order 10³, the effect of capillary number and viscosity ratio on the relative viscosity of emulsion is negligible, and the relative viscosity is only function of the particle volume fraction. In addition, we consider the case of suspensions that contain either deformable Hookian or rigid solid particles. We derive a model for these suspensions following the same approach as for emulsions. For both emulsions ($\lambda < \infty$) and suspensions ($\lambda \to \infty$), we find an excellent agreement between our model and experimental data over a wide range of viscosity ratio ($0 \leq \lambda \leq \infty$), particle volume fraction (0≤ψ<ψ _M ), and capillary number ($0 \leq Ca< \infty$) or finite Weissenberg number for Hookian solid suspensions. Finally, we discuss the application of the proposed model to predict the relative viscosity of multimodal emulsions in the limit of C a≪1.