1 Introduction

Because of the wide application of the streaming media, many multimedia data are delivered in the two different terminals. Those multimedia data include the image, video, and audio. Especially, the image data is an important data format in militarily, medical, and industrial areas. For example, a personal picture can illustrate the secret information of this person like health condition and personal habit [18, 46]. Therefore, the image files have the risk of unauthorized access. The protection scheme of the image files has become a serious problem. The image files are different with the text message. It is a typical two-dimensional data. Therefore, the data capacity of image is huge and the spatial distribution is complex. It is a disputed question that the encryption standard of text message is whether suitable to protect image data [5, 6, 18]. Besides, the image files without compression operation can occupy a huge resource of communication channels. These situations make the encryption algorithm needs to improve the security level of multimedia data transmission.

The chaotic systems have the properties of unpredictability, ergodicity, and sensitivity to their parameters. Therefore, chaotic systems have been widely used in different applications. In the security application area, most research objects are adopted different kinds of chaotic systems. These encryption schemes have wonderful security performance with a low calculation complexity [1, 4, 18, 23, 26, 27, 45]. Moreover, the DNA encode theory is applied to the chaotic-based encryption scheme [2, 22, 24, 39, 43]. The fractional-order chaotic system has more complex dynamical characteristics compared with the integer-order chaotic system [11, 16, 17, 25, 31, 32]. In the encryption algorithm, the order of the system can expend the key space of the algorithm. Also, the chaotic sequences of fractional-order chaotic system are random and the high-randomness sequence can cover the plain-text information more effectively. The related research can prove the fractional-order chaotic system has flexible and good characteristics in the encryption algorithm [21, 22, 34,35,36, 43].

The other problem is the size of the multimedia files. Firstly, the number of multimedia files in real-time transmitting is large. Secondly, it has to strictly comply with the law of sampling for the uncompressed multimedia data. Therefore, the resource of the signal channel is short and the transmitting cost is huge. The compression sensing technology is a new approach in the signal sampling theory. This scheme can generate the measured result by the measurement matrix. The size of the result is less than the original signal. It can save the storage space in the signal channel and reduce the transmitting cost. Moreover, the chaotic system is applied to build the measured matrix in the compressive sensing algorithm. This method can improve the security of transmission and compress the image file at the same time [7, 13, 30, 38, 40].

Based on the advantages of compression sensing, an image encryption algorithm based on the fractional-order chaotic system and compression sensing is proposed. The encryption algorithm is a combination of compression and encryption, the discrete chaotic system is applied to compress the image. The encryption scheme depends on the fractional-order chaotic system. The sequences of the fractional-order chaotic system are obtained by the CADM algorithm [15, 20, 25]. The contributions of this algorithm are listed as follows

  1. 1.

    Two different and independent chaotic systems are applied into the flow of compression and encryption. The final cipher image cannot be decoded without the complete initial condition.

  2. 2.

    The scrambling operation and diffusion calculation are carried out simultaneously. The purpose of this structure is to cover the statistical information of the plain-text image and change the arrangement of the pixel at the one round operation.

  3. 3.

    The secret key has two parts: the public key and the private key. The compression rate (CR) is public in the processing of transmission. The parameters of the chaotic system are the private key in this algorithm.

  4. 4.

    The new critical scores of the difference attack analyses are adopted in the security analyses [3, 10, 14, 42, 44].

The rest parts of this paper are structured as follows. The basic theory of compression sensing and the dynamical characteristics analyses of a fractional-order chaotic system are carried out in Sect. 2. The detail of the encryption algorithm and decryption workflow is described in Sect. 3. The encryption and decryption image is shown in Sect. 4. The results of performance analyses are given in Sect. 4 too. The important conclusion is given in Sect. 5.

2 Preliminaries

2.1 The basic theory of compression sensing

The basic structure of the compression sensing includes the three parts: the measurement matrix, the method of sparse signal, and the reconstruction algorithm. The complete flow of compression sensing can be presented as

$$\begin{aligned} y= \phi \cdot x=\phi \cdot \psi \cdot x, \end{aligned}$$
(1)

where x represents the original signal. The matrix \(\psi \) is the orthogonal transform matrix. This matrix is applied to the sparse the original signal matrix. Therefore, this matrix can be called the sparse base matrix. The common sparse method includes the discrete cosine transform (DCT) algorithm and the discrete wavelet transform (DWT) algorithm. The matrix \(\phi \) is called the measurement matrix. The size of the measurement matrix is \(M \times N\) and M is less than the pixel amount N in the row or column.

The reconstruction algorithm can present the solution of the optimization \(l_{0}\) problem. This problem can be denoted as

$$\begin{aligned} {\left\{ \begin{array}{ll} {\hat{x}} =argmin \Vert S \Vert _{0};\\ y= {\hat{\Theta }} x;\\ \end{array}\right. } \end{aligned}$$
(2)

where \(\Theta =\phi \cdot \psi \). The common reconstruction algorithms are orthogonal matching pursuit (OMP) algorithm, subspace pursuit (SP) algorithm and smoothed \(\ell _{0}\) norm (SL0) algorithm. The smoothed \(\ell _{0}\) (SL0) algorithm is applied in this encryption algorithm. The sparsest solutions are obtained by an under determined system of linear equations \(As = x\). Moreover, this algorithm tries to directly minimize the \(\ell _{0}\) norm [28, 29].

In this encryption algorithm, the sparse method is adopted the DWT scheme. The measurement matrix is constructed by the discrete chaotic system. To reduce the relevance among the column vectors, the first element of column vector is set \(\hat{\Phi (i,1)}=\lambda \cdot \Phi (i-1,1)\). The final measurement matrix is generated by

$$\begin{aligned} {\left\{ \begin{array}{ll} {\hat{\Phi }}(i,1)=\lambda \cdot \Phi (i-1,1)\\ {\hat{\Phi }}(i,2:end)=\lambda \cdot \Phi (i-1,1:end-1)\\ \end{array}\right. }. \end{aligned}$$
(3)

2.2 The dynamical characteristics of fractional-order chaotic system

The design concept of random-number generator in this encryption algorithm is based on the fractional-order Jerk chaotic system. The chaotic sequences are obtained by the CADM algorithm. Firstly, the integer-order Jerk chaotic system is present in Eq. (4)

$$\begin{aligned} {\left\{ \begin{array}{ll} {{\dot{x}}_1} = {x_2} \\ {{\dot{x}}_2} = a{x_3} \\ {{\dot{x}}_3} = -b{x_1} \cdot c{x_3} - d({e^{k{x_2}}} - {e^{ - {x_2}}}) \\ \end{array}\right. }. \end{aligned}$$
(4)

Based on the Caputo definition [15], the fractional-order system can be rewritten as

$$\begin{aligned} {\left\{ \begin{array}{ll} D_{t}^q {x_1}= {x_2} \\ D_{t}^q {x_2}= a{x_3} \\ D_{t}^q {x_3}= -b{x_1} \cdot c{x_3} - d({e^{k{x_2}}} - {e^{ - {x_2}}}) \\ \end{array}\right. }. \end{aligned}$$
(5)

At the first, Eq. (5) needs to be divided into the two blocks: the linear terms and the nonlinear terms

$$\begin{aligned} \begin{bmatrix} {L{x_1}} \\ {L{x_2}} \\ {L{x_3}} \\ \end{bmatrix}=\begin{bmatrix} {{x_2}} \\ {a{x_3}} \\ { - b{x_1} - c{x_3}} \\ \end{bmatrix}, \begin{bmatrix} {N{x_1}} \\ {N{x_2}} \\ {N{x_3}} \\ \end{bmatrix}=\begin{bmatrix} 0 \\ 0 \\ {-d({e^{k{x_2}}}-{e^{-{x_2}}})} \\ \end{bmatrix}.\nonumber \\ \end{aligned}$$
(6)

According to the calculation flow of CADM, the first five Adomian polynomials of the nonlinear term are calculated as follows:

$$\begin{aligned} \begin{array}{l} A_3^0 = {e^{kx_2^0}} - {e^{ - x_2^0}} \\ A_3^1 = kx_2^1{e^{kx_2^0}} + x_2^1{e^{ - x_2^0}} \\ A_3^2 = [kx_2^2 + \frac{1}{2}{k^2}{(x_2^1)^2}]{e^{kx_2^0}} - [ - x_2^2 + \frac{1}{2}{(x_2^1)^2}]{e^{ - x_2^0}} \\ A_3^3 = [kx_2^3 + {k^2}x_2^1x_2^2 + \frac{1}{6}{k^3}{(x_2^1)^3}]{e^{kx_2^0}} - [ - x_2^3 + x_2^1x_2^2 - \frac{1}{6}{(x_2^1)^3}]\\ A_3^3 =A_3^3 \cdot {e^{ - x_2^0}} - [ - x_2^3 + x_2^1x_2^2 - \frac{1}{6}{(x_2^1)^3}]{e^{ - x_2^0}}\\ A_3^4 = [kx_2^4 + {k^2}(x_2^3x_2^1 + \frac{1}{2}{(x_2^2)^2}) + \frac{1}{2}{k^3}{(x_2^1)^2}x_2^2 + \frac{1}{{24}}{k^4}{(x_2^1)^4}]\\ A_3^4 = {e^{kx_2^0}} A_3^4 - [ - x_2^4 + (x_2^3x_2^1 + \frac{1}{2}{(x_2^2)^2}) - \frac{1}{2}{(x_2^1)^2}x_2^2\\ \quad \quad \quad + \frac{1}{{24}}{(x_2^1)^4}]{e^{ - x_2^0}} \\ \end{array}.\nonumber \\ \end{aligned}$$
(7)

The initial conditions \(x_0\) is equal to [\(x_1(t^+_ 0)\) \(x_2(t^+_ 0)\) \(x_3(t^+_ 0)\)]. Therefore, the first item is:

$$\begin{aligned} \left\{ \begin{array}{l} x_1^0 = {x_1}(t_0^ + ) \\ x_2^0 = {x_2}(t_0^ + ) \\ x_3^0 = {x_3}(t_0^ + ) \\ \end{array} \right. . \end{aligned}$$
(8)

Letting \(x^0= c^0 = [c^0_ 1 c^0_ 2 c^0_ 3\)]. The second term is:

$$\begin{aligned} \left\{ \begin{array}{l} x_1^1 = c_2^0\frac{{{h^q}}}{q} \\ x_2^1 = ac_3^0\frac{{{h^q}}}{q} \\ x_3^1 = ( - bc_1^0 - cc_3^0 - d({e^{kc_2^0}} - {e^{ - c_2^0}}))\frac{{{h^q}}}{q} \\ \end{array} \right. , \end{aligned}$$
(9)

where the step size \(h=t-t_0\). Setting

$$\begin{aligned} \left\{ \begin{array}{l} c_1^1 = c_2^0 \\ c_2^1 = ac_3^0 \\ c_3^1 = - bc_1^0 - cc_3^0 - d({e^{kc_2^0}} - {e^{ - c_2^0}}) \\ \end{array} \right. , \end{aligned}$$
(10)

then \(x^1\) will be represented as \(x^1_ i = \frac{c^1h^q}{q}\) (\(i=1,2,3\)). Similarly, the other four coefficients of the rest terms are:

$$\begin{aligned}&\left\{ \begin{array}{l} c_1^2 = c_2^1 \\ c_2^2 = ac_3^1 \\ c_3^2 = - bc_1^1 - cc_3^1 - d(kc_2^1{e^{kc_2^0}} + c_2^1{e^{ - c_2^0}}) \\ \end{array} \right. , \end{aligned}$$
(11)
$$\begin{aligned}&\left\{ \begin{array}{l} c_1^3 = c_2^2 \\ c_2^3 = ac_3^2 \\ c_3^3 = - bc_1^2 - cc_3^2 - d((kc_2^2 + {(kc_2^1)^2}){e^{kc_2^0}}\\ \qquad + (c_2^2 - {(c_2^1)^2}){e^{ - c_2^0}}) \\ \end{array} \right. , \end{aligned}$$
(12)
$$\begin{aligned}&\left\{ \begin{array}{l} c_1^4 = c_2^3 \\ c_2^4 = ac_3^3 \\ c_3^4 = - bc_1^3 - cc_3^3 - d((kc_2^3 + 3{k^2}c_2^1c_2^2 + {k^3}{(c_2^1)^3}){e^{kc_2^0}}\\ \qquad + (c_2^3 - 3{k^2}c_2^1c_2^2 + {k^3}{(c_2^1)^3}){e^{ - c_2^0}}) \\ \end{array} \right. \ , \end{aligned}$$
(13)
$$\begin{aligned}&\begin{array}{l} c_1^5 = c_2^4 \\ c_2^5 = ac_3^4 \\ c_3^5 =- bc_1^4 - cc_3^4 - d((kc_2^4 + {k^2}(4c_2^3c_2^1+3{(c_2^2)^2})\\ \quad \quad \quad + 6{k^3}{(c_2^1)^2}c_2^2 + {k^4}{(c_2^1)^4}){e^{kc_2^0}}-(-c_2^4 + 4c_2^3c_2^1 +3{(c_2^2)^2}\\ \quad \quad \quad - 6{(c_2^1)^2}c_2^2 +{(c_2^1)^4}){e^{ - c_2^0}}) \\ \end{array}.\nonumber \\ \end{aligned}$$
(14)

So, the numerical solution of the FONJCS with six terms is

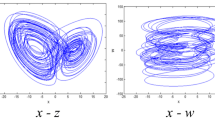
$$\begin{aligned} \ {{\tilde{x}}_j}= & {} c_j^0 + c_j^1\frac{{{h^q}}}{q} + c_j^2\frac{{{h^{2q}}}}{{2{q^2}}} + c_j^3\frac{{{h^{3q}}}}{{6{q^3}}}\nonumber \\&+ c_j^4\frac{{{h^{4q}}}}{{24{q^4}}} + c_j^5\frac{{{h^{5q}}}}{{120{q^5}}}. \end{aligned}$$
(15)

The system initial conditions are [1.9,0,0]; the system parameters are [a c d k q] = [1,0.5,\(2.72165*10^{-4}\),1,0.9]. The phase diagrams are shown in Fig. 1. Set the system parameters as \(a=1\), \(c=0.5\), \(k=1\), \(q=0.9\). The variable \(b\in [0.85,2.85]\). The Lyapunov exponent spectrum and the bifurcation diagram are shown in Fig. 2. This system suddenly transforms into two coexisting attractors when the parameter b = 0.965. Therefore, the curves of the max Lyapunov exponent and bifurcation diagram show the properties of two coexisting attractors. The widely chaotic range can be illustrated by Fig. 2a. Figure 2b can prove that this system has widely chaotic range from the max Lyapunov direction.

Fig. 1
figure 1

The phase diagram: a \(x-y\) (\(b=0.3\)), b \(x-z\) (\(b=0.3\)), c \(y-z\) (\(b=0.3\)), d \(x-y\) (\(b=1\)), e \(x-z\) (\(b=1\)), and f \(y-z\) (\(b=1\))

Full size image
Fig. 2
figure 2

The dynamical characteristics of the FONJCS. a Coexisting bifurcation diagram and b coexisting maximum Lyapunov exponent spectrum

Full size image

The DSP development board is selected as hardware platform to implement the fractional-order system in this paper. The parameters of six different type attractors are listed in Table 1. The experiment suit and the application environment are shown in Fig. 3. The simulation results are shown in Fig. 4.

Table 1 Attractor’s type
Full size table
Fig. 3
figure 3

DSP experimental platform

Full size image
Fig. 4
figure 4

Simulation results on the oscilloscope with different parameters [b, k, q]: a [1.01, 1, 41, 0.9], b [1.01, 1.51, 0.9], c [1.01, 1.51, 0.9], d [1.44, 2.31, 0.9], e [3.01, 2.62, 0.9], and f [1.6, 1.19, 0.691]

Full size image

2.3 The dynamical characteristics of the discrete chaotic system

The measurement matrix is obtained by the discrete chaotic system. Firstly, the size of the measurement matrix needs to control in a certain size. This measure can save the resource of the signal channel. The discrete chaotic system has low calculation cost and complex dynamical behaviors. It can satisfy this request. Moreover, the sequences of the discrete chaotic system have uniform distribution and zero correlation. Therefore, the discrete chaotic system has good promising applications in the encryption algorithm [4, 9, 44].

The 3D-SIMM system is a high-dimension (HD) discrete chaotic system. The mathematical model is

$$\begin{aligned} {\left\{ \begin{array}{ll} x_{i+1}=a_{1} \cdot \sin (b_{1}z_{i})\cdot \sin (\frac{c_{1}}{x_{i}}) \\ y_{i+1}=a_{1} \cdot \sin (b_{1}x_{i+1})\cdot \sin (\frac{c_{1}}{y_{i}}) \\ z_{i+1}=a_{1} \cdot \sin (b_{1}y_{i+1})\cdot \sin (\frac{c_{1}}{z_{i}}) \\ \end{array}\right. }. \end{aligned}$$
(16)
Fig. 5
figure 5

The dynamical behaviors of 3D-SIMM: a The phase diagram, b the Lyapunov spectrum, and c the bifurcation diagram

Full size image
Fig. 6
figure 6

The flow of encryption

Full size image

The phase diagram is shown in Fig. 5a. When the system parameters [a, b, c]=[1,\(2 \pi \),11.5], this system is in chaotic state. The 3D-SIMM has a wide hyper-chaotic range when variable \(a \in [0.33,5]\). The Lyapunov spectrum and bifurcation diagram are shown in Fig. 5b, c. It is obvious that this system has complex dynamical characteristics and a wide chaotic range [23]. Firstly, the hyper-chaotic state can maintain in the whole parameter range. This property is illustrated by Fig. 5c. Secondly, Fig. 5b can prove that this assumption is correct from other side. Therefore, the sequences of this system are applied to construct the measurement matrix.

Fig. 7
figure 7

The flow of decryption algorithm

Full size image

3 The description of encryption algorithm

The discussion point of this section is the concrete steps of the encryption algorithm. The flow is shown in Fig. 6.

The order of encryption is subject to the compression–encryption. In the encryption operation, the scrambling operation and the diffusion calculation are going at the same time. Besides, the encryption algorithm is based on the block cipher theory. Therefore, the length of the secret sequence is certain. It can reduce the time cost in chaotic sequences calculation. Moreover, the elements of the cipher block are dependent on the front of the cipher block, the plain-text block, and the chaotic sequences.

3.1 The flow of encryption algorithm

  1. 1.

    Sparse the image matrix. The sparse signal matrix is come from the plain-text image by DWT algorithm. The size of sparse signal matrix is equal to \(H \times W\), where H presents the number of rows, W is the number of columns.

  2. 2.

    Set the compression rate (CR). The measurement matrix is generated by the discrete chaotic system. The size of the measurement matrix is subject to the number of CR. The final measurement matrix is obtained by Eq. (3). This equation is used to reduce the relevance among the column vectors.

  3. 3.

    Compress the image matrix. The size of the new image matrix is equal to \(M \times W\), where the number of M is equal to \(CR \times H\). The elements of the new image matrix need to uniformization. The method of uniformization is

    $$\begin{aligned} {\left\{ \begin{array}{ll} Max = max(max(P) \\ Min = min(min(P)) \\ Q = round(255 * (P - Min) / (Max - Min)) \\ \end{array}\right. }\qquad \end{aligned}$$
    (17)

    where P is the new image matrix, Q is the compressed image.

  4. 4.

    The secret sequence is generated by the fractional-order Jerk chaotic system. The length of sequence is equal to the row vectors. The secret sequence is obtained by

    $$\begin{aligned} S=\lfloor (pow2(16)*Y) \rfloor \bmod L, \end{aligned}$$
    (18)

    where the L is present for the max gray level in the image matrix. Y is a chaotic sequence obtained by the fractional-order Jerk chaotic system. Besides, the scrambling matrix is generated by a sort chaotic sequence.

  5. 5.

    The size of cipher image is equal to \(H1 \times W1\). The encryption operation contains two directions: the blockchain diffusion and the elements scrambling in the group. These directions can be presented by one equation group as follows

    $$\begin{aligned} {\left\{ \begin{array}{ll} MDF(i) = P(Index1(i)) + S1(i) + S2(i)\\ MDF(i) = MDF(i) \bmod L\\ Cipher image(n,:) = MDF \qquad n = 1 \end{array}\right. }. \end{aligned}$$
    (19)

    The front matrix of diffusion (MDF) is start block in the chain diffusion. The secret sequences S1 and S2 respond to the change value of the pixel. The Index1 is generated by sorting the chaotic sequence. This sequence is applied to disorder the arrangement of pixel in group. The final results of MDF are embed into the first row of cipher image.

    $$\begin{aligned} {\left\{ \begin{array}{ll} MD(i)=MD1(Index1(i))+MD2(Index2(i)) \\ MD(i)=MD(i)+4*S1(i)+5*S2(i) \\ MD(i)=MD(i) \bmod L \\ Cipher image(n,:) = MD \qquad n \in [2, \cdots , H1] \end{array}\right. }. \end{aligned}$$
    (20)

    The matrix of diffusion (MD) is a basic unit in the encryption operation. The size of MD is equal to the column vector of plain-text image. The plain-text sequences P are named as MD1. The front cipher blocks C are named as MD2. Therefore, the value of the cipher group depends on the plain-text block, the secret sequence, and the front block of cipher image. The pixel of plain-text and the front cipher sequence are selected randomly. The select principle is subject to the Index matrix.

Table 2 The parameters of encryption algorithm
Full size table
Fig. 8
figure 8

The simulation result: a plain-text image, b cipher image, and c recover image

Full size image

3.2 The flow of decryption algorithm

The decryption algorithm is inverse flow compare with the encryption algorithm. The flow is shown in Fig. 7.

Firstly, the value and order of the cipher matrix are recovered by the block diffusion and the elements scrambling. The recovered matrix is regrouped by the divide algorithm. The reconstructed image is obtained by the smoothed \(\ell _{0}\) algorithm and the inverse DWT transform.

  1. 1.

    Recover the value of pixel. The principle of recovery is subject to Eqs. (21–22).

    $$\begin{aligned} {\left\{ \begin{array}{ll} MRF(Index1(i))=MDF(i)-S1(i)-S2(i)\\ MRF(Index1(i))=MRF(Index1(i)) \bmod L\\ \end{array}\right. }, \end{aligned}$$
    (21)

    Equation (21) is inverse algorithm of Eq. (19). The inverse algorithm of Eq. (20) as follows

    $$\begin{aligned} {\left\{ \begin{array}{ll} MR(Index1(i))=MR1(i)-MR2(Index2(i)) \\ -(4*S1(i)+5*S2(i)) \\ MR(Index1(j))=MR(Index1(j)) \bmod L\\ \end{array}\right. }. \end{aligned}$$
    (22)
  2. 2.

    Inverse uniformization of image matrix. The method of inverse uniformization as follows

    $$\begin{aligned} R=(Q*(Max-Min))/255 + Min, \end{aligned}$$
    (23)

    where the matrix R is recover image matrix.

  3. 3.

    Reconstruct the original image pixel. The smoothed \(\ell _{0}\) (SL0) algorithm is applied to reconstruct pixel of image matrix.

  4. 4.

    Inverse the DWT and obtain the final decrypted image.

4 The performance analysis

4.1 Simulation result

This section to test the decoded image is similar to the plain-text image, where some classical images are selected as the test images. The encryption parameters contain two parts: (1) the parameters of the chaotic system; (2) the initial parameters of the chaotic system. The structure of the secret key is listed in Table 2. The encryption and decryption results are shown in Fig. 8.

4.2 The key analyses

The secret key is decided the decoded image is correct. Also, the secret key can affect the security of the cipher image. Therefore, the security of secret key is an important character of encryption algorithm. This subsection has two directions need to discuss.

4.2.1 The key space analysis

The first discussion point is the key space. The space of secret key should approach or larger than \(2^{100}\) [5, 8, 12]. The large key space makes sure the cipher image has the ability to resist the brute-force attack. The key space of the proposed algorithm can approach \(2^{448}\). This result is satisfied with the request for key space. Table 3 demonstrates that the comparison result with another encryption scheme. Firstly, the proposed algorithm has enough key space to resist the brute-force attack. Secondly, compared with other algorithms, the key space of the proposed algorithm is large.

4.2.2 The key sensitivity analysis

The second discussion point is the sensitivity of the secret key. The image applied to test key sensitivity is Lena (\(256 \times 256\)). Set the change value \(\Delta \) equal to \(\pm 10^{-15}\); the new parameters encode the plain-text image. The test result is shown in Fig. 9. The difference between the two cipher images can be calculated by the number of pixels change rate (NPCR). The calculation method is shown as follows

$$\begin{aligned} NPCR = \frac{\sum _{i,j}^{} D(i,j)}{H \times W} \times 100 \%. \end{aligned}$$
(24)

Equation 25 is represented the symbolic function \(D( i , j )\).

$$\begin{aligned} D(i,j)={\left\{ \begin{array}{ll} 1 &{} C(i,j) \ne C_{1}(i,j) \\ 0 &{} C(i,j) = C_{1}(i,j) \\ \end{array}\right. }, \end{aligned}$$
(25)

where C (\( i \), \( j \)) is the original cipher matrix and C1 (\( i \), \( j \)) is the new cipher matrix. The size of image matrix can be considered as \(W \times H\). Besides, the new cipher matrix has come from the different parameters of encryption algorithm.

Table 4 shows the test results of NPCR with difference cipher image. It is obviously that the new cipher image is a different image compare with the original cipher image. The error key can’t recover the cipher image. In the encryption phase, the little change of secret key can obtain the difference cipher image.

Table 3 Key space
Full size table
Fig. 9
figure 9

The analysis result of key sensitivity: a The original cipher image, b the new cipher image, and c the result of image subtraction

Full size image

4.3 The anti-statistical attack ability analyses

The discussion point in this subsection is the anti-statistical attack ability. The discussion direction has three indexes, the histogram, the information entropy, and the adjacent point correlation analysis. These indexes can present the randomness of cipher image.

Table 4 NPCR between the new cipher image and the original cipher image
Full size table
Table 5 \(\chi ^{2}\)-value for different images
Full size table

4.3.1 The histogram analysis

The purpose of histogram analysis proves that the distribution of pixels is the uniform distribution. This hypothesis can be illustrated by \(\chi ^{2}\)-value. The different critical values with 10%, 5%, and 1% probability are 284.3360, 293.2478, and 310.4574, respectively. The analysis result is listed in Table 5. The values of \(\chi ^{2}\) can prove that the distribution cipher image is uniform. The histogram of the cipher image and the plain-text image is shown in Fig. 10.

Fig. 10
figure 10

The analysis result of histogram: a the test image, b the histogram of plain-text image, and c the histogram of cipher image

Full size image

4.3.2 Correlation analysis

The correlation analysis is aim to measure the correlation of adjacent pixel in different directions. The calculation equation of correlation coefficients is shown in Eq. (26–29).

$$\begin{aligned}&\!\!\gamma _{xy} = \frac{cov(x,y)}{\sqrt{D(X)D(Y)}}; \end{aligned}$$
(26)
$$\begin{aligned}&\!\!cov(x,y) = E{(X-E(X))-(Y-E(Y))}; \end{aligned}$$
(27)
$$\begin{aligned}&\!\!E(x) = \frac{1}{N} \sum _{i=1}^{N} x_{i}; \end{aligned}$$
(28)
$$\begin{aligned}&\!\!D(x) = \frac{1}{N} \sum _{i=1}^{N} [(x_{i}-E(x))]^2. \end{aligned}$$
(29)

This equation group has calculated the value of correlation coefficients of the image. The correlation coefficients of the cipher image are close to 0. It can prove that the adjacent pixel is not correlated. The adjacent pixel point distribution is shown in Fig. 11. The correlation coefficient results are listed in Table 6. The comparison results are shown in Table 7

Fig. 11
figure 11

The analysis result of pixel point distribution: a plain-text horizontal direction, b plain-text vertical direction correlation, c plain-text diagonal direction correlation, d ciphertext horizontal direction correlation, e ciphertext vertical direction correlation, and f ciphertext diagonal direction correlation

Full size image

Figure 11d–f illustrates that the correlation of adjacent pixels is reduced. The correlation coefficient with different directions can prove that the assumption is correct.

4.4 The compression ratio analyses

In this subsection, the mean structural similarity (MSSIM) and peak signal-to-noise ratio (PSNR) are applied to measure the quality of decode image with difference compression ratios.

4.4.1 The mean structural similarity (MSSIM) analysis

The structural similarity (SSIM) is used to measure the similarity between two images. The mean structural similarity (MSSIM) is applied to evaluate the performance of the encryption algorithm. The calculation method is defined as

Table 6 Correlation coefficients with different directions
Full size table
Table 7 Correlation coefficients with different algorithms
Full size table
Table 8 The compression results of MSSIM values with difference CR
Full size table
Fig. 12
figure 12

The analysis result of anti-noise attack: a MSE, b PSNR, and c cosine similarity

Full size image
$$\begin{aligned} {\left\{ \begin{array}{ll} I(X,Y)=\frac{2\mu _{x}\mu _{y}+C_{1}}{\mu _{x}^{2}+\mu _{y}^{2}+C_{1}}\\ c(X,Y)=\frac{2\sigma _{x}\sigma _{y}+C_{2}}{\sigma _{x}^{2}+\sigma _{y}^{2}+C_{2}}\\ s(X,Y)=\frac{\sigma _{xy}+C_{3}}{\sigma _{x}\sigma _{y}+C_{3}}\\ SSIM(X,Y)=I(X,Y) \times c(X,Y) \times s(X,Y)\\ MSSIM(X,Y)=\frac{1}{M}\sum _{k=1}^{M}SSIM(x_{k},y_{k})\\ \end{array}\right. }, \end{aligned}$$
(30)

where \(\mu _{x}\) and \(\mu _{y}\) represent the average values of plain image X and the decode image Y. \(\sigma _{x}\) and \(\sigma _{y}\) denote the variance values of X and Y. \(\sigma _{xy}\) is the covariance of X and Y. C1, C2 and \(C3=[(K_{1} \times 255)^{2},(K_{2} \times 255)^{2}, \frac{C_{2}}{2}\)] are constants, where \(k_{1}=0.01\) and \(k_{2}=0.03\). The total number of image blocks M is equal to 64. Table 8 lists the different images at the different compression.

The bigger MSSIM value can prove two different images have a good similarity. For the decrypted image, the value of MSSIM is bigger than 0.9. The analysis results illustrated that the decrypted image is similar to the plain-text image.

4.4.2 The peak signal-to-noise ratio (PSNR) analysis

The anti-noise attack ability is discussion point in this section. The cipher image might be disturbed by noise signal during transmission. Mean squared error (MSE) and peak signal-to-noise ratio (PSNR) are adopted to calculate the quality of decrypted image. The formula of MSE and PSNR is as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} MSE=\frac{\sum _{i=1}^n (y_{i}-x_{i})^2}{H*W}\\ PSNR=10\lg \frac{255^2}{MSE}\\ \end{array}\right. }, \end{aligned}$$
(31)

where \(x_{i}\) and \(y_{i}\) are the pixel value of plain-text image and decrypted image, respectively. The high score of PSNR can illustrate the high quality of decode image. On the contrary, the value of MSE has a low degree. The diagrams of MSE and PSNR are shown in Fig. 12a, b. The simulation condition is that the encrypted image is attacked by Gaussian white noise with the variance within the range of (\(10^{-7}\), \(10^{-5}\)). The distribution of MSE and PSNR displays that the noise signal could affect the quality of the decrypted image.

Table 9 The compression results of PSNR with difference CR
Full size table
Table 10 The NPCR result of different images
Full size table
Table 11 The UACI result of different images
Full size table

The other function of PSNR is to judge the quality of the recovered image. The Lean (\(256 \times 256\)) image is selected as the test image in this section. The comparison result is shown in Table 9.

The other index about image quality is cosine similarity. This index is applied to calculate the similarity between the decrypted image and the original image. The equation of cosine similarity is

$$\begin{aligned} \cos \theta =\frac{\sum _{i=1}^n (x_{i},y_{i})}{\sqrt{\sum _{i=1}^n x_{i}} \cdot \sqrt{\sum _{i=1}^n y_{i}}} , \end{aligned}$$
(32)

where \(x_{i}\) and \(y_{i}\) are present for the decrypted image with Gaussian noise signal and plain-text image, respectively. In the ideal conditions, the result of cosine similarity should be 1. The value of cosine similarity decrease when the cipher image is affected by the noise signal. The results of cosine similarity are shown in Fig. 12c.

The analysis results can prove that the encryption algorithm can resist the effect of the noise signal. The quality of the decrypted image is shown clearly. The similarity of cosine can prove that the cipher image is similar to the plain-text image.

4.5 The anti-difference attack ability

The NPCR (number of pixels change rate) and UACI (unified average changing intensity) are important index for measuring the ability for anti-difference attack. The equation of NPCR is present in Eq. (24–25). The calculation method of UACI is shown as follows

$$\begin{aligned} UACI= \frac{1}{L} \sum _{i,j} \frac{\vert C(i,j)-C_1(i,j) \vert }{256 }\times 100 \%, \end{aligned}$$
(33)

where C (\( i \), \( j \)) is the cipher matrix and C1 (\( i \), \( j \)) is the new cipher matrix. In this subsection, the pixel original plain-text image is changed randomly. The new plain-text image is obtained. Therefore, the new plain image is applied to encryption and obtained the new cipher image C1.

The criteria values of NPCR and UACI are applied to test the encryption algorithm. The critical score of NPCR is

$$\begin{aligned} N_{a}^{*} = \frac{G - \varPhi ^{-1} (a) \sqrt{\frac{G}{L}}}{G+1}, \end{aligned}$$
(34)

where \( G \) is the number of pixel points or coordinates in a plain matrix, L indicates the value of the gray level. Setting the significance level \(\alpha \), the NPCR value of the cipher image is greater than \(N_{*}^{a}\). It means that the encryption scheme can resist difference attack effectively. The critical range of UACI is obtained from Eq. (35)

$$\begin{aligned} {\left\{ \begin{array}{ll} u_{a}^{*-} = \mu _{u} - \varPhi ^{-1} (\frac{\alpha }{2}) \sigma _{u} \\ u_{a}^{*+} = \mu _{u} + \varPhi ^{-1} (\frac{\alpha }{2}) \sigma _{u} \\ \end{array}\right. }, \end{aligned}$$
(35)

where

$$\begin{aligned} \mu _{u} = \frac{G+2}{3G+4}, \end{aligned}$$
(36)

and

$$\begin{aligned} \sigma _{u} = \frac{(G+2)(G^2+2G+3)}{18(G+1)^2GL}. \end{aligned}$$
(37)

The UACI score of cipher images should fall into the interval of (\(u_{a}^{*-},u_{a}^{*+}\)). It can prove that the encryption algorithm passes the UACI test. The test results of NPCR and UACI are listed in Tables 10 and 11.

The test results can prove that the encryption algorithm has a high sensitivity of pixels change. It means that the encryption algorithm can resist the difference attack. The comparison result of other encryption schemes is shown in Table 12.

Table 12 Comparison results between other algorithms
Full size table

4.6 The anti-choose plain-text and Known plain-text attack analysis

In this section, the known plain-text attack and chosen plain-text attack are used to evaluate the security performance of the encryption algorithm. Based on the description in Ref. [14], the attacker can choose the random matrix to obtain the corresponding cipher and speculate the construction of the secret key. For measuring the algorithm performance of resisting the known plain-text attack and chosen plain-text attack, all-white and all-black pictures are selected as encryption object. The performance of anti-known plain-text and chosen plain-text attacks ability are shown in Fig. 13 and Table 13.

The encryption result and histogram are shown in Fig. 13a–c. Figure 13c can illustrate that the cipher picture is the uniform distribution. Besides, the \(\chi ^{2}\) value is 251.0833. It is satisfied with the critical stander of different freedom. It can prove that the proposed algorithm can resist known plain-text attack and chosen plain-text attack more effectively.

Fig. 13
figure 13

The analysis result: a the plain-text image, b the cipher image, and c the histogram of cipher image

Full size image
Table 13 The performance of anti-known plain-text attack
Full size table

5 Conclusion

This paper provided a novel image encryption algorithm. This algorithm is based on the fractional-order Jerk system, the discrete chaotic system and compression sensing theory. Firstly, the analysis of the dynamical characteristics shows that this chaotic system has a wide chaotic range. Therefore, the analysis results can prove that this system is suitable to apply to the encryption algorithm. Secondly, the block cipher theory is applied to the encryption algorithm. Therefore, the size of secret code sequences is small. It can reduce the time cost of chaotic sequences calculation. In the encryption operation, the value of the plain-text matrix and the arrangement of pixels are changed simultaneously. It can permute the pixels arrangement more effectively. Moreover, the current elements of the cipher block are based on the front cipher block and plain-text block. At the end, the security analyses show that this algorithm has good performance in resisting common attacks such as statistical, brute-force, and anti-differential attacks. Therefore, this encryption algorithm has good encryption properties and protects the plain information more effectively. Also, this algorithm provided another realization way for image security.

However, this algorithm still has few questions that need to be improved. The limitations of this algorithm are summarized as follows,

  1. 1.

    The one-dimensional measurement matrix is applied in the current algorithm. Therefore, the image size is only reduced in the row direction. The channel resource occupied problem cannot be overcome completely.

  2. 2.

    The two chaotic system can expend key space of secret key. Besides, these systems can provide different chaotic sequences. However, the calculation cost is bigger than the encryption algorithm based on the one chaotic system.

Therefore, the measurement matrix is two-dimensional in compression operation in the future. It can reduce the image size from two directions. The performance of compression has improved. On the other hand, the new chaotic sequence generator scheme is a new focus point in the future. The time cost of chaotic sequences calculation needs to decrease in the new scheme. This is an important index of new encryption algorithm.