1 Introduction

Existing chaotic maps can be classified into two categories: one-dimensional (1D) and HD chaotic maps. A 1D chaotic map has a few parameters and one variable, such as the Logistic, Tent, Chebyshev and Sine maps [1]. Due to the advantages of complexity [2, 3], implement efficiency, and simplicity of implementation, they have been widely applied to cryptography [4,5,6] and chaotic spread-spectrum communications [7]. However, with the development of Internet and cloud computing technology, a 1D chaotic map-based encryption system with simple orbits and small parameters space cannot ensure the information security [8,9,10], because its trajectories, parameters and initial conditions may be predicted by chaotic signal estimation technologies [11, 12]. Compared with 1D chaotic map, HD chaotic map, especially hyperchaotic map, has more complicated structure and better chaotic performance. Examples include Arnolds [13], Hénon [14] and Folded-Towel [15] maps, etc. However, their hardware implementations are more expensive.

In recent years, researchers have proposed some new or enhanced chaotic maps by methods like modeling [16], system cascading [17], dimension expansion [18,19,20,21] and so on [22, 23]. Some of them are derived from 1D chaotic map, while others are based on some special physical modes. For example, Sheng et al. [16] proposed a tangent-delay ellipse reflecting caving map system (TD-ERCS) by establishing a physical model of elliptical reflecting cavity. It has high complexity and zero correlation in total parameter range, but its structure is rather complex. Wang et al. [17] proposed Logistic-Logistic (LL), Logistic-Cubic (LC) and Logistic-Tent (LT) maps and proved that the cascade chaos can increase the LEs values, but their iteration costs are also increased. Li et al. [18] extended the 1D-Chebyshev into 2D-Chebyshev without any coupling between two equations. Thus, it cannot enhance the system complexity. Wu et al. [19] extended the classical 1D-Logistic map into 2D-Logistic by establishing a closed-loop coupling mechanism, which can further enhance the system complexity and hold a simple structure. Based on this method, Hua et al. [20] proposed a 2D Sine Logistic modulation map (2D-SLMM), and it has hyperchaotic behavior, but its MLE is relatively small. To address these problems, it is significant to design a chaotic map to meet the following requirements: high system dimension, excellent chaotic performances and a relative low iteration cost.

Complexity measure is an important indicator to analyze dynamics of a chaotic system. Currently, complexity measure methods include Kolmogorov entropy (KE) [24], approximate entropy (ApEn) [25], fuzzy entropy (FuzzyEn) [26] and permutation entropy (PE) [27], etc. Among them, PE algorithm is a proper choice to assess complexity of a time series because of its simplicity, extremely fast calculation, robustness and invariance to nonlinear monotonous transformations, and it is applied to measure the complexity of biomedical signals [28].

This paper focuses on how to construct a chaotic map with better performance. Derived from Sine map and ICMIC [29], SF-SIMM is obtained based on a closed-loop modulation coupling pattern. The rest of this paper is organized as follows. The mode of SF-SIMM is presented in Sect. 2. In Sect. 3, performances of 2D SF-SIMM are assessed by means of attractors, equilibrium points, Lyapunov exponent spectrum, bifurcations, complexity, distribution characteristic and correlation. Finally, we summarize results and indicate future directions.

2 Model of SF-SIMM

Consider an m-dimensional discrete-time system with a control parameter \(\omega \):

$$\begin{aligned} X(n+1)=Af[x_m(n), X(n+1),\omega ], \end{aligned}$$
(1)

where \(X(n) = [x_1(n), x_2(n), \ldots , x_m(n)]^\mathrm{T}\) with order \(m \ge 2\), and A is a \(m\times m\) control matrix. \(f[x_m(n), X(n+1), \omega ]\) is an uniformly bounded nonlinear feedback controller, which is given by

$$\begin{aligned}&f\;[{x_m}(n),\;X(n + 1),\;\omega ] \nonumber \\&= \left( {\begin{array}{*{20}{c}} {{f_1}[{x_1}(n + 1),\omega ]}\\ {{f_2}[{x_2}(n + 1),\omega ]}\\ \vdots \\ {{f_{m - 1}}[{x_{m - 1}}(n + 1),\omega ]}\\ {{f_m}[{x_m}(n),\omega ]} \end{array}} \right) , \end{aligned}$$
(2)

where \(\omega = [\omega , \omega , \ldots , \omega ]^\mathrm{T}\). Here, to hold a simple structure, \(f[x_m(n), X(n+1), \omega ]\) is chosen to the Sine map function, i.e.,

$$\begin{aligned} {f_i}[{x_i}(n),\omega ] = \sin [\omega {x_i}(n)],i = 1,2,\ldots ,m. \end{aligned}$$
(3)

Firstly, there are different patterns to establish a coupling mechanism between any two equations in system (1) for different forms of the control matrix A. Following the closed-loop coupling method reported in Ref. [30], A is chosen as the following form with a control parameter a:

$$\begin{aligned} A = {\left( {\begin{array}{*{20}{c}} 0&{}0&{} \cdots &{}0&{}a\\ a&{}0&{} \cdots &{}0&{}0\\ 0&{}a&{} \ddots &{} \vdots &{} \vdots \\ \vdots &{} \vdots &{}a&{}0&{}0\\ 0&{}0&{} \cdots &{}a&{}0 \end{array}} \right) _{m \times m}}. \end{aligned}$$
(4)

Secondly, a diagonal matrix B is applied to modulate the output of system (1) to enhance its nonlinearity and randomness. According to the rules above and Eqs. (1–4), a general form of the above m-dimensional controlled system is obtained as

$$\begin{aligned} X(n + 1)\; = \;BA\;f\;[x_m(n),\;X(n + 1),\;\omega ], \end{aligned}$$
(5)

where \(B = Diag\{g[x_1(n), c], g[x_2(n), c], \ldots , g[x_m(n), c]\}\).

Finally, to ensure the solution of system (5) to be bounded uniformly, \(g( \cdot )\) is chosen to be the ICMIC function [29], i.e.,

$$\begin{aligned} {g_i}[{x_i}(n),c] = \sin [c/{x_i}(n)],\;i\; = \;1,\;2,\;\ldots ,\;m. \end{aligned}$$
(6)

It follows from Eqs. (5) and (6) that

$$\begin{aligned} \begin{array}{l} \left( {\begin{array}{*{20}{c}} {{x_1}(n + 1)}\\ {{x_2}(n + 1)}\\ \vdots \\ {{x_m}(n + 1)} \end{array}} \right) \\ \; = {\left( {\begin{array}{*{20}{c}} {\sin [c/{x_1}(n)]}&{}0&{} \cdots &{}0\\ 0&{}{\sin [c/{x_2}(n)]}&{} \cdots &{}0\\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ 0&{}0&{} \cdots &{}{\sin [c/{x_m}(n)]} \end{array}} \right) _{m \times m}}\\ \qquad \times {\left( {\begin{array}{*{20}{c}} 0&{}0&{} \cdots &{}0&{}a\\ a&{}0&{} \cdots &{}0&{}0\\ 0&{}a&{} \ddots &{} \vdots &{} \vdots \\ \vdots &{} \vdots &{}a&{}0&{}0\\ 0&{}0&{} \cdots &{}a&{}0 \end{array}} \right) _{m \times m}}\left( {\begin{array}{*{20}{c}} {\sin [\omega {x_1}(n + 1)]}\\ {\sin [\omega {x_2}(n + 1)]}\\ \vdots \\ {\sin [\omega {x_{m - 1}}(n + 1)]}\\ {\sin [\omega {x_m}(n)]} \end{array}} \right) \end{array}. \end{aligned}$$
(7)

According to Eq. (7), the state equations of the m-dimensional controlled system are

$$\begin{aligned} \left\{ \begin{array}{l} {x_1}(n + 1) = a\sin [\omega {x_m}(n)]\sin [c/{x_1}(n)]\\ {x_2}(n + 1) = a\sin [\omega {x_1}(n + 1)]\sin [c/{x_2}(n)]\\ \begin{array}{*{20}{c}} {}&{}{}&{}{}&{}{\begin{array}{*{20}{c}} {}&{}{\begin{array}{*{20}{c}} {}&{}{}&{}{}&{}{}&{}{}&{}{}&{}{}&{}{}&{}{}&{}{}&{}{} \vdots \end{array}} \end{array}} \end{array}\\ {x_m}(n + 1) = a\sin [\omega {x_{m - 1}}(n + 1)]\sin [c/{x_m}(n)] \end{array} \right. , \end{aligned}$$
(8)

where \(a, \omega , c\) are system parameters, and \(a, \omega , c\in (0, +\infty )\). The closed-loop modulation coupling model of system (8) is established as shown in Fig. 1. It shows that ICMIC \(G_{i+1}\) is employed to modulate the output of Sine map \(F_i\) by a simple multiplication operation, \(i = 1, 2, \ldots , m-1\), and \(G_1\) is employed to modulate the output of \(F_m\). So all equations in system (8) are coupled in a closed loop. Furthermore, since Sine map is used in feedback controller, system (8) is named as SF-SIMM.

Fig. 1
figure 1

Closed-loop modulation coupling model of SF-SIMM

Full size image

3 Performances analysis of 2D SF-SIMM

In this section, performances of SF-SIMM are analyzed. To simplify research, we focus on the following 2D model (2D-SIMM):

$$\begin{aligned} \left\{ \begin{array}{l} x(n + 1) = a\sin [\omega y(n)]\sin [c/x(n)]\\ y(n + 1) = a\sin [\omega x(n + 1)]\sin [c/y(n)] \end{array} \right. , \end{aligned}$$
(9)

where x, y are the state variables of the system. a is the amplitude. \(\omega \) is the frequency. c is the internal perturbation frequency. It is worth noting that \(x_n, y_n \ne 0\). Otherwise, system (9) is meaningless. Thus, the initial condition \(x_0, y_0 \ne k\pi \) or \(c/k\pi \), \(k\in N\). In addition, when \(a = 1, \omega = \pi \) and \(c = 3\), the system is hyperchaotic as shown in Fig. 2 with Lyapunov exponents (LEs) (3.8307, 2.7737) and Lyapunov dimension (LD) 8.6044.

Fig. 2
figure 2

Attractor of 2D-SIMM with \(a = 1, \omega = \pi \) and \(c = 3\)

Full size image
Fig. 3
figure 3

Attractors of 2D-SIMM with different parameters a \(a = 2\), \(\omega = \pi \), \(c = 0.5\). b \(a = 2\), \(\omega = \pi \), \(c = 1\). c \(a = 2\), \(\omega = \pi \), \(c = 3\). d \(a = 2\), \(\omega = \pi \), \(c = 5\). e \(a = 2.5\), \(\omega = \pi \), \(c = 5\). f \(a = 3\), \(\omega = \pi \), \(c = 5\)

Full size image

3.1 Attractors

The attractors of 2D-SIMM with different parameters are shown in Fig. 3. When \(a = 2, \omega = \pi \), and c varies from 0.5 to 5, the attractor of system distributes in a larger region, and its density lines decrease as shown in Fig. 3a, c, which indicates the ergodicity and randomness of system increase with c increasing. When \(c = 5\), all density lines disappear in the evolution region. Furthermore, Fig. 3d–f shows that \(x, y\in [-a, a]\), and there are two sinusoidal borderlines differing T / 2 phase with amplitude a and angular frequency \(\omega \) as follows.

$$\begin{aligned} \left\{ \begin{array}{l} {Y_1}:y = a\sin (\omega x)\\ {Y_2}:y = a\sin (\omega x + T/2) \end{array} \right. , \end{aligned}$$
(10)

where \(T = 2\pi / \omega \), and \(\Delta \varphi = T/2 = \pi /\omega \). Here, we define that the region with \(Y_1\) and \(Y_2\) as double sinusoidal cavities (DSCs). Obviously, there are \(4a/T = 2a\omega /\pi \) DSCs within \(Y_1\) and \(Y_2\) at \([-a, a]\).

3.2 Equilibrium points

The equilibrium points of 2D-SIMM are calculated by

$$\begin{aligned} \left\{ \begin{array}{l} x = a\sin (\omega y)\sin (c/x)\\ y = a\sin (\omega x)\sin (c/y) \end{array} \right. , \end{aligned}$$
(11)

where \(x\ne 0, y\ne 0\). Because of the reflexivity between x and y in Eq. (11), it is equivalent to calculate the intersection points of the following two lines.

$$\begin{aligned} \left\{ \begin{array}{l} {Y_3}:y = x\\ {Y_4}:y = a\sin (\omega x)\sin (c/x) \end{array} \right. . \end{aligned}$$
(12)

As it is shown in Fig. 4, the red cycles represent the intersection points of \(Y_3\) and \(Y_4\) (equilibrium points). Obviously, when \(a = 1, \omega = 1\) and \(c = 3\), the system has no equilibrium point as shown in Fig. 4a. However, when \(\omega \) just increases to 1.01, it has infinite equilibrium points as shown in Fig. 4b. Furthermore, according to Fig. 4c, the collapses number of \(Y_4\) and equilibrium points increase with the increase of c.

Fig. 4
figure 4

Equilibrium points of 2D-SIMM with different parameters a \(a = 1\), \(\omega = 1\), \(c = 3\). b \(a = 1\), \(\omega = 1.01, c = 3\). c \(a = 1\), \(\omega = 1.01\), \(c = 10\)

Full size image

Theorem 1

When \(a\omega > 1\), 2D-SIMM has infinite equilibrium points \(S_k = (x_k, y_k) (k = 1, 2, \ldots )\).

Proof

According to Eq. (12), and supposing \(F(x) = x-a\mathrm{sin}(\omega x)sin(c/x)\), the equilibrium point is calculated by

$$\begin{aligned} \left\{ \begin{array}{l} y = x\\ F(x) = 0 \end{array} \right. . \end{aligned}$$
(13)

When \(x > 0\), and supposing \(A_k = c/(2k\pi )\), \(B_k = c/[\pi (0.5+2k)] < A_k, (k = 1, 2, \ldots )\), then \(F(A_k) = A_k > 0\), and \(F(B_k) = B_k-a\mathrm{sin}(\omega B_k)\). To determine the sign of \(F(B_k)\), and assuming \(G(x) = x-a\mathrm{sin}(\omega x)\), then \(G'(x) = 1-a\omega \mathrm{cos}(\omega x)\). It is easy to know that \(G(0) = 0\) and \(G'(0) = 1-a\omega < 0\). So, \(\exists \varepsilon > 0\), when \(x\in (0, \varepsilon )\), \(G(x) < 0\). Interestingly, there are countless \(A_k\), \(B_k\in (0, \varepsilon )\) meeting the conditions of \(F(B_k) = G(B_k) < 0\) and \(F(A_k)F(B_k) < 0\) when \(k \ge \) C (C is the minimum k meeting the conditions of \(B_k < \varepsilon \)). Therefore, there are infinite equilibrium points where \(x_k = y_k\in (B_k, A_k)\) (k = C, C + 1, ...) according to the Zero-point Theorem.

When \(x < 0\), a same conclusion can be obtained. \(\square \)

Theorem 2

When \(a\omega \le 1\), 2D-SIMM has no equilibrium point.

Proof

According to the above analysis, it is equivalent to prove that Eq. (13) has no solution. When \(x > 0\), since

$$\begin{aligned} \begin{array}{l} F(x) = x - a\sin (\omega x)\sin (c/x)\\ \quad \quad \qquad \ge x - a|\sin (\omega x)| \cdot |\sin (c/x)|\\ \quad \quad \qquad > x(1 - a\omega ) \ge 0 \end{array}, \end{aligned}$$
(14)

\(F(x)>0\) is true constantly. So Eq. (13) has no solution. When \(x=0\), F(x) is pointless. When \(x < 0\), since

$$\begin{aligned} \begin{array}{l} F(x) = x - a\sin (\omega x)\sin (c/x)\\ \quad \quad \qquad \le x + a|\sin (\omega x)| \cdot |\sin (c/x)|\\ \quad \quad \qquad < x + a|\omega x| = x(1 - a\omega ) \le 0 \end{array}, \end{aligned}$$
(15)

\(F(x)<0\) is true constantly. So it has no solution too. \(\square \)

Fig. 5
figure 5

LEs and bifurcation diagram of 2D-SIMM with \(\omega = \pi \), \(c = 3\) a LEs versus \(a\in (0, 4]\). b Bifurcation diagram versus \(a\in (0, 4]\)

Full size image
Fig. 6
figure 6

LEs and bifurcation diagram of 2D-SIMM with \(a = 1, c = 3\) a LEs versus \(\omega \in (0, 5]\). b Bifurcation diagram versus \(\omega \in (0, 5]\)

Full size image

3.3 Lyapunov exponent spectrum and bifurcations

As is well known, Lyapunov exponent spectrum and bifurcation diagram are the major indicators for different dynamical states, and LEs are employed to measure the exponential rates of convergence and divergence of nearby trajectories in state space. By using the QR decomposition method, two LEs \(\lambda _1\) and \(\lambda _2\) of 2D-SIMM are calculated with following cases.

  1. 1.

    Amplitude a varies

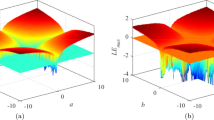
When \(\omega = \pi , c = 3\), LEs versus a and the corresponding bifurcation diagram are shown in Fig. 5, where the range of amplitude variable is \(a\in (0, 4]\) with an increment of \(\Delta a = 0.01\). It shows that 2D-SIMM is hyperchaotic when \(a\in (0.676, 0.704]\cup (0.82, 1.684]\cup (1.804, 1.932]\). However, when a varies from 1 to 4, \(\lambda _2\) decreases, and the corresponding \(\lambda _1\) is stable. So it eventually degenerates into chaos at \(a = 1.932\). Furthermore, there are several apparent periodic windows at the ranges \(a\in (0.704, 0.82]\cup (1.648, 1.804]\cup (2.636, 2.884]\).

  1. 2.

    Frequency \(\omega \) varies

When \(a = 1, c = 3\), LEs versus \(\omega \) and the corresponding bifurcation diagram are shown in Fig. 6, where the range of frequency variable is \(\omega \in (0, 5]\) with an increment of \(\Delta \omega = 0.01\). It shows that the system is divergent when \(\omega \in (0, 2]\), and it enters into hyperchaos when \(\omega > 2\).

  1. 3.

    Internal perturbation frequency c varies

When \(a = 1, \omega = \pi \), LEs versus c and the corresponding bifurcation diagram are shown in Fig. 7, where the range of internal perturbation frequency variable is \(c\in (0, 5]\) with an increment of \(\Delta c = 0.01\). It shows that the system is chaotic when \(c\in (0.840, 1.076]\). After that, it is hyperchaotic in most of the range c except a periodic window at (3.196, 3.256]. Furthermore, both the values of two LEs become larger when c is close to 5.

Fig. 7
figure 7

LEs and bifurcation diagram of 2D-SIMM with \(a = 1, \omega = \pi \) a LEs versus \(c\in (0, 5]\). b Bifurcation diagram versus \(c\in (0, 5]\)

Full size image

To observe the bifurcation behaviors, a periodic window is expanded with steps of 0.001 as shown in Fig. 8. Two sets of asymmetrical initial conditions (\(-0.7\), \(-0.7\)) and (\(-0.8\), \(-0.8\)) are selected for visualizing the pitchfork bifurcation, and the corresponding bifurcation diagram is plotted in blue and red in Fig. 8b, respectively. Obviously, three kinds of bifurcations exist in [0.7, 0.9], including a pitchfork bifurcation at \(c\cong 0.734\), a period-doubling bifurcation at \(c\cong 0.830\), and a tangent bifurcation at \(c\cong 0.836\).

Fig. 8
figure 8

LEs and bifurcation diagram of 2D-SIMM with \(a = 1, \omega = \pi \) a LEs versus \(c\in [0.7, 0.9]\). b Bifurcation diagram versus \(c\in [0.7, 0.9]\)

Full size image

Interestingly, multiple coexisting attractors occur in this system. To study the phenomenon of multiple attractor bifurcations, the single scalar definition of an attractor is described as follows [31].

$$\begin{aligned} \left\langle {r_x^2} \right\rangle = \mathop {\lim }\limits _{N \rightarrow \infty } \frac{1}{N}\sum \limits _{i = 1}^N {{{({x_i} - {x_r})}^2}}, \end{aligned}$$
(16)
$$\begin{aligned} \left\langle {r_y^2} \right\rangle = \mathop {\lim }\limits _{N \rightarrow \infty } \frac{1}{N}\sum \limits _{i = 1}^N {{{({y_i} - {y_r})}^2}}, \end{aligned}$$
(17)

which are the mean square deviations of attractor from the reference point \((x_r, y_r)\) projected onto x, y-axis, respectively. The computation of Eqs. (16) and (17) for different realizations of initial conditions gives different values of \(\left\langle {r_x^2} \right\rangle \) or \(\left\langle {r_y^2} \right\rangle \) clustering around distinct values, which indicate the multiple coexisting attractors. Abrupt change in its slope or value as a parameter indicates a discontinuous or continuous bifurcation, respectively. Here, (1, 1) is taken as the reference point, and initial conditions are chosen from a normal random distribution with mean 0 and variance 1.

Figure 9 shows multiple coexisting attractors in 2D-SIMM with \(a = 1, \omega = \pi \), and \(c = 0.839\) and 3.15, respectively. Obviously, there exist two pairs of odd symmetric attractors 1, 2 and 3, 4 in the system when \(c = 0.839\), and all attractors are limit cycles with 2 or 6 periods as shown in Fig. 10, where the initial conditions are \((x_0, y_0)\) = (\(-1\), \(-0.8\)), (\(-1\), \(-0.9\)), (\(-1\), \(-0.2\)) and (\(-0.8\), \(-1\)), respectively. Furthermore, limit cycles and chaotic attractors coexist when \(c = 3.15\).

Fig. 9
figure 9

Multiple coexisting attractors in 2D-SIMM with \(c=0.839\) and \(c=3.15\)

Full size image
Fig. 10
figure 10

Four coexisting attractors in 2D-SIMM with \(a = 1, \omega = \pi , c = 0.839\)

Full size image
Fig. 11
figure 11

PE distributions of 2D-SIMM with a \(\omega = \pi , c = 3\), b \(a = 1, c = 3\), and c \(a = 1, \omega = \pi \). d PE distributions of 2D-SIMM (a), 2D-SLMM (\(\alpha \)) and the 2D-Logistic (\(r-0.2\)), Sine (\(a_0\)) and Logistic (u / 4) maps

Full size image

3.4 Complexity analysis

For the PE calculation algorithm, given a time series x with a length N, each time series x is mapped into an n dimension space, and vectors \(X_i\) starting from time point i are constructed by selecting n equally spaced samples from x:

$$\begin{aligned} {X_i} = {[x(i),x(i + \tau ),\ldots ,x(i + (n - 1)\tau )]^\mathrm{T}}, \end{aligned}$$
(18)

where n is the embedding dimension, and \(\tau \) is the time lag. Then \(X_i\) are reshaped in an increasing order, and a new time series \(Xr_i\) with a symbol vector \(\pi = [i_1, i_2, \ldots , i_n]^\mathrm{T}\) is obtained as

$$\begin{aligned} X{r_i}&= [x(i + ({i_1} - 1)\tau ),x(i + ({i_2} - 1)\tau ),\ldots ,\nonumber \\&\quad x(i + ({i_n} - 1)\tau )]^\mathrm{T}, \end{aligned}$$
(19)

where \(\pi \) is the time sequence. The frequency of each possible \(\pi \) occurrence is indicated as \(P(\pi )\), which is normalized by \(N-(n-1)\tau \). Therefore, PE is defined by

$$\begin{aligned} H(n) = - \sum \limits _{i = 1}^{n!} {P({\pi _i})\log P({\pi _i})}, \end{aligned}$$
(20)

where n! is the number of the possible permutations. Theoretically, since H(n) can maximally reach log(n!), Eq. (20) is generally normalized as

$$\begin{aligned} h(n) = H(n)/\log (n!). \end{aligned}$$
(21)

In our experiments, PE of 2D-SIMM is calculated versus \(a, \omega \) and c with \(n = 5\) and \(\tau = 1\). Results are shown in Fig. 11a–c, respectively. As it is shown, PE of the system holds a less value in periodic windows, and it is close to the ideal value 1 for chaos. In addition, PEs of 2D-SIMM, 2D-SLMM, 2D-Logistic, Sine and Logistic maps versus their parameters are shown in Fig. 11d. Obviously, 2D-SIMM has larger PE complexity than that of others in most of the parameter range.

Table 1 PE of different chaotic maps
Full size table
Fig. 12
figure 12

The static \(\eta \) of 2D-SIMM with a \(\omega =\pi , c=3\), b \(a=1,c=3\), and c \(a=1, \omega =\pi \)

Full size image

By using three different initial conditions, PEs of some typical chaotic maps are illustrated in Table 1, and their average values \(\overline{PE}\) are calculated subsequently. Five ranks are applied to assess the PE complexity of these systems, including rank 1\(\sim \)rank 5: [0.9, 1], [0.8, 0.9), ..., [0.5, 0.6). Obviously, 2D-SIMM, ICMIC, TD-ERCS and LT have better PE complexity than that of other chaotic maps. Furthermore, although they belong to the same level, \(\overline{PE}\) of 2D-SIMM is up to 0.985, which is the largest.

Table 2 \(\eta \) of different chaotic maps
Full size table
Fig. 13
figure 13

Probability density curves of 2D-SIMM with a \(a=1, \omega =\pi , c=3\). b \(a=4, \omega =5\pi , c=3\)

Full size image
Fig. 14
figure 14

Cross-correlation coefficient curves of 2D-SIMM with \(a=1\) and \(b=\pi \) a \(R_1\) curve of 2D-SIMM. b \(R_2\) curve of 2D-SIMM

Full size image
Table 3 \(R_1\) and \(R_2\) for different chaotic maps
Full size table

3.5 Distribution characteristics

Ergodicity is a remarkable characteristic of chaos. In the limited number of iterations, chaotic sequence should distribute as possible as throughout the range of the variables. Here, the statistics of \(\chi ^2\) test (\(\eta \)) is used to measure the even distribution characteristic of 2D-SIMM, which is given by

$$\begin{aligned} \eta = \sum \limits _{i = 1}^m {\frac{{mv_i^2}}{n}} - n, \end{aligned}$$
(22)

where n is the number of sampling points. m is the number of smallest interval and \(v_i\) is the frequency in i-th interval. Obviously, the smaller the statistical result is, the better its probability distribution is. In our experiments, the test is carried out with \(m-1=50\), \(n=10^5\). Figure 12 shows the statistic \(\eta \) of 2D-SIMM with different parameter values. As is shown in Fig. 12a, b, the statistic \(\eta \) decreases with the increasing of parameter a or \(\omega \). Considering that we have obtained a conclusion that the number of DSCs is \(2a\omega /\pi \propto a\omega \) in Sect. 3.1, we can conclude that the distribution of 2D-SIMM is more uniform when the number of DSCs is larger. As is shown in Fig. 12c, the statistic \(\eta \) tends to stable with the increasing of parameter c, and its value is less when c is small. Thus, we choose parameters \((a,\omega ,c)=(4,5\pi ,3)\) to calculate the statistic \(\eta \) of 2D-SIMM as shown in Table 2, and the parameter values of other chaotic maps are listed as shown in Table 1. It shows that the statistic \(\eta \) of 2D-SIMM is less over 4 times than that of other maps.

In addition, the probability density curve of 2D-SIMM with \(a=1, \omega =\pi \) and \(c=3\) is shown in Fig. 13a. As is shown, the probability distribution of 2D-SIMM is not very ideal because the probability density is much large when |x| is close to 0. However, when parameters \((a,\omega )\) are increased to \((4,5\pi )\), the probability density curve tends to uniform distribution as shown in Fig. 13b, and its value is close to the ideal value \(1/(m-1)=0.02\).

3.6 Correlation analysis

The sensitivity to initials of chaotic systems is shown as the zero correlation between two adjacent iterative evolution sequences. The correlation is measured by the cross-correlation coefficient (R):

$$\begin{aligned} R = \frac{{\sum \limits _{i = 1}^N {({x_i} - \bar{x})({y_i} - \bar{y})} }}{{\sqrt{\sum \limits _{i = 1}^N {{{({x_i} - \bar{x})}^2}} \sum \limits _{i = 1}^N {{{({y_i} - \bar{y})}^2}} } }} \end{aligned}$$
(23)

where \(x_i\) and \(y_i\) represent the i-th pair of adjacent iterative sequences. \(\overline{x}\) and \(\overline{y}\) represent the average of sequence x and y, respectively. For 2D-SIMM, R of x(i) and \(x(i+1) (R_1)\) versus parameter c, and the corresponding R of x(i) and \(y(i) (R_2)\) are shown in Fig. 14. The average of \(R_1\) and \(R_2\) of 2D-SIMM are \(6.6059\times 10^{-4}\) and \(-2.1733\times 10^{-4}\), respectively, which are close to the ideal value 0 in total parameter range. The corresponding mean square errors are \(1.8242\times 10^{-4}\) and \(2.2423\times 10^{-4}\), respectively. Thus, each sequence of 2D-SIMM can be used as separate keys. In addition, from Table 3, we find that both the values of \(R_1, R_2\) of 2D-SIMM are smaller than that of other chaotic maps with the parameter values as listed in Table 1.

4 Conclusions

In this paper, a new HD chaotic map called SF-SIMM is proposed by employing a closed-loop modulation coupling pattern. It is derived from Sine map and ICMIC. Taking 2D-SIMM as an example, the basic dynamics of this map are analyzed by using LEs and bifurcation diagrams, which demonstrate hyperchaotic behaviors in the system. With the change of the internal perturbation frequency c, the system exhibits chaos, hyperchaos, multiple coexisting attractors and three typical bifurcations. So it has more complex dynamical behaviors than that of the original maps. Furthermore, this map has high complexity, uniform distribution and zero correlation in total parameter range. Future works will include its application in engineering such as pseudo-random sequence generator and image encryption.