3D reconstruction framework via combining one 3D scanner and multiple stereo trackers

Abstract

This paper presents a novel 3D reconstruction framework of large objects, where we adopt one 3D scanner to reconstruct partial sections of large objects, and employ multiple stereo trackers to extend reconstruction range. Both the 3D scanner and stereo trackers are fitted with infrared light-emitting diode (LED) lights. During reconstruction, the stereo trackers are placed one after another, their poses are estimated according to the LED lights, the 3D scanner is moved to reconstruct partial sections of a large object, and the LED lights on the 3D scanner are tracked by the stereo trackers to compute the poses of the 3D scanner for partial alignment. The experimental results show that this proposed method can accurately and effectively reconstruct large objects, and has its advantages for long-range reconstruction compared with similar existing methods.

1 Introduction

3D reconstruction is of great importance in numerous applications, such as industrial manufacturing, game production and film-making. However, rapid and accurate 3D reconstruction of large objects is still an open question because lots of difficulties may be simultaneously present.

Recently, a number of literatures have presented some 3D reconstruction methods. However, many of them have limitations because they are usually designed for special fields, and most of existing methods can only acquire 3D shapes for small objects. Existing 3D reconstruction methods can be roughly divided into two categories: passive and active methods. Passive methods use a sensor to reconstruct the radiance reflected or emitted by an object’s surface to infer its 3D structure. Some of the passive methods can acquire large scenes’ 3D structure [1,2,3,4,5,6,7,8] using feature-based alignment strategy. However, passive methods require an object with rich texture, and thus, they cannot reconstruct texture-less objects which usually exist in industrial manufacturing.

Active methods, which can be mainly categorized into time-of-flight (TOF) laser methods and structured light methods, usually reconstruct 3D shapes by projecting special light onto objects. Compared with passive methods, active methods can usually acquire more accurate and denser data in a rapid and stable manner.

TOF laser methods acquire 3D shape of an object using time of flight based on the known speed of light. Though traditional TOF laser techniques can obtain high-precision 3D data [9], they are usually time-consuming to perform a dense scanning of a large object because point-by-point scanning strategy is used. Recently, TOF camera [10], a kind of range imaging camera system that resolves distance according to the speed of light, has been widely used. By using TOF camera, an entire scene can be captured with lots of laser beams in one time, as opposed to point-by-point scanning with one laser beam [11, 12]. These TOF methods can obtain dense 3D data in real time. However, the 3D data captured with TOF cameras usually have very low data quality because the image resolution is rather limited and the level of random noise contained in the depth maps is very high [13,14,15]. Thus, it is difficult to accurately reconstruct the 3D shapes of large objects by TOF camera.

Compared with TOF laser methods, structured light methods can rapidly and accurately capture 3D data. Currently, several studies of structured light techniques have been conducted regarding the 3D reconstruction of large objects. The basic idea of these methods is: first reconstruct multiple partial sections of a large object and then align different sections together. According to alignment strategies, these methods can be roughly categorized into four types: shape-based method [16,17,18,19,20], marker-based method [21], guide rail-based method [22, 23] and tracker-based method [24, 25].

The shape-based methods in [16, 17] capture partial sections of a large scene using Kinect sensor and then align different sections by using a coarse-to-fine iterative closest point (ICP) algorithm. [18] designs a real-time volumetric surface reconstruction method, which supports live reconstruction of large scenes with fine geometric details. [19] presents a full 3D mapping system that utilizes a joint optimization algorithm combining visual features and shape-based alignment. Bylow et al. [20] present a method for real-time camera tracking and 3D reconstruction of indoor environments using an RGB-D sensor, where the camera pose can be estimated by minimizing the error of the depth images on the signed distance function. Because these methods require the reconstructed scene has complex surface geometries for alignment, they cannot be applied into large smooth objects, such as large bending plates used in ship manufacturing.

Barone et al. [21] propose a marker-based method, which needs to put fiducial markers on objects and reconstruct the 3D coordinates of fiducial markers that are used as references to align point clouds obtained by a 3D scanner. Though this method can accurately align different sections, it is also inconvenient and time-consuming because special markers are adopted.

Fig. 1

Illustration of system

Paoli and Razionale [22] present a guide rail-based method which is based on the integration of a robotic system with a 3D scanner. The position of the robotic system on two linear guides is determined by a laser total station, thus allowing the automatic multiple view data registration into a common reference frame. Though this method can reconstruct large objects, it is inconvenient to use. In [23], we present a guide rail-based method for large object reconstruction, which preforms partial alignment by computing the motion distance of a 3D scanner sliding on a guide rail via a laser range finder. This method can obtain good result. However, the 3D scanner must be moved in a straight line on the guide rail; otherwise, the alignment accuracy will be heavily influenced, which requires high quality of system manufacturing and brings some problems for system installation due to the use of a long guide rail.

[25] presents a tracker-based method which adopts one stereo tracker and one 3D scanner. The 3D scanner is used to reconstruct partial sections, and the stereo tracker detects retroreflective infrared markers rigidly connected to the 3D scanner for alignment of different partial views. Since the stereo tracker cannot clearly catch the infrared markers if the distance between the tracker and 3D scanner becomes larger, the reconstruction range is limited. In [24], we propose a tracker-based method, in which some high-brightness LED markers installed on the 3D scanner are used as tracking markers in order to extend the reconstruction range, and one stereo tracker is in charge of tracking the LED markers to estimate the poses of the 3D scanner for partial view alignment. This method is convenient and flexible to use, and can perform 3D reconstruction of large texture-less objects with simple surface geometries. However, the alignment accuracy may be reduced with the increase of moving distance because only one stereo tracker is used.

In summary, active methods can acquire more accurate and denser data compared with passive methods, and the tracker-based methods have advantages over the other active methods: firstly, it is not limited by the shapes and texture of objects; secondly, it does not need to paste markers on objects; thirdly, it is convenient and flexible to install the system. Thus, tracker-based methods are very suitable for applications in industrial manufacturing where objects to be reconstructed are usually smooth, large and texture-less.

In this paper, an active tracker-based framework is designed for industrial applications. In this framework, we make use of one 3D scanner and multiple stereo trackers; some infrared LED lights are rigidly connected to the 3D scanner; multiple stereo trackers are used instead of one to extend the reconstruction range. Compared with existing tracker-based methods, in this framework, we present a method of matching LED markers based on trajectory, a method of stereo tracker pose estimation, a method of partial section reconstruction and a method of partial section alignment. Overall, the proposed method has the following advantages over the existing methods: firstly, compared with feature-based methods, our method can reconstruct texture-less objects due to the use of structured light technique; secondly, compared with shape-based method, our method can reconstruct large objects with simple surface geometries because we integrate structured light technique with tracker-based alignment method; thirdly, compared with marker-based methods, our method is more convenient because it need not attach special markers on objects; fourthly, compared with guide rail-based methods, this method is easy for installation; finally, by comparison with the existing tracker-based methods, our method can obtain more accurate result for large object reconstruction because multiple stereo trackers make more remote tracking feasible. Certainly, like other methods based on LED lights, there is a limitation for the current method: If the LED markers on the 3D scanner are rotated with a large degree, they may be deformed in images, which will result in inaccurate detection. However, we think the current method is still useful for many industrial applications.

2 The proposed method

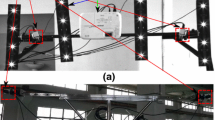
As Fig. 1 shows, our system is composed of one 3D scanner and multiple stereo trackers. The 3D scanner consists of one stereo vision system which includes two calibrated video cameras and one infrared line projector which can only emit an infrared line. To align different partial sections reconstructed by the 3D scanner, we place $n_{s}$ infrared LED lights on the 3D scanner as tracking markers. As previously mentioned, if we only use one stereo tracker, the reconstruction range is limited. In order to extend the reconstruction range, we adopt multiple stereo trackers which are used to remotely track the infrared LED markers on the 3D scanner. Each stereo tracker consists of two calibrated video cameras. We suppose n stereo trackers are used, and let $\tau _{k}$, $k\in \{1,\ldots ,n\}$, denote the kth stereo tracker. In order to locate the poses of the stereo trackers, we install $n_{\tau _k}$ infrared LED lights on $\tau _{k}$ (where $k\in \{2,\ldots ,n\}$).

Before reconstruction, firstly, infrared LED markers on $\tau _{k}$ ($k\in \{2,\ldots ,n\}$) and on the 3D scanner should be reconstructed and calibrated; secondly, we place the stereo trackers one after another so that the infrared LED markers on $\tau _{k}$ can be seen by $\tau _{k-1}$, and estimate the poses of the stereo trackers by computing the transformation $\varGamma _{\tau _{k}\tau _{k-1}}$ between coordinate systems of $\tau _{k}$ and $\tau _{k-1}$.

During reconstruction, firstly, we reconstruct partial sections of a large object using the 3D scanner; secondly, we align different partial sections based on the tracking of the 3D scanner using multiple stereo trackers.

2.1 Preparatory work before reconstruction

2.1.1 Reconstruct LED markers

The calculation of the LED markers’ 3D coordinates is an essential prerequisite for pose estimation of the 3D scanner and stereo trackers. Actually, the process of calculating LED markers’ 3D coordinates includes two subproblems, namely detecting LED markers and matching LED markers. We here use the method we presented in [24] to detect LED markers in the images captured by the stereo trackers, and this is not the focus of this paper and will not be discussed in detail.

Next, the key problem is how to match LED markers in the stereo images captured by the stereo trackers. When capturing images, we stop down the lenses of the stereo trackers to a small aperture in order to increase robustness; thus, the LED markers are bright points and other regions are very dark in the stereo images. In such a situation, there are no distinctive color, intensity or texture features for each LED marker. Therefore, it becomes a difficult problem to robustly match the LED markers in stereo images. To solve this problem, we propose a matching method based on trajectory. Next, we explain the basic idea. Firstly, without loss of generality, suppose $\tau _{1}$ is the working stereo tracker which directly tracks the 3D scanner, and suppose the coordinate of a LED marker on the 3D scanner is denoted by $M^{\tau _{1}s}_{i}(t)$ in the coordinate system of $\tau _{1}$ at time t, where $i\in \{1,\ldots ,n_s\}$. $M^{\tau _{1}s}_{i}(t)$ will be projected onto the rectified stereo image plane of $\tau _{1}$, and form two projected image points, denoted by $Q^l_{i}(t)=(x_{i}^{l}(t), y_{i}^{l}(t))^{\mathrm{T}}$ and $Q^r_{i}(t)=(x_{i}^{r}(t), y_{i}^{r}(t))^{\mathrm{T}}$. Secondly, suppose during time span $T(t)=\{t|1\le t \le T_0\}$, we move the 3D scanner in the FOV (field of view) of $\tau _{1}$, the projections $Q^l_{i}(t)$ and $Q^r_{i}(t)$ will form two trajectories in the rectified stereo image sequences, as Fig. 2 shows. We must ensure the LED markers on 3D scanner cannot be occluded due to large rotation, when we move the 3D scanner. Here, to construct the trajectories over time span T(t), we use Kanade–Lucas–Tomasi (KLT) tracker [26, 27] to track the LED markers in consecutive sequence of frames. Finally, we construct descriptors based on the trajectories during time span T(t) for LED markers $M^{\tau _{1}s}_{i}(t)$, and the descriptors can be denoted by $D^l_i(T(t))=(y_{i}^{l}(1),..,y_{i}^{l}(T_0))$ and $D^r_i(T(t))=(y_{i}^{r}(1),..,y_{i}^{r}(T_0))$. In theory, $y_{i}^{l}(t)$ should be equal to $y_{i}^{r}(t)$, which means the same LED marker in the stereo images has the same trajectory descriptor, and then the LED markers across views can be matched according to the descriptors. After matching LED markers, we can reconstruct $M^{\tau _{1}s}_{i}(t)$ in the coordinate system of $\tau _{1}$ using stereo triangulation.

In addition, we suppose, at time t, the coordinates of the LED markers on $\tau _{k}$ are denoted by $M^{\tau _{l}\tau _{k}}_{j}(t)$ in the coordinate system of $\tau _{l}$, where $k\in \{2,\ldots ,n\}$ and $l\le k$. Therefore, similarly, we can calculate $M^{\tau _{1}\tau _{k}}_{j}(t)$ using $\tau _{1}$ as well according to the above-mentioned method in the same way, where $j\in \{1,..,n_{\tau _{k}}\}$.

Fig. 2

Match LED markers by trajectories

2.1.2 Calibrate LED markers

Though $M^{\tau _{1}s}_{i}(t)$ and $M^{\tau _{1}\tau _{k}}_{j}(t)$ can be computed using $\tau _{1}$, they locate in the coordinate system of $\tau _{1}$. However, to compute the poses of the 3D scanner and stereo trackers, we need to transform $M^{\tau _{1}s}_{i}(t)$ from the coordinate system of $\tau _{1}$ to that of the 3D scanner, and suppose the corresponding coordinate is $M^{ss}_{i}$ after transformation. We also need to transform $M^{\tau _{1}\tau _{k}}_{j}(t)$ to that of $\tau _{k}$, and similarly we suppose the corresponding coordinate is $M^{\tau _{k}\tau _{k}}_{j}$ after transformation. The process of computing $M^{ss}_{i}$ and $M^{\tau _{k}\tau _{k}}_{j}$ is also called as LED marker calibration [24, 25].

Fig. 3

Compute the locations of LED markers in the coordinate system of 3D scanner

Next, we take the computation of $M^{ss}_{i}$ as an example to explain the process. As Fig. 3 shows, a calibration board is used to calibrate the LED markers. The calibration board is put in a place where both the 3D scanner and stereo tracker $\tau _{1}$ can see. Meanwhile, the LED markers on the 3D scanner must be seen by the stereo tracker. The calibration board is considered as the world coordinate system, which is denoted by $C_{\mathrm{W}}$. The coordinate systems of the 3D scanner and stereo tracker are represented by $C_{\mathrm{S}}$ and $C_{\mathrm{T}}$, respectively. The transformation between $C_{\mathrm{S}}$ and $C_{\mathrm{W}}$ is denoted by $T_{\mathrm{SW}}$, the transformation between $C_{\mathrm{T}}$ and $C_{\mathrm{W}}$ is denoted by $T_{\mathrm{TW}}$, and the transformation between $C_{\mathrm{T}}$ and $C_{\mathrm{S}}$ is denoted by $T_{\mathrm{TS}}$. $T_{\mathrm{SW}}$, $T_{\mathrm{TW}}$ and $T_{\mathrm{TS}}$ are matrix with 4 rows and 4 columns. To calibrate the LED markers, we must know $T_{\mathrm{TS}}$. According to the transformations among $C_{\mathrm{W}}$, $C_{\mathrm{S}}$ and $C_{\mathrm{T}}$, we have:

$$\begin{aligned} T_{\mathrm{TW}}=T_{\mathrm{TS}}~T_{\mathrm{SW}} \end{aligned}$$

(1)

Thus, we obtain:

$$\begin{aligned} T_{\mathrm{TS}}=T_{\mathrm{TW}}~T_{\mathrm{SW}}^{-1} \end{aligned}$$

(2)

Since $T_{\mathrm{TW}}$ and $T_{\mathrm{SW}}$ can be obtained by using the calibration board, we can obtain $T_{\mathrm{TS}}$.

Next, we compute the locations of LED markers in the 3D scanner’s coordinate system. Suppose $M^{ss}_{i}$ is homogeneous coordinates of the LED markers in $C_{\mathrm{S}}$, and $M^{\tau _{1}s}_{i}(t)$ is homogeneous coordinates of the LED markers in $C_{\mathrm{T}}$. Since $M^{\tau _{1}s}_{i}(t)$ is directly reconstructed by the stereo tracker $\tau _{1}$, we can transform $M^{\tau _{1}s}_{i}(t)$ to the 3D scanner’s coordinate system by Eq. (3):

$$\begin{aligned} M^{ss}_{i}=T_{\mathrm{TS}}~M^{\tau _{1}s}_{i}(t),\quad i\in \{1,\ldots ,n_s\} \end{aligned}$$

(3)

In the same way, we can calculate $M^{\tau _{k}\tau _{k}}_{j}$ according to $M^{\tau _{1}\tau _{k}}_{j}(t)$ based on the above-mentioned method.

2.1.3 Estimate the poses of stereo trackers

The steps of estimating the stereo trackers’ poses are as follows: firstly, we place the stereo trackers one after another, ensure the LED markers on $\tau _{k}$ can be seen by $\tau _{k-1}$, and regard the coordinate system of $\tau _{1}$ as the global coordinate system, as shown in Fig. 1; secondly, after $\tau _{k-1}$ has been placed, when we place $\tau _{k}$, $\tau _{k}$ will be moved in the FOV of $\tau _{k-1}$; meanwhile, we can compute $M^{\tau _{k-1}\tau _{k}}_{j}(t)$ using the trajectories generated by the motion of $\tau _{k}$ in the FOV of $\tau _{k-1}$; thirdly, we build two connected graphs according to $M^{\tau _{k}\tau _{k}}_{j}$ and $M^{\tau _{k-1}\tau _{k}}_{j}(t)$; fourthly, we match $M^{\tau _{k}\tau _{k}}_{j}$ and $M^{\tau _{k-1}\tau _{k}}_{j}(t)$ by graph matching. The concrete thought of connected graph matching will be elaborated in subsequent sections, and we here only suppose $M^{\tau _{k}\tau _{k}}_{j}$ and $M^{\tau _{k-1}\tau _{k}}_{j}(t)$ have been matched; fifthly, we can compute the transformation $\varGamma _{\tau _{k}\tau _{k-1}}$ between coordinates systems of $\tau _{k}$ and $\tau _{k-1}$ using:

$$\begin{aligned} \varGamma _{\tau _{k}\tau _{k-1}}=\arg \min _{\varGamma _{\tau _{k}\tau _{k-1}}}\left( \sum _{j}|\varGamma _{\tau _{k}\tau _{k-1}}M^{\tau _{k}\tau _{k}}_{j}- M^{\tau _{k-1}\tau _{k}}_{j}(t)|^2\right) \end{aligned}$$

(4)

Here,

$$\begin{aligned} \varGamma _{\tau _{k}\tau _{k-1}} = \left( \begin{array}{cc}{} \mathbf R ~~~~~~~~~~\mathbf t \\ \mathbf 0 ^{\mathrm{T}}~~~~~~~~~\mathbf 1 \end{array} \right) \end{aligned}$$

(5)

where $\mathbf R \in \mathbb {R}^{3\times 3}$, and $\mathbf t \in \mathbb {R}^{3}$. Finally, after the transformation between adjacent stereo trackers is obtained, the poses of stereo trackers can be estimated. For example, for the kth stereo tracker, if $k=2$, its pose can be represented by $\varGamma _{\tau _{2}\tau _{1}}$, and if $k\ge 3$, its pose can be represented by:

$$\begin{aligned} P^{\mathrm{T}}_k = \varGamma _{\tau _{2}\tau _{1}}\ldots \varGamma _{\tau _{k}\tau _{k-1}} \end{aligned}$$

(6)

Fig. 4

3D scanner. a Principle of 3D scanner, b rectified stereo images with projected lines, c one scanline with a cross section between the scanline and projected line, d Smoothed scanline

2.2 3D reconstruction

2.2.1 Reconstruct partial sections

As Fig. 4 shows, the 3D scanner is composed of two video cameras and one infrared line projector. The infrared line projector only casts one infrared line onto objects; therefore, the 3D scanner can only reconstruct one line at a time. We here use infrared light instead of visible light because this can reduce the effect of visible light and infrared light is harmless to human eyes. Furthermore, we use line projector which can only cast one line instead of video projector because of two reasons. One reason is that highly light-reflecting objects usually reflect light to the cameras with video projector so that captured images cannot be understood, but line projector will not result in large area reflection; another reason is that it is easier to match lines in rectified images due to only projecting one line on objects, which increases the system robustness. Figure 4a illustrates the principle of 3D scanner. During reconstruction, we use an infrared bandpass filter to filter useless light and meanwhile stop down the lens of video cameras to a small aperture. Under this circumstances, the projected line will be very distinct in rectified stereo images, as illustrated in Fig. 4b.

We detect lines in stereo images in three steps: firstly, for each scanline, there is a cross section between the projected infrared line and the scanline, as Fig. 4b shows. Figure 4c shows one scanline, where the trapezoid represents the cross section. We use one-dimensional difference of Gaussian (DOG) to filter each scanline (Fig. 4c) in rectified stereo images and obtain a smoothed scanline, as Fig. 4d illustrates. The one-dimensional DOG function can be represented as:

$$\begin{aligned} f(x;\mu ;\sigma _1;\sigma _2)= & {} \frac{1}{\sqrt{2\pi }}(\frac{1}{\sigma _1}\exp (-\frac{(x-\mu )^2}{2\sigma ^2_1})\nonumber \\&- \frac{1}{\sigma _2}\exp (-\frac{(x-\mu )^2}{2\sigma ^2_2})) \end{aligned}$$

(7)

Now, the cross section will change from trapezoid to paraboloid. Here, $\sigma _1$ is set to about the width of the projected infrared line, and $\sigma _2$ is set to about half of the width of the projected infrared line; secondly, for each pair of filtered lines, we detect the peak with the biggest gray value; as Fig. 4d shows, the peak can be considered as initial value of the center of cross section, and we here let $\mathbf x _{I}^l=(x^l,y^l)^{\mathrm{T}}$ and $\mathbf x _{I}^r=(x^r,y^r)^{\mathrm{T}}$ to represent the initial values of cross-sectional centers in the stereo images; finally, in order to obtain more accurate center for the cross section, we need to select some neighbor pixels around initial values. For example, some neighbor pixels of $\mathbf x _{I}^l$ form a point sequence $\{\ldots ,\mathbf x _{q},\mathbf x _{I}^l,\mathbf x _{q+1},\ldots \}$, we use the point sequence to fit a parabola $C^l$, and let the extremum value $\mathbf x _{e}^l$ of $C^l$ be the accurate center of cross section. Similarly, we can obtain the corresponding extremum value $\mathbf x _{e}^r$ of $\mathbf x _{I}^r$.

After detecting $\mathbf x _{e}^l$ and $\mathbf x _{e}^r$ in left and right rectified images, they are considered as the matching pair, and we compute the corresponding 3D coordinates using stereo triangulation [28]. In this way, we can reconstruct one line of an object using the 3D scanner. We here suppose, at time t, there are p 3D points reconstructed by the 3D scanner, let $\mathbf X ^{s(t)}=(X^{s(t)}_{1},\ldots ,X^{s(t)}_{i},\ldots .,X^{s(t)}_{p})^{\mathrm{T}}$ represent the reconstructed 3D point set, and $X^{s(t)}_{i}$ denote one 3D point in the 3D scanner’s coordinate system.

2.2.2 Align different partial sections

To align different partial sections, we need to compute the poses of 3D scanner using the stereo trackers. In order to track the 3D scanner in the FOV of the stereo trackers, we here present a method based on the integration of KLT tracking algorithm with graph matching algorithm.

At the beginning of 3D reconstruction (suppose, at time $t_0$), $\tau _{1}$ is the working tracker, and $n_s(t_0)$ LED lights on the 3D scanner can be seen by $\tau _{1}$, we suppose all LED lights can be seen at this time, and that means $n_s(t_0)$ is the number of LED markers installed on the 3D scanner. Meanwhile, we compute the 3D coordinates of the LED markers on the 3D scanner and then establish a connected graph in which LED markers are considered as vertices and the links between different vertices are regarded as edges. We here represent this connected graph by a matrix $G_{n_s(t_0)}$, where $G_{n_s(t_0)}$ is a $n_s(t_0)\times n_s(t_0)$ matrix with $d^{n_s(t_0)}_{ij}$ as its element in the ith row, jth column, $i\in \{1,\ldots ,n_s(t_0)\}$; $j\in \{1,\ldots ,n_s(t_0)\}$. $d^{n_s(t_0)}_{ij}$ denotes the Euclidean distance between the ith vertex $M^{\tau _{1}s}_{i}(t_0)$ and the jth vertex $M^{\tau _{1}s}_{j}(t_0)$. When we install the LED markers on the 3D scanner, we try our best to ensure the distance between every two LED markers is different; namely, it is better to make $d^{n_s(t_0)}_{ij}$ distinctive; in this case, it becomes more robust to track LED markers.

During 3D reconstruction, with the movement of the 3D scanner from the near to the distance, stereo tracker $\tau _{k}$, $k\in \{2,\ldots ,n\}$, will become the working tracker by detecting the emergence of the 3D scanner in stereo image sequence. For example, during tracking the 3D scanner using $\tau _{1}$, a thread of $\tau _{2}$ continuously detects its stereo image sequence until the 3D scanner emerges, and then, $\tau _{2}$ becomes the working stereo tracker until it is replaced by $\tau _{3}$. We here use a method similar with that in [29] to detect the emergence of the 3D scanner in stereo image sequence. After $\tau _{k}$ becomes the working tracker, $\tau _{k}$ will track the motion of the LED markers on the 3D scanner using KLT algorithm. However, some LED markers may frequently appear and disappear in the FOV of the stereo trackers due to occlusions. Thus, the number of detected and tracked LED markers may be smaller than $n_s(t_0)$. In this circumstance, tracking error may occur, and the system may be not robust if we only use the results tracked by KLT. Therefore, we combine KLT algorithm and graph matching, where KLT algorithm is adopted to match LED markers across views by computing trajectories of LED markers, and graph matching is adopted to compute the 3D scanner’s poses by matching the 3D coordinates of the LED markers captured at different time. Next, suppose, at time $t_1$, $n_s(t_1)$ LED markers are tracked by $\tau _{k}$, similarly, a connected graph $G_{n_s(t_1)}$ can be constructed as well. $G_{n_s(t_1)}$ is a $n_s(t_1)\times n_s(t_1)$ matrix with $d^{n_s(t_1)}_{hk}$ as its element in the hth row, kth column, $h\in \{1,2,\ldots ,n_s(t_1)\}$; $k\in \{1,2,\ldots ,n_s(t_1)\}$. And $d^{n_s(t_1)}_{hk}$ also denotes the Euclidean distance between the hth vertex $M^{\tau _{k}s}_{h}(t_1)$ and the kth vertex $M^{\tau _{k}s}_{k}(t_1)$.

Fig. 5

Experimental system. a 3D scanner with infrared LED markers, b stereo tracker $\tau _{1}$, c stereo tracker $\tau _{2}$ with infrared LED markers

The tracking of the 3D scanner can be performed by matching connected graph $G_{n_s(t_0)}$ and $G_{n_s(t_1)}$. The basic idea is: firstly, we build connected graph $G_{n_s(t_0)}$ and $G_{n_s(t_1)}$ according to $d^{n_s(t_0)}_{ij}$ and $d^{n_s(t_1)}_{hk}$; secondly, we create a KD tree for each row of $G_{n_s(t_0)}$; thirdly, for each element $d^{n_s(t_1)}_{hk}$ in the hth row of $G_{n_s(t_1)}$, we locate the nearest element $d^{n_s(t_0)}_{ij}$ in every row of $G_{n_s(t_0)}$ using KD tree; fourthly, we compute the distances between the hth row of $G_{n_s(t_1)}$ and every row of $G_{n_s(t_0)}$, and the distances can be denoted by $d_{<h,i>}$, where $i \in \{1,2,\ldots ,n_s(t_0)\}$; fifthly, we locate the smallest distance $d_{<h,i>}$, and the hth vertex in $G_{n_s(t_1)}$ and the ith vertex in $G_{n_s(t_0)}$ are considered as a matching pair if $d_{<h,i>}$ is smaller than a threshold value. By this method, even if some LED markers are invisible due to occlusions in the process of 3D scanner movement, while $n_s(t_1)$ is smaller than $n_s(t_0)$, we can match $G_{n_s(t_0)}$ and $G_{n_s(t_1)}$ very well. Next, we elaborate the proposed graph matching algorithm.

The threshold value $\sigma$ is set to $1\,\hbox {mm}$ in our method. Next, suppose the pose of 3D scanner at time $t_1$ is represented as $\varGamma _{s\tau _{k}}(t_1)$ which can be obtained using:

$$\begin{aligned} \varGamma _{s\tau _{k}}(t_1)= & {} \arg \min _{\varGamma _{s\tau _{k}}(t_1)}\left( \sum _{<i,h>}| \varGamma _{\tau _{2}\tau _{1}}\cdots \varGamma _{\tau _{k}\tau _{k-1}}\varGamma _{s\tau _{k}}(t_1)M^{\tau _{k}s}_{h}(t_1)\right. \nonumber \\&\quad \left. - M^{\tau _{1}s}_{i}(t_0)|^2\right) \end{aligned}$$

(8)

Thus, one reconstructed partial 3D point set $\mathbf X ^{s(t_1)}$ can be transformed into the coordinates system of $\tau _{1}$ by:

$$\begin{aligned} \mathbf X ^{\tau _{1}(t1)}=\varGamma _{\tau _{2}\tau _{1}}\cdot \cdot \cdot \varGamma _{\tau _{k}\tau _{k-1}}~\varGamma _{s\tau _{k}}(t_1)~ \mathbf X ^{s(t_1)} \end{aligned}$$

(9)

Fig. 6

Experiments of reconstructing large smooth texture-less objects. a An image of smooth texture-less bending plates, b region within the red rectangle in a captured by our method, c region within the red rectangle in a captured by KinectFusion, d, e reconstructed 3D point clouds viewed from different angles, f, g results, respectively, captured using [24, 25], h an image of a mat which is placed beside a large bending plate, i, j corresponding dense 3D point clouds of h

3 Results and evaluations

An experimental system is designed to validate the performance and effectiveness of the proposed method. Figure 5 illustrates the experimental system. Figure 5a shows the 3D scanner with LED markers, where the 3D scanner is composed of one infrared line projector to generate a 850 nm infrared line and two 5-million-pixel Bamuer video cameras to capture images. We make use of two stereo trackers due to our laboratory conditions, namely $\tau _{1}$ (Fig. 5b) and $\tau _{2}$ (Fig. 5c). All the video cameras are equipped with Japanese Computar lenses having a focal length of 16 mm, and the lenses are fitted with 850 nm filters. The FOV of video cameras is about 60$^\circ$, the FOV of 3D scanner is about 45$^\circ$, and the FOV of stereo trackers is about 50$^\circ$. The frame rate of video cameras is 15 fps, and we adopt an external trigger with a PLC (programmable logic controller) module to synchronously capture images. Twelve infrared LED lights are rigidly connected to 3D scanner and stereo tracker $\tau _{2}$. When we install these LED lights, we try our best to ensure the distance between every two LED markers is different, and ensure all LED lights are not in the same plane. In addition, a Leica FlexLine TS09 laser total station and two circular retroreflective markers are used to evaluate the system accuracy. The distance error of FlexLine TS09 laser total station is less than 1.5 mm for large object measurement. We calibrate the cameras of the 3D scanner and stereo trackers using the method in [30], and we calibrate the LED markers using the method described in Sect. 2.1.2.

Fig. 7

Experiments of reconstructing complex scenes with free form surfaces. a Image of a scene with free form surfaces, b, c results of the region within red rectangle in a captured, respectively, by our method and KinectFusion, d, e reconstructed 3D point clouds of a viewed from different angles, f, g results of a captured using [24, 25], respectively, h an image of a bear, i, j corresponding 3D point clouds of a viewed from different angles, k, l corresponding 3D point clouds of h captured by [24, 25], respectively, m an image with a straw hat and a porcelain horse, n, o corresponding 3D point clouds of m viewed from different angles

3.1 Experimental results

Two types of experiments are performed in this section, the size of reconstruction range is about $6.5\,\hbox {m}\times 1.6\,\hbox {m}$, and we put $\tau _{2}$ at a distance of about 3.5 m from $\tau _{1}$.

In the first type of experiments, we want to confirm the effectiveness of reconstructing large smooth texture-less objects used in industrial manufacturing. Figure 6a shows the image of smooth texture-less bending plates, and Fig. 6d, e illustrates the reconstructed 3D point clouds viewed from different angles. Figure 6b, c shows the results of the region within red rectangle in Fig. 6a, captured, respectively, by our method and KinectFusion [16], and we take advantage of Kinect 2.0 for Windows and the KinectFusion source code provided by Microsoft SDK. Figure 6f, g shows the results captured using [24, 25], respectively. We can see there is more noise on the reconstructed 3D data in the rectangular region in Fig. 6f, g compared with that in Fig. 6d, e, which means the alignment result becomes worse and worse with the movement of the 3D scanner for the method [24, 25]. Figure 6h shows an image of a mat which is placed beside a large bending plate, we here only show the mat in Fig. 6h because we want to illustrate the detailed information of the mat, and Fig. 6i, j shows the corresponding dense 3D point clouds. In summary, we can see that our method can obtain better experimental results.

In the second type of experiments, some large complex scenes are reconstructed. Figure 7a shows the image of a scene with free form surfaces, and Fig. 7d, e demonstrates the our reconstructed 3D point clouds viewed from different angles. Figure 7b, c shows the results of the region within red rectangle in Fig. 7a, captured, respectively, by our method and KinectFusion. Figure 7f, g shows the results captured using [24, 25], respectively. Figure 7h shows an image of a bear, we here only show the bear in Fig. 7h because we want to illustrate the detailed information of the bear, Fig. 7i, j shows the corresponding 3D point clouds viewed from different angles, and Fig. 7k, l shows the corresponding 3D point clouds captured by [24, 25], respectively. Figure 7m shows an image with a straw hat and a porcelain horse, and Fig. 7n, o shows the corresponding 3D point clouds viewed from different angles. From these experimental results, we can see that our method is effective for accurate 3D data acquisition of large complex objects, the results captured by KinectFusion are oversmoothed, while our results are more edge-preserving; there is more noise on the reconstructed 3D data captured by [24, 25], while our method can obtain better experimental results.

3.2 Evaluate pose estimation of long-range tracking

Next, another experiment is performed to validate the effectiveness of the 3D scanner’s pose estimation for long-range tracking. Because there is no groundtruth, it is difficult to evaluate 3D scanner’s pose estimation. However, if the LED marker tracking is accurate enough, the topology of connected graph formed by the tracked LED markers should never change during the reconstruction; under the circumstances, the pose estimation must be accurate. According to this thought, we evaluate the long-range tracking by estimating the topology change of the LED markers, and by this way we evaluate the accuracy of the 3D scanner’s pose estimation. Firstly, we put $\tau _{2}$ at a distance of 6 m from $\tau _{1}$, $\tau _{1}$ can see the infrared LED markers on $\tau _{2}$, and both $\tau _{1}$ and $\tau _{2}$ remain stationary. If the distance between the 3D scanner and $\tau _{1}$ is less than 7 m, $\tau _{1}$ is used as working tracker; if the distance is bigger than 7 m, $\tau _{2}$ will automatically replace $\tau _{1}$ as working tracker. Secondly, we put the 3D scanner at a distance of 2 m from $\tau _{1}$, $\tau _{1}$ can see the infrared LED markers on the 3D scanner. At time $t_0$, we compute the LED markers’ 3D coordinates $M^{\tau _{1}s}_{i}(t_0)$ in the coordinate system of $\tau _{1}$. The current location of the 3D scanner is considered as reference location. Thirdly, we compute $d^{n_s(t_0)}_{ij}$ according to vertices $M^{\tau _{1}s}_{i}(t_0)$ and $M^{\tau _{1}s}_{j}(t_0)$. Fourthly, we move the 3D scanner about 14 m from the near to the distance. Meanwhile, we track and calculate the 3D coordinates of the LED markers at intervals of one meter in the coordinate system of $\tau _{1}$. Here, we suppose all LED markers can be seen during the moving process, and compute $d^{n_s(t_k)}_{ij}$ according to $M^{\tau _{k}s}_{i}(t_k)$ and $M^{\tau _{k}s}_{j}(t_k)$ at time $t_k$, where $k\in \{1,\ldots ,n-1\}$. Finally, we evaluate the errors for long-range tracking according to the changes between $d^{n_s(t_0)}_{ij}$ and $d^{n_s(t_k)}_{ij}$ using $E_{t_k} = \frac{1}{H} \sum |d^{n_s(t_0)}_{ij}-d^{n_s(t_k)}_{ij}|$, where H is the number of edges of connected graph formed by LED markers. Here, $E_{t_k}$ is called as average tracking error at time $t_k$. Figure 8 shows the curves of computed average tracking error, and Fig. 9 shows the corresponding standard deviation.

For comparison, we perform an experiment of similar tracker-based method we presented in [24], where only stereo tracker $\tau _{1}$ is used, and the curve of tracking error is also shown in Figs. 8 and 9. We can see that the tracking accuracy using $\tau _{1}$ and $\tau _{2}$ is higher than that only using $\tau _{1}$, especially, when tracking distance is more than 7 m. In addition, we also implemented the similar tracker-based algorithm described in [25] proposed by Barone, and we here call it our implemented version. We take advantage of some low-brightness LED lights to simulate the reflective markers used in [25]. The corresponding curves are also shown in Figs. 8 and 9. As Fig. 8 shows, if the distance between the stereo tracker and 3D scanner is less than 6 m, the errors for two methods are similar. However, when distance is bigger than 6 m, the error of the method with low-brightness LED lights increases dramatically; this is because some LED lights cannot be located correctly due to the low brightness.

From this experiment, we can see that the pose estimation of the presented method is more accurate than those similar methods in [24, 25], and certainly our method is more suitable to reconstruct large object compared with the methods in [24, 25].

Fig. 8

Average tracking error

Fig. 9

Standard deviation

3.3 Evaluation of accuracy

Actually, it is very difficult to assess system accuracy because the reconstruction range is very large. Thus, to evaluate the system accuracy, we here make use of two circular retroreflective markers and one laser total station. Firstly, we paste two retroreflective markers on ground; secondly, we manually measure the distance between the centers of two markers using laser total station, and the measured distance can be considered as ground truth for accuracy evaluation; thirdly, we measure the distance between the two markers using our system, where we also put $\tau _{2}$ at a distance of 6 m from $\tau _{1}$, $\tau _{1}$ can see the infrared LED markers on $\tau _{2}$, and both $\tau _{1}$ and $\tau _{2}$ remain stationary. The distance between the first retroreflective marker and $\tau _{1}$ is about 2 m. During the measurement, we manually select the centers of retroreflective markers in images; fourthly, we measure the distance between markers only using one stereo tracker (the method in [24]) for comparison, where the distance between the first retroreflective marker and the stereo tracker is also about 2 m, and we also manually select the centers of retroreflective markers; fifthly, we measure the distance between markers using the method in [25] for comparison, where the distance between the first retroreflective marker and the stereo tracker is also about 2 m, and we manually select the centers of retroreflective markers as well; finally, we compare the measured values with ground truth. We here preform 5 tests by putting the markers at different places. The evaluation results are shown in Table 1. From the results, we can see that the proposed system is more accurate.

Table 1 1 Evaluation of accuracy (mm)

3.4 Evaluation of speed

The running time can be divided into three parts: One is the time of reconstructing one 3D line, another is the time of aligning one line into the global coordinate system, and the third one is the time of moving the 3D scanner. Here, the time of 3D scanner movement is not considered, because it is the same for the proposed method, the methods in [24, 25]. We process the method by a server that has one dual core 3.0 GHz CPU, 16G RAM and two GeForce GTX 690 NVIDIA graphics cards with 4096 MB GDDR5 memory. Based on the hardware, we test the running time for the three methods. All of the three methods need about 2.5 ms to reconstruct one 3D line, the proposed method needs about 1.5 ms to align one 3D line when two stereo trackers are used, and the methods in [24, 25] need about 1 ms to align one 3D line. When we reconstruct a 6-m-long area, if we reconstruct one line every five millimeters, which means we need to reconstruct 1200 3D lines. In this case, the proposed method costs about $1200\times (2.5+1.5)\hbox {ms}= 4.5\,\hbox {s}$, and the other two methods cost about $1200\times (2.5+1.0)\hbox {ms}= 4.2\,\hbox {s}$. That means the proposed method is a little bit slower than the methods in [24, 25]. However, we think it still fast enough for the large reconstruction in industrial manufacturing.

4 Conclusions

We present a 3D reconstruction framework for large objects. According to the experiments, this method can effectively reconstruct large objects and has its advantages compared with similar existing methods. Certainly, there exist some limitations: The current method is unsuitable to reconstruct objects with large occlusions which tend to require the 3D scanner to rotate a large degree. Under such circumstances, LED markers may be seriously deformed in the images of stereo trackers, which will result in inaccurate detection. In the future, we will solve this issue by redesigning the LED markers arrangement. However, we think the current method is still valuable for some applications.