1 Introduction

According to the relationship between inputs and outputs, the structural problems can be roughly classified into two categories: forward problems and inverse problems. Forward problems are defined as the problems to calculate the outputs based on the known inputs. In contrast with forward problems, inverse problems are defined as the problems to calculate the inputs through the outputs. Due to the increasing complexity of the structures and application environment, the measuring system inputs directly obtained by experiments are becoming harder in some of the complex structures and systems. Therefore, the inverse problem methods [1,2,3] are proposed to indirectly obtain the inputs through the system outputs which are available or more convenient to be measured. In practical engineering, many problems can be considered as inverse problems, such as crack identification and traffic accident reconstruction. In traditional inverse problems, the parameters in structures are measured as constants, thus those identified parameters will be constants. However, in practical engineering problems, uncertainties widely exist in geometric dimensions, loads and other material parameters. To obtain a reliable design, the uncertain inverse problems which comprehensively consider uncertain parameters in structures are gradually studied in the last few decades.

At present, the Bayesian method and the maximum likelihood estimation method are two important methods that are widely used to deal with uncertain inverse problems [4,5,6,7,8,9,10,11,12,13], and many uncertain analysis methods are also applied to uncertain inverse problems to improve the solution efficiency at the same time, such as perturbation method [7] and sensitivity matrix method [14]. However, those methods are all on the assumption that the probability distributions of uncertain parameters are already obtained [15,16,17,18,19,20,21]. However, this assumption may not always be true or sometimes requires expensive cost in practical engineering problems. Therefore, the non-probabilistic methods [22,23,24,25,26], which do not need the probability distributions of uncertain parameters, are proposed as beneficial supplements to the probability method. The interval method [22, 27, 28] is one of the non-probability methods, and because it only requires the lower and upper bounds of the uncertain parameters, fewer samples are required to construct an interval model compared with the probability method.

As a result, the inverse problem considering interval uncertainty called interval inverse problem is gradually investigated by many researchers. In the process of solving the interval inverse problem, usually, the forward propagation problem is repeatedly called by the interval identification process in a double-loop nested framework, which brings about lower computational efficiency. Therefore, the researches on improving computational efficiency are of great significance. At present, there are mainly two ways to improve the efficiency of the corresponding forward propagation: one is to construct surrogate models [29, 30]; the other is to apply interval analysis methods [31, 32]. Surrogate model methods mainly exist in the interval finite element modeling updating problems [33,34,35]. Fang et al. [36] proposed a special quadratic response surface method to construct the surrogate model, by which the interval function responses can be directly obtained by interval arithmetic. Deng et al. [37] applied the radial basis function neural networks to construct the surrogate model and then employed the perturbation technique to calculate the interval function responses. However, usually, the surrogate model methods need many sampling points to construct an accurate approximate model, and the accuracy of the surrogate model method strongly influences the results of the identified parameters. In addition to the surrogate model methods, interval analysis methods are widely applied to solve interval inverse problems. Jiang et al. [38] applied the first-order Taylor expansion interval analysis method to transform the inverse problem into deterministic inverse problems that can be calculated by traditional optimization and applied it to identify the material characterization of composites. Liu et al. [39] presented an inverse method that combines the interval analysis with regularization to stably identify the bounds of the dynamic load acting on the uncertain structures. Feng et al. [40] presented a new interval inverse method, which combines the Chebyshev inclusion function and multi-island genetic algorithm, and applied this method to deal with the suspension design of a vehicle vibration model. Liu et al. [41] proposed an interval inverse method based on high dimensional model representation and affine arithmetic to improve the efficiency of the interval inverse problem with the uncertainty that existed in responses and parameters.

In the above interval inverse methods, almost all of them concern with the uncertainties that existed in structure or system responses. The research of the interval inverse problem discussed in this paper is relatively few. However, this type of interval inverse problem discussed in this paper widely exists in practical engineering. For example, as for the vehicle accident reconstruction problem, the measured data of the deformation of the impacted vehicles in an accident is rare and deterministic and it is impossible to measure again, and some of the parameters such as the material parameters and friction factors are uncertain parameters. Under the influence of those uncertain parameters, the possible value of the vehicle speed and collision angle should be identified. Therefore, a kind of inverse problem for parameter identification will be discussed here, in which the experimental results are limited and fixed, and the intervals of some structural parameters should be identified under the influence of other structural parameters that are known yet described by intervals. In this paper, this kind of interval inverse problem is call model uncertainty inverse problem, and the parameters whose intervals have been obtained are called “interval parameters”, and the ones that should be identified are called “identified parameters”. Commonly, solving the model uncertainty problem encounters the double-loop problem where the outer loop is the uncertain propagation from uncertain parameters to identified parameters, and the inner loop is the deterministic inverse calculation.

To improve the efficiency of the model uncertainty problem, a novel inverse method based on the dimension-reduction interval method and adaptive collocation strategy is proposed. First, the interval inverse problem is transformed into the form of inverse-propagation function problem; and then the dimension-reduction interval method is used to transform the inverse-propagation function into several one-dimensional inverse-propagation functions; an adaptive collocation strategy is proposed to determine the collocation nodes in an interval, based on which, the one-dimensional inverse-propagation function is transformed into several deterministic inverse calculations which effectively avoids the time-consuming double-loop solution procedure and improves the efficiency of uncertain inverse calculation. The rest of this paper is as follows: Sect. 2 gives a problem statement of the inverse problem; Sect. 3 gives the formulation of the dimension-reduction method of the inverse function and the calculation strategy; afterward, three examples are utilized to demonstrate the feasibility and validity of the proposed method in Sect. 4; finally, Sect. 5 gives the conclusions of this paper.

2 Problem statement

A general inverse problem can be formulated as:

$${\mathbf{Z}} = {\mathbf{g}}\left( {\mathbf{X}} \right),Z_{i} = g_{i} \left( {X_{1} ,X_{2} ,...,X_{n} } \right),\;\;i = 1,2,...,m,$$
(1)

where \({\mathbf{X}}\) is an n-dimensional structural parameter vector that needs to be identified by inverse calculation; \({\mathbf{g}}\) is system function vector; m is the number of the functions; \({\mathbf{Z}}\) is the structural response vector which is known and obtained by measurement; m is the number of functions; n is the number of parameters to be identified. Generally speaking, m should be larger or equal to n to ensure the positive definite solution of Eq. (1). Supposing that there are uncertainties in some of the parameters or inputs of structures, and those uncertainties are modeled by intervals. The uncertain inverse problem can be formulated as:

$${\mathbf{Z}} = {\mathbf{g}}\left( {{\mathbf{X}},{\mathbf{U}}} \right),Z_{i} = g_{i} \left( {X_{1} ,X_{2} ,...,X_{n} ,U_{1} ,U_{2} ,...,U_{q} } \right),\;i = 1,2,...,m,$$
(2)

where:

$${\mathbf{U}} \in {\mathbf{U}}^{I} = \left[ {{\mathbf{U}}^{L} ,{\mathbf{U}}^{R} } \right],U_{k} = \left[ {U_{k}^{L} ,U_{k}^{R} } \right],\;k = 1,2,...,q,$$
(3)

where the interval vector \({\mathbf{U}}^{I}\) is used to describe the uncertainty of the parameter vector \({\mathbf{U}}\); The subscripts I, L and R are the interval, lower and upper bounds of the interval, respectively; q is the number of interval parameters; \({\mathbf{Z}}\) is the deterministic response vector. Eq. (2) is called model uncertainty inverse problem.

For a deterministic inverse problem, the identified parameters can be obtained through a deterministic inverse calculation. For interval parameters, the corresponding possible value of identified parameters will form a solution set, which in this paper is described by the interval vector. Therefore, the corresponding interval inverse problem can be further expressed as:

$$\left\{ {\begin{array}{*{20}c} {F:{\mathbf{U}}^{I} \to {\mathbf{X}}^{I} } \\ {{\mathbf{Z}} = {\mathbf{g}}\left( {{\mathbf{X}},{\mathbf{U}}} \right)} \\ \end{array} } \right.,$$
(4)

where \(F\) denotes the mapping relation of interval propagation from an uncertain parameter vector \({\mathbf{U}}^{I}\) to the identified parameter vector \({\mathbf{X}}^{I}\). Equation (4) is to calculate the intervals of identified parameters according to the interval parameters on the condition of \({\mathbf{Z}} = {\mathbf{g}}\left( {{\mathbf{X}},{\mathbf{U}}} \right)\). In practical engineering problems, the researchers always encounter the “ill-posed” problem where the inverse solution cannot be uniquely obtained. For this problem, the regularization method [39, 42, 43] can be usually applied to transform the “ill-posed” into a “well-posed” problem, and the inverse methods based on the “well-posed” inverse problem can be applied to solve the “ill-posed” inverse problem.

This paper mainly concentrates on the computational efficiency of Eq. (4) in which the double-loop nested problem always encounters in the solving process. The nested double-loop involves outer-loop and inner-loop, where the outer-loop is interval analyses and the inner loop is inverse calculations. In the process of solving this problem, the inverse calculation (inner-loop) is repeatedly called by interval propagation (outer-loop). Therefore, the computational process is very time-consuming and the computational efficiency is relatively low.

3 Interval assessment method for identified parameters

In this section, an efficient interval assessment method for identified parameters is proposed. The main strategy of the proposed method is to transform the interval inverse problem into several deterministic inverse problems. First, the interval inverse problem is transformed into an inverse function problem where the propagation direction is from an interval parameter vector and deterministic responses vector to the identified parameter vector. Then, the dimension-reduction method is introduced to transform the inverse function problem into several one-dimensional inverse-propagation problems. Moreover, an adaptive collocation strategy is proposed to obtain the lower and upper bounds of the identified parameters through a minimum number of collocation points.

3.1 The dimension-reduction model of the inverse function

Following the notation in interval mathematics [31, 32], an interval vector \({\mathbf{U}}^{I}\) can be rewritten in the following form:

$${\mathbf{U}}^{I} = \left[ {{\mathbf{U}}^{L} ,{\mathbf{U}}^{R} } \right] = \left[ {{\mathbf{U}}^{C} - {\mathbf{U}}^{W} ,{\mathbf{U}}^{C} + {\mathbf{U}}^{W} } \right] = {\mathbf{U}}^{C} + \left[ { - 1,1} \right]{\mathbf{U}}^{W} ,$$
(5)

where the subscripts \(C\) and \(W\) represent interval midpoint and interval radius, respectively; \({\mathbf{U}}^{C}\) and \({\mathbf{U}}^{W}\) can be obtained by:

$$\left\{ {\begin{array}{*{20}c} {{\mathbf{U}}^{C} = \frac{{{\mathbf{U}}^{L} + {\mathbf{U}}^{R} }}{2},U_{j}^{C} = \frac{{U_{j}^{L} + U_{j}^{R} }}{2},j = 1,2,...,n} \\ {{\mathbf{U}}^{W} = \frac{{{\mathbf{U}}^{R} - {\mathbf{U}}^{L} }}{2},U_{j}^{W} = \frac{{U_{j}^{R} - U_{j}^{L} }}{2},j = 1,2,...,n} \\ \end{array} } \right..$$
(6)

For the convenience of expression, the inverse-propagation expression of Eq. (2) can be transformed into:

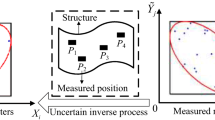
$${\mathbf{X}} = {\mathbf{\mathop{g}\limits^{\leftarrow} }}\left( {{\mathbf{Z}},{\mathbf{U}}} \right),$$
(7)

where \({\mathbf{\mathop{g}\limits^{\leftarrow} }}\) denotes the inverse function vector by which the identified vector \({\mathbf{X}}\) can be obtained by the deterministic response vector \({\mathbf{Z}}\) and the uncertain parameter vector \({\mathbf{U}}\). The explicit expression of \({\mathbf{\mathop{g}\limits^{\leftarrow} }}\) is usually non-existent, and it denotes a mapping relationship from the interval parameters \({\mathbf{U}}\) to identified parameters \({\mathbf{X}}\). For example, the mapping relation from two-interval parameters to two identified parameters is depicted as shown in Fig. 1.

Fig. 1
figure 1

The mapping relation from interval parameters to identified parameters

Full size image

In the probability analysis methods, the dimension-reduction method [44] is an efficient integration method to calculate the response moments, and this method is widely applied in the probability analysis problems [45,46,47] and uncertain design optimization problems [48, 49]. The main strategy of the dimension-reduction method is to deal with the uncertain parameters one by one, meanwhile transforms the original function into several one-dimensional functions. Solving those one-dimensional functions is more efficient than solving the original function. Therefore, the integration problem is simplified, and the calculation efficiency is improved. In current years, the dimension-reduction method is extended to the interval analysis field to efficiently calculate the bounds of function interval response [50,51,52], and those methods also achieved well performance both in accuracy and efficiency. Interval dimension-reduction model can be expressed as:

$$\tilde{f}_{{}} \left( {\mathbf{U}} \right){ = }f_{{}} \left( {U_{1} ,U_{2}^{C} ,...,U_{q}^{C} } \right) + f_{{}} \left( {U_{1}^{C} ,U_{2}^{{}} ,...,U_{q}^{C} } \right) + \cdots + f_{{}} \left( {U_{1}^{C} ,U_{2}^{C} ,...,U_{q}^{{}} } \right) - \left( {q - 1} \right)f\left( {{\mathbf{U}}^{C} } \right).$$
(8)

According to the Taylor series expansions of the original and dimension-reduction functions. The residual error of the dimension-reduction function can be expressed as:

$$\begin{aligned} f\left( {\mathbf{U}} \right) - \tilde{f}\left( {\mathbf{U}} \right) & { = }\sum\limits_{i = 1}^{q} {\sum\limits_{j = 1,j \ne i}^{q} {\frac{{\partial^{2} f\left( {U_{i}^{C} ,U_{j}^{C} } \right)}}{{\partial U_{i}^{{}} \partial U_{j}^{{}} }}\left( {U_{i}^{{}} - U_{i}^{C} } \right)\left( {U_{j}^{{}} - U_{j}^{C} } \right)} } \; + \sum\limits_{i = 1}^{q} {\sum\limits_{j = 1,j \ne i}^{q} {\frac{1}{2!}\frac{{\partial^{3} f\left( {U_{i}^{C} ,U_{j}^{C} } \right)}}{{\partial U_{i}^{2} \partial U_{j}^{{}} }}\left( {U_{i}^{{}} - U_{i}^{C} } \right)_{{}}^{2} \left( {U_{j}^{{}} - U_{j}^{C} } \right)} } \\ & + \sum\limits_{i = 1}^{q} {\sum\limits_{j = 1,j \ne i}^{q} {\sum\limits_{\substack{ k = 1,k \ne i, \\ k \ne j } }^{q} {\frac{{\partial^{3} f\left( {U_{i}^{C} ,U_{j}^{C} } \right)}}{{\partial U_{i}^{{}} \partial U_{j}^{{}} \partial U_{k}^{{}} }}\left( {U_{i}^{{}} - U_{i}^{C} } \right)\left( {U_{j}^{{}} - U_{j}^{C} } \right)\left( {U_{k}^{{}} - U_{k}^{C} } \right) + ...\;\;} } } . \\ \end{aligned}$$
(9)

It can be seen that the residual error of interval dimension reduction functions mainly lies in cross terms.

In this paper, the dimension-reduction interval method is extended to the interval inverse problem. Based on Eqs. (7) and (8), the inverse function can be transformed into the form of dimension-reduction:

$$\begin{gathered} {\mathbf{X}} = {\mathbf{\mathop{g}\limits^{\leftarrow} }}\left( {{\mathbf{Z}},{\mathbf{U}}} \right){ = }{\mathbf{\mathop{g}\limits^{\leftarrow} }}_{{\mathbf{1}}} \left( {{\mathbf{Z}},U_{1} ,U_{2}^{C} ,...,U_{q}^{C} } \right) + {\mathbf{\mathop{g}\limits^{\leftarrow} }}_{{\mathbf{2}}} \left( {{\mathbf{Z}},U_{1}^{C} ,U_{2}^{{}} ,...,U_{q}^{C} } \right) + ... \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} + {\mathbf{\mathop{g}\limits^{\leftarrow} }}_{q} \left( {{\mathbf{Z}},U_{1}^{C} ,U_{2}^{C} ,...,U_{q}^{{}} } \right) - \left( {q - 1} \right){\mathbf{\mathop{g}\limits^{\leftarrow} }}\left( {{\mathbf{Z}},U_{1}^{C} ,U_{2}^{C} ,...,U_{q}^{C} } \right), \hfill \\ \end{gathered}$$
(10)

where \({\mathbf{\mathop{g}\limits^{\leftarrow} }}\left( {{\mathbf{Z}},U_{1}^{C} ,U_{2}^{C} ,...,U_{q}^{C} } \right)\) is a deterministic inverse-propagation problem that can be directly obtained by a deterministic inverse calculation; \({\mathbf{\mathop{g}\limits^{\leftarrow} }}_{k} \left( {{\mathbf{Z}},U_{1}^{C} ,...,U_{k}^{{}} ,...,U_{q}^{C} } \right),k = 1,2,...,q\) is the one-dimensional inverse function. Equation (10) is called the dimension-reduction model of the inverse function. Based on the dimension-reduction interval method, Eq. (7) is transformed into the accumulation of multiply one-dimensional inverse functions, and the number of the one-dimensional inverse functions is determined by the number of interval parameters. For the simplicity of expression, \({\mathbf{X}}_{k} ,k = 1,2,...,q\) is defined as the output vector of the inverse function vector \({\mathbf{\mathop{g}\limits^{\leftarrow} }}_{k} ,k = 1,2,...,q\), and \({\mathbf{X}}^{C}\) is defined as the output vector of the inverse function vector \({\mathbf{\mathop{g}\limits^{\leftarrow} }}\left( {{\mathbf{Z}},U_{1}^{C} ,...,U_{k}^{C} ,...,U_{q}^{C} } \right)\) as follows:

$$\left\{ {\begin{array}{*{20}c} {{\mathbf{X}}_{k} { = }{\mathbf{\mathop{g}\limits^{\leftarrow} }}_{k} \left( {{\mathbf{Z}},U_{1}^{C} ,...,U_{k}^{{}} ,...,U_{q}^{C} } \right)} \\ {{\mathbf{X}}^{C} { = }{\mathbf{\mathop{g}\limits^{\leftarrow} }}\left( {{\mathbf{Z}},U_{1}^{C} ,...,U_{k}^{C} ,...,U_{q}^{C} } \right)} \\ \end{array} } \right..$$
(11)

The identified parameter vector \({\mathbf{X}}\) can be obtained by:

$${\mathbf{X}} = {\mathbf{X}}_{1} + {\mathbf{X}}_{2} + ...{\mathbf{X}}_{q} - \left( {q - 1} \right){\mathbf{X}}^{C} .$$
(12)

Based on Eq. (12), the identified interval parameter vector \({\mathbf{X}}\) is transformed into the summation of several interval vectors \({\mathbf{X}}_{k}\). Since each inverse-propagation problem \({\mathbf{\mathop{g}\limits^{\leftarrow} }}_{k} \left( {{\mathbf{Z}},U_{1}^{C} ,...,U_{k}^{{}} ,...,U_{q}^{C} } \right)\) contains an interval parameter \(U_{k}^{{}}\), the one-dimensional inverse-propagation problems \({\mathbf{\mathop{g}\limits^{\leftarrow} }}_{k} \left( {{\mathbf{Z}},U_{1}^{C} ,...,U_{k}^{{}} ,...,U_{q}^{C} } \right)\) can be solved separately, and the parallel computation also can be applied to solve Eq. (12).

Based on the dimension-reduction method, the interval inverse problem is transformed into several one-dimensional inverse problems. Although there are many interval analysis methods, few of them can be appropriately used to directly solve the inverse problem discussed in this paper for the strong nonlinear of the inverse function. Therefore, in the procedure of solving each one-dimensional inverse function \({\mathbf{\mathop{g}\limits^{\leftarrow} }}_{k} \left( {{\mathbf{Z}},U_{1}^{C} ,...,U_{k}^{{}} ,...,U_{q}^{C} } \right)\), the points in interval parameters \(U_{k}^{{}}\) are selected to calculate the possible values of the identified vector \({\mathbf{X}}_{k}^{{}}\). For example, \(a_{k}\) points selected in the interval parameter \(U_{k}^{{}}\) can obtain \(a_{k}\) possible vectors as:

$$\left\{ {\begin{array}{*{20}c} {{\mathbf{X}}_{k}^{1} { = }{\mathbf{\mathop{g}\limits^{\leftarrow} }}_{k} \left( {{\mathbf{Z}},U_{1}^{C} ,...,U_{k}^{1} ,...,U_{q}^{C} } \right)} \\ {{\mathbf{X}}_{k}^{2} { = }{\mathbf{\mathop{g}\limits^{\leftarrow} }}_{k} \left( {{\mathbf{Z}},U_{1}^{C} ,...,U_{k}^{2} ,...,U_{q}^{C} } \right)} \\ {...} \\ {{\mathbf{X}}_{k}^{{a_{k} }} { = }{\mathbf{\mathop{g}\limits^{\leftarrow} }}_{k} \left( {{\mathbf{Z}},U_{1}^{C} ,...,U_{k}^{{a_{k} }} ,...,U_{q}^{C} } \right)} \\ \end{array} } \right.,$$
(13)

where the subscribe of \(U_{k}^{{}}\) represents the point in the interval \(U_{k}^{{}}\). According to Eq. (13), it can be seen that \(a_{k}\) deterministic inverse calculations obtain \(a_{k}\) deterministic identified vectors \({\mathbf{X}}_{k}^{1} ,{\mathbf{X}}_{k}^{2} ,...,{\mathbf{X}}_{k}^{{a_{k} }}\). The obtained possible vector of identified vectors in Eq. (13) is assembled to a \(n \times a_{k}\) matrix as:

$${\mathbf{A}}_{k} = \left( {{\mathbf{X}}_{k}^{1} ,{\mathbf{X}}_{k}^{2} ,...,{\mathbf{X}}_{k}^{{{\text{a}}_{k} }} } \right),k = 1,2,...,q$$
(14)

The upper and lower bounds of each identified parameters \({\mathbf{X}}_{k}^{{}}\) are determined by the maximum and minimum values of each row of the matrix \({\mathbf{A}}_{k}\), respectively:

$$\left\{ {\begin{array}{*{20}c} {X_{k,1}^{L} = \min \left( {{\mathbf{A}}_{k,1} } \right),X_{k,1}^{R} = \max \left( {{\mathbf{A}}_{k,1} } \right)} \\ {X_{k,2}^{L} = \min \left( {{\mathbf{A}}_{k,2} } \right),X_{k,2}^{R} = \max \left( {{\mathbf{A}}_{k,2} } \right)} \\ {...} \\ {X_{k,n}^{L} = \min \left( {{\mathbf{A}}_{k,n} } \right),X_{k,n}^{R} = \max \left( {{\mathbf{A}}_{k,n} } \right),} \\ \end{array} } \right.$$
(15)

where \({\mathbf{A}}_{k,i} ,i = 1,2,...,n\) is the ith row of the matrix \({\mathbf{A}}_{k}\); \(X_{k,i}^{L}\) and \(X_{k,i}^{R}\) are the lower and upper bound of the ith identified parameter \(X_{i}^{{}}\) in the interval vector \({\mathbf{X}}_{k}^{{}}\), respectively. Based on Eq. (15), the lower and upper bound vectors of the interval vector \({\mathbf{X}}_{k}\) can be obtained according to Eq. (15):

$${\mathbf{X}}_{k} \in {\mathbf{X}}_{k}^{I} = \left[ {{\mathbf{X}}_{k}^{L} ,{\mathbf{X}}_{k}^{R} } \right],{\mathbf{X}}_{k}^{L} = \left[ {X_{k,1}^{L} ,X_{k,2}^{L} ,...,X_{k,n}^{L} } \right],{\mathbf{X}}_{k}^{R} = \left[ {X_{k,1}^{R} ,X_{k,2}^{R} ,...,X_{k,n}^{R} } \right],$$
(16)

Based on all the interval vector \({\mathbf{X}}_{k}^{I}\), the identified parameter interval vector \({\mathbf{X}}^{I}\) can be obtained by Eq. (12). The total number of the acquired points is:

$$f\left( {a_{k} ,q} \right) = \sum\limits_{k = 1}^{q} {a_{k} } ,$$
(17)

where \(a_{k}\) represents the number of selected points in the interval parameter \(U_{k}\). Based on Eq. (17), it can be seen that the computational efficiency depends on q and \(a_{k}\). At each point, the deterministic inverse problem can be constructed, and once the deterministic inverse calculation is implemented to obtain a possible value of the identified parameters. Therefore, \(\sum\nolimits_{k = 1}^{q} {a_{k} }\) deterministic inverse calculations are required to obtain the interval of identified parameters. In the practical calculation process, however, \(a_{k}\) is hard to be determined, and the accuracy of the results is strongly influenced by the number of \(a_{k}\). Therefore, an adaptive collocation strategy is proposed to determine the minimum number of points of each interval parameter on the premise of guaranteed accuracy.

3.2 Adaptive collocation strategy

The adaptive strategy is widely used in the reliability analysis method [53,54,55,56]. The strategy provides an effective way to improve the computational efficiency of the reliability analysis method. In this part, the idea of adaptive strategy is extended to the interval inverse-propagation analysis problem, and a novel computational strategy called adaptive collocation strategy is proposed to improve the computational efficiency of the interval inverse-propagation analysis.

The computational accuracy of the proposed method is determined by the number of points \(a_{k}\) in each interval parameter \(U_{k}\). Theoretically, the more points selected in an interval parameter will generally bring about better accuracy. However, the more points selected in an interval also need more deterministic inverse calculations, which will cause a larger computational cost. Therefore, it is desired to use a minimum number of points to achieve satisfying accuracy. The adaptive collocation strategy is proposed to determine the number of points in each interval parameter, through which the required points can be dramatically decreased and the efficiency of the inverse problem can be improved to a great extent.

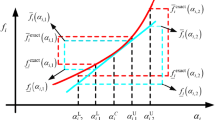
For example, the adaptive collocation strategy is operated to solve the one-dimensional inverse function problem \(\mathop{g}\limits^{\leftarrow} _{k} \left( {{\mathbf{Z}},U_{1}^{C} ,...,U_{k}^{{}} ,...,U_{q}^{C} } \right)\). As shown in Fig. 2, the first three iterative steps of this iterative mechanism are depicted: at the first iterative step, the midpoint and two vertex points of an interval parameter are selected (depicted as red circle dots) to calculate the interval vector of \({\mathbf{X}}_{k}^{{}}\); based on the three points, the interval inverse problem is transformed into three deterministic inverse problems, and the \({\mathbf{X}}_{k}^{L(1)}\) and \({\mathbf{X}}_{k}^{R(1)}\) can be obtained by Eqs. (14) and (15), where the superscript in bracket represents the iterative step; at the second iterative step, the midpoints of two adjacent red circle dots (depicted as black square dots) are added to calculate the \({\mathbf{X}}_{k}^{L(2)}\) and \({\mathbf{X}}_{k}^{R(2)}\), and only black square points are required to calculate; if the convergence criterion is satisfied, terminate the iteration and the \({\mathbf{X}}_{k}^{L(2)}\) and \({\mathbf{X}}_{k}^{R(2)}\) are the lower and upper bounds of \({\mathbf{X}}_{k}^{{}}\), respectively; otherwise, the midpoints of the existed adjacent points (depicted as green triangle dots in step 3) are added at the third iterative step. The iterative process will continue until the convergence criterion is satisfied as:

$$\left( {\left\| {{\mathbf{X}}_{k}^{{L\left( {s + 1} \right)}} - {\mathbf{X}}_{k}^{L\left( s \right)} } \right\| + \left\| {{\mathbf{X}}_{k}^{{R\left( {s + 1} \right)}} - {\mathbf{X}}_{k}^{R\left( s \right)} } \right\|} \right) \le \varepsilon ,$$
(18)

where \(s\) is the iterative step; \({\mathbf{X}}_{k}^{L\left( s \right)}\) and \({\mathbf{X}}_{k}^{R\left( s \right)}\) are the lower and upper bounds at the sth step, and \({\mathbf{X}}_{k}^{{R\left( {s + 1} \right)}}\) are the lower and upper bounds which are obtained at the (s + 1)th iterative step. \(\varepsilon\) is the small value, and set \(\varepsilon = 0.001\). Through Eq. (18), the lower and upper bounds \({\mathbf{X}}_{k}\) are guaranteed to be converged. In summary, the computational procedure can be described as follows:

Fig. 2
figure 2

Adaptive collocation strategy

Full size image

Step 1. As for the kth one-dimensional inverse-propagation problem \({\mathbf{\mathop{g}\limits^{\leftarrow} }}_{k} \left( {{\mathbf{Z}},U_{1}^{C} ,...,U_{k}^{{}} ,...,U_{q}^{C} } \right)\), set \(s = 1\);

Step 2. If \(s = 1\), the midpoint and two vertex points of an interval parameter are selected to calculate the lower and upper bound vector \({\mathbf{X}}_{k}^{L\left( s \right)}\) and \({\mathbf{X}}_{k}^{R\left( s \right)}\) of the identified parameter vectors \({\mathbf{X}}_{k}^{\left( s \right)}\); otherwise, add new points at the midpoints of the existed adjacent points and calculate the lower and upper bound vectors \({\mathbf{X}}_{k}^{L\left( s \right)}\) and \({\mathbf{X}}_{k}^{R\left( s \right)}\) of the identified parameter vectors \({\mathbf{X}}_{k}^{\left( s \right)}\), respectively;

Step 3. If the convergence criteria Eq. (18) is satisfied, terminate the iteration and obtain the upper and lower bound vectors \({\mathbf{X}}_{k}^{L\left( s \right)}\) and \({\mathbf{X}}_{k}^{R\left( s \right)}\), respectively; otherwise set \(s = s + 1\) and turn to step 2.

The iterative flowchart of one-dimensional inverse-propagation is depicted in Fig. 3. Based on \({\mathbf{X}}_{k}^{{}}\), \(k = 1,2,...,q\), the interval of identified parameters \({\mathbf{X}}_{{}}^{{}}\) can be obtained by Eq. (12). Generally, the adaptive collocation strategy takes only a few iterations to reach convergence and provides a solution with acceptable accuracy, which can be demonstrated in the following examples. Since the proposed method decouples the original interval inverse problem to several deterministic inverse problems, the double-loop strategy is successfully avoided and hence the high efficiency of the proposed method is guaranteed. In practical engineering problems, the uncertainties always are relatively small, therefore, the iterative mechanism can deal with most of the engineering problems. For the rest, particularly the complicated systems or structures, the proposed mechanism may encounter a convergence problem that may identify the local interval solution, and the reader should select enough points at the first iterative step to overcome the convergence problem as far as possible. Besides, the more samples selected in the first step, the more deterministic inverse calculations are acquired to obtain the identified interval, and the efficiency of the proposed method will be correspondingly reduced to a certain extent based on the number of the points at the first iterative step.

Fig. 3
figure 3

Iterative flowchart of one-dimensional inverse-propagation problem

Full size image

3.3 Solution of the deterministic inverse problem

When each interval parameter is replaced by the selected points determined by the adaptive collocation strategy, the interval inverse system Eq. (7) has degenerated to deterministic inverse problems as:

$${\mathbf{X}}_{k}^{{a_{k} }} { = }{\mathbf{\mathop{g}\limits^{\leftarrow} }}_{k} \left( {{\mathbf{Z}},U_{1}^{C} ,...,U_{k}^{{a_{k} }} ,...,U_{q}^{C} } \right) \Leftrightarrow {\mathbf{Z}} = {\mathbf{g}}\left( {{\mathbf{X}}_{k}^{{a_{k} }} ,U_{1}^{C} ,U_{2}^{C} ,...,U_{k}^{{a_{k} }} ,...,U_{q}^{C} } \right),i = 1,2,...,m$$
(19)

where \(U_{k}^{{(a_{k} )}}\) is a point in \(U_{k}^{{}}\). The least-square method can be used to construct deterministic optimization as:

$$\mathop {\min }\limits_{{{\mathbf{X}}_{k}^{{a_{k} }} }} \sum\limits_{i = 1}^{n} {\left( {Z_{i} - g_{i} \left( {{\mathbf{X}}_{k}^{{a_{k} }} ,U_{1}^{C} ,U_{2}^{C} ,...,U_{k}^{{a_{k} }} ,...,U_{n}^{C} } \right)} \right)^{2} }$$
(20)

Equation (20) is a deterministic optimization problem, and many traditional optimization methods can be applied to this unconstrained deterministic optimization problem. In this paper, the genetic algorithm (GA) [57] is selected to solve the Eq. (20) to obtain the global convergence solution for the deterministic inverse problem.

3.4 Iterative mechanism

The above section illustrates the adaptive collocation strategy and iterative procedure of a one-dimensional inverse function, and through the procedure, the one-dimensional inverse function can be efficiently solved. As for a multi-dimensional inverse problem, all the transformed one-dimensional inverse functions must be solved and then the solution results are assembled to obtain the identified parameters. The multi-dimensional inverse problem can be solved as shown in Fig. 4:

  1. Step 1.

    Transform the inverse problem into the inverse propagation problem as shown in Eq. (7) through the interval inverse analysis method;

  2. Step 2.

    Transform the inverse propagation problem into several one-dimensional inverse propagation problems as shown in Eq. (10) through the dimension-reduction method.

  3. Step 3.

    Solve all the one-dimensional inverse propagation problems by adaptive collocation strategy to obtain \({\mathbf{X}}_{k} { = }\overleftarrow {{\mathbf{f}}}_{k} \left( {{\mathbf{Z}},U_{1}^{C} ,...,U_{k}^{{}} ,...,U_{q}^{C} } \right)\);

  4. Step 4.

    Assemble all the \({\mathbf{X}}_{k} { = }\overleftarrow {{\mathbf{f}}}_{k} \left( {{\mathbf{Z}},U_{1}^{C} ,...,U_{k}^{{}} ,...,U_{q}^{C} } \right)\) to obtain the identified parameter vector as shown in Eq. (12).

Fig. 4
figure 4

Iterative mechanism

Full size image

In the processing of the iteration, the multi-dimensional inverse problem is transformed into several one-dimensional inverse propagation problems, and each one is independent of the others. Therefore, parallel compute methods [58,59,60,61] can be used to calculate all the transformed one-dimensional inverse propagation problems simultaneously, and further improve the efficiency of the interval inverse problem. The number of the deterministic inverse calculations of the proposed method for \(q\)-dimensional inverse problem can be expressed as:

$$f_{{\Pr {\text{o}}}} {(}s_{k} ,q{) = }1{ + }\sum\limits_{k = 1}^{q} {{2}^{{s_{k} }} } ,$$
(21)

where \(s_{k}\) represents the iterative step of the kth one-dimensional inverse-propagation problem. It can be seen that the number of the deterministic inverse calculations is the summation of the number of the q one-dimensional deterministic inverse calculations, and in each dimension, the calculation is \({2}^{{s_{k} }}\). Usually, in each one-dimensional inverse problem, only 2–3 iterative steps are required to achieve convergence. Therefore, the proposed method has a fine computational efficiency. To verify the accuracy of the obtained solutions, the results obtained by the Monte Carlo method [62] (MCS) are used to compare the results of the proposed method. The number of the deterministic inverse calculations of MCS is:

$$f_{{{\text{MCS}}}} (a_{k} ,q) = \prod\limits_{k = 1}^{q} {a_{k} } .$$
(22)

It can be seen that the number of the deterministic inverse calculations is the multiplication of the number of the q one-dimensional deterministic inverse calculations, and in each dimension, the calculation is \(a_{k}\). To ensure the accuracy of the reference solution, \(a_{k} = 100,\,\,k = 1,2,...,q\) is selected to assess the interval bounds. Therefore, MCS needs \(100^{q}\) deterministic inverse calculations.

4 Numerical examples and discussions

Two numerical examples and an engineering application are applied to verify the accuracy and efficiency of the proposed method. The results of the Monte Carlo method (MCS) [62] are selected as the reference solutions to verify the accuracy of the results obtained by the proposed method. To help readers clearly understand the proposed method, the computational process of this proposed method is detailedly illustrated in example one.

4.1 Numerical example 1

Consider the following numerical system equations:

$$\left\{ {\begin{array}{*{20}c} {Z_{1} = X_{1} + X_{2}^{2} + U_{1} } \\ {Z_{2} = e^{{X_{1} /2}} + 10/X_{2} - U_{2} } \\ \end{array} } \right.,$$
(23)

where \(X_{1}\) and \(X_{2}\) are the unknown parameters that should be identified; \(Z_{1}\) and \(Z_{2}\) are the system responses which are already measured as \(Z_{1} = 1\) and \(Z_{2} = 3\), respectively; \(U_{1}\) and \(U_{2}\) are the uncertain parameters which are quantified by intervals as \(U_{1} \in U_{1}^{I} = \left[ {5,7} \right]\) and \(U_{2} \in U_{2}^{I} = \left[ {8,9} \right]\), respectively. First, Eq. (23) can be transformed into the form of the interval inverse function as Eq. (7):

$$\left( {X_{1} ,X_{2} } \right)^{T} = {\mathbf{\mathop{g}\limits^{\leftarrow} }}\left( {Z_{1} ,Z_{2} ,U_{1} ,U_{2} } \right).$$
(24)

Based on the dimension-reduction method as Eq. (10), Eq. (24) can be transformed into two one-dimensional interval inverse function problems as:

$$\left( {X_{1} ,X_{2} } \right)^{T} = {\mathbf{\mathop{g}\limits^{\leftarrow} }}_{1} \left( {Z_{1} ,Z_{2} ,U_{1}^{{}} ,U_{2}^{C} } \right) + {\mathbf{\mathop{g}\limits^{\leftarrow} }}_{2} \left( {Z_{1} ,Z_{2} ,U_{1}^{C} ,U_{2} } \right) - {\mathbf{\mathop{g}\limits^{\leftarrow} }}\left( {Z_{1} ,Z_{2} ,U_{1}^{C} ,U_{2}^{C} } \right),$$
(25)

where \({\mathbf{\mathop{g}\limits^{\leftarrow} }}\left( {Z_{1} ,Z_{2} ,U_{1}^{C} ,U_{2}^{C} } \right)\) is a deterministic inverse problem and can be directly solved by the GA method [57]. By solving \({\mathbf{\mathop{g}\limits^{\leftarrow} }}\left( {Z_{1} ,Z_{2} ,U_{1}^{C} ,U_{2}^{C} } \right)\), \({\mathbf{X}}_{{}}^{C} = \left[ {3.7906,2.0638} \right]\) can be obtained. \({\mathbf{\mathop{g}\limits^{\leftarrow} }}_{1} \left( {Z_{1} ,Z_{2} ,U_{1}^{{}} ,U_{2}^{C} } \right)\) contains an interval parameter \(U_{1}^{{}}\), and it cannot be directly obtained by GA [57]. Therefore, the proposed adaptive collocation strategy is employed to solve this problem. First, three points \(U_{1}^{L}\), \(U_{1}^{R}\) and \(U_{1}^{C}\) are selected to estimate the possible values \({\mathbf{X}}_{1}\) according to the adaptive collocation strategy as:

$$\left\{ {\begin{array}{*{20}c} {{\mathbf{X}}_{1}^{1} = {\mathbf{\mathop{g}\limits^{\leftarrow} }}_{1} \left( {Z_{1} ,Z_{2} ,U_{1}^{L} ,U_{2}^{C} } \right) = \left( {3.7255,1.9769} \right)} \\ {{\mathbf{X}}_{1}^{2} = {\mathbf{\mathop{g}\limits^{\leftarrow} }}_{1} \left( {Z_{1} ,Z_{2} ,U_{1}^{C} ,U_{2}^{C} } \right) = \left( {3.7906,2.0638} \right)} \\ {{\mathbf{X}}_{1}^{3} = {\mathbf{\mathop{g}\limits^{\leftarrow} }}_{1} \left( {Z_{1} ,Z_{2} ,U_{1}^{R} ,U_{2}^{C} } \right) = \left( {3.8438,2.1432} \right)} \\ \end{array} } \right..$$
(26)

According to Eq. (14), the vectors in Eq. (26) are assembled to a matrix:

$${\mathbf{A}}_{1} = \left( {{\mathbf{X}}_{1}^{1} ,{\mathbf{X}}_{1}^{2} ,{\mathbf{X}}_{1}^{3} } \right) = \left[ {\begin{array}{*{20}l} {3.7255} \hfill & {3.7906} \hfill & {3.8438} \hfill \\ {1.9769} \hfill & {2.0638} \hfill & {2.1432} \hfill \\ \end{array} } \right]$$
(27)

Based on Eq. (27), the row vectors \({\mathbf{A}}_{1}\) are obtained as:

$$\left\{ {\begin{array}{*{20}c} {{\mathbf{A}}_{1,1} = \left( {\begin{array}{*{20}c} {3.7255} & {3.7906} & {3.8438} \\ \end{array} } \right)} \\ {{\mathbf{A}}_{1,2} = \left( {\begin{array}{*{20}c} {1.9769} & {2.0638} & {2.1432} \\ \end{array} } \right)} \\ \end{array} } \right..$$
(28)

Based on Eqs. (15) and (28), the lower and upper bounds of identified parameters \({\mathbf{X}}_{1}\) can be obtained as:

$$\left\{ {\begin{array}{*{20}c} {X_{1,1}^{L\left( 1 \right)} = \min \left( {{\mathbf{A}}_{1,1} } \right) = 3.7255} \\ {X_{1,1}^{R\left( 1 \right)} = \max \left( {{\mathbf{A}}_{1,1} } \right) = 3.8438} \\ {X_{1,2}^{L\left( 1 \right)} = \min \left( {{\mathbf{A}}_{1,2} } \right) = 1.9769} \\ {X_{1,2}^{R\left( 1 \right)} = \max \left( {{\mathbf{A}}_{1,2} } \right) = 2.1432} \\ \end{array} } \right.,$$
(29)

and the interval of \({\mathbf{X}}_{1}\) at the first step can be obtained as:

$${\mathbf{X}}_{1}^{\left( 1 \right)} = \left( {X_{1,1}^{\left( 1 \right)} ,X_{1,2}^{\left( 1 \right)} } \right),X_{1,1}^{\left( 1 \right)} \in X_{1,1}^{I\left( 1 \right)} = \left[ {3.7255,3.8438} \right],X_{1,2}^{\left( 1 \right)} \in X_{1,2}^{I\left( 1 \right)} = \left[ {1.9769,2.1432} \right].$$
(30)

Two new points between the existed points at the 2nd step are added as shown in Fig. 2, and the interval \({\mathbf{X}}_{1}\) can be updated to:

$$\left\{ {\begin{array}{*{20}c} {X_{1,1}^{I\left( 2 \right)} = \left[ {3.7255,3.8438} \right]} \\ {X_{1,2}^{I\left( 2 \right)} = \left[ {1.9769,2.1432} \right]} \\ \end{array} } \right..$$
(31)

At this step, the convergence criterion is satisfied and the iteration terminates. The intervals \(X_{1,1}^{I} = \left[ {3.7255,3.8438} \right]\) and \(X_{1,2}^{I} = \left[ {1.9769,2.1432} \right]\) are obtained. As the same to the \({\mathbf{\mathop{g}\limits^{\leftarrow} }}_{1} \left( {Z_{1} ,Z_{2} ,U_{1}^{{}} ,U_{2}^{C} } \right)\), the solution of \({\mathbf{\mathop{g}\limits^{\leftarrow} }}_{2} \left( {Z_{1} ,Z_{2} ,U_{1}^{C} ,U_{2} } \right)\) can be obtained by the adaptive collocation strategy as:

$$\left\{ {\begin{array}{*{20}c} {X_{2,1}^{I} = \left[ {3.6243,3.9433} \right]} \\ {X_{2,2}^{I} = \left[ {2.0507,2.0754} \right]} \\ \end{array} } \right..$$
(32)

Based on Eqs. (31) and (32), the lower and upper bounds of identified parameters can be obtained as:

$$\left\{ {\begin{array}{*{20}c} {X_{1}^{I} = X_{1,1}^{I} + X_{1,2}^{I} - X_{1}^{C} = \left[ {3.5592,3.9964} \right]} \\ {X_{2}^{I} = X_{2,1}^{I} + X_{2,2}^{I} - X_{2}^{C} = \left[ {1.9638,2.1550} \right]} \\ \end{array} } \right.$$
(33)

According to the above analysis, both one-dimensional inverse propagations are convergence at the second iterative step. Therefore, the proposed method only acquires 9 deterministic inverse calculations to obtain the interval solutions of the identified parameters \(X_{1}\) and \(X_{2}\) based on Eq. (21). To verify the accuracy of the interval solutions, the computational results obtained by MCS are used as a reference solution to compare with the ones obtained by the proposed method. According to Eq. (22), 10,000 deterministic inverse calculations to obtain the reference solution by MCS. It is demonstrated that the results obtained by MCS and those obtained by the proposed method are almost the same, which indicates that the proposed method has well performance in both accuracy and efficiency (see Table 1).

Table 1 The comparisons of accuracy and efficiency in example 1
Full size table

4.2 Numerical example 2

This example is the load identification problem of the cantilever. In this problem, the loads should be identified by the measurements of maximum stress of the fixed end and the deflection of the free end. The system equations of the cantilever can be expressed as:

$$\left\{ {\begin{array}{*{20}c} {\delta_{\max } = \frac{{6P_{X} L}}{{b^{2} h}} + \frac{{6P_{Y} L}}{{bh^{2} }}} \\ {D{ = }\frac{{4L^{3} }}{Ebh}\sqrt {\left( {\frac{{P_{X} }}{{h^{2} }}} \right)^{2} + \left( {\frac{{P_{Y} }}{{b^{2} }}} \right)^{2} } } \\ \end{array} } \right.,$$
(34)

where the length of the cantilever \(L\), the width of cross-section \(b\), the height of cross-section \(h\) and elastic modulus \(E\) are uncertain parameters and those uncertain parameters can be quantified by the intervals as \(L \in [970,1030][970,1030]\) mm, \(b \in \left[ {98,102} \right]\) mm, \(h \in \left[ {196,204} \right]\) mm and \(E \in \left[ {39,41} \right]\) Gpa, respectively. The maximum stress of the fixed end is measured as \(\delta_{\max } = 0.1{\text{Mpa}}\) and the deflection of the free end is measured as \(D = 10{\text{mm}}\). Based on the above information, the vertical load \(P_{Y}\) and horizontal load \(P_{X}\) should be identified.

The corresponding vertical load \(P_{Y}^{C} = 14.12\) and horizontal load \(P_{X}^{C} = 26.04\) can be obtained through one deterministic inverse calculation at the midpoints of uncertain parameters. The original problem is transformed into assessing effects from four uncertain parameters to two identified parameters. As shown in Table 2, the uncertainties propagate from uncertain parameters to horizontal load \(P_{X}\) are listed. \(P_{L,X}^{I}\) reflects the effect propagating from the uncertain length of the cantilever to horizontal load; \(P_{b,X}^{I}\) reflects the effect propagating from uncertain width of the cross-section to horizontal load; \(P_{h,X}^{I}\) reflects the effect propagating from the uncertain height of cross-section to horizontal load; \(P_{E,X}^{I}\) reflects the effect propagating from uncertain elastic modulus to horizontal load. It can be seen that the uncertainty of the width of the cross-section has the greatest influence on the identification of horizontal load. Therefore, in this aspect, the precision design requirement of the width of the cross-section should be higher than other uncertain parameters to minimize its influence on the identification of the horizontal load \(P_{X}\). As shown in Table 3, the uncertainties propagate from uncertain parameters to the vertical load \(P_{Y}\) are listed. \(P_{L,Y}^{I}\) reflects the effect propagating from the uncertain length of the cantilever to vertical load; \(P_{b,Y}^{I}\) reflects the effect propagating from uncertain width of the cross-section to vertical load; \(P_{h,Y}^{I}\) reflects the effect propagating from the uncertain height of cross-section to vertical load; \(P_{E,Y}^{I}\) reflects the effect propagating from uncertain elastic modulus to vertical load. It can be seen that the uncertainty of the length of the cantilever has the greatest influence on the identification of horizontal load. Therefore, in this aspect, the precision design requirement of the length of the cantilever should be higher than other uncertain parameters to minimize its influence on the identification of the vertical load \(P_{Y}\).

Table 2 The intervals of horizontal load \(P_{X}\) under the influence of uncertain parameters
Full size table
Table 3 The intervals of vertical load \(P_{Y}\) under the influence of uncertain parameters
Full size table

The obtained intervals of identified parameters by the proposed method are listed in Table 4, it can be seen that the results obtained by the proposed method are very close to the reference solutions. It can be seen that the proposed method only needs 17 deterministic inverse calculations, which demonstrates the high efficiency in solving the cantilever problem. Based on the results of the identified parameters, it can be concluded that the uncertainties of \(L\), \(b\), \(h\) and \(E\) have a stronger influence on the identification of the vertical load \(P_{Y}\) than the horizontal load \(P_{X}\).

Table 4 The comparisons of accuracy and efficiency in example 2
Full size table

4.3 Application to the occupant constraint system model

The occupant constraint system [6, 41] is an important device to protect the occupants when a vehicle collision accident happened. In current years, the safety of the occupants is paid more and more attention, and the constraint system is widely studied. Two dummy models, namely 50th percentile man, and 5th percentile women, are considered. The multi-body dynamic model is shown in Fig. 5, which includes dummy, seat belt, airbag and car body. The collision speed is 3.5 km/h, and the dimension parameter of the gas vent \(U\) is an interval parameter with an interval midpoint of 43 mm and an interval radius of 5 mm. The zoom factor and the ribbon stiffness \(X_{1}\) and \(X_{2}\) should be identified. The weighted injury criteria (WICs) [63] are selected as the measurement responses, and the expression of WIC can be written as [64]:

$${\text{WIC}} = 0.6\left( {{\text{HIC}}/1000} \right) + 0.35\left( {C_{{3\;{\text{ms}}}} /60} \right) + 0.05\left( {F_{{{\text{left}}}} + F_{{{\text{right}}}} } \right)/20.0,$$
(35)

where HIC is the head injury criterion; \(C_{{3\;{\text{ms}}}}\) is the chest injury criterion; \(F_{{{\text{left}}}}\) and \(F_{{{\text{right}}}}\) are the left leg strength index and right leg strength index, respectively (see Fig. 6).

Fig. 5
figure 5

Cantilever problem

Full size image
Fig. 6
figure 6

The occupant constraint system model [6, 41]

Full size image

To improve the computational efficiency the second-order response surfaces of the functions are constructed as:

$$\left\{ {\begin{array}{*{20}c} \begin{gathered} {\text{WIC}}_{1} = 0.7074 + 0.0971X_{1} - 0.3248X_{2} - 1.0934U - 0.0067X_{1}^{2} \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} + 0.1923X_{2}^{2} + 75.3548U^{2} - 0.0331X_{1} X_{2} + 0.0014X_{1} U - 5.3158X_{2} U \hfill \\ \end{gathered} \\ \begin{gathered} {\text{WIC}}_{2} = 0.8210 + 0.0743X_{1} - 0.7137X_{2} + 0.1177U - 0.0095X_{1}^{2} \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} + 0.3942X_{2}^{2} + 21.2557U^{2} - 0.0400X_{1} X_{2} - 0.0219X_{1} U - 3.8657X_{2} U \hfill \\ \end{gathered} \\ \end{array} } \right.,$$
(36)

where the \({\text{WIC}}_{1}\) denotes the WIC of 50th percentile man dummy, and it is measured as \({\text{WIC}}_{1} = 0.51629\); \({\text{WIC}}_{2}\) denotes the WIC of 5th percentile woman dummy, and it is measured as \({\text{WIC}}_{2} = 0.44425\).

The computational results of the proposed method are listed in Table 5. It can be seen that the proposed method only employs 5 deterministic inverse calculations to obtain a relatively accurate solution. Moreover, it should be noted that the variation of the identified parameter \(X_{1}^{I}\) is much larger than the variation of the identified parameter \(X_{2}^{I}\), which reflects that the uncertainty of the dimension parameter of the gas vent \(U\) has a stronger influence on the zoom factors \(X_{1}^{{}}\). Therefore, the designer could have a better and accurate understanding of the mass flow rate \(X_{2}^{{}}\), and more attention should be paid to the zoom factors \(X_{1}^{{}}\) in the analysis and design processing of the occupant restraint system model.

Table 5 The comparisons of accuracy and efficiency in example 3
Full size table

5 Conclusions

A kind of inverse problem called model uncertain inverse problem is proposed to assess the uncertainties of identified parameters with uncertainties in structural parameters and limited experimental data. To overcome the low efficiency of directly solving the problem, an efficient interval assessment method is proposed. First, the interval inverse problem is transformed into the inverse function problem, Based on which the dimension-reduction method is introduced to transform the inverse problem into several one-dimensional inverse problems. Afterward, an adaptive collocation strategy is proposed to determine the points in an interval to assess the interval of identified parameters, based on which the one-dimensional inverse-propagation problem is transformed into several deterministic inverse problems. Therefore, the double-loop problem of interval propagation and inverse calculations is decoupled, and the efficiency of the inverse problem can be improved. The results of the examples demonstrate that this proposed method has good performances both in accuracy and efficiency. Moreover, it should be aware that due to the disadvantages of the dimension reduction strategy, there might be an accuracy problem when the functions are strongly influenced by cross terms. In the future, we will focus on the possible problem and extend this efficient method to the inverse problems with hybrid uncertainty parameters, etc.