Abstract
This paper puts forward two new methods for reliability-based design optimization (RBDO) of complex engineering systems. The methods involve an adaptive-sparse polynomial dimensional decomposition (AS-PDD) of a high-dimensional stochastic response for reliability analysis, a novel integration of AS-PDD and score functions for calculating the sensitivities of the failure probability with respect to design variables, and standard gradient-based optimization algorithms, encompassing a multi-point, single-step design process. The two methods, depending on how the failure probability and its design sensitivities are evaluated, exploit two distinct combinations built on AS-PDD: the AS-PDD-SPA method, entailing the saddlepoint approximation (SPA) and score functions; and the AS-PDD-MCS method, utilizing the embedded Monte Carlo simulation (MCS) of the AS-PDD approximation and score functions. In both methods, the failure probability and its design sensitivities are determined concurrently from a single stochastic simulation or analysis. When applied in collaboration with the multi-point, single-step framework, the proposed methods afford the ability of solving industrial-scale design problems. Numerical results stemming from mathematical functions or elementary engineering problems indicate that the new methods provide more computationally efficient design solutions than existing methods. Furthermore, shape design of a 79-dimensional jet engine bracket was performed, demonstrating the power of the AS-PDD-MCS method developed to tackle practical RBDO problems.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Reliability-based design optimization, commonly referred to as RBDO, is an important prototype for solving engineering design problems in the presence of uncertainty, manifested by probabilistic descriptions of the objective and/or constraint functions (Kuschel and Rackwitz 1997; Tu et al. 1999; Du and Chen 2004; Chiralaksanakul and Mahadevan 2005; Agarwal and Renaud 2006; Liang et al. 2007; Rahman and Wei 2008). Formulated within a probabilistic framework, RBDO strives to achieve high reliability of an optimal design by fulfilling the probabilistic constraints at desired levels. With new formulations and methods appearing almost every year, RBDO, in conjunction with finite-element analysis (FEA), is becoming increasingly relevant and perhaps necessary for design of aerospace, civil, microelectronics, and automotive structures and systems.
The solution of an RBDO problem is heavily reliant on the methods employed for reliability analysis. Existing RBDO algorithms using surrogate methods for reliability analysis can be broadly classified into two groups: (1) the first-order reliability method or FORM-based methods (Kuschel and Rackwitz 1997; Tu et al. 1999; Du and Chen 2004; Chiralaksanakul and Mahadevan 2005; Agarwal and Renaud 2006; Liang et al. 2007) and (2) decomposition-based methods (Rahman and Wei 2008; Lee et al. 2008a, 2008b; Youn and Wang 2008; Lee et al. 2012). Depending on how reliability analysis and optimization iterations are integrated, the FORM-based RBDO algorithms can be further assorted into three kinds: double-loop algorithms (Tu et al. 1999), single-loop algorithms (Kuschel and Rackwitz 1997; Liang et al. 2007), and decoupled algorithms (Du and Chen 2004; Agarwal and Renaud 2006). For the double-loop RBDO, two equivalent approaches, known as the reliability index approach (RIA) and the performance measure approach (PMA), have emerged [2]. Nevertheless, a double-loop method is expensive, because for each design (outer) iteration, a set of reliability (inner) iterations involving costly function evaluations must be generated for locating the most probable point (MPP) required by FORM. To overcome high computational expense, single-loop formulations exploiting the Karush-Kuhn-Tucker optimality condition at MPP have appeared. In addition, several researchers have reformulated the nested RBDO problem to decouple reliability analysis from design optimization. However, a fundamental requirement of all three algorithms is FORM, which may not provide accurate reliability estimates in high dimensions and for highly nonlinear performance functions. Indeed, recent results from Rahman and Wei (2008) and Zou and Mahadevan (2006) reveal that the FORM-based RBDO process may produce infeasible or inaccurate designs. It should also be noted that no formal proof of convergence exists for either a single-loop or a decoupled algorithm (Royset et al. 2001).
More recently, Rahman and Wei (2008) proposed a univariate decomposition method for solving a general RBDO problem. Their method is rooted in a univariate truncation of the referential dimensional decomposition (RDD) (Rahman 2011, 2014) of a high-dimensional performance function. The resulting approximation, generated using the MPP as the reference point in the rotated standard Gaussian space of input variables, leads to accurate reliability and design sensitivity analysis. The computational effort for estimating failure probabilities and their design sensitivities required by RBDO has been markedly reduced owing to performing multiple yet one-dimensional integrations. A few other researchers adopted the same decomposition method under the synonym, the dimension-reduction method, and reported computationally efficient RBDO solutions (Lee et al. 2008a, 2008b; Youn Wang 2008; Lee et al. 2012). However, similar to the FORM-based methods, the decomposition or dimension-reduction method also requires finding the MPP, which can be unwieldy for noisy functions or even expensive for high-dimensional problems. Furthermore, a recent error analysis reveals the sub-optimality of RDD approximations, meaning that the RDD approximation, regardless of how the reference point is chosen, cannot be better than the analysis of variance (ANOVA) approximation for identical degrees of interaction (Rahman 2014; Yadav and Rahman 2013, 2014a). Therefore, approximations derived from the ANOVA dimensional decomposition (Efron and Stein 1981) or its polynomial variant, the polynomial dimensional decomposition (PDD) (Rahman 2008, 2009a), are expected to provide more accurate RBDO solutions at the same cost of existing decomposition-based methods. Although PDD-based reliability analysis is established (Rahman and Ren 2014), subsequent developments of PDD-based RBDO algorithms have yet to appear. More importantly, both the FORM- and decomposition-based methods discussed mandate new reliability and design sensitivity analysis at every design iteration. Consequently, a direct and straightforward integration of a reliability method — existing or new — with design optimization is expensive, depending on the cost of evaluating the objective and constraint functions and the requisite number of design iterations. The authors argue that not only are new computational methods needed for predicting reliability or design sensitivities, but also new or significantly improved design archetypes, possibly requiring a few stochastic simulations for solving the entire RBDO problem.
This paper presents two new methods — the adaptive-sparse PDD-saddlepoint approximation (SPA), or AS-PDD-SPA, method and the adaptive-sparse PDD-Monte Carlo simulation (MCS), or AS-PDD-MCS, method — for reliability-based design optimization of complex engineering systems. Both methods are based on (1) an adaptive-sparse PDD approximation of a high-dimensional stochastic response for reliability analysis; (2) a novel integration of the adaptive-sparse PDD approximation and score functions for calculating the sensitivities of the failure probability with respect to design variables; and (3) standard gradient-based optimization algorithms, encompassing a multi-point, single-step design process. Section 2 formally defines a general RBDO problem, including a concomitant mathematical statement. Section 3 starts with a brief exposition of PDD and explains how it leads up to the AS-PDD approximation. Section 4 formally introduces the AS-PDD-SPA and AS-PDD-MCS methods for reliability analysis. Exploiting score functions, Section 5 explains how the effort required to calculate the failure probability by these two methods also delivers its design sensitivities, sustaining no additional cost. The calculation of PDD expansion coefficients, required for reliability and design sensitivity analysis, is discussed in Section 6. Section 7 introduces a multi-point, single-step iterative scheme for RBDO and explains how the reliability analysis and design sensitivities from the AS-PDD-SPA and AS-PDD-MCS methods are integrated with a gradient-based optimization algorithm. Section 8 presents four numerical examples, including shape design of a 79-dimensional engine bracket problem, to evaluate the accuracy, convergence properties, and computational efforts of the proposed RBDO methods. Finally, the conclusions are drawn in Section 9.
2 Reliability-based design optimization
Let \(\mathbb {N}\), \(\mathbb {N}_{0}\), \(\mathbb {R}\), and \(\mathbb {R}_{0}^{+}\) represent the sets of positive integer (natural), non-negative integer, real, and non-negative real numbers, respectively. For \(k\in \mathbb {N}\), denote by \(\mathbb {R}^{k}\) the k-dimensional Euclidean space and by \(\mathbb {N}_{0}^{k}\) the k-dimensional multi-index space. These standard notations will be used throughout the paper.
Consider a measurable space \(({\Omega }_{\mathbf {d}},\mathcal {F}_{\mathbf {d}})\), where Ω d is a sample space and \(\mathcal {F}_{\mathbf {d}}\) is a σ-field on Ω d . Defined over \(({\Omega }_{\mathbf {d}},\mathcal {F}_{\mathbf {d}})\), let \(\{P_{\mathbf {d}}:\mathcal {F}\to [0,1]\}\) be a family of probability measures, where for \(M\in \mathbb {N}\) and \(N\in \mathbb {N}\), \(\mathbf {d}=(d_{1},\cdots ,d_{M})^{T}\in \mathcal {D}\) is an \(\mathbb {R}^{M}\)-valued design vector with non-empty closed set \(\mathcal {D}\subseteq \mathbb {R}^{M}\) and let \(\mathbf {X}:=(X_{1},\cdots ,X_{N})^{T}:({\Omega }_{\mathbf {d}},\mathcal {F}_{\mathbf {d}})\to (\mathbb {R}^{N},\mathcal {B}^{N})\) be an \(\mathbb {R}^{N}\)-valued input random vector with \(\mathcal {B}^{N}\) representing the Borel σ-field on \(\mathbb {R}^{N}\), describing the statistical uncertainties in loads, material properties, and geometry of a complex mechanical system. The probability law of X is completely defined by a family of the joint probability density functions (PDF) \(\{f_{\mathbf {X}}(\mathbf {x};\mathbf {d}),\:\mathbf {x}\in \mathbb {R}^{N},\:\mathbf {d}\in \mathcal {D}\}\) that are associated with probability measures \(\{P_{\mathbf {d}},\:\mathbf {d}\in \mathcal {D}\}\), so that the probability triple \(({\Omega }_{\mathbf {d}},\mathcal {F}_{\mathbf {d}},P_{\mathbf {d}})\) of X depends on d. A design variable d k can be any distribution parameter or a statistic — for instance, the mean or standard deviation — of X i .
Let y l (X), l=1,2,⋯ ,K, be a collection of K+1 real-valued, square-integrable, measurable transformations on \(({\Omega }_{\mathbf {d}},\mathcal {F}_{\mathbf {d}})\), describing performance functions of a complex system. It is assumed that \(y_{l}:(\mathbb {R}^{N},\mathcal {B}^{N})\to (\mathbb {R},\mathcal {B})\) is not an explicit function of d, although y l implicitly depends on d via the probability law of X. This is not a major limitation, as most RBDO problems involve means and/or standard deviations of random variables as design variables. Nonetheless, the mathematical formulation for RBDO in most engineering applications involving an objective function \(c_{0}:\mathbb {R}^{M}\to \mathbb {R}\) and probabilistic constraint functions \(c_{l}:\mathbb {R}^{M}\to \mathbb {R}\), where l=1,⋯ ,K and 1≤K<∞, requires one to
where Ω F,l (d) is the lth failure domain, 0≤p l ≤1 is the lth target failure probability, and d k,L and d k,U are the lower and upper bounds of the kth design variable d k . The objective function c 0 is commonly prescribed as a deterministic function of d, describing relevant system geometry, such as area, volume, and mass. In contrast, the constraint functions c l , l=1,2,⋯ ,K, are generally more complicated than the objective function. Depending on the failure domain Ω F,l , a component or a system failure probability can be envisioned. For component reliability analysis, the failure domain is often adequately described by a single performance function y l (X), for instance, Ω F,l :={x:y l (x)<0}, whereas multiple, interdependent performance functions y l,i (x), i=1,2,⋯ , are required for system reliability analysis, leading, for example, to Ω F,l :={x:∪ i y l,i (x)<0} and Ω F,l :={x:∩ i y l,i (x)<0} for series and parallel systems, respectively. In any case, the evaluation of the failure probability in (1) is fundamentally equivalent to calculating a high-dimensional integral over a complex failure domain.
The evaluation of probabilistic constraints c l (d), l=1,2,⋯ ,K, requires calculating component or system probabilities of failure defined by respective performance functions. Coupling with gradient-based optimization algorithms mandates that the gradients of c l (d) also be formulated, thus requiring design sensitivity analysis of failure probability. The focus of this work is to solve a general high-dimensional RBDO problem described by (1) for arbitrary functions y l (X), l=1,2,⋯ ,K, and arbitrary probability distributions of X.
3 Polynomial dimensional decomposition
Let y(X):=y(X 1,⋯ ,X N ) represent any one of the random functions y l , l=1,⋯ ,K, introduced in Section 2, and let \(\mathcal {L}_{2}({\Omega }_{\mathbf {d}},\mathcal {F}_{\mathbf {d}},P_{\mathbf {d}})\) represent a Hilbert space of square-integrable functions y with respect to the probability measure f X (x;d)d x supported on \(\mathbb {R}^{N}\). Assuming independent coordinates, the joint probability density function of X is expressed by the product, \(f_{\mathbf {\mathbf {X}}}(\mathbf {x};\mathbf {d})={{\prod }_{i=1}^{i=N}}f_{X_{i}}(x_{i};\mathbf {d})\), of marginal probability density functions \(f_{X_{i}}:\mathbb {R}\to \mathbb {R}_{0}^{+}\) of X i , i=1,⋯ ,N, defined on its probability triple \(({\Omega }_{i,\mathbf {d}},\mathcal {F}_{i,\mathbf {d}},P_{i,\mathbf {d}})\) with a bounded or an unbounded support on \(\mathbb {R}\). Then, for a given subset u⊆{1,⋯ ,N}, \(f_{\mathbf {X}_{u}}(\mathbf {x}_{u};\mathbf {d}):={\textstyle {\prod }_{p=1}^{|u|}}f_{i_{p}}(x_{i_{p}};\allowbreak \mathbf {d})\) defines the marginal density function of the subvector \(\mathbf {X}_{u}=(X_{i_{1}},\cdots ,X_{i_{|u|}})^{T}\) of X.
Let {ψ i j (X i ;d); j=0,1,⋯ } be a set of univariate orthonormal polynomial basis functions in the Hilbert space \(\mathcal {L}_{2}({\Omega }_{i,\mathbf {d}},\mathcal {F}_{i,\mathbf {d}},P_{i,\mathbf {d}})\) that is consistent with the probability measure P i,d of X i for a given design d, where i=1,⋯ ,N. For a given ∅≠u={i 1,⋯ ,i |u|}⊆{1,⋯ ,N}, 1≤|u|≤N, 1≤i 1<⋯<i |u|≤N, denote by \((\times _{p=1}^{p=|u|}{\Omega }_{i_{p},\mathbf {d}},\allowbreak \times _{p=1}^{p=|u|}\mathcal {F}_{i_{p},\mathbf {d}},\times _{p=1}^{p=|u|}P_{i_{p},\mathbf {d}})\) the product probability triple of the subvector X u . Since the probability density function of X u is separable (independent), the product polynomial \(\psi _{u\mathbf {j}_{|u|}}\allowbreak (\mathbf {X}_{u};\allowbreak \mathbf {d}):=\allowbreak {\prod }_{p=1}^{|u|}\allowbreak \psi _{i_{p}j_{p}}(X_{i_{p}};\mathbf {d})\), where \(\mathbf {j}_{|u|}=(j_{1},\cdots ,j_{|u|})\in \mathbb {N}_{0}^{|u|}\) is a |u|-dimensional multi-index, constitutes an orthonormal basis in \(\mathcal {L}_{2}(\allowbreak \times _{p=1}^{p=|u|}{\Omega }_{i_{p},\mathbf {d}},\times _{p=1}^{p=|u|}\allowbreak \mathcal {F}_{i_{p},\mathbf {d}},\times _{p=1}^{p=|u|}P_{i_{p},\mathbf {d}})\).
The PDD of a square-integrable function y represents a hierarchical expansion (Rahman 2008, 2009a)
in terms of a set of random multivariate orthonormal polynomials of input variables with increasing dimensions, where
and
are various expansion coefficients. The inner sum of (2) precludes j 1,⋯ ,j |u|≠0, that is, the individual degree of each variable X i in \(\psi _{u\mathbf {j}_{|u|}},\ i\in u\), can not be zero since \(\psi _{u\mathbf {j}_{|u|}}(\mathbf {X}_{u};\mathbf {d})\) is a zero-mean strictly |u|-variate function. Derived from the ANOVA dimensional decomposition (Efron and Stein 1981), (2) provides an exact representation because it includes all main and interactive effects of input variables. For instance, |u|=0 corresponds to the constant component function y ∅ , representing the mean effect of y; |u|=1 leads to the univariate component functions, describing the main effects of input variables, and |u|=S, 1<S≤N, results in the S-variate component functions, facilitating the interaction among at most S input variables \(X_{i_{1}},\cdots ,X_{i_{S}}\), 1≤i 1<⋯<i S ≤N. Further details of PDD are available elsewhere (Rahman 2008, 2009a).
Equation (2) contains an infinite number of coefficients, emanating from infinite numbers of orthonormal polynomials. In practice, the number of coefficients must be finite, say, by retaining finite-order polynomials and reduced-degree interaction among input variables. Doing so results in a truncated PDD and concomitant approximation, but there is more than one way to perform the truncation, described as follows.
3.1 Truncated PDD approximation
The PDD in (2) is grounded on a fundamental conjecture known to be true in many real-world applications: given a high-dimensional function y, its |u|-variate component functions decay rapidly with respect to |u|, leading to accurate lower-variate approximations of y. Furthermore, the largest order of polynomials in each variable can be restricted to a finite integer. Indeed, given the integers 0≤S<N and 1≤m<∞ for all 1≤|u|≤S and the ∞-norm ||j |u||| ∞ := max(j 1,⋯ ,j |u|), the truncated PDD (Rahman 2008, 2009a)
leads to the S-variate, mth-order PDD approximation, which for S>0 includes interactive effects of at most S input variables \(X_{i_{1}},\cdots ,X_{i_{S}}\), 1≤i 1<⋯<i S ≤N, on y. It is elementary to show that when S→N and/or m→∞, \(\tilde {y}_{S,m}\) converges to y in the mean-square sense, generating a hierarchical and convergent sequence of approximations of y. The truncation parameters S and m depend on the dimensional structure and nonlinearity of a stochastic response. The higher the values of S and m, the higher the accuracy, but also the computational cost that is endowed with an Sth-order polynomial computational complexity (Rahman 2008, 2009a). The S-variate, mth-order PDD approximation will be referred to as simply truncated PDD approximation in this paper.
3.2 Adaptive-sparse PDD approximation
In practice, the dimensional hierarchy or nonlinearity, in general, is not known apriori. Therefore, indiscriminately assigning the truncation parameters S and m is not desirable, nor is it possible to do so when a stochastic solution is obtained via complex numerical algorithms. In which case, one should perform these truncations adaptively by progressively drawing in higher-variate or higher-order contributions as appropriate. Furthermore, given 1≤S<N, all S-variate component functions of PDD may not contribute equally or even appreciably to be considered in the resulting approximation. Therefore, a sparse approximation, expelling component functions with negligible contributions, is possible. Indeed, addressing these issues, Yadav and Rahman (2014b) developed two AS-PDD approximations, but they have yet to be exploited for solving RBDO problems.
Based on the authors’ past experience, an S-variate PDD approximation, where S≪N, is adequate, when solving real-world engineering problems, with the computational cost varying polynomially (S-order) with respect to the number of variables (Rahman 2008, 2009a). As an example, consider the selection of S=2 for solving a stochastic problem in 100 dimensions by a bivariate PDD approximation, comprising 100×99/2=4950 bivariate component functions. If all such component functions are included, then the computational effort for even a full bivariate PDD approximation may exceed the computational budget allocated to solving this problem. But many of these component functions contribute little to the probabilistic characteristics sought and can be safely ignored. Similar conditions may prevail for higher-variate component functions. Henceforth, define an S-variate, partially AS-PDD approximation (Yadav and Rahman 2014b)
of y(X), where
defines the approximate m u th-order approximation of the global sensitivity index of y(X) for a subvector X u , ∅≠u⊆{1,⋯ ,N}, of input variables X and
defines the relative change in the approximate global sensitivity index when the largest polynomial order increases from m u −1 to m u , provided that 2≤m u <∞ and \(\tilde {G}_{u,m_{u}-1}\ne 0\). Here,
is the variance of y(X). Then the sensitivity indices \(\tilde {G}_{u,m_{u}}\) and \({\Delta }\tilde {G}_{u,m_{u}}\) provide an effective means to truncate the PDD in (2) both adaptively and sparsely. Equation (6) is attained by subsuming at most S-variate component functions, but fulfilling two inclusion criteria: (1) \(\tilde {G}_{u,m_{u}}>\epsilon _{1}\) for 1≤|u|≤S≤N, and (2) \({\Delta }\tilde {G}_{u,m_{u}}>\epsilon _{2}\) for 1≤|u|≤S≤N, where 𝜖 1≥0 and 𝜖 2≥0 are two non-negativetolerances. The resulting approximation is partially adaptive because the truncations are restricted to at most S-variate component functions of y. When S=N, (6) becomes the fully AS-PDD approximation (Yadav and Rahman 2014b). Figure 1 presents a computational flowchart to accomplish the numerical implementation of both variants of the AS-PDD approximation. The algorithmic details of the iterative process are available elsewhere (Yadav and Rahman 2014b) and are not included here for brevity.
A flowchart for constructing AS-PDD approximations (Yadav and Rahman 2014b)
The S-variate, partially AS-PDD approximation behaves differently from the S-variate, mth-order PDD approximation. While the latter approximation includes a sum containing at most S-variate component functions, the former approximation may or may not include all such component functions, depending on the tolerances 𝜖 1>0 and 𝜖 2>0. It is elementary to show that \(\bar {y}_{S}\) approaches \(\tilde {y}_{S,m}\) in the mean-square sense as 𝜖 1→0,𝜖 2→0, and m→∞. The S-variate, partially adaptive-sparse PDD approximation will be referred to as simply AS-PDD approximation in this paper.
It is important to note that the existing adaptive-sparse approximations, such as the one reported by Hu and Youn (2011), are based on polynomial chaos expansion (PCE). In a previous work (Rahman and Yadav 2011), the authors found the PDD method to be more accurate or computationally efficient than the PCE method. Therefore, for stochastic design optimization, an adaptive method rooted in PDD is preferred over that derived from PCE.
4 Reliability analysis
A fundamental problem in reliability analysis, required for evaluating the probabilistic constraints in (1), entails calculation of the failure probability
where Ω F is the failure domain and \(I_{{\Omega }_{F}}(\mathbf {x})\) is the associated indicator function, which is equal to one when x∈Ω F and zero otherwise. Depending on the failure domain, as explained in Section 2, Ω F :={x:y(x)<0} for component reliability analysis and Ω F :={x:∪ i y i (x)<0} and Ω F :={x:∩ i y i (x)<0} for series- and parallel-type system reliability analyses, respectively. In this section, two methods are presented for estimating the failure probability. The AS-PDD-SPA method, which blends the AS-PDD approximation with SPA, is described first. Then the AS-PDD-MCS method, which exploits the AS-PDD approximation for MCS, is elucidated.
4.1 The AS-PDD-SPA method
Let F y (ξ):=P d [y≤ξ] be the cumulative distribution function (CDF) of y(X). Assume that the PDF f y (ξ):=d F y (ξ)/d ξ exists and suppose that the cumulant generating function (CGF)
of y converges for \(t\in \mathbb {R}\) in some non-vanishing interval containing the origin. Using inverse Fourier transformation, exponential power series expansion, and Hermite polynomial approximation, Daniels (1954) developed an SPA formula to approximately evaluate f y (ξ). However, the success of such a formula is predicated on how accurately the CGF and its derivatives, if they exist, are calculated. In fact, determining K y (t) is immensely difficult because it is equivalent to knowing all higher-order moments of y. To mitigate this problem, consider the Taylor series expansion of
at t=0, where κ (r):=d r K y (0)/d t r,\(r\in \mathbb {N}\), is known as the rth-order cumulant of y(X). If some of these cumulants are effectively estimated, then a truncated Taylor series provides a useful means to approximate K y (t). For instance, assume that, given a positive integer Q<∞, the approximate raw moments \(\bar {m}_{S}^{(r)}(\mathbf {d}):={\int }_{\mathbb {R}^{N}}{\displaystyle \bar {y}_{S}^{r}(\mathbf {x})f_{\mathbf {X}}(\mathbf {x};\mathbf {d})d\mathbf {x}}=:\mathbb {E}_{\mathbf {d}}\left [\bar {y}_{S}^{r}(\mathbf {X})\right ]\) of order 1≤r≤Q have been calculated with sufficient accuracy using an S-variate, AS-PDD approximation \(\bar {y}_{S}(\mathbf {X})\) of y(X), involving integrations of elementary polynomial functions and requiring no expensive evaluation of the original function y(X). Nonetheless, because \(\bar {y}_{S}(\mathbf {X})\) is a superposition of at most S-variate component functions of independent variables, the largest dimension of the integrals is min(r S,N). Therefore, many high-dimensional integrations are involved if min(r S,N) is large, even though the \(\bar {y}_{S}(\mathbf {X})\) is known analytically. An alternative approach, adopted in the paper, is dimension-reduction integration, approximating the N-dimensional integral by
and hence involving at most T-dimensional lower-variate Gauss quadratures, where T≤N is a positive integer. When T≪N, the computational cost of statistical moment analysis is markedly reduced. Then the corresponding approximate cumulants are easily obtained from the well-known cumulant-moment relationship,
where the functional argument d serves as a reminder that the moments and cumulants all depend on the design vector d. Setting \(\kappa ^{(r)}=\bar {\kappa }_{S}^{(r)}\) for r=1,⋯ ,Q, and zero otherwise in (12), the result is an S-variate, AS-PDD approximation
of the Qth-order Taylor series expansion of K y (t). It is elementary to show that \(\bar {K}_{y,Q,S}(t;\mathbf {d})\to K_{y}(t)\) when 𝜖 1→0, 𝜖 2→0, S→N, and Q→∞.
Using the CGF approximation in (15), Daniels’ SPA leads to the explicit formula (Daniels 1954),
for the approximate PDF of y, where the subscript “APS” stands for AS-PDD-SPA and t s is the saddlepoint that is obtained from solving
with \(\bar {K}^{\prime }_{y,Q,S}(t;\mathbf {d}):=d\bar {K}{}_{y,Q,S}(t;\mathbf {d})/dt\) and \(\bar {K}^{\prime \prime }_{y,Q,S}(t;\mathbf {d}):=d^{2}\bar {K}{}_{y,Q,S}(t;\mathbf {d})/dt^{2}\) defining the first- and second-order derivatives, respectively, of the approximate CGF of y with respect to t. Furthermore, based on a related work of Lugannani and Rice (1980), the approximate CDF of y becomes
where Φ(⋅) and ϕ(⋅) are the CDF and PDF, respectively, of the standard Gaussian variable and sgn(t s )=+1,−1,or 0, depending on whether t s is positive, negative, or zero. According to (18), the CDF of y at a point ξ is obtained using solely the corresponding saddlepoint t s , that is, without the need to integrate (16) from −∞ to ξ.
Finally, using Lugannani and Rice’s formula, the AS-PDD-SPA estimate \(\bar {P}_{F,APS}(\mathbf {d})\) of the component failure probability P F (d):=P d [y(X)<0] is obtained as
the AS-PDD-SPA generated CDF of y at ξ=0. It is important to recognize that no similar SPA-based formulae are available for the joint PDF or joint CDF of dependent stochastic responses. Therefore, the AS-PDD-SPA method in the current form cannot be applied to general system reliability analysis.
The AS-PDD-SPA method contains several truncation parameters that should be carefully selected. For instance, if Q is too small, then the truncated CGF from (15) may spoil the method, regardless of how large is the S chosen in the AS-PDD approximation. On the other hand, if Q is overly large, then many higher-order moments involved may not be accurately calculated by the PDD approximation. More significantly, a finite-order truncation of CGF may cause loss of convexity of the actual CGF, meaning that the one-to-one relationship between ξ and t s in (17) is not ensured for every threshold ξ. Furthermore, the important property \(\bar {K}^{\prime \prime }_{y,Q,S}(t_{s};\mathbf {d})>0\) may not be maintained. To resolve this quandary, Yuen et al. (2007) presented for Q=4 several distinct cases of the cumulants, describing the interval (t l ,t u ), where −∞≤t l ≤0 and 0≤t u ≤∞, such that t l ≤t s ≤t u and \(\bar {K}^{\prime \prime }_{y,Q,S}(t_{s};\mathbf {d})>0\), ruling out any complex values of the square root in (16) or (18). If ξ falls into these specified thresholds, then the saddlepoint t s is uniquely determined from (17), leading to the CDF or reliability in (18) or (19). Otherwise, the AS-PDD-SPA method will fail to provide a solution. Further details of these thresholds can be found elsewhere (Rahman and Ren 2014).
4.2 The AS-PDD-MCS method
Depending on component or system reliability analysis, let \(\bar {\Omega }_{F,S}:=\{\mathbf {x}:\bar {y}_{S}(\mathbf {x})<0\}\) or \(\bar {\Omega }_{F,S}:=\{\mathbf {x}:\cup _{i}\bar {y}_{i,S}(\mathbf {x})<0\}\) or \(\bar {\Omega }_{F,S}:=\{\mathbf {x}:\cap _{i}\bar {y}_{i,S}(\mathbf {x})<0\}\) be an approximate failure set as a result of S-variate, AS-PDD approximations \(\bar {y}_{S}(\mathbf {X})\) of y(X) or \(\bar {y}_{i,S}(\mathbf {X})\) of y i (X). Then the AS-PDD-MCS estimate of the failure probability P F (d) is
where the subscript “APM” stands for AS-PDD-MCS, L is the sample size, x (l) is the lth realization of X, and \(I_{\bar {\Omega }_{F,S}}(\mathbf {x})\) is another indicator function, which is equal to one when \(\mathbf {x}\in \bar {\Omega }_{F,S}\) and zero otherwise.
Note that the simulation of the PDD approximation in (20) should not be confused with crude MCS commonly used for producing benchmark results. The crude MCS, which requires numerical calculations of y(x (l)) or y i (x (l)) for input samples x (l),l=1,⋯ ,L, can be expensive or even prohibitive, particularly when the sample size L needs to be very large for estimating small failure probabilities. In contrast, the MCS embedded in the AS-PDD approximation requires evaluations of simple polynomial functions that describe \(\bar {y}_{S}(\mathbf {x}^{(l)})\) or \(\bar {y}_{i,S}(\mathbf {x}^{(l)})\). Therefore, an arbitrarily large sample size can be accommodated in the AS-PDD-MCS method. In which case, the AS-PDD-MCS method also furnishes the approximate CDF \(\bar {F}_{y,PM}(\xi ;\mathbf {d})\allowbreak :=P_{\mathbf {d}}[\bar {y}_{S}(\mathbf {X})\le \xi ]\) of y(X) or even joint CDF of dependent stochastic responses, if desired.
Although the AS-PDD-SPA and AS-PDD-MCS methods are both rooted in the same PDD approximation, the former requires additional layers of approximations to calculate the CGF and saddlepoint. Therefore, the AS-PDD-SPA method, when it works, is expected to be less accurate than the AS-PDD-MCS method at comparable computational efforts. However, the AS-PDD-SPA method facilitates an analytical means to estimate the probability distribution and reliability — a convenient process not supported by the AS-PDD-MCS method. The respective properties of both methods extend to sensitivity analysis, presented in the following section.
5 Design sensitivity analysis
When solving RBDO problems employing gradient-based optimization algorithms, at least first-order derivatives of the failure probability with respect to each design variable are required. Therefore, the AS-PDD-SPA and AS-PDD-MCS methods for reliability analysis in Section 4 are expanded for sensitivity analysis of the failure probability in the following subsections.
5.1 Score functions
Let
be a generic probabilistic response, where h(d) and g(x) are either P F (d) and \(I_{{\Omega }_{F}}(\mathbf {x})\) for reliability analysis, or m (r)(d) and y r(x) for statistical moment analysis, where \(m^{(r)}(\mathbf {d})=\mathbb {E}_{\mathbf {d}}\left [{y_{S}^{r}}(\mathbf {X})\right ]\), r=1,⋯ ,Q, is the rth-order raw moment of y(X). Suppose that the first-order derivative of h(d) with respect to a design variable d k , 1≤k≤M, is sought. Taking the partial derivative of h(d) with respect to d k and then applying the Lebesgue dominated convergence theorem (Browder 1996), which permits the differential and integral operators to be interchanged, yields the sensitivity
provided that f X (x;d)>0 and the derivative ∂lnf X (x;d)/∂ d k exists. In the last line of (22), \(s_{d_{k}}^{(1)}(\mathbf {X};\mathbf {d})\allowbreak :=\allowbreak \partial \ln f_{\mathbf {X}}(\mathbf {X};\mathbf {d})\left /\partial d_{k}\right .\) is known as the first-order score function for the design variable d k (Rubinstein and Shapiro 1993; Rahman 2009b). According to (21) and (22), the generic probabilistic response and its sensitivities have both been formulated as expectations of stochastic quantities with respect to the same probability measure, facilitating their concurrent evaluations in a single stochastic simulation or analysis.
Remark 1
The evaluation of score functions, \(s_{d_{k}}^{(1)}(\mathbf {X};\mathbf {d})\), k=1,⋯ ,M, requires differentiating only the PDF of X. Therefore, the resulting score functions can be determined easily and, in many cases, analytically — for instance, when X follows classical probability distributions (Rahman 2009b). If the density function of X is arbitrarily prescribed, the score functions can be calculated numerically, yet inexpensively, since no evaluation of the performance function is involved.
When X comprises independent variables, as assumed here, \(\ln f_{\mathbf {X}}(\mathbf {X};\mathbf {d})=\sum \limits {}_{i=1}^{i=N}\ln f_{X_{i}}(x_{i};\mathbf {d})\) is a sum of N univariate log-density (marginal) functions of random variables. Hence, in general, the score function for the kth design variable, expressed by
is also a sum of univariate functions \(s_{ki}(X_{i};\mathbf {d}):=\partial \ln f_{X_{i}}\allowbreak (X_{i};\mathbf {d})\left /\partial d_{k}\right .\), i=1,⋯ ,N, which are the derivatives of log-density (marginal) functions. If d k is a distribution parameter of a single random variable \(X_{i_{k}}\), then the score function reduces to \(s_{d_{k}}^{(1)}(\mathbf {X};\mathbf {d})=\partial \ln f_{X_{i_{k}}}(X_{i_{k}};\mathbf {d})\allowbreak \left /\partial d_{k}\right .=:s_{ki_{k}}(X_{i_{k}};\mathbf {d})\), the derivative of the log-density (marginal) function of \(X_{i_{k}}\), which remains a univariate function. Nonetheless, combining (22) and (23), the sensitivity of the generic probabilistic response h(d) is obtained as
the sum of expectations of products comprising stochastic response and log-density derivative functions with respect to the probability measure P d , \(\mathbf {d}\in \mathcal {D}\).
5.2 The AS-PDD-SPA method
Suppose that the first-order derivative \(\partial \bar {F}_{y,APS}(\xi ;\mathbf {d})/\partial d_{k}\) of the CDF \(\bar {F}_{y,APS}(\xi ;\mathbf {d})\) of \(\bar {y}_{S}(\mathbf {X})\), obtained by the AS-PDD-SPA method, with respect to a design variable d k , is desired. Applying the chain rule on the derivative of (18),
is obtained via the partial derivatives
where the derivatives of moments, that is, \(\partial \bar {m}_{S}^{(r)}/\partial d_{k}\), r=1,⋯ ,Q, required to calculate the derivatives of cumulants, are also obtained by the dimension-reduction numerical integration. In which case,
requiring also at most T-dimensional lower-variate Gauss quadratures. The remaining two partial derivatives in (25) are expressed by
and
where
The expressions of the partial derivatives \(\partial \bar {K}_{y,Q,S}/\partial \bar {\kappa }_{S}^{(r)}\), \(\partial \bar {K}^{\prime }_{y,Q,S}/\partial \bar {\kappa }_{S}^{(r)}\), and \(\partial \bar {K}^{\prime \prime }_{y,Q,S}/\partial \bar {\kappa }_{S}^{(r)}\), not explicitly presented here, can be easily derived from (15) once the cumulants \(\bar {\kappa }_{S}^{(r)},\ r=1,\cdots ,Q\), and the saddlepoint t s are obtained.
Henceforth, the first-order derivative of the failure probability estimate by the AS-PDD-SPA method is easily determined from
the sensitivity of the CDF evaluated at ξ=0.
5.3 The AS-PDD-MCS method
Taking the partial derivative of the AS-PDD-MCS estimate of the failure probability in (20) with respect to d k and then following the same arguments in deriving (22) produces
where L is the sample size, x (l) is the lth realization of X, and \(I_{\bar {\Omega }_{F,S}}(\mathbf {x})\) is the AS-PDD-generated indicator function. Again, they are easily and inexpensively determined by sampling analytical functions that describe \(\bar {y}_{S}\) and \(s_{d_{k}}^{(1)}\). A similar sampling procedure can be employed to calculate the sensitivity of the AS-PDD-MCS-generated CDF \(\bar {F}_{y,APM}(\xi ;\mathbf {d}):=P_{\mathbf {d}}[\bar {y}_{S}(\mathbf {X})\le \xi ]\). It is important to note that the effort required to calculate the failure probability or CDF also delivers their sensitivities, incurring no additional cost. Setting S=1 or 2 in (20) and (34), the univariate or bivariate AS-PDD approximation of the failure probability and its sensitivities are determined.
Remark 2
The score function method has the nice property that it requires differentiating only the underlying PDF f X (x;d). The resulting score functions can be easily and, in most cases, analytically determined. If the performance function is not differentiable or discontinuous − for example, the indicator function that comes from reliability analysis − the proposed method still allows evaluation of the sensitivity if the density function is differentiable. In reality, the density function is often smoother than the performance function, and therefore the proposed sensitivity methods will be able to calculate sensitivities for a wide variety of complex mechanical systems.
Remark 3
The AS-PDD-SPA and AS-PDD-MCS methods, discussed in Sections 3 and 4, are predicated on the S-variate, AS-PDD approximation \(\bar {y}_{S}(\mathbf {X})\)(6) and are, therefore, new. The authors had developed in a prequel similar methods, called the PDD-SPA and PDD-MCS methods (Rahman and Ren 2014), employing the truncated PDD approximation \(\tilde {y}_{S,m}(\mathbf {X})\)(5). The new methods will be contrasted with the existing ones in the Numerical Examples section.
6 Expansion coefficients by dimension-reduction integration
The determination of AS-PDD expansion coefficients y ∅ (d) and \(C_{u\mathbf {j}_{|u|}}(\mathbf {d})\) is vitally important for reliability analysis, including its design sensitivities. As defined in (3) and (4), the coefficients involve various N-dimensional integrals over \(\mathbb {R}^{N}\). For large N, a multivariate numerical integration employing an N-dimensional tensor product of a univariate quadrature formula is computationally prohibitive and is, therefore, ruled out. An attractive alternative approach entails dimension-reduction integration, which was originally developed by Xu and Rahman (2004) for high-dimensional numerical integration. For calculating y ∅ and \(C_{u\mathbf {j}_{|u|}}\), this is accomplished by replacing the N-variate function y in (3) and (4) with an R-variate RDD approximation at a chosen reference point, where R≤N. The result is a reduced integration scheme, requiring evaluations of at most R-dimensional integrals.
Let \(\mathbf {c}=(c_{1},\cdots ,c_{N})^{T}\in \mathbb {R}^{N}\), which is commonly adopted as the mean of X, be a reference point, and y(x v ,c −v ) represent an |v|-variate RDD component function of y(x), where v⊆{1,⋯ ,N} (Rahman 2011, 2014). Given a positive integer S≤R≤N, when y(x) in (3) and (4) is replaced with its R-variate RDD approximation, the coefficients y ∅ (d) and \(C_{u\mathbf {j}_{|u|}}(\mathbf {d})\) are estimated from (Xu and Rahman 2004)
and
respectively, requiring evaluation of at most R-dimensional integrals. The reduced integration facilitates calculation of the coefficients approaching their exact values as R→N and is significantly more efficient than performing one N-dimensional integration, particularly when R≪N. Hence, the computational effort is significantly lowered using the dimension-reduction integration. For instance, when R=1 or 2, (35) and (36) involve one-, or at most, two-dimensional integrations, respectively. Nonetheless, numerical integrations are still required for performing various |v|-dimensional integrals over \(\mathbb {R}^{|v|}\), where 0≤|v|≤R. When R>1, the multivariate integrations involved can be approximated using full-grid and sparse-grid quadratures, including their combination, described as follows.
6.1 Full-grid integration
The full-grid dimension-reduction integration entails constructing a tensor product of the underlying univariate quadrature rules. For a given v⊆{1,⋯ ,N}, 1<|v|≤R, let v={i 1,⋯i |v|}, where 1≤i 1<⋯<i |v|≤N. Denote by \(\{x_{{\normalcolor i_{p}}}^{(1)},\cdots ,x_{i_{p}}^{(n_{v})}\}\subset \mathbb {R}\) a set of integration points of \(x_{i_{p}}\) and by \(\{w_{i_{p}}^{(1)},\cdots ,w_{i_{p}}^{(n_{v})}\}\) the associated weights generated from a chosen univariate quadrature rule and a positive integer \(n_{v}\in \mathbb {N}\). Denote by \(P^{(n_{v})}=\times _{p=1}^{p=|v|}\{x_{i_{p}}^{(1)},\cdots ,x_{i_{p}}^{(n_{v})}\}\) the rectangular grid consisting of all integration points generated by the variables indexed by the elements of v. Then the coefficients using dimension-reduction numerical integration with a full grid are approximated by
where \(\mathbf {x}_{v}^{(\mathbf {k}_{|v|})}=\{x_{i_{1}}^{(k_{1})},\cdots ,x_{i_{|v|}}^{(k_{|v|})}\}\) and \(w^{(\mathbf {k}_{|v|})}={\prod }_{p=1}^{p=|v|}\allowbreak w_{i_{p}}^{(k_{p})}\) is the product of integration weights generated by the variables indexed by the elements of v. For independent coordinates of X, as assumed here, a univariate Gauss quadrature rule is commonly used, where the integration points and associated weights depend on the probability distribution of X i . The quadrature rule is readily available, for example, as the Gauss-Hermite or Gauss-Legendre quadrature rule, when X i follows Gaussian or uniform distribution (Gautschi 2004). For an arbitrary probability distribution of X i , the Stieltjes procedure can be employed to generate the measure-consistent Gauss quadrature formulae (Gautschi 2004). An n v -point Gauss quadrature rule exactly integrates a polynomial of total degree at most 2n v −1.
The calculation of y ∅ and \(C_{u\mathbf {j}_{|u|}}\) from (37) and (38) involves at most R-dimensional tensor products of an n v -point univariate quadrature rule, requiring the following deterministic responses or function evaluations: y(c), \(y(\mathbf {x}_{v}^{(\mathbf {j}_{|v|})},\mathbf {c}_{-v})\) for i=0,⋯ ,R, v⊆{1,⋯ ,N}, |v|=R−i, and \(\mathbf {j}_{|v|}\in P^{(n_{v})}\). Accordingly, the total cost for estimating the PDD expansion coefficients entails
function evaluations, encountering a computational complexity that is Rth-order polynomial − for instance, linear or quadratic when R=1 or 2 − with respect to the number of random variables or integration points. For R<N, the technique alleviates the curse of dimensionality to an extent determined by R. The dimension-reduction integration in conjunction with the full-grid quadrature rule was used for constructing truncated PDD approximations (Rahman 2008, 2009a).
6.2 Sparse-grid integration
Although the full-grid dimension-reduction integration has been successfully applied to the calculation of the PDD expansion coefficients in the past (Rahman 2008, 2009a; Ren and Rahman 2013), it faces a major drawback when the polynomial order m u for a PDD component function y u needs to be modulated for adaptivity. As the value of m u is incremented by one, a completely new set of integration points is generated by the univariate Gauss quadrature rule, rendering all expensive function evaluations on prior integration points as useless. Therefore, a nested Gauss quadrature rule, such as the fully symmetric interpolatory rule capable of exploiting dimension-reduction integration, becomes desirable.
The fully symmetric interpolatory (FSI) rule, developed by Genz and his associates (Genz 1986; Genz and Keister 1996), is a sparse-grid integration technique for performing high-dimensional numerical integration. Applying this rule to the |v|-dimensional integrations in (35) and (36), the PDD expansion coefficients are approximated by
where v={i 1,⋯i |v|}, \(\mathbf {t}_{|v|}=(t_{i_{1}},\cdots ,t_{i_{|v|}})\), \(\mathbf {p}_{|v|}=(p_{i_{1}},\cdots ,p_{i_{|v|}})\), and
with \(\left \Vert \mathbf {p}_{|v|}\right \Vert :=\sum \limits {}_{r=1}^{|v|}p_{i_{r}}\) is the set of all distinct |v|-partitions of the integers \(0,1,\cdots ,\tilde {n}_{v}\), and \({\Pi }_{\mathbf {p}_{|v|}}\) is the set of all permutations of p |v|. The innermost sum over t |v| is taken over all of the sign combinations that occur when \(t_{i_{r}}=\pm 1\) for those values of i r with generators \(\alpha _{q_{i_{r}}}\ne 0\) (Genz and Keister 1996). The weight
where K is the number of nonzero components in p |v| and a i is a constant that depends on the probability measure of X i , for instance,
for i>0 and a 0=1 when X i follows the standard Gaussian distribution (Genz and Keister 1996). An \(\tilde {n}_{v}\)-parameter FSI rule exactly integrates a polynomial of degree at most \(2\tilde {n}_{v}-1\).
The number of function evaluations by the original FSI rule (Genz 1986) increases rapidly as |v| and \(\tilde {n}_{v}\) increase. To enhance the efficiency, Genz and Keister (1996) proposed an extended FSI rule in which the function evaluations are significantly reduced if the generator set is chosen such that some of the weights \(w_{\mathbf {\mathbf {p}_{|v|}}}\) are zero. The pivotal step in constructing such an FSI rule is to extend a (2β+1)-point Gauss-Hermite quadrature rule by adding 2γ points or generators ±α β+1,±α β+2,…,±α β+γ with the objective of maximizing the degree of polynomial exactness of the extended rule, where \(\beta \in \mathbb {N}\) and \(\gamma \in \mathbb {N}\). Genz and Keister (1996) presented a special case of initiating the FSI rule from the univariate Gauss-Hermite rule over the interval (−∞,∞). The additional generators in this case are determined as roots of the monic polynomial ζ 2γ+t γ−1 ζ 2γ−1+⋯+t 0, where the coefficients t γ−1,⋯ ,t 0 are obtained by invoking the condition
where γ>β. A new set of generators is propagated based on the prior rule and, therefore, as the polynomial degree of exactness of the rule increases, all the previous points and the expensive function evaluations over those points are preserved. A remarkable feature of the extended FSI rule is that the choice of generators is such that some of the weights \(w_{\mathbf {\mathbf {p}}_{|v|}}=0\) in each integration step of the extension (Genz and Keister 1996), thus eliminating the need for function evaluations at the integration points corresponding to zero weights, making the extended FSI rule significantly more efficient than its earlier version. The dimension-reduction integration in conjunction with the sparse-grid quadrature rule was used for constructing AS-PDD approximations of high-dimensional complex systems (Yadav and Rahman 2014b).
6.3 Combined sparse- and full-grids
The adaptive-sparse algorithm (Yadav and Rahman 2014b) described by Fig. 1, in tandem with the sparse-grid quadrature, should be employed to calculate the requisite AS-PDD expansion coefficients and hence determine the largest polynomial orders of PDD component functions retained. However, due to potential approximation errors, the expansion coefficients may need to be recalculated for at least two reasons.
The first source of error is low values of R set in the dimension-reduction integration. According to the algorithm, the largest polynomial orders maxu m u , ∅≠u⊆{1,⋯ ,N}, 1≤|u|≤S, associated with all S-variate PDD component functions, are determined using the expansion coefficients estimated by the dimension-reduction integration with R=|u|. For instance, the largest polynomial orders max{i}m {i}, i=1,⋯ ,N, of univariate (S=1) PDD component functions are ascertained employing the univariate expansion coefficients C i j , i=1,⋯ ,N, j=1,2,⋯, estimated with R=1 to keep the computational effort at minimum. However, from the authors’ recent experience, the setting R=1 is too low to warrant convergent solutions of complex RBDO problems, especially when the original function y contains significant interactive effects among input random variables. For an illustration, consider the function
of three independent standard Gaussian random variables X 1, X 2, and X 3 with zero means and unit variances. Selecting S=2 and sufficiently small tolerance parameters, let \(\bar {y}_{2}(X_{1},\allowbreak X_{2},\allowbreak X_{3})\) denote a bivariate, AS-PDD approximation, reproducing all terms of y(X 1,X 2,X 3). By definition, (4) yields the exact univariate, first-order coefficient C 11=7. However, setting R=1 for the dimension-reduction integration in (36), the adaptive-sparse algorithm produces an estimate of 5. The underestimation of C 11 originates from the failure to include the bivariate interactive term (1+X 1)2(1+X 2)2 of (46). Indeed, when R=2 is employed, (36) reproduces the exact value of 7. Therefore, the value of R must be raised to two to capture the two-variable interaction in this case and, in general, to S, which is the largest degree of interaction retained in a concomitant S-variate AS-PDD approximation. In other words, after the largest polynomial orders are determined by the adaptive-sparse algorithm, the AS-PDD coefficients need to be recalculated when S≥2. The authors propose doing so using full-grid dimension-reduction integration with R=S.
The second source of error is low-order Gauss quadrature. When calculating AS-PDD expansion coefficients \(C_{u\mathbf {j}_{|u|}}\) by (36), a low-order Gauss quadrature, selected merely according to the order of \(\psi _{u\mathbf {j}_{|u|}}(\mathbf {X}_{u};\mathbf {d})\) without accounting for maxu m u (reflecting the nonlinearity of y(x v ,c −v )), may result in inadequate or erroneous estimates. For example, consider the bivariate, first-order expansion coefficient C 1211 for the function in (46). According to (4), the exact value of C 1211=4. However, when the 2×2 Gauss quadrature is used in the dimension-reduction integration with R=2, the adaptive-sparse algorithm produces an estimate of 1. This is due to not accounting for the third-order term \({X_{1}^{3}}\) (max{1}m {1}=3) in (46), resulting in an under-integration by the order of Gauss quadrature chosen. Indeed, when the 3×2 Gauss quadrature is employed, the resulting estimate becomes 4, which is the exact value of C 1211. Therefore, the order of Gauss quadrature for the ith dimension in the dimension-reduction integration must be selected according to both maxi∈u m u and the order of the corresponding polynomial basis to accurately estimate all |u|-variate expansion coefficients. In other words, after the largest polynomial orders are determined by the adaptive-sparse algorithm, the AS-PDD coefficients need to be recalculated. Again, the authors propose doing so using full-grid dimension-reduction integration with a Gauss quadrature rule commensurate with maxi∈u m u .
6.4 Computational expense
For the AS-PDD approximation, the computational effort is commonly determined by the total number of original function evaluations required for calculating all necessary expansion coefficients. In solving an RBDO problem, which is presented in Section 7, the total computational effort stems from two types of calculations: (1) initial calculations involved in the adaptive-sparse algorithm to automatically determine the truncation parameters of PDD; and (2) final calculations of the AS-PDD expansion coefficients based on the knowledge of truncation parameters. The computational cost required by the initial calculations, that is, by the S-variate, adaptive-sparse algorithm, is discussed by Yadav and Rahman (2014b), although an explicit formula for the number of original function evaluations remains elusive. However, the computational cost can be bounded from above by
the number of function evaluations in the truncated S-variate, m maxth-order PDD approximation, where
is the largest order of polynomial expansions for all PDD component functions y u (X u ), ∅≠u⊆{1,⋯ ,N}, 1≤|u|≤S, such that \(\tilde {G}_{u,m_{u}}>\epsilon _{1}\), \({\Delta }\tilde {G}_{u,m_{u}}>\epsilon _{2}\). It is assumed here that the number of integration points at each dimension is m max+1. Therefore, the computational complexity of the S-variate AS-PDD approximation is at most an Sth-order polynomial with respect to the number of input variables or the largest order of polynomial. Therefore, S-variate AS-PDD approximation alleviates the curse of dimensionality to an extent determined by S, 𝜖 1, and 𝜖 2.
The number of original function evaluations required by the final calculations, that is, by recalculations of the AS-PDD expansion coefficients based on the known truncation parameters, can be obtained from another bound
when full-grid Gauss quadrature is employed. Here, the symbol ⌈t⌉ refers to the ceiling function, which is the smallest integer not less than t. Therefore, the recalculation of the expansion coefficients results in a computational expense in addition to that incurred by the adaptive-sparse algorithm. The total computational effort, measured in terms of the total number of function evaluations, is bounded by L I +L I I , and will be discussed in the Numerical Examples section.
7 Proposed RBDO methods
The PDD approximations described in the preceding sections provide a means to evaluate the constraint functions, including their design sensitivities, from a single stochastic analysis. No such approximation is required for the objective function, when it is a simple and explicit deterministic function of design variables. However, for complex mechanical design problems, for instance, Example 4 in the Numerical Examples section, the objective function is usually determined implicitly by intrinsic calculations from a computer-aided design code. In which case, the objective function and its design sensitivities may also be simultaneously evaluated by constructing PDD approximations of c 0(d) in the space of design variables d. Additional details of the PDD approximations of the objective function and its design sensitivities are not included here for brevity.
An integration of reliability analysis, design sensitivity analysis, and a suitable optimization algorithm should render a convergent solution of the RBDO problem in (1). However, new reliability and sensitivity analyses, entailing re-calculations of the PDD expansion coefficients, are needed at every design iteration. Therefore, a straightforward integration is expensive, depending on the cost of evaluating the objective and constraint functions and the requisite number of design iterations. In this section, a multi-point design process (Toropov et al. 1993; Ren and Rahman 2013), where a series of single-step, AS-PDD approximations are built on a local subregion of the design space, are presented for solving the RBDO problem.
7.1 Multi-point approximation
Let
be a rectangular domain, representing the design space of the RBDO problem defined by (1). For a scalar variable \(0<\beta _{k}^{(q)}\le 1\) and an initial design vector \(\mathbf {d}_{0}^{(q)}=(d_{1,0}^{(q)},\cdots ,d_{M,0}^{(q)})^{T}\), the subset
defines the qth subregion for q=1,2,⋯. Using the multi-point approximation (Toropov et al. 1993; Ren and Rahman 2013), the original RBDO problem in (1) is exchanged with a succession of simpler RBDO subproblems, expressed by
where \(\bar {c}_{0,S}^{(q)}(\mathbf {d})\), \(\bar {\Omega }_{F,l,S}^{(q)}(\mathbf {d})\) and \(\bar {c}_{l,S}^{(q)}(\mathbf {d})\) , l=1,2,⋯ ,K, are local S-variate, AS-PDD approximations of c 0(d), Ω F,l (d) and c l (d), respectively, at iteration q, where \(\bar {\Omega }_{F,l,S}^{(q)}(\mathbf {d})\) is defined using local, S-variate, AS-PDD approximations of \(\bar {y}_{l,S}^{(q)}(\mathbf {X})\) of y l (X), and \(d_{k,0}^{(q)}-\beta _{k}^{(q)}(d_{k,U}-d_{k,L})/2\) and \(d_{k,0}^{(q)}+\beta _{k}^{(q)}(d_{k,U}-d_{k,L})/2\), also known as the move limits, are the lower and upper bounds, respectively, of the kth coordinate of subregion \(\mathcal {D}^{(q)}\). In (52), the original objective and constraint functions are replaced with those derived locally from respective AS-PDD approximations. Since the PDD approximations are mean-square convergent (Rahman 2008, 2009a), they also converge in probability and in distribution. Therefore, given a subregion \(\mathcal {D}^{(q)}\), the solution of the associated RBDO subproblem also converges when 𝜖 1→0, 𝜖 2→0, and S→N.
7.2 Single-step procedure
The single-step procedure is motivated on solving each RBDO subproblem in (52) from a single stochastic analysis by sidestepping the need to recalculate the PDD expansion coefficients at every design iteration. It subsumes two important assumptions: (1) an S-variate, AS-PDD approximation \(\bar {y}_{S}\) of y at the initial design is acceptable for all possible designs in the subregion; and (2) the expansion coefficients for one design, derived from those generated for another design, are accurate.
Consider a change of the probability measure of X from f X (x;d)d x to f X (x;d ′)d x, where d and d ′ are two arbitrary design vectors corresponding to old and new designs, respectively. Let {ψ i j (X i ;d ′); j=0,1,⋯ } be a set of new orthonormal polynomial basis functions consistent with the marginal probability measure \(f_{X_{i}}(x_{i};\mathbf {d}^{\prime })dx_{i}\) of X i , producing new product polynomials \(\psi _{u\mathbf {j}_{|u|}}(\mathbf {X}_{u};\mathbf {d}^{\prime })={\prod }_{p=1}^{|u|}\psi _{i_{p}j_{p}}(X_{i_{p}};\mathbf {d}^{\prime })\), ∅≠u⊆{1,⋯ ,N}. Assume that the expansion coefficients, y ∅ (d) and \(C_{u\mathbf {j}_{|u|}}(\mathbf {d})\), for the old design have been calculated already. Then, the expansion coefficients for the new design are determined from
and
for all ∅≠u⊆{1,⋯ ,N} by recycling the old expansion coefficients and using orthonormal polynomials associated with both designs. The relationship between the old and new coefficients, described by (53) and (54), is exact and is obtained by replacing y in (3) and (4) with the right side of (2). However, in practice, when the S-variate, AS-PDD approximation (6) is used to replace y in (3) and (4), then the new expansion coefficients,
and
which are applicable for ∅≠u⊆{1,⋯ ,N}, 1≤|u|≤S, become approximate, although convergent. In the latter case, the integrals in (55) and (56) consist of finite-order polynomial functions of at most S variables and can be evaluated inexpensively without having to compute the original function y for the new design. Therefore, new stochastic analyses, all employing S-variate, AS-PDD approximation of y, are conducted with little additional cost during all design iterations, drastically curbing the computational effort in solving an RBDO subproblem.
7.3 The AS-PDD-SPA and AS-PDD-MCS methods
When the multi-point approximation is combined with the single-step procedure, the result is an accurate and efficient design process to solve the RBDO problem defined by (1). Depending on whether the AS-PDD-SPA or AS-PDD-MCS method is employed for reliability and design sensitivity analyses in the combined multi-point, single-step design process, two distinct RBDO methods are proposed: the AS-PDD-SPA method and the AS-PDD-MCS method. Using the single-step procedure in both methods, the design solution of an individual RBDO subproblem becomes the initial design for the next RBDO subproblem. Then, the move limits are updated, and the optimization is repeated iteratively until an optimal solution is attained. The method is schematically depicted in Fig. 2. Given an initial design d 0, a sequence of design solutions, obtained successively for each subregion \(\mathcal {D}^{(q)}\) and using the S-variate, AS-PDD approximation, leads to an approximate optimal solution \(\bar {\mathbf {d}}^{*}\) of the RBDO problem. In contrast, an AS-PDD approximation constructed for the entire design space \(\mathcal {D}\), if it commits large approximation errors, may possibly lead to a premature or an erroneous design solution. The multi-point approximation in the proposed methods overcomes this quandary by adopting smaller subregions and local AS-PDD approximations, whereas the single-step procedure diminishes the computational requirement as much as possible by recycling the PDD expansion coefficients.
When 𝜖 1→0, 𝜖 2→0, S→N, and q→∞, the reliability and its design sensitivities by the AS-PDD approximations converge to their exactness, yielding coincident solutions of the optimization problems described by (1) and (52). However, if the subregions are sufficiently small, then for finite and possibly low values of S and nonzero values of 𝜖 1 and 𝜖 2, (52) is expected to generate an accurate solution of (1), the principal motivation for developing the AS-PDD-SPA and AS-PDD-MCS methods.
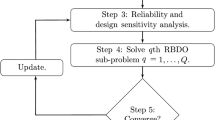
The AS-PDD-SPA and AS-PDD-MCS methods in conjunction with the combined multi-point, single-step design process is outlined by the following steps. The flow chart of this method is shown in Fig. 3.
- Step 1::
-
Select an initial design vector d 0. Define tolerances 𝜖 (1)>0, 𝜖 (2)>0, and 𝜖 (3)>0. Set the iteration q=1, \(\mathbf {d}_{0}^{(q)}=(d_{1,0}^{(q)},\cdots ,d_{M,0}^{(q)})^{T}=\mathbf {d}_{0}\). Define the subregion size parameters \(0<\beta _{k}^{(q)}\le 1\), k=1,⋯ ,M, describing \(\mathcal {D}^{(q)}=\times _{k=1}^{k=M}[d_{k,0}^{(q)}-\beta _{k}^{(q)}(d_{k,U}-d_{k,L})/2,d_{k,0}^{(q)}+\beta _{k}^{(q)}(d_{k,U}-d_{k,L})/2]\). Denote the subregion’s increasing history by a set H (0) and set it to empty. Set two designs d f =d 0 and d f,l a s t ≠d 0 such that ||d f −d f,l a s t ||2>𝜖 (1). Set \(\mathbf {d}_{*}^{(0)}=\mathbf {d}_{0}\), q f,l a s t =1 and q f =1. Usually, a feasible design should be selected to be the initial design d 0. However, when an infeasible initial design is chosen, a new feasible design can be obtained during the iteration if the initial subregion size parameters are large enough.
- Step 2::
-
Define tolerances 𝜖 1>0 and 𝜖 2>0. Use the adaptive PDD algorithm together with sparse-grid integration to obtain truncation parameters of c 0(d) and y l (X), l=1,⋯ ,K at current design \(\mathbf {d}_{0}^{(q)}\). Set \(\mathbf {d}_{AS}=\mathbf {d}_{0}^{(q)}\).
- Step 3::
-
Use (q>1) the PDD truncation parameters obtained in Step 2. At \(\mathbf {d}=\mathbf {d}_{0}^{(q)}\), generate the AS-PDD expansion coefficients, y ∅ (d) and \(\allowbreak C_{u\mathbf {j}_{|u|}}(\mathbf {d})\), where ∅≠u⊆{1,⋯ ,N}, 1≤|u|≤S, and \(\mathbf {j}_{|u|}\in \mathbb {N}_{0}^{|u|}\), j 1,⋯ ,j |u|≠0 was determined in Step 2, using dimension-reduction integration with R=S, leading to S-variate, AS-PDD approximations \(\bar {c}_{0,S}^{(q)}(\mathbf {d})\) of c 0(d) and \(\bar {y}_{l,S}^{(q)}(\mathbf {X})\) of y l (X), l=1,⋯ ,K.
- Step 4::
-
Evaluate \(\bar {c}_{l,S}^{(q)}(\mathbf {d})\) of c l (d), l=1,⋯ ,K, in (52) and their sensitivities by the AS-PDD-MCS or AS-PDD-SPA methods based on AS-PDD approximations \(\bar {y}_{l,S}^{(q)}(\mathbf {X})\) in Step 3.
- Step 5::
-
If q=1 and \(\bar {c}_{l,S}^{(q)}(\mathbf {d}_{0}^{(q)})<0\) for l=1,⋯ ,K, then go to Step 7. If q>1 and \(\bar {c}_{l,S}^{(q)}(\mathbf {d}_{0}^{(q)})<0\) for l=1,⋯ ,K, then set d f,l a s t =d f , \(\mathbf {\mathbf {d}}_{f}=\mathbf {d}_{0}^{(q)}\) , q f,l a s t =q f , q f =q and go to Step 7. Otherwise, go to Step 6.
- Step 6::
-
Compare the infeasible design \(\mathbf {d}_{0}^{(q)}\) with the feasible design d f and interpolate between \(\mathbf {d}_{0}^{(q)}\) and d f to obtain a new feasible design and set it as \(\mathbf {d}_{0}^{(q+1)}\). For dimensions with large differences between \(\mathbf {d}_{0}^{(q)}\) and d f , interpolate aggressively, that is, interpolate close to d f . Reduce the size of the subregion \(\mathcal {D}^{(q)}\) to obtain new subregion \(\mathcal {D}^{(q+1)}\). For dimensions with large differences between \(\mathbf {d}_{0}^{(q)}\) and d f , reduce aggressively. Also, for dimensions with large differences between the sensitivities of \(\bar {c}_{l,S}^{(q)}(\mathbf {d}_{0}^{(q)})\) and \(\bar {c}_{l,S}^{(q-1)}(\mathbf {d}_{0}^{(q)})\), reduce aggressively. Update q=q+1 and go to Step 3.
- Step 7::
-
If ||d f −d f,l a s t ||2<𝜖 (1) or \(|[\bar {c}_{0,S}^{(q)}(\mathbf {d}_{f})-\bar {c}_{0,S}^{(q_{f,last})}\allowbreak (\mathbf {d}_{f,last})]/\bar {c}_{0,S}^{(q)}(\mathbf {d}_{f})|<\epsilon ^{(3)}\), then stop and denote the final optimal solution as \(\bar {\mathbf {d}}^{*}=\mathbf {d}_{f}\). Otherwise, go to Step 8.
- Step 8::
-
If the subregion size is small, that is, \(\beta _{k}^{(q)}(d_{k,U}-d_{k,L})<\epsilon ^{(2)}\), and \(\mathbf {d}_{*}^{(q-1)}\) is located on the boundary of the subregion, then go to Step 9. Otherwise, go to Step 11.
- Step 9::
-
If the subregion centered at \(\mathbf {d}_{0}^{(q)}\) has been enlarged before, that is, \(\mathbf {d}_{0}^{(q)}\in H^{(q-1)}\), then set H (q)=H (q−1) and go to Step 11. Otherwise, set \(H^{(q)}=H^{(q-1)}\bigcup \{\mathbf {d}_{0}^{(q)}\}\) and go to Step 10.
- Step 10::
-
For coordinates of \(\mathbf {d}_{0}^{(q)}\) located on the boundary of the subregion and \(\beta _{k}^{(q)}(d_{k,U}-d_{k,L})<\epsilon ^{(2)}\), increase the sizes of corresponding components of \(\mathcal {D}^{(q)}\); for other coordinates, keep them as they are. Set the new subregion as \(\mathcal {D}^{(q+1)}\).
- Step 11::
-
Solve the design problem in (52) employing the single-step procedure. In so doing, recycle the PDD expansion coefficients obtained from Step 3 in (55) and (56), producing approximations of the objective and constraint functions that stem from single calculation of these coefficients. Denote the optimal solution by \(\mathbf {d}_{*}^{(q)}\) and set \(\mathbf {d}_{0}^{(q+1)}=\mathbf {d}_{*}^{(q)}\). Update q=q+1 and go to Step 12.
- Step 12::
-
If the form of a response function changes, go to Step 2; otherwise, go to Step 3. A threshold t∈[0,1] was used to determine whether the form changed. Only when the relative change of the objective function is greater than t, that is, \(|c_{0}(\mathbf {d}_{0}^{(q)})-c_{0}(\mathbf {d}_{AS})|/|c_{0}(\mathbf {d}_{AS})|>t\), then it is assumed that the form of the response function changes.
It is important to distinguish new contributions of this paper with those presented in past works (Yadav and Rahman 2014b; Rahman and Ren 2014; Ren and Rahman 2013). First, Yadav and Rahman (2014b) solved high-dimensional uncertainty quantification problems without addressing stochastic sensitivity analysis and design optimization. Second, Rahman and Ren (2014) conducted probabilistic sensitivity analysis based on non-adaptively truncated PDD and pre-assigned truncation parameters, which cannot capture automatically the hierarchical structure and/or nonlinearity of a complex system response. Third, the stochastic optimization performed by Ren and Rahman (2013) covered only RDO, not RBDO. Therefore, the unique contributions of this work include: (1) a novel integration of AS-PDD and score function for probabilistic RBDO sensitivity analysis; (2) a new AS-PDD-based RBDO design procedure for high-dimensional engineering problems; (3) a new combined sparse- and full-grid numerical integration to further improve the accuracy of the AS-PDD methods; and (4) construction of three new numerical examples.
8 Numerical examples
Four examples are presented to illustrate the AS-PDD-SPA and AS-PDD-MCS methods developed in solving various RBDO problems. The objective and constraint functions are either elementary mathematical functions or relate to engineering problems, ranging from simple structures to complex FEA-aided mechanical designs. Both size and shape design problems are included. In Examples 1 through 4, orthonormal polynomials, consistent with the probability distributions of input random variables, were used as bases. For the Gaussian distribution, the Hermite polynomials were used. For random variables following non-Gaussian probability distributions, such as the Lognormal distribution in Example 3 and truncated Gaussian distribution in Example 4, the orthonormal polynomials were obtained either analytically when possible or numerically, exploiting the Stieltjes procedure (Gautschi 2004). The value of S for AS-PDD approximation varies, depending on the function or the example, but in all cases the tolerances are as follows: 𝜖 1=𝜖 2=10−4. The AS-PDD expansion coefficients were calculated using dimension-reduction integration with R=S and the Gauss quadrature rule of the ith dimension consistent with maxi∈u m u . The moments and their sensitivities required by the AS-PDD-SPA method in Examples 1 and 2 were calculated using dimension-reduction integration with R=2. The sample size for the embedded simulation of the AS-PDD-MCS method is 106 in all examples. In Examples 1-3, the design sensitivities of the objective functions were obtained analytically. Since the objective function in Example 4 is an implicit function, the truncated PDD approximation of the objective function was employed to obtain design sensitivities. The multi-point, single-step PDD method was used in all examples. The tolerances, initial subregion size, and threshold parameters for the multi-point, single-step PDD method are as follows: (1) 𝜖 (1)=0.1 (Examples 1 and 2), 𝜖 (1)=0.01 (Example 3), 𝜖 (1)=0.2 (Example 4); 𝜖 (2)=2; 𝜖 (3)=0.005 (Examples 1, 2, and 3), 𝜖 (3)=0.05 (Example 4); (2) \(\beta _{1}^{(1)}=\cdots =\beta _{M}^{(1)}=0.5\); and (3) t=0.99 (Example 1-3); t=0.6 (Example 4). The optimization algorithm selected is sequential quadratic programming (DOT 2001) in all examples.
8.1 Example 1: optimization of a mathematical problem
Consider a mathematical example, involving a 100-dimensional random vector X, where X i , i=1,⋯ ,100, are independent and identically distributed Gaussian random variables, each with the mean value μ and the standard deviation s. Given the design vector d=(μ,s)T, the objective of this problem is to
where
is a random function. The design vector \(\mathbf {d}\in \mathcal {D}\), where \(\mathcal {D}=[-9,9]\times [0.5,4]\subset \mathbb {R}^{2}\). The exact solution of the RBDO problem in (57) is as follows: d ∗=(0,0.5)T; c 0(d ∗)=2.5; and c 1(d ∗)=Φ(−6)−10−3≈−10−3. The AS-PDD-SPA and AS-PDD-MCS methods with S=1 were employed to solve this elementary RBDO problem. The approximate optimal solution is denoted by \(\bar {\mathbf {d}}^{*}= (\bar {d}_{1}^{*},\bar {d}_{2}^{*})^{T}\).
Four different initial designs were selected to study the robustness of the proposed methods in obtaining optimal design solutions. The first two initial designs d 0=(−9,4)T and d 0=(−4.5,2)T lie in the feasible region, whereas the last two initial designs d 0=(9,4)T and d 0=(4.5,2)T are located in the infeasible region. Table 1 summarizes the optimization results, including the numbers of function evaluations, by the AS-PDD-SPA and AS-PDD-MCS methods for all four initial designs. The exact solution, existing for this particular problem, is also listed in Table 1 to verify the approximate solutions. From Table 1, the proposed methods, starting from four different initial designs, engender identical optima, which is the exact solution. Hence, each method can be used to solve this optimization problem, regardless of feasible or infeasible initial designs.
Figures 4 and 5 depict the iteration histories of the AS-PDD-SPA and AS-PDD-MCS methods, respectively, for all four initial designs. When starting from the feasible initial designs d 0=(−9,4)T and d 0=(−4.5,2)T, both methods experience nearly identical iteration steps. This is because at every step of the design iteration the AS-PDD-SPA method provides estimates of the failure probability and its design sensitivities very close to those obtained by the AS-PDD-MCS method. Consequently, both methods incur the same number of function evaluations in reaching respective optimal solutions. In contrast, when the infeasible initial designs d 0=(9,4)T and d 0=(4.5,2)T are chosen, there exist some discrepancies in the iteration paths produced by the AS-PDD-SPA and AS-PDD-MCS methods. This is primarily due to the failure of SPA, where the existence of the saddlepoint is not guaranteed for some design iterations. In which case, the MCS, instead of SPA, were used to calculate the failure probability and its design sensitivities. Therefore, the computational cost by the AS-PDD-SPA method should increase, depending on the frequency of the failure of SPA. Indeed, when the discrepancy is large, as exhibited for the initial design d 0=(9,4)T, nearly 900 more function evaluations are needed by the AS-PDD-SPA method. For the initial design d 0=(4.5,2)T, the discrepancy is small, and consequently, the AS-PDD-SPA method requires almost 300 more function evaluations than the AS-PDD-MCS method. In general, the AS-PDD-MCS method should be more efficient than the AS-PDD-SPA method in solving RBDO problems since an added layer of approximation is involved when evaluating CGF in the latter method.
8.2 Example 2: optimization of a speed reducer
The second example, studied by Lee and Lee (2005), entails RBDO of a speed reducer, which was originally formulated as a deterministic optimization problem by Golinski (1970). Seven random variables, as shown in Fig. 6, comprise the gear width X 1 (cm), the teeth module X 2 (cm), the number of teeth in the pinion X 3, the distances between bearings X 4 (cm) and X 5 (cm), and the axis diameters X 6 (cm) and X 7 (cm). They are independent Gaussian random variables with means \(\mathbb {E}_{\mathbf {d}}[X_{k}]\), k=1,⋯ ,7, and a standard deviation of 0.005. It is important to notice that in reality X 3 should be a discrete random variable, but here it is treated as a continuous Gaussian random variable. The design variables are the means of X, that is, \(d_{k}=\mathbb {E}_{\mathbf {d}}[X_{k}]\). The objective is to minimize the weight of the speed reducer subject to 11 probabilistic constraints, limiting the bending stress and surface stress of the gear teeth, transverse deflections of shafts 1 and 2, and stresses in shafts 1 and 2. Mathematically, the RBDO problem is formulated to
where
are 11 random performance functions and β l =3, l=1,⋯ ,11. The initial design vector is d 0=(3.1 cm,0.75 cm,22.5 ,7.8 cm,7.8 cm,3.4 cm,5.25 cm)T. The approximate optimal solution is denoted by \(\bar {\mathbf {d}}^{*}=(\bar {d}_{1}^{*},\bar {d}_{2}^{*},\allowbreak \cdots ,\bar {d}_{7}^{*})^{T}\).
Table 2 presents detailed optimization results generated by the AS-PDD-SPA and AS-PDD-MCS methods, each entailing S=1 and S=2, in the second through fifth columns. The optimal solutions by both proposed methods, regardless of S, are very close to each other, all indicating no constraints are active. The objective function values of optimal solutions by the AS-PDD-MCS method are slightly lower than those by the AS-PDD-SPA method. Although there is a constraint violation, that is, maxl c l >0 in the AS-PDD-MCS method with S=1, it is negligibly small. The results of both versions (S=1 and S=2) of the AS-PDD-SPA and AS-PDD-MCS methods confirm that the solutions obtained using the univariate (S=1), AS-PDD approximation are accurate and hence adequate. However, the numbers of function evaluations step up for the bivariate (S=2), AS-PDD approximation, as expected. When the univariate, AS-PDD approximation is employed, the respective numbers of function evaluations diminish by more than a factor of five, regardless of method selected.
Since this problem was also solved by the RIA, PMA, RIA envelope method, and PMA envelope method, comparing their reported solutions (Lee and Lee 2005), listed in the sixth through ninth columns of Table 2, with the proposed solutions should be intriguing. These existing methods are commonly used in conjunction with FORM for solving RBDO problems. It appears that RIA and PMA and their respective enhancements are also capable of producing optimal solutions similar to those obtained by the AS-PDD-SPA and AS-PDD-MCS methods, but by incurring computational costs markedly higher than those by the latter two methods. Comparing the numbers of function evaluations, the RIA and PMA methods are more expensive than the AS-PDD-SPA methods by factors of 20 to 120. These factors grow into 25 to 150 when graded against the AS-PDD-MCS methods. The dramatic reduction of computational cost by the proposed methods indicates that the AS-PDD approximations, in cooperation with the multi-point, single-step design process, should greatly improve the current state of the art of reliability-based design optimization.
8.3 Example 3: size design of a six-bay, twenty-one-bar truss
This example demonstrates how an RBDO problem entailing system reliability constraints can be efficiently solved by the AS-PDD-MCS method. A linear-elastic, six-bay, twenty-one-bar truss structure, with geometric properties shown in Fig. 7, is simply supported at nodes 1 and 12, and is subjected to four concentrated loads of 10,000 lb (44,482 N) at nodes 3, 5, 9, and 11 and a concentrated load of 16,000 lb (71,172 N) at node 7. The truss material is made of an aluminum alloy with the Young’s modulus E=107 psi (68.94 GPa). Considering the symmetry properties of the structure, the random input is selected as \(\mathbf {X}=(X_{1},\cdots ,X_{11})^{T}\allowbreak \in \mathbb {R}^{11}\), where X i , i=1,⋯ ,11 , is the cross-sectional areas of the ith truss member. The random variables are independent and lognormally distributed with means μ i in 2, and standard deviations σ i =0.1 in 2, i=1,⋯ ,11. From linear-elastic finite-element analysis (FEA), the maximum vertical displacement v max(X) and maximum axial stress σ max(X) occur at node 7 and member 3 or 12, respectively, where the permissible displacement and stress are limited to d allow=0.266 in (6.76 mm) and σ allow=37,680 psi (259.8 MPa), respectively. The system-level failure set is defined as Ω F :={x:{y 1(x)<0}∪{y 2(x)<0}}, where the performance functions
Due to symmetry, the design vector is \(\mathbf {d}=(\mu _{1},\cdots ,\mu _{11})^{T}\allowbreak \mathcal {\in D}\subset \mathbb {R}^{11}\). The objective is to minimize the volume of the truss structure subject to a system reliability constraint, limiting the maximum vertical displacement and the maximum axial stress. Therefore, the RBDO problem is formulated to
where V(d) is the total volume of the truss. The initial design is d 0=(15,15,15,15,15,15,15,15,15,15,15)T in2 (×2.542 cm 2). The approximate optimal solution is denoted by \(\bar {\mathbf {d}}^{*}=(\bar {d}_{1}^{*},\cdots ,\bar {d}_{11}^{*})^{T}\).
The second column of Table 3 presents detailed optimization results generated by the proposed AS-PDD-MCS method employing S=2. For comparison, the optimization results from the multi-point, single-step method using an existing truncated PDD-MCS approximation (S=2, m=2) for reliability and sensitivity analyses (Rahman and Ren 2014) are also tabulated in the third column. According to Table 3, both solutions reveal no constraint violations, but there are moderate to significant differences in the design variables at respective optima. This is possible because the surrogate approximations grounded in adaptive-sparse and truncated PDD approximations are not necessarily the same or even similar. Therefore, when the original performance functions in (72) are replaced by two different variants of the PDD approximation, the same initial condition may lead to distinct local optima, as found in this specific example. To seek further credibility to this reasoning, the RBDO problem, using these two optimal solutions as initial designs, was re-solved by crude MCS (106 samples) for evaluating the constraint and its design sensitivities in (73). The optimal solutions from crude MCS, listed in the fourth and fifth columns of Table 3, are the same as the initial designs, indicating that the optimal solutions generated by the proposed and existing RBDO methods pertain to two distinct local optima. Comparing the values of objective functions at the two optima, the proposed AS-PDD-MCS method yields a slightly lower volume of the truss than the existing method. Furthermore, the AS-PDD-MCS method accomplishes this feat by reducing the number of function evaluations by 42 percent.
It is important to recognize that the AS-PDD-SPA method can be applied to solve this RBDO problem involving series-system reliability analysis by interpreting the failure domain as Ω F :={x:y s y s (x)<0}, where y s y s (X):= min{y 1(X),y 2(X)} and then constructing an AS-PDD approximation of y s y s (X). In doing so, however, y s y s (X) is no longer a smooth function of X, meaning that the convergence properties of the resulting AS-PDD-SPA method can be significantly deteriorated. More importantly, the AS-PDD-SPA method is not suitable for a general system reliability problem involving multiple, interdependent component performance functions. This is the primary reason why the AS-PDD-SPA method was not used in this example.
8.4 Example 4: shape design of a jet engine bracket
The final example demonstrates the usefulness of the RBDO methods advocated in designing an industrial-scale mechanical component, known as a jet engine bracket, as shown in Fig. 8a. Seventy-nine random shape parameters, X i , i=1,⋯ ,79, resulting from manufacturing variability, describe the shape of a jet engine bracket in three dimensions, including two rounded quadrilateral holes introduced to reduce the mass of the jet engine bracket as much as possible. The design variables, \(d_{k}={\displaystyle \mathbb {E}_{\mathbf {d}}}[X_{k}]\), k=1,⋯ ,79, as shown in Fig. 9, are the means (mm) of these 79 independent random variables, with Figs. 8b–d depicting the initial design of the jet engine bracket geometry at mean values of the shape parameters. The centers of the four bottom circular holes are fixed. A deterministic horizontal force, F=43.091 kN, was applied at the center of the top circular hole with a 48∘ angle from the horizontal line, as shown in Fig. 8c, and a deterministic torque, T=0.1152 kN-m, was applied at the center of the top circular hole, as shown in Fig. 8d. These boundary conditions are determined from the interaction of the jet engine bracket with other mechanical components of the jet engine. The jet engine bracket is made of Titanium Alloy Ti-6Al-4V with deterministic material properties, as follows: mass density ρ=4430 kg/m3, elastic modulus E=113.8 GPa, Poisson’s ratio ν=0.342, fatigue strength coefficient \(\sigma _{f}^{\prime }=2030\) MPa, fatigue strength exponent b=−0.104, fatigue ductility coefficient \(\epsilon _{f}^{\prime }=0.841\), and fatigue ductility exponent c=−0.69. The performance of the jet engine bracket was determined by its fatigue durability obtained by (1) calculating maximum principal strain and mean stress at a point; and (2) calculating the fatigue crack-initiation life at that point from the well-known Coffin-Manson-Morrow equation (Stephens and Fuchs 2001). The objective is to minimize the mass of the jet engine bracket by changing the shape of the geometry such that the minimum fatigue crack-initiation life N min(X) exceeds a design threshold of N c =106 loading cycles with 99.865 % probability. Mathematically, the RBDO for this problem is defined to
where
is a high-dimensional random response function. The initial design d 0=(d 0,1,⋯ ,d 0,79)T mm; the upper and lower bounds of the design vector \(\mathbf {d}=(d_{1},\cdots ,d_{79})^{T}\in \mathcal {D}\subset \mathbb {R}^{79}\) are listed in Table 4. Figure 10 portrays the FEA mesh for the initial jet engine bracket design, which comprises 341,112 nodes and 212,716 ten-noded, quadratic, tetrahedral elements.
Due to their finite bounds, the random variables X i , i=1,⋯ ,79, were assumed to follow truncated Gaussian distributions with densities
when a i ≤x i ≤b i and zero otherwise, where Φ(⋅) and ϕ(⋅) are the cumulative distribution and probability density functions, respectively, of a standard Gaussian random variable; σ i =0.2 are constants; and a i =d i −D i and b i =d i +D i are the lower and upper bounds, respectively, of X i ; and D i =2.
The proposed AS-PDD-MCS method was applied to solve this jet engine bracket design problem employing S=1 since employing S≥2 demands a large number of FEAs leading to a prohibitive computational cost for this 79-dimensional problem. Figures 11a through d show the contour plots of the logarithm of fatigue crack-initiation life at mean shapes of several design iterations, including the initial design, throughout the RBDO process. Due to a conservative initial design, with fatigue life contour depicted in Fig. 11a, the minimum fatigue crack-initiation life of 0.665×1010 cycles is much larger than the required fatigue crack-initiation life of a million cycles. For the tolerance and subregion size parameters selected, 14 iterations and 2,808 FEA led to a final optimal design with the corresponding mean shape presented in Fig. 11d.
Table 4 exhibits the values of design variables, objective function, and constraint function for both the optimal and initial designs. The objective function c 0 is reduced from 2.9977 kg at initial design to 0.4904 kg at optimal design — an almost 84 percent change. At optimum, the constraint function c 1 is −1.35×10−3 and is, therefore, close to being active. Most of the design variables, except for d 12, d 18, and d 43, have undergone the most significant changes from their initial values, prompting substantial modifications of the shapes or sizes of the outer boundaries, rounded quadrilateral holes, and bottom surfaces of the engine bracket. The design variables d 12, d 18, and d 43, controlling minor features of outer boundaries, are virtually unchanged, because the associated initial values used are close to or the same as their lower or upper bounds, which the design process is seeking.
This final example demonstrates that the RBDO methods developed — in particular, the AS-PDD-MCS method — are capable of solving industrial-scale engineering design problems with reasonable computational cost. However, the “optimal” solution generated from the univariate AS-PDD approximation has yet to be verified with those obtained from bivariate or higher-variate AS-PDD approximations. The univariate solution reported here should be guardedly interpreted.
9 Conclusion
Two new methods, namely, the AS-PDD-SPA method and the AS-PDD-MCS method, are proposed for reliability-based design optimization of complex engineering systems. The methods involve an adaptive-sparse polynomial dimensional decomposition of a high-dimensional stochastic response for reliability analysis, a novel integration of AS-PDD and score functions for calculating the sensitivities of the probability failure with respect to design variables, and standard gradient-based optimization algorithms, encompassing a multi-point, single-step design process. The AS-PDD-SPA method capitalizes on a novel integration of AS-PDD, SPA, and score functions. The result is analytical formulae for calculating the failure probability and design sensitivities, solving component-level RBDO problems. In contrast, the AS-PDD-MCS method utilizes the embedded MCS of AS-PDD approximations and score functions. Unlike the AS-PDD-SPA method, however, the failure probability and design sensitivities in the AS-PDD-MCS method are estimated via efficient sampling of approximate stochastic responses, thereby affording the method the capability to address either component- or system-level RBDO problems. Furthermore, the AS-PDD-MCS method is not influenced by any added approximations, involving calculations of the saddlepoint and higher-order moments, of the AS-PDD-SPA method. Since both methods are rooted in the AS-PDD approximation, a dimension-reduction approach combining sparse- and full-grid quadratures is proposed to estimate the expansion coefficients more accurately than existing techniques. For the two methods developed, both the failure probability and its design sensitivities are determined concurrently from a single stochastic analysis or simulation. Consequently, the methods provide more computationally efficient design solutions than existing methods. Moreover, the multi-point, single-step design process embedded in the proposed methods facilitates a solution of an RBDO problem with a large design space. Precisely for this reason, the AS-PDD-MCS method developed is capable of solving high-dimensional practical engineering problems, as demonstrated by the shape design of a jet engine bracket with 79 design variables.
References
Agarwal H, Renaud J E (2006) New decoupled framework for reliability-based design optimization. AIAA J 44:1524–1531
Browder A (1996) Mathematical analysis: an introduction. Undergraduate texts in mathematics. Springer Verlag
Chiralaksanakul A, Mahadevan S (2005) First-order approximation methods in reliability-based design optimization. J Mech Des 127(5):851–857
Daniels H E (1954) Saddlepoint approximations in statistics. Ann Math Stat:631–650
DOT (2001) DOT – design optimization tools, user’s manual. Vanderplaats Research and Development Inc., Colorado Springs, CO
Du X P, Chen W (2004) Sequential optimization and reliability assessment method for efficient probabilistic design. J Mech Des 126(2):225–233
Efron B, Stein C (1981) The jackknife estimate of variance. Ann Stat 9(3):586–596
Gautschi W (2004) Orthogonal polynomials: computation and approximation. Numerical mathematics and scientific computation. Oxford University Press
Genz A (1986) Fully symmetric interpolatory rules for multiple integrals. SIAM J Numer Anal 23(6):1273–1283
Genz A, Keister B D (1996) Fully symmetric interpolatory rules for multiple integrals over infinite regions with Gaussian weight. J Comput Appl Math 71(2):299–309
Golinski J (1970) Optimal synthesis problems solved by means of nonlinear programming and random methods. J Mech 5(3):287–309
Hu C, Youn B D (2011) Adaptive-sparse polynomial chaos expansion for reliability analysis and design of complex engineering systems. Struct Multidiscip Optim 43(3):419–442
Kuschel N, Rackwitz R (1997) Two basic problems in reliability-based structural optimization. Math Methods Oper Res 46:309–333
Lee J J, Lee B C (2005) Efficient evaluation of probabilistic constraints using an envelope function. Eng Optim 37(2):185–200
Lee I, Choi K K, Du L, Gorsich D (2008a) Dimension reduction method for reliability-based robust design optimization. Comput Struct 86(13):1550–1562
Lee I, Choi K, Du L, Gorsich D (2008b) Inverse analysis method using MPP-based dimension reduction for reliability-based design optimization of nonlinear and multi-dimensional systems. Comput Methods Appl Mech Eng 198(1):14–27
Lee G, Yook S, Kang K, Choi D H (2012) Reliability-based design optimization using an enhanced dimension reduction method with variable sampling points. Int J Precis Eng Manuf 13(9):1609– 1618
Liang J H, Mourelatos Z P, Nikolaidis E (2007) A single-loop approach for system reliability-based design optimization. J Mech Des 129(12):1215–1224
Lugannani R, Rice S (1980) Saddle point approximation for the distribution of the sum of independent random variables. Adv Appl Probab 12:475–490
Rahman S (2008) A polynomial dimensional decomposition for stochastic computing. Int J Numer Methods Eng 76:2091–2116
Rahman S, Wei D (2008) Design sensitivity and reliability-based structural optimization by univariate decomposition. Struct Multidiscip Optim 35(3):245–261
Rahman S (2009a) Extended polynomial dimensional decomposition for arbitrary probability distributions. J Eng Mech 135(12):1439–1451
Rahman S (2009b) Stochastic sensitivity analysis by dimensional decomposition and score functions. Probab Eng Mech 24(3):278–287
Rahman S (2011) Decomposition methods for structural reliability analysis revisited. Probab Eng Mech 26 (2):357–363
Rahman S, Yadav V (2011) Orthogonal polynomial expansions for solving random eigenvalue problems. Int J Uncert Quant 1(2):163–187
Rahman S (2014) Approximation errors in truncated dimensional decompositions. Math Comput 83 (290):2799–2819
Rahman S, Ren X C (2014) Novel computational methods for high-dimensional stochastic sensitivity analysis. Int J Numerl Methods Eng 98:881–916
Ren X C, Rahman S (2013) Robust design optimization by polynomial dimensional decomposition. Struct Multidiscip Optim 48(1):127–148
Royset J O, Der Kiureghian A, Polak E (2001) Reliability-based optimal structural design by the decoupling approach. Reliab Eng Syst Safety 73(3):213–221
Rubinstein R Y, Shapiro A (1993) Discrete event systems: sensitivity analysis and stochastic optimization by the score function method. Wiley series in probability and mathematical statistics, Wiley
Stephens R, Fuchs H (2001) Metal fatigue in engineering. Wiley-Interscience
Toropov V V, Filatov A A, Polynkin A A (1993) Multiparameter structural optimization using FEM and multipoint explicit approximations. Struct Multidiscip Optim 6(1):7–14
Tu J, Choi K K, Park Y H (1999) A new study on reliability-based design optimization. J Mech Des Trans ASME 121(4):557–564
Xu H, Rahman S (2004) A generalized dimension-reduction method for multidimensional integration in stochastic mechanics. Int J Numer Methods Eng 61(12):1992–2019
Yadav V, Rahman S (2013) Uncertainty quantification of high-dimensional complex systems by multiplicative polynomial dimensional decompositions. Int J Numer Methods Eng 94(3):221–247
Yadav V, Rahman S (2014a) A hybrid polynomial dimensional decomposition for uncertainty quantification of high-dimensional complex systems. Probab Eng Mech 38:22–34
Yadav V, Rahman S (2014b) Adaptive-sparse polynomial dimensional decomposition for high-dimensional stochastic computing. Comput Methods Appl Mech Eng 274:56–83
Youn B, Wang P (2008) Bayesian reliability-based design optimization using eigenvector dimension reduction (EDR) method. Struct Multidiscip Optim 36(2):107–123
Yuen K V, Wang J, Au S K (2007) Application of saddlepoint approximation in reliability analysis of dynamic systems. Earthq Eng Eng Vibr 6(4):391–400
Zou T, Mahadevan S (2006) A direct decoupling approach for efficient reliability-based design optimization. Struct Multidiscip Optimn 31(3):190–200
Acknowledgments
The authors acknowledge financial support from the U.S. National Science Foundation under Grant No. CMMI-0969044.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Ren, X., Yadav, V. & Rahman, S. Reliability-based design optimization by adaptive-sparse polynomial dimensional decomposition. Struct Multidisc Optim 53, 425–452 (2016). https://doi.org/10.1007/s00158-015-1337-6
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00158-015-1337-6