1 Introduction

The analysis and applications of fractional calculus are an active and the fastest growing region for research in the last three decades. It has currently become an important tool owing to its wide applications in various scientific disciplines, such as physics, regular variation in thermodynamics, blood flow phenomenons, biophysics, electro-dynamics of complex medium, capacitor theory, chemistry, polymer rheology, dynamical systems, fitting of experimental data, etc. ([1,2,3, 7] and references therein). The increasing development of appropriate and efficient method to solve FDEs has aroused more interest of researchers in this field. Solving the nonlinear FDEs is relatively difficult compared to its linear type. In this regard, analytical methods such as, homotopy perturbation method (HPM), homotopy analysis method (HAM), new iterative methods and Adomian decomposition, have been used in the recent literature widely [8, 9, 11,12,13,14, 53] . On the other hands, some researchers such as Diethelm et al [2, 16] have developed standard numerical methods, such as Adams–Bashforth methods have been used for numerical integration of FDEs. Lakestani et al [54] have peresented The construction of operational matrix of fractional derivatives using B-spline functions, Application of Taylor series in obtaining the orthogonal operational matrix is proposed by Eslahchi and Dehghan [56], Kayedi-Bardeh et al have provided A method for obtaining the operational matrix of the fractional Jacobi functions and application [57].

Inclusion of delay in the differential equations of fractional order creates new perspectives especially in the field of bioengineering [6], because in bioengineering, the understanding of the dynamics that occur in biological tissues, is improved by fractional derivatives [4, 6].

In mathematics, delay differential equations (DDEs) are a type of differential equation in which the derivative of the unknown function at a certain time is given in terms of the values of the function at previous times. The DDEs are also called time-delay systems, systems with aftereffect or deed-time, hereditary systems, equations with deviating argument, or differential–difference equations [17].

Fractional delay differential equations differ from ordinary differential equations in that the derivative at any time depends on the solution (and in the case of neutral equations on the derivative) at prior times. Many events in the natural world can be modeled to form of fractional order of delay differential equations [7]. The fraction order of differential equations have many application in various scientific disciplines by modeling of various problem such as economy, electrodynamics, biology, control, finance, chemistry, physics and so on, for more detail, we refer the interested reader to [17,18,19,20,21,22,23].

In recent years, Margado et al in [24] analyzed numerical solution and approximated it for FDDEs. Cermak et al in [25], analyzed stability regions of FDDEs system. Stability for FDDEs systems by means of Gr\(\ddot{u}\)nwalds approach is analyzed by Lazarovic and Spansic [26]. Abbaszadeh and Dehghan have presented Numerical and analytical investigations for neutral delay fractional damped diffusion-wave equation based on the stabilized interpolating element free Galerkin (IEFG) method [55], Daftardar-Gejji et al in [12] have proposed a new predictor–corrector method and based on the realizer developed new iteration method presented by Daftardar-Gejji and Jafari [27] , for solving FDEs numerically. Bhalekar and Daftardar-Gejji proposed A predictor–corrector scheme to solve non-linear fractional-order delay differential equations in [10]. In [5], the author generalized the Adams–Bashforth–Moulton algorithm introduced in [2, 16, 28] to the delay FDEs. Varsha et al [6], have presented a new approach to solve non-linear fractional- order differential equations involving delay. Ghasemi et al [17], have employed Reproducing kernel Hilbert Space method to solve nonlinear delay differential equation of fractional order. Jhing and Daftardar-Gejji have presented a new numerical method to solve FDDEs [4].

Moreover, the spectral methods that basically depends on a set of orthogonal polynomials, are used to solve the differential equations of fractional-order. One of the most famous of them, is the classical Jacobi polynomials that shown as follows:

$$\begin{aligned} P_n^{(\alpha ,\beta )}(x)\,\,(n \ge 0,\,\alpha> -1 ,\, \beta > -1) . \end{aligned}$$

These polynomials have been used extensively in mathematical analysis and practical applications because it has the advantages of gaining the numerical solutions in \(\alpha \) and \(\beta \) parameters. Thus, it would be beneficial to carry out a systematic study via Jacobi polynomials with general indexes \( \alpha \) and \( \beta \) and this clearly considered one of the aims and the novelly of the time interval \( t\,\in [0,\,I] \) [15]. Furthermore, recently interest of researchers has increased in this field (field of variable fractional differential equations) [29, 30]. So, many methods are used to find the numerical solution of these equations [31,32,33].

Now, the aim of this paper is to generalize the orthogonal polynomials in the base of solution. In fact, this technique is introduced in [15] and we present a new shifted Jacobi operational matrix for the fractional derivative to solve the multi-terms variable-order FDDEs which as follows:

$$\begin{aligned}&\sum _{j=1}^{n}\alpha _{j} D^{\eta _{j}(t)} w(t)\, +\alpha _{n+1} w(t-\tau ) \nonumber \\&\quad =\, F\,(t,\, w(t),\, D^{\eta _{1}(t)} w(t), \nonumber \\&\qquad D^{\eta _{2}(t)} w(t) , \, \ldots ,\, D^{\eta _{n}(t)} w(t),w(t-\tau \,))\, , \, 0 \le t \le T\, ,\nonumber \\&\qquad w(t)=g(t),\,\, t \in [-\tau ,\,0],\nonumber \\&\qquad w(0)=w_{0}, \end{aligned}$$
(1)

where \( \alpha _{j}\, \in {\mathbb {R}} (j=1,2,\ldots ,n+1)\,,\alpha _{n+1}\ne 0,\,0<T\,.\) and \( D^{\eta _{j}(t)} w(t)\,(\,j\,=\,1 , 2,\ldots , n\,)\) are the derivatives of variable-order fractional in the Caputo sense.

Note 1

If \( \eta _{j}(t) \,(\,j\,=\,1 , 2,\ldots , n\,)\) are constants, then equation (1) will be as follows:

$$\begin{aligned}&\sum _{j=1}^{n}\alpha _{j} D^{\eta _{j}} w(t)\, +\alpha _{n+1} w(t-\tau ) \nonumber \\&\quad =\, F\,(t,\, w(t),\, D^{\eta _{1}} w(t),\, \nonumber \\&\qquad D^{\eta _{2}} w(t) , \, \ldots ,\, D^{\eta _{n}} w(t),w(t-\tau ))\, , \, 0 \le t \le T\, ,\nonumber \\&\qquad w(t)=g(t),\,\, t \in [-\tau ,\,0],\nonumber \\&\qquad w(0)=w_{0}, \end{aligned}$$
(2)

Also note that: we can use many polynomials such as Legendre polynomials, Gegenbauer polynomials, all Chebyshev polynomials, Lucas polynomials, Vieta-Lucas polynomials, and Fibonacci polynomials in our new suggestion technique.

The numerical results obtained for the mentioned equation in this study reveals that the present method is of highly accuracy. By focusing on numerical experiments gained by this method with other available methods, and comparing them, we can find that the proposed scheme capable of solving the variable-order fractional delay differential equation, playing role of a powerful effective and practical numerical technique.

2 Fundamentals and preliminaries

In the first part of this section, we review some of the basic and most important properties of fractional calculus theory. Then recall some important properties of the Jacobi polynomials which help us for developing the suggested technique. So we refuse to include duplicate concepts in other related articles and unnecessary content but for more detail, we refer the interested reader to [34, 37, 38].

2.1 The fractional derivative and integral

There are several used definitions for fractional derivatives but the three most usual are Riemann–Liouville, Gr\(\ddot{u}\)nwald-Letincov and Caputo definitions. This article is based on Caputo definition because ,as well as know, only the Caputo sense has the same form as integer-order differential equations in initial conditions.

Definition 2.1

The left- and right-sided Caputo fractional derivatives of order \(\eta \,(n-1<\eta \le n\,)\) are defined as

$$\begin{aligned} \begin{array}{c} D_+^{\eta } w(t)=\dfrac{1}{\Gamma (n-\eta )}\int _{0}^t \dfrac{U^{(n)}(\tau )}{(t-\tau )^{\eta -n+1}} d\tau , \\ D_-^{\eta } w(t)=\dfrac{(-1)^n}{\Gamma (n-\eta )}\int _{t}^T\dfrac{U^{(n)}(\tau )}{(\tau - t)^{\eta -n+1}} d\tau .\\ \end{array} \end{aligned}$$
(3)

that

$$\begin{aligned} D_+^{\eta } t^j= \left\{ \begin{array}{c} 0 \,\,, \, for \, j \in M_0 \, and \, j < \lceil \eta \rceil , \\ \dfrac{\Gamma (j+1)}{\Gamma (j-\eta +1)} t^{j-\eta }, \, for\, j \in M_0 \, and \,j > \lceil \eta \rceil . \end{array} \right. \end{aligned}$$
(4)

and

$$\begin{aligned}&D_-^{\eta } (T-t)^j \nonumber \\&\quad = \left\{ \begin{array}{c} 0\,\, , \, for \, j \in M_0 \, and \, j < \lceil \eta \rceil , \\ \dfrac{(-1)^{j}\Gamma (j+1)}{\Gamma (j-\eta +1)} (T-t)^{j-\eta }, \, for\, j \in M_0 \, and \,j > \lceil \eta \rceil . \end{array} \right. \end{aligned}$$
(5)

where \(\lceil . \rceil \) is the ceiling function and \(M_0= \lbrace 0, 1, 2, \cdots \rbrace .\)

Also

$$\begin{aligned} D_\pm ^{\eta }(\gamma \varphi (t)\,+ \,\delta \phi (t))\,=\,\gamma D_\pm ^{\eta }( \varphi (t))\,+\delta D_\pm ^{\eta }( \phi (t)). \end{aligned}$$

where \( \gamma \)and \(\delta \) are constants.

Definition 2.2

The Caputo fractional derivatives of variable-order \(\eta (t)\) for \( w(t) \in C^m[0,\,T] \) are given respectively as [30, 35]:

$$\begin{aligned}&D^{\eta (t)} w(t)=\dfrac{1}{\Gamma (1-\eta (t))}\int _{0^+}^t \dfrac{w^\prime (\tau )}{(t-\tau )^{\eta (t)}} d\tau \nonumber \\&\quad +\dfrac{w(0^+)-w(0^-)}{\Gamma (1-\eta (t))}t^{-\eta (t)}. \end{aligned}$$
(6)

At the beginning time and for \( 0< \eta (t)<1 \), we have:

$$\begin{aligned} D^{\eta (t)} w(t)=\dfrac{1}{\Gamma (1-\eta (t))}\int _{0^+}^t \dfrac{w^\prime (\tau )}{(t-\tau )^{\eta (t)}} d\tau . \end{aligned}$$
(7)

also, if a and b are constant then

$$\begin{aligned} D^{\eta (t)} (a\, w_1(t)+b \,w_2(t))=a\, D^{\eta (t)} w_1(t)+b\, D^{\eta (t)} w_2(t)\,. \end{aligned}$$
(8)

According to Eq. (6), we have:

$$\begin{aligned} D^{\eta (t)} C\, = \, 0, \, C \,\quad is \, a \, constant. \end{aligned}$$
(9)

On the other hand

$$\begin{aligned} D^{\eta (t)} t^k={\left\{ \begin{array}{ll} 0, &{} for \,k\, = \,0,\\ \dfrac{\Gamma (k+1)}{\Gamma (k+1-\eta (t))}t^{k-\eta (t)} &{} for \,k=1,2,\cdots \, . \end{array}\right. } \end{aligned}$$
(10)

2.2 Shifted Jacobi polynomials and their properties

Denote \( P_n^{(\alpha ,\beta )}(z) ;\, \alpha>-1 \,, \beta >-1\) as the \(n-\)th order Jacobi polynomial in z defined on \(\left[ -1,\,1\right] \).

As all classic orthogonal polynomials, \( P_n^{(\alpha ,\beta )}(z)\) form an orthogonal system with respect to weight function \( \omega ^{(\alpha ,\beta )}(z)\,=\,(1+z)^{\alpha }\,(1-z)^{\beta } \), in other words [34]:

$$\begin{aligned} \int _{-1}^1 P_i^{(\alpha ,\beta )}(z)\, P_j^{\alpha ,\beta )}(z)\omega ^{(\alpha ,\beta )}\, dz\,=\, h_{j}^{(\alpha ,\beta )}\delta _{i,j}, \end{aligned}$$
(11)

where \( \delta _{i,j} \) is the Kronecker function and

$$\begin{aligned} h_{j}^{(\alpha ,\beta )}\, = \,\dfrac{2^{\alpha +\beta +1}\Gamma (j+\alpha +1)\Gamma (j+\beta +1)}{(2j+ \alpha + \beta +1)j!\,\Gamma (j+\beta +\alpha +1)}, \end{aligned}$$

also the i-th order Jacobi polynomial has the following analytical form [15]

$$\begin{aligned} P_i^{(\alpha ,\beta )}(t)=\sum _{k=0}^i \dfrac{\Gamma (\alpha +i+1)\Gamma (\alpha +i+1+\beta +k)}{\Gamma (\alpha +\beta +i+1)\Gamma (\alpha +1+k)\Gamma (k+1)\Gamma (i-k+1)}\, \left( \dfrac{t-1}{2}\right) ^k , \end{aligned}$$
(12)

If we implement the change of variable \( z\, =\,(\dfrac{2t}{T}-1) \), then we can use the polynomial of Eq. (12) on the interval \( t\in [0,T] \). Therefore, we have so-called the shifted Jacobi polynomials \( P_n^{(\alpha ,\beta )}(\dfrac{2t}{T}-1)\) which denoted by \( P_{T,i}^{ (\alpha ,\beta )}(t) \). Then \( P_{T,i}^{ (\alpha ,\beta )}(t) \) form an orthogonal system with respect to weight function \( \omega _{T}^{(\alpha ,\beta )}(t)\,=\,t^{\alpha }\,(T-t)^{\beta } \) in the interval \( [0,\,T] \) with follow orthogonality trait:

$$\begin{aligned} \int _{0}^T P_{T,i}^{(\alpha ,\beta )}(t)\, P_{T,j}^{\alpha ,\beta )}(t)\omega _T^{(\alpha ,\beta )}\, dt\,=\, h_{T,j}^{(\alpha ,\beta )}\delta _{i,j}, \end{aligned}$$
(13)

where \( \delta _{i,j} \) is the Kronecker function and

$$\begin{aligned} h_{T,j}^{(\alpha ,\beta )}\, = \,\left( \dfrac{T}{2}\right) ^{\alpha +\beta +1}\,h_{j}^{(\alpha ,\beta )} , \end{aligned}$$

also the i-th order Shifted Jacobi polynomial has the following analytical form [15]

$$\begin{aligned}&P_{T,i}^{(\alpha ,\beta )}(t)=\sum _{k=0}^i (-1)^{i-k}\dfrac{\Gamma (\alpha +i+1)\Gamma (\alpha +\beta +k+i+1)}{\Gamma (\alpha +\beta +i+1)\Gamma (\alpha +1+k)\Gamma (k+1)\Gamma (i-k+1)T^k}\, t^k ,\nonumber \\&\quad =\sum _{k=0}^i \dfrac{\Gamma (\beta +i+1)\Gamma (\alpha +\beta +k+i+1)}{\Gamma (\alpha +\beta +i+1)\Gamma (\beta +1+k)\Gamma (k+1)\Gamma (i-k+1)T^k}\, (T-t)^k . \end{aligned}$$
(14)

And in the endpoint values are given as

$$\begin{aligned} \begin{array}{c} P_{T,i}^{(\alpha ,\beta )}(0)=(-1)^{i}\dfrac{\Gamma (\alpha +i+1)}{\Gamma (\alpha +1)\Gamma (k+1)}\, , \\ P_{T,i}^{(\alpha ,\beta )}(T)= \dfrac{\Gamma (\beta +i+1)}{\Gamma (\beta +1)\Gamma (k+1)}\, . \\ \end{array} \end{aligned}$$

Also, \( P_{T,i}^{(\alpha ,\beta )}(t) \) can be obtained via the recurrence relation, we refer the interested reader to [15].

Note 2

Furthermore, since the shifted Jacobi polynomials includes unlimited number of orthogonal polynomials such as the shifted Gegenbauer polynomials \( G_{T,i}^{(\alpha ,\beta )}(t) \), the shifted Legendre polynomials \( L_{T,i}^{(\alpha ,\beta )}(t) \), and the shifted Chebyshev polynomials of the first, second, third and fourth kinds \( T_{T,i}^{(\alpha ,\beta )}(t) \), \( U_{T,i}^{(\alpha ,\beta )}(t) \), \( V_{T,i}^{(\alpha ,\beta )}(t) \) and \( W_{T,i}^{(\alpha ,\beta )}(t) \), respectively. All these orthogonal polynomials are contacted with \( P_{T,i}^{(\alpha ,\beta )} (t)\) through the relations:

$$\begin{aligned}&L_{T,i}^{(\alpha ,\beta )}(t) =P_{T,i}^{(0,0)} (t),\\&G_{T,i}^{(\alpha ,\beta )}(t) =\dfrac{\Gamma (i+1)\Gamma \left( \alpha +\dfrac{1}{2}\right) }{\Gamma \left( \alpha +\dfrac{1}{2}+i\right) }P_{T,i}^{\left( \alpha -\dfrac{1}{2},\beta -\dfrac{1}{2}\right) } (t),\\&T_{T,i}^{(\alpha ,\beta )}(t) =\dfrac{\Gamma (i+1)\Gamma \left( \dfrac{1}{2}\right) }{\Gamma \left( \dfrac{1}{2}+i\right) }P_{T,i}^{\left( -\dfrac{1}{2}, -\dfrac{1}{2}\right) } (t), \\&U_{T,i}^{(\alpha ,\beta )}(t) =\dfrac{\Gamma (i+2)\Gamma \left( \dfrac{1}{2}\right) }{2 \Gamma \left( \dfrac{3}{2}+i\right) }P_{T,i}^{\left( \dfrac{1}{2}, \dfrac{1}{2}\right) } (t), \\&V_{T,i}^{(\alpha ,\beta )}(t) =\dfrac{2^{2i}\left( \Gamma (i+1)\right) ^{2}}{\Gamma (2i+1)}P_{T,i}^{\left( -\dfrac{1}{2}, \dfrac{1}{2}\right) } (t),\\&W_{T,i}^{(\alpha ,\beta )}(t) =\dfrac{2^{2i}(\Gamma (i+1))^{2}}{\Gamma (2i+1)}P_{T,i}^{\left( \dfrac{1}{2}, -\dfrac{1}{2}\right) } (t) . \end{aligned}$$

3 Function approximation by shifted Jacobi polynomials

The function w(t) , square integrable with respect to \( \omega _{T}^{(\alpha ,\beta )}(t) \) in \( [0,\, T] , \) can be expanded as the following expression [15, 34]:

$$\begin{aligned} w(t)\,=\,\sum _{i=0}^{\infty }a_i P_{T,i}^{(\alpha ,\beta )}(t), \end{aligned}$$
(15)

where \( a_i \) (the coefficients of the series) are obtained by

$$\begin{aligned} a_i =\dfrac{1}{h_{T,i}^{(\alpha ,\beta )}}\int _{0}^T \omega _T^{(\alpha ,\beta )}\, w(t)\, P_{T,i}^{(\alpha ,\beta )}(t) dt,\,\, i=0,1, \cdots . \end{aligned}$$
(16)

So, we can estimate the approximate solution by taking \((N+1)\)-terms of the series in Eq. (15) and we will have

$$\begin{aligned} w(t)\, \simeq w_N (t)\, =\,\sum _{i=0}^{N} a_i P_{T,i}^{(\alpha ,\beta )}(t)= \, A^T \Phi _{T,N}(t), \end{aligned}$$
(17)

where \( A \,=\,[ a_0,a_1, \cdots , a_N]^T\), and \( \Phi _{T,N}(t)\,=\,[P_{T,0}^{(\alpha ,\beta )}(t),P_{T,1}^{(\alpha ,\beta )}(t),\cdots , P_{T,N}^{(\alpha ,\beta )}(t)] ^T\).

Here, we suppose that

$$\begin{aligned} S(t)\, =\,[ 1,\, t,\, t^2,\, t^3, \cdots , t^N]^T. \end{aligned}$$
(18)

By Eq. (17), the vector \( \Phi _{T,N}(t)\,\) can be presented as

$$\begin{aligned} \Phi _{T,N}(t)\,=\, B_{(\alpha ,\beta )} S(t). \end{aligned}$$
(19)

where \( B_{(\alpha ,\beta )} \) is a square matrix of order \( (N+1) \times (N+1) \) that given as follows

$$\begin{aligned} b_{i+1,j+1}\,=\, \left\{ \begin{array}{l} (-1)^{i-j}\dfrac{(\alpha +i)!(\alpha +\beta +j+i)!}{(\alpha +\beta +i)!(\alpha +j)!(j!)(i-j)! \, T^j},\, i\ge j ,\\ \\ 0\, ,\, otherwise . \end{array}\right. \end{aligned}$$
(20)

for \( 0 \le i,j \le N \).

For example, if \(N=4,\, \alpha \, =\,\beta =\,0\), then B as follows

$$\begin{aligned} B_{(0,0)}\, = \, \dfrac{1}{T^i} \left[ \begin{array}{ccccc} 1&{}0&{}0&{}0&{}0\\ -1&{}2&{}0&{}0&{}0\\ 1&{}-6&{}6&{}0&{}0\\ -1&{}12&{}-30&{}20&{}0\\ 1&{}-20&{}90&{}-140&{}70\\ \end{array}\right] . \end{aligned}$$
(21)

Hence, using Eq. (19) , we get

$$\begin{aligned} S(t)\,=\, B_{(\alpha ,\beta )}^{-1}\,\Phi _{T,N}(t) . \end{aligned}$$
(22)

Note 3

Note that, we obtain this square matrix B for all other orthogonal polynomials as well. For example, if \(N=4,\, \alpha \, =\dfrac{1}{2},\,\beta =\,\dfrac{-1}{2}\) then the square matrix B for the fourth kind shifted Chebyshev polynomials as follows

$$\begin{aligned} B_{\left( \dfrac{1}{2},\dfrac{-1}{2}\right) }\, = \, \dfrac{1}{T^i} \left[ \begin{array}{ccccc} 1&{}0&{}0&{}0&{}0\\ -1&{}4&{}0&{}0&{}0\\ 1&{}-12&{}16&{}0&{}0\\ -1&{}24&{}-80&{}64&{}0\\ 1&{}-40&{}240&{}-448&{}256\\ \end{array}\right] . \end{aligned}$$
(23)

4 Shifted Jacobi polynomials operational matrix (SJOM)

Operational matrices, which are used in different areas of numerical analysis and they are especially important to solve a variety of problems in different fields such as integral equations, differential equations, integro-differential equations, ordinary and partial fractional differential equations and etc [31, 34,35,36, 39,40,41,42,43,44,45,46,47]. In this section, we investigate the (SJOM) of fractional variable-order to support the numerical solution of Eq. (1). Therefore, we convert the problem into the system of algebraic of equations which solved numerically in collocation points.

At first, \( D^{\eta _{i}(t)} \Phi _{T,N}(t) ,\,(i=1,2,\cdots ,n)\) can be deduced as the following:

since \( \Phi _{T,N}(t)\,=\, B_{(\alpha ,\beta )} S(t) \), then we have

$$\begin{aligned}&D^{\eta _{i}(t)} \Phi _{T,N}(t)\, = \, D^{\eta _{i}(t)}( B_{(\alpha ,\beta )} S(t)\,) \nonumber \\&\quad =\, B_{(\alpha ,\beta )} D^{\eta _{i}(t)}\,[1,t,\cdots , t^N ]^T ,\nonumber \\&\qquad i\, = \, 1, 2,\cdots , n. \end{aligned}$$
(24)

Combining Eqs. (10) and (24), it gives

$$\begin{aligned}&D^{\eta _{i}(t)} \Phi _{T,N}(t)\,=\, B_{(\alpha ,\beta )}D^{\eta _{i}(t)}( S(t)\,)\nonumber \\&\quad =\, B_{(\alpha ,\beta )} \,\left[ 0,\dfrac{\Gamma (2) t^{(1-\eta _{i}(t))}}{\Gamma (2-\eta _{i}(t))},\cdots , \dfrac{\Gamma (N+1) t^{(N-\eta _{i}(t))}}{\Gamma (N+1-\eta _{i}(t))} \right] ^T \nonumber \\&\quad = \,B_{(\alpha ,\beta )} \left[ \begin{array}{ccccc} 0&{}0&{}0&{}\cdots &{}0\\ 0&{}\dfrac{\Gamma (2) t^{-\eta _{i}(t)}}{\Gamma (2-\eta _{i}(t))}&{}0&{}\cdots &{}0\\ 0&{}0&{}\dfrac{\Gamma (3) t^{-\eta _{i}(t)}}{\Gamma (3-\eta _{i}(t))}&{}\cdots &{}0\\ \vdots &{}\vdots &{}\vdots &{}\vdots &{}\vdots \\ 0&{}0&{}0&{}\cdots &{}\dfrac{\Gamma (N) t^{-\eta _{i}(t)}}{\Gamma (N+1-\eta _{i}(t))}\\ \end{array}\right] \, \left[ \begin{array}{c} 1\\ t\\ t^2\\ \vdots \\ t^N\\ \end{array}\right] \nonumber \\&\quad =\, B_{(\alpha ,\beta )}Q_i(t) S(t) ,\,\, i\, = \, 1, 2,\cdots , n. \end{aligned}$$
(25)

where

$$\begin{aligned} Q_i (t)=\left[ \begin{array}{ccccc} 0&{}0&{}0&{}\cdots &{}0\\ 0&{}\dfrac{\Gamma (2) t^{-\eta _{i}(t)}}{\Gamma (2-\eta _{i}(t))}&{}0&{}\cdots &{}0\\ 0&{}0&{}\dfrac{\Gamma (3) t^{-\eta _{i}(t)}}{\Gamma (3-\eta _{i}(t))}&{}\cdots &{}0\\ \vdots &{}\vdots &{}\vdots &{}\vdots &{}\vdots \\ 0&{}0&{}0&{}\cdots &{}\dfrac{\Gamma (N) t^{-\eta _{i}(t)}}{\Gamma (N+1-\eta _{i}(t))}\\ \end{array}\right] ,\,\, i\, = \, 1, 2,\cdots , n. \end{aligned}$$
(26)

Using Eq. (22), then

$$\begin{aligned} D^{\eta _{i}(t)} \Phi _{T,N}(t)\, = \, B_{(\alpha ,\beta )} Q_i(t)\, B_{(\alpha ,\beta )}^{-1} \Phi _{T,N}(t) ,\,\, i\, = \, 1, 2,\cdots , n. \end{aligned}$$
(27)

The operational matrix of \( D^{\eta _{i}(t)} \Phi _{T,N}(t)\,,(i\, = \, 1, 2,\cdots , n.) \) is \( B_{(\alpha ,\beta )} Q_i(t)\, B_{(\alpha ,\beta )}^{-1} \).

Now, we can estimate the variable-order fractional of the approximated function that obtained in Eq. (17) as the following

$$\begin{aligned}&D^{\eta _{i}(t)} w(t)\, \simeq D^{\eta _{i}(t)}( A^{T} \Phi _{T,N}(t)\,)=\, A^{T} D^{\eta _{i}(t)}\Phi _{T,N}(t)\nonumber \\&\quad = A^{T} B_{(\alpha ,\beta )} Q_i(t)\, B_{(\alpha ,\beta )}^{-1} \Phi _{T,N}(t) ,\,\, i\, = \, 1, 2,\cdots , n. \end{aligned}$$
(28)

By using Eq. (28), hence the Eq. (1) is turned into

$$\begin{aligned}&\sum _{i=1}^{n}\alpha _{i} (A^{T} B_{(\alpha ,\beta )} Q_i(t)\, B_{(\alpha ,\beta )}^{-1} \Phi _{T,N}(t))\, \nonumber \\&\qquad +\alpha _{n+1} A^{T} \Phi _{T,N}(t-\tau ) \nonumber \\&\quad = F\,(t,\, A^{T} \Phi _{T,N}(t),\, (A^{T} B_{(\alpha ,\beta )} Q_1(t)\, B_{(\alpha ,\beta )}^{-1} \Phi _{T,N}(t)),\, \nonumber \\&\qquad (A^{T} B_{(\alpha ,\beta )} Q_2(t)\, B_{(\alpha ,\beta )}^{-1} \Phi _{T,N}(t)) , \, \ldots , \nonumber \\&\qquad (A^{T} B_{(\alpha ,\beta )} Q_n(t)\, B_{(\alpha ,\beta )}^{-1} \Phi _{T,N}(t)), \nonumber \\&\qquad A^{T} \Phi _{T,N}(t-\tau ))\, , \, 0 \le t \le T\, , \end{aligned}$$
(29)

Finally, we use \( t_j\,(j\, = \, 0,1, 2,\cdots , m.) \) where they are the roots of \(P_{T,m+1}^{(\alpha ,\beta )}(t)\). Then Eq. (29) can be converted into the following algebraic system

$$\begin{aligned}&\sum _{i=1}^{n}\alpha _{i} (A^{T} B_{(\alpha ,\beta )} Q_i(t_{j})\, B_{(\alpha ,\beta )}^{-1} \Phi _{T,N}(t_{j}))\, \nonumber \\&\qquad +\alpha _{n+1} A^{T} \Phi _{T,N}(t_{j}-\tau )\nonumber \\&\quad =F\,(t_{j},\, A^{T} \Phi _{T,N}(t_{j}),\, (A^{T} B_{(\alpha ,\beta )} Q_1(t_{j})\, B_{(\alpha ,\beta )}^{-1} \Phi _{T,N}(t_{j})),\, \nonumber \\&\qquad (A^{T} B_{(\alpha ,\beta )} Q_2(t_{j})\, B_{(\alpha ,\beta )}^{-1} \Phi _{T,N}(t_{j})) , \, \ldots , \nonumber \\&\qquad (A^{T} B_{(\alpha ,\beta )} Q_n(t_{j})\, B_{(\alpha ,\beta )}^{-1} \Phi _{T,N}(t_{j})), \nonumber \\&\qquad A^{T} \Phi _{T,N}(t_{j}-\tau ))\, ,\,\, j=0,1,2,\cdots , m. \end{aligned}$$
(30)

So, the system in Eq. (30) can be solved numerically for determining the unknown vector A. Therefore, the numerical solution that presented in Eq. (17) can be obtained.

5 Error analysis

In this part of paper, we estimate an upper bound of the absolute errors via using the Lagrange interpolation polynomials. Also, by using the current method (NSJOM) with error approximation and the residual correction method [48, 49], an efficient error approximation will be obtained for the variable-order fractional differential equations.

5.1 Error bound

Now, our aim is to gain an analytic expression of error norm for the best approximation of a smooth function \( w(t) \in [0,T] \) via its expansion in terms of Jacobi polynomials. Let

$$\begin{aligned} \prod _{N}^{\alpha ,\beta }= span\left\{ P_{T,i}^{(\alpha ,\beta )}(t), \, i=0,1,2,\cdots , N \right\} . \end{aligned}$$

In this part of the discussion, we always assume that \(w_{N}(t) \in \prod _{N}^{\alpha ,\beta }\) is the best approximation of w(t), then by definition of the best approximation, we have

$$\begin{aligned} \forall v_N (t)\in \prod _{N}^{\alpha ,\beta }\,\quad \Vert w(t)-w_N (t)\Vert _{\infty }\,\le \Vert w(t)-v_N (t)\Vert _{\infty }. \end{aligned}$$
(31)

It’s obvious that the above inequality is also true if \( v_N (t) \) be the interpolating polynomials at node points \( t_i \, (i=0,1,\cdots , m)\), where \( t_i \) are the roots of \(P_{T,m+1}^{(\alpha ,\beta )}(t)\). Then by the Lagrange interpolation polynomials formula and its error formula, we have

$$\begin{aligned} w(t)-v_N (t)=\dfrac{w^{(N+1)}(\xi )}{(N+1)!}\prod _{j=0}^{N}(t-t_j)\, , \end{aligned}$$
(32)

where \( \xi \in [0, T]\), and hence we obtain that

$$\begin{aligned}&\parallel w(t)-v_N (t)\parallel _{\infty }\le \max _{0\le t\le T}\mid w^{(N+1)}(\xi )\mid \nonumber \\&\quad \dfrac{\parallel \prod _{j=0}^{N}(t-t_j)\parallel _{\infty }}{(N+1)!}\, . \end{aligned}$$
(33)

We note that w(t) is a smooth function on \( [0,\,T] \), therefore, there exist a constant \( C_1 \), such that

$$\begin{aligned} \max _{0\le t\le T}\mid w^{(N+1)}(\xi )\mid \le C_1\, . \end{aligned}$$
(34)

By minimizing the factor \( \parallel \prod _{j=0}^{N}(t-t_j)\parallel _{\infty } \) as follows, we will have:

If use the one-to-one mapping \( t=\dfrac{T}{2}(z+1) \) between the interval \( [-1,\,1] \) and \( [0,\,T] \) to deduce that [34, 50]

$$\begin{aligned}&\min _{0\le t_j\le T} \max _{0\le t\le T}\mid \prod _{j=0}^{N}(t-t_j) \mid \nonumber \\&\quad =\min _{-1\le z_j\le 1}\max _{-1\le z\le 1}\mid \prod _{j=0}^{N}\dfrac{T}{2}(z-z_j) \mid \nonumber \\&\quad =\left( \dfrac{T}{2}\right) ^{N+1}\min _{-1\le z_j\le 1}\max _{-1\le z\le 1}\mid \prod _{j=0}^{N}(z-z_j) \mid \nonumber \\&\quad = \left( \dfrac{T}{2}\right) ^{N+1}\min _{-1\le z_j\le 1}\max _{-1\le z\le 1}\mid \dfrac{P_{N+1}^{(\alpha ,\beta )}(z)}{\lambda _{N}^{(\alpha ,\beta )}}\mid , \end{aligned}$$
(35)

where \( \lambda _{N}^{(\alpha ,\beta )}= \dfrac{\Gamma (2N+\alpha +\beta +1)}{2^{N}N! \Gamma (N+\alpha +\beta +1)} \) is the leading coefficient of \( P_{N+1}^{(\alpha ,\beta )}(z) \) and \( z_j \) are the roots of \( P_{N+1}^{(\alpha ,\beta )}(z) \). It is clear that

$$\begin{aligned} \max _{-1\le z\le 1}\mid P_{N+1}^{(\alpha ,\beta )}(z)\mid =P_{N+1}^{(\alpha ,\beta )}(1)=\dfrac{\Gamma (\beta +N+2)}{\Gamma (\beta +1)(N+1)!}\, , \end{aligned}$$

Using Eqs. (34) and (35), gives the following result

$$\begin{aligned} \parallel w(t)-w_N (t)\parallel _{\infty }\le C_{1} \dfrac{(\dfrac{T}{2})^{N+1} \Gamma (\beta +N+2)}{\lambda _{N}^{(\alpha ,\beta )} ((N+1)!)^{2}\, \Gamma (\beta +1)}\, . \end{aligned}$$
(36)

Then, we estimate an upper bound for absolute error of the exact and approximate solutions.

5.2 Error function estimation

In this subsection, we have introduced the error estimation based on the residual error function for the presented technique and the approximate solution (17) is refined via the residual correction scheme. The residual error estimation was used for the error estimation of some methods for different equations [36, 49, 51, 52].

At first, we denote \( e_{N}(t)\,=w_{N}(t)\,- w(t)\) as the error function of the NSJOM method approximation \( w_{N}(t) \) to w(t) , where w(t) is the exact solution of Eq. (1).

Therefore, \( w_{N}(t) \) satisfies the following equation

$$\begin{aligned}&\sum _{j=1}^{n}\alpha _{j} D^{\eta _{j}(t)} w_{N}(t)\, +\alpha _{n+1} w_{N}(t-\tau ) \nonumber \\&\quad = F\,(t,\, w_{N}(t),\, D^{\eta _{1}(t)} w_{N}(t),\, \nonumber \\&\qquad D^{\eta _{2}(t)} w_{N}(t) , \, \ldots ,\, D^{\eta _{n}(t)} w_{N}(t),w_{N}(t-\tau \,))\, + R_{N}(t),\nonumber \\&\qquad \, 0 \le t \le T\, ,\nonumber \\&\qquad w_{N}(0)=w_{0}, \end{aligned}$$
(37)

where \( R_{N}(t)\) is the residual function of Eq. (1), which is estimated by replacing the \( w_{N}(t) \) with w(t) in Eq. (1).

By subtract Eq. (1) from Eq. (37), the error problem is constructed as follows:

$$\begin{aligned}&\sum _{j=1}^{n}\alpha _{j} D^{\eta _{j}(t)} e_{N}(t)\, +\alpha _{n+1} e_{N}(t-\tau ) \nonumber \\&\quad =\, R_{N}(t)+R_{N,F}(t), \,\ \ \ \ 0 \le t \le T\,,\nonumber \\&\qquad e_{N}(0)=0, \end{aligned}$$
(38)

where

$$\begin{aligned}&R_{N,F}(t)=F\,(t,\, w_{N}(t),\, D^{\eta _{1}(t)} w_{N}(t),\,\nonumber \\&\quad D^{\eta _{2}(t)} w_{N}(t) , \, \ldots ,\, D^{\eta _{n}(t)} w_{N}(t),w_{N}(t-\tau \,))\nonumber \\&\quad -F\,(t,\, w(t),\, D^{\eta _{1}(t)} w(t),\, \nonumber \\&\quad D^{\eta _{2}(t)} w(t) , \, \ldots ,\, D^{\eta _{n}(t)} w(t),w(t-\tau \,)). \end{aligned}$$
(39)

Thus, the (38) can be solved in the same way as in the previous section and we obtain the following approximation to \( e_{N}(t) \).

$$\begin{aligned} \mathbf{e} _N (t)\, =\,\sum _{i=0}^{N} d_i P_{T,i}^{(\alpha ,\beta )}(t)= \, D^T \Phi _{T,N}(t), \end{aligned}$$
(40)

Then the maximum absolute error can be obtained approximately by

$$\begin{aligned} \mathbf{E} _N (t)\, =\,\max \lbrace \mathbf{e} _N (t)\, , 0 \le t \le T \rbrace . \end{aligned}$$
(41)

Note 4

Note that if the exact solution of the problem (1) is unknown, in real practical experiment, we have trouble with computing \(R_{N,F}\). But, the replacement strategy is to be approximated by its bound, say \(D_1|e_{N}(t)|+D_2|e_{N}(t-\tau )|\) with \(D_1\) and \(D_2\) as positive constants. In fact, it is possible by supposing that the nonlinear term F satisfies Lipschitz condition with respect to its all arguments.

The above estimation of error (41), depends on the convergence rates of expansions in Jacobi polynomial. Thus, it provides reasonable convergence rates in temporal discretizations [34, 52].

6 Numerical experiments

In this section, based on the previous discussion, some numerical examples are given to illustrate the accuracy, efficiency, applicability, generality and validity of the proposed technique. In all examples, the results of the present method are computed by Mathematica 10 software. In order to test our scheme, we compared it with other known methods in terms of absolute errors \( \mid w_{exact}(t)- w_{n}(t)\mid \), relative errors \( \mid \dfrac{ w_{exact}(t)- w_{n}(t)}{ w_{exact}(t)}\mid \) and the CPU time required for solving all examples.

Comparison of the results obtained by this scheme with the exact solution of each example shows that this new technique has a better agreement than other methods. The stability, consistency and easy implementation of this technique cause this method to be more applicable and reliable.

Example 6.1

[6, 10] Consider the following delay fractional order equation for \(0 <\eta \le 1\,,\tau >0\)

$$\begin{aligned}&D^{\eta } w(t)\, = \dfrac{2 w(t)^{1-\dfrac{\eta }{2}}}{\Gamma (3-\eta )}+ w(t-\tau )\, -w(t)+2 \tau \sqrt{w(t)}-\tau ^{2},\nonumber \\&w(t)=0,\,\, t \le 0. \end{aligned}$$
(42)

Note that \(w(t)=\,t^{2}\) is the exact solution and \(0 \le t \le T\,, T=2,\, \tau =0.3\,,\,\eta =0.6\).

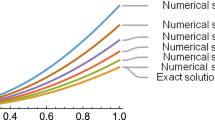
By the concepts presented in Sect. 4, we consider the approximate solution with \((N+1)\) finite terms that presented in Eq. (17) for this problem and substitute in main problem. Then by using Eq. (28), this problem is converted to form of the Eq. (29), finally using \(t_i\), therefore, a system of algebraic equations emerges which can be solved numerically to determine the unknown vector A with initial value \(w_0 =0\). The solution of the Eq. (42) approximated using new method compared to other methods, is in the best agreement with the exact solution. The absolute errors ( at some nodal points) of this method and methods in [6, 10] are presented and compared in Table 1, also the CPU time needed for these methods is given in this Table. From this Table, it is observed that the numerical results are very close to the exact solution and we achieved an excellent approximation for the exact solution by employing current scheme and it was found the our method in comparison with mentioned methods is better with view to utilization, accuracy and more time efficiency. Figure 1 compares the exact and approximated solution which confirms the reliability of NSJOM method. Moreover, in Fig. 2 we plot the absolute error for this example. Note that the Figs. 1 and 2 show a proper agreement between approximate and exact solutions. In this example for \( N=2 \) and \( N=7 \), we have \(A\,=[ 1.33333,2,0.66667]^T , \,A\,=[ 1.33333,2,0.66667,2.95496\times 10^{-16},8.71848\times 10^{-17},0,3.55601\times 10^{-16},-2.82553\times 10^{-16}]^T \), respectively.

Table 1 Comparison the absolute errors between results in [6, 10] and our results with \( \alpha \,=\,0, \beta \,=\,0 \) and \( T=2 \) for Ex.1
Full size table
Fig. 1
figure 1

Comparison of between approximate solution (\( w_{5}\)) of NSJOM method and exact solution for example 1

Full size image
Fig. 2
figure 2

The absolute errors comparison between numerical solution (\( w_{5}\)) and exact solution for Example 1

Full size image

Example 6.2

[4, 27] Consider the following delay fractional order equation for \(0 <\eta \le 1\,,\tau >0\)

$$\begin{aligned}&D^{0.9} w(t)\, = \dfrac{2 t^{1.1}}{\Gamma (2.1)}\,-\dfrac{ t^{0.1}}{\Gamma (1.1)}\nonumber \\&\quad + w(t-0.1)\, -w(t)+0.2 t-0.11,\nonumber \\&w(t)=0,\,\, t \le 0. \end{aligned}$$
(43)

In above problem \(w(t)=\,t^{2} -t\) is the exact solution and \(0 \le t \le T\,, T=10,\, \tau =0.1\,,\,\eta =0.9\).

Using the process mentioned in Ex. 1, we get the solution of this problem. The solution of the Eq. (43) approximated using current method compared to other methods, is in the best agreement with the exact solution. The absolute and relative errors ( at some nodal points) of this method and methods in [4, 27] are presented and compared in Tables 2, 3, also the CPU time needed for these methods is given in these Tables. From these Tables, it is observed that the numerical results are very close to the exact solution and we achieved an excellent approximation for the exact solution by employing new technique and it was found the current method in comparison with mentioned methods is better with view to utilization, accuracy and more time efficiency. Figure 3 compares the exact and approximated solution which confirms the reliability of NSJOM method. Moreover, in Fig. 4 we plot the absolute error for this example. Note that the Figs. 3 and 4 show a proper agreement between approximate and exact solution. In this example for \( N=2 \) and \( N=3 \), we have \(A\,=[ 28.33333,45,16.66667]^T , \,A\,=[ 28.33333,45,16.66667,0]^T \), respectively.

Table 2 Comparison the absolute errors between results in [4, 27] and our results with \( \alpha \,=\,0, \beta \,=\,0 \) and \( T=10 \) for Ex.2
Full size table
Table 3 Comparison the relative errors between results in [4, 27] and our results with \( \alpha \,=\,0, \beta \,=\,0 \) and \( T=10 \) for Ex.2
Full size table
Fig. 3
figure 3

Comparison of between approximate solution( \( w_{2}\)) of NSJOM method and exact solution for example 2

Full size image
Fig. 4
figure 4

The absolute errors comparison between numerical solution( \( w_{2}\)) and exact solution for Example. 2

Full size image

Example 6.3

[5] Consider the following delay fractional order equation for \(0 <\eta \le 1\,,\tau >0\)

$$\begin{aligned}&D^{\eta } w(t)\, = \dfrac{2 t^{2-\eta }}{\Gamma (3-\eta )}\,-\dfrac{ t^{1-\eta }}{\Gamma (2-\eta )}\, \nonumber \\&\quad + w(t-\tau ) \, -w(t)+2\tau t-\tau ^{2} -\tau ,\nonumber \\&w(t)=0,\,\, t \le 0. \end{aligned}$$
(44)

In this problem \(w(t)=\,t^{2} -t\) is the exact solution and \(0 \le t \le T\,\).

Like pervious examples, we get the solution of this problem in accordance with delay being constant or time varying. The solution of the Eq. (44) approximated using current method compared to other methods, is in the best agreement with the exact solution. The absolute (\( E _A \)) and relative errors (\( E _R \)) (at \(t=T \)) of this method and method in [5] are displayed and compared in Tables 4, 5. From these Tables, it is observed that the numerical results are very close to the exact solution and we gained an excellent approximation for the exact solution by employing new technique and it was found the current technique in comparison with mentioned method is better with view to utilization, accuracy and more time efficiency. Figures 5, 7 compare the exact and approximated solution which confirms the reliability of NSJOM method. Moreover, in Figs. 6, 8 we plot the absolute errors of this example in accordance with delay being constant or time varying. Note that the Figs. 5 ,6, 7 and 8 show a proper agreement between approximate and exact solution.

Table 4 Comparison the error treatment between results in [5] and our results with \( \alpha \,=\,0, \beta \,=\,0 ,\eta =0.9, \tau =0.01 \exp (-t)\) at \( t=T \) for Ex.3
Full size table
Table 5 Comparison the error treatment between results in [5] and our results with \( \alpha \,=\,0, \beta \,=\,0 ,\tau =0.1, \eta =0.9\) at \( t=T \) for Ex.3
Full size table
Fig. 5
figure 5

Comparison of between approximate solution( \( w_{2}\)) of NSJOM method and exact solution for example. 3. (\( \tau =0.1, \eta =0.9\))

Full size image
Fig. 6
figure 6

The absolute errors comparison between numerical solution( \( w_{2}\)) and exact solution for Example. 3. (\( \tau =0.1, \eta =0.9 \))

Full size image
Fig. 7
figure 7

Comparison of between approximate solution (\( w_{2}\)) of NSJOM method and exact solution for example. 3. (\( \tau =0.01 \exp\, (-t), \eta =0.9\))

Full size image
Fig. 8
figure 8

The absolute errors comparison between numerical solution( \( w_{2}\)) and exact solution for Example. 3. (\( \tau =0.01 \exp (-t), \eta =0.9\))

Full size image
Table 6 Absolute errors of w(t) with \( \alpha \,=\,0, \beta \,=\,0 \) and \( T=1 \) for Ex.4
Full size table
Table 7 Relative errors of w(t) with \( \alpha \,=\,0, \beta \,=\,0 \) and \( T=1 \) for Ex.4
Full size table
Table 8 Absolute errors of w(t) with \( \alpha \,=\,1, \beta \,=\,1 \) and \( T=1 \) for Ex.4
Full size table
Table 9 Relative errors of w(t) with \( \alpha \,=\,1, \beta \,=\,1 \) and \( T=1 \) for Ex.4
Full size table
Table 10 Absolute errors of w(t) with \( \alpha \,=\,\dfrac{1}{2}, \beta \,=\,\dfrac{1}{2} \) and \( T=1 \) for Ex.4
Full size table
Table 11 Relative errors of w(t) with \( \alpha \,=\,\dfrac{1}{2}, \beta \,=\,\dfrac{1}{2} \) and \( T=1 \) for Ex.4
Full size table

Example 6.4

[6, 10] As the last and general example, consider the following delay fractional order equation for \(0 <\eta (t) \le 1\,,\tau >0\)

$$\begin{aligned}&D^{\eta (t)} w(t)\, = \dfrac{2 w(t)^{1-\dfrac{\eta (t)}{2}}}{\Gamma (3-\eta (t))} \nonumber \\&\quad + w(t-\tau )\, -w(t)+2 \tau \sqrt{w(t)}-\tau ^{2},\nonumber \\&\quad w(t)=0,\,\, t \le 0. \end{aligned}$$
(45)

Note that \(w(t)=\,t^{2}\) is the exact solution and \(0 \le t \le T\,, T=1,\, \tau =0.3\,,\,\eta (t)=0.6 t \).

By the concepts presented in Sect. 4, we consider the approximate solution with \((N+1)\) finite terms that presented in Eq. (17) for this problem and substitute in main problem. Then by using Eq. (28), this problem is converted to form of the Eq. (29), finally using \(t_i\), therefore, a system of algebraic equations emerges which can be solved numerically to determine the unknown vector A. The solutions of the Eq. (45) approximated for various values of \( \alpha ,\,\beta \), via new method compared to other methods, is in the best agreement with the exact solution. The absolute and relative errors ( at some nodal points) of this method are shown in Tables 6, 7, 8, 9, 10, 11. From these Tables, it is observed that the numerical results are very close to the exact solution and we achieved an excellent approximation for the exact solution by employing current scheme and it was found the our method in comparison with mentioned methods is better with view to utilization, accuracy and more time efficiency. Figure 9 compares the exact and approximated solution which confirms the reliability of NSJOM method. Moreover, in Fig. 10 we plot the absolute error with \( \alpha =1 ,\,\beta =1 \) for this example . Note that the Figs. 9 and 10 show a proper agreement between approximate and exact solution. In this example, we have

$$\begin{aligned}&If\, \alpha \,=\,0, \,\beta \,=\,0 \,\, and \,\, N=2 ,\, then \\&\,A\,=[ 1.33333,2,0.66667]^T ,\, CPU\, time \,=\, 0\,s\,,\\&if \,\,\alpha \,=\,0, \,\beta \,=\,0 \,\, and \,\, N=5 ,\, then \\&\,A\,=[ 1.33333,2,0.66667, 1.77479\times 10^{-16},0, \\&\quad -1.44702 \times 10^{-16}]^T ,\, CPU\, time \,=\, 0.01560\, s\,,\\&if \,\,\alpha \,=\,\dfrac{1}{2}, \,\beta \,=\,\dfrac{1}{2} \,\, and \,\, N=2 ,\, then \\&\,A\,=[ 1.25,1.33333,0.4]^T ,\, CPU \,time \,=\, 0.01560\, s\,, \\&if \,\, \alpha \,=\,\dfrac{1}{2}, \,\beta \,=\,\dfrac{1}{2}\,\, and \,\, N=5 ,\, then \\&\,A\,=[ 1.25,1.33333,0.4,-2.66269\times 10^{-15},\\&\quad -3.52736\times 10^{-16},-1.04701\times 10^{-16}]^T ,\, \\&\quad CPU\, time \,=\, 0.21840\, s\,, \\&if \,\, \alpha \,=\,1, \,\beta \,=\,1 \,\, and \,\, N=2 ,\, then \\&\,A\,=[ 1.2,1,0.26667]^T ,\, CPU \,time \,=\, 0.01560\, s\,, \\&if \,\, \alpha \,=\,1, \,\beta \,=\,1 \,\, and \,\, N=5 ,\, then \\&\,A\,=[ 1.2,1,0.26667,7.94864\times 10^{-17},5.29022\times 10^{-17}, \\&\quad -7.42853\times 10^{-17}]^T ,\, CPU\, time \,=\, 0.21840\, s\,. \end{aligned}$$
Fig. 9
figure 9

Comparison of between approximate solution( \( w_{5}\)) of NSJOM method and exact solution for example. 4. (\( \tau =0.3, \eta (t)=0.6 \,t\))

Full size image
Fig. 10
figure 10

The absolute errors comparison between numerical solution( \( w_{5}\)) and exact solution for Example. 4. (\( \tau =0.3, \eta (t)=0.6 \,t\))

Full size image

7 Conclusions

In the current paper, we have proposed the novel shifted Jacobi operational matrix (NSJOM) scheme for variable-order fractional delay differential equations via reducing the main problem to an algebraic system of equations that can be solved numerically. We have shown that the proposed method has good convergence, is easy to implement and its concepts are simple. The obtained results are excellent compared to other methods. Finally, the numerical results have been presented to clarify the effectiveness and accuracy of this technique.