Optimization of weight and cost of cantilever retaining wall by a hybrid metaheuristic algorithm

Abstract

A retaining wall is a structure used to resist the lateral pressure of soil or any backfill material. Cantilever retaining walls provide resistance to overturning and sliding by using backfill weight. In this paper, the weight and cost of the cantilever retaining wall have been minimized using a hybrid metaheuristic optimization technique, namely, h-BOASOS. The algorithm has been developed by the ensemble of two popular metaheuristics, butterfly optimization algorithm (BOA) and symbiosis organism search (SOS) algorithm. BOA’s exploratory intensity is coupled with SOS’s greater exploitative capacity to find the superior algorithm h-BOASOS. The newly developed algorithm has been tested with a suite of 35 classical benchmark functions, and the results are compared with several state-of-the-art metaheuristic algorithms. The results are evaluated statistically by the Friedman rank test, and convergence curves measure the convergence speed of the algorithm. It is observed in both cases that h-BOASOS is superior to other algorithms. The suggested approach is then used to solve four real-world engineering design problems to examine the problem-solving capacity of the proposed algorithm, and the results are contrasted with a wide range of algorithms. The proposed h-BOASOS is considered to be the winner on each occasion. Finally, the newly suggested algorithm is applied to find the cost and weight of the cantilever retaining wall problems of two different heights, 3.2 m and 6.3 m. The obtained results are compared with the component algorithms and found that the new algorithm works better than the compared algorithms.

1 Introduction

Soil is unstable in many circumstances due to its integral angle of inclination. There are several procedures to make these slopes stable. One of the most popular methods to stabilize slopes is the use of retaining wall structures. The retaining wall is the structure that holds soil behind it and resists lateral pressure of the soil. Designing a retaining wall depends on three primary criteria: structural strength, geotechnical stability, and the economy. It generally uses a trial and error approach to satisfy these criteria simultaneously, and these criteria are checked against geotechnical and structural requirements. Thus, these approaches demand several repetitions, and there is no assurance that the final design is the best from an economic point of view.

Optimization algorithms can be exploited to reach a cost-effective design satisfying all the geotechnical and structural requirements simultaneously. It is extremely challenging to find a design that satisfies all the safety criteria, so it is essential to formulate the problem as one of the mathematical non-linear programming techniques. Because of these reasons, these approaches demand several repetitions, which are time-consuming, and there is no assurance that the final design obtained will be safe and best from an economic point of view. Existing optimization structural software used for retaining wall design lacks the ability to find out optimal design because of their deterministic nature, while stochastic methods adopted are not tailored specifically for retaining walls and massive concrete structures. To overcome these limitations and find out a cost-effective design, there is a need for an optimization algorithm to solve the retaining wall problem. Numerous studies have investigated the optimization of retaining walls using meta-heuristic algorithms. Hence, it is one of the most compelling research topics in geotechnical and structural optimization.

The retaining wall optimization problem comprises of structural strength and geotechnical stability requirements. The objective function is to minimize both the cost and weight of the retaining wall. To economize the cost, satisfying these situations, there is a need to vary the dimensions of the wall several times, which makes it very tedious and monotonous. It is incredibly challenging to find a design that satisfies all the safety criteria, so it is essential to formulate the problem as one of the mathematical non-linear programming techniques.

Retaining walls are the rigid wall which laterally supports the soil on both the sides at different levels. Retaining walls are further classified into gravity, cantilever, counterfort, and buttress retaining wall. In this study, the cantilever retaining wall problem is considered for optimization. The cantilever retaining wall is constructed of reinforced concrete with a thinner stem. Resistance to overturning and sliding is provided by utilizing the weight of backfill soil.

Due to the high complexity, such as highly non-linearity, multi-modal property, a large number of variables, and constraints of present-day optimization problems, the researchers are inclined to solve these problems by meta-heuristic optimization techniques as the available methods cannot cope with these types of complexities. Due to simplicity, meta-heuristic methods are gaining popularity day by day. The meta-heuristics are generally developed depending on some particular metaphors. These metaphor-based algorithms can be divided into groups based on the metaphors on which the methods are developed. These are evolutionary algorithms, swarm intelligence based algorithms, physics-based algorithms, immune algorithms, human-based algorithm, etc.

The working procedure of most of the algorithms is the same. These algorithms randomly generate some initial candidate solutions within the specific range and upgrade the solutions depending upon the metaphors they follow. In the process of up-gradation, each candidate solution upgrades itself locally and globally, which means the candidate explores new regions in the search space and exploit the region where they already obtained a potential solution. To develop an efficient meta-heuristic algorithm, proper balancing of exploration and exploitation is necessary. This is why the optimization community is developing hybrid methods to get a proper balance between these two characteristics. It has already been proved that, in many a case, a combination of two algorithms (maybe two meta-heuristics or parts of two meta-heuristics or one meta-heuristic combined with another heuristic or any other method) gives better results in solving optimization problem than the component algorithms. For the last two decades, hybrid meta-heuristic algorithms have been gaining popularity, and scientists are widely using these methods to solve real-life combinatorial and other complicated optimization problems.

Metaheuristics have wide applications in the field of structural engineering. Structural problems are non-linear and multi-modal under some complex constraints. To eliminate these complexities, many researchers are using metaheuristic algorithms to solve such types of problems. Dede [1] used JAYA algorithm to solve the size optimization problem for steel grillage structures. Baradaran and Madhkhan [2] used an improved genetic algorithm (GA) for the optimal design of planar steel frames, Kaveh and Farhadmanesh [3] employed colliding body optimization (CBO) and enhanced colliding body optimization (ECBO) for optimal seismic design of steel plate shear walls, Kaveh et al. [4] proposed modified dolphin monitoring operator for weight optimization of skeletal structures. Teaching-learning based optimization (TLBO), ECBO, CBO, vibrating particles system (VPS), and harmony search algorithm (HS) were used by Kaveh et al. [5] for the optimal design of multi-span pitched roof frames with tapered members.

Considering the huge ability of meta-heuristic algorithms, researchers use these algorithms to optimize structural problems like retaining wall problems in recent decades. For instance, particle swarm optimization (PSO) was used by Varaee [6] to optimize the cost and weight of a 4.5 m-high retaining wall. Again PSO with the passive congregation was utilized by Khajehzadeh et al. [7] in finding optimum cost design for 3 m and 5.5 m high retaining walls. Also, Khajehzadeh et al. [8] used modified particle swarm optimization (MPSO) in optimizing the cost of a 3 m-high retaining wall and sensitivity analysis of soil properties for a 4.5 m tall retaining wall. Gravitational search algorithm (GSA) was opted for finding the best cost design of 3 m and 5.5 m high retaining wall by Khajehzadeh and Eslami [9]. Yepes et al. [10] used simulated annealing (SA) for analyzing parameters of 4 m to 10 m retaining walls by considering soil properties variation. Ant colony optimization (ACO) was used by Bonab [11] for designing 3 m, 4 m, and 5 m-high retaining walls. Kaveh and Abadi [12] found out the optimal design of a 6.1 m high retaining wall by adopted harmony search (AHS), while the charged system search algorithm (CSS) was used for the same wall by Kaveh and Behnam [13]. Big bang big crunch (BBBC) was used by Camp and Akin [14] for optimizing cost and weight of 3 m-high and 4.5 m-high retaining walls, including a base shear key effect. The same problem was also solved by Gandomi et al. [15] by exploring swarm intelligence techniques efficiency with the same case studies. Nama et al. [21] incorporated HS, PSO, and TLBO for optimizing seismic active earth pressure coefficient. Optimum design of the tied-back retaining wall was accomplished by Jasim and Al-Yaqoobi [17] using GA. Differential evolution (DE) was used for the optimal design of the cantilever retaining wall by Kumar and Suribabu [18]. For retaining wall optimization, Bath et al. [19] used DE, and PSO was used for optimum design of reinforced concrete retaining walls by Moayyeri et al. [20]. Nama et al. [21] used an improved backtracking search algorithm (IBSA) to obtain the active earth pressure on retaining wall supporting c-$\phi$ backfill using the pseudo-dynamic method. Except for all the above cases, meta-heuristic algorithms were used for many applications in structural engineering. Some of those can be seen in [22,23,24,25,26,27,28,29,30,31,32].

The BOA [33] is a nature-based algorithm that mimics butterflies’ food and mating pair search behaviors. The system is focused primarily on the butterflies’ foraging technique, which uses their smelling sense to assess the nectar or mating partner. The global phase of BOA uses the best butterfly’s information to forage, and the local phase uses a random search or explores the domain for potential solutions. Both these phases make the BOA a suitable algorithm to apply in the different optimization problems. Although the literature indicates enough scope for the BOA to explore the search space, it faces some problems such as local optima stagnation, slow convergence, and skipping real solutions when solving real-life problems. That is why many articles have come up in the literature, improving the basic BOA so that the algorithm can perform better than the basic BOA. Some of the improved or modified algorithms of BOA can be found in [35]. Also, some of the hybrid methods where BOA is a component algorithm can be seen in [36,37,38].

The SOS [39] algorithm is implemented through the ecosystem’s interactive behavior of different organisms. SOS is considered one of the most common algorithms for solving complex real-world problems because of its simplicity and higher proficiency. For various optimization problems of different disciplines, SOS has already proven its effectiveness. The stages of mutualism and commensalism make good use of population data as these two stages use the position of its best organism as a point of reference, helping to exploit the possible solutions. Again, by changing the current solution to generate new solutions, the parasitism process eliminates the inferior solutions and helps to explore the entire search room, allowing the algorithm to be well balanced in both exploratory and exploitative competencies. The simplicity of the SOS makes it one of the most competitive swarm intelligence based algorithm. Motivated by the above claims, we believe that the effectiveness of SOS must be further improved by hybridizing with other efficient algorithms to make the algorithm more efficient, stable, and robust. Numerous works on SOS in literature have tried to improve the algorithm by modifying it in various manners to improve its performance. Some of the works on improving and hybridizing SOS can be found in [40,41,42,43]. For detailed improvement, hybridization, and applications of SOS, one can see [44].

The present study suggests a hybrid meta-heuristic, viz. h-BOASOS, combining BOA and SOS and applied it to solve the cantilever retaining wall problem. It is seen that the strength of BOA lies in its exploration capability whereas, SOS is known for its better exploitation capacities. To balance the exploration and exploitation of the algorithm, the search agents first search the entire region through the steps of BOA to discover the possible solutions throughout the entire search space. Once the possible solutions are obtained, the solutions are passed through the SOS steps to take advantage of the search space to find the optimal solution near the potential solutions already obtained by BOA. Thus the suggested h-BOASOS is assumed to be a well-balanced and robust algorithm that can find the optimal global solution. By applying the algorithm to solve a suite of 35 (thirty-five) benchmark functions of varying complexities, the efficacy of the proposed h-BOASOS was assessed and the results obtained are contrasted with 10 (ten) state-of-the-art algorithms. To prevent the error due to the algorithm’s stochastic nature, each function was executed for 30 runs with 10,000 iterations. For analysis, mean and standard deviation values are reported. The experimental results indicate that the algorithm proposed is more potent than those of the algorithms compared to h-BOASOS. For further study, the non-parametric Friedman rank test has been performed considering the mean values of the proposed and compared algorithms and found that the rank of h-BOASOS is the least among all compared algorithms. For all comparative algorithms, convergence graphs of selected functions are plotted to scrutinize the convergence velocity and find that the convergence rate of the proposed algorithm is more robust than that of other algorithms. It is also applied to solve 04 (four) real-world engineering design problems, namely, gear train design problem, cantilever beam design problem, car-side impact design problem, and three-bar truss design problem to assess the problem-solving skill of the h-BOASOS. The results obtained to support our assertion of h-BOASOS’ supremacy and argue that the proposed algorithm is better than some of the literature’s well-known meta-heuristics. Finally, h-BOASOS was used to obtain the optimum cost and weight of the cantilever retaining wall problem, a relatively complex problem with 12 (twelve) design variables and 16 (sixteen) constraints.

The remaining part of paper has been organized as follows: the two component algorithms, BOA and SOS have been described in Sects. 2 and  3 respectively. The proposed algorithm has been elaborated in Sect. 4. Section 5 deals with the experimental setup. Section 6 describes the results of the proposed algorithm. Applications of this hybrid method in different real-life problems are described in Sect. 7. Section 8 describes the cantilever retaining wall problem with its mathematical formulation. Section 9 discusses the results of the problem with the aid of the proposed h-BOASOS and some other methods. Finally the conclusion and future scope of this work has been presented in Sect. 10.

2 Butterfly optimization algorithm

Butterfly optimization algorithm (BOA) was introduced by Arora and Singh [33] in 2018, mimicking the food foraging and mating pair behavior of butterflies. In BOA, butterflies are used as search agents for the algorithm as BOA is a population-based iterative algorithm. The fragrance generated by a butterfly is propagated to all other butterflies in the region, and other butterflies sense the propagated fragrance through chemoreceptors scattered over the body of butterflies, which are used to smell the fragrance. Thus a collective social knowledge network is formed in BOA, which helped the algorithm to search the entire space effectively. The candidate butterflies are always moving towards the best butterfly once they smell the best butterfly’s fragrance. This is known as the global search phase of BOA.

On the other hand, when a butterfly does not smell the fragrance from any butterfly, a random movement is considered, which is termed as a local search phase in BOA. The basic concept of sense depends on three special parameters viz., sensory modality (c), stimulus intensity (I), and power exponent (a). In BOA, it is assumed that many butterflies release fragrance simultaneously, and by the sensory modality, butterflies sense and differentiate the fragrances. I characterizes the fitness of a butterfly in BOA, and a is the response compression. The behavior of butterflies depends on two imperative factors viz. variation of I, and formulation of f. In BOA, the stimulus intensity I of a butterfly is linked with the value of the objective function, and f is relative. Considering all these aspects, the fragrance is formulated in the following way:

$$\begin{aligned} f_i=c*I^a \end{aligned}$$

(1)

where, $f_i$ is the apparent magnitude of the fragrance of ith butterfly.

It has been already discussed that BOA consists of two crucial phases, viz., global search phase and local search phase. In the global phase, a butterfly moves towards the best butterfly in a particular iteration. Mathematically, it is represented as

$$\begin{aligned} X_i^{new}=X_i+(r^2*g^{best}-X_i )*f_i \end{aligned}$$

(2)

where, $X_i$ is the ith butterfly and $g^{best}$ represents the current best solution in a particular stage. The fragrance of $i^{th}$ butterfly is represented by $f_i$ and r is a random number in [0, 1].

The local search phase of BOA can be represented as

$$\begin{aligned} X_i^{new}=X_i+(r^2*X_j-X_k )*f_i \end{aligned}$$

(3)

where, $X_j$ and $X_k$ are the jth and kth butterflies from the solution space and selected randomly from the current population, and r is a random number in between 0 and 1.

3 Symbiosis organisms search

In 2014, Cheng and Prayogo [39] proposed SOS algorithm mimicking the interactive relationship among the organisms in an ecosystem. The SOS is executed in three steps: mutualism phase, commensalism phase, and parasitism phase. During the optimization process, a set of initial solution is generated randomly within the search space, and each solution is updated by the three phases. The details of SOS are summarized below:

3.1 Mutualism phase

In the mutualism phase, two organisms of the ecosystem interact mutually, and both get benefits from the interaction. An organism $X_i$ tries to interact with an organism $X_j$, where $X_j$ is randomly selected from the ecosystem. From the interaction, both the organisms try to improve their mutual survival benefit in the ecosystem. Mathematically, the new $X_i$ and $X_j$ are determined by Eqs. (4) and (5) and update in the ecosystem. The new organism will replace the old one if the new organism is better than its previous fitness value.

$$\begin{aligned} X_i^{new}= \,\,& {} X_i+r_1*(X_{best}-Mutual_{Vector}*BF_1 ) \end{aligned}$$

(4)

$$\begin{aligned} X_j^{new}= \,\,& {} X_j+r_2*(X_{best}-Mutual_{Vector}*BF_2 ) \end{aligned}$$

(5)

where,

$$\begin{aligned} Mutual_{Vector}= (X_i +X_j)/2 \end{aligned}$$

(6)

Here, $X_{best}$ represents the best organism in the ecosystem, the value of benefit factors ($BF_1$ and $BF_2$) are considered randomly as either 1 or 2. These factors represent the level of benefit to each organism, i.e., whether an organism partially or fully benefits from the interaction. ‘$Mutual_{Vector}$’ represents the characteristic of the relationship of the organism $X_i$ and $X_j$. $r_1$ and $r_2$ are two random numbers between 0 and 1.

3.2 Commensalism phase

When, in the interaction of two organisms, one gets benefited, and the other neither benefited nor harmed, this interaction is called commensalism. In the commensalism phase of SOS, an organism $X_i$ increases its beneficial advantage by interacting with another organism $X_j$ to a higher degree of adaptation in the ecosystem, but $X_j$ remains the same. The new fitness value of $X_i$ is determined by Eq. (7) and updates the new $X_i$ if its fitness value is better than the previous $X_i$.

$$\begin{aligned} X_i^{new}=X_i+r_3*(X_{best}-X_j ) \end{aligned}$$

(7)

where, $X_{best}$ is the best organism according to the fitness value in the ecosystem and $r_3$ is any random number between $-1$ and 1.

3.3 Parasitism phase

On the interaction of two organisms, if one organism gets benefited but the other organism gets harmed, then this interaction is called a parasitism relationship in an ecosystem. In the SOS algorithm, a parasite vector, namely $Parasite_{Vector}$ is determined by duplicating an organism $X_i$. The $Parasite_{Vector}$ is obtained in the following way:

$\bullet$ Select one dimension randomly from the dimensions of organism $X_i$ i.e. from 1, 2, 3, ...D.

$\bullet$ Randomly modify the selected dimension using Eq. (8) and replace the position of the dimension into $X_i$.

$$\begin{aligned} X_{i,d}=l_d+r_4*(u_d-l_d ) \end{aligned}$$

(8)

Where, $r_4$ is a random number between 0 and 1.

If the objective function value of the $Parasite_{Vector}$ is superior to that of $X_j$, $Parasite_{Vector}$ will replace $X_j$ in the ecosystem. If the reverse happens, $X_j$ is sustained and the $Parasite_{Vector}$ leaves the ecosystem.

4 Proposed methodology

An efficient and robust algorithm can be developed only when the balance between exploring new areas in search space and exploiting prior knowledge that has been already gathered in the search process is assured. When exploration is better than exploitation, diversification becomes poor and causes premature convergence. On the other hand, when exploitation is better than exploration, it causes poor intensification, and thus the algorithm’s convergence rate becomes slower. The proposed meta-heuristic seems to have a brilliant combination of exploration and exploitation using both the global and local phases of BOA together with mutualism, commensalism, and parasitism steps of SOS. The proposed h-BOASOS seems to have the co-ordination of exploring the global search process, together with the exploitation of the search process.

BOA uses a random number r in order to update the location of butterflies. The choice of the search process of butterflies depends on a factor known as switch probability. In the original BOA, the switch probability (p) was taken as 0.8. So, when the value of random number r is less than 0.8, the butterflies move into the global search phase, indicating that most butterflies move towards the global phase when a smaller number of butterflies choose the local search phase. This makes the algorithm weaker in exploration in the search space though it is relatively more robust in exploiting the search process.

On the other hand, SOS is known for its stronger local searchability. The mutualism and commensalism phases concentrate on generating new organisms and select the best organism for survival. Provided that a new solution is updated relied on the best organism, the convergence rate often speeds up; however, local solutions may occur. The mathematical equations of these two phases show that the algorithm allows the organisms to search in the domain to discover near the best solutions they already obtained in the search space, thereby improving the exploitation ability of the algorithm. Again, the parasitism phase enables the search process to avoid the solution from trapping in local optima, thus improving the exploration ability of the algorithm. The improvements happen because a new candidate solution, namely, $Parasite_{Vector}$ is generated in the ecosystem by replacing some random elements of the organism $X_i$ with other elements. Then $Parasite_{Vector}$ is compared to another randomly selected organism in the ecosystem. Also, in the mutualism phase, two organisms update their mutual existence from their interaction and the same organisms that already updated their position through mutualism again update their positions to attain the global optima in the commensalism phase. These double impacts help the algorithm to expedite the convergence rate and make the algorithm competitive than other meta-heuristic algorithms.

From the above observations, to overcome the lacunae of both the algorithms, we have tried to construct a better algorithm by combining the above two algorithms BOA and SOS to propose a novel hybrid algorithm for optimization and named it h-BOASOS. The descriptions of BOA and SOS has already been given in Sects. 2 and 3 for convenience.

The main objective of the proposed algorithm is to combine the exploration and exploitation skill of SOS with the exploration facility of BOA. The original SOS has great exploitation strength, and the reason behind it is already explained above, whereas, in contrast, the basic BOA has very efficient exploration capability as the majority of the butterflies in the swarm choose the global phase of the algorithm. Thus, the proposed h-BOASOS algorithm owns an excellent convergence speed, can come out from the possible entrapment in the local optima, and possesses an excellent computational ability. Pseudo-code and flowchart of the proposed h-BOASOS are given in Table 1 and Fig. 1 respectively.

Table 1 Pseudo-code of the proposed h-BOASOS algorithm

Fig. 1

Flowchart diagram of the proposed h-BOASOS

4.1 Parameters used in the proposed h-BOASOS

In the proposed hybrid h-BOASOS, the parameters of both the component algorithms, BOA and SOS are incorporated. The value of the parameters are given in Table 2.

Table 2 Values of parameters of the proposed algorithms

4.2 Iterative technique used in proposed h-BOASOS

The newly suggested h-BOASOS combines the concepts of BOA and SOS and generates solutions in every new generation by using different operators and mechanisms of BOA and SOS. The steps of the h-BOASOS can be described as follows:

Step 1: Generate the initial candidate solutions randomly to create an initial population.

Step 2: For each candidate solution, the fragrance is generated using the formulation as a function of the physical intensity of stimulus using Eq. 1.

Step 3: For the iterative phase, one random number r is generated and checked with the switching probability (p).

Step 4: If the global exploration has opted, the candidate solution gets updated using Eq. 2.

Step 5: If the local phase is selected, the candidate solution takes a random search and updates using Eq. 3.

Step 6: The fitness value of each candidate solution is checked with the previous one and replaced if needed.

Step 7: The updated solution goes for the mutualism phase by choosing a random solution from the search space and find the mutual Vector using Eq. 6.

Step 8: With the mutual Vector, both of the candidate solutions are updated by using Eqs. 4 and 5.

Step 9: In the commensalism phase, the opted candidate solution is updated using Eq. 7.

Step 10: In the parasitism phase, one $Parasite_{Vector}$ is formed and checked with the recent candidate solution and replaced if needed.

Step 11: The fitness of all the candidate solution is obtained and checked with the fitness of the previous one.

Step 12: The approach is stopped when the termination condition (maximum number of iterations) has been reached.

5 Experimental setup

In this section, the experimental set-up that we have performed to show the proposed algorithm’s superiority is discussed briefly.

To check the efficiency, the h-BOASOS algorithm is tested on 35 different benchmark functions of varying complexity as shown in Tables 3 and 4. These benchmark functions are chosen to examine various features of the algorithm such as convergence rate, attainment of a large number of optimal points, ability to jump out of local optima, and avoid premature convergence. The stopping criteria can be defined in different ways like maximum CPU time used, maximum iteration number reached, the maximum number of iterations with no improvement, a particular value of the error rate, or any other appropriate criteria. In our case, we have taken the maximum number of iteration as the stopping criterion.

Table 3 Unimodal classical benchmark functions

Table 4 Multimodal classical benchmark functions

6 Results and discussions

6.1 Comparison with some state-of-the-art algorithms

To measure the performance of a meta-heuristic, several tests should be conducted to approve an algorithm’s performance. As these algorithms are stochastic in nature, it should be carefully noticed that an appropriate and a sufficient number of test functions and case studies are engaged to assure that the obtained results are occurring through its solid mathematical base and not by chance.

In the present study, a set of 35 classical benchmark functions of varied complexities are considered from literature to examine the competence of the proposed h-BOASOS, and the performance is compared with some state-of-the-art meta-heuristics, including BOA and SOS. Knowing the meta-heuristics’s stochastic nature, each of the algorithms is run 30 times to avoid the variability of the results. For this comparative analysis, the population size is fixed at 50; the maximum number of iterations is taken as 10,000. The performance of h-BOASOS over the aforesaid benchmark functions is compared with 12 (twelve) state-of-the-art algorithms: two component algorithms (BOA and SOS) and 10 (ten) popular meta-heuristics DE [45], PSO [46] and JAYA [48] sine cosine algorithm (SCA) [49], artificial bee colony ABC [47], cuckoo search (CS) [51], firefly algorithm (FA) [52], GA [53], monarch butterfly optimization (MBO) [54], and moth flame optimization (MFO) [50]. To compare the performances of the algorithms, simulation results containing the average results (MEAN) and the corresponding standard deviations (STD) are recorded for each algorithm. Firstly, the results of h-BOASOS and six other algorithms (BOA, SOS, DE, PSO, JAYA, and SCA) are recorded in Tables 5 and 6 . Secondly, the newly suggested algorithm is compared with six other meta-heuristics (ABC, CS, FA, GA, MBO, and MFO), and the results are shown in Tables 7 and 8.

From the simulation results shown in Table 5, it can be interpreted that the performance of the proposed h-BOASOS is better than the basic BOA and SOS in terms of searching function minimum. From this table, it is found that h-BOASOS is superior to BOA and SOS in 17 and 16 benchmark functions, similar to 16 and 12 functions, and inferior in 2 and 7 occasions, respectively.

Table 5 Simulation results of h-BOASOS and other state-of-the-art algorithms for functions 1 to 28 with NP=50 and 30 execution each with 10,000 iterations

Table 6  Simulation results of h-BOASOS and other state-of-the-art algorithms for functions 29 to 35 with NP=50 and 30 execution each with 10,000 iterations

To evaluate the performance of proposed h-BOASOS, it is compared to ten other state-of-the-art algorithms, which are the best performing and produce a satisfactory performance when applied to global optimization problems. These algorithms are widely employed to compare the performance of optimization algorithms, and the results are recorded in Tables 5 and 7.

The observation can be made from Table 5, h-BOASOS obtained superior solution than DE, PSO, JAYA, and SCA in 23, 29, 24, and 33 functions, similar in 5, 3, 3, 1 cases and inferior in 7, 3, 6, 1 occasions.

By Table 7, it can be evaluated that h-BOASOS generate superior solution compared to ABC, CS, FA, GA, MBO, and MFO in 28, 33, 22,28, 29, and 15 benchmark functions. h-BOASOS obtained similar results with the said algorithms in 2, 1, 7, 2, 3, and 19 functions. Again, h-BOASOS is inferior to the algorithms in 5, 1, 6, 5, 3, and 1 occasions (Tables 9, 10).

Table 7 Simulation results of functions 1 to 27 of h-BOASOS and some other algorithms with NP=50 and 30 execution each with 10,000 iterations

Table 8 Simulation results of functions 28 to 35 functions of h-BOASOS and some other algorithms with  NP=50 and 30 execution each with 10,000 iterations

Table 9 Comparison of experimental results of Tables 5 and 6, where the numbers represent the number of functions

Table 10 Comparison of experimental results of Tables 7 and 8, where the numbers represent the number of functions

6.2 Statistical rank test

Also, to evaluate the statistical performance of the newly developed algorithm, we have introduced the Friedman rank test, a non-parametric statistical test considering all the algorithms and mean values found by the respective algorithms found on the Tables 5, 6, 7 and 8 . The mean rank found for all the algorithms after performing the Friedman’s test is given in Tables 11, 12. From these two tables, it is evident that the rank of the proposed hybrid h-BOASOS is minimum in both cases. Table 6 shows that the algorithms’ respective ranks are 1 for h-BOASOS with mean rank 2.29, 2 for SOS, 3 for BOA, 4 for DE, 5 for JAYA, and 6 for PSO from the Table 11. Also, from Table 12, it can be seen that the first mean rank holder is the proposed h-BOASOS, the second is ABC, third-GA, fourth-MBO, fifth-CS, sixth-MFO, and seventh is FA. Finally, an overall Friedman rank test is also performed considering all the compared algorithms, shown in Table 13. Evaluating Table 13, we can rank 1 for h-BOASOS with minimal mean rank (3.49), 2 for ABC with 3.78 mean rank, 3 for SOS with mean rank 4.40, followed by BOA, DE, JAYA, GA, MBO, CS, SCA, PSO, MFO, and FA. So it may be concluded that the proposed h-BOASOS is statistically superior to all of the compared algorithms.

Table 11 Friedman’s rank test with compared algorithms from Tables 5 and 6

Table 12 Friedman’s rank test with compared algorithms from Tables 7 and 8

Table 13 Friedman’s rank test with all of the compared algorithms

6.3 Convergence analysis

To verify the convergence speed of h-BOASOS, some of the convergence graphs with its component algorithms BOA and SOS, as well as with other five well-known algorithms DE PSO, JAYA, SCA, and MFO are presented in Fig. 2a–f. Different unimodal and multimodal functions for which convergence graphs are given here are Booth, Ackley, Branin, Dejong5, Griewank, Levy N.13, Schaffer 4, and Foxholes functions. The best candidate solution’s fitness value in each iteration is considered to draw convergence curves in these figures. From these figures, it can be concluded that the proposed h-BOASOS algorithm converges faster for both types of functions, which establishes that the exploration and exploitation capacities of the proposed algorithm are more balanced than the other chosen algorithms.

Fig. 2

Convergence graphs of h-BOASOS compared with BOA, SOS, DE, PSO, JAYA, and SCA

7 Real world problem

7.1 Gear train design problem

Gear Train Design Problem: The main objective of this engineering design problem is to minimize the gear ratio for a given set of four gears of a train. The number of teeth of the gears is the parameter here. It is an unconstrained problem, but the ranges of variables are considered as constraints. The schematic diagram of the system is shown in Fig. 7 The gear ratio is calculated as follows:

$$\begin{aligned} Gear\, ratio =\frac{(angular\, velocity\, of\, output\, shaft)}{(angular\, velocity\, of\,input\, shaft)} \end{aligned}$$

The mathematical formulation of this problem is as follows:

$$\begin{aligned} Minimize\,f(x)=\left( {\frac{1}{6.931}}-{\frac{x_cx_b}{x_ax_d}}\right) ^2 \end{aligned}$$

Subject to

$$\begin{aligned} 12 \le x_a,x_b,x_c,x_d\le 60 \end{aligned}$$

This problem is solved with h-BOASOS, and the results are compared to MFO, ABC, MBA, GA, CS, and ISA in Table 14. Table 14 shows that the h-BOASOS algorithm finds the better optimal gear ratio value than MFO, ABC, MBA, GA CS, and ISA. The obtained result proves that h-BOASOS can be useful in solving discrete problems as well. All the results except h-BOASOS have been taken from [55].

Table 14 Comparison of results on the gear train design problem

7.2 Cantilever beam design problem

A beam is a structural element that is capable of withstanding load primarily by resisting bending. Here the cantilever beam has five square-shaped hollow elements. Figure 8 depicts that each element acts as one variable with the thickness as constant, so there are five structural parameters in total. It may be seen from Fig. 8 that a vertical load also acts to the free end of the beam (node 6), and the right side of the beam (node 1) is rigidly supported. Minimizing the weight of the beam is the objective here. One vertical displacement constraint is there that should be taken care of by the final optimal design. The mathematical formulation of the problem may be represented as:

$$\begin{aligned}&Minimize f(x)= 0.06224(x_1 + x_2 + x_3+ x_4 + x_5); \\&\quad Subject\,to: g(x)= {61/x_1^3}+{ 37/x_2^3}+{19/x_3^3}+ {7/x_4^3}+{1/x_5^3}\le 1;\\&\quad \hbox {Where }0.01 \le x_1, x_2, x_3, x_4, x_5 \le 100; \end{aligned}$$

The problem has been solved by h-BOASOS, and the results are compared with some other methods viz., ALO, CS, SOS, CGA-I, CSA-II, and MMA. The results other than h-BOASOS are taken from [57]. It has been found from Table 15 that the proposed method shows better performance for this problem.

Table 15 Comparison of results on the cantilever beam design problem

7.3 Car side impact design problem

The objective of this problem is to minimize the car’s total weight using eleven mixed variables while maintaining safety performance according to the standard. These variables represent the thickness and material of critical parts of the car. The 8th and the 9th variables are discrete, and these are material design variables, while the rest of the variables are continuous and represents thickness design variables.

The symbols $a_1,a_2,a_3,a_4,a_5,a_6,a_7,a_8,a_9, a_{10}, a_{11}$ are used here to represent the variables thickness of B-pillar inner, the thickness of B-pillar reinforcement, the thickness of floor side inner, the thickness of cross members, the thickness of door beam, the thickness of door beltline reinforcement, the thickness of roof rail, the material of B-pillar inner, the material of floor side inner, barrier height, barrier hitting position respectively. The problem is subjected to ten inequality constraints. The car side impact design is considered a real case of a mechanical optimization problem with mixed discrete and continuous design variables. This problem can be mathematically described as:

$$\begin{aligned}&a =(a_1,a_2,a_3,a_4,a_5,a_6,a_7,a_8,a_9,a_{10},a_{11}) \\&\quad Min\; f(a)=1.98+4.90 a_1+6.67 a_2+6.98 a_3 \\&\quad +4.01 a_4+1.78 a_5+2.73 a_7 \\&\hbox {Subject to} \\&h_1 (a)=1.16-0.3717 a_2 a_4-0.00931 a_2 a_10-0.484 a_3 a_9\\&\quad + 0.01343 a_6 a_{10} \le 1 \\&h_2 (a)=0.261-0.0159 a_1 a_2-0.188 a_1 a_8-0.019 a_2 a_7 \\&\quad +0.0144 a_3a_5 \\&\quad + 0.0008757 a_5 a_10+0.080405 a_6 a_9+0.00139 a_8 a_11 \\&\quad + 0.00001575 a_{10} a_{11}\le 0.32 \\&h_3 (a)=0.214+0.00817 a_5-0.131 a_1 a_8\\&\quad -0.0704 a_1 a_9+0.03099 a_2 a_6 \\&\quad -0.018 a_2 a_7+0.0208 a_3 a_8+0.121 a_3 a_9-0.00364 a_5 a_6\\&\quad + 0.0007715 a_5 a_{10}-0.0005354 a_6 a_{10}\\&\quad +0.00121 a_8 a{11}\le 0.32\\&h_4 (a)=0.074-0.061 a_2-0.163 a_3 a_8\\&\quad +0.001232 a_3 a_{10}-0.166 a_7a_9 +0.227a_2^2 \le 0.32 \\&h_5 (a)=28.98+3.818 a_3-4.2a_1 a_2+0.0207a_5 a_{10}\\&\quad +6.63a_6 a_9-7.7 a_7 a_8+0.32 a_9 a_{10}\le 32 \\&h_6(a)=33.86+2.95 a_3+0.1792 a_{10}-5.05 a_1 a_2-11.0 a_2 a_8\\&\quad - 0.0215 a_5 a_{10}-9.98 a_7 a_8+22.0 a_8 a_9\le 32 \\&h_7 (a)=46.36-9.9 a_2-12.9 a_1 a_8+0.1107 a_3 a_{10}\le 32 \\&h_8 (a)=4.72-0.5 a_4-0.19 a_2 a_3-0.0122 a_4 a_{10}\\&\quad +0.009325 a_6 a_{10} +0.000191 a_{11}^2\le 4 \\&h_9(a)=10.58-0.674 a_1 a_2-1.95 a_2 a_8+0.02054 a_3 a_{10}\\&\quad -0.0198 a_4 a_{10}+0.028 a_6 a_{10}\le 9.9 \\&h_{10} (a)=16.45-0.489 a(3) a_7-0.843 a_5 a_6+0.0432 a_9 a_{10}\\&\quad -0.0556 a_9 a_{11}-0.000786 a_{11}^2\le 15.7 \\&\quad \hbox {where},\; 0.5\le a(1)-a(7)\le 1.5 \\&\quad a(8),a(9)\in (0.192,0.345) \\&\quad -30\le a(10),a(11)\le 30 \\ \end{aligned}$$

To judge the efficiency of the newly proposed h-BOASOS in the car side impact design problem, the results have been compared to that of 11 other state-of-the-art algorithms viz., WOAmM, ABC, PSO, MFO, ALO, ER-WCA, GWO, WCA, MBA, SSA, and WOA. Tables 15, 16 and 17 shows the result found by h-BOASOS and comparison with the results found in literature [55]. Results are taken using a population size of 35, and 850 is the maximum number of iterations in one run, whereas the proposed h-BOASOS find the minimum solution in 50 iterations. f(x) here represents the value of the optimal weight of the car.

Table 16 Comparison of results on the car-side impact design problem

Table 17 Comparison of results on car-side impact design problem

7.4 Three bar truss design problem

The purpose of the problem is to reduce the weight of the bar structures. Stress, deflection, and buckling constraints are the limitations of the problem. The objective function of the problem is a non-linear function with three non-linear limitations. The mathematical formulation of the problem is given below:

$$\begin{aligned} Minimize \;f(x)=L{x_2+2\sqrt{2} x_1 } \end{aligned}$$

where

$$\begin{aligned}&h_1 (x)=\frac{x_2}{(2x_2x_1+\sqrt{2}x_1^2 )} P-\rho \le 0 \\&h_2 (x)=\frac{x_2+\sqrt{2}x_1}{(2x_2x_1+\sqrt{2}x_1^2 )} P-\rho \le 0 \\&h_1 (x)=\frac{1}{(x_1+\sqrt{2}x_2 )} P-\rho \le 0 \\&\hbox {where}, \; 0\le x_1, x_2\le 1 \,\hbox {and}\, P=2, L=100, \rho =2. \end{aligned}$$

To evaluate the performance of the h-BOASOS on this problem, the result evaluated by the proposed method is compared to ten other algorithms, among which few are collected from the literature [50]. Table 18 contains the best value found by the h-BOASOS and other algorithms. Here to check the convergence speed of the proposed method total iteration has been set to 35 with 1000 iteration. It seems that the proposed method finds a new optimal solution, ‘150.451’, with a new set of parameters value, [0.41471 0.33153] to this problem.

Table 18 Comparison of results on three bar truss design problem

8 Cantilever retaining wall

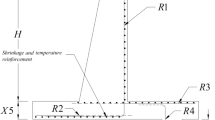
In the optimum design of the structure, three stages are generally considered: structural modeling, optimum design modeling, and the optimization algorithm. In the first stage, i.e., structural modeling, the formulation of the problem is done, and the objective function of the problem is defined without violating the constraints. The problem considered for optimization is solved in the past by using optimtool [58]. Figure 3 shows a sketch of the cantilever retaining wall model showing variables used for optimization.

8.1 Structural modeling

In most of the structural problems, the objective function is defined based on the weight and cost of the structure depending on some constraints. Weight is calculated by assuming a density of concrete and steel, and the cost is estimated as the combined cost of reinforcement and concrete. The optimization equation can be formulated as:

$$\begin{aligned}&\hbox {Minimize } f(x) \\&\hbox {Subject to} \\&g_i(x)=0.........i=1,2,....p \\&h_j(x)\le 0.........j=1,2,....m \\&L_k(x)\le X_k(x)\le U_k(x)....k=1,2,....n \end{aligned}$$

where, objective function is given by f(X), $g_i(X)$ and $h_j(X)$ are equality and inequality constraints respectively, $L_k$ and $U_k$ are lower and upper bounds of the kth variable.

8.2 Optimum design modeling

In this stage, the parameters of the problems are studied in-depth so that parameters, design variables, constraints, and the objective function can be decided.

8.2.1 Design variables

Figure 3 shows design variables for retaining wall, include: width of the base of retaining wall ($X_1$), toe projection ($X_2$), thickness at the bottom of the stem ($X_3$), thickness at the top of the stem ($X_4$), thickness of base slab ($X_5$), area of vertical reinforcement in the stem ($X_6$), area of horizontal reinforcement in the toe ($X_7$), area of horizontal reinforcement in the heel ($X_8$), distance from toe to the front of the shear key ($X_9$), shear key width ($X_{10}$), shear key depth ($X_{11}$), area of vertical reinforcement in the base shear key ($X_{12}$).

Fig. 3

Retaining wall model representing variables used for optimization

8.2.2 Constraints

Retaining structures seeks designs that provide safety and stability against different types of failure modes and meet the terms with concrete building code requirements. These requirements can be categorized into four general groups of design constraints: capacity, stability, reinforcement configuration, and geometric limitations. Design constraints are imposed as penalties on the objective functions and are non-zero only when violated. If the design is reasonable, the sum of the constraint penalties will be zero. The design constraints are based on geotechnical and structural requirements as per IS code 456:2000. There are different types of failure modes such as bearing capacity, sliding, and overturning, and for these modes of failure minimum factor of safety should be provided by retaining wall (Table 20).

Table 19 Lower and upper bounds of design variables

Table 20 Constraints of cantilever retaining wall

i. Overturning Failure Mode:

$$\begin{aligned} g_1(x)=F_0-(\sum M_{vo}/\sum M_{ho})\le 0 \end{aligned}$$

where, $F_o$ is Factor of safety against overturning, $\sum M_{vo}$ represents the total moment of vertical forces that resist overturning about toe, $\sum M_{ho}$ is the total horizontal moment of forces that tends to overturn about the toe.

ii. Bearing Capacity:

$$\begin{aligned}&g_2(x)=P_{min}\le 0 \\&g_3(x)=P_{max}-SBC\le 0 \end{aligned}$$

in which, $P_{min}$ and $P_{max}$ is minimum, and maximum contact pressure at the interface between the foundation soil and the wall structure and safe bearing capacity of the soil is represented as SBC.

iii. Sliding Failure Mode

$$\begin{aligned} g_4(x)=F_s-\left[ \left( \sum V*\mu +H_p\right) /\sum H\right] \le 0 \end{aligned}$$

where, $F_s$ represents factor of safety against sliding , $\sum H$ and $\sum V$ are total horizontal and vertical driving forces respectively and $H_p$ denotes horizontal passive pressure.

iv. Tension Failure Mode

$$\begin{aligned} g_5(x)=E-(B/6)\le 0 \end{aligned}$$

in which, eccentricity of the resultant force is given by E and base width of retaining wall by B.

v. Moment failure mode

The flexural strength $M_{rs}$ is computed as:

$$\begin{aligned}&M_{rs}=0.87A_s f_y(d_s-0.416X_u) \\&X_{u}=0.87A_s f_y(0.36f_{ck}b) \\&g_6(x)=M_s-M_{rs}\le 0 \end{aligned}$$

where, $X_u$ is the location of the neutral axis, $A_s$ is c/s area of steel, $d_s$ is effective depth of stem, $f_y$ is the yield strength of reinforcement, $M_s$ represents the maximum bending moment at the face of the wall, $M_{rs}$ is flexural strength of stem.

$$\begin{aligned}&g_7(x)=M_t-M_{rt}\le 0 \\&g_8(x)=M_h-M_{rh}\le 0 \\&g_9(x)=M_k-M_{rk}\le 0 \end{aligned}$$

where, $M_t$ and $M_h$ are maximum bending moment at the junction of the stem with toe slab and heel slab, Maximum bending moment at base shear key, $M_{rt}$ and $M_{rh}$ are Modulus of rupture of the toe slab, heel slab, $M_k$ is the moment at the base of the shear key.

vi. Shear failure mode

$$\begin{aligned}&g_{10}(x)=V_s-V_{us}\le 0 \\&g_{11}(x)=V_t-V_{ut}\le 0 \\&g_{12}(x)=V_h-V_{uh}\le 0 \\&g_{13}(x)=V_k-V_{uk}\le 0 \end{aligned}$$

where, $V_s$, $V_t$, $V_h$, and $V_k$ are the maximum shear carrying capacity of the stem, toe, heel, and shear key, respectively. Similarly, $V_{us}$, $V_{ut}$, $V_{uh}$ and $V_{uk}$ are the shear capacity of the concrete stem, toe, heel, and shear key.

vii. Criteria for minimum reinforcement

$$\begin{aligned}&g_{14}(x)=(0.12/100b)bD_s-A_s\le 0 \\&g_{15}(x)=(0.12/100b)bD_s-A_t\le 0 \\&g_{16}(x)=(0.12/100b)bD_s-A_h\le 0 \end{aligned}$$

where, the base width of the retaining wall is given by b, $D_s$ and D are thickness at the bottom of stem and base slab, $A_s$, $A_t$, and $A_h$ are the area of reinforcement in the stem, toe, and heel.

viii. Criteria for maximum reinforcement

$$\begin{aligned}&g_{17}(x)=A_s-(4/100)bD_S\le 0 \\&g_{18}(x)=A_t-(4/100)bD\le 0 \\&g_{19}(x)=A_h-(4/100)bD\le 0 \end{aligned}$$

ix. Additional geometric criteria

In order to prevent infeasible retaining wall dimensions, some additional geometrical constraints have been added.

$$\begin{aligned}&g_{20}(x)=X_2+X_3-X_1\le 0 \\&g_{21}(x)=X_9+X_{10}-X_1\le 0 \end{aligned}$$

x. Lower and upper bound constraints

The derived constraint expressions are found to be highly nonlinear in the design variables.

8.2.3 Objective function

As mentioned earlier, the objective of the problem is the minimization of weight and cost. The forms of two objective functions for this sort of optimization problem in structural engineering are reliable. The cost function f(cost) is given by:

$$\begin{aligned} f_{cost}=C_sW_s+C_cV_c \end{aligned}$$

where $C_s$ is the unit cost of steel and concrete, $W_s$ is the weight of reinforcement per unit length of the wall, and $V_c$ is the volume of concrete per unit length. The second objective function depends exclusively on the weight of the materials. The weight function f (weight) is:

$$\begin{aligned} f_{weight}=W_s+100V_c\gamma _c \end{aligned}$$

Where, $\gamma _c$ is the unit weight of concrete, and a factor of 100 is used for consistency of units

Table 21 Input parameters for the retaining wall problem

9 Results and Discussions

In this section, the results of minimum cost and minimum weight for cantilever retaining wall of height 3.2 m and 6.3 m are obtained by the newly proposed h-BOASOS algorithm, and some discussions on the obtained results are performed. Table 21 shows different input parameters for the cantilever retaining wall.

9.1 For 3.2 m and 6.3 m high retaining wall

For the retaining wall with a height of 3.2 m, lower and upper bounds of design variables for the two objective functions which are constructed to obtain cost and weight are presented in Table 19.

Values of design constraints for a 3.2 m high retaining wall are presented in Table 23. Again, Table 22 depicts the optimized weight and cost for the entire structure. Results obtained from the h-BOASOS algorithm for the optimized weight of steel and volume of concrete required for construction to be safe have been shown in Table 24. The minimum weight obtained using the h-BOASOS algorithm is 2630.8284 Kg/m, and the minimum cost is 1895.3257 Rs/m (1 $ = Rs.74.2 approx).

Table 22 Optimum values of design variables for 3.2 m high retaining wall

Table 23 Values of constraints at optimum values of design variables for 3.2 m high retaining wall

Table 24 Minimum values of objective function for 3.2 m high retaining wall

In Table 25, optimized results of design variables are presented for 6.3 m high retaining wall.

Table 25 Optimum values of design variables for 6.3 m high retaining wall

Values of design constraints for 6.3 m high retaining wall are presented in Tables 26 and 27 shows optimized weight and cost for the entire structure. Minimum weight obtained by using h-BOASOS algorithm is 9093.9172 Kg/m and minimum cost is Rs.3359.5348/m.

Table 26 Values of constraints at optimum values of design variables for 6.3 m high retaining wall

Table 27 Minimum values of objective function for 6.3 m high retaining wall

Figure 2 shows the optimum value of cost function and weight function at different heights of cantilever retaining wall from 3 m to 6 m obtained from the h-BOASOS Algorithm.

Fig. 4

Comparison of cost function at different stem height of cantilever retaining wall

The range of the stem height (3–6 m) shows that for higher values of height, the optimum cost and weight become more sensitive to variations in the stem height. This is more apparent for the cost function. Higher stem height produces higher values of the objective function. It is obvious that weight and cost will increase as the retaining wall’s height increases, which is reflected in Fig. 2. The optimum values for both objective models are shown for different heights from 3 to 6 m; the optimum weight increases 3.42 times while the optimum cost by 1.53 times.

Fig. 5

Comparison of optimum volume of concrete for both the objective function at different stem height of cantilever retaining wall

Figure 4 shows the optimum value of concrete required for both the objective functions at different heights of the cantilever retaining wall from 3 to 6 m. Although it does not follow a particular trend of increase or decrease, a weight function optimum volume of concrete for 6 m high retaining wall is almost 1.79 times greater than that of 3 m high. Similarly, for cost function, the optimum volume of concrete for a 6 m high retaining wall is almost 3.43 times greater than a 3 m high wall.

Fig. 6

Comparison of optimum weight of steel for both the objective function at different stem height of cantilever retaining wall

Figure 5 represents the optimum value of the weight of steel obtained for both objective functions at different heights of the cantilever retaining wall from 3 to 6 m. For the weight function, the optimum weight of steel for a 6 m high retaining wall is almost 0.73 times lesser than 3 m high. Similarly, for cost function, the optimum volume of concrete for a 6 m high retaining wall is almost 0.377 times greater than that of 3 m high (Fig. 6).

9.2 Comparison of results

In this section, the optimum values of design variables, the optimum volume of concrete, and optimum cost and weight of retaining wall obtained by h-BOASOS are compared with the optimtool, BOA, and SOS results.

Table 28 Comparison of results—optimum weight as objective function for 3.2 m high retaining wall

Table 29 Comparison of results—optimum cost as objective function for 3.2 m high retaining wall

Table 30 Comparison of results—optimum weight as objective function for 6.3 m high retaining wall

Table 31 Comparison of results—optimum weight as objective function for 6.3 m high retaining wall

Tables 19, 20, 21 and 22 present the comparison of results obtained from Optim tool [58], BOA, SOS and proposed methodology, i.e., h-BOASOS. Optimized geometrical parameters for which weight and cost are minimum, the optimum weight of steel, and the concrete volume are presented in Tables 19, 20, 21 and 22. From these tables, it is seen that the proposed algorithm h-BOASOS gives efficient results for both cost and weight function for 3.2 m and 6.3 m height of cantilever retaining wall. The optimum weight of the 3.2 m retaining wall obtained from the h-BOASOS algorithm is 3115.34 Kg/m, and its Optimum Cost is Rs.11895.33/m. While, Optimum Weight of 6.3 m is 3115.34 Kg/m and it’s Optimum Cost is 11895.33 Rs/m (1 $ = Rs.74.2 approx) (Tables 28, 29, 30, 31).

10 Conclusion

In this envisage, the cantilever retaining wall problem is solved by a newly proposed hybrid algorithm h-BOASOS. The proposed algorithm is tested on a suite of thirty-five classical benchmark functions. The obtained results are then compared with a wide variety of popular optimization algorithms and found that the proposed method outperforms the compared algorithms in numerical results. To support our claim, we have performed the Friedman rank test and found that the rank of the proposed algorithm is the least. To examine the convergence speed of the h-BOASOS, some of the convergence graphs are plotted and found that the proposed algorithm converges faster than the compared algorithms. Further, two real-world engineering design problems obtained from literature are also solved by the suggested algorithm. The experimental results prove the efficiency of the proposed algorithm over several state-of-the-art algorithms. Finally, the reduction of weight and cost of retaining wall is achieved successfully by the newly proposed algorithm. Using h-BOASOS, for 3.2 m and 6.3 m high retaining wall, approximately 8.75% and 5.43% material weight is reduced compared to the results obtained from the optimtool, 19.6% and 2.05% compared to SOS. Similarly, in the case of cost obtained from h-BOASOS, the cost saved for the retaining wall of heights 3.2 m and 6.3 m are 14.02% and 56.53% compared to results obtained from the optimtool. While, as compared to SOS, cost saved is 14.7% and 2.2%, respectively.

The researchers are always involved in exploring new hypotheses and simultaneously seeking to refine existing theories, so there is always space for finding new studies and improving existing research. Several further extensions can be made from the review of the research discussed in this article. Some of those are listed below:

• The present study may be upgraded by considering the adaptive or self-adaptive parameter setting of both the component algorithms. Specifically, the switching probability of BOA and the beneficial factors of SOS can be taken adaptively.

• The concept of fuzzy and its extensions may be incorporated in the parameter setting. For example, fuzzy-adaptive, neighborhood-based, fitness distance-based, etc., may be combined with this study to improve its efficiency further.

• The mathematical foundation of the metaheuristic algorithms has not been widely studied so far. So, mathematical analysis of stability, convergence, divergence, complexity, etc., may be done for better understanding.

• Depending upon the physiognomies of the design variables (integer, mixed-integer, binary, discrete, etc.), some modified algorithms can be established to solve real-life industrial problems.

• The proposed algorithm may further be extended to the multimodal and multi and many-objective scenario.

• The suggested algorithm may be applied to the optimization of complex systems such as designing the structures of civil engineering, business models, inventory control, transportation problems, power system problem, simulation and planning, controlling, and scheduling problems, etc.

Fig. 7

Schematic diagram of Gear Train Design Problem

Fig. 8

Cantilever beam design