Combining machine learning models via adaptive ensemble weighting for prediction of shear capacity of reinforced-concrete deep beams

Abstract

This study presents a novel artificial intelligence (AI) technique based on two support vector machine (SVM) models and symbiotic organisms search (SOS) algorithm, called “optimized support vector machines with adaptive ensemble weighting” (OSVM-AEW), to predict the shear capacity of reinforced-concrete (RC) deep beams. This ensemble learning-based system combines two supervised learning models—the support vector machine (SVM) and least-squares support vector machine (LS-SVM)—with the SOS optimization algorithm as the optimizer. In OSVM-AEW, SOS is integrated to simultaneously select the optimal parameters of SVM and LS-SVM, and control the coordination process of the learning outputs. Experimental results show that OSVM-AEW achieves the greatest evaluation criteria for coefficient of correlation (0.9620), coefficient of determination (0.9254), mean absolute error (0.3854 MPa), mean absolute percentage error (7.68%), and root-mean-squared error (0.5265 MPa). This paper demonstrates the successful application of OSVM-AEW as an efficient tool for helping structural engineers in the RC deep beams design process.

1 Introduction

As structural members, reinforced-concrete (RC) deep beams have often been used as load distribution elements such as in folded plate construction, foundation walls, transfer girders, and pile caps in tall buildings. Despite their usefulness and popularity, RC deep beams are difficult to design, because various parameters non-linearly affect their behavior and shear strength. Notably, shear stress is a dominant failure mode of RC deep beams that tends to result in sudden, severe collapse and human loss. For decades, quantitative studies have explored shear strength and analyzed the behavior of RC deep beams, including the strut-and-tie model [1, 2], mechanism analysis using the upper bound theorem of plasticity theory and finite-element analyses [3]. However, these design procedures are linear; thus, they often provide estimated values that are not close to the real strength of RC deep beams [4].

In general, a variety of bodies publish design code procedures that seek to calculate the ultimate shear strength of RC deep beams; these bodies include the American Concrete Institute (ACI) [5], the Construction Institute Research Information Association (CIRIA Guide 2) [6], and the Canadian Standard Association (CSA) [7]. However, these values, with respect to experimental tests, are at best conservative and at worst subpar. The following standard performance by the design code can be attributed to the large number of parameters and the non-linear relationships between the ultimate shear strength of the RC deep beam and the corresponding parameters. This ultimately leads to an inherent difficulty in creating a model that approximates mathematical shear strength.

In the past decades, artificial intelligence (AI) has been the subject of extensive research in the civil engineering field [8,9,10,11,12,13,14]. It has been reported that AI has successfully simulated the human inference process and, therefore, has become a powerful prediction technique. This enables civil engineers to predict the structural performance of concrete members. AI techniques have proven to be capable of capturing the complicated non-linear relationship between simply supported RC deep beams with its influencing parameters and providing highly accurate strength estimations.

Support vector machine (SVM) is a widely used machine learning technique that was proposed by Vapnik in 1995 [15]. As one of the most robust methods in the field of machine learning, the SVM algorithm belongs to the group of supervised models. Compared with other similar methods, SVM offers a range of beneficial characteristics, such as its above-average generalization performance, giving it the ability to produce top-quality decision boundaries based on a relatively small training data point subset. Furthermore, SVM offers the ability to model both non-linear and complex relations. It is, perhaps, for these reasons that SVM has shown effective levels of performance in a variety of real-world challenges and problems, even when applied to a variety of situations and applications.

Least-squares support vector machine (LS-SVM) is an extension of SVM that contains several advanced features demonstrated by its fast computation and generalized capacity [16]. LS-SVM has been used to tackle many complex and non-linear problems in engineering [17]. As part of the training process, LS-SVM uses a least-squares cost function method to derive a linear set of equations that exist in dual space. As such, the solution is derived using iterative methods, such as conjugate gradient, to efficiently solve linear equations.

The prevailing trend in AI techniques combines the merits of multiple models, the so-called “ensemble model,” to create a new ensemble model with significantly higher performance. Typically, an ensemble model can achieve superior performance when both the accuracy of its individual learners and the error diversity among the members are high. Therefore, compared with the method of using a single machine learner with a different subset of training data, or using a single machine learner with different training parameters, the method of using various machine learners is likely to create strong ensemble models with high generalizability, because different machine learners may efficiently avoid making the same error. Furthermore, the comprehensive training data can be fully employed in the training process, which is essential in the event of limited training data. Chou and Pham [18] found that an ensemble model combining two or more strong machine learners can markedly outperform individual learners. By combining multiple machine learners, problems with weak predictors can potentially be mitigated [19] and the variance of the results can be reduced, because the aggregate results of several learners can be less noisy than the single result of one learner. Another study conducted by Acar and Rais-Rohani [20] revealed that an ensemble of prediction models with optimized weighting coefficients always outperforms its stand-alone members.

Studies suggest that the ensemble models have been demonstrated to be superior to single AI models when employed to solve various civil engineering problems such as construction cost and schedule success [21], disputes prediction in public–private partnership projects [22], concrete compressive strength [18], and estimating the peak shear strength of discrete fiber-reinforced soils [23]. However, despite their success elsewhere, ensemble models have not yet been applied to RC deep beam-related problems. In addition, the ensemble weighting coefficients are set as average values [18], which is likely to diminish the ensemble model’s performance. Thus, the current study investigates the efficacy of combining two distinct machine learning techniques: SVM and LS-SVM.

To achieve the greatest success using the ensemble model of SVM and LS-SVM, the user must determine the appropriate parameter values for both ensemble members. A sub-optimal parameter setting may undermine model predictability, whereas an optimal parameter setting can increase the accuracy of the prediction model. Parameters from SVM that must be pre-specified include the regularization parameter (C) and RBF kernel parameter (γ₁). Meanwhile, the LS-SVM model parameters that must be pre-specified include the regularization parameter (γ₂) and RBF kernel parameter (σ²). In addition, it is worth noting that identification of the most suitable parameter values is a challenging task and represents an optimization problem [24,25,26,27,28]. Therefore, fusing SVM and LS-SVM with an optimization algorithm may produce an effective resolution to the above-mentioned issue. In addition, adding the adaptive weighting coefficient will be likely to boost the ensemble performance instead of setting an average weighting value.

Inspired by the symbioses of living organisms, Cheng and Prayogo [29] developed a metaheuristic-based optimization algorithm known as “symbiotic organisms search” (SOS). The SOS algorithm is relatively flexible and easy to use, even for beginners, due in part to a small number of control parameters. The initial research has shown that SOS is a superior algorithm as compared with others, especially in terms of identifying optimal solutions. Over the past years, SOS has been used to solve problems in different research fields [30,31,32,33,34,35,36,37]. In addition, SOS is a reliable tool when paired with other AI techniques [24, 25, 38, 39]. Thus, SOS can become a promising optimization tool when integrated with SVM and LS-SVM.

This study develops and investigates a new approach, called “optimized support vector machines with adaptive ensemble weighting” (OSVM-AEW), to predict the shear strength of RC deep beams. The OSVM-AEW’s output is created by dynamically aggregating prediction values of the SVM and LS-SVM models. The SOS optimization algorithm is integrated to autonomously identify the optimal parameter settings, ensuring that OSVM-AEW achieves the best performance. The benefits of this newly developed model include: (1) it can operate autonomously without AI knowledge and (2) it predicts shear strength more accurately than single models do.

2 Methodology

2.1 Support vector machine

First introduced by Vapnik [15], SVM is a binary classifier of the non-linear subset. As a supervised learning-based method, SVM is often useful in both regression and classification applications. In this study, SVM is used for regression applications. In formal terms, an SVM algorithm uses data points expressed as an (x_i, y_i) pair, where x_i represents the feature vector (x_i1, x_i2,…, x_ip), p represents the number of features, i = 1,…, n, and n represents how many training observations apply. For regression applications, y_i is scalar vector representing the output of the training data. Using each data point, the SVM algorithm works in high-dimensional vector spaces to construct linear separating hyperplanes.

The following equation represents the decision function of SVM:

$$y\left( x \right) = \omega^{T} \phi \left( x \right) + b,$$

(1)

where $x \in R^{n} ,y \in R,$ and $\phi \left( x \right):R^{n} \to R^{nh}$ is the mapping to the high-dimensional feature space and $b$ is the bias term.

For regression problem, the R function is formulated using a constrained optimization, as shown in Eq. (2), while $c$ denotes the regularization constant, which the user must optimize, and gives the relative weight of the second part as compared with the first part; $\varepsilon_{i}$ is the training data error:

$$\begin{array}{*{20}l} {{\text{Minimize:}}} \hfill & {R\left( {\omega ,\varepsilon ,b} \right) = \frac{1}{2}\omega^{2} + c\mathop \sum \limits_{i = 1}^{n} \varepsilon_{i}^{2} ,} \hfill \\ {{\text{Subjected}}\,{\text{to:}}} \hfill & {y_{i} = \omega^{T} \phi \left( {x_{i} } \right) + b + \begin{array}{*{20}c} {\varepsilon_{i} } \\ \end{array} ,\quad i = 1, \ldots ,n.} \hfill \\ \end{array}$$

(2)

Using each data point, the SVM algorithm for regression works in high-dimensional vector spaces to construct linear separating hyperplanes. The best hyperplane can be identified and defined as the hyperplane with the maximum distance to its training errors ($\varepsilon$). Due to the uses of training error $\varepsilon_{i}$, SVM for regression starts to penalize for errors that are greater than $\varepsilon$ in magnitude. In addition, using kernel function $\phi \left( x \right)$, a non-linear enlarging of the original space can result from the higher dimension of space.

However, the objective function from Eq. (2) can be unsolvable when $\omega$ is infinite. Thus, the Lagrange multiplier optimal programming method is used to handle this task, as shown in following equation:

$$L\left( {\omega ,b,\varepsilon ,\xi } \right) = R\left( {\omega ,\varepsilon ,b} \right) - \mathop \sum \limits_{i = 1}^{n} \xi_{i} (\omega^{T} \phi \left( {x_{i} } \right) + b + \varepsilon_{i} - y_{i} ),$$

(3)

where $\xi_{k}$ is the Lagrange multiplier. Following are the given conditions for optimality:

$$\left\{ \begin{aligned} \frac{\partial L}{\partial w} &= 0 \to \omega = \sum\limits_{k = 1}^{N} {\alpha_{k} \phi (x_{k} )} \hfill \\ \frac{\partial L}{\partial b} &= 0 \to \sum\limits_{k = 1}^{N} {\alpha_{k} = 0} \hfill \\ \frac{\partial L}{{\partial e_{k} }} &= 0 \to \alpha_{k} = \gamma e_{k} ,\quad \,k = 1, \ldots ,N \hfill \\ \frac{\partial L}{{\partial \alpha_{k} }} &= 0 \to \omega^{T} \phi (x_{k} ) + b + e_{k} - y_{k} = 0,\quad k = 1, \ldots ,N \hfill \\ \end{aligned} \right..$$

(4)

After eliminating $\varepsilon$ and $\omega$, the linear system is obtained as follows:

$$\left[ {\begin{array}{*{20}c} 0 & {1_{v}^{T} } \\ {1_{v} } & {\omega + 1/\gamma } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} b \\ \xi \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} 0 \\ y \\ \end{array} } \right],$$

(5)

where $y = y_{1} , \ldots ,y_{n} ,\begin{array}{*{20}c} {1_{v} } \\ \end{array} = \left[ {1; \ldots ;1} \right],$ and $\xi = [\xi_{1} ; \ldots ;\xi_{n} ]$. The kernel function is applied as follows:

$$\omega = \phi (x_{i} )^{T} \phi \left( {x_{k} } \right) = K\left( {x_{i,} x_{k} } \right).$$

(6)

Finally, the SVM model for regression is presented as Eq. (7):

$$y\left( x \right) = \mathop \sum \limits_{i = 1}^{n} \xi_{i} K\left( {x_{i} ,x_{k} } \right) + b ,$$

(7)

$$K\left( {x_{k} ,x_{l} } \right) = \exp \left( { - \frac{{x_{k} - x_{l}^{2} }}{{2\gamma^{2} }}} \right),$$

(8)

where $\xi_{k}$ and $b$ denote the solution to the linear system and $\gamma$ is the kernel function parameter. This study uses the radial basis function (RBF) as the kernel function, as shown in Eq. (8).

2.2 Least-squares support vector machine (LS-SVM)

First introduced by Suykens et al. [16], the LS-SVM is a variant of the SVM. The R function is formulated using a constrained optimization for the function estimation problem, as shown in Eq. (9), while $\gamma$ represents the regularization constant, which the user must optimize, and gives the relative weight of the second part as compared with the first part; $\varepsilon_{i}$ is the training data error:

$$\begin{array}{*{20}c} {{\text{Minimize:}}} & {R\left( {\omega ,\varepsilon ,b} \right) = \frac{1}{2}\left\| \omega \right\|^{2} + \frac{1}{2}\gamma \mathop \sum \limits_{i = 1}^{n} \varepsilon_{i}^{2} ,} \\ {{\text{Subjected}}\,{\text{to:}}} & {y_{i} = \omega^{T} \phi \left( {x_{i} } \right) + b + \begin{array}{*{20}c} {\varepsilon_{i} } \\ \end{array} ,\quad i = 1, \ldots ,n.} \\ \end{array}$$

(9)

It is worth noting that Eq. (9) is slightly similar to Eq. (2) from SVM’s decision function. As can be seen, the objective function R represents the sum of the squared fitting error and a regularization term similar to the standard procedure in training the feed-forward neural network and is related to a ridge regression. Nevertheless, this objective function can be unsolvable when $\omega$ is infinite. Thus, the Lagrange multiplier optimal programming method is used to handle this task, as shown in following equation:

$$L\left( {\omega ,b,\varepsilon ,\xi } \right) = R\left( {\omega ,\varepsilon ,b} \right) - \mathop \sum \limits_{i = 1}^{n} \xi_{i} (\omega^{T} \phi \left( {x_{i} } \right) + b + \varepsilon_{i} - y_{i} ),$$

(10)

Using a similar approach with the SVM described in previous section, the LS-SVM model for regression is presented as Eq. (11):

$$y\left( x \right) = \mathop \sum \limits_{i = 1}^{n} \xi_{i} K\left( {x_{i} ,x_{k} } \right) + b,$$

(11)

$$K\left( {x_{k} ,x_{l} } \right) = \exp \left( { - \frac{{\left\| {x_{k} - x_{l} } \right\|^{2} }}{{2\sigma ^{2} }}} \right),$$

(12)

where $\xi_{k}$ and $b$ denote the solution to the linear system and $\sigma^{2}$ is the kernel function parameter. This study uses the radial basis function (RBF) as the kernel function, as shown in Eq. (12). Hence, to attain success in establishing the LS-SVM model, two tuning parameters ($\gamma ,\begin{array}{*{20}c} {\sigma^{2} } \\ \end{array}$) must be determined. The current study, thus, employs SOS to identify the optimal values of $\gamma$ and $\sigma^{2}$.

2.3 Symbiotic organisms search (SOS)

Initially proposed by Cheng and Prayogo [29] as a population-based optimization algorithm, the SOS algorithm is now becoming widely used in solving many multidimensional optimization problems [40]. For the optimization routine, SOS utilizes three types of symbioses: mutualism, commensalism, and parasitism. The SOS algorithm uses organisms to represent potential solutions to the problem itself, with the organism’s fitness referring to the associated solution’s quality. Figure 1 shows the pseudo-code of SOS.

Fig. 1

SOS pseudo-code

During the mutualism phase, new potential improved organisms are generated by the mutualism symbiosis between two organisms, which benefits both sides. To improve the candidate organisms (new_X_i and new_X_j), the current organisms (X_i and X_j) simulate a mutualism interaction as modeled in the following equations:

$${\text{new}}\_X_{i} = \, X_{i} + \, rand\left( {0,1} \right) \times \left( {X_{\text{best}} {-}{\text{mutual}}\_{\text{vector }} \times {\text{ BF}}_{1} } \right),$$

(13)

$${\text{new}}\_X_{j} = X_{j} + rand\left( {0, 1} \right) \times \left( {X_{\text{best}} {-}{\text{mutual}}\_{\text{vector}} \times {\text{BF}}_{2} } \right),$$

(14)

$${\text{mutual}}\_{\text{vector}} = {\text{mean}}\left( {X_{i} + \, X_{j} } \right),$$

(15)

where mutual_vector represents the mutualism relationship between current organisms and BF₁ and BF₂ are random values of either 0 or 1, illustrating each interacting organism’s benefit level.

During the commensalism phase, a new potential improved organism is generated by the commensalism symbiosis between two organisms, which benefits only one side. To improve the candidate organism (X_i), the current organisms (X_i and X_j) simulate a mutualism interaction as modeled in the following equation:

$${\text{new}}\_X_{i} = \, X_{i} + rand\left( {{-} 1, 1} \right) \times \left( {X_{\text{best}} {-} \, X_{j} } \right).$$

(16)

During the parasitism phase, a new potential improved organism is generated by the parasitism symbiosis between two organisms, which benefits one side and is harmful for the other side. In this circumstance, organism X_i will generate a parasite_vector to threaten the existence of X_j. The parasite_vector is generated using the following equation:

$${\text{Parasite}}\_{\text{vector}} = F \times X_{i} + \left( {1{-}F} \right) \times \left[ {rand\left( {0,1} \right) \times \left( {{\text{up}}{-}{\text{low}}} \right) + {\text{low}}} \right],$$

(17)

where F and (1–F) represent the binary random generator and its inverse, respectively; up and low are the search space’s upper and lower boundaries, respectively.

2.4 Optimized support vector machine models with adaptive ensemble weighting (OSVM-AEW)

In machine learning, identification of the most suitable tuning parameter values is a critical issue and is recognized as an optimization problem [16, 29, 41]. For the ensemble model, besides having to determine the optimal parameter settings for individual models, users must concurrently find the combination coefficient values for individual models involved in the ensemble model. This is a high-dimension optimization problem and often beyond human ability. Hence, to maximize efficient performance, the current study uses the SOS search engine to optimize tuning parameters in construction of the developed OSVM-AEW. In multiple attempts to increase the AI-based inference model’s prediction accuracy, studies focusing on a combination of an ensemble model and a metaheuristic algorithm are surprisingly limited.

This section describes the operation of the proposed OSVM-AEW for estimating the shear of RC deep beams in detail, as shown in Fig. 2. The proposed OSVM-AEW was built in the MATLAB R2017b environment.

Fig. 2

Structure of OSVM-AEW

2.5 Data process

The range [0, 1] is used to normalize the training data using Eq. (18). This prevents the formation of numerical difficulties along with the problem of larger range numeric attributes dominating smaller range attributes. Next, the training data are randomly divided into ten distinct folds. While nine folds are used to construct an estimation model, the tenth fold is sequenced through validation tasks:

$$x_{i}^{n} = \frac{{x_{i} - x_{\text{min} } }}{{x_{\text{max} } - x_{\text{min} } }},$$

(18)

where x_i denotes any data point, x_min denotes the minimum value of the entire data set, x_max represents maximum value of the entire data set, and $x_{i}^{n}$ denotes the normalized value of the data point.

2.6 Parameter initialization

Before commencement of the searching loop within pre-defined ranges, six tuning parameters (C, γ₁, γ₂, σ², α, and β) must be generated as the initial values. Table 1 presents the settings for each parameter of the experiment in this study, as suggested by the previous studies [25, 28].

Table 1 Initial control parameter settings

2.7 SVM and LS-SVM prediction models

During this stage, SVM and LS-SVM carry out their training process using parameter values (C, γ₁, γ₂, and σ²) provided by the SOS search engine and then test the validation data. It is worth noting that these parameter values seek to achieve the highest prediction accuracy for the OSVM-AEW as opposed to individual models.

2.8 Ensemble learning system

The proposed ensemble model’s prediction value is the sum of individual models’ prediction values multiplied by their own ensemble weighting coefficients (α and β), as shown in Eq. (19). SOS searching produces the ensemble weighting coefficients (α and β). The literature reveals that these coefficients are subjectively set as average values [18], which is likely to diminish the ensemble model performance:

$$P_{i}^{{{\text{OSVM}} - {\text{EL}}}} = \alpha \times P_{i}^{\text{SVM}} + \beta \times P_{i}^{{{\text{LS}} - {\text{SVM}}}} ,$$

(19)

where $P_{i}^{{{\text{OSVM}} - {\text{EL}}}}$, $P_{i}^{\text{SVM}}$, and $P_{i}^{{{\text{LS}} - {\text{SVM}}}}$ indicate the prediction values of OSVM-AEW, SVM, and LS-SVM, respectively, and $\alpha$ and $\beta$ are the ensemble weighting coefficients of SVM and LS-SVM, respectively.

2.9 Evaluate ensemble model using fitness function

Through quantitative studies, a metaheuristic algorithm has been combined with a machine learner to create a hybrid algorithm. Nevertheless, all attempts have a common problem; the training error is often not optimally minimized during the training process. On the other hand, this well fitting of the training set could simply reflect the model’s complexity, which tends to face the over-fitting issue [42]. To combat the effects of over-fitting and to tune hyperparameters, one should consider validation of the training set during construction of the inference model. This study used k-fold cross-validation to partition the training data as commonly used in many studies [43, 44]. The number of folds is usually determined by the number of data points. In selecting the number of folds (k), one should ensure that the number of data points in the training subset and the validation subset contain sufficient variation and represent the same distribution. If a data set only contains 10 data points, then using tenfold cross-validation will result in only one data point in the validation subset. In this study, we used 67% as the proportion for training subset and 33% for the validation subset, which can be achieved by implementing the threefold cross-validation approach, to ensure that all subsets have the same distribution.

Because the present study uses threefold cross-validation, the ensemble model will be trained and validated three times for each set in the parameter optimizing process. As such, the objective function is arranged with the average validation error over the threefold. The prediction accuracy function for identifying the optimal tuning parameters is used as the SOS algorithm’s objective function and is shown as follows:

$$f = {\text{RMSE}}_{\text{validation}} ,$$

(20)

where ${\text{RMSE}}_{\text{validation}}$ indicates the average validating error of threefolds. In Eq. (20), root-mean-square error (RMSE) is used as the estimation error. The RMSE is computed using the following equation:

$${\text{RMSE}} = \sqrt {\left( {1/n} \right) \times \mathop \sum \limits_{i = 1}^{n} [p_{i} - y_{i} ]^{2} } ,$$

(21)

where p_i predicted value, y_i actual value, and n sample size.

2.10 SOS searching

For OSVM-AEW, the best tuning parameters, C, γ₁, γ₂, σ², α, and β, are identified by comparing the qualities of the fitness function or the objective function. In this way, the tuning parameters have values that progressively improve through each loop. The smaller the fitness function’s value, the better the tuning parameter values. Through the greedy selection of the SOS algorithm, optimal tuning parameters, which provide the smallest fitness function, can be selected.

2.11 Stopping criterion

Once the stopping criterion that the user has designated has been met, the optimization process is stopped. In this study, the criterion to stop the model is the maximum number of iterations (max_iter).

2.12 Optimal parameters

Once the stop criterion has been met, the loop terminates. This indicates that the tuning parameters, which include C, γ₁, γ₂, σ², α, and β, have reached an optimal set and are ready to predict a new and unseen input dataset.

3 Experimental results and discussion

3.1 Data set description

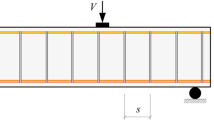
In this study, the data set comprised 214 deep beam test results conducted throughout the course of eight independent studies [2]. These studies included: 37 test patterns from Clark [45], 25 test patterns from Kong et al. [46], 52 test patterns from Smith and Vantsiotis [47], 12 test patterns from Anderson and Ramirez [48], 19 test patterns from Tan et al. [49], 53 test patterns from Oh and Shin [50], 4 test patterns from Aguilar et al. [51], and 12 test patterns from Quintero-Febres et al. [52]. The RC deep beams used in the experiments were simply supported; each test ran until failure. Figure 3 illustrates the details for an RC deep beam.

Fig. 3

Geometrical parameters of an RC deep beam

Following a review of the literature, eight essential factors affecting the shear strength of RC deep beams are selected [53]. The first seven influencing factors, used as input variables in the OSVM-AEW to estimate shear strength, are: effective depth (d); web width (b); main reinforcement ratio (ρ); concrete compressive strength (f_c); vertical shear reinforcement ratio (ρ_v); horizontal shear reinforcement ratio (ρ_h); and ratio of shear span to effective depth (a/d). The remaining factor is the ultimate shear strength of RC deep beam (V/bd). Table 2 and Fig. 4 present a statistical description of the input and output variables.

Table 2 Statistical description of any input and output variables used in this study

Fig. 4

Histogram of the input and output variables

3.2 Performance indicators

The performance of OSVM-AEW was compared with that of other models using the coefficient of correlation (R), coefficient of determination (R²), mean absolute percentage error (MAPE), mean absolute error (MAE), and root-mean-square error (RMSE). The coefficient R represents the correlation between the actual values and predicted values. The coefficient R² represents the level of explained variability between the actual values and predicted values. The closer the coefficients R and R² vary toward 1, the more similar the actual and predicted values become. Similarly, relatively low values for MAE, MAPE, and RMSE indicate a high level of accuracy in the values that the model predicts. Equations (22)–(26) show the mathematical formulation of the proposed performance evaluation criteria:

$${\text{RMSE}} = \sqrt {\left( {1/n} \right) \times \mathop \sum \limits_{i = 1}^{n} [p_{i} - y_{i} ]^{2} } ,$$

(22)

$${\text{MAE}} = \left( {1/n} \right) \times \mathop \sum \limits_{i = 1}^{n} \left( {\left| {p_{i} - y_{i} } \right|} \right),$$

(23)

$${\text{MAPE}} = \left( {1/n} \right)\mathop \sum \limits_{i = 1}^{n} \left( {\left| {p_{i} - y_{i} } \right|/y_{i} } \right) \times 100,$$

(24)

$$R = \frac{{n\mathop \sum \nolimits y_{i} \times p_{i} - \left( {\mathop \sum \nolimits y_{i} } \right)\left( {\mathop \sum \nolimits p_{i} } \right)}}{{\sqrt {n\left( {\mathop \sum \nolimits y_{i}^{2} } \right) - \left( {\mathop \sum \nolimits y_{i} } \right)^{2} } \times \sqrt {n\left( {\mathop \sum \nolimits p_{i}^{2} } \right) - \left( {\mathop \sum \nolimits p_{i} } \right)^{2} } }} ,$$

(25)

where p_i predicted value, y_i actual value, and n sample size:

$$R^{2} = \left( {\frac{{n\mathop \sum \nolimits y_{i} \times p_{i} - \left( {\mathop \sum \nolimits y_{i} } \right)\left( {\mathop \sum \nolimits p_{i} } \right)}}{{\sqrt {n\left( {\mathop \sum \nolimits y_{i}^{2} } \right) - \left( {\mathop \sum \nolimits y_{i} } \right)^{2} } \times \sqrt {n\left( {\mathop \sum \nolimits p_{i}^{2} } \right) - \left( {\mathop \sum \nolimits p_{i} } \right)^{2} } }}} \right)^{2} ,$$

(26)

where p_i predicted value, y_i actual value, and n sample size.

3.3 Experimental results

In this study, the data set was randomly partitioned to training and testing. The complete training and testing data sets can be seen at Appendix. A training partition was used to build the prediction model. The testing partition was used to test the established trained model. A total of 171 data points were selected randomly as a training partition and the remaining were used for testing. The training partition was further divided into two sub-data sets. The training set is primarily used for model fitting. The validation set is used to validate the previous training performance and to fine-tune the trained model. A threefold cross-validation approach is used in this study to mitigate any bias that might have occurred in the model training due to the randomness of selecting training and validation subsets [42].

3.4 Training phase and parameter selection

Through the cross-validation approach, the training data points were randomly grouped into three mutually exclusive subsets. During each iteration, one subset was used for the validation process, while the other two subsets were utilized in turn for the training process. In this way, the study ensured that each data set was used at least once during both the testing and training phases. As such, the average results of the three subsets represent a useful way of predicting the model’s overall performance.

The training results of the cross-validation approach and the convergence graphics of each fold’s RMSEs are depicted in Fig. 5. It can be seen that, through parameter optimization process by SOS, the average validation RMSE was improved in every iteration.

Fig. 5

Convergence graphics of RMSE_validation of each fold

The tuning process of hyperparameters by SOS is illustrated in Fig. 6. The achieved values of α and β properly vary to yield the best collaboration between SVM and LS-SVM rather than follow the 50:50 assumption rule of Chou and Pham [18]. Moreover, the sum of α and β in each fold is very close to 1, though this constraint was not applied in the model construction process.

Fig. 6

Tuning process of hyperparameters and ensemble learning coefficients

Finally, the optimal parameters obtained through the fine-tuning process are shown in Table 3. Figure 7 shows the training performance based on the obtained optimal parameters. According to the four performance indicators, OSVM-AEW produced high value of R and R² as well as low values of RMSE, MAPE, and MAE. Thus, these optimal parameters and model are ready to predict the new and unseen testing data set.

Table 3 Obtained optimal parameters of OSVM-AEW through training phase

Fig. 7

Training performance and result of OSVM-AEW

3.5 Testing phase and prediction results

Using the optimal parameters from Table 3 and the trained model, the testing result of OSVM-AEW is displayed in Fig. 8. It is observable that the OSVM-AEW earned relatively high values of R (≥ 0.95) for testing. This indicates that the OSVM-AEW is proficient at capturing the shear strength’s underlying function. Because of the reaping of low MAPE values (≤ 8%), the OSVM-AEW-estimated shear strength is reliable and trustworthy. Thus, it is acceptable for the design of RC deep beams. Furthermore, the statistical results show that the proposed method can avoid the over-fitting issue by attaining minor differences between performance evaluation values for the training and testing phases.

Fig. 8

Testing result of OSVM-AEW

3.6 Benchmark with other AI models

To better evaluate the developed OSVM-AEW’s capability, its performance was compared against those of other AI techniques, including: (1) the SVM model without any parameter tuning, (2) the LS-SVM model without any parameter tuning, (3) the optimized SVM model via SOS optimization, (4) the optimized LS-SVM model via SOS optimization, (5) the ensemble model of multiple linear regression and regression tree (MLR-RegTree), and (6) the ensemble model of SVM and linear SVM (SVM-LSVM) without involving any parameter tuning. The first five AI techniques were established in the MATLAB R2017b environment. The SVM model was adopted from LIBSVM toolbox [54], whereas the LS-SVM model was adopted from LS-SVMlab toolbox [55]. Meanwhile, the MLR-RegTree utilized “fitlm” and “fitrtree” function from MATLAB toolbox. The ensemble of SVM and LS-SVM was constructed using the IBM SPSS Modeler 18.1 platform. The parameters of these AI models are set to default as can be seen in Table 4. Table 5 reveals the results of competitive models with respect to average values and standard deviations.

Table 4 Features and parameters of AI methods used in this study

Table 5 Result comparisons with other AI approaches

One can see that the proposed model achieves the most desirable values of RMSE (0.5265), MAE (0.3854), MAPE (7.68), R (0.9620), and R² (0.9254). According to Table 5, the obtained results suggest that the OSVM-AEW outperforms other comparative AI models. The finding can be summarized as follows:

• The OSVM-AEW outperforms the SVM and LS-SVM. This indicates that parameter tuning plays an important role in establishing the prediction model. SVM and LS-SVM used a default parameter setting, while the proposed model utilized SOS for parameter optimization.

• The OSVM-AEW shows better performance than the optimized SVM and LS-SVM models. It can be concluded that the proposed ensemble learning system improves the performance of the single model in addition to the parameter tuning.

• The ensemble weighting coefficients are still needed to be optimized. Through the SOS optimization, OSVM-AEW is able to find the optimal weighting that results in the superior performance of OSVM-AEW over SVM-LSVM.

• According to Tables 3 and 5, the ensemble weighting coefficients of SVM (α) and LS-SVM (β) are 0.7992 and 0.2001, respectively, indicating that the SVM results dominate the ensemble’s prediction. The previous study conducted by Acar and Rais-Rohani [20] revealed that optimizing ensemble weighting coefficients based on mean-squared error of each member will yield the best accuracy in comparison with the other approaches. According to Table 5, the RMSE of optimized SVM is slightly better than those of optimized LS-SVM. Thus, it can be concluded that OSVM-AEW ensemble learning system favors the SVM model, because SVM has a better RMSE than LS-SVM.

3.7 Benchmark with literature results

An additional experiment was conducted to compare OSVM-AEW’s performance with those of two approaches widely applied in current structural design projects and research, including ACI 318-11 [5] and CSA [7], and genetic-simulated annealing (GSA) [53]. Table 6 shows the average and standard deviation values of models in terms of MAE, MAPE, and the actual value-to-estimated value ratio. In terms of V_actual/V_estimated, the ACI code and CSA code tend to provide shear strength values that are considerably lower than actual shear strength values, with average values of 1.766 and 1.637, and standard deviation values of 0.571 and 0.574, respectively. The GSA performed well by providing an average value of close to 1 (desirable value). However, its standard deviation value was relatively high compared with that of OSVM-AEW; thus, it is likely to deliver estimated values that are drastically different from the actual values. Regarding MAE and MAPE, the proposed model achieved the most desirable values for both the average and standard deviation, which are remarkably smaller than those of other approaches.

Table 6 Benchmark with the results from literature

The results show that both mathematical methods, including ACI code and CSA code, are insufficient to estimate the shear strength of RC deep beams. Interestingly, the proposed model is particularly accurate for RC deep beams with high shear strength capacity. In sum, the analysis results have amply demonstrated that OSVM-AEW is a promising new tool for the bridge engineer and capable of producing reliable estimation values for the shear strength of RC deep beams. The improvement in the estimation accuracy of shear strength implies benefits in terms of increased safety and cost savings in designing RC deep beams.

4 Conclusions

This study introduces a novel AI-inference model, called “optimized support vector machines with adaptive ensemble weighting” (OSVM-AEW), to predict the shear strength of RC deep beams. In OSVM-AEW, two individual prediction models, SVM and LS-SVM, are controlled by the SOS search engine, which uses an optimization process to provide the most appropriate set of parameter values (C, γ₁, γ₂, σ², α, and β). Thus, the proposed model can run autonomously without the need for human intervention and domain knowledge while still achieving the best performance.

This study is apparently the first to investigate the efficacy of an ensemble model for estimating shear strength for RC deep beams. A simulation involving 214 test beams shows that OSVM-AEW achieves the most desirable evaluation criteria values in terms of RMSE (0.5265 MPa), MAE (0.3854 MPa), MAPE (7.68%), and R (0.9620). This strongly indicates that OSVM-AEW is the most accurate model in terms of estimating shear strength for RC deep beams. These results indicate a drastic reduction in RMSE, MAE, and MAPE compared with other AI competitors and literature approaches. In sum, these findings fully justify the use of SVM, LS-SVM, and SOS to establish OSVM-AEW. Improvement of the estimation accuracy of shear strength implies increased safety in the design of RC deep beams.

Appendix 1

See Tables 7 and 8.

Table 7 Training data set

Table 8 Testing data set