A novel alternating-direction implicit spectral Galerkin method for a multi-term time-space fractional diffusion equation in three dimensions

Abstract

In this paper, we develop an efficient spectral Galerkin method for the three-dimensional (3D) multi-term time-space fractional diffusion equation. Based on the L2-1_σ formula for time stepping and the Legendre-Galerkin spectral method for space discretization, a fully discrete numerical scheme is constructed and the stability and convergence analyses are rigorously established. The results show that the fully discrete scheme is unconditionally stable and has second-order accuracy in time and optimal error estimation in space. In addition, we give the detailed implementation and apply the alternating-direction implicit (ADI) method to reduce the computational complexity. Furthermore, numerical experiments are presented to confirm the theoretical claims. As an application of the proposed method, the fractional Bloch-Torrey model is also solved.

1 Introduction

As is well known, the diffusion model is one of the most important mathematical models for description of the transport process. The classical diffusion model was obtained from Fick’s law, which rests on the assumption that particles move as Brownian motion. However, many experimental studies indicated that the Brownian motion assumption may not be appropriate to depict some physical processes such as transport process in environments that are not locally homogeneous. In these situations, classical Fick’s law is no longer obeyed and generalized Fick’s law should be developed. In this direction, fractional differential equations (FDEs), which are based on fractional Fick’s law, have gained considerable attention and popularity, and have been widely applied for modeling anomalously slow transport processes with memory and heredity in engineering, physics, biology and finance [3, 19, 24, 25, 28, 36,37,38, 61].

In general, FDEs can be classified into time-fractional differential equations (TFDEs), space-fractional differential equations (SFDEs) and time-space fractional differential equations (TSFDEs). For most FDEs, it is not feasible to obtain their exact solutions. Therefore, developing efficient numerical methods to solve FDEs has become essential.

In recent years, various efficient time-stepping schemes have been developed for solving TFDEs numerically. A typical approximation formula is the Grünwald–Letnikov approximation, which was considered initially in Oldham and Spanier [39] and further discussed in Lubich [33], Podlubny [40] and Liu et al. [29]. Many works have followed up along the line of the Grünwald–Letnikov formula (see [35, 49] for details). Another class of approximation formulae for the Caputo fractional derivative is based on the interpolation approximation, i.e. by replacing the integrand with its piecewise polynomial interpolation. The most widely used method is the L1 formula, which has convergence order O(τ^2−α) under the assumption that the given function is twice continuously differentiable [22, 48]. In addition, to improve the numerical accuracy to approximate the Caputo fractional derivative, the L1-2 formula [16] and L2-1_σ formula [1] have also been constructed by using quadratic interpolation.

All the above mentioned works were devoted to the numerical approximation of the single-term time-fractional derivative. Over the past few decades, the multi-term TFDEs have attracted more and more attention and have been successfully applied to model many processes in practice, such as the underlying processes with loss [34], viscoelastic damping [46], oxygen delivery through a capillary to tissues [47], anomalous diffusion in highly heterogeneous aquifers and complex viscoelastic materials [18] and in rheology [6]. It is noted that existing numerical methods for multi-term time-fractional derivatives are obtained mainly by applying directly the techniques which are used to handle the single-term time-fractional derivative (see [2, 9, 10, 12, 26, 32] for detail). In this paper, we adopt the L2-1_σ formula [13], which is proved to have second-order accuracy if the given function is cubic continuously differentiable, to discretize the multi-term time-fractional derivatives.

A number of numerical methods also have been developed to solve SFDEs, such as finite difference methods [5, 57, 62, 64, 65], finite element methods [8, 11, 30, 45], finite volume methods [20, 21, 27], spectral methods [55, 59, 60, 63] and meshfree methods [23, 31]. Most recent studies have looked at the numerical solutions of SFDEs in one or two dimensions. Although the three-dimensional fractional models are much more useful in real applications, numerical methods for the 3D SFDEs are still underdeveloped. In this paper, we consider the following three-dimensional multi-term time-space fractional diffusion equation

$$ \begin{array}{ll} \sum\limits_{i=0}^{s}K_{i}{~}^{\text{C}}{\mathcal{D}}_{t}^{\alpha_{i}}u(x,y,z,t)=&\ K_{x}\frac{\partial^{2{\upbeta}_{1}}u(x,y,z,t)}{\partial\lvert x\rvert^{2{\upbeta}_{1}}}+K_{y}\frac{\partial^{2{\upbeta}_{2}}u(x,y,z,t)}{\partial\lvert y\rvert^{2{\upbeta}_{2}}}\\ &+K_{z}\frac{\partial^{2{\upbeta}_{3}}u(x,y,z,t)}{\partial\lvert z\rvert^{2{\upbeta}_{3}}}+f(x,y,z,t), \end{array} $$

(1)

subject to initial condition

$$ u(x,y,z,0)=\phi(x,y,z),\qquad (x,y,z)\in {\Omega}, $$

(2)

and Dirichlet boundary condition:

$$ u(x,y,z,t)|_{\partial {\Omega}}=0, \qquad 0\leq t\leq T, $$

(3)

where 1 = α₀ > α₁ > α₂ > … > α_s > 0, 1/2 < β₁,β₂,β₃ ≤ 1, K_i > 0, (i = 0,1,…,s), Ω = [0,l₁] × [0,l₂] × [0,l₃] is a cuboid region. K_x, K_y, K_z > 0 are the diffusion coefficients in x, y, z directions, respectively. ∂Ω is the boundary of Ω. The Caputo fractional derivative ${~}^{\text {C}}{\mathcal {D}}_{t}^{\alpha _{i}}$ is defined as [29, 40]

$$ {~}^{\text{C}}_{~}{\mathcal{D}}_{t}^{\alpha_{i}} f(t):=\left\{ \begin{array}{llc} &\frac{1}{\Gamma(1-\alpha_{i})} {{\int}_{0}^{t}}(t-s)^{-\alpha_{i}} f'(s) \mathrm{d} s, \quad &0 <\alpha_{i} < 1,\\ &\frac{\partial f(t)}{\partial t}, \ &\alpha_{i}=1. \end{array} \right. $$

(4)

The Riesz space fractional derivative of order 2β₁ with respect to 0 ≤ x ≤ l₁, namely, $\frac {\partial ^{2{\upbeta }_{1}}}{\partial \lvert x\rvert ^{2{\upbeta }_{1}}}$, is defined as [29, 50]

$$\frac{\partial^{2{\upbeta}_{1}}f(x)}{\partial\lvert x\rvert^{2{\upbeta}_{1}}}:=-c_{{\upbeta}_{1}}\left( {~}^{~}_{0}{\mathcal{D}}_{x}^{2{\upbeta}_{1}}f(x) + {~}^{~}_{x}{\mathcal{D}}_{l_{1}}^{2{\upbeta}_{1}}f(x)\right),$$

where $c_{{\upbeta }_{1}}=\frac {1}{2\cos \limits (\pi {\upbeta }_{1})}$, ${~}^{~}_{0}{\mathcal {D}}_{x}^{2{\upbeta }_{1}}$ and ${~}^{~}_{x}{\mathcal {D}}_{l_{1}}^{2{\upbeta }_{1}}$ are the left- and right- Riemann–Liouville derivatives of order 2β₁ with respect to 0 ≤ x ≤ l₁, defined as

$$ {~}^{~}_{0}{\mathcal{D}}_{x}^{2{\upbeta}_{1}}f(x)= \frac{1}{\Gamma(2-2{\upbeta}_{1})}\frac{\partial^{2}}{\partial x^{2}}{{\int}_{0}^{x}}\frac{f(\xi)\mathrm{d}\xi}{(x-\xi)^{2{\upbeta}_{1}-1}}, \frac{1}{2}<{\upbeta}_{1}<1, $$

(5)

$$ {~}^{~}_{x}{\mathcal{D}}_{l_{1}}^{2{\upbeta}_{1}}f(x)= \frac{1}{\Gamma(2-2{\upbeta}_{1})}\frac{\partial^{2}}{\partial x^{2}}{\int}_{x}^{l_{1}}\frac{f(\xi)\mathrm{d}\xi}{(\xi-x)^{2{\upbeta}_{1}-1}},\frac{1}{2}<{\upbeta}_{1}<1. $$

(6)

Similarly, we can define the Riesz fractional derivatives $\frac {\partial ^{2{\upbeta }_{2}}}{\partial \lvert y\rvert ^{2{\upbeta }_{2}}}$ with respect to 0 ≤ y ≤ l₂ and $\frac {\partial ^{2{\upbeta }_{3}}}{\partial \lvert z\rvert ^{2{\upbeta }_{3}}}$ with respect to 0 ≤ z ≤ l₃.

The existence and uniqueness of the weak solution for the problem (1)-(3) can be guaranteed by the well-known Lax-Milgram lemma (one can refer to [51, 52]). In [51], based on the fractional integration by parts formula, Li and Xu derived the variational formulation of space-time fractional diffusion equation and then proved the well-posedness of the weak solution by the Lax-Milgram lemma. Through similar argument, Zheng, Liu, Anh and Turner [52] proved the well-posedness of variational solution for the multi-term time-fractional diffusion equations. In addition, one can prove the uniqueness of solution by the maximum principle (see the details in [53, 54]).

This present work is devoted to designing an efficient spectral Galerkin method for the 3D multi-term time-space fractional diffusion equation. Here, the Legendre-Galerkin spectral method is implemented for the space discretization and the L2-1_σ formula is applied to discretize the multi-term time-fractional derivatives. The stability and convergence are proved rigorously, which show that the proposed method is unconditionally stable and convergent with second-order accuracy in time, and the optimal spectral accuracy in space. In addition, to reduce the computational cost and memory requirement, we adopt the ADI method and provide the detailed implementation. Numerical experiments are carried out to verify the theoretical predictions, which are in good agreement with the theoretical analysis. Additionally, the proposed method is extended to solve the fractional Bloch–Torrey model, which is widely used to simulate anomalous diffusion in the human brain [41, 42, 58].

The paper is organized as follows. In Section 2, some definitions and lemmas on the spaces of fractional derivatives are introduced. In Section 3, we develop the L2-1_σ spectral Galerkin scheme for the 3D multi-term time-space fractional diffusion equation. The stability and convergence are rigorously proved in Section 4. In Section 5, we construct the ADI spectral Galerkin scheme and give its detailed implementation. In Section 6, the numerical experiments are shown to confirm the theoretical analysis, and the conclusions follow in Section 7.

2 Preliminaries

In this section, based on Ervin and Roop [7, 43], we present some definitions and lemmas on the spaces of fractional derivatives, which are useful for the rigorous analysis of stability and convergence.

We write (⋅,⋅) for the inner product on the space L²(Ω) with the L²norm $\lVert \cdot \rVert _{L^{2}({\Omega } )}$. For convenience, we denote $\lVert \cdot \rVert _{L^{2}({\Omega } )}$ as $\lVert \cdot \rVert$.

Definition 1

(Left fractional derivative space). For μ > 0, we define the semi-norm

$$ \begin{array}{@{}rcl@{}} \lvert u\rvert_{J_L^{\mu}({\Omega})}=\left( \lVert {~}^{~}_{0}{\mathcal{D}}_{x}^{\mu}u \rVert^2+\lVert {~}^{~}_{0}{\mathcal{D}}_{y}^{\mu}u \rVert^2+\lVert {~}^{~}_{0}{\mathcal{D}}_{z}^{\mu}u \rVert^2\right)^{1/2}, \end{array} $$

and the norm

$$ \begin{array}{@{}rcl@{}} \lVert u \rVert_{J_L^{\mu}({\Omega})}=\left( \lVert u \rVert^2+\lvert u\rvert_{J_L^{\mu}({\Omega})}^2\right)^{1/2}, \end{array} $$

and denote $J_{L}^{\mu }({\Omega })$ and $J_{L,0}^{\mu }({\Omega })$ as the closure of $C^{\infty }({\Omega })$ and $C_{0}^{\infty }({\Omega })$ with respect to $\lVert \cdot \rVert _{J_{L}^{\mu }({\Omega })}$, respectively.

Definition 2

(Right fractional derivative space). For μ > 0, we define the semi-norm

$$ \begin{array}{@{}rcl@{}} \lvert u\rvert_{J_R^{\mu}({\Omega})}=\left( \lVert {~}^{~}_{x}{\mathcal{D}}_{l_1}^{\mu}u \rVert^2+\lVert {~}^{~}_{y}{\mathcal{D}}_{l_2}^{\mu}u \rVert^2+\lVert {~}^{~}_{z}{\mathcal{D}}_{l_3}^{\mu}u \rVert^2 \right)^{1/2}, \end{array} $$

and the norm

$$ \begin{array}{@{}rcl@{}} \lVert u \rVert_{J_R^{\mu}({\Omega})}=\left( \lVert u \rVert^2+\lvert u\rvert_{J_R^{\mu}({\Omega})}^2\right)^{1/2}, \end{array} $$

and denote $J_{R}^{\mu }({\Omega })$ and $J_{R,0}^{\mu }({\Omega })$ as the closure of $C^{\infty }({\Omega })$ and $C_{0}^{\infty }({\Omega })$ with respect to $\lVert \cdot \rVert _{J_{R}^{\mu }({\Omega })}$, respectively.

Definition 3

(Symmetric fractional derivative space). Let μ > 0 and $\mu \neq n-\frac {1}{2},\ n\in \mathbb {N}$, we define the seminorm

$$ \begin{array}{@{}rcl@{}} \lvert u\rvert_{J_S^{\mu}({\Omega})}=\left( \lvert ({~}^{~}_{0}{\mathcal{D}}_{x}^{\mu}u, {~}^{~}_{x}{\mathcal{D}}_{l_1}^{\mu}u)\rvert+\lvert ({~}^{~}_{0}{\mathcal{D}}_{y}^{\mu}u, {~}^{~}_{y}{\mathcal{D}}_{l_2}^{\mu}u)\rvert+\lvert ({~}^{~}_{0}{\mathcal{D}}_{z}^{\mu}u, {~}^{~}_{z}{\mathcal{D}}_{l_3}^{\mu}u)\rvert \right)^{1/2}, \end{array} $$

and the norm

$$ \begin{array}{@{}rcl@{}} \lVert u \rVert_{J_S^{\mu}({\Omega})}=\left( \lVert u \rVert^2+\lvert u\rvert_{J_S^{\mu}({\Omega})}^2\right)^{1/2}, \end{array} $$

and denote $J_{S}^{\mu }({\Omega })$ and $J_{S,0}^{\mu }({\Omega })$ as the closure of $C^{\infty }({\Omega })$ and $C_{0}^{\infty }({\Omega })$ with respect to $\lVert \cdot \rVert _{J_{S}^{\mu }({\Omega })}$, respectively.

Definition 4

(Fractional Sobolev space). For μ > 0, we define the semi-norm

$$ \begin{array}{@{}rcl@{}} \lvert u\rvert_{H^{\mu}({\Omega})} =\lVert \lvert \xi\rvert^{\mu}\mathcal{F}(\hat{u})(\xi) \rVert_{L^2(\mathbb{R})}, \end{array} $$

and the norm

$$ \begin{array}{@{}rcl@{}} \lVert u \rVert_{H^{\mu}({\Omega})} =\left( \lVert u \rVert^2+\lvert u\rvert_{H^{\mu}({\Omega})}^2\right)^{\frac{1}{2}}. \end{array} $$

and denote H^μ(Ω) and $H_{0}^{\mu }({\Omega })$ as the closure of $C^{\infty }({\Omega })$ and $C_{0}^{\infty }({\Omega })$ with respect to $\lVert \cdot \rVert _{H^{\mu }({\Omega })}$, respectively. Here, $\mathcal {F}(\hat {u})(\xi )$ is the Fourier transformation of the function $\hat {u}$, and $\hat {u}$ is the zero extension of u outside Ω.

Lemma 1

[7] Suppose $\mu \neq n-\frac {1}{2},\ n\in \mathbb {N}$ and $u\in J_{L,0}^{\mu }({\Omega })\cap J_{R,0}^{\mu }({\Omega })\cap H^{\mu }({\Omega })$. Then there exist positive constants C₁ and C₂ independent of u such that

$$C_{1}\lvert u\rvert_{H^{\mu}({\Omega})}\leq\max\left\{\lvert u\rvert_{J_{L}^{\mu}({\Omega})},\lvert u\rvert_{J_{R}^{\mu}({\Omega})}\right\}\leq C_{2}\lvert u\rvert_{H^{\mu}({\Omega})}.$$

Lemma 2

[7] Suppose μ > 0 and $u\in J_{L,0}^{\mu }({\Omega })\cap J_{R,0}^{\mu }({\Omega })$, then we have

$$ \begin{array}{@{}rcl@{}} \begin{array}{lllll} &({~}^{~}_{0}{\mathcal{D}}_{x}^{\mu}u, {~}^{~}_{x}{\mathcal{D}}_{l_1}^{\mu}v)=\cos(\mu\pi)\lVert {~}^{~}_{-\infty}{\mathcal{D}}_{x}^{\mu}\hat{u} \rVert_{L^2(\mathbb{R}^3)}^2=\cos(\mu\pi)\lVert {~}^{~}_{x}{\mathcal{D}}_{\infty}^{\mu}\hat{u} \rVert_{L^2(\mathbb{R}^3)}^2,\\ &({~}^{~}_{0}{\mathcal{D}}_{y}^{\mu}u, {~}^{~}_{y}{\mathcal{D}}_{l_2}^{\mu}v)=\cos(\mu\pi)\lVert {~}^{~}_{-\infty}{\mathcal{D}}_{y}^{\mu}\hat{u} \rVert_{L^2(\mathbb{R}^3)}^2=\cos(\mu\pi)\lVert {~}^{~}_{y}{\mathcal{D}}_{\infty}^{\mu}\hat{u} \rVert_{L^2(\mathbb{R}^3)}^2,\\ &({~}^{~}_{0}{\mathcal{D}}_{z}^{\mu}u, {~}^{~}_{z}{\mathcal{D}}_{l_3}^{\mu}v)=\cos(\mu\pi)\lVert {~}^{~}_{-\infty}{\mathcal{D}}_{z}^{\mu}\hat{u} \rVert_{L^2(\mathbb{R}^3)}^2=\cos(\mu\pi)\lVert {~}^{~}_{z}{\mathcal{D}}_{\infty}^{\mu}\hat{u} \rVert_{L^2(\mathbb{R}^3)}^2, \end{array} \end{array} $$

where $\hat {u}$ is the extension of u by zero outside Ω.

Lemma 3

[43] Suppose 0 < ν < μ and $u\in H_{0}^{\mu }({\Omega })$, then we have the following fractional Poincar$\acute {e}$-Friedrichs inequalities

$$ \begin{array}{@{}rcl@{}} \begin{array}{lllll} &C_3\lVert u \rVert^2\leq\lVert {~}^{~}_{0}{\mathcal{D}}_{x}^{\nu}u \rVert\leq C_4\lVert {~}^{~}_{0}{\mathcal{D}}_{x}^{\mu}u \rVert,\\ &C_3\lVert u \rVert^2\leq\lVert {~}^{~}_{0}{\mathcal{D}}_{y}^{\nu}u \rVert\leq C_4\lVert {~}^{~}_{0}{\mathcal{D}}_{y}^{\mu}u \rVert,\\ &C_3\lVert u \rVert^2\leq\lVert {~}^{~}_{0}{\mathcal{D}}_{z}^{\nu}u \rVert\leq C_4\lVert {~}^{~}_{0}{\mathcal{D}}_{z}^{\mu}u \rVert, \end{array} \end{array} $$

where C₃ and C₄ are positive constants independent of u.

Remark 1

The above lemmas indicate that these fractional derivative spaces $J_{L}^{\mu }({\Omega })$, $J_{R}^{\mu }({\Omega })$, $J_{S}^{\mu }({\Omega })$ and H^μ(Ω) ($J_{L,0}^{\mu }({\Omega })$, $J_{R,0}^{\mu }({\Omega })$, $J_{S,0}^{\mu }({\Omega })$ and $H_{0}^{\mu }({\Omega })$) are equivalent with equivalent semi-norms and norms if $\mu \neq n-\frac {1}{2},\ n\in \mathbb {N}$.

Lemma 4

[7] Suppose 1/2 < μ ≤ 1. For any $u,\ v \in J_{L,0}^{2\mu }({\Omega })\cap J_{R,0}^{2\mu }({\Omega })$, we have

$$ \begin{array}{@{}rcl@{}} \begin{array}{lllll} &({~}^{~}_{0}{\mathcal{D}}_{x}^{2\mu}u, v)=({~}^{~}_{0}{\mathcal{D}}_{x}^{\mu}u, {~}^{~}_{x}{\mathcal{D}}_{l_1}^{\mu}v),\qquad &({~}^{~}_{x}{\mathcal{D}} _{l_1}^{2\mu}u, v)=({~}^{~}_{x}{\mathcal{D}}_{l_1}^{\mu}u, {~}^{~}_{0}{\mathcal{D}}_{x}^{\mu}v),\\ &({~}^{~}_{0}{\mathcal{D}}_{y}^{2\mu}u, v)=({~}^{~}_{0}{\mathcal{D}}_{y}^{\mu}u, {~}^{~}_{y}{\mathcal{D}}_{l_2}^{\mu}v),\qquad &({~}^{~}_{y}{\mathcal{D}} _{l_2}^{2\mu}u, v)=({~}^{~}_{y}{\mathcal{D}}_{l_2}^{\mu}u, {~}^{~}_{0}{\mathcal{D}}_{y}^{\mu}v),\\ &({~}^{~}_{0}{\mathcal{D}}_{z}^{2\mu}u, v)=({~}^{~}_{0}{\mathcal{D}}_{z}^{\mu}u, {~}^{~}_{z}{\mathcal{D}}_{l_3}^{\mu}v),\qquad &({~}^{~}_{z}{\mathcal{D}} _{l_3}^{2\mu}u, v)=({~}^{~}_{z}{\mathcal{D}}_{l_3}^{\mu}u, {~}^{~}_{0}{\mathcal{D}}_{z}^{\mu}v). \end{array} \end{array} $$

Finally, we define the spaces of functions mapping the time interval (0,T] to the fractional space X equipped with the norm $\lVert \cdot \rVert _{X}$.

Definition 5

For the space X with norm $\lVert \cdot \rVert _{X}$, define the spaces of functions as

$$ \begin{array}{@{}rcl@{}} L^{2}(0,T;X):=\{w:(0,T]\rightarrow X\ \text{measurable}: \lVert w(x,y,t) \rVert_{L^{2}(0,T;X)}<\infty\}, \end{array} $$

and

$$ \begin{array}{@{}rcl@{}} C(0,T;X):=\{w:(0,T]\rightarrow X\ \text{measurable}:\lVert w(x,y,t) \rVert_{C(0,T;X)}<\infty\}, \end{array} $$

with

$$ \begin{array}{@{}rcl@{}} \begin{array}{lllll} \lVert w(x,y,z,t) \rVert_{L^{2}(0,T;X)}^2:=&{\int}_0^T\lVert w(x,y,z,t) \rVert_X^2 \mathrm{d}t,\\ \lVert w(x,y,z,t) \rVert_{C(0,T;X)}:=&\max_{0\leq t\leq T} \{\lVert w(x,y,z,t) \rVert_X\}. \end{array} \end{array} $$

3 Numerical scheme

In this section, we present the numerical scheme for problem (1)-(3), which is based on the L2-1_σ formula for the time discretization and Legendre-spectral Galerkin method for the space discretization.

3.1 Variational formulation

Considering Lemma 4, we can drive the following variational formulation for problem (1): Find $u(\cdot , t) \in H_{0}^{{\upbeta }_{1}}({\Omega })\cap H_{0}^{{\upbeta }_{2}}({\Omega })\cap \ H_{0}^{{\upbeta }_{3}}({\Omega })$, such that

$$ \left( \sum\limits_{i=0}^{s}K_{i} {~}^{\mathrm{C}}{\mathcal{D}}_{t}^{\alpha_{i}} u,v\right)+\mathcal{A}(u,v)=(f,v),\qquad \forall v \in H_{0}^{\beta_{1}}({\Omega})\cap H_{0}^{\beta_{2}}({\Omega})\cap H_{0}^{\beta_{3}}({\Omega}), $$

(7)

where

$$ \begin{array}{@{}rcl@{}} \mathcal{A}(u,v) &=& \frac{K_{x}}{2\cos(\beta_{1}\pi)}\left( ({~}_{0}{\mathcal{D}}_{x}^{\beta_{1}}u, {~}_{x}{\mathcal{D}}_{l_{1}}^{\beta_{1}}v) + ({~}_{x}{\mathcal{D}}_{l_{1}}^{\beta_{1}}u, {~}_{0}{\mathcal{D}}_{x}^{\beta_{1}}v)\right)\\ &&+\frac{K_{y}}{2\cos(\beta_{2}\pi)}\left( ({~}_{0}{\mathcal{D}}_{y}^{\beta_{2}}u, {~}_{y}{\mathcal{D}}_{l_{2}}^{\beta_{2}}v) + ({~}_{y}{\mathcal{D}}_{l_{2}}^{\beta_{2}}u, {~}_{0}{\mathcal{D}}_{y}^{\beta_{2}}v)\right)\\ &&+\frac{K_{z}}{2\cos(\beta_{3}\pi)}\left( ({~}_{0}{\mathcal{D}}_{z}^{\beta_{3}}u, {~}_{z}{\mathcal{D}}_{l_{3}}^{\beta_{3}}v) + ({~}_{z}{\mathcal{D}}_{l_{3}}^{\beta_{3}}u, {~}_{0}{\mathcal{D}}_{z}^{\beta_{3}}v)\right). \end{array} $$

(8)

For a multi-index β = (β₁,β₂,β₃), we set

$$ {\upbeta}_{\max}=\max\{{\upbeta}_{1},{\upbeta}_{2},{\upbeta}_{3}\},\qquad{\upbeta}_{\min}=\min\{ {\upbeta}_{1},{\upbeta}_{2},{\upbeta}_{3}\}. $$

From Lemma 2, we know that $\mathcal {A}(v,v)\geq 0$. Then we define the semi-norm $\lvert \cdot \rvert _{\upbeta }$ and norm $\lVert \cdot \rVert _{\upbeta }$ as follows

$$ \lvert v\rvert_{\upbeta}=\sqrt{\mathcal{A}(v,v)},\qquad \lVert v \rVert_{\upbeta}=\sqrt{ \lVert v \rVert^{2}+\lvert v\rvert_{\upbeta}^{2}}. $$

The semi-norm $\lvert \cdot \rvert _{\upbeta }$ and norm $\lVert \cdot \rVert _{\upbeta }$ are equivalent if $v\in H_{0}^{{\upbeta }_{1}}({\Omega } )\cap H_{0}^{{\upbeta }_{2}}({\Omega } )\cap H_{0}^{{\upbeta }_{3}}({\Omega } )\ (\frac {1}{2}<{\upbeta }_{1},{\upbeta }_{2},{\upbeta }_{3}\leq 1)$, which is given in the following lemma.

Lemma 5

For $v\in H_{0}^{{\upbeta }_{\max \limits }}({\Omega })$, we have

$$ \lVert v \rVert^{2}\leq C_{5}\lvert v\rvert_{\upbeta}^{2}, $$

(9)

where C₅ is a positive constant independent of u.

Proof

One can easily obtain (9) from Lemmas 2 – 3 and Remark 1. □

Lemma 6

Suppose that Ω = (0,l₁) × (0,l₂) × (0,l₃), $v\in H_{0}^{{\upbeta }_{1}}({\Omega })\cap H_{0}^{{\upbeta }_{2}}({\Omega }) \cap H_{0}^{{\upbeta }_{3}}({\Omega })\ (\frac {1}{2}<{\upbeta }_{1},{\upbeta }_{2},{\upbeta }_{3}\leq 1)$. Then there exist positive constants C₆ < 1 and C₇ independent of u, such that

$$ C_6\lVert v \rVert_{\upbeta}\leq \lvert v\rvert_{\upbeta}\leq \lVert v \rVert_{\upbeta}\leq C_7\lvert v\rvert_{H^{{\upbeta}_{\max}}({\Omega})}. $$

Proof

The proof of this lemma is similar to that of Lemma 4.2 in [59], so we omit it here for simplicity. □

3.2 Time semi-discrete scheme

The existing approaches to approximate the multi-term time-fractional derivatives are mainly direct applications of the techniques which are used to handle the single-term time-fractional derivative, including the L1 approximation [2, 4, 11] and the Grü nwald–Letnikov approximation [14, 15, 56]. A disadvantage of the former approach lies in the lower order of numerical accuracy, while the latter one requires the continuous zero-extension of solutions when t < 0. Here, we adopt the L2-1_σ approximation [13], which can reach second-order accuracy and does not require the continuous zero-extension of solutions when t < 0. The core idea of the L2-1_σ formula is described below.

For any positive integer N_T, let τ be the time step size such that $\tau =\frac {T}{N_{T}}.$ We denote by {t_n = nτ, n = 0,1,...,N_T} a uniform partition of the time interval [0,T] and t_n− 1+σ = (n − 1 + σ)τ. For any function u(t), we denote uⁿ = u(t_n). For convenience, we introduce the following notation:

$$ u^{n-1+\sigma }=\sigma u^{n}+(1-\sigma )u^{n-1}, $$

where σ is the unique root of the equation

$$ F(\sigma )=\sum\limits_{i=0}^{s}\frac{K_{i}}{\Gamma (3-\alpha_{i})}\sigma^{1-\alpha_{i}}[\sigma -(1-\frac{\alpha_{i}}{2})]\tau^{2-\alpha_{i}}=0,\qquad 1-\frac{\alpha_{0}}{2}\leq \sigma \leq 1-\frac{\alpha_{s}}{2 }. $$

(10)

In addition, we define the linear and quadric interpolation operators over the time interval [t_k− 1,t_k] and [t_k− 1,t_k+ 1] as

$$ \begin{array}{@{}rcl@{}} L_{1,k}u(t)&=& \frac{t_{k}-t}{\tau}u(t_{k-1})+\frac{t-t_{k-1}}{t_{k}},\\ L_{2,k}u(t)&=& \frac{(t-t_{k})(t-t_{k+1})}{2\tau^{2}}u(t_{k-1})- \frac{(t-t_{k-1})(t-t_{k+1})}{\tau^{2}}u(t_{k})\\ &&+\frac{(t-t_{k-1})(t-t_{k})}{2\tau^{2}}u(t_{k+1}). \end{array} $$

(11)

Using the L2-1_σ formula, the multi-term time-fractional derivatives at time t = t_n− 1+σ can be approximated by

$$ \begin{array}{@{}rcl@{}} &&\sum\limits_{i=0}^{s} K_{i} {~}^{\mathrm{C}} {\mathcal{D}}_{t}^{\alpha_{i}} u (t_{n-1 + \sigma})\\ &=& \sum\limits_{i=0}^{s} \frac{K_{i}}{\Gamma (1-\alpha_{i})} \left[ \sum\limits_{k=1}^{n-1} {\int}_{t_{k-1}}^{t_{k}} \frac{\partial_{s} u (s)}{(t_{n-1+\sigma}-s)^{\alpha_{1}}}\mathrm{d}s + {\int}_{t_{n-1}}^{t_{n-1+\sigma}} \frac{\partial_{s} u (s)}{(t_{n-1+\sigma}-s)^{\alpha_{i}}}\mathrm{d}s \right] \\ &\approx& \sum\limits_{i=0}^{s} \frac{K_{i}}{\Gamma (1-\alpha_{i})} \left[ \sum\limits_{k=1}^{n-1} {\int}_{t_{k-1}}^{t_{k}} \frac{\partial_{s} L_{2,k} u (s)}{(t_{n-1+\sigma}-s)^{\alpha_{1}}}\mathrm{d}s + {\int}_{t_{n-1}}^{t_{n-1+\sigma}} \frac{\partial_{s} L_{1,n} (s)}{(t_{n-1+\sigma}-s)^{\alpha_{i}}}\mathrm{d}s \right] \\ &=& \sum\limits_{k=0}^{n-1} \left( \sum\limits_{i=0}^{s} \frac{K_{i} \tau^{-\alpha_{i}}}{\Gamma (2-\alpha_{i})} {c}_{k}^{(n,\alpha_{i})} \right) (u^{n-k} - u^{n-k-1})\\ &=& \sum\limits_{k=0}^{n-1} {\hat{c}}_{k}^{(n)} (u^{n-k} - u^{n-k-1} := {\mathbb{D}}_{t}^{\alpha} u^{n-1-\sigma}), \end{array} $$

(12)

where $c_{0}^{(1,\alpha _{i})}=a_{0}^{(\alpha _{i})}$ and for n ≥ 2,

$$ c_{k}^{(n,\alpha_{i})}=\left\{ \begin{array}{lllll} &a_{0}^{(\alpha_{i})}+b_{1}^{(\alpha_{i})},\qquad &k=0,\\ &a_{k}^{(\alpha_{i})}+b_{k+1}^{(\alpha_{i})}-b_{k}^{(\alpha_{i})},\qquad &1\leq k\leq n-2,\\ &a_{k}^{(\alpha_{i})}-b_{k}^{(\alpha_{i})},\qquad &k=n-1, \end{array}\right. $$

(13)

with

$$ \begin{array}{lllll} &a_{0}^{(\alpha_{i})}=\sigma^{1-\alpha_{i}},\qquad a_{k}^{(\alpha_{i})}=(k+\sigma)^{1-\alpha_{i}}-(k-1+\sigma)^{1-\alpha_{i}},\qquad \quad k\geq 1,\\ &b_{k}^{(\alpha_{i})}=[(k+\sigma)^{2-\alpha_{i}}-(k-1+\sigma)^{2-\alpha_{i}}]/(2- \alpha_{i})-[(k+\sigma)^{1-\alpha_{i}}+(k-1+\sigma)^{1-\alpha_{i}}]/2, \qquad k\geq 1. \end{array} $$

(14)

In particular, $c_{0}^{(n,1)}=1,\ c_{j}^{(n,1)}=0,\ 1\leq j\leq n-1.$

Lemma 7

[13] Given any non-negative integer s and positive constants K₀, K₁,…,K_s, for any α_i ∈ [0,1], i = 0,1,...,s, where at least one of α_i belongs to (0,1), it holds that

$$ \hat{c}_{1}^{(n)}>\hat{c}_{2}^{(n)}>\ldots>\hat{c}_{n-2}^{(n)}>\hat{c}_{n-1}^{(n)}>\sum\limits_{i=0}^{s}\frac{K_{i}\tau^{-\alpha_{i}}}{\Gamma(2-\alpha_{i})}\cdot\frac{1-\alpha_{i}}{2}(n-1+\sigma)^{-\alpha_{i}}. $$

(15)

Lemma 8

[13] Given any non-negative integer s and positive constants K₀, K₁,…,K_s, for any α_i ∈ [0,1], i = 0,1,...,s, where at least one of α_i belongs to (0,1), then there exists a number τ₀ > 0, such that

$$ (2\sigma-1)\hat{c}_{0}^{(n)}-\sigma \hat{c}_{1}^{(n)}>0, $$

(16)

when τ ≤ τ₀, n = 2,3,… and hence

$$ \hat{c}_{0}^{(n)}>\sigma \hat{c}_{1}^{(n)}. $$

(17)

Lemma 9

[13] Suppose u(t) ∈ C³(0,T). $\mathbb {D}_{t}^{\alpha }u^{n-1+\sigma }$ as defined in (12). Then, we have

$$ \left\lvert \sum\limits_{i=0}^{s} K_{i} {~}^{\text{C}}_{}{\mathcal{D}}{{~}_{t}^{\alpha_{i}}}u(t_{n-1+\sigma})-\mathbb{D}_{t}^{\alpha}u^{n-1+\sigma}\right\rvert\leq M\sum\limits_{i=0}^{s}\frac{K_{i}}{\Gamma(2-\alpha_{i})}\cdot\left( \frac{1-\alpha_{i}}{12}+\frac{\sigma}{6}\right)\sigma^{-\alpha_{i}}\tau^{3-\alpha_{i}}, $$

(18)

where $M=\max \limits _{0\leq t\leq T}\lvert u^{\prime \prime \prime }(t)\rvert$.

Lemma 10

For $v^{0},\ v^{1},\ v^{2},\ldots ,v^{n}\in H_{0}^{{\upbeta }_{\max \limits }}({\Omega })$, we have

$$ \begin{array}{@{}rcl@{}} &&\sum\limits_{j=0}^{n-1}\hat{c}_{j}^{(n)}(v^{n-j}-v^{n-j-1}, v^{n-1+\sigma})\geq\frac{1}{2}\sum\limits_{j=0}^{n-1}\hat{c}_{j}^{(n)}(\lVert v^{n-j} \rVert^{2}-\lVert v^{n-j-1} \rVert^{2}),\\ &&\sum\limits_{j=0}^{n-1}\hat{c}_{j}^{(n)}\mathcal{A}(v^{n-j}-v^{n-j-1},v^{n-1+\sigma})\geq\frac{1}{2}\sum\limits_{j=0}^{n-1}\hat{c}_{j}^{(n)}(\lvert v^{n-j}\rvert_{\upbeta}^{2}-\lvert v^{n-j-1}\rvert_{\upbeta}^{2}).\ \end{array} $$

(19)

Proof

Using Lemmas 7, 8 and Lemma 1, Corollary 1 in [1], we can easily obtain (19), so we skip the detailed proof. □

Discretizing the (12) at time t = t_n− 1+σ, we obtain the following time semi-discrete scheme: Find $u^{n} \in H_{0}^{{\upbeta }_{\max \limits }}({\Omega })$ satisfying

$$ \left( \mathbb{D}_{t}^{\alpha}u^{n-1+\sigma},v\right)+\mathcal{A} (u^{n-1+\sigma},v)=(f(t_{n-1+\sigma}),v),\qquad \forall v \in H_{0}^{{\upbeta}_{\max}}({\Omega}). $$

(20)

3.3 Fully discrete scheme

In this subsection, we use the spectral Galerkin method for the spatial discretization. For a fixed positive integer N, we denote by P_N(I_x) , P_N(I_y) and P_N(I_z) the spaces of polynomials defined on the intervals I_x = (0,l₁), I_y = (0,l₂) and I_z = (0,l₃) with the degree no greater than N, respectively. The approximation space S_N(Ω) is defined as

$$ S_{N}({\Omega} )=(P_{N}(I_{x})\otimes P_{N}(I_{y})\otimes P_{N}(I_{z}))\cap H_{0}^{{\upbeta}_{\max }}({\Omega} ). $$

Then the L2-1_σ/spectral Galerkin scheme of (1) can be expressed as follows: for n = 1,2,...,N_T, find ${u_{N}^{n}}\in S_{N}$ such that

$$ \left\{ \begin{array}{lllll} &\left( \mathbb{D}_{t}^{\alpha}u_{N}^{n-1+\sigma},v_{N}\right)+\mathcal{A}(u_{N} ^{n-1+\sigma},v_{N})=(f(t_{n-1+\sigma}),v_{N}), \qquad \forall v_{N}\in S_{N}({\Omega}),\\ &{u_{N}^{0}}=I_{N}\phi, \end{array}\right. $$

(21)

where I_N is the interpolation operator satisfying

$$ I_{N}u(x_{p},y_{q},z_{s})=u(x_{p},y_{q},z_{s}),\qquad p,q,s=0,1,{\ldots} ,N, $$

(22)

with {x_p} {y_q} {z_s} being the Legendre–Gauss–Lobatto (LGL) points in the domains [0,l₁], [0,l₂] and [0,l₃], respectively.

Lemma 11

[44] Suppose 0 ≤ μ ≤ r and u ∈ H^r(Ω), then

$$\begin{array}{lllll} &\lVert u-I_N u \rVert_{H^{\mu}({\Omega})}\leq C_8N^{\mu-r}\lVert u \rVert_{H^r({\Omega})}, &\lVert I_N u \rVert\leq C_9\lVert u \rVert, \end{array}$$

where the positive constants C₈ and C₉ are independent of N.

For the theoretical analysis, we also introduce the orthogonal projection operator ${\Pi }_{N}^{\upbeta ,0}$ from $H_{0}^{{\upbeta }_{{\max \limits } }}({\Omega } )$ to S_N(Ω), which satisfies

$$ \mathcal{A}(u-{\Pi}_{N}^{\upbeta ,0}u,v_{N})=0,\qquad \forall v_{N}\in S_{N}({\Omega} ). $$

(23)

The orthogonal projection operator has the following properties.

Lemma 12

Let β₁, β₂, β₃ and r be arbitrary real numbers satisfying $\frac {1}{2}< {\upbeta }_{1},\ {\upbeta }_{2},$ β₃ ≤ 1 < r. Then there exists a positive constant C₁₀ independent of N such that, for any $u\in H^{{\upbeta }_{\max \limits }}({\Omega })\cap H^{r}({\Omega })$, the following estimate holds:

$$ \lvert u-{\Pi}_{N}^{\upbeta,0} u\rvert_{\upbeta}\leq C_{10}N^{{\upbeta}_{\max}-r}\lVert u \rVert_{H^{r}({\Omega})}. $$

(24)

Proof

The proof of this lemma is similar to that of Lemma 4.4 in [59], so we skip it. □

Corollary 1

It follows from the “duality argument” method that if $u\in H_{0}^{{\upbeta }_{\max \limits }}({\Omega })\cap H^{r}({\Omega })$, then we have

$$ \lVert u-{\Pi}_{N}^{\upbeta,0} u \rVert\leq C_{11}N^{-r}\lVert u \rVert_{H^{r}({\Omega})}, $$

(25)

where C₁₁ is a constant independent of N.

4 Theoretical analysis

In this part, we discuss the stability and convergence of the fully discrete scheme (21).

4.1 Stability

Theorem 1

Suppose $\phi \in L^{2}({\Omega })\cap H^{{\upbeta }_{\max \limits }}({\Omega })$, f ∈ C(0,T, L²(Ω)), $\{{u_{N}^{n}}|{u_{N}^{n}}\in H_{0}^{{\upbeta }_{\max \limits }}({\Omega })\}|_{n=0}^{N_{T}}$ be the numerical solution of the L2-1_σ/spectral Galerkin scheme (21). Then for 1 ≤ n ≤ N_T, we have

$$ \begin{array}{@{}rcl@{}} \lVert {u_{N}^{n}} \rVert^{2}\leq {C_{9}^{2}}\lVert \phi \rVert^{2}+\frac{C_{5}}{\sum\limits_{i=0}^{s}\frac{K_{i}}{\Gamma(1-\alpha_{i})}}\lVert f \rVert_{C(0,T,L^{2}({\Omega}))}^{2}, \end{array} $$

$$ \begin{array}{@{}rcl@{}} \lvert {u_{N}^{n}}\rvert_{\upbeta}^{2}\leq {C_{7}^{2}}(1+{C_{8}^{2}})\lvert \phi\rvert_{H^{{\upbeta}_{\max}}({\Omega})}^{2}+\frac{1}{\sum\limits_{i=0}^{s}\frac{K_{i}}{\Gamma(1-\alpha_{i})}}\lVert f \rVert_{C(0,T,L^{2}({\Omega}))}^{2}. \end{array} $$

Proof

Firstly, choosing $v_{N}=u_{N}^{n-1+\sigma }$ in (21), we get

$$ \begin{array}{@{}rcl@{}} &&\sum\limits_{j=0}^{n-1}\hat{c}_{j}^{(n)}(u_{N}^{n-j}-u_{N}^{n-j-1},\sigma {u_{N}^{n}}+(1-\sigma)u_{N}^{n-1})+\mathcal{A}(u_{N}^{n-1+\sigma},u_{N}^{n-1+\sigma})\\ &=&\ (f(t_{n-1+\sigma}),u_{N}^{n-1+\sigma}). \end{array} $$

(26)

It follows from Lemma 10 that

$$ \sum\limits_{j=0}^{n-1}\hat{c}_{j}^{(n)}(u_{N}^{n-j}-u_{N}^{n-j-1},\sigma {u_{N}^{n}}+(1-\sigma)u_{N}^{n-1})\geq \frac{1}{2}\sum\limits_{j=0}^{n-1}\hat{c}_{j}^{(n)}(\lVert u_{N}^{n-j} \rVert^{2}-\lVert u_{N}^{n-j-1} \rVert^{2}). $$

(27)

Using Young’s inequality, we obtain

$$ \begin{array}{@{}rcl@{}} (f(t_{n-1+\sigma}),u_{N}^{n-1+\sigma})&\leq&\frac{C_{5}}{4}\lVert f(t_{n-1+\sigma}) \rVert^{2}+\frac{1}{C_{5}}\lVert u_{N}^{n-1+\sigma} \rVert^{2}\\ &\leq&\frac{C_{5}}{4}\lVert f(t_{n-1+\sigma}) \rVert^{2}+\lvert u_{N}^{n-1+\sigma}\rvert_{\upbeta}^{2}, \end{array} $$

(28)

where (9) was used in the last inequality.

Combining (26) and (27)-(28), we get

$$ \frac{1}{2}\sum\limits_{j=0}^{n-1}\hat{c}_{j}^{(n)}(\lVert u_{N}^{n-j} \rVert^{2}-\lVert u_{N}^{n-j-1} \rVert^{2})\leq \frac{C_{5}}{4}\lVert f(t_{n-1+\sigma}) \rVert^{2}, $$

(29)

i.e.

$$ \hat{c}_{0}^{(n)}\lVert {u_{N}^{n}} \rVert^{2}\leq {\sum}_{j=1}^{n-1}(\hat{c}_{j-1}^{(n)}-\hat{c}_{j}^{(n)})\lVert u_{N}^{n-j} \rVert^{2}+\hat{c}_{n-1}^{(n)}\lVert {u_{N}^{0}} \rVert^{2}+\frac{C_{5}}{2}\lVert f(t_{n-1+\sigma}) \rVert^{2}. $$

(30)

Noticing

$$ \hat{c}_{n-1}^{(n)}\geq \sum\limits_{i=0}^{s}\frac{K_{i}\tau^{-\alpha_{i}}}{\Gamma(2-\alpha_{i})}\cdot\frac{1-\alpha_{i}}{2}(n-1+\sigma)^{-\alpha_{i}}\geq\frac{1}{2}\sum\limits_{i=0}^{s}\frac{K_{i}}{T^{\alpha_{i}}{\Gamma}(1-\alpha_{i})}, $$

(31)

we can obtain that

$$ \begin{array}{@{}rcl@{}} \hat{c}_{0}^{(n)}\lVert {u_{N}^{n}} \rVert^{2}&\leq &\ {\sum}_{j=1}^{n-1}(\hat{c}_{j-1}^{(n)}-\hat{c}_{j}^{(n)})\lVert u_{N}^{n-j} \rVert^{2}\\ &&+\hat{c}_{n-1}^{(n)}\left( \lVert {u_{N}^{0}} \rVert^{2}+\frac{C_{5}}{\sum\limits_{i=0}^{s}\frac{K_{i}}{T^{\alpha_{i}}{\Gamma}(1-\alpha_{i})}}\lVert f(t_{n-1+\sigma}) \rVert^{2}\right). \end{array} $$

(32)

Next, by setting $v_{N}=-(K_{x}\frac {\partial ^{2{\upbeta }_{1}}}{\partial \lvert x\rvert ^{2{\upbeta }_{1}}}+K_{y}\frac {\partial ^{2{\upbeta }_{2}}}{\partial \lvert y\rvert ^{2{\upbeta }_{2}}}+K_{z}\frac {\partial ^{2{\upbeta }_{3}}}{\partial \lvert z\rvert ^{2{\upbeta }_{3}}})u_{N}^{n-1+\sigma }$ in (21), and noticing

$$ \begin{array}{@{}rcl@{}} &&\sum\limits_{j=0}^{n-1}\hat{c}_{j}^{(n)}\left( u_{N}^{n-j}-u_{N}^{n-j-1},-(K_{x}\frac{\partial^{2{\upbeta}_{1}}}{\partial \lvert x\rvert^{2{\upbeta}_{1}}}+K_{y}\frac{\partial^{2{\upbeta}_{2}}}{\partial \lvert y\rvert^{2{\upbeta}_{2}}}+K_{z}\frac{\partial^{2{\upbeta}_{3}}}{\partial \lvert z\rvert^{2{\upbeta}_{3}}})u_{N}^{n-1+\sigma}\right)\\ &=&\ \sum\limits_{j=0}^{n-1}\hat{c}_{j}^{(n)}\mathcal{A}\left( v^{n-j}-v^{n-j-1},\sigma v^{n}+(1-\sigma)v^{n-1}\right)\\ &\geq&\ \frac{1}{2}\sum\limits_{j=0}^{n-1}\hat{c}_{j}^{(n)}(\lvert v^{n-j}\rvert_{\upbeta}^{2}-\lvert v^{n-j-1}\rvert_{\upbeta}^{2}),\ \end{array} $$

(33)

$$ \begin{array}{@{}rcl@{}} &&-\mathcal{A}(u_{N}^{n-1+\sigma},(K_{x}\frac{\partial^{2{\upbeta}_{1}}}{\partial \lvert x\rvert^{2{\upbeta}_{1}}}+K_{y}\frac{\partial^{2{\upbeta}_{2}}}{\partial \lvert y\rvert^{2{\upbeta}_{2}}}+K_{z}\frac{\partial^{2{\upbeta}_{3}}}{\partial \lvert z\rvert^{2{\upbeta}_{3}}})u_{N}^{n-1+\sigma})\\ &=&\ \lVert (K_{x}\frac{\partial^{2{\upbeta}_{1}}}{\partial \lvert x\rvert^{2{\upbeta}_{1}}}+K_{y}\frac{\partial^{2{\upbeta}_{2}}}{\partial \lvert y\rvert^{2{\upbeta}_{2}}}+K_{z}\frac{\partial^{2{\upbeta}_{3}}}{\partial \lvert z\rvert^{2{\upbeta}_{3}}})u_{N}^{n-1+\sigma} \rVert^{2}, \end{array} $$

(34)

and

$$ \begin{array}{@{}rcl@{}} &&\left( f(t_{n-1+\sigma}),(K_{x}\frac{\partial^{2{\upbeta}_{1}}}{\partial \lvert x\rvert^{2{\upbeta}_{1}}}+K_{y}\frac{\partial^{2{\upbeta}_{2}}}{\partial \lvert y\rvert^{2{\upbeta}_{2}}}+K_{z}\frac{\partial^{2{\upbeta}_{3}}}{\partial \lvert z\rvert^{2{\upbeta}_{3}}})u_{N}^{n-1+\sigma}\right)\\ &\leq&\ \frac{1}{4}\lVert f(t_{n-1+\sigma}) \rVert^{2}+\lVert (K_{x}\frac{\partial^{2{\upbeta}_{1}}}{\partial \lvert x\rvert^{2{\upbeta}_{1}}} + K_{y}\frac{\partial^{2{\upbeta}_{2}}}{\partial \lvert y\rvert^{2{\upbeta}_{2}}}+K_{z}\frac{\partial^{2{\upbeta}_{3}}}{\partial \lvert z\rvert^{2{\upbeta}_{3}}})u_{N}^{n-1+\sigma} \rVert^{2},\qquad \end{array} $$

(35)

we get

$$ \begin{array}{@{}rcl@{}} \hat{c}_{0}^{(n)}\lvert {u_{N}^{n}}\rvert_{\upbeta}^{2}&\leq &\ \sum\limits_{j=1}^{n-1}(\hat{c}_{j-1}^{(n)}-\hat{c}_{j}^{(n)})\lvert u_{N}^{n-j}\rvert_{\upbeta}^{2}+\hat{c}_{n-1}^{(n)}\lvert {u_{N}^{0}}\rvert_{\upbeta}^{2}+\frac{1}{2}\lVert f(t_{n-1+\sigma}) \rVert^{2}\\& \leq &\ \hat{c}_{n-1}^{(n)}\left( \lvert {u_{N}^{0}}\rvert_{\upbeta}^{2}+\frac{1}{{\sum}_{i=0}^{s}\frac{K_{i}}{T^{\alpha_{i}}{\Gamma}(1-\alpha_{i})}}\lVert f(t_{n-1+\sigma}) \rVert^{2}\right)\\ &&\ +\sum\limits_{j=1}^{n-1}(\hat{c}_{j-1}^{(n)}-\hat{c}_{j}^{(n)})\lvert u_{N}^{n-j}\rvert_{\upbeta}^{2}. \end{array} $$

(36)

Applying mathematical induction to (32) and (36) will produce that

$$ \begin{array}{@{}rcl@{}} \lVert {u_{N}^{n}} \rVert^{2}&\leq& \lVert {u_{N}^{0}} \rVert^{2}+\frac{C_{5}}{{\sum}_{i=0}^{s}\frac{K_{i}}{\Gamma(1-\alpha_{i})}}\max_{1\leq n\leq N_{T}}\lVert f(t_{n-1+\sigma}) \rVert^{2}\\ &\leq& {C_{9}^{2}}\lVert \phi \rVert^{2}+\frac{C_{5}}{{\sum}_{i=0}^{s}\frac{K_{i}}{\Gamma(1-\alpha_{i})}}\lVert f \rVert_{C(0,T,L^{2}({\Omega}))}^{2}, \end{array} $$

(37)

and

$$ \begin{array}{@{}rcl@{}} \lvert {u_{N}^{n}}\rvert_{\upbeta}^{2}&\leq& \lvert {u_{N}^{0}}\rvert_{\upbeta}^{2}+\frac{1}{{\sum}_{i=0}^{s}\frac{K_{i}}{\Gamma(1-\alpha_{i})}}\max_{1\leq n\leq N_{T}}\lVert f(t_{n-1+\sigma}) \rVert^{2}\\ &\leq& (\lvert \phi\rvert_{\upbeta}^{2}+\lvert \phi-I_{N}\phi\rvert_{\upbeta}^{2})+\frac{1}{{\sum}_{i=0}^{s}\frac{K_{i}}{\Gamma(1-\alpha_{i})}}\lVert f \rVert_{C(0,T,L^{2}({\Omega}))}^{2}\\ &\leq& {C_{7}^{2}}(\lvert \phi\rvert_{H^{{\upbeta}_{\max}({\Omega})}}^{2}+\lvert \phi-I_{N}\phi\rvert_{H^{{\upbeta}_{\max}({\Omega})}}^{2})+\frac{1}{{\sum}_{i=0}^{s}\frac{K_{i}}{\Gamma(1-\alpha_{i})}}\lVert f \rVert_{C(0,T,L^{2}({\Omega}))}^{2}\\ &\leq& {C_{7}^{2}}(1+{C_{8}^{2}})\lvert \phi\rvert_{H^{{\upbeta}_{\max}}({\Omega})}^{2}+\frac{1}{{\sum}_{i=0}^{s}\frac{K_{i}}{\Gamma(1-\alpha_{i})}}\lVert f \rVert_{C(0,T,L^{2}({\Omega}))}^{2}. \end{array} $$

(38)

This completes the proof. □

Theorem 1 shows the unconditional stability of the spectral Galerkin scheme (21) with respect to the initial value function ϕ and the source term f. In the next subsection, we will prove the convergence of our scheme.

4.2 Convergence

Before giving the convergence analysis, we assume that the exact solution of the original problem (1) has the following regularities.

Assumption 1

The exact solution of (1) satisfies the following regularities:

$$ u, \sum\limits_{i=0}^{s} K_{i} {~}^{\mathrm{C}}{\mathcal{D}}_{t}^{\alpha_{i}} u \in C(0,T;H^{r}({\Omega})),\quad {\partial}_{t}^{2} u \in C(0,T;H^{2\beta_{\max}} ({\Omega})), \quad {\partial}_{t}^{3} u \in C(0,T;L^{2}({\Omega})). $$

(39)

In other words, there exist positive constants M₁, M₂, M₃ and M₄, such that

$$ \begin{array}{@{}rcl@{}} &&\lVert u \rVert_{C(0,T;H^{r}({\Omega}))}\leq M_{1}, \qquad \lVert \sum\limits_{i=0}^{s}K_{i}{~}^{\text{C}}_{}{\mathcal{D}}{{~}_{t}^{\alpha_{i}}}u \rVert_{C(0,T;H^{r}({\Omega}))}\leq M_{2},\\ &&\lVert u_{tt} \rVert_{C(0,T;H^{2{\upbeta}_{\max}}({\Omega}))}\leq M_{3}, \qquad \lVert u_{ttt} \rVert_{C(0,T;L^{2}({\Omega}))}\leq M_{4}. \end{array} $$

(40)

Corollary 2

Replacing the $\lvert \cdot \rvert$ in the proof of Lemma 9 (i.e. Theorem 2.1 in [13]) with the $\lVert \cdot \rVert$, we can easily obtain that the following estimate holds true if u(x, y, z, t) satisfies Assumption 1.

$$ \begin{array}{@{}rcl@{}} &&\lVert \sum\limits_{i=0}^{s} K_{i}{~}^{\text{C}}_{}{\mathcal{D}}{{~}_{t}^{\alpha_{i}}}u(t_{n-1+\sigma})-\mathbb{D}_{t}^{\alpha}u^{n-1+\sigma} \rVert\\ &\leq &\ M_{4}\sum\limits_{i=0}^{s}\frac{K_{i}}{\Gamma(2-\alpha_{i})}\cdot\left( \frac{1-\alpha_{i}}{12}+\frac{\sigma}{6}\right)\sigma^{-\alpha_{i}}\tau^{3-\alpha_{i}}. \end{array} $$

(41)

Theorem 2

Let β₁, β₂, β₃ and r be arbitrary real numbers satisfying $\frac {1}{2}<{\upbeta }_{1},{\upbeta }_{2},{\upbeta }_{3}\leq 1<r$. Suppose that the exact solution u(x, y, z, t) of the original problem (1) satisfies Assumption 1 and $\left \{{u_{N}^{n}}\right \}_{n=0}^{N_{T}}$ is the solution of the L2-1_σ/spectral Galerkin scheme (21), then there exist constant C₁₂ and C₁₃ independent of τ and N such that the following estimates hold true,

$$ \begin{array}{@{}rcl@{}} \lVert e^{n} \rVert\leq C_{12}(\tau^{2}+N^{-r}),\qquad \lvert e^{n}\rvert_{\upbeta}\leq C_{13}(\tau^{2}+N^{{\upbeta}_{\max}-r}), \end{array} $$

where $e^{n}=u(x,y,z,t_{n})-{u_{N}^{n}}(x,y,z).$

Proof

Splitting the error eⁿ into

$$ e^n=u^n-u_N^{n}=(u^n-{\Pi}_N^{\upbeta,0}u^n)+({\Pi}_N^{\upbeta,0}u^n-u_N^{n})=:\rho^n+\eta^n,\qquad 0\leq n\leq N_T.$$

Based on Lemma 12, Corollary 1 and (40), we obtain

$$ \begin{array}{@{}rcl@{}} &&\lVert \rho^{n} \rVert\leq C_{11}N^{-r}\lVert u \rVert_{C(0,T;H^{r}({\Omega}))}\leq C_{11}M_{1}N^{-r},\\ &&\lvert \rho^{n}\rvert_{\upbeta}\leq C_{10}N^{{\upbeta}_{\max}-r}\lVert u \rVert_{C(0,T;H^{r}({\Omega}))}\leq C_{10}M_{1}N^{{\upbeta}_{\max}-r}. \end{array} $$

(42)

When n = 0, it follows from Lemmas 6, 11 and 12 that

$$ \lVert \eta^{0} \rVert=\lVert {\Pi}_{N}^{\upbeta,0}\phi-I_{N}\phi \rVert\leq \lVert \phi-{\Pi}_{N}^{\upbeta,0}\phi \rVert+\lVert \phi-I_{N}\phi \rVert\leq (C_{8}+C_{11})N^{-r}\lVert \phi \rVert_{H^{r}({\Omega})}, $$

(43)

and

$$ \begin{array}{@{}rcl@{}} \lvert \eta^{0}\rvert_{\upbeta}=\lvert {\Pi}_{N}^{\upbeta,0}\phi-I_{N}\phi\rvert_{\upbeta}&\leq &\ \lvert \phi-{\Pi}_{N}^{\upbeta,0}\phi\rvert_{\upbeta}+\lvert \phi-I_{N}\phi\rvert_{\upbeta}\\ &\leq &\ C_{10}N^{{\upbeta}_{\max}-r}\lVert \phi \rVert_{H^{r}({\Omega})}+C_{7}\lVert \phi-I_{N}\phi \rVert_{H^{{\upbeta}_{\max}({\Omega})}}\\& \leq &\ (C_{10}+C_{7}C_{8})N^{{\upbeta}_{\max}-r}\lVert \phi \rVert_{H^{r}({\Omega})}. \end{array} $$

(44)

From now on, we consider the case of n ≥ 1. Subtracting the first equation of (21) from (7) and using the definition (23), we conclude that: ∀v_N ∈ S_N(Ω)

$$ \begin{array}{@{}rcl@{}} &&\left( \mathbb{D}_{t}^{\alpha}\eta^{n-1+\sigma},v_{N}\right)+\mathcal{A}(\eta^{n-1+\sigma},v_{N})\\ &=&\left( \sum\limits_{i=0}^{s} K_{i}{~}^{\text{C}}_{}{\mathcal{D}}{{~}_{t}^{\alpha_{i}}}u(t_{n-1+\sigma})-\mathbb{D}_{t}^{\alpha}u^{n-1+\sigma},v_{N}\right)\\ &&-\mathcal{A}(u(t_{n-1+\sigma})-u^{n-1+\sigma},v_{N})-\left( \mathbb{D}_{t}^{\alpha}\rho^{n-1+\sigma},v_{N}\right)\\ &=&:(RHS,v_{N}), \end{array} $$

(45)

where

$$ \begin{array}{@{}rcl@{}} RHS&=&\ \sum\limits_{i=0}^{s} K_{i}{~}^{\text{ C}}_{}{\mathcal{D}}{{~}_{t}^{\alpha_{i}}}u(t_{n-1+\sigma})-\mathbb{D}_{t}^{\alpha}u^{n-1+\sigma}-\mathbb{D}_{t}^{\alpha}\rho^{n-1+\sigma}\\ && - \left( K_{x}\frac{\partial^{2{\upbeta}_{1}}}{\partial\lvert x\rvert^{2{\upbeta}_{1}}}+K_{y}\frac{\partial^{2{\upbeta}_{2}}}{\partial\lvert y\rvert^{2{\upbeta}_{2}}}+K_{z}\frac{\partial^{2{\upbeta}_{3}}}{\partial\lvert z\rvert^{2{\upbeta}_{3}}}\right)(u(t_{n-1+\sigma})-u^{n-1+\sigma}). \end{array} $$

(46)

Before bounding $\lVert RHS \rVert$, we give the following estimates by using the Taylor formula and the Cauchy-Schwarz inequality:

$$ \begin{array}{@{}rcl@{}} &&\lVert {~}^{~}_{0}{\mathcal{D}}_{x}^{2{\upbeta}_{1}}(u(t_{n-1+\sigma})-u^{n-1+\sigma}) \rVert^{2}\\ &=&\ {\int}_{\Omega}\left\lvert \sigma{\int}_{t_{n-1+\sigma}}^{t_{n}}(t_{n}-t) {~}^{~}_{0}{\mathcal{D}}_{x}^{2{\upbeta}_{1}}u_{tt}(t)\mathrm{d}t+(1-\sigma){\int}_{t_{n-1}}^{t_{n-1+\sigma}}(t-t_{n-1}) {~}^{~}_{0}{\mathcal{D}}_{x}^{2{\upbeta}_{1}}u_{tt}(t)\mathrm{d}t\right\rvert^{2}\mathrm{d}{\Omega}\\ &\leq&\ 2\sigma^{2}{\int}_{\Omega}\left( {\int}_{t_{n-1+\sigma}}^{t_{n}}(t_{n}-t)^{2}\mathrm{d}t{\int}_{t_{n-1+\sigma}}^{t_{n}}\left( {~}^{~}_{0}{\mathcal{D}}_{x}^{2{\upbeta}_{1}} u_{tt}(t)\right)^{2}\mathrm{d}t\right)\mathrm{d}{\Omega}\\ &&\ +2(1-\sigma)^{2}{\int}_{\Omega}\left( {\int}_{t_{n-1}}^{t_{n-1+\sigma}}(t-t_{n-1})^{2}\mathrm{d}t{\int}_{t_{n-1}}^{t_{n-1+\sigma}}\left( {~}^{~}_{0}{\mathcal{D}}_{x}^{2{\upbeta}_{1}} u_{tt}(t)\right)^{2}\mathrm{d}t\right)\mathrm{d}{\Omega}\\ &\leq&\ \frac{2\tau^{3}}{3}\sigma^{2}(1-\sigma)^{2}{\int}_{\Omega}{\int}_{t_{n-1}}^{t_{n}}\left( {~}^{~}_{0}{\mathcal{D}}_{x}^{2{\upbeta}_{1}}u_{tt}(t)\right)^{2}\mathrm{d}t\mathrm{d}{\Omega}\\ &\leq&\ \frac{2\tau^{4}}{3}\sigma^{2}(1-\sigma)^{2}\lVert {~}^{~}_{0}{\mathcal{D}}_{x}^{2{\upbeta}_{1}}u_{tt} \rVert_{C(0,T;L^{2}({\Omega}))}^{2}. \end{array} $$

(47)

Similarly, the following estimates are true:

$$ \begin{array}{@{}rcl@{}} &&\lVert {~}^{~}_{x}{\mathcal{D}}_{l_{1}}^{2{\upbeta}_{1}}(u(t_{n-1+\sigma})-u^{n-1+\sigma}) \rVert^{2}\leq\frac{2\tau^{4}}{3}\sigma^{2}(1-\sigma)^{2}\lVert {~}^{~}_{x}{\mathcal{D}}_{l_{1}}^{2{\upbeta}_{1}}u_{tt} \rVert_{C(0,T;L^{2}({\Omega}))}^{2},\\ &&\lVert {~}^{~}_{0}{\mathcal{D}}{{~}_{y}^{2{\upbeta}_{2}}}(u(t_{n-1+\sigma})-u^{n-1+\sigma}) \rVert^{2}\leq\frac{2\tau^{4}}{3}\sigma^{2}(1-\sigma)^{2}\lVert {~}^{~}_{0}{\mathcal{D}}{{~}_{y}^{2{\upbeta}_{2}}}u_{tt} \rVert_{C(0,T;L^{2}({\Omega}))}^{2},\\ &&\lVert {~}^{~}_{y}{\mathcal{D}}{{~}_{l_{2}}^{2{\upbeta}_{2}}}(u(t_{n-1+\sigma})-u^{n-1+\sigma}) \rVert^{2}\leq\frac{2\tau^{4}}{3}\sigma^{2}(1-\sigma)^{2}\lVert {~}^{~}_{y}{\mathcal{D}}{{~}_{l_{2}}^{2{\upbeta}_{2}}}u_{tt} \rVert_{C(0,T;L^{2}({\Omega}))}^{2},\\ &&\lVert {~}^{~}_{0}{\mathcal{D}}{{~}_{z}^{2{\upbeta}_{3}}}(u(t_{n-1+\sigma})-u^{n-1+\sigma}) \rVert^{2}\leq\frac{2\tau^{4}}{3}\sigma^{2}(1-\sigma)^{2}\lVert {~}^{~}_{0}{\mathcal{D}}{{~}_{z}^{2{\upbeta}_{3}}}u_{tt} \rVert_{C(0,T;L^{2}({\Omega}))}^{2},\\ &&\lVert {~}^{~}_{z}{\mathcal{D}}{{~}_{l_{3}}^{2{\upbeta}_{3}}}(u(t_{n-1+\sigma})-u^{n-1+\sigma}) \rVert^{2}\leq\frac{2\tau^{4}}{3}\sigma^{2}(1-\sigma)^{2}\lVert {~}^{~}_{z}{\mathcal{D}}{{~}_{l_{3}}^{2{\upbeta}_{3}}}u_{tt} \rVert_{C(0,T;L^{2}({\Omega}))}^{2}. \end{array} $$

(48)

It follows from Corollaries 1 and 2 that

$$ \begin{array}{@{}rcl@{}} \lVert \mathbb{D}_{t}^{\alpha}\rho^{n-1+\sigma} \rVert&\leq& \ \lVert \mathbb{D}_{t}^{\alpha}\rho^{n-1+\sigma}-\sum\limits_{i=0}^{s}K_{i}{~}^{\text{ C}}_{}{\mathcal{D}}{{~}_{t}^{\alpha_{i}}}\rho(t_{n-1+\sigma}) \rVert+\lVert \sum\limits_{i=0}^{s}K_{i}{~}^{\text{C}}_{}{\mathcal{D}}{{~}_{t}^{\alpha_{i}}}\rho(t_{n-1+\sigma}) \rVert\\ &\leq&\ \lVert {\partial_{t}^{3}}\rho \rVert_{C(0,T,L^{2}({\Omega}))}\left( \sum\limits_{i=0}^{s}\frac{K_{i}}{\Gamma(2-\alpha_{i})}\cdot\left( \frac{1-\alpha_{i}}{12}+\frac{\sigma}{6}\right)\sigma^{-\alpha_{i}}\tau^{3-\alpha_{i}}\right)\\ &&\ +C_{11}N^{-r}\lVert \sum\limits_{i=0}^{s}K_{i}{~}^{\text{C}}_{}{\mathcal{D}}{{~}_{t}^{\alpha_{i}}}u(t_{n-1+\sigma}) \rVert_{H^{r}({\Omega})}\\ &\leq&\ C_{11}N^{-r}\lVert {\partial_{t}^{3}}u \rVert_{C(0,T,L^{2}({\Omega}))}\left( \sum\limits_{i=0}^{s}\frac{K_{i}}{\Gamma(2-\alpha_{i})}\cdot\left( \frac{1-\alpha_{i}}{12}+\frac{\sigma}{6}\right)\sigma^{-\alpha_{i}}\tau^{3-\alpha_{i}}\right)\\ &&\ +C_{11}N^{-r}\lVert \sum\limits_{i=0}^{s}K_{i}{~}^{\text{C}}_{}{\mathcal{D}}{{~}_{t}^{\alpha_{i}}}u \rVert_{C(0,T;H^{r}({\Omega}))}\\& \leq&\ C_{11}M_{4}N^{-r}\left( \sum\limits_{i=0}^{s}\frac{K_{i}}{\Gamma(2-\alpha_{i})}\cdot\left( \frac{1-\alpha_{i}}{12}+\frac{\sigma}{6}\right)\sigma^{-\alpha_{i}}\tau^{3-\alpha_{i}}\right)+C_{11}M_{2}N^{-r}. \end{array} $$

(49)

Combining Corollary 2 and (47)–(49), we can obtain the upper bound for $\lVert RHS \rVert$ as follows.

$$ \begin{array}{@{}rcl@{}} &&\lVert RHS \rVert\\ &\leq &\ \lVert \sum\limits_{i=0}^{s} K_{i}{~}^{\text{C}}_{}{\mathcal{D}}{{~}_{t}^{\alpha_{i}}}u(t_{n-1+\sigma})-\mathbb{D}_{t}^{\alpha}u^{n-1+\sigma} \rVert+\lVert \mathbb{D}_{t}^{\alpha}\rho^{n-1+\sigma} \rVert\\ &&\ -\frac{K_{x}}{\cos({\upbeta}_{1}\pi)}\left( \lVert {~}^{~}_{0}{\mathcal{D}}_{x}^{2{\upbeta}_{1}}(u(t_{n-1+\sigma})-u^{n-1+\sigma}) \rVert+\lVert {~}^{~}_{x}{\mathcal{D}}_{l_{1}}^{2{\upbeta}_{1}}(u(t_{n-1+\sigma})-u^{n-1+\sigma}) \rVert\right)\\ &&\ -\frac{K_{y}}{\cos({\upbeta}_{2}\pi)}\left( \lVert {~}^{~}_{0}{\mathcal{D}}{{~}_{y}^{2{\upbeta}_{2}}}(u(t_{n-1+\sigma})-u^{n-1+\sigma}) \rVert+\lVert {~}^{~}_{y}{\mathcal{D}}{{~}_{l_{2}}^{2{\upbeta}_{2}}}(u(t_{n-1+\sigma})-u^{n-1+\sigma}) \rVert\right)\\ &&\ -\frac{K_{z}}{\cos({\upbeta}_{3}\pi)}\left( \lVert {~}^{~}_{0}{\mathcal{D}}{{~}_{z}^{2{\upbeta}_{3}}}(u(t_{n-1+\sigma})-u^{n-1+\sigma}) \rVert+\lVert {~}^{~}_{z}{\mathcal{D}}{{~}_{l_{3}}^{2{\upbeta}_{3}}}(u(t_{n-1+\sigma})-u^{n-1+\sigma}) \rVert\right)\\ &\leq &\ (1+C_{11}N^{-r})M_{4}\left( \sum\limits_{i=0}^{s}\frac{K_{i}}{\Gamma(2-\alpha_{i})}\cdot\left( \frac{1-\alpha_{i}}{12}+\frac{\sigma}{6}\right)\sigma^{-\alpha_{i}}\tau^{3-\alpha_{i}}\right)\\ &&\ +C_{11}M_{2}N^{-r}+4\tau^{2}\sigma(1-\sigma)C_{2}C_{4}M_{3}\\ &\leq &\ \frac{(1+C_{11}N^{-r})M_{4}}{2}\left( \sum\limits_{i=0}^{s}\frac{K_{i}}{\Gamma(2-\alpha_{i})}\right)\tau^{2}+C_{11}M_{2}N^{-r}+\tau^{2}C_{2}C_{4}M_{3}\\ &\leq &\ \frac{(1+C_{11})M_{4}}{2}\left( \sum\limits_{i=0}^{s}\frac{K_{i}}{\Gamma(2-\alpha_{i})}\right)\tau^{2}+C_{11}M_{2}N^{-r}+\tau^{2}C_{2}C_{4}M_{3}, \end{array} $$

(50)

Similar to the proof of Theorem 1, we deduce that

$$ \begin{array}{@{}rcl@{}} \lVert \eta^{n} \rVert&\leq& \lVert \eta^{0} \rVert+\sqrt{\frac{C_{5}}{\sum\limits_{i=0}^{s}\frac{K_{i}}{\Gamma(1-\alpha_{i})}}}\lVert RHS \rVert,\\ \lvert \eta^{n}\rvert_{\upbeta}&\leq& \lvert \eta^{0}\rvert_{\upbeta}+\sqrt{\frac{1}{\sum\limits_{i=0}^{s}\frac{K_{i}}{\Gamma(1-\alpha_{i})}}}\lVert RHS \rVert. \end{array} $$

(51)

Combining the above equation and the triangle inequality, we derive that

$$ \begin{array}{@{}rcl@{}} \lVert e^{n} \rVert&\leq&\ \lVert \rho^{n} \rVert+\lVert \eta^{n} \rVert\\ &\leq &\ \left( C_{11}M_{1}+(C_{8}+C_{11})\lVert \phi \rVert_{H^{r}({\Omega})}+\sqrt{\frac{C_{5}}{\sum\limits_{i=0}^{s}\frac{K_{i}}{\Gamma(1-\alpha_{i})}}}C_{11}M_{2}\right)N^{-r}\\ &&\ +\sqrt{\frac{C_{5}}{\sum\limits_{i=0}^{s}\frac{K_{i}}{\Gamma(1-\alpha_{i})}}}\left( \frac{(1+C_{11})M_{4}}{2}\left( \sum\limits_{i=0}^{s}\frac{K_{i}}{\Gamma(2-\alpha_{i})}\right)+C_{2}C_{4}M_{3}\right)\tau^{2}, \end{array} $$

(52)

and

$$ \begin{array}{@{}rcl@{}} \lvert e^{n}\rvert_{\upbeta}&\leq&\ \lvert \rho^{n}\rvert_{\upbeta}+\lvert \eta^{n}\rvert_{\upbeta}\\ &\leq &\ \left( C_{10}M_{1}+(C_{10}+C_{7}C_{8})\lVert \phi \rVert_{H^{r}({\Omega})}+\sqrt{\frac{C_{5}}{\sum\limits_{i=0}^{s}\frac{K_{i}}{\Gamma(1-\alpha_{i})}}}C_{11}M_{2}\right)N^{{\upbeta}_{\max}-r}\\ &&\ +\sqrt{\frac{C_{5}}{\sum\limits_{i=0}^{s}\frac{K_{i}}{\Gamma(1-\alpha_{i})}}}\left( \frac{(1+C_{11})M_{4}}{2}\left( \sum\limits_{i=0}^{s}\frac{K_{i}}{\Gamma(2-\alpha_{i})}\right)+C_{2}C_{4}M_{3}\right)\tau^{2}. \end{array} $$

(53)

This completes the proof. □

5 Implementation

In this subsection, we will give the details of the implementation of the fully discrete scheme (21). The approximation space can be expressed as

$$ S_{N}=\text{span}\{\phi_{j}(x)\varphi_{k}(y)\psi_{l}(z):j,k,l=0,1,{\ldots} ,N-2\}, $$

in which ϕ_k(x), φ_l(y), ψ_m(z) are defined as

$$ \begin{array}{lllll} \phi_{k}(x)&=L_{k}(\hat{x})-L_{k+2}(\hat{x}),\ &\hat{x}\in [-1,1],\ \qquad &x=\frac{l_{1}(1+\hat{x})}{2},\\ \varphi_{l}(y)&=L_{l}(\hat{y})-L_{l+2}(\hat{y}),\ &\hat{y}\in [-1,1],\ \qquad &y=\frac{l_{2}(1+\hat{y})}{2},\\ \psi_{m}(z)&=L_{m}(\hat{z})-L_{m+2}(\hat{z}),\ &\hat{z}\in [-1,1],\ \qquad &z=\frac{l_{3}(1+\hat{z})}{2}, \end{array} $$

(54)

where $L_{k}(\hat {x}),\ L_{l}(\hat {y}),\ L_{m}(\hat {z})$ are the Legendre polynomials [44].

It is obvious that S_N is a subspace of $H_0^{{\upbeta }_{\max \limits }}({\Omega })$. The numerical solution $u_N^n\in S_N$ can be given by

$$ {u_{N}^{n}}=\sum\limits_{k=0}^{N-2}\sum\limits_{l=0}^{N-2}\sum\limits_{m=0}^{N-2}\hat{u} _{klm}^{n}\phi_{k}(x)\varphi_{l}(y)\psi_{m}(z). $$

(55)

Define the matrices $M^x,\ M^y,\ M^z,\ S^x,\ S^y,\ S^z\in \mathbb {R} ^{(N-1)\times (N-1)}$, which satisfy

$$ \begin{array}{@{}rcl@{}} &&(M^{x})_{k,l}=M^{x}_{kl}=(\phi_{l}(x),\phi_{k}(x)),\quad (M^{y})_{k,l}=M^{y}_{kl}=(\varphi_{l}(y),\varphi_{k}(y)),\\ &&(M^{z})_{k,l}=M^{z}_{kl}=(\psi_{l}(z),\psi_{k}(z)),\\ &&(S^{x})_{k,l}=S^{x}_{kl}=\frac{K_{x}}{2\cos(\beta_{1}\pi)} \left( \left( {~}_{0} {\mathcal{D}}_{x}^{\beta_{1}} \phi_{l}(x), {~}_{x} {\mathcal{D}}_{l_{1}}^{\beta_{1}} \phi_{k} (x)\right) + \left( {~}_{x} {\mathcal{D}}_{l_{1}}^{\beta_{1}} \phi_{l}(x), {~}_{0} {\mathcal{D}}_{x}^{\beta_{1}} \phi_{k} (x)\right)\right),\\ &&(S^{y})_{k,l}=S^{y}_{kl}=\frac{K_{y}}{2\cos(\beta_{2}\pi)} \left( \left( {~}_{0} {\mathcal{D}}_{y}^{\beta_{2}} \varphi_{l}(y), {~}_{y} {\mathcal{D}}_{l_{2}}^{\beta_{2}} \varphi_{k} (y)\right) + \left( {~}_{y} {\mathcal{D}}_{l_{2}}^{\beta_{2}} \varphi_{l}(y), {~}_{0} {\mathcal{D}}_{y}^{\beta_{2}} \varphi_{k} (y)\right)\right),\\ &&(S^{z})_{k,l}=S^{z}_{kl}=\frac{K_{z}}{2\cos(\beta_{3}\pi)} \left( \left( {~}_{0} {\mathcal{D}}_{z}^{\beta_{3}} \psi_{l}(z), {~}_{z} {\mathcal{D}}_{l_{3}}^{\beta_{3}} \psi_{k} (z)\right) + \left( {~}_{z} {\mathcal{D}}_{l_{3}}^{\beta_{3}} \psi_{l}(z), {~}_{0} {\mathcal{D}}_{z}^{\beta_{3}} \psi_{k} (z)\right)\right). \end{array} $$

Now, we compute the elements of the above matrices. Obviously, these matrices are symmetric. Considering the orthogonality of Legendre polynomials, we can verify that the elements of the matrix M^x are

$$ \begin{array}{@{}rcl@{}} {M}_{kl}^{x} &=& {\int}_{0}^{l_{1}} \phi_{l}(x)\phi_{k}(x) \mathrm{d}x \\ &=& \frac{l_{1}}{2} {\int}_{-1}^{1} \left( L_{l} (\hat{x}) - L_{l+2} (\hat{x}) \right) \left( L_{k} (\hat{x}) - L_{k+2} (\hat{x})\right)\mathrm{d}\hat{x}\\ &=& \left\{\begin{array}{lr} \displaystyle\frac{l_{1}}{2k+1} + \frac{l_{1}}{2k+5}, &\qquad l=k,\\ \displaystyle-\frac{l_{1}}{2k+5}, &\qquad l=k\pm2,\\ 0, & \qquad \text{otherwise}, \end{array} \right. \end{array} $$

(56)

which means that M^x is a 5 bandwidth matrix. Similarly, we can calculate the elements of the matrices M^y and M^z. Since the computations of the matrices S^y and S^z are almost the same as that of the matrix S^x, here we mainly concentrate on computing the elements of S^x. In this part, the following lemma will be used.

Lemma 13

[17] For 0 < μ < 1, we have

$$ \begin{array}{@{}rcl@{}} {~}^{~}_{-1}{\mathcal{D}}{{~}_{\hat{x}}^{\mu}}L_{n}(\hat{x})&=\frac{\Gamma(n+1)}{\Gamma(n-\mu+1)}(1+\hat{x})^{-\mu}J_{n}^{\mu,-\mu}(\hat{x}),\\ {~}^{~}_{\hat{x}}{\mathcal{D}}{{~}_{1}^{\mu}}L_{n}(\hat{x})&=\frac{\Gamma(n+1)}{\Gamma(n-\mu+1)}(1-\hat{x})^{-\mu}J_{n}^{-\mu,\mu}(\hat{x}), \end{array} $$

(57)

where $J_{n}^{a,b}(\hat {x})(a,b>-1, n=0,1,2,\ldots )$ are the Jacobi polynomials, which are orthogonal with respect to the weight function ω^{a, b} = (1 − x)^a(1 + x)^b over I = [− 1,1].

Since

$$ \left( {~}_{0} {\mathcal{D}}_{x}^{\beta_{1}} \phi_{l} (x), {~}_{x} {\mathcal{D}}_{l_{1}}^{\beta_{1}} \phi_{k}(x)\right) = \left( {~}_{0} {\mathcal{D}}_{x}^{\beta_{1}} (L_{1} (\hat{x}) - L_{l+2} (\hat{x})), {~}_{x} {\mathcal{D}}_{l_{1}}^{\beta_{1}} (L_{k} (\hat{x}) - L_{k+2} (\hat{x})) \right), $$

(58)

we only need to calculate $\left ({~}^{{\upbeta }_1}_{x}{\mathcal {D}}{{~}_{L}^{0}}_l(\hat {x}),{~}^{{\upbeta }_1}_{l_1}{\mathcal {D}}{{~}_{L}^{x}}_k(\hat {x})\right )$. It is easy to obtain

$$ \begin{array}{@{}rcl@{}} {~}_{0} {\mathcal{D}}_{x}^{\beta_{1}} L_{k} (\hat{x}) &=& \frac{1}{\Gamma (1-\beta_{1})} \frac{\mathrm{d}}{\mathrm{d}x} {\int}_{0}^{x} (x-s)^{-\beta_{1}} L_{k} (\hat{s}) \mathrm{d}s = \left( \frac{l_{1}}{2}\right)^{-\beta_{1}} {~}_{-1} {\mathcal{D}}_{\hat{x}}^{\beta_{1}} L_{k} (\hat{x}), \\ {~}_{x} {\mathcal{D}}_{l_{1}}^{\beta_{1}} L_{k} (\hat{x}) &=& \frac{1}{\Gamma (1-\beta_{1})} \frac{\mathrm{d}}{\mathrm{d}x} {\int}_{x}^{l_{1}} (s-x)^{-\beta_{1}} L_{k} (\hat{s}) \mathrm{d}s = \left( \frac{l_{1}}{2}\right)^{-\beta_{1}} {~}_{\hat{x}} {\mathcal{D}}_{1}^{\beta_{1}} L_{k} (\hat{x})\\ \end{array} $$

(59)

where we have used the transform $x=\frac {l_1\hat {x}+l_1}{2}\in [0,l_1]$ and $s=\frac {l_1\hat {s}+l_1}{2}\in [0,l_1]$. Based on Lemma 13 and the transform $x=\frac {l_1\hat {x}+l_1}{2}\in [0,l_1]$, we have

$$ \begin{array}{@{}rcl@{}} ({~}_{0} {\mathcal{D}_{x}^{\beta_{1}}} L_{l} (\hat{x}), {~}_{x} {\mathcal{D}_{l_{1}}^{\beta_{1}}} L_{k} (\hat{x})) &=& {\int}_{0}^{l_{1}} {~}_{0} {\mathcal{D}_{x}^{\beta_{1}}} L_{l} (\hat{x}) {~}_{x} {\mathcal{D}_{l_{1}}^{\beta_{1}}} L_{k} (\hat{x}) \mathrm{d}x\\ &=& \left( \frac{l_{1}}{2}\right)^{1-2\beta_{1}} {\int}_{-1}^{1} {~}_{-1} {\mathcal{D}_{\hat{x}}^{\beta_{1}}} L_{l} (\hat{x}) {~}_{\hat{x}} {\mathcal{D}_{1}^{\beta_{1}}} L_{k} (\hat{x}) \mathrm{d}\hat{x}\\ &=& \left( \frac{l_{1}}{2}\right)^{1-2\beta_{1}} \frac{\Gamma (k+1)}{\Gamma (k-\beta_{1} + 1)} \frac{\Gamma (l+1)}{\Gamma (l-\beta_{1}+1)}\\ &&\times {\int}_{-1}^{1} (1+\hat{x})^{-\beta_{1}} (1-\hat{x})^{-\beta_{1}} {J}_{l}^{\beta_{1},-\beta_{1}} (\hat{x}) {J}_{k}^{-\beta_{1},\beta_{1}} (\hat{x})\mathrm{d}\hat{x}.\\ \end{array} $$

(60)

To calculate the integral

$$ I(k,l,{\upbeta}_{1})={\int}_{-1}^{1}(1+\hat{x})^{-{\upbeta}_{1}}(1-\hat{x} )^{-{\upbeta}_{1}}J_{l}^{{\upbeta}_{1},-{\upbeta}_{1}}(\hat{x})J_{k}^{-{\upbeta}_{1},{\upbeta}_{1}}(\hat{x} )\mathrm{d}\hat{x}, $$

(61)

we use the following Jacobi-Gauss-Lobatto quadrature

$$ I(k,l,{\upbeta}_{1})\approx\sum\limits_{j=0}^{\hat{N}}\omega_{j}J_{k}^{-{\upbeta}_{1}, {\upbeta}_{1}}(x_{j})J_{l}^{{\upbeta}_{1},-{\upbeta}_{1}}(x_{j}), $$

(62)

where {x_j} are the Jacobi-Gauss nodes with respect to the weight function $\omega ^{-{\upbeta }_1,-{\upbeta }_1}=(1+x)^{-{\upbeta }_1}(1-x)^{-{\upbeta }_1}$ and {ω_j} are the corresponding weights. Note that the numerical integration (62) is exact for all 0 ≤ k, l ≤ N when $\hat {N} >N$. In conclusion, the detailed implementation of assembling the stiffness matrix S^x is shown Algorithm 1.It is noted that S^x, S^y and S^z are full, which is very different from the Galerkin spectral methods for the integer-order differential equation.

The fully discrete scheme (21) can be written in the matrix form as

$$ \begin{array}{lllll} &P\hat{U}^{n}=Q\hat{U}^{n-1}-{\sum}_{j=1}^{n-1}\hat{c}_{n,j}^{(\sigma)}(M^{x} \otimes M^{y}\otimes M^{z})(\hat{U}^{n-j}-\hat{U}^{n-j-1})+F^{n}, \end{array} $$

(63)

where

$$ \begin{array}{lllll} P=&\ \hat{c}_{n,0}^{(\sigma)}M^{x}\otimes M^{y}\otimes M^{z}\\ &\ +\sigma(S^{x}\otimes M^{y}\otimes M^{z}+M^{x}\otimes S^{y}\otimes M^{z}+M^{x}\otimes M^{y}\otimes S^{z}),\\ Q=&\ \hat{c}_{n,0}^{(\sigma)}M^{x}\otimes M^{y}\otimes M^{z}\\ &\ -(1-\sigma)(S^{x}\otimes M^{y}\otimes M^{z}+M^{x}\otimes S^{y}\otimes M^{z}+M^{x}\otimes M^{y}\otimes S^{z}), \end{array} $$

$$ \hat{U}^{n}=[\hat{u}_{1,1,1}^{n},\ldots,\hat{u}_{1,1,N-1}^{n},\ldots,\hat{u} _{1,N-1,N-1}^{n},\ldots,\hat{u}_{N-1,N-1,N-1}^{n}]^{T}, $$

and

$$ F^{n}=[F_{1,1,1}^{n},\ldots,F_{1,1,N-1}^{n},\ldots,F_{1,N-1,N-1}^{n}, \ldots,F_{N-1,N-1,N-1}^{n}]^{T}, $$

where $F_{k,l,m}^n=(f,\phi _k(x)\varphi _l(y)\psi _m(z)).$

Since P is a (N − 1)³ × (N − 1)³ dense matrix, it consumes a large amount of CPU time if we calculate (63) directly. To reduce the computational complexity, we introduce the alternating-direction implicit (ADI) method.

Firstly, for convenience, we introduce the following notations:

$$ F_{x}u=K_{x}\frac{\partial^{2{\upbeta}_{1}}u}{\partial \lvert x\rvert^{2{\upbeta}_{1}}} ,\ F_{y}u=K_{y}\frac{\partial^{2{\upbeta}_{2}}u}{\partial \lvert y\rvert^{2{\upbeta}_{2}} },\ F_{z}u=K_{z}\frac{\partial^{2{\upbeta}_{3}}u}{\partial \lvert z\rvert^{2{\upbeta}_{3}}}, $$

(64)

then the fully discrete scheme (21) can be rewritten as

$$ \left\{ \begin{array}{lll} &({u_{N}^{n}},v_{N})-\eta\tau\sigma\left( (F_{x}+F_{y}+F_{z}){u_{N}^{n}},v_{N}\right)\\ =&\ (u_{N}^{n-1},v_{N})+\eta\tau(1-\sigma)\left( (F_{x}+F_{y}+F_{z})u_{N}^{n-1},v_{N}\right)\\ &\ -\eta\tau\sum\limits_{j=1}^{n-1}\hat{c}_{n,j}^{(\sigma)}(u_{N}^{n-j}-u_{N}^{n-j-1},v_{N})+\eta\tau(f,v_{N}), \qquad \forall v_{N}\in {V_{N}^{0}},\\ &{u_{N}^{0}}=I_{N}\phi,&\ \end{array}\right. $$

(65)

where $\eta =\frac {1}{\hat {c}_{n,0}^{(\sigma )}\tau }$ is a bounded constant.

We add the perturbation term

$$ (\sigma^{2}\eta^{2}\tau^{3}(F_{x}F_{y}+F_{x}F_{z}+F_{y}F_{z})\delta_{t}u_{N}^{n-\frac{1}{2}}-\sigma^{2}\eta^{3}\tau^{3}F_{x}F_{y}F_{z}u_{N}^{n-1+\sigma },v_{N})=O(\tau^{3}) $$

(66)

to the left side of above equation which leads to the following ADI spectral Galerkin scheme:

$$ \begin{array}{@{}rcl@{}} \left\{ \begin{array}{lllll} &\left( (1-\sigma\eta\tau F_{x})(1-\sigma\eta\tau F_{y})(1-\sigma\eta\tau F_{z}){u_{N}^{n}},v_{N}\right)\\ =&\ \left( (1+(1-\sigma)\eta\tau F_{x})(1+(1-\sigma)\eta\tau F_{y})(1+(1-\sigma)\eta\tau F_{z})u_{N}^{n-1},v_{N}\right)\\ &\ +\eta^{2}\tau^{2}(2\sigma-1)\left( (F_{x}F_{y}+F_{x}F_{z}+F_{y}F_{z})u_{N}^{n-1}+\sigma^{2}\eta \tau F_{x}F_{y}F_{z}u_{N}^{n-1},v_{N}\right)\\ &\ -\eta\tau\sum\limits_{j=1}^{n-1}\hat{c}_{n,j}^{(\sigma)}(u_{N}^{n-j}-u_{N}^{n-j-1},v_{N})+\eta\tau(f,v_{N}),\qquad \forall v_{N}\in {V_{N}^{0}},\\ &{u_{N}^{0}}=I_{N}\phi. \end{array}\right. \end{array} $$

(67)

Next, we will give the details of the implementation of ADI scheme (67) . We denote P^x, P^y, P^z, Q^x, Q^y, Q^z as

$$ \begin{array}{lllll} &P^{x}=M^{x}+\sigma\eta\tau S^{x},\qquad &\qquad Q^{x}=M^{x}-(1-\sigma)\eta\tau S^{x},\\ &P^{y}=M^{y}+\sigma\eta\tau S^{y},\qquad &\qquad Q^{y}=M^{y}-(1-\sigma)\eta\tau S^{y},\\ &P^{z}=M^{z}+\sigma\eta\tau S^{z},\qquad &\qquad Q^{z}=M^{z}-(1-\sigma)\eta\tau S^{z}. \end{array} $$

For any $v=\phi _{k^{\prime }}(x)\varphi _{l^{\prime }}(y)\psi _{m^{\prime }}(z)$ in S_N,

$$ \begin{array}{@{}rcl@{}} &&\left( (1-\frac{\sigma\eta\tau}{2}F_{x})(1-\frac{\sigma\eta\tau}{2}F_{y})(1- \frac{\sigma\eta\tau}{2}F_{z}){u_{N}^{n}},v_{N}\right)\\ &=&{\sum}_{k=0}^{N-2}{\sum}_{l=0}^{N-2}{\sum}_{m=0}^{N-2}P_{k'k}^{x} \hat{u}_{klm}^{n}P_{l'l}^{y}P_{m'm}^{z}, \end{array} $$

(68)

$$ \begin{array}{@{}rcl@{}} G_{k'l'm'}^{n,1}&:=&\ \left( \left( 1+(1-\sigma)\eta\tau F_{x}\right)\left( 1+(1-\sigma)\eta\tau F_{y}\right)\left( 1+(1-\sigma)\eta\tau F_{z}\right)u_{N}^{n-1},v_{N}\right)\\ &=&\ \sum\limits_{k=0}^{N-2}\sum\limits_{l=0}^{N-2}\sum\limits_{m=0}^{N-2}Q_{k'k}^{x} \hat{u}_{klm}^{n-1}Q_{l'l}^{y}Q_{m'm}^{z}, \end{array} $$

(69)

$$ \begin{array}{@{}rcl@{}} G_{k'l'm'}^{n,2}:&=&(u_{N}^{n-j}-u_{N}^{n-j-1},v_{N})\\ &=&\sum\limits_{k=0}^{N-2}\sum\limits_{l=0}^{N-2}\sum\limits_{m=0}^{N-2}M_{k'k}^{x}(\hat{u}_{klm}^{n-j}-\hat{u}_{klm}^{n-j-1})M_{l'l}^{y}M_{m'm}^{z}, \end{array} $$

(70)

and

$$ \begin{array}{@{}rcl@{}} G_{k'l'm'}^{n,3}:&=&(f^{n-1+\sigma},v)\\ &\approx&\frac{ l_{1}l_{2}l_{3}}{8}\sum\limits_{p=0}^{N}\sum\limits_{q=0}^{N}\sum\limits_{s=0}^{N}f^{n-1+ \sigma}(x_{p},y_{q},z_{s})w_{p}w_{q}w_{s}\phi_{k'}(x_{p})\varphi_{l'}(y_{q})\psi_{m'}(z_{s}),\\ \end{array} $$

(71)

where $\{\hat {x}_{p}\}$, $\{\hat {y}_{q}\}$, $\{\hat {z}_{s}\}$ are the Legendre-Gauss-Lobatto nodes and {ω_j} are the corresponding weights. Letting $G_{k^{\prime }l^{\prime }m^{\prime }}^{n}:=G_{k^{\prime }l^{\prime }m^{\prime }}^{n,1}+G_{k^{\prime }l^{\prime }m^{\prime }}^{n,2}+G_{k^{\prime }l^{\prime }m^{\prime }}^{n,3}$, (67) can be calculated by the following equation:

$$ \sum\limits_{k=0}^{N-2}\sum\limits_{l=0}^{N-2}\sum\limits_{m=0}^{N-2}P_{k^{\prime }k}^{x}\hat{u} _{klm}^{n}P_{l^{\prime }l}^{y}P_{m^{\prime }m}^{z}=G_{k^{\prime }l^{\prime }m^{\prime }}^{n}. $$

(72)

Denote

$$ \sum\limits_{l=0}^{N-2}\sum\limits_{m=0}^{N-2}\hat{u}_{klm}^{n}P_{l^{\prime }l}^{y}P_{m^{\prime }m}^{z}=V_{kl^{\prime }m^{\prime }}^{n}, $$

$$ \sum\limits_{m=0}^{N-2}P_{m^{\prime }m}^{z}\hat{u}_{klm}^{n}=W_{kl^{\prime }m^{\prime }}^{n}, $$

equation (72) can be solved using the following three steps in one time step:

• Step 1: For fixed $l^{\prime },m^{\prime }$, compute ${\sum }_{k=0}^{N-2}P_{k^{\prime }k}^{x}V_{kl^{\prime }m^{\prime }}^{n}=G_{k^{\prime }l^{\prime }m^{\prime }}^{n};$

• Step 2: For fixed $k,m^{\prime }$, compute ${\sum }_{l=0}^{N-2}P_{l^{ \prime }l}^{y}W_{klm^{\prime }}^{n}=V_{kl^{\prime }m^{\prime }}^{n};$

• Step 3: For fixed k, l, compute ${\sum }_{m=0}^{N-2}P_{m^{\prime }m}^{z}\hat {u}_{k^{\prime }l^{\prime }m^{\prime }}^{n}=W_{klm^{\prime }}^{n}.$

To summarize, the ADI scheme (67) can be solved by the following algorithm:

Remark 2

Algorithm 2 shows that we just need to solve some algebraic systems of the form Ax = b (A = P^x,P^y,P^z) to get the numerical solutions, which can reduce the computational complexity significantly.

The perturbation term (66) is very small, which will not affect the error estimation. Using a similar method in Theorem 2, the convergence result of the ADI scheme (67) can be directly obtained as follows.

Theorem 3

Let β₁, β₂, β₃ and r be arbitrary real numbers satisfying $\frac {1}{2}<{\upbeta }_1,{\upbeta }_2,{\upbeta }_3\leq 1<r$. Suppose that the exact solution u(x, y, z, t) of the original problem (1) satisfies Assumption 1 and $\left \{u_N^{n}\right \}_{n=0}^{N_T}$ is the solution of the ADI scheme (67). Then there exist constant C₁₄ and C₁₅ independent of τ and N such that the following estimates hold true:

$$ \begin{array}{@{}rcl@{}} \lVert e^{n} \rVert\leq C_{14}(\tau^{2}+N^{-r}),\qquad \lvert e^{n}\rvert_{\upbeta}\leq C_{15}(\tau^{2}+N^{{\upbeta}_{\max}-r}), \end{array} $$

where $e^n=u(x,y,z,t_n)-u_N^n(x,y,z).$

6 Experimental results

In this section, two numerical examples are presented to illustrate the theoretical results. In addition, we will use our method to simulate the multi-term time-space fractional Bloch-Torrey model.

6.1 Example 1

We consider the following three-term time-space fractional diffusion equation [4] on the unit cube Ω = (0,1) × (0,1) × (0,1) :

$$ \left\{ \begin{array}{lr} \displaystyle K_{0} \frac{\partial u}{\partial t} + K_{1} {~}^{\mathrm{C}} {\mathcal{D}}_{t}^{\alpha_{1}} u + K_{2} {~}^{\mathrm{C}} {\mathcal{D}}_{t}^{\alpha_{2}} u = K_{x} \frac{\partial^{2\beta_{1}}}{\partial |x|^{2\beta_{1}}} + K_{y} \frac{\partial^{2\beta_{2}}}{\partial |y|^{2\beta_{2}}} + K_{z} \frac{\partial^{2\beta_{3}}u}{\partial |z|^{2\beta_{3}}} + f, & \text{in } {\Omega} \times (0,T],\\ u(x,y,z,0)=0, & \text{in } {\Omega},\\ u(x,y,z,t)=0, & \text{on } \partial {\Omega}\times (0,T], \end{array}\right. $$

(73)

where

$$ \begin{array}{@{}rcl@{}} &&f(x,y,z,t)\\ &=&\ 2^{12}(3K_{0}t^{2}+\frac{K_{1}{\Gamma}(4)}{\Gamma(4-\alpha_{1})}t^{3-\alpha_{1}}+ \frac{K_{2}{\Gamma}(4)}{\Gamma(4-\alpha_{2})}t^{3- \alpha_{2}})x^{2}(1-x)^{2}y^{2}(1-y)^{2}z^{2}(1-z)^{2}\\ &\ &+\frac{2^{12}K_{x}}{2\cos({\upbeta}_{1}\pi)}t^{3}y^{2}(1-y)^{2}z^{2}(1-z)^{2}g(x,{\upbeta}_{1})+ \frac{2^{12}K_{y}}{2\cos({\upbeta}_{2}\pi)}t^{3}x^{2}(1-x)^{2}z^{2}(1-z)^{2}g(y,{\upbeta}_{2})\\ &&\ +\frac{2^{12}K_{z}}{2\cos({\upbeta}_{3}\pi)}t^{3}x^{2}(1-x)^{2}y^{2}(1-y)^{2}g(z,{\upbeta}_{3}) \end{array} $$

and

$$ \begin{array}{@{}rcl@{}} g(s,\upbeta )&=& \ \frac{\Gamma (3)}{\Gamma (3-2\upbeta )}\left( s^{2-2\upbeta }+(1-s)^{2-2\upbeta }\right) \\ && \ -\frac{2{\Gamma} (4)}{\Gamma (4-2\upbeta )}\left( s^{3-2\upbeta }+(1-s)^{3-2\upbeta }\right)+\frac{\Gamma (5)}{\Gamma (5-2\upbeta )}\left( s^{4-2\upbeta }+(1-s)^{4-2\upbeta }\right). \end{array} $$

The exact solution of (73) is u(x, y, z, t) = 2¹²t³x²(1 − x)²y²(1 − y)²z²(1 − z)². We set K_i = K_x = K_y = K_z = 1, i = 0,1,2, and T = 1. The error function between the exact solution u(x, y, z, T) and the numerical solution $U_{N}^{N_{T}}(x,y,z)$ is given by $e(\tau ,N)(x,y,z)=u(x,y,z,T)-U_{N}^{N_{T}}(x,y,z)$. The convergence rates in time and space in the L²-norm on two successive time step sizes τ₁ and τ₂ and two successive polynomial degrees N₁ and N₂ are defined as

$$ \text{Rate}=\left\{ \begin{array}{lllll} &\frac{\log(\lVert e(\tau_{1},N) \rVert/\lVert e(\tau_{2},N) \rVert)}{\log(\tau_{1}/\tau_{2})}, & \text{in\ time},\\ &\frac{\log(\lVert e(\tau,N_{1}) \rVert/\lVert e(\tau,N_{2}) \rVert)}{\log(N_{1}/N_{2})}, & \text{in\ space.} \end{array}\right. $$

(74)

The convergence rates in the $L^{\infty }$-norm and H^β-seminorm can be defined similarly.

Set (α₁,α₂) = (0.8,0.6), (β₁,β₂,β₃) = (0.9,0.75,0.6) and time step τ = 10^− 3. The errors in the L²-norm and CPU time of L2-1_σ/spectral Galerkin scheme (21) and ADI scheme (67) are listed in Table 1. We see that both schemes can achieve the same precision and convergence rate of errors. Moreover, compared with the L2-1_σ/spectral Galerkin scheme without ADI, the ADI scheme can greatly reduce the CPU time and storage.

Table 1 The errors, rates and CPU time of L2-1_σ /spectral Galerkin scheme (21) and ADI scheme (67)

In the latter tests, we use the ADI scheme (67) to calculate the numerical solution. Firstly, we check the temporal convergence rate for different (α₁,α₂) by fixing polynomial degree N = 40 and (β₁,β₂,β₃) = (0.6,0.7,0.8). In Table 2, we present the errors and rates in the $L^{\infty }$-norm, L²-norm and H^β-seminorm and CPU time for (α₁,α₂) = (0.99,0.60) , (α₁,α₂) = (0.63,0.34) and (α₁,α₂) = (0.37,0.26). These results show that our method has second-order convergence in time, which is in accordance with our theoretical analysis in Theorem 3.

Table 2 The errors, rates and CPU time versus τ for (β₁,β₂,β₃) = (0.6,0.7,0.8) with different (α₁,α₂)

Then, we investigate the spatial convergence rate for different (β₁,β₂,β₃) by fixing time step τ = 10^− 3 and (α₁,α₂) = (0.8,0.3). The errors versus polynomial degree N for different (β₁,β₂,β₃) are displayed in Table 3. Here we test three cases, (β₁,β₂,β₃) = (0.80,0.80,0.80), (β₁,β₂,β₃) = (0.9,0.75,0.6) and (β₁,β₂,β₃) = (0.58,0.83,0.66), respectively. We observe that errors decay algebraically (not exponentially) in spatial direction. This is because that the function f(x, y, z, t) is singular on ∂Ω, which causes a loss of accuracy when calculating (71). Our results on spatial convergence rate are in agreement with the results of Example 6.1 in [59], which considered the two-dimensional space-fractional diffusion equation. The CPU time in Tables 2 and 3 shows the effectiveness of our algorithm.

Table 3 The errors, rates and CPU time versus N for (α₁, α₂) = (0.8,0.3) with different (β₁,β₂,β₃)

6.2 Example 2

We now consider the following 3D multi-term time-space fractional Bloch-Torrey equation [4]:

$$ \left\{ \begin{array}{lllll} \frac{\partial M_{x}}{\partial t}+\omega^{\alpha_{1}-1}\frac{\partial^{\alpha_{1}}M_{x}}{\partial t^{\alpha_{1}}}+\omega^{\alpha_{2}-1}\frac{\partial^{\alpha_{2}}M_{x}}{\partial t^{\alpha_{2}}}=&\ D\mu^{2{\upbeta}_{1}-2}\frac{\partial^{2{\upbeta}_{1}}M_{x}}{\partial \lvert x\rvert^{2{\upbeta}_{1}}}+D\mu^{2{\upbeta}_{2}-2}\frac{\partial^{2{\upbeta}_{2}}M_{x}}{\partial \lvert y\rvert^{2{\upbeta}_{2}}}\\ &\ +D\mu^{2{\upbeta}_{3}-2}\frac{\partial^{2{\upbeta}_{3}}M_{x}}{\partial \lvert z\rvert^{2{\upbeta}_{3}}}+\lambda(t)M_{y},\\ \frac{\partial M_{y}}{\partial t}+\omega^{\alpha_{1}-1}\frac{\partial^{\alpha_{1}}M_{y}}{\partial t^{\alpha_{1}}}+\omega^{\alpha_{2}-1}\frac{\partial^{\alpha_{2}}M_{y}}{\partial t^{\alpha_{2}}}=&\ D\mu^{2{\upbeta}_{1}-2}\frac{\partial^{2{\upbeta}_{1}}M_{y}}{\partial \lvert x\rvert^{2{\upbeta}_{1}}}+D\mu^{2{\upbeta}_{2}-2}\frac{\partial^{2{\upbeta}_{2}}M_{y}}{\partial \lvert y\rvert^{2{\upbeta}_{2}}}\\ & +D\mu^{2{\upbeta}_{3}-2}\frac{\partial^{2{\upbeta}_{3}}M_{y}}{\partial \lvert z\rvert^{2{\upbeta}_{3}}}-\lambda(t)M_{x}, \end{array}\right. $$

(75)

with the initial condition and boundary condition

$$ \left\{ \begin{array}{lllll} &M_{y}(x,y,z,0)=100,\qquad &(x,y,z,t)\in {\Omega}\times(0,T],\\ &M_{x}(x,y,z,0)=0,\qquad &(x,y,z,t)\in {\Omega}\times(0,T],\\ &M_{x}(x,y,z,t)=M_{y}(x,y,z,t)=0,\qquad &(x,y,z,t)\in \partial{\Omega}\times(0,T], \end{array}\right. $$

(76)

where λ(t) = t, Ω = (0,1) × (0,1) × (0,1) and T = 20.

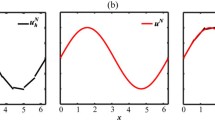
We choose ω = 2, D = 10^− 3, μ = 15, τ = 1/40,N = 24 to simulate the behaviour of the transverse magnetization $\lvert M_{xy}(x,y,z,t)\rvert =\sqrt { {M_{x}^{2}}(x,y,z,t)+{M_{y}^{2}}(x,y,z,t)}$. In Figs. 1 and 2, we illustrate the solution behaviour for M_x(x, y, z, t), M_y(x, y, z, t) at the point (x^∗,y^∗,z^∗) = (0.5,0.5,0.5) and normalized decay of the transverse magnetization for different (α₁,α₂) with fixed (β₁,β₂,β₃) = (0.6,0.7,0.8). It is observed that (α₁,α₂) has a significant impact on the solution behaviour; specifically, decreasing the time-fractional power can accelerate the evolution from (0,100) to (0,0) . The simulation results for different (β₁,β₂,β₃) with fixed (α₁,α₂) = (0.9,0.7) are displayed in Figs. 3 and 4, which show that the effects of (β₁,β₂,β₃) on the solution behaviour are not obvious; this is because the parameter D is very small.

Fig. 1

The solution behaviour versus t at point (x^∗,y^∗,z^∗) for different (α₁,α₂)

Fig. 2

The normalized decay of the transverse magnetization versus t at point (x^∗,y^∗,z^∗) for different (α₁,α₂)

Fig. 3

The solution behaviour versus t at point (x^∗,y^∗,z^∗) for different (β₁,β₂,β₃)

Fig. 4

The normalized decay of the transverse magnetization versust at point (x^∗,y^∗,z^∗) for different (β₁,β₂,β₃)

7 Conclusions

In this paper, we proposed an efficient spectral Galerkin method by using the L2-1_σ formula for time discretization and the Legendre-Galerkin spectral method for space discretization to solve the three-dimensional multi-term time-space fractional diffusion equation. The stability and convergence of the numerical scheme were rigorously established, which show that the fully discrete scheme is unconditionally stable and can reach second-order convergence in time and spectral convergence in space. The direct method to solve the fully discrete scheme is too time consuming; thus, we constructed an ADI spectral Galerkin scheme and gave the detailed implementation. Finally, numerical examples were presented to validate our theoretical analysis. As an application of our method, we solved the 3D multi-term time-space fractional Bloch–Torrey problem. The simulation results show that such problem can have very different dynamics with different values of the time-fractional power α.