1 Introduction

Researchers have developed and designed the number of new evolutionary multi-objective algorithms over the past few years to solve problems with more than two objectives [1,2,3]. multi-objective evolutionary algorithms (MOEAs) are a type of population based heuristics [4,5,6,7,8,9] that, during simulation runs, can get a group of solutions. Nonetheless, some real-life issues, such as vehicle engine tuning problems [10], water distribution systems [11], and land use management problems [12] and so on [13,14,15,16,17,18,19,20,21,22] also require a large number of objectives. MOEAs also face some challenges in tackling these multiple objectives. The selection methods are the reason behind the failure of most MOEAs. To converge the population to the Pareto front, such methods are useful. When the number of objectives increases, it is difficult to maintain the diversity, as the solutions are very sparsely allocated within the objective search space.

Non-dominated Sorting Genetic Algorithm (NSGA-II) [23] and Strength Pareto Evolutionary Algorithm 2 (SPEA2) [24] are the most popular multi-objective evolutionary algorithms. Both of these algorithms use dominance based selection strategy that fails to solve problems with more than three objectives.

To address this issue, researchers have developed new optimization algorithms to deal with a large number of objectives [25,26,27,28,29,30], also referred to as the Many-Objective Problems (MaOPs). The main challenges in MaOPs are:

  • Pareto’s front visualization in a search space requires special procedures [31].

  • The fact of the dominance resistance (DR), in which the gap between the solutions is caused by an increase in the amount of non-dominated solutions [32,33,34].

  • The number of solutions has increased exponentially to define the multi-dimensional Pareto front problems [35, 36].

Most of the MaOPs concentrate on maintaining diversity and enhancing convergence. Such algorithms are not about using preferences for many-objective problems. This is because the researchers may be interested in optimal Pareto solutions and less computational effort [37,38,39,40,41,42,43,44] to achieve a demonstrative subset of the Pareto front [45].

There are several evolutionary algorithms that have been developed to improve the effectiveness of algorithms to solve MaOPs [46,47,48]. Reference Vector Guided Evolutionary Algorithm (RVEA) [49] is a recently developed decomposition based approach that can produce optimal solutions using reference points for a Pareto subset of solutions. Such points of reference are useful for greater convergence. Despite this, the most common algorithm based on hypervolume indicator is the Hypervolume Estimation Algorithm (HypE) [50] which uses the Monte Carlo simulation to estimate the exact hypervolume values and maintain diversity.

The main contribution of this work is the development of a novel hybrid evolutionary algorithm using the principles of RVEA and HypE algorithms. The algorithm is called Reference Vector Guided Evolutionary Algorithm based on the Hypervolume indicator (H-RVEA). H-RVEA’s four main strategies are mating selection, variation, environmental selection, and adaptation strategy for reference vectors. The mating selection strategy is used to exchange information between individuals, and to select from the current population the most promising optimal solution. The variation method utilize operators of recombination and mutation to generate new offspring. It is the task of the environmental selection strategy to break and merge the strategies into non-dominated fronts. The Adaptation technique for the reference vector is used to enhance the search process and to decompose the problem into a sub-problem.

H-RVEA’s performance is tested on well-known benchmark test problems. The two performance measures, namely Inverted Generational Distance (IGD) [51] and Hypervolume (HV) [52], have been used to assess the algorithms. The results have been compared with five approaches such as Reference Vector Guided Evolutionary Algorithm (RVEA) [49], Hypervolume Estimation Algorithm (HypE) [50], Non-dominated Sorting Genetic Algorithm (NSGA-III) [53], Many-Objective Evolutionary Algorithm based on Dominance and Decomposition (MOEA/DD) [54], and Approximation-guided Evolutionary Algorithm (AGE-II) [55]. Therefore, to illustrate its usefulness, H-RVEA has been applied to two real-life many-objective problems.

The rest of the paper has the following structure: Sect. 2 represents the basics of many-objective problems and two many-objective evolutionary algorithms. Section 3 presents the motivation and brief description of proposed H-RVEA algorithm. Results and discussions of experiments are given in Sect. 4. Section 5 presents the performance of H-RVEA on two real-life problems followed by conclusions and future works in Sect. 6.

2 Background

In this section, the basic concepts of Multi-Objective Problems (MOPs) are presented. Then, the brief descriptions of RVEA and HypE algorithms are presented.

2.1 Basic concepts

Multi-Objective Optimization Problems (MOPs) involve more than one objective which is to be optimized. The MOPs can be formulated as follows:

$$\begin{aligned} \begin{aligned}&{\text {Minimize}}\quad f(\vec {x})=(f_1(\vec {x}), f_2(\vec {x}), f_3(\vec {x}),\ldots ,f_n(\vec {x}))\\&{\text {Subject to:}}\quad \vec {x} \,\in \, R \end{aligned} \end{aligned}$$
(1)

where n defines the number of objective functions and \(f(\vec {x})\) defines the objective function. However, the feasible space R is a subset of decision space (D), which consists the decision vectors \(\vec {x}=(\vec {x_1}, \vec {x_2}, \ldots , \vec {x_m})^\mathrm{T}\).

2.2 Reference Vector Guided Evolutionary Algorithm (RVEA)

Reference Vector Guided Evolutionary Algorithm (RVEA) is an evolutionary algorithm for many-objective optimization problems [49]. The main components of the RVEA algorithm are offspring production, guided selection of the reference vector, and strategies for adapting the reference vector. The genetic operators, as used in NSGA-III and HypE, are employed to build the offspring population. The guided selection method for the reference vector consists of four steps, namely objective value translation, population partitions, Angle Penalized Distance (APD) calculation and elitism selection [49]. RVEA uses their strategies of elitism and offspring as similar to the NSGA-III algorithm. Its selection strategy adopts a set of reference vectors. Angle Penalized Distance (APD) is used to align the convergence and diversity properly. An adaptive technique is used to modify the reference vectors to ensure a consistent distribution of solutions within the objective space. The preferential articulation method based on the reference vector is used to get optimal solutions in a chosen area uniformly distributed by Pareto. The RVEA is described in the Algorithm 1 [49].

figure a

2.3 Hypervolume Estimation Algorithm (HypE)

Bader and Zitzler [50] have proposed a MOEA based rapid hypervolume indicator, namely Hypervolume Estimation Algorithm (HypE). The main concept behind HypE is the rating by the hypervolume of solutions achieved. HypE uses a generalized technique of granting fitness. The hypervolume values are calculated using Monte-Carlo simulation. Mating selection, variation, and environmental selection are key components of HypE. Selection of binary tournament is used to select offspring. The variation employed operators of recombination and mutation to produce offspring. Throughout environmental selection, the populations of parents and children are integrated and decomposed into non-dominated fronts, and the new population is added with the best fronts. The HypE is described in Algorithm 2 [50].

figure b

3 Proposed H-RVEA Algorithm

This section describes the motivation and overall procedure of proposed H-RVEA algorithm.

3.1 Motivation

The researchers have pointed to difficulties of convergence and diversity with more than four objectives for real-life problems. Therefore, an algorithm must be established which maintains the convergence and diversity. In this paper the hypervolume indicator is used to preserve the diversity. The reason for preferring this measure over others is:

  1. 1.

    Hypervolume indicator removes the lack of selection pressure.

  2. 2.

    The value of this indicator is optimized directly, without the need for niching, which helps to maintain the diversity.

  3. 3.

    This indicator ensures that any approximation set with a high quality value for a specific problem includes all optimal objective vectors from Pareto [56].

Hypervolume calculation, however, requires a high computational effort. We have used fast HypE algorithm to solve this problem. HypE suffers from the overheads of having the information needed. We have used reference vector adaptation strategy to preserve the knowledge. The reference vector adaptation strategy is taken from RVEA algorithm. Therefore, a novel hybrid algorithm is proposed which employs both HypE and RVEA features.

3.2 Proposed algorithm

The intend to propose the H-RVEA is to solve problems that have a large number of objectives. The basic procedure of proposed H-RVEA is mentioned in Algorithm 3. The H-RVEA is inspired by RVEA and HypE algorithms (see Fig. 1). H-RVEA consists of four main components. These are mating selection (Algorithm 4), variation, environmental selection (Algorithm 8), and reference vector adaptation strategy (Algorithm 9). Initially, it starts with the randomly generated population P and N number of individuals. The mating selection procedure is used to select the promising solutions in a search space. The variation uses the mutation and recombination operators to generate the N number of offspring. The environmental selection procedure is used for the selection of the best optimal solution. Finally, the reference vector adaptation strategy is performed to obtain a uniformly distributed Pareto optimal solutions set.

figure c

3.2.1 Mating selection

The mating selection is a procedure for exchanging the information between individuals and to select the promising optimal solutions from the current population. The mating selection strategy of proposed H-RVEA is described in Algorithm 4. When the number of objectives is less than 3 (\(\le 3\)), then the computation of hypervolume is done through Computehypervolume procedure which is mentioned in Algorithm 5. Otherwise, the computation of hypervolume is done through the Estimatehypervolume procedure which is mentioned in Algorithm 7.

The Computehypervolume procedure uses the recursive function Slicing and returns a fitness assignment \(\alpha\) and a multi-set containing a pair (\(a, w_a\)), where \(w_a\) is fitness value and \(a \in P\). The Slicing procedure mentioned in Algorithm 6, recursively cut the dominated space into hyper-rectangles and returns a partial fitness assignment \(\alpha '\). The scanning process is performed at each recursive level l with \(u'\), where \(u'\) represents the current scan position. The scan positions are included in vector \((s_1, s_2, \ldots , s_n)\) which contains all the dimensions. The partial volume PV is updated and reference points are filtered out during whole the recursive process (Line 2 and 3). Example 1 is used to describe the working of Computehypervolume procedure.

The Estimatehypervolume procedure returns a fitness assignment \(\alpha\) corresponding to the estimated hypervolume as mentioned in Algorithm 7. The first step is to determine the sampling box S which is a superset of approximate hypervolumes. Thereafter, the volume of sampling space S is computed (Line 6). For sampling process the M objective vectors \((y_1, y_2, \ldots , y_M)\) are selected from S randomly. Based on the sampling point an estimation of hypervolume is done. The hypervolumes values are then updated during procedure call.

Example 1

(Hypervolume computation) Consider the population contains four solutions i.e., w, x, y, z with objective vectors \(f(w)=(-9, -2, -1), f(x)=(-7, 0, -7), f(y)=(-5, -7, -9), f(z)=(-3, -4, -10)\), fitness parameter \(f_{\text {p}}=2\) , reference points \(r=(-1, 0, 0)\), and \(y=(-1, -2, -3)\).

Firstly, call the Slicing procedure in which the value of l is set to 3 and U contains all objective vectors and reference points. According to the third vector components, the U with its elements are sorted in ascending order.

$$\begin{aligned} U= {\left\{ \begin{array}{ll} f(z)=(-3, -4, -10)\\ f(y)=(-5, -7, -9)\\ f(x)=(-7, 0, -7)\\ y=(-1, -2, -3)\\ f(w)=(-9, -2, -1)\\ r=(-1, 0, 0) \end{array}\right. } \end{aligned}$$

The variable \(u'\) assigned the third vector value of these elements to \(f_3(z)=-10, f_3(y)=-9, f_3(x)=-7, y_3=-3, f_3(w)=-1, r_3=0\). During iteration process, U is reduced and assign \(u'=f_3(x)=-7\) and update the value of \({\text {PV}}'=1\times (-3-(-7))=4\) with scan positions \((s_1, s_2, s_3)=(\infty , \infty , -7)\). Now, these values are passed to next recursion level \(l=2\) and process the Line 13 in Slicing procedure, where U is initialized.

In the next level, the sorting is performed according to second dimension of these elements.

$$\begin{aligned} U= {\left\{ \begin{array}{ll} f(y)=(-5, -7, -9)\\ f(z)=(-3, -4, -10)\\ y=(-1, -2, -3)\\ f(x)=(-7, 0, -7)\\ r=(-1, 0, 0) \end{array}\right. } \end{aligned}$$

Therefore, variable \(u'\) assigned the second vector value to \(f_2(y)=-7, f_2(z)=-4, y_2=-2, f_2(x)=0, r_2=0\). U is further reduced and assign \(u'=f_2(x)=0\). The value of \({\text {PV}}'=1\times 4\times (0-0)=0\) and scan positions \((s_1, s_2, s_3)=(\infty , 0, -7)\). For the next recursion level \(l=1\) in which the sorting is performed according to first vector, then the U is computed as follows.

$$\begin{aligned} U= {\left\{ \begin{array}{ll} f(x)=(-7, 0, -7)\\ f(y)=(-5, -7, -9)\\ f(z)=(-3, -4, -10)\\ r=(-1, 0, 0) \end{array}\right. } \end{aligned}$$

In the second iteration, variable \(u'\) assigned the first vector value to \(f_1(x)=-7, f_1(y)=-5, f_1(z)=-3, r_1=-1\) and holds \(u'=f_1(y)=-5\). The value of \({\text {PV}}'=1\times 4\times 0 \times (-3-(-5))=0\) and scan positions \((s_1, s_2, s_3)=(-5, 0, -7)\). Once the recursion level is reached at level 0 (\(l=0\)), the \(\beta\) is computed with N number of population size, fitness parameter \(f_{\text {p}}=2\), and hyperrectangle \({\text {RS}}=0\). Therefore, the whole procedure is applied to all slices to identifies all hyperrectangles of the search space.

Fig. 1
figure 1

Flowchart of the proposed H-RVEA algorithm

Full size image
figure d
figure e
figure f
figure g

3.2.2 Environmental selection

Environmental selection is a procedure to obtain a well-distributed population and to keep it in a memory. It chooses the best optimal solutions from the previous and newly created population. The proposed H-RVEA algorithm implements the environmental selection strategy with hypervolume subset selection problem [50]. Algorithm 8 describes the environmental selection strategy for creating a new population. Firstly, the nondominated sorting approach [23, 57] is used for partitioning the union of parent and offspring into disjoint partitions. The partition that fits into the new population is further processed [50]. The fitness value of each partition is computed and remove the individual with the worst fitness assignment. The parents and offsprings are merged into population P which truncates the non-fitted solutions. Therefore, the dominated solutions do not affect the overall value of hypervolume. Algorithm 8 is repeated until the desired size of a partition is not found and returns the generated new population T.

figure h

3.2.3 Reference vector adaptation strategy

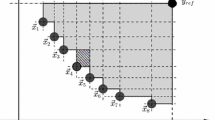
The proposed H-RVEA algorithm uses reference vector adaptation [49] strategy to obtain a set of Pareto optimal solutions as shown in Fig. 2.

Fig. 2
figure 2

Uniformly distributed reference vectors in 3D search space

Full size image

Algorithm 9 mentions this strategy. These solutions are the points of intersection between each reference vector and the Pareto front. However, when the objective function values are normalized in the same range, these reference vectors won’t produce uniformly distributed solutions. The range of the reference vectors will be modified as follows to eliminate this conflict:

$$\begin{aligned} \begin{aligned}&v_{k+1,j}= \dfrac{ v_{0,j}\circ (O_{k+1}^{\max }-O_{k+1}^{\min }) }{\mid \mid v_{0,j}\circ (O_{k+1}^{\max }-O_{k+1}^{\min })\mid \mid } \end{aligned} \end{aligned}$$
(2)

where \(j=1,2,\ldots ,N\), \(v_{k+1,j}\) defines the jth reference vector adapted for generation \(k+1\), \(v_{0,j}\) represents the jth uniformly distributed reference vector. \(O_{k+1}^{\min }\) and \(O_{k+1}^{\max }\) are the minimum and maximum values of objective function, respectively. The \(\circ\) operator indicates the Hadamard product that element-wise multiply the two vectors of same size [49]. The adaptation strategy for the reference vector is capable of obtaining uniformly distributed solutions even if the objective functions are not normalized in the same range.

figure i

There is a \(F_{\text {c}}\) controlling parameter which controls the frequency of use of the adaptation strategy. This parameter means that the reference vector adaptation strategy has to be carried out in a selected generation, since this strategy is not needed very often [58]. Example 2 illustrates the working of control parameter \(F_{\text {c}}\) in adaptation strategy.

Example 2

(Control parameter) For instance, the value of \(F_{\text {c}}\) is set to 0.4. The reference vector will be adapted only at \(k=0, k=0.4 \times {\text {Max}}_{\text {iteration}}, k=0.8 \times {\text {Max}}_{\text {iteration}}, k=0.12 \times {\text {Max}}_{\text {iteration}}\) and so forth.

3.3 Computational complexity

The computational complexity of the proposed algorithm is debated in this subsection. The proposed algorithm’s complexities in terms of time and space are given below.

3.3.1 Time complexity

  1. 1.

    H-RVEA population initialization needs \({\mathcal {O}}(M \times N)\) time, where M and N represent the number of objectives and population size, respectively.

  2. 2.

    The selection procedure for mating requires time of \({\mathcal {O}}(M\times N^2)\).

  3. 3.

    Variation procedure uses \({\mathcal {O}}(N)\) time. Environmental selection method uses \({\mathcal {O}}(N{\text {log}}N)\) and the adaptation technique for the reference vector includes \({\mathcal {O}}(N / F_{\text {c}})\) time, where \(F_{\text {c}}\) represents the control parameter.

The summary of the complexities of all the above steps and the total time complexity of H-RVEA for the maximum number of generations is therefore \({\mathcal {O}}(M \times N^2)+(N / F_{\text {c}})\times {\text {Max}}_{\text {iteration}})\).

3.3.2 Space complexity

H-RVEA algorithm’s space complexity is the cumulative amount of space that is perceived during its initialization process at any given point. Hence, the total space complexity of H-RVEA algorithm is \({\mathcal {O}}(M \times N)\).

4 Experimental results and discussions

The proposed algorithm H-RVEA is compared with five algorithms, namely Reference Vector Guided Evolutionary Algorithm (RVEA) [49], Hypervolume Estimation Algorithm (HypE) [50], Non-dominated Sorting Genetic Algorithm (NSGA-III) [53], Many-Objective Evolutionary Algorithm based on Dominance and Decomposition (MOEA/DD) [54], and Approximation-guided Evolutionary Algorithm (AGE-II) [55]. The well-known benchmark test problems from DTLZ test suite [59] are taken for experimentation. The findings are measured with two well-known performance measures such as Inverted Generational Distance (IGD) [51] and Hypervolume (HV) [52].

4.1 Benchmark test problems

The four (DTLZ1-DTLZ4) test functions from DTLZ [59] test suite are employed. The number of objectives is varied from 3 to 15, i.e., {3, 5, 10, 15}. The number of decision variables is set to \(n = m + r - 1\) for DTLZ test problems [59], where \(r=5\) for DTLZ1 and \(r=10\) for DTLZ2-DTLZ4.

4.2 Experimental setup

The mean and median solutions are reported in tables which are obtained in final iteration. The simulations are done in Matlab R2019a environment on Microsoft Windows 10 (64-bit) using Core i7 and 3.15 GHz processor with 16 GB main memory.

4.3 Performance evaluation on DTLZ test suite

Tables 1 and 2 display the values of IGD and HV obtained through the suggested and competitor algorithms for the DTLZ test suite of 3-, 5-, 10- and 15-objectives. The results reveal that for DTLZ1 test problem H-RVEA offers better values of IGD and HV. Except for H-RVEA, RVEA and MOEA/DD achieve better values of IGD and HV than the others. RVEA and MOEA/DD are therefore the second and third best algorithms, respectively. Whereas, NSGA-III’s output for all objectives is almost identical to the HypE algorithm on DTLZ1 test problem.

For test problem DTLZ2, H-RVEA gets a better value of IGD for 3- and 15-objectives. RVEA performs better results for these objectives than the other algorithms after H-RVEA. H-RVEA performs second best algorithm in terms of the performance measurement IGD for 5- and 10-objectives. RVEA provides better results for those objectives than all other approaches. H-RVEA generates optimal results for all objectives of the DTLZ2 test function for performance measurement HV. Whereas, for the efficiency indicator of HV, RVEA and HypE algorithms are very close to one another.

In terms of IGD and HV performance measures for all objectives, H-RVEA is significantly better than other algorithms on DTLZ3. Nonetheless, MOEA/DD and NSGA-III are the second and third strongest methods, respectively, for IGD efficiency assessment. The NSGA-III obtained the second best solution for HV efficiency estimation after the original H-RVEA algorithm.

For DTLZ4 test issue, H-RVEA’s success measurements for 3-, 5-, 10- and 15-objectives are higher than others in terms of IGD and HV. MOEA/DD and NSGA-III comprise the second and third best methods for IGD and HV.

From Tables 1 and 2 it has been found that H-RVEA’s consistency and efficiency is highest on most of the test functions. For IGD, H-RVEA performs well on 3 out of 4 assessment features. For values of HV, H-RVEA delivers the best results on 4 out of 4 test functions.

For visualization of the solutions, Figs. 3 and 4 display the non-dominated fronts obtained from the proposed H-RVEA and other 15- and 3-objectives competitor algorithms on the DTLZ test functions. RVEA and MOEA/DD have consistent convergence for 15-objectives DTLZ test functions but fail to reach certain regions of the Pareto front. HypE, NSGA-III, and AGE-II ensure good integration across most of Pareto’s fronts. Fig. 3 demonstrates that H-RVEA’s non-dominated front provides greater consistency and variety than other strategies. It has been observed for 3-objectives DTLZ test functions that the Pareto front obtained from H-RVEA, RVEA, NSGA-III, and MOEA/DD has uniform convergence and better diversity as shown in Fig. 4. Nonetheless, over the Pareto front HypE and AGE-II struggle to get a good coverage.

Table 1 The IGD values obtained by proposed H-RVEA and other competitor algorithms on DTLZ test suite
Full size table
Table 2 The HV values obtained by proposed H-RVEA and other competitor algorithms on DTLZ test suite
Full size table
Fig. 3
figure 3

The non-dominated fronts obtained from six algorithms for 15-objectives on DTLZ1, DTLZ2, DTLZ3, and DTLZ4 test functions

Full size image
Fig. 4
figure 4

The non-dominated solutions obtained from six algorithms for 3-objectives on DTLZ1, DTLZ2, DTLZ3, and DTLZ4 test functions

Full size image

4.4 Wilcoxon signed-rank test

It has been observed in the literature [60] that the performance measures IGD and HV do not provide any guarantee for better convergence and diversity, because sometimes the solutions obtained are not close to the optimal Pareto front. The Wilcoxon signed-rank test [61] is performed on the average value of performance measures of IGD and HV to solve this problem. For increasing issue the gap between each pair of average outcomes is calculated. Such variations are ordered in ascending order, and a rank is given from the smallest to the highest. If more than one discrepancy is equivalent, then each of them is given an average rank [61]. The ranks are subsequently converted to signed ranks. It is used in pair-wise analysis of H-RVEA to other algorithms. The positive rank is granted to the proposed algorithm if it is stronger for a specific output factor (i.e., IGD and HV) than the competitor algorithms. Otherwise, it is assigned negative rank. A meaning level is set to 0.10 for comparison and sums up all the positive and negative rank [61]. Tabulate the effects of the Wilcoxon test in Table 3, where \(+, -,\) and = mean that H-RVEA efficiency is superior, inferior, and equivalent to competitor algorithms, respectively. From Table 3, it is observed that H-RVEA outperforms with IGD and HV efficiency measures over all competitor algorithms except for NSGA-III which finds superior on the HV measure.

Table 3 Wilcoxon signed-rank test results between proposed H-RVEA and other algorithms based on average IGD and HV performance measures
Full size table

5 H-RVEA for real-life applications

In this section, the performance of proposed H-RVEA has been tested on two real-life problems namely, Multi-Objective Travelling Salesman Problem (MOTSP) and Car Side Impact Problem (CSI). These problems are used to show the efficiency and effectiveness of proposed H-RVEA in real-life problems.

5.1 Multi-objective travelling salesman problem (MOTSP)

The traveling salesman problem in combinatorial optimization is a difficult and most studied NP-hard issue. The number of cities and the cost of travel are provided in this problem. The challenge with the traveling salesman is to find the cheapest tour to reach each area precisely once and return to the point of departure (see Fig. 5).

Fig. 5
figure 5

Schematic view of multi-objective travelling salesman problem

Full size image

The mathematical formulation of multi-objective travelling salesman problem is as follows [62]: Given a set n cities and p cost \(c_{ij}^k, \quad k=1,2,\ldots , p\) to travel from city i to j. The main aim of MOTSP is to find a tour, i.e., a cyclic permutation R of n cities.

$$\begin{aligned} \begin{aligned}&{\text {Minimize}} \, f_k(R)=\sum _{i=1}^{n-1} c_{R(i),R(i+1)}^k + c_{R(n),R(1)}^k , \quad k=1,2,\ldots ,p \end{aligned} \end{aligned}$$
(3)

In this work, p is set to 3, 5, 10, and 15.

Table 4 shows the IGD value obtained from H-RVEA and other competitor algorithms of Multi-Objective Travelling Salesman Problem (MOTSP). H-RVEA can be seen performing better for all test objectives than other algorithms (i.e., 3, 5, 10, 15). For 3- and 5-objectives, H-RVEA has a best IGD value and the difference between H-RVEA and its competitor algorithms is statistically significant. RVEA is the second best algorithm for 3-objectives. The MOEA/DD is the second best performing algorithm for 5-objectives. H-RVEA outperforms the other five algorithms for the 10- and 15-objectives. RVEA is the second best algorithm for these test objectives. It is worth mentioning that H-RVEA consistently performing better than other algorithms for all four MOTSP test objectives.

Table 4 The IGD values obtained by proposed H-RVEA and other competitor algorithms on MOTSP
Full size table

5.2 Car side impact problem (CSI)

Car side impact problem is a constrained optimization problem to optimize the vehicle side crashworthiness [63]. This problem involves seven design variables namely thickness of B-Pillar inner, B-Pillar inner reinforcement, floor side inner, cross-members, door beam, door beltline reinforcement, and roof rail (see Fig. 6). There are three objective functions of this problem which are described as:

  • Weight of the car.

  • Pubic force experienced by a passenger.

  • Average velocity of the V-Pillar responsible for withstanding the impact load.

The mathematical formulation of this problem is described as follows:

$$\begin{aligned} \begin{aligned}&f_1(z) = 1.98 + 4.9z_1 + 6.67z_2 + 6.98z_3 + 4.01z_4 + 1.78z_5 + 0.00001z_6 + 2.73z_7,\\&f_2(z) = 4.72 - 0.5z_4 - 0.19z_2z_3,\\&f_3(z) = 0.5 \times (10.58 - 0.674z_1z_2 - 0.67275z_2 + 16.45 - 0.489z_3z_7 - 0.843z_5z_6),\\&{\text {Subject to:}}\\&g_1(z) = 1.16 - 0.3717z_2z_4 - 0.0092928z_3 \le 1.0,\\&g_2(z) = 0.261 - 0.0159z_1z_2 - 0.06486z_1 - 0.019z_2z_7 \\&\quad + 0.0144z_3z_5 + 0.0154464z_6 \le 0.32,\\&g_3(z) = 0.214 + 0.00817z_5 - 0.045195z_1 - 0.0135168z_1 \\&\quad +0.03099z_2z_6 - 0.018z_2z_7 + 0.007176z_3 \\&\quad + 0.023232z_3 - 0.00364z_5z_6 - 0.018z_2z_2 \le 0.32,\\&g_4(z) = 0.74 - 0.61z_2 - 0.031296z_3 - 0.031872z_7 + 0.227z_2z_2 \le 0.32,\\&g_5(z) = 28.98 + 3.818z_3 - 4.2z_1z_2 + 1.27296z_6 - 2.68065z_7 \le 0.32,\\&g_6(z) = 33.86 + 2.95z_3 - 5.057z_1z_2 - 3.795z_2 - 3.4431z_7 \\&\quad + 1.45728 \le 0.32,\\&g_7(z) = 46.36 - 9.9z_2 - 4.4505z_1 \le 0.32,\\&g_8(z) = 4.72 - 0.5z_4 - 0.19z_2z_3 \le 4.0,\\&g_9(z) = 10.58 - 0.674z_1z_2 - 0.67275z_2 \le 9.9,\\&g_{10}(z) = 16.45 - 0.489z_3z_7 - 0.843z_5z_6 \le 15.7,\\&\text {where,}\\&0.5 \le z_1, z_3, z_4 \le 1.5, \,0.4\le z_6, z_7 \le 1.2, \,0.45 \le z_2 \\&\quad \le 1.35,\,0.875 \le z_5 \le 2.625. \end{aligned} \end{aligned}$$
(4)
Fig. 6
figure 6

Schematic view of car side impact problem [64]

Full size image

The obtained IGD values by proposed and competitor algorithms are shown in Table 5. H-RVEA generates the smaller IGD value than the others. NSGA-III and HypE are the second and third best optimization algorithms, respectively. It can be seen that H-RVEA provides optimal results and very competitive than the other approaches for CSI problem.

Table 5 The IGD values obtained by proposed H-RVEA and other competitor algorithms on CSI
Full size table

6 Conclusions and future works

A novel hybrid many-objective evolutionary algorithm, named H-RVEA, is introduced in this article. H-RVEA uses the Hypervolume Estimation Algorithm (HypE) and Reference Vector Guided Evolutionary Algorithm (RVEA) methods. The proposed H-RVEA was applied and evaluated on well-known test functions. Comparing H-RVEA results to other algorithms, it was found that H-RVEA outperformed RVEA, HypE, NSGA-III, MOEA/DD, and AGE-II. The comparative work was carried out to demonstrate the statistical significance of proposed H-RVEA over benchmark test functions. The proposed H-RVEA was tested on two real-life constrained problems. The findings show that among all the successful algorithms H-RVEA has delivered better performance.

There are several research directions which can be recommended for future works. The variation in operators and selection procedure of the proposed H-RVEA algorithm can be the motivation of future work. Also, to extend this algorithm to solve more real-life constrained many-objective optimization problems can also be seen as a future contribution.