1 Introduction

As a novel functionally graded (FG) material, FG porous material have acquired a significant attention in recent years due to its improved characteristics such as flexibility of tailoring a desired design and excellent capability for energy dissipation and biomedical applications. Chen et al. [1] explored the nonlinear free vibrations of sandwich Timoshenko beams with FG porous core with different porosity distributions. Wang and Wu [2] performed a free vibration analysis for FG porous cylindrical shell subjected to various types of immovable boundary conditions. Wu et al. [3] used a computational scheme based on the finite element method to predict the free and forced vibration responses of FG porous beams. Karami et al. [4] investigated the size-dependent guided wave propagation in mounted FG porous nanoplates. Sahmani et al. [5,6,7] developed a size-dependent beam model for nonlinear mechanical behaviors of FG porous micro/nanobeams reinforced with graphene platelets. Gao et al. [8] presented an analytical solution on the basis of the method of multiple scales for the nonlinear primary resonance of FG porous cylindrical shells. Safaei et al. [9,10,11] analyzed the thermoelastic response of carbon-nanotube-reinforced sandwich plates. Qin et al. [12, 13] developed a unified solution for traveling wave analysis and vibrations of FG shallow shells under general boundary conditions.

Several unconventional continuum theories of elasticity have been proposed and employed to take different size dependencies into consideration [14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48]. Gurtin and Murdoch [49, 50] developed a theoretical framework based on the continuum mechanics including surface stress effect which has an excellent capability to incorporate the surface stress effect into the mechanical responses of nanostructures. Based on this type of continuum elasticity theory, the surface is simulated as a mathematical layer of zero thickness with different material properties derived from the underlying bulk material. A variety of problems at nanoscale have been analyzed on the basis of Gurtin–Murdoch elasticity theory. Herein, some of the investigations carried out about the effect of surface energy on the mechanical behaviors of nanostructures are cited.

Wang and Feng [51] investigated the free vibration response of microscale beam including surface effects on the basis of Euler–Bernoulli and Timoshenko beam theories, respectively. Lü et al. [52] presented a generalized refined theory incorporating the influence of surface stress for functionally graded films based on Gurtin–Murdoch elasticity theory. Fu et al. [53] studied the influences of surface energy on the free vibration and buckling behavior of nanobeams in both linear and nonlinear regimes using Galerkin technique. Ansari and Sahmani [54, 55] analyzed the surface stress effect on the free vibrations of nanoplates and bending of nanobeams. Gao et al. [56] considered the surface stress effect in the buckling analysis of nanowires on elastomeric substrates. Sahmani et al. [57] studied the free vibration characteristics of postbuckled functionally graded third-order shear deformable nanobeams using surface elasticity theory. Asemi and Farajpour [58] presented a vibration analysis of circular graphene sheets subjected to a thermo-mechanical loading condition based on the surface elasticity theory. Sahmani et al. [59] used Gurtin–Murdoch elasticity theory to develop a non-classical beam model to study the nonlinear forced vibrations of nanobeams including surface effects. Ghorbanpour Arani et al. [60] explored the surface stress effect on vibrations of bioliquid-filled microtubules embedded in cytoplasm. Sahmani et al. [61,62,63] examined the surface free energy effect on the nonlinear buckling and postbuckling behavior of cylindrical nanoshells under various loading conditions. Lu et al. [64] developed surface elastic Kirchhoff and Mindlin plate models for dynamic response of nanoplates. Sun et al. [65] presented an analytical solution for buckling of piezoelectric cylindrical nanoshells under combination of compressive mechanical loads and external voltages including surface stress effect. Attia and Abel Rahman [31] investigated the free vibration response of FG viscoelastic nanobeams based on the surface elasticity theory. Sarafraz et al. [66] studied the nonlinear secondary resonance of a silicon nanobeam on the basis of the surface elastic beam model. Dong et al. [67] proposed a refined beam model to describe the buckling characteristics of hallow metal nanowires encapsulating carbon nanotubes. Sahmani et al. [68] predicted the surface stress effect on the nonlinear buckling and postbuckling of cylindrical nanoshells under hydrostatic pressure. Lu et al. [69] introduced a unified size-dependent plate model including surface stress effect for buckling analysis of nanoplates. Yang et al. [70] analyzed a mode-III nanocrack at the interface between two bonded dissimilar under antiplane shear loading. Sahmani et al. [71] developed a surface elastic shell model for the nonlinear primary resonance of FG porous nanoshells including modal interactions.

The objective of the present study is to analyze the nonlinear secondary resonance of FG porous silicon nanobeams under hard excitation in the presence of surface free energy effects. Consequently, the Gurtin–Murdoch theory of elasticity is applied to the classical Euler–Bernoulli beam theory to construct a surface elastic beam model. With the aid of the multiple time scales method together with the Galerkin technique, the size-dependent nonlinear differential equation of motion is solved incorporating multiple vibration modes and interactions between them. The frequency response and amplitude response associated with the both subharmonic and superharmonic excitations are obtained corresponding to various beam thicknesses, boundary conditions, porosity coefficients and porosity dispersion patterns.

2 FG porous beam model based on the surface elasticity

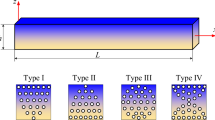
As it is displayed in Fig. 1, four different patterns for porosity dispersion are taken into consideration including the uniform porous material (Pattern A), and three FG porous materials with patterns B, C, and D. As a result, the Young’s modulus (\( E \)), shear modulus (\( G \)), and mass density (\( \rho \)) of the porous nanobeams can be extracted for each pattern as below

$$ \begin{aligned} E(z) & = \tilde{E}\left[ {1 - \varGamma_{p} s(z)} \right] \\ G(z) & = \frac{E(z)}{{\left( {2\left[ {1 - \nu (z)} \right]} \right)}} \\ \rho (z) & = \tilde{\rho }\left[ {1 - \varGamma_{m} s(z)}, \right] \\ \end{aligned} $$
(1)

where

$$ s(z) = \left\{ {\begin{array}{*{20}l} {s_{0} } \hfill & {{\text{for}}\;{\text{pattern}}\;{\text{A}}} \hfill \\ {\cos \left( {\frac{\pi z}{2h} + \frac{\pi }{4}} \right)} \hfill & {{\text{for}}\;{\text{pattern}}\;{\text{B}}} \hfill \\ {\cos \left( {\frac{\pi z}{h}} \right)} \hfill & {{\text{for}}\;{\text{pattern}}\;{\text{C}}} \hfill \\ {1 - \cos \left( {\frac{\pi z}{h}} \right)} \hfill & {{\text{for}}\;{\text{pattern}}\;{\text{D}}} \hfill \\ \end{array}, } \right. $$
(2)

where \( \tilde{E} \) and \( \tilde{\rho } \) represent the maximum Young’s modulus and maximum mass density of the FG porous silicon nanobeam.

Fig. 1
figure 1

Schematic representation of FG porous silicon nanobeam with surface layers under hard excitation

Full size image

On the basis of the Gaussian-random field scheme [72], all finite dimensional distributions are supposed to be multivariate normal distributions for any number of coordinates. Therefore, the mass density coefficient (\( \varGamma_{m} \)) can be introduced as a function of the porosity coefficient (\( \varGamma_{p} \)) as below:

$$ \varGamma_{m} = 1.121\left[ {1 - \left( {1 - \varGamma_{p} s(z)} \right)^{1/2.3} } \right]/s(z). $$
(3)

In addition, the Poisson’s ratio of the FG porous silicon can be obtained for each type of porosity dispersion pattern via the closed-cell Gaussian-random field scheme [58] as follows:

$$ \nu (z) = 0.221\left( {1 - \frac{\rho (z)}{{\tilde{\rho }}}} \right) + \tilde{\nu }\left[ {1 + 0.342\left( {1 - \frac{\rho (z)}{{\tilde{\rho }}}} \right)^{2} - 1.21\left( {1 - \frac{\rho (z)}{{\tilde{\rho }}}} \right)} \right]. $$
(4)

The proper value of \( s_{0} \) should be defined in such a way that the mass density of FG porous silicon becomes equal for all four different porosity dispersion patterns. Therefore, one will have

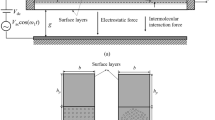
$$ s_{0} = \frac{1}{{\varGamma_{p} }}\left[ {1 - \left( {\frac{{\frac{1}{h}\mathop \int \nolimits_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} \frac{\rho (z)}{{\tilde{\rho }}}{\text{d}}z + 0.121}}{1.121}} \right)^{2.3} } \right]. $$
(5)

In accordance with Fig. 1, an FG porous silicon nanobeam of length \( L \), width \( b \) and thickness \( h \) under harmonic excitation is considered. It is assumed that the nanobeam consists of a bulk part and additional thin outer surface layers. Within the framework of the classical Euler–Bernoulli beam theory, the displacement field including mid-plane stretching effect can be expressed as

$$ u_{x} (x,t) = u(x,t) - z\frac{\partial w(x,t)}{\partial x},\quad u_{z} (x,t) = w(x,t), $$
(6)

where \( w \) denotes the middle surface displacements along \( z \)-axis, \( u \) represents the mid-plane stretching, and \( t \) stands for time.

Following the von Karman kinematics of nonlinearity, the strain–displacement relationship including the mid-plane stretching can be written as

$$ \varepsilon_{xx} = \frac{\partial u}{\partial x} - z\frac{{\partial^{2} w}}{{\partial x^{2} }} + \frac{1}{2}\left( {\frac{\partial w}{\partial x}} \right)^{2}. $$
(7)

Based upon the elastic constitutive law, the stress component related to the bulk part of the FG porous silicon nanobeam can be given as

$$ \sigma_{xx} = \left[ {\lambda (z) + 2\mu (z)} \right]\left( {\frac{1}{2}\left( {\frac{\partial w}{\partial x}} \right)^{2} + \frac{\partial u}{\partial x} - z\frac{{\partial^{2} w}}{{\partial x^{2} }}} \right) $$
(8)

in which \( \lambda (z) = E(z)\nu (z)/\left[ {1 - \nu^{2} (z)} \right] \), \( \mu (z) = E(z)/\left[ {2(1 + \nu (z))} \right] \) are Lame’s constants.

About the atomic features of nanostructures, there are always interactions between the elastic surface and bulk material. As a result, in-plane loads in various directions are applied to nanostructures. These in-plane loads on the free surface of a nanobeam make surface stresses. In accordance with Gurtin–Murdoch theory of elasticity, the surface stress components can be introduced in the following form [49, 50]

$$ \begin{array}{*{20}l} {\sigma_{ij}^{s} = \tau_{s} \delta_{ij} + \left( {\tau_{s} + \lambda_{s} } \right)\varepsilon_{kk} \delta_{ij} + 2\left( {\mu_{s} - \tau_{s} } \right)\varepsilon_{ij} + \tau_{s} u_{i,j}^{s} } \hfill \\ {\sigma_{iz}^{s} = \tau_{s} u_{z,i}^{s} } \hfill \\ \end{array} ; \;\;(i,j = x,y), $$
(9)

where \( \lambda_{s} \) and \( \mu_{s} \) denote the surface Lame’s constants and \( \tau_{s} \) represents the residual surface stress under unstrained conditions. Consequently, the surface stress components for an FG porous silicon nanobeam can be achieved in terms of the displacement components as follows

$$ \begin{aligned} \sigma_{xx}^{s} & = \left( {\lambda_{s} + 2\mu_{s} } \right)\left( {\frac{1}{2}\left( {\frac{\partial w}{\partial x}} \right)^{2} + \frac{\partial u}{\partial x} - z\frac{{\partial^{2} w}}{{\partial x^{2} }}} \right) + \tau_{s} - \frac{{\tau_{s} }}{2}\left( {\frac{\partial w}{\partial x}} \right)^{2} \\ \sigma_{xz}^{s} & = \tau_{s} \frac{\partial w}{\partial x} \\ \end{aligned} $$
(10)

In the classical continuum elasticity, it is assumed that \( \sigma_{zz} = 0, \) because this component of stress is so small compared to other ones. Nevertheless, this assumption does not satisfy the balance conditions on the free surface layer. To tackle this problem, it is supposed that the stress component \( \sigma_{zz} \) varies linearly through the thickness and satisfies the equilibrium necessities on the free surface of an FG porous silicon nanobeam. As a result, it yields

$$ \sigma_{zz} = \frac{{\left( {\frac{{\partial \sigma_{xz}^{S + } }}{\partial x} - \rho_{s}^{ + } \frac{{\partial^{2} w}}{{\partial t^{2} }}} \right) + \left( {\frac{{\partial \sigma_{xz}^{S - } }}{\partial x} - \rho_{s}^{ - } \frac{{\partial^{2} w}}{{\partial t^{2} }}} \right)}}{2} + \frac{{\left( {\frac{{\partial \sigma_{xz}^{S + } }}{\partial x} - \rho_{s}^{ + } \frac{{\partial^{2} w}}{{\partial t^{2} }}} \right) - \left( {\frac{{\partial \sigma_{xz}^{S - } }}{\partial x} - \rho_{s}^{ - } \frac{{\partial^{2} w}}{{\partial t^{2} }}} \right)}}{h}z, $$
(11)

where \( \rho_{s} \) is the surface mass density.

By inserting Eq. (10) in Eq. (11), one will have

$$ \sigma_{zz} = \frac{2z}{h}\left( {\tau_{s} \frac{{\partial^{2} w}}{{\partial x^{2} }} - \rho_{s} \frac{{\partial^{2} w}}{{\partial t^{2} }}} \right), $$
(12)

Thereafter, substitution \( \sigma_{zz} \) into the constitutive Eq. (8) yields

$$ \sigma_{xx} = \left[ {\lambda (z) + 2\mu (z)} \right]\left( {\frac{1}{2}\left( {\frac{\partial w}{\partial x}} \right)^{2} + \frac{\partial u}{\partial x} - z\frac{{\partial^{2} w}}{{\partial x^{2} }}} \right) + \frac{2\nu (z)z}{{\left( {1 - \nu (z)} \right)h}}\left( {\tau_{s} \frac{{\partial^{2} w}}{{\partial x^{2} }} - \rho_{s} \frac{{\partial^{2} w}}{{\partial t^{2} }}} \right) $$
(13)

Based upon the surface continuum theory of elasticity, the total strain energy of an FG porous nanobeam in the present of surface free energy effects can be expressed as

$$ \begin{aligned} \varPi_{s} & = \frac{1}{2}\mathop \int \limits_{x} \mathop \int \limits_{S} \sigma_{ij} \varepsilon_{ij} {\text{d}}x{\text{d}}S + \frac{1}{2}\left( {\mathop \int \limits_{{S^{ + } }} \sigma_{ij}^{s} \varepsilon_{ij} {\text{d}}S^{ + } + \mathop \int \limits_{{S^{ - } }} \sigma_{ij}^{s} \varepsilon_{ij} {\text{d}}S^{ - } } \right) \\ & = \frac{1}{2}\mathop \int \limits_{x} \left\{ {\left( {N_{xx} + \bar{N}_{xx} } \right)\left( {\frac{1}{2}\left( {\frac{\partial w}{\partial x}} \right)^{2} + \frac{\partial u}{\partial x}} \right) - \left( {M_{xx} + \bar{M}_{xx} } \right)\frac{{\partial^{2} w}}{{\partial x^{2} }}} \right\}{\text{d}}x, \\ \end{aligned} $$
(14)

in which

$$ \begin{aligned} N_{xx} & = b\mathop \int \limits_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} \sigma_{xx} {\text{d}}z = A_{11} \left( {\frac{1}{2}\left( {\frac{\partial w}{\partial x}} \right)^{2} + \frac{\partial u}{\partial x}} \right) - B_{11} \frac{{\partial^{2} w}}{{\partial x^{2} }} \\ \bar{N}_{xx} & = \bar{A}_{11} \left( {\frac{1}{2}\left( {\frac{\partial w}{\partial x}} \right)^{2} + \frac{\partial u}{\partial x}} \right) - \bar{B}_{11} \frac{{\partial^{2} w}}{{\partial x^{2} }} + 2b\tau_{s} - b\tau_{s} \left( {\frac{\partial w}{\partial x}} \right)^{2} + C^{*} \left( {\tau_{s} \frac{{\partial^{2} w}}{{\partial x^{2} }} - \rho_{s} \frac{{\partial^{2} w}}{{\partial t^{2} }}} \right) \\ M_{xx} & = b\mathop \int \limits_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} \sigma_{xx} z{\text{d}}z = B_{11} \left( {\frac{1}{2}\left( {\frac{\partial w}{\partial x}} \right)^{2} + \frac{\partial u}{\partial x}} \right) - D_{11} \frac{{\partial^{2} w}}{{\partial x^{2} }} \\ \bar{M}_{xx} & = \bar{B}_{11}^{*} \left( {\frac{1}{2}\left( {\frac{\partial w}{\partial x}} \right)^{2} + \frac{\partial u}{\partial x}} \right) - \bar{D}_{11}^{*} \frac{{\partial^{2} w}}{{\partial x^{2} }} + G^{*} \left( {\tau_{s} \frac{{\partial^{2} w}}{{\partial x^{2} }} - \rho_{s} \frac{{\partial^{2} w}}{{\partial t^{2} }}} \right) \\ \end{aligned} $$
(15)

and

$$ \begin{aligned} A_{11} & = b\mathop \int \limits_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} \left\{ {\lambda (z) + 2\mu (z)} \right\}{\text{d}}z,\quad \bar{A}_{11} = 2\left( {\lambda_{s} + 2\mu_{s} } \right)b \\ B_{11} & = b\mathop \int \limits_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} \left\{ {\lambda (z) + 2\mu (z)} \right\}z{\text{d}}z,\quad \bar{B}_{11} = \left( {\lambda_{s} + 2\mu_{s} } \right)bh \\ D_{11} & = b\mathop \int \limits_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} \left\{ {\lambda (z) + 2\mu (z)} \right\}z^{2} {\text{d}}z,\quad \bar{D}_{11} = \left( {\lambda_{s} + 2\mu_{s} } \right)\left( {\frac{{bh^{2} }}{2} + \frac{{h^{3} }}{6}} \right) \\ C^{*} & = b\mathop \int \limits_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} \left\{ {\frac{2\nu (z)z}{{\left( {1 - \nu (z)} \right)h}}} \right\}{\text{d}}z,\quad G^{*} = b\mathop \int \limits_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} \left\{ {\frac{{2\nu (z)z^{2} }}{{\left( {1 - \nu (z)} \right)h}}} \right\}{\text{d}}z \\ \end{aligned} $$
(16)

Moreover, the work \( \varPi_{P} \) done by the external harmonic distributed load \( f \) can be expressed in the following form:

$$ \varPi_{P} = \mathop \int \limits_{x} fw{\text{d}}x. $$
(17)

In addition, the kinetic energy of the nanobeam including surface free energy effects can be calculated as

$$ \begin{aligned} \varPi_{T} & = \frac{1}{2}\mathop \int \limits_{x} \mathop \int \limits_{S} \rho (z)\left\{ {\left( {\frac{{\partial u_{x} }}{\partial t}} \right)^{2} + \left( {\frac{{\partial u_{z} }}{\partial t}} \right)^{2} } \right\}{\text{d}}x{\text{d}}S \\ & \quad + \frac{1}{2}\left( \mathop \int \limits_{{S^{ + } }} \rho_{s} \left\{ {\left( {\frac{{\partial u_{x} }}{\partial t}} \right)^{2} + \left( {\frac{{\partial u_{z} }}{\partial t}} \right)^{2} } \right\}{\text{d}}S^{ + }\right.\\ &\left.\quad+ \mathop \int \limits_{{S^{ + } }} \rho_{s} \left\{ {\left( {\frac{{\partial u_{x} }}{\partial t}} \right)^{2} + \left( {\frac{{\partial u_{z} }}{\partial t}} \right)^{2} } \right\}{\text{d}}S^{ - } \right) \\ & = \frac{1}{2}\mathop \int \limits_{x} \left\{ {I_{0} \left[ {\left( {\frac{\partial u}{\partial t}} \right)^{2} + \left( {\frac{\partial w}{\partial t}} \right)^{2} } \right] - 2I_{1} \frac{\partial u}{\partial t}\frac{{\partial^{2} w}}{\partial x\partial t} + I_{2} \left( {\frac{{\partial^{2} w}}{\partial x\partial t}} \right)^{2} } \right\}{\text{d}}x, \\ \end{aligned} $$
(18)

where

$$ \begin{aligned} I_{0}^{*} & = b\mathop \int \limits_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} \rho (z){\text{d}}z + 2\rho_{s} (b + h),\\ I_{1}^{*} &= b\mathop \int \limits_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} \rho (z)z{\text{d}}z + \rho_{s} \left( {bh + \frac{{h^{2} }}{2}} \right) \\ I_{2}^{*} & = b\mathop \int \limits_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} \rho (z)z^{2} {\text{d}}z + \frac{{\rho_{s} \left( {3bh^{2} + h^{3} } \right)}}{6} \\ \end{aligned} $$
(19)

Now, using the Hamilton principle as below

$$ \delta \mathop \int \limits_{{{\text{t}}_{1} }}^{{{\text{t}}_{2} }} \left( {\varPi_{T} - \varPi_{s} + \varPi_{P} } \right){\text{d}}t = 0 $$
(20)

it yields

$$ \frac{\partial }{\partial x}\left( {N_{xx} + \bar{N}_{xx} } \right) = I_{0}^{*} \frac{{\partial^{2} u}}{{\partial t^{2} }} - I_{1}^{*} \frac{{\partial^{2} w}}{\partial x\partial t}. $$
(21a)
$$ \frac{\partial }{\partial x}\left[ {\left( {N_{xx} + \bar{N}_{xx} } \right)\frac{\partial w}{\partial x}} \right] + \frac{{\partial^{2} }}{{\partial x^{2} }}\left[ {M_{xx} + \bar{M}_{xx} } \right] = f + I_{0}^{*} \frac{{\partial^{2} w}}{{\partial t^{2} }} - I_{2}^{*} \frac{{\partial^{4} w}}{{\partial x^{2} \partial t^{2} }}. $$
(21b)

For the FG porous silicon material, it is assumed that

$$ A_{11}^{*} = A_{11} + \bar{A}_{11} ,\quad B_{11}^{*} = B_{11} + \bar{B}_{11} ,\quad D_{11}^{*} = D_{11} + \bar{D}_{11}. $$
(22)

Therefore, one will have

$$ \frac{\partial u}{\partial x} = \frac{{N_{xx} + \bar{N}_{xx} }}{{A_{11}^{*} }} + \left( {\frac{{b\tau_{s} }}{{A_{11}^{*} }} - \frac{1}{2}} \right)\left( {\frac{\partial w}{\partial x}} \right)^{2} - \frac{{2b\tau_{s} }}{{A_{11}^{*} }} + \frac{{B_{11}^{*} }}{{A_{11}^{*} }}\frac{{\partial^{2} w}}{{\partial x^{2} }} - \frac{{C^{*} }}{{A_{11}^{*} }}\left( {\tau_{s} \frac{{\partial^{2} w}}{{\partial x^{2} }} - \rho_{s} \frac{{\partial^{2} w}}{{\partial t^{2} }}} \right). $$
(23)

By integrating Eq. (23) and taking immovable end supports into account, it yields

$$ N_{xx} + \bar{N}_{xx} = 2b\tau_{s} + \left( {\frac{{A_{11}^{*} }}{2L} - \frac{{b\tau_{s} }}{L}} \right)\mathop \int \limits_{0}^{L} \left( {\frac{\partial w}{\partial x}} \right)^{2} {\text{d}}x - B_{11}^{*} \frac{{\partial^{2} w}}{{\partial x^{2} }} + C^{*} \left( {\tau_{s} \frac{{\partial^{2} w}}{{\partial x^{2} }} - \rho_{s} \frac{{\partial^{2} w}}{{\partial t^{2} }}} \right). $$
(24)

Substitution Eq. (24) into Eq. (21b) leads to the size-dependent nonlinear governing differential equation of motion for an FG porous nanobeam incorporating surface free energy effects as follows

$$ \begin{aligned} & - D_{11}^{*} \frac{{\partial^{4} w}}{{\partial x^{4} }} + G^{*} \left( {\tau_{s} \frac{{\partial^{2} w}}{{\partial x^{2} }} - \rho_{s} \frac{{\partial^{2} w}}{{\partial t^{2} }}} \right) \\ & \quad + \left[ \left( {\frac{{A_{11}^{*} }}{2L} - \frac{{b\tau_{s} }}{L}} \right)\mathop \int \limits_{0}^{L} \left( \frac{\partial w}{\partial x} \right)^{2} {\text{d}}x + 2b\tau_{s} - B_{11}^{*} \frac{{\partial^{2} w}}{{\partial x^{2} }}\right.\\ &\left.\quad + C^{*} \left( {\tau_{s} \frac{{\partial^{2} w}}{{\partial x^{2} }} - \rho_{s} \frac{{\partial^{2} w}}{{\partial t^{2} }}} \right) \right]\frac{{\partial^{2} w}}{{\partial x^{2} }} \\ & \quad = f + I_{0}^{*} \frac{{\partial^{2} w}}{{\partial t^{2} }} - I_{2}^{*} \frac{{\partial^{4} w}}{{\partial x^{2} \partial t^{2} }}. \\ \end{aligned} $$
(25)

3 Multiple time-scales solving process

To continue the solving process in a more general form, the following dimensionless parameters are introduced:

$$ \begin{aligned} W & = \frac{w}{h} ,\quad X = \frac{x}{L},\quad \xi = \frac{h}{L},\quad {\mathfrak{t}} = \frac{t}{L}\sqrt {\frac{{\lambda_{0} + 2\mu_{0} }}{\rho }} ,\quad F = \frac{{fL^{2} }}{{\left( {\lambda_{0} + 2\mu_{0} } \right)bh^{2} }} \\ \left\{ {\hat{I}_{0} ,\hat{I}_{2} } \right\} & = \left\{ {\frac{{I_{0}^{*} }}{{\rho_{0} bh}},\frac{{I_{2}^{*} }}{{\rho_{0} bh^{3} }}} \right\},\quad \hat{\tau } = \frac{{\tau_{s} }}{{\left( {\lambda_{0} + 2\mu_{0} } \right)h}},\quad \hat{\rho } = \frac{{\rho_{s} }}{{\rho_{0} h}} \\ \left\{ {a_{11}^{*} ,b_{11}^{*} ,d_{11}^{*} } \right\} & = \left\{ {\frac{{A_{11}^{*} }}{{\left( {\lambda_{0} + 2\mu_{0} } \right)bh}},\frac{{B_{11}^{*} }}{{\left( {\lambda_{0} + 2\mu_{0} } \right)bh^{2} }},\frac{{D_{11}^{*} }}{{\left( {\lambda_{0} + 2\mu_{0} } \right)bh^{3} }}} \right\},\quad \left\{ {c^{*} ,g^{*} } \right\} = \left\{ {\frac{{C^{*} }}{bh},\frac{{G^{*} }}{{bh^{2} }}} \right\} \\ \end{aligned} $$
(26)

where \( \lambda_{0} , \mu_{0} \), and \( \rho_{0} \) are, respectively, the elastic Lame constants and mass density for the silicon without porosity.

As a result, the dimensionless size-dependent nonlinear governing differential equation of motion takes the following form:

$$ \begin{aligned} & - d_{11}^{*} \xi^{2} \frac{{\partial^{4} W}}{{\partial X^{4} }} + g^{*} \left( {\hat{\hat{\tau }}\xi^{2} \frac{{\partial^{2} W}}{{\partial X^{2} }} - \hat{\rho }\frac{{\partial^{2} W}}{{\partial {\mathfrak{t}}^{2} }}} \right) \\ & \qquad + \left[ \frac{{\left( {a_{11}^{*} - 2\hat{\tau }} \right)\xi^{2} }}{2}\mathop \int \limits_{0}^{1} \left( {\frac{\partial W}{\partial X}} \right)^{2} {\text{d}}X + 2\hat{\tau } - b_{11}^{*} \xi^{2} \frac{{\partial^{2} W}}{{\partial X^{2} }}\right. \\&\left.\qquad + c^{*} \left( {\hat{\hat{\tau }}\xi^{2} \frac{{\partial^{2} W}}{{\partial X^{2} }} - \hat{\rho }\frac{{\partial^{2} W}}{{\partial {\mathfrak{t}}^{2} }}} \right) \right]\frac{{\partial^{2} W}}{{\partial X^{2} }} \\ & \quad = F + \hat{I}_{0} \frac{{\partial^{2} W}}{{\partial {\mathfrak{t}}^{2} }} - \hat{I}_{2} \frac{{\partial^{4} W}}{{\partial X^{2} \partial {\mathfrak{t}}^{2} }}. \\ \end{aligned} $$
(27)

Subsequently, with the aid of the Galerkin method, the solution of the problem can be written in discretized form. To this end, it is assumed that \( W(X, {\mathfrak{t}}) \) can be expressed as combination of the three first modes as follows:

$$ W(X,{\mathfrak{t}}) = \mathop \sum \limits_{n = 1}^{3} \varphi_{n} (X)q_{n} ({\mathfrak{t}}). $$
(28)

The analytical expressions for \( \varphi_{n} (X) \) corresponding to different types of boundary conditions are considered based on the linear vibration modes as follows:

  • For simply supported-simply supported boundary conditions:

    $$ \varphi_{n} (X) = \sin \left( {e_{n} X} \right),\quad e_{n} = n\pi. $$
    (29)

  • For clamped–clamped boundary conditions:

    $$ \begin{aligned} \varphi_{n} (X) & = \cos \left( {e_{n} X} \right) - \cos h\left( {e_{n} X} \right) \\ & \quad + \left( {\frac{{\cos \left( {e_{n} } \right) - \cos h\left( {e_{n} } \right)}}{{\sin \left( {e_{n} } \right) - \sin h\left( {e_{n} } \right)}}} \right)\left( {\sin h\left( {e_{n} X} \right) - \sin \left( {e_{n} X} \right)} \right) \\ e_{1} , e_{2} , e_{3} & = 4.7300, 7.8532, 10.9956. \\ \end{aligned} $$
    (30)

  • For simply supported-clamped boundary conditions:

    $$ \begin{aligned} \varphi_{n} (X) & = \cos \left( {e_{n} X} \right) - \cos h\left( {e_{n} X} \right) \\ & \quad + \left( {\frac{{\cos \left( {e_{n} } \right) - \cos h\left( {e_{n} } \right)}}{{\sin \left( {e_{n} } \right) - \sin h\left( {e_{n} } \right)}}} \right)\left( {\sin h\left( {e_{n} X} \right) - \sin \left( {e_{n} X} \right)} \right) \\ e_{1} , e_{2} , e_{3} & = 3.9266, 7.0686, 10.2102. \\ \end{aligned} $$
    (31)

  • For clamped-free boundary conditions:

    $$ \begin{aligned} \varphi_{n} (X) & = \cos \left( {e_{n} X} \right) - \cos h\left( {e_{n} X} \right) \\ & \quad + \left( {\frac{{\cos \left( {e_{n} } \right) - \cos h\left( {e_{n} } \right)}}{{\sin \left( {e_{n} } \right) - \sin h\left( {e_{n} } \right)}}} \right)\left( {\sin h\left( {e_{n} X} \right) - \sin \left( {e_{n} X} \right)} \right) \\ e_{1} , e_{2} , e_{3} & = 1.8751, 4.6941, 7.8547 \\ \end{aligned} $$
    (32)

In the case of hard excitation, the order of the external distributed load is higher than that of the damping and nonlinear terms. Consequently, by inserting Eq. (28) in the governing differential Eq. (27), one will have

$$ \begin{aligned} & \ddot{q}_{1} + \omega_{1}^{2} q_{1} + \alpha_{1} q_{1}^{3} + \alpha_{2} q_{2}^{3} + \alpha_{3} q_{3}^{3} + \alpha_{4} q_{2} q_{1}^{2} + \alpha_{5} q_{3} q_{1}^{2} \\ & \quad + \alpha_{6} q_{1} q_{2}^{2} + \alpha_{7} q_{3} q_{2}^{2} + \alpha_{8} q_{1} q_{3}^{2} + \alpha_{9} q_{2} q_{3}^{2} \\ & \quad + \alpha_{10} q_{1} q_{2} q_{3} = 2F\cos (\varOmega T) \\ \end{aligned} $$
(33a)
$$ \begin{aligned} & \ddot{q}_{2} + \omega_{2}^{2} q_{2} + \beta_{1} q_{1}^{3} + \beta_{2} q_{2}^{3} + \beta_{3} q_{3}^{3} + \beta_{4} q_{2} q_{1}^{2} \\ & \quad + \beta_{5} q_{3} q_{1}^{2} + \beta_{6} q_{1} q_{2}^{2} + \beta_{7} q_{3} q_{2}^{2} + \beta_{8} q_{1} q_{3}^{2} + \beta_{9} q_{2} q_{3}^{2} \\ & \quad + \beta_{10} q_{1} q_{2} q_{3} = 0 \\ \end{aligned} $$
(33b)
$$ \begin{aligned} & \ddot{q}_{3} + \omega_{3}^{2} q_{3} + \gamma_{1} q_{1}^{3} + \gamma_{2} q_{2}^{3} + \gamma_{3} q_{3}^{3} + \gamma_{4} q_{2} q_{1}^{2} + \gamma_{5} q_{3} q_{1}^{2} \\ & \quad + \gamma_{6} q_{1} q_{2}^{2} + \gamma_{7} q_{3} q_{2}^{2} + \gamma_{8} q_{1} q_{3}^{2} + \gamma_{9} q_{2} q_{3}^{2} \\ & \quad + \gamma_{10} q_{1} q_{2} q_{3} = 0. \\ \end{aligned} $$
(33c)

To continue the solution methodology, it is assumed that the external distributed load is a dissipative one, so the damping parameter can be defined as

$$ \vartheta = \frac{{{\mathcal{G}}\omega_{1}^{2} }}{{\omega_{L} }}, $$
(34)

in which \( \omega_{L} \) stands for the linear frequency of the system, and \( {\mathcal{G}} \) is a constant.

Furthermore, it is assumed that \( \hat{t} = \hat{\omega }_{1} {\mathfrak{t}} \), and \( \bar{q}_{i} = \varepsilon q_{i} ,\;\;\; i = 1,2,3 \), where \( \hat{\omega }_{1} \) represents the first frequency of the FG porous nanobeam in the absence of the surface stress effect. Therefore, scaling Eq. (33) and consideration of the hard excitation yield

$$ \begin{aligned} & \ddot{\bar{q}}_{1} + \left( {\frac{{2\varepsilon^{2} \vartheta }}{{\hat{\omega }_{1} }}} \right)\dot{\bar{q}}_{1} + \left( {\frac{{\omega_{1}^{2} }}{{\hat{\omega }_{1}^{2} }}} \right)\bar{q}_{1} \\ & \qquad + \left( {\frac{{\varepsilon^{2} }}{{\hat{\omega }_{1}^{2} }}} \right)\left( \alpha_{1} \bar{q}_{1}^{3} + \alpha_{2} \bar{q}_{2}^{3} + \alpha_{3} \bar{q}_{3}^{3} + \alpha_{4} \bar{q}_{2} \bar{q}_{1}^{2} + \alpha_{5} \bar{q}_{3} \bar{q}_{1}^{2} \right.\\&\left. \qquad+ \alpha_{6} \bar{q}_{1} \bar{q}_{2}^{2} + \alpha_{7} \bar{q}_{3} \bar{q}_{2}^{2} + \alpha_{8} \bar{q}_{1} \bar{q}_{3}^{2} + \alpha_{9} \bar{q}_{2} \bar{q}_{3}^{2} + \alpha_{10} \bar{q}_{1} \bar{q}_{2} \bar{q}_{3} \right) \\ & \quad = \frac{{2\varepsilon^{2} F}}{{\hat{\omega }_{1}^{2} }}\cos \left( {\frac{{\varOmega \hat{t}}}{{\hat{\omega }_{1} }}} \right) \\ \end{aligned} $$
(35a)
$$ \begin{aligned} & \ddot{\bar{q}}_{2} + \left( {\frac{{2\varepsilon^{2} \vartheta }}{{\hat{\omega }_{1} }}} \right)\dot{\bar{q}}_{2} + \left( {\frac{{\omega_{2}^{2} }}{{\hat{\omega }_{1}^{2} }}} \right)\bar{q}_{2} \\ & \quad + \left( {\frac{{\varepsilon^{2} }}{{\hat{\omega }_{1}^{2} }}} \right)\left( {\alpha_{1} \bar{q}_{1}^{3} + \alpha_{2} \bar{q}_{2}^{3} + \alpha_{3} \bar{q}_{3}^{3} + \alpha_{4} \bar{q}_{2} \bar{q}_{1}^{2} + \alpha_{5} \bar{q}_{3} \bar{q}_{1}^{2} + \alpha_{6} \bar{q}_{1} \bar{q}_{2}^{2} + \alpha_{7} \bar{q}_{3} \bar{q}_{2}^{2} + \alpha_{8} \bar{q}_{1} \bar{q}_{3}^{2} + \alpha_{9} \bar{q}_{2} \bar{q}_{3}^{2} + \alpha_{10} \bar{q}_{1} \bar{q}_{2} \bar{q}_{3} } \right) = 0 \\ \end{aligned} $$
(35b)
$$ \begin{aligned} & \ddot{\bar{q}}_{3} + \left( {\frac{{2\varepsilon^{2} \vartheta }}{{\hat{\omega }_{1} }}} \right)\dot{\bar{q}}_{3} + \left( {\frac{{\omega_{3}^{2} }}{{\hat{\omega }_{1}^{2} }}} \right)\bar{q}_{3} \\ & \quad + \left( {\frac{{\varepsilon^{2} }}{{\hat{\omega }_{1}^{2} }}} \right)\left( {\alpha_{1} \bar{q}_{1}^{3} + \alpha_{2} \bar{q}_{2}^{3} + \alpha_{3} \bar{q}_{3}^{3} + \alpha_{4} \bar{q}_{2} \bar{q}_{1}^{2} + \alpha_{5} \bar{q}_{3} \bar{q}_{1}^{2} + \alpha_{6} \bar{q}_{1} \bar{q}_{2}^{2} + \alpha_{7} \bar{q}_{3} \bar{q}_{2}^{2} + \alpha_{8} \bar{q}_{1} \bar{q}_{3}^{2} + \alpha_{9} \bar{q}_{2} \bar{q}_{3}^{2} + \alpha_{10} \bar{q}_{1} \bar{q}_{2} \bar{q}_{3} } \right) = 0. \\ \end{aligned} $$
(35c)

Thereafter, the following multiple time-scales summations are taken into account for \( \bar{q}_{i} (i = 1,2,3) \):

$$ \bar{q}_{1} \left( {\hat{t},\varepsilon } \right) = Q_{10} \left( {T_{0} ,T_{1} ,T_{2} } \right) + \varepsilon Q_{11} \left( {T_{0} ,T_{1} ,T_{2} } \right) + \varepsilon^{2} Q_{12} \left( {T_{0} ,T_{1} ,T_{2} } \right) $$
(36a)
$$ \bar{q}_{2} \left( {\hat{t},\varepsilon } \right) = Q_{20} \left( {T_{0} ,T_{1} ,T_{2} } \right) + \varepsilon Q_{21} \left( {T_{0} ,T_{1} ,T_{2} } \right) + \varepsilon^{2} Q_{22} \left( {T_{0} ,T_{1} ,T_{2} } \right) $$
(36b)
$$ \bar{q}_{3} \left( {\hat{t},\varepsilon } \right) = Q_{30} \left( {T_{0} ,T_{1} ,T_{2} } \right) + \varepsilon Q_{31} \left( {T_{0} ,T_{1} ,T_{2} } \right) + \varepsilon^{2} Q_{32} \left( {T_{0} ,T_{1} ,T_{2} } \right), $$
(36c)

where \( T_{0} = \hat{t} \), \( T_{1} = \varepsilon \hat{t} \), and \( T_{2} = \varepsilon^{2} \hat{t} \). After substitution Eq. (36) into Eq. (35), it is seen that the solution of the problem is not dependent on \( T_{1} \). Therefore, one will have

$$ O\left( {\varepsilon^{0} } \right):\left\{ {\begin{array}{*{20}l} {{\mathcal{D}}_{0}^{2} Q_{10} + \left( {\frac{{\omega_{1}^{2} }}{{\hat{\omega }_{1}^{2} }}} \right)Q_{10} = \frac{2F}{{\hat{\omega }_{1}^{2} }}\cos \left( {\frac{{\varOmega \hat{t}}}{{\hat{\omega }_{1} }}} \right)} \hfill \\ {{\mathcal{D}}_{0}^{2} Q_{20} + \left( {\frac{{\omega_{2}^{2} }}{{\hat{\omega }_{1}^{2} }}} \right)Q_{20} = 0} \hfill \\ {{\mathcal{D}}_{0}^{2} Q_{30} + \left( {\frac{{\omega_{3}^{2} }}{{\hat{\omega }_{1}^{2} }}} \right)Q_{30} = 0} \hfill \\ \end{array} } \right. $$
(37)
$$ O\left( {\varepsilon^{2} } \right):\left\{ {\begin{array}{*{20}c} {{\mathcal{D}}_{0}^{2} Q_{12} + \left( {\frac{{\omega_{1}^{2} }}{{\hat{\omega }_{1}^{2} }}} \right)Q_{12} = - 2{\mathcal{D}}_{0} {\mathcal{D}}_{2} Q_{10} - \left( {\frac{2\vartheta }{{\hat{\omega }_{1} }}} \right){\mathcal{D}}_{0} Q_{10} - \left( {\frac{{\alpha_{1} }}{{\hat{\omega }_{1}^{2} }}} \right)Q_{10}^{3} - \cdots - \left( {\frac{{\alpha_{1} }}{{\hat{\omega }_{1}^{2} }}} \right)Q_{10} Q_{20} Q_{30} } \\ {{\mathcal{D}}_{0}^{2} Q_{22} + \left( {\frac{{\omega_{2}^{2} }}{{\hat{\omega }_{1}^{2} }}} \right)Q_{22} = - 2{\mathcal{D}}_{0} {\mathcal{D}}_{2} Q_{20} - \left( {\frac{2\vartheta }{{\hat{\omega }_{1} }}} \right){\mathcal{D}}_{0} Q_{20} - \left( {\frac{{\alpha_{1} }}{{\hat{\omega }_{1}^{2} }}} \right)Q_{10}^{3} - \cdots - \left( {\frac{{\alpha_{1} }}{{\hat{\omega }_{1}^{2} }}} \right)Q_{10} Q_{20} Q_{30} } \\ {{\mathcal{D}}_{0}^{2} Q_{32} + \left( {\frac{{\omega_{3}^{2} }}{{\hat{\omega }_{1}^{2} }}} \right)Q_{32} = - 2{\mathcal{D}}_{0} {\mathcal{D}}_{2} Q_{30} - \left( {\frac{2\vartheta }{{\hat{\omega }_{1} }}} \right){\mathcal{D}}_{0} Q_{30} - \left( {\frac{{\alpha_{1} }}{{\hat{\omega }_{1}^{2} }}} \right)Q_{10}^{3} - \cdots - \left( {\frac{{\alpha_{1} }}{{\hat{\omega }_{1}^{2} }}} \right)Q_{10} Q_{20} Q_{30} } \\ \end{array} } \right. $$
(38)

in which \( {\mathcal{D}}_{i}^{j} = \frac{{{\text{d}}^{j} }}{{{\text{d}}T_{i}^{j} }} \) denote the time derivatives.

Now, the following parameters are introduced:

$$ \tilde{F} = \frac{F}{{\hat{\omega }_{1}^{2} }},\quad \tilde{\varOmega } = \frac{\varOmega }{{\hat{\omega }_{1} }}, \quad \left\{ {\begin{array}{*{20}c} {\tilde{\alpha }_{i} , \tilde{\beta }_{i} , \tilde{\gamma }_{i} } \\ {\tilde{\omega }_{1} ,\tilde{\omega }_{2} ,\tilde{\omega }_{3} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {\frac{{\alpha_{i} }}{{\hat{\omega }_{1}^{2} }},\frac{{ \beta_{i} }}{{\hat{\omega }_{1}^{2} }}, \frac{{\gamma_{i} }}{{\hat{\omega }_{1}^{2} }}} \\ {\frac{{\omega_{1} }}{{\hat{\omega }_{1} }},\frac{{\omega_{2} }}{{\hat{\omega }_{1} }},\frac{{\omega_{3} }}{{\hat{\omega }_{1} }} } \\ \end{array} } \right\}\quad i = 1,2, \ldots , 10 $$
(39)

On the basis of the Eq. (37), it can be written

$$ \begin{aligned} Q_{10} & = {\mathcal{A}}\left( {T_{1} ,T_{2} } \right)e^{{i\tilde{\omega }_{1} T_{0} }} + \Delta e^{{i\tilde{\varOmega }T_{0} }} + {\text{CC}} \\ Q_{20} & = {\mathcal{B}}\left( {T_{1} ,T_{2} } \right)e^{{i\tilde{\omega }_{2} T_{0} }} + {\text{CC}} \\ Q_{30} & = {\mathcal{C}}\left( {T_{1} ,T_{2} } \right)e^{{i\tilde{\omega }_{3} T_{0} }} + {\text{CC}} \\ \end{aligned} $$
(40)

in which \( {\text{CC}} \) denotes the complex conjugate part of the expression, and

$$ \Delta = \frac{{\tilde{F}}}{{\tilde{\omega }_{1}^{2} - \tilde{\varOmega }^{2} }}. $$
(41)

Thereby, after inserting Eq. (40) in Eq. (38), and performing some mathematical calculations, the secular terms associated with each type of the external excitation are extracted.

3.1 Superharmonic excitation

In accordance with the superharmonic excitation, one can write

$$ 3\tilde{\varOmega } = \tilde{\omega }_{1} + \varepsilon \varGamma, $$
(42)

where \( \varGamma \) is the detuning parameter. By setting the secular as well as small divisor terms equal to zero, one will have

$$ \begin{aligned} & - 2i\tilde{\omega }_{1} \frac{{\partial {\mathcal{A}}}}{{\partial T_{2} }}e^{{i\tilde{\omega }_{1} T_{0} }} - 2i\vartheta \tilde{\omega }_{1} {\mathcal{A}}e^{{i\tilde{\omega }_{1} T_{0} }} - 3\tilde{\alpha }_{1} {\mathcal{A}}^{2} {\bar{\mathcal{A}}}e^{{i\tilde{\omega }_{1} T_{0} }} \\ & \quad - 6\tilde{\alpha }_{1} {\mathcal{A}}\Delta^{2} e^{{i\tilde{\omega }_{1} T_{0} }} - \tilde{\alpha }_{1} \Delta^{3} e^{{3i\tilde{\omega }_{1} T_{0} }} - 2\tilde{\alpha }_{6} {\mathcal{A}\mathcal{B}\bar{\mathcal{B}}}e^{{i\tilde{\omega }_{1} T_{0} }} - 2\tilde{\alpha }_{8} {\mathcal{A}\mathcal{C}\bar{\mathcal{C}}}e^{{i\tilde{\omega }_{1} T_{0} }} = 0 \\ \end{aligned} $$
(43a)
$$ \begin{aligned} & - 2i\tilde{\omega }_{2} \frac{{\partial {\mathcal{B}}}}{{\partial T_{2} }}e^{{i\tilde{\omega }_{2} T_{0} }} - 2i\vartheta \tilde{\omega }_{2} {\mathcal{B}}e^{{i\tilde{\omega }_{2} T_{0} }} - 3\tilde{\beta }_{2} {\mathcal{B}}^{2} {\bar{\mathcal{B}}}e^{{i\tilde{\omega }_{2} T_{0} }} \\ & \quad - 2\tilde{\beta }_{4} {\mathcal{B}}\Delta^{2} e^{{i\tilde{\omega }_{2} T_{0} }} - 2\tilde{\beta }_{4} {\mathcal{A}\bar{\mathcal{A}}\mathcal{B}}e^{{i\tilde{\omega }_{2} T_{0} }} - 2\tilde{\beta }_{9} {\mathcal{B}\mathcal{C}\bar{\mathcal{C}}}e^{{i\tilde{\omega }_{2} T_{0} }} = 0 \\ \end{aligned} $$
(43b)
$$ \begin{aligned} & - 2i\tilde{\omega }_{3} \frac{{\partial {\mathcal{C}}}}{{\partial T_{2} }}e^{{i\tilde{\omega }_{3} T_{0} }} - 2i\vartheta \tilde{\omega }_{3} {\mathcal{C}}e^{{i\tilde{\omega }_{3} T_{0} }} - 3\tilde{\gamma }_{3} {\mathcal{C}}^{2} {\bar{\mathcal{C}}}e^{{i\tilde{\omega }_{3} T_{0} }} - 2\tilde{\gamma }_{5} {\mathcal{C}}\Delta^{2} e^{{i\tilde{\omega }_{3} T_{0} }} \\ & \quad - 2\tilde{\gamma }_{5} {\mathcal{A}\bar{\mathcal{A}}\mathcal{C}}e^{{i\tilde{\omega }_{3} T_{0} }} - 2\tilde{\gamma }_{7} {\mathcal{C}\mathcal{B}\bar{\mathcal{B}}}e^{{i\tilde{\omega }_{3} T_{0} }} = 0 \\ \end{aligned} $$
(43c)

Now, \( {\mathcal{A}}\left( {T_{1} ,T_{2} } \right),{ \mathcal{B}}(T_{1} ,T_{2} ) \) and \( {\mathcal{C}}(T_{1} ,T_{2} ) \) are considered in polar function form as below:

$$ \begin{aligned} {\mathcal{A}}\left( {T_{1} ,T_{2} } \right) & = \frac{1}{2}\fancyscript{a}\left( {T_{1} ,T_{2} } \right)e^{{i\varsigma \left( {T_{1} ,T_{2} } \right)}} \\ {\mathcal{B}}\left( {T_{1} ,T_{2} } \right) & = \frac{1}{2}\fancyscript{b}\left( {T_{1} ,T_{2} } \right)e^{{i\eta \left( {T_{1} ,T_{2} } \right)}} \\ {\mathcal{C}}\left( {T_{1} ,T_{2} } \right) & = \frac{1}{2}\fancyscript{c}\left( {T_{1} ,T_{2} } \right)e^{{i\psi \left( {T_{1} ,T_{2} } \right)}} \\ \end{aligned} $$
(44)

Inserting Eq. (44) in Eq. (43) leads to the following equations corresponding to each of the real and imaginary parts:

$$ \left\{ {\begin{array}{*{20}l} {\frac{{{\text{d}}\fancyscript{a}}}{{{\text{d}}T_{2} }} = - \vartheta \fancyscript{a} - \frac{{\tilde{\alpha }_{1} \Delta^{3} }}{{\tilde{\omega }_{1} }}\sin \left( {\varGamma T_{2} - \varsigma } \right)} \hfill \\ {\fancyscript{a}\frac{{{\text{d}}\varsigma }}{{{\text{d}}T_{2} }} = \frac{{3\tilde{\alpha }_{1} }}{{8\tilde{\omega }_{1} }}\fancyscript{a}^{3} + \frac{{3\tilde{\alpha }_{1} \Delta^{2} }}{{\tilde{\omega }_{1} }}\fancyscript{a} + \frac{{\tilde{\alpha }_{1} \Delta^{3} }}{{\tilde{\omega }_{1} }}\cos \left( {\varGamma T_{2} - \varsigma } \right)} \hfill \\ \end{array} } \right. $$
(45a)
$$ \left\{ {\begin{array}{*{20}l} {\frac{{{\text{d}}\fancyscript{b}}}{{{\text{d}}T_{2} }} = - \vartheta \fancyscript{b}} \hfill \\ {\fancyscript{b}\frac{{{\text{d}}\eta }}{{{\text{d}}T_{2} }} = \frac{{3\tilde{\beta }_{2} }}{{8\tilde{\omega }_{2} }}\fancyscript{b}^{3} + \frac{{\tilde{\beta }_{4} \Delta^{2} }}{{\tilde{\omega }_{2} }}\fancyscript{b} + \frac{{\tilde{\beta }_{4} \fancyscript{a}^{2} }}{{4\tilde{\omega }_{2} }}\fancyscript{b} + \frac{{\tilde{\beta }_{9} \fancyscript{c}^{2} }}{{4\tilde{\omega }_{2} }}\fancyscript{b}} \hfill \\ \end{array} } \right. $$
(45b)
$$ \left\{ {\begin{array}{*{20}l} {\frac{{{\text{d}}\fancyscript{c}}}{{{\text{d}}T_{2} }} = - \vartheta \fancyscript{c}} \hfill \\ {\fancyscript{c}\frac{{{\text{d}}\psi }}{{{\text{d}}T_{2} }} = \frac{{3\tilde{\gamma }_{3} }}{{8\tilde{\omega }_{3} }}\fancyscript{c}^{3} + \frac{{\tilde{\gamma }_{5} \Delta^{2} }}{{\tilde{\omega }_{3} }}\fancyscript{c} + \frac{{\tilde{\gamma }_{5} \fancyscript{a}^{2} }}{{4\tilde{\omega }_{3} }}\fancyscript{c} + \frac{{\tilde{\gamma }_{7} \fancyscript{b}^{2} }}{{4\tilde{\omega }_{3} }}\fancyscript{c}} \hfill \\ \end{array} } \right.. $$
(45c)

The oscillation amplitudes of a silicon nanobeam under superharmonic excitation are shown in Fig. 2 corresponding to the first three vibration modes. As it can be observed, the vibration amplitude of the first mode is so higher than those of the second and third modes. As a result, the values of \( \fancyscript{b} \) and \( \fancyscript{c} \) are so small in comparison with the value of \( \fancyscript{a} \), so it is possible to neglect them. Therefore, Eq. (45) reduces in the following form:

Fig. 2
figure 2

Variation of the oscillation amplitude with time for an FG porous silicon nanobeam under superharmonic excitation corresponding to different mode numbers (\( h = 2\;{\text{nm}}, h/L = 20 \), pattern A)

Full size image
$$ \left\{ {\begin{array}{*{20}l} {\frac{{{\text{d}}\fancyscript{a}}}{{{\text{d}}T_{2} }} = - \vartheta \fancyscript{a} - \frac{{\tilde{\alpha }_{1} \Delta^{3} }}{{\tilde{\omega }_{1} }}\sin \left( {\varGamma T_{2} - \varsigma } \right)} \hfill \\ {\fancyscript{a}\frac{{{\text{d}}\varsigma }}{{{\text{d}}T_{2} }} = \frac{{3\tilde{\alpha }_{1} }}{{8\tilde{\omega }_{1} }}\fancyscript{a}^{3} + \frac{{3\tilde{\alpha }_{1} \Delta^{2} }}{{\tilde{\omega }_{1} }}\fancyscript{a} + \frac{{\tilde{\alpha }_{1} \Delta^{3} }}{{\tilde{\omega }_{1} }}\cos \left( {\varGamma T_{2} - \varsigma } \right)} \hfill \\ \end{array} } \right.. $$
(46)

The purpose is now to obtain the steady-state solution, so the derivative terms on the left side of Eq. (46) are set to zero. As a result, it gives

$$ \begin{aligned} \left[ {\vartheta^{2} + \left( {\varGamma - \frac{{3\tilde{\alpha }_{1} \Delta^{2} }}{{\tilde{\omega }_{1} }} - \frac{{3\tilde{\alpha }_{1} \fancyscript{a}^{2} }}{{8\tilde{\omega }_{1} }}} \right)^{2} } \right]\fancyscript{a}^{2} = \frac{{\tilde{\alpha }_{1}^{2} \Delta^{6} }}{{\tilde{\omega }_{1}^{2} }}. \hfill \\ \hfill \\ \end{aligned} $$
(47)

Therefore, the size-dependent frequency response for an FG porous silicon nanobeam under superharmonic excitation can be expressed as

$$ \varGamma = \frac{{3\tilde{\alpha }_{1} \Delta^{2} }}{{\tilde{\omega }_{1} }} + \frac{{3\tilde{\alpha }_{1} \fancyscript{a}^{2} }}{{8\tilde{\omega }_{1} }} \pm \sqrt {\frac{{\tilde{\alpha }_{1}^{2} \Delta^{6} }}{{\fancyscript{a}^{2} \tilde{\omega }_{1}^{2} }} - \vartheta^{2} }. $$
(48)

On the other hand, Eq. (47) can be rewritten as

$$ \left( {\vartheta^{2} + \varGamma^{2} + \frac{{9\tilde{\alpha }_{1}^{2} \Delta^{4} }}{{\tilde{\omega }_{1}^{2} }} + \frac{{9\tilde{\alpha }_{1}^{2} \fancyscript{a}^{4} }}{{64\tilde{\omega }_{1}^{2} }} - \frac{{6\tilde{\alpha }_{1} \Delta^{2} \varGamma }}{{\tilde{\omega }_{1} }} - \frac{{3\tilde{\alpha }_{1} \fancyscript{a}^{2} \varGamma }}{{4\tilde{\omega }_{1} }} + \frac{{9\tilde{\alpha }_{1}^{2} \fancyscript{a}^{2} \Delta^{2} }}{{4\tilde{\omega }_{1}^{2} }}} \right)\fancyscript{a}^{2} = \frac{{\tilde{\alpha }_{1}^{2} \Delta^{6} }}{{\tilde{\omega }_{1}^{2} }}. $$
(49)

Thereby, it yields

$$ {\mathcal{S}}_{1} \Delta^{6} + {\mathcal{S}}_{2} \Delta^{4} + {\mathcal{S}}_{3} \Delta^{2} + {\mathcal{S}}_{4} = 0, $$
(50)

in which

$$ \begin{aligned} {\mathcal{S}}_{1} & = \frac{{\tilde{\alpha }_{1}^{2} }}{{\tilde{\omega }_{1}^{2} }},\quad {\mathcal{S}}_{2} = - \frac{{9\tilde{\alpha }_{1}^{2} \fancyscript{a}^{2} }}{{\tilde{\omega }_{1}^{2} }},\quad {\mathcal{S}}_{3} = \frac{{6\tilde{\alpha }_{1} \varGamma \fancyscript{a}^{2} }}{{\tilde{\omega }_{1} }} - \frac{{9\tilde{\alpha }_{1}^{2} \fancyscript{a}^{4} }}{{4\tilde{\omega }_{1}^{2} }} \\ {\mathcal{S}}_{4} & = - \left( {\vartheta^{2} + \varGamma^{2} + \frac{{9\tilde{\alpha }_{1}^{2} \fancyscript{a}^{4} }}{{64\tilde{\omega }_{1}^{2} }} - \frac{{3\tilde{\alpha }_{1} \fancyscript{a}^{2} \varGamma }}{{4\tilde{\omega }_{1} }}} \right)\fancyscript{a}^{2}. \\ \end{aligned} $$
(51)

The solution of Eq. (50) results in the size-dependent amplitude response of an FG porous silicon nanobeam under superharmonic excitation in the presence of surface stress effect.

3.2 Subharmonic excitation

In accordance with the subharmonic excitation, one can write

$$ \tilde{\varOmega } = 3\tilde{\omega }_{1} + \varepsilon \varGamma. $$
(52)

Afterwards, by eliminating the secular and small divisor terms, the following sets of equations can be obtained:

$$ \begin{aligned} & - 2i\tilde{\omega }_{1} \frac{{\partial {\mathcal{A}}}}{{\partial T_{2} }}e^{{i\tilde{\omega }_{1} T_{0} }} - 2i\vartheta \tilde{\omega }_{1} {\mathcal{A}}e^{{i\tilde{\omega }_{1} T_{0} }} - 3\tilde{\alpha }_{1} {\mathcal{A}}^{2} {\bar{\mathcal{A}}}e^{{i\tilde{\omega }_{1} T_{0} }} - 6\tilde{\alpha }_{1} {\mathcal{A}}\Delta^{2} e^{{i\tilde{\omega }_{1} T_{0} }} \\ & \quad - 3\tilde{\alpha }_{1} {\mathcal{A}}^{2} \Delta e^{{i\left( {\tilde{\varOmega } - 2\tilde{\omega }_{1} } \right)T_{0} }} - 2\tilde{\alpha }_{6} {\mathcal{A}\mathcal{B}\bar{\mathcal{B}}}e^{{i\tilde{\omega }_{1} T_{0} }} - 2\tilde{\alpha }_{8} {\mathcal{A}\mathcal{C}\bar{\mathcal{C}}}e^{{i\tilde{\omega }_{1} T_{0} }} = 0 \\ \end{aligned} $$
(53a)
$$ \begin{aligned} & - 2i\tilde{\omega }_{2} \frac{{\partial {\mathcal{B}}}}{{\partial T_{2} }}e^{{i\tilde{\omega }_{2} T_{0} }} - 2i\vartheta \tilde{\omega }_{2} {\mathcal{B}}e^{{i\tilde{\omega }_{2} T_{0} }} - 3\tilde{\beta }_{2} {\mathcal{B}}^{2} {\bar{\mathcal{B}}}e^{{i\tilde{\omega }_{2} T_{0} }} \\ & \quad - 2\tilde{\beta }_{4} {\mathcal{B}}\Delta^{2} e^{{i\tilde{\omega }_{2} T_{0} }} - 2\tilde{\beta }_{4} {\mathcal{A}\bar{\mathcal{A}}\mathcal{B}}e^{{i\tilde{\omega }_{2} T_{0} }} - 2\tilde{\beta }_{9} {\mathcal{B}\mathcal{C}\bar{\mathcal{C}}}e^{{i\tilde{\omega }_{2} T_{0} }} = 0 \\ \end{aligned} $$
(53b)
$$ \begin{aligned} & - 2i\tilde{\omega }_{3} \frac{{\partial {\mathcal{C}}}}{{\partial T_{2} }}e^{{i\tilde{\omega }_{3} T_{0} }} - 2i\vartheta \tilde{\omega }_{3} {\mathcal{C}}e^{{i\tilde{\omega }_{3} T_{0} }} - 3\tilde{\gamma }_{3} {\mathcal{C}}^{2} {\bar{\mathcal{C}}}e^{{i\tilde{\omega }_{3} T_{0} }} \\ & \quad - 2\tilde{\gamma }_{5} {\mathcal{C}}\Delta^{2} e^{{i\tilde{\omega }_{3} T_{0} }} - 2\tilde{\gamma }_{5} {\mathcal{A}\bar{\mathcal{A}}\mathcal{C}}e^{{i\tilde{\omega }_{3} T_{0} }} - 2\tilde{\gamma }_{7} {\mathcal{C}\mathcal{B}\bar{\mathcal{B}}}e^{{i\tilde{\omega }_{3} T_{0} }} = 0. \\ \end{aligned} $$
(53c)

For \( {\mathcal{A}}\left( {T_{1} ,T_{2} } \right),{ \mathcal{B}}\left( {T_{1} ,T_{2} } \right) \) and \( {\mathcal{C}}\left( {T_{1} ,T_{2} } \right) \), a polar function is assumed similar to Eq. (47), so one will have

$$ \left\{ {\begin{array}{*{20}l} {\frac{{{\text{d}}\fancyscript{a}}}{{{\text{d}}T_{2} }} = - \vartheta \fancyscript{a} - \frac{{3\tilde{\alpha }_{1} \fancyscript{a}^{2} \Delta }}{{4\tilde{\omega }_{1} }}\sin \left( {\varGamma T_{2} - 3\varsigma } \right)} \hfill \\ {\fancyscript{a}\frac{{{\text{d}}\varsigma }}{{{\text{d}}T_{2} }} = \frac{{3\tilde{\alpha }_{1} }}{{8\tilde{\omega }_{1} }}\fancyscript{a}^{3} + \frac{{3\tilde{\alpha }_{1} \Delta^{2} }}{{\tilde{\omega }_{1} }}\fancyscript{a} + \frac{{3\tilde{\alpha }_{1} \fancyscript{a}^{2} \Delta }}{{4\tilde{\omega }_{1} }}\cos \left( {\varGamma T_{2} - 3\varsigma } \right)} \hfill \\ \end{array} } \right. $$
(54a)
$$ \left\{ {\begin{array}{*{20}l} {\frac{{{\text{d}}\fancyscript{b}}}{{{\text{d}}T_{2} }} = - \vartheta \fancyscript{b}} \hfill \\ {\fancyscript{b}\frac{{{\text{d}}\eta }}{{{\text{d}}T_{2} }} = \frac{{3\tilde{\beta }_{2} }}{{8\tilde{\omega }_{2} }}\fancyscript{b}^{3} + \frac{{\tilde{\beta }_{4} \Delta^{2} }}{{\tilde{\omega }_{2} }}\fancyscript{b} + \frac{{\tilde{\beta }_{4} \fancyscript{a}^{2} }}{{4\tilde{\omega }_{2} }}\fancyscript{b} + \frac{{\tilde{\beta }_{9} \fancyscript{c}^{2} }}{{4\tilde{\omega }_{2} }}\fancyscript{b}} \hfill \\ \end{array} } \right. $$
(54b)
$$ \left\{ {\begin{array}{*{20}l} {\frac{{{\text{d}}\fancyscript{c}}}{{{\text{d}}T_{2} }} = - \vartheta \fancyscript{c}} \hfill \\ {\fancyscript{c}\frac{{{\text{d}}\psi }}{{{\text{d}}T_{2} }} = \frac{{3\tilde{\gamma }_{3} }}{{8\tilde{\omega }_{3} }}\fancyscript{c}^{3} + \frac{{\tilde{\gamma }_{5} \Delta^{2} }}{{\tilde{\omega }_{3} }}\fancyscript{c} + \frac{{\tilde{\gamma }_{5} \fancyscript{a}^{2} }}{{4\tilde{\omega }_{3} }}\fancyscript{c} + \frac{{\tilde{\gamma }_{7} \fancyscript{b}^{2} }}{{4\tilde{\omega }_{3} }}\fancyscript{c}} \hfill \\ \end{array} } \right.. $$
(54c)

The oscillation amplitudes of an FG porous silicon nanobeam subjected to subharmonic excitation are illustrated in Fig. 3 corresponding to the first three vibration modes. It is obvious that the oscillation amplitude of the first mode is so higher than those of the second and third modes. As a result, the values of \( \fancyscript{b} \) and \( \fancyscript{c} \) are so small in comparison with the value of \( \fancyscript{a} \), so it is possible to neglect them. Therefore, Eq. (54) reduces to the following form

Fig. 3
figure 3

Variation of the oscillation amplitude with time for an FG porous silicon nanobeam under subharmonic excitation corresponding to different mode numbers (\( h = 2\;{\text{nm}}, h/L = 20 \), pattern A)

Full size image
$$ \left\{ {\begin{array}{*{20}l} {\frac{{{\text{d}}\fancyscript{a}}}{{{\text{d}}T_{2} }} = - \vartheta \fancyscript{a} - \frac{{3\tilde{\alpha }_{1} \fancyscript{a}^{2} \Delta }}{{4\tilde{\omega }_{1} }}\sin \left( {\varGamma T_{2} - 3\varsigma } \right)} \hfill \\ {\fancyscript{a}\frac{{{\text{d}}\varsigma }}{{{\text{d}}T_{2} }} = \frac{{3\tilde{\alpha }_{1} }}{{8\tilde{\omega }_{1} }}\fancyscript{a}^{3} + \frac{{3\tilde{\alpha }_{1} \Delta^{2} }}{{\tilde{\omega }_{1} }}\fancyscript{a} + \frac{{3\tilde{\alpha }_{1} \fancyscript{a}^{2} \Delta }}{{4\tilde{\omega }_{1} }}\cos \left( {\varGamma T_{2} - 3\varsigma } \right)} \hfill \\ \end{array} } \right. .$$
(55)

The purpose is now to obtain the steady-state solution, so the derivative terms on the left side of Eq. (55) are set to zero. As a result, it gives

$$ 9\vartheta^{2} + \left( {\varGamma - \frac{{9\tilde{\alpha }_{1} \Delta^{2} }}{{\tilde{\omega }_{1} }} - \frac{{9\tilde{\alpha }_{1} \fancyscript{a}^{2} }}{{8\tilde{\omega }_{1} }}} \right)^{2} = \frac{{81\tilde{\alpha }_{1}^{2} \fancyscript{a}^{2} \Delta^{2} }}{{16\tilde{\omega }_{1}^{2} }}. $$
(56)

Consequently, the frequency response for an FG porous silicon nanobeam under subharmonic excitation and in the presence of surface free energy effect can be written as

$$ \varGamma = \frac{{9\tilde{\alpha }_{1} \Delta^{2} }}{{\tilde{\omega }_{1} }} + \frac{{9\tilde{\alpha }_{1} \fancyscript{a}^{2} }}{{8\tilde{\omega }_{1} }} \pm \sqrt {\frac{{81\tilde{\alpha }_{1}^{2} \fancyscript{a}^{2} \Delta^{2} }}{{16\tilde{\omega }_{1}^{2} }} - 9\vartheta^{2} } .$$
(57)

On the other hand, Eq. (56) can be rewritten as

$$ \left( {9\vartheta^{2} + \varGamma^{2} + \frac{{81\tilde{\alpha }_{1}^{2} \Delta^{4} }}{{\tilde{\omega }_{1}^{2} }} + \frac{{81\tilde{\alpha }_{1}^{2} \fancyscript{a}^{4} }}{{64\tilde{\omega }_{1}^{2} }} - \frac{{18\tilde{\alpha }_{1} \Delta^{2} \varGamma }}{{\tilde{\omega }_{1} }} - \frac{{9\tilde{\alpha }_{1} \fancyscript{a}^{2} \varGamma }}{{4\tilde{\omega }_{1} }} + \frac{{81\tilde{\alpha }_{1}^{2} \fancyscript{a}^{2} \Delta^{2} }}{{4\tilde{\omega }_{1}^{2} }}} \right) = \frac{{81\tilde{\alpha }_{1}^{2} \fancyscript{a}^{2} \Delta^{2} }}{{16\tilde{\omega }_{1}^{2} }}. $$
(58)

Therefore, it yields

$$ \fancyscript{p}_{1} \Delta^{4} + \fancyscript{p}_{2} \Delta^{2} + \fancyscript{p}_{3} = 0 $$
(59)

where

$$ \begin{aligned} \fancyscript{p}_{1} & = \frac{{81\tilde{\alpha }_{1}^{2} }}{{\tilde{\omega }_{1}^{2} }},\quad \fancyscript{p}_{2} = \frac{{243\tilde{\alpha }_{1}^{2} \fancyscript{a}^{2} }}{{16\tilde{\omega }_{1}^{2} }} - \frac{{18\tilde{\alpha }_{1} \varGamma }}{{\tilde{\omega }_{1} }} \\ \fancyscript{p}_{3} & = 9\vartheta^{2} + \varGamma^{2} + \frac{{81\tilde{\alpha }_{1}^{2} \fancyscript{a}^{4} }}{{64\tilde{\omega }_{1}^{2} }} - \frac{{9\tilde{\alpha }_{1} \fancyscript{a}^{2} \varGamma }}{{4\tilde{\omega }_{1}. }} \\ \end{aligned} $$
(60)

The solution of Eq. (59) is the size-dependent amplitude response for an FG porous silicon nanobeam subjected to subharmonic excitation.

4 Results and discussion

Herein, selected numerical results for the nonlinear secondary resonance of FG porous silicon nanobeams under harmonic excitation is analyzed in the presence of free surface energy effects and corresponding to simply supported-simply supported (SS–SS), clamped-simply supported (C-SS) and clamped–clamped (C–C) boundary conditions. The mechanical properties and surface elastic constants of silicon material are given in Table 1. It is assumed that \( L/h = 20, b = h, \) and \( \vartheta = 0.2 \). In addition, this point should be noted that the present analysis is based on this assumption that the values of frequencies corresponding to different vibration modes are not within the range that leads to internal resonance.

Table 1 Material properties of the silicon material [73, 74]
Full size table

To check the validity as well as accuracy of the current investigation, the natural frequency of silicon nanobeams with different thicknesses and boundary conditions in the presence of the surface stress are obtained and compared to those reported by Ansari et al. [75] using generalized differential quadrature methodology. A very good agreement is found which confirms the validity of the present solving process (Table 2).

Table 2 Comparison between the dimensionless natural frequencies of silicon nanobeams with different thicknesses in the presence of the surface stress effect
Full size table

In Figs. 4 and 5, the frequency response of porous silicon nanobeams with different thicknesses and uniform porosity dispersion (pattern A) is displayed corresponding to the subharmonic and superharmonic excitations, respectively. It is revealed that due to the higher surface to volume ratio for a nanobeam with lower thickness, reduction in the value of beam thickness causes to enhance the difference between the classical and non-classical frequency responses. In the case of superharmonic excitation, it is seen that the surface stress effect leads to decrease the both height of jump phenomenon and the associated nonlinearity effect to the hardening direction. As a result, the excitation frequency associated with the both bifurcation points increases by taking the surface stress effect into account. These anticipations are more significant for the SS–SS boundary conditions. Regarding the subharmonic excitation, it is seen that the surface stress effect leads to increase the value of the excitation frequency at the joint point of the two branches of the frequency response curve. However, by moving from SS–SS boundary conditions to C–C ones, the significance of this effect diminishes.

Fig. 4
figure 4

Frequency response of FG porous silicon nanobeams with different thicknesses under subharmonic excitation based on the classical and surface elastic beam models (\( \varGamma_{p} = 0.4 \), pattern A, \( \tilde{F} = 0.4 \))

Full size image
Fig. 5
figure 5

Frequency response of FG porous silicon nanobeams with different thicknesses under superharmonic excitation based on the classical and surface elastic beam models (\( \varGamma_{p} = 0.4 \), pattern A, \( \tilde{F} = 0.4 \))

Full size image

Figures 6 and 7 depict the amplitude-response of porous silicon nanobeams with different thicknesses and uniform porosity dispersion (pattern A) corresponding to the superharmonic and subharmonic excitations, respectively. It is found that for the subharmonic excitation, within a specific range of the excitation amplitude, the nanobeam is excited, and this range shifts to higher excitation amplitude with higher area by incorporating the surface free energy effects, especially for SS–SS boundary conditions. In addition, for the superharmonic excitation, by taking the surface stress effect into account, the excitation amplitude associated with the peak of vibration amplitude enhances. Also, the surface stress effect causes the bifurcation points occur at higher excitation amplitude.

Fig. 6
figure 6

Amplitude response of FG porous silicon nanobeams with different thicknesses under subharmonic excitation based on the classical and surface elastic beam models (\( \varGamma_{p} = 0.4 \), pattern A, \( \varGamma = 5 \))

Full size image
Fig. 7
figure 7

Amplitude response of FG porous silicon nanobeams with different thicknesses under superharmonic excitation based on the classical and surface elastic beam models (\( \varGamma_{p} = 0.4 \), pattern A, \( \varGamma = 5 \))

Full size image

The influence of the porosity dispersion pattern on the frequency response of FG porous silicon nanobeams with different end supports including surface stress effects is shown in Figs. 8 and 9 corresponding to the subharmonic and superharmonic excitations, respectively. In the subharmonic case, it is revealed that the value of the excitation frequency at the joint point of the two branches of the frequency-response curve for patterns D and C is maximum and minimum, respectively. However, this difference between various patterns of the porosity dispersion becomes negligible by changing the boundary conditions from SS–SS ones to C–C ones. In the superharmonic case, it is observed that the peak of the oscillation amplitude and the associated excitation frequency are maximum and minimum, respectively, for pattern D and pattern C of the porosity dispersion. This prediction is the same for all types of end supports.

Fig. 8
figure 8

Surface elastic frequency response of FG porous silicon nanobeams under subharmonic excitation corresponding to various porosity dispersion patterns (\( h = 5 \;{\text{nm}}, \varGamma_{p} = 0.6, \tilde{F} = 0.4 \))

Full size image
Fig. 9
figure 9

Surface elastic frequency response of FG porous silicon nanobeams under superharmonic excitation corresponding to various porosity dispersion patterns (\( h = 5\; {\text{nm}}, \varGamma_{p} = 0.6, \tilde{F} = 0.4 \))

Full size image

Figures 10 and 11 demonstrate the influence of the porosity dispersion pattern on the amplitude response of FG porous silicon nanobeams with different end supports including surface stress effects is corresponding to the subharmonic and superharmonic excitations, respectively. In the subharmonic case, it is found that by changing the porosity dispersion pattern from pattern A to pattern D, from pattern D to pattern B, and from pattern B to pattern C, the specific range of the excitation amplitude corresponding to which the FG porous nanobeams is excited, shifts to a higher value. In the superharmonic case, it is seen that the excitation amplitude associated with the peak of the oscillation amplitude is maximum and minimum for FG porous nanobeams with patterns C and A, respectively.

Fig. 10
figure 10

Surface elastic amplitude response of FG porous silicon nanobeams under subharmonic excitation corresponding to various porosity dispersion patterns (\( h = 5 \;{\text{nm}}, \varGamma_{p} = 0.6, \varGamma = 5 \))

Full size image
Fig. 11
figure 11

Surface elastic amplitude-response of FG porous silicon nanobeams under superharmonic excitation corresponding to various porosity dispersion patterns (\( h = 5\;{\text{nm}}, \varGamma_{p} = 0.6, \varGamma = 5 \))

Full size image

In Figs. 12 and 13, the influence of porosity coefficient on the frequency response of porous silicon nanobeams with uniform porosity dispersion (pattern A) and various end supports incorporating surface stress effects is shown corresponding to the subharmonic and superharmonic excitations, respectively. In the subharmonic case, it can be observed that by increasing the porosity coefficient, the value of the excitation frequency at the joint point of the two branches of the frequency-response curve reduces. This anticipation becomes more prominent by changing the boundary conditions from C–C ones to SS–SS ones. In the superharmonic case, it is indicated that an increment in the value of porosity coefficient leads to decrease the peak of the oscillation amplitude and the associated excitation frequency.

Fig. 12
figure 12

Surface elastic frequency response of FG porous silicon nanobeams under subharmonic excitation corresponding to various porosity coefficients (\( h = 5 \;{\text{nm}} \), pattern A, \( \tilde{F} = 0.4 \))

Full size image
Fig. 13
figure 13

Surface elastic frequency response of FG porous silicon nanobeams under superharmonic excitation corresponding to various porosity coefficients (\( h = 5 \;{\text{nm}} \), pattern A, \( \tilde{F} = 0.4 \))

Full size image

The influence of porosity coefficient on the amplitude response of porous silicon nanobeams with uniform porosity dispersion (pattern A) and various end supports incorporating surface stress effects is illustrated in Figs. 14 and 15 corresponding to the subharmonic and superharmonic excitations, respectively. In the subharmonic case, it is revealed that by increasing the value of porosity coefficient, the specific range of the excitation amplitude corresponding to which the porous silicon nanobeam is excited, shifts to higher value. In the superharmonic case, the increase in the value of porosity coefficient results in an increment in the excitation amplitude associated with the peak of the oscillation amplitude. These observations are similar for all types of boundary conditions.

Fig. 14
figure 14

Surface elastic amplitude response of FG porous silicon nanobeams under subharmonic excitation corresponding to various porosity coefficients (\( h = 5\;{\text{nm}} \), pattern A, \( \varGamma = 5 \))

Full size image
Fig. 15
figure 15

Surface elastic amplitude-response of FG porous silicon nanobeams under superharmonic excitation corresponding to various porosity coefficients (\( h = 5\;{\text{nm}} \), pattern A, \( \varGamma = 5 \))

Full size image

5 Concluding remarks

The prime aim of the current study was to investigate the nonlinear secondary resonance of hard excited FG porous silicon nanobeams in the presence of the surface free energy effects. Consequently, the Gurtin–Murdoch theory of elasticity was applied to the classical beam theory to construct a non-classical beam model having the capability to take surface stress effects into consideration. With the aid of the multiple time-scales method together with the Galerkin technique, the frequency response and amplitude response of the FG porous silicon nanobeams were obtained based upon the developed surface elastic beam model.

It was shown that due to the higher surface to volume ratio for a nanobeam with lower thickness, reduction in the value of beam thickness causes to enhance the difference between the classical and non-classical predictions for the nonlinear secondary resonance response. In the case of superharmonic excitation, it was revealed that the surface stress effect leads to decrease the both height of jump phenomenon and the associated nonlinearity effect to the hardening direction. As a result, the excitation frequency associated with the both bifurcation points increases by taking the surface stress effect into account. Regarding the subharmonic excitation, it was observed that the surface stress effect leads to increase the value of the excitation frequency at the joint point of the two branches of the frequency-response curve.

In the subharmonic case, it was indicated that by changing the porosity dispersion pattern from pattern A to pattern D, from pattern D to pattern B, and from pattern B to pattern C, the specific range of the excitation amplitude corresponding to which the FG porous nanobeams is excited, shifts to a higher value. In the superharmonic case, it was demonstrated that the excitation amplitude associated with the peak of the oscillation amplitude is maximum and minimum for FG porous nanobeams with porosity dispersion patterns C and A, respectively.