Free Vibration Analysis of Graphene Platelets–Reinforced Composites Plates in Thermal Environment Based on Higher-Order Shear Deformation Plate Theory

Abstract

As a first endeavor, this article presents the free vibration of composite plates reinforced with graphene platelets (GPLs) based on the higher-order shear deformation plate theory. Moreover, it is assumed that the material properties are temperature dependent and are graded in the thickness direction. It is assumed that GPLs randomly spread out in each individual composite layer reinforced with graphene platelets. The theoretical formulation is derived based on higher-order shear deformation plate theory and the initial thermal stresses are evaluated by solving the thermo-elastic equilibrium equations. The Halpin–Tsai micromechanical model is used to evaluate the effective material properties of every layer of composite plates reinforced GPLs. Further, the Navier solution has been used to derive the governing equations of motion and evaluate the natural frequencies and dynamic response of simply supported graphene platelet reinforced composite plates. Four different GPL distribution pattern is modeled to find out its effect on the frequency of the plate and the other parameters. The result asserted that subjoining GPL to composite plates has a significant reinforcing effect on the free vibration of Graphene platelet reinforced composite (GPLRC) plates.

1 Introduction

Recent researches justify the significant usage of various composites for different engineering applications like aerospace, biomedical, civil engineering, automotive engineering. As a result of greater advancement in science and technology, composite reinforced with carbon nanofillers have been a potential candidate in the recent past [1,2,3,4]. However, in contrast to the carbon nanofillers, a predominant influence of graphene or graphene platelets (GPLs) as reinforcement for composites is witnessed. This is due to the fact that GPLs have low production cost with high pacific surface areas up to 2630 m² g⁻² [5,6,7,8]. Graphene platelets with a tensile strength of 130 GPA are an appropriate candidate as reinforcement in composite materials [5,6,7,8]. The other point that convinced the researchers to use fillers in composite structures is that reinforcing even a minute amount of graphene or other fillers to base material can drastically improve its properties as thermal properties, mechanical properties, and electrical too [9,10,11,12,13,14,15].

To this end, the nanocomposites that reinforced with graphene and its derivatives become a widespread topic of researchers. To validate the claim that GPLs improve mechanical properties of composites, Rafiee et al. [16] through their study determined that 0.1% additional (wt%) GPLs in polymer composites improved the different properties of composites such as strength and stiffness. Additionally, King et al. [17] found that Young’s modulus of epoxy reinforced nanocomposites increases approximately 0.64 GPa by adding 6.0 wt% of GPLs as the fillers in the composite plate. According to recent researches, graphene as a filler and reinforcement for composites is compared to carbon nanotubes that are used widely. The results showed that graphene has superior material properties than CNTs,¹ such as high stiffness, high strength but low mass density [17, 18].

As a conclusion, nanocomposites reinforced with graphene and its derived forms have recently become a widespread topic of research efforts in composite materials [19]. Additionally, alumina ceramic composites reinforced with GPLs are studied by Liu et al. [20] and they found that the mechanical properties of these composites have been significantly improved too. Spanos et al. [21] incorporated FEM (finite element method) as a multiscale method to achieve atomistic molecular structural mechanics of composites reinforced with graphene. Ji et al. [22] investigated the stiffening effect of graphene sheets on polymer nanocomposites and they concluded that embedding even a low amount of graphene sheets can extremely increase the effective stiffness of the epoxy matrix.

Studying the various behavior of the structures reinforced with Carbon derivatives is of much importance as a matter of fact that they exhibit a unique mechanical response. In this regard, the linear and nonlinear free and forced vibration, bending, elastic buckling, post-buckling of composite structures reinforced CNTs have been widely probed by numerous pioneers [26,27,28,29,30]. Natural frequencies of polymer composites reinforced graphene have been presented by Chandra et al. [31] using continuum finite element method.

From the exhaustive literature survey, the necessity of accurate prediction of mechanical response of composite plates with graphene reinforcements has been realized. In addition, to the best of authors’ knowledge, it is witnessed that no work has been done at vibration analysis of GPLRC using higher-order shear deformation plate theory considering temperature-dependent material properties. Therefore, in this article, the non-uniformly distributed different GPL patterns are considered and their performance is carefully analyzed to decide the best pattern of distribution. Additionally, the differences between these patterns under vibrational loading and conditions are exclusively presented. Meanwhile, temperature variation is considered to illustrate the effect of the thermal environment on the vibrational behavior of GPLRC plates. It can be claimed that the novelty of this work lies in different parts such as assessing the thermal environment effects on vibrational treatment of GPLRC, different dispersion effects of pattern of GPLs on mechanical properties of structures and vibrational behaviors and results, using HSDT theory to solve the problem in the considered environment and structure conditions.

2 Multi-layer Composite Plates Reinforced GPLs Modeling

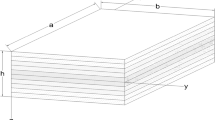
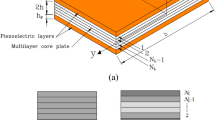
To have a complete study on the significance and applications of the proposed model, a multi-layer composite plates where GPLs are distributed in epoxy matrix layers. Figure 1 indicates the geometry of multi-layer GPLRC plates with length a, width b and thickness h. $N_{\text{L}}$ is the number of layers with the equal thickness. The weight fraction of every individual layer is different from another as depicted in Fig. 2 and the corresponding mathematical representations are shown in Eqs. (1–4).

Fig. 1

A multi-layer composite plate reinforced with graphene platelets

Fig. 2

Different GPL distribution pattern

Among the distribution patterns considered as depicted in Fig. 2, pattern 1 is an isotropic homogeneous plate case wherein GPLs (wt% of GPLs 1%) are regularly distributed. Pattern 2 shows that GPLs weight fraction (wt%) changes from layer to layer along the thickness. In other words, GPLs weight fraction is the highest in the mid-plane and decreases layer to layer when it moves to the top and bottom layer. In contrast to pattern 2, in pattern 3 both top and bottom layers are in the maximum weight fraction of GPLs and changes to the lowest by moving to mid-plane. Analogously, Pattern 4 is a non-symmetrical pattern where the weight fraction of GPLs increases linearly from top to the bottom surface.

The volume fraction functions of the four GPL distribution pattern depicted in Fig. 2 can be represented as:

$$ {\text{Pattern}}\;{ 1}\!:V_{\text{GPL}} \left( k \right) \, = V_{\text{GPL}}^{*} , $$

(1)

$$ {\text{Pattern }}\; 2\!:V_{\text{GPL}} = 2V_{\text{GPL}}^{*} \left| {2k - N_{\text{L}} - 1} \right|/N_{\text{L}} , $$

(2)

$$ {\text{Pattern }}\; 3\!: V_{\text{GPL}} = 2V_{\text{GPL}}^{*} (1 - \left| {2k - N_{\text{L}} - 1} \right|/N_{\text{L}} ), $$

(3)

$$ {\text{Pattern }}\; 4\!:V_{\text{GPL}} = 2V_{\text{GPL}}^{*} \left( {2k - 1} \right)/N_{\text{L}} , $$

(4)

where k is number of plate layers, k = 1, 2, …, $N_{\text{L}} = 10$ and $V_{\text{GPL}}^{*}$ is the total volume fraction of GPLs.

Based on the Halpin–Tsai model, the effective elastic modulus of GPLRC approximated by: [23,24,25]

$$ {\text{E}} = \frac{ 3}{ 8}\;E_{\text{L}} + \frac{5}{8}E_{\text{T}} , $$

(5)

where E is the effective modulus of GPLRC and $E_{\text{L}}$ is the longitudinal modulus for a unidirectional laminate calculated by the Halpin–Tsai model and $E_{\text{T}}$ is the transverse moduli of the laminate.

$$ E_{\text{L}} = \frac{{1 + \xi_{\text{L}} \eta_{\text{L}} V_{\text{f}} }}{{1\_\eta_{\text{L}} V_{\text{f}} }} \times E_{\text{m}} , $$

(6)

$$ E_{\text{T}} = \frac{{1 + \xi_{\text{t}} \eta_{\text{T}} V_{\text{f}} }}{{1 - \eta_{\text{T}} V_{\text{f}} }} \times E_{\text{m}} , $$

(7)

where

$$ \xi_{\text{L}} = 2\left( {l_{\text{GPL}} /h_{\text{GPL}} } \right), $$

(8)

$$ \xi_{\text{t}} = 2(w_{\text{GPL}} /h_{\text{GPL}} ), $$

(9)

where $l_{\text{GPL }}$, $h_{\text{GPL}}$, $w_{\text{GPL}}$ are GPLs dimensions.

$$ {\text{And}}\;\eta_{\text{L}} = \frac{{\left( {{\raise0.7ex\hbox{${E_{\text{GPL}} }$} \!\mathord{\left/ {\vphantom {{E_{\text{GPL}} } {E_{\text{M}} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${E_{\text{M}} }$}}} \right) - 1}}{{\left( {{\raise0.7ex\hbox{${E_{\text{GPL}} }$} \!\mathord{\left/ {\vphantom {{E_{\text{GPL}} } {E_{\text{M}} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${E_{\text{M}} }$}}} \right) + \xi_{\text{L}} }}, $$

(10)

$$ \eta_{\text{T}} = \frac{{\left( {{\raise0.7ex\hbox{${E_{\text{GPL}} }$} \!\mathord{\left/ {\vphantom {{E_{\text{GPL}} } {E_{\text{M}} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${E_{\text{M}} }$}}} \right) - 1}}{{\left( {{\raise0.7ex\hbox{${E_{\text{GPL}} }$} \!\mathord{\left/ {\vphantom {{E_{\text{GPL}} } {E_{\text{M}} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${E_{\text{M}} }$}}} \right) + \xi_{\text{t}} }}. $$

(11)

Using the rule of mixture, mass density $\rho_{\text{c}}$ and Possion’s ratio $\nu_{\text{c}}$ of the GPL/nanocomposite can be presented as:

$$ \rho_{\text{c}} = \rho_{\text{GPL}} V_{\text{GPL}} + \rho_{\text{M}} V_{\text{M}} , $$

(12)

$$ \nu_{\text{c}} = \nu_{\text{GPL}} V_{\text{GPL}} + \nu_{\text{M}} V_{\text{M}} , $$

(13)

where $V_{\text{M}}$ is the volume fraction of the epoxy matrix.

The governing equation of $V_{\text{GPL}}^{*}$ can be expressed as:

$$ V_{\text{GPL}}^{*} = \frac{{W_{\text{GPL}} }}{{W_{\text{GPL}} + (\rho_{\text{GPL}} /\rho_{\text{m}} )(1 - W_{\text{GPL}} )}}, $$

(14)

where $W_{\text{GPL}}$ is GPL weight fraction; $\rho_{\text{GPL}}$ and $\rho_{\text{M}}$ are the mass densities of GPLs and the epoxy matrix.

3 Governing Equation

According to the higher-order shear deformation plate theory [37], the displacement of the plate along x, y and z directions are represented as:

$$ \left\{ {\begin{array}{*{20}l} {u(x,y,z,t) = u_{0} (x,y,t) + z\phi_{x} (x,y,t) - c_{1} z^{3} \left[ {\phi_{x} (x,y,t) + \frac{{\partial w_{0} (x,y,t)}}{\partial x}} \right]} \\ {v(x,y,z,t) = v_{0} (x,y,t) + z\phi_{y} (x,y,t) - c_{1} z^{3} \left[ {\phi_{y} (x,y,t) + \frac{{\partial w_{0} (x,y,t)}}{\partial y}} \right]} \\ {w(x,y,z,t) = w_{0} (x,y,t)} \\ \end{array} } \right., $$

(15)

where $c_{1}$ is equal to $4/3h^{2}$ and where u and v are the in-plane displacements at any point (x,y,z) and $u_{0}$ and $v_{0}$ define the in-plane displacement of the point (x,y,0) on the mid-plane, w is the deflection, and $\phi_{x}$ and $\phi_{y}$ are the rotations of the normals to the mid-plane about the y and x axes.

According to the above theory the strain–displacement relationship at any point can be written as:

$$ \left\{ \begin{aligned} \varepsilon_{xx} \hfill \\ \varepsilon_{yy} \hfill \\ \gamma_{xy} \hfill \\ \gamma_{xz} \hfill \\ \gamma_{yz} \hfill \\ \end{aligned} \right\} = \left[ \begin{aligned} & \frac{{\partial u_{0} }}{\partial x} + z\frac{{\partial \phi_{x} }}{\partial x} - z^{3} c_{1} \left( {\frac{{\partial \phi_{x} }}{\partial x} + \frac{{\partial^{2} w_{0} }}{{\partial x^{2} }}} \right) \hfill \\ & \frac{{\partial v_{0} }}{\partial y} + z\frac{{\partial \phi_{x} }}{\partial y} - z^{3} c_{1} \left( {\frac{{\partial \phi_{y} }}{\partial y} + \frac{{\partial^{2} w_{0} }}{{\partial y^{2} }}} \right) \hfill \\ & \frac{{\partial u_{0} }}{\partial y} + \frac{{\partial v_{0} }}{\partial x} + z\left( {\frac{{\partial \phi_{x} }}{\partial y} + \frac{{\partial \phi_{y} }}{\partial x}} \right) - z^{3} c_{1} \left( {\frac{{\partial \phi_{x} }}{\partial y} + \frac{{\partial \phi_{y} }}{\partial x} + 2\frac{{\partial^{2} w_{0} }}{\partial x\partial y}} \right) \hfill \\ & (1 - 3z^{2} c_{1} )\left( {\phi_{x} + \frac{{\partial w_{0} }}{\partial x}} \right) \hfill \\ & (1 - 3z^{2} c_{1} )\left( {\phi_{y} + \frac{{\partial w_{0} }}{\partial y}} \right) \hfill \\ \end{aligned} \right]. $$

(16)

The stress components of the every individual layer of GPLRC plate in the thermal environment can be obtained as:

$$ \,\left\{ \begin{aligned} \sigma_{xx} \hfill \\ \sigma_{yy} \hfill \\ \sigma_{xy} \hfill \\ \sigma_{yz} \hfill \\ \sigma_{xz} \hfill \\ \end{aligned} \right\} = \left[ {\begin{array}{*{20}l} {C_{11} } & {C_{12} } & 0 & 0 & 0 \\ {C_{12} } & {C_{22} } & 0 & 0 & 0 \\ 0 & 0 & {C_{66} } & 0 & 0 \\ 0 & 0 & 0 & {C_{44} } & 0 \\ 0 & 0 & 0 & 0 & {C_{55} } \\ \end{array} } \right]\left\{ \begin{aligned} & \varepsilon_{xx} - \alpha_{xx} (T - T_{0} ) \hfill \\ & \varepsilon_{yy} - \alpha_{yy} (T - T_{0} ) \hfill \\ & 2\varepsilon_{xy} \hfill \\ & 2\varepsilon_{yz} \hfill \\ & 2\varepsilon_{xz} \hfill \\ \end{aligned} \right\}, $$

(17)

where

$$ C_{11} = C_{22} = \frac{{E}}{{1 - \nu_{\text{c}}^{2} }},C_{12} = \frac{{\nu_{\text{c}} E}}{{1 - \nu_{\text{c}}^{2} }},C_{44} = C_{55} = C_{66} = \frac{E}{{2(1 + \nu_{\text{c}} )}}, $$

(18)

and T₀ is the base temperature of GPLRCT as the temperature parameter is investigated as:

$$ T = T_{\text{in}} - \Delta T(1/2 + z/h), $$

(19)

$$ \Delta T = T_{\text{in}} - T_{\text{out}}. $$

(20)

On the assumption that the temperature varies linearly from $T_{\text{out}}$ at the outer surface to $T_{\text{in}}$ at the inner surface along the thickness, the governing equation of the temperature dependent GPLRC plate have been derived.

Based on Hamilton’s principle:

$$ \int\limits_{{t_{1} }}^{{t_{2} }} {(\delta T - \delta U + \delta W){\text{d}}t = 0} , $$

(21)

the governing equations of motion of GPLRC plates in the thermal environment can be derived as follows:

$$ \begin{aligned} & \delta u_{0} :\frac{{\partial N_{xx} }}{\partial x} + \frac{{\partial N_{xy} }}{\partial y} = I_{0} \frac{{\partial^{2} u_{0} }}{{\partial t^{2} }} + I_{1} \frac{{\partial^{2} \phi_{x} }}{{\partial t^{2} }} - I_{3} c_{1} \left( {\frac{{\partial^{2} \phi_{x} }}{{\partial t^{2} }} + \frac{{\partial^{3} w_{0} }}{{\partial t^{2} \partial x}}} \right), \\ & \delta v_{0} :\frac{{\partial N_{yy} }}{\partial y} + \frac{{\partial N_{xy} }}{\partial x} = I_{0} \frac{{\partial^{2} v_{0} }}{{\partial t^{2} }} + I_{1} \frac{{\partial^{2} \phi_{y} }}{{\partial t^{2} }} - I_{3} c_{1} \left( {\frac{{\partial^{2} \phi_{y} }}{{\partial t^{2} }} + \frac{{\partial^{3} w_{0} }}{{\partial t^{2} \partial y}}} \right), \\ & \delta w_{0} :c_{1} \frac{{\partial^{2} P_{xx} }}{{\partial x^{2} }} + c_{1} \frac{{\partial^{2} P_{yy} }}{{\partial y^{2} }} + 2c_{1} \frac{{\partial^{2} P_{xy} }}{\partial x\partial y} + \frac{{\partial Q_{xz} }}{\partial x} \hfill \\ &\qquad- 3c_{1} \frac{{\partial S_{xz} }}{\partial x} + \frac{{\partial Q_{yz} }}{\partial y} - 3c_{1} \frac{{\partial S_{yz} }}{\partial y} \hfill \\ & \qquad - N_{1}^{T} \left( {\frac{{\partial^{2} w}}{{\partial x^{2} }}} \right) - N_{2}^{T} \left( {\frac{{\partial^{2} w}}{{\partial y^{2} }}} \right) = c_{1} I_{3} \frac{{\partial^{3} u_{0} }}{{\partial x\partial t^{2} }} + c_{1} I_{4} \frac{{\partial^{3} \phi_{x} }}{{\partial x\partial t^{2} }}\hfill \\ &\qquad - I_{6} c_{1}^{2} \left( {\frac{{\partial^{3} \phi_{x} }}{{\partial x\partial t^{2} }} + \frac{{\partial^{4} w}}{{\partial t^{2} \partial x^{2} }}} \right) \hfill \\ & \qquad + c_{1} I_{3} \frac{{\partial^{3} v_{0} }}{{\partial y\partial t^{2} }} + c_{1} I_{4} \frac{{\partial^{3} \phi_{y} }}{{\partial y\partial t^{2} }} - I_{6} c_{1}^{2} \left( {\frac{{\partial^{3} \phi_{y} }}{{\partial y\partial t^{2} }} + \frac{{\partial^{4} w}}{{\partial t^{2} \partial y^{2} }}} \right) + \left( {I_{0} \frac{{\partial^{2} w_{0} }}{{\partial t^{2} }}} \right), \hfill \\ & \delta \phi_{x} :\frac{{\partial M_{xx} }}{\partial x} - c_{1} \frac{{\partial P_{xx} }}{\partial x} + \frac{{\partial M_{xy} }}{\partial y} - c_{1} \frac{{\partial P_{xy} }}{\partial y} - Q_{xz} + 3c_{1} S_{xz} \hfill \\ &\quad = + I_{1} \frac{{\partial^{2} u_{0} }}{{\partial t^{2} }} + I_{2} \frac{{\partial^{2} \phi_{x} }}{{\partial t^{2} }} - I_{4} c_{1} \left( {\frac{{\partial^{2} \phi_{x} }}{{\partial t^{2} }} + \frac{{\partial^{3} w}}{{\partial t^{2} \partial x}}} \right) \hfill \\ & \qquad - c_{1} I_{3} \frac{{\partial^{2} u_{0} }}{{\partial t^{2} }} - c_{1} I_{4} \frac{{\partial^{2} \phi_{x} }}{{\partial t^{2} }} + I_{6} c_{1}^{2} \left( {\frac{{\partial^{2} \phi_{x} }}{{\partial t^{2} }} + \frac{{\partial^{3} w}}{{\partial t^{2} \partial x}}} \right), \hfill \\ & \delta \phi_{y} :\frac{{\partial M_{yy} }}{\partial y} - c_{1} \frac{{\partial P_{yy} }}{\partial y} + \frac{{\partial M_{xy} }}{\partial x} - c_{1} \frac{{\partial P_{xy} }}{\partial x} - Q_{yz} + 3c_{1} S_{yz} \hfill \\ &\quad = I_{1} \frac{{\partial^{2} v_{0} }}{{\partial t^{2} }} + I_{2} \frac{{\partial^{2} \phi_{y} }}{{\partial t^{2} }} - I_{4} c_{1} \left( {\frac{{\partial^{2} \phi_{y} }}{{\partial t^{2} }} + \frac{{\partial^{3} w}}{{\partial t^{2} \partial y}}} \right) \hfill \\ & \qquad - c_{1} I_{3} \frac{{\partial^{2} v_{0} }}{{\partial t^{2} }} - c_{1} I_{4} \frac{{\partial^{2} \phi_{y} }}{{\partial t^{2} }} + I_{6} c_{1}^{2} \left( {\frac{{\partial^{2} \phi_{y} }}{{\partial t^{2} }} + \frac{{\partial^{3} w}}{{\partial t^{2} \partial y}}} \right). \hfill \\ \end{aligned} $$

(22)

The boundary condition equation of the simply supported plate in all edges can be written as:

$$ \begin{aligned} S - S\quad {\text{at}}\quad x = 0,a \to V = 0,\,W = 0,\,\,\,\phi_{y} = 0,\,\,\,N_{xx} = M_{xx} = 0, \hfill \\ S - S\quad {\text{at}}\quad y = 0,b \to U = 0,\,W = 0,\,\,\,\phi_{x} = 0,\,\,\,N_{yy} = M_{yy} = 0. \hfill \\ \end{aligned} $$

(23)

The equation of the motion of GPLRC plate in the thermal environment can be expressed as:

$$ \{ ([k] + \Delta T[k_{\text{T}} ]) - \omega^{2} [M]\} [d] = 0, $$

(24)

where $\{ d\} = \{ u_{mn} ,V_{mn} ,W_{mn} ,X_{mn} ,Y_{mn} \}$ is the displacement vector, ω is the natural frequency of the GPLRC plate, [M] is the mass matrix, also [k] is the stiffness matrix and [k_T] is the coefficients matrix of the temperature change, respectively. The equation can be solved by setting the determinant of the coefficients matrix equal to zero and the natural frequency and other mechanical properties of the GPLRC plate can be derived.

4 Solution Procedure

Navier solution is used to establish the solution for the free vibration motion equations of a GPLRC plate in the thermal environment. The behavior is studied for simply supported boundary condition whose constraints are shown in Eqs. (23).

The dimensionless displacements are represented as follows:

$$ \left\{ \begin{aligned} & u(x,y,z) \hfill \\ & v(x,y,z) \hfill \\ & w(x,y,z) \hfill \\ & \phi_{x} (x,y,z) \hfill \\ & \phi_{y} (x,y,z) \hfill \\ \end{aligned} \right\} = \sum\limits_{m = 1}^{\infty } {\sum\limits_{n = 1}^{\infty } {\left\{ \begin{aligned} U_{mn} \cos \frac{m\pi x}{a}\sin \frac{n\pi y}{b}e^{iwt} \hfill \\ V_{mn} \sin \frac{m\pi x}{a}\cos \frac{n\pi y}{b}e^{iwt} \hfill \\ W_{mn} \sin \frac{m\pi x}{a}\sin \frac{n\pi y}{b}e^{iwt} \hfill \\ X_{mn} \cos \frac{m\pi x}{a}\sin \frac{n\pi y}{b}e^{iwt} \hfill \\ Y_{mn} \sin \frac{m\pi x}{a}\cos \frac{n\pi y}{b}e^{iwt} \hfill \\ \end{aligned} \right\}} } , $$

(25)

where $U_{mn}$, $V_{mn}$, $W_{mn}$ are unknown functions of dimensionless time t. Further, m and n are the frequency mode numbers.

5 Results and Discussion

In this section, a parametric study is carried out to present the free vibration behavior of multi-layer GPLRC plate. Meanwhile, this study also considers evaluating the influence of the different distribution of GPL patterns, a total number of composite layers, dimensions of plate’s ratio, the weight fraction of GPLs, the dimensionless critical temperature on the dynamic response of GPLRC plate.

The plate dimensions are considered as a = 0.45 m, b = 0.45 m and h = 0.045 m. The material properties of the GPL as a reinforcement and epoxy are given in Table 1. To ease the understanding of the reader, both tabular and graphical forms of the numerical results are presented as follows.

Table 1 Material properties of epoxy and GPL

The dimensionless natural frequency of GPLRC plate with a different distribution of GPL are listed in Table 2 and compared with Song et al. [32]. It can be noticed from Table 2 that the results correlate with each other. It is noteworthy to mention that Song et al. [32] used first-order shear deformation plate theory to obtain the results for composite plates reinforced graphene platelets. However, the present study investigates numerical and analytical results based on higher-order shear deformation plate theory. Therefore, negligible discrepancies are observed. Meanwhile, the GPLRC plate is exposed to a thermal environment to study the influence of the thermal stresses and forces along with the different effects of the thermal environment on the dynamic behavior of GPLRC plate.

Table 2 Comparison of dimensionless natural frequencies of GPLRC with varying mode number and different distribution patterns (present study and Song et al. [32])

As shown in Table 2, it can be noticed that irrespective of the pattern considered, the natural frequencies of GPLRC plate increases by GPL weight fraction increasing in every individual layer.

It can also be witnessed that pattern 3 shows the highest amount of frequency when pattern 2 produced the lowest fundamental frequency. The most impressive way to consolidate plate stiffness is that distributing more GPL nanofillers as reinforcement, near the top and the bottom layer surfaces of the multi-layer GPLRC plate where the high normal stress amount is placed on the top and bottom. Additionally, results show that dispersing less reinforcement element near mid-plane makes the pattern more appropriate in mechanical properties and dynamic behavior. This is because of the very small normal stress placed there.

5.1 Dependence of Frequency of GPLRC Plate to GPL Weight Fraction

Figure 3 indicates that additional graphene platelet nanofillers as the reinforcement in composite plates improve the frequency of the plates. Results revealed that even a low amount of GPLs, resulted in a bigger dimensionless frequency of the GPLRC plate, than the epoxy plate. Therefore, it can be concluded that by increasing $g_{\text{GPL}}$, the relative frequency increased.

Fig. 3

Effect of GPL weight fraction on the percentage relative frequency for GPLRC plates with different GPLs dispersion patterns

5.2 Effect of Number of Layers of the Multi-layer Plate on Natural Frequency of GPLRC Plate

Figure 4 indicates the effect of the number of layers $N_{\text{L}}$ of multi-layer GPLRC plate on the relative frequency change with different GPL distribution patterns. The percentage denotes the relative frequency increase $(\omega_{\text{c}} - \omega_{\text{M}} )/\omega_{\text{M}}$, in which $\omega_{\text{c}}$ is the natural frequency of plate with GPLs and $\omega_{\text{M}}$ is the natural frequency of plate without GPLs, respectively. As expected, in pattern 1 the relative frequencies for the GPLRC plates are not affected by $N_{\text{L}}$ since they are homogeneous. In the non-uniformly dispersed GPLs patterns such as pattern 2 and 4, it can be noticed that their fundamental frequencies decreases by the total number of layers increasing up to $N_{\text{L}}$ = 10–15. However, the natural frequency then stabilizes as $N_{\text{L}}$ further increases.

Fig. 4

Effect of the number of layers ($N_{\text{L}} )$ on the relative frequency change for GPLRC plates

5.3 Effect of Temperature Rise on the Natural Frequency of GPLRC Plate

As shown in Fig. 5 by increasing temperature parameter ($\lambda_{\text{cr}}$) presented in Eq. (26), the natural frequency decreases at first, but increasing after the critical temperature point. The lowest point of this chart is the critical temperature that results in frequency = 0. By varying a/h ratio, $\lambda_{\text{cr}}$ varies too and Table 4 investigates less amount of critical temperature by a/h increasing

Fig. 5

Natural frequency of GPLRC modifications by temperature variation

$$ \lambda_{\text{cr}} = 10^{3} \alpha \Delta T_{\text{cr}} . $$

(26)

In this study, it is assumed that temperature varies linearly from $T_{\text{out}}$ at the outer surface to $T_{\text{in}}$ at the inner surface along the thickness.

Table 3 indicates temperature variation in addition to the a/h ratio variation. As shown in Table 3 by increasing the temperature, the frequency of multi-layer composite plates reinforced GPLs is decreasing continually. Additionally, when a/b ratio is changing to a bigger amount, the frequency is decreasing again. Logically, by making the width of plate smaller, the frequency reduces. Frequency is changing at a smaller rate as the a/h ratio increases. So Table 3 clearly presented a variational view of the frequency with different parameters.

Table 3 Comparison of different a/h ratio and different distribution patterns and a/b ratio and effects of these parameters on frequency of GPLRC

The comparison between Wu et al. [33] and Zhang et al. [34] which used local Kriging meshless method and Zhao et al. [35] which used kp-Ritz method and the present study are presented in Table 4.

Table 4 Comparison of critical temperature parameter ($\lambda_{\text{cr}}$) for simply supported isotropic plates ($a/b$ = 1,$\nu = 0.3$)

Critical temperature parameter for simply supported isotropic plates is presented in Table 4. The results reveal that by keeping a/b ratio and Poisson’s ratio constant and varying a/h ratio to the bigger amount the critical temperature decreases.

6 Conclusion

Vibrational behavior of the temperature-dependant GPLRC plate considering different distribution GPL patterns are investigated in the present theory. Higher-order shear deformation theory is used to model the composite plate. By implementing Hamilton’s principle, the governing differential equations and related boundary conditions in the thermal environment are derived. Finally, Navier’s solution is used to obtain the solution. Through a thorough parametric study and numerical examples, the effects of different parameters on the vibration of GPLRC plate, such as GPLs weight fraction, number of multi-layer GPLRC plate, temperature rise and plate dimensions ratio are investigated. Various important factors are considered in studying the dynamic behavior of multi-layer GPLRC plates.

The results of the present study can be written as:

• 1. The dimensionless frequency of GPLRC plate improves as the GPL weight fraction increases.

• 2. By increasing the length-to-thickness ratio of GPLRC plate (a/h), critical temperature parameter of simply supported GPLRC decreases.

• 3. Dimensionless natural frequency increases by adding graphene platelets to epoxy matrix irrespective of the GPL distribution pattern.

• 4. The frequency of GPLRC plate is increasing by a/h ratio decreasing.

• 5. By a/b ratio decreasing, the frequency of GPLRC plate is noticed to be increasing.

• 6. The frequency of GPLRC plates is the largest in pattern 3 with the maximum weight fraction on both top and bottom surfaces and the lowest in the mid-plane of the plate is the biggest amount of these four patterns.

• 7. The critical temperature of GPLRC in thermal environment resulted in the zero amount of frequency.

• 8. The natural frequency of GPLRC plate is decreasing by temperature increasing to the lowest amount and then increasing to the end point.

Appendix 1

$$ \begin{aligned} T & = \int\limits_{V} {\frac{1}{2}\rho \left[ {\left ( {\frac{\partial u}{\partial t}} \right)^{2} + \left( {\frac{\partial v}{\partial t}} \right)^{2} + \left( {\frac{\partial w}{\partial t}} \right)^{2} } \right]} {\text{d}}V: \hfill \\ \delta T & = \int\limits_{0}^{a} {\int\limits_{0}^{b} {\left[ \begin{aligned} & \left( { - I_{0} \frac{{\partial^{2} u_{0} }}{{\partial t^{2} }} - I_{1} \frac{{\partial^{2} \phi_{x} }}{{\partial t^{2} }} + I_{3} c_{1} \left( {\frac{{\partial^{2} \phi_{x} }}{{\partial t^{2} }} + \frac{{\partial^{3} w_{0} }}{{\partial t^{2} \partial x}}} \right)} \right)\delta u_{0} \hfill \\ & + \left( { - I_{1} \frac{{\partial^{2} u_{0} }}{{\partial t^{2} }} - I_{2} \frac{{\partial^{2} \phi_{x} }}{{\partial t^{2} }} + I_{4} c_{1} \left( {\frac{{\partial^{2} \phi_{x} }}{{\partial t^{2} }} + \frac{{\partial^{3} w}}{{\partial t^{2} \partial x}}} \right)} \right)\delta \phi_{x} \hfill \\ & + \left( {c_{1} I_{3} \frac{{\partial^{2} u_{0} }}{{\partial t^{2} }} + c_{1} I_{4} \frac{{\partial^{2} \phi_{x} }}{{\partial t^{2} }} - I_{6} c_{1}^{2} \left( {\frac{{\partial^{2} \phi_{x} }}{{\partial t^{2} }} + \frac{{\partial^{3} w}}{{\partial t^{2} \partial x}}} \right)} \right)\delta \phi_{x} \hfill \\ & + \left( { - c_{1} I_{3} \frac{{\partial^{3} u_{0} }}{{\partial x\partial t^{2} }} - c_{1} I_{4} \frac{{\partial^{3} \phi_{x} }}{{\partial x\partial t^{2} }} + I_{6} c_{1}^{2} \left( {\frac{{\partial^{3} \phi_{x} }}{{\partial x\partial t^{2} }} + \frac{{\partial^{4} w}}{{\partial t^{2} \partial x^{2} }}} \right)} \right)\delta w_{0} \hfill \\ & \left( { - I_{0} \frac{{\partial^{2} v_{0} }}{{\partial t^{2} }} - I_{1} \frac{{\partial^{2} \phi_{y} }}{{\partial t^{2} }} + I_{3} c_{1} \left( {\frac{{\partial^{2} \phi_{y} }}{{\partial t^{2} }} + \frac{{\partial^{3} w_{0} }}{{\partial t^{2} \partial y}}} \right)} \right)\delta v_{0} \hfill \\ & + \left( { - I_{1} \frac{{\partial^{2} v_{0} }}{{\partial t^{2} }} - I_{2} \frac{{\partial^{2} \phi_{y} }}{{\partial t^{2} }} + I_{4} c_{1} \left( {\frac{{\partial^{2} \phi_{y} }}{{\partial t^{2} }} + \frac{{\partial^{3} w}}{{\partial t^{2} \partial y}}} \right)} \right)\delta \phi_{y} \hfill \\ & + \left( {c_{1} I_{3} \frac{{\partial^{2} v_{0} }}{{\partial t^{2} }} + c_{1} I_{4} \frac{{\partial^{2} \phi_{y} }}{{\partial t^{2} }} - I_{6} c_{1}^{2} \left( {\frac{{\partial^{2} \phi_{y} }}{{\partial t^{2} }} + \frac{{\partial^{3} w}}{{\partial t^{2} \partial y}}} \right)} \right)\delta \phi_{y} \hfill \\ & + \left( { - c_{1} I_{3} \frac{{\partial^{3} v_{0} }}{{\partial y\partial t^{2} }} - c_{1} I_{4} \frac{{\partial^{3} \phi_{y} }}{{\partial y\partial t^{2} }} + I_{6} c_{1}^{2} \left( {\frac{{\partial^{3} \phi_{y} }}{{\partial y\partial t^{2} }} + \frac{{\partial^{4} w}}{{\partial t^{2} \partial y^{2} }}} \right)} \right)\delta w_{0} \hfill \\ & + \left( { - I_{0} \frac{{\partial^{2} w_{0} }}{{\partial t^{2} }}} \right)\delta w_{0} \hfill \\ \end{aligned} \right]} } \,{\text{d}}x\,{\text{d}}y, \hfill \\ \end{aligned} $$

$$ \left\{ {I_{{_{0} }} ,I_{1} ,I_{2} ,I_{3} ,I_{4} ,I_{5} ,I_{6} } \right\} = \sum\limits_{k = 1}^{{N_{L} }} {\int\limits_{ - h/2}^{h/2} {\rho^{k} } \left\{ {1,z,z^{2} ,z^{3} ,z^{4} ,z^{5} ,z^{6} } \right\}{\text{d}}z}, $$

$$ \begin{aligned} \delta U = & \frac{1}{2}\iiint\limits_{V} {\sigma _{{ij}} \delta \varepsilon _{{ij}} {\text{d}}V} \\ = & \iint\limits_{A} {\left[ {\begin{array}{*{20}l} {N_{{xx}} \frac{{\partial \delta u_{0} }}{{\partial x}} + M_{{xx}} \frac{{\partial \delta \phi _{x} }}{{\partial x}} - P_{{xx}} c_{1} \left( {\frac{{\partial \delta \phi _{x} }}{{\partial x}} + \frac{{\partial ^{2} \delta w_{0} }}{{\partial x^{2} }}} \right)} \hfill \\ {\;\; + N_{{yy}} \frac{{\partial \delta v_{0} }}{{\partial y}} + M_{{yy}} \frac{{\partial \delta \phi _{x} }}{{\partial y}} - P_{{yy}} c_{1} \left( {\frac{{\partial \delta \phi _{y} }}{{\partial y}} + \frac{{\partial ^{2} \delta w_{0} }}{{\partial y^{2} }}} \right)} \hfill \\ {\;\; + N_{{xy}} \frac{{\partial \delta u_{0} }}{{\partial y}} + N_{{xy}} \frac{{\partial \delta v_{0} }}{{\partial x}} + M_{{xy}} \left( {\frac{{\partial \delta \phi _{x} }}{{\partial y}} + \frac{{\partial \delta \phi _{y} }}{{\partial x}}} \right) - P_{{xy}} c_{1} \left( {\frac{{\partial \delta \phi _{x} }}{{\partial y}} + \frac{{\partial \delta \phi _{y} }}{{\partial x}} + 2\frac{{\partial ^{2} \delta w_{0} }}{{\partial x\partial y}}} \right)} \hfill \\ {\;\; + (Q_{{xz}} - 3S_{{xz}} c_{1} )\left( {\delta \phi _{x} + \frac{{\partial \delta w_{0} }}{{\partial x}}} \right) + (Q_{{yz}} - 3S_{{yz}} c_{1} )\left( {\delta \phi _{y} + \frac{{\partial \delta w_{0} }}{{\partial y}}} \right)} \hfill \\ \end{array} } \right]}{\text{d}}A \\ = & \iint\limits_{A} {\left[ {\begin{array}{*{20}l} { - \frac{\partial }{{\partial x}}N_{{xx}} \delta u_{0} - \frac{\partial }{{\partial x}}M_{{xx}} \delta \phi _{x} - c_{1} \left( { - \frac{\partial }{{\partial x}}P_{{xx}} \delta \phi _{x} + \frac{{\partial ^{2} }}{{\partial x^{2} }}P_{{xx}} \delta w_{0} } \right)} \hfill \\ { - \frac{\partial }{{\partial y}}N_{{yy}} \delta v_{0} - \frac{\partial }{{\partial y}}M_{{yy}} \delta \phi _{y} - c_{1} \left( { - \frac{\partial }{{\partial y}}P_{{yy}} \delta \phi _{y} + \frac{{\partial ^{2} }}{{\partial y^{2} }}P_{{yy}} \delta w_{0} } \right)} \hfill \\ { - \frac{\partial }{{\partial y}}N_{{xy}} \delta u_{0} - \frac{\partial }{{\partial x}}N_{{xy}} \delta v_{0} - \frac{\partial }{{\partial y}}M_{{xy}} \delta \phi _{x} - \frac{\partial }{{\partial x}}M_{{xy}} \delta \phi _{y} } \hfill \\ { - c_{1} \left( { - \frac{\partial }{{\partial y}}P_{{xy}} \delta \phi _{x} - \frac{\partial }{{\partial x}}P_{{xy}} \delta \phi _{y} + 2\frac{{\partial ^{2} }}{{\partial x\partial y}}P_{{xy}} \delta w_{0} } \right)} \hfill \\ {\;\; + Q_{{xz}} \delta \phi _{x} - \frac{\partial }{{\partial x}}Q_{{xz}} \delta w_{0} - 3c_{1} \left( {S_{{xz}} \delta \phi _{x} - \frac{\partial }{{\partial x}}S_{{xz}} \delta w_{0} } \right)} \hfill \\ {\;\; + Q_{{yz}} \delta \phi _{y} - \frac{\partial }{{\partial y}}Q_{{yz}} \delta w_{0} - 3c_{1} \left( {S_{{yz}} \delta \phi _{y} - \frac{\partial }{{\partial y}}S_{{yz}} \delta w_{0} } \right)} \hfill \\ \end{array} } \right]}{\text{d}}A \\ \end{aligned}. $$

$$ \begin{aligned} \left\{ {N_{xx} ,N_{yy} ,N_{xy} } \right\} & = \sum\limits_{k = 1}^{{N_{\text{L}} }} {\int_{z} {\left\{ {\sigma_{xx}^{k} ,\sigma_{yy}^{k} ,\sigma_{xy}^{k} } \right\}} } {\text{d}}z, \hfill \\ \left\{ {M_{xx} ,M_{yy} ,M_{xy} } \right\} & = \sum\limits_{k = 1}^{{N_{\text{L}} }} {\int_{z} {\left\{ {\sigma_{xx}^{k} ,\sigma_{yy}^{k} ,\sigma_{xy}^{k} } \right\}} } z{\text{d}}z, \hfill \\ \left\{ {P_{xx} ,P_{yy} ,P_{xy} } \right\} & = \sum\limits_{k = 1}^{{N_{\text{L}} }} {\int_{z} {\left\{ {\sigma_{xx}^{k} ,\sigma_{yy}^{k} ,\sigma_{xy}^{k} } \right\}} z^{3} } {\text{d}}z, \hfill \\ \left\{ {Q_{xz} ,Q_{yz} } \right\} & = \sum\limits_{k = 1}^{{N_{\text{L}} }} {\int_{z} {\left\{ {\sigma_{xz}^{k} ,\sigma_{xy}^{k} } \right\}} } {\text{d}}z, \hfill \\ \left\{ {S_{xz} ,S_{yz} } \right\} & = \sum\limits_{k = 1}^{{N_{\text{L}} }} {\int_{z} {\left\{ {\sigma_{xz}^{k} ,\sigma_{xy}^{k} } \right\}z^{2} } } {\text{d}}z, \hfill \\ \end{aligned} $$

$$\begin{aligned} N_{xx} & = A_{11} \frac{{\partial u_{0} }}{\partial x} + B_{11} \frac{{\partial \phi_{x} }}{\partial x} - D_{11} c_{1} \left( {\frac{{\partial \phi_{x} }}{\partial x} + \frac{{\partial^{2} w_{0} }}{{\partial x^{2} }}} \right)\\& \quad + A_{12} \frac{{\partial v_{0} }}{\partial y} + B_{12} \frac{{\partial \phi_{y} }}{\partial y} - D_{12} c_{1} \left( {\frac{{\partial \phi_{y} }}{\partial y} + \frac{{\partial^{2} w_{0} }}{{\partial y^{2} }}} \right), \\ N_{yy} & = A_{22} \frac{{\partial v_{0} }}{\partial y} + B_{22} \frac{{\partial \phi_{y} }}{\partial y} - D_{22} c_{1} \left( {\frac{{\partial \phi_{y} }}{\partial y} + \frac{{\partial^{2} w_{0} }}{{\partial y^{2} }}} \right)\\& \quad + A_{12} \frac{{\partial u_{0} }}{\partial x} + B_{12} \frac{{\partial \phi_{x} }}{\partial x} - D_{12} c_{1} \left( {\frac{{\partial \phi_{x} }}{\partial x} + \frac{{\partial^{2} w_{0} }}{{\partial x^{2} }}} \right), \\ N_{xy} & = A_{44} \frac{{\partial u_{0} }}{\partial y} + A_{44} \frac{{\partial v_{0} }}{\partial x} + B_{44} \left( {\frac{{\partial \phi_{x} }}{\partial y} + \frac{{\partial \phi_{y} }}{\partial x}} \right)\\& \quad - D_{44} c_{1} \left( {\frac{{\partial \phi_{x} }}{\partial y} + \frac{{\partial \phi_{y} }}{\partial x} + 2\frac{{\partial^{2} w_{0} }}{\partial x\partial y}} \right), \\ M_{xx} & = B_{11} \frac{{\partial u_{0} }}{\partial x} + C_{11} \frac{{\partial \phi_{x} }}{\partial x} - E_{11} c_{1} \left( {\frac{{\partial \phi_{x} }}{\partial x} + \frac{{\partial^{2} w_{0} }}{{\partial x^{2} }}} \right)\\& \quad + B_{12} \frac{{\partial v_{0} }}{\partial y} + C_{12} \frac{{\partial \phi_{y} }}{\partial y} - E_{12} c_{1} \left( {\frac{{\partial \phi_{y} }}{\partial y} + \frac{{\partial^{2} w_{0} }}{{\partial y^{2} }}} \right), \\ M_{yy} & = B_{22} \frac{{\partial v_{0} }}{\partial y} + C_{22} \frac{{\partial \phi_{y} }}{\partial y} - E_{22} c_{1} \left( {\frac{{\partial \phi_{y} }}{\partial y} + \frac{{\partial^{2} w_{0} }}{{\partial y^{2} }}} \right) \\& \quad + B_{12} \frac{{\partial u_{0} }}{\partial x} + C_{12} \frac{{\partial \phi_{x} }}{\partial x} - E_{12} c_{1} \left( {\frac{{\partial \phi_{x} }}{\partial x} + \frac{{\partial^{2} w_{0} }}{{\partial x^{2} }}} \right), \\ M_{xy} & = B_{44} \frac{{\partial u_{0} }}{\partial y} + B_{44} \frac{{\partial v_{0} }}{\partial x} + C_{44} \left( {\frac{{\partial \phi_{x} }}{\partial y} + \frac{{\partial \phi_{y} }}{\partial x}} \right)\\& \quad - E_{44} c_{1} \left( {\frac{{\partial \phi_{x} }}{\partial y} + \frac{{\partial \phi_{y} }}{\partial x} + 2\frac{{\partial^{2} w_{0} }}{\partial x\partial y}} \right), \\ p_{xx} & = D_{11} \frac{{\partial u_{0} }}{\partial x} + E_{11} \frac{{\partial \phi_{x} }}{\partial x} - G_{11} c_{1} \left( {\frac{{\partial \phi_{x} }}{\partial x} + \frac{{\partial^{2} w_{0} }}{{\partial x^{2} }}} \right)\\& \quad + D_{12} \frac{{\partial v_{0} }}{\partial y} + E_{12} \frac{{\partial \phi_{y} }}{\partial y} - G_{12} c_{1} \left( {\frac{{\partial \phi_{y} }}{\partial y} + \frac{{\partial^{2} w_{0} }}{{\partial y^{2} }}} \right), \\ p_{yy} & = D_{22} \frac{{\partial v_{0} }}{\partial y} + E_{22} \frac{{\partial \phi_{y} }}{\partial y} - G_{22} c_{1} \left( {\frac{{\partial \phi_{y} }}{\partial y} + \frac{{\partial^{2} w_{0} }}{{\partial y^{2} }}} \right) \\& \quad + D_{12} \frac{{\partial u_{0} }}{\partial x} + E_{12} \frac{{\partial \phi_{x} }}{\partial x} - G_{12} c_{1} \left( {\frac{{\partial \phi_{x} }}{\partial x} + \frac{{\partial^{2} w_{0} }}{{\partial x^{2} }}} \right), \\ p_{xy} & = D_{44} \frac{{\partial u_{0} }}{\partial y} + D_{44} \frac{{\partial v_{0} }}{\partial x} + E_{44} \left( {\frac{{\partial \phi_{x} }}{\partial y} + \frac{{\partial \phi_{y} }}{\partial x}} \right)\\& \quad - G_{44} c_{1} \left( {\frac{{\partial \phi_{x} }}{\partial y} + \frac{{\partial \phi_{y} }}{\partial x} + 2\frac{{\partial^{2} w_{0} }}{\partial x\partial y}} \right), \\ Q_{xz} & = (A_{55} - 3C_{55} c_{1} )\left( {\phi_{x} + \frac{{\partial w_{0} }}{\partial x}} \right), \\ S_{xz} & = (C_{55} - 3E_{55} c_{1} )\left( {\phi_{x} + \frac{{\partial w_{0} }}{\partial x}} \right), \\ Q_{yz} & = (A_{66} - 3C_{66} c_{1} )\left( {\phi_{y} + \frac{{\partial w_{0} }}{\partial y}} \right), \\ S_{yz} & = (C_{66} - 3E_{66} c_{1} )\left( {\phi_{y} + \frac{{\partial w_{0} }}{\partial y}} \right). \\ \end{aligned} $$

$$ \begin{aligned} &\left\{ {A_{11} ,B_{11} ,C_{11} ,D_{11} ,E_{11} ,F_{11} ,G_{11} } \right\} \\& \quad = \sum\limits_{k = 1}^{{N_{\text{L}} }} {\int\limits_{ - h/2}^{h/2} {Q_{11}^{k} \left\{ {1,z,z^{2} ,z^{3} ,z^{4} ,z^{5} ,z^{6} } \right\}} } {\text{d}}z, \hfill \\& \left\{ {A_{12} ,B_{12} ,C_{12} ,D_{12} ,E_{12} ,F_{12} ,G_{12} } \right\} \\& \quad = \sum\limits_{k = 1}^{{N_{\text{L}} }} {\int\limits_{ - h/2}^{h/2} {Q_{12}^{k} \left\{ {1,z,z^{2} ,z^{3} ,z^{4} ,z^{5} ,z^{6} } \right\}} } {\text{d}}z, \hfill \\& \left\{ {A_{22} ,B_{22} ,C_{22} ,D_{22} ,E_{22} ,F_{22} ,G_{22} } \right\} \\& \quad = \sum\limits_{k = 1}^{{N_{\text{L}} }} {\int\limits_{ - h/2}^{h/2} {Q_{22}^{k} \left\{ {1,z,z^{2} ,z^{3} ,z^{4} ,z^{5} ,z^{6} } \right\}} } {\text{d}}z, \hfill \\& \left\{ {A_{55} ,B_{55} ,C_{55} ,D_{55} ,E_{55} } \right\}\\& \quad = \sum\limits_{k = 1}^{{N_{\text{L}} }} {\int\limits_{ - h/2}^{h/2} {Q_{55}^{k} \left\{ {1,z,z^{2} ,z^{3} ,z^{4} } \right\}} } {\text{d}}z, \hfill \\ &\left\{ {A_{66} ,B_{66} ,C_{66} ,D_{66} ,E_{66} } \right\}\\& \quad = \sum\limits_{k = 1}^{{N_{\text{L}} }} {\int\limits_{ - h/2}^{h/2} {Q_{66}^{k} \left\{ {1,z,z^{2} ,z^{3} ,z^{4} } \right\}} } {\text{d}}z. \hfill \\\end{aligned}$$

$$ \delta W_{1} = \iint\limits_{A} {\left[ {N_{1}^{T} \frac{\partial w}{\partial x}\frac{\partial \delta w}{\partial x} + N_{2}^{T} \frac{\partial w}{\partial y}\frac{\partial \delta w}{\partial y}} \right]}\,{\text{d}}x{\text{d}}y, $$

$$ N_{1}^{\text{T}} = N_{2}^{\text{T}} = \int_{ - h/2}^{h/2} {E\,\alpha (T - T_{0} ){\text{d}}z}. $$

(27)