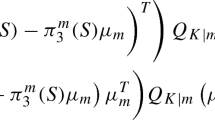Unequal Priors in Linear Discriminant Analysis

Abstract

Dealing with unequal priors in both linear discriminant analysis (LDA) based on Gaussian distribution (GDA) and in Fisher’s linear discriminant analysis (FDA) is frequently used in practice but almost described in neither any textbook nor papers. This is one of the first papers exhibiting that GDA and FDA yield the same classification results for any number of classes and features. We discuss in which ways unequal priors have to enter these two methods in theory as well as algorithms. This may be of particular interest if prior knowledge is available and should be included in the discriminant rule. Various estimators that use prior probabilities in different places (e.g. prior-based weighting of the covariance matrix) are compared both in theory and by means of simulations.

1 Introduction

This paper deals with methods of linear discriminant analysis (LDA) under the assumption of unequal priors. We concentrate on LDA based on Gaussian distribution (GDA) and a weighted version of Fisher’s LDA (FDA).

Several authors have different opinions about the equivalence of Gaussian and Fisher’s linear discriminant analysis, especially if unequal priors are present. One might state GDA and FDA are only identical if equal priors are assumed or given (Fahrmeir et al. 1996). Others show GDA and FDA are identical in special cases (Rencher 1995) and implicitly readers may guess they are not identical in other cases. The purpose of this paper is to get things straight concerning the similarities and differences of GDA and FDA in theory and application.

Therefore, we briefly review the theory of LDA in Section 2, more precisely, for both GDA (see Section 2.1) and FDA (see Section 2.2). Section 2.3 lists possible estimators applied in GDA and FDA. Subsequently, in Section 3, we prove that GDA and FDA yield the same classification results under some assumptions.

Afterwards, we shortly discuss implementations of GDA and FDA in Section 4, e.g. function lda from R package MASS (R Core Team 2016; Venables and Ripley 2002) as well as self-implemented versions of these methods (see Section 4.2). These functions are applied in simulations to compare GDA and FDA in conjunction with various estimators for the covariance matrix. Next, the design of the simulation study is explained in Section 4.3 and followed by the results in Section 4.4. Concluding, we summarise the substantial results of theory and simulation in Section 5.

2 Linear Discriminant Analysis

Assume G ≥ 2 non-empty, disjoint groups which should be discriminated. Each group g ∈{1,...,G} is represented by a p-dimensional random vector $\mathcal {X}_{g} = (\mathcal {X}_{g1},...,\mathcal {X}_{gp})^{\prime }$ with expected value μ_g and covariance matrix Σ_g. We imply $\mu _{g} \neq \mu _{g^{\prime }}$ for g≠g^′. Prior π_g specifies the probability that a randomly chosen observation x is an element of group g. It applies π_g ∈ (0,1) and ${\sum }_{g =1}^{G} \pi _{g} = 1$. For another random vector $\mathcal {X}$ which measures the same features as $\mathcal {X}_{g}$ an observation vector $x = (x_{1},...,x_{p})^{\prime } \in \mathbb {R}^{p}$ is given.

2.1 LDA Based on Gaussian Distribution

Linear discriminant analysis based on Gaussian distribution (GDA) is a special case of Bayes’ rule (Huberty 1994). We assume normal distribution within each class with expected value μ_g and covariance matrix Σ_g. Additionally, we assume Σ := Σ₁ = ... = Σ_G that is the covariance matrices are all equal, one of the main assumptions of LDA. Hence, the density function of group g is:

$$ f_{g}(x) = (2\pi)^{-\frac{p}{2}} (\det({\Sigma}))^{-\frac{1}{2}} \exp \left[- \frac{1}{2} (x - \mu_{g})^{\prime} {\Sigma}^{-1} (x - \mu_{g}) \right]. $$

(1)

The term

$$ {{d}_{g}^{2}}(x) = (x - {\mu}_{g})^{\prime} {\Sigma}^{-1} (x - \mu_{g}) $$

(2)

in the exponential function in Eq. 1 is the squared Mahalanobis distance (Mahalanobis 1936) between observation x and expected value μ_g. Given the covariance matrix is an identity matrix Σ = I_p, the squared Mahalanobis distance from Eq. 2 becomes the squared Euclidean distance ${\sum }_{j = 1}^{p} (x_{j} - {\mu }_{gj})^{2}$.

The discriminant rule of GDA is based on the idea of assigning an observation x to the group g with the highest posterior (Bayes 1763; Huberty 1994):

$$ \mathrm{P}(g|x) = \frac{\pi_{g} \exp[-\frac{1}{2}(x -\mu_{g})^{\prime} {\Sigma}^{-1} (x- \mu_{g})]}{{\sum}_{g^{\prime} = 1}^{G} \pi_{g^{\prime}} \exp [-\frac{1}{2} (x - \mu_{g^{\prime}})^{\prime}{\Sigma}^{-1}(x - \mu_{g^{\prime}}) ]}. $$

(3)

The denominator in Eq. 3 is identical for all groups and can be neglected. Taking the logarithm of the numerator in Eq. 3 results in the canonical classification function:

$$ L_{g}(x) = -\frac{1}{2} (x - \mu_{g})^{\prime}{\Sigma}^{-1}(x - \mu_{g}) + \log(\pi_{g}). $$

(4)

We assign an observation x to group

$$ g = \underset{g^{\prime} = 1,...,G}{\arg\max} L_{g^{\prime}}(x). $$

(5)

Multiplying the canonical discriminant function in Eq. 4 by − 2 changes the maximisation in Eq. 5 into a minimisation. Thus, we obtain an equivalent discriminant rule which assigns an observation x to group:

$$ g = \underset{g^{\prime} = 1,...,G}{\arg\min} {L}_{g^{\prime}}^{*}(x) $$

(6)

where

$$ {L}_{g^{\prime}}^{*}(x) = (x - \mu_{g^{\prime}})^{\prime}{\Sigma}^{-1}(x - \mu_{g^{\prime}}) - 2 \log(\pi_{g^{\prime}}). $$

(7)

2.2 Fisher’s Linear Discriminant Analysis

The idea of Fisher’s linear discriminant analysis (FDA) is to find r < p linear combinations

$$ \mathcal{Y}_{g} = \begin{pmatrix} \mathcal{Y}_{g1} \\ {\vdots} \\ \mathcal{Y}_{gr} \end{pmatrix} = \begin{pmatrix} \alpha_{1}^{\prime} \mathcal{X}_{g} \\ {\vdots} \\ \alpha_{r}^{\prime} \mathcal{X}_{g} \end{pmatrix} = \begin{pmatrix} \alpha_{1}^{\prime} \\ {\vdots} \\ \alpha_{r}^{\prime} \end{pmatrix} \mathcal{X}_{g} = \mathcal{A}^{\prime}\mathcal{X}_{g} $$

(8)

of the random vectors $\mathcal {X}_{g}$, g = 1,...,G, which separate the groups as much as possible (Fisher 1936; Huberty 1994). Thereby, $\alpha _{j} = (\alpha _{j1},...,\alpha _{jp})^{\prime } \in \mathbb {R}^{p}$ for j = 1,...,r and $\mathcal {A} = (\alpha _{1},..., \alpha _{r}) \in \mathbb {R}^{p \times r}$. First, we take a closer look at one specific linear transformation $\mathcal {Y}_{gj} = \alpha _{j}^{\prime }\mathcal {X}_{g}$ of the random vector of group g. The expected value of $\mathcal {Y}_{gj}$ is

$$ {\mu}_{_{\mathcal{Y}_{gj}}} := \mathrm{E}(\mathcal{Y}_{gj}) = \text{E}(\alpha_{j}^{\prime}\mathcal{X}_{g}) = \alpha_{j}^{\prime}\mu_{g} $$

(9)

and the variance of $\mathcal {Y}_{gj}$ is

$$ \sigma_{_{\mathcal{Y}_{gj}}}^{2} := \text{var}(\mathcal{Y}_{gj}) = \text{var}(\alpha_{j}^{\prime}\mathcal{X}_{g}) = \alpha_{j}^{\prime} {\Sigma} \alpha_{j} $$

(10)

for g = 1,...,G and j = 1,...,r. Since the covariance matrices are identical for all groups, the variances of the linear transformations $\mathcal {Y}_{gj}$ are all equal as well, so $\sigma ^{2}_{_{\mathcal {Y}_{j}}} := \sigma ^{2}_{_{\mathcal {Y}_{1j}}} = ... = \sigma ^{2}_{_{\mathcal {Y}_{Gj}}}$. Further, we refer to $\mu _{w} = {\sum }_{g = 1}^{G} \pi _{g} \mu _{g}$ as a weighted mean of the expected values. The linear transformations of μ_w are $\mu _{_{\mathcal {Y}_{wj}}} = \alpha _{j}^{\prime } \mu _{w}$ for j = 1,...,r.

In the following paragraph, we simply formulate the optimisation problem as a function of α. To obtain a suitable discrimination with the transformations in Eq. 8, the idea of Fisher is that the expected values $\mu _{_{\mathcal {Y}_{g}}} = \alpha ^{\prime }\mu _{g}$ need to differ as much as possible for all groups and the variance $\sigma _{_{\mathcal {Y}}}^{2} = \alpha ^{\prime } {\Sigma } \alpha$ should be as small as possible (Fisher 1936). For that purpose, consider the sum of squared difference between $\mu _{_{\mathcal {Y}_{g}}}$ and $\mu _{_{\mathcal {Y}_{w}}}$ weighted by the priors. This sum of weighted differences needs to be maximised whereas $\sigma _{_{\mathcal {Y}}}^{2}$ should be minimised. This is achieved by solving the weighted optimisation problem (Filzmoser et al. 2006):

$$ \max_{\alpha \in \mathbb{R}^{p}} \frac{{\sum}_{g = 1}^{G} \pi_{g} (\mu_{_{\mathcal{Y}_{g}}} - \mu_{_{\mathcal{Y}_{w}}})^{2}}{\sigma^{2}_{_{\mathcal{Y}}}} = \max_{\alpha \in \mathbb{R}^{p}} \frac{\alpha^{\prime} B_{\mu_{w}} \alpha}{\alpha^{\prime} {\Sigma} \alpha}. $$

(11)

The numerator in Eq. 11 contains the weighted covariance matrix between the groups:

$$ B_{\mu_{w}} = \sum\limits_{g = 1}^{G} \pi_{g} (\mu_{g} - \mu_{w})(\mu_{g} - \mu_{w})^{\prime}. $$

(12)

The eigenvectors of ${\Sigma }^{-1} B_{\mu _{w}}$ with corresponding positive eigenvalue yield the solution of the maximisation problem in Eq. 11 (Mukhopadhyay 2009). The solution is unique up to scalar multiplication, that is why in some literature it is mentioned that the optimisation problem in Eq. 11 is solved under the side condition α^′Σα = 1 (Johnson and Wichern 2007; Mukhopadhyay 2009).

We obtain r suitable solutions α_j, j = 1,...,r, from the optimisation problem in Eq. 11. Their derivation is explained below. The rank of a matrix is equal to the number of nonzero eigenvalues, i.e. $r := \text {rk}({\Sigma }^{-1} B_{\mu _{w}}) \leq \min \{ \text {rk}({\Sigma }^{-1}), \text {rk}(B_{\mu _{w}})\}$. The inverse covariance matrix Σ^− 1 is a p × p-dimensional matrix which has maximum rank p. This leads to $r \leq \min \{p, \text {rk}(B_{\mu _{w}})\}$. Further, the G vectors π_g(μ_g − μ_w), g = 1,...,G, contained in $B_{\mu _{w}}$ are linearly dependent because:

$$ \sum\limits_{g=1}^{G} \pi_{g}(\mu_{g} - \mu_{w}) = \sum\limits_{g=1}^{G} \pi_{g} \mu_{g} - \mu_{w} {\sum}_{g=1}^{G} \pi_{g} = \mu_{w} - \mu_{w} = 0. $$

(13)

Consequently, at least one of the vectors π_g(μ_g − μ_w) can be rewritten through the remaining G − 1 vectors. Thus, the space spanned by π₁(μ₁ − μ_w),..., π_G(μ_G − μ_w) is less than or equal G − 1. According to this, we receive r ≤ min{p,G − 1}.

The r ≤ min{p,G − 1} positive eigenvalues λ₁ ≥ ... ≥ λ_r > 0 of ${\Sigma }^{-1} B_{\mu _{w}}$ or identically of ${\Sigma }^{-\frac {1}{2}} B_{\mu _{w}}{\Sigma }^{-\frac {1}{2}}$ lead to the solution of the optimisation problem in Eq. 11. The matrices ${\Sigma }^{-1} B_{\mu _{w}}$ and ${\Sigma }^{-\frac {1}{2}} B_{\mu _{w}}{\Sigma }^{-\frac {1}{2}}$ have the same eigenvalues since

$$ {\Sigma}^{-\frac{1}{2}} B_{\mu_{w}} {\Sigma}^{-\frac{1}{2}} v_{j} = \lambda_{j} v_{j} \Leftrightarrow {\Sigma}^{-1} B_{\mu_{w}} {\Sigma}^{-\frac{1}{2}} v_{j} = \lambda_{j} {\Sigma}^{-\frac{1}{2}}v_{j} $$

(14)

for j = 1,...,r (Mukhopadhyay 2009). Let v₁,...,v_r denote the associated orthogonal and normalised eigenvectors of ${\Sigma }^{-\frac {1}{2}} B_{\mu _{w}}{\Sigma }^{-\frac {1}{2}}$. From these, the corresponding eigenvectors

$$ \alpha_{j} = {\Sigma}^{-\frac{1}{2}} v_{j} $$

(15)

of ${\Sigma }^{-1} B_{\mu _{w}}$ can be determined which satisfy $\alpha _{j}^{\prime } {\Sigma } \alpha _{j} = 1$ for j = 1,...,r and maximise the ratio in Eq. 11.

The vectors $\alpha _{1},...,\alpha _{r} \in \mathbb {R}^{p}$ in Eq. 15 are the so-called discriminant components. They transform the p-dimensional random vector $\mathcal {X}$ into an r-dimensional random vector $\mathcal {Y} = \mathcal {A}^{\prime }\mathcal {X}$. The linear transformations $\mathcal {Y}_{j} = \alpha _{j}^{\prime } \mathcal {X}$ are pairwise uncorrelated. It is $\text {cov}(\mathcal {Y}_{j}, \mathcal {Y}_{k}) = \alpha _{j}^{\prime } {\Sigma } \alpha _{k} = v_{j}^{\prime } {\Sigma }^{-\frac {1}{2}} {\Sigma } {\Sigma }^{-\frac {1}{2}} v_{k} = v_{j}^{\prime } v_{k} = 0$ for j,k ∈{1,...,r} with j≠k since the eigenvectors v₁,...,v_r are pairwise orthogonal.

The discriminant components are used for both dimension reduction and classification. To classify an object with observation vector $x \in \mathbb {R}^{p}$, the sum of the squared projected distance between the observation and the expected value of one group is considered (Rao 1948; Wald 1944). Besides, this sum can be adjusted with the associated prior of a group (Filzmoser et al. 2006). Fisher’s discriminant rule assigns observation x to group

$$ g = \underset{g^{\prime} = 1,...,G}{\arg\min} D_{g^{\prime}}(x) $$

(16)

where

$$ D_{g^{\prime}}(x) = \sum\limits_{j = 1}^{r} (\alpha_{j}^{\prime} (x - \mu_{g^{\prime}}))^{2} - 2 \log(\pi_{g^{\prime}}) $$

(17)

denotes Fisher’s discriminant score with penalty (Filzmoser et al. 2006). The penalty − 2log(π_g) in Eq. 17 is equal to that of the canonical discriminant function $L_{g}^{*}$ (see Eq. 7, Section 2.1). It penalises the distance between an observation and a group with higher prior less than the distance between an observation and a class with small prior. For the simple reason that π_g ∈ (0,1) for all g = 1,...,G, it holds 2log(π_g) < 0. Therefore, the higher a prior π_g, the smaller the penalty and the less is added to Fisher’s discriminant score of group g.

2.3 Estimation

In general, the expected values μ_g and covariance matrix Σ are unknown and must be estimated suitably. For this purpose, we need a sample $X = (X_{1}^{\prime },...,X_{G}^{\prime })^{\prime } \in \mathbb {R}^{n \times p}$ with known group membership. The sample of group g denotes $X_{g}^{\prime } = (x_{g1},...,x_{gn_{g}}) \in \mathbb {R}^{p \times n_{g}}$ with $x_{gi} \in \mathbb {R}^{p}$ for i = 1,...,n_g and g = 1,...,G. The total number of observations is $n = {\sum }_{g = 1}^{G} n_{g}$. The most common estimate for the expected value of group g is its mean:

$$ \hat{\mu}_{g} = \overline{x}_{g} = \frac{1}{n_{g}} \sum\limits_{i = 1}^{n_{g}} x_{gi} $$

(18)

for g = 1,...,G (Hastie et al. 2009). The covariance matrix Σ which is assumed to be identical for all groups is estimated by the pooled covariance matrix

$$ \hat{\Sigma} = S_{pool} = \frac{1}{n - G} W $$

(19)

with the estimated covariance matrix within the groups

$$ W= \sum\limits_{g=1}^{G} (n_{g} - 1) S_{g}. $$

(20)

S_g is the estimated covariance matrix of group g and is defined by:

$$ S_{g} = \frac{1}{n_{g} - 1} \sum\limits_{i = 1}^{n_{g}} (x_{gi} - \overline{x}_{g})(x_{gi} - \overline{x}_{g})^{\prime}. $$

(21)

Another estimate of the covariance matrix which is weighted by the priors is

$$ \hat{\Sigma} = S_{w} = \sum\limits_{g = 1}^{G} \pi_{g} S_{g} $$

(22)

with S_g as in Eq. 21 (Filzmoser et al. 2006). It can be shown that the estimators in Eqs. 19 and 22 are identical for equal priors $\pi _{1} = ... = \pi _{G} = \frac {1}{G}$ and class sizes $n_{1} = ... = n_{G} = \frac {n}{G}$:

$$ \begin{array}{@{}rcl@{}} S_{w} &=& \sum\limits_{g = 1}^{G} \pi_{g} S_{g} = \sum\limits_{g = 1}^{G} \frac{1}{G} S_{g} = \frac{1}{n-G} \sum\limits_{g = 1}^{G} \frac{n - G}{G} S_{g} \\ &=& \frac{1}{n-G} \sum\limits_{g = 1}^{G} \left( \frac{n}{G} -1\right) S_{g} = \frac{1}{n-G} \sum\limits_{g = 1}^{G} (n_{g} -1) S_{g} = S_{pool}. \end{array} $$

Additionally, in FDA, we need estimates for μ_w and $B_{\mu _{w}}$. The empirical equivalent for the weighted mean of the expected values can be defined as

$$ \hat{\mu}_{w} = \overline{x}_{w} = \sum\limits_{g = 1}^{G} \pi_{g} \overline{x}_{g} $$

(23)

with $\overline {x}_{g}$ as in Eq. 18 (Filzmoser et al. 2006). Various estimates for the covariance matrix between the groups have been proposed which differ in prefactor (Johnson and Wichern 2007; Krzanowski and Marriott 1995; Rao 1948) or weighting (Bryan 1951; Filzmoser et al. 2006; Krzanowski and Marriott 1995). One weighted estimate we refer to is (Filzmoser et al. 2006)

$$ \hat{B}_{\mu_{w}} = \sum\limits_{g = 1}^{G} \pi_{g} (\overline{x}_{g} - \overline{x}_{w})(\overline{x}_{g} - \overline{x}_{w})^{\prime}. $$

(24)

Nevertheless, the choice of the estimate for the covariance matrix between the groups is not as important as that of the covariance matrix within the groups. Especially in the case of two groups with two features we show (see Appendix) that the discriminant component only depends on the expected values and the covariance matrix within the groups. Hence, the estimate for the covariance matrix between the groups has no influence on the discriminant result.

In some cases, information about the priors is given by pre-test or other studies. If no prior information is disposable, we can assume a discrete uniform distribution, thus:

$$ \hat{\pi}_{g} = \frac{1}{G} $$

(25)

for g = 1,...,G (McLachlan 1992). An alternative is using the relative group frequencies (Huberty 1994). Then, the priors are estimated by

$$ \hat{\pi}_{g} = \frac{n_{g}}{n}. $$

(26)

In case that the groups are all of the same size, the two estimates in Eqs. 25 and 26 are identical.

3 Theoretical Comparison of GDA and FDA

To prove that GDA and FDA as described in the previous section yield the same results, one could compare the discriminant hyperplanes of the discriminant rules. In case we have G = p = 2 groups and features, we obtain a line which can be calculated easily. Therefore, we need the discriminant component $\alpha _{1} = \frac {{\Sigma }^{-1} (\mu _{2} - \mu _{1})}{((\mu _{1} - \mu _{2})^{\prime } {\Sigma }^{-1} (\mu _{2} - \mu _{1}))^{\frac {1}{2}} }$. For a detailed derivation, see Appendix. For increasing G or p, the analytical derivation of discriminant components becomes more difficult and thus the determination of hyperplanes as well. So, we concentrate on the discriminant rules while comparing GDA and FDA for any number of groups and features. Note that there is no straightforward way to get posterior probabilities from an FDA for further comparisons.

Consider Fisher’s discriminant rule with penalty and all p instead of r discriminant components (see Eq. 17, Section 2.2). To determine the discriminant components, we solve the eigenvalue equation for the matrix ${\Sigma }^{-\frac {1}{2}} B_{\mu _{w}} {\Sigma }^{-\frac {1}{2}}$. This is symmetric, positive semidefinite and has the eigenvalues λ₁ > ... > λ_r > 0 = λ_r+ 1 = ... = λ_p. The corresponding normalised eigenvectors $v_{1},...,v_{r},...,v_{p} \in \mathbb {R}^{p}$ are pairwise orthogonal according to the spectral theorem (Mukhopadhyay 2009). Hence, the matrix $\mathcal {V} =(v_{1},...,v_{r},...,v_{p}) \in \mathbb {R}^{p \times p}$ is orthogonal and it applies $\mathcal {V}^{\prime }\mathcal {V} = \mathcal {V}\mathcal {V}^{\prime } = I_{p}$. Let $\mathcal {A}^{*} = (\alpha _{1},...,\alpha _{r},...,\alpha _{p}) \in \mathbb {R}^{p \times p}$ denote the matrix of the p discriminant components (see Eq. 15, Section 2.2), then $\mathcal {A}^{*} = {\Sigma }^{-\frac {1}{2}} \mathcal {V}$. Contemplating Fisher’s discriminant score with penalty (see Eq. 17, Section 2.2) and p discriminant components this yields:

$$ \begin{array}{@{}rcl@{}} D^{*}_{g}(x) &=& {\sum}_{j = 1}^{p} (\alpha_{j}^{\prime} (x - \mu_{g}))^{2} - 2\log(\pi_{g}) \\ &=& \left( \begin{array}{c} \alpha_{1}^{\prime} (x - \mu_{g})\\ {\vdots} \\ \alpha_{p}^{\prime}(x - \mu_{g}) \end{array} \right)^{\prime} \left( \begin{array}{c} \alpha_{1}^{\prime} (x - \mu_{g})\\ {\vdots} \\ \alpha_{p}^{\prime}(x - \mu_{g}) \end{array} \right) - 2 \log(\pi_{g})\\ &=& \left( \left( \begin{array}{c} \alpha_{1}^{\prime}\\ {\vdots} \\ \alpha_{p}^{\prime} \end{array} \right) (x - \mu_{g}) \right)^{\prime} \left( \left( \begin{array}{c} \alpha_{1}^{\prime}\\ {\vdots} \\ \alpha_{p}^{\prime} \end{array} \right) (x - \mu_{g}) \right) - 2 \log(\pi_{g})\\ &=& (\mathcal{A}^{*\prime} (x - \mu_{g}))^{\prime} \mathcal{A}^{*\prime} (x - \mu_{g}) - 2 \log(\pi_{g}) \\ &=& (x - \mu_{g})^{\prime} \mathcal{A}^{*} \mathcal{A}^{*\prime} (x - \mu_{g}) - 2 \log(\pi_{g}) \\ &=& (x - \mu_{g})^{\prime} {\Sigma}^{-\frac{1}{2}} \mathcal{V} \mathcal{V}^{\prime} {\Sigma}^{-\frac{1}{2}} (x - \mu_{g}) - 2 \log(\pi_{g}) \\ &=& (x - \mu_{g})^{\prime} {\Sigma}^{-1} (x - \mu_{g}) - 2 \log(\pi_{g}) = L^{*}_{g}(x). \end{array} $$

Thus, Fisher’s weighted discriminant score with all p discriminant components is equal to the canonical discriminant score (see Eq. 7, Section 2.1).

Usually Fisher’s discriminant rule (see Eqs. 16 and 17, Section 2) only uses the first r discriminant components. However, using r or p discriminant components in Fisher’s discriminant score does not change the assignment of an observation into one of the G groups. Because the last (p − r) terms of the sum $\alpha _{j}^{\prime }(x - \mu _{g})$ are equal for all μ_g, g = 1,...,G, they do not contribute to the assignment. We take a closer look at the last discriminant components α_j for j = r + 1,...,p. These are eigenvectors for the matrix ${\Sigma }^{-1}B_{\mu _{w}}$ with corresponding eigenvalues λ_r+ 1 = ... = λ_p = 0. Therefore, it applies

$$ {\Sigma}^{-1}B_{\mu_{w}}\alpha_{j} = {\Sigma}^{-1} \sum\limits_{g = 1}^{G} \pi_{g}(\mu_{g} - \mu_{w})(\mu_{g} - \mu_{w})^{\prime} \alpha_{j} = \lambda_{j} \alpha_{j} = 0 \alpha_{j} = 0 $$

(27)

for j = r + 1,...,p. This implies that the last (p − r) eigenvectors α_j with corresponding eigenvalue 0 and the vectors (μ_g − μ_w) for all g = 1,...,G are orthogonal. Thus, α_j and $(\mu _{g} - \mu _{w}) - (\mu _{g^{\prime }} - \mu _{w}) = (\mu _{g} - \mu _{g^{\prime }})$ for g,g^′ = 1,...,G are orthogonal. Hence $0 = \alpha _{j}^{\prime } (\mu _{g} - \mu _{g^{\prime }}) = \mu _{_{\mathcal {Y}_{gj}}} - \mu _{_{\mathcal {Y}_{g^{\prime }j}}}$ and therefore:

$$ \begin{array}{@{}rcl@{}} 0 &=& \mu_{\mathcal{Y}_{gj}} - \mu_{\mathcal{Y}_{g^{\prime}j}} \Leftrightarrow \mu_{\mathcal{Y}_{g^{\prime}j}} = \mu_{\mathcal{Y}_{gj}} \Leftrightarrow \alpha_{j}^{\prime} \mu_{g^{\prime}} = \alpha_{j}^{\prime} \mu_{g} \\ \Leftrightarrow \alpha_{j}^{\prime} x - \alpha_{j}^{\prime} \mu_{g^{\prime}} &=& \alpha_{j}^{\prime} x - \alpha_{j}^{\prime} \mu_{g} \Leftrightarrow \alpha_{j}^{\prime} (x - \mu_{g^{\prime}}) = \alpha_{j}^{\prime} (x - \mu_{g}) \end{array} $$

for j = r + 1,...,p. The last (p − r) projected distances between an observation x and the expected value μ_g are equal for all groups g = 1,...,G. Then:

$$ \sum\limits_{j = r + 1}^{p} \alpha_{j}^{\prime}(x - \mu_{g}) = \sum\limits_{j = r + 1}^{p} \alpha_{j}^{\prime} (x - \mu_{g^{\prime}}) $$

(28)

for all g,g^′ = 1,...,G, meaning the sum of the last (p − r) projected distances is constant for all G groups and consequently can be neglected in the discriminant rule without changing the assignment.

To sum up, we have two remarkable results. First, Fisher’s weighted discriminant rule is the same for a number of r,r + 1,...,p discriminant components. Second, Fisher’s discriminant score with penalty and p discriminant components is identical to the canonical discriminant score. All in all, we obtain the discriminant rule which assigns observation x to group:

$$ g = \underset{g^{\prime} = 1,..., G}{\arg\min} D_{g^{\prime}}(x) = \underset{g^{\prime} = 1,...,G}{\arg\min} D^{*}_{g^{\prime}}(x) = \underset{g^{\prime} = 1,...,G}{\arg\min} L^{*}_{g^{\prime}}(x) = \underset{g^{\prime} = 1,...,G}{\arg\max} L_{g^{\prime}}(x). $$

(29)

That means the discriminant rules of FDA and GDA yield the same results for any number of groups and features. This is valid for the presence of unequal priors as well, but only when applying Fisher’s discriminant score with penalty.

4 Implementation

In practice, the expected values and covariances are generally unknown and have to be estimated (see Section 2.3). Various implementations in statistical software systems exist, those of the probably most frequently used systems are briefly described in Section 4.1. In the preceding sections, we described various methods to estimate the theoretical moments. Using these estimators in GDA and LDA, we may observe different results. Hence, we implemented these as described in Section 4.2. In the simulation study (see Section 4.3) implemented in R (R Core Team 2016), we investigate how large the actual differences between the various combinations of estimators and methods are.

4.1 Implementations in Statistical Software Systems

4.1.1 R

The R package MASS contains the function lda which performs Fisher’s LDA (see Section 2.2) (Venables and Ripley 2002). Herbrandt (2012) provides the only detailed description of the algorithms implemented in this function and the associated predict-method. The covariance matrix Σ is estimated by the pooled covariance matrix S_pool (see Eq. 19, Section 2.3). Unlike in Section 2.3 (see Eq. 24), lda uses the following estimate (Herbrandt 2012; Venables and Ripley 2002) for the covariance matrix between the groups:

$$ \tilde{B}_{\mu_{w}} = \frac{1}{G-1} \sum\limits_{g = 1}^{G} \pi_{g} n (\overline{x}_{g} - \overline{x}_{w}) (\overline{x}_{g} - \overline{x}_{w})^{\prime}. $$

(30)

The predict-method for lda classifies new observations under the assumption of a normal distribution (Herbrandt 2012). This method function utilises the discriminant components from the lda-output and calculates a centred projection of the observations (Herbrandt 2012; Venables and Ripley 2002). These centred and projected observations are plugged in an adapted version of the canonical discriminant function (see Eq. 7, Section 2.1). Then, the posterior probabilities (see Eq. 3, Section 2.1) can be calculated. Hence, training and prediction with lda form a mixture of FDA and GDA.

4.1.2 SAS

SAS offers two procedures for LDA: DISCRIM and CANDISC.

The CANDISC procedure performs discriminant analysis as a dimension reduction technique (SAS Institute Inc. 2018). Although the ‘CAN’ part of CANDISC stands for ‘canonical’, we do not use it here as it does not match our definition of canonical used in this paper. Given an input sample X and a dummy variable Y describing the known group membership and the total sample covariance matrix:

$$S = \begin{pmatrix} S_{X,X} & S_{X,Y} \\ S_{Y,X} & S_{Y,Y} \end{pmatrix}$$

an eigenvalue decomposition of the matrix:

$$\hat{\Sigma}^{-\frac{1}{2}} S_{X,Y} S_{Y,Y}^{-1} S_{Y,X}\hat{\Sigma}^{-\frac{1}{2}}$$

is performed. The pooled covariance matrix $\hat {\Sigma }$ is estimated as in Eq. 19.

One can prove $S_{X,Y} S_{Y,Y}^{-1} S_{Y,X} = \frac {n}{n-1}\hat B_{\mu _{w}}$ if the priors are estimated by relative group frequencies (26). Therefore, the resulting eigenvectors are identical to those of the FDA case described by $\mathcal {V}$ (see Section 2.2). The resulting coefficients (discriminant components) α_j, j = 1,…,r (see Eq. 15, Section 2.2) are the columns of $\mathcal {A} = \hat {\Sigma }^{-\frac {1}{2}} \mathcal {V}$. The scores given by CANDISC are not in the quadratic form of our previous descriptions of the discriminant scores. Unfortunately, the CANDISC procedure does not allow for prediction as it is focused on dimension reduction.

The DISCRIM procedure in SAS can be used to perform LDA based on the multivariate normal distribution when using the (default) option METHOD=NORMAL and (default) option POOL=YES (SAS Institute Inc. 2018). In this case, linear discriminant functions are derived based on the density functions (see Eq. 1, Section 2.1) with the pooled covariance matrix $\hat {\Sigma }$ (see Eq. 19, Section 2.3). The PRIORS statement can be set to equal (default) or proportional in order to assign equal (25) or proportional (26) priors for the classes. Priors can also be specified individually. Therefore, the DISCRIM procedure with settings mentioned above performs GDA by solving the minimisation problem given in Eq. 6.

4.1.3 SPSS

In SPSS, the command DISCRIMINANT (IBM Corp 2015; Leech et al. 2005) allows for linear discriminant analysis. The documentation of the underlying algorithm (IBM Corp 2016) suggests a GDA approach is used for the classification functions while the command also allows for variable selection and other sorts of discriminant analyses. The PRIORS subcommand can be set to EQUAL (default) or SIZE in order to assign equal (25) or proportional (26) priors for the classes. Priors can also be specified individually.

4.2 Implementations of Alternative Methods

Henceforth, we focus on the implementation in R. For evaluation, we construct a grid of observations in the space of the explanatory variables for the discriminant analysis. The results of applying lda and self-implemented versions of both GDA (gda, wgda) and FDA (fda, wfda) for all observations on the grid are compared using the estimators described in Section 2.3.

The functions gda and fda are based on the estimator S_pool (see Eq. 19, Section 2.3) whereas wgda and wfda make use of S_w (see Eq. 22, Section 2.3). Furthermore, predict-methods for these self-implemented functions are implemented. The one for GDA applies the canonical discriminant function given in Eq. 4 or Eq. 7 (see Section 2.1), the one for FDA utilises Fisher’s discriminant score with penalty (see Eq. 17, Section 2.3).

4.3 Design of the Simulation Study

We simulate the behaviour of FDA and GDA to support theoretical findings from the previous sections. For data generation, we choose fixed class means and rather change the shape of the ‘landscape’ by choosing various (even rather extreme) covariance matrices. We generate different settings for priors by varying the class probabilities, because setting priors correctly and having penalties based on priors is essential according to the theoretical findings. Further on, different settings of priors are used for estimating GDA and FDA on each of the simulated situations. With these settings of rather extreme variances and also unequal priors, we should be able to detect differences between FDA and GDA in case there were any.

In order to graphically visualise the results a two-dimensional classification problem with G = 3 classes is considered. The chosen expected values of the three classes are μ₁ = (1,1)^′, μ₂ = (4,3)^′ and μ₃ = (2,5)^′. They are selected in such a way that they differ without leading to possible perfect linear separation. We construct a covariance matrix Σ which is equal for all three classes

$$ {\Sigma} = \begin{pmatrix} 1~ & \rho \\ \rho~ & 1 \end{pmatrix} $$

(31)

while the covariance ρ corresponds to the correlation and we choose ρ ∈{− 0.9,− 0.5, − 0.1,0,0.3,0.6,0.8}. Thus, various correlation structures between variables are covered, including uncorrelated variables. For each scenario, we generate 100 training data sets with n = 150 random numbers from bivariate normal distributions with the described parameters μ₁, μ₂, μ₃ and Σ for each ρ. On the one hand, we assume equal class sizes n₁ = n₂ = n₃ = 50, and on the other hand, we generate training data sets with different class sizes, i.e. n₁ = 15, n₂ = 30 and n₃ = 105.

Table 1 contains the selected combinations of priors for the three groups. We consider equal priors in combination I as well as three situations with unequal priors in combinations II–IV. The combinations II and III cover the cases of one high prior ($\frac {1}{2}$ vs. $\frac {1}{4}$) as well as two high ones ($\frac {2}{5}$ vs. $\frac {1}{5}$). Thereby, in each instance, there are two priors of the same size. Furthermore, in combination IV, the priors of all three groups differ and they are equal to the relative group frequencies of n₁ = 15, n₂ = 30 and n₃ = 105.

Table 1 Combinations of considered priors for three classes

Consider one training data set with fixed class sizes n₁,n₂,n₃, one value of ρ, and one combination of priors. Based on this training data set and the given priors, a discriminant rule is estimated with each function (lda, gda, fda, wgda, wfda). Next, a two-dimensional grid is generated which exists of 12321 lattice points, i.e. {− 3.0,− 2.9,...,8.0}×{− 3.0,− 2.9,...,8.0}. Each grid point is classified by all five estimated discriminant rules. The classified grid points are compared pairwise and the relative number of differently classified lattice points is calculated. Overall, there are 10 function comparisons. Similarly, the remaining 99 training data sets for the contemplated combination which are based on the same ρ are processed. The relative numbers of differently classified grid points are averaged over the number of training data sets. On the basis of this relative number of differently classified grid points, the differences between the methods and the different estimators are compared. This procedure is repeated for each combination of priors and ρ.

4.4 Results of the Simulation Study

The results for equal as well as unequal class sizes are exemplarily given in Tables 2 and 3 for ρ = − 0.9 and ρ = 0. Here, 0^∗ indicates that at most two of 12321 grid points are classified differently in 100 repetitions. These small values only appear in comparisons with lda (see Tables 2 and 3, rows 1–4) and their occurrence may change when using a different operating system, hardware or R version.

Table 2 Mean relative numbers of differently classified grid points based on 100 training data sets with equal and unequal class sizes and correlation ρ = − 0.9. Further, 0^∗ indicates that at most two of 12321 grid points are classified differently

Table 3 Mean relative numbers of differently classified grid points based on 100 training data sets with equal and unequal class sizes and correlation ρ = 0. Further, 0^∗ indicates that at most two of 12321 grid points are classified differently

This numerical difference can be neglected and is probably based on the different numerical implementations of lda and our self-implemented functions. Thus, lda yields the same classification results as gda and fda (see Tables 2 and 3, rows 1 and 3) although our self-implemented function fda uses another estimator $B_{\mu _{w}}$ for the covariance matrix between groups than lda. Note that lda, gda and fda apply S_pool as an estimator for the covariance matrix Σ and the functions wgda and wfda apply S_w. Hence, in the comparisons lda vs. wgda and lda vs. wfda for ρ = − 0.9, the mean relative number of differently classified grid points is not larger than 0.0322 for equal class sizes (see Table 2, column 4) and not larger than 0.0332 for unequal class sizes (see Table 2, column 5).

Provided that equal priors and class sizes are present, all lattice points are classified into the same class by each discrimination function (see Tables 2 and 3, column 1) because the estimators S_pool and S_w are identical in this case (see Section 2.3). In all situations, when focussing on the comparisons fda vs. gda and wfda vs. wdga, the mean relative numbers of differently classified lattice points are 0 (see Tables 2 and 3, rows 6 and 9). Thus, GDA and FDA yield identical results when using the same estimator for the covariance matrix Σ. This closely resembles our theoretical result in Section 3.

We have to distinguish several cases if different estimators for the covariance matrix Σ are used:

• If we consider unequal priors, the results of the methods are not identical in general.

• If we consider equal priors and unequal numbers of observations for different classes, the results of the methods are not identical in general.

• If we consider equal priors and an equal number of observations for different classes, the results of the methods are identical.

In Tables 2 and 3, non-identical results can thus be seen for the six comparisons lda vs. wfda, lda vs. wgda, fda vs. wfda, fda vs. wgda, wfda vs. gda and gda vs. wgda.

In addition, the more the priors resemble the relative group frequencies, the smaller the mean relative number of differently classified grid points and the smaller the differences between the classification results of the distinct functions (see Tables 2 and 3, column 1 and 8). Similar results are obtained from the simulations with ρ ∈{− 0.5,− 0.1,0.3,0.6,0.8}.

Knowing that results of different methods are identical if exactly one of S_pool or S_w is used, we can focus on comparisons based on S_pool and S_w independent of the methods. Figure 1 illustrates an example of estimated hyperplanes based on one training data set with equal class sizes and ρ = 0 using the estimate S_pool (gda, fda) on the left and S_w (wgda, wfda) on the right. Each plot shows two sets of hyperplanes: one for priors $\pi _{1} = \pi _{2} = \pi _{3} = \frac {1}{3}$ (dashed) and one for priors $\pi _{1} = \frac {1}{10}$, $\pi _{2} = \frac {1}{5}$, $\pi _{3} = \frac {7}{10}$ (dotted). If we utilise the estimate S_pool and assume equal priors and class sizes, the hyperplanes are identical to those obtained with S_w (see Fig. 1, dashed).

Fig. 1

Estimated hyperplanes based on one training data set with ρ = 0, equal class sizes n₁ = n₂ = n₃ = 50 using the estimate S_pool (left) and S_w (right). Each plot shows two sets of hyperplanes: one for priors $\pi _{1} = \pi _{2} = \pi _{3} = \frac {1}{3}$ (dashed) and one for priors $\pi _{1} = \frac {1}{10}$, $\pi _{2} = \frac {1}{5}$, $\pi _{3} = \frac {7}{10}$ (dotted)

The estimated hyperplanes of estimate S_pool for unequal priors run parallel to the ones based on equal priors (see Fig. 1, left). In this instance, changing the priors changes the intercepts of the hyperplanes but not the slopes. Thus, the hyperplanes of S_pool have an intuitive behaviour by assigning a larger surface to a class with higher prior.

This is not the case if we consider S_w as we can see on the right of Fig. 1. The estimated hyperplanes based on unequal priors (dotted) have both different intercepts and slopes compared to those for equal priors (dashed). Unlike S_pool, the estimate S_w depends on the priors.

In practice, GDA and FDA yield the same results for both unequal priors and class sizes, provided the same estimator is used for the covariance matrix Σ. Thereby, the choice of an estimator for the covariance matrix between the groups $B_{\mu _{w}}$ does not affect the outcome.

5 Conclusion

We resolve the misconceptions of the similarities and differences of linear discriminant analysis based on Gaussian distribution (GDA) and Fisher’s linear discriminant analysis (FDA).

We prove that GDA and FDA are identical even if unequal priors are present (see Section 3) given an appropriate penalty in Fisher’s discriminant score is introduced (see Eq. 17, Section 2.2). We focus on the comparison of the discriminant rules of both methods, because there is no straightforward way to get posterior probabilities from an FDA for further comparisons. Without the penalty, the same results can only be obtained if we assume equal priors.

Necessarily, in applications, the estimator for the covariance matrix must be the same (see Section 4.4). Otherwise, identical results can only be obtained if equal priors and equal class sizes are given. We show that different estimators for the covariance matrix can yield different hyperplanes. Whereas, the choice of an estimator for the covariance matrix between the groups does not matter.

Appendix: Comparison for two groups and two features

Assume G = p = 2 groups and features. Hence, in FDA, the number of discriminant components is r ≤ min{p,G − 1} = min{2, 1} = 1 (see Section 2.2). We obtain at most one discriminant component $\alpha _{1} = (\alpha _{11}, \alpha _{12})^{\prime } \in \mathbb {R}^{2}$. Hereinafter, this is derived.

First, we take a closer look at the weighted covariance matrix between the groups $B_{\mu _{w}}$. In case of two classes and features, this can be rewritten as:

$$ \begin{array}{@{}rcl@{}} B_{\mu_{w}} &=& \sum\limits_{g = 1}^{2} \pi_{g} (\mu_{g} - \mu_{w}) (\mu_{g} - \mu_{w})^{\prime}\\ & = & \pi_{1} (\mu_{1} -\mu_{w}) (\mu_{1} -\mu_{w})^{\prime} + \pi_{2} (\mu_{2} - \mu_{w}) (\mu_{2} - \mu_{w})^{\prime} \\ & =& \pi_{1}(\mu_{1}\mu_{1}^{\prime} - \mu_{1}\mu_{w}^{\prime} - \mu_{w} \mu_{1}^{\prime} + \mu_{w}\mu_{w}^{\prime}) + \pi_{2} (\mu_{2} \mu_{2}^{\prime} - \mu_{2}\mu_{w}^{\prime} -\mu_{w}\mu_{2}^{\prime} +\mu_{w}\mu_{w}^{\prime})\\ & =& (\pi_{1} + \pi_{2}) \mu_{w}\mu_{w}^{\prime} - (\pi_{1}\mu_{1} +\pi_{2} \mu_{2})\mu_{w}^{\prime} - \mu_{w}(\pi_{1} \mu_{1} + \pi_{2} \mu_{2})^{\prime} + \pi_{1}\mu_{1}\mu_{1}^{\prime} + \pi_{2} \mu_{2} \mu_{2}^{\prime} \\ & =& \mu_{w}\mu_{w}^{\prime} - \mu_{w}\mu_{w}^{\prime} - (\pi_{1} \mu_{1} + \pi_{2}\mu_{2})(\pi_{1} \mu_{1} + \pi_{2} \mu_{2})^{\prime} + \pi_{1} \mu_{1}\mu_{1}^{\prime} + \pi_{2} \mu_{2} \mu_{2}^{\prime} \\ & =& \pi_{1} \mu_{1}\mu_{1}^{\prime} + \pi_{2} \mu_{2} \mu_{2}^{\prime} - {\pi_{1}^{2}} \mu_{1} \mu_{1}^{\prime} - \pi_{1} \pi_{2} \mu_{1} \mu_{2}^{\prime} - \pi_{1} \pi_{2} \mu_{2} \mu_{1}^{\prime} - {\pi_{2}^{2}} \mu_{2} \mu_{2}^{\prime}\\ & =& (1 - \pi_{1}) \pi_{1} \mu_{1}\mu_{1}^{\prime} + (1 - \pi_{2}) \pi_{2} \mu_{2} \mu_{2}^{\prime} - \pi_{1} \pi_{2} \mu_{1} \mu_{2}^{\prime} - \pi_{1} \pi_{2} \mu_{2} \mu_{1}^{\prime} \\ & =& \pi_{1} \pi_{2} \mu_{1}\mu_{1}^{\prime}- \pi_{1} \pi_{2} \mu_{1} \mu_{2}^{\prime} - \pi_{1} \pi_{2} \mu_{2} \mu_{1}^{\prime} + \pi_{1} \pi_{2} \mu_{2} \mu_{2}^{\prime} = \pi_{1} \pi_{2} (\mu_{1} - \mu_{2}) (\mu_{1} - \mu_{2})^{\prime} \\ & =& \pi_{1} \pi_{2} (\mu_{2} - \mu_{1}) (\mu_{2} - \mu_{1})^{\prime}. \end{array} $$

As previously mentioned (see Section 2.2), the optimisation problem in Eq. 11 is solved by the eigenvector v₁ with the corresponding highest eigenvalue λ₁ of the matrix ${\Sigma }^{-\frac {1}{2}}B_{\mu _{w}} {\Sigma }^{-\frac {1}{2}} = \pi _{1} \pi _{2} {\Sigma }^{-\frac {1}{2}} (\mu _{2} - \mu _{1}) (\mu _{2} - \mu _{1})^{\prime } {\Sigma }^{-\frac {1}{2}}$. Therefore, the biggest eigenvalue λ₁ and the corresponding normalised eigenvector v₁ are determined.

The number of eigenvalues unequal zero of a matrix is equal to the rank of this matrix. So, we have:

$$ \begin{array}{@{}rcl@{}} \text{rk}\left( {\Sigma}^{-\frac{1}{2}} B_{\mu_{w}} {\Sigma}^{-\frac{1}{2}} \right) & = &\text{rk}\left( \pi_{1} \pi_{2} {\Sigma}^{-\frac{1}{2}} (\mu_{2} - \mu_{1}) (\mu_{2} - \mu_{1})^{\prime} {\Sigma}^{-\frac{1}{2}}\right) \\ & \leq & \min \left\{ \text{rk}({\Sigma}^{-\frac{1}{2}}), \text{rk}(\pi_{1} \pi_{2} (\mu_{2} - \mu_{1})), \text{rk}((\mu_{2} - \mu_{1})^{\prime}), \text{rk}({\Sigma}^{-\frac{1}{2}}) \right\} = 1 \end{array} $$

because rk(π₁π₂(μ₂ − μ₁)) = 1 as well as rk((μ₂ − μ₁)^′) = 1 . The rank of ${\Sigma }^{-\frac {1}{2}}B_{\mu _{w}} {\Sigma }^{-\frac {1}{2}}$ is 1 or 0. Whereas the zero matrix is the only matrix which has rank 0, it applies $\text {rk}\left ({\Sigma }^{-\frac {1}{2}} B_{\mu _{w}} {\Sigma }^{-\frac {1}{2}} \right ) = 0$ if and only if $(\mu _{2} - \mu _{1}) (\mu _{2} - \mu _{1})^{\prime } = 0 \in \mathbb {R}^{2 \times 2}$ thus $\mu _{2} - \mu _{1} = 0 \in \mathbb {R}^{2}$. This contradicts the assumption of different expected values of the groups (see Section 2).

The trace of a matrix is equal to the sum of its eigenvalues. So, we reveal the eigenvalue

$$ \begin{array}{@{}rcl@{}} \lambda_{1} &=& \text{tr}\left( {\Sigma}^{-\frac{1}{2}} B_{\mu_{w}} {\Sigma}^{-\frac{1}{2}} \right) = \text{tr}\left( {\Sigma}^{-\frac{1}{2}} \pi_{1} \pi_{2}(\mu_{2} - \mu_{1}) (\mu_{2} - \mu_{1})^{\prime} {\Sigma}^{-\frac{1}{2}} \right) \\ &=& \text{tr}\left( \pi_{1} \pi_{2}(\mu_{2} - \mu_{1})^{\prime} {\Sigma}^{-1} (\mu_{2} - \mu_{1})\right) = \pi_{1} \pi_{2}(\mu_{2} - \mu_{1})^{\prime} {\Sigma}^{-1} (\mu_{2} - \mu_{1}). \end{array} $$

Since the priors are non-negative and the covariance matrix Σ is positive semidefinite λ₁ > 0 is the biggest eigenvalue of ${\Sigma }^{-\frac {1}{2}} B_{\mu _{w}} {\Sigma }^{-\frac {1}{2}}$. Therefore, the corresponding eigenvector is $v_{1} = \frac {{\Sigma }^{-\frac {1}{2}} (\mu _{2} - \mu _{1})}{((\mu _{2} - \mu _{1})^{\prime } {\Sigma }^{-1} (\mu _{2} - \mu _{1}))^{\frac {1}{2}}}$. It satisfies the two conditions

$$ \begin{array}{@{}rcl@{}} {\Sigma}^{-\frac{1}{2}} B_{\mu_{w}} {\Sigma}^{-\frac{1}{2}}v_{1} &=& {\Sigma}^{-\frac{1}{2}} \pi_{1}\pi_{2}(\mu_{2} - \mu_{1})(\mu_{2}-\mu_{1})^{\prime} {\Sigma}^{-\frac{1}{2}} \frac{{\Sigma}^{-\frac{1}{2}} (\mu_{2} - \mu_{1})}{((\mu_{2} - \mu_{1})^{\prime} {\Sigma}^{-1} (\mu_{2} - \mu_{1}))^{\frac{1}{2}}} \\ &=& \frac{{\Sigma}^{-\frac{1}{2}}(\mu_{2} - \mu_{1}) \pi_{1}\pi_{2} (\mu_{2}-\mu_{1})^{\prime} {\Sigma}^{-1} (\mu_{2} - \mu_{1})}{((\mu_{2} - \mu_{1})^{\prime} {\Sigma}^{-1} (\mu_{2} - \mu_{1}))^{\frac{1}{2}}} \\ &=& \frac{{\Sigma}^{-\frac{1}{2}}(\mu_{2} - \mu_{1}) \lambda_{1}}{((\mu_{2} - \mu_{1})^{\prime} {\Sigma}^{-1} (\mu_{2} - \mu_{1}))^{\frac{1}{2}}} = \lambda_{1} v_{1} \end{array} $$

and

$$ \begin{array}{@{}rcl@{}} v_{1}^{\prime}v_{1} &=& \left( \frac{{\Sigma}^{-\frac{1}{2}} (\mu_{2} - \mu_{1})}{((\mu_{2} - \mu_{1})^{\prime} {\Sigma}^{-1} (\mu_{2} - \mu_{1}))^{\frac{1}{2}}} \right)^{\prime} \frac{{\Sigma}^{-\frac{1}{2}} (\mu_{2} - \mu_{1})}{((\mu_{2} - \mu_{1})^{\prime} {\Sigma}^{-1} (\mu_{2} - \mu_{1}))^{\frac{1}{2}}} \\ &=& \frac{(\mu_{2} - \mu_{1})^{\prime} {\Sigma}^{-1}(\mu_{2} - \mu_{1})}{(\mu_{2} - \mu_{1})^{\prime} {\Sigma}^{-1} (\mu_{2} - \mu_{1})} =1. \end{array} $$

Hence, the discriminant component which is the eigenvector of the matrix ${\Sigma }^{-1}B_{\mu _{w}}$ is constituted by:

$$ \begin{array}{@{}rcl@{}} \alpha_{1} = {\Sigma}^{-\frac{1}{2}} v_{1} = {\Sigma}^{-\frac{1}{2}}\frac{{\Sigma}^{-\frac{1}{2}} (\mu_{2} - \mu_{1})}{((\mu_{1} - \mu_{2})^{\prime} {\Sigma}^{-1} (\mu_{2} - \mu_{1}))^{\frac{1}{2}} } = \frac{{\Sigma}^{-1} (\mu_{2} - \mu_{1})}{((\mu_{1} - \mu_{2})^{\prime} {\Sigma}^{-1} (\mu_{2} - \mu_{1}))^{\frac{1}{2}} }. \end{array} $$

The discriminant component α₁ only depends on the expected values of the groups μ₁, μ₂ and the covariance matrix Σ or rather its inverse. Notice, α₁ is independent from the covariance matrix between the groups $B_{\mu _{w}}$.

In order to determine the hyperplane of Fisher’s discriminant rule, the scores of the two groups D₁ and D₂ (see Eq. 17, Section 2.2) are equated:

$$ \begin{array}{@{}rcl@{}} &\qquad& D_{1}(x) \stackrel{!}{=} D_{2} (x) \\ &\Leftrightarrow& (\alpha_{1}^{\prime}(x - \mu_{1}))^{2} - 2\log(\pi_{1}) \stackrel{!}{=} (\alpha_{1}^{\prime}(x - \mu_{2}))^{2} - 2\log(\pi_{2}) \\ &\Leftrightarrow& -2(\log(\pi_{1})-\log(\pi_{2})) \stackrel{!}{=} (\alpha_{1}^{\prime}(x - \mu_{2}))^{2} - (\alpha_{1}^{\prime}(x - \mu_{1}))^{2} \\ &\Leftrightarrow& -2(\log(\pi_{1})-\log(\pi_{2})) \stackrel{!}{=} (\alpha_{1}^{\prime}(x - \mu_{2}) + \alpha_{1}^{\prime}(x - \mu_{1}))(\alpha_{1}^{\prime}(x - \mu_{2}) -\alpha_{1}^{\prime}(x - \mu_{1})) \\ &\Leftrightarrow& -2(\log(\pi_{1})-\log(\pi_{2})) \stackrel{!}{=} \alpha_{1}^{\prime}(x - \mu_{2} + x - \mu_{1})\alpha_{1}^{\prime}(x - \mu_{2} - x + \mu_{1}) \\ &\Leftrightarrow& -2(\log(\pi_{1})-\log(\pi_{2})) \stackrel{!}{=} \alpha_{1}^{\prime}(2x - \mu_{1} - \mu_{2})\alpha_{1}^{\prime}(\mu_{1} -\mu_ 2) \\ &\Leftrightarrow& -2(\log(\pi_{1})-\log(\pi_{2})) \stackrel{!}{=} -2\alpha_{1}^{\prime}\left( \frac{\mu_{1} + \mu_{2}}{2} - x\right)\alpha_{1}^{\prime}(\mu_{1} - \mu_{2}) \\ &\Leftrightarrow& \log(\pi_{1})-\log(\pi_{2}) \stackrel{!}{=} \alpha_{1}^{\prime}(\mu - x)\alpha_{1}^{\prime}(\mu_{1} - \mu_{2}) \\ &\Leftrightarrow& \frac{\log(\pi_{1})-\log(\pi_{2})}{\alpha_{1}^{\prime}(\mu_{1} - \mu_{2})} \stackrel{!}{=} \alpha_{1}^{\prime}\mu - \alpha_{1}^{\prime}x \\ &\Leftrightarrow& -\alpha_{1}^{\prime}\mu+ \frac{\log(\pi_{1})-\log(\pi_{2})}{\alpha_{1}^{\prime}(\mu_{1} - \mu_{2})} \stackrel{!}{=} -\alpha_{1}^{\prime}x = -\alpha_{11}x_{1} - \alpha_{12}x_{2} \\ &\Leftrightarrow& \alpha_{11}x_{1} + \alpha_{12}x_{2} \stackrel{!}{=} \alpha_{1}^{\prime}\mu -\frac{\log(\pi_{1})-\log(\pi_{2})}{\alpha_{1}^{\prime}(\mu_{1} - \mu_{2})} \\ &\Leftrightarrow& x_{2} \stackrel{!}{=} - \frac{\alpha_{11}}{\alpha_{12}} x_{1} + \frac{\alpha_{1}^{\prime}\mu}{\alpha_{12}} + \frac{\log(\pi_{1}) - \log(\pi_{2})}{\alpha_{12} (\alpha_{1}^{\prime}(\mu_{2} - \mu_{1}))} \\ &\Leftrightarrow& x_{2} \stackrel{!}{=} -\frac{\alpha_{11}}{\alpha_{12}}x_{1} + \frac{\alpha_{1}^{\prime}\mu}{\alpha_{12}} +\frac{\log(\pi_{1}) - \log(\pi_{2})}{\alpha_{12} ((\mu_{2} - \mu_{1})^{\prime}{\Sigma}^{-1}(\mu_{2} - \mu_{1}))^{\frac{1}{2}}}. \end{array} $$

Before we equate the canonical discriminant scores of group 1 and 2 those will rearranged.

$$ \begin{array}{@{}rcl@{}} L_{g}(x) &=& -\frac{1}{2} (x - \mu_{g})^{\prime}{\Sigma}^{-1}(x - \mu_{g}) + \log(\pi_{g}) \\ &=& -\frac{1}{2}((x - \mu_{g})^{\prime}{\Sigma}^{-1} x - (x - \mu_{g})^{\prime}{\Sigma}^{-1}\mu_{g}) + \log(\pi_{g}) \\ &=&-\frac{1}{2}(x^{\prime} {\Sigma}^{-1} x - \mu_{g}^{\prime} {\Sigma}^{-1} x - x^{\prime}{\Sigma}^{-1}\mu_{g} + \mu_{g}^{\prime} {\Sigma}^{-1}\mu_{g}) + \log(\pi_{g}) \\ &=& -\frac{1}{2}(x^{\prime} {\Sigma}^{-1} x - 2 \mu_{g}^{\prime}{\Sigma}^{-1} x + \mu_{g}^{\prime} {\Sigma}^{-1}\mu_{g}) + \log(\pi_{g}) \\ &=& -\frac{1}{2}x^{\prime} {\Sigma}^{-1} x + \mu_{g}^{\prime}{\Sigma}^{-1} x - \frac{1}{2} \mu_{g}^{\prime} {\Sigma}^{-1}\mu_{g} + \log(\pi_{g}) \end{array} $$

The term $-\frac {1}{2}x^{\prime } {\Sigma }^{-1} x$ is the same for all groups g = 1,...,G and can be neglected. Thus, we obtain

$$ \begin{array}{@{}rcl@{}} \tilde{L}_{g}(x) &=& \mu_{g}^{\prime}{\Sigma}^{-1} x - \frac{1}{2} \mu_{g}^{\prime} {\Sigma}^{-1}\mu_{g} + \log(\pi_{g})\\ & = & ({\Sigma}^{-1}\mu_{g})^{\prime}x - \frac{1}{2} \mu_{g}^{\prime} {\Sigma}^{-1}\mu_{g} + \log(\pi_{g}) =: b_{g}^{\prime}x + c_{g} \end{array} $$

with b_g := (Σ^− 1μ_g)^′ and $c_{g} := - \frac {1}{2} \mu _{g}^{\prime } {\Sigma }^{-1}\mu _{g} + \log (\pi _{g})$. The hyperplane of the discriminant rule of GDA results by:

$$ \begin{array}{@{}rcl@{}} &\quad& \tilde{L}_{1}(x) = b_{1}^{\prime}x + c_{1} \stackrel{!}{=} b_{2}^{\prime}x + c_{2} = \tilde{L}_{2}(x) \\ &\Leftrightarrow~& (b_{2} - b_{1})^{\prime}x \stackrel{!}{=} c_{1} - c_{2} \\ &\Leftrightarrow& ({\Sigma}^{-1}\mu_{2} - {\Sigma}^{-1}\mu_{1})^{\prime}x \stackrel{!}{=} -\frac{1}{2}\mu_{1}^{\prime}{\Sigma}^{-1}\mu_{1} + \log(\pi_{1}) + \frac{1}{2}\mu_{2}^{\prime}{\Sigma}^{-1}\mu_{2} - \log(\pi_{2}) \\ &\Leftrightarrow& {\Sigma}^{-1}(\mu_{2} - \mu_{1})^{\prime}x \stackrel{!}{=} -\frac{1}{2}(\mu_{1}^{\prime}{\Sigma}^{-1}\mu_{1} - \mu_{2}^{\prime}{\Sigma}^{-1}\mu_{2}) + \log(\pi_{1}) - \log(\pi_{2}) \\ &\Leftrightarrow& {\Sigma}^{-1}(\mu_{2} - \mu_{1})^{\prime}x \stackrel{!}{=} -\frac{1}{2}(\mu_{1}^{\prime}{\Sigma}^{-1}\mu_{1} +\mu_{1}^{\prime}{\Sigma}^{-1}\mu_{2} -\mu_{2}^{\prime}{\Sigma}^{-1}\mu_{1} - \mu_{2}^{\prime}{\Sigma}^{-1}\mu_{2})\\ &&+ \log \left( \frac{\pi_{1}}{\pi_{2}} \right) \\ &\Leftrightarrow& {\Sigma}^{-1}(\mu_{2} - \mu_{1})^{\prime}x \stackrel{!}{=} -\frac{1}{2}(\mu_{1}^{\prime}{\Sigma}^{-1}(\mu_{1} + \mu_{2}) -\mu_{2}^{\prime}{\Sigma}^{-1}(\mu_{1} + \mu_{2}))\\ &&+ \log(\pi_{1}) - \log(\pi_{2}) \\ &\Leftrightarrow& {\Sigma}^{-1}(\mu_{2} - \mu_{1})^{\prime}x \stackrel{!}{=} -\frac{1}{2}(\mu_{1}^{\prime} -\mu_{2}^{\prime}){\Sigma}^{-1}(\mu_{1} + \mu_{2}) + \log(\pi_{1}) - \log(\pi_{2}) \\ &\Leftrightarrow& {\Sigma}^{-1}(\mu_{2} - \mu_{1})^{\prime}x \stackrel{!}{=} (\mu_{2} - \mu_{1})^{\prime} {\Sigma}^{-1} \left( \frac{\mu_{1} + \mu_{2}}{2} \right)+ \log(\pi_{1}) - \log(\pi_{2}) \\ &\Leftrightarrow& \alpha_{1}^{\prime}x \stackrel{!}{=} \alpha_{1}^{\prime}\mu+\frac{\log(\pi_{1}) - \log(\pi_{2})}{((\mu_{2} - \mu_{1})^{\prime}{\Sigma}^{-1}(\mu_{2} - \mu_{1}))^{\frac{1}{2}}} \\ &\Leftrightarrow& x_{2} \stackrel{!}{=} -\frac{\alpha_{11}}{\alpha_{12}}x_{1} + \frac{\alpha_{1}^{\prime}\mu}{\alpha_{12}} +\frac{\log(\pi_{1}) - \log(\pi_{2})}{\alpha_{12} ((\mu_{2} - \mu_{1})^{\prime}{\Sigma}^{-1}(\mu_{2} - \mu_{1}))^{\frac{1}{2}}}. \end{array} $$

In case of two groups and features, GDA and FDA have the same hyperplane:

$$ h(x_{1}) := -\frac{\alpha_{11}}{\alpha_{12}}x_{1} + \frac{\alpha_{1}^{\prime}\mu}{\alpha_{12}} +\frac{\log(\pi_{1}) - \log(\pi_{2})}{\alpha_{12} ((\mu_{2} - \mu_{1})^{\prime}{\Sigma}^{-1}(\mu_{2} - \mu_{1}))^{\frac{1}{2}}}. $$

Thus, GDA and FDA yield the same results even for unequal priors π₁ and π₂.