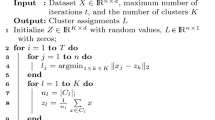A Modified k-Means Clustering Procedure for Obtaining a Cardinality-Constrained Centroid Matrix

Abstract

k-means clustering is a well-known procedure for classifying multivariate observations. The resulting centroid matrix of clusters by variables is noted for interpreting which variables characterize clusters. However, between-clusters differences are not always clearly captured in the centroid matrix. We address this problem by proposing a new procedure for obtaining a centroid matrix, so that it has a number of exactly zero elements. This allows easy interpretation of the matrix, as we may focus on only the nonzero centroids. The development of an iterative algorithm for the constrained minimization is described. A cardinality selection procedure for identifying the optimal cardinality is presented, as well as a modified version of the proposed procedure, in which some restrictions are imposed on the positions of nonzero elements. The behaviors of our proposed procedure were evaluated in simulation studies and are illustrated with three real data examples, which demonstrate that the performances of the procedure is promising.

1 Introduction

k-means clustering is one of the most popular procedures for classifying the rows of an observations × variables data matrix into a small number of clusters (Aggarwal and Reddy 2013). The k-means clustering procedure is widely used for classification purposes and recent advances in its development can be found in Steinley (2006). Various extensions and related procedures of the k-means clustering exist, fuzzy versions (Miyamoto et al. 2008), probabilistic models (Bock 1996), and variable selection procedures (Brusco and Cradit 2001), for example. Applications of k-means clustering can be found in various fields of sciences, such as biology (Jetti et al. 2014), environmental science (Dalton et al. 2016), agricultural science (Hyland et al. 2016), engineering (Peng et al. 2013), applied psychology (Cortina and Wasti 2005; Kuerbis et al. 2014), and experimental psychology (Schloss et al. 2015; Alsius et al. 2016; Slobodenyuk et al. 2015).

For the n-observations × p-variable data matrix X, k-means clustering is formulated as minimizing the least squares loss function

$$ f(\mathbf{M}, \mathbf{Y}) = \sum\limits_{i,l}m_{il}||\mathbf{x}_{(i)}^{\prime} - \mathbf{y}_{l}||^{2} = ||\mathbf{X} - \mathbf{M}\mathbf{Y}^{\prime}||^{2} $$

(1)

over M and Y. Here, M = {m_il}(i = 1, ⋯ ,n;l = 1, ⋯ ,k) is an n-observations × k-clusters binary membership matrix and Y = {y_jl}(j = 1, ⋯ ,p) is a p-variables × k-cluster centroid matrix. x_(i) and y_l denote the i-th row vector and l-th column vector of X and Y, respectively. The operator $||\mathbf {X}||^{2} = {\text {tr}(\mathbf {X}^{\prime }\mathbf {X})}$ denotes the sum of the squared elements in X. The minimization of Eq. 1 can be attained by using the iterative algorithm proposed by MacQueen (1967), in which M and Y are alternately updated.

The resulting membership matrix M shows how observations are classified into clusters. In the interpretation of what variables characterize the clusters, the centroid matrix Y plays a key role. Let us illustrate such an interpretation process with Adachi’s (2006) 13 (jobs) × 12 (attributes) data matrix X called job impression data in this article, which describes the extent to which the jobs are described by the impression attributes. We applied k-means clustering to the column-centered version of the data matrix, with the number of clusters set to 4. Table 1 shows the resulting centroid matrix. Its j-th row equals the average vector of the observations classified into the l-th cluster and represents the variables that characterize the l-th cluster. For example, the third cluster (C3) is characterized by the impressions of “powerful,” “strong,” and “fast,” as the elements for them in C3 show larger values than those in the other clusters, where police, journalist, sailor, and athlete are classified into C3. The within-column and between-column contrasts in the centroids help to capture which variables feature clusters, although these contrasts are not always observed clearly in the centroid matrix.

Table 1 Estimated centroid matrix by k-means with four clusters to job impression data

A typical strategy to clarify the contrasts is to ignore the elements close to zeros (those less than 0.4 in absolute value, for example) in the centroid matrix and regard them as zeros. For example, we can consider that the first cluster (C1) is characterized by the “useful,” “stubborn,” and “busy” impression, by ignoring the elements having absolute values less than 0.4. This strategy is not desirable, however, because which elements can be ignored depends on the users’ decisions. Such decisions are both subjective and potentially erroneous, because, in fact, they weaken the initial fit achieved by the centroid matrix in an intuitive manner.

In this article, considering the above problem of the interpretability of the resulting centroid matrix, we propose a new clustering procedure that produces an easily interpreted centroid matrix. We call this procedure cardinality-constrained k-means clustering (CCKM). In CCKM, a number of the elements in the centroid matrix Y are constrained to be zeros, where Card(Y) for the cardinality of Y, i.e., its number of nonzero elements. The constraint is expressed as

$$ Card(\mathbf{Y}) = c $$

(2)

with c a pre-specified integer. That is, our proposed CCKM is formulated as minimizing Eq. 1 subject to Eq. 2. Here, it should be noted that it is unknown which elements in Y are zero/nonzero. They are also estimated optimally in CCKM. This provides the centroid matrix with pk − c zero elements, which facilitates the interpretation of Y, as we may ignore the zero elements in Y. Here, it is noteworthy that no subjective decision is involved in what elements are ignored; as described above, which elements are to be zeros is estimated optimally.

The classic work Gordon (1973) firstly introduced constrained clustering procedure, in which a priori information as to clusters are incorporated to clustering. Such a priori information is thoroughly discussed in DeSarbo and Mahajan (1984); some pairs of objects are constrained to be in the same or different cluster, for example. These constraints are helpful for obtaining interpretable and valid clusters. The related works can be found in Steinley and Hubert (2008) and Basu et al. (2008). These procedures require clearly defined information as to cluster structures although is often unavailable before applying clustering in the case of exploratory data analysis. The proposed procedure in this paper does not require such external information with combination of cardinality selection procedure introduced in Section 3.

The proposed procedure is also related to variable selection technique in clustering (Brusco and Cradit 2001). These procedures are designed to obtain appropriate cluster structure even if some musking variables (Fowlkes and Mallows 1983) exist, which often spoils clustering result. In order to accomplish this, variable selection procedure specifies the set of variables which manifest cluster structure by various strategies, which are detailed and compared in Steinley and Brusco (2008). CCKM differs from the variable selection procedures in that it is aimed to improve interpretability of cluster centroids and therefore, the set of variable corresponds to clusters are not always identical.

The remaining parts of this paper are organized as follows. In the following section, we present the algorithm for minimizing Eq. 1 under the cardinality constraint (2). In Section 3, a cardinality selection procedure is proposed, in which the best c is chosen with an information criterion. In Section 4, a modified version of CCKM is presented, in which cardinality constraints are imposed row/column-wise, although Eq. 2 is imposed matrix-wise. Two numerical simulations and three real data examples are presented in Sections 5 and 6, respectively, in order to assess and illustrate the performances of the proposed procedure. Section 7 is devoted to a general discussion.

1.1 Related Method: Factor Rotation

Interpretability of solutions is of importance also in the multivariate analysis procedures other than clustering. Factor rotation is a well-known technique to obtain interpretable solutions in factor analysis (FA), in which its initial solution is transformed into more interpretable one of simple structure (Browne 2001). It is based on the rotational indeterminacy of the FA solution, which allows a factor loading matrix be transformed in a post hoc manner. Varimax rotation (Kaiser 1974), Oblimin rotation (Harman 1976), and Promax rotation (Hendrickson and White 1964) are known as common procedures for factor rotation. More generally, rotation can be applied to some other multivariate analysis techniques, not limited for factor analysis; Yamashita (2012) and Satomura and Adachi (2013) proved that solutions can be rotated in canonical correlation analysis.

In clustering, however, such post hoc transformations of solutions are not feasible. We therefore propose CCKM for improving the interpretability of solutions in clustering, and it is surely beneficial for practical users. Also, as a special case of CCKM, we propose RC-CCKM to produce the centroid matrix having a simple structure, by means of restricting the row/column cardinality of the centroid matrix. Such a structure is desired also in FA (Thurstone 1947; Ullman 2006).

2 Algorithm

The optimization algorithm for CCKM is outlined in Section 2.1. It is composed of two steps called the M- and Y-steps, which are iteratively alternated until convergence is reached. These steps are described in detail in Section 2.2.

2.1 Outline: Whole Algorithm

Our proposed CCKM is formulated as

$$ minimize\ f(\mathbf{M},\mathbf{Y}) = ||\mathbf{X} - \mathbf{M}\mathbf{Y}^{\prime}||^{2}\ over\ \mathbf{M}\ and\ \mathbf{Y} $$

(3)

subject to the cardinality constraint (2) and the membership constraint imposed on M such that

$$ m_{il} \in \{0,1\}\ and\ \sum\limits_{l}m_{il}=1. $$

(4)

Two parameter matrices are alternately updated in the M- and Y-steps, respectively, starting from multiple sets of initial values in order to avoid accepting a local minimum as a final solution. In each step, Eq. 1 is minimized over M or Y with the other parameter matrix kept fixed. The CCKM algorithm is thus summarized as follows.

Step 1.:

Set t = 0.

Step 2.:

Set initial values for M and Y.

Step 3.:

(M-step) Update M to that which minimizes f(M,Y) subject to Eq. 4 with Y fixed.

Step 4.:

(Y-step) Update Y to that which minimizes f(M,Y) subject to Eq. 2 with M fixed.

Step 5.:

If the current M has an empty column filled with zeros, return to Step 2.

Step 6.:

Increase t by one and go to Step 7, if the decrease in the Eq. 1 value from the previous round is less than 1.0 × 10^− 7; otherwise, return to Step 3.

Step 7.:

Update $\hat {\mathbf {M}}$ and $\hat {\mathbf {Y}}$ by the current M and Y if $f(\hat {\mathbf {M}}, \hat {\mathbf {Y}}) > f(\mathbf {M}, \mathbf {Y})$ or t = 1.

Step 8.:

If t = t_max, accept $\hat {\mathbf {M}}$ and $\hat {\mathbf {Y}}$ as the final solution; otherwise, return to Step 2.

The purpose of Step 5 is to avoid a solution with an empty cluster to which no observations belong. In order to avoid accepting a local minimum, Steps 2 to 6 are repeated t_max times starting from different initial values. Among the resulting multiple solutions, that with the lowest (1) value is selected as the optimal solution. The update formulas used in the M- and Y-steps are presented in the following section.

2.2 Optimization in M-Step and Y-Step

For the M-step, the corresponding step in the k-means clustering (MacQueen 1967) can be used: for fixed Y, the optimal M = {m_il} minimizing Eq. 1 is given by

$$ \begin{array}{@{}rcl@{}} m_{il}= \left\{\begin{array}{lll} 1\ \ (l = \underset{{l}}{\text{arg min }} f(\mathbf{M}, \mathbf{Y}))\\ 0\ \ (otherwise) \end{array}\right., \end{array} $$

(5)

for i = 1, ⋯ ,n.

The problem in the Y-step cannot be solved straightforwardly and we therefore need a trick. As such a one, we use the fact that Eq. 1 can be decomposed as

$$ f(\mathbf{M}, \mathbf{Y}) = ||\mathbf{X} - \mathbf{MA}^{\prime}||^{2} + ||\textbf{D}^{1/2}(\textbf{A} - \mathbf{Y})||^{2} . $$

(6)

Here, D = diag{d₁₁, ⋯ ,d_ll, ⋯ ,d_kk} denotes the k × k diagonal matrix with d_ll the number of the observations classified into the l-th cluster (l = 1, ⋯ ,k), while A is defined as

$$ \textbf{A} = \mathbf{X}^{\prime}\mathbf{M}(\mathbf{M}^{\prime}\mathbf{M})^{-1}, $$

(7)

the l-th column of which contains the averages of the observation in the l-th cluster. The identity in Eq. 6 can be proved as follows. Equation 1 can be rewritten as

$$ \begin{array}{@{}rcl@{}} f(\mathbf{M}, \mathbf{Y}) &=& ||\mathbf{X} - \mathbf{M}\mathbf{Y}^{\prime}||^{2} \\ &=& ||\mathbf{X} - \mathbf{MA}^{\prime} + \mathbf{MA}^{\prime} - \mathbf{M}\mathbf{Y}^{\prime}||^{2}\\ &=& ||\mathbf{X} - \mathbf{MA}^{\prime}||^{2} + ||\textbf{D}^{1/2}(\textbf{A} - \mathbf{Y})||^{2} - {\text{tr}\{(\mathbf{X} - \mathbf{MA}^{\prime})^{\prime}(\mathbf{MA}^{\prime} - \mathbf{M}\mathbf{Y}^{\prime})\}} \end{array} $$

(8)

with its last term vanishing as

$$ \begin{array}{@{}rcl@{}} & & {\text{tr}\{(\mathbf{X} - \mathbf{MA}^{\prime})^{\prime}(\mathbf{MA}^{\prime} - \mathbf{M}\mathbf{Y}^{\prime})\}} \\ &=& {\text{tr}\{\mathbf{X}^{\prime}\mathbf{M}(\mathbf{M}^{\prime}\mathbf{M})^{-1}\mathbf{M}^{\prime}\mathbf{X}\} - \text{tr}\{\mathbf{X}^{\prime}\mathbf{M}(\mathbf{M}^{\prime}\mathbf{M})^{-1}\mathbf{M}^{\prime}\mathbf{X}\} - \text{tr}(\mathbf{X}^{\prime}\mathbf{M}^{\prime}\mathbf{M}) + \text{tr}(\mathbf{X}^{\prime}\mathbf{M}^{\prime}\mathbf{M})}\\ &=& 0 . \end{array} $$

(9)

In the right-hand side of Eq. 6, only g(Y) = ||D^1/2(A −Y)||² is relevant to Y. Thus, our task is to minimize g(Y) subject to Eq. 2. The minimum can be found using the fact that g(Y) satisfies the following identity and inequality:

$$ g(\mathbf{Y}) = \sum\limits_{(j,l)\in Z}d_{ll}^{1/2}a_{jl}^{2} + \sum\limits_{(j,l)\in Z^{\bot}}d_{ll}^{1/2}(a_{jl} - y_{jl})^{2} \geq \sum\limits_{(j,l)\in Z}d_{ll}^{1/2}a_{jl}^{2}, $$

(10)

where Z denotes the set of pk − c pairs (j,l)s for the elements y_jls to be zero, while Z^⊥ is the complement of Z. The inequality in Eq. 10 shows that g(Y) attains its lower limit ${\sum }_{(j,l)\in Z}d_{ll}^{1/2}a_{jl}^{2}$ when the elements y_jls in the second term in Eq. 10 is equal to zero, that is, when the y_jls with (j,l) ∈ Z^⊥ is set equal to zero. Further, the limit ${\sum }_{(j,l)\in Z}d_{ll}^{1/2}a_{jl}^{2}$ is minimal when Z contains the indices for the pk − c smallest $a_{jl}^{2}$s among all squared elements in A. Therefore, the optimal Y is obtained as

$$ y_{jl} = \left\{\begin{array}{ll} 0\ \ (\textit{iff}\ a_{jl}^{2} \leq a_{[pk-c]}^{2})\\ a_{jl}\ \ (otherwise) \end{array}\right. $$

(11)

for l = 1, ⋯ ,k and j = 1, ⋯ ,p, where $a_{[pk-c]}^{2}$ denotes the (pk − c)-th smallest value among all $a_{jl}^{2}s$.

Equations 5 and 11 are used for the updates in M- and Y-steps, respectively. They guarantee the monotonic decrement in the the f(M,Y) value. In the following simulation studies and real data examples, we used 300 different initial values for M and Y; i.e., t_max = 300.

3 Cardinality Selection Based on Information Criteria

In the CCKM algorithm, the cardinality of centroid matrix Y has to be set to a positive integer c, as in Eq. 2. In this article, the minimum and maximum of c, c_min, c_max, are defined as

$$ c_{min} = p,\ \ c_{max} = pk. $$

(12)

It should be noted that Y has p non-zero elements when Y has a perfect cluster structure; i.e., each variable is associated with only one cluster. The selection of the number of non-zero elements in Y can be viewed as a model selection problem, since the selection partially specifies the model part of CCKM, $\mathbf {M}\mathbf {Y}^{\prime }$, fitted to the given data matrix X. Thus, information criteria, such as Akaike information criterion (AIC) and Bayesian information criterion (BIC), for the model selection problem can be suitable for determining c, which directly constrains the cardinality of the model fitted to the dataset. In this study, we propose using AIC and BIC to select the “best” c among the interval [c_min,c_max].

Let E = {e_ij} be the matrix of errors defined as $\mathbf {E} = \mathbf {X}-\mathbf {M}\mathbf {Y}^{\prime }$ and assume that data matrix X is modeled as $\mathbf {X} = \mathbf {M}\mathbf {Y}^{\prime }+\mathbf {E}$ with e_ij distributed independently and identically according to N(0,σ²) for all i and j. Here, N(0,σ²) represents normal distribution with its mean zero and variance σ². Then, it can be shown that the least squares and maximum likelihood estimates for CCKM are equivalent. Under the above assumption, the log-likelihood function to be maximized in ML estimation is expressed as

$$ l(\mathbf{M},\mathbf{Y}) = -\frac{np}{2}\log||\mathbf{X} - \mathbf{M}\mathbf{Y}^{\prime}||^{2}. $$

(13)

Its maximization is equivalent to minimizing least squares function (1). For a positive integer c, the maximum of l(M,Y) is attained as

$$ l(\mathbf{M},\mathbf{Y}) \leq -\frac{np}{2}\log f_{min}(c). $$

(14)

where f_min(c) denotes the attained function value of Eq. 1. Using Eq. 14, the information criteria AIC(c) and BIC(c) for a specific c are defined as

$$ \begin{array}{@{}rcl@{}} AIC(c) &=& np\times\log f_{min}(c) + 2\nu(c), \end{array} $$

(15)

$$ \begin{array}{@{}rcl@{}} BIC(c) &=& np\times\log f_{min}(c) + \log(np)\times\nu(c), \end{array} $$

(16)

where ν(c) denotes the number of parameters to be estimated and equals the sum of the numbers of the memberships in M, the nonzero elements in Y, and error variance σ²:

$$ \nu(c) = n + c + 1. $$

(17)

Therefore, the best c can be given by $c = \underset {c_{min} \leq c \leq c_{max}}{\text {arg min}} AIC(c)\ \text {or}\ BIC(c)$. AIC and BIC were originally proposed as model selection criteria and also used for cardinality selection in studies in the literature Adachi and Trendafilov (2015, 2017). This approach is not considered to be computationally efficient, however, because CCKM involves the optimization with respect to a binary membership matrix, as in the standard k-means, and therefore is sensitive to local minima. To select c with AIC(c) or BIC(c) is not feasible because a heavy computational load is required for all runs, especially when the data matrix is large (i.e., X contains many objects and variables). In such a situation, the centroid matrix to be estimated is also large, although CCKM must facilitate the interpretation of such a large matrix.

In order to find a suitable c value with a lower computational cost, we propose the following algorithm.

Step 1.:

Set S_initial and S_decrease to an integer within the range [0,1]. Set c_current = c_min and S = c_max × S_initial.

Step 2.:

Repeat Steps 2 and 3 for S > 1.

Step 3.:

(Forward search) Repeat (a) to (c).

(a):

Set c = c_current and compute

$$ {\Delta} AIC(c) = AIC(c+1) - AIC(c) $$

(18)

or

$$ {\Delta} BIC(c) = BIC(c+1) - BIC(c). $$

(19)

(b):

If ΔAIC(c) or ΔBIC(c) is smaller than 0, set c_current = c_current + S and return to Step 2; otherwise, proceed to (c).

(c):

Set S = S × S_decrease and proceed to the backward search.

Step 4.:

(Backward search) Repeat (a) to (c).

(a):

Set c = c_current and compute ΔAIC(c) or ΔBIC(c).

(b):

If ΔAIC(c) or ΔBIC(c) is greater than 0, set c_current = c_current − S and return to Step 4; otherwise proceed to (c).

(c):

Set S = S × S_decrease and proceed to the forward search.

Step 5.:

If the previous step is forward search, repeat backward search with S = 1 until ΔAIC(c) or ΔBIC(c) becomes positive; otherwise, repeat forward search until ΔAIC(c) or ΔBIC(c) becomes negative.

The above algorithm seeks c that minimizes AIC(c) or BIC(c) within the range [m_min,m_max] by repeating the forward and backward searches and reducing the step size S through iteration. The rate of decrement in the step size is controlled by S_decrease and the initial step size is defined as c_max × S_initial. The total computational cost is therefore dramatically reduced in comparison with that incurred by performing CCKM with computation of AIC(c) or BIC(c) for all c s. In the following simulation and real data examples, we set S_initial = 0.9 and S_decrease = 0.7, settings that were empirically confirmed to behave well.

4 CCKM with Row/Column-Wise Cardinality Constraint (RC-CCKM)

While a matrix-wise cardinality is constrained by cardinality parameter c in CCKM, we can also consider its modified version subject to row- and column-wise cardinality constraints. By combining row- and column-wise constraints, we can restrict both the cardinality of the centroid matrix and the positions of the nonzero elements, so that the resulting matrix approximates a simple structure. The utility of this approach can be illustrated with an example of a 5 variables × 3 clusters centroid matrix that has several zero elements, but is not easily interpretable:

$$ \mathbf{Y} = \left[ \begin{array}{ccc} & & * \\ * & * & * \\ & & * \\ * & * & * \\ & & * \end{array} \right]. $$

(20)

Here, the cardinality is 10 and ∗ represents a nonzero element. Although this matrix has more zero elements than unconstrained ones, it is still difficult to interpret in that the centroid matrix has a column (the third column) filled with non-zero elements, which indicates that all the variables are associated with the third cluster. To interpret of such a cluster, abstraction and integration of all variables are required, and it is not always straightforward to name the cluster. Similarly, the second and fourth rows are filled with non-zeros. We therefore prefer the centroid matrix

$$ \mathbf{Y} = \left[ \begin{array}{ccc} * & * & \\ * & * & \\ & * & * \\ * & & * \\ & * & * \end{array} \right] $$

(21)

because it does not contain any row/column vector filled with non-zeros in spite of its cardinality equaling that of Eq. 20. In order to obtain a centroid matrix as in Eq. 21, the positions of nonzero elements, in other words, the cardinality of rows and columns, have to be restricted. Such constraints are defined as

$$ Card(\mathbf{y}_{(j)}) = r(j),\ Card(\mathbf{y}_{l}) = c(l) $$

(22)

where r(j) and c(l) denote the cardinality of the row and column of Y, respectively.

To find the matrices M and Y that minimize Eq. 1 under the above constraint, the Y-step in Section 2.2 can be modified as follows. To minimize Eq. 1 subject to the constraint Card(y_(j)) = r(j), the set Z is redefined as

$$ Z = \{(j,l)| a^{2}_{jl} \leq a^{2}_{j[r(j)]} \}, $$

(23)

where $\{a^{2}_{j[k-r(j)]}\}$ denotes the {k − r(j)}-th smallest element among $a^{2}_{j1},\cdots ,a^{2}_{jk}$ for j = 1, ⋯ ,p. Each row is therefore updated by using the above Z and referencing the squared elements of A in Eq. 7. In a parallel manner, under Card(y_l) = c(l), Z is redefined as

$$ Z = \{(j,l)| a^{2}_{jl} \leq a^{2}_{[c(l)]l} \} $$

(24)

with $a^{2}_{[p-c(l)]l}$ the {p − c(l)}-th smallest element among $a^{2}_{1l},\cdots ,a^{2}_{pl}$ for l = 1, ⋯ ,k.

We refer to the above procedure as CCKM with row/column-cardinality constraint (RC-CCKM). The performance of the procedure is demonstrated later in one of the real data examples.

5 Simulation Studies

In order to assess the behaviors of the CCKM algorithm presented in Section 2 and the AIC/BIC-based cardinality selection procedure presented in Section 3, we performed two numerical simulation studies. The behaviors to be assessed are the following two. (1) The correctness of the identification of the true cardinality is identified by the cardinality selection procedure and (2) the recovery by CCKM of the true parameters from which artificial datasets are synthesized. Therefore, the purpose of the first simulation study was to assess the accuracy of the cardinality selection, and of the second to evaluate the performance of the parameter recovery.

5.1 Accuracy of Cardinality Selection

First, we examined the accuracy of true cardinality in the cardinality selection procedure. A hundred data matrices X of n = 100 by p = 30 were randomly generated with setting k = 3, as follows.

Step 1.:

A positive integer c_T was randomly drawn from the interval [0.1 × pk,0.9 × pk] and used for the true cardinality of a centroid matrix.

Step 2.:

The c_T nonzero elements in Y were drawn from the uniform distribution U(1,5), with their positions and signs randomly chosen.

Step 3.:

The true membership matrix M was formed by randomly assigning n observations to k clusters.

Step 4.:

The elements of n × p error matrix E were drawn from the standard normal distribution N(0,1).

Step 5.:

Data matrix X of n-observations × p-variables was synthesized with

$$ \mathbf{X} = \mathbf{M}\mathbf{Y}^{\prime} + \mu(\rho)\mathbf{E} $$

(25)

where μ(ρ) is defined as

$$ \mu(\rho) = \sqrt{\frac{1-\rho}{\rho} \times \frac{||\mathbf{M}\mathbf{Y}^{\prime}||^{2}}{||\mathbf{E}||^{2}}} $$

(26)

with ρ being the rate of the variance explained.

In Step 5, μ(ρ) was used for controlling the level of errors, so that ρ approximated the proportion of the variances in ||X||² accounted for by the model part $\mathbf {M}\mathbf {Y}^{\prime }$ (Adachi 2009; Yamashita and Mayekawa 2015). We considered the medium error level with ρ = 0.70, which represents the 70% of the variance of X explained by $\mathbf {M}\mathbf {Y}^{\prime }$. For each of 100 X s, the best cardinality was selected with AIC and BIC: c_AIC and c_BIC were used for the selected cardinality, respectively. The bias of the estimated cardinality was evaluated with the standardized difference (SD) defined as

$$ SD(m) = (pk)^{-1}(c_{T} - c). $$

(27)

Figure 1 shows the boxplots of the resulting SD(c_AIC) and SD(c_BIC) in the medium-error condition. The SD values are found to approximate zero in the BIC-based cardinality selection, which indicates that the BIC-based procedure almost perfectly specifies the true cardinality, although it slightly overestimates it in a few cases. Conversely, the AIC-based selection tended to considerably underestimate the true cardinality, which is seen in the result that the discrepancy between the true and estimated cardinality is over 7% of all entries in Y at 50 percentile of SD(c). These results show that the BIC-based is more precise than the AIC-based selection, suggesting that the former should be used.

Fig. 1

Boxplots of SD(c_AIC) and SD(c_BIC) as indices of discrepancy between true and estimated cardinality by AIC and BIC criterion

5.2 Accuracy of Parameter Estimation

In order to assess how well the parameter matrices are recovered in the CCKM algorithm, we considered the cases where (n,p) = (100,30) and (30,100) and three error levels (ρ = 0.90,0.70,0.50). A hundred artificial datasets X were generated as described in the previous section. Next, CCKM was applied to X with its cardinality set as c = c_T (identical to the true cardinality), c = c_T − 0.05 × pk (5% fewer than the true cardinality), and c = c_T + 0.05 × pk (5% more than the true cardinality) in order to assess the sensitivity to cardinality misidentification. For each of 2 (dimension of data matrix; (n,p) = (100,30),(30,100)) × 3 (error level; ρ = 0.90,0.70,0.50) × 3 (cardinality setting; 5% fewer, identical to true cardinality, and 5% more) combinations, we generated 100 datasets in the manner described in the previous section. The resulting parameters $(\hat {\mathbf {M}},\hat {\mathbf {Y}})$ were compared to their true counterparts and the accuracy of their recovery was evaluated by the following indices. For the membership matrix, we compared $\hat {\mathbf {M}}$ and M in terms of the Adjusted Rand Index (ARI) (Rand 1971; Hubert and Arabie 1985) of these matrices, ranged from 0 to 1 with ARI = 1 representing the perfect coherence of the two partitions shown by $\hat {\mathbf {M}}$ and M. The proximity between $\hat {\mathbf {Y}}=\{\hat {y}_{jl}\}$ and its true counterpart Y = {y_jl} was evaluated with Averaged Absolute Error (AAE) defined as $AAE(\hat {\mathbf {Y}}, \mathbf {Y})=(pk)^{-1}{\sum }_{j,l}|\hat {y}_{jl} - y_{jl}|$, which indicates the averaged discrepancy between the pk elements in $\hat {\mathbf {Y}}$ and Y. It should be noted that, before computing the four indices, we must choose the k × k permutation matrix that minimizes $||\hat {\mathbf {Y}}\mathbf {P} - \mathbf {Y}||^{2}$, to eliminate the freedom of row-permutation of $\hat {\mathbf {Y}}$ shown as $||\mathbf {X} - \mathbf {M}\mathbf {Y}^{\prime }||^{2} = ||\mathbf {X} - (\mathbf {M}\mathbf {P})(\mathbf {Y}\mathbf {P})^{\prime }||$. Therefore, the permutation of P was chosen that minimizes $||\hat {\mathbf {Y}}\mathbf {P} - \mathbf {Y}||^{2}$ among all possible p! permutation matrices. We use $\hat {\mathbf {M}}\mathbf {P}$ for $\hat {\mathbf {M}}$ and $\hat {\mathbf {Y}}\mathbf {P}$ for $\hat {\mathbf {Y}}$ with the chosen P.

The CCKM algorithm is run starting from t_max different initial values in order to avoid accepting a local minimum as the final solution. In this simulation, we ran the CCKM algorithm from 300 different initial values; i.e., t_max = 300.

Figures 2 and 3 show the parameter recovery results in the two cases of data sizes. Overall, the parameters were correctly recovered by CCKM, in that the ARI indices attained their maximum 1 in almost all cases, and that the discrepancy between $\hat {\mathbf {Y}}$ and Y indicated by the AAE values are sufficiently small. Even in the case where ρ = 0.50, where the error variance amounts to the half of the total variance of the dataset, the AAE value is lower than 0.3 at 50 percentile. Further, even if the cardinality is misidentified, the levels of the ARI and AAE values are still satisfactory. Thus, it can be considered that the true cardinality can be identified fairly accurately in CCKM. These results allow us to conclude that the performances of CCKM is suitable for dealing with practical problems, in that the CCKM almost perfectly recovers the true parameters.

Fig. 2

Boxplot of ARI (adjusted Rand index) and $AAE(\hat {\mathbf {Y}},\mathbf {Y})$ values in the case with (n,p) = (100,30)

Fig. 3

Boxplot of ARI (adjusted Rand index) and $AAE(\hat {\mathbf {Y}},\mathbf {Y})$ values in the case with (n,p) = (30,100)

6 Real Data Examples

In this section, we illustrate CCKM with the cardinality selection procedure, using three real data examples. Further, the modified version of CCKM with row/column-cardinality constraints are finally illustrated with an additional example.

6.1 Example 1: Fisher’s Iris Data

CCKM was applied to Fisher’s (1936) Iris data, in which the 150 observations sampled from 3 species were measured with respect to 4 variables. Note that the data matrix was column-wise standardized beforehand. In order to find the optimal cardinality, the BIC-based cardinality selection procedure was used and the results suggested that c = 8 is the best. We also applied k-means clustering to the dataset for comparison. The estimated centroid matrices are shown in Table 2.

Table 2 Estimated centroid matrices by CCKM with c = 10 (left) and k-means (right); a blank cell shows exact-zero element

In the centroid matrix estimated by CCKM in Table 2, we can find that the first cluster is contrasted to the second one for Sepal.Length and Sepal.Width. Further, the second cluster is different from the other clusters for Sepal.Width, with Versicolor in the second cluster characterized by narrow sepals. The contrast between clusters is clearer in the centroid matrix of CCKM than in that of the resulting k-means clustering, because the former has exactly zero elements. Further, as shown in Table 3, the three clusters are associated with the three species, Setosa, Versicolor, and Virginica, respectively. It can be seen that the estimated memberships correspond to the species, since (49 + 37 + 42)/150 = 85.3% of 150 observations are correctly classified into the true species, while (50 + 39 + 36)/150 = 83.3% in the k-means clustering. The ARI (with its 95 % confidence interval by Steinley et al. (2016)) between the partition obtained by CCKM for the three species was 0.645 ([0.626,0.664]), while ARI = 0.620 ([0.601,0.638]) for k-means clustering. Also, ARI for the two partitions was 0.832 ([0.813, 0.851]), and it suggests that two partitions obtained by CCKM and k-means are similar, even if the cardinality of centroid matrix is restricted in CCKM. These results demonstrate that CCKM yields an easily interpreted centroid matrix subject to the cardinality constraint, and the classification accuracy is improved.

Table 3 Contingency table for species vs. the estimated partitions by CCKM and k-means

6.2 Example 2: Wine Data

The second example is that of the Wine data available at the UCI machine learning repository, in which the 178 types of wine are evaluated in terms of 13 chemical features. Note that the data matrix was column-wise standardized beforehand. CCKM was performed for the dataset with c = 35 selected by the BIC-based procedure. Table 4 shows the estimated centroid matrix. It can be seen that each cluster is characterized by a small number of chemical features, which highlights the contrasts among clusters. For example, the contrast between the fourth and fifth clusters can be found in “Malic acid” and “Hue”; the observations classified into the fourth cluster are characterized by lower “Malic acid” and higher “Hue.” Similarly, the other contrast between clusters can be found in several variables, such as “Ash,” “Total phenols,” and “Nonflavonoid phenols,” which are clearly highlighted by the cardinality constrained estimation of nonzero and exact-zero elements.

Table 4 Centroid matrix obtained by CCKM with cardinality of r = 35. The exact-zero elements are shown as blank cells

Originally, the wines in the dataset are classified into three categories. In Table 5, we compare these categories and the clusters obtained by CCKM and k-means. Note that the number of clusters in k-means was set at 5 for comparison. It is interesting that clusters obtained by the two procedures are fairly similar, as indicated that ARI = 0.715 with its 95% interval [0.700, 0.731] for the two partitions. For both procedures, the first and fifth clusters correspond to Category 1 and 3, respectively. Further, the wines in Category 2 is splitted into three clusters (second, third, and fourth clusters). It suggests that even if CCKM reduces cardinality of centroid matrix, it produces similar cluster structure to k-means clustering.

Table 5 Contingency table for wine categories vs. the estimated partitions by CCKM and k-means

6.3 Example 3: Job Impression Data

Here, we illustrate RC-CCKM by using the job impression dataset that was also used in Section 1. Note that the data matrix was column-wise centered beforehand. Row- and column-wise cardinalities were set to r(j) = k/2 = 2 and c(l) = p/2 = 6 for j = 1, ⋯ , 12, l = 1, ⋯ ,4. This implies “Each row should contain at least one zero and each column should contain at least k zeros,” which is a property of an easily interpreted matrix (Thurstone 1947).

The estimated centroid matrix is presented in Table 6. The resulting cardinality of the centroid matrix is 19, which is 19/48 ≈ 39.6% of all entries. As in the previous two examples, we can see clear differences between clusters and the homogeneity in each cluster. As the row-wise cardinality was set at 2, each row has at least two zero elements and the remaining nonzero elements show the contrast of extreme positive and negative values, as found in the rows of “powerful” and “strong,” for example. Furthermore, each cluster corresponds to fewer variables, as compared with the results of k-means in Table 1, which facilitates the interpretation of clusters. It should be noted that the proportion of the variance explained by the CCKM is 60.8%, which is not substantially lower than the proportion of 68.9% in the k-means solution. Further, the memberships estimated in CCKM perfectly correspond to those in the k-means clustering. These results demonstrate promising performances of RC-CCKM: it gives easily interpreted solutions while the goodness of fit to data is retained.

Table 6 Estimated centroid matrix by CCKM with row/column-cardinality constraint and four clusters for job impression data; exact-zero elements are shown as blank cells

7 Concluding Remarks

In this paper, we addressed the difficulty in interpreting the centroid matrix resulting from the standard k-means clustering. We proposed a new procedure called CCKM in which the cardinality of the centroid matrix is directly constrained ti improve its interpretability. CCKM produces a centroid matrix with reduced cardinality and its interpretation is easier than that of the standard k-means clustering, because between-cluster contrasts are highlighted by exact-zero elements. We also proposed a cardinality selection procedure and modified version of CCKM. The results of the simulation studies show that the BIC-based cardinality selection is more accurate than the AIC-based one, and the parameter estimation of CCKM is not sensitive to error contamination and misidentification of cardinality. Real data examples were presented to demonstrate the promising performance of CCKM and its modified version.

In clustering, the interpretability of solutions is of importance, as well as the classification accuracy. Thus, the cardinality constraint is considered to be useful for users in that the number of non-zero elements is directly associated with interpretability. Further, users can control the balance of low cardinality and model fit by tuning the cardinality parameter c within a restricted range. Therefore, we can conclude that the proposed procedure is suitable for extracting interpretable clusters.