An experimental apparatus for generating homogeneous isotropic turbulence

Abstract

An experimental apparatus using synthetic jets to generate zero mean flow homogeneous isotropic turbulence (HIT) in the center of a cubic water tank is presented. Pumps drive jets at the corners and midpoints of the tank edges, producing center-facing flow to generate turbulence. The array of synthetic jets is controlled by a random forcing algorithm (Variano et al. in Exp Fluids 37:613–615, 2004) to optimize generation of turbulence while minimizing mean and secondary flows. We explore different combinations of mean percentage of jets on, $\varPhi _\textrm{on}$, mean on-time, $T_\textrm{on}$, and pump outlet velocity, $V_P$, to determine their respective roles in turbulence generation. Particle image velocimetry (PIV) and acoustic Doppler velocimetry (ADV) are used to measure the velocity in the central isotropic region of the tank to determine turbulence statistics including mean velocities, mean flow strength, turbulent kinetic energy, spectra, integral scales, dissipation rates, Kolmogorov scales, Taylor microscales, and the Taylor-scale Reynolds number. We identified a range of input parameters to vary energy and length scales of the flow while maintaining homogeneity and isotropy in the central core of the facility. Magnitudes of the Taylor-scale Reynolds number ranged from 68 to 176 in the apparatus. Negligible mean recirculations were found, with mean flow strength values ranging from 1.26 to 2.99%, while ratios of root mean square turbulent velocities remained between 0.93 and 0.98, indicating a high degree of isotropy.

1 Introduction

Homogeneous isotropic turbulence (HIT) with zero mean flow is a form of fundamental turbulence that is statistically independent of position and invariant of direction. By creating laboratory facilities to study HIT with zero mean flow, we can isolate the underlying role of turbulence in complex flows to quantify its role in processes such as ice melting, sediment transport, flocculation, diffusivity and mixing without needing to incorporate the effects of mean shear, density stratification, and boundary layers. It is necessary to quantify the role of turbulence via laboratory studies to improve our understanding of transport phenomena that can be difficult to quantify in field settings yet remain critical to the success of numerical simulations or predictive models. For example, some numerical models of melting rely on empirical constants to incorporate the role of turbulence (Jackson et al. 2020). Obtaining in situ measurements at ice–ocean interfaces or seafloor beds to better define model parameters can be difficult and costly. Moreover, processes in natural scenarios are highly interconnected and difficult to study independently. Idealized laboratory experiments allow for individual parameters in complex fluid dynamical processes to be investigated separately in order to validate numerical models and improve simulations of energetic physical processes.

The earliest experimental apparatus designed to generate zero mean flow HIT in a laboratory were grid stirred tanks (GSTs), in which wakes generated via oscillating grids in otherwise quiescent water or air chambers produced turbulence. GSTs were first developed by Rouse and Dodu (1955) to study mixing and entrainment rates in water with low mean flows across a horizontal density interface. Given the planar forcing of a GST, these facilities have commonly been used to characterize boundary layers (Brumley and Jirka 1987) and stratified mixing (Turner and Kraus 1967). For example, various studies investigated turbulent structures (Thompson and Turner 1975), entrainment (Hopfinger and Toly 1976), and sediment motion (Medina et al. 2001) using these oscillating grids.

Despite their popularity and relative ease of use, the main drawback of GSTs is the generation of significant means flows inherent to these facilities, due to the uniform planar forcing (McKenna and McGillis 2004). Many GST studies assume no significant mean flows are produced, although this approach has been questioned by several experimentalists (Fernando and De Silva 1993; Hopfinger and Toly 1976; Mcdougall 1979). McKenna and McGillis (2004) showed mean flow strength—the ratio of mean velocities to root mean square velocities of turbulent fluctuations—were often as strong as 25%, suggesting persistent recirculations. The advective transport that can occur in the secondary flows in GSTs can greatly reduce the reliability of experimental results.

Variano et al. (2004) explored using randomly driven jets to generate HIT with small mean flows. A 3 $\times$ 3 array of solenoid valves was positioned at the base of a water tank. When these valves opened, synthetic jets were formed due to upward momentum driven via a single centrifugal pump. The on-time for each jet was determined by an algorithm that randomly selects a value from a normal distribution. Using this random jet forcing algorithm, Variano et al. (2004) found generated mean flow strength values to be significantly less compared to those produced by GSTs. Variano and Cowen (2008) continued this work and developed a randomly actuated synthetic jet array (RASJA) that produces approximately HIT with low mean and secondary flows. A random jet forcing code, termed the “sunbathing” algorithm, controlled an 8 $\times$ 8 array of upwards facing jets to investigate the effect of HIT on gas transfer across a free surface. In a recent study, Johnson and Cowen (2018) in separate experiments used both 8 $\times$ 8 and 16 $\times$ 16 downward-facing jet arrays with the “sunbathing” algorithm to generate horizontally homogeneous and approximately isotropic turbulence with negligible mean shear to study the turbulent boundary layer at a stationary bed.

Numerous facilities have used horizontal or vertical planar arrays of jets to generate zero mean flow HIT in regions away from boundaries using the “sunbathing” algorithm. For example, the apparatus of Bellani and Variano (2013) had two vertical planar arrays of jets facing each other, each consisting of 64 pumps generating synthetic jets in the horizontal direction. Similarly, Petersen et al. (2019) used multi-planar jet arrays to study particle clustering in zero mean flow HIT in air. Pérez-Alvarado et al. (2016) investigated how turbulence downstream of a jet array is affected by spatial configurations imposed in the jet control algorithm. Turbulence with negligible mean flow was found to be produced with the randomized “sunbathing” algorithm without spatially correlating the operating of the jets.

Other unique apparatus have used synthetic jets and various devices in both air and water to produce turbulence in the centers of facilities, without boundary layers, in particular by mounting actuators symmetrically at the vertices of tanks. For example, Birouk et al. (1996) used 8 vertex-mounted fans to generate HIT in a cube air chamber, whereas Hwang and Eaton (2004) generated a region of HIT in a cube air tank using 8 center-facing loudspeakers driven with sine waves at random frequency and phase values, acting as synthetic jets. In a study to investigate evaporating droplets, Goepfert et al. (2010) deployed 6 loudspeakers as pulsed synthetic jets to generate HIT with weak mean flows in air. Webster et al. (2004) built a facility to study zooplankton in turbulent flow, in which HIT was produced in a water tank via 8 center-facing, corner-mounted synthetic jets driven by woofer speakers. Bounoua et al. (2018) used 8 rotating disks arranged at the corners of a cube water tank to study the rotation of neutrally buoyant fibers in turbulence in a central core of HIT generated via rotating disks.

The development of these vertex-forced synthetic jet facilities, along with evidence of the benefits of the “sunbathing” algorithm highlighted in the recent review of Ghazi et al. (2023), inspired the design of the experimental apparatus developed in this study. It was our objective to design a zero mean flow homogeneous isotropic turbulence tank with a large region of turbulence, relative to the integral length scale, using stochastically forced jets generated by pumps for refined control of turbulence characteristics. Specifically, we aim to generate flows in which the turbulence levels (e.g., turbulent kinetic energy, Reynolds number) approximate the energetics of environmental flows such as rivers, the coastal nearshore, submerged discharges, and others. The new facility consists of a cube tank filled with water with 20 pumps located at the tank corners and edge midpoints, controlled by a random forcing algorithm. Because this is the first zero mean flow HIT tank with pumps as the actuators in the corners of the facility, as opposed to loudspeakers (Hwang and Eaton 2004; Goepfert et al. 2010) or rotating disks (Bounoua et al. 2018), among others, the new facility required significant testing and iterative design to create an ideal turbulent environment with negligible mean flow while maintaining a sizeable region of HIT. While many studies explore the parameters of the sunbathing algorithm, including the mean on-time and percentage of active jets (e.g., Variano and Cowen 2008; Carter et al. 2016; Johnson and Cowen 2018), there is relatively little information regarding the role of outlet jet velocity on the resultant turbulence in zero mean flow facilities. Thus, we incorporated jet velocity as an additional variable to investigate the relative importance of these controls.

Initial flow visualizations were completed to determine the penetration length and spread of an individual jet, varying jet outlet velocity and on-time, to ensure individual jets did not penetrate the targeted HIT region at high momentum. The results of these tests informed subsequent nozzle design for the pump outlets, along with testing of a variety of parameter combinations of the jet forcing algorithm to ultimately inform HIT generation using the random jet array. Similar to the approach of de Jong et al. (2009) who used an HIT facility to evaluate different methods for computing dissipation, we use our experimental facility to test common assumptions (i.e., symmetry, isotropy, continuity) made by many experimental researchers directly calculating the dissipation rate of turbulent kinetic energy, a highly three-dimensional process, from planar velocity data, in order to evaluate how these assumptions affect the magnitude of resultant statistics. In addition, we compare several different metrics to evaluate isotropy in order to characterize flow behavior.

The manuscript is structured as follows. Details regarding the turbulence tank, nozzle design, and measurement techniques are presented in Sect. 2. Measured turbulence statistics, including the integral length scale, dissipation rate, and others, are presented in Sect. 3. A summary of findings and conclusions is presented in Sect. 4.

2 Experimental facility

2.1 Apparatus

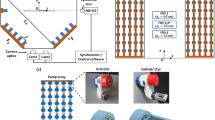
Laboratory experiments were performed in a novel turbulence generating facility at the University of Texas at Austin. The apparatus consists of a tank with inner base dimensions of 44.6 cm by 44.6 cm and a height of 50.4 cm. Tank walls are acrylic with a thickness of 1.27 cm. Inside the tank is a custom PVC frame with 20 Rule iL200 submersible inline pumps (3.3 gpm, 12V, 2.8 Amp) secured along the edges and corners of the exterior sidewalls (Figs. 1 and 2). During the tank design process, the pumps were fitted with two different types of custom 3D-printed nozzles (details below) to direct the outlet jet flows to the center of the tank. For experiments conducted in this study, the water within the tank had a measured temperature of 20.5$^\circ$C. Negligible temperature change (i.e., ± 0.1°C) was recorded during experiments.

The random forcing of the pumps uses the “sunbathing” algorithm (Variano and Cowen 2008) to minimize mean and secondary flows within the tank. The “sunbathing” algorithm uses MATLAB to create jet operation matrices, using Gaussian distributions to select the pump on/off states from user-input values of mean on-time ($T_\textrm{on}$) and the mean percentage of jet activity at any instant ($\varPhi _\textrm{on}$), where $\varPhi _\textrm{on} = \frac{T_\textrm{on}}{T_\textrm{on}+T_\textrm{off}}$, and the on-time and off-time standard deviations, $\sigma _\textrm{on}$ and $\sigma _\textrm{off}$, are set as one-third of $T_\textrm{on}$ and $T_\textrm{off}$, respectively, as in Variano and Cowen (2008). An Arduino Mega 2560 microcontroller sends the on/off states to Texas Instruments SN74HC595N shift registers on custom-designed control boards fabricated by PJC Solutions that trigger each pump (Johnson and Cowen 2018).

The experimental facility uses an AMETEK programmable power supply (Model number XG12-70MEB) that allows the user to select the voltage to power the pumps. Whereas a majority of the existing stochastically driven zero mean flow HIT facilities use a single pump outlet velocity ($V_P$) and rely solely upon algorithm parameters $T_\textrm{on}$ and $\varPhi _\textrm{on}$ to modify the turbulent flow conditions, incorporating additional control of the pump outlet velocity allows for further refinement of flow statistics (Pratt et al. 2017). Given that the relationship between the supplied voltage and $V_P$ is approximately linear, we have considerable control over the outlet flows generated.

Fig. 1

Photograph of the experimental apparatus

Fig. 2

Side view schematic drawing of the turbulence facility with vertex-mounted jets facing the center of the tank

Ideally, each jet interacts with other jet flows and with the ambient flow to generate approximately homogeneous isotropic turbulence with negligible mean flow. To aim the pump outlet flows toward the center of the tank, custom nozzles were designed to re-direct the flow at 90 and 45 degree angles for the midpoint and corner pumps, respectively. These nozzles have an exit diameter of 1.15 cm. The distance between a corner nozzle outlet and an adjacent edge-midpoint jet nozzle orifice is 19 cm. Along with the size of the outlet, the jet forcing parameters $T_\textrm{on}$ and $V_P$ specify the distance the jets travel. Together with $\varPhi _\textrm{on}$, these parameters control the development of HIT and statistics of the resultant turbulence in the center of the tank. The pump inlets are positioned along the edges of the tank, with suction flows parallel to the tank walls so as to minimally influence flows in the center of the facility.

A series of experiments was completed to visualize a single jet within the experimental apparatus under a combination of jet control parameters using a single jet nozzle. To visualize the distance the jet travels from the edge to the center of the tank, a mixture of water with fluorescein salt was injected into the pump inlet just prior to operation, using a variety of $T_\textrm{on}$ and $V_P$ combinations. The fluorescent jet was illuminated by ultraviolet lights surrounding the tank, and timelapse images captured the evolution of the jet. From the jet visualization tests and preliminary velocity analysis using the single-outlet nozzle, we determined this setup significantly constrained the size of the HIT region due to narrow spreading. Thus, we designed a nozzle with an outlet head that splits into four adjacent orifice openings (Fig. 3) to attach to each single-outlet nozzle. Each of the outlets on this nozzle has the same inner diameter of 1.15 cm. The spacing between the 4 orifices is 2.2 cm, while the space between the center of a corner nozzle and the center of an adjacent midpoint nozzle is 15 cm. The use of this new nozzle results in momentum being distributed across a larger cross-sectional area, such that the overall flow spreads more readily to generate a larger region of HIT without direct impingement of individual jets. All results presented herein are for data collected with the four-outlet nozzles affixed to each pump.

Fig. 3

Photograph of the four-nozzle extension for each pump outlet

2.2 Measurement techniques

2.2.1 Particle image velocimetry

Particle image velocimetry (PIV; Adrian 1991) was used to collect velocity measurements in the center of the tank. The baseline flow conditions determined from PIV were used to identify and characterize the region of HIT. The PIV was two-dimensional, two-component (2D2C), providing velocities U and W aligned with the x- and z-directions of the 2D field of view (FOV), respectively, where x and z describe the horizontal and vertical axes, respectively, in the Cartesian coordinate system (Fig. 4). A LRS-0532 DPSS Laser System from Laserglow Technologies illuminated the FOV. An Imperx CMOS camera (Model PIV01882 from TSI Inc.), fitted with a Nikon Nikkor 50-mm lens (f/4), recorded image pairs at a sampling rate of 1 Hz for 20 min with the time between each image within a pair, $\varDelta T$, ranging from 5.5 to 6.5 ms, depending on the jet forcing conditions. The FOV had a width of 14 cm and height of 10 cm, in which we identified a region of approximately 10 cm by 10 cm centered within the measurement region found to satisfy conditions of homogeneity and isotropy (details below) for the selected forcing parameters. We note that for all analysis, velocity statistics are reported only within the 10 cm by 10 cm HIT region.

Fig. 4

Diagram of the PIV setup including the laser, camera, and tank

ORGASOL (R) 2002 ES 3 Nat 3 Polyamide 12 nylon particles from Arkema Group were used to seed the tank for velocity measurements. The particles have a specific gravity (S) of 1.03 and an average batch diameter ($D_p$) of 29.4 μm, with 8% greater than 40 μm and 5% less than 20 $\mu$m. The Stokes number, $St = \frac{\tau _R}{\tau }$, where $\tau _R$ and $\tau$ are the relaxation time scale $\frac{(S) D_p^2}{18 \nu }$ and the Kolmogorov time scale, respectively, was found to be less than 0.01, confirming the seeding particles to be passive tracers of the turbulent flow. The kinematic viscosity was selected for water at 20.5$^\circ$C.

To analyze the images from the PIV measurements, PIVlab was used (Thielicke and Stamhuis 2014, 2019). To improve image quality for analysis, an artificial minimum background image was first constructed by determining the minimum illumination at every pixel in the FOV. This background image was subtracted from all raw images. Images were further pre-processed by using a high-pass filter built into PIVlab, increasing the contrast between the background and illuminated seeding particles. In PIVlab, the subwindow sizes selected were 64 × 64 pixels for two passes and 32 × 32 pixels for an additional two passes with 50% overlap. The spatial resolution for the images was 0.0036 cm/pixel and the vector-to-vector resolution was 0.058 cm for the final interrogation. Post-processing included an adaptive Gaussian window (AGW; Cowen and Monismith 1997) filter to remove erroneous high magnitude vectors and a spatial median filter to remove additional erroneous vectors (Johnson and Cowen 2018). After the AGW and spatial median filters were applied, 96% of valid data remained in the data sets. To compute the uncertainty bounds on the turbulence statistics, we used the bootstrap method of Efron and Tibshirani (1993) to obtain 95% confidence intervals. The 97.5 percentile and 2.5 percentile statistics were used to compute the 95% confidence interval.

2.2.2 Acoustic Doppler velocimetry

A Nortek Vectrino acoustic Doppler velocimeter (ADV) with “plus” firmware was used to collect temporally resolved velocity measurements at a single point at the center of the tank. The ADV had a transmit length of 1.8 mm and a sample volume length of 7 mm. Velocity measurements were recorded in the x and y coordinate directions only, orthogonal to the vertical tank walls. Data were collected at 200 Hz for a total of 10 min. Invalid vectors were removed with the AGW filter, and filtered data points were linearly interpolated to obtain a full temporal record for computation of energy spectra.

3 Results

We present resulting mean velocities and turbulence metrics in response to changing the turbulence driving parameters, $T_\textrm{on}$, $\varPhi _\textrm{on}$, and $V_\textrm{P}$. We evaluate isotropy via several statistical metrics, and we present a comparison of common assumptions used in estimating dissipation from planar PIV data.

3.1 Mean and fluctuating velocities

Reynolds decomposition, $U_i (x,y,z,t) = \langle U_i (x,y,z,t) \rangle +u_i (x,y,z,t)$, is used to consider the mean and fluctuating velocities separately, where $U_i$ is the instantaneous velocity, $u_i$ is the fluctuating velocity, and $\langle \rangle$ denotes the temporal mean. Values that have been temporally and spatially averaged are indicated with an overbar. The horizontal, lateral (i.e., normal to the PIV measurement plane), and vertical velocities are denoted with $i=1$, $i=2$, and $i=3$, which correspond to the x-, y-, and z-directions.

The root mean square (RMS) velocity is a metric of the turbulence velocity fluctuations, calculated as $u_i' = \sqrt{\langle u_i^2 \rangle }$. Turbulent kinetic energy is defined as:

$$\begin{aligned} k = \frac{1}{2}\left( u_1'^2 + u_2'^2+u_3'^2\right) \end{aligned}$$

(1)

Given 2D PIV measurements, only the $u_1'^2$ and $u_3'^2$ terms can be directly measured. Thus, we assume $u_2'^2$ is statistically equal to $u_1'^2$ due to the symmetric design of the tank, and confirmed via ADV data. As a result, we compute k as:

$$\begin{aligned} k = u_1'^2 + \frac{1}{2} u_3'^2. \end{aligned}$$

(2)

Summary values of mean velocities, fluctuating velocities, and turbulent kinetic energy across all tests are presented in Table 1. There was no strong correlation observed between the mean velocities and changing the individual jet parameters, but some trends were noted. For instance, increasing $V_P$ typically resulted in a slight increase of mean flows, $\overline{{U_1}}$ and $\overline{{U_3}}$. By contrast, an increase in $\varPhi _\textrm{on}$ resulted in a reduction of $\overline{{U_1}}$ and $\overline{{U_3}}$, indicating that increasing $\varPhi _\textrm{on}$ likely results in a damping mechanism that reduces mean flows, even at larger values of $V_P$. Considering Fig. 5, we see an overall trend that as energy input within the tank was enhanced by increasing $V_P$ and $T_\textrm{on}$, the magnitudes of the turbulent kinetic energy were generally observed to be higher, consistent with observations presented in Carter et al. (2016), Pratt et al. (2017), and Johnson and Cowen (2018). For tests conducted with $\varPhi _\textrm{on}$ = 15%, both $V_P$ and $T_\textrm{on}$ are positively correlated with k. However, whereas the turbulent kinetic energy increased with $\varPhi _\textrm{on}$ for the case in which $V_P$ = 217 cm/s, k subsequently decreased with an increase in $\varPhi _\textrm{on}$ at higher $V_P$ values of 248 and 279 cm/s, again suggesting a damping mechanism if the forcing is sufficiently strong. During development of a planar random jet array, Variano and Cowen (2008) identified fluctuating velocities were maximized when $\varPhi _\textrm{on}$ was set to 12.5% and subsequently decreased as $\varPhi _\textrm{on}$ was further increased, consistent with our findings. Similarly, Pérez-Alvarado et al. (2016) found a significant increase in RMS velocities when $\varPhi _\textrm{on}$ was reduced from 50 to 10% in a facility driven by a planar jet array. Given the different geometric setup of the cube facility presented herein, we expect $\varPhi _\textrm{on}$ to be optimal at a different value as compared to planar jet arrays, and perhaps to vary with the additional control parameter $V_P$.

Table 1 The spatial median of the time-averaged values for the mean velocities, RMS velocities, and turbulent kinetic energy for a combination of jet control parameters. 95% confidence intervals shown in square brackets. All values are determined from PIV data

Fig. 5

Variation of turbulent kinetic energy with jet outlet velocity for trials in which $T_\textrm{on}$ = 1.0 s, $\varPhi _\textrm{on}$ = 15% (pink filled circle); $T_\textrm{on}$ = 1.4 s, $\varPhi _\textrm{on}$ = 15% (black open circle); and $T_\textrm{on}$ = 1.0 s, $\varPhi _\textrm{on}$ = 30% (blue filled square)

The ratio of $u_3'$ to $u_1'$ provides one metric of isotropy, where a value of 1 indicates isotropic turbulence. We found values of $\frac{u_3'}{u_1'}$ ranging from 0.93 to 0.98 for all combinations of jet parameters, indicating high isotropy in comparison with many other laboratory facilities designed to generate zero mean flow turbulence (Ghazi et al. 2023). To evaluate homogeneity, we calculated the homogeneity deviation $\frac{2 \overline{\sigma _{u_i'}}}{\overline{u_i'}}$ proposed by Carter et al. (2016) of $u'$ and $w'$ at each elevation ($HD_{u', z}$ or $HD_{w', z}$) and at each lateral position ($HD_{u', x}$ or $HD_{w', x}$) across the entire PIV measurement region. Within the central 10 cm by 10 cm region of the FOV, results showed the median homogeneity deviation to be less than 10% for almost all jet parameter cases, with a few values of $HD_{w', x}$ reaching slightly over 10% (see Table 2). This is within the threshold range proposed by Carter et al. (2016); thus, flows within the central 10 cm by 10 cm of the facility can be considered homogeneous. The size of the HIT region is equivalent to 5.17% of the total cross-sectional area through the central plane of the tank. Similar facilities with center-facing synthetic jets or vertex-mounted rotating disks reported the HIT region to facility cross-sectional area to be 0.95% (Hwang and Eaton 2004), 1.27% (Webster et al. 2004), 0.52% (Goepfert et al. 2010), and 4.69% (Bounoua et al. 2018).

The mean flow strength for the horizontal and vertical directions, $M_1$ and $M_3$ , respectively, indicates the magnitude of secondary flows relative to the turbulence. $M_1$ is determined from the ratio $\left| \langle U_1\rangle \right| /\langle u_1' \rangle$, and likewise $M_3 = \left| \langle U_3\rangle \right| /\langle u_3' \rangle$. The relative mean flow strength, $M^*$, is defined as the ratio of mean kinetic energy to turbulent kinetic energy (Eq. 3). Summary values of mean flow strength are presented in Table 2. For all jet parameter combinations tested herein, all values of $M_3$ are less than 10%, indicating negligible strength of vertically oriented mean flows in the facility (Esteban et al. 2019). Despite values of $M_1$ ranging from 2 to 18%, showing that some combinations of test parameters result in potentially strong lateral flows in the facility (especially at high $V_\textrm{P}$), $M^*$ fell between 1 and 3% for all conditions. Given a threshold level of $M^*$ = 5% determined by Variano and Cowen (2008) for which mean flows are negligible, our findings indicate sufficiently energetic turbulence relative to mean recirculations.

$$\begin{aligned} M^* = \frac{\left( \langle U_1\rangle ^2+ \frac{1}{2}\langle U_3\rangle ^2 \right) }{\langle k \rangle } \end{aligned}$$

(3)

Table 2 The spatial median of the time-averaged values for isotropy (ratio of RMS velocities), mean flow strength, and relative mean flow strength for a combination of jet control parameters. All values are determined from PIV data

3.2 Dissipation

The dissipation rate, $\epsilon$, is calculated via two different approaches—using the second-order structure function and using the direct method. We first compute the longitudinal second-order structure function:

$$\begin{aligned} D_\textrm{LL}(x,r) = \left\langle [U\left( x_c-\frac{1}{2}r\right) - U\left( x_c+\frac{1}{2}r\right) ]^2\right\rangle \end{aligned}$$

(4)

at every height in the FOV, where r indicates the lateral separation between two points and $x_c$ describes the vertical centerline at x = 0. Similarly, the second-order transverse structure function, $D_\textrm{NN}$, is computed using the vertical velocity record with lateral separation r. Following determination of $D_\textrm{LL}$, dissipation is computed at every height in the FOV via

$$\begin{aligned} \epsilon _\textrm{LL}(r) = \frac{1}{r}\left( \frac{D_\textrm{LL}}{C_2}\right) ^\frac{3}{2} \end{aligned}$$

(5)

where $C_2$ is a constant equal to 2.0 (Pope 2000) in the inertial subrange. Given the highly isotropic flow, according to the ratio of RMS velocities, we invoke the relationship $D_\textrm{NN} = \frac{4}{3}D_\textrm{LL}$, in order to compute dissipation from the transverse structure function as:

$$\begin{aligned} \epsilon _\textrm{NN}(r) = \frac{1}{r}\left( \frac{3}{4}\frac{D_\textrm{LL}}{C_2}\right) ^\frac{3}{2} \end{aligned}$$

(6)

The relationships for $\epsilon _\textrm{LL}(r)$ and $\epsilon _\textrm{NN}(r)$ apply in the inertial subrange, from which median values can be determined to estimate the magnitude of dissipation throughout the FOV. The profiles of dissipation (see Fig. 6) computed from the longitudinal and transverse structure functions, while somewhat noisy, are relatively constant with z. Profiles of both $\epsilon _\textrm{LL}$ and $\epsilon _\textrm{NN}$ are subsequently averaged in z to produce estimates of dissipation, as presented in Table 4. The mean ratio of $\epsilon _\textrm{LL}$ to $\epsilon _\textrm{NN}$ is equal to 1.07 across all experiments, again showing high isotropy. From the estimates of $\epsilon _\textrm{LL}$, we can approximate the Kolmogorov length scale, $\eta _\textrm{LL} \equiv (\nu ^3/ \overline{\epsilon _\textrm{LL}})^{1/4}$. As presented in Table 4, values of $\eta _\textrm{LL}$ range from 0.015 to 0.023 cm, with no clear dependence on the jet forcing parameters.

Fig. 6

Dissipation profiles $\epsilon _\textrm{LL}$ (– green) and $\epsilon _\textrm{NN}$ (– orange) using the structure function method. $V_P$ = 185 cm/s, $\varPhi _\textrm{on}$ = 15%, and $T_\textrm{on}$ = 1 s

Following estimation of dissipation via the structure function, we subsequently compute dissipation directly as $\epsilon _d\equiv 2 \nu \langle S_{ij}S_{ij} \rangle$, where the strain rate $S_{ij}$ is defined as

$$\begin{aligned} S_{ij} \equiv \frac{1}{2} \left( \frac{\partial u_i}{\partial x_j}+\frac{\partial u_j}{\partial x_i} \right) \end{aligned}$$

(7)

where velocity gradients are determined from PIV data. PIV spatial resolution is of concern when using the direct method to calculate dissipation. If the spatial resolution is smaller than the smallest length scales of the turbulence, the noise in the data is amplified. Alternatively, when the PIV interrogation subwindows are too large, the turbulent length scales are erroneously averaged, resulting in an underestimation of the dissipation rate. Given our estimate of $\eta _\textrm{LL}$ above, we found the spatial resolution of our PIV measurements to range from 2.5 to 3.9 $\eta _\textrm{LL}$ across all tests. In order to evaluate whether the spatial resolution of the PIV data were adequate to measure dissipation in this way, we follow the methodology of Cowen and Monismith (1997) and referenced the integration of the universal spectrum of Pao (1965). Given the resolution of the PIV data relative to $\eta _\textrm{LL}$, we find our data sufficient to capture $>99$% of the total dissipation using the direct method.

Due to the symmetry of the facility, there are six different choices regarding which assumptions can be made to approximate the out-of-plane velocities and velocity gradients from the PIV data. Specifically, to determine $\frac{\partial u_1}{\partial x_2}$ and $\frac{\partial u_2}{\partial x_1}$, we can either assume radial symmetry about the z-axis, or radial symmetry about the x-axis. In order to estimate $\frac{\partial u_2}{\partial x_2}$, we can assume continuity (Cowen and Monismith, 1997; Doron et al., 2001), or we can assume isotropy about either the x- or z-axis to directly relate out-of-plane velocities and gradients with in-plane measurements. The combinations of assumptions and the total direct dissipation equations we considered are presented in Table 3.

Fig. 7

The individual components of the total dissipation for jet parameters of $V_P$ = 185 cm/s, $\varPhi _\textrm{on}$ = 15%, and $T_\textrm{on}$ = 1 s. Due to fluctuations in the profiles, a local median smoothing filter was applied to the vertical profiles of each component. $\overline{\left( \frac{\partial u}{\partial x}\right) ^2}$ (– light blue), $\overline{\left( \frac{\partial w}{\partial z}\right) ^2}$ (- - blue), $\overline{\left( \frac{\partial u}{\partial z}\right) ^2}$ (– orange), $\overline{\left( \frac{\partial w}{\partial x}\right) ^2}$ (- - green), $\overline{\left( \frac{\partial u}{\partial x} \frac{\partial w}{\partial z}\right) }$ (– pink), and $\overline{\left( \frac{\partial u}{\partial z} \frac{\partial w}{\partial x}\right) }$ (- - black)

Representative vertical profiles of the individual dissipation components are shown in Fig. 7. In the example shown (and consistent across all tests), we find the $(\frac{\partial u_1}{\partial x_1})^2$ and $(\frac{\partial u_3}{\partial x_3})^2$ terms are roughly 17% less in magnitude than the $(\frac{\partial u_1}{\partial x_3})^2$ and $(\frac{\partial u_3}{\partial x_1})^2$ terms, while the $\frac{\partial u_1}{\partial x_3}\frac{\partial u_3}{\partial x_1}$ and $\frac{\partial u_1}{\partial x_1}\frac{\partial u_3}{\partial x_3}$ products are significantly smaller in magnitude. Among the six different combinations of assumptions, it appears that, in this relatively isotropic turbulent flow, the assumptions of radial symmetry and isotropy are interchangeable and the total dissipation values are approximately independent of the selection of axis (i.e., x or z) about which out-of-plane velocities or velocity gradients are determined. However, specifically for determination of $\frac{\partial u_2}{\partial x_2}$, the assumption of continuity plays a more significant role, resulting in dissipation magnitudes roughly 10% greater than in comparable calculations based upon isotropy, as apparent in Fig. 8, which shows a comparison of the total dissipation for all six assumption combinations. In the interest of consistency with prior literature, we choose to report $\epsilon _d$ as the spatial median value based on assumptions of continuity and z-axis symmetry throughout the remainder of calculations that incorporate dissipation (Table 4).

Comparing dissipation between test cases, we observe an overall trend that $\epsilon _d$ increases with $V_P$, as we expect due to prior studies of Pratt et al. (2017). Similarly, $\epsilon _d$ increases with $T_\textrm{on}$, consistent with the findings of Johnson and Cowen (2018). Although an increase in $\varPhi _\textrm{on}$ resulted in a reduction of RMS velocities, it resulted in an increase in two of the $\epsilon _d$ values for the presented test cases.

For comparable $Re_\lambda$ in de Jong et al. (2009), the ratio of dissipation when determined via the second-order structure function as compared to the direct method, without corrections, is approximately 0.5. By contrast, Johnson (2016) found this ratio to be approximately 0.8 at higher $Re_\lambda$. We find this ratio to range from 0.16 to 0.35. Given our relatively high spatial resolution of PIV data relative to $\eta _\textrm{LL}$, we choose to use the estimates of $\epsilon _d$ as representative of the true dissipation within the facility. We subsequently recalculate the Kolmogorov length scale $\eta _d$ using $\epsilon _d$, seeing a reduction in magnitudes, as shown in Table 4. Even with a reduction in the Kolmogorov length scale (compared to $\eta _\textrm{LL}$), we remain in the range of spatial resolution to adequately measure dissipation directly, without corrections (Cowen and Monismith 1997; Pao 1965).

Considering the dissipation profiles in Fig. 8, we note variability up to 30% of $\epsilon _d$ with z in the FOV. This inhomogeneity is observed in spite of the symmetric forcing design, and having found $HD<$ 10% based on RMS velocities across the measurement plane in both the x- and z-directions. To explore this spatial variability further, we calculated the homogeneity deviation of the isotropy ratio $\frac{u'_3}{u'_1}$ (recall Table 2), with values ranging from 7 to 17%, and thus deviating beyond the accepted 10% threshold for HD of RMS velocities. The homogeneity deviation is a common method for evaluating flow, upon which we base our statement of achieving sufficient homogeneity within the facility (based on RMS velocities), yet this variability in dissipation and in the isotropy ratio reinforces the notion that there are various metrics for evaluating flow that may yield contradictory findings, and may not encompass the complex behaviors within a single facility.

Table 3 Combinations of six different radial symmetry and isotropy assumptions to select the velocity gradients to calculate the total dissipation using a 2D direct formulation

Fig. 8

Dissipation profiles reported using 6 assumptions for the total dissipation calculation for jet parameters of $V_P$ = 185 cm/s, $\varPhi _\textrm{on}$ = 15%, and $T_\textrm{on}$ = 1 s. Due to fluctuations in the profiles, a local median smoothing filter was applied to the vertical profiles of dissipation. Radial symmetry (z-axis) and continuity (– green); radial symmetry (x-axis) and continuity (- - blue); radial symmetry (z-axis) and isotropy (x-axis) (– black); radial symmetry (x-axis) and isotropy (x-axis) (–$\cdot$ orange); radial symmetry (z-axis) and isotropy (z-axis) (– pink); radial symmetry (x-axis) and isotropy (z-axis) (- - light blue)

Table 4 Turbulence statistical quantities including the median of the time-averaged values for dissipation, Taylor-scale Reynolds number, Taylor microscale, Kolmogorov length, and time scales for a combination of jet control parameters

3.3 Length and time scales

To obtain the integral length scale, the longitudinal and transverse spatial autocorrelation functions were calculated using both horizontal and vertical separation, r, for the vertical and horizontal velocity data as:

$$\begin{aligned} a_{ij,k}(r)={\langle u_i(x_c+{1 \over 2}r_k)u_j(x_c-{1 \over 2}r_k) \rangle \over \sqrt{\langle u_i(x_c+{1 \over 2}r_k)^2\rangle \langle u_j(x_c-{1 \over 2}r_k) ^2\rangle }}. \end{aligned}$$

(8)

The integral length scale of the turbulence, $L_{ij,k}$, is defined as the integral of the autocorrelation:

$$\begin{aligned} {\mathcal {L}}_{ij,k} = \int a_{ij,k}(r)dr \end{aligned}$$

(9)

For the longitudinal integral length scales, ${\mathcal {L}}_{L}$, where i, j, and k are equal to one another, a(r) does not consistently converge to zero due to the size of our FOV, and so, a direct integration of the autocorrelation data would underestimate the integral length scale. Thus, an exponential curve is fit to the autocorrelation results as in Johnson and Cowen (2018) such that:

$$\begin{aligned} a_{L}(r)=e^{-r \over {\mathcal {L}}_{L}} \end{aligned}$$

(10)

Values of ${\mathcal {L}}_{L}$ are determined directly from the exponent of the best fit curve (Eq. 10) to determine a vertical profile of ${\mathcal {L}}_{11,1}$ and lateral profile of ${\mathcal {L}}_{33,3}$. The median values from these profiles are reported in Table 5.

For the transverse integral length scales, in which $i,j \ne k$, the autocorrelation data reached values of $a(r) = 0$ within the measurement region; thus, no curve-fitting was required and we integrated the autocorrelation functions to directly determine lateral and vertical profiles of the transverse integral length scales, ${\mathcal {L}}_{11,3}$ and ${\mathcal {L}}_{33,1}$, respectively. Median values are reported in Table 5.

For isotropic turbulence, we expect the ratio between the longitudinal and transverse integral length scale to have a value of approximately 2 (Pope 2000). This is an additional metric we can compare with the isotropy ratio presented above as $\frac{u_3'}{u_1'}$. Surveying the literature on similarly designed facilities, relatively few studies report both longitudinal and transverse integral length scale values. For those that do present this information, it is common for either the ratio of RMS velocities or the ratio of integral length scales to satisfy conditions of isotropy, but not both. For example, Carter et al. (2016) presented integral length scale ratio values ranging from 1.75 to 2.23, satisfying conditions for isotropy, whereas RMS velocity ratios consistently exceeded 1.28. Across all jet parameters tested for our facility, we found the ratio ${\mathcal {L}}_{11,1}/{\mathcal {L}}_{11,3}$ ranged from 1.39 to 1.60, while values of ${\mathcal {L}}_{33,3}/{\mathcal {L}}_{33,1}$ ranged from 1.68 to 1.88. While these values show some departure from the target of 2, these ratios suggest a notable improvement to isotropy in comparison with several other HIT facilities that used synthetic jet arrays. For example, in tests with a planar jet array, Variano and Cowen (2008) found integral length scale ratios to be 1.18, and Johnson and Cowen (2018) measured a ratio of 1.29.

Given the symmetry of our experimental facility, we are uniquely positioned to consider a third set of ratios to evaluate isotropy: $\frac{{\mathcal {L}}_{11,1}}{{\mathcal {L}}_{33,3}}$ and $\frac{{\mathcal {L}}_{11,3}}{{\mathcal {L}}_{33,1}}$. We expect both of these ratios to be equal to unity for isotropic turbulence (Carter et al. 2016). Across all tests, $\frac{{\mathcal {L}}_{11,1}}{{\mathcal {L}}_{33,3}}$ ranges from 0.92 to 1.0, showing excellent isotropy; however, values of $\frac{{\mathcal {L}}_{11,3}}{{\mathcal {L}}_{33,1}}$ range from 1.22 to 1.29, again showing a departure from the idealized condition.

The width of our region of HIT was equivalent to approximately 2.9${\mathcal {L}}_{11,1}$ across all of the test cases considered, with some variability given the range of integral scales that we were able to generate via modifications to the forcing algorithm and outlet velocity. Similar facilities with center-facing actuators reported ratios of HIT region width to integral length scale of approximately 1.3 (Webster et al. 2004), 1.5 (Goepfert et al. 2010), and 2.2 (Bounoua et al. 2018), making our region of HIT among the largest to date, relative to turbulence length scales.

Table 5 The median of the time-averaged values for the integral length and time scales for a combination of jet control parameters

The integral time scale is estimated using the spatial median of the integral length scale and turbulent kinetic energy (Peters 1999) $\tau _{{int}} = \frac{{\overline{{\mathcal{L}}} }}{{\sqrt {\bar{k}} }}$. As shown in Table 5, $\tau _{int}$ is consistently less than 1 s, indicating independent sampling via 1 Hz PIV measurements.

The Taylor microscale, $\lambda$, which gives us a measure of an intermediate length scale of the turbulence, is calculated as $\lambda = \sqrt {10} \eta _{d}^{{\frac{2}{3}}} \overline{{{\mathcal{L}}_{{11,1}} }} ^{{\frac{1}{3}}}$. The Taylor-scale Reynolds number is calculated as $Re_\lambda = \left( {2 \over 3}\overline{k} \right) \sqrt{{15 \over \nu \overline{\epsilon _d}}}$. The Kolmogorov time scale, $\tau$, is found via $(\nu / \overline{\epsilon _d})^{1/2}$. As reported in Table 4, the ranges for the Taylor microscale and the Kolmogorov length and time scales were $\lambda$ = 0.24 to 0.27 cm, $\eta _d$ = 0.012 to 0.015 cm, and $\tau$ = 0.014 to 0.024 s. Distinct trends for $\lambda$, $\eta _d$, and $\tau$ based on selected jet parameters were not observed.

Across our experimental conditions, $Re_\lambda$ ranges from 68 to 176, increasing with higher $V_P$ and $T_\textrm{on}$, but decreasing as $\varPhi _\textrm{on}$ increases. In other facilities that used synthetic jet arrays, $Re_\lambda$ tended to have higher values of 314 (Variano and Cowen 2008), 334 (Pérez-Alvarado et al. 2016), and 277 to 378 (Johnson and Cowen 2018). While increasing $V_P$ and $T_\textrm{on}$ in our facility could potentially result in higher $Re_\lambda$ values, we note that $M^*$ also increases with $V_P$ and $T_\textrm{on}$, implying there may be a limit to the maximum attainable $Re_\lambda$ with this setup. Ghazi et al. (2023) found that $Re_\lambda$ appears to be limited by facility size across all zero mean flow HIT facilities, regardless of the strength of the actuators, hence the smaller $Re_\lambda$ in our facility relative to the above-mentioned facilities. Consequently, to maintain negligible mean flows, we limited values of $V_P$ and $T_\textrm{on}$ to those presented herein.

3.4 Temporal spectra

The temporal spectra can be calculated from ADV data using:

$$\begin{aligned} S_{U_iU_i} = \left| {(fft (U_i))^2\over N f_s}\right| , \end{aligned}$$

(11)

where fft is the fast Fourier transform, $f_s$ is the sampling frequency, and N is the total number of samples within the velocity record. The spectra are plotted up to the Nyquist frequency, $k_{ny}$, showing only 1-side of the spectra in Fig. 9. The frequency spectra are normalized by multiplying by 2 such that the integral of the spectra over the entire domain is equal to the variance of the velocity signal. Slopes of -5/3 are observed in the inertial subrange of the spectra plots for both the horizontal and lateral velocity signals, indicating the presence of well-developed homogeneous isotropic turbulence (Kolmogorov 1941). Whereas the spectrum from the $u_2$ velocity shows noise beyond a frequency of roughly 10 Hz, we see the $u_1$ spectrum exhibits a -3 slope, potentially indicative of the dissipation region of the spectrum for this energetic flow.

Fig. 9

Frequency spectra of the $u_1$ (– green) and $u_2$ (... blue) velocity from ADV measurements at $(x_1,x_2,x_3 )$ = (0, 0, 0), using 50 ensemble averages, and overlaying slopes of -5/3 (– black) and -3 (- - black). $V_P$ = 185 cm/s, $\varPhi _\textrm{on}$ = 15%, and $T_\textrm{on}$ = 1 s

4 Conclusions

A new experimental apparatus was developed to produce homogeneous isotropic turbulence with negligible mean and secondary flows in the center of a water tank. The apparatus is the first of its kind to use center-facing pumps controlled by a random forcing algorithm to generate HIT. The array consists of 20 vertex- and edge-mounted jets in which the mean percentage of jets on, jet mean on-time, and pump outlet velocity are independently varied. PIV and ADV measurements were completed to obtain flow statistics and aid in making adjustments to the design of the tank.

We initially explored a wide range of jet parameter combinations and experimented with different jet nozzle configurations to produce HIT with negligible mean flows within the facility. The first iteration of jet nozzle had a single outlet that directed the pump flow toward the tank center, which limited the spread of the jets and resulted in poor isotropy in the central core of turbulence. A nozzle with four adjacent orifice openings was subsequently designed to distribute the momentum input from each source. Incorporation of this nozzle was found to significantly increase homogeneity while simultaneously decreasing $M^*$ in the 10 cm by 10 cm central region of the tank. Turbulence levels were adjusted by the jet control parameters, and characteristics of the turbulence were quantified using PIV and ADV measurements. Increases to $T_\textrm{on}$ and $V_P$ each resulted in greater values of k, consistent with observations in comparable facilities. However, increases to $\phi _\textrm{on}$ resulted in both increases and decreases to k, suggesting there may be an optimal average number of active jets to maximize turbulent kinetic energy. Values of turbulent kinetic energy for the jet parameter combinations we explored ranged from 12.1 $\hbox {cm}^2$ $\hbox {s}^{-2}$ to 51.1 $\hbox {cm}^2$ $\hbox {s}^{-2}$, while $Re_\lambda$ ranged from 68 to 176.

Isotropy was quantified via ratios of RMS velocities, dissipation rates, and integral length scales. Ratios of $\frac{u_3'}{u_1'}$ were between 0.93 and 0.98, indicating highly isotropic flow, given a target of unity. Similarly, $\frac{\epsilon _\textrm{LL}}{\epsilon _\textrm{NN}}$ ranged from 1.0 to 1.1 across all tests, close to the target of 1. The ratios between the longitudinal and transverse integral length scales (i.e., $\frac{{\mathcal {L}}_{11,1}}{{\mathcal {L}}_{11,3}}$ and $\frac{{\mathcal {L}}_{33,3}}{{\mathcal {L}}_{33,1}}$; recalling a target value of 2) ranged from 1.39 to 1.60 and 1.68 to 1.88, respectively. Meanwhile, we further computed $\frac{{\mathcal {L}}_{11,1}}{{\mathcal {L}}_{33,3}}$ and $\frac{{\mathcal {L}}_{11,3}}{{\mathcal {L}}_{33,1}}$ (recalling a target value of unity for both), which ranged from 0.92 to 1.09 and 1.22 to 1.29, respectively. Together, these values suggest that the turbulence within this facility can overall be characterized as isotropic, despite some disparities across the different metrics considered. The isotropic region comprises about 5.2% of the entire 44 cm by 44 cm cross-sectional area of the facility, and the length of the region is approximately equivalent to 2.9${\mathcal {L}}_{11,1}$. The homogeneity deviation of $u_1'$ and $u_3'$ in both the $x_1$ and $x_3$ direction was below 10% for the majority of cases, indicating a high degree of homogeneity was achieved across the full measurement region. Calculation of temporal spectra from ADV data revealed slopes of -5/3 and -3 in the inertial and dissipation regions of the spectra plots, indicating well-developed HIT. Last, $M^*$ values were less than 3% for all cases, indicating secondary flows were negligible relative to the turbulence.

Given suitable degrees of homogeneity and isotropy of the turbulent flow, we evaluated six different combinations of common assumptions made when computing dissipation directly from planar PIV, to account for velocities and velocity gradients in the y-direction (i.e., the out-of-plane direction given our coordinate system). To estimate $\frac{\partial u_1}{\partial x_2}$ and $\frac{\partial u_2}{\partial x_1}$, we explored assumptions of radial symmetry about both the z and x axes. To estimate $\frac{\partial u_2}{\partial x_2}$, we considered continuity as well as isotropy about the x and z axes. In the cases in which we assumed continuity, total dissipation values were approximately 10% greater than resultant values based on isotropy. However, changes in the total dissipation calculation based on assumptions for radial symmetry to estimate $\frac{\partial u_1}{\partial x_2}$ or $\frac{\partial u_2}{\partial x_1}$ and isotropy to estimate $\frac{\partial u_2}{\partial x_2}$ resulted in nearly identical dissipation estimates. Dissipation values based on assumptions of continuity and z-axis symmetry, which we selected to be consistent with prior literature, ranged from 17.7 to 56.5 $\hbox {cm}^2$/$\hbox {s}^3$.