Micro-PIV characterization of the flow in a milli-labyrinth-channel used in drip irrigation

Abstract

The baffle-fitted labyrinth-channel is largely used in drip irrigation systems. The existing baffles, which play an important role for generating head losses and ensure the flow regulation on the irrigation network, produce vorticity regions where the velocity is low or equal to zero. These vortices are likely to favor the deposition of particles or biochemical development causing dripper clogging which drastically reduces its performance. Flow topology in the dripper labyrinth-channel must be described to analyze dripper clogging sensibility and the effect on irrigation efficiency. Also, a question remains about the regime of this low Reynolds number flow. In the present study, the flow is characterized experimentally by micro-particle image velocimetry (micro-PIV) technique on ten-pattern repeating baffles used in drip irrigation dripper. Square cross-section is of about 1.4 mm$^2$. Studied inlet Reynolds number varies from 345 to 690, which is equivalent to 1.4–2.8 l h$^{-1}$. The mean velocity distribution and turbulence quantities within the labyrinth-channel flow are presented and discussed in this paper. The results underline that flow regime is turbulent and non-isotropic.

Graphical abstract

1 Introduction

Drip irrigation is a system which serves to distribute the water through a network of pipes under low pressure, bringing the water to an immediate vicinity of the cultivated plants (Lamm et al. 2007). It is considered the most efficient method of providing water to plants; water efficiency varies from 0.7 to 0.95. This efficiency refers to the ratio of the amount of water used by the crop to the amount of water supplied from the water source (Howell 2003; Hsiao et al. 2007). Drip irrigation has many advantages such as economical in terms of human labor, water and energy, and has good sanitary conditions when wastewater is used (Oron et al. 1999; Lazarova and Bahri 2015). Despite its advantages, drip irrigation is sensitive to clogging which depends on water quality. Clogging restricts the application of drip irrigation system, and is an important factor affecting dripper life and drip irrigation benefits (Nakayama and Bucks 1991; Yavuz et al. 2010). Good understanding of the flow characteristics in the dripper is required to analyze and prevent clogging mechanism. Flow visualization and characterization may be performed by experimental and/or numerical methods. It is important to highlight that drippers generate flow rates between 0.5 and 8 l h$^{-1}$ for pressures between 50 and 400 kPa (Goldberg et al. 1976) and labyrinth-channel cross-section of about 1 mm$^2$. Therefore, Reynolds numbers, based on the mean velocity and hydraulic diameter, are in the range of 300–2220. So, the flow has a rather low Reynolds number. However, it is often considered as being turbulent because of the complexity of labyrinth-channels (Nishimura et al. 1984). In the literature, almost all studies conducted on the labyrinth-channel dripper geometry have used numerical modeling to obtain results with lower time and cost (Date 2005). Most of these studies use turbulence models such as the k–$\epsilon$ model or similar two-equation models (Wei et al. 2006, 2012; Dazhuang et al. 2007; Ali 2013). However, these models assume the turbulent flow is isotropic, while the Reynolds-stress model (RSM) which is used by Zhang et al. (2007, 2010) and Philipova et al. (2009) takes into account non-isotropic effects. Other more complex models such as the LES model (large eddy simulations) have been used by Wu et al. (2013). LES is very expensive in time and memory, and, for some complex flows, computations do not converge easily. Low-Reynolds number k–$\epsilon$ models have been explored by Al-Muhammad et al. (2016). The choice of numerical models is not fixed so far. This emphasizes the importance and the strong need to use an experimental approach to visualize and characterize the flow in the labyrinth-channel as a first step, and to define the flow regime and validate the numerical model as a second step.

Presently, only a few experimental studies that characterize the flow in the labyrinth-channel dripper are available. This shortage of experimental studies can be justified by the geometry complexity. Thus, critical experimental conditions must be taken into account in order to carry out experiments in a correct way. The LDV method is used by Zhang et al. (2007) on an arch-type labyrinth-channel. Then, the digital particle image velocimetry (DPIV or PIV) is used by Li et al. (2008) to assess flow characteristics in the labyrinth flow path. Fluorescent particles constructed from polystyrene (density of polystyrene is 1050 kg m$^{-3}$) are used with an average diameter of 1–1.5 $\times \,10^{-5}$ m. Image number is not specified, and no attention is paid to data convergence. Li et al. (2008) compare experimental results with numerical ones obtained with the k–$\epsilon$ model as turbulence model. Based on the numerical velocity distribution, they conclude that the prediction of flow process in the central cross-section dripper flow path is relatively similar to that estimated by PIV experiments. Likewise, they find that the mainstream flow is turbulent at pressures between 10 and 150 kPa, which corresponds to Reynolds numbers 70–1000, without clear analysis about transition from laminar to turbulent flow. Next, Liu et al. (2010), a co-author of the work Li et al. (2008), analyze experimentally the flow within two geometries for which the basic labyrinth-channel units are rectangular and triangular. Liu et al. (2010) focus on the same experimental conditions as those studied by Li et al. (2008). In the work of Liu et al. (2010), only 50 pairs of images are considered to compute velocity with a vector resolution of 0.08 mm $\times$ 0.11 mm. They analyze the flow characteristics in three different positions within the labyrinth-channel. The micro-PIV technique is also used by Wei et al. (2012) to visualize the water flow with suspended sand particles inside the labyrinth-channel under the pressure range 40–150 kPa on two geometries. $\hbox {Al}_{2}\hbox {O}_{3}$ powder is selected to trace the liquid phase with a particle diameter of 5 $\upmu$ m and density of 3950 kg m$^{-3}$; which is almost four times that of water so that particles will sediment. However, tracer sedimentation effects are not discussed by the authors. They use the RNG k–$\epsilon$ model to perform simulations and conclude that computational fluid dynamics (CFD) simulation results show reasonable agreement with their experimental results on the basis of the curve for the pressure–discharge relationship. The average of flow rate deviations is about $4\%$. But these analyses are still mostly qualitative considering the PIV protocols: too few images are taken to ensure convergence and heavy particles are used for seeding the flow. Consequently, one cannot be confident in their analysis of the turbulent quantities.

In the present study, the micro-PIV technique is used to characterize the flow in a square cross-section labyrinth-channel. The experimental protocol is first introduced. Then, a detailed discussion about the choice of setting parameters is presented and their influence on experimental data accuracy is analyzed. Next, the data treatment is explained. Finally, the experimental results are presented and discussed.

Fig. 1

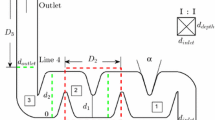
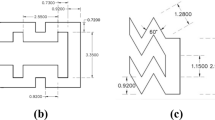
Dripper studied. a Industrial dripper geometry with a zoom of the basic unit made of three baffles (labyrinth-channel unit). b Dripper prototype used to perform the micro-PIV analysis. c Ten baffles labyrinth-channel constitutive of the dripper prototype: a straight $D_1$ length is added to the existing distance at the inlet and the outlet of the real labyrinth-channel of the dripper to operate the micro-PIV experiments and ensure developed flow before entering the labyrinth-channel. The points $P_1$ and $P_2$, the colored lines and rectangles represent the zones where the results will be analyzed. The origin of a Cartesian coordinate system is arbitrarily specified so that the bottom wall is at $y=0$ for the vertical lines 1–3 and the bottom of the channel (green-colored zone) corresponds to $z=0$

Table 1 The labyrinth-channel dimensions

2 Materials and methods

2.1 Geometry of studied dripper

The studied labyrinth-channel geometry is an integrated dripper with uniform section which generates a turbulent flow as a result of the direction changes. This industrial dripper is the most widespread in drip irrigation (namely GR dripper which is not a pressure-compensating one), as displayed in Fig. 1a. The original dripper is composed of 60 baffles (labyrinth-channel units). Each three baffles pattern composes the basic unit which is repeated 20 times.

For the present laboratory experiments, a ten-pattern labyrinth-channel is fabricated by machining. To allow optical access for micro-PIV, the material is transparent (PMMA: poly-methyl methacrylate). Sealing is ensured by pressing the two PMMA plates between two 5-mm-thick steel plates (Fig. 1b). A detailed geometry in 2D of the labyrinth-channel used for micro-PIV experiments is shown in Fig. 1c. All the dimensions are presented in Table 1, while the line coordinates are presented in Table 2.

2.2 Hydraulic equipments

The hydraulic scheme is presented in Fig. 2. It is composed of different elements to filter and pump the fluid. Flow rate, pressure losses and relative pressure are measured. The experimental setup is shown in Fig. 4. Pump type is a diaphragm metering pump (SIMDOS 10). Pump accuracy is of $2\%$ of the set value of the flowrate. It circulates water from a 1-l tank. The water quantity in the pipes and the labyrinth-channel is about 50 ml. The pump provides a flow rate between 10 and 100 ml min$^{-1}$ (or 0.6–6 l h$^{-1}$).

Fig. 2

Hydraulic scheme

Just before the pump, there is an in-line filter to protect it, especially during seeding to keep a good performance and to avoid the pump cleaning which must be done by specialists. The pump induces flow pulsations. These flow pulsations must be absorbed before the fluid goes through the studied prototype. To avoid them, two dampers are added to the circuit. A commercial damper of type: PML 9962-FPD10, with a maximum efficiency of $97\%$ is firstly checked. However, with this damper, the pulsations are not completely damped. For this reason, a second, hand-made, damper is constituted of a pipe containing air to completely damp the pump pulsations. As a result, peak-to-peak amplitude decreases from 9.4 ml min$^{-1}$ with no pulsation dampers to 1.8 ml min$^{-1}$ when both dampers are used, for a flow rate of 48 ml min$^{-1}$ (Fig. 3). Variation rms values are calculated for both systems, it is found $Q_{\text {rms}}$ = 0.20 ml min$^{-1}$ and 2.82 ml min$^{-1}$ for the system with dampers and without dampers, respectively. The average flowrate decreases from 48.64 ml min$^{-1}$ to 48.15 ml min$^{-1}$ when dampers are used, which is related to the device head losses (Fig. 4).

Table 2 Line coordinates

Fig. 3

Flowrate profiles when dampers are used (blue) or not (red). In this figure, the data are plotted for a period of 40 s for visualization. However, the flowrate data are recorded for a period of 800 s

Fig. 4

Experimental scheme. The laser light sheet is introduced from the inlet side of the channel. Almost all experiments are performed in the middle plane except for the analysis of roughness; see Table 2

2.3 Micro-PIV components

The micro-PIV equipment is composed of a laser source [Litron Nd-YAG Laser of 135 mJ, doubled in frequency (532 nm)] and a HiSense 4M camera. The minimum thickness of the light sheet reaches 1 mm. The minimum thickness must be in the studied zone to ensure maximal light intensity. The distance between the laser and the prototype is changed depending on the studied baffle. The Dantec Dynamics HiSense 4M camera offers high resolution ($2048 \times 2048$ pixels) combined with high sensitivity, with a pixel size of $7.4 ~\upmu$m.

This camera is equipped with a Canon MP-E 65 mm f/2.8 lens. The lens provides a magnification of up to $M=5~\times$ for which the depth of field is 0.048 mm. Three extension rings (extension tube) of 12, 20 and 32 mm have been added to increase magnification up to 6.9 and thus to visualize 1 $\upmu$m-PIV particles. The flow is seeded by fluorescent particles. The green laser light (532 nm) is filtered on the camera reception to catch only the fluorescent particle emission ($\lambda =607$ nm).

The correlation depth, defined as the depth over which particles significantly contribute to the correlation function (Olsen and Adrian 2000), is equal simply to $2 z_{\text {corr}}$. $z_{\text {corr}}$ is calculated using Eq. (1) defined by Olsen and Adrian (2000):

$$\begin{aligned} z_{\text {corr}} =\left[ \frac{(1-\sqrt{\epsilon })}{\sqrt{\epsilon }} \left( f^{\# 2} d_{\text {p}}^2 + \frac{5.95 (M+1)^2 \lambda ^2 f^{\#4} }{M^2} \right) \right] ^{1/2}, \end{aligned}$$

(1)

where $d_{\text {p}}$ is the diameter of the particle (m), $f^\#$ is the f-number of the objective lens defined by $f^\#=f/D_{\text {a}}$, where f is the focal distance (m), and $D_{\text {a}}$ is the aperture lens diameter (m). In the present experiment, $f^\#=2.8$, $\epsilon$ is the ratio between the weighting function of a particle that does not contribute to the correlation and the weighting function at the object plane. As advised by Wereley et al. (1999), we fix $\epsilon =0.01$. This yields $2 z_{\text {corr}}= 82 \,\upmu$m.

The resolving power of a lens is defined as the minimum transverse distance between two point sources of light, r, that can be resolved using the Rayleigh criterion (Jenkins and White 1957). The resolving power is given by Eq. (2) (Meinhart and Wereley 2003):

$$\begin{aligned} r =1.22 f^{\#} \lambda . \end{aligned}$$

(2)

In the present experiments, we obtain 2.074 $\upmu$m. r is almost twice the diameter of particles and/or almost twice the pixel size. This means two particles located on two neighboring pixels will be seen as one large particle (Fig. 5).

2.4 Experimental setting

2.4.1 Type and concentration of seeding particles

Polystyrene-based (PS) particles are preferred because their density (1050 kg m$^{-3}$) is closer to the water density than PMMA particles (1190 kg m$^{-3}$). These particles are hydrophobic (and insoluble in acids and bases). PS fluorescent particles are used to improve sensitivity and detectability in presence of nearby walls and to have a bright feature with high-contrast colors. In this work, particles with a diameter of 1 $\upmu$m are used. Fluorescent components are Rhodamine B. The absorption and emission wavelengths are $\lambda _{\text {abs}}=530$ nm and $\lambda _{\text {em}}=607$ nm, respectively. The supplier is microParticles GmbH.

The choice of the particles size is based on three criteria. The first criterion is the Stokes number (Eq. 3) which is defined as the ratio of the characteristic time of a particle (Eq. 4) to a characteristic time of the flow, namely, the Kolmogorov time scale (Eq. 5).

Table 3 Turbulent dissipation rate and Kolmogorov length scale, as obtained numerically by the RSM model (Al-Muhammad 2016)

$$\begin{aligned} {\text {St}}=\frac{\tau _{\text {p}}}{\tau _\text {k}}, \end{aligned}$$

(3)

where $\tau _{\text {p}}$ is the characteristic time of a particle (s), $\tau _\text {k}$ is the Kolmogorov time scale (s),

$$\begin{aligned} \tau _{\text {p}}=d_{\text {p}}^2\frac{\rho _{\text {p}}}{18 \mu }, \end{aligned}$$

(4)

where $\mu$ is the dynamic viscosity of the fluid (Pa s), and $\rho _{\text {p}}$ is the particle density (kg m$^{-3})$.

$$\begin{aligned} \tau _\text {k}=\left( \frac{\nu }{\epsilon }\right) ^{1/2}, \end{aligned}$$

(5)

where $\nu$ is the kinematic viscosity of the fluid (m$^2$ s$^{-1})$, and $\epsilon$ is dissipation of turbulence kinetic energy (m$^2$ s$^{-3})$.

For $d_{\text {p}}=1\,\upmu$m, Stokes numbers for the flow rates reported in Table 3 are $4.5 \times 10^{-4}$ and $13 \times 10^{-4}$ for $Re=400$ and $Re=800$, respectively. The average dissipation rate $\epsilon$ is obtained by the RSM model (Al-Muhammad 2016) in the plane located at the middle of the channel in the z-direction (Table 3). The Stokes number values, thus, tend toward zero, since $\tau _{\text {p}}$ is indeed, as expected, much smaller than $\tau _\text {k}$.

The second criterion is related to the sedimentation velocity $U_g=d_{\text {p}}^2 \frac{\left( \rho _{\text {p}} - \rho \right) }{18 \mu } g=3 \times 10^{-8}$ m s$^{-1}$, where g is the gravitational acceleration (m s$^{-2})$. It is indeed a very low velocity because the particles density is selected to be very close to that of water. Typical velocities in the channel are in the order of 0.1–3 m s$^{-1}$ (Al-Muhammad et al. 2016; Li et al. 2008; Wu et al. 2013). These estimations show that the particle response time is faster than the smallest time scale of the flow. Particles, consequently, follow fluid streamlines closely without be derived by the sedimentation velocity. Therefore, the particles behave like tracers.

The third criterion is the particle concentration. If it is too large, the particles are not discernible on the images. However, if the concentration is too low, the particles are not distributed along the entire channel, and it is then difficult to estimate the velocity distribution in each point of the studied field. In practice, particles are added to the water until there are about 8–10 particles by interrogation window (Lu and Sick 2013). This concentration is obtained by mixing 1 ml of raw solution charged with particles added to 150 ml of pure water.

2.4.2 Experimental conditions

The temperature is that of ambient room, ${T}=20\,^\circ \text {C}$. The water used for the experiments is distilled water for which pH is 5.8. The refractive index of water is $n = 1.32580$ (Hale and Querry 1973). The refractive index of PMMA (prototype constitutive material) is $n=1.49253$ (Beadie et al. 2015). With this volume illumination, despite these refractive index differences no reflection nor shadows affect the studied zone (Fig. 5).

The present experiments are conducted with three flow rates $q_1=24$ ml min$^{-1}$ (1.44 l h$^{-1})$, $q_2=36$ ml min$^{-1}$ (2.16 l h$^{-1})$ and $q_3=48$ ml min$^{-1}$ (2.88 l h$^{-1})$; where $q_1$ and $q_3$ are chosen symmetrically around $q_2$ which corresponds to the nominal flow rate of such a dripper. These flow rates correspond to Reynolds numbers of 345, 520 and 690 (see Table 1). Image quality is not good enough from the third baffle when 1 $\upmu$-m particles are used. The laser light sheet is refracted and dispersed, which induces too low signal-to-noise ratio (SNR) values (see Appendix 1 for more details).

Fig. 5

a Raw image. b Arithmetic image

Table 4 Acquisition configuration

Table 5 Time delays between two laser pulses inferred from numerical results

2.4.3 Micro-PIV settings

Time delays between laser pulses In general, the time delay is adjusted to the flow velocity:

$$\begin{aligned} \Delta t =\frac{\Delta x}{|{\bar{u}}|}, \end{aligned}$$

(6)

where $\Delta x= \text {window size}/4$ is a typical particle displacement (m) (Raffel et al. 1998), and $|{\bar{u}}|$ is the flow velocity modulus (m s$^{-1})$.

The difficulty for choosing the time delay is that the labyrinth-channel flow is complex. It is in particular composed of two distinct regions, one, namely the mainstream flow, having a relatively high velocity value, and the other one, the recirculation zone, having a much smaller velocity value (Al-Muhammad et al. 2016). A typical velocity profile (along the line 3 presented in Fig. 1c) is plotted in Fig. 6. This profile corresponds to the modeling results obtained by the RSM model for a Reynolds number $Re=800$ (Al-Muhammad 2016). Two velocities corresponding to the extreme values are taken for estimating $\Delta t$. Then, $\Delta t$ is calculated from Eq. 6 in order that a particle moves a quarter of interrogation window (Tables 4, 5).

Fig. 6

Velocity modulus profile for $Re=800$ along the line 3 (see line position on Fig. 1c) (Al-Muhammad 2016)

It is important to underline that the values presented in Table 5, for the RSM model, are only indicative and serve as a first guess. Tests are carried out to determine which time delay would be better for micro-PIV experiments. It is observed (see Al-Muhammad 2016 for more details) that the measured velocity profiles do not evolve anymore when the time delay is lower than that corresponding to the mainstream flow, i.e., 15 $\upmu$s for the flow rate of 48 ml min$^{-1}$. Therefore, the time values 12, 8 and 6 $\upmu$s have been selected to perform the experiments for 24, 36 and 48 ml min$^{-1}$, respectively.

Acquisition frequency The acquisition frequency fr of image pairs is calculated by taking into account that velocity fields have to be non-correlated. The distance and the spatially averaged velocity in the recirculation zone allow to calculate this time, and thus the frequency. We thus fix fr $=1~\text {Hz}$.

2.4.4 Micro-PIV processing

Once the micro-PIV images are acquired, the instantaneous particle-displacement fields are calculated using the auto-correlation definition within the data acquisition software (Dantec Dynamic Studio). Firstly, a mask is applied manually. This mask is used to hide the outside of the flow. The average image is calculated. The background noise is removed by subtracting the average image from each image (image arithmetic). The subtraction of background noise is justified by the deposition of the seeding particles. The peak detection and vector validation are, then, processed using the Dantec software. Finally, a Matlab program is developed to plot velocity vectors and calculate derived statistical quantities such as velocity mean values and variances or the turbulence kinetic energy using only valid vectors (see Appendix 2).

Cross-correlation The technique of micro-PIV is based on image cross-correlation. In the present study, adaptive correlation is chosen to treat micro-PIV images. The adaptive correlation vector is based on the definition of offset from the previous offset. This results in a more accurate calculation of the average displacement. An overlap of $50\%$ is chosen. Process is performed in three steps starting from a first treatment with an interrogation area of $256 \times 256$ pixels until $32 \times 32$ pixels for 1-$\upmu$m-diameter particles.

Since the overall field of view is large, and it covers the whole baffle, the average spatial resolution of the vectors is limited to 17.2 $\upmu$m. Hence, the resolved scale is larger than the Kolmogorov length scale $\eta =(\frac{\nu ^3}{\epsilon })^{(1/4)}$, calculated for two flowrates and given in Table 3.

Vector validation The validation of peak correlation chosen is the relative height of the highest peak compared to that of the second highest peak. It is often quite satisfactory to use 1.1. If a very strict validation is required a value as high as 2 can be used. In our case, we fix a validation at 1.1. However, the percentage of non-valid vectors is about of 0–5%. Then, the post-processing is performed on the valid vectors only (the number of valid vectors is then $N_\text {v}$).

Micro-PIV measurement errors Some measurement errors may occur during acquisition, processing of acquired data, and/or errors due to the devices used (precision device). For example, the error due to flowmeter device is given, by the manufactures, as equal to $2\%$ of the set value in the operation manual. The effect of peak-locking, due to the sensor geometry in digital camera, is analyzed (see Appendix 1). Results for the peak-locking analysis show that there is no peak-locking when estimating velocity in the x and y directions in the third baffle, since the degree of peak-locking (C) remains lower than the critical value of 0.2 ($0.04\le C \le 0.09$). Therefore, the second-order moments of the fluctuating velocities are not biased by peak-locking. However, an inherent error of 0.01 pixel is produced by the software which is equivalent to 0.0027 m s$^{-1}$.

2.4.5 Data convergence and image number

The number of image pairs is chosen to ensure convergence criteria toward the mean velocity components u and v together with the three second-order moments of the fluctuating velocities. Its determination allows to reduce the recording time, to optimize the computer memory load and to avoid treatment of a huge amount of data.

The convergence of instantaneous velocities u and v, and fluctuating velocities towards the mean velocity are calculated and plotted in Figs. 7 and 8 for 750 pairs of images at two points in the flow, one is in the mainstream flow and the other is in the recirculation zone. Based on these results, 500 pairs of images are considered to be enough and an optimal choice when micro-PIV experiments are performed.

The quantitative convergence study is based on two types of residues:

• The residues calculated from the mean velocities $\overline{u}$, $\overline{v}$ and $\vert \overline{u} \vert$.

• The residues calculated from the second-order moments of fluctuating velocities $\overline{u^{\prime 2}}$, $\overline{v^{\prime 2}}$ and $\overline{u^{\prime } v^{\prime }}$.

Fig. 7

u and v velocity components, $Re=690$, pairs of images number $N=750$, where $N_\text {v}=596$, $N_\text {v}=710$ for P1 and P2, respectively. a Point P1 (− 5.5, 1.5). b Point P2 (− 6.5, 1.7)

Fig. 8

The second-order moments of the fluctuating velocity, $Re=690$, pairs of images number $N=750$, where $N_\text {v}=596$, $N_\text {v}=710$ for P1 and P2, respectively. a Point P1 (− 5.5,1.5). b Point P2 (− 6.5,1.7)

Fig. 9

Residues for the mean velocity, $Re=690$, number of pairs of images N = 500. a ${\text {log}}_{10}(\mathcal {R}_\text {u})$. b ${\text {log}}_{10}(\mathcal {R}_\text {v})$

Fig. 10

Residues for the second-order moments of the fluctuating velocities, $Re=690$, number of pairs of images N = 500. a log$_{10}(\mathcal {R}_\text {u}^{\prime 2})$. b log$_{10}(\mathcal {R}_\text {v}^{\prime 2})$ (c) log$_{10}(\mathcal {R}_{{\text {u}}^{\prime } {\text {v}}^{\prime }})$

Mean velocity The formula used to calculate the residue value, $\mathcal {R}$, for the mean velocity, is the following one:

$$\begin{aligned} \mathcal {R}_{{\text {u}}_{i_{N_\text {v}}}}= \frac{\left[ \frac{1}{N_\text {v}} \sum \nolimits ^{N_\text {v}}_{k=1} u_{i_\text {k}} -\frac{1}{N_\text {v}-1}\sum \nolimits ^{N_\text {v}}_{k=2} u_{i_{k-1}} \right] ^2}{\left[ \frac{1}{N_\text {v}} \sum \nolimits ^{N_\text {v}}_{k=1} u_{i_\text {k}} \right] ^2} \ , \end{aligned}$$

(7)

where $i=1, 2$ for x, y; k is the image number; $N_\text {v}$ is the valid image number which is different from the total image number N. It is important to emphasize that the valid image number varies from one interrogation window to another. The percentage is $96\%$ at the point [− 8.25, 2], whereas it reaches $98\%$ at the point [− 8.1, 1.4] when 1 $\upmu$m-particles are used. The position of both points is marked by signs (+) in Fig. 9. The logarithmic values of mean velocity residues are plotted for the data acquired in Fig. 9. The residue values are globally about $10^{-7}$ with 500 pairs of images. The red-colored regions (Fig. 9) are those for which the residues are larger than $10^{-2}$. In fact, these maxima are due to almost zero values of velocity fields.

Fluctuating velocity The second-order moments of fluctuating velocities residues are calculated by the formula:

$$\begin{aligned} \mathcal {R}_{{{{u}}^{\prime }_i u^{\prime }_j}_{N_\text {v}}}= \frac{\left[ \frac{1}{N_\text {v}}\sum \nolimits _{k=1}^{N_\text {v}} u^{\prime }_{i_\text {k}} u^{\prime }_{j_\text {k}}- \frac{1}{N_\text {v}-1}\sum \nolimits _{k=2}^{N_\text {v}} u^{\prime }_{i_{k-1}} u^{\prime }_{j_{k-1}} \right] ^2}{\left[ \frac{1}{N_\text {v}}\sum \nolimits _{k=1}^{N_\text {v}} u^{\prime }_{i_\text {k}} u^{\prime }_{j_\text {k}}\right] ^2} \ , \end{aligned}$$

(8)

where $i, j=1, 2$ for x, y.

The values obtained by this formula are plotted on Fig. 10. The residues values according to the second-order moments of fluctuating velocities are larger than for the mean velocity. The second-order moments of fluctuating velocities reach a stable value in the mainstream part of the flow. However, such a behavior is slightly not achieved in the recirculation zone for $\overline{u^{\prime } v^{\prime }}$ for which the residue values are about $10^{-5}$.

3 Results and discussion

3.1 Mean flow characterization inside the baffles

The mean velocity modulus field and streamlines inside the first and third baffles are shown in Figs. 11 and 12. Behind the obstacle, namely the tip herein, the flow is composed of two small vortices for the first baffle and a single large vortex for the third baffle. This region is called a recirculation zone (red ellipse, Fig. 11) which is characterized by a very low velocity. The mean velocity modulus varies from 0.05 to 0.2 m s$^{-1}$ for $Re=345$ (respectively, 0.1–0.4 m s$^{-1}$ for $Re=690$). The mainstream flow is interrupted by a stagnation zone (black circle) in the first baffle that may favor particle deposit or biofilm development. The vortex form of the recirculation zone, inside the third baffle (Fig. 12), is not changed when increasing the flow rate. The vortex center moves a little towards the bottom wall for $Re=345$. The vortex center is located at x = − 8.78 mm and $y = 0.66$ mm for $Re=345$ and then at $x = -\,8.78$ mm and $y = 0.76$ mm for $Re=690$ (Fig. 12b, d). In the middle of the labyrinth-channel, the flow has a high velocity reaching 1.2 m s$^{-1}$ (2.2 m s$^{-1}$) for $Re=345$ ($Re=690$) inside the third baffle. This narrow zone is called the mainstream flow. This description of the velocity regions is in agreement with the description cited by several numerical works such as Al-Muhammad et al. (2016).

Fig. 11

Mean velocity modulus fields and streamlines (m s$^{-1})$ inside the first baffle, $Re=345$ (a, b), $Re=690$ (c, d). a Mean velocity modulus. b Mean velocity streamlines. c Mean velocity modulus. d Mean velocity streamlines

The experimental velocity profiles (normalized mean velocity modulus and components inside the baffle) are, then, plotted on the three lines (1, 2 and 3, see Fig. 1c) for both Reynolds numbers $Re = 345$ and $Re = 690$ (Fig. 13). The velocity $\overline{u}$ is negative in the mainstream flow because the flow is in the opposite direction of the x-axis. $\overline{u}$ is positive in the lower part of the recirculation zone. $\overline{v}$ is negative in the mainstream flow for the second and the third baffles and is positive in the first baffle. The flow for $Re = 690$ is developed faster than for $Re = 345$ where the velocity evolves more between the line 2 and the line 3.

Fig. 12

Mean velocity modulus fields and streamlines (m s$^{-1})$ inside the third baffle, $Re=345$ (a, b), $Re=690$ (c, d). a Mean velocity modulus. b Mean velocity streamlines. c Mean velocity modulus. d Mean velocity streamlines

Fig. 13

Normalized mean velocity profiles for the first three baffles, $Re=345$ (a–c), $Re=690$ (d–f); see Table 1. a $\vert \overline{u} \vert$. b $\overline{u}$. c $\overline{v}$. d $\vert \overline{u} \vert$. e $\overline{u}$. f$\overline{v}$

3.2 Reynolds stresses

This paragraph presents results for the Reynolds stresses and relates them with the mean velocity gradient in the labyrinth-channel. Reynolds stresses $\overline{u^{\prime 2}}$, $\overline{v^{\prime 2}}$ and $\overline{u^\prime v^\prime }$ are calculated and plotted inside the third baffles for $Re=345$ and $Re=690$ (Fig. 14). It can be observed that the Reynolds stresses are 3–4 times higher for $Re=690$ in comparison with $Re=345$ (Fig. 14). For both Re, $\overline{u^{\prime 2}}$ and $\overline{v^{\prime 2}}$ are maximum in the mainstream flow near the separation zone. Reynolds stresses are weak ($\overline{u^{\prime 2}}$ and $\overline{v^{\prime 2}}$) and even close to zero ($\overline{u^\prime v^\prime }$) in the vortex zones ($y \le 1.5$ mm, or $y/d_2 \le 0.54$, Fig. 15). Combined with low mean velocity, particle deposition and dripper clogging are likely to occur in these zones. The magnitude scales of fluctuating velocity second-order moments are, in the first baffle, small when compared with the second and the third baffle, e.g., normalized $\overline{u^{\prime 2}}$ is, respectively, equal to 0.19, 0.67 and 0.71 for $Re=690$.

Fig. 14

Fluctuating velocity second-order moments fields inside the third baffle, $Re=345$ (a–c), $Re=690$ (d–f). a $\overline{u^{\prime 2}}$. b $\overline{v^{\prime 2}}$. c $\overline{u^\prime v^\prime }$. d $\overline{u^{\prime 2}}$. e $\overline{v^{\prime 2}}$. f $\overline{u^\prime v^\prime }$

Fig. 15

Normalized fluctuating velocity second-order moments profiles for the first three baffles, $Re=345$ (a–c), $Re=690$ (d–f). a $\overline{u^{\prime 2}}$. b $\overline{v^{\prime 2}}$. c $\overline{u^\prime v^\prime }$. d $\overline{u^{\prime 2}}$. e $\overline{v^{\prime 2}}$. f $\overline{u^\prime v^\prime }$

In turbulent flows, the mean shear stress is composed of two terms, $\tau =\tau _\text {visc}+\tau _\text {tur}$, where $\tau _\text {visc}=\mu \left( \frac{\partial \overline{u}}{\partial y} + \frac{\partial \overline{v}}{\partial x} \right)$ and $\tau _\text {tur}=-\rho \overline{u^\prime v^\prime }$. $\overline{u^\prime v^\prime }$ can be related to the mean velocity gradient, through Boussinesq’s hypothesis :

$$\begin{aligned} -\, \rho \overline{u^\prime v^\prime }= \mu _t \left( \frac{\partial \overline{u}}{\partial y} + \frac{\partial \overline{v}}{\partial x} \right). \end{aligned}$$

(9)

In the first cell located at the wall, where the turbulent viscosity is zero, $\tau = \mu \left( \frac{\partial \overline{u}}{\partial y}\right) _{y=0}$ when the flow is parallel to the x-axis. In the flow stream, the shear stress is given as: $\tau =- \rho \overline{u^\prime v^\prime }$ neglecting $\tau _\text {visc}$ in comparison with $\tau _\text {tur}$.

The profiles of $\frac{\partial \overline{u}}{\partial y}$ and $\frac{\partial \overline{v}}{\partial x}$ are plotted on the line 3 to determine the dominant term and/or the term values along this line (Fig. 16). $\frac{\partial \overline{u}}{\partial y}$ and $\frac{\partial \overline{v}}{\partial x}$ have the same magnitude. In near-wall region, when $y=0$, $\frac{\partial \overline{u}}{\partial y}$ is equal to 2200 and 5000 $s^{-1}$, and thus $\tau =2.2$ and 5 Pa, for $Re=345$ and $Re=690$, respectively. As a consequence, $- \overline{u^\prime v^\prime }$ values are equal to 0.0022 and 0.005 m$^2$ s$^{-2}$.

For both Reynolds numbers, $\overline{u^\prime v^\prime }$ values are almost zero in the recirculation zone ($0<y/d_2<0.54$). Then, in the flow core, they are positive for $0.54<y/d_2<0.64$ and negative for $y/d_2>0.64$. For $y/d_2\le ~0.54$, one of the two terms eliminates the other, therefore, $\overline{u^\prime v^\prime }$ is almost zero. From $y/d_2=0.54$ to $y/d_2=0.71$ ($1.5<y($mm$)<2$mm), the value of $\frac{\partial \overline{u}}{\partial y}$ is responsible for the positive value of $\overline{u^\prime v^\prime }$, while for $y/d_2>0.71$ ($y>2$ mm) both terms accumulate and give the strong negative value of $\overline{u^\prime v^\prime }$. We can conclude that $\overline{u^\prime v^\prime }$ values are well correlated with the mean velocity gradient values and therefore depend on the different regions which have been already distinguished.

Fig. 16

Mean velocity derivatives along the line 3. a $Re=345$. b $Re=690$

3.3 Vertical evolution of the flow

As mentioned above, the labyrinth-channel is fabricated by machining and thus its bottom surface is not smooth. The surface roughness is characterized using an optical profilometer. The roughness average, $\mathcal {R}_{\text {a}}$, is the most widely used one-dimensional roughness parameter. This parameter is the arithmetic average of the absolute values. When measuring $\mathcal {R}_{\text {a}}$ for the fabricated labyrinth-channel, we found that $\mathcal {R}_{\text {a}}=4.65\,\upmu$ m. The normalized mean and fluctuating velocity profiles are plotted in Figs. 17 and 18, for the third baffle at $z_n=z/d_\text {{depth}}=[0.20; 0.50; 0.60]$ above the rough wall. Velocity profiles for $z_n=0.50$ and $z_n=0.60$ are superimposed; while some differences are remarked at $z_n=0.20$ in the recirculation zone ($0<y/d_2<0.54$) for $\overline{v}$, and consequently $\vert \overline{u}\vert$ and $\overline{v^{\prime 2}}$ (Fig. 17). Indeed, the recirculation zone shape is changed. The recirculation center (minimum of $\vert \overline{u}\vert$ for $0<y/d_2<0.54$) moves closer to wall: 0.3 for $z_n$ = 0.20 against 0.4 for $z_n$ = 0.50 and 0.60 (Fig. 17a). Some points on the fluctuating velocity profiles are outlier due particles stick on the wall that alterate the signal at $z_n = 0.20$.

Fig. 17

Normalized mean velocity profiles along the line 3 for three normalized vertical positions $z_n=z/d_{\text {depth}}$ ($Re=690$). a $\vert \overline{u} \vert / \vert \overline{u} \vert _{\text {inlet}}$. b $\overline{u}/ \vert \overline{u} \vert _{\text {inlet}}$. c $\overline{v}/ \vert \overline{u} \vert _{\text {inlet}}$

Fig. 18

Normalized fluctuating velocity second-order moments profiles along the line 3 for three normalized vertical positions $z_n=z/d_{\text {depth}}$ ($Re=690$). a $\overline{u^{\prime 2}}/ \vert \overline{u} \vert ^2_{\text {inlet}}$. b $\overline{v^{\prime 2}}/ \vert \overline{u} \vert ^2_{\text {inlet}}$. c $\overline{u^\prime v^\prime }/ \vert \overline{u} \vert ^2_{\text {inlet}}$

3.4 Flow isotropy

The ratio $\overline{u^{\prime 2}}$/$\overline{v^{\prime 2}}$ is calculated within the third baffle to determine whether the flow can be considered as isotropic or not; this is presented in Fig. 19a. In order to better distinguish contour values, the high scale (dark red) is fixed to be 3. However, the value of $\overline{u^{\prime 2}}$/$\overline{v^{\prime 2}}$ reaches about 10 near the wall. This is due to the values of $\overline{v^{\prime 2}}$ which are almost zero. The red zones highlight the zones where $\overline{u^{\prime 2}}$/$\overline{v^{\prime 2}}$ is greater than 3.

In practice, the boundary condition $\vert \overline{u} \vert =0$ at the wall determines the way in which the Reynolds stresses depart from zero for small wall distances. The logarithmic value of $\overline{u^{\prime 2}}/\overline{v^{\prime 2}}$ is, then, calculated and represented in Fig. 19b. In Fig. 19b, the positive values of $\text {log}_{10}(\overline{u^{\prime 2}}/\overline{v^{\prime 2}})$ correspond to the regions where $\overline{u^{\prime 2}}$ is superior to $\overline{v^{\prime 2}}$ while the negative values are for the opposite case. The peak value is $\text {log}_{10}(\overline{u^{\prime 2}}/\overline{v^{\prime 2}})$ = 0.8 which gives $\overline{u^{\prime 2}}/\overline{v^{\prime 2}}$ = 6.31. This indicates that the flow is strongly anisotropic, with periodic switching of major contributions from u and v, as seen very close to the walls (where red and blue levels alternate), due to the orientation of the wall.

Fig. 19

Anistropy of the flow in the third baffle, $Re=690$. a $\overline{u^{\prime 2}}/\overline{v^{\prime 2}}$. b $\text {log}_{10}(\overline{u^{\prime 2}}/\overline{v^{\prime 2}})$

4 Conclusion

As far as we know, it is the first time that such a micro-PIV technique is developed to analyze the flow in a baffle-fitted labyrinth-channel constituting irrigation drippers. The characterization of the flow in a milli-labyrinth-channel by the micro-PIV technique is presented and detailed in this paper. The results demonstrate that micro-PIV is a technique which is relevant to determine with high accuracy the mean and fluctuating velocity fields inside the labyrinth-channel. The main conclusions are as follows :

• In the present configuration, the experimental investigation is difficult from the third baffle owing to the light dispersion through several labyrinth-channel walls;

• 500 pairs of images are considered to calculate properly the mean velocity fields;

• The present study confirms some numerical results obtained by Al-Muhammad et al. (2016) for which the flow is composed of a mainstream flow and a recirculation zone;

• Velocity profiles are measured at three vertical positions ($z_n$) from the bottom wall. The observed differences for $z_n = 0.20$, by comparison to $z_n = 0.50$ and 0.60, are resulting from the wall presence which impacts the recirculation zone ($0<y/d_2<0.54$). The mean velocities and fluctuating velocities second-order moments are the same in the flow core;

• The flow regime inside the labyrinth-channel is turbulent and non-isotropic. Therefore, it is advised to use a numerical model which can take into account anisotropic effects.

These experimental results will allow, in future work, to restrict the choice of a turbulence model to study the flow in the labyrinth-channel with high accuracy. Next, detecting the recirculation zones, which are mainly responsible for clogging problems in drip irrigation systems, and analyzing them in a quantitative way, is one of the main objectives of future work based on micro-PIV data. Finally, these analyses and results will be used as a basis for studying two-phase flow by injecting sand particles. Moreover, having a precise and comprehensive aspect on the clogging topology and formation mechanism is essential to optimize an anti-clogging dripper.

Appendices

Appendix 1: Uncertainly analysis

1.1 Peak locking

The peak-locking effect is due to the sensor geometry in digital cameras. This phenomenon occurs when particle images are much smaller than the pixel size, so that the displacement tends to be biased towards discrete pixel values (Westerweel 2000). Peak-locking significantly reduces the accuracy of micro-PIV measurements although the effects on the mean velocities may be within acceptable limits. Indeed, the mean velocities are the only statistics that are insensitive to peak locking as it was found by Christensen (2004). The peak-locking effect can lead to awkward results for instantaneous spatial derivative data such as velocity gradient and also for turbulent velocity fluctuations. The easiest way to analyze this phenomenon is to plot an histogram of the fractional part of velocity components (displacements) which is between $-\,0.5$ and $+\,0.5$ pixel units. In the present study, the pixel size, due to the magnification, is equivalent to 1.074 $\upmu$m, which is close to the particles diameter. The histograms of displacements are presented in Fig. 20. The degree of peak locking can be quantified as:

$$\begin{aligned} C=1-\frac{N_{\text {min}}}{N_{\text {max}}}, \end{aligned}$$

(A.1)

where $N_{\text {min}}$ (minimum of $\%$) and $N_{\text {max}}$ (maximum of $\%$) are the lowest and highest percent of counts in the fractional histogram. Hence, if $C=0$, this indicates the absence of peak-locking, whereas $C=1$ indicates very strong peak locking. Four levels of peak-locking can be distinguished (Overmars et al. 2010):

• $C<0.2$, virtually no peak-locking occurs,

• $0.2<C<0.4$ mild peak-locking occurs,

• $0.4<C<0.6$ strong peak-locking occurs,

• $C>0.6$ severe peak-locking.

1.2 Signal-to-noise ratio (SNR)

The choice of the optimal diameter for seeding particles is a compromise between an adequate tracer response of the particles in the fluid, which requires small diameters, and a high signal-to-noise ratio (SNR) of the scattered light signal, which requires large diameters. The cross-correlation SNR is based on the measure of the primary peak ratio (PPR), namely the ratio between the highest correlation peak and the second tallest peak (Kumar and Hassebrook 1990). The optical properties may be deteriorated when choosing 1 $\upmu$m diameter, even though there is no peak-locking effect which could induce erroneous estimates for mean velocities and fluctuating velocity second-order moments. In practice, for 1 $\upmu$m diameter, the SNR from the fourth baffle is less than 4, which is the threshold value for correct detection. Therefore, it is not possible to use the 1 $\upmu$m particles to conduct the micro-PIV experiments for baffles farther than the third one. The labyrinth-channel prototype is illuminated by the right side where $x> 0$ (Fig. 1c). As a consequence, the laser light-sheet is more diffused by the 1-$\upmu$m particles and even more when the laser light-sheet moves deeper into the labyrinth-channel.

Fig. 20

The subpixel analysis in the third baffle, $Re=345$ (a, b), $Re=690$ (c, d). a u subpixel. b v subpixel. c u subpixel. d v subpixel

Appendix 2: Data processing

Fig. 21

Chart of micro-PIV data processing

See Fig. 21.