Introduction

Micro-irrigation is an irrigation system characterized by low water flow rates. Water drops near the plants through emitters. This type of irrigation improves efficiency by reducing energy consumption, evaporation, drift, runoff and deep percolation losses when compared with the other techniques such as sprinkler irrigation. In this technique, the emitters are the most important and critical component. They work with weak flow rate between 0.5 and 0.8 l h−1 for pressure between 50 and 400 kPa. The emitter flow rate increases with static pressure in a lateral pipe according to a power-law relation (Karmeli 1977):

$$q=K P^x$$
(1)

where q is the flow rate of emitter ( l h−1), K is the constant of proportionality that characterizes each emitter, P is the pressure head (kPa) and x is the emitter discharge exponent. The value of this exponent depends on emitter conception. Indeed, manufacturers try to design emitters for which the flow rate is not directly dependent on the pressure head (\(x<0.5\)). To reach this goal, they introduce some elements in the emitter such as a labyrinth channel which generates local pressure head losses. The problem is that this labyrinth channel is very sensitive to the clogging phenomenon, which reduces micro-irrigation system efficiency. Clogging is partially governed by hydrodynamics (Li et al. 2008). Therefore, it is necessary to analyze the flow. Flow analysis in the labyrinth channel is focused on the swirl zones at the downstream side of the baffles where the velocities are very low, thus favoring the deposition mechanism for particles. Therefore, when designing emitters, clogging can be prevented or at least significantly reduced by decreasing, as much as possible, the size of the swirl zones. The shape of the swirling region can be predicted by computational fluid dynamic (CFD) modeling. The Reynolds number \(Re=U_\mathrm{mean} d_\mathrm{h}/\nu\), based on the mean velocity \(U_\mathrm{mean}\) and on the hydraulic diameter \(d_\mathrm{h}\), is low (around 500). So the flow should be laminar. But, as the channel is narrow and wavy, some authors postulate a laminar to turbulent transition at lower Reynolds number: around 350 Nishimura et al. (1984) or between 100 and 700 Pfahler et al. (1990). Thus, it appears that the question is still open on the characteristics of such a flow and consequently on the choice of the model, i.e., turbulent or not.

CFD modeling differs from one study to another. For example, Palau Salvador et al. (2004) employ the laminar model, while Wei et al. (2006) choose the standard k–\(\varepsilon\) model. They consider that this model is typically used for most engineering calculations even if it has been developed for fully turbulent flows. While Wei et al. (2012) and Mohammed Ali (2013) employ the RNG k–\(\varepsilon\) model, the realizable k–\(\varepsilon\) model is used by Dazhuang et al. (2007). The RNG k–\(\varepsilon\) model generally improves the accuracy for rapidly strained and swirling flows. These features make the RNG k–\(\varepsilon\) model more accurate and reliable for a wider class of flows than the standard k–\(\varepsilon\) model. The realizable k–\(\varepsilon\) model is effectively applied in various flow simulations, including vortex steady shear flow, free flow containing jet and mixed flow, pipe flow, boundary layer flow, and segregated flow. But all of these models calculate the turbulent stress with isotropic turbulent viscosity assumption, and the variation of surface curvature along the channel is not taken into account. That is why Reynolds Stress Model (RSM) is also used in several studies (Zhang et al. 2007, 2010;  Philipova et al. 2009). This model can account for the effects of streamline curvature, swirl, rotation and rapid changes in strain rate in a more rigorous way. Other more complex simulations such as LES model (Large Eddy Simulation) can be found (Wu et al. 2013). However, LES still requires substantially finer meshes than those typically used for Reynolds-Averaged Naviers–Stokes equations (RANS) calculations. In addition, LES has to be run for a sufficiently long flow-time to obtain stable statistics. As a result, the computational cost involved with LES is usually some orders of magnitude higher than that for steady RANS calculations in terms of memory and Central Processing Unit (CPU) time. Therefore, high-performance computing is a necessity for LES, especially for industrial applications. The objective of this study is to develop the simplest numerical model that will be used to better define flow regions that generate pressure losses. Therefore, it is limited to turbulence models (no LES model). The use of high-Reynolds number models is not always justified or accurate. Especially, in the case of flow with separation, as it is found by Grasso and Falconi (1993). In addition, unsatisfactory results are obtained with this type of model for flows with recirculation. Considering that the flow rate is weak and then that the Reynolds number is low, the present study introduces the low-Reynolds number k–\(\varepsilon\) models in order to model the flow in labyrinth channel. Such models have another advantage as they eliminate the wall functions and modify model equations directly to take into account the near-wall region turbulence. This avoids inappropriate choice of the wall function. Several turbulence models are examined in the paper: the standard k–\(\varepsilon\), RNG k–\(\varepsilon\) and low-Reynolds number k–\(\varepsilon\) models. The adapted model, simple and fairly inexpensive in computation time, will be used in the future to optimize the baffles shape in terms of discharge/pressure loss and limit the areas where low velocity is likely to generate emitter clogging.

The next sections of the paper present the numerical models and procedure to simulate and validate the flow within a narrow labyrinth representative of emitter. The numerical results are discussed and compared to experimental measurements. The main objective of the paper is to determine the simplest and most efficient model to improve emitter conception. The emitter baffles are used to generate head losses to dissipate flow energy and thus to regulate the flow. That is why, in the results section, we focus on pressure head losses and we try to numerically understand the respective contributions of wall shear stress and turbulent and mean flow dissipation rates.

Materials and methods

Governing equations

In this study, incompressible steady-state flow is assumed. Buoyancy and gravity are not taken into account. Therefore, the RANS equations, according to these approximations, are:

$$\frac{{\partial u_{i} }}{{\partial x_{i} }} = 0,$$
(2)
$$\rho \frac{\partial }{{\partial x_{j} }}\left( {u_{i} u_{j} } \right) = - \frac{{\partial p}}{{\partial x_{i} }} + \frac{\partial }{{\partial x_{j} }}\left[ {\mu \left( {\frac{{\partial u_{i} }}{{\partial x_{j} }} + \frac{{\partial u_{j} }}{{\partial x_{i} }}} \right)} \right] + \frac{\partial }{{\partial x_{j} }}\left[ { - \rho \overline{{u_{i}^{\prime } u_{j}^{\prime } }} } \right],$$
(3)

where i and j are indices denoting Cartesian coordinate directions, \(u_i\) and \(u_j\) are the averaged velocities (m s−1), \(\rho\) is the fluid density \((\text{kg}\,\text{m}^{-3})\), \(\mu\) is the dynamic fluid viscosity \((\text{kg}\,\text{m}^{-1}\,\text{s}^{-1})\), p is the fluid averaged pressure (Pa), and \(u^\prime _i\) and \(u^\prime _j\) are the velocity fluctuations (m s−1).

The last term in Eq. 3, which is called the Reynolds stress tensor, must be modeled in order to close the equation system. A common method is to refer to the Boussinesq hypothesis Pope (2000) to relate the Reynolds stresses to the mean velocity gradients:

$$- \rho \overline{{u_{i}^{\prime } u_{j}^{\prime } }} = \mu_{\rm t} \left( {\frac{{\partial u_{i} }}{{\partial x_{j} }} + \frac{{\partial u_{j} }}{{\partial x_{i} }}} \right) - \frac{2}{3}\rho k\delta _{{ij}} ,$$
(4)

where \(\mu _{\rm t}\) is the turbulent viscosity \((\text {kg}\,\text {m}^{-1}\,\text {s}^{-1})\), k is the turbulent kinetic energy \((\text {m}^2\,\text {s}^{-2})\), \(k=\frac{1}{2} \overline{u^\prime _i u^\prime _i}\) and \(\delta _{ij}\) is the Kronecker delta.

This hypothesis is employed in several turbulent models, such as k–\(\varepsilon\) models. Momentum equation for all the models using the Boussinesq approximation is then given by the following formula:

$$\rho u_{j} \frac{{\partial u_{i} }}{{\partial x_{j} }} = - \frac{{\partial p}}{{\partial x_{i} }} + \frac{\partial }{{\partial x_{j} }}\left[ {\left( {\mu + \mu_{\rm t} } \right)\left( {\frac{{\partial u_{i} }}{{\partial x_{j} }} + \frac{{\partial u_{j} }}{{\partial x_{i} }}} \right)} \right]$$
(5)

k–\(\varepsilon\) models are based on the Eqs. 2, 5 and two additional equations for computing the turbulent kinetic energy (k) and its dissipation rate (\(\varepsilon\)), \(\varepsilon =\nu \overline{\frac{\partial u^\prime _i}{\partial x_j} \frac{\partial u^\prime _i}{\partial x_j}}\), where \(\nu {\,}(\text {m}^2\,\text {s}^{-1})\) is the kinematic viscosity. There are two types of k–\(\varepsilon\) models, namely, high-Reynolds number k–\(\varepsilon\) models and low-Reynolds number k–\(\varepsilon\) models.

k–\(\varepsilon\) models

High-Reynolds number k–\(\varepsilon\) models

The standard k–\(\varepsilon\) model is initially proposed by Launder and Spalding (1972). Then, it is developed by Launder and Jones (1972). This model is derived by assuming that the flow is fully turbulent. Therefore, the effects of molecular viscosity are negligible Launder and Spalding (1972). The standard k–\(\varepsilon\) model is recommended for high Reynolds number flows Launder and Spalding (1974). It is considered as a powerful tool for prediction of many complex flow problems including jets, wakes or wall flows. Another model is the RNG k–\(\varepsilon\) model which uses a technique, namely the renormalization group theory, described by Yakhot and Orszag (1986). The effect of swirl is accounted for in the RNG k–\(\varepsilon\) model, which enhances the accuracy for swirling flows. The RNG k–\(\varepsilon\) model uses an analytically derived differential formula for the effective turbulent viscosity which is adapted for low-Reynolds number flows. So, the RNG k–\(\varepsilon\) model is generally considered as more accurate and more reliable than the standard k–\(\varepsilon\) model for a wider range of flows. However, for wall-bounded flows, these models require additional semi-empirical parameterization, namely wall functions detailed in “Damping and wall functions” section.

Low-Reynolds number k–\(\varepsilon\) models

The standard k–\(\varepsilon\) model is modified, in the low-Reynolds number k–\(\varepsilon\) models, to account for the low-Reynolds number effects. There are quite a few low-Reynolds number k–\(\varepsilon\) models. The following low-Reynolds number k–\(\varepsilon\) models are used in this paper: [Abid] Abid (1991), [LS] Launder and Sharma (1974), [AKN] Abe et al. (1994) and [CHC] Chang et al. (1995).

k–\(\varepsilon\) equations

The modeled equations for the turbulent kinetic energy k and the dissipation rate \(\varepsilon\), for k–\(\varepsilon\) models, are then:

$$\begin{aligned}&\underbrace{\rho u_j \frac{\partial {k}}{\partial {x_j}}}_{\text{adv}_{k}} =\underbrace{\frac{\partial {}}{\partial {x_j}}\left[ \left( \mu +\frac{\mu_{\rm t}}{\sigma _{k}} \right) \frac{\partial {k}}{\partial {x_j}}\right] }_{\text{diff}_{k}} + \underbrace{G_{\rm k}}_{\text{prod}_{k}}-\underbrace{\rho \varepsilon }_{\text{diss}_{k}} \nonumber \\&\quad - \underbrace{D}_{\text{source}{\,}term_{k}}; \end{aligned}$$
(6)
$$\begin{aligned}&\underbrace{\rho u_j \frac{\partial {\varepsilon }}{\partial {x_j}}}_{\text{adv}_{\varepsilon }} =\underbrace{\frac{\partial {}}{\partial {x_j}}\left[ \left( \mu +\frac{\mu_{\rm t}}{\sigma _{\varepsilon }}\right) \frac{\partial {\varepsilon }}{\partial {x_j}}\right] }_{\text{diff}_{\varepsilon }}+\underbrace{C_{1 \varepsilon } f_1 \frac{\varepsilon }{k}G_{\rm k}}_{\text{prod}_{\varepsilon }}-\underbrace{C_{2 \varepsilon } f_2 \rho \frac{\varepsilon ^2}{k}}_{\text{diss}_{\varepsilon }} \nonumber \\&\quad +\underbrace{E}_{\text{source}{\,}\text{term}_{\varepsilon }}. \end{aligned}$$
(7)

\(G_{\rm k}\) represents the generation (or production) of turbulent kinetic energy due to the mean velocity gradients:

$$\begin{aligned} G_{\rm k} =-\rho \overline{{u^\prime _i}{u^\prime _j}}\frac{\partial {u_j}}{\partial {x_i}}= \mu_{\rm t} S^2; \end{aligned}$$
(8)

where S is the modulus of the mean rate-of-strain tensor, defined as:

$$\begin{aligned} S=\sqrt{2 S_{ij} S_{ij}}; \end{aligned}$$
(9)

and

$$\begin{aligned} S_{ij}=\frac{1}{2} \left( \frac{\partial u_j}{\partial x_i}+ \frac{\partial u_i}{\partial x_j} \right). \end{aligned}$$
(10)

The turbulent viscosity can be written as a general term multiplied by a damping function, \(f_{\mu }\):

$$\begin{aligned} \mu _{\rm t} =\rho f_{\mu } C_\mu \frac{k^2}{\varepsilon }. \end{aligned}$$
(11)

The model constants for all k–\(\varepsilon\) models used in this work are summarized in Table 1, while the damping functions are discussed in “Damping and wall functions” section and summarized in Table 2 Footnote 1 It is worth noting (see Pope 2000 for more details) that, in Eq. 6 for k, only the diffusion term is modeled on a global basis and the production term modeling only involves the use of Eq. 4 to obtain Eq. 8, while all terms except the advection term are modeled on a global basis in Eq. 7 for \(\varepsilon\). For any specific flow geometry, such as the present labyrinth channel configuration, analyzing the relative contributions of the terms in these equations provides insight into the turbulence mechanisms which dominate. For Eq. 6, this is usually named as analyzing the turbulent kinetic energy budget (see “Turbulent kinetic energy budgets” section).

Table 1 The constants involved in all k–\(\varepsilon\) models used in this study
Full size table

Damping and wall functions

Turbulent flows are significantly affected by the presence of walls since molecular viscosity effects become more and more predominant relative to turbulence effects—which vanish at the wall—as the wall is approached. The mean velocity field must satisfy the non-slip condition at the wall. However, the turbulence is also changed by the presence of the wall. Very close to the wall, viscous damping reduces the tangential velocity fluctuations, while kinematic blocking reduces the normal fluctuations. Toward the outer part of the near-wall region; however, the turbulence is rapidly augmented by the production of turbulent kinetic energy due to the large gradients in mean velocity. The wall region involves three sub-regions, namely the viscous sub-layer, the buffer layer, and the fully turbulent region. In the viscous sub-layer, the flow is almost laminar, and molecular viscosity plays a dominant role. In the fully turbulent region, turbulence plays the major role. Finally, there is a region between the viscous sub-layer and the fully turbulent layer where the effects of molecular viscosity and turbulence are equally important. This region is called the buffer region. In these regions, we use \(u^+ = u / u_{\tau }\) which is the dimensionless velocity: the velocity u parallel to the wall (function of Y which is the distance from the wall), divided by the friction velocity \(u_{\tau }\).

The law of the wall, in the near-wall regions, can be written as follows:

$$\begin{aligned} u^{+}=f(Y^{+}), \end{aligned}$$
(12)

with \(Y^+ = Y \rho u_{\tau }/ \mu\), \(u_{\tau }=\sqrt{\frac{\tau _w}{\rho }}\),

\(Y^+\) is the wall coordinate: the distance Y to the wall, made dimensionless with \(u_{\tau }\), \(\mu\) and \(\rho\); \(\tau _w\) is the wall shear stress. The \(\mu _{\rm t}\), k and \(\varepsilon\) equations are modified using algebraic functions to represent physical reality. Near the wall, \(Re_{\rm t}\) (defined in Eq. 13) and \(\mu _{\rm t}\) tend toward zero, therefore, \(\varepsilon \simeq\) diffusion of k. While further from the wall, \(\mu _{\rm t} \gg \mu\), therefore, \(\varepsilon \simeq\) production of k. In addition, very close to the wall, k tends toward zero, but \(\varepsilon\) has a non-zero defined value. In order to take into account these complex effects, one must adapt the standard equations by adding the damping functions. Indeed, the equations are integrated to the wall without assuming an universal law for the velocity profile and an equilibrium condition for k and \(\varepsilon\). The damping functions \(f_{\mu }\), \(f_{1}\) and \(f_{2}\) for low-Reynolds number k–\(\varepsilon\) models are summarized in Table 2. The damping functions are written in terms of the turbulence Reynolds numbers:

$$Re_{{\text{t}}} = \frac{{\rho k^{2} }}{{\mu \varepsilon }},$$
(13)
$$Re_{Y} = \frac{{\rho Y\sqrt k }}{\mu },$$
(14)

and

$$Re_{\varepsilon } = \frac{{\rho \left( {\mu \varepsilon /\rho } \right)^{{1/4}} Y}}{\mu }.$$
(15)

This approach based on modeled equations for k and for \(\varepsilon\) together with damping functions is developed for low-Reynolds number flows. But, when high-Reynolds number flows are considered, and especially for complex flows, the mesh grid cannot in general be refined sufficiently in the near-wall region for this approach to be implemented. For such situations, the so-called enhanced wall treatment is then used, which involves a two-layer model and wall functions. For \(Re_Y>200\), the flow is assumed to be fully turbulent and the k–\(\varepsilon\) models are used. Otherwise, for \(Re_Y<200\), the one-equation model of Wolfshtein (1969). The turbulent kinetic energy is then calculated with a transport equation, but the turbulent viscosity is determined using a characteristic length scale \(\ell _{\rm t}\), so that \(\mu _{\rm t}=\rho C_{\mu } \ell _{\rm t} \sqrt{k}\) where \(\ell _{\rm t}\) is given by \(\ell _{\rm t}=Y C_\ell (1-exp({-Re_Y/A_{\mu }}))\), with \(A_{\mu }\) a constant. On the contrary, \(\varepsilon\) is not computed with a transport equation, but it is evaluated through an algebraic relation, namely, \(\varepsilon =k^{3/2}/\ell _{\varepsilon }\) where the length scale \(\ell _{\varepsilon }\) is inferred from a relation similar to that for \(\ell _{\rm t}\), but with a constant \(A_{\varepsilon }\) instead of \(A_{\mu }\) (see Hanjalic and Launder 2011).

Fig. 1
figure 1

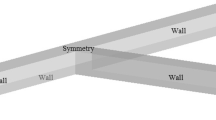
The emitter and the geometry studied. The dashed square and lines define the zones where the mean velocity and turbulent quantities are more deeply analyzed in “Results” section

Full size image
Table 2 The damping functions of all k–\(\varepsilon\) models used in this study, where \(\eta =S k/\varepsilon\), \(\eta _0 = 4.38\) and \(\beta = 0.012\)
Full size table

Geometry of the study and numerical approach

Geometry of the study

The emitter selected is integrated within the drip-line and is characterized by labyrinth channel features with an emitter discharge exponent of 0.59 (see Eq. 1). For this numerical study, only the repeating pattern of the labyrinth channel is simulated (Fig. 1). All dimensions are defined in Table 3.

Table 3 The labyrinth channel dimensions
Full size table

Numerical approach

The study is performed using commercial computational fluid dynamics software where the models studied are implemented: ANSYS/Fluent V14. Simulations are performed in two (2D) and three (3D) dimensions. The main advantage of 2D is that it runs faster than 3D. However, the real labyrinth is narrow and thus considering that the walls in the transverse direction are very distant from the simulated plane could result in wrong predictions. That is why 2D and 3D results are compared.

Firstly, the geometry is designed. Secondly, the mesh is generated and its quality is examined. The skewness, based on the deviation from a normalized equilateral angle, is around 0.75 and 0.56 in two and three dimensions, respectively, which states that mesh quality is acceptable. For all models, we opted for a quadratic-dominant (in two dimensions) and prism with quadrilateral base (in three dimensions) mesh type. The mesh is chosen with \(Y^+ <5\) for high-Reynolds number k–\(\varepsilon\) models. Low-Reynolds number k–\(\varepsilon\) models require fine mesh, \(Y^+\le 1\) at the wall-adjacent cell. Modeling by low-Reynolds number k–\(\varepsilon\) models requires more mesh refinement close to the wall in order to have a sufficient number of points in the region \(0<Y^+ <10\).

The independence of the results to the meshing has been verified. The velocity modulus profiles are plotted on line 2 for different mesh cell numbers (Fig. 2). The variation of the velocity is weak when the mesh cell number is at least \(1.33\times 10^{5}\) and then the smallest mesh size is \(15.6{\,}\mu m\). Therefore, the effect of mesh can be neglected. The chosen cell numbers are, for all models, \(1.33\times 10^{5}\) and \(2.2\times 10^{6}\) in two and three dimensions respectively. That way, the results will not depend on meshing to ensure that the differences will be due to the model.

Fig. 2
figure 2

The velocity modulus (\(\text{m}\,\text{s}^{-1}\)) for four mesh cell sizes; [LS] k–\(\varepsilon\) model for \(Re=800\) on line 2 defined in Fig. 1

Full size image

Inlet and outlet sections are offset from the studied region in order to prevent perturbations. In addition, a low turbulent intensity (\(5\,\%\)) and a hydraulic diameter (\(D_{\rm H} = 2{\,}\) and \(1{\,}\text{mm}\), in two dimensions and three dimensions, respectively) are chosen for the specification method. The simulation, for high-Reynolds number and low-Reynolds number k–\(\varepsilon\) models, is performed with an initial inlet flow rate of \(1.4{\,}\text{l}\,\text{h}^{-1}\); then, it is regularly increased until \(2.9{\,}\text{l}\,\text{h}^{-1}\); which corresponds to a Reynolds number ranging from 400 to 800.

To solve the pressure-velocity coupling and to interpolate face pressure, we choose respectively the “SIMPLE” and “STANDARD” methods which are robust and valid for a large flow range. “Third-order MUSCL” discretization is selected to solve momentum, turbulent kinetic energy and turbulent dissipation rate equations because this method is accurate and adapted for all mesh types.

The convergence accuracy is not fixed. It changes from one model to another. However, it is always less than \(10^{-6}\) and can reach \(10^{-12}\) in some cases. The objective is to have stable computation residuals. Results reported hereafter are plotted and compared on two transversal lines which cross through a swirling region at its center, line 2 and line 3 (Fig. 1).

Experimental validation

In order to validate the modeling results, an experiment has been developed to determine the pressure head loss Fig. 3a, b. The repeating-pattern labyrinth-channel prototype which is composed of three baffles has been fabricated from a plexiglas plate. Then, it has been covered by another plate. One of these two plates contains pressure ports as well as inlet and outlet points (Fig. 3c). A diaphragm metering pump (SIMDOS 10 with an accuracy of \(2\,\%\) of the set value) pumps water from a \(1{\,}l\) tank. Then, two dampers, a hand-made damper (which is constituted by a pipe which contains air) and a commercial damper (type: PML 9962-FPD10, with a maximum efficiency of \(97\,\%\)), absorb the flow pulsations, before going through a flow meter (Mc Millan, accuracy of \({\pm}3{\,}\text{ml}\,\text{min}^{-1}\)) and the labyrinth-channel prototype. The pressure at the inlet as well as the pressure drop is measured by two highly precise pressure transmitters (PR-33x/80794 and PD-33x/80920, accuracy of \(0.01{\,}\%\)). The test duration is fixed to \(10{\,}\text{min}\). The hydraulic circuit is turned on \(30{\,}\text{min}\) before acquiring the data to ensure that the flow has reached its steady state. The number of measuring points is about 20,000. Then, the averaged value of each parameter (pressure drop and flow rate) is calculated. This test is repeated three times in three different days. The pressure drop for each flow rate is measured by pressure transmitter between the points b and e, \(\Delta p_{\rm be}\) Fig. 3c. It contains three contributions, namely, the pressure drop caused by the labyrinth-channel \(\Delta p_{\rm cd}\) compared with numerical results in “The pressure loss and discharge” section, the pressure drop between b and c, and the pressure drop between d and e. The measured pressure drop \(\Delta p_{\rm be}\) can be written as:

$$\begin{aligned} \Delta p_{\rm be}= \Delta p_{\rm bc} + \Delta p_{\rm cd} +\Delta p_{\rm de}, \end{aligned}$$
(16)

with

$$\Delta p_{{{\text{bc}}}} = f_{{{\text{bc}}}} \frac{{\ell _{{{\text{bc}}}} }}{{D_{{{\text{bc}}}} }}\rho \frac{{U_{{{\text{bc}}}}^{2} }}{2},$$
(17)
$$\Delta p_{{{\text{de}}}} = f_{{{\text{de}}}} \frac{{\ell _{{{\text{de}}}} }}{{D_{{{\text{de}}}} }}\rho \frac{{U_{{{\text{de}}}}^{2} }}{2},$$
(18)

where \(f_{\rm bc}=f_{\rm de}=48/Re{\,}\)(square section), hydraulic diameters \(D_{\rm bc}=d_{\rm inlet}=1{\,}\text{mm}\), \(D_{\rm de}=\frac{4{\,}d_{\rm outlet}\times d_{\rm depth}}{2{\,}d_{\rm outlet}+2{\,}d_{\rm depth}}=1.09{\,}mm\), \(\ell _{\rm bc}=\ell _{\rm de}=10{\,}mm\) and \(U= q_1/A_{\rm section}\). The two previous equations can be written as:

$$\begin{aligned} \Delta p_{\rm bc}= 4 \times q_1 \end{aligned}$$
(19)
$$\begin{aligned} \Delta p_{\rm de}= 2.825 \times q_1 \end{aligned}$$
(20)

where \(\Delta p_{\rm bc}\) and \(\Delta p_{de}\) are pressure drops in (Pa), and \(q_1\) is the measured flow rate \((\text{ml}\,\text{min}^{-1})\).

Fig. 3
figure 3

General scheme of experiment and experimental set-up. a Scheme of the experiment. b Experimental set-up. c A prototype design

Full size image

Results

The pressure loss and discharge

The discharge-pressure loss curves (\(q=f(\Delta P)\)) where \(\Delta P\) stands for the inlet/outlet pressure losses) are plotted for each turbulence model in 2D and two models in 3D and compared with the experimental data (Fig. 4). In the paper of Karmeli (1977), it can be noted that for long-path emitters, which are used for our study, the emitter discharge exponent is between 1 and 0.5, the values, respectively, for laminar and rough fully turbulent wall flows. In 2D (Fig. 4a), the exponents of the standard and RNG k–\(\varepsilon\) models are those of rough fully turbulent regime (for which the friction factor \(C_{\rm f}\), which is proportional to \(\Delta P / q^2\), does not depend anymore on the Reynolds number Re) and they are close to, but slightly smaller than, the exponents of the (LS) k–\(\varepsilon\) model and the experiments (0.57–0.59, such that \(C_{\rm f}\) slightly decreases with Re, see White (2010)). [Abid], [AKN] and [CHC] k–\(\varepsilon\) models have a laminar behavior since the exponents of these models are close to 1 and therefore such that \(C_{\rm f}\) strongly decreases with Re (see Table 4). It appears that when the flow rate increases, all the models predict almost the same pressure drop. Even though it is quite difficult to comment and analyze in detail the results presented in Fig. 4a, b, a clear distinction can be made between the three types of flow regimes, with the [LS] k–\(\varepsilon\) model being the only model which can simulate the turbulent regime for which \(C_{\rm f}\)

Fig. 4
figure 4

Discharge-pressure loss curves in two dimensions (2D) (a) and three dimensions (3D) (b) (a) 2D. b 3D

Full size image

slightly decreases with Re.

Table 4 The exponent values in the Eq. 1 for all models plotted in Fig. 4
Full size table

From now, the numerical results of three models are more deeply analyzed: the standard k–\(\varepsilon\) model as a high Reynolds number model, the [LS] k–\(\varepsilon\) model as a low-Reynolds number k–\(\varepsilon\) model which behaves like a high-Reynolds number model and the [CHC] k–\(\varepsilon\) model as a low- Reynolds number k–\(\varepsilon\) model which tends to a laminar behavior.

In three dimensions, two models are chosen: the standard k–\(\varepsilon\) model and the [LS] k–\(\varepsilon\) model. [CHC] k–\(\varepsilon\) model is not converged even when refining the mesh until \(2 \times 10^6\) cells. Therefore, it is not represented on the Fig. 4b. It can be observed that the curve exponents, in 3D, are close to 0.5. These results confirm that the flow is turbulent. Differences can be observed between experimental and numerical values. One could suspect that this is due to the 2D hypothesis (Fig. 4a). However, looking at 3D results, a larger gap is noted (Fig. 4b): pressure losses are larger than in 2D. Deeper analysis of the main drivers of head losses is proposed in “Pressure losses” section. The exponents of the standard and [LS] k–\(\varepsilon\) models are 0.5 and 0.54, respectively in 3D. Therefore, with fine mesh and to avoid wall function, the [LS] model is recommended.

The mean velocity fields

The mean velocity fields obtained from the CFD simulations for the minimum and the maximum flow rates, \(Re=400\) and 800 respectively, are shown on Fig. 5, for the three turbulence models chosen in two dimensions. The velocity fields show that there are two regions. One is the main flow characterized by large velocity values. The other is the swirl region characterized by a low velocity value and negative velocity values (Fig. 6). It can also be observed (Fig. 5) that the maximum velocity is at the corner of the labyrinth channel, where the water hits the wall in the different baffles. The swirl regions are approximately identical for the standard and [LS] k–\(\varepsilon\) models (Fig. 5). The swirl region form, for the [CHC] k–\(\varepsilon\) model, is changed from \(Re=400\) (Fig. 5c), where the swirl region is large, to \(Re=800\) (Fig. 5f), where it is smaller and closer to the shape for standard and [LS] models. It seems, as observed on discharge/pressure losses curves, that at higher Reynolds number, the different models predict almost the same flow.

Fig. 5
figure 5

The mean velocity fields in the dashed square (defined in Fig. 1) in 2D, \((\text{m}\,\text{s}^{-1})\). a Standard. b LS. c CHC. d Standard e LS. f CHC

Full size image
Fig. 6
figure 6

The x and y velocities on line 3 defined in Fig. 1 for \(Re=400\), standard k–\(\varepsilon\) model

Full size image

In order to better understand and analyze the velocity field within the labyrinth-channel unit, normalized mean velocity profiles, in both 2D and 3D, are plotted along the lines 2 and 3 shown in Fig. 1, allowing to compare results for \(Re=400\) and \(Re=800\). All mean velocity profiles have two peaks and one trough which is located in the center of the swirling zone (Fig. 7). The peak as well as the trough values vary from one model to another. Such comparison of normalized mean velocity profiles on two lines positioned at the same position in the labyrinth-channel unit helps to determine whether the flow is developed for the different baffles or whether it still undergoes evolution and is not yet developed. The mean velocity is larger in the flow mainstream when the swirling zone is larger, in accordance with the mass conservation as the velocity in the swirling zone has a negative value (Fig. 6). In addition, velocity reaches higher values in 3D than in 2D. In any case, the mean velocity is high on line 2 and it generally decreases on line 3. However, this diminution is more or less notable according to the model. For example, only a small diminution is observed for the standard k–\(\varepsilon\) model in 2D and 3D for \(Re=400\) and \(Re=800\), while, for the [LS] k–\(\varepsilon\) model, the velocity varies more for \(Re=400\) than for \(Re=800\). For the [CHC] k–\(\varepsilon\) model, the velocity profile significantly evolves between lines 2 and 3 (Fig. 7e, f). Therefore, the flow is not yet developed and it evolves from one baffle to another. It can be noted that all the turbulence models studied herein have the same velocity profile at \(Re=800\) on line 3 (Fig. 7).

Fig. 7
figure 7

Evolution of the normalized mean velocity modulus profile on lines 2 and 3 defined in Fig. 1. a Standard k–\(\varepsilon\) model, \(Re=400\). b Standard k–\(\varepsilon\) model, \(Re=800\). c LS k–\(\varepsilon\) model, \(Re=400\). d LS k–\(\varepsilon\) model, \(Re=800\). e CHC k–\(\varepsilon\) model, \(Re=400\). f CHC k–\(\varepsilon\) model, \(Re=800\)

Full size image

It has been underlined that the flow for the low-Reynolds number [CHC] k–\(\varepsilon\) model, in 2D, is not yet developed. Therefore, a fourth baffle was added to analyze the flow characteristics on this baffle and compare it with the other baffles. Figure 8 shows the mean velocity fields for two turbulence models. The flow modeled by the [LS] k–\(\varepsilon\) model is fully developed. This is seen when comparing the velocity profiles on lines 3 and 5 (Fig. 9a). On the contrary, it clearly appears, on Fig. 9b, that the velocity profile on line 5 is different from that on line 3. This confirms the previous observation that the flow modeled by the [CHC] k–\(\varepsilon\) model is no yet developed at the third baffle. [Abid] and [AKN] k–\(\varepsilon\) models, not shown, are similar to the [CHC] k–\(\varepsilon\) model. This is in line with the results reported in Table 4 which indicate that the exponent values in Eq. 1 are very close for these three models, and much larger than the other values.

Fig. 8
figure 8

The mean velocity fields, [CHC] (top) and [LS] (bottom) k–\(\varepsilon\) models and \(Re=400\)

Full size image
Fig. 9
figure 9

The mean velocity modulus profiles for [LS] (a) and [CHC] (b) k–\(\varepsilon\) models on the lines 3 and 5 (defined in Fig. 8) in the case of four baffles compared with the line 3 in the case of three baffles and \(Re=400\). a LS k–\(\varepsilon\) model, \(Re=400\). b CHC k–\(\varepsilon\) model, \(Re=400\)

Full size image

Turbulent kinetic energy budgets

The fields of the normalized turbulent kinetic energy (k) and the normalized dissipation rate (\(\varepsilon\)) are shown on Figs. 10 and 11 for \(Re=400\) and \(Re=800\). Such normalization helps to better visualize and compare k and \(\varepsilon\) data. It is equivalent to the use of the Reynolds number for comparing flow properties which may vary as a function of velocity and/or length scale. It allows, in particular, to have almost the same levels for different Reynolds numbers, but also to analyze in a quantitative way departure of the present results from results obtained for wall flows with standard geometries. As an example, Pope (2000) shows that the dissipation term magnitude is about 0.5, with the maximum value of about 1 attained at the wall, for a turbulent flow over a flat and smooth plate. Similarly, the normalized turbulence level \(k/u_{\tau }^2\) is about 5, corresponding to a maximum turbulence intensity \(k/U^2\) of about 0.1, which is not very different from what is obtained in our case since \(U/U_{inlet}\) can be as large as 3.5 (Fig. 7e) (which is therefore compatible with values of \(k/U_{\rm inlet}^2\) larger than 1).

Fig. 10
figure 10

The normalized turbulent kinetic energy in 2D, \(k/U^2_{\rm inlet}\). a Standard. b LS. c CHC. d Standard. e LS. f CHC

Full size image
Fig. 11
figure 11

The normalized dissipation rate in 2D, where the red-colored regions have the values \(3>\varepsilon / \frac{U_{inlet}^3}{d_{inlet}}>5\) in order to visualize the transition between the main flow and the swirl region. a Standard. b LS. c CHC. d Standard. e LS. f CHC

Full size image

It can be observed that k and \(\varepsilon\) for the standard and [LS] k–\(\varepsilon\) models no longer evolve from just after the first baffle until the end, which has already been observed for the mean velocity fields (Fig. 7). For the [CHC] k–\(\varepsilon\) model, k and \(\varepsilon\) are not impacted by the first baffle. The increase in k and \(\varepsilon\) can be observed only after the third and the second baffle for \(Re=400\) and \(Re=800\) respectively (Fig. 10c, f). This could be linked to the mean velocity value in the principal flow which is high as the turbulence is not well developed (Fig. 7). The other models dissipate flow energy from the first baffle, whereas the [CHC] k–\(\varepsilon\) model dissipates a large amount of energy only after the second baffle.

The evolutions of each term of the k equation are then plotted for the line 3 (Fig. 12), for the standard, [LS] and [CHC] k–\(\varepsilon\) models. To allow quantitative comparison between results obtained for different flow rates, all of these terms are normalized by \(\frac{\rho U_{\rm inlet}^3}{d_{\rm inlet}}\) (since they obviously all have the same dimension, namely, that of \(\rho \varepsilon\)). The k budget-equation is composed of several terms which promote or destroy the turbulent kinetic energy. The contribution of each term to the production or the dissipation of k is signaled by the positive (source term) or negative (sink term) sign. Therefore, the production term, anywhere, has positive values, while the dissipation term (−\(\varepsilon\)) has, on the contrary, negative values. The signs of other terms change according to the local flow conditions.

In the middle of the flow, the normalized diffusion terms, in k equation, for the standard, [LS] and [CHC] k–\(\varepsilon\) models give the same profile for \(Re=800\). For \(Re=400\), this term is different for [CHC] model. Far from the wall, the damping functions are equal to 1. Therefore, these factors do not affect the k-budget; hence, they are the same for all models. The production term for k equation is identical for the different models. It has two peaks (Fig. 6): one is in the middle of the main flow and the other is at the contact between the main flow and the swirl region due to the shear rate. The advection term is also the same for all models: It is positive between the main flow and the center of the swirl region. That is due to the negative values of the velocity components (Fig. 6) and the gradients of k. Otherwise, the turbulent kinetic energy increases from the wall and the main flow to the center of the swirling region. The main difference is the treatment at the wall: in the [CHC] k–\(\varepsilon\) model, the boundary conditions imposed at the wall are \(k=0 , \varepsilon =2\nu \left( \frac{\partial \sqrt{k}}{\partial Y} \right) ^2\); therefore, the dissipation at the wall has a high value. It can be linked with the high value of the dissipation term for k equation which is related to \(\varepsilon\). Consequently, the diffusion term of the turbulent kinetic budget-equation for the [LS] and [CHC] k–\(\varepsilon\) models reaches a significant value at the wall (Fig. 12d, f), as this term is then in equilibrium with the dissipation term.

Fig. 12
figure 12

Normalized terms of turbulent kinetic energy budget-equation in 2D, where y s is the radial position of the center of the swirl. a Standard with Re = 400. b Standard with Re = 800. c LS with Re = 400. d LS with Re = 800. e CHC with Re = 400. f CHC with Re = 800

Full size image

Pressure losses

In a pipe flow, two processes may dissipate the mean flow kinetic energy, the first is by volume dissipation or the internal dissipation and the second is by friction at the wall (Chassaing 2000; White 2010). In general, these two mechanisms occur together. Pressure drop is related to tube length. It can be written as:

$$\begin{aligned} \frac{\text{d}p}{\text{d}x}\approx \frac{\rho }{Q_v} \int \varepsilon _t \times \text{d}S + \frac{\tau _{\rm w}}{R_{\rm h}} \end{aligned}$$
(21)

with \(\varepsilon _t=\bar{\varepsilon }+\varepsilon\)

In Eq. 21, the sign \((\approx )\) is set instead of \((=)\) because it is assumed that turbulent production equals turbulent dissipation. The term, on the left-hand side, is the pressure drop absolute value per length unit. On the right-hand side, the first term is the dissipation rate integrated on the cross-section, where \(Q_v= U_{\rm mean} \times S_{\rm section}\) is the volumetric flow rate \((\text{m}^3\,\text{s}^{-1})\), \(S_{\rm section}\) is the cross-section surface \((\text{m}^2)\). The total dissipation rate, \(\varepsilon _t\), is also composed of two contributions. The first contribution, \(\bar{\varepsilon }\), is the dissipation due to the mean flow: in general, it is of order \(Re^{-1}\) compared with the other terms, and therefore negligible. The second contribution, \(\varepsilon\), is the dissipation due to the fluctuating flow. \(\varepsilon\) is the variable in Eq. 7 and \(\bar{\varepsilon }\) is defined by the formula: \(\bar{\varepsilon }=\nu {S}^2\), where S is the modulus of the mean rate-of-strain tensor (Eq. 9) in the flow core. The second term is the energy dissipated at the wall, by friction, divided by the hydraulic radius \(R_{\rm h}\). The wall friction is given by formula: \(\tau _{\rm w}=\mu S\), where S is the modulus of the mean rate-of-strain tensor at the wall (Eq. 9). The volume of fluid V, in the labyrinth channel, can be written by different ways:

$$\begin{aligned} V=S_{\rm section}\times L=A_{\rm area} \times d_{\rm depth} =\ell _{\rm mean} \times L \times d_{\rm depth}, \end{aligned}$$
(22)

where L is the path length of the fluid (m), and \(\ell _{\rm mean}=A_{\rm area}/L{\,}\) is the mean width over the entire area of the labyrinth channel (m). \(A_{\rm area}=32.44{\,}\text{mm}^2\) and \(L=26.48{\,}\text{mm}\). Therefore, \(\ell _{\rm mean}=1.22{\,}\text{mm}\) (Eq. 22). By multiplying and handling Eq. 21 by the total volume of fluid V, we obtain:

$$\begin{aligned}&\left( p_{\rm inlet} \times d_{\rm inlet}-p_{\rm outlet} \times d_{\rm outlet} \right) \times d_{\rm depth} \approx \nonumber \\&\quad \left( \bar{\varepsilon }+\varepsilon \right) \frac{\rho A_{\rm area}}{U_{\rm mean}} \times d_{\rm depth} + \frac{\tau _{\rm w} \times S_{\rm section}\times L}{R_h} \end{aligned}$$
(23)

where \(R_h=S_{\rm section}/P\); P is the wetted perimeter of the cross-section. Generally, in 2D, where \(d_{\rm depth} \gg d_{\rm inlet}\) and \(S_{\rm section}=d_{\rm inlet} \times d_{\rm depth}\), \(R_h=d_{\rm inlet}/2\). Therefore, \(S_{\rm section}/R_h=2d_{\rm depth}\). The previous equation can be written as:

$$\begin{aligned}&p_{\rm inlet} \times d_{\rm inlet}-p_{\rm outlet} \times d_{\rm outlet}\approx \left( \bar{\varepsilon }+\varepsilon \right) \frac{\rho A_{\rm area}}{U_{\rm mean}}+ \nonumber \\&\quad \tau _{\rm w} \times L_{\rm wall} \end{aligned}$$
(24)

with \(L_{\rm wall}=2 L\).

In 3D, Eq. 23 can be written as:

$$\begin{aligned}&p_{\rm inlet} \times S_{\rm inlet}-p_{\rm outlet} \times S_{\rm outlet}\approx \left( \bar{\varepsilon }+\varepsilon \right) \frac{\rho V}{U_{\rm mean}}+ \nonumber \\&\quad \tau _{\rm w} \times A_{\rm wall} \end{aligned}$$
(25)

with \(A_{\rm wall}= \left( 2 \ell _{\rm mean} + 2d_{\rm depth} \right) \times L\).

The dissipation rate and the wall friction for the standard, [LS] and [CHC] k–\(\varepsilon\) models are calculated and presented in Table 5, in 2D, and in Table 6, in 3D, for the standard and [LS] k–\(\varepsilon\) models, for \(Re=400\) and \(Re=800\) which are the extreme values for the performed simulations. The percentage is calculated as the ratio of each contribution to the pressure drop divided by the sum of the three contributions to the pressure drop. It can be observed that the turbulent dissipation rate for the [CHC] k–\(\varepsilon\) model is higher than for the other models (Fig. 11c, f)), which induces a pressure loss which is significantly larger (almost double for \(Re=400\) see Table 5). The pressure drop generated by the turbulent dissipation is dominant, and even greater than the wall friction. Therefore, turbulent dissipation is the main phenomenon which explains the pressure drop, unlike what is observed for standard channel flows. This dissipation is due to the large swirling regions where wall friction is minimal. The pressure drop for each part of labyrinth channel is also calculated in Tables 7, 8 and 9 for the intermediate Reynolds number (i.e., \(Re=600\)). The pressure drop calculated by the numerical modeling is a function of \(\varepsilon\), \(\bar{\varepsilon }\) and \(\tau _w\). The gaps between the measured data and numerical results could be explained by the over-estimation of \(\varepsilon\) contribution (in relation to the assumption that turbulent production and dissipation are equal) which is the main responsible of pressure drop (70–80 %, for the high flow rates). When comparing the curves plotted in Fig. 4a, b), it is found that the pressure drop is increased in the 3D case. One can see from the Tables 7, 8 and 9 that the pressure drop due to the wall friction is greater in 3D. That is to say that the 3D modeling generates a larger contribution of the wall friction, which is not surprising since the two lateral walls are then considered, while this is not the case for the 2D modeling. A significant shear-strain increase is observed with respect to the dissipation. The ratio of turbulent dissipation / shear-strain, for the [LS] k–\(\varepsilon\) model, is decreased from 4.6 / 1, in 2D, to 2 / 1, in 3D for \(Re=800\) and from 3.3 / 1, in 2D, to 0.75 / 1, in 3D for \(Re=400\).

Normalized terms of turbulent kinetic energy budget-equation in 2D, where \(y_{s}\) is the radial position of the center of the swirl (a) Standard with \(Re=400\). (b) Standard with \(Re=800\). (c) LS with \(Re=400\) (d) LS with \(Re=800\) (e) CHC with \(Re=400\). (f) CHC with \(Re=800\).

Table 5 The pressure drop \(\Delta p\) with \(\varepsilon\), \(\bar{\varepsilon }\) and \(\tau _{\rm w}\), in 2D
Full size table
Table 6 The pressure drop \(\Delta P\) with \(\varepsilon\), \(\bar{\varepsilon }\) and \(\tau _{\rm w}\), in 3D
Full size table
Table 7 Standard k–\(\varepsilon\) model for \(Re=600\), in 2D
Full size table
Table 8 [LS] k–\(\varepsilon\) model for \(Re=600\), in 2D
Full size table
Table 9 [CHC] k–\(\varepsilon\) model for \(Re=600\), in 2D
Full size table

Discussion

The paper reports the assessment of several turbulent models compared with experimental data. In the literature, the choice of turbulent model is not yet established. Several models as the k–\(\varepsilon\), RSM and LES models are studied. As LES model is not well adapted to simulate wall-bounded flows and as it is time consuming, RANS models were chosen to perform the present study: high-Reynolds number k–\(\varepsilon\) and low-Reynolds number k–\(\varepsilon\) models. But the high-Reynolds number k–\(\varepsilon\) models require wall functions. Using wall functions to treat the flow near the wall can cause errors because the wall function is applicable only for parallel walls within a certain range of derivation Li et al. (2008). The complex structure of the labyrinth-channel flow can thus produce errors. Therefore, other models such as low -Reynolds number \(k- \varepsilon\) models are also studied.

The validation method is based on the discharge-pressure curves. This method is used by Wei et al. (2012) to validate the choice of turbulent or laminar model. In addition, this curve defines the hydraulic performance of emitter. That allows to optimize the emitter geometry. Mathematically, Philipova et al. (2009) calculated the emitter discharge related to the pressure head losses (Eq. 1), using a polynominal depending on the geometric parameters of the baffle.

In the present paper, these losses are calculated numerically by the simulation, based on dissipation rate and wall friction. The turbulence effect is clearly underlined. In Tables 5 and 6, the pressure losses due to the turbulent dissipation \(\varepsilon\) indeed are dominant. They are about 79–81 % for \(Re=800\). As expected, this effect decreases when Re decreases to \(Re=400\) (70.8–71.4 %). The percent of dissipation rate due to the mean flow is weak, about 3.6–4.6 % for Re=800 and it increases when Re decreases. The wall shear stress contribution increases when Re decreases. This is due to the friction factor increase which is related to the Reynolds number through the Blasius relationship for a smooth wall: \(f=0.3164 \times Re^{-1/4}\). In 3D, the results are more influenced by the presence of walls and the percent increases until reaching 37–42 %. The turbulence effects decrease by comparison with 2D. To our knowledge, this analysis is quite innovative as it is the first time that it is conducted. The numerical tools will be used to optimize the labyrinth geometry, with the objective of minimizing the swirl regions where particle deposition is likely to occur, while maintaining a sufficiently large pressure loss.

In addition, the flow seems to be established after the first baffle, with the [LS] model, where the flow becomes fully turbulent (Fig. 11). This is confirmed by the study of Takahiro and Shougo (2006) on a symmetric channel with expanded grooves, in 2D and for small low-Reynolds number. As also shown by the present results, these authors concluded that the flow characteristics within each unit are identical when the flow is fully developed. This observation is of interest for manufacturers who could adjust the number of labyrinth units according to the discharge they want to achieve, in order to meet the plant needs.

Conclusion and perspectives

CFD simulations of the flow in a narrow labyrinth channel have been carried out. The results of the [LS] k–\(\varepsilon\) model follow the high-Reynolds models (standard and RNG k–\(\varepsilon\) models), and their predicted curve exponents are close to the experimental data. The other low-Reynolds number k–\(\varepsilon\) models ([Abid], [AKN] and [CHC]) reproduce a laminar tendency. The flow modeled by the [CHC] k–\(\varepsilon\) model is not yet developed. The damping functions are able to solve the sub-layer and inner layer by modifying the equations with damping factors. That helps to obtain accurate results, without using wall functions at the vicinity of the wall, which are important for pressure loss predictions (“Damping and wall functions” section). The turbulent dissipation rate is the major responsible for the pressure losses in labyrinth channel (2D/3D) by comparison with the dissipation due to the mean flow and the friction at the wall. In addition, this confirms that the flow is turbulent, so that a turbulence model has to be used.

In order to avoid the wall functions and decrease the calculation time, the [LS] k–\(\varepsilon\) model, in 2D, will be used for future studies. Using this model, we could track particles inside the labyrinth channel. Finally, the results of modeling will be compared with the results of Particle Image Velocimetry (PIV) experiments, which allow to visualize the velocity field, characterize the swirl region and determine the mean velocity field as well as turbulent quantities.