1 Introduction

Over the past decades, the evolution properties of laser beams propagating through atmospheric turbulence, oceanic turbulence and non-Kolmogorov turbulence media have been widely studied because of their wide applications in free-space optical communication and sensing. The propagation properties of single laser beam propagating in turbulent media have been widely studied, such as dark hollow and flat-topped beams [1], elegant Hermite–Gaussian beam [2], partially coherent beam [3], electromagnetic concentric rings Schell-model beam [4], multi-Gaussian–Schell-model vortex beam [5], radially polarized multi-cosine Gaussian–Schell-model beams [6], square multi-Gaussian–Schell-model beam [7], Laguerre–Gaussian-correlated Schell-model beam [8], elegant Hermite–Gaussian-correlated Schell-model beam [9], Hankel–Bessel–Schell beam [10], Bessel–Gaussian beam [11], partially coherent Bessel–Gaussian beams carrying optical vortices [12], stochastic electromagnetic beam [13] and random electromagnetic multi-Gaussian–Schell-model vortex beam [14] etc.

On the other hand, the application of single laser beam is limited because of the lower beam power. In this situation, the beam array is produced to obtain the higher beam power. The properties of beam array propagating in turbulent media have been investigated, such as those of ring Airy Gaussian beams with optical vortices [15], Gaussian array beams [16, 17], radial phased-locked partially coherent Lorentz–Gauss array beam [18], radial phased-locked partially coherent flat-topped vortex beam array [19], radial phased-locked partially coherent anomalous hollow beam array [20], partially coherent Hermite–Gaussian linear array beams [21], radial phased-locked partially coherent standard Hermite–Gaussian beam [22], radial Gaussian–Schell-model array beam [23], and radial Gaussian beam array [24]. However, to the best of our knowledge, the propagation properties of the radial phase-locked partially coherent elegant Laguerre–Gaussian (PCELG) beam array have not been reported. Thus, in this paper, the model of the radial phase-locked PCELG beam array has first been introduced, and the average intensity properties and the spectral degree of coherence properties of a radial phase-locked PCELG beam array propagating in non-Kolmogorov medium have been studied using numerical examples.

2 Radial phase-locked PCELG beam array

The electric field distribution of elegant Laguerre–Gaussian beam in cylindrical coordinate can be expressed as [25]

$${E_{nm}}\left( {r,\theta ,0} \right)={\left( {\frac{r}{{{w_0}}}} \right)^m}L_{n}^{m}\left( {\frac{{{r^2}}}{{w_{0}^{2}}}} \right)\exp \left( { - \frac{{{r^2}}}{{w_{0}^{2}}}} \right)\exp \left( {im\theta } \right),$$
(1)

where \(r\) and \(\theta\) are the radial and azimuthal (angle) coordinates, respectively, \(L_{n}^{m}\) denotes the Laguerre polynomial with mode orders \(n\) and \(m\), \({w_0}\) is the beam width of fundamental Gaussian mode. By use the following relation [25]:

$$\exp \left( {im\theta } \right){\rho ^m}L_{n}^{m}\left( {{\rho ^2}} \right)=\frac{{{{\left( { - 1} \right)}^n}}}{{{2^{2n+m}}n!}}\sum\limits_{{t=0}}^{n} {\sum\limits_{{s=0}}^{m} {{i^s}} } \left( {\begin{array}{*{20}{c}} n \\ t \end{array}} \right)\left( {\begin{array}{*{20}{c}} m \\ s \end{array}} \right){H_{2t+m - s}}\left( x \right){H_{2n - 2t+s}}\left( y \right).$$
(2)

In the above equation, \({H_n}\left( x \right)\) is the n order Hermite polynomial, which can be expressed as [26]

$${H_n}\left( x \right)=\sum\limits_{{l=0}}^{{\left[ {\frac{n}{2}} \right]}} {\frac{{{{\left( { - 1} \right)}^l}n!}}{{l!\left( {n - 2l} \right)!}}} {\left( {2x} \right)^{n - 2l}}.$$
(3)

Based on the theory of coherence [27], the cross-spectral density function of partially coherent beam generated by a Gaussian–Schell-model source as the source plane z = 0 can be written as

$$\begin{aligned} W\left( {{\mathbf{r}_{10}},{\mathbf{r}_{20}},0} \right)= & \left\langle {E\left( {{\mathbf{r}_{10}},0} \right)E_{{}}^{ * }\left( {{\mathbf{r}_{20}},0} \right)} \right\rangle \\ = & \sqrt {I\left( {{\mathbf{r}_{10}},0} \right)I\left( {{\mathbf{r}_{20}},0} \right)} \exp \left[ { - \frac{{{{\left( {{x_{10}} - {x_{20}}} \right)}^2}}}{{2\sigma _{x}^{2}}} - \frac{{{{\left( {{y_{10}} - {y_{20}}} \right)}^2}}}{{2\sigma _{y}^{2}}}} \right], \\ \end{aligned}$$
(4)

where \({\sigma _x}\) and \({\sigma _y}\) are the coherence lengths in x-axis and y-axis, respectively.

Submitting Eqs. (1) into (4) and considering Eq. (2), the cross-spectral density function of radial phase-locked PCELG beam array generated by a Gaussian–Schell-model source can be written as

$$\begin{aligned} W\left( {{r_{10}},{r_{20}},0} \right)= & \sum\limits_{{{q_1}=1}}^{Q} {\sum\limits_{{{q_2}=1}}^{Q} {\exp \left[ {i\left( {{\varphi _{q1}} - {\varphi _{{q_2}}}} \right)} \right]} } \frac{{{{\left( { - 1} \right)}^n}}}{{{2^{2n+m}}n!}}\sum\limits_{{{t_1}=0}}^{n} {\sum\limits_{{{s_1}=0}}^{m} {{i^{{s_1}}}} } \left( {\begin{array}{*{20}{c}} n \\ {{t_1}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} m \\ {{s_1}} \end{array}} \right)\frac{{{{\left( { - 1} \right)}^n}}}{{{2^{2n+m}}n!}}\sum\limits_{{{t_2}=0}}^{n} {\sum\limits_{{{s_2}=0}}^{m} {{{\left( { - i} \right)}^{{s_2}}}} } \left( {\begin{array}{*{20}{c}} n \\ {{t_2}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} m \\ {{s_2}} \end{array}} \right) \\ & \times {H_{2{t_1}+m - {s_1}}}\left( {\frac{{{x_{10}} - {r_{q1x}}}}{{{w_0}}}} \right){H_{2n - 2{t_1}+{s_1}}}\left( {\frac{{{y_{10}} - {r_{q1y}}}}{{{w_0}}}} \right)\exp \left[ { - \frac{{{{\left( {{x_{10}} - {r_{q1x}}} \right)}^2}+{{\left( {{y_{10}} - {r_{q1y}}} \right)}^2}}}{{w_{0}^{2}}}} \right] \\ & \times {H_{2{t_2}+m - {s_2}}}\left( {\frac{{{x_{20}} - {r_{q2x}}}}{{{w_0}}}} \right){H_{2n - 2{t_2}+{s_2}}}\left( {\frac{{{y_{20}} - {r_{q2y}}}}{{{w_0}}}} \right)\exp \left[ { - \frac{{{{\left( {{x_{20}} - {r_{q2x}}} \right)}^2}+{{\left( {{y_{20}} - {r_{q2y}}} \right)}^2}}}{{w_{0}^{2}}}} \right] \\ & \times \exp \left\{ { - \frac{{{{\left[ {\left( {{x_{10}} - {r_{q1x}}} \right) - \left( {{x_{20}} - {r_{q2x}}} \right)} \right]}^2}}}{{2\sigma _{x}^{2}}} - \frac{{{{\left[ {\left( {{y_{10}} - {r_{q1y}}} \right) - \left( {{y_{20}} - {r_{q2y}}} \right)} \right]}^2}}}{{2\sigma _{y}^{2}}}} \right\}, \\ \end{aligned}$$
(5)

with

$${\varphi _q}=q\frac{{2\pi }}{Q}\quad e=1,2,3 \ldots Q,$$
(6)
$${r_{qx}}=R\sin {\varphi _q},$$
(7)
$${r_{qy}}=R\cos {\varphi _q}.$$
(8)

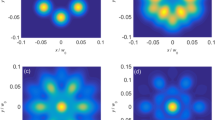
Figure 1 illustrates the contour graphs of a radial phased-locked PCELG beam array with \({w_0}=1\;{\text{cm}}\) and \(R=3\;{\text{cm}}\) at the source plane z = 0 for the different Q, n and m. From Fig. 1, it is found that the radial phased-locked PCELG beam consists of Q equal elegant Laguerre–Gaussian beamlets, which are located symmetrically on a ring with a radius \(R\); and when the parameters n and m change, the beamlet is the elegant Laguerre–Gaussian beam with the mode orders n and m.

Fig. 1
figure 1

The contour graphs of a radial phase-locked PCELG beam array at the source plane. a Q = 4, n = 1, m = 1, b Q = 5, n = 1, m = 1, c Q = 4, n = 3, m = 1, d Q = 4, n = 1, m = 3

Full size image

3 Propagation theory

The cross-spectral density function of the partially coherent beam propagating through non-Kolmogorov medium can be expressed by the extended Huygens–Fresnel principle [5,6,7,8,9,10,11,12,13]:

$$\begin{aligned} W\left( {{\mathbf{r}_1},{\mathbf{r}_2},z} \right)= & \frac{{{k^2}}}{{4{\pi ^2}{z^2}}}\int_{{ - \infty }}^{{+\infty }} {\int_{{ - \infty }}^{{+\infty }} {\int_{{ - \infty }}^{{+\infty }} {\int_{{ - \infty }}^{{+\infty }} {W\left( {{\mathbf{r}_{10}},{\mathbf{r}_{20}},0} \right)} } } } \\ & \times \exp \left[ { - \frac{{ik}}{{2z}}{{\left( {{\mathbf{r}_1}-{\mathbf{r}_{10}}} \right)}^2}+\frac{{ik}}{{2z}}{{\left( {{\mathbf{r}_2}-{\mathbf{r}_{20}}} \right)}^2}} \right] \\ & \times \left\langle {\exp \left[ {\psi \left( {{\mathbf{r}_{10}},{\mathbf{r}_1}} \right)+{\psi ^ * }\left( {{\mathbf{r}_{20}},{\mathbf{r}_2}} \right)} \right]} \right\rangle {\text{d}}{\mathbf{r}_{10}}{\text{d}}{\mathbf{r}_{20}} \\ \end{aligned}$$
(9)

where \(k={{2\pi } \mathord{\left/ {\vphantom {{2\pi } \lambda }} \right. \kern-0pt} \lambda }\) is the wave number with \(\lambda\) being the wavelength; \(\mathbf{r}=\left( {x,y} \right)\) and \({\mathbf{r}_0}=\left( {{x_0},{y_0}} \right)\) denotes the position vector at the receiver plane z and source plane z = 0, respectively; \(\psi \left( {{\mathbf{r}_0},\mathbf{r}} \right)\) is the complex phase perturbation; in the above equation, the last term can be written as [5,6,7,8,9,10,11,12,13]

$$\left\langle {\exp \left[ {\psi \left( {{\mathbf{r}_{10}},{\mathbf{r}_1}} \right)+{\psi ^ * }\left( {{\mathbf{r}_{20}},{\mathbf{r}_2}} \right)} \right]} \right\rangle =\exp \left\{ { - \frac{{{\pi ^2}{k^2}z}}{3}\int\limits_{0}^{\infty } {{\text{d}}\kappa {\kappa ^3}} \Phi \left( {\kappa ,\alpha } \right)\left[ {{{\left( {{\mathbf{r}_{10}} - {\mathbf{r}_{20}}} \right)}^2}+\left( {{\mathbf{r}_{10}} - {\mathbf{r}_{20}}} \right)\left( {{\mathbf{r}_1} - {\mathbf{r}_2}} \right)+{{\left( {{\mathbf{r}_1} - {\mathbf{r}_2}} \right)}^2}} \right]} \right\},$$
(10)

where \(\Phi \left( {\kappa ,\alpha } \right)\) is the spatial power spectrum of the refractive index fluctuations of the turbulent medium, \(\kappa\) is the magnitude to two-dimensional spatial frequency, and \(\alpha\) is the power-law exponent. And when the turbulent is governed by non-Kolmogorov statistics, \(\Phi \left( {\kappa ,\alpha } \right)\) can be expressed as

$$\Phi \left( {\kappa ,\alpha } \right)=A\left( \alpha \right)C_{n}^{2}\frac{{\exp \left( { - {{{\kappa ^2}} \mathord{\left/ {\vphantom {{{\kappa ^2}} {\kappa _{m}^{2}}}} \right. \kern-0pt} {\kappa _{m}^{2}}}} \right)}}{{{{\left( {{\kappa ^2}+\kappa _{0}^{2}} \right)}^{{\alpha \mathord{\left/ {\vphantom {\alpha 2}} \right. \kern-0pt} 2}}}}}0 \leq \kappa <\infty ,\quad 3<\alpha <4,$$
(11)

where \(C_{n}^{2}\) is a generalized index-of-refraction structure constant with units \({m^{3 - \alpha }}\); \({\kappa _0}={{2\pi } \mathord{\left/ {\vphantom {{2\pi } {{L_0}}}} \right. \kern-0pt} {{L_0}}}\), \({L_0}\) being the outer scale of turbulence; \({\kappa _m}={{c\left( \alpha \right)} \mathord{\left/ {\vphantom {{c\left( \alpha \right)} {{l_0}}}} \right. \kern-0pt} {{l_0}}}\), \({l_0}\) being the inner scale of turbulence; and

$$A\left( \alpha \right)=\frac{1}{{4{\pi ^2}}}\Gamma \left( {\alpha - 1} \right)\cos \left( {\frac{{\alpha \pi }}{2}} \right),$$
(12)
$$c\left( \alpha \right)={\left[ {\frac{{2\pi }}{3}\Gamma \left( {5 - \frac{\alpha }{2}} \right)A\left( \alpha \right)} \right]^{\frac{1}{{\alpha - 5}}}}.$$
(13)

In Eq. (12), \(\Gamma \left( x \right)\) is the Gamma function. In Eq. (10), we can define

$${1 \mathord{\left/ {\vphantom {1 {\rho _{0}^{2}=}}} \right. \kern-0pt} {\rho _{0}^{2}=}}{\pi ^2}{k^2}zT/3,$$
(14)

with

$$T=\int\limits_{0}^{\infty } {{\text{d}}\kappa {\kappa ^3}} \Phi \left( {\kappa ,\alpha } \right)=\frac{1}{{{\text{2}}\left( {\alpha - 2} \right)}}A\left( \alpha \right)C_{n}^{2}\left[ {\beta \kappa _{m}^{{2 - \alpha }}\exp \left( {\frac{{\kappa _{0}^{2}}}{{\kappa _{m}^{2}}}} \right)\Gamma \left( {2 - \frac{\alpha }{2},\frac{{\kappa _{0}^{2}}}{{\kappa _{m}^{2}}}} \right) - 2\kappa _{0}^{{4 - \alpha }}} \right],$$
(15)

with \(\beta ={\text{2}}\kappa _{{\text{0}}}^{{\text{2}}}{\text{-2}}\kappa _{m}^{2}+\alpha \kappa _{m}^{2}\). And \(\Gamma \left( {x,y} \right)\) is the incomplete Gamma function.

Submitting Eq. (5) into Eq. (9), the cross-spectral density function of a radial phase-locked PCELG beam array propagating in non-Kolmogorov medium can be derived as

$$\begin{aligned} W\left( {{\mathbf{r}_1},{\mathbf{r}_2},z} \right)= & \frac{{{k^2}}}{{4{\pi ^2}{z^2}}}\exp \left[ { - \frac{{ik}}{{2z}}\left( {x_{1}^{2}+y_{1}^{2}} \right)+\frac{{ik}}{{2z}}\left( {x_{2}^{2}+y_{2}^{2}} \right)} \right]\exp \left[ { - \frac{{{{\left( {{x_1} - {x_2}} \right)}^2}+{{\left( {{y_1} - {y_2}} \right)}^2}}}{{\rho _{0}^{2}}}} \right] \\ & \times \sum\limits_{{{q_1}=1}}^{Q} {} \sum\limits_{{{q_2}=1}}^{Q} {\exp \left[ {i\left( {{\varphi _{q1}} - {\varphi _{{q_2}}}} \right)} \right]} \frac{{{{\left( { - 1} \right)}^n}}}{{{2^{2n+m}}n!}}\sum\limits_{{{t_1}=0}}^{n} {\sum\limits_{{{s_1}=0}}^{m} {{i^{{s_1}}}} } \left( {\begin{array}{*{20}{c}} n \\ {{t_1}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} m \\ {{s_1}} \end{array}} \right)\frac{{{{\left( { - 1} \right)}^n}}}{{{2^{2n+m}}n!}}\sum\limits_{{{t_2}=0}}^{n} {\sum\limits_{{{s_2}=0}}^{m} {{{\left( { - i} \right)}^{{s_2}}}} } \left( {\begin{array}{*{20}{c}} n \\ {{t_2}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} m \\ {{s_2}} \end{array}} \right) \\ & \times W\left( {x,z} \right)W\left( {y,z} \right), \\ \end{aligned}$$
(16)

where

$$\begin{aligned} W\left( {x,z} \right)= & \exp \left[ { - \frac{{{{\left( {{r_{{q_1}x}} - {r_{{q_2}x}}} \right)}^2}}}{{\rho _{0}^{2}}}} \right]\exp \left[ { - \frac{{ik}}{{2z}}r_{{{q_1}x}}^{2}} \right]\left[ {\frac{{ik}}{{2z}}r_{{{q_2}x}}^{2}} \right]\exp \left[ {2\frac{{ik}}{{2z}}{x_1}{r_{{q_1}x}}} \right]\exp \left[ {-2\frac{{ik}}{{2z}}{x_2}{r_{{q_2}x}}} \right] \\ & \times \exp \left[ { - \frac{{\left( {{x_1} - {x_2}} \right)\left( {{r_{{q_1}x}} - {r_{{q_2}x}}} \right)}}{{\rho _{0}^{2}}}} \right]\sum\limits_{{l=0}}^{{\left[ {\frac{{2{t_1}+m - {s_1}}}{2}} \right]}} {\frac{{{{\left( { - 1} \right)}^l}\left( {2{t_1}+m - {s_1}} \right)!}}{{l!\left( {2{t_1}+m - {s_1} - 2l} \right)!}}} {\left( {\frac{2}{{{w_0}}}} \right)^{2{t_1}+m - {s_1} - 2l}} \\ & \times \left( {2{t_1}+m - {s_1} - 2l} \right)!\sqrt {\frac{\pi }{{{a_x}}}} {\left( {\frac{1}{{{a_x}}}} \right)^{2{t_1}+m - {s_1} - 2l}}\exp \left\{ {\frac{1}{{{a_x}}}{{\left[ {\frac{{ik}}{{2z}}\left( {{x_1} - {r_{{q_1}x}}} \right) - \frac{{\left( {{x_1} - {x_2}} \right)+2\left( {{r_{{q_1}x}} - {r_{{q_2}x}}} \right)}}{{2\rho _{0}^{2}}}} \right]}^2}} \right\} \\ & \times \sum\limits_{{u=0}}^{{\left[ {\frac{{2{t_2}+m - {s_2}}}{2}} \right]}} {\frac{{{{\left( { - 1} \right)}^u}\left( {2{t_2}+m - {s_2}} \right)!}}{{u!\left( {2{t_2}+m - {s_2} - 2u} \right)!}}} {\left( {\frac{2}{{{w_0}}}} \right)^{2{t_2}+m - {s_2} - 2u}}\sum\limits_{{k=0}}^{{\left[ {\frac{{2{t_1}+m - {s_1} - 2l}}{2}} \right]}} {\frac{1}{{k!\left( {2n - 2{t_1}+{s_1} - 2l - 2k} \right)!}}} {\left( {\frac{{{a_x}}}{4}} \right)^k} \\ & \times \sum\limits_{{h=0}}^{{2{t_1}+m - {s_1} - 2l - 2k}} {\frac{{\left( {2{t_1}+m - {s_1} - 2l - 2k} \right)!}}{{h!\left( {2{t_1}+m - {s_1} - 2l - 2k - h} \right)!}}\left[ {\frac{{ik}}{{2z}}\left( {{x_1} - {r_{{q_1}x}}} \right) - \frac{{\left( {{x_1} - {x_2}} \right)+2\left( {{r_{{q_1}x}} - {r_{{q_2}x}}} \right)}}{{2\rho _{0}^{2}}}} \right]} _{{}}^{{2{t_1}+m - {s_1} - 2l - 2k - h}} \\ & \times {\left( {\frac{1}{{\rho _{0}^{2}}}+\frac{1}{{2\sigma _{x}^{2}}}} \right)^h}\sqrt {\frac{\pi }{{{b_x}}}} {2^{ - \left( {2{t_2}+m - {s_2} - 2u+h} \right)}}{i^{2{t_2}+m - {s_2} - 2u+h}} \\ & \times \exp \left( {\frac{{c_{x}^{2}}}{{{b_x}}}} \right){\left( {\frac{1}{{{b_x}}}} \right)^{0.5\left( {2{t_2}+m - {s_2} - 2u+h} \right)}}{H_{2{t_2}+m - {s_2} - 2u+h}}\left( { - \frac{{i{c_x}}}{{\sqrt {{b_x}} }}} \right) \\ \end{aligned}$$
(17)

with

$${a_x}=\frac{1}{{w_{0}^{2}}}+\frac{1}{{2\sigma _{x}^{2}}}+\frac{1}{{\rho _{0}^{2}}}+\frac{{ik}}{{2z}},$$
(18)
$${b_x}=\frac{1}{{w_{0}^{2}}}+\frac{1}{{2\sigma _{x}^{2}}}+\frac{1}{{\rho _{0}^{2}}} - \frac{{ik}}{{2z}} - \frac{1}{{{a_x}}}{\left( {\frac{1}{{2\sigma _{x}^{2}}}+\frac{1}{{\rho _{0}^{2}}}} \right)^2},$$
(19)
$$\begin{aligned} {c_x}= & \frac{{ik}}{{2z}}{r_{{q_2}x}} - \frac{{ik}}{{2z}}{x_2}+\frac{{\left( {{x_1} - {x_2}} \right)+2\left( {{r_{{q_1}x}} - {r_{{q_2}x}}} \right)}}{{2\rho _{0}^{2}}} \\ & +\frac{1}{{{a_x}}}\left[ {\frac{{ik}}{{2z}}\left( {{x_1} - {r_{{q_1}x}}} \right) - \frac{{\left( {{x_1} - {x_2}} \right)+2\left( {{r_{{q_1}x}} - {r_{{q_2}x}}} \right)}}{{2\rho _{0}^{2}}}} \right]\left( {\frac{1}{{2\sigma _{x}^{2}}}+\frac{1}{{\rho _{0}^{2}}}} \right), \\ \end{aligned}$$
(20)

and

$$\begin{aligned} W\left( {y,z} \right)= & \exp \left[ { - \frac{{{{\left( {{r_{{q_1}y}} - {r_{{q_2}y}}} \right)}^2}}}{{\rho _{0}^{2}}}} \right]\exp \left[ { - \frac{{ik}}{{2z}}r_{{{q_1}y}}^{2}} \right]\left[ {\frac{{ik}}{{2z}}r_{{{q_2}y}}^{2}} \right]\exp \left[ {2\frac{{ik}}{{2z}}{y_1}{r_{{q_1}y}}} \right]\exp \left[ {-2\frac{{ik}}{{2z}}{y_2}{r_{{q_2}y}}} \right] \\ & \times \exp \left[ { - \frac{{\left( {{y_1} - {y_2}} \right)\left( {{r_{{q_1}y}} - {r_{{q_2}y}}} \right)}}{{\rho _{0}^{2}}}} \right]\sum\limits_{{l=0}}^{{\left[ {\frac{{2n - 2{t_1}+{s_1}}}{2}} \right]}} {\frac{{{{\left( { - 1} \right)}^l}\left( {2n - 2{t_1}+{s_1}} \right)!}}{{l!\left( {2n - 2{t_1}+{s_1} - 2l} \right)!}}} {\left( {\frac{2}{{{w_0}}}} \right)^{2n - 2{t_1}+{s_1} - 2l}} \\ & \times \left( {2n - 2{t_1}+{s_1} - 2l} \right)!\sqrt {\frac{\pi }{{{a_y}}}} {\left( {\frac{1}{{{a_y}}}} \right)^{2n - 2{t_1}+{s_1} - 2l}}\exp \left\{ {\frac{1}{{{a_y}}}{{\left[ {\frac{{ik}}{{2z}}\left( {{y_1} - {r_{{q_1}y}}} \right) - \frac{{\left( {{y_1} - {y_2}} \right)+2\left( {{r_{{q_1}y}} - {r_{{q_2}y}}} \right)}}{{2\rho _{0}^{2}}}} \right]}^2}} \right\} \\ & \times \sum\limits_{{u=0}}^{{\left[ {\frac{{2n - 2{t_2}+{s_2}}}{2}} \right]}} {\frac{{{{\left( { - 1} \right)}^u}\left( {2n - 2{t_2}+{s_2}} \right)!}}{{u!\left( {2n - 2{t_2}+{s_2} - 2u} \right)!}}} {\left( {\frac{2}{{{w_0}}}} \right)^{2n - 2{t_2}+{s_2} - 2u}}\sum\limits_{{k=0}}^{{\left[ {\frac{{2n - 2{t_1}+{s_1} - 2l}}{2}} \right]}} {\frac{1}{{k!\left( {2n - 2{t_1}+{s_1} - 2l - 2k} \right)!}}} {\left( {\frac{{{a_y}}}{4}} \right)^k} \\ & \times \sum\limits_{{h=0}}^{{2n - 2{t_1}+{s_1} - 2l - 2k}} {\frac{{\left( {2n - 2{t_1}+{s_1} - 2l - 2k} \right)!}}{{h!\left( {2n - 2{t_1}+{s_1} - 2l - 2k - h} \right)!}}\left[ {\frac{{ik}}{{2z}}\left( {{y_1} - {r_{{q_1}y}}} \right) - \frac{{\left( {{y_1} - {y_2}} \right)+2\left( {{r_{{q_1}y}} - {r_{{q_2}y}}} \right)}}{{2\rho _{0}^{2}}}} \right]} _{{}}^{{2n - 2{t_1}+{s_1} - 2l - 2k - h}} \\ & \times {\left( {\frac{1}{{\rho _{0}^{2}}}+\frac{1}{{2\sigma _{y}^{2}}}} \right)^h}\sqrt {\frac{\pi }{{{b_y}}}} {2^{ - \left( {2n - 2{t_2}+{s_2} - 2u+h} \right)}}{i^{2n - 2{t_2}+{s_2} - 2u+h}} \\ & \times \exp \left( {\frac{{c_{y}^{2}}}{{{b_y}}}} \right){\left( {\frac{1}{{{b_y}}}} \right)^{0.5\left( {2n - 2{t_2}+{s_2} - 2u+h} \right)}}{H_{2n - 2{t_2}+{s_2} - 2u+h}}\left( { - \frac{{i{c_y}}}{{\sqrt {{b_y}} }}} \right) \\ \end{aligned}$$
(21)

with

$${a_y}=\frac{1}{{w_{0}^{2}}}+\frac{1}{{2\sigma _{y}^{2}}}+\frac{1}{{\rho _{0}^{2}}}+\frac{{ik}}{{2z}},$$
(22)
$${b_y}=\frac{1}{{w_{0}^{2}}}+\frac{1}{{2\sigma _{y}^{2}}}+\frac{1}{{\rho _{0}^{2}}} - \frac{{ik}}{{2z}} - \frac{1}{{{a_y}}}{\left( {\frac{1}{{2\sigma _{y}^{2}}}+\frac{1}{{\rho _{0}^{2}}}} \right)^2},$$
(23)
$$\begin{aligned} {c_y}= & \frac{{ik}}{{2z}}{r_{{q_2}y}} - \frac{{ik}}{{2z}}{y_2}+\frac{{\left( {{y_1} - {y_2}} \right)+2\left( {{r_{{q_1}y}} - {r_{{q_2}y}}} \right)}}{{2\rho _{0}^{2}}} \\ & +\frac{1}{{{a_y}}}\left[ {\frac{{ik}}{{2z}}\left( {{y_1} - {r_{{q_1}y}}} \right) - \frac{{\left( {{y_1} - {y_2}} \right)+2\left( {{r_{{q_1}y}} - {r_{{q_2}y}}} \right)}}{{2\rho _{0}^{2}}}} \right]\left( {\frac{1}{{2\sigma _{y}^{2}}}+\frac{1}{{\rho _{0}^{2}}}} \right). \\ \end{aligned}$$
(24)

The following equation has been applied in the derivations of the above equations [26]:

$$\int_{{ - \infty }}^{{+\infty }} {{x^n}\exp \left( { - p{x^2}+2qx} \right){\text{d}}x} =n!\exp \left( {\frac{{{q^2}}}{p}} \right){\left( {\frac{q}{p}} \right)^n}\sqrt {\frac{\pi }{p}} \sum\limits_{{k=0}}^{{\left[ {\frac{n}{2}} \right]}} {\frac{1}{{k!\left( {n - 2k} \right)!}}} {\left( {\frac{p}{{4{q^2}}}} \right)^k}.$$
(25)

In Eq. (16), let \({\mathbf{r}_1}={\mathbf{r}_2}=\mathbf{r}\), the average intensity of a radial phase-locked PCELG beam array propagating in non-Kolmogorov medium at the plane z can be obtained as [27]

$$I\left( {\mathbf{r},z} \right)=W\left( {\mathbf{r},\mathbf{r},z} \right).$$
(26)

The spectral degree of spatial coherence of two points \({\mathbf{r}_1}=({x_1},{y_1})\) and \({\mathbf{r}_2}=({x_2},{y_2})\) for the partially coherent beam can be expressed as [27]

$$\mu \left( {{\mathbf{r}_1},{\mathbf{r}_2},z} \right)=\frac{{W\left( {{\mathbf{r}_1},{\mathbf{r}_2},z} \right)}}{{{{\left[ {W\left( {{\mathbf{r}_1},{\mathbf{r}_1},z} \right)W\left( {{\mathbf{r}_2},{\mathbf{r}_2},z} \right)} \right]}^{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}}}}.$$
(27)

4 Numerical results and analyses

In this section, the average intensity and spectral degree of coherence properties of a radial phased-locked PCELG beam array composed of Q beamlets propagating through non-Kolmogorov medium are studied using the derived formulae in the above section. The initial parameters are set as \(\lambda =800\;{\text{nm}}\), \({w_0}=1\;{\text{cm}}\), \(R=3\;{\text{cm}}\), \(\alpha =3.8\), \({L_0}=1\;{\text{cm}}\), \({l_0}=1\;{\text{mm}}\) and \(C_{n}^{2}={10^{ - 14}}{{\text{m}}^{3 - \alpha }}\) through the paper, unless the different values are specified.

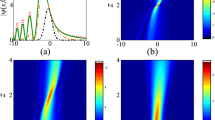
The 3D average intensity and contour graphs of the normalized intensity of a radial phased-locked PCELG beam array propagating in non-Kolmogorov medium for Q = 4 and Q = 5 are shown in Figs. 2 and 3, respectively. By comparing Figs. 1, 2 and 3, it is found that the radial phased-locked PCELG beam array can keep the initial beam profile with the Q beamlets at the short propagation distance (Figs. 2a, 3a), and each beamlet can almost remain the Laguerre–Gaussian beam profile. As the propagation distance increases, each beamlet will lose the Laguerre–Gaussian beam profile and coincide with the adjacent beamlet (Fig. 2b); the radial phased-locked PCELG beam array will evolve into flat-topped beam (Figs. 2e, 3c) and evolve into a solid beam with Gaussian-like distribution (Figs. 2f, 3d) in the far field. From the previous work, we known the radial phased-locked PCELG beam array propagation in non-Kolmogorov media has the similar evolution properties with the other radial phased-locked beam propagating in turbulent media [18, 20, 28].

Fig. 2
figure 2

The average intensity and contour graphs of normalized intensity of a radial phase-locked PCELG beam array with Q = 4 propagating in non-Kolmogorov medium. a \(z=100\;{\text{m}}\), b \(z=300\;{\text{m}}\), c \(z=700\;{\text{m}}\), d \(z=1500\;{\text{m}}\), e \(z=4000\;{\text{m}}\), f \(z=12,000\;{\text{m}}\)

Full size image
Fig. 3
figure 3

The average intensity and contour graphs of normalized intensity of a radial phase-locked PCELG beam array with Q = 5 propagating in non-Kolmogorov medium. a \(z=100\;{\text{m}}\), b \(z=2000\;{\text{m}}\), c \(z=5000\;{\text{m}}\), d \(z=12,000\;{\text{m}}\)

Full size image

The influences of initial beam parameters of coherence length \(\sigma\), n and m on the normalized intensity of a radial phased-locked PCELG beam array with Q = 4 propagating in non-Kolmogorov medium are shown in Figs. 4, 5 and 6, respectively. From Fig. 4, one can find that the radial phased-locked PCELG beam array with smaller coherence length will first lose the initial beam profile at the short propagation, and will evolve into a solid beam with Gaussian-like distribution more rapidly, while the fully coherent beam (\(\sigma {\text{=infinity}}\)) can remain the initial beam profile better at the short propagation distance, and evolve into a solid beam with Gaussian-like distribution slower than the partially coherent beam. From Figs. 5 and 6, one can find that the radial phase-locked PCELG beam array with smaller n and m can remain the initial beam profile better, while in the far field, the radial phased-locked PCELG beam array with larger n and m will have a larger beam spot.

Fig. 4
figure 4

The cross section of normalized intensity of a radial phase-locked PCELG beam array with Q = 4 propagating in non-Kolmogorov medium for the different \(\sigma\). a \(z=300\;{\text{m}}\), b \(z=1000\;{\text{m}}\), c \(z=5000\;{\text{m}}\), d \(z=12,000\;{\text{m}}\)

Full size image
Fig. 5
figure 5

The cross section of normalized intensity of a radial phase-locked PCELG beam array with Q = 4 propagating in non-Kolmogorov medium for the different n. a \(z=100\;{\text{m}}\), b \(z=500\;{\text{m}}\), c \(z=2000\;{\text{m}}\), d \(z=10,000\;{\text{m}}\)

Full size image
Fig. 6
figure 6

The cross section of normalized intensity of a radial phase-locked PCELG beam array with Q = 4 propagating in non-Kolmogorov medium for the different m. a \(z=200\;{\text{m}}\), b \(z=500\;{\text{m}}\), c \(z=1000\;{\text{m}}\), d \(z=5000m\)

Full size image

The influences of the parameters of non-Kolmogorov medium \(C_{n}^{2}\), \(\alpha\), \({L_0}\), and \({l_0}\) on the normalized intensity of a radial phase-locked PCELG beam array with Q = 4 propagating in non-Kolmogorov medium are shown in Figs. 7, 8, 9 and 10, respectively. From Fig. 7, one sees that, the radial phase-locked PCELG beam array with Q = 4 propagating in non-Kolmogorov medium with larger \(C_{n}^{2}\) will lose the initial beam profile faster. And the radial phase-locked PCELG beam array with Q = 4 propagating in non-Kolmogorov medium with smaller \(\alpha\) will evolve into a solid beam with Gaussian-like distribution more rapidly in the far field (Fig. 8). In the studies of the influences of \({L_0}\) (Fig. 9), and \({l_0}\) (Fig. 10) on the evolution properties of a radial phase-locked PCELG beam array, it is found that the a radial phase-locked PCELG beam array propagating in non-Kolmogorov medium with larger \({L_0}\) or smaller \({l_0}\) will evolve into a solid beam with Gaussian-like distribution more rapidly, while comparing to the parameter \(\alpha\), the influences of the parameters \({L_0}\) and \({l_0}\) on the spreading properties of a radial phase-locked PCELG beam array are not evident in the far filed.

Fig. 7
figure 7

The cross section of normalized intensity of a radial phase-locked PCELG beam array with Q = 4 propagating in non-Kolmogorov medium for the different \(C_{n}^{2}\). a \(z=1200\;{\text{m}}\), b \(z=1000\;{\text{m}}\), c \(z=5000\;{\text{m}}\), d \(z=10,000\;{\text{m}}\)

Full size image
Fig. 8
figure 8

The cross section of normalized intensity of a radial phase-locked PCELG beam array with Q = 4 propagating in non-Kolmogorov medium for the different \(\alpha\). a \(z=1200\;{\text{m}}\), b \(z=5000\;{\text{m}}\)

Full size image
Fig. 9
figure 9

The cross section of normalized intensity of a radial phase-locked PCELG beam array with Q = 4 propagating in non-Kolmogorov medium for the different \({L_0}\). a \(z=200\;{\text{m}}\), b \(z=5000\;{\text{m}}\)

Full size image
Fig. 10
figure 10

The cross section of normalized intensity of a radial phase-locked PCELG beam array with Q = 4 propagating in non-Kolmogorov medium for the different \({l_0}\). a \(z=200\;{\text{m}}\), b \(z=5000\;{\text{m}}\)

Full size image

Figure 11 gives the spectral degree of coherence of a radial phase-locked PCELG beam array with Q = 4 propagating in non-Kolmogorov medium for the different propagation distances. One can find that the spectral degree of coherence for the same two points is not the same at the different propagation distances, and the spectral degree of coherence has a function with oscillatory phenomenon at the different propagation distance, and which is not a function decreasing with the increase of x. The similar phenomenon can be found in the previous reports [19].

Fig. 11
figure 11

The spectral degree of coherence of a radial phase-locked PCELG beam array with Q = 4 propagating in non-Kolmogorov medium for the different propagation distances

Full size image

5 Conclusions

In this paper, the average intensity properties and spectral degree of coherence properties for a radial phase-locked PCELG beam array with Q beamlets propagating in non-Kolmogorov medium have been studied in details. One can find that the radial phase-locked PCELG beam array can keep the initial beam profile with the Q beamlets at the short propagation distance, and the beam array will evolve into a solid beam with Gaussian-like distribution in the far field. One can also find that the radial phase-locked PCELG beam array with smaller n and m can remain the initial beam profile better, and the beam array with larger n and m will have a larger beam spot in the far field. In the studies of the influences of non-Kolmogorov on the properties, it is found that the beam array propagating in non-Kolmogorov medium with larger \({L_0}\) or smaller \({l_0}\) or smaller \(\alpha\) will evolve into a solid beam with Gaussian-like distribution more rapidly.