Effects of Bi and Mn codoping on the physical properties of barium titanate: investigation via DFT method

Abstract

The current study employs density functional theory to explore the physical properties of Ba_1−xBi_xTi_1−xMn_xO₃ (x = 0, 0.3, and 0.4). A detailed analysis of structural, electronic, and mechanical properties is carried out in order to assess the impact of metal (Bi, Mn) doping at varying concentrations. The optimized lattice parameters vary with the incremental doping of metal, which is consistent with the experimental data. The band structure calculation shows that it is feasible to modify the band structure of BaTiO₃ by partially substituting Bi and Mn at Ba- and Ti-sites, respectively. With the increase of doping level, the accumulation of electron carriers near the Fermi level increases, which reveal the metallic characteristics of the doped compounds. The density of states calculation completely justifies the alteration of the band structures. The investigation of mechanical properties ensures the mechanical stability of both undoped and doped systems as well as exhibits a brittle to ductile transition after doping. In addition, the anisotropy factors reveal a considerable variation of elastic anisotropy between pure and doped systems, demonstrating the impacts of metal doping.

1 Introduction

Perovskite titanates (ATiO₃; A = Ca, Sr, Ba) have gained substantial attention in recent years because of its photocatalytic, dielectric, ferroelectric, and piezoelectric properties [1,2,3]. Considering the huge demand, this type of materials is one of the core compounds for theoretical and computational studies [4,5,6,7,8]. Theoretical studies of pure perovskites can be accomplished almost effortlessly and can achieve satisfactory results [4, 7]. But, when a pure system is being doped, the structure and properties undergo dramatic changes [9,10,11,12,13,14,15,16]. Doping of ATiO₃ with transition metal is frequently executed as it allows modifying and controlling the material’s properties [13,14,15,16,17]. In the midst of them BaTiO₃ is a phenomenal dielectric ceramic material with a considerable bandgap [18]. It has a broad range of application fields containing capacitors, transducers, positive temperature coefficient thermistors, ferroelectric nonvolatile memories, piezoelectric sensors, optoelectronic devices, actuators, and so on [19,20,21,22]. Therefore, BaTiO₃ ceramics are usually modified by special dopants to improve the basic properties and usability [23]. Over the last few years, researchers have been experimenting on the doped BaTiO₃ by isovalent or aliovalent cation substitution in either A-site and/or B-site [24,25,26,27,28,29,30]. The results have shown that doping brings prominent changes on the dielectric and ferromagnetic properties [27, 30]. Doping with transition metal, such as manganese (Mn) converts BaTiO₃ into a magnetic material and room temperature ferromagnetism can be detected in Mn-doped BaTiO₃ [31, 32]. The coercive field of BaTiO₃ can be enhanced by doping in the B-site, while the magnetization can be amplified by A-site substitution [33]. The previous researches also evidenced that the resistivity of BaTiO₃ was increased by doping with Mn [34, 35]. The acceptor doping reduces the charged vacancies of BaTiO₃ with ionic compensation [36]. However, doping with a donor dopant, such as bismuth (Bi) results in a significant increase in conductivity by decreasing bandgap [37]. It also increased the positive temperature coefficient of resistance [38]. In the recent years, metal-doped BaTiO₃ has gained popularity in energy storage systems using in compact electronics and electrical power systems [39, 40]. Moreover, the addition of Bi and Mn ions increased the dc electrical conductivity of BaTiO₃ [41]. The above discussions provide some significant information and application areas of pure and doped BaTiO₃ based on the experimental findings. Moreover, the physical properties of pure BaTiO₃ were also studied via the theoretical investigations [1, 4,5,6,7,8, 42], but such study is yet available on the Bi and Mn-codoped BaTiO₃. This motivates to choose this material in the present work to explore its physical properties, so that the effects of adding Bi and Mn can be predicted. Moreover, it is found that the incorporation of Bi and Mn in BaTiO₃ lead the stabilization of new perovskites with increased electrical conductivity and dielectric properties [41]. Therefore, it is required to investigate the detailed physical properties in order to get a whole picture about the electronic and mechanical behaviors in such systems for the feasible application fields. Recently, the first-principles scheme inaugurated on the density functional theory (DFT) has been the most convincing theoretical approach for investigating the physical and chemical properties of materials [43,44,45,46]. Therefore, the DFT method is exploited to pursue the structural, electronic, mechanical, and anisotropic properties of Ba_1−xBi_xTi_1−xMn_xO₃ (x = 0, 0.3, and 0.4) in this study.

2 Computational methods

The calculations are carried out using the Cambridge Serial Total Energy Package (CASTEP) in the context of DFT [47,48,49]. In this case, the orbital shape approximations are totally neglected [50, 51]. The electronic interaction and correlation energy are evaluated by using the general gradient approximation (GGA) with the functional of Perdew–Berke–Emzerhof (PBE) [52]. The electron–ion interaction is dealt with the Vanderbilt-type ultrasoft pseudopotential [53]. The cutoff energy is chosen as 900 eV and k- point mesh is set to 16 × 16 × 16 grid under the outline of Monkhorst–Pack [54] for the best fit to converge into the ground state. The convergence tolerance for energy, maximum force, maximum stress, and maximum atomic displacement of 5 × 10⁻⁶ eV/atom, 0.01 eV/Å, 0.02 GPa, and 5 × 10⁻⁴ Å, respectively, are used for the present calculations. The Broyden–Fletcher–Goldfarb–Shanno (BFGS) algorithm is used for optimizing the structure [55]. The lattice parameter and the atomic positions were relaxed while being optimized [56, 57]. Moreover, the virtual crystal approximation (VCA) compiled within the CASTEP code is also utilized to incorporate Bi and Mn atoms at A- and B-site, respectively. This method was successfully employed in various disordered systems, including silicates, perovskites, ferroelectric ceramics, superconductors, and MAX phases [58,59,60,61,62]. After optimization, electronic and mechanical properties are calculated by using the aforementioned measures. The elastic constants are estimated by employing the finite-strain method [63] in the CASTEP code. Furthermore, the 2D and 3D anisotropy contour plots of Young’s modulus, shear modulus, and Poisson’s ratio are obtained using the ELATE program [64]. The Young’s modulus is a function of single unit vector a (E (a)) and can be parameterized by two angles in spherical coordinates (0 ≤ θ ≤ π, and 0 ≤ φ ≤2π) as follows.

$$a = \left( \begin{gathered} {\text{sin}}\left( \theta \right){\text{cos}}\left( \varphi \right) \hfill \\ {\text{sin}}\left( \theta \right){\text{sin}}\left( \varphi \right) \hfill \\ {\text{cos}}\left( \theta \right) \hfill \\ \end{gathered} \right)$$

On the other hand, the shear modulus and Poisson’s ratio depend on two orthogonal unit vectors a and b (the direction of applied stress and measurement, respectively) and can be parameterized by three angles, so that b is written as,

$$b = \left( \begin{gathered} \cos \left( \theta \right)\cos \left( \varphi \right)\cos \left( \chi \right) - \sin \left( \phi \right){\text{sin}}\left( \chi \right) \hfill \\ \cos \left( \theta \right)\sin \left( \varphi \right)\cos \left( \chi \right) + \cos \left( \phi \right){\text{sin}}\left( \chi \right) \hfill \\ - {\text{sin}}\left( \theta \right){\text{cos}}\left( \chi \right) \hfill \\ \end{gathered} \right)$$

3 Results and discussion

3.1 Structural properties

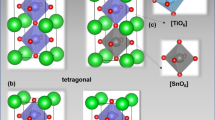
The optimized crystal structure of Ba_1−xBi_xTi_1−xMn_xO₃(x = 0, 0.3, and 0.4) is shown in Fig. 1, which has the similar structural feature to the experimental findings [41]. It has cubic perovskite phase with the space group $Pm\overline{3}m$(#221), in which A-site cations Ba/Bi are located at the corner with the Wyckoff position 1a (0, 0, 0), B-site cations Ti/Mn occupy the body center with the Wyckoff position 1b (0.5, 0.5, 0.5), and O anion is placed at the face center of the crystal with the Wyckoff position 3c (0, 0.5, 0.5). The B-site cation forms octahedral TiO₆ and (Ti/Mn)O₆ for pure and doped compounds, respectively. The calculated lattice constants and bond lengths of Ba_1−xBi_xTi_1−xMn_xO₃ in this study are listed in Table 1, comparing with the previous experimental and theoretical results [4, 41, 42]. The deviation of estimated lattice parameters and bond lengths from available reported results is negligible, justifying the accuracy of present simulation process. It is well known that when an atom in a material is partially substituted, it has a noticeable effect on the inter-planner distance, resulting in a significant change of lattice parameters [65,66,67]. Table 1 also manifests that the lattice parameters are slightly changed by the partial replacement of Ba and Ti with Bi and Mn, respectively. Since, the compound Ba_1−xBi_xTi_1−xMn_xO₃ (x = 0, 0.3, and 0.4) has already been synthesized [41], there should no remaining suspicion about its structural stability. Therefore, the stability of this doped system is not discussed in this study.

Fig. 1

The optimized crystal structure of Ba_1−xBi_xTi_1−xMn_xO₃ for a x = 0, b x = 0.3, and c x = 0.4

Table 1 The calculated lattice constant, a (Å) and bond lengths (Å) of Ba_1−xBi_xTi_1−xMn_xO₃ (x = 0, 0.3, and 0.4)

3.2 Electronic properties

In order to understand the electronic properties of a material, it is necessary to analysis the band structure, density of states (DOS), and charge density [43, 68]. Figure 2 demonstrates the electronic band structure of Ba_1−xBi_xTi_1−xMn_xO₃ (x = 0, 0.3, and 0.4), in which the horizontal dotted line at 0 eV denotes the Fermi level (E_F). The purely valence and conduction bands are indicated by blue lines, while the colored lines indicate the bands crossing the E_F. Figure 2a illustrates that the valence band maximum and conduction band minimum are found at R and G point points of the Brillouin zone, respectively, indicating an indirect bandgap (E_g) of pure BaTiO₃ with a value of 1.723 eV. The equivalent E_g value (1.75 eV) of BaTiO₃ [4], revealing the validity of the current computations utilizing the GGA-PBE approximations.

Fig. 2

Band structures of Ba_1−xBi_xTi_1−xMn_xO₃ for a x = 0, b x = 0.3, and c x = 0.4

The predicted energy bandgap of BaTiO₃ underestimates the experimentally evaluated value [69] because of the limitation of GGA-PBE approach. It is well known that the GGA-PBE sometimes underestimate the bandgap and it is expected that the inclusion of Hubbard parameter (U) with GGA or hybrid functional could give a better approximation [70]. However, it has been noted that a hybrid functional only cause the shift of the conduction band toward the higher energy and consequently increase the bandgap, whereas the other characteristics of the band structure remain unchanged [70]. The experimental bandgap of our considered compounds has been reported in the literature [41] and the reported values may be utilized for other explanations. Therefore, we have not considered the hybrid functional in bandgap calculation to avoid repeating the calculations rather than focusing to explore unknown properties like mechanical and anisotropic properties. It is also seen from Fig. 2b and c that the valence and conduction bands are shifted toward the E_F and overlapped with each other for doped compounds. As a result, the doped systems may show metallic behavior because of the accelerated transmission of electrons from the valence band to conduction band. The overlapping of Ba_0.6Bi_0.4Ti_0.6Mn_0.4O₃ is relatively more intensive, hence it is more conductive than that of Ba_0.7Bi_0.3Ti_0.7Mn_0.3O₃. Moreover, the increasing doping concentration of Bi and Mn is also responsible for tuning the band structure of Ba_1−xBi_xTi_1−xMn_xO₃. The most significant feature is observed at R and M points, where the separation between the valence and conduction bands is remarkably reduced by increasing the doping concentration from 30 to 40%.

To explicate the tuning of band structure because of metal doping, the total density of states (TDOS) and partial density of states (PDOS) are calculated and plotted in Fig. 3, where the vertical dotted line at 0 eV represents the E_F. According to Fig. 3a, the signature of energy E_g for undoped BaTiO₃ is also found in the DOS diagram. In the valence band, the main contribution comes from O-2p states along with small contribution of Ti-3d states, whereas the conduction band is mainly composed of Ti-3d states with a minor contribution of O-2p states. The valence band maximum and conduction band minimum are originated from O-2p and Ti-3d, respectively. As can be seen from Fig. 3b and c that, the DOS profile of BaTiO₃ is modified after metal (Bi, Mn) doping and no E_g is found. The valence band maximum for Bi-6p and conduction band minimum for Mn-3d are overlapped, hence no E_g is existed. However, the contribution of Bi-6p becomes prominent in making the valence band with a noticeable participation of O-2p, and Mn-3d, but the contribution of Ti-3d remains small. Interestingly, some of the valence bands are stacked together at ~2.5 eV, which is also evident from the band structure because of highly dispersive bands originated from Bi-6p and O-2p states at the same energy region. The conduction band is shifted toward the lower energy region and a flat peak is observed contributed by the Mn-3d states. The substantial shift of conduction bands toward the E_F is mainly contributed by Mn-3d, Bi-6p, and O-2p. Interestingly, the TDOS value of Ba_0.6Bi_0.4Ti_0.6Mn_0.4O₃ near the E_F is significantly higher, which makes it more conductive than that of Ba_0.7Bi_0.3Ti_0.7Mn_0.3O₃.

Fig. 3

DOS diagrams of Ba_1-xBi_xTi_1-xMn_xO₃ for a x = 0, b x = 0.3, and c x = 0.4

Moreover, the charge density difference mapping of Ba_1−xBi_xTi_1−xMn_xO₃ (Fig. 4) along the (100) crystallographic plane is also analyzed with the help of a charge density scale. In the scale, higher and lower electron density is indicated by blue and red color, respectively. It is evident from Fig. 4a that the electron density is very high for O and low for Ba atoms. At the same time, there is no overlapping between the electron density of Ba and O, which indicates the ionic nature of Ba–O bond in pure BaTiO₃. On the other hand, the Ba–O bond distance is clearly reduced and showing tendency to overlap, when 30% Ba is replaced by Bi atoms. Interestingly, a clear overlapping can be observed between Ba/Bi and O atoms, when the doping concentration is increased to 40%. Therefore, it can be concluded that the bonding nature of Ba/Bi-O is less ionic in Ba_0.7Bi_0.3Ti_0.7Mn_0.3O₃ than that of Ba–O in pure BaTiO₃, while the covalent bonding exists between Ba/Bi and O atoms in Ba_0.6Bi_0.4Ti_0.6Mn_0.4O₃.

Fig. 4

Charge density mappings of Ba_1−xBi_xTi_1−xMn_xO₃ for a x = 0, b x = 0.3, and c x = 0.4

3.3 Mechanical properties

The mechanical stability and various mechanical properties of Ba_1−xBi_xTi_1−xMn_xO₃ (x = 0, 0.3, and 0.4) are determined and discussed in this section. The calculated elastic constants C_ij and the Cauchy pressure (C₁₂–C₄₄) of titled compounds are listed in Table 2. If Hook’s law is applied to lattice dynamics, only three independent constants (C₁₁, C₁₂, and C₄₄) can be found for cubic compounds by combining the lattice symmetry. It is evident that the elastic constants of a compound must obey the following Born stability criteria for showing its mechanical stability [71].

$$C_{{{11}}} > 0,C_{{{44}}} > 0,C_{{{11}}} - C_{{{12}}} > 0,{\text{and}}\;C_{{{11}}} + {2}C_{{{12}}} > 0$$

(1)

Table 2 The calculated elastic constants C_ij (GPa) and Cauchy pressure C₁₂–C₁₄ (GPa) of Ba_1−xBi_xTi_1−xMn_xO₃ (x = 0, 0.3, and 0.4)

As the elastic constants of pure and doped compounds perfectly satisfy the Born stability criteria, they are mechanically stable. In addition, the calculated elastic constants of undoped BaTiO₃ accord well with the previous study [4], demonstrating the reliability of this calculation method once again.

The calculated C₁₁ of pure and doped compounds are larger than C₁₂, which is responsible for higher incompressibility along the crystallographic a-axis than that of b-axis. Therefore, the bonding along the [100] direction is harder than that of [011] direction. Moreover, it is worth mentioning that the C₁₁ is much higher than C₄₄, indicating that Ba_1−xBi_xTi_1−xMn_xO₃ has stronger resistance to the unidirectional compression than that of the shear deformation. The Cauchy pressure (C₁₂–C₄₄) can be used to describe the materials brittleness and ductility. The negative value of C₁₂–C₄₄ implies a material’s brittle nature and vice versa [72]. In this study, the calculated C₁₂–C₄₄ is negative for pure BaTiO₃, implying that it is brittle, while the positive C₁₂–C₄₄ of Ba_1−xBi_xTi_1−xMn_xO₃ (x = 0.3 and 0.4) reveals the ductility of doped compounds. Therefore, a transition from brittle to ductile nature of BaTiO₃ is observed after doping and Ba_0.6Bi_0.4Ti_0.6Mn_0.4O₃ would be more ductile than that of Ba_0.7Bi_0.3Ti_0.7Mn_0.3O₃ because of having larger positive C₁₂–C₄₄ (Table 2).

The fundamental mechanical properties, such as bulk modulus (B), shear modulus (G), Young’s modulus (E), Poisson’s ratio (ʋ), Pugh’s ratio (B/G), Vicker’s hardness (H_V), and machinability index (µ_M) of Ba_1−xBi_xTi_1−xMn_xO₃ (x = 0, 0.3, and 0.4), are also calculated and summarized in Table 3. The B and G are calculated using the well-known Voigt–Reuss approximation [73]. For cubic lattices, Voigt bulk modulus (B_V) and Voigt shear modulus (G_V) are defined as follows.

$$B_{V} = { }\frac{1}{3}\left( {C_{11} + { }2C_{12} } \right)$$

(2)

$$G_{V} = { }\frac{1}{5}\left( {C_{11} - C_{12} + 3C_{44} } \right)$$

(3)

Table 3 Calculated bulk modulus B (GPa), shear modulus G (GPa), Young’s modulus E (GPa), Poisson’s ratio ʋ, Pugh’s ratio B/G, Vicker’s hardness H_V (GPa), and machinability index µ_M of Ba_1−xBi_xTi_1−xMn_xO₃ (x = 0, 0.3, and 0.4)

In addition, the Reuss bulk modulus (B_R) and Reuss shear modulus (G_R) for cubic lattices are given by the following expressions.

$$B_{R} = B_{V} = \frac{1}{3}\left( {C_{11} + 2C_{12} } \right)$$

(4)

$$G_{R} = \frac{{5C_{44} \left( {C_{11} - C_{12} } \right)}}{{\left[ {4C_{44} + 3\left( {C_{11} - C_{12} } \right)} \right]}}$$

(5)

According to the Hill’s theory [74], the arithmetic mean of the Voigt and Reuss equations is used to estimate the B and G. Therefore, the following equations are practically used to estimate the bulk modulus (B_H) and shear modulus (G_H).

$$B_{H} = \frac{1}{2}\left( {B_{v} + B_{R} } \right)$$

(6)

$$G_{H} = \frac{1}{2}\left( {G_{v} + G_{R} } \right)$$

(7)

Moreover, the Young’s modulus (E), Poisson’s ratio (ʋ), Vicker’s hardness (H_V), and machinability index (µ_M) are given by following expressions [75, 76].

$$E = \frac{9BG}{{3B + G }}$$

(8)

$$\upsilon = \frac{3B - E}{{6B}}$$

(9)

$$H_{V} = \frac{{\left( {1 - 2\upsilon } \right)E}}{{6\left( {1 + \upsilon } \right)}}$$

(10)

$$\mu_{M} = \frac{B}{{C_{44} }}$$

(11)

The B and G represent the resistance to fracture and deformation, respectively [77]. Therefore, the pure BaTiO₃ is more resistant to fracture and deformation as compared to the doped compounds, because of having higher B and E. Moreover, E can be used to determine the stiffness of a material; the greater the value of E, the stiffer the material. Hence, BaTiO₃ is expected to be stiffer than that of Ba_0.7Bi_0.3Ti_0.7Mn_0.3O₃ and Ba_0.6Bi_0.4Ti_0.6Mn_0.4O₃. Since, the calculated E of BaTiO₃ becomes lower after doping, it is expected that the doped materials have better quality for thermal barrier coating. The computed B, G, and E of undoped BaTiO₃ are found similar to those of prior theoretical investigation [4].

Poisson’s ratio (v) is an important parameter for predicting the ductile/brittle nature of a solid. The limiting value of v is 0.26; the higher and lower value than 0.26 disclose the ductile and brittle nature, respectively [77]. Table 3 clearly exhibits that pure BaTiO₃ is brittle in nature, but it switches to ductile nature when Ba and Ti atoms are partially doped with Bi and Mn, respectively. The ratio of bulk modulus to shear modulus, B/G is another important parameter known as Pugh’s ratio, which has a marginal value of 1.75. A material is supposed to be ductile above 1.75, otherwise it is brittle [78]. It is obvious from Table 3 that the pure BaTiO₃ reflects brittle nature, while the doped Ba_1−xBi_xTi_1−xMn_xO₃ (x = 0.3 and 0.4) shows ductile nature. The Ba_0.6Bi_0.4Ti_0.6Mn_0.4O₃ is found to be more ductile than that of Ba_0.7Bi_0.3Ti_0.7Mn_0.3O₃. The findings of ʋ and B/G completely support the prediction of brittle/ductile nature of Ba_1−xBi_xTi_1−xMn_xO₃ (x = 0, 0.3, and 0.4) provided by the Cauchy pressure. Moreover, the value of ν should be in the range of 0.25–0.5 to detect the presence of central force within a crystal [79]. It is seen from Table 3 that the value of ν lies within 0.25–0.5 for doped phases but not for pure compound, confirming the presence of central force inside Ba_0.7Bi_0.3Ti_0.7Mn_0.3O₃ and Ba_0.6Bi_0.4Ti_0.6Mn_0.4O₃.

The calculated hardness is listed in Table 3, indicating that the partial replacement of Ba and Ti by Bi and Mn, respectively, greatly reduced the hardness of BaTiO₃, which is responsible for increasing the machinability of this compound. The machinability index (µ_M) is a measurement of a material’s plasticity and lubricating properties [80]. A greater µ_M indicates good lubrication, minimal feed friction, and increased plastic strain. According to this investigation, the doping of Bi and Mn significantly increases the machinability of BaTiO₃. However, the machinability of Ba_0.6Bi_0.4Ti_0.6Mn_0.4O₃ is much better than that of pure BaTiO₃ and doped Ba_0.7Bi_0.3Ti_0.7Mn_0.3O₃, which would have significant impact in the industrial applications. The variation of Hv and µ_M of BaTiO₃ under the effect of doping is presented in Fig. 5.

Fig. 5

Variation in hardness and machinability of Ba_1−xBi_xTi_1−xMn_xO₃ under various doping concentration of Bi and Mn

3.4 Elastic anisotropy

Various physical properties, such as plastic deformation in crystals, microscale cracking, crack propagation, texture in nanoscale shape memory alloys, and plastic relaxation in thin-film metallics, are influenced by the elastic anisotropy [81,82,83,84,85]. It is critical to be able to observe the impact of elastic anisotropy on these properties. The shear anisotropic factor can be used to determine the degree of anisotropy in bonding strength of atoms in different crystallographic planes. Three shear anisotropic factors can be found along the {100}, {010}, and {001} planes [86,87,88]. These three factors are given by the following equations.

$$A_{1} = \frac{{4C_{44} }}{{C_{11} + C_{33} - 2C_{13} }}$$

(12)

$$A_{2} = \frac{{4C_{55} }}{{C_{22} + C_{33} - 2C_{23} }}$$

(13)

$$A_{3} = \frac{{4C_{66} }}{{C_{11} + C_{22} - 2C_{12} }}$$

(14)

For cubic symmetry,

$$A_{1} = A_{2} = A_{3} = \frac{{4C_{44} }}{{C_{11} + C_{33} - 2C_{13} }} = \frac{{2C_{44} }}{{C_{11} - C_{13} }}$$

(15)

Which is similar to the Zener Anisotropy factor, A that can be denoted as follows [89, 90].

$$A = \frac{{2C_{44} }}{{C_{11} - C_{12} }}$$

(16)

For an isotropic material, A = A₁ = A₂ = A₃ = 1 and the deviation from unity corresponds to the anisotropy of a material [81]. The calculated values of A, A₁, A₂, and A₃ are listed in Table 4, manifesting the anisotropy of both pure and doped compounds. The percent anisotropy indices of compression (A_B) and shear (A_G) are expressed as follows [91].

$$A_{B} = \frac{{B_{V} - B_{R} }}{{B_{V} + B_{R} }}$$

(17)

$$A_{G} = \frac{{G_{V} - G_{R} }}{{2G_{H} }}$$

(18)

Table 4 Shear anisotropic factors (A₁, A₂, and A₃), Zener anisotropic factor A, anisotropy in compressibility A_B, anisotropy in shear A_G, universal log-Euclidean index A^L, and the universal anisotropy index A^U of Ba_1−xBi_xTi_1−xMn_xO₃ (x = 0, 0.3, and 0.4)

In the case of isotropic materials, A_B = A_G = 0. For cubic crystal A_B = 0 [B_V = B_R], which indicates the isotropic compression of compounds. Another key aspect in determining the type of material configuration (layered/non-layered) is the universal log-Euclidean index (A^L). The log-Euclidean formula is also defined as the universal log-Euclidean index [81, 91, 92], which is expressed as follows.

$$A^{L} = \sqrt {[\ln \left( {\frac{{B_{V} }}{{B_{R} }}} \right)]^{2} + 5[\ln \left( {\frac{{G_{V} }}{{G_{R} }}} \right)]^{2} }$$

(19)

For a cubic system, the above formula can be written as,

$$A^{L} = \sqrt {5[\ln \left( {\frac{{G_{V} }}{{G_{R} }}} \right)]^{2} } = \sqrt 5 \ln \left( {\frac{{G_{V} }}{{G_{R} }}} \right)$$

(20)

Since, the value of A^L is zero for isotropic materials; the studied compound Ba_1−xBi_xTi_1−xMn_xO₃ (x = 0, 0.3, and 0.4) is anisotropic (Table 4). Moreover, a compound with higher and lower A^L reveals the strong layered and non-layered structural feature, respectively [81]. Therefore, it can be concluded that both the pure and doped BaTiO₃ are non-layered materials.

To provide an accurate measure of anisotropy, the universal anisotropy factor (A^U) was first derived by Ranganathan and Ostoja-Starzewski [81, 93, 94]. Since A^U can apply to all the crystal symmetries, it is referred to as universal anisotropy factor and can be written as,

$$A^{U} = 5\frac{{G_{V} }}{{G_{R} }} + \frac{{B_{V} }}{{B_{R} }} - 6 \ge 0$$

(21)

But for cubic system,

$$A^{U} = 5\frac{{G_{V} }}{{G_{R} }} - 5 \ge 0$$

(22)

A^U is 0 for isotropic materials [80, 92]. The nonzero values of A^U (Table 4) indicate the anisotropic nature of both pure and doped compounds. After 30% doping the anisotropy of BaTiO₃ increases and greatly reduced when doping with 40%.

To visually interpret the anisotropy, 2D and 3D contour plots of Young’s modulus (E), shear modulus (G), and Poisson’s ratio (ʋ) are presented in Figs. 6, 7, and 8, respectively. The 2D and 3D constructions should be circular and spherical, respectively, for an isotropic crystal, while the degree of anisotropy is determined by the deviation of circular and spherical surface [95]. The anisotropy of pure and doped BaTiO₃ is clearly visualized in Figs. 6, 7, and 8. The minimum and maximum values of these three parameters at different crystallographic directions are also calculated and summarized in Table 5, from which the order of anisotropy can be written as $\nu > G > E$.

Fig. 6

Anisotropy contour plots of Young’s modulus of Ba_1−xBi_xTi_1−xMn_xO₃ under various doping concentrations of Bi and Mn

Fig. 7

Anisotropy contour plots of shear modulus of Ba_1−xBi_xTi_1−xMn_xO₃ under various doping concentrations of Bi and Mn

Fig. 8

Anisotropy contour plots of Poisson’s ratio of Ba_1−xBi_xTi_1−xMn_xO₃ under various doping concentrations of Bi and Mn

Table 5 The minimum and maximum limits of Young’s modulus (E), shear modulus (B), and Poisson’s ratio (ʋ) of Ba_1−xBi_xTi_1−xMn_xO₃ (x = 0, 0.3, and 0.4)

4 Conclusions

The effects of metal (Mn, Bi) doping on the structural, electronic, and mechanical properties of BaTiO₃ have been comprehensively explored by applying DFT-based first-principle calculations. The optimized lattice parameters are varied after codoping with Bi and Mn, providing analogy with the experimental data. The compound becomes metallic from semiconducting nature under the doping of Bi and Mn in place of Ba and Ti, respectively. To explain this behavior, the total and partial density of states are discussed briefly. The elastic constants perfectly satisfy the Born stability factors, which confirm the mechanical stability of pure and doped phases. The calculated values of Cauchy pressure, Poisson’s ratio, and Pugh’s ratio exhibit brittle to ductile transition, revealing the influence of doping. The anisotropic nature is also exhibited for pure and doped materials by several anisotropy factors. Finally, it is anticipated that this theoretical study may open up new avenues for the development of functional materials and their potential applications.