Biaxial experimental and analytical characterization of a dielectric elastomer

Abstract

Electroactive polymers (EAPs) have emerged as a strong contender for use in low-cost efficient actuators in multiple applications especially related to biomimetic and mobile-assistive devices. Dielectric elastomers (DE), a subcategory of these smart materials, have been of particular interest due to their large achievable deformation and favourable mechanical and electro-mechanical properties. Previous work has been completed to understand the behaviour of these materials; however, their properties require further investigation to properly integrate them into real-world applications. In this study, a biaxial tensile experimental evaluation of 3M™ VHB 4905 and VHB 4910 is presented with the purpose of illustrating the elastomers’ transversely isotropic mechanical behaviours. These tests were applied to both tapes for equibiaxial stretch rates ranging between 0.025 and 0.300 s⁻¹. Subsequently, a dynamic planar biaxial visco-hyperelastic constitutive relationship was derived from a Kelvin–Voigt rheological model and the general Hooke’s law for transversely isotropic materials. The model was then fitted to the experimental data to obtain three general material parameters for either tapes. The model’s ability to predict tensile stress response and internal energy dissipation, with respect to experimental data, is evaluated with good agreement. The model’s ability to predict variations in mechanical behaviour due to changes in kinematic variables is then illustrated for different conditions.

1 Introduction

Over the last two decades, technological advancements have allowed researchers to develop many novel self-independent mobile systems such as human mobility assistive devices. Powered by electrical motors and/or hydraulic and pneumatic cylinders, they provide a considerable improvement to human physical abilities. Their development is not, however, without its limitations. The success of these devices is greatly restricted by the operational times currently achievable, as well as their unfavourable weight and volume [1, 2]. This has led to new interests in the application of smart materials to produce novel types of actuation. As part of this newer class of materials, electroactive polymers (EAP) have emerged as a strong contender for use in low-cost efficient actuators. Among their many appealing properties, they have proven particularly useful for soft robotic and assistive device applications due to their similar mechanical behaviour to human muscle [1, 3]. A subcategory of these polymers, namely dielectric elastomers (DE), has shown very promising properties for these types of applications. Their structures have revealed large achievable deformation while their material composition has demonstrated high dielectric strength [4,5,6,7].

As to be expected by any rubber-like material, DE demonstrate a proportional sensitivity to strain rate, as well as a clear dissipation of internal energy during a load–unload tensile test. For this reason, their mechanical (uniaxial) tensile behaviours have required investigation to adequately design, predict, and optimize DE-based actuators [8, 9]. No multi-axis experimental results have been found in the literature to demonstrate the materials’ behaviour under complex tensile loading. In most cases, the material behaviour is assumed to be isotropic based on its elastomeric structure. Acrylic-based DE are typically always pre-stretched for their use as an EAP. In most cases, this stretching is applied biaxially. It is, therefore, of particular interest to quantify the materials’ behaviour from a biaxial perspective, to validate its mechanical properties under these conditions.

Researchers have also proposed several constitutive models to characterize the behaviour of these materials. To predict the electro-mechanically coupled behaviour of an actuator, the mechanical constitutive behaviour must first be studied. This relationship between the stress and stretch ratio provides the foundation to all further design and analysis of DE-based actuators. Being rubber-like materials, the elastic response of acrylic-based DE are highly nonlinear, and therefore necessitate more complex stress–stretch ratio characterization. Several hyperelastic strain energy functions have been proposed to characterize these types of materials, from both phenomenological and micro-mechanical considerations. Steinmann [10] and Hossain [11] have reviewed and compared 25 of these models. Among the surveyed candidates, they have demonstrated the accuracies of Neo-Hooke [12], Ogden [13], and Yeoh [14] models, which have been used by various research groups [15,16,17,18,19,20] to model the mechanical and electro-mechanical response of DE films and actuators.

Although hyperelastic models provide good insight of the material’s elastic behaviour in tension, they unfortunately neglect its time-dependent viscoelastic properties. To include these behaviours as part of the constitutive models, several groups [21,22,23,24,25] have adapted both hyper- and visco-hyperelastic models such as Mooney-Rivlin [12], Gent [26], and Bergström-Boyce [27] to predict the DE films/actuator mechanical behaviour. Viscoelastic constitutive models yield high accuracy when describing static time-dependent responses such as stress relaxation and creep. They are also very effective in precise analysis applications such as computational finite element modelling. Such alternatives are not, however, as practical for design purposes due to their high complexity, and lack of ability to effectively model continuous/alternating loading conditions. This is in-part due to the fact that the damping aspect of elastomers, particularly VHB tapes, is highly nonlinear and, therefore, difficult to represent analytically. For this reason, certain groups have adopted other approaches, based on rheological models [28,29,30,31] or quasi-linear viscoelasticity [32, 33], to provide a more intuitive physical representation. Further developments, such as the works of Sabran et al. [34] and Zhang et al. [35] have implemented rheological approaches for dynamic applications, which demonstrates their potential for high-frequency applications such as DE actuators.

One such approach has been proposed by Lochmatter et al. [28], to provide a more straightforward method for DE-based planar actuator design and analysis. This alternative makes use of a three-dimensional network of fluid-filled cuboids, where their frame-segments are comprised of enhanced Kelvin–Voigt rheological model (also known as a Standard Linear Solid model). The model aimed to describe the mechanical behaviour of visco-hyperelastic elastomers to provide an investigative tool for actuators under continuous cyclical electro-mechanical activation.

Further development by Wang et al. [29] re-expressed this model with a dynamic energy dissipation parameter. The group introduced a rate-dependent frequency to the equivalent (lumped) modulus of the aforementioned Kelvin–Voigt segments. As the polymer’s stress response is also dependent on stretch rate, this allowed the model to reflect the variations in mechanical response due to changes in rate of deformation. Wang’s new approach has proven successful in agreeing with experimental values. It has also demonstrated the ability to represent variations in energy loss and changes in peak stresses due to the effects of changing the kinematic parameters. The model’s mathematical structure is also more illustrative of mechanical behaviour, which is advantageous for the design and evaluation of DE actuators. The aforementioned models have not, however, taken into consideration the behaviour of the DE under biaxial loading. This type of modelling would seem nonetheless imperative to both the assembly and subsequent actuation modelling of several DE-based actuator configurations. In particular, configurations such as the bow-tie [36] or diamond-shape [37], where both planar axes are coupled by a rigid outer-frame.

This study firstly provides a comprehensive experimental evaluation of 3M™ VHB polyacrylic dielectric elastomer under biaxial tensile loading which, to the author’s knowledge, is the first of its kind. The viscoelastic rate- and time-dependent responses of the polymer are studied for different loading conditions at various stretch rates. The study then proposes a novel modification to the rheological constitutive model to characterize the material’s tensile response in biaxial conditions. The model is fitted to experimental data and then evaluated based on modifying kinematic variables.

2 Methods

2.1 Equipment and experimental protocol

To characterize the transversely isotropic tensile behaviour of 3M™ VHB tape, a series of biaxial tests were performed. To achieve these experiments, CellScale’s BioTester (CellScale, Waterloo) was used. The BioTester machine makes use of tungsten rakes to mount samples to its 23-N load cells. The rakes used for all experiments had a tine diameter of 305 µm, tine spacing of 1.0 mm and puncture depth of 1.9 mm [38].

Samples for VHB 4905 and 4910 tapes were cut down to a 10-mm square specimen and mounted to the rakes for tensile tests. The load–unload tensile testing was performed at six different synchronous stretch rates: 0.025, 0.050, 0.075, 0.100, 0.200, and 0.300 s⁻¹. These tests consisted of a constant stretch rate elongation phase to a peak stretch ratio of $\lambda =2$ (i.e. 100% strain), followed by a mirrored release phase. In all cases, experiments were set to equibiaxial conditions (i.e. stretch ratios ${\lambda _1}={\lambda _2}=\lambda$). Each experimental stretch rate was repeated for five different samples. The data in the current work are reflective of a single loading cycle, which represents the material’s initial response. It should be noted that cyclical loading of highly viscous elastomers, such as VHB tape, results in the eventual convergence of its mechanical behaviour and will produce a stable, reproducible stress–stretch curve [39, 40]. This should thus be taken into account for the context of actuator modelling, as the current study does not reflect the steady-state properties of VHB tape.

CellScale’s LabJoy image tracking software was used to evaluate the specimen’s true stretch ratio for the biaxial load–unload tests. This additional step was taken as precaution due to possible inaccurate representation of the material’s deformation based on grip displacements [41, 42].

To track the specimen’s true displacement, methods similar to the ones reported by Labrosse et al. [41] were used, where a 9 by 9 node square grid was manually selected within the central portion of its surface. After running the tracking software, the localized stretch ratios were observed for each of the 64 square elements and a single element was selected based on the region’s most relatively homogeneous strain. The displacement of all four nodes forming the chosen square element are then exported in terms of the planar axes coordinates for further processing.

To determine the displacement of the element along either axis, a method of iso-parametric mapping was utilized. Similar to the method described by Humphrey [43] and Labrosse et al. [41, 44], this involves transformations between a quadrilateral element’s nodal coordinates and a set of natural coordinates, based on the reference coordinate system of its analogous parent geometry.

Following displacement tracking and calculations, the true stress acting on both axes of the specimen were calculated by introducing the Cauchy Stress tensor. A MATLAB code was written to process these calculations, as well as plot the final data.

2.2 Analytical model

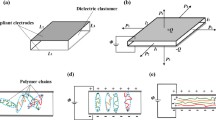
The model proposed by Wang et al. [29] is a visco-hyperelastic constitutive model based on an enhanced Kelvin–Voigt model, as shown in Fig. 1. The spring-damper element model was first proposed by Lochmatter et al. [28] as a suitable general description of VHB tape’s characteristic viscoelastic mechanical behaviour.

Fig. 1

Representation of dielectric elastomer model and enhanced Kelvin–Voigt element

It can be seen that the polymer is analyzed within a three-dimensional micro-level framework. The film is divided into cuboid elements, each consisting of individual segments comprised of an enhanced Kelvin–Voigt element. This element is comprised of a serial spring of stiffness ${k_{\text{s}}}$, and a parallel spring-damper element with coefficients of ${k_{\text{p}}}$ and ${d_{\text{p}}}$, respectively. The cuboids are further described as being filled with an incompressible fluid that exerts a hydrostatic pressure $p$ on their walls when deformed. The combination of the segments’ spring-damper configuration and the incompressible fluidic cuboid cores ensure that the model represents VHB’s visco-hyperelastic properties in all three principal directions. It additionally ensures the mechanical coupling of the spatial deformation due to incompressibility. Three main assumptions are made for this model:

• The segments of the cuboid elements are mass-free, which implies a neglection of internal wave propagation (i.e. effects of inertia)

• The cuboid geometry is maintained under deformation, which is a requirement for laterally compliant boundary conditions

• Only uniformly distributed normal loads are considered, discounting all shearing effects

The film is broken up into a large number of ${N_i}$ segments (i.e., ${N_i} \gg 1$), where $i=1,~2,~3$ (or x, y, z). The sample’s global dimensions are represented by $L_{i}^{{(0)}}$ and ${L_i}$, as the initial (undeformed) and final deformed lengths, respectively, in all three directions of space. Similarly, each cuboid’s dimensions are also represented as initial and deformed lengths $s_{i}^{{(0)}}$ and ${s_i}$, respectively. When loaded, the net true stresses exerted on the film can be expressed as:

$${\sigma _i}={\lambda _i}{\sigma _{{\text{syste}}{{\text{m}}_i}}} - p,{\text{ }}i=1,{\text{ }}2,{\text{ }}3$$

(1)

where ${\lambda _i}$ is the stretch ratio of the deformed geometry, defined by ${\lambda _i}={L_i}/L_{i}^{{(0)}}$. Under the assumption that deformation of coaxial segments of all cuboids is equal, this implies that ${\lambda _i}={s_i}/s_{i}^{{(0)}}$ as well. ${\sigma _{{\text{syste}}{{\text{m}}_i}}}$ are the nominal stresses of the spring-damper segments of the uncoupled frameworks, and $p$ is the previously mentioned hydrostatic pressure exerted on the cuboid walls.

Based on the enhanced Kelvin–Voigt model, the spring-damper element’s modulus can be expressed as a single equivalent parameter in terms of the serial modulus of elasticity, parallel moduli of elasticity and viscosity loss are ${E_{{{\text{s}}_i}}}={k_{{{\text{s}}_i}}}/s_{i}^{{(0)}}$, ${E_{{{\text{p}}_i}}}={k_{{{\text{p}}_i}}}/s_{i}^{{(0)}}$, and ${D_{{{\text{p}}_i}}}={d_{{{\text{p}}_i}}}/s_{i}^{{(0)}}$, respectively. To provide a more explicit physical representation of the material’s dynamic response, the model is expressed in the frequency domain as a complex modulus:

$$E_{{{\text{e}}{{\text{q}}_i}}}^{{\text{*}}}=\frac{{{E_{{{\text{s}}_i}}}\left( {{E_{{{\text{p}}_i}}}+j{\omega _i}{D_{{{\text{p}}_i}}}} \right)}}{{\left( {{E_{{{\text{s}}_i}}}+{E_{{{\text{p}}_i}}}} \right)+j{\omega _i}{D_{{{\text{p}}_i}}}}},{\text{ }}i=1,{\text{ }}2,{\text{ }}3$$

(2)

where ${\omega _i}$ is the angular frequency of the alternating stress (or strain) applied to the system, in direction $i$.

To simplify the experimental conditions, the material was tested through a rudimentary ramp load–unload tensile test, at a constant stretch rate. This uniform motion is then approximated to be the first half-cycle of the harmonic motion. Based on this approximation, the experimental angular frequency can be expressed as:

$${\omega _i}=\frac{{2\pi }}{{{T_i}}} \approx \frac{{\pi {{\dot {\lambda }}_i}}}{{2\left( {{\lambda _{{{\text{m}}_i}}} - 1} \right)}},~\quad ~i=1,~2,~3$$

(3)

where ${\dot {\lambda }_i}={\text{d}}{\lambda _i}/{\text{d}}t$ is the stretch rate, and ${\lambda _{{{\text{m}}_i}}}$ is the maximum achieved stretch ratio during the cycle. Finally, the system’s nominal stress ${\sigma _{{\text{syste}}{{\text{m}}_i}}}$ in each direction can be represented as:

$${\sigma _{{\text{syste}}{{\text{m}}_i}}}=E_{{{\text{e}}{{\text{q}}_i}}}^{{\text{*}}}{\varepsilon _i}=E_{{{\text{e}}{{\text{q}}_i}}}^{{\text{*}}}\left( {{\lambda _i} - 1} \right),\quad i=1,{\text{ }}2,{\text{ }}3$$

(4)

where ${\varepsilon _i}$ is the strain in direction $i$.

For the case where the strains are both periodically and dynamically changing based on time and angular frequency, ${\varepsilon _i}$ can be expressed as ${\varepsilon _i}={\varepsilon _{{{\text{m}}_i}}}{e^{j\omega t}}$ (or ${\varepsilon _i}={\varepsilon _{{{\text{m}}_i}}}{\text{sin}}(\omega t)$) where ${\varepsilon _{{{\text{m}}_i}}}$ is the strain amplitude. Applying this relationship to (4), under the assumption that the stresses and strains vary at the same frequency, with a certain phase shift ${\delta _i}$, the nominal stresses can then be expressed as:

$${\sigma _{{\text{syste}}{{\text{m}}_i}}}=\left| {E_{{{\text{e}}{{\text{q}}_i}}}^{{\text{*}}}} \right|{\varepsilon _{{m_i}}}{e^{j({\omega _i}t+{\delta _i})}},\quad i=1,{\text{ }}2,{\text{ }}3$$

(5)

where $\left| {E_{{e{q_i}}}^{*}} \right|$ is the magnitude of the complex modulus (i.e. the absolute modulus), and ${\delta _i}$ denotes the lag angle of the strain relative to the stress. Through general conventions for complex numbers, the absolute modulus can be expressed as:

$$\left| {E_{{{\text{e}}{{\text{q}}_i}}}^{*}} \right|=\frac{{{E_{{{\text{s}}_i}}}\sqrt {\left( {E_{{{{\text{p}}_i}}}^{2}+\omega _{i}^{2}D_{{{{\text{p}}_i}}}^{2}} \right)} }}{{\sqrt {{{\left( {{E_{{{\text{s}}_i}}}+{E_{{{\text{p}}_i}}}} \right)}^2}+\omega _{i}^{2}D_{{{{\text{p}}_i}}}^{2}} }},~\quad i=1,~2,~3$$

(6)

The variable $\eta$ is a measure of a viscoelastic material’s intrinsic damping property, which is defined by the ratio between the imaginary and real parts of the complex modulus [45]. This value can be used to illustrate the internal energy dissipation of the elastomer. From this, the lag angle is derived as:

$${\delta _i}=\arctan {\eta _i}=\arctan \frac{{\operatorname{Im} \left[ {E_{{{\text{e}}{{\text{q}}_i}}}^{*}} \right]}}{{\operatorname{Re} \left[ {E_{{{\text{e}}{{\text{q}}_i}}}^{*}} \right]}}$$

$${\delta _i}=\arctan \left( {\frac{{E_{{{{\text{s}}_i}}}^{2}{D_{{{\text{p}}_i}}}{\omega _i}}}{{E_{{{{\text{s}}_i}}}^{2}{E_{{{\text{p}}_i}}}+{E_{{{\text{s}}_i}}}E_{{{{\text{p}}_i}}}^{2}+{E_{{{\text{s}}_i}}}D_{{{{\text{p}}_i}}}^{2}\omega _{i}^{2}}}} \right),\quad i=1,{\text{ }}2,{\text{ }}3$$

(7)

The lag angle ${\delta _i}$ creates a phase shift between the stress and the strain of the system. This shift will create the enclosed hysteresis curve (as demonstrated in [29]), which will represent the expected internal energy dissipation of the elastomer.

Under biaxial tensile loading, the film is being elongated along both ${\lambda _1}$ and ${\lambda _2}$ axes, implying a free boundary condition only along its thickness (${\lambda _3}$). Due to the loads applied on axes $i=1,~2$, the moduli for either axes will be processed independently. An assumption of isotropy will need to be introduced for the biaxial model, to allow mathematical derivations with a solvable number of unknown variables. In other words, the complex modulus $E_{{{\text{e}}{{\text{q}}_i}}}^{*}:=E_{{{\text{eq}}}}^{*}$ for $i=1,~2,~3$. Taking an ideal biaxial tension along directions $i=1,2$, the true stress can be expressed as:

$${\sigma _i}={\lambda _i}{\sigma _{{\text{syste}}{{\text{m}}_i}}} - p={\sigma _{{\text{ex}}{{\text{t}}_i}}},\quad i=1,2$$

(8)

where ${\sigma _{{\text{ex}}{{\text{t}}_i}}}$ are the external stresses applied to the system, at stretch ratios of ${\lambda _1}$ and ${\lambda _2}$. The thickness will have free boundary conditions, and its true stress will necessarily be zero (${\sigma _3}=0$). It follows that the net normal stress equation is:

$${\sigma _3}={\lambda _3}{\sigma _{{\text{syste}}{{\text{m}}_3}}} - p=0$$

(9)

From the incompressibility condition, a relationship between the three stretch ratios can be drawn, as ${\lambda _3}=1/({\lambda _1}{\lambda _2})$. Knowing that the hydrostatic pressures will be equal along all axes, and recalling the value of nominal stress for a free boundary from (4), $p$ can be expressed as:

$$p=E_{{{\text{eq}}}}^{*}[{\left( {{\lambda _1}{\lambda _2}} \right)^{ - 2}} - {\left( {{\lambda _1}{\lambda _2}} \right)^{ - 1}}]$$

(10)

Due to the change in loading conditions, the currently proposed model will make use of the generalized Hooke’s law for biaxial loading to express nominal stresses along $i=1,2$. This will allow the nominal stresses to reflect the overall deformation of the elastomer in terms of both ${\lambda _1}$ and ${\lambda _2}$. Neglecting the effects of shear, the system nominal stresses for an isotropic material is, therefore, by convention:

$$\left\{ {\begin{array}{*{20}{c}} {{\sigma _{{\text{syste}}{{\text{m}}_1}}}} \\ {{\sigma _{{\text{syste}}{{\text{m}}_2}}}} \end{array}} \right\}=\frac{1}{{1 - {\nu ^2}}}\left[ {\begin{array}{*{20}{c}} {E_{{{\text{eq}}}}^{{\text{*}}}}&{\nu E_{{{\text{eq}}}}^{{\text{*}}}} \\ {\nu E_{{{\text{eq}}}}^{{\text{*}}}}&{E_{{{\text{eq}}}}^{{\text{*}}}} \end{array}} \right]\left\{ {\begin{array}{*{20}{c}} {({\lambda _1} - 1)} \\ {({\lambda _2} - 1)} \end{array}} \right\}$$

(11)

where Poisson’s ratio $\nu =0.49$ for both VHB 4905 and VHB 4910 tapes [46]. Inserting (11) to (8), and equating the hydrostatic pressures will give the final expression for normal stress along axes of deformation:

$$p=E_{{{\text{eq}}}}^{*}\left[ {{{\left( {{\lambda _i}{\lambda _j}} \right)}^{ - 2}} - {{\left( {{\lambda _i}{\lambda _j}} \right)}^{ - 1}}} \right]=\frac{{{\lambda _i}E_{{{\text{eq}}}}^{*}}}{{1 - {\nu ^2}}}\left[ {\left( {{\lambda _i} - 1} \right)+\nu \left( {{\lambda _j} - 1} \right)} \right] - {\sigma _i}$$

$$\left\{ {\begin{array}{*{20}{c}} {{\sigma _1}=\frac{{{\lambda _1}E_{{{\text{eq}}}}^{*}}}{{1 - {\nu ^2}}}\left[ {\left( {{\lambda _1} - 1} \right)+\nu \left( {{\lambda _2} - 1} \right)} \right]+E_{{{\text{eq}}}}^{*}\left[ {{{\left( {{\lambda _1}{\lambda _2}} \right)}^{ - 1}} - {{\left( {{\lambda _1}{\lambda _2}} \right)}^{ - 2}}} \right]} \\ {{\sigma _2}=\frac{{{\lambda _2}E_{{{\text{eq}}}}^{*}}}{{1 - {\nu ^2}}}\left[ {\left( {{\lambda _2} - 1} \right)+\nu \left( {{\lambda _1} - 1} \right)} \right]+E_{{{\text{eq}}}}^{*}\left[ {{{\left( {{\lambda _2}{\lambda _1}} \right)}^{ - 1}} - {{\left( {{\lambda _2}{\lambda _1}} \right)}^{ - 2}}} \right]} \end{array}} \right.$$

(12)

The strain of the system, in both directions of deformation, will change over time, and can thus be expressed as:

$${\varepsilon _i}\left( t \right)={\lambda _i}\left( t \right) - 1={\varepsilon _{{m_i}}}{e^{j{\omega _i}t}},\quad ~i=1,2$$

(13)

Then, (12) can be expressed in terms of time: to correlate the experimental values to the time-dependent equation, only the variables’ sizes are considered, such that:

$$\left\{ {\begin{array}{*{20}{c}} {\left| {{\sigma _1}} \right|=\left| {E_{{{\text{eq}}}}^{*}} \right|\left[ {\frac{{{\lambda _1}}}{{1 - {\nu ^2}}}\left( {\left( {{\lambda _1} - 1} \right)+\nu \left( {{\lambda _2} - 1} \right)} \right)+\left( {{{\left( {{\lambda _1}{\lambda _2}} \right)}^{ - 1}} - {{\left( {{\lambda _1}{\lambda _2}} \right)}^{ - 2}}} \right)} \right]} \\ {\left| {{\sigma _2}} \right|=\left| {E_{{{\text{eq}}}}^{*}} \right|\left[ {\frac{{{\lambda _2}}}{{1 - {\nu ^2}}}\left( {\left( {{\lambda _2} - 1} \right)+\nu \left( {{\lambda _1} - 1} \right)} \right)+\left( {{{\left( {{\lambda _1}{\lambda _2}} \right)}^{ - 1}} - {{\left( {{\lambda _1}{\lambda _2}} \right)}^{ - 2}}} \right)} \right]} \end{array}} \right.$$

(14)

Having derived the equation for $\left| {E_{{{\text{eq}}}}^{*}} \right|$ in (6), the parameters can be determined by fitting the model to experimental data. It will then be possible to analyze the dynamic behaviour of the DE film quantitatively, at various stretch rates.

3 Results and discussion

3.1 Experimental stress–strain plots

An example of the experimental results achieved for this study are displayed in the following section. Figure 2 depicts the data for VHB 4910 tape, being stretched at a rate of $\lambda =0.300\,{{\text{s}}^{ - 1}}$. The graph shows a clear hysteresis loop, demonstrating the expected energy loss within the material during its elongation. Further analysis of the superimposed curves also shows an almost parallel behaviour of the stress versus stretch ratio on both axes of tension. This similarity of the normal stresses confirms that the material behaves in a transversely isotropic manner.

Fig. 2

Comparison of biaxial tensile load–unload curves for VHB 4910 tape at $\dot {\lambda }=0.300\,\,{{\text{s}}^{ - 1}}$

The material’s tensile response also exhibited rate-dependent behaviour between tests. It can be seen that the stretch rate has a proportional influence on the energy loss, as the samples with greater rates all exhibited larger overall hysteresis. The peak stress increases by almost 60%, based on the variation of stretch rate. In all cases, for both tape types, the peak stress exerted on the sample increased as the strain rate was accelerated. For VHB 4905 tape, the peak stresses ranged from 0.22 to 0.42 MPa, whereas for VHB 4910 tape, their values increased from 0.19 to 0.37 MPa.

It can be noted that none of the experiments achieved a peak stretch ratio of $\lambda =2$, enforced during the experimental protocol. Due to the polymer’s high viscosity, and deformation around rake attachments, samples achieved peak elongations of $~{\lambda _{{\text{max}}}} \approx 1.7 - 1.8$. These relatively smaller total elongations resulted in experimental curves not reaching expected exponential behaviour typical of elastomers at high stretch ratios. This is because the material has not reached a point of strain-hardening.

Certain inconsistencies can also be noticed with respect to a portion of the experiments, and can be attributed to a variety of factors. These include noise during experimentation, accuracy of image tracking, the apparatus’ tensile fixtures, and overall material deformation relative to the attachment points. Post-experiment data smoothing did provide sufficient filtering to present consistent data in most cases.

3.2 Theoretical material constants

Using the equations previously derived in (14), the experimental data were fitted to the biaxial model in MATLAB using the Levenberg–Marquardt (L–M) method through a two-step approach similar to that of [29]. The first round of optimizations provided the individual experiments’ dynamic moduli with respect to their independent angular frequencies. The second optimization was then run to find global parameters for the materials. In this step, the individual angular frequencies were related to their respective complex moduli by finding a set of constants for all cases. This yielded a set of final parameters that apply to all stretch rates for the materials.

The complex modulus is obtained for either axis independently, despite the assumption that the material is isotropic. Achieving this allowed the results for both axes to be compared to verify whether the assumption is in fact supportable from a transverse perspective.

An example of these curve fittings is illustrated in Fig. 3. It can be seen that the curve fitting yielded values of reasonably high precision. It should be noted that due to limitations brought on by the experimental instrumentation, the material was unable to be elongated to a biaxial stretch ratio sufficient to demonstrate a discernable exponential behaviour. This affected the overall accuracy of the model parameter fitting, as it is of exponential nature.

Fig. 3

Example of curve fitting for individual biaxial experiments at ${\dot {\lambda }_1}=0.100\,\,{{\text{s}}^{ - 1}}$ for VHB 4910 tape trial

The goodness of fit was calculated through the ${R^2}$ coefficient. The averaged values for the results of the first parameter fitting, along with the standard deviations for both the angular frequency and complex modulus, are displayed in Tables 2 and 3 of Appendix. It can be noted that, in all cases, a clear proportional increase in dynamic modulus was observed with respect to the stretch rate of the experiment. This correlation was expected, as it is reflective of the viscoelastic response of the elastomer.

The standard deviation for all angular frequencies is negligible. This level of accuracy illustrates the consistency in experimental results for the stretch ratio and stretch rates achieved. The equivalent values of deviation between ${\lambda _1}$ and ${\lambda _2}$ axes in most cases also demonstrate the experiments’ ability to maintain equibiaxial stretch ratio, despite sample deformation due to experimental fixation techniques. The values for complex moduli among similar experiments were found to have slightly higher standard deviations, with values ranging between 0.01 and 0.02 MPa. These results are attributed to the greater fluctuations in experimental stresses. Despite these disparities, the overall mechanical trends in (averaged) dynamic modulus growth were consistent with the actual mechanical response of the material and proved very representative during final parameter fitting.

Lastly, the goodness of fit for the stress–stretch ratio curves all averaged above 0.82 (or 82% accuracy). This signifies that the polynomial fitting has a good accuracy and reliability.

As with the dynamic modulus fitting, the overall parameters for the model were fitted to either axes separately to provide distinct values for comparison. A depiction of the optimizations can be seen in Fig. 4, which demonstrates the averaged dynamic moduli, including standard deviations, plotted against their respective angular frequencies. The optimized theoretical curve based on these values is drawn in the figure.

Fig. 4

Curve fitting for averaged dynamic moduli and angular frequencies under biaxial loading for VBH 4910 tape along λ ₁ axis

It can be seen that the nonlinear optimizer was able to fit the final parameters of the model with accuracy. The curves of the optimized values fell within good agreement to the dynamic moduli obtained for each stretch rate. The values obtained from the final parameter fitting of both tapes can be found in Table 1.

Table 1 Final optimized spring and damper moduli for VHB 4905 and VHB 4910 tapes under biaxial tensile consideration

3.3 Reproducibility of equibiaxial results

To evaluate the model’s accuracy when simulating visco-hyperelastic response, the final averaged parameters for both VHB tapes were used to plot load–unload curves under various conditions.

That is to say that, for VHB 4905 tape ${E_{\text{s}}}=0.1304~{\text{MPa}}$, ${E_{\text{p}}}=0.2421~{\text{MPa}}$, and ${D_{\text{p}}}=1.9575~{\text{MPa}}$. For VHB 4910 tape, ${E_{\text{s}}}=0.1163~{\text{MPa}}$, ${E_{\text{p}}}=0.2054~{\text{MPa}}$, and ${D_{\text{p}}}=1.4708~{\text{MPa}}$. Data for experiments possessing similar stretch rate were averaged for each axis independently, and then plotted next to a theoretical curve of the same stretch rate. In either case, the stretch rate and maximum stretch ratio were calculated to reflect the experimental deformation, and the stresses for either axis was subsequently plotted using these values. Due to the phase shift applied to create the hysteresis loop, the data calculated from the model parameters were zeroed prior to plotting. Figure 5 illustrates a comparison for VHB 4910 tape at ${\dot {\lambda }_{1,2}}=0.025$ and $0.200\,\,{{\text{s}}^{ - 1}}$, respectively.

Fig. 5

Theoretical and experimental plots for biaxial tensile tests of VHB 4910 tape at a ${\dot {\lambda }_{1,2}}=0.025\,\,{{\text{s}}^{ - 1}}$ and b ${\dot {\lambda }_{1,2}}=0.200\,\,{{\text{s}}^{ - 1}}$ (where black curves represent ${\lambda _1}$ axis, and grey represents ${\lambda _2}$ axes)

It can be seen that peak stresses for both axes are predicted with good qualitative agreement. Due to the experiments’ lack of demonstrable exponential growth, the model has difficulty replicating exact experimental behaviour for the current data. Behaviours deviating from a purely exponential progression will be misrepresented owing to the mathematical simplicity of the current model. It can also be seen that the theoretical data exhibit the same variation in energy loss prediction as the uniaxial model introduced in [29].

3.4 Variation of kinematic variables

The change in loss factor with respect to angular frequency can be seen in Fig. 6 for VHB 4910 tape. The trend reflects those expected from previous findings in [29]. The thresholds of internal dissipation are $\eta =0.217~{\text{and}}~0.226$ for VHB 4905 and VHB 4910 tapes, respectively. This peak in value is explained through the physical principles at a macroscopic level. At lower angular frequencies, the polymeric chains within the elastomer are able to adjust to the elongation of the film. As the frequency is increased, these chains will gradually lose their ability to comply with the deformation, thus increasing the loss factor, and resulting in a viscoelastic response. At a certain peak value, the frequency will reach a threshold where the internal macrostructure will no longer be capable of adapting to the elongation, which will lead the polymer to exhibit behaviour similar to its properties in glassy state. This will cause the loss factor to decrease, as the polymer’s internal dissipation will be minimized [29, 47].

Fig. 6

Distribution of loss factor variation with respect to angular frequency for VHB 4910 tape

The model was plotted while modifying one of two kinematic experimental variables to demonstrate the changes in internal dissipation and visco-hyperelastic response. Figure 7 provides an example of the model elongated to ${\lambda _{1,2({\text{max}})}}=1.3,~1.5,~{\text{and}}~1.7$, at a constant stretch rate of $\dot {\lambda }=0.025\,\,{{\text{s}}^{ - 1}}$. It can be seen that it manages to portray the effects of percent-elongation on the behaviour of the material. For both tapes, a beginning of exponential mechanical behaviour starts to show as the stretch ratio increases. The VHB 4905 tape also reaches higher peak stresses due to its stiffer overall behaviour. The change in internal dissipation is reflected in the plots as well.

Fig. 7

Theoretical plot of biaxial tensile test at various maximum stretch ratios $({\dot {\lambda }_{1,2}}=0.025\,\,{{\text{s}}^{ - 1}})$ for VHB 4905 tape

An additional simulation for VHB 4910 tape was plotted at stretch ratios well above the achieved experimental results. Figure 8 represents the model’s ability to still demonstrate proportionally increasing nonlinear response with respect to maximum elongation. This illustrates the model’s capacity to provide an accurate portrayal of the elastomer’s mechanical response, with parameters optimized to a greater value of experimental stretch ratios.

Fig. 8

Theoretical plot of biaxial tensile test at various large maximum stretch ratios for VHB 4910 tape $({\dot {\lambda }_{1,2}}=0.050\,\,{{\text{s}}^{ - 1}})$

The next plot (Fig. 9) represents the model under varying stretch rates of ${\dot {\lambda }_{1,2}}=0.030,~0.060,~\,\,{\text{and}}\,\,~0.090\,\,{{\text{s}}^{ - 1}}$. For both tapes, a clear correlation between the stretch rate and peak stresses is observed. This demonstrates the model’s ability to predict the elastomer’s viscoelastic response to an increase in rate of elongation. It can be seen that the variation in loss factor is also demonstrated with respect to the change in angular frequency.

Fig. 9

Theoretical plot of biaxial tensile test for various stretch rates at ${\lambda _{{\text{max}}}}=$ 1.7 for VHB 4905

Other general errors in the model’s behaviour can be attributed in part to the approximation of harmonic motion based on linear ramp-type experimental data. In addition to this, the model was fit to a smaller spectrum of stretch ratios. Although this provided the model with a good range of angular frequencies for fitting purposes, the experimental data did not illustrate the elastomer’s intrinsic nonlinear exponential response. This decreased the model’s ability to give accurate stress curve trends for various loading conditions.

A last series of tests was performed to evaluate the model under non-equibiaxial tension. The model was then applied to this experimental data to evaluate its abilities of simulating kinematic parameters that maybe more representative of true DE-based actuator configuration. The tests were arranged for two stretch ratios along ${\lambda _1}$. Specifically, ${\dot {\lambda }_1}=0.025$ and $0.300\,\,{{\text{s}}^{ - 1}}$. Three cases for each stretch rate were applied; the maximum stretch ratios for either axes were set to ${\lambda _{1(\hbox{max} )}}~ \times ~{\lambda _{2(\hbox{max} )}}=2~ \times ~1.25$, $2~ \times ~1.50$, and $2~ \times ~1.75$. The stretch rate ${\dot {\lambda }_2}$ was calculated to ensure a paralleled motion between the two axes. An example can be found in Fig. 10.

Fig. 10

Theoretical plot of biaxial tensile test for various non-equibiaxial stretch rates for VHB 4910 tape at ${\dot {\lambda }_1}=0.025\,\,{{\text{s}}^{ - 1}}$ and ${\lambda _{{\text{max}}}}=2 \times 1.25$

The model demonstrates the ability to adjust the axes stresses according to the change in parameters for both stretch rates. Unlike the equibiaxial conditions, the theoretical stresses undershoot the peak experimental stress values, particularly for the higher stretch rate. The energy dissipation is also less accurate to that of the experimental data. This ability to predict such behaviour is greatly valuable for design purposes. In many cases, DE will not be stretched to equibiaxial configurations for applications in actuators. It is, therefore, important to understand their behaviour under uneven tensile loading.

4 Conclusion

4.1 Experimental results

The results of the biaxial load–unload tensile testing fall in line with the expected trends for this type of material, and illustrated a transversely isotropic tensile behaviour within agreeable limits. Despite the fact that the samples did not reach maximum stretch ratio of the experimental protocol, the VHB tapes still demonstrated viscoelastic response to a biaxial tensile load–unload cycle. They exhibited a proportional sensitivity to stretch-rate through both their achieved peak stresses as well as their distinguishable energy loss. The viscoelastic behaviours observed in these tests agree with the previous uniaxial results in literature, and are all typical of rubber-like materials.

4.2 Biaxial visco-hyperelastic model

The newly developed biaxial visco-hyperelastic model has demonstrated a simple and straightforward approach to analytically characterize the mechanical behaviour of an acrylic-based dielectric elastomer. Through the use of a simple mathematical structure based on the generalized Hooke’s law (for isotropic materials) under biaxial tensile loading, it has proven effective at anticipating the material’s mechanical response variations relative to changes in stretch rate and maximum elongation. The model maintained expected peak stress values for the variations of kinematic parameters. It has also proven effective at providing general mechanical response for non-equibiaxial tension. This, along with the aforementioned predictive abilities, proves promising for design considerations. The model also provides the foundation for a biaxial electro-mechanical model, which would enable the forecasting of dielectric elastomer behaviour under electro-mechanical coupling.

Future work will consist of the development of newer fixation methods for tensile tests, to allow greater maximum stretch ratios. The model will also be expanded to consider effects of inertia, to provide a more suitable foundation for high-frequency applications.

Appendix: Parameter fitting values

See Tables 2 and 3.

Table 2 VHB 4905 tape averaged angular frequencies and optimized dynamic complex moduli for biaxial tensile experiments

Table 3 VHB 4910 tape averaged angular frequencies and optimized dynamic complex moduli for biaxial tensile experiments