1 Introduction

Dielectric elastomer (DE) is a new type of smart soft material. When a flexible electrode is coated on the surface of the DE film and a voltage is applied, the deformation including in-plane expansion and thickness contraction will occur. Based on such a performance, a large number of sensors (Ref 1, 2), actuators (Ref 3, 4) and energy harvesters (Ref 5) have been developed from the DEs. It is worth noting that the DEs often withstand mechanical, electrical, or even electro-mechanically coupled cyclic loads in service. It is very important to systematically investigate and accurately model the electro-mechanically coupled cyclic deformation of DEs. At present, the VHB DEs produced by 3 M company in the United States are widely used. Many scholars have studied their mechanical and electro-mechanically coupled deformation from the experimental and theoretical perspectives.

For examples, Wissler et al. (Ref 6) and Hossain et al. (Ref 7) performed basic mechanical tests (including tension-unloading, relaxation and creep tests) to investigate the uniaxial viscoelastic deformation of VHB 4910 DE; Helal et al. (Ref 8) investigated the transversely isotropic mechanical behaviors of VHB 4910 and VHB 4905 DEs in a biaxial deformation mode; Ahmad et al. (Ref 9, 10) studied the critical mechanical properties (such as fracture toughness and failure stress) of VHB 4910 DE in a biaxial deformation mode, and explored the stress–strain response of VHB 4910 DE in a pure-shear deformation mode; Liao et al. (Ref 11) and Zhang et al. (Ref 12) explored, respectively, the effects of temperature and humidity on the tensile stress of VHB DEs in a uniaxial deformation mode; Hossain et al. (Ref 13) revealed the electro-mechanically coupled tension-unloading, single-step and multi-step relaxation curves of VHB 4910 DE in a pure-shear deformation mode; Mehnert et al. (Ref 14) used the specimen with a size of 7:10 to explore the stress–strain curves of VHB 4905 DE with different voltages in a deformation mode between uniaxial and pure-shear ones; Mehnert et al. (Ref 15) further revealed the tension-unloading curves of VHB 4905 DE under mechanical, thermo-mechanically, electro-mechanically and thermo-electro-mechanically coupled loading conditions by using the specimen with a size of 7:10. From such existing references, it can be concluded that the experimental studies (especially the tension-unloading test) of VHB DEs have been relatively sufficient.

There are also some researches on the cyclic deformation of DEs. For examples, Sahu and Patra (Ref 16) carried out the strain-controlled cyclic deformation tests with 7 cycles in a uniaxial deformation mode, and explored the strain-controlled cyclic deformation and its strain rate-dependence of VHB 4910 DE; Thylander et al. (Ref 17) conducted the strain-controlled cyclic deformation tests with 10 cycles in a uniaxial deformation mode, and studied the effects of strain rate and strain level on the cyclic deformation of VHB 4910 DE. More recently, Chen et al. (Ref 18) and Huang et al. (Ref 19) performed a series of strain-controlled and stress-controlled cyclic deformation tests on the VHB 4910 DE in pure-shear and uniaxial deformation modes, respectively, and revealed the cyclic softening and ratchetting of VHB 4910 DE as well as their dependences on the stress- and strain-levels, loading rate and holding time. Furthermore, Chen et al. (Ref 20) revealed the electro-mechanically coupled cyclic deformation characteristics of laterally pre-stretched VHB 4910 DE with applying a constant voltage and cyclic voltage in a pure-shear deformation mode. Thus, the literature survey here demonstrates that the mechanical cyclic deformation of DEs has been investigated in both the uniaxial and pure-shear deformation modes, but the research on the electro-mechanically coupled cyclic deformation of DEs is limited only to the pure-shear deformation mode.

As observed in the existing tests, the VHB DEs exhibit obvious visco-hyperelasticity, which should be considered in the construction of constitutive model. For instances, Wissler et al. (Ref 6) and Patra et al. (Ref 21) theoretically described the visco-hyperelasticity of VHB 4910 DE by using relaxation function; Hossain et al. (Ref 7) proposed a modified visco-hyperelastic constitutive model, and reasonably predicted the tension-unloading, single-step and multi-step relaxation behaviors of VHB 4910 DE; Zhang et al. (Ref 22) used the combined Kelvin-Voigt-Maxwell model to capture the initial instantaneous elastic deformation and subsequent viscoelastic deformation of VHB 4910 DE, and then verified the rationality of the model by using the correspondent experimental results; Chen et al. (Ref 23) considered the plastic deformation of VHB 4910 DE observed in the pure-shear cyclic tests and proposed a visco-hyperelastic-plastic model by employing a linear viscosity, which reasonably predicted the unrecoverable deformation observed in the cyclic tests. However, due to the strong viscosity of VHB DEs, it is necessary to consider the nonlinear viscosity in the constitutive model, which has not been reasonably involved in the above-mentioned models.

In addition, it has been revealed from the existing experimental observations that the VHB DEs present a significant electro-mechanically coupled effect when a voltage is applied. However, early research (Ref 24) simply equated the action of voltage to a stress, the Maxwell stress, in the construction of constitutive model. To overcome such a shortcoming, based on the thermodynamic theory, Suo (Ref 25) reasonably described the transformation between electric field energy and strain energy in the process of electro-mechanically coupled deformation, and obtained a widely recognized constitutive model. Recently, Mehnert et al. (Ref 26) proposed an electro-mechanically coupled model by assuming the material parameters to be the functions of electric field strength. Subsequently, based on Hossain et al. (Ref 7), Mehnert et al. (Ref 14) further proposed a model by coupling the effect of electric field, and then reasonably reproduced the electro-mechanically coupled tension-unloading and relaxation experimental results of VHB 4095 DE. Mehnert et al. (Ref 27) also proposed a thermo-electro-mechanically coupled constitutive model of DEs based on the continuum mechanics. Thylander et al. (Ref 28) introduced a micromechanically driven incompressible constitutive model to simulate the electro-mechanically coupled deformation of VHB 4910 DE. More recently, Chen et al. (Ref 23) considered the change of dielectric constant with deformation, and obtained an electro-mechanically coupled visco-hyperelastic-plastic model to reproduce the electro-mechanically coupled cyclic deformation of VHB 4910 DE in a pure-shear deformation mode. However, the existing electro-mechanically coupled constitutive models are not validated by the correspondent cyclic experimental results in a uniaxial deformation mode, which is different from that observed in a pure-shear deformation mode as discussed by Huang et al. (Ref 19).

Therefore, a series of electro-mechanically coupled deformation tests are first carried out on the VHB 4905 DE in a uniaxial deformation mode, including tension-unloading, relaxation, creep, strain-controlled and stress-controlled cyclic tests. Then, based on the obtained experimental results, the proposed electro-mechanically coupled visco-hyperelastic constitutive model by Chen et al. (Ref 23) is modified by considering the significant nonlinear viscosity of VHB 4905 DE. Finally, considering the additional deformation caused by the applied voltage, the modified model is validated by comparing the predictions with correspondent experimental results. The improved electro-mechanically coupled constitutive model can help the analysis on the service performance and life-prediction of DE devices in the future.

2 Experimental Observations

2.1 Experimental Conditions

The experimental material is the VHB 4905 DE with a thickness of 0.5 mm and produced by 3 M Company in the United States. The conductive carbon grease is MG chemical 846-80G. The experimental instruments are shown in Fig. 1, which include the waveform generator (BNC-645), the voltage amplifier (TREK-610E) and the mechanical test system (CARE-IPBF-500). The waveform generator is used to generate the specified signal, which is amplified by the voltage amplifier to obtain the required voltage.

Fig. 1
figure 1

Experimental instruments: (a) the waveform generator and voltage amplifier; (b) the mechanical test system

Full size image

In the uniaxial tests, two pieces of VHB 4905 DE films with the same size of 100 mm × 50 mm are used in each test. Because the VHB 4905 DE is very soft and sticky, the fabrication of the specimen has considerable challenge. Thus, the corresponding fixture and auxiliary splint are specially designed as shown in Fig. 2(a) and (b), respectively. When the conductive carbon grease is coated on the surface of the specimen, a 5 mm blank is needed on both sides of the specimen to prevent the electric breakdown after applying a voltage. Due to the requirement of leaving a certain blank in width, the specimen with the size of 50 mm × 10 mm used in the previous uniaxial pure mechanical tests (Ref 19) is not suitable for the uniaxial electro-mechanically coupled tests. In Appendix, the effect of specimen size on the deformation mode is explored and the specimen of VHB 4905 DE with the size of 100 mm × 50 mm is verified to be able to meet the requirement of uniaxial electro-mechanically coupled experimental conditions. Thus, the region with coated carbon grease is 40 mm in width and the coated ratio is 80%. The experimental details are shown in Fig. 2(c).

Fig. 2
figure 2

Experimental details: (a) the fixture; (b) the auxiliary splint; (c) the assembly diagram

Full size image

To avoid the influence of applied voltage on the initial state of the specimen, the voltage is applied only when the strain of the specimen increases to about 0.5 in the first beginning of loading stage in all the uniaxial electro-mechanically coupled tests. And, the nominal stress and nominal strain are used here, i.e., \(\sigma = {F \mathord{\left/ {\vphantom {F {A_{0}^{{}} }}} \right. \kern-0pt} {A_{0}^{{}} }}\), \(\varepsilon = \lambda - 1\), where F is the force, A0 is the initial cross-section area of the specimen, \(\lambda\) is the principal elongation in the tensile direction. To keep the repeatability and credibility of experimental data, all the tests are repeated 3 times for each loading case. The experimental results presented in the related figures are obtained from the average of the results in the three repeated tests.

2.2 Experimental Results and Discussions

In the experimental observations, the electro-mechanically coupled basic property tests (including tension-unloading, relaxation and creep tests) are first performed, and then the electro-mechanically coupled strain-controlled and stress-controlled cyclic tests of VHB 4905 DE are conducted in a uniaxial deformation mode.

2.2.1 Observations on Electro-Mechanically Coupled Basic Property

2.2.1.1 Tension-Unloading Curves

At first, the tension-unloading tests of VHB 4905 DE are performed with and without applying a constant voltage of 4 kV. Figure 3 shows the experimental stress–strain curves (with the error-bars in certain date points) obtained at a strain rate of 0.03 s−1 and with a peak strain of 3.0. It is found from Fig. 3 that with applying a constant voltage of 4 kV, the stress is lower than that without any voltage at the same strain, but the value of stress difference is small. When the specimen is unloaded to a zero-stress state, the strain does not immediately recover completely, and the remained value obtained in the case with a constant voltage is slightly larger than that without any voltage.

Fig. 3
figure 3

Experimental stress–strain curves of VHB 4905 DE in the tension-unloading tests with and without applying a voltage

Full size image

As depicted in Fig. 3, the effect of applied voltage on the tensile stress–strain curves of VHB 4905 DE is not so remarkable in a uniaxial deformation mode. Although the effect of applied voltage can be increased by increasing the value of voltage, the electric breakdown of the DE film will become more easily and cannot obtain a stable stress–strain response in the electro-mechanically coupled cyclic deformation of VHB 4095 DE at higher voltage. So, in the subsequent electro-mechanically coupled deformation tests, only a voltage of 4 kV is applied on the tested specimen.

2.2.1.2 Relaxation and Creep Behaviors

Figure 4(a) and (b) depict the experimental curves (with the error-bars in certain date points) obtained in the typical relaxation (at a strain rate of 0.03 s−1 and with a holding strain of 1.0) and creep tests (at a stress rate of 1.0 kPa· s−1 and with a holding stress of 50 kPa), respectively. It is concluded from Fig. 4 that with applying a constant voltage of 4 kV, both the stress relaxation and creep deformation of VHB 4905 DE are apparently different from that without any voltage, that is, the relaxed stress is smaller but the creep strain is larger than that without any voltage.

Fig. 4
figure 4

Uniaxial stress and strain evolution curves obtained in: (a) relaxation tests; (b) creep tests

Full size image

The VHB 4905 DE film becomes thinner with applying a constant voltage, which makes the electric field strength further increase; meanwhile, the increased electric field strength can make the DE film become further thinner. Thus, if the stress in the DE film cannot resist the compressive stress generated by the applied electric field, an electro-mechanically coupled instability (Ref 29) will occur in the DE film. According to the existing research (Ref 30), such an instable phenomenon can be eliminated by pre-stretching to an enough magnitude. In addition, because the applied strain and stress are remained at their peak values in the whole relaxation and creep processes, the electric breakdown phenomenon will occur more frequently than that in the cyclic deformation tests. So, the applied voltage cannot be increased further to enlarge the difference between the stress and strain responses of VHB 4905 DE in the relaxation and creep tests with and without applying a voltage.

Note that, it can be seen from the error bars given in Fig. 3 and 4 that the repeatability of experimental results obtained in this work is good, which can ensure the reliability of the experimental data. So, the error bars are no longer given in the subsequent figures illustrating the electro-mechanically coupled cyclic deformation of VHB 4905 DE to keep them more concise.

2.2.2 Observations on Electro-Mechanically Coupled Cyclic Deformation

To investigate the effect of applied voltage on the cyclic deformation of VHB 4905 DE, the strain-controlled and stress-controlled cyclic tests are, respectively, performed in a uniaxial deformation mode with and without applying a constant voltage, which will be discussed in the next two subsections.

2.2.2.1 Strain-Controlled Cyclic Deformation

Figure 5 gives the results obtained in the uniaxial strain-controlled cyclic deformation tests (at a strain rate of 0.03 s−1 and with a peak strain of 2.0) of VHB 4905 DE with and without applying a voltage. Figure 5(a) depicts the experimental stress–strain curve with applying a voltage of 4.0 kV, and Fig. 5(b)-(e) show the evolution curves of peak stress (the stress at the maximum strain), valley strain (the strain when the stress is unloaded to 0), dissipated energy density (the area of stress–strain hysteresis loop) and apparent modulus (the slope between the maximum and minimum strains in the unloading stage per cycle) with the cyclic number, respectively. It is found from Fig. 5 that: (1) the evolution trends of specific variables obtained with and without applying a voltage are basically consistent with each other, but apparent difference can be found in the values of such specific variables, as shown in Fig. 5(b)-(e); (2) similar to that observed in the tension-unloading tests, the peak stress of VHB 4905 DE is smaller but the valley strain is larger when a voltage is applied, as shown in Fig. 5(b) and (c); (3) the dissipation energy density and apparent modulus obtained with applying a voltage are smaller than that without applying a voltage, as shown in Fig. 5(d) and (e). To sum up, although the differences of such specific variables obtained in the tests with and without applying a voltage tend to increase gradually with the increase of cyclic number, they are not so remarkable due to the limitation caused by the uniaxial deformation mode and discussed in Sect. 2.2.1.

Fig. 5
figure 5

Experimental results obtained in the strain-controlled cyclic tests with and without applying a voltage: (a) stress–strain curves in some specific cycles; (b) evolution curves of peak stress; (c) evolution curves of valley strain; (d) evolution curves of dissipative energy density; (e) evolution curves of apparent modulus

Full size image
2.2.2.2 Stress-Controlled Cyclic Deformation

Figure 6 presents the experimental results obtained in the uniaxial stress-controlled cyclic tests of VHB 4905 DE (at a stress rate of 0.6 kPa· s−1 and with a stress-level of 40 ± 30 kPa, which means that the applied mean stress is 40 kPa and stress amplitude is 30 kPa) with and without applying a voltage. Figure 6(a) depicts the experimental stress–strain curve with applying a voltage of 4.0 kV, and Fig. 6(b)-(e) give the evolution curves of ratchetting strain (the average value of peak and valley strains), peak/valley strain (the strain at the maximum/minimum stress), dissipated energy density and apparent modulus with the cyclic number, respectively. It is concluded from Fig. 6 that: (1) with applying a constant voltage, the ratchetting strain and peak/valley strain of VHB 4905 DE are larger than that in the cyclic tests without any voltage, as shown in Fig. 6(b) and (c); (2) the dissipation energy density is larger in the stress-controlled cyclic tests with applying a constant voltage, as shown in Fig. 6(d), which is opposite to that in the strain-controlled cyclic tests; (3) the evolution of the apparent modulus in the stress-controlled cyclic tests of VHB 4905 DE is similar to that in the strain-controlled cyclic tests, but the value of apparent modulus obtained in the tests with applying a voltage is lower than that without any voltage. It is further observed from Fig. 6(b) that with the increase of cyclic number, the difference of ratchetting strain in the cyclic tests with and without applying a voltage becomes larger and larger, which is similar to the evolution trend of creep strain shown in Fig. 4(b). The reason is that the thickness of VHB 4905 DE film will gradually decrease due to the continuous increase of axial ratchetting strain in the stress-controlled cyclic tests, which increases the electric field strength and then makes the effect of voltage become more and more obvious.

Fig. 6
figure 6

Experimental results obtained in the stress-controlled cyclic tests with and without applying a voltage: (a) stress–strain curves in some specific cycles; (b) evolution curves of ratchetting strain; (c) evolution curves of peak/valley strain; (d) evolution curves of dissipative energy density; (e) evolution curves of apparent modulus

Full size image

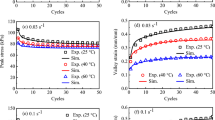
Furthermore, the ratchetting of VHB 4905 DE is investigated at different stress rates (with a stress-level of 40 ± 30 kPa and at the stress rates of 0.4, 0.6 and 1.0 kPa· s−1) and with different stress-levels (at a stress rate of 0.6 kPa· s−1, with the stress-levels of 30 ± 30, 40 ± 30, 50 ± 30 kPa), as well as with and without applying a voltage. The evolution curves of ratchetting strain are shown in Fig. 7. It is depicted that: (1) the increase of stress rate hinders the evolution of ratchetting strain, that is, the larger the stress rate is, the smaller the ratchetting strain is, as shown in Fig. 7(a); (2) the increase of stress-level promotes the evolution of ratchetting strain, and the effect of stress-level on the ratchetting is significant, as shown in Fig. 7(b); (3) at all the stress rates and with all the stress-levels discussed here, the ratchetting strain of VHB 4905 DE obtained with applying a constant voltage of 4.0 kV is larger than that without any voltage, as shown in Fig. 7.

Fig. 7
figure 7

Evolution curves of ratchetting strain: (a) at different stress rates; (b) with different stress-levels

Full size image

In addition, compared with the pure-shear electro-mechanically coupled cyclic deformation of VHB DE investigated by Chen et al. (Ref 20), it is found that the electro-mechanically coupled deformation characteristics of VHB DE in the uniaxial and pure-shear deformation modes are consistent with each other in the evolution trend; however, the applied voltage has less influence on the electro-mechanically coupled deformation of VHB DE in the uniaxial deformation mode than that in the pure-shear one. The main reason is that the VHB DE film is less constrained by the boundary conditions in the uniaxial deformation mode than that in the pure-shear one, and the effect of applied voltage on the tensile direction of the VHB DE film is weakened by relatively free boundary.

3 Constitutive Model and Its Validations

From the experimental observations, it is concluded that the VHB 4905 DE exhibits an obvious nonlinear visco-hyperelasticity, and an additional deformation will be caused by the electro-mechanically coupled effect of the DE with applying a voltage. Therefore, considering both the two characteristics, the electro-mechanically coupled visco-hyperelastic constitutive model is proposed to predict the uniaxial electro-mechanically coupled deformation of VHB 4905 DE.

3.1 Electro-Mechanically Coupled Visco-Hyperelastic Constitutive Model

3.1.1 Main Constitutive Equations

Figure 8 depicts the rheological model representing all the branches of the proposed visco-hyperelastic constitutive model, where branch A is a hyperelastic spring, and branches B1 to Bn are composed of a series of parallel Maxwell elements (each of which consists of a spring and a dashpot).

Fig. 8
figure 8

Rheological model for the proposed visco-hyperelastic constitutive model

Full size image

For the above rheological model, the total deformation gradient is

$${\mathbf{F}} = {\mathbf{F}}_{A}^{{}} = {\mathbf{F}}_{Bi}^{{}}$$
(1)

where i = 1, 2, 3, … n. For the branch B, the deformation gradient can be divided into \({\mathbf{F}}_{B}^{{\text{e}}}\) of the spring and \({\mathbf{F}}_{B}^{{\text{v}}}\) of the dashpot, i.e.,

$${\mathbf{F}}_{B}^{{}} { = }{\mathbf{F}}_{B}^{{\text{e}}} {\mathbf{F}}_{B}^{{\text{v}}}$$
(2)

Then the right Cauchy-Green deformation tensors are introduced as \({\mathbf{C}} = {\mathbf{F}}_{{}}^{{\text{T}}} {\mathbf{F}}\),\({\mathbf{C}}_{A}^{{}} = {\mathbf{C}} = {\mathbf{F}}_{{}}^{{\text{T}}} {\mathbf{F}}\),\({\mathbf{C}}_{B}^{{\text{e}}} { = }{\mathbf{F}}_{B}^{{\text{e T}}} {\mathbf{F}}_{B}^{{\text{e}}}\), and \({\mathbf{C}}_{B}^{{\text{v}}} { = }{\mathbf{F}}_{B}^{{\text{v T}}} {\mathbf{F}}_{B}^{{\text{v}}}\), respectively.

Its free energy density WM is the sum of that for the branches A and B, i.e.,

$$W_{M}^{{}} { = }W_{A}^{{}} + W_{B}^{{}}$$
(3)

where WA is related to the deformation tensor C, and WB is related to the deformation tensor \(\, {\mathbf{C}}_{Bi}^{{\text{e}}}\), namely,

$$W_{A}^{{}} = W_{A}^{{}} \left( {\mathbf{C}} \right)$$
(4)
$$W_{B}^{{}} = \sum\limits_{{i{ = 1}}}^{n} {W_{Bi}^{{}} \left( {{\mathbf{C}}_{Bi}^{{\text{e}}} } \right)}$$
(5)

The electro-mechanically coupled deformation behavior of DE can also be described by the free energy density function WEM, which is related to the deformation tensor C and the electric field strength E, and can be taken the form as

$$W_{EM}^{{}} = W_{EM}^{{}} \left( {{\mathbf{C}},{\mathbf{\rm E}}} \right)$$
(6)

So, the total free energy density function W is the sum of the visco-hyperelastic part WM and the electro-mechanically coupled part WEM, that is,

$$W = W_{M}^{{}} + W_{EM}^{{}} = W_{A}^{{}} \left( {\mathbf{C}} \right) + \sum\limits_{{i{ = 1}}}^{n} {W_{Bi}^{{}} \left( {{\mathbf{C}}_{Bi}^{{{\rm e}}} } \right)} + W_{EM}^{{}} \left( {{\mathbf{C}},{\mathbf{E}}} \right)$$
(7)

For the branch A, the second Piola stress tensor TRRA can be obtained according to the theory of continuum mechanics, i.e.,

$${\mathbf{T}}_{RRA}^{{}} = 2\frac{{\partial W_{A}^{{}} \left( {\mathbf{C}} \right)}}{{\partial {\mathbf{C}}}}$$
(8)

For the branch B, the dissipative energy inequality should be satisfied, that is,

$${\mathbf{T}}_{RRB} :\frac{1}{2}{\mathbf{C}}^{\prime } - W_{B}^{\prime } \ge 0$$
(9)

And \(\, {\mathbf{C}}_{B}^{{\text{e}}} { = }{\mathbf{F}}_{B}^{{\text{v - T}}} {\mathbf{CF}}_{B}^{{\text{v - 1}}}\), so

$$\left( {{\mathbf{T}}_{RRB}^{{}} - {2}\sum\limits_{{i{ = 1}}}^{n} {{\mathbf{F}}_{Bi}^{{\text{v - 1}}} \frac{{\partial W_{Bi}^{{}} }}{{\partial {\mathbf{C}}_{Bi}^{{\text{e}}} }}{\mathbf{F}}_{Bi}^{{\text{v - T}}} } } \right):\frac{1}{2}{\mathbf{C^{\prime}}} - \sum\limits_{{i{ = 1}}}^{n} {\frac{{\partial W_{Bi}^{{}} }}{{\partial {\mathbf{C}}_{Bi}^{{\text{e}}} }}:\left( {\left( {{\mathbf{F}}_{Bi}^{{\text{v - T}}} } \right)^{\prime } {\mathbf{CF}}_{Bi}^{{\text{v - 1}}} { + }{\mathbf{F}}_{Bi}^{{\text{v - T}}} {\mathbf{C}}\left( {{\mathbf{F}}_{Bi}^{{\text{v - 1}}} } \right)^{\prime } } \right)} \ge 0$$
(10)

The second Piola stress tensor TRRB can be obtained as

$${\mathbf{T}}_{RRB}^{{}} { = 2}\sum\limits_{{i{ = 1}}}^{n} {{\mathbf{F}}_{Bi}^{{\text{v - 1}}} \frac{{\partial W_{Bi}^{{}} }}{{\partial {\mathbf{C}}_{Bi}^{{\text{e}}} }}{\mathbf{F}}_{Bi}^{{\text{v - T}}} }$$
(11)

And the dissipative energy inequality is obtained as

$$- \sum\limits_{{i{ = 1}}}^{n} {\frac{{\partial W_{Bi}^{{}} }}{{\partial {\mathbf{C}}_{Bi}^{{\text{e}}} }}:\left( {\left( {{\mathbf{F}}_{Bi}^{{\text{v - T}}} } \right)^{\prime } {\mathbf{CF}}_{Bi}^{{\text{v - 1}}} { + }{\mathbf{F}}_{Bi}^{{\text{v - T}}} {\mathbf{C}}\left( {{\mathbf{F}}_{Bi}^{{\text{v - 1}}} } \right)^{\prime } } \right)} \ge 0$$
(12)

According to Reese and Govindjee (Ref 31), the above dissipative energy inequality can be further rewritten as

$$- \sum\limits_{i = 1}^{n} {{{\varvec{\uptau}}}_{Bi}^{{\text{e}}} :{\mathbf{F}}\left( {{\mathbf{C}}_{Bi}^{{\text{v - 1}}} } \right)^{\prime } {\mathbf{F}}_{{}}^{{\text{T}}} } {\mathbf{B}}_{Bi}^{{\text{e - 1}}} \ge {0}$$
(13)

where

$${\mathbf{B}}_{Bi}^{{\text{e}}} { = }{\mathbf{F}}_{Bi}^{{\text{e}}} {\mathbf{F}}_{Bi}^{{\text{e T}}}$$
(14)
$${{\varvec{\uptau}}}_{Bi}^{{\text{e}}} { = 2}{\mathbf{F}}_{Bi}^{{\text{e}}} \frac{{\partial W_{Bi}^{{}} }}{{\partial {\mathbf{C}}_{Bi}^{{\text{e}}} }}{\mathbf{F}}_{Bi}^{{\text{e T}}}$$
(15)

And the evolution equations of the dashpots are

$${{\varvec{\uptau}}}_{Bi}^{{\text{e}}} = - \frac{{\eta_{i}^{{}} }}{{2}}{\mathbf{F}}\left( {{\mathbf{C}}_{Bi}^{{\text{v - 1}}} } \right)^{\prime } {\mathbf{F}}_{{}}^{{\text{T}}} {\mathbf{B}}_{Bi}^{{\text{e - 1}}}$$
(16)

Note that, the above evolution equations are nonlinear and can satisfy the dissipation inequality. \(\eta_{i}^{{}}\) represents the viscosity strength of branch Bi. The nonlinearity of viscoelastic part is mainly reflected by the nonlinearities of both the spring and the dashpot.

Similarly, for the electro-mechanically coupled part, the second Piola stress tensor TRREM can be obtained as

$$\varvec{T}_{{RREM}}^{{}} = 2\frac{{\partial W_{{EM}}^{{}} \left( {\varvec{C},\varvec{E}} \right)}}{{\partial \varvec{C}}}$$
(17)

The nominal stress used in the tests is the first Piola stress, which satisfies the relation \({\mathbf{T}}_{R}^{{}} = {\mathbf{T}}_{RR}^{{}} {\mathbf{F}}\).

3.1.2 Principal Elongation Form

The constitutive model needs to be written in a principal elongation form before verifying its rationality. For easy explanation, the tensile direction is taken as the direction 1, the electric field direction is taken as the direction 3, and the direction 2 is the free boundary. Generally, the VHB 4905 DE can be approximated as an incompressible material, namely, \(J = 1\). Obviously, if the elongation in the direction 1 is taken as \(\, \lambda_{1}^{{}}\), the deformation gradient in the uniaxial deformation mode is

$$\left[ {\mathbf{F}} \right] = \left[ {\begin{array}{*{20}c} {\lambda_{1}^{{}} } & 0 & 0 \\ 0 & {\lambda_{1}^{ - 0.5} } & 0 \\ 0 & 0 & {\lambda_{1}^{ - 0.5} } \\ \end{array} } \right]$$
(18)

From the above deformation gradient, it can be observed that the deformation gradient in the uniaxial deformation mode is only related to the principal elongation in the direction 1.

Although the VHB 4905 DE samples are approximately set in a uniaxial deformation mode before a voltage is applied, a deviation occurs after a voltage is applied. If the strain in the direction 1 is kept constant, the direction 3 is further compressed and the direction 2 has a certain expansion; if the stress in the direction 1 is kept constant, the direction 3 is further compressed, the direction 1 is further elongated, and the direction 2 also produces corresponding deformation. Therefore, the practical deformation in the VHB 4905 DE samples with applying a voltage deviates from the perfect uniaxial deformation mode. The principal elongations in the tensile direction \(\left( {\lambda_{1}^{{}} } \right)\) and electric field direction \(\left( {\lambda_{3}^{{}} } \right)\) should be both considered to depict the additional deformation caused by the electric field. So, the practical deformation gradient becomes as

$$\left[ {\mathbf{F}} \right]{ = }\left[ {\begin{array}{*{20}c} {\lambda_{1}^{{}} } & 0 & 0 \\ 0 & {\lambda_{1}^{ - 1} \lambda_{3}^{ - 1} } & 0 \\ 0 & 0 & {\lambda_{3}^{{}} } \\ \end{array} } \right]$$
(19)

When there is no electric field, \(\lambda_{3}^{{}} = \lambda_{1}^{ - 0.5}\), the deformation gradient above degenerates into the perfect uniaxial one. When an electric field is applied, \(\lambda_{3}^{{}} \ne \lambda_{1}^{ - 0.5}\), there is a certain deviation from the uniaxial deformation gradient, which is observed in the tests. Therefore, the additional deformation caused by the applied electric field can be described by considering the principal elongations in two directions as depicted in Eq 19.

The constitutive model is composed of three parts: the hyperelastic, viscoelastic and electro-mechanically coupled ones. For the branch A, i.e., the hyperelastic part, it is found that the Ogden model (Ref 32) based on the principal elongation form can describe the experimental results well. The strain energy density is

$$W_{A}^{{}} \left( {\mathbf{C}} \right) = \sum\limits_{m = 1}^{\infty } {\frac{{\mu_{{A_{m}^{{}} }} }}{{\alpha_{{A_{m}^{{}} }} }}\left( {\lambda_{1}^{{{\alpha_{{A_{m}{}} }}^{{}} }} + \lambda_{1}^{{{ - \alpha_{{A_{m}{}} }}^{{}} }} \lambda_{3}^{{{ - \alpha_{{A_{m}{}} }}^{{}} }} + \lambda_{3}^{{{\alpha_{{A_{m}{}} }}^{{}} }} - 3} \right)}$$
(20)

Here m is the number of terms, and it is taken as m = 2. So, the first Piola stresses TRA in the directions 1 and 3 are

$$T_{RA1}^{{}} = \sum\limits_{m = 1}^{2} {\mu_{{A_{m}^{{}} }}^{{}} \left( {\lambda_{1}^{{{\alpha_{{A_{m}{}} }}^{{}} - 1}} - \lambda_{3}^{{{ - \alpha_{{A_{m}{}} }}^{{}} }} \lambda_{1}^{{{ - \alpha_{{A_{m}{}} }}^{{}} - 1}} } \right)}$$
(21)
$$T_{RA3}^{{}} = \sum\limits_{m = 1}^{2} {\mu_{{A_{m}^{{}} }}^{{}} \left( {\lambda_{3}^{{{\alpha_{{A_{m}{}} }}^{{}} - 1}} - \lambda_{1}^{{{ - \alpha_{{A_{m}{}} }}^{{}} }} \lambda_{3}^{{{ - \alpha_{{A_{m}{}} }}^{{}} - 1}} } \right)}$$
(22)

For the branch B, i.e., the viscoelastic part, it is considered that the spring has the same strain energy form as the branch A, namely, the Ogden model. And, three viscous branches are selected to describe the strong nonlinear viscosity of VHB 4905 DE. Similarly, the first Piola stresses TRB in the directions 1 and 3 are

$$T_{{RB{1}}}^{{}} = \sum\limits_{n = 1}^{3} {\mu_{{B_{n}^{{}} }}^{{}} \left( {\lambda_{{n{\text{ e1}}}}^{{{\alpha_{{B_{n}{}} }}^{{}} - 1}} - \lambda_{{n{\text{ e}}3}}^{{{ - \alpha_{{B_{n}{}} }}^{{}} }} \lambda_{{n{\text{ e}}1}}^{{{ - \alpha_{{B_{n}{}} }}^{{}} - 1}} } \right)\lambda_{{n{\text{ v1}}}}^{ - 1} }$$
(23)
$$T_{RB3}^{{}} = \sum\limits_{n = 1}^{3} {\mu_{{B_{n}^{{}} }}^{{}} \left( {\lambda_{{n{\text{ e3}}}}^{{{\alpha_{{B_{n}{}} }}^{{}} - 1}} - \lambda_{{n{\text{ e1}}}}^{{{ - \alpha_{{B_{n}{}} }}^{{}} }} \lambda_{{n{\text{ e3}}}}^{{{ - \alpha_{{B_{n}{}} }}^{{}} - 1}} } \right)\lambda_{{n{\text{ v3}}}}^{ - 1} }$$
(24)

And the evolution equations of internal variables are

$$\lambda_{{n{\text{ v1}}}}^{\prime } { = }\frac{{\mu_{{B_{n} }} }}{{\eta_{{B_{n} }} }}\left( {\lambda_{{n{\text{ e1}}}}^{{\alpha_{{B_{n} }} }} - \lambda_{{n{\text{ e}}3}}^{{ - \alpha_{{B_{n} }} }} \lambda_{{n{\text{ e}}1}}^{{ - \alpha_{{B_{n} }} }} } \right)\lambda_{{n{\text{ v1}}}}$$
(25)
$$\lambda_{{n{\text{ v3}}}}^{\prime } { = }\frac{{\mu_{{B_{n} }} }}{{\eta_{{B_{n} }} }}\left( {\lambda_{{n{\text{ e3}}}}^{{\alpha_{{B_{n} }} }} - \lambda_{{n{\text{ e1}}}}^{{ - \alpha_{{B_{n} }} }} \lambda_{{n{\text{ e3}}}}^{{ - \alpha_{{B_{n} }} }} } \right)\lambda_{{n{\text{ v3}}}}$$
(26)

For the electro-mechanically coupled part, the whole system can be considered as a capacitor. When the voltage U is applied on the both sides of DE, the energy stored is

$$W_{EM}^{{}} = \frac{1}{2}CU^{2} ,\;C{ = }\frac{{\varepsilon_{0}^{{}} \varepsilon_{{\text{r}}}^{{}} S}}{d}$$
(27)

where, C is capacitance;\(\varepsilon_{0}^{{}}\) is vacuum dielectric constant;\(\varepsilon_{r}^{{}}\) is relative dielectric constant; S is the area of the capacitor; d is the distance between two sides of capacitor. Note that, the real electric field strength e = U/d; the nominal electric field strength \(E{ = }\lambda e\); and \(\lambda\) is the principal elongation in the electric field direction. So, the energy density is

$$W_{EM}^{{}} = \frac{1}{2}J\varepsilon_{0}^{{}} \varepsilon_{{\text{r}}}^{{}} \lambda_{{}}^{ - 2} E_{{}}^{2}$$
(28)

where J = det(F), and J = 1 for the incompressible materials. It is extended to a three-dimensional case so as to obtain the same strain energy density form as that used in Dorfmann and Ogden (Ref 33), namely,

$$W_{EM}^{{}} \left( {\varvec{C},{\mathbf{E}}} \right){ = }\frac{1}{2}J\varepsilon_{0} \varepsilon_{r} \varvec{C}^{ - 1} {:}\left[ {{\mathbf{E}} \otimes {\mathbf{E}}} \right]$$
(29)

In addition, the relative dielectric constant of VHB DEs decreases gradually with the increase of principal elongation (Ref 34) and can be approximated as a quasi-linear polarization (Ref 35), i.e.,

$$\varepsilon_{r} \left( \varvec{C} \right){ = }\overline{\varepsilon }_{r} \left( {1{ + }aI_{0} } \right)$$
(30)

where \(\, I_{0} { = }\lambda_{1} { + }\lambda_{2} { + }\lambda_{3} - 3\),\(\overline{\varepsilon }_{r}\) is the relative dielectric constant of the un-deformed DE,\(\alpha \,\) is the material constant. The first Piola stresses TREM in the directions 1 and 3 are

$$T_{{REM{1}}}^{{}} { = }\frac{1}{2}\varepsilon_{0} \overline{\varepsilon }_{r} \alpha \left( {1 - \lambda_{{1}}^{ - 2} \lambda_{3}^{ - 1} } \right)\lambda_{3}^{ - 2} E_{{}}^{2}$$
(31)
$$T_{REM3}^{{}} = \frac{1}{2}\varepsilon_{0} \overline{\varepsilon }_{r} \alpha \left( {1 - \lambda_{3}^{ - 2} \lambda_{1}^{ - 1} } \right)\lambda_{3}^{ - 2} E_{{}}^{2} - \varepsilon_{0} \varepsilon_{r} \lambda_{3}^{ - 3} E_{{}}^{2}$$
(32)

It can be found that the change of dielectric constant causes the electrostrictive stress, which contributes to both the directions 1 and 3. While the Maxwell stress generated by the electric field only contributes to the direction 3. The first Piola stress in the tensile direction is obtained by adding three parts of the stress in the direction 1, i.e.,

$$\begin{aligned} T_{{R1}}^{{}} = & \;T_{{RA1}}^{{}} + T_{{RB1}}^{{}} + T_{{REM1}}^{{}} \\ = & \;\sum\limits_{{m = 1}}^{2} {\mu _{{A_{m}^{{}} }}^{{}} \left( {\lambda _{1}^{{\alpha _{{A_{m} }} ^{{}} - 1}} - \lambda _{3}^{{ - \alpha _{{A_{m} }} ^{{}} }} \lambda _{1}^{{ - \alpha _{{A_{m} }} ^{{}} - 1}} } \right)} \\ & \; + \sum\limits_{{n = 1}}^{3} {\mu _{{B_{n}^{{}} }}^{{}} \left( {\lambda _{{n{\text{ e1}}}}^{{\alpha _{{B_{n} }} ^{{}} - 1}} - \lambda _{{n{\text{ e}}3}}^{{ - \alpha _{{B_{n} }} ^{{}} }} \lambda _{{n{\text{ e}}1}}^{{ - \alpha _{{B_{n} }} ^{{}} - 1}} } \right)\lambda _{{n{\text{ v1}}}}^{{ - 1}} } \\ & \; + \frac{1}{2}\varepsilon _{0} \bar{\varepsilon }_{r} \alpha \left( {1 - \lambda _{1}^{{ - 2}} \lambda _{3}^{{ - 1}} } \right)\lambda _{3}^{{ - 2}} E_{{}}^{2} \\ \end{aligned}$$
(33)

The influence of applied electric field in the tensile direction includes two aspects: (1) the electrostrictive stress in the direction 1 reflected by the third item on the right side of Eq 33; (2) the electrostrictive stress in the direction 3 and the Maxwell stress work together to produce a compression deformation, which makes the principal elongation in the direction 3 deviate from the perfect uniaxial deformation mode. Then the hyperelastic stress of the first term and the viscoelastic stress of the second term change accordingly. It is inferred that the electrostrictive stress in the direction 3 and Maxwell stress affect the stress in the direction 1 through the correspondent deformation. If the additional deformation is ignored, it will only be subjected to an electrostrictive stress in the direction 1. Thus, it is very reasonable to consider the effect of the electric field by introducing the additional deformation.

Thus, if \(\, \lambda_{1}^{{}}\) and \(\, \lambda_{3}^{{}}\) are given, the stress in the direction 1 can be obtained. That is, in the tests, besides measuring the principal elongation in the tensile direction, the principal elongation in the electric field direction should be measured simultaneously. However, due to the limitation of experimental conditions, only the principal elongation \(\, \lambda_{1}^{{}}\) in the tensile direction can be measured, and the principal elongation \(\, \lambda_{3}^{{}}\) in the electric field direction cannot be measured. It is noted that the hyperelastic stress and viscoelastic stress are balanced with the stress generated by the electric field in the direction 3, that is,\(\, T_{RA3}^{{}} + T_{RB3}^{{}} = T_{REM3}^{{}}\), namely,

$$\sum\limits_{{m = 1}}^{2} {\mu _{{A_{m}^{{}} }}^{{}} \left( {\lambda _{3}^{{\alpha _{{A_{m} }} ^{{}} - 1}} - \lambda _{1}^{{ - \alpha _{{A_{m} }} ^{{}} }} \lambda _{3}^{{ - \alpha _{{A_{m} }} ^{{}} - 1}} } \right)} + \sum\limits_{{n = 1}}^{3} {\mu _{{B_{n}^{{}} }}^{{}} \left( {\lambda _{{n{\text{ e3}}}}^{{\alpha _{{B_{n} }} ^{{}} - 1}} - \lambda _{{n{\text{ e1}}}}^{{ - \alpha _{{B_{n} }} ^{{}} }} \lambda _{{n{\text{ e3}}}}^{{ - \alpha _{{B_{n} }} ^{{}} - 1}} } \right)\lambda _{{n{\text{ v3}}}}^{{ - 1}} } = \frac{1}{2}\varepsilon _{0} \bar{\varepsilon }_{r} \alpha \left( {1 - \lambda _{3}^{{ - 2}} \lambda _{1}^{{ - 1}} } \right)\lambda _{3}^{{ - 2}} E_{{}}^{2} - \varepsilon _{0} \varepsilon _{r} \lambda _{3}^{{ - 3}} E_{{}}^{2}$$
(34)

In Eq 34, the unknown variable is only \(\, \lambda_{3}^{{}}\), which can be solved numerically by dichotomy. Then, the principal elongation \(\, \lambda_{3}^{{}}\) in the direction 3 can be obtained successfully from the requirement of stress balance.

3.1.3 Material Parameters

There are many methods to determine the visco-hyperelastic parameters used in the proposed constitutive model. Simply, it can be obtained by fitting the relaxation curves, or the creep curves, or even the tension-unloading curves of the materials. One issue that cannot be ignored is that the visco-hyperelastic parameters obtained by the above methods are usually different. And different parameters can well predict the experimental results for a certain case. Unfortunately, although many parameters can fit the relaxation, creep and tension-unloading results well, respectively, most of them cannot reproduce the cyclic deformation results well. The reason is that the basic mechanical properties (i.e., relaxation, creep and tension-unloading response) are relatively simple when compared with the cyclic deformation characteristics (i.e., the cyclic softening and ratchetting). For the complex cyclic deformation of VHB DEs, it is not appropriate to determine the parameters only by the basic mechanical experimental data. Specific variables related to the cyclic deformation should be introduced to optimize the model parameters. Therefore, the material parameters used in the proposed visco-hyperelastic constitutive model are obtained by fitting the stress–strain curves in the first cycle obtained in the cyclic deformation tests and introducing the evolution of specific variables with the cyclic number simultaneously, so as to simulate the results of cyclic deformation better.

The electrical parameters of the electro-mechanically coupled part can be directly obtained from the reference (Ref 35), and the hyperelastic, viscoelastic and electrical parameters used in the proposed model are finally determined, as shown in Table 1.

Table 1 Parameters used in the constitutive model
Full size table

3.2 Validations and Discussions

In this section, the uniaxial electro-mechanically coupled deformation of VHB 4905 DE revealed in the tests is numerically simulated by using the above proposed constitutive model. The rationality of the improved constitutive model is investigated by comparing the simulations with the experimental results.

3.2.1 Simulations on Electro-Mechanically Coupled Basic Property

3.2.1.1 Simulations on Tension-Unloading Response

Figure 9 demonstrates the comparison between the experimental and simulated stress–strain curves in the tension-unloading tests with and without applying a voltage. Overall, it is depicted that the improved constitutive model can describe the experimental results well. The simulated results can reflect the phenomena of stress softening, the decrease of peak stress and the increase of valley strain with applying a voltage, which also indicate that the applied voltage has little effect on the stress in the uniaxial deformation mode.

Fig. 9
figure 9

Comparison of experimental and simulated stress–strain curves in the tension-unloading tests

Full size image
3.2.1.2 Simulations on Relaxation and Creep

Figure 10 presents the comparison of experimental and simulated relaxed stresses and creep strains for the correspondent relaxation and creep tests of VHB 4905 DE. It is found from Fig. 10 that the proposed electro-mechanically coupled visco-hyperelastic constitutive model can capture the strong nonlinear viscosity and visible electro-mechanically coupled effect of VHB 4905 DE in the uniaxial deformation mode, and can predict the relaxed stress and creep strain and their evolutions with the increase of time in the cases with or without applying a voltage very well.

Fig. 10
figure 10

Comparison of experimental and simulated relaxed stresses and creep strains: (a) for relaxation tests; (b) for creep tests

Full size image

3.2.2 Simulations on Electro-Mechanically Coupled Cyclic Deformation

3.2.2.1 Simulations on Strain-Controlled Cyclic Deformation

Figure 11 shows the comparison between the simulated and experimental results of the strain-controlled cyclic deformation of VHB 4905 DE. From Fig. 11, it is concluded that: (1) the simulated stress–strain curves by the proposed model shown in Fig. 11(a) are in good agreement with the experimental ones shown in Fig. 5(a); (2) the simulations can well reproduce the evolution curves of peak stress, valley strain, dissipated energy density and apparent modulus with the cyclic number observed in the cyclic tests with and without applying a voltage in both the trend and magnitude, respectively.

Fig. 11
figure 11

Comparison of simulated and experimental results in the strain-controlled cyclic deformation tests: (a) stress–strain curves; (b) evolution curves of peak stress; (c) evolution curves of valley strain; (d) evolution curves of dissipative energy density; (e) evolution curves of apparent modulus

Full size image

It can be summarized that the improved electro-mechanically coupled visco-hyperelastic constitutive model here can reproduce well the strain-controlled cyclic deformation characteristics of VHB 4905 DE with and without applying a voltage. This is because the VHB 4905 DE mainly exhibits the electro-mechanically coupled hyperelasticity and strong viscosity, which are fully considered in the proposed model, especially by using a nonlinear viscosity equation to describe such a strong viscosity.

3.2.2.2 Simulations on Stress-Controlled Cyclic Deformation

Figure 12 shows the comparison between the simulated and experimental results of the stress-controlled cyclic deformation of VHB 4905 DE with and without applying a voltage. It should be noted that in Fig. 12(c), the letters V and P represent the valley strain and peak strain, respectively. It can be observed from Fig. 12 that: (1) the simulated stress–strain curves (Fig. 12a) are in good agreement with the experimental ones (shown in Fig. 6a), including the ratchetting strain and its evolution trend with the increase of cyclic number in the cases with or without applying a voltage as shown in Fig. 12(b); (2) there are good descriptions to the evolution curves of peak/valley strain, dissipated energy density and apparent modulus in both the trend and magnitude.

Fig. 12
figure 12

Comparison between the simulated and experimental results of stress-controlled cyclic deformation in the cases with a stress-level of 40 ± 30 kPa and at a stress rate of 0.6 kPa· s−1 as well as with and without applying a voltage: (a) stress–strain curves; (b) evolution curves of ratchetting strain; (c) evolution curves of peak/valley strain; (d) evolution curves of dissipative energy density; (e) evolution curves of apparent modulus

Full size image

Although the effect of applied voltage (4.0 kV) is not so significant, the simulations can still accurately reproduce the electro-mechanically coupled ratchetting of VHB 4905 DE, which demonstrates that it is reasonable to capture the effect of applied voltage on the uniaxial ratchetting by introducing the principal elongations in two directions into the simulations by the proposed constitutive model.

Then, the capability of proposed constitutive model is further validated by reproducing the rate- and stress-level-dependent uniaxial ratchetting of VHB 4905 with and without applying a voltage. Figure 13 demonstrates the comparison between the experimental and simulated results for the ratchetting of VHB 4905 DE obtained at different stress rates. It can be found from Fig. 13 that the ratchetting strains of VHB 4905 DE and their rate-dependence are well predicted in the cases with and without applying a voltage, since a nonlinear viscosity is incorporated in the proposed electromechanically coupled visco-hyperelastic constitutive model.

Fig. 13
figure 13

Comparison between the simulated and experimental results of stress-controlled cyclic deformation in the cases with a stress-level of 40 ± 30 kPa and at various stress rates as well as with and without applying a voltage: (a) evolution curves of ratchetting strain at a stress rate of 0.4 kPa· s−1; (b) evolution curves of ratchetting strain at a stress rate of 0.6 kPa· s−1; (c) evolution curves of ratchetting strain at a stress rate of 1.0 kPa· s.−1

Full size image

Figure 14 presents the comparison between the experimental and simulated results for the ratchetting strain of VHB 4905 DE obtained with different stress-levels. It is concluded from Fig. 14 that the ratchetting of VHB 4905 DE and its stress-level-dependence in the uniaxial deformation mode are well reproduced by the proposed model, and the simulated ratchetting strains are consistent with the correspondent experimental results.

Fig. 14
figure 14

Comparison between the simulated and experimental results of stress-controlled cyclic deformation in the cases with various stress-levels and at a stress rate of 0.6 kPa· s−1 as well as with and without applying a voltage: (a) evolution curves of ratchetting strain with a stress-level of 30 ± 30 kPa; (b) evolution curves of ratchetting strain with a stress-level of 40 ± 30 kPa; (c) evolution curves of ratchetting strain with a stress-level of 50 ± 30 kPa

Full size image

In this work, the uniaxial electro-mechanically coupled deformation characteristics of VHB 4905 DE are investigated experimentally and theoretically. In the experimental part, the uniaxial electro-mechanically coupled experimental data of VHB 4905 DE are sufficiently supplied, which can provide a good reference for the engineering applications of VHB 4905 DE. Moreover, in the theoretical part, the strong nonlinear viscosity of VHB 4905 DE is fully considered by adopting the nonlinear viscosity equation and the electro-mechanically coupled effect of VHB 4905 DE is reasonably predicted by introducing the additional deformation caused by the applied voltage. However, since the VHB 4905 DE is prone to electrical breakdown in the uniaxial electro-mechanically coupled deformation mode, the applied voltage can just reach to a constant voltage of 4.0 kV, leading to a slight effect on the deformation in the tensile direction. Furthermore, the effects of higher voltages and cyclic voltage on the cyclic deformation of VHB 4905 DE are not considered yet. In addition, as a soft polymer material, the VHB 4905 DE will exhibit an obvious temperature-dependence. The influence of ambient temperature on the electro-mechanically coupled cyclic deformation of VHB 4905 DE has also not been involved yet in this work. These issues should be further explored in the future work.

4 Conclusions

In this work, the uniaxial electro-mechanically coupled deformation tests of VHB 4905 DE are first carried out in a uniaxial deformation mode to reveal the correspondent deformation characteristics. Then, an electro-mechanically coupled visco-hyperelastic constitutive model is proposed to reproduce the uniaxial electro-mechanically coupled deformation of VHB 4905 DE. The main conclusions are obtained as follows:

From the experimental observations, it gives: (1) the stress in the tensile direction is decreased with applying a voltage, but the applied voltage has a slight effect on the deformation in the uniaxial deformation mode; (2) the applied voltage does not change the evolution trends of specific variables, but the values obtained with a constant voltage are different from those without applying a voltage; (3) the cyclic softening is enhanced and the evolution of ratchetting is accelerated by applying a voltage; (4) the ratchetting strain exhibits obvious rate- and stress-level-dependence, and the differences of ratchetting strain with and without applying a voltage becomes gradually remarkable with the increase of cyclic number.

For the proposed constitutive model, it includes: (1) the nonlinear evolution equation is used in the visco-hyperelastic constitutive model to describe the strong nonlinear viscosity of VHB 4905 DE, which accurately captures the viscoelastic characteristics revealed by the tests; (2) by introducing the principal elongations in two directions to consider the additional deformation caused by the applied voltage, the uniaxial electro-mechanically coupled cyclic deformation of VHB 4905 DE is also well predicted by the proposed constitutive model.