Hill Four-Body Problem with Oblate Bodies: An Application to the Sun–Jupiter–Hektor–Skamandrios System

Abstract

We consider a restricted four-body problem, with a precise hierarchy between the bodies: two larger bodies and a smaller one, all three of oblate shape, and a fourth, infinitesimal body, in the neighborhood of the smaller of the three bodies. The three heavy bodies are assumed to move in a plane under their mutual gravity, and the fourth body to move in the three-dimensional space under the gravitational influence of the three heavy bodies, but without affecting them. We first find that the triangular central configuration of the three heavy oblate bodies is a scalene triangle (rather than an equilateral triangle as in the point mass case). Then, assuming that these three bodies are in such a central configuration, we perform a Hill approximation of the equations of motion describing the dynamics of the infinitesimal body in a neighborhood of the smaller body. Through the use of Hill’s variables and a limiting procedure, this approximation amounts to sending the two larger bodies to infinity. Finally, for the Hill approximation, we find the equilibrium points for the motion of the infinitesimal body and determine their stability. As a motivating example, we identify the three heavy bodies with the Sun, Jupiter, and the Jupiter’s Trojan asteroid Hektor, which are assumed to move in a triangular central configuration. Then, we consider the dynamics of Hektor’s moonlet Skamandrios.

1 Introduction

The discovery of binary asteroids has led to considering dynamical models formed by four bodies, the other two bodies being typically the Sun and Jupiter. Among possible four-body models (see also Howell and Spencer 1986; Scheeres 1998; Gabern and Jorba 2003; Scheeres and Bellerose 2005; Alvarez-Ramirez and Vidal 2009; Burgos-García and Delgado 2013a, b; Burgos-García 2016; Kepley and Mireles James 2019), a relevant role is played by those in which three bodies lie on a triangular central configuration. Given that asteroids have often a (very) irregular shape, it is useful to assume in our model that the smaller body is oblate. For a more complete study, we also assume that the larger bodies are oblate as well. Among the different questions that this model may rise, we concentrate on the existence of equilibrium points and the corresponding linear stability analysis.

We focus on the specific example of the Trojan asteroid 624 Hektor, which is located close to the Lagrangian point $L_4$ of the Sun–Jupiter system, and its small moonlet Skamandrios. Hektor is the largest Jupiter Trojan and has one of the most elongated shapes among the bodies of its size in the Solar system. Its moonlet appears to have a complicated orbit, which is close to 1:10 and 2:21 orbit/spin resonances; a small change could potentially eject the moonlet or make it collide with the asteroid (Marchis et al. 2014).

Another example of a four-body problem is the Patroclus–Menoetius system. This is a binary system in the proximity of the Lagrangian point $L_5$, whose components are roughly of similar size; see, e.g., Noll et al. (2017).

Of related interest is the study of Earth’s trojans. See, e.g., Dvorak et al. (2012) for stability regions of trojans around the Earth, and Lhotka and Celletti (2015) for dissipative effects around the triangular Lagrangian points.

Besides the interest from the aspect of planetary dynamics, another motivation to study the motion of an infinitesimal body near a Trojan asteroid comes from astrodynamics. NASA prepares the first mission, Lucy, to the Jupiter’s Trojans, which is planned to be launched in October 2021 and visit seven different asteroids: a Main Belt asteroid and at least five Trojans, including the Patroclus–Menoetius system.

As our model for the Sun–Jupiter–Hektor, we consider a system of three bodies of masses $m_1 \geqslant m_2 \gg m_3$, which move in circular orbits under mutual gravity, and form a triangular central configuration. We refer to these bodies as the primary, the secondary, and the tertiary, respectively. We assume that all three bodies are oblate. We describe their gravitational potential in terms of the second-order zonal harmonic. We show the existence of a corresponding triangular central configuration, which turns out to be a scalene triangle. We note that triangles corresponding to different values of the moment of inertia are in general not similar to one another.

If the oblateness of all three bodies is made to be zero, the central configuration becomes the well-known equilateral triangle Lagrangian central configuration. We stress that when the bodies are oblate, the central configuration is not the same as in the non-oblate case, since the overall gravitational field is no longer Newtonian. It is well known that central configurations depend on the nature of the gravitational field (see, e.g., Corbera et al. 2004; Arredondo and Perez-Chavela 2013; Diacu et al. 2018; Martínez and Simó 2017). We note that there are papers in the literature (e.g., Asique et al. 2016), which consider systems of three bodies, with one of the bodies non-spherical, which are assumed to form an equilateral triangle central configuration. Such assumption, while it may lead to very good approximations, is not physically correct.

The moonlet Skamandrios is represented by a fourth body, of infinitesimal mass, which moves in a vicinity of $m_3$ under the gravitational influence of $m_1, m_2, m_3$, but without affecting their motion. We consider the motion of the infinitesimal mass taking place in the three-dimensional space, not confined to the plane of motion of the three heavy bodies. This situation is referred to as the spatial circular restricted four-body problem and can be described by an autonomous Hamiltonian system of 3 degrees of freedom.

We ‘zoom-in’ on the dynamics in a small neighborhood of $m_3$ by performing a Hill’s approximation of the restricted four-body problem. This is done by rescaling the distances by a factor of $m_3^{1/3}$, writing the associated Hamiltonian in the rescaled coordinates as a power series in $m_3^{1/3}$, and neglecting all the terms of order $O(m_3^{1/3})$ in the expansion, since such terms are small when $m_3$ is small. This yields an approximation of the motion of the infinitesimal mass in an $O(m_3^{1/3})$-neighborhood of the tertiary, while the primary and the secondary are ‘sent to infinity’ through the rescaling.

The resulting model is an extension of the classical lunar Hill problem (Hill 1878), as well as of Hill’s approximation of the restricted four-body problem derived in Burgos-García and Gidea (2015). The novelty of our model is that it assumes that the heavy bodies have oblate shapes.

The main advantage of the Hill approximation is that it yields a much simpler Hamiltonian then the one for the circular restricted four-body problem, since in the former the contribution of the primary and the secondary to the gravitational potential is given by a quadratic polynomial, while in the latter is given by singular terms; see Sect. 5.1. Having a simpler Hamiltonian also allows us to compute analytically the equilibrium points of the system and determine their stability; see Sect. 6. The Hill approximation is also more advantageous for numerical computations with realistic parameters. In the restricted four-body problem, there is a large difference of scales among the relevant parameters, i.e., the mass of Hektor is much smaller than the masses of the other two heavy bodies. The rescaling involved in the Hill approximation reduces the difference of scales to more manageable quantities. More precisely, in normalized units the oblateness effect in the restricted four-body problem is of the order $O(10^{-15})$, while in the Hill approximation is of the order $O(10^{-7})$; see Sect. 5.2 for details.

Once we have established the model, we study the equilibrium points and their linear stability. Relative to a coordinate system with the origin at the center of mass of $m_3$, we find that there are 2 pairs of symmetric equilibrium points on each of the x-, y-, and z-coordinate axes, respectively. The equilibrium points on the x- and y-coordinate axes are a continuation of the corresponding ones for the Hill four-body problem with spherical bodies (Burgos-García and Gidea 2015). The equilibrium points on the z-coordinate axis are a novel feature of the model that does not appear in Burgos-García and Gidea (2015). They are a continuation of the corresponding ones that appear in the $J_2$ problem (see Sect. 2.2).

We remark that for certain shapes, e.g., for rotational ellipsoids, ‘out-of-plane’ equilibrium points are not physically possible, as there is no other force that can balance the gravitation in the vertical direction; see Nan et al. (2018). However, certain non-convex shapes can have true ‘out-of-plane’ equilibrium points. For this reason, we consider the presence of equilibrium points of the z-coordinate axis (very close to the barycenter of $m_3$) as an interesting feature of our model.

This work is organized as follows: In Sect. 2 we provide data on the Sun–Jupiter–Hektor system, and also describe the gravitational potential of a non-spherical body. We determine triangular central configurations formed by three oblate bodies in Sect. 3. The equations of motion of the restricted four-body problem when the three heavy bodies are oblate are given in Sect. 4. The Hill’s approximation is derived in Sect. 5. The corresponding equilibria and their stability are given in Sect. 6. We summarize our results in Sect. 7. The existence of ‘out-of-plane’ equilibria is discussed in “Appendix B.”

2 Preliminaries

We provide orbital and physical values for the Sun, Jupiter, the asteroid Hektor, and its moon Skamandrios, in Sect. 2.1. We give the equations of the gravitational field of a non-spherical body that we will use in our model, in Sect. 2.2.

2.1 Data on the Sun–Jupiter–Hektor–Skamandrios System

The models which we will develop below will be illustrated in the case of the Sun–Jupiter–Hektor–Skamandrios system. We extract the data for this system from JPL Solar System Dynamics (2018), Lunar and Planetary Science (2020), Marchis et al. (2014) and Descamps (2015).

Hektor is approximately located at the Lagrangian point $L_4$ of the Sun–Jupiter system. According to Descamps (2015), Hektor is approximately $416 \times 131 \times 120$ km in size, and its shape can be approximated by a dumb-bell figure; the equivalent radius (i.e., the radius of a sphere with the same volume as the asteroid) is $R_H=92$ km.¹

We also note that the inclination of Hektor is approximately $18.17^\circ$ (see JPL Solar System Dynamics 2018). Although a more refined model should include a nonzero inclination, we will assume that Sun–Jupiter–Hektor move in the same plane. We will further assume that the axis of rotation of Hektor is perpendicular to the plane of motion.

The moonlet Skamandrios orbits around Hektor are at a distance of approximately 957.5 km, with an orbital period of 2.965079 days; see Descamps (2015). Its orbit is highly inclined, at approximately $50.1^\circ$ with respect to the orbit of Hektor, which justifies choosing as a model the spatial restricted four-body problem rather than the planar one; see Marchis et al. (2014).

For the masses of Sun, Jupiter, and Hektor, we use the values of $M_1= 1.989\times 10^{30}$ kg, $M_2=1.898\times 10^{27}$, and $M_3=7.91\times 10^{18}$ kg, respectively. For the average distance Sun–Jupiter, we use the value $778.5\times 10^6$ km.

In Fig. 1 we provide a comparison between the strength of the different forces acting on the moonlet: the Newtonian gravitational attraction of Hektor, Sun, Jupiter, and the effect of the non-spherical shape of the asteroid, limited to the second-order zonal harmonic of the spherical harmonic expansion, which will be given in Sect. 2.2.

Fig. 1

Order of magnitude of the different perturbations acting on the moonlet as a function of its distance from Hektor. The terms GM, Sun and Jupiter denote, respectively, the monopole terms of the gravitational influence of Hektor, the attraction of the Sun and that of Jupiter. $J_2$ represents the perturbation due to the non-spherical shape of Hektor. The actual distance of the moonlet is indicated by a vertical line

2.2 The Gravitational Field of a Non-spherical Body

It is well known that the gravitational potential of a general (non-spherical) shape can be expanded in terms of spherical harmonics (see, e.g., Celletti and Gales 2018). In this paper, we will only use the truncation up to second-order zonal harmonic. This amounts to approximating the body by an an oblate shape (i.e., an ellipsoid of revolution obtained by rotating an ellipse about its minor axis). Relative to a reference frame centered at the barycenter of the body, this potential is given in spherical coordinates $(r,\phi ,\lambda )$ by

$$\begin{aligned} V(r,\phi ,\lambda ) =\frac{\mathcal {G}m}{r}+ \frac{\mathcal {G}m}{r} \left( \frac{R}{r}\right) ^2 \left( \frac{C_{20}}{2}\right) \left( 3\sin \phi ^2 -1\right) , \end{aligned}$$

(2.1)

where $\mathcal {G}$ is the gravitational constant, m is the mass of the body, R is its average radius, and $C_{20}$ is a dimensionless quantity representing the coefficient of the second-order zonal harmonic. For an oblate body $C_{20}$ is a negative number. The positive quantity $-C_{20}$ is often denoted by $J_2$, and the study of the motion of particle relative to the gravitational field (2.1) is referred to as the $J_2$ problem.

In the case of an ellipsoid of semi-axes $a\geqslant b\geqslant c$, we have the following explicit formula (Boyce 1997):

$$\begin{aligned} C_{20}=\frac{c^2-\frac{a^2}{2}-\frac{b^2}{2}}{5R_H^2}. \end{aligned}$$

(2.2)

For Hektor, taking $a=208$ km, $b=65.5$ km, $c=60$ km, $R_H=92$ km, as in Descamps (2015) (see Sect. 2.1), we obtain

$$\begin{aligned}C^3_{20}=-0.476775.\end{aligned}$$

Note that the value of $C^3_{20}$ computed above is different from the corresponding value of 0.15 reported in Marchis et al. (2014). The reason is that we use different estimates for the size of Hektor, following Descamps (2015) (see Sect. 2.1).

For the oblateness coefficient of Sun, we use $C^1_{20}=-5.00 \times 10^{-6}$. The oblateness of the Sun is a subject of active debate, and several different values can be found in the literature. Here we use the measurements from Kuhn et al. (2012).

For Jupiter’s oblateness coefficient, we use the value $C^2_{20}=-14{,}736\times 10^{-6}$.

3 Central Configurations for the Three-Body Problem with Three Oblate Bodies

In this section, we show the existence and uniqueness of triangular central configurations of three oblate bodies, and we compute the positions of the bodies in such a central configuration relative to some rotating frame.

3.1 Existence and Uniqueness of Triangular Central Configurations of Three Oblate Bodies

We now consider only the three heavy, oblate bodies, of normalized masses $m_1 \geqslant m_2 \geqslant m_3$, that is $m_1+m_2+m_3=1$. For each body $m_i$ we denote by $C^i_{20}$ the oblateness coefficient in the expression of the potential (2.1). The corresponding gravitational potential in Cartesian coordinates is:

$$\begin{aligned} \begin{aligned} V_i(x,y,z)&=\frac{m_i}{r}+\frac{m_i}{r} \left( \frac{R_i}{r}\right) ^2 \left( \frac{C^i_{20}}{2}\right) \left( 3 \left( \frac{z}{r}\right) ^2 -1\right) \end{aligned} \end{aligned}$$

(3.1)

where $m_i$ is the normalized mass of the i-th body, $R_i$ is its average radius in normalized units, and the gravitational constant is also normalized $\mathcal {G}=1$.

We want to find the triangular central configurations formed by $m_1$, $m_2$, $m_3$; we will follow the approach in Arredondo and Perez-Chavela (2013). Since for a central configuration the three bodies lie in the same plane, we choose an inertial frame centered at the barycenter of the three bodies, and in the gravitational field (3.1) we let $z=0$, obtaining

$$\begin{aligned} V_i(q)=\frac{m_i}{r}- \frac{m_iC_i}{r^3}, \end{aligned}$$

(3.2)

where $q=(x,y)$ is the position vector of an arbitrary point in the plane, $r=\Vert q\Vert$ is the distance from $m_i$, and we denote

$$\begin{aligned} C_i=R_i^2C^i_{20}/2<0. \end{aligned}$$

(3.3)

Combining the gravitational potentials (3.2), the equations of motion of the three bodies are

$$\begin{aligned} m_i\ddot{q}_i=\sum _{j\ne i}{m_im_j(q_j-q_i)}\left[ \frac{1}{\Vert q_j-q_i\Vert ^3}-\frac{C_{ij}}{\Vert q_j-q_i\Vert ^5}\right] \end{aligned}$$

(3.4)

where $q_i$ is the position vector of the mass $m_i$, for $i=1,2,3$, and

$$\begin{aligned} C_{ij}=C_i+C_j \text { for } i\ne j\in \{1,2,3\}. \end{aligned}$$

(3.5)

Denote $r_{ij}=\Vert q_i-q_j\Vert$, for $i\ne j$, $\mathbf{q}=(q_1,q_2,q_3)$, and

$$\begin{aligned} \mathbf{M}=\text {diag}(m_1, m_1,m_2 ,m_2, m_3, m_3) \end{aligned}$$

the $6\times 6$ matrix with 2 copies of each mass along the diagonal. Then, (3.4) can be written as

$$\begin{aligned} {\mathbf{M}}\ddot{\mathbf{q}}=\nabla U(\mathbf{q}), \end{aligned}$$

(3.6)

where

$$\begin{aligned} U(\mathbf{q})=\sum _{i\ne j}{m_im_j}\left( \frac{1}{r_{ij}}-\frac{C_{ij}}{r_{ij}^3}\right) \end{aligned}$$

(3.7)

is the potential for the three-body problem with oblate masses.

Let us assume that the center of mass is fixed at the origin, i.e.,

$$\begin{aligned} \mathbf{M}\mathbf{q}= \sum _{i=1}^3 m_iq_i=0. \end{aligned}$$

(3.8)

We are interested in relative equilibrium solutions for the motion of the three bodies, which are characterized by the fact they become equilibrium points in a uniformly rotating frame.

Denote by $R(\theta )$ the $6\times 6$ block diagonal matrix consisting of 3 diagonal blocks the form

$$\begin{aligned} \left( \begin{array}{rr} \cos (\theta ) &{} -\sin (\theta ) \\ \sin (\theta ) &{} \cos (\theta ) \\ \end{array} \right) \in SO(2). \end{aligned}$$

Substituting $\mathbf{q}(t)=R(\omega t)\mathbf{z}(t)$ for some $\omega \in \mathbb {R}$ in (3.6), where $\mathbf{z}=(z_1,z_2,z_3)\in \mathbb {R}^6$, we obtain

$$\begin{aligned} \mathbf{M}\left( {\ddot{\mathbf{z}}}-2\omega \mathbf{{J}}\dot{\mathbf{z}}-\omega ^2\mathbf{z}\right) =\nabla U (\mathbf{z}), \end{aligned}$$

where $\mathbf{{J}}$ is the block diagonal matrix consisting of 3 diagonal blocks the form

$$\begin{aligned} J=\left( \begin{array}{rr} 0 &{} 1 \\ -1 &{} 0 \\ \end{array} \right) . \end{aligned}$$

(3.9)

The condition for an equilibrium point of (3.1) yields the algebraic equation

$$\begin{aligned} \nabla U(\mathbf{z})+\omega ^2 \mathbf{M}\mathbf{z}=0. \end{aligned}$$

(3.10)

A solution $\mathbf{z}$ of the three-body problem satisfying (3.10) is referred to as a central configuration. This is equivalent to ${\ddot{z}}_i=-\omega ^2 z_i$, for $i=1,2,3$, meaning that the accelerations of the masses are proportional to the corresponding position vectors, and all accelerations are pointing toward the center of mass. Thus, the solution $\mathbf{q}(t)$ is a relative equilibrium solution if and only if $\mathbf{q}(t)=R(\omega t)\mathbf{z}(t)$ with $\mathbf{z}(t)$ being a central configuration solution, and the rotation $R(\omega t)$ being a circular solution of the Kepler problem.

Let $I(\mathbf{z})=\mathbf{z}^T M \mathbf{z}=\sum _{i} m_i \Vert z_i\Vert ^2$ be the moment of inertia. It is easy to see that this is a conserved quantity for the motion, that is, $I(\mathbf{z}(t))={\bar{I}}$ for some ${\bar{I}}$ at all t. Using Lagrange’s second identity (see, e.g., Gidea and Niculescu 2012), and that $\mathbf{M}\mathbf{z}=0$, normalizing the masses so that $\sum _{i=1}^3 m_i=1$, the moment of inertia can be written as:

$$\begin{aligned} I(\mathbf{z})=\sum _{1\leqslant i<j\leqslant 3} m_{i}m_{j} \Vert z_i-z_j\Vert ^2 =\sum _{1\leqslant i<j\leqslant 3} m_{i}m_{j} r_{ij}^2.\end{aligned}$$

(3.11)

Thus, central configurations correspond to critical points of the potential U on the sphere $\mathbf{z}^TM\mathbf{z}=1$, which can be obtained by solving the Lagrange multiplier problem

$$\begin{aligned} \nabla f(\mathbf{z})=0,\qquad I(\mathbf{z})-\bar{I}=0, \end{aligned}$$

(3.12)

where $f(\mathbf{z})=U(\mathbf{z})+\frac{1}{2}\omega ^2(I(\mathbf{z})-\bar{I})$. In the above, we used the fact that $\nabla I(\mathbf{z})=2\mathbf{M}\mathbf{z}$.

We solve this problem in the variables $r_{ij}=\Vert z_i-z_j\Vert$ for $1\leqslant i<j\leqslant 3$, since both U and I can be written in terms of these variables. This reduces the dimension of the system (3.12) from 7 equations to 4 equations. Denote $\mathbf{r}=(r_{12}, r_{13},r_{23})$, and let $\tilde{f}(\mathbf{r})$ be the function f expressed in the variable $\mathbf{r}$, that is $\tilde{f}(\mathbf{r}(\mathbf{z}))=f(\mathbf{z})$. By the chain rule, $\nabla _r \tilde{f} \cdot \left( \frac{\partial \mathbf{r}}{\partial \mathbf{z}} \right) =\nabla _\mathbf{z}f(\mathbf{z})$. It is easy to see that the rank of the matrix $\left( \frac{\partial \mathbf{r}}{\partial \mathbf{z}} \right)$ is maximal provided that $z_1,z_2,z_3$ are not collinear (for details, see Corbera et al. 2004; Arredondo and Perez-Chavela 2013). As we are looking for triangular central configurations, this condition is satisfied.

Thus, $\nabla _r \tilde{f}(\mathbf{r})=0$ if and only if $\nabla _\mathbf{z}f(\mathbf{z})=0$. This is equivalent to the following system of equations:

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \frac{1}{r_{12}^3}-\frac{3C_{12}}{r_{12}^5}=\omega ^2,\\ \displaystyle \frac{1}{r_{13}^3}-\frac{3C_{13}}{r_{13}^5}=\omega ^2,\\ \displaystyle \frac{1}{r_{23}^3}-\frac{3C_{23}}{r_{23}^5}=\omega ^2,\\ \displaystyle m_1m_2r_{12}^2+m_1m_3r_{13}^2+m_2m_3r_{23}^2=\bar{I}. \end{array} \right. \end{aligned}$$

(3.13)

Note that the function

$$\begin{aligned} h(r)=\frac{1}{r^3}-\frac{3C}{r^5}-\omega ^2 \end{aligned}$$

(3.14)

has negative derivative

$$\begin{aligned} h'(r)=-\frac{3}{r^4}+\frac{15C}{r^6}<0 \end{aligned}$$

for $r>0$ and $C<0$; hence, h is injective as a function of r. Also, $\lim _{r\rightarrow 0}h(r)=+\infty$ and $\lim _{r\rightarrow \infty }=-\omega ^2<0$. Thus, for each of the first three equations (3.13), and for a fixed $\omega$, there is a unique solution $r_{ij}=r_{ij}(\omega )$.

From the first equation of the system (3.13), implicit differentiation with respect to $\omega$ yields

$$\begin{aligned} \begin{aligned}&\frac{3}{r_{12}^{4}}\frac{dr_{12}}{d\omega }-\frac{15 C_{12}}{r_{12}^6}\frac{dr_{12}}{d\omega }=-2\omega ,\quad \text {implying}\\&\frac{dr_{12}}{d\omega }=\frac{-2\omega }{\frac{3}{r_{12}^4}-\frac{15C_{12}}{r_{12}^6}}. \end{aligned} \end{aligned}$$

(3.15)

For $r_{12}>0$ and $C_{12}<0$, we have $\frac{dr_{12}}{d\omega }<0$, provided $\omega >0$. Similarly, we obtain $\frac{dr_{13}}{d\omega }<0$, and $\frac{dr_{23}}{d\omega }<0$.

The right-hand side of the last equation of the system (3.13) as a function of $\omega$ is

$$\begin{aligned} F(\omega )=m_1m_2r_{12}^2 (\omega )+m_2m_3r_{23}^2 (\omega )+m_1m_3r_{13}^2(\omega ) \end{aligned}$$

(3.16)

and its derivative with respect to $\omega$ is

$$\begin{aligned} F'(\omega ) =2m_1m_2r_{12}\frac{dr_{12}}{d\omega }+2m_1m_3r_{13}\frac{dr_{13}}{d\omega }+2m_2m_3r_{23}\frac{dr_{23}}{d\omega } \end{aligned}$$

(3.17)

Since $\frac{dr_{ij}}{d\omega }<0$, we have $F^\prime (\omega )<0$. Hence, there exists a unique $\omega$ such that $F(\omega )=\bar{I}$.

Now we study the dependence on the unique solution $r_{ij}$ on $C_{ij}$. If r is the unique solution of

$$\begin{aligned} \frac{1}{r^3}-\frac{3C}{r^5}=\omega ^2 \end{aligned}$$

implicit differentiation with respect to C yields

$$\begin{aligned} \frac{dr}{dC}=-\frac{r}{r^2-5C}<0, \end{aligned}$$

thus r is a decreasing function in C. If the $C_i$’s satisfy some ordering, e.g., $C_2\leqslant C_1 \leqslant C_3$, then $C_{12} \leqslant C_{23}\leqslant C_{13}$; hence, $r_{13}\leqslant r_{23}\leqslant r_{12}$.

Thus, we have proved the following result:

Proposition 3.1

In the three-body problem with all bodies oblate, for every fixed value $\bar{I}$ of the moment of inertia, there exists a unique central configuration, which is in general a scalene triangle.

Moreover, the body with the larger $C_i$ is opposite to the longer side of the triangle.

The last statement of Proposition 3.1 is similar to the elementary geometry theorem saying that in a triangle, the largest angle is opposite the longest side.

Surprisingly, the masses of the bodies do not play a role in the ordering of the sides.

Note that in the special case when $C_1=C_2$ we have $C_{13}=C_1+C_3=C_2+C_3=C_{23}$. In this case, the second and third equations of the system (3.13) are identical, and, since the function h defined in (3.14) is injective as a function of r, it follows that $r_{13}=r_{23}$, so the central configuration is an isosceles triangle. This situation occurs, for example, if we assume that only the body $m_3$ is oblate, i.e., $C^1_{20}=C^2_{20}=0$. We have thus obtained the following:

Corollary 3.2

In the three-body problem with one oblate body $m_3$, for every fixed value $\bar{I}$ of the moment of inertia, there exists a unique central configuration, which is an isosceles triangle with $r_{13}=r_{23}$.

Remark 3.3

The triangular central configurations corresponding to different values of $\omega$ are not similar to one another, as shown by the following counterexample. Let $C_{12}=-0.1$, $C_{13}=-0.2$, and $C_{23}=-0.3$. For $\omega =1$, solving (3.13) yields $r_{12}=1.07937$, $r_{13}=1.13577$, $r_{23}=1.18063$. For $\bar{\omega }=2$, solving (3.13) yields $\bar{r}_{12}=0.730867$, $\bar{r}_{13}=0.788914$, $\bar{r}_{23}=0.831688$. We have

$$\begin{aligned} \frac{r_{12}}{\bar{r}_{12}}=1.47683,\, \frac{r_{13}}{\bar{r}_{13}}=1.43967,\, \frac{r_{23}}{\bar{r}_{23}}=1.41956. \end{aligned}$$

This situation is very different from the case of point masses (no oblateness), when all triangular central configurations are equilateral triangles.

Remark 3.4

If the unit of distance is rescaled by a factor of $\alpha$, that is, the quantities $r_{ij}$ and $R_{i}$ get rescaled by a factor of $\alpha$, then $C_i$ and $C_{ij}$ get rescaled by a factor of $\alpha ^2$ due to (3.3) and (3.5). Therefore, $\omega$ gets rescaled by a factor of $\alpha ^{-3/2}$, and $\bar{I}$ gets rescaled by a factor of $\alpha ^2$ due to (3.13).

3.2 Location of the Bodies in the Triangular Central Configuration

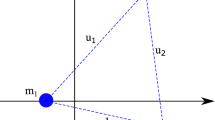
We now compute the locations of the three bodies in the triangular central configuration, relative to a synodic frame that rotates together with the bodies with the center of mass fixed at the origin, with $m_1$ on the negative x-semi-axis. We assume that the masses lie in the $z=0$ plane. Instead of fixing the value $\bar{I}$ of the moment of inertia, we fix $r_{12}=1$, and let $r_{13}=u$, and $r_{23}=v$, where u and v are uniquely determined by (3.13). For convenience, denote $w=1+u^2-v^2$. Then, we obtain the following result:

Fig. 2

Triangular central configuration

Proposition 3.5

In the synodic reference frame, the coordinates of the three bodies in the triangular central configuration, satisfying the constraints

$$\begin{aligned} (x_2-x_1)^2+(y_2-y_1)^2= & {} 1, \end{aligned}$$

(3.18)

$$\begin{aligned} (x_3-x_1)^2+(y_3-y_1)^2= & {} u^2,\end{aligned}$$

(3.19)

$$\begin{aligned} (x_3-x_2)^2+(y_3-y_2)^2= & {} v^2,\end{aligned}$$

(3.20)

$$\begin{aligned} m_1x_1+m_2x_2+m_3x_3= & {} 0,\end{aligned}$$

(3.21)

$$\begin{aligned} m_1y_1+m_2y_2+m_3y_3= & {} 0,\end{aligned}$$

(3.22)

$$\begin{aligned} m_1+m_2+m_3= & {} 1,\end{aligned}$$

(3.23)

$$\begin{aligned} y_1= & {} 0, \end{aligned}$$

(3.24)

are given by

$$\begin{aligned} \begin{aligned} x_1&=-\sqrt{m_2^2+wm_2m_3+u^2m_3^2},\\ y_1&=0,\\ x_2&=\frac{-2m_2^2-2u^2m_3^2-2wm_2m_3+2m_2+wm_3}{2\sqrt{m_2^2+w m_2m_3+u^2m_3^2}},\\ y_2&=-\frac{1}{2}\sqrt{\frac{(4u^2-w^2)m_3^2}{m_2^2+w m_2m_3+u^2m_3^2}},\\ x_3&= \frac{-2m_2^2-2u^2m_3^2 -2wm_2m_3+wm_2+2u^2m_3}{2\sqrt{m_2^2+w m_2m_3+u^2m_3^2}},\\ y_3&=+\frac{1}{2}\sqrt{\frac{(4u^2-w^2)m_2^2}{m_2^2+w m_2m_3+u^2m_3^2}}. \end{aligned} \end{aligned}$$

(3.25)

Proof

Denote $x_2-x_1=A$ and $x_3-x_1=B$. Also denote $m_2/m_3=m$. From (3.24) and (3.22), we have $y_3=-my_2$. From (3.18) and (3.19) we have $x_2-x_1=\sqrt{1-y_2^2}=A$ and $x_3-x_1=\sqrt{u^2-m^2y_2^2}=B$. So, by subtracting we obtain $x_3-x_2=-\sqrt{1-y_2^2}+\sqrt{u^2-m^2y_2^2}$. From (3.20) we have $x_3-x_2=\pm \sqrt{v^2-(1+m)^2y_2^2}$. Equating the two expressions of $x_3-x_2$ and solving for $y_2^2$ yield the value of

$$\begin{aligned} y_2^2=\frac{(4u^2-w^2)m_3^2}{4(m_2^2+w m_2m_3+u^2m_3^2)}. \end{aligned}$$

Solving for $y_2$ and choosing the negative solution to be in agreement with the convention in Fig. 2 yield the formula for $y_2$ as in (3.25). Since $y_3=-(m_2/m_3)y_2$, we obtain the formula for $y_3$ as in (3.25). Note that the sign of $y_3$ agrees with the convention in Fig. 2. Now we can substitute $y_2$ in A and B obtaining

$$\begin{aligned} \begin{aligned} A=\frac{2m+w}{2\sqrt{m^2+wm+u^2}},\quad B=\frac{wm+2u^2}{2\sqrt{m^2+wm+u^2}}. \end{aligned} \end{aligned}$$

Substituting $x_2=x_1+A$ and $x_3=x_1+B$ in (3.21) and using (3.23), we obtain $x_1=-m_2A-m_3B=m_3(-mA-B)$. After simplification, we obtain the formula for $x_1$ from (3.25). Then by substituting $x_1$ in $x_2=x_1+A$ and $x_3=x_1+B$, we obtain the formulas for $x_2$ and $x_3$ from (3.25). $\square$

Remark 3.6

For future reference, we note that if we let $m_3\rightarrow 0$ in (3.25), we obtain

$$\begin{aligned} \begin{array}{ll} x_1=-m_2, &{} y_1=0, \\ x_2=-m_2+1,&{} y_2=0,\\ x_3=-m_2+\frac{w}{2}, &{} y_3=\frac{1}{2}\sqrt{4u^2-w^2}. \end{array} \end{aligned}$$

(3.26)

Remark 3.7

In the case when only the mass $m_3$ is oblate, by Corollary 3.2 we have $r_{13}=u=r_{23}=v$, so $w=1+u^2-v^2=1$, so the formulas (3.25) become

$$\begin{aligned} x_1&=-\sqrt{m_2^2+m_2m_3+u^2m_3^2},\nonumber \\ y_1&=0,\nonumber \\ x_2&=\frac{-2m_2^2-2u^2m_3^2-2 m_2m_3+2m_2+ m_3}{2\sqrt{m_2^2+ m_2m_3+u^2m_3^2}},\nonumber \\ y_2&=-\frac{1}{2}\sqrt{\frac{(4u^2-1)m_3^2}{m_2^2+ m_2m_3+u^2m_3^2}},\nonumber \\ x_3&= \frac{-2m_2^2-2u^2m_3^2 -2 m_2m_3+m_2+2u^2m_3}{2\sqrt{m_2^2+ m_2m_3+u^2m_3^2}},\nonumber \\ y_3&=\frac{1}{2}\sqrt{\frac{(4u^2-1)m_2^2}{m_2^2+ m_2m_3+u^2m_3^2}}. \end{aligned}$$

(3.27)

Remark 3.8

In the case when none of the bodies are oblate we have $u=v=1$ and $w=1$, so in (3.27) we obtain the Lagrangian equilateral triangle central configuration $r_{12}=r_{23}=r_{13}=1$. The position given (3.27) is equivalent to the following formulas (see, e.g., Baltagiannis and Papadakis 2013):

$$\begin{aligned} \begin{aligned} x_1&=\frac{-|K |\sqrt{m_2^2+m_2 m_3+m_3^2}}{K},\\ y_1&=0,\\ x_2&=\frac{|K |[(m_2-m_3)m_3+m_1(2m_2+m_3)]}{2K\sqrt{m_2^2+m_2m_3+m_3^2}},\\y_2&=-\frac{\sqrt{3}m_3}{2\sqrt{m_2^2+m_2m_3+m_3^2}},\\ x_3&=\frac{|K |}{2\sqrt{m_2^2+m_2m_3+m_3^2}},\\ y_3&=\frac{\sqrt{3}m_2}{2\sqrt{m_2^2+m_2m_3+m_3^2}}, \end{aligned} \end{aligned}$$

(3.28)

where $K=m_2(m_3-m_2)+m_1(m_2+2m_3)$.

Notice that the equations (3.28) are expressed in terms of $m_1,m_2,m_3$, while (3.25) are expressed in terms of $m_2, m_3$; we obtain corresponding expressions that are equivalent when we substitute $m_1=1-m_2-m_3$ in (3.28). One minor difference is that in (3.28) the position of $x_1$ is not constrained to be on the negative x-semi-axis, as we assumed for (3.25); the position of $x_1$ in (3.28) depends on the quantity $\text {sign}(K)$; when $\text {sign}(K)>0$, we have $|K|/K=1$, and the equations (3.25) become equivalent with the equation (3.28).

We remark that when $m_3\rightarrow 0$, the limiting position of the three masses in (3.28) is given by:

$$\begin{aligned} \begin{array}{lll} x_1 =-m_2, &{} y_1 = 0, &{} z_1 =0,\\ x_2 =1-m_2,&{} y_2 =0,&{} z_2=0,\\ x_3= \frac{1-2m_2}{2},&{}y_3=\frac{\sqrt{3}}{2},&{}z_3=0, \end{array} \end{aligned}$$

(3.29)

with $(x_1,y_1)$ and $(x_2,y_2)$ representing the position of the masses $m_1$ and $m_2$, respectively, and $(x_3,y_3)$ representing the position of the equilibrium point $L_4$ in the planar circular restricted three-body problem.

4 eqnarrays of Motion for the Restricted Four-Body Problem with Three Oblate Bodies

In this section, we consider the dynamics of an infinitesimal mass under the influence of the three heavy bodies. For example, this fourth body represents the moonlet Skamandrios orbiting around Hektor. We model the dynamics of the fourth body by the spatial, circular, restricted four-body problem, meaning that the moonlet is moving under the gravitational attraction of Hektor, Jupiter, and the Sun, without affecting their motion which remains on circular orbits and forming a triangular central configuration as in Sect. 3.

The equations of motion of the infinitesimal mass relative to a synodic frame of reference that rotates together with the three heavy bodies are given by

$$\begin{aligned} \begin{aligned} \ddot{x}-2\omega \dot{y}&=\frac{\partial {\tilde{\Omega }}}{\partial x}={\tilde{\Omega }}_x\\ \ddot{y}+2\omega \dot{x}&=\frac{\partial {\tilde{\Omega }}}{\partial x}={\tilde{\Omega }}_y\\ \ddot{z}&=\frac{\partial {\tilde{\Omega }}}{\partial z}={\tilde{\Omega }}_z, \end{aligned} \end{aligned}$$

(4.1)

where the effective potential $\tilde{\Omega }=\tilde{\Omega }(x,y,z)$ is given by

$$\begin{aligned} {\tilde{\Omega }} = \frac{1}{2}\omega ^2(x^2+y^2)+\sum _{i=1}^{3}\left( \frac{m_i}{r_i}+ \frac{m_i}{r_i} \left( \frac{R_i}{r_i}\right) ^2\left( \frac{C^i_{20}}{2}\right) (3\sin ^2{\phi _i}-1)\right) \end{aligned}$$

with $(x_i, y_i,z_i)$ representing the (x, y, z)-coordinates in the synodic reference frame of the body of mass $m_i$, $r_{i} = \left( (x-x_{i})^2+(y-y_{i})^2+z^2\right) ^{\frac{1}{2}}$ is the distance from the infinitesimal body to the mass $m_i$, $\sin \phi _i=z/r_i$, $\omega$ is the angular velocity of the system of three bodies around the center of mass, and $C^i_{20}$ is the oblateness coefficient of mass $m_i$, for $i=1,2,3$. Note that $\omega$ depends on the oblateness parameters. Since $r_{12}=1$, $r_{13}=u$ and $r_{23}=v$, from (3.13) we have that the angular velocity is given by

$$\begin{aligned} \begin{aligned} \omega =\sqrt{1-3C_{12}}, \end{aligned} \end{aligned}$$

(4.2)

where we recall that $C_{12}=C_1+C_2=R_1^2C^1_{20}/2+R_2^2C^2_{20}/2$.

We rescale the time $t=s/\omega$ so that relative to the new time s the mean motion is normalized to 1, obtaining

$$\begin{aligned} \begin{aligned} \ddot{x}-2\dot{y}&=\frac{\partial {\Omega }}{\partial {x}}=\Omega _{x},\\ \ddot{y}+2\dot{x}&=\frac{\partial {\Omega }}{\partial {y}}=\Omega _{y},\\ \ddot{z}&=\frac{\partial {\Omega }}{\partial {z}}=\Omega _{z}, \end{aligned} \end{aligned}$$

(4.3)

with the effective potential $\Omega =\Omega (x,y,z)$ given by

$$\begin{aligned} \Omega =\frac{1}{2}(x^2+y^2)+\frac{1}{\omega ^2}\sum _{i=1}^{3}\left( { \frac{m_i}{r_i}}+ \frac{m_i}{r_i} \left( \frac{R_i}{r_i}\right) ^2\left( \frac{C^i_{20}}{2}\right) (3\sin ^2{\phi _i}-1)\right) . \end{aligned}$$

(4.4)

We switch to the Hamiltonian setting via the transformation $\dot{x}=p_x+y$, $\dot{y}=p_y-x$ and $\dot{z}=p_z$, thus passing to the symplectic coordinates $(x,y,z,p_x,p_y,p_z)$ relative to the symplectic form $\varpi =x\wedge p_x+y\wedge p_y+z\wedge p_z$. We obtain:

$$\begin{aligned} \begin{aligned} H=&\, \frac{1}{2} ((p_{x}+y)^2+(p_{y}-x)^2+p_{z}^2)-\frac{1}{2}(x^2+y^2)\\&-\frac{1}{\omega ^2}\left( \sum _{i=1}^{3}\frac{m_i}{r_i}+ \frac{m_i}{r_i}\left( \frac{R_i}{r_i}\right) ^2\left( \frac{C^i_{20}}{2}\right) (3\sin ^2{\phi _i}-1)\right) \\ =&\, \frac{1}{2}(p_{x}^2+p_{y}^2+p_{z}^2)+yp_{x}-xp_{y}\\ {}&-\frac{1}{\omega ^2}\sum _{i=1}^{3} \left( \frac{m_i}{r_i}+ \frac{m_i}{r_i^3} C_i (3\sin ^2{\phi _i}-1)\right) , \end{aligned} \end{aligned}$$

(4.5)

where $C_i={R_i}^2C^i_{20}/2$. Thus, the equations of motion (4.1) are equivalent to Hamilton’s equations for the Hamiltonian given by (4.5).

Remark 4.1

In the special case when only the body $m_2$ is oblate and $m_3=0$, we have

$$\begin{aligned} \omega =\sqrt{1-3C^2_{20}}=\sqrt{1-\frac{3R_2^2C^2_{20}}{2}}. \end{aligned}$$

The resulting model is the circular restricted three-body problem with one oblate body, and the above formula agrees with the one in McCuskey (1963), Sharma and Subba Rao (1976) and Arredondo et al. (2012). Further, if $m_2$ has no oblateness, i.e., $C^2_{20}=0$, we have $\omega =1$, and the resulting model is the classical circular restricted three-body problem.

Other models of the restricted three-body problems which involve oblate primaries, relativistic and radiation effects are studied in Bello and Singh (2016) and Bello and Umar (2018).

5 Hill Four-Body Problem with Three Oblate Bodies

In this section, we derive the Hill approximation of the spatial, circular, restricted four-body problem with oblate bodies. Through the use of rescaled variables and a limiting procedure, the masses $m_1$ and $m_2$ are ‘sent to infinite distance’, so that a neighborhood of $m_3$ can be studied in detail.

5.1 Hill’s Approximation

The main result is the following:

Theorem 5.1

Transform the Hamiltonian (4.5) as follows:

• (i) shift the origin of the reference frame so that it coincides with $m_3$;

• (ii) perform a conformal symplectic scaling given by

  $$\begin{aligned} (x,y,z,p_{x},p_{y},p_{z})\rightarrow m_{3}^{1/3}(x,y,z,p_{x},p_{y},p_{z}); \end{aligned}$$

• (iii) rescale the average radius of each heavy body as $R_i=m_3^{1/3}\rho _i$ for $i=1,2,3$;

• (iv) expand the resulting Hamiltonian as a power series in $m_3^{1/3}$, and

• (v) neglect all the terms of order $O(m_3^{1/3})$ in the expansion.

Then, we obtain the following Hamiltonian describing the Hill four-body problem with three oblate bodies:

$$\begin{aligned} \begin{aligned} H&= \frac{1}{2}(p_x^2+p_y^2+p_z^2)+yp_x-xp_y\\&\quad -\frac{1}{2}\left[ \left( \frac{(1-\mu )\left( \frac{3w^2}{4}-1\right) }{u^5}+\frac{\mu \left( \frac{3(2-w)^2}{4}-1\right) }{v^5}\right) x^2\right. \\&\quad +\left( \frac{(1-\mu )\left( \frac{3(4u^2-w^2)}{4}-1\right) }{u^5}+\frac{\mu \left( \frac{3(4u^2-w^2)}{4}-1\right) }{v^5} \right) y^2\\&\quad \left. +\left( \frac{(1-\mu )\frac{6w\sqrt{4u^2-w^2}}{4}}{u^5}-\frac{\mu \frac{6(2-w)\sqrt{4u^2-w^2}}{4}}{v^5}\right) xy -\left( \frac{(1-\mu )}{u^3}+\frac{\mu }{v^3}\right) z^2 \right] \\&\quad -\left[ \left( \frac{(1-\mu )c_1}{u^3}\right) \left( 3\left( \frac{z}{u}\right) ^2-1\right) + \left( \frac{\mu c_2}{v^3}\right) \left( 3\left( \frac{z}{v}\right) ^2-1\right) \right. \\&\quad \left. +\frac{1}{(x^2+y^2+z^2)^{\frac{1}{2}}}+\frac{c_3}{(x^2+y^2+z^2)^{\frac{3}{2}}}\left( \frac{3z^2}{x^2+y^2+z^2}-1\right) \right] , \end{aligned}\nonumber \\ \end{aligned}$$

(5.1)

where 1, u, v represent the sides of the triangular central configuration as in Sect. 3.2, $w=1+u^2-v^2$, $\mu =\frac{m_2}{m_1+m_2}$, and $c_i :=\rho _i^2C^i_{20}/2=m_3^{-\frac{2}{3}}R^i_3C^i_{20}/2$, $i=1,2,3$.

Proof

We start by shifting the origin of the coordinate system (x, y, z) to the location of the mass $m_3$ (representing Hektor), via the change of coordinates

$$\begin{aligned} \begin{array}{lll} \xi =x-x_3, &{} \eta =y-y_3, &{} \zeta =z,\\ p_\xi =p_x+y_3, &{} p_\eta =p_y-x_3, &{} p_\zeta =p_z . \end{array} \end{aligned}$$

The Hamiltonian corresponding to (4.5) becomes

$$\begin{aligned} \begin{aligned} H =&\,\frac{1}{2} \left( (p_\xi -y_3)^2+(p_\eta +x_3)^2+p_\zeta ^2\right) \\ {}&+(\eta +y_3)(p_\xi -y_3)-(\xi +x_3)(p_\eta +x_3)\\&-\frac{1}{\omega ^2}\sum _{i=1}^{3}\left( \frac{m_i}{\bar{r}_i}+\frac{m_i}{\bar{r}_i}\left( \frac{R_i}{\bar{r}_i}\right) ^2 \left( \frac{C^i_{20}}{2}\right) (3\sin ^2{\phi _i}-1)\right) \\ =&\,\frac{1}{2}(p_\xi ^2+p_\eta ^2+p_\zeta ^2)+\eta p_\xi -\xi p_\eta -(\xi x_3+\eta y_3)-\frac{1}{2}(x_3^2+y_3^2)\\&-\frac{1}{\omega ^2}\sum _{i=1}^{3}\left( \frac{m_i}{\bar{r}_i}+ \frac{m_i}{\bar{r}_i} \left( \frac{R_i}{\bar{r}_i}\right) ^2\left( \frac{C^i_{20}}{2}\right) (3\sin ^2{\phi _i}-1)\right) , \end{aligned} \end{aligned}$$

(5.2)

where $\bar{r}_i^2=(\xi -\bar{x}_i)^2+(\eta -\bar{y}_i)^2+\zeta ^2=(\xi +x_3-x_i)^2+(\eta +y_3-y_i)^2+\zeta ^2$, with $\bar{x}_i=x_i-x_3$, $\bar{y}_i=y_i-y_3$. Note that $\bar{r}_3=r_3$. Since $-\frac{1}{2}(x_3^2+y_3^2)$ is a constant term, it plays no role in the Hamiltonian equations and it will be dropped in the following calculation.

Since $\sin {\phi _i}=\frac{\zeta }{\bar{r}_i}$ for each mass $m_i$, we have

$$\begin{aligned} \begin{aligned} H =&\,\frac{1}{2} (p_{\xi }^2+p_{\eta }^2+p_{\zeta }^2)+\eta p_{\xi }-\xi p_{\eta }-(\xi x_3+\eta y_3)\\&-\frac{1}{\omega ^2}\sum _{i=1}^{3}\left[ \frac{m_i}{\bar{r}_i}+\frac{m_i}{\bar{r}_i}\left( \frac{R_i}{\bar{r}_i}\right) ^2 \left( \frac{C^i_{20}}{2}\right) \left( 3\left( \frac{\zeta }{\bar{r}_i}\right) ^2-1\right) \right] . \end{aligned} \end{aligned}$$

(5.3)

We expand the terms $\displaystyle \frac{1}{\bar{r}_1}$ and $\displaystyle \frac{1}{\bar{r}_2}$ in Taylor series around the new origin of coordinates, obtaining

$$\begin{aligned} \begin{aligned} f^1:=\frac{1}{\bar{r}_1}=\sum _{k\geqslant 0}{P_k^1(\xi ,\eta ,\zeta )},\\ f^2:=\frac{1}{\bar{r}_2}=\sum _{k\geqslant 0}{P_k^2(\xi ,\eta ,\zeta )}, \end{aligned} \end{aligned}$$

where $P_k^j(\xi ,\eta ,\zeta )$ is a homogeneous polynomial of degree k, for $j=1,2$.

Straightforward computations yield

$$\begin{aligned} P_0^i&= (\bar{x_i}^2+\bar{y_i}^2)^{-\frac{1}{2}}=r_{i3}^{-1},\nonumber \\ P^i_1&= \frac{\bar{x}_i}{r_{i3}^3}\xi +\frac{\bar{y}_i}{r_{i3}^3}\eta \nonumber \\ P^i_2&=\frac{1}{2}\left( \frac{3\bar{x}^2_i}{r_{i3}^5}-\frac{1}{r_{i3}^3}\right) \xi ^2+\frac{1}{2}\left( \frac{3\bar{y}^2_i}{r_{i3}^5}-\frac{1}{r_{i3}^3}\right) \eta ^2+\frac{1}{2}\left( -\frac{1}{r_{i3}^3}\right) \zeta ^2\nonumber \\&+\left( \frac{3\bar{x}_i\bar{y}_i}{r_{i3}^5}\right) \xi \eta , \end{aligned}$$

(5.4)

for $i=1,2$, where $r_{13}=((x_1-x_3)^2+(y_1-y_3)^2)^{1/2}=u$, and $r_{23}=((x_2-x_3)^2+(y_2-y_3)^2)^{1/2}=v$.

We note that $P_0^1$ and $P_0^2$ are constant terms and play no role in the Hamiltonian equations, so they will be dropped from (5.3) in the following calculations.

We now perform the following conformal symplectic scaling with multiplier $m_3^{-2/3}$, given by

$$\begin{aligned} \begin{aligned} \xi&=m_3^{\frac{1}{3}} x\ ,\qquad \eta =m_3^{\frac{1}{3}} y\ ,\qquad \zeta =m_3^{\frac{1}{3}}z,\\ p_\xi&=m_3^{\frac{1}{3}} p_x\ ,\qquad p_\eta =m_3^{\frac{1}{3}} p_y\ ,\qquad p_\zeta =m_3^{\frac{1}{3}} p_z, \end{aligned} \end{aligned}$$

(5.5)

where, with an abuse of notation, we call again the new variables x, y, z, $p_x$, $p_y$, $p_z$.

Consistently with this scale change, we also introduce the scaling transformation of the average radius of the three bodies

$$\begin{aligned} R_i^2 =(m_3^{1/3}\rho _i)^2 =m_3^{2/3}\rho _i^2, \text { with } \rho _i=m_3^{-1/3}R_i,\,\text { for }i=1,2,3. \end{aligned}$$

(5.6)

The choice of the power of $m_3$ is motivated by the fact that in this way the gravitational force becomes of the same order of the centrifugal and Coriolis forces (see, e.g., Meyer and Schmidt 1982).

Due to the conformal symplectic scaling with multiplier $m_3^{-2/3}$, the Hamiltonian in the new variables, which we still denote by H, is given by

$$\begin{aligned} H(x,y,z,p_x,p_y,p_z)=m_3^{-2/3}H( m_3^{\frac{1}{3}} x, m_3^{\frac{1}{3}}y,m_3^{\frac{1}{3}}z,m_3^{\frac{1}{3}}p_x,m_3^{\frac{1}{3}}p_y,m_3^{\frac{1}{3}}p_z). \end{aligned}$$

The resulting Hamiltonian H takes the form

$$\begin{aligned} \begin{aligned} H =&\,\frac{1}{2}(p_x^2+p_y^2+p_z^2)+yp_x-xp_y-m_3^{-\frac{1}{3}}xx_3-m_3^{-\frac{1}{3}}yy_3\\&-\frac{1}{\omega ^2}\left( m_3^{-\frac{1}{3}} m_1 P_1^1(x,y,z)+m_3^{-\frac{1}{3}} m_2 P_1^2(x,y,z)\right. \\&+\sum _{k\geqslant 2}m_3^{\frac{k-2}{3}}m_1P_k^1(x,y,z)+\sum _{k\geqslant 2}m_3^{\frac{k-2}{3}}m_2P_k^2(x,y,z)\\&+\frac{m_1}{\bar{r}_1}\left( \frac{\rho _1}{\bar{r}_1}\right) ^2 \left( \frac{C_{20}^{1}}{2}\right) \left( 3\left( \frac{z}{\bar{r}_1}\right) ^2-1\right) \\&+\frac{m_2}{\bar{r}_2}\left( \frac{\rho _2}{\bar{r}_2}\right) ^2 \left( \frac{C_{20}^{2}}{2}\right) \left( 3\left( \frac{z}{\bar{r}_2}\right) ^2-1\right) \\&\left. +\frac{1}{\bar{r}_3}+\frac{1}{\bar{r}_3}\left( \frac{\rho _3^2}{\bar{r}_3^2}\right) \left( \frac{C_{20}^{3}}{2}\right) \left( 3\left( \frac{z}{\bar{r}_3}\right) ^2-1\right) \right) . \end{aligned} \end{aligned}$$

(5.7)

The purpose of the subsequent calculation is that after the above substitutions, we expand the resulting Hamiltonian as a power series in $m_3^{1/3}$. Then, we will neglect all the terms of order $O(m_3^{1/3})$ in the expansion, as in the classical Hill theory of lunar motion (Meyer and Schmidt 1982).

We now compute the contribution of the different terms in (5.7). Using (5.4) and (3.13) we obtain

$$\begin{aligned} \begin{aligned} -m_3^{-\frac{1}{3}}&\left[ xx_3+yy_3+ \frac{m_1 P_1^1}{\omega ^2} +\frac{m_2 P_1^2}{\omega ^2}\right] \\ =&-m_3^{-\frac{1}{3}}\left[ \left( x_3+\frac{m_1\bar{x}_1}{\omega ^2u^3}+\frac{m_2\bar{x}_2}{\omega ^2v^3}\right) x +\left( y_3+\frac{m_1 \bar{y}_1}{\omega ^2 u^3}+\frac{m_2\bar{y}_2}{\omega ^2 v^3}\right) y\right] \\ =&-m_3^{-\frac{1}{3}}\left[ \left( x_3+ {m_1\bar{x}_1}\left( 1+\frac{3C_{13}}{\omega ^2 u^5}\right) +{m_2\bar{x}_2}\left( 1+\frac{3C_{23}}{\omega ^2v^5}\right) \right) x\right. \\&\left. + \left( y_3+ {m_1\bar{y}_1}\left( 1+\frac{3C_{13}}{\omega ^2 u^5}\right) +{m_2\bar{y}_2}\left( 1+\frac{3C_{23}}{\omega ^2v^5}\right) \right) y\right] \\ =&-m_3^{-\frac{1}{3}}\left[ \left( x_3+m_1\bar{x}_1+m_2\bar{x}_2+m_1\bar{x}_1\frac{3C_{13}}{\omega ^2u^5} +m_2\bar{x}_2\frac{3C_{23}}{\omega ^2v^5}\right) x \right. \\&\left. +\left( y_3+m_1\bar{y}_1+m_2\bar{y}_2+m_1\bar{y}_1\frac{3C_{13}}{\omega ^2u^5} +m_2\bar{y}_2\frac{3C_{23}}{\omega ^2v^5}\right) y\right] \end{aligned} \end{aligned}$$

(5.8)

Using (3.21) and (3.23) we have

$$\begin{aligned} \begin{aligned} x_3+m_1\bar{x}_1+m_2\bar{x}_2= x_3+m_1(x_1-x_3)+m_2(x_2-x_3)=0 \end{aligned} \end{aligned}$$

(5.9)

and similarly, using (3.22) and (3.23) we have

$$\begin{aligned}y_3+m_1\bar{y}_1+m_2\bar{y}_2=0.\end{aligned}$$

Thus, (5.8) becomes

$$\begin{aligned} \begin{aligned} -m_3^{-\frac{1}{3}}\left[ \left( m_1\bar{x}_1\frac{3C_{13}}{\omega ^2u^5}+m_2\bar{x}_2 \frac{3C_{23}}{\omega ^2v^5}\right) x+\left( m_1\bar{y}_1\frac{3C_{13}}{\omega ^2 u^5}+m_2\bar{y}_2\frac{3C_{23}}{\omega ^2v^5}\right) y\right] . \end{aligned}\nonumber \\ \end{aligned}$$

(5.10)

Recalling the $C_{ij}$ notation, we obtain

$$\begin{aligned} \begin{aligned} C_{ij}=&\,C_{i}+C_{j}=\left( \frac{R_i^2C_{20}^i}{2}+\frac{R_j^2C_{20}^j}{2}\right) = m_3^{\frac{2}{3}}\left( \frac{\rho _i^2C_{20}^i}{2}+\frac{\rho _j^2C_{20}^j}{2}\right) \\ :=&\,m_3^{\frac{2}{3}}K_{ij} \end{aligned} \end{aligned}$$

(5.11)

for $i\ne j$.

From (3.13), $\omega ^2= 1-3C_{12} =1-m_3^{\frac{2}{3}}K_{12}$; hence,

$$\begin{aligned} \frac{1}{\omega ^2}= \frac{1}{1-m_3^{\frac{2}{3}}K_{12}}=1+m_3^{\frac{2}{3}}K_{12}+O(m_3^{\frac{4}{3}}). \end{aligned}$$

(5.12)

Neglecting the higher-order terms in (5.12), (5.10) becomes

$$\begin{aligned} m_3^{-\frac{1}{3}}\left[ \left( m_1\bar{x}_1\frac{3m_3^{\frac{2}{3}}K_{13}}{u^5} +m_2\bar{x}_2\frac{3m_3^{\frac{2}{3}}K_{23}}{v^5}\right) x +\left( m_1\bar{y}_1\frac{3m_3^{\frac{2}{3}}K_{13}}{u^5}+m_2\bar{y}_2\frac{3m_3^{\frac{2}{3}}K_{23}}{v^5} \right) y\right] .\nonumber \\ \end{aligned}$$

(5.13)

Since in the Hill approximation we are neglecting all terms of order of $m_3^{1/3}$, it follows that the above expression and hence the one (5.8), get neglected.

Now we combine the corresponding terms for the second-degree polynomials $P^i_2$ in the Hamiltonian (5.7). Using (5.12), we obtain

$$\begin{aligned} -\frac{1}{\omega ^2}&\left( m_1P_2^1+m_2P_2^2\right) \nonumber \\&=-\frac{1}{\omega ^2}\left[ \frac{m_1}{2}\left( \frac{3\bar{x}_1^2}{r_{13}^5}-\frac{1}{r_{13}^3}\right) x^2+\frac{m_1}{2}\left( \frac{3\bar{y}_1^2}{r_{13}^5}- \frac{1}{r_{13}^3}\right) y^2\right. \nonumber \\&\quad +\frac{m_1}{2}\left( -\frac{1}{r_{13}^3}\right) z^2+ m_1\left( \frac{3\bar{x_1}\bar{y}_1}{r_{13}^5}\right) xy\nonumber \\&\quad +\frac{m_2}{2}\left( \frac{3\bar{x}_2^2}{r_{23}^5}-\frac{1}{r_{23}^3}\right) x^2+\frac{m_2}{2} \left( \frac{3\bar{y}_2^2}{r_{23}^5}-\frac{1}{r_{23}^3}\right) y^2\nonumber \\&\quad \left. +\frac{m_2}{2}\left( -\frac{1}{r_{23}^3}\right) z^2+m_2\left( \frac{3\bar{x}_2\bar{y}_2}{r_{23}^5}\right) xy\right] \nonumber \\&=-\frac{1}{2}\left[ \left( \frac{3m_1\bar{x}_1^2}{u^5}+\frac{3m_2\bar{x}_2^2}{v^5}-\frac{m_1}{u^5} -\frac{m_2}{v^5}\right) x^2\right. \nonumber \\&\quad +\left( \frac{3m_1\bar{y}_1^2}{u^5}+\frac{3m_2\bar{y}_2^2}{v^5}-\frac{m_1}{u^5}-\frac{m_2}{v^5}\right) y^2\nonumber \\&\quad +\left( \frac{6m_1\bar{x}_1\bar{y}_1}{u^5}+\frac{6m_2\bar{x}_2\bar{y}_2}{v^5}\right) xy+\left. \left( -\frac{m_1}{u^3}-\frac{m_2}{v^3}\right) z^2 \right] . \end{aligned}$$

(5.14)

This is a quadratic polynomial in which the quantities $\bar{x}_1$, $\bar{x}_2$, $\bar{y}_1$, $\bar{y}_2$ depend on $m_3$. We use (3.26) to evaluate the corresponding quantities when the terms of order of $m_3^{1/3}$ are neglected,

$$\begin{aligned} \bar{x}_1=-\frac{w}{2},\, \bar{x}_2=\frac{2-w}{2},\, \bar{y}_1=\bar{y}_2=-\frac{1}{2}\sqrt{4u^2-w^2}, \end{aligned}$$

(5.15)

where we recall that $w=1+u^2-v^2$.

Thus, the quadratic polynomial (5.14) becomes

$$\begin{aligned} \begin{aligned} -\frac{1}{2}&\left[ \left( \frac{m_1\left( \frac{3w^2}{4}-1\right) }{u^5}+\frac{m_2 \left( \frac{3(2-w)^2}{4}-1\right) }{v^5}\right) x^2\right. \\&\,\,+\left( \frac{m_1\left( \frac{3(4u^2-w^2)}{4}-1\right) }{u^5}+\frac{m_2\left( \frac{3(4u^2-w^2)}{4}-1\right) }{v^5} \right) y^2\\&\,\, \left. +\left( \frac{m_1\frac{6w\sqrt{4u^2-w^2}}{4}}{u^5}-\frac{m_2\frac{6(2-w)\sqrt{4u^2-w^2}}{4}}{v^5}\right) xy -\left( \frac{m_1}{u^3}+\frac{m_2}{v^3}\right) z^2 \right] . \end{aligned} \end{aligned}$$

(5.16)

The Taylor expressions of $f^i$, $i=1,2$, of order $k\geqslant 3$ in the Hamiltonian are of the form

$$\begin{aligned} \sum _{k\geqslant 3}m_3^{\frac{k-2}{3}}m_1P_k^1(x,y,z)+\sum _{k\geqslant 3}m_3^{\frac{k-2}{3}}m_2P_k^2(x,y,z),\end{aligned}$$

and they can be written in terms of positive powers of $m_3^{1/3}$, so they are neglected in the Hill approximation.

The rest of the terms in the Hamiltonian (5.7) become

$$\begin{aligned} \begin{aligned}&-\left[ \left( \frac{m_1\rho _1^2}{\bar{r}_1^3}\right) \left( \frac{C_{20}^1}{2}\right) \left( 3\left( \frac{z}{\bar{r}_1}\right) ^2 -1\right) +\left( \frac{m_2\rho _2^2}{\bar{r}_2^3}\right) \left( \frac{C_{20}^2}{2}\right) \left( 3\left( \frac{z}{\bar{r}_2}\right) ^2-1\right) \right. \\&\quad \left. +\frac{1}{\bar{r}_3}+\left( \frac{\rho _3^2}{\bar{r}_3^3}\right) \left( \frac{C_{20}^3}{2}\right) \left( 3\left( \frac{z}{\bar{r}_3}\right) ^2-1\right) \right] . \end{aligned}\nonumber \\ \end{aligned}$$

(5.17)

The terms $\bar{r}_1$ and $\bar{r}_2$ also depend on $m_3$. When we let $m_3\rightarrow 0$, we obtain $\bar{r}_1\rightarrow u$ and $\bar{r}_2\rightarrow v$. Recall $\bar{r}_3=r_3=(x^2+y^2+z^2)^{\frac{1}{2}}$ which we now denote by r.

Therefore, when we neglect all terms of order $m_3^{\frac{1}{3}}$ in (5.7), we obtain the following Hamiltonian:

$$\begin{aligned} \begin{aligned} H=&\frac{1}{2}(p_x^2+p_y^2+p_z^2)+yp_x-xp_y\\&-\left[ \left( \frac{(1-\mu )\left( \frac{3w^2}{4}-1\right) }{u^5}+\frac{\mu \left( \frac{3(2-w)^2}{4}-1\right) }{v^5}\right) \frac{x^2}{2}\right. \\&+\left( \frac{(1-\mu )\left( \frac{3(4u^2-w^2)}{4}-1\right) }{u^5}+\frac{\mu \left( \frac{3(4u^2-w^2)}{4}-1\right) }{v^5} \right) \frac{y^2}{2}\\&+\left( \frac{(1-\mu )\frac{6w\sqrt{4u^2-w^2}}{4}}{u^5}-\frac{\mu \frac{6(2-w)\sqrt{4u^2-w^2}}{4}}{v^5}\right) \frac{xy}{2}\\&-\left( \frac{(1-\mu )}{u^3}+\frac{\mu }{v^3}\right) \frac{z^2}{2} \\&+ \left( \frac{(1-\mu )c_1}{u^3}\right) \left( 3\left( \frac{z}{u}\right) ^2-1\right) + \left( \frac{\mu c_2}{v^3}\right) \left( 3\left( \frac{z}{v}\right) ^2-1\right) \\&\left. +\frac{1}{r}+\left( \frac{c_3}{r^3}\right) \left( 3\left( \frac{z}{r}\right) ^2- 1\right) \right] , \end{aligned} \end{aligned}$$

(5.18)

where we denote $\mu =m_2/(m_1+m_2)$, $r=(x^2+y^2+z^2)^{\frac{1}{2}}$, and $c_i:=\rho _i^2C^i_{20}/2=m_3^{-\frac{2}{3}}R^i_3C^i_{20}/2$. $\square$

We refer to the Hamiltonian (5.18) as the Hill’s approximation. It can be thought of as the limiting Hamiltonian, when the primary and the secondary are sent at an infinite distance. It provides an approximation of the motion of the infinitesimal particle in an $O(m_3^{1/3})$ neighborhood of $m_3$. Remarkably, the angular velocity $\omega$ associated with the triangular central configuration does not appear in the limiting Hamiltonian.

We introduce the gravitational potential as

$$\begin{aligned} \begin{aligned} {\widehat{U}}(x,y,z)=&\left( \frac{(1-\mu )\left( \frac{3w^2}{4}-1\right) }{u^5}+\frac{\mu \left( \frac{3(2-w)^2}{4}-1\right) }{v^5}\right) \frac{x^2}{2} \\&\,+\left( \frac{(1-\mu )\left( \frac{3(4u^2-w^2)}{4}-1\right) }{u^5}+\frac{\mu \left( \frac{3(4u^2-w^2)}{4}-1\right) }{v^5} \right) \frac{y^2}{2}\\&\,+\left( \frac{(1-\mu )\frac{6w\sqrt{4u^2-w^2}}{4}}{u^5}-\frac{\mu \frac{6(2-w)\sqrt{4u^2-w^2}}{4}}{v^5}\right) \frac{xy}{2}\\&\,-\left( \frac{(1-\mu )}{u^3}+\frac{\mu }{v^3}\right) \frac{z^2}{2} \\&\, + \left( \frac{(1-\mu )c_1}{u^3}\right) \left( 3\left( \frac{z}{u}\right) ^2-1\right) + \left( \frac{\mu c_2}{v^3}\right) \left( 3\left( \frac{z}{v}\right) ^2-1\right) \\&\, +\frac{1}{r}+\left( \frac{c_3}{r^3}\right) \left( 3\left( \frac{z}{r}\right) ^2- 1\right) \end{aligned} \end{aligned}$$

(5.19)

and the effective potential as

$$\begin{aligned} \begin{aligned} {\widehat{\Omega }}(x,y,z)&=\frac{1}{2}(x^2+y^2)+{\widehat{U}}(x,y,z). \end{aligned} \end{aligned}$$

(5.20)

The equations of motion associated with (5.18) can thus be written as:

$$\begin{aligned}\begin{aligned} \ddot{x}-2\dot{y}&={\widehat{\Omega }}_x,\\ \ddot{y}+2\dot{x}&={\widehat{\Omega }}_y,\\ \ddot{z}&={\widehat{\Omega }}_z.\end{aligned} \end{aligned}$$

Remark 5.2

One of the main advantages of the Hill approximation is that it yields a much simpler Hamiltonian than for the circular restricted four-body problem. In the latter, the effective potential (4.4) has three singularities, corresponding to the positions of the three heavy bodies. In the former, there is only one singularity, corresponding to the position of the tertiary, while the effect of the primary and the secondary in the effective potential (5.20) is represented by a quadratic polynomial in x, y, z.

Remark 5.3

In the case when $C^i_{20}=0$ for $i=1,2,3$, we have that $u=v=w=1$ and the Hamiltonian in (5.18) is the same as the one obtained in Burgos-García and Gidea (2015). Also, its quadratic part coincides with the quadratic part of the expansion of the Hamiltonian of the restricted three-body problem centered at the Lagrange libration point $L_{4}$. If, in addition, we make $\mu =0$, we obtain the classical lunar Hill problem, after some rotation of the coordinate axes as in Sect. 5.2.

Remark 5.4

Our model is an extension of the classical Hill’s approximation of the restricted three-body problem, with the major differences that we consider a four-body problem which takes into account the effect of the oblateness coefficients $C^i_{20}$, $i=1,2,3$; compare with Hill (1878), Meyer and Schmidt (1982) and Burgos-García and Gidea (2015).

We remark that an approach similar to ours was adopted in Markellos et al. (2001), where a Hill’s three body problem with oblate primaries has been considered.

5.2 Hill’s Approximation Applied to the Sun–Jupiter–Hektor System

In the case of the Sun–Jupiter–Hektor system, we have the following data (see Sect. 2.1):

	$C_{20}$	Average radius (km)	Mass (kg)
Sun	$C^1_{20}=-5.00 \times 10^{-6}$	$R_1=695{,}700$	$M_1=1.989\times 10^{30}$
Jupiter	$C^2_{20}=-14{,}736\times 10^{-6}$	$R_2=69{,}911$	$M_2=1.898\times 10^{27}$
Hektor	$C^3_{20}=-0.476775$	$R_3=92$	$M_3=7.91\times 10^{18}$

In the normalized units, where we use the average distance Sun–Jupiter $778.5\times 10^6$ km as the unit of distance, and the mass of Sun–Jupiter–Hektor $1.990898\times 10^{30}$ kg as the unit of mass, we have $R_1=8.936416\times 10^{-4}$, $R_2=8.980218\times 10^{-5}$, $R_3=1.18176\times 10^{-7}$, $m_1=0.9990467$, $m_2=9.533386\times 10^{-4}$, $m_3= 3.97308\times 10^{-12}$.

If we set $r_{12}=1$, from (3.13) we obtain $r_{13}=u=1- 5.94154\times 10^{-11}$ and $r_{23}=v= 1-1.99318\times 10^{-12}$. In terms of the unit distance $r_{12}=1$ (the Sun–Jupiter distance is $778.5\times 10^6$ km), the distance $r_{13}$ differs from $r_{12}$ by 0.0462549 km, and the distance $r_{23}$ differs from $r_{12}$ by 0.00155169 km, Practically, the scalene triangle central configuration is almost an equilateral triangle.

The parameters that appear in the Hamiltonian (5.18) are

$$\begin{aligned} \begin{aligned} c_1&= m_3^{-\frac{2}{3}}R_1^2 C^1_{20}/2=-7.958816\times 10^{-5},\\ c_2&= m_3^{-\frac{2}{3}}R_2^2 C^2_{20}/2= -2.368673\times 10^{-3},\\ c_3&= m_3^{-\frac{2}{3}}R_3^2 C^3_{20}/2= -1.327161\times 10^{-7}. \end{aligned} \end{aligned}$$

(5.21)

The mass ratio that appears in the Hill approximation is $\mu =m_2/(m_1+m_2)=0.0009533386$.

We remark that if we consider the restricted four-body problem (without the Hill approximation) described by the Hamiltonian (4.5), the oblateness effect is given by the coefficients

$$\begin{aligned} \begin{aligned} C_1&=R_1^2C^1_{20}/2= -1.996488\times 10^{-12},\\ C_2&=R_2^2C^2_{20}/2= -5.941874\times 10^{-11} ,\\ C_3&=R_3^2C^3_{20}/2=-3.32921544\times 10^{-15}, \end{aligned} \end{aligned}$$

(5.22)

which are much smaller than the corresponding normalized values $c_i$, $i=1,2,3$ in (5.21). As the numerical values of the parameters involved are relatively larger, the Hill approximation is more convenient to use for numerical computations.

We also note that we have the ordering

$$\begin{aligned}C_{2}<C_{1}<C_{3},\end{aligned}$$

and the corresponding ordering

$$\begin{aligned}r_{13}=u<r_{23}=v<r_{12}=1.\end{aligned}$$

The matching between these two orderings is in agreement with Proposition 3.1.

5.3 Hill’s Approximation in Rotated Coordinates

In this section we write the Hamiltonian of the Hill approximation in a reference frame that is rotated, so that the quadratic part of the effective potential (5.20) is diagonalized.

Corollary 5.5

The Hamiltonian (5.1) is equivalent, via a rotation of the coordinate axes that diagonalizes the quadratic part of the effective potential, to the Hamiltonian

$$\begin{aligned} \begin{aligned} H&=\frac{1}{2}(p_x^2+p_y^2+p_z^2)+y p_x-xp_y\\&\quad +\left( \frac{1-\lambda _2}{2}\right) x^2+\left( \frac{1-\lambda _1}{2}\right) y^2+ \frac{1}{2}\left( \frac{(1-\mu )}{u^3}+\frac{\mu }{v^3}\right) z^2\\&\quad - \left( \frac{(1-\mu )c_1}{u^3}\right) \left( 3\left( \frac{z}{u}\right) ^2-1\right) - \left( \frac{\mu c_2}{v^3}\right) \left( 3\left( \frac{z}{v}\right) ^2-1\right) \\&\quad -\frac{1}{(x^2+y^2+z^2)^{1/2}}- \frac{c_3}{(x^2+y^2+z^2)^{3/2}} \left( \frac{3z^2}{ x^2+y^2+z^2 }- 1\right) , \end{aligned} \end{aligned}$$

(5.23)

where $\lambda _2$ and $\lambda _1$ are the eigenvalues corresponding to the rotation transformation in the xy-plane, given by (5.26).

Proof

We perform a rotation on the xy-plane and rewrite the Hamiltonian in (5.1) in the rotated coordinates, which are more suitable for the subsequent analysis. We adopt the following notation

$$\begin{aligned} \begin{aligned}&U=\frac{3w^2}{4}-1,\quad V=\frac{3(2-w)^2}{4}-1,\quad Z=\frac{3(4u^2-w^2)}{4}-1,\\&W_1=\frac{6w\sqrt{4u^2-w^2}}{4},\quad W_2=\frac{6(2-w)\sqrt{4u^2-w^2}}{4}. \end{aligned} \end{aligned}$$

(5.24)

The planar effective potential restricted to the xy-plane (i.e., $z=0$) is given by

$$\begin{aligned}\begin{aligned} {\widehat{\Omega }} (x,y)=&\left( 1+\frac{(1-\mu )U}{u^5}+\frac{\mu V}{v^5}\right) \frac{x^2}{2}+\left( 1+\frac{(1-\mu )Z}{u^5}+\frac{\mu Z}{v^5} \right) \frac{y^2}{2}\\&\,+\left( \frac{(1-\mu )W_1}{u^5}-\frac{\mu W_2}{v^5}\right) \frac{xy}{2} \\&\, - \left( \frac{(1-\mu )c_1}{u^3}\right) - \left( \frac{\mu c_2}{v^3}\right) +\frac{1}{r}-\left( \frac{c_3}{r^3}\right) . \end{aligned} \end{aligned}$$

which can be written in matrix notation as

$$\begin{aligned} {\widehat{\Omega }} = \frac{1}{2}q^TMq- \left( \frac{(1-\mu )c_1}{u^3}\right) - \left( \frac{\mu c_2}{v^3}\right) +\frac{1}{\Vert q \Vert }- \frac{c_3}{ \Vert q \Vert ^3}, \end{aligned}$$

where $q=(x,y)^T$ and

$$\begin{aligned} M= \left( {\begin{array}{ll} 1+\frac{(1-\mu )U}{u^5}+\frac{\mu V}{v^5} &{} \frac{1}{2}\left( \frac{(1-\mu )W_1}{u^5}-\frac{\mu W_2}{v^5} \right) \\ \frac{1}{2}\left( \frac{(1-\mu )W_1}{u^5}-\frac{\mu W_2}{v^5} \right) &{} 1+\frac{(1-\mu )Z}{u^5}+\frac{\mu Z}{v^5} \end{array} } \right) . \end{aligned}$$

(5.25)

We find the eigenvalues of M by solving the characteristic equation: $\det ( M-\lambda I )=0$, which gives

$$\begin{aligned} \begin{aligned}&\lambda ^2-\left( 2+\frac{(1-\mu )(U+Z)}{u^5}+\frac{\mu (V+Z)}{v^5} \right) \lambda \\&\quad + \left( 1+\frac{(1-\mu )U}{u^5}+\frac{\mu V}{v^5}\right) \left( 1+\frac{(1-\mu )Z}{u^5}+\frac{\mu Z}{v^5} \right) \\&\quad -\frac{1}{4} \left( \frac{(1-\mu )W_1}{u^5}-\frac{\mu W_2}{v^5} \right) ^2=0,\\&\lambda _1=\frac{1}{2}\left( 2-\frac{2(1-\mu )}{u^5}-\frac{2\mu }{v^5}+\frac{3(1-\mu )}{u^3}+\frac{3\mu }{v^3} -\frac{3}{u^3v^3}\sqrt{\Delta }\right) ,\\&\lambda _2=\frac{1}{2}\left( 2-\frac{2(1-\mu )}{u^5}-\frac{2\mu }{v^5}+\frac{3(1-\mu )}{u^3}+\frac{3\mu }{v^3} +\frac{3}{u^3v^3}\sqrt{\Delta }\right) . \end{aligned} \end{aligned}$$

(5.26)

where

$$\begin{aligned} \Delta =(\mu u^3+(1-\mu )v^3)^2-\mu (1-\mu )uv\left( -u^4-v^4+2u^2+2v^2+2u^2v^2-1\right) . \end{aligned}$$

When u and v are close to 1, which is the case when $c_1,c_2,c_3$ are close to 0, we have that $\lambda _1,\lambda _2>0$ and $\lambda _1\ne \lambda _2$.

Since the matrix M is symmetric, its eigenvalues $\lambda _1$ and $\lambda _2$ are real, and the corresponding eigenvectors are orthogonal. Let $v_1$ be an eigenvector for $\lambda _1$, i.e., $Mv_1=\lambda _1v_1$, such that $\Vert v_1 \Vert =1$, and $v_2$ be an eigenvector for $\lambda _2$, i.e., $Mv_2=\lambda _2v_2$, such that $\Vert v_2 \Vert =1$. The expressions of these eigenvalues are given in “Appendix A.” The associated matrix $C=\text {col}(v_2,v_1)$ is orthogonal, i.e., $C^{T}=C^{-1}$, so C defines a rotation in the xy-plane.

The equations of motion for the planar case can be written as

$$\begin{aligned} \ddot{q}-2 J \dot{q}=M q-\frac{q}{\Vert q\Vert ^3} +\frac{{3c_3}q}{\Vert q \Vert ^5}, \end{aligned}$$

where

$$\begin{aligned} J= \left( {\begin{array}{cc} 0 &{} 1 \\ -1 &{} 0 \ \end{array} } \right) . \end{aligned}$$

Consider the linear change of variable $q=C\bar{q}$ with $\bar{q} = (\bar{x},\bar{y})^T$. By substituting the new variable and multiplying $C^{-1}$ from the left, we obtain

$$\begin{aligned} C^{-1}C\ddot{\bar{q}}-2C^{-1} J C\dot{\bar{q}}=C^{-1}MC\bar{q}-\frac{C^{-1}C\bar{q}}{\Vert \bar{q} \Vert ^3}+ \frac{3c_3C^{-1}C\bar{q}}{\Vert \bar{q} \Vert ^5}. \end{aligned}$$

Notice that $D=C^{-1}MC$ is the diagonal matrix $D=\text {diag}(\lambda _2,\lambda _1)$, that is $\Vert C \bar{q} \Vert ^3=\Vert \bar{q} \Vert ^3$. Therefore, the equation becomes

$$\begin{aligned} \ddot{\bar{q}}-2C^{-1} J C\dot{\bar{q}}=D\bar{q} -\frac{\bar{q}}{\Vert \bar{q} \Vert ^3}+ \frac{3c_3\bar{q}}{\Vert \bar{q} \Vert ^5}. \end{aligned}$$

Recall that $v_1=(v_{11},v_{12})^T$, $v_2=(v_{21},v_{22})^T$ and $C=\text {col}(v_2,v_1)$. Since C is unitary, we have $C^{-1}=C^{T}$ and moreover

$$\begin{aligned} C^{-1} J C= \left( {\begin{array}{cc} 0 &{} v_{12}v_{21}-v_{11}v_{22} \\ -(v_{12}v_{21}-v_{11}v_{22}) &{} 0 \ \end{array} } \right) . \end{aligned}$$

A direct computation shows that $v_{12}v_{21}-v_{11}v_{22}=1$, which implies $C^{-1} J C= J$. Since $C^{-1} J C=C^T J C=J$, the matrix C is symplectic by definition. Therefore, the change of coordinates is symplectic. Thus, the equations of motion can be written as

$$\begin{aligned} \ddot{\bar{q}}-2 J\dot{\bar{q}}=D\bar{q}-\frac{\bar{q}}{\Vert \bar{q} \Vert ^3}+ \frac{3c_3\bar{q}}{\Vert \bar{q} \Vert ^5}. \end{aligned}$$

For $\mu \in [0,\frac{1}{2})$, we obtain the equations

$$\begin{aligned} \begin{aligned}&\ddot{\bar{x}}-2\dot{\bar{y}}=\bar{\Omega }_{\bar{x}}\\&\ddot{\bar{y}}+2\dot{\bar{x}}=\bar{\Omega }_{\bar{y}} \end{aligned} \end{aligned}$$

(5.27)

with

$$\begin{aligned} \begin{aligned} \bar{\Omega }(\bar{x},\bar{y}) =&\frac{1}{2}(\lambda _2\bar{x}^2+\lambda _1\bar{y}^2) -\frac{(1-\mu )c_1}{u^3}- \frac{\mu c_2}{v^3} +\frac{1}{\Vert \bar{q}\Vert }-\frac{c_3}{\Vert \bar{q}\Vert ^3}. \end{aligned} \end{aligned}$$

(5.28)

From the expressions for $\bar{\Omega }_{\bar{x}}$ and $\bar{\Omega }_{\bar{y}}$, we notice the symmetry properties:

$$\begin{aligned} \bar{\Omega }_{\bar{x}}(\bar{x},-\bar{y})=\bar{\Omega }_{\bar{x}}(\bar{x},\bar{y})\ ,\qquad \bar{\Omega }_{\bar{y}}(\bar{x},-\bar{y})=-\bar{\Omega }_{\bar{x}}(\bar{x},\bar{y}). \end{aligned}$$

Using these properties, we see that the equations (5.27) are invariant under the transformations $\bar{x}\rightarrow \bar{x}$, $\bar{y} \rightarrow -\bar{y}$, $\dot{{\bar{x}}}\rightarrow -\dot{{\bar{x}}}$, $\dot{{\bar{y}}} \rightarrow \dot{{\bar{y}}}$, $\ddot{{\bar{x}}} \rightarrow \ddot{{\bar{x}}}$ and $\ddot{{\bar{y}}}\rightarrow -\ddot{{\bar{y}}}$.

If we now go back to the spatial problem, we need to replace ${\bar{\Omega }}$ by

$$\begin{aligned} \begin{aligned} \bar{\Omega }(\bar{x},\bar{y},\bar{z})=&\frac{1}{2}(\lambda _2\bar{x}^2+\lambda _1\bar{y}^2)-\frac{1}{2}\left( \frac{(1-\mu )}{u^3}+\frac{\mu }{v^3}\right) {\bar{z}^2} \\&\, + \left( \frac{(1-\mu )c_1}{u^3}\right) \left( 3\left( \frac{\bar{z}}{u}\right) ^2-1\right) + \left( \frac{\mu c_2}{v^3}\right) \left( 3\left( \frac{\bar{z}}{v}\right) ^2-1\right) \\&\, +\frac{1}{r}+\left( \frac{c_3}{r^3}\right) \left( 3\left( \frac{\bar{z}}{r}\right) ^2- 1\right) . \end{aligned} \end{aligned}$$

(5.29)

We can write $\bar{\Omega }(\bar{x},\bar{y},\bar{z})=\frac{1}{2}\bar{x}^2+\frac{1}{2}\bar{y}^2+{\bar{U}}(\bar{x},\bar{y},\bar{z})$, with ${\bar{U}}$ given by

$$\begin{aligned} \begin{aligned} \bar{U}(\bar{x},\bar{y},\bar{z})=&\left( \frac{\lambda _2-1}{2}\right) \bar{x}^2+\left( \frac{\lambda _1-1}{2}\right) \bar{y}^2 -\frac{1}{2}\left( \frac{(1-\mu )}{u^3}+\frac{\mu }{v^3}\right) {\bar{z}^2}\\&+ \left( \frac{(1-\mu )c_1}{u^3}\right) \left( 3\left( \frac{\bar{z}}{u}\right) ^2-1\right) + \left( \frac{\mu c_2}{v^3}\right) \left( 3\left( \frac{\bar{z}}{v}\right) ^2-1\right) \\&+\frac{1}{r} - \frac{c_3 }{ r^{3}} +\frac{3c_3 \bar{z}^2}{r^{5}}. \end{aligned} \end{aligned}$$

(5.30)

In conclusion, the Hamiltonian in these new coordinates is given by the following expression (we omit the bars for x, y and z to simplify the notation):

$$\begin{aligned} \begin{aligned} H(x,y,z,p_x,p_y,p_z)&=\frac{1}{2}(p_x^2+p_y^2+p_z^2)+y p_x-xp_y\\&\quad +\left( \frac{1-\lambda _2}{2}\right) x^2+\left( \frac{1-\lambda _1}{2}\right) y^2 +\frac{1}{2}\left( \frac{(1-\mu )}{u^3}+\frac{\mu }{v^3}\right) {{z}^2}\\&\quad - \left( \frac{(1-\mu )c_1}{u^3}\right) \left( 3\left( \frac{{z}}{u}\right) ^2-1\right) - \left( \frac{\mu c_2}{v^3}\right) \left( 3\left( \frac{{z}}{v}\right) ^2-1\right) \\&\quad -\frac{1}{r} + \frac{c_3}{ r^{3}} -\frac{3c_3{z}^2}{r^{5}}. \end{aligned} \end{aligned}$$

Substituting $r=(x^2+y^2+z^2)^{\frac{1}{2}}$, we obtain (5.23). $\square$

Remark 5.6

If we let $C^i_{20}=0$ for $i=1,2,3$ and $\mu =0$ in (5.23), we obtain the Hamiltonian for the classical lunar Hill problem, see, e.g., Meyer and Schmidt (1982).

6 Linear Stability Analysis of the Hill Four-Body Problem with Oblate Bodies

In this section we determine the equilibrium points associated with the potential in (5.29) and we analyze their linear stability.

6.1 The Equilibrium Points of the System

To find the equilibrium points of (5.23), we have to solve the system:

$$\begin{aligned} \left. \begin{array}{ll} \Omega _{x} = 0\\ \Omega _{y} = 0\\ \Omega _{z} = 0 \end{array} \right\} \Rightarrow \left. \begin{array}{ll} \displaystyle \left( \lambda _2 -\frac{1}{r^3}+\frac{3c_3}{r^5}-\frac{15c_3 z^2}{r^7}\right) x:=Ax =0\\ \displaystyle \left( \lambda _1 -\frac{1}{r^3}+\frac{3c_3}{r^5}-\frac{15c_3 z^2}{r^7} \right) y :=B y= 0\\ \displaystyle \left( \gamma -\frac{1}{r^3}+\frac{9c_3}{r^5}-\frac{15c_3z^2}{r^7} \right) z:=C z = 0 \end{array} \right\} \end{aligned}$$

where $\Omega$ is the effective potential (5.29) (again we omit the bars), and

$$\begin{aligned} \gamma :=-\left[ \frac{(1-\mu )}{u^3}+\frac{\mu }{v^3}\right] +\frac{6(1-\mu )c_1}{u^5}+\frac{6 \mu c_2}{v^5}. \end{aligned}$$

(6.1)

In the above expressions A and B cannot simultaneously equal to 0 since

$$\begin{aligned} A-B=\lambda _2-\lambda _1 \end{aligned}$$

and $\lambda _1\ne \lambda _2$. Also, A and C, or B and C, cannot simultaneously equal to 0, since

$$\begin{aligned}A-C=\lambda _2+\frac{(1-\mu )}{u^3}+\frac{\mu }{v^3} - \frac{6(1-\mu )c_1}{u^5}-\frac{6 \mu c_2}{v^5}-\frac{6c_3}{r^5} >0\end{aligned}$$

because $c_i \leqslant 0$ for $i=1,2,3$, and $\lambda _1,\lambda _2>0$. A similar argument holds for B and C. This implies that for example, if $A= 0$, then $B\ne 0$ and $C\ne 0$, so $y=z=0$ and x is given by the equation $A=0$; the same reasoning applies for the other combinations of variables. Thus, all equilibrium points must lie on the x-, y-, z-coordinate axes. Precisely, we have the following results.

(i):

Equilibrium points on the x-axis: In the case $A= 0$, $B\ne 0$, $C\ne 0$, we must have $y=z=0$. From $A=0$ and $z=0$ we infer

$$\begin{aligned} h_A(r):=\lambda _2-\frac{1}{r^3}+\frac{3c_3 }{r^5}=0. \end{aligned}$$

We have $\displaystyle h'_A(r)= \frac{3}{r^4}-\frac{15c_3}{r^6}>0$, since $c_3<0$; also, $\lim _{r\rightarrow 0}h_A(r)=-\infty$ and $\lim _{r\rightarrow \infty }h_A(r)=\lambda _2>0$. Hence, the equation $h_A(r)=0$ has a unique solution $r^*_x>0$, yielding the equilibrium points $(\pm r^*_x,0,0)$.

(ii):

Equilibrium points on the  y-axis: In the case $B= 0$, $A\ne 0$, $C\ne 0$, we must have $x=z=0$. From $B=0$ and $z=0$ we infer

$$\begin{aligned} h_B(r):=\lambda _1-\frac{1}{r^3}+\frac{3c_3}{r^5}=0. \end{aligned}$$

We have $\displaystyle h'_B(r)= \frac{3}{r^4}-\frac{15c_3}{r^6}>0$, since $c_3<0$; also, $\lim _{r\rightarrow 0}h_B(r)=-\infty$ and $\lim _{r\rightarrow \infty }h_B(r)=\lambda _1>0$. Hence, the equation $h_B(r)=0$ has a unique solution $r^*_y>0$, yielding the equilibrium points $(0,\pm r^*_y,0)$.

(iii):

Equilibrium points on the  z-axis: In the case $C= 0$, $A\ne 0$, $B\ne 0$, we must have $x=y=0$, so $z=\pm r$. Hence, $C=0$ implies

$$\begin{aligned} \gamma -\frac{1}{r^3}-\frac{6c_3}{r^5} =\frac{\gamma r^5-r^2-6c_3}{r^5} =0.\end{aligned}$$

Since $c_1,c_2\leqslant 0$ we have that $\gamma <0$. Let $h_C(r)=\gamma r^5-r^2-6c_3$. We have $h'_C(r)=5\gamma r^4-2r<0$; also, $\lim _{r\rightarrow 0} h_C(r)=-6c_3 >0$ and $\lim _{r\rightarrow +\infty } h_C(r)=-\infty$. Hence, the equation $h_C(r)=0$ has a unique solution $r^*_z>0$, yielding the equilibrium points $(0,0,\pm r^*_z)$.

In the case of the Sun–Jupiter–Hektor system, in normalized units, we obtain $\lambda _1=0.002144499689960222$, $\lambda _2=2.9978555002506795$ and the equilibrium points location are given as follows:

	x	y	z
x-equilibria	$\pm 0.6935267570$	0	0
y-equilibria	0	$\pm 7.7545750772$	0
z-equilibria	0	0	$\pm 0.0008923544$

We remark that in the case of the Hill’s four-body problem with non-oblate bodies (i..e., point masses), the x-equilibria and the y-equilibria also exist, see Burgos-García and Gidea (2015); their locations, in the case of Hektor, are very close to the ones in the case of an oblate tertiary. Precisely, we have the following

	x	y	z
x-equilibria	$\pm 0.6935265657$	0	0
y-equilibria	0	$\pm 7.7545747024$	0

This result leads us to conclude that the x-equilibria and the y-equilibria for the Hill’s problem with oblate bodies are continuations of the ones for the Hill problem with non-oblate bodies.

On the other hand, the z-equilibria do not exist for the Hill’s problem with non-oblate bodies. However, these z-equilibria are a continuation of the equilibria that appear in the $J_2$-problem; see Sect. 2.2. From the $J_2$-problem it can be derived that the distance from the z-equilibrium points to the center is given by ${\hat{r}}_z= R_3(-3C_{20})^{1/2}$. When we apply this formula in the case of Hektor, the numerical result is very close to the one found above.

To summarize, the Hill three-body problem has 2 equilibrium points, Hill’s four-body problem has 4 equilibrium points, and the Hill four-body problem with oblate bodies has 6 equilibrium points.

To convert to real units, the distances from the equilibrium points to the center need to be multiplied by $m_3^{1/3}$—due to the rescaling involved in the Hill procedure—, and by the unit of distance which in this case is the distance Sun–Jupiter. It follows that the x-equilibrium points are at a distance of 85, 512.774 km from the barycenter of Hektor, the y-equilibrium points are at 956, 149.451 km and the z-equilibrium points are at 110.028 km. As the smallest semi-minor axis of Hektor is 60 km, the z-equilibrium points are outside but very close to the body of the asteroid. The above computation uses the value of $C^3_{20}=-0.476775$ from Sect. 2.2 Instead, if we use $C^3_{20}=-0.15$, as provided by Marchis et al. (2014), we obtain that the z-equilibrium points are at 62 km from the barycenter, basically at the surface of the asteroid.

Since the shape of an asteroid and its oblateness are difficult to determine precisely, it is worth studying a range of values of the oblateness parameter. In Fig. 3 we plot the dependence on the $C^3_{20}$ of the distance from the z-equilibrium point to the barycenter (in km). The corresponding parameter $C^3_{20}$ ranges between $-\,0.001$ and $-\,0.95$. Note that for some values, the z-equilibrium points are outside the Brillouin sphere (which is the smallest sphere that contains the body), while for some others they are inside. The z-equilibria that are outside are an artifact of the model, as they do not make physical sense. However, the z-equilibria that are inside the Brillouin sphere of the asteroid are physically possible. See “Appendix B.”

Fig. 3

The dependence of the z-equilibrium point distance on $C^3_{20}$

6.2 Linear Stability of the Equilibrium Points

We study the linear stability of the equilibrium points in the case of Hektor.

The Hamiltonian (5.23) yields the following system of equations

$$\begin{aligned}&\dot{x}=v_x,&\dot{v}_x=2v_y+ \Omega _x,\\&\dot{y}=v_y,&\dot{v}_y=-v_x+ \Omega _y,\\&\dot{z}=v_z,&\dot{v}_z= \Omega _z, \end{aligned}$$

where $\Omega$ is the effective potential given by (5.29) (again, we omit the overline bar on the variables).

The second-order derivatives of $\Omega$ are given by

$$\begin{aligned} \begin{aligned} \Omega _{xx}&=\lambda _2-\frac{1}{r^3}+\frac{3x^2}{r^5}+\frac{3c_3}{r^5} -\frac{15c_3 x^2}{r^7}-\frac{15c_3 z^2}{r^7}+\frac{105c_3 z^2x^2}{r^9},\\ \Omega _{yy}&=\lambda _1-\frac{1}{r^3}+\frac{3y^2}{r^5}+\frac{3c_3}{r^5} -\frac{15c_3 y^2}{r^7}-\frac{15c_3 z^2}{r^7}+\frac{105c_3 z^2y^2}{r^9},\\ \Omega _{zz}&=\gamma -\frac{1}{r^3}+\frac{3z^2}{r^5}+\frac{9c_3}{r^5}-\frac{90c_3 z^2}{r^7}+\frac{105c_3 z^4}{r^9},\\ \Omega _{xy}&=\frac{3xy}{r^5}-\frac{15c_3 xy}{r^7}+\frac{105c_3 z^2xy}{r^9},\\ \Omega _{xz}&=\frac{3xz}{r^5}-\frac{45c_3 xz}{r^7}+\frac{105c_3 z^3x}{r^9},\\ \Omega _{yz}&=\frac{3yz}{r^5}-\frac{45c_3 yz}{r^7}+\frac{105c_3 z^3y}{r^9}. \end{aligned}\end{aligned}$$

(6.2)

The Jacobian matrix describing the linearized system is

$$\begin{aligned} \mathscr {J}=\left( \begin{array}{r@{\quad }r@{\quad }r@{\quad }r@{\quad }r@{\quad }r} 0 &{} 0 &{} 0 &{} 1 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 1 \\ \Omega _{xx} &{} \Omega _{xy} &{} \Omega _{xz} &{} 0 &{} 2 &{} 0 \\ \Omega _{yx} &{} \Omega _{yy} &{} \Omega _{yz} &{}-2 &{} 0 &{} 0 \\ \Omega _{zx} &{} \Omega _{zy} &{} \Omega _{zz} &{} 0 &{} 0 &{} 0 \\ \end{array} \right) . \end{aligned}$$

(6.3)

Since the equilibria are of the form $(\pm r^*_x,0,0)$, $(0,\pm r^*_y,0)$, $(0,0,\pm r^*_z)$, the mixed second-order partial derivatives $\Omega _{xy}$, $\Omega _{xz}$, $\Omega _{yz}$ vanish at each of the equilibrium points. Hence, Jacobian matrix (6.3) evaluated at the equilibria is of the form:

$$\begin{aligned} \mathscr {J}=\left( \begin{array}{r@{\quad }r@{\quad }r@{\quad }r@{\quad }r@{\quad }r} 0 &{} 0 &{} 0 &{} 1 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 1 \\ \Omega _{xx} &{}0 &{} 0 &{} 0 &{} 2 &{} 0 \\ 0 &{} \Omega _{yy} &{} 0 &{}-2 &{} 0 &{} 0 \\ 0 &{} 0 &{} \Omega _{zz} &{} 0 &{} 0 &{} 0 \\ \end{array} \right) , \end{aligned}$$

(6.4)

The characteristic equation of (6.4) is

$$\begin{aligned} (\rho ^2-\Omega _{zz})(\rho ^4+(4-\Omega _{xx}-\Omega _{yy})\rho ^2+\Omega _{xx}\Omega _{yy})=0. \end{aligned}$$

(6.5)

The stability of the equilibria depends on the signs of $\Omega _{zz}$ and of A, B, and D. We find the following stability character of the equilibrium positions in the case of the Sun–Jupiter–Hektor system:

i):

Eigenvalues of x-equilibria at $(\pm 0.6935267570, 0 ,0)$:

$$\begin{aligned}&2.5069424783&-2.5069424783,\\&2.0704830660 i,&-2.0704830660 i,\\&1.9995877290 i,&-1.9995877290 i. \end{aligned}$$

 Stability type: center $\times$ center $\times$ saddle.

ii):

Eigenvalues of y-equilibria at $(0, \pm 7.7545750772,0)$

$$\begin{aligned}&0.9890157325 i,&- 0.9890157325 i,\\&0.1403687326 i ,&- 0.1403687326 i,\\&1.0013166944 i,&-1.0013166944 i \end{aligned}$$

Stability type: center $\times$ center $\times$ center.

iii):

Eigenvalues of z-equilibria at $(0,0,\pm 0.0008923544)$:

$$\begin{aligned}&-37514.04321 + 0.9999999997 i&-37514.04321 - 0.9999999997 i\\&37514.04321 + 0.9999999997 i&37514.04321 - 0.9999999997 i\\&53052.86869 i&- 53052.86869 i \end{aligned}$$

Stability type: center $\times$ complex saddle.

Note that for the z-equilibria the imaginary part of the ‘Krein quartet’ of eigenvalues of z-equilibria is approximately $\pm 1$. This means that the infinitesimal motion around the equilibrium point is close to the 1 : 1 resonance with the rotation of the primary and the secondary. In Fig. 4 we show that for a range of $r^*_z$ values between $z= 0.0008923544$ (corresponding to the value for Hektor $c_3=-1.327161 \times 10^{-7}$) and $z=0.009999$ (corresponding to $c_3= -1.666271\times 10^{-5}$), the real part and the imaginary part of the ‘Krein quartet’ of eigenvalues; the imaginary part stays close to $\pm 1$.

Fig. 4

The dependence of the real part (left) and imaginary part (right) of the Krein quartet of eigenvalues on the z-equilibrium point. The horizontal axis represents the distance $r^*_z$ from the equilibrium point to the origin, the vertical axis the real part (left), and the absolute value of the imaginary part (right) of the eigenvalues. The former never changes sign, and the latter stays within $4\times 10^{-7}$ from 1

In Sect. 6.3.1 we will provide an analytic argument that the real part of the ‘Krein quartet’ of eigenvalues is always nonzero, and the imaginary part is close to $\pm 1$ for $r^*_z$ sufficiently small; this result will help us to explain the behavior observed in Fig. 4.

6.3 Analytical Results on the Linear Stability of Equilibria

We provide some analytical arguments for the linear stability of the equilibria. The problem has three parameters, $c_1,c_2,c_3$, which make the analysis quite complicated. To simplify, in this section we will assume that $c_1=c_2=0$ and study the stability of the equilibria for varying $c_3<0$. This simplifying assumption is justified by the fact that in the Hill problem, the contribution to the gravitational potential (5.19) of the term containing $c_3$ in a small neighborhood of the tertiary, that is, for $r\ll 1$, is much bigger than the contributions of the terms containing $c_1$ and $c_2$.

Also, we will rescale the sides of the triangular central configuration (3.13) differently, namely $r_{13}=r_{23}=1$ and $r_{12}=\upsilon$. Note that the triangular central configuration does not change when we rescale the unit of distance, only the constant $c_3$ get rescaled by a factor; see Remark 3.4. With this rescaling, the computations turn out to be somewhat easier. In this case, the eigenvalues of the matrix M in (5.25) are given by

$$\begin{aligned} \begin{aligned} \lambda _1&=\frac{3}{2}\left[ 1- \sqrt{1-(\mu -\mu ^2)\upsilon ^2(4-\upsilon ^2)}\right] ,\\ \lambda _2&=\frac{3}{2}\left[ 1+ \sqrt{1-(\mu -\mu ^2)\upsilon ^2(4-\upsilon ^2)}\right] , \end{aligned} \end{aligned}$$

(6.6)

and the constant $\gamma$ in (6.1) becomes $\gamma =-1$.

6.3.1 Linear Stability of the Equilibria on the z-Axis

The z-equilibrium points are of the form $(0,0,\pm r^*_z)$, with

$$\begin{aligned} -(r^*_z)^5-(r^*_z)^2-6c_3 =0, \end{aligned}$$

(6.7)

which yields

$$\begin{aligned} c_3=\frac{-(r^*_z)^2- (r^*_z)^5}{6}. \end{aligned}$$

(6.8)

Evaluating $\Omega _{xx}$, $\Omega _{yy}$, $\Omega _{zz}$ at the equilibrium point yields:

$$\begin{aligned}\begin{aligned} \Omega _{xx}&= \lambda _2 - (r^*_z)^{-3}-12c_3 (r^*_z)^{-5},\\ \Omega _{yy}&= \lambda _1 - (r^*_z)^{-3}-12c_3 (r^*_z)^{-5},\\ \Omega _{zz}&= -1+2(r^*_z)^{-3}+24c_3 (r^*_z)^{-5}. \end{aligned}\end{aligned}$$

Substituting (6.8) we obtain

$$\begin{aligned} \begin{aligned} \Omega _{xx}&=2+\lambda _2+(r^*_z)^{-3},\\ \Omega _{yy}&=2+\lambda _1+(r^*_z)^{-3},\\ \Omega _{zz}&=-5-2(r^*_z)^{-3}. \end{aligned}\end{aligned}$$

(6.9)

Using (5.26) and denoting $d:=\sqrt{1-(\mu -\mu ^2)\upsilon ^2(4-\upsilon ^2)}$ we can write

$$\begin{aligned} \begin{aligned} \lambda _1=\frac{3}{2}(1-d),\\ \lambda _2=\frac{3}{2}(1+d). \end{aligned} \end{aligned}$$

(6.10)

Also for $c_3=0$ we have $d_0=\sqrt{1-3(\mu -\mu ^2)}$ and

$$\begin{aligned} \begin{aligned} \lambda _{10}&=\frac{3}{2}(1-d_0),\\ \lambda _{20}&=\frac{3}{2}(1+d_0). \end{aligned} \end{aligned}$$

(6.11)

This is in agreement with the results in Burgos-García and Gidea (2015).

For future reference, we expand d as a power series in the parameter $c_3$ as

$$\begin{aligned} d=d_0+d_1 c_3+ O(c_3^2), \end{aligned}$$

(6.12)

where the coefficient $d_1$ can be obtained from the Taylor’s theorem around $c_3 = 0$ as

$$\begin{aligned} d_1=-\frac{2(\mu -\mu ^2)}{d_0}. \end{aligned}$$

(6.13)

From the characteristic equation (6.5), we obtain that the pair of eigenvalues $\rho _{1,2}=\pm (\Omega _{zz})^{1/2}$ is purely imaginary, since by (6.9), $\Omega _{zz}<0$.

The ‘Krein quartet’ eigenvalues are given by

$$\begin{aligned} \rho _{3,4,5,6}= \pm \sqrt{\frac{-A\pm \sqrt{A^2-4B}}{2}}, \end{aligned}$$

(6.14)

where

$$\begin{aligned} \begin{array}{lllll} A&{}=&{}\displaystyle 4-\Omega _{xx}-\Omega _{yy}&{}=&{}-3-\frac{2}{(r^*_z)^3},\\ B&{}=&{}\Omega _{xx}\Omega _{yy}&{}=&{}\displaystyle 10+{9\over 4} \upsilon ^2(4-\upsilon ^2)(\mu -\mu ^2) +\frac{7}{(r^*_z)^3}+\frac{1}{(r^*_z)^6}. \end{array} \end{aligned}$$

Then, we have

$$\begin{aligned} D:=A^2-4B= d^2-40-\frac{16}{(r^*_z)^3}=-31-9\upsilon ^2(4-\upsilon ^2)(\mu -\mu ^2)-\frac{16}{(r^*_z)^3}<0. \end{aligned}$$

Since $-A>0$ and $D<0$, we obtain that the eigenvalues $\rho _{3,4,5,6}$ are complex numbers, non-real, non-purely-imaginary, for all parameter values. Let $\rho =a+ib$ be such that $\rho ^2=-\frac{A}{2}\pm \frac{\sqrt{4B-A^2}}{2}i:=\alpha +i\beta$. We have

$$\begin{aligned} a+ib=\left( \frac{(\alpha ^2+\beta ^2)^{\frac{1}{2}}+\alpha }{2}\right) ^{\frac{1}{2}}+ \text {sign}(\beta )\left( \frac{(\alpha ^2+\beta ^2)^{\frac{1}{2}}-\alpha }{2}\right) ^{\frac{1}{2}}\ i. \end{aligned}$$

To show that b is approximately $\pm 1$, or $b^2\approx 1$, for $r^*_z\approx 0$, note that

$$\begin{aligned}\begin{aligned} b^2=&\frac{(\alpha ^2+\beta ^2)^{\frac{1}{2}}-\alpha }{2}=\frac{A}{4}+\frac{\sqrt{B}}{2}\\ =&-\frac{3}{4}+\frac{1}{2}\left[ \left( 10+\frac{9}{4}\Upsilon +\frac{7}{(r^*_z)^3}+ \frac{1}{(r^*_z)^6} \right) ^{\frac{1}{2}}-\frac{1}{(r^*_z)^3}\right] \\ =&-\frac{3}{4}+\frac{1}{2}\frac{10+\frac{9}{4}\Upsilon +\frac{7}{(r^*_z)^3}+ \frac{1}{(r^*_z)^6} -\frac{1}{(r^*_z)^6}}{\left( 10+\frac{9}{4}\Upsilon +\frac{7}{(r^*_z)^3}+ \frac{1}{(r^*_z)^6} \right) ^{\frac{1}{2}}+\frac{1}{(r^*_z)^3}}\\ =&-\frac{3}{4}+\frac{1}{2}\frac{10+\frac{9}{4}\Upsilon +\frac{7}{(r^*_z)^3}}{\left( 10+\frac{9}{4}\Upsilon +\frac{7}{(r^*_z)^3}+ \frac{1}{(r^*_z)^6} \right) ^{\frac{1}{2}}+\frac{1}{(r^*_z)^3}}, \end{aligned} \end{aligned}$$

where $\Upsilon :=\upsilon ^2(4-\upsilon ^2)(\mu -\mu ^2)$. Since

$$\begin{aligned} \lim _{r^*_z\rightarrow 0} \frac{10+\frac{9}{4}\Upsilon +\frac{7}{(r^*_z)^3}}{\left( 10+\frac{9}{4}\Upsilon +\frac{7}{(r^*_z)^3}+ \frac{1}{(r^*_z)^6} \right) ^{\frac{1}{2}}+\frac{1}{(r^*_z)^3}} = \frac{7}{2}, \end{aligned}$$

we have that $\lim _{r^*_z\rightarrow 0} b^2=-\frac{3}{4}+\frac{7}{4}=1$, so $b^2\approx 1$ for $r^*_z\approx 0$, as in the case of Hektor.

We obtained the following result:

Proposition 6.1

Consider the equilibria on the z-axis. For $\mu \in (0,1/2]$, $\Omega _{zz}$, A and D are negative. Consequently, one pair of eigenvalues is purely imaginary, and the two other pairs of eigenvalues are complex conjugate, with the imaginary part close to $\pm i$ for $c_1=c_2=0$ and for $c_3$ negative and sufficiently small. The linear stability is of center $\times$ complex-saddle type.

6.3.2 Linear Stability of the Equilibria on the y-Axis

The y-equilibrium points are of the form $(0,\pm r^*_y,0)$, with

$$\begin{aligned} \lambda _1 (r^*_y)^5-(r^*_y)^2+3c_3=0, \end{aligned}$$

(6.15)

which yields

$$\begin{aligned} c_3=\frac{(r^*_y)^2-\lambda _1 (r^*_y)^5}{3}. \end{aligned}$$

(6.16)

Evaluating $\Omega _{xx}$, $\Omega _{yy}$, $\Omega _{zz}$ at the equilibrium point yields:

$$\begin{aligned} \begin{aligned} \Omega _{xx}&=\lambda _2-\frac{1}{(r^*_y)^3}+\frac{3c_3}{(r^*_y)^5},\\ \Omega _{yy}&=\lambda _1+\frac{2}{(r^*_y)^3}-\frac{12c_3}{(r^*_y)^5}, \\ \Omega _{zz}&= -1-\frac{1}{(r^*_y)^3}+\frac{9c_3}{(r^*_y)^5}. \end{aligned}\end{aligned}$$

(6.17)

Substituting $c_3$ from (6.16) we obtain

$$\begin{aligned} \begin{aligned} \Omega _{xx}&=\lambda _2-\lambda _1 ,\\ \Omega _{yy}&= 5\lambda _1-\frac{2}{(r^*_y)^3}, \\ \Omega _{zz}&= -1-3\lambda _1+\frac{2}{(r^*_y)^3}, \end{aligned}\end{aligned}$$

(6.18)

We also expand $r^*_y$ as a power series in the parameter $c_3$ as

$$\begin{aligned} r^*_y=r_{y0}+r_{y1} c_3+O(c_3^2), \end{aligned}$$

(6.19)

where $\pm r_{y0}$ is the position of the y-equilibrium in the case when $c_3=0$, which is given by $r_{y0}^3=1/\lambda _{10}$; this is in agreement with Burgos-García and Gidea (2015). The computation of $r_{y1}$ yields

$$\begin{aligned} r_{y1}= \frac{-1 +(1/2)d_1r_{y0}^5}{r_{y0}}, \end{aligned}$$

(6.20)

with $d_1$ as in (6.13).

We will also need $\frac{1}{(r^*_y)^3}$ as a power series in the parameter $c_3$

$$\begin{aligned} \frac{1}{(r^*_y)^3}=\alpha +\beta c_3+O(c_3^2), \end{aligned}$$

(6.21)

and a simple calculation yields

$$\begin{aligned} \begin{aligned} \alpha&=\frac{1}{r_{y0}^3},\\ \beta&= -\frac{3r_{y1}}{r_{y0}^4}. \end{aligned} \end{aligned}$$

(6.22)

For $\mu =1/2$, we have $d_0=\frac{1}{2}$, $\lambda _{10}=\frac{3}{4}$, $d_1=-m_3^{2/3}$, $r_{y0}=\left( \frac{4}{3}\right) ^{1/3}$. It is easy to see that dominant part $d_0$ of d is a strictly decreasing function with respect to $\mu \in (0,1/2]$ and takes values in [1/2, 1). The dominant part $\lambda _{10}$ of $\lambda _1$ is increasing with respect to $\mu \in (0,1/2]$ and takes values in (0, 3/4] . Also, the dominant part $r_{y0}$ of $r^*_y$ is a strictly decreasing function in $\mu \in (0,1/2]$, where $r_{y0}(1/2)=\root 3 \of {4/3}$ and $r_{y0}\rightarrow \infty$ when $\mu \rightarrow 0$; as a consequence, the values of $r_{y0}$ are in the interval $[\root 3 \of {4/3},\infty )$.

From (6.17) we have

$$\begin{aligned}\begin{aligned} \Omega _{zz}&=-1-\frac{1}{(r^*_y)^3}+\frac{9c_3}{(r^*_y)^5}\\&= -\frac{1}{(r^*_y)^5}((r^*_y)^5+(r^*_y)^2-9c_3)\\&< 0 \end{aligned}\end{aligned}$$

since $r^*_y>0$ and $c_3$ is negative. Therefore, $\Omega _{zz}<0$ for all admissible values of $\mu$.

For $A=4-\Omega _{xx}-\Omega _{yy}$, using (6.11) and the expansions (6.12) and (6.21), we obtain

$$\begin{aligned}\begin{aligned} A&= 1-3\lambda _1 +\frac{2}{(r^*_y)^3}\\&= 1-3\lambda _{10}+\frac{2}{(r_{y0})^3}+O(c_3)\\&= 1-3\lambda _{10}+2\lambda _{10}+O(c_3)\\&> 0 \end{aligned}\end{aligned}$$

for $c_3$ small.

For $B=\Omega _{xx}\Omega _{yy}$ using (6.11) and the expansions (6.12) and (6.21), we obtain

$$\begin{aligned}\begin{aligned} B&= (\lambda _2-\lambda _1)\left( 5\lambda _1 -\frac{2}{(r^*_y)^3}\right) \\&= (3d)\left( \frac{15}{2} -\frac{15d}{2} -\frac{2}{(r^*_y)^3}\right) \\&= (3d_0)\left( 5\lambda _{10}-\frac{2}{r_{y0}^3}\right) +O(c_3)\\&= (3d_0)\left( 5\lambda _{10}-2\lambda _{10}\right) +O(c_3)\\&> 0 \end{aligned}\end{aligned}$$

for $c_3$ small.

For $D=A^2-4B$, using (6.11) and the expansions (6.12) and (6.21), we have

$$\begin{aligned} \begin{aligned} D&=\left( 1-3\lambda _{10}+\frac{2}{r_{y0}^3}\right) ^2-4(3d_0)\left( 5\lambda _{10}-\frac{2}{r_{y0}^3}\right) +O(c_3)\\&=\left( 1-\lambda _{10}\right) ^2-12(3-2\lambda _{10})\lambda _{10}+O(c_3). \end{aligned} \end{aligned}$$

For $\mu \approx 0$ we have $D\approx 1+O(c_3)$ and for $\mu =1/2$ we have $D=-\frac{215}{16}+O(c_3)$. The intermediate value theorem implies that D changes its sign from positive to negative for $\mu \in (0,1/2]$, provided $c_3$ is small. We have thus proved the following result:

Proposition 6.2

Consider the equilibria on the y-axis. For $\mu \in (0,1/2]$ for $c_1=c_2=0$ and for $c_3$ negative and sufficiently small, $\Omega _{zz}$ is always negative, the coefficients A and B are always positive, and the value of the discriminant D changes from positive to negative values. Consequently, one pair of eigenvalues is always purely imaginary, and there exists $\mu _*$, depending on $c_3$, where the other two pairs of eigenvalues change from being purely imaginary to being complex conjugate. The linear stability changes from center $\times$ center $\times$ center type to center $\times$ complex-saddle type.

6.3.3 Linear Stability of the Equilibria on the x-Axis

The x-equilibrium points are of the form $(\pm r^*_x, 0,0)$, with

$$\begin{aligned} \lambda _2(r^*_x)^5-(r^*_x)^2+3c_3=0, \end{aligned}$$

(6.23)

which yields

$$\begin{aligned} c_3=\frac{(r^*_x)^2-\lambda _2 (r^*_x)^5}{3}. \end{aligned}$$

(6.24)

Evaluating $\Omega _{xx}$, $\Omega _{yy}$, $\Omega _{zz}$ at the equilibrium point yields:

$$\begin{aligned} \begin{aligned} \Omega _{xx}&=\lambda _2+\frac{2}{(r^*_x)^3}-\frac{12c_3}{(r^*_x)^5},\\ \Omega _{yy}&=\lambda _1-\frac{1}{(r^*_x)^3}+\frac{3c_3}{(r^*_x)^5}, \\ \Omega _{zz}&= -1-\frac{1}{(r^*_x)^3}+\frac{9c_3}{(r^*_x)^5}. \end{aligned} \end{aligned}$$

(6.25)

Substituting $c_3$ from (6.24) we obtain

$$\begin{aligned} \begin{aligned} \Omega _{xx}&=5\lambda _2-\frac{2}{(r^*_x)^3} ,\\ \Omega _{yy}&= \lambda _1-\lambda _2, \\ \Omega _{zz}&= -1-3\lambda _2+\frac{2}{(r^*_x)^3}, \end{aligned} \end{aligned}$$

(6.26)

We expand $r^*_x$ as a power series in the parameter $c_3$ as

$$\begin{aligned} r^*_x=r_{x0}+r_{x1} c_3+ O(c_3^2), \end{aligned}$$

(6.27)

where $\pm r_{x0}$ is the position of the x-equilibrium in the case when $c_3=0$, which is given by $r_{x0}^3=1/\lambda _{20}$; see Burgos-García and Gidea (2015). The computation of $r_{x1}$ yields

$$\begin{aligned} r_{x1}= \frac{-1-(1/2)d_1r_{x0}^5}{r_{x0}}. \end{aligned}$$

(6.28)

We will also need $\frac{1}{(r^*_x)^3}$ as a power series in the parameter $c_3$

$$\begin{aligned} \frac{1}{(r^*_x)^3}=\alpha '+\beta ' c_3+O(c_3^2), \end{aligned}$$

(6.29)

and a simple calculation yields

$$\begin{aligned} \begin{aligned} \alpha ' =&\frac{1}{r_{x0}^3},\\ \beta ' =&-\frac{3r_{x1}}{r_{x0}^4}. \end{aligned} \end{aligned}$$

(6.30)

From (6.25) we have

$$\begin{aligned} \begin{aligned} \Omega _{zz}&= -1-\frac{1}{(r^*_x)^3}+\frac{9c_3}{(r^*_x)^5}\\&=-\frac{1}{(r^*_x)^5}((r^*_x)^5+(r^*_x)^2-9c_3)\\&<0 \end{aligned} \end{aligned}$$

since $r^*_x>0$ and $c_3<0$. Therefore, $\Omega _{zz}<0$ for all admissible values of $\mu$.

For $A=4-\Omega _{xx}-\Omega _{yy}$, using (6.11) and the expansions (6.12) and (6.29), we obtain

$$\begin{aligned}\begin{aligned} A&= 1-3\lambda _{20}+\frac{2}{(r_{x0})^3}+O(c_3)\\&= 1-\lambda _{20}+O(c_3)\\&=-\frac{1}{2}-\frac{3}{2}d_0+O(c_3)\\&< 0 \end{aligned}\end{aligned}$$

for $c_3$ small.

For $B=\Omega _{xx}\Omega _{yy}$, using (6.11) and the expansions (6.12) and (6.29), we obtain

$$\begin{aligned} \begin{aligned} B&= -(3d_0)\left( 5\lambda _{20}-\frac{2}{r_{x0}^3}\right) +O(c_3)\\&= -(3d_0)\left( 5\lambda _{20}-2\lambda _{20}\right) +O(c_3)\\&=-9d_0\left( \frac{3}{2}+\frac{3}{2}d_0\right) \\&< 0 \end{aligned} \end{aligned}$$

for $c_3$ small.

For $D=A^2-4B$, using (6.11) and the expansions (6.12) and (6.29), we have

$$\begin{aligned}\begin{aligned} D&=\left( 1-\lambda _{20}\right) ^2+36d_0\lambda _{20}+O(c_3)\\&>0. \end{aligned}\end{aligned}$$

for $c_3$ small.

We have proved the following result:

Proposition 6.3

Consider the equilibria on the x-axis. For $\mu \in (0,1/2]$, for $c_1=c_2=0$ and for $c_3$ negative and sufficiently small, $\Omega _{zz}$ is negative, A and B are negative, and the value of the discriminant D is always positive. Consequently, two pairs of eigenvalues are purely imaginary, and one pair of eigenvalues are real (one positive and one negative). The linear stability is of center $\times$ center $\times$ saddle type.

7 Conclusions

In this paper we have developed a rigorous model of a Hill four-body problem with oblate bodies, which can be used for analytical studies.

In Proposition 3.1 we determined the triangular central configurations of three oblate bodies, which are found to be scalene triangles. Triangles corresponding to different moments of inertia are not necessarily similar to one another. This situation is very different from the case when the bodies are point-masses, when the central configurations are equilateral triangles.

Assuming that the three heavy bodies are in such a triangular central configurations, in Theorem 5.1 we derived, starting from the spatial circular restricted four-body problem, the Hill approximation. Our Hill approximation is different from the one in the case when the bodies are point-masses, due to the different type of triangular central configuration and of the oblateness effects. The Hill approximation acts like a ‘magnifying glass’ in a neighborhood of the smallest body, by sending the two larger bodies at infinite distance via a limiting procedure. The effect of the two larger bodies is represented in the Hamiltonian by a quadratic polynomial, while in the restricted four-body problem, their effect is represented by singular terms.

The fact that the Hamiltonian for the Hill approximation has a simpler form allows us to study analytically the equilibrium points and their stability, as in Proposition 6.1, Proposition 6.3, and Proposition 6.2. By contrast, in the restricted four-body problem such a study is only possible numerically.

An interesting feature of our model is the presence of ‘out-of-plane’ equilibria. These may be physically possible only when they are very close to the barycenter of the smallest body, and only for certain shapes. We describe a toy-model that has true ‘out-of-plane’ equilibria in “Appendix B.”

Appendices

Appendix A: Expressions for the Eigenvectors of the Matrix M in (5.25)

Below we provide the expressions of the eigenvectors $v_1$, $v_2$ associated with the eigenvalues (5.26), respectively. Denote

$$\begin{aligned} \Theta :=\sqrt{-u^4-v^4+2 u^2+2 v^2+2 u^2 v^2-1}.\end{aligned}$$

We have

$$\begin{aligned} \begin{aligned} v_1=&\left[ -\left( (1-\mu )(-v^7+(1+u^2)v^5)-\mu (-u^7+(1+v^2)u^5)\right) \Theta ,\right. \\&\quad (1-\mu )(v^9-2(1+u^2)v^7+v^5(1+u^4))\\&\quad +\mu (u^9-2(1+v^2)u^7+u^5(1+v^4))\\&\quad \left. - \sqrt{2}u^2v^2\sqrt{((1-\mu )v^3+\mu u^3)^2-\mu (1-\mu )uv\Theta ^2}\right] ,\\ v_2=&\left[ -\left( (1-\mu )(-v^7+(1+u^2)v^5)-\mu (-u^7+(1+v^2)u^5)\right) \Theta ,\right. \\&\quad (1-\mu )(v^9-2(1+u^2)v^7+v^5(1+u^4))\\&\quad +\mu (u^9-2(1+v^2)u^7+u^5(1+v^4))\\&\quad \left. + \sqrt{2}u^2v^2\sqrt{((1-\mu )v^3+\mu u^3)^2-\mu (1-\mu )uv\Theta ^2}\right] \end{aligned} \end{aligned}$$

(A.1)

Appendix B: Existence of ‘Out-of Plane’ Equilibria

The existence of ‘out-of-plane’ equilibria near an oblate asteroid, such as the z-equilibrium points found in Sect. 6.2, does not agree with the physical intuition, as it seems that the combined gravitational force acting on the infinitesimal mass must be pointing toward the $\{z=0\}$ plane.

Such ‘out-of-plane’ equilibria appear due to the $J_2$-approximation of the gravitational potential. The $J_2$-approximation is a truncation of the spherical harmonic series expansion of the gravitational potential. Such expansion is known to be convergent outside the Brillouin sphere (which is the smallest sphere that contains the body), while the nature of the series inside the Brillouin sphere is unknown in general. (For certain shapes, e.g., for ellipsoids, the series is divergent inside the Brillouin sphere).

Nan et al. (2018) shows analytically that ‘out-of-plane’ equilibrium points do not physically exist in the restricted three-body problem when one primary is a rotational ellipsoid. They note that the same conclusion can be drawn if both primaries are rotational ellipsoids. Their argument can also be carried out for the Hill four-body problem when all heavy bodies are rotational ellipsoids.

However, we shall note that for non-convex shapes, ‘out-of-plane’ equilibria are physically possible. We show a ‘rubble pile’-model that has true ‘out-of-plane’ equilibria. The model consists of six balls, with four identical larger balls of radius R and two identical smaller balls of radius r, arranged as in the left side of Fig. 5. The centers of the larger balls are at $(\pm 1,0, \pm R)$, and the centers of the smaller balls are at $(\pm r,0,0)$. The condition that the balls in the configuration are tangent is $r = 1/(2(1 + R))$. The right side of Fig. 5 represents the plot of the gravitational force along the z-axis, computed by direct numerical integration. The intersection points with the horizontal axis in this plot correspond to the z-values of the ‘out-of-plane’ equilibria. We note that such ‘out-of-plane’ equilibria exist only for certain ranges of values of R, and disappear through a saddle-node bifurcation. We plan to study families of such configurations in future works.

Fig. 5

Left: Six-ball ‘rubble-pile’ model. Right: the sgravitational force along the z-axis

Many small bodies in the solar system are believed to be ‘rubble piles’, consisting of smaller elements separated by voids. Moreover, many known asteroids have highly irregular shapes. Hence, the study of ‘out-of-plane’ equilibria for asteroids is an interesting problem, with possible applications to missions targeting asteroids.