Central Configurations of the Curved N-Body Problem

Abstract

We consider the N-body problem of celestial mechanics in spaces of nonzero constant curvature. Using the concept of effective potential, we define the moment of inertia for systems moving on spheres and hyperbolic spheres and show that we can recover the classical definition in the Euclidean case. After proving some criteria for the existence of relative equilibria, we find a natural way to define the concept of central configuration in curved spaces using the moment of inertia and show that our definition is formally similar to the one that governs the classical problem. We prove that, for any given point masses on spheres and hyperbolic spheres, central configurations always exist. We end with results concerning the number of central configurations that lie on the same geodesic, thus extending the celebrated theorem of Moulton to hyperbolic spheres and pointing out that it has no straightforward generalization to spheres, where the count gets complicated even for two bodies.

1 Introduction

Central configurations for the N-body problem of celestial mechanics were introduced by Pierre-Simon Laplace in 1789 in connection with the discovery of Eulerian and Lagrangian orbits and via Kepler’s laws in the flat case (Euler 1764; Lagrange 1772; Laplace 1891). But a first systematic study of this concept appeared only in 1900, when Dziobek (1900) published a fundamental paper on central configurations. Research in this direction has continued ever since, showing over the past decades that central configurations are essential for understanding the N-body problem. Although breakthroughs are rare in this difficult area of mathematics, some recent progress has been made on the Wintner–Smale conjecture, which we will discuss later.

1.1 Motivation

In 1772 Joseph Louis Lagrange found the equilateral solutions of the three-body problem and rediscovered the collinear orbits, whose existence Leonhard Euler had proved a decade earlier. These motions, called homographic because they stay similar to themselves for all time, can be decomposed into homothetic and relative equilibrium solutions. The former are dilations and/or contractions of the particle system without rotation, whereas the latter are rotations without dilations or contractions, such that the mutual distances remain constant during the motion. Starting from the homothetic Lagrangian orbits, Laplace noticed that it may be simpler to seek the configurations that remain similar to themselves, which we now call central configurations, instead of looking for the homographic solutions to the differential equations (Wintner 1947). Central configurations do not involve the time variable and are given by the system

$$\begin{aligned} \nabla U({\mathbf {q}})=\lambda \nabla I({\mathbf {q}}), \end{aligned}$$

where ${\mathbf {q}}$ provides the positions of the bodies, U is the force function (the negative of the potential), I is the moment of inertia as defined in (2) below, $\lambda$ is a constant, and $\nabla$ denotes the gradient. In this case, central configurations provide classes of relative equilibrium, homothetic, and homographic orbits by reducing the dynamical question of finding solutions of a differential equation to solving algebraic systems.

1.2 Importance

Research done since 1900 has shown that the concept of central configuration opens a path towards understanding the N-body problem. Not only it offers a method for finding periodic solutions, but it appears in various other circumstances. For instance, when three or more bodies tend to a simultaneous collision, or when the system becomes unbounded and the mutual distances between bodies tend to infinity, the system tends asymptotically to a central configuration (Saari 1980, 2005).

But finding central configurations is far from easy. Basic questions related to them are often difficult. The Wintner–Smale conjecture, for instance, became notorious after Steven Smale placed it sixth on his list of open problems for the twenty-first century (Smale 1998). The problem asks whether, for given N positive masses, the number of planar central configurations is finite or not. So far, the conjecture has been solved only for $N=3,4,$ and 5, see Moeckel (2006) and Albouy and Kaloshin (2012). In all these cases the answer is that the set of central configurations is finite. But it is possible that for more than five bodies this set is infinite. If so, it may be countable or contain a continuum, as it actually happens when some masses are negative or charges are embedded in the system (Alfaro and Pérez-Chavela 2002; Roberts 1999).

1.3 Our Goal

We consider here the motion of N point masses in spaces of constant Gaussian curvature $\kappa \ne 0$, namely spheres for $\kappa >0$ and hyperbolic spheres for $\kappa <0$ in a non-relativistic context. This problem stems from the work of János Bolyai and Nikolai Lobachevsky, done in the 1830s, who independently had the idea of generalizing celestial mechanics to hyperbolic space, being among the first to understand that the laws of physics are related to the geometry of the universe (Bolyai and Bolyai 1913; Lobachevsky 1949). The problem was further pursued by Schering (1870, 1873), Killing (1880), Liebmann (1902, 1903), and others. More recent work in this direction appears in Kozlov and Harin (1992), Shchepetilov (2006), Diacu (2011, 2012a, b, 2013a, b, 2017, 2016), Diacu and Kordlou (2013), Diacu et al. (2013), Diacu and Pérez-Chavela (2011), Diacu et al. (2005, 2012a, b, c, 2018), Diacu and Popa (2014), Diacu and Thorn (2015), García-Naranjo et al. (2016), Martínez and Simó (2013, 2017), Montanelli and Gushterov (2016), Pérez-Chavela and Reyes Victoria (2012), Tibboel (2013a, b, 2014), Zhu (2014) and Zhu and Zhao (2017). A history of the problem and reasons why it is worth studying can be found in Diacu (2012b).

In this paper we extend the concept of central configuration to the N-body problem in spaces of constant Gaussian curvature. Our idea was to find a formal definition that resembles the classical one. To achieve this goal we had to formulate first the correct definition of the moment of inertia for 3-spheres and hyperbolic 3-spheres, such that it agrees with the standard definition known in the Euclidean space. This step proved more difficult than we expected, also because of a terminological mix-up that had occurred in the past few decades in the literature pertaining to the Newtonian N-body problem. A main obstacle was that, in the three-dimensional case, the definition of the moment of inertia we considered suitable for our purposes did not match the one in the Euclidean space when the curvature takes the value zero. But in the end we found a way out with the help of the concept of effective potential and thus clarified the semantic confusion that had occurred in recent years.

We also wanted to develop some criteria for the existence of central configurations and apply them towards finding new classes of such mathematical objects. The reward was higher than expected when we understood that any central configuration on a 3-sphere delivers two classes of relative equilibria, whereas any central configuration on hyperbolic 3-spheres provides three such classes. Unlike in the Euclidean case, however, central configurations do not lead to homothetic orbits, in general. The loss of this property is not only because spheres and hyperbolic spheres are not vector spaces, so the concept of similarity does not make much sense, but also for dynamical reasons. In Euclidean space, bodies released from a central configuration with zero initial velocities collide simultaneously. While this happens in some highly symmetric cases in curved space as well, it does not happen in general. For example, for fixed points on spheres, which are central configurations, the bodies do not move at all.

We also include in this first paper on central configurations of the curved N-body problem a complete proof that for any masses on spheres and hyperbolic spheres central configurations exist. Finally, we add some results on the number of geodesic central configurations, in the spirit of the classical theorem proved by Forest Ray Moulton in the classical case (Moulton 1910).

2 The Moment of Inertia in Euclidean Space

In this section we discuss the moment of inertia in Euclidean space, aiming to find later a proper definition of this concept for an N-body system in spaces of constant curvature. At this stage we do not need any equations of motion, since the moment of inertia does not depend on them. The reason for dealing with this issue here is related to the fact that we will use this concept later in the definition of central configurations.

2.1 The Physical Concept

The moment of inertia first appeared in one of Euler’s works of 1765, p. 166. The term apparently made it into dictionaries sometime between 1820 and 1830 (Dictionary 2015). In the spirit of Euler, we can define this concept as follows.

Definition 1

The moment of inertia is the sum of the products of the mass and the square of the perpendicular distance to the axis of rotation of each particle in a body rotating about an axis.

According to the above definition, given for a rigid body, the moment of inertia I for a system of N positive point masses, $m_1,\dots , m_N$, relative to the z-axis in some xyz-coordinate system of the Euclidean space ${\mathbb {R}}^3$, must be of the form

$$\begin{aligned} I=\sum _{i=1}^N m_i\left( x_i^2+y_i^2\right) , \end{aligned}$$

(1)

where the position of the body $m_i$ is given by the vector $\mathbf{q}_i=(x_i,y_i,z_i)$. The moment of inertia has the same expression (1) if we restrict the motion to the plane ${\mathbb {R}}^2$ and assume that the rotation takes place about the origin of some xy-coordinate system, where the position vector for the body $m_i$ is now $\mathbf{q}_i=(x_i,y_i)$.

In celestial mechanics, as long as the motion is restricted to ${\mathbb {R}}^2$, the moment of inertia is taken as in (1) or, sometimes, as half this quantity. We will soon clarify the reason for which some authors introduce the factor $\frac{1}{2}$, but it is more important for now to note that in celestial mechanics the moment of inertia is taken in ${\mathbb {R}}^3$ as

$$\begin{aligned} I=\sum _{i=1}^n m_i\left( x_i^2+y_i^2+z_i^2\right) \end{aligned}$$

(2)

or as half this quantity. The usual physical interpretation of formula (2) given in the field is that the moment of inertia provides a crude measure for the distribution of the bodies in space, with $I=0$ at total collision and I large if at least one body is far away from the others. So not only there is no match between Definition 1 and formula (2), but the celestial mechanics literature never hints at any connection between the moment of inertia thus defined and the rotation of the bodies about an axis.

We thought that we might find a reason for this mismatch in the original works where formula (2) appeared. The moment of inertia for the classical N-body problem has been historically known for its presence in the Lagrange–Jacobi equation,

$$\begin{aligned} {\ddot{I}}=(2\alpha +4)U+4h, \end{aligned}$$

where I is defined as in (2), U is the force function (i.e. the negative of the potential energy),

$$\begin{aligned} U:{\mathbb {R}}^{3N}\rightarrow (0,\infty ),\ \ U(\mathbf{q}_1,\dots , \mathbf{q}_N)=\sum _{1\le i<j\le N}\frac{m_im_j}{|\mathbf{q}_i-\mathbf{q}_j|^\alpha }, \end{aligned}$$

h is the energy constant, and $\alpha >0$ is also a constant. The physical units are chosen such that the gravitation constant is 1. Since the right-hand side of the Lagrange–Jacobi formula has a factor of 2, some researchers in celestial mechanics prefer to introduce the factor $\frac{1}{2}$ in the definition of I, but this detail is irrelevant. So a good place to start our attempt at answering the above question was the first work that contained the Lagrange–Jacobi equation.

2.2 Jacobi’s Approach

In the winter semester of 1842–1843 at the University of Königsberg in East Prussia, Carl Gustav Jacobi gave a lecture series on the N-body problem, which was very well received, so he published it as a book entitled Vorlesungen über Dynamik in 1848 (Jacobi 1884). On page 22, the Lagrange–Jacobi equation appears for the first time as $\sum m_ir_i^2,$ where $r_i^2=x_i^2+y_i^2+z_i^2.$ Jacobi never attached a name to this sum, as he did for other important concepts, such as kinetic energy, which he called “lebendige Kraft” (living force). Between pages 22 and 24 he referred to $\sum m_ir_i^2$ as “Ausdruck” (expression), “Summe” (sum), or “Grösse” (quantity), but never hinted that it has anything to do with the moment of inertia defined in physics. Recall that this concept had been defined in 1765 and was already in dictionaries around 1830, so Jacobi should have been aware of it by the time of his lectures.

In the first paragraph on page 24, he mentioned that, at the origin of the coordinate system, $\sum m_ir_i^2$ reaches its minimum value and, when $\sum m_ir_i^2$ is constant, the bodies can be thought of lying on the same sphere. So he formulated there our current physical interpretation of the moment of inertia in celestial mechanics as a crude measure of the bodies’ distribution in space. And this is all he wrote relative to $\sum m_ir_i^2$. It is thus reasonable to think that he made no connection between this expression and the rotation of the bodies about a fixed axis.

2.3 Wintner’s Terminology

A century later, Aurel Wintner published the first edition of his influential book on the analytical foundations of celestial mechanics, updated in a second edition that appeared in 1947 (Wintner 1947). On page 234, the quantity $J=\sum m_i\xi _i^2$ was introduced (with $\xi _i$ having the same meaning as Jacobi’s $r_i$ mentioned above), which finally bears a name; he called it the polar inertia momentum. In modern parlance, the polar moment of inertia, or the polar moment of area, is a quantity used to predict an object’s resistance to torsion. Physicists warn, however, that the polar moment of inertia should not be confused with the moment of inertia, which characterizes an object’s angular acceleration due to torque. So though related, the concepts of torque and torsion mean different things.

2.4 Recent Developments

Since the publication of Wintner’s book, researchers in celestial mechanics got apparently mixed up in terminology. Though the two physical concepts are identical in the classical N-body problem as long as I is defined in the plane ${\mathbb {R}}^2$, in ${\mathbb {R}}^3$ we must distinguish between the polar moment of inertia, (2), and the moment of inertia, (1). This remark is important to us for reasons related to the definition we will give for central configurations in spaces of constant curvature and to the fact that we can recover the classical definition when the curvature tends to zero.

In spite of a misleading terminology, the polar moment of inertia was understood in terms of a rotation when considered in the context of relative equilibria (orbits that maintain constant mutual distances between the bodies all along the motion) defined by central configurations, as we will explain later. But the central configurations leading to relative equilibria must be planar (see Wintner 1947, p. 287). As there are no spatial relative equilibria in ${\mathbb {R}}^3$, the mix-up between concepts was harmless. In the next section, we will provide and justify the correct definition of the moment of inertia for spheres and hyperbolic spheres and later find another way to back up our findings.

3 The Moment of Inertia in Spaces of Constant Curvature

In this section we first introduce the definition of relative equilibria in the context of mechanical systems with symmetry. We use the language of geometric mechanics (Abraham and Marsden 1987; Marsden 2009; Marsden and Ratiu 1999; Smale 1998) to show that finding relative equilibria of mechanical systems in spheres and hyperbolic spheres is equivalent to finding the critical points of the corresponding effective potentials. The effective potentials corresponding to different relative equilibria have the same form, a fact that motivates our definition of the moment of inertia in spheres and hyperbolic spheres. Throughout this paper, vectors are all column vectors, but written as row vectors in the text, and the masses $m_1,\dots , m_N$ are all positive.

3.1 Relative Equilibria

We begin with some definitions for general mechanical systems. The first is from Smale (1998), whereas the second is from Smale (1970b).

Definition 2

A mechanical system with symmetry consists of a 4-tuple (M, K, V, G), where M is a manifold, K the kinetic energy, V the potential energy, and G a Lie group acting on M preserving K and V with all data smooth.

For each $\varvec{\xi }$ in the Lie algebra ${\mathfrak {g}}$ of G, there is a vector field $\varvec{\xi }_M$ on M given by

$$\begin{aligned} \varvec{\xi }_M ({\mathbf {q}}) := \frac{d}{\mathrm{d}t}\Bigg |_{t=0} \left( \exp (\varvec{\xi }t) {\mathbf {q}}\right) . \end{aligned}$$

We denote by $\varvec{\xi }_M({\mathbf {q}})$ the vector at ${\mathbf {q}}\in M$, and by $\exp (\varvec{\xi }t){\mathbf {q}}$ the action of $\exp (\varvec{\xi }t)$ on ${\mathbf {q}}$.

Definition 3

A solution of the mechanical system with symmetry (M, K, V, G) is called a relative equilibrium if it is also an integral curve of the vector field $\varvec{\xi }_M$. In other words, a relative equilibrium is a solution in the form of $\exp (\varvec{\xi }t){\mathbf {q}}$. The curve $\exp (\varvec{\xi }t)\in G$ is called a one-parameter subgroup of G.

Recall that a $4\times 4$ matrix A is in the orthogonal Lie group O(4) if it preserves the inner product in the four-dimensional Euclidean space, that is, if

$$\begin{aligned} A\mathbf{u}\cdot A\mathbf{v}=\mathbf{u}\cdot \mathbf{v}, \quad \mathrm{for \ any \ }\quad \mathbf{u}, \mathbf{v}\in \mathbb R^4. \end{aligned}$$

O(4) is a matrix Lie group that has two components. The component containing the identity matrix I, i.e. the set of matrices with determinant one, denoted by SO(4), is the special orthogonal group. The tangent space at I, the Lie algebra of O(4), is a six-dimensional linear space and is denoted by $\mathfrak so(4)$. A $4\times 4$ matrix X is in $\mathfrak so(4)$ if $X^T=-\,X$.

Also recall that a $4\times 4$ matrix A is in O(3, 1) if it preserves the inner product in the four-dimensional Minkowski space, that is, if

$$\begin{aligned} A\mathbf{u}\cdot A\mathbf{v}=\mathbf{u}\cdot \mathbf{v}, \quad \mathrm{for \ any \ }\quad \mathbf{u}, \mathbf{v}\in \mathbb R^{3,1}. \end{aligned}$$

O(3, 1) is a matrix Lie group with four components (Naber 1991). The two components with determinant one form SO(3, 1), out of which the component containing I, denoted by $SO^+(3,1)$, is the Lorentz group. The tangent space at I, the Lie algebra of O(3, 1), is a six-dimensional linear space and denoted by $\mathfrak so(3,1)$. A $4\times 4$ matrix X belongs to $\mathfrak so(3,1)$ if $\psi X^T\psi =-X$, where $\psi =\mathrm{diag} (1,1,1,-\,1)$.

Let us return to mechanical systems in spheres and hyperbolic spheres. We embed them either in the standard Euclidean space, ${\mathbb {R}}^{4}$, or in the Minkowski space, ${\mathbb {R}}^{3,1}$. More precisely, for vectors ${\mathbf {q}}_1=(x_1,y_1,z_1,w_1)$ and ${\mathbf {q}}_2=(x_2,y_2,z_2,w_2)$ in $\mathbb R^4$ or $\mathbb R^{3,1}$, the inner products are given by

$$\begin{aligned} {\mathbf {q}}_1\cdot {\mathbf {q}}_2 = x_1x_2+y_1y_2+z_1z_2 +\sigma w_1w_2, \end{aligned}$$

where $\sigma =1$ for $\mathbb R^4$ and $\sigma =-1$ for $\mathbb R^{3,1}$. Then the family of manifolds is

$$\begin{aligned} \mathbb M_\kappa ^3:= \{(x,y,z,w)\in {\mathbb {R}}^4\ |\ x^2+y^2+z^2+\sigma w^2=\kappa ,\ \kappa \ne 0\}, \end{aligned}$$

with $w>0$ for $\kappa <0$. For $\kappa >0$, the manifolds are 3-spheres, which we denote by $\mathbb S_\kappa ^3$, whereas for $\kappa <0$, the manifolds are hyperbolic 3-spheres, which we denote by $\mathbb H_\kappa ^3$.

Given positive masses $m_1,\ldots , m_N$, whose positions are described by the configuration ${\mathbf {q}}=({\mathbf {q}}_1,\ldots ,{\mathbf {q}}_N)\in (\mathbb M_\kappa ^3)^N$, ${\mathbf {q}}_i=(x_i,y_i,z_i,w_i),\ i=\overline{1,N}$, we define the singularity set

$$\begin{aligned} \Delta =\cup _{1\le i<j\le N}\left\{ {\mathbf {q}}\in (\mathbb M^3)^N\ ; \ {\mathbf {q}}_i=\pm {\mathbf {q}}_j\right\} . \end{aligned}$$

We take the kinetic energy as

$$\begin{aligned} K({\dot{{\mathbf {q}}}})= \sum _{1\le i\le N}\frac{1}{2}m_i {\dot{{\mathbf {q}}}}_i \cdot {\dot{{\mathbf {q}}}}_i. \end{aligned}$$

We assume that the potential energy is invariant under the O(4) (O(3, 1)) action. For instance, $V=\sum _{1\le i<j\le N} m_i m_j f(d_{ij})$, where $d_{ij}$ is the distance between ${\mathbf {q}}_i$ and ${\mathbf {q}}_j$.

Now let us consider the relative equilibrium of such a mechanical system that consists of the 4-tuple

$$\begin{aligned} \left( (\mathbb M^3_\kappa )^N{\setminus } \Delta , \ K(\dot{{\mathbf {q}}}) , \ V({\mathbf {q}}), O(4) (O(3,1))\right) . \end{aligned}$$

(3)

Proposition 1

A one-parameter subgroup of SO(4) is of the form $PA_{\alpha , \beta }(t)P^{-1}$, with $P\in SO(4)$ and

$$\begin{aligned} A_{\alpha , \beta }(t)= \begin{bmatrix} \cos \alpha t&\quad -\,\sin \alpha t&\quad 0&\quad 0\\ \sin \alpha t&\quad \cos \alpha t&\quad 0&\quad 0\\ 0&\quad 0&\quad \cos \beta t&\quad -\,\sin \beta t\\ 0&\quad 0&\quad \sin \beta t&\quad \cos \beta t \end{bmatrix}, \ \alpha , \beta \in \mathbb R. \end{aligned}$$

We call these rotations positive elliptic–elliptic if $\alpha \ne 0$ and $\beta \ne 0$, and positive elliptic if only one of them is zero. We call the corresponding relative equilibria positive elliptic–elliptic relative equilibria and positive elliptic relative equilibria, respectively.

Proposition 2

A one-parameter subgroup of $SO^+(3,1)$ is of the form $PB_{\alpha , \beta }(t)P^{-1}$ or $PC_\eta (t)P^{-1}$, with $P\in SO(3,1)$, and

$$\begin{aligned} B_{\alpha , \beta }(t)= & {} \begin{bmatrix} \cos \alpha t&\quad -\sin \alpha t&\quad 0&\quad 0\\ \sin \alpha t&\quad \cos \alpha t&\quad 0&\quad 0\\ 0&\quad 0&\quad \cosh \beta t&\quad \sinh \beta t\\ 0&\quad 0&\quad \sinh \beta t&\quad \cosh \beta t \end{bmatrix},\\ C_\eta (t)= & {} \begin{bmatrix} 1&\quad 0&\quad 0&\quad 0\\ 0&\quad 1&\quad -\,\eta t&\quad \eta t\\ 0&\quad \eta t&\quad 1-\eta t^2/2&\quad \eta t^2\\ 0&\quad \eta t&\quad -\,\eta t^2&\quad 1+\eta t^2/2 \end{bmatrix}, \end{aligned}$$

where $\alpha$, $\beta ,\ \eta \in \mathbb R$.

Similarly, the negative elliptic, negative hyperbolic, negative elliptic–hyperbolic, and parabolic transformations correspond to $\alpha \ne 0$ and $\beta =0$, $\alpha = 0$ and $\beta \ne 0$, $\alpha \ne 0$ and $\beta \ne 0$, and $\eta \ne 0$, respectively. We call the corresponding relative equilibria negative elliptic relative equilibria, negative hyperbolic relative equilibria, negative elliptic–hyperbolic relative equilibria, and parabolic relative equilibria, respectively.

We can easily check that

$$\begin{aligned} A_{\alpha , \beta }(t)=\exp ( \varvec{\xi }_1t),\quad B_{\alpha , \beta }(t)=\exp ( \varvec{\xi }_2t),\quad C_\eta (t)=\exp ( \varvec{\xi }_3t), \end{aligned}$$

where $\varvec{\xi }_1\in \mathfrak {so}(4)$, $\varvec{\xi }_2$, $\varvec{\xi }_3$ $\in \mathfrak {so}(3,1)$, and

$$\begin{aligned} \varvec{\xi }_1 = \begin{bmatrix}0&\quad -\,\alpha&\quad 0&\quad 0\\ \alpha&\quad 0&\quad 0&\quad 0\\ 0&\quad 0&\quad 0&\quad -\,\beta \\0&\quad 0&\quad \beta&\quad 0 \end{bmatrix}, \quad \varvec{\xi }_2 = \begin{bmatrix}0&\quad -\alpha&\quad 0&\quad 0\\ \alpha&\quad 0&\quad 0&\quad 0\\ 0&\quad 0&\quad 0&\quad \beta \\0&\quad 0&\quad \beta&\quad 0 \end{bmatrix}, \quad \varvec{\xi }_3 = \begin{bmatrix}0&\quad 0&\quad 0&\quad 0\\ 0&\quad 0&\quad -\,\eta&\quad \eta \\ 0&\quad \eta&\quad 0&\quad 0\\0&\quad \eta&\quad 0&\quad 0 \end{bmatrix}. \end{aligned}$$

It is easy to see that for any $\phi$ in the isometry group, ${\mathbf {q}}(t)$ solves the mechanical system (3) if and only if $\phi {\mathbf {q}}(t)$ does. Thus, we cover all possible relative equilibria for the mechanical system if we define them in terms of the three normal forms of the one-parameter subgroup. To simplify the notation, we will denote initial positions without any argument and attach the argument t to functions depending on time.

Definition 4

Let ${\mathbf {q}}=({\mathbf {q}}_1,\dots ,{\mathbf {q}}_N)$ be an initial configuration of the masses $m_1,\dots ,m_N$, $N\ge 2$ in $(\mathbb {M_\kappa }^3)^N{\setminus } \Delta$, where the initial position vectors are ${\mathbf {q}}_i=(x_i, y_i, z_i, w_i)$, $i=\overline{1,N}$. Then a solution of the form

$$\begin{aligned} {\mathbf {q}}(t)=Q(t){\mathbf {q}}:= (Q(t){\mathbf {q}}_1,\dots ,Q(t){\mathbf {q}}_N) \end{aligned}$$

of system (3), with Q(t) being $A_{\alpha , \beta }(t)$, $B_{\alpha , \beta }(t)$, or $C_\eta (t)$, is called a relative equilibrium of the mechanical system (3).

It was proved in Diacu (2012b) that parabolic relative equilibria do not exist for system (3).

3.2 Effective Potentials and Moment of Inertia

First recall the following result.

Theorem 1

(Smale 1970b) Suppose (M, K, V, G) is a mechanical system with symmetry and $\varvec{\xi }\in {\mathfrak {g}}$. Then $\exp (\varvec{\xi }t){\mathbf {q}}$ is a relative equilibrium if and only if ${\mathbf {q}}$ is a critical point of the real valued function on M which sends ${\mathbf {q}}$ into $V({\mathbf {q}}) - K(\varvec{\xi }_M ({\mathbf {q}}),\varvec{\xi }_M ({\mathbf {q}}))$, the effective potential corresponding to $\varvec{\xi }$.

Theorem 2

Consider system (3). Let ${\mathbf {q}}=({\mathbf {q}}_1,\dots ,{\mathbf {q}}_N)$, ${\mathbf {q}}_i=(x_i,y_i,z_i,w_i), \ i=\overline{1,N},$ be a configuration in $(\mathbb M_\kappa ^3)^N{\setminus } \Delta$. In $(\mathbb S_\kappa ^3)^N{\setminus } \Delta$, $\exp (\varvec{\xi }_1t){\mathbf {q}}=A_{\alpha , \beta }(t){\mathbf {q}}$ is a relative equilibrium if and only if this configuration satisfies the equation

$$\begin{aligned} \frac{\alpha ^2-\beta ^2}{2}\nabla _{{\mathbf {q}}_i} \left( \sum _{i=1}^Nm_i(x_i^2+y_i^2) \right) =\nabla _{{\mathbf {q}}_i} V({\mathbf {q}}), \ i=\overline{1,N}. \end{aligned}$$

In $(\mathbb H_\kappa ^3)^N{\setminus } \Delta$, $\exp (\varvec{\xi }_2t){\mathbf {q}}=B_{\alpha , \beta }(t){\mathbf {q}}$ is a relative equilibrium if and only if this configuration satisfies the equations

$$\begin{aligned} \frac{\alpha ^2+\beta ^2}{2}\nabla _{{\mathbf {q}}_i} \left( \sum _{i=1}^Nm_i(x_i^2+y_i^2) \right) =\nabla _{{\mathbf {q}}_i} V({\mathbf {q}}), \ i=\overline{1,N}. \end{aligned}$$

Proof

The action of $\exp (\varvec{\xi }_it)$ is $\exp (\varvec{\xi }_it){\mathbf {q}}=(\exp (\varvec{\xi }_it){\mathbf {q}}_1, \ldots ,\exp (\varvec{\xi }_it){\mathbf {q}}_N).$ Thus, the vector fields generated by $\varvec{\xi }_1$ and $\varvec{\xi }_2$ on $(\mathbb S_\kappa ^3)^N$ and $(\mathbb H_\kappa ^3)^N$ are $\varvec{\xi }_1{\mathbf {q}}=(\varvec{\xi }_1{\mathbf {q}}_1,\ldots ,\varvec{\xi }_1{\mathbf {q}}_N)$ and $\varvec{\xi }_2{\mathbf {q}}=(\varvec{\xi }_2{\mathbf {q}}_1,\ldots ,\varvec{\xi }_2{\mathbf {q}}_N)$, respectively.

Recall that the kinetic energy is $K(\dot{\mathbf{q}}, \dot{\mathbf{q}})=\sum _{i=1}^{N}\frac{1}{2}m_i \dot{\mathbf{q}}_i \cdot \dot{\mathbf{q}}_i$. In $\mathbb S_\kappa ^3$, using the fact ${\mathbf {q}}_i\cdot {\mathbf {q}}_i =1$, we obtain

$$\begin{aligned} K(\varvec{\xi }_1{\mathbf {q}},\varvec{\xi }_1{\mathbf {q}})= & {} \sum _{i=1}^{N}\frac{1}{2}m_i \varvec{\xi }_1{\mathbf {q}}_i \cdot \varvec{\xi }_1{\mathbf {q}}_i\\= & {} \sum _{i=1}^{N}\frac{1}{2}m_i (-\alpha y_i, \alpha x_i, -\beta w_i, \beta z_i) \cdot (-\alpha y_i, \alpha x_i, -\beta w_i, \beta z_i)\\= & {} \sum _{i=1}^{N}\frac{1}{2}m_i \left( \alpha ^2 (x_i^2 +y^2_i) +\beta ^2 (\kappa -x_i^2 -y^2_i)\right) \\= & {} \frac{\alpha ^2-\beta ^2 }{2}\sum _{i=1}^Nm_i\left( x_i^2+y_i^2\right) + \frac{\kappa \beta ^2 }{2}\sum _{i=1}^Nm_i. \end{aligned}$$

In $\mathbb H_\kappa ^3$, by using ${\mathbf {q}}_i\cdot {\mathbf {q}}_i =\kappa$, we similarly obtain

$$\begin{aligned} K(\varvec{\xi }_2{\mathbf {q}},\varvec{\xi }_2{\mathbf {q}})= \frac{\alpha ^2+\beta ^2 }{2}\sum _{i=1}^Nm_i\left( x_i^2+y_i^2\right) - \frac{\kappa \beta ^2 }{2}\sum _{i=1}^Nm_i. \end{aligned}$$

Ignoring the constant, the effective potentials with respect to $\varvec{\xi }_1$ and $\varvec{\xi }_2$ are

$$\begin{aligned} \begin{aligned} V({\mathbf {q}})- \sum _{i=1}^ N \frac{m_i}{2} \left( \alpha ^2-\beta ^2\right) \left( x_i^2+y_i^2\right) , \quad V({\mathbf {q}})- \sum _{i=1}^ N \frac{m_i}{2} \left( \alpha ^2+\beta ^2\right) \left( x_i^2+y_i^2\right) . \end{aligned} \end{aligned}$$

So $\exp (\varvec{\xi }_i t){\mathbf {q}}$ is a relative equilibrium if and only if ${\mathbf {q}}$ is a critical point of these effective potentials, which is equivalent to the equations. This remark completes the proof. $\square$

The effective potentials depend on the parameters $\alpha , \beta$ in such a manner since the spheres are three-dimensional. Note that the quantity $\sum _{i=1}^ N m_i(x_i^2+y_i^2)$, which has the same form as the moment of inertia in $\mathbb R^3$, see Definition 1, is related to relative equilibria of system (3) in the same way as the moment of inertia is related to relative equilibria of mechanical systems in $\mathbb R^3$. We can now introduce the natural definition of the moment of inertia for the mechanical systems in $(\mathbb M_\kappa ^3)^N{\setminus } \Delta$.

Definition 5

Consider a mechanical system that is determined by the 4-tuple (3). Assume that their configuration is given by the vectors ${\mathbf {q}}_i=(x_i, y_i, z_i,w_i)\in \mathbb M_\kappa ^3, \ i=\overline{1,N}$. Then the moment of inertia of the particle system is the function

$$\begin{aligned} I({\mathbf {q}}):=\sum _{i=1}^Nm_i(x_i^2+y_i^2). \end{aligned}$$

(4)

4 Equations of Motion

In this section we introduce the N-body problem in spaces of constant nonzero curvature, which we will refer to as the curved N-body problem. It is the study of motion of particle systems under Newton-like attraction. We will call its analogue in Euclidean space the Newtonian N-body problem.

As in Diacu (2012b), we set the curved N-body problems $\mathbb M_{\pm 1}^3$, which we will simply denote by $\mathbb S^3$ and $\mathbb H^3$. For convenience, we will also use the notation

$$\begin{aligned} \mathbb M^3:= \{(x,y,z,w)\in {\mathbb {R}}^{4}\ |\ x^2+y^2+z^2+\sigma w^2=\sigma , \ \mathrm{with}\ w>0\ \mathrm{for}\ \sigma =-1\}. \end{aligned}$$

Given the positive masses $m_1,\dots , m_N$, whose positions are described by the configuration ${\mathbf {q}}=({\mathbf {q}}_1,\ldots ,{\mathbf {q}}_N)\in (\mathbb M^3)^N$, ${\mathbf {q}}_i=(x_i,y_i,z_i,w_i),\ i=\overline{1,N}$, we define the singularity set

$$\begin{aligned} \Delta =\cup _{1\le i<j\le N}\{{\mathbf {q}}\in (\mathbb M^3)^N\ ; \ {\mathbf {q}}_i\cdot {\mathbf {q}}_j=\pm \sigma \}. \end{aligned}$$

If $d_{ij}$ is the geodesic distance between the point masses $m_i$ and $m_j$, we define the force function U ($-U$ being the potential function) on $(\mathbb M^3)^N{\setminus }\Delta$ as

$$\begin{aligned} U({\mathbf {q}}):=\sum _{1\le i<j\le N}m_im_j\text {ctn}d_{ij}, \end{aligned}$$

where $\text {ctn}(x)$ stands for $\cot (x)$ in $\mathbb S^3$ and $\coth (x)$ in $\mathbb H^3$. We would like to mention that there are many other choices of the potential, but this potential is coherent with the Newtonian N-body problem, see Diacu (2012b). We also introduce two more notations, which unify the trigonometric and hyperbolic functions,

$$\begin{aligned} \text {sn}(x)= \sin (x) \ \mathrm{or}\ \sinh (x), \quad \text {csn}(x)= \cos (x) \ \mathrm{or}\ \cosh (x). \end{aligned}$$

Then the distance $d_{ij}$ is given by the expression $d_{ij}:=\text {arccsn}(\sigma {\mathbf {q}}_i\cdot {\mathbf {q}}_j),$ where $\text {arccsn}(x)$ is the inverse function of $\text {csn}(x)$. We define the kinetic energy as

$$\begin{aligned} T({\mathbf {p}})= \sum _{1\le i\le N}m_i {\dot{{\mathbf {q}}}}_i \cdot {\dot{{\mathbf {q}}}}_i=\sum _{1\le i\le N}m_i^{-1}{\mathbf {p}}_i\cdot {\mathbf {p}}_i, \end{aligned}$$

where ${\mathbf {p}}_i:=m_i{\dot{{\mathbf {q}}}}_i$ is the momentum of $m_i$. We also denote the momentum of the particle system by ${\mathbf {p}}=({\mathbf {p}}_1,\ldots ,{\mathbf {p}}_N).$ Then the curved N-body problem is given by the Hamiltonian system on $T^*((\mathbb M^3)^N{\setminus }\Delta )$, with

$$\begin{aligned} \ H({\mathbf {q}},{\mathbf {p}}):=T({\mathbf {q}},{\mathbf {p}})-U({\mathbf {q}}). \end{aligned}$$

Let us derive the equations of motion for the Hamiltonian system in $\mathbb S^3$. The Hamiltonian is

$$\begin{aligned} H= \sum _{1\le i\le N}\frac{1}{2} m_i^{-1}{\mathbf {p}}_i\cdot {\mathbf {p}}_i- \sum _{1\le i<j\le N}m_im_j\cot d_{ij}. \end{aligned}$$

Here U is defined on $(\mathbb S^3)^N{\setminus }\Delta$, with the set of singularities $\Delta =\Delta ^-\cup \Delta ^+$, where

$$\begin{aligned} \begin{aligned} \Delta ^-:&= \cup _{1\le i<j\le N}\{{\mathbf {q}}\in (\mathbb S^3)^N: \ {\mathbf {q}}_i=-{\mathbf {q}}_j\}{\setminus } \cup _{1\le i<j\le N}\{{\mathbf {q}}\in (\mathbb S^3)^N: \ {\mathbf {q}}_i={\mathbf {q}}_j\}, \\ \Delta ^+:&= \cup _{1\le i<j\le N}\{{\mathbf {q}}\in (\mathbb S^3)^N: \ {\mathbf {q}}_i={\mathbf {q}}_j\}{\setminus } \cup _{1\le i<j\le N}\{{\mathbf {q}}\in (\mathbb S^3)^N: \ {\mathbf {q}}_i=-{\mathbf {q}}_j\}. \end{aligned} \end{aligned}$$

(5)

We will call $\Delta ^-$ the antipodal singularity set and $\Delta ^+$ the collision singularity set. Using constrained Hamiltonian dynamics, we obtain the equations describing the motion of the bodies,

$$\begin{aligned} {\left\{ \begin{array}{ll} {\dot{{\mathbf {q}}}}_i=m_i^{-1}{\mathbf {p}}_i\\ {\dot{{\mathbf {p}}}} _i=\nabla _{{\mathbf {q}}_i} U-m_i^{-1}({\mathbf {p}}_i\cdot {\mathbf {p}}_i){\mathbf {q}}_i=\nabla _{{\mathbf {q}}_i} U-m_i(\dot{{\mathbf {q}}}_i\cdot \dot{{\mathbf {q}}}_i){\mathbf {q}}_i\\ {\mathbf {q}}_i\cdot {\mathbf {q}}_i=1,\ \ {\mathbf {p}}_i\cdot {\mathbf {q}}_i=0, \ \ i=\overline{1,N}, \end{array}\right. } \end{aligned}$$

where $\nabla _{{\mathbf {q}}_i} U$ stands for the gradient of U on the manifold $(\mathbb S^3)^N$. Notice that $\nabla _{{\mathbf {q}}_i} U$ can be interpreted as the attractive force on ${\mathbf {q}}_i$ produced by all other particles, and $-m_i^{-1}({\mathbf {p}}_i\cdot {\mathbf {p}}_i){\mathbf {q}}_i$ can be viewed as the constraint force keeping the particles on the sphere. Thus, we denote $\nabla _{{\mathbf {q}}_i} U$ and $\nabla _{{\mathbf {q}}_i} m_im_j \cot d_{ij}$ by ${\mathbf {F}}_i$ and ${\mathbf {F}}_{ij}$, respectively. We have

$$\begin{aligned} {\mathbf {F}}_{ij}=\frac{-m_im_j}{\sin ^2 d_{ij}}\nabla _{{\mathbf {q}}_i} d_{ij}=\frac{-m_im_j}{\sin ^2 d_{ij}}\nabla _{{\mathbf {q}}_i} \cos ^{-1}{\mathbf {q}}_i\cdot {\mathbf {q}}_j = \frac{m_im_j}{\sin ^3 d_{ij}}\nabla _{{\mathbf {q}}_i} {\mathbf {q}}_i\cdot {\mathbf {q}}_j. \end{aligned}$$

The gradient of ${\mathbf {q}}_i\cdot {\mathbf {q}}_j$ on the manifold $(\mathbb S^3)^N$ can be computed as follows. We extend any function $f:(\mathbb S^3)^N \rightarrow \mathbb R$ to the ambient space ${\bar{f}}:(\mathbb R^4)^N\rightarrow \mathbb R$,

$$\begin{aligned} {\bar{f}}({\mathbf {q}})= f\left( \frac{{\mathbf {q}}_1}{\sqrt{{\mathbf {q}}_1\cdot {\mathbf {q}}_1}}, \ldots , \frac{{\mathbf {q}}_N}{\sqrt{{\mathbf {q}}_N\cdot {\mathbf {q}}_N}}\right) . \end{aligned}$$

Then ${\bar{f}}(\lambda {\mathbf {q}})={\bar{f}}({\mathbf {q}})$ for $\lambda >0$, i.e. ${{\bar{f}}}$ is a homogeneous function of degree zero. Let $\widetilde{\nabla }$ be the gradient in the ambient space and $\frac{\partial }{\partial n_i}$ the unit normal vector of the ith unit sphere. Since $\frac{\partial {\bar{f}}}{\partial r_i}=0$, we obtain $(\widetilde{\nabla }_{{\mathbf {q}}_i}{\bar{f}})|_{(\mathbb S^3)^N}=\nabla _{{\mathbf {q}}_i} f+ \frac{\partial {\bar{f}}}{\partial r_i}\frac{\partial }{\partial n_i}=\nabla _{{\mathbf {q}}_i} f$. Thus,

$$\begin{aligned} \begin{aligned} {\mathbf {F}}_{ij}&= \frac{m_im_j}{\sin ^3 d_{ij}}\widetilde{\nabla }_{{\mathbf {q}}_i} \frac{{\mathbf {q}}_i\cdot {\mathbf {q}}_j}{\sqrt{{\mathbf {q}}_i\cdot {\mathbf {q}}_i}\sqrt{{\mathbf {q}}_j\cdot {\mathbf {q}}_j}} =\frac{m_im_j}{\sin ^3 d_{ij}} \frac{\sqrt{{\mathbf {q}}_i\cdot {\mathbf {q}}_i}\sqrt{{\mathbf {q}}_j\cdot {\mathbf {q}}_j} {\mathbf {q}}_j- {\mathbf {q}}_i\cdot {\mathbf {q}}_j \frac{\sqrt{{\mathbf {q}}_j\cdot {\mathbf {q}}_j}}{\sqrt{{\mathbf {q}}_i\cdot {\mathbf {q}}_i}} {\mathbf {q}}_i}{(\sqrt{{\mathbf {q}}_i\cdot {\mathbf {q}}_i}\sqrt{{\mathbf {q}}_j\cdot {\mathbf {q}}_j})^2}\\&= \frac{m_im_j [{\mathbf {q}}_j-\cos d_{ij}{\mathbf {q}}_i]}{\sin ^3 d_{ij}}. \end{aligned} \end{aligned}$$

Thus, the equations of motion for the curved N-body problem in $\mathbb S^3$ are

$$\begin{aligned} {\left\{ \begin{array}{ll} {\dot{{\mathbf {q}}}}_i=m_i^{-1}{\mathbf {p}}_i\\ {\dot{{\mathbf {p}}}} _i=\mathop {\sum }\nolimits _{j=1,j\ne i}^N\frac{m_im_j [{\mathbf {q}}_j-\cos d_{ij}{\mathbf {q}}_i]}{\sin ^3 d_{ij}} -m_i(\dot{{\mathbf {q}}}_i\cdot \dot{{\mathbf {q}}}_i){\mathbf {q}}_i\\ {\mathbf {q}}_i\cdot {\mathbf {q}}_i=1,\ \ {\mathbf {p}}_i\cdot {\mathbf {q}}_i=0, \ \ i=\overline{1,N}. \end{array}\right. } \end{aligned}$$

Gravitation law in $\mathbb S^3$ A mass $m_2$ at ${\mathbf {q}}_2 \in \mathbb S^3$ attracts another mass $m_1$ at ${\mathbf {q}}_1\in \mathbb S^3$ (${\mathbf {q}}_1\ne \pm {\mathbf {q}}_2$) along the minimal geodesic connecting the two points with a force whose magnitude is $\frac{m_1m_2}{\sin ^2 d_{12}}$. More precisely,

$$\begin{aligned} {\mathbf {F}}_{12}= \frac{m_1m_2 [{\mathbf {q}}_2-\cos d_{12}{\mathbf {q}}_1]}{\sin ^3 d_{12}}. \end{aligned}$$

Similarly, we can derive the equations of motion for the Hamiltonian system in $\mathbb H^3$. The Hamiltonian is

$$\begin{aligned} H=T({\mathbf {q}},{\mathbf {p}})-U({\mathbf {q}})= \sum _{1\le i\le N}\frac{1}{2} m_i^{-1}{\mathbf {p}}_i\cdot {\mathbf {p}}_i- \sum _{1\le i<j\le N}m_im_j\coth d_{ij}. \end{aligned}$$

Here U is defined on $(\mathbb H^3)^N{\setminus }\Delta$, and the set of singularities is

$$\begin{aligned} \Delta := \cup _{1\le i<j\le N}\{{\mathbf {q}}\in (\mathbb H^3)^N: \ {\mathbf {q}}_i={\mathbf {q}}_j\}. \end{aligned}$$

We interpret $\nabla _{{\mathbf {q}}_i} U$ and $\nabla _{{\mathbf {q}}_i} m_im_j \coth d_{ij}$ as ${\mathbf {F}}_i$ and ${\mathbf {F}}_{ij}$, respectively. Similar computations lead to

$$\begin{aligned} \mathbf{F}_{ij}= \frac{m_im_j [{\mathbf {q}}_j-\cosh d_{ij}{\mathbf {q}}_i]}{\sinh ^3 d_{ij}}, \end{aligned}$$

and the equations of motion for the curved N-body problem in $\mathbb H^3$ are

$$\begin{aligned} {\left\{ \begin{array}{ll} {\dot{{\mathbf {q}}}}_i=m_i^{-1}{\mathbf {p}}_i\\ {\dot{{\mathbf {p}}}} _i=\mathop {\sum }\nolimits _{j=1,j\ne i}^N\frac{m_im_j [{\mathbf {q}}_j-\cosh d_{ij}{\mathbf {q}}_i]}{\sinh ^3 d_{ij}} +m_i(\dot{{\mathbf {q}}}_i\cdot \dot{{\mathbf {q}}}_i){\mathbf {q}}_i\\ {\mathbf {q}}_i\cdot {\mathbf {q}}_i=-1,\ \ {\mathbf {p}}_i\cdot {\mathbf {q}}_i=0, \ \ i=\overline{1,N}. \end{array}\right. } \end{aligned}$$

Gravitation law in $\mathbb H^3$ A mass $m_2$ at ${\mathbf {q}}_2 \in \mathbb H^3$ attracts another mass $m_1$ at ${\mathbf {q}}_1\in \mathbb H^3$ (${\mathbf {q}}_1\ne {\mathbf {q}}_2$) along the minimal geodesic connecting the two points with a force whose magnitude is $\frac{m_1m_2}{\sinh ^2 d_{12}}$. More precisely,

$$\begin{aligned} {\mathbf {F}}_{12}= \frac{m_1m_2 [{\mathbf {q}}_2-\cosh d_{12}{\mathbf {q}}_1]}{\sinh ^3 d_{12}}. \end{aligned}$$

Using the functions $\text {sn}(x)$ and $\text {csn}(x)$ introduced earlier, we can blend the two systems of equations into one system in $(\mathbb M^3)^N{\setminus }\Delta$ (Diacu 2012b, 2013a),

$$\begin{aligned} {\left\{ \begin{array}{ll} {\dot{{\mathbf {q}}}}_i=m_i^{-1}{\mathbf {p}}_i\\ {\dot{{\mathbf {p}}}} _i=\mathop {\sum }\nolimits _{j=1,j\ne i}^N\frac{m_im_j [{\mathbf {q}}_j-\text {csn}d_{ij}{\mathbf {q}}_i]}{\text {sn}^3 d_{ij}}-\sigma m_i(\dot{{\mathbf {q}}}_i\cdot \dot{{\mathbf {q}}}_i){\mathbf {q}}_i\\ \mathbf{q}_i\cdot { {\mathbf {q}}_i}=\sigma , \ \ {\mathbf {p}}_i\cdot {\mathbf {q}}_i=0, \ \ i=\overline{1,N}. \end{array}\right. } \end{aligned}$$

(6)

Remark 1

If we derive the equation of motion in $\mathbb M^3_\kappa$, we would see that the gravitational law is

$$\begin{aligned} {\mathbf {F}}_{12}= \frac{m_1m_2 |\kappa |^\frac{3}{2}[{\mathbf {q}}_2-\text {csn}|\kappa |^\frac{1}{2} d_\kappa ({\mathbf {q}}_1, {\mathbf {q}}_2){\mathbf {q}}_1]}{\text {sn}^3\left( |\kappa |^\frac{1}{2} d_\kappa ({\mathbf {q}}_1, {\mathbf {q}}_2)\right) }, \end{aligned}$$

(Diacu 2012b, p. 29), where $d_\kappa ({\mathbf {q}}_1, {\mathbf {q}}_2)$ is the distance between the two particles in $\mathbb M^3_\kappa$. Formally, it tends to the gravitational law in $\mathbb R^3$ when $\kappa \rightarrow 0$, which again shows that the potential is coherent with the Newtonian potential.

Some researchers studied the curved N-body problem in $\mathbb M^3_\kappa$ with curvature $\kappa \ne \pm \,1$ (Kilin 1999). This is not necessary since it has been shown in Diacu (2012b) that there are coordinate and time-rescaling transformations,

$$\begin{aligned} {\mathbf {q}}_i = |\kappa |^{-1/2}{} \mathbf{r}_i, \quad i=\overline{1,N}\ \ \mathrm{and}\ \ \tau = |\kappa |^{3/4} t, \end{aligned}$$

which bring the systems from $\mathbb S_\kappa ^3$ and $\mathbb H_\kappa ^3$ to systems to $\mathbb S^3$ and $\mathbb H^3$, respectively.

4.1 Total Angular Momentum Integrals

The Hamiltonian function is invariant under the action of SO(4) and SO(3, 1) for motions in $\mathbb S^3$ and $\mathbb H^3,$ respectively. These symmetries lead to six integrals, which stand for the generalized version of the usual total angular momentum conservation laws in ${\mathbb {R}}^3,$

$$\begin{aligned} \omega _{uv}=\sum _{i=1}^Nm_i(\dot{u}_iv_i-u_i\dot{v}_i), \end{aligned}$$

where u, v is any combinations of x, y, z, w, a fact shown in Diacu (2012b) and Diacu (2013a). We refer to them as angular momentum integrals.

5 Relative Equilibria and Central Configurations

We can apply Theorem 2 to derive the criteria for relative equilibria of the curved N-body problem. They are equivalent to the criteria given in Diacu (2012b) and Diacu (2013a), but differ significantly in form. We then define central configuration of the curved N-body problem and discuss the relationships between central configurations and solutions of the curved N-body problem.

5.1 Criterion for Relative Equilibria in $\mathbb M^3$

Let ${\mathbf {q}}=({\mathbf {q}}_1,\ldots ,{\mathbf {q}}_N),\ \ {\mathbf {q}}_i=(x_i,y_i,z_i,w_i)$, $i=\overline{1,N},$ be a non-singular configuration and $Q(t){\mathbf {q}}$ a relative equilibrium, where Q(t) is $A_{\alpha , \beta }(t)$ or $B_{\alpha , \beta }(t)$. Again, we denote initial positions and velocities without any argument and attach the argument t to functions depending on time.

We first substitute ${\mathbf {q}}_i(t)=Q(t){\mathbf {q}}_i,\ i=\overline{1,N}$, into Eq. (6) and obtain

$$\begin{aligned} m_i\ddot{Q}(t){\mathbf {q}}_i=\nabla _{{\mathbf {q}}_i} U(t)-\sigma m_i[\dot{Q}(t){\mathbf {q}}_i\cdot \dot{Q}(t){\mathbf {q}}_i]Q(t){\mathbf {q}}_i, \quad i=\overline{1,N}. \end{aligned}$$

Since U is invariant under the isometry group, it is easy to see that $Q^{-1}(t)\nabla _{{\mathbf {q}}_i} U(t)= \nabla _{{\mathbf {q}}_i} U$. Multiplying to the left by $Q^{-1}(t)$ yields

$$\begin{aligned} m_iQ^{-1}(t)\ddot{Q}(t){\mathbf {q}}_i=\nabla _{{\mathbf {q}}_i} U-\sigma m_i[\dot{Q}(t){\mathbf {q}}_i\cdot \dot{Q}(t){\mathbf {q}}_i]{\mathbf {q}}_i. \end{aligned}$$

(7)

Theorem 3

Let ${\mathbf {q}}=({\mathbf {q}}_1,\dots ,{\mathbf {q}}_N), {\mathbf {q}}_i=(x_i,y_i,z_i,w_i),\ i=\overline{1,N}$, be a non-singular configuration in $\mathbb S^3$. Then $A_{\alpha , \beta }(t){\mathbf {q}}$ is a relative equilibrium if and only if this configuration satisfies the equations

$$\begin{aligned} m_i(\beta ^2-\alpha ^2) \begin{bmatrix} x_i(w_i^2 +z_i^2)\\ y_i(w_i^2 +z_i^2)\\ -z_i(x_i^2 +y_i^2)\\ -w_i(x_i^2 +y_i^2) \end{bmatrix}=\nabla _{{\mathbf {q}}_i} U,\quad i=\overline{1,N}. \end{aligned}$$

(8)

Proof

Using the fact that $A_{\alpha , \beta }(t)=\exp ( \varvec{\xi }_1t)$ and that $\exp (\varvec{\xi }_1 t)$ and $\varvec{\xi }_1$ commute, straightforward computations show that

$$\begin{aligned} \begin{aligned} A^{-1}_{\alpha , \beta }(t)\ddot{A}_{\alpha , \beta }(t)&= \mathrm{diag}(-\alpha ^2, -\alpha ^2, -\beta ^2, -\beta ^2),\\ \dot{A}_{\alpha , \beta }(t){\mathbf {q}}_i\cdot \dot{A}_{\alpha , \beta }(t){\mathbf {q}}_i&=\alpha ^2(x_i^2+y_i^2)+\beta ^2(z_i^2+w_i^2). \end{aligned} \end{aligned}$$

Substituting these expressions into Eq. (7), we obtain that

$$\begin{aligned} m_i ( -\alpha ^2x_i, -\alpha ^2y_i, -\beta ^2z_i, -\beta ^2w_i )= & {} \nabla _{{\mathbf {q}}_i} U - m_i[\alpha ^2(x_i^2+y_i^2) +\beta ^2(z_i^2+w_i^2)] {\mathbf {q}}_i,\\ i= & {} \overline{1,N}. \end{aligned}$$

Using in the above equations the identity ${\mathbf {q}}_i \cdot {\mathbf {q}}_i=1$, we can obtain Eq. (8), a remark that completes the proof. $\square$

Similarly, we can prove the following criterion for relative equilibria in $\mathbb H^3$.

Theorem 4

Let ${\mathbf {q}}=({\mathbf {q}}_1,\dots ,{\mathbf {q}}_N)$, ${\mathbf {q}}_i=(x_i,y_i,z_i,w_i), \ i=\overline{1,N},$ be a non-singular configuration in $\mathbb H^3$. Then $B_{\alpha , \beta }(t){\mathbf {q}}$ is a relative equilibrium if and only if this configuration satisfies the equations

$$\begin{aligned} -m_i(\alpha ^2+\beta ^2) \begin{bmatrix} x_i(w_i^2 -z_i^2)\\ y_i(w_i^2 -z_i^2)\\ z_i(x_i^2 +y_i^2)\\ w_i(x_i^2 +y_i^2) \end{bmatrix}=\nabla _{{\mathbf {q}}_i} U, \quad i=\overline{1,N}. \end{aligned}$$

(9)

Theorem 2 and the above two theorems are equivalent. For example, in $\mathbb S^3$, define $f(x,y,z,w)=x^2+y^2$ as a function from $\mathbb S^3$ to $\mathbb R$. To find the gradient of f, we employ the trick used to derive $\nabla _{{\mathbf {q}}_i} {\mathbf {q}}_i \cdot {\mathbf {q}}_j$ in Sect. 4. Extend f to a homogeneous function ${{\bar{f}}}$ of degree zero in the ambient space $\mathbb R^4$,

$$\begin{aligned} {\bar{f}}(x,y,z,w):= \frac{x^2+y^2}{x^2+y^2+z^2+w^2}. \end{aligned}$$

Let $\widetilde{\nabla }$ be the gradient in the ambient space, and let $\frac{\partial }{\partial n}$ be the unit normal vector of the unit sphere. Since $\frac{\partial {\bar{f}}}{\partial r}=0$, we obtain $(\widetilde{\nabla }{\bar{f}})|_{\mathbb S^3}=\nabla f+ \frac{\partial {\bar{f}}}{\partial r}\frac{\partial }{\partial n}=\nabla f$. Thus, straightforward computations show that

$$\begin{aligned} \begin{aligned} \nabla f(x,y,z,w)= 2\left( x(w^2+ z^2), y(w^2+ z^2), - z(x^2+ y^2), - w(x^2+ y^2) \right) . \end{aligned} \end{aligned}$$

Hence, we can conclude that

$$\begin{aligned} \nabla _{{\mathbf {q}}_i} I({\mathbf {q}})= 2m_i \left( x_i(w_i^2+ z_i^2), y_i(w_i^2+ z_i^2), - z_i(x_i^2+ y_i^2), - w_i(x_i^2+ y_i^2) \right) . \end{aligned}$$

Thus, the right-hand side of (8) is $\frac{\beta ^2-\alpha ^2}{2}\nabla _{{\mathbf {q}}_i} \left( \sum _{i=1}^Nm_i(x_i^2+y_i^2) \right)$. Theorem 2 matches Theorem 3. Similarly, in $\mathbb H^3$,

$$\begin{aligned} \nabla _{{\mathbf {q}}_i} I({\mathbf {q}})= 2m_i \left( x_i(w_i^2- z_i^2), y_i(w_i^2- z_i^2), z_i(x_i^2+ y_i^2), w_i(x_i^2+ y_i^2) \right) . \end{aligned}$$

Thus, Theorem 2 also matches Theorem 4.

5.2 Central Configurations and Relative Equilibria

We are now motivated to study the equation

$$\begin{aligned} \nabla _{{\mathbf {q}}_i}U({\mathbf {q}})=\lambda \nabla _{{\mathbf {q}}_i}\left[ \sum _{i=1}^Nm_i(x_i^2+y_i^2)\right] , i=\overline{1,N}. \end{aligned}$$

Definition 6

Assume that the point masses $m_1,\ldots , m_N$ in $\mathbb M^3$ have the non-singular positions given by the vector ${\mathbf {q}}=({\mathbf {q}}_1,\ldots ,{\mathbf {q}}_N),\ {\mathbf {q}}_i=(x_i,y_i,z_i,w_i), \ i=\overline{1,N}.$ Then ${\mathbf {q}}$ is a central configuration of the curved N-body problem in $\mathbb M^3$ if it satisfies the equations

$$\begin{aligned} \nabla _{{\mathbf {q}}_i}U({\mathbf {q}})=\lambda \nabla _{{\mathbf {q}}_i} I({\mathbf {q}}),\quad i=\overline{1,N}, \end{aligned}$$

(10)

where $\lambda \in \mathbb R$ is a constant and I is the moment of inertia. We call (10) the central configuration equations.

Explicitly, the central configuration equations (10) are

$$\begin{aligned} \sum _{j\ne i, j=1}^N \frac{m_jm_i {\mathbf {q}}_j}{\text {sn}^3 d_{ij}}- \sum _{j\ne i, j=1}^N \frac{m_jm_i \text {csn}d_{ij}}{\text {sn}^3 d_{ij}} {\mathbf {q}}_i=\lambda \nabla _{{\mathbf {q}}_i} I, \ i=\overline{1,N}. \end{aligned}$$

(11)

Proposition 3

The ith equation of the central configuration equations (11) holds if and only if there is a constant $\theta _i$ such that

$$\begin{aligned} \sum _{j\ne i, j=1}^N \frac{m_jm_i {\mathbf {q}}_j}{\text {sn}^3 d_{ij}}- \theta _i{\mathbf {q}}_i=\lambda \nabla _{{\mathbf {q}}_i} I. \end{aligned}$$

(12)

Proof

Multiply (12) by ${\mathbf {q}}_i$. Since ${\mathbf {q}}_i\cdot {\mathbf {q}}_j = \sigma \text {csn}d_{ij}$, ${\mathbf {q}}_i\cdot {\mathbf {q}}_i = \sigma$, and ${\mathbf {q}}_i\cdot \nabla _{{\mathbf {q}}_i}I = 0$, we obtain $\theta _i = \sum _{j\ne i, j=1}^N \frac{m_jm_i \text {csn}d_{ij}}{\text {sn}^3 d_{ij}}.$ Thus, (12) is equivalent to the ith equation of (11). $\square$

The following class of central configurations exists in $\mathbb S^3$ only (Diacu 2012b, 2013a).

Definition 7

Consider the positive masses $m_1,\ldots , m_N$ in $\mathbb S^3$. Then a configuration ${\mathbf {q}}=({\mathbf {q}}_1,\ldots ,{\mathbf {q}}_N),\ {\mathbf {q}}_i=(x_i,y_i,z_i,w_i), \ i=\overline{1,N},$ is called a special central configuration if it is a critical point of the force function U, i.e.

$$\begin{aligned} \nabla _{{\mathbf {q}}_i}U({\mathbf {q}})=0,\quad i=\overline{1,N}. \end{aligned}$$

In other words, ${\mathbf {F}}_i=0, i=\overline{1,N}.$ To avoid any confusion, we will call ordinary central configurations those central configurations that are not special.

Here is one remark on terminology. These special central configurations were introduced in Diacu (2012b, 2013a) under the name of fixed points. Given such a configuration ${\mathbf {q}}$, we see with the help of Theorem 3 that $A_{0,0}(t) {\mathbf {q}}$ is an associated relative equilibrium, which is a fixed-point solution: ${\mathbf {q}}(t)={\mathbf {q}}$, ${\mathbf {p}}(t)=0$. This explains the old terminology. Let us introduce some new terminology as well.

Definition 8

A central configuration ${\mathbf {q}}$ of the curved N-body problem is called

• a geodesic central configuration if it is lying on a geodesic;

• an $\mathbb S^2$ central configuration if it is lying on a great 2-sphere;

• an $\mathbb H^2$ central configuration if it is lying on a great hyperbolic 2-sphere;

• an $\mathbb S^3$ central configuration if it is not lying on any great 2-sphere;

• an $\mathbb H^3$ central configuration if it is not lying on any great hyperbolic 2-sphere.

Central configurations will play an important role in the study of the curved N-body problem. They influence the topology of the integral manifolds (Marsden 2009; Smale 1970b). Now we discuss the connection between them and the motions of the curved N-body problem. Let

$$\begin{aligned} \begin{aligned} \mathbb S^1_{xy}:=&\, \{(x,y,z,w)\in \mathbb R^4| x^2+y^2=1, z=w=0\},\\ \mathbb S^1_{zw}:=&\, \{(x,y,z,w)\in \mathbb R^4| z^2+w^2=1, x=y=0\}, \\ \mathbb H^1_{zw}:=&\, \{(x,y,z,w)\in \mathbb R^4| z^2-w^2=-1, x=y=0\}. \end{aligned} \end{aligned}$$

Lemma 1

In $(\mathbb S^3)^N$, we have that $\nabla _{{\mathbf {q}}_i}I=0 \ \mathrm{if \ and \ only\ if}\ {\mathbf {q}}_i\in \mathbb S^1_{xy}\cup \mathbb S^1_{zw}.$ Similarly, in $(\mathbb H^3)^N$, we have that $\nabla _{{\mathbf {q}}_i}I=0 \ \mathrm{if \ and \ only\ if}\ {\mathbf {q}}_i\in \mathbb H^1_{zw}.$

Proof

In $(\mathbb S^3)^N$, recall that

$$\begin{aligned} \nabla _{{\mathbf {q}}_i} I = 2m_i\left( x_i\left( w_i^2+ z_i^2\right) , y_i\left( w_i^2+ z_i^2\right) , - z_i\left( x_i^2+ y_i^2\right) , - w_i\left( x_i^2+ y_i^2\right) \right) . \end{aligned}$$

On the one hand, if $\nabla _{{\mathbf {q}}_i} I$ is a zero vector, then

$$\begin{aligned} \left( x_i\left( w_i^2+ z_i^2\right) \right) ^2+\left( y_i\left( w_i^2+ z_i^2\right) \right) ^2=\left( x_i^2+ y_i^2\right) \left( w_i^2+ z_i^2\right) ^2=0, \end{aligned}$$

which means that ${\mathbf {q}}_i\in \mathbb S^1_{xy}$ or $\mathbb S^1_{zw}$. On the other hand, if ${\mathbf {q}}_i\in \mathbb S^1_{xy}\cup \mathbb S^1_{zw}$, then $\nabla _{{\mathbf {q}}_i} I=0$.

In $(\mathbb H^3)^N$, recall that

$$\begin{aligned} \nabla _{{\mathbf {q}}_i} I = 2m_i\left( x_i\left( w_i^2- z_i^2\right) , y_i\left( w_i^2- z_i^2\right) , z_i\left( x_i^2+ y_i^2\right) , w_i\left( x_i^2+ y_i^2\right) \right) . \end{aligned}$$

Again, on the one hand, if $\nabla _{{\mathbf {q}}_i} I$ is a zero vector, then

$$\begin{aligned} \left( x_i\left( w_i^2- z_i^2\right) \right) ^2+\left( y_i\left( w_i^2- z_i^2\right) \right) ^2=\left( x_i^2+ y_i^2\right) \left( w_i^2- z_i^2\right) ^2=0, \end{aligned}$$

which means that $x_i=y_i=0$, since $w_i^2- z_i^2 = 1+x_i^2+y_i^2\ne 0$. Thus, we obtain that ${\mathbf {q}}_i\in \mathbb H^1_{zw}$. On the other hand, if ${\mathbf {q}}_i\in \mathbb H^1_{zw}$, then $\nabla _{{\mathbf {q}}_i} I=0$. $\square$

Corollary 1

Consider a central configuration ${\mathbf {q}}=({\mathbf {q}}_1,\ldots ,{\mathbf {q}}_N)$, ${\mathbf {q}}_i=(x_i,y_i,z_i,w_i),$ $i=\overline{1,N},$ in $\mathbb M^3$. Let $\lambda$ be the constant in the central configuration equations

$$\begin{aligned} \nabla _{{\mathbf {q}}_i}U({\mathbf {q}})=\lambda \nabla _{{\mathbf {q}}_i} I({\mathbf {q}}). \end{aligned}$$

• 1. If ${\mathbf {q}}$ is an ordinary central configuration in $\mathbb S^3$, then it gives rise to a one-parameter family of relative equilibria: $A_{\alpha , \beta }(t){\mathbf {q}}$ with $\lambda =\frac{\beta ^2-\alpha ^2}{2}$.

• 2. If ${\mathbf {q}}$ is in $\mathbb H^3$, then it gives rise to a one-parameter family of relative equilibria: $B_{\alpha , \beta }(t){\mathbf {q}}$ with $\lambda =-\frac{\alpha ^2+\beta ^2}{2}$.

• 3. If ${\mathbf {q}}$ is a special central configuration in $\mathbb S^3$ and not all the particles are on $\mathbb S^1_{xy}\cup \mathbb S^1_{zw}$, then it gives rise to a one-parameter family of relative equilibria: $A_{\alpha , \beta }(t){\mathbf {q}}$ with $0=\beta ^2-\alpha ^2$.

• 4. If ${\mathbf {q}}$ is a special central configuration in $\mathbb S^3$ and all the particles are on $\mathbb S^1_{xy}\cup \mathbb S^1_{zw}$, then it gives rise to a two-parameter family of relative equilibria: $A_{\alpha , \beta }(t){\mathbf {q}}$ with $\alpha ,\beta \in \mathbb R$.

Before proving this corollary, let us make the following remark on terminology. In the literature, the concept of relative equilibrium stands for both central configurations and the rigid motions associated with them (Marsden 2009; Smale 1970b). In this paper, however, we use the term relative equilibrium only for the associated motion.

Proof

The first two claims are obvious by Theorem 2. If ${\mathbf {q}}$ is a special central configuration in $\mathbb S^3$, then by Theorem 2, $A_{\alpha , \beta }(t){\mathbf {q}}$ is an associated relative equilibrium if and only if $\frac{\beta ^2-\alpha ^2}{2}\nabla _{{\mathbf {q}}_i}I=0$ for $i=\overline{1,N}$.

There are two possibilities: first, if there exists some ${\mathbf {q}}_i$ with $\nabla _{{\mathbf {q}}_i}I\ne 0$, i.e. there is some ${\mathbf {q}}_i\notin \mathbb S^1_{xy}\cup \mathbb S^1_{zw},$ then $0=\beta ^2-\alpha ^2$, i.e. there is a one-parameter family of relative equilibria associated with the special central configuration ${\mathbf {q}}$: $A_{\alpha , \beta }(t){\mathbf {q}}$ with $0=\beta ^2-\alpha ^2$; second, if $\nabla _{{\mathbf {q}}_i}I=0$ for all i, that is, ${\mathbf {q}}_i\in \mathbb S^1_{xy}\cup \mathbb S^1_{zw}$ for all i, then there is no limitation for $\alpha ,\beta$, i.e. there is a two-parameter family of relative equilibria associated with the special central configuration ${\mathbf {q}}$: $A_{\alpha , \beta }(t){\mathbf {q}}$ with $\alpha , \beta \in \mathbb R$. $\square$

Remark 2

There is a gap in the proof. For a central configuration in $\mathbb H^3$, we do not have a one-parameter family of relative equilibria, as claimed, unless we can show that the value of $\lambda$ is always negative. This fact will be proved in Sect. 6.

Notice that while three-dimensional central configurations of the Newtonian N-body problem do not have associated relative equilibria (Wintner 1947), all central configurations of the curved N-body problem have associated relative equilibria.

In the class of relative equilibria associated with one central configuration, there are motions of different types. In $\mathbb S^3$, the relative equilibria can be positive elliptic and positive elliptic–elliptic. In $\mathbb H^3$, they can be negative elliptic, negative hyperbolic, and negative elliptic–hyperbolic. These solutions can be periodic, quasi-periodic, or different. For an ordinary central configuration in $\mathbb S^3$, the intersections of the hyperbola $\lambda =\frac{\beta ^2-\alpha ^2}{2}$ and the line $\beta =k\alpha$, k rational, in the $\alpha \beta$ plane, give periodic motions; otherwise, the motions are quasi-periodic. For a special central configuration in $\mathbb S^3$ that not all particles are on $\mathbb S^1_{xy}\cup \mathbb S^1_{zw}$, the relative equilibria are always periodic. If ${\mathbf {q}}$ is on $\mathbb S^1_{xy}\cup \mathbb S^1_{zw}$, then any points on the line $\beta =k\alpha$, k rational in the $\alpha \beta$ plane give periodic motions; otherwise, the motions are quasi-periodic. For an ordinary central configuration in $\mathbb H^3$, the relative equilibria are periodic if and only if $\beta =0$. Some negative hyperbolic solutions can be mere hyperbolic rotations, which are neither periodic nor quasi-periodic.

However, unlike in the Newtonian N-body problem, central configurations do not provide us with homothetic solutions, which occur only in vector spaces, since they require similarity (Wintner 1947). Actually, since there is no centre of masses, it makes no sense to talk about homothetic solutions. For a special central configuration, if we set the particles at rest at $t=0$, then we obtain a fixed-point solution.

6 Central Configurations

In this section we prove some basic facts about central configurations. We first write the central configuration equations in another form, then give their physical description, which justifies their name, and finally define equivalent classes of central configurations.

6.1 The Central Configuration Equations

In the previous section we introduced the central configuration equations in different forms, such as (10), (11), and (12). We now derive another form of the central configuration equations, which will be useful. Define

$$\begin{aligned} r_i:=(x_i^2+y_i^2)^{1/2},\quad \rho _i:=(\sigma z_i^2+w_i^2)^{1/2}, \quad i=\overline{1,N}. \end{aligned}$$

Then, in $\mathbb H^3$, we have $r_i^2+\sigma \rho _i^2=\sigma$ and $rho_i^2>0$. Recall that the ith equation of (11) is $\sum _{j\ne i, j=1}^N \frac{m_jm_i {\mathbf {q}}_j}{\text {sn}^3 d_{ij}}- \sum _{j\ne i, j=1}^N \frac{m_jm_i \text {csn}d_{ij}}{\text {sn}^3 d_{ij}} {\mathbf {q}}_i=\lambda \nabla _{{\mathbf {q}}_i} I.$

Proposition 4

Consider the positive masses $m_1,\dots , m_N$ on $\mathbb S^3$ at the configuration ${\mathbf {q}}=({\mathbf {q}}_1,\ldots ,{\mathbf {q}}_N)$, where ${\mathbf {q}}_i=(x_i,y_i,w_i)$. If ${\mathbf {q}}_i=(x_i,y_i,z_i,w_i) \notin \mathbb S^1_{xy} \cup \mathbb S^1_{zw}$, then the ith equations of (11) can be written as

$$\begin{aligned} {\left\{ \begin{array}{ll} &{}\mathop {\sum }\limits _{j=1,j\ne i}^N\dfrac{m_j(x_ix_j + y_iy_j -r_i^2\cos d_{ij})}{\sin ^3 d_{ij}}=2\lambda r_i^2\rho _i^2\\ &{}\mathop {\sum }\limits _{j=1,j\ne i}^N\dfrac{m_j(x_iy_j-x_jy_i)}{\sin ^3 d_{ij}}=0\\ &{}\mathop {\sum }\limits _{j=1,j\ne i}^N\dfrac{m_j(z_iw_j-z_jw_i)}{\sin ^3 d_{ij}}=0. \end{array}\right. } \end{aligned}$$

(13)

Proof

Since ${\mathbf {q}}_i\notin \mathbb S^1_{xy} \cup \mathbb S^1_{zw}$, the following four vectors

$$\begin{aligned} \mathbf{v}_{i1}= (x_i,y_i,0,0),\quad \mathbf{v}_{i2}= (-\,y_i, x_i,0, 0),\quad \mathbf{v}_{i3}= (0,0,z_i,w_i),\quad \mathbf{v}_{i4}= (0,0,-w_i,z_i)\ \end{aligned}$$

form an orthogonal basis of $T_{{\mathbf {q}}_i} \mathbb R^4$. Recall that

$$\begin{aligned} \nabla _{{\mathbf {q}}_i} U= \sum _{j=1, j\ne i}^{N}m_im_j\frac{{\mathbf {q}}_j -\cos d_{ij} {\mathbf {q}}_i}{\sin ^3 d_{ij}}, \quad \nabla _{{\mathbf {q}}_i} I= 2m_i(x_i \rho _i^2, y_i \rho _i^2, -z_i r_i^2, -w_i r_i^2 ). \end{aligned}$$

Then $\nabla _{{\mathbf {q}}_i} U=\lambda \nabla _{{\mathbf {q}}_i} I$ is equivalent to $\nabla _{{\mathbf {q}}_i} U \cdot \mathbf{v}_{ik}=\lambda \nabla _{{\mathbf {q}}_i} I \cdot \mathbf{v}_{ik}, k=1,2,3,4.$ Thus,

$$\begin{aligned}&\sum _{j=1,j\ne i}^N\frac{m_im_j}{\sin ^3 d_{ij}} (x_ix_j +y_iy_j -r_i^2 \cos d_{ij}) =\lambda 2m_i r_i^2 \rho _i^2, \\&\sum _{j=1,j\ne i}^N\frac{m_im_j}{\sin ^3 d_{ij}} (x_iy_j -y_ix_j)=0,\\&\sum _{j=1,j\ne i}^N\frac{m_im_j}{\sin ^3 d_{ij}} ( z_iz_j+w_iw_j - \rho _i^2\cos d_{ij}) =-\lambda 2m_i r_i^2 \rho _i^2, \\&\sum _{j=1,j\ne i}^N\frac{m_im_j}{\sin ^3 d_{ij}} (z_iw_j -w_iz_j)=0. \end{aligned}$$

Adding the first and the third equations we obtain an identity. $\square$

Similarly, we can prove the following result.

Proposition 5

Consider the positive masses $m_1,\ldots , m_N$ in $\mathbb H^3$ at the configuration ${\mathbf {q}}=({\mathbf {q}}_1,\ldots ,{\mathbf {q}}_N)$, where ${\mathbf {q}}_i=(x_i,y_i,w_i)$. If ${\mathbf {q}}_i\notin \mathbb H^1_{zw}$, then the ith equations of (11) can be written as

$$\begin{aligned} {\left\{ \begin{array}{ll} &{}\mathop {\sum }\limits _{j=1,j\ne i}^N\dfrac{m_j(x_ix_j + y_iy_j -r_i^2\cosh d_{ij})}{\sinh ^3 d_{ij}}=2\lambda r_i^2\rho _i^2\\ &{}\mathop {\sum }\limits _{j=1,j\ne i}^N\dfrac{m_j(x_iy_j-x_jy_i)}{\sinh ^3 d_{ij}}=0\\ &{}\mathop {\sum }\limits _{j=1,j\ne i}^N\dfrac{m_j(z_iw_j-z_jw_i)}{\sinh ^3 d_{ij}}=0. \end{array}\right. } \end{aligned}$$

Now we consider the value of $\lambda$ in the central configuration equations. In this section, let M be the matrix $\mathrm{diag}(m_1, m_1, m_1, m_1,\ldots ,m_N, m_N, m_N, m_N )$. Introduce a metric in $(\mathbb R^{4})^N$ $\left( (\mathbb R^{3,1})^N\right)$:

$$\begin{aligned} \langle {\mathbf {q}}, {\mathbf {q}}\rangle =\sum _{i=1}^N m_i {\mathbf {q}}_i \cdot {\mathbf {q}}_i= {\mathbf {q}}\cdot M{\mathbf {q}}. \end{aligned}$$

For ordinary central configurations we have

$$\begin{aligned} \langle M^{-1} \nabla U, M^{-1} \nabla I \rangle = \lambda \langle M^{-1} \nabla I, M^{-1} \nabla I \rangle . \end{aligned}$$

Proposition 6

Let ${\mathbf {q}}$ be an ordinary central configuration, then the value of $\lambda$ in the central configuration equation is $\frac{\langle M^{-1} \nabla U, M^{-1} \nabla I \rangle }{\langle M^{-1} \nabla I, M^{-1} \nabla I \rangle }.$ For central configurations in $\mathbb H^3$, we have $\lambda <0$.

Proof

Since ${\mathbf {q}}$ is an ordinary central configuration, $\nabla I \ne 0$ and $\langle M^{-1} \nabla I, M^{-1} \nabla I \rangle \ne 0$. Thus, the value of $\lambda$ for an ordinary central configuration ${\mathbf {q}}$ is $\frac{\langle M^{-1} \nabla U, M^{-1} \nabla I \rangle }{\langle M^{-1} \nabla I, M^{-1} \nabla I \rangle }.$

In $\mathbb H^3$, using the identities $\cosh d_{ij}=w_iw_j-(x_ix_j +y_iy_j+z_iz_j )$ and $x_i^2 +y_i^2+z_i^2-w_i^2=-1$, the denominator is

$$\begin{aligned} \langle M^{-1} \nabla I, M^{-1} \nabla I \rangle = 4\sum _{i=1}^N m_i r_i^2 \rho _i^2 \end{aligned}$$

and the numerator is

$$\begin{aligned} \begin{aligned}&\sum _{i=1}^N m_i \left( \sum _{j\ne i}^N m_j \frac{{\mathbf {q}}_j }{\sinh ^3 d_{ij} } \cdot \frac{\nabla _{{\mathbf {q}}_i} I}{m_i} \right) \\&\quad = 2\sum _{ 1\le i<j \le N} m_im_j \frac{ (x_ix_j +y_iy_j )(\rho _i^2+\rho _j^2)+(z_iz_j-w_iw_j)(r_i^2 +r_j^2)}{\sinh ^3 d_{ij} }\\&\quad =2\sum _{ 1\le i<j \le N} m_im_j \frac{ 2 x_i x_j +2y_iy_j -(r_i^2 +r_j^2)\cosh d_{ij} }{\sinh ^3 d_{ij} }\\&\quad =-2\sum _{ 1\le i<j \le N} m_im_j \frac{ (x_i-x_j)^2 +(y_i-y_j)^2+(r_i^2 +r_j^2)(\cosh d_{ij}-1) }{\sinh ^3 d_{ij} }<0,\\ \end{aligned} \end{aligned}$$

a remark that completes the proof. $\square$

This proposition fills the gap in the proof of Corollary 1. It also implies that there are no special central configurations in $\mathbb H^3$ and that there is no such central configuration with ${\mathbf {q}}_i\in \mathbb H^1_{zw}$ for all $i=\overline{1,N}$, since in either case we have $\lambda =0$.

In $\mathbb S^3$, the value of $\lambda$ could be positive, zero, or negative, see examples in Sect. 9. The case $\lambda =0$ corresponds to special central configurations.

6.2 A Physical Description of Central Configurations

It turns out that the moment of inertia I has geometric meaning, a fact that brings some insight into the problem and provides a physical description of central configurations.

Lemma 2

If $A=(x,y,z,w)$ is a point in $\mathbb S^3$, then $z^2+w^2= \cos ^2 d(A, \mathbb S^1_{zw})$. If $A=(x,y,z,w)$ is a point in $\mathbb H^3$, then $-z^2+w^2= \cosh ^2 d(A, \mathbb H^1_{zw})$, where $d(A,\mathcal M):= \inf _{B\in \mathcal M}d(A,B)$, with A, B representing points and $\mathcal M$ being a smooth manifold.

Proof

View A as a vector in $\mathbb R^4$. Denote by $\mathbb R^3_A$ the three-dimensional (or two-dimensional) subspace spanned by A, $e_z=(0,0,1,0)$, and $e_w=(0,0,0,1)$. Denote by $\mathbb R^2_{zw}$ the two-dimensional subspace spanned by $e_z$ and $e_w$.

In $\mathbb S^3$, the minimal geodesic connecting A and $\mathbb S^1_{zw}$ is on the great 2-sphere $\mathbb S^2_A=\mathbb R^3_A\cap \mathbb S^3$. Let $\theta =d(A, \mathbb S^1_{zw})$. Then $A=A_v+A_h\in (\mathbb R^2_{zw})^\bot \oplus \mathbb R^2_{zw}$ with $||A_v||=\sin \theta$ and $||A_h||=\cos \theta$. Hence, we obtain

$$\begin{aligned} \cos ^2 d(A,\mathbb S^1_{zw})=||A_h||^2=|| (A\cdot e_z ) e_z+(A\cdot e_w) e_w ||^2=|| z e_z+w e_w ||^2=z^2+w^2. \end{aligned}$$

In $\mathbb H^3$, the minimal geodesic connecting A and $\mathbb H^1_{zw}$ is on the great hyperbolic 2-sphere $\mathbb H^2_A=\mathbb R^3_A\cap \mathbb H^3$. Let $\theta =d(A, \mathbb H^1_{zw})$. Then similarly we have $A=A_v+A_h\in (\mathbb R^2_{zw})^\bot \oplus \mathbb R^2_{zw}$ with $||A_v||=\sinh \theta$ and $||A_h||=\cosh \theta$. Hence, we obtain

$$\begin{aligned} \begin{aligned} \cosh ^2 d(A,\mathbb H^1_{zw})&=||A_h||^2=\left| \left| \frac{A\cdot e_z}{e_z\cdot e_z} e_z+\frac{A\cdot e_w}{e_w\cdot e_w} e_w \right| \right| ^2\\&=|| z e_z-(-w) e_w ||^2=|(z e_z+w e_w)\cdot (z e_z+w e_w) |\\&=|z^2-w^2|=-z^2+w^2. \end{aligned} \end{aligned}$$

$\square$

Theorem 5

A non-singular configuration ${\mathbf {q}}=({\mathbf {q}}_1,\ldots ,{\mathbf {q}}_N),\ {\mathbf {q}}_i=(x_i,y_i,z_i,w_i), \ i=\overline{1,N}$, in $\mathbb M^3$ is a central configuration if and only if

$$\begin{aligned} \begin{aligned} \nabla _{{\mathbf {q}}_i}U({\mathbf {q}})&=\lambda m_i \sin [2 d({\mathbf {q}}_i, \mathbb S^1_{zw})]\nabla _{{\mathbf {q}}_i}d({\mathbf {q}}_i, \mathbb S^1_{zw}),\ i=\overline{1,N}, \ \mathrm{in}\ \mathbb S^3,\\ \nabla _{{\mathbf {q}}_i}U({\mathbf {q}})&=\lambda m_i \sinh [2 d({\mathbf {q}}_i, \mathbb H^1_{zw})]\nabla _{{\mathbf {q}}_i}d({\mathbf {q}}_i, \mathbb H^1_{zw}),\ i=\overline{1,N}, \ \mathrm{in}\ \mathbb H^3, \end{aligned} \end{aligned}$$

(14)

where $\lambda \in \mathbb R$ is a constant.

Proof

By Lemma 2, we obtain $x_i^2+y_i^2= \sin ^2 d({\mathbf {q}}_i, \mathbb S^1_{zw})$ in $\mathbb S^3$ and $x_i^2+y_i^2= \sinh ^2 d({\mathbf {q}}_i, \mathbb H^1_{zw})$ in $\mathbb H^3$. Thus,

$$\begin{aligned} I=\sum _{1\le i\le N} m_i \sin ^2 d({\mathbf {q}}_i, \mathbb S^1_{zw}) \ \mathrm{in \ } \mathbb S^3, \ \ I=\sum _{1\le i\le N} m_i \sinh ^2 d({\mathbf {q}}_i, \mathbb H^1_{zw})\ \mathrm{in \ } \mathbb H^3. \end{aligned}$$

Then the central configuration equations (10) can be written as (14). $\square$

By definition, special central configurations are arrangements of the particles for which the forces acting on each particle cancel. By the above theorem, ordinary central configurations are special arrangements of the particles with the property that the gravitational force produced on each particle by all the other particles points towards the geodesic $\mathbb S^1_{zw}$ $(\mathbb H^1_{zw})$ and is proportional to $m_i\sin [2 d({\mathbf {q}}_i, \mathbb S^1_{zw})]$ $(m_i\sinh [2 d({\mathbf {q}}_i, \mathbb H^1_{zw})])$.

Define

$$\begin{aligned} \mathbb H^2_{xyw}:= & {} \{(x,y,z,w)\in \mathbb R^4| x^2+y^2-w^2=-1, z=0\},\\ \mathbb S^2_{xyz}:= & {} \{(x,y,z,w)\in \mathbb R^4| x^2+y^2+z^2=1, w=0\}. \end{aligned}$$

Recall that in the Newtonian N-body problem, central configurations are those arrangements of particles such that all ${\mathbf {F}}_i$ are pointing towards the centre of mass (Wintner 1947). In the curved N-body problem, instead of a point, all ${\mathbf {F}}_i$ are pointing towards a geodesic. Furthermore, it was shown in Zhu and Zhao (2017) that all central configurations in $\mathbb H^3$ lie on a submanifold $\mathbb H^2_{xyw}$ and we will prove that all ordinary $\mathbb S^2$ central configurations lie on a submanifold $\mathbb S^2_{xyz}$. The intersection of $\mathbb H^2_{xyw}$ and $\mathbb H^1_{zw}$ is (0, 0, 0, 1), and the intersections of $\mathbb S^2_{xyz}$ and $\mathbb S^1_{zw}$ are $(0,0,\pm 1,0)$. It is easy to see that the minimal path connecting ${\mathbf {q}}_i$ on $\mathbb H^2_{xyw}$ ($\mathbb S^2_{xyz}$) and the geodesic $\mathbb H^1_{zw}$ ($\mathbb S^1_{zw}$) lies on the two submanifolds. Thus, we can say that for all central configurations in $\mathbb H^3$, all ${\mathbf {F}}_i$ are pointing towards one point; for all ordinary $\mathbb S^2$ central configurations, all ${\mathbf {F}}_i$ are pointing towards one of two points. The vector fields $\nabla (x^2+y^2)$ on the two submanifolds are sketched in Fig. 1.

Fig. 1

$\nabla (x^2+y^2)$ on $\mathbb S_{xyz}^2$ (left) and $\mathbb H_{xyw}^2$ (right)

6.3 Equivalent Central Configurations

Recall that central configurations in the Newtonian N-body problem are invariant under translations, rotations, reflections, and scaling (Wintner 1947). In the curved N-body problem, U is invariant under the symmetry group O(4) or O(3, 1). We can check by the formula of $\nabla _{{\mathbf {q}}_i}U$ that $\nabla _{{\mathbf {q}}_i}U|_{{\mathbf {q}}'=\chi {\mathbf {q}}} = \chi \nabla _{{\mathbf {q}}_i}U|_{\mathbf {q}}$ for any $\chi$ in the symmetry group. Though I is not invariant under all elements of the symmetry group, it is invariant under a subgroup $O(2)\times O(2)$ $\left( O(2)\times O(1,1) \right)$. Let $\chi =(\chi _1, \chi _2)\in O(2)\times O(2)$ $\left( O(2)\times O(1,1) \right)$. The action is

$$\begin{aligned} \chi {\mathbf {q}}= (\chi {\mathbf {q}}_1, \ldots , \chi {\mathbf {q}}_N), \quad \chi {\mathbf {q}}_i=(\chi _1 (x_i,y_i)^T, \chi _2 (z_i,w_i)^T ). \end{aligned}$$

Then, by using the formula of $\nabla _{{\mathbf {q}}_i}I$ or Lemma 2, we can see that $\nabla _{{\mathbf {q}}_i}I|_{{\mathbf {q}}'=\chi {\mathbf {q}}} = \chi \nabla _{{\mathbf {q}}_i}I|_{\mathbf {q}}$.

There is no other obvious transform that keeps the central configuration equations. Also note that I is not involved in the equation of special central configurations. Thus, we introduce the following definition.

Definition 9

Let ${\mathbf {q}}=({\mathbf {q}}_1,\ldots ,{\mathbf {q}}_N),\ {\mathbf {q}}_i=(x_i,y_i,z_i,w_i),\ i=\overline{1,N},$ and ${\mathbf {q}}'=({\mathbf {q}}'_1,\ldots ,{\mathbf {q}}'_N)$, $q'_i=(x'_i,y'_i,z'_i,w'_i),\ i=\overline{1,N},$ be two central configurations in $\mathbb M^3$.

• 1. If they are special central configurations in $\mathbb S^3$, then they are equivalent if there is a $\chi \in SO(4)$ such that ${\mathbf {q}}=\chi {\mathbf {q}}'$.

• 2. If they are ordinary central configurations, then they are equivalent if there is a $\chi =(\chi _1, \chi _2)\in SO(2)\times SO(2)$ $\left( SO(2)\times SO(1,1) \right)$ such that ${\mathbf {q}}=\chi {\mathbf {q}}'$.

We use $SO(2)\times SO(2)$ $\left( SO(2)\times SO(1,1) \right)$ instead of $O(2)\times O(2)$ $(O(2)\times O(1,1))$. We adopt this definition to keep consistency with the critical point characterization of central configurations, which will be introduced in Sect. 8.

Example 1

(Lagrangian central configuration on $\mathbb S^2_{xyz}$). Let three equal masses $m_1=m_2=m_3=1$ be at

$$\begin{aligned} {\mathbf {q}}= & {} ({\mathbf {q}}_1,{\mathbf {q}}_2, {\mathbf {q}}_3),\quad {\mathbf {q}}_j=(x_j,y_j,z_j,w_j),\quad j=1,2,3,\\ x_j= & {} \sqrt{1-c^2}\cos \beta _j,\quad y_j=\sqrt{1-c^2}\sin \beta _j,\quad z_j=c,\quad w_j=0,\quad \beta _j = \frac{2\pi (j-1)}{3}, \end{aligned}$$

where c could have any value between $-\,1$ and 1, see Fig. 2. By symmetry, we see that $\nabla _{{\mathbf {q}}_i}U$ is pointing towards the north pole if $c>0$, or towards the south pole if $c<0$. Comparing with Fig. 1, we get that there must be some constant $\lambda$ such that $\nabla _{{\mathbf {q}}_i}U=\lambda \nabla _{{\mathbf {q}}_i}I$ for $1\le i\le 3$. Note that $d_{12}=d_{13}=d_{23}$, which is reminiscent of the three-body central configuration in the Newtonian N-body problem found by Lagrange (Wintner 1947). We call them Lagrangian central configurations.

By the convention we introduced, rotating the central configurations in the xy-plane does not lead to new central configurations, and the rotated ones still remain on the original 2-sphere; rotating them in the zw-plane does not lead to new central configurations either, although they will not remain on the original 2-sphere. Though these central configurations, for different values of c, are similar in some sense, there does not exist an element in $SO(2)\times SO(2)$ to relate any two of them. Thus, we see that there is a continuum of central configurations.

Fig. 2

Lagrangian central configurations on $\mathbb S^2_{xyz}$

In Sect. 8, we will see that, for any given masses, there is a continuum of central configurations.

7 Some Properties of Central Configurations

In this section we provide some lemmas and theorems that will be useful in the study of central configurations. We first prove a property that is analogous to the relationship $\sum _{i=1}^{N}m_i{\mathbf {q}}_i=0$ for central configurations of the Newtonian N-body problem (Moeckel 1994). We then focus on lower-dimensional ordinary central configurations, namely geodesic central configurations, $\mathbb S^2$ central configurations, and $\mathbb H^2$ central configurations. We show that any geodesic central configuration in $\mathbb H^3$ is equivalent to some central configuration on $\mathbb H^1_{xw}$. We also show that any $\mathbb S^2$ central configuration in $\mathbb S^3$ can be found on $\mathbb S^2_{xyz}$ and that any geodesic central configuration in $\mathbb S^3$ is equivalent to some central configuration on $\mathbb S^1_{xz}$.

Theorem 6

Let ${\mathbf {q}}=({\mathbf {q}}_1,\ldots ,{\mathbf {q}}_N),\ {\mathbf {q}}_i=(x_i,y_i,z_i,w_i),\ i=\overline{1,N},$ be an ordinary central configuration. Then we have the relationships

$$\begin{aligned} \sum _{i=1}^Nm_ix_iz_i=\sum _{i=1}^Nm_ix_iw_i=\sum _{i=1}^Nm_iy_iz_i=\sum _{i=1}^Nm_iy_iw_i=0. \end{aligned}$$

(15)

Proof

We first prove (15) in $\mathbb S^3$. Let $\mathbf{v}_{i1}=(z_i, 0, -x_i, 0)$. Take the inner product of both sides of the ith equation of (11) with $\mathbf{v}_{i1}$. Since

$$\begin{aligned} {\mathbf {q}}_j\cdot \mathbf{v}_{i1}=z_ix_j-x_iz_j, \quad {\mathbf {q}}_i\cdot \mathbf{v}_{i1}=0, \quad \nabla _{{\mathbf {q}}_i}I\cdot \mathbf{v}_{i1}=2m_ix_iz_i({\mathbf {q}}_i\cdot {\mathbf {q}}_i)=2m_ix_iz_i, \end{aligned}$$

we obtain $\sum _{j=1,j\ne i}^N\frac{m_im_j}{\sin ^3 d_{ij} } (z_ix_j-x_iz_j) = 2\lambda m_ix_iz_i.$ Summing over all i leads to

$$\begin{aligned} 2\lambda \sum _{i=1}^N m_ix_iz_i= \sum _{i=1}^N\sum _{j=1,j\ne i}^N\frac{m_im_j}{\sin ^3 d_{ij} } (z_ix_j-x_iz_j)=0. \end{aligned}$$

Since ${\mathbf {q}}$ is an ordinary central configuration, we have $\lambda \ne 0$, so $\sum _{i=1}^Nm_ix_iz_i=0$. The other relationships in $\mathbb S^3$ can be obtained by considering the inner product of (11) with

$$\begin{aligned} \mathbf{v}_{i2}= (w_i,0,0,- x_i), \quad \mathbf{v}_{i3}= (0, z_i,-y_i,0), \quad \mathbf{v}_{i4}= (0,w_i,0,- y_i). \end{aligned}$$

The relationships in $\mathbb H^3$ can be obtained by considering the inner product of (11) with

$$\begin{aligned} \mathbf{v}_{i1}=(z_i, 0, -x_i, 0),\quad \mathbf{v}_{i2}= (w_i,0,0, x_i),\quad \mathbf{v}_{i3}= (0, z_i,-y_i,0), \quad \mathbf{v}_{i4}= (0,w_i,0,y_i), \end{aligned}$$

a remark that completes the proof. $\square$

An obvious application of Eq. (15) is that of showing with little computational effort why certain configurations are not ordinary central configurations.

Recall that a (hyperbolic) 2-sphere means a sphere (hyperbolic sphere) isometric to the unit sphere (hyperbolic sphere) in $\mathbb R^3$ ($\mathbb R^{2,1}$). This is the non-empty intersection of $\mathbb M^3$ with a three-dimensional linear subspace, $\{ (x,y,z,w) \in \mathbb R^4\ |\ ax+by+cz+ dw=0 \}$ (Bridson and Haefliger 1999). Similarly, a geodesic is the non-empty intersection of a (hyperbolic) 2-sphere with a two-dimensional linear subspace.

Lemma 3

Assume that the intersection of $\mathbb S^3$ $(\mathbb H^3)$ and the three-dimensional linear space $V=\{ (x,y,z,w) \in \mathbb R^4\ |\ ax+by+cz+ dw=0 \}$ is non-empty. Let ${\mathbf {q}}=({\mathbf {q}}_1, \ldots , {\mathbf {q}}_N)$, $N\ge 2,$ be a non-singular configuration on the (hyperbolic) 2-sphere $V \cap \mathbb M^3$. If $\nabla _{{\mathbf {q}}_i} I$ are not all zero, then $\nabla _{{\mathbf {q}}_i} I\in V, i=\overline{1,N},$ if and only if $a=b=0$ or $c=d=0$.

Proof

Recall that

$$\begin{aligned} \nabla _{{\mathbf {q}}_i} I=2m_i\left( x_i\left( w_i^2+ \sigma z_i^2\right) ,y_i\left( w_i^2+ \sigma z_i^2\right) , -\sigma z_i\left( x_i^2+ y_i^2\right) , - \sigma w_i\left( x_i^2+ y_i^2\right) \right) . \end{aligned}$$

Then $\nabla _{{\mathbf {q}}_i} I\in V, i=\overline{1,N}$ if and only if

$$\begin{aligned} \begin{aligned} 0&=ax_i\left( w_i^2+ \sigma z_i^2\right) +by_i\left( w_i^2+ \sigma z_i^2\right) -c\sigma z_i\left( x_i^2+ y_i^2\right) -d \sigma w_i\left( x_i^2+ y_i^2\right) \\&=\left( ax_i+by_i\right) \left( w_i^2+ \sigma z_i^2\right) +\sigma \left( ax_i+by_i\right) \left( x_i^2+ y_i^2\right) =(ax_i+by_i). \end{aligned} \end{aligned}$$

Thus, $cz_i+dw_i=0$. Consider the matrix $A:=\begin{bmatrix} a&b&c&d\\ a&b&0&0\\ 0&0&c&d \end{bmatrix}.$ Then $({\mathbf {q}}_1,\ldots ,{\mathbf {q}}_N)\in \mathrm{ker} A$. Since ${\mathbf {q}}_i$ and ${\mathbf {q}}_j$ are linearly independent, we obtain rank(ker A)$\ge 2$, which implies that $\mathrm{rank}\ A= 1$. Therefore, we have either $a=b=0$ or $c=d=0$. $\square$

Now we turn to central configurations in $\mathbb H^3$. The following result is from Zhu and Zhao (2017).

Theorem 7

Each central configuration in $\mathbb H^3$ is equivalent to some central configuration on $\mathbb H^2_{xyw}$.

Thus, there are no $\mathbb H^3$ central configurations. However, there exist both special $\mathbb S^3$ central configurations and ordinary $\mathbb S^3$ central configurations, so the set of central configurations in $\mathbb S^3$ is richer and more interesting than in $\mathbb H^3$ (Zhu and Zhao 2017).

Define $\mathbb H_{xw}^1:=\{(x,y,z,w) \in \mathbb H^3\ | \ y=z=0\}$.

Corollary 2

Each geodesic central configuration in $\mathbb H^3$ is equivalent to some central configuration on $\mathbb H^1_{xw}$.

Proof

By Theorem 7, every geodesic central configuration is equivalent to some geodesic central configuration on $\mathbb H^2_{xyw}$. A geodesic on $\mathbb H^2_{xyw}$ is the non-empty intersection of a two-dimensional linear space V and $\mathbb H^2_{xyw}$. Suppose that V is defined by $\{ ax +by+ dw=0\}$ and that a central configuration ${\mathbf {q}}$ is on $V\cap \mathbb H^2_{xyw}$. Then $\nabla _{{\mathbf {q}}_i}U$ lies in V for all i. It implies that each $\nabla _{{\mathbf {q}}_i}I$ belongs to V. As in Lemma 3, we can show that it is sufficient and necessary to require $d=0$.

Then any geodesic central configuration is equivalent to some central configuration on a geodesic $\{ (x,y,w)\in \mathbb H^2_{xyw}\ |\ ax+by=0 \}$ and there is some element in $SO(2)\times SO(1,1)$ that moves the geodesic to $\mathbb H^1_{xw}$. This remark completes the proof. $\square$

Now we discuss the $\mathbb S^2$ ordinary central configurations and geodesic ordinary central configurations in $\mathbb S^3$. Define

$$\begin{aligned} \mathbb S_{xzw}^2:=\{(x,y,z,w) \in \mathbb S^3\ | \ y=0\}, \quad \mathbb S_{xz}^1:=\{(x,y,z,w) \in \mathbb S^3\ | \ w=y=0\}. \end{aligned}$$

Theorem 8

Any $\mathbb S^2$ ordinary central configuration is equivalent to some ordinary central configuration on $\mathbb S_{xyz}^2$ or on $\mathbb S_{xzw}^2$. Furthermore, there is a one-to-one correspondence between the central configurations on $\mathbb S_{xyz}^2$ and the central configurations on $\mathbb S_{xzw}^2$.

Proof

Lemma 3 implies that any $\mathbb S^2$ ordinary central configuration is either on $\mathbb S^3\cap \{ax+by=0 \}$ or on $\mathbb S^3\cap \{cz+dw=0 \}$. It is easy to see that there is some element in $SO(2)\times SO(2)$ that would move these 2-spheres to either $\mathbb S^2_{xyz}$ or $\mathbb S^2_{xzw}$. Thus, any $\mathbb S^2$ ordinary central configuration is equivalent to some ordinary central configuration on $\mathbb S_{xyz}^2$ or on $\mathbb S_{xzw}^2$.

Let ${\mathbf {q}}$ be a central configuration on $\mathbb S^2_{xyz}$, i.e. $\nabla _{{\mathbf {q}}_i}U({\mathbf {q}}) -\lambda \nabla _{{\mathbf {q}}_i}I({\mathbf {q}})=0, i=\overline{1,N}$. Consider the orthogonal transformation $\varphi (x_i,y_i,z_i,w_i)=(z_i,w_i,x_i,y_i).$ Then we have that ${\mathbf {q}}'=({\mathbf {q}}_1',...,{\mathbf {q}}_N')=\varphi {\mathbf {q}}=(\varphi {\mathbf {q}}_1, ..., \varphi {\mathbf {q}}_N)$ is a configuration on $\mathbb S^2_{xzw}$. Note that for ${\mathbf {q}}_i'=(x'_i,y'_i,z'_i,w'_i )= (z_i,w_i,x_i,y_i)$ we have

$$\begin{aligned} I({\mathbf {q}}')= & {} \sum _{i=1}^N m_i({x'}_i^2+{y'}_i^2)=\sum _{i=1}^N m_i(1-x_i^2-y_i^2)\\= & {} \sum _{i=1}^N m_i -I({\mathbf {q}})\ \mathrm{and} \ U({\mathbf {q}}')=U({\mathbf {q}}). \end{aligned}$$

Then $\nabla U ({\mathbf {q}}')=\varphi \nabla U ({\mathbf {q}})$ and $\nabla I ({\mathbf {q}}')=-\varphi \nabla I ({\mathbf {q}})$. Here $\nabla U ({\mathbf {q}}')$ and $\nabla I ({\mathbf {q}}')$ mean the gradient of U and I at ${\mathbf {q}}'$, respectively. Thus, ${\mathbf {q}}'$ satisfies the central configuration equations $\nabla _{{\mathbf {q}}_i}U({\mathbf {q}}') +\lambda \nabla _{{\mathbf {q}}_i}I({\mathbf {q}}')=0, i=\overline{1,N}.$ This remark completes the proof. $\square$

The proof of the following statement is similar to that of Corollary 2.

Corollary 3

Each ordinary geodesic central configuration in $\mathbb S^3$ is equivalent to some central configuration on $\mathbb S^1_{xz}$.

8 Existence of Ordinary Central Configurations

In this section we interpret central configurations as critical points of functions related to U and prove the existence of ordinary central configurations for any given masses. Then we discuss the Wintner–Smale conjecture for the curved N-body problem.

8.1 Central Configurations as Critical Points

From the first central configuration equations,

$$\begin{aligned} \nabla _{{\mathbf {q}}_i}U({\mathbf {q}})-\lambda \nabla _{{\mathbf {q}}_i}I({\mathbf {q}})=0, \end{aligned}$$

we can derive the following property.

Proposition 7

Central configurations in $\mathbb M^3$ are critical points of the function

$$\begin{aligned} U-\lambda I: (\mathbb M^3)^N{\setminus }\Delta \rightarrow \mathbb R. \end{aligned}$$

In $\mathbb H^3$, $\lambda$ is a negative constant; in $\mathbb S^3$, $\lambda$ could be any real number, and the case $\lambda =0$ corresponds to special central configurations.

We can also see that an ordinary central configuration is a critical point of the restriction of U subject to the constraint $I=constant$. From this point of view, $-\lambda$ is a Lagrange multiplier. More precisely, let us denote

$$\begin{aligned} S_c:=\{ {\mathbf {q}}\in (\mathbb M^3)^N{\setminus }\Delta \ | \ I({\mathbf {q}})=c\}. \end{aligned}$$

Proposition 8

Ordinary central configurations in $\mathbb M^3$ are critical points of $U|_{S_c}$, i.e. critical points of

$$\begin{aligned} U : \ S_c \rightarrow \mathbb R. \end{aligned}$$

Let ${\mathbf {q}}$ be an ordinary central configuration and $\phi$ an element of $SO(2)\times SO(2)$ or $SO(2)\times SO(1,1)$. Then $\phi {\mathbf {q}}$ is also a central configuration. Thus, it follows that the critical points of $U|_{S_c}$ are not isolated, but rather occur as manifolds of critical points. Similarly, these special central configurations are not isolated either. This fact suggests that we can further look at central configurations as critical points of U subject to a factorization. Note that both U and $(\mathbb M^3)^N$ are invariant under the isometry group and the set $S_c$ is invariant under the subgroup $SO(2)\times SO(2)$ or $SO(2)\times SO(1,1)$. We thus have the following property.

Proposition 9

There is a one-to-one correspondence between the classes of central configurations and the critical points of the force function ${\hat{U}}$ induced by U on the quotient set

• (1) $((\mathbb S^3)^N{\setminus } \Delta ) /SO(4)$ for special central configurations in $\mathbb S^3$,

• (2) $S_c/(SO(2)\times SO(2))$ for ordinary central configurations in $\mathbb S^3$, and

• (3) $S_c/(SO(2)\times SO(1,1))$ for central configurations in $\mathbb H^3$.

Let ${\mathbf {q}}$ in the quotient set be a critical point of ${\hat{U}}$. In the case of special central configuration on $\mathbb S^3$, the Hessian of ${\hat{U}}$ at ${\mathbf {q}}$, $D^2{\hat{U}}({\mathbf {q}})$, is an invariant symmetric bilinear form on $T_{{\mathbf {q}}} ((\mathbb S^3)^N{\setminus } \Delta ) /SO(4) )$. For ordinary central configurations in $\mathbb S^3$ and $\mathbb H^3$, $D^2{\hat{U}}({\mathbf {q}})$ is an invariant symmetric bilinear form on $T_{{\mathbf {q}}} {\hat{S}}_c$, where $\hat{S_c}$ is the quotient set in either (2) or (3) of Proposition 9. The index of $D^2{\hat{U}}({\mathbf {q}})$ is the maximal dimension of a subspace of the tangent space on which this form is negative definite. A critical point ${\mathbf {q}}$ of ${\hat{U}}$ is degenerate whenever the Hessian has a non-trivial null-space.

We can now formally introduce the following two concepts.

Definition 10

A central configuration is degenerate (non-degenerate) provided that the corresponding critical point ${\mathbf {q}}$ of ${\hat{U}}$ is degenerate (non-degenerate).

8.2 The Structure of $I^{-1}(c)$

Unlike in the Newtonian N-body problem, where $I=c>0$ is always a $(3N-1)$-dimensional ellipsoid, the set $I^{-1}(c)$ may not be a smooth manifold. To understand the structure of this set, we need the classical regular value theorem, which we further recall for completeness. Let ${\mathcal {M}}, {\mathcal {N}}$ be differentiable manifolds and $f:{\mathcal {M}}\rightarrow {\mathcal {N}}$ a differentiable function. Then f is called a submersion at $x\in {\mathcal {M}}$ if its differential, $Df_x:T_x{\mathcal {M}}\rightarrow T_{f(x)}{\mathcal {N}}$, is surjective. In this case, x is called a regular point and f(x) a regular value. Otherwise, x is called a critical point and f(x) a critical value. We can now state the following well-known result (Hirsch 1976).

$\mathbf{Regular \ Value\ Theorem}$ Let $f:{\mathcal {M}}\rightarrow {\mathcal {N}}$ be a $C^r$ -map, $r\ge 1$. If $y\in f({\mathcal {M}})$ is a regular value, then $f^{-1}(y)$ is a $C^r$ -submanifold of ${\mathcal {M}}$.

If we further regard the moment of inertia as the smooth map

$$\begin{aligned} I:(\mathbb M^3)^N\rightarrow [0,\infty ), \end{aligned}$$

we have the following properties.

Lemma 4

Assume that the masses $m_1,\dots , m_N$ are in $\mathbb S^3$, and consider $c\ge 0$, not of the form $c=\sum _{i=1}^Nm_i\mu _i$, where $\mu _1,\dots , \mu _N\in \{0,1\}$. Then the set $I^{-1}(c)$ is a smooth manifold.

Proof

Suppose that $c\ge 0$ is a critical value for I. This is equivalent to saying that there exists a ${\mathbf {q}}=({\mathbf {q}}_1,\dots ,{\mathbf {q}}_N)$ such that ${\mathbf {q}}\in I^{-1}(c)$ and

$$\begin{aligned} \nabla _{{\mathbf {q}}_1}I({\mathbf {q}})=\dots =\nabla _{{\mathbf {q}}_N}I({\mathbf {q}})=\mathbf 0, \end{aligned}$$

which implies that ${\mathbf {q}}_i\in \mathbb S^1_{xy}\cup \mathbb S^1_{zw}$ by Lemma 1 in Sect. 6. Then $x_i^2+y_i^2=0$ or 1 and $c=\sum _{i=1}^Nm_i\mu _i$, where $\mu _1,\dots , \mu _N\in \{0,1\}$, a remark that completes the proof. $\square$

Lemma 5

Assume that the masses $m_1,\ldots ,m_N$ are in $\mathbb H^3$, and consider $c\ge 0$. Then $I^{-1}(c)$ is always a smooth manifold.

Proof

Suppose that $c\ge 0$ is a critical value for I. This is equivalent to saying that there exists a ${\mathbf {q}}=({\mathbf {q}}_1,\dots ,{\mathbf {q}}_N)$ such that ${\mathbf {q}}\in I^{-1}(c)$ and

$$\begin{aligned} \nabla _{{\mathbf {q}}_1}I({\mathbf {q}})=\cdots =\nabla _{{\mathbf {q}}_N}I({\mathbf {q}})=\mathbf 0, \end{aligned}$$

which implies that ${\mathbf {q}}_i\in \mathbb H^1_{zw}$ by Lemma 1 in Sect. 6. Then $x_i^2+y_i^2=0$ and $c=0$. Moreover, $I^{-1}(0)= (\mathbb H^1_{zw})^N$, which is homeomorphic with $\mathbb R^N$, a remark that completes the proof. $\square$

8.3 The Existence Result

The characterization of central configurations as critical points provides an easy way to see that ordinary central configurations exist, i.e. that the complicated criteria developed earlier always have solutions for $\lambda \ne 0$.

Theorem 9

Assume that the masses $m_1,\dots ,m_N$ are in $\mathbb S^3$ or $\mathbb H^3$. Then for any positive values these masses take, there is at least one ordinary central configuration in $\mathbb S^3$ and at least one ordinary central configuration in $\mathbb H^3$.

Proof

Let us first prove the result in $\mathbb H^3$. In general, the manifold $I^{-1}(c)$ is not compact in this case. However, things change if we confine all masses to the hyperbolic circle $\mathbb H^1_{xw}$, since the set $I=c>0$ is homeomorphic to an ellipsoid. Then U defines a smooth function on the open subset $S_c$, and the boundary of $S_c$ is composed of points in the singularity set. Since the ellipsoid is compact and $U\rightarrow +\,\infty$ as ${\mathbf {q}}$ approaches the boundary of $S_c$, it follows that U attains a minimum at some non-singular configuration ${\mathbf {q}}$. This will be a critical point of U on $S_c$ and hence an ordinary central configuration.

In $\mathbb S^3$, we need to construct a connected component of $S_c$ on whose boundary U approaches $+\,\infty$. Recall that there are two kinds of singularities, collision singularities in $\Delta ^+$ and antipodal singularities in $\Delta ^-$. U approaches $+\,\infty$ as the configuration approaches $\Delta ^+$, but approaches $-\,\infty$ as the configuration approaches $\Delta ^-$. Thus, we need to construct a connected component of $S_c$ whose boundary lies only in $\Delta ^+$.

We confine the particles to $\mathbb S_{xyz}^2$ and order the masses as $0<m_1\le \ldots \le m_N,$. Let $0<c<m_1$. Then $S_c$ is a smooth manifold. Let us further choose a configuration ${\mathbf {q}}\in S_c$ with all bodies lying near the North Pole (0, 0, 1), i.e. $z_i>0,\ i=\overline{1,N}$. Denote by ${\mathcal {J}}$ the connected component of the manifold $S_c$ that contains the configuration ${\mathbf {q}}$. We claim that the boundary of ${\mathcal {J}}$ contains only points from $\Delta ^+$.

To prove this claim, we define the sets ${\mathcal {U}}=\{(x,y,z)\in \mathbb S_{xyz}^2\ |\ x^2+y^2<c/m_1,\ z>0\}$ and ${\mathcal {V}}=\{(x,y,z)\in \mathbb S_{xyz}^2\ |\ x^2+y^2<c/m_1,\ z\le 0\}.$ Since $I({\mathbf {q}})=\sum _{i=1}^Nm_i(x_i^2+y_i^2)\ge m_1(x_i^2+y_i^2),$ it follows that $x_i^2+y_i^2\le c/m_1, \ i=\overline{1,N},$ which means that for any configuration ${\mathbf {q}}\in {\mathcal {J}}$ each body lies either in ${\mathcal {U}}$ or in ${\mathcal {V}}$.

Fig. 3

${\bar{{\mathbf {q}}}}_1$, ${\bar{{\mathbf {q}}}}_2$ (left) and ${\mathbf {q}}_1, {\mathbf {q}}_2$ (right) on $\mathbb S^2_{xyz}$

Let us now suppose that $\partial {\mathcal {J}}\cap \Delta ^-\ne \emptyset$. Then there must exist a configuration ${\bar{{\mathbf {q}}}}=({\bar{{\mathbf {q}}}}_1,\dots ,{\bar{{\mathbf {q}}}}_N)\in {\mathcal {J}}$ such that one body is in ${\mathcal {U}}$ and the another in ${\mathcal {V}}$, say, ${\bar{{\mathbf {q}}}}_1\in {\mathcal {U}}$ and ${\bar{{\mathbf {q}}}}_2\in {\mathcal {V}}$, see Fig. 3. Since ${\mathcal {J}}$ is connected, it is also path-connected. Then there is a path in ${\mathcal {J}}$ connecting ${\mathbf {q}}$ and ${\bar{{\mathbf {q}}}}$, so there is a path that connects ${\mathbf {q}}_2\in {\mathcal {U}}$ and ${\bar{{\mathbf {q}}}}_2\in {\mathcal {V}}$. But this is impossible since ${\mathcal {U}}\cap {\mathcal {V}}=\emptyset$. Thus, ${\mathcal {J}}$ is a connected component of the manifold $S_c$ whose boundary consists only of points from $\Delta ^+$. Therefore, $U\rightarrow +\infty$ as ${\mathbf {q}}$ approaches $\partial {\mathcal {J}}$. It follows that U attains a minimum at some configuration ${\mathbf {q}}$, which is then a critical point of U on $S_c$, hence an ordinary central configuration. $\square$

8.4 The Wintner–Smale Conjecture in Spaces of Constant Curvature

Recall that three equal masses on $\mathbb S^2_{xyz}$ possess a continuum of central configurations, see Example 1. Notice that these central configurations are on different $S_c$. In general, there is no obvious way to relate central configurations in $S_{c_1}$ and central configurations in $S_{c_2}$. Thus, we consider them as belonging to different classes of central configurations. Notice that the existence proof of ordinary central configurations works for other constant values of I. Hence, there always exist central configurations on $S_c$ for c belonging to some open intervals. So we have the following obvious consequence.

Corollary 4

Assume that the masses $m_1,\dots ,m_N$ are in $\mathbb S^3$ or $\mathbb H^2$. Then for any positive values of these masses, the set of ordinary central configurations has the power of the continuum.

Recall that the Wintner–Smale problem (Smale’s 6th problem) asks whether for some given masses, $m_1,\dots ,m_N>0$, the number of classes of planar central configurations for the Newtonian N-body problem is finite or not. If we extend the problem to the curved N-body problem in the following way: whether for some given masses, $m_1,\dots ,m_N>0$, the number of classes of central configurations for the curved N-body problem is finite or not, then this extension has an obvious and uninteresting answer. So we modify the problem as follows for ordinary central configurations.

Question 1

In the curved N-body problem, for given masses $m_1,\ldots , m_N$ and all possible values of c, is the number of ordinary central configurations on $S_c$ finite?

From now on, we say that several masses possess a continuum of ordinary central configurations if the continuum of central configurations is on a certain set $S_c$. We will see in Sect. 10 that even for two equal masses, $m_1=m_2=:m$, there is a continuum of central configurations on $S_m$.

For special central configurations in $\mathbb S^3$, we also pose a similar question:

Question 2

In the curved N-body problem in $\mathbb S^3$, for given masses $m_1,\dots , m_N$, is the number of special central configurations finite?

9 Examples

In this section we produce examples of central configurations of the curved N-body problem in $\mathbb S^3$ and $\mathbb H^3$ and discuss the associated relative equilibria. Some examples will concern special and ordinary central configurations for $N=3$ that lie on the great sphere $\mathbb S^2_{xyz}$ and the great hyperbolic sphere $\mathbb H^2_{xyw}$. In the Newtonian N-body problem there are only two classes of central configurations for $N=3$, the Lagrangian (equilateral triangles) and the Eulerian (collinear configurations). For nonzero constant curvature, however, the set of central configurations (and therefore that of relative equilibria) is richer, as we will further show. We also include in this section examples of central configurations for $N>3$. Unless otherwise stated, the relative equilibria associated with all these central configurations were already found in Diacu (2012b) and Diacu (2013a).

The stability question for some relative equilibria of the curved N-body problem was studied by several authors (Diacu et al. 2013, 2018; Martínez and Simó 2013). In particular, the paper Diacu et al. (2018) is about the relative equilibria associated with the special central configurations mentioned in Sect. 9.1.

9.1 Acute Triangle Special Central Configurations on $\mathbb S^1_{xy}$

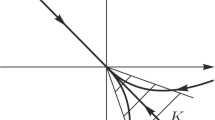
Let us assume that three masses, $m_1=\frac{\sin ^2 \alpha }{\sin ^2 \beta }$, $m_2=\frac{\sin ^2 \alpha }{\sin ^2 (\alpha +\beta )}$, and $m_3=1$, form an acute scalene triangle on $\mathbb S^1_{xy}$. In the complex coordinates of the xy-plane, i.e. $q_j=x_j+ i y_j\in {\mathbb {C}}$, the configuration is given by

$$\begin{aligned} {\mathbf {q}}_1= 1, \quad {\mathbf {q}}_2= e^{i\alpha },\quad {\mathbf {q}}_3= e^{i(\alpha +\beta )},\ \end{aligned}$$

for any fixed $0<\alpha<\pi , 0<\beta<\pi , \pi<\alpha +\beta <2\pi$, see Fig. 4. Then it is easy to verify that $\nabla _{{\mathbf {q}}_i} U=0$ for each $i=1,2,3$, [22].

Fig. 4

An acute triangle special central configuration

Since these special central configurations are confined to $\mathbb S^1_{xy}\cup \mathbb S^1_{zw}$, they give rise to two-parameter families of associated relative equilibria: $A_{\alpha ,\beta }(t){\mathbf {q}}$, $\alpha ,\beta \in \mathbb R$. The rotation in zw-plane does not affect the configuration, which will stay on $\mathbb S^1_{xy}$, thus forming a one-parameter family of associated relative equilibria, $A_{\alpha ,0}(t){\mathbf {q}}$, $\alpha \in \mathbb R$.

9.2 Regular Tetrahedron Special Central Configurations on $\mathbb S_{xyz}^2$

Let us assume that four masses, $m_1=m_2=m_3=m_4=m$, form a regular tetrahedron on $\mathbb S_{xyz}^2$, see Fig. 5. By symmetry, it is easy to see that this is a special central configuration.

Fig. 5

Regular tetrahedron special central configuration

Since this special central configuration is not confined to $\mathbb S^1_{xy}\cup \mathbb S^1_{zw}$, it gives rise to a one-parameter family of associated relative equilibria, $A_{\alpha ,\pm \alpha }(t){\mathbf {q}}$, $\alpha \in \mathbb R$. They are periodic orbits, but the motion is not confined to $\mathbb S^2_{xyz}$.

9.3 Regular Pentatope Special Central Configurations in $\mathbb S^3$

Let us assume that five masses, $m_1=m_2=m_3=m_4=m_5=m$, form a regular pentatope in $\mathbb S^3$. By symmetry, it is easy to see that $\sum _{j=1,j\ne i}^4 {\mathbf {F}}_{ij}=\nabla _{{\mathbf {q}}_i} U=0$ for $i=1,2,3,4,5$, and thus this is a special central configuration. Since this special central configuration is not confined to $\mathbb S^1_{xy}\cup \mathbb S^1_{zw}$, it gives rise to a one-parameter family of associated relative equilibria, $A_{\alpha ,\pm \alpha }(t){\mathbf {q}}$, $\alpha \in \mathbb R$, which are periodic orbits.

9.4 Pair of Equilateral Triangle Special Central Configuration in $\mathbb S^3$

Let us assume that six masses, $m_1=m_2=m_3=m_4=m_5=m_6=m$, in $\mathbb S^3$ form two equilateral triangles on complementary great circles: $\mathbb S^1_{xy}$ and $\mathbb S^1_{zw}$.

To see that $\sum _{j=1,j\ne i}^6 {\mathbf {F}}_{ij}=\nabla _{{\mathbf {q}}_i} U=0$ for $i=1,2,3,4,5,6$, it suffices to check that for $m_1$. That is,

$$\begin{aligned} {\mathbf {F}}_1={\mathbf {F}}_{12}+{\mathbf {F}}_{13}+{\mathbf {F}}_{14}+{\mathbf {F}}_{15}+{\mathbf {F}}_{16}=0. \end{aligned}$$

By symmetry, we obtain that ${\mathbf {F}}_{12} +{\mathbf {F}}_{13}=0$. For $i=4,5,6$, since ${\mathbf {q}}_1\cdot {\mathbf {q}}_i =0$, we have $d_{1i}= \pi /2$ and ${\mathbf {F}}_{1i}=\frac{m^2 ({\mathbf {q}}_i-\cos d_{1i}{\mathbf {q}}_1)}{\sin ^3 d_{1i}} =m^2 {\mathbf {q}}_i$. Then

$$\begin{aligned} {\mathbf {F}}_{14}+{\mathbf {F}}_{15}+{\mathbf {F}}_{16}= m^2({\mathbf {q}}_4+{\mathbf {q}}_5+{\mathbf {q}}_6)=0; \end{aligned}$$

hence, this is a special central configuration. Since this special central configuration is on $\mathbb S^1_{xy}\cup \mathbb S^1_{zw}$, it gives rise to a two-parameter family of associated relative equilibria, $A_{\alpha ,\beta }(t){\mathbf {q}}$, $\alpha ,\beta \in \mathbb R$. They are periodic orbits if $\alpha /\beta$ is rational, but quasi-periodic orbits if $\alpha /\beta$ is irrational.

9.5 Lagrangian central configurations in $\mathbb S_{xyz}^2$

Let us assume that three equal masses, $m_1=m_2=m_3=m$, form an equilateral configuration on $\mathbb S_{xyz}^2$, parallel with the xy-plane, so the coordinates are given by

$$\begin{aligned} {\mathbf {q}}_1=(r, 0, z, 0), \quad {\mathbf {q}}_2=\left( -r/2, r\sqrt{3}/2, z, 0\right) , \quad {\mathbf {q}}_3=\left( -r/2, -r\sqrt{3}/2, z, 0\right) , \end{aligned}$$

where $r^2+z^2=1$, $r\in (0,1)$, see Fig. 2. By symmetry, we notice that ${\mathbf {F}}_i$ is pointing towards the North or South Poles and that $|{\mathbf {F}}_i|=|{\mathbf {F}}_j|$. Comparing this with the vector field $\nabla (x^2+y^2)$ on $\mathbb S_{xyz}^2$, see Fig. 1, we see that the central configuration equations $\nabla _{{\mathbf {q}}_i} U=\lambda \nabla _{{\mathbf {q}}_i} I$ are satisfied for $i=1,2,3$.

To find the value of $\lambda$, we use the expression obtained in Proposition 6. For any $i\ne j$, we obtain that $\sin ^3 d_{ij}=3\sqrt{3}r^3\left( 1-\frac{3r^2}{4}\right) ^{3/2}, x_ix_j+y_iy_j=-r^2/2.$ Then

$$\begin{aligned} \begin{aligned} \lambda&= \sum _{1\le i\le N} \sum _{j=1,j\ne i}^N\frac{m_im_j(2x_ix_j+2y_iy_j-(r_i^2+r_j^2)\cos d_{ij})}{\sin ^3d_{ij}}/\left( 2 \sum _{1\le i\le N} m_i r_i^2 \rho _i^2 \right) \\&=\frac{3m}{2\sin ^3d}= -\frac{m}{2\sqrt{3}r^3\left( 1-\frac{3r^2}{4}\right) ^{3/2}}<0. \end{aligned} \end{aligned}$$

These central configurations give rise to a one-parameter family of associated relative equilibria, $A_{\alpha , \beta }(t){\mathbf {q}}$ with $\lambda =\frac{\beta ^2-\alpha ^2}{2}$.

9.6 Geodesic Central Configurations on $\mathbb S^1_{xz}$

Let the coordinates of the three bodies of masses $m_1=m_2=m_3=m$ be given by

$$\begin{aligned} {\mathbf {q}}_1=(0, 0, 1, 0), \quad {\mathbf {q}}_2=(r, 0, z, 0), \quad {\mathbf {q}}_3=(-r, 0, z, 0), \end{aligned}$$

with $r>0$, $z\in (-1,0)\cup (0,1)$ and $r^2+z^2=1$, see Fig. 6 (left). Given the many zeroes that occur in the above coordinates, it is not difficult to check that the central configuration equations are satisfied for $i=1,2,3$.

To find the value of $\lambda$, we use the expressions obtained in Proposition 6, so we have

$$\begin{aligned} d_{12}= & {} d_{13}, \quad r_1^2=0,\quad r_2^2=r_3^2=r^2,\quad \sin ^3 d_{12}=r^3,\quad \sin ^3 d_{23}=8r^3|z|^3,\\&\quad x_1x_2+y_1y_2=x_1x_3+y_1y_3=0, \quad x_2x_3+y_2y_3=-r^2. \end{aligned}$$

Then

$$\begin{aligned} \begin{aligned} \lambda&= \frac{1}{4mr^2z^2}\left( \frac{m^2(-r^2 \cos d_{12})}{\sin ^3d_{12}} +\frac{m^2(-r^2 \cos d_{13})}{\sin ^3d_{13}} +\frac{m^2(-2r^2-2r^2 \cos d_{23})}{\sin ^3d_{23}}\right) \\&=\frac{-m}{2z^2}\left( \frac{\cos d_{12}}{\sin ^3d_{12}} +\frac{1+\cos d_{23}}{\sin ^3d_{23}}\right) =\frac{-m}{2r^3}\left( \frac{1}{z} +\frac{1}{4|z|^3}\right) . \end{aligned} \end{aligned}$$

It is easy to see that $\lambda <0$ for $z\in ( -1/2,0)\cup (0,1)$, $\lambda >0$ for $z\in (-1,-1/2)$, and $\lambda =0$ for $z= -1/2$, which shows the connection with the special central configuration discussed in the first example.

Fig. 6

Geodesic central configurations on $\mathbb S^1_{xz}$

All ordinary geodesic central configurations of three masses on $\mathbb S^1_{xz}$ were found in Zhu (2014). Some interesting examples were given there, such as the one in which three distinct masses form an equilateral triangle. In the complex coordinates of the xz-plane, i.e. $q_j=x_j+ i z_j\in {\mathbb {C}}$, for instance, one such central configuration is given by

$$\begin{aligned} {\mathbf {q}}_1= e^{i\frac{3\pi }{4}}, \quad {\mathbf {q}}_2= e^{i\frac{17\pi }{12}},\quad {\mathbf {q}}_3= e^{i\frac{\pi }{12}}, \end{aligned}$$

and the masses are $m_1=2, m_2=1, m_3=3$, see Fig. 6 (right).

We could also verify that the central configuration equations are satisfied and $\lambda =-\frac{8}{3}.$ We can actually find many such examples. For any three unequal masses $m_1, m_2, m_3$, we can find $\lambda \ne 0$ and $\theta$ such that the equations

$$\begin{aligned} \sin 2\theta = -\frac{4}{3\lambda }(m_3-m_2), \quad \cos 2\theta = \frac{4\sqrt{3}}{9\lambda } (2m_1-m_3-m_2) \end{aligned}$$

hold. Then the configuration

$$\begin{aligned} {\mathbf {q}}_1= e^{i\theta }, \quad {\mathbf {q}}_2= e^{i\left( \theta + \frac{2\pi }{3}\right) },\quad {\mathbf {q}}_3= e^{i \left( \theta + \frac{4\pi }{3}\right) } \end{aligned}$$

is a central configuration.

9.7 Isosceles Central Configuration in $\mathbb S^2_{xyz}$

Let us assume that three masses, $m_1=-2\cos \varphi$, with $\varphi \in (\pi /2,\pi )$, $m_2=m_3=1$, form an isosceles triangle on the sphere $\mathbb S^2_{xyz}$, parallel with the xy-plane. The configuration is given by

$$\begin{aligned} {\mathbf {q}}_1= & {} (\sin \theta , 0, \cos \theta , 0), \ {\mathbf {q}}_2=(\sin \theta \cos \varphi , \sin \theta \sin \varphi , \cos \theta , 0),\\ {\mathbf {q}}_3= & {} (\sin \theta \cos \varphi , -\sin \theta \sin \varphi , \cos \theta , 0), \end{aligned}$$

with $\theta$ chosen such that $\cos ^2\theta =1+\frac{2}{(\cos \varphi -1)(2\cos \varphi +3)}$ (Fig. 7).

Fig. 7

Isosceles central configuration on $\mathbb S^2_{xyz}$

By straightforward computations, we can see that the central configuration equations are satisfied, and

$$\begin{aligned} \lambda =-\frac{2-2\cos \varphi }{2\sin ^3d_{12}}=-\frac{2-2\cos \varphi }{2\sin ^3\theta (1-\cos \varphi )^{3/2}(1+\sin ^2\theta \cos \varphi +\cos ^2\theta )^{3/2}}. \end{aligned}$$

The existence of the associated relative equilibria was proved in Diacu (2016). Some interesting details concerning this type of central configuration will be given in a future paper (Zhu and Diacu, to appear).

9.8 Lagrangian Central Configurations in $\mathbb H_{xyw}^2$

Let us assume that three equal masses, $m_1=m_2=m_3=m$, form an equilateral configuration in $\mathbb H^2_{xyw}$, parallel with the xy-plane, and the coordinates are given by

$$\begin{aligned} {\mathbf {q}}_1=(r, 0, 0, w), \quad {\mathbf {q}}_2=(-\,r/2, r\sqrt{3}/2, 0,w), \quad {\mathbf {q}}_3=(-\,r/2, -\,r\sqrt{3}/2, 0,w), \end{aligned}$$

where $r^2-w^2=-1$, $w\in (1,+\infty )$, see Fig. 8 (left). By symmetry, we notice that ${\mathbf {F}}_i$ is pointing towards (0, 0, 0, 1) and $|{\mathbf {F}}_i|=|{\mathbf {F}}_j|$. Comparing with the vector field $\nabla (x^2+y^2)$ on $\mathbb H^2_{xyw}$ (see Fig. 1), we see that the central configuration equations $\nabla _{{\mathbf {q}}_i} U=\lambda \nabla _{{\mathbf {q}}_i} I$ are satisfied for $i=1,2,3$.

To find the value of $\lambda$, we use the expression obtained in Proposition 6. For any $i\ne j$, we obtain that $\sinh ^3 d_{ij}=3\sqrt{3}r^3\left( 1+\frac{3r^2}{4}\right) ^{3/2}, x_ix_j+y_iy_j=-\,r^2/2.$ Then

$$\begin{aligned} \begin{aligned} \lambda&= \sum _{1\le i\le N} \sum _{j=1,j\ne i}^N\frac{m_im_j(2x_ix_j+2y_iy_j-(r_i^2+r_j^2)\cosh d_{ij})}{\sinh ^3d_{ij}}/\left( 2 \sum _{1\le i\le N} m_i r_i^2 \rho _i^2 \right) \\&=\frac{3m}{2\sinh ^3d}= -\frac{m}{2\sqrt{3}r^3\left( 1+\frac{3r^2}{4}\right) ^{3/2}}. \end{aligned} \end{aligned}$$

Each of these central configurations gives rise to a one-parameter family of associated relative equilibria: $B_{\alpha , \beta }(t){\mathbf {q}}$ with $\lambda =-\frac{\beta ^2+\alpha ^2}{2}$. These orbits are a new discovery that has been missed in previous studies, a fact that shows the power of the central configuration approach for finding relative equilibria.

Fig. 8

Lagrangian central configurations on $\mathbb H^2_{xyw}$ and the associated relative equilibria in the Poincaré ball

Although we build the whole theory of negative curvature spaces on the hyperbolic sphere model $\mathbb H^3$, it is convenient to visualize the associated relative equilibria in the Poincaré ball model. Recall that the Poincaré ball model is given by

$$\begin{aligned} \left( {\bar{x}}^2+{\bar{y}}^2+{\bar{z}}^2<1, \ \mathrm{d}s^2=\frac{4(\mathrm{d}{\bar{x}}^2+\mathrm{d}{\bar{y}}^2+\mathrm{d}{\bar{z}}^2)}{1-({\bar{x}}^2+{\bar{y}}^2+{\bar{z}}^2)} \right) , \end{aligned}$$

which can be seen as the perspective projection of the upper three-dimensional hyperboloid viewed from $(0,0,0,-\,1)$. The projection mapping is

$$\begin{aligned} {\bar{x}}=\frac{x}{1+w}, \quad {\bar{y}}=\frac{y}{1+w}, \quad {\bar{z}}=\frac{z}{1+w}. \end{aligned}$$

This projection mapping shows that the isometries of the SO(2) rotations in the xy-plane become the rotations in the ${\bar{x}}{\bar{y}}$-plane and that the isometries of the SO(1, 1) rotations in the zw-plane become action moving points from $(0,0,-\,1)$ to (0, 0, 1) or in the opposite direction. Thus, the relative equilibria $B_{\alpha ,\beta }(t){\mathbf {q}}$ in the Poincaré ball model can be viewed as bodies that rotate around the ${\bar{z}}$-axis and move up or down along the projection of the hyperbolic cylinder

$$\begin{aligned} \mathbf{C}_{r\rho }:=\{(x,y,z,w)\in \mathbb H^3\ | \ x^2+y^2=r^2 \}, \end{aligned}$$

a spindle-shaped surface (within the framework of this model) for which the hyperbolic distance from the ${{\bar{z}}}$-axis is constant, see Fig. 8 (right), hence the name “hyperbolic cylinder” previously given to $\mathbf{C}_{r\rho }$ (Diacu 2012b, 2013a).

9.9 Geodesic Central Configurations in $\mathbb H^1_{xw}$

Let the three bodies of masses $m_1=m_2=m_3=:m$ have the coordinates

$$\begin{aligned} {\mathbf {q}}_1=(0, 0, 0,1), \quad {\mathbf {q}}_2=(r, 0, 0, w), \quad {\mathbf {q}}_3=(-\,r, 0, 0,w), \end{aligned}$$

with $r>0$ and $r^2-w^2=-1$, see Fig. 9 (left). It is easy to check that system (11) is satisfied.

To find the value of $\lambda$, we use the expression obtained in Proposition 6. We have

$$\begin{aligned} d_{12}= & {} d_{23}, \quad r_1^2=0,\quad r_2^2=r_3^2=r^2,\quad \sinh ^3 d_{12}=r^3,\quad \sinh ^3 d_{23}=8r^3w^3, \\ x_1x_2+y_1y_2= & {} x_1x_3+y_1y_3=0, \quad x_2x_3+y_2y_3=-r^2, \end{aligned}$$

which yield

$$\begin{aligned} \begin{aligned} \lambda&= \frac{1}{4mr^2z^2}\left[ \frac{m^2(-r^2 \cosh d_{12})}{\sinh ^3d_{12}} +\frac{m^2(-r^2 \cosh d_{13})}{\sinh ^3d_{13}} +\frac{m^2(-2r^2-2r^2 \cosh d_{23})}{\sinh ^3d_{23}}\right] \\&=-\frac{m}{2w^2}\left( \frac{\cosh d_{12}}{\sinh ^3d_{12}} +\frac{1+\cosh d_{23}}{\sinh ^3d_{23}}\right) =-\frac{m}{2r^3}\left( \frac{1}{w} +\frac{1}{4w^3}\right) . \end{aligned} \end{aligned}$$

Fig. 9

Geodesic central configurations on $\mathbb H^1_{xw}$ and the associated relative equilibria in the Poincaré ball

As in the last example, we can also represent the associated relative equilibria in the Poincaré ball model, see Fig. 9 (right), where the bodies rotate around the ${\bar{z}}$-axis and move up or down, one along the ${{\bar{z}}}$-axis, and the other two along the projection of the hyperbolic cylinder $\mathbf{C}_{r\rho }$, thus maintaining constant mutual distances.

10 Moulton’s Theorem

In 1910, Forest Ray Moulton sought to extend Euler’s results about the collinear central configurations in the Newtonian N-body problem to any number N of point masses. He showed that for a given ordering of the bodies on a straight line, there is exactly one class of central configurations (Moulton 1910). In this section we are asking whether Moulton’s theorem has a natural correspondent in spaces of nonzero constant curvature. As we will further prove, this extension is true on geodesics of $\mathbb H^3$, but not on geodesics of $\mathbb S^3$, where even the case $N=2$ leads to a complicated count.

Before we get to the curved N-body problem, let us make some comments about the Euclidean case. The class of central configurations in the above statement of the theorem is meant as the set of central configurations factorized to homotheties. So another equivalent way of stating Moulton’s result is to say that, for every ordering of any given masses with $I({\mathbf {q}})=$ constant, there is exactly one central configuration. This new formulation is the one we adopt here, since the value of $I({\mathbf {q}})$ could never be the same for central configurations with different sizes, as the definition of equivalent central configurations implies.

10.1 Geodesic Central Configurations in $\mathbb H^3$

Corollary 2 states that every geodesic central configuration in $\mathbb H^3$ is equivalent to some geodesic central configuration on $\mathbb H^1_{xw}$. Thus, we assume that the point masses $m_1,\dots ,m_N$ lie on $\mathbb H^1_{xw}$. Expressing the position of each mass $m_i$ in terms of the oriented hyperbolic distance $\theta _i\in \mathbb R, \ i=\overline{1,N}$, measured from the vertex, (0, 0, 0, 1), we can represent the position vectors and the distances between bodies as

$$\begin{aligned} {\mathbf {q}}_i=(\sinh \theta _i, 0, 0, \cosh \theta _i),\quad d_{ij}=|\theta _i-\theta _j|, \quad i,j=\overline{1,N}, \end{aligned}$$

respectively. Then the force function and the moment of inertia can be written as

$$\begin{aligned} U({\mathbf {q}})=\sum _{1\le i<j\le N}m_im_j\coth d_{ij}\ \ \mathrm{and}\ \ I({\mathbf {q}})=\sum _{i=1}^Nm_i\sinh ^2\theta _i. \end{aligned}$$

By the critical point characterization of central configurations introduced in Sect. 8, we only need to find the number of critical points of ${\hat{U}}$ on $\hat{S_c}$ for a constant $c>0$. In this case, we have

$$\begin{aligned} \hat{S_c}= S_c/ SO(2)\times SO(1,1)=S_c=\{{\mathbf {q}}\in (\mathbb H^1_{xw})^N{\setminus }\Delta \ |\ I({\mathbf {q}})=c\},\ \ {\hat{U}}=U, \end{aligned}$$

where $\Delta$ denotes the collision set. Equivalently, we only need to find the number of critical points of $U -\lambda I$ in $(\mathbb H^1_{xw})^N{\setminus }\Delta$, where $\lambda$ is fixed. We can now state and prove the following result.

Theorem 10

For any given point masses $m_1,\dots ,m_N>0$ in $\mathbb H^3$ and each $c>0$, there are exactly N! / 2 geodesic central configurations with $I({\mathbf {q}})=c$, one for each ordering of the masses on the geodesic.

Proof

We follow the idea used to prove the classical theorem of Moulton (Abraham and Marsden 1987; Moeckel 1994) and show first that the manifold $S_c$ contains N! components, each homeomorphic to an $(N-1)$-dimensional disc. We will then prove that the critical points of ${\hat{U}}$, or equivalently, of U, are local minima on these discs, and finally show that there is just one minimum on each such disc.

To prove that each ordering corresponds to an $(N-1)$-dimensional open disc, it suffices to consider one of the orderings, $\theta _1<\cdots <\theta _N$. Denote the corresponding component by $S_c'$, see Fig. 10. Consider the homeomorphism $\phi : (\mathbb H^1_{xw})^N \rightarrow \mathbb R^N$, $\phi (\theta _1, \ldots , \theta _N)=(x_1, \ldots , x_N)$, where $x_i=\sinh \theta _i$. Then $S_c'$ is homeomorphic to

$$\begin{aligned} \left\{ (x_1,\dots ,x_N)\in \mathbb R^N\ | \ x_1<\cdots <x_N, \ \ \sum _{i=1}^N m_ix_i^2=c\right\} , \end{aligned}$$

which is an $(N-1)$-dimensional open disc [45]. Thus, the set $S_c$ has exactly N! components, each homeomorphic to an $(N-1)$-dimensional open disc. By an argument similar to the one in the proof of Theorem 9, we can establish the existence of a critical point, or a central configuration, on each component. Denote such a critical point by ${\mathbf {q}}'$. We will show that ${\mathbf {q}}'$ must be a local minimum of U in $S_c$. For this, we first prove that ${\mathbf {q}}'$ is a local minimum of $U({\mathbf {q}})-\lambda I({\mathbf {q}})$ in $(\mathbb H_{xw}^1)^N{\setminus } \Delta$, where $\lambda =\lambda ({\mathbf {q}}')<0$ is a constant. To reach this goal, we compute the Hessian of $U({\mathbf {q}})-\lambda I({\mathbf {q}})$ and show that it is positive definite. By straightforward computations, we obtain

Fig. 10

A configuration of N-masses on $\mathbb H^1_{xw}$

$$\begin{aligned} \mathrm{Hess}_{\mathbf {q}}&=\ D^2 U({\mathbf {q}}) -\lambda D^2I({\mathbf {q}})\\&= 2\begin{bmatrix} \sum \limits _{\begin{array}{c} j=1, j\ne 1 \end{array}}^N \frac{m_1m_j\cosh d_{1j}}{\sinh ^3d_{1j}}&\quad -\frac{m_1m_2\cosh d_{12}}{\sinh ^3d_{12}}&\quad \cdots&\quad -\frac{m_1m_N\cosh d_{1N}}{\sinh ^3d_{1N}}\\ -\frac{m_2m_1\cosh d_{12}}{\sinh ^3d_{12}}&\quad \sum \limits _{\begin{array}{c} j=1,j\ne 2 \end{array}}^N \frac{m_2m_j\cosh d_{2j}}{\sinh ^3d_{2j}}&\quad \cdots&\quad -\frac{m_2m_N\cosh d_{2N}}{\sinh ^3d_{2N}}\\ \cdots&\quad \cdots&\quad \cdots&\quad \cdots \\ -\frac{m_1m_N\cosh d_{1N}}{\sinh ^3d_{1N}}&\quad \cdots&\quad \cdots&\quad \sum \limits _{\begin{array}{c} j=1, j\ne N \end{array}}^N \frac{m_Nm_j\cosh d_{Nj}}{\sinh ^3d_{Nj}} \end{bmatrix}\\&\quad -2\lambda \begin{bmatrix} m_1 \cosh 2\theta _1&\quad 0&\quad \cdots&\quad 0\\ 0&\quad m_2 \cosh 2\theta _2&\quad \cdots&\quad 0\\ \cdots&\quad \cdots&\quad \cdots&\quad \cdots \\ 0&\cdots&\quad \cdots&m_N \cosh 2\theta _N\ \end{bmatrix}. \end{aligned}$$

Notice first that $-\,\lambda D^2I({\mathbf {q}})$, the second term in $\mathrm{Hess}_{\mathbf {q}}$, is positive definite. Indeed, the matrix $D^2I({\mathbf {q}})$ is obviously positive definite, and the coefficient $-\,\lambda$ is positive.

For the first term, $D^2U$, let us take any nonzero vector $\mathbf{v}=(v_1,\ldots , v_N)$ in the tangent space $T_{{\mathbf {q}}'}\left( (\mathbb H_{xw}^1)^N{\setminus } \Delta \right)$. Regarding $D^2U$ as a bilinear form, we obtain

$$\begin{aligned} \mathbf{v}^T (D^2U)\mathbf{v}=\sum _{i=1}^N\sum _{j=1}^N(D^2 U)_{ij} v_iv_j=&2\sum _{i=1}^{N}\sum \limits _{\begin{array}{c} j=1\\ j\ne i \end{array}}^N \frac{m_im_j\cosh d_{ij}}{\sinh ^3d_{ij}}v_i^2\ 2\sum _{i=1}^N\sum \limits _{\begin{array}{c} j=1\\ j\ne i \end{array}}^N \frac{m_im_j\cosh d_{ij}}{\sinh ^3d_{ij}}v_iv_j =&\sum _{i=1}^N\sum \limits _{\begin{array}{c} j=1\\ j\ne i \end{array}}^N \frac{m_im_j\cosh d_{ij}}{\sinh ^3d_{ij}}(v_i-v_j)^2 \ge 0. \end{aligned}$$

We can conclude that $\text{ Hess }_{\mathbf {q}}(\mathbf{v},\mathbf{v})>0$ for all $\mathbf{v}\in T_{{\mathbf {q}}'}(\mathbb H_{xw}^1)^N{\setminus } \Delta$, so ${\mathbf {q}}'$ is a local minimum of $U({\mathbf {q}})-\lambda I({\mathbf {q}})$ on $(\mathbb H_{xw}^1)^N{\setminus } \Delta$. Then ${\mathbf {q}}'$ is also a local minimum of the new function $U({\mathbf {q}})-\lambda I({\mathbf {q}})+\lambda c$ restricted to the submanifold $S_c$. Note that, on $S_c$, this new function becomes U. Consequently ${\mathbf {q}}'$ is a local minimum of U on $S_c$.

We show that such a minimum of U is unique on each $(N-1)$-dimensional open disc. Assume that there are two such minima. Connect these two points with a continuous family of curves. As the two ends are local minima, there must be a local maximum on each curve. Then the minimum of all these maxima must be a saddle point of U, in contradiction with the positive definiteness of the Hessian.

Note that a $180^\circ$ rotation in the xy-plane does not change the ordering, which means that we counted each case twice, so there are exactly N! / 2 classes of geodesic central configurations, a remark that completes the proof. $\square$

10.2 Geodesic Central Configurations in $\mathbb S^3$

Unlike in the hyperbolic case, Moulton’s theorem has no straightforward generalization to $\mathbb S^3$. We give an example of geodesic central configurations for two masses to show that the number of central configurations on $S_c$ depends on the value of c. This example also provides some degenerate central configurations, as defined in Sect. 8, and means that the corresponding critical points of ${\hat{U}}$ on $\hat{S_c}$ are degenerate.

According to Corollary 3, any geodesic central configuration in $\mathbb S^3$ is equivalent to some geodesic central configuration on $\mathbb S^1_{xz}$. The example we will exhibit is that of central configurations for two masses on $\mathbb S^1_{xz}$. Special central configurations cannot exist under these circumstances since any non-singular configuration would force the two masses to lie inside a semicircle, which turns out to be impossible because such a configuration cannot generate relative equilibria, as proved in Diacu (2012b). Expressing the positions of $m_1$ and $m_2$ in terms of the oriented spherical distance, $\theta _i\in [0,2\pi ], \ i=1,2$, measured from (0, 0, 1, 0), see Fig. 11, we can write the position vectors as

$$\begin{aligned} {\mathbf {q}}_1=(-\sin \theta _1,0,\cos \theta _1,0),\quad {\mathbf {q}}_2=(-\sin \theta _2,0,\cos \theta _2,0), \quad 0\le \theta _1<\theta _2\le 2\pi . \end{aligned}$$

Then the force function and the moment of inertia have the form

$$\begin{aligned} U({\mathbf {q}})=m_1m_2\cot d_{12}\ \ \mathrm{and}\ \ I({\mathbf {q}})=m_1\sin ^2\theta _1+m_2\sin ^2\theta _2, \end{aligned}$$

respectively, where $d_{12}=\min \{\theta _2-\theta _1, 2\pi -\theta _2+\theta _1\}$ is the distance between the bodies. We can also assume, without loss of generality, that $\theta _1\in [0,\pi /2]$. This is all the preparation we need to state and prove the following result.

Fig. 11

A configuration of two masses on $\mathbb S^1_{xz}$

Theorem 11

Consider two masses $m_1$ and $m_2$ on $\mathbb S^1_{xz}$ with positions ${\mathbf {q}}_1$ and ${\mathbf {q}}_2$ as above. Then these bodies can form a central configuration if and only if

$$\begin{aligned} m_1 \sin 2\theta _1+ m_2 \sin 2\theta _2=0 \ \mathrm{with}\ \sin 2\theta _1\ne 0. \end{aligned}$$

(16)

The number of geodesic central configurations depends on the size $I({\mathbf {q}})=c$ of each configuration and is given in the table below, where $M:=m_1+m_2$. The table on the left is for $m_1<m_2$, whereas the table on the right is for the $m_1=m_2=:m$.

When the masses are equal and $c=m$, all central configurations are degenerate critical points of U on $S_{m}$ and the set they form has the power of the continuum.

Proof

In this case, the central configuration equations $\nabla _{{\mathbf {q}}_i}U=\lambda \nabla _{{\mathbf {q}}_i}I, i=1,2$, reduce to

$$\begin{aligned} \frac{\partial U}{\partial \theta _1} = \lambda \frac{\partial I}{\partial \theta _1} \ \ \mathrm{and}\ \ \frac{\partial U}{\partial \theta _2} = \lambda \frac{\partial I}{\partial \theta _2}, \end{aligned}$$

which implies that

$$\begin{aligned} \frac{\pm m_1m_2}{\sin ^2(\theta _2-\theta _1)}=\lambda m_1 \sin 2\theta _1\ \ \mathrm{and}\ \ \frac{{\mp } m_1m_2}{\sin ^2(\theta _2-\theta _1)}=\lambda m_2 \sin 2\theta _2, \end{aligned}$$

where the signs depend on whether $d_{12}$ equals $\theta _2-\theta _1$ or $2\pi -\theta _2+\theta _1$. From these equations we obtain the condition

$$\begin{aligned} m_1 \sin 2\theta _1+ m_2 \sin 2\theta _2=0 \ \mathrm{with}\ \sin 2\theta _1\ne 0. \end{aligned}$$

This relationship implies that $\theta _1\in \left( 0, \frac{\pi }{2}\right)$ and $\theta _2 \in \left( \frac{1}{2}\pi ,\pi \right)$ or $\theta _2\in \left( \frac{3}{2}\pi ,2\pi \right)$.

To find the number of central configurations on $S_c$, we solve the system

$$\begin{aligned} {\left\{ \begin{array}{ll} m_1\sin ^2\theta _1+m_2\sin ^2\theta _2=c\\ m_1 \sin 2\theta _1+ m_2 \sin 2\theta _2=0 \end{array}\right. } \end{aligned}$$

and obtain

$$\begin{aligned} \sin ^2\theta _2 = \frac{c(m_1-c)}{m_2(M-2c)} \ \ \text{ and }\ \ \sin ^2\theta _1 = \frac{c(m_2-c)}{m_1(M-2c)}. \end{aligned}$$

Notice that $\sin 2\theta _i\ne 0$, so let

$$\begin{aligned} 0<\frac{c(m_1-c)}{m_2(M-2c)}<1, \ \ 0<\frac{c(m_2-c)}{m_1(M-2c)}<1. \end{aligned}$$

We are then led to

$$\begin{aligned} 0<c<m_1, \ \ m_2<c<M, \end{aligned}$$

a fact that can also be seen in the graphs of Fig. 12, where a typical function of the form $\frac{c(m_1-c)}{m_2(M-2c)}$ is represented for $m_1<m_2$ (left) and $m_1=m_2$ (right).

Fig. 12

Graphs of $\sin ^2\theta _2 = \frac{c(m_1-c)}{m_2(M-2c)}$ for $m_1<m_2$ (left) and $m_1=m_2=:m$ (right) in coordinates $(c,\sin ^2\theta _2$)

Thus, having c in this range, we can obtain the values for $\sin ^2 \theta _i<1, i=1,2$. Using the fact that $\theta _1\in \left( 0, \frac{\pi }{2}\right)$ and $\theta _2 \in \left( \frac{1}{2}\pi ,\pi \right)$ or $\theta _2 \in \left( \frac{3}{2}\pi ,2\pi \right)$, we see that there are exactly two central configurations for each c:

$$\begin{aligned} (\theta _1, \theta _2) \in \left( 0, \frac{\pi }{2}\right) \times \left( \frac{1}{2}\pi ,\pi \right) \ \mathrm{and}\ \ (\theta _1, \theta _2 + \pi ) \in \left( 0, \frac{\pi }{2}\right) \times \left( \frac{3}{2}\pi ,2\pi \right) . \end{aligned}$$

If $m_1=m_2=m$ and $I=m$, we have

$$\begin{aligned} {\hat{S}}_m=S_m=\{ (\theta _1,\theta _2)\in (0,\pi /2)\times [0,2\pi ] \ | \ \theta _1<\theta _2,\ \sin ^2\theta _1+\sin ^2\theta _2=1\}, \end{aligned}$$

which implies that

$$\begin{aligned}{\hat{S}}_m=\{ \theta _1 \in (0,\pi /2),\ \theta _2=\theta _1 +\pi /2 \ \ \text{ or } \ \ \theta _2=\theta _1 +3\pi /2\}. \end{aligned}$$

Thus, $d_{12}=\pi /2$ and ${\hat{U}}=U=m_1m_2\cot d_{12}=0$ on $S_m$, which means that all elements of this set are degenerate critical points of U on $S_m$, so they are degenerate central configurations. This remark justifies the values in the above tables and completes the proof. $\square$

The related problem of finding relative equilibria on $\mathbb S_{xz}^1$ has also been considered by A.A. Kilin, who obtained the same criterion given in the first part of Theorem 11 (Kilin 1999).

Remark 3

The complicated count of geodesic central configurations in $\mathbb S^3$ is a consequence of two facts: the boundary of some components in $S_c$ may contain points in $\Delta ^+$ and $\Delta ^-$, which can destroy the existence of critical points on those components, and the geodesic central configurations are not necessarily minima of U on $S_c$.

11 Conclusions

So far, the only classes of solutions found for the N-body problem in spaces of constant curvature have been relative equilibria and rotopulsators, the latter allowing dilations and contractions of the configuration, which, of course, fail to maintain similarity, Diacu and Kordlou (2013), although, very recently, some numerical results have pointed out the existence of choreographies, including the figure-eight solution on the sphere $\mathbb S^2$ (Montanelli and Gushterov 2016). However, these studies are only at the beginning, and the current paper shows that the approach we took here offers another way to answer some of the natural problems that occur in the qualitative study of the equations of motion and the dynamics of the solutions.

But most questions related to central configurations are far from easy, as it also happens in the Euclidean case. Even finding all the central configurations in the curved three-body problem, which has been settled in the classical case long time ago, is not trivial in curved space and requires a separate study. As we have already seen, new central configurations, such as the isosceles triangles, or the scalene triangles on the equator of the sphere, none of which have correspondents in the Euclidean case, show up. So far, all these central configurations on $\mathbb S^2_{xyz}$ lie in planes parallel with the xy-plane, except for the geodesic ones. But at this point we have some indication that most triangular central configurations do not lie in planes parallel with the xy-plane and hope to be able to prove this statement in the near future. So even for only three bodies, the set of central configurations of the curved problem is significantly richer than in the Euclidean case, especially in the case of the sphere.

These investigations hint at the rich dynamics of the curved N-body problem and show that the questions occurring from its study allow us to view the classical case from a new perspective. Having now extended the concept of central configuration to the curved problem, we have a new tool and a new direction of research, which will hopefully shed more light on the equations of motion that govern this mathematical model.