Picker routing in scattered storage warehouses: an evaluation of solution methods based on TSP transformations

Abstract

To optimize their order fulfillment processes, many e-commerce warehouses employ a storage assignment strategy known as scattered or mixed-shelves storage. Under this approach, unit loads of homogeneous products are divided, and individual pieces are stored in various shelves throughout the warehouse. This arrangement ensures that products that appear together on unpredictable pick lists are stored in close proximity somewhere in the huge warehouses, reducing the travel distance for pickers. Despite these advancements, efficiently guiding pickers through the warehouse remains a significant planning challenge. Since the same products can be found in multiple storage positions, the traditional picker routing problem becomes more complex, as an additional selection task arises regarding which shelf to retrieve each requested product from. While previous research has developed several tailor-made solution algorithms, we demonstrate that known transformation schemes used for different variants of the well-known Traveling Salesman Problem (TSP) can be utilized to convert the single picker routing problem with scattered storage (SPRP-SS) into a classical TSP. This approach enables us to leverage the extensive array of state-of-the-art TSP solvers. The purpose of this paper is to explore the performance of these solvers when applied to solving the SPRP-SS. Through our computational study, we found that existing TSP solvers exhibit good performance, allowing near-optimal solutions to be obtained in less than a second for real-world scale SPRP-SS instances. Moreover, the efficiency of these TSP solvers remains unaffected by the number of cross aisles in the warehouse. Consequently, we exploit this flexibility to investigate the impact of cross aisles on picking performance in scattered storage warehouses.

1 Introduction

For years, the retail sector has been undergoing a structural transformation. Most recently, driven by the pandemic, e-commerce has been experiencing steady growth, which is expected to continue in the future (see, e.g., Lone et al. 2021). As a result, online retailers of all sizes are facing the challenge of managing an increasing number of small and heterogeneous orders, putting increased pressure on their supply chains. Marketing-induced trends such as next-day or same-day deliveries further amplify this effect, making warehouse operations highly time-critical (Boysen et al. 2019). Consequently, efficient order fulfillment processes play a crucial role in the success of e-commerce.

Accordingly, novel warehousing systems have been developed and implemented for e-commerce operations. Among these, scattered storage (also known as mixed-shelves storage) has emerged as a highly successful and widely adopted approach, suitable for picker-to-parts warehouses of all sizes due to its low investment costs and high scalability. In these facilities, batched orders are picked by human pickers who traverse the warehouse, following a similar approach to classical picker-to-parts warehousing. However, the key distinction lies in the storage strategy. Unlike the traditional setup, stock keeping units (SKUs) are not assigned to specific dedicated storage positions; instead, they are scattered in small quantities throughout the warehouse. The fragmentation of trading units and the distribution of single pieces lead to a more work-intensive replenishment process. However, it ensures that a piece of any demanded SKU is always within proximity, regardless of the picker’s current position within the warehouse. For small, heterogeneous, and hardly predictable orders, as commonly occurring in e-commerce, this storage scheme significantly reduces the length of picking tours (see, e.g., Weidinger 2018). Considering the high time pressure during order picking in comparison to restocking, the additional effort during replenishment is a price gladly paid by e-commerce retailers, as can be seen in the broad acceptance of scattered storage in practice. Further, this concept fits seamlessly into the tradition of warehouse optimization, as classical storage assignment strategies, for example, are based on the same principle.

Regardless of its numerous advantages in e-commerce warehousing, scattered storage has a significant drawback: its higher reliance on human labor compared to other warehousing strategies often applied in this area. Compared to robotic mobile fulfillment systems, picking assisted by automated guided vehicles, and advanced picking stations, for example, scattered storage makes little use of modern automation technologies, such that labor costs constitute a substantial portion of operational expenses in direct comparison (see Boysen et al. 2019). To reduce these expenses, one crucial aspect is optimizing the order picking process (De Koster et al. 2007), during which pickers traverse the warehouse and visit storage positions to retrieve the demanded SKUs. Although the concept of scattered storage aims to reduce unproductive picker travel, it is still worthwhile to optimize the route taken by pickers. This not only maximizes the potential benefits of the overall concept, thereby reducing costs, but also accelerates order assembly, enabling the fulfillment of short-term delivery promises. The problem of determining the shortest route through the warehouse, starting and ending at a depot while visiting a given set of storage positions, is widely known as the picker routing problem (see, e.g., Boysen et al. 2019). In traditional picker-to-parts warehouses, this problem is equivalent to the well-known Traveling Salesman Problem (TSP). However, in scattered storage warehouses, an additional selection problem arises, as pickers must decide from which alternative storage positions a demanded product should be obtained (Daniels et al. 1998). In the following, we refer to this problem as the single picker routing problem with scattered storage (SPRP-SS).

In recent years, several solution algorithms have been proposed for the SPRP-SS (e.g., Weidinger 2018; Weidinger et al. 2019; Heßler and Irnich 2023). However, in this paper, our objective is not to develop a new tailor-made algorithm. Instead, we leverage the solution power of existing state-of-the-art TSP solvers. To achieve this, we utilize known transformation schemes that reduce various extended TSP variants to the standard TSP. Specifically, we apply transformations from the generalized TSP to the clustered TSP, then to the asymmetric TSP, and finally to the symmetric TSP, and show that they are also applicable to the SPRP-SS. By employing generic TSP solvers, we gain the following main advantages:

(i) Previous tailor-made solution approaches for the SPRP-SS exploit that the routing subproblem can efficiently be solved once all storage positions to be visited are fixed. They utilize the dynamic program of Ratliff and Rosenthal (1983), or one of its extensions developed over the years, to solve the TSP within the parallel-aisle structure of a warehouse in polynomial time. This allows for an extremely fast solution of the routing subproblem, but it restricts the applicability of the tailor-made algorithms to warehouses with a given parallel-aisle structure. However, some e-commerce warehouses deviate from this standard and, for instance, allow pickers to change levels in their multi-level mezzanine warehouses (Boysen et al. 2019; Tadumadze et al. 2023) or store products also within cross aisles (Jang and Sun 2011). Generic TSP solvers are not bound to specially structured distance matrices, induced by the parallel-aisle structure, and can also handle non-standard warehouse layouts.

(ii) Additionally, an extension of the algorithm proposed by Ratliff and Rosenthal (1983), developed by Pansart et al. (2018), enables the solution of the TSP within parallel-aisle structures with an arbitrary (yet fixed) number of cross aisles in polynomial time. However, the runtime of this algorithm is heavily influenced by the number of cross aisles. In contrast, generic TSP solvers are not affected by the number of cross aisles, allowing us to leverage their capabilities to investigate the impact of different numbers of cross aisles on picking performance in scattered storage warehouses.

(iii) Being one of the classics of operations research, extensive research efforts have been devoted to the TSP over several decades (for a survey, e.g., refer to Laporte 1992). As a result, the research community has developed highly efficient exact and heuristic TSP solvers. By utilizing these solvers, we can effectively solve the SPRP-SS with good performance without any implementation effort and, additionally, link the research stream of the SPRP-SS with that of the TSP, so that novel methods for solving the TSP can also be applied to the SPRP-SS. Our computational study demonstrates that, while being outperformed by tailor-made SPRP-SS solvers, current TSP solvers derive near-optimal solutions for real-world scale SPRP-SS instances in less than a second.

Therefore, this paper is dedicated to examining the performance of state-of-the-art TSP solvers when applied to the SPRP-SS. In this context, the paper makes the following key contributions:

• Transformation of SPRP-SS into TSP: We demonstrate how to transform the SPRP-SS into the TSP. This transformation is straightforward and based on known schemes for cases where each order line on a pick list corresponds to a unique SKU and requires only a single piece. For scenarios involving multi-piece demands and storage positions with multiple pieces of the same SKU in stock, new transformation schemes are proposed and evaluated.

• Performance evaluation of TSP Solvers: We evaluate the performance of state-of-the-art TSP solvers when solving the SPRP-SS. The experimental results show that these solvers can efficiently handle real-world-sized instances of the problem, yielding near-optimal solutions.

• Impact of cross aisles: By leveraging the flexibility of generic TSP solvers, which are not affected by the number of cross aisles in a warehouse, we investigate the optimal number of cross aisles for scattered storage warehouses.

The remaining sections of the paper are organized as follows: Sect. 2 provides a summary of the related literature. The formal definition of the problem and the proposed solution approach based on transformation schemes are presented in Sects. 3 and 4, respectively. In Sect. 5, we conduct a computational study to evaluate the solution procedure and address managerial aspects such as determining the optimal number of cross aisles in scattered storage warehouses. Finally, Sect. 6 concludes the paper.

2 Literature review

The field of e-commerce warehousing has received significant attention in recent years due to the growing importance of e-commerce. In this literature overview, we will focus on works closely related to our approach. For a comprehensive review of the warehousing literature, we recommend referring to the following in-depth literature reviews: De Koster et al. (2007); Gu et al. (2007, 2010); Van Gils et al. (2018); Azadeh et al. (2019); Boysen et al. (2019); Masae et al. (2020a). Plenty of recent research addresses the storage assignment in scattered storage warehouses, deciding on the placement of products in the shelves (e.g. Weidinger and Boysen 2018; Xu and Ren 2022; Albán et al. 2024). We, however, assume a given storage assignment and concentrate our literature survey on related routing research.

Many studies have addressed the picker routing problem (without scattered storage), which is one of the key operational planning problems in traditional warehousing research. Several rule-based heuristics have been proposed for this problem, including the traversal, midpoint, and largest gap strategies (Hall 1993), which have been further expanded with the return and composite heuristics (Petersen 1997). As the picker routing problem is a special case of the TSP, algorithms developed for the TSP, such as the procedure introduced by Lin and Kernighan (1973), can also be applied. Their performance in the warehousing context has, for instance, been explored by Theys et al. (2010). Extensions of the basic problem have been studied to address additional challenges, such as congestion (Chen et al. 2013) or precedence constraints, e.g., induced by fragility of products (Chabot et al. 2017).

An exact optimization approach for the picker routing problem (without scattered storage) within the parallel-aisle structure of warehouses with cross aisles at the front and back has been provided by Ratliff and Rosenthal (1983). Their dynamic program solves the resulting special case of the TSP, which is well-known to be strongly $\mathcal{N}\mathcal{P}$-hard for generals graphs, in polynomial time. Several extensions of this algorithm have been developed, including decentralized handover of picked products onto conveyors in the cross aisles (De Koster and Van der Poort 1998), handling precedence constraints (Žulj et al. 2018), incorporating turn penalties (Çelik and Süral 2016), and accommodating dynamic order picking (Lu et al. 2016). The algorithm of Ratliff and Rosenthal (1983) has also been extended to warehouses with an additional middle aisle (Roodbergen and De Koster 2001b), middle aisles containing storage positions (Jang and Sun 2011), and arbitrary start- and endpoints (Masae et al. 2020b). Pansart et al. (2018) demonstrate that the TSP in the parallel-aisle structure can still be solved in polynomial time for an arbitrary (but fixed) number of cross aisles. A recent extension focuses on incorporating four attributes present in modern warehouses, namely multi-block layouts, multiple depots, dynamic batching policies, and cartless subtours (Schiffer et al. 2022). Furthermore, other exact approaches have been developed using techniques such as branch-and-bound (Roodbergen and De Koster 2001a), branch-and-cut (Chabot et al. 2017), and adapted TSP formulations (Scholz et al. 2016; Goeke and Schneider 2021). However, all of these approaches address traditional picker routing, where each SKU is located at a unique storage position.

Daniels et al. (1998) introduce the concept of picker routing where SKUs can be available at multiple storage positions, thus modeling the single picker routing problem with scattered storage (SPRP-SS). They propose heuristic approaches based on nearest neighbor, shortest arc, and tabu search. Building upon this work, Weidinger (2018) proves the $\mathcal{N}\mathcal{P}$-hardness of the problem, even for the special case of parallel-aisle warehouses, and proposes a decomposition heuristic based on the approach of Ratliff and Rosenthal (1983). An exact solution approach based on a mixed integer programming (MIP) model is suggested by Goeke and Schneider (2021). Also exploiting the structural properties proven by Ratliff and Rosenthal (1983) in a network flow model, Heßler and Irnich (2023) provide an exact solution approach for SPRP-SS, which is even faster than the one of Goeke and Schneider (2021) in most cases. While the aforementioned approaches are tailored for warehouses with cross aisles at the front and back, Su et al. (2023) suggest a MIP that can accommodate an arbitrary number of cross aisles. Finally, an integration of non-disjunct batching and multiple depots is investigated by Weidinger et al. (2019), while the combined problem of batching orders, batch assignment to pickers, and picker routing is tackled by Rasmi et al. (2022), both focusing on heuristic solutions. However, all of these approaches are either restricted to parallel-aisle warehouses or rely on complex MIP formulations.

In conclusion, none of the three main contributions of this paper, as outlined in the introduction, have been previously addressed in the literature. Specifically, no prior research has focused on the transformation of SPRP-SS into the TSP, the exploration of state-of-the-art TSP solvers for solving SPRP-SS, or the determination of the optimal number of cross aisles in scattered storage warehouses.

3 The single picker routing problem with scattered storage

This section is devoted to defining the SPRP-SS, which is a combined selection and sequencing problem (Weidinger 2018). Among the storage positions that hold a requested SKU, a subset of positions to be visited must be selected to satisfy the total demand of the SKU. Additionally, the selected storage positions for all SKUs must be sequenced to create the shortest feasible picking tour, wherein all selected positions are visited, and a closed tour without any subtours is constructed.

This problem setting can be modeled as a MIP (quoted from Weidinger 2018), consisting of objective function (3.1) and constraints (3.2) to (3.8), based on the symbols defined in Table 1.

Table 1 Notation for SPRP-SS MIP

$$\begin{array}{*{20}c} {{\text{SPRP - SS MIP:}}} & {{\text{Min}}{\text{. }}Z({\mathbf{x}}) = \sum\limits_{{i \in N}} {\sum\limits_{{j \in N}} {d_{{i,j}} } } \cdot x_{{i,j}} } \\ \end{array}$$

(3.1)

$$\begin{array}{*{20}c} {{\text{subject to}}\sum\limits_{{i \in N}} {x_{{i,j}} } = 1} & {\forall j \in N} \\ \end{array}$$

(3.2)

$$\begin{aligned}&\sum _{j \in N}x_{i,j}=1 \qquad \forall i \in N&\end{aligned}$$

(3.3)

$$\begin{aligned}&\sum _{i \in N_k} q_i \cdot x_{i,i} \le I_k-r_k \qquad \forall k \in M&\end{aligned}$$

(3.4)

$$\begin{aligned}&\sum _{i \in N_k \setminus \{j\}} q_i \cdot x_{i,i} + I_k \cdot x_{j,j} \ge I_k - r_k - q_j + 1 \qquad \forall k \in M,j \in N_k&\end{aligned}$$

(3.5)

$$\begin{aligned}&v_i-v_j+ |N| \cdot x_{i,j} - |N| \cdot (x_{i,i}+x_{j,j}) \le |N|-1 \qquad \forall i,j \in N \setminus \{0\}&\end{aligned}$$

(3.6)

$$\begin{aligned}&v_i \ge 0 \qquad \forall i \in N&\end{aligned}$$

(3.7)

$$\begin{aligned}&x_{i,j} \in \{0,1\} \qquad \forall i,j \in N&\end{aligned}$$

(3.8)

Objective function (3.1) minimizes the total travel length of the picking tour, by summing up the individual distances between selected and successively visited positions. Constraints (3.2) and (3.3) make sure that each position, represented by a node of the graph, has an input and output degree of one. This is either because it is part of the tour and therefore visited exactly once, or because it is not visited at all. In the latter case, the node is connected to itself by a loop. Constraints (3.4) ensure that the storage positions visited hold a sufficient number of pieces for each SKU to be picked. In contrast, optional constraints (3.5) guarantee that the picker does not visit more storage positions than needed to fulfill the demand of each SKU, as they make sure that demand cannot be fully satisfied if any selected storage position is deleted from the tour. Constraints (3.6) and (3.7) are subtour elimination constraints similar to the approach of Miller et al. (1960), but extended by the fact that not all storage positions must be part of the tour. Constraint (3.8), finally, defines the domain of binary variables ${\textbf{x}}$. Recall that strong $\mathcal{N}\mathcal{P}$-hardness has been proven by Weidinger (2018), even if the parallel-aisle structure of warehouses holds.

Note that scattered storage warehouses in general hold multiple SKUs per storage position. If more than one demanded SKU is stored within the same storage position, the presented model and all following solution procedures are still applicable by introducing a position for each demanded SKU representing the same real-world storage position. By setting the distance between these newly introduced storage positions to zero, instances with the described setup can be solved without introducing additional complexity.

Several assumptions commonly made in the context of the single picker routing problem are also incorporated in this model formulation. These assumptions are as follows:

• 1. Tours start and end at a depot: It is assumed that the picking tour starts and ends at a depot. Hereby, start and end depot do not have to be identical if the distance matrix is adapted accordingly such that this assumption results in little limitation.

• 2. Order batching not considered: It is assumed that order batching has either already occurred, and the batches are fixed and unchangeable, or solving the picker routing problem is a subroutine of the order batching process, used to evaluate the quality of the batching decision. In both cases, the batches cannot be altered, and the demand to be picked remains fixed.

• 3. No interference between pickers: In a typical warehouse setting, multiple pickers work in parallel. However, for wide aisle warehouses where pickers can pass each other, it is generally assumed that pickers do not impede each other’s progress. Additionally, conflicts among pickers competing for the same SKUs are assumed to have been resolved during the upstream batching planning stage.

• 4. No impact of picking times: It is assumed that once the demand for SKUs on a pick list is determined, the picking times for those SKUs remain fixed. This implies that the picking times for a specific product do not vary across alternative picking positions. In the absence of varying picking times, minimizing the total travel time becomes the primary lever to influence picking performance (De Koster et al. 2007). However, if some positions provide significantly more SKUs than others, increased search time for the demanded product might occur. To avoid this, many warehouses restrict the maximum number of different SKUs per position in business practice. Alternatively, one could still interpret the distance parameter as a time value and summarize picking and travel times in d.

• 5. Deterministic data: It is assumed that distances and inventory values are static and known with certainty.

On top of these widely applied picker routing assumptions, a further critical assumption is the following:

• 6. Sufficient inventory per storage position: Since most online orders are small and demand only one or two pieces (Boysen et al. 2019), it often occurs that the entire demand for each SKU can be fulfilled by visiting a single storage position that provides that SKU. Using the notation introduced in Table 1, this means that condition $q_i \ge r_k \; \forall i \in N_k, k \in M$ holds. Naturally, this assumption holds for pick lists which demand just a single piece per SKU. Thus, we refer to this case and the SPRP-SS instances where this assumption holds as the single-demand case and instances, respectively. However, there may still be instances where orders demand multiple pieces of some SKU that exceed the quantity of pieces stored at certain storage positions. In this case, it depends on the number of pieces per SKU stored at the single storage positions, which and how many positions must be visited to satisfy a multi-demand.

Whether or not this assumption holds (and whether we are in the single-demand or multi-demand case) strongly affects the TSP transformation. We will discuss this differentiation in the following section.

4 A solution approach for the SPRP-SS based on TSP transformations

If the single-demand assumption holds, then only one of the storage positions that store a demanded SKU needs to be visited by the picker. As a result, single-demand SPRP-SS instances can be directly transformed into the well-known generalized TSP (GTSP). Therefore, existing transformation schemes from the literature can be applied to convert this problem into the TSP. This approach is explained in detail in Sect. 4.1. For multi-demand cases, i.e., multiple storage positions holding a demanded SKU may need to be visited, the direct translation into the GTSP becomes more complex. In such cases, modified transformation schemes are required, which we discuss in Sect. 4.2.

4.1 Single-demand case

The SPRP-SS under the single-demand assumption, as described in the previous section, is an extension of the classical TSP, which is one of the most extensively studied problems in optimization (see, e.g., Flood 1956). Consequently, there exists a vast body of literature and proposed solution approaches for the TSP, all aiming to find the shortest connected circular tour through a set of nodes in a weighted graph. Recall that, unlike the SPRP-SS, the classical TSP requires visiting all nodes in the tour. The proposed solution approach for the SPRP-SS builds upon the existing research on the TSP by transforming SPRP-SS instances into TSP instances. This approach has been mentioned in the literature (Heßler and Irnich 2023) but has not been thoroughly pursued yet. By leveraging this transformation, we can take advantage of the established TSP research stream to address the SPRP-SS.

In the subsequent sections, we first demonstrate that, under the single-demand assumption, the SPRP-SS is equivalent to GTSP. We then proceed to transform the GTSP into the Clustered TSP (CTSP), which is further converted into an Asymmetric TSP (ATSP). Although these transformation techniques have been previously presented by Noon and Bean (1993), we have made adaptations specific to our problem. The resulting ATSP can be addressed using various established TSP solvers. However, we go on to present a translation of the ATSP into the Symmetric TSP, which is the typical version referred to when discussing the TSP (as we do in this paper). Notably, the widely acclaimed Concorde solver (Applegate et al. 2003) specializes in solving TSP instances but is unable to handle ATSP instances.

4.1.1 SPRP-SS to GTSP

For the GTSP, it is not necessary to visit all nodes. Instead, the set of nodes V is partitioned into |C| disjoint subsets $V_c \subseteq V \; \forall c \in C$ (with $\cup _{c \in C} V_c = V$ and $V_c \cap V_{c'} = \emptyset \; \forall c, c' \in C: c \ne c'$), and exactly one node per subset must be part of the tour (Gutin and Punnen 2006). Under the single-demand assumption, a one-to-one mapping exists between GTSP and SPRP-SS, as each storage position that provides a demanded SKU is sufficient to fulfill the total demand for that SKU. This mapping involves introducing a partition for each demanded SKU and the depot. Each storage position that provides a specific SKU, represented by partition $c \in C$, is assigned to set $V_c$ setting up a corresponding node. The depot itself forms its own dedicated partition. It is important to note that storage positions not supplying any demanded SKU should not be visited and are therefore eliminated from the problem data. As a result, a one-to-one mapping between GTSP and SPRP-SS instances is established, provided that the single-demand assumption is valid.

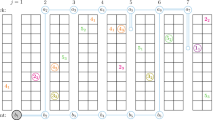
Example: Fig. 1 illustrates an instance of the SPRP-SS (a), where one storage position each for SKU A and SKU B needs to be visited. The proposed transformation scheme results in the GTSP instance shown in subfigure (b), where storage positions are indexed from left to right and distances are measured by counting squares. Note that, for simplicity, only edges incident to vertices A1 and A2 are displayed in the figure. As an example, the edge $\{D,A2\}$ is assigned a weight of 6, representing the distance between the depot and the central storage position A2 of SKU A.

4.1.2 GTSP to CTSP

For the CTSP, the set of nodes V is still divided into disjoint subsets, referred to as clusters ($V_c$). In this variation of the TSP, all nodes must be included in the tour, and nodes within the same cluster must be visited consecutively. Given binary variables $x_{i,j}$, where $x_{i,j}$ equals one iff node j directly follows node i in the current tour (as discussed in Sect. 3), the following constraint must be satisfied for the CTSP:

$$\begin{aligned} x_{i,k} \cdot x_{k,j} \cdot {\textbf{1}}_{V_c}(i) \cdot {\textbf{1}}_{V_c}(j) \le {\textbf{1}}_{V_c}(k) \qquad \forall i,j,k \in V, c \in C \text {,} \end{aligned}$$

where ${\textbf{1}}_{V_c}(i)$ represents the indicator function, which equals 1 if $i\ \in V_c$. Note that there are linear formulations available for this constraint, but for the sake of brevity, we opt not to present them here.

Different transformations schemes for different TSP variants have previously been addressed in literature (Chisman 1975; Noon and Bean 1993). In the following, we outline the procedure proposed by Noon and Bean (1993). The general idea of the transformation is to construct zero-weighted Hamilton paths for each cluster by adding edges such that visiting all nodes within the cluster incurs no additional cost. Let $\pi _c$ be an ordering of the nodes belonging to cluster c, and let $\pi _c(n)$ be the n-th node in that order. By adding zero-weighted edges $(\pi _c(n), \pi _c(n+1)) \; \forall n = 1, \ldots , (|V_c|-1)$ as well as edge $(\pi _c(|V_c|), \pi _c(1))$, it is possible to visit all nodes of a cluster cost-neutrally in the predefined sequence, after having entered via a cluster-node (see Fig. 1c). As each node can be visited only once, however, cluster c visited at node n will be left at node $\textbf{mod}(n-2,|V_c|) + 1$, with $\textbf{mod}$ being the modulo function. In consequence, weights leaving the cluster must be adapted such that the updated weight for edge $(\pi _c(n),v)$ is identical to the initial weight of edge $(\pi _c(\textbf{mod}(n,|V_c|)+1),v) \; \forall c \in C; n = 1,\ldots ,|V_c|; v \in V {\setminus } V_c$. Note that the transformation described introduces directed edges, regardless of whether the original problem was symmetric or asymmetric. As a result, the distance matrices to be considered become asymmetric. However, while the zero-weighted edges allow to visit all nodes of a cluster in direct succession without additional cost under the CTSP, this means that only the node where a cluster is entered is actually visited under the GTSP. The result is a polynomial-time transformation scheme between GTSP and CTSP.

Example (cont.): In the transformation from GTSP to CTSP, the nodes within a cluster are connected by circular directed edges (Fig. 1c). For simplicity, only the additional edges incident to nodes A1 and A2 are shown. Concerning the inter-cluster edges, undirected edges are divided into two opposing directed edges. The weights of incoming edges, originating from clusters with only one node (e.g., the depot cluster), remain unchanged. For instance, the weight of the edge from D to A2 is still weighted by 6. However, for outgoing edges, the weights are adjusted according to the aforementioned procedure. As a result, the edge from A1 to D is assigned a weight of 6, resembling the weight of the edge $\{A2,D\}$ in the GTSP instance (see Fig. 1b). It is important to mention that the weights of incoming edges might also change if they originate from a cluster with more than one node. For that cluster, the edges are outgoing and therefore require weight adaptation. This is the case for edge (B2, A2). Being an incoming edge for cluster A, it is not affected by the transformation regarding cluster A. However, as cluster B has more than one node, the weight of edge (B2, A2) needs to be set to 12, representing edge $\{B1,A2\}$ of the GTSP instance.

Fig. 1

Transformation schemes from SPRP-SS to TSP (only edges incident to A1 and A2 are depicted)

4.1.3 CTSP to ATSP

In contrast to the CTSP, nodes can be sequenced in an arbitrary order in the ATSP (Asymmetric Traveling Salesman Problem), requiring a complete graph. However, when transforming a CTSP instance into an ATSP instance, it is necessary to ensure that the optimal solution for the ATSP is feasible for the CTSP, meaning that nodes within a cluster are visited consecutively. By slightly modifying the transformation proposed by Noon and Bean (1993), the weights of inter-cluster edges in the CTSP are adjusted, and intra-cluster edges with prohibitively high weights are introduced to connect nodes within each cluster. Clearly, inter-cluster edges need to be selected for a feasible solution without subtours. However, by increasing the weights of the inter-cluster edges by a sufficiently large value $\beta$ (see Fig. 1d), they become comparatively costly, ensuring that inter-cluster edges are selected only when necessary. This guarantees that the cluster condition of the CTSP is satisfied in the ATSP version of the instance for any near-optimal solution. To determine an appropriate value of $\beta$, it is sufficient to set it equal to the sum of the weights of the most expensive (outgoing) inter-cluster edge per cluster, that is, $\beta = \sum _{c \in C} \max _{v \in V_c, v' \in V {\setminus } V_c}\{d_{v,v'}\}$. Preliminary tests have shown that the exact value of $\beta$ does not significantly affect the performance of standard solvers like Gurobi, as long as it is small enough to ensure computational stability. Since there are |C| inter-cluster edges in a feasible solution, the objective value achieved by the ATSP is increased by $|C| \cdot \beta$ compared to the CTSP, making $|C| \cdot \beta$ a lower bound for the objective value of the ATSP. With the definition provided for $\beta$ above, an upper bound for the objective value achieved by the ATSP can be determined as $(|C|+1) \cdot \beta$. As a result, intra-cluster edges, which should be assigned prohibitively high weights, can be assigned a weight of $\beta$, effectively excluding them from the range of near optimal solutions.

Example (cont.): Given our previous example, the transformation to ATSP (see Fig. 1d) results in additional edges per cluster, all weighted by $\beta$ (e.g., edge (A2, A1)). Additionally, the weights of inter-cluster edges are increased by $\beta$.

4.1.4 ATSP to TSP

In contrast to the ATSP, the distance matrix of an TSP instance is symmetric, i.e., $d_{v,v'} = d_{v',v} \; \forall v,v' \in V: v \ne v'$. Nevertheless, a symmetric instance can be obtained from an asymmetric instance by doubling the number of vertices. Based on Kumar and Li (1996), a transformation can be executed as follows: An auxiliary distance matrix $D'$ is created by adapting the edge weights:

$$\begin{aligned} d'_{v,v'} = {\left\{ \begin{array}{ll}\ 0, &{} \text {if}\ v = v'\text {,}\\ d_{v,v'}, &{} \text {if}\ (4 \cdot d_{min} - 3 \cdot d_{max}) > 0 \text { and } v \ne v'\text {,}\\ d_{v,v'} + (3d_{max}-4d_{min}+\epsilon ) = d_{v,v'} + \omega , &{} \text {otherwise,} \end{array}\right. } \end{aligned}$$

(4.1)

with $d_{min} = \min _{v,v' \in V: v \ne v'}\{d_{vv'}\}$ and $d_{max} = \max _{v,v' \in V: v \ne v'}\{d_{vv'}\}$ denoting the minimum and maximum edge weight between two nodes and $\epsilon > 0$ representing a small positive number. To abbreviate formulations, we substitute $(3d_{max}-4d_{min}+\epsilon )$ by $\omega$ in the following. For every (so-called) real node $v \in V$ of the asymmetric instance, a corresponding virtual node ${\bar{v}}$ is created, resulting in node set ${\bar{V}}$ with cardinality $|{\bar{V}}| = 2\cdot |V|$. By defining

$$\begin{aligned} {\bar{d}}_{v,v'} = {\bar{d}}_{{\bar{v}},{\bar{v}}'} = \infty , \; {\bar{d}}_{v, {\bar{v}}'} = {\bar{d}}_{{\bar{v}}, v'} = d'_{v,v'},\; {\bar{d}}_{v,{\bar{v}}} = {\bar{d}}_{{\bar{v}},v} = 0 \quad \forall v, v' \in V \end{aligned}$$

with ${\bar{v}}$ being the virtual node corresponding to real node v, a symmetric distance matrix ${\bar{D}}$ of dimension $|{\bar{V}}| \times |{\bar{V}}|$ is created. Based on distance matrix ${\bar{D}}$, for any near optimal solution to the TSP problem in graph ${\bar{G}} = (V \cup {\bar{V}},{\bar{E}})$ real and complementary virtual nodes are visited alternately, as $\infty$ represents a prohibitively high edge weight. Note that $|{\bar{V}}| \cdot \max _{v,v' \in {\bar{v}}}\{{\bar{d}}_{v,v'}\}$ is a sufficiently large edge weight for this purpose. By combining real and corresponding virtual nodes, these solutions also represent feasible solutions to the corresponding ATSP instance. However, the objective value of the TSP instance is higher, due to the transformation scheme. By inverting the above-mentioned equation (4.1) the objective value of the corresponding ATSP solution can be derived, i.e., in case $(4 \cdot d_{min} - 3 \cdot d_{max}) > 0$, we subtract $|V| \cdot \omega$.

Example (cont.): The TSP instance resulting from the final transformation is presented in Fig. 1e for our example. Again, only edges incident to nodes A1 and A2 are depicted. For all edges connecting two real or two virtual nodes, prohibitively high weights are applied (e.g., $\{A1,A2\}$). Edges connecting a real and the corresponding virtual node are weighted by zero (e.g., $\{A1,{\bar{A1}}\}$). For all remaining edges, $\omega$ is added in line with Formula (4.1).

With the described transformations, it becomes possible to convert any instance of the SPRP-SS into an (A)TSP instance. This allows for the utilization of a wide range of state-of-the-art TSP solvers. The transformations are not restricted to a particular warehouse layout and are further suitable for non-standard warehouses violating the parallel-aisle structure such that a highly flexible solution approach for the SPRP-SS with single-demand is at hand.

4.2 Multi-demand case

In this section, we adapt the transformation-based solution approach from the previous section to address the multi-demand case. In the multi-demand case, pick lists may require multiple pieces of a SKU, and the number of pieces available at a storage position influences which and how many positions holding the demanded SKU need to be visited.

Example: In Fig. 2a, an example for the multi-demand case is displayed. The warehouse contains five storage positions holding SKU A with the supply at the different positions being one, two, or three.

Unfortunately, under the multi-demand case, equivalence between SPRP-SS and GTSP no longer holds. Unlike the single-demand case where the transformation from SPRP-SS to TSP is exact, we now encounter a modeling gap. Our approximate transformation schemes from SPRP-SS lead to GTSP instances with a more constrained solution space. Therefore, the subsequent chain of transformations from GTSP to TSP ultimately yields only a heuristic solution for SPRP-SS. In the following, we present four different approximate transformation schemes from SPRP-SS, assuming the multi-demand scenario, to GTSP:

Fig. 2

Different transformation schemes for multi-demand SPRP-SS instances. The stock level of a storage position is given at the bottom right

• No-split: Only storage positions holding a sufficient number of pieces to completely satisfy the demand of the respective SKU on the pick list are considered in the transformation. All other storage positions with a lower stock level than the demanded quantity are deleted from the instance. Applying the notation of Table 1, this approach results in a reduction of sets $N_k$ for all $k \in M: r_k > 1$ during preprocessing such that $N_k:= \{i \in N_k: q_i \ge r_k\}$. If no such positions exist for at least one demanded SKU, i.e., if $\exists k \in M: \{i \in N_k: q_i \ge r_k\} = \emptyset$, this transformation scheme returns infeasibility, although a feasible solution for the actual SPRP-SS instance may exist.

  Example (cont.): Referring to the example depicted in Fig. 2, transformation scheme No-split only considers the three storage positions holding more than the demanded $r_{A}=2$ pieces of SKU A, and ignores all the remaining positions (see Fig. 2b).

• SKU-split: Under this transformation scheme, each unit of demand $r_k$ of a SKU k is represented individually by one of $r_k$ virtual SKUs, whose single-unit demand on the pick list must be satisfied by visiting one of the storage positions of SKU k, which are partitioned among the virtual SKUs. The picker must then visit one storage position of each virtual SKU in order to collect $r_k$ pieces of original SKU k. If less than $r_k$ storage positions contain a demanded SKU, this transformation scheme returns infeasibility, although a feasible solution for the actual SPRP-SS instance may exist. There are various ways to partition the storage positions among the virtual SKUs. We apply the following straightforward approach: storage positions are indexed from bottom to top along the aisle, iterating through the aisles from left to right, before being assigned to partition $i' \; \textbf{mod} \; r_k$ based on index $i'$.

  Example (cont.): To fulfill a demand of $r_{A}=3$ pieces of SKU A, SKU-split: introduces three virtual SKUs A1, A2, and A3 to the pick list each having a demand of one. The actual storage positions are partitioned among these virtual SKUs as depicted in Fig. 2c and their stock level is set to one.

• Position-split: For this approach, storage positions providing the same SKU are divided into subsets, similarly than for the SKU-split approach. However, here, the subsets $\kappa$ are built according to the current stock of the single storage positions, enabling the procedure to consider all pieces of a SKU stored at a specific storage position. Formally, with $q(\kappa _l)$ being a function determining the minimum supply of a SKU within all storage positions assigned to subset $\kappa _l$, each storage position i gets assigned to a preliminary subset $\kappa _l$ such that $q_i = q(\kappa _l)$. The set of preliminary partitions K is then ordered in a descending way regarding the supply such that $K = \{\kappa _1,\kappa _2,\ldots , \kappa _z \}$ with $q(\kappa _1)>q(\kappa _2)>\ldots >q(\kappa _z)$. To determine the final subsets, which are aligned to the demand of the considered SKU, the supply values of the preliminary subsets are summarized in the previously defined order until the demand is met, i.e., $\psi$ is minimized considering $q(\kappa _1)+q(\kappa _2)+\ldots +q(\kappa _\psi ) \ge r_k$ such that $\kappa _\psi$ is the subset that is critical to fulfill the demand. If this method leads to overpicking, i.e., $\sum _{j = 1}^{\psi }q(\kappa _j) > r_k$, it is evaluated whether, instead of visiting a position of subset $\kappa _\psi$, the demand could also be fulfilled by visiting a position of another partition $\kappa _\xi$ with a smaller supply. It is searched for the largest $\xi$ for which $\sum _{j = 1}^{\psi - 1}q(\kappa _j) + q(\kappa _\xi ) \ge r_k$ still holds. Since demand can be satisfied irrespective if a position in $\kappa _\psi$ or, if existent, in $\kappa _{\psi +1},\ldots ,\kappa _\xi$ is visited, those subsets can be united. By neglecting all remaining subsets $\kappa _{\xi +1}, \ldots , \kappa _z$ and uniting the subsets $\kappa _\psi ,\ldots ,\kappa _\xi$, a final partition is determined by ${\bar{K}}=\{\kappa _1, \kappa _2,\ldots ,\kappa _\psi \cup \kappa _{\psi +1} \cup \ldots \cup \kappa _{\xi -1} \cup \kappa _{\xi }\}$. Again, a virtual SKU with a demand of one is introduced for each partition such that our transformation scheme ends in a picking tour visiting one storage position of each subset and hereby is able to collect a sufficient number of pieces per SKU.

  However, there are cases for which such a partition does not exist. Then, the approach subdivides partitions by additionally splitting $\kappa _l$ into $s_l$ subsets, starting with $l=1$ and $s_1 = 2$. If the demand still cannot be satisfied, $s_l$ is iteratively incremented by one, creating additional partitions, until a sufficient number of pieces is available. If $|\kappa _l|$ partitions are created, i.e., every storage position of subset $\kappa _l$ needs to be visited by the picker, but the demand still cannot be met, l is incremented by one and $s_l$ is reset to two, i.e., the next subset is split. It is worth mentioning that this method can ultimately result in a dedicated partition for each storage position, and therefore always finds a feasible solution for a feasible initial SPRP-SS instance.

  Example (cont.): Fig. 2d shows the transformation of Position-split for a demand of $r_{A} = 4$. Since storage positions holding SKU A with a supply of three, two, and one exist, Position-split creates three preliminary subsets, the first one containing the two storage positions with $q_i = 3$, the second one the position with $q_i = 2$, etc. The demand is attempted to be fulfilled by sorting the subsets in descending order such that the second subset is critical, i.e., $\kappa _\psi = \kappa _2$ with $q(\kappa _2) = 2$ because $\sum _{j = 1}^{\psi } q(\kappa _j) = 3 + 2 \ge 4 = r_{A}$. Clearly, visiting a position of subset $\kappa _3$ (with $q(\kappa _3) = 1$) instead of $\kappa _2$ would be sufficient to fulfill the demand of four as well such that $\kappa _2$ and $\kappa _3$ can be united. Eventually, the final partition in this example can be expressed by ${\bar{K}}=\{\kappa _1, \kappa _2 \cup \kappa _3\}$, i.e., the picker needs to visit one storage position containing three pieces and one storage position containing either two pieces or one piece to fulfill the demand. An example in which a further subdivision of the subsets is necessary can be created by increasing the demand for SKU A to nine (see Fig. 2e). Since the preliminary division can only fulfill a demand of $q(\kappa _1) + q(\kappa _2) + q(\kappa _3) = 6$, $\kappa _1$ is further split into two subsets containing one position with a supply of three each. Since $q(\kappa _1^{(1)}) + q(\kappa _1^{(2)}) + q(\kappa _2) + q(\kappa _3) \ge 9 = r_{A}$, the demand is met after one subdivision and the procedure terminates. As a result, the partition ${\bar{K}}=\{\kappa _1^{(1)}, \kappa _1^{(2)}, \kappa _2, \kappa _3\}$ contains two subsets each providing three pieces, as well as one subset providing two pieces and one piece respectively.

• Full-split: Our fourth transformation scheme extends the SKU-split as well as the Position-split scheme. Again, we introduce $r_k$ virtual SKUs with single-unit demands for each unit of demand of the original SKU k. However, we also introduce virtual storage positions whenever a position holds more than a single piece of stock, and partition all resulting virtual storage positions among the virtual SKUs. Thus, we introduce a set ${\tilde{N}}_i$ of $q_i$ virtual storage positions for every position i where a demanded SKU is located. By defining the distances as $d_{{\tilde{i}}, {\tilde{j}}} = 0\ \; \forall {\tilde{i}},{\tilde{j}} \in {\tilde{N}}_i$ and $d_{{\tilde{i}}, j} = d_{j, {\tilde{i}}} = d_{i,j}\ \; \forall {\tilde{i}} \in \tilde{N_i}, j \in N {\setminus } \tilde{N_i}$, it is made sure that visiting a virtual storage position ${\tilde{i}}$ induces the same costs as visiting the corresponding real storage position i. These storage positions are sequenced by the same pattern applied for SKU-split and the virtual SKUs are assigned to the sequence in alternating order with a stock of one per storage position. Note that this scheme always leads to a feasible solution (if one exists for the original SPRP-SS instance), but is still heuristic and comes at the price of many virtual SKUs that may need to be added.

  Example (cont.): As depicted in Fig. 2f, Full-split transforms the multi-demand instance by introducing virtual storage positions with zero distance among each other for each position containing more than one piece of SKU A. Furthermore, virtual SKUs A1,...,A5 are created and assigned in alternating order to the virtual positions each having a stock level of one. The pick demand for A1,...,A5 is set to one as well. This way, the picker has to visit as many (virtual) storage positions as pieces demanded by the original pick list such that full demand is met.

5 Computational study

This section presents our computational study. First, we introduce its setup in Sect. 5.1. Then, we compare the performance of state-of-the-art TSP solvers for SPRP-SS under the single- and multi-demand cases in Sects. 5.2 and 5.3, respectively. Finally, we apply the best performing TSP solver, which is unaffected by the number of cross aisles in the warehouse, to explore the optimal warehouse layout concerning the number of cross aisles used in scattered storage warehouses.

All computational experiments were implemented using C# (Visual Studio 2022) and executed on a 64-bit computer with an Intel Core i7–8700K (12 x 3.70 GHz) CPU and 64 GB main memory using Windows 10 Professional.

5.1 Setup of study

Our computational tests are based on the data instances provided by Heßler and Irnich (2023). Specifically, we use those instances that represent warehouses with cross aisles at the front and back and five (ten) picking aisles each with a length of 30 (60) equally sized storage positions. For these two warehouse dimensions, pick lists with 3, 7, 15, and 30 SKUs were created. The total number of SKUs was determined such that each SKU occurs twice on average within the warehouse (scatter factor of two), considering a skewed demand where A-, B-, and C-products account for 80%, 15%, and 5% of the demand, respectively. Hereby, 20% of the SKUs were defined as A-, 30% as B-, and the remaining 50% as C-products. The storage positions are then assigned as follows: First a demand class is randomly chosen based on the demand pattern, then a SKU is selected with equal distribution from the chosen demand class. For a detailed description of these instances, please refer to Heßler and Irnich (2023). By combining all parameters in a full factorial approach and generating 50 instances per parameter combination, Heßler and Irnich (2023) provide a test bed of 400 instances for the described configuration. Note that proven optimal solutions are known for all instances, provided by the tailor-made SPRP-SS solver of Heßler and Irnich (2023), limited to the parallel-aisle structure.

Using these basic SPRP-SS instances, we apply the transformation schemes detailed in Sect. 4. The resulting ATSP and TSP instances are then solved with the following state-of-the-art TSP solvers:

• Off-the-shelf solver Gurobi (2023, version 9.5.2,) solving the MIP of Miller et al. (1960) for the ATSP. We dub this exact solution approach $\hbox {Gurobi}_{\text {ATSP}}$.

• Exact TSP solver Concorde in version 03.12.19 (see Applegate et al. 2003) solving the TSP. We denote this exact solution method $\hbox {Concorde}_\text {TSP}$.

• The Lin–Kernighan–Helsgaun (LKH) heuristic (Helsgaun 2017) solving the ATSP (dubbed $\hbox {LKH}_\text {ATSP}^n$). As the LKH heuristic has a stochastic component, it is repeatedly executed in a best-of-n approach, with the number of iterations n given in superscript.

Additionally, we provide solutions attained from Gurobi solving the SPRP-SS MIP model presented in Sect. 3 and cited from Weidinger (2018). We refer to this approach by $\hbox {Gurobi}_\text {MIP}$. All solution approaches have been executed with a time limit of one hour per instance.

5.2 Benchmark results for the single-demand case

The section presents the benchmark results for the single-demand case. In this case, we assume that each storage position contains sufficient inventory to fulfill the entire demand for the corresponding SKU. Consequently, only one storage position needs to be selected for each SKU, and the transformation from SPRP-SS to (A)TSP is exact. Thus, provided that the transformed (A)TSP instance is solved to proven optimality, we obtain an exact solution for SPRP-SS.

First, we compare the performance of the three exact approaches: $\hbox {Gurobi}_\text {ATSP}$, $\hbox {Concorde}_\text {TSP}$, and $\hbox {Gurobi}_\text {MIP}$. Table 2 presents the average runtimes in seconds ($\mu _t$) and the standard deviation of runtimes ($\sigma _t$) for these approaches. Additionally, the table provides information about the average gap to the optimal solution (‘gap’) and the percentage of proven optimal solutions (‘% opt’). The results are differentiated based on warehouse dimensions (i.e., the number of picking aisles ‘#aisles’ and the length of aisles measured in storage positions ‘sp/aisle’) as well as the pick list length (‘picks’). Each row in Table 2 represents aggregations over 50 instances.

The results show that the approaches based on transforming the instances into an TSP, i.e., $\hbox {Gurobi}_\text {ATSP}$ and $\hbox {Concorde}_\text {TSP}$, are able to provide more proven optima in less average time. Only for the smallest instances with a pick list length of three, $\hbox {Gurobi}_\text {MIP}$ was able to outperform the other two opponents. Regarding the transformation-based procedures, it can be observed that $\hbox {Gurobi}_\text {ATSP}$ outperforms $\hbox {Concorde}_\text {TSP}$ for 3 and 7 picks, with lower mean runtimes and smaller standard deviations. $\hbox {Gurobi}_\text {ATSP}$ provides proven optimal solutions in less than 15.67 s for all instances of this size. However, this performance trend reverses for 15 and 30 picks. In these cases, $\hbox {Concorde}_\text {TSP}$ outperforms $\hbox {Gurobi}_\text {ATSP}$, despite solving a symmetric problem with twice the number of vertices compared to the asymmetric version solved by $\hbox {Gurobi}_\text {ATSP}$. Interestingly, both approaches perform better for larger warehouses. Although the average number of storage positions to be selected remains the same for different warehouse sizes according to the instance generation scheme (see Sect. 5.1), larger warehouse dimensions result in the same number of vertices on average for the (A)TSP, but with a higher variance in edge weights. Both solvers appear to exploit this higher variance to find better bounds.

Table 2 Performance of exact solution approaches $\hbox {Gurobi}_\text {ATSP}$, $\hbox {Concorde}_\text {TSP}$, and $\hbox {Gurobi}_\text {MIP}$

For 10 aisles and 15 picks, $\hbox {Concorde}_\text {TSP}$ can find and prove all optimal solutions in approximately four minutes on average. However, for smaller warehouse dimensions and/or longer pick lists, the performance in finding proven optimal solutions significantly decreases. In the case of pick lists with a length of 30 picks, $\hbox {Concorde}_\text {TSP}$ can only prove 4% of optimal solutions, while $\hbox {Gurobi}_\text {ATSP}$ cannot prove optimality for any of the instances. All three exact approaches exceed runtimes of 1000 s for these instance sizes, making them impractical for use in a productive setting. For instances where all solvers fail to prove optimality, $\hbox {Gurobi}_{\text {MIP}}$ delivers the lowest optimality gaps. However, if proven optimality is no longer required, other (heuristic) (A)TSP solvers might be preferable. Finally, note that there is a trend of decreasing runtimes of all exact solvers if the size of the warehouse increases (for a constant number of picks). A reason for this (on first sight counterintuitive) behavior of the black-box solvers could be the following: Any additional picking aisle adds distance among subsets of picking positions (i.e., among those of different aisles), which adds information to solvers to prefer picking positions of the same aisles as potential successors. Seemingly, this allows the solvers to reduce the solution space.

We conclude that seeking exact SPRP-SS solutions via state-of-the-art (A)TSP solvers is not competitive with tailor-made SPRP-SS solvers. They only solve instances with up to 10 aisles and 15 picks to proven optimality. On the positive side, these (A)TSP solvers are readily available without additional implementation effort.

Next, we demonstrate that the previous conclusion does not hold for state-of-the-art heuristic ATSP solvers. To achieve significantly faster solutions of good quality, a heuristic approach can be employed to solve the transformed ATSP instances. Table 3 presents average runtimes and optimality gaps, as defined above, for applying the LKH heuristic ($\hbox {LKH}_\text {ATSP}^n$) in a best-of-n approach for the same instances used in the previous test. Recall that $\hbox {LKH}_\text {ATSP}^n$ cannot prove optimality, which is why the respective columns are not included in Table 3.

Table 3 Performance of the LKH heuristic with $n \in \{1,10,100\}$ iterations

These results show that even with a single iteration ($\hbox {LKH}_\text {ATSP}^1$), LKH is capable of finding near-optimal solutions with an average optimality gap of only 0.22% in approximately 0.17 s on average. For 376 out of a total of 400 instances, optimal solutions are found. If a higher solution quality is desired, several repetitions of LKH can be performed in a best-of-n approach. With ten repetitions ($\hbox {LKH}_\text {ATSP}^{10}$), all but four instances are solved optimally, with only a slight increase in runtime to a still reasonable average of 0.97 s. By performing even more iterations, all instances can be solved optimally ($\hbox {LKH}_\text {ATSP}^{100}$). Note that Appendix 1 provides detailed performance data for LKH on a larger instance set of Heßler and Irnich (2023) including 2400 instances and even larger warehouses. The results displayed there are comparable to the ones discussed in this paragraph. Even for the largest of these instances with 50 picking aisles of a length of 180 storage positions each, the runtime of $\hbox {LKH}_\text {ATSP}^1$ never reaches one second and the gap is still well below 0.3% on average. We conclude that if only heuristic solutions are aspired and good solutions need to be obtained quickly, then applying a state-of-the-art ATSP solver such as LKH seems the perfect choice for the single-demand case. Without additional implementation effort, solutions to SPRP-SS instances of real-world size can be obtained in less than a second and with negligible optimality gaps.

5.3 Benchmark results for the multi-demand cases

In this section, we switch to the multi-demand case and benchmark our alternative transformation schemes (see Sect. 4.2), if pick lists may require multiple pieces of some SKUs. To test our transformation schemes, the multi-demand version of the previously applied test bed with a pick list length of 3 and 7 is employed (see Heßler and Irnich 2023). By generating two additional parameters, namely the stock available at each position and the pick demand for each SKU at the pick list, the single demand instances can be transformed into multi-demand ones. For the instances of Heßler and Irnich (2023), the current stock is drawn independently from ${\mathcal {U}}(1,3)$ for each position, with ${\mathcal {U}}$ representing the uniform distribution. A similar approach is implemented for the pick demand, which is drawn from ${\mathcal {U}}(1,\min {\{6,\sum _{i\in N_k}q_i\}})$ for each demanded SKU. Providing further insights into the performance of the procedures, we derive multiple versions of each instance by trimming the maximum demand for a SKU to $r_{max} \in \{2,3,4,5,6\}$. As Heßler and Irnich (2023) provide proven optimal solutions for instances with a maximal demand of six pieces per SKU only, we determine optimal solutions for the trimmed versions of the instances employing Gurobi solving the MIP model of Weidinger (2018) without time limit.

The results of the tests are presented in Table 4. Here, the average gap to the optimal solution value (gap), the number of optimal solutions found (opt.), as well as the number of feasible solutions found (feas.) is given for the different approaches. Additionally, the columns combined present the performance indicators for a best-of-four approach, representing the best solution found among all four procedures. For all approaches, the resulting ATSP instances have been solved employing the $\hbox {LKH}_{\text {ATSP}}^{100}$ approach.

As can be seen in the data, the proposed approaches provide good results even for multi-demand cases with up to six demanded pieces per SKU. While solution quality decreases for higher demands per SKU, the average optimality gap for all evaluated settings is at most 2%, while at least 80% of the instances are solved to optimality if the combined approach is applied. Hereby, especially, the approach Full-split delivers good-quality solutions with an optimality gap of only 1.95% on average over all scenarios and a success rate of 81.5% for finding optimal solutions. By combining the approaches No-split, Position-split, and Full-split, these results can further be improved to an optimality gap of only about 1.1% on average and more than 88% optimal solutions. Note that the SKU-split procedure never provides a best solution, that has not been found by at least one of the other approaches as well.

After conducting our study, we once again conclude that using a state-of-the-art heuristic ATSP solver, such as LKH, yields nearly optimal solutions in a reasonable amount of time, even for the multi-demand case. Therefore, for practical applications where small optimality gaps are acceptable, there appears to be no need to employ tailor-made SPRP-SS solvers.

Table 4 Optimality gaps, no. optimal solutions found, and no. solvable instances by the different approaches for different warehouse dimensions and maximum demands per SKU ($r_{max}$)

5.4 Cross aisles

In an additional test, the flexibility of the approach is exploited to study the influence of the number of cross aisles on the average length of picking tours. The number of cross aisles has two antagonistic main effects on the evaluation criteria, i.e., the average length of picking tours. Introducing more cross aisles allows for greater flexibility in changing picking aisles, which tends to reduce average tour lengths (effect 1). However, additional cross aisles also require more floor space, leading to larger warehouses and therefore longer average picking tours (effect 2). This tradeoff has gathered significant attention from both the scientific community and practitioners (Vaughan and Petersen 1999; Roodbergen and De Koster 2001a). To address this tradeoff in a scattered storage warehouse, we again employ the dataset of Heßler and Irnich (2023) with a scatter factor of two. To provide more insights, however, instances with five and ten aisles, aisle lengths of 30 and 60 storage positions, and differing pick list lengths have been tackled in a full factorial approach. For each of the 50 instances per warehouse size and pick list length, we started with a classical one-block layout, i.e., two cross aisles (see Fig. 1a). For that basic layout, we attained a solution using the $\hbox {LKH}_\text {ATSP}^{100}$ approach. Incrementing the number of cross aisles iteratively by one, and solving the resulting instances again with the same approach, i.e., $\hbox {LKH}_\text {ATSP}^{100}$, we kept track of the solution values obtained for identical instances with differing number of cross aisles. The procedure has been repeated until the average tour length reached a minimum and started to increase again (i.e., effect 2 outweighs effect 1). Once the minimum has been exceeded by more than 2%, the procedure has been terminated and a binary search was started to identify the number of cross aisles, for which the average tour length exceeds the value for two cross aisles only.

Note that we arrange the cross aisle as equidistantly as possible within the picking aisles. However, due to the non-divisibility of the storage positions, a perfect equidistant distribution of cross aisles could not be achieved for all settings.

Table 5 (Near) optimal number of cross aisles (#CA*), avg. picking tour length relative to tour length with two cross aisles (mean rel. length), and mean number of cross aisles leading to longer avg. tours than a one-block layout (${\#}\text{CA}^{\nabla}$) discriminated by different warehouse dimensions and pick lists

The results of the tests are presented in Table 5, discriminated by the number of picking aisles, the length of picking aisles measured in storage positions per aisle, as well as the length of the pick lists. To account for the flat optima observed in the data, we report the number of cross aisles, which exceeded the minimum average tour length by less than one percent (#CA*). We further provide the interval of average tour lengths achieved (mean rel. length), set in relation to the average tour length obtained by the traditional one-block layout, which has cross aisles only at the front and back (see Fig. 1a). Finally, the minimum number of cross aisles for which the average tour length exceeds the benchmark of a classical one-block layout is given in column ${\#}\text{CA}^{\nabla}$. Note, that for some settings, such a value could not be identified. Analyzing the data reveals the following key findings:

• Potential savings are higher for larger warehouses and longer pick lists: As the size of the warehouse increases, the number and/or length of the picking aisles also increases. In these scenarios, additional shortcuts have a greater potential to reduce the length of picking tours. The same principle applies to longer pick lists. Since the average tour length increases with longer pick lists, there are more opportunities to utilize shortcuts, leading to increased benefits from additional cross aisles.

• The optimal number of cross aisles depends on interaction effects: Although all examined parameters have some influence on the optimal number of cross aisles, interaction effects can be observed. While the length of the pick list does not have major effects on the optimal number of cross aisles for the smallest warehouses tackled (for instance, 5 cross aisles are within the #CA*-interval for all pick list lengths in 5×30 warehouses), the factor importance increases for larger warehouses. In tendency, larger warehouses (and longer pick lists in larger warehouses) come with a demand for more cross aisles.

• Negative effects prevail only for an extremely high number of cross aisles: Across all experiments, the decreasing effect of an excessively large number of cross aisles could be observed. However, the point where more cross aisles even fall behind the traditional warehouse with just two cross aisles is only reached (if at all) at an unrealistically high number of cross aisles for all settings.

Based on these initial results, it can be assumed that the optimal number of cross aisles evaluated by the average length of picking tours tends to be higher than what is commonly observed in real-world facilities. During many visits to warehouses, the authors found most often only a handful of cross aisles within comparable storage areas. Therefore, warehouse managers should not shy away from implementing an adequate number of cross aisles due to concerns about increased floor space, at least if the average picking tour length is the benchmark value and additional floor space is easily available, e.g., if a warehouse is newly built on a green field. Clearly, in business practice, additional decision criteria must be evaluated, i.e., the costs of implementing and maintaining additional floor space. Seeing that the optimal number of cross aisles for a 10x30 warehouse increased floor space by about 19% in our tests (see Appendix 2, Fig. 4), these costs might be significant. Still, on the positive side a reduction of unproductive walking times by nearly 30% is promised. Based on these results, the most profitable decision must be made for each particular setting, as operating and labor costs are highly fluctuating, and therefore optimal decisions might vary for differing locations and time periods.

5.5 Non-rectangular warehouse layouts

In the last computational test of this study, we tackle non-rectangular warehouse layouts to provide insights into the solution performance of the proposed approaches in such environments. For these tests, the instances of Heßler and Irnich (2023) have been transformed into two widely known non-rectangular layouts, namely the flying-V and the fishbone layout (see, e.g., Pohl et al. 2009; Clark and Meller 2013; Çelk and Süral 2014; Cardona et al. 2015). As for the flying-V layout, we add diagonal cross aisles such that each cross aisle starts at the (centered) depot and connects the picking aisles to the left and right at a $\hbox {45}^{\circ }$ angle (see Fig. 3b). The resulting triangular picking areas are additionally reflected across a diagonal line for the fishbone layout (see Fig. 3c). Note that due to Concorde’s limitation to integer parameters, we approximate a diagonal movement of one square by $\sqrt{2} \approx 1.4$ such that we can attain integrity by applying factor five to the distance values. To ensure comparability, we use this procedure for all solution approaches.

Fig. 3

An SPRP-SS instance in different warehouse layouts

These transformations have been applied to the 200 instances of Heßler and Irnich (2023) with five picking aisles of length 30 and a scatter factor of two. Each of the resulting instances has been solved employing $\hbox {Gurobi}_{\text {ATSP}}$, $\hbox {Concorde}_{\text {TSP}}$, $\hbox {Gurobi}_{\text {MIP}}$, and $\hbox {LKH}^{100}_{\text {ATSP}}$ with a time limit of one hour each per instance. Table 6 presents the mean runtimes ($\mu _t$), standard deviation of runtimes ($\sigma _t$), gap to the best known solution (gap), and percentage of proven optimal solutions attained (% opt.), discriminated by the different approaches, layouts, and pick list lengths (picks) and averaged over 50 instances per cell. As can be seen based on the results, the presented approaches can be applied to non-rectangular layouts without any decrease in performance. Again, both TSP-based solution procedures outperform the SPRP-SS MIP model solved by Gurobi. While the single values vary a bit, no significant differences in performance can be identified, such that again $\hbox {Gurobi}_{\text {ATSP}}$ is preferable for short pick lists and $\hbox {Concorde}_{\text {TSP}}$ should be applied for longer pick lists. Remarkable is (once again) the outstanding solution quality of the $\hbox {LKH}^{100}_{\text {ATSP}}$ approach, which finds all best known solutions in only a fraction of the time of the exact approaches.

Table 6 Performance of solution approaches for non-rectangular warehouse layouts

It can be concluded that the presented solution approaches are highly flexible and, according to the first tests conducted, robust regarding solution performance and time over differing layouts.

6 Conclusion

This paper is dedicated to proposing a flexible approach for solving the single picker routing problem with scattered storage (SPRP-SS) either exact or heuristically, by providing transformation schemes of the problem into a classical (asymmetric) TSP. This transformation allows us to address all possible warehouse layouts and establishes a connection between SPRP-SS and TSP. By doing so, we can leverage the extensive array of powerful TSP solvers available to tackle the SPRP-SS effectively.

Through an extensive computational study, the novel approach demonstrates remarkable potential and achieves excellent performance by delivering near-optimal solutions in less than a second, even for warehouses of realistic sizes. On the managerial front, the approach provides initial insights into the optimal number of cross aisles required in mixed-shelves storage warehouses. Specifically, it identifies the size of the warehouse, rather than the length of the pick lists, as a key driver influencing the optimal number of cross aisles.

Based on the ideas presented in this paper, future research should primarily concentrate on benchmarking additional TSP solvers, while leveraging the transformation schemes proposed in this study. Moreover, it is essential to acknowledge that many real-world scattered storage warehouses expand beyond the basic SPRP-SS to encompass various other complexities. These complexities may include dynamic batching of bins on the cart, cartless subtours, or the integration of stowing products in the shelves before transitioning to picking (see Boysen et al. 2019). Therefore, it becomes imperative for future research to investigate whether these extended problem settings necessitate the development of new tailor-made routing algorithms or if existing solvers for standard routing tasks can be adapted and effectively reused, especially for subproblems. Further, the results of this paper can be employed to extend analytical frameworks for the  TSP towards scattered storage picker routing. Finally, a more comprehensive analysis of the costs and benefits of cross aisles is an interesting research question.

Appendices

Appendix 1: Detailed results of the Lin–Kernighan–Helsgaun heuristic

See Table 7.

Table 7 Mean optimality gaps and solution times for the Lin–Kernighan–Helsgaun heuristic with 1, 10, and 100 iterations for the whole dataset

Appendix 2: Cross aisles: performance gain versus space utilization

See Fig. 4.

Fig. 4

Impact of cross aisles on the lengths of picking tours and the resulting warehouse size for a warehouse with 10 aisles with a length of 30 storage positions per aisle and a pick list length of 30. All values are set in relation to a classical one-block layout with two cross aisles only