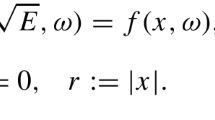Determining a Random Schrödinger Operator: Both Potential and Source are Random

Abstract

We study an inverse scattering problem associated with a Schrödinger system where both the potential and source terms are random and unknown. The well-posedness of the forward scattering problem is first established in a proper sense. We then derive two unique recovery results in determining the rough strengths of the random source and the random potential, by using the corresponding far-field data. The first recovery result shows that a single realization of the passive scattering measurements uniquely recovers the rough strength of the random source. The second one shows that, by a single realization of the backscattering data, the rough strength of the random potential can be recovered. The ergodicity is used to establish the single realization recovery. The asymptotic arguments in our study are based on techniques from the theory of pseudodifferential operators and microlocal analysis.

1 Introduction

1.1 Mathematical formulations

In this paper, we are mainly concerned with the following random Schrödinger system

where $\mathrm {i} := \sqrt{-1}$, and $\omega$ in (1.1a) is a random sample belonging to $\Omega$ with $(\Omega ,{\mathcal {F}},{\mathbb {P}})$ being a complete probability space, and $f(x,\omega )$ and $q(x,\omega )$ are independently distributed generalized Gaussian random fields with zero-mean and are supported in bounded domains $D_f$ and $D_q$, respectively. $E\in {\mathbb {R}}_+$ is the energy level. In the sequel, we follow the convention to replace E with $k^2$, namely $k := \sqrt{E} \in {\mathbb {R}}_+$, which can be understood as the wave number. In (1.1b), ${d \in {\mathbb {S}}^2:=\{ x \in {\mathbb {R}}^3 \,;\, |x| = 1 \}}$ signifies the incident direction of the plane wave, and $\alpha$ takes the value of either 0 or 1 to impose or suppress the incident wave, respectively. $u^{sc}$ in (1.1b) is the scattered wave field, which is also random due to the randomness of the source and potential. The limit (1.1c) is the Sommerfeld Radiation Condition (SRC) [10] that characterizes the outgoing nature of the scattered field $u^{sc}$. The random system (1.1) describes the quantum scattering [13, 16] associated with a source f and a potential q at the energy level $k^2$.

f and q in equation (1.1a) are assumed to be generalized Gaussian random fields. It means that f is a random distribution and the mapping

$$\begin{aligned} \omega \in \Omega \ \mapsto \ \langle {f(\cdot ,\omega ),\varphi } \rangle \in {\mathbb {C}} \end{aligned}$$

is a Gaussian random variable whose probabilistic measure depends on the test function $\varphi$. The same notation applies to q. There are different types of generalized Gaussian random fields [32]. In our setting, we assume that f and q are two microlocally isotropic generalized Gaussian random (m.i.g.r. for short) functions/distributions; see Definition 2.1 in the following. The m.i.g.r. model has been under intensive studies; see, e.g., [8, 23,24,25]. Two important parameters of a m.i.g.r. distribution are its rough order and rough strength. Roughly speaking, the rough order, which is a real number, determines the degree of spatial roughness of the m.i.g.r. distribution, and the rough strength, which is a real-valued function, indicates its spatial correlation length and intensity. The rough strength also captures the micro-structure of the object in interest [24]. We shall give a more detailed introduction to this random model in Sect. 2.2.

In this work, we denote the rough order of f (resp. q) as $-m_f$ (resp. $-m_q$), and the rough strength as $\mu _f(x)$ (resp. $\mu _q(x)$). The main purpose of this work is to recover the rough strengths of both the source and the potential using either passive or active far-field measurements associated with (1.1).

1.2 Statement of the main results

In order to study the inverse scattering problem, i.e., the recovery of $\mu _f$ and $\mu _q$, we first need to have a thorough understanding of the direct scattering problem. For the case where both the source and the potential are deterministic and $L^\infty$ functions with compact supports, the well-posedness of the direct problem of system (1.1) is known; see, e.g., [10, 13, 29]. Moreover, there holds the following asymptotic expansion of the outgoing radiating field $u^{sc}$ as $|x| \rightarrow +\infty$,

$$\begin{aligned} u^{sc}(x) = \frac{e^{\mathrm {i}k |x|}}{|x|} u^\infty ({\hat{x}}, k, d) + {\mathcal {O}} \left( \frac{1}{|x|^2} \right) . \end{aligned}$$

$u^\infty ({\hat{x}}, k, d)$ is referred to as the far-field pattern, which encodes information of the potential and the source. ${\hat{x}}:=x/|x|$ and d in $u^\infty ({\hat{x}}, k, d)$ are unit vectors and they respectively stand for the observation direction and the impinging direction of the incident wave. When $d = -{\hat{x}}$, $u^\infty ({\hat{x}}, k, -{\hat{x}})$ is called the backscattering far-field pattern.

In the random setting, however, due to the randomness inherited in the source and potential terms, the regularities of the corresponding scattering wave field are much worse [8, 24]. This makes those standard PDE theories invalid for the direct problem of system (1.1). To tackle this issue, we shall reformulate the direct problem and show that the direct problem is still well-posed in a proper sense. Therefore, our direct problem can be formulated as

$$\begin{aligned} \displaystyle { (f, q) \rightarrow \{u^{sc}({\hat{x}}, k, d, \omega ), u^\infty ({\hat{x}}, k, d, \omega ) \,;\, \omega \in \Omega ,\, {\hat{x}} \in {\mathbb {S}}^2, k \in {\mathbb {R}}_+,\, d \in {\mathbb {S}}^2 \}. } \end{aligned}$$

The well-posedness of the direct scattering problem enables us to explore our inverse problems. Due to the fact that the precise values of a random function provide little information about its statistical properties, we are interested in the recovery of the rough strengths of the source and the potential by knowledge of the far-field patterns.

In the recovery procedure, we recover $\mu _f$ and $\mu _q$ in a sequential way by knowledge of the associated far-field pattern measurements $u^\infty ({\hat{x}}, k, d, \omega )$. By sequential, we mean that $\mu _f$ and $\mu _q$ are recovered by the corresponding far-field data sets one-by-one. In addition to this, in the recovery procedure, both the passive and active measurements are utilized. When $\alpha = 0$, the incident wave is suppressed and the scattering is solely generated by the unknown source. The corresponding far-field pattern is referred to as the passive measurement. In this case, the far-field pattern is independent of the incident direction d, and we denote it as $u^\infty ({\hat{x}}, k, \omega )$. When $\alpha = 1$, the scattering is generated by both the active source and the incident wave, and the far-field pattern is referred to as the active measurement, and is denoted as $u^\infty ({\hat{x}}, k, d, \omega )$.

With the above discussion, our inverse problems can be formulated as

$$\begin{aligned} \displaystyle { \left\{ \begin{aligned} {\mathcal {M}}_f(\omega )&:= \ \{u^\infty ({\hat{x}}, k, \omega ) \,;\, \forall \hat{x} \in {\mathbb {S}}^2,\, \forall k \in {\mathbb {R}}_+\}&\rightarrow \quad \mu _f, \\ {\mathcal {M}}_q(\omega )&:= \ \{u^\infty ({\hat{x}}, k, -{\hat{x}}, \omega ) \,;\, \forall \hat{x} \in {\mathbb {S}}^2,\, \forall k \in {\mathbb {R}}_+\}&\rightarrow \quad \mu _q. \end{aligned} \right. } \end{aligned}$$

The data set ${\mathcal {M}}_f(\omega )$ (abbr. ${\mathcal {M}}_f$) corresponds to the passive measurement ($\alpha = 0$), while the data set ${\mathcal {M}}_q(\omega )$ (abbr. ${\mathcal {M}}_q$) corresponds to the active measurement ($\alpha = 1$). Different random samples $\omega$ generate different data sets. Our study shows that in certain general scenarios the data sets ${\mathcal {M}}_f(\omega )$, ${\mathcal {M}}_q(\omega )$ with a fixed $\omega \in \Omega$ can uniquely recover $\mu _f$ and $\mu _q$, respectively.

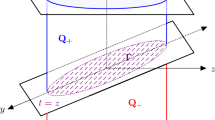
With the potential term being unknown, the inverse source problem, i.e., the recovery of $\mu _f$, becomes highly nonlinear and thus more challenging. One possibility to tackle this situation is to put some geometrical assumption on the locations of the source and the potential. In what follows, we assume that there is a positive distance between the convex hulls of the supports of f and q, i.e.,

$$\begin{aligned} \mathop {\mathrm{dist}}({\mathcal {CH}}(D_f), {\mathcal {CH}}(D_q)) := \inf \{\, |x - y| \,;\, x \in {\mathcal {CH}}(D_f),\, y \in {\mathcal {CH}}(D_q) \,\} > 0, \end{aligned}$$

(1.2)

where ${\mathcal {CH}}$ means taking the convex hull of a domain. Therefore, one can find a plane which separates $D_f$ and $D_q$. In what follows, in order to simplify the exposition, we assume that $D_f$ and $D_q$ are convex domains and hence ${\mathcal {CH}}(D_f)=D_f$ and ${\mathcal {CH}}(D_q)=D_q$. Moreover, we let ${\varvec{n}}$ denote the unit normal vector of the aforementioned plane that separates $D_f$ and $D_q$, pointing from the half-space containing $D_f$ into the half-space containing $D_q$.

In system (1.1), both the source and the potential are assumed to be unknown. Moreover, the source and the potential are generalized random functions of the same type. These issues make the decoupling of $\mu _f$ and $\mu _q$ far more difficult. However, some a-priori information about the rough orders of f and q can help us to achieve the recoveries. Now we are ready to state our main recovery results of the inverse problems.

Theorem 1.1

Suppose that f and q in system (1.1) are m.i.g.r. distributions of order $-m_f$ and $-m_q$, respectively, satisfying

$$\begin{aligned} {2< m_f< 4, \ m_f < 5m_q - 11.} \end{aligned}$$

(1.3)

Assume that (1.2) is satisfied and ${\varvec{n}}$ is defined as above. Then, independent of $\mu _q$, the data set ${\mathcal {M}}_f(\omega )$ for a fixed $\omega \in \Omega$ can uniquely recover $\mu _f$ almost surely. Moreover, the recovering formula is given by

$$\begin{aligned} \displaystyle { {{\widehat{\mu }}}_f(\tau {\hat{x}}) = \left\{ \begin{aligned}&\lim _{K \rightarrow +\infty } \frac{4\sqrt{2\pi }}{K} \int _K^{2K} k^{m_f} \overline{u^\infty ({\hat{x}},k,\omega )} u^\infty ({\hat{x}},k+\tau ,\omega ) \,\mathrm {d}{k}, \quad \hat{x} \cdot {\varvec{n}} \ge 0, \\&\ \overline{{{\widehat{\mu }}}_f(-\tau {\hat{x}})}, \quad \hat{x} \cdot {\varvec{n}} < 0, \end{aligned}\right. } \end{aligned}$$

(1.4)

where $\tau \ge 0$ and $u^\infty ({\hat{x}},k,\omega ) \in \mathcal M_f(\omega )$.

Remark 1.1

In Theorem 1.1, $\mu _f$ can be uniquely recovered without a-priori knowledge of q. Moreover, since $\alpha =0$ in ${\mathcal {M}}_f(\omega )$, Theorem 1.1 indicates that $\mu _f$ can be uniquely recovered by a single realization of the passive scattering measurement. Due to the requirement ${\hat{x}} \cdot {\varvec{n}} \ge 0$, only half of all the observation directions are needed. Besides, for the sake of simplicity, we set the wave number k in the definition of ${\mathcal {M}}_f$ to be running over all the positive real numbers. But, according to (1.4), it is sufficient to let k be greater than any fixed positive number. These remarks also apply to Theorem 1.2 in what follows. Moreover, it is noted that in the definition of m.i.g.r. distribution (cf. Definition 2.1), $\mu$ is defined as a real-valued function. Therefore, ${{\widehat{\mu }}}_f$ in Theorem 1.1 (and ${{\widehat{\mu }}}_q$ in Theorem 1.2 below) is a conjugate-symmetric function. It is worth mentioning that the a-priori requirement $2< m_f < 4$ comes from (3.22)–(3.23) and (4.6), while the a-priori requirement $m_f < 5 m_q - 11$ comes from (4.8) in our subsequent analysis.

To recover $\mu _q$, the active scattering measurement shall be needed in our recovery procedure.

Theorem 1.2

Under the same condition as that in Theorem 1.1 with an additional assumption that $m_q < m_f$, and independent of $\mu _f$, the data set ${\mathcal {M}}_q(\omega )$ for a fixed $\omega \in \Omega$ can uniquely recover $\mu _q$ almost surely. Moreover, the recovering formula is given by

$$\begin{aligned} \displaystyle { {{\widehat{\mu }}}_q(\tau {\hat{x}}) = \left\{ \begin{aligned}&\lim _{K \rightarrow +\infty } \frac{4\sqrt{2\pi }}{K} \int _K^{2K} k^{m_q} \overline{u^\infty ({\hat{x}},k,-{\hat{x}},\omega )} u^\infty ({\hat{x}},k\!+\! \tfrac{\tau }{2},-{\hat{x}},\omega ) \,\mathrm {d}{k}, \ \hat{x} \cdot {\varvec{n}} \ge 0, \\&\ \overline{{{\widehat{\mu }}}_f(-\tau {\hat{x}})}, \quad \hat{x} \cdot {\varvec{n}} < 0, \end{aligned}\right. } \end{aligned}$$

(1.5)

where $\tau \ge 0$ and $u^\infty ({\hat{x}},k,-{\hat{x}},\omega ) \in {\mathcal {M}}_q(\omega )$.

Remark 1.2

It is emphasized that the recovery result in Theorem 1.2 is independent of $\mu _f$. Moreover, we only make use of a single realization of the active backscattering measurement. We would also like to point out that the additional a-priori requirement $m_q < m_f$ comes from (5.9) in our subsequent analysis.

1.3 Discussion and connection to the existing results

There is abundant literature for inverse scattering problems associated with either passive or active measurements. Given a known potential, the recovery of an unknown source term by the corresponding passive measurement is referred to as the inverse source problem. We refer to [2,3,4, 9, 15, 18,19,20, 22, 33, 36] and references therein for both theoretical uniqueness/stability results and computational methods for the inverse source problem in the deterministic setting. The simultaneous recovery of an unknown source and its surrounding potential was also investigated in the literature. In [21, 27], motivated by applications in thermo- and photo-acoustic tomography, the simultaneous recovery of an unknown source and its surrounding medium parameter was considered. This type of inverse problems also arise in the magnetic anomaly detections using geomagnetic monitoring [11, 12]. The studies in [11, 12, 21, 27] were confined to the deterministic setting and associated mainly with the passive measurement. For the random/stochastic case, the determination of a random source by the corresponding passive measurement was also recently studied in [1, 25, 28, 35]. In [25], the homogeneous Helmholtz system with a random source is studied. Compared with [25], system (1.1) in this paper comprises of both unknown source and unknown potential, making the corresponding study radically more challenging. The determination of a random potential by the corresponding active measurement, with the source term being zero, was established in [8]. We also refer to [5,6,7, 23, 24] and references therein for more relevant studies on random inverse medium problems.

We are particularly interested in the case with a single realization of the random sample, namely the $\omega$ is fixed in the recovery of the source and potential; see the recovery formulae (1.4)–(1.5). In our approach, we assume that the backscattering far-field data $u^\infty ({\hat{x}}, k, -{\hat{x}}, \omega )$ for different observation directions are generated by a single realization of the random sample [8]. Intuitively, a particular realization of f or q provides us little information about their statistical properties. However, our study indicates that a single realization of the far-field measurement can be used to uniquely recover the rough strength in certain scenarios. A crucial assumption to make the single realization recovery possible is that the randomness is independent of the wave number k. Indeed, there are variant applications in which the randomness changes slowly or is independent of time [8, 24], and by temporal Fourier transforming into the frequency domain, they actually correspond to the aforementioned situation. The single realization recovery has been studied in the literature; see, e.g., [8, 23, 24, 26]. The idea of this article is mainly motivated by [8, 26].

Compared with our previous work [26], the result of this paper has two major differences. First, the random models are different. In [26], the random part of the source is assumed to be a Gaussian white noise, while in system (1.1), the potential and the source are assumed to be m.i.g.r. distributions. The m.i.g.r. distribution can fit larger range of randomness by tuning its rough order. Second, in system (1.1), both the source and potential are random, while in [26], the potential is assumed to be deterministic. These two facts make this work much more challenging than that in [26]. The techniques used in the estimates of higher order terms (see Sect. 3) are pseudodifferential operators and microlocal analysis, which are more technically involved compared to that in [26].

The rest of this paper is organized as follows. In Sect. 2, we first give an introduction to the random model and present some preliminary and auxiliary results. Then we show the well-posedness of the direct scattering problem. Section 3 establishes the asymptotics of different terms appeared in the recovery formula. In Sect. 4, we recover the rough strength of the source. Section 5 is devoted to the recovery of the rough strength of the potential.

2 Mathematical Analysis of the Direct Problem

In this section, we show that the direct problem is well-posed in a proper sense. Before that, we first present some preliminaries for the subsequent use and give the introduction to our random model.

2.1 Preliminary and auxiliary results

For convenient reference and self-containedness, we first present some preliminary and auxiliary results in what follows. In this paper, we mainly focus on the three-dimensional case. Nevertheless, some of the results derived also hold for higher dimensions and in those cases, we choose to present the results in the general dimension $n\ge 3$ since they might be useful in other studies.

The Fourier transform and inverse Fourier transform of a function $\varphi$ are respectively defined as

$$\begin{aligned} {\mathcal {F}}\varphi (\xi )&= {{\widehat{\varphi }}}(\xi ) := (2\pi )^{-n/2} \int e^{-{\text {i}}x\cdot \xi } \varphi (x) \,\mathrm {d}{x}, \\ {\mathcal {F}}^{-1} \varphi (\xi )&:= (2\pi )^{-n/2} \int e^{{\text {i}}x\cdot \xi } \varphi (x) \,\mathrm {d}{x}. \end{aligned}$$

Set

$$\begin{aligned} \Phi (x,y) = \Phi _k(x,y) := \frac{e^{{\text {i}}k|x-y|}}{4\pi |x-y|}, \quad x\in {\mathbb {R}}^3\backslash \{y\}. \end{aligned}$$

$\Phi _k$ is the outgoing fundamental solution, centered at y, to the differential operator $-\Delta -k^2$. Define the resolvent operator ${{\mathcal {R}}_{k}}$,

$$\begin{aligned} ({{\mathcal {R}}_{k}}\varphi )(x) := \int _{{\mathbb {R}}^3} \Phi _k(x,y) \varphi (y) \,\mathrm {d}{y}, \quad x \in {\mathbb {R}}^3, \end{aligned}$$

(2.1)

where $\varphi$ can be any measurable function on ${\mathbb {R}}^3$ as long as (2.1) is well-defined for almost all x in ${\mathbb {R}}^3$.

Write $\langle {x} \rangle := (1+|x|^2)^{1/2}$ for $x \in {{\mathbb {R}}^n}$, $n\ge 1$. We introduce the following weighted $L^p$-norm and the corresponding function space over ${{\mathbb {R}}^n}$ for any $\delta \in {\mathbb {R}}$,

$$\begin{aligned} \begin{aligned} \Vert {\varphi } \Vert _{L_\delta ^p({{\mathbb {R}}^n})}&:= \Vert { \langle {\cdot } \rangle ^{\delta } \varphi (\cdot )} \Vert _{L^p({{\mathbb {R}}^n})} = \big ( \int _{{{\mathbb {R}}^n}} \langle {x} \rangle ^{p\delta } |\varphi |^p \,\mathrm {d}{x} \big )^{\frac{1}{p}},\\ L_\delta ^p({{\mathbb {R}}^n})&:= \{\, \varphi \in L_{loc}^1({{\mathbb {R}}^n}) \,;\, \Vert {\varphi } \Vert _{L_\delta ^p({{\mathbb {R}}^n})} < +\infty \,\}. \end{aligned} \end{aligned}$$

(2.2)

We also define $L_\delta ^p(S)$ for any subset S in ${{\mathbb {R}}^n}$ by replacing ${{\mathbb {R}}^n}$ in (2.2) with S. In what follows, we may write $L_\delta ^2({\mathbb {R}}^3)$ as $L_\delta ^2$ for short without ambiguities. Let I be the identity operator and define

$$\begin{aligned} \Vert {f} \Vert _{H_\delta ^{s,p}({{\mathbb {R}}^n})}:= & {} \Vert {(I-\Delta )^{s/2} f} \Vert _{L_\delta ^p({{\mathbb {R}}^n})}, \\ H_\delta ^{s,p}({{\mathbb {R}}^n})= & {} \{ f \in {\mathscr {S}}'({{\mathbb {R}}^n}); \Vert {f} \Vert _{H_\delta ^{s,p}({{\mathbb {R}}^n})} < +\infty \}, \end{aligned}$$

where ${\mathscr {S}}'({{\mathbb {R}}^n})$ stands for the dual space of the Schwartz space ${\mathscr {S}}({{\mathbb {R}}^n})$. The space $H_\delta ^{s,2}({{\mathbb {R}}^n})$ is abbreviated as $H_\delta ^s({{\mathbb {R}}^n})$, and $H_0^{s,p}({{\mathbb {R}}^n})$ is abbreviated as $H^{s,p}({{\mathbb {R}}^n})$. It can be verified that

$$\begin{aligned} \Vert {f} \Vert _{H_\delta ^s({{\mathbb {R}}^n})} = \Vert { \langle {\cdot } \rangle ^s {\widehat{f}}(\cdot )} \Vert _{H^\delta ({{\mathbb {R}}^n})}. \end{aligned}$$

(2.3)

Let $m \in (-\infty ,+\infty )$. We define $S^m$ to be the set of all functions $\sigma (x,\xi ) \in C^{\infty }({{\mathbb {R}}^n},{{\mathbb {R}}^n};{\mathbb {C}})$ such that for any two multi-indices $\alpha$ and $\beta$, there is a positive constant $C_{\alpha , \beta }$, depending on $\alpha$ and $\beta$ only, for which

$$\begin{aligned} \big | (D_{x}^{\alpha }D_{\xi }^{\beta }\sigma )(x,\xi ) \big | \le C_{\alpha , \beta }(1+|\xi |)^{m-|\beta |}, \quad \forall x, \xi \in {{\mathbb {R}}^n}. \end{aligned}$$

We call any function $\sigma$ in $\bigcup _{m \in {\mathbb {R}}} S^m$ a symbol. A principal symbol of $\sigma$ is an equivalent class $[\sigma ] = \{ {{\tilde{\sigma }}} \in S^m \,;\, \sigma - {{\tilde{\sigma }}} \in S^{m-1} \}$. In what follows, we may use one representative ${{\tilde{\sigma }}}$ in $[\sigma ]$ to represent the equivalent class $[\sigma ]$. Let $\sigma$ be a symbol. Then the pseudo-differential operator T, defined on ${\mathscr {S}}({{\mathbb {R}}^n})$ and associated with $\sigma$, is defined by

$$\begin{aligned} (T_{\sigma }\varphi )(x)&:= (2\pi )^{-n/2} \int _{{{\mathbb {R}}^n}} e^{{\text {i}}x \cdot \xi } \sigma (x,\xi ) {\hat{\varphi }}(\xi ) \,\mathrm {d}{\xi } \\&= (2\pi )^{-n} \iint _{{{\mathbb {R}}^n}\times {{\mathbb {R}}^n}} e^{{\text {i}}(x-y) \cdot \xi } \sigma (x,\xi ) \varphi (y) \,\mathrm {d}{y} \,\mathrm {d}{\xi }, \quad \forall \varphi \in {\mathscr {S}}({{\mathbb {R}}^n}). \end{aligned}$$

In the sequel, we write ${\mathcal {L}}({\mathcal {A}}, {\mathcal {B}})$ to denote the set of all the bounded linear mappings from a normed vector space ${\mathcal {A}}$ to a normed vector space ${\mathcal {B}}$. For any mapping ${\mathcal {K}} \in {\mathcal {L}}({\mathcal {A}}, {\mathcal {B}})$, we denote its operator norm as $\Vert {{\mathcal {K}}} \Vert _{{\mathcal {L}}({\mathcal {A}}, \mathcal B)}$. We also use C and its variants, such as $C_D$, $C_{D,f}$, to denote some generic constants whose particular values may change line by line. For two quantities, we write ${\mathcal {P}}\lesssim {\mathcal {Q}}$ to signify ${\mathcal {P}}\le C {\mathcal {Q}}$ and ${\mathcal {P}} \simeq {\mathcal {Q}}$ to signify ${\widetilde{C}}{\mathcal {Q}}\le {\mathcal {P}} \le C {\mathcal {Q}}$, for some generic positive constants C and ${\widetilde{C}}$. We write “almost everywhere” as “a.e.” and “almost surely” as “a.s.” for short. We use $|{\mathcal {S}}|$ to denote the Lebesgue measure of any Lebesgue-measurable set ${\mathcal {S}}$.

2.2 The random model

As already mentioned in Sect. 1.1, a generalized Gaussian random field maps test functions to random variables. Assume h is a generalized Gaussian random field. Then both $\langle {h(\cdot ,\omega ),\varphi } \rangle$ and $\langle {h(\cdot ,\omega ),\psi } \rangle$ are random variables for $\varphi$, $\psi \in {\mathscr {S}}({{\mathbb {R}}^n})$. From a statistical point of view, the covariance between these two random variables,

$$\begin{aligned} {\mathbb {E}}_\omega ( \langle {\overline{h(\cdot ,\omega )},\varphi } \rangle \langle {h(\cdot ,\omega ),\psi } \rangle ), \end{aligned}$$

(2.4)

can be understood as the covariance of h, where the $\mathbb E_\omega$ means to take expectation on the argument $\omega$. Formula (2.4) induces an operator ${\mathfrak {C}}_h$,

$$\begin{aligned} {\mathfrak {C}}_h :\varphi \in {\mathscr {S}}({{\mathbb {R}}^n}) \ \mapsto \ \mathfrak C_h \varphi \in {\mathscr {S}}'({{\mathbb {R}}^n}), \end{aligned}$$

in a way that

$$\begin{aligned} {\mathfrak {C}}_h \varphi :\psi \in {\mathscr {S}}({{\mathbb {R}}^n}) \ \mapsto \ ({\mathfrak {C}}_h \varphi )(\psi ) = {\mathbb {E}}_\omega ( \langle {\overline{h(\cdot ,\omega )},\varphi } \rangle \langle {h(\cdot ,\omega ),\psi } \rangle ) \in {\mathbb {C}}. \end{aligned}$$

The operator ${\mathfrak {C}}_h$ is called the covariance operator of h. See also [8, 24] for reference.

We adopt the definition of the m.i.g.r. distribution from [8] with some modifications to fit our mathematical setting.

Definition 2.1

A generalized Gaussian random function h on ${{\mathbb {R}}^n}$ is called microlocally isotropic (m.i.g.r.) with rough order $-m$ and rough strength $\mu (x)$ in D, if the following conditions hold:

• (1) the expectation ${\mathbb {E}} h$ is in $C_c^\infty ({{\mathbb {R}}^n})$ with $\mathop {\mathrm{supp}}{\mathbb {E}} h \subset D$;

• (2) h is supported in D a.s.;

• (3) the covariance operator ${\mathfrak {C}}_h$ is a pseudodifferential operator of order $-m$;

• (4) ${\mathfrak {C}}_h$, regarded as a pseudo-differential operator, has a principal symbol of the form $\mu (x)|\xi |^{-m}$ with $\mu \in C_c^\infty ({{\mathbb {R}}^n};{\mathbb {R}})$, $\mathop {\mathrm{supp}}\mu \subset D$ and $\mu (x) \ge 0$ for all $x \in {{\mathbb {R}}^n}$.

Here, $\mu (x)|\xi |^{-m}$ is a representative of the principal symbol of ${\mathfrak {C}}_h$. Throughout this work, the principal symbol of the covariance operator of the $f(\cdot ,\omega )$ in (1.1) is assumed to be $\mu _f(x) |\xi |^{-m_f}$ and that of the $q(\cdot ,\omega )$ in (1.1) is denoted as $\mu _q(x)|\xi |^{-m_q}$.

Lemma 2.1

Let h be a m.i.g.r. distribution of rough order $-m$ in D. Then, $h \in H^{{-s},p}({{\mathbb {R}}^n})$ almost surely for any $1< {p} < +\infty$ and $s > (n-m)/2$.

Proof of Lemma 2.1

See Proposition 2.4 in [8]. $\quad \square$

Lemma 2.1 shows the regularity of h according to its rough order.

By the Schwartz kernel theorem (see Theorem 5.2.1 in [17]), there exists a kernel $K_h(x,y)$ with $\mathop {\mathrm{supp}}K_h \subset D \times D$ such that

$$\begin{aligned} ({\mathfrak {C}}_h \varphi )(\psi ) = {\mathbb {E}}_\omega ( \langle {\overline{h(\cdot ,\omega )},\varphi } \rangle \langle {h(\cdot ,\omega ),\psi } \rangle ) = \iint K_h(x,y) \varphi (x) \psi (y) \,\mathrm {d}{x} \,\mathrm {d}{y}, \end{aligned}$$

(2.5)

for all $\varphi$, $\psi \in {\mathscr {S}}({{\mathbb {R}}^n})$. It is easy to verify that $K_h(x,y) = \overline{K_h(y,x)}$. Denote the symbol of $\mathfrak C_h$ as $c_h$, then it can be verified [8] that the equalities

hold in the distributional sense, and the integrals in (2.6) shall be understood as oscillatory integrals. Despite the fact that h usually is not a function, intuitively speaking, however, it is helpful to keep in mind the following correspondence,

$$\begin{aligned} K_h(x,y) \sim {\mathbb {E}}_\omega \big ( \overline{h(x,\omega )} h(y,\omega ) \big ). \end{aligned}$$

2.3 The well-posedness of the direct problem

We first derive two important quantitative estimates.

Theorem 2.1

For any $0< s < 1/2$ and $\epsilon > 0$, when $k > 2$,

$$ \Vert {{{\mathcal {R}}_{k}}\varphi } \Vert _{H_{-1/ 2 - \epsilon }^s({\mathbb {R}}^3)} \le C_{\epsilon ,s} k^{-(1 - 2s)} \Vert {\varphi } \Vert _{H_{1/2 + \epsilon }^{-s}({\mathbb {R}}^3)}, \quad \varphi \in H_{1/2 + \epsilon }^{-s}({\mathbb {R}}^3). $$

Theorem 2.2

Assume that $q(\cdot ,\omega )$ is microlocally isotropic of order $-m$. Then in any dimension $n \ge 3$ and for every $s > (n-m)/2$ and every $\epsilon \in (0, 3/2]$, $q :H_{-1/2 - \epsilon }^s({{\mathbb {R}}^n}) \rightarrow H_{1/2 + \epsilon }^{-s}({{\mathbb {R}}^n})$ is bounded almost surely,

$$\begin{aligned} \Vert {q(\cdot ,\omega ) \varphi (\cdot )} \Vert _{H_{1/2 + \epsilon }^{-s}({\mathbb {R}}^3)} \le C_{\epsilon ,s}(\omega ) \Vert {\varphi } \Vert _{H_{-1/2 - \epsilon }^s({{\mathbb {R}}^n})}, \quad \varphi \in H_{1/2 + \epsilon }^{-s}({{\mathbb {R}}^n}), \quad {\text { a.e. }}\omega \in \Omega . \end{aligned}$$

The random variable $C_{\epsilon ,s}(\omega )$ is finite almost surely.

The arguments in proving Theorems 2.1 and 2.2 are inspired by [8] and [Sect. 29,  [13]].

Proof of Theorem 2.1

Define an operator

$$\begin{aligned} {{\mathcal {R}}_{k,\tau } \varphi (x) := (2\pi )^{-3/2} \int _{{\mathbb {R}}^3} e^{{\text {i}}x\cdot \xi } \frac{{{\hat{\varphi }}}(\xi )}{|\xi |^2 - k^2 - \text {i}\tau } \,\mathrm {d}{\xi },} \end{aligned}$$

(2.7)

where $\tau \in {\mathbb {R}}_+$. Fix a function $\chi$ satisfying

$$\begin{aligned} \left\{ \begin{aligned}&\chi \in C_c^\infty ({{\mathbb {R}}^n}),\, 0 \le {\chi } \le 1, \\&\chi (x) = 1 \hbox { when } |x| \le 1, \\&\chi (x) = 0 \hbox { when } |x| \ge 2. \end{aligned}\right. \end{aligned}$$

(2.8)

Write ${\mathfrak {R}} \psi (x) := \psi (-x)$. Fix $p \in (1,+\infty )$, we have

$$\begin{aligned}&({\mathcal {R}}_{k,\tau } \varphi ,\psi )_{L^2({\mathbb {R}}^3)} \nonumber \\&\quad = \int _{{\mathbb {R}}^3} {\mathcal {R}}_{k,\tau } \varphi (x) \overline{\psi (x)} \,\mathrm {d}{x} = \int _{{\mathbb {R}}^3} {\mathcal {F}}\{{\mathcal {R}}_{k,\tau } \varphi \} (\xi ) \cdot {\mathcal {F}}\{{\mathfrak {R}} {{\overline{\psi }}}\}(\xi ) \,\mathrm {d}{\xi }\nonumber \\&\quad = \int _0^\infty \frac{(1 - \chi ^2(r - k))}{r^2 - k^2 - {\text {i}}\tau } \,\mathrm {d}{r} \cdot \int _{|\xi | = r} {{\hat{\varphi }}} (\xi ) \cdot \widehat{{\mathfrak {R}} {{\overline{\psi }}}}(\xi ) \,\mathrm {d}{S(\xi )} \nonumber \\&\qquad + \int _0^\infty \frac{ \langle {r} \rangle ^{1/p}\, r^2 \chi ^2(r - k)}{r^2 - k^2 - {\text {i}}\tau } \,\mathrm {d}{r} \cdot \int _{{\mathbb {S}}^2} [ \langle {k} \rangle ^{\frac{-1}{2p}} {{\hat{\varphi }}} (k\omega )] [ \langle {k} \rangle ^{\frac{-1}{2p}} \widehat{{\mathfrak {R}} {{\overline{\psi }}}}(k\omega )] \,\mathrm {d}{S(\omega )} \nonumber \\&\qquad + \int _0^\infty \frac{ \langle {r} \rangle ^{1/p}\, r^2 \chi ^2(r - k)}{r^2 - k^2 - {\text {i}}\tau } \,\mathrm {d}{r} \cdot \int _{{\mathbb {S}}^2} \{ [ \langle {r} \rangle ^{\frac{-1}{2p}} {{\hat{\varphi }}} (r\omega )] [ \langle {r} \rangle ^{\frac{-1}{2p}} \widehat{{\mathfrak {R}} {{\overline{\psi }}}}(r\omega )] \nonumber \\&\qquad - [ \langle {k} \rangle ^{\frac{-1}{2p}} {{\hat{\varphi }}} (k\omega )] [ \langle {k} \rangle ^{\frac{-1}{2p}} \widehat{{\mathfrak {R}} \overline{\psi }}(k\omega )] \} \,\mathrm {d}{S({\omega })} \nonumber \\&\quad =: \ I_1(\tau ) + I_2(\tau ) + I_3(\tau ). \end{aligned}$$

(2.9)

Now we estimate $I_1(\tau )$. By Young’s inequality we have

$$\begin{aligned} ab \le a^p/p + b^q/q \quad \Rightarrow \quad (p^{1/p} q^{1/q}) a^{1/p} b^{1/q} \le a + b \end{aligned}$$

(2.10)

for $a,b> 0,\, p,q > 1,\, 1/p + 1/q = 1$. Note that $|r - k| > 1$ in the support of the function $1 - \chi ^2(r - k)$ and $|\widehat{{\mathfrak {R}} {{\overline{\psi }}}}(\xi )| = |{{\hat{\psi }}}(\xi )|$, one can compute

$$\begin{aligned} |I_1(\tau )|&\le \int _0^\infty \frac{1 - \chi ^2(r - k)}{1 \cdot |(r + 1) + (k - 1)|} \,\mathrm {d}{r} \cdot \int _{|\xi | = r} |{{\hat{\varphi }}} (\xi )| \cdot |\widehat{{\mathfrak {R}} {{\overline{\psi }}}}(\xi )| \,\mathrm {d}{S(\xi )} \nonumber \\&\le \int _0^\infty \frac{1 - \chi ^2(r - k)}{1 \cdot p^{1/p} q^{1/q} (r+1)^{1/p} (k-1)^{1/q}} \,\mathrm {d}{r} \nonumber \\&\quad \cdot \int _{|\xi | = r} |\hat{\varphi }(\xi )| \cdot |{{\hat{\psi }}}(\xi )| \,\mathrm {d}{S(\xi )} \quad (\text {by } (2.10)) \nonumber \\&\le C_p k^{-1/q} \int _0^\infty \langle {r} \rangle ^{-1/p} \,\mathrm {d}{r} \cdot \int _{|\xi | = r} |{{\hat{\varphi }}} (\xi )| \cdot |{{\hat{\psi }}}(\xi )| \,\mathrm {d}{S(\xi )} \nonumber \\&\le C_p k^{1/p - 1} \Vert {\varphi } \Vert _{H_\delta ^{-1/(2p)}({\mathbb {R}}^3)} \Vert {\psi } \Vert _{H_\delta ^{-1/(2p)}({\mathbb {R}}^3)}, \end{aligned}$$

(2.11)

where $1< p < +\infty$ and $\delta > 0$ and the $C_p$ is independent of $\tau$.

We next estimate $I_2(\tau )$. One has

$$\begin{aligned} I_2(\tau )&= \int _{{\mathbb {S}}^2} [ \langle {k} \rangle ^{\frac{-1}{2p}} {{\hat{\varphi }}} (k\omega )] [ \langle {k} \rangle ^{\frac{-1}{2p}} \widehat{{\mathfrak {R}} {{\overline{\psi }}}}(k\omega )] \int _0^\infty \frac{ \langle {r} \rangle ^{\frac{1}{p}} r^2 \chi ^2(r - k) \,\mathrm {d}{r}}{r^2 - k^2 - {\text {i}}\tau } \,\mathrm {d}{S(\omega )}. \end{aligned}$$

(2.12)

Let $\tau _0 \in (0,1)$ be a fixed number whose value shall be specified later. Write $p_\tau (r) := p(r) = r^2 - k^2 - {\text {i}}\tau$. Recall that $\chi (r-k) = 0$ when $|r - k| > 2$. When $\tau _0 \le |r - k| \le 2$, we have

$$\begin{aligned} |p(r)| \ge |\mathfrak {R}p(r)| = |r - k| |r + k| \ge \tau _0 (2k - 2) \ge \tau _0 k. \end{aligned}$$

(2.13)

Write $\Gamma _{k,\tau _0} := \{r \in {\mathbb {C}} ; |r - k| = \tau _0, \mathfrak {I}r \le 0 \}$. When $r \in \Gamma _{k,\tau _0}$, we have

$$\begin{aligned} \forall \tau \in (0,\tau _0) , \quad |p_\tau (r)| \ge |r-k| \,|2k + (r-k)| - \tau _0 = \tau _0 (2k - \tau _0) - \tau _0 \ge \tau _0 k.\quad \end{aligned}$$

(2.14)

Combining (2.13) and (2.14), we conclude that $\forall \tau \in (0,\tau _0), \forall k > 2$,

$$\begin{aligned} |p_\tau (r)| \ge \tau _0 k, \quad {~\forall \,}r \in \{ r \in {\mathbb {R}}_+; 2 \ge |r - k| \ge \tau _0 \} \cup \Gamma _{k,\tau _0},\, \forall \tau \in (0,\tau _0). \end{aligned}$$

(2.15)

By using Cauchy’s integral theorem, we change the integral domain w.r.t. r in (2.12) from ${\mathbb {R}}_+$ to $\{ r \in {\mathbb {R}}_+; 2 \ge |r - k| \ge \tau _0 \} \cup \Gamma _{k,\tau _0}$. Combining this with the estimate (2.15) and noting that $\chi (r - k) = 1$ when $r \in \{ r \in {\mathbb {R}}; |r-k| \le 1 \}$, we have

$$\begin{aligned} |I_2(\tau )|&\le \int _{|\xi |=k} \langle {\xi } \rangle ^{\frac{-1}{2p}} |{{\hat{\varphi }}} (\xi )| \cdot \langle {\xi } \rangle ^{\frac{-1}{2p}} |{{\hat{\psi }}}(\xi )| \big ( \int _{\{ r \in {\mathbb {R}}_+ \,;\, 2 \ge |r - k| \ge \tau _0 \}} \frac{ \langle {r} \rangle ^{\frac{1}{p}} (r/k)^2}{\tau _0 k} \,\mathrm {d}{r} \big ) \,\mathrm {d}{S(\xi )} \nonumber \\&\quad + \int _{|\xi |=k} \langle {\xi } \rangle ^{\frac{-1}{2p}} |{{\hat{\varphi }}} (\xi )| \cdot \langle {\xi } \rangle ^{\frac{-1}{2p}} |{{\hat{\psi }}}(\xi )| \big ( \int _{\Gamma _{k,\tau _0}} \frac{(1+|r|^2)^{\frac{1}{2p}} (|r|/k)^2}{\tau _0 k} \,\mathrm {d}{r} \big ) \,\mathrm {d}{S(\xi )} \end{aligned}$$

(2.16)

for all $\tau \in (0,\tau _0)$ and for all $k > 2$.

Note that in $\{ r \in {\mathbb {R}}_+; 2 \ge |r - k| \ge \tau _0 \}$ we have

$$\begin{aligned} \langle {r} \rangle ^{2s} \le 5^s \langle {k} \rangle ^{2s}, \quad 1 \le (r/k)^2 \le 4. \end{aligned}$$

(2.17)

For $r \in \Gamma _{k,\tau _0}$ the complex number $(1+r^2)$ can be expressed as $R(r) e^{{\text {i}}\theta (r)}$ for real valued functions R(r) and $\theta (r)$. Now we choose $\tau _0$ small enough such that $|\theta (r)| < \frac{\pi }{10}$ in $\Gamma _{2,\tau _0}$, then $|\theta (r)| < \frac{\pi }{10}$ in $\Gamma _{k,\tau _0}$ for all $k \ge 2$. This can be easily seen from the geometric view. Thus $(1+r^2)^s$ is well-defined for all $|s| \le 2$, and

$$\begin{aligned} \forall r \in \Gamma _{k,\tau _0}, \quad |(1+r^2)^s| = |1+r^2|^s \le (1+|r|^2)^s \le \langle {k+\tau _0} \rangle ^{2s} \le C_{\tau _0} \langle {k} \rangle ^{2s} \end{aligned}$$

(2.18)

for some constant $C_{\tau _0}$ independent of $\tau$ when $0< \tau < \tau _0$. Similarly, we have

$$\begin{aligned} \forall r \in \Gamma _{k,\tau _0}, \quad |r/k|^2 \le (k+\tau _0)^2/k^2 \le C_{\tau _0} \end{aligned}$$

(2.19)

for some constant $C_{\tau _0}$ independent of $\tau$. Hence by (2.17), (2.19) and Remark 13.1 in [13], we can continue (2.16) as

$$\begin{aligned} |I_2(\tau )|&\le C_{\tau _0} \int _{|\xi |=k} \langle {\xi } \rangle ^{\frac{-1}{2p}} |\hat{\varphi }(\xi )| \langle {\xi } \rangle ^{\frac{-1}{2p}} |{{\hat{\psi }}}(\xi )| \nonumber \\&\quad \big (\int _{\Gamma _{k,\tau _0} \cup \{ r \in {\mathbb {R}}_+; 2 \ge |r - k| \ge \tau _0 \}} \frac{ \langle {k} \rangle ^{1/p}}{\tau _0 k} \,\mathrm {d}{r} \big ) \,\mathrm {d}{S(\xi )} \nonumber \\&\le C_{\tau _0} k^{1/p - 1} \Vert { \langle {\cdot } \rangle ^{-1/(2p)} {{\hat{\varphi }}}(\cdot )} \Vert _{H^{1/2 + \epsilon }({\mathbb {R}}^3)} \Vert { \langle {\cdot } \rangle ^{-1/(2p)} \hat{\psi }(\cdot )} \Vert _{H^{1/2 + \epsilon }({\mathbb {R}}^3)} \nonumber \\&\le C_{\tau _0,\epsilon } k^{1/p - 1} \Vert {\varphi } \Vert _{H_{1/2 + \epsilon }^{-1/(2p)}({\mathbb {R}}^3)} \Vert {\psi } \Vert _{H_{1/2 + \epsilon }^{-1/(2p)}({\mathbb {R}}^3)}, \end{aligned}$$

(2.20)

where the constant $C_{\tau _0,\epsilon }$ is independent of $\tau$. It should be pointed out that the presence of the infinitesimal number $\epsilon$ in $\Vert {\cdot } \Vert _{H^{1/2 + \epsilon }}$ in (2.20) comes from the requirement that the order of the Sobolev space should be strictly greater than 1/2; see Remark 13.1 in [13] for more relevant discussion. Here, in deriving the last inequality in (2.20), we have made use of (2.3).

Finally, we estimate $I_3(\tau )$. Denote ${\mathbb {F}}(r\omega ) = {\mathbb {F}}_r(\omega ) := \langle {r} \rangle ^{-1/(2p)} {{\hat{\varphi }}}(r\omega )$ and ${\mathbb {G}}(r\omega ) = {\mathbb {G}}_r(\omega ) := \langle {r} \rangle ^{-1/(2p)} \widehat{{\mathfrak {R}} {\bar{\psi }}}(r\omega )$. One can compute

$$\begin{aligned} |I_3(\tau )|&= \big | \int _0^\infty \frac{ \langle {r} \rangle ^{1/p}\, r^2 \chi ^2(r - k)}{r^2 - k^2 - {\text {i}}\tau } \,\mathrm {d}{r} \cdot \int _{{\mathbb {S}}^2} ({\mathbb {F}}_r {\mathbb {G}}_r - {\mathbb {F}}_k {\mathbb {G}}_k) \,\mathrm {d}{S(\omega )} \big | \nonumber \\&\le \int _0^\infty \frac{ \langle {r} \rangle ^{1/p} \chi ^2(r - k)}{|r^2 - k^2|} \cdot \Vert {{\mathbb {F}}_r} \Vert _{L^2({\mathbb {S}}_r^2)} \cdot \big ( r^2 \int _{{\mathbb {S}}^2} |{\mathbb {G}}_r - {\mathbb {G}}_k|^2 \,\mathrm {d}{S(\omega )} \big )^{\frac{1}{2}} \,\mathrm {d}{r} \nonumber \\&\quad + \int _0^\infty \frac{ \langle {r} \rangle ^{1/p} \chi ^2(r - k)}{|r^2 - k^2|} \cdot \big ( r^2 \int _{{\mathbb {S}}^2} |{\mathbb {F}}_r - \mathbb F_k|^2 \,\mathrm {d}{S(\omega )} \big )^{\frac{1}{2}} \nonumber \\&\quad \cdot \big (\frac{r}{k} \big )^2 \Vert {{\mathbb {G}}_k} \Vert _{L^2({\mathbb {S}}_k^2)} \,\mathrm {d}{r}, \end{aligned}$$

(2.21)

where ${\mathbb {S}}_r^2$ signifies the central sphere of radius r. Combining both Remark 13.1 and (13.28) in [13] and (2.3) and (2.10), we can continue (2.21) as

$$\begin{aligned} |I_3(\tau )|&\le C_{\alpha ,\epsilon } \int _0^\infty \frac{ \langle {r} \rangle ^{1/p} \chi ^2(r - k)}{|r - k| (r+k)} \cdot \Vert {{\mathbb {F}}} \Vert _{H^{1/2+\epsilon }({\mathbb {R}}^3)} \cdot |r - k|^\alpha \cdot \Vert {{\mathbb {G}}} \Vert _{H^{1/2+\epsilon }({\mathbb {R}}^3)} \,\mathrm {d}{r} \nonumber \\&\le C_{\alpha ,\epsilon ,p} \int _0^\infty \frac{ \langle {r} \rangle ^{1/p} \chi ^2(r - k)}{|r - k|^{1-\alpha } (r+1)^{1/p} (k-1)^{1-1/p}} \,\mathrm {d}{r}\nonumber \\&\quad \cdot \Vert {{\mathbb {F}}} \Vert _{H^{1/2+\epsilon }({\mathbb {R}}^3)} \Vert {{\mathbb {G}}} \Vert _{H^{1/2+\epsilon }({\mathbb {R}}^3)} \nonumber \\&\le C_{\alpha ,\epsilon ,p} k^{1/p-1} \int _0^\infty \frac{\chi ^2(r - k)}{|r - k|^{1-\alpha }} \,\mathrm {d}{r} \cdot \Vert {\varphi } \Vert _{H_{1/2+\epsilon }^{-1/(2p)}({\mathbb {R}}^3)} \cdot \Vert {\psi } \Vert _{H_{1/2+\epsilon }^{-1/(2p)}({\mathbb {R}}^3)} \nonumber \\&\le C_{\alpha ,\epsilon ,p} k^{1/p-1} \Vert {\varphi } \Vert _{H_{1/2+\epsilon }^{-1/(2p)}({\mathbb {R}}^3)} \cdot \Vert {\psi } \Vert _{H_{1/2+\epsilon }^{-1/(2p)}({\mathbb {R}}^3)}, \end{aligned}$$

(2.22)

where the $\epsilon$ can be any positive real number and the $\alpha$ satisfies $0< \alpha < \epsilon$, and the constant $C_{\alpha ,\epsilon ,p}$ is independent of $\tau$.

Combining (2.9), (2.11), (2.20) and (2.22), we arrive at

$$\begin{aligned}&|({\mathcal {R}}_{k,\tau } \varphi ,\psi )_{L^2({\mathbb {R}}^3)}| \le |I_1(\tau )| + |I_2(\tau )| + |I_3(\tau )| \\&\quad \le C k^{1/p - 1} \Vert {\varphi } \Vert _{H_{1/2 + \epsilon }^{-1/(2p)}({\mathbb {R}}^3)} \Vert {\psi } \Vert _{H_{1/2 + \epsilon }^{-1/(2p)}({\mathbb {R}}^3)}, \end{aligned}$$

which implies that

$$\begin{aligned} \Vert {{\mathcal {R}}_{k,\tau } \varphi } \Vert _{H_{-1/2 - \epsilon }^{1/(2p)}({\mathbb {R}}^3)} \le C k^{1/p - 1} \Vert {\varphi } \Vert _{H_{1/2 + \epsilon }^{-1/(2p)}({\mathbb {R}}^3)} \end{aligned}$$

(2.23)

for some constant C independent of $\tau$.

Next we study the limiting case $\lim \limits _{\tau \rightarrow 0^+} {\mathcal {R}}_{k,\tau } \varphi$. For any two positive real numbers $\tau _1, \tau _2 < {{\tilde{\tau }}}$, we study $|I_j(\tau _1) - I_j(\tau _2)|$ for $j = 1,2,3$.

Similar to our previous derivation, we have

$$\begin{aligned}&|I_1(\tau _1) - I_1(\tau _2)|\nonumber \\&\quad \le \int _0^\infty \frac{|\tau _1 - \tau _2| (1 - \chi ^2(r - k))}{|r^2 - k^2| \cdot p^{\frac{1}{p}} q^{\frac{1}{q}} (r+1)^{\frac{1}{p}} (k-1)^{\frac{1}{q}}} \,\mathrm {d}{r} \cdot \int _{|\xi | = r} |{{\hat{\varphi }}} (\xi )| \cdot |{{\hat{\psi }}}(\xi )| \,\mathrm {d}{S(\xi )} \nonumber \\&\quad \le {{\tilde{\tau }}} \, C_p k^{1/p - 1} \Vert {\varphi } \Vert _{H_\delta ^{-1/(2p)}({\mathbb {R}}^3)} \Vert {\psi } \Vert _{H_\delta ^{-1/(2p)}({\mathbb {R}}^3)}, \end{aligned}$$

(2.24)

and

$$\begin{aligned}&|I_2(\tau _1) - I_2(\tau _2)|\nonumber \\&\quad \le C \int _{|\xi |=k} \langle {\xi } \rangle ^{\frac{-1}{2p}} |{{\hat{\varphi }}} (\xi )| \langle {\xi } \rangle ^{\frac{-1}{2p}} |{{\hat{\psi }}}(\xi )| \big ( \int _{\{ r \in {\mathbb {R}}_+; 2 \ge |r - k| \ge \tau _0 \}} \frac{|\tau _1 - \tau _2| \langle {k} \rangle ^{\frac{1}{p}}}{(\tau _0 k)^2} \,\mathrm {d}{r} \big ) \,\mathrm {d}{S(\xi )} \nonumber \\&\qquad + C \int _{|\xi |=k} \langle {\xi } \rangle ^{\frac{-1}{2p}} |{{\hat{\varphi }}} (\xi )| \langle {\xi } \rangle ^{\frac{-1}{2p}} |{{\hat{\psi }}}(\xi )| \big ( \int _{\Gamma _{k,\tau _0}} \frac{|\tau _1 - \tau _2| \langle {k} \rangle ^{\frac{1}{p}}}{(\tau _0 k)^2} \,\mathrm {d}{r} \big ) \,\mathrm {d}{S(\xi )} \nonumber \\&\quad \le {{\tilde{\tau }}} \, C k^{1/p - 1} \Vert {\varphi } \Vert _{H_{1/2 + \epsilon }^{-1/(2p)}({\mathbb {R}}^3)} \Vert {\psi } \Vert _{H_{1/2 + \epsilon }^{-1/(2p)}({\mathbb {R}}^3)}. \end{aligned}$$

(2.25)

To analyze $I_3(\tau )$ as $\tau$ goes to zero, we note that by (2.10) one has

$$\begin{aligned} C_\beta (\mathfrak {R}z)^\beta (\mathfrak {I}z)^{1-\beta } \le |z|, \quad \forall z \in {\mathbb {C}}, \end{aligned}$$

which holds for all $\beta \in (0,1)$ and some constant $C_\beta$. Without loss of generality, we assume $\tau _1 \le \tau _2$. Hence we can compute

$$\begin{aligned} \big | \frac{1}{r^2 - k^2 - {\text {i}}\tau _1} - \frac{1}{r^2 - k^2 - {\text {i}}\tau _2} \big |&\le \frac{1}{|r^2 - k^2|} \cdot \frac{C \tau _2}{|r^2 - k^2|^\beta \cdot \tau _2^{1-\beta }} \le \frac{C \tau _2^\beta }{|r^2 - k^2|^{1+\beta }}. \end{aligned}$$

Thus

$$\begin{aligned}&\ |I_3(\tau _1) - I_3(\tau _2)| \nonumber \\&\quad \lesssim \ \tau _2^\beta \int _0^\infty \frac{ \langle {r} \rangle ^{\frac{1}{p}} \chi ^2(r - k)}{|r-k|^{1+\beta } (r+1)^{\frac{1}{p}} (k-1)^{1 - \frac{1}{p}}} \nonumber \\&\qquad \cdot |r-k|^\alpha \cdot \Vert {{\mathbb {F}}} \Vert _{H^{\frac{1}{2} + \epsilon }({\mathbb {R}}^3)} \cdot \Vert {{\mathbb {G}}} \Vert _{H^{\frac{1}{2} + \epsilon }({\mathbb {R}}^3)} \,\mathrm {d}{r} \nonumber \\&\quad \lesssim \ {{\tilde{\tau }}}^\beta k^{1/p - 1} \Vert {\varphi } \Vert _{H_{1/2 + \epsilon }^{-1/(2p)}({\mathbb {R}}^3)} \Vert {\psi } \Vert _{H_{1/2 + \epsilon }^{-1/(2p)}({\mathbb {R}}^3)}, \end{aligned}$$

(2.26)

where the last inequality holds when $0< \beta < \alpha$.

From (2.24), (2.25) and (2.26) we arrive at

$$\begin{aligned} \Vert {{\mathcal {R}}_{k,\tau _1} \varphi - {\mathcal {R}}_{k,\tau _2} \varphi } \Vert _{H_{-1/2 - \epsilon }^{-1/(2p)}({\mathbb {R}}^3)} \lesssim {{\tilde{\tau }}} \Vert {\varphi } \Vert _{H_{1/2 + \epsilon }^{-1/(2p)}({\mathbb {R}}^3)}, \quad \forall \tau _1,\tau _2 \in (0,{{\tilde{\tau }}}), \end{aligned}$$

(2.27)

and thus ${\mathcal {R}}_{k,{{\tilde{\tau }}}} \varphi$ converges and

$$\begin{aligned} \lim _{{{\tilde{\tau }}} \rightarrow 0^+} {\mathcal {R}}_{k,{{\tilde{\tau }}}} \varphi = {{\mathcal {R}}_{k}}\varphi \quad \text { in }\quad H_{-1/2 - \epsilon }^{1/(2p)}({\mathbb {R}}^3). \end{aligned}$$

(2.28)

The relationships (2.27) and (2.28) sometimes refer to as the limiting absorption principle. Hence from (2.23) and (2.28) we conclude that

$$ \Vert {{{\mathcal {R}}_{k}}\varphi } \Vert _{H_{-1/2 - \epsilon }^{1/(2p)}({\mathbb {R}}^3)} \le C_{\epsilon ,p} k^{-(1 - 1/p)} \Vert {\varphi } \Vert _{H_{1/2 + \epsilon }^{-1/(2p)}({\mathbb {R}}^3)} $$

holds for any $1< p < +\infty$ and any $\epsilon > 0$.

The proof is complete. $\quad \square$

Proof of Theorem 2.2

Let $\varphi ,\psi \in {\mathscr {S}}({{\mathbb {R}}^n})$ and define $\langle {q \varphi ,\psi } \rangle := \langle {q,\varphi \psi } \rangle$. Choose a function $\chi$ such that $\chi \in C_c^\infty ({{\mathbb {R}}^n})$ and $\chi (x) = 1$ when $x \in \mathop {\mathrm{supp}}q$. Choose $s'$ satisfying $-s' < (m-n)/2$ and $p, p'$ satisfying $1< p < +\infty ,\, 1/{p'} + 1/p = 1$. Then according to [Proposition 2.4, [8]], $\Vert {q} \Vert _{H^{-s',p'}({\mathbb {R}}^n)} < +\infty$ almost surely. Denote $\Vert {q} \Vert _{H^{-s',p'}({\mathbb {R}}^n)}$ as $C_s(\omega )$. One can compute

$$\begin{aligned} | \langle {q \varphi ,\psi } \rangle |&= | \langle {q,(\chi \varphi ) (\chi \psi )} \rangle | = | \langle {(I-\Delta )^{-s'} q,(I-\Delta )^{s'} \big ( (\chi \varphi ) (\chi \psi ) \big ) } \rangle | \nonumber \\&\le \Vert {q} \Vert _{H^{-s',p'}({\mathbb {R}}^n)} \cdot \Vert {(I-\Delta )^{s'} \big ( (\chi \varphi ) (\chi \psi ) \big ) } \Vert _{L^p({\mathbb {R}}^n)} \nonumber \\&= C_s(\omega ) \Vert {(I-\Delta )^{s'} \big ( (\chi \varphi ) (\chi \psi ) \big ) } \Vert _{L^p({\mathbb {R}}^n)}. \end{aligned}$$

(2.29)

According to the fractional Leibniz rule [14], when $1/p = 1/2 + 1/q$, one has

$$\begin{aligned} \Vert {(I-\Delta )^{s'} \big ( (\chi \varphi ) (\chi \psi ) \big ) } \Vert _{L^p({\mathbb {R}}^n)}&\le C_s(\omega ) \big ( \Vert {\chi \varphi } \Vert _{L^2({\mathbb {R}}^n)} \Vert {\chi \psi } \Vert _{H^{s',q}({\mathbb {R}}^n)} \nonumber \\&\quad + \Vert {\chi \psi } \Vert _{L^2({\mathbb {R}}^n)} \Vert {\chi \varphi } \Vert _{H^{s',q}({\mathbb {R}}^n)} \big ). \end{aligned}$$

(2.30)

By (2.29)–(2.30) and noting the Sobolev embedding $H^s({\mathbb {R}}^n) \hookrightarrow H^{s',q}({\mathbb {R}}^n)$ when $s - n/2 \ge s' - n/q$, $s > s'$, we can continue (2.29) as

$$\begin{aligned} | \langle {q \varphi ,\psi } \rangle |&\lesssim C_s(\omega ) \big ( \Vert {\chi \varphi } \Vert _{L^2({\mathbb {R}}^n)} \cdot \Vert {\chi \psi } \Vert _{H^{s',q}({\mathbb {R}}^n)} + \Vert {\chi \psi } \Vert _{L^2({\mathbb {R}}^n)} \cdot \Vert {\chi \varphi } \Vert _{H^{s',q}({\mathbb {R}}^n)} \big ) \nonumber \\&\lesssim C_s(\omega ) \Vert {\chi \varphi } \Vert _{H^s({\mathbb {R}}^n)} \cdot \Vert {\chi \psi } \Vert _{H^s({\mathbb {R}}^n)}. \end{aligned}$$

(2.31)

Because $1< p' < +\infty$ and $s' > -\frac{m-n}{2}$, the real number s should satisfy

$$ s \ge s' + \frac{n}{2} - \frac{n}{q} = s' + \frac{n}{2} - n(\frac{1}{p} - \frac{1}{2}) = s' + n - \frac{n}{p} = s' + \frac{n}{p'} \ge s' > \frac{n-m}{2}. $$

Next we adapt the proof of Lemma 3.7 in [8] to show that

$$\begin{aligned} \Vert {\chi \varphi } \Vert _{H^s({\mathbb {R}}^n)} \le C \Vert {\varphi } \Vert _{H_{-2}^s({\mathbb {R}}^n)}, \quad \varphi \in {\mathscr {S}}({{\mathbb {R}}^n}). \end{aligned}$$

(2.32)

Rewriting the right-hand side of (2.32) in terms of the $L^2$-norm form, we obtain

$$\begin{aligned} \Vert {\chi \varphi } \Vert _{H^s({\mathbb {R}}^n)} \le C \Vert { \langle {\cdot } \rangle ^{-2} (I - \Delta )^{s/2} \varphi } \Vert _{L^2({\mathbb {R}}^n)}. \end{aligned}$$

Write $\psi (x) := \langle {x} \rangle ^{-2} (I - \Delta )^{s/2} \varphi (x)$. Obviously, $\varphi \in {\mathscr {S}}({{\mathbb {R}}^n})$ is equivalent to $\psi \in {\mathscr {S}}({{\mathbb {R}}^n})$. Define $T_a \psi := \chi \cdot (I - \Delta )^{-s/2} ( \langle {\cdot } \rangle ^2 \psi )$. Then $\chi \varphi = T_a \psi$ and (2.32) is equivalent to

$$\begin{aligned} \Vert {T_a \psi } \Vert _{H^s({\mathbb {R}}^n)} \le C \Vert {\psi } \Vert _{L^2({\mathbb {R}}^n)}. \end{aligned}$$

(2.33)

$T_a$ is a pseudo-differential operator with

$$ a(x,\xi ) := \chi (x) \big ( \langle {x} \rangle ^2 \langle {\xi } \rangle ^{-s} - 2{\text {i}}x \cdot \nabla _\xi \langle {\xi } \rangle ^{-s} - \Delta _\xi \langle {\xi } \rangle ^{-s} \big ) $$

as its symbol. It is easy to see that $a \in S^{-s}$, and thus according to the properties of pseudo-differential operators [13], (2.33) holds, and so does (2.32).

We can continue the estimates in (2.31) as

$$\begin{aligned} | \langle {q \varphi ,\psi } \rangle |&\lesssim C_s(\omega ) \Vert {\chi \varphi } \Vert _{H^s({\mathbb {R}}^n)} \cdot \Vert {\chi \psi } \Vert _{H^s({\mathbb {R}}^n)} \lesssim C_s(\omega ) \Vert {\varphi } \Vert _{H_{-2}^s({\mathbb {R}}^n)} \cdot \Vert {\psi } \Vert _{H_{-2}^s({\mathbb {R}}^n)} \\&\le C_s(\omega ) \Vert {\varphi } \Vert _{H_{-1/2 - \epsilon }^s({\mathbb {R}}^n)} \cdot \Vert {\psi } \Vert _{H_{-1/2 - \epsilon }^s({\mathbb {R}}^n)}, \quad \forall \varphi , \psi \in {\mathscr {S}}({{\mathbb {R}}^n}), \end{aligned}$$

where $0 < \epsilon \le 3/2$, which implies that

$$\begin{aligned} \Vert {q \varphi } \Vert _{H_{1/2 + \epsilon }^{-s}({\mathbb {R}}^n)} \le C_{\epsilon ,s}(\omega ) \Vert {\varphi } \Vert _{H_{-1/2 - \epsilon }^s({\mathbb {R}}^n)}, \quad \forall \varphi \in {\mathscr {S}}({{\mathbb {R}}^n}). \end{aligned}$$

(2.34)

We proceed to show that ${\mathscr {S}}({{\mathbb {R}}^n})$ is dense in $H_{-1/2 - \epsilon }^s({\mathbb {R}}^n)$. Fix a function $\chi$ satisfying (2.8). Now we assume that $\varphi \in H_{-1/2 - \epsilon }^s({\mathbb {R}}^n)$, and hence we have $\langle {\cdot } \rangle ^{-1/2 - \epsilon } (I - \Delta )^{s/2} \varphi \in L^2({{\mathbb {R}}^n})$. Then for any $\delta > 0$ there exists a constant M, depending on $\varphi$, such that $\Vert { \langle {\cdot } \rangle ^{-1/2 - \epsilon } (I - \Delta )^{s/2} \varphi - \varphi ^{(1)}} \Vert _{L^2({{\mathbb {R}}^n})} < \frac{\delta }{2}$, where $\varphi ^{(1)} = \chi (\cdot /M) \langle {\cdot } \rangle ^{-1/2 - \epsilon } (I - \Delta )^{s/2} \varphi$. Note that $\varphi ^{(1)} \in L^2({{\mathbb {R}}^n})$ with a compact support. Furthermore, there exists a sufficiently small constant $\zeta \in {\mathbb {R}}_+$ such that $\Vert {\varphi ^{(1)} - \varphi ^{(2)}} \Vert _{L^2({{\mathbb {R}}^n})} < \frac{\delta }{2}$, where $\varphi ^{(2)} = (\frac{1}{\zeta ^n} \chi (\frac{\cdot }{\zeta })) *\varphi ^{(1)}$. The function $\varphi ^{(2)}$ is in $C^\infty ({{\mathbb {R}}^n})$ with a compact support, thus is in ${\mathscr {S}}({{\mathbb {R}}^n})$. Write $\varphi ^{(3)} = (I - \Delta )^{-s/2} \big ( \langle {\cdot } \rangle ^{1/2 + \epsilon } \varphi ^{(2)} \big )$. Hence $\varphi ^{(3)} \in {\mathscr {S}}({{\mathbb {R}}^n})$ and

$$\begin{aligned} \Vert {\varphi - \varphi ^{(3)}} \Vert _{H_{-1/2 - \epsilon }^s({\mathbb {R}}^n)}&= \Vert { \langle {\cdot } \rangle ^{-1/2 - \epsilon } (I - \Delta )^{s/2} \varphi - \langle {\cdot } \rangle ^{-1/2 - \epsilon } (I - \Delta )^{s/2} \varphi ^{(3)}} \Vert _{L^2({{\mathbb {R}}^n})} \\&\le \Vert { \langle {\cdot } \rangle ^{-1/2 - \epsilon } (I - \Delta )^{s/2} \varphi - \varphi ^{(1)}} \Vert _{L^2({{\mathbb {R}}^n})} + \Vert {\varphi ^{(1)} - \varphi ^{(2)}} \Vert _{L^2({{\mathbb {R}}^n})} \\&< \delta /2 + \delta /2 = \delta . \end{aligned}$$

Therefore ${\mathscr {S}}({{\mathbb {R}}^n})$ is dense in $H_{-1/2 - \epsilon }^s({\mathbb {R}}^n)$. Since $H_{-1/2 - \epsilon }^s({\mathbb {R}}^n)$ is a Banach space, and hence by a density argument, the inequality (2.34) can be extended to all $\varphi \in H_{-1/2 - \epsilon }^s({\mathbb {R}}^n)$.

The proof is complete. $\quad \square$

We are now in a position to study the well-posedness of the direct scattering problem. To that end, we reformulate (1.1) into the Lippmann-Schwinger equation formally (cf. [10]) to obtain

$$\begin{aligned} (I - {{\mathcal {R}}_{k}}q) u^{sc} = \alpha {{\mathcal {R}}_{k}}q u^i - {{\mathcal {R}}_{k}}f. \end{aligned}$$

(2.35)

Theorem 2.3

When k is large enough such that $\Vert {{{\mathcal {R}}_{k}}q} \Vert _{{\mathcal {L}}(H_{1/2+\epsilon }^{-s}({\mathbb {R}}^3), H_{1/2+\epsilon }^{-s}({\mathbb {R}}^3))} < 1$, there exists a unique stochastic process $u^{sc}(\cdot ,\omega ) :{\mathbb {R}}^3 \rightarrow {\mathbb {C}}$ such that $u^{sc}(x)$ satisfies (2.35) almost surely. Moreover,

$$\begin{aligned} \Vert {u^{sc}(\cdot ,\omega )} \Vert _{H_{1/2+\epsilon }^{-s}({\mathbb {R}}^3)} \lesssim \Vert {\alpha {{\mathcal {R}}_{k}}q u^i - {{\mathcal {R}}_{k}}f} \Vert _{H_{1/2+\epsilon }^{-s}({\mathbb {R}}^3)} \quad a.s. \end{aligned}$$

(2.36)

for any $\epsilon \in {\mathbb {R}}_+$.

Proof

The condition (1.3) implies $m_q > 2$, and hence there exists ${s \in (\max \{(3 - m_q)/}{2, 0\} , 1/2)}$ such that Theorem 2.1 can apply. By Theorems 2.1 and 2.2, we know

$$\begin{aligned} F := \alpha {{\mathcal {R}}_{k}}q u^i - {{\mathcal {R}}_{k}}f \in H_{1/2+\epsilon }^{-s}({\mathbb {R}}^3). \end{aligned}$$

From Theorems 2.1 and 2.2, we also know that the operator $I - {{\mathcal {R}}_{k}}q$ is invertible from $H_{1/2+\epsilon }^{-s}({\mathbb {R}}^3)$ to itself, and the right-hand side of (2.35) belongs to $H_{1/2+\epsilon }^{-s}({\mathbb {R}}^3)$.

Let $u^{sc} := (I - {{\mathcal {R}}_{k}}q)^{-1} F \in H_{1/2+\epsilon }^{-s}({\mathbb {R}}^3)$, then $u^{sc}$ fulfills the requirements of the theorem. The existence of the solution is proved. (2.36) can be verified easily from Theorems 2.1, 2.2 and (2.35). The uniqueness follows readily from (2.36).

The proof is complete. $\quad \square$

3 Asymptotic Analysis of High-order Terms

We intend to recover $\mu _f$, $\mu _q$ from the data via the correlation formula of the following form

$$\begin{aligned} \frac{1}{K} \int _K^{2K} k^m \overline{u^\infty (k,\omega )} u^\infty (k+\tau ,\omega ) \,\mathrm {d}{k}, \end{aligned}$$

(3.1)

where $u^\infty (k,\omega )$ stands for the far-field pattern $u^\infty ({\hat{x}},k,\omega ) \in {\mathcal {M}}_f$ in the case of $\alpha = 0$ and stands for $u^\infty ({\hat{x}},k,-{\hat{x}},\omega ) \in \mathcal M_q$ in the case of $\alpha = 1$. The Lippmann-Schwinger equation corresponding to (1.1) is

$$\begin{aligned} (I - {{\mathcal {R}}_{k}}q)u^{sc}(k,\omega ) = \alpha {{\mathcal {R}}_{k}}q u^i {-} {{\mathcal {R}}_{k}}f. \end{aligned}$$

(3.2)

When k is large enough such that $\Vert {{{\mathcal {R}}_{k}}q} \Vert _{{\mathcal {L}} (H_{-1/2 - \epsilon }^s,H_{-1/2 - \epsilon }^s)} < 1$, from (3.2) we obtain

$$\begin{aligned} u^{sc}(k,\omega )&= {-\sum _{j \ge 0} {{\mathcal {R}}_{k}}\big ( (q {{\mathcal {R}}_{k}})^j f \big ) + \alpha \sum _{j \ge 0} {{\mathcal {R}}_{k}}\big ( (q {{\mathcal {R}}_{k}})^j qu^i \big )}, \end{aligned}$$

(3.3)

$$\begin{aligned} u^\infty (k,\omega )&= (4\pi )^{-1} \sum _{j=0,1,2} F_j({\hat{x}},k,\omega ) + \alpha (4\pi )^{-1} \sum _{j=0,1,2} G_j({\hat{x}},k,\omega ), \end{aligned}$$

(3.4)

where

$$\begin{aligned} \left\{ \begin{aligned} F_j({\hat{x}},k,\omega )&:= {-}\int _{{\mathbb {R}}^3} e^{-\text {i}k{\hat{x}} \cdot z} \big [ (q{{\mathcal {R}}_{k}})^j f \big ](z) \,\mathrm {d}{z}, \quad j = 0,1 \\ F_2({\hat{x}},k,\omega )&:= {-} \sum _{j \ge 2} \int _{{\mathbb {R}}^3} e^{-\text {i}k{\hat{x}} \cdot z} \big [ (q{{\mathcal {R}}_{k}})^j f \big ](z) \,\mathrm {d}{z}, \\ G_j({\hat{x}},k,d,\omega )&:= \int _{{\mathbb {R}}^3} e^{-\text {i}k{\hat{x}} \cdot z} {\big [ (q {{\mathcal {R}}_{k}})^j q u^i \big ](z)} \,\mathrm {d}{z}, \quad j = 0,1 \\ G_2({\hat{x}},k,d,\omega )&:= \sum _{j \ge 2} \int _{{\mathbb {R}}^3} e^{-\text {i}k{\hat{x}} \cdot z} {\big [ (q {{\mathcal {R}}_{k}})^j q u^i \big ](z)} \,\mathrm {d}{z}. \end{aligned}\right. \end{aligned}$$

(3.5)

Substituting (3.4) into (3.1), we obtain several crossover terms comprised by $F_j$ and $G_j$. To recover $\mu _f$ and $\mu _q$, it is necessary to establish the asymptotics of $F_j$ and $G_j$ in terms of k. The asymptotic analyses of $G_j\, (j=0,1,2)$ are established in [8].

This section is devoted to the asymptotic analysis of $F_1$ and $F_2$, which are given in Lemmas 3.3 and 3.5, respectively. These two lemmas shall play key roles in the proofs to Theorems 1.1 and 1.2.

3.1 Asymptotics of $F_1$

In order to establish the asymptotics of $F_1$, we need to derive two auxiliary lemmas. First, let us recall the notion of the fractional Laplacian [30] of order $s \in (0,1)$ in ${\mathbb {R}}^n$ ($n\ge 3$),

$$\begin{aligned} (-\Delta )^{s/2} \varphi (x) := (2\pi )^{-n} \iint e^{{\text {i}}(x-y) \cdot \xi } |\xi |^s \varphi (y) \,\mathrm {d}{y} \,\mathrm {d}{\xi }, \end{aligned}$$

(3.6)

where the integration is defined as an oscillatory integral. When $\varphi \in {\mathscr {S}}({{\mathbb {R}}^n})$, (3.6) can be understood as a usual Lebesgue integral if one integrates w.r.t. y first and then integrates w.r.t. $\xi$. By duality arguments, the fractional Laplacian can be generalized to act on wider range of functions and distributions (cf. [34]). It can be verified that the fractional Laplacian is self-adjoint.

In the following two lemmas, we present the results in a more general form where the space dimension n can be arbitrary but greater than 2, though only the case $n=3$ shall be used subsequently.

Lemma 3.1

For any $s \in (0,1)$, we have

$$\begin{aligned} (-\Delta _\xi )^{s/2} (e^{{\text {i}}x \cdot \xi }) = |x|^s e^{{\text {i}}x \cdot \xi } \end{aligned}$$

in the distributional sense.

Proof

For any $\varphi \in {\mathscr {S}}({\mathbb {R}}^n)$, because $(-\Delta _\xi )^{s/2}$ is self-adjoint, we have

$$\begin{aligned} \big ( (-\Delta _\xi )^{s/2} (e^{{\text {i}}x \cdot \xi }), \varphi (\xi ) \big )&= \big ( e^{{\text {i}}x \cdot \xi }, (-\Delta _\xi )^{s/2} \varphi (\xi ) \big ) \\&= \int e^{{\text {i}}x \cdot \xi } \cdot \big [ (2\pi )^{-n} \iint e^{{\text {i}}(\xi -y) \cdot \eta } |\eta |^s \varphi (y) \,\mathrm {d}{y} \,\mathrm {d}{\eta }\big ] \,\mathrm {d}{\xi }\\&= \int e^{{\text {i}}x \cdot \xi } \cdot \big \{ (2\pi )^{-n/2} \int \big [ (2\pi )^{-n/2} \\&\quad \int e^{{\text {i}}(\xi -y) \cdot \eta } |\eta |^s \,\mathrm {d}{\eta }\big ] \varphi (y) \,\mathrm {d}{y} \big \} \,\mathrm {d}{\xi }\\&= (2\pi )^{-n/2} \int e^{{\text {i}}x \cdot \xi } \cdot \int {\mathcal {F}}^{-1}\{ |\cdot |^s \}(\xi -y) \cdot \varphi (y) \,\mathrm {d}{y} \,\mathrm {d}{\xi }\\&= (2\pi )^{-n/2} \iint e^{{\text {i}}x \cdot \xi } {\mathcal {F}}^{-1}\{ |\cdot |^s \}(\xi -y) \cdot \varphi (y) \,\mathrm {d}{y} \,\mathrm {d}{\xi }\\&= \int \big [ (2\pi )^{-n/2} \int e^{{\text {i}}x \cdot \xi } {\mathcal {F}}^{-1}\{ |\cdot |^s \}(\xi -y) \,\mathrm {d}{\xi }\big ] \cdot \varphi (y) \,\mathrm {d}{y} \\&= \int e^{{\text {i}}x \cdot y} \big [ (2\pi )^{-n/2} \int e^{-{\text {i}}(-x) \cdot \xi } {\mathcal {F}}^{-1} \{ |\cdot |^s \}(\xi ) \,\mathrm {d}{\xi }\big ] \cdot \varphi (y) \,\mathrm {d}{y} \\&= \int e^{{\text {i}}x \cdot y} {\mathcal {F}}{\mathcal {F}}^{-1} \{ |\cdot |^s \}(-x) \cdot \varphi (y) \,\mathrm {d}{y} \\&= \int |x|^s e^{{\text {i}}x \cdot y} \cdot \varphi (y) \,\mathrm {d}{y} \\&= \big ( |x|^s e^{{\text {i}}x \cdot \xi }, \varphi (\xi ) \big ). \end{aligned}$$

It is noted that in the derivation above, some integrals should be understood as oscillatory integrals. $\quad \square$

Lemma 3.2

For any $m < 0$, $s \in (0,1)$ and $c(x,\xi ) \in S^m$, we have

$$\begin{aligned} |\big ( (-\Delta _\xi )^{s/2} c \big ) (x,\xi )| \le C \langle {\xi } \rangle ^{m-s}, \end{aligned}$$

where the constant C is independent of x, $\xi$.

Proof

The proof is divided into two steps.

Step 1: The case $|\xi | \ge 1$.

In this step, we set $|\xi |$ to be greater than 1. By the definition (3.6), we have

$$\begin{aligned} \big ( (-\Delta _\xi )^{s/2} c \big ) (x,\xi )&\simeq \iint e^{{\text {i}}(\xi - \eta ) \cdot \gamma } |\gamma |^s\, c(x,\eta ) \,\mathrm {d}{\eta }\,\mathrm {d}{\gamma }\nonumber \\&= \iint e^{-{\text {i}}\eta \cdot \gamma } |\gamma |^s\, c(x,\eta + \xi ) \,\mathrm {d}{\eta }\,\mathrm {d}{\gamma }\nonumber \\&= \iint e^{-{\text {i}}\eta \cdot \gamma } \big | \frac{\gamma }{|\xi |} \big |^s\, c(x,|\xi |\eta + \xi ) \,\mathrm {d}{(}|\xi |\eta ) \,\mathrm {d}{(}\gamma /|\xi |) \nonumber \\&\simeq |\xi |^{-s} \iint e^{-{\text {i}}\eta \cdot \gamma } |\gamma |^s\, c(x,|\xi |(\eta + {{\hat{\xi }}})) \,\mathrm {d}{\eta }\,\mathrm {d}{\gamma }, \end{aligned}$$

(3.7)

where ${{\hat{\xi }}} = \xi / |\xi |$. Fix a function $\chi _0 \in C_c^\infty ({\mathbb {R}})$ with $\chi _0(|x|) \equiv 1$ when $1/2 \le |x| \le 3/2$ and $\chi _0(|x|) \equiv 1$ when $|x| \le 0$ or $|x| \ge 2$. We can continue (3.7) as

$$\begin{aligned} \big ( (-\Delta _\xi )^{s/2} c \big ) (x,\xi )&\simeq |\xi |^{m-s} \iint e^{-{\text {i}}\eta \cdot \gamma } \chi _0(|\eta |) |\gamma |^s\, c(x,|\xi |(\eta + {{\hat{\xi }}}))\, |\xi |^{-m} \,\mathrm {d}{\eta }\,\mathrm {d}{\gamma }\nonumber \\&\quad + |\xi |^{m-s} \iint e^{-{\text {i}}\eta \cdot \gamma } \big ( 1 - \chi _0(|\eta |)\big )\, |\gamma |^s\, c(x,|\xi |(\eta + {{\hat{\xi }}}))\, |\xi |^{-m} \,\mathrm {d}{\eta }\,\mathrm {d}{\gamma }\nonumber \\&:= |\xi |^{m-s} ({\mathcal {B}}_1 + {\mathcal {B}}_2). \end{aligned}$$

(3.8)

We estimate ${\mathcal {B}}_1$, ${\mathcal {B}}_2$ seperately. For $\mathcal B_1$, one can compute

$$\begin{aligned} {\mathcal {B}}_1&= \iint e^{-{\text {i}}(\eta - {{\hat{\xi }}}) \cdot \gamma } \chi _0(|\eta - {{\hat{\xi }}}|) |\gamma |^s\, c(x,|\xi |\eta )\, |\xi |^{-m} \,\mathrm {d}{\eta }\,\mathrm {d}{\gamma }\nonumber \\&= \int e^{{\text {i}}{{\hat{\xi }}} \cdot \gamma } |\gamma |^s \big ( \int e^{-{\text {i}}\eta \cdot \gamma } \chi _0(|\eta - {{\hat{\xi }}}|)\, c(x,|\xi |\eta )\, |\xi |^{-m} \,\mathrm {d}{\eta }\big ) \,\mathrm {d}{\gamma }\nonumber \\&=: \int e^{{\text {i}}{{\hat{\xi }}} \cdot \gamma } |\gamma |^s J(\gamma ;|\xi |,x) \,\mathrm {d}{\gamma }, \end{aligned}$$

(3.9)

where $J(\gamma ;|\xi |,x) = \int e^{-{\text {i}}\eta \cdot \gamma } \chi _0(|\eta - {{\hat{\xi }}}|)\, c(x,|\xi |\eta )\, |\xi |^{-m} \,\mathrm {d}{\eta }.$ We claim that the $J(\gamma ;|\xi |,x)$ is rapidly decaying w.r.t. $|\gamma |$, that is

$$\begin{aligned} \forall N \in {\mathbb {N}}, \quad |\gamma |^{2N}\, |J(\gamma ;|\xi |,x)| \le C_N < +\infty , \end{aligned}$$

(3.10)

for some constant $C_N$ independent of $\gamma$, $\xi$ and x. This can be seen from

$$\begin{aligned} |\gamma |^{2N}\, |J(\gamma ;|\xi |,x)|&\simeq \big | \int \Delta _\eta ^N (e^{-{\text {i}}\eta \cdot \gamma }) \cdot \chi _0(|\eta - {{\hat{\xi }}}|)\, c(x,|\xi |\eta )\, |\xi |^{-m} \,\mathrm {d}{\eta }\big | \nonumber \\&= \big | \int e^{-{\text {i}}\eta \cdot \gamma } \cdot \Delta _\eta ^N \big ( \chi _0(|\eta - {{\hat{\xi }}}|)\, c(x,|\xi |\eta ) \big )\, |\xi |^{-m} \,\mathrm {d}{\eta }\big | \nonumber \\&\le \int _{\frac{1}{2} \le |\eta - {{\hat{\xi }}}| \le 2} |\Delta _\eta ^N \big ( \chi _0(|\eta - {{\hat{\xi }}}|)\, c(x,|\xi |\eta )| \cdot |\xi |^{-m} \,\mathrm {d}{\eta }\nonumber \\&\lesssim \int _{\frac{1}{2} \le |\eta - {{\hat{\xi }}}| \le 2} \sum _{|\alpha | \le 2N} |(\partial _\xi ^\alpha c) (x,|\xi |\eta )| \cdot |\xi |^{|\alpha |-m} \,\mathrm {d}{\eta }\nonumber \\&\lesssim \sum _{|\alpha | \le 2N} \int _{\frac{1}{2} \le |\eta - \hat{\xi }| \le 2} (1 + |\xi |\,|\eta |)^{m - |\alpha |} \cdot |\xi |^{|\alpha |-m} \,\mathrm {d}{\eta }\nonumber \\&= \sum _{|\alpha | \le 2N} \int _{\frac{1}{2} \le |\eta - {{\hat{\xi }}}| \le 2} (|\xi |^{-1} + |\eta |)^{m - |\alpha |} \,\mathrm {d}{\eta }, \end{aligned}$$

(3.11)

where N is an arbitrary non-negative integer. The condition $|\xi | \ge 1$ gives

$$\begin{aligned} (|\xi |^{-1} + |\eta |)^{m - |\alpha |} \le {\left\{ \begin{array}{ll} (1 + |\eta |)^{m - |\alpha |}, &{}\hbox {when}~ |\alpha | \le m, \\ |\eta |^{m - |\alpha |}, &{}\hbox {when}~ |\alpha | > m. \end{array}\right. } \end{aligned}$$

(3.12)

By (3.11) and (3.12), we obtain (3.10).

Therefore, $J(\gamma ;|\xi |,x)$ is indeed rapidly decaying. Now, combining (3.9) and (3.10), we arrive at

$$\begin{aligned} |{\mathcal {B}}_1| \lesssim \int _{|\gamma | \ge 1} |\gamma |^s \,\mathrm {d}{\gamma }+ \int _{|\gamma | > 1} |\gamma |^s |\gamma |^{-4} \,\mathrm {d}{\gamma }\le C < +\infty , \end{aligned}$$

(3.13)

for some constant C independent of x, $\xi$.

To estimate ${\mathcal {B}}_2$,

we split ${\mathcal {B}}_2$ into two terms, say, ${\mathcal {B}}_{21}$ and ${\mathcal {B}}_{22}$, in the following way,

$$\begin{aligned} {\mathcal {B}}_2&= \iint _{\gamma \le 1} e^{-\text {i}\eta \cdot \gamma } \big ( 1 - \chi _0(|\eta |)\big )\, |\gamma |^s\, c(x,|\xi |(\eta + {{\hat{\xi }}}))\, |\xi |^{-m} \,\mathrm {d}{\eta }\,\mathrm {d}{\gamma }\nonumber \\&\quad + \iint _{\gamma > 1} e^{-\text {i}\eta \cdot \gamma } \big ( 1 - \chi _0(|\eta |)\big )\, |\gamma |^s\, c(x,|\xi |(\eta + {{\hat{\xi }}}))\, |\xi |^{-m} \,\mathrm {d}{\eta }\,\mathrm {d}{\gamma }\nonumber \\&=: {\mathcal {B}}_{21} + {\mathcal {B}}_{22}. \end{aligned}$$

(3.14)

Define the differential operator $L := (\gamma /|\gamma |^2) \cdot \nabla _{\eta }$.

The term ${\mathcal {B}}_{21}$ can be estimated as follows,

$$\begin{aligned} |{\mathcal {B}}_{21}|&\le \int _{|\gamma | \le 1} |\gamma |^s \cdot \big | \int e^{-\text {i}\eta \cdot \gamma } \big ( 1 - \chi _0(|\eta |)\big )\, c(x,|\xi |(\eta + {{\hat{\xi }}}))\, |\xi |^{-m} \,\mathrm {d}{\eta }\big | \,\mathrm {d}{\gamma }\nonumber \\&\simeq \int _{|\gamma | \le 1} |\gamma |^{s} \cdot \big | \int L^{n} (e^{-\text {i}\eta \cdot \gamma })\, \big ( 1 - \chi _0(|\eta |)\big )\, c(x,|\xi |(\eta + {{\hat{\xi }}}))\, |\xi |^{-m} \,\mathrm {d}{\eta }\big | \,\mathrm {d}{\gamma }\nonumber \\&\lesssim \int _{|\gamma | \le 1} |\gamma |^{s} |\gamma |^{-n} \cdot \big | \int e^{-\text {i}\eta \cdot \gamma }\, \nabla _{\eta }^{n} \Big ( \big ( 1 - \chi _0(|\eta |)\big )\, c(x,|\xi |(\eta + {{\hat{\xi }}})) \Big )\, |\xi |^{-m} \,\mathrm {d}{\eta }\big | \,\mathrm {d}{\gamma }\nonumber \\&\le \int _{|\gamma | \le 1} |\gamma |^{s-n} \int \Big | \nabla _\eta ^{n} \Big ( \big ( 1 - \chi _0(|\eta |)\big )\, c(x,|\xi |(\eta + {{\hat{\xi }}})) \Big ) \Big | \cdot |\xi |^{-m} \,\mathrm {d}{\eta }\,\mathrm {d}{\gamma }\nonumber \\&\lesssim \int _{|\gamma | \le 1} |\gamma |^{s-n} \int _{|\eta | \not \in (\frac{1}{2}, \frac{3}{2})} (1+|\xi | \cdot |\eta + \hat{\xi }|)^{m-n} \cdot |\xi |^{n-m} \,\mathrm {d}{\eta }\,\mathrm {d}{\gamma }\nonumber \\&= \int _{|\gamma | \le 1} |\gamma |^{s-n} \int _{|\eta | \not \in (\frac{1}{2}, \frac{3}{2})} (|\xi |^{-1} + |\eta + {{\hat{\xi }}}|)^{m-n} \,\mathrm {d}{\eta }\,\mathrm {d}{\gamma }\nonumber \\&\le \int _{|\gamma | \le 1} |\gamma |^{s-n} \int _{|\eta | \not \in (\frac{1}{2}, \frac{3}{2})} |\eta + {{\hat{\xi }}}|^{m-n} \,\mathrm {d}{\eta }\,\mathrm {d}{\gamma }\nonumber \\&\le C < +\infty , \end{aligned}$$

(3.15)

for some constant C independent of x, $\xi$. Here, it is noted that in (3.15) n is the space dimension. The last two inequalities in (3.15) make use of the following three facts: $s - n > -n$, $m - n < -n$, and the restriction $|\eta | \not \in (1/2, 3/2)$ that makes $|\eta +{{\hat{\xi }}}|\ge 1/2$.

To estimate ${\mathcal {B}}_{22}$, we proceed in a way similar to (3.15), but replacing $L^{n}$ with $L^{n+1}$,

$$\begin{aligned} |{\mathcal {B}}_{22}|&\lesssim \int _{|\gamma |> 1} |\gamma |^{s-1-n} \int \Big | \nabla _\eta ^{n+1} \Big ( \big ( 1 - \chi _0(|\eta |)\big )\, c(x,|\xi |(\eta + {{\hat{\xi }}})) \Big ) \Big | \cdot |\xi |^{-m} \,\mathrm {d}{\eta }\,\mathrm {d}{\gamma }\nonumber \\&\lesssim \int _{|\gamma |> 1} |\gamma |^{s-1-n} \int _{|\eta | \not \in (\frac{1}{2}, \frac{3}{2})} (|\xi |^{-1} + |\eta + {{\hat{\xi }}}|)^{m-1-n} \,\mathrm {d}{\eta }\,\mathrm {d}{\gamma }\nonumber \\&\le \int _{|\gamma | > 1} |\gamma |^{s-1-n} \int _{|\eta | \not \in (\frac{1}{2}, \frac{3}{2})} |\eta + {{\hat{\xi }}}|^{m-1-n} \,\mathrm {d}{\eta }\,\mathrm {d}{\gamma }\nonumber \\&\le C < +\infty , \end{aligned}$$

(3.16)

for some constant C independent of x, $\xi$. Also, the last two inequality in (3.16) take advantage of the following three facts: $s - 1 - n < -n$, $m - 1 - n < -n$, and the restriction $|\eta | \not \in (1/2, 3/2)$ that makes $|\eta +{{\hat{\xi }}}| \ge 1/2$.

Finally, by (3.8), (3.13), (3.14), (3.15) and (3.16), we arrive at

$$\begin{aligned} |\big ( (-\Delta _\xi )^{s/2} c \big ) (x,\xi )| \le C |\xi |^{m-s}, \quad \text {for all} \quad |\xi | \ge 1. \end{aligned}$$

(3.17)

Step 2: The case $|\xi | < 1$.

In this step, $|\xi |$ is set to be smaller than 1. We differentiate $\big ( (-\Delta _\xi )^{s/2} c \big ) (x,\xi )$ formally w.r.t. $\xi$, and follow the arguments similar to (3.15)–(3.16),

$$\begin{aligned} |\partial _{\xi _j} \big ( (-\Delta _\xi )^{s/2} c \big ) (x,\xi )|&\simeq |\partial _{\xi _j} \iint e^{\text {i}(\xi - \eta ) \cdot \gamma } |\gamma |^s\, c(x,\eta ) \,\mathrm {d}{\eta }\,\mathrm {d}{\gamma }| \nonumber \\&\lesssim |\iint _{|\gamma | \le 1} L^{1+n} (e^{\text {i}(\xi - \eta ) \cdot \gamma }) |\gamma |^s \gamma _j\, c(x,\eta ) \,\mathrm {d}{\eta }\,\mathrm {d}{\gamma }| \nonumber \\&\quad + |\iint _{|\gamma |> 1} L^{2 +n} (e^{\text {i}(\xi - \eta ) \cdot \gamma }) |\gamma |^s \gamma _j\, c(x,\eta ) \,\mathrm {d}{\eta }\,\mathrm {d}{\gamma }| \nonumber \\&\lesssim \int _{|\gamma | \le 1} |\gamma |^{s-n} \int \langle {\eta } \rangle ^{m-1-n} \,\mathrm {d}{\eta }\,\mathrm {d}{\gamma }\nonumber \\&\quad + \int _{|\gamma | > 1} |\gamma |^{s-1-n} \int \langle {\eta } \rangle ^{m-2-n} \,\mathrm {d}{\eta }\,\mathrm {d}{\gamma }\nonumber \\&\le C < +\infty , \end{aligned}$$

(3.18)

where the constant C is independent of x and $\xi$.

Therefore, $\big ( (-\Delta _\xi )^{s/2} c \big ) (x,\xi )$ is continuous w.r.t. $\xi$ in ${\mathbb {R}}^n$. Moreover, the gradient w.r.t. x and $\xi$ is bounded. Therefore, $\big ( (-\Delta _\xi )^{s/2} c \big ) (x,\xi )$ is uniformly bounded for all $x \in {{\mathbb {R}}^n}$ and all $|\xi | \le 1$. Combining this with (3.17), we arrive at the conclusion.

The proof is complete. $\quad \square$

By the commutability between $(-\Delta _\xi )^{s/2}$ and differential operators, we can readily obtain the following corollary.

Corollary 3.1

For any $m < 0$ and $s \in (0,1)$, we have

$$\begin{aligned} \big ( (-\Delta _\xi )^{s/2} c \big ) (x,\xi ) \in S^{m-s} \quad \text {for any} \quad c(x,\xi ) \in S^m. \end{aligned}$$

Proof

Write ${{\tilde{c}}}(x,\xi ) = (-\Delta _\xi )^{s/2} c(x,\xi )$. Then

$$\begin{aligned} \partial _x^\alpha \partial _\xi ^\beta {{\tilde{c}}}(x,\xi )&\simeq \partial _x^\alpha \partial _\xi ^\beta \iint e^{\text {i}(\xi - \eta ) \cdot \gamma } |\gamma |^s\, c(x,\eta ) \,\mathrm {d}{\eta }\,\mathrm {d}{\gamma }\nonumber \\&\simeq \partial _x^\alpha \partial _\xi ^\beta \int e^{\text {i}\xi \cdot \gamma } |\gamma |^s\, {\mathcal {F}}_{\xi \rightarrow \gamma } \{c\}(x,\gamma ) \,\mathrm {d}{\gamma }\nonumber \\&\simeq \partial _x^\alpha \int e^{\text {i}\xi \cdot \gamma } |\gamma |^s\, \gamma ^\beta {\mathcal {F}}_{\xi \rightarrow \gamma } \{c\}(x,\gamma ) \,\mathrm {d}{\gamma }\nonumber \\&\simeq \partial _x^\alpha \int e^{\text {i}\xi \cdot \gamma } |\gamma |^s\, {\mathcal {F}}_{\xi \rightarrow \gamma } \{\partial _\xi ^\beta (c)\}(x,\gamma ) \,\mathrm {d}{\gamma }\nonumber \\&\simeq \partial _x^\alpha \iint e^{\text {i}(\xi - \eta ) \cdot \gamma } |\gamma |^s\, (\partial _\xi ^\beta c)(x,\eta ) \,\mathrm {d}{\eta }\,\mathrm {d}{\gamma }\nonumber \\&= \iint e^{\text {i}(\xi - \eta ) \cdot \gamma } |\gamma |^s\, (\partial _x^\alpha \partial _\xi ^\beta c)(x,\eta ) \,\mathrm {d}{\eta }\,\mathrm {d}{\gamma }\nonumber \\&= \big ( (-\Delta _\xi )^{s/2} (\partial _x^\alpha \partial _\xi ^\beta c) \big ) (x,\xi ). \end{aligned}$$

Applying Lemma 3.2, we obtain

$$\begin{aligned} |\partial _x^\alpha \partial _\xi ^\beta {{\tilde{c}}}(x,\xi )| \le C_{\alpha ,\beta } \langle {\xi } \rangle ^\beta . \end{aligned}$$

The proof is complete. $\quad \square$

Recall the definition of the unit normal vector ${\varvec{n}}$ after (1.2). The asymptotic estimate associated with the term $F_1$ is established in the following lemma.

Lemma 3.3

We have

$$\begin{aligned} {\mathbb {E}} (|F_1({\hat{x}},k,\cdot )|^2) \le C k^{-4},\quad {~\forall \,}k >1, \end{aligned}$$

(3.19)

for all ${\hat{x}}$ with ${\hat{x}} \cdot {\varvec{n}} \ge 0$, and the constant C in (3.19) is independent of ${\hat{x}}$, k.

In what follows, we shall use ${{\mathcal {C}}(\cdot )}$ and its variants, such as ${{{{\mathcal {C}}}}}(\cdot )$, ${{\mathcal {C}}_{a,b}(\cdot )}$ etc., to represent some generic smooth scalar/vector functions, within $C_c^\infty ({\mathbb {R}}^3)$ or $C_c^\infty ({\mathbb {R}}^{3 \times 4})$, whose particular definition may change line by line.

Proof of Lemma 3.3

Using (2.5) and (2.6), one can show that

$$\begin{aligned}&{\mathbb {E}} (|F_1({\hat{x}},k,\cdot )|^2) \nonumber \\&\quad = {\mathbb {E}} \big ( \int _{{\mathbb {R}}^3} e^{-\text {i}k{\hat{x}} \cdot y} q(y,\cdot ) \int _{{\mathbb {R}}^3} \frac{e^{\text {i}k|y-s|}}{4\pi |y-s|} f(s,\cdot ) \,\mathrm {d}{s} \,\mathrm {d}{y} \nonumber \\&\qquad \cdot \int _{{\mathbb {R}}^3} e^{\text {i}k{\hat{x}} \cdot z} \overline{q}(z,\cdot ) \int _{{\mathbb {R}}^3} \frac{e^{-\text {i}k|z-t|}}{4\pi |z-t|} {\overline{f}}(t,\cdot ) \,\mathrm {d}{t} \,\mathrm {d}{z} \big ) \nonumber \\&\quad \simeq \int e^{-\text {i}k{\hat{x}} \cdot (y-z)} \frac{e^{\text {i}k(|y-s|-|z-t|)}}{|y-s| \cdot |z-t|} \cdot {\mathbb {E}} \big ( q(y,\cdot ) {\overline{q}}(z,\cdot ) \big ) \cdot {\mathbb {E}} \big ( f(s,\cdot ) {\overline{f}}(t,\cdot ) \big ) \,\mathrm {d}{(s, y, t, z)} \nonumber \\&\quad \simeq \int e^{\text {i}k\varphi (y,s,z,t)} \big ( \int e^{\text {i}(z-y) \cdot \xi } c_q(z,\xi ) \,\mathrm {d}{\xi }\big ) \big ( \int e^{\text {i}(t-s) \cdot \eta } c_f(t,\xi ) \,\mathrm {d}{\eta }\big ) \cdot {\mathcal {C}}\cdot \,\mathrm {d}{(s, y, t, z)}, \end{aligned}$$

(3.20)

where $\varphi (y,s,z,t) := -{\hat{x}} \cdot (y-z) - |y-s| + |z-t|$, and the $\,\mathrm {d}{(s, y, t, z)}$ is a short notation for $\,\mathrm {d}{s} \,\mathrm {d}{y} \,\mathrm {d}{t} \,\mathrm {d}{z}$. We omit the repeated integral symbols and the integral domain in the calculation for simplicity. The term ${\mathcal {C}}(y,z,s,t)$ in (3.20) belongs to $C_c^\infty ({\mathbb {R}}^{3 \times 4})$ due to the fact that q and f are compactly supported and ${\mathop {\mathrm{dist}}({\mathcal {CH}}(D_f), {\mathcal {CH}}(D_q)) > 0}$.

Next we are about to differentiate the term $e^{\text {i}k\varphi (y,s,z,t)}$ by two differential operators, in order to obtain the decay w.r.t. the argument k. To that end, we introduce the aforesaid two differential operators with $C^\infty$-smooth coefficients as follows,

$$\begin{aligned} L_1 := \frac{(y-s) \cdot \nabla _s}{\text {i}k|y-s|}, \quad L_2 = L_{2,{\hat{x}}} := \frac{\nabla _y \varphi \cdot \nabla _y}{\text {i}k|\nabla _y \varphi |}, \end{aligned}$$

where ${\nabla _y \varphi = \frac{s-y}{|s-y|} - {\hat{x}}}$. The operator $L_{2,{\hat{x}}}$ depends on ${\hat{x}}$ because $\nabla _y \varphi$ does. Due to the fact that $y \in D_q$ while $s \in D_f$, the operator $L_1$ is well-defined. It can be verified there is a positive lower bound of $|\nabla _y \varphi |$ for all ${\hat{x}}\in \{{\hat{x}} \in {\mathbb {S}}^2 :{\hat{x}} \cdot {\varvec{n}} \ge 0\}$. It can also be verified that

$$\begin{aligned} L_1 (e^{\text {i}k\varphi (y,s,z,t)}) = L_2 (e^{\text {i}k\varphi (y,s,z,t)}) = e^{\text {i}k\varphi (y,s,z,t)}. \end{aligned}$$

By using integration by parts, one can compute

$$\begin{aligned}&{\mathbb {E}} (|F_1({\hat{x}},k,\cdot )|^2) \nonumber \\&\quad = \int \big ( L_1^2 L_2^2 \big ) (e^{\text {i}k\varphi (y,s,z,t)}) \cdot \big ( \int e^{\text {i}(z-y) \cdot \xi } c_q(z,\xi ) \,\mathrm {d}{\xi }\big ) \nonumber \\&\qquad \cdot \big ( \int e^{\text {i}(t-s) \cdot \eta } c_f(t,\eta ) \,\mathrm {d}{\eta }\big ) \cdot {\mathcal {C}}(y,z,s,t) \,\mathrm {d}{(s, y, t, z)} \nonumber \\&\quad \simeq \ k^{-4} \int _{{\mathcal {D}}} e^{\text {i}k\varphi (y,s,z,t)} \big [{\mathcal {J}}_1\, ({\mathcal {K}}_1\, {\mathcal {C}}+ {{\mathcal {K}}}_2 \cdot {{\mathcal {C}}} + \sum _{a,b=1,2,3} {\mathcal {K}}_{3;a,b}\, {\mathcal {C}}_{a,b}) \nonumber \\&\qquad + \sum _{c=1,2,3} {\mathcal {J}}_{2;c}\, ({\mathcal {K}}_1\, {\mathcal {C}}_c + {{\mathcal {K}}}_2 \cdot {{\mathcal {C}}}_c + \sum _{a,b=1,2,3} \mathcal K_{3;a,b}\, {\mathcal {C}}_{a,b,c}) \nonumber \\&\qquad + \sum _{a',b'=1,2,3} {\mathcal {J}}_{3;a',b'} ({\mathcal {K}}_1\, {\mathcal {C}}_{a',b'} + {{\mathcal {K}}}_2 \cdot {{\mathcal {C}}}_{a',b'}\nonumber \\&\qquad +\sum _{a,b=1,2,3} {\mathcal {K}}_{3;a,b}\, {\mathcal {C}}_{a,b,a',b'}) \big ] \,\mathrm {d}{(s, y, t, z)}, \end{aligned}$$

(3.21)

where the integral domain ${\mathcal {D}} \subset {\mathbb {R}}^{3 \times 4}$ is bounded and

$$\begin{aligned} {\mathcal {J}}_1&:= \int e^{\text {i}(t-s) \cdot \eta }\, c_f(t,\eta ) \,\mathrm {d}{\eta }, \quad {\mathcal {K}}_1 := \int e^{\text {i}(z-y) \cdot \xi }\, c_q(z,\xi ) \,\mathrm {d}{\xi }, \\ {{\mathcal {J}}}_2&:= \nabla _s \int e^{\text {i}(t-s) \cdot \eta }\, c_f(t,\eta ) \,\mathrm {d}{\eta }, \quad {{\mathcal {K}}}_2 := \nabla _y \int e^{\text {i}(z-y) \cdot \xi }\, c_q(z,\xi ) \,\mathrm {d}{\xi }, \\ {\mathcal {J}}_{3;a,b}&:= \partial _{s_a,s_b}^2 \int e^{\text {i}(t-s) \cdot \eta }\, c_f(t,\eta ) \,\mathrm {d}{\eta }, \quad {\mathcal {K}}_{3;a,b} := \partial _{y_a,y_b}^2 \int e^{\text {i}(z-y) \cdot \xi }\, c_q(z,\xi ) \,\mathrm {d}{\xi }, \end{aligned}$$

and ${\mathcal {J}}_{2;c}$ (resp. ${\mathcal {K}}_{2;c}$) is the c-th component of the vector ${{\mathcal {J}}}_2$ (resp. ${\mathcal K}_2$).

For the case with $s \ne t$, these three quantities, $\mathcal J_1$, ${{\mathcal {J}}}_2$ and ${\mathcal {J}}_{3;a,b}$, can be estimated as follows,

$$\begin{aligned} |{\mathcal {J}}_1|&= |\int e^{\text {i}(t-s) \cdot \eta }\, c_f(t,\eta ) \,\mathrm {d}{\eta }| = |s-t|^{-2} \cdot |\int \Delta _\eta (e^{\text {i}(s-t) \cdot \eta })\, c_f(t,\eta ) \,\mathrm {d}{\eta }| \nonumber \\&= |s-t|^{-2} \cdot |\int e^{\text {i}(t-s) \cdot \eta } (\Delta _\eta c_f) (t,\eta ) \,\mathrm {d}{\eta }| \le |s-t|^{-2} \int |(\Delta _\eta c_f) (t,\eta )| \,\mathrm {d}{\eta }\nonumber \\&\lesssim |s-t|^{-2} \int \langle {\eta } \rangle ^{-m_f-2} \,\mathrm {d}{\eta }\lesssim |s-t|^{-2}, \end{aligned}$$

(3.22)

and

$$\begin{aligned} |{{\mathcal {J}}}_{2;c}|&= |\partial _{s_c} \int e^{\text {i}(t-s) \cdot \eta }\, c_f(t,\eta ) \,\mathrm {d}{\eta }| = |\int e^{\text {i}(t-s) \cdot \eta } \cdot c_f(t,\eta ) \eta _c \,\mathrm {d}{\eta }| \nonumber \\&= |s-t|^{-2} \cdot |\int \Delta _\eta (e^{\text {i}(t-s) \cdot \eta })\, c_f(t,\eta ) \eta _c \,\mathrm {d}{\eta }| = |s-t|^{-2}\nonumber \\&\quad \cdot |\int e^{\text {i}(t-s) \cdot \eta } \Delta _\eta (c_f(t,\eta ) \eta _c) \,\mathrm {d}{\eta }| \nonumber \\&\lesssim |s-t|^{-2} \int \langle {\eta } \rangle ^{-m_f+1-2} \,\mathrm {d}{\eta }\lesssim |s-t|^{-2}, \end{aligned}$$

(3.23)

and similarly

$$\begin{aligned} {\mathcal {J}}_{3;a,b}&\simeq \int e^{\text {i}(t-s) \cdot \eta } \cdot c_f(t,\eta ) \eta _a \eta _b \,\mathrm {d}{\eta }\simeq |s-t|^{-2} \int \Delta _\eta (e^{\text {i}(t-s) \cdot \eta }) \cdot c_f(t,\eta ) \eta _a \eta _b \,\mathrm {d}{\eta }\nonumber \\&= |s-t|^{-2} \int e^{\text {i}(t-s) \cdot \eta } \cdot \Delta _\eta (c_f(t,\eta ) \eta _a \eta _b) \,\mathrm {d}{\eta }. \end{aligned}$$

(3.24)

Here, in deriving the last two inequalities respectively in (3.22) and (3.23), we have made use of the a-priori requirement $m_f > 2$ in (1.3); see also the discussion at the end of Remark 1.1.

Now, if we further differentiate the term $e^{\text {i}(t-s) \cdot \eta }$ in (3.24) by $\frac{\text {i}(s-t) \cdot }{|s-t|^2} \nabla _\eta$ and then transfer the operator $\nabla _\eta$ onto $\Delta _\eta (c_f(t,\eta ) \eta _a \eta _b)$ by using integration by parts, we would arrive at

$$\begin{aligned} |{\mathcal {J}}_{3;a,b}| \lesssim |s-t|^{-3} \int |\nabla _\eta \Delta _\eta (c_f(t,\eta ) \eta _a \eta _b)| \,\mathrm {d}{\eta }\le |s-t|^{-3} \int \langle {\eta } \rangle ^{-m_f-1} \,\mathrm {d}{\eta }. \end{aligned}$$

The term $\int \langle {\eta } \rangle ^{-m_f-1} \,\mathrm {d}{\eta }$ is absolutely integrable now, but the term $|s-t|^{-3}$ is not integrable at the hyperplane $s = t$ in ${\mathbb {R}}^3$. To circumvent this dilemma, the fractional Laplacian can be applied as follows. By using Lemmas 3.1 and 3.2, we can continue (3.24) as

$$\begin{aligned} |{\mathcal {J}}_{3;a,b}|&\simeq |s-t|^{-2} \cdot \big | |s-t|^{-s} \int (-\Delta _\eta )^{s/2} (e^{\text {i}(t-s) \cdot \eta }) \cdot \Delta _\eta (c_f(t,\eta ) \eta _j \eta _\ell ) \,\mathrm {d}{\eta }\big | \nonumber \\&= |s-t|^{-2-s} \cdot |\int e^{\text {i}(t-s) \cdot \eta } \cdot (-\Delta _\eta )^{s/2} \big ( \Delta _\eta (c_f(t,\eta ) \eta _j \eta _\ell ) \big ) \,\mathrm {d}{\eta }| \nonumber \\&\lesssim |s-t|^{-2-s} \int \langle {\eta } \rangle ^{-m_f+2-2-s} \,\mathrm {d}{\eta }= |s-t|^{-2-s} \int \langle {\eta } \rangle ^{-m_f-s} \,\mathrm {d}{\eta }, \end{aligned}$$

(3.25)

where the number s is chosen to satisfy $\max \{0, 3 - m_f\}< s < 1$, and the existence of such a number s is guaranteed by noting that $m_f > 2$. Therefore, we have

Thanks to the condition (3.26a), we can continue (3.25) as

$$\begin{aligned} |{\mathcal {J}}_{3;a,b} |&\lesssim |s-t|^{-2-s} \int \langle {\eta } \rangle ^{-m_f-s} \,\mathrm {d}{\eta }\lesssim |s-t|^{-2-s}. \end{aligned}$$

(3.27)

Using similar arguments, we can also conclude that

$$\begin{aligned} \left\{ \begin{aligned} |{\mathcal {K}}_1|,\, |{{\mathcal {K}}}_2|&\lesssim |y-z|^{-2}, \\ |{\mathcal {K}}_{3;a,b}|&\lesssim |y-z|^{-2-s}. \end{aligned}\right. \end{aligned}$$

(3.28)

Combining (3.21), (3.22), (3.23), (3.27) and (3.28), we arrive at

$$\begin{aligned}&{\mathbb {E}} (|F_1({\hat{x}},k,\cdot )|^2) \nonumber \\&\quad \lesssim \ k^{-4} \int _{{\mathcal {D}}} (|{\mathcal {J}}_1| + |{{\mathcal {J}}}_2| + \sum _{a',b'=1,2,3} |{\mathcal {J}}_{3;a',b'}|) \cdot (|{\mathcal {K}}_1| + |{{\mathcal {K}}}_2| \nonumber \\&\qquad + \sum _{a,b=1,2,3} |{\mathcal {K}}_{3;a,b}|) \,\mathrm {d}{(s, y, t, z)} \nonumber \\&\quad \lesssim \ k^{-4} \int _{{\mathcal {D}}} |s - t|^{-2-s} \cdot |y - z|^{-2-s} \,\mathrm {d}{(s, y, t, z)} \nonumber \\&\quad \lesssim \ k^{-4} \int _{\widetilde{{\mathcal {D}}}} |s - t|^{-2-s} \,\mathrm {d}{s} \,\mathrm {d}{t} \cdot \int _{\widetilde{{\mathcal {D}}}} |y - z|^{-2-s} \,\mathrm {d}{y} \,\mathrm {d}{z} \end{aligned}$$

(3.29)

for some sufficiently large but bounded domain $\widetilde{\mathcal D} \subset {\mathbb {R}}^{3 \times 2}$ satisfying ${\mathcal {D}} \subset \widetilde{{\mathcal {D}}} \times \widetilde{{\mathcal {D}}}$. Note that the integral (3.29) should be understood as a singular integral because of the presence of the singularities occuring when $s = t$ and $y = z$. By (3.29) and (3.26b), we can finally conclude (3.19).

The proof is complete. $\quad \square$

3.2 Asymptotics of $F_2$

The following lemma is necessary for the estimates of $F_2({\hat{x}},k,\omega )$.

Lemma 3.4

Assume that $\epsilon > 0$. For $\forall s \in {\mathbb {R}}$, $\forall k \in {\mathbb {R}}$ and $\forall {\hat{x}} \in {\mathbb {S}}^{n-1}$, we have

$$\begin{aligned} \Vert {e^{-\text {i}k{\hat{x}} \cdot (\cdot )} \varphi } \Vert _{H_{-1/2-\epsilon }^s} \le C_{s,\varphi } \langle {k} \rangle ^s, \quad \forall \varphi \in C_c^\infty ({{\mathbb {R}}^n}), \end{aligned}$$

where the constant $C_{s,\varphi }$ depends on s and $\varphi$, but is independent of ${\hat{x}}$, k.

Proof

By the Plancherel theorem and Peetre’s inequality, one has

$$\begin{aligned} \Vert {e^{-\text {i}k{\hat{x}} \cdot (\cdot )} \varphi } \Vert _{H_{-1/2-\epsilon }^s}^2&= \int \langle {x} \rangle ^{-1-2\epsilon } |(I - \Delta )^{s/2} \big ( e^{-\text {i}k{\hat{x}} \cdot (\cdot )} \varphi \big ) (x)|^2 \,\mathrm {d}{x} \nonumber \\&\le \int |(I - \Delta )^{s/2} \big ( e^{-\text {i}k{\hat{x}} \cdot (\cdot )} \varphi \big ) (x)|^2 \,\mathrm {d}{x} \nonumber \\&\simeq \int \langle {\xi } \rangle ^{2s} |{\mathcal {F}}\big \{ e^{-\text {i}k{\hat{x}} \cdot (\cdot )} \varphi \big \} (\xi )|^2 \,\mathrm {d}{\xi }= \int \langle {\xi } \rangle ^{2s} |{{\widehat{\varphi }}}(\xi + k{\hat{x}})|^2 \,\mathrm {d}{\xi }\nonumber \\&= \int \langle {\xi - k{\hat{x}}} \rangle ^{2s} |{{\widehat{\varphi }}}(\xi )|^2 \,\mathrm {d}{\xi }\le \langle {k} \rangle ^{2s} \int \langle {\xi } \rangle ^{2|s|} |{{\widehat{\varphi }}}(\xi )|^2 \,\mathrm {d}{\xi }. \end{aligned}$$

${{\widehat{\varphi }}}$ is rapidly decaying because $\varphi \in C_c^\infty ({{\mathbb {R}}^n})$. Thus, the integral $\int \langle {\xi } \rangle ^{2|s|} |{{\widehat{\varphi }}}(\xi )|^2 \,\mathrm {d}{\xi }$ is a finite number depending on s, $\varphi$. The proof is done. $\quad \square$

Lemma 3.5

For every $s \in (\frac{3-m_q}{2},\frac{1}{2})$, there exists a subset $\Omega _s \subset \Omega$ with ${\mathbb {P}}(\Omega _s) = 0$ such that for $\forall \, \omega \in \Omega \backslash \Omega _s$, the inequality

$$\begin{aligned} |F_2({\hat{x}},k,\omega )| \le C_s(\omega ) k^{5s-2} \end{aligned}$$

(3.30)

holds uniformly for $\forall {\hat{x}} \in {\mathbb {S}}^2$ and $\forall k > 1$, where $C_s(\omega )$ is finite almost surely.

Proof

First, we note that the condition (1.3) implies $(3-m_q)/2 < 1/2$, and hence $(\frac{3-m_q}{2},\frac{1}{2})$ is a non-empty open interval. We define $\chi _q$ (resp. $\chi _f$) as a function in $C_c^\infty ({\mathbb {R}}^3)$ with $\chi _q(x) = 1$ (resp. $\chi _f(x) = 1$) for $\forall x \in \mathop {\mathrm{supp}}q$ (resp. $\forall x \in \mathop {\mathrm{supp}}f$). From (3.5), Theorems 2.1, 2.2 and Lemma 3.4, one can compute

$$\begin{aligned} |F_2({\hat{x}},k,\omega )|&\le \sum _{j \ge 2} \big | \int _{{\mathbb {R}}^3} e^{-\text {i}k{\hat{x}} \cdot z} \chi _q(z) \big [ (q{{\mathcal {R}}_{k}})^j f \big ](z) \,\mathrm {d}{z} \big | \nonumber \\&\le \Vert {e^{-\text {i}k{\hat{x}} \cdot (\cdot )} \chi _q} \Vert _{H_{-1/2-\epsilon }^s} \sum _{j \ge 2} \Vert {(q{{\mathcal {R}}_{k}})^j (f \cdot \chi _q)} \Vert _{H_{1/2+\epsilon }^{-s}} \nonumber \\&\le C_s \cdot \langle {k} \rangle ^s \cdot C_{\epsilon ,s}(\omega ) \sum _{j \ge 2} k^{-j(1-2s)} \Vert {f \cdot \chi _q} \Vert _{H_{1/2+\epsilon }^{-s}} \nonumber \\&\le C_{\epsilon ,s}(\omega ) \cdot \langle {k} \rangle ^s \cdot k^{-2(1-2s)} \Vert {f \cdot \chi _q} \Vert _{H_{1/2+\epsilon }^{-s}} \nonumber \\&\le C_{\epsilon ,s}(\omega ) k^{5s-2} \Vert {\chi _q} \Vert _{H_{-1/2-\epsilon }^{s}}, \end{aligned}$$

(3.31)

with a random variable $C_{\epsilon ,s}(\omega )$ that is finite almost surely. The last inequality in (3.31) utilizes the fact that $f(\cdot ,\omega )$ is microlocally isotropic of order $m_f$ so that Theorem 2.2 holds for $f(\cdot ,\omega )$. Let $\epsilon = 1/2$ in (3.31), we arrive at (3.30).

The proof is complete. $\quad \square$

4 Recovery of the Source

In this section, we focus on the recovery of $\mu _f(x)$ associated with the random source term. In the recovering procedure, only a single realization of the passive scattering measurement is used. Thus, $\alpha$ in (1.1) is set to be 0, and the random sample $\omega$ is fixed. The data set $\mathcal M_f(\omega )$ is used to achieve the unique recovery.

We first present the following auxiliary lemma.

Lemma 4.1

For any stochastic process $\{g(k,\omega )\}_{k \in {\mathbb {R}}_+}$ satisfying

$$\begin{aligned} \int _1^{+\infty } k^{m-1} {\mathbb {E}} (|g(k,\cdot )|) \,\mathrm {d}{k} < +\infty , \end{aligned}$$

it holds that

$$\begin{aligned} \lim _{K \rightarrow +\infty } \frac{1}{K} \int _K^{2K} k^m g(k,\omega ) \,\mathrm {d}{k} = 0, \ {\text { a.s. }}\omega \in \Omega . \end{aligned}$$

Proof

By $\int _1^{+\infty } k^{m-1} {\mathbb {E}} (|g(k,\cdot )|) \,\mathrm {d}{k} < +\infty$ and Fubini’s Theorem, we know

$$\begin{aligned} \int _1^{+\infty } k^{m-1} |g(k,\omega )| \,\mathrm {d}{k} < +\infty , \quad {\text { a.s. }}\omega \in \Omega , \end{aligned}$$

(4.1)

which implies that $g(k,\omega )$ is almost everywhere finite in terms of k. Now we define a function $g_K(k,w) := \frac{\chi _{(K,2K)}(k)}{2K} k^m g(k,\omega )$, where $\chi _{(K,2K)}(k)$ is the characteristic function of the interval (K, 2K). For almost surely every fixed $\omega$, we have

$$\begin{aligned} {\lim _{K \rightarrow + \infty } g_K(k,\omega ) = 0 \quad {\text { a.e. }}\quad k \in [1,+\infty ).} \end{aligned}$$

Moreover, the function series $\{g_K(k,\omega )\}_{K}$ is dominated, in the argument k, by the function $k^{m-1} g(k,\omega )$. Thus, from (4.1) and the dominated convergence theorem, we can conclude

$$\begin{aligned} \lim _{K \rightarrow +\infty } \int _1^{+\infty } g_K(k,\omega ) \,\mathrm {d}{k} = 0 \ {\text { a.s. }}\omega \in \Omega . \end{aligned}$$

The proof is complete. $\quad \square$

We are ready to establish the recovery of $\mu _f(x)$.

Proof of Theorem 1.1

This proof depends on Lemma 3.3, which requires ${\hat{x}} \cdot {\varvec{n}} \ge 0$. Hence, we assume that ${\hat{x}} \cdot {\varvec{n}} \ge 0$ unless otherwise stated.

Recall the definition of $F_p~(p=0,1,2)$ in (3.5). As already mentioned at the beginning of Sect. 3, we correlate the data in the following form

$$\begin{aligned}&\frac{1}{K} \int _K^{2K} k^{m_f} 16\pi ^2 \overline{u^\infty ({\hat{x}},k,\omega )} u^\infty ({\hat{x}},k+\tau ,\omega ) \,\mathrm {d}{k} \nonumber \\&\quad = \sum _{p,q=0}^2 \frac{1}{K} \int _K^{2K} k^{m_f} \overline{F_p({\hat{x}},k,\omega )} F_q({\hat{x}},k+\tau ,\omega ) \,\mathrm {d}{k} \nonumber \\&\quad =: \sum _{p,q=0}^2 I_{p,q}({\hat{x}},K,\tau ,\omega ). \end{aligned}$$

(4.2)

According to Corollary 4.4 in [8], for $\forall \tau \ge 0$ and $\forall {\hat{x}} \in {\mathbb {S}}^2$, there exists $\Omega _{\tau ,{\hat{x}}}^{0,0} \subset \Omega$, with $\mathbb P(\Omega _{\tau ,{\hat{x}}}^{0,0}) = 0$, such that

$$\begin{aligned} \forall \omega \in \Omega \backslash \Omega _{\tau ,{\hat{x}}}^{0,0}, \quad \lim _{K \rightarrow +\infty } I_{0,0}({\hat{x}},K,\tau ,\omega ) = (2\pi )^{3/2} {{\widehat{\mu }}}_f(\tau {\hat{x}}), \end{aligned}$$

(4.3)

which also implies that

$$\begin{aligned} \forall \omega \in \Omega \backslash \Omega _{\tau ,{\hat{x}}}^{0,0}, \quad \lim _{K \rightarrow +\infty } \frac{1}{K} \int _K^{2K} k^{m_f} |F_0({\hat{x}},k,\omega )|^2 \,\mathrm {d}{k} = (2\pi )^{3/2} {{\widehat{\mu }}}_f(0). \end{aligned}$$

(4.4)

We next estimate the higher order terms. The Cauchy-Schwarz inequality yields

$$\begin{aligned} |I_{p,q}| \le \big ( \frac{1}{K} \int _K^{2K} k^{m_f} |F_p({\hat{x}},k,\omega )|^2 \,\mathrm {d}{k} \big )^{\frac{1}{2}} \cdot \big ( \frac{1}{K} \int _K^{2K} k^{m_f} |F_q({\hat{x}},k+\tau ,\omega )|^2 \,\mathrm {d}{k} \big )^{\frac{1}{2}}. \end{aligned}$$

(4.5)

Recall that $m_f < 3$. From the condition (1.3) and Lemma 3.3 we have

$$\begin{aligned} \int _1^{+\infty } k^{m_f-1} {\mathbb {E}} (|F_1({\hat{x}},k,\cdot )|^2) \,\mathrm {d}{k} \lesssim \int _1^{+\infty } k^{m_f-1} k^{-4} \,\mathrm {d}{k} < +\infty . \end{aligned}$$

(4.6)

By (4.6) and Lemma 4.1, we conclude that

$$\begin{aligned} \lim _{K \rightarrow +\infty } \frac{1}{K} \int _K^{2K} k^{m_f} |F_1({\hat{x}},k,\omega )|^2 \,\mathrm {d}{k} = 0 \quad {\text { a.s. }}\omega \in \Omega . \end{aligned}$$

(4.7)

For every $s \in ((3-m_q)/2,1/2)$, Lemma 3.5 gives

$$\begin{aligned} \frac{1}{K} \int _K^{2K} k^{m_f} |F_2({\hat{x}},k,\omega )|^2 \,\mathrm {d}{k} \le \frac{C_s(\omega )}{K} \int _K^{2K} k^{m_f} k^{2(5s-2)} \,\mathrm {d}{k} \le \frac{C_s(\omega )}{K^{4-m_f-10s}}. \end{aligned}$$

(4.8)

Recalling the condition (1.3), we know $(3-m_q)/2 < (4 - m_f)/{10}$.

Choosing any $s \in \big ( (3-m_q)/2, (4 - m_f)/{10} \big )$, we have ${4 - m_f - 10s > 0}$. Combining this with (4.8), we conclude that

$$\begin{aligned} \lim _{K \rightarrow +\infty } \frac{1}{K} \int _K^{2K} k^{m_f} |F_2({\hat{x}},k,\omega )|^2 \,\mathrm {d}{k} = 0 \quad {\text { a.s. }}\omega \in \Omega . \end{aligned}$$

(4.9)

Formula (4.9) easily implies that

$$\begin{aligned} \lim _{K \rightarrow +\infty } \frac{1}{K} \int _K^{2K} k^{m_f} |F_2({\hat{x}},k+\tau ,\omega )|^2 \,\mathrm {d}{k} = 0 \quad {\text { a.s. }}\omega \in \Omega , \end{aligned}$$

(4.10)

for every fixed $\tau \in {\mathbb {R}}$.

Write ${\mathcal {A}} := \{ (p,q) \,;\, 0 \le p,q \le 2 \} \backslash \{(0,0)\}$. By (4.5), (4.4), (4.7) and (4.10) we have that, for $\forall \tau \ge 0$ and $\forall {\hat{x}} \in {\mathbb {S}}^2$ there exists $\Omega _{\tau ,{\hat{x}}}^{p,q} \subset \Omega : \mathbb P(\Omega _{\tau ,{\hat{x}}}^{p,q}) = 0$, $\Omega _{\tau ,{\hat{x}}}^{p,q}$ depending on $\tau$ and ${\hat{x}}$, such that

$$\begin{aligned} \forall (p,q) \in {\mathcal {A}}, \quad \forall \omega \in \Omega \backslash \Omega _{\tau ,{\hat{x}}}^{p,q}, \quad \lim _{K \rightarrow +\infty } I_{p,q}({\hat{x}},K,\tau ,\omega ) = 0. \end{aligned}$$

(4.11)

Write $\Omega _{\tau {\hat{x}}} := \cup _{(p,q) \in {\mathcal {A}} \cup \{(0,0)\}} \Omega _{\tau , {\hat{x}}}^{p,q}$, thus $\mathbb P(\Omega _{\tau {\hat{x}}}) = 0$. Then (4.11) gives

$$\begin{aligned} \forall \omega \in \Omega \backslash \Omega _{\tau {\hat{x}}}, \quad \forall (p,q) \in {\mathcal {A}}, \quad \lim _{K \rightarrow +\infty } I_{p,q}({\hat{x}},K,\tau ,\omega ) = 0. \end{aligned}$$

(4.12)

Combining (4.2), (4.3) and (4.12), we arrive at the following statement:

$$\begin{aligned} \begin{aligned}&\forall \, y \in {\mathbb {R}}^3, {~\exists \,}\Omega _y \subset \Omega :{\mathbb {P}}(\Omega _y) = 0, {\text { s.t. }}\forall \omega \in \Omega \backslash \Omega _y, \text { we have} \\&\lim _{K \rightarrow +\infty } \frac{1}{K} \int _K^{2K} k^{m_f} 16\pi ^2 \overline{u^\infty ({\hat{x}},k,\omega )} u^\infty ({\hat{x}},k+\tau ,\omega ) \,\mathrm {d}{k} = (2\pi )^{3/2} {{\widehat{\mu }}}_f(\tau {\hat{x}}). \end{aligned} \end{aligned}$$

(4.13)

To prove Theorem 1.1, the logical order between y and $\omega$ should be exchanged. Denote the usual Lebesgue measure on ${\mathbb {R}}^3$ as ${\mathbb {L}}$ and the product measure ${\mathbb {L}} \times {\mathbb {P}}$ as $\mu$, and construct the product measure space ${\mathbb {M}} := ({\mathbb {R}}^3 \times \Omega , {\mathcal {G}}, \mu )$ in the canonical way, where ${\mathcal {G}}$ is the corresponding complete $\sigma$-algebra. Define

$$ Z(y, \omega ) := \lim _{K \rightarrow +\infty } \frac{1}{K} \int _K^{2K} k^{m_f} 16\pi ^2 \overline{u^\infty ({\hat{y}},k,\omega )} u^\infty ({\hat{y}},k+|y|,\omega ) \,\mathrm {d}{k} - (2\pi )^{3/2} {{\widehat{\mu }}}_f(y). $$

Write ${\mathcal {A}} := \{ (y,\omega ) \in {\mathbb {R}}^3 \times \Omega \,;\, Z(y, \omega ) \ne 0 \}$. Then ${\mathcal {A}}$ is a subset of $\mathbb M$. Set $\chi _{\mathcal {A}}$ as the characteristic function of ${\mathcal {A}}$ in ${\mathbb {M}}$. By (4.13) we obtain

$$\begin{aligned} \int _{R^3} \big ( \int _\Omega \chi _{{\mathcal {A}}}(y,\omega ) \,\mathrm {d}{{\mathbb {P}}(\omega )} \big ) \,\mathrm {d}{{\mathbb {L}}(y)} = 0. \end{aligned}$$

(4.14)

By (4.14) and Corollary 7 in Sect. 20.1 in [31], we obtain

$$\begin{aligned} \int _{{\mathbb {M}}} \chi _{{\mathcal {A}}}(y,\omega ) \,\mathrm {d}{\mathbb \mu } = \int _\Omega \big ( \int _{R^3} \chi _{{\mathcal {A}}}(y,\omega ) \,\mathrm {d}{{\mathbb {L}}(y)} \big ) \,\mathrm {d}{{\mathbb {P}}(\omega )} = 0. \end{aligned}$$

(4.15)

Since $\chi _{{\mathcal {A}}}(y,\omega )$ is nonnegative, (4.15) implies

$$\begin{aligned} {~\exists \,}\Omega _0 :{\mathbb {P}} (\Omega _0) = 0, {\text { s.t. }}\forall \, \omega \in \Omega \backslash \Omega _0,\, \int _{R^3} \chi _{\mathcal A}(y,\omega ) \,\mathrm {d}{{\mathbb {L}}(y)} = 0. \end{aligned}$$

(4.16)

Formula (4.16) further implies for every $\omega \in \Omega \backslash \Omega _0$,

$$\begin{aligned} {~\exists \,}S_\omega \subset {\mathbb {R}}^3 :{\mathbb {L}} (S_\omega ) = 0, {\text { s.t. }}\forall \, y \in {\mathbb {R}}^3 \backslash S_\omega , \ Z(y,\omega ) = 0. \end{aligned}$$

(4.17)

Now Theorem 1.1 is proved by (4.17) for the case where ${\hat{x}} \cdot {\varvec{n}} \ge 0$.

Note that $\mu _f$ is real-valued, and hence ${{\widehat{\mu }}}_f(\tau {\hat{x}}) = \overline{{{\widehat{\mu }}}_f(-\tau {\hat{x}})}$ when ${\hat{x}} \cdot {\varvec{n}} < 0$.

The proof is complete. $\quad \square$

5 Recovery of the Potential

This section is devoted to the recovery of $\mu _q(x)$ associated with the the random potential. The data set ${\mathcal {M}}_q(\omega )$ is utilized to achieve the recovery. Throughout this section, $\alpha$ in (1.1) is set to be 1.

Proof of Theorem 1.2

Similar to the proof of Theorem 1.1, the case where ${\hat{x}} \cdot {\varvec{n}} < 0$ can be proved by utilizing the fact that $\mu _q$ is real-valued. In what follows, we assume that ${\hat{x}} \cdot {\varvec{n}} \ge 0$ unless otherwise stated.

From (3.4) we have

$$\begin{aligned}&\frac{1}{K} \int _K^{2K} k^{m_q} 16\pi ^2 \overline{u^\infty ({\hat{x}},k,-{\hat{x}},\omega )} u^\infty ({\hat{x}},k+\tau ,-{\hat{x}},\omega ) \,\mathrm {d}{k} \nonumber \\&\quad = \sum _{p,q=0}^2 \frac{1}{K} \int _K^{2K} k^{m_q} \sum _{p=0}^2 [ \overline{F_p({\hat{x}},k,\omega )} + \overline{G_p({\hat{x}},k,\omega )}]\nonumber \\&\qquad \cdot \sum _{q=0}^2 [F_q({\hat{x}},k+\tau ,\omega ) + G_q({\hat{x}},k+\tau ,\omega )] \,\mathrm {d}{k} \nonumber \\&\quad =: \sum _{p,q=0,1,2} \big [ I'_{p,q}({\hat{x}},K,\tau ,\omega ) + J_{p,q}({\hat{x}},K,\tau ,\omega ) \nonumber \\&\qquad + L_{p,q}^1({\hat{x}},K,\tau ,\omega ) + L_{p,q}^2({\hat{x}},K,\tau ,\omega ) \big ], \end{aligned}$$

(5.1)

where

$$\begin{aligned} \left\{ \begin{aligned} I'_{p,q}({\hat{x}},K,\tau ,\omega )&:= \frac{1}{K} \int _K^{2K} k^{m_q} \overline{F_p({\hat{x}},k,\omega )} F_q({\hat{x}},k+\tau ,\omega ) \,\mathrm {d}{k}, \\ J_{p,q}({\hat{x}},K,\tau ,\omega )&:= \frac{1}{K} \int _K^{2K} k^{m_q} \overline{G_p({\hat{x}},k,\omega )} G_q({\hat{x}},k+\tau ,\omega ) \,\mathrm {d}{k}, \\ L_{p,q}^1({\hat{x}},K,\tau ,\omega )&:= \frac{1}{K} \int _K^{2K} k^{m_q} \overline{F_p({\hat{x}},k,\omega )} G_q({\hat{x}},k+\tau ,\omega ) \,\mathrm {d}{k}, \\ L_{p,q}^2({\hat{x}},K,\tau ,\omega )&:= \frac{1}{K} \int _K^{2K} k^{m_q} \overline{G_p({\hat{x}},k,\omega )} F_q({\hat{x}},k+\tau ,\omega ) \,\mathrm {d}{k}. \end{aligned}\right. \end{aligned}$$

(5.2)

Note that $I'_{p,q}$ differs from $I_{p,q}$, defined in (4.2), in that the power of k in the definition of $I'_{p,q}$ is $m_q$ while that of $I_{p,q}$ is $m_f$.

It is shown in [8] that there exists $\Omega _J \subset \Omega :{\mathbb {P}}(\Omega _J) = 0$ such that

$$\begin{aligned}&\forall \omega \in \Omega \backslash \Omega _J, \quad \lim _{K \rightarrow +\infty } J_{0,0}({\hat{x}},K,\tau ,\omega ) = (2\pi )^{3/2} {{\widehat{\mu }}}_q(2\tau {\hat{x}}), \end{aligned}$$

(5.3)

$$\begin{aligned}&\forall \omega \in \Omega \backslash \Omega _J, \quad \lim _{K \rightarrow +\infty } J_{p,q}({\hat{x}},K,\tau ,\omega ) = 0, \quad (p,q) \in {\mathcal {A}}. \end{aligned}$$

(5.4)

We conclude that there exists $\Omega _{I'} \subset \Omega :{\mathbb {P}}(\Omega _{I'}) = 0$ such that

$$\begin{aligned} \forall \omega \in \Omega \backslash \Omega _{I'}, \quad \lim _{K \rightarrow +\infty } \sum _{p,q=0}^2 I'_{p,q}({\hat{x}},K,\tau ,\omega ) = 0. \end{aligned}$$

(5.5)

The reason for (5.5) to hold is that

$$\begin{aligned} \big | \sum _{p,q=0}^2 I'_{p,q}({\hat{x}},K,\tau ,\omega ) \big |&\le \frac{1}{K^{m_f - m_q}} \sum _{p,q=0}^2 \Big [ \big ( \frac{1}{K} \int _K^{2K} k^{m_f} |F_p({\hat{x}},k,\omega )|^2 \,\mathrm {d}{k} \big )^{\frac{1}{2}} \nonumber \\&\quad \cdot \big ( \frac{1}{K} \int _K^{2K} k^{m_f} |F_p({\hat{x}},k+\tau ,\omega )|^2 \,\mathrm {d}{k} \big )^{\frac{1}{2}} \Big ]. \end{aligned}$$

(5.6)

By (4.4), (4.7) and (4.9)-(4.10), as well as a similar argument that exchanges the logical order between $\omega$ and y, we can prove that there exists $\Omega _0 :{\mathbb {P}}(\Omega _0) = 0$ such that for every $\omega \in \Omega \backslash \Omega _0$, one can find $S_\omega \subset {\mathbb {R}}^3 :{\mathbb {L}} (S_\omega ) = 0$ fulfilling that for $\forall y \in {\mathbb {R}}^3 \backslash S_\omega$, there holds

Combining (5.6)–(5.7), we arrive at (5.5).

We next analyze $\sum _{p,q=0}^2 L_{p,q}^1({\hat{x}},K,\tau ,\omega )$,

$$\begin{aligned} \big | \sum _{p,q=0}^2 L_{p,q}^1({\hat{x}},K,\tau ,\omega ) \big |&\le \frac{1}{K^{m_f - m_q}} \sum _{p,q=0}^2 \Big [ \big ( \frac{1}{K} \int _K^{2K} k^{m_f} |F_p({\hat{x}},k,\omega )|^2 \,\mathrm {d}{k} \big )^{\frac{1}{2}} \nonumber \\&\quad \cdot \big ( \frac{1}{K} \int _K^{2K} k^{m_f} |G_p({\hat{x}},k+\tau ,\omega )|^2 \,\mathrm {d}{k} \big )^{\frac{1}{2}} \Big ]. \end{aligned}$$

(5.8)

By (5.2)–(5.4), (5.7) and (5.8) and the a-priori requirement $m_q < m_f$, we conclude that

$$\begin{aligned} \lim _{K \rightarrow +\infty } \big | \sum _{p,q=0}^2 L_{p,q}^1({\hat{x}},K,\tau ,\omega ) \big | \lesssim \lim _{K \rightarrow +\infty } \frac{|{{\widehat{\mu }}}_f(0)|}{K^{m_f - m_q}} = 0, \quad {\text { a.s. }}\end{aligned}$$

(5.9)

Similarly, we can show

$$\begin{aligned} \lim _{K \rightarrow +\infty } \big | \sum _{p,q=0}^2 L_{p,q}^2({\hat{x}},K,\tau ,\omega ) \big | = 0, \quad {\text { a.s. }}\end{aligned}$$

(5.10)

Combining (5.1), (5.3)–(5.5) and (5.9)–(5.10), we arrive at

$$\begin{aligned} \lim _{K \rightarrow +\infty } \frac{1}{K} \int _K^{2K} k^{m_q} 16\pi ^2 \overline{u^\infty ({\hat{x}},k,-{\hat{x}},\omega )} u^\infty ({\hat{x}},k+\tau ,-{\hat{x}},\omega ) \,\mathrm {d}{k} = (2\pi )^{3/2} {{\widehat{\mu }}}_q(2\tau {\hat{x}}). \end{aligned}$$

The proof is complete. $\quad \square$