Abstract
In this article, we prove that on any compact spin manifold of dimension \(m \equiv 0,6,7 \mod 8\), there exists a metric, for which the associated Dirac operator has at least one eigenvalue of multiplicity at least two. We prove this by “catching” the desired metric in a subspace of Riemannian metrics with a loop that is not homotopically trivial. We show how this can be done on the sphere with a loop of metrics induced by a family of rotations. Finally, we transport this loop to an arbitrary manifold (of suitable dimension) by extending some known results about surgery theory on spin manifolds.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction and statement of the results
For this entire article, let \((M, \Theta )\) be a closed Riemannian spin manifold of dimension m and \(\Theta :\widetilde{{\text {GL}}}^{+}M \rightarrow {\text {GL}}^{+}M\) be a fixed topological spin structure on M. For any Riemannian metric g on M, we denote by \(\Sigma ^g_{{{\mathrm{\mathbb {K}}}}} M \rightarrow M\) the spinor bundle with respect to g and \({{\mathrm{\mathbb {K}}}}\in \{{{\mathrm{\mathbb {R}}}}, \mathbb {C}\}\). The associated Dirac operator is denoted by  . We think of this operator as an unbounded operator
. We think of this operator as an unbounded operator

densely defined on the first order Sobolev space \(H^1(\Sigma ^g_{{{\mathrm{\mathbb {K}}}}} M)\) of sections of \(\Sigma ^g_{{{\mathrm{\mathbb {K}}}}} M\). In that sense the operator has a spectrum  . One is usually interested in the case \({{\mathrm{\mathbb {K}}}}=\mathbb {C}\). In terms of a local orthonormal frame, the Dirac operator is given by
. One is usually interested in the case \({{\mathrm{\mathbb {K}}}}=\mathbb {C}\). In terms of a local orthonormal frame, the Dirac operator is given by  and its spectrum comprises of those \(\lambda \in {{\mathrm{\mathbb {R}}}}\) for which there exists a non-trivial spinor field \(\psi \in \Gamma (\Sigma ^g_{{{\mathrm{\mathbb {K}}}}} M) \) such that
and its spectrum comprises of those \(\lambda \in {{\mathrm{\mathbb {R}}}}\) for which there exists a non-trivial spinor field \(\psi \in \Gamma (\Sigma ^g_{{{\mathrm{\mathbb {K}}}}} M) \) such that

The Eq. (1.1) is called the Dirac equation and our main result about it is as follows.
Main Theorem
(Existence of higher multiplicities) Let \((M, \Theta )\) be a closed spin manifold of dimension \(m \equiv 0,6,7 \mod 8\). There exists a Riemannian metric \({\tilde{g}}\) on M such that the complex Dirac operator  has at least one eigenvalue of multiplicity at least two. In addition, \({\tilde{g}}\) can be chosen such that it agrees with an arbitrary metric g outside an arbitrarily small open subset on the manifold.
has at least one eigenvalue of multiplicity at least two. In addition, \({\tilde{g}}\) can be chosen such that it agrees with an arbitrary metric g outside an arbitrarily small open subset on the manifold.
1.1 Dahl’s conjecture
The result of the Main Theorem fits nicely into the context of a conjecture by Dahl [9], which deals with the question of what sequences of real numbers can occur as Dirac spectra. In general, the Dirac spectrum depends on the metric and even on the spin structure, see [10]. On the other hand, all Dirac spectra have certain properties in common.
Lemma 1.1
(Properties of Dirac spectra) Let \((M,\Theta )\) be a closed spin manifold and g be any Riemannian metric on M. Then  is a self-adjoint elliptic first order differential operator and its spectrum satisfies the following properties:
is a self-adjoint elliptic first order differential operator and its spectrum satisfies the following properties:
-
(D1)
 is discrete and unbounded from both sides.
is discrete and unbounded from both sides. -
(D2)
In case \(m \equiv 2,3,4 \mod 8\), there exists a quaternionic structure on the spinor space (hence and all eigenspaces are even-dimensional over \(\mathbb {C}\)).
-
(D3)
In case \(m \not \equiv 3 \mod 4\), the Dirac spectrum is symmetric about zero including multiplicities.
-
(D4)
The kernel of the Dirac operator satisfies the estimate

Here, \(\hat{A}(M)\) denotes the \(\hat{A}\)-genus and \(\alpha (M)\) denotes the \(\alpha \)-genus.
-
(D5)
The growth of the Dirac eigenvalues satisfies a certain Weyl’s law.
For a proof of these elementary facts as well as for an introduction into spin geometry in general, the reader is referred to [11, 16, 24].
Lemma 1.1 raises the question whether or not one can prescribe Dirac spectra artibrarily as long as one does not violate its assertions.
Conjecture 1.2
([9]) Let \(k \in {{\mathrm{\mathbb {N}}}}, \Lambda _1, \Lambda _2 \in {{\mathrm{\mathbb {R}}}}, \Lambda _1 < \Lambda _2\), and \((M,\Theta )\) be a compact spin manifold. For any non-zero \(\lambda _1 \le \cdots \le \lambda _k \in ]\Lambda _1, \Lambda _2[\) satisfying (D2) and (D3), there exists a metric g on M such that

where the eigenvalues are counted with multiplicities.
In the same article, Dahl also gives a proof of this conjecture in the case where all eigenvalues are simple, see [9, Thm. 1]. In this context, an eigenvalue \(\lambda \) is called simple if its multiplicitiy

is equal to 1. Here, \(\mathbb {H}\) denotes the quaternions.
Remark 1.3
(Multiplicities) Denote by  the multiplicity of an eigenvalue \(\lambda \) over \({{\mathrm{\mathbb {K}}}}\in \{{{\mathrm{\mathbb {R}}}}, \mathbb {C}\}\). Then the various notions of multiplicity are related by
the multiplicity of an eigenvalue \(\lambda \) over \({{\mathrm{\mathbb {K}}}}\in \{{{\mathrm{\mathbb {R}}}}, \mathbb {C}\}\). Then the various notions of multiplicity are related by
We will be primarily concerned with the case \(m \equiv 0,6,7 \mod 8\), where all these notions agree, see also Remark 1.4.
The question what one can say about Conjecture 1.2 in case of higher multiplicities has been open ever since. One would guess that one can prescribe eigenvalues of arbitrary finite multiplicity. Unfortunately, the proof of Conjecture 1.2 in case of simple multiplicities does not carry over to higher multiplicities. Therefore, the aim of this article is to introduce some new techniques to approach Conjecture 1.2 in case of higher multiplicities, which will allow us to prove the Main Theorem.
Remark 1.4
(Real vs. complex spin geometry) The restriction in the dimension in the assertion of the Main Theorem stems from the fact that we need tools from real and from complex spin geometry. In dimensions \(m \equiv 0,6,7 \mod 8\), complex spin geometry is the complexification of real spin geometry. More precisely, the complexification of an irreducible real representation of the real Clifford algebra will be an irreducible complex representation of the complex Cilfford algebra. This follows from the explicit classification of real and complex Clifford algebras, see for instance [24, I.§4]. Hence the complexification of the real spinor representation is a complex one. This behavior under complexification goes through for all other structures on the spinor bundle, in particular Clifford multiplication, the spinorial connection and the Dirac operator. Thus, in dimensions \(m \equiv 0,6,7 \mod 8\), we can jump back and forth between the real and the complex spin geometry.
Remark 1.5
(Neighborhood) The precise nature of the neighborhood mentioned in the Main Theorem will become clear in the proof. It will be a surgery disc around a point, where we perform a connected sum, see in Fig. 5. However, \({\tilde{g}}\) will typically not be in a small \(\mathcal {C}^1\)-neighborhood of g in the space \({{\mathrm{\mathcal {R}}}}(M)\) of Riemannian metrics on M.
1.2 Proof strategy
The key idea to prove the Main Theorem is the following simple topological reasoning to which we will refer to as the Lasso Lemma, see Fig. 1.
Lemma 1.6
(“Lasso Lemma”) Let X be a simply connected topological space and let \(Y \subset X\) be any subspace. Let \(\gamma :S^1 \rightarrow Y\) be a loop and \(E \rightarrow Y\) be a vector bundle such that \(\gamma ^* E \rightarrow S^1\) is not trivial. Then \(X {\setminus } Y\) is not empty.
Proof
Since X is simply connected, there exists a homotopy \(H:I^2 \rightarrow X\) from \(\gamma \) to the constant loop. Since \(\gamma ^*E \rightarrow S^1\) is not trivial, \(\gamma \) cannot be null-homotopic in Y. Thus, there has to be at least one point in \(X {\setminus } Y\) that is hit by H, hence \(X {\setminus } Y \ne \emptyset \). \(\square \)
Remark 1.7
Of course we can identify \(I^2\) with \(D^2\) and obtain that any extension \(H:D^2 \rightarrow X\) of \(\gamma :S^1 \rightarrow Y\) satisfies \(H(p) \in X {\setminus } Y \) for at least one \(p \in D^2\).
We will apply this reasoning in the following way: We set \(X(M) := ({{\mathrm{\mathcal {R}}}}(M), \mathcal {C}^1)\), the space of all Riemannian metrics on M endowed with \(\mathcal {C}^1\)-topology. The set Y(M) will be a subspace of metrics tailor-made such that \(X(M) {\setminus } Y(M) \ne \emptyset \) directly implies the existence of an eigenvalue of higher multiplicity. (The set Y(M) contains the set of all metrics for which all eigenvalues are simple, see Definition 3.1. We use Y(M) instead of this simpler set for technical reasons.) The bundle \(E := E(M)\) consists of the span of the eigenspinors corresponding to a certain finite set of eigenvalues, see Definition 3.1. For the loop \(\gamma \) we will have to construct a suitable loop \(\mathbf {g}:S^1 \rightarrow Y(M)\) of Riemannian metrics.
Unfortunately, we will not be able to construct this loop directly. Therefore, we will use the following strategy: In Sect. 4.1, we consider loops of spin diffeomorphisms \((f_{\alpha })_{\alpha \in S^1}\) on M and study loops of metrics induced by setting \(g_{\alpha } := (f^{-1}_{\alpha })^* g, \alpha \in S^1, g \in {{\mathrm{\mathcal {R}}}}(M)\). We will work out a criterion when this loop induces a non-orientable bundle over \(S^1\) as desired, see Theorem 4.12. This reduces the problem of finding a loop of metrics to finding a loop of spin diffeomorphisms (which might be even harder in general). In Sect. 4.2, we will show that the family of rotations by degree \(\alpha \) on the sphere \(S^m\) will suit our purpose, if we start with a metric \(g_0\) that is obtained from the round metric by a small perturbation. This will give us the desired loop of metrics on the sphere \(S^m\).
Finally, we will have to transport the loop of metrics on the sphere \(S^m\) to our original manifold M. Any smooth m-manifold M is diffeomorphic to \(M \sharp S^m\), where \(\sharp \) denotes a connected sum, which is a special type of surgery. In Sect. 4.3, we will review the concept of surgery in the setting of Riemannian spin geometry and ultimately show that the existence of a suitable loop of metrics is stable under certain surgeries, see Theorem 4.26. Applying this to the connected sum will yield the desired result, see also Fig. 5.
1.3 Comparison to results for Laplace, Schrödinger and other operators
One should note that Conjecture 1.2 has not only been formulated for the Dirac operator. The Laplace operator on functions and the Schrödinger operator has been studied by Colin de Verdiére [6–8]. Some parts of these articles are formulated for more general classes of self-adjoint positive operators (notice however that the Dirac operator is not positive). These results were generalized later by Jammes [18–21] to the case of a Hodge Laplacian acting on p-forms and even to the Witten Laplacian.
It is interesting to note how the research on the problem of prescribing the eigenvalues of the Laplace operator has progressed: Jammes started with simple eigenvalues, advanced to double eigenvalues and finally considered eigenvalues of arbitrary multiplicity. Therefore, we think that a similar approach for the Dirac operator is reasonable.
A similar problem is given by the Laplace operator \(\Delta _{\Omega } = - \sum _i \partial _i^2\) on a domain \(\Omega \subset {{\mathrm{\mathbb {R}}}}^m\) with Dirichlet boundary conditions. The spectrum \(\{\lambda _j(\Omega )\}_{j \in {{\mathrm{\mathbb {N}}}}}\) of \(\Delta _{\Omega }\) depends on \(\Omega \), but it cannot be prescribed arbitrarily by varying \(\Omega \) among all domains of \({{\mathrm{\mathbb {R}}}}^m\) with a fixed volume. By the theorem of Faber-Krahn, the Ball B of volume c satisfies \(\lambda _1(B) = \min \{ \lambda _1(\Omega ) \mid \Omega \mathring{\subset }{{\mathrm{\mathbb {R}}}}^m, |\Omega | = c \}\). Analogously, by the theorem of Kran-Szegö, the minimum of \(\lambda _2(\Omega )\) among all bounded open subsets of \({{\mathrm{\mathbb {R}}}}^m\) with given volume is achieved by the union of two identical balls. A proof of these results (and many more results in this direction) can be found in [14].
While it is possible to prescribe eigenvalues of higher multiplicity for the Laplace operator, there are other physically motivated operators L for which \(Lu = \lambda u\) always implies that \(\lambda \) is simple. For instance, consider the Sturm–Liouville operator \( L u := - \Big ( \frac{d}{dx} \left( p \cdot \frac{d}{dx} \right) + q \Big )u = \lambda u\) on \(L^2([a,b])\) subject to the boundary conditions
for some fixed constants \(c_a, d_a, c_b, d_b \in {{\mathrm{\mathbb {R}}}}\). Here, p is differentiable and positive and q is continuous. As a domain for L we can choose the closure of the \(\mathcal {C}^2\) functions satisfying the boundary conditions (1.2) under the \(L^2\)-scalar product. Then L is an elliptic self-adjoint operator of second order depending on the functions p and q. However, any eigenvalue \(\lambda \) of L is always simple regardless of the choice of p and q, see for instance [12, Thm 4.1].
2 Construction of the set
The construction of a subset Y(M) suitable to apply Lemma 1.6 needs a consistent enumeration of the spectrum for all metrics by globally defined continuous functions. This is possible by the following result.
Theorem 2.1
([26, Main Thm. 2]) There exists a family of continuous functions \(\{\lambda _j:{{\mathrm{\mathcal {R}}}}(M) \rightarrow {{\mathrm{\mathbb {R}}}}\}_{j \in {{\mathrm{\mathbb {Z}}}}}\) such that for all \(g \in {{\mathrm{\mathcal {R}}}}(M)\), the sequence \((\lambda _j(g))_{j \in {{\mathrm{\mathbb {Z}}}}}\) represents all the eigenvalues of  (counted with multiplicities) and is non-decreasing, i.e. all \(g \in {{\mathrm{\mathcal {R}}}}(M)\) satisfy \(\lambda _j(g) \le \lambda _k(g)\), if \(j \le k\).
(counted with multiplicities) and is non-decreasing, i.e. all \(g \in {{\mathrm{\mathcal {R}}}}(M)\) satisfy \(\lambda _j(g) \le \lambda _k(g)\), if \(j \le k\).
We fix one such family for the entire article.
Definition 2.2
(Construction of Y(M)) Let \(k \in 2 {{\mathrm{\mathbb {N}}}}+1 \) be a fixed number (whose precise value will be specified later, see Remark 4.15). Then
i.e. Y(M) is the set of all metrics, where at least one of the eigenvalues with index \(1, \ldots , k\) is of odd multiplicity.
Remark 2.3
One might wonder, why we define Y(M) in such a complicated manner. For the moment we recall that \(X(M) = {{\mathrm{\mathcal {R}}}}(M)\) and convince ourselves that
Therefore, if we can show that \(X(M) {\setminus } Y(M)\) is not empty, we have shown the existence of an eigenvalue of higher multiplicity.
3 Construction of the bundle
3.1 Definition of E(M) as a set
The construction of the vector bundle E(M) as a set is straightforward.
Definition 3.1
(Construction of E(M)) Let k be a fixed number as in Definition 2.2. We define

where the bundle projection simply maps a \(\psi \in H^1(\Sigma ^g_{{{\mathrm{\mathbb {R}}}}} M)\) to g. That means that at each \(g \in Y(M)\), the bundle \(E^g(M)\) is spanned by the eigenspaces corresponding to the eigenvalues \(\lambda _1(g), \ldots , \lambda _k(g)\) mentioned in Definition 2.2.
Remark 3.2
Recall that \(\{\lambda _j\}_{j \in {{\mathrm{\mathbb {Z}}}}}\) evaluated at any \(g \in {{\mathrm{\mathcal {R}}}}(M)\) is a non-decreasing enumeration of the Dirac spectrum  counted with multiplicities. This is why we had to add the conditions \(\lambda _0(g) < \lambda _1(g)\) and \(\lambda _k(g) < \lambda _{k+1}(g)\) in (2.1); they ensure that the vector spaces defined in (3.1) have constant dimension, thus E(M) has constant rank.
counted with multiplicities. This is why we had to add the conditions \(\lambda _0(g) < \lambda _1(g)\) and \(\lambda _k(g) < \lambda _{k+1}(g)\) in (2.1); they ensure that the vector spaces defined in (3.1) have constant dimension, thus E(M) has constant rank.
Notice that E(M) consists of real vector spaces, since they are spanned by real eigenspinors of the real Dirac operator. We want to use E(M) to make a conclusion about the complex Dirac operator, so we will have to jump between the real and the complex spin geometry as discussed in Remark 1.4.
3.2 Topologization of E(M)
It remains only to topologize E(M) and show that it is a continuous vector bundle. The topology will be the subspace topology of a universal spinor field bundle. The continuity claim will follow from standard arguments of functional analysis.
For the definition of a topology on E(M), we need to compare the spinors in spinor bundles formed with respect to two different metrics, let’s say \(g,h \in {{\mathrm{\mathcal {R}}}}(M)\). The problem is that the the two Dirac operators  and
and  cannot be compared directly, because not only the operators depend on the metric, but also their domains. Therefore, the expression
cannot be compared directly, because not only the operators depend on the metric, but also their domains. Therefore, the expression  does not make any sense. A solution to this problem is to systematically construct identification isomorphisms (of Hilbert spaces)
does not make any sense. A solution to this problem is to systematically construct identification isomorphisms (of Hilbert spaces)
for any two metrics g and h and use these maps to pull back one Dirac operator to the domain of definition of the other. In the Riemannian case, this program has been carried out in [5] by means of a connection, but can also be described using only the Lifting Theorem, see [25]. There is also an alternative approach using generalized cylinders that also works in the Lorentz case, see [3]. We will apply these results in the following way.
Theorem 3.3
(Universal spinor field bundle) The universal spinor field bundle defined by
has a unique topology as a Hilbert bundle such that for any \(g \in {{\mathrm{\mathcal {R}}}}(M)\),
is a global trivialization. Here, \(\bar{\beta }_{h,g}\) is the identification isomorphism (3.2).
Proof
We fix a metric \(g \in {{\mathrm{\mathcal {R}}}}(M)\) and define the topology on \(L^2(\Sigma _{{{\mathrm{\mathbb {K}}}}} M)\) by simply declaring \(\bar{\beta }^g\) to be a trivialization. To see that this topology is independent of g, one has to show that the identification isomorphisms \(\bar{\beta }_{h,g}\) themselves depend \(\mathcal {C}^1\)-continuously on the metric. This is clear from the construction, but a bit tedious to carry out, see [27, Chapter 4] for details.
\(\square \)
Theorem 3.4
(Continuity of eigenbundles) Let \(Y \subset {{\mathrm{\mathcal {R}}}}(M)\) be any subspace and \(k \in {{\mathrm{\mathbb {N}}}}\) such that
Then the eigenbundle

is a continuous vector bundle of rank k over \({{\mathrm{\mathbb {K}}}}\), when endowed with the subspace topology inherited from the universal spinor field bundle \(L^2(\Sigma ^g_{{{\mathrm{\mathbb {K}}}}} M)\) from Theorem 3.3.
Proof
For any g in Y, we can find a simple closed curve \(c:S^1 \rightarrow \mathbb {C}\) such that \(\lambda _1(g), \ldots , \lambda _k(g)\) lie inside the area enclosed by c and the rest of the spectrum lies outside this area. Since the \(\lambda _j\)’s are continuous, the same holds in a small neighborhood of g. We obtain that the expression

depends continuously on g. It is shown in [22, Theorem 6.17, p. 178] that \(P^g\) and \({{\mathrm{id}}}- P^g\) define operators with spectrum \(\lambda _1(g), \ldots , \lambda _k(g)\) respectively \(\{\lambda _j(g), j \ne 1, \ldots , k\}\). Since the Dirac operator is self-adjoint, it follows that (3.3) is actually the spectral projection onto the sum of eigenspaces spanned by \(\lambda _1(g), \ldots , \lambda _k(g)\). As a result the images of the various \(P^g\)’s assemble to a continuous vector bundle, see [27, Thm. 4.5.2] for more details.\(\square \)
Corollary 3.5
(Topologization of E(M)) The bundle \(E(M) \rightarrow Y(M)\) from Definition 3.1 is a continuous vector bundle of rank k
3.3 Triviality of vector bundles over \(S^1\)
Ultimately, we want to apply Lemma 1.6 and therefore, we will have to verify that a real vector bundle over \(S^1\) is not trivial. The question whether or not a vector bundle is trivial can in general be approached by various topological machineries. But we are mainly interested in vector bundles over \(S^1\) and here the situation is very simple: The set of isomorphism classes of vector bundles of rank k over \(S^1\) has only two elements, see for instance [13, p.25]. One class represents the trivial, hence orientable bundles, the other class consists of vector bundles that are non-orientable, hence non-trivial.
Remark 3.6
(Sign of a vector bundle) A neat criterion to check when a real vector bundle \(E \rightarrow S^1\) of rank k is not orientable is the following: Let \({{\mathrm{GL}}}E \rightarrow S^1\) be the principal \({{\mathrm{GL}}}_k\)-bundle of frames of E. Let \(I := [0,1]\) be the unit interval and denote by \(\pi _{S^1}:I \rightarrow S^1\) the canonical projection. Since I is contractible, \(\pi _{S^1}^*({{\mathrm{GL}}}E) \rightarrow I\) has a global section \(\Psi \). For any such section \(\Psi \), there exists \(A \in {{\mathrm{GL}}}_k\) such that \(\Psi (1)=\Psi (0).A\). Clearly,
We define \({{\mathrm{sgn}}}(E) := {{\mathrm{sgn}}}(\Psi ) := {{\mathrm{sgn}}}(\det (A)) \in {{\mathrm{\mathbb {Z}}}}_2:=\{\pm 1 \}\) to be the sign of E.
It will be very important that the sign of a vector bundle is stable under small deformations of the bundle in the following sense.
Theorem 3.7
(Sign stability) Let \(\mathcal {H} \rightarrow X\) be a Hilbert bundle and \(E,{\tilde{E}} \rightarrow X\) be two k-dimensional subbundles of \(\mathcal {H}\) with induced metric. Denote by \(S {\tilde{E}} \rightarrow X\) the bundle of unit spheres of \({\tilde{E}}\). If
then \(E \cong {\tilde{E}}\). In particular, if \(X=S^1\), then \({{\mathrm{sgn}}}(E) = {{\mathrm{sgn}}}({\tilde{E}})\).
Proof
Let \(P:\mathcal {H} \rightarrow \mathcal {H}\) be the orthogonal projection onto E. Let \(x \in X, {\tilde{v}} \in S {\tilde{E}}_x\) be arbitrary and assume \(P_x({\tilde{v}}) = 0\). By definition, this simply means that \({\tilde{v}}\) is perpendicular to \(E_{x}\). This implies
which contradicts our assumption (3.4). Consequently, \(P|_{{\tilde{E}}}: {\tilde{E}} \rightarrow E\) is an isomorphism.
\(\square \)
4 Construction of the loop
4.1 Loops of metrics via loops of diffeomorphisms
In this section, we introduce a technique to produce certain loops of metrics via loops of spin diffeomorphisms. We denote by \({{\mathrm{Diff}}}(M)\) the diffeomorphism group of M endowed with the usual \(\mathcal {C}^{\infty }\)-topology, see for instance [17, Chpt. 2.1]. We will also use this topology on all the other mapping spaces.
Definition 4.1
(Associated loops of metrics) Let \(f:S^1 \rightarrow {{\mathrm{Diff}}}(M)\) be a loop of diffeomorphisms and \(g \in {{\mathrm{\mathcal {R}}}}(M)\) be any Riemannian metric. The family of metrics
is called an associated loop of metrics.
We are primarily interested in loops spin diffeomorphisms. Since there exist slightly different conventions, we fix the following notion.
Definition 4.2
(Spin diffeomorphism) An orientation-preserving diffeomorphism f of M is a spin diffeomorphism (or just “is spin”), if there exists \(\hat{f}\) such that

commutes. We say \(\hat{f}\) is a spin lift of f. We define
the spin diffeomorphism group (with lift).
Notice that in case M is connected and f is spin, there are always two spin lifts \(\hat{f}_{\pm }\) of f and \(\hat{f}_{-} = \hat{f}_{+}.(-1)\), where \(.(-1)\) denotes the action of \(-1 \in \widetilde{{\text {GL}}}^{+}_m\). With a bit more work, one can show the following relation.
Theorem 4.3
Let M be connected. The canonical projection

is a 2 : 1 covering space.
Proof
This follows essentially from the fact that \(\Theta :\widetilde{{\text {GL}}}^{+}M \rightarrow {\text {GL}}^{+}M\) is a 2 : 1-covering and that locally \(f_* = \Theta \circ \hat{f} \circ \Theta ^{-1}\). A detailed proof can be found in [27, Thm. 2.6.4].\(\square \)
Definition 4.4
(Odd/even) A loop of spin diffeomorphisms \(f:S^1 \rightarrow {{\mathrm{Diff}}}^{{{\mathrm{spin}}}}(M)\) is even, if there exists a loop \(\hat{f}\) such that

commutes. A loop is odd, if it is not even.
Remark 4.5
(Associated isotopy) Recall that we think of \(S^1\) as \(I / \sim \) and that \(\pi _{S^1}:I \rightarrow S^1\) denotes the canonical projection. Clearly, \(h := f \circ \pi _{S^1}:I \rightarrow {{\mathrm{Diff}}}^{{{\mathrm{spin}}}}\) is a path. By the path lifting property of covering spaces, there exists a lift \(\hat{h}:I \rightarrow \widehat{{{\mathrm{Diff}}}}^{{{\mathrm{spin}}}}(M)\) of h. Nevertheless, \(\hat{h}\) will in general only be a path, but not a loop:

We say h is the isotopy associated to f.
Definition 4.6
(Sign) Let \(f:S^1 \rightarrow {{\mathrm{Diff}}}^{{{\mathrm{spin}}}}(M)\) be a loop and h be its associated isotopy. The unique number \({{\mathrm{sgn}}}(f) \in {{\mathrm{\mathbb {Z}}}}_2\) such that \(\hat{h}(0) = {{\mathrm{sgn}}}(f) \hat{h}(1)\) is called the sign of f.
The sign of f does not depend on the choice of the lift \(\hat{h}\). Apparently, f is even if and only if \({{\mathrm{sgn}}}(f)=+1\). One can show that the sign has the following abstract characterization.
Lemma 4.7
The map \({{\mathrm{pr}}}^{{{\mathrm{spin}}}}:\widehat{{{\mathrm{Diff}}}}^{{{\mathrm{spin}}}}(M) \rightarrow {{\mathrm{Diff}}}^{{{\mathrm{spin}}}}(M)\) is a principal \({{\mathrm{\mathbb {Z}}}}_2\)-bundle. The connecting homomorphism \(\delta \) from its long exact homotopy sequence

satisfies \(\delta (f) = ({{\mathrm{id}}}_M, {{\mathrm{sgn}}}(f) {{\mathrm{id}}}_{\widetilde{{\text {GL}}}^{+}M})\) for any loop \(f:(S^1,0) \rightarrow ({{\mathrm{Diff}}}^{{{\mathrm{spin}}}}(M), {{\mathrm{id}}}_M)\).
Proof
Any 2 : 1-covering is normal, hence a principal \({{\mathrm{\mathbb {Z}}}}_2\)-bundle. Therefore, the claim follows from the definition of the connecting homomorphism \(\delta \).\(\square \)
Lemma 4.8
The sign induces a group homomorphism
and the elements of \(\ker {{\mathrm{sgn}}}\) are precisely the homotopy classes of even loops.
Proof
It follows from Lemma 4.7 that \({{\mathrm{sgn}}}\) is well-defined on homotopy classes. To see that \({{\mathrm{sgn}}}\) is a group homomorphism, let \(f^{(1)}, f^{(2)} \in \pi _1({{\mathrm{Diff}}}^{{{\mathrm{spin}}}}(M), {{\mathrm{id}}}_M)\) and consider
Let \(\hat{f}^{(1)}\) be a lift of \(f^{(1)}\) starting at the identity and \(\hat{f}^{(2)}\) be a lift of \(f^{(2)}\) starting hat \(\hat{f}^{(1)}(1)\). Then \(\hat{f} = \hat{f}^{(2)} * \hat{f}^{(1)}\) is a lift of f and
thus \({{\mathrm{sgn}}}(f) = {{\mathrm{sgn}}}(f^{(2)}) {{\mathrm{sgn}}}(f^{(1)})\). Clearly, the constant map \(S^1 \rightarrow {{\mathrm{Diff}}}^{{{\mathrm{spin}}}}(M), \alpha \mapsto {{\mathrm{id}}}_M\), lifts to the constant map \(\alpha \mapsto ({{\mathrm{id}}}_M, {{\mathrm{id}}}_{\widetilde{{\text {GL}}}^{+}M})\), so \({{\mathrm{sgn}}}\) is a group homomorphism as claimed.
\(\square \)
Remark 4.9
Although one cannot just replace the isotopy h associated to the loop f by the loop f itself in (4.1), there always exists a lift \({\tilde{f}}\) such that

commutes. Here, \(\cdot 2\) denotes the non-trivial double cover of \(S^1\). This follows from the fact that due to Lemma 4.8, we have \({{\mathrm{sgn}}}(f \circ \cdot 2) = {{\mathrm{sgn}}}(f)^2 = +1\) and thus, \(f \circ \cdot 2\) is even (although f itself might not be even).
Remark 4.10
In the special case where \(f:S^1 \rightarrow {{\mathrm{Diff}}}^{{{\mathrm{spin}}}}(M)\) is a group action, the notions of odd and even in the sense of Definition 4.4 coincide with the notions of an odd and even group action in the sense of [24, IV.§3, p.295].
Remark 4.11
Let \(f:S^1 \rightarrow {{\mathrm{Diff}}}^{{{\mathrm{spin}}}}(M)\) be a loop and h be its associated isotopy as in Remark 4.5. For any \(t \in I\), we get an induced isometry
between all the spinor bundles \(\Sigma ^{g_t}_{{{\mathrm{\mathbb {K}}}}} M\). The induced map on sections, denoted by \(\bar{h}_{t}\), satisfies

and therefore maps eigenspinors to eigenspinors.
The following will be crucial to verify the hypothesis of Lemma 1.6.
Theorem 4.12
Let \(Y \subset {{\mathrm{\mathcal {R}}}}(M)\) be any subset, \(f:S^1 \rightarrow {{\mathrm{Diff}}}^{{{\mathrm{spin}}}}(M)\) be a loop of spin diffeomorphisms and \(g \in {{\mathrm{\mathcal {R}}}}(M)\) such that the associated loop of metrics \(\alpha \mapsto (f_{\alpha }^{-1})^* g\) is a map \(\mathbf {g}:S^1 \rightarrow Y\). Furthermore, let \(E \subset L^2(\Sigma _{{{\mathrm{\mathbb {R}}}}} M) \rightarrow Y\) be a vector bundle of rank k. Let \(\bar{h}_t\) be the map induced by f as in Remark 4.11 and assume \(\bar{h}_t(E) \subset E\) for any \(t \in I\). Then \({\mathbf {g}}^*E \rightarrow S^1\) is not orientable if and only if f is odd and k is odd, i.e.
where \({{\mathrm{sgn}}}\) is as in Remark 3.6.
Proof
For any basis \((0,(\psi _1, \ldots , \psi _k)) \in {\mathbf {g}}^*E|_0\), the curve
is a curve of frames for \({\mathbf {g}}^*E \rightarrow S^1\) as in Remark 3.6. By definition, we have \(\bar{h}_1 = {{\mathrm{sgn}}}(f) \bar{h}_0\). Consequently, \(\Psi (1)=\Psi (0).A\), where \(A = {{\mathrm{sgn}}}(f) {{\mathrm{{\text {I}}}}}_k\), which has determinant \({{\mathrm{sgn}}}(f)^{k}\). By definition,
which implies the result.\(\square \)
4.2 The sphere
We have not yet shown that there exists an odd loop \(f:S^1 \rightarrow {{\mathrm{Diff}}}^{{{\mathrm{spin}}}}(M)\) and in general it is very difficult to construct non-trivial loops of spin diffeomorphisms. Fortunately, the most obvious candidate on the sphere does the job.
Theorem 4.13
For any \(\alpha \in {{\mathrm{\mathbb {R}}}}, m \in {{\mathrm{\mathbb {N}}}}\), we define the rotation
The map \(f:S^1 \rightarrow {{\mathrm{Diff}}}^{{{\mathrm{spin}}}}(S^m), \alpha \mapsto R_{2 \pi \alpha }|_{S^m}\), is an odd loop of spin diffeomorphisms.
Proof
Chose the round metric \(g^{\circ }\) on \(S^m\). In this case, the spin structure on \(S^m\) is simply given by the universal cover \(\vartheta _{m+1}: {{\mathrm{Spin}}}_{m+1} \rightarrow {{\mathrm{SO}}}_{m+1}\). By a tedious calculation carried out in [27, Lem. 5.4.5], one can check that the lift \(\hat{f}\) of f is given by
It follows from this explicit formula that f is odd.\(\square \)
To obtain an associated loop of metrics \(g_{\alpha } = (f^{-1}_{\alpha })^*g_0\), we need a start metric \(g_0\). Obviously, we cannot take the round metric \(g^{\circ }\), since rotations are an isometry with respect to \(g^{\circ }\), so the resulting loop would be trivial. A way out is provided by the following.
Theorem 4.14
(Odd neighborhood theorem) Let \((M,\Theta )\) be a closed spin manifold of dimension \(m \equiv 0,6,7 \mod 8\) and \(g_0\) be any Riemannian metric on M. In every \(\mathcal {C}^1\)-neighborhood of \(g_0 \in {{\mathrm{\mathcal {R}}}}(M)\), there exists \(g \in {{\mathrm{\mathcal {R}}}}(M)\) such that  has an eigenvalue \(\lambda \) of odd multiplicity.
has an eigenvalue \(\lambda \) of odd multiplicity.
Proof
The idea of this proof is as follows: By [9, Thm. 1], there exists a metric \(g_1 \in {{\mathrm{\mathcal {R}}}}(M)\) such that  has an eigenvalue of multiplicity 1, which is odd. Connect the metric \(g_0\) with \(g_1\), i.e. define the path \(g_t := tg_1 + (1-t)g_0, t \in I\), see Fig. 2. This path is real-analytic. As explained in [15, Lem. A.0.16], the Dirac operators
has an eigenvalue of multiplicity 1, which is odd. Connect the metric \(g_0\) with \(g_1\), i.e. define the path \(g_t := tg_1 + (1-t)g_0, t \in I\), see Fig. 2. This path is real-analytic. As explained in [15, Lem. A.0.16], the Dirac operators  are the restriction of a self-adjoint holomorphic family of type (A) onto I. Therefore, the eigenvalues of
are the restriction of a self-adjoint holomorphic family of type (A) onto I. Therefore, the eigenvalues of  can be described by a real-analytic family of functions \(\{ \lambda _j:I \rightarrow {{\mathrm{\mathbb {R}}}}\}_{j \in {{\mathrm{\mathbb {N}}}}}\). This means that for any \(t \in I\), the sequence \((\lambda _j(t))_{j \in {{\mathrm{\mathbb {N}}}}}\) represents all the eigenvalues of
can be described by a real-analytic family of functions \(\{ \lambda _j:I \rightarrow {{\mathrm{\mathbb {R}}}}\}_{j \in {{\mathrm{\mathbb {N}}}}}\). This means that for any \(t \in I\), the sequence \((\lambda _j(t))_{j \in {{\mathrm{\mathbb {N}}}}}\) represents all the eigenvalues of  counted with multiplicity (but possibly not ordered by magnitude). To prove the claim, we argue by contradiction: If the claim is wrong, there exists an open neighborhood around 0 in which all metrics \(g_t\) have only eigenvalues of even multiplicity. Since the eigenvalue functions \(\lambda _j\) are real analytic, this behavior extends to all of I and therefore, all the eigenvalues of \(g_1\) have even multiplicity as well. But this contradicts the choice of \(g_1\). The technical details of this last argument are a bit cumbersome and can be found in [27, Thm. 5.4.6].\(\square \)
counted with multiplicity (but possibly not ordered by magnitude). To prove the claim, we argue by contradiction: If the claim is wrong, there exists an open neighborhood around 0 in which all metrics \(g_t\) have only eigenvalues of even multiplicity. Since the eigenvalue functions \(\lambda _j\) are real analytic, this behavior extends to all of I and therefore, all the eigenvalues of \(g_1\) have even multiplicity as well. But this contradicts the choice of \(g_1\). The technical details of this last argument are a bit cumbersome and can be found in [27, Thm. 5.4.6].\(\square \)
Remark 4.15
(Choice of k ) We define the number k to be the dimension of the eigenspace of the eigenvalue of odd multiplicitiy, whose existence is asserted by Theorem 4.14.
Remark 4.16
By Theorem 4.14, Theorem 4.12 and Theorem 3.4, we have verified the hypothesis of Lemma 1.6 on the sphere, i.e. we have verified a sufficient criterion, which implies that the sphere admits a metric for which at least one eigenvalue is of higher multiplicity (which is well known). We will show in the next section that this criterion is stable under certain surgeries, which will allow us to verify it on much more general manifolds than just the sphere.
4.3 Surgery and eigenbundles
We introduce some basic notions concerning the surgery theory of spin manifolds and recall some well known results by Bär and Dahl [2]. Similar techniques are also used in [1]. We denote by \(S^l\) the l-dimensional unit sphere and by \(D^l\) the open unit ball.
Definition 4.17
(Surgery) Let N be a smooth n-manifold, let \(f:S^l \times \overline{D}^{n-l} \rightarrow N, 0 \le l \le n\), be a smooth embedding and set \(S:=f(S^l \times \{0\}), U := f(S^l \times D^{n-l})\). The manifold
where \(\sim \) is the equivalence relation generated by
is obtained by surgery in dimension l along S from N. The number \(n-l\) is the codimension of the surgery. The map f is the surgery map and S is the surgery sphere.
Remark 4.18
The space \({\tilde{N}}\) is again a smooth manifold (see for instance [23, IV.1] for a very detailed discussion of the connected sum). The manifold \({\tilde{N}}\) is always of the form
where \({\tilde{U}} \subset {\tilde{N}}\) is open. Here, by slight abuse of notation, \((N {\setminus } U) \subset N\) also denotes the image of \(N {\setminus } U\) in the quotient \({\tilde{N}} \), see Fig. 3.
Remark 4.19
(Spin structures and surgery) It can be shown that if one performs surgery in codimension \(n-l \ge 3\), the spin structure on N always extends uniquely (up to equivalence) to a spin structure on \({\tilde{N}}\), if \(l \ne 1\). In case \(l=1\), the boundary \(S^l \times S^{n-l-1}\) has two different spin structures, but only one of them extends to \(D^{l+1} \times S^{n-l-1}\). Adopting the convention from [2, p. 56], we assume that the map f is chosen such that it induces the spin structure that extends. Also, we will only perform surgeries in codimension \(n-l \ge 3\).
It is natural to ask how the Dirac spectra of a spin manifold before and after surgery are related to one another. The result is roughly that a finite part of the spectrum before surgery is arbitrarily close to the spectrum after surgery. For a precise statement, the following notion is useful.
Definition 4.20
( \((\Lambda _1, \Lambda _2, \varepsilon )\)-spectral close) Let \(T: H \rightarrow H\) and \(T':H' \rightarrow H'\) be two densely defined operators on Hilbert spaces H and \(H'\) (over \({{\mathrm{\mathbb {K}}}}\)) with discrete spectrum. Let \(\varepsilon > 0\) and \(\Lambda _1, \Lambda _2 \in {{\mathrm{\mathbb {R}}}}, \Lambda _1 < \Lambda _2\). Then T and \(T'\) are \((\Lambda _1, \Lambda _2, \varepsilon )\)-spectral close if
-
(i)
\( \Lambda _1, \Lambda _2 \notin ({{\mathrm{spec}}}T \cup {{\mathrm{spec}}}T')\).
-
(ii)
The operators T and \(T'\) have the same number k of eigenvalues in \(\mathopen {]} \Lambda _1, \Lambda _2 \mathclose {[}\), counted with \({{\mathrm{\mathbb {K}}}}\)-multiplicities.
-
(iii)
If \(\{\lambda _1 \le \cdots \le \lambda _k \}\) are the eigenvalues of T in \(\mathopen {]} \Lambda _1, \Lambda _2 \mathclose {[}\) and \(\{\lambda _1' \le \cdots \le \lambda _k' \}\) are the eigenvalues of \(T'\) in \(\mathopen {]} \Lambda _1, \Lambda _2 \mathclose {[}\), then
$$\begin{aligned} \forall 1 \le j \le k: |\lambda _j - \lambda _j'| < \varepsilon . \end{aligned}$$
Using this terminology, a central result is the following
Theorem 4.21
([2, Thm. 1.2]) Let \((N^n, g, \Theta ^g)\) be a closed Riemannian spin manifold, let \(0 \le l \le n-3\) and \(f:S^l \times \overline{D}^{n-l} \rightarrow N\) be any surgery map with surgery sphere S as in Definition 4.17. For any \(\varepsilon > 0\) (sufficiently small) and any  , there exists a Riemannian spin manifold \(({\tilde{N}}^{\varepsilon }, {\tilde{g}}^{\varepsilon })\), which is obtained from (N, g) by surgery such that
, there exists a Riemannian spin manifold \(({\tilde{N}}^{\varepsilon }, {\tilde{g}}^{\varepsilon })\), which is obtained from (N, g) by surgery such that  and
and  are \((-\Lambda , \Lambda , \varepsilon )\)-spectral close. This manifold is of the form \({\tilde{N}}^{\varepsilon } = (N {\setminus } U_{\varepsilon }) \dot{\cup }{\tilde{U}}_{\varepsilon }\), where \(U_{\varepsilon }\) is an (arbitrarily small) neighborhood of S and the metric \({\tilde{g}}^{\varepsilon }\) can be chosen such that \({\tilde{g}}|_{N {\setminus } U_{\varepsilon }} = g|_{N {\setminus } U_{\varepsilon }}\).
are \((-\Lambda , \Lambda , \varepsilon )\)-spectral close. This manifold is of the form \({\tilde{N}}^{\varepsilon } = (N {\setminus } U_{\varepsilon }) \dot{\cup }{\tilde{U}}_{\varepsilon }\), where \(U_{\varepsilon }\) is an (arbitrarily small) neighborhood of S and the metric \({\tilde{g}}^{\varepsilon }\) can be chosen such that \({\tilde{g}}|_{N {\setminus } U_{\varepsilon }} = g|_{N {\setminus } U_{\varepsilon }}\).
We will need not only the statement of Theorem 4.21, but also some arguments from the proof, which relies on estimates of certain Rayleigh quotients and these are very useful in their own right. One of the technical obstacles here is that the spinors on N and the spinors on \({\tilde{N}}^{\varepsilon }\) cannot be compared directly, since they are defined on different manifolds. A simple yet effective tool to solve this problem are cut-off functions adapted to the surgery.
Definition 4.22
(Adapted cut-off functions) In the situation of Theorem 4.21, assume that for each \(\varepsilon > 0\) (sufficiently small), we have a decomposition of N into \(N = U_{\varepsilon } \dot{\cup }A_{\varepsilon } \dot{\cup }V_{\varepsilon }\), where
for some \(r_{\varepsilon }, r'_{\varepsilon } > 0\). A family of cut-off functions \(\chi ^{\varepsilon } \in \mathcal {C}^\infty _c(N)\) is adapted to these decompositions, if
-
(i)
\(0 \le \chi ^{\varepsilon } \le 1\),
-
(ii)
\(\chi ^{\varepsilon } \equiv 0 \text { on a neighborhood of } \bar{U}_{\varepsilon }\),
-
(iii)
\(\chi ^{\varepsilon } \equiv 1 \text { on } V_{\varepsilon }\),
-
(iv)
\(|\nabla \chi ^{\varepsilon }| \le \tfrac{c}{r_{\varepsilon }} \text { on }N\) for some constant \(c>0\).
In case \({\tilde{N}}^{\varepsilon } = (N {\setminus } U_{\varepsilon }) \dot{\cup }{\tilde{U}}_{\varepsilon }\) is obtained from N by surgery, the restriction \(\chi ^{\varepsilon }|_{N {\setminus } U_{\varepsilon }}\) can be extended smoothly by zero to a function \(\chi ^{\varepsilon } \in \mathcal {C}_c^\infty ({\tilde{N}}^{\varepsilon })\). The situation is depicted in Fig. 4.
Remark 4.23
(Cutting off spinor fields) We can use the cut-off functions from Definition 4.22 to transport spinor fields from (N, g) to \(({\tilde{N}}^{\varepsilon }, {\tilde{g}}^{\varepsilon })\) and vice versa: For any \(\psi \in L^2(\Sigma ^g_{{{\mathrm{\mathbb {K}}}}} N)\), we can think of \(\chi ^{\varepsilon } \psi \) as an element in \(L^2(\Sigma ^{{\tilde{g}}}_{{{\mathrm{\mathbb {K}}}}} {\tilde{N}}^{\varepsilon })\) by extending \(\chi ^{\varepsilon } \psi \) to all of \({\tilde{N}}^{\varepsilon }\) by zero. Analogously, for any \({\tilde{\psi }} \in L^2(\Sigma ^{{\tilde{g}}}_{{{\mathrm{\mathbb {K}}}}} {\tilde{N}}^{\varepsilon })\), we can think of \(\chi ^{\varepsilon } {\tilde{\psi }}\) as an element in \(L^2(\Sigma ^g_{{{\mathrm{\mathbb {K}}}}} N)\) by extending \(\chi ^{\varepsilon } {\tilde{\psi }}|_{N {\setminus } {\tilde{U}}_{\varepsilon }}\) by zero to N. This correspondence is not an isomorphism, but one does not loose “too much”: It preserves smoothness and it is shown in [2] that under the assumptions of Theorem 4.21, for each eigenspinor \({\tilde{\psi }}^{\varepsilon } \in L^2(\Sigma ^{{\tilde{g}}^{\varepsilon }}_{{{\mathrm{\mathbb {K}}}}} {\tilde{N}}^{\varepsilon })\) to an eigenvalue \({\tilde{\lambda }}^{\varepsilon } \in ]-\Lambda , \Lambda [\), the spinor field \(\psi ^{\varepsilon } := \chi ^{\varepsilon } {\tilde{\psi }}^{\varepsilon } \in L^2(\Sigma ^g_{{{\mathrm{\mathbb {K}}}}} N)\) satisfies


The proof of Eqs. (4.6) and (4.7) is an integral part of the proof of Theorem 4.21, see [2, p. 69]. In combination, they imply the following crucial estimate for the Rayleigh quotient

This estimate is then used to apply the min–max principle, see Theorem 6.1, which gives the conclusion of Theorem 4.21.
We will need the following version of Theorem 4.21 that is slightly more general.
Theorem 4.24
Let \((N,\Theta )\) be a closed spin manifold of dimension \(n \ge 3\), let \(0 \le l \le n-3\) and f be a surgery map with surgery sphere \(S \subset N\) of dimension l as in Definition 4.17. Let \((Z,\tau _Z)\) be a compact topological space,
be a continuous family of Riemannian metrics and let \(\Lambda _1, \Lambda _2 \in \mathcal {C}^0(Z,{{\mathrm{\mathbb {R}}}}), \Lambda _1 < \Lambda _2\), such that

Then the following hold:
-
(i)
For any \(\varepsilon > 0\) (sufficiently small), there exists a spin manifold \(({\tilde{N}}^{\varepsilon }, {\tilde{\Theta }}^{\varepsilon })\), and a continuous family of Riemannian metrics
$$\begin{aligned} \tilde{\mathbf {g}}^{\varepsilon }:(Z, \tau _Z) \rightarrow ({{\mathrm{\mathcal {R}}}}({\tilde{N}}^{\varepsilon }), \mathcal {C}^2) \end{aligned}$$such that for each \(z \in Z\), the manifold \(({\tilde{N}}^{\varepsilon }, {\tilde{g}}^{\varepsilon }_{z})\) is obtained from \((N, g_{z})\) by surgery along S and such that for all \(z \in Z\), the operators
 and
and  are \((\Lambda _1(z), \Lambda _2(z), \varepsilon )\)-spectral close.
are \((\Lambda _1(z), \Lambda _2(z), \varepsilon )\)-spectral close. -
(ii)
For any open neighborhood \(U \subset N\) of the surgery sphere, one can choose \({\tilde{\mathbf {g}}^{\varepsilon }}\) such that
$$\begin{aligned} \forall z \in Z: {\tilde{g}}^{\varepsilon }_{z}|_{N {\setminus } U} = g_{z}|_{N {\setminus } U}. \end{aligned}$$(4.9) -
(iii)
If \({\tilde{\psi }}^{\varepsilon }_{z} \in L^2(\Sigma ^{{\tilde{g}}^{\varepsilon }_{z}}_{{{\mathrm{\mathbb {K}}}}} {\tilde{N}}^{\varepsilon }), z \in Z\), is in the span of the eigenspinors corresponding to eigenvalues in \([\Lambda _1(z), \Lambda _2(z)]\) and \(\chi ^{\varepsilon }_{z}\) is the cut-off function from Definition 4.22, the spinor field \(\psi ^{\varepsilon }_{z} := \chi ^{\varepsilon }_{z} {\tilde{\psi }}^{\varepsilon }_{z}\) satisfies
 (4.10)
(4.10)where \(c_z:= \tfrac{1}{2}(\Lambda _1(z) + \Lambda _2(z)), l_z := \tfrac{1}{2}|\Lambda _2(z) - \Lambda _1(z)|\).
Remark 4.25
Theorem 4.24 generalizes Theorem 4.21 in the following ways.
-
(i)
The metric g is replaced by a compact \(\mathcal {C}^2\)-continuous family of metrics. It has already been observed by Dahl in a later paper, see [9, Thm. 4], that the proof of Theorem 4.21 goes through in this case.
-
(ii)
The interval \([-\Lambda , \Lambda ]\) is replaced by the interval \([\Lambda _1, \Lambda _2]\), which might not be symmetric around zero. This is why one has to introduce c and l in (4.10).
-
(iii)
The field is \({{\mathrm{\mathbb {K}}}}\in \{{{\mathrm{\mathbb {R}}}}, \mathbb {C}\}\). This simply makes no difference in the proof.
-
(iv)
We replaced the constants \(\Lambda _1, \Lambda _2\) by continuous functions on Z. This is possible, since their key function in the proof is to ensure that at any \(z \in Z\) no eigenvalues enter or leave the spectral interval \([\Lambda _1(z), \Lambda _2(z)]\). Since they are continuous, they are also bounded, so uniform estimates are possible. (This generalization is not really needed in our proof of the Main Theorem.)
These generalizations are all straightforward, but some more arguments can be found in [27, A.8].
We are now able to prove the main result of this section (which will be applied for \(Z=S^1\) below) (Fig. 5).
Theorem 4.26
(surgery stability) Assume the hypothesis of Theorem 4.24 and in addition that \(\mathbf {g}:Z \rightarrow Y(N)\), where Y(N) is as in Definition 3.1 and let \(E(N) \rightarrow Y(N)\) be the corresponding eigenbundle as in Theorem 3.4. Let \({\tilde{\mathbf {g}}}^{\varepsilon }:Z \rightarrow {{\mathrm{\mathcal {R}}}}({\tilde{N}}^{\varepsilon })\) be the family from the conclusion of Theorem 4.24. Then for \(\varepsilon \) small enough, \({\tilde{\mathbf {g}}}^{\varepsilon }:Z \rightarrow Y({\tilde{N}}^{\varepsilon })\) and the corresponding eigenbundle \(E({\tilde{N}}^{\varepsilon }) \rightarrow Y({\tilde{N}}^{\varepsilon })\) satisfies
as vector bundles over Z.
Proof
The idea of the proof is to show that the situation of the Lasso Lemma (Lemma 1.6) still holds, if one perturbs everything a bit, see Fig. 6.
Step 1 \({\tilde{\mathbf {g}}}^{\varepsilon }:Z \rightarrow Y({\tilde{N}}^{\varepsilon })\): By the conclusion of Theorem 4.24, we obtain that for each \(z \in Z\), the operators  and
and  are \((\Lambda _1(z), \Lambda _2(z), \varepsilon )\)-spectral close. We fix some \(z_0 \in Z\) and take an enumeration of
are \((\Lambda _1(z), \Lambda _2(z), \varepsilon )\)-spectral close. We fix some \(z_0 \in Z\) and take an enumeration of  such that \({\tilde{\lambda }}_1^{\varepsilon }({\tilde{g}}^{\varepsilon }_{z_0})\) is the smallest eigenvalue \( > \Lambda _1(z_0)\). Let \(\{{\tilde{\lambda }}_j^{\varepsilon }\}_{j \in {{\mathrm{\mathbb {Z}}}}}\) be the corresponding enumeration of eigenvalues on \({\tilde{N}}^{\varepsilon }\) as in Theorem 2.1. We obtain, that for \(\varepsilon \) small enough
such that \({\tilde{\lambda }}_1^{\varepsilon }({\tilde{g}}^{\varepsilon }_{z_0})\) is the smallest eigenvalue \( > \Lambda _1(z_0)\). Let \(\{{\tilde{\lambda }}_j^{\varepsilon }\}_{j \in {{\mathrm{\mathbb {Z}}}}}\) be the corresponding enumeration of eigenvalues on \({\tilde{N}}^{\varepsilon }\) as in Theorem 2.1. We obtain, that for \(\varepsilon \) small enough
Therefore, for each \(z \in Z\), there are k eigenvalues between \(\Lambda _1(z)\) and \(\Lambda _2(z)\). Since k is odd, at least one eigenvalue must have odd multiplicity. Hence \({\tilde{\mathbf {g}}}^{\varepsilon }:Z \rightarrow {\tilde{Y}}^{\varepsilon }(N)\).
Step 2 (Passing from \({\tilde{N}}^{\varepsilon }\) to N): Let \(L^2(\Sigma _{{{\mathrm{\mathbb {K}}}}} N) \rightarrow {{\mathrm{\mathcal {R}}}}(N)\) be the universal spinor field bundle, see Theorem 3.3, E(N) be the bundle from Definition 3.1 and define
For any \(z \in Z\), let \(\chi ^{\varepsilon }_z\), be the canonical cut-off functions from Definition 4.22. These functions can be chosen such that \(\chi ^{\varepsilon }_z\) depends continuously on z. We consider the map
see also Remark 4.23. In case \(P({\tilde{\psi }}^{\varepsilon }_z) = 0\), we obtain \({\tilde{\psi }}^{\varepsilon }_z = 0\) by the weak unique continuation property for Dirac type operators, see [4, Rem. 2.3c)]. Therefore, this is a continuous morphism of vector bundles that is fibrewise injective. Hence, P has constant rank and its image \(E^{\varepsilon } := P({\tilde{E}}^{\varepsilon }) \subset \mathcal {H} \rightarrow Z\) is a continuous vector bundle isomorphic to \({\tilde{E}}^{\varepsilon }\).
Step 3 (Analyze Rayleigh quotients): We consider the \(\lambda _j\)’s as functions on Z by pulling them back via \(\mathbf {g}\) (and analogously for \({\tilde{\lambda }}_j^{\varepsilon }\)). For any \(z \in Z\), if \(\lambda _1(z), \ldots , \lambda _k(z)\) are the eigenvalues of  in \([\Lambda _1(z), \Lambda _2(z)]\), then \((\lambda _1(z)-c_z)^2, \ldots , (\lambda _k(z) - c_z)^2\) are the eigenvalues of
in \([\Lambda _1(z), \Lambda _2(z)]\), then \((\lambda _1(z)-c_z)^2, \ldots , (\lambda _k(z) - c_z)^2\) are the eigenvalues of  in \([0,l(z)^2]\), where \(c_z := \tfrac{1}{2} \left( \Lambda _1(z) + \Lambda _2(z) \right) \) and \(l_z := \tfrac{1}{2} |\Lambda _2(z) - \Lambda _1(z)|\). The span of their collective eigenspinors is the same space \(E_z\). It follows from (4.10) that the Rayleigh quotients satisfy
in \([0,l(z)^2]\), where \(c_z := \tfrac{1}{2} \left( \Lambda _1(z) + \Lambda _2(z) \right) \) and \(l_z := \tfrac{1}{2} |\Lambda _2(z) - \Lambda _1(z)|\). The span of their collective eigenspinors is the same space \(E_z\). It follows from (4.10) that the Rayleigh quotients satisfy

Now, choose \(\varepsilon \) small enough such that for all \(z \in Z\), we have \(l_z + \varepsilon < \rho _{k+1}(z)\), where \(\rho _{k+1}(z)\) is the \((k+1)\)-th eigenvalue of  . This is possible due to the continuity of \(\mathbf {g}\) and since
. This is possible due to the continuity of \(\mathbf {g}\) and since
by hypothesis. By Theorem 6.2, we obtain
By Theorem 3.7, we obtain that \(E \cong E^{\varepsilon } \cong {\tilde{E}}^{\varepsilon }\).
All in all, we have verified the hypothesis of Lemma 1.6 for \(E({\tilde{N}}^{\varepsilon }) \rightarrow Y({\tilde{N}}^{\varepsilon })\) and \({\tilde{\mathbf {g}}}^{\varepsilon }\) , which proves the claim.\(\square \)
Remark 4.27
Theorem 4.26 holds also for other sets than Y(N). For instance it holds for the larger set
with essentially the same proof. It does not hold for arbitrary subsets of \({{\mathrm{\mathcal {R}}}}(N)\) though. For instance, if one replaces the condition \(\exists 1 \le j \le k: \lambda _j \in 2 {{\mathrm{\mathbb {N}}}}+1\) by \(\exists 1 \le j \le k: \lambda _j \in 2 {{\mathrm{\mathbb {N}}}}\), the first step of the proof no longer holds, because an eigenvalue of even multiplicity might split up into two eigenvalues of odd multiplicity.
5 Proof of the Main Theorem
We are now in a position to put all the results together to prove the Main Theorem (stated below again for convenience).
Main Theorem
(Existence of higher multiplicities) Let \((M, \Theta )\) be a closed spin manifold of dimension \(m \equiv 0,6,7 \mod 8\). There exists a Riemannian metric \({\tilde{g}}\) on M such that the complex Dirac operator  has at least one eigenvalue of multiplicity at least two. In addition, \({\tilde{g}}\) can be chosen such that it agrees with an arbitrary metric g outside an arbitrarily small open subset on the manifold.
has at least one eigenvalue of multiplicity at least two. In addition, \({\tilde{g}}\) can be chosen such that it agrees with an arbitrary metric g outside an arbitrarily small open subset on the manifold.
Proof
The idea is to apply the surgery stability theorem Theorem 4.26, to the connected sum \(M \sharp S^m\), see Fig. 5.
Step 1 (Build lasso on the sphere): By Theorem 4.13, there exists an odd loop of spin diffeomorphisms on \(S^m\). By Theorem 4.14, there exists a metric on \(S^m\), for which at least one eigenvalue \(\lambda \) has an odd multiplicity k. The associated loop of metrics \(\mathbf {g}_{S^m}\) is a \(\mathcal {C}^2\)-continuous map \(\mathbf {g}_{S^m}:S^1 \rightarrow Y(S^m)\), where \(Y(S^m)\) is as in Definition 2.2. We obtain the associated real eigenbundle \(E(S^m)\) as in Definition 3.1. By Theorem 3.4, \(E(S^m) \rightarrow Y(S^m)\) is a continuous vector bundle of rank k. By Theorem 4.12, this bundle it not trivial. This verifies the hypothesis of Lemma 1.6 on the sphere.
Step 2 (Prepare M for surgery): Define the manifold \(N := M \amalg S^m\). Choose any metric \({\tilde{g}}\) on M. We obtain the loop \(\mathbf {g} := {\tilde{g}} \amalg \mathbf {g}_{S^m}:S^1 \rightarrow {{\mathrm{\mathcal {R}}}}(N)\). In case \(\lambda \in {{\mathrm{spec}}}{\tilde{g}}\), we first scale \(\mathbf {g}_{S^m}\) a little such that \(\lambda \notin {{\mathrm{spec}}}{\tilde{g}}\). We obtain that \({{\mathrm{spec}}}g_z\) is constant with respect to \(z \in S^1\). Since the spectrum is also discrete, we can certainly find continuous (even constant) functions \(\Lambda _1, \Lambda _2: S^1 \rightarrow {{\mathrm{\mathbb {R}}}}\) such that
It follows that \(\mathbf {g}:S^1 \rightarrow Y(N)\). We get that \(E(N) \rightarrow Y(N)\) is a non-trivial vector bundle of real rank k, since it is isomorphic to the pullback of \(E(M) \rightarrow Y(M)\) along the map \({{\mathrm{\mathcal {R}}}}(N) \rightarrow {{\mathrm{\mathcal {R}}}}(M), g \amalg h \mapsto g\).
Step 3 (Perform surgery): We extend the loop \(\mathbf {g}:S^1 \rightarrow Y(N)\) to a disc \(D^2 \rightarrow {{\mathrm{\mathcal {R}}}}(N)\), which is still denoted by \(\mathbf {g}\), and set \(Z := D^2\). We apply Theorem 4.24 to N in dimension \(l=0\) for \({{\mathrm{\mathbb {K}}}}= {{\mathrm{\mathbb {R}}}}\), i.e. we obtain a connected sum \({\tilde{N}}^{\varepsilon } = M \sharp S^m\) together with a resulting family \({\tilde{\mathbf {g}}}^{\varepsilon }:D^2 \rightarrow {{\mathrm{\mathcal {R}}}}({\tilde{N}}^{\varepsilon })\) of metrics. By Theorem 4.26, this gives a loop \({\tilde{\mathbf {g}}}^{\varepsilon }|_{S^1}:S^1 \rightarrow Y({\tilde{N}}^{\varepsilon })\) and the corresponding bundle \(E({\tilde{N}}^{\varepsilon }) \rightarrow Y({\tilde{N}}^{\varepsilon })\) satisfies \(({\tilde{\mathbf {g}}}^{\varepsilon }|_{S^1})^* E({\tilde{N}}^{\varepsilon }) \cong (\mathbf {g}|_{S^1})^*(E(N))\), thus it is also not trivial.
All in all, we have verified the hypothesis of Lemma 1.6 on \({\tilde{N}}^{\varepsilon } = M \sharp S^m\), which is spin diffeomorphic to M. This proves the first part of the Main Theorem. Recall from Remark 1.7 that our metric lies somewhere on the disc \({\tilde{\mathbf {g}}}^{\varepsilon }:D^2 \rightarrow {{\mathrm{\mathcal {R}}}}(M)\). Therefore, the second claim follows from (4.9).\(\square \)
Abbreviations
- \({\bar{\beta }}_{g,h}\) :
-
Identification isomorphism \(L^2(\Sigma ^g_{{{\mathrm{\mathbb {K}}}}} M) \rightarrow L^2(\Sigma ^h_{{{\mathrm{\mathbb {K}}}}} M)\)
- \(D^l\) :
-
Euclidean unit disc
- \({\widehat{{{\mathrm{Diff}}}}}^{{{\mathrm{spin}}}}(M)\) :
-
Group of spin diffeomorphisms with lift
- \({{\mathrm{Diff}}}(M)\) :
-
The diffeomorphism group of M
- \({{\mathrm{Diff}}}^{{{\mathrm{spin}}}}(M)\) :
-
group of spin diffeomorphisms
-
 :
: -
Dirac operator w.r.t. g over \({{\mathrm{\mathbb {K}}}}\)
- E(M):
-
A finite dimensional bundle over Y(M)
- \(\Gamma (\Sigma ^g_{{{\mathrm{\mathbb {K}}}}} M)\) :
-
Smooth spinor fields
- \(H^1(\Sigma ^g_{{{\mathrm{\mathbb {K}}}}} M)\) :
-
First order Sobolev space of sections of \(\Sigma ^g_{{{\mathrm{\mathbb {K}}}}} M\)
- I :
-
\(I := [0,1] \subset {{\mathrm{\mathbb {R}}}}\) is the unit interval
- K :
-
\(\mathbb {C}\) or \(\mathbb {H}\)
- \({{\mathrm{\mathbb {K}}}}\) :
-
\({{\mathrm{\mathbb {R}}}}\) or \(\mathbb {C}\)
- \(L^2(\Sigma ^g_{{{\mathrm{\mathbb {K}}}}} M)\) :
-
\(L^2\) spinor fields
- \(L^2(\Sigma _{{{\mathrm{\mathbb {K}}}}} M)\) :
-
Universal spinor field bundle
- \(\lambda _j(g)\) :
-
j-th eigenvalue of

- M :
-
A closed spin manifold of dimension m
- \(\mu (\lambda )\) :
-
Multiplicitiy of the eigenvalue \(\lambda \)
- \(\mu _{{{\mathrm{\mathbb {K}}}}}(\lambda )\) :
-
Multiplicitiy of the eigenvalue \(\lambda \) over \({{\mathrm{\mathbb {K}}}}\)
- \({{\mathrm{\mathbb {N}}}}\) :
-
The natural numbers \({{\mathrm{\mathbb {N}}}}=\{0,1,2, \ldots \}\)
- \(\pi _{S^1}:I \rightarrow S^1\) :
-
Canonical projection
- \({{\mathrm{pr}}}^{{{\mathrm{spin}}}}\) :
-
Projection \(\widehat{{{\mathrm{Diff}}}}^{{{\mathrm{spin}}}}(M) \rightarrow {{\mathrm{Diff}}}^{{{\mathrm{spin}}}}(M)\)
- \(R_{\alpha }\) :
-
Rotation by an angle \(\alpha \)
- \({{\mathrm{\mathcal {R}}}}(M)\) :
-
Space of Riemannian metrics on M with \(\mathcal {C}^1\)-topology
- \(S^l\) :
-
Euclidean unit sphere
- \({{\mathrm{sgn}}}(E)\) :
-
Sign of a vector bundle
- \({{\mathrm{sgn}}}(f)\) :
-
Sign of a loop
- \(\Sigma ^g_{{{\mathrm{\mathbb {K}}}}} M\) :
-
Spinor bundle over M w.r.t. g
-
 :
: -
Dirac spectrum
- \(\Theta \) :
-
A topological spin structure
- \(\mathcal {T}(M)\) :
-
Smooth vector fields on M
- X(M):
-
\(X(M) = {{\mathrm{\mathcal {R}}}}(M)\)
- Y(M):
-
A subset of Riemannian metrics
- \({{\mathrm{\mathbb {Z}}}}_2\) :
-
\(\{\pm 1\}\)
References
Ammann, B., Dahl, M., Humbert, E.: Surgery and harmonic Spinors. Adv. Math. 220(2), 523–539 (2009). doi:10.1016/j.aim.2008.09.013
Bär, C., Dahl, M.: Surgery and the spectrum of the Dirac operator. J. Reine Angew. Math. 552, 53–76 (2002). doi:10.1515/crll.2002.093
Bär, C., Gauduchon, P., Moroianu, A.: Generalized cylinders in semi-Riemannian and spin geometry. Math. Z. 249(3), 545–580 (2005). doi:10.1007/s00209-004-0718-0
Booss-Bavnbek, B., Marcolli, M., Wang, B.-L.: Weak UCP and perturbed monopole equations. Int. J. Math. 13(9), 987–1008 (2002). doi:10.1142/S0129167X02001551
Bourguignon, J.-P., Gauduchon, P.: Spineurs, opérateurs de Dirac et variations de métriques. Commun. Math. Phys. 144(3), 581–599 (1992)
Colin de Verdière, Y.: Multiplicités des valeurs propres. Laplaciens discrets et laplaciens continus. Rend. Math. Appl. (7) 13.3, 433–460 (1993)
Colin de Verdière, Y.: Sur la multiplicité de la première valeur propre non nulle du laplacien. Comment. Math. Helv. 61(2), 254–270 (1986). doi:10.1007/BF02621914
Colin de Verdière, Y.: Construction de laplaciens dont une partie finie du spectre est donnée. Ann. Sci. École Norm. Sup. 20, 599–615 (1987)
Dahl, M.: Prescribing eigenvalues of the Dirac operator. Manuscr. Math. 118(2), 191–199 (2005). doi:10.1007/s00229-005-0583-0
Friedrich, T.: Zur Abhängigkeit des Dirac-operators von der Spin-Struktur. Colloq. Math. 48(1), 57–62 (1984)
Friedrich, T.: Dirac Operators in Riemannian geometry. Vol. 25. Graduate Studies in Mathematics. Translated from the 1997 German original by Andreas Nestke, pp. xvi+195. American Mathematical Society, Providence (2000)
Hartman, P.: Ordinary Differential Equations, pp. xiv+612. Wiley, New York (1964)
Hatcher, A.: Vector bundles and K-theory. http://www.math.cornell.edu/~hatcher/VBKT/VBpage.html (2009)
Henrot, A.: Extremum problems for eigenvalues of elliptic operators. Front. Math. Birkhäuser Verlag, Basel, pp. x+202 (2006)
Hermann, A.: Dirac eigenspinors for generic metrics. Ph.D. thesis. url: http://epub.uni-regensburg.de/25024/. 26 June 2012
Hijazi, O.: Spectral properties of the Dirac operator and geometrical structures. In: Campo, H.O., Rayes, A., Paycha, S. (eds.) Proceedings of the Summer School on Geometric Methods for Quantum Field Theory, pp. 116–169. World Scientific Publishing Co. (1999). doi:10.1142/9789812810571_0002
Hirsch, M.W.: Differential Topology. Vol. 33. Graduate Texts in Mathematics. Corrected reprint of the 1976 original, pp. x+222. Springer, New York (1994)
Jammes, P.: Prescription du spectre du laplacien de Hodge-de Rham dans une classe conforme. Comment. Math. Helv. 83(3), 521–537 (2008). doi:10.4171/CMH/134
Jammes, P.: Construction de valeurs propres doubles du laplacien de Hodge-de Rham. J. Geom. Anal. 19(3), 643–654 (2009). doi:10.1007/s12220-009-9079-6
Jammes, P.: Prescription de la multiplicité des valeurs propres du laplacien de Hodge- de Rham. Comment. Math. Helv. 86(4), 967–984 (2011). doi:10.4171/CMH/245
Jammes, P.: Sur la multiplicité des valeurs propres du laplacien deWitten. Trans. Am. Math. Soc. 364(6), 2825–2845 (2012). doi:10.1090/S0002-9947-2012-05363-3
Kato, T.: Perturbation Theory for Linear Operators. Classics in Mathematics. Reprint of the 1980 edition, pp. xxii+619. Springer, Berlin (1995)
Kosinski, A.A.: Differential Manifolds. Vol. 138. Pure and Applied Mathematics, pp. xvi+248. Academic Press Inc., Boston (1993)
Lawson Jr, H.B., Michelsohn, M.-L.: Spin Geometry. Vol. 38. Princeton Mathematical Series, pp. xii+427. Princeton University Press, Princeton (1989)
Maier, S.: Generic metrics and connections on Spin- and Spin\(\chi \)-manifolds. Commun. Math. Phys. 188(2), 407–437 (1997). doi:10.1007/s002200050171
Nowaczyk, N.: Continuity of Dirac spectra. Ann. Glob. Anal. Geom. 44(4), 541–563 (2013). doi:10.1007/s10455-013-9381-1
Nowaczyk, N.: Dirac eigenvalues of higher multiplicity. Ph.D. thesis. url: http://epub.uni-regensburg.de/31209/. 14 Jan 2015
Reed, M., Simon, B.: Methods of Modern Mathematical Physics. IV. Analysis of operators, pp. xv+396. Academic Press [Harcourt Brace Jovanovich Publishers], New York (1978)
Acknowledgments
I would like to thank Bernd Ammann for interesting discussions. I’m also grateful to Mattias Dahl for explaining parts of his previous work to me. This research was kindly supported by the Studienstiftung des deutschen Volkes and the DFG Graduiertenkolleg GRK 1692 “Curvature, Cycles and Cohomology”.
Author information
Authors and Affiliations
Corresponding author
Appendix: Rayleigh quotients and the min–max principle
Appendix: Rayleigh quotients and the min–max principle
In this section, we provide a version of the min–max principle suitable for our needs, see also [28, XIII.1].
Theorem 6.1
(Min–max principle) Let H be a Hilbert space and \(T: {{\mathrm{\mathcal {D}}}}(T) \subset H \rightarrow H\) be a densely defined self-adjoint operator with compact resolvent. Assume that the spectrum of T satisfies \(b \le \lambda _1 \le \lambda _2 \le \cdots \) for some lower bound \(b \in {{\mathrm{\mathbb {R}}}}\). Then for any \(k \in {{\mathrm{\mathbb {N}}}}\), we have
where the \(\min \) is taken over all linear subspaces \(U \subset {{\mathrm{\mathcal {D}}}}(T)\) of dimension k.
Theorem 6.2
Let H be a Hilbert space, \(T:H \rightarrow H\) be a densely defined operator, self-adjoint with compact resolvent. Let \(\Lambda > 0\) and \(k \in {{\mathrm{\mathbb {N}}}}\) and assume that the first \(k+1\) distinct eigenvalues of T satisfy
Define \(E^{(\nu )} := \ker (T-\lambda _{\nu }), V := \bigoplus _{\nu =1}^{k}{E^{(\nu )}}\), and let \(x \in {{\mathrm{\mathcal {D}}}}(T), \Vert x\Vert =1\), such that \(\langle Tx, x \rangle \le \Lambda + \varepsilon \). Then the distance between x and V satisfies \({{\mathrm{dist}}}(V,x)^2 \le \frac{\Lambda + \varepsilon }{\lambda _{k+1}}\).
Proof
Consider the orthogonal decomposition
By hypothesis
Let \(P_V:H \rightarrow H\) be the orthogonal projection onto V. We obtain
\(\square \)
Rights and permissions
About this article
Cite this article
Nowaczyk, N. Existence of Dirac eigenvalues of higher multiplicity. Math. Z. 284, 285–307 (2016). https://doi.org/10.1007/s00209-016-1657-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00209-016-1657-2



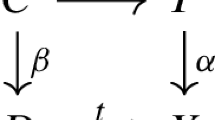
 is discrete and unbounded from both sides.
is discrete and unbounded from both sides.




 and
and  are
are 


 :
:
 :
: