A New Formulation of the 3D Compressible Euler Equations with Dynamic Entropy: Remarkable Null Structures and Regularity Properties

Abstract

We derive a new formulation of the 3D compressible Euler equations exhibiting remarkable null structures and regularity properties. Our results hold for an arbitrary equation of state (which yields the pressure in terms of the density and the entropy) in non-vacuum regions where the speed of sound is positive. Our work here is an extension of our prior joint work with J. Luk, in which we derived a similar new formulation in the special case of a barotropic fluid, that is, when the equation of state depends only on the density. The new formulation comprises covariant wave equations for the Cartesian components of the velocity and the logarithmic density coupled to a transport equation for the specific vorticity (defined to be vorticity divided by density), transport equations for the entropy and its gradient, and some additional transport–divergence–curl-type equations involving special combinations of the derivatives of the solution variables. The good geometric structures in the equations allow one to use the full power of the vectorfield method in treating the “wave part” of the system. In a forthcoming application, we will use the new formulation to give a sharp, constructive proof of finite-time shock formation, tied to the intersection of acoustic “wave characteristics,” for solutions with nontrivial vorticity and entropy at the singularity. In the present article, we derive the new formulation and provide an overview of the central role that it plays in the proof of shock formation. Although the equations are significantly more complicated than they are in the barotropic case, they enjoy many of same remarkable features, including: (i) all derivative-quadratic inhomogeneous terms are null forms relative to the acoustical metric, which is the Lorentzian metric driving the propagation of sound waves and (ii) the transport–divergence–curl-type equations allow one to show that the entropy is one degree more differentiable than the velocity and that the vorticity is exactly as differentiable as the velocity, assuming that the initial data enjoy the same gain in regularity. This represents a gain of one derivative compared to standard estimates. This gain of a derivative, which seems to be new for the entropy, is essential for closing the energy estimates in our forthcoming proof of shock formation, since the second derivatives of the entropy and the first derivatives of the vorticity appear as inhomogeneous terms in the wave equations.

1 Introduction and Summary of Main Results

Our main result in this article is Theorem 1, in which we provide a new formulation of the compressible Euler equations with vorticity and dynamic entropy that exhibits astoundingly good null structures and regularity properties. We consider only the physically relevant case of three spatial dimensions, though similar results hold in any number of spatial dimensions. Our results hold for an arbitrary equation of state in non-vacuum regions where the speed of sound is positive. By “equation of state,” we mean the function yielding the pressure in terms of the density and the entropy. Our results are an extension of our previous joint work with J. Luk [21], in which we derived a similar new formulation of the equations in the special case of a barotropic fluid, that is, when the equation of state depends only on the density. Our work [21] was in turn inspired by Christodoulou’s remarkable proofs [6, 9] of shock formation for small-data solutions to the compressible Euler equations in irrotational (that is, vorticity-free) and isentropic (that is, with constant entropy) regions as well as our prior work [28] on shock formation for general classes of wave equations; we describe these works in more detail below.

A principal application of the new formulation is that it serves as the starting point for our forthcoming work, in which we plan to give a sharp proof of finite-time shock formation for an open set of initial conditions without making any symmetry assumptions, irrotationality assumption, isentropic assumption, or barotropic equation of state assumption. The forthcoming work will be an extension of our recent work with J. Luk [22], in which we proved a similar shock formation result for barotropic fluids in the case of two spatial dimensions.

Our new formulation of the compressible Euler equations comprises covariant wave equations, transport equations, and transport–divergence–curl-type equations involving special combinations of solution variables [see Def. 3]. As we mentioned earlier, the inhomogeneous terms exhibit good null structures, which we characterize in our second main result, Theorem 2. Its proof is quite simple given Theorem 1. As we mentioned above, in [21], we derived a similar new formulation of the equations under the assumption that the fluid is barotropic. The barotropic assumption, though often made in astrophysics, cosmology, and meteorology, is generally unjustified because it entails neglecting thermal dynamics and their effect on the fluid. Compressible fluid models that are more physically realistic feature equations of state that depend on the density and a second thermodynamic state-space variable, such as the temperature, which satisfies an evolution equation that is coupled to the other fluid equations. In the present article, we allow for an arbitrary physical equation of state in which, for mathematical convenience, we have chosen the second thermodynamic variable to be the entropy per unit mass (which we refer to as simply the “entropy” from now on).¹

1.1 Paper Outline

In the remainder of Section 1, we summarize some of our notation, provide some standard background material on the compressible Euler equations, define the solution variables that we use in formulating our main results, roughly summarize our main results, and provide some preliminary context. In Section 2, we define some geometric objects that we use in formulating our main results and provide some basic background on Lorentzian geometry and null forms. In Section 3, we give precise statements of our main results, namely Theorems 1 and 2, and give the simple proof of the latter. In Section 4, we provide an overview of our forthcoming proof of shock formation, highlighting the roles that Theorems 1 and 2 will play. In Section 5, we prove Theorem 1 via a series of calculations in which we observe many important cancellations.

1.2 Notation

Throughout $\lbrace x^{\alpha } \rbrace _{\alpha =0,1,2,3}$ denotes a standard Cartesian coordinate system on ${\mathbb {R}}^{1+3} \simeq {\mathbb {R}} \times {\mathbb {R}}^3$.² More precisely, $x^0 \in {\mathbb {R}}$ is the time coordinate and $(x^1,x^2,x^3) \in {\mathbb {R}}^3$ are spatial coordinates. We use the notation $\displaystyle \partial _{\alpha } := \frac{\partial }{\partial x^{\alpha }}$ to denote the corresponding Cartesian coordinate partial derivative vectorfields. We often use the alternate notation $x^0 = t$ and $\partial _0 = \partial _t$. Greek “spacetime” indices such as $\alpha$ vary over 0, 1, 2, 3, while Latin “spatial” indices such as a vary over 1, 2, 3. We use Einstein’s summation convention in that repeated indices are summed over their respective ranges. $\varSigma _t$ denotes the usual flat hypersurface of constant Cartesian time t. If V is a vectorfield and f is a function, then $Vf := V^{\alpha } \partial _{\alpha } f$ denotes the derivative of f in the direction V.

1.3 Background on the Compressible Euler Equations

In this subsection, we provide some basic background on the compressible Euler equations and provide definitions that we will use throughout the article.

1.3.1 Equations of State

We study the compressible Euler equations for a perfect fluid in three spatial dimensions under any equation of state with positive sound speed [see definition (1.3.9)]. The equation of state is the function (which we assume to be given) that determines the pressure p in terms of the density $\varrho \ge 0$ and the entropy $s\in {\mathbb {R}}$:

$$\begin{aligned} p = p(\varrho ,s). \end{aligned}$$

(1.3.1)

Given the equation of state, the compressible Euler equations can be formulated as evolution equations for the velocity $v:{\mathbb {R}}^{1+3} \rightarrow {\mathbb {R}}^3$, the density $\varrho :{\mathbb {R}}^{1+3} \rightarrow [0,\infty )$, and the entropy $s:{\mathbb {R}}^{1+3} \rightarrow (-\infty ,\infty )$.

1.3.2 Some Definitions

We use the following notation for the Euclidean divergence and curl of a $\varSigma _t-$tangent vectorfield V with Cartesian components $\lbrace V^a \rbrace _{a=1,2,3}$:³

$$\begin{aligned} \hbox {div}V := \partial _a V^a, \qquad (\hbox {curl}V)^i := \varepsilon _{iab} \partial _a V^b. \end{aligned}$$

(1.3.2)

In (1.3.2) and throughout, $\varepsilon _{ijk}$ denotes the fully antisymmetric symbol normalized by

$$\begin{aligned} \varepsilon _{123} = 1. \end{aligned}$$

(1.3.3)

The vorticity $\omega : {\mathbb {R}}^{1+3} \rightarrow {\mathbb {R}}^3$ is the vectorfield with the following Cartesian components, ($i=1,2,3$):

$$\begin{aligned} \omega ^i&:= (\hbox {curl}v)^i. \end{aligned}$$

(1.3.4)

Rather than formulating the equations in terms of the density and the vorticity, we find it convenient to use the logarithmic density$\uprho$ and the specific vorticity$\varOmega$; some of the equations that we study take a simpler form when expressed in terms of these variables.

To define these quantities, we first fix a constant “background density” ${\bar{\varrho }}$ such that

$$\begin{aligned} {\bar{\varrho }} > 0. \end{aligned}$$

(1.3.5)

In applications, one may choose any convenient value of ${\bar{\varrho }}$.⁴

Definition 1

(Logarithmic density and specific vorticity) We define the logarithmic density $\uprho$, which is a scalar function, and the specific vorticity $\varOmega$, which is a $\varSigma _t-$tangent vectorfield, as follows:

$$\begin{aligned} \uprho&:= \ln \left( \frac{\varrho }{{\bar{\varrho }}} \right) , \qquad \varOmega := \frac{\omega }{(\varrho /{\bar{\varrho }})} = \frac{\omega }{\exp \uprho }. \end{aligned}$$

(1.3.6)

We assume throughout that⁵

$$\begin{aligned} \varrho > 0. \end{aligned}$$

(1.3.7)

In particular, the variable $\uprho$ is finite assuming (1.3.7).

In the study of shock formation, to obtain sufficient top-order regularity for the entropy, it is important to work with the $\varSigma _t$-tangent vectorfield $S$ provided by the next definition; see Remark 1 for further discussion.

Definition 2

(Entropy gradient vectorfield) We define the Cartesian components of the $\varSigma _t$-tangent entropy gradient vectorfield$S$ as follows, ($i=1,2,3$):

$$\begin{aligned} S^i&:= \delta ^{ia} \partial _a s= \partial _i s. \end{aligned}$$

(1.3.8)

Remark 1

(The need for$S$and transport-div-curl estimates in controlling$s$) In our forthcoming proof of shock formation, we will control the top-order derivatives of $s$ by combining estimates for transport equations with div-curl-type elliptic estimates for $S$ and its higher derivatives. At first glance, it might seem like the div-curl elliptic estimates could be replaced with simpler elliptic estimates based on controlling $\varDelta s$, in view of the simple identity $\varDelta s= \hbox {div}S$. Although this is true for $\varDelta s$ itself, in our proof of shock formation, the Euclidean Laplacian $\varDelta$ is not compatible with the differential operators that we must use to commute the equations when obtaining estimates for the solution’s higher derivatives. Specifically, like all prior works on shock formation in more than one spatial dimension, our forthcoming proof is based on commuting the equations with geometric vectorfields (see Section 4.3 for an overview) that are adapted to the acoustic wave characteristics of the compressible Euler equations.⁶ The acoustic characteristics have essentially no relation to the operator $\varDelta$. For this reason, the geometric vectorfields exhibit very poor commutation properties with $\varDelta$ and in fact, would generate uncontrollable error terms if commuted with it. In contrast, in carrying out our transport–divergence–curl-type estimates, we only have to commute the geometric vectorfields through first-order operators, including a transport operator, $\hbox {div}$, and $\hbox {curl}$; it turns out that commuting the geometric vectorfields through first-order operators, as long as they are weighted with an appropriate geometric weight, leads to controllable error terms, compatible with following the solution all the way to the singularity.⁷ We explain this issue in more detail in Steps 1 and 2 of Section 4.3.

Notation 11

(Differentiation with respect to state-space variables via semicolons) If $f = f(\uprho ,s)$ is a scalar function, then we use the following notation to denote partial differentiation with respect to $\uprho$ and $s$: $\displaystyle f_{;\uprho } := \frac{\partial f}{\partial \uprho }$ and $\displaystyle f_{;s} := \frac{\partial f}{\partial s}$. Moreover, $\displaystyle f_{;\uprho ;s} := \frac{\partial ^2 f}{\partial s\partial \uprho }$, and we use similar notation for other higher-order partial derivatives of f with respect to $\uprho$ and $s$.

1.3.3 Speed of Sound and an Assumption on the Equation of State

The scalar function $c\ge 0$ defined by

$$\begin{aligned} c&:= \sqrt{\frac{\partial p}{\partial \varrho }\left| \right. _{s}} = \sqrt{\frac{1}{{\bar{\varrho }}}\exp (-\uprho ) p_{;\uprho }} \end{aligned}$$

(1.3.9)

is a fundamental quantity known as the speed of sound.⁸ To obtain the last equality in (1.3.9), we used the chain rule identity $\displaystyle \frac{\partial }{\partial \varrho } \left| \right. _{s} = \frac{1}{{\bar{\varrho }}} \exp (-\uprho ) \frac{\partial }{\partial \uprho } \left| \right. _{s}$. From now on, we view $c$ as a function of the logarithmic density and the entropy:

$$\begin{aligned} c&= c(\uprho ,s). \end{aligned}$$

(1.3.10)

Assumption on the equation of state

We make the following physical assumption, which ensures the hyperbolicity of the system when $\varrho > 0$:

We assume that $c> 0$ when $\varrho > 0$. Equivalently, we assume that $c> 0$ whenever $\uprho \in (-\infty ,\infty )$.

1.3.4 A Standard First-order Formulation of the Compressible Euler Equations

We now state a standard first-order formulation of the compressible Euler equations; these equations form the starting point of our new formulation. Specifically, relative to Cartesian coordinates, the compressible Euler equations can be expressed as follows, where we again stress that $\uprho$ denotes the logarithmic density:⁹

$$\begin{aligned} B\uprho&= - \hbox {div}v, \end{aligned}$$

(1.3.11a)

$$\begin{aligned} Bv^i&= - c^2 \delta ^{ia} \partial _a \uprho - \exp (-\uprho ) \frac{p_{;s}}{{\bar{\varrho }}} \delta ^{ia} \partial _a s, \end{aligned}$$

(1.3.11b)

$$\begin{aligned} Bs&= 0. \end{aligned}$$

(1.3.11c)

Above and throughout, $\delta ^{ab}$ denotes the standard Kronecker delta, and

$$\begin{aligned} B&:= \partial _t + v^a \partial _a \end{aligned}$$

(1.3.12)

denotes the material derivative vectorfield. We stress already that $B$ plays a critical role in the ensuing discussion. Readers can consult, for example, [9] for discussion behind the physics of the equations and for a first-order formulation of them in terms of $\varrho$, $\lbrace v^i \rbrace _{i=1,2,3}$, and $s$, which can easily seen to be equivalent to (1.3.11a)–(1.3.11c).

1.3.5 Modified Fluid Variables

Although it is not obvious, the quantities that we provide in the following definition satisfy transport equations with a good structure; see (3.1.3b) and (3.1.4a). When combined with elliptic estimates, the transport equations allow one to prove that the specific vorticity and entropy are one degree more differentiable than naive estimates would yield, assuming that these quantities initially have the extra differentiability. This gain of regularity is essential in our forthcoming proof of shock formation since it is needed to control some of the source terms in the wave equations for the velocity, density, and entropy, specifically, the first products on RHSs (3.1.1a)–(3.1.1c). In addition, the source terms in the transport equations have a good null structure, which is also essential in the study of shock formation. We discuss these issues in more detail in Section 4.

Definition 3

(Modified fluid variables) We define the Cartesian components of the $\varSigma _t$-tangent vectorfield ${\mathcal {C}}$ and the scalar function ${\mathcal {D}}$ as follows, ($i=1,2,3$):

$$\begin{aligned} {\mathcal {C}}^i&:= \exp (-\uprho ) (\hbox {curl}\varOmega )^i + \exp (-3\uprho ) c^{-2} \frac{p_{;s}}{{\bar{\varrho }}} S^a \partial _a v^i - \exp (-3\uprho ) c^{-2} \frac{p_{;s}}{{\bar{\varrho }}} (\partial _a v^a) S^i, \end{aligned}$$

(1.3.13a)

$$\begin{aligned} {\mathcal {D}}&:= \exp (-2 \uprho ) \hbox {div}S- \exp (-2 \uprho ) S^a \partial _a \uprho . \end{aligned}$$

(1.3.13b)

1.4 A Brief Summary of Our Main Results

For the reader’s convenience, we now provide a brief, informal version of our main results.

Summary of the main results. The compressible Euler equations (1.3.11a)–(1.3.11c) can be reformulated as a system of covariant wave equations for the Cartesian components $\lbrace v^i \rbrace _{i=1,2,3}$ of the velocity and the logarithmic density $\uprho$ coupled to a transport equation for the entropy $s$, transport equations for the Cartesian components $\lbrace S^i \rbrace _{i=1,2,3}$ of the entropy gradient, transport equations for the Cartesian components $\lbrace \varOmega ^i \rbrace _{i=1,2,3}$ of the specific vorticity, transport equations for the modified fluid variables of Def. 3, and identities for $\hbox {div}\varOmega$ and $(\hbox {curl}S)^i$; see Theorem 1 for the equations.¹⁰ Moreover, the inhomogeneous terms exhibit remarkable structures, including good null form structures tied to the acoustical metricg (which is the Lorentzian metric corresponding to the propagation of sound waves, see Def. 4); see Theorem 2 for the precise statement.

1.5 Some Preliminary Context for the Main Results

In this subsection, we provide some preliminary context for our main results, with a focus on the special null structures exhibited by the inhomogeneous terms in our new formulation of the compressible Euler equations and their relevance for the study of shock formation. The presence of special null structures in the equations might seem surprising since they are often associated with equations that admit global solutions; see, for example, Klainerman’s work [18] on small-data global existence for wave equations satisfying his “classic” null condition. However, as we explain below, the good null structures are in fact key to proving that the shock forms. Several works have contributed to our understanding of the important role that the null structures play in the proof of shock formation, including [6, 14, 21, 22, 28]. Below we will review these works and some related ones and, for the results in more than one spatial dimension, we will highlight the role that the presence of good geo-analytic structures and null structures played in the proofs.

The famous work of Riemann [26], in which he invented the Riemann invariants, yielded the first general proof of shock formation for solutions to the compressible Euler equations in one spatial dimension. More precisely, for such solutions, the velocity and density remain bounded, even though their first-order Cartesian coordinate partial derivatives blow up in finite time. This type of singularity formation is also known as wave breaking in the literature. The standard proof of this phenomenon is elementary and is essentially based on identifying a Riccati-type blowup-mechanism for the solution’s first derivatives; see Section 4.1 for a review of these ideas in the context of simple plane wave solutions.

In all prior proofs of shock formation in more than one spatial dimension, there also was a Riccati-type mechanism that drove the blowup of the solution’s derivatives. However, in the analysis, the authors encountered many new kinds of error terms that are much more complicated than the ones encountered by Riemann. A key aspect of the proofs was showing that the additional error terms do not interfere with the Riccati-type blowup-mechanism. This is where the special null structure mentioned above enters into play: terms that enjoy the special null structure are weak compared to the Riccati-type terms that drive the singularity, at least near the shock. In order to explain this in more detail, we now review some prior works on shock formation in more than one spatial dimension.

Alinhac was the first [1,2,3,4] to prove shock formation results for quasilinear hyperbolic PDEs in more than one spatial dimension.¹¹ Specifically, in two and three spatial dimensions, he proved shock formation results for scalar quasilinear wave equations of the form

$$\begin{aligned} (g^{-1})^{\alpha \beta }(\partial \varPhi ) \partial _{\alpha } \partial _{\beta } \varPhi = 0 \end{aligned}$$

(1.5.1)

whenever the nonlinearities fail to satisfy Klainerman’s “classic” null condition and the data are small, smooth, compactly supported, and verify a non-degeneracy condition.¹² We clarify that the classic null condition refers to structures adapted to the Minkowski metric and thus is distinct from the good null structures appearing in our new formulation of the compressible Euler equations; we refer to the good null structures appearing in the new formulation as the “strong null condition” (relative to the acoustical metric g) in Theorem 2.

Although Alinhac’s work significantly advanced our understanding of singularity formation in solutions to quasilinear wave equations, the most robust and precise framework for proving shock formation in solutions to quasilinear wave equations was developed by Christodoulou in his groundbreaking work [6]. More precisely, Christodoulou [6] proved a small-data shock formation result for irrotational and isentropic solutions to the equations of compressible relativistic fluid mechanics. In the irrotational and isentropic case, the equations are equivalent to an Euler–Lagrange equation for a potential function $\varPhi$, which can be expressed in the form (1.5.1). It turns out that for all fluid equations of state except for one, the quasilinear wave equation for the potential function fails to satisfy the classic null condition, leading to the presence of nonlinear terms that can drive finite-time shock formation; the exceptional equation of state was identified in [6] in the case of the relativistic Euler equations and in [9] in the case of the non-relativistic compressible Euler equations. Christodoulou’s sharp geometric framework relied on a reformulation of the wave equation (1.5.1) that exhibits good geo-analytic structures [see equation (1.5.2)], and his approach yielded information that is not accessible via Alinhac’s approach. In particular, Christodoulou’s framework is able to reveal information about the structure of the maximal classical development of the initial data, all the way up to the boundary, information that is essential for properly setting up the shock development problem in compressible fluid mechanics.¹³ Roughly, the shock development problem is the problem of weakly continuing the solution past the singularity under suitable jump conditions. We note that even if the data are irrotational, vorticity can be generated to the future of the first singularity. Thus, in the study of the shock development problem, one must consider the full compressible Euler equations with vorticity and entropy. The shock development problem remains open in full generality and is expected to be very difficult. However, Christodoulou–Lisibach recently made important progress: in [8], they solved the problem in spherical symmetry in the relativistic case.

Christodoulou’s shock formation results for the irrotational and isentropic relativistic compressible Euler equations were extended to the non-relativistic irrotational and isentropic compressible Euler equations by Christodoulou–Miao in [9], to general classes of wave equations [28] by the author, and to other solution regimes in [24, 25, 29]. In all cases, the formation of the shock singularity was driven by the presence of Riccati-type interactions, similar in spirit to the ones found in Riemann’s aforementioned work [26] in the case of one spatial dimension and in the famous class of genuinely nonlinear hyperbolic systems. Readers can consult the survey article [14] for an extended overview of some of these works. We remark that a similar Riccati-type blowup-mechanism was also present in our aforementioned proof of shock formation [22] for the compressible Euler equations with vorticity under a barotropic equation of state, and that a similar mechanism drives the blowup in our forthcoming proof of shock formation for general equations of state. Of the above works, the ones [6, 9] are most relevant for the present article. In those works, the authors proved small-data shock formation results for the compressible Euler equations in irrotational and isentropic regions by studying the wave equation for the potential function $\varPhi$. The wave equation can be written in the (non-Euler–Lagrange) form (1.5.1) relative to Cartesian coordinates, where the Cartesian components $g_{\alpha \beta } = g_{\alpha \beta }(\partial \varPhi )$ are determined by the fluid equation of state.¹⁴ In the context of fluid mechanics, the Lorentzian metric g in (1.5.1) is known as the acoustical metric because it drives the propagation of sound waves. We note that the acoustical metric also plays a fundamental role in the main results of this article (see Def. 4), even when the vorticity and entropy are non-zero.

A simple – but essential – step in Christodoulou’s proof [6] of shock formation was to differentiate the wave equation (1.5.1) with the Cartesian coordinate partial derivative vectorfields $\partial _{\nu }$, which led to the following system of covariant wave equations, ($\nu = 0,1,2,3$):

$$\begin{aligned} \square _{{\widetilde{g}}(\vec {\varPsi })} \varPsi _{\nu }&= 0. \end{aligned}$$

(1.5.2)

In (1.5.2), $\vec {\varPsi } := (\varPsi _0,\varPsi _1,\varPsi _2,\varPsi _3)$ is the array of scalar functions $\varPsi _{\nu } := \partial _{\nu } \varPhi$ (with $\partial _{\nu }$ denoting a Cartesian coordinate partial derivative), ${\widetilde{g}}$ is a Lorentzian metric conformal to g, $\square _{{\widetilde{g}}(\vec {\varPsi })}$ is the covariant wave operator of ${\widetilde{g}}$ (see Def. 9), and $\varPsi _{\nu }$ is treated as a scalar function under covariant differentiation in (1.5.2).¹⁵ A key feature of the system (1.5.2) is that all of the terms that drive the shock formation are on the left-hand side, hidden in the lower-order terms generated by the operator $\square _{{\widetilde{g}}(\vec {\varPsi })}$. That is, if one expands $\square _{{\widetilde{g}}(\vec {\varPsi })} \varPsi _{\nu }$ relative to the standard Cartesian coordinates, one encounters Riccati-type terms of the schematic form $\partial \vec {\varPsi } \cdot \partial \vec {\varPsi }$ that fail to satisfy the classic null condition and thus are able to drive the blowup of a certain tensorial component of $\partial \vec {\varPsi }$, while $\vec {\varPsi }$ itself remains uniformly bounded up to the singularity; roughly, this is what it means for solutions to (1.5.2) to form a shock.¹⁶ Readers can consult Section 4.1 for a more detailed description of how the Riccati-type terms lead to blowup for simple isentropic plane wave solutions to the compressible Euler equations.

The presence of a covariant wave operator on LHS (1.5.2) was crucial for Christodoulou’s analysis. The reason is that he was able to construct, with the help of an eikonal function (see Section 4.2), a collection of geometric, solution-dependent vectorfields that enjoy good commutation properties with $\square _{{\widetilde{g}}(\vec {\varPsi })}$. He then used the vectorfields to differentiate the wave equations and to obtain estimates for the solution’s higher derivatives, much like in his celebrated proof [7], joint with Klainerman, of the global nonlinear (dynamic) stability of Minkowski spacetime as a solution to the Einstein-vacuum equations. Indeed, in more than one spatial dimension, the main technical challenge in the proof of shock formation is to derive sufficient energy estimates for the geometric vectorfield derivatives of the solution that hold all the way up to the singularity. In the context of shock formation, this step is exceptionally technical, and we discuss it in more detail in Section 4. It is important to note that the standard Cartesian coordinate partial derivatives $\partial _{\nu }$ generate uncontrollable error terms when commuted through $\square _{{\widetilde{g}}(\vec {\varPsi })}$ and thus the geometric vectorfields and their good commutation properties with the operator $\square _{{\widetilde{g}}(\vec {\varPsi })}$ are essential ingredients in the proof.

In [28], we showed that if one considers a general wave equation of type (1.5.1), not necessarily of the Euler–Lagrange type considered by Christodoulou [6] and Christodoulou–Miao [9], then upon differentiating it with $\partial _{\nu }$, one does not generate a system of type (1.5.2), but rather an inhomogeneous system of the form

$$\begin{aligned} \square _{g(\vec {\varPsi })} \varPsi _{\nu }&= {\mathrm {f}}(\vec {\varPsi }){\mathfrak {Q}}(\partial \vec {\varPsi },\partial \varPsi _{\nu }), \end{aligned}$$

(1.5.3)

where ${\mathrm {f}}$ is smooth and ${\mathfrak {Q}}$ is a standard null form relative to the acoustical metricg; see Def. 8. We then showed that the null forms relative to g have precisely the right structure such that they do not interfere with or prevent the shock formation processes, at least for suitable data. The ${\mathfrak {Q}}$ are canonical examples of terms that enjoy the good null structure that we mentioned at the beginning of this subsection. In particular, the term ${\mathfrak {Q}}$ on RHS (1.5.3) is not strong enough to overcome derivative-quadratic terms on LHS (1.5.3), which become visible upon expanding $\square _{g(\vec {\varPsi })} \varPsi _{\nu }$ relative to the Cartesian coordinates and which, exceptional cases aside, do not enjoy the same good null structure featured on RHS (1.5.3). More generally, we refer to the good null structure on RHS (1.5.3) as the strong null condition; see Def. 7 and Prop. 1. We stress that the full nonlinear structure of the null forms ${\mathfrak {Q}}$ is critically important. This is quite different from Klainerman’s classic null condition (see Footnote 12), which he formulated in his study of wave equations in three spatial dimensions that enjoy small-data global existence [18]; in Klainerman’s classic null condition, the structure of cubic and higher order terms is not even taken into consideration since, in the small-data regime that he studied, wave dispersion causes the cubic terms to decay fast enough that their precise structure is typically not important. The reason that the full nonlinear structure of the null forms ${\mathfrak {Q}}$ is of critical importance in the study of shock formation is that they are adapted to the acoustical metric g and enjoy the following key property: each ${\mathfrak {Q}}$ is linear in the tensorial component of $\partial \vec {\varPsi }$ that blows up. Therefore, near the singularity, ${\mathfrak {Q}}$ is small relative to the quadratic terms $\partial \vec {\varPsi } \cdot \partial \vec {\varPsi }$ that drive the singularity formation (which we again stress are hidden in the definition of $\square _{g(\vec {\varPsi })} \varPsi _{\nu }$). Roughly, this linear dependence on the singular terms is the crux of the strong null condition. In contrast, a typical quadratic inhomogeneous term $\partial \vec {\varPsi } \cdot \partial \vec {\varPsi }$, if present on RHS (1.5.3), would distort the dynamics near the singularity and could in principle prevent it from forming or change its nature. Moreover, in the context of shock formation, cubic or higher-order terms such as $\partial \vec {\varPsi } \cdot \partial \vec {\varPsi } \cdot \partial \vec {\varPsi }$ are expected to become dominant in regions where $\partial \vec {\varPsi }$ is large and it is therefore critically important that there are no such terms on RHS (1.5.3). These observations suggest that proofs of shock formation are less stable under perturbations of the equations compared to more familiar perturbative proofs of global existence.

The equations in our new formulation of the compressible Euler equations (see Theorem 1) are drastically more complicated than the homogeneous wave equations (1.5.2) that Christodoulou encountered in his study of irrotational and isentropic compressible fluid mechanics and the inhomogeneous equations (1.5.3) that we encountered in [28]. The equations of Theorem 1 are even considerably more complicated than the equations we derived in [21] in our study of the barotropic fluids with vorticity. However, the equations of Theorem 1 exhibit many of the same good structures enjoyed by the equations of [21], as well as some remarkable new ones. Specifically, in the present article, we derive geometric equations whose inhomogeneous terms are either null forms relative to the acoustical metric g, similar to the ones on RHS (1.5.3), or less dangerous terms that are at most linear in the solution’s derivatives. We find the presence of this null structure to be somewhat miraculous in view of the sensitivity of proofs of shock formation under perturbations of the equations, as we described in the previous paragraph. Moreover, in Theorem 1, we also exhibit special combinations of the solution variables that solve equations with good source terms, allowing, with the help of elliptic estimates, for a proof that the vorticity is one degree more differentiable than one might expect, assuming that the gain in differentiability is present in the initial data; see Def. 3 for the special combinations, which we refer to as “modified fluid variables.”¹⁷ The gain in differentiability for the vorticity has long been known relative to Lagrangian coordinates, in particular because it has played an important role in proofs of local well-posedness [10,11,12, 15, 16] for the compressible Euler equations for data featuring a physical vacuum-fluid boundary. However, the gain in differentiability for the vorticity with respect to arbitrary vectorfield differential operators (with coefficients of sufficient regularity relative to the solution) seems to originate in [21]. The freedom to gain the derivative relative to general vectorfield differential operators is important because Lagrangian coordinates are not adapted to the wave characteristics, whose intersection corresponds to the formation of a shock. Therefore, Lagrangian coordinates are not suitable for following the solution all the way to the shock; instead, as we describe in Sections 4.2 and 4.3 , one needs a system of geometric coordinates constructed with the help of an eikonal function, as well as the aforementioned geometric vectorfields, which are closely related to the geometric coordinates. We remark that in the barotropic case [21], the “special combinations” of solution variables were simpler than they are in the present article. Specifically, in the barotropic case, the specific vorticity and its curl satisfied good transport equations; compare this with the more complicated expression (1.3.13a). Similarly, we can prove that the entropy is one degree more differentiable than one might expect by studying a rescaled version of its Laplacian; see (1.3.13b).¹⁸ To the best of our knowledge, the gain in regularity for the entropy is a new result.

As we mentioned above, we exhibit the special null structure of the inhomogeneous terms in Theorem 2. Given Theorem 1, the proof of Theorem 2 is simple and is essentially by observation. However, it is difficult to overstate its profound importance in the study of shock formation since, as we described above, the good null structures are essential for showing that the inhomogeneous terms are not strong enough to interfere with the shock formation processes (at least for suitable open sets of initial data). The gain of differentiability mentioned in the previous paragraph is also essential for our forthcoming work on shock formation since we need it to control some of the source terms in the wave equations.

2 Geometric Background and the Strong Null Condition

In this section, we define some geometric objects and concepts that we need in order to precisely state our main results.

2.1 Geometric Tensorfields Associated to the Flow

Roughly, there are two kinds of motion associated to compressible Euler flow: the transporting of vorticity and entropy and the propagation of sound waves. We now discuss the tensorfields associated to these phenomena.

We start by recalling that the material derivative vectorfield $B$, defined in (1.3.12), is associated to the transporting of vorticity and entropy; the equations of Theorem 1 justify this remark.

We now define the Lorentzian metric g corresponding to the propagation of sound waves; again, the equations of Theorem 1 justify this remark.

Definition 4

(The acoustical metricand its inverse) We define the acoustical metricg and the inverse acoustical metric$g^{-1}$ relative to the Cartesian coordinates as follows:¹⁹

$$\begin{aligned} g&:= - \mathrm{{d}}t \otimes \mathrm{{d}}t + c^{-2} \sum _{a=1}^3(\mathrm{{d}}x^a - v^a \mathrm{{d}}t) \otimes (\mathrm{{d}}x^a - v^a \mathrm{{d}}t), \end{aligned}$$

(2.1.1a)

$$\begin{aligned} g^{-1}&:= - B\otimes B+ c^2 \sum _{a=1}^3 \partial _a \otimes \partial _a. \end{aligned}$$

(2.1.1b)

Remark 2

One can easily check that $g^{-1}$ is the matrix inverse of g, that is, we have $(g^{-1})^{\mu \alpha } g_{\alpha \nu } = \delta _{\nu }^{\mu }$, where $\delta _{\nu }^{\mu }$ is the standard Kronecker delta.

The vectorfield $B$ enjoys some simple but important geometric properties, which we provide in the next lemma. We repeat the simple proof from [21] for the reader’s convenience.

Lemma 1

(Basic geometric properties of $B)$$B$ is g-timelike,²⁰ future-directed,²¹$g-$orthogonal to $\varSigma _t$, and g-unit-length²²:

$$\begin{aligned} g(B,B)&= - 1. \end{aligned}$$

(2.1.2)

Proof

Clearly $B$ is future-directed. The identity (2.1.2) (which also implies that $B$ is g-timelike) follows from a simple calculation based on (1.3.12) and (2.1.1a). Similarly, we compute that $\displaystyle g(B,\partial _i) := g_{\alpha i}B^{\alpha } = 0$ for $i=1,2,3$, from which it follows that $B$ is $g-$orthogonal to $\varSigma _t$. $\quad \square$

2.2 Decompositions Relative to Null Frames

The special null structures found in our new formulation of the compressible Euler equations, which we briefly described in Section 1.5, are intimately connected to the notion of a null frame.

Definition 5

(Standardg-Null frame) Let g be a Lorentzian²³ metric on ${\mathbb {R}}^{1+3}$.²⁴ A standard g-null frame (“null frame” for short, when the metric is clear) at a point q is a set of vectors

$$\begin{aligned} {\mathscr {N}} := \lbrace L,\underline{L},e_1,e_2 \rbrace \end{aligned}$$

(2.2.1)

belonging to the tangent space of ${\mathbb {R}}^{1+3}$ at q such that

$$\begin{aligned} g(L,L)&= g(\underline{L},\underline{L}) = 0,&\end{aligned}$$

(2.2.2a)

$$\begin{aligned} g(L,\underline{L})&= -2,&\end{aligned}$$

(2.2.2b)

$$\begin{aligned} g(L,e_A)&= g(\underline{L},e_A) = 0,&(A=1,2), \end{aligned}$$

(2.2.2c)

$$\begin{aligned} g(e_A,e_B)&= \delta _{AB},&(A,B=1,2), \end{aligned}$$

(2.2.2d)

where $\delta _{AB}$ is the standard Kronecker delta.

The following lemma is a straightforward consequence of Def. 5; we omit the simple proof:

Lemma 2

(Decomposition of $g^{-1}$ relative to a standard g-null frame) Relative to an arbitrary standard $g-$null frame, we have

$$\begin{aligned} g^{-1}&= - \frac{1}{2} L\otimes \underline{L}- \frac{1}{2} \underline{L}\otimes L+ \sum _{A=1}^2 e_A \otimes e_A. \end{aligned}$$

(2.2.3)

Definition 6

(Decomposition of a derivative-quadratic nonlinear term relative to a null frame) Let

$$\begin{aligned} \vec {V}&:= (\uprho ,v^1,v^2,v^3,s,\varOmega ^1,\varOmega ^2,\varOmega ^3,S^1,S^2,S^3) \end{aligned}$$

(2.2.4)

be the array of unknowns in the below system (3.1.1a)–(3.1.4b) (see Footnote 30). We label the components of $\vec {V}$ as follows:

$$\begin{aligned} V^0 :=\uprho , V^i :=v^i, V^4 := s, V^{i+4} :=\varOmega ^i, \hbox { and } V^{i+7} :=S^i, \hbox { for } i=1,2,3. \end{aligned}$$

(2.2.5)

Let ${\mathcal {N}}(\vec {V},\partial \vec {V})$ be a smooth nonlinear term that is quadratically nonlinear in $\partial \vec {V}$. That is, we assume that ${\mathcal {N}}(\vec {V},\partial \vec {V}) ={\mathrm {f}}(\vec V)_{\varTheta \varGamma }^{\alpha \beta } (\partial _{\alpha } V^\varTheta ) \partial _{\beta } V^\varGamma$, where ${\mathrm {f}}(\vec V)_{\varTheta \varGamma }^{\alpha \beta }$ is symmetric in $\varTheta$ and $\varGamma$ and is a smooth function of $\vec V$ (not necessarily vanishing at 0) for $\alpha ,\beta =0,1,2,3$ and $\varTheta ,\varGamma =0,1,\ldots ,10$.²⁵ Given a standard g-null frame ${\mathscr {N}}$ as defined in Def. 5, we denote

$$\begin{aligned} {\mathscr {N}} := \lbrace e_1, e_2, e_3:= \underline{L}, e_4 := L\rbrace . \end{aligned}$$

Moreover, we let $M_{\alpha }^A$ denote the scalar functions corresponding to expanding the Cartesian coordinate partial derivative vectorfield $\partial _{\alpha }$ at q relative to the null frame, that is,

$$\begin{aligned} \partial _{\alpha } = M_{\alpha }^A e_A := \sum _{A=1}^4 M_{\alpha }^A e_A. \end{aligned}$$

Then

$$\begin{aligned} {\mathcal {N}}_{{\mathscr {N}}}&:={\mathrm {f}}(\vec V)_{\varTheta \varGamma }^{\alpha \beta } M_{\alpha }^A M_{\beta }^B (e_A V^\varTheta ) e_B V^\varGamma \end{aligned}$$

(2.2.6)

denotes the nonlinear term obtained by expressing ${\mathcal {N}}(\vec {V},\partial \vec {V})$ in terms of the derivatives of $\vec {V}$ with respect to the elements of ${\mathscr {N}}$, that is, by expanding $\partial \vec {V}$ as a linear combination of the derivatives of $\vec {V}$ with respect to the elements of ${\mathscr {N}}$ and substituting the expression for the factor $\partial \vec {V}$ in ${\mathcal {N}}(\vec {V},\partial \vec {V})$.

2.3 Strong Null Condition and Standard Null Forms

In Section 1.5, we roughly described the special null structure enjoyed by the inhomogeneous terms in our new formulation of the compressible Euler equations. We precisely define the special null structure in the next definition, which we recall from [21].

Definition 7

(Strong null condition) Let ${\mathcal {N}}_{{\mathscr {N}}} :={\mathrm {f}}(\vec V)_{\varTheta \varGamma }^{\alpha \beta } M_{\alpha }^A M_{\beta }^B (e_A V^\varTheta ) e_B V^\varGamma$ be as in Def. 6. We say that ${\mathcal {N}}(\vec {V},\partial \vec {V})$ verifies the strong null condition relative to g if the following condition holds: for every standard g-null frame ${\mathscr {N}}$, ${\mathcal {N}}_{{\mathscr {N}}}$ can be expressed in a form that depends linearly (or not at all) on $L\vec {V}$ and $\underline{L}\vec {V}$. That is, for $A,B=1,2,3,4$ and $\varTheta ,\varGamma = 0,1,\ldots ,10$, there exist scalar functions ${\overline{{\mathrm {f}}}}_{\varTheta \varGamma }^{AB}(\vec V)$ and ${\underline{{\mathrm {f}}}}_{\varTheta \varGamma }^{AB}(\vec V)$, depending on the null frame, such that the following hold:

$$\begin{aligned} {\overline{{\mathrm {f}}}}_{\varTheta \varGamma }^{33}(\vec V)&= {\overline{{\mathrm {f}}}}_{\varTheta \varGamma }^{44}(\vec V)=0,&{\underline{{\mathrm {f}}}}_{\varTheta \varGamma }^{33}(\vec V) = {\underline{{\mathrm {f}}}}_{\varTheta \varGamma }^{44}(\vec V) = 0,&\varTheta , \varGamma = 0,1,\ldots ,10, \end{aligned}$$

(2.3.1)

and

$$\begin{aligned} \begin{aligned} {\mathrm {f}}(\vec V)_{\varTheta \varGamma }^{\alpha \beta } M_{\alpha }^3 M_{\beta }^3 (e_3 V^\varTheta ) e_3 V^\varGamma&= {\overline{{\mathrm {f}}}}_{\varTheta \varGamma }^{AB}(\vec V)(e_A V^\varTheta ) e_B V^\varGamma ,\\ {\mathrm {f}}(\vec V)_{\varTheta \varGamma }^{\alpha \beta } M_{\alpha }^4 M_{\beta }^4 (e_4 V^\varTheta ) e_4 V^\varGamma&={\underline{{\mathrm {f}}}}_{\varTheta \varGamma }^{AB}(\vec V)(e_A V^\varTheta ) e_B V^\varGamma . \end{aligned} \end{aligned}$$

(2.3.2)

Put differently, (2.3.1)–(2.3.2) state that ${\mathcal {N}}_{{\mathscr {N}}}$ can be re-expressed in such a way that terms proportional to $(LV^\varTheta ) LV^\varGamma$ and $(\underline{L}V^\varTheta ) \underline{L}V^\varGamma$ are completely absent.

Remark 3

(Some comments on the strong null condition) Equation (2.3.2) allows for the possibility that one uses external PDEs²⁶ to algebraically substitute for terms on LHS (2.3.2), thereby generating the good terms on RHS (2.3.2), which verify the essential condition (2.3.1). As our proof of Prop. 1 below shows, this kind of substitution is not needed for null forms relative to the acoustical metric g, which can directly be shown to exhibit the desired structure, without the help of external PDEs. That is, for null forms ${\mathfrak {Q}}$ relative to g, one can directly show that ${\mathrm {f}}(\vec V)_{\varTheta \varGamma }^{\alpha \beta } M_{\alpha }^3 M_{\beta }^3 = {\mathrm {f}}(\vec V)_{\varTheta \varGamma }^{\alpha \beta } M_{\alpha }^4 M_{\beta }^4 = 0$. In the present article, the formulation of the equations that we provide (see Theorem 1) is such that all derivative-quadratic terms are null forms relative to g. Readers might then wonder why our definition of the strong null condition allows for the more complicated scenario in which one uses external PDEs for algebraic substitution to detect the good null structure. The reason is that in our work [21] on the barotropic case, we encountered the inhomogeneous terms $\displaystyle \varepsilon _{iab} \left\{ (\partial _a \varOmega ^d) \partial _d v^b - (\partial _a v^d) \partial _d \varOmega ^b \right\}$, which are not null forms. To show that these terms had the desired null structure, we used the compressible Euler equations for substitution and therefore relied on the full scope of Def. 7. In the present article, we encounter the same terms, but we treat them in a different way and show that in fact, $\displaystyle \varepsilon _{iab} \left\{ (\partial _a \varOmega ^d) \partial _d v^b - (\partial _a v^d) \partial _d \varOmega ^b \right\}$ is equal to a null form plus other terms that are either harmless or that can be incorporated into our definition of the modified fluid variables from Def. 3; see the identity (5.1.14) and the calculations below it.

A key feature of our new formulation of the compressible Euler equations is that all derivative-quadratic inhomogeneous terms are linear combinations of the standard null forms relative to the acoustical metric g, which verify the strong null condition relative to g (see Prop. 1). We now recall their standard definition.

Definition 8

(Standard null forms) The standard null forms ${\mathfrak {Q}}^{(g)}(\cdot ,\cdot )$ (relative to g) and ${\mathfrak {Q}}_{(\alpha \beta )}(\cdot ,\cdot )$, ($0 \le \alpha < \beta \le 3$), act on pairs $(\phi ,{\widetilde{\phi }})$ of scalar-valued functions as follows:

$$\begin{aligned} {\mathfrak {Q}}^{(g)}(\partial \phi , \partial {\widetilde{\phi }})&:= (g^{-1})^{\alpha \beta } (\partial _{\alpha } \phi ) \partial _{\beta } {\widetilde{\phi }}, \end{aligned}$$

(2.3.3a)

$$\begin{aligned} {\mathfrak {Q}}_{(\alpha \beta )}(\partial \phi , \partial {\widetilde{\phi }})&:= (\partial _{\alpha } \phi ) \partial _{\beta } {\widetilde{\phi }} - (\partial _{\alpha } {\widetilde{\phi }}) \partial _{\beta } \phi . \end{aligned}$$

(2.3.3b)

Proposition 1

(The standard null forms satisfy the strong null condition) Let ${\mathfrak {Q}}$ be a standard null form relative to g and let $\phi$ and ${\widetilde{\phi }}$ be any two entries of the array $\vec {V}$ from Def. 6. Let ${\mathrm {f}}= {\mathrm {f}}(\vec {V})$ be a smooth scalar-valued function of the entries of $\vec {V}$. Then ${\mathrm {f}}(\vec {V}) {\mathfrak {Q}}(\partial \phi , \partial {\widetilde{\phi }})$ verifies the strong null condition relative to g, as defined in Def. 7.

Proof

In the case of the null form ${\mathfrak {Q}}^{(g)}$, the proof is a direct consequence of the identity (2.2.3).

In the case of the null form ${\mathfrak {Q}}_{(\alpha \beta )}$ defined in (2.3.3b), we consider any g-null frame (2.2.1), and we label its elements as follows: ${\mathscr {N}} := \lbrace e_1, e_2, e_3:= \underline{L}, e_4 := L\rbrace$. Since ${\mathscr {N}}$ spans the tangent space at each point where it is defined, there exist scalar functions $M_{\alpha }^A$ such that the following identity holds for $\alpha = 0,1,2,3$:

$$\begin{aligned} \partial _{\alpha } = \sum _{A=1}^4 M_{\alpha }^A e_A. \end{aligned}$$

(2.3.4)

From (2.3.3b) and (2.3.4), we deduce

$$\begin{aligned} {\mathfrak {Q}}_{(\alpha \beta )}(\partial \phi ,\partial {\widetilde{\phi }}) = \sum _{A,B=1}^4 \left\{ M_{\alpha }^A M_{\beta }^B - M_{\alpha }^B M_{\beta }^A \right\} (e_A \phi ) e_B {\widetilde{\phi }}. \end{aligned}$$

The key point is that the terms in braces are antisymmetric in A and B. It follows that the sum does not contain any diagonal terms, that is, terms proportional to $(e_A \phi ) e_A {\widetilde{\phi }}$ (in the previous expression, we do not sum over A). In particular, terms proportional to $(\underline{L}\phi ) \underline{L}{\widetilde{\phi }}$ and $(L\phi ) L{\widetilde{\phi }}$ are not present, which is the desired result. $\quad \square$

3 Precise Statement of the Main Results

In this section, we precisely state our two main theorems and give the simple proof of the second one. We start by recalling the standard definition of the covariant wave operator $\square _g$.

Definition 9

(Covariant wave operator) Let g be a Lorentzian metric. The covariant wave operator $\square _g$ acts on scalar-valued functions $\phi$ as follows:²⁷

$$\begin{aligned} \square _g \phi := \frac{1}{\sqrt{|\hbox {det} g|}} \partial _{\alpha } \left\{ \sqrt{|\hbox {det} g|} (g^{-1})^{\alpha \beta } \partial _{\beta } \phi \right\} . \end{aligned}$$

(3.0.1)

3.1 The New Formulation of the Compressible Euler Equations with Vorticity and Entropy

Our first main result is Theorem 1, which provides the new formulation of the compressible Euler equations. We postpone its lengthy proof until Section 5.

Remark 4

(Explanation of the different kinds of inhomogeneous terms) In the equations of Theorem 1, there are many inhomogeneous terms that are denoted by decorated versions of “${\mathfrak {Q}}$.” These terms are linear combinations of standard null forms relative to g that, in our forthcoming proof of shock formation, can be controlled in the energy estimates without elliptic estimates. Similarly, in the equations of Theorem 1, decorated versions of the symbol “${\mathfrak {L}}$” denote terms that are at most linear in the derivatives of the solution and that can be controlled in the energy estimates without elliptic estimates. In our forthcoming proof of shock formation, the ${\mathfrak {Q}}$’s and ${\mathfrak {L}}$’s will be simple error terms. The equations of Theorem 1 also feature additional null form inhomogeneous terms depending on $\partial \varOmega$ and $\partial S$, which we explicitly display (i.e., we do not incorporate them into the “${\mathfrak {Q}}$’s”) because one needs elliptic estimates along $\varSigma _t$ to control them in the energy estimates. For this reason, in the proof of shock formation, these terms are substantially more difficult to control compared to the ${\mathfrak {Q}}$’s and ${\mathfrak {L}}$’s. Similarly, terms that are linear in $\partial \varOmega$, $\partial S$, ${\mathcal {C}}$, or ${\mathcal {D}}$ can be controlled only with the help of elliptic estimates along $\varSigma _t$.

Theorem 1

(The geometric wave-transport–divergence–curl formulation of the compressible Euler equations) Let ${\bar{\varrho }} > 0$ be any constant background density [see (1.3.5)], and assume that $(\uprho ,v^1,v^2,v^3,s)$ is a $C^3$ solution to the compressible Euler equations (1.3.11a)–(1.3.11c) in three spatial dimensions under an arbitrary equation of state (1.3.1) with positive sound speed $c$ [see (1.3.9)].²⁸ Let $B$ be the material derivative vectorfield defined in (1.3.12), let g be the acoustical metric from Def. 4, and let ${\mathcal {C}}$ and ${\mathcal {D}}$ be the modified fluid variables from Def. 3. Then the scalar-valued functions $\uprho$ and $v^i$, $\varOmega ^i$, $s$, $S^i$, $\hbox {div}\varOmega$, ${\mathcal {C}}^i$, ${\mathcal {D}}$, and $(\hbox {curl}S)^i$, ($i=1,2,3$), also solve the following equations, where the Cartesian component functions$v^i$are treated as scalar-valued functions under covariant differentiation on LHS (3.1.1a):

Covariant wave equations

$$\begin{aligned} \square _g v^i&= - c^2 \exp (2 \uprho ) {\mathcal {C}}^i + {\mathfrak {Q}}_{(v)}^i + {\mathfrak {L}}_{(v)}^i, \end{aligned}$$

(3.1.1a)

$$\begin{aligned} \square _g \uprho&= - \exp (\uprho ) \frac{p_{;s}}{{\bar{\varrho }}} {\mathcal {D}}+ {\mathfrak {Q}}_{(\uprho )} + {\mathfrak {L}}_{(\uprho )}, \end{aligned}$$

(3.1.1b)

$$\begin{aligned} \square _g s&= c^2 \exp (2 \uprho ) {\mathcal {D}}+ {\mathfrak {L}}_{(s)}. \end{aligned}$$

(3.1.1c)

Transport equations ²⁹

$$\begin{aligned} B\varOmega ^i&= {\mathfrak {L}}_{(\varOmega )}^i, \end{aligned}$$

(3.1.2a)

$$\begin{aligned} Bs&= 0, \end{aligned}$$

(3.1.2b)

$$\begin{aligned} BS^i&= {\mathfrak {L}}_{(S)}^i. \end{aligned}$$

(3.1.2c)

Transport–divergence–curl system for the specific vorticity

$$\begin{aligned} \hbox {div}\varOmega&= {\mathfrak {L}}_{(\hbox {div}\varOmega )}, \end{aligned}$$

(3.1.3a)

$$\begin{aligned} B{\mathcal {C}}^i&= - 2 \delta _{jk} \varepsilon _{iab} \exp (-\uprho ) (\partial _a v^j) \partial _b \varOmega ^k + \varepsilon _{ajk} \exp (-\uprho ) (\partial _a v^i) \partial _j \varOmega ^k \\&\quad + \exp (-3 \uprho ) c^{-2} \frac{p_{;s}}{{\bar{\varrho }}} \left\{ (BS^a) \partial _a v^i - (Bv^i) \partial _a S^a \right\} \nonumber \\&\quad + \exp (-3 \uprho ) c^{-2} \frac{p_{;s}}{{\bar{\varrho }}} \left\{ (Bv^a) \partial _a S^i - ( BS^i) \partial _a v^a \right\} \nonumber \\&\quad + {\mathfrak {Q}}_{({\mathcal {C}})}^i + {\mathfrak {L}}_{({\mathcal {C}})}^i. \nonumber \end{aligned}$$

(3.1.3b)

Transport–divergence–curl system for the entropy gradient

$$\begin{aligned} B{\mathcal {D}}&= 2 \exp (-2 \uprho ) \left\{ (\partial _a v^a) \partial _b S^b - (\partial _a S^b) \partial _b v^a \right\} + \exp (-\uprho ) \delta _{ab} (\hbox {curl}\varOmega )^a S^b\nonumber \\&\quad + {\mathfrak {Q}}_{({\mathcal {D}})}, \end{aligned}$$

(3.1.4a)

$$\begin{aligned} (\hbox {curl}S)^i&= 0. \end{aligned}$$

(3.1.4b)

Above, ${\mathfrak {Q}}_{(v)}^i$, ${\mathfrak {Q}}_{(\uprho )}$, ${\mathfrak {Q}}_{({\mathcal {C}})}^i$, and ${\mathfrak {Q}}_{({\mathcal {D}})}$ are the null forms relative tog defined by

$$\begin{aligned} {\mathfrak {Q}}_{(v)}^i&:= - \left\{ 1 + c^{-1} c_{;\uprho } \right\} (g^{-1})^{\alpha \beta } (\partial _{\alpha } \uprho ) \partial _{\beta } v^i, \end{aligned}$$

(3.1.5a)

$$\begin{aligned} {\mathfrak {Q}}_{(\uprho )}&:= - 3 c^{-1} c_{;\uprho } (g^{-1})^{\alpha \beta } (\partial _{\alpha } \uprho ) \partial _{\beta } \uprho + \left\{ (\partial _a v^a) \partial _b v^b - (\partial _a v^b) \partial _b v^a \right\} , \end{aligned}$$

(3.1.5b)

$$\begin{aligned} {\mathfrak {Q}}_{({\mathcal {C}})}^i&:= \exp (-3 \uprho ) c^{-2} \frac{p_{;s}}{{\bar{\varrho }}} S^i \left\{ (\partial _a v^b) \partial _b v^a - (\partial _a v^a) \partial _b v^b \right\} \\&\quad + \exp (-3 \uprho ) c^{-2} \frac{p_{;s}}{{\bar{\varrho }}} S^b \left\{ (\partial _a v^a) \partial _b v^i - (\partial _a v^i) \partial _b v^a \right\} \nonumber \\&\quad + 2 \exp (-3 \uprho ) c^{-2} \frac{p_{;s}}{{\bar{\varrho }}} S^a \left\{ (\partial _a \uprho ) Bv^i - (\partial _a v^i) B\uprho \right\} \nonumber \\&\quad + 2 \exp (-3 \uprho ) c^{-3} c_{;\uprho } \frac{p_{;s}}{{\bar{\varrho }}} S^a \left\{ (\partial _a \uprho ) Bv^i - (\partial _a v^i) B\uprho \right\} \nonumber \\&\quad + \exp (-3 \uprho ) c^{-2} \frac{p_{;s;\uprho }}{{\bar{\varrho }}} S^a \left\{ (\partial _a v^i) B\uprho - (\partial _a \uprho ) Bv^i \right\} \nonumber \\&\quad + \exp (-3 \uprho ) c^{-2} \frac{p_{;s;\uprho }}{{\bar{\varrho }}} S^i \left\{ (Bv^a) \partial _a \uprho - (B\uprho ) \partial _a v^a \right\} \nonumber \\&\quad + 2 \exp (-3 \uprho ) c^{-2} \frac{p_{;s}}{{\bar{\varrho }}} S^i \left\{ (B\uprho ) \partial _a v^a - (Bv^a) \partial _a \uprho \right\} \nonumber \\&\quad + 2 \exp (-3 \uprho ) c^{-3} c_{;\uprho } \frac{p_{;s}}{{\bar{\varrho }}} S^i \left\{ (B\uprho ) \partial _a v^a - (Bv^a) \partial _a \uprho \right\} , \nonumber \end{aligned}$$

(3.1.5c)

$$\begin{aligned} {\mathfrak {Q}}_{({\mathcal {D}})}&:= 2 \exp (-2 \uprho ) S^a \left\{ (\partial _a v^b) \partial _b \uprho - (\partial _a \uprho ) \partial _b v^b \right\} . \end{aligned}$$

(3.1.5d)

In addition, the terms ${\mathfrak {L}}_{(v)}^i$, ${\mathfrak {L}}_{(\uprho )}$, ${\mathfrak {L}}_{(s)}$, ${\mathfrak {L}}_{(\varOmega )}^i$, ${\mathfrak {L}}_{(S)}^i$, ${\mathfrak {L}}_{(\hbox {div}\varOmega )}$, and ${\mathfrak {L}}_{({\mathcal {C}})}^i$,

which are at most linear in the derivatives of the unknowns, are defined as follows:

$$\begin{aligned} {\mathfrak {L}}_{(v)}^i&:= 2 \exp (\uprho ) \varepsilon _{iab} (Bv^a) \varOmega ^b - \frac{p_{;s}}{{\bar{\varrho }}} \varepsilon _{iab} \varOmega ^a S^b \\&\quad - \frac{1}{2} \exp (-\uprho ) \frac{p_{;\uprho ;s}}{{\bar{\varrho }}} S^a \partial _a v^i \nonumber \\&\quad - 2 \exp (-\uprho ) c^{-1} c_{;\uprho } \frac{p_{;s}}{{\bar{\varrho }}} (B\uprho ) S^i + \exp (-\uprho ) \frac{p_{;s;\uprho }}{{\bar{\varrho }}} (B\uprho ) S^i, \nonumber \end{aligned}$$

(3.1.6a)

$$\begin{aligned} {\mathfrak {L}}_{(\uprho )}&:= - \frac{5}{2} \exp (-\uprho ) \frac{p_{;s;\uprho }}{{\bar{\varrho }}} S^a \partial _a \uprho - \exp (-\uprho ) \frac{p_{;s;s}}{{\bar{\varrho }}} \delta _{ab} S^a S^b, \end{aligned}$$

(3.1.6b)

$$\begin{aligned} {\mathfrak {L}}_{(s)}&:= c^2 S^a \partial _a \uprho - cc_{;\uprho } S^a \partial _a \uprho - cc_{;s} \delta _{ab} S^a S^b, \end{aligned}$$

(3.1.6c)

$$\begin{aligned} {\mathfrak {L}}_{(\varOmega )}^i&:= \varOmega ^a \partial _a v^i - \exp (-2 \uprho ) c^{-2} \frac{p_{;s}}{{\bar{\varrho }}} \varepsilon _{iab} (Bv^a) S^b, \end{aligned}$$

(3.1.6d)

$$\begin{aligned} {\mathfrak {L}}_{(S)}^i&:= - S^a \partial _a v^i + \varepsilon _{iab} \exp (\uprho ) \varOmega ^a S^b, \end{aligned}$$

(3.1.6e)

$$\begin{aligned} {\mathfrak {L}}_{(\hbox {div}\varOmega )}&:= - \varOmega ^a \partial _a \uprho , \end{aligned}$$

(3.1.6f)

$$\begin{aligned} {\mathfrak {L}}_{({\mathcal {C}})}^i&:= 2 \exp (-3 \uprho ) c^{-3} c_{;s} \frac{p_{;s}}{{\bar{\varrho }}} (Bv^i) \delta _{ab} S^a S^b \\&\quad - 2 \exp (-3 \uprho ) c^{-3} c_{;s} \frac{p_{;s}}{{\bar{\varrho }}} \delta _{ab} S^a (Bv^b) S^i \nonumber \\&\quad + \exp (-3 \uprho ) c^{-2} \frac{p_{;s;s}}{{\bar{\varrho }}} \delta _{ab} (Bv^a) S^b S^i \nonumber \\&\quad - \exp (-3 \uprho ) c^{-2} \frac{p_{;s;s}}{{\bar{\varrho }}} (Bv^i) \delta _{ab} S^a S^b.\nonumber \end{aligned}$$

(3.1.6g)

Remark 5

(Comparison to the results of [21]) For barotropic fluids, we have $p_{;s} \equiv 0$, and consequently, the variables $s$ and $S^i$ do not influence the dynamics of the remaining solution variables. For such fluids, one can check that equations (3.1.1a)–(3.1.1b), (3.1.2a), and (3.1.3a)–(3.1.3b) are equivalent to the equations that we derived in [21]. However, one needs some observations described in Remark 3 in order to see the equivalence.

Remark 6

(The data for the system (3.1.1a)–(3.1.4b)) The “fundamental” initial data for the compressible Euler equations (1.3.11a)–(1.3.11c) are $\uprho |_{t=0}$, $\lbrace v^i|_{t=0} \rbrace _{i=1,2,3}$, and $s|_{t=0}$. On the other hand, to solve the Cauchy problem for the system (3.1.1a)–(3.1.4b), one also needs the data $\partial _t \uprho |_{t=0}$, $\lbrace \partial _t v^i|_{t=0} \rbrace _{i=1,2,3}$, $\partial _t s|_{t=0}$, $\lbrace \varOmega ^i|_{t=0} \rbrace _{i=1,2,3}$, and $\lbrace S^i|_{t=0} \rbrace |_{i=1,2,3}$. These data can be obtained by differentiating the fundamental initial data with respect to the Cartesian coordinate spatial partial derivative vectorfields $\lbrace \partial _i \rbrace _{i=1,2,3}$ and by using equations (1.3.11a)–(1.3.11c) to algebraically solve for time derivatives.

3.2 The Structure of the Inhomogeneous Terms

The next theorem is our second main result. In the theorem, we characterize the structure of the inhomogeneous terms in the equations Theorem 1. The most important part of the theorem is the null structure of the Type $\mathbf{iii }$ terms.

Theorem 2

(The structure of the inhomogeneous terms) Let

$$\begin{aligned} \vec {V} := (\uprho ,v^1,v^2,v^3,s,\varOmega ^1,\varOmega ^2,\varOmega ^3,S^1,S^2,S^3) \end{aligned}$$

denote the array of unknowns in the equations of Theorem 1.³⁰ The inhomogeneous terms on the right-hand sides of equations (3.1.1a)–(3.1.4b) consist of three types:

• i. Terms of the form ${\mathrm {f}}(\vec {V})$, where ${\mathrm {f}}$ is smooth and vanishes when $S= \varOmega \equiv 0$.

• ii. Terms of the form ${\mathrm {f}}(\vec {V}) \cdot \partial \vec {V}$ where ${\mathrm {f}}$ is smooth, that is, terms that depend linearly on the elements of $\partial \vec {V}$.

• iii. Terms of the form ${\mathrm {f}}(\vec {V}) {\mathfrak {Q}}(\partial \phi ,\partial {\widetilde{\phi }})$, where ${\mathrm {f}}$ is smooth, $\phi$ and ${\widetilde{\phi }}$ are elements of $\vec {V}$, and ${\mathfrak {Q}}$ is a standard null form relative to the acoustical metric g from Def. 8. By Prop. 1, these terms satisfy the strong null condition relative to g.

Proof

It is easy to see that ${\mathfrak {Q}}_{(v)}^i$, ${\mathfrak {Q}}_{(\uprho )}$, ${\mathfrak {Q}}_{({\mathcal {C}})}^i$, and ${\mathfrak {Q}}_{({\mathcal {D}})}$ are Type $\mathbf{iii }$ terms, and that the same is true for the products on the first through third lines of RHS (3.1.3b) and the terms in braces on the first line of RHS (3.1.4a). Similarly, it is easy to see that ${\mathfrak {L}}_{(v)}^i$, ${\mathfrak {L}}_{(\uprho )}$, ${\mathfrak {L}}_{(s)}$, ${\mathfrak {L}}_{(\varOmega )}^i$, ${\mathfrak {L}}_{(S)}^i$, ${\mathfrak {L}}_{(\hbox {div}\varOmega )}$, and ${\mathfrak {L}}_{({\mathcal {C}})}^i$ are sums of terms of type Type ${\mathbf{i }}$ and Type $\mathbf{ii }$, while the first product on RHS (3.1.1a), the first product on RHS (3.1.1b), the first product on RHS (3.1.1c), and the second product on RHS (3.1.4a) are, in view of Def. 3, Type $\mathbf{ii }$. $\quad \square$

4 Overview of the Roles of Theorems 1 and 2 in Proving Shock Formation

As we mentioned in Section 1, in forthcoming work, we plan to use the results of Theorems 1 and 2 as the starting point for a proof of finite-time shock formation for an open set of solutions to the compressible Euler equations. In this section, we provide an overview of the main ideas in the proof and highlight the role that Theorems 1 and 2 play. We plan to study a convenient open set of initial conditions in three spatial dimensions whose solutions typically have non-zero vorticity and non-constant entropy: perturbations (without symmetry assumptions) of simple isentropic (that is, constant entropy³¹) plane waves.³² We note that in our joint work [29] on scalar wave equations in two spatial dimensions, we proved shock formation for solutions corresponding to a similar set of nearly plane symmetric initial data. The advantage of studying perturbations of simple isentropic plane waves is that it allows us to focus our attention on the singularity formation without having to confront additional evolutionary phenomena that are often found in solutions to wave-like systems. For example, nearly plane symmetric solutions do not exhibit wave dispersion because their dynamics are dominated by 1D-type wave behavior.³³ In particular, our forthcoming analysis will not feature time weights or radial weights.

4.1 Blowup for Simple Isentropic Plane Waves

Simple isentropic plane waves are a subclass of plane symmetric solutions. By “plane symmetric solutions,” we mean solutions that depend only on t and $x^1$ and such that $v^2 \equiv v^3 = 0$. To further explain simple isentropic plane wave solutions, we will present some standard material without providing proofs. Readers can consult, for example, [5, 13] for additional details. We start by defining the Riemann invariants:

$$\begin{aligned} {\mathcal {R}}_{\pm }&:= v^1 \pm F(\uprho ). \end{aligned}$$

(4.1.1)

The function F in (4.1.1) solves the following initial value problem, where $c$ is the speed of sound (and we suppress the dependence of $c$ on $s$ since $s$ is constant by assumption):

$$\begin{aligned} \frac{\mathrm{{d}}}{\mathrm{{d}}\uprho } F(\uprho )&= c(\uprho ),&F(\uprho =0) = 0, \end{aligned}$$

(4.1.2)

where $F(\uprho =0) = 0$ is a convenient normalization condition. In one spatial dimension, in terms of ${\mathcal {R}}_{\pm }$, the compressible Euler equations (1.3.11a)–(1.3.11c) with constant entropy are equivalent to the system

$$\begin{aligned} \underline{L}{\mathcal {R}}_-&= 0,&L{\mathcal {R}}_+ = 0, \end{aligned}$$

(4.1.3)

where

$$\begin{aligned} L&:= \partial _t + (v^1 + c) \partial _1,&\underline{L}:= \partial _t + (v^1 - c) \partial _1 \end{aligned}$$

(4.1.4)

are null vectorfields relative to the acoustical metric of Def. 4. That is, one can easily check that $g(L, L) = g(\underline{L},\underline{L}) = 0$. The initial data are ${\mathcal {R}}_{\pm }|_{t=0}$ (together with the initial constant value of the entropy, which we suppress for the rest of the discussion). A simple isentropic plane wave is a solution such that one of the Riemann invariants, say ${\mathcal {R}}_-$, completely vanishes. Note that by the first equation in (4.1.3), the condition ${\mathcal {R}}_- = 0$ is propagated by the flow of the equations if it is verified at time 0.

The simple isentropic plane wave solutions described in the previous paragraph typically form a shock in finite time via the same mechanism that leads to singularity formation in solutions to Burgers’ equation. For illustration, we now quickly sketch the argument. We assume the simple isentropic plane wave condition ${\mathcal {R}}_- \equiv 0$, which implies that the system (4.1.3) reduces to $\lbrace \partial _t + f({\mathcal {R}}_+) \partial _1 \rbrace {\mathcal {R}}_+ = 0$, where f is a smooth function determined by F. It can be shown that f is not a constant-valued function of ${\mathcal {R}}_+$, except in the case of the equation of state of a Chaplygin gas, which is $\displaystyle p = p(\varrho )=C_0-\frac{C_1}{\varrho }$, where $C_0\in {\mathbb {R}}$ and $C_1>0$. We now take a $\partial _1$ derivative of the evolution equation for ${\mathcal {R}}_+$ to deduce the equation $\lbrace \partial _t + f({\mathcal {R}}_+) \partial _1 \rbrace \partial _1 {\mathcal {R}}_+ = - f'({\mathcal {R}}_+) (\partial _1 {\mathcal {R}}_+)^2$. Since ${\mathcal {R}}_+$ is constant along the integral curves of $\partial _t + f({\mathcal {R}}_+) \partial _1$ (which are also known as “characteristics” in the present context), the above equation can be viewed as a Riccati-type ODE for $\partial _1 {\mathcal {R}}_+$ along the characteristics, specifically the ODE

$$\begin{aligned} \frac{\mathrm{{d}}}{\mathrm{{d}}t} \partial _1 {\mathcal {R}}_+&= k (\partial _1 {\mathcal {R}}_+)^2, \end{aligned}$$

(4.1.5)

where the constant k is equal to $- f'({\mathcal {R}}_+)$ evaluated at the point on the $x^1$-axis from which the characteristic emanates. Thus, we can easily deduce that for initial data such that $\partial _1 {\mathcal {R}}_+$ and k have the same (non-zero) sign at some point along the $x^1$ axis, the solution $\partial _1 {\mathcal {R}}_+$ to (4.1.5) will blow up in finite time along the corresponding characteristic, even though ${\mathcal {R}}_+$ remains bounded; this is essentially the crudest picture of the formation of a shock singularity. Note that there is no blowup in the case of the Chaplygin gas since $f' \equiv 0$ in that case; see Footnote 43 for related remarks.

4.2 Fundamental Ingredients in the Proof of Shock Formation in More than One Spatial Dimension

We can view the simple isentropic plane waves described in Section 4.1 as solutions in three spatial dimension that have symmetry. In our forthcoming work on shock formation in three spatial dimensions, we will study perturbations (without symmetry assumptions) of simple isentropic plane waves, and we will prove that the shock formation illustrated in Section 4.1 is stable. For technical convenience, instead of considering data on ${\mathbb {R}}^3$, we will consider initial data on the spatial manifold

$$\begin{aligned} \varSigma := {\mathbb {R}} \times {\mathbb {T}}^2, \end{aligned}$$

where the factor of ${\mathbb {T}}^2$ (equal to the two-dimensional torus) corresponds to perturbations away from plane symmetry. This allows us to circumvent some technical difficulties, such as the fact that non-trivial plane wave solutions have infinite energy when viewed as solutions with symmetry on the spacetime ${\mathbb {R}}^{1+3}$.

Although the method of Riemann invariants allows for an easy proof of shock formation for simple isentropic plane waves, the method is not available in more than one spatial dimension. Another key feature of the study of shock formation in more than one spatial dimension is that all known proofs rely on sharp estimates that provide much more information compared to the proof of blowup for simple plane waves from Section 4.1. Therefore, in our forthcoming proof of shock formation for perturbations of simple isentropic plane waves, we will use the geometric formulation of the equations provided by Theorem 1.³⁴ We will show that these equations have the right structure such that they can be incorporated into an extended version of the paradigm for proving shock formation initiated by Alinhac [1,2,3,4] and significantly advanced by Christodoulou [6].

The most fundamental ingredient in the approaches of Alinhac and Christodoulou is a system of geometric coordinates

$$\begin{aligned} (t,u,\vartheta ^1,\vartheta ^2) \end{aligned}$$

(4.2.1)

that are dynamically adapted to the solution. We denote the corresponding partial derivative vectorfields as follows:

$$\begin{aligned} \left\{ \frac{\partial }{\partial t}, \frac{\partial }{\partial u}, \frac{\partial }{\partial \vartheta ^1}, \frac{\partial }{\partial \vartheta ^2} \right\} . \end{aligned}$$

(4.2.2)

Here, t is the standard Cartesian time function, while u is an eikonal function adapted to the acoustical metric. That is, u solves the following fully nonlinear hyperbolic PDE, known as the eikonal equation:

$$\begin{aligned} (g^{-1})^{\alpha \beta } (\partial _{\alpha } u) \partial _{\beta } u&= 0,&\partial _t u&> 0, \end{aligned}$$

(4.2.3a)

$$\begin{aligned} u|_{t=0} = 1 - x^1. \end{aligned}$$

(4.2.3b)

Above and throughout the rest of the article, g is the acoustical metric from Def. 4. We construct the geometric torus coordinates $\vartheta ^A$ by solving the transport equations

$$\begin{aligned} (g^{-1})^{\alpha \beta } (\partial _{\alpha } u) \partial _{\beta } \vartheta ^A&= 0, \end{aligned}$$

(4.2.4a)

$$\begin{aligned} \vartheta ^1|_{t=0}&= x^2, \qquad \vartheta ^2|_{t=0} = x^3, \end{aligned}$$

(4.2.4b)

where $x^2$ and $x^3$ are standard (locally defined) Cartesian coordinates on ${\mathbb {T}}^2$; see Footnote 2 regarding the Cartesian coordinates in the present context. For various reasons, when differentiating the equations to obtain estimates for the solution’s derivatives, one needs to use geometric vectorfields, described below, rather than the partial derivative vectorfields in (4.2.2). For this reason, the coordinates $(\vartheta ^1,\vartheta ^2)$ play only a minor role in the analysis, and we will downplay their significance for most of the remaining discussion.

Note that the Cartesian components $g_{\alpha \beta }$ depend on the fluid variables $\uprho$, $v^i$, and $s$ [see (2.1.1a)]. Therefore, the regularity properties of the eikonal function are tied to that of the fluid solution; below we will further discuss this crucial issue. The initial conditions (4.2.3b) are adapted to the approximate plane symmetry of the solutions that we plan to study.³⁵ The level sets of u are known as the “characteristics,” the “wave characteristics,” or the “acoustic characteristics,” and we denote them by ${\mathcal {P}}_u$. The ${\mathcal {P}}_u$ are null hypersurfaces relative to the acoustical metric g. As we further explain below, the intersection of the level sets of the function u (viewed as an ${\mathbb {R}}$-valued function of the Cartesian coordinates) corresponds to the formation of a shock singularity and the blowup of the first-order Cartesian coordinate partial derivatives of the density and velocity. As we will explain below, u can be viewed as a “sharp coordinate” that is dynamically adapted to the fluid flow, that can be used to reveal special structures in the equations, and that can be used to construct geometric objects adapted to the characteristics. The price that one pays for the precision is that the top-order regularity theory for u is very complicated and tensorial in nature. As we later explain, the regularity theory is especially difficult near the shock and leads to degenerate high-order energy estimates for the fluid.

The first use of an eikonal function in proving a global result for a nonlinear hyperbolic system occurred in the celebrated proof [7] of the stability of the Minkowski spacetime as a solution to the Einstein-vacuum equations.³⁶ Eikonal functions have also played a central role in proofs of low-regularity well-posedness for quasilinear hyperbolic equations, most notably the recent Klainerman–Rodnianski–Szeftel proof of the bounded $L^2$ curvature conjecture [20].

The paradigm for proving shock formation originating in the works [1,2,3,4, 6] can be summarized as follows:

To the extent possible, prove “long-time-existence-type” estimates for the solution relative to the geometric coordinates and then recover the formation of the shock singularity as a degeneration between the geometric coordinates and the Cartesian ones. In particular, prove that the solution remains many times differentiable relative to the geometric coordinates, even though the first-order Cartesian coordinate partial derivatives of the density and velocity blow up.

The most important quantity in connection with the above paradigm for proving shock formation is the inverse foliation density.

Definition 10

(Inverse foliation density of the${\mathcal {P}}_u$) We define the inverse foliation density $\upmu > 0$ of the characteristics ${\mathcal {P}}_u$ as follows:

$$\begin{aligned} \upmu&:= \frac{-1}{(g^{-1})^{\alpha \beta } (\partial _{\alpha } t) \partial _{\beta } u}. \end{aligned}$$

(4.2.5)

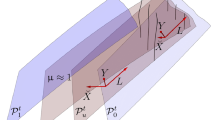
$\displaystyle \frac{1}{\upmu }$ is a measure of the density of the characteristics ${\mathcal {P}}_u$ relative to the constant-time hypersurfaces $\varSigma _t$. When $\upmu$ vanishes, the density becomes infinite, the characteristics intersect, and, as it turns out, the first-order Cartesian coordinate partial derivatives of the density and velocity blow up in finite time. See Fig. 1 for a depiction of a solution for which the characteristics have almost intersected. Note that by (2.1.1b), (4.2.3a), and (4.2.3b), we have $\upmu |_{t=0} \approx 1$.³⁷ Christodoulou was the first to introduce $\upmu$ in the context of proving shock formation in more than one spatial dimension [6]. However, before Christodoulou’s work, quantities in the spirit of $\upmu$ had been used in one spatial dimension, for example, by John in his proof [17] of blowup for solutions to a large class of quasilinear hyperbolic systems. In short, to prove a shock formation result under Christodoulou’s approach, one must control the solution all the way up until the time of first vanishing of $\upmu$.

Fig. 1

The vectorfield frame $\mathscr {Z}$ at two distinct points in ${\mathcal {P}}_u$ and the integral curves of $B$ (along which $\varOmega$, $s$, and $S$ are transported), with one spatial dimension suppressed

4.3 Summary of the Proof of Shock Formation

Having introduced the geometric coordinates and the inverse foliation density, we are now ready to summarize the main ideas in the proof of shock formation for perturbations of simple isentropic plane wave solutions to the compressible Euler equations in three spatial dimensions with spatial topology $\varSigma = {\mathbb {R}} \times {\mathbb {T}}^2$. For convenience, we will study solutions with very small initial data given along a portion of the characteristic ${\mathcal {P}}_0$ and “interesting” data (whose derivatives can be large in directions transversal to the characteristics) along a portion of $\varSigma _0 \simeq {\mathbb {R}} \times {\mathbb {T}}^2$; see Fig. 1 for a schematic depiction of the setup.

Given the structures revealed by Theorems 1 and 2, much of the proof is based on frameworks developed in prior works, as we now quickly summarize. The bulk of the framework originated in Christodoulou’s groundbreaking work [6] in the irrotational case, with some key contributions (especially the idea to rely on an eikonal function) coming from Alinhac’s earlier work [1,2,3,4] on scalar wave equations. The relevance of the strong null condition in the context of proving shock formation was first recognized in [14, 28]. The crucial new ideas needed to handle the transport equations and the elliptic operators/estimates originated in [21, 22]. Three key contributions of the present work are showing (i) that one can gain a derivative for the entropy $s$, which is needed to ensure that all terms in our new formulation of the compressible Euler equations have a consistent amount of regularity (see Step 8 below for further discussion); (ii) the inhomogeneous terms generated by including $s$ in our new formulation all have a good null structure; and (iii) that in the context of shock formation, one needs to rely on transport-div-curl estimates for the entropy gradient $S$ in order to avoid uncontrollable error terms; see Remark 1 and Step 2 below for further discussion on this last point.

We now summarize the main ideas behind our forthcoming proof of shock formation. Most of the discussion will be at a rough, schematic level.

• 1. (Commutation vectorfields adapted to the characteristics). With the help of the eikonal function u (see Section 4.2), construct a set of geometric vectorfields

  $$\begin{aligned} \mathscr {Z}&:= \lbrace L, \breve{X}, Y_1, Y_2 \rbrace \end{aligned}$$

  (4.3.1)

  that are adapted to the characteristics ${\mathcal {P}}_u$; see Fig. 1. Readers can consult [14, 21, 22] for details on how to use u to construct $\mathscr {Z}$. Here, we only note some basic properties of these vectorfields. The subset

  $$\begin{aligned} \mathscr {P}&:= \lbrace L, Y_1, Y_2 \rbrace \end{aligned}$$

  (4.3.2)

  spans the tangent spaces of ${\mathcal {P}}_u$, while the vectorfield $\breve{X}$ is transversal to ${\mathcal {P}}_u$. $L$ is a g-null (that is, $g(L,L) = 0$) generator of ${\mathcal {P}}_u$ normalized by $Lt = 1$, while $\displaystyle \breve{X}= \frac{\partial }{\partial u} + \hbox {Error}$, where $\hbox {Error}$ is a small vectorfield tangent to the co-dimension-two tori ${\mathcal {P}}_u \cap \varSigma _t$. The vectorfields $\lbrace Y_1, Y_2 \rbrace$ span the tangent spaces of ${\mathcal {P}}_u \cap \varSigma _t$.

  The elements of $\mathscr {Z}$ are designed to have good commutation properties with each other and also, as we describe below, with $\upmu \square _g$. In particular, one can show that we have the following schematic relations:³⁸

  $$\begin{aligned}{}[\mathscr {Z}, \mathscr {Z}] \sim \mathscr {P}. \end{aligned}$$

  (4.3.3)

  In the rest of the discussion, Z denotes a generic element of $\mathscr {Z}$ and $P$ denotes a generic element of $\mathscr {P}$ or, more generally, a ${\mathcal {P}}_u$-tangent differential operator. It is straightforward to derive the following relationships, which are key to understanding the shock formation, where $\partial$ schematically denotes linear combinations of the Cartesian coordinate partial derivative vectorfields:³⁹

  $$\begin{aligned} P&\sim \partial ,&\breve{X}\sim \upmu \partial . \end{aligned}$$

  (4.3.4)

  We also note the complementary schematic relation

  $$\begin{aligned} \upmu \partial \sim \breve{X}+ \upmu P, \end{aligned}$$

  (4.3.5)

  which we will refer to in Step 2. At the end of Step 5, we will clarify the role of the second relation in (4.3.4) in tying the vanishing of the inverse foliation density $\upmu$ (see Def. 10) to the blowup of the solution’s first-order Cartesian coordinate partial derivatives. In the proof of shock formation, one uses the elements of $\mathscr {Z}$ to differentiate the equations and to obtain estimates for the solution’s derivatives. The goal is to show that up to a sufficiently high order, the $\mathscr {Z}$-derivatives of the solution remain uniformly bounded, all the way up to the time of first vanishing of $\upmu$. Note that by (4.3.4), we have $|P| = {\mathcal {O}}(1)$, while $|\breve{X}| = {\mathcal {O}}(\upmu )$. The relation $|\breve{X}| = {\mathcal {O}}(\upmu )$ implies that deriving uniform bounds for the solution’s $\breve{X}$-derivatives is tantamount to having only very weak estimates in regions where $\upmu$ is small (i.e., near the shock); one might think of the boundedness of the solution’s $\breve{X}$-derivatives as “degenerate estimates” for the solution’s ${\mathcal {P}}_u$-transversal derivatives, consistent with an order-unity-length transversal derivative of the solution blowing up like $\displaystyle \frac{1}{\upmu }$ as $\upmu \rightarrow 0$. In contrast, the relation $|P| = {\mathcal {O}}(1)$ implies that uniform bounds for the derivatives of the solution with respect to the elements of $\mathscr {P}$ yield non-degenerate estimates for the ${\mathcal {P}}_u$-tangential derivatives of the solution. We will revisit these crucial issues in Step 3. We now note that one can derive the relations $\displaystyle L= \frac{\partial }{\partial t}$, $\displaystyle \breve{X}= \frac{\partial }{\partial u} + \hbox {Error}$, $\displaystyle Y_A = \frac{\partial }{\partial \vartheta ^A} + \hbox {Error}$, $A=1,2$, where $\hbox {Error}$ denotes small vectorfields that are tangent to the tori ${\mathcal {P}}_u \cap \varSigma _t$. Hence, deriving estimates for the $\mathscr {Z}$-derivatives of the solution is equivalent to deriving estimates for the derivatives of the solution relative to the geometric coordinates. The elements of (4.3.1) are replacements for the geometric coordinate partial derivative vectorfields (4.2.2) that, as it turns out, enjoy better regularity properties. Specifically, an important point, which is not at all obvious, is that the elements of $\displaystyle \left\{ \frac{\partial }{\partial u}, \frac{\partial }{\partial \vartheta ^1}, \frac{\partial }{\partial \vartheta ^2} \right\}$, when commuted through the covariant wave operator $\square _g$ from LHSs (3.1.1a)–(3.1.1c), generate error terms that lose a derivative and thus are uncontrollable at the top-order. In contrast, the elements $Z \in \mathscr {Z}$ are adapted to the acoustical metric g in such a way that the commutator operator $[\upmu \square _g,Z]$ generates controllable error terms. We note that one includes the factor of $\upmu$ in the previous commutator because it leads to essential cancellations. Although achieving control of the commutator error terms at the top-order derivative level is possible, it is quite difficult and in fact constitutes the main step in the proof. The difficulty is that the Cartesian components of $Z \in \mathscr {Z}$ depend on the Cartesian coordinate partial derivatives of u, which we can schematically depict as follows: $Z^{\alpha } \sim \partial u$. Therefore, the regularity of the vectorfields Z themselves depends on the regularity of the fluid solution through the dependence of the eikonal equation (4.2.3a) on the fluid variables. In fact, some of the commutator terms generated by $[\upmu \square _g,Z]$appear, at first glance, to suffer from the loss of a derivative. Fortunately, the derivative loss can be overcome using ideas originating in [7, 19] and, in the context of shock formation, in [6]. However, as we explain in Step 7, one pays a steep price in overcoming the loss of a derivative: the only known procedure for gaining back the derivative leads to degenerate estimates in which the high-order energies are allowed to blow up as $\upmu \rightarrow 0$. On the other hand, to close the proof and show that the shock forms, one must prove that the low-order energies remain bounded all the way up to the singularity. Establishing this hierarchy of energy estimates is the main technical step in the proof.

• 2. (Multiple speeds and commuting geometric vectorfields through first-order operators). The compressible Euler equations with vorticity and entropy feature two kinds of characteristics: the acoustic characteristics ${\mathcal {P}}_u$ and the integral curves of the material derivative vectorfield $B$; see Fig. 1. That is, the system features multiple characteristic speeds, which creates new difficulties compared to the case of the scalar wave equations treated in the works [1,2,3,4, 6, 9, 21, 22, 25, 29]. Another new difficulty compared to the scalar wave equation case is the presence of the operators $\hbox {div}$ and $\hbox {curl}$ in the equations of Theorem 1. The first proof of shock formation for a quasilinear hyperbolic system in more than one spatial dimension featuring multiple speeds and the operators $\hbox {div}$ and $\hbox {curl}$ was our prior work [21, 22] on the compressible Euler equations in the barotropic case. We now review the main difficulties corresponding to the presence multiple speeds and the operators $\hbox {div}$ and $\hbox {curl}$. We will then explain how to overcome them; it turns out that essentially the same strategy can be used to handle all of these first-order operators. Since the formation of a shock is tied to the intersection of the wave characteristic ${\mathcal {P}}_u$ (as we clarify in Step 5), our construction of the geometric vectorfields $Z \in \mathscr {Z}$ from Step 1 was, by necessity, adapted to g; indeed, this seems to be the only way to ensure that the commutator terms $[\upmu \square _g,Z]$ are controllable up to the shock. This begs the question of what kind of commutation error terms are generated upon commuting the Z through first-order operators such as $B$, $\hbox {div}$, and $\hbox {curl}$. The resolution was provided by the following key insight from [21, 22]: the elements of $\mathscr {Z}$ have just enough structure such that their commutator with an appropriately weighted, but otherwise arbitrary, first-order differential operator produces controllable error terms, consistent with the solution remaining bounded relative to the geometric coordinates at the lower derivative levels.⁴⁰ Specifically, one can show that we have the schematic commutation relation

  $$\begin{aligned}{}[\upmu \partial _{\alpha }, \mathscr {Z}] \sim \breve{X}+ P, \end{aligned}$$

  (4.3.6)

  which is suggested by the schematic relations (4.3.3) and (4.3.5). The important point is that RHS (4.3.6) does not feature any singular factor of $\displaystyle \frac{1}{\upmu }$. The above discussion suggests the following strategy for treating the first-order equations of Theorem 1: weight them with a factor of $\upmu$ so that the principal part is of the schematic form $\upmu \partial$. Then by (4.3.6), upon commuting the weighted equation with elements of $\mathscr {Z}$, we generate only commutator terms that do not feature any damaging factor of $\displaystyle \frac{1}{\upmu }$. We stress that the property (4.3.6) does not generalize to typical second-order operators. That is, we have the schematic relation $\displaystyle [\upmu \partial _{\alpha } \partial _{\beta }, \mathscr {Z}] \sim \frac{1}{\upmu } \mathscr {Z}\mathscr {Z}+ \cdots$, which features uncontrollable factors of $\displaystyle \frac{1}{\upmu }$. This is the reason that in deriving elliptic estimates for the entropy $s$, we work the divergence and curl of the entropy gradient vectorfield $S^i = \partial _i s$ instead of $\varDelta s$ (see also Remark 1); the div-curl formulation allows us to avoid commuting the elements of $\mathscr {Z}$ through the (second-order) flat Laplacian $\varDelta$ and therefore to avoid uncontrollable error terms.

• 3. ($L^{\infty }$bootstrap assumptions). Formulate appropriate uniform$L^{\infty }$ bootstrap assumptions for the $\mathscr {Z}$-derivatives of the solution, up to order approximately 10, on a region on which the solution exists classically. In particular, these $\mathscr {Z}$-derivatives of the solution will not blow up, even as the shock forms. We now describe some crucial implications of these uniform bounds. We start by recalling the following facts, which we alluded to just below (4.3.5): the Cartesian components of the element $\breve{X}$ in $\mathscr {Z}$ are of size ${\mathcal {O}}(\upmu )$, while the elements $L,Y_1,Y_2$ of the ${\mathcal {P}}_u$-tangent subset $\mathscr {P}$ of $\mathscr {Z}$ have Cartesian components of size ${\mathcal {O}}(1)$. This leads to the following point, which is central for all aspects of the proof of shock formation:

  Uniform $L^{\infty }$ bounds for the solution’s $\mathscr {P}$-derivatives imply that the derivatives of the solution with respect to any order-unity-length vectorfield that is tangent to the acoustic characteristics ${\mathcal {P}}_u$ remain uniformly bounded all the way up to the shock.⁴¹ In contrast, a uniform $L^{\infty }$ bound for the solution’s $\breve{X}$-derivative allows for the possibility that order-unity-length derivatives of the solution in directions transversal to ${\mathcal {P}}_u$ can blow up like ${\mathcal {O}}(1/\upmu )$ as $\upmu \rightarrow 0$. This is in direct analogy to the behavior exhibited by solutions to Burgers’ equation, in which the derivatives of the solution in directions tangent to the characteristics remain bounded, while the solution’s transversal derivatives can blow up.⁴²

  Just below equation (4.3.11g), we explain why the proof requires so many derivatives. The bootstrap assumptions are tensorial in nature and involve several parameters measuring the size of various directional derivatives of the solution. We will not discuss the bootstrap assumptions in detail here. Instead, we simply note that they reflect our expectation that the solution remains a small perturbation of a simple isentropic plane wave at the lower $\mathscr {Z}$-derivative levels; readers can consult [21, 22] for more details on the bootstrap assumptions in the barotropic case and keep in mind that in our forthcoming work, we will make similar bootstrap assumptions, the new feature being smallness assumptions on the derivatives of $s$.

• 4. (The role of Theorem 2). We now clarify the importance of the good null structures revealed by Theorem 2, thereby fleshing out the discussion from Section 1.5. Let $\vec {V}$ denote the solution array (2.2.4). As we alluded to above, before commuting the equations of Theorem 1 with elements of $\mathscr {Z}$, we first multiply the equations by a factor of $\upmu$. The main point is that by Theorem 2, all derivative-quadratic inhomogeneous terms (more precisely, the Type iii terms in theorem) in $\upmu$-weighted versions of the equations of Theorem 1 can be decomposed in the following schematic form, where we ignore the order-unity coefficients:

  $$\begin{aligned} \upmu \partial \vec {V} \cdot \partial \vec {V} = \breve{X}\vec {V} \cdot P\vec {V} + \upmu P\vec {V} \cdot P\vec {V}, \end{aligned}$$

  (4.3.7)

  where $P$ is as in Step 1. The decomposition (4.3.7) is precisely what is afforded by the strong null condition, which is available in view of Prop. 1. The reader might have noticed that Def. 7 of the strong null condition is based on decompositions relative to standard g-null frames, while the terms on RHS (4.3.7) are decomposed relative to the elements of $\mathscr {Z}$. That is, one needs some minor observations in order to translate the strong null condition into the statement (4.3.7). The main idea is to consider the strong null condition under a null frame (2.2.1) in which $L$ is the vectorfield from (4.3.1) and the vectorfields $\lbrace e_1, e_2 \rbrace$ have the same span as $\lbrace Y_1, Y_2 \rbrace$, in which case both of the sets $\lbrace L, e_1, e_2 \rbrace$ and $\lbrace L, Y_1, Y_2 \rbrace$ span the tangent spaces of ${\mathcal {P}}_u$. From these considerations, it is easy to see that given any derivative-quadratic term verifying the strong null condition, we can decompose it into factors such that each factor contains at least one ${\mathcal {P}}_u$-tangent differentiation, which is precisely what is indicated on RHS (4.3.7). In particular, on RHS (4.3.7), there are no terms proportional to $\breve{X}\vec {V} \cdot \breve{X}\vec {V}$, which, by signature considerations, would have to be multiplied by an uncontrollable factor of$\displaystyle \frac{1}{\upmu }$ that would blow up at the shock. Such a term, had it have been present, would have completely obstructed the goal of obtaining regular estimates for the solution’s low-level $\mathscr {Z}$-derivatives that hold all the way up to the shock. We have therefore explained the good structure of Type iii terms from Theorem 2. The only other kind of inhomogeneous terms that one encounters in the $\upmu$-weighted equations of Theorem 1 are at most linear in $\partial \vec {V}$, that is, $\upmu$-weighted versions of the Type i and Type ii terms from Theorem 2. The linear terms $\upmu \partial \vec {V}$ can be decomposed (schematically) as

  $$\begin{aligned} \upmu \partial \vec {V} = \breve{X}\vec {V} + \upmu P\vec {V}, \end{aligned}$$

  (4.3.8)

  the key point being that RHS (4.3.8) does not feature any singular factor of $\displaystyle \frac{1}{\upmu }$. For this reason, all linear terms $\upmu \partial \vec {V}$ remain uniformly bounded all the way up to the shock and are admissible within the scope of our approach. Similar remarks of course apply to terms that depend on $\vec {V}$ but not $\partial \vec {V}$.

• 5. (Tying the singularity formation to the vanishing of$\upmu$). Derive the following evolution equation for $\upmu$, written in schematic form:⁴³

  $$\begin{aligned} \displaystyle \frac{\partial }{\partial t} \upmu \sim \frac{\partial }{\partial u} v^1 + \hbox {Error}. \end{aligned}$$

  (4.3.9)

  Then, using the $L^{\infty }$ bootstrap assumptions from Step 3, show that for data near that of a simple plane wave, $\displaystyle \frac{\partial }{\partial u} v^1$ is negative and approximately constant in time (relative to the geometric coordinates) and that $\hbox {Error}$ is small in $L^{\infty }$, all the way up to the shock. Thus, from (4.3.9), we deduce that $\upmu$ will vanish in finite time. Moreover, since $\breve{X}v^1$ and $\displaystyle \frac{\partial }{\partial u} v^1$ agree up to small error terms and since $\displaystyle \frac{\partial }{\partial u} v^1$ is strictly non-zero at any point where $\upmu$ vanishes, it follows from the second relation in (4.3.4) that $\displaystyle \left| \partial v^1 \right| \sim \frac{1}{\upmu }$ in a past neighborhood of any point where $\upmu$ vanishes. In particular, some first-order Cartesian coordinate partial derivative of $v^1$ must blow up like $\displaystyle \frac{1}{\upmu }$ at points where $\upmu$ vanishes.

• 6. (Pointwise estimates and sharp estimates for$\upmu$). Commute all of the equations of Theorem 1 up to top-order (i.e., up to approximately 20 times) with the elements of $\mathscr {Z}$, and similarly for the transport equations verified by $\upmu$ and the Cartesian components $L^i$, ($i=1,2,3$).⁴⁴ For brevity, we do not provide these transport equations in detail here [we schematically displayed the one for $\upmu$ in (4.3.9)]. Instead, we only note that the inhomogeneous terms in the transport equations exhibit structures similar to the ones enjoyed by the simple Type i and type Type ii terms from Theorem 2. The reason that we must estimate the derivatives of $\upmu$ and $L^i$ is that they appear as source terms when we commute the equations of Theorem 1 with the elements $Z \in \mathscr {Z}$ [see (4.3.1)]. After commuting the equations, one uses the $L^{\infty }$ bootstrap assumptions from Step 3 to derive suitable pointwise estimates for all of the error terms and inhomogeneous terms in the equations up to top-order. A key point is that all good null structures, such as the structure displayed in (4.3.7), are preserved under differentiations of the equations with the elements of $\mathscr {Z}$. Moreover, since the elements $Z \in \mathscr {Z}$ are adapted to $\upmu \square _g$, the commutator terms corresponding to the operator $[\upmu \square _g,Z]$ also exhibit a similar good null structure. Another key step in the proof is to derive very sharp pointwise estimates for $\upmu$, capturing exactly how it vanishes. More precisely, through a detailed study of equation (4.3.9), one can show that for the solutions under study, $\displaystyle \frac{\partial }{\partial t} \upmu$ is quantitatively negative in regions where $\upmu$ is near 0, which implies that $\upmu$ vanishes linearly. It turns out that these facts are crucial for closing the energy estimates.

• 7. (Energy estimates). Using the pointwise estimates and the sharp estimates for $\upmu$ from Step 6, derive energy estimates up to top-order. This is the main technical step in the proof. Null structures such as (4.3.7) are again critically important for the energy estimates, since our energies (described below) are designed to control error integrals that are generated by special products of the form of RHS (4.3.7) and their higher-order analogs. To control some of the terms in the energy estimates, we also need elliptic estimates along $\varSigma _t$, which we describe in Step 8. As a preliminary step, we now briefly describe, from the point of view of regularity, why our proof fundamentally relies on the transport-div-curl-type equations (3.1.3a)–(3.1.4b) and elliptic estimates. In reality, we need elliptic estimates only to control the solution’s top-order derivatives, that is, after commuting the equations many times with the elements of $\mathscr {Z}$. However, for convenience, here we ignore the need to commute the equations and instead focus our discussion on how to derive a consistent amount of Sobolev regularity for solutions to the non-commuted equations. In proving shock formation, we are primarily interested in deriving estimates for solutions to the wave equations (3.1.1a)–(3.1.1b); given suitable estimates for their solutions, the rest of the proof of the formation of the shock is relatively easy. To proceed, we first note that the inhomogeneous terms ${\mathcal {C}}$ and ${\mathcal {D}}$ (see Def. 3) on the right-hand sides of the wave equations (3.1.1a)–(3.1.1b) are, from the point of view of regularity, at the level of $\partial \varOmega$ and $\partial S$, plus easier terms that can be treated using energy estimates for wave equations (and that we will therefore ignore in the present discussion). On the other hand, the transport equations (3.1.2a) and (3.1.2c) for $\varOmega$ and $S$ have source terms that depend on $\partial v$ and $\partial \uprho$. Since solutions to transport equations are typically only as regular as their source terms, this falsely suggests that $\varOmega$ and $S$ have the same Sobolev regularity as $\partial v$ and $\partial \uprho$ (and therefore that $\partial \varOmega$ and $\partial S$ have the same Sobolev regularity as $\partial ^2 v$ and $\partial ^2 \uprho$) which, from the point of view of regularity, would be inconsistent with the presence of the inhomogeneous terms $\partial \varOmega$ and $\partial S$ on the right-hand side of the wave equations; the inconsistency would come from the fact that energy estimates for the wave equations yield $L^2$-control only over $\partial v$ and $\partial \uprho$ and thus $\partial v$ and $\partial \uprho$ cannot have more $L^2$ regularity than the wave equation source terms $\partial \varOmega$ and $\partial S$. To circumvent this difficulty, one needs to rely on the transport-div-curl-type equations (3.1.3a)–(3.1.4b) and elliptic estimates to control $\partial \varOmega$ and $\partial S$ in $L^2(\varSigma _t)$, using only that $\partial v^i$ and $\partial \uprho$ are in $L^2(\varSigma _t)$. We further explain this in Step 8. A key reason behind the viability of this approach is that even though equations (3.1.3a)–(3.1.4b) are obtained by differentiating the transport equations (3.1.2a) and (3.1.2c) (which feature inhomogeneous terms of the schematic form $\partial v$), the inhomogeneous terms on RHSs (3.1.3a)–(3.1.4b) do not feature the terms$\partial ^2 v$or$\partial ^2 \uprho$; this is a surprising structural feature of the equations that is based on the observation of cancellations and that should not be taken for granted. The main technical difficulty that one encounters in the proof of shock formation is that the best energy estimates that we know how to derive allow for the possibility that the high-order energies might blow up as the shock forms. This makes it difficult to justify the uniform (non-degenerate) $L^{\infty }$ bootstrap assumptions from Step 3, which play a crucial role in showing that the shock forms and in deriving the pointwise estimates from Step 6. It turns out that the maximum possible energy blowup-rates can be expressed in terms of negative powers of⁴⁵

  $$\begin{aligned} \upmu _{\star }(t)&:= \min _{\varSigma _t} \lbrace 1, \upmu \rbrace . \end{aligned}$$

  (4.3.10)

  Note that the formation of the shock corresponds to $\upmu _{\star } \rightarrow 0$. Just below, we will roughly describe the hierarchy of energy estimates. The energy estimates involve energies ${\mathbb {E}}_{(Wave)}$ for the “wave variables” $\lbrace \uprho , v^1, v^2, v^3 \rbrace$ as well as energies ${\mathbb {E}}_{(Transport)}$ for the “transport variables” $\lbrace s, \varOmega ^1, \varOmega ^2, \varOmega ^3, S^1, S^2, S^3, {\mathcal {C}}^1, {\mathcal {C}}^2, {\mathcal {C}}^3, {\mathcal {D}}\rbrace$. We use the notation ${\mathbb {E}}_{(Wave);Top}$ to denote a wave energy that controls the top-order $\mathscr {Z}$-derivatives⁴⁶ of the wave variables (here we are not specific about how many derivatives correspond to top-order), ${\mathbb {E}}_{(Wave);Top-1}$ denote a just-below-top-order wave energy, ${\mathbb {E}}_{(Wave);Mid}$ denote a mid-order wave energy (we also are not specific about how many derivatives correspond to mid-order), ${\mathbb {E}}_{(Wave);1}$ correspond to the energy after a single commutation,⁴⁷ and similarly for the transport equation energies. The hierarchy of energy estimates that one can derive roughly has the following structure, where $K \approx 20$ is a universal constant (independent of the specific structure of the compressible Euler equations) and $\mathring{\upepsilon }$ is a small parameter representing the size of a seminorm that, roughly speaking, measures how far the initial data are from the data of a simple isentropic plane wave:⁴⁸

  $$\begin{aligned} \mathbb {E}_{(Wave);Top}(t), \, \mathbb {E}_{(Transport);Top}(t)&\lesssim \mathring{\upepsilon }^2 \upmu _{\star }^{-K}(t), \end{aligned}$$

  (4.3.11a)
  $$\begin{aligned} \mathbb {E}_{(Wave);Top-1}(t), \, \mathbb {E}_{(Transport);Top-1}(t)&\lesssim \mathring{\upepsilon }^2 \upmu _{\star }^{2-K}(t), \end{aligned}$$

  (4.3.11b)
  $$\begin{aligned} \mathbb {E}_{(Wave);Top-2}(t), \, \mathbb {E}_{(Transport);Top-2}(t)&\lesssim \mathring{\upepsilon }^2 \upmu _{\star }^{4-K}(t), \end{aligned}$$

  (4.3.11c)
  $$\begin{aligned}&\cdots , \end{aligned}$$

  (4.3.11d)
  $$\begin{aligned} \mathbb {E}_{(Wave);Mid}(t), \, \mathbb {E}_{(Transport);Mid}(t)&\lesssim \mathring{\upepsilon }^2, \end{aligned}$$

  (4.3.11e)
  $$\begin{aligned}&\cdots , \end{aligned}$$

  (4.3.11f)
  $$\begin{aligned} \mathbb {E}_{(Transport);1}(t)&\lesssim \mathring{\upepsilon }^2. \end{aligned}$$

  (4.3.11g)

  The difficult parts of the proof are controlling the maximum possible top-order blowup-rate $\upmu _{\star }^{-K}(t)$ as well as establishing the “descent scheme” showing that the below-top-order energies become successively less degenerate until one reaches the level (4.3.11e), below which the energies do not blow up.⁴⁹ Descent schemes of this type originated in the works [1,2,3,4, 6] of Alinhac and Christodoulou and have played a key role in all prior works on shock formation in more than one spatial dimension. From the non-degenerate energy estimates (4.3.11e)–(4.3.11g), Sobolev embedding, and a smallness assumption on the data-size parameter $\mathring{\upepsilon }$, one can justify (that is, improve) the non-degenerate $L^{\infty }$ bootstrap assumptions from Step 3. To close the proof, we need the energies to remain uniformly bounded (up to the singularity) starting at a level representing, roughly, slightly more than half of the top-order number of derivatives. Consequently, the proof requires a lot of regularity, and “top-order” corresponds to commuting the equations roughly 20 times with the elements of $\mathscr {Z}$ (see Footnote 46). The precise numerology behind the hierarchy (4.3.11a)–(4.3.11g) is complicated, but the following two features seem fundamental: (i) The top-order blowup-rate $\upmu _{\star }^{-K}(t)$, since, as we explain below, the blowup-exponent K is tied to universal structural constants in the equations that are independent of the number of times that we commute them. (ii) An improvement of precisely $\upmu _{\star }^2(t)$ at each step in the descent, which is tied to the fact that $\upmu _{\star }(t)$ vanishes linearly (as we mentioned at the end of Step 6). To construct energies that result in controllable error terms, we must weight various energy integrand terms with factors of $\upmu$, a difficulty that lies at the heart of the analysis. For example, the energies ${\mathbb {E}}_{(Wave)}$ for the “wave variables” $\varPsi \in \lbrace \uprho , v^1, v^2, v^3 \rbrace$ are constructed⁵⁰ so that, at the level of the undifferentiated equations, we have, relative to the geometric coordinates (4.2.1) and the vectorfields in (4.3.1), the following schematic relation:⁵¹

  $$\begin{aligned} {\mathbb {E}}_{(Wave)}[\varPsi ](t)&{\sim } \int _{\varSigma _t} \left\{ (\breve{X}\varPsi )^2 + \upmu \left( (L\varPsi )^2 + (Y_1 \varPsi )^2 + (Y_2 \varPsi )^2 \right) \right\} \, d \vartheta ^1 d \vartheta ^2 du. \end{aligned}$$

  (4.3.12)

  The energy ${\mathbb {E}}_{(Wave);Top}(t)$ on LHS (4.3.11a) schematically represents one of the quantities ${\mathbb {E}}_{(Wave)}[\mathscr {Z}^{N_{top}} \varPsi ](t)$, where $N_{top} \approx 20$ is the maximum number of times that we need to commute the equations in order to close the estimates. The factor of $\upmu$ in (4.3.12) is chosen so that only controllable error terms are generated in the energy identities (it is true, though not obvious, that RHS (4.3.12) has the right strength). Note that some components of the energies become very weak near the shock (that is, in regions where $\upmu$ is small), namely the products on RHS (4.3.12) that are explicitly $\upmu$-weighted. This makes it difficult to control the dangerous non-$\upmu$-weighted error terms that one encounters in the energy identities. To control such “strong” error terms, one uses, in addition to the energies (4.3.12), energies along ${\mathcal {P}}_u$ (known as “null fluxes” or “characteristic fluxes”) as well as a coercive friction-type spacetime integral, which is available because $\displaystyle \frac{\partial }{\partial t} \upmu$ is quantitatively negative in the difficult region where $\upmu$ is small (as we described in Step 6). These aspects of the proof, though of fundamental importance, are quite technical and have been well-understood since Christodoulou’s work [6]. These issues are described in more detail in [21, 22, 29], and we will not further discuss them here. We must also derive energy estimates for the transport equations in Theorem 1. Specifically, to control the transport variables $\varPhi \in \lbrace s, \varOmega ^1, \varOmega ^2, \varOmega ^3, S^1, S^2, S^3, {\mathcal {C}}^1, {\mathcal {C}}^2, {\mathcal {C}}^3, {\mathcal {D}}\rbrace$, we rely on energies with the following strength:⁵²

  $$\begin{aligned} {\mathbb {E}}_{(Transport)}[\varPhi ](t)&\sim \int _{\varSigma _t} \upmu \varPhi ^2 \, d \vartheta ^1 d \vartheta ^2 du. \end{aligned}$$

  (4.3.13)

  As in the case of the wave variable energies, the factor of $\upmu$ in (4.3.13) is chosen so that only controllable error terms are generated in the energy identities. We now sketch some of the most important steps in the proof of the degenerate top-order energy estimate (4.3.11a). We will focus only on the wave equation energy estimates since the transport equation energy estimates are much easier to derive.⁵³ The basic difficulty is that, on the basis of energy identities, the following integral inequality is the best that we are able to obtain:

  $$\begin{aligned} {\mathbb {E}}_{(Wave);Top}(t)&\le C \mathring{\upepsilon }^2 + A \int _{s=0}^t \left\{ \sup _{\varSigma _s} \left| \frac{\frac{\partial }{\partial s} \upmu }{\upmu } \right| \right\} {\mathbb {E}}_{(Wave);Top}(s) \, ds + \cdots , \end{aligned}$$

  (4.3.14)

  where A is a universal positive constant that is independent of the equation of state and the number of times that the equations are commuted, and $\cdots$ denotes similar or less degenerate error terms. Below, we explain the origin of the degenerate factor $\displaystyle \left| \frac{\frac{\partial }{\partial s} \upmu }{\upmu } \right|$ on RHS (4.3.14) (which blows up as the shock forms), whose presence is tied to an issue that we highlighted earlier: the required top-order regularity properties of the eikonal function are difficult to derive. To apply Gronwall’s inequality to the inequality (4.3.14), we need the following crucial estimate:

  $$\begin{aligned} \int _{s=0}^t \sup _{\varSigma _s} \left| \frac{\frac{\partial }{\partial s} \upmu }{\upmu } \right| \, ds \sim \left| \ln \upmu _{\star }^{-1} \right| , \end{aligned}$$

  (4.3.15)

  where $\upmu _{\star }$ is defined in (4.3.10). The estimate (4.3.15) can be derived with the help the estimates

  $$\begin{aligned} \upmu _{\star }(t)&\sim 1 - \mathring{\updelta }_{*}t, \end{aligned}$$

  (4.3.16)
  $$\begin{aligned} \left\| \frac{\partial }{\partial t} \upmu \right\| _{L^{\infty }(\varSigma _t)}&\sim \mathring{\updelta }_{*}, \end{aligned}$$

  (4.3.17)

  stop where $\mathring{\updelta }_{*}> 0$ is a data-dependent parameter that, roughly speaking, measures the $L^{\infty }$ size of the term $\displaystyle \frac{\partial }{\partial u} v^1$ on RHS (4.3.9). We note that to close the proof, one needs to consider initial data such that $\mathring{\upepsilon }$ is small relative to $\mathring{\updelta }_{*}$ (though $\mathring{\updelta }_{*}$ might be small in an absolute sense). We also note that the estimates (4.3.16)–(4.3.17) fall under the scope of the sharp estimates for $\upmu$ from Step 6. Moreover, we point out that the aforementioned fact that $\upmu _{\star }$ vanishes linearly is important for deriving (4.3.15). Finally, we note that (4.3.15) is just a quasilinear version of the estimate $\displaystyle \int _{s=t}^1 \frac{1}{s} \, ds \le \ln (t^{-1})$, in which $s=0$ represents the time of first vanishing of $\upmu _{\star }$ and $s=1$ represents the “initial” data time. After we have derived (4.3.14) and (4.3.15), we can apply Gronwall’s inequality [ignoring the terms $\cdots$ on RHS (4.3.14)] to obtain the following bound:

  $$\begin{aligned} {\mathbb {E}}_{(Wave);Top}(t)&\le C \mathring{\upepsilon }^2 \upmu _{\star }^{-A}(t). \end{aligned}$$

  (4.3.18)

  The bound (4.3.18) is essentially the top-order energy estimate (4.3.11a). However, in reality, the blowup-exponent K on RHS (4.3.11a) is larger than the blowup-exponent A on RHS (4.3.18) because the correct estimate (4.3.11a) is influenced by additional difficult error terms that we have ignored in deriving (4.3.18). We now briefly explain the origin of the difficult error integral on RHS (4.3.14). Let $\vec {\varPsi } := \lbrace \uprho , v^1, v^2, v^3 \rbrace$ denote the array of “wave variables,” and let $\varPsi$ denote any element of $\vec {\varPsi }$. The difficulty arises from the worst commutator error terms that are generated when one commutes the elements of $\mathscr {Z}$ [see (4.3.1)] through the wave operator $\upmu \square _g$ in the wave equation satisfied by $\varPsi$. To explain the main ideas, we consider only the wave equation verified by $Y^N \varPsi$, where $Y^N$ schematically denotes an order N differential operator corresponding to repeated differentiation with respect to elements of the set $\lbrace Y_1, Y_2 \rbrace$; similar difficulties arise upon commuting $\upmu \square _g$ with other strings of vectorfields from $\mathscr {Z}$. Specifically, one can show that upon commuting any of the $\upmu$-weighted wave equations (3.1.1a)–(3.1.1b) with $Y^N$, we obtain an inhomogeneous wave equation of the schematic form

  $$\begin{aligned} \upmu \square _g Y^N \varPsi&= (\breve{X}\vec {\varPsi }) Y^N {\hbox {tr}_{g \! /\, }}\upchi + \cdots . \end{aligned}$$

  (4.3.19)

  The term $\upchi$ on RHS (4.3.19) is the null second fundamental form of the co-dimension-two tori ${\mathcal {P}}_u \cap \varSigma _t$, that is, the symmetric type $\left( {\begin{array}{c}0\\ 2\end{array}}\right)$ tensorfield on ${\mathcal {P}}_u \cap \varSigma _t$ whose components are $\displaystyle \upchi _{\frac{\partial }{\partial \vartheta ^A} \frac{\partial }{\partial \vartheta ^B}} = g(\mathscr {D}_{\frac{\partial }{\partial \vartheta ^A}} L, \frac{\partial }{\partial \vartheta ^B})$, where $\mathscr {D}$ is the Levi–Civita connection of g. Moreover, ${\hbox {tr}_{g \! /\, }}\upchi$ is the trace of $\upchi$ with respect to the Riemannian metric $g \! /\,$ induced on ${\mathcal {P}}_u \cap \varSigma _t$ by g. Geometrically, ${\hbox {tr}_{g \! /\, }}\upchi$ is the null mean curvature of ${\mathcal {P}}_u$. Analytically, $Y^N {\hbox {tr}_{g \! /\, }}\upchi$ is a difficult commutator term in which the maximum possible number of derivatives falls on the eikonal function (recall that $L\sim \partial u$ and thus $\upchi \sim \partial ^2 u$). As we mentioned earlier, the main difficulty is that a naive treatment of terms involving the maximum number of derivatives of the eikonal function would lead to the loss of a derivative and obstruct the closure of the top-order energy estimates. This difficulty is visible directly from the evolution equation satisfied by $Y^N {\hbox {tr}_{g \! /\, }}\upchi$, which can be derived from geometric considerations⁵⁴ and which takes the following schematic form [recall that $P$ schematically denotes elements of the ${\mathcal {P}}_u$-tangent set $\mathscr {P}$ defined in (4.3.2)]:

  $$\begin{aligned} \frac{\partial }{\partial t} Y^N {\hbox {tr}_{g \! /\, }}\upchi&= {\varDelta \! /\,}Y^N \vec {\varPsi } + \frac{\partial }{\partial t} PY^N \vec {\varPsi } + l.o.t, \end{aligned}$$

  (4.3.20)

  where ${\varDelta \! /\,}$ is the covariant Laplacian induced on ${\mathcal {P}}_u \cap \varSigma _t$ by $g \! /\,$ and l.o.t. denotes terms with an allowable amount of regularity, involving, for example, $\le N+1$ derivative of $\vec {\varPsi }$.⁵⁵ The difficulty with equation (4.3.20) is that the two explicitly displayed terms on RHS (4.3.20) depend on $N+2$ derivatives of $\vec {\varPsi }$, which is one more than we can control by energy estimates for the wave equation (4.3.19). That is, the two terms on RHS (4.3.20) seem to lose a derivative. To overcome this difficulty for the second term $\displaystyle \frac{\partial }{\partial t} PY^N \vec {\varPsi }$, we can simply bring it over to the left so that equation (4.3.20) becomes $\displaystyle \frac{\partial }{\partial t} \left\{ Y^N {\hbox {tr}_{g \! /\, }}\upchi - PY^N \vec {\varPsi } \right\} = {\varDelta \! /\,}Y^N \vec {\varPsi } + l.o.t$. To handle the term ${\varDelta \! /\,}Y^N \vec {\varPsi }$, we can use a similar – but more complicated – strategy, first employed in [19] in the context of low-regularity local well-posedness and later by Christodoulou [6] in the context of shock formation: by decomposing the principal parts of the $Y^N$-commuted wave equations (3.1.1a)–(3.1.1b), we can obtain the following algebraic relation, written in schematic form: $\displaystyle \upmu {\varDelta \! /\,}Y^N \vec {\varPsi } = \frac{\partial }{\partial t} \left\{ \breve{X}Y^N \vec {\varPsi } + \upmu PY^N \vec {\varPsi } \right\} + l.o.t.$, where $P\in \mathscr {P}$. Bringing the perfect time derivative term $\frac{\partial }{\partial t} \left\{ \breve{X}Y^N \vec {\varPsi } + \upmu PY^N \vec {\varPsi } \right\}$ over to LHS (4.3.20) as well, and accounting for the factor of $\upmu$, we obtain

  $$\begin{aligned} \frac{\partial }{\partial t} \left\{ \upmu Y^N {\hbox {tr}_{g \! /\, }}\upchi - \breve{X}Y^N \vec {\varPsi } - \upmu PY^N \vec {\varPsi } \right\}&= l.o.t. \end{aligned}$$

  (4.3.21)

  The key point is that all inhomogeneous terms on RHS (4.3.21) now feature an allowable amount of regularity, which implies that we can gain back the derivative by deriving estimates for a “modified” quantity with the following schematic structure:⁵⁶

  $$\begin{aligned} \upmu Y^N {\hbox {tr}_{g \! /\, }}\upchi - \breve{X}Y^N \vec {\varPsi } - \upmu PY^N \vec {\varPsi }. \end{aligned}$$

  (4.3.22)

  We have therefore explained how to avoid the derivative loss that was threatened by the term $Y^N {\hbox {tr}_{g \! /\, }}\upchi$ on RHS (4.3.19). However, our approach comes with a large price: the inhomogeneous term on RHS (4.3.19) involves the factor $Y^N {\hbox {tr}_{g \! /\, }}\upchi$, while (4.3.21) yields an evolution equation only for the modified version of $\upmu Y^N {\hbox {tr}_{g \! /\, }}\upchi$ stated in (4.3.22); the discrepancy factor of $\upmu$ is what leads to the dangerous factor of $\displaystyle \frac{1}{\upmu }$ on RHS (4.3.14). Moreover, from a careful analysis that takes into account the evolution equation for $\upmu$ as well as the precise structure of the factor $\breve{X}\vec {\varPsi }$ on RHS (4.3.19) and the terms on LHS (4.3.21), one can deduce the presence of the factor $\displaystyle \frac{\partial }{\partial s} \upmu$ on RHS (4.3.14), whose precise form is important for the proof of the estimate (4.3.15). We have therefore explained the main ideas behind the origin of the main error integral displayed on RHS (4.3.14). Having provided an overview of the derivation of the top-order energy estimate (4.3.11a), we now describe why the below-top-order energies become successively less singular as one descends below top-order, that is, how to implement the energy estimate descent scheme resulting in the estimates (4.3.11b)–(4.3.11g); recall that the non-degenerate energy estimates (4.3.11e)–(4.3.11g) are needed to improve, by Sobolev embedding and a small-data assumption, the $L^{\infty }$ bootstrap assumptions from Step 2, which are central to the whole process. A key ingredient in the energy estimate descent scheme is the following estimate, valid for constants $b > 0$, which shows that integrating the singularity in time reduces its strength:

  $$\begin{aligned} \int _{s=0}^t \upmu _{\star }^{-b}(s) \, ds \lesssim \upmu _{\star }^{1-b}(t)+1. \end{aligned}$$

  (4.3.23)

  The estimate (4.3.23) is easy to obtain thanks to the sharp information that we have about the linear vanishing rate of $\upmu _{\star }$ [see (4.3.16)]. We note that (4.3.23) is just a quasilinear version of the estimate $\int _{s=t}^1 s^{-b} \, ds \lesssim t^{1 - b}$ for $0< t < 1$, where $s=0$ represents the vanishing of $\upmu _{\star }$. A second key ingredient in implementing the descent scheme is to exploit that below top-order, we can estimate the difficult term $Y^N {\hbox {tr}_{g \! /\, }}\upchi$ on RHS (4.3.19) in a different way; recall that this term was the main driving force behind the degenerate top-order energy estimates. Specifically, for N below top-order, we can directly estimate $Y^N {\hbox {tr}_{g \! /\, }}\upchi$ by integrating the transport equation (4.3.20) in time, without going through the procedure that led to equation (4.3.21) in the top-order case. This approach results in a loss of one derivative (which is permissible below top-order) caused by the two explicitly displayed terms on RHS (4.3.20) and therefore couples the below-top-order energy estimates to the top-order ones. However, the integration in time allows one to employ the estimate (4.3.23), which implies that below top-order, $Y^N {\hbox {tr}_{g \! /\, }}\upchi$ is less singular than RHS (4.3.20); this is the crux of the descent scheme. We also note that this procedure allows one to avoid the difficult factor of $\upmu$, which in the top-order case appeared on LHS (4.3.21) and which drove the blowup-rate of the top-order energies. We have thus explained one step in the descent. One can continue the descent, noting that at each stage, we can directly estimate the difficult term $Y^N {\hbox {tr}_{g \! /\, }}\upchi$ by integrating the transport equation (4.3.20) in time and allowing the loss of one derivative coming from the terms on RHS (4.3.20). This procedure couples the energy estimates at a given derivative level to the estimates for the (already controlled) next-highest-energy, but it nonetheless allows one to derive the desired improvement in the energy blowup-rate by downward induction, thanks to the integration in time and the estimate (4.3.23).

• 8. (Elliptic estimates along$\varSigma _t$). We now confront an important issue that we ignored in Step 7: to close the energy estimates, we are forced to control some of the inhomogeneous terms in the equations using elliptic estimates along $\varSigma _t$. This major difficulty is not present in works on shock formation for wave equations; it was encountered for the first time in our earlier work on shock formation [21] for barotropic fluids with vorticity. A key aspect of the difficulty is that elliptic estimates along $\varSigma _t$ necessarily involve controlling the derivatives of the solution in a direction transversal to the acoustic characteristics ${\mathcal {P}}_u$, that is, in the singular direction. We need elliptic estimates to control the source terms on RHSs (3.1.3b) and (3.1.4a) that depend on ${\underline{\partial }} \varOmega$ and ${\underline{\partial }} S$, where ${\underline{\partial }}$ denotes the gradient with respect to the Cartesian spatial coordinates. More precisely, we need the elliptic estimates only at the top derivative level, but we will ignore that issue and instead focus on the main issue: the degeneracy of the elliptic estimates with respect to $\upmu$. The elliptic estimates can easily be derived relative to the Cartesian coordinates and the Euclidean volume form $\mathrm{{d}}x^1 \mathrm{{d}}x^2 \mathrm{{d}}x^3$ on $\varSigma _t$. However, in order to compare the strength of the elliptic estimates to that of the wave energies (4.3.12) and the transport energies (4.3.13), we need to understand the relationship between the Euclidean volume form and the volume form $\mathrm{{d}}u \mathrm{{d}} \vartheta ^1 \mathrm{{d}} \vartheta ^2$ featured in the energies. Specifically, by studying the Jacobian of the change of variables map between the geometric and the Cartesian coordinates, one can show that there is an ${\mathcal {O}}(\upmu )$ discrepancy factor between the two forms:

  $$\begin{aligned} \mathrm{{d}}x^1 \mathrm{{d}}x^2 \mathrm{{d}}x^3&\sim \upmu \, \mathrm{{d}}u \mathrm{{d}} \vartheta ^1 \mathrm{{d}} \vartheta ^2. \end{aligned}$$

  (4.3.24)

  In the rest of this discussion, our notion of an $L^2(\varSigma _t)$ norm is in terms of the volume form $\mathrm{{d}}u \mathrm{{d}} \vartheta ^1 \mathrm{{d}} \vartheta ^2$. That is, we set

  $$\begin{aligned} \Vert f \Vert _{L^2(\varSigma _t)}^2 := \int f^2(t,u,\vartheta ^1,\vartheta ^2) \, \mathrm{{d}}u \mathrm{{d}} \vartheta ^1 \mathrm{{d}} \vartheta ^2. \end{aligned}$$

  (4.3.25)

  We now further explain some aspects of the elliptic estimates. For convenience, we focus on the estimates for ${\underline{\partial }} S$, where as before, ${\underline{\partial }}$ denotes the gradient with respect to the Cartesian spatial coordinates. One also needs similar elliptic estimates to obtain control over ${\underline{\partial }} \varOmega$, but we omit those details; see [21] for an overview of how to control ${\underline{\partial }} \varOmega$ in the barotropic case. Our elliptic estimates are essentially standard div-curl estimates of the form⁵⁷

  $$\begin{aligned} \int _{\varSigma _t} \left| {\underline{\partial }} S\right| ^2 \, \mathrm{{d}}x^1 \mathrm{{d}}x^2 \mathrm{{d}}x^3 \lesssim \int _{\varSigma _t} \left| \hbox {div}S\right| ^2 \, \mathrm{{d}}x^1 \mathrm{{d}}x^2 \mathrm{{d}}x^3 + \int _{\varSigma _t} \left| \hbox {curl}S\right| ^2 \, \mathrm{{d}}x^1 \mathrm{{d}}x^2 \mathrm{{d}}x^3. \end{aligned}$$

  (4.3.26)

  With the help of (4.3.24) and (4.3.25), we can re-express (4.3.26) as follows:

  $$\begin{aligned} \Vert \sqrt{\upmu } {\underline{\partial }} S\Vert _{L^2(\varSigma _t)}&\lesssim \Vert \sqrt{\upmu } \hbox {div}S\Vert _{L^2(\varSigma _t)} + \Vert \sqrt{\upmu } \hbox {curl}S\Vert _{L^2(\varSigma _t)}. \end{aligned}$$

  (4.3.27)

  We now explain the role that (4.3.27) plays in closing the energy estimates. Our main goal is to show how to derive the bound

  $$\begin{aligned} \Vert \sqrt{\upmu } {\underline{\partial }} S\Vert _{L^2(\varSigma _t)}^2&\lesssim \mathring{\upepsilon }^2 \upmu _{\star }^{- {\widetilde{\upsigma }}}(t) + \cdots , \end{aligned}$$

  (4.3.28)

  where ${\widetilde{\upsigma }} > 0$ is a small constant and $\cdots$ denotes error terms that can be controlled without elliptic estimates (for example, via the wave equation energies). We stress that (4.3.28) is meant to be interpreted as representing the kind of estimate that one needs at the top derivative level, since below top-order, one can avoid using elliptic estimates.⁵⁸ We also stress that, since (4.3.11a) implies that the top-order wave energies can be very degenerate, some of the terms in $\cdots$ on RHS (4.3.28) can in fact blow up at a much worse rate than the one $\upmu _{\star }^{- {\widetilde{\upsigma }}}(t)$ that we have explicitly displayed. The point of writing the estimate for $\Vert \sqrt{\upmu } {\underline{\partial }} S\Vert _{L^2(\varSigma _t)}^2$ in the form (4.3.28) is that this form emphasizes the following point: the self-interaction terms in the elliptic estimates are not the ones driving the blowup-rate of the top-order derivatives of$S$; instead, the blowup-rate of $\Vert \sqrt{\upmu } {\underline{\partial }} S\Vert _{L^2(\varSigma _t)}^2$ is driven by the blowup-rate of the top-order derivatives of the wave variables $\lbrace \uprho , v^1, v^2, v^3 \rbrace$, which are hidden in the $\cdots$ terms on RHS (4.3.28). It turns out that, as a consequence, the blowup-rates for the top-order wave energies are exactly the same as they are in the irrotational and isentropic case. That is, our approach to energy estimates yields the same blowup-exponent K in the energy hierarchy (4.3.11a)–(4.3.11g) compared to the exponent that our approach would yield in the irrotational and isentropic case. To explain how to derive (4.3.28), we start by discussing energy estimates for the transport equation (3.1.4a) for ${\mathcal {D}}$. We again remind the reader that the elliptic estimate approach to deriving (4.3.28) is needed mainly at the top-order, but for convenience, we discuss here only the non-differentiated equations. Specifically, by deriving standard transport equation energy estimates for the weighted transport equation $\upmu \times$ (3.1.4a), by using the $L^{\infty }$ bootstrap assumptions of Step 3 (which in particular can be used to derive the bound $\Vert \upmu \partial _a v^b \Vert _{L^{\infty }(\varSigma _t)} \lesssim 1$), and taking into account definition (4.3.10), one can obtain the following integral inequality:

  $$\begin{aligned} \Vert \sqrt{\upmu } {\mathcal {D}}\Vert _{L^2(\varSigma _t)}^2&\le \upgamma \int _{s=0}^t \frac{1}{\upmu _{\star }(s)} \Vert \sqrt{\upmu } {\underline{\partial }} S\Vert _{L^2(\varSigma _s)}^2 \, \mathrm{{d}}s + \cdots . \end{aligned}$$

  (4.3.29)

  In (4.3.29), $\cdots$ denotes simpler error terms that can be treated without elliptic estimates and, by judicious use of Young’s inequality, it can be arranged that $\upgamma$ is a small positive constant.⁵⁹ Substituting the estimate (4.3.27) into (4.3.29) and using equation (3.1.4b), we obtain

  $$\begin{aligned} \Vert \sqrt{\upmu } {\mathcal {D}}\Vert _{L^2(\varSigma _t)}^2&\le \upgamma \int _{s=0}^t \frac{1}{\upmu _{\star }(s)} \Vert \sqrt{\upmu } \hbox {div}S\Vert _{L^2(\varSigma _s)}^2 \, \mathrm{{d}}s + \cdots , \end{aligned}$$

  (4.3.30)

  where $\cdots$ is as above. From the $L^{\infty }$ bootstrap assumptions of Step 3, one can show that $\exp (2 \uprho ) \lesssim 1$. Thus, in view of definition (1.3.13b), we deduce $\Vert \sqrt{\upmu } \hbox {div}S\Vert _{L^2(\varSigma _s)}^2 \lesssim \Vert \sqrt{\upmu } {\mathcal {D}}\Vert _{L^2(\varSigma _s)}^2 + \cdots$, where $\cdots$ denotes terms that can be controlled without elliptic estimates, that is, via energy estimates for the wave equations (3.1.1a)–(3.1.1b) and the transport equations (3.1.2a)–(3.1.2c). From these considerations and (4.3.30), we deduce

  $$\begin{aligned} \Vert \sqrt{\upmu } {\mathcal {D}}\Vert _{L^2(\varSigma _t)}^2&\le \upgamma \int _{s=0}^t \frac{1}{\upmu _{\star }(s)} \Vert \sqrt{\upmu } {\mathcal {D}}\Vert _{L^2(\varSigma _s)}^2 \, \mathrm{{d}}s + \cdots , \end{aligned}$$

  (4.3.31)

  where we again emphasize that $\upgamma > 0$ can be chosen to be a small constant. Then from (4.3.16), (4.3.31), Gronwall’s inequality, and an appropriate ${\mathcal {O}}(\mathring{\upepsilon })$-size small-data assumption, we deduce that

  $$\begin{aligned} \Vert \sqrt{\upmu } {\mathcal {D}}\Vert _{L^2(\varSigma _t)}^2&\lesssim \mathring{\upepsilon }^2 \upmu _{\star }^{- {\widetilde{\upgamma }}}(t) + \cdots , \end{aligned}$$

  (4.3.32)

  where ${\widetilde{\upgamma }} > 0$ is a small constant whose smallness is controlled by $\upgamma$. Again using (1.3.13b) and the bound $\exp (2 \uprho ) \lesssim 1$, we deduce from (4.3.32) that⁶⁰

  $$\begin{aligned} \Vert \sqrt{\upmu } \hbox {div}S\Vert _{L^2(\varSigma _t)}^2&\lesssim \mathring{\upepsilon }^2 \upmu _{\star }^{- {\widetilde{\upgamma }}}(t) + \cdots . \end{aligned}$$

  (4.3.33)

  One can obtain similar – but much simpler – estimates for $\Vert \sqrt{\upmu } \hbox {curl}S\Vert _{L^2(\varSigma _t)}^2$ directly from equation (3.1.4b).⁶¹ Then inserting these bounds into (4.3.27), we finally obtain the desired bound (4.3.28). We have therefore presented the main ideas behind the elliptic estimates. This completes our overview of our forthcoming proof of shock formation.

5 Proof of Theorem 1

In this section, we prove Theorem 1. The theorem is a conglomeration of Lemmas 3, 4, 5, 6, 8, 9, and 10, in which we separately derive the equations stated in the theorem. Actually, to obtain Theorem 1 from the lemmas, one must slightly reorganize the terms in the equations and relabel some of the indices; we omit those minor details.

Throughout Section 5, we freely use the following identity [see (1.3.6)]:

$$\begin{aligned} \omega ^i&= \exp (\uprho ) \varOmega ^i. \end{aligned}$$

(5.0.1)

5.1 Deriving the Transport and Transport-div-curl Equations

In this subsection, we derive the transport and transport–divergence–curl equations in Theorem 1.

5.1.1 Deriving the Transport Equations for $\lbrace \varOmega ^i \rbrace _{i=1,2,3}$

We now establish the transport equations (3.1.2a) for the Cartesian components $\lbrace \varOmega ^i \rbrace _{i=1,2,3}$.

Lemma 3

(Transport equations for $\varOmega ^i)$ For $C^2$ solutions of the compressible Euler equations (1.3.11a)–(1.3.11c), the Cartesian components $\lbrace \varOmega ^i \rbrace _{i=1,2,3}$ of the specific vorticity vectorfield from Def. 1 verify the following transport equations:

$$\begin{aligned} B\varOmega ^i&= \varOmega ^a \partial _a v^i - \exp (-2 \uprho ) c^{-2} \frac{p_{;s}}{{\bar{\varrho }}} \varepsilon _{iab} (Bv^a) S^b. \end{aligned}$$

(5.1.1)

Proof

We first note the following chain rule identity, which follows easily from definitions (1.3.6) and (1.3.9): $\displaystyle \frac{1}{{\bar{\varrho }}} \exp (-\uprho ) \partial _i p = c^2 \delta ^{ia} \partial _a \uprho + \exp (-\uprho ) \frac{p_{;s}}{{\bar{\varrho }}} \delta ^{ia} \partial _a s$. It follows that $\displaystyle \left( {\mathrm{RHS}} ({\mathrm{1.3.11b}})\right) ^i = - \frac{1}{{\bar{\varrho }}} \exp (-\uprho ) \partial _i p$. Hence, applying $\exp (-\uprho ) \hbox {curl}$ to (1.3.11b) and using definition (1.3.8), the antisymmetry of $\varepsilon _{\dots }$, and the symmetry property $\partial _a \partial _b p = \partial _b \partial _a p$, we deduce the following identity:

$$\begin{aligned} \exp (-\uprho ) \left( \hbox {curl}{\mathrm{RHS}}({\mathrm{1.3.11b}}) \right) ^i&= \exp (-2 \uprho ) \frac{p_{;s}}{{\bar{\varrho }}} \varepsilon _{iab} (\partial _a \uprho ) \partial _b s\nonumber \\&= \exp (-2 \uprho ) \frac{p_{;s}}{{\bar{\varrho }}} \varepsilon _{iab} (\partial _a \uprho ) S^b. \end{aligned}$$

(5.1.2)

Next, in view of the definition (1.3.6) of $\varOmega$, we commute equation (1.3.11b) with the operator $\displaystyle \exp (-\uprho )\hbox {curl}$ and use equations (1.3.11a) and (1.3.12), the antisymmetry of $\varepsilon _{\dots }$, the identity $\varepsilon _{iab} \epsilon _{deb} = \delta _{id} \delta _{ae} - \delta _{ie} \delta _{ad}$, and the identity (5.1.2) to deduce

$$\begin{aligned} B\varOmega ^i&= - \exp (-\uprho ) \varepsilon _{iab} (\partial _a v^d) \partial _d v^b - \exp (-\uprho ) (B\uprho ) \omega ^i + \exp (-2 \uprho ) \frac{p_{;s}}{{\bar{\varrho }}} \varepsilon _{iab} (\partial _a \uprho ) S^b \\&= - \exp (-\uprho ) \varepsilon _{iab} (\partial _a v^d) \partial _d v^b + (\partial _a v^a) \varOmega ^i + \exp (-2 \uprho ) \frac{p_{;s}}{{\bar{\varrho }}} \varepsilon _{iab} (\partial _a \uprho ) S^b \nonumber \\&= - \exp (-\uprho ) \varepsilon _{iab} (\partial _a v^d) (\partial _d v^b - \partial _b v^d) + (\partial _a v^a) \varOmega ^i \nonumber \\&\quad + \exp (-2 \uprho ) \frac{p_{;s}}{{\bar{\varrho }}} \varepsilon _{iab} (\partial _a \uprho ) S^b \nonumber \\&= - \varepsilon _{iab} \epsilon _{dbe} \varOmega ^e (\partial _a v^d) + (\partial _a v^a) \varOmega ^i + \exp (-2 \uprho ) \frac{p_{;s}}{{\bar{\varrho }}} \varepsilon _{iab} (\partial _a \uprho ) S^b \nonumber \\&= \varepsilon _{iab} \epsilon _{deb} \varOmega ^e (\partial _a v^d) + (\partial _a v^a) \varOmega ^i + \exp (-2 \uprho ) \frac{p_{;s}}{{\bar{\varrho }}} \varepsilon _{iab} (\partial _a \uprho ) S^b \nonumber \\&= (\delta _{id} \delta _{ae} - \delta _{ie} \delta _{ad}) \varOmega ^e \partial _a v^d + (\partial _a v^a) \varOmega ^i + \exp (-2 \uprho ) \frac{p_{;s}}{{\bar{\varrho }}} \varepsilon _{iab} (\partial _a \uprho ) S^b \nonumber \\&= \varOmega ^a (\partial _a v^i) + \exp (-2 \uprho ) \frac{p_{;s}}{{\bar{\varrho }}} \varepsilon _{iab} (\partial _a \uprho ) S^b. \nonumber \end{aligned}$$

(5.1.3)

Next, we use equation (1.3.11b), the definition $S^i = \partial _i s$, and the antisymmetry of $\varepsilon _{\dots }$ to derive the identity $\varepsilon _{iab} (\partial _a \uprho ) S^b = - c^{-2} \varepsilon _{iab} (Bv^a) S^b$. Substituting this identity into the last product on RHS (5.1.3), we arrive at (5.1.1). $\quad \square$

5.1.2 Deriving the Transport Equations for $s$ and $\lbrace S^i \rbrace _{i=1,2,3}$

We now establish the transport equations (3.1.2b)–(3.1.2c) for $s$ and the Cartesian components $\lbrace S^i \rbrace _{i=1,2,3}$.

Lemma 4

(Transport equations for $s$ and $S^i)$ For $C^2$ solutions of the compressible Euler equations (1.3.11a)–(1.3.11c), the entropy $s$ and the Cartesian components $\lbrace S^i \rbrace _{i=1,2,3}$ of the entropy gradient vectorfield defined in (1.3.8) verify the following transport equations:

$$\begin{aligned} Bs&= 0, \end{aligned}$$

(5.1.4a)

$$\begin{aligned} BS^i&= - S^a \partial _a v^i + \exp (\uprho ) \varepsilon _{iab} \varOmega ^a S^b. \end{aligned}$$

(5.1.4b)

Proof

Equation (5.1.4a) is just a restatement of (1.3.11c).

To derive (5.1.4b), we first commute equation (5.1.4a) with $\partial _i$ and use definition (1.3.12), the definition $S^i = \partial _i s$, and the identity (5.0.1) to obtain

$$\begin{aligned} BS^i&= - \delta _{ab}(\partial _i v^a) S^b \\&= - \delta _{ab}(\partial _a v^i) S^b + \delta _{ab}(\partial _a v^i - \partial _i v^a) S^b \nonumber \\&= - S^a \partial _a v^i + \varepsilon _{aij} \omega ^j S^a \nonumber \\&= - S^a \partial _a v^i + \exp (\uprho ) \varepsilon _{aij} \varOmega ^j S^a. \nonumber \end{aligned}$$

(5.1.5)

Equation (5.1.4b) now follows from (5.1.5) and the antisymmetry of $\varepsilon _{\dots }$. $\quad \square$

5.1.3 Deriving the Transport–Divergence–Curl Equations for ${\mathcal {D}}$ and $\lbrace (\mathrm{curl}S)^i \rbrace _{i=1,2,3}$

We now establish the transport–divergence–curl equations (3.1.4a)–(3.1.4b) for ${\mathcal {D}}$ and the Cartesian components $\lbrace (\hbox {curl}S)^i \rbrace _{i=1,2,3}$.

Lemma 5

(Transport–divergence–curl equations for ${\mathcal {D}}$ and $\hbox {curl}S^i)$ For $C^3$ solutions of the compressible Euler equations (1.3.11a)–(1.3.11c), the modified fluid variable ${\mathcal {D}}$ defined in (1.3.13b) and the Cartesian components $\lbrace (\hbox {curl}S)^i \rbrace _{i=1,2,3}$ of the curl of the entropy gradient vectorfield defined in (1.3.8) verify the following transport–divergence–curl equations:

$$\begin{aligned} B{\mathcal {D}}&= 2 \exp (-2 \uprho ) \left\{ (\partial _a v^a) \partial _b S^b - (\partial _a v^b) \partial _b S^a \right\} \nonumber \\&\quad + 2 \exp (-2 \uprho ) \left\{ S^a (\partial _a v^b) \partial _b \uprho - (\partial _a v^a) S^b \partial _b \uprho \right\} \nonumber \\&\quad + \exp (-\uprho ) \delta _{ab} (\hbox {curl}\varOmega )^a S^b, \end{aligned}$$

(5.1.6a)

$$\begin{aligned} (\hbox {curl}S)^i&= 0. \end{aligned}$$

(5.1.6b)

Proof

Equation (5.1.6b) is a simple consequence of the fact that $S$ is a (spatial) gradient vectorfield.

To derive (5.1.6a), we first commute the already established equation (5.1.4b) with $\partial _i$ and use definition (1.3.12) and to deduce

$$\begin{aligned} B\hbox {div}S&= - 2 (\partial _a v^b) \partial _b S^a - S^a \partial _a \hbox {div}v + \exp (\uprho ) \varepsilon _{iab} (\partial _i \uprho ) \varOmega ^a S^b \nonumber \\&\quad + \exp (\uprho ) \varepsilon _{iab} (\partial _i \varOmega ^a) S^b + \exp (\uprho )\varepsilon _{iab} \varOmega ^a \partial _i S^b. \end{aligned}$$

(5.1.7)

From equation (5.1.6b), we see that the last product on RHS (5.1.7) vanishes. Also noting that $\varepsilon _{iab} (\partial _i \varOmega ^a) = (\hbox {curl}\varOmega )^b$, we deduce from (5.1.7) that

$$\begin{aligned} B\hbox {div}S&= - S^a \partial _a \hbox {div}v - 2 (\partial _a v^b) \partial _a S^b + \exp (\uprho ) \varepsilon _{iab} (\partial _i \uprho ) \varOmega ^a S^b \nonumber \\&\quad + \exp (\uprho ) \delta _{ab} (\hbox {curl}\varOmega )^a S^b. \end{aligned}$$

(5.1.8)

Next, using equation (1.3.11a) to substitute for the term $\hbox {div}v$ on RHS (5.1.8) and using equation (1.3.12), we find that

$$\begin{aligned} B\hbox {div}S&= S^a \partial _a (B\uprho ) - 2 (\partial _a v^b) \partial _b S^a + \exp (\uprho ) \varepsilon _{iab} (\partial _i \uprho ) \varOmega ^a S^b \nonumber \\&\quad + \exp (\uprho ) \delta _{ab} (\hbox {curl}\varOmega )^a S^b \nonumber \\&= B(S^a \partial _a \uprho ) + S^a (\partial _a v^b) \partial _b \uprho - (BS^a) \partial _a \uprho - 2 (\partial _a v^b) \partial _b S^a \nonumber \\&\quad + \exp (\uprho ) \varepsilon _{iab} (\partial _i \uprho ) \varOmega ^a S^b + \exp (\uprho ) \delta _{ab} (\hbox {curl}\varOmega )^a S^b. \end{aligned}$$

(5.1.9)

Using equation (5.1.4b) to substitute for the factor $BS^a$ on RHS (5.1.9), we deduce

$$\begin{aligned} B\hbox {div}S&= B(S^a \partial _a \uprho ) - 2 (\partial _a v^b) \partial _b S^a + 2 S^a (\partial _a v^b) \partial _b \uprho + \exp (\uprho ) \delta _{ab} (\hbox {curl}\varOmega )^a S^b. \end{aligned}$$

(5.1.10)

Bringing the term $B(S^a \partial _a \uprho )$ on RHS (5.1.10) over to the left and then commuting the equation with $\exp (-2\uprho )$, we obtain

$$\begin{aligned}&B\left\{ \exp (-2 \uprho ) \hbox {div}S- \exp (-2 \uprho ) S^a \partial _a \uprho \right\} \nonumber \\&= - 2 \exp (-2 \uprho ) (\partial _a v^b) \partial _b S^a - 2 \exp (-2 \uprho ) (B\uprho ) \hbox {div}S\nonumber \\&\quad + 2 \exp (-2 \uprho ) S^a (\partial _a v^b) \partial _b \uprho + 2 \exp (-2 \uprho ) (B\uprho ) S^a \partial _a \uprho \nonumber \\&\quad + \exp (-\uprho ) \delta _{ab} (\hbox {curl}\varOmega )^a S^b. \end{aligned}$$

(5.1.11)

Finally, using equation (1.3.11a) to substitute for the two factors of $B\uprho$ on RHS (5.1.11) and referring to definition (1.3.13b), we arrive at the desired equation (5.1.6a). $\quad \square$

5.1.4 Deriving the Transport–Divergence–Curl Equations for $\mathrm{div} \varOmega$ and $\lbrace {\mathcal {C}}^i \rbrace _{i=1,2,3}$

We now establish the transport–divergence–curl equations (3.1.3a)–(3.1.3b) for $\hbox {div}\varOmega$ and the Cartesian components $\lbrace {\mathcal {C}}^i \rbrace _{i=1,2,3}$.

Lemma 6

(Transport–divergence–curl equations for $\hbox {div}\varOmega$ and ${\mathcal {C}}^i)$ For $C^3$ solutions of the compressible Euler equations (1.3.11a)–(1.3.11c), the Cartesian components $\lbrace {\mathcal {C}}^i \rbrace _{i=1,2,3}$ of the modified fluid variable defined in (1.3.13a) and the divergence of the specific vorticity vectorfield defined in (1.3.6) verify the following transport–divergence–curl equations:

$$\begin{aligned} \hbox {div}\varOmega&= - \varOmega ^a \partial _a \uprho , \end{aligned}$$

(5.1.12a)

$$\begin{aligned} B{\mathcal {C}}^i&= - 2 \delta _{jk} \varepsilon _{iab} \exp (-\uprho ) (\partial _a v^j) \partial _b \varOmega ^k + \varepsilon _{ajk} \exp (-\uprho ) (\partial _a v^i) \partial _j \varOmega ^k \\&\quad + \exp (-3 \uprho ) c^{-2} \frac{p_{;s}}{{\bar{\varrho }}} \left\{ (BS^a) \partial _a v^i - (Bv^i) \partial _a S^a \right\} \nonumber \\&\quad + \exp (-3 \uprho ) c^{-2} \frac{p_{;s}}{{\bar{\varrho }}} \left\{ (Bv^a) \partial _a S^i - (\partial _a v^a) BS^i \right\} \nonumber \\&\quad + \exp (-3 \uprho ) c^{-2} \frac{p_{;s}}{{\bar{\varrho }}} S^i \left\{ (\partial _a v^b) \partial _b v^a - (\partial _a v^a) \partial _b v^b \right\} \nonumber \\&\quad + \exp (-3 \uprho ) c^{-2} \frac{p_{;s}}{{\bar{\varrho }}} \left\{ (\partial _a v^a) S^b \partial _b v^i - S^a (\partial _a v^b) \partial _b v^i \right\} \nonumber \\&\quad + 2 \exp (-3 \uprho ) c^{-2} \frac{p_{;s}}{{\bar{\varrho }}} \left\{ S^a (\partial _a \uprho ) Bv^i - (B\uprho ) S^a \partial _a v^i \right\} \nonumber \\&\quad + 2 \exp (-3 \uprho ) c^{-3} c_{;\uprho } \frac{p_{;s}}{{\bar{\varrho }}} \left\{ S^a (\partial _a \uprho ) Bv^i - (B\uprho ) S^a \partial _a v^i \right\} \nonumber \\&\quad + \exp (-3 \uprho ) c^{-2} \frac{p_{;s;\uprho }}{{\bar{\varrho }}} \left\{ (B\uprho ) S^a \partial _a v^i - S^a (\partial _a \uprho ) Bv^i \right\} \nonumber \\&\quad + \exp (-3 \uprho ) c^{-2} \frac{p_{;s;\uprho }}{{\bar{\varrho }}} S^i \left\{ (Bv^a) \partial _a \uprho - (B\uprho ) \partial _a v^a \right\} \nonumber \\&\quad + 2 \exp (-3 \uprho ) c^{-2} \frac{p_{;s}}{{\bar{\varrho }}} S^i \left\{ (B\uprho ) \partial _a v^a - (Bv^a) \partial _a \uprho \right\} \nonumber \\&\quad + 2 \exp (-3 \uprho ) c^{-3} c_{;\uprho } \frac{p_{;s}}{{\bar{\varrho }}} S^i \left\{ (B\uprho ) \partial _a v^a - (Bv^a) \partial _a \uprho \right\} \nonumber \\&\quad + 2 \exp (-3 \uprho ) c^{-3} c_{;s} \frac{p_{;s}}{{\bar{\varrho }}} (Bv^i) \delta _{ab} S^a S^b - 2 \exp (-3 \uprho ) c^{-3} c_{;s} \frac{p_{;s}}{{\bar{\varrho }}} \delta _{ab} S^a (Bv^b) S^i \nonumber \\&\quad + \exp (-3 \uprho ) c^{-2} \frac{p_{;s;s}}{{\bar{\varrho }}} \delta _{ab} (Bv^a) S^b S^i - \exp (-3 \uprho ) c^{-2} \frac{p_{;s;s}}{{\bar{\varrho }}} (Bv^i) \delta _{ab} S^a S^b. \nonumber \end{aligned}$$

(5.1.12b)

Proof

Equation (5.1.12a) follows easily from applying the operator $\hbox {div}$ to equation (5.0.1) and noting that since $\omega = \hbox {curl}v$, we have $\hbox {div}\omega = 0$.

We now derive (5.1.12b). First, commuting the already established equation (5.1.1) with the operator $\hbox {curl}$ and using definitions (1.3.8) and (1.3.12) and equation (5.0.1), we compute that

$$\begin{aligned} B(\hbox {curl}\varOmega )^i&= \varOmega ^a \partial _a \omega ^i + \varepsilon _{iab} (\partial _a \varOmega ^d) \partial _d v^b - \varepsilon _{iab} (\partial _a v^d) \partial _d \varOmega ^b \nonumber \\&\quad - \varepsilon _{iab} \epsilon _{bjk} \partial _a \left\{ \exp (-2 \uprho ) c^{-2}\frac{p_{;s}}{{\bar{\varrho }}} (Bv^j) S^k \right\} \nonumber \\&= (\exp \uprho ) \varOmega ^a \partial _a \varOmega ^i + (\exp \uprho ) \varOmega ^i \varOmega ^a \partial _a \uprho \nonumber \\&\quad + \varepsilon _{iab} (\partial _a \varOmega ^d) \partial _d v^b - \varepsilon _{iab} (\partial _a v^d) \partial _d \varOmega ^b \nonumber \\&\quad + 2 \varepsilon _{iab} \epsilon _{bjk} (\partial _a \uprho ) \left\{ \exp (-2 \uprho ) c^{-2} \frac{p_{;s}}{{\bar{\varrho }}} (Bv^j) S^k \right\} \nonumber \\&\quad + 2 \varepsilon _{iab} \epsilon _{bjk} (\partial _a \uprho ) \left\{ \exp (-2 \uprho ) c^{-3} c_{;\uprho } \frac{p_{;s}}{{\bar{\varrho }}} (Bv^j) S^k \right\} \nonumber \\&\quad + 2 \varepsilon _{iab} \epsilon _{bjk} S^a \left\{ \exp (-2 \uprho ) c^{-3} c_{;s} \frac{p_{;s}}{{\bar{\varrho }}} (Bv^j) S^k \right\} \nonumber \\&\quad - \varepsilon _{iab} \epsilon _{bjk} (\partial _a \uprho ) \left\{ \exp (-2 \uprho ) c^{-2} \frac{p_{;s;\uprho }}{{\bar{\varrho }}} (Bv^j) S^k \right\} \nonumber \\&\quad - \varepsilon _{iab} \epsilon _{bjk} S^a \left\{ \exp (-2 \uprho ) c^{-2} \frac{p_{;s;s}}{{\bar{\varrho }}} (Bv^j) S^k \right\} \nonumber \\&\quad - \varepsilon _{iab} \epsilon _{bjk} \left\{ \exp (-2 \uprho ) c^{-2} \frac{p_{;s}}{{\bar{\varrho }}} (\partial _a v^d) (\partial _d v^j) S^k \right\} \nonumber \\&\quad - \varepsilon _{iab} \epsilon _{bjk} \left\{ \exp (-2 \uprho ) c^{-2} \frac{p_{;s}}{{\bar{\varrho }}} (B\partial _a v^j) S^k \right\} \nonumber \\&\quad - \varepsilon _{iab} \epsilon _{bjk} \left\{ \exp (-2 \uprho ) c^{-2} \frac{p_{;s}}{{\bar{\varrho }}} (Bv^j) \partial _a S^k \right\} . \end{aligned}$$

(5.1.13)

Next, using the identity $\varepsilon _{iab} \epsilon _{jdb} = \delta _{ij}\delta _{ad} - \delta _{id} \delta _{aj}$ and the antisymmetry of $\varepsilon _{\cdots }$, we rewrite the third and fourth terms on RHS (5.1.13) as follows:

$$\begin{aligned}&\varepsilon _{iab} (\partial _a \varOmega ^d) \partial _d v^b - \varepsilon _{iab} (\partial _a v^d) \partial _d \varOmega ^b \nonumber \\&\quad = - 2 \delta _{jk} \varepsilon _{iab} (\partial _a v^j) \partial _b \varOmega ^k \nonumber \\&\qquad + \varepsilon _{iab} (\partial _a \varOmega ^d) (\partial _d v^b - \partial _b v^d) + \varepsilon _{iab} (\partial _a v^d) (\partial _b \varOmega ^d - \partial _d \varOmega ^b) \nonumber \\&\quad = - 2 \delta _{jk} \varepsilon _{iab} (\partial _a v^j) \partial _b \varOmega ^k + \varepsilon _{iab} \epsilon _{jdb} (\partial _a \varOmega ^d) \omega ^j + \varepsilon _{iab} \epsilon _{jbd} (\partial _a v^d) (\hbox {curl}\varOmega )^j \nonumber \\&\quad = - 2 \delta _{jk} \varepsilon _{iab} (\partial _a v^j) \partial _b \varOmega ^k + \exp (\uprho ) (\hbox {div}\varOmega ) \varOmega ^i - \exp (\uprho ) \varOmega ^a \partial _a \varOmega ^i \nonumber \\&\qquad + (\hbox {curl}\varOmega )^a \partial _a v^i - (\partial _a v^a) (\hbox {curl}\varOmega )^i. \end{aligned}$$

(5.1.14)

Substituting RHS (5.1.14) for the third and fourth terms on RHS (5.1.13), using equation (5.1.12a) for substitution, and using the identities $(\hbox {curl}\varOmega )^a \partial _a v^i = \varepsilon _{ajk} (\partial _a v^i) \partial _j \varOmega ^k$ and $\varepsilon _{iab} \epsilon _{bjk} = \delta _{ij}\delta _{ak} - \delta _{ik} \delta _{aj}$, we compute that

$$\begin{aligned}&B(\hbox {curl}\varOmega )^i \nonumber \\&\quad = - 2 \delta _{jk} \varepsilon _{iab} (\partial _a v^j) \partial _b \varOmega ^k - (\partial _a v^a) (\hbox {curl}\varOmega )^i + \varepsilon _{ajk} (\partial _a v^i) \partial _j \varOmega ^k \nonumber \\&\qquad + 2 \exp (-2 \uprho ) c^{-2} \frac{p_{;s}}{{\bar{\varrho }}} S^a (\partial _a \uprho ) Bv^i - 2 \exp (-2 \uprho ) c^{-2} \frac{p_{;s}}{{\bar{\varrho }}} (Bv^a) (\partial _a \uprho ) S^i \nonumber \\&\qquad + 2 \exp (-2 \uprho ) c^{-3} c_{;\uprho } \frac{p_{;s}}{{\bar{\varrho }}} S^a (\partial _a \uprho ) Bv^i - 2 \exp (-2 \uprho ) c^{-3} c_{;\uprho } \frac{p_{;s}}{{\bar{\varrho }}} (Bv^a) (\partial _a \uprho ) S^i \nonumber \\&\qquad + 2 \exp (-2 \uprho ) c^{-3} c_{;s} \frac{p_{;s}}{{\bar{\varrho }}} (Bv^i) \delta _{ab} S^a S^b - 2 \exp (-2 \uprho ) c^{-3} c_{;s} \frac{p_{;s}}{{\bar{\varrho }}} \delta _{ab} S^a (Bv^b) S^i \nonumber \\&\qquad + \exp (-2 \uprho ) c^{-2} \frac{p_{;s;\uprho }}{{\bar{\varrho }}} (Bv^a) (\partial _a \uprho ) S^i - \exp (-2 \uprho ) c^{-2} \frac{p_{;s;\uprho }}{{\bar{\varrho }}} S^a (\partial _a \uprho ) Bv^i \nonumber \\&\qquad + \exp (-2 \uprho ) c^{-2} \frac{p_{;s;s}}{{\bar{\varrho }}} \delta _{ab} (Bv^a) S^b S^i - \exp (-2 \uprho ) c^{-2} \frac{p_{;s;s}}{{\bar{\varrho }}} (Bv^i) \delta _{ab} S^a S^b \nonumber \\&\qquad + \exp (-2 \uprho ) c^{-2} \frac{p_{;s}}{{\bar{\varrho }}} (\partial _a v^b) (\partial _b v^a) S^i - \exp (-2 \uprho ) c^{-2} \frac{p_{;s}}{{\bar{\varrho }}}S^a (\partial _a v^b) \partial _b v^i \nonumber \\&\qquad + \exp (-2 \uprho ) c^{-2} \frac{p_{;s}}{{\bar{\varrho }}} (B\partial _a v^a) S^i - \exp (-2 \uprho ) c^{-2} \frac{p_{;s}}{{\bar{\varrho }}} S^a B\partial _a v^i \nonumber \\&\qquad + \exp (-2 \uprho ) c^{-2} \frac{p_{;s}}{{\bar{\varrho }}} (Bv^a) \partial _a S^i - \exp (-2 \uprho ) c^{-2} \frac{p_{;s}}{{\bar{\varrho }}} (Bv^i) \partial _a S^a. \end{aligned}$$

(5.1.15)

We now bring the terms $\displaystyle \exp (-2 \uprho ) c^{-2} \frac{p_{;s}}{{\bar{\varrho }}} (B\partial _a v^a) S^i - \exp (-2 \uprho ) c^{-2} \frac{p_{;s}}{{\bar{\varrho }}} S^a B\partial _a v^i$ from the next-to-last line of RHS (5.1.15) over to the left under the transport operator $B$, which generates some additional commutator terms on the RHS (note that by (1.3.11c), the additional terms that feature a factor of $Bs$ completely vanish). In total, we obtain

$$\begin{aligned}&B\left\{ (\hbox {curl}\varOmega )^i + \exp (-2 \uprho ) c^{-2} \frac{p_{;s}}{{\bar{\varrho }}} S^a \partial _a v^i - \exp (-2 \uprho ) c^{-2} \frac{p_{;s}}{{\bar{\varrho }}} (\partial _a v^a) S^i \right\} \nonumber \\&\quad = - (\partial _a v^a) (\hbox {curl}\varOmega )^i \nonumber \\&\qquad - 2 \delta _{jk} \varepsilon _{iab} (\partial _a v^j) \partial _b \varOmega ^k + \varepsilon _{ajk} (\partial _a v^i) \partial _j \varOmega ^k \nonumber \\&\qquad - 2 \exp (-2 \uprho ) c^{-2} \frac{p_{;s}}{{\bar{\varrho }}} (B\uprho ) S^a \partial _a v^i - 2 \exp (-2 \uprho ) c^{-3} c_{;\uprho } \frac{p_{;s}}{{\bar{\varrho }}} (B\uprho ) S^a \partial _a v^i \nonumber \\&\qquad + \exp (-2 \uprho ) c^{-2} \frac{p_{;s;\uprho }}{{\bar{\varrho }}} (B\uprho ) S^a \partial _a v^i \nonumber \\&\qquad + \exp (-2 \uprho ) c^{-2} \frac{p_{;s}}{{\bar{\varrho }}} (BS^a) \partial _a v^i \nonumber \\&\qquad + 2 \exp (-2 \uprho ) c^{-2} \frac{p_{;s}}{{\bar{\varrho }}} (B\uprho )(\partial _a v^a) S^i + 2 \exp (-2 \uprho ) c^{-3} c_{;\uprho } \frac{p_{;s}}{{\bar{\varrho }}} (B\uprho )(\partial _a v^a) S^i \nonumber \\&\qquad - \exp (-2 \uprho ) c^{-2} \frac{p_{;s;\uprho }}{{\bar{\varrho }}} (B\uprho ) (\partial _a v^a) S^i \nonumber \\&\qquad - \exp (-2 \uprho ) c^{-2} \frac{p_{;s}}{{\bar{\varrho }}} (\partial _a v^a) BS^i \nonumber \\&\qquad + 2 \exp (-2 \uprho ) c^{-2} \frac{p_{;s}}{{\bar{\varrho }}} S^a (\partial _a \uprho ) Bv^i - 2 \exp (-2 \uprho ) c^{-2} \frac{p_{;s}}{{\bar{\varrho }}} (Bv^a) (\partial _a \uprho ) S^i \nonumber \\&\qquad + 2 \exp (-2 \uprho ) c^{-3} c_{;\uprho } \frac{p_{;s}}{{\bar{\varrho }}} S^a (\partial _a \uprho ) Bv^i - 2 \exp (-2 \uprho ) c^{-3} c_{;\uprho } \frac{p_{;s}}{{\bar{\varrho }}} (Bv^a) (\partial _a \uprho ) S^i \nonumber \\&\qquad + 2 \exp (-2 \uprho ) c^{-3} c_{;s} \frac{p_{;s}}{{\bar{\varrho }}} (Bv^i) \delta _{ab} S^a S^b - 2 \exp (-2 \uprho ) c^{-3} c_{;s} \frac{p_{;s}}{{\bar{\varrho }}} \delta _{ab} S^a (Bv^b) S^i \nonumber \\&\qquad + \exp (-2 \uprho ) c^{-2} \frac{p_{;s;\uprho }}{{\bar{\varrho }}} (Bv^a) (\partial _a \uprho ) S^i - \exp (-2 \uprho ) c^{-2} \frac{p_{;s;\uprho }}{{\bar{\varrho }}} S^a (\partial _a \uprho ) Bv^i \nonumber \\&\qquad + \exp (-2 \uprho ) c^{-2} \frac{p_{;s;s}}{{\bar{\varrho }}} \delta _{ab} (Bv^a) S^b S^i - \exp (-2 \uprho ) c^{-2} \frac{p_{;s;s}}{{\bar{\varrho }}} (Bv^i) \delta _{ab} S^a S^b \nonumber \\&\qquad + \exp (-2 \uprho ) c^{-2} \frac{p_{;s}}{{\bar{\varrho }}} (\partial _a v^b) (\partial _b v^a) S^i - \exp (-2 \uprho ) c^{-2} \frac{p_{;s}}{{\bar{\varrho }}}S^a (\partial _a v^b) \partial _b v^i \nonumber \\&\qquad + \exp (-2 \uprho ) c^{-2} \frac{p_{;s}}{{\bar{\varrho }}} (Bv^a) \partial _a S^i - \exp (-2 \uprho ) c^{-2} \frac{p_{;s}}{{\bar{\varrho }}} (Bv^i) \partial _a S^a. \end{aligned}$$

(5.1.16)

Next, we add $\displaystyle - \exp (-2 \uprho ) c^{-2} \frac{p_{;s}}{{\bar{\varrho }}}(\partial _a v^a) S^b \partial _b v^i + \exp (-2 \uprho ) c^{-2} \frac{p_{;s}}{{\bar{\varrho }}}(\partial _a v^a)^2 S^i$ to the first line of RHS (5.1.16), subtract the same terms on a different line, use equation (1.3.11a) to substitute $\partial _a v^a$ with $- B\uprho$ for some factors, and rearrange the terms to deduce

$$\begin{aligned}&B\left\{ (\hbox {curl}\varOmega )^i + \exp (-2 \uprho ) c^{-2} \frac{p_{;s}}{{\bar{\varrho }}} S^a \partial _a v^i - \exp (-2 \uprho ) c^{-2} \frac{p_{;s}}{{\bar{\varrho }}} (\partial _a v^a) S^i \right\} \nonumber \\&\quad = (B\uprho ) \left\{ (\hbox {curl}\varOmega )^i + \exp (-2 \uprho ) c^{-2} \frac{p_{;s}}{{\bar{\varrho }}} S^a \partial _a v^i - \exp (-2 \uprho ) c^{-2} \frac{p_{;s}}{{\bar{\varrho }}} (\partial _a v^a) S^i \right\} \nonumber \\&\qquad + \exp (-2 \uprho ) c^{-2} \frac{p_{;s}}{{\bar{\varrho }}} (BS^a) \partial _a v^i - \exp (-2 \uprho ) c^{-2} \frac{p_{;s}}{{\bar{\varrho }}} (Bv^i) \partial _a S^a \nonumber \\&\qquad + \exp (-2 \uprho ) c^{-2} \frac{p_{;s}}{{\bar{\varrho }}} (Bv^a) \partial _a S^i - \exp (-2 \uprho ) c^{-2} \frac{p_{;s}}{{\bar{\varrho }}} (\partial _a v^a) BS^i \nonumber \\&\qquad - 2 \delta _{jk} \varepsilon _{iab} (\partial _a v^j) \partial _b \varOmega ^k + \varepsilon _{ajk} (\partial _a v^i) \partial _j \varOmega ^k \nonumber \\&\qquad + \exp (-2 \uprho ) c^{-2} \frac{p_{;s}}{{\bar{\varrho }}}(\partial _a v^b) (\partial _b v^a) S^i - \exp (-2 \uprho ) c^{-2} \frac{p_{;s}}{{\bar{\varrho }}}(\partial _a v^a)^2 S^i \nonumber \\&\qquad + \exp (-2 \uprho ) c^{-2} \frac{p_{;s}}{{\bar{\varrho }}}(\partial _a v^a) S^b \partial _b v^i - \exp (-2 \uprho ) c^{-2} \frac{p_{;s}}{{\bar{\varrho }}}S^a (\partial _a v^b) \partial _b v^i \nonumber \\&\qquad + 2 \exp (-2 \uprho ) c^{-2} \frac{p_{;s}}{{\bar{\varrho }}} S^a (\partial _a \uprho ) Bv^i - 2 \exp (-2 \uprho ) c^{-2} \frac{p_{;s}}{{\bar{\varrho }}} (B\uprho ) S^a \partial _a v^i \nonumber \\&\qquad + 2 \exp (-2 \uprho ) c^{-3} c_{;\uprho } \frac{p_{;s}}{{\bar{\varrho }}} S^a (\partial _a \uprho ) Bv^i - 2 \exp (-2 \uprho ) c^{-3} c_{;\uprho } \frac{p_{;s}}{{\bar{\varrho }}} (B\uprho ) S^a \partial _a v^i \nonumber \\&\qquad + \exp (-2 \uprho ) c^{-2} \frac{p_{;s;\uprho }}{{\bar{\varrho }}} (B\uprho ) S^a \partial _a v^i - \exp (-2 \uprho ) c^{-2} \frac{p_{;s;\uprho }}{{\bar{\varrho }}} S^a (\partial _a \uprho ) Bv^i \nonumber \\&\qquad + \exp (-2 \uprho ) c^{-2} \frac{p_{;s;\uprho }}{{\bar{\varrho }}} (Bv^a) (\partial _a \uprho ) S^i - \exp (-2 \uprho ) c^{-2} \frac{p_{;s;\uprho }}{{\bar{\varrho }}} (B\uprho ) (\partial _a v^a) S^i \nonumber \\&\qquad + 2 \exp (-2 \uprho ) c^{-2} \frac{p_{;s}}{{\bar{\varrho }}} (B\uprho )(\partial _a v^a) S^i - 2 \exp (-2 \uprho ) c^{-2} \frac{p_{;s}}{{\bar{\varrho }}} (Bv^a) (\partial _a \uprho ) S^i \nonumber \\&\qquad + 2 \exp (-2 \uprho ) c^{-3} c_{;\uprho } \frac{p_{;s}}{{\bar{\varrho }}} (B\uprho )(\partial _a v^a) S^i - 2 \exp (-2 \uprho ) c^{-3} c_{;\uprho } \frac{p_{;s}}{{\bar{\varrho }}} (Bv^a) (\partial _a \uprho ) S^i \nonumber \\&\qquad + 2 \exp (-2 \uprho ) c^{-3} c_{;s} \frac{p_{;s}}{{\bar{\varrho }}} (Bv^i) \delta _{ab} S^a S^b - 2 \exp (-2 \uprho ) c^{-3} c_{;s} \frac{p_{;s}}{{\bar{\varrho }}} \delta _{ab} S^a (Bv^b) S^i \nonumber \\&\qquad + \exp (-2 \uprho ) c^{-2} \frac{p_{;s;s}}{{\bar{\varrho }}} \delta _{ab} (Bv^a) S^b S^i - \exp (-2 \uprho ) c^{-2} \frac{p_{;s;s}}{{\bar{\varrho }}} (Bv^i) \delta _{ab} S^a S^b. \end{aligned}$$

(5.1.17)

We now multiply both sides of (5.1.17) by $\exp (-\uprho )$ and bring the factor of $\exp (-\uprho )$ under the operator $B$ on the LHS. The commutator term $(B\exp (-\uprho )) \times \cdots$ completely cancels the first line of RHS (5.1.17), which therefore yields

$$\begin{aligned}&B\left\{ \exp (-\uprho ) (\hbox {curl}\varOmega )^i + \exp (-3 \uprho ) c^{-2} \frac{p_{;s}}{{\bar{\varrho }}} S^a \partial _a v^i - \exp (-3 \uprho ) c^{-2} \frac{p_{;s}}{{\bar{\varrho }}} (\partial _a v^a) S^i \right\} \nonumber \\&\quad = - 2 \delta _{jk} \varepsilon _{iab} \exp (-\uprho ) (\partial _a v^j) \partial _b \varOmega ^k + \varepsilon _{ajk} \exp (-\uprho ) (\partial _a v^i) \partial _j \varOmega ^k \nonumber \\&\qquad + \exp (-3 \uprho ) c^{-2} \frac{p_{;s}}{{\bar{\varrho }}} (BS^a) \partial _a v^i - \exp (-3 \uprho ) c^{-2} \frac{p_{;s}}{{\bar{\varrho }}} (Bv^i) \partial _a S^a \nonumber \\&\qquad + \exp (-3 \uprho ) c^{-2} \frac{p_{;s}}{{\bar{\varrho }}} (Bv^a) \partial _a S^i - \exp (-3 \uprho ) c^{-2} \frac{p_{;s}}{{\bar{\varrho }}} (\partial _a v^a) BS^i \nonumber \\&\qquad + \exp (-3 \uprho ) c^{-2} \frac{p_{;s}}{{\bar{\varrho }}}(\partial _a v^b) (\partial _b v^a) S^i - \exp (-3 \uprho ) c^{-2} \frac{p_{;s}}{{\bar{\varrho }}}(\partial _a v^a)^2 S^i \nonumber \\&\qquad + \exp (-3 \uprho ) c^{-2} \frac{p_{;s}}{{\bar{\varrho }}}(\partial _a v^a) S^b \partial _b v^i - \exp (-3 \uprho ) c^{-2} \frac{p_{;s}}{{\bar{\varrho }}}S^a (\partial _a v^b) \partial _b v^i \nonumber \\&\qquad + 2 \exp (-3 \uprho ) c^{-2} \frac{p_{;s}}{{\bar{\varrho }}} S^a (\partial _a \uprho ) Bv^i - 2 \exp (-3 \uprho ) c^{-2} \frac{p_{;s}}{{\bar{\varrho }}} (B\uprho ) S^a \partial _a v^i \nonumber \\&\qquad + 2 \exp (-3 \uprho ) c^{-3} c_{;\uprho } \frac{p_{;s}}{{\bar{\varrho }}} S^a (\partial _a \uprho ) Bv^i - 2 \exp (-3 \uprho ) c^{-3} c_{;\uprho } \frac{p_{;s}}{{\bar{\varrho }}} (B\uprho ) S^a \partial _a v^i \nonumber \\&\qquad + \exp (-3 \uprho ) c^{-2} \frac{p_{;s;\uprho }}{{\bar{\varrho }}} (B\uprho ) S^a \partial _a v^i - \exp (-3 \uprho ) c^{-2} \frac{p_{;s;\uprho }}{{\bar{\varrho }}} S^a (\partial _a \uprho ) Bv^i \nonumber \\&\qquad + \exp (-3 \uprho ) c^{-2} \frac{p_{;s;\uprho }}{{\bar{\varrho }}} (Bv^a) (\partial _a \uprho ) S^i - \exp (-3 \uprho ) c^{-2} \frac{p_{;s;\uprho }}{{\bar{\varrho }}} (B\uprho ) (\partial _a v^a) S^i \nonumber \\&\qquad + 2 \exp (-3 \uprho ) c^{-2} \frac{p_{;s}}{{\bar{\varrho }}} (B\uprho )(\partial _a v^a) S^i - 2 \exp (-3 \uprho ) c^{-2} \frac{p_{;s}}{{\bar{\varrho }}} (Bv^a) (\partial _a \uprho ) S^i \nonumber \\&\qquad + 2 \exp (-3 \uprho ) c^{-3} c_{;\uprho } \frac{p_{;s}}{{\bar{\varrho }}} (B\uprho )(\partial _a v^a) S^i - 2 \exp (-3 \uprho ) c^{-3} c_{;\uprho } \frac{p_{;s}}{{\bar{\varrho }}} (Bv^a) (\partial _a \uprho ) S^i \nonumber \\&\qquad + 2 \exp (-3 \uprho ) c^{-3} c_{;s} \frac{p_{;s}}{{\bar{\varrho }}} (Bv^i) \delta _{ab} S^a S^b - 2 \exp (-3 \uprho ) c^{-3} c_{;s} \frac{p_{;s}}{{\bar{\varrho }}} \delta _{ab} S^a (Bv^b) S^i \nonumber \\&\qquad + \exp (-3 \uprho ) c^{-2} \frac{p_{;s;s}}{{\bar{\varrho }}} \delta _{ab} (Bv^a) S^b S^i - \exp (-3 \uprho ) c^{-2} \frac{p_{;s;s}}{{\bar{\varrho }}} (Bv^i) \delta _{ab} S^a S^b. \end{aligned}$$

(5.1.18)

From equation (5.1.18) and definition (1.3.13a), we conclude the desired equation (5.1.12b). $\quad \square$

5.2 Deriving the Covariant Wave Equations

In this subsection, we derive the covariant wave equations in Theorem 1.

5.2.1 An Explicit Expression for the Covariant Wave Operator in Cartesian Coordinates

Recall that the covariant wave operator $\square _g$ is defined in Def. 9. In the next lemma, we provide an explicit expression for $\square _g \phi$ that holds relative to the Cartesian coordinates.

Lemma 7

$(\square _g$ relative to the Cartesian coordinates) Let g be the acoustical metric from Def. 4. The covariant wave operator $\square _g$ acts on scalar functions $\phi$ via the following identity, where RHS (5.2.1) is expressed in Cartesian coordinates:

$$\begin{aligned} \square _g \phi&= - BB\phi + c^2 \delta ^{ab} \partial _a \partial _b \phi \\&\quad + 2 c^{-1} c_{;\uprho } (B\uprho ) B\phi - (\partial _a v^a) B\phi - c^{-1} c_{;\uprho } (g^{-1})^{\alpha \beta } (\partial _{\alpha } \uprho ) \partial _{\beta } \phi \nonumber \\&\quad - cc_{;s} S^a \partial _a \phi + 3 c^{-1} c_{;s} (Bs) B\phi . \nonumber \end{aligned}$$

(5.2.1)

Proof

It is straightforward to compute using equations (2.1.1a)–(2.1.1b) that relative to Cartesian coordinates, we have

$$\begin{aligned} \hbox {det} g&= - c^{-6} \end{aligned}$$

(5.2.2)

and hence

$$\begin{aligned} \sqrt{|\hbox {det} g|} g^{-1}&= - c^{-3} B\otimes B+ c^{-1} \sum _{a=1}^3 \partial _a \otimes \partial _a. \end{aligned}$$

(5.2.3)

Using definition (1.3.8) and equations (3.0.1), (5.2.2), and (5.2.3), we compute that

$$\begin{aligned} \square _g \phi&= - c^3 \left( B^{\alpha } \partial _{\alpha } (c^{-3}) \right) B^{\beta } \partial _{\beta } \phi - (\partial _{\alpha } B^{\alpha }) B^{\beta } \partial _{\beta } \phi - (B^{\alpha } \partial _{\alpha } B^{\beta }) \partial _{\beta } \phi \\&\quad - B^{\alpha } B^{\beta } \partial _{\alpha } \partial _{\beta } \phi + c^2 \delta ^{ab} \partial _a \partial _b \phi - cc_{;\uprho } \delta ^{ab} (\partial _a \uprho ) \partial _b \phi - cc_{;s} S^a \partial _a \phi . \nonumber \end{aligned}$$

(5.2.4)

Finally, from (5.2.4), the expression (1.3.12) for $B$, the expression (2.1.1b) for $g^{-1}$, and simple calculations, we arrive at (5.2.1). $\quad \square$

5.2.2 Deriving the Covariant Wave Equation for $\uprho$

In the next lemma, we derive the covariant wave equation (3.1.1b) for $\uprho$.

Lemma 8

(Covariant wave equation for $\uprho )$ For $C^2$ solutions of the compressible Euler equations (1.3.11a)–(1.3.11c), the logarithmic density variable $\uprho$ from Def. 1 verifies the following covariant wave equation, where on RHS (5.2.5), ${\mathcal {D}}$ is the modified fluid variable from Def. 3:

$$\begin{aligned} \square _g \uprho&= - \exp (\uprho ) \frac{p_{;s}}{{\bar{\varrho }}} {\mathcal {D}}- 3 c^{-1} c_{;\uprho } (g^{-1})^{\alpha \beta } (\partial _{\alpha } \uprho ) \partial _{\beta } \uprho + \left\{ (\partial _a v^a) \partial _b v^b - (\partial _a v^b) \partial _b v^a \right\} \\&\quad - \frac{5}{2} \exp (-\uprho ) \frac{p_{;s;\uprho }}{{\bar{\varrho }}} S^a \partial _a \uprho - \exp (-\uprho ) \frac{p_{;s;s}}{{\bar{\varrho }}} \delta _{ab} S^a S^b. \nonumber \end{aligned}$$

(5.2.5)

Proof

First, using (5.2.1) with $\phi = \uprho$, equation (1.3.11a), and equation (1.3.11c) (which implies that the last product on RHS (5.2.1) vanishes), we compute that

$$\begin{aligned} \square _g \uprho&= - BB\uprho + c^2 \delta ^{ab} \partial _a \partial _b \uprho + 2 c^{-1} c_{;\uprho } (B\uprho )^2 + (\partial _a v^a)^2 \\&\quad - c^{-1} c_{;\uprho } (g^{-1})^{\alpha \beta } (\partial _{\alpha } \uprho ) \partial _{\beta } \uprho - cc_{;s} S^a \partial _a \uprho . \nonumber \end{aligned}$$

(5.2.6)

Next, we use definitions (1.3.8) and (1.3.12), equations (1.3.11a)–(1.3.11c), the chain rule identity $\displaystyle 2 cc_{;s} = (c^2)_{;s} = \left( \frac{1}{{\bar{\varrho }}} \exp (-\uprho ) p_{;\uprho } \right) _{;s} = \exp (-\uprho ) \frac{p_{;\uprho ;s}}{{\bar{\varrho }}}$, and the identity $p_{;\uprho ;s} = p_{;s;\uprho }$ to compute that

$$\begin{aligned} BB\uprho&= - \partial _a (Bv^a) + (\partial _a v^b) \partial _b v^a \nonumber \\&= c^2 \delta ^{ab} \partial _a \partial _b \uprho + \delta ^{ab} (\partial _a c^2) \partial _b \uprho + \partial _a \left\{ \exp (-\uprho ) \frac{p_{;s}}{{\bar{\varrho }}} \delta ^{ab} \partial _b s\right\} + (\partial _a v^b) \partial _b v^a \nonumber \\&= c^2 \delta ^{ab} \partial _a \partial _b \uprho + \exp (-\uprho ) \frac{p_{;s}}{{\bar{\varrho }}} \delta ^{ab} \partial _a \partial _b s+ 2 cc_{;\uprho } \delta ^{ab} (\partial _a \uprho ) \partial _b \uprho \nonumber \\&\quad + 2 cc_{;s} \delta ^{ab} (\partial _a \uprho ) \partial _b s- \exp (-\uprho ) \frac{p_{;s}}{{\bar{\varrho }}} \delta ^{ab} (\partial _a \uprho ) \partial _b s\nonumber \\&\quad + \exp (-\uprho ) \frac{p_{;s;\uprho }}{{\bar{\varrho }}} \delta ^{ab} (\partial _a \uprho ) \partial _b s+ \exp (-\uprho ) \frac{p_{;s;s}}{{\bar{\varrho }}} \delta ^{ab} (\partial _a s) \partial _b s+ (\partial _a v^b) \partial _b v^a \nonumber \\&= c^2 \delta ^{ab} \partial _a \partial _b \uprho + \exp (-\uprho ) \frac{p_{;s}}{{\bar{\varrho }}} \hbox {div}S+ 2 cc_{;\uprho } \delta ^{ab} (\partial _a \uprho ) \partial _b \uprho + (\partial _a v^b) \partial _b v^a \nonumber \\&\quad + 2 \exp (-\uprho ) \frac{p_{;s;\uprho }}{{\bar{\varrho }}} S^a \partial _a \uprho - \exp (-\uprho ) \frac{p_{;s}}{{\bar{\varrho }}} S^a \partial _a \uprho + \exp (-\uprho ) \frac{p_{;s;s}}{{\bar{\varrho }}} \delta _{ab} S^a S^b. \end{aligned}$$

(5.2.7)

Finally, using (5.2.7) to substitute for the term $- BB\uprho$ on RHS (5.2.6), using the identity $(B\uprho ) B\uprho - c^2 \delta ^{ab} (\partial _a \uprho ) \partial _b \uprho = - (g^{-1})^{\alpha \beta } (\partial _{\alpha } \uprho ) \partial _{\beta } \uprho$ [see (2.1.1b)], using definition (1.3.13b) to algebraically substitute for the factor of $\hbox {div}S$ on RHS (5.2.7), and using the aforementioned chain rule identity to express the last term $- cc_{;s} S^a \partial _a \uprho$ on RHS (5.2.6) as $- \frac{1}{2} \exp (-\uprho ) \frac{p_{;\uprho ;s}}{{\bar{\varrho }}} S^a \partial _a \uprho$, we arrive at the desired expression (5.2.5).

$\square$

5.2.3 Deriving the Covariant Wave Equations for $\lbrace v^i \rbrace _{i=1,2,3}$

In the next lemma, we derive the covariant wave equations (3.1.1a) verified by the Cartesian component functions $\lbrace v^i \rbrace _{i=1,2,3}$.

Lemma 9

(Covariant wave equations for $\lbrace v^i \rbrace _{i=1,2,3})$ For $C^2$ solutions of the compressible Euler equations (1.3.11a)–(1.3.11c), the scalar-valued Cartesian component functions $\lbrace v^i \rbrace _{i=1,2,3}$ verify the following covariant wave equations, where on RHS (5.2.8), $\lbrace {\mathcal {C}}^i \rbrace _{i=1,2,3}$ denotes the Cartesian components of the modified fluid variable from Def. 3:

$$\begin{aligned} \square _g v^i&= - c^2 \exp (2\uprho ) {\mathcal {C}}^i - \left\{ 1+c^{-1} c' \right\} (g^{-1})^{\alpha \beta } (\partial _{\alpha } \uprho ) \partial _{\beta } v^i\nonumber \\&\quad + 2 \exp (\uprho ) \varepsilon _{iab} (Bv^a) \varOmega ^b - \frac{p_{;s}}{{\bar{\varrho }}} \varepsilon _{iab} \varOmega ^a S^b \nonumber \\&\quad - \frac{1}{2} \exp (-\uprho ) \frac{p_{;\uprho ;s}}{{\bar{\varrho }}} S^a \partial _a v^i \nonumber \\&\quad - 2 \exp (-\uprho ) c^{-1} c_{;\uprho } \frac{p_{;s}}{{\bar{\varrho }}} (B\uprho ) S^i + \exp (-\uprho ) \frac{p_{;s;\uprho }}{{\bar{\varrho }}} (B\uprho ) S^i. \end{aligned}$$

(5.2.8)

Proof

First, we use equation (5.2.1) with $\phi = v^i$, definition (1.3.8), equation (1.3.11b), and equation (1.3.11c) (which implies that the last product on RHS (5.2.1) vanishes), to compute

$$\begin{aligned} \square _g v^i&= - BBv^i + c^2 \delta ^{ab} \partial _a \partial _b v^i - 2 cc_{;\uprho } (B\uprho ) \delta ^{ia} \partial _a \uprho - 2 \exp (-\uprho ) c^{-1} c_{;\uprho } \frac{p_{;s}}{{\bar{\varrho }}} (B\uprho ) S^i \\&\quad - (\partial _a v^a) Bv^i - c^{-1} c_{;\uprho } (g^{-1})^{\alpha \beta } (\partial _{\alpha } \uprho ) \partial _{\beta } v^i - cc_{;s} S^a \partial _a v^i. \nonumber \end{aligned}$$

(5.2.9)

Next, we use definitions (1.3.8) and (1.3.12), equations (1.3.11a)–(1.3.11c), and the already established equation (5.1.4b) to compute that

$$\begin{aligned} BBv^i&= - c^2 \delta ^{ia} B\partial _a \uprho - 2 cc_{;\uprho } (B\uprho ) \delta ^{ia} \partial _a \uprho \\&\quad + \exp (-\uprho ) \frac{p_{;s}}{{\bar{\varrho }}} (B\uprho ) S^i - \exp (-\uprho ) \frac{p_{;s;\uprho }}{{\bar{\varrho }}} (B\uprho ) S^i - \exp (-\uprho ) \frac{p_{;s}}{{\bar{\varrho }}} BS^i \nonumber \\&= - c^2 \delta ^{ia} \partial _a (B\uprho ) + c^2 \delta ^{ia} (\partial _a v^b) \partial _b \uprho - 2 cc_{;\uprho } (B\uprho ) \delta ^{ia} \partial _a \uprho \nonumber \\&\quad + \exp (-\uprho ) \frac{p_{;s}}{{\bar{\varrho }}} (B\uprho ) S^i - \exp (-\uprho ) \frac{p_{;s;\uprho }}{{\bar{\varrho }}} (B\uprho ) S^i \nonumber \\&\quad + \exp (-\uprho ) \frac{p_{;s}}{{\bar{\varrho }}} S^a \partial _a v^i - \varepsilon _{iab} \frac{p_{;s}}{{\bar{\varrho }}} \varOmega ^a S^b \nonumber \\&= c^2 \delta ^{ia} \delta _d^b \partial _a (\partial _b v^d) - \delta ^{ia} \delta _{bd} (\partial _a v^b) Bv^d \nonumber \\&\quad - \exp (-\uprho ) \frac{p_{;s}}{{\bar{\varrho }}} \delta ^{ij} \delta _{ab} (\partial _j v^a) S^b - 2 cc_{;\uprho } (B\uprho ) \delta ^{ia} \partial _a \uprho \nonumber \\&\quad + \exp (-\uprho ) \frac{p_{;s}}{{\bar{\varrho }}} (B\uprho ) S^i - \exp (-\uprho ) \frac{p_{;s;\uprho }}{{\bar{\varrho }}} (B\uprho ) S^i \nonumber \\&\quad + \exp (-\uprho ) \frac{p_{;s}}{{\bar{\varrho }}} S^a \partial _a v^i - \varepsilon _{iab} \frac{p_{;s}}{{\bar{\varrho }}} \varOmega ^a S^b \nonumber \\&= c^2 \delta ^{ab} \partial _a \partial _b v^i + c^2 \delta ^{ia} \partial _d (\partial _a v^d - \partial _d v^a) \nonumber \\&\quad - (Bv^a) \partial _a v^i + (Bv^a)(\partial _a v^i - \partial _i v^a) \nonumber \\&\quad + \exp (-\uprho ) \frac{p_{;s}}{{\bar{\varrho }}} S^a (\partial _a v^i - \partial _i v^a) - 2 cc_{;\uprho } (B\uprho ) \delta ^{ia} \partial _a \uprho \nonumber \\&\quad + \exp (-\uprho ) \frac{p_{;s}}{{\bar{\varrho }}} (B\uprho ) S^i - \exp (-\uprho ) \frac{p_{;s;\uprho }}{{\bar{\varrho }}} (B\uprho ) S^i - \frac{p_{;s}}{{\bar{\varrho }}} \varepsilon _{iab} \varOmega ^a S^b. \nonumber \end{aligned}$$

(5.2.10)

Next, we use definitions (1.3.4) and (1.3.8), the identity (5.0.1), equation (1.3.11b), and the antisymmetry of $\varepsilon _{\cdots }$ to derive the identities

$$\begin{aligned} c^2 \delta ^{ia} \partial _d (\partial _a v^d - \partial _d v^a)&= c^2 \varepsilon _{iab} \partial _a \omega ^b = c^2 \hbox {curl}\omega ^i \nonumber \\&= c^2 \exp (\uprho ) \hbox {curl}\varOmega ^i + c^2 \exp (\uprho ) \varepsilon _{iab} \varOmega ^b \partial _a \uprho \nonumber \\&= c^2 \exp (\uprho ) \hbox {curl}\varOmega ^i - \exp (\uprho ) \varepsilon _{iab} (Bv^a) \varOmega ^b \nonumber \\&\quad + \frac{p_{;s}}{{\bar{\varrho }}} \varepsilon _{iab} \varOmega ^a S^b, \end{aligned}$$

(5.2.11)

$$\begin{aligned} \exp (-\uprho ) \frac{p_{;s}}{{\bar{\varrho }}} S^a (\partial _a v^i - \partial _i v^a)&= \frac{p_{;s}}{{\bar{\varrho }}} \varepsilon _{bai} S^a \varOmega ^b = \frac{p_{;s}}{{\bar{\varrho }}} \varepsilon _{iab} \varOmega ^a S^b, \end{aligned}$$

(5.2.12)

$$\begin{aligned} (Bv^a)(\partial _a v^i - \partial _i v^a)&= \exp (\uprho ) \varepsilon _{bai} (Bv^a) \varOmega ^b = - \exp (\uprho ) \varepsilon _{iab} (Bv^a) \varOmega ^b. \end{aligned}$$

(5.2.13)

Substituting the RHSs of (5.2.11)–(5.2.13) for the relevant terms on RHS (5.2.10), we obtain

$$\begin{aligned} BBv^i&= c^2 \delta ^{ab} \partial _a \partial _b v^i + c^2 \exp (\uprho ) \hbox {curl}\varOmega ^i - 2 \exp (\uprho ) \varepsilon _{iab} (Bv^a) \varOmega ^b + \frac{p_{;s}}{{\bar{\varrho }}} \varepsilon _{iab} \varOmega ^a S^b \nonumber \\&\quad - (Bv^a) \partial _a v^i - 2 cc_{;\uprho } (B\uprho ) \delta ^{ia} \partial _a \uprho \nonumber \\&\quad + \exp (-\uprho ) \frac{p_{;s}}{{\bar{\varrho }}} (B\uprho ) S^i - \exp (-\uprho ) \frac{p_{;s;\uprho }}{{\bar{\varrho }}} (B\uprho ) S^i. \end{aligned}$$

(5.2.14)

Next, substituting −RHS (5.2.14) for the term $- BBv^i$ on RHS (5.2.9), and using the chain rule identity $\displaystyle cc_{;s} = \frac{1}{2} (c^2)_{;s} = \frac{1}{2} \left( \frac{1}{{\bar{\varrho }}} \exp (-\uprho ) p_{;\uprho } \right) _{;s} = \frac{1}{2} \exp (-\uprho ) \frac{p_{;\uprho ;s}}{{\bar{\varrho }}}$, we compute that

$$\begin{aligned} \square _g v^i&= - c^2 \exp (\uprho ) (\hbox {curl}\varOmega )^i + 2 \exp (\uprho ) \varepsilon _{iab} (Bv^a) \varOmega ^b - \frac{p_{;s}}{{\bar{\varrho }}} \varepsilon _{iab} \varOmega ^a S^b \nonumber \\&\quad + \left\{ (Bv^a) \partial _a v^i - (\partial _a v^a) Bv^i \right\} - c^{-1} c_{;\uprho } (g^{-1})^{\alpha \beta } (\partial _{\alpha } \uprho ) \partial _{\beta } v^i \nonumber \\&\quad - \frac{1}{2} \exp (-\uprho ) \frac{p_{;\uprho ;s}}{{\bar{\varrho }}} S^a \partial _a v^i \nonumber \\&\quad - 2 \exp (-\uprho ) c^{-1} c_{;\uprho } \frac{p_{;s}}{{\bar{\varrho }}} (B\uprho ) S^i - \exp (-\uprho ) \frac{p_{;s}}{{\bar{\varrho }}} (B\uprho ) S^i \nonumber \\&\quad + \exp (-\uprho ) \frac{p_{;s;\uprho }}{{\bar{\varrho }}} (B\uprho ) S^i. \end{aligned}$$

(5.2.15)

We now rewrite the terms in braces on RHS (5.2.15). Specifically, we use definitions (1.3.8) and (2.1.1b) and equations (1.3.11a)–(1.3.11b) to obtain

$$\begin{aligned} (Bv^a) \partial _a v^i - (\partial _a v^a) Bv^i&= - c^2 \delta ^{ab} (\partial _b \uprho ) \partial _a v^i - \exp (-\uprho ) \frac{p_{;s}}{{\bar{\varrho }}} S^a \partial _a v^i + (B\uprho ) Bv^i \\&= - \exp (-\uprho ) \frac{p_{;s}}{{\bar{\varrho }}} S^a \partial _a v^i -(g^{-1})^{\alpha \beta } (\partial _{\alpha } \uprho ) \partial _{\beta } v^i. \nonumber \end{aligned}$$

(5.2.16)

Next, substituting (5.2.16) into (5.2.15), we deduce that

$$\begin{aligned} \square _g v^i&= - c^2 \exp (\uprho ) (\hbox {curl}\varOmega )^i - \left\{ 1+c^{-1} c_{;\uprho } \right\} (g^{-1})^{\alpha \beta } (\partial _{\alpha } \uprho ) \partial _{\beta } v^i \nonumber \\&\quad + 2 \exp (\uprho ) \varepsilon _{iab} (Bv^a) \varOmega ^b - \frac{p_{;s}}{{\bar{\varrho }}} \varepsilon _{iab} \varOmega ^a S^b \nonumber \\&\quad - \exp (-\uprho ) \frac{p_{;s}}{{\bar{\varrho }}} S^a \partial _a v^i - \frac{1}{2} \exp (-\uprho ) \frac{p_{;\uprho ;s}}{{\bar{\varrho }}} S^a \partial _a v^i \nonumber \\&\quad - 2 \exp (-\uprho ) c^{-1} c_{;\uprho } \frac{p_{;s}}{{\bar{\varrho }}} (B\uprho ) S^i - \exp (-\uprho ) \frac{p_{;s}}{{\bar{\varrho }}} (B\uprho ) S^i \nonumber \\&\quad + \exp (-\uprho ) \frac{p_{;s;\uprho }}{{\bar{\varrho }}} (B\uprho ) S^i. \end{aligned}$$

(5.2.17)

Finally, we use equation (1.3.13a) to algebraically substitute for the term $(\hbox {curl}\varOmega )^i$ on RHS (5.2.17) and equation (1.3.11a) to replace the term $\displaystyle - \exp (-3\uprho ) c^{-2} \frac{p_{;s}}{{\bar{\varrho }}} (\partial _a v^a) S^i$ on RHS (1.3.13a) with $\displaystyle \exp (-3\uprho ) c^{-2} \frac{p_{;s}}{{\bar{\varrho }}} (B\uprho ) S^i$, which in total yields the desired equation (5.2.8). $\quad \square$

5.2.4 Deriving the Covariant Wave Equation for $s$

In the next lemma, we derive the covariant wave equation (3.1.1c) for $s$, thereby completing the proof of Theorem 1.

Lemma 10

(Covariant wave equation for $s)$ For $C^2$ solutions of the compressible Euler equations (1.3.11a)–(1.3.11c), the entropy variable $s$ verifies the following covariant wave equation, where on RHS (5.2.18), ${\mathcal {D}}$ is the modified fluid variable from Def. 3:

$$\begin{aligned} \square _g s&= c^2 \exp (2 \uprho ) {\mathcal {D}}+ c^2 S^a \partial _a \uprho - cc_{;\uprho } S^a \partial _a \uprho - cc_{;s} \delta _{ab} S^a S^b. \end{aligned}$$

(5.2.18)

Proof

First, we use equation (5.2.1) with $\phi = s$, definition (1.3.8), the expression (2.1.1b), and equation (1.3.11c) (which in particular implies that many products on RHS (5.2.1) vanish) to compute

$$\begin{aligned} \square _g s&= c^2 \hbox {div}S- cc_{;\uprho } S^a \partial _a \uprho - cc_{;s} \delta _{ab} S^a S^b. \end{aligned}$$

(5.2.19)

We then use equation (1.3.13b) to algebraically substitute for the factor of $\hbox {div}S$ on RHS (5.2.19), which immediately yields the desired equation (5.2.18). $\quad \square$