1 Introduction

A (1-dimensional) \((N,w,\lambda _a,\lambda _c)\) optical orthogonal code (OOC) is a family of binary sequences (codewords) of length N, and constant Hamming weight w satisfying the following two conditions:

  • (off-peak auto-correlation property) for any codeword \(c=(c_0,c_1,\ldots ,c_{N-1})\) and for any integer \(1\le t \le N-1\), we have \(\displaystyle \sum \nolimits _{i=1}^{N-1}c_ic_{i+t}\le \lambda _a\),

  • (cross-correlation property) for any two distinct codewords \(c,c'\) and for any integer \(0\le t \le N-1\), we have \(\displaystyle \sum \nolimits _{i=0}^{N-1}c_ic'_{i+t}\le \lambda _c\),

where each subscript is reduced modulo N.

An \((N,w,\lambda _a,\lambda _c)\) OOC with \(\lambda _a=\lambda _c\) is denoted an \((N,w,\lambda )\) OOC. The number of codewords is the size, or capacity of the code. For fixed values of N, w, \(\lambda _a\) and \(\lambda _c\), the largest capacity of an \((N,w,\lambda _a,\lambda _c)\)-OOC, C, is denoted \(\Phi (N,w,\lambda _a,\lambda _c)\), or \( \Phi (C) \). An \((N,w,\lambda _a,\lambda _c)\)-OOC with capacity \(\Phi (N,w,\lambda _a,\lambda _c)\) is said to be optimal.

A family of \( (N,w,\lambda _a,\lambda _c) \) OOCs is called asymptotically optimal if

$$\begin{aligned} \lim _{N\rightarrow \infty } \frac{|C|}{\Phi (C)}=1. \end{aligned}$$
(1)

Since the work of Salehi et al. [23, 24], OOCs have been employed within optical code division multiple access (OCDMA) networks. OCDMA networks are widely employed due to their strong performance with multiple users. They are ideally suited for bursty, asynchronous, concurrent traffic. In applications, optimal OOCs facilitate the largest possible number of asynchronous users to transmit information efficiently and reliably. In order to maintain low correlation values the code length must increase quite rapidly with the number of users, reducing bandwidth utilization.

The 1-D OOCs spread the input data bits only in the time domain. Technologies such as wavelength-division-multiplexing (WDM) and dense-WDM enable the spreading of codewords in both space and time [21], or in wave-length and time [15]. Hence, codewords may be considered as \(\Lambda \times T\) (0, 1)-matrices. These codes are referred to in the literature as multiwavelength, or multiple-wavelength, or wavelength-time hopping, or 2-dimensional OOCs (2-D OOCs).

This addition of another dimension allows codes with off-peak autocorrelation zero, thereby improving the OCDMA performance in comparison with 1-D OCDMA. For optimal constructions of 2-D OOCs see [7, 13, 17], and for asymptotically optimal constructions see [18, 19, 28,29,30]. Later, a third dimension was added which gave a further increase in the performance of the codes [2, 11]. In 3-D OCDMA the optical pulses are spread in three domains, space, wave-length, and time. These 3-dimensional codes are referred to as space/wavelength/time spreading codes, or 3-D OOC. In [8], coherent fibre-optic communication systems are discussed, whereby both quadratures and both polarizations of the electromagnetic field are used, resulting in a four-dimensional signal space.

In the present work we bridge these developments to the next stage, introducing constructions and bounds on n-dimensional OOCs, for all \( n\ge 1 \). In Sect. 2 we introduce n-dimensional OOCs. We develop some upper bounds on these codes based on the Johnson Bound. We also develop bounds on higher dimensional ideal codes (\( \lambda _a=0 \)). In Sect. 3 we establish methods by which lower dimensional OOCs can produce higher dimensional codes. In particular we provide conditions under which (asymptotic) optimality is maintained when transforming to higher dimensional codes. In Sect. 4 we present two constructions of new infinite families of ideal codes; one optimal, and another which is asymptotically optimal.

2 n-D OOCs and bounds

2.1 n-D OOCs

Denote by \(( \Lambda _1\times \Lambda _2 \cdots \times \Lambda _{n-1} \times T,w, \lambda _a, \lambda _c)\) an n dimensional Optical Orthogonal Code (n-D OOC) with constant weight w, i’th spreading length \( \Lambda _i \), \( 1\le i \le {n-1} \), and time-spreading length T. Each codeword may be considered as an n-dimensional \(\Lambda _1\times \Lambda _2 \cdots \times \Lambda _{n-1} \times T\) binary array. The off-peak autocorrelation, and cross correlation of an \((\Lambda _1\times \Lambda _2 \cdots \times \Lambda _{n-1} \times T,w, \lambda _a, \lambda _c)\,n \)-D OOC have the following properties.

  • (off-peak auto-correlation property) for any codeword \(A=(a_{i_1,i_2,\ldots ,i_n})\) and for any integer \(1\le t \le T-1\), we have \(\displaystyle \sum \nolimits _{i_1=0}^{\Lambda _1-1}\sum \nolimits _{i_2=0}^{\Lambda _2-1} \cdots \sum \nolimits _{i_{n-1}=0}^{\Lambda _{n-1}-1}\sum \nolimits _{i_n=1}^{T-1}a_{i_1,i_2,\ldots ,i_n}a_{i_1,i_2,\ldots ,i_n+t}\le \lambda _a\),

  • (cross-correlation property) for any two distinct codewords \(A=(a_{i_1,i_2,\ldots ,i_n})\), \(B=(b_{i_1,i_2,\ldots ,i_n})\) and for any integer \(0 \le t \le T-1\), we have \(\displaystyle \sum \nolimits _{i_1=0}^{\Lambda _1-1}\sum \nolimits _{i_2=0}^{\Lambda _2-1} \cdots \sum \nolimits _{i_{n-1}=0}^{\Lambda _{n-1}-1}\sum \nolimits _{i_n=1}^{T-1}a_{i_1,i_2,\ldots ,i_n}b_{i_1,i_2,\ldots ,i_n+t}\le \lambda _c\),

where each subscript is reduced modulo T. In the case that \( \lambda _a=\lambda _c \), C is denoted an \(( \Lambda _1\times \Lambda _2 \cdots \times \Lambda _{n-1} \times T,w, \lambda )\) OOC.

We note that taking all but \( t-1 \) of the \( \Lambda _i \)’s to be 1 results in a t-dimensional OOC. With practical applications in mind we shall take minimal correlation values to be most desirable. Codes satisfying \( \lambda _a=0 \) will be said to be ideal.

As it is of interest to construct codes with maximal capacity, we now discuss some upper bounds on the capacity of codes.

2.2 Bounds

We shall require the following notation. By an \( (N,w,\lambda )_{m+1} \)-code, we denote a (conventional) code of length N, with constant weight w, and maximum Hamming correlation (the number of non-zero agreements between the two codewords) of \( \lambda \) over an alphabet of size \( m+1 \). We assume with no loss of generality that the alphabet contains zero. For binary codes (\( m=1 \)) the subscript 2 is typically dropped. Let \( A(N,w,\lambda )_{m+1}\) denote the maximum capacity of an \( (N,w,\lambda )_{m+1} \)-code. In [2], the following bound is established.

Theorem 2.1

([2], Generalized Johnson Bound)

$$\begin{aligned} A(N,w,\lambda )_{m+1} \le \left\lfloor \frac{m N}{w} \left\lfloor \frac{m(N-1)}{w-1}\left\lfloor \cdots \left\lfloor \frac{ m(N-\lambda )}{w-\lambda }\right\rfloor \right\rfloor \cdots \right\rfloor \right. . \end{aligned}$$
(2)

If \( w^2>mN\lambda \) then

$$\begin{aligned} A(N,w,\lambda )_{m+1}\le \text { min } \left\{ mN,\left\lfloor \frac{mN(w-\lambda )}{w^2-mN\lambda } \right\rfloor \right\} . \end{aligned}$$
(3)

We note that the first bound (2) may also be found in [18]. As observed in [9], given a 1-D \( (N,w,\lambda ) \)-OOC, C,, the collection of codewords, along with each of the \( N-1 \) distinct non-trivial cyclic shifts of codewords comprise a binary \( (N,w,\lambda ) \) code with capacity N|C| . Applying the bound (2) with \( m=1 \) we immediately obtain

$$\begin{aligned} \Phi (N,w,\lambda )\le J(N,w,\lambda )&=\left\lfloor \frac{1}{w} \left\lfloor \frac{N-1}{w-1}\left\lfloor \frac{N-2}{w-2} \left\lfloor \cdots \left\lfloor \frac{N-\lambda }{w-\lambda }\right\rfloor \right\rfloor \cdots \right\rfloor \right. \right. \end{aligned}$$
(4)
$$\begin{aligned}&:= \left\lfloor f(N,w,\lambda )\right\rfloor . \end{aligned}$$
(5)

To obtain bounds on higher dimensional OOCs, we observe that by choosing any fixed linear ordering of the array entries, each codeword from a \( (\Lambda _1\times \Lambda _2 \cdots \times \Lambda _{n-1} \times T,w,\lambda )\,n \)-D OOC, C, can be viewed as a binary constant weight (w) code of length \( N=\Lambda _1 \Lambda _2 \cdots \Lambda _{n-1} T \). Moreover, by including the T distinct cyclic shifts of each codeword we obtain a corresponding constant weight binary code of size \( T \cdot |C| \). It follows that

$$\begin{aligned} |C|\le \left\lfloor \frac{A(N, w, \lambda )}{T}\right\rfloor \end{aligned}$$
(6)

From the Eq. (6) and Theorem 2.1 we obtain the following bounds for n-D OOCs.

Theorem 2.2

(Johnson Bound for n-D OOCs) If C is an \( (\Lambda _1\times \Lambda _2 \cdots \times \Lambda _{n-1} \times T, w, \lambda ) \) OOC, then

$$\begin{aligned} \Phi (C)&\le J(\Lambda _1\times \Lambda _2 \cdots \times \Lambda _{n-1} \times T, w, \lambda ) \end{aligned}$$
(7)
$$\begin{aligned}&= \left\lfloor \frac{N}{Tw} \left\lfloor \frac{N-1}{w-1}\left\lfloor \cdots \left\lfloor \frac{ N -\lambda }{w-\lambda }\right\rfloor \right\rfloor \cdots \right\rfloor \right. \end{aligned}$$
(8)
$$\begin{aligned}&:= \left\lfloor f(\Lambda _1\times \Lambda _2 \cdots \times \Lambda _{n-1} \times T, w, \lambda )\right\rfloor , \end{aligned}$$
(9)

where \( N=\Lambda _1 \Lambda _2 \cdots \Lambda _{n-1}T \). If \( w^2> N \lambda \) then

$$\begin{aligned} \Phi (C) \le \text { min } \left\{ \frac{N}{T},\left\lfloor \frac{\frac{N}{T}(w-\lambda )}{w^2- N\lambda } \right\rfloor \right\} . \end{aligned}$$
(10)

We note that the bounds in Theorem 2.2 subsume the Johnson type bounds on 1, 2, and 3-dimensional codes, such as those found in [7, 9, 20]. Moreover, we can see from the theorem, that in a certain sense, maximum capacity is more intrinsically linked to the time spreading length than to the other dimensions.

Corollary 2.3

If \(N=\Lambda _1\cdot \Lambda _2\cdots \Lambda _{s-1} \cdot T=\Lambda '_1\cdot \Lambda '_2\cdots \Lambda '_{t-1} \cdot T\) where \( s , t \ge 1 \) then

$$\begin{aligned} J(\Lambda _1\times \cdots \times \Lambda _{s-1} \times T,w,\lambda )= J(\Lambda '_1\times \cdots \times \Lambda '_{t-1} \times T,w,\lambda ) \end{aligned}$$
(11)

Some easy arithmetic gives the following.

Lemma 2.4

If \(N=\Lambda _1\cdot \Lambda _2\cdots \Lambda _{n-1} \cdot T\), then

$$\begin{aligned} \frac{N}{T}\cdot J(N,w,\lambda )&\le J(\Lambda _1\times \cdots \times \Lambda _{n-1} \times T,w,\lambda ) \end{aligned}$$
(12)
$$\begin{aligned}&\le \frac{N}{T}\cdot J(N,w,\lambda )+\frac{N}{T}-1 \end{aligned}$$
(13)

In particular, if \(f(N,w,\lambda )-J(N,w,\lambda )<\frac{T}{N}\) (such as the case in which \(f(N,w,\lambda )\) is integral) then

$$\begin{aligned} \frac{N}{T}\cdot J(N,w,\lambda )= J(\Lambda _1\times \cdots \times \Lambda _{n-1} \times T,w,\lambda ). \end{aligned}$$
(14)

Corollary 2.5

Let \(N=\Lambda _1\cdot \Lambda _2\cdots \Lambda _{n-1} \cdot T\) where \(T=\Lambda _n\cdot T'\). If \(f(\Lambda _1\times \cdots \times \Lambda _{n-1} \times T ,w,\lambda )-J(\Lambda _1\times \cdots \times \Lambda _{n-1} \times T ,w,\lambda )<\frac{1}{\Lambda _n}\), then

$$\begin{aligned} \Lambda _n\cdot J(\Lambda _1\times \cdots \times \Lambda _{n-1} \times T ,w,\lambda )&= J(\Lambda _1\times \cdots \times \Lambda _{n-1}\Lambda _n \times T' ,w,\lambda ) \end{aligned}$$
(15)
$$\begin{aligned}&=J(\Lambda _1\times \cdots \times \Lambda _{n-1}\times \Lambda _n \times T' ,w,\lambda ). \end{aligned}$$
(16)

Generalizing the approach in [2] for 3-dimensional OOCs, observe that an n-D OOC C with \( \lambda _a=0 \) can be viewed as a constant weight (w) code of length \( \frac{N}{T} =\Lambda _1 \Lambda _2 \cdots \Lambda _{n-1} \) over an alphabet of size \( T+1\) containing zero. By including the T distinct cyclic shifts of each codeword we obtain a corresponding constant weight code of size \( T \cdot |C| \).

It follows that

$$\begin{aligned} |C|\le \left\lfloor \frac{A(\frac{N}{T}, w, \lambda )_{T+1}}{T}\right\rfloor . \end{aligned}$$
(17)

From Theorem 2.1 and the Eq. (17) we obtain the following bound for ideal n-D OOCs.

Theorem 2.6

(Johnson Bound for Ideal n-D OOC) Let C be an \( (\Lambda _1\times \cdot \times \Lambda _{n-1} \times T,w,0,\lambda _c) \) OOC, then

$$\begin{aligned} \Phi (C)&\le J(Ideal) \nonumber \\&= \left\lfloor \frac{N}{Tw} \left\lfloor \frac{ N-T}{w-1} \left\lfloor \frac{N-2T}{w-2} \left\lfloor \cdots \left\lfloor \frac{N-\lambda T}{w-\lambda _c}\right\rfloor \right\rfloor \cdots \right\rfloor \right. \right. \end{aligned}$$
(18)

where \(N=\Lambda _1\cdot \Lambda _2\cdots \Lambda _{n-1} \cdot T\). In particular, if C has (maximal) weight \(w = \frac{N}{T} \), then \( \Phi (C)\le T^\lambda \).

Note that the bound (18) is tight in certain cases, see e.g. the codes constructed in [17].

2.3 Ideal codes and sections

Suppose A is a codeword from an n-dimensional \( (\Lambda _1\times \Lambda _2\times \cdot \times \Lambda _{n-1} \times T,w,\lambda _a,\lambda _c) \) OOC. For any fixed i, \( 1\le i \le n-1 \), a \( \Lambda _i \) plane of A may be considered as an \( (n-1) \)-dimensional array. Such a plane is called a \( \Lambda _i \)section, or an i-section of A.

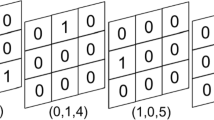
For \( i\ne j \), the intersection of an i-section and a j-section is a section of degree 2, denoted an (i, j) -section. A section of degree \( t\ge 3 \) is defined in the analogous way, denoted an \( (i_1,i_1,\ldots ,i_t) \)-section. See Fig. 1.

Fig. 1
figure 1

Sections of a 3-D, \( \Lambda \times S\times T \) (\( =\Lambda _1\times \Lambda _2 \times T \)) codeword: b a 1-section; c a 2-section; d a (1,2)-section

Full size image

One way to ensure an n-D OOC is ideal, is to restrict the code to having at most one pulse peri-section, for some fixed i. Such a code is said to be AMOPS(i) . For 2-D OOCs these are commonly called At Most One Pulse Per Wavelength (AMOPW) codes [7, 13, 17]. For 3-D codes these are commonly called At-Most-One-Pulse-per-Plane (AMOPP) codes [6, 25,26,27].

If an n-D OOC, C, is restricted to having at most one pulse per \( (i_1,i_2,\ldots ,i_j) \)-section, where \( 1\le j \le n-1 \), then C will be ideal. Such a code is said to have at most one pulse per section of degree j, and is denoted an AMOPS\((i_1,i_2,\ldots ,i_j)\) code. If such a code has exactly one pulse per \((i_1,i_2,\ldots ,i_j) \)-section, then it is said to have a single pulse per section of degree j, and is denoted an SPS\((i_1,i_2,\ldots ,i_j)\) code. An ideal n-dimensional OOC is necessarily AMOPS\( (1,2,\ldots ,n-1) \).

An approach entirely similar to that in Sect. 2.2 shows that an AMOPS\((i_1,i_2,\ldots ,i_j) \) corresponds to a constant weight 1-dimensional code of length \( m=\Lambda _{i_1}\cdot \Lambda _{i_2} \cdots \Lambda _{i_j} \) over an alphabet of size \( \frac{N}{m}+1 \) (containing zero). Consequently, we obtain the following bounds on AMOPS codes.

Theorem 2.7

(Johnson Bound for AMOPS codes) Let C be an (ideal) \( (\Lambda _1\times \cdot \times \Lambda _{n-1} \times T,w,0,\lambda ) \)-AMOPS\({(i_1,i_2,\ldots ,i_j)}\) OOC, where \( j\ge 1 \) then

$$\begin{aligned} \Phi (C)&\le J(AMOPS) \nonumber \\&= \left\lfloor \frac{N}{Tw} \left\lfloor \frac{ N\left( 1-\frac{1}{M}\right) }{w-1} \left\lfloor \frac{ N\left( 1-\frac{2}{M}\right) }{w-2} \left\lfloor \cdots \left\lfloor \frac{ N\left( 1-\frac{\lambda }{M}\right) }{w-\lambda }\right\rfloor \right\rfloor \cdots \right\rfloor \right. \right. \nonumber \\&\le J(Ideal) \end{aligned}$$
(19)

where \(N=\Lambda _1\cdot \Lambda _2\cdots \Lambda _{n-1} \cdot T\), and \( M=\Lambda _{i_1}\cdot \Lambda _{i_2}\cdots \Lambda _{i_{j}} \). In the extremal case where \( w = M \), the bound (19) simplifies to \(\displaystyle \frac{N^{\lambda +1}}{TM^{\lambda +1}}\).

In particular, if C is an \( (\Lambda _1\times \cdot \times \Lambda _{n-1} \times T,w,0,\lambda ) \)-AMOPS(i) OOC, then

$$\begin{aligned} \Phi (C)&\le \left\lfloor \frac{N}{Tw} \left\lfloor \frac{ N\left( 1-\frac{1}{\Lambda _i}\right) }{w-1} \left\lfloor \frac{ N\left( 1-\frac{2}{\Lambda _i}\right) }{w-2} \left\lfloor \cdots \left\lfloor \frac{ N\left( 1-\frac{\lambda }{\Lambda _i}\right) }{w-\lambda }\right\rfloor \right\rfloor \cdots \right\rfloor \right. \right. \end{aligned}$$
(20)

where \(N=\Lambda _1\cdot \Lambda _2\cdots \Lambda _{n-1} \cdot T\). In the extremal case where \( w = \Lambda _i \), the bound (20) simplifies to \(\displaystyle T^\lambda \prod \nolimits _{j\ne i}\Lambda _j^{\lambda +1} \).

The bound (19) is tight in certain cases, see e.g. the codes constructed in [2, 7, 12,13,14, 25]. We also note that the bound (19) reduces to the bound in Theorem 2.6 when \( j=n-1. \)

3 Iterative constructions of optimal n-D OOCs

Suppose C is a \( (\Lambda \times T, w , \lambda _a,\lambda _c) \) 2-D OOC where \( \Lambda =\Lambda _1\cdot \Lambda _2 \). Each codeword in C can be considered as a \( \Lambda \times T \) array. Let \( X\in C \) where \( X=(x_{i,j}) \). We may construct a corresponding 3-D \( \Lambda _1\times \Lambda _2\times T \) codeword \( Y_x=(y_{i,j,k}) \), \( 0\le i<\Lambda _1,0\le j<\Lambda _2, 0\le k<T \), where

$$\begin{aligned} y_{i,j,k} = c_{i+j\Lambda _1,k}. \end{aligned}$$
(21)

It is readily verified that \( C'=\{Y_x\mid x\in C\} \) is a \( (\Lambda _1\times \Lambda _2\times T, w, \lambda _a,\lambda _c) \) 3-D OOC with \( |C'|=|C|\). Inductively we arrive at the following.

Lemma 3.1

Let \( \Lambda =\Lambda _1\cdot \Lambda _2\cdots \Lambda _{s-1} \) be a positive integral factorisation. There exists an \( (\Lambda \times T, w, \lambda _a,\lambda _c) \) 2-D OOC with capacity M if and only if there exists an \( (\Lambda _1\times \Lambda _2\cdots \times \Lambda _{s-1} \times T, w, \lambda _a,\lambda _c) \)s-D OOC with capacity M.

An n-D OOC meeting any of the Johnson-type bounds established in the previous sections is referred to as a J-optimal code. With reference to Lemma 3.1 along with Corollary 2.3 we observe that a higher dimensional OOC with time spreading length T, obtained from a J-optimal lower dimensional OOC by factoring the \( \Lambda _i \)’s will always be J-optimal. For example, each of the optimal codes in Table 1 give rise to optimal codes of dimension 4 or more.

Table 1 Some J-optimal ideal \( (\Lambda _1\times \Lambda _2\times T) \) 3-D OOCs that give rise to J-optimal ideal codes of dimension \( n>3 \). Unless stated otherwise, \( \lambda _c=1 \)
Full size table

On the other hand, a J-optimal n-D OOC may correspond to an s-D OOC with \( s<n \) that is strictly asymptotically optimal. For example, from the bound (19), we see that a J-optimal \( (5\times 5\times 5,5,0,1) \)-AMOPS(1) OOC has capacity 125, whereas a J-optimal \( (25 \times 5,5,0,1) \)-AMOPS(1) OOC has capacity 150.

Corollary 3.2

Let \( \Lambda =\Lambda _1\cdot \Lambda _2\cdots \Lambda _{n-1} \) be a positive integral factorisation.

  1. 1.

    If there exists a (resp. asymptotically) J-optimal \( (\Lambda \times T, w, \lambda _a,\lambda _c) \) 2-D OOC then there exists a (resp. asymptotically) J-optimal \( (\Lambda _1\times \Lambda _2\cdots \times \Lambda _{n-1} \times T, w, \lambda _a,\lambda _c) \)n-D OOC.

  2. 2.

    If there exists a (resp. asymptotically) J-optimal \( (\Lambda _1\times \Lambda _2\cdots \times \Lambda _{n-1} \times T, w, \lambda _a,\lambda _c) \)n-D OOC, then there exists a \( (\Lambda \times T, w, \lambda _a,\lambda _c) \) 2-D OOC which is at least asymptotically J-optimal.

Theorem 3.3

Let C be an \((\Lambda _1\times \Lambda _2\times \cdots \times \Lambda _{n-1} \times T,w,\lambda _a,\lambda _c)\)n-D OOC, \( n\ge 1 \). For any positive integral factorization \( T=T_1\cdot T_2 \), there exists an \((T_1\Lambda _1\times \Lambda _2\times \cdots \times \Lambda _{n-1} \times T_2,w,\lambda _a',\lambda _c')\)n-D OOC, \(C'\) with \(\lambda _a'\le \lambda _a \), \( \lambda _c'\le max\{\lambda _a,\lambda _c\}\), and \(|C'|= T_1\cdot |C|\).

Proof

For \( n=1,2 \) see Theorems 3 and 5 in [5]. The result then follows from Lemma 3.1. \(\square \)

There are many constructions of optimal 1-dimensional OOCs. From the Theorem 3.3 we see that in some cases optimal 1-dimensional OOCs give optimal n-D OOCs.

Corollary 3.4

Let C be an \((N,w,\lambda )\) OOC with \(N=\Lambda _1\cdot \Lambda _2\cdots \Lambda _{n-1}\cdot T\).

  1. 1.

    If C is J-optimal and \(f(N,w,\lambda )-J(N,w,\lambda )<\frac{T}{N}\), then a J-optimal \(((\Lambda _1\times \Lambda _2\times \cdots \times \Lambda _{n-1}\times T, w, \lambda )\)n-D OOC exists.

  2. 2.

    If C is a member of a J-optimal (or asymptotically J-optimal) family then a family of \((\Lambda _1\times \Lambda _2\times \cdots \times \Lambda _{n-1}\times T, w, \lambda )\)n-D OOCs exists which is (at least) asymptotically optimal.

Proof

Follows from Theorem 3.3, (taking \( n=1 \)), Lemma 2.4, and the bounds in Theorem 2.2. \(\square \)

In [9], by considering orbits of lines in finite projective spaces, it is shown that for any prime power q,  an infinite family of J-optimal \( (\frac{q^{k+1-1}}{q-1}, q+1,1) \) OOCs exits. From Corollary 3.4 we now see that for any positive integral factorisation \( \frac{q^{k+1-1}}{q-1}=\Lambda _1\cdot \Lambda _2\cdots \Lambda _{n-1}\cdot T \), an optimal \( (\Lambda _1\times \Lambda _2\times \cdots \times \Lambda _{n-1}\times T, q+1,1) \)n-D OOC exists.

For dimensions \( n>1 \), we may also construct new optimal codes from others.

Corollary 3.5

Let C be an \((\Lambda _1\times \Lambda _2\times \cdots \times \Lambda _{n-1} \times T,w,\lambda )\)n-D OOC with \(T=T_1\cdot T_2\) a positive integral factorisation.

  1. 1.

    If C is J-optimal and \(f(\Lambda _1\times \Lambda _2\times \cdots \times \Lambda _{n-1} \times T,w,\lambda )-J(\Lambda _1\times \Lambda _2\times \cdots \times \Lambda _{n-1} \times T,w,\lambda )<\frac{1}{T_1}\) (in particular, if \(f(\Lambda _1\times \Lambda _2\times \cdots \times \Lambda _{n-1} \times T,w,\lambda )\) is integral), then a J-optimal \((T_1\Lambda _1\times \Lambda _2\times \cdots \times \Lambda _{n-1} \times T_2,w,\lambda , w, \lambda )\)n-D OOC exists.

  2. 2.

    If C is a member of a J-optimal family, or an asymptotically J-optimal family then a family of \((T_1\Lambda _1\times \Lambda _2\times \cdots \times \Lambda _{n-1} \times T_2,w,\lambda )\)n-D OOCs exists which is (at least) asymptotically optimal.

Proof

Follows from Theorem 3.3, Corollary 2.5, and the bounds in Theorem 2.2. \(\square \)

4 New optimal and asymptotically optimal codes

4.1 Preliminaries

Our techniques will rely heavily on the properties of finite projective and affine spaces. Such techniques have been used successfuly in the construction of infinite families of optimal OOCs of one dimension, [1, 3, 4, 9, 16], two dimensions [5, 7], and three dimensions [2, 6]. We start with a brief overview of the necessary concepts. By PG(k, q) we denote the classical (or Desarguesian) finite projective geometry of dimension k and order q. PG(k, q) may be modeled with the affine (vector) space \(AG(k+1,q)\) of dimension \(k+1\) over the finite field GF(q). Under this model, points of PG(k, q) correspond to 1-dimensional subspaces of AG(k, q), projective lines correspond to 2-dimensional affine subspaces, and so on. A d-flat\(\Pi \) in PG(k, q) is a subspace isomorphic to PG(d, q); if \(d=k-1\), the subspace \(\Pi \) is called a hyperplane. Elementary counting shows that the number of d-flats in PG(k, q) is given by the Gaussian coefficient

$$\begin{aligned} \left[ \begin{array}{c} k+1 \\ d+1 \\ \end{array} \right] _q = \frac{(q^{k+1}-1)(q^{k+1}-q)\cdots (q^{k+1}-q^{d})}{(q^{d+1}-1)(q^{d+1}-q)\cdots (q^{d+1}-q^{d})}. \end{aligned}$$
(22)

In particular, the number of points of PG(k, q) is given by \(\theta (k,q)=\frac{q^{k+1}-1}{q-1}\). We will use \(\theta (k)\) to represent this number when q is understood to be the order of the field. Further, we shall denote by \( \mathcal {L}(k) \) the number of lines in PG(k, q) .

A Singer group of PG(k, q) is a cyclic group of automorphisms acting sharply transitively on the points. The generator of such a group is known as a Singer cycle. Singer groups are known to exist in classical projective spaces of any order and dimension and their existence follows from that of primitive elements in a finite field.

Here, we make use of a Singer group that is most easily understood by modelling a finite projective space using a finite field. If we let \(\beta \) be a primitive element of \(GF(q^{k+1})\), the points of \(\Sigma =PG(k,q)\) can be represented by the field elements \(\beta ^0=1,\beta ,\beta ^2,\ldots ,\beta ^{n-1}\), where \(n=\theta (k)\).

The non-zero elements of \(GF(q^{k+1})\) form a cyclic group under multiplication. Multiplication by \(\beta \) induces an automorphism, or collineation, on the associated projective space PG(k, q) (see e.g. [22]). Denote by \(\phi \) the collineation of \(\Sigma \) defined by \(\beta ^i \mapsto \beta ^{i+1}\). The map \(\phi \) clearly acts sharply transitively on the points of \(\Sigma \).

As observed in [5], we can construct 2-dimensional codewords by considering orbits under some subgroup of G. Let \(n=\theta (k)=\Lambda \cdot T\) where G is the Singer group of \(\Sigma =PG(k,q)\). Since G is cyclic there exists an unique subgroup H of order T (H is the subgroup with generator \(\phi ^\Lambda \)).

Definition 1

Let \(\Lambda , T\) be integers such that \(n=\theta (k)=\Lambda \cdot T\). For an arbitrary pointset S in \(\Sigma =PG(k,q)\) we define the \(\Lambda \times T\) incidence matrix \(A=(a_{i,j})\), \(0\le i\le \Lambda -1\), \( 0\le j \le T-1 \) where \(a_{i,j}=1\) if and only if the point corresponding to \(\beta ^{i+\Lambda j}\) is in S.

If S is a pointset of \(\Sigma \) with corresponding \(\Lambda \times T\) incidence matrix W of weight w, then \(\phi ^\Lambda \) induces a cyclic shift on the columns of W. For any such set S, consider its orbit \(Orb_H(S)\) under the group H generated by \(\phi ^\Lambda \). The set S has full H-orbit if \(|Orb_H(S)|=T=\frac{n}{\Lambda } \) and short H-orbit otherwise. If S has full H-orbit then a representative member of the orbit and corresponding 2-dimensional codeword is chosen. The collection of all such codewords gives rise to a \((\Lambda \times T,w,\lambda _a,\lambda _c)\) 2-D OOC, where \(\lambda _a\) is determined by

$$\begin{aligned} \max _{1\le i<j \le \;T} \left\{ |\phi ^{\Lambda \cdot i}(S)\cap \phi ^{\Lambda \cdot j}(S)| \right\} \end{aligned}$$

and \(\lambda _c\) is determined by

$$\begin{aligned} \max _{1\le i,j \le \;T} \left\{ |\phi ^{\Lambda \cdot i}(S) \cap \phi ^{\Lambda \cdot j} (S')| \right\} . \end{aligned}$$

4.2 Construction

Let \(\Sigma =PG(k,q)\) where \(G=\langle \phi \rangle \) is the Singer group of \(\Sigma \) as in the previous section. Our work will rely on the following results about orbits of flats.

Theorem 4.1

(Rao [22], Drudge [10]) In \(\Sigma =PG(k,q)\), there exists a short G-orbit of d-flats if and only if \(gcd(k+1,d+1)\ne 1\). In the case that \( d+1 \) divides \( k+1 \) there is a short orbit \(\mathcal {S}\) which partitions the points of \(\Sigma \) (i.e. constitutes a d-spread of \(\Sigma \)). There is precisely one such orbit, and the G-stabilizer of any \(\Pi \in \mathcal {S}\) is \(Stab_G(\Pi )=\langle \phi ^{\frac{\theta (k)}{\theta (d)}}\rangle \).

4.2.1 Construction 1

For our first construction we mimic the methods of [2], whereby codewords correspond to lines that are not contained in any element of a d-spread of \( \Sigma \).

For \( d\ge 1 \), let \( k>1 \) such that \( d+1 \) divides \( k+1 \). Let \(G=\langle \phi \rangle \) be the Singer group of \( \Sigma =PG(k,q) \), as detailed above, and let \(\mathcal {S}\) be the d-spread determined (as in Theorem 4.1) by G, where say \(Stab_G(\mathcal {S})=H = \left\langle \phi ^\Lambda \right\rangle \), where \( \Lambda =\frac{\theta (k)}{\theta (d)} \).

Let \( \ell \) be a line not contained in any spread element (a d-flat in \( \mathcal {S}\)), and let A be the \( \Lambda \times \theta (d)\) projective incidence array corresponding to \( \ell \). Observe that \( \ell \) has a full H-orbit. H acts sharply transitively on the points of each spread element. It follows that A, considered as a \( \Lambda \times \theta (d)\) codeword, satisfies \( \lambda _a = 0 \). For each such line \( \ell \), we choose a representative element of it’s H-orbit, and include its corresponding incidence array as a codeword. The aggregate of these codewords gives an ideal \( (\Lambda \times \theta (d), q+1, 0, 1) \)-3-D OOC, C. Elementary counting gives

$$\begin{aligned} |C|&= \frac{\mathcal {L}(k)-\mathcal {L}(d)\cdot \frac{\theta (k)}{\theta (d)}}{\theta (d)} \nonumber \\&= \frac{\theta (k)\theta (k-1)}{\theta (d)(q+1)} - \frac{\theta (d-1)\theta (k)}{\theta (d)(q+1)} \nonumber \\&= \frac{\theta (k)}{\theta (d)(q+1)}\left[ \theta (k-1)-\theta (d-1)\right] . \end{aligned}$$
(23)

Comparing (23) with the bound in Theorem 2.6 shows these codes to be optimal.

Theorem 4.2

For \( d+1\) a proper divisor of \( k+1 \), there exists a J-optimal \( (\frac{\theta (k)}{\theta (d)} \times \theta (d), q+1, 0, 1) \) 2-D OOC.

With the observation that \( \frac{\theta {(k)}}{\theta (d)} =\theta (m-1,q^{d+1}) \), we have shown the following.

Corollary 4.3

For \( d\ge 1 \), \( m>1 \), and for any positive integral factorisation \( \Lambda _1\cdot \Lambda _2\cdots \Lambda _{n-1} =\theta (m-1,q^{d+1}) \), there exists a J-optimal (ideal) \( (\Lambda _1\times \Lambda _2\times \cdots \times \Lambda _{n-1} \times \theta (d), q+1, 0, 1) \)\( n-\)D OOC .

Table 2 will perhaps place this construction in context. Each of the optimal \( \Lambda \times T \) constructions described in the table gives rise to optimal higher dimensional OOCs, with dimensions limited by the number of distinct factors in \( \Lambda \).

Table 2 J-optimal families of ideal 2-D OOCs that give rise to higher dimensional optimal codes
Full size table

4.2.2 Construction 2

In our second construction, codewords correspond to conics, and lines in \( \Sigma =PG(3,q) \). An m-arc in PG(2, q) is a collection of \(m>2\) points such that no 3 points are incident with a common line. In PG(2, q), a (non-degenerate) conic is a \((q+1)\)-arc. Elementary counting shows that this arc is complete (of maximal size) when q is odd. The \((q+2)\)-arcs (hyperovals) exist in PG(2, q) if q is even and they are necessarily complete. Conics are a special case of the so called normal rational curves. We will be interested in the existence of large collections of arcs pairwise intersecting in at most two points. From Theorem 8 of [1], and its proof, we obtain the following.

Theorem 4.4

([1]) In \( \Pi =PG(2,q) \) there exists a family \( \mathcal {F} \) of conics, pairwise intersecting in at most 2 points, where \( |\mathcal {F}|=q^3-q^2 \). Moreover, there is a distinguished line \( \ell \) in \( \Pi \) disjoint from each member of \( \mathcal {F} \).

Let \(G=\langle \phi \rangle \) be the Singer group as above, and let \(\mathcal {S}\) be the 1-spread determined (as in Theorem 4.1) by G where say \(Stab_G(\mathcal {S})=H = \left\langle \phi ^\Lambda \right\rangle \) where \( \Lambda =\frac{\theta (3)}{q+1}=q^2+1 \).

Through each line \( \ell \) of \( \mathcal {S}\), choose a plane \( \pi (\ell ) \). As the members of \( \mathcal {S}\) are disjoint, each such plane contains precisely one member of \( \mathcal {S}\) (and therefore meets \( q^2 \) further members of \( \mathcal {S}\) in precisely one point). As H acts sharply transitively on the points of each line in \( \mathcal {S}\), each such plane has full H orbit. A dimension argument shows that any two elements in the H-orbit of \( \pi (\ell ) \) meet precisely in \( \ell \). In each \( \pi (\ell ) \), let \( \mathcal {F}(\ell ) \) be a family of conics as in Theorem 4.4. Denote by \( \mathcal {F}=\cup \mathcal {F}(\ell ) \), where the union is taken over all spread lines.

Let \( \mathcal {C}\in \mathcal {F}\) be a conic, and let A be the \( (q^2+1) \times (q+1)\) incidence array corresponding to \( \ell \). From the above, it follows that A, considered as a codeword, satisfies \( \lambda _a = 0 \). For each such conic, choose a representative element of it’s H-orbit, and include its corresponding incidence array as a codeword. The aggregate of these codewords gives an ideal \( ( q^2+1 \times q+1, q+1, 0, 2) \)-2D OOC, \( C_1 \). Note that \( \lambda _c=2 \) follows from the fact that two conics in \( \mathcal {F}\) are either coplanar, and therefore meet in at most two points, or are not coplanar, in which case their intersection lies on the line common to the two planes.

Note that as in Construction 1, the H-orbits of non-spread lines of \( \Sigma \) correspond to an ideal \( ( q^2+1 \times q+1, q+1, 0, 1) \)-2D OOC, \( C_2 \). Since a line and a conic meet in at most two points, we have \( C= C_1\cup C_2 \) is an ideal \( ( q^2+1 \times q+1, q+1, 0, 2) \)-2D OOC. Moreover

$$\begin{aligned} |C|= (q^2+1)\cdot (q^3-q^2)+\frac{\mathcal {L}(3)-(q^2+1)}{q+1}=q(q^2+1)(q^2-q+1) \end{aligned}$$
(24)

Comparing 24 to the bound in Theorem 2.6 shows C to be asymptotically optimal.

Theorem 4.5

For q a prime power, there exists an asymptotically optimal \( (q^2+1 \times q+1, q+1, 0, 2) \) 2-D OOC.

Corollary 4.6

For any positive integral factorisation \( \Lambda _1\cdot \Lambda _2\cdots \Lambda _{n-1} = q^{2}+1 \), there exists an asymptotically optimal (ideal) \( (\Lambda _1\times \Lambda _2\times \cdots \times \Lambda _{n-1} \times q+1, q+1, 0, 2) \)\( n-\)D OOC .

5 Conclusion

Here, we have generalized to higher dimensions the notions of optical orthogonal codes. We establish bounds on the capacity of general n-dimensional OOCs, as well as specific types of ideal codes. The bounds presented subsume existing bounds on codes of dimension three or less appearing in the literature.

In Sect. 2.2 we observe that, barring any imposed structural requirements on the remaining domains, the maximum capacity of a code is intrinsically linked to the length of the time spreading domain only. From an implementation standpoint, there is great advantage in constraining the structure of codewords to guarantee an off-peak auto-correlation of zero (ideal codes). We establish bounds for ideal codes, and in Sect. 4 provide constructions of ideal codes. One construction furnishes an infinite family of optimal codes for each dimension \( n\ge 2 \), and another which provides an asymptotically optimal family for each dimension \( n\ge 2 \).

Our constructions are iterative, in that they start with a construction of 2-D OOC, the wavelength domain is then factored to produce higher dimensional codes. The literature seems quite sparse of constructions of infinite families of higher dimensional OOCs that do not arise (at least indirectly) from 2-D OOCs. Perhaps combinatorial design techniques such as those in [26, 27] may be fruitful in this regard.