1 Introduction

Periodic arrays with good correlation properties are useful for applications in multiple target recognition, optical communications, and digital watermarking. In previous work we used the multidimensional periodicity of the generalization of the Welch Costas array to generate a new family of 3-D optical orthogonal codes (OOC) [1]. Although the periodic Welch Costas construction produces one single array, since for the application of optical orthogonal codes we only need periodicity in one of the three dimensions of the array, we obtain families of optical orthogonal codes from a single multi periodic array.

In [2] Moreno and Maric presented a construction of a large family of arrays based on the extended rational cycle (ERC) [3] that have near-perfect correlation values and periodicity for frequency hopping applications. Because of these properties, in [4] Tirkel et al. extended the construction to produce 2-D arrays for digital watermarking. Recently Gomez et al. [5] presented a construction of 3-D pseudo-noise arrays based on the composition of a ERC with a 2-D Legendre array for digital watermarking applications. The ERC has also been used by Moreno et al. to produce 2-D constant weight codes [3], and more recently by Omrani et al. to produce 2-D OOCs [6].

Optical Code Division Multiple Access (OCDMA) networks are particularly attractive for their ability to support bursty, asynchronous, concurrent communications, besides their good performance in the presence of multiple users.

In this work, we present new families of 3-D wave-length/space/time codes based on the ERC used to construct the well known 2-D Moreno-Maric arrays. These new codes have 0 out-of-phase autocorrelation, and near-perfect cross-correlation value 2. Similar to our previous construction based on the Welch Costas construction, the new families presented in this paper are asymptotically optimal with respect to the Johnson bound. More constructions of 3-D OOC can be found in [1, 7,8,9,10]. Table 1 summarizes the few constructions of 3-D wave-length/space/time OOCs.

Table 1 Summary of constructions of 3-D OOCs
Full size table

The new families of 3-D OOC have parameters (code length = wave-length × space × time, Hamming weight, autocorrelation, cross-correlation) = (p × S × p, S, 0, 2), with 2 ≤ S ≤ p2 + 1 and family size p(p2 + 1)(p2 − 1), and (p × p × (p2 + 1), p2, 0, 2) with family size p2(p2 − 1).

The paper is organized as follows: Section 1.1 reviews the definitions of 3-D OOCs and the Johnson bound. Section 2 describes the construction of 3-D periodic arrays based on the ERC. Section 3 describes the construction of the new 3-D OOCs, Section 3.1 their family size, and Section 3.2 their correlation constraints. Section 3.3 summarizes the new 3-D OOCs. Section 4 has conclusions.

1.1 Optical orthogonal codes

The first optical orthogonal code (OOC) [11] was proposed as a 1-D set of binary sequences, where one period of transmission clock is divided into a given number of small temporal segments. The out-of-phase autocorrelation of 1-D OOCs cannot be zero because there is more than one pulse within one period. This is a limitation because in order to achieve out-of-phase autocorrelation 1, the code length increases as the number of users increases. To overcome this limitation, the addition of a second dimension (2-D OOC) allows to have a single pulse per row [6, 12,13,14,15], and thus it achieves out-of-phase autocorrelation 1. In 2-D OOCs the optical pulses are spread in space and time [12], or in wave-length and time [6, 13].

Later, the three dimensional optical orthogonal code (3-D OOC) is implemented to increase the family size and the performance of the code [7]. In the implementation of 3-D OCDMA, the optical pulses are spread in three domains: space, wave-length, and time; which is a combination of the two spreading domains used in 2-D OOCs.

Definition 1

An (l × m × n, ω, λa, λc) 3-D Optical Orthogonal Code (3-D OOC) [7] C where 0 ≤ λa, λc ≤ ω ≤ lmn, is a family of {0,1}- (l × m × n) matrices, each of Hamming weight ω, maximum autocorrelation λa, and maximum cross-correlation λc satisfying:

  • Autocorrelation,

    $$ \begin{array}{@{}rcl@{}} \sum\limits_{i=0}^{l-1}\sum\limits_{j=0}^{m-1}\sum\limits_{k=0}^{n-1}x(i,j,k)x(i, j, k \oplus_{n} \tau) & = \omega & \text{for } \tau = 0, and \\ & \le \lambda_{a} & \text{for } 1 \le \tau \le n-1 \end{array} $$
    (1)

for every x in C, and ⊕n denotes addition modulo n.

  • Cross-correlation,

    $$ \begin{array}{@{}rcl@{}} \sum\limits_{i=0}^{l-1}\sum\limits_{j=0}^{m-1}\sum\limits_{k=0}^{n-1}x(i,j,k)y(i, j, k \oplus_{n} \tau) & \le \lambda_{c} & \text{for } 0 \le \tau \le n-1 \end{array} $$
    (2)

for every pair of codewords x, y in C where x ≠ y, and ⊕n denotes addition modulo n.

In Definition 1, the addition modulo n implies periodicity only in the n (time) dimension. There is another definition of 3-D OOCs that spreads the signal in time, wavelength, and polarization. The definition is similar to Definition 1, but the polarization domain is of length 2, and requires periodicity in the polarization and time domains [6, 16].

The definition of a family of 3-D periodic arrays is similar to that of a 3-D OOC but with periodicity in the three (l × m × n) dimensions. We simply need to add addition modulo l(i ⊕lβ, β ≤ l − 1), and addition modulo m(i ⊕mα, α ≤ m − 1) in the first and second dimensions, i.e. in the space and wave-length domains.

In previous work [1, 14] we presented an upper bound for 3-D OOCs Φ(l × m × n, ω, λ) derived from the Johnson Bound [17] on the cardinality of constant weight codes A(nml, ω, λ) which states that a 3-D OOC C of family size P is optimal when:

$$ P \le {\varPhi}(l \times m \times n, \omega, \lambda) \le \left \lfloor{\frac{A(lmn, \omega, \lambda)}{n}} \right \rfloor $$
(3)

and asymptotically optimal if:

$$ \displaystyle{\lim_{n\to\infty} \frac{P}{{\varPhi}(nml, \omega, \lambda)} = 1} $$
(4)

Theorem 1

(Johnson Bound A for 3-D OOC) [1]

$$ \begin{array}{@{}rcl@{}} \lefteqn{{\varPhi}(l \times m \times n, \omega, \lambda) \le} \\ & & { \left \lfloor \frac{lm}{\omega} { \left \lfloor \frac{ (lmn) -1}{\omega -1} { \left \lfloor \frac{(lmn)-2}{\omega-2} {\dots} { \left \lfloor \frac{(lmn) - \lambda}{\omega - \lambda} \right \rfloor } \right \rfloor } \right \rfloor } \right \rfloor } \end{array} $$
(5)

In Theorem 2 of [8], Shum presents a similar upper bound that also derives from the Johnson Bound, to bound at most one pulse per plane (AMOPP) 3-D OOCs. Although in this work we present new AMOPP 3-D OOCs, we stick to the general upper bound that applies to any 3-D OOC. It can be noted that if the construction is asymptotically optimal using the general upper bound, it will also be asymptotically optimal for the special case.

1.2 2-D periodic Moreno-Maric construction

In this section we review the Moreno-Maric construction for frequency hopping applications. In the following sections we describe how we use this construction to construct 3-D arrays.

Lemma 1

Moreno-Maric [2, 18]: Whenever x2 + x + α is irreducible, and α is a primitive root of GF(q), q = pn, the rational function\(\frac {-\alpha }{(x+1)}\)gives a cycle (permutation) of length and period q + 1. The permutation sequence x(i) is generated with the recursion:

$$ x(i+1) = {\frac{-\alpha}{(x(i) + 1)}} \text{ for } i=1, \ldots, q-1 \text{; } x(0) = 0, x(q) = \infty. $$
(6)

Example 1

Moreno-Maric sequence with elements in GF(q), q = p2.

Let q = 32, and α be the root of the polynomial x2 + 2x + 2, the recursion: \(x(i+1) = \frac {-\alpha }{x(i) + 1}\) generates the sequence \(0, 2\alpha , \alpha + 1, 2\alpha + 2, 1, \alpha , 2\alpha + 1, \alpha + 2, 2,\infty \).

Lemma 2

Moreno Maric family [2] There are q − 1 distinct linear transformations of periodic arrays of length q + 1 with auto- and cross-correlation 2.

This construction produces periodic arrays with near-perfect correlation constraints that have been used to produce arrays for applications in multiple target recognition, 2-D optical orthogonal codes, and digital watermarking.

2 3-D periodic Moreno-Maric construction

In this section we describe how to construct a family of 3-D periodic (p × p × (p2 + 1), p2, 2) frequency hop arrays with family size p2 − 1. The family is obtained by using the 2-tuple representation of the elements of the Moreno-Maric sequence with elements in GF(q), q = p2. Note that Gomez et al. [5] presented a construction of 3-D pseudo-noise arrays based on the composition of an ERC with a 2-D Legendre array. The algebraic construction presented in this section does not use composition of 2-D arrays. In Section 3, we show how to construct them for the application of optical communications.

Construction 1

Given a Moreno-Maric sequence with elements in GF(q), q = p2, construct a 3D Moreno-Maric periodic array by mapping elements of the sequence x into the array s as follows:

$$ s_{a,b} = i \text{ if and only if } x(i) = a\alpha + b $$
(7)

Example 2

3-D Moreno-Maric frequency hopping array obtained from mapping the sequence \(0, 2\alpha , \alpha + 1, 2\alpha + 2, 1, \alpha , 2\alpha + 1, \alpha + 2, 2,\infty \) from Example 1 into a (3 × 3) array.

$$ \begin{array}{@{}rcl@{}} s_{(0,0)} = 0 & s_{(0,1)} = 4 & s_{(0,2)} = 8 \\ s_{(1,0)} = 5 & s_{(1,1)} = 2 & s_{(1,2)} = 7 \\ s_{(2,0)} = 1 & s_{(2,1)} = 6 & s_{(2,2)} = 3 \\ s_{\infty} = 9 && \end{array} $$

The following is the 2-D representation of the 3-D Moreno-Maric array. The 3-D representation would have a 1 in position (a, b, i) if sa, b = i. Note that the last element \(\infty \) would leave an empty plane in the 3-D representation. Refer to Fig. 1 to see its 3-D binary representation.

$$ \textbf{s} =\left( \begin{array}{c c c} 0 & 4 & 8 \\ 5 & 2 & 7 \\ 1 & 6 & 3 \end{array}\right) $$
Fig. 1
figure 1

Binary 3-D representation of the array \(\protect s_{f^{(0)}}\) of Example 4. Note that the 10th plane does not contain a 1. This empty plane represents the \(\infty \) element of the array and is necessary to keep periodicity in the third dimension

Full size image

Using sequence x of Example 1, and Lemma 2 we can construct a family of arrays of size q − 1 applying the transformation f(k)(x) = αkx, for \(k = 0 {\dots } q-2\).

Construction 2

Given a family of q − 1 sequences obtained from the Moreno-Maric construction with elements in GF(q), q = p2, apply Construction 1 to each of the sequences in the family to construct a family of 3-D periodic (p × p × (p2 + 1), p2,2) frequency hop arrays with family size p2 − 1.

Theorem 2

The family of 3-D periodic frequency hop arrays with family size p2 − 1 obtained from Construction 2 have auto and cross-correlation 2.

The proof of Theorem 2 follows from the proof of Theorem 2 in [2], and from Lemma 4.2 in [5]. Note that there is only one pulse per plane, in different coordinates of the planes, given by the mapping of the original Moreno-Maric sequence of elements in GF(p2). Thus the auto and cross-correlation, i.e. the number of times the pulses of the planes of one array will coincide with the pulses of the planes of another array, will also be given by the number of repetitions of the periodic differences between the elements in GF(p2) of the corresponding sequences at a fixed distance.

Example 3

The following are the 8 sequences obtained by applying the transformation f(k)(x) = αkx, for \(k = 0 {\dots } q-2\).

$$ \begin{array}{@{}rcl@{}} f^{(0)}(x) & = & 0, 2\alpha, \alpha + 1, 2\alpha + 2, 1, \alpha, 2\alpha + 1, \alpha + 2, 2,\infty \\ f^{(1)}(x) & = & 0, 2\alpha + 2, 2\alpha + 1, \alpha + 2, \alpha, \alpha + 1, 2, 1, 2\alpha, \infty \\ f^{(2)}(x) & = & 0, \alpha + 2, 2, 1, \alpha + 1, 2\alpha + 1, 2\alpha, \alpha, 2\alpha + 2, \infty \\ f^{(3)}(x) & = & 0, 1, 2\alpha, \alpha, 2\alpha + 1, 2, 2\alpha + 2, \alpha + 1, \alpha + 2, \infty \\ f^{(4)}(x) & = & 0, \alpha, 2\alpha + 2, \alpha + 1, 2, 2\alpha, \alpha + 2, 2\alpha + 1, 1, \infty \\ f^{(5)}(x) & = & 0, \alpha + 1, \alpha + 2, 2\alpha + 1, 2\alpha, 2\alpha + 2, 1, 2, \alpha, \infty \\ f^{(6)}(x) & = & 0, 2\alpha + 1, 1, 2, 2\alpha + 2, \alpha + 2, \alpha, 2\alpha, \alpha + 1,\infty \\ f^{(7)}(x) & = & 0, 2, \alpha, 2\alpha, \alpha + 2, 1, \alpha + 1, 2\alpha + 2, 2\alpha + 1,\infty \\ \end{array} $$

Example 4

The following are the 2-D representations of the eight 3-D periodic arrays obtained from applying Construction 2 to the sequences of Example 3.

$$ \begin{array}{@{}rcl@{}} s_{f^{(0)}} =\left( \begin{array}{ c c c } 0 & 4 & 8 \\ 5 & 2 & 7 \\ 1 & 6 & 3 \end{array}\right)& s_{f^{(1)}} = \left( \begin{array}{ c c c } 0 & 7 & 6 \\ 4 & 5 & 3 \\ 8 & 2 & 1 \end{array}\right)& s_{f^{(2)}} = \left( \begin{array}{ c c c } 0 & 3 & 2 \\ 7 & 4 & 1 \\ 6 & 5 & 8 \end{array}\right)\\ s_{f^{(3)}} = \left( \begin{array}{ c c c } 0 & 1 & 5 \\ 3 & 7 & 8 \\ 2 & 4 & 6 \end{array}\right)& s_{f^{(4)}} = \left( \begin{array}{ c c c } 0 & 8 & 4 \\ 1 & 3 & 6 \\ 5 & 7 & 2 \end{array}\right)& s_{f^{(5)}} = \left( \begin{array}{ c c c } 0 & 6 & 7 \\ 8 & 1 & 2 \\ 4 & 3 & 5 \end{array}\right)\\ s_{f^{(6)}} = \left( \begin{array}{ c c c } 0 & 2 & 3 \\ 6 & 8 & 5 \\ 7 & 1 & 4 \end{array}\right)& s_{f^{(7)}} = \left( \begin{array}{ c c c } 0 & 5 & 1 \\ 2 & 6 & 4 \\ 3 & 8 & 7 \end{array}\right)& \end{array} $$

Remark 1

Note that Constructions 1 and 2 can be easily extended to (m + 1) dimensions by using the Moreno-Maric construction with elements in GF(q) and q = pm.

Figure 1 contains the (3 × 3 × 10) 3-D binary representation of the first array of Example 4. Note that the 3-D Moreno-Maric arrays are at most one pulse per plane (AMOPP) arrays, because by definition there is at most only one pulse (or one) in the p × p planes.

3 New 3-D optical orthogonal codes

3-D OOC periodicity is only required in the time domain. This has two direct implications. First, given a family, F of periodic AMOPP (l × m × n) arrays with correlation λ, one may generate the codewords of a 3-D OOC, C, by considering as codewords each distinct periodic shift in the non-time domains. Second, the correlation values of C will be equal to that of the original family F, and observe that |C| = lm|F|.

Also observe that because F is periodic in all its domains the codewords of F can also be represented as a family of periodic (m × n × l) arrays or a family of periodic (n × l × m) arrays, thus one can similarly generate the codewords of 3-D OOCs with the same correlation values and sizes |C| = mn|F|, and |C| = nl|F| respectively.

We now describe how to obtain families of 3-D Optical Orthogonal Codes from the 3-D Moreno-Maric construction. We begin by describing the family sizes of the new families and then proceed to discuss their correlation properties.

3.1 New 3-D OOC family size

The three dimensional Moreno-Maric construction produces p2 − 1 periodic arrays. Since by definition the 3-D OOC requires periodicity only in the time domain we can periodically shift the p2 − 1 arrays of the Moreno-Maric family construction in two of its three dimensions such that for each (p × p × p2 + 1) 3-D periodic Moreno-Maric family of arrays:

  • we can construct a 3-D OOCs with parameters (p × (p2 + 1) × p, p2, 0, 2) and family size p(p2 + 1)(p2 − 1), when the dimensions shifted are one dimension of length p and the dimension with length p2 + 1;

  • 3-D OOCs with parameter (p × p × (p2 + 1), p2, 0, 2) and family size p2(p2 − 1), when the dimensions shifted are the two dimensions of length p.

Because for 3-D OOC periodicity is only required in the time domain, we can first generate the codewords of the 3-D OOC shifting periodically the space and wave-length domains, and then decrease the length of the space or wave-length domain (by removing planes). We select a length from 1 to p or from 1 to p2 + 1 if the domain to be cut is of length p or length p2 + 1 respectively. This is similar to the case of 3-D OOCs obtained from the Welch construction in [1]. For both, the 3-D OOCs based on the Welch construction and the 3-D OOCs presented in this work, one of the three domains is considerably greater than the others, thus decreasing the length of the space or wave-length domains when its length is p2 + 1 could be particularly useful in the applications. This change does not affect the auto and cross-correlation constraints nor the cardinality of the family.

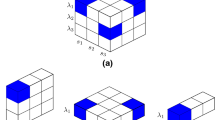
Figure 2 contains examples of 4 of the 30 codewords of the 3-D OOC with parameters (3 × 10 × 3, 9, 0, 2) obtained from shifting the first 3-D Moreno-Maric array from Example 4. In this example s(i, j,0) means s shifted i times in the space domain, j times in the wave-length domain, and 0 times in the time domain.

Fig. 2
figure 2

3-D representation of 4 of the 30 codewords of the 3-D OOC obtained from shifting the array \(\protect s_{f^{(0)}}\) of Example 4

Full size image

A total of 30 × 8 = 240 codewords would be obtained from the 8 arrays of the 3-D Moreno-Maric family construction with p = 3.

3.2 3-D OOC correlation constraints

Ultimately the correlation constraints of 3-D OOCs, which provide synchronization and user identification, will determine the system performance [12, 19]. The best correlation constraints that a 3-D OOC can achieve are out-of-phase autocorrelation λa = 0, and peak cross-correlation λc = 1. For the constructions presented in this paper the peak cross-correlation value is λc = 2.

3.2.1 Autocorrelation

The codes of our constructions are AMOPP; and for AMOPP codes the peak out-of-phase autocorrelation is always zero. Therefore the autocorrelation of the families presented in this work is λa = 0.

3.2.2 Cross-correlation

Lemma 3

The cross-correlation value of our new families of 3-D OOCs is λc = 2.

Proof

The codewords of the new families correspond to periodic shifts of the original Moreno-Maric arrays in the non-time domains. Hence, they have cross-correlation value equal to that of the original periodic Moreno-Maric array, which satisfies λc = 2. □

3.3 New families of 3D-OOC

We summarize the new families of 3D-OOCs in the following theorem:

Theorem 3

Given a family of periodic Moreno-Maric arrays with elements in GF(p2) the following families of asymptotically optimal 3-D OOC can be constructed:

  1. 1.

    Families of 3-D OOC with parameters (p × p × (p2 + 1), p2, 0, 2) and family size p4 − p2.

  2. 2.

    Families of 3-D OOC with parameters (p × (p2 + 1) × p, p2, 0, 2) and family size p5 − p.

  3. 3.

    Families of 3-D OOC with parameters ((p2 + 1) × p × p, p2, 0, 2) and family size p5 − p.

  4. 4.

    Families of 3-D OOC with parameters (W × p × p, W, 0, 2), where 2 ≤ W ≤ p2 + 1 and family size p5 − p.

  5. 5.

    Families of 3-D OOC with parameters (p × S × p, S, 0, 2) where 2 ≤ S ≤ p2 + 1 and family size p5 − p.

Using Theorem 1 and Eq. 4 it is easy to proof that the families in Theorem 3 are asymptotically optimal.

4 Conclusions

In this work we presented new constructions of 3-D Optical Orthogonal Codes with near-perfect correlation constraints for Optical CDMA (λa = 0, λc = 2). The constructions are based on periodic 3-dimensional Moreno-Maric arrays. The new 3-D OOCs are shown to be asymptotically optimal. These constructions find applications in digital watermarking and are likely to find applications in other fields.