Assigning pollution permits: are uniform auctions efficient?

Abstract

We study the efficiency of the uniform auction as an allocation mechanism for emission permits among polluting firms. In our model, firms have private information about their abatement costs, which differ across firms and across units, and bidders’ demands are linear. We show that there is a continuum of interior Bayesian Nash equilibria, and only one is efficient, minimizing abatement costs. We find that the existence of many bidders is not a sufficient condition to guarantee an efficient equilibrium in the uniform auction. Additionally, bidders’ types have to be uncorrelated.

1 Introduction

Emissions trading, or cap and trade, is an increasingly popular environmental policy instrument used to encourage firms to reduce pollution, with the European Emission Trading system (EU ETS) being the leading example. A permit represents the right to emit a specific amount of a pollutant. Firms are required to hold a number of permits equivalent to their emissions and are legally forced to reduce them, from their business as usual level, i.e., their emissions in the absence of regulation, to the number of permits they hold, and bear any associated abatement costs. The main objective of this policy approach is to achieve the emission target reduction at the lowest economic cost, i.e., to achieve an efficient allocation of permits between polluting firms.

In this paper, we analyze the efficiency of the uniform auction format as an assignment mechanism of emission permits. In the auction, each bidder, typically a polluting firm, submits a demand function for permits. The auctioneer aggregates the individual demands and determines the stop-out price from the usual market clearing condition, given the exogenous and ex ante known quantity of permits to be auctioned. All quantities demanded at or above the stop-out price are awarded and, under a uniform format, paid at the stop-out price. In the absence of a secondary market, if a polluting firm gets in the auction less permits than its business as usual level of pollution, it must exert an abatement effort for the difference, which is costly for the firm. The auction is efficient whenever the allocation of permits resulting from the auction minimizes the total—sum across firms—abatement cost.

In our model, the abatement cost functions exhibit decreasing returns to scale and differ across firms. The differences are parametrized by a scalar, the firm’s type, the standard terminology in games of incomplete information. As it is usual in those games, each type is a random draw privately observed by the corresponding firm prior to bidding. We assume that the firm’s marginal abatement cost function shifts upward as its type increases. This implies that an efficient allocation of permits is characterized by higher type firms getting more permits than lower type ones, by a precise amount so that marginal abatement costs are equalized across firms.

We question whether the theory predicts that the uniform auction is that precise. Generally, the efficiency of auctions as allocations mechanisms is a rather unexplored field. In single-unit auctions, efficiency follows because bidding functions are real valued increasing functions, from valuations into bids, so that the bidder with the highest valuation makes the highest bid and wins. Many theoretical models of multi-unit multi-bid auctions, as those motivated by Treasury auctions, assume common value, that is, the value of all the units on sale is constant both across units and bidders, even though bidders might have private information on that value, and therefore efficiency is not an issue. In contrast, the auctions for emission permits are multi-unit multi-bid auctions in which the valuations are determined by the abatement cost, and thus, the common value assumption is no longer valid. The closest paper to ours is by Ausubel et al. (2014), who analyze the efficiency of different multi-unit multi-bid auctions, including the uniform auction. Our model contains two departures from the common value assumption: first, bidders’ valuations are not constant across units; and second, valuations are not constant across bidders. Ausubel et al. (2014) consider separately each of those departures, while in our paper we take them jointly.

Two additional aspects of our model should be noted. First, we follow Wilson (1979) share auctions approach, in which the good auctioned is assumed to be perfectly divisible, and bidders bid a continuous demand schedule. Second, the marginal abatement cost (MAC) function is assumed to be linear, with a slope common to all firms, and the firm’s type being its vertical intercept, corresponding to the marginal cost of achieving a zero-level of pollution. With linear MAC functions that only differ on the vertical intercept, the natural candidates to conform an equilibrium are strategies that map type realizations into linear demand functions. More specifically, we restrict ourselves to linear demand functions in which the quantity demanded when the price is zero (the demand’s horizontal intercept) depends on the firm’s type, whereas the slope does not.

We use an ex-post efficiency concept, as Ausubel et al. (2014), so that the efficient allocation of permits depends on the firms’ types. A profile of strategies conforming an equilibrium is efficient if it leads to an efficient allocation for any realization of the vector of types. To simplify the analysis, we only consider a subspace of parameter values under which the allocation, given a strategy profile, is interior with probability one (w.p.1). In an efficient interior allocation, all firms win some permits at the auction and exert some abatement effort. We show that interior allocations are characterized by two inequalities, implying that that neither the range of types’ variation nor the total quantity of permits to be assigned are too large. Finally, we assume that the probability distribution of types is common knowledge and that bidders are symmetric in the sense that the probability distribution of rivals’ types, conditional on the own type, is identical across bidders. Given this symmetry, we consider symmetric equilibria, in which all bidders play the same strategy or, equivalently, any two bidders with the same type submit the same demand function. In what follows, a strategy conforming a symmetric equilibrium leading to an interior allocation w.p.1 is simply an equilibrium.

Our main results can be classified in two groups: the characterization of equilibria and the allocation efficiency, respectively. On the characterization of equilibria, we show that the bidding behavior under any equilibrium strategy can be interpreted in terms of marginal valuation and price. As the number of bidders tends to infinity, the bidder’s valuation for the last unit that he wins at the auction equals the expected auction price. However, with two bidders, the bidder’s valuation for the last unit is larger than the expected auction price.

We also show that there are multiple equilibria, but that multiplicity can be conveniently indexed as follows. First, recall that we consider strategies under which bidders submit a linear demand function such that only the intercept depends on the bidder’s type. We show that, in our model with linear MAC functions, such strategies can lead to an efficient allocation only if that intercept is itself a linear function of the bidder’s type. Let us denote that family of strategies as linear strategies. For linear strategies, we denote by $\kappa _1$ the coefficient of the bidder’s type. Restricting to linear strategies while allowing for nonlinear responses, we prove that the set of equilibria can be indexed by $\kappa _1$. Specifically, there exists a bounded open interval in the real line such that each value of $\kappa _1$ in the interval corresponds to an equilibrium. This indexing is particularly useful for the analysis of efficiency, as we further prove that any linear strategy is efficient if and only if $\beta \kappa _1 = 1$ is satisfied, where $\beta$ is the absolute value of the slope of the MAC function, common to all firms. Moreover, firms with higher types that have higher abatement costs, bid more aggressively and thus get more permits than firms with lower types whenever $\kappa _1 >0$ holds. However, if $\beta \kappa _1 <1$ holds, firms with higher types are under-assigned: they do not get enough permits in the sense that, under the auction allocation, their marginal abatement cost for the last unit is still higher than for firms with lower types. Intuitively, if $\kappa _1 >0$ holds, firms react to types in the right direction, but if $\beta \kappa _1 < 1$, not enough. In contrast, if $\beta \kappa _1 >1$ holds, there is over-assignment for firms with higher types: they get too many permits.

In order to further analyze efficiency, we impose some additional structure on the distribution of types. We consider separately two different families of probability distributions: a pure private value case, in which the bidders’ types are mutually independent, and a mineral right model, in which bidders’ types are positively correlated.¹ Both cases lie within the ex ante symmetric bidder scenario.

For both the private value case and the mineral right model, we prove that the strategy that induces efficiency, that is, the strategy in which $\beta \kappa _1 = 1$ holds, is an equilibrium for any number of bidders equal or greater than two. In the case of independent types, for a small number of bidders (we prove our result for two bidders), there are other equilibria besides the efficient equilibrium. All equilibria satisfy that firms with higher types get more permits than firms with lower types ($\kappa _1 >0$), but in some of them there is under-assignment ($\beta \kappa _1 <1$) while in some others there is over-assignment ($\beta \kappa _1 >1$) for the firms with higher types. The same typology of equilibria arises for the correlated-type case for a small number of bidders. What is, then, the qualitative difference between independent and correlated types? We show that as the number of bidders grows large, and so does the total amount of permits while the ratio of both magnitudes stays constant and within the subspace of parameter values in which the efficient allocation is interior, only the efficient strategy can be sustained as an equilibrium in the independent-type case. In contrast, for the correlated-type case there are inefficient equilibria surviving this limit scenario.

In order to derive policy implication, two additional comments must be considered. First, in the EU ETS there is a secondary market for permits that runs in parallel to the auctions that is ignored in our paper. It is well established in the literature that if the secondary market is perfectly competitive, those firms that can reduce emissions most cheaply will do so, which ensures that the equilibrium allocation will be efficient.² If this is the case, the allocation of permits resulting form the auction only matters for the distribution of the gains from trade but is irrelevant to achieve efficiency. On the other hand, as first noted by Hahn (1984), if the secondary market for emission permits is not perfectly competitive, the initial allocation of permits—the auction—matters.³ Second, we have restricted ourselves to interior allocations, reached when firms have similar abatement costs. This could be a reasonable assumption at this stage in the EU ETS, given that auctions’ participants are mainly big firms from the power generating sector, that since 2013 must buy all their allowances,⁴ and that have similar abatement costs.

Another paper close to ours is Ausubel and Cramton (2002), analyzing efficiency of a uniform price auction in a pure private value model in which bidders’ marginal values are decreasing in quantity.⁵ They conclude that there does not exist an ex-post efficient equilibrium. The main difference with our model is that they impose bidding strategies such that bidders bid their valuation for the first unit, which implies that the bid curves lie strictly below the marginal-value curve at all positive quantities. We obtain such an equilibria in our model, that, as in their case, is not efficient because there is differential bid shading. However, allowing more general linear equilibria, we show that there are efficient equilibria in the uniform auction.

We aim at filling a gap in the theoretical literature regarding auctions of emission permits. Some authors have addressed permit auctioning from a descriptive point of view (see. e.g., Hepburn et al. (2006) or Cramton and Kerr (2002)) or by means of experimental studies (see, e.g., Ledyard and Szakaly-Moore (1994); Godby (1999, 2000); Muller et al. (2002) or Goeree et al. (2010)). Also some theoretical approximations have been made. Antelo and Bru (2009) compare auctioning and grandfathering in a permit market with a dominant firm when the government is concerned both about cost-effectiveness and public revenue. Alvarez and André (2015) and Alvarez and André (2016) also compare auctioning and grandfathering when there is a secondary market with market power and firms have private information on their own abatement technologies. Kline and Menezes (1999) examine a stylized version of EPA double auctions between buyers and sellers. Nevertheless, none of these studies address multi-unit, multi-bid auctions of permits as we do, using a standard auction theory approach. Antelo and Bru (2009) assume perfect information and hence omit one of the main ingredients of auctions. Alvarez and André (2015) consider that the bidders act non-strategically and in Alvarez and André (2016) only one firm (the dominant one) bids strategically. Kline and Menezes (1999) do not address the use of auctions to make the initial allocation of permits by the environmental authority (as it is done in the UE ETS), but only consider the exchange of permits among firms. Moreover, they use a single-unit approach and restrict themselves to perfect information except for two specific examples under complete information. So, apart from addressing the specific question on efficiency, our aim is to contribute to the theoretical literature by providing a sound model for permit auctioning and bidding.

This paper is organized as follows. In Sect. 2, we present the model, and in Sect. 3 we characterize the equilibria in Proposition  1, show that the set of interior equilibria conformed by linear strategies can be indexed by a parameter in Proposition 2, and establish the existence and multiplicity of equilibria in Proposition 3. In Sect. 4, we analyze the efficiency of the equilibria, when bidders’ types are independent in Proposition 5 and when types are correlated in Proposition 6. Finally, Sect. 5 concludes the paper. “Appendix” contains all proofs.

2 The model

Assume that Q perfectly divisible permits are inelastically supplied in a uniform auction with I bidders, the polluting firms, indexed by $i \in \lbrace 1,\dots ,I \rbrace$, with $I \ge 2$.

Bidder i’s marginal abatement cost is linear, defined by

$$\begin{aligned} \phi \left( e; \tilde{\alpha _i}\right) := \tilde{\alpha }_i - \beta e \end{aligned}$$

(1)

where $\tilde{\alpha }_i$ is a bidder-specific random variable, his type, e is the bidder’s emission level, and $\beta$ is some positive constant.⁶ Types are drawn from a joint continuous distribution, which is common knowledge. The realization of $\tilde{\alpha }_i$ is privately observed by bidder i before the auction, i.e., each firms knows his marginal abatement cost function before the auction, but not his rivals’. We assume that the marginal probability distribution of types is identical across types, i.e., bidders are ex ante symmetric, and has support $\Omega \equiv \left[ \underline{\alpha }, \overline{\alpha } \right]$.

Note that Eq. (1) implies that bidders have marginal values for additional permits that are decreasing in the quantity received. As Ausubel et al. (2014) point out, this is an aspect of multi-unit demands not present in auctions of unit demands.⁷

Let $C(q_i;\alpha _i )$ denote bidder i’s total cost of complying with the emission cap when his type is $\alpha _i$ and he wins $q_i$ permits at the auction. The $q_i$ permits won at the auction give the bidder the right to pollute $q_i$ units, and he has to incur in the cost of reducing pollution from his business as usual emission level, that is, bidder i’s emission level in the absence of environmental regulation, to $q_i$. Let $e^{*}(\alpha _i)$ denote bidder’s i business as usual emission level when his type is $\alpha _i$. Since $\phi$ is strictly decreasing in e, it is defined as the value of e that solves $\phi (e;\alpha _i)=0$; from (1), it is $e^{*}(\alpha _i)= \alpha _i/\beta$. Bidder i’s total cost is the sum of the auction payment and his abatement cost. Under the uniform format, bidders pay the same price for all permits, the auction stop-out price, p, defined as the maximum price at which all permits are sold, so that bidder i’s total cost is defined by

$$\begin{aligned} C(q_i;\alpha _i) := p q_i + \int _{q_i}^{e^{*} (\alpha _i)} \phi (e;\alpha _i)\mathrm{d}e \end{aligned}$$

(2)

The first term in (2) is bidder i’s auction payment under the uniform format given stop-out price p, and the second term is his abatement cost.

We follow Wilson (1979) share auctions approach: we assume that the Q permits are perfectly divisible, and bidders’ strategies are a continuous demand schedule that we define next.

Definition 1

(Strategy) Bidder i’s strategy at the auction is a demand function, $\gamma _i(\alpha _i,p)$, that for each realizations of his type, $\alpha _i \in \Omega$, specifies the quantity demanded at different price levels, p:

$$\begin{aligned} \gamma _i: \Omega \times \mathcal {R}_+ \rightarrow \mathcal {R}_+ \end{aligned}$$

Denote by $\Gamma$ the strategy space, which we restrict to the class of functions that are continuous and non-increasing in p.

A profile of strategies is a vector $\varvec{\gamma }:=(\gamma _1,\dots ,\gamma _I)$, which specifies a strategy for each bidder. We alternatively write $\varvec{\gamma }=(\gamma _i,\varvec{\gamma }_{-i})$, where $\varvec{\gamma }_{-i}$ is the vector of strategies played by all bidders except i.

Bidder i’s best response to $\varvec{\gamma }_{-i}$ is the strategy $\gamma _i$ that minimizes his expected cost:

$$\begin{aligned} E \lbrace C(q_i;\alpha _i) \mid \gamma _i,\varvec{\gamma }_{-i} \rbrace \end{aligned}$$

where the expectation is taken with respect to $\varvec{\alpha }_{-i}$, his rivals’ types.

The game is a simultaneous game of incomplete information, for which the standard equilibrium concept is Bayesian Nash equilibrium, that we define next.

Definition 2

(Equilibrium) A profile of strategies $(\gamma _1^{*},\dots ,\gamma _I^{*})$ is an equilibrium if and only if, for all $i \in \lbrace 1,\dots ,I \rbrace$, $\gamma _i \in \Gamma$ and $\alpha _i \in \Omega$, it is

$$\begin{aligned} E \lbrace C(q_i;\alpha _i) \mid \gamma _i^{*},\varvec{\gamma }_{-i}^{*} \rbrace \le E \lbrace C(q_i;\alpha _i) \mid \gamma _i,\varvec{\gamma }_{-i}^{*} \rbrace \end{aligned}$$

that is, $\gamma _i^{*}$ is a best response to $\varvec{\gamma }_{-i}^{*}$: bidder i cannot lower his expected cost by deviating from $\gamma _i^{*}$ when all other bidders are playing $\gamma _{-i}^{*}$.

We focus on symmetric equilibria of the form $(\gamma ^{*},\dots ,\gamma ^{*})$; i.e., any two bidders with the same type submit the same demand function. In the sequel, we refer to a Bayesian Nash symmetric equilibrium simply as an equilibrium. When $(\gamma ^{*},\dots ,\gamma ^{*})$ is an equilibrium, we say that $\gamma ^{*}$ is the equilibrium strategy. Moreover, $p^{*}$ and $q_i^{*}$ refer hereafter to the auction’s stop-out price and to bidder i’s allocation under an equilibrium strategy; these values depend on the vector of bidder’s types.

3 Characterization of equilibria

In this section, we characterize the auction equilibria. We consider demands that are additively separable in bidder’s type and price and that are linear in price.⁸ Specifically, we consider equilibria conformed by strategies of the form

$$\begin{aligned} \gamma (\alpha _i,p) = \tau (\alpha _i) - \delta p \end{aligned}$$

(3)

where $\tau$ is an arbitrary function of the bidder’s observed type and $\delta$ is some positive constant. Both $\tau \left( \cdot \right)$ and $\delta$ are to be determined at the equilibrium. We must remark that the strategy space is not restricted to this class of strategies, i.e., arbitrary responses within $\Gamma$ are allowed.

Furthermore, we restrict ourselves to interior equilibria. We say that an allocation of permits is interior if each bidder receives a positive amount of permits and has strictly positive abatement cost. An equilibrium is interior if the stop-out price is nonnegative and generates an interior allocation with probability one, that is, for almost all vector of types’ realizations. The motivation to focus on interior equilibria will be clear from the analysis, particularly from Proposition 3, as we argue in Introduction.

Our approach to characterize equilibria rests on the fact that, under the uniform format, a bidder’s auction payment depends only on the stop-out price and the quantity demanded at that price. We proceed as follows. Select an arbitrary bidder, i. First, we characterize the stop-out price that minimizes bidder i’s expected total cost, given that all of his rivals are playing some (and the same) arbitrary strategy as in (3). Then, we characterize the expected stop-out price if all bidders, including i, follow that strategy. That strategy is the equilibrium strategy if and only if, for each $\alpha _i \in \Omega$, the expected stop-out price when all bidders play the strategy is equal to the stop-out price that minimizes bidder i’s expected total cost, both expectations being conditional on $\alpha _i$. The next proposition characterizes the equilibrium strategy. All proofs are left to “Appendix”.

Proposition 1

Consider an strategy $\gamma$, as in (3). At any interior equilibrium, the following equality holds for all $i \in \lbrace 1,\dots ,I \rbrace$ with probability 1

$$\begin{aligned} \alpha _i \!- \beta \left( \frac{I-1}{I} \right) \left( \tau (\alpha _i) - \delta E \lbrace p_{-i}^{*} \mid \gamma , \; \alpha _i \rbrace \right) \!=\! \frac{2}{I} \times \frac{\tau (\alpha _i)}{\delta } + \left( \frac{I-2}{I} \right) \times E \lbrace p_{-i}^{*} \mid \gamma , \; \alpha _i \rbrace \end{aligned}$$

(4)

where $E \lbrace p_{-i}^{*} \mid \gamma , \; \alpha _i \rbrace$ is the expected stop-out price if all bidders but i follow $\gamma$ and bidder i bids zero.

To interpret (4), consider first the case in which there is a large number of bidders, $I \rightarrow \infty$. With many bidders, each bidder’s contribution to aggregate demand is small, and thus $E \lbrace p_{-i}^{*} \mid \gamma , \; \alpha _i \rbrace$ tends to the expected auction price, $E \lbrace p_{-i}^{*} \mid \gamma , \; \alpha _i \rbrace \rightarrow E \lbrace p^{*} \mid \gamma , \; \alpha _i \rbrace$ as $I \rightarrow \infty$. Then Eq. (4) is

$$\begin{aligned} \alpha _i - \beta \left( \tau (\alpha _i) - \delta E \lbrace p^{*} \mid \gamma , \; \alpha _i \rbrace \right) = E \lbrace p^{*} \mid \gamma , \; \alpha _i \rbrace \end{aligned}$$

(5)

The left-hand side of (5) is the marginal abatement cost bidder i has to pay under his expected allocation in the auction,⁹$\tau (\alpha _i) - \delta E \lbrace p^{*} \mid \gamma , \; \alpha _i \rbrace$. At the equilibrium, that expected marginal cost, his saving on abatement cost from the last unit, equals the expected auction price, the right-hand size of (5). The intuition behind this result is that the presence of many bidders eliminates strategical aspects from the bidders’ strategies, and bidders bid to equalize their expected marginal abatement cost of the last unit won at the auction to the expected price.

Next, consider a finite number of bidders, $I \ge 2$, with bidders acting strategically. The left-hand side of (4) is still an estimation of the highest marginal abatement cost bidder i has to pay under his expected equilibrium allocation. To see this, assume that all bidders but i follow some strategy $\gamma$ as in (3). Let $p^{*}_{-i}$ and $p^{*}$ denote the auction’s stop-out price considering the demand of all bidders but the i and all bidders, respectively. Thus, $p^{*}_{-i}$ satisfies $\sum _{j \ne i}\tau (\alpha _j)-(I-1)\delta p^{*}_{-i}=Q$ whereas $p^{*}$ satisfies $\sum _{j}\tau (\alpha _j)-I\delta p^{*}=Q$. From the linearity in price of the previous equations, it follows $\frac{I-1}{I}\left( \tau (\alpha _i) -\delta p^{*}_{-i} \right) = \tau (\alpha _i)-\delta p^{*}$. The term multiplying $\beta$ on the left-hand side of (4) is therefore bidder i’s expected allocation, so that the left-hand side is bidder i’s highest expected marginal abatement cost.

To interpret the right-hand side of (4), assume that bidder i expects to win some permits in the auction by following $\gamma$ when all other bidders follow $\gamma$ as well. In that case, he expects the auction price to be strictly above $E \lbrace p^{*}_{-i} \mid \gamma , \; \alpha _i \rbrace$ and strictly below $\tau (\alpha _i)/\delta$, this latter being the highest price—under $\gamma$—at which he demands a nonnegative quantity. The right-hand side of (4) is a convex combination of those lower and upper bounds, with the upper bound having less weight as I increases. This is illustrated in Fig. 1. In the figure, $D_{-i}(p)$ is the demand of all bidders but the i, and $p^{*}_{-i}$ the corresponding stop-out price, determined by the intersection of $D_{-i}(p)$ and the vertical line representing the inelastic supply of Q permits. Bidder i’s demand is $\tau (\alpha _i)- \delta p$. The aggregate demand is D(p), and the corresponding stop-out price is $p^{*}$. The figure shows that bidder i wins permits at the auction if and only if $p^{*}$ satisfies $p^{*}_{-i}< p^{*} < \frac{\tau (\alpha _i)}{\delta }$. The quantity of permits awarded to bidder i at the equilibrium is $q_i^{*}$, which satisfies $\tau (\alpha _i)-\delta p^{*} = q_i^{*} = \frac{I-1}{I}\left( \tau (\alpha _i)-\delta p^{*}_{-i} \right)$.¹⁰ Therefore, the right-hand side of (4) is bidder i’s estimate of the stop-out price at an interior equilibrium.

Note that with two bidders, $I=2$, the right-hand side of (4) is $\tau (\alpha _i)/\delta$, which is the upper bound for the expected auction price whenever bidder i wins permits at the auction. In contrast with the many bidders case, when there are only two bidders, the expected abatement cost of the last unit the bidder wins at the auction (left side of 4) is larger than the expected auction’s price. Therefore, with I finite there is an strategic component in bidding, that disappears when $I\rightarrow \infty$.

Fig. 1

Supply of permits is the vertical line at Q, and $D_{-i}(p)$ is the demand of all bidders but the i; the intersection determines the corresponding stop-out price, $p^{*}_{-i}$. Bidder i’s demand is $\tau (\alpha _i)- \delta p$. The aggregated demand is D(p), and $p^{*}$ the corresponding stop-out price. Bidder i wins permits at the auction if and only if $p^{*}$ satisfies $p^{*}_{-i}< p^{*} < \frac{\tau (\alpha _i)}{\delta }$. The quantity awarded to bidder i at the equilibrium is $q_i^{*}$

Next, we focus on equilibria that are linear in both bidder’s type and price, that is, such that the strategy conforming an equilibrium is linear in both arguments, $\alpha _i$ and p. Apart from its simplicity, linear strategies are natural candidates to conform an equilibrium as the marginal abatement cost function—which defines the valuation of the permits auctioned—is assumed to be linear. Moreover, our analysis will illustrate that if the marginal abatement cost and the strategies conforming the equilibria have similar shapes, there is a straightforward way to analyze efficiency.

The next Lemma characterizes necessary and sufficient conditions for a linear strategy (not necessarily conforming an equilibrium) to generate an interior allocation.

Lemma 1

Consider an arbitrary linear strategy

$$\begin{aligned} \gamma (\alpha _i,p) = \kappa _0 + \kappa _1 \alpha _i - \delta p \end{aligned}$$

where $\kappa _0$, $\kappa _1$ and $\delta$ are constants. Assume that all bidders play $\gamma$. Under $\gamma$, each bidder demands a positive quantity at the stop-out price and the stop-out price is positive (with probability one) if and only if

$$\begin{aligned} I(\kappa _0+\kappa _1 \underline{\alpha })> Q > (I-1)\kappa _1 \left( \overline{\alpha }-\underline{\alpha } \right) \end{aligned}$$

(6)

Furthermore, under the auction allocation, each bidder’s marginal abatement cost is nonnegative (with probability one) if and only if

$$\begin{aligned} \frac{\beta Q }{I } \le {\left\{ \begin{array}{ll} \underline{\alpha } &{} \text { if }\beta \kappa _1 \le \frac{I}{I-1} \\ \overline{\alpha }- \beta \kappa _1\frac{I-1}{I}\left( \overline{\alpha } - \underline{\alpha } \right) &{} \text { otherwise} \\ \end{array}\right. } \end{aligned}$$

(7)

The first inequality in (6) gives the condition under which the stop-out price is strictly positive with probability one: if all bidders get the lowest possible signal, $\underline{\alpha }$, the aggregate quantity demanded at price 0, $I(\kappa _0+\kappa _1\underline{\alpha })$, has to be greater than Q. The second inequality gives the condition under which each bidder demands a positive quantity of permits at the stop-out price with probability one: the worst scenario is that all bidders but one get the highest signal, $\overline{\alpha }$, and one of them gets the lowest one, $\underline{\alpha }$; in that case, the last kink in the aggregate demand is at a price equal to the vertical intercept of the demand of the bidder with the lowest signal, $\dfrac{\kappa _0 }{\delta }+\dfrac{\kappa _1 }{\delta }\underline{\alpha }$, with a quantity demanded equal to $(I-1)\kappa _1 \left( \overline{\alpha }-\underline{\alpha } \right)$. The second inequality in (6) states that Q has to be greater than that quantity. Note that it imposes that the dispersion of types, $\overline{\alpha } - \underline{\alpha }$ has to be low enough. Finally, condition (7) states that each bidder has a positive abatement cost if the number of permits auctioned is low enough.

Next, we characterize the set of linear and interior equilibria. We assume hereafter that the expected value of rivals’ types conditional on the own observed type is linear. Therefore, for any two bidders, i and j, it is

$$\begin{aligned} E \lbrace \tilde{\alpha }_j \mid \alpha _i \rbrace = \left( 1-\lambda \right) E \lbrace \tilde{\alpha }_i \rbrace + \lambda \alpha _i \end{aligned}$$

(8)

where $\lambda$ denotes the linear correlation between $\tilde{\alpha }_i$ and $\tilde{\alpha }_j$, which we assume to be common for any pair of types. In the sequel we assume $\lambda \in \left[ 0,1 \right]$. Recall that, additionally, we assume equal marginal distribution of types.

The next proposition shows that the set of interior equilibria conformed by linear strategies can be indexed by $\kappa _1$, the type’s coefficient on the strategy’s horizontal intercept: there is a one-to-one mapping from the values of $\kappa _1$ to the set of interior equilibria conformed by linear strategies. This is important for two reasons. First, regarding the positive properties of the equilibrium, its existence and uniqueness can be easily studied within the real line (as $\kappa _1$ is real valued) instead of the more complex space of linear strategies. Second, there is a normative side: we will show that the efficiency of any equilibrium strategy depends only on $\kappa _1$.

Proposition 2

There exists a unique pair of two real valued differentiable functions, $\left( g_0,g_{\delta } \right)$, such that a linear strategy with coefficients $\left( \kappa _0,\kappa _1,\delta \right)$, conforms an interior equilibrium only if $\kappa _0=g_0(\kappa _1)$ and $\delta = g_{\delta }(\kappa _1)$. Moreover, $g_{\delta }$ is strictly increasing, with $g_{\delta }(0)=0$.

From Proposition 2, it is easy to prove that $\delta >0$ for all $\lambda \in \left[ 0,1 \right]$, i.e., the equilibrium strategy is downward sloping. Given the properties of $g_{\delta }$, this implies that $\kappa _1>0$, i.e., the equilibrium strategy’s horizontal intercept is increasing in $\alpha _i$. Therefore, for any two firms i and j such that $\alpha _i > \alpha _j$, the demand of the less efficient firm, i, lies to the right of the demand of the more efficient firm, i.e., the former bids a higher price for each given amount of permits than his rival.

Note that the equilibrium strategies considered by Ausubel and Cramton (2002) and Ausubel et al. (2014) correspond to $\kappa _1=\delta$ and $\kappa _0=0$. Imposing $\kappa _1=\delta$, $g_0(\kappa _1)$ from Proposition 2 implies $\kappa _0=0$, i.e., our equilibria includes theirs.¹¹

The next Proposition analyzes the existence of equilibria conformed by linear strategies.

Proposition 3

Assume that

$$\begin{aligned} \overline{\alpha }-\underline{\alpha }< \frac{\beta Q}{I} < \underline{\alpha } . \end{aligned}$$

(9)

Then there exists a non-empty interval, say $(\kappa _1^l,\kappa _1^u)$, with $(\kappa _1^l,\kappa _1^u) \subset (0,\infty )$ and a subinterval $[0,\lambda ^u) \subset [0,1)$, such that, if $\lambda \in [0,\lambda ^u)$, for any $\kappa _1' \in (\kappa _1^l,\kappa _1^u)$ the linear strategy with coefficients $\left( \kappa _0,\kappa _1,\delta \right) = \left( g_0(\kappa _1'),\kappa _1', g_{\delta }(\kappa _1')\right)$ constitutes an interior equilibrium, where $g_0$ and $g_{\delta }$ are defined in Proposition 2.

Proposition 3 states a condition for the existence of interior equilibria: the range of types, $\overline{\alpha } - \underline{\alpha }$, has to be low in comparison with the infimum of $\Omega$, $\underline{\alpha }$. Intuitively, if we allow for too different types across bidders, under a symmetric equilibrium it might occur that the bidder with the lowest type gets no permits. In the analysis that follows we will make use of (9) or stronger though qualitatively similar conditions.

Additionally, Proposition 3 states that even with linear strategies there is a continuum of equilibria, that is, there are multiple equilibria for the uniform auction. The values of $\kappa _1$ defining an equilibrium belong to an open interval in the real line, while the functions that map each value of $\kappa _1$ into the associated values of $(\kappa _0,\delta )$ are continuous, as stated in Proposition 2. It is important to notice that, in some sense, the equilibria are close to one another, since we are considering interior equilibria.

4 Efficiency

We use an ex-post efficiency concept, as in Ausubel et al. (2014). Given a vector of types’ realizations and a total amount of permits, Q, the efficient allocation of permits minimizes the total abatement cost among the I firms. The formal definition is presented next.

Definition 3

(Efficient allocation) Given a total amount of permits, Q, and a vector of types realizations, $\varvec{\alpha }=\left( \alpha _1,\dots ,\alpha _I \right)$, an assignment of the Q permits among bidders, $\mathbf {q^o}=\left( q_{1}^o,\dots ,q_{I}^o\right)$, is ex-post efficient if it minimizes the total abatement cost:¹²

$$\begin{aligned} \mathbf {q^o} \equiv \mathrm{arg min}_{\lbrace q_{1},\dots ,q_{I} \rbrace } \left\{ \sum _{i=1}^{I} \int _{q_i}^{e^{*}_i(\alpha _i)} \phi _i(e;\alpha _i)\mathrm{d}e \mid \sum _{i=1}^{I} q_i\le Q \right\} \end{aligned}$$

The definition of efficiency is contingent on Q, the quantity of permits auctioned: we do not define the efficient quantity of permits to be auctioned but take that quantity as exogenous and focus on its efficient distribution. This concept of efficiency is usually termed as cost-effective in environmental economics. Since in our model the marginal abatement cost for each firm and each type realization is strictly decreasing, that cost-minimizing or efficient allocation is unique.

Fig. 2

Geometry of the efficient allocation for $I=2$ in the $\overline{q_1 q_2}$ plane. The feasible allocations of permits are delimited by the triangle $\lbrace (0,0), (0,Q), (Q,0) \rbrace$. The dashed lines are type dependent. The line $\alpha _1-\beta q_1 = \alpha _2 -\beta q_2$ changes its intercept as the difference $\alpha _2-\alpha _1$ changes. If $| \alpha _2 -\alpha _1 |$ is big, that line shifts too much either upward or downward so that the optimal allocation is to assign all permits to the highest type firm. Furthermore, if too many permits are available, that is, Q is too large, the point A, which corresponds to the business as usual emission level, lies inside the feasible triangle, so that the efficient allocation is A, under which the marginal abatement costs are zero. Finally, if $| \alpha _2 -\alpha _1 |$ and Q are both small enough, the efficient allocation, E, is interior. We arbitrarily have selected a realization of types such that $\alpha _2 - \alpha _1 <0$

We restrict the analysis to parameter values for which the cost-minimizing allocation is interior with probability one. Under an interior allocation, each firm buys permits at the auction and has positive abatement costs. If the efficient allocation is interior, marginal abatement costs are equalized across bidders, that is, $\phi (q_i^o;\alpha _i)=\phi (q_j^o;\alpha _j)$ for any i and j in $\lbrace 1, \dots , I \rbrace$. The next Lemma characterizes the subspace of parameter values for which the efficient allocation is interior with probability one. We use the following terminology. An strategy is efficient if the permits allocation when all bidders play it is the efficient allocation with probability one. The Lemma also gives necessary and sufficient conditions for a strategy as in (3) to be efficient.

Lemma 2

• 1. The efficient allocation is interior with probability one iff

  $$\begin{aligned} (I-1)(\overline{\alpha }-\underline{\alpha }) \le \beta Q \le I \underline{\alpha } \end{aligned}$$

• 2. Assume that the efficient allocation is interior and consider an strategy $\gamma$ as in (3). Then $\gamma$ is efficient if and only if $\tau$ is linear, $\tau (\alpha ) = \kappa _0 + \kappa _1 \alpha$, with $\beta \kappa _1=1$.

Figure 2 shows the geometry of part 1 of Lemma 2 when there are two bidders, in the $\overline{q_1 q_2}$ plane. The feasible allocations of permits are delimited by the triangle $\lbrace (0,0), (0,Q), (Q,0) \rbrace$. The dashed lines are type dependent. The line $\alpha _1-\beta q_1 = \alpha _2 -\beta q_2$, which represents allocations for which marginal abatement cost are equal across bidders, changes its intercept as the difference between types, $\alpha _2-\alpha _1$, changes. If the types are too different, i.e., if $| \alpha _2 -\alpha _1 |$ is too big, that line shifts too much either upward or downward so that the optimal allocation is to assign all permits to the highest type firm. Furthermore, if too many permits are available, that is, if Q is too large, the point A, which represents the business as usual emission level, lies inside the feasible triangle, so that the efficient allocation is A, and abatement cost is zero. Finally, if $| \alpha _2 -\alpha _1 |$ and Q are both small enough, the efficient allocation, E, is an interior allocation: both bidders buy permits at the auction and have positive abatement costs. We arbitrarily have selected a realization of types such that $\alpha _2 - \alpha _1 <0$, so that at the efficient allocation bidder 2 buys less permits than bidder 1.

Part 2 of Lemma 2 states that ex-post efficient strategies are easily characterized in our model: $\kappa _1$, the type’s coefficient in the strategy played by all bidders, has to be equal to $\frac{1}{\beta }$, the inverse of the slope of the marginal abatement cost function. To understand this condition, assume that all firms play an strategy $\gamma$ as in Lemma 1, and that the corresponding equilibrium allocation is $\left( q_1^{*},...,q_I^{*} \right)$. Consider any two firms, i and j, such that $\alpha _i > \alpha _j$, i.e., such that firm i has higher marginal abatement cost for any emission level than his rival. If $\kappa _1>0$, the less efficient firm, firm i, bids more aggressively and thus gets more permits at the auction than his rival. Still, the less efficient firm might not obtain the efficient amount of permits. Given $\gamma$, the difference in marginal abatement costs among firms is

$$\begin{aligned} \phi (q_i^{*};\alpha _i) - \phi (q_j^{*};\alpha _j) = (1-\beta \kappa _1)(\alpha _i-\alpha _j) \end{aligned}$$

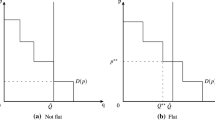
Clearly, equality of the marginal abatement costs is ex-post guaranteed only if $\kappa _1$ satisfies $1-\beta \kappa _1 = 0$. Contrarily, if $\kappa _1>0$ and $1-\beta \kappa _1>0$, the highest type firm has higher marginal abatement cost than his rival at the equilibrium. In other words, the highest type firm gets more permits that his rival, but fails to get enough permits as to equalize marginal abatement costs. We say that the less efficient firm is under-assigned in the auction with respect to the efficient allocation. Analogously, the case $\kappa _1>0$ and $1-\beta \kappa _1<0$ leads to an over-assignment of the less efficient firm. These departures from the efficient strategy are depicted in Fig. 3, for the case of two bidders. In the figure, we represent in both panels the marginal abatement cost function, $\phi$, for two bidders, 1 and 2, such that $\alpha _1>\alpha _2$ and $q_1^{*}>q_2^{*}$, which necessarily rests on strategies (which are not plotted) with $\kappa _1>0$. However, the marginal abatement cost at the equilibrium is not equal across firms, as efficiency requires. Panel (a) represents a permit allocation and the corresponding marginal abatement costs when $1-\beta \kappa _1 > 0$, and thus the less efficient firm (firm with type $\alpha _1$) is under-assigned, so that $\phi (q_1^{*};\alpha _1)>\phi (q_2^{*};\alpha _2)$. Panel (b) represents a case in which the less efficient firm is over-assigned.

Fig. 3

For $I=2$, efficiency requires $\phi \left( q_1^{*}; \alpha _1 \right) = \phi \left( q_2^{*}; \alpha _2 \right)$. If both bidders play a strategy as in Lemma 1 (not plotted), efficiency requires $1-\beta \kappa _1 = 0$. Panel (a) represents a permit allocation $\left( q_1^{*}, q_2^{*}\right)$ and the corresponding marginal abatement costs when $1-\beta \kappa _1 > 0$, and thus the less efficient firm (firm with type $\alpha _1$) is under-assigned, so that $\phi (q_1^{*};\alpha _1)>\phi (q_2^{*};,\alpha _2)$. Panel (b) represents a case in which the less efficient firm is over-assigned. a$1-\beta \kappa _1 > 0$. b$1-\beta \kappa _1 < 0$

Next, we analyze equilibrium strategies. The two essential questions analyzed in this section are as follows. First, does the efficient strategy belong to the set of equilibria?¹³ And second, if there other equilibria besides the efficient equilibrium, what sort of inefficiency characterize those equilibria?

As we use an ex-post concept of efficiency, the distribution of types is irrelevant for the efficient allocation. However, the distributional assumptions matter for the equilibria. If all bidders have the same type with probability one, which corresponds to $\lambda = 1$ in (8), under any symmetric equilibrium, all bidders submit the same demand function, permits are equally shared among bidders, and since types are identical, the allocation is efficient. In short, with $\lambda = 1$ any symmetric equilibrium is efficient. This is the case analyzed by Ausubel et al. (2014). But things are not that simple if types vary across bidders. Section 4.1 analyzes the case of independent types, that is, $\lambda = 0$, and Sect. 4.1considers an special case of positively correlated types, $\lambda = 1/2$.

4.1 Independent types

In this subsection, we consider the case of independent types, i.e., $\lambda = 0$ in (8). Using the standard terminology in auction theory, this is a pure private value case, as the valuations (marginal abatement costs in our model) are privately observed and independent across bidders. The basic idea to analyze efficiency follows from the previous section. From Proposition 2, we know that the set of interior equilibria is indexed by $\kappa _1$, while from Lemma 2 we know that any linear strategy is characterized by $\beta \kappa _1 = 1$. Both results combined make the analysis of efficiency tractable, as it simply requires to find out the equilibrium values of a real valued parameter, $\kappa _1$. The next proposition characterized interior equilibria.

Proposition 4

Assume (9) and $\lambda = 0$. Then, there exists some $\kappa _1^{*}$ satisfying $\kappa _1^{*}< \frac{1}{\beta }\frac{I}{I-1}$, such that a linear strategy constitutes an interior equilibrium if and only if $\kappa _1 \in \left( \kappa _1^{*}, \frac{1}{\beta }\frac{I}{I-1}\right)$. Furthermore, there exists some finite value of I, say $I^0$, such that for any $I>I^0$: (i) $\kappa _1^{*}$ increases as $E \lbrace \tilde{\alpha }_i \rbrace$, $E \lbrace \tilde{\alpha }_i \rbrace - \underline{\alpha }$ or Q increase (considering each of those variations separately), and (ii) the efficient equilibrium, characterized by $\beta \kappa _1 = 1$, is an interior equilibrium.

The basic message from Proposition 4 is that the set of (interior) equilibria is convex in the dimension of $\kappa _1$. In other words, the set of values of $\kappa _1$ defining an equilibrium is an open interval, which depends on parameters related to the types’ distribution and the number of bidders, I. The next proposition analyzes this latter dependence and defines efficient equilibria.

Proposition 5

Assume $\lambda = 0$ and

$$\begin{aligned} \frac{I}{I-1}\left( \overline{\alpha } - \underline{\alpha } \right) \le \frac{\beta Q}{I-1} \le \underline{\alpha } \end{aligned}$$

(10)

Then:

• 1. For all $I \ge 2$ the efficient strategy is an interior equilibrium strategy, given by

  $$\begin{aligned} \gamma _{0}^{*} (\alpha _i,p) = \frac{1}{\beta } \left( E \lbrace \tilde{\alpha }_i \rbrace - \frac{1}{I-1} \beta Q + \alpha _i - 2p \right) \end{aligned}$$

  For any bidder i and any $\alpha _i \in \Omega$, it satisfies

  $$\begin{aligned} E \lbrace p^{*} \mid \alpha _i \rbrace \le E \lbrace \phi (q_i^{*},\alpha _i) \mid \alpha _i \rbrace \end{aligned}$$

  (11)

  where $p^{*}$ is the auction’s stop-out price and $q_i^{*}$ is bidder i’s allocation of permits.

• 2. Consider $I \rightarrow \infty$ and $Q \rightarrow \infty$ while $\frac{Q}{I}$ remains constant. Then the unique interior equilibrium is the efficient strategy.

• 3. For the case $I=2$, there exists some $b^{0} \in (0,1)$ such that any $\kappa _1$ with $\beta \kappa _1 \in (b^{0},2)$ defines an equilibrium strategy. Additionally, in all equilibria, for any bidder i and any $\alpha _i \in \Omega$, (11) is satisfied.

Part 1 of Proposition 5 presents the efficient strategy, that is an equilibrium strategy for all $I \ge 2$. From Proposition 2, given the value for $\kappa _1$ that characterizes the efficient strategy, $\beta \kappa _1=1$, there exists unique values for $(\kappa _0,\delta )$ that define the corresponding equilibrium strategy. The comparative statics properties of the efficient equilibrium strategy are straightforward. Under (10), for each possible type’s realization, the relative position of the efficient equilibrium strategy, $\gamma$, and the marginal abatement cost function, $\phi$, in the usual price-quantity axis, is as depicted in Fig. 4: the efficient strategy has a lower vertical intercept and a higher horizontal intercept than the marginal abatement cost function, i.e., given that bidders are restricted to bid a linear strategy, the efficient equilibrium strategy is such that bid shading is decreasing as q increases, and is negative (bidders bid more that their valuation for those units) for q large enough.

Even if bidders bid higher than their valuation for some units, for all $I \ge 2$, at the efficient equilibrium, bidders expect to have a positive surplus: the expected auction’s stop-out price is not greater than the marginal abatement cost of the last permit bought at the auction, as stated on condition (11). This is illustrated in Fig. 4, for the realized stop-out price, $p^{*}$, and marginal abatement cost of the last unit won, $\phi (q^{*}_i;\alpha _i)$. In the figure, given $p^{*}$, $\gamma$ determines the assignment at the auction, $q^{*}_i$, which in turn determines the marginal saving in the abatement cost of the last unit won at the auction, $\phi (q^{*}_i;\alpha _i)$. According to (2), the bidder’s total cost is the payment in the auction (blue area¹⁴) plus the abatement cost, the area below $\phi$ from his assignment of permits, $q^{*}_i$, up to $e^{*}(\alpha _i)$ (orange). If the firm had no permits, his total cost would be the whole area below $\phi$ from zero to $e^{*}(\alpha _i)$. Thus, his realized surplus from participating in the auction is the green area. Notice that $p^{*} \le \phi (q^{*}_i,\alpha _i)$ implies a positive surplus: under the uniform auction format, a sufficient condition to have a positive surplus is that the auction’s stop-out price, $p^{*}$, is not larger than the marginal saving in the abatement cost of the last unit won at the auction, $\phi (q^{*}_i,\alpha _i)$.

Fig. 4

An arbitrary linear strategy, $\gamma$, and the marginal abatement cost function, $\phi$, are represented given the firm’s type, $\alpha _i$. The auction’s stop-out price, $p^{*}$, and $\gamma$ determine the assignment in the auction, $q^{*}_i$, which in turn determines the marginal saving in the abatement cost of the last unit won at the auction, $\phi (q^{*}_i;\alpha _i)$. The bidder total cost is the payment in the auction (blue area) plus the abatement cost, the area below $\phi$ from his assignment of permits up to $e^{*}(\alpha _i)$ (orange). If the firm had no permits, his total cost would be the whole area below $\phi$ from zero to $e^{*}(\alpha _i)$. Thus, his realized surplus from the auction is the green area. Notice that $p^{*} \le \phi (q^{*}_i,\alpha _i)$ implies a positive surplus

Part 2 of Proposition 5 states an interesting property of the set of interior equilibria. As $I\rightarrow \infty$ keeping the ratio Q / I constant, the only interior equilibrium is the efficient equilibrium: in a private value model, an increase in the number of bidders drives the auction toward the efficient equilibrium. This is not the case for I finite, as we illustrate on part 3 of Proposition 5, considering the case $I=2$. With only two bidders, there are inefficient equilibria. In terms of the notation previously introduced, under some of those inefficient equilibria the firm with highest type is under-assigned while under some other equilibria it is over-assigned. In all of those equilibria condition (11) holds, i.e., bidders expect to have a positive surplus when participating in the auction.

4.2 Correlated types: mineral right model

In this subsection, we consider a specific probabilistic structure that implies private values with positively correlated types. The basic idea is to split the bidders’ type into a common term plus a bidder-specific term, so that the correlation among different types arises from the common term. This corresponds to the mineral rights model, using auction theory terminology.¹⁵ In addition, we specify a probability distributions for both terms so that the marginal distribution is identical across types, has finite support and the conditional expectation of types is linear, as in (8).

Specifically, we assume that for all i

$$\begin{aligned} \tilde{\alpha }_i = \theta + \tilde{a} + \tilde{u}_i \end{aligned}$$

(12)

where $\theta$ is a parameter, and $\lbrace \tilde{a},\tilde{u}_1,\dots , \tilde{u}_I \rbrace$ is a set of globally independent and identically distributed zero-mean random variables. With this specification, $\tilde{a}$ is the common term for all types while the u’s are bidder specific. Moreover, we assume that all the random variables are uniformly distributed in some finite interval $[-\sigma ,\sigma ]$, with $\sigma$ fixed, which implies that the marginal distribution is identical across types, with the support of $\tilde{\alpha }_i$ being $[\theta - 2\sigma ,\theta + 2 \sigma ]$. Straightforward calculation shows that the unconditional expectation is given by $E \lbrace \tilde{\alpha }_i \rbrace = \theta$, and, additionally,

$$\begin{aligned} E \lbrace \tilde{\alpha }_j \mid \alpha _i \rbrace = \frac{1}{2} \left( \theta + \alpha _i \right) \end{aligned}$$

(13)

i.e., the expectation of the rivals’ type conditional on the own type is linear, as required in our model. A direct comparison between (8) and (13) shows that the latter conveys $\lambda =\frac{1}{2}$. For our purposes, any probabilistic structure leading to the same correlation value among types is essentially equivalent to the one presented here.

Next, we analyze efficiency and equilibria when $\lambda = 1/2$. We focus on the comparison to the independent case presented on the previous Subsection. The next proposition summarizes our main results.

Proposition 6

Assume (10), $\lambda = 1/2$ and

$$\begin{aligned} \frac{2}{I-1} \beta Q \le E \lbrace \tilde{\alpha }_i \rbrace \qquad 2(\overline{\alpha }-\underline{\alpha }) \le \frac{\beta Q}{I} \le 2 \underline{\alpha } - \overline{\alpha } \end{aligned}$$

(14)

Then:

• 1. For all $I \ge 2$ the efficient strategy is an interior equilibrium strategy, given by

  $$\begin{aligned} \gamma _{1/2}^{*} (\alpha _i,p) = \frac{1}{\beta } \left( \frac{1}{I+1}E \lbrace \tilde{\alpha }_i \rbrace - \frac{2}{(I+1)(I-1)} \beta Q + \alpha _i - \frac{I+2}{I+1}p \right) \end{aligned}$$

  For any bidder i and any $\alpha _i \in \Omega$, it satisfies (11).

• 2. Consider $I \rightarrow \infty$ and $Q \rightarrow \infty$ while $\frac{Q}{I}$ remains constant. Then there exists some $b^1 \in (0,1)$ such that $\kappa _1$ defines an equilibrium strategy if and only if $\beta \kappa _1 \in (b^1,2)$. Additionally, in all equilibria, for any i and $\alpha _i \in \Omega$, (11) is satisfied.

Similar to part 1 of Proposition 5, part 1 of Proposition 6 presents the efficient strategy, that is an equilibrium strategy for all $I\ge 2$. As it is the case for $\lambda =0$, in the efficient equilibria condition (11) holds, and bidders expect to have a positive surplus from participating in the auction.

Part 2 of Proposition 6 states that, in contrast to the case of private values, there are many equilibria besides the efficient equilibrium when types are correlated and I and $Q\rightarrow \infty$, so that the ratio Q / I stays constant. In all of them condition (11) holds, and bidders expect to have a positive surplus from participating in the auction. This is one of the main results of our analysis: the existence of many bidders is not a sufficient condition to guarantee an efficient equilibrium in the uniform auction. Additionally, bidders’ types have to be uncorrelated. The next Corollary presents an example of an equilibrium that is not efficient when $I \rightarrow \infty$ and $\lambda = \frac{1}{2}$.

Corollary 1

Assume $I \rightarrow \infty$ and $Q \rightarrow \infty$ while $\frac{Q}{I}$ remains constant, and $\lambda = \frac{1}{2}$. An interior equilibrium is characterized by $\beta \kappa _1 = \frac{3}{2}$. The equilibrium strategy is

$$\begin{aligned} \gamma _{1/2}(\alpha _i,p)=\frac{3}{\beta }\left( \frac{E \lbrace \alpha _i \rbrace + \alpha _i}{2} - p \right) \end{aligned}$$

(15)

The stop-out price and the equilibrium allocation for bidder i are, respectively, $p^{*}=E\lbrace \tilde{\alpha }_i \rbrace - \frac{\beta Q}{3I}$ and $q^{*} = \frac{3}{2\beta }(\alpha _i - E\lbrace \tilde{\alpha }_i \rbrace ) + \frac{Q}{I}$.

In the equilibrium presented in Corollary 1, all bidders with types $\alpha _i$ such that $\alpha _i < E\lbrace \tilde{\alpha }_i \rbrace$ bid more than their valuations for all units, and even if they expect to have a positive surplus participating in the auction, their realized surplus is negative. Only bidders with high types end up having a positive surplus, even if they are over-assigned, given that $1-\beta \kappa _1<0$.

Finally, to conclude the analysis, the next Corollary compares efficient equilibrium strategies as I and $Q\rightarrow \infty$ so that the ratio Q / I stays constant for $\lambda =0$ and $\lambda =1/2$.

Corollary 2

Assume $I \rightarrow \infty$ and $Q \rightarrow \infty$ while $\frac{Q}{I}$ remains constant. Denote by $\gamma _{\lambda }^{*}$ for $\lambda \in \lbrace 0, \frac{1}{2} \rbrace$ the efficient equilibrium strategy at the limiting value of I when the correlation between types is $\lambda$. It is

$$\begin{aligned} \gamma _0^{*}(\alpha _i,p)=\frac{1}{\beta }\left( E \lbrace \alpha _i \rbrace - \frac{\beta Q}{I} + \alpha _i -2p \right) \qquad \gamma _{1/2}^{*}(\alpha _i,p)=\frac{1}{\beta } \left( \alpha _i - p \right) \end{aligned}$$

(16)

For $\lambda \in \lbrace 0, \frac{1}{2} \rbrace$ the stop-out price and the equilibrium allocation for bidder i are, respectively, $p^{*}=E\lbrace \tilde{\alpha }_i \rbrace - \frac{\beta Q}{I}$ and $q^{*} = \frac{1}{\beta }(\alpha _i - E\lbrace \tilde{\alpha }_i \rbrace ) + \frac{Q}{I}$.

Figure 5 shows the relative position of the efficient equilibrium strategy, $\gamma _{\lambda }$, for $\lambda =0$ on panel (a), and for $\lambda = \frac{1}{2}$ on panel (b), and the marginal abatement cost function, $\phi (q;\alpha _i)$, common to both panels, as $I \rightarrow \infty$. Also common to both panels are the stop-out price, $p^{*}$ and the equilibrium allocation for bidder i, $q_i^{*}$. When types are uncorrelated, $\lambda =0$, the unique interior equilibrium is such that bidders bid lower than their marginal abatement cost for that particular unit for all quantities lower than $q_i^{*}$, and bid higher than their marginal abatement cost for that particular unit for all quantities greater than $q_i^{*}$. In contrast, when types are correlated, $\lambda = \frac{1}{2}$, in the efficient equilibrium bidders bid their marginal abatement cost for all units, and the equilibrium strategy is the inverse of the marginal abatement cost function. For both cases, uncorrelated and correlated types, bidder i’s total cost is the same, the shaded area in the figure, equal to the auction’s payment, $p^{*}q_i^{*}$, plus the abatement cost.

From the expression for the efficient allocation in Corollary 2, note that bidders whose type, $\alpha _i$, is greater than the a priori expected value of types, $E\lbrace \tilde{\alpha }_i\rbrace$, get more permits at the auction than they would get if permits were equally shared among bidders, $\frac{Q}{I}$, while bidder whose type is lower than the a priori expected value of types, get less.

Fig. 5

Relative position of the efficient equilibrium strategy, $\gamma _{\lambda }^{*}$, for $\lambda =0$ on panel (a), and for $\lambda = \frac{1}{2}$ on panel (b), and the marginal abatement cost function, $\phi (q;\alpha _i)$, common to both panels, as $I \rightarrow \infty$. The auction stop-out price is $p^{*}$ and the equilibrium allocation for bidder i is $q_i^{*}$. The bidder’s total cost is the shaded area, equal to the auction’s payment, $p^{*}q_i^{*}$, plus the abatement cost. a Uncorrelated types, $\lambda = 0$. b Uncorrelated types, $\lambda = 1/2$

5 Concluding remarks

This paper aims to provide a theoretical assessment for the efficiency of a uniform auction as a primary allocation mechanism of emission permits. Despite the fact that the issue of efficiency has a simple answer within single-unit auction settings, our analysis reveals that for multi-unit multi-bid non-common value auctions the question is more complex.

We consider a given total amount of permits to be allocated. Polluting firms, the bidders at the auction, must exert abatement costs by the amount of the business as usual pollution level not covered by their post-auction holdings of permits. An allocation of permits between firms is efficient when it minimizes the total sum across firms of abatement costs. The auction is modeled as a Bayesian game of incomplete information, in which bidders have some private information, their type, on their abatement technologies prior to bidding. In our model, a high type means a less efficient abatement technology. For most cases, we obtain multiplicity of equilibria. In all of the equilibria, the firms with higher types get more permits than the firms with lower types, but all but one of the equilibria are inefficient in the sense that firms with higher types get either too many or too few permits as compared to the efficient allocation. We also prove that an scenario with many bidders and statistically independent types is sufficient to sustain the efficient allocation of permits as a unique equilibrium. Furthermore, we show that if types are correlated, inefficient equilibria survive even as the number of bidders grows large.

The uniform auction format is currently the primary assignment mechanism for emission permits in the European Union (EU ETS). A closer look to this example suggests a number of possible extensions to this paper. An obvious one is to consider the interaction between the auction and the secondary market for permits, that runs in parallel to the auction, which is of particular interest as long as this secondary market is not perfectly competitive, see Hahn (1984). Additionally, we have restricted our analysis to interior allocations, in which all bidders get some permits at the auction and must exert some abatement costs. This is a natural scenario when bidders have similar abatement cost functions, which could be the case in the EU ETS general allowances auctions at this stage, given that auctions’ participants are mainly firms from the power generating sector, with similar abatement technologies. However, as other sectors begin to participate more actively in the auctions, given the differences on marginal abatement cost across industries,¹⁶ the analysis of corner solution equilibria could be relevant. Finally, from a more general perspective, other auction formats are being currently used for pollution permits, as for instance the discriminatory format in the Environmental Protection Agency EPA Sulphur Dioxide emissions trading program. In this regard, to identify the comparative advantage of different auction formats in terms of its efficiency might be of interest for policy makers.

Appendix: Proofs

The following notation is convenient for several of the proofs, while it is omitted from the main text to ease the overall exposition.

$$\begin{aligned} \mu :=(1-\lambda )E \lbrace \tilde{\alpha }_i \rbrace \end{aligned}$$

(17)

And (8) can be rewritten as

$$\begin{aligned} E \lbrace \tilde{\alpha }_j \mid \alpha _i \rbrace = \mu + \lambda \alpha _i \end{aligned}$$

Proof of Proposition 1

Assume that all bidders but i follow some—and the same—linear strategy, as in (3). The residual supply for bidder i at price p is

$$\begin{aligned} S_{-i}(p) = Q- \sum _{j \ne i} \tau ( \alpha _j) + (I-1)\delta p \end{aligned}$$

(18)

where $\sum _{j \ne i} \tau ( \alpha _j)$ depends on the types of all bidders but the i. For an arbitrary stop-out price p, bidder i’s realized cost is $C(S_{-i}(p),\alpha _i )$. After some algebra from (1), (2) and (18), we have

$$\begin{aligned} E \lbrace C(S_{-i}(p),\alpha _i ) \mid \ \varvec{\gamma }_{-i} \rbrace&= \left( -\alpha _i (I-1)\delta + (Q-\hat{\rho }(\alpha _i))(1+\beta (I-1)\delta ) \right) p\nonumber \\&\quad + \left( \frac{1}{2}\beta (I-1)\delta + 1 \right) (I-1)\delta p^2 + \theta \end{aligned}$$

(19)

where $\theta$ contains terms that do not depend on p and $\hat{\rho }(\alpha _i):=E \lbrace \sum _{j \ne i} \tau ( \alpha _j) \mid \alpha _i \rbrace$. It is

$$\begin{aligned} \theta = \alpha _i+\left( Q-\hat{\rho }(\alpha _i)\right) -\dfrac{\beta }{2}\left( e^*+\left( Q-\hat{\rho }(\alpha _i)\right) ^2\right) \end{aligned}$$

(20)

Under the uniform format, bidder i’s cost depends only on the stop-out price and on the quantity demanded at that price and, given a residual supply, there is a one-to-one mapping between that price and that quantity. Thus, given a residual supply and $\alpha _i$, choosing the stop-out price is equivalent to choosing the quantity demanded at that price. Given $\alpha _i$ and the rivals’ strategy, the stop-out price that minimizes bidder i’s expected cost is

$$\begin{aligned} \min _{p} E \lbrace C(S_{-i}(p),\alpha _i) \mid \varvec{\gamma }_{-i} \rbrace \end{aligned}$$

Denote by $p^{*}(\alpha _i,\varvec{\gamma }_{-i})$ the solution to that problem. From (19), first-order conditions of bidder’s i minimization problem imply that

$$\begin{aligned} p^{*}(\alpha _i,\varvec{\gamma }_{-i}) = \frac{\alpha _i(I-1)\delta -(Q-\hat{\rho }(\alpha _i))(1+\beta (I-1)\delta )}{(2+\beta (I-1)\delta )(I-1)\delta } \end{aligned}$$

(21)

Assuming that all bidders (including i) play $\gamma$ defined in (3), bidder i has no incentives to deviate if and only if, for each $\alpha _i \in \Omega$, the expected stop-out price when all bidders are playing $\gamma$, conditional on $\alpha _i$, is precisely $p^{*}(\alpha _i,\varvec{\gamma }_{-i})$.

On the other hand, if all bidders follow $\gamma$ defined in (3), the stop-out price can be characterized as the solution in p to

$$\begin{aligned} S_{-i}(p) = \tau (\alpha _i)-\delta p \end{aligned}$$

Solving this latter equation in p, denoting the solution by $p_o$, and taking expectations conditional on $\alpha _i$, we get

$$\begin{aligned} E \lbrace p_o \mid \alpha _i, \gamma \rbrace = \frac{1}{\delta I}\left( \hat{\rho }(\alpha _i) + \tau (\alpha _i)-Q\right) \end{aligned}$$

(22)

Thus, $\gamma$ is an equilibrium if and only if $(\tau ,\delta )$ satisfy

$$\begin{aligned} p^{*}(\alpha _i,\varvec{\gamma }_{-i}) = E \lbrace p_o \mid \alpha _i, \gamma \rbrace \qquad \forall \alpha _i \in \Omega \end{aligned}$$

(23)

Using (21) and (22), we can rewrite (23) as

$$\begin{aligned} \alpha _i = \frac{\xi }{I} \times \frac{\tau (\alpha _i)}{\delta } + \left( 1- \frac{\xi }{I} \right) \times \frac{1}{I-1}\frac{1}{\delta } \left( (\hat{\rho }(\alpha _i) -Q\right) \end{aligned}$$

(24)

where $\xi := 2 + \beta (I-1)\delta$. Consider the equation $S_{-i}(p)=0$, where $S_{-i}(p)$ is given by (18), and denote its solution by $p_{-i}$. It is

$$\begin{aligned} E \lbrace p_{-i} \mid \gamma , \; \alpha _i \rbrace = \frac{1}{I-1}\frac{1}{\delta } ((\hat{\rho }(\alpha _i) -Q) \end{aligned}$$

which substituted in (24) leads to

$$\begin{aligned} \alpha _i = \frac{\xi }{I} \times \frac{\tau (\alpha _i)}{\delta } + \left( 1- \frac{\xi }{I} \right) \times E \lbrace p_{-i} \mid \gamma , \; \alpha _i \rbrace \end{aligned}$$

This latter equality can be easily rewritten as in the statement in the proposition. $\square$

Proof of Lemma 1

Assuming that all players demand some positive quantity at the stop-out price, the market clearing condition is

$$\begin{aligned} \sum _i \gamma (\alpha _i,p) = Q \iff p = \frac{1}{\delta } \left( \kappa _0 + \kappa _1 \frac{1}{I}\sum _i \alpha _i - \frac{Q}{I} \right) \end{aligned}$$

where the last equality characterizes the auction’s stop-out price. Recall that the support of $\tilde{\alpha }_i$ is $[\underline{\alpha },\overline{\alpha }]$. The auction’s stop-out price is positive with probability 1 if and only if¹⁷

$$\begin{aligned} \kappa _0 + \kappa _1 \underline{\alpha } - \frac{Q}{I} > 0 \end{aligned}$$

(25)

The quantity demanded by bidder i at the stop-out price is

$$\begin{aligned} \begin{aligned} \gamma _i(\alpha _i,p)&= \kappa _0 + \kappa _1 \alpha _i - \left( \kappa _0 + \kappa _1 \frac{1}{I}\sum _i \alpha _i - \frac{Q}{I} \right) \\&= \kappa _1 \left( \alpha _i - \frac{1}{I}\sum _i \alpha _i \right) + \frac{Q}{I}\\&= \frac{I-1}{I} \kappa _1 \left( \alpha _i - \frac{1}{I-1}\sum _{j \ne i} \alpha _j \right) + \frac{Q}{I} \end{aligned} \end{aligned}$$

Thus

$$\begin{aligned} \gamma _i> 0 \iff (I-1)\kappa _1 \left( \alpha _i - \frac{1}{I-1}\sum _{j \ne i} \alpha _j \right) + Q > 0 \end{aligned}$$

The latter equality holds with probability 1 iff

$$\begin{aligned} (I-1)\kappa _1 (\underline{\alpha }-\overline{\alpha }) + Q > 0 \end{aligned}$$

(26)

Combining (25) and (26) we obtain (6).

Next, we give conditions for a nonnegative marginal abatement cost. It is

$$\begin{aligned} \phi (e;\alpha _i) \ge 0 \iff \alpha _i - \beta (\kappa _0+\kappa _1 \alpha _i - \delta p) \ge 0 \end{aligned}$$

Substituting p from the market clearing condition for interior solution and collecting terms in $\alpha$’s, the latter inequality becomes

$$\begin{aligned} \left( 1 - \beta \kappa _1 \left( 1 - \frac{1}{I} \right) \right) \alpha _i + \beta \kappa _1 \frac{1}{I} \sum _{j \ne i} \alpha _j \ge \frac{\beta Q}{I} \end{aligned}$$

The most adverse case on the second term on the left is $\alpha _j=\underline{\alpha }$ for all $j \ne i$, so that the inequality becomes

$$\begin{aligned} \left( 1 - \beta \kappa _1 \left( 1 - \frac{1}{I} \right) \right) \alpha _i + \beta \kappa _1 \frac{I-1}{I}\underline{\alpha } \ge \frac{\beta Q}{I} \end{aligned}$$

(27)

The coefficient of $\alpha _i$ in (27) is nonnegative if and only if

$$\begin{aligned} \beta \kappa _1 \le \frac{I}{I-1} \end{aligned}$$

(28)

Thus, if (28) holds, the most adverse case of $\alpha _i$ for inequality (27) is $\alpha _i = \underline{\alpha }$. Substituting this value of $\alpha _i$, the inequality (27) becomes

$$\begin{aligned} \underline{\alpha } \ge \frac{\beta Q}{I} \end{aligned}$$

On the other hand, if the inequality in (28) does not hold, the most adverse case of $\alpha _i$ for inequality (27) is $\alpha _i = \overline{\alpha }$. Substituting this value of $\alpha _i$, the inequality (27) becomes

$$\begin{aligned} \overline{\alpha }-\beta \kappa _1 \frac{I-1}{I}\left( \overline{\alpha }-\underline{\alpha }\right) \ge \frac{\beta Q}{I} \end{aligned}$$

Inequality (7) summarizes these latter two inequalities. $\square$

Proof of Proposition 2

Assume that $\tau$ is linear, i.e., we restrict to equilibria in which $\gamma$ is linear in both arguments, $\alpha _i$ and p:

$$\begin{aligned} \tau (\alpha ) = \kappa _0 + \kappa _1 \alpha \end{aligned}$$

(29)

Using (29), (8) and (17), we can write

$$\begin{aligned} \hat{\rho }(\alpha _i) = (I-1)(\kappa _0+\kappa _1\mu ) + (I-1)\kappa _1 \lambda \alpha _i \end{aligned}$$

In turn, with the above expression for $\hat{\rho }(\alpha _i)$, both sides of (23) are linear on $\alpha _i$. Specifically, substituting in (21) we have

$$\begin{aligned} \begin{aligned} p^{*}(\alpha _i,\varvec{\gamma }_{-i})&= \frac{1}{2+\beta (I-1)\delta } \left( 1 + (1+\beta (I-1)\delta )\frac{\lambda \kappa _1}{\delta } \right) \alpha _i\\&\quad + \frac{1+\beta (I-1)\delta }{(2+\beta (I-1)\delta )(I-1)\delta } \left( (I-1)(\kappa _0+\kappa _1\mu )- Q\right) \end{aligned} \end{aligned}$$

and from (22)

$$\begin{aligned} E \lbrace p_o \mid \alpha _i, \gamma \rbrace = \frac{1}{I\delta } (\lambda (I-1)+1)\kappa _1\alpha _i + \frac{1}{I\delta }((I-1)(\kappa _0+\kappa _1\mu )+\kappa _0 - Q) \end{aligned}$$

Using these expressions, from (23), the coefficients of $\alpha _i$ and the intercept on both expressions have to be equal. Equalizing the coefficients of $\alpha _i$ we obtain the following equation

$$\begin{aligned} \frac{1}{\beta (I-1)} - \left( \frac{2}{\beta (I-1)} + \lambda \kappa _1 \right) \frac{1}{\xi } = \frac{1}{I}(1-\lambda )\kappa _1 \end{aligned}$$

(30)

where $\xi := 2 + \beta (I-1) \delta$, as in the proof of Proposition 1. Notice that there is a one-to-one mapping between $\xi$ (or $\xi ^{-1}$) and $\delta$. Equalizing the intercepts (the terms that do not depend on $\alpha _i$), we obtain the following equation

$$\begin{aligned} \left( \frac{1}{I-1}Q -(\kappa _0+\kappa _1 \mu ) \right) \frac{1}{\xi } + \frac{1}{I}\kappa _1 \mu = \frac{1}{I(I-1)}Q \end{aligned}$$

(31)

Equations (30) and (31) characterize the equilibrium parameters for any linear strategy $\gamma$. The unknowns are $\kappa _0$, $\kappa _1$ and $\xi ^{-1}$. From (30), we have that

$$\begin{aligned} \frac{1}{\xi } = m(\kappa _1) \end{aligned}$$

(32)

where we have denoted

$$\begin{aligned} m(\kappa _1) := \frac{I-\beta (I-1)(1-\lambda )\kappa _1}{2I+\beta (I-1)I\lambda \kappa _1} \end{aligned}$$

(33)

It follows that

$$\begin{aligned} \delta =g_{\delta }\left( \kappa _1 \right) = \left( \frac{1}{m(\kappa _1)}-2 \right) \frac{1}{\beta (I-1)} \end{aligned}$$

(34)

Clearly, m is differentiable. Straightforward computations show that $m'(\kappa _1) <0$ if $\lambda \ge 0$ and $m(0)=\frac{1}{2}$. The properties of $g_{\delta }$ follow from the properties of m.

Substituting (32) into (31) and solving for $\kappa _0$, we get

$$\begin{aligned} \kappa _0 = g_{0}\left( \kappa _1 \right) = \left( 1 - \frac{1}{Im(\kappa _1)}\right) \left( \frac{1}{I-1}Q-\kappa _1\mu \right) \end{aligned}$$

(35)

The right-hand side of Eq. (35) defines $g_{0}$. $\square$

Proof of Proposition 3

Consider the first inequality in (6), substitute the expression for $\kappa _0$ given in (35) and reorder terms to obtain

$$\begin{aligned} \left( 1-\frac{1}{m(\kappa _1)}\right) \frac{1}{I-1}Q + \left( \underline{\alpha } + \mu \left( \frac{1}{Im(\kappa _1)}-1\right) \right) I\kappa _1 \ge 0 \end{aligned}$$

(36)

Step 1. We show that (36) neither holds for $\kappa _1=0$ nor for $\kappa _1 \rightarrow \infty$. If $\kappa _1=0$, using that $m(0)=1/2$, (36) collapses to

$$\begin{aligned} -\frac{1}{I-1} Q \ge 0 \end{aligned}$$

which does not hold. Furthermore, as $\kappa _1 \rightarrow \infty$, we have $m(\kappa _1) \rightarrow -\frac{1-\lambda }{I\lambda }$. For $\lambda \ne 1$, the sign of the left-hand side in (36) as $\kappa _1 \rightarrow \infty$ is given by the coefficient of $\kappa _1$ with $m(\kappa _1)$ at its limiting value:

$$\begin{aligned} \underline{\alpha } - \mu \frac{1}{1-\lambda } = \underline{\alpha } - E \lbrace \tilde{\alpha } \rbrace \end{aligned}$$

(37)

where we have used (17). The expression on the right-hand side of (37) is clearly negative.

Step 2. Consider $\kappa _1^p$, defined by $\beta \kappa _1(I-1)=I$. It is

$$\begin{aligned} m \left( \kappa _1^p \right) = \frac{\lambda }{2 + \lambda I} \end{aligned}$$

For $\kappa _1=\kappa _1^p$, taking limits in (36) as $\lambda \rightarrow 0$ we have

$$\begin{aligned} -\frac{1}{I-1}Q + \mu \kappa _1^p \ge 0 \end{aligned}$$

where $\mu \rightarrow E \lbrace \tilde{\alpha }_i \rbrace$ as $\lambda \rightarrow 0$. Using the expression for $\kappa _1^p$, the latter inequality becomes

$$\begin{aligned} \frac{\beta Q}{I} \le E \lbrace \tilde{\alpha }_i \rbrace \end{aligned}$$

(38)

Now consider the second inequality in (6) for $\kappa _1=\kappa _1^p$. It is

$$\begin{aligned} (I-1)\kappa _1^p (\overline{\alpha }-\underline{\alpha }) \le Q \iff \overline{\alpha }-\underline{\alpha } \le \frac{\beta Q}{I} \end{aligned}$$

(39)

Finally, condition (7) for $\kappa _1=\kappa _1^p$ becomes

$$\begin{aligned} \frac{\beta Q }{I} \le \underline{\alpha } \end{aligned}$$

(40)

which is more restrictive than (38). Combining (39) and (40) we obtain (9). Using a continuity argument, it follows the existence of an interval containing $\kappa _1^p$ and some non-empty interval in $[0,\lambda ^u)$. $\square$

Proof of Lemma 2

• 1. We solve the problem that characterizes the efficient allocation for a given vector of type realizations, say $\varvec{\alpha }=\left( \alpha _1,\dots ,\alpha _I \right)$. We define the Lagrangian

  $$\begin{aligned} \mathcal {L} = \sum _{i=1}^{I} \int _{q_i}^{e^{*}_i(\alpha _i)} \phi (e;\alpha _i)\mathrm{d}e + \theta \left( \sum _{i=1}^{I} q_i- Q \right) \end{aligned}$$

  where nonnegativity constraints are omitted for sake of simplicity and $\theta$ denotes the multiplier. The Kuhn–Tucker conditions are

  $$\begin{aligned} \phi (q_i;\alpha _i)= & {} \theta \qquad i \in \lbrace 1,\dots , I \rbrace \nonumber \\&\qquad \theta \left( \sum _{i=1}^{I} q_i- Q \right) = 0 \qquad \theta \ge 0 \end{aligned}$$

  (41)

  An interior allocation occurs when $\phi (q_i;\alpha _i) >0$ holds, which implies $\theta >0$ and thus

  $$\begin{aligned} \sum _{i=1}^{I} q_i- Q = 0 \end{aligned}$$

  (42)

  Next, we solve in q’s the set of equations given by (41) and (42). These equations conform a system of linear equations which can be solved using standard linear algebra. Alternatively, consider any $i \ne 1$ and use (41) to write

  $$\begin{aligned} q_1 - q_i = \frac{1}{\beta } (\alpha _1-\alpha _i) \end{aligned}$$

  (43)

  Substituting in (42) for any $i \ne 1$ and then solving (42) for $q_1$ we have

  $$\begin{aligned} q_1 = \frac{Q}{I} - \frac{1}{\beta I} \left( \sum _{i \ne 1}\alpha _i - (I-1)\alpha _1 \right) \end{aligned}$$

  Substituting back in (43) and solving for $q_i$ we obtain

  $$\begin{aligned} q_i = \frac{Q}{I} - \frac{1}{\beta I} \left( \sum _{j \ne i}\alpha _j - (I-1)\alpha _i \right) \end{aligned}$$

  (44)

  for any $i \in \lbrace 1,\dots ,I \rbrace$. Using (44), the nonnegativity requirement can be written

  $$\begin{aligned} q_i \ge 0 \iff Q \ge \frac{1}{\beta } \left( \sum _{j \ne i} \alpha _j - (I-1)\alpha _i\right) \end{aligned}$$

  Considering the most adverse realizations, the latter inequality becomes

  $$\begin{aligned} Q \ge \frac{1}{\beta }(I-1) \left( \overline{\alpha } - \underline{\alpha } \right) \end{aligned}$$

  (45)

  Analogously, using (44), the nonnegativity of the marginal abatement cost (equivalently, the condition for $\theta >0$) can be written

  $$\begin{aligned} \phi (q_i;\alpha _i) \ge 0 \iff Q \le \frac{1}{\beta } \sum _i \alpha _i \end{aligned}$$

  Considering the most adverse realizations, the latter inequality becomes

  $$\begin{aligned} Q \le \frac{1}{\beta } I \underline{\alpha } \end{aligned}$$

  (46)

  This part of the Lemma follows trivially from the combination of (45) and (46).

• 2. If the efficient allocation is interior, from (41), for any $i,j \in \lbrace 1,\dots , I \rbrace$, it is

  $$\begin{aligned} \alpha _i - \alpha _j = \beta (q_i-q_j) \end{aligned}$$

  Now assume that q’s in this latter equality come from an equilibrium in the auction in which all bidders play a strategy as in (3) and that leads to an interior allocation, that is, for any $h \in \lbrace 1,\dots , I \rbrace$ it is

  $$\begin{aligned} q_h = \tau (\alpha _h) - \delta p^{*} \end{aligned}$$

  where $p^{*}$ is the stop-out price in the auction. Combining the previous two equalities, we have

  $$\begin{aligned} \frac{1}{\beta } = \frac{\tau (\alpha _i)-\tau (\alpha _j)}{\alpha _i-\alpha _j} \end{aligned}$$

  This latter equality holds for any arbitrary pair of realizations $\alpha _i$ and $\alpha _j$ in $[\underline{\alpha },\overline{\alpha }]$ if and only if it is $\tau (\alpha )= \kappa _0 + \beta ^{-1}\alpha$, where $\kappa _0$ is an arbitrary parameter. $\square$

Proof of Proposition 4

Write the inequalities that characterize interior equilibria for $\lambda = 0$. First, take $\lambda = 0$ in (33) and substitute into (36) to obtain

$$\begin{aligned} \left( 1 - \frac{2}{1-x} \right) \frac{\beta Q}{I} + \left( I \underline{\alpha } + \mu \left( \frac{2}{1-x} - I \right) \right) x \ge 0 \end{aligned}$$

(47)

where we have denoted $x := \beta \frac{I-1}{I}\kappa _1$. From Proposition 2, interior equilibria are indexed by $\kappa _1$, so they are equivalently indexed by x. Recall that this latter inequality is the first inequality in (6). Using the definition of x, the second inequality in (6) becomes:

$$\begin{aligned} \frac{\beta Q}{I} \ge x (\overline{\alpha }-\underline{\alpha }) \end{aligned}$$

(48)

Finally, the condition (7) can be written

$$\begin{aligned} \frac{\beta Q }{I } \le {\left\{ \begin{array}{ll} \underline{\alpha } &{} \text { if }x \le 1 \\ \overline{\alpha }- x\left( \overline{\alpha } - \underline{\alpha } \right) &{} \text { otherwise} \\ \end{array}\right. } \end{aligned}$$

(49)

Thus, for $\lambda =0$, x defines an interior equilibrium if and only if it satisfies (47) to (49).

Rewrite (47) as

$$\begin{aligned} \frac{\beta Q}{I} + I (\underline{\alpha }-\mu )x + \left( \mu x - \frac{\beta Q}{I} \right) \frac{2}{1-x} \ge 0 \end{aligned}$$

(50)

where we must recall that $x := \beta \frac{I-1}{I}\kappa _1$. Notice that for $x = 1$ this latter inequality collapses to

$$\begin{aligned} \mu \ge \frac{\beta Q}{I} \end{aligned}$$

which is implied by (9). In addition, for $x=1$ (48) and (49) collapse to (9). Thus, under (9) there is an interior equilibrium for $x=1$ or, equivalently

$$\begin{aligned} \kappa _1 = \frac{1}{\beta } \frac{I}{I-1} \end{aligned}$$

Now consider $1-x >0$. Write (50) as

$$\begin{aligned} I (\mu - \underline{\alpha })x^2 + \left( 2 \mu - I(\mu - \underline{\alpha }) - \frac{\beta Q}{I} \right) x - \frac{\beta Q}{I} \ge 0 \end{aligned}$$

(51)

Let us denote by h a function of x such that (51) is $h(x) \ge 0$. Clearly, h is quadratic, convex since $\mu - \underline{\alpha } >0$ holds and it satisfies $h(0)<0$ and $h(1)=2\left( \mu - \frac{\beta Q}{I} \right) >0$. Thus, there is a unique value of x in (0, 1), say $x^{*}$, such that (51) holds if and only if $x \in [x^{*},1]$. More concretely, $h(x)=0$ has necessarily two real roots and $x^{*}$ is the largest (and the only positive) root. Notice also that (48) and (49) are implied by (9) for any $x<1$.

If $1-x <0$, then from (50) we obtain $h(x) \le 0$, where h is still the left-hand side of (51). Thus, this latter inequality cannot hold for $x>1$. Therefore, the set of interior equilibria are characterized by $x \in [x^{*},1]$. Denoting $\kappa _1^{*}$ such that $x^{*} = \beta \frac{I-1}{I}\kappa _1^{*}$, the interior equilibria are characterized equivalently by $\kappa _1 \in \left( \kappa _1^{*}, \frac{1}{\beta }\frac{I}{I-1}\right)$.

The sensitivity analysis of $\kappa _1^{*}$ is equivalent to $x^{*}$. Consider first a variation in $\mu$ keeping all other parameters constant. Taking total differential in the latter equality, we have

$$\begin{aligned} \left( 2 + I(x^{*}-1) \right) x^{*} d \mu + \left( 2 \mu + I(\mu - \underline{\alpha })(2x^{*}-1) - \frac{\beta Q}{I} \right) dx^{*} = 0 \end{aligned}$$

(52)

Since $x^{*} <1$ holds, the coefficient of $d\mu$ is negative if I is large enough. To analyze the sign of the coefficient of dx we must notice first that (9) implies $2\mu - \frac{\beta Q}{I} >0$, so a sufficient condition for that coefficient to be positive is $2x^{*}-1 >0$ or, equivalently, $x^{*} > \frac{1}{2}$. It is

$$\begin{aligned} h \left( \frac{1}{2} \right) = \mu - \frac{1}{4} I (\mu - \underline{\alpha }) - \frac{3}{2} \frac{\beta Q }{I} \end{aligned}$$

Thus, $h \left( \frac{1}{2} \right) <0$ holds if I is large enough, which in turn implies that $x^{*} > \frac{1}{2}$. Therefore, for I large enough, the coefficient of $d \mu$ is negative whereas the coefficient of dx is positive, which implies $d \mu$ and $dx^{*}$ must have the same sign.

Let $s:= \mu - \underline{\alpha }$. Consider a variation in s keeping all other parameters (in particular $\mu$) constant. Taking total differential in $h(x^{*})=0$ we have

$$\begin{aligned} Ix^{*}(x^{*}-1)ds + \left( 2 \mu + Is(2x^{*}-1)-\frac{\beta Q}{I} \right) dx^{*} = 0 \end{aligned}$$

The coefficient of ds in the previous expression is negative since $x^{*}<1$, whereas, following an argument as above, the coefficient of $dx^{*}$ is positive if I is large enough. Thus, for I large enough ds and $dx^{*}$ must have the same sign.

Consider a variation in Q keeping all other parameters constant. Taking total differential in $h(x^{*})=0$ we have

$$\begin{aligned} - \frac{1}{I}(x^{*}+1) \beta dQ + \left( 2 \mu - \frac{\beta Q}{I} + I (\mu - \underline{\alpha })(2x^{*}-1) \right) dx^{*} = 0 \end{aligned}$$

Using an analogous reasoning, when I is large enough we obtain that dQ and $dx^{*}$ must have the same sign.

It rests to prove that the efficient equilibrium, $\beta \kappa _1 = 1$, belongs to the set of interior equilibrium for I large enough. Notice that $\beta \kappa _1 = 1$ implies $x = \frac{I-1}{I}$. It conforms an interior equilibrium if and only if it satisfies (47) to (49). Substituting in (47), we have

$$\begin{aligned} \frac{I-1}{2I-1} (\underline{\alpha } + \mu ) \ge \frac{\beta Q}{I} \end{aligned}$$

(53)

whereas substituting in (48) and (49) we have

$$\begin{aligned} \underline{\alpha } \ge \frac{\beta Q}{I} \ge \frac{I-1}{I} (\overline{\alpha }-\underline{\alpha }) \end{aligned}$$

(54)

For any I finite, (54) is implied by (9). In addition, (53) is also implied by (9) if

$$\begin{aligned} \frac{I-1}{2I-1} (\underline{\alpha } + \mu ) \ge \underline{\alpha } \end{aligned}$$

The coefficient of $\underline{\alpha } + \mu$ in this latter inequality is strictly increasing and continuous in I. It converges to $\frac{1}{2}$ as $I \rightarrow \infty$. The inequality clearly holds at the limiting value of that coefficient; thus, it must hold for any I larger than some finite threshold. $\square$

Proof of Proposition 5

• 1. The necessary and sufficient conditions for $\kappa _1$ to constitute an interior equilibrium are (47) to (49), in Proposition 4, where $x=\beta \frac{I-1}{I}\kappa _1$. Taking $\beta \kappa _1=1$, (47) becomes

  $$\begin{aligned} \underline{\alpha } + \mu \ge \left( 1 + \frac{I}{I-1} \right) \frac{\beta Q}{I} \end{aligned}$$

  (55)

  Also (48) and (49) become

  $$\begin{aligned} \overline{\alpha } - \underline{\alpha } \le \frac{\beta Q}{I-1} \le \frac{I}{I-1} \underline{\alpha } \end{aligned}$$

  (56)

  The inequalities (55) and (56) are implied by (10) just noting that $\lambda =0$ implies $\mu = E \lbrace \tilde{\alpha } \rbrace > \underline{\alpha }$. The efficient equilibrium strategy follows from taking $\kappa _1 = \beta ^{-1}$ and $\lambda = 0$ in (32) to (35), in the proof of Proposition 2. To show that the efficient strategy satisfies (11) is left to the part 4 of this proof.

• 2. Take again the characterization of equilibrium as (47) to (49). We write $I \rightarrow \infty$ to represent: $I \rightarrow \infty$ and $Q \rightarrow \infty$ while $\frac{Q}{I}$ remains constant. If $I \rightarrow \infty$ for $\beta \kappa _1 \ne 1$, then (47) converges to

  $$\begin{aligned} \left( \underline{\alpha } - \mu \right) x \ge 0 \end{aligned}$$

  which cannot hold: $\underline{\alpha } - \mu <0$ holds for any non-degenerated distribution of types, while $x>0 \iff \kappa _1>0$ and, from Proposition 2, this latter equality must hold at any equilibrium under which firms submit downward sloping demand functions. In addition, for $\beta \kappa _1 = 1$, the conditions for an interior equilibrium are (55) and (56), which hold in the limiting case $I \rightarrow \infty$ under (10).

• 3. Take $I=2$ and let $\beta \kappa _1$ be arbitrary. Using (32) to (35), in the proof of Proposition 2, we have

  $$\begin{aligned} m(\kappa _1) = \frac{1}{4} (2-\beta \kappa _1); \; \kappa _0 = \frac{\beta \kappa _1}{2 - \beta \kappa _1} \left( \kappa _1 \mu - Q \right) ; \; \delta = \frac{2 \kappa _1}{2 - \beta \kappa _1} \end{aligned}$$

  (57)

  From the latter equality, we have a downward sloping demand if and only if $\beta \kappa _1 \in (0,2)$. The conditions for an interior equilibrium in Lemma 1, for $I=2$, can be written as follows. (6) is

  $$\begin{aligned} \beta \kappa _0+ \beta \kappa _1 \underline{\alpha }> \frac{\beta Q}{2} > \frac{1}{2}\beta \kappa _1 \left( \overline{\alpha }-\underline{\alpha } \right) \end{aligned}$$

  (58)

  In addition, since $\beta \kappa _1 \le 2$, the condition (7) is

  $$\begin{aligned} \frac{\beta Q}{2} \le \underline{\alpha } \end{aligned}$$

  (59)

  The second equality in (58) and (59) is implied by (10). Use the expression for $\kappa _0$ above to write the first inequality in (58) as

  $$\begin{aligned} \beta \kappa _1 \mu + (2-\beta \kappa _1) \underline{\alpha } \ge \left( \frac{2}{\beta \kappa _1} + 1 \right) \frac{\beta Q}{2} \end{aligned}$$

  The left-hand side of the previous inequality is continuous and strictly increasing in $\beta \kappa _1$ as $\mu > \underline{\alpha }$ holds. The right-hand side is continuous and strictly decreasing. Clearly, the inequality fails to hold as $\beta \kappa _1 \rightarrow 0$, whereas it is implied by (10) at $\beta \kappa _1 = 1$. Thus, under (10), there must exist a unique $b^{0} \in (0,1)$ such that for any $\beta \kappa _1 \in (0,2)$ the inequality holds iff $\beta \kappa _1 \in (b^{0},2)$.

• 4. We prove (11) for $I=2$ and $\beta \kappa _1 \in (0,2)$. For any linear strategy, the stop-out price in the auction is defined by the market clearing condition

  $$\begin{aligned} 2 \kappa _0 + \kappa _1 \sum _i \alpha _i -2 \delta p^{*} = Q \end{aligned}$$

  Using the expressions for $\kappa _0$ and $\delta$ in (57), we have

  $$\begin{aligned} p^{*}(\hat{\alpha }) = \frac{1}{\beta \delta } \left( \beta \kappa _0 - \frac{1}{2} \beta Q + \beta \kappa _1 \hat{\alpha } \right) \end{aligned}$$

  (60)

  where $\hat{\alpha }$ denotes the sample mean of types and the notation emphasizes that the stop-out price depends on it. Denoting by $q^{*}_i$ the auction assignment for bidder i, his marginal saving on abatement cost is

  $$\begin{aligned} \phi _i(q^{*}_i, \alpha _i) = \alpha _i - \beta q^{*}_i = \alpha _i - \beta \left( \kappa _0 + \kappa _1 \alpha _i - \delta p^{*}(\hat{\alpha }) \right) \end{aligned}$$

  (61)

  Taking expectations in (61), substituting in (11) and re-arranging terms, (11) is equivalent to

  $$\begin{aligned} (1-\beta \delta ) E \lbrace p^{*}(\hat{\alpha }) \mid \alpha _i \rbrace \le (1 - \beta \kappa _1) \alpha _i - \beta \kappa _0 \end{aligned}$$

  (62)

  Taking expectations in (60) and substituting into (62), we can rewrite (62) as

  $$\begin{aligned} \left( \frac{1}{\beta \delta }-1 \right) \left( \beta \kappa _0 - \frac{1}{2}\beta Q + \frac{1}{2}\beta \kappa _1 \left( \alpha _i + E \lbrace \tilde{\alpha }_i \rbrace \right) \right) \le (1 - \beta \kappa _1) \alpha _i - \beta \kappa _0 \end{aligned}$$

  where we have used that, since bidder i only observes his own type and types are independent, it is

  $$\begin{aligned} E \lbrace \hat{\alpha } \mid \alpha _i \rbrace = \frac{1}{2} \left( \alpha _i + E \lbrace \tilde{\alpha }_i \rbrace \right) \end{aligned}$$

  The latter inequality is equivalent to

  $$\begin{aligned}&\frac{1}{\beta \delta } \beta \kappa _0 -\frac{1}{2} \left( \frac{1}{\beta \delta } -1 \right) \beta Q + \left( \left( \frac{1}{\beta \delta } -1 \right) \frac{1}{2} \beta \kappa _1 - 1 + \beta \kappa _1 \right) \alpha _i \\&\qquad + \frac{1}{2}\left( \frac{1}{\beta \delta } -1 \right) \beta \kappa _1 E \lbrace \tilde{\alpha }_i \rbrace \le 0 \end{aligned}$$

  Using the expression for $\delta$ in this latter inequality yields

  $$\begin{aligned} \frac{2-\beta \kappa _1}{2 \beta \kappa _1} \beta \kappa _0 - \frac{2-3 \beta \kappa _1}{4 \beta \kappa _1} \beta Q - \frac{1}{4}(2-\beta \kappa _1)\alpha _i + \frac{1}{4} \left( 2-3 \beta \kappa _1 \right) E \lbrace \tilde{\alpha }_i \rbrace \le 0 \end{aligned}$$

  Finally, using the expression for $\kappa _0$ in this latter inequality yields

  $$\begin{aligned} - \frac{2 - \beta \kappa _1}{4} \left( \frac{\beta Q}{\beta \kappa _1} + \alpha _i - E \lbrace \tilde{\alpha }_i \rbrace \right) \le 0 \end{aligned}$$

  since $\beta \kappa _1 \in (0,2)$, the latter inequality is equivalent to

  $$\begin{aligned} \beta Q \ge \beta \kappa _1 \left( E \lbrace \tilde{\alpha }_i \rbrace - \alpha _i \right) \end{aligned}$$

  (63)

  But (63) is implied by the first inequality in (10) since $\beta \kappa _1 \le 2$ and $\overline{\alpha } > E \lbrace \tilde{\alpha }_i \rbrace$. Finally, we prove (11) for $I > 2$ and $\beta \kappa _1 = 1$. Notice that in this case (11) can still be written as (62). The efficient strategy satisfies $\beta \kappa _1 =1$. In addition, using the value for $\kappa _0$ and $\delta$ for the efficient strategy, in the part 1 of the proposition, we can rewrite (62) as

  $$\begin{aligned} E \lbrace p^{*} (\hat{\alpha }) \mid \alpha _i \rbrace \ge E \lbrace \tilde{\alpha }_i \rbrace - \frac{I}{I-1} \frac{\beta Q}{I} \end{aligned}$$

  (64)

  To obtain the stop-out price, we consider the market clearing condition

  $$\begin{aligned} \sum _i \gamma (\alpha _i,p) = Q \end{aligned}$$

  Use the expression for $\gamma$ in the part 1 of the proposition, solve for p, to obtain

  $$\begin{aligned} p^{*}(\hat{\alpha }) = \frac{1}{2} \left( E \lbrace \tilde{\alpha }_i \rbrace + \hat{\alpha } \right) - \frac{1}{2} \left( \frac{I}{I-1}+1 \right) \frac{\beta Q}{I} \end{aligned}$$

  where, as before, $\hat{\alpha }$ denotes the sample mean of types. Analogously to the two-bidder case, notice that

  $$\begin{aligned} E \lbrace \hat{\alpha } \mid \alpha _i \rbrace = \frac{I-1}{I} E \lbrace \tilde{\alpha }_i \rbrace + \frac{1}{I} \alpha _i \end{aligned}$$

  Taking conditional expectations on the previous expression for $p^{*}(\hat{\alpha })$, substituting in (64) and re-arranging terms, (64) is equivalent to

  $$\begin{aligned} \frac{\beta Q}{I-1} > E \lbrace \tilde{\alpha }_i \rbrace - \alpha _i \end{aligned}$$

  This latter inequality is clearly implied by the first inequality in (10) just noting that it is

  $$\begin{aligned} E \lbrace \tilde{\alpha }_i \rbrace - \alpha _i \le \overline{\alpha } - \underline{\alpha } \end{aligned}$$

$\square$

Proof of Proposition 6

• 1. We write the inequalities that characterize interior equilibria for $\lambda = 1/2$. Note that $\lambda =1/2$ implies $\mu = \frac{E\lbrace \tilde{\alpha _i}\rbrace }{2}$. First, (33) is

  $$\begin{aligned} m(\kappa _1) = \frac{1-x}{2+Ix} \end{aligned}$$

  where $x := \beta \frac{I-1}{2I}\kappa _1$. From Proposition 2, interior equilibria are indexed by $\kappa _1$, so they are equivalently indexed by x. Substitute the expressions for $m(\kappa _1)$ and $\mu$ into (36) to obtain

  $$\begin{aligned} \left( 1-\frac{2+Ix}{1-x}\right) \frac{\beta Q}{2I} + \left( I\underline{\alpha } + \frac{E \lbrace \tilde{\alpha _i} \rbrace }{2} \left( \frac{ 2+Ix}{1-x}-I\right) \right) x \ge 0 \end{aligned}$$

  (65)

  Recall that this latter inequality is the first inequality in (6). Using the definition of x, the second inequality in (6) becomes:

  $$\begin{aligned} \frac{\beta Q}{I} \ge 2 x (\overline{\alpha }-\underline{\alpha }) \end{aligned}$$

  (66)

  Finally, condition (7) can be written

  $$\begin{aligned} \frac{\beta Q }{I } \le {\left\{ \begin{array}{ll} \underline{\alpha } &{} \text { if }x \le 1/2 \\ \overline{\alpha }- 2x\left( \overline{\alpha } - \underline{\alpha } \right) &{} \text { otherwise} \\ \end{array}\right. } \end{aligned}$$

  (67)

  Thus, for $\lambda =1/2$, x defines an interior equilibrium if and only if it satisfies (65) to (67). Take $\beta \kappa _1 = 1$. Then

  $$\begin{aligned} \frac{2+Ix}{1-x} = \frac{I(I+3)}{I+1} \end{aligned}$$

  Thus, (65) can be written

  $$\begin{aligned} \underline{\alpha } + \frac{1}{2} E \lbrace \tilde{\alpha }_i \rbrace \left( \frac{I+3}{I+1}-1 \right) \ge \left( \frac{I+3}{I+1}- \frac{1}{I} \right) \frac{\beta Q}{I-1} \end{aligned}$$

  or, equivalently,

  $$\begin{aligned} \underline{\alpha } + \frac{1}{I+1} E \lbrace \tilde{\alpha }_i \rbrace \ge \frac{\beta Q}{I} + \frac{2}{I+1} \frac{\beta Q}{I-1} \end{aligned}$$

  Using (10), it suffices to add the first inequality in (14) for this latter inequality to hold. In addition, (66) and (67), for $\beta \kappa _1 = 1$, collapse to

  $$\begin{aligned} \frac{I-1}{I} \left( \overline{\alpha } - \underline{\alpha } \right) \le \frac{\beta Q}{I} \le \underline{\alpha } \end{aligned}$$

  These latter two inequalities are implied by (10). The efficient equilibrium strategy follows from taking $\kappa _1 = \beta ^{-1}$ and $\lambda = \frac{1}{2}$ in (32) to (35), in the proof of Proposition 2. As in the proof of Proposition 5, we can write (11) as (62). For the case $\lambda = \frac{1}{2}$, the efficient equilibrium strategy is presented in the part 1 of this proposition, in particular

  $$\begin{aligned} \kappa _0 = \frac{1}{\beta }\frac{1}{I+1} \left( E \lbrace \tilde{\alpha }_i \rbrace - 2 \frac{I}{I-1} \frac{\beta Q}{I} \right) ; \qquad \kappa _1 = \frac{1}{\beta }: \qquad \delta = \frac{1}{\beta } \frac{I+2}{I+1} \end{aligned}$$

  Substituting in (62) and re-arranging terms, it is

  $$\begin{aligned} E \lbrace p^{*} \left( \hat{\alpha }\right) \mid \alpha _i \rbrace \ge E \lbrace \tilde{\alpha }_i \rbrace -2 \frac{I}{I-1} \frac{\beta Q}{I} \end{aligned}$$

  (68)

  In the other hand, the stop-out price follows from the usual market clearing condition, as in the proof of Proposition 5, leading to

  $$\begin{aligned} p^{*} (\hat{\alpha }) = \frac{1}{\beta \delta } \left( \beta \kappa _0 + \beta \kappa _1 \hat{\alpha } - \frac{\beta Q}{I} \right) \end{aligned}$$

  (69)

  where $\hat{\alpha }$ denotes the sample mean of the types. Under $\lambda = \frac{1}{2}$, it is

  $$\begin{aligned} E \lbrace \hat{\alpha } \mid \alpha _i \rbrace = \frac{I-1}{I} E \lbrace \tilde{\alpha }_j \mid \alpha _i \rbrace + \frac{1}{I} \alpha _i = \frac{I-1}{2I} E \lbrace \tilde{\alpha }_i \rbrace + \frac{I+1}{2I} \alpha _i \end{aligned}$$

  (70)

  where $j \ne i$. Taking the conditional expectation on the stop-out price, using the parameter values of the equilibrium strategy and substituting into (68), we can rewrite it as

  $$\begin{aligned}&\left( \frac{2I}{I-1}{-} \frac{I+1}{I+2} \left( \frac{1}{I+1} \frac{2I}{I-1} + 1 \right) \right) \frac{\beta Q}{I} \ge \left( 1{-} \frac{I+1}{I+2} \left( \frac{1}{I+1}{+}\frac{I-1}{2I} \right) \right) \\&\qquad E \lbrace \tilde{\alpha }_i \rbrace - \frac{I+1}{I+2}\frac{I+1}{2I}\alpha _i \end{aligned}$$

  or, equivalently

  $$\begin{aligned} \frac{\beta Q}{I-1} \ge \frac{1}{2} \left( E \lbrace \tilde{\alpha }_i \rbrace - \alpha _i \right) \end{aligned}$$

  which is implied for all $\alpha _i \in \Omega$ by the first inequality in (10).

• 2. In the remainder of the proof, we write $I \rightarrow \infty$ to represent: $I \rightarrow \infty$ and $Q \rightarrow \infty$ while $\frac{\beta Q}{I}$ remains constant. Taking $I \rightarrow \infty$, $x \rightarrow \frac{\beta \kappa _1}{2}$. Additionally, considering $x\ne 0$, equation (65) converges to

  $$\begin{aligned} \underline{\alpha } + \frac{1}{2}v(x) \ge 0 \end{aligned}$$

  (71)

  where we have denoted

  $$\begin{aligned} v(x) := \frac{1}{1-x} \left( E\lbrace \tilde{\alpha _i}\rbrace \left( 2x-1 \right) - \frac{\beta Q}{I}\right) \end{aligned}$$

  Note that v is unbounded at $x=1$. Under (9), it is

  $$\begin{aligned} E\lbrace \tilde{\alpha _i}\rbrace - \frac{\beta Q}{I}> \underline{\alpha } - \frac{\beta Q}{I} > 0 \end{aligned}$$

  Thus, as $x \rightarrow 1$ from the left and from the right, it is $\lim _{x \rightarrow 1^{-}}v(x)= \infty$ and $\lim _{x \rightarrow 1^{+}}v(x)= -\infty$, respectively. Furthermore

  $$\begin{aligned} v'(x) = \frac{1}{(1-x)^2} \left( E\lbrace \tilde{\alpha _i}\rbrace - \frac{\beta Q}{I}\right) \end{aligned}$$

  which is positive from (9). In turn, (9) is implied by (10). In fact, in the remainder of this part of the proof it will suffice to use (9) instead of (10). Note that $\lim _{x \rightarrow \infty } v(x) = -2 E \lbrace \tilde{\alpha }_i \rbrace$. Using this latter limit in (71) and taking into account that v is strictly increasing, (71) cannot hold for any $x > 1$. Equivalently, there cannot be interior equilibrium for any $\kappa _1$ such that $\beta \kappa _1 >2$ holds as $I \rightarrow \infty$. Note that $v(1/2)= -2 \frac{\beta Q}{I}$. Thus, (71) holds with strict inequality under (9) for $x=1/2$. Taking into account that v is strictly increasing, (71) holds for any $x \in [1/2,1]$. Notice that (66) and (67) are unaffected by taking $I \rightarrow \infty$. For $x=1/2$, (66) and (67) are implied by (9), so that $x=1/2$, or equivalently $\beta \kappa _1=1$, that is, the efficient allocation, constitutes an interior equilibrium. Within $x \in (1/2,1]$, the most restrictive case for (66) and (67) to hold is at $x=1$. For that value of x, (66) and (67) are equivalent to the second and third inequalities in (14). Now consider $x \in \left( 0, \frac{1}{2}\right)$. (66) and (67) are implied by (9). Under (9), (71) holds with strict inequality for $x=1/2$. Since v is continuous and increasing at any $x \le 1/2$, (71) must also hold if and only if $x \in (x^{*},1/2)$, for some $x^{*} \in (0,1/2)$. The relation between $x^{*}$ and $b^1$ follows from $x \rightarrow \frac{\beta \kappa _1}{2}$ as $I \rightarrow \infty$. As in the proof of Proposition 5, we can write (11) as (62). Combining with the expression of the stop-out price, in (69), we can write (11) as

  $$\begin{aligned} \frac{1}{\beta \delta } \beta \kappa _0 + \left( \frac{1}{\beta \delta } -1 \right) \left( \beta \kappa _1 E \lbrace \hat{\alpha } \mid \alpha _i \rbrace - \frac{\beta Q}{I} \right) \le (1-\beta \kappa _1) \alpha _i \end{aligned}$$

  Taking limits as $I \rightarrow \infty$ in (70) and substituting in the later inequality, we can rewrite it as

  $$\begin{aligned} \frac{1}{\beta \delta } \beta \kappa _0 + \left( \frac{1}{\beta \delta } -1 \right) \left( \frac{1}{2} \beta \kappa _1 E \lbrace \tilde{\alpha }_i \rbrace - \frac{\beta Q}{I} \right) \le \left( 1-\beta \kappa _1 - \left( \frac{1}{\beta \delta } -1 \right) \frac{1}{2} \beta \kappa _1 \right) \alpha _i \end{aligned}$$

  (72)

  Next, we use the expressions in (32) to (35), in the proof of Proposition 2. Taking $\lambda = \frac{1}{2}$ and $I \rightarrow \infty$, it is

  $$\begin{aligned} \lim _{I \rightarrow \infty } \frac{I}{\xi } = \lim _{I \rightarrow \infty } I m(\kappa _1) \iff \frac{1}{\beta \delta } = \frac{2-\beta \kappa _1}{\beta \kappa _1}; \end{aligned}$$

  and

  $$\begin{aligned} \lim _{I \rightarrow \infty } \beta \kappa _0 = \left( 1- \frac{\beta \kappa _1}{2-\beta \kappa _1} \right) \left( \frac{\beta Q}{I} - \frac{1}{2} E \lbrace \tilde{\alpha }_i \rbrace \beta \kappa _1 \right) \end{aligned}$$

  Using these limit values into (72), we have $0 \le 0$ for any $\beta \kappa _1 \ne 0$.

$\square$

Proof of Corollary 1

With $\beta \kappa _1 = \frac{3}{2}$, x, as defined in the proof of Proposition (6) is $x = \frac{3(I-1)}{4I}$, so that $m(\kappa _1) = \frac{I+3}{I(3I+5)}$. From the definition of $\xi$ in the proof of Proposition 2, substituting in Eq. (32)

$$\begin{aligned} \delta = \frac{I(3I+5)-2(I+3)}{\beta (I+3)(I-1)} \end{aligned}$$

(73)

that tends to $\frac{3}{\beta }$ as $I \rightarrow \infty$. From (35)

$$\begin{aligned} \kappa _0 = \left( 1-\frac{3I+5}{I+3} \right) \left( \frac{1}{I-1}Q-\frac{3}{2\beta }\frac{E \lbrace \tilde{\alpha }_i \rbrace }{2} \right) \end{aligned}$$

(74)

that tends to $\frac{3}{2\beta }E \lbrace \tilde{\alpha }_i \rbrace$ as $I \rightarrow \infty$. $\square$

Proof of Corollary 2

It follows from the definition of $\xi$ in the proof of the Proposition 2, substitution of the corresponding value of $\lambda$ and $\kappa _1=1/\beta$ in Eqs. (32) to (35), and then taking limits as $I \rightarrow \infty$, $Q \rightarrow \infty$ and $\frac{Q}{I}$ stays constant. $\square$