Population dynamics of tax avoidance with crowding effects

Abstract

There are two ways for taxpayers to avoid paying taxes: legal tax optimization and illegal tax evasion. The government reacts by altering the law, and by conducting audits, respectively. These phenomena are modeled as a strategic interaction between all taxpayers: the more taxpayers optimize, the lower the optimization result as a consequence of the government tightening the tax law. The more taxpayers evade, the higher the risk of detection because of the tax agencies increasing the audit probability. It emerges that, in equilibrium, the population shares of optimizers and evaders are not interdependent; rather, they both increase to the detriment of the share of non-optimizing taxpayers. If the government reacts to changed optimization behavior with too large a delay, an equilibrium tax law cannot be reached. Tax codes should be updated rapidly in order to avoid a permanent change of the tax law, which is costly both for the legislator and the taxpayers facing legal uncertainty.

1 Introduction

In the tax game, the main forces at play are taxpayers’ efforts to avoid paying taxes and the tax authority’s effort to enforce tax compliance. These forces act via two channels: first, the government needs to establish a tax code that regulates the details of liability for taxation and ensures horizontal and vertical equity. To reach this goal, tax codes have to consider many real-world eventualities and grant tax exemptions where appropriate. Such tax shelters are used (and misused) by taxpayers. Also, since tax codes typically are complicated and to some extent inconsistent, taxpayers are able legally to avoid tax payments by searching for “loopholes”. Second, taxpayers can illegally avoid taxes by simply not reporting their income to the tax authority or by reporting nonexistent expenses. The tax authority, in turn, conducts audits in order to detect and punish tax evaders.

This second channel has featured heavily in economic theory, starting with the seminal work of Allingham and Sandmo (1972), who regard tax evasion as a portfolio optimization approach, with the amount of evaded tax being the risky asset. Given that taxpayers feature decreasing absolute risk aversion, increasing the tax rate affects the taxpayers’ reporting decisions in two ways: an income effect by trend reduces the amount of tax evasion (because higher tax payments make taxpayers less wealthy and, thus, more risk-averse), while a substitution effect makes tax evasion more lucrative. Yitzhaki (1974) shows that, if the penalty is levied upon the evaded tax rather than upon the evaded tax base, the substitution effect vanishes, leaving us with the rather counterintuitive result that tax compliance increases with higher tax rates.

Their work was extended to cover the tax authority’s reaction and public goods provision by Cowell and Gordon (1988) who, amongst others, find that tax compliance may increase with increasing tax rates if public goods are over-provided. Reinganum and Wilde (1986) develop a game theoretical tax compliance model that assumes taxpayers with heterogenous income to play against the tax authority. The authors construct a separating equilibrium in which all taxpayers reduce their true income by a certain amount and the tax authority audits taxpayers with a certain probability, which decreases with reported income. As a main result they find that individuals with higher income evade by less.¹Erard and Feinstein (1994) extend the model by introducing a budget constraint for the tax authority and by assuming a certain fraction of taxpayers to be inherently honest. The complexity of the solution increases considerably. In equilibrium, both the taxpayers’ income reports and the audit schedule depend on the taxpayers’ income distribution. Since the model is not analytically solvable, the authors perform simulations. They find that the tax authority’s net tax and penalty revenue rises rather slowly with an increasing share of honest taxpayers. Another string of literature relies on a principal-agent framework to analyze tax compliance issues. Assuming lump-sum taxes and penalties, Reinganum and Wilde (1985) find that random audit schedules where the audit probability is unconditional upon reported income are dominated by an audit policy in which the tax authority (the principal) sets a cutoff level, with lower reports always audited and higher reports never audited. They assume that the tax authority can commit to a certain schedule.²

With regard to the first channel mentioned above – legal tax optimization – the literature is less extensive, however. Mayshar (1991) generalizes the Allingham-Sandmo model by introducing the notion of a “tax technology”, formally, a function which takes as arguments the tax base, the taxpayer’s tax-shielding effort and a vector of tax instruments adopted by the tax authority and gives as output the tax payment. The function is kept general, the tax technology is thus a “black box”, and the tax-shielding effort can be interpreted as any kind of legal or illegal measure the taxpayer might take in order to reduce their tax burden. Taxpayers choose labor effort and tax-shielding effort whereas the tax authority chooses (costly) tax instruments. The model aims at providing a framework capable of giving a cost-benefit analysis of administrative tax instruments. Slemrod (2001) specifies the tax technology by assuming a linear tariff. Tax avoidance is modeled as a reduction of the tax base by a certain amount at costs that depend on the true income and the extent of avoidance. The model’s main focus lies on explaining behavioral responses to taxation, namely, the taxpayer’s choice of labor supply and tax avoidance effort, and the interdependence between both. Cowell (1990) distinguishes between (illegal) tax evasion and (legal) tax sheltering. He argues that taxpayers will either evade or shelter parts of their income: since the tax sheltering function is publicly known, tax sheltering implicitly causes taxpayers to reveal information about their true income to the fiscal authority. It follows that there can be a complete polarization between shelterers and evaders, with the “rich” sheltering and the “poor” evading.³

The models mentioned above focus on individual taxpayer characteristics: the authors investigate how taxpayers choose labor effort, tax avoidance effort, and, in the case of tax evasion, the amount of tax evaded. As with tax evasion, the fiscal authority’s reaction (i. e., audit probability) is based on the taxpayer’s income report. As with tax avoidance, the government may choose certain tax instruments. However, the economic damage of both legal and illegal tax avoidance is heavily determined by the number of taxpayers applying such strategies, and so may be the tax authority’s reaction. Formally, the tax agency’s audit function (concerning tax evasion) and the “tax technology” function (concerning tax avoidance) may take as arguments the number of taxpayers applying either strategy. If so, an individual taxpayer’s benefit from tax optimization or tax evasion is determined by the behavior of their fellow taxpayers rather than by the tax agency’s reaction to an individual tax report: the game is no longer played between an individual taxpayer and the tax agency, but rather between all taxpayers.

This paper presents three main contributions: (1) while previous literature either ignored strategic interaction (e. g., Allingham and Sandmo 1972), or required a very high level of taxpayer rationality (e. g., Reinganum and Wilde 1986) the evolutionary approach adopted here not only captures the effect of an individual’s behavior onto the society, but also allows for assuming myopic taxpayers who simply need to compare their own payoff to another person’s payoff; (2) next, the model allows for both tax avoidance and tax evasion as alternative (mutually exclusive) strategies; (3) finally, the model takes into account the reaction time of the participating institutions.

Below, I will argue that the individual taxpayer’s benefit from tax avoidance or tax evasion declines in the number of taxpayers who avoid or evade taxes, respectively. I will refer to this phenomenon as “crowding effect”.

Concerning tax evasion, this crowding effect can be motivated as follows: tax agencies, while auditing a set of tax reports, should be able to estimate the share of tax evaders based on the detection rate rather easily. It seems reasonable to assume that auditing activities are broadened if it turns out that there are many tax evaders, while auditing is cut down if the taxpayers turn out to be predominantly honest. The relationship is kept general in this paper, however, for lack of empirical evidence on its shape.

As with tax avoidance, there are several potential reasons for a crowding effect. First, the government is unaware of the necessity to close loopholes until they are exploited by a sufficiently large number of taxpayers. Also, if loopholes are used by a small fraction of taxpayers only, closing them is simply not profitable because tax leakages are small compared to the (political) costs of altering the law. However, governments have to intervene if too many taxpayers save on taxes in a way that is legal though not the intention of the legislator. They do so by altering the tax law, or by adding additional legal norms. For example, most tax codes contain thin-capitalization rules which limit the companies’ possibilities of exploiting interest tax shields. Currently, the OECD “base erosion and profit shifting” (BEPS) project aims at prohibiting prominent structures such as the “Double Irish with a Dutch Sandwich”. Moreover, many tax authorities impose general anti-tax-avoidance doctrines, which are not necessarily part of the tax law. They restrict tax avoidance directly by limiting the resulting tax savings.⁴ Examples are the business purpose doctrine or the economic substance doctrine. Basically, such doctrines state that transactions will not be regarded by the tax law if their only purpose is a reduction of the tax liability. The presence of anti-tax-avoidance doctrines and legal norms that prohibit the usage of certain tax avoidance schemes reduces the taxpayers’ profit from engaging in legal tax optimization. However, a tight tax law is also costly. Both the government and the taxpayers suffer bureaucracy costs from a high level of tax complexity. Also, multinational companies might refrain from investing in countries with tight tax laws. Hence, in part, countries could compete over the laxness of the tax law rather than over tax rates. Indeed, countries such as the United States, Spain and Ireland recently weakened or abolished their thin capitalization rules (Haufler and Runkel 2012). This shows that governments basically have incentives to laxen their tax laws, if possible. In other words, if no one would optimize, governments would desire a tax law that is both uncomplicated and allows for generous tax savings. If such a lenient tax law is then heavily exploited by taxpayers, however, governments would need to tighten it again.⁵ Another explanation for a crowding effect could be the government’s aim to reach a certain budget target. For example, consider a government’s budget target of $ 90. Legal tax avoidance / tax optimization is interpreted as taxpayers applying for tax refunds. If ten taxpayers each pay taxes of $ 10, the total tax revenue exceeds the budget by $ 10. The excess amount is divided among the optimizing taxpayers. If only one taxpayer optimizes they receive the whole amount of $ 10. However, if five taxpayers optimize, each get a tax refund of $ 2. Again, for lack of knowledge on the shape of the relation between the number of tax avoiders and the “profit” from tax avoidance, apart from being negative, it is kept general.

I develop the model in two steps: first, taxpayers can choose between regular tax payment and (legal) avoidance, only. In part, this is done for expositional reasons. However, the two-strategy model can also be seen as displaying situations where tax evasion is not a viable strategy (e. g., for large companies that have internal controls in place) or where tax evasion is simply not possible (e. g., in the case of withholding taxes). In a second step, the model is modified to allow for tax evasion as a third possible strategy. The extended model applies to all taxpayer clienteles who are prone to both tax avoidance and tax evasion (e. g., small companies that have a high number of cash transfers).

Strategic interactions where an individual plays against a whole society rather than a limited number of other individuals are referred to as population games (Hofbauer and Sigmund 1998). Then, a Nash equilibrium is given not by a strategy choice of single individuals, but by population shares that each play pure strategies. In the basic model developed in this paper, taxpayers decide between two strategies, “optimization” and “non-optimization”. “Optimization” involves tax planning costs that depend on the amount of pre-tax income. Tax planning then leads to a certain tax refund. The size of the tax refund depends negatively on the share of optimizing taxpayers, as motivated above. There exists only one Nash equilibrium that involves a certain share of taxpayers who optimize while the remainder do not optimize. It turns out that the share of optimizing taxpayers increases with increasing tax rates, decreasing optimization costs and a generally higher optimization result. A dynamic version of the game is implemented by applying a pairwise proportional revision protocol. That is, when receiving an opportunity to update their strategy, a taxpayer meets another taxpayer at random and adopts their strategy with probability proportional to the payoff difference if the latter is positive. The evolution of the whole population’s behavior can then be approximated by the replicator dynamic (Schlag 1998), which was originally developed by Taylor and Jonker (1978) to capture the evolution of species by survival and reproduction of the fittest. Applying the replicator dynamic, it is shown that the Nash equilibrium is the only stable rest point and thus a good prediction for the outcome of the game. Since in reality the legislative process is rather slow, next a delay is introduced to the tax law reaction function, which causes the population share of optimizing and non-optimizing taxpayers to oscillate over time. If the delay is small, the oscillation is dampened and over time the system approaches the Nash equilibrium. If the delay exceeds a certain threshold, however, the population state continues to oscillate. This result is especially interesting because of two points: first, it shows that the structure of the tax law can change “endogenously” without a change in institutional parameters such as the cost of tax complexity or cost of tax optimization. Second, looking only at the Nash equilibrium but neglecting the dynamic adaption process, the very result of an oscillating population state would not be found, giving a fundamentally different prediction for the outcome of the game. In reality, the process of legislative amendments is costly. Moreover, a permanently changing tax law creates legal uncertainty.⁶ One potential policy implication is that the legislative process should be accelerated in order to reach an equilibrium and avoid having to amend the law incessantly.

In the next step, the taxpayers are allowed to choose to evade taxes illegally as a third possible strategy. As explained above, in contrast to other tax evasion models, the audit probability is assumed to depend not on the tax return but on the share of evading taxpayers within a population. Because of that, tax evasion is an all-or-none decision: taxpayers always report an income of zero once they choose the “evasion” strategy. Depending on parameter relations, two possible Nash equilibria can be identified. The first equilibrium requires that all three strategies are played by positive population shares. Then, the population share of optimizers is the same as in the two-strategy case, and the share of evaders increases to the detriment of the share of non-optimizing taxpayers if the penalty rate decreases or if the audit function generally decreases. As to the dynamic case, the Nash equilibrium again is the only stable rest point. If the parameters are chosen such that the payoff from non-optimization is lower than both the payoffs form tax optimization and tax evasion, the “non-optimization” strategy becomes extinct. Then, both increasing the tax rate and the penalty rate causes the share of optimizers to increase to the detriment of the share of tax evaders.⁷ Introducing a delay into the tax law reaction function causes the population state to oscillate over time, as in the two-strategy case. Again, if the delay is below a certain threshold, the Nash equilibrium is reached over time, whereas if the delay is too large, the system keeps oscillating.

The remainder of this paper is structured as follows. In the next section, a basic model with the two strategies, “optimization” and “non-optimization”, is presented; the game’s equilibrium is characterized and a dynamic approach including a delayed government’s reaction is outlined. Section 3 extends the model to allow for (tax) “evasion” as a third strategy. Again, the game is analyzed as a static and dynamic model. The paper closes with a brief summary.

2 Basic model

2.1 Framework with two strategies

Consider a population of risk-neutral taxpayers as defined by the set $P=\{1,\ldots ,N\}$. Every period, each taxpayer plays against the whole population of taxpayers. The set of strategies available to the taxpayers is denoted by $S=\{o,n\}$, where o denotes legal tax optimization and non-optimization is denoted by n. Let $x_{s}$ denote the share of the population that chooses strategy $s\in S$. The population state is given by $X=\{x \in \mathbb {R}_{+}^{2}: {\sum }_{s\in S}x_{s}= 1\}$. The reaction of the government is not considered explicitly. Instead its actions are reflected by the payoff functions, that is, it is assumed that the state of the tax law is a function of the number of agents who try to reduce their tax burden in a legal manner: the more agents optimize, the less can be gained through optimization by an individual taxpayer.

Formally, tax savings as a fraction of the tax rate are denoted by a continuous, strictly decreasing function $o(x_{o})$ with $o(1)= 0$ and $o(0)= 1$.⁸ If all taxpayers optimize (x_o = 1), the tax code takes a state that allows for no more tax savings. By contrast, if no one optimizes (x_o = 0), the first taxpayer to optimize can reduce their tax rate to zero.⁹ The payoff vector field $F:X\rightarrow \mathbb {R}^{2}$ consists of the following continuous payoff functions.

The payoff from tax optimization is given as

$$\begin{array}{@{}rcl@{}} F_{o}(x)=y-\tau(1-o(x_{o}))y-c(y) , \end{array} $$

(1)

where y is a taxpayer’s income before tax, $\tau$ is the tax rate and $c(y)$ denotes the cost of tax optimization as a function of income. It seems reasonable to assume that $c^{\prime }(y)>0$ and $c^{\prime \prime }(y)\leq 0$: it is more expensive to “hide” higher income from the tax authority, the marginal tax planning costs decrease, however, because of economies of scale.¹⁰ This can also be interpreted in the way that taxpayers with higher income are well-educated and thus find it easier to optimize taxes at the margin. Moreover, marginal optimization costs can also be constant with lower costs representing greater knowledge of the tax law, or higher capability. An optimizer can expect to receive the fraction o(x_o) of their tax liability as a tax refund. As described above, the success of their optimization activities depends on the total number of optimizing agents. If a large number of taxpayers reduce their tax liabilities using loopholes in the law, the government will close these loopholes by adopting additional laws, thus complicating the tax code. Optimization activities will then be less successful.

Non-optimization delivers the payoff

$$\begin{array}{@{}rcl@{}} F_{n}=y(1-\tau) , \end{array} $$

(2)

which is certain and does not depend on the actions of other taxpayers. Note that optimizing may be never a beneficial strategy, even if only one taxpayer chooses “optimization” and hence $o(x_{o})\rightarrow 1$. Still, it is possible that $y-c(y)<y(1-\tau )$, i. e., the cost of tax optimization is higher than its benefit. Given the concave cost structure introduced above, this could happen for low values of y. A strategy that is never beneficial will become extinct in equilibrium. Since a trivial solution involving all taxpayers paying their taxes without optimization is of little interest, it is assumed that $c(y)<\tau y$ below; i. e., optimization costs are lower than the tax payment and thus tax optimization can (though need not always) be beneficial.

F is a potential game (Monderer and Shapley 1996) since there exists a potential function $f:X\rightarrow \mathbb {R}$ that satisfies $\nabla f(x)=F(x) \forall x\in X$:

$$\begin{array}{@{}rcl@{}} f(x)=x_{n} y(1-\tau)+x_{o} (y(1-\tau)-c(y)) + \tau y {\int}_{0}^{x_{o}} o(z) \mathrm{d} z . \end{array} $$

Since f is concave,¹¹ all Nash equilibria are maximizers of f (see Sandholm 2010, p. 60).

2.2 Equilibrium

The only Nash equilibrium of the game is given by the population state $\{x_{o}^{\star },x_{n}^{\star }\}$ that satisfies the conditions

$$\begin{array}{@{}rcl@{}} \tau o(x_{o}^{\star})-\frac{c(y)}{y} = &~ 0, \end{array} $$

(3)

$$\begin{array}{@{}rcl@{}} x_{o}^{\star}+x_{n}^{\star}= &~ 1. \end{array} $$

(4)

Equation 3 is intuitive: the beneficial decrease in the tax rate due to optimization activities has to equate the cost of optimization relating to income. Equation 4 ensures that each taxpayer chooses either optimization or non-optimization. Note that, in equilibrium, the payoff of the strategy “optimization” is equal to the outcome of the strategy “non-optimization”, $y(1-\tau )$. Hence, legal tax avoidance is not profitable. This is not surprising but rather a requirement for a Nash equilibrium: if in some population state $x^{\prime }$ one of the strategies is profitable, other taxpayers will adopt this strategy until there is no more excess return; the system converges to state x^⋆.¹²

Proposition 1

In equilibrium, the share of optimizing taxpayers increases with

• a) increasing tax rates,

• b) generally decreasing optimization costs $c_{L}(y)<c(y)\forall y$ ,

• c) generally higher optimization results $o_{H}(x_{o})>o(x_{o})\forall x_{o}\neq 0,1$ , and

• d) higher income iff $\tau o(x_{o}^{\star })>c^{\prime }(y)$ .

Proof

The derivative of the equilibrium share of optimizing taxpayers $x_{o}^{\star }$ with respect to the tax rate

$$\begin{array}{@{}rcl@{}} \frac{\partial x_{o}^{\star}}{\partial \tau}= \frac{o(x_{o}^{\star})}{-\tau o^{\prime}(x_{o}^{\star})} \end{array} $$

is unambiguously positive. This result is driven by the optimization costs that depend on income y only, but do not increase in the tax rate $\tau$. Parts b) and c) of Proposition 1 are immediately evident from Eq. 3. Deriving (3) with respect to income y delivers

$$\begin{array}{@{}rcl@{}} \frac{\partial x_{o}^{\star}}{\partial y}=\frac{c(y) - y c^{\prime}(y)}{-\tau y^{2} o^{\prime}(x_{o}^{\star})} , \end{array} $$

(5)

which is positive as long as the average costs exceed marginal costs: $c(y)/y > c^{\prime }(y)$. Making use of Eq. 3, the condition can be rewritten as $\tau o(x_{o}^{\star })>c^{\prime }(y)$: as long as marginal optimization costs are smaller than the optimization effect, the share of optimizing taxpayers will increase if income increases. If costs are assumed to be linear, the equilibrium share of optimizing taxpayers does not depend on the amount of income. If costs decrease with increasing income (possibly because better-educated individuals with higher income find it easier to shelter income from taxation), increasing income increases the share of optimizers. The same is true if costs are assumed to be constant. □

In equilibrium, the tax code will allow tax savings of

$$\begin{array}{@{}rcl@{}} o(x^{\star}_{o})=\frac{c(y)}{\tau y} \end{array} $$

(6)

generating a total tax revenue of

$$\begin{array}{@{}rcl@{}} T&= & \sum\limits_{i\in P:s=n} \tau y+ \sum\limits_{i\in P:s=o} \tau y(1-o(x_{o}^{\star}))\\ &= & N\left( \tau y-x_{o}^{\star} c(y)\right) , \end{array} $$

(7)

where N is the number of all taxpayers. An optimizing taxpayer’s tax payment is given by $\tau y-c(y)$. The tax authority hence loses exactly the optimization cost $c(y)$ measured by the share of optimizing taxpayers.

2.3 Replicator dynamics

The Nash equilibrium derived in the previous section is a static concept. So far, there is no explanation of how the equilibrium population state is actually reached. The taxpayers’ behavior at the micro-level is modeled using the notion of a revision protocol (Sandholm 2010, p. 121). Hereby, the evolutionary process for a number of N taxpayers is described by a Markov process. It is assumed that individuals receive opportunities to change their strategies at certain points in time. The time lags between the arrivals of revision opportunities are distributed independently according to an exponential distribution with rate $\lambda$. If a revision opportunity arrives, an individual taxpayer switches from strategy i to strategy j with probability $r_{ij}/\lambda$, where $r_{ij}$ is called conditional switch rate. In this article, the revision protocol known as proportional imitation will be applied (Schlag 1998), defining the conditional switch rate as $r_{ij}=x_{j}\left [ F_{j}(x)-F_{i}(x) \right ]_{+}$. For the two-strategy game introduced above, the conditional switch rate from non-optimization to optimization is given by $r_{no}=x_{o}\left [ F_{o}(x)-F_{n}\right ]_{+}$. Intuitively, a non-optimizing taxpayer with the opportunity to switch strategies meets another taxpayer at random. With probability $x_{o}$ they will meet an optimizer. If this is the case, the taxpayer will switch strategies only if the (observed) payoff from optimization exceeds the payoff from non-optimization (otherwise, $[\cdot ]_{+}= 0=r_{no}$). Given that, the conditional switch rate is defined to increase in the payoff difference; that is, the more “optimization” outperforms “non-optimization”, the higher the likelihood that the taxpayer switches. This way of modeling the taxpayers’ decision making has the pleasant feature that they need not be informed about properties such as the population state x, the population’s average payoff or other individuals’ payoffs (except the payoff of the one taxpayer met at random). This is especially desirable in view of the fact that tax returns are undisclosed in most countries.

Note that, if no one optimizes, i. e., $x_{o}= 0$, the probability of switching to the optimization strategy is zero for all taxpayers, that is, strategies that are currently not played by a positive population share will not be invented under the proportional imitation protocol.

Given the pairwise proportional imitation revision protocol explained above, the behavior of the Markov process can be approximated as follows: As the revision opportunities are assumed to be distributed according to an exponential distribution with cumulative distribution function $P(\text {``revision opportunity''}\leq t)= 1-e^{-\lambda t}$, the expected number of revision opportunities arriving in the short time interval $[0, \mathrm {d}t]$ is given by $P(\text {``revision opportunity''}\leq \mathrm {d}t)= 1-e^{-\lambda \mathrm {d}t}\approx \lambda \mathrm {d}t$ (by means of a Taylor approximation, see Sandholm (2010, p. 378). Thus, the number of revision opportunities received by non-optimizing agents in this time span is given by $N x_{n} \lambda \mathrm {d}t$, and a number of $N x_{o} \lambda \mathrm {d}t$ optimizers receive revision opportunities. By definition, individuals switch from strategy i to strategy j with probability $r_{ij}/\lambda$. Hence, the number of agents who switch from optimization to non-optimization is given by $\frac {r_{on}}{\lambda } N x_{o} \lambda \mathrm {d}t = Nx_{o} r_{on}\mathrm {d}t$, while $\frac {r_{no}}{\lambda } N x_{n} \lambda \mathrm {d}t = Nx_{n} r_{no} \mathrm {d}t$ agents agents switch from non-optimization to optimization. Consequently, the expected change in the population share (i. e., dividing by N) of non-optimizing agents is given by the difference between the inflow and the outflow, $(x_{o} r_{on}-x_{n} r_{no}) \mathrm {d}t$. Thus, denoting by $\dot {x_{i}}=\frac {d}{d t}x_{i}$ the time derivative, $\dot {x}_{n}= x_{o} r_{on}-x_{n} r_{no}$. Applying the pairwise imitation protocol, one obtains

$$\begin{array}{@{}rcl@{}} \dot{x}_{n}&=&x_{o} x_{n}[F_{n}-F_{o}(x)]_{+}-x_{n} x_{o}[F_{o}(x)-F_{n}]_{+} \\ &=&x_{n} x_{o}\left( [F_{n}-F_{o}(x) ]_{+} - [ F_{o}(x)-F_{n}]_{+} \right) \\ &=& x_{n} x_{o} \left( 1_{\{ F_{n} > F_{o}(x) \}}F_{n} - 1_{\{ F_{n} > F_{o}(x) \}} F_{o}(x) -1_{\{ F_{n} < F_{o} (x)\}} F_{o}(x) + 1_{\{ F_{n} < F_{o}(x) \}} F_{n} \right)\\ &=& x_{n} (x_{o} F_{n}- x_{o} F_{o}(x) ), \end{array} $$

which can be rewritten as $\dot {x}_{n}= x_{n} (F_{n}- (x_{n} F_{n} + x_{o} F_{o}(x) ) )$. $\dot {x}_{o}$ is derived similarly.¹³ This gives the dynamic

$$\begin{array}{@{}rcl@{}} \dot{x}_{o} &=& x_{o}\left( F_{o}(x)-x^{T}F(x)\right)\\ \dot{x}_{n} &=& x_{n}\left( F_{n}-x^{T}F(x)\right) , \end{array} $$

(8)

where $x^{T}$ is the transposed vector of the population state. The system (8) is the well-known replicator dynamic. At a macro level, the relative rate of change of a strategy is given by the difference between its own payoff and the mean payoff.

A fixed point is reached when the change over time is zero; hence $\dot {x}_{o}=\dot {x_{n}}= 0$ has to be fulfilled simultaneously. The replicator dynamic (8) features three fixed points

$$\begin{array}{@{}rcl@{}} && \left\{x_{n}= 0,x_{o}= 1\right\},\\ && \left\{x_{n}= 1,x_{o}= 0\right\},\\ &&\left\{x_{n}=x_{n}^{\star},x_{o}=x_{o}^{\star}\right\}. \end{array} $$

The first two are corner solutions in which the whole population either optimizes or doesn’t optimize, respectively. The third fixed point is the Nash equilibrium shown above. It is easily shown that the Nash equilibrium is the only stable fixed point of the system. Starting from $x_{o}= 0,~\dot {x}_{o}= 0$, if a single taxpayer, for whatever reason, starts optimizing, the rate of change $\dot {x}_{o}$ becomes positive since

$$\begin{array}{@{}rcl@{}} \left.\frac{\partial \dot{x}_{o}}{\partial x_{o}}\right|_{x_{o}= 0}=\tau y-c(y)>0 \end{array} $$

is positive by an assumption made earlier in this article. Thus, more taxpayers start optimizing until the Nash equilibrium is reached and one has $x_{o}=x_{o}^{\star },~\dot {x}_{o}= 0$. If the whole population optimizes, that is, $x_{o}= 1,~\dot {x}_{o}= 0$ but one taxpayer decides to pay their taxes regularly, the rate of change $\dot {x}_{o}$ becomes negative since

$$\begin{array}{@{}rcl@{}} \left.\frac{\partial \dot{x}_{o}}{\partial x_{o}}\right|_{x_{o}= 1}=c(y)>0. \end{array} $$

Thus, more taxpayers refrain from optimizing and $x_{o}$ decreases until the Nash equilibrium is reached again. The same kind of reasoning applies for the share of non-optimizing taxpayers since $x_{n}= 1-x_{o}$. Figure 1 illustrates the situation. Over time the system converges to the Nash equilibrium from (almost) all initial population states. Only if all taxpayers optimize (all taxpayers don’t optimize) will the respective alternative strategy never be “invented”. As described above, however, these states are not robust to small perturbations. Figure 2 shows the evolution of the population state for different initial conditions. All illustrations below are plotted choosing the reaction functions and parameters stated in Appendix A.1.

Fig. 1

Rate of change of the “optimization” strategy, $\dot {x}_{o}$, depending on the population share of optimizing taxpayers x_o

Fig. 2

Evolution of the share of optimizing taxpayers x_o over time for initial conditions varying from (almost) zero to (almost) one in steps of 0.125

2.4 Delayed amendments

In the previous section, the sequence of the game could be thought of as follows: first, all taxpayers simultaneously choose their respective strategies. The tax authority then observes the population state and chooses the state of the tax law. Third, taxes are collected and tax refunds are granted according to $o(x_{o})$. It is, however, a strong assumption to demand that tax law be adjusted immediately depending on the number of optimizing taxpayers. It would be more realistic to assume that the tax authority amends the legislation in the subsequent period. In reality, however, amendments can take even longer. This phenomenon is captured by a delay parameter $\delta$, where $\delta$ is a positive real number that is interpreted as the time the tax authority needs to amend the tax code. Suppose that at time $t^{\prime }$ the tax code is in a lax state, and, consequently, there is a high number of taxpayers optimizing. The government realizes that the tax code needs to be tightened. Yet, the new code is not in place until $t^{\prime }+\delta$. Hence, any taxpayer who is optimizing at time $t^{\prime }+\delta$ is confronted with the tax code that was adapted to the number of optimizers at time $t^{\prime }+\delta -\delta = t^{\prime }$. The other way round, from the perspective of any point in time t, a taxpayer deciding to optimize receives a tax refund according to the tax code that was optimal for the taxpayer behavior at time $t-\delta$. Denoting the population state as a function of time, the modified payoff vector field can be written as

$$\begin{array}{@{}rcl@{}} \hat{F}(x(t))=\left( \begin{array}{ll} \hat{F}_{o}(x(t))\\ F_{n} \end{array}\right)=\left( \begin{array}{ll} y-\tau(1-o(x_{o}(t-\delta)))y-c(y)\\ y(1-\tau) \end{array}\right) \end{array} $$

(9)

and the modified replicator dynamic is then given by the system

$$\begin{array}{@{}rcl@{}} \dot{x}_{o}(t) &= & x_{o}(t)\left( \hat{F}_{o}(x(t))-x(t)^{T}\hat{F}(x(t))\right)\\ \dot{x}_{n}(t) &= & x_{n}(t)\left( F_{n}-x(t)^{T}\hat{F}(x(t))\right). \end{array} $$

(10)

Introducing a delay causes the population state to oscillate over time. It can be shown that the system over time converges to the Nash equilibrium if the delay is not too large:

Proposition 2

If the strategy “optimization” is delayed by$\delta$,the system (10) is asymptotically stable for all$0\leq \delta <\overline {\delta }$,where

$$\begin{array}{@{}rcl@{}} \overline{\delta}=\frac{\pi}{2 x_{o}^{\star} (1-x_{o}^{\star}) \tau y (-o^{\prime}(x_{o}^{\star}))}. \end{array} $$

Otherwise, the system doesn’t converge and continues to oscillate.

Proof

See Appendix A.2. □

In an economic context, this means that if it takes too long to amend the tax code to reflect changed taxpayer behavior, an equilibrium tax law and equilibrium population shares of optimizers and non-optimizers cannot be reached. Figure 3 illustrates the population’s evolution for different values of delay. If there is no delay, the share of optimizers approaches the Nash equilibrium and remains there. If the delay is small, the oscillation around the equilibrium is dampened after some time. In both cases, the tax code is not amended any more once the equilibrium is reached. For delay values that are greater than the critical delay $\overline {\delta }$ the population share of optimizers continues to oscillate. Accordingly, the tax code keeps changing, too. In reality, tax codes are updated on a regular basis. In the context of this model, this phenomenon can be explained by real-world governments reacting too slowly to changed taxpayer behavior, implying that a stable equilibrium tax law cannot be reached.¹⁴

3 Extended model with tax evasion

3.1 Framework with three strategies

Taxpayers may also attempt to reduce their tax burden in an illegal manner. The economic difference between (illegal) tax evasion and (legal) tax optimization is that the latter involves paying optimization costs in advance, which can be either costs for engaging a professional tax consultant, opportunity costs for having to cope with the tax code, or a disutility from doing so, or a mixture of all three. By contrast, tax evasion does not require an ex ante payment. The taxpayer just reports less income and thus generates tax savings immediately. Afterwards, they are confronted with a certain probability of being audited and having to pay a penalty fee. Many other analytical models of tax evasion assume that the audit probability is exogenous.¹⁵ or conditional on reported income¹⁶ However, I do not assume that the detection probability depends on the amount evaded / reported by an individual but on the proportion of the population that evades taxes. This assumption is taken in order to fade out the effects of the reported amount in favor of shedding light on the population effects which are of interest in this article. In addition, the tax authority can estimate the population rate of evaders since the latter should be almost identical – but at least highly correlated – with the detection rate. It seems plausible for the tax authority to increase its audit effort when it realizes that tax evasion behavior is starting to spread within society.

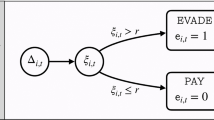
The extended set of strategies is denoted by $\bar S=\{e,o,n\}$, where e denotes the “tax evasion” strategy.¹⁷ The population state is now given by $\bar X=\{x \in \mathbb {R}_{+}^{3}: {\sum }_{s\in S}x_{s}= 1\}$. As with tax optimization, the tax authority’s reaction to tax evasion is reflected by the payoff function. Audit probability is denoted by the function $p(x_{e})$, which strictly increases in the share of evading taxpayers $x_{e}$. Further, it is assumed that $p(1)= 1$ and $p(0)= 0$: if the whole population evades, it is reasonable for the tax authority to always audit. By contrast, if no one evades, it is rational to never audit. Since the audit probability does not depend on the amount that is evaded, a risk-neutral taxpayer will report “all or nothing”. Thus, choosing the evasion-strategy implies that a taxpayer will report an income of zero. An evading taxpayer receives their pre-tax income y if no audit takes place; if audited, they receive their pre-tax income y minus tax payment minus penalty payment. Evading taxes illegally delivers an expected payoff of

$$\begin{array}{@{}rcl@{}} F_{e}(x)=p\left( x_{e}\right) \left( y - \tau y - \theta \tau y \right)+(1-p(x_{e})) y , \end{array} $$

(11)

where $\theta >0$ is the penalty rate. Note that the penalty is imposed on the amount of taxes evaded, $\tau y$, as proposed by Yitzhaki (1974). If the whole population evades, the “tax evasion” strategy is always dominated by non-optimization since $\tau (1+\theta )>\tau$. If no one evades, the “evasion” strategy dominates non-optimization: $y>y(1-\tau )$. The payoff functions of the “optimization” and “non-optimization” strategies are given by Eqs. (1) and (2), respectively, giving the new payoff vector field $\bar F(x) = \left (\begin {array}{ll} F_{e}(x),F_{o}(x),F_{n} \end {array}\right )^{T}$. The potential function of the extended game is given by

$$\begin{array}{@{}rcl@{}} \bar f(x) &=& (x_{e}+x_{o}+x_{n})y - (x_{o}+x_{n})\tau y - x_{o} c(y)+ \tau y {\int}_{0}^{x_{o}} o(z) \mathrm{d}z \\ && - \,y\tau (1+\theta) {\int}_{0}^{x_{e}} p(z) \mathrm{d}z . \end{array} $$

Again, $\bar f(x)$ is concave,¹⁸ implying that all Nash equilibria are maximizers of $\bar f$.

3.2 Equilibrium

3.2.1 Survival of three strategies

Consider first the case where all strategies are played by positive population shares in equilibrium. The only Nash equilibrium is denoted by the population state $\left \{x_{e}^{*},x_{o}^{*},x_{n}^{*}\right \}$ satisfying the conditions

$$\begin{array}{@{}rcl@{}} p(x_{e}^{*})-\frac{1}{1+\theta} = & ~0, \end{array} $$

(12)

$$\begin{array}{@{}rcl@{}} \tau o(x_{o}^{*})-\frac{c(y)}{y} = &~ 0, \end{array} $$

(13)

$$\begin{array}{@{}rcl@{}} x_{e}^{*}+x_{o}^{*}+x_{n}^{*}= & ~1, \end{array} $$

(14)

where Eq. 13 is similar to Eq. 3. The comparative statics with respect to $x_{o}^{*}$ derived from the two strategy game (Proposition 1) are therefore still valid.

Proposition 3

In the three-strategy game, where all strategies are played by positive population shares, the share of tax evaders increases to the detriment of the share of non-optimizers with

• a) a decreasing penalty rate, and

• b) generally lower audit rates $p_{L}(x_{e}) < p(x_{e})\forall x_{e} \neq 0,1$ .

Proof

Deriving (12) with respect to $\theta$ delivers

$$\begin{array}{@{}rcl@{}} \frac{\partial x_{e}^{*}}{\partial \theta}= -\frac{1}{(1 + \theta)^{2} p^{\prime}(x_{e}^{*})}<0. \end{array} $$

Part b) of Proposition 3 can be seen immediately from Eq. 12. The share of optimizers is not affected since $x_{o}^{*}$ depends neither on $\theta$ nor on $p()$, while $x_{n}^{*}= 1-x_{e}^{*}-x_{o}^{*}$. □

Interestingly – in contrast to most other analytical tax compliance models – the share of evading taxpayers does not depend on the tax rate. Instead, the only parameter that affects tax evasion behavior is the penalty rate $\theta$. Increasing the penalty causes taxpayers to switch from tax evasion to non-optimization, ignoring the possibility of legal optimization.

In summary, increasing optimization costs cause the share of optimizers to shrink while the share of non-optimizers increases. By contrast, a higher tax rate causes taxpayers to switch from non-optimization to legal optimization behavior. If income y changes, the shift takes place between the share of non-optimizing and optimizing taxpayers; the direction is, however, not distinct. Increasing y may cause optimization activities to increase to the detriment of non-optimization (part d) of Proposition 1). Still, this would not yet be a theoretical explanation for anecdotical evidence that the “rich” are more involved in legal tax optimization than the “poor”, since in this model all taxpayers are identical. If income rises, then it rises by the same amount for all taxpayers. Instead, the reason for this effect would be the concave optimization cost structure.

In equilibrium, the tax code allows for tax savings according to Eq. (6) and audits will happen with probability

$$\begin{array}{@{}rcl@{}} p(x_{e}^{*})=\frac{1}{1+\theta}. \end{array} $$

The tax authority’s total tax revenue

$$\begin{array}{@{}rcl@{}} \bar T &= &~ \sum\limits_{i\in P:s=n} \tau y + \sum\limits_{i \in P:s=o} \tau y(1-o(x_{o}^{*}))+ \sum\limits_{i\in P:s=e} p(x_{e}^{*})\tau y (1 + \theta)\\ &= & ~N(\tau y - x_{o}^{*}c(y)) \end{array} $$

is identical to Eq. 7 since the share of optimizing taxpayers is not altered by introducing the possibility to evade taxes. Further, the tax authority loses nothing through tax evasion: in equilibrium, tax evasion is not beneficial to taxpayers (again, by definition of the Nash equilibrium) because expected tax savings equate expected penalty payments. This result of course no longer holds if one assumes audits to be costly to the tax authority, or if penalty payments are not part of tax revenue.

3.2.2 Extinction of non-optmization

Depending on the choice of parameters, the “non-optimization” strategy may become extinct over time. This is the case if the payoff of either “evasion” or “optimization” in equilibrium exceeds the payoff of “non-optimization”. The section above demonstrates that an increase in the shares of both evaders (possibly caused by a decrease in the penalty rate) and optimizers (possibly caused by an increase in the tax rate) goes entirely to the detriment of the share of non-optimizing taxpayers. If $x_{n}$ reaches zero, it cannot decrease any further. Hence, if the share of evaders (optimizers) were to increase to a greater degree, then the share of optimizers (evaders) would decrease, respectively. This would cause the payoff of the “optimization” (“evasion”) strategy to increase. In equilibrium, these two payoffs have to balance again, that is, $F_{e}(x)=F_{o}(x)>F_{n}$. This equilibrium is denoted by the population state $\left \{ x^{\dagger }_{e},x^{\dagger }_{o},0 \right \}$ that fulfills the conditions

$$\begin{array}{@{}rcl@{}} \tau y (1+\theta)p(x^{\dagger}_{e})&= &\tau y \left( 1- o(x^{\dagger}_{o})\right) + c(y), \end{array} $$

(15)

$$\begin{array}{@{}rcl@{}} x^{\dagger}_{e}+x^{\dagger}_{o}&= &1. \end{array} $$

(16)

This is the Nash equilibrium if only “evasion” and “optimization” are chosen by positive population shares.¹⁹ The condition for non-optimization to become extinct can be derived from either one of the equivalent conditions

$$\begin{array}{@{}rcl@{}} F_{e}(x^{\dagger}_{e}) &\geq & F_{n} \Longleftrightarrow \theta \leq \frac{1-p(x^{\dagger}_{e})}{p(x^{\dagger}_{e})}, \end{array} $$

(17)

$$\begin{array}{@{}rcl@{}} F_{o}(x^{\dagger}_{o}) &\geq & F_{n} \Longleftrightarrow c(y) \leq \tau y o(x^{\dagger}_{o}). \end{array} $$

(18)

Proposition 4

In the three-strategy game, where only “optimization” and “evasion” are played by positive population shares, the share of optimizers increases with

• a) increasing tax rates,

• b) increasing penalty rates, and,

• c) increasing income iff average costs exceed marginal costs.

Proof

Deriving (15) with respect to $\tau$, making use of the fact that $\partial x^{\dagger }_{e} / \partial \tau + \partial x^{\dagger }_{o} / \partial \tau = 0$, and introducing $o(x_{o}^{\dagger })$ as obtained from Eq. 15 delivers

$$\begin{array}{@{}rcl@{}} -\frac{\partial x^{\dagger}_{e}}{\partial \tau}=\frac{\partial x^{\dagger}_{o}}{\partial \tau}= \frac{c(y)}{\tau^{2} y \left( -o^{\prime}\left( x^{\dagger}_{o}\right)+(1+\theta ) p^{\prime}\left( x^{\dagger}_{e}\right)\right)}, \end{array} $$

which is positive. The derivative with respect to $\theta$,

$$\begin{array}{@{}rcl@{}} -\frac{\partial x^{\dagger}_{e}}{\partial \theta}=\frac{\partial x^{\dagger}_{o}}{\partial \theta}= \frac{p\left( x^{\dagger}_{e}\right)}{-o^{\prime}\left( x^{\dagger}_{o}\right) + (1 + \theta) p^{\prime}\left( x^{\dagger}_{e}\right)}, \end{array} $$

is positive as well. Finally, deriving (15) with respect to y and rearranging gives

$$\begin{array}{@{}rcl@{}} -\frac{\partial x^{\dagger}_{e}}{\partial y}=\frac{\partial x^{\dagger}_{o}}{\partial y}= \frac{c(y)-y c^{\prime}(y)}{\tau y^{2} \left( -o^{\prime}\left( x^{\dagger}_{o}\right)+(1+\theta) p^{\prime}\left( x^{\dagger}_{e}\right)\right)}, \end{array} $$

which is positive if average costs exceed marginal costs, if costs decrease with income, or if costs are constant. □

Increasing the tax rate causes the population share of optimizers to increase. This effect can be explained as follows: since this model employs the penalty structure of Yitzhaki (1974) there is no substitution effect in the “evasion” strategy. As taxpayers are assumed to be risk-neutral, neither is an income effect. Since the optimization cost does not depend on the tax rate, however, optimization becomes more beneficial with increasing tax rates.

It is not possible to give a closed-form solution for both $p(x^{\dagger }_{e})$ and $o(x^{\dagger }_{o})$. Hence, the government’s total tax revenue cannot be stated explicitly either. However, since the taxpayers’ equilibrium payoffs increase, the government’s total tax revenue has to be smaller than above. Formally,

$$\begin{array}{@{}rcl@{}} \bar T &= & \sum\limits_{i \in P:s=o} \tau y(1-o(x^{\dagger}_{o}))+ \sum\limits_{i\in P:s=e} p(x^{\dagger}_{e})\tau y (1 + \theta)\\ &= & n \left( \tau y - x^{\dagger}_{o} c(y) +c(y)-\tau y o\left( x^{\dagger}_{o}\right)\right). \end{array} $$

(19)

Equations 15 and 16 are used. Comparing (19) with (7) one finds that the former is smaller than the latter if

$$\begin{array}{@{}rcl@{}} c(y)\left( 1-x^{\dagger}_{o}+x_{o}^{*}\right)<\tau y o\left( x^{\dagger}_{o}\right). \end{array} $$

Comparing (15) and (13) one ascertains that $o\left (x^{\dagger }_{o}\right )<o\left (x_{o}^{*}\right )$ if Eq. 17 holds strictly, hence $x^{\dagger }_{o}>x_{o}^{*}$. Thus, $(1-x^{\dagger }_{o}+x_{o}^{*})<1$. If Condition (18) holds strictly, then the inequality is fulfilled, that is, tax revenue decreases if the “non-optimization” strategy is not played.

3.3 Replicator dynamics with three strategies

The model of individual taxpayer’s behavior described in Section 2.3 is applied to the three strategy-case: upon receiving an opportunity to update their strategy, a taxpayer meets another taxpayer at random and compares payoffs. As with tax evasion, however, recall that Eq. 11 is an expected payoff. At the micro-level, in contrast, there are two distinct types of tax evaders: those who were audited, incurred a punishment and thus “lost”, receiving a payoff of ${F_{e}^{L}}=y(1-\tau (1+\theta ))$, and those who “won”, receiving ${F_{e}^{W}}=y$. Applying the proportional imitation protocol having regard to these additional instances, weighting each with the probabilities $p(x_{e})$ and $(1-p(x_{e}))$, respectively, the new replicator dynamic with three strategies is given by the system

$$\begin{array}{@{}rcl@{}} \dot{x}_{e} &=& x_{e}\left( F_{e}(x)-x^{T}\bar F(x)\right)\\ \dot{x}_{o} &=& x_{o}\left( F_{o}(x)-x^{T}\bar F(x)\right)\\ \dot{x}_{n} &=& x_{n}\left( F_{n}-x^{T}\bar F(x)\right) , \end{array} $$

(20)

which has seven fixed points.²⁰ Three of them,

$$\begin{array}{@{}rcl@{}} && \left\{x_{e}= 1,x_{o}= 0,x_{n}= 0\right\},\\ && \left\{x_{e}= 0,x_{o}= 1,x_{n}= 0\right\},\\ && \left\{x_{e}= 0,x_{o}= 0,x_{n}= 1\right\}, \end{array} $$

are corner solutions in which the whole population either evades, optimizes or non-optimizes, respectively. It turns out that all corner solutions are unstable source nodes. Both alternative strategies deliver excess return; thus, the population shares of taxpayers playing these strategies would increase to their equilibrium values $x_{e}^{*}$ and $x_{o}^{*}$ once some taxpayers started to play these strategies. Then there is one fixed point,

$$\begin{array}{@{}rcl@{}} \left\{x_{e}= 0,x_{o}= x_{o}^{*},x_{n}= 1-x_{o}^{*}\right\}, \end{array} $$

in which the population share $x_{o}^{*}$ optimizes and the rest of the population non-optimizes with no one evading. This is the Nash equilibrium of the two-strategy game elaborated on in Section 2. In the three-strategy model, it is an unstable saddle point: excess return could be generated by evading taxes. Thus, $x_{e}$ would reach $x_{e}^{*}$ once a single taxpayer started tax evasion. Another fixed point,

$$\begin{array}{@{}rcl@{}} \left\{x_{e}= x_{e}^{*},x_{o}= 0,x_{n}= 1-x_{e}^{*}\right\}, \end{array} $$

is given for a population share of $x_{e}^{*}$ evading taxes and the rest non-optimizing with no one optimizing. This would be the Nash equilibrium of a two-strategy model without the possibility to “optimize”, but the strategies “evasion” and “non-optimization” only. This fixed point is also an unstable saddle point in the three-strategy model because optimizing delivers excess return. If no one non-optimizes, the fixed point

$$\begin{array}{@{}rcl@{}} \left\{ x_{e}=x^{\dagger}_{e},x_{o}=x^{\dagger}_{o},x_{n}= 0 \right\} \end{array} $$

can be reached. This fixed point is stable if Conditions (17) and (18) hold, that is, if the parameters are such that the “non-optimization” strategy in equilibrium delivers a payoff that is worse than “evasion” and “optimization”, and thus “non-optimization” becomes extinct. Otherwise, the fixed point is an unstable saddle point because “non-optimization” delivers excess return. Finally, the Nash equilibrium

$$\begin{array}{@{}rcl@{}} \left\{x_{e}= x_{e}^{*},x_{o}= x_{o}^{*},x_{n}= 1-x_{o}^{*}-x_{e}^{*}\right\} \end{array} $$

elaborated on above is a stable fixed point of the system (20). See Appendix A.3.1 for a detailed stability analysis of all fixed points. Figure 4 shows the flow pattern in the three-strategy space. At the corners of the simplex, the whole population either evades, optimizes or non-optimizes, respectively. The respective corner solutions (A, E, C) are source nodes: all arrows point away from the corners. All population states on the edges require the strategy of the opposite corner to be non-existent within the population. In this example, the Nash equilibrium requires all three strategies to be played by positive population shares. Thus, all rest points on the edges (B, D, F) are saddle points. The arrows point from the corners towards those rest points; however, they are unstable. If the third strategy is played by a single individual, the population state moves towards the Nash equilibrium indicated by a black circle in the bottom-left corner of the simplex (G), which involves all strategies to be played by a fraction of all individuals.

Fig. 4

Flow pattern for the three-strategy game. Red (blue) colors indicate fast (slow) movement. White circles indicate the unstable rest points; the black circle shows the stable rest point. The figure was created using the Mathematica application “Dynamo” by Sandholm et al. (2012)

While the saddle point (B) on the right-hand edge of Fig. 4 – where no one optimizes – is not stable if the “optimization” strategy is available, it would be stable if such an alternative did not exist. The “optimization” strategy can also be interpreted in a more specific way as a particular (legal) tax avoidance model rather than general tax planning. A popular example of such a model is the Double Irish arrangement. The former tax law reaction function $o(x_{o})$ could then be interpreted as the probability of such a model being accepted by the tax authority. The assumption that $o(x_{o})$ is strictly decreasing would still be reasonable: the more prominent such a model becomes, the higher the probability that it will be rejected by the tax authority or a fiscal court. $F_{o}$ would then be the expected value of the (uncertain) income after tax. The model can then capture the behavior of the population if a specific tax savings model is invented by a single taxpayer at time $t^{\star }$. Figure 5 (top) illustrates the behavior of the system over time for a population of 4 000 taxpayers. Starting from an (arbitrarily chosen) initial population state of $1/2$ evaders and $1/2$ non-optimizing taxpayers, the system approaches the rest point with $x_{e}^{*}$ evaders and $1-x_{e}^{*}$ non-optimizing individuals and remains there. At time $t^{\star }$ one formerly non-optimizing taxpayer develops a particular tax optimization model. Since the initial population share of optimizers is only $1/4\,000$, some time elapses until the strategy starts to spread to other parts of the population. Then, $x_{o}$ increases quickly and the population state approaches the Nash equilibrium of the three-strategy game. The equilibrium population share of evaders is the same in both the two-strategy (evasion and non-optimization only) and the three-strategy game. There is just a small dent in $x_{e}$ shortly after the invention of the optimization model during the adjustment process towards the new equilibrium. The equilibrium share of optimizers goes entirely to the detriment of the share of non-optimizing taxpayers. Figure 5 (bottom-left) shows a situation where the system is out of equilibrium at the time of the invention of the optimization strategy, $t^{\star }$, with $0.01-1/4\,000$ evading, 0.99 non-optimizing (bottom-right: vice versa), and $1/4\,000$ optimizing. The situation with an initially very high share of tax evaders (bottom-right) shows that the evolution can be surprising: the invention of the optimization strategy causes the share tax evaders to drop and the share of non-optimizers to rise very fast, initially; shortly after the invention of “optimization”, an observer could suspect that this (also) promotes non-optimizing behavior (which might be preferable from the viewpoint of the government). Yet, after some time, the share of non-optimizers declines as taxpayers “learn” to optimize.

Fig. 5

Evolution of the population state over time for 4 000 individuals. Top: the initial population state is $\frac {1}{2}$ evaders and $\frac {1}{2}$ non-optimizing taxpayers. At time t^⋆ the optimization strategy is invented by one formerly non-optimizing taxpayer. Bottom-left: the population initially consists of 39 evaders, 3 960 non-optimizers, and 1 optimizer. Bottom-right: the population initially consists of 3 960 evaders, 39 non-optimizers, and 1 optimizer

3.4 Delayed amendments and tax evasion

In Section 2.4 it was argued that the tax authority may not be able to amend the tax code immediately. Thus, a delay $\delta$ is introduced to the “optimization” strategy in the extended model, too. Of course, the tax authority may not be able to adjust the audit rate immediately as well, since the population share of evaders is not known before actually having audited the population. On the other hand, adjusting the audit rate seems to be far easier than amending the code. If the tax authority, while auditing, realizes that a lot of tax reports are incorrect, it could immediately decide to broaden its audit activities, possibly following a Bayesian updating inference. Therefore, in this section it is assumed that the audit rate can be adjusted instantly, whereas the tax code is adjusted with delay.²¹ This gives the new payoff vector field $\bar F_{\delta }=\left (\begin {array}{ll} F_{e}(x),\hat {F}_{o}(x),F_{n} \end {array}\right )^{T}$ where $\hat {F}_{o}(x)$ includes the delay $\delta$ as stated in Eq. 9. The replicator dynamic including delay is given by the system

$$\begin{array}{@{}rcl@{}} \dot{x}_{e} & =& x_{e}\left( F_{e}-x^{T}\bar F_{\delta}(x)\right)\\ \dot{x}_{o} & =& x_{o}\left( \hat{F}_{o}-x^{T}\bar F_{\delta}(x)\right)\\ \dot{x}_{n} & =& x_{n}\left( F_{n}-x^{T}\bar F_{\delta}(x)\right). \end{array} $$

(21)

Again, introducing a delay to the “optimization” strategy causes the population state to oscillate over time. The analysis is carried out for the case that in equilibrium all three strategies are played by positive population shares, i. e., it is assumed that the Conditions (17) and (18) do not hold.

Proposition 5

If the strategy “optimization” is delayed by$\delta$,the system (21) is asymptotically stable for all$0\leq \delta <\hat {\delta }$,

$$\begin{array}{@{}rcl@{}} \hat{\delta}= \frac{1 }{\omega_{+}} \text{arccot} \left( \frac{\omega_{+} (d-a l)}{a d+l \omega_{+}^{2}} \right), \end{array} $$

where

$$\begin{array}{@{}rcl@{}} a &=& \left( 1-x_{e}^{*} \right) x_{e}^{*} \tau (1 + \theta) y p^{\prime}\left( x_{e}^{*}\right)>0,\\ l &=& \left( 1-x_{o}^{*}\right) x_{o}^{*} \tau y \left( - o^{\prime}\left( x_{o}^{*}\right) \right) >0,\\ d &= & x_{e}^{*} x_{o}^{*} \left( 1-x_{e}^{*} - x_{o}^{*}\right) (1+ \theta) \tau^{2} y^{2} \left( -o^{\prime}\left( x_{o}^{*}\right)\right) p^{\prime}\left( x_{e}^{*}\right)>0,\\ \omega_{+} &= & \left( \frac{1}{2}\left( (l^{2}-a^{2}) + \sqrt{ (l^{2}-a^{2})^{2} + 4d^{2} }\right) \right)^{1/2}>0. \end{array} $$

For higher delay values$\delta >\hat {\delta }$thesystem becomes unstable and stability cannot be regained with increasing delayfurther.

Proof

See Appendix A.3.2. □

Figure 6 shows the evolution of the population state for different values of delay. While the main shift takes place between optimizers and non-optimizers, the adaption process causes the share of evaders to oscillate, as well. Whereas the state of the tax law is hard to measure empirically, the fraction of tax evaders is easy to assess. Thus, it is an empirically testable hypothesis whether tax evasion rates oscillate over time. In the sense of this model, such a finding could be an indication that (hard-to-observe) optimization activities and the (almost unobservable) state of the tax law also change over time.

Fig. 6

Evolution of the population state x(t) for different values of delay

4 Conclusion

This article aims to contribute to the scarce theoretical literature on the strategic interdependency between taxpayers and tax authority relating to legal tax avoidance. It is assumed that taxpayers can legally avoid taxes by searching for appropriate legal norms in the tax code, which is associated with optimization costs. The tax authority reacts by closing certain loopholes if they are exploited by too many taxpayers. It emerges that the share of optimizing taxpayers increases if the tax rate increases, optimization costs decrease and tax law gets less tight. If the legislation reacts to changed taxpayer behavior with a delay, the population shares of optimizers and the tax law oscillate over time. It is shown that the tax law can change endogenously by explicitly modeling the adaption process towards equilibrium. If the delay is not too large, the oscillation is dampened over time. Otherwise, however, the population state keeps oscillating and the Nash equilibrium cannot be reached. As a policy implication, it is recommended to accelerate the legislation process in order to avoid costly repeated amendments to the tax code.

Then, tax evasion is introduced as a third strategy. Depending on parameter values, there exist two Nash equilibria. The first equilibrium consists of all three strategies being played by positive population shares. It turns out that the population shares of optimizers and evaders are not interdependent; instead, an increase in both groups goes fully to the detriment of the share of non-optimizing taxpayers. A second equilibrium is reached if the payoff to non-optimization is worse than the payoffs of both optimization and evasion; then, no one applies the “non-optimization”-strategy. The share of optimizers increases to the detriment of the share of evaders if the tax rate or the penalty rate increase. Introducing a delay again causes the population shares and the tax law to oscillate over time. The oscillation is not dampened if the delay exceeds a certain threshold. This confirms the policy implication found above.

Of course, there are several limitations to the model. First, if the crowding effect in the “optimization”-strategy is interpreted as tax complexity, the fact is neglected that increasing tax complexity also affects the payoffs of non-optimizing taxpayers and of audited evading taxpayers since they need to spend more resources on coping with a complex tax code. This holds no longer, however, if the reduction in tax savings after an increase in the share of optimizers is interpreted as anti-tax avoidance doctrines or legal norms that reduce the profitability of certain tax shelters but do not bother individuals who pay their taxes regularly. The assumption that the tax law reaction function is continuous is also a simplified one. A more realistic tax law reaction function would be likely to jump if the number of optimizers exceeds a certain threshold. Future research could implement a discontinuous tax law reaction function. Then, the assumptions that tax savings possibilities decrease if more taxpayers optimize and that audit probability increases if more taxpayers evade taxes are not empirically tested. However, neither is it certain that the crucial assumption of some other tax compliance models is valid, namely, that audit probability depends on the amount of reported income. Both assumptions taken in this model seem plausible; whether or not they are true is ultimately an empirical question.

The main results of this paper could also be empirically tested: increasing the tax rate ought to leave the extent of tax evasion unaffected; instead, optimization activities – which could be measured by offsets of tax consultancy costs – ought to increase. While the state of the tax law is hard to measure, amendments to the tax code are easy to observe. It can also be empirically tested if audit rates vary over time, which could be an indirect indication of a changing tax law.

Future research should allow taxpayers to be heterogenous with respect to their income and possibly other individual characteristics, such as risk aversion. Also, a social disutility from behaving “immorally” could be integrated. Finally, it would be desirable to drop the mean field assumption and instead to incorporate a social network model.

Appendix

1.1 A Exemplary reaction functions and parameters

The reaction functions and parameters used for illustration purposes in this article are chosen according to Table 1.

Table 1 Reaction functions and parameters used in the illustrations

1.2 B.1 Stability of the replicator dynamic with two strategies and delay

Since $x_{n}= 1-x_{o}$, it suffices to study the stability of $\dot {x}_{o}$. Let $z(t)=x_{o}(t)-x_{o}^{\star }$. The linear variational system of (10) is then

$$\begin{array}{@{}rcl@{}} z^{\prime}(t) + x_{o}^{\star} (1-x_{o}^{\star}) \tau y (-o^{\prime}(x_{o}^{\star})) z(t-\delta )= 0. \end{array} $$

(22)

The fixed point $\{x_{n}=x_{n}^{\star },x_{o}=x_{o}^{\star }\}$ is asymptotically stable for the system (10) if the trivial solution of Eq. 22 is asymptotically stable (Bellman and Cooke 1963, p. 336). As shown by Freedman and Kuang (1991, p. 195), (22) is stable if $\delta <\overline {\delta }$, where

$$\begin{array}{@{}rcl@{}} \overline{\delta}=\frac{\pi}{2 x_{o}^{\star} (1-x_{o}^{\star}) \tau y (-o^{\prime}(x_{o}^{\star}))}. \end{array} $$

1.3 B.2 Replicator dynamic with three strategies

1.3.1 B.2.1 Stability without delay

To evaluate the stability of the fixed points of the system (20), it suffices to study the system of two equations, $\dot {x}_{e}$ and $\dot {x}_{o}$ only, where x_n = 1 − x_e − x_o. Since $\dot {x}_{n}=\dot {x}_{e}-\dot {x}_{o}$ it must be that $\dot {x}_{n}$ is stable whenever $\dot {x}_{e}$ and $\dot {x}_{o}$ are stable. The eigenvalues of the Jacobian $J(x_{e},x_{o})$ of the system are examined at the respective fixed points (Bellman and Cooke 1963, p. 338).

The first fixed point requires all taxpayers to evade. The eigenvalues of $J(1,0)$ are given by $\{\theta \tau y,(1+ \theta ) \tau y-c(y)\}$. Since $\tau y>c(y)$ by assumption, all eigenvalues are positive; the first fixed point is an unstable source node.

The second fixed point is reached if all taxpayers optimize. It is also a source node since the eigenvalues of $J(0,1)$, $\{c(y),\tau y + c(y)\}$, are positive.

The third corner solution requires all taxpayers to non-optimize: the shares of evaders and optimizers are zero. The eigenvalues of $J(0,0)$ are given by $\{\tau y,\tau y-c(y)\}$. Since they are positive, the population state with all taxpayers non-optimizing is an unstable source node, as well.

The next fixed point requires the share $x_{o}^{*}$ to optimize whereas the remainder, $1-x_{o}^{*}$, non-optimizes with no one evading. The eigenvalues of $J(0,x_{o}^{*})$ are given by $\left \{\tau y,\tau \left (1-x_{o}^{*}\right ) x_{o}^{*} y o^{\prime }\left (x_{o}^{*}\right )\right \}$. The first eigenvalue is positive, the second is negative; the fourth fixed point is thus an unstable saddle point.

Another fixed point is given if the share $x_{e}^{*}$ evades and the remainder, $1-x_{e}^{*}$, non-optimizes. The eigenvalues of $J(x_{e}^{*},0)$ are given by $\{\tau y-c(y), -(1+ \theta ) \tau y \left (1-x_{e}^{*}\right ) x_{e}^{*} p^{\prime }\left (x_{e}^{*}\right )\}$. Again, the eigenvalues have opposite signs. The fifth fixed point is thus also a saddle point.

If no one non-optimizes, a fixed point can be reached in which the share $x^{\dagger }_{e}$ evades and the share $x^{\dagger }_{o}= 1-x^{\dagger }_{e}$ optimizes. The eigenvalues of $J(x^{\dagger }_{e},x^{\dagger }_{o})$ are given by

$$\begin{array}{@{}rcl@{}} \left\{\tau y \left( (1+ \theta) p\left( x^{\dagger}_{e}\right)-1\right), \tau y \left( 1-x^{\dagger}_{e}\right) x^{\dagger}_{e} \left( o^{\prime}\left( 1-x^{\dagger}_{e}\right)-(1+\theta ) p^{\prime}\left( x^{\dagger}_{e}\right)\right)\right\}. \end{array} $$

The second eigenvalue is always negative. The first is negative if the condition (17) holds strictly. The fixed point is then a stable sink node; it is an unstable saddle point otherwise.

Finally, the eigenvalues of $J(x_{e}^{*},x_{o}^{*})$ are given by $\{ \psi - \sqrt {\varphi }, \psi +\sqrt {\varphi } \}$, where

$$\begin{array}{@{}rcl@{}} \psi= - \frac{1}{2}\tau y \left( (1-x_{e}^{*}) x_{e}^{*} (1+\theta) p^{\prime}(x_{e}^{*}) + (1-x_{o}^{*}) x_{o}^{*} (-o^{\prime}(x_{o}^{*}))\right) \end{array} $$

is clearly negative and the sign of

$$\begin{array}{@{}rcl@{}} \varphi &= & \tau^{2} y^{2}\frac{1}{4} \left( \left( -(1-x_{o}^{*}) x_{o}^{*} o^{\prime}(x_{o}^{*})+(1-x_{e}^{*}) x_{e}^{*} (1+\theta ) p^{\prime}(x_{e}^{*})\right)^{2} \right.\\ &&\left. -\,4 x_{e}^{*} x_{o}^{*} (1 - x_{e}^{*} - x_{o}^{*}) (1+\theta ) \left( - o^{\prime}(x_{o}^{*})\right) p^{\prime}(x_{e}^{*})\right) \end{array} $$

is not distinct. If $\varphi$ is positive then $\psi -\sqrt {\varphi }$ is always negative. Further, $\psi +\sqrt {\varphi }$ is negative if $\sqrt {\varphi }<-\psi \Leftrightarrow \varphi <\psi ^{2}$. This gives the condition

$$\begin{array}{@{}rcl@{}} x_{e}^{*} (1+\theta) x_{o}^{*} \tau^{2} y^{2} (1-x_{e}^{*}-x_{o}^{*}) (-o^{\prime}(x_{o}^{*})) p^{\prime}(x_{e}^{*})>0 , \end{array} $$

which is always fulfilled. It can be concluded that the fixed point is stable if $\varphi$ is positive, that is, if the eigenvalues of $J(x_{e}^{*},x_{o}^{*})$ are real. If $\varphi$ is negative, the eigenvalues take the form $\{ \psi -i\sqrt {-\varphi },\psi +i\sqrt {-\varphi }\}$. Since the eigenvalues have negative real parts, the system behaves as a damped oscillator; the fixed point is also stable.

1.3.2 B.2.2 Stability with delay in the strategy “optimization”

Again, only the stability of $\dot {x}_{e}$ and $\dot {x}_{o}$ needs to be studied. Let $u(t)=x_{e}(t)-x_{e}^{*}$ and $v(t)=x_{o}(t)-x_{o}^{*}$. The variational system of (21) about $x^{*}$ is given by

$$\begin{array}{@{}rcl@{}} u^{\prime}(t)& = & -a u(t) + b v(t-\delta )\\ v^{\prime}(t)& = & k u(t)-l v(t-\delta ) \end{array} $$

(23)

(Bellman and Cooke 1963, p. 339), where

$$\begin{array}{@{}rcl@{}} a &=& \left( 1-x_{e}^{*} \right) x_{e}^{*} \tau (1 + \theta) y p^{\prime}\left( x_{e}^{*}\right)>0,\\ b &=& x_{e}^{*} x_{o}^{*} \tau y \left( - o^{\prime}\left( x_{o}^{*}\right) \right)>0,\\ k &=& x_{e}^{*} x_{o}^{*} \tau (1 + \theta) y p^{\prime}\left( x_{e}^{*}\right)>0,\\ l &=& \left( 1-x_{o}^{*}\right) x_{o}^{*} \tau y \left( - o^{\prime}\left( x_{o}^{*}\right) \right) >0. \end{array} $$

The system (23) can be written as

$$\begin{array}{@{}rcl@{}} v^{\prime\prime}(t) +a v^{\prime}(t) +l v^{\prime}(t-\delta ) + d v(t-\delta ) = 0, \end{array} $$

(24)

where $d=(a l -k b)$. The characteristic equation (Laplace transform) of Eq. 24 is given by

$$\begin{array}{@{}rcl@{}} \lambda^{2}+a \lambda+l \lambda e^{-\lambda \delta}+d e^{-\lambda \delta}= 0. \end{array} $$

(25)

The roots of Eq. 25 are given by $\lambda =i\omega ,\omega >0$. From equation (4.6) in Freedman and Kuang (1991, p. 199) one has

$$\begin{array}{@{}rcl@{}} \omega^{2}_{\pm} = \frac{1}{2}\left( (l^{2}-a^{2}) \pm \sqrt{ (l^{2}-a^{2})^{2} + 4d^{2} }\right). \end{array} $$

Theorem 4.1 of Freedman and Kuang (1991, p. 202) is applied. $d \neq 0$ if

$$\begin{array}{@{}rcl@{}} (\tau y-c(y)) (\tau y-(1+\theta) c(y)) \neq 0. \end{array} $$

τy > c(y) by an assumption made in Section 2.1. The additional assumption $\tau y \neq (1+\theta ) c(y)$ has to be made. Since $0<d^{2}$ only one imaginary root exists (Freedman and Kuang 1991, p. 200). Hence the system is stable if $\delta <\hat {\delta }$, and unstable afterwards, with

$$\begin{array}{@{}rcl@{}} \hat{\delta}=\frac{\eta}{\omega_{+}}, \end{array} $$

where

$$\begin{array}{@{}rcl@{}} \cos \eta &= & -\frac{a l \omega^{2}_{+} -d \omega^{2}_{+}}{l^{2}\omega^{2}_{+} +d^{2}},\\ \sin \eta &= & \frac{d a \omega_{+} + l \omega_{+}^{3}}{l^{2}\omega_{+}^{2}+d^{2}} \end{array} $$

according to equations (4.13) and (4.14) of Freedman and Kuang (1991, p. 201); thus,

$$\begin{array}{@{}rcl@{}} \eta=\text{arccot} \left( \frac{\omega_{+} (d-a l)}{a d+l \omega_{+}^{2}} \right). \end{array} $$

1.3.3 B.2.3 Stability with delay in the strategy “evasion”

The procedure is similar to Appendix A.3.2. A delay $\gamma$ is introduced to the “evasion”-strategy. Thus, at time t, the tax authority audits with a probability according to the number of tax evaders at time $t-\gamma$. Setting $\delta = 0$ and introducing $\gamma$ as described above, the variational system of (21) about $x^{*}$ is given by

$$\begin{array}{@{}rcl@{}} u^{\prime}(t)& = & -a u(t-\gamma) + b v(t )\\ v^{\prime}(t)& = & k u(t-\gamma)-l v(t ) \end{array} $$

(26)

which can be written as

$$\begin{array}{@{}rcl@{}} u^{\prime\prime}(t) + l u^{\prime}(t)+a u^{\prime}(t-\gamma) + d u(t-\gamma) = 0. \end{array} $$

(27)

Comparing (27) with (24), one finds that the variables a and l are simply inverted. Thus,

$$\begin{array}{@{}rcl@{}} \omega^{2}_{\pm} = \frac{1}{2}\left( (a^{2}-l^{2}) \pm \sqrt{ (a^{2}-l^{2})^{2} + 4d^{2} }\right), \end{array} $$

and the critical delay is given by

$$\begin{array}{@{}rcl@{}} \hat{\gamma} = \frac{\text{arccot} \left( \frac{ \omega_{+}(d-al) }{ dl + a \omega_{+}^{2} } \right)}{ \omega_{+} } . \end{array} $$