GNSS best integer equivariant estimation using multivariant t-distribution: a case study for precise point positioning

Abstract

A key prerequisite for fast and reliable solution convergence time in precise point positioning with ambiguity resolution is the successful determination of the initial integer ambiguity parameters. In this contribution, a reliable approach of partial ambiguity resolution based on the BIE using the t-distribution (BIE-td) is proposed and compared against existing algorithms, such as the partial ambiguity resolution-based LAMBDA method (PAR-Ps) and the iFlex method proposed by the Trimble Navigation company. A 31-day set of GNSS measurements, collected in 2018 from 17 globally distributed GNSS continuously operating reference stations (CORS), were processed to determine the best-fit distribution for the GNSS measurements. It is found that the t-distribution with three degrees of freedoms provides a better fit compared to the Gaussian distribution. The authors then propose a method for selecting the integer ambiguity candidates when using the BIE-td approach. This method is based on the differences of unknown parameters of interest (i.e. receiver’s coordinates) determined at two consecutive processing steps. Finally, another 30-day set of GNSS measurements, collected in 2019 from the same CORS, confirm that the iFlex method outperforms the PAR-Ps method in the sense of minimizing the position errors of a simulated kinematic test. In particular, compared to the PAR-Ps method for 99th percentile of errors, the iFlex method has an improved convergence time of about 10 min. In addition, the positioning performance using the BIE-td and iFlex methods is comparable, with a similar positioning accuracy for both horizontal and vertical coordinate components.

1 Introduction

A significant limitation of the precise point positioning (PPP) technique is slow solution convergence time. Tens of minutes are required for solutions to converge to decimetre-level accuracy, even with carrier phase ambiguity resolution (PPP-AR) (Collins and Bisnath 2011; Ge et al. 2008; Geng et al. 2010a; Laurichesse et al. 2009, 2010). This constrains PPP uptake for real-time applications. Recent research shows that utilization of next generation Global Navigation Satellite System (GNSS) satellites transmitting on three or more frequencies is an essential requirement for reducing the convergence time of PPP solutions (Duong et al. 2019a; El-Mowafy et al. 2016; Geng et al. 2018; Laurichesse and Banville 2018).

Multi-frequency multi-constellation GNSS brings opportunities and challenges. The benefit of combining systems is to improve satellite geometry, redundancy, and atmospheric delay estimability. A challenge for multi-frequency and multi-GNSS solutions is that it is not always possible to fix all carrier-phase ambiguities reliably. This is because multi-frequency multi-GNSS observations introduce more ambiguities, and the probability of correct integer estimation (also known as the “success rate”) may decrease when more ambiguities are involved (Teunissen 1999; Teunissen et al. 1999). However, there may be a subset of (linear functions of) ambiguities that can successfully be fixed to integers. Hence, partial ambiguity resolution (PAR) methods were developed to improve the reliability of ambiguity resolution and to “fix” a subset of the ambiguities.

Several PAR approaches have been proposed, differing in the criterion used to select the ambiguities to be fixed. Teunissen et al. (1999) introduced the first PAR method in order to select a subset of ambiguities based on a minimum success rate. Another strategy attempted to only fix the ambiguities with longer wavelengths such as (extra) wide-lane linear combinations in the case of two or more frequencies (Cao et al. 2007; Li et al. 2010). Other selection criteria included ambiguities from satellites above a certain elevation angle, or ambiguities visible for a specific period (Takasu and Yasuda 2010). Another approach selected ambiguities associated with a specified signal-to-noise ratio cutoff (Parkins 2011). Dai et al. (2007) selected a subset of integer ambiguities (or linear combinations of them), which proved to be identical in terms of the best and second-best results obtained using the Least-squares Ambiguity Decorrelation Adjustment (LAMBDA) algorithm. However it is doubtful whether this is an appropriate selection criterion since those ambiguities might be identical but still be wrong in the presence of high noise or large biases (Verhagen et al. 2011). Another PAR strategy comprised sequentially discarding satellites until passing a critical value in the ratio test (Duong et al. 2019b; Li and Zhang 2015; Wang and Feng 2013). Note, however, that the use of the ratio test with a fixed threshold value often results in either unacceptably high failure rates or is overly conservative (Verhagen and Teunissen 2013).

Most of the existing PAR methods involve an iterative procedure where many different subsets are evaluated, such as discarding satellites, which will impact processing time, especially for a multi-GNSS scenario (Verhagen et al. 2012). Based on its success rate, the PAR method (Teunissen 2001a; Teunissen et al. 1999) is widely used by GNSS researchers because it requires less computational time compared with other PAR methods. Another advantage is that this approach is easy to implement and allows users to specify the minimum required success rate. Furthermore, this method inherently includes an automatic procedure for deciding when to include newly risen satellites. This PAR method is based on decorrelation and bootstrapping and was implemented in the LAMBDA software package. For convenience this method is denoted here as “PAR-Ps”, but note that its success rate is driven by the underlying model and not by the actual measurements (Teunissen and Verhagen 2008). Any undetected biases, such as multipath effects and atmosphere biases in the observation model, may affect the data-driven success rate, while the model-driven success rate can still be high (Li and Zhang 2015). Even setting a high threshold for the success rate in the PAR-Ps method does not guarantee correct fixing of ambiguities (Teunissen 2001b; Verhagen and Li 2012).

Several studies conducted by Trimble Navigation Limited, and described in patents (Talbot and Vollath 2013; Vollath 2014; Vollath and Talbot 2013), have proposed an alternative approach, namely the “iFlex” method. This method was originally inspired by the “best integer equivariant estimator” (BIE) algorithm described by Teunissen (2003). The Trimble authors claim the iFlex method results in reliable ambiguity resolution. Moreover, since the iFlex method is a weighted combination of possible integer ambiguity candidates, a position solution using iFlex will converge more rapidly to correct values compared with the float solution (Vollath and Talbot 2013). Nevertheless, details of the improvement, in terms of convergence time between the PAR-Ps and the iFlex methods, has not been investigated. In addition, recent GNSS literature claim that multivariate t-distributions, which are generalizations of the classical univariate Student t-distributions, can offer a more viable alternative representation of the GNSS measurement and navigation errors than the normal distribution, particularly because its tails are more realistic (Madrid 2016). However, it is not clear how the multivariate t-distributions can be applied for high positioning accuracy GNSS applications.

In this contribution, the authors propose a reliable approach for partial fixing ambiguity based on the best integer equivariant estimator using multivariate t-distributions (BIE-td). The positioning performance of the proposed approach is then compared against existing methods such as the iFlex method (Vollath and Talbot 2013) and the PAR-Ps method (Teunissen 1999, 2001a; Teunissen et al. 1999). Although this contribution is motivated by the ambiguity resolution problem of PPP as a case study, there are no restrictions to applying these ambiguity resolution methods for other GNSS techniques having unknown integer parameters as well as real-valued parameters in their observational models, such as the differential real-time-kinematic (RTK) techniques. Furthermore, the proposed method can be applied to both single and multi-constellation multi-frequency GNSS measurement to achieve fast and reliable positioning solution. Thus, our PPP model will utilize multi-frequency GNSS signals to provide relevant insights into the achievable PPP positioning performance.

This paper is organized as follows. First, we present a quick overview of GNSS observation model followed by a review of GNSS carrier phase ambiguity resolution methods such as the integer least-squares estimation, PAR-Ps, the BIE and the iFlex ambiguity resolution methods. Next, we explain the proposed GNSS best integer equivariant estimation using multivariant t-distribution including GNSS data processing strategy, distribution of GNSS measurements, selection of integer candidate sets and the BIE-td approach. Then, we present the results of the proposed method against existing ambiguity resolution methods, using multi-frequency and multi-constellation PPP-AR as a case study. The paper ends with discussion and conclusions.

2 GNSS observational model

The functional models of between-satellite single-differenced (SD) code and phase measurements on the ith frequency at the ${\kappa }$th epoch are given by Leick et al. (2015):

$${P}_{i,\left(\kappa \right)}^{bs}={\left({\rho }^{bs}-{ct}^{bs}+{\mu }_{i}{I}_{1}^{bs}+{T}^{bs}+{\xi }_{\mathrm{code},i}^{bs}+{\varepsilon }_{\mathrm{code},i}^{bs}\right)}_{\left(\kappa \right)}$$

(1)

$${L}_{i,\left(\kappa \right)}^{bs}={\left({\rho }^{bs}-{ct}^{bs}-{\mu }_{i}{I}_{1}^{bs}+{T}^{bs}+{\lambda }_{i}{\xi }_{\mathrm{phase},i}^{bs}+{\lambda }_{i}{N}_{i}^{bs}+{\varepsilon }_{\mathrm{phase},i}^{bs}\right)}_{\left(\kappa \right)}$$

(2)

where ${P}_{i}^{bs}$ and ${L}_{i}^{bs}$ are the SD code and phase measurement vectors on the ${i}^{th}$ frequency (in units of meters), respectively; the superscript bs represents single-differencing between two satellites (the reference satellite b and any other s); ${\rho }^{bs}$ is the SD receiver-satellite geometric distance vector (m); c is the speed of light in vacuum (m/s); ${t}^{bs}$ is the SD satellite clock error (s); ${f}_{i}$ is the ith frequency (MHz); ${\lambda }_{i}$ is the wavelength of the carrier-phase on the ith frequency (m); ${I}_{1}^{bs}$ is the vector of SD the first order ionospheric delays on the first frequency (m); ${\mu }_{i}=\frac{{f}_{1}^{2}}{{f}_{i}^{2}}$ is the ionosphere coefficient; ${T}^{bs}$ is the vector of SD tropospheric delays (m); ${\xi }_{\mathrm{code},i}^{bs}$ is the vector of SD satellite code biases (m); ${\lambda }_{i}{\xi }_{\mathrm{phase},i}^{bs}$ is the vector of SD satellite phase biases (m); ${N}_{i}^{bs}$ is the vector of SD integer ambiguities on the ${i}$th frequency (cycles); and ${\varepsilon }_{\mathrm{code},i}^{bs}$ and ${\varepsilon }_{\mathrm{phase},i}^{bs}$ denote the vector of remaining unmodeled errors such as multipath effects on the SD code and phase measurements (m), respectively. Note that the receiver clock error and the receiver phase and code biases are eliminated via differencing in (1) and (2).

Standard PPP with “float ambiguities”, which is a combination of the integer ambiguity terms and the satellite and receiver hardware biases, usually requires tens of minutes, or even several hours, in order to obtain centimeter-level accuracy. Significant efforts from GNSS researchers since 2007 have made progress in addressing the challenge of resolving carrier-phase ambiguities in PPP. In general, two classes of methods have been proposed to resolve carrier-phase ambiguities: the “Uncalibrated Hardware Delays” method (Bertiger et al. 2010; Ge et al. 2008); and the “Integer-Recovery-Clocks” (Laurichesse et al. 2009) or “Decoupled Clock Model” (Collins 2008) methods. It has been demonstrated that the ambiguity-fixed position estimates from these methods are theoretically equivalent (Geng et al. 2010b; Shi 2012; Teunissen and Khodabandeh 2014).

By using Radio Technical Commission for Maritime Services (RTCM) State-Space Representation (SSR) correction products (e.g., CLK93 real-time stream), the satellite errors, including clocks, orbits, code and phase biases, for multi-frequency multi-GNSS measurements can be minimized. Since 2010 these RTCM-SSR corrections have provided a unified framework for the satellite errors, which can be used for PPP-AR. In particular the satellite code and phase biases are defined as quantities (one value per observable) to be added to the raw GNSS measurements. More importantly, the integer nature of phase measurements is preserved, and the integer ambiguities can be estimated regardless of which linear combinations is chosen by the user’s software (Laurichesse 2015; Laurichesse and Blot 2016). These RTCM-SSR corrections have been publicly provided by several service providers, including Natural Resources Canada (NRCan), Center for Orbit Determination in Europe (CODE), Centre National d’Études Spatiales (CNES) and Wuhan University (WHU). These enable high accuracy single-receiver positioning with PPP, using precise satellite orbits, clocks, code and phase biases are provided to users so as to correct code and phase measurements. The corrected observations at the ${\kappa }$th epoch can be written as:

$${\stackrel{-}{P}}_{i,\left(\kappa \right)}^{bs}={\left({P}_{i}^{bs}+{ct}^{bs}-{\xi }_{\mathrm{code},i}^{bs}\right)}_{\left(\kappa \right)}{=\left({\rho }^{bs}+{\mu }_{i}{I}_{1}^{bs}+{T}^{bs}+{\varepsilon }_{\mathrm{code},i}^{bs}\right)}_{\left(\kappa \right)}$$

(3)

$${\stackrel{-}{L}}_{i,\left(\kappa \right)}^{bs}={\left({L}_{i}^{bs}+{ct}^{bs}-{\lambda }_{i}{\xi }_{\mathrm{phase},i}^{bs}\right)}_{\left(\kappa \right)}={\left({\rho }^{bs}-{\mu }_{i}{I}_{1}^{bs}+{T}^{bs}+{\lambda }_{i}{N}_{i}^{bs}+{\varepsilon }_{\mathrm{phase},i}^{bs}\right)}_{\left(\kappa \right)}$$

(4)

The SD receiver-satellite geometric distance vector ${\rho }^{bs}$ is not parameterized in terms of receiver coordinates for reasons of clarity. Note, however, that our analyses will use the geometry-based model where ${\rho }^{bs}$ is parametrized in terms of receiver coordinates.

3 A review of GNSS carrier phase ambiguity resolution methods

The goal of geometry-based AR is to estimate the integer ambiguities and thereby reduce positioning convergence time. Assuming that GNSS signals are transmitted on f frequencies, the linearized GNSS observation equations corresponding to (3) and (4) can be expressed as:

$$y=\left[\begin{array}{c}\stackrel{-}{P}\\ \stackrel{-}{L}\end{array}\right]=Aa+Bb+\epsilon ;\quad a\in {Z}^{n},\; b\in {R}^{p}$$

(5)

where y is the GNSS data vector of $\left[m\times 1\right]$ comprising the observed-minus-computed pseudorange (code) and phase observations accumulated over all observation epochs; $\stackrel{-}{P}={\left[{\stackrel{-}{P}}_{1}^{\mathrm{T}}\dots {\stackrel{-}{P}}_{f}^{\mathrm{T}}\right]}^{\mathrm{T}}$ and $\stackrel{-}{L}={\left[{\stackrel{-}{L}}_{1}^{\mathrm{T}}\dots {\stackrel{-}{L}}_{f}^{\mathrm{T}}\right]}^{\mathrm{T}}$ with ${\stackrel{-}{P}}_{i}$ and ${\stackrel{-}{L}}_{i}$ containing, respectively, the code and phase observations on the ith frequency over all the epochs; vector $a$ $\left[n\times 1\right]$ contains all carrier-phase ambiguities ${\left[{\stackrel{-}{N}}_{1}^{\mathrm{T}}\dots {\stackrel{-}{N}}_{f}^{\mathrm{T}}\right]}^{\mathrm{T}}$, expressed in units of cycles; vector b $\left[p\times 1\right]$ comprises the remaining unknown parameters, such as receiver coordinates and atmospheric delay parameters; $A \left[m\times n\right]$ and $B \left[m\times p\right]$ are the corresponding design matrices; $\epsilon =\left[\begin{array}{c}{\varepsilon }_{\mathrm{code}}\\ {\varepsilon }_{\mathrm{phase}}\end{array}\right]$ is the noise vector accumulated over all observation epochs; ${\varepsilon }_{\mathrm{code}}={\left[{\varepsilon }_{\mathrm{code},1}^{\mathrm{T}}\dots {\varepsilon }_{code,f}^{\mathrm{T}}\right]}^{\mathrm{T}}$ and ${\varepsilon }_{phase}={\left[{\varepsilon }_{\mathrm{phase},1}^{\mathrm{T}}\dots {\varepsilon }_{\mathrm{phase},f}^{\mathrm{T}}\right]}^{\mathrm{T}}$ with ${\varepsilon }_{\mathrm{code},i}$ and ${\varepsilon }_{\mathrm{phase},i}$ contain, respectively, the unmodeled errors of code and phase observations on the ${i}$th frequency over all observation epochs.

3.1 Integer least squares estimation

To solve (5), the least-squares adjustment will be used to calculate the unknown parameters and the integer SD ambiguities (Teunissen 1995).

$$\underset{a,b}{\mathrm{min}}{\Vert y-Aa-Bb\Vert }_{{Q}_{y}}^{2}; \quad \in {Z}^{n},\; b\in {R}^{p}$$

(6)

where ${\Vert \cdot \Vert }_{{Q}_{y}}^{2}={\left(\cdot \right)}^{T}{Q}_{y}^{-1}\left(\cdot \right)$, the parameter estimation usually will be required in three following steps.

Float Solution the minimization of (6) is carried out with $a\in {R}^{n}$ and $b\in {R}^{p}.$ Note that ambiguities are estimated not accounting for their integer nature ($a\in {Z}^{n}$). Real-valued numbers for both a and b, along with their variance–covariance matrices will be obtained.

$$\left[\begin{array}{c}{\widehat{a}}\\ {\widehat{b}}\end{array}\right],\left[\begin{array}{cc}{Q}_{{\widehat{a}}{\widehat{a}}}& {Q}_{{\widehat{a}}{\widehat{b}}}\\ {Q}_{{\widehat{b}}{\widehat{a}}}& {Q}_{{\widehat{b}}{\widehat{b}}}\end{array}\right]$$

(7)

Integer ambiguity resolution the float ambiguity estimate ${\widehat{a}}$ is used to compute the corresponding integer ambiguity estimate ${\check{a}}$. The integer least-squares (ILS) problem is introduced such that.

$$\underset{a}{\mathrm{min}}{\Vert {\widehat{a}}-{\check{a}}\Vert }_{{Q}_{{\widehat{a}}{\widehat{a}}}}^{2}\;\; \mathrm{with}\; a\in {Z}^{n}$$

(8)

Although different integer estimators exist (i.e., integer rounding or integer bootstrapping), ILS provides the optimal result in the sense of maximizing the probability of correct integer estimation (success rate) (Teunissen 1999). The ILS problem is resolved using well-known LAMBDA method (De Jonge and Tiberius 1996; Teunissen 1993). Ambiguity resolution should only be applied when there is enough confidence in its results, which means that the success rate should be very close to one. If this is not the case, a user will prefer the float solution.

Fixed solution once the integer ambiguities are computed, they are used in the third step to finally correct the ‘float’ estimate of b. As a result, one obtains the fixed solution

$${\check{b}}={\widehat{b}}-{Q}_{{\widehat{b}}{\widehat{a}}}{Q}_{{\widehat{a}}{\widehat{a}}}^{-1}\left({\widehat{a}}-{\check{a}}\right)$$

(9)

$${Q}_{{\check{b}}{\check{b}}}={Q}_{{\widehat{b}}{\widehat{b}}}-{Q}_{{\widehat{b}}{\widehat{a}}}{Q}_{{\widehat{a}}{\widehat{a}}}^{-1}{Q}_{{\widehat{a}}{\widehat{b}}}$$

(10)

where ${Q}_{{\widehat{b}}{\widehat{a}}}^{\mathrm{T}}={Q}_{{\widehat{a}}{\widehat{b}}}$ is the float covariance matrix. Centimeter-level positioning accuracy could be achieved with the carrier-phase observables in the precise positioning if the successful determination of the initial integer ambiguity parameters.

3.2 PAR-based LAMBDA

The reliability of integer ambiguity fixing depends on several factors, including the strength of the underlying GNSS model and the ambiguity resolution method that is used. Consequently, it is not always possible to reliably fix all GNSS ambiguities. One could, however, still fix a subset of the phase ambiguities (or linear functions of them) with sufficient confidence (Teunissen et al. 1999; Verhagen et al. 2012). This strategy for AR is referred to as partial AR (PAR). This PAR method is based on decorrelation and bootstrapping and has been implemented in the Least-squares Ambiguity Decorrelation Adjustment (LAMBDA) software package. A subset of the decorrelated ambiguities is fixed, with a corresponding bootstrapped success rate larger than or equal to a minimum specified value ${P}_{0}$. Hence, the goal is to select the largest possible subset such that:

$$\prod_{j=q}^{n}\left(2\Phi \left(\frac{1}{2{\sigma }_{{{\widehat{z}}}_{j|I}}}-1\right)\right)\ge {P}_{0}$$

(11)

where $q\ge 1$. $\Phi \left({\rm M}\right)=\frac{1}{\sqrt{2\pi }}{\int }_{-\infty }^{\rm M}\mathrm{exp}\left(-\frac{1}{2}{t}^{2}\right)\mathrm{d}t$ is the cumulative normal distribution; ${\sigma }_{{{\widehat{z}}}_{j|I}}$ is the conditional standard deviation of the decorrelated ambiguities ${\widehat{z}}={Z}^{\mathrm{T}}{\widehat{a}}$ when using a decorrelating Z-transformation $\left(Z\right)$; and ${\widehat{a}}$ is the float ambiguities. Hence, only the last $n-q+1$ entries of the vector ${\widehat{z}}$, denoted by ${{\widehat{z}}}_{s}$, are fixed. Adding more ambiguities implies multiplication with another probability which, by definition, is smaller than or equal to 1. Hence, q is chosen such that the inequality in (11) holds, while a smaller q (i.e., larger subset) would result in an unacceptably low success rate. Note that the fixed solution, in terms of the original ambiguities and the corresponding fixed remaining unknown parameters, can be obtained after applying the back-transformation as (Verhagen and Li 2012):

$${{\check{a}}}_{\mathrm{PAR}}={Z}^{-\mathrm{T}}{{\check{z}}}_{\mathrm{PAR}}$$

(12)

$${\check{b}}={\widehat{b}}-{Q}_{{\widehat{b}}{\widehat{a}}}{Q}_{{\widehat{a}}{\widehat{a}}}^{-1}\left({\widehat{a}}-{{\check{a}}}_{\mathrm{PAR}}\right)$$

(13)

where ${\widehat{b}}$ and ${\check{b}}$ are the vectors of the float and fixed solution of the remaining unknown parameters, respectively; and ${{\check{a}}}_{\mathrm{PAR}}$ will generally not contain integer entries, since it is a linear function of the decorrelated ambiguities ${{\check{z}}}_{\mathrm{PAR}}$, which are not all integer-valued. The corresponding precision improvement of the remaining unknown parameters is:

$${Q}_{{\check{b}}{\check{b}}}={Q}_{{\widehat{b}}{\widehat{b}}}-{Q}_{{\widehat{b}}{{\widehat{z}}}_{s}}{Q}_{{{\widehat{z}}}_{s}{{\widehat{z}}}_{s}}^{-1}{Q}_{{{\widehat{z}}}_{s}{\widehat{b}}}$$

(14)

where ${Q}_{{\widehat{b}}{{\widehat{z}}}_{s}}$ and ${Q}_{{{\widehat{z}}}_{s}{{\widehat{z}}}_{s}}$ are the submatrices of ${Q}_{{\widehat{b}}{\widehat{z}}}={Q}_{{\widehat{b}}{\widehat{a}}}Z$ and ${Q}_{{\widehat{z}}{\widehat{z}}}={{Z}^{\mathrm{T}}Q}_{{\widehat{a}}{\widehat{a}}}Z$, respectively, relating to ${{\widehat{z}}}_{s}$. ${Q}_{{\check{b}}{\check{b}}}$ and ${Q}_{{\widehat{a}}{\widehat{a}}}$ is the variance–covariance matrix of the unknown parameters and ambiguities, respectively; and ${Q}_{{\widehat{b}}{\widehat{a}}}$ and ${Q}_{{\widehat{a}}{\widehat{b}}}$ are submatrices. In general, ${Q}_{{\check{b}}{\check{b}}}\ll {Q}_{{\widehat{b}}{\widehat{b}}}$. However, incorrect integer ambiguity fixing may have the opposite effect in terms of positioning accuracy. That is, rather than an accuracy improvement, an incorrect ambiguity solution can cause substantial position errors, exceeding those of the float solution.

3.3 Best integer equivariant estimation

In the case of PAR with a low success rate, the BIE estimator should be used as an alternative algorithm instead of the fixed solution because it provides better convergence time. Further, the BIE estimator will approximate the float solution if the precision is low, and the fixed solution when the probability density function (PDF) is high (Verhagen and Teunissen 2005). Therefore, the BIE estimator is a compromise between float and fixed solutions. Consider the following arbitrary linear function of the unknown parameters a and b (cf. 5):

$$\theta ={l}_{a}^{\mathrm{T}}a+{l}_{b}^{\mathrm{T}}b$$

(15)

where ${l}_{a}\in {R}^{n}$ and ${l}_{b}\in {R}^{p}$. If ${l}_{b}=0$ then $\theta$ is a linear function of the ambiguities only; whereas if ${l}_{a}=0$ then $\theta$ is a linear function of the remaining real-valued parameters (i.e., receiver’s coordinates and atmospheric delays). The BIE estimator of $\theta$ is then given by (Teunissen 2003):

$${\widehat{\theta }}_{\mathrm{BIE}}=\frac{\sum_{z\in {Z}^{n}}{\int }_{{R}^{p}}\left({l}_{a}^{\mathrm{T}}z+{l}_{b}^{\mathrm{T}}\beta \right){p}_{y}\left(y+A\left(a-z\right)+B\left(b-\beta \right)\right)\mathrm{d}\beta }{\sum_{z\in {Z}^{n}}{\int }_{{R}^{p}}{p}_{y}\left(y+A\left(a-z\right)+B\left(b-\beta \right)\right)d\beta }$$

(16)

where $y\in {R}^{m}$ is the observation vector in (5) with the mean $E\left\{y\right\}=Aa+Bb$ and the PDF ${p}_{y}\left(y\right).$ $\beta$ is the remaining unknown parameters, such as receiver coordinates and atmospheric delay parameters of a single receiver (i.e. PPP), with $E\left\{\beta \right\}=b.$ As (16) shows, the BIE estimator is equal to a weighted sum over all integer set vectors, and the weights depend on the PDF of the observations. BIE method advantages include: (1) there is no need to fix the integer ambiguities at one point; hence, the risk of wrongly fixing the integer ambiguities is eliminated; (2) there is no need for a validation test because the outcome of the BIE estimator is obtained by weighting all integer set vectors and the predefined PDF of the observations; and (3), the precision of the remaining unknown parameters (i.e. receiver’s coordinates) using the BIE estimator is always better in the minimum mean squared error (MMSE) sense than, or at least as good as, the precision of its ‘float’ and ‘fixed’ counterparts.

In a special case, when the observations follow a Gaussian distribution, the PDF of a m-dimensional normally distributed random vector y with mean vector $E\left\{y\right\}=Aa+Bb$ and the variance–covariance matrix ${Q}_{y}$ is given by:

$${p}_{y}\left(y\right)=\frac{1}{({2\pi )}^{\frac{m}{2}}\sqrt{\mathrm{det}{Q}_{y}}}\mathrm{exp}\left\{-\frac{1}{2}{\Vert y-Aa-Bb\Vert }_{{Q}_{y}}^{2}\right\}$$

(17)

where $\mathrm{det}$ denotes the determinant operator. As shown by Teunissen (2003), when the vector of observations y follows a Gaussian distribution, the BIE estimators of ambiguities a and the remaining real-valued parameters b are simplified to:

$$\left\{\begin{array}{l}{{\widehat{a}}}_{\mathrm{BIE}}=\frac{{\sum }_{z\in {Z}^{n}}z\mathrm{exp}\left(-\frac{1}{2}{\Vert {\widehat{a}}-z\Vert }_{{Q}_{{\widehat{a}}}}^{2}\right)}{{\sum }_{z\in {Z}^{n}}\mathit{exp}\left(-\frac{1}{2}{\Vert {\widehat{a}}-z\Vert }_{{Q}_{{\widehat{a}}}}^{2}\right)}={\sum }_{z\in {Z}^{n}}z{w}_{z}\left({\widehat{a}}\right) \\ {{\widehat{b}}}_{\mathrm{BIE}}={\widehat{b}}-{Q}_{{\widehat{b}}{\widehat{a}}}{Q}_{{\widehat{a}}}^{-1}\left({\widehat{a}}-{{\widehat{a}}}_{\mathrm{BIE}}\right)\end{array}\right.$$

(18)

with the weighting factor ${w}_{{z}_{j}}\left({\widehat{a}}\right)=\frac{\mathrm{exp}\left(-\frac{1}{2}{\Vert {\widehat{a}}-{z}_{j}\Vert }_{{Q}_{{\widehat{a}}}}^{2}\right)}{{\sum }_{z\in {Z}^{n}}\mathrm{exp}\left(-\frac{1}{2}{\Vert {\widehat{a}}-z\Vert }_{{Q}_{{\widehat{a}}}}^{2}\right)}\le 1$, $\forall {z}_{j}\in {Z}^{n}$ satisfying ${\sum }_{z\in {Z}^{n}}{w}_{z}\left({\widehat{a}}\right)=1$.

3.4 iFlex method

The iFlex method, as described by Vollath and Talbot (2013), originally relies on the BIE algorithm when the vector of observations $(y)$ follows a Gaussian distribution. The method is a weighted combination of some possible integer ambiguity candidates, but not all (within the infinite region). Vollath and Talbot (2013) claim the iFlex method converges more rapidly to correct values in a reasonable computational time compared with the convergence time of the float solution. The weighting factor of each integer candidate is influenced by the different distribution of the GNSS observations. Vollath and Talbot (2013) introduced empirical formulas, namely the Laplace or a Minmax distribution, which can be used to calculate the weighting factor of (18) according to the following expressions:

$${w}_{{z}_{j}}\left({\widehat{a}}\right)=\frac{\mathrm{exp}\left(-\alpha \sqrt{{\Vert {\widehat{a}}-{z}_{j}\Vert }_{{Q}_{{\widehat{a}}}}^{2}}\right)}{{\sum }_{z\in {Z}^{n}}\mathrm{exp}\left(-\alpha \sqrt{{\Vert {\widehat{a}}-z\Vert }_{{Q}_{{\widehat{a}}}}^{2}}\right)} \quad \left(\mathrm{Laplace}\right)$$

(19)

$${w}_{{z}_{j}}\left({\widehat{a}}\right)=\frac{\mathrm{exp}\left(-\mathrm{max}\left|{\widehat{a}}-{z}_{j}\right|\right)}{{\sum }_{z\in {Z}^{n}}\mathrm{exp}\left(-\mathrm{max}\left|{\widehat{a}}-z\right|\right)}\quad \left(\mathrm{Minmax}\right)$$

(20)

where α is a scaling factor used to tune the weights and $\left|\cdot \right|$ is the absolute value. The three weighting functions (including Gaussian, Laplace, and Minmax distribution) are summarized in Table 1. A one-hour GNSS session at one CORS, ALBY in Australia 2019 (DOY 100), was analyzed. The data sampling interval was one second. Additionally, the LAMBDA software was used to output the estimated integer candidates, after using a decorrelating Z-transformation for the ambiguities. This software also generated corresponding ambiguity residual squared norm. Two different marking epochs, 100th and 300th, were used for the comparison.

Table 1 Weighting function comparison of Gaussian distribution (18), Laplace distribution (19) and Minmax distribution (20) at the 100th and 300th epochs

Significantly, the first integer candidate’s weight is always dominant among a total of eight candidate sets output in the Gaussian distribution case. In particular, its weight at the 300th epoch is more than 0.999 while other candidate weights are extremely small (or equal to zero). This means the AR performance of the BIE method for the Gaussian case is very similar to the PAR-Ps solution. It converged too quickly or often resulted in false fixes at the initial epochs, especially when the stochastic model was incorrect (i.e., precisions were too optimistic); and this leads to incorrect position estimates. Deficiencies in stochastic modeling can be caused by incorrect modeling of satellite corrections (i.e., clock, orbit, or code and phase biases).

However, the mathematically non-rigorous Laplace or Minmax distribution case, as shown in (19) and (20) respectively, results in more weight being given to other candidate sets, which is one way to guard against incorrect fixing of ambiguities. According to Vollath and Talbot (2013), these distributions are effectively the broadened distributions and have less weight for the first best integer candidate set compared with the Gaussian distribution. Introducing the square root of the squared-norm distance, such as the Laplace case of (19), effectively spreads the probability function over a more extensive search space. Consequently, validation of the fixed solution is extended and delayed, with the added benefit of extra reliability.

In Sect. 3, we have reviewed the existing ambiguity resolution methods. The limitations of these methods have been also discussed. Overall, the success rate in PAR-Ps method is driven by the underlying model and not by the actual measurements (Teunissen and Verhagen 2008). Even setting a high threshold for the success rate in the PAR-Ps method does not guarantee correct fixing of ambiguities (Teunissen 2001b; Verhagen and Li 2012). As discussed in Sect. 3.3, the general BIE formula (16) can only be applied once the PDF of the observations is known. In addition, the AR performance of the BIE method for the Gaussian case is very similar to the PAR-Ps solution. It either converged too quickly or often resulted in false fixes at the initial epochs, especially when deficiencies exist in the stochastic model. The iFlex method using Laplace or Minmax function, as shown in (19) and (20) respectively, results in more weight being given to other candidate sets, which is one way to guard against incorrect fixing of ambiguities. They are however not mathematically rigorous. Therefore, in the next section we propose a more reliable and rigorous ambiguity resolution method derived from the general BIE formula.

4 GNSS best integer equivariant estimation using multivariant t-distribution

Using the geometry-fixed model, GNSS observations made by 17 CORS for a period of 31 days in 2018 were used to verify the distribution of the GNSS measurements. Next, BIE using the distribution determined from previous step was investigated. Furthermore, the positioning performance in terms of convergence time and positioning accuracy was assessed using an independent GNSS dataset in 2019 (Sect. 5). All GNSS observations were corrected using SSR products such as precise satellite orbits, clocks, code and phase biases from the Centre National d’Etudes Spatiales (CNES) CLK93 real-time stream.

4.1 Data collection and processing strategy

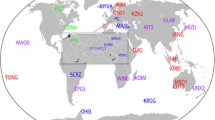
To evaluate the PPP-AR performance using different ambiguity resolution methods, real GNSS measurements from 17 GNSS CORS worldwide over a 30 consecutive day period from April 10 to May 10, 2019 (DOY 100 to 130) were processed. The reference stations were selected based on two criteria: (1) the receiver must simultaneously track three GPS signal frequencies (L1 + L2 + L5), three BeiDou signal frequencies (B1 + B2 + B3) and four Galileo signal frequencies (E1 + E5a + E5b + E6); and (2), the selected stations should be globally distributed. Thus, a total of 3102 datasets were analyzed. An independent GNSS dataset collected from the same 17 CORS for a period of 31 days in 2018 were used to verify the GNSS measurement distributions.

Figure 1 shows the locations of the GNSS stations used in this study. Figure 2 is a plot of the number of satellites observed from each point of a global grid, with a combination of different satellite constellations. At the time of writing (February 2020), more than 15 GNSS satellites were transmitting three or more signals were visible in the Asia–Pacific region, from which the following measurement were available: GPS L1 + L2 + L5 Galileo E1 + E5a + E5b + E6 and BeiDou B1 + B2 + B3. Twelve GPS Block IIF satellites were transmitting the third signal L5 in addition to the L1 and L2 signals. The first GPS Block III satellite was launched on 23 December 2018. More GPS Block III satellites will be launched in the coming years. There were 22 Galileo operational satellites which broadcast healthy signals and valid navigation messages (https://www.gsc-europa.eu/system-status/Constellation-Information). The BeiDou constellation currently provides signal coverage in the Asia–Pacific region and comprises five geostationary Earth orbiting (GEO) satellites, six inclined geosynchronous orbiting (IGSO) satellites and three medium Earth orbiting (MEO) satellites (http://mgex.igs.org/). Due to significant system biases in the BeiDou GEO satellites at present (Guo et al. 2017), only the BeiDou IGSO and MEO satellites were used in this study.

Fig. 1

Distribution of selected GNSS stations tracking GPS (L1 + L2 + L5) Galileo (E1 + E5a + E5b + E6) and BeiDou (B1 + B2 + B3) satellites

Fig. 2

Number of multi-frequency GPS + Galileo + BeiDou satellites observed worldwide on May 10, 2019 at 00:00UT

It should, however, be pointed out that the number of GNSS satellites transmitting three or more signal frequencies was limited during some periods of the day. In this study, all available frequencies from the three GNSS constellations were used.

A modified version of the RTKLIB software (Takasu 2013) was used to stream the GNSS measurements and output corrected observables free of the PPP systematic effects (i.e. phase wind-up). A MATLAB-based GNSS PPP software with Kalman filter estimator was developed to process corrected observables using the multi-frequency uncombined (UC) observation model for GPS, Galileo and BeiDou. Note that, henceforth, the phrase “uncombined observation models” implies that no ionosphere-free linear combination of measurements was created and that the ionospheric delay was estimated together with the other parameters using the SD measurements.

The commonly used variance functions for phase observations, which depend on the satellite elevation angle $\theta$, are (Dach et al. 2015; Luo 2013, Chap. 3, pp. 85):

$${\sigma }_{L}^{2}=\frac{{\sigma }_{{L}_{0}}^{2}}{{\mathrm{sin}}^{2}\theta }$$

(21)

where the standard deviation of GPS and Galileo phase observations for the zenith direction $\left({\sigma }_{{L}_{0}}\right)$ was chosen to be 3 mm. The measurement error ratio between code and carrier-phase observations $\left(\frac{{\sigma }_{P}}{{\sigma }_{L}}\right)$ was assumed to be 100, except for the BeiDou observations for which a value of 200 was adopted (Nadarajah et al. 2018; Pan et al. 2017; Zhou et al. 2019). Considering the stochastic information of the real-time satellite orbit, satellite clock and bias products, (21) is extended:

$${\tilde{\sigma }}_{L}^{2}=\left(\frac{{\sigma }_{{L}_{0}}^{2}}{{\mathrm{sin}}^{2}\theta }\right)+{\sigma }_{\mathrm{clk}}^{2}+{\sigma }_{\mathrm{orb}}^{2}+{\sigma }_{\mathrm{bias}}^{2}$$

(22)

where ${\sigma }_{\mathrm{clk}}^{2}$ is the satellite clock variance, ${\sigma }_{\mathrm{orb}}^{2}$ is the satellite orbit variance, and ${\sigma }_{\mathrm{bias}}^{2}$ is the satellite phase and code biases variance. The user equivalent range error (UERE) can also be used in (22) to combine the errors in the satellite’s orbit, clock and biases, and projected in the satellite-user direction (Laurichesse and Blot 2016). When forming the PPP model, UERE is the accumulated error the user experiences when modeling the GNSS measurements. In this study, the values of UERE were set as 1 cm, 5 cm and 5 cm for GPS, Galileo and BeiDou, respectively (Laurichesse and Blot 2016). Triple-frequency GPS + BeiDou and quad-frequency Galileo measurements were processed. The igs14_2013.atx file, which contains the frequency-dependent phase-center offsets and variations (PCO/PCV) for GPS, Galileo and BeiDou, was used in this study. Since the satellite antenna correction value for the GPS L5 signal is not available, the PCO/PCV of GPS L2 was used instead due to the closeness of frequency value between the GPS L2 and L5 signals. In addition there were no Galileo and BeiDou-specific ground-receiver-antenna calibrations available, hence the correction values (PCO/PCV) for GPS were employed for both Galileo and BeiDou, as approximations, and the third frequency signals had the same corrections as those for L2.

It should be noted one could have used a stronger model when working with calibrated inter-system biases (ISBs) (Odijk et al. 2017). The authors however had no access to the ISBs receiver-satellite frequency information from service providers (such as CNES). Furthermore, in practice the calibrated ISBs may not available for many GNSS receiver types. Hence in this study the authors have decided to use the ‘reference satellite per system’ method instead of the calibrated ISBs to combine GPS, Galileo and BeiDou measurements in a triple-frequency PPP-AR model. Table 2 summarizes the processing strategy that was employed.

Table 2 Multi-frequency multi-GNSS PPP-AR processing strategy

It should be noted that our PPP analyses were carried out in a well-known Kalman filter. However, the Kalman filter and its derivation presented in the literature usually require that the mean of the random initial state vector and the initial state-vector variance matrix to be known (or specified). Such derivations of the Kalman filter are indeed not appropriate in case when the mean of the random state vector is unknown, a situation that applies to most engineering applications. Thus instead of working with known state-vector means, we relax the model and assume these means to be unknown (Teunissen and Khodabandeh 2013). In this case, one needs to make use of prediction methods such as the recursive best linear unbiased prediction (BLUP) principle or best integer equivariant prediction (BIEP) principle as shown in Teunissen (2007), rather than the recursive Kalman filter. As proven by Teunissen (2007), the best integer equivariant estimator (BIEE) may be considered a special case of the BIEP. In the sense of minimum mean squared error (MMSE) prediction, the error variance of the BIEP is smaller than that of the BLUP (or MMSE(BIEP) ≤ MMSE(BLUP)). Further, when the predictor (or unobservable) ${y}_{0}\in {R}^{{m}_{0}}$ and the observable $y\in {R}^{m}$ have a joint normal distribution, the BIEP takes a form which is similar to the BLUP. Note that the recursive BLUP is shown to follow the Kalman filter. However, in the initialization step, while the BLUP does not require the known-mean, the information of the mean of the random initial state vector is required for the Kalman filter (Teunissen and Khodabandeh 2013).

To apply the BIEE in this study, the Kalman filter has been modified according to the BLUP principle as follows: we only keep ambiguities constant in time where no random process noise or dynamic models are considered. Thus, the recursive BIE solution at each epoch will be based upon the recursive least-squares adjusted ambiguities from the previous epoch and the observations of the current epoch. We hereby remark that the obtained BIE solution is not equivalent to its counterpart based on the observations of all the epochs (the batch solution). In other words, the BLUP error is never more precise than that of the Kaman filter. This is due to additional uncertainty caused by having to estimate $x={\left[\begin{array}{cc}a& b\end{array}\right]}^{\mathrm{T}}$ as well (Teunissen and Montenbruck 2017). The BLUP in this context is similar to the Kaman filter applied for real-time-kinematic applications. In this case, the user does not have any knowledge or information about receiver’s coordinates or even atmospheric delays (if local atmospheric model is not available) at each epoch, except for the ambiguity, which will be constant if no cycle slips occur.

4.2 Distribution of GNSS ambiguity

As shown in (16), the BIE only can be used when the PDF of $y$ is known. In GNSS applications it is often assumed that $y$ is normally distributed. In this case, the float ambiguities are also expected to be normally distributed (Teunissen 1998) the PDF of $y$ takes the form of (17) (Teunissen 2003). However, Madrid (2016) stated that the $t$-distribution is heavy-tailed and is a more realistic representation of the measurement and navigation errors than the Gaussian distribution; hence, it was used in order to improve the robustness of navigation filters against outliers. The PDF of a $m$-dimensional $t$-distributed random vector $y$ with $\nu$ degrees of freedom, mean vector $E\left\{y\right\}=Aa+Bb$ and the variance–covariance matrix ${Q}_{y}$, is given by:

$${p}_{y}\left(y\right)=\frac{\Gamma ((v+m)/2)}{({\pi v)}^{\frac{m}{2}}\Gamma (v/2)\sqrt{\mathrm{det}{Q}_{y}}}{\left[1+\frac{1}{v}{\Vert y-Aa-Bb\Vert }_{{Q}_{y}}^{2}\right]}^{-\frac{v+m}{2}}$$

(23)

$\mathrm{with }\,\, \Gamma \,\,(\cdot)$ denoting the gamma function. To validate the distribution of the GNSS measurements (i.e. GPS, BeiDou and Galileo observations), the ambiguity residuals were analyzed, i.e., differences between float ambiguities and their integer values resolved using the multi-epoch (1-h) geometry-fixed model. Real measurements from 17 GNSS stations (Fig. 1) over 31 consecutive days from September 25 to October 25, 2018 (DOY 268 to 298) were processed. The receiver positions at the CORS were fixed to their known coordinate values. Further, as discussed in the BIE section, the BIE estimation using (16) can only be used with a recursive solution, such as a Kalman filter with no dynamic models applied. Therefore the float solution obtained from the Kalman filter is designed to satisfy two criteria: (a) the ambiguities are kept time-constant; and (b) no dynamic models are applied for the atmospheric delays (i.e., troposphere and ionosphere). From a one-hour observation dataset, the model in (5) is sufficiently robust, and all ambiguities could be successfully fixed.

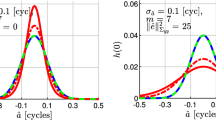
Let the float ambiguities and their corresponding ambiguity variance–covariance matrix at a particular CORS $\left(r\right)$ in a certain session $\left(s\right)$ be denoted by ${{\widehat{a}}}_{\left(r,s\right)}={\left[{{\widehat{a}}}_{1}\dots {{\widehat{a}}}_{n}\right]}^{\mathrm{T}}$ and ${Q}_{{{\widehat{a}}}_{\left(r,s\right)}}$, respectively. The fixed ambiguities from a 1-h solution are also written as ${{\check{a}}}_{\left(r,s\right)}={\left[{{\check{a}}}_{1}\dots {{\check{a}}}_{n}\right]}^{\mathrm{T}}$. Assuming that the GNSS observation errors follow a normal distribution, the ambiguity residuals are also expected to follow a normal distribution, i.e., ${\Delta a}_{\left(r,s\right)}={{\widehat{a}}}_{\left(r,s\right)}-{{\check{a}}}_{\left(r,s\right)}\sim {\mathbb{N}}\left(0, {Q}_{{{\widehat{a}}}_{\left(r,s\right)}}\right)$. The ambiguities are highly correlated and the variance–covariance matrix ${Q}_{{{\widehat{a}}}_{\left(r,s\right)}}$ is usually fully populated. A Cholesky’s factorization can normalize the ambiguity residuals concerning their variances. The resulting ambiguity residuals, referred to as “standardized” ambiguity residuals, will then have the identity matrix as their variance–covariance matrix. The normalization procedure is summarized as follows. First, Cholesky decomposition of the variance–covariance matrix as ${Q}_{{{\widehat{a}}}_{\left(r,s\right)}}=G{G}^{\mathrm{T}}$ is applied. The ambiguity residuals ${\Delta a}_{\left(r,s\right)}$ are then transformed using the Cholesky factor $\left(G\right)$ as $\Delta {\stackrel{\sim }{a}}_{\left(r,s\right)}={G}^{-1}{\Delta a}_{\left(r,s\right)}$, with the distribution ${\Delta \stackrel{\sim }{a}}_{\left(r,s\right)}\sim {\mathbb{N}}\left(0,{I}_{n}\right)$. The histogram of the standardized ambiguity residuals $\Delta {\stackrel{\sim }{a}}_{\left(r,s\right)}$ are plotted in Fig. 3.

Fig. 3

Standardized ambiguity residuals. These combined statistics are based on PPP-AR results from 17 CORS selected over 31 consecutive days in 2018

In the case that GNSS observation errors follow a normal distribution, the standardized ambiguity residuals shown in Fig. 3 will also exhibit a standard normal distribution. The MATLAB toolbox function “Distribution filter” was used to determine the actual distribution of the GNSS ambiguity residuals ${\Delta \stackrel{\sim }{a}}_{\left(r,s\right)}$. The $t$-distribution was shown to be a good model for the measurement errors compared with the normal distribution (Madrid 2016). In addition, these distributions are available in MATLAB toolbox function, namely “Distribution filter”. Consequently, they were employed for generating the best-fit PDFs of the GNSS ambiguity residuals. As shown in Fig. 3, the red and blue solid lines are generated, representing the best-fit PDFs of the standard normal distribution in (17) and the t-distribution in (23), respectively. Interestingly, the t-distribution with three degrees of freedoms $\left(\nu \simeq 3\right)$ shown in Fig. 3 provides a better fit compared with the Gaussian distribution for this GNSS data sample.

4.3 Selection of integer candidate sets

The BIE estimator ${{\widehat{a}}}_{\mathrm{BIE}}$, and thus ${{\widehat{b}}}_{\mathrm{BIE}}$, in (18) cannot be computed precisely because of the infinite sum over integers. If the infinite sum is replaced by a sum over a finite set of integers, this might result in a non-integer equivariant estimator. In GNSS applications it is necessary to find an approximate solution of this estimator while retaining the property of integer equivariance. Hence, when implementing (18) in any software package, the size of the integer sets must be set beforehand to reduce computational burden. Similarly, the number of integer candidates must be set in the iFlex method, as this method was initially inspired by the BIE formula under the assumption of Gaussian distribution of errors (shown in Eq. 18). Vollath and Talbot (2013) state that when forming the weighted average of the iFlex method, selecting too many candidate sets does not substantially improve the convergence of the iFlex method, but increases the computational burden. To address this problem they proposed a method to limit the size of integer candidate sets based on applying an empirical threshold (i.e. critical values) to only include candidate sets with significant weight concerning the best (first) integer candidate (the one with the shortest squared-norm distance), such that:

$$\frac{{w}_{{z}_{j}}\left({\widehat{a}}\right)}{{w}_{{z}_{1}}\left({\widehat{a}}\right)}>\gamma $$

(24)

where ${w}_{{z}_{1}}\left({\widehat{a}}\right)$ is the weight of the first candidate set of the ambiguities $\left({z}_{1}\right)$; and ${w}_{{z}_{j}}\left({\widehat{a}}\right)$ represents the weight of the ${j}^{th}$ candidate set. This means that the discarded integer candidate vectors have a weight at least γ times less than the first integer candidate set. Hence, as more integer vectors are required when forming the weighted combination, the smaller the γ value is set in (24). γ is an empirical value and set to 0.001 or 0.01 (Banville 2016; Vollath and Talbot 2013). Introducing (18) into (24) gives the criterion for selecting integer candidate sets for Gaussian, Laplace and Minmax distributions, respectively:

$${\Vert {\widehat{a}}-{z}_{j}\Vert }_{{Q}_{{\widehat{a}}}}^{2}<{\Vert {\widehat{a}}-{z}_{1}\Vert }_{{Q}_{{\widehat{a}}}}^{2}-2\mathrm{ln}(\gamma )$$

(25)

$${\Vert {\widehat{a}}-{z}_{j}\Vert }_{{Q}_{{\widehat{a}}}}^{2}<{\left[\sqrt{{\Vert {\widehat{a}}-{z}_{1}\Vert }_{{Q}_{{\widehat{a}}}}^{2}}-\frac{1}{\alpha }\mathrm{ln}(\gamma )\right]}^{2}$$

(26)

$$\mathrm{max}\left|{\widehat{a}}-{z}_{j}\right|<\left[\mathrm{max}\left|{\widehat{a}}-{z}_{1}\right|-\mathrm{ln}(\gamma )\right]$$

(27)

Since the LAMBDA software can output the estimated integer candidates sorted in ascending order according to corresponding squared norms, with the best candidate first, a minor modification of this software for the BIE analysis was made to select only the number of integer candidate vectors according to equations (25), (26) or (27).

As the ultimate goal of ambiguity resolution is to obtain a better positioning accuracy, the integer candidate selection criterion can be derived based on the positioning parameters. One way to limit the number of integer candidates (16) is by using the differences of the unknown parameters of interest (i.e. receiver’s coordinates) estimated at two consecutive processing steps; so that when the number of integer candidates $\left(g\right)$ and $\left(g-1\right)$ is significantly small use a threshold such as $\upepsilon =\left|{b}_{{\left(X,Y,Z\right)}_{\left(g\right)}}-{b}_{{\left(X,Y,Z\right)}_{\left(g-1\right)}}\right|\le 0.0001$ m to terminate the processing cycle.

4.4 BIE using the multivariant t-distribution

As demonstrated in Sect. 4.2, the PDF of y is more likely to take the form of the t-distribution. Thus, this section will provide further information on how to implement the BIE using the multivariate t-distribution (BIE-td). Two examples will be given to illustrate the procedure of calculating interested unknown parameters (i.e. ambiguity terms or receiver’s coordinates).

We begin with the procedure for implementing the BIE-td and describe them by first substituting (17) into (16):

$${\widehat{\theta }}_{\mathrm{BIE}}=\frac{\sum_{z\in {Z}^{n}}{\int }_{{R}^{p}}\left({l}_{a}^{\mathrm{T}}z+{l}_{b}^{\mathrm{T}}\beta \right){\left[1+\frac{1}{v}{\Vert y-Az-B\beta \Vert }_{{Q}_{y}}^{2}\right]}^{-\frac{v+m}{2}}\mathrm{d}\beta }{\sum_{z\in {Z}^{n}}{\int }_{{R}^{p}}{\left[1+\frac{1}{v}{\Vert y-Az-B\beta \Vert }_{{Q}_{y}}^{2}\right]}^{-\frac{v+m}{2}}\mathrm{d}\beta }$$

(28)

Note that the BIE estimator can also be written as:

$${\widehat{\theta }}_{\mathrm{BIE}}={l}_{a}^{T}{{\widehat{a}}}_{\mathrm{BIE}}+{l}_{b}^{T}{{\widehat{b}}}_{\mathrm{BIE}}$$

(29)

In addition, when applying least-squares adjustment, the term ${\Vert y-Az-B\beta \Vert }_{{Q}_{y}}^{2}$ in (28) will be denoted as:

$${\Vert y-Az-B\beta \Vert }_{{Q}_{y}}^{2}={\Vert A\left({\widehat{a}}-z\right)+B\left({\widehat{b}}-\beta \right)+\widehat{\epsilon }\Vert }_{{Q}_{y}}^{2}={\Vert K\left(z\right)-B\beta \Vert }_{{Q}_{y}}^{2}$$

(30)

with $K\left(z\right)=A\left({\widehat{a}}-z\right)+B{\widehat{b}}+\widehat{\epsilon }$. If one is only interested in the ambiguities and receiver coordinates, the ${{\widehat{a}}}_{\mathrm{BIE}}$ and ${{\widehat{b}}}_{\mathrm{BIE}}$ can be written as:

$${{\widehat{a}}}_{\mathrm{BIE}}=\frac{\sum_{z\in {Z}^{n}}z{\int }_{{R}^{3}}{\left[1+\frac{1}{v}{\Vert K\left(z\right)-B\beta \Vert }_{{Q}_{y}}^{2}\right]}^{-\frac{v+m}{2}}\mathrm{d}\beta }{\sum_{z\in {Z}^{n}}{\int }_{{R}^{3}}{\left[1+\frac{1}{v}{\Vert K\left(z\right)-B\beta \Vert }_{{Q}_{y}}^{2}\right]}^{-\frac{v+m}{2}}\mathrm{d}\beta }={\sum }_{z\in {Z}^{n}}z{w}_{z}\left(y\right)$$

(31)

$${{\widehat{b}}}_{\mathrm{BIE}}=\frac{\sum_{z\in {Z}^{n}}{\int }_{{R}^{3}}\beta {\left[1+\frac{1}{v}{\Vert K\left(z\right)-B\beta \Vert }_{{Q}_{y}}^{2}\right]}^{-\frac{v+m}{2}}\mathrm{d}\beta }{\sum_{z\in {Z}^{n}}{\int }_{{R}^{3}}{\left[1+\frac{1}{v}{\Vert K\left(z\right)-B\beta \Vert }_{{Q}_{y}}^{2}\right]}^{-\frac{v+m}{2}}\mathrm{d}\beta }$$

(32)

with the weighting factor ${w}_{{z}_{j}}\left(y\right)=\frac{{\int }_{{R}^{3}}{\left[1+\frac{1}{v}{\Vert K\left(z\right)-B\beta \Vert }_{{Q}_{y}}^{2}\right]}^{-\frac{v+m}{2}}\mathrm{d}\beta }{\sum_{z\in {Z}^{n}}{\int }_{{R}^{3}}{\left[1+\frac{1}{v}{\Vert K\left(z\right)-B\beta \Vert }_{{Q}_{y}}^{2}\right]}^{-\frac{v+m}{2}}\mathrm{d}\beta }\le 1$, $\forall {z}_{j}\in {Z}^{n}$, satisfying ${\sum }_{z\in {Z}^{n}}{w}_{z}\left(y\right)=1$. $\beta ={\left[{\beta }_{1}, {\beta }_{2},{\beta }_{3}\right]}^{\mathrm{T}}$ are the three-dimensional coordinate components (X, Y and Z respectively) of a single receiver. ${w}_{{z}_{j}}\left(y\right)$ is an integral function evaluated from lower limit of $\beta$ to upper limit of $\beta$.

Unlike the use of BIE in the normal distribution case as shown in (18), the ambiguities and the three-dimensional coordinate components can be calculated separately. In particular, the updated receiver’s coordinates ${({\widehat{b}}}_{\mathrm{BIE}})$ can be computed using (32) by adding every integer candidate to its summation. In fact, as the ultimate goal of ambiguity resolution is to obtain a high positioning accuracy, it is necessary to eliminate an intermediate step (i.e. ambiguity resolution using (31)). When using (32), the empirical criterion such as gamma $\left(\gamma \right)$ as shown in (24) is not suitable for selecting integer candidate due to the presence of the variable $\beta$ on the numerator. Instead, the proposed criterion based on position (Sect. 4.3) can be applied to select integer candidates.

Assume that the range of $\beta$ was set from -infinite (-Inf) to + infinite (Inf) in the MATLAB-based GNSS PPP software and the degrees of freedoms $\left(\nu \right)$ of the $t$-distribution was set as three (as discussed in Sect. 4.2). The same one-hour GNSS session used in Sect. 3.3 was then reprocessed using the BIE-td. Table 3 shows updated vector of corrections $\left(\delta X,\delta Y\,\text{and}\,\delta Z\right)$ to the station position (X, Y, and Z) when adding every integer candidate to Eq. (32). The last column is the Euclidean norm of the vector corrections to receiver’s coordinates, which can be used to terminate the processing cycle. As can be seen from the table, if a threshold such as $\upepsilon =\left|{\delta D}_{{\left(X,Y,Z\right)}_{\left(50\right)}}-{\delta D}_{{\left(X,Y,Z\right)}_{\left(49\right)}}\right|\le 0.0001$ m is set, 50 integer candidates are required for the BIE-td computation, whereas more integer candidates (53 and 56) are required for the Laplace or Minmax distribution cases, respectively, using the empirical criterion $\left(\gamma =0.001\right)$.

Table 3 Three-dimensional coordinate corrections of a single receiver of BIE using $t$-distribution at the 300th epoch

If one is interested in the ambiguities, Table 4 represents the weighting function of BIE-td at the 100th and 300^th epochs. In general, an important characteristic of BIE-td weights is that it is similar to those of the mathematically non-rigorous Laplace or Minmax distribution cases, as shown in (19) and (20) respectively. Spreading out the weights for other candidates by using these broadened distributions is one way to minimize wrong fixing of ambiguities.

Table 4 Weighting function of BIE using $t$-distribution at the 100th and 300th epochs

Although the BIE solutions (i.e. BIE-td or iFlex) concentrate on the whole ambiguity vector and not just a subset of it, the nature and mechanism of these methods can be categorized as a PAR approach. Consider eight integer candidates to calculate the BIE solutions, with ten ambiguities in each integer vector. Furthermore, assuming that the first five out of ten ambiguities have exactly the same integer value for all eight integer candidates, one can then obtain a subset of the five of ten fixed ambiguities using the BIE-td or iFlex method.

5 Performance analysis of PPP results

The focus in this section is to validate the correctness of the proposed BIE-td method against the existing methods presented in Sect. 3. In addition, we aim to also verify the Trimble authors’ claim whether a reliable ambiguity resolution result can be achieved using the iFlex method. To investigate the impact of different AR methods on PPP convergence, the triple-frequency (GPS + BeiDou) and quad-frequency (Galileo) measurements were processed using three different AR methods: (a) the PAR-Ps method; (b) the iFlex method using two different weighting functions in (19) and (20), referred to as “iFlex-Laplace” and “iFlex-Minmax”, respectively; and (c) BIE estimation (see 16) with GNSS data errors assumed to follow the t-distribution (BIE-td). Note that the AR performance of the BIE method for the Gaussian case is very similar to the PAR-Ps method, as shown in Sect. 3.3. Thus, two different weighting functions in (19) and (20) were assumed for the iFlex method.

The convergence time was used to evaluate the performance of the different AR methods. The convergence in these PPP-AR comparisons means that the position estimates steadily approach a specific accuracy level, and do not deviate from this level after reaching it. Statistical measures such as root-mean-square error (RMSE) and percentiles are computed based on the differences between the “known” coordinates of the 17 stations and the PPP-AR solutions. The t-distribution with 3 degrees of freedom was used because it was a better fit for this GNSS data sample analysis (see Sect. 4.2). Table 5 lists the critical values for the AR methods used.

Table 5 Threshold values for ambiguity resolution methods

5.1 PAR-based LAMBDA and iFlex method

This section compares the performance of partial ambiguity resolution-based LAMBDA method (PAR-Ps) with the iFlex method using settings listed in Tables 2 and 5. Figure 4 and Table 6 show the 68th and 99th percentiles for the RMSEs calculated from these two ambiguity estimators. Note that two different weighting functions (Laplace and Minmax) for the iFlex method were included in the analyses. The 68th percentile curves highlight the benefit of the iFlex method, which converges to 0.1 m (for the horizontal component) and 0.2 m (for the vertical component) in about 10 min. The PAR-Ps method requires 17 and 11 min to reach the same level of accuracy, respectively. In the 99th percentile curves, both the iFlex and the PAR-Ps methods have improved horizontal positioning accuracy and shorter convergence time compared with the float solution. In addition, the iFlex method has a slight advantage over the PAR-Ps method in the case of horizontal component. However, the iFlex method has a significant advantage over the float and the PAR-Ps method in the case of the vertical component. The vertical error in the PAR-Ps case is not stable until the 40-min mark. This is caused by several sessions with incorrectly fixed ambiguities, resulting in a large position error. This again confirms the limitation of using PAR-Ps method. Specifically, setting a high threshold for the success rate in the PAR-Ps method does not guarantee correct fixing of ambiguities because its success rate is driven by the underlying model and not by the actual measurements (Teunissen and Verhagen 2008). Significantly, the horizontal and vertical position solutions require 40 min to converge to within 0.1 m and 0.2 m, respectively. When compared with the PAR-Ps method, the iFlex method had an improved convergence time of about 10 min.

Fig. 4

Time series of 68th (top) and 99th (bottom) percentile of the horizontal and vertical errors based on the combined GPS + Galileo + BeiDou (G + E + C) measurements used for two different PPP-AR methods, namely the iFlex method and the PAR-based LAMBDA method (PAR-Ps). The blue and magenta solid line represents the results of the iFlex method using Laplace and Minmax, respectively. The dashed red line refers to the PAR-Ps results. The black line illustrates the float solution. The RMS statistics are based on the PPP-AR results from all reference stations selected over all consecutive days. The horizontal and vertical errors with a y-axis maximum limit of 0.5 m (68th-top), and horizontal and vertical errors with y-axis maximum limits of 1 m (99th-bottom), respectively

Table 6 Positioning convergence time with combined results from seventeen selected stations: iFlex methods and PAR-Ps

5.2 BIE estimation using ${\varvec{t}}$-distribution and iFlex methods

In the previous section it can be seen that the numerical results indicated that the iFlex method outperformed the PAR-Ps method due to shorter solution convergence times. In this subsection the AR performance of the iFlex method was compared with the BIE estimation using the t-distribution (BIE-td). Again, two different weighting functions for the iFlex method (Laplace and Minmax) together with the settings as per Table 5 were considered. As discussed in Sect. 4.1, the BIE estimation in (16) can be used with a Kalman filter in which: (a) only a dynamic model was applied for the ambiguities; and (b) no dynamic models were applied for the remaining unknown parameters. For both the iFlex and BIE-td estimation methods, the ambiguities were assumed time-constant and the remaining unknown parameters (i.e., ionosphere, troposphere and receiver’s coordinates) were considered uncorrelated in time.

Figure 5 and Table 7 show the 68th and 99th percentiles of the RMSEs calculated with these two ambiguity estimators. Overall, the two different AR methods have very similar positioning errors. In the 68th percentile, the BIE-td gains a slight advantage over the iFlex method. Both methods converge to 0.1 m (horizontal component) and 0.2 m (vertical component) in about 10 min. The 99th percentile curves confirm these findings. The two methods have similar performance for the horizontal and vertical position components. That is, the horizontal and vertical position solutions require nearly 50 min to converge to within 0.1 m and 0.2 m, respectively. This is an improvement over an ambiguity float solution where at least more than 60 min is required to reach the same level of accuracy.

Fig. 5

Time series of 68th (top) and 99th (bottom) percentile of the horizontal and vertical errors based on the combined GPS + Galileo + BeiDou (G + E + C) measurements used for two different PPP-AR methods, namely the BIE estimator (BIE-td) and the iFlex methods. The red and magenta dashed line represents the results for the iFlex method using Laplace and Minmax function, respectively. The solid blue line refers to the BIE-td solutions. The black line illustrates the float solution. These combined RMS statistics are based on the PPP-AR results from all reference stations selected over all consecutive days. The horizontal and vertical error with a y-axis maximum limit of 0.5 m (68th-top), and horizontal and vertical errors with y-axis maximum limits of 1 m (99th-bottom), respectively. The notation “w/d” in the legend means without using any dynamic models for the unknown parameters, except for the ambiguities

Table 7 Positioning convergence time with combined results from seventeen selected stations: BIE-td and iFlex methods

To evaluate the computational performance using different partial ambiguity resolution methods, we implemented the iFlex and BIE-td method given in Sects. 3 and 4 in MATLAB. In addition, we performed numerical simulations to compare the CPU running time of PAR-Ps, iFlex and BIE-td methods. The LAMBDA MATLAB, version 3.0 package, which is available from the GNSS Research Centre at Curtin University (http://gnss.curtin.edu.au/research/lambda-and-ps-lambda-software-packages/). All computations were performed in MATLAB R2020a on an Intel dual core i7-9750, 2.6 GHz PC with 32 GB memory running Windows 10 64-bit Professional. Significantly, the computational time using the iFlex methods and the BIE-td are approximately 3–4 times and 10 times longer than that using PAR-Ps, respectively (see Table 8). In fact, the results of the BIE-td method involved a recursive calculation of integral functions, as shown in (16). As a result, both the iFlex and BIE-td methods take longer computational time compared to the PAR-Ps method as implemented in the PPP-AR software. The computational time as presented in Table 8 can be reduced significantly when the different partial ambiguity resolution algorithms such as BIE-td or iFlex method are written in C or C++ programming language. The reason is that C/C++ language usually has higher speed performance in terms of data processing compared to MATLAB.

Table 8 Computational time for each single one-hour session using different partial ambiguity resolution methods

6 Concluding remarks

New-generation GNSS satellites offer additional signal frequencies for measurements that facilitate improved solution convergence time in PPP solutions. In multi-frequency and multi-GNSS scenarios, there is a need for quick and reliable ambiguity resolution to improve the GNSS receiver position solution. In this contribution, that authors assessed three different carrier-phase ambiguity resolution methods for reliable multi-frequency multi-GNSS PPP, namely: the PAR-based LAMBDA method (PAR-Ps), the iFlex method, and the BIE estimation using the t-distribution (BIE-td). Thirty-one days of real GNSS measurements collected from 17 globally distributed GNSS stations in 2018 were processed to determine the best-fit distribution of the GNSS ambiguity residuals. It was concluded that the t-distribution with three degrees of freedoms provided a better fit than the Gaussian distribution for this GNSS data sample. A new method to select integer candidates was proposed based on the differences of the unknown parameters of interest (i.e., receiver’s coordinates) determined at two consecutive processing steps. If the differences over two consecutive steps were smaller than a threshold of 0.0001 m, the calculation was terminated. It has been demonstrated that the BIE-td method or the non-rigorous iFlex’s algorithms are categorized as a PAR approach to provide a reliable multi-frequency and multi-GNSS PPP solution. Analysis of another 30-day GNSS measurement set collected in 2019 from the same CORS confirmed that the iFlex method outperformed the PAR-Ps method and float solution by minimizing position errors in a simulated kinematic test. When compared with the PAR-Ps method for the 99th percentile of errors, the iFlex method had shortened the convergence time to about 10 min. In addition, without applying dynamic constraints on all parameters except that the ambiguities were estimated as time-constants, the BIE-td and the iFlex methods had similar positioning accuracy, for both the horizontal and vertical position components. With an improved accuracy of the Galileo and BeiDou satellite correction products, provision of precise atmospheric delay corrections, and, in the near future, a likely increase in the number of multi-frequency multi-GNSS satellites (and hence better satellite geometry), faster PPP centimeter-level solutions can be achieved.