A stochastic Stackelberg differential reinsurance and investment game with delay in a defaultable market

Abstract

In this paper, we investigate a stochastic Stackelberg differential reinsurance and investment game problem with delay for a reinsurer and an insurer in a defaultable market, which consists of a risk-free asset, a risky asset and a defaultable bond. As the leader, the reinsurer can determine reinsurance premium price and investment strategy to maximize the expected exponential utility of its terminal wealth with delay. As the follower, the insurer can select reinsurance proportion and investment strategy to maximize the expected exponential utility of its terminal wealth with delay. By using the idea of backward induction and the dynamic programming approach, we solve the leader’s and follower’s optimization problems sequentially and derive the Stackelberg equilibrium strategy explicitly. Then, we provide the corresponding verification theorem. Finally, we present some numerical examples to illustrate the influence of model parameters on the equilibrium strategy and draw some economic interpretations from these results. We find that the pre-default value functions are higher than the post-default value functions and the influence of delay weight on equilibrium strategy depends on the length of delay time. Moreover, when the Stackelberg equilibrium is achieved in the interior case, the optimal reinsurance premium follows the variance premium principle and the influence of delay weight on the optimal reinsurance premium strategy is just opposite to that on other strategies.

1 Introduction

Reinsurers and insurers, as special financial institutions, not only face the investment risk in the financial market, but also face the risk of future random claims in the insurance market. The study of optimal reinsurance and investment problem has become a hot issue in actuarial and mathematical finance research. The existing literature is mainly based on a single perspective of the insurer, while the interest of the reinsurer is often ignored. For example, Browne (1995), Bai and Guo (2008), Li et al. (2012), Yi et al. (2013), Bensoussan et al. (2014), Liang et al. (2016), Hu et al. (2018), Zhou et al. (2019), Zhou et al. (2019) and so on. Since any reinsurance contract is obviously a mutual agreement between the insurer and the reinsurer, a reinsurance strategy that only considers the interest of one party may be unacceptable to the other party. To address this problem, we investigate the reinsurer’s premium pricing and investment optimization problem as well as insurer’s reinsurance-investment optimization problem.

The existing literature on two-party optimization problems is generally carried out under the framework of game, such as zero-sum game (e.g., Zeng (2010), Taksar and Zeng (2011), Li et al. (2015), etc.) and non-zero-sum game (e.g., Bensoussan et al. (2014), Meng et al. (2015), Guan and Liang (2016), Zhou et al. (2021), etc.). However, both parties considered in the above literature are insurers, and the interest of the reinsurer is not considered. Under utility maximization criteria, Chen and Shen (2018) first constructed a Stackelberg stochastic differential game model to analyze optimal reinsurance problem from joint interests of the insurer and the reinsurer. By solving the optimization problems of both parties in turn, they obtained the optimal premium price strategy and the optimal retained proportion under special circumstances. Based on this study, many literatures have conducted extensive research in different market environments, such as, Chen and Shen (2019), Bai et al. (2020), Bai et al. (2021), etc. In view of the more extensive investment channels of insurance funds, this paper studies a stochastic Stackelberg differential reinsurance and investment game problem for a reinsurer and an insurer in the defaultable market.

Although the default risk has been understood as one of the significant trigger of the global credit crisis, defaultable bonds are still sought after because of the relative high profits. With respect to maximizing the expected utility of the terminal wealth, Bielecki and Jang (2006) studied a portfolio optimization problem with a defaultable security; Zhu et al. (2015) analyzed the optimal proportional reinsurance and investment problem in a defaultable market under the Heston’s stochastic volatility model. Deng et al. (2018) derived the Nash equilibrium reinsurance-investment policy with default risk under the non-zero-sum game framework. More studies on defaultable bond can be found in Zhao et al. (2016), Li et al. (2017) and Wang et al. (2019a) and so on.

Traditionally, the optimal reinsurance-investment decision-making problem based on current information has been studied, ignoring the past wealth performance. However, the decisions of managers often depend on the past information in the real system, and delays arise naturally. It would be more practical to consider such a delay period. Recently, delay has been explicitly discussed in the literature on stochastic control (e.g., Chang et al. (2011), Federico (2011), Shen and Zeng (2014), Wang et al. (2019b), etc.). With the optimality criterion of maximizing the expected exponential utility of the combination of terminal wealth and average performance wealth, Chunxiang and Li (2015) and Chunxiang et al. (2018) studied optimal investment and excess-of-loss reinsurance problems with delay. Motivated by the above studies, we consider the wealth processes with delay to characterize the bounded memory feature in the framework of stochastic Stackelberg differential game.

The main work of this study is summarized as follows. We build a stochastic Stackelberg differential reinsurance and investment game model between a reinsurer and an insurer. Both of the insurer and the reinsurer can invest their wealth in a defaultable market. Moreover, we consider the wealth processes with delay. By using the idea of backward induction and the dynamic programming approach, we solve the reinsurer’s and insurer’s optimization problems sequentially, and derive the Stackelberg equilibrium reinsurance-investment strategy and value functions explicitly. Then, we prove the corresponding verification theorem, and analyze the properties of the equilibrium strategy and value functions. Finally, we provide some numerical simulations and sensitivity analysis to show the impact of the model parameters on the Stackelberg equilibrium strategy and verify our theoretical results. We have the following findings. Firstly, we find the pre-default value functions are higher than the post-default value functions and the difference between two cases stands for the loss in objectives due to the default event. Secondly, if the proportional reinsurance is applied, the variance premium principle is an ideal candidate among all possible premium principles when the equilibrium is achieved in the interior case. Thirdly, the influence of delay weight on equilibrium strategy depends on the length of delay time, and the influence of delay weight on the equilibrium reinsurance premium strategy is opposite to that on other strategies.

Different from the existing literature, this paper has the following contributions. (1) We first consider the default risk in the framework of stochastic Stackelberg differential reinsurance and investment game model. (2) Compared with the existing research on the stochastic Stackelberg differential game in the field of actuarial and strategic optimization, we consider not only the reinsurance game between the reinsurer and the insurer, but also the optimal investment problem. (3) We consider the delay factor in the Stackelberg game model to characterize the bounded memory feature of wealth processes.

The remainder of this paper is organized as follows. In Sect. 2, we construct a stochastic Stackelberg differential reinsurance and investment game model considering the default risk and delay. In Sect. 3, we derive the Stackelberg equilibrium reinsurance-investment strategy and value functions explicitly and prove the corresponding verification theorem. In Sect. 4, we give some numerical examples to illustrate the influence of model parameters on the Stackelberg equilibrium strategy and draw some economic interpretations. Finally, we summarize the conclusions of this paper.

2 Model setup

In this section, we describe the model in details. Let [0, T] be a finite time horizon, over which reinsurance and investment activities can occur. The uncertainty in markets is represented by a probability space $\left( \Omega ,{\mathcal {F}},{\mathbb {P}}\right)$, where ${\mathbb {P}}$ is the real world probability measure; ${\mathcal {F}}=\left\{ {\mathcal {F}}_t\right\} _{t\ge 0}$ is the right-continuous, ${\mathbb {P}}$-complete filtration generated by two standard Brownian motions W(t) and $W_F(t)$. We assume that W(t) and $W_F(t)$ are independent of each other. We denote by ${\mathcal {H}}=\left\{ {\mathcal {H}}_t\right\} _{t\ge 0}$ the filtration of a default process, which is driven by a Poisson process. We assume that ${\mathcal {H}}$ and ${\mathcal {F}}$ are independent of each other. Let ${\mathcal {G}}=\left\{ {\mathcal {G}}_t\right\} _{t\ge 0}$ be the enlarged filtration of ${\mathcal {F}}$ and ${\mathcal {H}}$, i.e., ${\mathcal {G}}_t={\mathcal {F}}_t\vee {\mathcal {H}}_t$.

2.1 Dynamics of the financial assets

We consider a financial market that consists of a risk-free asset, a risky asset (i.e., a stock) and a corporate zero coupon bond that is defaultable. The price process of the risk-free asset, $\{S_0(t)\}_{t\ge 0}$, is given by the following ordinary differential equation (ODE):

$$\begin{aligned} dS_0(t)=r_0S_0(t)dt,\quad S_0(0)=1, \end{aligned}$$

(2.1)

where $r_0>0$ is the constant risk-free interest rate. The stock price process, $\{S(t)\}_{t\ge 0}$, follows a constant elasticity of variance (CEV) model (refer to Cox and Ross (1976), Emanuel and Macbeth (1982) and Gu et al. (2010)):

$$\begin{aligned} dS(t)=S(t)\left[ rdt+\sigma S^\beta (t) dW(t)\right] ,\quad S(0)=s_0, \end{aligned}$$

(2.2)

where r, $\sigma S^\beta (t)$ and $\beta$ denote the expected return rate, the volatility and the constant elasticity parameter of the risky asset, respectively; $r>r_0$, $\sigma >0$. $\beta$ is a constant parameter. As in Emanuel and Macbeth (1982) and Gu et al. (2010), we assume $\beta \ge 0$ to keep the stock price process positive. If $\beta =0$, the CEV model reduces to the geometric Brownian motion (GBM) model. If $\beta >0$, the volatility $\sigma S^\beta (t)$ increases as the stock price increases.

Referring to Chapter 5 and Chapter 8 in Bielecki and Rutkowski (2002), we adopt the reduced-form approach to modeling the default risk. Assume $T_1>T$ is the maturity date of the defaultable bond and the default time is denoted by $\tau$ which is a nonnegative random variable and the first jump time of a Poisson process with constant intensity $h^P>0$ under the real world probability measure ${\mathbb {P}}$. Define the default process by $H(t)={\mathbf {I}}_{\{\tau \le t\}}$, where ${\mathbf {I}}$ denotes the indicator function that equals one if there exists a jump and zero otherwise. Then, $H(t)=0$ and $H(t)=1$ correspond to the pre-default case ${\{\tau > t\}}$ and the post-default case ${\{\tau \le t\}}$, respectively.

Assume that the investor would recover a fraction of the market value of the defaultable bond prior to default and the value of the defaultable bond after default is zero. Then, we use $0<\zeta \le 1$ to denote the constant loss rate when a default occurs, and $1-\zeta$ is the default recovery rate. According to Bielecki and Jang (2006), Zhu et al. (2015), Zhao et al. (2016) and Wang et al. (2019a), the dynamics of the defaultable bond price, $\{S_1(t,T_1)\}_{t\ge 0}$, under measure ${\mathbb {P}}$ is given by the following stochastic differential equation (SDE):

$$\begin{aligned} dS_1(t,T_1)=S_1(t-,T_1)\left[ r_0dt+(1-H(t-))\eta (1-\Delta )dt-(1-H(t-))\zeta dM^P(t)\right] , \end{aligned}$$

(2.3)

where

$$\begin{aligned} M^P(t)=H(t)-\int _0^t(1-H(u-))h^Pdu \end{aligned}$$

(2.4)

is a ${\mathcal {G}}$-martingale under ${\mathbb {P}}$; $\frac{1}{\Delta }=\frac{h^Q}{h^P}$ denotes the default risk premium; $h^Q$ is the default intensity under the risk-neutral measure ${\mathbb {Q}}$; $\eta =h^Q\zeta$ denotes the credit spread. Duffie and Singleton (2003) indicated that the probability of default occurring under risk-neutral measure ${\mathbb {Q}}$ is higher than that under the real world probability measure ${\mathbb {P}}$. Therefore, we assume that $\frac{1}{\Delta }\ge 1$ throughout this paper.

2.2 Dynamics of the surplus processes

We consider an insurance market that consists of one huge reinsurer and one small insurer. For the convenience of calculation, we use the diffusion approximation model proposed by Grandell (1990) to describe the surplus process. The surplus process of the insurer, $\{X_F(t)\}_{t\ge 0}$, is denoted by

$$\begin{aligned} dX_F(t)&=c_Fdt-\lambda _F\mu _Fdt+\sqrt{\lambda _F({\tilde{\sigma }}_F)^2}dW_F(t),\quad X_F(0)=x_F^0, \end{aligned}$$

(2.5)

where $x_F^0>0$ is the insurer’s initial surplus, $c_F\ge 0$ is the premium rate, $\lambda _F>0$ is the claim intensity, $0<\mu _F<+\infty$ and $({\tilde{\sigma }}_F)^2<+\infty$ are the first moment and second moment of the claim size, respectively. The insurance premium rate $c_F$ is assumed to be determined by the expected value premium principle, i.e., $c_F=(1+\theta _F)\lambda _F\mu _F$, where $\theta _F>0$ is the insurer’s safety loading.

The insurer can purchase proportional reinsurance protection continuously from the reinsurer to manage its claim risks. Denote $\{q(t),t\ge 0\}$ the reinsurance strategy of the insurer, where $q(t)\in [0,1]$. Then, the reinsurer will cover $(1-q(t))100\%$ of the claims while the insurer will cover the remaining at time t. The price of the reinsurance premium at time t is $p(t)\in [c_F,{\bar{c}}]$, where ${\bar{c}}=(1+{\bar{\theta }})\lambda _F\mu _F$, ${\bar{\theta }}$ is an upper bound of the reinsurer’s relative safety loading and satisfies ${\bar{\theta }}>\theta _F$. The larger safety loading aims at avoiding cheap reinsurance, in which case the insurer transfers the complete risk and still earns something. Introducing proportional reinsurance strategy q(t) into Eq. (2.5), then

$$\begin{aligned} dX_F(t) =[\theta _Fa-(p(t)-a)(1-q(t))]dt+q(t)\sigma _FdW_F(t), \end{aligned}$$

(2.6)

where $a=\lambda _F\mu _F$, $\sigma _F=\sqrt{\lambda _F({\tilde{\sigma }}_F)^2}$. The surplus process of the reinsurer associated to this contract with the above insurer, $\{X_L(t)\}_{t\ge 0}$, can be expressed:

$$\begin{aligned} dX_L(t) =(p(t)-a)(1-q(t))dt+(1-q(t))\sigma _FdW_F(t),\quad X_L(0)=x_L^0, \end{aligned}$$

(2.7)

where $x_L^0>x_F^0$. In other words, the huge reinsurer has more initial wealth than the small insurer.

2.3 Wealth processes with delay and default risk

In this paper, we assume that the insurer and the reinsurer can invest in the risk-free asset, the stock and the corporate zero coupon bond continuously. Suppose that there are no transaction costs or taxes for investment and reinsurance; short-selling of the risky asset is allowed; the corporate bond is not traded after default, and these investments are not enough to affect the prices of the stock and defaultable bond. The investment horizon is [0, T] and $T<T_1$. Let $b_F(t)$ and $b_L(t)$ represent the dollar amount that the insurer and the reinsurer invest in the stock at time t, respectively. Let $b_{F1}(t)$ and $b_{L1}(t)$ represent the dollar amount that the insurer and the reinsurer invest in the corporate bond at time t, respectively. Then, the remaining wealth $X_F^{\pi _F}(t)-b_F(t)-b_{F1}(t)$ and $X_L^{\pi _L}(t)-b_L(t)-b_{L1}(t)$ are invested in the risk-free asset. Let $\pi _F(t)=(q(t),b_F(t),b_{F1}(t))$ and $\pi _L(t)=(p(t),b_L(t),b_{L1}(t))$. Thus, in the defaultable financial market described above, the wealth processes of the insurer and the reinsurer are given by (2.8) and (2.9), respectively.

$$\begin{aligned} dX_F^{\pi _F}(t) =&\frac{X_F^{\pi _F}(t)-b_F(t)-b_{F1}(t)}{S_0(t)}dS_0(t)+\frac{b_F(t)}{S(t)}dS(t) +\frac{b_{F1}(t)}{S_1(t-,T_1)}dS_1(t,T_1)\nonumber \\&+[\theta _Fa-(p(t)-a)(1-q(t))]dt+q(t)\sigma _FdW_F(t)\nonumber \\ =&\big [\theta _Fa-(p(t)-a)(1-q(t))+r_0X_F^{\pi _F}(t)\nonumber \\&+(r-r_0)b_F(t) +(1-H(t-))\eta (1-\Delta )b_{F1}(t)\big ]dt\nonumber \\&+q(t)\sigma _FdW_F(t)+b_F(t)\sigma S^\beta (t) dW(t)-b_{F1}(t)(1-H(t-))\zeta dM^P(t), \end{aligned}$$

(2.8)

$$\begin{aligned} dX_L^{\pi _L}(t)=&\frac{X_L^{\pi _L}(t)-b_L(t)-b_{L1}(t)}{S_0(t)}dS_0(t)+\frac{b_L(t)}{S(t)}dS(t) +\frac{b_{L1}(t)}{S_1(t-,T_1)}dS_1(t,T_1)\nonumber \\&+(p(t)-a)(1-q(t))dt+(1-q(t))\sigma _FdW_F(t)\nonumber \\ =&\left[ (p(t)-a)(1-q(t))+r_0X_L^{\pi _L}(t)\nonumber \right. \\&\left. +(r-r_0)b_L(t)+(1-H(t-))\eta (1-\Delta )b_{L1}(t)\right] dt\nonumber \\&+(1-q(t))\sigma _FdW_F(t)+b_L(t)\sigma S^\beta (t) dW(t)-b_{L1}(t)(1-H(t-))\zeta dM^P(t). \end{aligned}$$

(2.9)

In fact, due to the bounded memory characteristic, the decisions of the reinsurer and the insurer depend on the exogenous capital instantaneous inflow into or outflow from current wealth. Motivated by Chunxiang and Li (2015), we consider the wealth processes with delay. Let $Y_F(t)$ and $Z_F(t)$ be the integrated and pointwise delayed information of the insurer’s wealth in the past horizon $[t-h_F,t]$, respectively. Correspondingly, the integrated and pointwise delayed information of the reinsurer in the time interval $[t-h_L,t]$ is denoted as $Y_L(t)$ and $Z_L(t)$, respectively. That is, for $\forall t\in [0,T]$,

$$\begin{aligned} Y_F(t)&=\int _{-h_F}^0e^{\alpha _F s}X_F^{\pi _F}(t+s)ds,\quad Z_F(t)=X_F^{\pi _F}(t-h_F), \end{aligned}$$

(2.10)

$$\begin{aligned} Y_L(t)&=\int _{-h_L}^0e^{\alpha _L s}X_L^{\pi _L}(t+s)ds,\quad Z_L(t)=X_L^{\pi _L}(t-h_L), \end{aligned}$$

(2.11)

where $\alpha _L\ge 0$ and $\alpha _F\ge 0$ are average parameters; $h_L>0$ and $h_F>0$ are delay time parameters. Let $f_F(t,X_F^{\pi _F}(t)-Y_F(t),X_F^{\pi _F}(t)-Z_F(t))$ and $f_L(t,X_L^{\pi _L}(t)-Y_L(t),X_L^{\pi _L}(t)-Z_L(t))$ represent the capital inflow/outflow amount of the insurer and the reinsurer, respectively; where $X_F^{\pi _F}(t)-Y_F(t)$, $X_L^{\pi _L}(t)-Y_L(t)$ represent the average performance and $X_F^{\pi _F}(t)-Z_F(t)$, $X_L^{\pi _L}(t)-Z_L(t)$ represent the absolute performance. To make the problem solvable, we assume

$$\begin{aligned} f_F(t,X_F^{\pi _F}(t)-Y_F(t),X_F^{\pi _F}(t)-Z_F(t))&=B_F(X_F^{\pi _F}(t)-Y_F(t))+C_F(X_F^{\pi _F}(t)-Z_F(t)),\\ f_L(t,X_L^{\pi _L}(t)-Y_L(t),X_L^{\pi _L}(t)-Z_L(t))&=B_L(X_L^{\pi _L}(t)-Y_L(t))+C_L(X_L^{\pi _L}(t)-Z_L(t)), \end{aligned}$$

where $B_F$, $C_F$, $B_L$ and $C_L$ are nonnegative constants. In other words, the amount of the capital inflow/outflow is the linear weighted sum of the average performance and the absolute performance. Then, considering capital inflow/outflow functions $f_F(t,X_F^{\pi _F}(t)-Y_F(t),X_F^{\pi _F}(t)-Z_F(t))$ and $f_L(t,X_L^{\pi _L}(t)-Y_L(t),X_L^{\pi _L}(t)-Z_L(t))$, the wealth processes of the insurer and the reinsurer are governed by the following stochastic differential delay equations (SDDEs), respectively:

$$\begin{aligned} dX_F^{\pi _F}(t) =&\big [\theta _Fa-(p(t)-a)(1-q(t))+A_FX_F^{\pi _F}(t)+B_FY_F(t)+C_FZ_F(t)+(r-r_0)b_F(t)\nonumber \\&+(1-H(t-))\eta (1-\Delta )b_{F1}(t)\big ]dt+q(t)\sigma _FdW_F(t)\nonumber \\&+b_F(t)\sigma S^\beta (t) dW(t)-b_{F1}(t)(1-H(t-))\zeta dM^P(t), \end{aligned}$$

(2.12)

$$\begin{aligned} dX_L^{\pi _L}(t) =&\big [(p(t)-a)(1-q(t))+A_LX_L^{\pi _L}(t)+B_LY_L(t)+C_LZ_L(t)+(r-r_0)b_L(t)\nonumber \\&+(1-H(t-))\eta (1-\Delta )b_{L1}(t)\big ]dt+(1-q(t))\sigma _FdW_F(t)\nonumber \\&+b_L(t)\sigma S^\beta (t) dW(t)-b_{L1}(t)(1-H(t-))\zeta dM^P(t), \end{aligned}$$

(2.13)

where $A_F=r_0-B_F-C_F$ and $A_L=r_0-B_L-C_L$. In addition, we assume that the insurer is endowed with the initial wealth $x_F^0$ at time $-h_F$ and does not start the business (insurance/reinsurance/investment) until time 0, i.e., $X_F^{\pi _F}(t)=x_F^0,\forall t\in [-h_F,0]$. Correspondingly, suppose that $X_L^{\pi _L}(t)=x_L^0>0,\forall t\in [-h_L,0]$. Then, $Y_F(0)=\frac{x_F^0}{\alpha _F}(1-e^{-\alpha _Fh_F})$ and $Y_L(0)=\frac{x_L^0}{\alpha _L}(1-e^{-\alpha _Lh_L})$.

For any fixed $t\in [0,T]$, denote $X_L^{\pi _L}(t)=x_L$, $X_F^{\pi _F}(t)=x_F$, $Y_L(t)= y_L$, $Y_F(t)=y_F$, $Z_L(t)=z_L$, $Z_F(t)=z_F$, $S(t)=s$ and $H(t)=h$. Then, we define the admissible strategy as follows.

Definition 1

(Admissible strategy) $\pi (\cdot )=\pi _L(\cdot )\times \pi _{F}(\cdot ) =(p(\cdot ),b_L(\cdot ),b_{L1}(\cdot ))\times (q(\cdot ),b_{F}(\cdot ),b_{F1}(\cdot ))$ is said to be admissible, if

• (i) $\{\pi _L(t)\}_{t\in [0,T]}$ and $\{\pi _{F}(t)\}_{t\in [0,T]}$ are ${\mathcal {G}}$-progressively measurable processes, such that $p(t)\in [c_F,{\bar{c}}]$ and $q(t)\in [0,1]$ for any $t\in [0,T]$;

• (ii) $E\big [\int _t^T[(b_L(\ell ))^2(S^\beta (\ell ))^2+(b_{L1}(\ell ))^2]d\ell \big ]<+\infty$ and $E\big [\int _t^T[(b_F(\ell ))^2(S^\beta (\ell ))^2+(b_{F1}(\ell ))^2]d\ell \big ]<+\infty$, $\forall \ell \in [t,T]$;

• (iii) the state equation (2.13) associated with $\pi _L(\cdot )$ has a unique strong solution, which satisfies

  $\{E_{t,x_L,y_L,s,h}[\sup |X_L^{\pi _L}(\ell )|^2]\}^{\frac{1}{2}}<+\infty$, for $\forall (t,x_L,y_L,s,h)\in [0,T]\times {\mathbb {R}}\times {\mathbb {R}}\times {\mathbb {R}}\times \{0,1\}$, $\forall \ell \in [t,T]$;

• (iv) the state equation (2.12) associated with $\pi _{F}(\cdot )$ has a unique strong solution, which satisfies

  $\{E_{t,x_F,y_F,s,h}[\sup |X_F^{\pi _F}(\ell )|^2]\}^{\frac{1}{2}}<+\infty$, for $\forall (t,x_F,y_F,s,h)\in [0,T] \times {\mathbb {R}}\times {\mathbb {R}}\times {\mathbb {R}}\times \{0,1\}$, $\forall \ell \in [t,T]$.

Let $\Pi =\Pi _L\times \Pi _{F}$ be the set of all admissible strategies, where $\Pi _L$ and $\Pi _F$ denote the set of all admissible strategies of the reinsurer and the insurer, respectively.

2.4 Formulation of a stochastic Stackelberg differential game

In this paper, we consider a stochastic Stackelberg differential reinsurance-investment game with default risk and delay, in which the reinsurer is the leader and the insurer is the follower. The goal of the game is to seek the Stackelberg equilibrium by solving the leader’s and follower’s optimization problems sequentially. According to Yong (2002), Chen and Shen (2018) and Chen and Shen (2019), the procedure of solving the Stackelberg game adopts the idea of backward induction. Specifically, the procedure can be divided into the following three steps:

• Step 1 The leader (i.e., the reinsurer) moves first by announcing one admissible strategy $\pi _L(\cdot )=(p(\cdot ),b_L(\cdot ),b_{L1}(\cdot ))$;

• Step 2 The follower (i.e., the insurer) observes the reinsurer’s strategy and obtains its optimal strategy $q^{*}(\cdot )=\alpha ^{*}(\cdot ,p(\cdot ),b_L(\cdot ),b_{L1}(\cdot ))$, $b_F^{*}(\cdot )=\beta ^{*}(\cdot ,p(\cdot ),b_L(\cdot ),b_{L1}(\cdot ))$ and $b_{F1}^{*}(\cdot )=\beta _1^{*}(\cdot ,p(\cdot ),b_L(\cdot ),b_{L1}(\cdot ))$ by solving its own optimization problem;

• Step 3 Knowing that the insurer would execute $\alpha ^{*}(\cdot ,p(\cdot ),b_L(\cdot ),b_{L1}(\cdot ))$, $\beta ^{*}(\cdot ,p(\cdot ),b_L(\cdot ), b_{L1}(\cdot ))$ and $\beta _1^{*}(\cdot ,p(\cdot ),b_L(\cdot ),b_{L1}(\cdot ))$, the reinsurer then decides on its admissible strategy $(p^{*}(\cdot ),b^{*}_L(\cdot ), b^{*}_{L1}(\cdot ))$ by solving its own optimization problem.

Due to the bounded memory feature, we suppose that both the reinsurer and the insurer are concerned with not only the terminal wealth, but also the integrated delayed information. In other words, the objective of the reinsurer is to find a premium pricing strategy and investment strategies such that the expected utility of $X_L^{\pi _L}(T)+\eta _LY_L(T)$ is maximized, where the constant $\eta _L\in (0,1)$ is the reinsurer’s delay weight, representing the sensitivity of the reinsurer to past wealth. Correspondingly, the objective of the insurer is to find a reinsurance strategy and investment strategies such that the expected utility of $X_F^{\pi _F}(T)+\eta _FY_F(T)$ is maximized, where the constant $\eta _F\in (0,1)$ is the insurer’s delay weight, representing the sensitivity of the insurer to past wealth. Then, the Stackelberg game problem is given by Problem 1.

Problem 1

The insurer’s problem is the following optimization problem: for any $\pi _L(\cdot )=(p(\cdot ),b_L(\cdot ),b_{L1}(\cdot )) \in \Pi _L(\cdot )$, find a map $(q^{*}(\cdot ),b_F^{*}(\cdot ),b_{F1}^{*}(\cdot )) =(\alpha ^{*}(\cdot ,p(\cdot ),b_L(\cdot ),b_{L1}(\cdot )), \beta ^{*}(\cdot ,p(\cdot ),b_L(\cdot ),b_{L1}(\cdot )), \beta _1^{*}(\cdot ,p(\cdot ),b_L(\cdot ), b_{L1}(\cdot ))) :[0,T]\times \Omega \times \Pi _L\rightarrow \Pi _F$ such that the following value function holds:

$$\begin{aligned}&V^F\big (t,x_F,y_F,s,h;p(\cdot ),b_L(\cdot ),b_{L1}(\cdot ), \alpha ^{*}(\cdot ,p(\cdot ),b_L(\cdot ),b_{L1}(\cdot )),\nonumber \\&\qquad \beta ^{*}(\cdot ,p(\cdot ),b_L(\cdot ),b_{L1}(\cdot )),\beta _1^{*}(\cdot ,p(\cdot ),b_L(\cdot ),b_{L1}(\cdot ))\big )\nonumber \\&\quad =\sup _{(q(\cdot ),b_F(\cdot ),b_{F1}(\cdot ))\in \Pi _F}V^F\big (t,x_F,y_F,s,h; p(\cdot ),b_L(\cdot ),b_{L1}(\cdot ),q(\cdot ),b_F(\cdot ),b_{F1}(\cdot )\big )\nonumber \\&\quad =\sup _{(q(\cdot ),b_F(\cdot ),b_{F1}(\cdot ))\in \Pi _F}E_{t,x_F,y_F,s,h} \big [U_F\big (X_F^{\pi _F}(T)+\eta _FY_F(T)\big )\big ], \end{aligned}$$

(2.14)

where $U_F$ is a strictly increasing and strictly concave utility function for the insurer. The reinsurer’s problem is the following optimization problem: find a $(p^{*}(\cdot ),b_L^{*}(\cdot ),b_{L1}^{*}(\cdot ))\in \Pi _L$ such that the following value function holds:

$$\begin{aligned}&V^L\big (t,x_L,y_L,s,h;p^{*}(\cdot ),b_L^{*}(\cdot ),b_{L1}^{*}(\cdot ), \alpha ^{*}(\cdot ,p^{*}(\cdot ),b_L^{*}(\cdot ),b_{L1}^{*}(\cdot )),\nonumber \\&\qquad \beta ^{*}(\cdot ,p^{*}(\cdot ),b_L^{*}(\cdot ),b_{L1}^{*}(\cdot )), \beta _1^{*}(\cdot ,p^{*}(\cdot ),b_L^{*}(\cdot ),b_{L1}^{*}(\cdot ))\big )\nonumber \\&\quad =\sup _{(p(\cdot ),b_L(\cdot ),b_{L1}(\cdot ))\in \Pi _L}V^L\big (t,x_L,y_L,s,h;p(\cdot ),b_L(\cdot ),b_{L1}(\cdot ), \alpha ^{*}(\cdot ,p(\cdot ),b_L(\cdot ),b_{L1}(\cdot )),\nonumber \\&\qquad \beta ^{*}(\cdot ,p(\cdot ),b_L(\cdot ),b_{L1}(\cdot )), \beta _1^{*}(\cdot ,p(\cdot ),b_L(\cdot ),b_{L1}(\cdot ))\big )\nonumber \\&\quad =\sup _{(p(\cdot ),b_L(\cdot ),b_{L1}(\cdot ))\in \Pi _L}E_{t,x_L,y_L,s,h} \big [U_L\big (X_L^{\pi _L}(T)+\eta _LY_L(T)\big )\big ]. \end{aligned}$$

(2.15)

where $U_L$ is a strictly increasing and strictly concave utility function for the reinsurer.

Definition 2

The six-tuple $\big (p^{*}(\cdot ),b_L^{*}(\cdot ),b_{L1}^{*}(\cdot ), \alpha ^{*}(\cdot ,p^{*}(\cdot ),b_L^{*}(\cdot ),b_{L1}^{*}(\cdot )), \beta ^{*}(\cdot ,p^{*}(\cdot ),b_L^{*}(\cdot ),b_{L1}^{*}(\cdot )), \beta _1^{*}(\cdot ,p^{*}(\cdot ),b_L^{*}(\cdot ), b_{L1}^{*}(\cdot ))\big )$ is called an equilibrium solution to the Stackelberg game problem 1.

Furthermore, if there is no risk of confusion, when the equilibrium strategy of the Stackelberg game is adopted, $V^F\big (t,x_F,y_F,s,h;p^{*}(\cdot ),b_L^{*}(\cdot ),b_{L1}^{*}(\cdot ), \alpha ^{*}(\cdot ,p^{*}(\cdot ),b_L^{*}(\cdot ),b_{L1}^{*}(\cdot )), \beta ^{*}(\cdot ,p^{*}(\cdot ),b_L^{*}(\cdot ),b_{L1}^{*}(\cdot )), \beta _1^{*}(\cdot ,p^{*}(\cdot ),b_L^{*}(\cdot ), b_{L1}^{*}(\cdot ))\big )$ is also called the value function of the insurer’s problem.

3 Solution to the Stackelberg game for CARA preference

Compared with individual investors, insurers and reinsurers have considerable wealth. Therefore, the risk aversion coefficient is relatively stable and can be regarded as a constant. Moreover, the wealth of the insurer and the reinsurer are likely to be negative due to the randomness of future claims, which could lead to bankruptcy. In view of these facts, we assume that the insurer and the reinsurer have exponential utility preferences, i.e., both the insurer and the reinsurer are constant absolute risk aversion (CARA) agents:

$$\begin{aligned} U_F(x_F+\eta _Fy_F)&=-\frac{1}{\gamma _F}\exp [-\gamma _F(x_F+\eta _Fy_F)], \end{aligned}$$

(3.16)

$$\begin{aligned} U_L(x_L+\eta _Ly_L)&=-\frac{1}{\gamma _L}\exp [-\gamma _L(x_L+\eta _Ly_L)], \end{aligned}$$

(3.17)

where $\gamma _F>0$ and $\gamma _L>0$ are the constant absolute risk aversion coefficients of the insurer and the reinsurer, respectively.

According to existing literature, the optimal control problem with delay is infinite-dimensional in general. The stochastic control problem with delay can be transformed into a finite-dimensional Markov system when the drift and diffusion terms in (2.12) (or (2.13)) are linear with respect to $X_F^{\pi _F}(t)$, $Y_F(t)$ and $Z_F(t)$ (or $X_L^{\pi _L}(t)$, $Y_L(t)$ and $Z_L(t)$), and the coefficients satisfy a certain relationship (refer to Elsanosi et al. (2000), Elsanousi and Larssen (2001), Larssen (2002)). In order to deal with this problem, the existing literature (for example, Chunxiang and Li (2015), Chunxiang et al. (2018) etc.) generally assumes the following relationships:

$$\begin{aligned}&C_L=\eta _Le^{-\alpha _Lh_L}, \quad B_Le^{-\alpha _Lh_L}=(\alpha _L+A_L+\eta _L)C_L, \end{aligned}$$

(3.18)

$$\begin{aligned}&C_F=\eta _Fe^{-\alpha _Fh_F}, \quad B_Fe^{-\alpha _Fh_F}=(\alpha _F+A_F+\eta _F)C_F. \end{aligned}$$

(3.19)

Note that although conditions (3.18) and (3.19) lose some generality, they are one of the sufficient conditions for the optimal control problem with delay to have analytic solution. In fact, (3.18) and (3.19) can be regarded as the conditions given in advance by the reinsurer and the insurer. That is, the reinsurer (the insurer) can calculate the average performance and the absolute performance by selecting average parameter and delay time parameter, then select delay weight parameter, and use the condition (3.18) (or (3.19)) to calculate $B_L$ and $C_L$ ($B_F$ and $C_F$) as the average performance and the absolute performance proportional parameters to regulate the inflow and outflow of wealth from the reinsurer (the insurer). From the explicit forms of $B_L$ and $C_L$ ($B_F$ and $C_F$), we can see that, the shorter the delay time considered by managers, the greater the absolute performance weight; the longer the delay time, the greater the average performance weight. The nature of the parameters reflects that this setting is also common sense.

Based on the dynamic programming technique, for $\forall t\in [0,T]$, we derive Hamilton-Jacobi-Bellman (HJB) equations for the insurer and the reinsurer as follows:

$$\begin{aligned}&\left\{ \begin{array}{ccl} \sup _{\pi _F\in \Pi _F}{\mathcal {A}}^FV^F(t,x_F,y_F,s,h)=0,\\ V^F(T,x_F,y_F,s,h)=U_F(x_F+\eta _Fy_F); \end{array} \right. \end{aligned}$$

(3.20)

$$\begin{aligned}&\left\{ \begin{array}{ccl} \sup _{\pi _L\in \Pi _L}{\mathcal {A}}^LV^L(t,x_L,y_L,s,h)=0,\\ V^L(T,x_L,y_L,s,h)=U_L(x_L+\eta _Ly_L); \end{array} \right. \end{aligned}$$

(3.21)

where

$$\begin{aligned}&{\mathcal {A}}^FV^F(t,x_F,y_F,s,h)\nonumber \\&\quad =\frac{\partial V^F(t,x_F,y_F,s,h)}{\partial t} + \big [\theta _Fa-(p(t)-a)(1-q(t))\nonumber \\&\qquad +A_Fx_F+B_Fy_F+C_Fz_F+(r-r_0)b_F(t)\nonumber \\&\qquad +(1-h)\eta b_{F1}(t)\big ]\frac{\partial V^F(t,x_F,y_F,s,h)}{\partial x_F}\nonumber \\&\qquad +\frac{1}{2}\big [(q(t))^2\sigma _F^2+(b_F(t))^2\sigma ^2s^{2\beta }\big ]\frac{\partial V^F(t,x_F,y_F,s,h)}{\partial x_F^2}\nonumber \\&\qquad +(x_F-\alpha _Fy_F-e^{-\alpha _Fh_F}z_F)\frac{\partial V^F(t,x_F,y_F,s,h)}{\partial y_F}\nonumber \\&\qquad +rs\frac{\partial V^F(t,x_F,y_F,s,h)}{\partial s}+\frac{1}{2}\sigma ^2s^{2\beta +2}\frac{\partial V^F(t,x_F,y_F,s,h)}{\partial s^2}\nonumber \\&\qquad +b_F(t)\sigma ^2s^{2\beta +1} \frac{\partial V^F(t,x_F,y_F,s,h)}{\partial x_F\partial s}+\big [V^F(t,x_F-b_{F1}(t)\zeta ,y_F,s,h+1)\nonumber \\&\qquad -V^F(t,x_F,y_F,s,h)\big ]h^P(1-h), \end{aligned}$$

(3.22)

$$\begin{aligned}&{\mathcal {A}}^LV^L(t,x_L,y_L,s,h)\nonumber \\&\quad =\frac{\partial V^L(t,x_L,y_L,s,h)}{\partial t} + \big [(p(t)-a)(1-q^{*}(t))+A_Lx_L\nonumber \\&\qquad +B_Ly_L+C_Lz_L+(r-r_0)b_L(t)\nonumber \\&\qquad +(1-h)\eta b_{L1}(t)\big ]\frac{\partial V^L(t,x_L,y_L,s,h)}{\partial x_L}\nonumber \\&\qquad +\frac{1}{2}\big [(1-q^{*}(t))^2\sigma _F^2+(b_L(t))^2\sigma ^2s^{2\beta }\big ]\frac{\partial V^L(t,x_L,y_L,s,h)}{\partial x_L^2}\nonumber \\&\qquad +(x_L-\alpha _Ly_L-e^{-\alpha _Lh_L}z_L)\frac{\partial V^L(t,x_L,y_L,s,h)}{\partial y_L}\nonumber \\&\qquad +rs\frac{\partial V^L(t,x_L,y_L,s,h)}{\partial s}+\frac{1}{2}\sigma ^2s^{2\beta +2}\frac{\partial V^L(t,x_L,y_L,s,h)}{\partial s^2}\nonumber \\&\qquad +b_L(t)\sigma ^2s^{2\beta +1} \frac{\partial V^L(t,x_L,y_L,s,h)}{\partial x_L\partial s}+\big [V^L(t,x_L-b_{L1}(t)\zeta ,y_L,s,h+1)\nonumber \\&\qquad -V^L(t,x_L,y_L,s,h)\big ]h^P(1-h). \end{aligned}$$

(3.23)

Next, we will deduce the solutions of HJB equations (3.20) and (3.21) according to the steps of solving the Stackelberg game proposed in Sect. 2.4. Then, we will construct the verification theorem to prove that the equilibrium strategy obtained by the above steps is optimal in $\Pi _L\times \Pi _{F}$ and the solutions are the value functions of the insurer and reinsurer, respectively. We split the original value functions into two pieces that represent the pre-default (i.e., $h=0$) value functions and post-default (i.e., $h=1$) value functions.

3.1 Equilibrium strategy and value functions after default

After the default of the corporate zero-coupon bond, which corresponds to the case of $h=1$. In this section, we address the stochastic Stackelberg differential reinsurance-investment game after default, and provide explicit expressions of the equilibrium strategy and associated value functions. The relevant results are given by Theorem 1.

Table 1 $p^{*}(t)$ and $q^{*}(t)$ under different cases

Theorem 1

(Post-default) For $\forall t\in [\tau \wedge T,T]$, the equilibrium strategy of the Stackelberg game problem 1 is $(p^{*}(t),b^{*}_L(t),b^{*}_{L1}(t),q^{*}(t),b^{*}_F(t),b^{*}_{F1}(t))$, where $p^{*}(t)$ and $q^{*}(t)$ under different cases are given by Table 1; the equilibrium investment strategies of the reinsurer and the insurer are described by

$$\begin{aligned} b^{*}_L(t)&=\frac{(r-r_0)s^{-2\beta }}{\gamma _L\varphi ^L(t)\sigma ^2}-\frac{2\beta g_{1}^L(t)s^{-2\beta }}{\gamma _L\varphi ^L(t)}, \end{aligned}$$

(3.24)

$$\begin{aligned} b^{*}_{L1}(t)&=0, \end{aligned}$$

(3.25)

$$\begin{aligned} b^{*}_F(t)&=\frac{(r-r_0)s^{-2\beta }}{\gamma _F\varphi ^F(t)\sigma ^2}-\frac{2\beta g_{1}^F(t)s^{-2\beta }}{\gamma _F\varphi ^F(t)}, \end{aligned}$$

(3.26)

$$\begin{aligned} b^{*}_{F1}(t)&=0, \end{aligned}$$

(3.27)

where p is any value in the interval $[c_F,{\bar{c}}]$, $\varphi ^L(t)$, $\varphi ^F(t)$, $g_{1}^L(t)$ and $g_{1}^F(t)$ are given by

$$\begin{aligned} \varphi ^L(t)=&\exp [(A_L+\eta _L)(T-t)], \end{aligned}$$

(3.28)

$$\begin{aligned} \varphi ^F(t)=&\exp [(A_F+\eta _F)(T-t)], \end{aligned}$$

(3.29)

$$\begin{aligned} g^L_1(t)=&g^F_1(t)=-\frac{1}{4\beta r_0}(\frac{r-r_0}{\sigma })^2\{1-\exp [-2\beta r_0(T-t)]\}, \end{aligned}$$

(3.30)

K(t), $N^{\theta _F}(t)$ and $N^{{\bar{\theta }}}(t)$ are given by

$$\begin{aligned} K(t)=\frac{\gamma _F\varphi ^F(t)+\gamma _L\varphi ^L(t)}{2\gamma _F\varphi ^F(t)+\gamma _L\varphi ^L(t)},\quad N^{\theta _F}(t)=\frac{\theta _Fa}{\gamma _F\sigma _F^2\varphi ^F(t)},\quad N^{{\bar{\theta }}}(t)=\frac{{\bar{\theta }}a}{\gamma _F\sigma _F^2\varphi ^F(t)}. \end{aligned}$$

(3.31)

The post-default value function of the reinsurer is given by

$$\begin{aligned} V^L(t,x_L,y_L,s,1) =&-\frac{1}{\gamma _L}\exp [-\gamma _L\varphi ^L(t)(x_L+\eta _Ly_L)\nonumber \\&+g^L_1(t)s^{-2\beta }+g^{L}_2(t)], \end{aligned}$$

(3.32)

and, the post-default value function of the insurer is given by

$$\begin{aligned} V^F(t,x_F,y_F,s,1) =&-\frac{1}{\gamma _F}\exp [-\gamma _F\varphi ^F(t)(x_F+\eta _Fy_F)\nonumber \\&+g^F_1(t)s^{-2\beta }+g^{F}_2(t)], \end{aligned}$$

(3.33)

where $g^{L}_2(t)$ and $g^{F}_2(t)$ under different cases are given by Table 2; $g^{La}_2$, $g^{Lb1}_2(t)$, $g^{Lb2}_2(t)$,$g^{Lb3}_2(t)$, $g^{Fa}_2(t)$, $g^{Fb1}_2(t)$, $g^{Fb2}_2(t)$ and $g^{Fb3}_2(t)$ are given by

$$\begin{aligned} g^{La}_2(t)=&-\frac{(2\beta +1)(r-r_0)^2}{4r_0}(T-t)+\frac{(2\beta +1)(r-r_0)^2}{8\beta r_0^2}\{1-\exp [-2\beta r_0(T-t)]\}, \end{aligned}$$

(3.34)

$$\begin{aligned} g^{Lb1}_2(t)=&g^{La}_2(t) +\frac{\gamma _L^2\sigma _F^2}{4(A_L+\eta _L)}[(\varphi ^L(t))^2-1]\nonumber \\&-\int _T^t ({\bar{\theta }}a)^2[\frac{\gamma _L\varphi ^L(u)}{\gamma _F\sigma _F^2\varphi ^F(u)} +\frac{1}{2}\frac{\gamma _L^2(\varphi ^L(u))^2}{\gamma _F^2\sigma _F^2(\varphi ^F(u))^2}]du\nonumber \\&+\int _T^t({\bar{\theta }}a)[\gamma _L\varphi ^L(u) +\frac{\gamma _L^2(\varphi ^L(u))^2}{\gamma _F(\varphi ^F(u))}]du, \end{aligned}$$

(3.35)

$$\begin{aligned} g^{Lb2}_2(t)=&g^{La}_2(t) +\frac{\gamma _L^2\sigma _F^2}{4(A_L+\eta _L)}[(\varphi ^L(t))^2-1]\nonumber \\&-\int _T^t (\theta _Fa)^2[\frac{\gamma _L\varphi ^L(u)}{\gamma _F\sigma _F^2\varphi ^F(u)} +\frac{1}{2}\frac{\gamma _L^2(\varphi ^L(u))^2}{\gamma _F^2\sigma _F^2(\varphi ^F(u))^2}]du\nonumber \\&+\int _T^t(\theta _Fa)[\gamma _L\varphi ^L(u) +\frac{\gamma _L^2(\varphi ^L(u))^2}{\gamma _F(\varphi ^F(u))}]du, \end{aligned}$$

(3.36)

$$\begin{aligned} g^{Lb3}_2(t)=&g^{La}_2(t) +\frac{\gamma _L^2\sigma _F^2}{4(A_L+\eta _L)}[(\varphi ^L(t))^2-1]\nonumber \\&+\int _T^tK(u)\gamma _F\sigma _F^2\varphi ^F(u)[\gamma _L\varphi ^L(u) +\frac{\gamma _L^2(\varphi ^L(u))^2}{\gamma _F(\varphi ^F(u))}]du\nonumber \\&-\int _T^t (K(u)\gamma _F\sigma _F^2\varphi ^F(u))^2[\frac{\gamma _L\varphi ^L(u)}{\gamma _F\sigma _F^2\varphi ^F(u)}\nonumber \\&+\frac{1}{2}\frac{\gamma _L^2(\varphi ^L(u))^2}{\gamma _F^2\sigma _F^2(\varphi ^F(u))^2}]du, \end{aligned}$$

(3.37)

$$\begin{aligned} g^{Fa}_2(t)=&g^{La}_2(t)-\frac{\gamma _F\theta _Fa}{A_F+\eta _F}(\varphi ^F(t)-1) +\frac{\gamma _F^2\sigma _F^2}{4(A_F+\eta _F)}[(\varphi ^F(t))^2-1], \end{aligned}$$

(3.38)

$$\begin{aligned} g^{Fb1}_2(t)=&g^{La}_2(t) +\frac{\gamma _Fa({\bar{\theta }}-\theta _F)}{A_F+\eta _F}(\varphi ^F(t)-1) -\frac{({\bar{\theta }}a)^2}{2\sigma _F^2}(T-t), \end{aligned}$$

(3.39)

$$\begin{aligned} g^{Fb2}_2(t)=&g^{La}_2(t) -\frac{(\theta _Fa)^2}{2\sigma _F^2}(T-t), \end{aligned}$$

(3.40)

$$\begin{aligned} g^{Fb3}_2(t)=&g^{La}_2(t)-\frac{\gamma _F\theta _Fa}{A_F+\eta _F}(\varphi ^F(t)-1) -\gamma _F\int _T^t\varphi ^F(u)K(u)\gamma _F\sigma _F^2\varphi ^F(u)du\nonumber \\&+\frac{1}{2\sigma _F^2}\int _T^t[K(u)\gamma _F\sigma _F^2\varphi ^F(u)]^2du. \end{aligned}$$

(3.41)

Table 2 $g^{L}_2(t)$ and $g^{F}_2(t)$ under different cases

Proof

The proof is similar to the proof of Theorem 2, therefore we omit it here. $\square$

Remark 1

Note that the amount of money invested in the defaultable bond is 0, (i.e., $b^{*}_{L1}(t)=0$ and $b^{*}_{F1}(t)=0$) because the defaultable bond can not be traded after default.

3.2 Equilibrium strategy and value functions before default

Before the default of the corporate zero-coupon bond, which corresponds to the case of $h=0$. In this section, we derive the Stackelberg equilibrium reinsurance-investment strategy before default. Theorem 2 describes the pre-default equilibrium strategy and its associated value functions.

Theorem 2

(Pre-default) For $\forall t\in [0,\tau \wedge T)$, the equilibrium strategy of the Stackelberg game problem 1 is $(p^{*}(t),b^{*}_L(t),b^{*}_{L1}(t),q^{*}(t),b^{*}_F(t),b^{*}_{F1}(t))$, where $b_{L1}^{*}(t)$ and $b_{F1}^{*}(t)$ are given by

$$\begin{aligned} b^{*}_{L1}(t)&=\frac{ln(\frac{1}{\Delta }) +(ln\frac{1}{\Delta }+\Delta -1)[e^{-\frac{\eta }{\zeta }(T-t)}-1]}{\gamma _L\varphi ^L(t)\zeta }, \end{aligned}$$

(3.42)

$$\begin{aligned} b^{*}_{F1}(t)&=\frac{ln(\frac{1}{\Delta }) +(ln\frac{1}{\Delta }+\Delta -1)[e^{-\frac{\eta }{\zeta }(T-t)}-1]}{\gamma _F\varphi ^F(t)\zeta }; \end{aligned}$$

(3.43)

$p^{*}(t)$, $q^{*}(t)$, $b_{L}^{*}(t)$ and $b_{F}^{*}(t)$ are the same as that in Theorem 1. The pre-default value function of the reinsurer is given by

$$\begin{aligned} V^L(t,x_L,y_L,s,0) =&-\frac{1}{\gamma _L}\exp \{-\gamma _L\varphi ^L(t)(x_L+\eta _Ly_L)+g^L_1(t)s^{-2\beta }+g^{L}_2(t)+G_2(t)\}\nonumber \\ =&V^L(t,x_L,y_L,s,1)e^{G_2(t)}, \end{aligned}$$

(3.44)

and, the pre-default value function of the insurer is given by

$$\begin{aligned} V^F(t,x_F,y_F,s,0) =&-\frac{1}{\gamma _F}\exp \{-\gamma _F\varphi ^F(t)(x_F+\eta _Fy_F)+g^F_1(t)s^{-2\beta }+g^{F}_2(t)+G_2(t)\}\nonumber \\ =&V^F(t,x_F,y_F,s,1)e^{G_2(t)}, \end{aligned}$$

(3.45)

where

$$\begin{aligned} G_2(t) =(ln\frac{1}{\Delta }+\Delta -1)[e^{-\frac{\eta }{\zeta }(T-t)}-1]. \end{aligned}$$

(3.46)

Proof

See Appendix A. $\square$

Combining Theorems 1 and 2, we obtain the following result directly.

Theorem 3

The equilibrium strategy of the Stackelberg game problem 1 is $(p^{*}(t),b^{*}_L(t),b^{*}_{L1}(t),q^{*}(t),b^{*}_F(t), b^{*}_{F1}(t))$, where $p^{*}(t)$ and $q^{*}(t)$ under different cases are given by Table 1; $b_{L}^{*}(t)$ and $b_{F}^{*}(t)$ are given by (3.24) and (3.26); $b_{L1}^{*}(t)$ and $b_{F1}^{*}(t)$ are given by

$$\begin{aligned} b^{*}_{L1}(t)=\left\{ \begin{array}{cll} \frac{ln(\frac{1}{\Delta })e^{-\frac{\eta }{\zeta }(T-t)} +(1-\Delta )[1-e^{-\frac{\eta }{\zeta }(T-t)}]}{\gamma _L\varphi ^L(t)\zeta },&{} t\in [0,\tau \wedge T),\\ 0,&{} t\in [\tau \wedge T,T]. \end{array} \right. \end{aligned}$$

(3.47)

and

$$\begin{aligned} b^{*}_{F1}(t)=\left\{ \begin{array}{cll} \frac{ln(\frac{1}{\Delta })e^{-\frac{\eta }{\zeta }(T-t)} +(1-\Delta )[1-e^{-\frac{\eta }{\zeta }(T-t)}]}{\gamma _F\varphi ^F(t)\zeta },&{} t\in [0,\tau \wedge T),\\ 0,&{} t\in [\tau \wedge T,T]. \end{array} \right. \end{aligned}$$

(3.48)

respectively; $\varphi ^F(t)$ and $\varphi ^L(t)$ are given by (3.29) and (3.28), respectively.

The value function of the reinsurer is given by

$$\begin{aligned} V^L(t,x_L,y_L,s,0) =&-\frac{1}{\gamma _L}\exp \{-\gamma _L\varphi ^L(t)(x_L+\eta _Ly_L)\nonumber \\&+g^L_1(t)s^{-2\beta }+g^{L}_2(t)+(1-h)G_2(t)\}, \end{aligned}$$

(3.49)

and, the value function of the insurer is given by

$$\begin{aligned} V^F(t,x_F,y_F,s,0) =&-\frac{1}{\gamma _F}\exp \{-\gamma _F\varphi ^F(t)(x_F+\eta _Fy_F)\nonumber \\&+g^F_1(t)s^{-2\beta }+g^{F}_2(t)+(1-h)G_2(t)\}, \end{aligned}$$

(3.50)

where $g^L_1(t)$, $g^F_1(t)$ and $G_2(t)$ are given by (3.30) and (3.46), respectively; $g^{L}_2(t)$ and $g^{F}_2(t)$ under different cases are given by Table 2.

From Theorem 3, we find that the Stackelberg equilibrium reinsurance-investment strategy is independent of the current wealth, which is caused by the choice of exponential utility. Furthermore, the equilibrium investment strategies are independent with the reinsurer’s premium pricing strategy and the insurer’s reinsurance strategy. Moreover, we find that the insurer’s optimal reinsurance strategy can be expressed as the optimal reinsurance premium strategy. That is,

$$\begin{aligned} q^{*}(t) =\frac{p^{*}(t)-a}{\gamma _F\sigma _F^2\varphi ^F(t)} \wedge 1. \end{aligned}$$

(3.51)

Remark 2

Similar to Chen and Shen (2018), when the Stackelberg equilibrium is achieved in the interior case (i.e., Case (4) in Table 1), the optimal reinsurance premium follows the variance premium principle. That is, for every one unit of risk, the total instantaneous reinsurance premium associated with the ceded proportion $(1-q^{*}(t))$ can be written as

$$\begin{aligned} (1-q^{*}(t))p^{*}(t) =a(1-q^{*}(t))+(1-q^{*}(t))^2\sigma _F^2[\gamma _L\varphi ^L(t)+\gamma _F\varphi ^F(t)], \end{aligned}$$

(3.52)

where the first term accounts for the mean component, and the second for the variance component. This implies that the variance premium principle is an ideal candidate among all possible premium principles when the proportional reinsurance is applied. In fact, this conclusion has a dual conclusion: proportional reinsurance is the optimal form of reinsurance when the variance premium principle is adopted, which can be seen from Proposition 3.2 in Chen and Shen (2019).

Table 3 The properties of $p^{*}(t)$ and $q^{*}(t)$

Corollary 1

When the Stackelberg equilibrium is achieved in the interior case (i.e., Case (4) in Table 1)), some of the properties of $p^{*}(t)$ and $q^{*}(t)$ are given in Table 3, (3.53) and (3.54).

$$\begin{aligned} \frac{\partial p^{*}(t)}{\partial \alpha _L}=\left\{ \begin{array}{rcl}<0, &{} {\alpha _L>-\frac{1}{h_L}ln\frac{1}{h_L};}\\ =0,&{} {\alpha _L=-\frac{1}{h_L}ln\frac{1}{h_L};}\\>0, &{} {\alpha _L<-\frac{1}{h_L}ln\frac{1}{h_L}.} \end{array} \right. \frac{\partial q^{*}(t)}{\partial \alpha _F}=\left\{ \begin{array}{rcl}>0, &{} {\alpha _F>-\frac{1}{h_F}ln\frac{1}{h_F};}\\ =0,&{} {\alpha _F=-\frac{1}{h_F}ln\frac{1}{h_F};}\\<0, &{} {\alpha _F<-\frac{1}{h_F}ln\frac{1}{h_F}.} \end{array} \right. \end{aligned}$$

(3.53)

If $r_0+\alpha _L<1$, we have

$$\begin{aligned} \frac{\partial p^{*}(t)}{\partial \eta _L}=\left\{ \begin{array}{rcl}<0, &{} {h_L<-\frac{1}{\alpha _L}ln(1-r_0-\alpha _L);}\\ =0,&{} {h_L=-\frac{1}{\alpha _L}ln(1-r_0-\alpha _L);}\\>0, &{} {h_L>-\frac{1}{\alpha _L}ln(1-r_0-\alpha _L).} \end{array} \right. \frac{\partial q^{*}(t)}{\partial \eta _F}=\left\{ \begin{array}{rcl}>0,&{} {h_F<-\frac{1}{\alpha _F}ln(1-r_0-\alpha _F);}\\ =0,&{} {h_F=-\frac{1}{\alpha _F}ln(1-r_0-\alpha _F);}\\ <0,&{} {h_F>-\frac{1}{\alpha _F}ln(1-r_0-\alpha _F).} \end{array} \right. \end{aligned}$$

(3.54)

Proof

See Appendix B. $\square$

The Eq. (3.53) shows that the optimal reinsurance premium strategy and the optimal reinsurance strategy are quadratic in relation to their average parameters. The equation (3.54) shows that the influence of delay weight on optimal reinsurance premium strategy or optimal reinsurance strategy is related to the length of delay time. For the optimal reinsurance premium strategy, when the delay time exceeds a given value, the greater the delay weight, the higher the reinsurance premium; when the delay time is lower than this given value, the greater the delay weight, the lower the reinsurance premium. For the optimal reinsurance strategy, when the delay time exceeds a given value, the larger the delay weight is, the lower the reservation proportion of the insurer is; when the delay time is lower than this given value, the larger the delay weight is, the higher the reservation proportion of the insurer is.

Corollary 2

 

• (1) If $\frac{1}{\Delta }=1$, for $\forall t\in [0,T]$, we have

  $$\begin{aligned}&b^{*}_{L1}(t)=0,\quad b^{*}_{F1}(t)=0, \end{aligned}$$

  (3.55)
  $$\begin{aligned}&V^L(t,x_L,y_L,s,0)=V^L(t,x_L,y_L,s,1), \end{aligned}$$

  (3.56)
  $$\begin{aligned}&V^F(t,x_F,y_F,s,0)=V^F(t,x_F,y_F,s,1). \end{aligned}$$

  (3.57)

• (2) If $\frac{1}{\Delta }> 1$, for $\forall t\in [0,T]$, we have

  $$\begin{aligned}&b^{*}_{L1}(t)> 0,\quad b^{*}_{F1}(t)>0, \end{aligned}$$

  (3.58)
  $$\begin{aligned}&V^L(t,x_L,y_L,s,0)>V^L(t,x_L,y_L,s,1), \end{aligned}$$

  (3.59)
  $$\begin{aligned}&V^F(t,x_F,y_F,s,0)>V^F(t,x_F,y_F,s,1). \end{aligned}$$

  (3.60)

Proof

See Appendix C. $\square$

The risk premium refers to the premium investors demand for average risk investment relative to the risk-free interest rate. If $\frac{1}{\Delta }=1$, then investors cannot get the default risk premium. In this case, the reinsurer and the insurer will not buy defaultable bonds. Furthermore, we find that when $\frac{1}{\Delta }>1$, the pre-default value functions of the reinsurer and the insurer are higher than the post-default value functions, respectively. The difference between two cases stands for the loss in the reinsurer’s and the insurer’s objectives due to the default event. For the analysis of the nature of the optimal investment strategies of the reinsurer and the insurer, we have the following conclusions.

Table 4 The properties of $b_L^{*}(t)$, $b^{*}_{L1}(t)$, $b_F^{*}(t)$ and $b^{*}_{F1}(t)$

Corollary 3

For $\forall t\in [0,T]$, if $\frac{1}{\Delta }>1$ and $\beta >0$, some properties of $b_L^{*}(t)$, $b^{*}_{L1}(t)$, $b_F^{*}(t)$ and $b^{*}_{F1}(t)$ are given in Table 4, (3.61) and (3.63).

$$\begin{aligned} \frac{\partial b_L^{*}(t)}{\partial \alpha _L}= & {} \left\{ \begin{array}{rcl}>0, &{} {\alpha _L>-\frac{1}{h_L}ln\frac{1}{h_L};}\\ =0,&{} {\alpha _L=-\frac{1}{h_L}ln\frac{1}{h_L};}\\<0, &{} {\alpha _L<-\frac{1}{h_L}ln\frac{1}{h_L}.} \end{array} \right. \frac{\partial b_F^{*}(t)}{\partial \alpha _F}=\left\{ \begin{array}{rcl}>0, &{} {\alpha _F>-\frac{1}{h_F}ln\frac{1}{h_F};}\\ =0,&{} {\alpha _F=-\frac{1}{h_F}ln\frac{1}{h_F};}\\<0, &{} {\alpha _F<-\frac{1}{h_F}ln\frac{1}{h_F}.} \end{array} \right. \end{aligned}$$

(3.61)

$$\begin{aligned} \frac{\partial b_{L1}^{*}(t)}{\partial \alpha _L}= & {} \left\{ \begin{array}{rcl}>0, &{} {\alpha _L>-\frac{1}{h_L}ln\frac{1}{h_L};}\\ =0,&{} {\alpha _L=-\frac{1}{h_L}ln\frac{1}{h_L};}\\<0, &{} {\alpha _L<-\frac{1}{h_L}ln\frac{1}{h_L}.} \end{array} \right. \frac{\partial b_{F1}^{*}(t)}{\partial \alpha _F}=\left\{ \begin{array}{rcl}>0, &{} {\alpha _F>-\frac{1}{h_F}ln\frac{1}{h_F};}\\ =0,&{} {\alpha _F=-\frac{1}{h_F}ln\frac{1}{h_F};}\\<0, &{} {\alpha _F<-\frac{1}{h_F}ln\frac{1}{h_F}.} \end{array} \right. \end{aligned}$$

(3.62)

Furthermore, if $r_0+\alpha _L<1$ and $r_0+\alpha _F<1$, then

$$\begin{aligned} \frac{\partial b_L^{*}(t)}{\partial \eta _L}= & {} \left\{ \begin{array}{rcl}>0, &{} {h_L<-\frac{1}{\alpha _L}ln(1-r_0-\alpha _L);}\\ =0,&{} {h_L=-\frac{1}{\alpha _L}ln(1-r_0-\alpha _L);}\\<0, &{} {h_L>-\frac{1}{\alpha _L}ln(1-r_0-\alpha _L).} \end{array} \right. \nonumber \\ \frac{\partial b_F^{*}(t)}{\partial \eta _F}= & {} \left\{ \begin{array}{rcl}>0,&{} {h_F<-\frac{1}{\alpha _F}ln(1-r_0-\alpha _F);}\\ =0,&{} {h_F=-\frac{1}{\alpha _F}ln(1-r_0-\alpha _F);}\\ <0,&{} {h_F>-\frac{1}{\alpha _F}ln(1-r_0-\alpha _F).} \end{array} \right. \end{aligned}$$

(3.63)

$$\begin{aligned} \frac{\partial b_{L1}^{*}(t)}{\partial \eta _L}= & {} \left\{ \begin{array}{rcl}>0, &{} {h_L<-\frac{1}{\alpha _L}ln(1-r_0-\alpha _L);}\\ =0,&{} {h_L=-\frac{1}{\alpha _L}ln(1-r_0-\alpha _L);}\\<0, &{} {h_L>-\frac{1}{\alpha _L}ln(1-r_0-\alpha _L).} \end{array} \right. \nonumber \\ \frac{\partial b_{F1}^{*}(t)}{\partial \eta _F}= & {} \left\{ \begin{array}{rcl}>0,&{} {h_F<-\frac{1}{\alpha _F}ln(1-r_0-\alpha _F);}\\ =0,&{} {h_F=-\frac{1}{\alpha _F}ln(1-r_0-\alpha _F);}\\ <0,&{} {h_F>-\frac{1}{\alpha _F}ln(1-r_0-\alpha _F).} \end{array} \right. \end{aligned}$$

(3.64)

Proof

The proof of this corollary is similar to that of Corollary 1. $\square$

Similar to the analysis of Corollary 1, we find that the optimal investment strategy presents a quadratic relationship with the average parameter, and the effect of delay weight on the optimal investment strategy depends on the length of delay time. Furthermore, we find that the influence of delay weight on the equilibrium reinsurance premium strategy is just opposite to that on other strategies.

When the Stackelberg reinsurance-investment game in the defaultable market does not consider the effects of delay factors, Theorem 3 can be reduced to the following conclusions.

Table 5 $p^{*}(t)$ and $q^{*}(t)$ under different cases

Corollary 4

If $\eta _L=0$ and $\eta _F=0$, the equilibrium strategy of the Stackelberg game is $(p^{*}(t),b^{*}_L(t),b^{*}_{L1}(t),q^{*}(t), b^{*}_F(t), b^{*}_{F1}(t))$, where $p^{*}(t)$ and $q^{*}(t)$ under different cases are given by Table 5;

$$\begin{aligned} K^0(t)=\frac{\gamma _F+\gamma _L}{2\gamma _F+\gamma _L},\quad N^{\theta _{F0}}(t)=\frac{\theta _Fae^{-r_0(T-t)}}{\gamma _F\sigma _F^2},\quad N^{{\bar{\theta }}_0}(t)=\frac{{\bar{\theta }}ae^{-r_0(T-t)}}{\gamma _F\sigma _F^2}. \end{aligned}$$

$b_{L}^{*}(t)$, $b_{L1}^{*}(t)$, $b_{F}^{*}(t)$ and $b_{F1}^{*}(t)$ are given by

$$\begin{aligned} b^{*}_L(t)&=\frac{(r-r_0)e^{-r_0(T-t)}}{\gamma _L\sigma ^2s^{2\beta }}\{1+\frac{r-r_0}{2r_0}[1-e^{-2\beta r_0(T-t)}]\}, \end{aligned}$$

(3.65)

$$\begin{aligned} b^{*}_{L1}(t)&=\left\{ \begin{array}{cll} \frac{e^{-r_0(T-t)}}{\gamma _L\zeta }[(ln\frac{1}{\Delta }+\Delta -1)e^{-\frac{\eta }{\zeta }(T-t)} +1-\Delta ],&{} t\in [0,\tau \wedge T),\\ 0,&{} t\in [\tau \wedge T,T]. \end{array} \right. \end{aligned}$$

(3.66)

and

$$\begin{aligned} b^{*}_F(t)&=\frac{\gamma _L}{\gamma _F}b^{*}_L(t),\quad b^{*}_{F1}(t)=\frac{\gamma _L}{\gamma _F}b^{*}_{L1}(t), \end{aligned}$$

(3.67)

respectively.

It can be seen from Corollary 4 that when the Stackelberg reinsurance-investment game without delay, the optimal reinsurance premium price strategy and the optimal reservation ratio are consistent with Proposition 5.2 in Chen and Shen (2018), the strategy of investing in the defaultable bond is consistent with that in Zhu et al. (2015).

3.3 Verification theorem

In order to prove that the Stackelberg equilibrium strategy given in Theorem 3 is indeed optimal for both sides of the Stackelberg game and verify that the smooth candidate solutions derived in the previous section are the value functions of the insurer and reinsurer, we give a verification theorem in this section.

Lemma 1

Let $\tau _i$ be the exiting time from the open set ${\mathcal {M}}_{i}$, where ${\mathcal {M}}_i\subset {\mathcal {M}}={\mathbb {R}}\times {\mathbb {R}}\times {\mathbb {R}}\times \{0,1\}$ such that ${\mathcal {M}}_i\subset {\mathcal {M}}_{i+1}\subset {\mathcal {M}},i=1,2,\cdots$, and ${\mathcal {M}}=\cup _i{\mathcal {M}}_{i}$. Then, for any $\epsilon >1$, $i=1,2,\cdots$, we have

$$\begin{aligned}&\sup _iE\big \{\mid V^{F}(\tau _i\wedge T,X_F(\tau _i\wedge T),Y_F(\tau _i\wedge T),S(\tau _i\wedge T),H(\tau _i\wedge T))\mid ^{\epsilon }\big \}<+\infty , \end{aligned}$$

(3.68)

$$\begin{aligned}&\sup _iE\big \{\mid V^{L}(\tau _i\wedge T,X_L(\tau _i\wedge T),Y_L(\tau _i\wedge T),S(\tau _i\wedge T),H(\tau _i\wedge T))\mid ^{\epsilon }\big \}<+\infty . \end{aligned}$$

(3.69)

Proof

The proof of this lemma is similar to the proof of Lemma 4.1 of Deng et al. (2018), so we omitted it. $\square$

Theorem 4

(Verification theorem) Under the CARA utility function, let $J^F$ and $J^L$ be solutions to HJB equations (3.20) and (3.21), respectively. Then, the equilibrium strategy $(p^{*}(t),b^{*}_L(t),b^{*}_{L1}(t), q^{*}(t),b^{*}_F(t),b^{*}_{F1}(t))$ described in Theorem 3 achieves optimality in $\Pi _L\times \Pi _F$; $J^F$ and $J^L$ are value functions of the insurer and reinsurer, respectively.

Proof

See Appendix D. $\square$

4 Sensitivity analysis

In order to illustrate the sensitivity of the Stackelberg equilibrium strategy $(p^{*}(t),b^{*}_L(t), b^{*}_{L1}(t), q^{*}(t),b^{*}_F(t), b^{*}_{F1}(t))$ to the model parameters, we present some numerical experiments in this section. In the following, unless otherwise stated, the basic model parameters are given in Tables 6, 7 and 8.

Table 6 The parameter values of the financial assets

Table 7 The parameter values of the insurer

Table 8 The parameter values of the reinsurer

4.1 Sensitivity analysis of the equilibrium investment strategy

Figure 1 shows the influence of risk aversion parameters on the equilibrium investment strategy. Figure 1a depicts the impact of the reinsurer’s risk aversion coefficient $\gamma _L$ on its optimal investment strategies $b_L^{*}(t)$ and $b_{L1}^{*}(t)$. Accordingly, Fig. 1b describes the impact of the insurer’s risk aversion coefficient $\gamma _F$ on its optimal investment strategies $b_F^{*}(t)$ and $b_{F1}^{*}(t)$. As can be seen from Fig. 1, the amount invested in the risky asset and the amount invested in the defaultable bond will decrease with the increase of risk aversion coefficient. In other words, the more risk-averse (i.e., conservative) investors are, the less willing they are to invest their idle assets in the risky asset and the bond with default risk, which is also consistent with the actual situation.

Fig. 1

Effects of risk aversion coefficients on the equilibrium investment strategy

Fig. 2

Effects of the defaultable bond coefficients on the equilibrium investment strategy

Figure 2 describes the effects of the coefficients of the defaultable bond on the equilibrium investment strategy at $t=0$. Figure 2a shows the effect of the default risk premium $\frac{1}{\Delta }$ on $b_{L1}^{*}(0)$ and $b_{F1}^{*}(0)$. We note that the amount of money invested in the defaultable bond increases as the default risk premium $\frac{1}{\Delta }$ increases and the slopes of the curves decrease as the default risk premium $\frac{1}{\Delta }$ increases. It is intuitive that the reinsurer and the insurer would invest more wealth in a corporate bond with a higher default risk premium. In addition, we find that the amount of money invested in the defaultable bond is zero when the defaultable bond’s risk premium is 1(i.e., $h^P=h^Q$). Figure 2b shows the sensitivity of the equilibrium investment strategy with respect to the loss rate $\zeta$. The curves in Fig.  2b mean that the amount of money invested in the defaultable bond decreases with the increase of the loss rate $\zeta$. This is easy to understand because a larger loss rate $\zeta$ results in a lower recovery rate; this implies that the reinsurer’s and the insurer’s potential losses become greater at a higher loss rate. As a result, the reinsurer and the insurer will reduce their investment in the defaulted bond when the loss rate is high.

Figure 3 presents the impacts of the constant elasticity parameter $\beta$ on equilibrium investment strategy at $t=0$. As shown in Fig. 3, the amount invested in the risk asset will increase with the increase of the elasticity parameter, and the increasing trend tends to be more and more flat. This indicates that both the reinsurer and the insurer will reduce investment in the risky asset as $\beta$ decreases to hedge the volatility risk.

Fig. 3

Effects of $\beta$ on the equilibrium investment strategy

Fig. 4

Effects of delay coefficients on the equilibrium investment strategy

Figure 4 illustrates the effects of delay coefficients (i.e., $\eta _L$, $h_L$, $\eta _F$ and $h_F$) on equilibrium investment strategy at $t=0$. Four subgraphs in Fig. 4 show that the investment strategy will decrease as the delay time increases, i.e., $\frac{\partial b_{L}^{*}(t)}{\partial h_L}<0$, $\frac{\partial b_{L1}^{*}(t)}{\partial h_L}<0$, $\frac{\partial b_{F}^{*}(t)}{\partial h_L}<0$ and $\frac{\partial b_{F1}^{*}(t)}{\partial h_L}<0$, which is consistent with the conclusions in Table 4. In addition, when the delay time is within a certain time range, the investment strategy has a positive correlation with the delay weight; when the delay time exceeds this range, a negative correlation is presented, which is consistent with (3.63) and (3.64).

Fig. 5

Effect of t on $p^{*}(t)$ and $q^{*}(t)$

4.2 Sensitivity analysis of the equilibrium premium strategy and reinsurance strategy

Table 9 Numerical results corresponding to Fig. 5

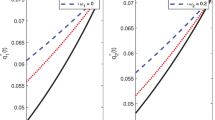
Figure 5 presents the changes of the equilibrium premium strategy and the equilibrium reinsurance strategy over time, and Table 9 shows the corresponding numerical results. From Table 9, we find that when $t\le 3$, the condition of Case (2) in Table 1 (i.e., $N^{{\bar{\theta }}}(t)\le K(t)$) is satisfied, then $p^{*}(t)={\bar{c}}$ and $q^{*}(t)=N^{{\bar{\theta }}}(t)$; when $t\ge 4$, the condition of Case (4) in Table 1 (i.e., $N^{\theta _F}(t)<K(t)<N^{{\bar{\theta }}}(t)$) is satisfied, then $p^{*}(t)=a+K(t)\gamma _F\sigma _F^2\varphi ^F(t)$ and $q^{*}(t)=K(t)$. Figure 5 clearly shows the trends of the equilibrium premium strategy and the equilibrium reinsurance strategy in these two cases.

Since Case (4) in Table 1 is the most general situation in this paper, we will analyze the sensitivity of the equilibrium premium strategy and the equilibrium reinsurance strategy in Case (4) in Table 1 with respect to model parameters. Therefore, in order to ensure that the condition of Case (4) is satisfied, we select the equilibrium strategy at $t=8$ for analysis.

Fig. 6

Effects of $\gamma _L$ and $\gamma _F$ on $p^{*}(8)$ and $q^{*}(8)$

Figure 6 depicts the effects of $\gamma _L$ and $\gamma _F$ on $p^{*}(8)$ and $q^{*}(8)$. From Fig. 6, we have the following findings. Firstly, the more risk-averse the reinsurer or the insurer is, the more expensive the reinsurance premium will be. Secondly, the more the reinsurer is risk-averse or the more the insurer prefers the risks, the higher the reserve level of the insurer will be. When the reinsurer is more risk-averse, it will reduce the compensation risk by raising the reinsurance premium price, and correspondingly the insurer will reduce the reinsurance proportion in the reinsurance contract (i.e., the insurer’s reserved proportion will increase). When the insurer is more risk-averse, it will reduce the compensation risk by reducing its reserved proportion (that is, increasing the proportion of reinsurance in the reinsurance contract), and accordingly the reinsurer will increase the price of reinsurance premium. These phenomena are consistent with the actual situation and the mathematical conclusions in Table 3.

Fig. 7

Effects of $\eta _L$, $h_L$, $\eta _F$ and $h_F$ on $p^{*}(8)$ and $q^{*}(8)$

Figure 7 illustrates the effects of delay coefficients (i.e., $\eta _L$, $h_L$, $\eta _F$ and $h_F$) on $p^{*}(8)$ and $q^{*}(8)$. Figure 7a shows that the premium strategy will increase as the delay time increases. In addition, when the delay time is within a certain time range, the premium strategy and the delay weight show a negative correlation; when the delay time exceeds this range, it shows a positive correlation. Figure 7b shows that the reinsurance strategy will decrease as the delay time increases. In addition, when the delay time is within a certain time range, the reinsurance strategy has a positive correlation with the delay weight; when the delay time exceeds this range, a negative correlation is presented. Combined with Fig. 4, we can find that the influence of delay weight on the equilibrium reinsurance premium strategy is just opposite to that on other strategies, which is consistent with Corollary 1 and Corollary 3.

5 Conclusion

In the paper, we study a stochastic Stackelberg differential reinsurance and investment game between a reinsurer and an insurer, in which the reinsurer is the leader and the insurer is the follower. Assuming that both the reinsurer and the insurer can invest their wealth in a financial market consisting of a risk-free asset, a risky asset and a defaultable bond. We consider the delay factor to characterize the bounded memory feature of wealth processes. The objective of the reinsurer is to determine the optimal reinsurance premium strategy and the optimal investment strategy to maximize the expected CARA utility of the combination of its terminal wealth and integrated performance. The objective of the insurer is to select the optimal reinsurance strategy and the optimal investment strategy to maximize the expected CARA utility of the combination of its terminal wealth and integrated performance. Based on the idea of backward induction and the dynamic programming approach, We derive the Stackelberg equilibrium reinsurance and investment strategy explicitly and prove the corresponding verification theorem. Finally, we present some numerical examples to illustrate the influence of model parameters on the equilibrium reinsurance and investment strategy and draw some economic interpretations.

The main findings are as concluded as follows: (1) When the Stackelberg equilibrium is achieved in the interior case (i.e., Case (4) in Theorem 1), the optimal reinsurance premium follows the variance premium principle, which implies the variance premium principle is an ideal candidate among all possible premium principles when the proportional reinsurance is applied. (2) The pre-default value functions of the reinsurer and the insurer are higher than the post-default value functions, respectively; which implies that the difference between two cases stands for the loss in the reinsurer’s and the insurer’s objectives due to the default event. (3) The influence of delay weight on equilibrium strategy depends on the length of delay time, and the influence of delay weight on the equilibrium reinsurance premium strategy is just opposite to that on other strategies.

Because the goal of minimizing the ruin probabilities is very important for reinsurers and insurers, it is also interesting to study the reinsurance-investment strategy aiming at minimizing ruin probabilities under the Stackelberg game framework, which can be seemed as an expansion of this paper in the future.

Appendices

Appendix A Proof of Theorem 2

Proof

Step 1 In the stochastic Stackelberg differential game, the reinsurer takes action first by announcing its any admissible strategy $\pi _L(\cdot )=(p(\cdot ),b_L(\cdot ),b_{L1}(\cdot ))\in \Pi _L$.

Step 2 Based on the reinsurer’s strategy $\pi _L(\cdot )=(p(\cdot ),b_L(\cdot ),b_{L1}(\cdot ))\in \Pi _L$, we solve the insurer’s optimization problem (2.14) under the CARA utility function.

When $h=0$, the HJB equation of the insurer becomes

$$\begin{aligned} 0=&\sup _{(q(\cdot ),b_F(\cdot ),b_{F1}(\cdot ))\in \Pi _F}\big \{\frac{\partial V^F(t,x_F,y_F,s,0)}{\partial t} \nonumber \\&+ \big [\theta _Fa-(p(t)-a)(1-q(t))+A_Fx_F+B_Fy_F+C_Fz_F\nonumber \\&+(r-r_0)b_F(t)+\eta b_{F1}(t)\big ]\frac{\partial V^F(t,x_F,y_F,s,0)}{\partial x_F}\nonumber \\&+\frac{1}{2}\big [(q(t))^2\sigma _F^2+(b_F(t))^2\sigma ^2s^{2\beta }\big ]\frac{\partial V^F(t,x_F,y_F,s,0)}{\partial x_F^2}\nonumber \\&+(x_F-\alpha _Fy_F-e^{-\alpha _Fh_F}z_F)\frac{\partial V^F(t,x_F,y_F,s,0)}{\partial y_F}\nonumber \\&+rs\frac{\partial V^F(t,x_F,y_F,s,0)}{\partial s}+\frac{1}{2}\sigma ^2s^{2\beta +2}\frac{\partial V^F(t,x_F,y_F,s,0)}{\partial s^2}\nonumber \\&+b_F(t)\sigma ^2s^{2\beta +1} \frac{\partial V^F(t,x_F,y_F,s,0)}{\partial x_F\partial s}\nonumber \\&+\big [V^F(t,x_F-b_{F1}(t)\zeta ,y_F,s,1)-V^F(t,x_F,y_F,s,0)\big ]h^P\big \}, \end{aligned}$$

(A.70)

with the boundary condition $V^F(T,x_F,y_F,s,0)=U_F(x_F+\eta _Fy_F)$. To solve this equation, we conjecture that

$$\begin{aligned} V^F\big (t,x_F,y_F,s,0\big ) =&-\frac{1}{\gamma _F}\exp [-\gamma _F\varphi ^F(t)(x_F+\eta _Fy_F) +g^F_{01}(t)s^{-2\beta }+g^F_{02}(t)], \end{aligned}$$

(A.71)

where $\varphi ^F(t)$, $g^F_{01}(t)$ and $g^F_{02}(t)$ are deterministic, continuously differentiable functions with boundary conditions $\varphi ^F(T)=0$, $g^F_{01}(T)=0$ and $g^F_{02}(T)=0$. Then, we can get that

$$\begin{aligned} \frac{\partial V^F(t,x_F,y_F,s,0)}{\partial t}&=V^F(t,x_F,y_F,s,0)[-\gamma _F\frac{d\varphi ^F(t)}{d t}(x_F+\eta _Fy_F) \\&\quad +\frac{d g^F_{01}(t)}{d t}s^{-2\beta }+\frac{d g^F_{02}(t)}{d t}],\\ \frac{\partial V^F(t,x_F,y_F,s,0)}{\partial x_F}&=V^F(t,x_F,y_F,s,0)[-\gamma _F\varphi ^F(t)],\\ \frac{\partial V^F(t,x_F,y_F,s,0)}{\partial x_F^2}&=V^F(t,x_F,y_F,s,0)(\gamma _F)^2[\varphi ^F(t)]^2,\\ \frac{\partial V^F(t,x_F,y_F,s,0)}{\partial y_F}&=V^F(t,x_F,y_F,s,0)[-\gamma _F\eta _F\varphi ^F(t)],\\ \frac{\partial V^F(t,x_F,y_F,s,0)}{\partial s}&=V^F(t,x_F,y_F,s,0)[-2\beta g^F_{01}(t)s^{-2\beta -1}],\\ \frac{\partial V^F(t,x_F,y_F,s,0)}{\partial s^2}&=V^F(t,x_F,y_F,s,0)[4\beta ^2 (g^F_{01}(t))^2s^{-4\beta -2}+2\beta (2\beta +1) g^F_{01}(t)s^{-2\beta -2}],\\ \frac{\partial V^F(t,x_F,y_F,s,0)}{\partial x_F\partial s}&=V^F(t,x_F,y_F,s,0)\gamma _F\varphi ^F(t)2\beta g^F_{01}(t)s^{-2\beta -1}. \end{aligned}$$

Substituting the above differential forms into the HJB equation (A.70) leads the following differential equation:

$$\begin{aligned} 0=&V^F(t,x_F,y_F,s,0)\Big \{ \gamma _Fx_F\big (-\frac{d\varphi ^F(t)}{dt}-\varphi ^F(t)A_F-\varphi ^F(t)\eta _F\big )\nonumber \\&+\gamma _Fy_F\big (-\frac{d\varphi ^F(t)}{dt}\eta _F-\varphi ^F(t)B_F+\varphi ^F(t)\eta _F\alpha _F\big )\nonumber \\&+\gamma _F\varphi ^F(t)z_F\big (-C_F+\eta _Fe^{-\alpha _Fh_F}\big )\nonumber \\&+s^{-2\beta }\big [\frac{dg^F_{01}(t)}{dt}-2\beta rg^F_{01}(t)+2\sigma ^2\beta ^2(g^F_{01}(t))^2\big ] +\beta (2\beta +1)\sigma ^2g^F_{01}(t)\nonumber \\&+\frac{dg^F_{02}(t)}{dt}-\gamma _F\varphi ^F(t)\theta _Fa\nonumber \\&+\inf _{q(t)\in [0,1]}\big [\gamma _F\varphi ^F(t)(p(t)-a)(1-q(t)) +\frac{1}{2}\gamma ^2_F\sigma _F^2(\varphi ^F(t))^2(q(t))^2\big ]\nonumber \\&+\inf _{b_F(t)}\big [-\gamma _F\varphi ^F(t)(r-r_0)b_F(t) +\frac{1}{2}\gamma ^2_F\sigma ^2(\varphi ^F(t))^2s^{2\beta }(b_F(t))^2\nonumber \\&+2\beta \sigma ^2\gamma _F\varphi ^F(t)g^F_{01}(t)b_F(t)\big ]\nonumber \\&+\inf _{b_{F1}(t)}\big [-\gamma _F\varphi ^F(t)\eta b_{F1}(t)\nonumber \\&+h^P(e^{\gamma _F\varphi ^F(t)b_{F1}(t)\zeta +(g^F_{1}(t)-g^F_{01}(t))s^{-2\beta }+(g^F_{2}(t)-g^F_{02}(t))}-1)\big ]\Big \}. \end{aligned}$$

(A.72)

The first-order conditions for a regular interior minimizer of (A.72) gives that

$$\begin{aligned} q^{*}(t,p(t))&=\alpha ^{*}(t,p(t)) =\frac{p(t)-a}{\gamma _F\sigma _F^2\varphi ^F(t)}\vee 0 \wedge 1, \end{aligned}$$

(A.73)

$$\begin{aligned} b^{*}_F(t)&=\frac{(r-r_0)s^{-2\beta }}{\gamma _F\varphi ^F(t)\sigma ^2}-\frac{2\beta g_{01}^F(t)s^{-2\beta }}{\gamma _F\varphi ^F(t)}, \end{aligned}$$

(A.74)

$$\begin{aligned} b^{*}_{F1}(t)&=\frac{ln(\frac{1}{\Delta }) -(g^F_{1}(t)-g^F_{01}(t))s^{-2\beta } -(g^F_{2}(t)-g^F_{02}(t))}{\gamma _F\varphi ^F(t)\zeta }. \end{aligned}$$

(A.75)

It is observed that the optimal investment strategies $b^{*}_{F}(t)$ and $b^{*}_{F1}(t)$ have nothing to do with the reinsurer’s strategy, and the optimal reinsurance strategy $q^{*}(t)$ depends on the reinsurer’s premium pricing strategy. Furthermore, the optimal strategies $q^{*}(t,p(t))$, $b^{*}_F(t)$ and $b^{*}_{F1}(t)$ do not depend on state variables $x_F$, $y_F$ and $z_F$. Substitute $b^{*}_F(t)$ and $b^{*}_{F1}(t)$ into (A.72), we can get that

$$\begin{aligned} 0=&V^F(t,x_F,y_F,s,0)\Big \{ \gamma _Fx_F\big (-\frac{d\varphi ^F(t)}{dt}-\varphi ^F(t)A_F-\varphi ^F(t)\eta _F\big )\nonumber \\&+\gamma _Fy_F\big (-\frac{d\varphi ^F(t)}{dt}\eta _F-\varphi ^F(t)B_F+\varphi ^F(t)\eta _F\alpha _F\big )\nonumber \\&+\gamma _F\varphi ^F(t)z_F\big (-C_F+\eta _Fe^{-\alpha _Fh_F}\big )\nonumber \\&+s^{-2\beta }\big [\frac{dg^F_{01}(t)}{dt}-2\beta r_0g^F_{01}(t)\nonumber \\&-\frac{1}{2}\frac{(r-r_0)^2}{\sigma ^2}+\frac{\eta }{\zeta }(g^F_{1}(t)-g^F_{01}(t))\big ]\nonumber \\&+\frac{dg^F_{02}(t)}{dt} +\beta (2\beta +1)\sigma ^2g^F_{01}(t)+\frac{\eta }{\zeta }(g^F_{2}(t)-g^F_{02}(t)) +h^P(\frac{1}{\Delta }-1)\nonumber \\&-\frac{\eta }{\zeta }ln(\frac{1}{\Delta }) -\gamma _F\varphi ^F(t)\theta _Fa\nonumber \\&+\big [\gamma _F\varphi ^F(t)(p(t)-a)(1-q^{*}(t,p(t))) +\frac{1}{2}\gamma ^2_F\sigma _F^2(\varphi ^F(t))^2(q^{*}(t,p(t)))^2\big ]\Big \}. \end{aligned}$$

(A.76)

Then, we can derive (A.76) into the following differential equations:

$$\begin{aligned} 0=&\gamma _Fx_F\big (-\frac{d\varphi ^F(t)}{dt}-\varphi ^F(t)A_F-\varphi ^F(t)\eta _F\big )\nonumber \\&+\gamma _Fy_F\big (-\frac{d\varphi ^F(t)}{dt}\eta _F-\varphi ^F(t)B_F+\varphi ^F(t)\eta _F\alpha _F\big )\nonumber \\&+\gamma _F\varphi ^F(t)z_F\big (-C_F+\eta _Fe^{-\alpha _Fh_F}\big ), \end{aligned}$$

(A.77)

$$\begin{aligned} 0=&s^{-2\beta }\big [\frac{dg^F_{01}(t)}{dt}-2\beta r_0g^F_{01}(t)-\frac{1}{2}\frac{(r-r_0)^2}{\sigma ^2}+\frac{\eta }{\zeta }(g^F_{1}(t)-g^F_{01}(t))\big ], \end{aligned}$$

(A.78)

$$\begin{aligned} 0=&\frac{dg^F_{02}(t)}{dt} +\beta (2\beta +1)\sigma ^2g^F_{01}(t)+\frac{\eta }{\zeta }(g^F_{2}(t)-g^F_{02}(t)) +h^P(\frac{1}{\Delta }-1) -\frac{\eta }{\zeta }ln(\frac{1}{\Delta })\nonumber \\&-\gamma _F\varphi ^F(t)\theta _Fa+\big [\gamma _F\varphi ^F(t)(p(t)-a)(1-q^{*}(t,p(t)))\nonumber \\&+\frac{1}{2}\gamma ^2_F\sigma _F^2(\varphi ^F(t))^2(q^{*}(t,p(t)))^2\big ], \end{aligned}$$

(A.79)

with boundary conditions $\varphi ^F(T)=0$, $g^F_{01}(T)=0$ and $g^F_{02}(T)=0$. Due to (3.19), we have

$$\begin{aligned} \varphi ^F(t)=&\exp [(A_F+\eta _F)(T-t)]. \end{aligned}$$

(A.80)

Let $G_1^F(t)=g^F_{01}(t)-g^F_{1}(t)$, and $G_1^F(t)$ is differentiated w.r.t. t. From (3.30) and (A.78), we obtain:

$$\begin{aligned} \frac{dG_1^F(t)}{dt}=\frac{dg^F_{01}(t)}{dt}-\frac{dg^F_{1}(t)}{dt}=(2\beta r_0+\frac{\eta }{\zeta })G_1^F(t), \end{aligned}$$

(A.81)

with boundary conditions $G_1^F(T)=g^F_{01}(T)-g^F_{1}(T)=0$. Then, $G_1^F(t)=0$, i.e., $g^F_{01}(t)=g^F_{1}(t)$.

Similarly, let $G_2^{F}(t)=g^F_{02}(t)-g^F_{2}(t)$, and $G_2^{F}(t)$ is differentiated w.r.t. t. From the process of calculating the value functions in Theorem 1, we know that

$$\begin{aligned} 0=&\frac{dg^F_{2}(t)}{dt} +\beta (2\beta +1)\sigma ^2g^F_{1}(t) -\gamma _F\varphi ^F(t)\theta _Fa\nonumber \\&+\gamma _F\varphi ^F(t)(p(t)-a)(1-q^{*}(t,p(t)))\nonumber \\&+\frac{1}{2}\gamma ^2_F\sigma _F^2(\varphi ^F(t))^2(q^{*}(t,p(t)))^2. \end{aligned}$$

(A.82)

From (A.82) and (A.79), we have:

$$\begin{aligned} \frac{dG_2^F(t)}{dt}=&\frac{dg^F_{02}(t)}{dt}-\frac{dg^F_{2}(t)}{dt}\nonumber \\&=\frac{\eta }{\zeta }G_2^F(t)+\frac{\eta }{\zeta }ln(\frac{1}{\Delta })-h^P(\frac{1}{\Delta }-1), \end{aligned}$$

(A.83)

with boundary conditions $G_2^F(T)=g^F_{02}(T)-g^F_{2}(T)=0$. Then,

$$\begin{aligned} G_2^F(t) =(ln\frac{1}{\Delta }+\Delta -1)[e^{-\frac{\eta }{\zeta }(T-t)}-1]. \end{aligned}$$

(A.84)

That is $g^F_{02}(t)=g^F_{2}(t)+G_2^{F}(t)$.

Then, from (A.74) and (A.75), the optimal investment strategies for the insurer are given by

$$\begin{aligned} b^{*}_F(t)&=\frac{(r-r_0)s^{-2\beta }}{\gamma _F\varphi ^F(t)\sigma ^2}-\frac{2\beta g_{1}^F(t)s^{-2\beta }}{\gamma _F\varphi ^F(t)}, \end{aligned}$$

(A.85)

$$\begin{aligned} b^{*}_{F1}(t)&=\frac{ln(\frac{1}{\Delta }) +(ln\frac{1}{\Delta }+\Delta -1)(e^{-\frac{\eta }{\zeta }(T-t)}-1)}{\gamma _F\varphi ^F(t)\zeta }. \end{aligned}$$

(A.86)

From the form of $\varphi ^F(t)$ and the range of reinsurance premium price p(t), we know that $q^{*}(t,p(t))=\frac{p(t)-a}{\gamma _F\sigma _F^2\varphi ^F(t)}>0$. Next, we will discuss the size relationship between reinsurance strategy $q^{*}(t,p(t))$ and 1.

• Case (Fa) If $\frac{p(t)-a}{\gamma _F\sigma _F^2\varphi ^F(t)}\ge 1$, then $q^{*}(t,p(t))=1$.

  Substituting $q^{*}(t,p(t))$ into Eq. (A.79) gives

  $$\begin{aligned} 0=&\frac{dg^F_{02}(t)}{dt} +\beta (2\beta +1)\sigma ^2g^F_{01}(t)+\frac{\eta }{\zeta }(g^F_{2}(t)-g^F_{02}(t))\nonumber \\&+h^P(\frac{1}{\Delta }-1) -\frac{\eta }{\zeta }ln(\frac{1}{\Delta })\nonumber \\&-\gamma _F\varphi ^F(t)\theta _Fa+ \frac{1}{2}\gamma ^2_F\sigma _F^2(\varphi ^F(t))^2. \end{aligned}$$

  (A.87)

  The integral from T to t gives that

  $$\begin{aligned} g^F_{02}(t)=g^{Fa}_{02}(t)\doteq g^{Fa}_{2}(t)+G_2^{F}(t). \end{aligned}$$

  (A.88)

• Case (Fb) If $\frac{p(t)-a}{\gamma _F\sigma _F^2\varphi ^F(t)}<1$, then $q^{*}(t,p(t))=\frac{p(t)-a}{\gamma _F\sigma _F^2\varphi ^F(t)}$. Substituting $q^{*}(t,p(t))$ into Eq. (A.79) and integrating from T to t gives

  $$\begin{aligned} 0=&\frac{dg^F_{02}(t)}{dt} +\beta (2\beta +1)\sigma ^2g^F_{01}(t)+\frac{\eta }{\zeta }(g^F_{2}(t)-g^F_{02}(t))\nonumber \\&+h^P(\frac{1}{\Delta }-1) -\frac{\eta }{\zeta }ln(\frac{1}{\Delta })\nonumber \\&-\gamma _F\varphi ^F(t)\theta _Fa+\gamma _F\varphi ^F(t)(p(t)-a) -\frac{1}{2\sigma _F^2}(p(t)-a)^2. \end{aligned}$$

  (A.89)

  The integral from T to t gives that

  $$\begin{aligned} g^F_{02}(t)=g^{Fb}_{02}(t)\doteq g^{Fb}_{2}(t)+G_2^{F}(t). \end{aligned}$$

  (A.90)

Step 3

When $h=0$, the HJB equation of the reinsurer becomes

$$\begin{aligned} 0=&\sup _{(p(\cdot ),b_L(\cdot ),b_{L1}(\cdot ))\in \Pi _L}\big \{\frac{\partial V^L(t,x_L,y_L,s,0)}{\partial t} \nonumber \\&+ \big [(p(t)-a)(1-q^{*}(t))+A_Lx_L+B_Ly_L+C_Lz_L\nonumber \\&+(r-r_0)b_L(t)+\eta b_{L1}(t)\big ]\frac{\partial V^L(t,x_L,y_L,s,0)}{\partial x_L}\nonumber \\&+\frac{1}{2}\big [(1-q^{*}(t))^2\sigma _F^2+(b_L(t))^2\sigma ^2s^{2\beta }\big ]\frac{\partial V^L(t,x_L,y_L,s,0)}{\partial x_L^2}\nonumber \\&+(x_L-\alpha _Ly_L-e^{-\alpha _Lh_L}z_L)\frac{\partial V^L(t,x_L,y_L,s,0)}{\partial y_L}+rs\frac{\partial V^L(t,x_L,y_L,s,0)}{\partial s}\nonumber \\&+\frac{1}{2}\sigma ^2s^{2\beta +2}\frac{\partial V^L(t,x_L,y_L,s,0)}{\partial s^2} +b_L(t)\sigma ^2s^{2\beta +1} \frac{\partial V^L(t,x_L,y_L,s,0)}{\partial x_L\partial s}\nonumber \\&+\big [V^L(t,x_L-b_{L1}(t)\zeta ,y_L,s,1)-V^L(t,x_L,y_L,s,0)\big ]h^P\big \}. \end{aligned}$$

(A.91)

with the boundary condition $V^L(T,x_L,y_L,s,0)=U_L(x_L+\eta _Ly_L)$. To solve this equation, we conjecture that

$$\begin{aligned} V^L\big (t,x_L,y_L,s,0\big ) =&-\frac{1}{\gamma _L}\exp [-\gamma _L\varphi ^L(t)(x_L+\eta _Ly_L) +g^L_{01}(t)s^{-2\beta }+g^L_{02}(t)], \end{aligned}$$

(A.92)

where $\varphi ^L(t)$, $g^L_{01}(t)$ and $g^L_{02}(t)$ are deterministic, continuously differentiable functions with boundary conditions $\varphi ^L(T)=0$, $g^L_{01}(T)=0$ and $g^L_{02}(T)=0$. Then, we can get that

$$\begin{aligned}&\frac{\partial V^L(t,x_L,y_L,s,0)}{\partial t} =V^L(t,x_L,y_L,s,0)\\&\qquad \qquad \left[ -\gamma _L\frac{d\varphi ^L(t)}{d t}(x_L+\eta _Ly_L) +\frac{d g^L_{01}(t)}{d t}s^{-2\beta }+\frac{d g^L_{02}(t)}{d t}\right] ,\\&\frac{\partial V^L(t,x_L,y_L,s,0)}{\partial x_L}=V^L(t,x_L,y_L,s,0)[-\gamma _L\varphi ^L(t)],\\&\frac{\partial V^L(t,x_L,y_L,s,0)}{\partial x_L^2}=V^L(t,x_L,y_L,s,0)(\gamma _L)^2(\varphi ^L(t))^2,\\&\frac{\partial V^L(t,x_L,y_L,s,0)}{\partial y_L}=V^L(t,x_L,y_L,s,0)[-\gamma _L\eta _L\varphi ^L(t)],\\&\frac{\partial V^L(t,x_L,y_L,s,0)}{\partial s}=V^L(t,x_L,y_L,s,0)[-2\beta g^L_{01}(t)s^{-2\beta -1}],\\&\frac{\partial V^L(t,x_L,y_L,s,0)}{\partial s^2}=V^L(t,x_L,y_L,s,0)[4\beta ^2 (g^L_{01}(t))^2s^{-4\beta -2}+2\beta (2\beta +1) g^L_{01}(t)s^{-2\beta -2}],\\&\frac{\partial V^L(t,x_L,y_L,s,0)}{\partial x_L\partial s}=V^L(t,x_L,y_L,s,0)\gamma _L\varphi ^L(t)2\beta g^L_{01}(t)s^{-2\beta -1}. \end{aligned}$$

Substituting the above differential forms into the HJB equation (A.91) leads the following differential equation:

$$\begin{aligned} 0=&V^L(t,x_L,y_L,s,0)\Big \{ \gamma _Lx_L\big (-\frac{d\varphi ^L(t)}{dt}-\varphi ^L(t)A_L-\varphi ^L(t)\eta _L\big )\nonumber \\&+\gamma _Ly_L\big (-\frac{d\varphi ^L(t)}{dt}\eta _L-\varphi ^L(t)B_L+\varphi ^L(t)\eta _L\alpha _L\big )\nonumber \\&+\gamma _L\varphi ^L(t)z_L\big (-C_L+\eta _Le^{-\alpha _Lh_L}\big )\nonumber \\&+s^{-2\beta }\big [\frac{dg^L_{01}(t)}{dt}-2\beta rg^L_{01}(t)+2\sigma ^2\beta ^2(g^L_{01}(t))^2\big ]\nonumber \\&+\beta (2\beta +1)\sigma ^2g^L_{01}(t) +\frac{dg^L_{02}(t)}{dt}\nonumber \\&+\inf _{p(t)\in [c_F,{\bar{c}}]}\big [-\gamma _L\varphi ^L(t)(p(t)-a)(1-q^{*}(t,p(t)))\nonumber \\&+\frac{1}{2}\gamma ^2_L\sigma _F^2(\varphi ^L(t))^2(1-q^{*}(t,p(t)))^2\big ]\nonumber \\&+\inf _{b_L(t)}\big [-\gamma _L\varphi ^L(t)(r-r_0)b_L(t)\nonumber \\&+\frac{1}{2}\gamma ^2_L\sigma ^2(\varphi ^L(t))^2s^{2\beta }(b_L(t))^2 +2\beta \sigma ^2\gamma _L\varphi ^L(t)g^L_{01}(t)b_L(t)\big ]\nonumber \\&+\inf _{b_{L1}(t)}\big [-\gamma _L\varphi ^L(t)\eta b_{L1}(t)\nonumber \\&+h^P(e^{\gamma _L\varphi ^L(t)b_{L1}(t)\zeta +(g^L_{1}(t)-g^L_{01}(t))s^{-2\beta }+(g^L_{2}(t)-g^L_{02}(t))}-1)\big ]\Big \}. \end{aligned}$$

(A.93)

Since the premium strategy and investment strategies are independent of each other, the first-order conditions for a regular interior minimizer of (A.93) about $b^{*}_L(t)$ and $b^{*}_{L1} (t)$ give that

$$\begin{aligned} b^{*}_L(t)&=\frac{(r-r_0)s^{-2\beta }}{\gamma _L\varphi ^L(t)\sigma ^2}-\frac{2\beta g_{01}^L(t)s^{-2\beta }}{\gamma _L\varphi ^L(t)}, \end{aligned}$$

(A.94)

$$\begin{aligned} b^{*}_{L1}(t)&=\frac{ln(\frac{1}{\Delta }) -(g^L_{1}(t)-g^L_{01}(t))s^{-2\beta } -(g^L_{2}(t)-g^L_{02}(t))}{\gamma _L\varphi ^L(t)\zeta }. \end{aligned}$$

(A.95)

Substitute $b^{*}_L(t)$ and $b^{*}_{L1}(t)$ into (A.93), we can get that

$$\begin{aligned} 0=&V^L(t,x_L,y_L,s,0)\Big \{ \gamma _Lx_L\big (-\frac{d\varphi ^L(t)}{dt}-\varphi ^L(t)A_L-\varphi ^L(t)\eta _L\big )\nonumber \\&+\gamma _L\varphi ^L(t)z_L\big (-C_L+\eta _Le^{-\alpha _Lh_L}\big )\nonumber \\&+\gamma _Ly_L\big (-\frac{d\varphi ^L(t)}{dt}\eta _L-\varphi ^L(t)B_L+\varphi ^L(t)\eta _L\alpha _L\big )\nonumber \\&+s^{-2\beta }\big [\frac{dg^L_{01}(t)}{dt}-2\beta r_0g^L_{01}(t)-\frac{1}{2}\frac{(r-r_0)^2}{\sigma ^2}\nonumber \\&+\frac{\eta }{\zeta }(g^L_{1}(t)-g^L_{01}(t))\big ] +\frac{dg^L_{02}(t)}{dt} +\beta (2\beta +1)\sigma ^2g^L_{01}(t)\nonumber \\&+\frac{\eta }{\zeta }(g^L_{2}(t)-g^L_{02}(t)) +h^P(\frac{1}{\Delta }-1) -\frac{\eta }{\zeta }ln(\frac{1}{\Delta }) \nonumber \\&+\inf _{p(t)\in [c_F,{\bar{c}}]}\big [-\gamma _L\varphi ^L(t)(p(t)-a)(1-q^{*}(t,p(t)))\nonumber \\&+\frac{1}{2}\gamma ^2_L\sigma _F^2(\varphi ^L(t))^2(1-q^{*}(t,p(t)))^2\big ]\Big \}. \end{aligned}$$

(A.96)

Then, we can derive (A.96) into the following differential equations:

$$\begin{aligned} 0=&\gamma _Lx_L\big (-\frac{d\varphi ^L(t)}{dt}-\varphi ^L(t)A_L-\varphi ^L(t)\eta _L\big )\nonumber \\&+\gamma _Ly_L\big (-\frac{d\varphi ^L(t)}{dt}\eta _L-\varphi ^L(t)B_L+\varphi ^L(t)\eta _L\alpha _L\big )\nonumber \\&+\gamma _L\varphi ^L(t)z_L\big (-C_L+\eta _Le^{-\alpha _Lh_L}\big ), \end{aligned}$$

(A.97)

$$\begin{aligned} 0=&s^{-2\beta }\big [\frac{dg^L_{01}(t)}{dt}-2\beta r_0g^L_{01}(t)-\frac{1}{2}\frac{(r-r_0)^2}{\sigma ^2}+\frac{\eta }{\zeta }(g^L_{1}(t)-g^L_{01}(t))\big ], \end{aligned}$$

(A.98)

$$\begin{aligned} 0=&\frac{dg^L_{02}(t)}{dt} +\beta (2\beta +1)\sigma ^2g^L_{01}(t)+\frac{\eta }{\zeta }(g^L_{2}(t)-g^L_{02}(t))\nonumber \\&+h^P(\frac{1}{\Delta }-1) -\frac{\eta }{\zeta }ln(\frac{1}{\Delta }) \nonumber \\&+\inf _{p(t)\in [c_F,{\bar{c}}]}\big [-\gamma _L\varphi ^L(t)(p(t)-a)(1-q^{*}(t,p(t)))\nonumber \\&+\frac{1}{2}\gamma ^2_L\sigma _F^2(\varphi ^L(t))^2(1-q^{*}(t,p(t)))^2\big ]. \end{aligned}$$

(A.99)

with boundary conditions $\varphi ^L(T)=0$, $g^L_{1}(T)=0$ and $g^L_{2}(T)=0$. Due to (3.18), we have

$$\begin{aligned} \varphi ^L(t)=&\exp [(A_L+\eta _L)(T-t)]. \end{aligned}$$

(A.100)

Let $G_1^L(t)=g^L_{01}(t)-g^L_{1}(t)$, and $G_1^L(t)$ is differentiated w.r.t. t. From (3.30) and (A.98), we obtain:

$$\begin{aligned} \frac{dG_1^L(t)}{dt}=\frac{dg^L_{01}(t)}{dt}-\frac{dg^L_{1}(t)}{dt}=(2\beta r_0+\frac{\eta }{\zeta })G_1^L(t), \end{aligned}$$

(A.101)

with boundary condition $G_1^L(T)=g^L_{01}(T)-g^L_{1}(T)=0$. Then, $G_1^L(t)=0$, i.e., $g^L_{01}(t)=g^L_{1}(t)$.

Similarly, let $G_2^{L}(t)=g^L_{02}(t)-g^L_{2}(t)$, and $G_2^{L}(t)$ is differentiated w.r.t. t. From the process of calculating the value functions in Theorem 1, we know that

$$\begin{aligned} 0=&\frac{dg^L_{2}(t)}{dt}+\beta (2\beta +1)\sigma ^2g^L_{1}(t) +\inf _{p(t)\in [c_F,{\bar{c}}]}\big [-\gamma _L\varphi ^L(t)(p(t)-a)(1-q^{*}(t,p(t))) \nonumber \\&+\frac{1}{2}\gamma ^2_L\sigma _F^2(\varphi ^L(t))^2(1-q^{*}(t,p(t)))^2\big ]. \end{aligned}$$

(A.102)

From (A.102) and (A.99), we have:

$$\begin{aligned} \frac{dG_2^L(t)}{dt}=\frac{dg^L_{02}(t)}{dt}-\frac{dg^L_{2}(t)}{dt} =\frac{\eta }{\zeta }G_2^L(t)+\frac{\eta }{\zeta }ln(\frac{1}{\Delta })-h^P(\frac{1}{\Delta }-1), \end{aligned}$$

(A.103)

with boundary conditions $G_2^L(T)=g^L_{02}(T)-g^L_{2}(T)=0$. Then,

$$\begin{aligned} G_2^L(t) =(ln\frac{1}{\Delta }+\Delta -1)[e^{-\frac{\eta }{\zeta }(T-t)}-1]. \end{aligned}$$

(A.104)

That is $g^L_{02}(t)=g^L_{2}(t)+G_2^{L}(t)$.

Then, from (A.94) and (A.95), the optimal investment strategies for the reinsurer are given by

$$\begin{aligned} b^{*}_L(t)&=\frac{(r-r_0)s^{-2\beta }}{\gamma _L\varphi ^L(t)\sigma ^2}-\frac{2\beta g_{1}^L(t)s^{-2\beta }}{\gamma _L\varphi ^L(t)}, \end{aligned}$$

(A.105)

$$\begin{aligned} b^{*}_{L1}(t)&=\frac{ln(\frac{1}{\Delta }) +(ln\frac{1}{\Delta }+\Delta -1)[e^{-\frac{\eta }{\zeta }(T-t)}-1]}{\gamma _L\varphi ^L(t)\zeta }. \end{aligned}$$

(A.106)

For premium strategy p(t), we discuss it in the following categories:

• Case (La) If $\frac{p(t)-a}{\gamma _F\sigma _F^2\varphi ^F(t)}\ge 1$, then $q^{*}(t,p(t))=1$. Substituting $q^{*}(t,p(t))$ into Eq. (A.99), we have

  $$\begin{aligned} 0=&\frac{dg^L_{02}(t)}{dt} +\beta (2\beta +1)\sigma ^2g^L_{01}(t)+\frac{\eta }{\zeta }(g^L_{2}(t)-g^L_{02}(t))\nonumber \\&+h^P(\frac{1}{\Delta }-1) -\frac{\eta }{\zeta }ln(\frac{1}{\Delta }). \end{aligned}$$

  (A.107)

  with the boundary condition $g^L_{02}(T)=0$. We can get that $p^{*}(t)=p$, where p is an arbitrary value in the interval $[c_F,{\bar{c}}]$. Then, $q^{*}(t,p^{*}(t))=1$. The precondition $\frac{p(t)-a}{\gamma _F\sigma _F^2\varphi ^F(t)}\ge 1$ becomes $N^{\theta _F}(t)\ge 1$. From (3.34) and (A.107), we have

  $$\begin{aligned} g^L_{02}(t)=g^{La}_{02}(t)\doteq g^{La}_{2}(t)+G_2^{L}(t). \end{aligned}$$

  (A.108)

• Case (Lb) If $\frac{p(t)-a}{\gamma _F\sigma _F^2\varphi ^F(t)}<1$, then $q^{*}(t,p(t))=\frac{p(t)-a}{\gamma _F\sigma _F^2\varphi ^F(t)}$. Substituting $q^{*}(t,p(t))$ into Eq. (A.99), we have

  $$\begin{aligned} 0=&\frac{dg^L_{02}(t)}{dt} +\beta (2\beta +1)\sigma ^2g^L_{01}(t)+\frac{\eta }{\zeta }(g^L_{2}(t)-g^L_{02}(t)) +h^P(\frac{1}{\Delta }-1) -\frac{\eta }{\zeta }ln(\frac{1}{\Delta }) \nonumber \\&+\inf _{p(t)\in [c_F,{\bar{c}}]} \big \{(p(t)-a)^2[\frac{\gamma _L\varphi ^L(t)}{\gamma _F\sigma _F^2\varphi ^F(t)} +\frac{1}{2}\frac{\gamma _L^2(\varphi ^L(t))^2}{\gamma _F^2\sigma _F^2(\varphi ^F(t))^2}]\nonumber \\&-(p(t)-a)[\gamma _L\varphi ^L(t)+\frac{\gamma _L^2(\varphi ^L(t))^2}{\gamma _F(\varphi ^F(t))}]+\frac{1}{2}\gamma _L^2(\varphi ^L(t))^2\sigma _F^2 \big \}. \end{aligned}$$

  (A.109)

  with boundary condition $g^L_{02}(T)=0$. The first-order conditions for a regular interior minimizer of (A.109) gives that

  $$\begin{aligned} p^{*}(t)=[a+K(t)\gamma _F\sigma _F^2\varphi ^F(t)]\vee c_F \wedge {\bar{c}}. \end{aligned}$$

  (A.110)

• Subcase (Lb1) When $a+K(t)\gamma _F\sigma _F^2\varphi ^F(t)\ge {\bar{c}}$, we have $p^{*}(t)={\bar{c}}$, $q^{*}(t,p^{*}(t))=N^{{\bar{\theta }}}(t)$. Then, the precondition $\frac{p(t)-a}{\gamma _F\sigma _F^2\varphi ^F(t)}<1$ becomes $N^{{\bar{\theta }}}(t)<1$, which is definitely true in this case due to $K(t)<1$. Then, by Eq. (A.109), we can get that

  $$\begin{aligned} 0=&\frac{dg^L_{02}(t)}{dt} +\beta (2\beta +1)\sigma ^2g^L_{01}(t)+\frac{\eta }{\zeta }(g^L_{2}(t)-g^L_{02}(t))\nonumber \\&+h^P(\frac{1}{\Delta }-1) -\frac{\eta }{\zeta }ln(\frac{1}{\Delta }) \nonumber \\&+({\bar{\theta }}a)^2[\frac{\gamma _L\varphi ^L(t)}{\gamma _F\sigma _F^2\varphi ^F(t)} +\frac{1}{2}\frac{\gamma _L^2(\varphi ^L(t))^2}{\gamma _F^2\sigma _F^2(\varphi ^F(t))^2}]\nonumber \\&-({\bar{\theta }}a)[\gamma _L\varphi ^L(t)+\frac{\gamma _L^2(\varphi ^L(t))^2}{\gamma _F(\varphi ^F(t))}] +\frac{1}{2}\gamma _L^2(\varphi ^L(t))^2\sigma _F^2. \end{aligned}$$

  (A.111)

  From (3.35) and (A.111), we have

  $$\begin{aligned} g^L_{02}(t)=g^{Lb1}_{02}(t)\doteq&g^{Lb1}_{2}(t)+G^L_2(t). \end{aligned}$$

  (A.112)

  And, Eq. (A.90) becomes

  $$\begin{aligned} g^{Fb}_{02}(t)=g^{Fb1}_{02}(t)\doteq&g^{Fb1}_{2}(t)+G^L_2(t). \end{aligned}$$

  (A.113)

• Subcase (Lb2) When $a+K(t)\gamma _F\sigma _F^2\varphi ^F(t)\le c_F$, we have $p^{*}(t)=c_F$, $q^{*}(t,p^{*}(t))=N^{\theta _F}(t)$. Then, the precondition $\frac{p(t)-a}{\gamma _F\sigma _F^2\varphi ^F(t)}<1$ becomes $N^{\theta _F}(t)<1$. Then, by Eq. (A.109), we can get that

  $$\begin{aligned} 0=&\frac{dg^L_{02}(t)}{dt} +\beta (2\beta +1)\sigma ^2g^L_{01}(t)+\frac{\eta }{\zeta }(g^L_{2}(t)-g^L_{02}(t)) +h^P(\frac{1}{\Delta }-1) -\frac{\eta }{\zeta }ln(\frac{1}{\Delta }) \nonumber \\&+(\theta _Fa)^2[\frac{\gamma _L\varphi ^L(t)}{\gamma _F\sigma _F^2\varphi ^F(t)} +\frac{1}{2}\frac{\gamma _L^2(\varphi ^L(t))^2}{\gamma _F^2\sigma _F^2(\varphi ^F(t))^2}]\nonumber \\&-(\theta _Fa)[\gamma _L\varphi ^L(t)+\frac{\gamma _L^2(\varphi ^L(t))^2}{\gamma _F(\varphi ^F(t))}] +\frac{1}{2}\gamma _L^2(\varphi ^L(t))^2\sigma _F^2. \end{aligned}$$

  (A.114)

  From (3.36) and (A.114), we have

  $$\begin{aligned} g^L_{02}(t)=g^{Lb2}_{02}(t)\doteq&g^{Lb2}_{2}(t)+G^L_2(t). \end{aligned}$$

  (A.115)

  And, Eq. (A.90) becomes

  $$\begin{aligned} g^{Fb}_{02}(t)=g^{Fb2}_{02}(t)\doteq&g^{Fb2}_{2}(t)+G^L_2(t). \end{aligned}$$

  (A.116)

• Subcase (Lb3) When $c_F\le a+K(t)\gamma _F\sigma _F^2\varphi ^F(t)\le {\bar{c}}$, we have $p^{*}(t)=a+K(t)\gamma _F\sigma _F^2\varphi ^F(t)$, $q^{*}(t,p^{*}(t))=K(t)$. Then, the precondition $\frac{p(t)-a}{\gamma _F\sigma _F^2\varphi ^F(t)}<1$ becomes $K(t)<1$, which is obviously true. Then, by Eq. (A.109), we can get that

  $$\begin{aligned} 0=&\frac{dg^L_{02}(t)}{dt} +\beta (2\beta +1)\sigma ^2g^L_{01}(t)+\frac{\eta }{\zeta }(g^L_{2}(t)-g^L_{02}(t))\nonumber \\&+h^P(\frac{1}{\Delta }-1) -\frac{\eta }{\zeta }ln(\frac{1}{\Delta })+\frac{1}{2}\gamma _L^2(\varphi ^L(t))^2\sigma _F^2 \nonumber \\&+(K(t)\gamma _F\sigma _F^2\varphi ^F(t))^2[\frac{\gamma _L\varphi ^L(t)}{\gamma _F\sigma _F^2\varphi ^F(t)} +\frac{1}{2}\frac{\gamma _L^2(\varphi ^L(t))^2}{\gamma _F^2\sigma _F^2(\varphi ^F(t))^2}]\nonumber \\&-(K(t)\gamma _F\sigma _F^2\varphi ^F(t))[\gamma _L\varphi ^L(t)+\frac{\gamma _L^2(\varphi ^L(t))^2}{\gamma _F(\varphi ^F(t))}] . \end{aligned}$$

  (A.117)

  From (3.37) and (A.117), we have

  $$\begin{aligned} g^L_{02}(t)=g^{Lb3}_{02}(t)\doteq&g^{Lb3}_{2}(t)+G^L_2(t). \end{aligned}$$

  (A.118)

  And, Eq. (A.90) becomes

  $$\begin{aligned} g^{Fb}_{02}(t)=g^{Fb3}_{02}(t)\doteq&g^{Fb3}_{2}(t)+G^L_2(t). \end{aligned}$$

  (A.119)

Then, the proof is complete. $\square$

Appendix B Proof of Corollary 1

Proof

The conclusions in Table 3 can be obtained by taking partial derivatives of $p^{*}(t)$ and $q^{*}(t)$ with corresponding variables, respectively. From $A_L=r_0-B_L-C_L$, $C_L=\eta _Le^{-\alpha _Lh_L}$, $B_Le^{-\alpha _Lh_L}=(\alpha _L+A_L+\eta _L)C_L$, we can get that

$$\begin{aligned} A_L=\frac{1}{1+\eta _L}[r_0-(\alpha _L+\eta _L)\eta _L-\eta _Le^{-\alpha _Lh_L}]. \end{aligned}$$

Put $A_L$ into $p^{*}(t)$ of Case (4) in Table 1, and take the derivative with respect to $\eta _L$ and $\alpha _L$, respectively. We can get that

$$\begin{aligned} \frac{\partial p^{*}(t)}{\partial \eta _L}&=\frac{(\gamma _F\sigma _F\varphi ^F(t))^2\gamma _L\varphi ^L(t)(T-t)}{[2\gamma _F\varphi ^F(t)+\gamma _L\varphi ^L(t)]^2}\frac{1}{(1+\eta _L)^2}[1-r_0-\alpha _L-e^{-\alpha _Lh_L}],\\ \frac{\partial p^{*}(t)}{\partial \alpha _L}&=\frac{(\gamma _F\sigma _F\varphi ^F(t))^2\gamma _L\varphi ^L(t)(T-t)}{[2\gamma _F\varphi ^F(t)+\gamma _L\varphi ^L(t)]^2}\frac{\eta _L}{1+\eta _L}[h_Le^{-\alpha _Lh_L}-1]. \end{aligned}$$

Thus, the left side of Eqs. (3.53) and (3.54) is established. Following similar derivations, we can get that the right side of Eqs. (3.53) and (3.54) are true. $\square$

Appendix C Proof of Corollary 2

Proof

The conclusions of (1) can be obtained by bringing $\frac{1}{\Delta }=1$ into the expressions of $b^{*}_{L1}(t)$, $b^{*}_{F1}(t)$, $V^L(t,x_L,y_L,s,0)$ and $V^F(t,x_F,y_F,s,0)$. If $\frac{1}{\Delta }>1$, $b^{*}_{L1}(t)\ge 0$ and $b^{*}_{F1}(t)\ge 0$ are clearly true. Furthermore, we have $\Delta +ln(\frac{1}{\Delta })>1$, then

$$\begin{aligned} G_2(t)=(1-\Delta -ln(\frac{1}{\Delta }))[1-e^{-\frac{\eta }{\zeta }(T-t)}]<0. \end{aligned}$$

(C.120)

Due to $V^F(t,x_F,y_F,s,1)<0$ and $V^L(t,x_L,y_L,s,1)<0$, then (3.59) and (3.60) are established. Then, the proof is complete. $\square$

Appendix D Proof of Theorem 4

Proof

We first prove that the six-tuple $(p^{*}(t),b^{*}_L(t),b^{*}_{L1}(t), q^{*}(t),b^{*}_F(t), b^{*}_{F1}(t))$ obtained in Theorem 3 is an admissible strategy. Since $p^{*}(t),b^{*}_L(t),b^{*}_{L1}(t),q^{*}(t),b^{*}_F(t),b^{*}_{F1}(t)$ are deterministic functions of time t and some constant parameters, and the premium strategy satisfies $p^{*}(t)\in [c_F,{\bar{c}}]$ and the reinsurance strategy satisfies $q^{*}(t)\in [0,1]$, so the six-tuple satisfies (i) and (ii) of Definition 1. According to (2.12) and (2.13), the drift and diffusion terms satisfy the Lipschitz condition and the linear growth condition. Then, the six-tuple satisfies (iii) and (iv) of Definition 1. Therefore, $(p^{*}(t),b^{*}_L(t),b^{*}_{L1}(t),q^{*}(t),b^{*}_F(t), b^{*}_{F1}(t))\in \Pi _L\times \Pi _F$.

Next, we show the optimality of $(p^{*}(t),b^{*}_L(t),b^{*}_{L1}(t),q^{*}(t),b^{*}_F(t),b^{*}_{F1}(t))$ in $\Pi _L\times \Pi _F$. From the construction of $\tau _i$, we know that $\tau _i\wedge T\rightarrow T$ when $i\rightarrow +\infty$. For $\forall (p(t),b_L(t),b_{L1}(t),q(t),b_F(t),b_{F1}(t))\in \Pi _L\times \Pi _F$ and $\forall \iota \in [t,T]$, we apply Itô’s formula to $J^F(t,x_F,y_F,s,h)$ and deduce

$$\begin{aligned}&J^F(\tau _i\wedge T,X_F(\tau _i\wedge T),Y_F(\tau _i\wedge T),S(\tau _i\wedge T),H(\tau _i\wedge T))\\&\quad =J^F(t,x_F,y_F,s,h) +\int _t^{\tau _i\wedge T}{\mathcal {A}}^{F}J^F(\iota ,X_F(\iota ),Y_F(\iota ),S(\iota ),H(\iota ))d\iota \\&\qquad +\int _t^{\tau _i\wedge T}q^{*}(\iota )\sigma _F\frac{\partial J^F(\iota ,x_F,y_F,s,h)}{\partial x_F}dW_F(\iota )\\&\qquad +\int _t^{\tau _i\wedge T}b_F^{*}(\iota )\sigma S^{\beta }(\iota ) \frac{\partial J^F(\iota ,x_F,y_F,s,h)}{\partial s}dW(\iota )\\&\qquad +\int _t^{\tau _i\wedge T} \big (J^F(\iota ,X_F(\iota )-b_{F1}^{*}(\iota )\zeta ,Y_F(\iota ),S(\iota ),1)\\&\qquad -J^F(\iota ,X_F(\iota ),Y_F(\iota ),S(\iota ),0)\big )dM^P(\iota ). \end{aligned}$$

From the theory of the Itô integral,

$$\begin{aligned} \int _t^{\tau _i\wedge T}q^{*}(\iota )\sigma _F\frac{\partial J^F(\iota ,x_F,y_F,s,h)}{\partial x_F}dW_F(\iota ) \end{aligned}$$

and

$$\begin{aligned} \int _t^{\tau _i\wedge T}b_F^{*}(\iota )\sigma S^{\beta }(\iota ) \frac{\partial J^F(\iota ,x_F,y_F,s,h)}{\partial s}dW(\iota ) \end{aligned}$$

are Itô integrals with respect to Brownian motions $W_F(\cdot )$ and $W(\cdot )$, respectively. Since $q^{*}(\cdot )$ and $b_F^{*}(\cdot )$ are square-integrable and the partial derivatives are continuous, these two terms are square-integrable martingales with zero expectations. Because $M^P(\cdot )$ is a martingale, referring to Section 3.3 in Zhu et al. (2015) and Section 4.3 in Deng et al. (2018), we know that the last term is also a square-integrable martingale with zero expectation. For given $(t,x_F,y_F,s,h)$, taking conditional expectations on both sides of the above equation, we have

$$\begin{aligned}&E_{t,x_F,y_F,s,h}[J^F(\tau _i\wedge T,X_F(\tau _i\wedge T),Y_F(\tau _i\wedge T),S(\tau _i\wedge T),H(\tau _i\wedge T))]\\&\quad =J^F(t,x_F,y_F,s,h) +E_{t,x_F,y_F,s,h}\big [\int _t^{\tau _i\wedge T}{\mathcal {A}}^{F}J^F(\iota ,X_F(\iota ),Y_F(\iota ),S(\iota ),H(\iota ))d\iota \big ]\\&\quad \le J^F(t,x_F,y_F,s,h). \end{aligned}$$

From Lemma 1, we have uniform integrability of $J^F(\tau _i\wedge T,X_F(\tau _i\wedge T),Y_F(\tau _i\wedge T),S(\tau _i\wedge T),H(\tau _i\wedge T))$, and

$$\begin{aligned}&\sup _{(q(\cdot ),b_F(\cdot ),b_{F1}(\cdot ))\in \Pi _F}E_{t,x_F,y_F,s,h} \big [U_F\big (X_F^{\pi _F}(T)+\eta _FY_F(T)\big )\big ]\\&\quad =\lim _{i\rightarrow +\infty }E_{t,x_F,y_F,s,h}[V^F(\tau _i\wedge T,X_F(\tau _i\wedge T),Y_F(\tau _i\wedge T),S(\tau _i\wedge T),H(\tau _i\wedge T))]\\&\quad \le J^F(t,x_F,y_F,s,h). \end{aligned}$$

When $(q(\cdot ),b_F(\cdot ),b_{F1}(\cdot ))=(q^{*}(\cdot ),b_F^{*}(\cdot ),b_{F1}^{*}(\cdot ))$, the inequality in the above formula becomes an equality, and thus

$$\begin{aligned} \sup _{(q(\cdot ),b_F(\cdot ),b_{F1}(\cdot ))\in \Pi _F}E_{t,x_F,y_F,s,h} \big [U_F\big (X_F^{\pi _F}(T)+\eta _FY_F(T)\big )\big ]= J^F(t,x_F,y_F,s,h). \end{aligned}$$

Following similar derivations, we can obtain

$$\begin{aligned} \sup _{(q(\cdot ),b_L(\cdot ),b_{L1}(\cdot ))\in \Pi _L}E_{t,x_L,y_L,s,h} \big [U_L\big (X_L^{\pi _L}(T)+\eta _LY_L(T)\big )\big ]\le J^L(t,x_L,y_L,s,h). \end{aligned}$$

And when $(p(\cdot ),b_L(\cdot ),b_{L1}(\cdot ))=(p^{*}(\cdot ),b_L^{*}(\cdot ),b_{L1}^{*}(\cdot ))$, the above inequality becomes an equality. Then, the proof is complete. $\square$