Optimal mean–variance reinsurance and investment in a jump-diffusion financial market with common shock dependence

Abstract

In this paper, we study the optimal reinsurance-investment problems in a financial market with jump-diffusion risky asset, where the insurance risk model is modulated by a compound Poisson process, and the two jump number processes are correlated by a common shock. Moreover, we remove the assumption of nonnegativity on the expected value of the jump size in the stock market, which is more economic reasonable since the jump sizes are always negative in the real financial market. Under the criterion of mean–variance, based on the stochastic linear–quadratic control theory, we derive the explicit expressions of the optimal strategies and value function which is a viscosity solution of the corresponding Hamilton–Jacobi–Bellman equation. Furthermore, we extend the results in the linear–quadratic setting to the original mean–variance problem, and obtain the solutions of efficient strategy and efficient frontier explicitly. Some numerical examples are given to show the impact of model parameters on the efficient frontier.

1 Introduction

In the past decade, optimal reinsurance and optimal investment problems for various risk models have gained a lot of interest in the actuarial literature, and the technique of stochastic control theory and the corresponding Hamilton–Jacobi–Bellman equation are frequently used to cope with these problems. See, for example, Schmidli (2001), Irgens and Paulsen (2004), Promislow and Young (2005), Liang et al. (2011) and Liang and Bayraktar (2014). The main popular criteria include maximizing the expected utility of the terminal wealth, minimizing the ruin probability of the insurer, and so on.

Mean–variance criterion, as another one of the popular criteria proposed by Markowitz (1952), has become one of the milestone in mathematical finance. In Markowitz (1952), the author was to seek a best allocation among a number of (risky) assets in order to achieve the optimal trade-off between the expected return and its risk (say, variance) over a fixed time horizon. From then on, mean–variance criterion becomes a rather popular criterion to measure the risk in finance theory. By now there exist numerous papers on the mean–variance problem and its extension in finance. See for example, Li and Ng (2000) developed an embedding technique to change the originally mean–variance problem into a stochastic linear–quadratic (LQ) control problem in a discrete-time setting. This technique was extended in Zhou and Li (2000), along with an indefinite stochastic LQ control approach, to the continuous time case. Before 2005, all the applications with mean–variance criterion focus on classical financial portfolio allocation problems. Bäuerle (2005) first pointed out that mean–variance criterion could also be of interest in insurance application, and then he studied the optimal reinsurance strategy problem for the classical compound Poisson insurance risk model. Under the mean–variance framework, by using the stochastic LQ control theory, the explicit solutions of the efficient strategy and efficient frontier are given. Further extensions and improvements in insurance applications were carried out. See for example, Bi and Guo (2013) considered the optimal reinsurance and optimal investment with a jump-diffusion risky asset for the compound Poisson risk model, by the technique of viscosity solution, the efficient frontier and efficient strategy were obtained; Ming and Liang (2016) studied the optimal reinsurance for the compound Poisson risk model with common shock dependence, and the optimal results were also derived.

Most of the literature about investment optimization is based on the assumption that the price of the stock follows a diffusion-type process, in particular a geometric Brownian motion. But in the real financial market, information often comes as a surprise, this usually leads to a jump in the price of stock. Therefore, in a jump-diffusion model the stock’s price may jump to a new level and then follow a geometric Brownian motion. Besides, the published papers with jump-diffusion risky asset always have some constraints on the jump sizes. See, for example, Alvarez et al. (2014) only considered the negative shocks, i.e., download jumps to study the optimal stopping problems; while Bi and Guo (2013) assumed that the expected value of the jump size in the stock market is nonnegative. In this paper, we remove all these constraints mentioned above, and allow the expected value of jump sizes to be negative as well as positive, which is more economic reasonable in the real financial market, and thus we have to discuss the optimization problem within five different cases. Moreover, we assume that the aggregate claim and the stock price are correlated by a common shock. This kind of model assumes that there exists a common shock affecting the stock market as well as the insurance market. In reality, a common component can depict the effect of a natural disaster which causes various kinds of risk including the one in financial market. It generalizes the model of Bi and Guo (2013) from the independent financial market to the case where aggregate claim process and risky asset process are correlated by a common shock. Under the mean–variance criterion, based on the framework of stochastic LQ control theory and the corresponding Hamilton–Jacobi–Bellman (HJB) equation, we derive the explicit expressions of the optimal strategies and value function, which is the viscosity solution of the HJB equation. Furthermore, we extend the results in the LQ-setting to the original mean–variance problem, and obtain the explicit solutions of the efficient strategy and efficient frontier.

The rest of the paper is organized as follows. In Sect. 2, the model and the mean–variance problem are presented. The main results and the explicit expressions for the optimal values are derived in Sect. 3. In Sect. 4, we extend the optimal results in the LQ-setting to the original mean–variance problem, and obtain the solutions of the efficient strategy and efficient frontier explicitly. Some numerical examples are shown to illustrate the impact of some model parameters on the efficient frontier in Sect. 5, and Sect. 6 concludes the paper.

2 Model and problem formulation

Let $(\Omega , {\mathcal {F}}, P)$ be a probability space with filtration $\{{\mathcal {F}}_{t}\}$ containing all objects defined in the following.

We consider the financial market where the assets are traded continuously on a finite time horizon [0, T]. There are a risk-free asset (bond) and a risky asset (stock) in the financial market. The price of the bond is given by

$$\begin{aligned} \left\{ \begin{aligned}&{ dB}(t)=r(t)B(t){ dt},&t\in [0,T],\\&B(0)=1,&\end{aligned}\right. \end{aligned}$$

where $r(t)(>0)$ is the interest rate of the bond.

The price of the stock is modeled by the following jump-diffusion process

$$\begin{aligned} \left\{ \begin{aligned}&{ dS}(t)=S(t-)\left[ b(t){ dt}+\sigma (t){ { dW}}(t)+d\sum \nolimits _{i=1}^{K_{2}(t)}{Y_{i}}\right] ,&t\in [0,T],\\&S(0)=S_{0},&\end{aligned}\right. \end{aligned}$$

(1)

where $S_{0}$ is the deterministic initial price, $b(t)({>}r(t))$ is the appreciation rate and $\sigma (t)>0$ is the volatility coefficient. We denote $a(t):=b(t)-r(t)>0$. $\{W(t)\}_{t\ge 0}$ is a standard $\{{\mathcal {F}}_{t}\}_{t\ge 0}$-adapted Brownian motion. We assume that r(t), b(t) and $\sigma (t)$ are deterministic, Borel-measurable and bounded on [0, T]. $\{K_{2}(t)\}_{t\ge 0}$ is a Poisson process with intensity parameter $\lambda _2+\lambda >0$. The jump sizes $\{Y_{i}, i\ge 1\}$ are assumed to be an i.i.d. sequence with values in $(-1, +\infty )$, the assumption that $Y_i>-1$ leads always to positive values of the stock prices. Y is a generic random variable which has the same distribution as $Y_i, i\ge 1$. Let $F_{Y}(\cdot )$ denote the cumulative distribution function of Y. We assume that $E[Y]=\mu _{21}$ and $E[Y^2]=\mu _{22}$. $\{W(t)\}_{t\ge 0}$, $\{K_{2}(t)\}_{t\ge 0}$ and $\{Y_{i}, i\ge 1\}$ are mutually independent.

The diffusion component in Eq. (1) characterizes the normal fluctuation in the stock’s price, due to gradual changes in economic conditions or the arrival of new information which causes marginal changes in the stock’s price. The jump component describes the sudden changes in the stock’s price due to the arrival of important new information which has a large effect on the stock’s price. By Protter (2004, Chapter V), a unique solution exists for stochastic differential equation (SDE) (1).

The risk process $\{U(t)\}_{t\ge 0}$ of the insurer is modeled by

$$\begin{aligned} { dU}(t)={ cdt}-d\sum _{i=1}^{K_{1}(t)}{X_{i}},\quad U(0)=U_{0}, \end{aligned}$$

(2)

where $U_{0}$ is the deterministic initial reserve of the insurer and the constant c is the premium rate. $\{K_{1}(t)\}_{t\ge 0}$ is a Poisson process with intensity $\lambda _1+\lambda >0$ which represents the number of claims occurring in time interval [0, t]. $X_{i}$ is the size of the $i\hbox {th}$ claim and $\{X_{i}, i\ge 1\}$ are assumed to be an i.i.d. sequence and independent of $\{K_{1}(t)\}_{t\ge 0}$. Thus the compound Poisson process $\sum _{i=1}^{K_{1}(t)}{X_{i}}$ represents the cumulative amount of claims in time interval [0, t]. X is a generic random variable which has the same distribution as $X_i, i\ge 1$. Let $F_{X}(\cdot )$ denote the cumulative distribution function of X. The expectation of X is $E[X]=\mu _{11}>0$ and the second moment of X is $E[X^{2}]=\mu _{12}>0$. Throughout this paper, we assume that the premium is calculated according to the expected value principle. That is, $c=(1+\tilde{\theta }_1)a_1$ with $a_1=(\lambda _1+\lambda )\mu _{11}$, where $\tilde{\theta }_1(>0)$ is the safety loading for insurer. The risk process defined in Eq. (2), from the perspective of the insurer, is really a pay-off process associated with the (insurance) contracts he (or she) has entered. The two number processes $\{K_{1}(t)\}_{t\ge 0}$ and $\{K_{2}(t)\}_{t\ge 0}$ are correlated in the way that

$$\begin{aligned} K_{1}(t)=N_1(t)+N(t) \quad \text{ and } \quad K_{2}(t)=N_2(t)+N(t), \end{aligned}$$

with $N_1(t)$, $N_2(t)$, and N(t) being three independent Poisson processes with parameters $\lambda _1$, $\lambda _2$, and $\lambda$, respectively. It is obvious that the dependence between the financial risky asset and the aggregate claim processes is due to a common shock governed by the counting process N(t). Moreover, $\{W(t)\}_{t\ge 0}$, $\{N_{1}(t)\}_{t\ge 0}$, $\{X_{i},i\ge 1\}$, $\{N_{2}(t)\}_{t\ge 0}$, $\{Y_{i},i\ge 1\}$ and $\{N(t)\}_{t\ge 0}$ are mutually independent.

We assume that, at time t, the insurer is allowed to invest all of his (or her) wealth R(t) into the financial market. Let $\xi (t)$ and $\eta (t)$ denote the total market value of the agent’s wealth in the bond and stock, respectively, and $\xi (t)+\eta (t)=R(t)$. An important restriction we will consider in this paper is the prohibition of short-selling of the stock, i.e., $\eta (t)\ge 0$. But $\xi (t)$ is not constrained. We assume that the insurer can purchase new business in addition to investment. Let $q(t)(\ge 0)$ represents the retention level of new business acquired at time t. It means that the insurer pays q(t)X of a claim occurring at time t and the new businessman pays $(1-q(t))X$. For this business, the premium has to be paid at rate $\delta (q(t))=(1+\theta )(1-q(t))a_1$, where $\theta$ is the safety loading for the new business. Without loss of generality, we assume that $\theta \ge \tilde{\theta }_1$. Note that for the insurance company, $q(t)\in [0,1]$ corresponds to a reinsurance cover and $q(t)>1$ would mean that the company can take an extra insurance business from other companies (i.e., act as a reinsurer for other cedents). A strategy $\pi (t)=(\eta (t),q(t))$ is said to be admissible if $\eta (t)$ and q(t) are $\mathcal {F}_{t}$-predictable processes, and satisfy $\eta (t)\ge 0$, $q(t)\ge 0$, $E[\int _{0}^{t}(\eta (s))^{2}{} { ds}]<\infty$ and $E[\int _{0}^{t}(q(s))^{2}{} { ds}]<\infty$ for all $t\ge 0$. We denote the set of all admissible strategies by $\Pi$. Then the resulting surplus process R(t) is given by

$$\begin{aligned} \left\{ \begin{aligned} { dR}(t)&=\left[ r(t)R(t-)+a(t)\eta (t)+c-\delta (q(t))\right] { dt}+\eta (t)\sigma (t){ dW}(t)\\&\quad +\eta (t)d\sum \nolimits _{i=1}^{K_{2}(t)}{Y_{i}}-q(t)d\sum \nolimits _{i=1}^{K_{1}(t)}{X_{i}}\\ R(0)&=R_{0}. \end{aligned}\right. \end{aligned}$$

(3)

Corresponding to an admissible trading strategy $\pi (\cdot )$ and a deterministic initial capital $R_{0}$, there exists a unique $R(\cdot )$ satisfying (3).

Let $R^{\pi }(T)$ denote the terminal wealth when the strategy $\pi (\cdot )$ is applied. Then the mean–variance problem is to maximize the expected terminal wealth $E[R^{\pi }(T)]$ and, in the meantime, to minimize the variance of the terminal wealth ${\mathrm{Var}}[R^{\pi }(T)]$ over $\pi (\cdot )\in \Pi$. This is a multi-objective optimization problem with two conflicting criteria, which can be formulated as follows:

$$\begin{aligned} \begin{aligned}&\text{ min } \quad (J_{1}(\pi (\cdot )),J_{2}(\pi (\cdot ))):=({\mathrm{Var}}[R^{\pi }(T)],-E[R^{\pi }(T)])\\&\text{ subject } \text{ to } \left\{ \begin{aligned}&\pi \in \Pi \\&(R(\cdot ), \pi (\cdot )) \text{ satisfy } (3). \end{aligned} \right. \end{aligned} \end{aligned}$$

(4)

Definition 2.1

For the multi-objective optimization problem (4), an admissible strategy $\pi ^{*}(\cdot )$ is called an efficient strategy if there exists no admissible portfolio $\pi (\cdot )\in \Pi$ such that

$$\begin{aligned} J_{1}(\pi (\cdot ))\le J_{1}(\pi ^{*}(\cdot )),\quad J_{2}(\pi (\cdot ))\le J_{2}(\pi ^{*}(\cdot )) \end{aligned}$$

with at least one of the inequalities holding strictly. In this case, $(J_{1}(\pi ^{*}(\cdot )),-J_{2}(\pi ^{*}(\cdot )))\in {\mathbb {R}}^{2}$ is called an efficient point. The set of all efficient points is called the efficient frontier.

We firstly consider the problem of finding an admissible strategy such that the expected terminal wealth satisfies $E[R^{\pi }(T)]=k$, where k is a constant, while the risk measured by the variance of the terminal wealth

$$\begin{aligned} {{\mathrm{Var}}}[R^{\pi }(T)]=E\left[ R^{\pi }(T)-E[R^{\pi }(T)]\right] ^{2} =E\left[ (R^{\pi }(T)-k)^{2}\right] \end{aligned}$$

is minimized. This variance minimizing problem can be formulated as the following optimization problem

$$\begin{aligned} \begin{aligned}&\text{ min } \quad {\mathrm{Var}}[R^{\pi }(T)]=E[R^{\pi }(T)-k]^{2}\\&\text{ subject } \text{ to } \left\{ \begin{aligned}&E[R^{\pi }(T)]=k\\&\pi \in \Pi \\&(R(\cdot ), \pi (\cdot )) \text{ satisfy } (3). \end{aligned} \right. \end{aligned} \end{aligned}$$

(5)

Definition 2.2

For the variance minimizing problem (5), the optimal strategy $\pi ^*(\cdot )$ (corresponding to a fixed k) is called a variance minimizing strategy, and the set of all points $({\mathrm{Var}}[R^{\pi ^*}(T)],k)$, where ${\mathrm{Var}}[R^{\pi ^*}(T)]$ denotes the optimal value of (5) corresponding to a fixed k, is called the variance minimizing frontier.

An efficient strategy is one for which there does not exist another strategy that has higher mean and no higher variance, and/or has lower variance and no lower mean at the terminal time T. In other words, an efficient strategy is one that is Pareto optimal. By Definitions 2.1 and 2.2, we know that the efficient frontier is a subset of the variance minimizing frontier. In the following context, we will discuss the variance minimizing problem firstly.

Since (5) is a convex optimization problem, the constraint $ER^{\pi }(T)=k$ can be dealt with by introducing a Lagrange multiplier $\beta \in {\mathbb {R}}$. In this way, problem (5) can be solved via the following optimal stochastic control problem (for every fixed $\beta$)

$$\begin{aligned} \begin{aligned}&\text{ min } \quad E\left[ (R^{\pi }(T)-k)^{2}+2\beta (E[R^{\pi }(T)]-k)\right] ,\\&\text{ subject } \text{ to } \left\{ \begin{aligned}&\pi \in \Pi \\&(R(\cdot ), \pi (\cdot )) \text{ satisfy } (3), \end{aligned} \right. \end{aligned} \end{aligned}$$

(6)

where the factor 2 in the front of $\beta$ is introduced in the objective function just for convenience. After solving problem (6), to obtain the optimal value and optimal strategy for problem (5), we need to maximize the optimal value in (6) over $\beta \in \mathbb {R}$ according to Lagrange duality theorem (see Luenberger 1968). Clearly, problem (6) is equivalent to

$$\begin{aligned} \begin{aligned}&\text{ min } \quad E\left[ (R^{\pi }(T)-(k-\beta ))^{2}\right] ,\\&\text{ subject } \text{ to } \left\{ \begin{aligned}&\pi \in \Pi \\&(R(\cdot ), \pi (\cdot )) \text{ satisfy } (3), \end{aligned} \right. \end{aligned} \end{aligned}$$

(7)

in the sense that the two problems have exactly the same optimal control for fixed $\beta$. For simplicity, we omit the superscript $\pi$ of $R^{\pi }(\cdot )$ from now on.

3 The HJB equation and optimal results

We firstly solve an auxiliary LQ problem. Consider the following controlled linear stochastic differential equation

$$\begin{aligned} \left\{ \begin{aligned} d\hat{R}(t)&=[r(t)\hat{R}(t-)+a(t)\eta (t)+c(t)-\delta (q(t))]{ dt}+\eta (t)\sigma (t){ dW}(t)\\&\quad +\eta (t)d\sum \nolimits _{i=1}^{K_{2}(t)}{Y_{i}}-q(t)d\sum \nolimits _{i=1}^{K_{1}(t)}{X_{i}}\\ \hat{R}(0)&=\hat{R}_{0}, \end{aligned}\right. \end{aligned}$$

(8)

and the problem

$$\begin{aligned} \begin{aligned}&\text{ min } \quad E\left[ \frac{1}{2}(\hat{R}(T))^{2}\right] ,\\&\text{ subject } \text{ to } \left\{ \begin{aligned}&\pi \in \Pi \\&(\hat{R}(\cdot ), \pi (\cdot )) \text{ satisfy } (8), \end{aligned} \right. \end{aligned} \end{aligned}$$

(9)

where r(t), a(t), c(t) and $\sigma (t)$ are deterministic, Borel-measurable functions and bounded on [0, T]. Note that if we set $\hat{R}(t)=R(t)-(k-\beta )$, then $R(t)=\hat{R}(t)+(k-\beta )$, $R(0)=\hat{R}(0)+(k-\beta )$, and $c(t)=c+(k-\beta )r(t)$ in (8), we can get (3) from (8). So we solve the auxiliary LQ problem (8)–(9) firstly.

We define the associated value function by

$$\begin{aligned} J(t,x):=\mathop {\inf }_{\pi \in \Pi } E\left[ \frac{1}{2}(\hat{R}(T))^{2}\big |\hat{R}(t)=x\right] . \end{aligned}$$

This is a stochastic LQ problem, in which the two controls are constrained to take nonnegative values. In the following, we will solve this problem with the help of the HJB equation.

According to Fleming and Soner (1993), the corresponding HJB equation of problem (8)–(9) is the following partial differential equation

$$\begin{aligned} \left\{ \begin{aligned}&\mathop {\inf }_{\pi }\biggl \{V_{t}(t,x)+[r(t)x+a(t)\eta +c(t)-\delta (q)]V_{x}(t,x)+\frac{1}{2}\sigma (t)^{2}\eta ^2V_{xx}(t,x)\\&\qquad +\lambda _{2} E[V(t,x+\eta Y)-V(t,x)]+\lambda _{1} E[V(t,x-qX)-V(t,x)]\\&\qquad +\lambda E[V(t, x+\eta Y-qX)-V(t,x)]\biggr \}=0\\&V(T,x)=\frac{1}{2}x^{2}. \end{aligned} \right. \end{aligned}$$

(10)

Here $V_{t}(t,x)$, $V_{x}(t,x)$ mean the partial derivatives of V(t, x). For function f(t, x), let $C^{1,2}([0,T]\times {\mathbb {R}})$ denote the space of f(t, x) such that f and its partial derivatives $f_{t}$, $f_{x}$, $f_{xx}$ are continuous on $[0,T]\times {\mathbb {R}}$. If the optimal value function $J(\cdot ,\cdot )\in C^{1,2}([0,T]\times {\mathbb {R}})$, it will satisfy Eq. (10). But in most of the examples this is not the case, so we study the viscosity solutions of Eq. (10). Next we will give the definition of viscosity solution according to Fleming and Soner (1993).

Definition 3.1

Let $V\in C([0,T]\times {\mathbb {R}})$, which consists of functions continuous on $[0,T]\times {\mathbb {R}}$.

• (1) We say V is a viscosity subsolution of (10) in $(t,x)\in [0,T]\times {\mathbb {R}}$, if for each $\varphi \in C^{1,2}([0,T]\times {\mathbb {R}})$,

  

  at every $(\bar{t},\bar{x})\in [0,T]\times {\mathbb {R}}$ which is a maximizer of $V-\varphi$ on $[0,T]\times {\mathbb {R}}$ with $V(\bar{t},\bar{x})=\varphi (\bar{t},\bar{x})$.

• (2) We say V is a viscosity supersolution of (10) in $(t,x)\in [0,T]\times {\mathbb {R}}$, if for each $\varphi \in C^{1,2}([0,T]\times {\mathbb {R}})$,

  

  at every $(\bar{t},\bar{x})\in [0,T]\times {\mathbb {R}}$ which is a minimizer of $V-\varphi$ on $[0,T]\times {\mathbb {R}}$ with $V(\bar{t},\bar{x})=\varphi (\bar{t},\bar{x})$.

• (3) We say V is a viscosity solution of (10) in $(t,x)\in [0,T]\times {\mathbb {R}}$, if it is both a viscosity subsolution and a viscosity supersolution of (10) in $(t,x)\in [0,T]\times {\mathbb {R}}.$

In the following context, we will give a detailed analysis for the continuously differentiable viscosity solution to the HJB Eq. (10).

Suppose that the HJB Eq. (10) has a solution which has the following form

$$\begin{aligned} V(t,x)=\frac{1}{2}P(t)x^{2}+Q(t)x+L(t). \end{aligned}$$

(11)

The boundary condition in (10) implies that $P(T)=1$, $Q(T)=0$, and $L(T)=0$. Inserting the ansatz (11) into (10) and rearranging yields

$$\begin{aligned} \begin{aligned}&\inf _{\pi }\biggl \{(\eta a(t)+(1+\theta )a_1 q)(P(t)x+Q(t))+\frac{1}{2}P(t)\sigma (t)^{2}\eta ^2\\&\quad +\lambda _1\left[ -(P(t)x+Q(t))q\mu _{11} +\frac{1}{2}P(t)q^2\mu _{12}\right] \\&\quad +\lambda _2\left[ (P(t)x+Q(t))\eta \mu _{21}+\frac{1}{2}P(t)\eta ^2\mu _{22}\right] \\&\quad +\lambda (P(t)x+Q(t))(\eta \mu _{21}-q\mu _{11}) +\frac{1}{2}P(t)\lambda (\eta ^2\mu _{22}-2\eta q\mu _{11}\mu _{21}+q^2\mu _{12})\biggr \}\\&\quad +\frac{1}{2}P_t(t) x^2+Q_t(t) x+L_t(t)+(r(t)x+c(t)-(1+\theta )a_1)(P(t)x+Q(t))=0. \end{aligned} \end{aligned}$$

(12)

Let

$$\begin{aligned} \begin{aligned} f(\eta , q)&=\left[ \eta a(t)+(1+\theta )a_1q\right] (P(t)x+Q(t))+\frac{1}{2}P(t)\sigma (t)^{2}\eta ^2\\&\quad +\lambda _1\left[ -(P(t)x+Q(t))q\mu _{11}+\frac{1}{2}P(t)q^2\mu _{12}\right] \\&\quad +\lambda _2\left[ (P(t)x+Q(t))\eta \mu _{21}+\frac{1}{2}P(t)\eta ^2\mu _{22}\right] \\&\quad +\lambda (P(t)x+Q(t))(\eta \mu _{21}-q\mu _{11})+\frac{1}{2}P(t)\lambda (\eta ^2\mu _{22}-2\eta q\mu _{11}\mu _{21}+q^2\mu _{12}). \end{aligned} \end{aligned}$$

We have

$$\begin{aligned} \left\{ \begin{array}{ll} \frac{\partial f}{\partial \eta }=\left[ \left( \sigma ^2(t)+(\lambda _2+\lambda )\mu _{22}\right) \eta -\lambda \mu _{11}\mu _{21}q\right] P(t)+(P(t)x+Q(t))(a(t)+(\lambda _2+\lambda )\mu _{21}),\\ \frac{\partial f}{\partial q}=\left[ (\lambda _1+\lambda )\mu _{12}q-\lambda \mu _{11}\mu _{21}\eta )\right] P(t)+(P(t)x+Q(t))\theta a_1,\\ \frac{\partial ^2 f}{\partial \eta ^2}=\left[ \sigma ^2(t)+(\lambda _2+\lambda )\mu _{22}\right] P(t),\\ \frac{\partial ^2 f}{\partial q^2}=(\lambda _1+\lambda )P(t)\mu _{12},\\ \frac{\partial ^2 f}{\partial \eta \partial q}=\frac{\partial ^2 f}{\partial q\partial \eta }=-\lambda P(t)\mu _{11}\mu _{21}. \end{array} \right. \end{aligned}$$

Let

$$\begin{aligned} \mathbf A =\left( \begin{array}{ccc} &{}P(t)\left( \sigma ^2(t)+\lambda _2\mu _{22}\right) &{} 0 \\ &{}0 &{} P(t)\lambda _1\mu _{12} \end{array}\right) , \quad \mathbf B =\left( \begin{array}{ccc} &{}P(t)\mu _{22} &{} -P(t)\mu _{11}\mu _{21}\\ &{}-P(t)\mu _{11}\mu _{21} &{} P(t)\mu _{12} \end{array}\right) . \end{aligned}$$

Then, the Hessian matrix of $f(\eta , q)$ can be decomposed as

$$\begin{aligned} \left( \begin{array}{ccc}&{}\frac{\partial ^2f(\eta , q)}{\partial \eta ^2} \quad &{} \frac{\partial ^2f(\eta , q)}{\partial \eta \partial q} \\ &{}\frac{\partial ^2f(\eta , q)}{\partial q \partial \eta } \quad &{} \frac{\partial ^2f(\eta , q)}{\partial q^2} \end{array}\right) =\mathbf A +\lambda \cdot \mathbf B . \end{aligned}$$

It is easy to see that $\mathbf A$ is a positive definite matrix. Furthermore, by the Cauchy$-$Schwarz inequality, it is not difficult to prove that $\mathbf B$ is a nonnegative definite matrix, and thus, the Hessian matrix is a positive definite matrix. Therefore, the minimizer $(\eta , q)$ of $f(\eta , q)$ satisfies the following equations

$$\begin{aligned} \left\{ \begin{array}{ll} &{}\left[ \left( \sigma ^2(t)+(\lambda _2+\lambda )\mu _{22}\right) \eta -\lambda \mu _{11}\mu _{21}q\right] P(t)+(P(t)x+Q(t))\\ &{}\quad \quad \left[ a(t)+(\lambda _2+\lambda )\mu _{21}\right] =0,\\ &{}\left[ (\lambda _1+\lambda )\mu _{12}q-\lambda \mu _{11}\mu _{21}\eta \right] P(t)+(P(t)x+Q(t))\theta a_1=0. \end{array} \right. \end{aligned}$$

(13)

Solving the equations (13) gives

$$\begin{aligned} \left\{ \begin{array}{ll} \check{\eta }=\Delta _1(t)\left( x+\frac{Q(t)}{P(t)}\right) ,\\ \check{q}=\Delta _2(t)\left( x+\frac{Q(t)}{P(t)}\right) , \end{array} \right. \end{aligned}$$

(14)

where

$$\begin{aligned} \left\{ \begin{array}{ll} \Delta _1(t)=-\frac{(a(t)+(\lambda _2+\lambda )\mu _{21})(\lambda _1+\lambda )\mu _{12}+\theta a_1\lambda \mu _{11}\mu _{21}}{\left( \sigma ^2(t)+(\lambda _2+\lambda )\mu _{22}\right) (\lambda _1+\lambda )\mu _{12}-\lambda ^2\mu _{11}^2\mu _{21}^2},\\ \Delta _2(t)=-\frac{(a(t)+(\lambda _2+\lambda )\mu _{21})\lambda \mu _{11}\mu _{21}+\theta a_1\left( \sigma ^2(t)+(\lambda _2+\lambda )\mu _{22}\right) }{\left( \sigma ^2(t)+(\lambda _2+\lambda )\mu _{22}\right) (\lambda _1+\lambda )\mu _{12}-\lambda ^2\mu _{11}^2\mu _{21}^2}. \end{array} \right. \end{aligned}$$

(15)

Let

$$\begin{aligned} \begin{array}{ll} \theta _1(t)=-\frac{(a(t)+(\lambda _2+\lambda )\mu _{21})(\lambda _1 +\lambda )\mu _{12}}{a_1\lambda \mu _{11}\mu _{21}},\\ \theta _2(t)=-\frac{(a(t)+(\lambda _2+\lambda )\mu _{21})\lambda \mu _{11} \mu _{21}}{a_1\left( \sigma ^2(t)+(\lambda _2+\lambda )\mu _{22}\right) }. \end{array} \end{aligned}$$

Before we discuss the optimal strategies based on the constraints of $(\eta , q)$, we first give the following lemma which plays a key role in this paper.

Lemma 3.1

For any $0\le t\le T$, when $-\frac{a(t)}{\lambda _2+\lambda }<\mu _{21}<0$, we have $0<\theta _2(t)<\theta _1(t)$; when $-1<\mu _{21}<-\frac{a(t)}{\lambda _2+\lambda }$ or $\mu _{21}>0$, we have $\theta _1(t)<\theta _2(t)<0$.

Proof

By the Cauchy$-$Schwarz inequality, it is not difficult to see that

$$\begin{aligned} \left( \sigma ^2(t)+(\lambda _2+\lambda )\mu _{22}\right) (\lambda _1 +\lambda )\mu _{12}>\lambda ^2\mu _{11}^2\mu _{21}^2. \end{aligned}$$

When $-\frac{a(t)}{\lambda _2+\lambda }<\mu _{21}<0$, we have $a(t)+(\lambda _2+\lambda )\mu _{21}>0$, and thus

$$\begin{aligned} \begin{array}{ll} &{}\left( \sigma ^2(t)+(\lambda _2+\lambda )\mu _{22}\right) (\lambda _1+\lambda )\mu _{12}>\lambda ^2\mu _{11}^2\mu _{21}^2\\ &{}\quad \Leftrightarrow \left( \sigma ^2(t)+(\lambda _2+\lambda )\mu _{22}\right) (\lambda _1 +\lambda )\mu _{12}(a(t)+(\lambda _2+\lambda )\mu _{21})\\ &{}\quad >\lambda ^2\mu _{11}^2\mu _{21}^2(a(t)+(\lambda _2+\lambda )\mu _{21})\\ &{}\quad \Leftrightarrow \frac{(a(t)+(\lambda _2+\lambda )\mu _{21})(\lambda _1+\lambda )\mu _{12}}{a_1\lambda \mu _{11} \mu _{21}}<\frac{(a(t)+(\lambda _2+\lambda )\mu _{21})\lambda \mu _{11}\mu _{21}}{a_1\left( \sigma ^2(t)+(\lambda _2+\lambda )\mu _{22}\right) }\\ &{}\quad \Leftrightarrow -\frac{(a(t)+(\lambda _2+\lambda )\mu _{21})(\lambda _1+\lambda )\mu _{12}}{a_1\lambda \mu _{11}\mu _{21}}>-\frac{(a(t)+(\lambda _2+\lambda )\mu _{21})\lambda \mu _{11}\mu _{21}}{a_1\left( \sigma ^2(t)+(\lambda _2+\lambda )\mu _{22}\right) },\\ \end{array} \end{aligned}$$

which proves that $\theta _2(t)<\theta _1(t)$.

Along the same lines, we can prove the results for the cases of $-1<\mu _{21}<-\frac{a(t)}{\lambda _2+\lambda }$ and $\mu _{21}>0$. $\square$

From (15), it is easy to see that $\Delta _1(t)>0$ and $\Delta _2(t)<0$ for $\mu _{21}=-\frac{a(t)}{\lambda _2+\lambda }$; $\Delta _1(t)<0$ and $\Delta _2(t)<0$ for $\mu _{21}=0$. Therefore, based on the results of Lemma 3.1, we will discuss the optimal results from the following five cases:

• Case 1: $-\frac{a(t)}{\lambda _2+\lambda }<\mu _{21}<0$, $0<\theta \le \theta _2(t)<\theta _1(t)$ (i.e., $\Delta _1(t)<0$, $\Delta _2(t)\ge 0$),

• Case 2: $-\frac{a(t)}{\lambda _2+\lambda }<\mu _{21}<0$, $0<\theta _2(t)<\theta \le \theta _1(t)$ (i.e., $\Delta _1(t)\le 0$, $\Delta _2(t)<0$),

• Case 3: $-\frac{a(t)}{\lambda _2+\lambda }<\mu _{21}<0$, $0<\theta _2(t)<\theta _1(t)<\theta$ (i.e., $\Delta _1(t)>0$, $\Delta _2(t)<0$),

• Case 4: $-1<\mu _{21}\le -\frac{a(t)}{\lambda _2+\lambda }$, $\theta >0$ (i.e., $\Delta _1(t)>0$, $\Delta _2(t)<0$),

• Case 5: $\mu _{21}\ge 0$, $\theta >0$ (i.e., $\Delta _1(t)<0$, $\Delta _2(t)<0$).

Remark 3.1

When $-\frac{a(t)}{\lambda _2+\lambda }<-1$, inequality $-\frac{a(t)}{\lambda _2+\lambda }<\mu _{21}$ always holds for any $t\in [0, T]$, then we only need to discuss Cases 1, 2, 3 and 5.

Case 1    $-\frac{a(t)}{\lambda _2+\lambda }<\mu _{21}<0$ and $0<\theta \le \theta _2(t)<\theta _1(t)$.

In this case, $\Delta _1(t)<0$ and $\Delta _2(t)\ge 0$. If $x+\frac{Q(t)}{P(t)}\le 0$, then $\check{\eta }\ge 0$ and $\check{q}\le 0$. Because of the restriction of $\pi ^*\in \Pi$, we have to choose $q^*=0$. Inserting $q^*$ into (12) with $\frac{\partial f(\eta , 0)}{\partial \eta }=0$, we obtain

$$\begin{aligned} \tilde{\eta }=-\frac{a(t)+(\lambda _2+\lambda )\mu _{21}}{\sigma ^2(t)+(\lambda _2+\lambda )\mu _{22}}\left( x+\frac{Q(t)}{P(t)}\right) \ge 0, \end{aligned}$$

then we get $\eta ^*=\tilde{\eta }$. Thus, the minimizer of the $f(\eta , q)$ is $\pi ^*=(\eta ^*, q^*)=(\tilde{\eta }, 0)$. Plugging $\pi ^*=(\tilde{\eta }, 0)$ back into (12) and separating the variables with and without x lead to the following systems of ODEs:

$$\begin{aligned} \left\{ \begin{array}{ll} \frac{1}{2}P_t+M_1(t)P(t)+r(t)P(t)=0,\\ Q_t+2M_1(t)Q(t)+r(t)Q(t)+(c(t)-(1+\theta )a_1)P(t)=0,\\ L_t+(c(t)-(1+\theta )a_1)Q(t)+M_1(t)\frac{Q^2(t)}{P(t)}=0, \end{array} \right. \end{aligned}$$

with the boundary conditions $P(T)=1$, $Q(T)=0$, $L(T)=0$, where

$$\begin{aligned} M_1(t)=-\frac{1}{2}\cdot \frac{(a(t)+(\lambda _2+\lambda ) \mu _{21})^2}{\sigma ^2(t)+(\lambda _2+\lambda )\mu _{22}}. \end{aligned}$$

Then we have

$$\begin{aligned} \left\{ \begin{array}{ll} \begin{aligned} P(t)&{}=e^{\int _t^T2(M_1(s)+r(s)){ ds}},\\ Q(t)&{}=e^{\int _t^T(2M_1(s)\,+\,r(s)){ ds}}\times \int _t^T(c(s)-(1+\theta )a_1)e^{\int _s^Tr(z){ dz}}{} { ds},\\ L(t)&{}=\int _{t}^{T}(c(s)-(1+\theta )a_1)e^{\int _{s}^{T}(2M_1(v)+r(v)){ dv}} \int _{s}^{T}(c(z)-(1+\theta )a_1)e^{\int _{z}^{T}r(v){ dv}}{} { { dz}}{} { ds}\\ &{}\quad +\int _{t}^{T}M_1(s)e^{\int _{s}^{T}M_1(v){ dv}}\left[ \int _{s}^{T}(c(z)-(1+\theta )a_1)e^{\int _{z}^{T}r(v){ dv}}{} { dz}\right] ^2{ ds}. \end{aligned} \end{array} \right. \end{aligned}$$

Note that

$$\begin{aligned} x+\frac{Q(t)}{P(t)}=x+e^{-\int _{t}^{T}r(s){ ds}}\int _{t}^{T}(c(s) -(1+\theta )a_1)e^{\int _{s}^{T}r(z){ dz}}{} { ds}, \end{aligned}$$

then we have

$$\begin{aligned} \left\{ \begin{array}{ll} &{}\eta ^{*}(t,x)=-\frac{a(t)+(\lambda _2+\lambda )\mu _{21}}{\sigma ^2(t) +(\lambda _2+\lambda )\mu _{22}}\cdot \left[ x+e^{-\int _{t}^{T}r(s){ ds}}\int _{t}^{T}(c(s) -(1+\theta )a_1)e^{\int _{s}^{T}r(z){ dz}}{} { ds}\right] ,\\ &{}q^{*}(t,x)=0. \end{array} \right. \end{aligned}$$

Substituting the solutions into (11), and rearranging, we obtain

$$\begin{aligned} V(t,x)=\frac{1}{2}e^{\int _t^T2M_1(s){ ds}} \left\{ x e^{\int _{t}^{T}r(s){ ds}} +\int _{t}^{T}(c(s)-(1+\theta )a_1)e^{\int _{s}^{T}r(z){ dz}}{} { ds}\right\} ^2. \end{aligned}$$

   If $x+\frac{Q(t)}{P(t)}>0$, then $\check{\eta }<0$ and $\check{q}\ge 0$. For the restriction of $\pi ^* \in \Pi$, we choose $\eta ^*=0$, by the same manner as above, we get

$$\begin{aligned} \tilde{q}=-\frac{\theta a_1}{(\lambda _1+\lambda )\mu _{12}}\left( x+\frac{Q(t)}{P(t)}\right) <0. \end{aligned}$$

Therefore, the minimizer of $f(\eta , q)$ is $\pi ^*=(\eta ^*, q^*)=(0, 0)$, and thus we get

$$\begin{aligned} V(t,x)=\frac{1}{2}\left\{ xe^{\int _t^Tr(s){ ds}}+\int _t^T(c(s) -(1+\theta )a_1)e^{\int _s^Tr(z){ dz}}{} { ds}\right\} ^2. \end{aligned}$$

Along the same lines, we can derive the minimizers and solutions of Eq. (11) for the other four cases as follows:

Case 2    $-\frac{a(t)}{\lambda _2+\lambda }<\mu _{21}<0$ and $0<\theta _2(t)<\theta \le \theta _1(t)$.

The minimum of the left-hand side of the Eq. (10) is attained at

$$\begin{aligned} \pi ^*(t) ={\left\{ \begin{array}{ll} (\bar{\eta }(t, x),\, \bar{q}(t, x)),&{}{\text {if}} \quad x+e^{-\int _{t}^{T}r(s){ ds}}\int _{t}^{T}(c(s)-(1+\theta )a_1)e^{\int _{s}^{T}r(z){ dz}}{} { ds}\le 0,\\ (0,\,0),&{}{\text {if}} \quad x+e^{-\int _{t}^{T}r(s){ ds}}\int _{t}^{T}(c(s)-(1+\theta )a_1)e^{\int _{s}^{T}r(z){ dz}}{} { ds}>0, \end{array}\right. } \end{aligned}$$

and the solution of Eq. (10) is

$$\begin{aligned} V(t,x) ={\left\{ \begin{array}{ll} \frac{1}{2}e^{\int _t^T2M_2(s){ ds}}\left\{ x e^{\int _{t}^{T}r(s){ ds}} +\int _{t}^{T}(c(s)-(1+\theta )a_1)e^{\int _{s}^{T}r(z){ dz}}{} { ds}\right\} ^2,\\ \quad \quad \quad \quad \quad {\text {if}} \quad x+e^{-\int _{t}^{T}r(s){ ds}} \int _{t}^{T}(c(s)-(1+\theta )a_1)e^{\int _{s}^{T}r(z){ dz}}{} { ds}\le 0,\\ \frac{1}{2}\left\{ x e^{\int _{t}^{T}r(s){ ds}} +\int _{t}^{T}(c(s)-(1+\theta )a_1)e^{\int _{s}^{T}r(z){ dz}}{} { ds}\right\} ^2, \\ \quad \quad \quad \quad \quad \text {if} \quad x+e^{-\int _{t}^{T}r(s){ ds}}\int _{t}^{T}(c(s)-(1+\theta )a_1)e^{\int _{s}^{T}r(z){ dz}}{} { ds}>0, \end{array}\right. } \end{aligned}$$

where

$$\begin{aligned} \left\{ \begin{array}{ll} \bar{\eta }(t, x)=\Delta _1(t)\left\{ x+e^{-\int _{t}^{T}r(s){ ds}}\int _{t}^{T}(c(s) -(1+\theta )a_1)e^{\int _{s}^{T}r(z){ dz}}{} { ds}\right\} ,\\ \bar{q}(t, x)=\Delta _2(t)\left\{ x+e^{-\int _{t}^{T}r(s){ ds}}\int _{t}^{T}(c(s) -(1+\theta )a_1)e^{\int _{s}^{T}r(z){ dz}}{} { ds}\right\} , \end{array} \right. \end{aligned}$$

(16)

and

$$\begin{aligned} M_2(t)=-\frac{1}{2}\cdot \frac{m^2(\lambda _1+\lambda )\mu _{12}+2m\theta a_1\lambda \mu _{11}\mu _{21}+\theta ^2a_1^2\left( \sigma ^2(t) +(\lambda _2+\lambda )\mu _{22}\right) }{\left( \sigma ^2(t)+(\lambda _2 +\lambda )\mu _{22}\right) (\lambda _1+\lambda )\mu _{12}-\lambda ^2\mu _{11}^2\mu _{21}^2}, \end{aligned}$$

with $m=a(t)+(\lambda _2+\lambda )\mu _{21}$. It is not difficult to see that $M_2(t)<0$ for any $t\in [0, T]$ when $-\frac{a(t)}{\lambda _2+\lambda }<\mu _{21}<0$ and $0<\theta _2(t)<\theta \le \theta _1(t)$.

Case 3    $-\frac{a(t)}{\lambda _2+\lambda }<\mu _{21}<0$, $0<\theta _2(t)<\theta _1(t)<\theta$.

The minimum of the left-hand side of the Eq. (10) is attained at

$$\begin{aligned} \pi ^*(t) ={\left\{ \begin{array}{ll} \left( 0,\, -\frac{\theta a_1}{(\lambda _1+\lambda )\mu _{12}}\left\{ x+e^{-\int _{t}^{T}r(s){ ds}}\int _{t}^{T}(c(s)-(1+\theta )a_1)e^{\int _{s}^{T}r(z){ dz}}{} { ds}\right\} \right) ,\\ \quad \quad \quad \quad {\text {if}} \quad x+e^{-\int _{t}^{T}r(s){ ds}}\int _{t}^{T}(c(s)-(1+\theta )a_1)e^{\int _{s}^{T}r(z){ dz}}{} { ds}\le 0,\\ (0,\,0), \quad {\text {if}} \quad x+e^{-\int _{t}^{T}r(s){ ds}}\int _{t}^{T}(c(s)-(1+\theta )a_1)e^{\int _{s}^{T}r(z){ dz}}{} { ds}>0, \end{array}\right. } \end{aligned}$$

and the solution of Eq. (10) is

$$\begin{aligned} V(t,x) ={\left\{ \begin{array}{ll}\frac{1}{2}e^{\int _t^T2M_3(s){ ds}}\left\{ x e^{\int _{t}^{T}r(s){ ds}} +\int _{t}^{T}(c(s)-(1+\theta )a_1)e^{\int _{s}^{T}r(z){ dz}}{} { ds}\right\} ^2,\\ \quad \quad \quad \quad \quad {\text {if}} \quad x+e^{-\int _{t}^{T}r(s){ ds}}\int _{t}^{T}(c(s)-(1+\theta )a_1)e^{\int _{s}^{T}r(z){ dz}}{} { ds}\le 0,\\ \frac{1}{2}\left\{ x e^{\int _{t}^{T}r(s){ ds}} +\int _{t}^{T}(c(s)-(1+\theta )a_1)e^{\int _{s}^{T}r(z){ dz}}{} { ds}\right\} ^2, \\ \quad \quad \quad \quad \quad {\text {if}} \quad x+e^{-\int _{t}^{T}r(s){ ds}}\int _{t}^{T}(c(s)-(1+\theta )a_1)e^{\int _{s}^{T}r(z){ dz}}{} { ds}>0, \end{array}\right. } \end{aligned}$$

where $M_3(t)=-\frac{1}{2}\frac{\theta ^2a_1^2}{(\lambda _1+\lambda )\mu _{12}}$.

Case 4    $-1<\mu _{21}\le -\frac{a(t)}{\lambda _2+\lambda }$, $\theta >0$.

The minimum of the left-hand side of the Eq. (10) is attained at

$$\begin{aligned} \pi ^*(t) ={\left\{ \begin{array}{ll}\left( 0,\, -\frac{\theta a_1}{(\lambda _1+\lambda )\mu _{12}}\left\{ x+e^{-\int _{t}^{T}r(s){ ds}}\int _{t}^{T}(c(s)-(1+\theta )a_1)e^{\int _{s}^{T}r(z){ dz}}{} { ds}\right\} \right) ,\\ \quad \quad \quad \quad \quad {\text {if}} \quad x+e^{-\int _{t}^{T}r(s){ ds}}\int _{t}^{T}(c(s)-(1 +\theta )a_1)e^{\int _{s}^{T}r(z){ dz}}{} { ds}\le 0,\\ \left( -\frac{a(t)+(\lambda _2+\lambda )\mu _{21}}{\sigma ^2(t) +(\lambda _2+\lambda )\mu _{22}}\cdot \left\{ x+e^{-\int _{t}^{T}r(s){ ds}}\int _{t}^{T}(c(s)-(1 +\theta )a_1)e^{\int _{s}^{T}r(z){ dz}}{} { ds}\right\} ,\,0\right) ,\\ \quad \quad \quad \quad \quad {\text {if}} \quad x+e^{-\int _{t}^{T}r(s){ ds}} \int _{t}^{T}(c(s)-(1+\theta )a_1)e^{\int _{s}^{T}r(z){ dz}}{} { ds}>0, \end{array}\right. } \end{aligned}$$

and the solution of Eq. (10) is

$$\begin{aligned} V(t,x) ={\left\{ \begin{array}{ll}\frac{1}{2}e^{\int _t^T2M_3(s){ ds}}\left\{ x e^{\int _{t}^{T}r(s){ ds}} +\int _{t}^{T}(c(s)-(1+\theta )a_1)e^{\int _{s}^{T}r(z){ dz}}{} { ds}\right\} ^2,\\ \quad \quad \quad \quad \quad {\text {if}} \quad x+e^{-\int _{t}^{T}r(s){ ds}}\int _{t}^{T}(c(s) -(1+\theta )a_1)e^{\int _{s}^{T}r(z){ dz}}{} { ds}\le 0,\\ \frac{1}{2}e^{\int _t^T2M_1(s){ ds}}\left\{ xe^{\int _t^Tr(s){ ds}} +\int _t^T(c(s)-(1+\theta )a_1)e^{\int _s^Tr(z){ dz}}{} { ds}\right\} ^2,\\ \quad \quad \quad \quad \quad {\text {if}} \quad x+e^{-\int _{t}^{T}r(s){ ds}}\int _{t}^{T}(c(s)-(1+\theta )a_1)e^{\int _{s}^{T}r(z){ dz}}{} { ds}>0. \end{array}\right. } \end{aligned}$$

Case 5    $\mu _{21}\ge 0$, $\theta >0$.

The results in this case is exactly the same as in Case 2.

To summarize, we have

Theorem 3.1

Let $\Delta _1(t)$ and $\Delta _2(t)$ be given as in (15), $\bar{\eta }(t, x)$ and $\bar{q}(t, x)$ be given as in (16). For any $t\in [0,T]$, we have

• (i) when $-1<\mu _{21}\le -\frac{a(t)}{\lambda _2+\lambda }$, the minimizer of the left-hand side of the Eq. (12) is attained at

  $$\begin{aligned} \pi ^*(t) ={\left\{ \begin{array}{ll}\left( 0,\,-\frac{\theta a_1}{(\lambda _1+\lambda )\mu _{12}}\left\{ x+e^{-\int _{t}^{T}r(s){ ds}}\int _{t}^{T}(c(s)-(1+\theta )a_1)e^{\int _{s}^{T}r(z){ dz}}{} { ds}\right\} \right) ,\\ \quad \quad \quad \quad \quad {\text {if}} \quad x+e^{-\int _{t}^{T}r(s){ ds}}\int _{t}^{T}(c(s)-(1+\theta )a_1)e^{\int _{s}^{T}r(z){ dz}}{} { ds}\le 0,\\ \left( -\frac{a(t)+(\lambda _2+\lambda )\mu _{21}}{\sigma ^2(t)+(\lambda _2+\lambda )\mu _{22}} \left\{ x+e^{-\int _{t}^{T}r(s){ ds}}\int _{t}^{T}(c(s)-(1+\theta )a_1)e^{\int _{s}^{T}r(z){ dz}}{} { ds}\right\} ,\, 0\right) ,\\ \quad \quad \quad \quad \quad {\text {if}} \quad x+e^{-\int _{t}^{T}r(s){ ds}}\int _{t}^{T}(c(s)-(1+\theta )a_1)e^{\int _{s}^{T}r(z){ dz}}{} { ds}>0, \end{array}\right. } \end{aligned}$$

  (17)

  and the solution of the HJB-Eq. (10) is given by

  $$\begin{aligned} V(t, x) ={\left\{ \begin{array}{ll}\frac{1}{2}e^{\int _t^T2M_3(s){ ds}}\left\{ x e^{\int _{t}^{T}r(s){ ds}} +\int _{t}^{T}(c(s)-(1+\theta )a_1)e^{\int _{s}^{T}r(z){ dz}}{} { ds}\right\} ^2,\\ \quad \quad \quad \quad \quad {\text {if}} \quad x+e^{-\int _{t}^{T}r(s){ ds}}\int _{t}^{T}(c(s)-(1+\theta )a_1)e^{\int _{s}^{T}r(z){ dz}}{} { ds}\le 0,\\ \frac{1}{2}e^{\int _t^T2M_1(s){ ds}}\left\{ x e^{\int _{t}^{T}r(s){ ds}} +\int _{t}^{T}(c(s)-(1+\theta )a_1)e^{\int _{s}^{T}r(z){ dz}}{} { ds}\right\} ^2,\\ \quad \quad \quad \quad \quad {\text {if}} \quad x+e^{-\int _{t}^{T}r(s){ ds}}\int _{t}^{T}(c(s)-(1+\theta )a_1)e^{\int _{s}^{T}r(z){ dz}}{} { ds}> 0; \end{array}\right. } \end{aligned}$$

  (18)

• (ii) when $-\frac{a(t)}{\lambda _2+\lambda }<\mu _{21}<0$, the minimizer of the left-hand side of the Eq. (12) is attained at

  $$\begin{aligned} \pi ^*(t) ={\left\{ \begin{array}{ll}(\eta _1^*,\, q_1^*),&{}x+e^{-\int _{t}^{T}r(s){ ds}}\int _{t}^{T}(c(s)-(1+\theta )a_1)e^{\int _{s}^{T}r(z){ dz}}{} { ds}\le 0,\\ (0,\, 0),&{}x+e^{-\int _{t}^{T}r(s){ ds}}\int _{t}^{T}(c(s)-(1+\theta )a_1)e^{\int _{s}^{T}r(z){ dz}}{} { ds}>0, \end{array}\right. } \end{aligned}$$

  (19)

  where

  $$\begin{aligned} (\eta _1^*,\, q_1^*)= {\left\{ \begin{array}{ll}\left( -\frac{a(t)+(\lambda _2+\lambda )\mu _{21}}{\sigma ^2(t)+(\lambda _2 +\lambda )\mu _{22}}\cdot \left\{ x+e^{-\int _{t}^{T}r(s){ ds}}\int _{t}^{T}(c(s) -(1+\theta )a_1)e^{\int _{s}^{T}r(z){ dz}}{} { ds}\right\} ,\, 0\right) ,&{}0<\theta \le \theta _2(t)<\theta _1(t),\\ (\bar{\eta }(t, x) ,\, \bar{q}(t, x)),&{}0<\theta _2(t)<\theta \le \theta _1(t),\\ \left( 0,\, -\frac{\theta a_1}{(\lambda _1+\lambda )\mu _{12}}\left\{ x+e^{-\int _{t}^{T}r(s){ ds}}\int _{t}^{T}(c(s)-(1+\theta )a_1)e^{\int _{s}^{T}r(z){ dz}}{} { ds}\right\} \right) ,&{}0<\theta _2(t)<\theta _1(t)<\theta . \end{array}\right. } \end{aligned}$$

  Moreover, the solution of the HJB-Eq. (10) is given by

  $$\begin{aligned} V(t, x) ={\left\{ \begin{array}{ll}V_1(t, x),&{}x+e^{-\int _{t}^{T}r(s){ ds}}\int _{t}^{T}(c(s)-(1+\theta )a_1)e^{\int _{s}^{T}r(z){ dz}}{} { ds}\le 0,\\ V_2(t, x),&{}x+e^{-\int _{t}^{T}r(s){ ds}}\int _{t}^{T}(c(s)-(1+\theta )a_1)e^{\int _{s}^{T}r(z){ dz}}{} { ds}>0, \end{array}\right. } \end{aligned}$$

  (20)

  where

  $$\begin{aligned} V_1(t, x) ={\left\{ \begin{array}{ll} \frac{1}{2}e^{\int _t^T2M_1(s){ ds}}\left\{ x e^{\int _{t}^{T}r(s){ ds}} +\int _{t}^{T}(c(s)-(1+\theta )a_1)e^{\int _{s}^{T}r(z){ dz}}{} { ds}\right\} ^2,&{}0<\theta \le \theta _2(t)<\theta _1(t),\\ \frac{1}{2}e^{\int _t^T2M_2(s){ ds}}\left\{ x e^{\int _{t}^{T}r(s){ ds}} +\int _{t}^{T}(c(s)-(1+\theta )a_1)e^{\int _{s}^{T}r(z){ dz}}{} { ds}\right\} ^2,&{}0<\theta _2(t)<\theta \le \theta _1(t),\\ \frac{1}{2}e^{\int _t^T2M_3(s){ ds}}\left\{ x e^{\int _{t}^{T}r(s){ ds}} +\int _{t}^{T}(c(s)-(1+\theta )a_1)e^{\int _{s}^{T}r(z){ dz}}{} { ds}\right\} ^2,&{}0<\theta _2(t)<\theta _1(t)<\theta , \end{array}\right. } \end{aligned}$$

  and

  $$\begin{aligned} V_2(t, x)=\frac{1}{2}\left\{ x e^{\int _{t}^{T}r(s){ ds}} +\int _{t}^{T}(c(s)-(1+\theta )a_1)e^{\int _{s}^{T}r(z){ dz}}{} { ds}\right\} ^2; \end{aligned}$$

• (iii) When $\mu _{21}\ge 0$, the minimizer of the left-hand side of the Eq. (12) is attained at

  $$\begin{aligned} \pi ^{*}(t) = {\left\{ \begin{array}{ll} (\bar{\eta }(t, x),\, \bar{q}(t, x)),&{}x+e^{-\int _{t}^{T}r(s){ ds}}\int _{t}^{T}(c(s)-(1+\theta )a_1)e^{\int _{s}^{T}r(z){ dz}}{} { ds}\le 0,\\ (0,\, 0),&{}x+e^{-\int _{t}^{T}r(s){ ds}}\int _{t}^{T}(c(s)-(1+\theta )a_1)e^{\int _{s}^{T}r(z){ dz}}{} { ds}>0, \end{array}\right. } \end{aligned}$$

  (21)

  and the solution of the HJB-Eq. (10) is given by

  $$\begin{aligned} V(t, x) ={\left\{ \begin{array}{ll}\frac{1}{2}e^{\int _t^T2M_2(s){ ds}}\left\{ x e^{\int _{t}^{T}r(s){ ds}} +\int _{t}^{T}(c(s)-(1+\theta )a_1)e^{\int _{s}^{T}r(z){ dz}}{} { ds}\right\} ^2,\\ \quad \quad \quad \quad \quad {\text {if}} \quad x+e^{-\int _{t}^{T}r(s){ ds}}\int _{t}^{T}(c(s)-(1+\theta )a_1)e^{\int _{s}^{T}r(z){ dz}}{} { ds}\le 0,\\ \frac{1}{2}\left\{ x e^{\int _{t}^{T}r(s){ ds}} +\int _{t}^{T}(c(s)-(1+\theta )a_1)e^{\int _{s}^{T}r(z){ dz}}{} { ds}\right\} ^2,\\ \quad \quad \quad \quad \quad {\text {if}} \quad x+e^{-\int _{t}^{T}r(s){ ds}}\int _{t}^{T}(c(s)-(1+\theta )a_1)e^{\int _{s}^{T}r(z){ dz}}{} { ds}> 0. \end{array}\right. } \end{aligned}$$

  (22)

Now we define regions $\Gamma _{1}$, $\Gamma _{2}$, and $\Gamma _{3}$ in the (t, x) plane as

$$\begin{aligned}&\Gamma _{1}:=\left\{ (t,x)\in [0,T]\times {\mathbb {R}}\big |x+e^{-\int _{t}^{T}r(s){ ds}}\int _{t}^{T}(c(s) -(1+\theta )a_1)e^{\int _{s}^{T}r(z){ dz}}{} { ds}<0\right\} ,\\&\Gamma _{2}:=\left\{ (t,x)\in [0,T]\times {\mathbb {R}}\big |x+e^{-\int _{t}^{T}r(s){ ds}}\int _{t}^{T}(c(s)-(1+\theta )a_1)e^{\int _{s}^{T}r(z){ dz}}{} { ds}>0\right\} ,\\&\Gamma _{3}:=\left\{ (t,x)\in [0,T]\times {\mathbb {R}}\big |x+e^{-\int _{t}^{T}r(s){ ds}}\int _{t}^{T}(c(s)-(1+\theta )a_1)e^{\int _{s}^{T}r(z){ dz}}{} { ds}=0\right\} . \end{aligned}$$

Some simple calculations show that in $\Gamma _{1}$ and $\Gamma _{2}$, V(t, x) is sufficiently smooth for the derivatives in (10). The non-smoothness of V(t, x) occurs in the switching curve $\Gamma _{3}$.

Explicitly, in $\Gamma _{1}$ and $\Gamma _{2}$, $V(t,x)=\frac{1}{2}P(t)x^{2}+Q(t)x+L(t)$ is sufficiently smooth for the terms in (10) with

$$\begin{aligned}&V_{t}(t,x)=\frac{1}{2}P_t(t)x^{2}+Q_t(t)x+L_t(t),\\&V_{x}(t,x)=P(t)x+Q(t),\\&V_{xx}(t,x)=P(t). \end{aligned}$$

While the switching curve $\Gamma _{3}$ is where the non-smoothness of V(t, x) occurs. On $\Gamma _{3}$,

$$\begin{aligned} V(t,x)=\frac{1}{2}P(t)x^{2}+Q(t)x+L(t)=0, \end{aligned}$$

so V(t, x) is continuous at points on $\Gamma _{3}$. In addition, we also easily obtain

$$\begin{aligned} \left\{ \begin{aligned}&V_{t}(t,x)=\frac{1}{2}P_t(t)x^{2}+Q_t(t)x+L_t(t)=0,\\&V_{x}(t,x)=P(t)x+Q(t)=0. \end{aligned} \right. \end{aligned}$$

That is, V(t, x) is also continuously differentiable at the point on $\Gamma _{3}$. However, $V_{xx}(t, x)$ does not exist on $\Gamma _{3}$, since the values of P(t) in $\Gamma _{1}$ and $\Gamma _{2}$ are different (it is not difficult to see from the results in Theorem 3.1). This means that V(t, x) does not possess the necessary smoothness properties to qualify as a classical solution of the HJB Eq. (10). For this reason, we are required to work within the framework of viscosity solutions.

By Definition 3.1, it is not difficult to prove that V(t, x) given in Theorem 3.1 is a viscosity solution of the HJB Eq. (10). Then the verification theorem within the framework of the viscosity solution is given as follows:

Theorem 3.2

Let $\Delta _1(t)$ and $\Delta _2(t)$ be given as in (16), $\hat{R}^{*}(s):=\hat{R}^{\pi ^{*}}(s)$ and $c_1(s):=c(s)-(1+\theta )a_1$.

If the initial reserve x satisfies

$$\begin{aligned} x+e^{-\int _{t}^{T}r(s){ ds}}\int _{t}^{T}c_1(s)e^{\int _{s}^{T}r(z){ dz}}{} { ds}>0 \end{aligned}$$

for the initial time t, the optimal investment and reinsurance strategy of problem (9) at any $s\in [t, T]$ is given by

• (i) When $-1<\mu _{21}\le -\frac{a(t)}{\lambda _2+\lambda }$ ,

  $$\begin{aligned} \pi ^{*}(s) ={\left\{ \begin{array}{ll} \left( -\frac{a(s)+(\lambda _2+\lambda )\mu _{21}}{\sigma ^2(s)+(\lambda _2+\lambda )\mu _{22}} \left\{ \hat{R}^{*}(s-)+e^{-\int _{s}^{T}r(z){ dz}}\int _{s}^{T}c_1(v)e^{\int _{v}^{T}r(z){ dz}}{} { dv}\right\} , \, 0 \right) , &{}t\le s < T\wedge \tau _1, \\ \left( 0,\,-\frac{\theta a_1}{(\lambda _1+\lambda )\mu _{12}} \left\{ \hat{R}^*(s-)+e^{-\int _{s}^{T}r(z){ dz}}\int _{s}^{T}c_1(v)e^{\int _{v}^{T}r(z){ dz}}{} { dv}\right\} \right) , &{}T\wedge \tau _1\le s < T\wedge \tau _2, \end{array}\right. } \end{aligned}$$

  where

  $$\begin{aligned} \tau _1:={\mathrm{inf}}\left\{ s>t:\hat{R}^*(s)+e^{-\int _{s}^{T}r(z){ dz}} \int _{s}^{T}c_1(v)e^{\int _{v}^{T}r(z){ dz}}{} { dv}\le 0\right\} , \end{aligned}$$

  and

  $$\begin{aligned} \tau _2:={\mathrm{inf}}\left\{ s>\tau _1:\hat{R}^*(s)+e^{ -\int _{s}^{T}r(z){ dz}}\int _{s}^{T}c_1(v)e^{\int _{v}^{T}r(z){ dz}}{} { dv}>0\right\} . \end{aligned}$$

  For the optimal strategy at $s\in [T\wedge \tau _2, T]$, we give the explanation in the following Remark 3.2;

• (ii) When $-\frac{a(t)}{\lambda _2+\lambda }<\mu _{21}<0$ or $\mu _{21}\ge 0$,

  $$\begin{aligned} \pi ^{*}(s)=(\eta ^*(s, \hat{R}^*(s)), q^*(s, \hat{R}^*(s)))=(0 ,\, 0). \end{aligned}$$

If the initial reserve x satisfies

$$\begin{aligned} x+e^{-\int _{t}^{T}r(s){ ds}}\int _{t}^{T}c_1(s)e^{\int _{s}^{T}r(z){ dz}}{} { ds}\le 0, \end{aligned}$$

for the initial time t, the optimal investment and reinsurance strategy of problem (9) at any $s\in [t, T]$ is given as follows.

• (i) When $-1<\mu _{21}\le -\frac{a(t)}{\lambda _2+\lambda }$,

  $$\begin{aligned} \pi ^{*}(s) ={\left\{ \begin{array}{ll} \left( 0,\,-\frac{\theta a_1}{(\lambda _1+\lambda )\mu _{12}} \left\{ \hat{R}^*(s-)+e^{-\int _{s}^{T}r(z){ dz}}\int _{s}^{T}c_1(v) e^{\int _{v}^{T}r(z){ dz}}{} { dv}\right\} \right) , &{}t\le s < T\wedge \tau _3,\\ \left( -\frac{a(s)+(\lambda _2+\lambda )\mu _{21}}{\sigma ^2(s)+(\lambda _2+\lambda )\mu _{22}} \left\{ \hat{R}^*(s-)+e^{-\int _{s}^{T}r(z){ dz}}\int _{s}^{T}c_1(v)e^{\int _{v}^{T}r(z){ dz}}{} { dv}\right\} , \, 0\right) , &{}T\wedge \tau _3\le s < T\wedge \tau _4; \end{array}\right. } \end{aligned}$$

  where

  $$\begin{aligned} \tau _3:={\mathrm{inf}}\left\{ s>t:\hat{R}^*(s)+e^{ -\int _{s}^{T}r(z){ dz}}\int _{s}^{T}c_1(v)e^{\int _{v}^{T}r(z){ dz}}{} { dv}>0\right\} , \end{aligned}$$

  and

  $$\begin{aligned} \tau _4:={\mathrm{inf}}\left\{ s>\tau _3:\hat{R}^*(s)+e^{ -\int _{s}^{T}r(z){ dz}}\int _{s}^{T}c_1(v)e^{\int _{v}^{T}r(z){ dz}}{} { dv}\le 0\right\} . \end{aligned}$$

  Again, for the optimal strategy at $s\in [T\wedge \tau _4, T]$, please see the explanation in the following Remark 3.2;

• (ii) When $-\frac{a(t)}{\lambda _2+\lambda }<\mu _{21}<0$,

  $$\begin{aligned} \pi ^{*}(s)=(\eta ^*(s, \hat{R}^*(s)), q^*(s, \hat{R}^*(s))), \end{aligned}$$

  where

  $$\begin{aligned} \eta ^*(s, \hat{R}^*(s)) ={\left\{ \begin{array}{ll}-\frac{a(s)+(\lambda _2+\lambda )\mu _{21}}{\sigma ^2(s)+(\lambda _2+\lambda )\mu _{22}}\cdot \left\{ \hat{R}^*(s-)+e^{-\int _{s}^{T}r(z){ dz}}\int _{s}^{T}c_1(v)e^{\int _{v}^{T}r(z){ dz}}{} { dv}\right\} ,&{} 0<\theta \le \theta _2(t)<\theta _1(t),\\ \Delta _1(s) \left\{ \hat{R}^*(s-)+e^{-\int _{s}^{T}r(z){ dz}}\int _{s}^{T}c_1(v)e^{\int _{v}^{T}r(z){ dz}}{} { dv}\right\} ,&{}0<\theta _2(t)<\theta \le \theta _1(t),\\ 0,&{}0<\theta _2(t)<\theta _1(t)<\theta , \end{array}\right. } \end{aligned}$$

  and

  $$\begin{aligned} q^*(s, \hat{R}^*(s)) ={\left\{ \begin{array}{ll} 0,&{}0<\theta \le \theta _2(t)<\theta _1(t),\\ \Delta _2(s) \left\{ \hat{R}^*(s-)+e^{-\int _{s}^{T}r(z){ dz}}\int _{s}^{T}c_1(v)e^{\int _{v}^{T}r(z){ dz}}{} { dv} \right\} ,&{}0<\theta _2(t)<\theta \le \theta _1(t),\\ -\frac{\theta a_1}{(\lambda _1+\lambda )\mu _{12}} \left\{ \hat{R}^*(s-)+e^{-\int _{s}^{T}r(z){ dz}}\int _{s}^{T}c_1(v)e^{\int _{v}^{T}r(z){ dz}}{} { dv}\right\} ,&{} 0<\theta _2(t)<\theta _1(t)<\theta \end{array}\right. } \end{aligned}$$

  for any $t\le s < T\wedge \tau _3$, and

  $$\begin{aligned} \pi ^{*}(s)=(\eta ^*(s, \hat{R}^*(s)), q^*(s, \hat{R}^*(s)))=(0, \, 0) \end{aligned}$$

  for any $T\wedge \tau _3\le s < T$;

• (iii) When $\mu _{21}\ge 0$ ,

  $$\begin{aligned} \pi ^{*}(s)=(\eta ^*(s, \hat{R}^*(s)), q^*(s, \hat{R}^*(s))), \end{aligned}$$

  where

  $$\begin{aligned} \eta ^*(s, \hat{R}^*(s)) ={\left\{ \begin{array}{ll} \Delta _1(s) \left\{ \hat{R}^*(s-)+e^{-\int _{s}^{T}r(z){ dz}}\int _{s}^{T}c_1(v)e^{\int _{v}^{T}r(z){ dz}}{} { dv}\right\} , &{}t\le s < T\wedge \tau _3,\\ 0, &{}T\wedge \tau _3\le s < T, \end{array}\right. } \end{aligned}$$

  and

  $$\begin{aligned} q^*(s, \hat{R}^*(s)) ={\left\{ \begin{array}{ll} \Delta _2(s) \left\{ \hat{R}^*(s-)+e^{-\int _{s}^{T}r(z){ dz}}\int _{s}^{T}c_1(v)e^{\int _{v}^{T}r(z){ dz}}{} { dv}\right\} , &{}t\le s < T\wedge \tau _3,\\ 0,&{}T\wedge \tau _3\le s < T. \end{array}\right. } \end{aligned}$$

Furthermore, the value function J(t, x) satisfies $J(t,x)=V(t,x)$, where V(t, x) is the same as shown in Theorem 3.1.

Along the same lines as in Section 4 of Bi and Guo (2013), we can prove the verification theorem. Therefore, we omit it here.

Remark 3.2

For the optimal strategies in the case of $-1<\mu _{21}\le -\frac{a(t)}{\lambda _2+\lambda }$, we only give two parts for the period of [t, T]. Actually, there are possibly more than two parts in this case. For example, during the period of $[\tau _2\wedge T, T]$, the value of

$$\begin{aligned} \hat{R}^*(s-)+e^{-\int _{s}^{T}r(z){ dz}}\int _{s}^{T}c_1(v)e^{\int _{v}^{T}r(z){ dz}}{} { dv} \end{aligned}$$

maybe reach to the negative value, then return back to the positive value, and then back to negative value again, and so on. Therefore, we have to make the choice of optimal strategies based on the value of

$$\begin{aligned} \hat{R}^*(s-)+e^{-\int _{s}^{T}r(z){ dz}}\int _{s}^{T}c_1(v)e^{\int _{v}^{T}r(z){ dz}}{} { dv}. \end{aligned}$$

That is, when

$$\begin{aligned} \hat{R}^*(s-)+e^{-\int _{s}^{T}r(z){ dz}}\int _{s}^{T}c_1(v)e^{\int _{v}^{T}r(z){ dz}}{} { dv}\le 0, \end{aligned}$$

the optimal strategies are

$$\begin{aligned} \pi ^*(s)=\left( 0,\,-\frac{\theta a_1}{(\lambda _1+\lambda )\mu _{12}} \left\{ \hat{R}^*(s-)+e^{-\int _{s}^{T}r(z){ dz}}\int _{s}^{T}c_1(v)e^{\int _{v}^{T}r(z){ dz}}{} { dv}\right\} \right) ; \end{aligned}$$

when

$$\begin{aligned} \hat{R}^*(s-)+e^{-\int _{s}^{T}r(z){ dz}}\int _{s}^{T}c_1(v)e^{\int _{v}^{T}r(z){ dz}}{} { dv}>0, \end{aligned}$$

the optimal strategies are

$$\begin{aligned} \pi ^*(s)=\left( -\frac{a(s)+(\lambda _2+\lambda )\mu _{21}}{\sigma ^2(s)+(\lambda _2+\lambda )\mu _{22}} \left\{ \hat{R}^*(s-)+e^{-\int _{s}^{T}r(z){ dz}}\int _{s}^{T}c_1(v)e^{\int _{v}^{T}r(z){ dz}}{} { dv}\right\} , \, 0\right) . \end{aligned}$$

4 The efficient strategy and efficient frontier

In this section, we apply the results in Sect. 3 to solve the mean–variance problem, and derive the efficient strategy and efficient frontier of problem (4). Here we only give the detailed analysis for the case of $-\frac{a(t)}{\lambda _2+\lambda }<\mu _{21}<0$.

Since we have set $\hat{R}(t)=R(t)-(k-\beta )$, then $R(t)=\hat{R}(t)+(k-\beta )$ and $R(0)=\hat{R}(0)+(k-\beta )$. Besides, $c(t)=c+(k-\beta )r(t)$ in (8). We can get

$$\begin{aligned} E\left[ \frac{1}{2}(\hat{R}(T)))^2\right] =\frac{1}{2}E[(R(T)-k)^2+2\beta (E[R(T)]-k)+\beta ^2]. \end{aligned}$$

Therefore, for every fixed $\beta$, we have

$$\begin{aligned} \begin{matrix} \min \limits _{\pi \in \Pi }E[(R(T)-k)^2+2\beta (E[R(T)]-k)]\\ \quad ={\left\{ \begin{array}{ll} \left\{ R_0 e^{\int _{0}^{T}r(s){ ds}} +(c-(1+\theta )a_1)\int _{0}^{T}e^{\int _{s}^{T}r(z){ dz}}{} { ds}-(k-\beta )\right\} ^2-\beta ^2,\\ \quad \quad \quad \quad \quad {\text {if}} \quad R_0-(k-\beta )e^{-\int _0^Tr(s){ ds}}+(c-(1+\theta )a_1)\int _{0}^{T}e^{\int _{s}^{T}r(z){ dz}}{} { ds}>0,\\ 2V_1(0, R_0)-\beta ^2,\\ \quad \quad \quad \quad \quad {\text {if}} \quad R_0-(k-\beta )e^{-\int _0^Tr(s){ ds}}+(c-(1+\theta )a_1)\int _{0}^{T}e^{\int _{s}^{T}r(z){ dz}}{} { ds}\le 0, \end{array}\right. } \end{matrix} \end{aligned}$$

(23)

where

$$\begin{aligned} \begin{matrix} 2V_1(0, R_0)-\beta ^2\\ \quad ={\left\{ \begin{array}{ll} e^{\int _0^T2M_1(s){ ds}}\left\{ R_0 e^{\int _{0}^{T}r(s){ ds}} +(c-(1+\theta )a_1)\int _{0}^{T}e^{\int _{s}^{T}r(z){ dz}}{} { ds} -(k-\beta )\right\} ^2-\beta ^2,&{}0<\theta \le \theta _2(t)<\theta _1(t),\\ e^{\int _0^T2M_2(s){ ds}}\left\{ R_0 e^{\int _{0}^{T}r(s){ ds}} +(c-(1+\theta )a_1)\int _{0}^{T}e^{\int _{s}^{T}r(z){ dz}}{} { ds}-(k-\beta )\right\} ^2-\beta ^2, &{}0<\theta _2(t)<\theta \le \theta _1(t),\\ e^{\int _0^T2M_3(s){ ds}}\left\{ R_0 e^{\int _{0}^{T}r(s){ ds}} +(c-(1+\theta )a_1)\int _{0}^{T}e^{\int _{s}^{T}r(z){ dz}}{} { ds}-(k-\beta )\right\} ^2-\beta ^2,&{}0<\theta _2(t)<\theta _1(t)<\theta . \end{array}\right. } \end{matrix} \end{aligned}$$

Note that the above value still depends on the Lagrange multiplier $\beta$, we denote it by $W(\beta )$. To obtain the minimum ${\mathrm{Var}}[R(T)]$ and the optimal strategy for the original control problem (4), it is sufficient to maximize the value in (23) over $\beta \in {\mathbb {R}}$ by the Lagrange duality theorem. Some calculations show that $W(\beta )$ attains its maximum value

$$\begin{aligned} W(\beta ^{*}) ={\left\{ \begin{array}{ll} \frac{\left[ R_{0}e^{\int _{0}^{T}r(s){ ds}}+(c-(1+\theta )a_1)\int _{0}^{T}e^{\int _{v}^{T}r(s){ ds}}{} { dv}-k\right] ^{2}}{e^{-\int _{0}^{T}2M_1(s){ ds}}-1}, &{}0<\theta \le \theta _2(t)<\theta _1(t),\\ \frac{\left[ R_{0}e^{\int _{0}^{T}r(s){ ds}}+(c-(1+\theta )a_1)\int _{0}^{T}e^{\int _{v}^{T}r(s){ ds}}{} { dv}-k\right] ^{2}}{e^{-\int _{0}^{T}2M_2(s){ ds}}-1},&{}0<\theta _2(t)<\theta \le \theta _1(t),\\ \frac{\left[ R_{0}e^{\int _{0}^{T}r(s){ ds}}+(c-(1+\theta )a_1)\int _{0}^{T}e^{\int _{v}^{T}r(s){ ds}}{} { dv}-k\right] ^{2}}{e^{-\int _{0}^{T}2M_3(s){ ds}}-1},&{}0<\theta _2(t)<\theta _1(t)<\theta , \end{array}\right. } \end{aligned}$$

at

$$\begin{aligned} \beta ^{*} ={\left\{ \begin{array}{ll} \frac{R_{0}e^{\int _{0}^{T}r(s){ ds}}+(c-(1+\theta )a_1)\int _{0}^{T}e^{\int _{v}^{T}r(s){ ds}}{} { dv}-k}{e^{-\int _{0}^{T}2M_1(s){ ds}}-1}, &{}0<\theta \le \theta _2(t)<\theta _1(t),\\ \frac{R_{0}e^{\int _{0}^{T}r(s){ ds}}+(c-(1+\theta )a_1)\int _{0}^{T}e^{\int _{v}^{T}r(s){ ds}}{} { dv}-k}{e^{-\int _{0}^{T}2M_2(s){ ds}}-1}, &{}0<\theta _2(t)<\theta \le \theta _1(t),\\ \frac{R_{0}e^{\int _{0}^{T}r(s){ ds}}+(c-(1+\theta )a_1)\int _{0}^{T}e^{\int _{v}^{T}r(s){ ds}}{} { dv}-k}{e^{-\int _{0}^{T}2M_3(s){ ds}}-1}, &{}0<\theta _2(t)<\theta _1(t)<\theta , \end{array}\right. } \end{aligned}$$

which leads to the following theorem.

Theorem 4.1

When $-\frac{a(t)}{\lambda _2+\lambda }<\mu _{21}<0$, the efficient frontier for problem (4) with expected terminal wealth $E[R(T)]=k$ is determined by

$$\begin{aligned} {\mathrm{Var}}[R(T)] ={\left\{ \begin{array}{ll} \frac{\left[ R_{0}e^{\int _{0}^{T}r(s){ ds}}+(c-(1+\theta )a_1)\int _{0}^{T}e^{\int _{v}^{T}r(s){ ds}}{} { dv}-E[R(T)]\right] ^{2}}{e^{-\int _{0}^{T}2M_1(s){ ds}}-1}, &{}0<\theta \le \theta _2(t)<\theta _1(t),\\ \frac{\left[ R_{0}e^{\int _{0}^{T}r(s){ ds}}+(c-(1+\theta )a_1)\int _{0}^{T}e^{\int _{v}^{T}r(s){ ds}}{} { dv}-E[R(T)]\right] ^{2}}{e^{-\int _{0}^{T}2M_2(s){ ds}}-1},&{}0<\theta _2(t)<\theta \le \theta _1(t),\\ \frac{\left[ R_{0}e^{\int _{0}^{T}r(s){ ds}}+(c-(1+\theta )a_1)\int _{0}^{T}e^{\int _{v}^{T}r(s){ ds}}{} { dv}-E[R(T)]\right] ^{2}}{e^{-\int _{0}^{T}2M_3(s){ ds}}-1},&{}0<\theta _2(t)<\theta _1(t)<\theta , \end{array}\right. } \end{aligned}$$

where

$$\begin{aligned} E[R(T)]\ge R_0e^{\int _0^Tr(s){ ds}}+(c-(1+\theta )a_1)\int _{0}^{T}e^{\int _{s}^{T}r(z){ dz}}{} { ds}. \end{aligned}$$

Moreover, the efficient strategy is given by

$$\begin{aligned} \pi ^{*}(t,R(t))= (\eta ^{*}(t,R(t)),q^{*}(t,R(t))) ={\left\{ \begin{array}{ll} (\tilde{\eta }^{*}(t,R(t)), \, 0), &{}0<\theta \le \theta _2(t)<\theta _1(t),\\ (\hat{\eta }^{*}(t,R(t)), \hat{q}^{*}(t,R(t))),&{}0<\theta _2(t)<\theta \le \theta _1(t),\\ (0, \, \tilde{q}^{*}(t,R(t))),&{}0<\theta _2(t)<\theta _1(t)<\theta , \end{array}\right. } \end{aligned}$$

for any $0\le t < T\wedge \hat{\tau }_{\pi ^*}$; and

$$\begin{aligned} \pi ^{*}(t,R(t))= (\eta ^{*}(t,R(t)),q^{*}(t,R(t)))=(0, \, 0) \end{aligned}$$

for any $T\wedge \hat{\tau }_{\pi ^*}\le t <T$. Where

$$\begin{aligned} \left\{ \begin{array}{ll} \tilde{\eta }^{*}(t,R(t))=-\frac{a(t)+(\lambda _2+\lambda )\mu _{21}}{\sigma ^2(t)+(\lambda _2+\lambda )\mu _{22}}\cdot \frac{R(t-)-ke^{-\int _{t}^{T}r(s){ ds}}+\int _{t}^{T}(c-(1+\theta )a_1)e^{-\int _{t}^{v}r(z){ dz}}{} { dv}}{1-e^{-\int _t^T2M_1(s){ ds}}},\\ \tilde{q}^{*}(t,R(t))=-\frac{\theta a_1}{(\lambda _1+\lambda )\mu _{12}}\frac{R(t-)-ke^{-\int _{t}^{T}r(s){ ds}}+\int _{t}^{T}(c-(1+\theta )a_1)e^{-\int _{t}^{v}r(z){ dz}}{} { dv}}{1-e^{-\int _t^T2M_3(s){ ds}}},\\ \hat{\eta }^{*}(t,R(t))=\Delta _1(t)\frac{R(t-)-ke^{-\int _{t}^{T}r(s){ ds}}+\int _{t}^{T}(c-(1+\theta )a_1)e^{-\int _{t}^{v}r(z){ dz}}{} { dv}}{1-e^{-\int _t^T2M_2(s){ ds}}},\\ \hat{q}^{*}(t,R(t))=\Delta _2(t)\frac{R(t-)-ke^{-\int _{t}^{T}r(s){ ds}}+\int _{t}^{T}(c-(1+\theta )a_1)e^{-\int _{t}^{v}r(z){ dz}}{} { dv}}{1-e^{-\int _t^T2M_2(s){ ds}}}, \end{array} \right. \end{aligned}$$

(24)

and

$$\begin{aligned} \hat{\tau }_{\pi ^{*}}:=\mathrm{inf}\left\{ s>t: R^*(s)-ke^{-\int _{s}^{T}r(z){ dz}}+\int _{s}^{T}(c-(1+\theta )a_1)e^{-\int _{s}^{v}r(z){ dz}}{} { dv}<0\right\} . \end{aligned}$$

Along the same lines, we can directly get the efficient frontier and efficient strategy for the other two cases as follows:

Theorem 4.2

• (i) When $-1<\mu _{21}\le -\frac{a(t)}{\lambda _2+\lambda }$, for any $\theta >0$, the efficient frontier for problem (4) with expected terminal wealth $E[R(T)]=k$ is given by

  $$\begin{aligned} {\mathrm{Var}}[R(T)]= \frac{\left[ R_{0}e^{\int _{0}^{T}r(s){ ds}}+(c-(1+\theta )a_1)\int _{0}^{T}e^{\int _{v}^{T}r(s){ ds}}{} { dv}-E[R(T)]\right] ^{2}}{e^{-\int _{0}^{T}2M_3(s){ ds}}-1}, \end{aligned}$$

  where

  $$\begin{aligned} E[R(T)]\ge R_0e^{\int _0^Tr(s){ ds}}+(c-(1+\theta )a_1)\int _{0}^{T}e^{\int _{s}^{T}r(z){ dz}}{} { ds}. \end{aligned}$$

  Moreover, the efficient strategy is

  $$\begin{aligned} \pi ^{*}(t,R(t))= \left\{ \begin{array}{ll} \left( 0, \, \tilde{q}^{*}(t,R(t))\right) , &{} 0\le t < T\wedge \hat{\tau }_{\pi ^*}, \\ \left( \tilde{\eta }^{*}(t,R(t)), \, 0 \right) , &{} T\wedge \hat{\tau }_{\pi ^*}\le t < T\wedge \tilde{\tau }_{\pi ^{*}}, \end{array} \right. \end{aligned}$$

  where

  $$\begin{aligned} \tilde{\tau }_{\pi ^{*}}:=\mathrm{inf}\left\{ s> \hat{\tau }_{\pi ^*}: R^*(s)-ke^{-\int _{s}^{T}r(z){ dz}}+\int _{s}^{T}(c-(1+\theta )a_1)e^{-\int _{s}^{v}r(z){ dz}}{} { dv} \ge 0\right\} . \end{aligned}$$

  For the efficient strategy in interval $[T\wedge \tilde{\tau }_{\pi ^{*}}, T]$, we can have the same analysis as mentioned in Remark 3.2.

• (ii) When $\mu _{21}\ge 0$, for any $\theta >0$, the efficient frontier for problem (4) with expected terminal wealth $E[R(T)]=k$ is given by

  $$\begin{aligned} {\mathrm{Var}}[R(T)]= \frac{\left[ R_{0}e^{\int _{0}^{T}r(s){ ds}}+(c-(1+\theta )a_1)\int _{0}^{T}e^{\int _{v}^{T}r(s){ ds}}{} { dv}-E[R(T)]\right] ^{2}}{e^{-\int _{0}^{T}2M_2(s){ ds}}-1}, \end{aligned}$$

  where

  $$\begin{aligned} E[R(T)]\ge R_0e^{\int _0^Tr(s){ ds}}+(c-(1+\theta )a_1)\int _{0}^{T}e^{\int _{s}^{T}r(z){ dz}}{} { ds}. \end{aligned}$$

  Moreover, the efficient strategy is

  $$\begin{aligned} \pi ^{*}(t,R(t))=(\hat{\eta }^{*}(t, R(t)), \hat{q}^{*}(t,R(t))), \end{aligned}$$

  where $(\hat{\eta }^{*}(t,R(t))$ are given in (24).

Remark 4.1

Note that the inequality

$$\begin{aligned} R_0-(k-\beta ^*)e^{-\int _0^Tr(s){ ds}}+(c-(1+\theta )a_1)\int _{0}^{T}e^{\int _{s}^{T}r(z){ dz}}{} { ds}\le 0 \end{aligned}$$

is equivalent to

$$\begin{aligned} R_0-ke^{-\int _0^Tr(s){ ds}}+(c-(1+\theta )a_1)\int _{0}^{T}e^{\int _{s}^{T}r(z){ dz}}{} { ds}\le 0, \end{aligned}$$

which can be rewritten as

$$\begin{aligned} k\ge R_0e^{\int _0^Tr(s){ ds}}+(c-(1+\theta )a_1)\int _{0}^{T}e^{\int _{s}^{T}r(z){ dz}}{} { ds}. \end{aligned}$$

This is the natural consequence which means that the investor expects higher terminal wealth k by investing in the stock market than the terminal wealth

$$\begin{aligned} R_{0}e^{\int _{0}^{T}r(s){ ds}}+(c-(1+\theta )a_1)\int _{0}^{T}e^{\int _{v}^{T}r(s){ ds}}{} { dv} \end{aligned}$$

by only investing in the bond market and $q(t)=0$. It also implies that the investor has to take risk to meet his/her investment target.

Remark 4.2

In this paper, when we assume that the two jump number processes $\{K_1(t)\}_{t\ge 0}$ and $\{K_2(t)\}_{t\ge 0}$ are independent, i.e., the parameter $\lambda =0$, and when we assume that $\mu _{21}$ are always nonnegative, we can get the same results as in Bi and Guo (2013).

5 Numerical examples

In this section, we give some numerical examples to illustrate our results.

Example 5.1

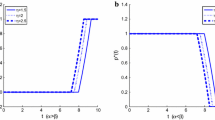
In this example, we set $R_0=10$, $T=1$, $r(t)\equiv 0.04$, $a(t)\equiv 0.01$, $\sigma (t)\equiv 0.03$, $\tilde{\theta }_1=0.2$, $\theta =0.8$, $\mu _{11}=0.01$, $\mu _{12}=0.002$, $\mu _{21}=0.005$, $\mu _{22}=0.0015$. The results are shown in Figs. 1 and 2.

Fig. 1

Efficient-frontier of problem (4) for different $\lambda$

Fig. 2

Efficient-frontier of problem (4) for different $\lambda _1$

From Fig. 1 with $\lambda =0, 8, 15$, $\lambda _1=3$, and $\lambda _2=1$, we can see that if ${\mathrm{Var}}[R(T)]$ is small enough, the smaller $\lambda$ the larger E[R(T)] with the same ${\mathrm{Var}}[R(T)]$. If ${\mathrm{Var}}[R(T)]$ is larger than some value, the reverse is true. This same property is shown in Fig. 2 with $\lambda =5$, $\lambda _1=1, 5, 10$, and $\lambda _2=1$. This is the natural consequence since $\mu _{21}>0$ means that the expected value of the jump size for the risky asset is positive, and thus the larger frequency (say, $\lambda _i (i=1, 2)$ and $\lambda$) of this kind of jump, the larger expected return.

Example 5.2

In this example, we set $R_0=10$, $T=1$, $r(t)\equiv 0.04$, $a(t)\equiv 0.01$, $\sigma (t)\equiv 0.03$, $\tilde{\theta }_1=0.2$, $\theta =0.8$, $\mu _{11}=0.01$, $\mu _{12}=0.002$, $\mu _{21}=0.02$. The results are shown in Fig. 3a–d.

Fig. 3

Efficient-frontier of problem (4) for different $\lambda$

Fig. 4

Efficient-frontier of problem (4) for different $\theta$

Figure 3 further investigates the influence of the common shock dependence, i.e., the parameter $\lambda$ on efficient frontier when the values of $\lambda _1+\lambda$ and $\lambda _2+\lambda$ are fixed. In Fig. 3a, b, the values of $\lambda _1+\lambda$ and $\lambda _2+\lambda$ are fixed by 16 and 20, respectively; In Fig. 3c, d, the values of $\lambda _1+\lambda$ and $\lambda _2+\lambda$ are fixed by 8 and 5, respectively. From Fig. 3b, d with $\mu _{22}=0.0025$, we can see that the larger $\lambda$ the larger E[R(T)] with the same ${\mathrm{Var}}[R(T)]$. Whereas, when $\mu _{22}$ is large enough, say, $\mu _{22}=0.025$, we find from Fig. 3a, c that the value of $\lambda$ almost has no impact on the efficient frontier. This suggests that the efficient frontier is less sensitive to the common shock dependence when $\lambda _1+\lambda$ and $\lambda _2+\lambda$ are fixed, which is also the natural consequence of Theorems 4.1 and 4.2.

Example 5.3

In this example, we set $R_0=10$, $T=1$, $r(t)\equiv 0.04$, $a(t)\equiv 0.01$, $\sigma (t)\equiv 0.03$, $\tilde{\theta }_1=0.2$, $\mu _{11}=0.01$, $\mu _{12}=0.002$, $\mu _{22}=0.0015$, $\lambda _2=1$, $\lambda _1=3$, $\lambda =5$. The results are shown in Figs. 4 and 5.

From Fig. 4 with $\mu _{21}=0.005$ and $\theta =0.2, 0.5, 0.8$, we can see that if ${\mathrm{Var}}[R(T)]$ is small enough, the smaller $\theta$ the larger E[R(T)] with the same ${\mathrm{Var}}[R(T)]$. If ${\mathrm{Var}}[R(T)]$ is larger than some value, the reverse is true. From Fig. 5 with $\theta =0.8$ and $\mu _{21}=0.005, 0.01, 0.015$, we conclude that the bigger $\mu _{21}$ the bigger E[R(T)] with the same ${\mathrm{Var}}[R(T)]$, and this phenomenon is not obvious when ${\mathrm{Var}}[R(T)]$ is small enough. This is the natural consequence since $\mu _{21}>0$ means that the expected value of the jump size for the risky asset is positive, and thus the larger $\mu _{21}$ the larger expected return.

Fig. 5

Efficient-frontier of problem (4) for different $\mu _{21}$

6 Conclusions

We first recap the main results of the paper. We consider mean–variance optimal problem for an insurer with investment and reinsurance in a jump-diffusion financial market where the aggregate claim process and the risky asset process are correlated by a common shock. Furthermore, we assume that the expected value of the jump size in the risky asset is not necessary nonnegative, therefore, we have to discuss the optimization problem on the five different cases because of the constraints on the investment and reinsurance control variables. Under the mean–variance criterion, using the technique of stochastic control theory and the corresponding Hamilton–Jacobi–Bellman equation, within a framework of viscosity solution, we derive the explicit expressions of the optimal strategies and the value function. Besides, we extend the optimal results to the original mean–variance optimization problem, and obtain the solutions of efficient frontier and efficient strategies explicitly.

For the future research, there are several interesting problems that deserve investigation. Firstly, we can extend the financial asset model to the one with Markov regime switching, such as the interest rate r(t), the appreciation rate b(t) and the volatility coefficient $\sigma (t)$ of the stock in our model can be changed from deterministic functions to a general stochastic processes with Markov regime switching; Secondly, we can consider portfolio problem with some constraints, such as the value of the dynamic wealth would be no less than a pre-given level c, or with no-bankruptcy constraint; Thirdly, transaction costs can also be considered in this optimization problem. Even though these kind of problems are challenging problems, they are meaningful and more realistic to be discussed, and they are also our future research work directions.