Continuous-time Markov decision processes with risk-sensitive finite-horizon cost criterion

Abstract

This paper studies continuous-time Markov decision processes with a denumerable state space, a Borel action space, bounded cost rates and possibly unbounded transition rates under the risk-sensitive finite-horizon cost criterion. We give the suitable optimality conditions and establish the Feynman–Kac formula, via which the existence and uniqueness of the solution to the optimality equation and the existence of an optimal deterministic Markov policy are obtained. Moreover, employing a technique of the finite approximation and the optimality equation, we present an iteration method to compute approximately the optimal value and an optimal policy, and also give the corresponding error estimations. Finally, a controlled birth and death system is used to illustrate the main results.

1 Introduction

Continuous-time Markov decision processes (CTMDPs) have been widely studied since they have wide applications, such as the controlled queueing system, the control of the epidemic, and telecommunication; see, for instance, Puterman (1994), Kitaev and Rykov (1995), Guo and Hernández-Lerma (2009), Prieto-Rumeau and Lorenzo (2010), Prieto-Rumeau and Hernández-Lerma (2012), Guo and Zhang (2014) and Guo et al. (2015). The time interval in real life is always finite, so the finite-horizon optimality criterion is a commonly used criterion. The existence of optimal policies under the finite-horizon expected total cost criterion has been discussed under the different sets of optimality conditions; see, for instance, Miller (1968), Wei and Chen (2014) and Guo et al. (2015). However, the finite-horizon expected total cost criterion is risk-neutral and cannot reflect the attitude of a decision-maker to the risk. In the real-world applications, a decision-maker is usually risk-sensitive, that is, he/she is either risk-seeking or risk-averse. Thus, it is necessary for us to take the risk-sensitivity of a decision-maker into consideration in the definition of the optimality criterion. The risk-sensitive optimality criteria employ the exponential utility function to characterize the risk-sensitivity of a decision-maker. When the risk-sensitivity coefficient of the exponential utility function takes positive (negative) values, the decision-maker is risk-averse (risk-seeking). For discrete-time MDPs, the risk-sensitive optimality criteria have been widely studied; see, for instance, Di Masi and Stettner (2007), Jaśkiewicz (2007), Cavazos-Cadena and Hernández-Hernández (2011) and the references therein. But there exist few works on the risk-sensitive optimality criteria for CTMDPs. Ghosh and Saha (2014) studied the risk-sensitive finite-horizon cost criterion and the risk-sensitive infinite-horizon discounted cost and average cost criteria for CTMDPs. More precisely, Ghosh and Saha (2014) also used the exponential utility function to characterize the risk-sensitivity of a decision-maker, dealt with the case of a denumerable state space, a positive risk-sensitivity coefficient, the nonnegative and bounded cost rates and the bounded transition rates, and obtained the existence of optimal policies. The positive risk-sensitivity coefficient indicates that the decision-maker is risk-averse in Ghosh and Saha (2014). However, the decision-maker may be risk-seeking in real life. Moreover, the transition rates in the controlled queueing system and the control of epidemic are usually unbounded; see, for instance, Guo and Hernández-Lerma (2009), Prieto-Rumeau and Lorenzo (2010), Prieto-Rumeau and Hernández-Lerma (2012), Guo and Zhang (2014) and Guo et al. (2015). Therefore, it is desirable for us to investigate the risk-sensitive optimality criteria for CTMDPs in which the risk-sensitivity coefficient can take positive and negative values and the transition rates are allowed to be unbounded.

In this paper we further study the risk-sensitive finite-horizon cost criterion for CTMDPs in Ghosh and Saha (2014). The state space is denumerable and the action space is a Borel space. The cost rates and the risk-sensitivity coefficient can take positive and negative values. The transition rates are allowed to be unbounded. Under the drift condition on the transition rates and the boundedness condition on the cost rates, we obtain the Feynman–Kac formula for CTMDPs which plays a crucial role in the proof of the existence of optimal policies (see Theorem 3.1). Besides the conditions for the Feynman–Kac formula, the standard continuity and compactness conditions are required for the existence of optimal policies. Under these mild conditions, we show the existence and uniqueness of the solution to the optimality equation via constructing an approximating sequence of bounded transition rates and using the Feynman–Kac formula, and then obtain the existence of an optimal deterministic Markov policy from the optimality equation (see Theorem 4.1).

On the other hand, we cannot obtain the precise forms of the optimal value and an optimal policy in general. Thus, it is of great importance for us to study the numerical methods. There are a few works dealing with the approximate computations of the risk-neutral optimality criteria for CTMDPs with the denumerable states and unbounded transition rates. van Dijk (1988, 1989) gave an approximate method for the finite-horizon expected total cost criterion via a technique of time discretization. Prieto-Rumeau and Lorenzo (2010) and Prieto-Rumeau and Hernández-Lerma (2012) studying the expected average reward criterion and the expected discounted reward criterion, respectively, proposed the numerical approximations by employing the finite truncation approach. Guo and Zhang (2014) discussed the finite approximation for the discounted CTMDPs with constraints by using a technique of occupation measures and the finite truncation method. In this paper we focus on the approximate computations of the optimal value and an optimal policy for the risk-sensitive finite-horizon cost criterion, which are not involved in Ghosh and Saha (2014). Since the state space is a denumerable set and the set of all admissible actions may be uncountable in the original control model ${\mathcal {M}}$, we construct a sequence of the control models $\{{\mathcal {M}}_n,n\ge 1\}$ with finite states and finite admissible actions to design a tractable numerical method. More specifically, applying the technique of the finite truncation in Prieto-Rumeau and Lorenzo (2010), Prieto-Rumeau and Hernández-Lerma (2012) and Guo and Zhang (2014) to the state space and the transition rates of the model ${\mathcal {M}}$, we give the corresponding elements of the model ${\mathcal {M}}_n$. Moreover, by choosing the set of all admissible actions of the model ${\mathcal {M}}_n$ satisfying a certain condition, we show that the optimal value of the model ${\mathcal {M}}_n$ converges to that of the model ${\mathcal {M}}$ and obtain the corresponding error estimation under the conditions which are stronger than those for the existence of optimal policies (see Theorem 5.1). Basing on this convergence and employing the optimality equation, we present an iteration method for the approximate computations of the optimal value and an optimal policy of the model ${\mathcal {M}}$ and give the corresponding error estimations (see Theorem 5.2). It should be mentioned that all the results on the numerical method for the risk-sensitive finite-horizon cost criterion are new. Finally, a controlled birth and death system which satisfies all the conditions in this paper is used to illustrate the applications of the risk-sensitive finite-horizon cost criterion and the numerical method.

The rest of this paper is organized as follows. In Sect. 2, we introduce the control model and the risk-sensitive finite-horizon cost criterion. In Sect. 3, we give the optimality conditions and establish the Feynman–Kac formula. In Sect. 4, we prove the existence of optimal policies via the optimality equation approach. In Sect. 5, we present an iteration method for the approximate computations of the optimal value and an optimal policy. In Sect. 6, we use a controlled birth and death system to illustrate the main results. In Sect. 7, we conclude with some remarks.

2 The control model

The control model under consideration is a five-tuple

$$\begin{aligned} {\mathcal {M}}:=\{S, A, (A(i), i\in S), q(j|i,a), c(i,a)\}. \end{aligned}$$

• The state space S is the set of all nonnegative integers.

• The action space A is a Borel space with the Borel $\sigma$-algebra $\mathcal {B}(A)$.

• $A(i)\in \mathcal {B}(A)$ denotes the set of all admissible actions in state $i\in S$. Let $K:=\{(i,a)|i\in S, a\in A(i)\}$.

• The transition rate q(j|i, a) is measurable in $a\in A(i)$ for each fixed $i,j\in S$. It satisfies $q(j|i,a)\ge 0$ for all $(i,a)\in K$ and $j\ne i$. Moreover, we assume that the transition rate is conservative and stable, i.e., $\sum _{j\in S} q(j|i,a)=0$ for all $(i,a)\in K$, and $q^*(i):=\sup _{a\in A(i)}|q(i|i,a)|<\infty$ for all $i\in S$.

• The real-valued cost rate function c(i, a) is measurable in $a\in A(i)$ for each $i\in S$.

Set $S_{\infty }:=S\cup \{i_{\infty }\}$ with an isolated point $i_{\infty }\notin S, {\mathbb {R}}_+:=(0,+\infty )$, $\Omega ^0:=(S\times {\mathbb {R}}_+)^{\infty }$ and $\Omega :=\Omega ^0\cup \{(i_0, \theta _1,i_1, \ldots , \theta _{m-1},i_{m-1}, \infty , i_{\infty },\infty , i_{\infty },\ldots )| i_0\in S, \ i_l\in S, \ \theta _l\in {\mathbb {R}}_+ \ \mathrm{for \ each} \ 1\le l\le m-1, \ m\ge 2\}$. Thus, we obtain a measurable space $(\Omega , \mathcal {F})$ in which $\mathcal {F}$ denotes the Borel $\sigma$-algebra of $\Omega$. For each $\omega =(i_0, \theta _1, i_1, \ldots )\in \Omega$, define $X_0(\omega ):=i_0$, $T_0(\omega ):=0$, $X_m(\omega ):=i_m$, $T_m(\omega ):=\theta _1+\theta _2+\cdots +\theta _m$ for $m\ge 1$, $T_{\infty }(\omega ):=\lim _{m\rightarrow \infty }T_m(\omega )$, and the state process

$$\begin{aligned} \xi _t(\omega ):=\sum _{m\ge 0}I_{\{T_m\le t<T_{m+1}\}}i_m+I_{\{T_{\infty }\le t\}}i_{\infty }\quad \mathrm{for} \ t\ge 0, \end{aligned}$$

where $I_D$ represents the indicator function of a set D. The process after $T_{\infty }$ is regarded to be absorbed in the state $i_{\infty }$. Hence, we write $q(i_{\infty }|i_{\infty }, a_{\infty })=0$, $c(i_{\infty }, a_{\infty })=0$, $A(i_{\infty }):=\{a_{\infty }\}$, $A_{\infty }:=A\cup \{a_{\infty }\}$, where $a_{\infty }$ is an isolated point. Let $\mathcal {F}_t:=\sigma (\{T_m\le s, X_m=i\}: i\in S, s\le t, m\ge 0)$ for $t\ge 0$, $\mathcal {F}_{s-}:=\bigvee _{0\le t<s}\mathcal {F}_t$, and $\mathcal {P}:=\sigma (\{D\times \{0\}, D\in \mathcal {F}_0\}\cup \{D\times (s,\infty ), D\in \mathcal {F}_{s-}, s>0\})$ which denotes the $\sigma$-algebra of predictable sets on $\Omega \times [0,\infty )$ related to $\{\mathcal {F}_t\}_{t\ge 0}$.

In order to define the optimality criterion, we introduce the definition of a policy below.

Definition 2.1

A $\mathcal {P}$-measurable transition probability $\pi (\cdot |\omega ,t)$ on $(A_{\infty }, \mathcal {B}(A_{\infty }))$, concentrated on $A(\xi _{t-}(\omega ))$ is called a randomized Markov policy if there exists a kernel $\varphi$ on $A_{\infty }$ given $S_{\infty }\times [0,\infty )$ such that $\pi (\cdot |\omega ,t)=\varphi (\cdot |\xi _{t-}(\omega ),t)$. A policy $\pi$ is said to be deterministic Markov if there exists a measurable function f on $[0,\infty )\times S_{\infty }$ satisfying $f(t,i)\in A(i)$ for all $(t,i)\in [0,\infty )\times S_{\infty }$ and $\pi (\cdot |\omega , t)=\delta _{f(t,\xi _{t-}(\omega ))}(\cdot )$, where $\delta _x(\cdot )$ is the Dirac measure concentrated at the point x.

The class of all randomized Markov policies and the class of all deterministic Markov policies are denoted by $\Pi$ and $\Pi ^D$, respectively.

For each $\pi \in \Pi$, we define the random measure

$$\begin{aligned} \nu ^{\pi }(\omega , dt,j):=\int _Aq(j|\xi _{t-}(\omega ),a)\pi (da|\xi _{t-}(\omega ),t)I_{\{j\ne \xi _{t-}(\omega )\}}dt \end{aligned}$$

for all $j\in S$, which is predictable and satisfies $\nu ^{\pi }(\omega , \{t\}\times S)=\nu ^{\pi }(\omega , [T_{\infty },\infty )\times S)=0$. Hence, for any $\pi \in \Pi$ and any initial state $i\in S$, employing Theorem 4.27 in Kitaev and Rykov (1995), we obtain the existence of a unique probability measure $P_i^{\pi }$ on $(\Omega ,\mathcal {F})$. Moreover, with respect to $P_i^{\pi }$, $\nu ^{\pi }$ is the dual predictable projection of the random measure on ${\mathbb {R}}_+\times S$

$$\begin{aligned} \mu (\omega , dt,j)=\sum _{m\ge 1}I_{\{T_m<\infty \}}I_{\{X_m=j\}}\delta _{T_m}(dt) \end{aligned}$$

for all $j\in S$. Let $E_i^{\pi }$ be the expectation operator with respect to $P_i^{\pi }$.

For each $\lambda \ne 0$, the exponential utility function $U_{\lambda }$ on ${\mathbb {R}}:=(-\infty ,\infty )$ is given by $U_{\lambda }(x)=sgn(\lambda )e^{\lambda x}$ for all $x\in {\mathbb {R}}$, where $sgn(\lambda )$ is the sign function, i.e., if $\lambda >0$, $sgn(\lambda )=1$; if $\lambda <0$, $sgn(\lambda )=-1$. The constant $\lambda$ is called the risk-sensitivity coefficient. If $\lambda >0$ ($\lambda <0$), the decision-maker is risk-averse (risk-seeking); see the detailed discussions in Cavazos-Cadena and Hernández-Hernández (2011).

Fix an arbitrary risk-sensitivity coefficient $\lambda \ne 0$ and the length of the horizon $T>0$ throughout the paper. Following the ideas for the definitions of the discrete-time risk-sensitive optimality criteria in Cavazos-Cadena and Hernández-Hernández (2011), for any $\pi \in \Pi$, $i,j\in S$ and $t\in [0,T]$, the risk-sensitive $(T-t)$-horizon cost criterion $V^{\pi }(t,i)$ with respect to the utility function $U_{\lambda }$ is defined by

$$\begin{aligned} V^{\pi }(t,i):=\frac{1}{\lambda }\ln E_j^{\pi }\left[ \exp \left( \lambda \int _t^T\int _Ac(\xi _{s},a)\pi (da|\xi _{s},s)ds\right) \bigg |\xi _t=i\right] . \end{aligned}$$

(2.1)

The corresponding optimal value function is given by

$$\begin{aligned} V^*(t,i):=\inf _{\pi \in \Pi }V^{\pi }(t,i) \quad \mathrm{for \ all} \quad (t,i)\in [0,T]\times S. \end{aligned}$$

Note that for each $\pi \in \Pi$, $\{\xi _t, t\ge 0\}$ is a Markov jump process. Hence, $V^{\pi }(t,i)$ does not depend on the state $j\in S$. Moreover, since the risk-sensitivity coefficient $\lambda$ in (2.1) can take any nonzero value, the risk-sensitive finite-horizon cost criterion in this paper takes the risk-averse and risk-seeking cases into consideration. Thus, (2.1) is a generalization of the risk-sensitive finite-horizon cost criterion in Ghosh and Saha (2014) which only deals with the positive risk-sensitivity coefficient.

Definition 2.2

A policy $\pi ^*\in \Pi$ is said to be optimal if $V^{\pi ^*}(0,i)=V^*(0,i)$ for all $i\in S$.

There are three main goals in this paper: (1) Give the optimality conditions and establish the optimality equation and the existence of optimal policies for CTMDPs with the unbounded transition rates. (2) Present a tractable numerical method for the approximate computations of an optimal policy and the optimal value. (3) Analyze the accuracy of the numerical method and obtain the corresponding error estimations.

3 Preliminaries

In this section, we give the optimality conditions for the existence of the optimal policies and obtain the Feynman–Kac formula which is very useful in proving the main results.

To avoid the explosion of the state process $\{\xi _t,t\ge 0\}$ and ensure the finiteness of the value function $V^*$, we introduce the following assumption consisting of the drift condition on the transition rates and the boundedness condition on the cost rates; see, for instance, Guo and Hernández-Lerma (2009), Prieto-Rumeau and Lorenzo (2010), Prieto-Rumeau and Hernández-Lerma (2012), Wei and Chen (2014), Guo and Zhang (2014) and Guo et al. (2015).

Assumption 3.1

There exist a function $w\ge 1$ on S and constants $\rho _1>0$, $d_1\ge 0, R>0$ and $M>0$ such that

• (i) $\sum _{j\in S}w(j)q(j|i,a)\le \rho _1w(i)+d_1$ for all $(i,a)\in K$;

• (ii) $q^*(i)\le Rw(i)$ for all $i\in S$;

• (iii) $|c(i,a)|\le M$ for all $(i,a)\in K$.

To ensure the existence of the optimal policies, we also need the following assumption, which is called the standard continuity and compactness conditions; see, for instance, Puterman (1994), Kitaev and Rykov (1995), Guo and Hernández-Lerma (2009), Prieto-Rumeau and Lorenzo (2010), Prieto-Rumeau and Hernández-Lerma (2012), Wei and Chen (2014), Ghosh and Saha (2014), Guo and Zhang (2014) and Guo et al. (2015).

Assumption 3.2

• (i) For each $i\in S$, the set A(i) is compact.

• (ii) For each $i,j\in S$, the functions c(i, a) and q(j|i, a) are continuous in $a\in A(i)$.

Let w be as in Assumption 3.1. A real-valued function u on $[0,T]\times S$ is called w-bounded if it satisfies the norm $\Vert u\Vert _{w}:=\sup _{(t,i)\in [0,T]\times S}\frac{|u(t,i)|}{w(i)}<\infty$. Denote by $B_{w}([0,T]\times S)$ the set of all w-bounded measurable functions on $[0,T]\times S$ and by $B([0,T]\times S)$ the set of all bounded measurable functions u on $[0,T]\times S$ with the norm $\Vert u\Vert :=\sup _{(t,i)\in [0,T]\times S}|u(t,i)|<\infty$. Let $\mathcal {L}([0,T]\times S):=\{u\in B([0,T]\times S): \mathrm{for \ each } \ i\in S, \ u(\cdot ,i) \ \mathrm{is \ differentiable \ on} \ [0,T] \ \mathrm{and} \ \frac{\partial u}{\partial t}\in B_{w}([0,T]\times S)\}$, where $\frac{\partial u}{\partial t}$ denotes the derivative of u with respect to the variable t.

Below we give the Feynman–Kac formula for CTMDPs with the unbounded transition rates, which plays a crucial role in proving the existence of optimal policies.

Theorem 3.1

Suppose that Assumption 3.1 is satisfied. Then for each $u\in \mathcal {L}([0,T] \times ~S)$, $i,j\in S$, $\pi \in \Pi$ and $0\le s\le t\le T$, we have

$$\begin{aligned}&E_j^{\pi }\left[ \exp \left( \lambda \int _s^t\int _Ac(\xi _v,a)\pi (da|\xi _v,v)dv\right) u(t,\xi _t)\bigg |\xi _s=i\right] -u(s,i)\\&\quad =E_j^{\pi }\bigg [\int _s^t\exp \left( \lambda \int _s^r\int _Ac(\xi _v,a)\pi (da|\xi _v,v)dv\right) \bigg (\lambda \int _Ac(\xi _r,a)\pi (da|\xi _r,r)u(r,\xi _r)\\&\quad \qquad +\frac{\partial u}{\partial r}(r,\xi _r) +\sum _{k\in S}u(r,k)\int _Aq(k|\xi _r,a)\pi (da|\xi _r,r)\bigg )dr\bigg |\xi _s=i\bigg ]. \end{aligned}$$

Proof

Fix any $i,j\in S$, $\pi \in \Pi$ and $0\le s\le t\le T$. Let $L:=\sup _{(v,k)\in [0,T]\times S}|u(v,k)|$. Then by Assumption 3.1 and Lemma 6.3 in Guo and Hernández-Lerma (2009), we obtain

$$\begin{aligned}&E_j^{\pi }\left[ \exp \left( \lambda \int _s^t\int _Ac(\xi _v,a)\pi (da|\xi _v,v)dv\right) |u(t,\xi _t)|\bigg |\xi _s=i\right] \le Le^{|\lambda |MT} \ \mathrm{and}\\&E_j^{\pi }\bigg [\int _s^t\exp \left( \lambda \int _s^r\int _Ac(\xi _v,a)\pi (da|\xi _v,v)dv\right) \bigg (\bigg |\lambda \int _Ac(\xi _r,a)\pi (da|\xi _r,r)u(r,\xi _r)\bigg |\\&\qquad +\left| \frac{\partial u}{\partial r}(r,\xi _r)\right| +\sum _{k\in S}|u(r,k)|\int _A|q(k|\xi _r,a)|\pi (da|\xi _r,r)\bigg )dr\bigg |\xi _s=i\bigg ]\\&\quad \le e^{|\lambda |MT}\left[ |\lambda |ML+\left\| \frac{\partial u}{\partial t}\right\| _{w}+2LR\right] E_j^{\pi }\left[ \int _s^tw(\xi _r)dr\bigg |\xi _s=i\right] \\&\quad \le e^{|\lambda |MT}\left[ |\lambda |ML+\left\| \frac{\partial u}{\partial t}\right\| _{w}+2LR\right] \int _s^t\left[ e^{\rho _1(r-s)}w(i) +\frac{d_1}{\rho _1}\left( e^{\rho _1(r-s)}-1\right) \right] dr\\&\quad \le Te^{|\lambda |MT}\left[ |\lambda |ML+\left\| \frac{\partial u}{\partial t}\right\| _{w}+2LR\right] \left( w(i)+\frac{d_1}{\rho _1}\right) e^{\rho _1T}<\infty . \end{aligned}$$

Since u belongs to $\mathcal {L}([0,T]\times S)$, the differential mean value theorem yields that for any $0\le t_1<t_2\le T$, there exists a constant $\widetilde{t}\in (t_1,t_2)$ such that

$$\begin{aligned} |u(t_2,i)-u(t_1,i)|=(t_2-t_1)\left| \frac{\partial u}{\partial t}(\widetilde{t},i)\right| \le (t_2-t_1)\left\| \frac{\partial u}{\partial t}\right\| _{w}w(i). \end{aligned}$$

(3.1)

Similarly, for any $0\le t_2<t_1\le T$, we can get

$$\begin{aligned} |u(t_2,i)-u(t_1,i)|\le (t_1-t_2)\left\| \frac{\partial u}{\partial t}\right\| _{w}w(i). \end{aligned}$$

(3.2)

Thus, combining (3.1) and (3.2), we obtain

$$\begin{aligned} |u(t_1,i)-u(t_2,i)|\le \left\| \frac{\partial u}{\partial t}\right\| _{w}w(i)|t_1-t_2| \end{aligned}$$

for all $t_1,t_2\in [0,T]$, i.e., $u(\cdot ,i)$ is Lipschitz continuous on [0, T]. Hence, it follows from the result in Royden (1988, p. 112) that $u(\cdot , i)$ is absolutely continuous on [0, T]. Moreover, we have

$$\begin{aligned}&E_j^{\pi }\bigg [\int _s^T\sum _{k\in S}\left| u(r,k)-u(r,\xi _{r-})\right| \mu (dr,k)\bigg |\xi _s=i\bigg ]\\&\quad \le 2LE_j^{\pi }[\mu ((s,T]\times S)|\xi _s=i]\\&\quad =2LE_j^{\pi }[\nu ^{\pi }((s,T]\times S)|\xi _s=i]\\&\quad =2LE_j^{\pi }\bigg [\int _s^T\int _A|q(\xi _{r}|\xi _{r},a)|\pi (da|\xi _r,r)dr\bigg |\xi _s=i\bigg ]\\&\quad \le 2LRE_j^{\pi }\bigg [\int _s^Tw(\xi _r)dr\bigg |\xi _s=i\bigg ]\\&\quad \le 2LRT\left( w(i)+\frac{d_1}{\rho _1}\right) e^{\rho _1T}, \end{aligned}$$

where the first equality is due to the fact that $\nu ^{\pi }$ is the dual predictable projection of $\mu$, and the last inequality follows from Lemma 6.3 in Guo and Hernández-Lerma (2009). Thus, direct calculations give

$$\begin{aligned}&E_j^{\pi }\bigg [\int _s^t \lambda \exp \left( \lambda \int _s^r\int _Ac(\xi _v,a) \pi (da|\xi _v,v)dv\right) \nonumber \\&\quad \int _Ac(\xi _r,a)\pi (da|\xi _r,r)u(r,\xi _r) dr\bigg |\xi _s=i\bigg ]\nonumber \\&\quad =E_j^{\pi }\bigg [\exp \left( \lambda \int _s^t\int _Ac(\xi _v,a) \pi (da|\xi _v,v)dv\right) u(t,\xi _t)\bigg |\xi _s=i\bigg ]-u(s,i)\nonumber \\&\qquad -E_j^{\pi }\bigg [\int _s^t\exp \left( \lambda \int _s^r\int _Ac(\xi _v,a) \pi (da|\xi _v,v)dv\right) du(r,\xi _r)\bigg |\xi _s=i\bigg ]\nonumber \\&\quad =E_j^{\pi }\bigg [\exp \left( \lambda \int _s^t\int _Ac(\xi _v,a) \pi (da|\xi _v,v)dv\right) u(t,\xi _t)\bigg |\xi _s=i\bigg ]-u(s,i)\nonumber \\&\qquad -E_j^{\pi }\bigg [\int _s^t\exp \left( \lambda \int _s^r\int _Ac(\xi _v,a) \pi (da|\xi _v,v)dv\right) \nonumber \\&\qquad \times \bigg (\frac{\partial u}{\partial r}(r,\xi _r)+\sum _{k\in S}u(r,k)\int _Aq(k|\xi _r,a) \pi (da|\xi _r,r)\bigg )dr\bigg |\xi _s=i\bigg ]\nonumber \\&\qquad -E_j^{\pi }\bigg [\int _s^t\exp \left( \lambda \int _s^r\int _Ac(\xi _v,a) \pi (da|\xi _v,v)dv\right) \nonumber \\&\qquad \times \sum _{k\in S}\big (u(r,k)-u(r,\xi _{r-})\big )\big (\mu (dr,k)-\nu ^{\pi }(dr,k)\big ) \bigg |\xi _s=i\bigg ]\nonumber \\&\quad =E_j^{\pi }\bigg [\exp \left( \lambda \int _s^t\int _Ac(\xi _v,a) \pi (da|\xi _v,v)dv\right) u(t,\xi _t)\bigg |\xi _s=i\bigg ]-u(s,i)\nonumber \\&\qquad -E_j^{\pi }\bigg [\int _s^t\exp \left( \lambda \int _s^r\int _Ac(\xi _v,a) \pi (da|\xi _v,v)dv\right) \nonumber \\&\qquad \times \bigg (\frac{\partial u}{\partial r}(r,\xi _r)+\sum _{k\in S}u(r,k) \int _Aq(k|\xi _r,a)\pi (da|\xi _r,r)\bigg )dr\bigg |\xi _s=i\bigg ], \end{aligned}$$

(3.3)

where the first equality is due to the integration by parts, the second one follows from the equation (2.9) in Confortola and Fuhrman (2014), and the third one is due to the fact that $\nu ^{\pi }$ is the dual predictable projection of $\mu$. Hence, the desired assertion follows from (3.3).$\square$

4 The existence of optimal policies

In this section, we establish the optimality equation and the existence of optimal policies for the risk-sensitive finite-horizon cost criterion with the unbounded transition rates.

Theorem 4.1

Under Assumptions 3.1 and 3.2, the following statements hold.

• (a) $|V^{\pi }(t,i)|\le MT$ and $|V^*(t,i)|\le MT$ for all $\pi \in \Pi$ and $(t,i)\in [0,T]\times S$.

• (b) There exists a unique solution in $\mathcal {L}([0,T]\times S)$ to the following equation:

  $$\begin{aligned} \left\{ \begin{array}{ll} -\frac{\partial u}{\partial t}(t,i)=sgn(\lambda )\inf _{a\in A(i)} sgn(\lambda )\left\{ \lambda c(i,a)u(t,i) +\sum _{j\in S}u(t,j)q(j|i,a)\right\} , \\ u(T,i)=1, \end{array}\right. \nonumber \\ \end{aligned}$$

  (4.1)

  for all $(t,i)\in [0,T]\times S$. Moreover, we have $u(t,i)=e^{\lambda V^*(t,i)}$ for all $(t,i)\in [0,T]\times S$.

• (c) There exists $f^*\in \Pi ^D$ satisfying

  $$\begin{aligned} \lambda e^{\lambda V^*(t,i)}\frac{\partial V^*}{\partial t}(t,i)+\lambda c(i,f^*(t,i))e^{\lambda V^*(t,i)} +\sum _{j\in S}e^{\lambda V^*(t,j)}q(j|i,f^*(t,i))=0 \end{aligned}$$

  (4.2)

  for all $(t,i)\in [0,T]\times S$ and $f^*$ is an optimal deterministic Markov policy.

Proof

(a) By Assumption 3.1(iii), we have

$$\begin{aligned} e^{-|\lambda |MT}\le E_j^{\pi }\left[ \exp \left( \lambda \int _t^T \int _Ac(\xi _{s},a)\pi (da|\xi _{s},s)ds\right) \bigg |\xi _t=i\right] \le e^{|\lambda |MT} \end{aligned}$$

for all $i,j\in S$, $\pi \in \Pi$ and $t\in [0,T]$, which gives the desired assertion.

(b) We only prove the case $\lambda <0$ because the arguments for the case $\lambda >0$ are similar. For each integer $m\ge 1$, let $S_m:=\{k\in S: w(k)\le m \}$ and we have $S_m\uparrow S$. For each $(i,a)\in K$, define

$$\begin{aligned} q^{(m)}(j|i,a):=\left\{ \begin{array}{ll} q(j|i,a), &{}\text {if}\; i\in S_m,\\ 0, &{}\text {if}\; i\notin S_m, \end{array}\right. \end{aligned}$$

(4.3)

and an operator $\Gamma _m$ on $B([0,T]\times S)$ as follows:

$$\begin{aligned} \Gamma _mg(t,i):=e^{\alpha t}+e^{\alpha t}\int _t^T e^{-\alpha s}\sup _{a\in A(i)}\left\{ \lambda c(i,a)g(s,i) +\sum _{j\in S}g(s,j)q^{(m)}(j|i,a)\right\} ds \end{aligned}$$

for all $g\in B([0,T]\times S)$, where $\alpha$ is an arbitrary positive constant. Then using Assumption 3.1, we obtain

$$\begin{aligned} |\Gamma _mg(t,i)|\le e^{\alpha T}+Te^{\alpha T}(|\lambda | M+2Rm)\Vert g\Vert \end{aligned}$$

for all $(t,i)\in [0,T]\times S$, which implies that $\Gamma _m$ is a map from $B([0,T]\times S)$ into itself. On the other hand, for any $g_1,g_2\in B([0,T]\times S)$, we have

$$\begin{aligned}&|\Gamma _mg_1(t,i)-\Gamma _mg_2(t,i)|\\&\quad \le e^{\alpha t}\int _t^T e^{-\alpha s}\sup _{a\in A(i)}\bigg |\lambda c(i,a)\big (g_1(s,i)-g_2(s,i)\big )\\&\qquad +\sum _{j\in S}\big (g_1(s,j)-g_2(s,j)\big )q^{(m)}(j|i,a)\bigg |ds\\&\quad \le \frac{(|\lambda | M+2Rm)}{\alpha }\Vert g_1-g_2\Vert \end{aligned}$$

for all $(t,i)\in [0,T]\times S$. Thus, taking $\alpha =|\lambda | M+2Rm+1$, we see that $\Gamma _m$ is a contraction operator on $B([0,T]\times S)$. Hence, it follows from the Banach fixed point theorem that there exists $g^{(m)}\in B([0,T]\times S)$ satisfying

$$\begin{aligned} g^{(m)}(t,i)=e^{\alpha t} +e^{\alpha t}\int _t^T e^{-\alpha s}\sup _{a\in A(i)}\left\{ \lambda c(i,a)g^{(m)}(s,i)+\sum _{j\in S}g^{(m)}(s,j)q^{(m)}(j|i,a)\right\} ds \end{aligned}$$

for all $(t,i)\in [0,T]\times S$ and $\alpha =|\lambda | M+2Rm+1$. Let $u^{(m)}(t,i):=e^{-(|\lambda | M+2Rm+1)t}g^{(m)}(t,i)$. The last equality can be rewritten as

$$\begin{aligned} u^{(m)}(t,i)=1+\int _t^T \sup _{a\in A(i)}\left\{ \lambda c(i,a)u^{(m)}(s,i) +\sum _{j\in S}u^{(m)}(s,j)q^{(m)}(j|i,a)\right\} ds. \end{aligned}$$

(4.4)

Note that for each $i\in S$, $u^{(m)}(\cdot ,i)$ is absolutely continuous on [0, T] and $u^{(m)}(T,i)=1$. Moreover, it follows from Assumption 3.2 that for each $i\in S$,

$$\begin{aligned} \sup _{a\in A(i)}\left\{ \lambda c(i,a)u^{(m)}(s,i) +\sum _{j\in S}u^{(m)}(s,j)q^{(m)}(j|i,a)\right\} \end{aligned}$$

is continuous in $s\in [0,T]$. Thus, the equality (4.4) gives

$$\begin{aligned} -\frac{\partial u^{(m)}}{\partial t}(t,i)=\sup _{a\in A(i)}\left\{ \lambda c(i,a)u^{(m)}(t,i) +\sum _{j\in S}u^{(m)}(t,j)q^{(m)}(j|i,a)\right\} \end{aligned}$$

(4.5)

and $\left| \frac{\partial u^{(m)}}{\partial t}(t,i)\right| \le (|\lambda | M+2R)\Vert g^{(m)}\Vert w(i)$ for all $(t,i)\in [0,T]\times S$. Hence, we have $u^{(m)}\in \mathcal {L}([0,T]\times S)$ for all $m\ge 1$. For each $i\in S$, $\pi \in \Pi$ and $m\ge 1$, denote by $P^{\pi ,m}_i$ the probability measure corresponding to $q^{(m)}(j|i,a)$ and by $E^{\pi ,m}_i$ the expectation operator with respect to $P^{\pi ,m}_i$. On one hand, Assumption 3.2 and the measurable selection theorem in Hernández-Lerma and Lasserre (1999, p. 50) give the existence of a measurable function $f_m$ on $[0,T]\times S$ satisfying

$$\begin{aligned} -\frac{\partial u^{(m)}}{\partial t}(t,i)=\lambda c(i,f_m(t,i))u^{(m)}(t,i) +\sum _{j\in S}u^{(m)}(t,j)q^{(m)}(j|i,f_m(t,i)) \end{aligned}$$

for all $(t,i)\in [0,T]\times S$. Then using the last equality, we obtain

$$\begin{aligned}&-E_j^{f_m,m}\left[ \int _t^T\exp \left( \lambda \int _t^sc(\xi _v,f_m(v,\xi _v))dv\right) \frac{\partial u^{(m)}}{\partial s}(s,\xi _s)ds\bigg |\xi _t=i\right] \\&\quad =E_j^{f_m,m}\bigg [\int _t^T\exp \left( \lambda \int _t^sc(\xi _v,f_m(v,\xi _v))dv\right) \bigg (\lambda c(\xi _s,f_m(s,\xi _s))u^{(m)}(s,\xi _s)\\&\qquad +\sum _{k\in S}u^{(m)}(s,k)q^{(m)}(k|\xi _s,f_m(s,\xi _s))\bigg )ds\bigg |\xi _t=i\bigg ], \end{aligned}$$

which together with Theorem 3.1 and $u^{(m)}(T,i)=1$ yields

$$\begin{aligned} u^{(m)}(t,i)=E_j^{f_m,m}\left[ \exp \left( \lambda \int _t^Tc\big (\xi _s,f_m(s,\xi _s)\big )ds\right) \bigg |\xi _t=i\right] \end{aligned}$$

(4.6)

for all $i,j\in S$ and $t\in [0,T]$. On the other hand, for any $\pi \in \Pi$, by (4.5) we have

$$\begin{aligned} -\frac{\partial u^{(m)}}{\partial s}(s,\xi _s)&\ge \lambda \int _A c(\xi _s,a)\pi (da|\xi _s,s)u^{(m)}(s,\xi _s)\\&\quad +\sum _{j\in S}u^{(m)}(s,j)\int _Aq^{(m)}(j|\xi _s,a)\pi (da|\xi _s,s) \end{aligned}$$

for all $s\in [0,T]$. Then employing the last inequality and following the similar arguments of (4.6), we obtain

$$\begin{aligned} u^{(m)}(t,i)\ge E_j^{\pi ,m}\left[ \exp \left( \lambda \int _t^T\int _Ac (\xi _s,a)\pi (da|\xi _s,s)ds\right) \bigg |\xi _t=i\right] \end{aligned}$$

(4.7)

for all $i,j\in S$, $t\in [0,T]$ and $\pi \in \Pi$. Thus, combining (4.6) and (4.7), we get

$$\begin{aligned} u^{(m)}(t,i) =\sup _{\pi \in \Pi }E_j^{\pi ,m}\left[ \exp \left( \lambda \int _t^T\int _Ac(\xi _s,a) \pi (da|\xi _s,s)ds\right) \bigg |\xi _t=i\right] , \end{aligned}$$

which implies

$$\begin{aligned} 0<u^{(m)}(t,i)\le e^{|\lambda | MT} \end{aligned}$$

(4.8)

for all $i,j\in S$ and $t\in [0,T]$. Moreover, observe that Assumption 3.1(i) and (ii) still hold with $q^{(m)}(j|i,a)$ in lieu of q(j|i, a). By Assumption 3.1 and (4.8), we have

$$\begin{aligned} \left| \sup _{a\in A(i)}\left\{ \lambda c(i,a)u^{(m)}(t,i) +\sum _{j\in S}u^{(m)}(t,j)q^{(m)}(j|i,a)\right\} \right| \le (|\lambda | M+2R w(i))e^{|\lambda | MT} \end{aligned}$$

(4.9)

for all $(t,i)\in [0,T]\times S$. Let $M_i:=(|\lambda | M+2R w(i))e^{|\lambda | MT}$. Then for each $i\in S$ and any $\varepsilon >0$, there exists $\eta :=\frac{\varepsilon }{M_i}>0$ such that

$$\begin{aligned}&|u^{(m)}(t_1,i)-u^{(m)}(t_2,i)|\\&\quad \le \int _{\min \{t_1,t_2\}}^{\max \{t_1,t_2\}} \left| \sup _{a\in A(i)}\left\{ \lambda c(i,a)u^{(m)}(s,i) +\sum _{j\in S}u^{(m)}(s,j)q^{(m)}(j|i,a)\right\} \right| ds\\&\quad \le M_i|t_1-t_2|\le \varepsilon \end{aligned}$$

for all $m\ge 1$, $t_1,t_2\in [0,T]$ and $|t_1-t_2|\le \eta$, where the first and second inequalities follow from (4.4) and (4.9), respectively. Thus, for each $i\in S$, $\{u^{(m)}(\cdot ,i),m\ge 1\}$ is uniformly bounded and equicontinuous. Hence, employing the Ascoli–Arzela theorem in Royden (1988, p. 169) and the denumerability of S, we obtain the existence of a subsequence of $\{m\}$ (still denoted by $\{m\}$) such that $\lim _{m\rightarrow \infty }u^{(m)}(t,i)=:u(t,i)$, $\Vert u\Vert \le e^{|\lambda | MT}$ and $u(T,i)=1$ for all $(t,i)\in [0,T]\times S$. Below we will show that for each $(t,i)\in [0,T]\times S$,

$$\begin{aligned}&\lim _{m\rightarrow \infty }\sup _{a\in A(i)}\left\{ \lambda c(i,a)u^{(m)}(t,i) +\sum _{j\in S}u^{(m)}(t,j)q^{(m)}(j|i,a)\right\} \nonumber \\&\quad =\sup _{a\in A(i)}\left\{ \lambda c(i,a)u (t,i) +\sum _{j\in S}u (t,j)q (j|i,a)\right\} . \end{aligned}$$

(4.10)

For each $(t,i)\in [0,T]\times S$ and $m\ge 1$, Assumption 3.2 implies that there exists $a_m^{t,i}\in A(i)$ satisfying

$$\begin{aligned}&\sup _{a\in A(i)}\left| \lambda c(i,a)u^{(m)}(t,i) +\sum _{j\in S}u^{(m)}(t,j)q^{(m)}(j|i,a)-\lambda c(i,a)u (t,i)\right. \nonumber \\&\qquad \left. -\sum _{j\in S}u (t,j)q (j|i,a)\right| =\left| \lambda c(i,a_m^{t,i})u^{(m)}(t,i)+\sum _{j\in S}u^{(m)}(t,j)q^{(m)}(j|i,a_m^{t,i})\right. \nonumber \\&\qquad -\left. \lambda c(i,a_m^{t,i})u (t,i) -\sum _{j\in S}u (t,j)q (j|i,a_m^{t,i})\right| . \end{aligned}$$

(4.11)

Then we have

$$\begin{aligned}&\bigg |\lambda c(i,a_m^{t,i})u^{(m)}(t,i) +\sum _{j\in S}u^{(m)}(t,j)q^{(m)}(j|i,a_m^{t,i}) -\lambda c(i,a_m^{t,i})u (t,i)\nonumber \\&\quad -\sum _{j\in S}u (t,j)q (j|i,a_m^{t,i})\bigg |\rightarrow 0 \end{aligned}$$

(4.12)

as $m\rightarrow \infty$. In fact, if (4.12) does not hold, there exist $\varepsilon _0>0$ and a subsequence $\{m_l\}$ of $\{m\}$ such that

$$\begin{aligned}&\bigg |\lambda c(i,a_{m_l}^{t,i})u^{(m_l)}(t,i) +\sum _{j\in S}u^{(m_l)}(t,j)q^{(m_l)}(j|i,a_{m_l}^{t,i}) -\lambda c(i,a_{m_l}^{t,i})u (t,i)\nonumber \\&\quad -\sum _{j\in S}u (t,j)q (j|i,a_{m_l}^{t,i})\bigg |\ge \varepsilon _0. \end{aligned}$$

(4.13)

The compactness of A(i) gives the existence of a subsequence of $\{m_l\}$ (still denoted by $\{m_l\}$) such that $a_{m_l}^{t,i}$ converges to some $a^{t,i}\in A(i)$. Thus, it follows from Assumption 3.2(ii) and (4.3) that

$$\begin{aligned}&\bigg |\lambda c(i,a_{m_l}^{t,i})u^{(m_l)}(t,i) +\sum _{j\in S}u^{(m_l)}(t,j)q^{(m_l)}(j|i,a_{m_l}^{t,i}) -\lambda c(i,a_{m_l}^{t,i})u (t,i)\nonumber \\&\quad -\sum _{j\in S}u (t,j)q (j|i,a_{m_l}^{t,i})\bigg |\rightarrow 0 \end{aligned}$$

as $l\rightarrow \infty$, which yields a contradiction to (4.13). Hence, (4.12) is true. Therefore, (4.11), (4.12) and the inequality

$$\begin{aligned}&\bigg |\sup _{a\in A(i)}\bigg \{\lambda c(i,a)u^{(m)}(t,i) +\sum _{j\in S}u^{(m)}(t,j)q^{(m)}(j|i,a)\bigg \}\\&\qquad -\sup _{a\in A(i)}\bigg \{\lambda c(i,a)u (t,i) +\sum _{j\in S}u (t,j)q (j|i,a)\bigg \}\bigg |\\&\quad \le \sup _{a\in A(i)}\left| \lambda c(i,a)u^{(m)}(t,i) +\sum _{j\in S}u^{(m)}(t,j)q^{(m)}(j|i,a)-\lambda c(i,a)u (t,i)\right. \\&\qquad \left. -\sum _{j\in S}u (t,j)q (j|i,a)\right| \end{aligned}$$

for all $(t,i)\in [0,T]\times S$, imply (4.10). Moreover, employing (4.4), (4.9), (4.10) and the dominated convergence theorem, we get

$$\begin{aligned} u(t,i)=1+\int _t^T\sup _{a\in A(i)}\left\{ \lambda c(i,a)u(s,i) +\sum _{j\in S}u(s,j)q(j|i,a)\right\} ds, \end{aligned}$$

which together with Assumption 3.2 yields that the derivative of u(t, i) with respect to the variable t exists for all $(t,i)\in [0,T]\times S$. Thus, (4.1) follows from the last equality. Note that Assumption 3.1, $\Vert u\Vert \le e^{|\lambda | MT}$ and (4.1) imply

$$\begin{aligned} \left| \frac{\partial u}{\partial t}(t,i)\right| \le (|\lambda | M+2R)e^{|\lambda | MT}w(i) \end{aligned}$$

for all $(t,i)\in [0,T]\times S$. Hence, we obtain $u\in \mathcal {L}([0,T]\times S)$. Using (4.1) and following the similar arguments of (4.6) and (4.7), there exists $f^*\in \Pi ^D$ satisfying

$$\begin{aligned} \frac{\partial u}{\partial t}(t,i)+\lambda c(i,f^*(t,i))u(t,i) +\sum _{j\in S}u(t,j)q(j|i,f^*(t,i))=0 \end{aligned}$$

(4.14)

and

$$\begin{aligned} u(t,i)=e^{\lambda V^{f^*}(t,i)}\ge E_j^{\pi }\left[ \exp \left( \lambda \int _t^T\int _Ac(\xi _s,a) \pi (da|\xi _s,s)ds\right) \bigg |\xi _t=i\right] \end{aligned}$$

(4.15)

for all $i,j\in S, t\in [0,T]$ and $\pi \in \Pi$. Thus, it follows from (4.14) and (4.15) that $u(t,i)=e^{\lambda V^*(t,i)}=e^{\lambda V^{f^*}(t,i)}$ for all $(t,i)\in [0,T]\times S$, and $f^*$ is optimal and satisfies (4.2). Finally, the uniqueness of the solution to (4.1) follows from the similar arguments of (4.6) and (4.7).

(c) The assertion follows directly from the proof of part (b). $\square$

Remark 4.1

The optimality equation of the risk-sensitive finite-horizon cost criterion has been established in Ghosh and Saha (2014) for the case of a positive risk-sensitivity coefficient, nonnegative and bounded cost rates and bounded transition rates. Theorem 4.1 extends the results in Ghosh and Saha (2014) to the case in which the risk-sensitivity coefficient and the cost rates can take positive and negative values, and the transition rates are allowed to be unbounded.

5 Finite approximation

In this section, we use the optimality equation established in Theorem 4.1 to give a finite approximation method for the approximate computations of an optimal policy and the optimal value. In order to obtain the error estimations of the approximate computations, we introduce the following conditions which are stronger than those in Sect. 3.

Assumption 5.1

• (i) The function w in Assumption 3.1 is nondecreasing and satisfies $\lim _{i\rightarrow \infty }w(i)=\infty$.

• (ii) There exist constants $\rho _2>0$ and $d_2\ge 0$ such that

  $$\begin{aligned} \sum _{j\in S}w^2(j)q(j|i,a)\le \rho _2w^2(i)+d_2 \quad \mathrm{for \ all} \quad (i,a)\in K. \end{aligned}$$

• (iii) For any $i,j\in S$, there exist constants $L_i>0$ and $L_{ij}>0$ such that

  $$\begin{aligned} |c(i,a)-c(i,b)|\le L_id_A(a,b) \quad \mathrm{and} \quad |q(j|i,a)-q(j|i,b)|\le L_{ij}d_A(a,b) \end{aligned}$$

  for all $a,b\in A(i)$, where $d_A$ represents the metric of the space A. For each integer $n\ge 1$, we define the control model

  $$\begin{aligned} {\mathcal {M}}_n:=\{S_n, A, (A_n(i), i\in S_n), q_n(j|i,a), c(i,a)\}. \end{aligned}$$

  • The state space is given by $S_n:=\{0,1,\ldots , j_n\}$ and the increasing sequence $\{j_n, n\ge 1\}$ satisfies $\lim _{n\rightarrow \infty }j_n=\infty$.

  • The action space is given by A as in the model ${\mathcal {M}}$.

  • The set of all admissible actions in the state $i\in S_n$ is given by an arbitrary finite set $A_n(i)$.

  • For each $(i,a)\in K_n:=\{(i,a)|i\in S_n, a\in A_n(i)\}$ and $j\in S_n$, the transition rate $q_n(j|i,a)$ is given by

    $$\begin{aligned} q_n(j|i,a):=\left\{ \!\begin{array}{l@{\quad }l} q(j|i,a), &{}\text {if}\; j\ne j_n,\\ \mathop {\sum }\limits _{k\ge j_n} q(k|i,a), &{}\text {if}\; j=j_n. \end{array}\right. \end{aligned}$$

    (5.1)

  • The cost rate function is given by the restriction of c in the model ${\mathcal {M}}$ to $K_n$.

Let $\Pi _n$ and $\Pi ^D_n$ be the set of all randomized Markov policies and the set of all deterministic Markov policies for ${\mathcal {M}}_n$, respectively. For each $i\in S_n$ and $\pi \in \Pi _n$, Theorem 4.27 in Kitaev and Rykov (1995) gives the existence of a probability measure $P_n^{i,\pi }$ associated with the model ${\mathcal {M}}_n$. Let $E_n^{i,\pi }$ be the expectation operator with respect to $P_n^{i,\pi }$. Moreover, replacing $E_i^{\pi }$ and $\Pi$ by $E_n^{i,\pi }$ and $\Pi _n$ in the definitions of $V^{\pi }$ and $V^{*}$, we can define the functions $V_n^{\pi }$ and $V^{*}_n$ on $[0,T]\times S_n$. Denote by $\mathcal {C}$ the set of all closed subsets of A. Recall that the Hausdorff metric on $\mathcal {C}$ is defined by

$$\begin{aligned} d_H(B_1,B_2):=\max \left\{ \sup _{a\in B_1}\inf _{b\in B_2}d_A(a,b), \ \sup _{b\in B_2}\inf _{a\in B_1}d_A(a,b)\right\} \end{aligned}$$

for all $B_1,B_2\in \mathcal {C}$.

Then we have the following statement about the error estimation between $V^*$ and $V^*_n$.

Theorem 5.1

Suppose that Assumptions 3.1, 3.2(i) and 5.1 are satisfied. If there exists a constant $\widetilde{M}>0$ such that for each $n\ge 1$ and $i\in S_n$,

$$\begin{aligned} d_H(A(i), A_n(i))\le \frac{\widetilde{M}w^2(i)}{e^{|\lambda |MT}\left( | \lambda |L_i+2\sum _{j=0}^{j_n-1}L_{ij}\right) w(j_n)}, \end{aligned}$$

(5.2)

then we have

$$\begin{aligned} |V_n^*(t,i)-V^*(t,i)|\le \frac{R_1w^2(i)}{w(j_n)} \end{aligned}$$

for all $t\in [0,T]$, where $R_1{=}\frac{Te^{2|\lambda |MT}}{|\lambda |}\left[ \widetilde{M}+e^{|\lambda |MT}(\rho _1+d_1+R)\right] \times \left[ e^{\rho _2T}+\frac{d_2}{\rho _2}e^{\rho _2T}\right]$.

Proof

Fix any $n\ge 1$, $i\in S_n$ and $t\in [0,T]$. Then it follows from Theorem 4.1 that there exists $f^*\in \Pi ^D$ satisfying

$$\begin{aligned} -\lambda e^{\lambda V^*(t,i)}\frac{\partial V^*}{\partial t}(t,i)&=\lambda c(i,f^*(t,i))e^{\lambda V^*(t,i)} +\sum _{j\in S}e^{\lambda V^*(t,j)}q(j|i,f^*(t,i))\nonumber \\&=\lambda c(i,f^*(t,i))e^{\lambda V^*(t,i)}\nonumber \\&\quad +\sum _{j=0}^{j_n-1}\left( e^{\lambda V^*(t,j)}-e^{\lambda V^*(t,j_n)}\right) q(j|i,f^*(t,i))\nonumber \\&\quad +\sum _{j>j_n} \left( e^{\lambda V^*(t,j)}-e^{\lambda V^*(t,j_n)}\right) q(j|i,f^*(t,i)). \end{aligned}$$

(5.3)

By Theorem 4.1, the monotonicity of w and Assumption 3.1, we obtain

$$\begin{aligned}&\sum _{j>j_n} \left( e^{\lambda V^*(t,j)}-e^{\lambda V^*(t,j_n)}\right) q(j|i,f^*(t,i))\nonumber \\&\quad \ge -e^{|\lambda |MT}\sum _{j>j_n}q(j|i,f^*(t,i))\nonumber \\&\quad \ge -\frac{e^{|\lambda |MT}}{w(j_n)}\sum _{j>j_n}w(j)q(j|i,f^*(t,i))\nonumber \\&\quad \ge -\frac{e^{|\lambda |MT}}{w(j_n)}\left[ \sum _{j\in S}w(j)q(j|i,f^*(t,i))-w(i)q(i|i,f^*(t,i))\right] \nonumber \\&\quad \ge -e^{|\lambda |MT}(\rho _1+d_1+R)\frac{w^2(i)}{w(j_n)}. \end{aligned}$$

(5.4)

Moreover, for each $s\in [0,T]$, there exists $\widetilde{f}(s,i)\in A_n(i)$ such that

$$\begin{aligned} d_A(f^*(s,i), \widetilde{f}(s,i))=\min _{a\in A_n(i)}d_A(f^*(s,i),a)\le d_H(A(i),A_n(i)). \end{aligned}$$

Thus, employing the last inequality, Assumption 5.1 and Theorem 4.1, we have

$$\begin{aligned} \lambda c(i,f^*(t,i))e^{\lambda V^*(t,i)}-\lambda c(i,\widetilde{f}(t,i))e^{\lambda V^*(t,i)}\ge&-|\lambda |e^{|\lambda |MT}L_id_A(f^*(t,i), \widetilde{f}(t,i))\nonumber \\ \ge&-|\lambda |e^{|\lambda |MT}L_i d_H(A(i),A_n(i)) \end{aligned}$$

and

$$\begin{aligned}&\sum _{j=0}^{j_n-1}\left( e^{\lambda V^*(t,j)}-e^{\lambda V^*(t,j_n)}\right) \left( q(j|i,f^*(t,i))-q(j|i,\widetilde{f}(t,i))\right) \nonumber \\&\quad \ge -2e^{|\lambda |MT}\sum _{j=0}^{j_n-1}\left| q(j|i,f^*(t,i))-q(j|i,\widetilde{f}(t,i))\right| \nonumber \\&\quad \ge -2e^{|\lambda |MT}d_A(f^*(t,i),\widetilde{f}(t,i))\sum _{j=0}^{j_n-1}L_{ij}\nonumber \\&\quad \ge -2e^{|\lambda |MT}d_H(A(i),A_n(i))\sum _{j=0}^{j_n-1}L_{ij}, \end{aligned}$$

which together with (5.1)–(5.4) give

$$\begin{aligned}&-\lambda e^{\lambda V^*(t,i)}\frac{\partial V^*}{\partial t}(t,i)\nonumber \\&\quad \ge \lambda c(i,\widetilde{f}(t,i))e^{\lambda V^*(t,i)} +\sum _{j=0}^{j_n-1}\left( e^{\lambda V^*(t,j)}-e^{\lambda V^*(t,j_n)}\right) q(j|i,\widetilde{f}(t,i))\nonumber \\&\qquad -e^{|\lambda |MT}d_H(A(i),A_n(i))\left( |\lambda |L_i+2\sum _{j=0}^{j_n-1}L_{ij}\right) -e^{|\lambda |MT}(\rho _1+d_1+R)\frac{w^2(i)}{w(j_n)}\nonumber \\&\quad \ge \lambda c(i,\widetilde{f}(t,i))e^{\lambda V^*(t,i)} +\sum _{j\in S_n}e^{\lambda V^*(t,j)}q_n(j|i,\widetilde{f}(t,i))\nonumber \\&\qquad -\left[ \widetilde{M}+e^{|\lambda |MT}(\rho _1+d_1+R)\right] \frac{w^2(i)}{w(j_n)}. \end{aligned}$$

(5.5)

Observe that (5.1), Assumptions 3.1 and 5.1 yield

$$\begin{aligned} \sum _{j\in S_n}w^l(j)q_n(j|i,a)\le \rho _lw^l(i)+d_l \quad \mathrm{and} \quad q^*_n(i):=\sup _{a\in A_n(i)}|q_n(i|i,a)|\le Rw(i) \end{aligned}$$

(5.6)

for all $a\in A_n(i)$ and $l=1,2$. By (5.5), Theorems 3.1 and 4.1(b), we get

$$\begin{aligned}&E_n^{j,\widetilde{f}}\left[ \exp \left( \lambda \int _t^Tc(\xi _s,\widetilde{f}(s,\xi _s))ds\right) \bigg |\xi _t=i\right] -e^{\lambda V^*(t,i)}\\&\quad \le \frac{\widetilde{M}+e^{|\lambda |MT}(\rho _1+d_1+R)}{w(j_n)}\\&\qquad \times \,E_n^{j,\widetilde{f}}\left[ \int _t^T\exp \left( \lambda \int _t^rc(\xi _v,\widetilde{f}(v,\xi _v))dv\right) w^2(\xi _r)dr\bigg |\xi _t=i\right] \end{aligned}$$

for all $j\in S_n$. Then it follows from (5.6), Lemma 6.3 in Guo and Hernández-Lerma (2009), Assumption 3.1(iii) and the last inequality that

$$\begin{aligned} e^{\lambda V_n^{\widetilde{f}}(t,i)}-e^{\lambda V^*(t,i)}&\le \frac{\left[ \widetilde{M}+e^{|\lambda |MT}(\rho _1+d_1+R)\right] e^{|\lambda |MT}}{w(j_n)}\int _t^TE_n^{j,\widetilde{f}}\left[ w^2(\xi _r)\Bigg |\xi _t=i\right] dr\\&\le \frac{\left[ \widetilde{M}+e^{|\lambda |MT}(\rho _1+d_1+R)\right] e^{|\lambda |MT}}{w(j_n)}\int _t^T\left[ e^{\rho _2(r-t)}w^2(i)\right. \\&\quad \,\left. +\frac{d_2}{\rho _2}e^{\rho _2(r-t)}\right] dr\\&\le \frac{\left[ \widetilde{M}+e^{|\lambda |MT}(\rho _1+d_1+R)\right] T e^{|\lambda |MT}}{w(j_n)}\left[ e^{\rho _2T}+\frac{d_2}{\rho _2}e^{\rho _2T}\right] w^2(i). \end{aligned}$$

Hence, letting $\widetilde{R}:=Te^{|\lambda |MT}\left[ \widetilde{M}+e^{|\lambda |MT}(\rho _1+d_1+R)\right] \times \left[ e^{\rho _2T}+\frac{d_2}{\rho _2}e^{\rho _2T}\right]$, we have

$$\begin{aligned} e^{\lambda V_n^*(t,i)}-e^{\lambda V^*(t,i)}\le \frac{\widetilde{R}w^2(i)}{w(j_n)}\quad \mathrm{for } \quad \lambda >0. \end{aligned}$$

(5.7)

Following the similar arguments of (5.7), we can obtain

$$\begin{aligned} \left| e^{\lambda V^*_n(t,i)}-e^{\lambda V^*(t,i)}\right| \le \frac{\widetilde{R}w^2(i)}{w(j_n)}\quad \mathrm{for } \quad \lambda \ne 0. \end{aligned}$$

(5.8)

Moreover, employing the differential mean value theorem and Theorem 4.1(a), we get

$$\begin{aligned} \left| e^{\lambda V^*_n(t,i)}-e^{\lambda V^*(t,i)}\right| \ge |\lambda |e^{-|\lambda | MT}|V^*_n(t,i)-V^*(t,i)|, \end{aligned}$$

which together with (5.8) implies the assertion. $\square$

For each integer $m\ge 1$, we divide the interval [0, T] into m equal parts with the following discrete points: $t_0:=T$ and $t_l:=t_0-\frac{T}{m}l$ for all $l=1,\ldots , m$. For each integer $n\ge 1$, define the iteration to compute approximately the optimal value as follows:

$$\begin{aligned} W_m(t_l,i)&:=W_m(t_{l-1},i)+sgn(\lambda )\frac{T}{m}\min _{a\in A_n(i)}sgn(\lambda ) \bigg \{\lambda c(i,a)W_m(t_{l-1},i)\nonumber \\&\quad \,+\sum _{j\in S_n}W_m(t_{l-1},j)q_n(j|i,a)\bigg \} \end{aligned}$$

(5.9)

with $W_m(t_0,i)=1$ for all $i\in S_n$ and $l=1,\ldots , m$. For each $n\ge 1$, $m\ge 1$, $i\in S_n$ and $l\in \{1,\ldots , m\}$, denote by $\mathcal {D}_{n,l}(i)$ the set of all the minimizers attaining the minimum of (5.9), and by $\mathcal {O}_{n,m}$ the set of all the policies with the following form:

$$\begin{aligned} f_{n,m}(t,i):=\left\{ \begin{array}{ll} h_{n,m}(i), &{}\text {if}\; t\in [0, t_{m-1}],\\ h_{n,l}(i), &{}\text {if}\; t\in (t_{l}, t_{l-1}] (l=1,\ldots ,m-1),\\ a^*, &{}\text {if}\; t>T, \end{array}\right. \end{aligned}$$

(5.10)

where $h_{n,l}(i)$ belongs to $\mathcal {D}_{n,l}(i)$ and $a^*\in A_n(i)$ is arbitrarily fixed.

Below we give the error estimations on the approximate computations of the optimal value and an optimal policy via employing the iteration defined by (5.9).

Theorem 5.2

Let $R_1$ be as in Theorem 5.1. Under the conditions in Theorem 5.1, the following statements hold.

• (a) $\left| e^{\lambda V^*_n(t_l,i)}-W_m(t_l,i)\right| \le \frac{TR_2}{m} w(j_n) \left( e^{T(|\lambda |M+2R) w(j_n)}-1\right)$ for all $n\ge 1$, $i\in S_n$, $m\ge 1$ and $l=0,1,\ldots ,m$, where $R_2=(|\lambda |M+2R)e^{|\lambda |MT}$.

• (b) For any $n\ge 1$ and $\tau \in (0,1)$, there exists a positive integer $m_{\tau }$ such that

  $$\begin{aligned}&(1-\tau )e^{-|\lambda |MT}\le W_m(0,i)\le (1+\tau )e^{|\lambda |MT} \quad and \\&\left| V^*(0,i)-\frac{1}{\lambda }\ln W_m(0,i)\right| \le \frac{R_1w^2(i)}{w(j_n)}\\&\quad + \frac{TR_2e^{|\lambda |MT}}{m|\lambda |(1-\tau )} w(j_n)\left( e^{T(|\lambda |M+2R)w(j_n)}-1\right) \end{aligned}$$

  for all $i\in S_n$ and $m\ge m_{\tau }$.

• (c) For any $n\ge 1$, $m\ge m_{\tau }$ and $f_{n,m}\in \mathcal {O}_{n,m}$, we have

  $$\begin{aligned}&\left| V^*(0,i)-V_n^{f_{n,m}}(0,i)\right| \le \frac{R_1w^2(i)}{w(j_n)}\\&\quad + \frac{2TR_2e^{|\lambda |MT}}{m|\lambda |(1-\tau )} w(j_n)\left( e^{T(|\lambda |M+2R)w(j_n)}-1\right) \end{aligned}$$

  for all $i\in S_n$.

Proof

(a) Fix any $n\ge 1$, $i\in S_n$, $m\ge 1$ and $l\in \{1,\ldots , m\}$. It follows from (5.1) and (5.6) that the conditions in Theorem 4.1 are satisfied for the control model ${\mathcal {M}}_n$. Then by Theorem 4.1 we have $V_n^*(T,i)=0$ and

$$\begin{aligned}&-\lambda e^{\lambda V^*_n(t,i)}\frac{\partial V^*_n}{\partial t}(t,i)\nonumber \\&\quad = sgn(\lambda )\min _{a\in A_n(i)} sgn(\lambda )\left\{ \lambda c(i,a)e^{\lambda V^*_n(t,i)}+\sum _{j\in S_n}e^{\lambda V^*_n(t,j)}q_n(j|i,a)\right\} \end{aligned}$$

(5.11)

for all $t\in [0,T]$. Thus, employing (5.6) and (5.11) we obtain

$$\begin{aligned}&\left| e^{\lambda V^*_n(t,i)}-e^{\lambda V^*_n(s,i)}\right| \nonumber \\&\quad =\left| \int _t^ssgn(\lambda )\min _{a\in A_n(i)} sgn(\lambda )\left\{ \lambda c(i,a)e^{\lambda V^*_n(r,i)}+\sum _{j\in S_n}e^{\lambda V^*_n(r,j)}q_n(j|i,a)\right\} dr\right| \nonumber \\&\quad \le (|\lambda |M+2R)e^{|\lambda |MT}w(i)|t-s| \end{aligned}$$

(5.12)

for all $s,t\in [0,T]$. Moreover, we have

$$\begin{aligned}&\left| e^{\lambda V^*_n(t_l,i)}-W_m(t_l,i)\right| \\&\quad =\bigg |e^{\lambda V^*_n(t_{l-1},i)}+\int _{t_l}^{t_{l-1}} sgn(\lambda )\min _{a\in A_n(i)} sgn(\lambda )\bigg \{\lambda c(i,a)e^{\lambda V^*_n(t,i)}\\&\qquad +\sum _{j\in S_n}e^{\lambda V^*_n(t,j)}q_n(j|i,a)\bigg \}dt\\&\qquad -W_m(t_{l-1},i)-sgn(\lambda )\frac{T}{m}\min _{a\in A_n(i)}sgn(\lambda ) \bigg \{\lambda c(i,a)W_m(t_{l-1},i)\\&\qquad +\sum _{j\in S_n}W_m(t_{l-1},j)q_n(j|i,a)\bigg \}\bigg |\\&\quad \le \left| e^{\lambda V^*_n(t_{l{-}1},i)}{-}W_m(t_{l-1},i)\right| {+}\int _{t_l}^{t_{l{-}1}} \max _{a\in A_n(i)}\left| \lambda c(i,a)\left( e^{\lambda V^*_n(t,i)}{-}W_m(t_{l{-}1},i)\right) \right| dt\\&\qquad +\int _{t_l}^{t_{l-1}} \max _{a\in A_n(i)}\left| \sum _{j\in S_n}\left( e^{\lambda V^*_n(t,j)}{-}W_m(t_{l{-}1},j)\right) q_n(j|i,a)\right| dt\\&\quad \le \left| e^{\lambda V^*_n(t_{l-1},i)}{-}W_m(t_{l-1},i)\right| {+}|\lambda |M \int _{t_l}^{t_{l-1}}\left| e^{\lambda V^*_n(t,i)}{-}e^{\lambda V^*_n(t_{l{-}1},i)}\right| dt\\&\qquad +\frac{T}{m}|\lambda |M\left| e^{\lambda V^*_n(t_{l-1},i)}-W_m(t_{l-1},i)\right| +\int _{t_l}^{t_{l-1}} \max _{a\in A_n(i)}\left| \sum _{j\in S_n}\left( e^{\lambda V^*_n(t,j)}\right. \right. \\&\qquad \left. \left. -e^{\lambda V^*_n(t_{l-1},j)}\right) q_n(j|i,a)\right| dt\\&\qquad +\frac{T}{m} \max _{a\in A_n(i)}\left| \sum _{j\in S_n}\left( e^{\lambda V^*_n(t_{l-1},j)}-W_m(t_{l-1},j)\right) q_n(j|i,a)\right| \\&\quad \le \left| e^{\lambda V^*_n(t_{l-1},i)}-W_m(t_{l-1},i)\right| +\left( \frac{T}{m}\right) ^2(|\lambda |M+2R)^2e^{|\lambda |MT}w^2(j_n)\\&\qquad +\frac{T}{m}(|\lambda |M+2R)w(i)\max _{j\in S_n}\left| e^{\lambda V^*_n(t_{l-1},j)}-W_m(t_{l-1},j)\right| , \end{aligned}$$

where the last inequality follows from (5.6) and (5.12). Hence, we obtain

$$\begin{aligned}&\max _{j\in S_n}\left| e^{\lambda V^*_n(t_l,j)}-W_m(t_l,j)\right| \\&\quad \le \bigg [1+\frac{T}{m}(|\lambda |M+2R) w(j_n)\bigg ] \max _{j\in S_n}\left| e^{\lambda V^*_n(t_{l-1},j)}-W_m(t_{l-1},j)\right| \\&\qquad +\left( \frac{T}{m}\right) ^2(|\lambda |M+2R)^2e^{|\lambda |MT} w^2(j_n)\\&\quad =\bigg [1+\frac{T}{m}(|\lambda |M+2R) w(j_n)\bigg ]\times \bigg [\max _{j\in S_n} \left| e^{\lambda V^*_n(t_{l-1},j)}-W_m(t_{l-1},j)\right| \\&\qquad +\frac{T}{m}(|\lambda |M+2R) e^{|\lambda |MT} w(j_n)\bigg ]-\frac{T}{m}(|\lambda |M+2R) e^{|\lambda |MT} w(j_n). \end{aligned}$$

Employing the last inequality and the induction, we get

$$\begin{aligned} \max _{j\in S_n}\left| e^{\lambda V^*_n(t_l,j)}-W_m(t_l,j)\right| \le&\frac{T}{m}(|\lambda |M+2R)e^{|\lambda |MT} w(j_n) \left( e^{\frac{T}{m}l(|\lambda |M+2R) w(j_n)}-1\right) \\ \le&\frac{T}{m}(|\lambda |M+2R)e^{|\lambda |MT} w(j_n) \times \,\left( e^{T(|\lambda |M+2R) w(j_n)}-1\right) . \end{aligned}$$

Therefore, the assertion holds.

(b) Fix any $n\ge 1$ and $i\in S_n$. By part (a), we have $\lim _{m\rightarrow \infty }W_m(0,i)=e^{\lambda V_n^*(0,i)}$, which implies that for any $\tau \in (0,1)$, there exists a positive integer $m_{\tau }$ satisfying

$$\begin{aligned} e^{\lambda V_n^*(0,i)}- \tau e^{-|\lambda | MT} \le W_m(0,i)\le e^{\lambda V_n^*(0,i)}+ \tau e^{-|\lambda | MT} \end{aligned}$$

for all $m\ge m_{\tau }$. Thus, employing the last inequalities we obtain

$$\begin{aligned} (1-\tau )e^{-|\lambda |MT} \le W_m(0,i)\le (1+\tau )e^{|\lambda |MT} \quad \mathrm{for \ all} \quad m\ge m_{\tau }. \end{aligned}$$

(5.13)

Below we discuss the cases $\lambda >0$ and $\lambda <0$ separately. Note that

$$\begin{aligned} \frac{1}{\lambda }\ln (1+\tau )\le \frac{1}{\lambda }\ln \frac{1}{1-\tau } \ \mathrm{for} \ \lambda >0 \quad \mathrm{and} \quad \frac{1}{\lambda }\ln (1+\tau )\ge \frac{1}{\lambda }\ln \frac{1}{1-\tau }\ \mathrm{for} \ \lambda <0. \end{aligned}$$

(5.14)

Case 1: $\lambda >0$. For each $m\ge m_{\tau }$, by (5.13) and (5.14) we get

$$\begin{aligned} -MT+\frac{1}{\lambda }\ln (1-\tau )\le \frac{1}{\lambda }\ln W_m(0,i)\le MT+\frac{1}{\lambda }\ln (1+\tau )\le MT-\frac{1}{\lambda }\ln (1-\tau ). \end{aligned}$$

Case 2: $\lambda <0$. For each $m\ge m_{\tau }$, employing (5.13) and (5.14) we have

$$\begin{aligned} -MT-\frac{1}{\lambda }\ln (1{-}\tau )\le -MT{+}\frac{1}{\lambda }\ln (1{+}\tau ) \le \frac{1}{\lambda }\ln W_m(0,i) \le MT+\frac{1}{\lambda }\ln (1-\tau ). \end{aligned}$$

Hence, we obtain

$$\begin{aligned} -MT+\frac{1}{|\lambda |}\ln (1-\tau )\le \frac{1}{\lambda }\ln W_m(0,i) \le MT-\frac{1}{|\lambda |}\ln (1-\tau ) \end{aligned}$$

(5.15)

for all $m\ge m_{\tau }$ and $\lambda \ne 0$. Moreover, it follows from the differential mean value theorem and (5.15) that

$$\begin{aligned} \left| e^{\lambda V^*_n(0,i)}-W_m(0,i)\right| \ge |\lambda | (1-\tau )e^{-|\lambda |MT} \left| V_n^*(0,i)-\frac{1}{\lambda }\ln W_m(0,i)\right| , \end{aligned}$$

which together with part (a) implies

$$\begin{aligned}&\left| V_n^*(0,i)-\frac{1}{\lambda }\ln W_m(0,i)\right| \le \frac{T}{m|\lambda |(1-\tau )}\\&\quad \times \left( |\lambda |M+2R \right) e^{2|\lambda |MT} w(j_n)\left( e^{T(|\lambda |M+2R)w(j_n)}-1\right) \end{aligned}$$

for all $m\ge m_{\tau }$. Therefore, the desired result follows from the last inequality, Theorem 5.1 and the inequality $\left| V^*(0,i)-\frac{1}{\lambda }\ln W_m(0,i)\right| \le \left| V^*(0,i)-V^*_n(0,i)\right| +\left| V_n^*(0,i)-\frac{1}{\lambda }\ln W_m(0,i)\right| .$

(c) Fix any $n\ge 1$, $m\ge m_{\tau }$ and $f_{n,m}\in \mathcal {O}_{n,m}$. Define an operator $\widetilde{\Gamma }$ on $B([0,T]\times S_n)$ as follows:

$$\begin{aligned} \widetilde{\Gamma }g(t,i):&=e^{\overline{\alpha } t}+e^{\overline{\alpha } t}\int _t^Te^{-\overline{\alpha } s}\bigg (\lambda c(i,f_{n,m}(s,i))g(s,i)\\&\quad +\sum _{j\in S_n}g(s,j)q_n(j|i,f_{n,m}(s,i))\bigg )ds \end{aligned}$$

for all $g\in B([0,T]\times S_n)$, where $\overline{\alpha }$ is an arbitrary positive constant. Then by (5.6) and Assumption 5.1(i) we have $|\widetilde{\Gamma }g(t,i)|\le e^{\overline{\alpha } T}+Te^{\overline{\alpha } T}(|\lambda |M+2Rw(j_n))\Vert g\Vert$ for all $(t,i)\in [0,T]\times S_n$, which yields that $\widetilde{\Gamma }$ is a map from $B([0,T]\times S_n)$ into itself. Moreover, for any $g_1,g_2\in B([0,T]\times S_n)$, direct calculations give

$$\begin{aligned} |\widetilde{\Gamma }g_1(t,i)-\widetilde{\Gamma }g_2(t,i)|\le \frac{|\lambda |M+2Rw(j_n)}{\overline{\alpha }}\Vert g_1-g_2\Vert \end{aligned}$$

for all $(t,i)\in [0,T]\times S_n$. Hence, letting $\overline{\alpha }=|\lambda |M+2Rw(j_n)+1$, we obtain that $\widetilde{\Gamma }$ is a contraction operator on $B([0,T]\times S_n)$. Therefore, the Banach fixed point theorem implies the existence of a function $\widetilde{g}\in B([0,T]\times S_n)$ satisfying

$$\begin{aligned} \widetilde{g}(t,i)&=e^{\overline{\alpha } t}+e^{\overline{\alpha } t}\int _t^Te^{-\overline{\alpha } s}\bigg (\lambda c(i,f_{n,m}(s,i))\widetilde{g}(s,i)\nonumber \\&\quad +\sum _{j\in S_n}\widetilde{g}(s,j)q_n(j|i,f_{n,m}(s,i))\bigg )ds \end{aligned}$$

(5.16)

for all $(t,i)\in [0,T]\times S_n$ and $\overline{\alpha }=|\lambda |M+2Rw(j_n)+1$. Set $\widetilde{u}(t,i):=e^{-(|\lambda |M+2Rw(j_n)+1)t}\widetilde{g}(t,i)$. Then by (5.16) we have

$$\begin{aligned} \widetilde{u}(t,i)=1+\int _t^T\bigg (\lambda c(i,f_{n,m}(s,i))\widetilde{u}(s,i)+\sum _{j\in S_n}\widetilde{u}(s,j)q_n(j|i,f_{n,m}(s,i))\bigg )ds \end{aligned}$$

(5.17)

for all $(t,i)\in [0,T]\times S_n$. Thus, the last equality yields that for each $i\in S_n$, $\widetilde{u}(\cdot ,i)$ is absolutely continuous on [0, T] and

$$\begin{aligned} -\frac{\partial \widetilde{u}}{\partial t}(t,i)=\lambda c(i,f_{n,m}(t,i))\widetilde{u}(t,i)+\sum _{j\in S_n}\widetilde{u}(t,j)q_n(j|i,f_{n,m}(t,i)) \end{aligned}$$

(5.18)

for a.e. $t\in [0,T]$. Moreover, from the proof of Theorem 3.1, we conclude that the Feynman–Kac formula is also applicable to the function $\widetilde{u}$. Hence, employing (5.18) and following the similar arguments of (4.6), we have $\widetilde{u}(t,i)=e^{\lambda V_n^{f_{n,m}}(t,i)}$ for all $(t,i)\in [0,T]\times S_n$. Therefore, by (5.17) we get

$$\begin{aligned} e^{\lambda V_n^{f_{n,m}}(t,i)}&=1+\int _t^T\bigg (\lambda c(i,f_{n,m}(s,i))e^{\lambda V_n^{f_{n,m}}(s,i)}\\&\quad +\sum _{j\in S_n}e^{\lambda V_n^{f_{n,m}}(s,j)}q_n(j|i,f_{n,m}(s,i))\bigg )ds \end{aligned}$$

for all $(t,i)\in [0,T]\times S_n$. Then using the last equality and following the same techniques in the proofs of parts (a) and (b), we obtain

$$\begin{aligned} \left| V_n^{f_{n,m}}(0,i)-\frac{1}{\lambda } \ln W_m(0,i)\right| \le \frac{TR_2e^{|\lambda |MT}}{m|\lambda |(1-\tau )} w(j_n)\left( e^{T(|\lambda |M+2R)w(j_n)}-1\right) \end{aligned}$$

for all $i\in S_n$, which together with part (b) gives the assertion.$\square$

Remark 5.1

(a) Theorems 5.1 and 5.2 are new for the risk-sensitive finite-horizon cost criterion. The iteration defined by (5.9) provides a numerical method to compute approximately the optimal value and an optimal policy of the model ${\mathcal {M}}$.

(b) For the control model ${\mathcal {M}}$ with finite states and finite actions, there exists a positive constant $\widehat{R}$ such that $q^*(i)\le \widehat{R}$ for all $i\in S$. Moreover, we do not need to construct a sequence of the control models $\{{\mathcal {M}}_n,n\ge 1\}$. Thus, employing the same technique used in the proof of Theorem 5.2, we obtain that for any $\tau \in (0,1)$, there exists a positive integer $m_{\tau }$ such that

$$\begin{aligned} \left| V^*(0,i)-\frac{1}{\lambda }\ln W_m(0,i)\right|&\le \frac{T}{m|\lambda |(1-\tau )}(|\lambda |M\\&\quad +2\widehat{R})e^{2|\lambda |MT}\left( e^{T(|\lambda |M +2\widehat{R})}-1\right) \ \mathrm{and}\\ \left| V^*(0,i)-V^{f_m}(0,i)\right|&\le \frac{2T}{m|\lambda |(1-\tau )}(|\lambda |M\\&\quad +2\widehat{R})e^{2|\lambda |MT}\left( e^{T(|\lambda |M+2\widehat{R})}-1\right) \end{aligned}$$

for all $i\in S$ and $m\ge m_{\tau }$, where the policy $f_m$ is as in (5.10). Hence, the last two inequalities yield that the accuracy of the approximation given by (5.9) and (5.10) is of order $m^{-1}$.

6 An example

In this section, we illustrate the application of our main results with a controlled birth and death system and use the iteration in Sect. 5 to compute approximately the optimal value.

Example 6.1

[A controlled birth and death system in Guo and Hernández-Lerma (2009)] Consider a controlled birth and death system in which the state variable represents the population size. Let the positive constants $\beta$ and $\gamma$ denote the natural birth and death rates, respectively. Suppose that the immigration parameter denoted by $a_1$ and the emigration parameter denoted by $a_2$ can be controlled by a decision-maker. When the population size of the system is not less than one, the decision-maker chooses an immigration parameter from a given set $[0,\kappa ]$ ($\kappa >0$) and an emigration parameter from a given set $[\zeta _1,\zeta _2]$ ($\zeta _2>\zeta _1>0$) to control the population size. When the population size equals zero, the decision-maker only needs to choose an immigration parameter from the set $[0,\kappa ]$ and it is natural to take $a_2\equiv 0$. Moreover, we assume that there exists a positive integer $i^*$ such that the cost of regulating the system is too high when the population size exceeds the integer $i^*$. Thus, we suppose that the cost takes a large enough positive value Q when the population size is greater than $i^*$. If the population size is $i\in \{0,1,2,\ldots ,i^*\}$, we suppose that this state and the action $(a_1,a_2)$ incur a cost $(|a_1-\eta _1|+|a_2-\eta _2|)i$, where $\eta _1$ and $\eta _2$ are given positive constants.

Now we formulate the above controlled birth and death system as a CTMDP with the state space given by $S=\{0,1,2\ldots \}$, the sets of all admissible actions given by $A(0)=[0,\kappa ]\times \{0\}$ and $A(i)=[0,\kappa ]\times [\zeta _1,\zeta _2]$ for all $i\ge 1$, the transition rate given by $q(1|0,(a_1,0))=-q(0|0,(a_1,0))=a_1$ for all $a_1\in [0,\kappa ]$ and

$$\begin{aligned} q(j|i,a)=\left\{ \begin{array}{ll} \beta i+a_1, &{}\text {if}\; j=i+1,\\ -(\beta +\gamma )i-a_1-a_2, &{}\text {if}\; j=i,\\ \gamma i+a_2, &{}\text {if}\; j=i-1,\\ 0, &{}\text {otherwise}, \end{array}\right. \end{aligned}$$

for all $i\ge 1$ and $a=(a_1,a_2)\in A(i)$, and the cost given by

$$\begin{aligned} c(i,a)=\left\{ \begin{array}{ll} (|a_1-\eta _1|+|a_2-\eta _2|)i, &{}\text {if}\; 0\le i\le i^*,\\ Q, &{}\text {if}\; i>i^*,\\ \end{array}\right. \end{aligned}$$

for all $a=(a_1,a_2)\in A(i)$.

Then we have the following statement.

Proposition 6.1

The controlled birth and death system in Example 6.1 satisfies Assumptions 3.1, 3.2 and 5.1. Hence, (by Theorem 4.1), there exists an optimal deterministic Markov policy.

Proof

Take $w(i)=i+1$ for all $i\in S$. Then Assumption 5.1(i) holds. Moreover, by the description of the model, we obtain

$$\begin{aligned} q^*(i)&\le (\beta +\gamma )i+\kappa +\zeta _2\le \max \{\beta +\gamma , \kappa +\zeta _2\}w(i),\\ \sum _{j\in S}w(j)q(j|i,a)&=(\beta -\gamma )i+a_1-a_2\le \beta w(i)+\kappa ,\\ \sum _{j\in S}w^2(j)q(j|i,a)&=2(\beta -\gamma )i^2+(3\beta -\gamma +2a_1-2a_2)i+3a_1-a_2\\&\le (5\beta +2\kappa )w^2(i)+3\kappa \end{aligned}$$

for all $i\ge 1$ and $a=(a_1,a_2)\in A(i)$, and

$$\begin{aligned}&q^*(0)\le \kappa w(0)\le \max \{\beta +\gamma , \kappa +\zeta _2\}w(0),\\&\sum _{j\in S}w(j)q(j|0,a)=a_1\le \beta w(0)+\kappa ,\\&\sum _{j\in S}w^2(j)q(j|0,a)=3a_1\le (5\beta +2\kappa )w^2(0)+3\kappa \end{aligned}$$

for all $a=(a_1,a_2)\in A(0)$. Hence, Assumptions 3.1(i), (ii), 5.1(ii) are satisfied with $\rho _1=\beta$, $d_1=\kappa$, $\rho _2=5\beta +2\kappa$, $d_2=3\kappa$ and $R=\max \{\beta +\gamma , \kappa +\zeta _2\}$. Moreover, we have $|c(i,a)|\le \max \{(\kappa +\zeta _2+\eta _1+\eta _2)i^*,Q\}$. Thus, Assumption 3.1(iii) holds with $M=\max \{(\kappa +\zeta _2+\eta _1+\eta _2)i^*,Q\}$. Furthermore, direct calculations give $|c(i,a)-c(i,b)|\le (|a_1-b_1|+|a_2-b_2|)i$ for all $0\le i\le i^*$, $|c(i,a)-c(i,b)|\le |a_1-b_1|+|a_2-b_2|$ for all $i>i^*$ and $\left| q(j|i,a)-q(j|i,b)\right| \le |a_1-b_1|+|a_2-b_2|$ for all $i,j\in S$ and $a=(a_1,a_2), b=(b_1,b_2)\in A(i)$, which together with the description of the model imply that Assumptions 3.2 and 5.1(iii) are satisfied with $L_i=i$ for $0\le i\le i^*$, $L_i=1$ for $i>i^*$ and $L_{ij}=1$. Therefore, we complete the proof of the proposition.$\square$

For each $n\ge 1$, the control model ${\mathcal {M}}_n$ is given by $S_n=\{0,1,\ldots ,n\}$, $A_n(0)=\{\frac{\kappa l}{n^2}:l=0,1,\ldots ,n^2\}\times \{0\}$, $A_n(i)=\{\frac{\kappa l}{n^2}:l=0,1,\ldots ,n^2\}\times \{\zeta _1+\frac{(\zeta _2-\zeta _1) l}{n^2}:l=0,1,\ldots ,n^2\}$ for all $i=1,2,\ldots ,n$. Then for each $n\ge 1$ and $i\in S_n$, direct calculations give

$$\begin{aligned} d_H(A(i),A_n(i))\le \frac{\kappa +\zeta _2-\zeta _1}{n^2}\le \frac{2e^{|\lambda |MT}(|\lambda |i^*+2) (\kappa +\zeta _2-\zeta _1)w^2(i)}{e^{|\lambda |MT}\left( |\lambda |L_i+2\sum _{j=0}^{n-1}L_{ij}\right) w(n)}. \end{aligned}$$

Hence, (5.2) in Theorem 5.1 holds with $\widetilde{M}=2e^{|\lambda |MT}(|\lambda |i^*+2) (\kappa +\zeta _2-\zeta _1)$.

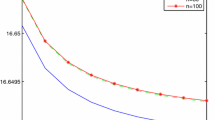
For a numerical experimentation of Example 6.1, we take the following values of the parameters: $T=5$, $\lambda =0.1$, $\beta =0.9$, $\gamma =1$, $\kappa =1$, $\zeta _1=0.4$, $\zeta _2=1$, $\eta _1=1.1$, $\eta _2=1.2$, $i^*=10{,}000$, $Q=1{,}000{,}000$. For $n=50$, 75, 100 and $m=10{,}000, \ldots , 80{,}000$, via the iteration defined by (5.9), we obtain the values of $\ln W_m^{10}(0,3)$ as displayed in Fig. 1. Empirically, the convergence is faster than that given in Theorem 5.2. This is due to the fact that the bounds used to obtain the error estimations in Theorem 5.2 are very conservative. Moreover, as can be seen in Fig. 1, the value of $V^*(0,3)$ approximately equals 4.62277.

Fig. 1

Value $\ln W^{10}_m(0,3)$ of the model ${\mathcal {M}}_n$ for $n=50, 75, 100$ and $m=10{,}000,\ldots ,80{,}000$

7 Concluding remarks

In this paper we have studied the risk-sensitive finite-horizon cost criterion for CTMDPs with the denumerable states, bounded cost rates and possibly unbounded transition rates. The risk-sensitivity coefficient can take any nonzero value. Under the suitable conditions, we have established the existence and uniqueness of the solution to the optimality equation and shown the existence of an optimal deterministic Markov policy. Moreover, we have proposed a tractable numerical method for the approximate computations of an optimal policy and the optimal value, and obtained the corresponding error estimations. It should be mentioned that the Feynman–Kac formula plays a crucial role in the study of the risk-sensitive finite-horizon cost criterion. The Feynman–Kac formula in Theorem 3.1 is only applicable to the case of the bounded cost rates and bounded optimal value function. For the case of the unbounded cost rates, the corresponding optimal value function is also unbounded. Hence, in order to study the risk-sensitive finite-horizon cost criterion with the unbounded cost rates, we need to extend the Feynman–Kac formula in Theorem 3.1 to the case which is applicable to the unbounded cost rates and unbounded optimal value function. How to extend the Feynman–Kac formula remains an open problem.