Spatial competition on 2-dimensional markets and networks when consumers don’t always go to the closest firm

Abstract

We investigate the strategic behavior of firms in a Hotelling spatial setting. The innovation is to combine two important features that are ubiquitous in real markets: (1) the location space is two-dimensional, often with physical restrictions on where firms can locate; (2) consumers with some probability shop at firms other than the nearest. We characterise convergent Nash equilibria (CNE), in which all firms cluster at one point, for several alternative markets. In the benchmark case of a square convex market, we provide a new direct geometric proof of a result by Cox (Am J Political Sci 31:82–108, 1987) that CNE can arise in a sufficiently central part of the market. The convexity of the square space is of restricted realism, however, and we proceed to investigate grids, which more faithfully represent a stylised city’s streets. We characterise CNE, which exhibit several new phenomena. CNE in more central locations tend to be easier to support, echoing the unrestricted square case. However, CNE on the interior of edges differ substantially from CNE at nodes and follow quite surprising patterns. Our results also highlight the role of positive masses of indifferent consumers, which arise naturally in a network setting. In most previous models, in contrast, such masses cannot exist or are assumed away as unrealistic.

1 Introduction

The classical Hotelling (1929) model of spatial competition can be generalised in several directions. Hotelling (and many researchers after him) assumed that both firms and consumers are located on the unit interval [0, 1], representing “Main Street”. In the simplest model, customers patronise the closest firm and the firms set an identical mill price of the good they provide, hence firms compete only by choosing their locations. Hotelling showed that for two competing firms the unique equilibrium is convergent and both firms locate at the midpoint of the interval. For three firms, no equilibria exist, and for four or more firms the equilibria are characterised by Eaton and Lipsey (1975)—they are non-convergent with candidates occupying a rather diverse set of positions.

One important direction of generalisation was to change the nature of the location space. Salop (1979) considered, rather than a line, a circle. Eaton and Lipsey (1975) believed that, if the number of firms is more than two, Nash equilibria on a bounded two-dimensional location space are unlikely to exist. Okabe and Suzuki (1987) investigated this hypothesis computationally and Aoyagi and Okabe (1993) studied how the shape of the two-dimensional market affects the existence of equilibrium.

On reflection, a two-dimensional location space also lacks realism. Indeed, the map of any city shows that it is structured as a network, with both firms and customers located along the city streets. In Sarkar et al. (1997), a network represents spatially separated markets with consumers located at nodes only. Pálvölgyi (2011) and Fournier and Scarsini (2019) consider the classical location game on a network (where customers and firms may locate anywhere)—when the number of firms is large enough, a pure strategy non-convergent Nash equilibrium exists and they show how to construct it. Fournier (2019) considers approximate equilibria under more general consumer distributions on the network.¹

All the above work assumes that consumers buy from the closest store. Relaxing this assumption is a second direction of generalisation of the basic model, pioneered by Cox (1987, 1990) and further investigated by Cahan and Slinko (2017, 2018) and Cahan et al. (2018). Cox suggested that, while a consumer usually shops at the closest firm, there is some probability of shopping at more distant firms. Let the number of firms be m and $\mathbf{p} =({p}_1,\ldots ,{p}_{m})$ be a vector of probabilities, where $p _i$ is the probability that a consumer buys from the ith most distant firm, $p_1\ge p_2\ge \cdots \ge p_m$, and $p_1>p_m$.^2,3 The classical Hotelling model and most of the previous literature (including, to our knowledge, all papers on networks) then corresponds to the special case where the probability vector is given by $\mathbf{p}=(1,0,\ldots ,0)$.⁴ Cox showed that, under more general probability vectors, CNE on a range of markets exist if and only if $c(\mathbf {p},m)\le \nicefrac {1}{2}$, where $c(\mathbf{p},m)=\frac{p_ 1-{\bar{p}}}{p_ 1-p_ m}$ and ${\overline{p}}=\frac{1}{m}(p_ 1+\ldots +p_ m)$. The parameter $c(\mathbf{p},m)$, also called the c-value, is always between 0 and 1 and is a measure of the dominating incentives (Myerson 1999). If $c(\mathbf{p},m)$ is high, consumers have a strong tendency to go to the closest firms only and, therefore, the incentive for the firm is to differentiate itself as the closest for as many consumers as possible. When $c(\mathbf{p},m)$ is low, consumers are quite happy to shop at more distant firms, so it becomes relatively less important to stand out as the closest firm for a large number of consumers. In different contexts, different $\mathbf{p}$ will make sense. Convenience shops tend to be visited by consumers who seek a particular product that can be found at any convenience shop. It would therefore be rare to need to go beyond the closest shop. With clothing shops, in contrast, many consumers like to browse through an assortment of products until finding something they want to buy, so are quite likely to go beyond the closest shop.

Here we combine the two directions of generalisation above. We show how both the market shape and consumer shopping behaviour influence the equilibrium location choosing behaviour of firms, in particular, their tendency to agglomerate at a single location. We begin with the benchmark case of a two-dimensional convex square market—any location in the square can be chosen by a firm to set up shop without restrictions. We provide a new direct geometric characterisation of Cox (1987) indirect description of convergent Nash equilibria (CNE), where all firms locate at the same point. Given $\mathbf{p}$, CNE may exist in a central region of the market bounded by hyperbolas that expands as $c(\mathbf{p},m)$ decreases.

Noting that a city’s layout is decidedly non-convex and has more in common with a network of nodes and edges, we then proceed to study the properties of CNE on networks. New considerations arise. Firstly, instead of Euclidean distances, we must analyse shortest paths between points on the network. Secondly, while previous papers study settings where positive masses of indifferent consumers do not arise, or disregard the possibility as unrealistic, on a network they occur naturally (see, e.g., Fig. 1) and add another layer of complexity to the analysis. We study in detail the case of a square grid, which illustrates explicitly these phenomena. In general, more central areas are supported as CNE for a broader range of probability vectors $\mathbf{p}$, as in the case of the unrestricted two-dimensional square. However, at a more local level, the equilibrium properties of edges (interior locations on streets) exhibit quite different patterns and are more irregular compared to those on nodes (intersections of streets). Counterintuitively, two locations that are very close (on opposite sides of an intersection) can have quite different equilibrium properties, which is not at all evident from the square convex market case. The practical implication is that, while at a very broad level the square convex market may be a reasonable approximation for the grid—this is not true locally. There is a time and place for both levels of thinking. Developers considering a new mall may initially consider whether a general neighborhood is likely to support CNE. Next, a specific location within that neighborhood needs to be selected, at which point a more detailed thinking is required. On top of our characterisation of CNE for grids, the results also suggest that a greater focus on atomic distributions, even on unidimensional spaces, may be an important and fruitful direction for future research.

Before we proceed, it is important to note that much of the spatial competition literature is framed in terms of electoral competition between political candidates (Hotelling 1929; Downs 1957). The political interpretation of probability vector $\mathbf{p}$ is a class of voting systems called scoring rules that includes plurality rule, antiplurality and Borda rule, among others Cox (1987).⁵ There, $p_i$ represents the number of “points” assigned to the ith ranked candidate on a voter’s ballot, although a probabilistic interpretation is also possible.

We focus on the firm interpretation, where we believe grids are the most natural. That said, our results for the convex square market and general networks are relevant for political competition as well. There are cases where the political space may have a network structure, even if not a grid. In Fig. 1, for example, the vertical line could represent an issue that is only relevant for voters at the center left of the ideological space. This might be some question about how to implement a certain policy that is only relevant, to a first approximation, to voters with this particular ideology. To the left or right of this point, voters may not consider the issue important or may be unanimous in their views. Another example is a star network with k edges, which we will return to in Example 1. This could represent a “tribalised society” in which k groups compete for power. A location along a given edge represents a level of favouritism of one group over the others—from full favouritism, at the outside end of the edge, to no favouritism, at the center of the star. In both examples, masses of indifferent voters are possible and affect equilibrium outcomes.

Fig. 1

On this network, all consumers on the vertical line—a positive mass—are indifferent between points u and v

2 CNE for measurable metric location spaces

2.1 General results

In this section we give a general result on the existence of CNE. Later we investigate in detail two specific markets—a convex square space and a grid.

The location space, I, is where both consumers and firms locate. It is assumed that the location of a consumer is fixed while the firms compete by choosing locations (and that the relocation costs are negligible). We assume that I is a measurable metric space. The metric determines preferences: if there are m competing firms located on I in positions ${u}_1,\ldots ,{u}_{m}$ and $v\in I$ is the location of a consumer, then the consumer has a linear preference order $\succeq$ induced by v on the set of firms determined by distance along the shortest path and visits the ith closest firm with probability $p_i$. Again, $p_1\ge \cdots \ge p_m$ and $p_1>p_m$. Consumers break ties by randomisation.

It is important to note that the probabilistic description of consumer behavior here is ordinal in nature—it only depends on rank and not on absolute distance. This is a simplification of reality and a limitation of the model, but it significantly improves tractability. We also believe that ordinal information does matter to an extent that is comparable with absolute distance, something that is not captured in many probabilistic models that do incorporate a dependence on absolute distance.⁶

There is a measure $\mu$ defined on I that gives the density of consumers on subsets of I. We assume I has finite measure, i.e., $\mu (I)<\infty$. We introduce the following notation:

$$\begin{aligned} \qquad \qquad \qquad \qquad K_{u\succ v}&=\mu (\{\text { consumers } \text { with } \text { strict } \text { preference } \text { for } u~ \text{ over } v\}), \\ \end{aligned}$$

where $u,v\in I$. $K_{u\sim v}$, analogously, is the set of indifferent consumers.⁷ The measure $\mu$ is assumed to be such that these sets are always measurable.

Given a vector of probabilities $\mathbf{p}$, each firm then calculates the expected measure of customers who will patronise it. Firms choose their locations simultaneously so as to maximise this expected measure of customers. Our focus is convergent Nash equilibria (CNE), in which all firms adopt the same location. This is a natural starting point as the most basic manifestation of firm agglomeration. Non-convergent Nash equilibria (NCNE) may also be possible, but are substantially more difficult to analyse and we leave them for future research.⁸

For any $u\in I$, we define

$$\begin{aligned} K(u)=\sup _{v\in I}\frac{K_{v\succ u}}{K_{u\succ v}}. \end{aligned}$$

This is the maximal achievable ratio of consumers preferring some other point v to u over consumers that prefer u to v.

The main result of this section is Theorem 1. Subsequently when we focus on the convex square market and grids we will focus on uniform measures for tractability, but Theorem 1 holds in general.⁹ For the special case of a square convex market case, the corresponding result was proven by Cox (1987). Theorem 1 is more general, however, because it applies on other spaces where the measure of consumers indifferent between two points may be non-zero. In fact, this generality is critical for our study because non-zero measures of indifferent consumers are a regular and natural occurrence on networks.

Theorem 1

Given a location space I with m competing firms and probability vector $\mathbf{p}$, a point $u\in I$ is a CNE if and only if

$$\begin{aligned} K(u) \le \frac{1}{c(\mathbf{p},m)}-1, \end{aligned}$$

(1)

where $c(\mathbf{p},m)=\frac{p_ 1-{\bar{p}}}{p_ 1-p_ m}$.

Proof

If all firms are located at u, each of them will get ${\overline{p}}\mu (I)$ consumers. If a single firm deviates from u to location v, then all customer will be split into three sets: those who are closer to v than to u, those equidistant from v and u and those who are closer to u than to v. The expected number of customers shopping at the deviating firm would be $p_1 K_{v\succ u}+{\overline{p}} K_{u\sim v}+p_m K_{u\succ v}$.

Thus, for any $v\in I$, for the deviation to v not to be profitable, we must have

$$\begin{aligned} p_1 K_{v\succ u}+{\overline{p}} K_{u\sim v}+p_m K_{u\succ v}\le {\overline{p}}\mu (I)= {\overline{p}}( K_{v\succ u}+ K_{u\sim v}+ K_{u\succ v}). \end{aligned}$$

This rearranges to

$$\begin{aligned} \frac{K_{v\succ u}}{K_{u\succ v}}\le \frac{{\overline{p}}-p_m}{p_1-{\overline{p}}}=\frac{p_1-p_m+{\overline{p}}-p_1}{p_1-{\overline{p}}}=\frac{1}{c(\mathbf{p},m)}-1. \end{aligned}$$

For u to be a CNE, even the best deviation should not be profitable, hence we take the supremum of the left-hand side in (1). $\square$

Note that the value K(u) is not always defined, e.g., when u is a leaf on a network. Then we set $K(u)=\infty$. Hence Theorem  1 rules out a CNE at a leaf.

If the measure of indifferent consumers is always zero, which will be the case on a line or a two-dimensional square (but not on grids), it will be more convenient to use the value $W(u):=\sup _{v\in G}\frac{K_{v\succ u}}{\mu (I)}=\frac{K(u)}{1+K(u)}$, where $\mu (I)$ is the total measure of consumers. Then condition (1) can be rewritten as

$$\begin{aligned} W(u)\le 1-c(\mathbf{p},m). \end{aligned}$$

(2)

Let us consider several examples.

Example 1

(Linear, circular and star markets) For a linear market $I=[0,1]$ with a uniform distribution of consumers, CNE exist if and only if $c(\mathbf {p},m)\le 1/2$. Any location $x\in I$ such that $c(\mathbf{p},m)\le x\le 1-c(\mathbf{p},m)$ can support a CNE (Cox 1987).

For a circular market I with a uniform distribution of consumers, a CNE exists if and only if $c(\mathbf {p},m)\le {1/2}$ In such a case every location can support a CNE.

Indeed, deviating to a point $v\ne u$, a deviating firm gets half of the customers, so $K(u)=1$.

Consider a star graph $S_k$ with $k\ge 2$ edges and $k+1$ nodes where each edge has measure 1 of consumers. The central node u is a CNE if and only if $W(u)=1/k \le 1-c(\mathbf {p},m)$. This is because the best deviation for any firm would be to deviate marginally towards one of the leaves. In particular, in the classical case with $\mathbf{p}=(1,0,\ldots ,0)$, it is a CNE if and only if $m\le k$, i.e., the number of firms does not exceed the number of edges. For any worst-punishing or intermediate $\mathbf{p}$, it is always a CNE. If u is on an edge at distance $\epsilon$ away from the central node, then the best deviation will be to deviate to the point v marginally towards the central node, in which case $K_{v\succ u}=k-1+\epsilon$ and $W(u)=1-\frac{1-\epsilon }{k}$.

Then (2) tells us that for u to be a CNE we must have $c(\mathbf{p},m)\le \frac{1-\epsilon }{k}$. In particular, it will never be a CNE for $\mathbf{p}=(1,0,\ldots ,0)$, but for $\mathbf{p}=(1,\ldots ,1,0)$ it will always be when the number of firms is large enough: $k\le m(1-\epsilon )$.¹⁰

A consequence of Theorem 1 is that, for any point $u\in I$, unless K(u) is not defined, there is always a threshold value of $c(\mathbf{p},m)$, ${\overline{c}}(u)=1/(K(u)+1)$, below which no CNE exist. That is, the set of all rules $\mathbf{p}$ with $c(\mathbf{p},m) > {\overline{c}}(u)$ do not admit CNE at u, while the set of all rules $\mathbf{p}$ with $c(\mathbf{p},m) \le {\overline{c}}(u)$ do admit CNE at u.

Thus agglomeration at any point (except where $K(u)=\infty$) can constitute a CNE provided $\mathbf{p}$ is such that $c(\mathbf{p},m)$ is low enough. That is, provided the consumers’ shopping behaviour exhibits sufficient lack of favouritism for the closest firms over more distant firms. On the other hand, when $c(\mathbf{p},m)$ is high enough, no CNE can be supported at any point—consumers favour the closest firms strongly enough that there is always an incentive to deviate away from the cluster. As $c(\mathbf{p},m)$ decreases, the set of possible CNE cannot get smaller.

2.2 Two-dimensional square market

We start by considering a two-dimensional square, $I=[0,1]^2$, without any restrictions on where firms can locate as perhaps the most basic extension of the linear model. This serves as a benchmark for our subsequent study of what happens when restrictions are placed on where firms and consumers are located, i.e., when we look at a grid. This case has previously been studied by Cox (1987), who showed that CNE exist if and only if $c(\mathbf {p},m)\le 1/2$. However, this indirect result does not explicitly describe the set of points that can support CNE for a given probability vector—here, we provide a direct, geometric result.

There cannot be a positive measure of consumers indifferent between two points, so for a point $u=(x,y)$, we only need to calculate the simpler $W(u)=\sup _{v\in I} K_{v\succ u}/\mu (I)=\sup _{v\in I} K_{v\succ u}$ (normalising the total measure of consumers to $\mu (I)=1$). We assume without loss of generality that $u \in I_1 = [0,{1/2}]^2$, as we can obtain all other CNE in the other quadrants $I_2=[{1/2},1]\times [0,{1/2}]$, $I_3=[{1/2},1]^2$ and $I_4=[0,{1/2}]\times [{1/2},1]$ by symmetry.

For any two points $u,v\in I$, the sets $K_{v\succ u}$ and $K_{u\succ v}$ are separated by a straight line passing through the midpoint of the line segment between u and v and perpendicular to it. It is therefore clear that the best deviation by a single firm from u is to a point infinitesimally close to u in some direction. Then W(u) will be the area of one of the regions which appear when a line through u divides the square into two parts.

Lemma 1

Let $\lambda$ be a line through u in the interior of $I_1$ dividing the square into regions $\alpha$ and $\beta$ so that $\mu (\beta )=W(u)$ and $\mu (\alpha ) = 1 - W(u)$. Then $\alpha$ is a triangle.

Proof

Since $\mu (\alpha )\le \mu (\beta )$, then $\alpha$ can be either triangle or a trapezium. Let $\lambda$ be a line through u such that it forms a trapezium with the parallel bases being parts of each of the top and bottom sides of the square and one of the lateral sides being a side of the square. Now consider the line through u and the top left corner (0, 1). Clearly the two light grey triangles (see Fig. 2) formed are similar. The “height" of the upper triangle (i.e., the distance from u to the upper side) is equal to $1-y$, but, as $y \le 1/2$, we know $1-y \ge y$. Since y is the height of the lower triangle, the upper one is larger. This means that the triangle ABC must have smaller area than the trapezium ABDE, which shows that $\lambda \ne ED$. Therefore, $\alpha$ cannot be a trapezium. The arguments for horizontal trapeziums (see Fig. 2) are symmetric. Therefore we must have that $\alpha$ is a triangle. $\square$

Fig. 2

Dividing the square into triangles and trapeziums

Lemma 2

For any $u=(x,y) \in I_1$ we have $W(u) = 1 - 2xy$.

Proof

If $y={1/2}$ the result is clear. Suppose now that u is in the interior of $I_1$. We let $\lambda$ be the line through u which bounds $\alpha$, the region as defined in the previous lemma. From Lemma 1 we also know that $\alpha$ must be a triangle, so we know that $\lambda$ crosses the x- and y-axes. Let b be the intersection of $\lambda$ with the y-axis and let a be the intersection with the x-axis, so that $\mu (\alpha ) = \frac{1}{2} ab$. The gradient of $\lambda$ is $m = \frac{y- b}{x}$, so that $\lambda = \{(x,y) \in I: y=mx+b\}$. We then have $0=\frac{y -b}{x}a+b$, which is equivalent to $a=\frac{bx}{b-y}$. Therefore

$$\begin{aligned} \mu (\alpha ) = \frac{1}{2}ab = \frac{b^2x}{2(b - y)} \text {, hence } \ \ \frac{\partial \mu (\alpha )}{\partial b} = \frac{x}{2}\left( \frac{2b}{b-y} - \frac{b^2}{(b -y)^2}\right) . \end{aligned}$$

So then $\frac{\partial \mu (\alpha )}{\partial b} = 0$ if and only if $\frac{2b}{b-y} = \frac{b^2}{(b - y)^2}$, or equivalently $b = 2y$, and hence $a = 2x$. Therefore $\mu (\alpha ) = \frac{1}{2}ab = 2xy$, and hence $W(u) = 1 - 2xy$, as required. $\square$

This means that we have our desired explicit formula for W(u), namely $W(u) = 1 - 2xy$ for $u \in I_1$. And since I is symmetric we have similar formulas for u in the other quadrants as well. This allows us to fully characterise CNE geometrically in the square market.

Theorem 2

For a given probability vector p with $c(\mathbf{p},m) \le \frac{1}{2}$, the profile $(u, \dots , u)$ is a CNE if and only if $u \in R = \bigcup \{R_1, \, R_2, \, R_3, \, R_4\}$, where:

$$\begin{aligned} R_1&= \{(x,y) \in I_1 : 2x y \ge c(\mathbf{p},m) \}; \\ R_2&= \{(x,y) \in I_2 : 2(1-x) y \ge c(\mathbf{p},m) \}; \\ R_3&= \{(x,y) \in I_3 : 2(1-x) (1-y) \ge c(\mathbf{p},m) \}; \text { and} \\ R_4&= \{(x,y) \in I_4 : 2x (1-y) \ge c(\mathbf{p},m) \}. \end{aligned}$$

Proof

If $u = (\frac{1}{2},\frac{1}{2})$ then by Lemma 2u is a CNE. If $u \in I_1$, then by Theorem 1 and Lemma 2 we must have that u is a CNE if and only if $2 xy \ge c(\mathbf{p},m)$, or equivalently $u \in R_1$. Since R must be symmetric about the axis of symmetry of I, we must have that if $u \in I_2 = \{z \in I :\frac{1}{2} \le z_1 \le 1, 0 \le z_2 \le \frac{1}{2}\}$ then u is a CNE if and only if $u \in R_2$ too. Similarly for all i if $u\in I_i$ then u is a CNE if and only if $u \in R_i$. $\square$

Fig. 3

Illustrating the area R of CNE for $c(\mathbf{p},m) = 1/4$

Therefore we have found a region in I bounded by four hyperbolas for which all points inside support CNE and all points outside do not. The region in which CNE exist is illustrated in Fig. 3. When $c(\mathbf {p},m)>{1/2}$, no CNE exist. At $c(\mathbf {p},m)={1/2}$, the center of the square is the first point to support CNE. As $c(\mathbf{p},m)$ decreases, the region R expands. Moreover, except for a point on the boundary, any point can be a CNE for low enough $c(\mathbf{p},m)$, although more central points are easier to support (allow CNE for a wider range of $\mathbf{p}$). This makes sense at an intuitive level. The more willing consumers are to travel to more distant firms, the easier it is to imagine a cluster of firms far from the city center—a cluster of clothing shops is probably the most viable at the city center, but that does not rule out clusters at distant locations like an outlet mall.¹¹ This pattern will turn out to be roughly reflected when we restrict the space to a grid, but not exactly—the non-convexity of the grid, specifically the fact that you can only reach a firm through a limited number of paths, will give rise to new equilibrium phenomena.

2.3 Grids

A grid is perhaps the most natural network to represent a stylised district of the city. Unlike the convex square, this market imposes the more realistic assumption that activity in the city occurs along streets – firms cannot locate anywhere they please, and consumers do not travel as the crow flies. Grids have so far been studied only in settings where consumers always go to the closest firm. Existence of NCNE is assured when the number of firms is large enough (Pálvölgyi 2011; Fournier and Scarsini 2019). In a Voronoi game context, Sun et al. (2020) show that NCNE exist for four firms when the grid is sufficiently narrow.¹²

Let G be a square grid with sides that are M edges long. Thus, it has $(M+1)^2$ nodes (equivalently, vertices or intersections of streets) and $2M(M+1)$ edges in total. To keep things simple, we will focus on the case where M is even—insights are similar in the case of M odd. Let $u\in G$ be a location in the northeast quadrant of the grid (by symmetry, there is no loss of generality). We write $u=(x,y)$, where $x\ge 0$ is the horizontal distance from u to the central node and $y\ge 0$ is the vertical distance. Thus, the central node is at coordinates (0, 0) and the northeast corner is at (M/2, M/2). Since the network includes edges as well as nodes, either x or y can be a non-integer, but not both.

We assume a uniform distribution of consumers over the grid, normalised so that one edge has measure 1. According to graph theory, the distance between two points on a graph is the length of the shortest path connecting them.

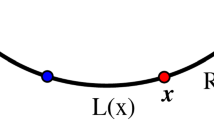
Consider nodes $u=(x,y)$ and $u'=(x-1,y-1)$ where $y, x\ge 1$. Note that consumers in the northwest and southeast corners of the grid are indifferent between u and $u'$ (see Fig. 4). Let us introduce the notation:

$$\begin{aligned} NW(u)&= \{(x',y')\in K_{u\sim u'}: x'\le x \text{ and } y'\ge y\};\\ SE(u)&= \{(x',y')\in K_{u\sim u'}: x \le x' \text{ and } y \ge y'\}. \end{aligned}$$

Though functions of u, we usually just write NW and SE when no confusion can emerge. We can write down an explicit formula for the number of consumers in each of these sets:

$$\begin{aligned} |NW|&= ({M/2}+x-1)({M/2}-y+1)+({M/2}+x)({M/2}-y), \\ |SE|&=({M/2}+y)({M/2}-x)+({M/2}+y-1)({M/2}-x+1). \end{aligned}$$

In a similar way, note that the consumers in the northeast portion of the grid described in Fig. 4 strictly prefer u over $u'$, while those in the southwest portion prefer $u'$ over u. We use the notation $|SW|=|K_{u'\succ u}|$ and $|NE|=|K_{u\succ u'}|$. We have the following formulas for these areas:

$$\begin{aligned} |SW|&=2({M/2}+x)({M/2}+y),\\ |NE|&=2({M/2}-x+1)({M/2}-y+1). \end{aligned}$$

Fig. 4

Thick black lines indicate consumers preferring $u'$ to u; thin black lines: consumers preferring u to $u'$; dotted lines: consumers indifferent between $u'$ and u

Theorem 3 is our characterisation of CNE at the nodes of the grid. To prove a point is a CNE, we need to show that no firm could profitably deviate to another position. By Theorem 1, this means finding the point $u'$ that maximises the ratio ${K_{u'\succ u}}/{K_{u\succ u'}}.$ In principle, then, we need to check every possible deviation, which appears a daunting task. Much of the work involves ruling out all but one or several potential “best deviations” that dominate all other possible deviations. Once we know these best deviations we calculate K(u) and thus determine whether a CNE is possible at point u.

Theorem 3

Let $u=(x,y)$ be a node with $x,y\ge 0$ and m firms co-located at u. Then the deviation $u'$ that maximises the ratio ${K_{u'\succ u}}/{K_{u\succ u'}}$ is among the following:

• (i) If $x>0$ and $y>0$, the point $(x-1,y-1)$ or just to the east or north of it.

• (ii) If $y=0$ and $x>0$, the point $(x-1,y)$. By symmetry, the point $(x,y-1)$ if $x=0$ and $y>0$.

• (iii) If $u=(0,0)$, either (1, 0) or (0, 1).

In case (i),

$$\begin{aligned} K(u)=\max \left\{ \frac{|NW|+|SW|}{|NE|+|SE|},\frac{|SW|}{|NE|},\frac{|SW|+|SE|}{|NW|+|NE|}\right\} .\end{aligned}$$

(3)

In case (ii),

$$\begin{aligned} K(u)=\frac{M^2+(2M+1)\max (x,y)-{1/2}}{M^2+2M-(2M+1)\max (x,y)+{1/2}}.\end{aligned}$$

(4)

In case (iii),

$$\begin{aligned} K(u)=\frac{M^2-{1/2}}{M^2+2M+{1/2}}.\end{aligned}$$

(5)

Thus, by Theorem 1, u can be supported as a CNE if and only if $K(u)\le \frac{1}{c(\mathbf{p},m)}-1$ and the threshold value of $c(\mathbf{p},m)$ below which u can be supported as a CNE is ${\overline{c}}(u)=\frac{1}{K(u)+1}$.

Proof

To determine whether u is a CNE we want to calculate K(u). This requires finding the point $u'$ at which the ratio ${K_{u'\succ u}}/{K_{u\succ u'}}$ is maximised. First, suppose $u=(x,y)$ is a node with positive integers x, y. We claim that the horizontal move (keeping y constant) that maximises ${K_{u'\succ u}}/{K_{u\succ u'}}$ is to the node $(x-1,y)$, rather than to a point in the interior of the edge, i.e., to a point $(x-\epsilon ,y)$, where $0<\epsilon <1$. In Fig. 5a, the customers on bold segments strictly prefer $u'$ over u, while those on thinly shaded edges strictly prefer u to $u'$. The set of indifferent consumers has measure zero in such a configuration. Consider a point slightly to the left of $u'$, i.e., $u''=(x-\epsilon -\eta , y)$, where $\eta >0$ is very small. We compare the score of i upon deviation to $u'$ with the score upon deviation to $u''$. We can see that $u''$ looks more attractive than $u'$ because the firm gains $\frac{\eta }{2}$ consumers from M edges and loses $\frac{\eta }{2}$ from only one edge (the one on which it is moving). Thus, the ratio ${K_{u'\succ u}}/{K_{u\succ u'}}$ is increasing as $u'$ moves to the left. By the same logic, the firm would want to continue left until reaching node $(x-1,y)$ as there is no discontinuity of the score when reaching this node.¹³

Fig. 5

Possible deviations from a point u in case (i). Thick black lines indicate consumers preferring $u'$ to u; thin black lines: consumers preferring u to $u'$

However, the best horizontal may not be the best move overall. Consider a move to a point $u'=(x-1,y-\epsilon )$, where $0<\epsilon <1$. Consider also a point $u''=(x-1,y-\epsilon -\eta )$ where $\eta >0$ is small (see Fig. 5(b)). Moving from $u'$ to $u''$, i is gaining from each edge $(x-1,z)$ where $z<y$ but losing at the same rate from each edge $(x-1,z)$, where $z\ge y$. Because $y>0$, there are more edges from which i is gaining, so $u''$ looks better than $u'$. Thus, ${K_{u'\succ u}}/{K_{u\succ u'}}$ increases as i moves towards the next node $(x-1,y-1)$.

By a similar argument, firm i could also have, instead of initially moving horizontally from u, moved down vertically from u to the node $(x,y-1)$ and then across towards $(x-1,y-1)$ from the right.

However, whether i should actually arrive at the node $(x-1,y-1)$ itself is not clear, since there is a potential discontinuity in the score. The reason is that, at $(x-1,y-1)$, the areas NW and SE will be indifferent between this node and u (the dotted edges in Fig. 4), and these are sets of positive measure. We therefore need to compare the ratio ${K_{u'\succ u}}/{K_{u\succ u'}}$ for three possible deviations: $u'=(x-1,y-1)$, the limiting point just north of $(x-1,y-1)$ and the limiting point just east of $(x-1,y-1)$.¹⁴

Next, consider the cases where we are on one of the central axes, i.e., $u=(x,0)$ or $u=(0,y)$. If $x>0$ and $y=0$, a deviation to $u'$ between u and $(x-1,0)$ results in a higher value of ${K_{u'\succ u}}/{K_{u\succ u'}}$ if $u'$ is further from u. In fact, the best move would be to the point $(x-1,0)$. Finally, if $u=(0,0)$, similar reasoning leads to the conclusion that the best move is to $u'=(1,0)$ or $u'=(0,1)$. $\square$

The main implication, to be discussed further in Corollary 1, is that, at least as far as nodes go, more central nodes support CNE for a larger range of consumer shopping behaviour. This is consistent in nature with what we saw for the square convex market.

Example 2

Let us consider the example of $M=6$, displayed in Fig.  6. We calculate the threshold ${\overline{c}}(u)$ for each node in the top right quadrant in Fig. 6 (the remaining nodes follow by symmetry). As we can see, the further out from the center of the grid, the more difficult it becomes to support a node as a CNE. The easiest point to support a CNE is the central node (0, 0), which has a threshold ${\overline{c}}(u)=0.577$. It is interesting to note that this means the central node on the grid is easier to support as a CNE than the center of the two-dimensional convex square, which has a threshold of ${\overline{c}}(u)=0.5$. This does not say anything about whether CNE exist on interior points of an edge (non-nodes)—we will consider this next.

Fig. 6

CNE on nodes in the case of $M = 6$. The numbers at the nodes of the grid indicate the threshold values ${\overline{c}}(u)$ corresponding to those nodes

Next, we turn our attention to points interior to an edge. It is so far not clear when a point on an edge between two nodes would be a CNE—whether this would be easier or harder to support than a node. Let $u=(x-\epsilon ,y)$, where $x, y\ge 1$ and $0< \epsilon <1$, and let $u'=(x-1,y-1+\epsilon )$. Given these two points, again the grid can be partitioned into four regions: two regions of indifferent consumers in the northwest and southeast and, in the northeast and southwest, consumers preferring u and $u'$, respectively (see Fig. 15a). Let $NW'$, $NE'$, $SE'$ and $SW'$ denote these regions and let NW, NE, SE and SW be the areas defined above during the comparison of (x, y) with $(x-1,y-1)$. Then we have the following formulas:

$$\begin{aligned} |NW'|&=|NW|+\epsilon (M+x-y-1); \quad |SE'| =|SE| ;\\ |SW'|&=|SW|-\epsilon ({M/2}+x-1); \quad |NE'| =|NE|-\epsilon ({M/2}-y). \end{aligned}$$

Note that the case where $u=(x,y-\epsilon )$ follows by symmetry.

Another important point to consider will be $u'=(x-1-\epsilon , y-1)$, when $x>1$ and $y\ge 1$. In a similar fashion, we again partition the grid into areas of indifferent consumers in the northwest and southeast, consumers who prefer u in the northeast and consumers who prefer $u'$ in the southwest (see Fig. 15b). The number of consumers in these areas, denoted $NW''$, $SW''$, $SE''$ and $NE''$, are given by the following formulas:

$$\begin{aligned}|NW''|&=|NW|-M+2y-1; \quad |SE''| =|SE| ;\\ |SW''|&=|SW|-\epsilon ; \quad |NE''| =|NE|+M-2y+1+\epsilon . \end{aligned}$$

With these definitions, Theorem 4 provides an analogous characterisation of CNE to Theorem 3, but for points interior to edges rather than nodes.

Theorem 4

Let $u=(x-\epsilon , y)$, where $x>0$ and $0<\epsilon <1$, be occupied by m firms. The deviation $u'$ of a single firm that maximises ${K_{u'\succ u}}/{K_{u\succ u'}}$ is among the following:

• (i) If $y>0$ and $x>1$, the point $(x-1,y-1+\epsilon )$, just to the north it, or the point just to the east of $(x-1-\epsilon , y-1)$.

• (ii) If $y>0$ and $x=1$, the point $(x-1,y-1+\epsilon )$, just north of it, or the point $(x-1,y-1)$.

• (iii) If $y=0$, the point $(x-1,0)$.

• (iv) Cases that are symmetric to (i)–(iii).

Therefore, in case (i),

$$\begin{aligned} K(u)=\max \left\{ \frac{|NW'|+|SW'|}{|NE'|+|SE'|},\frac{|SW'|}{|NE'|},\frac{|SW''|+|SE''|}{|NW''|+|NE''|}\right\} .\end{aligned}$$

(6)

In case (ii),

$$\begin{aligned} K(u)=\max \left\{ \frac{|NW'|+|SW'|}{|NE'|+|SE'|},\frac{|SW'|}{|NE'|},\frac{K_{{\overline{u}}\succ u}}{K_{u\succ {\overline{u}}}}\right\} , \end{aligned}$$

(7)

where ${\overline{u}}=(x-1,y-1)$ and

$$\begin{aligned} \frac{K_{{\overline{u}}\succ u}}{K_{u\succ {\overline{u}}}}=\frac{({M/2}+y)(2M+1) -{1/2}(M+\epsilon )}{({M/2}-y)(2M+1)+{3M/2}+{\epsilon /2}}.\end{aligned}$$

(8)

In case (iii),

$$\begin{aligned} K(u)=\frac{({M/2}+x)(2M+1)-{M/2}-{1/2}+{\epsilon (M-1)/2}}{({M/2}-x)(2M+1)+{3M/2}+{1/2}-{\epsilon (M-1)/2}}.\end{aligned}$$

(9)

Thus, by Theorem 1, u is a CNE if and only if $K(u)\le \frac{1}{c(\mathbf{p},m)}-1$ and the threshold value of $c(\mathbf{p},m)$ below which u can be supported as a CNE is ${\overline{c}}(u)=\frac{1}{K(u)+1}$.

Proof

See Appendix. $\square$

Theorem 4 has a number of implications. First, Corollary 1 presents some properties of K(u) that follow from both Theorems 3 and 4. It says that, at any point u except for the central node (0, 0), increasing M increases the threshold ${\overline{c}}(u)$—u becomes easier to support, as it is increasingly central. Increasing x or y, for fixed M, on the other hand, decreases ${\overline{c}}(u)$. This similarly makes sense—we reach less central points that can be supported for a smaller range of probability vectors $\mathbf{p}$. For $u=(0,0)$, increasing M makes the central node more difficult to support. This is because, as M increases, the best deviation from the center becomes increasingly attractive: in the limit you essentially get half the consumers, and the small difference in the number of consumers preferring point u over $u'$ becomes negligible.

Corollary 1

Let u be a point on the grid. Then K(u) is:

• (i) Increasing in M, holding $u=(0,0)$ fixed;

• (ii) Decreasing in M, holding $u\ne (0,0)$ fixed;

• (iii) Increasing in x or y, holding M fixed.

At all points u, K(u) converges towards 1 as M tends to infinity.

Proof

See Appendix.$\square$

When comparing nodes to interior points on edges, Theorem 4’s formulas for K(u) resemble those obtained in Theorem 3 except that there is an additional $\epsilon$ term on the numerator and denominator. Consider how K(u) depends on $\epsilon$. This is important because it tells us which end of a given edge is more likely to support a CNE. We might expect, based on our previous results, a CNE to be easiest to support at the end of the edge closer to the center of the grid. However, the dynamics are surprisingly complex, and the patterns are not unambiguous. What matters for whether u is a CNE is its position relative to $u'$, the best deviation from u. As $\epsilon$ increases within an edge, the best deviation may change in several ways. First, the point(s) around which the best deviation is located themselves may depend on $\epsilon$ (Theorem 4(i), (ii)). Second, in our expressions (6) and (7) for K(u), which of the arguments attains the maximum may switch. Third, as in Theorem 4(iii), the best move may not actually change when $\epsilon$ changes. As a consequence, it turns out that, within an edge, K(u) maybe increasing or decreasing in $\epsilon$.

In many cases, within an edge, as $c(\mathbf{p},m)$ decreases, the set of CNE “grows inwards” towards the center. That is, points further away from the center or a central axis can be easier to support than points closer to the center. This seemingly counterintuitive result can be understood by considering the example where $u=(x-\epsilon ,0)$. Then the best move is to $u'=(x-1,0)$. As $\epsilon$ increases, more of the consumers on the edge between u and $u'$ start to prefer u over $u'$. However, along the horizontal edges between $(x-1,z)$ and (x, z) for $z\ne 0$, more consumers along these paths begin to prefer $u'$. This makes $u'$ look relatively more attractive (more precisely, the ratio $K_{u'\succ u}/K_{u\succ u'}$ increases) as $\epsilon$ increases, so u will be harder to support as a CNE.

Fig. 7

CNE on edges in the case of $M = 6$. For points in the interior of an edge (non-nodes), the arrows indicate the direction of decrease of the threshold values within the given edge

Example 3

We return to the case of $M=6$ and consider edges. Using Theorem 4 we can calculate how the threshold value ${\overline{c}}(u)$ varies along edges. The arrows in Fig. 7 point in the direction of decreasing ${\overline{c}}(u)$, i.e., from points with higher thresholds towards points with lower thresholds. In general, within a given edge, as we move “towards the center” of the grid, points become harder to support. However, not for the outermost edges (where $y={M/2}$ or $x={M/2}$), on which, within an edge, it actually becomes harder to support points as we move away from the axes towards the diagonal. Figures 8, 9, 10 and 11 plots the threshold value of $c(\mathbf{p},m)$ as x and $\epsilon$ change for fixed values of y.

Fig. 8

Threshold ${\overline{c}}(u)$ along the segment from (0, 0) to (3, 0)

Fig. 9

Threshold ${\overline{c}}(u)$ along the segment from (0, 1) to (3, 1)

Fig. 10

Threshold ${\overline{c}}(u)$ along the segment from (0, 2) to (3, 2)

Fig. 11

Threshold ${\overline{c}}(u)$ along the segment from (0, 3) to (3, 3). The jump at the point (0, 3) is not to scale—it would be too small to distinguish. The key point is that there is a jump down from the limiting value as x approaches 0 and the value at (0, 3)

Another striking feature apparent in Figs. 8, 9, 10 and 11 are the discontinuities in the threshold value of $c(\mathbf{p},m)$ at nodes when $\epsilon$ approaches 1. This implies that within in a small region near an intersection of city streets, some points are predicted to exhibit CNE substantially more often than others, despite their proximity. This is formalised in the following corollary.

Corollary 2

The threshold ${\overline{c}}(u)$:

• (i) Is continuous as $\epsilon$ approaches 0 at nodes (x, y), $x\ge 1$. That is, $\lim _{\epsilon \rightarrow 0}{\overline{c}}(x-\epsilon ,y)={\overline{c}}(x,y)$.

• (ii) Is not in general continuous as $\epsilon$ approaches 1 at nodes (x, y). That is, $\lim _{\epsilon \rightarrow 1}{\overline{c}}(x-\epsilon ,y)$ is not generally equal to ${\overline{c}}(x,y)$.

Example 4

For several illustrative values of $c({\mathbf {p}},m)$, the set of CNE, including edges, is displayed in Fig. 12. As $c({\mathbf {p}},m)$ decreases, the set of CNE expands. For high values of $c({\mathbf {p}},m)$, CNE do not exist. The first point to support a CNE is the central node which, as noted in Example 2, is easier to support as a CNE than the center of the two-dimensional convex square. The next easiest points to support are the nodes (0, 1), (1, 0), $(-1,0)$ and $(0,-1)$. As far as nodes go, this is what we expect, as these are the next most central nodes. However, the edges connecting these nodes to (0, 0) are not yet CNE, despite being seemingly more central. Moreover, on one of these edges, the end of the edge that more easily supports CNE is the end further from the center of the grid, illustrating how the set of CNE may “grow inwards” along edges towards the center of the grid.

It is also interesting to note that there may be some intervals in the value of $c({\mathbf {p}},m)$ over which there is no change in the set of equilibria. For example, consider the bottom two cases displayed in Fig. 12. Every point on the edge between (2, 2) and (3, 2) has become a CNE once $c({\mathbf {p}},m)$ reaches 0.051, but points on the edge from (2, 3) to (3, 3) do not start becoming CNE until $c({\mathbf {p}},m)$ reaches about 0.290. For $c({\mathbf {p}},m)$ between these values, there is no change in the set of CNE.

Finally, on the square convex market the boundaries of the market cannot be supported as CNE for any $\mathbf{p}$. On the grid, in contrast, every point can eventually be supported as a CNE, when $c(\mathbf{p},m)$ is low enough. This is because, for any two points, each always has a positive measure of consumers preferring it over the other point.

Fig. 12

CNE in the case of $M=6$ for different values of $c(\mathbf{p },m)$. Not exactly to scale

3 Conclusion

In a real city firms are typically not restricted to just a linear “Main Street” when deciding where to set up shop, but rather the space of possible locations is two-dimensional. Even then, they are two-dimensional in a very restricted sense—firms locate along streets, the same streets that consumers must travel in order to shop. At the same time, most previous papers assume that consumers always purchase from the nearest firm when, more realistically, they are only more likely to.

We study the existence and properties of CNE in a spatial setting that incorporates both of these more realistic elements. The results, aside from providing detailed new characterisations of CNE, point to interesting new phenomena that future research should look to explore further in a broader range of contexts. For example, in our study of networks, positive masses of indifferent consumers arise and play an important role. This suggests that allowing for the possibility of point masses of consumers, which are often assumed away in the previous literature, may be important more generally. In the workhorse one-dimensional Main Street model, for example, it may make sense to allow atomic distributions of customers if there are certain access points through which consumers arrive to the market, which may be fiercely contested by the firms. In the political interpretation, too, there may be point masses of voters at certain natural policy positions (far left, center left, etc.).

Future work may also investigate other extensions in combination with one or both of the two features studied here. Examples include price competition (Heijnen and Soetevent 2018), other consumer distributions (Tarbush 2018; Fournier 2019), network externalities (Ahlin and Ahlin 2012; Peters et al. 2018), and Voronoi game settings. Additionally, our results are informative about the forces that lead to the clustering of firms at a single commercial center, but do not shed light on non-convergent equilibria and how their existence and properties depend on network structure and consumer shopping behaviour—intuitively, we might expect multiple commercial centers to arise in more spread out, loosely connected cities. This is non-trivial even in the unit interval case (Cahan and Slinko 2017; Cahan et al. 2018), but remains important to our understanding of clustering in real cities. Even more ambitious would be to study a model where the network itself endogenously arises as the firms compete. Finally, some of the implications of our model might be amenable, in principle, to an empirical analysis of the prevalence of clustering at different locations as a function of city layout and shopping behaviour (proxied by firm type).

Appendix

Proof of Theorem 4

First, let us consider case (i). Consider the point $u=(x-\epsilon ,y)$, where $x>1$ and $y>0$ are integers and $0<\epsilon <1$. Consider a firm deviating to $(x-\epsilon -\eta ,y)$, where $\eta >0$ is small. As in the case where u is the node (x, y), it would be better to deviate to the node $(x-1,y)$, because by moving to the left the firm is gaining from consumers along multiple edges and is losing from only one edge.

Fig. 13

Comparing the move just north of $(x-1,y-1+\epsilon )$ to the move just west of $(x-1-\epsilon ,y-1)$. Thick black lines indicate consumers preferring $u'$ to u; thin black lines: consumers preferring u to $u'$

Upon reaching the node, the firm would then want to continue deviating towards $(x-1,y-1)$ because, again, there are more edges from which the firm is gaining consumers than from which it is losing. However, the firm will continue to gain only until it reaches the point $(x-1,y-1+\epsilon )$, at which point the northwest and southeast corners become indifferent (see Fig. 15a). Therefore, the move that maximises ${K_{u'\succ u}}/{K_{u\succ u'}}$ could be $(x-1,y-1+\epsilon )$, just to the north, or just south of it. However, the latter move is actually dominated since by continuing to move down the edge towards $(x-1,y-1)$ the number of edges from which the firm is gaining consumers exceeds those from which it is losing consumers. Even on reaching $(x-1,y-1)$, since $x>1$, there is a further incentive to deviate west, to the point $(x-1-\epsilon ,y-1)$. Here, there is another discontinuity in the score (see Fig. 15b) so the following points could also potentially be the best deviation: $(x-1-\epsilon ,y-1)$, just to the east, or west of it.

It turns out, however, that of the latter three points, only the point just east of $(x-1-\epsilon ,y-1)$ is not dominated by another deviation. To see this, first consider the deviation to a point inifinitesimally west of $(x-1-\epsilon ,y-1)$. This is dominated by the deviation infinitesimally north of $(x-1,y-1+\epsilon )$. This can clearly be seen by comparing the two panels in Fig. 13.¹⁵

As for the deviation to precisely the point $(x-1-\epsilon , y-1)$, it is dominated by the move precisely to $(x-1,y-1+\epsilon )$. To see this, we show that ${|SW'|}/{|NE'|}>{|SW''|}/{|NE''|}$. That is,

$$\begin{aligned}\frac{|SW|-\epsilon ({M/2}+x-1)}{|NE|-\epsilon ({M/2}-y)}>\frac{|SW|-\epsilon }{|NE|+M-2y+1+\epsilon }. \end{aligned}$$

This can be expressed as

$$\begin{aligned}&|SW|(2+\epsilon ) ({M/2}-y+1)+2\epsilon |NE| >\epsilon ^2({M/2}-y)\nonumber \\&\quad +\epsilon ({M/2}+x-1)(M-2y+1+\epsilon )+\epsilon |NE|({M/2}+x). \end{aligned}$$

(10)

That inequality (10) is true follows from the following three facts: (a) $2|SW|({M/2}-y+1)> \epsilon |NE| ({M/2}+x)$; (b) $\epsilon |SW| ({M/2}-y+1)> \epsilon ({M/2}+x-1)(M-2y+1+\epsilon )$; and, (c) $2\epsilon |NE|>\epsilon ^2({M/2}-y).$ Inequality (a) can be written as

$$\begin{aligned}4({M/2}\!+\!x)({M/2}\!+\!y)({M/2}\!-\!y\!+\!1)>2\epsilon ({M/2}-x\!+\!1)({M/2}\!-\!y+1)({M/2}+x)\end{aligned}$$

which, cancelling terms, is clearly true. Inequality (b) can be rewritten as

$$\begin{aligned}2({M/2}+x)({M/2}+y)({M/2}-y+1)> 2({M/2}+x-1)({M/2}-y+{(1+\epsilon )/2}).\end{aligned}$$

Again, this is clearly true. Finally, (c) states that $2\epsilon ({M/2}-x+1)({M/2}-y+1)>\epsilon ^2({M/2}-y)$, also true.

Hence, there are three possibilities for the best deviation from u: the move to $(x-1,y-1+\epsilon )$, just north of it, or just east of $(x-1-\epsilon ,y-1)$. Thus, K(u) will be given by Eq. (6) and we have proven case (i).

Fig. 14

Possible deviation from a point u. Thick black lines indicate consumers preferring $u'$ to u; thin black lines: consumers preferring u to $u'$

For case (ii), where $x=1$ and $y>0$, the argument is similar to above. Two possibilities for the best deviation are the point $(x-1,y-1+\epsilon )$ and the point just north of it. The third possibility is the point ${\overline{u}}=(x-1,y-1)$—the firm would not continue west this time because it would gain and lose consumers from the same number of edges (see Fig. 14e). In case (ii), therefore, we have equations (7) and (8).

For case (iii), $u=(x-\epsilon ,0)$, where $x>0$ and $0<\epsilon <1$. We show the move that maximises $\nicefrac {K_{u'\succ u}}{K_{u\succ u'}}$ is to the point $(x-1,0)$. Consider a deviation by i to a point further along the same edge $(x-\epsilon -\eta ,0)$ for very small $\eta >0$. This is not the best deviation because i could continue further towards the node $(x-1,0)$ and gain customers from all the parallel horizontal edges, while only losing customers from the edge on which it is located. It follows that the best deviation would be to $u'=(x-1,0)$. In this case,

$$\begin{aligned} K(u) =\frac{|K_{u'\succ u}|}{|K_{u\succ u'}|}&=\frac{({M/2}+x-1)(M+1)+({M/2}+x)M+M-(M-1)(1-\epsilon )/2}{({M/2}-x+1)M+({M/2}-x)(M+1)+1+(M-1)(1-\epsilon )/2}\\ {}&=\frac{M^2+(2M+1)x-{1/2}+{\epsilon (M-1)/2}}{M^2+2M-(2M+1)x+{1/2}-{\epsilon (M-1)/2}}. \end{aligned}$$

$\square$

Fig. 15

Possible deviations from a point u in the interior of an edge. Thick black lines indicate consumers preferring $u'$ to u; thin black lines: consumers preferring u to $u'$; dotted lines: consumers indifferent between $u'$ and u

Proof of Corollary 1

Case (i) follows by simply differentiating (5) with respect to M. For (ii), we first show that each of the arguments in the maximum function in equation (6) is decreasing in M. From this, the case where u is a node follow by setting $\epsilon =0$ because (6) reduces to (3) (in fact, in the following proof (6) would be decreasing in M even allowing $x=1$, which corresponds to nodes where $x=1$).

Consider $|SW'|/|NE'|$. Differentiating with respect to M, the derivative is negative if and only if

$$\begin{aligned} (M-x&-y-{\epsilon /2}+2)(2({M/2}+x)({M/2}+y) -\epsilon ({M/2}+x-1))\\ {}&-(M+x+y-{\epsilon /2})(2({M/2}-x+1)({M/2}-y+1)-\epsilon ({M/2}-y))>0. \end{aligned}$$

This can be rewritten as

$$\begin{aligned} 2(x+y-1)(M(M+2)-\epsilon (M-x+y+3) +2(x+y-2xy)+{\epsilon ^{2}/2})>0, \end{aligned}$$

which is equivalent to

$$\begin{aligned}(x+y-1)(M^2+2M-\epsilon M+\epsilon x-\epsilon y-3\epsilon +2x+2y-4xy+{\epsilon ^{2}/2})>0.\end{aligned}$$

By assumption $x+y-1> 0$ and the term in the second set of brackets can be written as

$$\begin{aligned} (M^2-4xy) +M(2-\epsilon )+y(1-\epsilon )+(2x+y-3\epsilon )+\epsilon x+{\epsilon ^{2}/2}. \end{aligned}$$

That this is positive follows from the facts that $1\le x, y\le {M/2}$ and $0\le \epsilon <1$.

Next, consider ${(|NW'|+|SW'|)/(|NE'|+|SE'|)}$. This can be simplified to

$$\begin{aligned}\frac{({M/2}+x)(2M+1)-{M/2}+y-1+\epsilon ({M/2}-y)}{({M/2}-x+1)(2M+1)-{M/2}-y-\epsilon ({M/2}-y)}.\end{aligned}$$

Differentiating with respect to M, the derivative is negative if and only if

$$\begin{aligned}M^2(4x+\epsilon -2)+(4M+2)(x+y(1-\epsilon )-1)>0,\end{aligned}$$

which is certainly true.

Similarly, consider $(|SW''|+|SE''|)/(|NW''|+|NE''|)$. This can be simplified to

$$\begin{aligned}\frac{M^2+2My+x+y-\epsilon -1}{M^2-2My+2M-x-y+1+\epsilon }.\end{aligned}$$

Differentiating with respect to M, the derivative is negative if and only if

$$\begin{aligned} (2y-1)M^2+2M(x-\epsilon )+2M(y-1)+x+y-1-\epsilon >0. \end{aligned}$$

Given $y>0$, $x>1$ and $0\le \epsilon <1$, this is certainly true.

Next consider the case where $u=(x-\epsilon , y)$ where $y>0$ and $x=1$. It is straightforward to show that, in a similar fashion to the above, (8) is decreasing in M. In particular, its derivative is negative if and only if

$$\begin{aligned}(4y-2)M^2+4My+2y(\epsilon +1)-\epsilon >0,\end{aligned}$$

which is evidently true in this case.

Last, we consider the case where, without loss of generality, $y=0$. The derivative of (9) will be negative if and only if

$$\begin{aligned}M^2(4x+\epsilon -2)+(2M+1)(2x-1-\epsilon )>0,\end{aligned}$$

which is always true.

To prove (iii), if $x>0$, it is easy to see that $|SW'|$, $|NW'|+|SW'|$ and $|SW''|+|SE''|$ are all increasing in x, while $|NW'|$, $|NE'|+|SE'|$ and $|NW''|+|NE''|$ are decreasing in x. Thus, the ratios in (6) are all increasing. This is true even when $\epsilon =0$ and when $x=1$, so the case of nodes follows. The same holds true when y increases. We also need to check the case where $x=1$, i.e., $u=(1-\epsilon , y)$. Two of the arguments in the maximum in (7) are the same as in the previous case, hence increasing in x, and it can also be shown that (8) is less than ${(|SW''(v)|+|SE''(v)|)/(|NW''(v)|+|NE''(v)|)}$ for $v=(2-\epsilon ,y)$. Thus, (8) will be less than K(v).

When $y=0$, it is clear that (9) is increasing in x. Finally, we need to show that K(u) is increasing when $x=0$ and $y>1$. By symmetry, consider instead $u=(x-\epsilon , 0)$ and $v=(x-\epsilon ,1)$. We show that $K(u)< K(v)$. Consider a deviation from v to just north of $v'=(x-1, y-1+\epsilon )$. For this move,

$$\begin{aligned}\frac{K_{v'\succ v}}{K_{v\succ v'}}=\frac{|NW'(v)|+|SW'(v)|}{|NE'(v)|+|SE'(v)|}\le K(v).\end{aligned}$$

Using Eq. (9), after a bit of algebra it can be shown that $K(u)<K(v)$. $\square$