Spatial Cournot Competition

Abstract

This chapter reviews the literature on spatial Cournot competition with endogenous firms’ locations in the past 30 years, which started from Hamilton et al. (Spatial Discrimination: Bertrand vs. Cournot in a Model of Location Choice. Regional Science and Urban Economics, 19, 87–102, 1989) and Anderson and Neven (Cournot Competition Yields Spatial Agglomeration. International Economic Review, 32, 793–808, 1991). Linear markets and circular markets are two main streams in the spatial Cournot models. Overall speaking, spatial Cournot models can capture the real-world regularity (agglomeration at the market center) observed by Harold Hotelling and escape from the undercutting trap in Hotelling (Stability in Competition. Economic Journal, 39, 41–57, 1929). Moreover, diverse location patterns are shown in circular markets.

1 Introduction

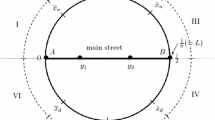
Competitive location theory started with Hotelling (1929),¹ who assumed that there are two identical firms selling homogenous goods to consumers living along a linear market with unit length (the “main street”). These consumers are uniformly distributed along this main street, and each buys exactly one unit of the product from the firm with the lowest full price (mill price plus linear transport cost). Firms pursue maximization of their own profits. They decide their locations simultaneously in the first stage of the game. In the second stage, they simultaneously determine the prices of their products. Hotelling (1929) “showed” that in equilibrium, these two firms will locate at the center of the linear market and share the market equally.

At first glance, Hotelling’s model seems correct, so his model was later heavily cited, and there were many extended studies, such as Lerner and Singer (1937), Smithies (1941), and Downs (1957). However, 50 years later, D’Aspremont et al. (1979) proved that Hotelling’s equilibrium result is invalid. The reason is that when the two firms locate close to one another, the price equilibrium provided by Hotelling (1929) cannot be sustained, because one of them will undercut the other and monopolize the entire market. In this situation, the profit of the undercutting firm is higher than what it would earn under co-existence, so the equilibrium of the Hotelling (1929) model is invalid; in fact, it is wrong.² D’Aspremont et al. (1979) proposed to use quadratic transport cost functions instead of linear transport cost functions, in order to make the game structure be correct, such that a price equilibrium exists for any location pair. However, their modification needs to pay a price, that is, the equilibrium locations will be at the two ends of the linear market, which is very different from Hotelling’s observation about the reality.³

Since the Hotelling (1929) model had already been misused for 50 years at the time of d’Aspremont et al.’s work in 1979, once the model was proved to be wrong, its impact on the academic world was foreseeable. Many scholars have tried to save the Hotelling (1929) model with slight modifications or directly switch to using quadratic transport cost functions to avoid the game structure problem. Several attempts will be briefly introduced in the following, where spatial Cournot competition will be highlighted.

2 Attempts to Save the Hotelling (1929) Model

2.1 Non-Cournot Models

First, Graitson (1980) employed the max-min strategy for the two firms and thus changed the game structure. In his model, even though the opponent’s price is reduced to zero, one firm can keep some parts of the market (and have a positive profit) by pricing just below the rival’s price at its own position, or it can relocate to a point far enough away from the opponent’s location that its rival will not undercut its price, and both firms can co-exist in the market. As a result, he found that the co-existence scenario dominates the max-min scenario and the final equilibrium locations fall at a quantile from both ends of the market.

Osborne and Pitchik (1987) allowed the firms in the Hotelling (1929) model to take mixed strategies in the price subgame. By way of their complex calculation process (solving a number of highly non-linear equations and some inequalities), they found approximate price equilibrium solutions for any combination of locations, although they couldn’t really prove these price equilibria. This is because under mixed strategies, the strategy space of any price is a continuous interval, which made them unable to completely describe these mixed strategy equilibria. Even though they did not provide an analytical proof for the price equilibria that they proposed, the rigor of their arguments prevented the academic community from questioning the correctness of these price equilibria. Returning to the first stage (the location stage), if the location behavior is limited to pure strategies, they confirmed that there is (in a symmetrical sense) a unique subgame perfect equilibrium, where the firms’ locations fall at about 0.27 from the two endpoints, respectively. Finally, they also calculated that if these firms are allowed to use mixed strategies in the location stage, then there is only one equilibrium in the symmetric case. Their greatest contribution was “confirming” (although they were unable to prove) that the Hotelling (1929) model has a unique location-price equilibrium as long as the firms are allowed to adopt mixed strategies.

Vogel (2008) concluded that because the profit functions of the Hotelling (1929) model are not globally quasi-concave, there is no pure-strategy equilibrium in some of the price subgames, so the Hotelling (1929) model does not have a pure-strategy subgame perfect Nash equilibrium (SPNE). Vogel (2008) constructed a model with several heterogeneous firms located on a unit circle and introduced an auxiliary game to redefine the indifferent consumers. He showed that when the difference of marginal production costs between any two adjacent firms is sufficiently small, there always exists an indifferent consumer between them, so a pure-strategy price equilibrium in each subgame exists.

Vogel (2008) also proved that as long as the marginal cost between firms is small enough, the auxiliary game’s profit is an upper bound on the real game and any unilateral deviation strategy is unprofitable. In short, Vogel (2008) did not directly calculate the equilibrium solution of the Hotelling (1929) model (in fact, it does not exist), but indirectly obtained the equilibrium of the model by redefining the indifferent consumers, which is quite clever.

Anderson (1988) used the linear-quadratic transport cost function and found that unless the two firms are at the same point (and thus the equilibrium price is zero), undercutting always exists. Therefore, the linear-quadratic transport cost functions still cannot solve the problem of undercutting.

In a larger sense, all the above attempts either failed in the agglomerate result (say Graitson 1980; Anderson 1988) or used abstract mathematical methodology (say Osborne and Pitchik 1987; Vogel 2008), and thus none are fully satisfactory.

2.2 Spatial Cournot Models

2.2.1 Linear Models

It was not until Anderson and Neven (1991)⁴ adopted the spatial Cournot competition model that the problem of inconsistency between the observation of reality and the mathematical problem of the Hotelling (1929) model was properly solved.⁵ Anderson and Neven (1991) assumed that the demand at every point x ∈ [0, 1]⁶ of the market is elastic:

$$ p(x)=a-b\left({q}_1(x)+{q}_2(q)\right), $$

where p is the market price, a > 0, b > 0 are parameters; and q _i(x), i = 1, 2 are the quantity at x supplied by firm i, where their locations are x₁ ∈ [0, 1] and x₂ ∈ [0, 1], respectively. Shipping costs are also linear in distance. They proved that the two firms (even in the case of n firms) will choose the same location at the center of the market (i.e., x₁ = x₂ = 1/2). The critical contribution of Anderson and Neven (1991) is that the agglomeration regularity in the real world was supported from a theoretical aspect while keeping the linear transport rate the same as that in Hotelling (1929), but without any game structure problem.⁷

For x ∈ [0, 1], the profit functions are π_i(x) = [a − bQ(x) − t(x − x_i)] · q_i(x), i = 1, 2, where Q(·) = q₁(·) + q₂(·). Then we can solve for

$$ {q}_i(x)=\frac{a+t\left(|{x}_j-x|\right)-2t\left(|{x}_i-x|\right)}{3b},\vspace*{-12pt} $$

(2.1)

$$ p(x)=\frac{a+t\left(|{x}_i-x|\right)+t\left(|{x}_j-x|\right)}{3}, \vspace*{-12pt}$$

(2.2)

$$ Q(x)=\frac{2a-t\left(|{x}_i-x|\right)-t\left(|{x}_j-x|\right)}{3b}, \vspace*{-12pt}$$

(2.3)

$$ {\displaystyle\begin{array}{l}{\pi}_i(x)=\frac{{\left[a+t\left(|{x}_j-x|\right)-2t\left(|{x}_i-x|\right)\right]}^2}{9b},\kern1em i=1,2,\kern1em j=1,2,\kern1em i\ne j.\end{array}} $$

(2.4)

The total profit for firm i is

$$ {\displaystyle \begin{array}{c}{\Pi}_i(x)=\underset{0}{\overset{x_1}{\int }}{\pi}_i\left(x;{x}_1,{x}_2\right) dx+\underset{x_1}{\overset{x_2}{\int }}{\pi}_i\left(x;{x}_1,{x}_2\right)\\ {}+\underset{x_2}{\overset{1}{\int }}{\pi}_i\left(x;{x}_1,{x}_2\right) dx,\kern1em i=1,2.\end{array}} $$

(2.5)

When the transport cost function is linear in distance, we can solve ∂Π₁/∂x ₁ = 0 and ∂Π₂/∂x ₂ = 0 simultaneously, yielding ${x}_1^{\ast }={x}_2^{\ast }=1/2$. This agglomeration result is also valid when there are n firms.

Ever since Anderson and Neven (1991) obtained an agglomeration equilibrium, many scholars have tried to obtain dispersed location equilibria under the spatial Cournot setting. The first attempt was by Chamorro-Rivas (2000a), who proved that if the reservation price in Anderson and Neven (1991) model is low enough, there is a dispersed location equilibrium in addition to the equilibrium in which firms agglomerate at the center of the market.

In Anderson and Neven (1991), the reservation price for each consumer (a) is assumed to be large (a > 2t) to ensure all market areas are served by the two firms. Chamorro-Rivas (2000a) discussed the scenarios of t ≤ α ≤ 2t, such that some areas are only served by one of the firms.⁸ In other words, the whole market can be divided into monopoly areas and duopoly areas, and the percentage of the former will increase as α decreases. After some calculations, he concluded that there exists a unique equilibrium location pair: $\left({x}_1^{\ast },{x}_2^{\ast}\right)=\left(1/2,1/2\right)$, when $\frac{3}{2}t\le \alpha \le 2$; there exist two equilibrium location pairs, $\left({x}_1^{\ast },{x}_2^{\ast}\right)=\left(1/2,1/2\right)$ and $\left({x}_1^{\ast },{x}_2^{\ast}\right)=\left(\frac{2 \alpha-t}{4t},1-\frac{2\alpha -t}{4t}\right)$, when $\frac{11}{10}t\le \alpha \le \frac{3t}{2}$; and when $t\le \alpha \le \frac{11}{10}t$, there exist two equilibrium location pairs: $\left({x}_1^{\ast },{x}_2^{\ast}\right)=\left(1/2,1/2\right)$, and ${x}_1^{\ast }=\frac{1}{434t}\left(208t-46\alpha -4\sqrt{-117{t}^2+540\alpha t-356{\alpha}^2}\right)$, ${x}_2^{\ast }=1-{x}_1^{\ast }$.

Chen and Lai (2008) further extended Chamorro-Rivas (2000a) to include zoning policy, where the government can prohibit firms from locating in the area (z, 1 − z) in order to preserve the amenities in this area. They showed that firms will locate at the boundary of the zoning area, that is, $\left({x}_1^{\ast },{x}_2^{\ast}\right)=\left[z,1-z\right]$. They also calculated the optimal zoning policy under different reservation prices. After some calculations, their results can be summarized as in Fig. 2.1, where $\beta \equiv \frac{\alpha }{t}$ and β ≥ 1. The results obtained in Chamorro-Rivas (2000a) (i.e., no zoning) are plotted by dashed lines, and the optimal zoning varies with β. From Fig. 2.1, it is noticed that the government can enact a proper zoning policy to improve social welfare.

Fig. 2.1

The results in Chen and Lai (2008)

Pal and Sarkar (2002) extended Anderson and Neven (1991) to allow each firm to choose multiple stores. They showed that every store will locate at its quantity-median point, where the total transport costs to its right-hand-side market equal those of its left-hand-side market. If m is the number of stores for firm 1 and n is the number of stores for firm 2, then their numerical analysis showed that ${x}_1^{\ast }=1/2$, ${y}_1^{\ast }=1/2$ when m = n = 1; ${x}_1^{\ast }=1/4={y}_1^{\ast }$, ${x}_2^{\ast }=3/4={y}_2^{\ast }$ when m = 2, n = 2, and when m = 1, n = 2, ${x}_1^{\ast }=1/2$ and ${y}_1^{\ast }=a-\sqrt{a^2-\frac{a}{2}+\frac{1}{8}}$, ${y}_2^{\ast }=1-{y}_2^{\ast }$. Note that their model obtained agglomeration location equilibrium and separation location equilibrium, depending on the number of plants.

Matsumura and Shimizu (2005) explored the welfare effects of the spatial Cournot model. They calculated the consumer surplus at each point of the market, and the profit of two (or more) firms, and found that the socially optimal locations are farther away than the equilibrium locations. However, the equilibrium locations will be farther away than the locations where the consumer surplus is maximized.

Mayer (2000) showed that firms agglomerate at the center when the production costs are identical at every point of the linear market or when the production costs are minimized at the center. Firms do not agglomerate at the center when the production costs have a globally concave distribution with the highest production costs at the center.

Gupta et al. (1997) examined the location equilibrium in Anderson and Neven (1991) with non-uniform population density functions. They showed that the agglomeration equilibrium is robust in most scenarios.

2.2.2 Circular Markets

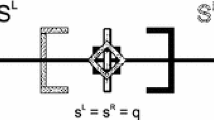
Another breakthrough path for spatial Cournot competition started when Pal (1998) modified the Anderson and Neven (1991) model into a unit-length circular market and proved that the firms’ locations are maximally separated, that is, the firms will locate at both ends of a diameter. Pal (1998) assumed a unit-length circular market, and assumed x ₂ = 1/2, while 0 ≤ x ₁ ≤ 1/2. For x ∈ (0, 1), the profit of firm 1 is

$$ {\pi}_1\left(x;{x}_1,{x}_2\right)=\frac{{\left(\alpha -2t|{x}_1-x|+t|{x}_2-x|\right)}^2}{9b}. $$

(2.6)

In the first stage, firm 1’s objective is

$$ \underset{x_1}{\max }{\Pi}_1\left({x}_1,{x}_2\right)={\int}_0^1{\pi}_1\left(x;{x}_1,{x}_2\right) dx. $$

(2.7)

Given x ₂ = 1/2 and 0 ≤ x ₁ ≤ 1/2, we have

$$ {\displaystyle \begin{array}{c}{\Pi}_1\left({x}_1,\frac{1}{2}\right)=\underset{0}{\overset{x_1}{\int }}\frac{{\left[\alpha -2t\left({x}_1-x\right)+t\left(\frac{1}{2}-x\right)\right]}^2}{9b}\; dx\\ {}+\underset{x_1}{\overset{\frac{1}{2}}{\int }}\frac{{\left[\alpha -2t\left(x-{x}_1\right)+t\left(\frac{1}{2}-x\right)\right]}^2}{9b}\; dx\\ {}+\underset{x_1}{\overset{\frac{1}{2}}{\int }}\frac{{\left[\alpha -2t\left(x-{x}_1\right)+t\left(\frac{1}{2}-x\right)\right]}^2}{9b}\; dx\\ {}+\underset{\frac{1}{2}+{x}_1}{\overset{1}{\int }}\frac{{\left[\alpha -2t\left(1-x+{x}_1\right)+t\left(x-\frac{1}{2}\right)\right]}^2}{9b}\; dx.\end{array}} $$

(2.8)

The first-order condition and the second-order condition are solved as follows:

$$ \frac{d{\varPi}_1\left({x}_1,\frac{1}{2}\right)}{d{x}_1}=\frac{4{t}^2{x}_1\left(2{x}_1-1\right)}{9b}, $$

(2.9)

$$ \frac{d{\varPi}_1^2\left({x}_1,\frac{1}{2}\right)}{d{x}_1^2}=\frac{4{t}^2\left(4{x}_1-1\right)}{9b}. $$

(2.10)

Only x ₁ = 0 satisfies both the first-order condition (f.o.c.) and second-order condition (s.o.c.). Therefore, the unique locational solution is $\left({x}_1^{\ast },{x}_2^{\ast}\right)=\left(0,1/2\right)$. The result of Pal (1998) seems to hint that in spatial Cournot competition, the shape of the market plays a decisive role. That is, in a linear market, all firms will agglomerate at the center of the market, but in a circular market, they will stay away from each other.⁹ This conjecture was quickly broken by Matsushima (2001), who proved when there are n firms (and n is even) locating in a circular market, $\frac{n}{2}$ firms locating at point 0 and the other $\frac{n}{2}$ firms locating at point $\frac{1}{2}$ is an equilibrium. His result means that the shape of the market is not necessarily a key factor to determine the location of the firms. This finding has led many scholars to devote efforts to find the decisive factors in the location game with two or more firms. With endeavors by many scholars, this academic competition was soon ended.

Gupta et al. (2004) basically solved the problem of n firms’ location selections (n can be either odd or even). They found that the firms’ location choices should satisfy the “aggregate cost median condition” (see Eq. (2.20) later). Therefore, the equilibrium locations may be separated, aggregated, or partially dispersed and partially aggregated.¹⁰

Gupta et al. (2004) did not solve the equilibrium locations directly. Obviously, as the number of firms increases, the number of the market segments also increases exponentially, making the solution process more tedious and more difficult.

Following the same settings as Pal (1998), assume that the consumer is homogeneously distributed on a circle with a circumference of one. Considering that n manufacturers engage in Cournot competition, where n ≥ 2, q_i and x_i indicate the number of products and the location of firm i, i ∈ {1, …, n}. The quantities and locations of these n firms are represented by ${\left({q}_i\right)}_{i=1}^n$ and ${\left({x}_i\right)}_{i=1}^n$, respectively. They assumed a unit transport rate; therefore the profit function for firm i at x is

$$ {\pi}_i\left({x}_1,{x}_2,\dots, {x}_n,x\right)=\left({p}_i(x)-|x-{x}_i|\right){q}_i(x),\kern1em i=1,\dots, n,\vspace*{-6pt} $$

(2.11)

After some calculations, they obtained the equilibrium quantities and profits in the second stage

$$ {q}_i\left({x}_1,{x}_2,\dots, {x}_n,x\right)=\frac{1}{n+1}\!\left(\!\alpha +\sum_{j=1}^n|x-{x}_j|-\left(n+1\right)|x-{x}_i|\!\right)\!, $$

(2.12)

and

$$ {\pi}_i\left({x}_1,{x}_2,\dots, {x}_n,x\right)={q}_i{\left({x}_1,{x}_2,\dots, {x}_n,x\right)}^2,\kern1em i=1,\dots, n. $$

(2.13)

Back to the first stage, given the position of other vendors, the objective of firm i is

$$ {\displaystyle \begin{array}{l}\max \kern0.37em {\Pi}_i\left({x}_1,{x}_2,\dots, {x}_n\right)=\underset{0}{\overset{1}{\int }}{\pi}_i\left({x}_1,{x}_2,\dots, {x}_n,x\right)\; dx,\\ {}\mathrm{s}.\mathrm{t}.\kern4.5em {x}_i\in \left[0,1\right),\kern1em i=1,\dots, n.\end{array}} $$

(2.14)

In Firm i’s profit function, Eq. (2.5) can be expanded to

$$ {\displaystyle \begin{array}{c}{\Pi}_i\left({x}_1,\dots, {x}_n\right)=\underset{0}{\overset{x_i}{\int }}{\pi}_i\left({x}_1,\dots, {x}_n,x\right) dx\\ {}+\underset{x_i}{\overset{x_i+\frac{1}{2}}{\int }}{\pi}_i\left({x}_1,\dots, {x}_n,x\right) dx+\underset{x_i+\frac{1}{2}}{\overset{1}{\int }}{\pi}_i\left({x}_1,\dots, {x}_n,x\right) dx.\end{array}} $$

Divide π_i(x₁, …, x_n) to x_i

$$ \vspace*{-2pt}\frac{\partial {\pi}_i\left({x}_1,\dots, {x}_n,x\right)}{\partial {x}_i}=2{q}_i\left({x}_1,\dots, {x}_n,x\right)\frac{\partial {q}_i\left({x}_1,\dots, {x}_n,x\right)}{\partial {x}_i},\vspace*{-2pt} $$

(2.15)

where

$$ \vspace*{-2pt}{\displaystyle \begin{array}{c}\frac{\partial {q}_i\left({x}_1,\dots, {x}_n,x\right)}{\partial {x}_i}=-\frac{n}{n+1}\left(\frac{\partial \left|x-{x}_i\right|}{\partial {x}_i}\right)\\ {}=\left\{\begin{array}{ll}-\frac{n}{n+1}\cdotp \frac{\partial \left({x}_i-x\right)}{\partial {x}_i}=\frac{-n}{n+1},& \forall x\in \left[0,{x}_i\right)\cup \left[{x}_i+\frac{1}{2},1\right),\\ {}-\frac{n}{n+1}\cdotp \frac{\partial \left(x-{x}_i\right)}{\partial {x}_i}=\frac{n}{n+1},& \forall x\in \left[{x}_i,{x}_i+\frac{1}{2}\right).\end{array}\right.\end{array}}\vspace*{-2pt} $$

(2.16)

Therefore, the first-order condition of Π_i(x₁, …, x_n) for x_i is

$$ \vspace*{-2pt}{\displaystyle \begin{array}{c}\frac{\partial {\Pi}_i\left({x}_1,\dots, {x}_n\right)}{\partial {x}_i}=\underset{0}{\overset{x_i}{\int }}\frac{\partial {\pi}_i\left({x}_1,\dots, {x}_n,x\right)}{\partial {x}_i} dx+\underset{x_i}{\overset{x_i+\frac{1}{2}}{\int }}\frac{\partial {\pi}_i\left({x}_1,\dots, {x}_n,x\right)}{\partial {x}_i} dx+\underset{x_i+\frac{1}{2}}{\overset{1}{\int }}\frac{\partial {\pi}_i\left({x}_1,\dots, {x}_n,x\right)}{\partial {x}_i} dx\\ {}=\frac{2n}{n+1}\left\{-\underset{0}{\overset{x_i}{\int }}{q}_i\left({x}_1,\dots, {x}_n,x\right) dx+\underset{x_i}{\overset{x_i+\frac{1}{2}}{\int }}{q}_i\left({x}_1,\dots, {x}_n,x\right) dx\right.\left.-\underset{x_i+\frac{1}{2}}{\overset{1}{\int }}{q}_i\left({x}_1,\dots, {x}_n,x\right) dx\right\}\end{array}}.\vspace*{-2pt} $$

(2.17)

Therefore, the first-order condition for the total profit is satisfied if and only if the following equation is valid:

$$ {\begin{array}{ll}\displaystyle\int_{x_i}^{x_i+\frac{1}{2}}{q}_i\left(x\_1,\dots, x_n,x\right) dx&=\displaystyle\int_0^{x_i}{q}_i\left({x}_1,\dots, {x}_n,x\right) dx\\&\quad \displaystyle+\int_{x_i+\frac{1}{2}}^1{q}_i\left({x}_1,\dots, {x}_n,x\right) dx.\end{array}} $$

(2.18)

Equation (2.18) implies that the optimal location for any firm must be consistent with the quantity-median of its products. In a circular market, the number of the median conditions can be further simplified. Notice that in a circular market, for any ${x}_i\in \left[0,\frac{1}{2}\right]$, we have

$$ {\begin{array}{ll}\displaystyle\int_{x_i}^{x_i+\frac{1}{2}}\alpha -n\left(|x-x_i|\right) dx&=\displaystyle\int_0^{x_i}\alpha -n\left(|x-{x}_i|\right) dx\\&\quad +\displaystyle\int_{x_i+\frac{1}{2}}^1\alpha -n\left(|x-{x}_i|\right) dx,\end{array}} $$

(2.19)

because the term of α − n(| x − x_i| ) in Eq. (2.19) is the same for each half circle. From the above Eqs. (2.12), (2.18), and (2.19), the first-order condition can be simplified to

$$ \vspace*{-2.5pt}{\begin{array}{ll}\displaystyle\int_{x_i}^{x_i+\frac{1}{2}}\sum_{j\ne i}^n\mid x-{x}_j\mid dx&=\displaystyle\int_0^{x_i}\sum_{j\ne i}^n\mid x-{x}_j\mid dx\\&\quad +\displaystyle\int_{x_i+\frac{1}{2}}^1\sum_{j\ne i}^n\mid x-{x}_j\mid dx.\end{array}}\vspace*{-2.5pt} $$

(2.20)

Defining Eq. (2.20) as the aggregate cost median condition, it is a necessary condition for the optimal location for each firm.

Let LHS and RHS represent the left-hand side and the right-hand side of the aggregate cost median condition, respectively. That is, for any x_i ∈ [0, 1/2],

$$ \vspace*{-2.5pt}\mathrm{LHS}\equiv \underset{x_i}{\overset{x_i+\frac{1}{2}}{\int }}\sum \limits_{j\ne i}^n\mid x-{x}_j\mid dx, \vspace*{-15pt}$$

$$ \mathrm{RHS}\equiv \underset{0}{\overset{x_i}{\int }}\sum \limits_{j\ne i}^n\mid x-{x}_j\mid dx+\underset{x_i+\frac{1}{2}}{\overset{1}{\int }}\sum \limits_{j\ne i}^n\mid x-{x}_j\mid dx.\vspace*{-2.5pt} $$

Given (x₁, x₂, …, x_i − 1, x_i + , x_n) and ${x}_i\in \left[0,\frac{1}{2}\right]$, the sign of $\frac{\partial^2{\varPi}_i}{\partial {x}_i^2}$ is the same as the sign of the first derivative of LHS with respect to x_i. That is,

$$ {\displaystyle \begin{array}{c}\frac{\partial^2{\Pi}_i\left({x}_1,\dots, {x}_n\right)}{\partial {x}_i^2}\\=\frac{2n}{n+1}\!\left\{\!\frac{n}{n+1}+\!\left(\!2{q}_i\left({x}_1,\dots, {x}_n,x\right)\!\left|{}_{x={x}_i+\frac{1}{2}}\right.-2{q}_i\left({x}_1,\dots, {x}_n,x\right)\!\left|{}_{x={x}_i}\right.\!\right)\!\right\}\\ {}=\frac{4{n}^2}{{\left(n+1\right)}^2}\left(\sum \limits_{j\ne i}^n|{x}_i+\frac{1}{2}-{x}_j\left|-\sum \limits_{j\ne i}^n|{x}_i-{x}_j\right|\right)\gtreqless 0\\ {}\iff \kern0.5em h\overset{def}{=}\frac{\partial LHS}{\partial {x}_i}=\sum \limits_{j\ne i}^n\mid {x}_i+\frac{1}{2}-{x}_{\!j}\left|-\sum \limits_{j\ne i}^n|{x}_i-{x}_j\right|\gtreqless 0,\end{array}} $$

which implies that LHS must be a negative slope at the optimal position ${x}_i^{\ast }$. In fact, instead of calculating the complicated f.o.c. and s.o.c., LHS and RHS are sufficient to imply whether any combination of locations is an equilibrium. After some calculations, they obtained the following Table 2.1. The contribution of Gupta et al. (2004) is significant, because it demonstrated various types of equilibrium location patterns and also triggered many subsequent studies and further discussion.

Table 2.1 Partial numerical solution of Cournot competition in circular market

Matsumura and Matsushima (2012) introduced discontinuous transportation costs to re-examine the various equilibriums of Gupta et al. (2004). They use the linear-quadratic transport cost function T(x, x_i) ≡ t · d(x, x_i) + τ · d(x, x_i)², t > 0, τ >  − t, where x is a point in the market, x_i is the location of firm i, d is the distance, and t and τ are the unit transport rates. When τ = 0, then this model degenerates to Gupta et al. (2004). If t ≠ 0, τ > (<)0, then the transportation rate is convex (concave). They finally proved that for the various equilibrium location patterns in Gupta et al. (2004), as long as τ ≠ 0 (i.e., the transport cost function is non-linear), only symmetric equilibrium patterns will be sustained, and asymmetric equilibria will no longer be valid.

Matsumura et al. (2005) explored firms’ locations in terms of the type of transport costs (convex, linear, and concave) and found that the Pal-type equilibrium always exists, while the Matsushima-type equilibrium can only be established under certain conditions.

Matsumura and Shimizu (2006) showed that the Pal (1998)-type equilibrium (maximal differentiation) always appears in equilibrium if the transport rate is non-decreasing with distance.

Chamorro-Rivas (2000b) assumed that each of the duopolists can choose to open up, at most, two plants and the location patterns can be either neighboring ((A,2) next to (A,1) and (B,2) next to (B,1)) or intertwined ((A,1) locates between (B,1) and (B,2)). They showed that for the equilibrium locations, all plants are equally spaced and paired in the market (Fig. 2.2).

Fig. 2.2

The equilibrium location pattern in Chamorro-Rivas (2000b)

Pal and Sarkar (2006) generalized the Chamorro-Rivas (2000b) model to a multiple (m) plants and multiple firms (n) and showed that all plants (and plants of each firm) being located equidistantly is a unique SPNE when n = 2 and m = 1 and it is very likely results in multiple SPNE locations for other cases. Moreover, the SPNE may not be unique, because firms may choose different numbers of plants.

Sun (2010) employed the directional constraint in a circular market with Cournot competition,¹¹ where firms can only choose one direction (clockwise or counter-clockwise) to serve the whole market. This assumption is justified in reality, because each shipping journey involves some fixed costs, which is double when the shipping job is done by two trucks with different directions. Moreover, when two trucks deliver the products starting from the location of a firm with two opposite directions, the two trucks will meet at the point opposite to the firm’s location, and they should return to the initial point with an empty load, which is a wasteful travel. He showed that when firms choose different directions, their locations will be at one point, while if they choose the same direction, then their locations will be the two endpoints of a diameter.

Cheng and Lai (2018) obtain the same location-direction equilibria with a different assumption from Sun (2010), instead of assuming a “first-entrant-takes-all” rule to capture the “one-house-one-outlet” phenomenon in water, electricity, natural gas, telephone, Internet, cable TV, and other service industries. Interestingly, their model is suitable for explaining the Treaty of Tordesillas in 1494 between Spain and Portugal, where both sides agreed to divide the newly discovered lands outside Europe along a meridian about 1770 km west of Cape Verde Island.

Yu (2007) showed that in a circular market with discrimination, the location equilibria in price competition are the same as those in quantity. That is, all the location equilibria in price competition, given the same number of firms, are identical to the equilibria in quantity competition.

Matsushima and Matsumura (2003) proved that when there are n private firms and a public firm, the public firm locating at one endpoint of a diameter, while all the private firms agglomerate at the other end of this diameter, is a location equilibrium.

Sun et al. (2017) considered scenarios of Cournot competition in which the maximal service range of a truck is less than half of the perimeter of a circular market, and thus each of the duopoly firms should initiate more than two dispatches to serve the whole market. For example, supposing the maximal service range (r) is 1/3, a firm may either initiate four dispatches (Fig. 2.3) or three dispatches (Fig. 2.4) to serve the whole market. They found that when the fixed cost of a transportation vehicle is sufficiently low, there exists a unique outcome with the same location pattern as that in Pal (1998), and each firm delivers its products with four dispatches. When the fixed cost is sufficiently high, there exists a unique outcome such that firms’ locations are less than the maximal difference, and each firm initiates three dispatches.

Fig. 2.3

Four dispatches with maximal service range r = 1/3 in Sun et al. (2017)

Fig. 2.4

Three dispatches with maximal service range r = 1/3 in Sun et al. (2017)

Guo and Lai (2019) analyzed the fully symmetric location equilibrium in two intersecting circular markets (see Fig. 2.5). Both circular markets are served by two homogenous firms which engage in Cournot competition at each point of these two circular markets. They showed that each firm locating at each of the intersecting points is the unique fully symmetric location equilibrium. The intuition of their result is clear: If a firm does not locate at an intersecting point, say x ₁ = 0 for firm 1, then it should deliver its product to the Y market through the section [0, s] in the X market, which produces no revenue and thus is a wasteful trip. Their model highlights the importance of traffic hubs, which can attract firms.

Fig. 2.5

Two intersecting circular markets in Guo and Lai (2019)

2.3 Linear Plus Circular Markets

Since the equilibrium location pattern in a linear market is quite different from that in a circular market, what is the location pattern if these two types of markets are combined? Ebina et al. (2011) developed a very smart method to integrate circular and linear markets. They assumed that there is a circular market with a unit length the same as Pal (1998). When products are shipped through the “0” point, an additional cost of β ∈ [0, 1] is generated. This cost can be seen as a tariff; when β = 0, the model degenerates to Pal (1998). When β is large enough, the vendor will never pass through the “0” point, which is equivalent to degenerating to a linear model like Anderson and Neven (1991). They proved that when β is small or large, the equilibrium location patterns are unique, but when β is in the middle range, there exist multiple location patterns, and in a large part of the range of β, the location equilibrium is concentrated at the market center, while the dispersed location pattern is valid only when β = 0. Therefore, they believed that some asymmetric location patterns in a circular market are balanced on a knife’s edge (i.e., unlikely to appear or not easily sustained).

In addition, Guo and Lai (2015) combined a linear market and a circular market such that a linear main street connects to an outer belt road. In particular, they allowed the main street to have a higher demand density than that of the outer belt road. When the demand in all markets is identical, the firms will locate at the two ends of the main street, which is the same as the result of Pal (1998), but as the demand density of the main street increases, the equilibrium locations gradually move toward the center of the main street to form results close (or equivalent) to Anderson and Neven (1991) (Fig. 2.6).

Fig. 2.6

A linear-circular market in Guo and Lai (2015)

3 Conclusions

Spatial Cournot competition with endogenous firms’ locations of Hamilton et al. (1989) and Anderson and Neven (1991) is one of the literature streams avoiding the undercutting trap in Hotelling (1929). This stream is more successful than other attempts in that most equilibrium patterns in spatial Cournot models are very intuitive and fit the real-world phenomenon, namely, that all firms will agglomerate at the market center in most linear market, a fact observed by Harold Hotelling. In this chapter, the development of spatial Cournot competition in the past 30 years was analyzed along the two major axes of the linear market and the circular market (see Fig. 2.7). We believe that spatial Cournot competition will continue to develop and match the reality in the future.

Fig. 2.7

Map of the spatial Cournot competition literature