Impartial achievement and avoidance games for generating finite groups

Abstract

We study two impartial games introduced by Anderson and Harary and further developed by Barnes. Both games are played by two players who alternately select previously unselected elements of a finite group. The first player who builds a generating set from the jointly selected elements wins the first game. The first player who cannot select an element without building a generating set loses the second game. After the development of some general results, we determine the nim-numbers of these games for abelian and dihedral groups. We also present some conjectures based on computer calculations. Our main computational and theoretical tool is the structure diagram of a game, which is a type of identification digraph of the game digraph that is compatible with the nim-numbers of the positions. Structure diagrams also provide simple yet intuitive visualizations of these games that capture the complexity of the positions.

1 Introduction

Anderson and Harary (1987) introduced two impartial games in which two players alternately select previously unselected elements of a finite group until the group is generated by the chosen elements. The first player who builds a generating set from the jointly selected elements wins the achievement game denoted by ${\mathsf{GEN}}$. The first player who cannot select an element without building a generating set loses the avoidance game denoted by $\mathsf{DNG}$.

In the original description of the avoidance game given in Anderson and Harary (1987), the game ends when a generating set is built. This suggests misère-play convention. We want to study both the achievement and the avoidance game under normal-play convention. So, our version of the avoidance game does not allow the creation of a generating set, and the game ends when there are no available moves. Our version of the avoidance game has the same outcome as the original, and so the difference is immaterial since Anderson and Harary do not consider game sums.

The outcome of both games was determined for finite abelian groups in Anderson and Harary (1987). Barnes (1988) provides criteria for determining the outcome of each game for an arbitrary finite group. Barnes applies his criteria to determine the outcome of some of the more familiar finite groups, including abelian, dihedral, symmetric, and alternating groups, although his analysis is incomplete for alternating groups in the avoidance game.

Brandenburg studies related games in Brandenburg (2017). In one of the variations, two players alternate moves, where a move consists of picking some non-identity element from a finitely generated abelian group. The game then continues with a group that results by taking the quotient by the subgroup generated by the chosen element. The player with the last possible move wins.

The fundamental problem in the theory of impartial combinatorial games is the determination of the nim-number of the game. This allows for the calculation of the nim-numbers of game sums and the determination of the outcome of the games. The major aim of this paper is the development of some theoretical tools that allow the calculation of the nim-numbers of the achievement and avoidance games for a variety of familiar groups.

The paper is organized as follows. In Sect. 2, we review the basic terminology of impartial games and establish our notation. We further our general study of avoidance and achievement games in Sects. 3 and 4, respectively. In particular, we introduce the structure diagram of a game, which is an identification digraph of the game digraph that is compatible with the nim-numbers of the positions. Structure diagrams also provide simple but intuitive visualizations of these games that capture the complexity of the positions. By making further identifications, we obtain the simplified structure diagram of a game, which will be our main computational and theoretical tool in the remainder of the paper. The main result of Sect. 3 states that the nim-number of the avoidance game is 0, 1, or 3 for an arbitrary finite group (see Corollary 3.21). Analogously, in Sect. 4, we show that if the order of a group is odd, then the nim-number of the corresponding achievement game is 1 or 2 (see Corollary 4.8). We conjecture that if the group is of even order, then the nim-number of the achievement game is in $\{0,1,2,3,4\}$ (see Conjecture 4.9). Sect. 5 describes the algorithms we implemented via a computer program to generate our initial conjectures and verify our results. Sects. 6, 7, and 8 contain a complete analysis of the nim-numbers for cyclic, dihedral, and abelian groups, respectively. In Sect. 9, we study the symmetric and alternating groups. In particular, we provide a description of the nim-numbers for the avoidance game for the symmetric groups. In addition, we provide a partial characterization for the achievement game for the symmetric groups, as well as both games for the alternating groups. We conclude with several open questions in Sect. 10.

The authors thank Bret Benesh and the anonymous referee for suggestions that greatly improved the paper.

2 Preliminaries

We briefly recall the basic terminology of impartial games to introduce our notation. A comprehensive treatment of impartial games can be found in Albert et al. (2007), Aaron (2013). For our purposes, an impartial game is a finite set X of positions together with a starting position and a collection $\{{\text {Opt}}(P)\subseteq X\mid P\in X\}$ of possible options. Two players take turns choosing one of the available options in ${\text {Opt}}(P)$ of the current position P. The player who encounters an empty option set cannot move and therefore loses. All games must come to an end in finitely many turns, so we do not allow infinite lines of play. There are two possible outcomes for an impartial game. The game is an N-position if the next player (i.e., the player that is about to move) wins and it is a P-position if the previous player (i.e., the player that just moved) wins.

The minimum excludant ${\text {mex}}(A)$ of a set A of ordinals is the smallest ordinal not contained in the set. The nim-number ${\text {nim}}(P)$ of a position P is the minimum excludant of the set of nim-numbers of the options of P. That is,

$$\begin{aligned} {\text {nim}}(P):={\text {mex}}({\text {nOpt}}(P)), \end{aligned}$$

where ${\text {nOpt}}(P):=\{{\text {nim}}(Q)\mid Q\in {\text {Opt}}(P)\}$. Note that the minimum excludant of the empty set is 0, and so the terminal positions of a game have nim-number 0. The nim-number of a game is the nim-number of its starting position. The nim-number of a game determines the outcome of a game since a position P is a P-position if and only if ${\text {nim}}(P)=0$.

The sum of the games P and R is the game $P+R$ whose set of options is

$$\begin{aligned} {\text {Opt}}(P+R):=\left\{ Q+R\mid Q\in {\text {Opt}}(P)\}\cup \{P+S\mid S\in {\text {Opt}}(R)\right\} . \end{aligned}$$

This means that in each turn a player makes a valid move either in game P or in game Q. The nim-number of the sum of two games can be determined as the nim-sum

$$\begin{aligned} {\text {nim}}(P+R)={\text {nim}}(P)\oplus {\text {nim}}(R), \end{aligned}$$

which requires binary addition without carry.

We write $P=R$ if the outcome of $P+T$ and $R+T$ is the same for every game T. The one pile NIM game with n stones is denoted by the nimber $*n$. The set of options of $*n$ is ${\text {Opt}}(*n)=\{*0,\ldots ,*(n-1)\}$. The following fundamental result shows the significance of the nimbers.

Theorem 2.1

(Sprague–Grundy) If P is an impartial game, then $P=*{\text {nim}}(P)$.

We now recall a few well-known group-theoretic results and definitions that will be useful in the remainder of the paper. The subgroup of a group G generated by the subset S is the intersection of all subgroups of G containing S. Note that the empty set generates the trivial subgroup.

A maximal proper subgroup of a group G is called a maximal subgroup of G. It is clear that every proper subgroup of a finite group is contained in a maximal subgroup. Note that the finite requirement is necessary. For example, the group $(\mathbb {Q},+)$ has no maximal subgroups. Maximal subgroups play an important role for us because of the following easy fact.

Proposition 2.2

A subset S of a finite group is a generating set if and only if S is not contained in any maximal subgroup.

Next, we provide a more precise overview of the achievement and avoidance games. Let G be a finite group. We define the avoidance game $\mathsf{DNG}(G)$ as follows. The first player chooses $x_{1}\in G$ such that $\langle x_{1}\rangle \ne G$ and at the kth turn, the concerned player selects $x_{k}\in G{\setminus }\{x_{1},\ldots ,x_{k-1}\}$, such that $\langle x_{1},\ldots ,x_{k}\rangle \ne G$. That is, a position in $\mathsf{DNG}(G)$ is a set of jointly selected elements that must be a non-generating subset of G. The player who cannot select an element without building a generating set loses the game.

In the achievement game ${\mathsf{GEN}}(G)$, the first player chooses any $x_{1}\in G$ and at the kth turn, the concerned player selects $x_{k}\in G{\setminus }\{x_{1},\ldots ,x_{k-1}\}$. That is, a position in ${\mathsf{GEN}}(G)$ is a set of jointly selected elements. A player wins on the nth turn as soon as $\langle x_{1},\ldots ,x_{n}\rangle =G$.

In this paper, we use $\mathbb {Z}_{n}:=\{0,1,\ldots ,n-1\}$ to denote the cyclic group of order n under addition modulo n, so that $\mathbb {Z}_{n}\cong \mathbb {Z}/n\mathbb {Z}$.

Example 2.3

The trivial group $\mathbb {Z}_{1}$ has no maximal subgroups. We cannot play $\mathsf{DNG}(\mathbb {Z}_{1})$ since every subset of the group, including the empty set, is a generating set. The only position of ${\mathsf{GEN}}(\mathbb {Z}_{1})$ is the empty set, and so the second player wins before the first player can make a move. This implies that ${\mathsf{GEN}}(\mathbb {Z}_{1})=*0$.

Example 2.4

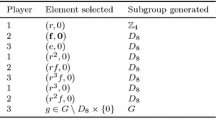
Consider the avoidance game on the cyclic group $\mathbb {Z}_{4}$. No player can choose either 1 or 3 since these elements individually generate the group. If the first player chooses 0, then the only option for the second player is 2. After this move, the first player has no available options. We arrive at the same conclusion if the first player chooses 2 on the opening move. Regardless, the second player wins $\mathsf{DNG}(\mathbb {Z}_{4})$, which implies that $\mathsf{DNG}(\mathbb {Z}_{4})=*0$. The game digraph for $\mathsf{DNG}(\mathbb {Z}_{4})$ is given in Fig. 1a. In the digraph, the vertices are the positions of the game, every position is connected to its options by arrows, and every position is labeled by the nimber of the corresponding position.

For the achievement game, it is easy to see that the first player can win on the opening move by choosing 1 or 3. However, if the first player happens to choose 0 or 2 on the opening move, then the second player may choose 1, 3, or the opposite choice that the first player made on the opening move. The second player wins the game if they choose either 1 or 3. However, if the second player makes the opposite choice between 0 and 2 that the first player made, then the first player wins by choosing either 1 or 3. The game digraph for ${\mathsf{GEN}}(\mathbb {Z}_{4})$ is given in Fig. 1b. By looking at the top node of the digraph, we see that ${\mathsf{GEN}}(\mathbb {Z}_{4})=*1$.

Fig. 1

Game digraphs of $\mathsf{DNG}(\mathbb {Z}_{4})$ and ${\mathsf{GEN}}(\mathbb {Z}_{4})$, and representative game digraph for ${\mathsf{GEN}}(\mathbb {Z}_{4})$. Nimbers corresponding to each position of the game are included. The second digraph can be created from the first by adding the dotted arrows that represent options that create terminal positions

We call two subsets P and Q of a group G automorphism equivalent if there is an automorphism $\phi$ of G such that $\phi (P)=Q$. It is clear that an automorphism $\phi$ of G induces an automorphism of the game digraph, and so ${\text {nim}}(P)={\text {nim}}(Q)$ if P and Q are automorphism equivalent. For simplicity, we can eliminate some of the positions of a game digraph without changing the nim-numbers of the remaining positions. For each position P, the set ${\text {Opt}}(P)$ of options is partitioned into automorphism equivalence classes. We delete all but one representative from each of these classes. The resulting digraph will be referred to as a representative game digraph.

Example 2.5

Consider the achievement game on the cyclic group $\mathbb {Z}_{4}$. It is clear that the subsets $\{3\}$, $\{0,3\}$, $\{2,3\}$, and $\{0,2,3\}$ are automorphism equivalent to $\{1\}$, $\{0,1\}$, $\{1,2\}$, and $\{0,1,3\}$, respectively. As a result, one possible representative game digraph for ${\mathsf{GEN}}(\mathbb {Z}_{4})$ is provided in Fig. 1c.

We define ${\text {pty}}(n):=n\bmod 2$. The parity of a subset of a group is defined to be the parity of the size of the subset. Observe that an option of a position in both $\mathsf{DNG}$ and ${\mathsf{GEN}}$ has the opposite parity.

3 Avoidance games

In this section we study the avoidance game $\mathsf{DNG}(G)$ on a finite group G. In Anderson and Harary (1987), Anderson and Harary proved the following criterion for determining the outcome of $\mathsf{DNG}(G)$ for a finite abelian group.

Proposition 3.1

Let G be a finite abelian group. The first player wins $\mathsf{DNG}(G)$ if and only if G is nontrivial of odd order or $G\cong \mathbb {Z}_{2k}$ with k odd. The second player wins otherwise.

Barnes (1988) reproved this result using the following criterion for determining the outcome of $\mathsf{DNG}(G)$ for an arbitrary finite group G. Recall that an involution in a group is an element of order 2.

Proposition 3.2

Let G be a nontrivial finite group. Then the first player wins $\mathsf{DNG}(G)$ if and only if there exists $\alpha \in G$ such that $\alpha$ has odd order and $\langle \alpha ,\beta \rangle =G$ for every involution $\beta \in G$.

Note that the last condition of the previous proposition vacuously holds if the order of G is odd. Since the first player wins precisely when $\mathsf{DNG}(G)\ne *0$, we immediately have the following corollary of Proposition 3.1.

Corollary 3.3

Let G be a nontrivial finite abelian group. Then $\mathsf{DNG}(G)\ne *0$ if and only if G has odd order or $G\cong \mathbb {Z}_{2k}$ with k odd.

The next proposition follows immediately from Proposition 2.2.

Proposition 3.4

The positions of $\mathsf{DNG}(G)$ are the subsets of the maximal subgroups of G and the terminal positions of $\mathsf{DNG}(G)$ are the maximal subgroups of G.

It turns out that positions that are contained in the same collection of maximal subgroups are closely related. This motivates the next two definitions.

Definition 3.5

Let $\mathcal {M}$ be the set of maximal subgroups of G. The set of intersection subgroups is defined to be the set

$$\begin{aligned} \mathcal {I}:=\{\cap \mathcal {N}\mid \emptyset \not =\mathcal {N\subseteq \mathcal {M}}\} \end{aligned}$$

containing all the possible intersections of some maximal subgroups.

Note that the elements of $\mathcal {I}$ are in fact subgroups of G. If G is nontrivial, then the smallest intersection subgroup is the Frattini subgroup $\Phi (G)$. Not every subgroup of G is an intersection subgroup. For example, $\Phi (G)$ may not be trivial. The set $\mathcal {I}$ of intersection subgroups is partially ordered by inclusion. We use interval notation to denote certain subsets of $\mathcal {I}$. For example, if $I\in \mathcal {I}$, then $(-\infty ,I):=\{J\in \mathcal {I}\mid J\subset I\}$.

Definition 3.6

For each $I\in \mathcal {I}$ let

$$\begin{aligned} X_{I}:=\mathcal {P}(I){\setminus }\cup \{\mathcal {P}(J)\mid J\in (-\infty ,I)\} \end{aligned}$$

be the collection of those subsets of I that are not contained in any other intersection subgroup smaller than I. We let $\mathcal {X}:=\{X_{I}\mid I\in \mathcal {I}\}$ and call an element of $\mathcal {X}$ a structure class.

The largest element of $X_{I}$ is I. The starting position $\emptyset$ is in $X_{\Phi (G)}$. We say that $X_{I}$ is terminal if I is terminal. The parity of a structure class is defined to be ${\text {pty}}(X_{I}):={\text {pty}}(I)$.

Example 3.7

The subset $P=\{0\}$ generates the trivial subgroup of $G=\mathbb {Z}_{4}$. If $I=\Phi (G)=\{0,2\}$ is the Frattini subgroup of G, then $P\in X_{I}$ since $P\subseteq I$ and $(-\infty ,I)$ is empty. This shows that $P\in X_{I}$ does not imply that P generates I.

Proposition 3.8

If I and J are different elements of $\mathcal {I}$, then $X_{I}\cap X_{J}=\emptyset$.

Proof

Assume $P\in X_{I}\cap X_{J}$ and let $K:=I\cap J\in \mathcal {I}$. Since $I\ne J$, we must have $K\ne I$ or $K\ne J$. Without loss of generality, assume that $K\ne I$. Then $P\subseteq K\in (-\infty ,I)$, which contradicts $P\in X_{I}$. $\square$

Corollary 3.9

The set $\mathcal {X}$ of structure classes is a partition of the set of game positions of $\mathsf{DNG}(G)$.

As we shall see, the structure classes play a pivotal role in the remainder of this paper. Proposition 3.10 and Corollary 3.11 imply that the collection of structure classes is compatible with the option relationship between game positions. This will allow us to define the structure digraph of $\mathsf{DNG}(G)$ (see Definition 3.12), which will capture the option relationship among structure classes. Then in Proposition 3.15, we show that two elements of a structure class have the same nim-number if and only if they have the same parity. In other words, each structure class is associated with two nim-numbers. By appending this data to the corresponding structure digraph, we can visualize the nim-number relationship among structure classes using a structure diagram. By defining an appropriate equivalence relation on the collection of structure classes (see Definition 3.17), we will be able to make identifications that allow us to greatly simplify the task of computing the nim-number of $\mathsf{DNG}(G)$ for a wide class of groups.

Proposition 3.10

Assume $X_{I},X_{J}\in \mathcal {X}$ and $P\in X_{I}\not =X_{J}$. Then ${\text {Opt}}(P)\cap X_{J}\not =\emptyset$ if and only if ${\text {Opt}}(I)\cap X_{J}\not =\emptyset$.

Proof

First, assume that ${\text {Opt}}(P)\cap X_{J}\not =\emptyset$. Then there exists a $g\in G{\setminus } P$ such that $P\cup \{g\}\in X_{J}$. That is, $P\cup \{g\}\subseteq J$ but $P\cup \{g\}$ is not contained in any $K\in (-\infty ,J)$. This implies that $I\subset J$, otherwise we would have $P\subseteq I\cap J\in (-\infty ,I)$, contradicting $P\in X_{I}$. There is no K satisfying $I\cup \{g\}\subseteq K\in (-\infty ,J)$ since we would then have $P\cup \{g\}\subseteq I\cup \{g\}\subseteq K\in (-\infty ,J)$, which contradicts $P\cup \{g\}\in X_{J}$. Thus, $I\cup \{g\}\in X_{J}$, which shows that ${\text {Opt}}(I)\cap X_{J}\not =\emptyset$.

Now, assume that ${\text {Opt}}(I)\cap X_{J}\not =\emptyset$. Then $I\cup \{g\}\in X_{J}$ for some $g\in J{\setminus } I$, that is, $I\cup \{g\}\subseteq J$ but $I\cup \{g\}$ is not contained in any $K\in (-\infty ,J)$. Then clearly $P\cup \{g\}\subseteq J$. There is no K satisfying $P\cup \{g\}\subseteq K\in (-\infty ,J)$, otherwise we would have $P\subseteq K\cap I\in (-\infty ,I)$ contradicting $P\in X_{I}$. Hence $P\cup \{g\}\in X_{J}$, and so ${\text {Opt}}(P)\cap X_{J}\not =\emptyset$, as desired. $\square$

Corollary 3.11

Assume $X_{I},X_{J}\in \mathcal {X}$ and $P,Q\in X_{I}\ne X_{J}$. Then ${\text {Opt}}(P)\cap X_{J}\not =\emptyset$ if and only if ${\text {Opt}}(Q)\cap X_{J}\ne \emptyset$.

This motivates the following definition.

Definition 3.12

We say that $X_{J}$ is an option of $X_{I}$ and we write $X_{J}\in {\text {Opt}}(X_{I})$ if ${\text {Opt}}(I)\cap X_{J}\not =\emptyset$. The structure digraph of $\mathsf{DNG}(G)$ has vertex set $\{X_{I}\mid I\in \mathcal {I}\}$ and edge set $\{(X_{I},X_{J})\mid X_{J}\in {\text {Opt}}(X_{I})\}$.

If $I\not =P\in X_{I}$, then $P\cup \{g\}\in {\text {Opt}}(P)\cap X_{I}$ for all $g\in I{\setminus } P\not =\emptyset$. So, I is the only element of $X_{I}$ without an option in $X_{I}$. Note that there are no loops in the structure digraph and $X_{\Phi (G)}$ is the only source vertex.

Example 3.13

The set of maximal subgroups of $G=\mathbb {Z}_{6}$ is $\mathcal {M}=\{\{0,2,4\},\{0,3\}\}$. The intersection subgroups are in $\mathcal {I}=\{\{0\},\{0,2,4\},\{0,3\}\}$. Note that $\Phi (G)=\{0\}$. The elements of $\mathcal {X}$ are

$$\begin{aligned}&\displaystyle X_{\{0,2,4\}}=\{\{2\},\{4\},\{0,2\},\{0,4\},\{2,4\},\{0,2,4\}\}\\&\displaystyle X_{\{0\}}=\{\emptyset , \{0\}\}, X_{\{0,3\}}=\{\{3\},\{0,3\}\}. \end{aligned}$$

The structure digraph is visualized by

$$\begin{aligned} X_{\{0,2,4\}}\longleftarrow X_{\{0\}}\longrightarrow X_{\{0,3\}}. \end{aligned}$$

The following lemma will be useful in the proof of Proposition 3.15.

Lemma 3.14

Let A and B be subsets of $\{0,1,2,\ldots \}$ such that ${\text {mex}}(A)\in B$. Then ${\text {mex}}(A\cup \{{\text {mex}}(B)\})={\text {mex}}(A)$.

Proof

Since ${\text {mex}}(A)\in B$, ${\text {mex}}(B)\not ={\text {mex}}(A)$. This implies that ${\text {mex}}(A\cup \{{\text {mex}}(B)\})={\text {mex}}(A)$. $\square$

Fig. 2

Unfolded structure diagrams for Proposition 3.15. We define $a:={\text {nim}}(Q)$, $b:={\text {nim}}(T)$ and $c:={\text {nim}}(S)$. Shading types represent parities

Proposition 3.15

If $P,Q\in X_{I}\in \mathcal {X}$ and ${\text {pty}}(P)={\text {pty}}(Q)$, then ${\text {nim}}(P)={\text {nim}}(Q)$.

Proof

We proceed by structural induction. Our inductive hypothesis states that if ${\text {pty}}(M)={\text {pty}}(N)$ and either $M,N\in X_{I}$ with $|M|,|N|>\min \{|P|,|Q|\}$ or $M,N\in X_{J}\in {\text {Opt}}(X_{I})$ for some $J\in \mathcal {I}$, then ${\text {nim}}(M)={\text {nim}}(N)$. Without loss of generality, assume that $|P|\le |Q|$.

We will consider two cases indicated by the diagrams in Fig. 2: $Q\ne I$ and $Q=I$. Each figure is referred to as an “unfolded structure diagram” and is meant to help visualize the structure of the proof. In the figures, each triangle represents a structure class and each horizontal band represents the collection of subsets from the given structure class that have the same size. An arrow from one set to another in the figure indicates that the second set is an option of the first set. In the first case ($Q\ne I$), we will show that ${\text {nOpt}}(P)={\text {nOpt}}(Q)$. The second case ($Q=I$) is more complicated as we will only have ${\text {nOpt}}(Q)\subseteq {\text {nOpt}}(P)$. In this case, we will make use of Lemma 3.14 to conclude that we still have ${\text {mex}}({\text {nOpt}}(P))={\text {mex}}({\text {nOpt}}(I))$.

First, assume that $Q\ne I$. Every option of P is either an element of $X_{I}$ or of some $X_{J}\in {\text {Opt}}(X_{I})$. If $T\in {\text {Opt}}(P)\cap X_{I}$, then we can choose $\widetilde{T}\in {\text {Opt}}(Q)\cap X_{I}$. By induction, ${\text {nim}}(T)={\text {nim}}(\widetilde{T})$ since ${\text {pty}}(T)={\text {pty}}(\tilde{T})$. On the other hand, if $S\in {\text {Opt}}(P)\cap X_{J}$ for some $X_{J}\in {\text {Opt}}(X_{I})$, then by Corollary 3.11, there exists $\tilde{S}\in {\text {Opt}}(Q)\cap X_{J}$. Since ${\text {pty}}(S)={\text {pty}}(\tilde{S})$, we must have ${\text {nim}}(S)={\text {nim}}(\tilde{S})$ by induction. We have shown that ${\text {nOpt}}(P)\subseteq {\text {nOpt}}(Q)$. A similar argument shows that ${\text {nOpt}}(Q)\subseteq {\text {nOpt}}(P)$.

Now, assume that $Q=I$. If $P=Q=I$, then the desired result follows trivially, so assume that $P\ne Q=I$. Note that this implies that $|P|<|Q|$. In this case, we might not have ${\text {nOpt}}(Q)={\text {nOpt}}(P)$ because ${\text {Opt}}(I)\cap X_{I}=\emptyset$. Instead we fix a $T^{\prime }\in X_{I}$ such that $I\in {\text {Opt}}(T^{\prime })$. Such a $T'$ exists since $I\not =\emptyset$. We are going to show that ${\text {nOpt}}(P)={\text {nOpt}}(I)\cup \{{\text {nim}}(T')\}$.

First, we verify ${\text {nOpt}}(P)\subseteq {\text {nOpt}}(I)\cup \{{\text {nim}}(T')\}$. Every option of P is either an element of $X_{I}$ or of some $X_{J}\in {\text {Opt}}(X_{I})$. In the latter case, if $S\in {\text {Opt}}(P)\cap X_{J}$ for some $X_{J}\in {\text {Opt}}(X_{I})$, then there exists $\tilde{S}\in {\text {Opt}}(Q)\cap X_{J}$ by Corollary 3.11. Since ${\text {pty}}(S)={\text {pty}}(\tilde{S})$, we must have ${\text {nim}}(S)={\text {nim}}(\tilde{S})\in {\text {nOpt}}(I)$ by induction. In the former case, if $T\in {\text {Opt}}(P)\cap X_{I}$, then ${\text {nim}}(T)={\text {nim}}(T')$ by induction and ${\text {nim}}(T)\in \{{\text {nim}}(T')\}$.

Now, we verify ${\text {nOpt}}(P)\supseteq {\text {nOpt}}(I)\cup \{{\text {nim}}(T')\}$. Suppose $\widetilde{S}\in {\text {Opt}}(I)$. Then $\widetilde{S}\in X_{J}$ for some $X_{J}\in {\text {Opt}}(X_{I})$ since the only options of I must exist outside $X_{I}$. Then by Corollary 3.11, there exists $S\in {\text {Opt}}(P)\cap X_{J}$. Since ${\text {pty}}(\widetilde{S})={\text {pty}}(S)$, we must have ${\text {nim}}(\widetilde{S})={\text {nim}}(S)$ by induction. This implies that ${\text {nOpt}}(I)\subseteq {\text {nOpt}}(P)$. Since $P\ne I$, there exits $T\in {\text {Opt}}(P)\cap X_{I}$. By induction, ${\text {nim}}(T')={\text {nim}}(T)$ and so $\{{\text {nim}}(T')\}\subseteq {\text {nOpt}}(P)$ by induction.

Finally

$$\begin{aligned} \begin{aligned}{\text {nim}}(P)&={\text {mex}}({\text {nOpt}}(P))={\text {mex}}({\text {nOpt}}(I)\cup \{{\text {nim}}(T')\})\\&={\text {mex}}({\text {nOpt}}(I)\cup \{{\text {mex}}({\text {nOpt}}(T'))\})\\&={\text {mex}}({\text {nOpt}}(I))={\text {nim}}(Q) \end{aligned} \end{aligned}$$

by Lemma 3.14 since ${\text {mex}}({\text {nOpt}}(I))={\text {nim}}(I)\in {\text {nOpt}}(T')$. $\square$

The upshot of Proposition 3.15 is that each structure class is associated with two nim-numbers. In light of this, we can append this information to a structure digraph to form a (folded) structure diagram, which is visualized as follows. A structure class $X_{I}$ is represented by a triangle pointing down if I is odd and by a triangle pointing up if I is even. The triangles are divided into a smaller triangle and a trapezoid. The smaller triangle represents the odd positions of $X_{I}$ and the trapezoid represents the even positions of $X_{I}$. The numbers are the nim-numbers of these positions. There is a directed edge from $X_{I}$ to $X_{J}$ provided $X_{J}\in {\text {Opt}}(X_{I})$.

For a nontrivial group G, $\Phi (G)$ and $\Phi (G){\setminus }\{e\}$ are positions in $X_{\Phi (G)}$. Hence $X_{\Phi (G)}$ contains both even and odd positions. Corollary 3.11 now implies that every structure class contains both even and odd positions. The nim-number of the game can be easily read from the structure diagram. It is the number in the trapezoid part of the triangle representing the source vertex of the structure digraph.

Fig. 3

Representative game digraph, unfolded structure diagram, and structure diagram for $\mathsf{DNG}(\mathbb {Z}_{9})$

Example 3.16

Figure 3 shows a representative game digraph and the corresponding unfolded and folded structure diagrams for $\mathsf{DNG}(\mathbb {Z}_{9})$. Since $\mathbb {Z}_{9}$ only has a single maximal subgroup, there is a unique structure class. The small triangle in the structure diagram represents the collection of odd positions with nim-number 0. This collection includes the representative positions $\{0,3,6\},\{3\}$, and $\{0\}$. The trapezoid represents the collection of even positions with nim-number 1. This collection includes positions $\{3,6\},\{0,3\}$, and $\emptyset$. Every position in a collection is connected to another position on the next level. The chain shown in the figure ends on an odd level with the terminal position $I=\{0,3,6\}$. This is why the large triangle representing $X_{I}$ points down and the small triangle representing the odd positions is on the bottom.

The structure diagram can be used to find the nim-numbers. Since the only terminal position is in the smaller triangle, these positions have nim-number 0. The positions in the trapezoid are only connected to the positions in the smaller triangle so they have nim-number ${\text {mex}}\{0\}=1$. The non-terminal positions in the smaller triangle are only connected to positions in the trapezoid so they have nim-number ${\text {mex}}\{1\}=0$. We conclude that $\mathsf{DNG}(\mathbb {Z}_{9})=*1$.

We want to recognize similar structure classes.

Definition 3.17

The type of the structure class $X_{I}$ is the triple

$$\begin{aligned} {\text {type}}(X_{I}):=({\text {pty}}(I),{\text {nim}}(P),{\text {nim}}(Q)) \end{aligned}$$

where $P,Q\in X_{I}$ with ${\text {pty}}(P)=0$ and ${\text {pty}}(Q)=1$. The option type of $X_{I}$ is the set

$$\begin{aligned} {\text {otype}}(X_{I}):=\{{\text {type}}(X_{K})\mid X_{K}\in {\text {Opt}}(X_{I})\}, \end{aligned}$$

and the full option type of $X_{I}$ is the set

$$\begin{aligned} {\text {Otype}}(X_{I}):={\text {otype}}(X_{I})\cup \{{\text {type}}(X_{I})\}. \end{aligned}$$

We say $X_{I}$ and $X_{J}$ are type equivalent if ${\text {type}}(X_{I})={\text {type}}(X_{J})$ and ${\text {Otype}}(X_{I})={\text {Otype}}(X_{J})$.

Fig. 4

Visualization of structure classes and their corresponding types

Once the structure digraph is known, the types of the structure classes can be computed recursively from the bottom up using the formulas ${\text {type}}(X_{I})=({\text {pty}}(I),a,b)$, where

$$\begin{aligned} \begin{aligned} A=\{\tilde{a}\mid (\epsilon ,\tilde{a},\tilde{b})\in {\text {otype}}(X_{I})\},\quad B=\{\tilde{b}\mid (\epsilon ,\tilde{a},\tilde{b})\in {\text {otype}}(X_{I})\},\\ a:={\text {mex}}(B),\,b:={\text {mex}}(A\cup \{a\})\text { if }{\text {pty}}(I)=0\\ b:={\text {mex}}(A),\,a:={\text {mex}}(B\cup \{b\})\text { if }{\text {pty}}(I)=1. \end{aligned} \end{aligned}$$

Figure 4 shows the type-dependent visualization of structure classes that occur as nodes of a structure diagram. Note that if $X_{I}$ is terminal, then ${\text {type}}(X_{I})$ must be either (0, 0, 1) or (1, 1, 0) depending on the parity of $X_{I}$. A structure digraph can be quite complicated, but we can simplify it by identifying some vertices.

Definition 3.18

The simplified structure digraph of $\mathsf{DNG}(G)$ is built from the structure digraph of $\mathsf{DNG}(G)$ by the identification of type equivalent structure classes followed by the removal of any resulting loops. The simplified structure diagram is built from the structure diagram using the same identification process.

Fig. 5

The process for obtaining the simplified structure diagram for $\mathsf{DNG}(\mathbb {Z}_{6}\times \mathbb {Z}_{3})$. The double headed arrow $X_{\Phi (G)}\twoheadrightarrow X_{\mathbb {Z}_{2}}$ indicates that $X_{\Phi (G)}$ is also connected to the options of $X_{\mathbb {\mathbb {Z}}_{2}}$

Example 3.19

Figure 5 illustrates the main steps of finding the simplified structure diagram of $\mathsf{DNG}(G)$ with $G=\mathbb {Z}_{6}\times \mathbb {Z}_{3}$. Subfigure (a) shows the Hasse diagram of the poset of intersection subgroups. For this group every proper subgroup is an intersection subgroup. Each intersection subgroup corresponds to a structure class shown in Subfigure (b).

The arrows coming out of a structure class $X_{I}$ are determined by finding the structure classes containing $I\cup \{g\}$ for $g\in G{\setminus } I$ according to Definition 3.12. Next, we compute ${\text {type}}(X_{I})$ and ${\text {otype}}(X_{I})$ for all $X_{I}$. These values are also shown in Subfigure (b). For example, $X_{\Phi (G)}$ is the structure class at the top of the diagram with ${\text {type}}(X_{\Phi (G)})=(1,0,1)$ and ${\text {otype}}(X_{\Phi (G)})=\{(0,0,1),(1,3,2)\}$.

Subfigure (c) depicts ${\text {Otype}}(X_{I})$ for all $X_{I}$, which are computed as the union of ${\text {type}}(X_{I})$ and ${\text {otype}}(X_{I})$. Note that each structure class $X_{I}$ with ${\text {type}}(X_{I})=(0,0,1)$ have the same ${\text {Otype}}(X_{I})$ even though they do not have the same ${\text {otype}}(X_{I})$.

The final step is the identification of the structure classes according to ${\text {type}}$ and ${\text {Otype}}$. This results in the simplified structure diagram of Subfigure (d). We have shaded the triangles in the simplified structure diagram to signify that we have identified type equivalent structure classes. In addition, if more than one structure class has been identified, the boundary of the corresponding triangle is bold.

Proposition 3.20

The type of a structure class $X_{I}$ of $\mathsf{DNG}(G)$ is in

$$\begin{aligned} T=\{t_{1}:=(0,0,1),t_{2}:=(1,0,1),t_{3}:=(1,1,0),t_{4}:=(1,3,2)\}. \end{aligned}$$

Proof

Recall that the type of a terminal structure class is either $t_{1}$ or $t_{3}$. We show that if ${\text {otype}}(X_{I})\subseteq T$, then ${\text {type}}(X_{I})\in T$, as well. This implies the statement by structural induction.

If $X_{J}$ is an option of $X_{I}$, then I is a subgroup of J, and so ${\text {pty}}(X_{J})=1$ implies ${\text {pty}}(X_{I})=1$. Hence if $(1,a,b)\in {\text {otype}}(X_{I})$ for some a and b, then ${\text {type}}(X_{I})$ must be of the form (1, c, d). The following table shows the possibilities for ${\text {otype}}(X_{I})$ and ${\text {type}}(X_{I})$:

We show the calculation for the case ${\text {otype}}(X_{I})=\{t_{4}\}$ which is the fourth case in the first column of the table. Since a structure class with type $t_{4}=(1,3,2)$ is odd, $X_{I}$ must be odd, and so ${\text {type}}(X_{I})=(1,c,d)$ as shown below:

We know that a position and any of its option have the opposite parity. So, $d={\text {mex}}\{3\}=0$, and hence $c={\text {mex}}\{d,2\}={\text {mex}}\{0,2\}=1$. Thus, ${\text {type}}(X_{I})=(1,1,0)=t_{3}$.

Now we show the calculation for the case ${\text {otype}}(X_{I})=\{t_{1},t_{4}\}$ which is the second case in the second table. Again since $t_{4}\in {\text {otype}}(X_{I})$, ${\text {type}}(X_{I})$ is of the form (1, c, d). Then $d={\text {mex}}\{0,3\}=1$, and hence $c={\text {mex}}\{d,1,2\}={\text {mex}}\{1,2\}=0$. Thus, ${\text {type}}(X_{I})=(1,0,1)=t_{2}$.

The rest of the calculations in the table are done similarly. $\square$

The next three results strengthen Corollary 3.3.

Corollary 3.21

The nim-number of $\mathsf{DNG}(G)$ is 0, 1, or 3.

Proof

The nim-number of $\mathsf{DNG}(G)$ is the second digit of ${\text {type}}(X_{\Phi (G)})$. $\square$

Proposition 3.22

If G is nontrivial with odd order, then the simplified structure diagram of $\mathsf{DNG}(G)$ is

and hence $\mathsf{DNG}(G)=*1$.

Proof

It is clear that every structure class is odd. Structural induction on the structure classes shows that ${\text {type}}(X_{I})=(1,1,0)$ and ${\text {Otype}}(X_{I})=\{(1,1,0)\}$ for all $X_{I}\in \mathcal {X}$. $\square$

Proposition 3.23

If G has an even Frattini subgroup, then the simplified structure diagram of $\mathsf{DNG}(G)$ is

and hence $\mathsf{DNG}(G)=*0$.

Proof

Every structure class is even since every intersection subgroup contains the Frattini subgroup. Structural induction on the structure classes shows that ${\text {type}}(X_{I})=(0,0,1)$ and ${\text {Otype}}(X_{I})=\{(0,0,1)\}$ for all $X_{I}\in \mathcal {X}$. $\square$

4 Achievement games

In this section we study the achievement game ${\mathsf{GEN}}(G)$ on the finite group G. For achievement games, we must include an additional structure class $X_{G}$ containing terminal positions. A subset $S\subseteq G$ belongs to $X_{G}$ whenever S generates G while $S{\setminus }\{s\}$ does not for some $s\in S$. Note that this is a slightly abusive notation because, for example, $X_{G}$ does not always contain G. For nontrivial groups, the positions of ${\mathsf{GEN}}(G)$ are the positions of $\mathsf{DNG}(G)$ together with the elements of $X_{G}$. If G is the trivial group, then $\Phi (G)=G$ is not a game position of ${\mathsf{GEN}}(G)=*0$ and $X_{G}=\{\emptyset \}$ is the only structure class. The following is immediate.

Proposition 4.1

The set $\mathcal {Y}:=\mathcal {X}\cup \{X_{G}\}$ is a partition of the set of game positions of ${\mathsf{GEN}}(G)$.

We show that the partition $\mathcal {Y}$ is compatible with the option relationship between positions. The next result is analogous to Proposition 3.10.

Proposition 4.2

Assume $X_{I},X_{J}\in \mathcal {Y}$ and $P\in X_{I}\ne X_{J}$ . Then ${\text {Opt}}(P)\cap X_{J}\not =\emptyset$ if and only if ${\text {Opt}}(I)\cap X_{J}\not =\emptyset$.

Proof

It suffices to consider the case when $J=G$ since the proofs of the other cases are the same as that of Proposition 3.10. We show that ${\text {Opt}}(P)\cap X_{G}\not =\emptyset$ for $P\in X_{I}$ if and only if ${\text {Opt}}(I)\cap X_{G}\not =\emptyset$. Note that ${\text {Opt}}(P)\cap X_{G}\not =\emptyset$ when there exists a $g\in G{\setminus } I$ such that $P\cup \{g\}$ generates G.

First, assume that ${\text {Opt}}(I)\cap X_{G}=\emptyset$. Then $\langle P\cup \{g\}\rangle \subseteq \langle I\cup \{g\}\rangle \not =G$ for all $g\in G{\setminus } I$ and so ${\text {Opt}}(P)\cap X_{G}=\emptyset$.

Now, assume that ${\text {Opt}}(I)\cap X_{G}\not =\emptyset$. Then $I\cup \{g\}\in X_{G}$ for some $g\in G{\setminus } I$, so that $\langle I\cup \{g\}\rangle =G$. For a contradiction, assume that ${\text {Opt}}(P)\cap X_{G}=\emptyset$. Then $H:=\langle P\cup \{g\}\rangle$ is a proper subgroup of G, and so H is contained is some maximal subgroup M. This implies that I is not a subset of M since $g\in M$ and $I\cup \{g\}$ generates G. Hence $P\subseteq M\cap I\in (-\infty ,I)$, which contradicts $P\in X_{I}$. $\square$

Corollary 4.3

Assume $X_{I},X_{J}\in \mathcal {Y}$ and $P,Q\in X_{I}\ne X_{J}$. Then ${\text {Opt}}(P)\cap X_{J}\not =\emptyset$ if and only if ${\text {Opt}}(Q)\cap X_{J}\not =\emptyset$.

As with $\mathsf{DNG}(G)$, it is convenient to append the nim-number data for each structure class to the structure digraph for ${\mathsf{GEN}}(G)$, which we visualize in a structure diagram. The following proposition guarantees that we may define the simplified structure diagram of ${\mathsf{GEN}}(G)$ analogously to that of $\mathsf{DNG}(G)$.

Proposition 4.4

If $P,Q\in X_{I}\in \mathcal {Y}$ and ${\text {pty}}(P)={\text {pty}}(Q)$, then ${\text {nim}}(P)={\text {nim}}(Q)$.

Proof

The proof is analogous to that of Proposition 3.15 using Corollary 4.3. $\square$

Given a structure class $X_{I}$, we define ${\text {type}}(X_{I})$, ${\text {otype}}(X_{I})$, and ${\text {Otype}}(X_{I})$ as before. Note that by definition the type of the terminal structure class $X_{G}$ is ${\text {type}}(X_{G})=({\text {pty}}(G),0,0)$. As in the avoidance games, we define $X_{I}$ and $X_{J}$ to be type equivalent if ${\text {type}}(X_{I})={\text {type}}(X_{J})$ and ${\text {Otype}}(X_{I})={\text {Otype}}(X_{J})$. The simplified structure digraph of ${\mathsf{GEN}}(G)$ is the identification digraph of the structure digraph with respect to type equivalence. The simplified structure diagram is visualized as expected, but the structure class $X_{G}$ will be denoted by 0, regardless of the parity of $X_{G}$.

Example 4.5

Figure 6 shows a simplified structure diagram for ${\mathsf{GEN}}(\mathbb {Z}_{6}\times \mathbb {Z}_{3})=*0$. Note that in the simplified structure diagram of $\mathsf{DNG}(\mathbb {Z}_{6}\times \mathbb {Z}_{3})$, shown in Fig. 5d, all the classes with type (0, 0, 1) were identified. This is not the case in the simplified structure digraph of ${\mathsf{GEN}}(\mathbb {Z}_{6}\times \mathbb {Z}_{3})$ since some of these classes are connected to terminal positions while others are not. The use of the dotted arrows is to emphasize that these arrows are not present in $\mathsf{DNG}(\mathbb {Z}_{6}\times \mathbb {Z}_{3})$.

Fig. 6

Simplified structure diagram for ${\mathsf{GEN}}(\mathbb {Z}_{6}\times \mathbb {Z}_{3})$

Definition 4.6

We call a structure class $X_{I}$ semi-terminal if the terminal class $X_{G}$ is an option of $X_{I}$. We call $X_{I}$ non-terminal if $X_{I}$ is neither terminal nor semi-terminal.

Note that if I is a maximal subgroup, then $X_{I}$ is semi-terminal. However, $X_{I}$ may be semi-terminal even if I is not a maximal subgroup. For example, $X_{\langle (0,1)\rangle }$ is semi-terminal in ${\mathsf{GEN}}(\mathbb {Z}_{6}\times \mathbb {Z}_{3})$ but $\langle (0,1)\rangle \cong \mathbb {Z}_{3}$ is not a maximal subgroup of $\mathbb {Z}_{6}\times \mathbb {Z}_{3}$, as shown in Figs. 5a and 6. Also note that a semi-terminal structure class cannot have a non-terminal option since if $X_{J}$ is an option of $X_{I}$, then $I\le J$.

Proposition 4.7

If G is a nontrivial group with |G| odd, then the type of a structure class $X_{I}$ of ${\mathsf{GEN}}(G)$ is in

$$\begin{aligned} T=\{t_{0}:=(1,0,0),t_{1}:=(1,1,0),t_{2}:=(1,2,0),t_{3}:=(1,2,1)\}. \end{aligned}$$

Proof

First, it is clear that ${\text {type}}(X_{I})=t_{0}$ if and only if $X_{I}$ is terminal. Now, we use structural induction to argue that ${\text {type}}(X_{I})=t_{3}$ if $X_{I}$ is semi-terminal and ${\text {type}}(X_{I})\in \{t_{1},t_{2}\}$ if $X_{I}$ is non-terminal.

If $X_{I}$ is semi-terminal, then every option of $X_{I}$ is either terminal or semi-terminal, and so ${\text {otype}}(X_{I})=\{t_{0}\}$ or ${\text {otype}}(X_{I})=\{t_{0},t_{3}\}$ by induction. In both cases the type of $X_{I}$ must be $t_{3}$.

If $X_{I}$ is non-terminal, then no option of $X_{I}$ has type $t_{0}$ and so ${\text {otype}}(X_{I})\subseteq \{t_{1},t_{2},t_{3}\}$. In each case, ${\text {type}}(X_{I})\in \{t_{1},t_{2}\}$. The following table shows the possibilities for ${\text {otype}}(X_{I})$ and ${\text {type}}(X_{I})$: $\square$

Corollary 4.8

If G is nontrivial with |G| odd, then the nim-number of ${\mathsf{GEN}}(G)$ is 1 or 2.

The computer experiments Ernst and Sieben (2013) of the next section hint at the following.

Conjecture 4.9

If |G| is even, then the nim-number of ${\mathsf{GEN}}(G)$ is in $\{0,1,2,3,4\}$.

The techniques used to prove Proposition 4.7 do not seem to be sufficient to settle this conjecture. A proof probably requires a more careful analysis of the forbidden configurations in a structure diagram.

5 Algorithms

We developed a software package that computes the simplified structure digraph of $\mathsf{DNG}(G)$ and ${\mathsf{GEN}}(G)$. We used GAP The GAP Group (2013) to get the maximal subgroups and the rest of the computation is implemented in C++. The software is efficient enough to allow us to compute the nim-numbers for the smallest 100, 000 groups which includes all groups up to size 511. The result is available on our companion web page Ernst and Sieben (2013). The algorithms used are shown in Figs. 7 and 8. Both are based on the results of this section.

Fig. 7

Algorithm to compute the simplified structure digraph of $\mathsf{DNG}(G)$

Fig. 8

Algorithm to compute the simplified structure digraph of ${\mathsf{GEN}}(G)$

If I and J are intersection subgroups, it is useful to define $\mathcal {K}:=\{K\in \mathcal {I}\mid I\subseteq K\text { and }J\not \subseteq K\}$.

Lemma 5.1

If $I,J\in \mathcal {I}$ with $I\le J$, then $[I,J)=\{J\cap K\mid K\in \mathcal {K}\}$.

Proof

Let $L\in [I,J)$. Then $L=\bigcap \mathcal {N}$ with some $\mathcal {N}\subseteq \mathcal {M}$ such that $I\subseteq L\subset J$, and so $L\in \mathcal {K}$. This implies that $[I,J)\subseteq \mathcal {K}$. Now, suppose $K\in \mathcal {K}$. Then $K\cap J\in [I,J)$, and hence $\{K\cap J\mid K\in \mathcal {K}\}\subseteq [I,J)$. Therefore, $[I,J)=\{J\cap K\mid K\in \mathcal {K}\}$. $\square$

The following result is used by the algorithms in Figs. 7 and 8.

Proposition 5.2

Let $I,J\in \mathcal {I}$. We have $X_{J}\in {\text {Opt}}(X_{I})$ if and only if $I\subseteq J$ and $J{\setminus }\bigcup \mathcal {K}\not =\emptyset$.

Proof

Assume $I\le J$. First, assume that $X_{J}\in {\text {Opt}}(X_{I})$. Then there exists $g\in G{\setminus } I$ such that $I\cup \{g\}\in X_{J}$. This means there exists $g\in J{\setminus } I$ such that $I\cup \{g\}\subseteq J$ but $I\cup \{g\}\nsubseteq L$ for any $L\in (-\infty ,J)$. Let $K\in \mathcal {K}$, so that $I\subseteq K$ and $J\nsubseteq K$. Then by Lemma 5.1, $J\cap K\in [I,J)\subseteq (-\infty ,J)$. Then it must be the case that $I\cup \{g\}\nsubseteq K$ for all $K\in \mathcal {K}$, which implies that $g\notin K$ for all $K\in \mathcal {K}$. Hence $g\notin \bigcup \mathcal {K}$. But since $g\in J$, $J{\setminus }\bigcup \mathcal {K}\ne \emptyset$.

Now, assume that there exist $g\in J{\setminus }\bigcup \mathcal {K}$. Then $I\cup \{g\}\subseteq J$ since $I\le J$. Moreover, since $g\in J{\setminus }\bigcup \mathcal {K}$, $g\notin K$ for all $K\in \mathcal {K}$. But then $g\notin J\cap K$ for all $K\in \mathcal {K}$. Thus, $X_{J}\in {\text {Opt}}(X_{I})$, as desired. $\square$

6 Cyclic groups

In this section we study the avoidance game $\mathsf{DNG}(G)$ and the achievement game ${\mathsf{GEN}}(G)$ for a cyclic group G. First, we recall some general results about maximal subgroups.

According to (Dlab 1960, Theorem 2) and (Suzuki (1982), Exercise 7 on page 144), we can decompose the Frattini subgroup of a direct product.

Proposition 6.1

If G and H are finite groups, then $\Phi (G\times H)=\Phi (G)\times \Phi (H)$.

The following result can be found in (Dlab 1960, Corollary 2) and (Dixon 1967, Problem 8.1) and is a consequence of Proposition 6.1.

Proposition 6.2

If n has prime factorization $n=p_{1}^{n_{1}}\cdots p_{k}^{n_{k}}$, then the Frattini subgroup of $\mathbb {Z}_{n}$ is generated by $p_{1}\cdots p_{k}$ and so it is isomorphic to the cyclic group of order $p_{1}^{n_{1}-1}\cdots p_{k}^{n_{k}-1}$.

The next result follows from (Dummit and Foote 2004, Exercise 6.1.4) and (Rose 1994, Problem 140(v)).

Proposition 6.3

A subgroup of a finite abelian group is maximal if and only if it has prime index.

Now we are ready to prove our first result about nim-numbers for finite cyclic groups.

Fig. 9

Simplified structure diagrams for cyclic groups assuming $k\ge 1$

Proposition 6.4

If $k\ge 1$, then the simplified structure diagram of $\mathsf{DNG}(\mathbb {Z}_{4k})$ is the one shown in Fig. 9a, and hence $\mathsf{DNG}(\mathbb {Z}_{4k})=*0$.

Proof

The result follows from Proposition 3.23 since $\Phi (\mathbb {Z}_{4k})$ is even by Proposition 6.2. $\square$

Proposition 6.5

If $k\ge 1$, then the simplified structure diagram of $\mathsf{DNG}(\mathbb {Z}_{4k+2})$ is the one shown in Fig. 9c, and hence $\mathsf{DNG}(\mathbb {Z}_{4k+2})=*3$.

Proof

Define the following collection of sets that form a partition of $\mathcal {X}$:

$$\begin{aligned} \begin{aligned} \mathcal {S}_{1}&:=\{X_{I}\in \mathcal {X}\mid I=\langle 2\rangle \};\\ \mathcal {S}_{2}&:=\{X_{I}\in \mathcal {X}\mid X_{I}\text { is even}\};\\ \mathcal {S}_{3}&:=\{X_{I}\in \mathcal {X}\mid X_{I}\text { is odd but }I\ne \langle 2\rangle \}. \end{aligned} \end{aligned}$$

We use structural induction on the structure classes to show that these sets are nonempty and are the type equivalence classes of the structure classes, and that

$$\begin{aligned} {\text {type}}(X_{I})={\left\{ \begin{array}{ll} (1,1,0), &{} \quad X_{I}\in \mathcal {S}_{1}\\ (0,0,1), &{} \quad X_{I}\in \mathcal {S}_{2}\\ (1,3,2), &{} \quad X_{I}\in \mathcal {S}_{3}. \end{array}\right. } \end{aligned}$$

First, note that $\langle 2\rangle$ has order $2k+1$, and hence index 2. By Proposition 6.3, $\langle 2\rangle$ is a maximal subgroup, which implies that $X_{\langle 2\rangle }\in \mathcal {S}_{1}$ is a terminal structure class. Since $\langle 2\rangle$ is odd, ${\text {type}}(X_{\langle 2\rangle })=(1,1,0)$. Hence ${\text {Otype}}(X_{\langle 2\rangle })=\{(1,1,0)\}$.

Next, let q be an odd prime divisor of $4k+2$. Then $\langle q\rangle$ has index q, and so $\langle q\rangle$ is a maximal subgroup by Proposition 6.3. Moreover, $\langle q\rangle$ has even order. It follows that $X_{\langle q\rangle }\in \mathcal {S}_{2}$, and hence $\mathcal {S}_{2}\ne \emptyset$. Let $X_{I}\in \mathcal {S}_{2}$. If $X_{I}$ is terminal, then ${\text {type}}(X_{I})=(0,0,1)$ and ${\text {otype}}(X_{I})=\emptyset$. If $X_{I}$ is not terminal, then any option of $X_{I}$ must be even since $X_{I}$ is even. In this case, ${\text {otype}}(X_{I})=\{(0,0,1)\}$ by induction. In both cases, ${\text {type}}(X_{I})=(0,0,1)$, and so ${\text {Otype}}(X_{I})=\{(0,0,1)\}$.

For the final case, suppose $4k+2$ has prime factorization $2p_{1}^{n_{1}}\cdots p_{r}^{n_{r}}$, where the $p_{i}$’s are distinct odd primes. By Proposition 6.2, $\Phi (\mathbb {Z}_{4k+2})$ is generated by $2p_{1}\cdots p_{r}$ and is isomorphic to the cyclic group of odd order $p_{1}^{n_{1}-1}\cdots p_{r}^{n_{r}-1}\ne 2k+1$. This implies that $\Phi (\mathbb {Z}_{4k+2})\ne \langle 2\rangle$. Hence $\Phi (\mathbb {Z}_{4k+2})\in \mathcal {S}_{3}$, and so $\mathcal {S}_{3}\ne \emptyset$. Let $X_{I}\in \mathcal {S}_{3}$ so that I is an odd intersection subgroup different from $\langle 2\rangle$. Since the Frattini subgroup is a subgroup of I, $I=\langle 2a\rangle$ for some $a\ne 1$ that divides $p_{1}\cdots p_{r}$. This implies that $\langle I\cup \{2\}\rangle =\langle 2\rangle$, and so $X_{\langle 2\rangle }\in \mathcal {S}_{1}$ is an option of $X_{I}$. Now, let p be a prime divisor of a, which is odd. Then $\langle I\cup \{p\}\rangle =\langle p\rangle$ has index p, and hence is an even maximal subgroup by Proposition 6.3. This implies that $X_{\langle p\rangle }\in \mathcal {S}_{2}$ is an option of $X_{I}$. Thus, ${\text {otype}}(X_{I})$ is either $\{(1,1,0),(0,0,1)\}$ or $\{(1,1,0),(0,0,1),(1,3,2)\}$ by induction. In both cases, ${\text {type}}(X_{I})=(1,3,2)$. Therefore, ${\text {Otype}}(X_{I})=\{(1,1,0),(0,0,1),(1,3,2)\}$.

It follows that the simplified structure diagram of $\mathsf{DNG}(\mathbb {Z}_{4k+2})$ is the one shown in Fig. 9(c), and so $\mathsf{DNG}(\mathbb {Z}_{4k+2})=*3$. $\square$

Example 6.6

Figure 10 shows a representative game digraph and the simplified structure diagram for $\mathsf{DNG}(\mathbb {Z}_{6})$.

Fig. 10

A representative game digraph and the simplified structure diagram for $\mathsf{DNG}(\mathbb {Z}_{6})$

An easy calculation in the $\mathbb {Z}_{2}$ case together with Propositions 6.4, 6.5, and 3.22 immediately yield the following result.

Corollary 6.7

The nim-number of $\mathsf{DNG}(\mathbb {Z}_{2})$ is 1. If $n\ge 3$, then

$$\begin{aligned} \mathsf{DNG}(\mathbb {Z}_{n})={\left\{ \begin{array}{ll} *1, &{} \quad n\equiv _{2}1\\ *0, &{} \quad n\equiv _{4}0\\ *3, &{} \quad n\equiv _{4}2 \end{array}\right. }. \end{aligned}$$

Proposition 6.8

The nim-number of ${\mathsf{GEN}}(\mathbb {Z}_{n})$ with $n\ge 2$ is one larger than the nim-number of $\mathsf{DNG}(\mathbb {Z}_{n})$.

Proof

The game digraph of ${\mathsf{GEN}}(\mathbb {Z}_{n})$ is an extension of the game digraph of $\mathsf{DNG}(\mathbb {Z}_{n})$. In this extension every old vertex in the game digraph of $\mathsf{DNG}(\mathbb {Z}_{n})$ gets a new option that is a generating set since $\mathbb {Z}_{n}$ is cyclic. These generating sets are terminal positions with nim-number 0. Figure 1a, b show this extension for $\mathbb {Z}_{4}$. After the extension, the nim-number of every old vertex is increased by one. Figure 9 shows how the structure diagrams change during the extension. $\square$

Corollary 6.9

The nim-number of ${\mathsf{GEN}}(\mathbb {Z}_{2})$ is 2. If $n\ge 3$, then

$$\begin{aligned} {\mathsf{GEN}}(\mathbb {Z}_{n})={\left\{ \begin{array}{ll} *2, &{} n\equiv _{2}1\\ *1, &{} n\equiv _{4}0\\ *4, &{} n\equiv _{4}2 \end{array}\right. }. \end{aligned}$$

7 Dihedral groups

In this section we study the avoidance game $\mathsf{DNG}(G)$ and the achievement game ${\mathsf{GEN}}(G)$ for a dihedral group G. The following result is folklore.

Proposition 7.1

The subgroups of the dihedral group $\mathbb {D}_{n}=\langle r,f{\mid } r^{n}=f^{2}=e,rf=fr^{n-1}\rangle$ are either dihedral or cyclic. The maximal subgroups of $\mathbb {D}_{n}$ are the cyclic group $\langle r\rangle$ and the dihedral groups of the form $\langle r^{p},r^{i}f\rangle \cong \mathbb {D}_{n/p}$ with prime divisors p of n.

The following result can be found in (Dixon 1967, Problem 8.1).

Proposition 7.2

If n has prime factorization $n=p_{1}^{n_{1}}\cdots p_{k}^{n_{k}}$, then the Frattini subgroup of $\mathbb {D}_{n}$ is a cyclic group of order $p_{1}^{n_{1}-1}\cdots p_{k}^{n_{k}-1}$.

Proposition 7.3

If $k\ge 1$, then the simplified structure diagrams of $\mathsf{DNG}(\mathbb {D}_{4k})$ and $\mathsf{DNG}(\mathbb {D}_{4k+2})$ are the ones shown in Fig. 11a, c, respectively, and hence $\mathsf{DNG}(\mathbb {D}_{2k+2})=*0$.

Proof

The Frattini subgroup of $\mathbb {D}_{4k}$ is even by Proposition 7.2. Thus, the simplified structure diagram of $\mathsf{DNG}(\mathbb {D}_{4k})$ is the one depicted in Fig. 11a by Proposition 3.23.

Fig. 11

Simplified structure diagrams for the dihedral groups assuming $k\ge 1$

The terminal structure classes of $\mathsf{DNG}(\mathbb {D}_{4k+2})$ are even since the maximal subgroups are even by Proposition 7.1. On the other hand, the Frattini subgroup is odd by Proposition 7.2. Structural induction on the structure classes shows that ${\text {type}}(X_{I})=(0,0,1)$ and ${\text {Otype}}(X_{I})=\{(0,0,1)\}$ if $X_{I}$ is even, while ${\text {type}}(X_{I})=(1,0,1)$ and ${\text {Otype}}(X_{I})=\{(1,0,1)\}$ if $X_{I}$ is odd. Every position that is not terminal has a terminal option since by Proposition 7.1 we can add an appropriate rotation to the position that creates a terminal position. Therefore, the simplified structure diagram of $\mathsf{DNG}(\mathbb {D}_{4k+2})$ is the one depicted in Fig. 11c. $\square$

Proposition 7.4

If $k\ge 1$, then the simplified structure diagram of $\mathsf{DNG}(\mathbb {D}_{2k+1})$ is the one shown in Fig. 11b, and hence $\mathsf{DNG}(\mathbb {D}_{2k+1})=*3$.

Proof

This argument is essentially the same as the one for $\mathsf{DNG}(\mathbb {Z}_{4k+2})$ (see the proof of Proposition 6.5), where we replace 2 with r. The only maximal subgroup with odd order is $\langle r\rangle$. Every other maximal subgroup has even order. $\square$

Corollary 7.5

For $n\ge 3$, we have

$$\begin{aligned} \mathsf{DNG}(\mathbb {D}_{n})={\left\{ \begin{array}{ll} *3, &{} n\equiv _{2}1\\ *0, &{} n\equiv _{2}0 \end{array}\right. }. \end{aligned}$$

The outcome of ${\mathsf{GEN}}(\mathbb {D}_{4k})$ can be determined using (Barnes 1988, Section 3.3). We provide information about the structure diagram of the game.

Proposition 7.6

If $k\ge 1$, then the simplified structure diagram of ${\mathsf{GEN}}(\mathbb {D}_{4k})$ is the one shown in Fig. 11d, and hence ${\mathsf{GEN}}(\mathbb {D}_{4k})=*0$.

Proof

Define the following collection of sets that form a partition of $\mathcal {Y}$:

$$\begin{aligned} \begin{aligned} \mathcal {S}_{1}&:=\{X_{I}\in \mathcal {Y}\mid X_{I}\text { is terminal}\};\\ \mathcal {S}_{2}&:=\{X_{I}\in \mathcal {Y}\mid X_{I}\text { is semi-terminal}\};\\ \mathcal {S}_{3}&:=\{X_{I}\in \mathcal {Y}\mid X_{I}\text { is non-terminal}\}. \end{aligned} \end{aligned}$$

We use structural induction on the structure classes to show that these sets are nonempty and are the type equivalence classes of the structure classes, and that

$$\begin{aligned} {\text {type}}(X_{I})={\left\{ \begin{array}{ll} (0,0,0), &{} X_{I}\in \mathcal {S}_{1}\\ (0,1,2), &{} X_{I}\in \mathcal {S}_{2}\\ (0,0,2), &{} X_{I}\in \mathcal {S}_{3} \end{array}\right. }. \end{aligned}$$

First, observe that the Frattini subgroup has even order by Proposition 7.2. This implies that every structure class is even, as well.

It is clear that $\mathcal {S}_{1}=\{X_{G}\}\ne \emptyset$ and ${\text {type}}(X_{G})=(0,0,0)$.

Consider the even maximal subgroup $R=\langle r\rangle$ of $\mathbb {D}_{4k}$. Then $X_{R}\in \mathcal {S}_{2}$ since $\langle R\cup \{f\}\rangle =\mathbb {D}_{4k}$, and so $\mathcal {S}_{2}\ne \emptyset$. If $X_{I}\in \mathcal {S}_{2}$, then $X_{I}$ is semi-terminal, and so ${\text {otype}}(X_{I})$ is either $\{(0,0,0)\}$ or $\{(0,0,0),(0,1,2)\}$ by induction. In either case, ${\text {type}}(X_{I})=(0,1,2)$, and so ${\text {Otype}}(X_{I})=\{(0,0,0),(0,1,2)\}$.

For the final case, observe that $\mathcal {S}_{3}\ne \emptyset$ since the empty position is non-terminal and belongs to $X_{\Phi (\mathbb {D}_{4k})}$. If $X_{I}\in \mathcal {S}_{3}$, then every option of $X_{I}$ must be semi-terminal or non-terminal, and so ${\text {otype}}(X_{I})$ is either $\{(0,0,2)\}$ or $\{(0,0,2),(0,1,2)\}$ by induction. In either case, ${\text {type}}(X_{I})=(0,0,2)$, and hence ${\text {Otype}}(X_{I})=\{(0,0,2),(0,1,2)\}$.

It follows that the simplified structure diagram of ${\mathsf{GEN}}(\mathbb {D}_{4k})$ is the one shown in Fig. 11d, and so ${\mathsf{GEN}}(\mathbb {D}_{4k})=*0$. $\square$

Proposition 7.7

If $k\ge 1$, then the simplified structure diagram of ${\mathsf{GEN}}(\mathbb {D}_{2k+1})$ is the one shown in Fig. 11e, and hence ${\mathsf{GEN}}(\mathbb {D}_{2k+1})=*3$.

Proof

Let $G:=\mathbb {D}_{2k+1}$. Define the following collection of sets that form a partition of $\mathcal {Y}$:

$$\begin{aligned} \begin{aligned} \mathcal {S}_{1}&:=\{X_{I}\in \mathcal {Y}\mid X_{I}\text { is terminal}\};\\ \mathcal {S}_{2}&:=\{X_{I}\in \mathcal {Y}\mid X_{I}\text { is odd and semi-terminal}\};\\ \mathcal {S}_{3}&:=\{X_{I}\in \mathcal {Y}\mid X_{I}\text { is even and semi-terminal}\};\\ \mathcal {S}_{4}&:=\{X_{I}\in \mathcal {Y}\mid X_{I}\text { is non-terminal}\}. \end{aligned} \end{aligned}$$

We use structural induction on the structure classes to show that these sets are nonempty and are the type equivalence classes of the structure classes, and that

$$\begin{aligned} {\text {type}}(X_{I})={\left\{ \begin{array}{ll} (0,0,0), &{} X_{I}\in \mathcal {S}_{1}\\ (1,2,1), &{} X_{I}\in \mathcal {S}_{2}\\ (0,1,2), &{} X_{I}\in \mathcal {S}_{3}\\ (1,3,0), &{} X_{I}\in \mathcal {S}_{4} \end{array}\right. }. \end{aligned}$$

It is clear that $\mathcal {S}_{1}=\{X_{G}\}\ne \emptyset$ and ${\text {type}}(X_{G})=(0,0,0)$.

Next, consider the maximal subgroup $R=\langle r\rangle$ of G. The only odd maximal subgroup is R by Proposition 7.1, and so $\mathcal {S}_{2}=\{X_{R}\}$. Any $T\in {\text {Opt}}(R)$ generates G since R is a maximal subgroup. So R has no option in a semi-terminal structure class, and hence ${\text {otype}}(X_{R})=\{(0,0,0)\}$. Thus, ${\text {type}}(X_{R})=(1,2,1)$, and so ${\text {Otype}}(X_{R})=\{(0,0,0),(1,2,1)\}$.

For the third case, consider the even subgroup $F=\langle f\rangle$. Then F is a position of an even semi-terminal structure class since $\langle F\cup \{r\}\rangle =G$, and so $\mathcal {S}_{3}\ne \emptyset$. Suppose $X_{I}\in \mathcal {S}_{3}$. Since $X_{I}$ is semi-terminal, ${\text {otype}}(X_{I})$ is either $\{(0,0,0)\}$ or $\{(0,0,0),(0,1,2)\}$ by induction. In either case, ${\text {type}}(X_{I})=(0,1,2)$, and so ${\text {Otype}}(X_{I})=\{(0,0,0),(0,1,2)\}$.

For the final case, note that $\Phi (G)$ is a proper subgroup of $\langle r\rangle$ by Proposition 7.2. If g is a rotation in G, then $\Phi (G)\cup \{g\}$ generates a subgroup of $\langle r\rangle$. If g is a reflection in G, then $\Phi (G)\cup \{g\}$ generates a subgroup H of G. It is easy to see that H is isomorphic to a dihedral group whose order is twice the order of $\Phi (G)$. Thus $H\ne G$ which means $X_{\Phi (G)}\in \mathcal {S}_{4}$, and so $\mathcal {S}_{4}\ne \emptyset$. Let $X_{I}\in \mathcal {S}_{4}$. Since $X_{I}$ is non-terminal, I does not contain r or any reflections. Then $X_{I}$ must be odd by Cauchy’s Theorem because there are no even order rotations in G. Hence $\langle I\cup \{r\}\rangle =\langle r\rangle$ is an option of $X_{I}$ in $\mathcal {S}_{2}$ and $\langle I\cup \{f\}\rangle$ is an option of $X_{I}$ in $\mathcal {S}_{3}$. So ${\text {otype}}(X_{I})$ is either $\{(1,2,1),(0,1,2)\}$ or $\{(1,2,1),(0,1,2),(1,3,0)\}$ by induction. In either case, ${\text {type}}(X_{I})=(1,3,0)$, and hence ${\text {Otype}}(X_{I})=\{(1,2,1),(0,1,2),(1,3,0)\}$.

It follows that the simplified structure diagram of ${\mathsf{GEN}}(G)$ is the one shown in Fig. 11e, and so ${\mathsf{GEN}}(G)=*3$. $\square$

Example 7.8

Figure 12 shows a representative game digraph for ${\mathsf{GEN}}(\mathbb {D}_{3})$ and Fig. 11e shows the simplified structure diagram for ${\mathsf{GEN}}(\mathbb {D}_{3})$.

Fig. 12

Representative game digraph of ${\mathsf{GEN}}(\mathbb {D}_{3})$. We use permutation notation after the identification of $\mathbb {D}_{3}$ with $S_{3}$

Proposition 7.9

If $k\ge 1$, then the simplified structure diagram of ${\mathsf{GEN}}(\mathbb {D}_{4k+2})$ is the one shown in Fig. 11f, and hence ${\mathsf{GEN}}(\mathbb {D}_{4k+2})=*1$.

Proof

Let $G:=\mathbb {D}_{4k+2}$. Define the following collection of sets that form a partition of $\mathcal {Y}$:

$$\begin{aligned} \begin{aligned} \mathcal {S}_{1}&:=\{X_{I}\in \mathcal {Y}\mid X_{I}\text { is terminal}\};\\ \mathcal {S}_{2}&:=\{X_{I}\in \mathcal {Y}\mid X_{I}\text { is semi-terminal}\};\\ \mathcal {S}_{3}&:=\{X_{I}\in \mathcal {Y}\mid X_{I}\text { is even and non-terminal}\};\\ \mathcal {S}_{4}&:=\{X_{I}\in \mathcal {Y}\mid X_{I}\text { is odd and non-terminal without any even non-terminal option}\};\\ \mathcal {S}_{5}&:=\{X_{I}\in \mathcal {Y}\mid X_{I}\text { is odd and non-terminal with an even non-terminal option}\}. \end{aligned} \end{aligned}$$

We use structural induction on the structure classes to show that these sets are nonempty and are the type equivalence classes of the structure classes and that

$$\begin{aligned} {\text {type}}(X_{I})={\left\{ \begin{array}{ll} (0,0,0), &{} \quad X_{I}\in \mathcal {S}_{1}\\ (0,1,2), &{} \quad X_{I}\in \mathcal {S}_{2}\\ (0,0,2), &{} \quad X_{I}\in \mathcal {S}_{3}\\ (1,1,0), &{} \quad X_{I}\in \mathcal {S}_{4}\\ (1,1,2), &{} \quad X_{I}\in \mathcal {S}_{5} \end{array}\right. }. \end{aligned}$$

As usual, we have $\mathcal {S}_{1}=\{X_{G}\}\ne \emptyset$ and ${\text {type}}(X_{G})=(0,0,0)$.

Next, consider the even maximal subgroup $R:=\langle r\rangle$. Then $X_{R}\in \mathcal {S}_{2}$ since $\langle R\cup \{f\}\rangle =G$, and so $\mathcal {S}_{2}\ne \emptyset$. Suppose $X_{I}\in \mathcal {S}_{2}$. Then $I=R$ or I contains a reflection, and so $X_{I}$ must be even. Since $X_{I}$ is semi-terminal, ${\text {otype}}(X_{I})$ is one of $\{(0,0,0)\}$ and $\{(0,0,0),(0,1,2)\}$ by induction. In either case, ${\text {type}}(X_{I})=(0,1,2)$, and so ${\text {Otype}}(X_{I})=\{(0,0,0),(0,1,2)\}$.

For the third case, consider the even subgroup $Q=\langle r^{2k+1}\rangle =\{e,r^{2k+1}\}$. Then $Q\in \mathcal {S}_{3}$ since for all $h\in G$, $\langle Q\cup \{h\}\rangle \ne G$, and so $\mathcal {S}_{3}\ne \emptyset$. Let $X_{I}\in \mathcal {S}_{3}$. Then every option of $X_{I}$ is even. Moreover, it must be the case that $\langle I\cup \{x\}\rangle$ is an option in a structure class belonging to $\mathcal {S}_{2}$ exactly when x is a reflection or x is a rotation such that $\langle I\cup \{x\}\rangle$ is the full rotation subgroup. Otherwise, $\langle I\cup \{x\}\rangle$ is an option in a structure class belonging to $\mathcal {S}_{3}$. This shows that ${\text {otype}}(X_{I})$ is either $\{(0,1,2)\}$ or $\{(0,1,2),(0,0,2)\}$ by induction. In either case, ${\text {type}}(X_{I})=(0,0,2)$, and hence ${\text {Otype}}(X_{I})=\{(0,1,2),(0,0,2)\}$.

To show that $\mathcal {S}_{4}\ne \emptyset$, consider the odd subgroup $P=\langle r^{2}\rangle$ and let x be any even order element of G. Then either x is a reflection or equal to $r^{m}$, where m is odd. In either case, $\langle P\cup \{x\}\rangle$ is maximal, and hence $\langle P\cup \{x\}\rangle$ must be an element of a semi-terminal structure class in $\mathcal {S}_{2}$. Hence $P\in \mathcal {S}_{4}$. Now, let $X_{I}\in \mathcal {S}_{4}$, so that $X_{I}$ is an odd non-terminal structure class without any even non-terminal options. We see that $\langle I\cup \{r\}\rangle$ contains the maximal subgroup $\langle r\rangle$, which has even order. So $X_{I}$ has an option in $\mathcal {S}_{2}$. Next, we show that $X_{I}$ has no option in $\mathcal {S}_{5}$. For a contradiction, suppose $X_{I}$ has an option $X_{J}$ in $\mathcal {S}_{5}$. By the definition of $\mathcal {S}_{5}$, $X_{J}$ has an option $X_{H}$ in $\mathcal {S}_{3}$. Let t be an element of order 2 in H and let $I\cup \{t\}\in X_{K}$. Then K is even and $K\le H\le G$. So $X_{K}$ is an option of $X_{I}$ in $\mathcal {S}_{3}$, which is a contradiction. This shows that ${\text {otype}}(X_{I})$ is either $\{(0,1,2)\}$ or $\{(0,1,2),(1,1,0)\}$ by induction. In either case, ${\text {otype}}(X_{I})=\{(1,1,0)\}$, and hence ${\text {Otype}}(X_{I})=\{(0,1,2),(1,1,0)\}$.

For the final case, consider the non-terminal structure class $X_{\Phi (G)}$, which contains the empty position $\emptyset$ and is odd by Proposition 7.2. We see that $\langle \emptyset \cup \{r^{2k+1}\}\rangle =\{e,r^{2k+1}\}$ is an option in a structure class belonging to $\mathcal {S}_{3}$. This shows that $X_{\Phi (G)}\in \mathcal {S}_{5}$, and so $\mathcal {S}_{5}\ne \emptyset$. Suppose $X_{I}\in \mathcal {S}_{5}$. Since I is of odd order, it must be a subgroup of $\langle r^{2}\rangle$. However, since $\langle r^{2}\rangle$ is an element of a structure class belonging to $\mathcal {S}_{4}$, I must be a proper subgroup of $\langle r^{2}\rangle$. We see that $\langle I\cup \{r\}\rangle =\langle r\rangle$ and $\langle I\cup \{r^{2}\}\rangle =\langle r^{2}\rangle$, which are elements of structure classes belonging to $\mathcal {S}_{2}$ and $\mathcal {S}_{4}$, respectively. As a consequence, ${\text {otype}}(X_{I})$ is either $\{(0,0,2),(1,1,0),(0,1,2)\}$ or $\{(0,0,2),(1,1,0),(0,1,2),(1,1,2)\}$ by induction. In either case, ${\text {type}}(X_{I})=(1,1,2)$, and hence ${\text {Otype}}(X_{I})=\{(0,0,2),(1,1,0),(0,1,2),(1,1,2)\}$.

It follows that the simplified structure diagram of ${\mathsf{GEN}}(G)$ is the one shown in Fig. 11f, which implies that ${\mathsf{GEN}}(G)=*1$. $\square$

Corollary 7.10

For $n\ge 3$, we have

$$\begin{aligned} {\mathsf{GEN}}(\mathbb {D}_{n})={\left\{ \begin{array}{ll} *3, &{} n\equiv _{2}1\\ *0, &{} n\equiv _{4}0\\ *1, &{} n\equiv _{4}2 \end{array}\right. }. \end{aligned}$$

The simplified structure diagrams for ${\mathsf{GEN}}(\mathbb {D}_{n})$ are shown in Fig. 11.

8 Abelian groups

In this section, we study the avoidance game $\mathsf{DNG}(G)$ and the achievement game ${\mathsf{GEN}}(G)$ for a finite abelian group G. The following result is from (Suzuki 1982, Corollary on page 141).

Proposition 8.1

If G and H are finite groups of relatively prime orders, then any subgroup of $G\times H$ is of the form $K\times L$ for some subgroups $K\le G$ and $L\le H$.

The next result completely characterizes the nim-numbers for $\mathsf{DNG}(G)$ for finite abelian groups G.

Proposition 8.2

If G is a finite abelian group, then

$$\begin{aligned} \mathsf{DNG}(G)={\left\{ \begin{array}{ll} *1, &{} \quad G\text { is nontrivial of odd order}\\ *1, &{} \quad G\cong \mathbb {Z}_{2}\\ *3, &{} \quad G\cong \mathbb {Z}_{2}\times \mathbb {Z}_{2k+1}\text { with }k\ge 1\\ *0, &{} \quad \text {else} \end{array}\right. }. \end{aligned}$$

Proof

The case when G is nontrivial of odd order is proved in Proposition 3.22. Corollary 6.7 covers both the $G\cong \mathbb {Z}_{2}$ and $G\cong \mathbb {Z}_{2}\times \mathbb {Z}_{2k+1}$ cases. In every other case, $\mathsf{DNG}(G)=*0$ since the second player has a winning strategy as was shown in (Anderson and Harary 1987, Section 3) and in (Barnes 1988, Section 2.1) (see Proposition 3.1). $\square$

The remainder of this section tackles ${\mathsf{GEN}}(G)$ for finite abelian groups G. Our analysis involving groups with non-zero nim-numbers handles three cases, which are addressed in Propositions 8.11, 8.14, and 8.15.

Recall that every finite abelian group G has an invariant factor decomposition $G\cong \mathbb {Z}_{\alpha _{1}}\times \cdots \times \mathbb {Z}_{\alpha _{k}}$ where the positive non-unit elementary divisors $\alpha _{1},\ldots ,\alpha _{k}$ are uniquely determined by G and satisfy $\alpha _{i}\mid \alpha _{i+1}$ for $i\in \{1,\ldots ,k-1\}$. Our proof of Proposition 8.11 requires the following notion and the lemmas that follow.

Definition 8.3

We define the spread ${\text {spr}}(G)$ of the finite abelian group G to be the number of elementary divisors in the invariant factor decomposition of G.

Note that the trivial group has spread ${\text {spr}}(\mathbb {Z}_{1})=0$. If $G=\mathbb {Z}_{p_{1}^{r_{1}}}\times \cdots \times \mathbb {Z}_{p_{k}^{r_{k}}}$ is an abelian group with primes $p_{1},\ldots ,p_{k}$, then ${\text {spr}}(G)=\max \{n_{i}\mid i\in \{1,\ldots ,k\}\}$ where $n_{i}:=|\{j\mid p_{i}=p_{j}\}|$. In this case, G is isomorphic to the direct product of ${\text {spr}}(G)$-many cyclic groups, but it is not isomorphic to the direct product of fewer cyclic groups. It follows that the spread of G is the minimum size of a generating set of G.

Example 8.4

Let $G=\mathbb {Z}_{3}\times \mathbb {Z}_{9}\times \mathbb {Z}_{5}\times \mathbb {Z}_{49}\times \mathbb {Z}_{7}$. Then ${\text {spr}}(G)=2$. If $g=(1,1,0,1,0)$, then $G/\langle g\rangle \cong \mathbb {Z}_{3}\times \mathbb {Z}_{5}\times \mathbb {Z}_{7}$, and so ${\text {spr}}(G/\langle g\rangle )=1={\text {spr}}(G)-1$. If $h=(0,3,1,1,0)$, then $G/\langle h\rangle \cong \mathbb {Z}_{3}\times \mathbb {Z}_{3}\times \mathbb {Z}_{7}$, and so ${\text {spr}}(G/\langle h\rangle )=2={\text {spr}}(G)$. If $k=(1,3,1,0,1)$, then $G/\langle k\rangle \cong \mathbb {Z}_{9}\times \mathbb {Z}_{49}$, and so ${\text {spr}}(G/\langle k\rangle )=1={\text {spr}}(G)-1$.

The following is an easy consequence of the definitions.

Lemma 8.5

Let $G=\mathbb {Z}_{p_{1}^{r_{1}}}\times \cdots \times \mathbb {Z}_{p_{k}^{r_{k}}}$ be an abelian group with primes $p_{1},\ldots ,p_{k}$. If $g=(g_{1},\ldots ,g_{k})$ with

$$\begin{aligned} g_{i}:={\left\{ \begin{array}{ll} 1, &{} \quad i=\min \{j\mid p_{i}=p_{j}\}\\ 0, &{} \quad \text {else} \end{array}\right. }, \end{aligned}$$

then ${\text {spr}}(G/\langle g\rangle )={\text {spr}}(G)-1$.

Definition 8.6

If A is an $m\times n$ integer matrix, then we define ${\text {Grp}}(A)$ to be the abelian group with generators $g_{1},\ldots ,g_{n}$ satisfying the relations

$$\begin{aligned} A\left[ \begin{array}{l}g_{1}\\ \vdots \\ g_{n} \end{array}\right] =\left[ \begin{array}{l}0\\ \vdots \\ 0 \end{array}\right] . \end{aligned}$$

It is well-known that ${\text {Grp}}(A)\cong {\text {Grp}}({\text {Snf}}(A))$ where ${\text {Snf}}(A)$ is the Smith Normal Form of A. The diagonal entries $\alpha _{1},\ldots ,\alpha _{k}$ of ${\text {Snf}}(A)$ can be calculated as $\alpha _{1}=d_{1}(A)$ and $\alpha _{i}=d_{i}(A)/d_{i-1}(A)$ for $i\in \{2,\ldots ,k\}$, where $d_{i}(A)$ is the greatest common divisor of all $i\times i$ minors of A (Jacobson 1985, Theorem 3.9). Elementary integer row and column operations can be used on A to get ${\text {Snf}}(A)$. The non-unit diagonal elements of ${\text {Snf}}(A)$ are the invariant factors of ${\text {Grp}}(A)$ and so ${\text {spr}}({\text {Grp}}(A))$ is the number of non-unit elements of $\{\alpha _{1},\ldots ,\alpha _{k}\}$.

The truncated Smith Normal Form ${\text {tSnf}}(A)$ of A is created from ${\text {Snf}}(A)$ by removing every zero row and every column containing a single nonzero entry equal to 1. We clearly have ${\text {Grp}}(A)\cong {\text {Grp}}({\text {tSnf}}(A))$. It is also clear that ${\text {spr}}({\text {Grp}}(A))$ is equal to the size of ${\text {tSnf}}(A)$.

Example 8.7

Let $G=\mathbb {Z}_{3}\times \mathbb {Z}_{15}\cong {\text {Grp}}\left( \left[ {\begin{matrix}3 &{}\quad \! 0\\ 0 &{}\quad \! 15 \end{matrix}}\right] \right)$. Then ${\text {spr}}(G)=2$. Now, let $g=(1,2)\in G$ and $A=\left[ {\begin{matrix}3 &{}\quad \! 0\\ 0 &{}\quad \! 15\\ 1 &{}\quad \! 2 \end{matrix}}\right]$. Then ${\text {Snf}}(A)=\left[ {\begin{matrix}1 &{}\quad \! 0\\ 0 &{}\quad \! 3\\ 0 &{}\quad \! 0 \end{matrix}}\right]$ and ${\text {tSnf}}(A)=\left[ {\begin{matrix}3\end{matrix}}\right]$, and so $G/\langle g\rangle \cong {\text {Grp}}(A)\cong {\text {Grp}}({\text {Snf}}(A))\cong \mathbb {Z}_{3}$. Hence ${\text {spr}}(G/\langle g\rangle )=1={\text {spr}}(G)-1$.

Definition 8.8

Let $\mathbb {Z}_{r_{1}}\times \cdots \times \mathbb {Z}_{r_{k}}$ be the invariant factor decomposition of G and $e_{i}:=(0,\ldots ,0,1,0,\ldots ,0)$ for $i\in \{1,\ldots ,k\}$, where 1 occurs in the ith component. For $g\in G$ we let $\hat{g}:=\left[ \begin{array}{lll}\hat{g}_{1}&\cdots&\hat{g}_{k}\end{array}\right] \in \mathbb {Z}^{1\times k}$ such that $\hat{g_{i}}$ is the smallest nonnegative integer satisfying

$$\begin{aligned} g=\sum \hat{g_{i}}e_{i}. \end{aligned}$$

Lemma 8.9

If g is an element of the abelian group G, then ${\text {spr}}(G/\langle g\rangle )\ge {\text {spr}}(G)-1$.

Proof

Let $\mathbb {Z}_{r_{1}}\times \cdots \times \mathbb {Z}_{r_{k}}$ be the invariant factor decomposition of G. Note that $1\ne r_{1}\mid r_{2}\mid \cdots \mid r_{k}$. Then $G\cong {\text {Grp}}(A)$ with $A={\text {diag}}(r_{1},\ldots ,r_{k})$ and $G/\langle g\rangle \cong {\text {Grp}}(B)\cong {\text {Grp}}({\text {Snf}}(B))$ where

$$\begin{aligned} B=\left[ \begin{array}{c} A\\ \hline \hat{g} \end{array}\right] =\left[ \begin{array}{ccc} r_{1} &{} &{} 0\\ &{} \ddots \\ 0 &{} &{} r_{k}\\ \hat{g}_{1} &{} \cdots &{} \hat{g}_{k} \end{array}\right] . \end{aligned}$$

Let $\alpha _{1},\ldots ,\alpha _{k}$ be the diagonal elements of ${\text {Snf}}(B)$. If ${\text {spr}}(G/\langle g\rangle )\le {\text {spr}}(G)-2=k-2$, then $d_{1}(B)=\alpha _{1}=\alpha _{2}=1$. This is impossible since it is easy to see that every $2\times 2$ minor of B is divisible by $r_{1}$ and so $\alpha _{2}=d_{2}(B)/d_{1}(B)=d_{2}(B)$ is divisible by $r_{1}$. $\square$

Proposition 8.10

If H is a subgroup and g is an element of the finite abelian group G, then

$$\begin{aligned} {\text {spr}}(G/\langle H\cup \{g\}\rangle )\ge {\text {spr}}(G/H)-1. \end{aligned}$$

Proof

Let $\mathbb {Z}_{r_{1}}\times \cdots \times \mathbb {Z}_{r_{k}}$ be the invariant factor decomposition of G and $H=\{h_{1},\ldots ,h_{m}\}$. Then $G\cong {\text {Grp}}(A)$ with $A={\text {diag}}(r_{1},\ldots ,r_{k})$ and $G/H\cong {\text {Grp}}(B)\cong {\text {Grp}}({\text {tSnf}}(B))$ with

$$\begin{aligned} B=\left[ \begin{array}{c} A\\ \hline \phantom {\int ^{\int }}\hat{H} \end{array}\right] \text { and }\hat{H}=\left[ \begin{array}{c} \widehat{\ h_{1}}\\ \hline \vdots \\ \hline \phantom {\int ^{\int ^{\int }}}\widehat{h_{m}} \end{array}\right] . \end{aligned}$$

Note that $\widehat{h_{i}}=\left[ \begin{array}{lll}\widehat{h_{i}}_{_{1}}&\cdots&\widehat{h_{i}}_{_{m}}\end{array}\right]$. Applying elementary integer row and column operations gives

$$\begin{aligned} G/\langle H\cup \{g\}\rangle \cong {\text {Grp}}\left[ \begin{array}{c} B\\ \hline \hat{g} \end{array}\right] \cong {\text {Grp}}\left[ \begin{array}{c|c} I &{} 0\\ \hline 0 &{} {\text {tSnf}}(B)\\ \hline 0 &{} \tilde{g} \end{array}\right] \cong {\text {Grp}}\left[ \begin{array}{c} {\text {tSnf}}(B)\\ \hline \tilde{g} \end{array}\right] \end{aligned}$$

for some $\tilde{g}$. So, $G/\langle H\cup \{g\}\rangle$ is isomorphic to a quotient of G / H by a cyclic subgroup. The result now follows as in the proof of Lemma 8.9. $\square$

Fig. 13

Simplified structure diagrams for ${\mathsf{GEN}}(G)$ with $G=\mathbb {Z}_{p_{1}^{r_{1}}}\times \cdots \times \mathbb {Z}_{p_{k}^{r_{k}}}$ and odd primes $p_{1},\ldots ,p_{k}$

Proposition 8.11

If $G=\mathbb {Z}_{p_{1}^{r_{1}}}\times \cdots \times \mathbb {Z}_{p_{k}^{r_{k}}}$ is an abelian group with odd primes $p_{1},\ldots ,p_{k}$, then the simplified structure diagram of ${\mathsf{GEN}}(G)$ is one of the diagrams shown in Fig. 13, and hence

$$\begin{aligned} {\mathsf{GEN}}(G)={\left\{ \begin{array}{ll} *0, &{} {\text {spr}}(G)=0\\ *2, &{} 1\le {\text {spr}}(G)\le 2\\ *1, &{} 3\le {\text {spr}}(G) \end{array}\right. }. \end{aligned}$$

Proof

The Frattini subgroup is $\Phi (G)\cong \mathbb {Z}_{p_{1}^{r_{1}-1}}\times \cdots \times \mathbb {Z}_{p_{k}^{r_{k}-1}}$ by Propositions 6.1 and 6.2, and so $G/\Phi (G)\cong \mathbb {Z}_{p_{1}}\times \cdots \times \mathbb {Z}_{p_{k}}$. One can show that this implies that every proper subgroup of G containing $\Phi (G)$ is an intersection subgroup. We use structural induction on the structure classes to show that the simplified structure diagram is only dependent on ${\text {spr}}(G)$ as shown in Fig. 13, and

$$\begin{aligned} {\text {type}}(X_{I})={\left\{ \begin{array}{ll} t_{0}:=(1,0,0), &{} \quad {\text {spr}}(G/I)=0\\ t_{1}:=(1,2,1), &{} \quad {\text {spr}}(G/I)=1\\ t_{2}:=(1,2,0), &{} \quad {\text {spr}}(G/I)=2\\ t_{3}:=(1,1,0), &{} \quad {\text {spr}}(G)\ge {\text {spr}}(G/I)\ge 3 \end{array}\right. }. \end{aligned}$$

The statement is clearly true when ${\text {spr}}(G/I)=0$, that is, $I=G$. Assume ${\text {spr}}(G/I)=i\ge 1$. Then $X_{I}$ has an option $X_{K}$ such that ${\text {spr}}(G/K)=i-1$ by Lemma 8.5 and the proof of Proposition 8.10. Now, suppose $g\in G{\setminus } I$. By Proposition 8.10, ${\text {spr}}(G/\langle I\cup \{g\}\rangle )\ge {\text {spr}}(G/I)-1$, which implies that if $X_{J}$ is an option of $X_{I}$, then ${\text {spr}}(G/J)\in \{{\text {spr}}(G/I),{\text {spr}}(G/I)-1\}$.

First, assume $j:={\text {spr}}(G/I)\in \{1,2,3\}$. Then ${\text {otype}}(X_{I})=\{t_{j-1}\}$ or ${\text {otype}}(X_{I})=\{t_{j-1},t_{j}\}$ by induction. In either case, ${\text {type}}(X_{I})=t_{j}$, and so ${\text {Otype}}(X_{I})=\{t_{j-1},t_{j}\}$. Now, assume ${\text {spr}}(G/I)\ge 4$. Then ${\text {otype}}(X_{I})=\{t_{3}\}$ by induction. Hence ${\text {type}}(X_{I})=t_{3}$, and so ${\text {Otype}}(X_{I})=\{t_{3}\}$. $\square$

Fig. 14

Simplified structure diagrams for ${\mathsf{GEN}}(\mathbb {Z}_{2}^{n})$

Example 8.12

It is easy to check that the simplified structure diagram of ${\mathsf{GEN}}(\mathbb {Z}_{2}^{n})$, shown in Fig. 14, follows a pattern somewhat similar to that of ${\mathsf{GEN}}(\mathbb {Z}_{p_{1}^{r_{1}}}\times \cdots \times \mathbb {Z}_{p_{k}^{r_{k}}})$, shown in Fig. 13. Note that the only odd order subgroup is the Frattini subgroup, which is the trivial subgroup.

The following result of Barnes (1988) is an easy consequence of the Third Isomorphism Theorem.

Lemma 8.13

If I is a proper intersection subgroup of the abelian group G, then $X_{I}$ is semi-terminal in ${\mathsf{GEN}}(G)$ if and only if G / I is cyclic.

Fig. 15

Simplified structure diagram for ${\mathsf{GEN}}(\mathbb {Z}_{2}\times \mathbb {Z}_{2}\times \mathbb {Z}_{m}\times \mathbb {Z}_{k})$ with odd m and k

Proposition 8.14

If $G=\mathbb {Z}_{2}\times \mathbb {Z}_{2}\times \mathbb {Z}_{m}\times \mathbb {Z}_{k}$ such that m and k are odd and relatively prime, then the simplified structure diagram of ${\mathsf{GEN}}(G)$ is the one shown in Fig. 15(a), and hence ${\mathsf{GEN}}(G)=*1$.

Proof

Define the following collection of sets that form a partition of $\mathcal {Y}$:

$$\begin{aligned} \begin{aligned} \mathcal {S}_{1}&:=\{X_{I}\in \mathcal {Y}\mid X_{I}\text { is terminal}\};\\ \mathcal {S}_{2}&:=\{X_{I}\in \mathcal {Y}\mid X_{I}\text { is semi-terminal}\};\\ \mathcal {S}_{3}&:=\{X_{I}\in \mathcal {Y}\mid X_{I}\text { is non-terminal}\}. \end{aligned} \end{aligned}$$

We use structural induction on the structure classes to show that these sets are nonempty and are the type equivalence classes of the structure classes, and that

$$\begin{aligned} {\text {type}}(X_{I})={\left\{ \begin{array}{ll} (0,0,0), &{} X_{I}\in \mathcal {S}_{1}\\ (0,1,2), &{} X_{I}\in \mathcal {S}_{2}\\ (1,1,0), &{} X_{I}\in \mathcal {S}_{3} \end{array}\right. }. \end{aligned}$$

First, note that since the orders of $\mathbb {Z}_{2}\times \mathbb {Z}_{2}$ and $\mathbb {Z}_{m}\times \mathbb {Z}_{k}$ are relatively prime, every subgroup is of the form $I=H\times K$ for some $H\le \mathbb {Z}_{2}\times \mathbb {Z}_{2}$ and $K\le \mathbb {Z}_{m}\times \mathbb {Z}_{k}$ by Proposition 8.1.

We show that if I is an intersection subgroup, then $X_{I}$ is even if and only if $X_{I}$ is semi-terminal. Suppose that $X_{I}$ is even. Then H is nontrivial, which implies that $(\mathbb {Z}_{2}\times \mathbb {Z}_{2})/H$ is isomorphic to $\langle 0\rangle$ or $\mathbb {Z}_{2}$. Since m and k are relatively prime, $\mathbb {Z}_{m}\times \mathbb {Z}_{k}$ is cyclic, and hence $(\mathbb {Z}_{m}\times \mathbb {Z}_{k})/K$ is cyclic, as well. This implies that

$$\begin{aligned} G/I=G/(H\times K)\cong (\mathbb {Z}_{2}\times \mathbb {Z}_{2})/H\times (\mathbb {Z}_{m}\times \mathbb {Z}_{k})/K \end{aligned}$$

is cyclic since the orders of $(\mathbb {Z}_{2}\times \mathbb {Z}_{2})/H$ and $(\mathbb {Z}_{m}\times \mathbb {Z}_{k})/K$ are relatively prime and each group is cyclic. Hence $X_{I}$ is semi-terminal by Lemma 8.13. On the other hand, if $X_{I}$ is semi-terminal, reversing the above argument presents no difficulties, so $X_{I}$ is even.

It is clear that $\mathcal {S}_{1}=\{X_{G}\}\ne \emptyset$ and ${\text {type}}(X_{G})=(0,0,0)$.

The maximal subgroup $R=\langle 0\rangle \times \mathbb {Z}_{2}\times \mathbb {Z}_{m}\times \mathbb {Z}_{k}$ is even. Hence $X_{R}\in \mathcal {S}_{2}$, and so $\mathcal {S}_{2}\ne \emptyset$. Let $X_{I}\in \mathcal {S}_{2}$. Then by the above, $X_{I}$ is even. Hence ${\text {otype}}(X_{I})$ is either $\{(0,0,0)\}$ or $\{(0,0,0),(0,1,2)\}$ by induction. In either case, ${\text {type}}(X_{I})=(0,1,2)$, and so ${\text {Otype}}(X_{I})=\{(0,0,0),(0,1,2)\}$.

For the final case, observe that $X_{\Phi (G)}\in \mathcal {S}_{3}$ since $\Phi (G)$ is odd by Propositions 6.1 and 6.2, and so $\mathcal {S}_{3}\ne \emptyset$. Let $X_{I}\in \mathcal {S}_{3}$. Then $X_{I}$ must be odd. Moreover, $I\cup \{(1,0,0,0)\}$ is an option of I that lies in a semi-terminal structure class. Hence ${\text {otype}}(X_{I})$ is either $\{(0,1,2)\}$ or $\{(0,1,2),(1,1,0)\}$ by induction. In either case, ${\text {type}}(X_{I})=(1,1,0)$, and hence ${\text {Otype}}(X_{I})=\{(0,1,2),(1,1,0)\}$.

It follows that the simplified structure diagram of ${\mathsf{GEN}}(G)$ is the one shown in Fig. 15a, and so ${\mathsf{GEN}}(G)=*1$. $\square$

Proposition 8.15

If $G=\mathbb {Z}_{2}\times \mathbb {Z}_{2}\times \mathbb {Z}_{m}\times \mathbb {Z}_{k}$ such that m and k are odd and not relatively prime, then the simplified structure diagram of ${\mathsf{GEN}}(G)$ is the one shown in Fig. 15b, and hence ${\mathsf{GEN}}(G)=*1$.

Proof

Define the following collection of sets that form a partition of $\mathcal {Y}$:

$$\begin{aligned} \begin{aligned} \mathcal {S}_{1}&:=\{X_{I}\in \mathcal {Y}\mid X_{I}\text { is terminal}\};\\ \mathcal {S}_{2}&:=\{X_{I}\in \mathcal {Y}\mid X_{I}\text { is semi-terminal}\};\\ \mathcal {S}_{3}&:=\{X_{I}\in \mathcal {Y}\mid X_{I}\text { is even and non-terminal}\};\\ \mathcal {S}_{4}&:=\{X_{I}\in \mathcal {Y}\mid X_{I}\text { is odd and non-terminal without any even non-terminal option}\};\\ \mathcal {S}_{5}&:=\{X_{I}\in \mathcal {Y}\mid X_{I}\text { is odd and non-terminal with an even non-terminal option}\}. \end{aligned} \end{aligned}$$

We use structural induction on the structure classes to show that these sets are nonempty and are the type equivalence classes of the structure classes and that

$$\begin{aligned} {\text {type}}(X_{I})={\left\{ \begin{array}{ll} (0,0,0), &{} X_{I}\in \mathcal {S}_{1}\\ (0,1,2), &{} X_{I}\in \mathcal {S}_{2}\\ (0,0,2), &{} X_{I}\in \mathcal {S}_{3}\\ (1,1,0), &{} X_{I}\in \mathcal {S}_{4}\\ (1,1,2), &{} X_{I}\in \mathcal {S}_{5} \end{array}\right. }. \end{aligned}$$

It is clear that $\mathcal {S}_{1}=\{X_{G}\}\ne \emptyset$ and ${\text {type}}(X_{G})=(0,0,0)$.

Next, consider the even maximal subgroup $R=\langle 0\rangle \times \mathbb {Z}_{2}\times \mathbb {Z}_{m}\times \mathbb {Z}_{k}$. Then $X_{R}\in \mathcal {S}_{2}$ since $\langle R\cup \{(1,0,0,0)\}\rangle =G$, and so $\mathcal {S}_{2}\ne \emptyset$. Let $X_{I}\in \mathcal {S}_{2}$. Note that the orders of $\mathbb {Z}_{2}\times \mathbb {Z}_{2}$ and $\mathbb {Z}_{m}\times \mathbb {Z}_{k}$ are relatively prime, so $I=H\times K$ for some $H\le \mathbb {Z}_{2}\times \mathbb {Z}_{2}$ and $K\le \mathbb {Z}_{m}\times \mathbb {Z}_{k}$ by Proposition 8.1. Since $X_{I}$ is semi-terminal, the quotient

$$\begin{aligned} G/I=G/(H\times K)\cong (\mathbb {Z}_{2}\times \mathbb {Z}_{2})/H\times (\mathbb {Z}_{m}\times \mathbb {Z}_{k})/K \end{aligned}$$

is cyclic by Lemma 8.13. This happens only if

$$\begin{aligned} H\in \{\langle 0\rangle \times \mathbb {Z}_{2},\mathbb {Z}_{2}\times \langle 0\rangle ,\langle (1,1)\rangle ,\mathbb {Z}_{2}\times \mathbb {Z}_{2}\}, \end{aligned}$$

which shows that $X_{I}$ must be even. Hence ${\text {otype}}(X_{I})$ is either $\left\{ (0,0,0)\right\}$ or $\left\{ (0,0,0),(0,1,2)\right\}$ by induction since $X_{I}$ is semi-terminal. In either case, ${\text {type}}(X_{I})=(0,1,2)$, and hence ${\text {Otype}}(X_{I})=\left\{ (0,0,0),(0,1,2)\right\}$.

For the third case, consider the even subgroups $R_{1}=\mathbb {Z}_{2}\times \langle 0\rangle \times \langle 0\rangle \times \langle 0\rangle$, $R_{2}=\langle 0\rangle \times \mathbb {Z}_{2}\times \langle 0\rangle \times \langle 0\rangle$, and $R_{3}=\langle (1,1)\rangle \times \langle 0\rangle \times \langle 0\rangle$. Let $X_{I_{i}}$ be the structure class containing $R_{i}$. Since m and k are not relatively prime, we can choose $m'$ and $k'$ such that $m/m'=k/k'$ is a prime. Then $I_{i}$ is contained in the sets

$$\begin{aligned} \begin{aligned}M&:=\mathbb {Z}_{2}\times \mathbb {Z}_{2}\times \langle m/m'\rangle \times \mathbb {Z}_{k}\cong \mathbb {Z}_{2}\times \mathbb {Z}_{2}\times \mathbb {Z}_{m'}\times \mathbb {Z}_{k}\\ N&:=\mathbb {Z}_{2}\times \mathbb {Z}_{2}\times \mathbb {Z}_{m}\times \langle k/k'\rangle \cong \mathbb {Z}_{2}\times \mathbb {Z}_{2}\times \mathbb {Z}_{m}\times \mathbb {Z}_{k'}. \end{aligned} \end{aligned}$$

By Proposition 6.3, M and N are maximal subgroups. Since $M\cap N\cong \mathbb {Z}_{2}\times \mathbb {Z}_{2}\times \mathbb {Z}_{m'}\times \mathbb {Z}_{k'}$, $G/M\cap N\cong \mathbb {Z}_{m/m'}^{2}$ is not cyclic. Hence each $G/I_{i}$ is not cyclic. So each $X_{I_{i}}$ is even and non-terminal by Lemma 8.13. Thus each $R_{i}$ is an element of an even non-terminal structure class, which shows that $\mathcal {S}_{3}\ne \emptyset$. Let $X_{I}\in \mathcal {S}_{3}$. We show that $X_{I}$ has an option in $\mathcal {S}_{2}$. Since I is even, at least one of $R_{1}$, $R_{2}$, or $R_{3}$ is a subgroup of I. Let $h_{3}=(0,0,1,0)$. Since $\gcd (2,k)=1$, each $G/\langle R_{i}\cup \{h_{3}\}\rangle \cong \mathbb {Z}_{2}\times \mathbb {Z}_{m}$ is cyclic. This implies that $G/\langle I\cup \{h_{3}\}\rangle$ is cyclic, and hence $I\cup \{h_{3}\}$ is an element of an even semi-terminal structure class. It is clear that every option of $X_{I}$ is in $\mathcal {S}_{2}\cup \mathcal {S}_{3}$. Therefore, ${\text {otype}}(X_{I})$ is either $\left\{ (0,1,2)\right\}$ or $\left\{ (0,1,2),(0,0,2)\right\}$ by induction. In either case, ${\text {type}}(X_{I})=(0,0,2)$, and so ${\text {Otype}}(X_{I})=\{(0,1,2),(0,0,2)\}$.

For the fourth case, consider the odd subgroup $Q:=\langle 0\rangle \times \langle 0\rangle \times \mathbb {Z}_{m}\times \langle 0\rangle$. Then Q is contained in an odd structure class $X_{J}$ since Q is a subset of the maximal subgroups $\langle 0\rangle \times \mathbb {Z}_{2}\times \mathbb {Z}_{m}\times \mathbb {Z}_{k}$ and $\mathbb {Z}_{2}\times \langle 0\rangle \times \mathbb {Z}_{m}\times \mathbb {Z}_{k}$. We show that $X_{J}\in \mathcal {S}_{4}$. For a contradiction, assume that $Q\cup \{h\}$ is in a structure class inside $\mathcal {S}_{3}$ for some h. Then $\langle Q\cup \{h\}\rangle \cong \mathbb {Z}_{2}\times \mathbb {Z}_{m}\times U$, where $U\le \mathbb {Z}_{k}$. This implies that $G/\langle Q\cup \{h\}\rangle \cong \mathbb {Z}_{2}\times (\mathbb {Z}_{k}/U)$, which is cyclic since k is odd. Then $Q\cup \{h\}$ is in a structure class in $\mathcal {S}_{2}$ by Lemma 8.13. This is a contradiction, and so $\mathcal {S}_{4}\ne \emptyset$. Now consider $X_{I}\in \mathcal {S}_{4}$. If $h_{4}$ is any element of G with even order, then $I\cup \{h_{4}\}$ is contained in an even semi-terminal structure class by the definition of $\mathcal {S}_{4}$. So $X_{I}$ has an option in $\mathcal {S}_{2}$. Next, we show that $X_{I}$ has no option in $\mathcal {S}_{5}$. For a contradiction, suppose $X_{I}$ has an option $X_{J}$ in $\mathcal {S}_{5}$. By the definition of $\mathcal {S}_{5}$, $X_{J}$ has an option $X_{H}$ in $\mathcal {S}_{3}$. Let t be an element of order 2 in H and let $I\cup \{t\}\in X_{K}$. Then K is even and $K\le H\le G$. So $X_{K}$ is an option of $X_{I}$ in $\mathcal {S}_{3}$, which is a contradiction. Hence any option of $X_{I}$ is in $\mathcal {S}_{2}$ or $\mathcal {S}_{4}$. Thus, ${\text {otype}}(X_{I})$ is either $\left\{ (0,1,2)\right\}$ or $\left\{ (0,1,2),(1,1,0)\right\}$ by induction. In either case, ${\text {type}}(X_{I})=(1,1,0)$ and so ${\text {Otype}}(X_{I})=\{(0,1,2),(1,1,0)\}$.

To show that $\mathcal {S}_{5}\ne \emptyset$, consider the empty position $\emptyset$, which is an element of the odd structure class $X_{\Phi (G)}$. Since G is not cyclic, $X_{\Phi (G)}$ must be a non-terminal structure class. Let $g_{3}:=(1,0,0,0)$. The empty position has the option $\{g_{3}\}$ that belongs to a structure class in $\mathcal {S}_{3}$ by Lemma 8.13, since

$$\begin{aligned} G/\langle \{g_{3}\}\rangle =G/(\mathbb {Z}_{2}\times \langle 0\rangle \times \langle 0\rangle \times \langle 0\rangle )\cong \mathbb {Z}_{2}\times \mathbb {Z}_{m}\times \mathbb {Z}_{k} \end{aligned}$$

is not cyclic as $\gcd (m,k)\ne 1$. Hence $X_{\Phi (G)}\in \mathcal {S}_{5}$. Next, let $X_{I}\in \mathcal {S}_{5}$. Let $g_{2}=(1,0,1,0)$ and $g_{4}=(0,0,1,0)$. Then $I\cup \{g_{2}\}$ belongs to an even semi-terminal structure class by Lemma 8.13 since $G/\langle I\cup \{g_{2}\}\rangle$ is cyclic. This implies that $X_{I}$ has an option in $\mathcal {S}_{2}$. Lastly, we will show that $I\cup \{g_{4}\}$ is an option of I in a structure class in $\mathcal {S}_{4}$. We see that Q is a subgroup of $\langle I\cup \{g_{4}\}\rangle$. We know from the fourth case that $\langle g_{4}\rangle =Q\in X_{J}\in \mathcal {S}_{4}$. Hence the odd structure class containing $I\cup \{g_{4}\}$ belongs to $\mathcal {S}_{4}$. As a consequence, ${\text {otype}}(X_{I})$ is either $\{(0,0,2),(1,1,0),(0,1,2)\}$ or $\{(0,0,2),(1,1,0),(0,1,2),(1,1,2)\}$ by induction. In either case, ${\text {type}}(X_{I})=(1,1,2)$, and hence ${\text {Otype}}(X_{I})=\{(0,0,2),(1,1,0),(0,1,2),(1,1,2)\}$.

It follows that the simplified structure diagram of ${\mathsf{GEN}}(G)$ is the one shown in Fig. 15b, which implies that ${\mathsf{GEN}}(G)=*1$. $\square$

It is interesting to notice that the simplified structure diagram from the previous theorem is the same as that of ${\mathsf{GEN}}(\mathbb {D}_{4k+2})$ shown in Fig. 11f.

Corollary 8.16

If G is a finite abelian group, then

$$\begin{aligned} {\mathsf{GEN}}(G)={\left\{ \begin{array}{ll} *2, &{} \quad |G|\text { is odd and }1\le {\text {spr}}(G)\le 2\\ *1, &{} \quad |G|\text { is odd and }{\text {spr}}(G)\ge 3\\ *2, &{} \quad G\cong \mathbb {Z}_{2}\\ *1, &{} \quad G\cong \mathbb {Z}_{4k}\text { with }k\ge 1\\ *4, &{} \quad G\cong \mathbb {Z}_{4k+2}\text { with }k\ge 1\\ *1, &{} \quad G\cong \mathbb {Z}_{2}\times \mathbb {Z}_{2}\times \mathbb {Z}_{m}\times \mathbb {Z}_{k}\text { for }m,k\text { odd}\\ *0, &{} \quad \text {else} \end{array}\right. }. \end{aligned}$$

Proof

By (Barnes 1988, Section 3.2), the first player wins ${\mathsf{GEN}}(G)$ exactly when G is cyclic, odd, or isomorphic to $\mathbb {Z}_{2}\times \mathbb {Z}_{2}\times \mathbb {Z}_{m}\times \mathbb {Z}_{k}$ with odd m and k. We already proved the result in these cases. In every other case the second player wins, so in these cases ${\mathsf{GEN}}(G)=*0$. $\square$

9 Symmetric and alternating groups

Fig. 16

Nimbers for $\mathsf{DNG}(S_{n})$ and $\mathsf{DNG}(A_{n})$

According to (Barnes 1988, Section 2.3), the second player wins $\mathsf{DNG}(S_{n})$ for $n\ge 4$. Hence $\mathsf{DNG}(S_{n})=*0$ for $n\ge 4$. We already studied the remaining cases. In particular, we know that $\mathsf{DNG}(S_{2})=\mathsf{DNG}(\mathbb {Z}_{2})=*1$ and $\mathsf{DNG}(S_{3})=\mathsf{DNG}(\mathbb {D}_{3})=*3$. These results are summarized in Fig. 16.

The $\mathsf{DNG}(A_{n})$ games remain a bit of a mystery. There is an incomplete analysis of $\mathsf{DNG}(A_{n})$ in (Barnes 1988, Section 2.4) that involves some fairly deep group-theoretic results. By Proposition 3.22, we know $\mathsf{DNG}(A_{3})=\mathsf{DNG}(\mathbb {Z}_{3})=*1$. Some additional computer calculated values are listed in Fig. 16.

By (Barnes 1988, Section 3.4), the first player wins ${\mathsf{GEN}}(S_{n})$ for $n\ge 5$ and ${\mathsf{GEN}}(A_{n})$ for all $n\ge 4$. On the other hand, ${\mathsf{GEN}}(S_{2})={\mathsf{GEN}}(\mathbb {Z}_{2})=*2$, ${\mathsf{GEN}}(S_{3})={\mathsf{GEN}}(\mathbb {D}_{3})=*3$, ${\mathsf{GEN}}(A_{3})={\mathsf{GEN}}(\mathbb {Z}_{3})=*2$, and computer calculations show that ${\mathsf{GEN}}(S_{4})=*0$.

Fig. 17

Known and conjectured values and simplified structure diagrams for ${\mathsf{GEN}}(S_{n})$ and ${\mathsf{GEN}}(A_{n})$

Conjecture 9.1

For $n\ge 5$, we have ${\mathsf{GEN}}(S_{n})=*1={\mathsf{GEN}}(A_{n})$.

We have verified the conjecture for $n\in \{5,6,7,8\}$ using our software. The conjectured simplified structure diagrams are shown in Fig. 17.

10 Further questions

We conclude with a few open problems that may not be out of reach.

• 1. Is it possible to have a directed cycle in the simplified structure digraph? This never happens for the groups we have considered, but are there groups for which this is possible?

• 2. Does Conjecture 9.1 about ${\mathsf{GEN}}(S_{n})$ and ${\mathsf{GEN}}(A_{n})$ hold? Structural induction on the structure classes could work to show that the simplified structure diagram of Fig. 17 is correct.

• 3. What are the remaining nim-numbers for $\mathsf{DNG}(A_{n})$? The partial results of (Barnes 1988, Theorem 2) are quite complicated. Settling this question likely requires some sophisticated group theory arguments.

• 4. What are the nim-numbers of other families of groups? In particular, what are the nim-numbers of generalized dihedral groups of the form $A\rtimes \mathbb {Z}_{2}$ where A is a finite abelian group?

• 5. Are there any general results regarding quotient groups and direct products of groups? A positive answer would be very helpful in the study of more complicated groups.

• 6. Does Conjecture 4.9 about the spectrum of ${\mathsf{GEN}}(G)$ hold? Is the set $\{{\text {nim}}({\mathsf{GEN}}(G))\mid G\text { is a finite group}\}$ at least bounded?

• 7. Can the structure diagram approach be generalized to study $\mathsf{DNG}$ and ${\mathsf{GEN}}$ on other algebraic structures with generators (e.g., semigroups, inverse semigroups) and compute their corresponding nim-numbers?

• 8. The Sprague-Grundy theory is generalized to infinite loopy games in Fraenkel and Perl (1975); Smith (1966). A recent description of the theory can be found in (Aaron 2013, IV.4). Can our techniques be generalized to find the loopy nim-numbers of some families of infinite groups?