Regional club convergence in the EU: evidence from a panel data analysis

Abstract

We investigate club convergence in income per capita in 194 European NUTS-2 regions using a nonlinear, time-varying factor model that allows for individual and transitional heterogeneity. Moreover, we extend an existing club clustering algorithm with two post-clustering merging algorithms that finalize club formation. We also apply an ordered response model to assess the role of initial and structural conditions, as well as geographic factors. Our results indicate the presence of four convergence clubs in the EU-15 countries. In support of the club convergence hypothesis, we find that initial conditions matter for the resulting income distribution. Geographic clustering is quite pronounced; besides a north-to-south division, we detect high-income clusters for capital cities. We conclude that the main supranational policy challenge is the politically sensitive handling of a multi-speed Europe.

1 Introduction

Regional convergence is an important topic in the political agenda of the European Union (EU). In the financial framework for 2007–2013, cohesion expenditure amounted to 350 billion euro, representing 36 % of the EU budget (European Commission 2015). A central argument in favor of European cohesion and integration is that all regions should be enabled to enter a common growth path, thereby generating economic gains for every EU citizen. Thus, a pivotal question is whether European integration has led to per capita income convergence. However, absolute income convergence might be virtually beyond reach in the presence of club convergence. This concept was put forward by Azariadis and Drazen (1990), Azariadis (1996), and Galor (1996) and essentially states that a region’s long-run growth path is also determined by initial conditions. Hence, questions on whether regions in the EU converge to the same income level or constitute convergence clubs are highly relevant for policy makers and academics.

Income convergence as a theoretical concept is related to neoclassical growth theory, according to which income between units converges as long as structural characteristics are the same, regardless of the initial level of income and capital stock. Besides Baumol (1986), who were the first to test for income catch-up processes, methodological landmarks have been achieved by Barro and Sala-i Martin (1992) and Mankiw et al. (1992), who translated the Solow model into an empirical test for convergence. Islam (1995) eventually proposed a panel specification of the Solow model. These regression approaches allow the detection of converging behavior in a group of units whose technological progress evolves homogeneously across time and units.

If technological progress is actually heterogeneous across units, the assumption of a homogeneous slope coefficient will lead to inconsistent parameter estimates (Robertson and Symons 1992; Pesaran and Smith 1995). Proposals to overcome this inconsistency problem include nonparametric and semiparametric approaches (Li and Stengos 1996; Baltagi and Li 2002; Cai and Li 2008), and incorporation of a country-specific production function into the augmented Solow model (Durlauf et al. 2001). Phillips and Sul (2003) widened the discussion and pointed to the important role of heterogeneity over time. They later proposed a nonlinear time-varying factor model that accommodates individual and transitional heterogeneity (hereafter called the PS model; Phillips and Sul 2007). In this context, factor representation circumvents potential endogeneity and omitted variable bias, which might arise in the use of a steady-state proxy vector (Phillips and Sul 2009).

The aim of the present study is to find convergence patterns in per capita GDP for 194 NUTS-2 regions in the EU-15. To take heterogeneous technological progress into account, we use the PS factor model and the PS convergence and cluster methodology. Factorization allows separation of unit-specific transitional factors from common factors to reveal the long-run growth trend for the underlying time series. We augment the existing club clustering algorithm of Phillips and Sul (2007, 2009) with two post-clustering merging algorithms to improve and complete the decision rules for club formation. This novel extension avoids ambiguity in the club merging process proposed by Phillips and Sul (2009). We then analyze the factors influencing membership of a certain club using an ordered response model as proposed by Bartkowska and Riedl (2012). We test the club convergence hypothesis stating that units with similar structural characteristics converge in the long run if initial conditions are in the same basin of attraction (Galor 1996). Unlike previous work, the ordered response model is augmented with further geographic explanatory variables.

Our results indicate strong and robust evidence in favor of four convergence clubs in the EU-15 countries. The ordered response model confirms the pivotal role of initial factors and hence corroborates the club convergence hypothesis. We also find a clear regional north-to-south decline in income, as well as a strong effect of capital cities. Overall, our results contribute to existing research on European income convergence that also uses the PS procedure but mainly draws on national data (Apergis et al. 2010; Fritsche and Kuzin 2011; Monfort et al. 2013; Borsi and Metiu 2015).

The remainder of the paper is organized as follows. Section 2 gives an overview of empirical studies on national and regional convergence in Europe. Our estimation strategy, which follows and extends the PS methodology, is outlined in Sect. 3. Results for the log t tests and the ordered logit model are provided in Sect. 4, followed by robustness tests in Sect. 5. Section 6 contains a summary of our findings and some concluding remarks.

2 Literature on European regional convergence

A number of empirical studies on economic growth adopt the nonlinear time-varying PS factor model to determine convergence clubs. Out of these studies, several authors have investigated income convergence within Europe (see Table 1 for an overview). Borsi and Metiu (2015) use national income per capita data for the EU-27 and find no absolute convergence, but club convergence, with the formation of four convergence clubs. Their sample also includes the newly joined countries from Eastern and Central Europe. Clubs are formed along geographic regions (in particular, southeast vs. northwest), but are not linked to Eurozone membership.

Monfort et al. (2013) investigate national income per worker in the EU-27 (except for Luxembourg, Malta, and Cyprus). They find four convergence clubs, of which two belong to the EU-15 and two to the new Eastern European members. For the two EU-15 clubs, they do not find any clustering along geographic lines or with respect to Eurozone membership. However, the latter factor seems to play a role in the clustering of the two Eastern European clubs.¹ Two convergence clubs within the EU-15 are also detected by Apergis et al. (2010), who use national income per capita data. One of these clubs consists of the so-called GIPS countries² plus Germany, which is clearly a remarkable if not questionable result in light of recent developments in the Eurozone. Overall, heterogeneity with respect to technological conditions in general and labor productivity in particular are identified as the most decisive factors for the absence of absolute convergence. Fritsche and Kuzin (2011) investigate convergence in prices, labor costs, productivity, and income per capita among EU-15 countries. With respect to income, they find three convergence clubs, with Italy and Germany not belonging to any of these clusters.

Table 1 Convergence literature using the log t test for European data

Despite these studies at the national level, application of the PS procedure at the regional level is rare, which surprises in light of the importance of European regional development for policy makers. An exception is the study by Bartkowska and Riedl (2012), who apply the PS log t test and clustering method for 206 NUTS-2 regions over the period 1990–2002. They identify six convergence clubs, but cannot reject convergence across subsequent ordered fractions of neighboring clubs. Moreover, using an ordered logit model, they reveal that initial conditions do play a role, indicating the applicability of the club convergence hypothesis.

The PS factor model is usually applied to aggregate income data. Hence, the role of sectoral dynamics (Fiaschi and Lavezzi 2007) is neglected. Furthermore, the methodology does not explicitly model spatial interaction, which is in particular relevant with respect to spatial dynamics in the accumulation of knowledge. However, the appealing feature of the PS method is that growth determinants and spatial influences are captured in a more flexible way, with both common and idiosyncratic factor loadings.

In light of the importance of spatial factors, we provide a brief summary of regional convergence research adopting methodologies other than the PS factor model. One strand of the literature examines regional convergence using variations of the regression approach of Barro and Sala-i Martin (1992). For example, Fischer and Stirböck (2006) determine club convergence within a spatial econometric framework for 256 NUTS-2 regions over the period 1995–2000. Their three-step procedure includes local clustering as proposed by Getis and Ord (1992), standard Barro-style convergence testing within the clusters, and a test of a spatial error specification. They find evidence of the presence of two spatial regimes. Procedures comprising spatial filtering techniques before the actual regression analysis are also proposed by Badinger et al. (2004) and Battisti and Vaio (2008) with, however, differing results: across European NUTS-2 regions, Badinger et al. (2004) find evidence for conditional convergence, whereas Battisti and Vaio ’s (2008) mixture regression approach suggests that the majority of European regions shows no tendency to converge.

Ramajo et al. (2008) explicitly consider spatial heterogeneity and spatial autocorrelation in their regression framework. They find that regions in Ireland, Greece, Portugal, and Spain (so-called cohesion-fund countries) converged separately compared to the rest of the EU in the period 1981–1996. Postiglione et al. (2010) use a modified regression tree approach (Durlauf and Johnson 1995), which takes spatial autocorrelation into account. They identify five convergence clubs across 191 NUTS-2 data over the period 1980–2002. More recently, Postiglione et al. (2013) have employed a spatial Durbin model as an objective function of two cluster algorithms. In a panel of 187 NUTS-2 regions from 1981 to 2004, they find four convergence clubs.

Other researchers do not explicitly consider spatial factors. For example, Lopez-Rodriguez (2008) adopts a fixed-effects panel data regression model to assess convergence in Europe at different regional levels (NUTS-1, NUTS-2, NUTS-3) over the period 1982–1999. He shows that regional steady-state incomes changed over time and drifted apart, leading to overall divergence in Europe, although the conditional convergence relationship might hold. Different cross-section and panel specifications used by Arbia et al. (2008) show that the inclusion of spatial factors does not necessarily lead to different results. Moreover, all of their approaches indicate that convergence across 183 European NUTS-2 regions cannot be rejected.

Besides the regression approach, regional convergence tests have also been based on distributional dynamics and on unit root and cointegration methods. Fiaschi and Lavezzi (2007) show that the distribution of labor productivity has two peaks, which implies two income clubs across NUTS-2 regions during 1980–2002. Furthermore, they investigate the determinants of club membership via descriptive statistics and nonlinear regression. Fischer and Stumpner (2008) apply a model of distribution dynamics to 257 NUTS-2 regions of the EU-27 over the period 1995–2003. They extend an existing distribution approach framework to spatially filtered kernel estimation and thereby identify two groups, with the high-income metropolitan group growing faster than the group comprising the other regions. Canova (2004) proposes a clustering methodology based on predictive densities. His methodology is a unified approach that is rooted in the tradition of Bayesian inference. However, it does not allow for spatial dependencies. Similarly, Cuaresma and Feldkircher (2013) use a Bayesian model averaging method to detect convergence clubs.

Another important contribution is made by Corrado et al. (2005), who use a multivariate stationarity test to endogenously identify regional club clustering. The method explicitly detects the impact of spatial factors, including knowledge spillovers from neighboring regions. In the context of knowledge accumulation, Olejnik (2008) uses a spatial autoregressively distributed lag model for 228 NUTS-2 regions and illustrates the importance of considering spatial interaction in regional growth analyses and the pivotal role of human capital as a factor for growth.

In comparison with the PS methodology, most of the (spatial) above-mentioned studies do not consider technological heterogeneity across both, regions and time. Given this fact and our potentially heterogeneous panel, we believe that the PS method is most appropriate for detecting convergence clusters.

3 Estimation strategy

3.1 Log t convergence test

Phillips and Sul (2007) explain log income as the product of a time-varying idiosyncratic factor loading $\delta _{it}$, which also absorbs the error terms $\varepsilon _{it}$, and a common factor $\mu _t$, which determines the common growth path, according to the relation

$$\begin{aligned} \log y_{it} = \delta _{it} \mu _t , \end{aligned}$$

(1)

where $\delta _{it}$ acts as a unit-specific measure of the share of or distance to the common growth path $\mu _t$. Clearly, it will change size in transition to the common growth path. For subsequent hypothesis testing, the relative transition coefficient $h_{it}$ needs to be constructed, given by log income for a unit in relation to the panel average at time t:

$$\begin{aligned} h_{it} =\frac{\log y_{it}}{N^{-1}\sum _{i=1}^{N}\log y_{it}}=\frac{\delta _{it}}{N^{-1}\sum _{i=1}^{N}\delta _{it}}. \end{aligned}$$

(2)

As Eq. (2) shows, the common component $\mu _t$ drops out, so $h_{it}$ is defined as the relation of the factor loading $\delta _{it}$ for a unit to the average $\delta _t$.

Convergence implies that an individual unit approaches the sample average over time. Therefore, it holds that the transition coefficient $\delta _{it}$ converges toward $\delta$ as $t \rightarrow \infty$. This is equivalent to convergence of the relative transition coefficient $h_{it}$ toward unity as $t \rightarrow \infty$. The latter in turn implies that the cross-sectional variance of $h_{it}$, $H_t$, converges toward zero as $t \rightarrow \infty$. In summary, convergence in a panel is given by the following conditions:

$$\begin{aligned}&\displaystyle \delta _{it} \rightarrow \delta \quad \text { for all } i \text { as } t \rightarrow \infty \end{aligned}$$

(3)

$$\begin{aligned}&\displaystyle h_{it} \rightarrow 1 \quad \text { for all } i \text { as } t \rightarrow \infty \end{aligned}$$

(4)

$$\begin{aligned}&\displaystyle H_t = N^{-1}\sum \limits _{i=1}^{N}(h_{it}-1)^2 \rightarrow 0 \quad \text { for all } i \text { as } t \rightarrow \infty . \end{aligned}$$

(5)

However, these three equations need to be treated with caution. The cross-sectional variance of a sample might decrease even if there is no overall convergence and only local convergence within certain subgroups. To account for such potential nonstationary transitional behavior, Phillips and Sul (2007) propose the following semiparametric specification of $\delta _{it}$:

$$\begin{aligned} \delta _{it} = \delta _i + \sigma _i \xi _{it}L(t)^{-1}t^{-\alpha }, \end{aligned}$$

(6)

where $\delta _i$ is the time-invariant part of the country-specific factor loading $\delta _{it}$, L(t) is a slowly varying increasing function (with $L(t) \rightarrow \infty \text { as } t \rightarrow \infty$), $\alpha$ is the decay rate (i.e., the speed of convergence), and $\xi _{it}$ is a weakly autocorrelated random error variable ($\xi _{it} \text { is } iid(0,1)$).

On the basis of these preliminary considerations, the PS log t convergence test examines the following hypotheses:

$$\begin{aligned} H_0: \delta _i = \delta \quad \text {and} \quad \alpha \ge 0 \qquad \text {vs.} \qquad H_1: \delta _i \ne \delta \quad \text {for all}\,i,\, \text {or} \,\, \alpha < 0. \end{aligned}$$

(7)

The testing procedure involves the following three steps.

• 1. Calculation of the cross-sectional variance ratio $H_1 / H_t$ (cp. Eq. 5).

• 2. Estimation of the following OLS regression:

  $$\begin{aligned} \log \left( \frac{H_1}{H_t} \right) \,-\,2\log L(t)\,=\,{\hat{a}} + {\hat{b}} \log \,t + {\hat{u}}_t\nonumber \\ \text {for } t=[rT],[rT]+1,\ldots ,T \quad \text { for some } r>0. \end{aligned}$$

  (8)

• 3. One-sided t test for $\alpha \ge 0$ using ${\hat{b}}$ (${\hat{b}}=2{\hat{\alpha }}$) and a HAC standard error.

r ($r\in (0,1)$) is a truncation parameter that shortens the regression by a certain fraction of the first observations. Monte Carlo simulations by Phillips and Sul (2007) suggest the use of $r=0.3$ and $L(t)=\text {log } t$ for samples up to $T=50$. Given the assumptions outlined by Phillips and Sul (2007), the standard critical values can be applied such that the null hypothesis of convergence is rejected at the 5 % level if $t_{{\hat{b}}}<-1.65$.

3.2 Club clustering algorithm

The log t test is rejected for samples that do not converge overall. Phillips and Sul (2007) developed a club clustering algorithm to detect both convergence clubs and diverging regions. The algorithm consists of the following four steps:

• 1. Last observation ordering: The panel observations are sorted in descending order with respect to the last observations.

• 2. Core group formation: The log t test is conducted for the first $k=2$ regions. If $t_{{\hat{b}}}(k=2) > -1.65$, both regions establish the core group $G_k$. Subsequently, the log t test is conducted for $G_k$ plus the next region. If $t_{{\hat{b}}}(k=3) > t_{{\hat{b}}}(k=2)$, the region is added to $G_k$. This procedure is performed as long as $t_{{\hat{b}}}(k) > t_{{\hat{b}}}(k-1)$ for all $N > k \ge 2$. If $t_{{\hat{b}}}(N) > t_{{\hat{b}}}(N-1)$, the whole remaining panel converges. If $t_{{\hat{b}}} > -1.65$ does not hold for the first two units chosen, the first unit is dropped and the loop is performed for the remaining units. If $t_{{\hat{b}}} > -1.65$ does not hold for any two units chosen, the whole panel diverges.

• 3. Sieve individuals for club membership: After the core group $G_k$ is formed, log t tests on $G_k$ with each remaining unit are conducted. All units for which $t_{{\hat{b}}}$ is greater than a certain critical value c are pooled in a subgroup. If the log t test on $G_k$ combined with the subgroup is greater than $-1.65$, all units of the subgroup are added to $G_k$. If not, the critical value has to be increased and the procedure is repeated.

• 4. Stopping rule: If by now only one unit is left, this unit diverges. Otherwise, a log t test for all remaining units is conducted. If $t_{{\hat{b}}} > -1.65$, all remaining units constitute their own convergence club. If $t_{{\hat{b}}} < -1.65$, steps 1–3 need to be performed for all remaining units to find another convergence club. If no further convergence club is found, the remaining regions diverge.

3.3 Club merging algorithm

The number of clubs identified in a given sample depends on choice of the critical value c. A high c value corresponds to conservative sieving for further club members. This in turn might lead to identification of more clubs than actually exist. To remedy this, Phillips and Sul (2009) proposed log t tests for adjacent clubs after the club clustering algorithm. If $t_{{\hat{b}}} > -1.65$, the respective clubs are merged at the 5 % significance level.

For a total number of C initially identified clubs, a total series of $C-1$ log t tests between adjacent clubs needs to be calculated. In this context, it is possible that a sequence of log t tests will not be able to reject the convergence hypothesis. One explanation would be that all clubs in this sequence indeed converge to the same steady-state growth path. However, in the presence of transition across clubs (Phillips and Sul 2009), it could be possible that a certain club contains elements converging toward the next higher club and elements converging toward the next lower club. Therefore, simple amalgamation of all adjacent clubs with significant t values might form clubs in cases in which the log t test for convergence is rejected. The point becomes clear for the extreme case in which all $C-1$ log t tests between adjacent clubs are significant; only in certain cases is this caused by actual convergence of all clubs. Hence, if the club clustering algorithm identifies many similar clubs (owing to a wide sample or a conservative critical value c), manual ex-post merging might become ambiguous. For these reasons, we propose the following algorithm.

• 1. Merging vector: Starting with P clubs, a log t test for adjacent clubs is performed to obtain an $(M\times 1)$ vector of convergence test statistics $t_{{\hat{b}}}$ (with $m = 1,2,\ldots ,M$ and $M = P-1$).

• 2. Merging rule: The rule starts with the first element of the club merging vector. If $t_{{\hat{b}}}(m) > -1.65$ and $t_{{\hat{b}}}(m) > t_{{\hat{b}}}(m+1)$, then the two clubs determining $t_{{\hat{b}}}(m)$ are merged and the algorithm starts again at step 1. If $t_{{\hat{b}}}(m) < -1.65$ and/or $t_{{\hat{b}}}(m) < t_{{\hat{b}}}(m+1)$, the merging rule is then performed for all following pairs of $t_{{\hat{b}}}(m)$.

• 3. Last element: If $t_{{\hat{b}}}(m = M) > -1.65$, the last two clubs are merged.

3.4 Merging algorithm for diverging regions

Application of the club clustering and club merging algorithm delivers statistically significant clubs and avoids overdetermination of the number of clubs. However, units identified as diverging according to the PS cluster algorithm might not necessarily be still diverging if the club merging algorithm has formed new clubs. For example, for a given panel, a conservative critical value c in the PS clustering algorithm will lead to the formation of comparatively more clubs. Accordingly, the number of club mergers in the club merging algorithm will be comparatively large. It might well be the case that convergence of formerly diverging regions with the consolidated clubs cannot be rejected by the log t test criterion. In this case, we also need to test whether the remaining diverging regions form their own convergence club. For this purpose, we propose the following algorithm.

• 1. Divergence club: A log t test for all diverging regions (left) is performed. If $t_{{\hat{b}}} > -1.65$, the diverging regions form their own club and the algorithm stops.

• 2. Merging table: A log t test is performed for each diverging region and each club at a time. The results are saved in a $(d \times p)$ matrix, where each row d represents a diverging region and each column p a convergence club.

• 3. Merging rule: If the highest $t_{{\hat{b}}}$ in the table is greater than a certain critical value e, the respective diverging region is added to the respective club. Subsequently, the algorithm starts again at step 1.

• 4. Stopping rule: The algorithm stops as soon as the merging table for diverging regions does not contain any $t_{{\hat{b}}} > e$. All regions left are truly diverging regions.

For consistency, we set the critical value e equal to the t value at the chosen level of significance ($e=-1.645$ at the 5 % significance level).

3.5 Ordered logit model

The approach of Phillips and Sul (2007) clusters regions according to their transition paths, which are revealed through factorizing the log of income. However, this does not prove the club convergence hypothesis (Azariadis and Drazen 1990; Azariadis 1996; Galor 1996). For this reason, we follow Bartkowska and Riedl (2012), who propose a two-step procedure: the first step is the PS clustering and the second is application of an ordered logit model to identify variables that drive club formation. The club convergence hypothesis postulates that the starting conditions matter for the income distribution of an economy. By contrast, conditional convergence studies suggest that structural characteristics (such as time preferences or economic policy) determine the long-run growth path, independent of the starting conditions. On the basis of these theoretical considerations, we include both the initial conditions and the structural characteristics as variables in the regression equation to find the determinants of clustering. To strengthen robustness, we also control for geographic factors.

The ordered logit model assigns each region to one convergence club, denoted as $c=1,\ldots ,C$, which is a categorical variable. We model the determinants of region membership to one of these C alternatives. The alternatives can be ranked in a logical way according to the steady-state per capita income of each club. We assume that there is an underlying latent variable that drives the choice between different clubs. This is consistent with a latent variable equation of the form

$$\begin{aligned} y_i^* = x_i^{\prime }\,\beta + \varepsilon _i , \end{aligned}$$

(9)

where $y_i^*$ is the unobserved dependent variable and $\varepsilon _i$ has a logistic distribution.³ The observed variable is the ordinal variable $y_i = 1,\ldots ,C$, corresponding to $y_i^*< \gamma _1, \gamma _1 \le y_i^* < \gamma _2,\ldots$ and $y_i^* \ge \gamma _C$ respectively. The joint estimation of the unknown parameters $\gamma$ and $\beta$ is based on maximum likelihood (ML).

The vector $x_i$ includes the potential determinants of club membership by region i and a constant term. In contrast to their sign, the size of the coefficients $\beta$ has no sensible economic interpretation. Therefore, we compute the implied probability that a given region belongs to a certain convergence club (e.g., to Club $c=4$), which is called the predicted probability. It follows from the logistic distribution that the probability is given by

$$\begin{aligned} P \, \{y_i = 4\, |\, x_i \} = \frac{1}{1+exp\left( -\gamma _3 + x_i^{\prime }\,\beta \right) } - \frac{1}{1+exp\left( -\gamma _2 + x_i^{\prime }\,\beta \right) } . \end{aligned}$$

(10)

Predicted probabilities are evaluated for the means of all remaining variables and are hence higher the larger a club is and the closer it is to the sample average. To assess the importance of certain variables in determining club membership, we calculate the marginal effects of the predicted probabilities. The marginal effects estimate how a unit change in the explanatory variable changes the probability that an average region belongs to the respective club, while holding all other variables fixed at their sample averages. Lastly, as a goodness-of-fit measure, we report McFadden’s $R^2$, which is often used as a likelihood ratio index.

3.6 Data

Our main data source is the European Regional Database of Cambridge Econometrics and the variable of interest is gross value added (GVA) per capita at the NUTS-2 level. We use per capita values to focus on cross-unit income convergence. Other studies have used GVA per worker as a measure for productivity. We assess this seemingly small difference as pivotal for estimation results and inference; since a region’s GVA and its number of workers are likely to be positively correlated, changes in GVA might simply be caused by changes in the number of workers. Hence, to assess income catch-up and income convergence processes and to infer policy conclusion and welfare considerations, we are advised to use per capita values. Besides Cambridge Econometrics, we use data from the European Transport Policy Information System (ETIS) for average longitude and latitude values for the NUTS-2 regions. Finally, to measure human capital in the ordered logit section, we use a new dataset of Barro and Lee (2013).

Our panel considers 194 regions of 14 EU countries over the period 1980–2011 ($T=31$). It comprises all member states as of 2003 (the so-called EU-15) except Luxembourg, before Eastern European member states joined the EU. Table 2 provides a brief overview of the panel. It reveals that a country’s size does not always coincide with the number of regions. For example, although Germany is much larger than the UK with respect to area and population, the UK has more NUTS-2 regions. This is because the NUTS segmentation is based on an administrative and not a functional classification. For reasons of data availability, we use NUTS-2 data.

Table 2 Overview of sample of EU-15 regions, 1980–2011

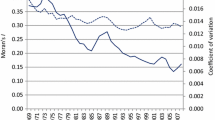
The two columns on the right of Table 2 report the coefficient of variation (CV) for the start and end of the period. CV is a measure of income dispersion among NUTS-2 regions within a country. Since the CVs are normalized values, they can be directly compared across regions and over time. Thus, a CV that decreases over time is equivalent to $\sigma$ convergence within a country. Table 2 reveals that CVs decrease for seven out of 14 countries over time, which indicates the presence of $\sigma$ convergence within these countries. Interestingly, all GIPS countries experienced a substantial decrease in CVs, whereas core European countries such as Germany, France, the Netherlands, and Denmark have quite stable CVs. Conversely, Sweden and Finland have a strongly increasing income variation over the sample period. However, the CVs for some countries have to be treated with caution owing to a low number of NUTS-2 regions, such as the case for Ireland.

An alternative way of describing the data in our sample is the scatter plot in Fig. 1. The slope of the fitted line in Fig. 1 represents the coefficient of an unconditional $\beta$ convergence regression. The estimated coefficient is statistically significant and yields a convergence speed of ${\hat{\beta }}=.009$ (0.9 %). This is considerably smaller than existing empirical evidence on unconditional convergence processes, with rates close to 2 % per annum reported (Abreu et al. 2005). However, it is evident from Fig. 1 that fitting lines for regions in certain countries or country groups would reveal faster $\beta$ convergence in the sense of conditional convergence.

Fig. 1

$\beta$ convergence: scatter plot of initial log GVA per capita and annual growth rate during 1980–2011, $N=194$

The scatter plot also illustrates within-country heterogeneity. For example, log GVA per capita in 1980 and the subsequent growth rate substantially differ within Greece. Furthermore, the scatter plot shows that Greece is a special case in the sense that all of its regions except one lie below the fitted line, indicating that the average growth rates for Greek regions lie below the sample average. By contrast, all of the Scandinavian regions are located above the fitted line. Within countries or country groups, regional log GVA substantially differed in 1980. This was not always accompanied by different subsequent growth rates in the sense of catching up; for example, starting with similar regional output, some Greek regions grew, whereas other shrank on average. However, it is not clear whether these developments are the result of divergence or transitional dynamics. Finally, one outlier can clearly be identified, Inner London, represented by the dot in the upper right corner of Fig. 1.

4 Estimation results

4.1 Convergence clubs

Since we are interested in long-run growth behavior, we used the Hodrick–Prescott (HP) filter to separate the time series into trend and cyclical components (Hodrick and Prescott 1997). The smoothing parameter was chosen according to the method proposed by Ravn and Uhlig (2002), such that the rescaled value for the smoothing parameter is 6.25. Only the trend component was used when applying the log t test. As discussed by Phillips and Sul (2007), the HP filter is common in this type of work.

The log t test applied to the whole panel suggests that the null hypothesis of overall convergence is rejected at the 1 % significance level (−2.326). Thus, we performed the PS club clustering procedure.⁴ Table 3 reports summary results for the club clustering algorithm.

Table 3 Results of the log t test, 1980–2011

Four clubs can be identified, with a fairly large difference with respect to the end-of-period average income (last column). Moreover, we find one diverging region (Inner London). The club merging algorithm and the merging algorithm for diverging regions do not lead to any amalgamation of clubs or regions, so Table 3 shows the final club classification. However, both newly proposed algorithms are applied and refine the results of the robustness tests, as described in Sect. 5. The panel contains one low-income, two medium-income, and one high-income club. The ${\hat{b}}$ values for Clubs 1, 2, and 4 are neither negative nor greater than 2. This indicates that the members of these clubs neither diverge nor converge to the same level, but converge conditionally and diverge with respect to their income levels. The ${\hat{b}}$ value for Club 3 is negative, but is not statistically different from zero. Following Phillips and Sul (2009), we take this as evidence that Club 3 is a weaker convergence club compared to the other clubs. The convergence speeds ${\hat{\alpha }}$ substantially differ across clubs. Regions in Club 1 converge at a rate of 4.8 %, whereas the convergence speed in Clubs 2 and 4 is close to 21 %. An interpretation of ${\hat{\alpha }}$ for Club 3 does not apply, since its ${\hat{b}}$ value lacks statistical significance.

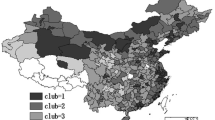
The map in Fig. 2 illustrates the club clustering results. Geographic effects seem to be very pronounced and point to a North-South division in regional income clubs. Moreover, the highly significant Moran’s I statistic of the club variable for several distance bands indicate that the clustering has also been influenced by spatial effects. We take this as evidence that the factorization done in the PS procedure is indeed capable of capturing a variety of effects, including spatial ones.

Fig. 2

Club clustering in the EU-15 panel (1980–2011)

Club 1 contains many cities and metropolitan areas, including Vienna, Salzburg, Brussels, Munich, Hamburg, Frankfurt, Copenhagen, Helsinki, Paris, Dublin, Groningen, Utrecht, Amsterdam, Stockholm, Bristol, Edinburgh, Aberdeen, and the regions west of London. All remaining regions in this club (seven in total) border on these (capital) cities (except the Finish Aland islands and Cheshire, although the latter is adjacent to Manchester and Liverpool).

Club 2 has a more scattered geographic distribution. On the one hand, around two-thirds of the Scandinavian regions are part of it. On the other hand, nearly half of the regions in the UK belong to this club. Larger cities in the south (Madrid, Bilbao, Athens) and wealthier regions and cities in Central Europe (parts of Austria, Belgium, Germany, and the Netherlands) complete the club.

More than half of the sample’s regions belong to Club 3, which covers most parts of Central Europe. It contains all of the French regions except Paris, most parts of Belgium and West Germany, northern Italian regions, and coastal areas in Spain. The remaining Austrian, Danish, Dutch, and British regions, as well as Lisbon, the Algarve coast (Portugal), and the southern Aegean islands (Greece) are included. Notably, all regions in Club 4 belong to the so-called GIPS countries. Apart from Greece, for which 85 % of all regions fall in Club 4, southern Italy and remaining regions in Portugal and Spain are also included.

Some remarks with respect to the UK and Ireland are in order. Regions in both countries are quantitatively fairly evenly distributed among Clubs 1, 2, and 3. In addition, the UK contains the only diverging region (Inner London) in the whole sample. We conclude that the UK and Ireland might be treated as special cases, not least because of their insular characteristics. In summary, we identify the following four geographical clubs: (1) Western cities, (2) high-income Northern and Central Europe hotspots, (3) Central Europe, and (4) Southern peripheral Europe.

4.2 Transitional behavior

Figure 3 shows the relative transition paths for regions within their respective club. The transition path is given by the relative transition coefficient $h_{it}$, as defined in Eq. (2). The graphs show that the transition paths for all clubs clearly form a funnel. The regions in Club 3, which is the largest club with 98 regions, exhibit less strong convergence within their club, as indicated by relatively time-constant transition paths. Furthermore, the transition mostly took place in the period up to 2000, and narrowing of the curves is less evident in the period 2000–2011.

Fig. 3

Relative transition path by club during 1980–2011, $N=194$

Figure 4 illustrates club formation in a scatter plot of log GVA per capita in 1980 versus log GVA per capita in 2011. The distance between each data point and the 45 degree line illustrates the average growth rate over the period. Not surprisingly, the different clubs are vertically staggered according to their income; regions belonging to higher-income clubs had higher growth rates on average. Moreover, growth rates within the clubs are higher for regions that were comparatively poor in 1980. Both findings indicate the presence of catch-up effects and conditional convergence in the sense that regions converge to different steady states. The graph also reveals a horizontal order of clubs. The lower the income in 1980, the lower the income club on average. This might be a first indication of the club convergence hypothesis. Finally, Fig. 4 similarly illustrates the within-club convergence process seen in Fig. 3. Income dispersion within each club is constantly higher in 1980 than in 2011 (e.g., log GVA per capita for Club 2 lies between 2.4 and 3.5 in 1980, but narrowed to the range 2.9–3.6 in 2011).

Fig. 4

Scatter plot of club formation, $N=194$

4.3 Convergence factor testing

We now discuss results for the ordered logit model introduced in Sect. 3.5. The marginal probabilities for the model are shown in Table 4. The sample consists of 193 NUTS-2 regions (without Inner London, which is a diverging region). An overview of the variables and sources used in the ordered logit model is provided in Table 9. The summary statistics in Table 10 show that the average region has a log income of 2.71 euro and a labor force participation rate of 45 percentage points. The dependent variable is the categorical variable ‘Club membership’, which varies from 1 to 4 with an average value of 2.58 and a median of 3, since Club 3 is the largest club.

Table 4 Marginal effects on probabilities (ordered logit)

Overall, the pattern for the results suggests that initial income per capita and initial human capital, measured in years of schooling, are the most important drivers of club membership. The interpretation is that a one-unit higher log initial income in 1980 increases a region’s probability of belonging to Club 1 by 26.6 % (Column 1). A 1-year increase in average schooling duration increases the probability of belonging to Club 1 by 9.9 % and decreases the probability of belonging to Club 4 by 3.9 %. With respect to structural characteristics, there is a statistically significant effect of industry and of service share on club membership. A one-unit increase in the initial industry or service share is associated with a higher probability of belonging to Club 1 or 2, and a lower probability of belonging to the lower-income clubs.

The sign of the marginal effect of initial physical capital seems peculiar, since it implies that a one-unit increase in the 1980 per capita gross fixed capital formation decreases the probability of belonging to the higher-income Clubs 1 or 2. A closer look shows that this result is driven by the British regions, because of the low physical capital endowment of high-income regions.⁵ If the ordered logit procedure is conducted without British regions, the sign of the physical capital variable becomes positive for Club 1 and 2 and negative for Club 3 and 4. A further analysis of this feature is beyond the scope of this paper. It should, however, be addressed by future research, perhaps under consideration of the agglomeration effects brought on by Great Britain’s structural transformation from a production-based economy to a system dominated by the service and finance sectors. The results are mostly in line with Bartkowska and Riedl (2012), who find coefficients similar in size but less pronounced in terms of statistical significance. In summary, the findings in Table 4 confirm that the initial conditions are relevant in explaining club membership and that log income is the most dominant driver of club membership.

The results in Sect. 4 (with a visual map in Fig. 2) suggest that geographic factors might play a role in determining the club membership of a region. Hence, we added latitude, a dummy ($=$1) indicating if the capital city is located in a region, and a dummy ($=$1) for metropolitan areas to the ordered logit model (Table 12). Except for minor deviations, the coefficients for the baseline model are robust to the inclusion of geographic variables. The main insight is that latitude and the capital dummy are statistically significant drivers of club membership. The highly significant coefficient for latitude confirms the previously described north–south division within Europe; in other words, the probability of belonging to a higher-income club increases with northerly latitude for a region. The coefficient for the capital dummy suggests that the probability of belonging to Club 1 is 19 % higher for regions that include the capital city.

It is important to note that geographic variables in the ordered logit regression serve as control variables which consider geography-related institutional differences. They do not measure the degree of spatial interaction and mutual dependencies between regions, as done by spatial Durbin or a spatial autoregressive models. Nevertheless, spatial effects are not neglected in our analysis, as already mentioned above; the factor representation of the preceding PS methodology implicitly incorporates any effect or influence, also spatial ones, although it does not explicitly measures them. An explicit analysis of possible spatial relationships (Ertur et al. 2006; Basile 2008) is beyond the scope of this paper.

5 Robustness

Robustness checks of the PS procedure can involve the robustness of the club number and composition, and the robustness of the parameter estimates. We checked for both types of robustness using the following twists in our estimation: (1) variation in the time period and the truncation parameter, (2) variation in the level of significance, and (3) estimation for a Eurozone panel.

To verify whether the global financial crisis from 2008 onwards had an effect on club formation, we use a panel over the period 1980–2007. The PS procedure leads to the formation of eight clubs. However, our club merging algorithm as described in Sect. 3.3 decreases the number of clubs to four. Summary results are provided in Table 5.

Table 5 Results of the log t test, 1980–2007

Compared to our baseline results, exclusion of the crisis years does not substantially change the average income structure across both panels. However, the club composition changes slightly, as summarized in Table 6.

Table 6 Stability of club composition: change in length of panel

Three points are noteworthy. First, the stability of the initial club membership is quite pronounced for the two lower-income clubs. For example, 95 % of regions belonging to Club 3 in the longer panel belong to the same club for the shorter panel. This does not hold for Club 1, which loses nearly half of its regions to Club 2. Second, changes in club membership on panel shortening only occur in one direction, toward lower-income clubs. This is directly linked to the third point: the two higher-income clubs shrink and the two lower-income clubs gain in overall club size. Whether the crisis itself caused the higher-income clubs to increase in size is a question for further research.

The convergence speed within clubs substantially changes across both panels (although in both panels we estimate a negative and insignificant t value for Club 3). For example, although Club 4 only gains five more regions when clustering the shorter panel (with all the ‘old’ members remaining in the club), the convergence speed decreases from 20.5 to 2.1 %. The test statistic $t_{{\hat{b}}}$ also decreases from 15.9 to 1.1, and hence becomes nonsignificant. We take this as evidence that the convergence speed must be interpreted with caution. The reason is that inclusion of further regions in a certain club might be justified by the log t test, but might worsen the test statistic and thus the parameter estimates to such an extent that inference is no longer valid. Further research could try to improve the clustering algorithm by excluding the possibility of relatively high jumps in the test statistic.

We apply the PS procedure to two shorter versions of our initial panel. The first covers the period 1990–2011, which excludes all observations before the fall of the Iron Curtain. After use of the proposed club and diverging regions’ merging algorithms (Sects. 3.3, 3.4), the final number of clubs decreases to seven and the number of diverging regions to one. The second panel covers 1990–2007, so data during both the Cold War and the global financial crisis are dropped. After running all three algorithms, we detect eight clubs and one diverging region. For both time spans, the parameter estimates for four clubs are not significantly different from zero, thereby pointing to weaker convergence clubs. Summary results for both panels are provided in the “Appendix” (Tables 13, 14). We take the results for both subpanels as an indication of the rapid increase in discriminatory power of the log t test as the sample size decreases.

Besides changing the input panel, we also change the truncation parameter r in the log t test. Phillips and Sul (2007) propose $r=0.3$, which we used in all our previous regressions. To check for robustness, we use $r=0.2$ and $r=0.4$. For $r=0.2$, we estimate five clubs, with a clustering pattern quite different to the pattern of our baseline results (Table 15). For $r=0.4$, the algorithm generates four clubs with remarkable size and composition similarities to our baseline clubs (Tables 16, 17). The convergence speed is close to the baseline result for Clubs 1 and 2, but sharply differs for Clubs 3 and 4.

We also test for robustness with respect to the level of significance. It should be noted that the PS procedure does not use the significance level as a post-estimation measure to classify the validity of a result. Instead, the significance level is used in the clustering algorithm to increase or decrease the discriminatory power of the procedure. The higher the significance level, the higher is the discriminatory power of the algorithm in the sense that membership of a certain existing club becomes less likely for a certain region. Accordingly, use of a low significance level usually leads to detection of fewer clubs.

Besides our baseline value of 5 %, we apply significance levels of 0.1, 1, 10, and 25 %. The results do not change, except for the 25 % level; in this case, the size and parameters of Clubs 2–4 alter, as illustrated in Table 7.⁶ Interestingly, the size of the two medium-income clubs nearly balances. Although Club 2 increases by 25 regions, its speed of convergence remains stable at 21 %. Club 3 now has a positive and significant speed of convergence of 7 %. However, the parameter estimate for Club 4 becomes nonsignificant, pointing to a weaker convergence club.

Table 7 Results of the log t test, 1980–2011, sign.level=$25\%$

Finally, we calculate estimates for a Eurozone panel containing 145 NUTS-2 regions for the same time span (1980–2011). When applying the PS club clustering algorithm, we have to increase the critical value to $c=2.7$. Table 8 summarizes the clustering algorithm results.⁷

Table 8 Results of the log t test, 1980–2011, Eurozone panel

In the Eurozone case, four clubs are eventually detected. The clubs with the lowest and highest income are quite stable in size, membership, and average income compared to the baseline estimation. Nevertheless, both clubs are classified as weak owing to their nonsignificant ${\hat{b}}$ coefficients. Moreover, a majority of regions clustered in Club 3 in the EU panel enter Club 2 in the Eurozone panel, accompanied by a substantial change in parameter estimates.

Overall, this section illustrates that the number of clubs is very stable across different panel specifications. The same largely holds for size, average income, and membership stability of the lowest-income club. There is, however, much volatility among coefficients for the remaining clubs. Future research could investigate whether these differences are associated with major political or economic shocks, or whether the methodology applied is appropriate for identifying the speed of convergence. In this respect, the PS clustering algorithm could be refined to take into account the relative effect of single regions joining a core group or a club.

6 Discussion and conclusion

We investigated the presence of club convergence in income per capita for NUTS-2 regions in Europe. To this end, we adopted a nonlinear time-varying factor model and the log t test proposed by Phillips and Sul (2007). The PS model tests whether the transition coefficient $\delta _{it}$, which measures distance to a common growth path $\mu _t$, converges toward the panel average $\delta$ as $t \rightarrow \infty$. Thus, in contrast to previous methods, the PS approach allows for transitional heterogeneity and divergence from the actual growth path.

We also applied the PS club clustering algorithm, which groups individual regions in certain convergence clubs according to the log t test. We augmented the existing methodology with two post-clustering algorithms of particular interest for wider and/or shorter samples when the PS club clustering algorithm leads to a comparatively large number of convergence clubs and diverging regions. Our estimation results in Sect. 5 show that both algorithms have an impact and finalize club formation. After identifying convergence clubs purely based on income per capita, we tested further explanatory convergence factors using an ordered response model. The underlying questions are whether initial or structural conditions determine a region’s membership in a given club.

Our main result is the identification of four convergence clubs along geographic lines: (1) Western cities, (2) high-income Northern and Central Europe hotspots, (3) Central Europe, and (4) southern peripheral Europe. The number of income clubs is robust for various specifications of the baseline model. However, the variation of coefficients in the robustness tests indicates that the PS club clustering procedure might need some refinements. In particular, researchers should ensure that inclusion of a certain region in an existing club does not substantially change the club transition coefficients.

Application of the ordered logit model corroborates the club convergence hypothesis in the sense that the initial conditions play a role in club membership. The probability of belonging to one of the two higher-income clubs increases with the initial labor force participation rate, the initial human capital, and the log initial income per capita. Extension of the ordered logit model using geographic variables confirms the conjecture of strong positive metropolitan effects and a north-to-south decline in income.

These results differ in part from findings in empirical studies using the PS procedure. Bartkowska and Riedl (2012), whose testing agenda we partly follow, use income per worker data in 206 NUTS-2 regions of the EU-15 over the period 1990–2002. They identify six convergence clubs, although these are geographically scattered. We suspect that use of per-worker values has a cushioning effect such that clustering is less pronounced. Moreover, our robustness tests revealed that the number of clubs increases if panels become too short. This might explain the higher number of clubs detected by Bartkowska and Riedl (2012) in their comparatively short panel. Based on NUTS-2 data, we find robust results in favor of four convergence clubs and a clear geographic pattern. By contrast, Monfort et al. (2013) and Apergis et al. (2010), who use national data over a time span similar to ours, find only one and two convergence clubs.

Our results suggest that club convergence holds within the EU, indicating a multi-speed Europe along geographic lines. Income growth paths differ substantially among Northern, Central, and Southern Europe. Although overall income convergence does not hold, European regional policy has not necessarily failed. On the one hand, policy measures need time to make a measurable impact. On the other hand, even perfectly equalized opportunities are likely to lead to region-specific growth paths if different initial conditions matter or if differences in region-specific structural characteristics prevail. In these cases, all efforts to achieve absolute income convergence have a natural limit. In light of a multi-speed Europe, the policy question is what income differences European citizens are willing to accept. Given our results European regional and structural policy should strive to support regions in converging within their respective income club for the time being.

There are several directions for further research. The PS log t test can be applied to datasets not yet considered, such as NUTS-1 data. In this respect, the question of the most suitable level of investigation is not fully answered. Comparison of results between national and NUTS-1, NUTS-2, and NUTS-3 data for the same area over the same period might be a first step in answering this question. From a methodological perspective, improvement, simplification, or merger of the three algorithms used in this study might be of interest. Finally, the stagnating income transition within clubs from 2000 onwards (Fig. 3) calls for a thorough investigation.

Appendix

See Tables 9, 10, 11, 12, 13, 14, 15, 16, 17, 18 and 19.

Table 9 Variables and sources

Table 10 Summary statistics

Table 11 Average p.c. gross fixed capital formation in 1980 (in Euro)

Table 12 Robustness: marginal effects on probabilities (ordered logit) with geographic controls

Table 13 Results of the log t test, 1990–2011

Table 14 Results of the log t test, 1990–2007

Table 15 Results of the log t test, 1980–2011, $r=0.2$

Table 16 Results of the log t test, 1980–2011, $r=0.4$

Table 17 Stability of club composition: change in the truncation parameter

Table 18 Stability of club composition: change in the significance level

Table 19 Stability of club composition: Eurozone panel