Covariance matrix testing in high dimension using random projections

Abstract

Estimation and hypothesis tests for the covariance matrix in high dimensions is a challenging problem as the traditional multivariate asymptotic theory is no longer valid. When the dimension is larger than or increasing with the sample size, standard likelihood based tests for the covariance matrix have poor performance. Existing high dimensional tests are either computationally expensive or have very weak control of type I error. In this paper, we propose a test procedure, CRAMP (covariance testing using random matrix projections), for testing hypotheses involving one or more covariance matrices using random projections. Projecting the high dimensional data randomly into lower dimensional subspaces alleviates of the curse of dimensionality, allowing for the use of traditional multivariate tests. An extensive simulation study is performed to compare CRAMP against asymptotics-based high dimensional test procedures. An application of the proposed method to two gene expression data sets is presented.

1 Introduction

In multivariate analysis, hypothesis tests involving the first two moments - mean and covariance matrix have been extensively studied. Consider a random variable $\mathbf {X}$ with mean $\varvec{\mu }= \mathbb {E}(\mathbf {X})$ and covariance matrix $\Sigma = \mathbb {E} \left\{ (\mathbf {X}- \varvec{\mu }) (\mathbf {X}- \varvec{\mu })^{\top } \right\}$. There is a vast amount of literature for inference involving the mean $\varvec{\mu }$, starting with the Hotelling’s $T^2$ statistic. Refer to Ayyala (2020), Hu and Bai (2016) for an extensive review of methods for the mean vector testing. In this article, we focus on inference on the covariance matrix. Given a random sample from a p-dimensional Gaussian distribution with mean $\varvec{\mu }$ and variance $\Sigma$, we are interested in testing the hypothesis

$$\begin{aligned} H_0 : \Sigma = \Sigma _0 \text{ vs. } H_A : \Sigma \ne \Sigma _0, \end{aligned}$$

(1)

for some known $p \times p$ matrix $\Sigma _0$. Of specific interest is when $\Sigma _0$ corresponds to a particular geometric shape: $\Sigma _0 = \sigma ^2 \mathcal {I}_p, \sigma \in \mathbb {R}$ for a spherical normal distribution or $\Sigma _0 = \mathrm{diag}(\sigma _{1}, \ldots , \sigma _{p})$ for independent components. Other forms, such as block diagonal can be helpful in testing the presence of subgroups of elements of $\mathbf {X}$ that are independent. In the two sample case, it is of interest to compare the covariance matrices $\Sigma _1$ and $\Sigma _2$ of two populations $\mathbf {X}$ and $\mathbf {Y}$ respectively. Equality of covariance matrices implies the distributions of $\mathbf {X}$ and $\mathbf {Y}$ have the same shape, but are centered at different locations. Importance of the problem of testing equality of covariance matrices for Gaussian models lies in the network interpretation of the covariance matrix. The inverse of the covariance matrix, called the precision matrix is used to construct undirected graphical network models with elements of the variable as nodes (Cai et al. 2012; Zhao et al. 2014).

For both the one and two sample hypotheses, traditional likelihood ratio tests are developed and studied in great detail (Anderson 2003). However the tests are valid only when $p < n$ and p is fixed. For high dimensional data, i.e. when p increases with n or when $p > n$, the asymptotic properties of these tests are no longer valid. This is because the sample covariance matrix $\mathcal {S}$ has rank $\min (p, n - 1)$, where n is the sample size. Therefore unconstrained estimation will lead to rank-deficient and inconsistent estimators when $p > n$. To avoid this problem, test statistics can be constructed based on a real-valued functional of $\mathcal {S}$. This approach is very commonly used in high dimensional inference for the mean (Ayyala 2020). The main idea is to have the functional equal to zero under $H_0$ and non-zero under $H_A$. For example in the one-sample hypothesis in (1), $f(\Sigma ) = \mathrm{tr}\left( \Sigma - \Sigma _0 \right) ^2$ can be used as the functional. The rejection region is determined by studying the asymptotic properties of the sampling distribution of $f(\mathcal {S})$. Appropriate functionals for the two-sample case can be constructed similarly.

An approach that is gaining prominence in other domains of high dimensional inference but has not been implemented explicitly in covariance matrix testing is the use of random projections. A computationally intensive approach, a random projection (RP) based inference involves embedding the original p-dimensional data into a lower k-dimensional space using linear projections. Dimension of the embedded space k can be chosen to be smaller than n, thereby upholding the assumptions of traditional multivariate methods. Validity of this method is guaranteed by the Johnson-Lindenstrauss lemma (Johnson and Lindenstrauss 1984).

In recent times, there is increasing interest in using random projections in various data mining and machine learning problems. Random projection methods have been used in ensemble machine learning methods such as classification (Schclar and Rokach 2009; Cannings and Samworth 2017; Cannings 2021). In linear regression, (Thanei et al. 2017) studied theoretical properties of RP based linear regression models and how they perform compared to ridge and principal component regression. In statistical inference, random projections have been used for the mean vector testing problem (Lopes et al. 2011; Srivastava et al. 2014). For the two sample covariance matrix testing problem, Wu and Li (2020) proposed a test procedure by randomly projecting the data into a one-dimensional space. The one-sample problems of test for sphericity and uniformity have not been addressed.

In this paper, we propose CRAMP - covariance matrix testing using random matrix projections. The rest of the article is organized as follows. In Sect. 2, we introduce two specific one sample tests and the two sample test hypotheses. A literature review of existing test procedures in both traditional and high-dimensional settings is also provided. Random projection based tests is introduced in Sect. 3. Theoretical details and algorithms for the one and two sample tests are also explicitly described. In Sect. 4, an extensive simulation study comparing the different methods is presented. We applied CRAMP to test equivalence of gene networks, which are represented by the covariance matrices using gene expression data. Results from the analysis of these data sets are presented in Sect. 5.

2 Hypotheses for covariance matrices

2.1 One sample tests

Consider a random sample $\mathbf {X}_1, \ldots , \mathbf {X}_n$ from a p-dimensional continuous distribution $\mathcal {F}_p$ with mean $\varvec{\mu }$ and variance $\Sigma$. The parameter of interest for this study is $\Sigma$, the covariance matrix. We are interested in testing the hypotheses

$$\begin{aligned}&H_{0I} : \Sigma = \mathcal {I}_p \text{ vs. } H_{1I} : \Sigma \ne \mathcal {I}_p, \end{aligned}$$

(2)

$$\begin{aligned}&H_{0S} : \Sigma = \sigma ^2 \mathcal {I}_p \text{ vs. } H_{1S} : \Sigma \ne \sigma ^2 \mathcal {I}_p, \end{aligned}$$

(3)

where $\mathcal {I}_p$ is the identity matrix of dimension p and $\sigma > 0$ is an unknown parameter. The hypotheses in Eqs. (2) and (3) are commonly referred to as tests for identity and sphericity respectively. The general test for $H_0 : \Sigma = \Sigma _0$ for some known matrix $\Sigma _0$ can be viewed as a test for identity when the data is transformed as $\mathbf {X}\mapsto \Sigma _0^{-1/2} \mathbf {X}$. The hypotheses can be equivalently stated in terms of the eigenvalues of $\Sigma$ as follows. If $\lambda _1, \ldots , \lambda _p$ denote the eigenvalues of $\Sigma$, then Eqs. (2) and (3) can be stated as

$$\begin{aligned} H_{0I} : \lambda _i = 1 \,\,\, \forall \,\,\, i \text{ vs. } H_{1I} : \lambda _i \le 1 \text{ for } \text{ at } \text{ least } \text{ one } i, \\ H_{0S} : \lambda _1 = \ldots = \lambda _p \text{ vs. } H_{1S} : \lambda _i \ne \lambda _j \text{ for } \text{ some } i \ne j. \end{aligned}$$

Let $\mathcal {S} = n^{-1} \sum \nolimits _{i = 1}^n \left( \mathbf {X}_i - \overline{\mathbf {X}} \right) \left( \mathbf {X}_i - \overline{\mathbf {X}} \right) ^{\top }$ denote the sample covariance matrix, where $\overline{\mathbf {X}} = n^{-1} \sum \nolimits _{i=1}^n \mathbf {X}_i$ is the sample mean. When $\mathcal {F}_p$ is the Gaussian distribution, $\mathcal {S}$ is the maximum likelihood estimator which follows a Wishart distribution. The likelihood ratio test statistics for the two hypotheses are given by

$$\begin{aligned}&LRT_{I} = (n - 1) \left\{ 1 - \frac{1}{6n - 7} \left( 2p + 1 - \frac{2}{p + 1} \right) \right\} \left[ -\log (|\mathcal {S}|) + \mathrm{tr}(\mathcal {S}) - p \right] , \nonumber \\&LRT_{S} = - \left\{ n - 1 - \frac{2p^2 + p + 2}{6p} \right\} \left[ p \log p + \sum \limits _{i = 1}^p \log \lambda _i - p \log \left( \sum \limits _{i = 1}^p \lambda _i \right) \right] .\nonumber \\ \end{aligned}$$

(4)

Under the null hypothesis, $LRT_I$ and $LRT_S$ are approximately distributed as a $\chi ^2$ distribution with degrees of freedom $\nu = p(p + 1)/2$ and $\nu = p(p + 1)/2 - 1$, respectively (Rencher and Christensen 2012).

Another approach to test the hypotheses is to construct a functional of the covariance matrix which will be zero under the null hypothesis and non-zero under the alternative. For sphericity and identity, it is straightforward to see that the functionals

$$\begin{aligned} \mathcal {U} = \frac{1}{p} \mathrm{tr}\left\{ \frac{\Sigma }{\mathrm{tr}\Sigma /p} - \mathcal {I}_p \right\} ^2, \mathcal {V} = \frac{1}{p} \mathrm{tr}\left\{ \Sigma - \mathcal {I}_p \right\} ^2, \end{aligned}$$

are non-negative and are equal to zero under $H_{0S}$ and $H_{0I}$ respectively. Using these functionals, John (1972) and Nagao (1973) proposed the following test statistics by plugging in the sample covariance matrix estimate to test $H_{0S}$ and $H_{0I}$ respectively:

$$\begin{aligned} U_{John} = \frac{1}{p} \mathrm{tr}\left\{ \frac{ \mathcal {S}}{\mathrm{tr}\mathcal {S}/p} - \mathcal {I}_p \right\} ^2, V_{Nagao} = \frac{1}{p} \mathrm{tr}\left\{ \mathcal {S} - \mathcal {I}_p \right\} ^2. \end{aligned}$$

(5)

It is shown that under the null hypothesis, $U_{John}$ and $V_{Nagao}$ are asymptotically distributed as chi-squared random variables with $p(p + 1)/2 - 1$ degrees of freedom. When the sample size is small, Nagao (1973) also provided second-order corrections to the p-values for both test statistics. While these tests are constructed assuming normality of the samples, they are applicable even when $\mathcal {S}$ is singular, unlike the likelihood ratio tests which involves inverting the sample covariance matrix. However, these tests fail when the data is high-dimensional, i.e. when p is larger than n. While the tests can be applied in practice, the asymptotic properties fail to hold unless p is assumed to be fixed with respect to n.

Under high dimensional setting, Ledoit and Wolf (2002) studied the properties of $U_{John}$ and $V_{Nagao}$ for high-dimensional models when $p/n \rightarrow c \in (0, \infty )$. They observed that $U_{John}$ is consistent for high-dimensional data, whereas $V_{Nagao}$ fails when p increases with n. Modifying $V_{Nagao}$, they proposed

$$\begin{aligned} V_{LW} = \frac{1}{p} \mathrm{tr}\left\{ \mathcal {S} - \mathcal {I}_p \right\} ^2 - \frac{p}{n} \left\{ \frac{ \mathrm{tr}\mathcal {S} }{p} \right\} ^2 + \frac{p}{n}. \end{aligned}$$

(6)

Under $H_{0I}$, $V_{LW}$ is shown to asymptotically follow a $\chi ^2$ distribution with $p(p + 1)/2$ degrees of freedom. The asymptotic distribution is derived under a normal distribution model for the observations.

With increased interest in high dimensional inference, several other tests have been proposed for the hypotheses in Eqs. (2) and (3). By modifying the estimators of $\mathrm{tr}\Sigma$ and $\mathrm{tr}\Sigma ^2$ in $\mathcal {U}$ and $\mathcal {V}$, Srivastava et al. (2014) proposed a test statistic is given by

$$\begin{aligned} U_{SYK} = \frac{n - 1}{2} \left[ \frac{\widehat{a}_2}{\widehat{a}_1} - 1 \right] , V_{SYK} = \frac{n - 1}{2} \left[ \widehat{a}_2 - 2 \widehat{a}_1 + 1 \right] , \end{aligned}$$

(7)

where $\widehat{a}_1 = \mathrm{tr}\left( \mathcal {S} \right) /p$, $\widehat{a}_2 = \left\{ pn(n - 1)(n - 2)(n - 3) \right\} ^{-1} \bigg [ (n - 1)^3(n - 2) \mathrm{tr}\mathcal {S}^2 - n(n - 1)^3 \mathrm{tr}\left( \mathcal {D}_{\mathcal {S}}^2 \right) + (n - 1)^2 \mathrm{tr}\left( \mathcal {S}^2 \right) \bigg ]$ and $\mathcal {D}_{\mathcal {S}} = \mathrm{diag}(\mathcal {S})$ denotes the diagonal of the sample covariance matrix. The test statistics are shown to be asymptotically normally distributed under $H_{0S}$ and $H_{0I}$ respectively. The statistics in (7) are based on comparing the arithmetic means of the eigenvalues of $\Sigma ^k$ for $k = 1, 2$. Extending the result to higher order powers, Fisher (2012), Fisher et al. (2010) expanded it to the fourth powers of $\Sigma$ and Qian et al. (2020) extended the results to the sixth power.

Chen et al. (2010) used Hoeffding’s U-statistics to estimate $\mathrm{tr}\Sigma$ and $\mathrm{tr}\Sigma ^2$. Their test statistics are given by

$$\begin{aligned} U_{CZZ} = p \left( \frac{T_{2,n}}{T_{1,n}^2} \right) - 1, V_{CZZ} = \frac{1}{p}T_{2,n} - \frac{2}{p} T_{1,n} + 1, \end{aligned}$$

(8)

where $T_{1,n} = n^{-1} \sum _{i=1}^n \mathbf {X}_i^{\top } \mathbf {X}_i - \{ n(n-1)\}^{-1} \sum _{i \ne j} \mathbf {X}_i^{\top } \mathbf {X}_j$ is the U-estimator for $\mathrm{tr}\Sigma$ and

$$\begin{aligned} T_{2,n}= & {} \frac{ \sum \nolimits _{i \ne j} \left( \mathbf {X}_i^{\top } \mathbf {X}_j \right) ^2}{n(n-1)} - \frac{2 \sum \nolimits _{i \ne j \ne k} \mathbf {X}_i^{\top } \mathbf {X}_j \mathbf {X}_j^{\top } \mathbf {X}_k }{n(n-1)(n-2)} \\&+ \frac{\sum \nolimits _{i \ne j\ne k \ne l} \mathbf {X}_i^{\top } \mathbf {X}_j \mathbf {X}_k^{\top } \mathbf {X}_l}{n(n-1)(n-2)(n-3)} \end{aligned}$$

is the U-estimator for $\mathrm{tr}\Sigma ^2$. Under the null hypotheses, the test statistics $nU_{CZZ}/2$ and $nV_{CZZ}/2$ both asymptotically follow a standard normal distribution.

2.2 Two sample tests

In the two sample case, our interest lies in comparing the covariance matrices of two independent populations. Let $\mathbf {X}_1, \ldots , \mathbf {X}_n$ and $\mathbf {Y}_1, \ldots , \mathbf {Y}_m$ be random samples drawn from p-dimensional distributions $\mathcal {F}_p$ and $\mathcal {G}_p$ respectively. Denoting the covariances of the two populations by $\Sigma _1$ and $\Sigma _2$ respectively, the hypothesis of interest is

$$\begin{aligned} H_{0T} : \Sigma _1 = \Sigma _2 \quad \text{ vs. } \quad H_{1T} : \Sigma _1 \ne \Sigma _2. \end{aligned}$$

(9)

Let $\mathcal {S}_1 = n^{-1} \sum \nolimits _{i = 1}^n \left( \mathbf {X}_i - \overline{\mathbf {X}} \right) \left( \mathbf {X}_i - \overline{\mathbf {X}} \right) ^{\top }$ and $\mathcal {S}_2 = m^{-1} \sum \nolimits _{i = 1}^m \left( \mathbf {Y}_i - \overline{\mathbf {Y}} \right) \left( \mathbf {Y}_i - \overline{\mathbf {Y}} \right) ^{\top }$ denote the sample covariance matrices of the two populations respectively. Let $\mathcal {S}_{pl} = (n \mathcal {S}_1 + m \mathcal {S}_2)/(n + m)$ denote the pooled sample covariance matrix. When $p < \min (m, n)$ and both $\mathcal {F}_p$ and $\mathcal {G}_p$ are assumed to be Gaussian, the likelihood ratio test is constructed using

$$\begin{aligned} \mathcal {M} = \frac{ \left| \mathcal {S}_1 \right| ^{n - 1} \left| \mathcal {S}_2\right| ^{m - 1} }{ \left| \mathcal {S}_{pl} \right| ^{n + m - 2} }. \end{aligned}$$

(10)

Under $H_{0T}$, $T = -2 (1 - c_1) \mathcal {M}$ is asymptotically $\chi ^2$-distributed with $p(p + 1)/2$ degrees of freedom, where $c_1 = (1/n + 1/m - 1/(n + m)) \frac{2p^2 + 3p - 1}{6(p + 1)}$. This test, called the Box’s $\mathcal {M}$-test, also has an approximation yielding an F distribution in the limit. For lower dimensional models ($p < n$), a Wald-type test can also be constructed as

$$\begin{aligned} T_{Wald} = \frac{1}{2} \bigg [ n \mathrm{tr}\left( \mathcal {S}_1 \mathcal {S}_{pl} \right) ^2 + m \mathrm{tr}\left( \mathcal {S}_2 \mathcal {S}_{pl}^{-1} \right) ^2 - \frac{ n m}{(n + m)} \mathrm{tr}\left( \mathcal {S}_1 \mathcal {S}_{pl}^{-1} \mathcal {S}_2 \mathcal {S}_{pl}^{-1} \right) \bigg ], \end{aligned}$$

(11)

which follows a $\chi ^2$ distribution asymptotically with $p(p + 1)/2$ degrees of freedom under $H_{0T}$.

However, the above two tests fail for high dimensional models with $p > n$. Similar to the one-sample tests, one way to avoid specifying a distribution model to the two groups is by constructing a functional of $\Sigma _1$ and $\Sigma _2$ which is zero under $H_{0T}$ and non-zero otherwise. The Wald-test in (11) can be thought of as being based on this principle with $\mathrm{tr}\left( \Sigma _1 \Sigma _2^{-1} \right)$ as the functional. However in high dimensional inference, sample covariance matrices are singular and hence matrix inversion is usually avoided. Instead, a more commonly used functional to compare covariance matrices is $\mathrm{tr}\left( \Sigma _1 - \Sigma _2 \right) ^2$, the Frobenius norm of the difference $\Sigma _1 - \Sigma _2$.

When the samples are normally distributed, Schott (2007) proposed a test statistic when $p/n \rightarrow b \in [0, \infty )$. Under the assumption that $\lim \mathrm{tr}(\Sigma _i^k)/p = b \in (0, \infty )$ for $i = 1, 2$ and $k = 1, \ldots , 8$, the test statistic

$$\begin{aligned} T_{Sch}&= \mathrm{tr}\left( \mathcal {S}_1 - \mathcal {S}_2 \right) ^2 - \frac{n - 2}{(n + 1)(n - 1)} \left\{ (n - 1)(n - 3) \mathrm{tr}\left( \mathcal {S}_1^2 \right) + (n - 1) \mathrm{tr}\left( \mathcal {S}_1 \right) ^2 \right\} \nonumber \\&\quad - \frac{m - 2}{(m + 1)(m - 1)} \left\{ (m - 1)(m - 3) \mathrm{tr}\left( \mathcal {S}_2^2 \right) + (m - 1)^2 \mathrm{tr}\left( \mathcal {S}_2 \right) ^2 \right\} \end{aligned}$$

(12)

is shown to be asymptotically normal under $H_{0T}$. This test statistic is still restrictive in terms of the distributional assumption required to derive the asymptotic properties.

Relaxing the normality assumption, Srivastava et al. (2014) considered a factor linear model of the form $\mathbf {X}= \varvec{\mu }+ \varvec{F} \varvec{u}$, for some $p \times m$ matrix $\varvec{F}$ and $m \times 1$ random vector $\varvec{u}$. The distributional assumption on $\mathbf {X}$ is replaced by conditions on the moments of elements of $\varvec{u}$. The test statistic, which is constructed based on the function $\mathrm{tr}\left( \mathcal {S}_1 - \mathcal {S}_2 \right) ^2$, is given by

$$\begin{aligned}&T_{SYK} = \frac{ \Delta _1 + \Delta _2 - 2 p^{-1} \mathrm{tr}\left( \mathcal {S}_1 \mathcal {S}_2 \right) }{ 2 \left( \frac{1}{n - 1} + \frac{1}{m - 1} \right) \frac{ (n - 1) \Delta _1 + (m - 1) \Delta _2}{n + m - 2} }, \end{aligned}$$

(13)

where

$$\begin{aligned} \Delta _k = \frac{ \left\{ (n_k - 1)^3 (n_k - 2) \mathrm{tr}\left( \mathcal {S}_k^2 \right) - n_k (n_k - 1)^3 \mathrm{tr}\left( D_{\mathcal {S}_k}^2 \right) + (n_k - 1)^2 \mathrm{tr}\left( \mathcal {S}_k \right) ^2 \right\} }{ \{p n_k (n_k - 1)(n_k - 2)(n_k - 3) \}}, \end{aligned}$$

for k = 1, 2 with $n_1 = n$ and $n_2 = m$. The dimension is allowed to increase at a polynomial rate with respect to the sample size, $p = O(n^{\delta })$ for $1/2< \delta < 1$. Under $H_{0T}$, the test statistic is shown to converge to a standard normal distribution.

Using $\mathrm{tr}\left( \Sigma _1 - \Sigma _2 \right) ^2$ as the functional, Li and Chen (2012) developed a test statistic. The main idea behind the test statistic is to use Hoeffding’s U-statistics to construct unbiased estimators for the functional. Asymptotic properties of this estimator are used to develop the test procedure. The test statistic is given by

$$\begin{aligned} T_{LC} = \frac{ \mathcal {A}_{n,1} + \mathcal {A}_{m,2} - 2 \mathcal {C}_{n m}}{ \sigma _{n,m}}, \end{aligned}$$

(14)

where for $h = 1, 2$,

$$\begin{aligned} A_{n, h}&= \frac{1}{n(n - 1)} \sum \limits _{i \ne j} \left( \mathbf {X}_{hi}^{\top } \mathbf {X}_{hj} \right) ^2 - \frac{2}{n (n - 1)(n - 2)} \sum \limits _{i \ne j \ne k} \mathbf {X}_{hi}^{\top } \mathbf {X}_{hj} \mathbf {X}_{hi}^{\top } \mathbf {X}_{hk} \\&\quad + \frac{1}{n(n - 1)(n - 2)(n - 3)} \sum \limits _{i \ne j \ne k \ne \ell } \mathbf {X}_{hi}^{\top } \mathbf {X}_{hj} \mathbf {X}_{hk}^{\top } \mathbf {X}_{h \ell }, \end{aligned}$$

with $\mathbf {X}_{1i} = \mathbf {X}_{i}$ and $\mathbf {X}_{2i} = \mathbf {Y}_{i}$ and

$$\begin{aligned} C_{n, m}= & {} \frac{1}{nm} \sum \limits _{i = 1}^n \sum \limits _{j = 1}^m \left( \mathbf {X}_i^{\top } \mathbf {Y}_j \right) ^2 - \frac{1}{n (n - 1) m} \sum \limits _{i \ne j} \sum \limits _k \mathbf {X}_i^{\top } \mathbf {Y}_k \mathbf {X}_j^{\top } \mathbf {Y}_k \\&\quad - \frac{1}{m ( m - 1) n} \sum \limits _{i \ne j} \sum \limits _k \mathbf {Y}_i^{\top } \mathbf {X}_k \mathbf {Y}_j^{\top } \mathbf {X}_k + \frac{1}{n(n-1)m(m - 1)} \sum \limits _{i \ne k} \sum \limits _{j \ne \ell } \mathbf {X}_i^{\top } \mathbf {Y}_j \mathbf {X}_k^{\top } \mathbf {Y}_{\ell }. \end{aligned}$$

Under regularity conditions on the covariance matrices, $T_{LC}$ is asymptotically normal under $H_{0T}$. One of the main advantages of $T_{LC}$ over $T_{SYK}$ and $T_{Sch}$ is that a direct relationship between n and p has been relaxed.

In the above two test statistics, the aggregate difference between $\Sigma _1$ and $\Sigma _2$ is measured using the Frobenius norm. Cai et al. (2013) proposed a test based on the maximum difference between elements. The test statistic, given by

$$\begin{aligned} T_{CLX} = \max \limits _{1 \le i < j \le p} \frac{ \left( \mathcal {S}_{1, ij} - \mathcal {S}_{2, ij} \right) ^2}{ \frac{ \omega _{1, ij}}{n} + \frac{\omega _{2, ij}}{m} }, \end{aligned}$$

(15)

where $\omega _{1, ij} = n^{-1} \sum \nolimits _{k=1}^n \left\{ (\mathbf {X}_{ki} - \overline{\mathbf {X}}_i) (\mathbf {X}_{kj} - \overline{\mathbf {X}}_j) - \mathcal {S}_{1, ij} \right\} ^2$ and $\omega _{2, ij} = m^{-1}$ $\sum \nolimits _{k=1}^m \left\{ (\mathbf {Y}_{ki} - \overline{\mathbf {Y}}_i) (\mathbf {Y}_{kj} - \overline{\mathbf {Y}}_j) - \mathcal {S}_{2, ij} \right\} ^2$. Under $H_{0T}$, the limiting distribution of $T_{CLX}$ is shown to be an extreme value distribution of type I. In comparison with the Frobenius norm based tests, $T_{CLX}$ is shown to be more powerful at detecting difference between the covariance matrices when the differences are sparse, i.e. they differ in very small number of elements.

3 Projection based test

Conventional methods discussed for testing equality of covariance matrices usually fail in high-dimensional data settings because the sample covariance matrix does not converge to its population counterpart. Test statistics comparing covariance matrices are mainly based on matrix functions, such as eigenvalues, trace, Frobenius norm, etc., which also lose consistency in high dimensions. Thus performance of methods for comparison of covariance matrices worsens with increasing dimension. Test methods for covariance matrices in lower case enjoy many appealing properties. For example, $U_{John}$ test is invariant and is also the locally most powerful. The high dimensional methods are shown perform well, but they fail to achieve the theoretical properties of $U_{John}$. The LRT in the two sample case is also robust and has good asymptotic properties when the dimension is smaller than the sample size. To preserve the properties of traditional multivariate methods, an attractive approach is to embed the data and model into a lower dimension such that the hypothesis and inference are preserved.

When embedding data into lower-dimensional subspaces for parametric inference, the mapping should be such that the local topology of the data is preserved. Since the parameter of interest is the covariance matrix, which is a measure of spread, the mapping should preserve pairwise distances between observations. The existence of such a mapping is given by the Johnson-Lindenstrauss lemma (Johnson and Lindenstrauss 1984), which says that any linear mapping from the original space into the lower-dimensional space satisfies this condition. Hence we consider linear projection mappings from $\mathbb {R}^p$ into $\mathbb {R}^k$ for $k < p$ of the form $\mathbf {X}\mapsto \mathcal {R} \mathbf {X}$ where $\mathcal {R} \in \mathbb {R}^{k \times p}$ is the projection matrix. This paper’s main motivation is to develop test methods for covariance matrices for high-dimensional data that enjoy the appealing properties of tests for covariance matrices for lower dimensional data. The most natural path to mimic the tests for covariance matrices for lower data, such as $U_{John}$ test is to project high-dimensional data onto a space of dimension smaller than the sample size.

When considering dimension reduction techniques, principal component analysis (PCA) is the most popular and commonly used. While PCA is used very frequently for graphical representation and has good geometric properties, it is not ideal for projection-based hypothesis testing in high dimensions. For example, consider the two-sample test. When using PCA-based projection, variance of the data projected onto the first m principal component is given by the first m eigenvalues. While the data is embedded in the lower dimension, the hypothesis is not preserved. Equality of the first m eigenvalues does not guarantee that the two covariance matrices are equal. Extending to include all the p eigenvalues will also not work since the sample covariance matrix is singular and yields only $n - 1$ non-zero eigenvalues. Other data-driven projection methods such as t-SNE (van der Maaten and Hinton 2008) will also not work for similar reasons. To avoid these shortcomings, random projection (RP) of data is a popular method to alleviate the curse of dimensionality.

A random projection matrix $R = (r_{ij}) \in \mathbb {R}^{k \times p}$ is a matrix with randomly generated elements, and is not generated from a matrix-valued distribution. The elements $r_{ij}$ are randomly and independently generated thereby resulting in a much lower computational cost. Structural constraints such as sparsity and orthogonality can be imposed later as desired. There are various methods to generate the elements of the random projection matrix - (Achlioptas 2001; Srivastava et al. 2014) generate sparse projection matrices by structuring the matrix to have a large proportion of zeros. Another approach is to impose structure by generating orthogonal matrices to preserve geometrical properties in the data. RP-based inference procedure is along the same lines as a union-intersection test, where the null hypothesis is equivalently written as the intersection of a family of hypotheses and the alternative is expressed as a union. The principle remains the same - we reject the null hypothesis if at least one random projection presents evidence in favor of rejection.

Using the principle of random projections, Wu and Li (2020) developed a test procedure by projecting the data onto a one-dimensional space ($k = 1$). For the one sample hypothesis of $H_0^{(1)} : \Sigma = \mathcal {I}$, the chi-squared test statistic can be used on the projected data. Conditional on the random projection matrix R, the test statistic will have a chi-squared distribution with 1 degree of freedom. For the two sample hypothesis in (9), the standard F test statistic was used. To combine the results of M random projection matrices, the maximum was used. The test statistics for the one and two sample cases are given by

$$\begin{aligned} \begin{aligned}&T_{M, n} = \max \limits _{1 \le i \le M} \chi ^2 \left( R_i \mathbf {X}_1, \ldots , R_i \mathbf {X}_n \right) , \\&T_{M, n, m} = \max \limits _{1 \le i \le M} F \left( R_i \mathbf {X}_1, \ldots , R_i \mathbf {X}_n; R_i \mathbf {Y}_1, \ldots , R_i \mathbf {Y}_m \right) , \end{aligned} \end{aligned}$$

(16)

where $R_1, \ldots , R_M$ are independently generated random matrices. The critical values for rejection $H_0$ are derived using type I extreme value (Gumbel) distribution. Projecting into the one-dimensional space is convenient because the standard $\chi ^2$ and F test statistics have exact distributions. However, there are a few limitations to this method. First, the effect of sample size on the performance of the test statistic is not extensively studied. The Gumbel distribution can have poor performance when the sample size is small, $n + m < 40$. In contrast, the simulation studies reported in Wu and Li (2020) use $n = m = 100$. Second, the projected space sounds very restrictive to translate the entire information from p dimensions to a single dimension.

3.1 Proposed test procedure

Using more than one dimension, we propose projecting the data from p to k dimensions using a random matrix $R \in \mathbb {R}^{k \times p}$, where $k > 1$ is smaller than sample size $n + m$. First consider the one sample hypotheses. For $k < p$, let $\mathcal {R} \in \mathbb {R}^{k \times p}$ be a projection matrix and define $\mathbf {X}^*_i = \mathcal {R} \mathbf {X}_i, i = 1, \ldots n$ as the projected data. If the mean and variance of $\mathbf {X}$ are given by $\varvec{\mu }$ and $\Sigma$ respectively, then we have $\varvec{\mu }^* = \mathbb {E} (\mathbf {X}^*_i) = \mathcal {R} \varvec{\mu }$ and $\Sigma ^* = \mathrm{var}(\mathbf {X}^*_i) = \mathcal {R} \Sigma \mathcal {R}^{\top }$. Under the null hypothesis of identity, the variance of $\mathbf {X}^*$ becomes $\mathrm{var}(\mathbf {X}^*| H_{0I} ) = \mathcal {R} \Sigma \mathcal {R}^{\top } = \mathcal {R} \mathcal {R}^{\top }$. Similarly under the null hypothesis of sphericity, we have $\mathrm{var}(\mathbf {X}^*| H_{0S}) = \sigma ^2 \mathcal {R} \mathcal {R}^{\top }$. If we choose the projection matrix $\mathcal {R}$ to be of full row rank and semi-orthogonal, i.e. $\mathcal {R} \mathcal {R}^{\top } = \mathcal {I}_k$, then the null hypotheses are preserved under the projection. Using $\mathbf {X}^*_1, \ldots , \mathbf {X}^*_n$ as the data, the hypotheses of interest will be

$$\begin{aligned}&H_{0I}^* : \Sigma ^* = \mathcal {I}_k \text{ vs. } H_{1I} : \Sigma ^* \ne \mathcal {I}_k, \\&H_{0S}^* : \Sigma ^* = \sigma ^2 \mathcal {I}_k \text{ vs. } H_{1S} : \Sigma ^* \ne \sigma ^2 \mathcal {I}_k. \end{aligned}$$

If the data $\mathbf {X}$ is assumed to follow a normal distribution, the projected observations $\mathbf {X}^*$ will also be normally distributed. Hence likelihood ratio tests can be used to test $H_{0I}^*$ and $H_{0S}^*$. Also, the functional based tests, $U_{John}$ and $V_{Nagao}$ in (5) can be used since the projection ensures $k < n$. Defining the sample covariance matrix $\mathcal {S}^* = n^{-1} \sum \nolimits _{i = 1}^n \left( \mathbf {X}^*_i - \overline{\mathbf {X}^*} \right) \left( \mathbf {X}^*_i - \overline{\mathbf {X}^*} \right) ^{\top }$, we have

$$\begin{aligned} U_{John}^* = \frac{1}{k} \mathrm{tr}\left\{ \frac{ \mathcal {S}^*}{\mathrm{tr}\mathcal {S}^*/k} - \mathcal {I}_k \right\} ^2, V_{Nagao}^* = \frac{1}{k} \mathrm{tr}\left\{ \mathcal {S}^* - \mathcal {I}_k \right\} ^2. \end{aligned}$$

(17)

Asymptotically, these tests will have a chi-squared distribution with $\nu = k(k + 1)/2 - 1$ degrees of freedom. Hence the p-values are given by

$$\begin{aligned} \pi _U = \chi ^2_{\nu } \left( U_{John}^* \right) , \pi _{V} = \chi ^2_{\nu } \left( V_{Nagao}^* \right) , \end{aligned}$$

(18)

which can be used to reject the null hypotheses.

The equivalence between $H_{0I}$ and $H_{0I}^*$ (similarly between $H_{0S}$ and $H_{0S}^*$) holds irrespective of the choice of the projection matrix $\mathcal {R}$. Basing the inference on a single instance of $\mathcal {R}$ may lead to erroneous conclusions. For example, if we take $k = p/2$ and $\Sigma = \begin{bmatrix} \mathcal {I}_k &{} \mathbf {0} \\ \mathbf {0} &{} \Omega \end{bmatrix}$ for some symmetric positive definite matrix $\Omega$, then setting $\mathcal {R} = \begin{bmatrix} \mathcal {I}_k&\mathbf {0} \end{bmatrix}$ satisfies $H_{0I}^*$ but not $H_{0I}$. To avoid this issue, the cumulative decision based on multiple random projections needs to be considered. Combining the decisions of multiple random projections is a common practice when doing random projection based inference. In mean vector tests, Srivastava et al. (2014) used average p-values to combine the M projections, while Wu and Li (2020) proposed using the maximum test statistic of the M projections. We consider the average of p-values to make inference as the mean is more robust to extreme projections causing extreme p-values, although they have a very low probability of occurring.

Let $\mathcal {R}_1, \ldots , \mathcal {R}_M$ be M independent random projection matrices. Let $\pi _1, \ldots , \pi _M$ denote the respective p-values for the m projections. We reject the null hypothesis if the average p-value is small,

$$\begin{aligned} \overline{\pi } \le q_{\alpha }, \end{aligned}$$

where $q_{\alpha }$ is the $\alpha$-level critical value of the sampling distribution of $\overline{\pi }$. Note that the significance level $\alpha$ is not used directly for comparison against $\overline{\pi }$, rather the level $\alpha$ critical is used. This is because the sampling distribution of $\overline{\pi }$ is not uniform and is unknown. The significance level $\alpha$ can be used directly only when we perform a single random projection ($M = 1$). However, as discussed above, multiple projections are needed to establish equivalence between $H_0$ and $H_0^*$’s. Therefore, we need to use the distribution of $\overline{\pi }$ to compute the $\alpha$-level critical value $q_{\alpha }$.

To compute $q_{\alpha }$, an asymptotic approximation for the distribution of $\overline{\pi }$ can be derived using the fact that the p-values are independent conditional on the observations. However, such an approximation can introduce additional error into the test procedure. To avoid this error, critical values are computed by simulating the empirical distribution of $\overline{\pi }$ under the null hypothesis. Algorithm 1 outlines the test procedure for $H_{0S}$. For $H_{0I}$, the algorithm is similar with $U_{John}^*$ and $\pi _{U}$ replaced by $V_{Nagao}^*$ and $\pi _{V}$ respectively.

Generating data under $H_{0I}$ is straightforward as the observations are generated from $\mathcal {N}_p \left( \mathbf {0}, \mathcal {I} \right)$. Under $H_{0S}$, the $\mathbf {Z}$ are generated from $\mathcal {N}_p \left( \mathbf {0}, \sigma ^2 \mathcal {I} \right)$ for some $\sigma \in \mathbb {R}$. As rejecting or accepting $H_{0S}$ is independent of the sphericity parameter, the choice of $\sigma$ should not affect the null distribution of $\overline{\pi }_{U}$. The following result establishes invariance of the distribution of $\overline{\pi }_{U}$ under $H_{0S}$. For practical implementation, the null distribution of $\overline{\pi }_U$ can therefore be constructed using Algorithm 1 by generating $\mathbf {Z}_1, \ldots , \mathbf {Z}_n$ from $\mathcal {N}(\mathbf {0}, \mathcal {I}_p)$.

Theorem 1

Let $\mathbf {X}_1, \ldots , \mathbf {X}_n$ be a random sample from $\mathcal {N}_p \left( \mathbf {0}, \sigma ^2 \mathcal {I} \right)$. Let $U_{John}^*$ and $\pi _{U}$ be as defined in (18). Let $\mathcal {R}_1, \ldots , \mathcal {R}_M$ be independent random projection matrices of dimension $k \times p$ yielding p-values $\pi _1, \ldots , \pi _M$. If we define $\overline{\pi }_U$ as the mean of $\pi _1, \ldots , \pi _M$, then the distribution of $\overline{\pi }$ is independent of $\sigma$.

Proof

See Appendix $\square$

3.2 Two sample testing

To test the equality of covariance matrices of two normal populations, the likelihood ratio test (10) or the Wald-type test (11) can be used when $p < n + m$. For high-dimensional data, these tests can be applied by projecting the data into lower-dimensional subspace. For a random semi-orthogonal matrix $\mathcal {R} \in \mathbb {R}_{k \times p}$ of full row rank, let $\mathbf {X}^*_i = \mathcal {R} \mathbf {X}_i, i =1, \ldots , n$ and $\mathbf {Y}^*_j = \mathcal {R} \mathbf {Y}_j, j = 1, \ldots , m$ denote the projected observations from the two populations respectively. The hypothesis of equality of covariance matrices in (9) can be equivalently stated as $H_{0T} : \Sigma _1 - \Sigma _2 = 0$ versus $H_{1T} : \Sigma _1 - \Sigma _2 \ne 0$. In the projected subspace, the two-sample hypothesis will become

$$\begin{aligned} H_{0T} : \mathcal {R} \left( \Sigma _1 - \Sigma _2 \right) \mathcal {R}^{\top } = 0 \text{ vs. } H_{1T} : \mathcal {R} \left( \Sigma _1 - \Sigma _2 \right) \mathcal {R}^{\top } \ne 0. \end{aligned}$$

Let $\mathcal {S}_1^*, \mathcal {S}_2^*$ and $\mathcal {S}_{pl}^*$ denote the sample covariance matrices of the two groups and the pooled covariance matrix respectively. Then the projected Box-M test statistic and the Wald-type test statistic will be

$$\begin{aligned} \begin{aligned} \mathcal {M}^*&= \frac{ \left| \mathcal {S}_1^* \right| ^{n - 1} \left| \mathcal {S}_2^*\right| ^{m - 1} }{ \left| \mathcal {S}_{pl}^* \right| ^{n + m - 2} }, \\ T_{Wald}^*&= \frac{n + m}{2} \bigg [ \frac{n}{n + m} \mathrm{tr}\left( \mathcal {S}_1^* \mathcal {S}_{pl}^* \right) ^2 + \frac{m}{n + m} \mathrm{tr}\left( \mathcal {S}_2^* \mathcal {S}_{pl}^{*^{-1}} \right) ^2 \\&\quad - \frac{ n m}{(n + m)^2} \mathrm{tr}\left( \mathcal {S}_1^* \mathcal {S}_{pl}^{*^{-1}} \mathcal {S}_2^* \mathcal {S}_{pl}^{*^{-1}} \right) \bigg ]. \end{aligned}\nonumber \\ \end{aligned}$$

(19)

The p-values are calculated using the $\chi ^2_{\eta }$ approximation with $\eta = k(k + 1)/2$. For $\mathcal {M}^*$, finite-sample correction terms as described in Sect. 2 can be used to improve performance.

As in the case of one-sample tests, the aggregate decision from multiple random projections should be used to accept or reject $H_{0T}$. For M independent random projection matrices $\mathcal {R}_{\ell }, {\ell } = 1, \ldots , M$ with corresponding p-values $\pi _{1}, \ldots , \pi _M$, let $\overline{\pi }$ denote the average p-value. To determine the $\alpha$-level critical value $q_{\alpha }$, the sampling distribution of $\overline{\pi }$ under $H_{0T}$ is required. Under the null hypothesis, it is only known that the two covariance matrices are equal. Thus, the empirical sampling distribution can be generated using any $\Sigma _1 = \Sigma _2 = \Sigma$ for any symmetric positive definite matrix $\Sigma$. The following theorem provides invariance of the sampling distribution of $\overline{\pi }$ to the choice of parameters under $H_{0T}$.

Theorem 2

Let $\mathbf {X}_i \sim \mathcal {N} \left( \varvec{\mu }_1, \Sigma \right) , i = 1, \ldots , n$ and $\mathbf {Y}_j \sim \mathcal {N} \left( \varvec{\mu }_2, \Sigma \right) , j = 1, \ldots , m$ be two groups of independent observations. Let $\mathcal {M}^*$ be as defined in (19) and $\pi _{\ell }$ denote the p-value obtained when using the random projection $\mathcal {R}_{\ell }, \ell = 1, \ldots , M$. If $\overline{\pi }_{\mathcal {M}}$ denotes the average of the M p-values, then the sampling distribution of $\overline{\pi }_{\mathcal {M}}$ is independent of $\varvec{\mu }_1, \varvec{\mu }_2$ and $\Sigma$.

Proof

See Appendix. $\square$

The above result indicates that random samples from standard normal distribution can be used to generate the empirical critical value. Implementation of the method is described in Algorithm 2.

3.3 Specifying parameters

In Algorithms 1 and 2, there are three parameters which are not data driven and are user-specified: number of iterations M and N, and dimension of projection space k. These quantities affect accuracy of the results and the computation cost of the algorithms.

• 1. The term N represents the number of random samples drawn when determining the sampling distribution of the test statistic under $H_0$. Consequently, it can be seen as the sample size for determining the empirical distribution and the critical value under $H_0$. Using small values of N will yield highly variable critical values. As N increases, the empirical distribution of the test statistic under $H_0$ becomes more stable and hence yields consistent critical values.

• 2. The quantity M is the number of random projections for each set of data, used in both determining the sampling distribution under $H_0$ as well as calculating the test statistic. It affects consistency of the average p-value as small values of M may result in the random projection matrices being generated from different subspaces. As M increases, the average p-value becomes less variable, resulting in a smaller sampling effect on the results.

• 3. Dimension of the projected space k is chosen to be smaller than $n + m$ so that the model becomes full rank. Theoretically, the idea of random projections is motivated by Johnson-Lindenstrauss (J-L) lemma (Johnson and Lindenstrauss 1984). For any $\varepsilon , \delta > 0$, by J-L lemma there exists a constant $c > 0$ and $k \ge c\varepsilon ^{-2} \log (1/\delta )$ such that

  $$\begin{aligned} \mathbb {P} \left[ (1 - \varepsilon ) \Vert \mathbf {X}\Vert _2^2 \le \Vert \mathcal {R} \mathbf {X}\Vert _2^2 \le (1 + \varepsilon ) \Vert \mathbf {X}\Vert _2^2 \right] > 1 - \delta , \end{aligned}$$

  for any projection matrix $\mathcal {R} \in \mathbb {R}^{k \times p}$. To compute k, Burr et al. (2018) provide an optimal bound as $k = 4 \varepsilon ^{-2} \log (1/\delta )$. However, the trade-off between error ($\varepsilon , \delta$) and dimension (k) is extremely high. For example, to have $\varepsilon = \delta = 10^{-2}$, the projected dimension will be $k = 4 \log (10^2) \times 10^4 \approx 1.8 \times 10^5$. Furthermore, the direct implication of J-L lemma on hypothesis testing is not very clearly understood.

In our simulation study and data illustrations, we used $N = M = 1000$. A brief simulation study demonstrating the effect of the parameters on consistency of critical values and the type I error are presented in Sect. 4.3.

4 Simulation study

To study the performance of the random projection based tests in comparison against the high-dimensional tests, we performed an extensive simulation study for both the one and two sample cases. Type I error and power are computed under different scenarios, for various values of sample sizes n and m, dimension of the original sample space p and projected spaces k, respectively. To study the effect of sample size and dimensions, we set $n \in \{20, 40, 50, 60\}$, $p \in \{ 100, 200, 500, 1000, 2000 \}$ and $k \in \{ 5, 10, 15\}$. Empirical size and power are computed at the nominal significance level of $\alpha = 0.05$.

4.1 One sample results

For the hypotheses of identity $H_{0I}$, we have the three high dimensional test statistics - $V_{CZZ}, V_{LW}$ and $V_{SYK}$, and three random projection based tests - $LRT_{I}$, $V_{John}$ and $V_{LW}$. For all the studies, observations are randomly generated from a normal distribution with mean $\varvec{\mu }$ and covariance matrix $\Sigma = (\sigma _{ij})_{1 \le i, j \le p}$. Elements of the mean vector were generated uniformly, $\mu _k \sim \mathrm{Unif}(-3, 3), i = 1, \ldots , p$. For computing type I error, the covariance matrix is set as identity matrix of dimension p. Power was computed under four scenarios (Power I–Power IV) under the alternative, with the difference from identity matrix defined in two ways—a band matrix with non-zero diagonal elements and a diagonal matrix with elements different from 1. For Power I and II, we set $\sigma _{ij} = \rho ^{|i - j|}$ for $|i - j| \le B$ for some bandwidth B and zero otherwise. For Power III and IV, we define $\Sigma$ as diagonal with $\sigma _{ii} = 1$ for $i \le B$ and $\sigma _{ii} = 1 + \varepsilon$ for $B < i \le p$. Table 1 presents the type I error for $k = 5$ and $k = 15$.

Among the high dimensional tests, only $V_{CZZ}$ preserves type I error at $5\%$ significance level. Both $V_{SYK}$ and $V_{LW}$ always reject the null hypothesis. When randomly projecting to $k = 5$ and $k = 15$ dimensions, all the three lower-dimensional tests control type I error rate, with the performance being slightly better for $k = 15$ than $k = 5$. Across all combinations of n and p, the RP-based $LRT_I$ and $V_{John}$ for both values of k outperform $V_{CZZ}$. As $V_{SYK}$ and $V_{LW}$ fail to preserve type I error, only $V_{CZZ}$ and the lower dimensional tests are compared in the power studies for the four scenarios, results of which are presented in Table 2. In Power I and II, all the tests have comparable power for small dimensions ($p = 100, 200 ,500$). For fixed sample size, the power decreases with dimension. The power of the RP-based tests increase when the projected dimension M is increased. For small sample size, $V_{LW}$ has higher power than $LRT_I$ and $V_{John}$ , with the likelihood ratio test achieving higher power than $V_{LW}$ as n increases to 50. In Power III and IV, the random projection tests have greater power, with $V_{LW}$ outperforming all the tests. Overall, $V_{LW}$ with random projection consistently outperforms the other tests across all comparisons.

Table 1 Type I error of the three one-sample high dimensional tests ($V_{CZZ}$, $V_{SYK}$, $V_{LW}$) and the RP based tests ($LRT_I, V_{LW}, V_{John}$) for projected dimensions $k = 5$ and $k = 15$. The results are for various combinations of sample size and dimension, averaged over 1000 replicates

Table 2 Power of the one-sample high dimensional test ($V_{CZZ}$) and the RP based tests ($LRT_I, V_{LW}, V_{John}$) for projected dimensions $k = 5$ and $k = 15$. The results are for various combinations of sample size and dimension under four different scenarios averaged over 1000 replicates

4.2 Two sample results

For the two sample test in (9), we have four high dimensional tests—$T_{Sch}$, $T_{SYK}$, $T_{LC}$ and $T_{CLX}$. For the random projection based tests, we have two standard dimension tests—Box’s $\mathcal {M}$ and Wald’s test; and the high-dimensional Wu-Li test. All the random samples are generated from p-dimensional normal distributions with means $\varvec{\mu }_1 = \varvec{\mu }_2 = \mathbf {0}$ and covariance matrices $\Sigma _1$ and $\Sigma _2$, respectively. For type I error, we set both $\Sigma _1$ and $\Sigma _2$ to be the identity matrix. The results are presented in Table 3. We considered a total of 8 settings (Power I–Power VIII) to compare the power of the high dimensional tests and the RP-based tests. We considered two models for differentiating the covariance matrices—unequal values along the diagonal and band matrices. For Power I–IV, we set $\Sigma = \mathcal {I}_p$ and $\Sigma _2 = \mathrm{diag}(\sigma _{21}, \ldots , \sigma _{2p})$, where $\sigma _{2k} = 1$ for $k \le [Bp]$ and $\sigma _{2k} \sim \Gamma (4,2)$ for $k = [Bp]+1, \ldots , p$. The bandwidth B is varied over the 4 scenarios. For Power V–VIII, we set $\Sigma = \mathrm{diag}(\sigma _{11}, \ldots , \sigma _{1p})$ with $\sigma _{1k} \sim \mathrm{Unif}(1, 3)$ and $\Sigma _2 = \Sigma _1^{1/2} \Omega \Sigma _1^{1/2}$, where $\Omega$ is set as a band matrix with $\Omega _{ij} = \rho ^{|i - j|}$ for $|i - j| \le Bp$ and 0 otherwise. The parameter B determines the width of the band matrix $\Omega$.

Results for the type I error comparison are presented in Table 3. At the nominal $5 \%$ significance level, none of the high dimensional tests preserve type I error for the chosen combinations of p and n. Amongst the RP-tests, both the Box’s $\mathcal {M}$-test and Wald test after random projections consistently preserves type I error rate for all values of k. It is interesting to note that the Wu-Li test, which is also based on random projections onto one dimension, fails to control type I error. This indicates that RP-based work well so long as the projected dimension is not very low. Tables 4 and 5 present the power of the Box’s $\mathcal {M}$-test and Wald test respectively for the eight power scenarios. We did not include the high dimensional methods as they failed to control type I error.

For all eight scenarios, the RP-based tests seem to achieve reasonable power, with the power decreasing with increase in p and increasing with increase in n. The trend with respect for k for a given p is different though - for Power I–IV, the power decreases whereas for Power V–VIII the power increases. This is because for Power I–IV, the number of parameters different between $\Sigma _1$ and $\Sigma _2$ is k (only along the diagonal). As the Box-M test has $k(k - 1)/2$ degrees of freedom, the power as a function of k can be perceived as $\chi ^2_{k(k - 1)/2}(k)$ which is a decreasing function of k. For Power V–VIII, $\Sigma _1$ and $\Sigma _2$ differ by $k(k - 1)$ parameters, yielding a power of the form $\chi ^2_{k(k - 1)/2}(k(k - 1))$ which increases with k.

Table 3 Type I error of the four two-sample high dimensional tests ($T_{CLX}$, $T_{SYK}$, $T_{CW}$, $T_{Sch}$) and the RP based tests for projected dimensions $k = 5, 10, 15$. The results are for various combinations of sample size and dimension, averaged over 1000 replicates

Table 4 Power of the RP based Box-$\mathcal {M}$ test for projected dimensions $k = 5, 10, 15$. The results are for various combinations of sample size and dimension under different scenarios averaged over 1000 replicates

Table 5 Power of the RP based Wald test for projected dimensions $k = 5, 10, 15$. The results are for various combinations of sample size and dimension under different scenarios averaged over 1000 replicates

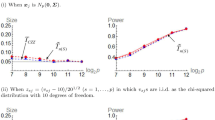
4.3 Effect of N and M

As described in Sect. 3.3, performance of the test statistics is determined by three parameters: k, N and M. We have seen in Tables 2, 3, 4 and 5 how k affects the performance of RP-based tests. To illustrate the effects of N and M, we repeated the simulation study for one sample hypothesis test described in Sect. 4.1. We fixed $n = 40$ and $p = 1000$ for generating data and $k = 5$ for the projection dimension. Critical value under the null distribution, empirical p-value and run-times for different values of (N, M) are computed. The calculations are repeated 1000 times and three measures are calculated: (i) standard deviation of critical values for consistency of the empirical null distribution; (ii) type I error for consistency of the rejection rule; and (iii) average run time to determine the computational cost. The values of N and M are chosen from the sets $\{1, 25, 100, 500, 1000\}$. The results are presented in Fig. 1. The two measures of consistency improve as both N and M increases. However, the computational cost also increases with N and M. From the standard deviation and type I error plots, we can that N smaller than 100 has particularly poor performance. Although it is not possible to determine an optimal value for N and M, we would recommend using large values, e.g. $N = M = 1000$.

Fig. 1

The three measures of consistency: standard deviation of critical values, type I and average runtimes for different values of N and M based on the one sample hypothesis test model. All results are based on average of 1000 replicates

5 Data analysis

To study how RP-based tests and high dimensional test statistics perform when applied to real data, we considered two data sets. The first data set is a gene expression data from 62 colon tissues - $n = 22$ normal and $m = 40$ tumor samples (Alon et al. 1999). Gene expression intensities of $p = 2000$ genes with highest minimal intensity were reported.¹ We refer to this data set as colon henceforth For the second illustration, we have gathered data on breast cancer subjects from the cancer genome atlas (TCGA).² Gene expression data from the RNA-Seq protocol are downloaded for patients from Stages IA, IIB and IIIC, resulting in samples of sizes 91, 291 and 70 respectively. The top $p = 2000$ genes with highest minimal intensity are kept in the final data set, which will be called breast henceforth.

5.1 colon data

For the colon data, we did two analyses to compare the type I error rate and power of the test statistics in detecting differences in covariance matrices. First, the $n = 40$ tumor samples were randomly divided into two equal groups and tested for equality of covariance matrices. Since the sub-samples are from the same population, we expect the tests to not detect a significant difference between the covariance matrices of the two groups. We repeated this process $N = 1000$ times and the average number of false rejections is calculated. Second, we compared the normal and tumor samples. It is widely accepted that in addition to the signals, co-expression networks also vary with disease. Hence we expect to detect a significant difference between the two covariance matrices. Results are presented in Table 6, and we expect a method to have very low type I error rate under $H_0$and reject $H_0$ when comparing the two groups. From the table, type I error calculations indicate that the random projection tests do not falsely reject the null hypothesis and correctly differentiate between the two groups. $T_{Sch}$ also correctly identified the difference between tumor and normal samples, however it falsely rejected the null hypothesis in a small ($3.5\%$) number of models. The $T_{SYK}$ and Wu-Li tests have a very high type I error. $T_{CLX}$ and $T_{LC}$ also controls type I error reasonably, however they could not detect the difference between normal and tumor samples.

Table 6 Results for type I error comparing sub-samples within the tumor samples and power for comparison between tumor and colon samples from the colon data set. The results are based on 1000 bootstrap samples

5.2 breast data

In breast data, the samples are divided into three groups based on the cancer stage. Similar to the colon data, we compared both type I error and power of the tests. First, we compared the type I error within each stage. Two samples of size 40 each are drawn to represent the two groups of observations. Since the observations correspond to the same stage, we expect the tests to not reject the null hypothesis. Proportion of rejections in $N = 1000$ repetitions will indicate the type I error within each cancer stage. Second, we compared the power of detecting difference between the stages. Using samples from different stages, power of the tests are similarly calculated. Results for both type I error and power are presented in Table 7. All the high dimensional methods have inflated type I error rates whereas the RP-based Box $\mathcal {M}$-test and Wald test have very low false positives for stages IA and IIIC. It is interesting to note that for Stage IIB, all the test procedures have inflated type I error including the RP-based tests. This is a strong indication that there is potentially high heterogeneity within the samples resulting in the hypotheses being rejected. The RP-based tests achieve very high power when comparing between the cancer stages.

Table 7 Results for type I error comparing sub-samples from within the three cancer stages and power for comparison between the three pairs of cancer stages from the breast data set. The results are based on 1000 bootstrap samples

6 Conclusion

Hypothesis tests for covariance matrices in high dimension are challenging. RP based tests are known to be very efficient for mean vector testing in high dimensions. In this paper, we have developed the random projection based tests for the covariance matrix for both one and two sample tests. Standard multivariate tests such as LRT for the one sample test and Box-$\mathcal {M}$ and Wald test for the two sample hypothesis have been studied after random projection into lower-dimensional space. Inference is based on the average p-value of M random projections, where the rejection region is determined by the empirical critical values simulated under the null hypothesis using fixed covariance matrices. Through Theorems 1 and 2, we have shown that the empirical null distributions can be generated using identity matrices for the fixed covariance matrices. Simulation results have shown that RP based methods control type I error rates and achieve very good power over a wide range of models, whereas high dimensional methods have very inflated type I error rates. For the RP based methods, increasing the projection dimension k lowers the type I error and increases power. In our limited simulation study, we have observed that a dimension of $k = 15$ achieves very good results. We applied the test procedures to two gene expression data sets with $p = 2000$ genes. The results show that RP based tests preserve type I error even in real data applications whereas the current existing test procedures have inflated type I error rates. An interesting observation in the breast data is that all the tests have consistently high type I error for Stage IIB breast cancer data. This could be an indication that there is potentially high levels of heterogeneity in the data that is not captured by the covariance matrix alone.

RP based methods are known to be computationally intensive - with the computational cost being linear in N and M. Typically, $N = M = 1000$ is large enough to obtain consistent results. Efficient methods for generating random matrices and parallelization can reduce the computational cost significantly. In spite of involving a matrix decomposition step, orthogonal random matrix generation is efficient since the matrix being decomposed is of low dimension ($k \times k$) and the projected dimension k is generally chosen to be smaller than the sample size. Parallelizing the computations for different random projections matrices can achieve a significant reduction in the overall computational time. To this effect, we have developed an R package cramp, which is available to download from https://github.com/dnayyala/cramp. Through efficient parallelization, cramp achieves very good computation times. Table 8 present the run times to calculate the average p-values of the two sample RP-based test statistics for different combinations of n, p and k based on $N = 10^3$ random projections. All computations were done on R (ver. 4.0.2) running on a 3.6 GHz AMD Ryzen7 1800X processor with 64 GB RAM, parallelized on 12 cores. The runtime increases very slow with respect to all three quantities, with the maximum time being 10.97 seconds.

Table 8 Computation times (in seconds) of the RP-based test statistics for different values of n, p and k based on $K = 10^3$ random projections

Appendix

Proof of Theorem 1

The proof of Theorem 1 is along the same lines as the proof of Theorem 2 in Srivastava et al. (2014). To show that the distribution of $\overline{\pi }_U$ is independent of $\sigma$, define $\mathbf {X}^*_{m; i} = \mathcal {R}_m \mathbf {X}_i, i = 1, \ldots , n, m = 1, \ldots , M$ as the projection of the $i^\mathrm{th}$ observation using the $m^\mathrm{th}$ random projection matrix. Then we have

$$\begin{aligned} \mathrm{var} \left( \mathbf {X}_{m;1}, \ldots , \mathbf {X}_{m; n} \right) = \mathcal {S}^*_m = \mathcal {R}_m \mathcal {S} \mathcal {R}_m^{\top }, \end{aligned}$$

where $\mathcal {S}$ and $\mathcal {S}_m^*$ are the sample covariance matrices of the original and projected observations respectively. From equation (17), the p-values based on M i.i.d. random projection matrices are

$$\begin{aligned} \pi _m = 1 - \chi ^2_{\nu } \left( \frac{1}{k} \mathrm{tr}\left\{ \frac{\mathcal {S}_m^*}{ \mathrm{tr}\mathcal {S}_m^* / k} - \mathcal {I}_k \right\} ^2 \right) . \end{aligned}$$

Firstly since the random matrices are independent, conditional on the data $\mathcal {X} = \{\mathbf {X}_1, \ldots , \mathbf {X}_n\}$ and $\mathcal {Y} = \{\mathbf {Y}_1, \ldots , \mathbf {Y}_m \}$, the p-values $\pi _1, \ldots , \pi _M$ are independent and identically distributed. This is because of the orthogonality of the projection matrices which preserves the covariance matrix structure ($\mathcal {R} \left( \sigma ^2 \mathcal {I}_p \right) \mathcal {R}^{\top } = \sigma ^2 \mathcal {I}_k$). Additionally, we can write

$$\begin{aligned} P \left[ \overline{\pi }< u \right] = \mathbb {E}_{\mathcal {X}, \mathcal {Y}} \left\{ P_{\mathcal {R}} \left[ \overline{\pi } < u | \mathcal {X}, \mathcal {Y} \right] \right\} , \end{aligned}$$

(A.20)

where the expected value is with respect to the distribution of the observations and the probability is with respect to the randomness of the projection matrix.

By the conditional independence of $\pi _1, \ldots , \pi _M$ and the central limit theorem, we have a normal approximation to the probability in (A.20)

$$\begin{aligned} \lim \limits _{M \rightarrow \infty } \left| P \left[ \overline{\pi } < u \right] - \Phi \left( \frac{u - \mathbb {E}_{\mathcal {R}} \left[ u | \mathcal {X}, \mathcal {Y} \right] }{ \mathrm{var}_{\mathcal {R}} \left[ u | \mathcal {X}, \mathcal {Y} \right] } \right) \right| = 0. \end{aligned}$$

(A.21)

Hence the probability $P \left[ \overline{\pi } < u \right]$ can be approximated only using the moments of $U | \mathcal {X}, \mathcal {Y}$. Under the null hypothesis $H_{0S}$, the variable $U | \mathcal {X}, \mathcal {Y}$ is defined as

$$\begin{aligned} U | \mathcal {X}, \mathcal {Y}&= 1 - \chi ^2_{\nu } \left( U | \mathcal {X}, \mathcal {Y} \right) = 1 - F_{\chi ^2_{\nu }} \left( \mathrm{tr}\left\{ \frac{\mathcal {S}_m^*}{ \mathrm{tr}\mathcal {S}_m^* / k} - \mathcal {I}_k \right\} ^2 | \mathcal {X}, \mathcal {Y} \right) \nonumber \\&\sim \mathrm{Unif}(0,1). \end{aligned}$$

(A.22)

The uniform distribution is from the standard property of p-value under the null hypothesis, which is independent of $\sigma ^2$. Using this property, we shall show that the distribution of $E_{\mathcal {R}} \left[ U | \mathcal {X}, \mathcal {Y} \right]$ and $\mathrm{var}_{\mathcal {R}} \left[ U | \mathcal {X}, \mathcal {Y} \right]$ with respect to $\mathcal {X}, \mathcal {Y}$ are also independent of $\sigma ^2$.

Let W denote the expected value of $U | \mathcal {X}, \mathcal {Y}$ with respect to $\mathcal {R}$,

$$\begin{aligned} W = \mathbb {E}_{\mathcal {R}} \left[ U | \mathcal {X}, \mathcal {Y} \right]&= \int u \, dP_{\mathcal {R}} \nonumber \\&= \int \left[ 1 - F_{\chi ^2_{\nu }} \left( \mathrm{tr}\left\{ \frac{\mathcal {S}_m^*}{ \mathrm{tr}\mathcal {S}_m^* / k} - \mathcal {I}_k \right\} ^2 | \mathcal {X}, \mathcal {Y} \right) \right] \, dP_{\mathcal {R}} \end{aligned}$$

(A.23)

where the integral is with respect to the distribution of the random projection matrix $\mathcal {R}$. While the exact integral is not of importance, it should be noted that from equation (A.22), the integrand is independent of $\sigma ^2$. As the random projection matrices are generated independent of the distribution of the observations, we can conclude that the variable W is independent of $\sigma ^2$. For any $m \ge 1$, the $\mathrm{m}\mathrm{th}$ moment of W is given by

$$\begin{aligned} \mathbb {E}_{\mathcal {X}, \mathcal {Y}} \left[ W^m \right] = \int W^m \, dF_{\mathcal {X}, \mathcal {Y}}&= \int \mathbb {E}_{\mathcal {R}} \left[ U| \mathcal {X}, \mathcal {Y} \right] ^m \, dF_{\mathcal {X}, \mathcal {Y}} \\&= \int \mathbb {E}_{\mathcal {R}} \left[ U| \mathcal {X}, \mathcal {Y} \right] \times \cdots \times \mathbb {E}_{\mathcal {R}} \left[ U| \mathcal {X}, \mathcal {Y} \right] \, dF_{\mathcal {X}, \mathcal {Y}} \\&= \int \left\{ \int U_{\mathcal {R}_1} \, dP_{\mathcal {R}_1} \right\} \cdots \left\{ \int U_{\mathcal {R}_m} \, dP_{\mathcal {R}_m} \right\} \, dF_{\mathcal {X}, \mathcal {Y}} \end{aligned}$$

Interchanging the integrals by Fubini’s theorem, we have

$$\begin{aligned} \mathbb {E}_{\mathcal {X}, \mathcal {Y}} \left[ W^m \right] = \int \cdots \int \left\{ \int U_{\mathcal {R}_1} \ldots U_{\mathcal {R}_m} \, dF_{\mathcal {X}, \mathcal {Y}} \right\} \, dP_{\mathcal {R}_1} \cdots dP_{\mathcal {R}_m} \end{aligned}$$

(A.24)

By the construction of U in equation (A.22), the integral $\left\{ \int U_{\mathcal {R}_1} \ldots U_{\mathcal {R}_m} \, dF_{\mathcal {X}, \mathcal {Y}} \right\}$ is independent of $\sigma ^2$. Therefore, all moments of W are independent of $\sigma ^2$ which implies that the distribution of W is independent of $\sigma ^2$.

Similarly, it can be shown that the distribution of $\mathrm{var}_{\mathcal {R}} \left( U| \mathcal {X}, \mathcal {Y} \right)$ is also independent of $\sigma ^2$. From the independence of the mean and variance, we have the distributions of

$$\begin{aligned} \Phi \left[ \frac{ u - \mathbb {E}_{\mathcal {R}} \left\{ U | \mathcal {X}, \mathcal {Y} \right\} }{ \mathrm{var}_{\mathcal {R}} \left\{ U | \mathcal {X}, \mathcal {Y} \right\} } \right] \text{ and } \quad \mathbb {E}_{\mathcal {X}, \mathcal {Y}} \left\{ \Phi \left[ \frac{ u - \mathbb {E}_{\mathcal {R}} \left\{ U | \mathcal {X}, \mathcal {Y} \right\} }{ \mathrm{var}_{\mathcal {R}} \left\{ U | \mathcal {X}, \mathcal {Y} \right\} } \right] \right\} \end{aligned}$$

(A.25)

are independent of $\sigma ^2$. Finally, combining this independence with equation (A.21), we have

$$\begin{aligned}&\lim \limits _{M \rightarrow \infty } P_\mathcal {R} \left\{ \overline{\pi } | \mathcal {X}, \mathcal {Y} \right\} = \Phi \left[ \frac{ u - \mathbb {E}_{\mathcal {R}} \left\{ U | \mathcal {X}, \mathcal {Y} \right\} }{ \mathrm{var}_{\mathcal {R}} \left\{ U | \mathcal {X}, \mathcal {Y} \right\} } \right] , \end{aligned}$$

with the right hand side independent of $\sigma ^2$. Taking expected values with respect to $\mathcal {X}$ and $\mathcal {Y}$, we have

$$\begin{aligned} \lim \limits _{M \rightarrow \infty } P \left[ \overline{\pi } < u \right] = \mathbb {E}_{\mathcal {X}, \mathcal {Y}} \left\{ \Phi \left[ \frac{ u - \mathbb {E}_{\mathcal {R}} \left\{ U | \mathcal {X}, \mathcal {Y} \right\} }{ \mathrm{var}_{\mathcal {R}} \left\{ U | \mathcal {X}, \mathcal {Y} \right\} } \right] \right\} . \end{aligned}$$

(A.26)

By equation (A.25), the right hand side in (A.26) is also independent of $\sigma ^2$, completing the proof. $\square$

Proof of Theorem 2

Invariance of the distribution of the two-sample test statistic can be shown similar to the above proof. Besides computation of the test statistic, rest of the argument remains the same since the Box M test statistic also follows a standard uniform distribution under the null hypothesis. Hence in Algorithm 2, $\pi _m \sim \mathrm{Unif}(0, 1)$ under $H_0$, which is independent of the choice of $\Sigma$. $\square$